Article contents
Concentrated matrix exponential distributions with real eigenvalues
Published online by Cambridge University Press: 26 August 2021
Abstract
Concentrated random variables are frequently used in representing deterministic delays in stochastic models. The squared coefficient of variation (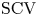 $\mathrm {SCV}$) of the most concentrated phase-type distribution of order
$\mathrm {SCV}$) of the most concentrated phase-type distribution of order 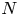 $N$ is
$N$ is 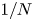 $1/N$. To further reduce the
$1/N$. To further reduce the 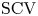 $\mathrm {SCV}$, concentrated matrix exponential (CME) distributions with complex eigenvalues were investigated recently. It was obtained that the
$\mathrm {SCV}$, concentrated matrix exponential (CME) distributions with complex eigenvalues were investigated recently. It was obtained that the 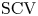 $\mathrm {SCV}$ of an order
$\mathrm {SCV}$ of an order 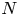 $N$ CME distribution can be less than
$N$ CME distribution can be less than 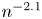 $n^{-2.1}$ for odd
$n^{-2.1}$ for odd 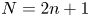 $N=2n+1$ orders, and the matrix exponential distribution, which exhibits such a low
$N=2n+1$ orders, and the matrix exponential distribution, which exhibits such a low 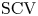 $\mathrm {SCV}$ has complex eigenvalues. In this paper, we consider CME distributions with real eigenvalues (CME-R). We present efficient numerical methods for identifying a CME-R distribution with smallest SCV for a given order
$\mathrm {SCV}$ has complex eigenvalues. In this paper, we consider CME distributions with real eigenvalues (CME-R). We present efficient numerical methods for identifying a CME-R distribution with smallest SCV for a given order 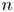 $n$. Our investigations show that the
$n$. Our investigations show that the 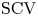 $\mathrm {SCV}$ of the most concentrated CME-R of order
$\mathrm {SCV}$ of the most concentrated CME-R of order 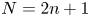 $N=2n+1$ is less than
$N=2n+1$ is less than 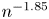 $n^{-1.85}$. We also discuss how CME-R can be used for numerical inverse Laplace transformation, which is beneficial when the Laplace transform function is impossible to evaluate at complex points.
$n^{-1.85}$. We also discuss how CME-R can be used for numerical inverse Laplace transformation, which is beneficial when the Laplace transform function is impossible to evaluate at complex points.
Keywords
Information
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 36 , Issue 4 , October 2022 , pp. 1171 - 1187
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by

