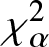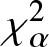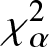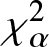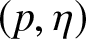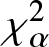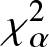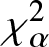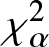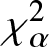1. Introduction
Information theory is one of the most important branches of science and engineering and has attracted significant attention of numerous researchers over the past seven decades. In information theory, several information-theoretic divergence measures between two probabilistic models have been introduced and then used in many fields including information theory, statistics, engineering and physics. Among the most important information, divergence measures are the Kullback–Leibler and chi-square divergence measures. These two information quantities have found many key applications in information theory, economics, statistics, physics and electrical engineering. In the literature, some extensions of Kullback–Leibler and chi-square divergence measures have appeared during the last three decades. For pertinent details, one may refer to [Reference Basu, Harris, Hjort and Jones5, Reference Cover and Thomas7, Reference Kharazmi and Balakrishnan11, Reference Nielsen and Nock18].
The chi-square divergence has several extensions, such as the symmetric chi-square, triangular divergence, generalized chi-square and Balakrishnan and Sanghvi divergence measures. Each of these measures has its own properties and applications in different fields.
In this work, we first consider chi-square (χ 2) and generalized chi-square (![]() $\chi_{\alpha}^2$) divergence measures and then propose relative-
$\chi_{\alpha}^2$) divergence measures and then propose relative-![]() $\chi_{\alpha}^2$ and two Jensen versions of
$\chi_{\alpha}^2$ and two Jensen versions of ![]() $\chi_{\alpha}^2$ (Jensen-
$\chi_{\alpha}^2$ (Jensen-![]() $\chi_{\alpha}^2$ and (p, w)-Jensen-
$\chi_{\alpha}^2$ and (p, w)-Jensen-![]() $\chi_{\alpha}^2$) divergence measure. We further examine a possible connection between the proposed information measures and also discuss some potential applications of them.
$\chi_{\alpha}^2$) divergence measure. We further examine a possible connection between the proposed information measures and also discuss some potential applications of them.
The proposed relative-![]() $\chi_{\alpha}^2$,
$\chi_{\alpha}^2$, ![]() $D_{\alpha}^{\psi}(\,f:g)$ divergence, provides a measure of the difference between two probability distributions, f and g, that is weighted by the density function
$D_{\alpha}^{\psi}(\,f:g)$ divergence, provides a measure of the difference between two probability distributions, f and g, that is weighted by the density function ![]() $\psi(x)$. The weight density function
$\psi(x)$. The weight density function ![]() $\psi(x)$ allows the divergence to be tailored to specific features and characteristics of the data, for the two models that are being compared.
$\psi(x)$ allows the divergence to be tailored to specific features and characteristics of the data, for the two models that are being compared.
The parameter α controls the sensitivity of the divergence to differences between f and g. For example, when α = 1, the divergence reduces to the L 2 distance, which measures the difference between f and g in terms of their squared deviations. When α = 0, the divergence measure reduces to half of the chi-square divergence measure. The weight density function ![]() $\psi(x)$ can be chosen to emphasize or de-emphasize certain regions of the data. For example, a weight function that down-weighs the tails of the distributions could be used to make the divergence more robust to outliers. Alternatively, a weight function that emphasizes a particular region of the data could be used to highlight differences in that region of the data.
$\psi(x)$ can be chosen to emphasize or de-emphasize certain regions of the data. For example, a weight function that down-weighs the tails of the distributions could be used to make the divergence more robust to outliers. Alternatively, a weight function that emphasizes a particular region of the data could be used to highlight differences in that region of the data.
Overall, the choice of α and the weight density function ![]() $\psi(x)$ can be tailored to suit the specific characteristics and features of the data for the two models that are being compared, allowing for greater sensitivity and flexibility in the comparison process, and the
$\psi(x)$ can be tailored to suit the specific characteristics and features of the data for the two models that are being compared, allowing for greater sensitivity and flexibility in the comparison process, and the ![]() $D_{\alpha}^{\psi}(\,f:g)$ measure has potential uses in various fields, as listed below:
$D_{\alpha}^{\psi}(\,f:g)$ measure has potential uses in various fields, as listed below:
• Statistics: It can be used in goodness-of-fit tests and model selection criteria, for example, chi-square divergence (α = 0) is commonly used in contingency table analysis.
• Machine learning: The proposed divergence measure can be used as a divergence measure in machine learning algorithms, such as clustering, classification and anomaly detection.
• Information theory: The proposed divergence can be used to measure the difference between probability distributions and to quantify the amount of information gained or lost in a data compression or transmission process.
• Signal processing:
 $D_{\alpha}^{\psi}(\,f:g)$ divergence measure can be used to compare the strength signals in signal processing applications.
$D_{\alpha}^{\psi}(\,f:g)$ divergence measure can be used to compare the strength signals in signal processing applications.• Image processing: The proposed
 $D_{\alpha}^{\psi}(\,f:g)$ divergence measure can be used to compare image histograms and textures in image processing applications.
$D_{\alpha}^{\psi}(\,f:g)$ divergence measure can be used to compare image histograms and textures in image processing applications.
One of the main motivations behind the development of ![]() $D_{{\alpha}}^{\psi}(\,f:g)$ divergence is that it encompasses several popular divergence measures as special cases, including the symmetric chi-square, triangular divergence, generalized chi-square, and Balakrishnan and Sanghvi divergence measures. This property makes the
$D_{{\alpha}}^{\psi}(\,f:g)$ divergence is that it encompasses several popular divergence measures as special cases, including the symmetric chi-square, triangular divergence, generalized chi-square, and Balakrishnan and Sanghvi divergence measures. This property makes the ![]() $D_{{\alpha}}^{\psi}(\,f:g)$ divergence measure a versatile tool for comparing probability distributions in a variety of fields and facilitates the integration of different divergence measures into a unified framework.
$D_{{\alpha}}^{\psi}(\,f:g)$ divergence measure a versatile tool for comparing probability distributions in a variety of fields and facilitates the integration of different divergence measures into a unified framework.
Furthermore, it should also be noted that the proposed Jensen-![]() $\chi_{\alpha}^2$ and (p, w)-Jensen-
$\chi_{\alpha}^2$ and (p, w)-Jensen-![]() $\chi_{\alpha}^2$ divergence measures are extensions of
$\chi_{\alpha}^2$ divergence measures are extensions of ![]() $D_{{\alpha}}^{\psi}(\,f:g)$ measure based on a convex combination. These extensions allow for the incorporation of additional divergence measures into the framework, further increasing the flexibility and applicability of the method. By combining different divergence measures in a convex form, these Jensen-type divergence measures can provide a more comprehensive and nuanced comparison of probability distributions.
$D_{{\alpha}}^{\psi}(\,f:g)$ measure based on a convex combination. These extensions allow for the incorporation of additional divergence measures into the framework, further increasing the flexibility and applicability of the method. By combining different divergence measures in a convex form, these Jensen-type divergence measures can provide a more comprehensive and nuanced comparison of probability distributions.
In addition, in this paper, we also establish a new generalized mixture density and specifically show that the proposed model provides optimal information under three different optimization problems associated with ![]() $\chi_{\alpha}^2$ divergence measure. Moreover, some results on these information measures and their connections to other well-known information measures are also provided.
$\chi_{\alpha}^2$ divergence measure. Moreover, some results on these information measures and their connections to other well-known information measures are also provided.
First, a diversity measure between two density functions f and g on common support ![]() ${\cal X}$, known as chi-square divergence, is defined as
${\cal X}$, known as chi-square divergence, is defined as
 \begin{eqnarray}
\chi^{2}(\,f:g)=\int_{\cal X} \frac{(\, f(x)-g(x))^{2}}{f(x)}\,{\rm d}x.
\end{eqnarray}
\begin{eqnarray}
\chi^{2}(\,f:g)=\int_{\cal X} \frac{(\, f(x)-g(x))^{2}}{f(x)}\,{\rm d}x.
\end{eqnarray} Similarly, we can define ![]() $\chi^{2}(g:f).$
$\chi^{2}(g:f).$
A generalized version of χ 2 divergence measure, denoted by ![]() $\chi_{\alpha}^2$, between two densities f and g, for
$\chi_{\alpha}^2$, between two densities f and g, for ![]() $\alpha\geq 0$, considered by [Reference Basu, Harris, Hjort and Jones5], is defined as
$\alpha\geq 0$, considered by [Reference Basu, Harris, Hjort and Jones5], is defined as
 \begin{eqnarray}
\chi_{\alpha}^{2}(\,f:g)=\frac{\alpha+1}{2}\int_{\cal X} \frac{\big(\,f(x)-g(x)\big)^2}{f^{1-\alpha}(x)}\, {\rm d}x.
\end{eqnarray}
\begin{eqnarray}
\chi_{\alpha}^{2}(\,f:g)=\frac{\alpha+1}{2}\int_{\cal X} \frac{\big(\,f(x)-g(x)\big)^2}{f^{1-\alpha}(x)}\, {\rm d}x.
\end{eqnarray}Balakrishnan and Sanghvi [Reference Balakrishnan and Sanghvi4] introduced another version of the chi-square divergence in Eq. (1.1) as
 \begin{eqnarray}
\chi_{\rm BS}^2(\,f:g)=\int_{\cal X} \left(\frac{f(x)-g(x)}{f(x)+g(x)}\right)^2 f(x) \,{\rm d}x=E_f\left[\frac{f(X)-g(X)}{f(X)+g(X)}\right]^2,
\end{eqnarray}
\begin{eqnarray}
\chi_{\rm BS}^2(\,f:g)=\int_{\cal X} \left(\frac{f(x)-g(x)}{f(x)+g(x)}\right)^2 f(x) \,{\rm d}x=E_f\left[\frac{f(X)-g(X)}{f(X)+g(X)}\right]^2,
\end{eqnarray}where E denotes expectation taken with respect to density f on support ![]() ${\cal X}$, assuming it exists. This information measure is known as Balakrishnan–Sanghvi divergence measure.
${\cal X}$, assuming it exists. This information measure is known as Balakrishnan–Sanghvi divergence measure.
Moreover, a symmetric version of chi-square divergence measure of the form
 \begin{eqnarray}
\chi_{T}^2(\,f:g)=\int_{\cal X} \frac{\big(\,f(x)-g(x)\big)^2}{{f(x)+g(x)}}\,{\rm d}x=8E_h\left[\frac{f(X)-g(X)}{f(X)+g(X)}\right]^2
\end{eqnarray}
\begin{eqnarray}
\chi_{T}^2(\,f:g)=\int_{\cal X} \frac{\big(\,f(x)-g(x)\big)^2}{{f(x)+g(x)}}\,{\rm d}x=8E_h\left[\frac{f(X)-g(X)}{f(X)+g(X)}\right]^2
\end{eqnarray}has been introduced by [Reference Le Cam12]. Here, E denotes expectation under mixture density  $h(x)=\frac{f(x)+g(x)}{2}$. The divergence measure in Eq. (1.4) is known as triangular divergence measure. Throughout this paper, we will suppress
$h(x)=\frac{f(x)+g(x)}{2}$. The divergence measure in Eq. (1.4) is known as triangular divergence measure. Throughout this paper, we will suppress ![]() ${\cal X}$ in the integration with respect to X, unless a distinction becomes necessary.
${\cal X}$ in the integration with respect to X, unless a distinction becomes necessary.
The rest of this paper is organized as follows. In Section 2, we first examine the connection between ![]() $\chi_{\alpha}^2$ divergence measure and q-Fisher information measure. Here, based on the
$\chi_{\alpha}^2$ divergence measure and q-Fisher information measure. Here, based on the ![]() $\chi_{\alpha}^2$ divergence measure, we introduce a relative-
$\chi_{\alpha}^2$ divergence measure, we introduce a relative-![]() $\chi_{\alpha}^2$ divergence measure, which includes other well-known versions of chi-square divergence as special cases. We propose Jensen-
$\chi_{\alpha}^2$ divergence measure, which includes other well-known versions of chi-square divergence as special cases. We propose Jensen-![]() $\chi_{\alpha}^2$ divergence measure in Section 3. We then show that Jensen-
$\chi_{\alpha}^2$ divergence measure in Section 3. We then show that Jensen-![]() $\chi_{\alpha}^2$ divergence is a mixture of the proposed relative-
$\chi_{\alpha}^2$ divergence is a mixture of the proposed relative-![]() $\chi_{\alpha}^2$ divergence measures. Further, we show that a lower bound for Jensen-
$\chi_{\alpha}^2$ divergence measures. Further, we show that a lower bound for Jensen-![]() $\chi_{\alpha}^2$ divergence can be given by Jensen–Shannon entropy measure. In Section 4, we first introduce (p, w)-Jensen-
$\chi_{\alpha}^2$ divergence can be given by Jensen–Shannon entropy measure. In Section 4, we first introduce (p, w)-Jensen-![]() $\chi_{\alpha}^2$ divergence measure and then discuss some of its properties. Next, the relative-
$\chi_{\alpha}^2$ divergence measure and then discuss some of its properties. Next, the relative-![]() $\chi_{\alpha}^2$ divergence measure of escort and arithmetic densities are studied in Section 5. We then introduce
$\chi_{\alpha}^2$ divergence measure of escort and arithmetic densities are studied in Section 5. We then introduce ![]() $(p,\eta)$-mixture density in Section 6 and show that this mixture distribution involves optimal information under three different optimization problems associated with
$(p,\eta)$-mixture density in Section 6 and show that this mixture distribution involves optimal information under three different optimization problems associated with ![]() $\chi_{\alpha}^2$ divergence measure. In Section 7, we study the relative-
$\chi_{\alpha}^2$ divergence measure. In Section 7, we study the relative-![]() $\chi_{\alpha}^2$ divergence measure of order statistics and mixed reliability systems. Next, in Section 8, we use a real example in image processing and present some numerical results in this regard in terms of Jensen-
$\chi_{\alpha}^2$ divergence measure of order statistics and mixed reliability systems. Next, in Section 8, we use a real example in image processing and present some numerical results in this regard in terms of Jensen-![]() $\chi_{\alpha}^2$ divergence measure. We specifically show that this divergence could serve as an useful measure of similarity between two images. Finally, we make some concluding remarks in Section 9.
$\chi_{\alpha}^2$ divergence measure. We specifically show that this divergence could serve as an useful measure of similarity between two images. Finally, we make some concluding remarks in Section 9.
2. Relative- $\chi_{\alpha}^2$ divergence measure and connection between
$\chi_{\alpha}^2$ divergence measure and connection between  $\chi_{\alpha}^2$ divergence measure and q-Fisher information
$\chi_{\alpha}^2$ divergence measure and q-Fisher information
In this section, we first show that the ![]() $\chi_{\alpha}^2$ divergence measure in Eq. (1.2) has a close connection to
$\chi_{\alpha}^2$ divergence measure in Eq. (1.2) has a close connection to ![]() $q-$Fisher information of mixing parameter of a given arithmetic mixture distribution. Next, we introduce a relative-
$q-$Fisher information of mixing parameter of a given arithmetic mixture distribution. Next, we introduce a relative-![]() $\chi_{\alpha}^2$ divergence measure and show that it includes some of the well-known chi-square-type divergence measures as special cases.
$\chi_{\alpha}^2$ divergence measure and show that it includes some of the well-known chi-square-type divergence measures as special cases.
2.1. Connection between  $\chi_{\alpha}^2$ divergence measure and q-Fisher information
$\chi_{\alpha}^2$ divergence measure and q-Fisher information
The q-Fisher information of a density function fθ about parameter θ, defined by [Reference Lutwak, Lv, Yang and Zhang14], is given by
 \begin{eqnarray}
{\cal I}_q(\theta)=\int \left(\frac{\partial \,\log_q f_{\theta}(x)}{\partial \theta}\right)^2 f_{\theta}(x)\,{\rm d}x,
\end{eqnarray}
\begin{eqnarray}
{\cal I}_q(\theta)=\int \left(\frac{\partial \,\log_q f_{\theta}(x)}{\partial \theta}\right)^2 f_{\theta}(x)\,{\rm d}x,
\end{eqnarray}where ![]() $\log_q (x)$ is the q-logarithmic function defined as
$\log_q (x)$ is the q-logarithmic function defined as
 \begin{eqnarray}
\log_q(x)=\frac{x^q-1}{q}\quad \big( x\in \Re,\ q\neq 0\big)
\end{eqnarray}
\begin{eqnarray}
\log_q(x)=\frac{x^q-1}{q}\quad \big( x\in \Re,\ q\neq 0\big)
\end{eqnarray}for more details, see [Reference Furuichi9, Reference Masi15, Reference Yamano23]. Then, we have the following result.
Theorem 2.1. Let f 1 and f 2 be two density functions. Then, the q-information measure of mixing parameter p in the two-component mixture model
is given by
 \begin{eqnarray*}
{{\cal I}_q}(p) = \frac{8}{2q+1} \mathcal{M}_{\frac{1}{2}}\left({\chi_{2q}^{2}(\,f_{p}, f_{1})},{\chi_{2q}^{2}(\,f_{p}, f_{2})} \right),
\end{eqnarray*}
\begin{eqnarray*}
{{\cal I}_q}(p) = \frac{8}{2q+1} \mathcal{M}_{\frac{1}{2}}\left({\chi_{2q}^{2}(\,f_{p}, f_{1})},{\chi_{2q}^{2}(\,f_{p}, f_{2})} \right),
\end{eqnarray*}where  $M_{\frac{1}{2}}(.,.)$ is the power mean with exponent
$M_{\frac{1}{2}}(.,.)$ is the power mean with exponent ![]() $\frac{1}{2}$, defined as
$\frac{1}{2}$, defined as  $\mathcal{M}_{\frac{1}{2}}(x,y)=\left(\frac{x^{\frac{1}{2}}}{2}+\frac{y^{\frac{1}{2}}}{2}\right)^{2}$ for positive x and y.
$\mathcal{M}_{\frac{1}{2}}(x,y)=\left(\frac{x^{\frac{1}{2}}}{2}+\frac{y^{\frac{1}{2}}}{2}\right)^{2}$ for positive x and y.
Proof. From the mixture model in Eq. (2.3), we readily see that
 \begin{eqnarray}
f_1(x)-f_2(x)=\frac{f_1(x)-f_{p}(x)}{1-p}=\frac{f_p(x)-f_2(x)}{p}.
\end{eqnarray}
\begin{eqnarray}
f_1(x)-f_2(x)=\frac{f_1(x)-f_{p}(x)}{1-p}=\frac{f_p(x)-f_2(x)}{p}.
\end{eqnarray}Now, from the definition of q-Fisher information measure in Eq. (2.1), we find
 \begin{equation}
{{\cal I}_q}(p)=\int \frac{\big(\,f_{1}(x)-f_{2}(x)\big)^2}{f_{p}^{1-2q}(x)}\,{\rm d}x
=\left\{
\begin{array}{ll}
\frac{2}{{(1+2q)(1-p)^2}}\chi_{2q}^{2}(\,f_p: f), & f=f_{1}, \\ \\
\frac{2}{{(1+2q)p^2}}\chi_{2q}^{2}(\,f_p: f), & f=f_{2},
\end{array}
\right.
\end{equation}
\begin{equation}
{{\cal I}_q}(p)=\int \frac{\big(\,f_{1}(x)-f_{2}(x)\big)^2}{f_{p}^{1-2q}(x)}\,{\rm d}x
=\left\{
\begin{array}{ll}
\frac{2}{{(1+2q)(1-p)^2}}\chi_{2q}^{2}(\,f_p: f), & f=f_{1}, \\ \\
\frac{2}{{(1+2q)p^2}}\chi_{2q}^{2}(\,f_p: f), & f=f_{2},
\end{array}
\right.
\end{equation}which readily yields
 \begin{eqnarray*}
{{\cal I}_q}(p)&=&\frac{2}{1+2q}\left(\sqrt{\chi_{2q}^{2}(\,f_{p}:f_{1})}+\sqrt{\chi_{2q}^{2}(\,f_{p}: f_{2})}\right)^{2}\\
&=&\frac{8}{1+2q}\left(\frac{1}{2}\sqrt{\chi_{2q}^{2}(\,f_{p}:{f_{1}})}+\frac{1}{2}\sqrt{\chi_{2q}^{2}(\,f_{p}: f_{2})}\right)^{2}\\
&=&\frac{8}{1+2q} \mathcal{M}_{\frac{1}{2}}\left({\chi_{2q}^{2}(\,f_{p}:f_{1})},{\chi_{2q}^{2}(\,f_{p}:f_{2})} \right),
\end{eqnarray*}
\begin{eqnarray*}
{{\cal I}_q}(p)&=&\frac{2}{1+2q}\left(\sqrt{\chi_{2q}^{2}(\,f_{p}:f_{1})}+\sqrt{\chi_{2q}^{2}(\,f_{p}: f_{2})}\right)^{2}\\
&=&\frac{8}{1+2q}\left(\frac{1}{2}\sqrt{\chi_{2q}^{2}(\,f_{p}:{f_{1}})}+\frac{1}{2}\sqrt{\chi_{2q}^{2}(\,f_{p}: f_{2})}\right)^{2}\\
&=&\frac{8}{1+2q} \mathcal{M}_{\frac{1}{2}}\left({\chi_{2q}^{2}(\,f_{p}:f_{1})},{\chi_{2q}^{2}(\,f_{p}:f_{2})} \right),
\end{eqnarray*}as required.
2.2. Relative- $\chi_{\alpha}^2$ divergence measure
$\chi_{\alpha}^2$ divergence measure
In this subsection, we introduce a relative-![]() $\chi_{\alpha}^2$ divergence measure and show that it includes some of the well-known chi-square-type divergence measures as special cases. Further, we show that the special case of the proposed measure, when α = 0, is connected to the variance of density ratios.
$\chi_{\alpha}^2$ divergence measure and show that it includes some of the well-known chi-square-type divergence measures as special cases. Further, we show that the special case of the proposed measure, when α = 0, is connected to the variance of density ratios.
Definition 2.2. Let f and g be two density functions on support ![]() ${\cal X}$. Then, a relative version of
${\cal X}$. Then, a relative version of ![]() $\chi_{\alpha}^2$ divergence measure between f and g with respect to density function ψ on support
$\chi_{\alpha}^2$ divergence measure between f and g with respect to density function ψ on support ![]() ${\cal X}$, denoted by R-
${\cal X}$, denoted by R-![]() $\chi_{\alpha}^2$, for
$\chi_{\alpha}^2$, for ![]() $\alpha\geq 0$, is defined as
$\alpha\geq 0$, is defined as
 \begin{eqnarray}
D_{{\alpha}}^{\psi}(\,f:g)=\frac{1+\alpha}{2}\int_{{\cal X}} \frac{\big({f(x)-g(x)}\big)^2}{\psi^{1-\alpha}(x)}\,{\rm d}x,
\end{eqnarray}
\begin{eqnarray}
D_{{\alpha}}^{\psi}(\,f:g)=\frac{1+\alpha}{2}\int_{{\cal X}} \frac{\big({f(x)-g(x)}\big)^2}{\psi^{1-\alpha}(x)}\,{\rm d}x,
\end{eqnarray} provided the involved integral exists. In addition, the special case of R-![]() $\chi_{\alpha}^2$ divergence measure, when α = 0, is of the form
$\chi_{\alpha}^2$ divergence measure, when α = 0, is of the form
 \begin{eqnarray}
D_{{\alpha=0}}^{\psi}(\,f:g)=\frac{1}{2}\int_{{\cal X}} \frac{\big({f(x)-g(x)}\big)^2}{\psi(x)}\,{\rm d}x.
\end{eqnarray}
\begin{eqnarray}
D_{{\alpha=0}}^{\psi}(\,f:g)=\frac{1}{2}\int_{{\cal X}} \frac{\big({f(x)-g(x)}\big)^2}{\psi(x)}\,{\rm d}x.
\end{eqnarray} Moreover, it is useful to note that ![]() $D_{{\alpha}}^{\psi}(\,f:g)$ reduces to
$D_{{\alpha}}^{\psi}(\,f:g)$ reduces to ![]() $\chi_{\alpha}^2(\,f:g)$ when
$\chi_{\alpha}^2(\,f:g)$ when ![]() $\psi=f.$ It is easily seen from Eq. (2.6) that R-
$\psi=f.$ It is easily seen from Eq. (2.6) that R-![]() $\chi_{\alpha}^2$ divergence measure can be expressed based on two expectations under densities f and g to be
$\chi_{\alpha}^2$ divergence measure can be expressed based on two expectations under densities f and g to be
 \begin{eqnarray*}
D_{{\alpha}}^{\psi}(\,f:g)&=&\frac{1+\alpha}{2}\int_{{\cal X}} \frac{\big({f(x)-g(x)}\big)^2}{\psi^{1-\alpha}(x)}\,{\rm d}x\\
&=&\frac{1+\alpha}{2}E_f\left(\frac{f(X)-g(X)}{\psi^{1-\alpha}(X)}\right)+\frac{1+\alpha}{2}E_g\left(\frac{g(X)-f(X)}{\psi^{1-\alpha}(X)}\right).
\end{eqnarray*}
\begin{eqnarray*}
D_{{\alpha}}^{\psi}(\,f:g)&=&\frac{1+\alpha}{2}\int_{{\cal X}} \frac{\big({f(x)-g(x)}\big)^2}{\psi^{1-\alpha}(x)}\,{\rm d}x\\
&=&\frac{1+\alpha}{2}E_f\left(\frac{f(X)-g(X)}{\psi^{1-\alpha}(X)}\right)+\frac{1+\alpha}{2}E_g\left(\frac{g(X)-f(X)}{\psi^{1-\alpha}(X)}\right).
\end{eqnarray*} From the definition of ![]() $D_{{\alpha}}^{\psi}(\,f:g)$, the weight density function,
$D_{{\alpha}}^{\psi}(\,f:g)$, the weight density function, ![]() $\psi(x)$, can be utilized to assign varying degrees of importance to different regions of the dataset. For instance, a weight function that places less emphasis on extreme values can be employed to make the divergence measure more robust to outliers. On the other hand, a weight function that highlights a specific region of the data can be used to detect dissimilarities within that region of the data.
$\psi(x)$, can be utilized to assign varying degrees of importance to different regions of the dataset. For instance, a weight function that places less emphasis on extreme values can be employed to make the divergence measure more robust to outliers. On the other hand, a weight function that highlights a specific region of the data can be used to detect dissimilarities within that region of the data.
In general, ![]() $D_{{\alpha}}^{\psi}(\,f:g)$ divergence provides a flexible and powerful framework for assessing the differences between probability distributions in a wide range of applications. The parameters α and
$D_{{\alpha}}^{\psi}(\,f:g)$ divergence provides a flexible and powerful framework for assessing the differences between probability distributions in a wide range of applications. The parameters α and ![]() $\psi(x)$ can be adjusted to suit the specific characteristics and features of the data for the two models that are being compared, offering greater sensitivity and flexibility in the comparison process.
$\psi(x)$ can be adjusted to suit the specific characteristics and features of the data for the two models that are being compared, offering greater sensitivity and flexibility in the comparison process.
(i) If α = 1, then
 $D_{\alpha=1}^{\psi}(\,f:g)=L_2(\,f:g)=\int \big(\,f(x)-g(x)\big)^2{\rm d} x$.
$D_{\alpha=1}^{\psi}(\,f:g)=L_2(\,f:g)=\int \big(\,f(x)-g(x)\big)^2{\rm d} x$.(ii) If
 $\psi(x)=f(x)$, then
$\psi(x)=f(x)$, then  $D_{\alpha=0}^{\psi}(\,f:g)={\chi_{0}^2(\,f,g)}=\frac{\chi^2(\,f,g)}{2}$.
$D_{\alpha=0}^{\psi}(\,f:g)={\chi_{0}^2(\,f,g)}=\frac{\chi^2(\,f,g)}{2}$.(iii) If
 $\psi(x)=g(x)$, then
$\psi(x)=g(x)$, then  $D_{\alpha=0}^{\psi}(\,f:g)={\chi_{0}^2(g,f)}=\frac{\chi^2(g,\,f)}{2}$.
$D_{\alpha=0}^{\psi}(\,f:g)={\chi_{0}^2(g,f)}=\frac{\chi^2(g,\,f)}{2}$.(iv) If
 $\psi(x)=p f(x)+(1-p) g(x)$, then
$\psi(x)=p f(x)+(1-p) g(x)$, then  $D_{\alpha=0}^{\psi}(\,f:g)=\frac{1}{2(1-p)^2}\chi^2\big(\psi:f\big)=\frac{1}{2p^2}\chi^2(\psi:g)$.
$D_{\alpha=0}^{\psi}(\,f:g)=\frac{1}{2(1-p)^2}\chi^2\big(\psi:f\big)=\frac{1}{2p^2}\chi^2(\psi:g)$.(v) If
 $\psi(x)= \frac{f(x)+g(x)}{2}$, then
$\psi(x)= \frac{f(x)+g(x)}{2}$, then  $D_{\alpha=0}^{\psi}(\,f:g)=\chi_{T}^2(\,f:g)$, where
$D_{\alpha=0}^{\psi}(\,f:g)=\chi_{T}^2(\,f:g)$, where  $\chi_{T}^2(\,f:g)$ is the triangular divergence defined in Eq. (1.4).
$\chi_{T}^2(\,f:g)$ is the triangular divergence defined in Eq. (1.4).(vi) If
 $\psi(x)= \frac{f(x)+g(x)}{2}$, then
$\psi(x)= \frac{f(x)+g(x)}{2}$, then  $D_{\alpha=0}^{\psi}(\,f:g)= \chi_{\rm BS}^2(\,f:g)+\chi_{\rm BS}^2(g:f)$, where
$D_{\alpha=0}^{\psi}(\,f:g)= \chi_{\rm BS}^2(\,f:g)+\chi_{\rm BS}^2(g:f)$, where  $D_{\rm BS}(\,f:g)$ is the Balakrishnan–Sanghvi divergence measure defined in Eq. (1.3).
$D_{\rm BS}(\,f:g)$ is the Balakrishnan–Sanghvi divergence measure defined in Eq. (1.3).
Theorem 2.4. Let ψ be a density function. Then,  $D_{\alpha=0}^{\psi}(\,f:g)$ divergence measure in Eq. (2.7) can be expressed as
$D_{\alpha=0}^{\psi}(\,f:g)$ divergence measure in Eq. (2.7) can be expressed as
 \begin{eqnarray}
D_{\alpha=0}^{\psi}(\,f:g)&=&\frac{Var_\psi\left(\frac{f(X)}{\psi(X)}\right)+Var_\psi\left(\frac{g(X)}{\psi(X)}\right)}{2}-E_\psi\left(\frac{f(X)g(X)}{\psi^2(X)}\right)+1.
\end{eqnarray}
\begin{eqnarray}
D_{\alpha=0}^{\psi}(\,f:g)&=&\frac{Var_\psi\left(\frac{f(X)}{\psi(X)}\right)+Var_\psi\left(\frac{g(X)}{\psi(X)}\right)}{2}-E_\psi\left(\frac{f(X)g(X)}{\psi^2(X)}\right)+1.
\end{eqnarray}Proof. From the definition of  $D_{\alpha=0}^{\psi}(\,f:g)$, we have
$D_{\alpha=0}^{\psi}(\,f:g)$, we have
 \begin{eqnarray*}
2 D_{\alpha=0}^{\psi}(\,f:g)&=&
\int \frac{f^2(x)}{\psi(x)}\,{\rm d}x-\left(\int{f(x)}{\rm d}x\right)^2\\
&&+\int \frac{g^2(x)}{\psi(x)}\,{\rm d}x-\left(\int{g(x)}{\rm d}x\right)^2
-2\int\frac{f(x)g(x)}{\psi(x)}\,{\rm d}x+2\\
&=&Var_\psi\left(\frac{f(X)}{\psi(X)}\right)+Var_\psi\left(\frac{g(X)}{\psi(X)}\right)-2E_\psi\left(\frac{f(X)g(X)}{\psi^2(X)}\right)+2,
\end{eqnarray*}
\begin{eqnarray*}
2 D_{\alpha=0}^{\psi}(\,f:g)&=&
\int \frac{f^2(x)}{\psi(x)}\,{\rm d}x-\left(\int{f(x)}{\rm d}x\right)^2\\
&&+\int \frac{g^2(x)}{\psi(x)}\,{\rm d}x-\left(\int{g(x)}{\rm d}x\right)^2
-2\int\frac{f(x)g(x)}{\psi(x)}\,{\rm d}x+2\\
&=&Var_\psi\left(\frac{f(X)}{\psi(X)}\right)+Var_\psi\left(\frac{g(X)}{\psi(X)}\right)-2E_\psi\left(\frac{f(X)g(X)}{\psi^2(X)}\right)+2,
\end{eqnarray*}as required.
3. Jensen- $\chi_{\alpha}^2$ divergence measure
$\chi_{\alpha}^2$ divergence measure
In this section, we first introduce Jensen-![]() $\chi_{\alpha}^2$ divergence measure and then establish some of its properties.
$\chi_{\alpha}^2$ divergence measure and then establish some of its properties.
In fact, the Jensen-![]() $\chi_{\alpha}^2$ divergence measure is an expansion of
$\chi_{\alpha}^2$ divergence measure is an expansion of ![]() $D_{{\alpha}}^{\psi}(\,f:g)$ that is established based on a convex combination. This extension allows for the incorporation of additional divergence measures into the framework, further increasing the flexibility and applicability of the method.
$D_{{\alpha}}^{\psi}(\,f:g)$ that is established based on a convex combination. This extension allows for the incorporation of additional divergence measures into the framework, further increasing the flexibility and applicability of the method.
Definition 3.1. Let ![]() $X_{1}, X_{2}$ and Y be random variables with density functions
$X_{1}, X_{2}$ and Y be random variables with density functions ![]() ${f}_{1},{f}_{2}$ and ψ, respectively, Then, the Jensen-
${f}_{1},{f}_{2}$ and ψ, respectively, Then, the Jensen-![]() $\chi_{\alpha}^2$ (J-
$\chi_{\alpha}^2$ (J-![]() $\chi_{\alpha}^2$) divergence measure, for
$\chi_{\alpha}^2$) divergence measure, for ![]() $p\in (0,1)$, is defined as
$p\in (0,1)$, is defined as
 \begin{eqnarray}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\textbf{P}}\big)&=& p\chi_{\alpha}^{2}(\psi:f_1)+(1-p)\chi_{\alpha}^{2}(\psi:f_2)-\chi_{\alpha}^{2}\big(\psi:pf_1+(1-p)f_2\big).
\end{eqnarray}
\begin{eqnarray}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\textbf{P}}\big)&=& p\chi_{\alpha}^{2}(\psi:f_1)+(1-p)\chi_{\alpha}^{2}(\psi:f_2)-\chi_{\alpha}^{2}\big(\psi:pf_1+(1-p)f_2\big).
\end{eqnarray}Lemma 3.2. The J-![]() $\chi_{\alpha}^2$ divergence measure in Eq. (3.1) is non-negative.
$\chi_{\alpha}^2$ divergence measure in Eq. (3.1) is non-negative.
Proof. As ![]() $\phi(x)=x^2$ is a convex function, by using Jensen’s inequality, we readily find
$\phi(x)=x^2$ is a convex function, by using Jensen’s inequality, we readily find
 \begin{eqnarray*}
\frac{2}{1+\alpha}{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)&=&p\int \frac{\big(\,f_1(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} \,{\rm d}x+(1-p)\int \frac{\big(\,f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)}\, {\rm d}x\\
&&- \int \frac{\big(pf_1(x)+(1-p)f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} \,{\rm d}x\\
&=& p\int \frac{f_{1}^{2}(x)}{\psi^{1-\alpha}(x)}\,{\rm d}x+(1-p)\int \frac{f_{2}^{2}(x)}{\psi^{1-\alpha}(x)}\,{\rm d}x-\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)^2}{\psi^{1-\alpha}(x)}\,{\rm d}x,\\
&\geq& 0,
\end{eqnarray*}
\begin{eqnarray*}
\frac{2}{1+\alpha}{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)&=&p\int \frac{\big(\,f_1(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} \,{\rm d}x+(1-p)\int \frac{\big(\,f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)}\, {\rm d}x\\
&&- \int \frac{\big(pf_1(x)+(1-p)f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} \,{\rm d}x\\
&=& p\int \frac{f_{1}^{2}(x)}{\psi^{1-\alpha}(x)}\,{\rm d}x+(1-p)\int \frac{f_{2}^{2}(x)}{\psi^{1-\alpha}(x)}\,{\rm d}x-\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)^2}{\psi^{1-\alpha}(x)}\,{\rm d}x,\\
&\geq& 0,
\end{eqnarray*}where the last expression follows from the fact that
 \begin{eqnarray*}
\big(pf_1(x)+(1-p)f_2(x)\big)^2\leq pf_{1}^2(x)+(1-p)f_{2}^2(x).
\end{eqnarray*}
\begin{eqnarray*}
\big(pf_1(x)+(1-p)f_2(x)\big)^2\leq pf_{1}^2(x)+(1-p)f_{2}^2(x).
\end{eqnarray*}Theorem 3.3. A representation for  ${\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)$, based on variance of the ratio of densities, is given by
${\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)$, based on variance of the ratio of densities, is given by
 \begin{eqnarray*}
{\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)=\frac{1}{2}\left\{p\, Var_\psi\left(\frac{f_1(X)}{\psi(X)}\right)+(1-p)Var_\psi\left(\frac{f_2(X)}{\psi(X)}\right)-Var_\psi\left(\frac{pf_1(X)+(1-p)f_2(X)}{\psi(X)}\right)\right\}.
\end{eqnarray*}
\begin{eqnarray*}
{\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)=\frac{1}{2}\left\{p\, Var_\psi\left(\frac{f_1(X)}{\psi(X)}\right)+(1-p)Var_\psi\left(\frac{f_2(X)}{\psi(X)}\right)-Var_\psi\left(\frac{pf_1(X)+(1-p)f_2(X)}{\psi(X)}\right)\right\}.
\end{eqnarray*}Proof. From the definition of  ${\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)$, we have
${\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)$, we have
 \begin{eqnarray*}
2{\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)&=&p\int \frac{\big(\,f_1(x)-\psi(x)\big)^2}{\psi(x)} {\rm d}x+(1-p)\int \frac{\big(\,f_2(x)-\psi(x)\big)^2}{\psi(x)} {\rm d}x\\
&&- \int \frac{\big(pf_1(x)+(1-p)f_2(x)-\psi(x)\big)^2}{\psi(x)} {\rm d}x\\
&=& p\int \frac{f_{1}^{2}(x)}{\psi(x)}{\rm d}x+(1-p)\int \frac{f_{2}^{2}(x)}{\psi(x)}{\rm d}x-\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)^2}{\psi(x)}{\rm d}x\\
&=&p\left\{\int \frac{f_{1}^{2}(x)}{\psi(x)}{\rm d}x-1\right\}+(1-p)\left\{\int \frac{f_{2}^{2}(x)}{\psi(x)}{\rm d}x-1\right\}\\
&&-\left\{\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)^2}{\psi(x)}{\rm d}x-1\right\}\\
&=&p\,Var_\psi\bigg(\frac{f_1(X)}{\psi(X)}\bigg)+(1-p)Var_\psi\bigg(\frac{f_2(X)}{\psi(X)}\bigg)-Var_\psi\left(\frac{pf_1(X)+(1-p)f_2(X)}{\psi(X)}\right),
\end{eqnarray*}
\begin{eqnarray*}
2{\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)&=&p\int \frac{\big(\,f_1(x)-\psi(x)\big)^2}{\psi(x)} {\rm d}x+(1-p)\int \frac{\big(\,f_2(x)-\psi(x)\big)^2}{\psi(x)} {\rm d}x\\
&&- \int \frac{\big(pf_1(x)+(1-p)f_2(x)-\psi(x)\big)^2}{\psi(x)} {\rm d}x\\
&=& p\int \frac{f_{1}^{2}(x)}{\psi(x)}{\rm d}x+(1-p)\int \frac{f_{2}^{2}(x)}{\psi(x)}{\rm d}x-\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)^2}{\psi(x)}{\rm d}x\\
&=&p\left\{\int \frac{f_{1}^{2}(x)}{\psi(x)}{\rm d}x-1\right\}+(1-p)\left\{\int \frac{f_{2}^{2}(x)}{\psi(x)}{\rm d}x-1\right\}\\
&&-\left\{\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)^2}{\psi(x)}{\rm d}x-1\right\}\\
&=&p\,Var_\psi\bigg(\frac{f_1(X)}{\psi(X)}\bigg)+(1-p)Var_\psi\bigg(\frac{f_2(X)}{\psi(X)}\bigg)-Var_\psi\left(\frac{pf_1(X)+(1-p)f_2(X)}{\psi(X)}\right),
\end{eqnarray*}as required.
Theorem 3.4. Let the random variables X 1 and X 2 have density functions f 1 and f 2, respectively. Then,  ${\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)$ measure is a mixture of R-
${\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)$ measure is a mixture of R-![]() $\chi_{\alpha}^{2}$ divergence measures of the form
$\chi_{\alpha}^{2}$ divergence measures of the form
 \begin{eqnarray*}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)=p D_{\alpha}^{\psi}(\,f_1:f_T)+(1-p)D_{\alpha}^{\psi}(\,f_2:f_T),
\end{eqnarray*}
\begin{eqnarray*}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)=p D_{\alpha}^{\psi}(\,f_1:f_T)+(1-p)D_{\alpha}^{\psi}(\,f_2:f_T),
\end{eqnarray*}where ![]() $D_{\alpha}^{\psi}(\,f_i:f_T)$ is the divergence measure in Eq. (2.6), with
$D_{\alpha}^{\psi}(\,f_i:f_T)$ is the divergence measure in Eq. (2.6), with ![]() $f_{T}=pf_1+(1-p)f_2$ being the two-component mixture density.
$f_{T}=pf_1+(1-p)f_2$ being the two-component mixture density.
Proof. With ![]() $f_{T}=pf_1+(1-p)f_2$, we first find
$f_{T}=pf_1+(1-p)f_2$, we first find
 \begin{eqnarray*}
\frac{2}{1+\alpha}{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)
&=&p\int \frac{\big(\,f_1(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x+(1-p)\int \frac{\big(\,f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&- \int \frac{\big(pf_1(x)+(1-p)f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=& p\int \frac{f_{1}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+(1-p)\int \frac{f_{2}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x.\\
\end{eqnarray*}
\begin{eqnarray*}
\frac{2}{1+\alpha}{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)
&=&p\int \frac{\big(\,f_1(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x+(1-p)\int \frac{\big(\,f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&- \int \frac{\big(pf_1(x)+(1-p)f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=& p\int \frac{f_{1}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+(1-p)\int \frac{f_{2}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x.\\
\end{eqnarray*} On the other hand, with ![]() $k=pD_{\alpha}^{\psi}(\,f_1:f_T)+(1-p)D_{\alpha}^{\psi}(\,f_2:f_T)$, we also have
$k=pD_{\alpha}^{\psi}(\,f_1:f_T)+(1-p)D_{\alpha}^{\psi}(\,f_2:f_T)$, we also have
 \begin{eqnarray*}
\frac{2}{1+\alpha}k&=& p\int \frac{\big(\,f_1(x)-f_T(x)\big)^2}{{\psi^{1-\alpha}(x)}} {\rm d}x+(1-p)\int \frac{\big(\,f_2(x)-f_T(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&p\int \frac{f_{1}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-2p\int \frac{f_1(x)f_T(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ p\int \frac{f_{T}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&&+(1-p)\int \frac{f_{2}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-2(1-p)\int \frac{f_2(x)f_T(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ (1-p)\int \frac{f_{T}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&p\int \frac{f_{1}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ (1-p)\int \frac{f_{2}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-2\int \frac{f_{T}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+\int \frac{f_{T}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&p\int \frac{f_{1}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ (1-p)\int \frac{f_{2}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-\int \frac{f_{T}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x,
\end{eqnarray*}
\begin{eqnarray*}
\frac{2}{1+\alpha}k&=& p\int \frac{\big(\,f_1(x)-f_T(x)\big)^2}{{\psi^{1-\alpha}(x)}} {\rm d}x+(1-p)\int \frac{\big(\,f_2(x)-f_T(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&p\int \frac{f_{1}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-2p\int \frac{f_1(x)f_T(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ p\int \frac{f_{T}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&&+(1-p)\int \frac{f_{2}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-2(1-p)\int \frac{f_2(x)f_T(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ (1-p)\int \frac{f_{T}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&p\int \frac{f_{1}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ (1-p)\int \frac{f_{2}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-2\int \frac{f_{T}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+\int \frac{f_{T}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&p\int \frac{f_{1}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ (1-p)\int \frac{f_{2}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-\int \frac{f_{T}^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x,
\end{eqnarray*}which establishes the required result.
Theorem 3.5. A connection between  ${\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)$ with
${\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)$ with  $\psi=\frac{f_1+f_2}{2}$ and Balakrishnan–Sanghvi divergence measure is given by
$\psi=\frac{f_1+f_2}{2}$ and Balakrishnan–Sanghvi divergence measure is given by
 \begin{eqnarray*}
{\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)=p\left\{\chi_{\rm BS}^2(\,f_1:f_T)+\chi_{\rm BS}^2(\,f_T:f_1)\right\}+(1-p)\left\{\chi_{\rm BS}^2(\,f_2:f_T)+\chi_{\rm BS}^2(\,f_T:f_2)\right\},
\end{eqnarray*}
\begin{eqnarray*}
{\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)=p\left\{\chi_{\rm BS}^2(\,f_1:f_T)+\chi_{\rm BS}^2(\,f_T:f_1)\right\}+(1-p)\left\{\chi_{\rm BS}^2(\,f_2:f_T)+\chi_{\rm BS}^2(\,f_T:f_2)\right\},
\end{eqnarray*}where ![]() $f_{T}=pf_1+(1-p)f_2$ is the two-component mixture density.
$f_{T}=pf_1+(1-p)f_2$ is the two-component mixture density.
Proof. With ![]() $f_{T}=pf_1+(1-p)f_2$ and from Part (vi) of Remark 2.3 and Theorem 3.4, we have
$f_{T}=pf_1+(1-p)f_2$ and from Part (vi) of Remark 2.3 and Theorem 3.4, we have
 \begin{eqnarray*}
{\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)&=&p D_{\alpha=0}^{\psi}(\,f_1:f_T)+(1-p)D_{\alpha=0}^{\psi}(\,f_2:f_T)\\
&=&p\left\{\chi_{\rm BS}^2(\,f_1:f_T)+\chi_{\rm BS}^2(\,f_T:f_1)\right\}+(1-p)\left\{\chi_{\rm BS}^2(\,f_2:f_T)+\chi_{\rm BS}^2(\,f_T:f_2)\right\},
\end{eqnarray*}
\begin{eqnarray*}
{\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)&=&p D_{\alpha=0}^{\psi}(\,f_1:f_T)+(1-p)D_{\alpha=0}^{\psi}(\,f_2:f_T)\\
&=&p\left\{\chi_{\rm BS}^2(\,f_1:f_T)+\chi_{\rm BS}^2(\,f_T:f_1)\right\}+(1-p)\left\{\chi_{\rm BS}^2(\,f_2:f_T)+\chi_{\rm BS}^2(\,f_T:f_2)\right\},
\end{eqnarray*}as required.
Theorem 3.6. We have
 \begin{eqnarray}
\frac{-1}{2}\,\frac{\partial^2}{\partial p^2}{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)= D_{\alpha}^{\psi}(\,f_1:f_2).
\end{eqnarray}
\begin{eqnarray}
\frac{-1}{2}\,\frac{\partial^2}{\partial p^2}{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)= D_{\alpha}^{\psi}(\,f_1:f_2).
\end{eqnarray}Proof. From the definition  ${\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\textbf{P}}\big)$ in Eq. (3.1) and making use of the dominated convergence theorem, we have
${\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\textbf{P}}\big)$ in Eq. (3.1) and making use of the dominated convergence theorem, we have
 \begin{eqnarray*}
\frac{-1}{2}\,\frac{\partial^2}{\partial p^2}{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)&=&-\frac{1+\alpha}{4}\,\frac{\partial}{\partial p}\left(\int\frac{\big(\,f_1(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x+\int \frac{\big(\,f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\right)\\
&&+\frac{1+\alpha}{2}\,\frac{\partial}{\partial p}\left(\int\big(\,f_1(x)-f_2(x)\big) \frac{pf_1(x)+(1-p)f_2(x)-\psi(x)}{\psi^{1-\alpha}(x)} {\rm d}x \right)\\
&=&\frac{1+\alpha}{2}\int\frac{\big(\,f_1(x)-f_2(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&D_{\alpha}^{\psi}(\,f_1:f_2),
\end{eqnarray*}
\begin{eqnarray*}
\frac{-1}{2}\,\frac{\partial^2}{\partial p^2}{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},{f}_{2}; {\bf{P}}\big)&=&-\frac{1+\alpha}{4}\,\frac{\partial}{\partial p}\left(\int\frac{\big(\,f_1(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x+\int \frac{\big(\,f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\right)\\
&&+\frac{1+\alpha}{2}\,\frac{\partial}{\partial p}\left(\int\big(\,f_1(x)-f_2(x)\big) \frac{pf_1(x)+(1-p)f_2(x)-\psi(x)}{\psi^{1-\alpha}(x)} {\rm d}x \right)\\
&=&\frac{1+\alpha}{2}\int\frac{\big(\,f_1(x)-f_2(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&D_{\alpha}^{\psi}(\,f_1:f_2),
\end{eqnarray*}as required.
We now extend the definition of Jensen-![]() $\chi_{\alpha}^{2}$ divergence measure in Eq. (3.1) to the case of n + 1 random variables. Let
$\chi_{\alpha}^{2}$ divergence measure in Eq. (3.1) to the case of n + 1 random variables. Let ![]() $X_{1},\ldots,X_{n}$ and Y be random variables with density functions
$X_{1},\ldots,X_{n}$ and Y be random variables with density functions ![]() ${f}_{1},\ldots,{f}_{n}$ and ψ, respectively, and
${f}_{1},\ldots,{f}_{n}$ and ψ, respectively, and ![]() $p_{1},\ldots,p_{n}$ be non-negative real numbers such that
$p_{1},\ldots,p_{n}$ be non-negative real numbers such that ![]() $\sum_{i=1}^{n}p_{i}=1$. Then, the Jensen-
$\sum_{i=1}^{n}p_{i}=1$. Then, the Jensen-![]() $\chi_{\alpha}^{2}$ measure is defined as
$\chi_{\alpha}^{2}$ measure is defined as
 \begin{eqnarray}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\textbf{P}}\big)&=& \sum_{i=1}^{n}p_i\chi_{\alpha}^{2}(\psi:f_i)-\chi_{\alpha}^{2} \left(\psi:\sum_{i=1}^{n}p_i f_i\right).
\end{eqnarray}
\begin{eqnarray}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\textbf{P}}\big)&=& \sum_{i=1}^{n}p_i\chi_{\alpha}^{2}(\psi:f_i)-\chi_{\alpha}^{2} \left(\psi:\sum_{i=1}^{n}p_i f_i\right).
\end{eqnarray} The special case of Jensen-![]() $\chi_{\alpha}^2$ divergence measure, when α = 0, has the representation
$\chi_{\alpha}^2$ divergence measure, when α = 0, has the representation
 \begin{eqnarray*}
{\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\textbf{P}}\big)&=&{\frac{1}{2}} \sum_{i=1}^{n}p_i\chi^{2}(\psi:f_i)-{\frac{1}{2}}\chi^{2}\left(\psi:\sum_{i=1}^{n}p_i f_i\right)\\
&=&{\frac{1}{2}}\sum_{i=1}^{n}p_i Var_\psi\left(\frac{f_i(X)}{\psi(X)}\right)-{\frac{1}{2}} Var_\psi\left(\frac{\sum_{i=1}^{n}p_if_i(X)}{\psi(X)}\right).
\end{eqnarray*}
\begin{eqnarray*}
{\cal {J}}_{\alpha=0}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\textbf{P}}\big)&=&{\frac{1}{2}} \sum_{i=1}^{n}p_i\chi^{2}(\psi:f_i)-{\frac{1}{2}}\chi^{2}\left(\psi:\sum_{i=1}^{n}p_i f_i\right)\\
&=&{\frac{1}{2}}\sum_{i=1}^{n}p_i Var_\psi\left(\frac{f_i(X)}{\psi(X)}\right)-{\frac{1}{2}} Var_\psi\left(\frac{\sum_{i=1}^{n}p_if_i(X)}{\psi(X)}\right).
\end{eqnarray*}Corollary 3.7. The  ${\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\textbf{P}}\big)$ measure in Eq. (3.3) is a mixture of
${\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\textbf{P}}\big)$ measure in Eq. (3.3) is a mixture of ![]() $D_{\alpha}^{\psi}$ measures in Eq. (2.6) of the form
$D_{\alpha}^{\psi}$ measures in Eq. (2.6) of the form
 \begin{eqnarray*}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\bf{P}}\big)&=&\sum_{i=1}^{n}p_i
D_{\alpha}^{\psi}(\,f_i:f_T).
\end{eqnarray*}
\begin{eqnarray*}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\bf{P}}\big)&=&\sum_{i=1}^{n}p_i
D_{\alpha}^{\psi}(\,f_i:f_T).
\end{eqnarray*}Theorem 3.8. The  ${\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\textbf{P}}\big)$ measure in Eq. (3.3) is a mixture of
${\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\textbf{P}}\big)$ measure in Eq. (3.3) is a mixture of ![]() $D_{\alpha}^{\psi}$ measures in Eq. (2.6) of the form
$D_{\alpha}^{\psi}$ measures in Eq. (2.6) of the form
 \begin{eqnarray*}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\bf{P}}\big)&=&2\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j D_{\alpha}^{\psi}(\,f_i:f_j).
\end{eqnarray*}
\begin{eqnarray*}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\bf{P}}\big)&=&2\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j D_{\alpha}^{\psi}(\,f_i:f_j).
\end{eqnarray*}Proof. From Corollary 3.7 and making use of the identity ([Reference Steele21], pp. 95–96)
 \begin{equation*}\sum_{i=1}^{n}w_i\big(x_i-\bar{x}_w\big)^2={\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}w_i w_j\big(x_i-x_j\big)^2,\qquad\bar{x}_w=\sum_{i=1}^{n}w_ix_i,\ \sum_{i=1}^{n}w_i=1,\end{equation*}
\begin{equation*}\sum_{i=1}^{n}w_i\big(x_i-\bar{x}_w\big)^2={\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}w_i w_j\big(x_i-x_j\big)^2,\qquad\bar{x}_w=\sum_{i=1}^{n}w_ix_i,\ \sum_{i=1}^{n}w_i=1,\end{equation*}we obtain
 \begin{eqnarray*}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\bf{P}}\big)&=&\sum_{i=1}^{n}p_i
D_{\alpha}^{\psi}(\,f_i:f_T)\\
&=&\frac{1+\alpha}{2}\sum_{i=1}^{n}p_i\int \frac{\big(\,f_i (x) -\sum_{j=1}^{n}p_j f_j(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&\frac{({1+\alpha})}{4}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j \int \frac{\big(\,f_i(x)-f_j(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j D_{\alpha}^{\psi}(\,f_i:f_j),
\end{eqnarray*}
\begin{eqnarray*}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\bf{P}}\big)&=&\sum_{i=1}^{n}p_i
D_{\alpha}^{\psi}(\,f_i:f_T)\\
&=&\frac{1+\alpha}{2}\sum_{i=1}^{n}p_i\int \frac{\big(\,f_i (x) -\sum_{j=1}^{n}p_j f_j(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&\frac{({1+\alpha})}{4}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j \int \frac{\big(\,f_i(x)-f_j(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j D_{\alpha}^{\psi}(\,f_i:f_j),
\end{eqnarray*}as required.
Theorem 3.9. Let  $f_i\geq \frac{\psi^{1-\alpha}}{2}, i=1,\ldots,n$. Then, a lower bound for
$f_i\geq \frac{\psi^{1-\alpha}}{2}, i=1,\ldots,n$. Then, a lower bound for  ${\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\textbf{P}}\big)$ is given by
${\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\textbf{P}}\big)$ is given by
 \begin{eqnarray*}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\bf{P}}\big)\geq \frac{1+\alpha}{4} JS_{{\bf{P}}}(\,f_1,\ldots,f_n),
\end{eqnarray*}
\begin{eqnarray*}
{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\bf{P}}\big)\geq \frac{1+\alpha}{4} JS_{{\bf{P}}}(\,f_1,\ldots,f_n),
\end{eqnarray*}where ![]() $JS_{{\textbf{P}}}(\,f_1,\ldots,f_n)$ is the Jensen–Shannon entropy; see [Reference Lin13].
$JS_{{\textbf{P}}}(\,f_1,\ldots,f_n)$ is the Jensen–Shannon entropy; see [Reference Lin13].
Proof. From the assumption, Theorem 3.8 and by making use of the identity
 \begin{equation*}\sum_{i=1}^{n}w_i\big(x_i-\bar{x}_w\big)^2={\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}w_i w_j\big(x_i-x_j\big)^2,\end{equation*}
\begin{equation*}\sum_{i=1}^{n}w_i\big(x_i-\bar{x}_w\big)^2={\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}w_i w_j\big(x_i-x_j\big)^2,\end{equation*}and then setting ![]() $w_i=p_i$,
$w_i=p_i$, ![]() $w_j=p_j$,
$w_j=p_j$, ![]() $x_i=f_i(x)$,
$x_i=f_i(x)$, ![]() $x_j=f_j(x)$ and
$x_j=f_j(x)$ and ![]() $\bar{x}_w=\sum_{i=1}^{n}p_i f_i(x)$ , we find
$\bar{x}_w=\sum_{i=1}^{n}p_i f_i(x)$ , we find
 \begin{eqnarray*}
\frac{2}{1+\alpha}{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\bf{P}}\big)
&=&\sum_{i=1}^{n}p_i\int \frac{\big(\,f_i (x) -\sum_{j=1}^{n}p_j f_j(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&{\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j \int \frac{\big(\,f_i(x)-f_j(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&{\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j \int \frac{\big(\,f_i(x)-f_j(x)\big)^2}{f_i(x)}\frac{f_i(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&\geq& {\frac{1}{2}} \sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j \int \frac{\big(\,f_i(x)-f_j(x)\big)^2}{f_i(x)} {\rm d}x\\
&\geq& {\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j \int f_i(x)\log\bigg(\frac{f_i(x)}{f_j(x)}\bigg) {\rm d}x\\
&=&{\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j KL(\,f_i:f_j)\\
&\geq&{\frac{1}{2}} JS_{{\bf{P}}}(\,f_1,\ldots,f_n),
\end{eqnarray*}
\begin{eqnarray*}
\frac{2}{1+\alpha}{\cal {J}}_{\alpha}^{\psi}\big({f}_{1},\ldots,{f}_{n}; {\bf{P}}\big)
&=&\sum_{i=1}^{n}p_i\int \frac{\big(\,f_i (x) -\sum_{j=1}^{n}p_j f_j(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&{\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j \int \frac{\big(\,f_i(x)-f_j(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&{\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j \int \frac{\big(\,f_i(x)-f_j(x)\big)^2}{f_i(x)}\frac{f_i(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&\geq& {\frac{1}{2}} \sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j \int \frac{\big(\,f_i(x)-f_j(x)\big)^2}{f_i(x)} {\rm d}x\\
&\geq& {\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j \int f_i(x)\log\bigg(\frac{f_i(x)}{f_j(x)}\bigg) {\rm d}x\\
&=&{\frac{1}{2}}\sum_{i=1}^{n}\sum_{j=1}^{n}p_ip_j KL(\,f_i:f_j)\\
&\geq&{\frac{1}{2}} JS_{{\bf{P}}}(\,f_1,\ldots,f_n),
\end{eqnarray*}where the second inequality follows from the fact that ![]() $\log(x) \lt x-1, x \gt 0$, and the last inequality follows from [Reference Asadi, Ebrahimi, Soofi and Zohrevand3].
$\log(x) \lt x-1, x \gt 0$, and the last inequality follows from [Reference Asadi, Ebrahimi, Soofi and Zohrevand3].
4. ( p, w)-Jensen- $\chi_{\alpha}^2$ divergence measure
$\chi_{\alpha}^2$ divergence measure
In this section, we first review the definition of (p, w)-Jensen–Shannon divergence measure. Then, we introduce (p, w)-Jensen-![]() $\chi_{\alpha}^2$ divergence measure in a way similar to (p, w)-Jensen–Shannon divergence. Furthermore, we establish some results for this extended divergence measure. Let f and g be two density functions. Then, the Kullback–Leibler divergence between f and g is defined as
$\chi_{\alpha}^2$ divergence measure in a way similar to (p, w)-Jensen–Shannon divergence. Furthermore, we establish some results for this extended divergence measure. Let f and g be two density functions. Then, the Kullback–Leibler divergence between f and g is defined as
 \begin{eqnarray*}
KL(\,f,g)=\int f(x)\,\log\left(\frac{f(x)}{g(x)}\right){\rm d}x,
\end{eqnarray*}
\begin{eqnarray*}
KL(\,f,g)=\int f(x)\,\log\left(\frac{f(x)}{g(x)}\right){\rm d}x,
\end{eqnarray*}where log denotes the natural logarithm. The (p, w)-Jensen–Shannon divergence between two density functions f 1 and f 2, for α and p ![]() $\in (0,1)$, is defined as
$\in (0,1)$, is defined as
 \begin{eqnarray*}
JS_{(p,w)}(\,f_1,f_2)&=& H\big((1-{\bar{s}})f_1+{\bar{s}}f_2\big)-w H\big((1-p)f_1+p f_2\big)-(1-w)H\big(p f_1+(1-p) f_2\big)\\
&=& wKL\left((1-p)f_1+p f_2: (1-\bar{s})f_1+\bar{s}f_2\right)\\
&&+(1-w)KL\left(p f_1+(1-p) f_2: (1-{\bar{s}})f_1+{\bar{s}}f_2\right),
\end{eqnarray*}
\begin{eqnarray*}
JS_{(p,w)}(\,f_1,f_2)&=& H\big((1-{\bar{s}})f_1+{\bar{s}}f_2\big)-w H\big((1-p)f_1+p f_2\big)-(1-w)H\big(p f_1+(1-p) f_2\big)\\
&=& wKL\left((1-p)f_1+p f_2: (1-\bar{s})f_1+\bar{s}f_2\right)\\
&&+(1-w)KL\left(p f_1+(1-p) f_2: (1-{\bar{s}})f_1+{\bar{s}}f_2\right),
\end{eqnarray*}where ![]() ${\bar{s}}=wp+(1-w)(1-p)$. For more details, one may refer to [Reference Melbourne, Talukdar, Bhaban, Madiman and Salapaka16, Reference Nielsen17].
${\bar{s}}=wp+(1-w)(1-p)$. For more details, one may refer to [Reference Melbourne, Talukdar, Bhaban, Madiman and Salapaka16, Reference Nielsen17].
Definition 4.1. Let ![]() $X_{1}, X_{2}$ and Y be random variables with density functions
$X_{1}, X_{2}$ and Y be random variables with density functions ![]() ${f}_{1},{f}_{2}$ and ψ, respectively, Then, the (p, w)-Jensen-
${f}_{1},{f}_{2}$ and ψ, respectively, Then, the (p, w)-Jensen-![]() $\chi_{\alpha}^2$ divergence measure, for w and p
$\chi_{\alpha}^2$ divergence measure, for w and p ![]() $\in (0,1)$, is defined as
$\in (0,1)$, is defined as
 \begin{eqnarray*}
{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)&=& w\chi_{\alpha}^{2}\big(\psi:(1-p)f_1+p f_2\big)+(1-w)\chi_{\alpha}^{2}\big(\psi:p f_1+(1-p) f_2\big)\\
&&-\chi_{\alpha}^{2}\big(\psi:(1-{\bar{s}})f_1+{\bar{s}}f_2\big),
\end{eqnarray*}
\begin{eqnarray*}
{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)&=& w\chi_{\alpha}^{2}\big(\psi:(1-p)f_1+p f_2\big)+(1-w)\chi_{\alpha}^{2}\big(\psi:p f_1+(1-p) f_2\big)\\
&&-\chi_{\alpha}^{2}\big(\psi:(1-{\bar{s}})f_1+{\bar{s}}f_2\big),
\end{eqnarray*}where ![]() ${\bar{s}}=wp+(1-w)(1-p)$.
${\bar{s}}=wp+(1-w)(1-p)$.
Theorem 4.2. Let the random variables X 1 and X 2 have density functions f 1 and f 2, respectively. Then,  ${\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)$ is a mixture of relative measures in Eq. (2.6) of the form
${\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)$ is a mixture of relative measures in Eq. (2.6) of the form
 \begin{align}
{\cal {J}}_{\alpha}^\psi\big(\,{f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)=wD_{\alpha}^{\psi}\left((1-p)f_1+p f_2:f_{{\bar{s}}}^{T}\right)+(1-w)D_{\alpha}^{\psi}\left(p f_1+(1-p) f_2:f_{{\bar{s}}}^{T}\right),
\end{align}
\begin{align}
{\cal {J}}_{\alpha}^\psi\big(\,{f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)=wD_{\alpha}^{\psi}\left((1-p)f_1+p f_2:f_{{\bar{s}}}^{T}\right)+(1-w)D_{\alpha}^{\psi}\left(p f_1+(1-p) f_2:f_{{\bar{s}}}^{T}\right),
\end{align}with ![]() $f_{{\bar{s}}}^{T}=(1-{\bar{s}})f_1+{\bar{s}}f_2$ is the two-component mixture density.
$f_{{\bar{s}}}^{T}=(1-{\bar{s}})f_1+{\bar{s}}f_2$ is the two-component mixture density.
Proof. With ![]() $f_{{\bar{s}}}^{T}=(1-{\bar{s}})f_1+{\bar{s}}f_2$, we find
$f_{{\bar{s}}}^{T}=(1-{\bar{s}})f_1+{\bar{s}}f_2$, we find
 \begin{eqnarray*}
&&{\frac{2}{1+\alpha}}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)\\
&=&w\int \frac{\big((1-p)f_1(x)+p f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x+(1-w)\int \frac{\big(p f_1(x)+(1-p) f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&- \int \frac{\big((1-{\bar{s}})f_1(x)+{\bar{s}}f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=& w\int \frac{\big((1-p)f_1(x)+p f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+(1-w)\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&&-\int \frac{\big((1-{\bar{s}})f_1(x)+{\bar{s}}f_2(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x.\\
\end{eqnarray*}
\begin{eqnarray*}
&&{\frac{2}{1+\alpha}}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)\\
&=&w\int \frac{\big((1-p)f_1(x)+p f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x+(1-w)\int \frac{\big(p f_1(x)+(1-p) f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&- \int \frac{\big((1-{\bar{s}})f_1(x)+{\bar{s}}f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=& w\int \frac{\big((1-p)f_1(x)+p f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+(1-w)\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&&-\int \frac{\big((1-{\bar{s}})f_1(x)+{\bar{s}}f_2(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x.\\
\end{eqnarray*}On the other hand, letting
 \begin{equation*}\frac{1+\alpha}{2}k=wD_{\alpha}^{\psi}\left((1-p)f_1+p f_2:f_{{\bar{s}}}^{T}\right)+(1-w)D_{\alpha}^{\psi}\left(p f_1+(1-p) f_2:f_{{\bar{s}}}^{T}\right)\end{equation*}
\begin{equation*}\frac{1+\alpha}{2}k=wD_{\alpha}^{\psi}\left((1-p)f_1+p f_2:f_{{\bar{s}}}^{T}\right)+(1-w)D_{\alpha}^{\psi}\left(p f_1+(1-p) f_2:f_{{\bar{s}}}^{T}\right)\end{equation*}and using the fact that
 \begin{eqnarray*}
f_{{\bar{s}}}^{T}(x)&=&(1-{\bar{s}})f_1(x)+{\bar{s}}f_2(x)\\
&=&\big(1-(wp+(1-w)(1-p))\big)f_1(x)+(wp+(1-w)(1-p))f_2(x)\\
&=&w\big((1-p)f_1(x)+p f_2(x)\big)+(1-w)\big(p f_1(x)+(1-p)f_2(x)\big),
\end{eqnarray*}
\begin{eqnarray*}
f_{{\bar{s}}}^{T}(x)&=&(1-{\bar{s}})f_1(x)+{\bar{s}}f_2(x)\\
&=&\big(1-(wp+(1-w)(1-p))\big)f_1(x)+(wp+(1-w)(1-p))f_2(x)\\
&=&w\big((1-p)f_1(x)+p f_2(x)\big)+(1-w)\big(p f_1(x)+(1-p)f_2(x)\big),
\end{eqnarray*}we find
 \begin{eqnarray*}
k&=& w\int \frac{\big((1-p)f_1(x)+p f_2(x)-f_{{\bar{s}}}^{T}(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x+(1-w)\int \frac{\big(p f_1(x)+(1-p) f_2(x)-f_{{\bar{s}}}^{T}(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&w\int \frac{\big((1-p)f_1(x)+p f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-2w\int \frac{\big((1-p) f_1(x)+p f_2(x)\big)f_{{\bar{s}}}^{T}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ \int \frac{\big(\,f_{{\bar{s}}}^{T}(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&&+(1-w)\int \frac{\big((pf_1(x)+(1-p)f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-2(1-w)\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)f_{{\bar{s}}}^{T}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&w\int \frac{\big((1-p)f_1(x)+p f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ (1-w)\int \frac{\big((pf_1(x)+(1-p)f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&&+\int \frac{\big(\,f_{{\bar{s}}}^{T}(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x.
\end{eqnarray*}
\begin{eqnarray*}
k&=& w\int \frac{\big((1-p)f_1(x)+p f_2(x)-f_{{\bar{s}}}^{T}(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x+(1-w)\int \frac{\big(p f_1(x)+(1-p) f_2(x)-f_{{\bar{s}}}^{T}(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&w\int \frac{\big((1-p)f_1(x)+p f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-2w\int \frac{\big((1-p) f_1(x)+p f_2(x)\big)f_{{\bar{s}}}^{T}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ \int \frac{\big(\,f_{{\bar{s}}}^{T}(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&&+(1-w)\int \frac{\big((pf_1(x)+(1-p)f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x-2(1-w)\int \frac{\big(pf_1(x)+(1-p)f_2(x)\big)f_{{\bar{s}}}^{T}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&w\int \frac{\big((1-p)f_1(x)+p f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x+ (1-w)\int \frac{\big((pf_1(x)+(1-p)f_2(x)\big)^{2}(x)}{\psi^{1-\alpha}(x)}{\rm d}x\\
&&+\int \frac{\big(\,f_{{\bar{s}}}^{T}(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x.
\end{eqnarray*}Now, from the above results, we have
 \begin{eqnarray*}
{{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)=\frac{1+\alpha}{2}k=wD_{\alpha}^{\psi}\left((1-p)f_1+p f_2:f_{{\bar{s}}}^{T}\right)+(1-w)D_{\alpha}^{\psi}\left(p f_1+(1-p) f_2:f_{{\bar{s}}}^{T}\right),}
\end{eqnarray*}
\begin{eqnarray*}
{{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)=\frac{1+\alpha}{2}k=wD_{\alpha}^{\psi}\left((1-p)f_1+p f_2:f_{{\bar{s}}}^{T}\right)+(1-w)D_{\alpha}^{\psi}\left(p f_1+(1-p) f_2:f_{{\bar{s}}}^{T}\right),}
\end{eqnarray*}which establishes the required result.
From Definitions 3.1 and 4.1, we readily have the following Corollary.
Corollary 4.3. A connection between  ${\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)$ and
${\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)$ and  ${\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};\textbf{w}\big)$ measures is given by
${\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};\textbf{w}\big)$ measures is given by
 \begin{equation*}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)={\cal {J}}_{\alpha}^{\psi}\bigg((1-p){f}_{1}+p{f}_{2}: p{f}_{1}+(1-p){f}_{2}; \textbf{w}\bigg).\end{equation*}
\begin{equation*}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)={\cal {J}}_{\alpha}^{\psi}\bigg((1-p){f}_{1}+p{f}_{2}: p{f}_{1}+(1-p){f}_{2}; \textbf{w}\bigg).\end{equation*}Theorem 4.4. We have
(i)
 \begin{eqnarray*}
\frac{-1}{2}\,\frac{\partial^2}{\partial w^2}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)= D_{\alpha}^{\psi}\left((1-p){f}_{1}+pf_2:p{f}_{1}+(1-p)f_2\right);
\end{eqnarray*}
\begin{eqnarray*}
\frac{-1}{2}\,\frac{\partial^2}{\partial w^2}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\textbf{P}},\textbf{w}\big)= D_{\alpha}^{\psi}\left((1-p){f}_{1}+pf_2:p{f}_{1}+(1-p)f_2\right);
\end{eqnarray*}(ii)
 \begin{eqnarray*}
\frac{-1}{2}\,\frac{\partial^2}{\partial p^2}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\bf{P}},\bf{w}\big)= D_{\alpha}^{\psi}\left((1-w){f}_{1}+wf_2:w{f}_{1}+(1-w)f_2\right)-D_{\alpha}^{\psi}\big(\,f_1:f_2\big).
\end{eqnarray*}
\begin{eqnarray*}
\frac{-1}{2}\,\frac{\partial^2}{\partial p^2}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\bf{P}},\bf{w}\big)= D_{\alpha}^{\psi}\left((1-w){f}_{1}+wf_2:w{f}_{1}+(1-w)f_2\right)-D_{\alpha}^{\psi}\big(\,f_1:f_2\big).
\end{eqnarray*}
Proof. From Theorem 3.6 and Corollary 4.3, we have
 \begin{eqnarray*}
\frac{-1}{2}\,\frac{\partial^2}{\partial w^2}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\bf{P}},\bf{w}\big)&=&\frac{-1}{2}\,\frac{\partial^2}{\partial w^2}{\cal {J}}_{\alpha}^\psi\left((1-p){f}_{1}+pf_2,p{f}_{2}+(1-p)f_1,{\bf{w}}\right)\\
&=& D_{\alpha}^{\psi}\left((1-p){f}_{1}+pf_2:p{f}_{1}+(1-p)f_2\right),
\end{eqnarray*}
\begin{eqnarray*}
\frac{-1}{2}\,\frac{\partial^2}{\partial w^2}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\bf{P}},\bf{w}\big)&=&\frac{-1}{2}\,\frac{\partial^2}{\partial w^2}{\cal {J}}_{\alpha}^\psi\left((1-p){f}_{1}+pf_2,p{f}_{2}+(1-p)f_1,{\bf{w}}\right)\\
&=& D_{\alpha}^{\psi}\left((1-p){f}_{1}+pf_2:p{f}_{1}+(1-p)f_2\right),
\end{eqnarray*}which proves Part (i). From Corollary 4.3 and using the facts that
 \begin{eqnarray*}
f_{{\bar{s}}}^{T}(x)&=&
w\big((1-p)f_1(x)+p f_2(x)\big)+(1-w)\big(p f_1(x)+(1-p)f_2(x)\big)
\end{eqnarray*}
\begin{eqnarray*}
f_{{\bar{s}}}^{T}(x)&=&
w\big((1-p)f_1(x)+p f_2(x)\big)+(1-w)\big(p f_1(x)+(1-p)f_2(x)\big)
\end{eqnarray*}and
we find
 \begin{eqnarray*}
\frac{-1}{2}\,\frac{\partial^2}{\partial p^2}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\bf{P}},\bf{w}\big)&=&\frac{-1}{2}\,\frac{\partial^2}{\partial p^2}{\cal {J}}_{\alpha}^{\psi}\left((1-p){f}_{1}+pf_2,p{f}_{1}+(1-p)f_2; \bf{w}\right)\\
&=&-w\frac{\alpha+1}{4}\,\frac{\partial^2}{\partial p^2}\int \frac{\big((1-p)f_1(x)+p f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&-(1-w)\frac{\alpha+1}{4}\,\frac{\partial^2}{\partial p^2}\int \frac{\big(p f_1(x)+(1-p) f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&+\frac{\alpha+1}{4}\,\frac{\partial^2}{\partial p^2}\int \frac{\big(\,f_{\bar{s}}^{T}(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&\frac{\alpha+1}{2}\int \frac{\left(w(\,f_2(x)-f_1(x))+(1-w)(\,f_1(x)-f_2(x))\right)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&-\frac{\alpha+1}{2}\int \frac{\big(\,f_2(x)-f_1(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&\frac{\alpha+1}{2}\int \frac{\left((1-w){f}_{1}(x)+wf_2(x) -\big(w{f}_{1}(x)+(1-w)f_2(x)\big)\right)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&-\frac{\alpha+1}{2}\int \frac{\big(\,f_2(x)-f_1(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&D_{\alpha}^{\psi}\left((1-w){f}_{1}+wf_2:w{f}_{1}
+(1-w)f_2\right)-D_{\alpha}^{\psi}\big(\,f_1:f_2\big) ,
\end{eqnarray*}
\begin{eqnarray*}
\frac{-1}{2}\,\frac{\partial^2}{\partial p^2}{\cal {J}}_{\alpha}^\psi\big({f}_{1},{f}_{2};{\bf{P}},\bf{w}\big)&=&\frac{-1}{2}\,\frac{\partial^2}{\partial p^2}{\cal {J}}_{\alpha}^{\psi}\left((1-p){f}_{1}+pf_2,p{f}_{1}+(1-p)f_2; \bf{w}\right)\\
&=&-w\frac{\alpha+1}{4}\,\frac{\partial^2}{\partial p^2}\int \frac{\big((1-p)f_1(x)+p f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&-(1-w)\frac{\alpha+1}{4}\,\frac{\partial^2}{\partial p^2}\int \frac{\big(p f_1(x)+(1-p) f_2(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&+\frac{\alpha+1}{4}\,\frac{\partial^2}{\partial p^2}\int \frac{\big(\,f_{\bar{s}}^{T}(x)-\psi(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&\frac{\alpha+1}{2}\int \frac{\left(w(\,f_2(x)-f_1(x))+(1-w)(\,f_1(x)-f_2(x))\right)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&-\frac{\alpha+1}{2}\int \frac{\big(\,f_2(x)-f_1(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&\frac{\alpha+1}{2}\int \frac{\left((1-w){f}_{1}(x)+wf_2(x) -\big(w{f}_{1}(x)+(1-w)f_2(x)\big)\right)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&&-\frac{\alpha+1}{2}\int \frac{\big(\,f_2(x)-f_1(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&D_{\alpha}^{\psi}\left((1-w){f}_{1}+wf_2:w{f}_{1}
+(1-w)f_2\right)-D_{\alpha}^{\psi}\big(\,f_1:f_2\big) ,
\end{eqnarray*}which proves Part (ii). Hence, the theorem.
5.  $D_{\alpha}^{\psi}$ divergence measure of escort and arithmetic mixture densities
$D_{\alpha}^{\psi}$ divergence measure of escort and arithmetic mixture densities
In this section, we examine ![]() $D_{\alpha}^{\psi}$ divergence measure of escort and arithmetic mixture densities.
$D_{\alpha}^{\psi}$ divergence measure of escort and arithmetic mixture densities.
5.1.  $D_{\alpha}^{\psi}$ divergence measure of escort and generalized escort densities
$D_{\alpha}^{\psi}$ divergence measure of escort and generalized escort densities
The escort distribution is a key concept in nonextensive statistical mechanics and coding theory and is closely associated with Tsallis and Rényi entropy measures. Bercher [Reference Bercher6] studied some connections between coding theory and the measure of complexity in nonextensive statistical mechanics in terms of escort distributions.
Let f be a density function. Then, the escort density with order η > 0, associated with f, is defined as
 \begin{eqnarray}
f_{\eta}(x)=\frac{f^\eta(x)}{\int f^\eta(x) {\rm d}x}.
\end{eqnarray}
\begin{eqnarray}
f_{\eta}(x)=\frac{f^\eta(x)}{\int f^\eta(x) {\rm d}x}.
\end{eqnarray}Theorem 5.1. Let f and g be two density functions and fα be the escort density corresponding to f. Then, for ![]() $0\leq\eta\leq1$ and
$0\leq\eta\leq1$ and ![]() $\psi(x)=f_{\eta}(x)$, we have
$\psi(x)=f_{\eta}(x)$, we have
 \begin{eqnarray}
D_{\alpha}^{\psi}(\,f:g)=\frac{1+\alpha}{1+\beta}G_{\eta}^{1-\alpha}(\,f)\chi_{\beta}^{2}(\,f:g),
\end{eqnarray}
\begin{eqnarray}
D_{\alpha}^{\psi}(\,f:g)=\frac{1+\alpha}{1+\beta}G_{\eta}^{1-\alpha}(\,f)\chi_{\beta}^{2}(\,f:g),
\end{eqnarray}where ![]() $\beta=1-\eta(1-\alpha)$ and
$\beta=1-\eta(1-\alpha)$ and ![]() $G_{\eta}(\,f)$ is the information generating function of density f with order η defined as
$G_{\eta}(\,f)$ is the information generating function of density f with order η defined as
 \begin{eqnarray}
G_{\eta}(\,f)=\int f^{\eta}(x) {\rm d}x.
\end{eqnarray}
\begin{eqnarray}
G_{\eta}(\,f)=\int f^{\eta}(x) {\rm d}x.
\end{eqnarray}Proof. From the definition of ![]() $D_{\alpha}^{\psi}(\,f:g)$ and the assumption that
$D_{\alpha}^{\psi}(\,f:g)$ and the assumption that ![]() $\psi(x)=f_{\eta}(x)$, we have
$\psi(x)=f_{\eta}(x)$, we have
 \begin{eqnarray*}
D_{\alpha}^{\psi}(\,f:g)&=&\frac{1+\alpha}{2}\int \frac{\big(\,f(x)-g(x)\big)^2}{f_{\eta}^{1-\alpha}(x)} {\rm d}x\\
&=&\frac{1+\alpha}{2}\left(\int f^{\eta}(x){\rm d}x\right)^{1-\alpha}\int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta(1-\alpha)}(x)}}{\rm d}x\\
&=&\frac{1+\alpha}{2} G_{\eta}^{1-\alpha}(\,f)\int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta(1-\alpha)}(x)}}{\rm d}x\\
&=&\frac{1+\alpha}{1+\beta}G_{\eta}^{1-\alpha}(\,f)\chi_{\beta}^{2}(\,f:g),
\end{eqnarray*}
\begin{eqnarray*}
D_{\alpha}^{\psi}(\,f:g)&=&\frac{1+\alpha}{2}\int \frac{\big(\,f(x)-g(x)\big)^2}{f_{\eta}^{1-\alpha}(x)} {\rm d}x\\
&=&\frac{1+\alpha}{2}\left(\int f^{\eta}(x){\rm d}x\right)^{1-\alpha}\int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta(1-\alpha)}(x)}}{\rm d}x\\
&=&\frac{1+\alpha}{2} G_{\eta}^{1-\alpha}(\,f)\int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta(1-\alpha)}(x)}}{\rm d}x\\
&=&\frac{1+\alpha}{1+\beta}G_{\eta}^{1-\alpha}(\,f)\chi_{\beta}^{2}(\,f:g),
\end{eqnarray*}where ![]() $\beta=1-\eta(1-\alpha),$ as desired.
$\beta=1-\eta(1-\alpha),$ as desired.
Next, let f and g be two density functions. Then, the generalized escort density, for ![]() $1 \gt \eta \gt 0$, is defined as
$1 \gt \eta \gt 0$, is defined as
 \begin{eqnarray}
h_{\eta}(x)=\frac{f^\eta(x) g^{1-\eta}(x)}{\int f^\eta(x) g^{1-\eta}(x) {\rm d}x}.
\end{eqnarray}
\begin{eqnarray}
h_{\eta}(x)=\frac{f^\eta(x) g^{1-\eta}(x)}{\int f^\eta(x) g^{1-\eta}(x) {\rm d}x}.
\end{eqnarray} Let ![]() $\psi(x)=h_{\eta}(x)$. We then have
$\psi(x)=h_{\eta}(x)$. We then have
 \begin{eqnarray}
2 D_{\alpha=0}^{\psi}(\,f:g)&=&\int \frac{\big(\,f(x)-g(x)\big)^2}{h_{\eta}(x)} {\rm d}x=\int \frac{\big(\,f(x)-g(x)\big)^2}{\frac{f^\eta(x) g^{1-\eta}(x)}{\int f^\eta(x) g^{1-\eta}(x) {\rm d}x}}{\rm d}x\\
&=&\left(\int f^{\eta}(x) g^{1-\eta}(x){\rm d}x\right) \int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta}(x)g^{1-\eta}(x)}}{\rm d}x\\
&=& R_{\eta}(\,f:g)\int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta}(x)g^{1-\eta}(x)}}{\rm d}x,
\end{eqnarray}
\begin{eqnarray}
2 D_{\alpha=0}^{\psi}(\,f:g)&=&\int \frac{\big(\,f(x)-g(x)\big)^2}{h_{\eta}(x)} {\rm d}x=\int \frac{\big(\,f(x)-g(x)\big)^2}{\frac{f^\eta(x) g^{1-\eta}(x)}{\int f^\eta(x) g^{1-\eta}(x) {\rm d}x}}{\rm d}x\\
&=&\left(\int f^{\eta}(x) g^{1-\eta}(x){\rm d}x\right) \int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta}(x)g^{1-\eta}(x)}}{\rm d}x\\
&=& R_{\eta}(\,f:g)\int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta}(x)g^{1-\eta}(x)}}{\rm d}x,
\end{eqnarray}where ![]() $R_{\eta}(\,f:g)$ is the relative information-generating function between density functions f and g defined as
$R_{\eta}(\,f:g)$ is the relative information-generating function between density functions f and g defined as
 \begin{eqnarray}
R_{\eta}(\,f:g)=\int f^{\eta}(x)g^{1-\eta}(x){\rm d}x.
\end{eqnarray}
\begin{eqnarray}
R_{\eta}(\,f:g)=\int f^{\eta}(x)g^{1-\eta}(x){\rm d}x.
\end{eqnarray}Theorem 5.2. A lower bound for  $D_{\alpha=0}^{\psi}(\,f:g)$ in Eq. (5.5) is given by
$D_{\alpha=0}^{\psi}(\,f:g)$ in Eq. (5.5) is given by
 \begin{eqnarray*}
D_{\alpha=0}^{\psi}(\,f:g)\geq \frac{R_{\eta}(\,f, g)}{2(1-\eta)^2}\chi^2(\,f_\eta:f),
\end{eqnarray*}
\begin{eqnarray*}
D_{\alpha=0}^{\psi}(\,f:g)\geq \frac{R_{\eta}(\,f, g)}{2(1-\eta)^2}\chi^2(\,f_\eta:f),
\end{eqnarray*}where ![]() $f_\eta=\eta f+(1-\eta)g$ is the two-component mixture density,
$f_\eta=\eta f+(1-\eta)g$ is the two-component mixture density, ![]() $\chi^2(.:.)$ is the chi-square divergence, and
$\chi^2(.:.)$ is the chi-square divergence, and ![]() $ R_{\eta}(\,f:g)$ is as defined in Eq. (5.6).
$ R_{\eta}(\,f:g)$ is as defined in Eq. (5.6).
Proof. From the definition of ![]() $D_{\alpha}^{\psi}(\,f:g)$ and the assumption that
$D_{\alpha}^{\psi}(\,f:g)$ and the assumption that
 \begin{equation*}\psi(x)=h_\eta(x)=\frac{f^\eta(x) g^{1-\eta}(x)}{\int f^\eta(x) g^{1-\eta}(x) {\rm d}x},\end{equation*}
\begin{equation*}\psi(x)=h_\eta(x)=\frac{f^\eta(x) g^{1-\eta}(x)}{\int f^\eta(x) g^{1-\eta}(x) {\rm d}x},\end{equation*}for ![]() $0\leq \eta \leq1$, and using the geometric mean-arithmetic mean inequality between densities f and g given by
$0\leq \eta \leq1$, and using the geometric mean-arithmetic mean inequality between densities f and g given by
and the fact that  $g(x)-f(x)=\frac{1}{1-\eta}(\,f_\eta(x)-f(x))$, we obtain
$g(x)-f(x)=\frac{1}{1-\eta}(\,f_\eta(x)-f(x))$, we obtain
 \begin{eqnarray*}
2D_{\alpha=0}^{\psi}(\,f:g)&=&\int \frac{\big(\,f(x)-g(x)\big)^2}{h_{\eta}(x)} {\rm d}x\\
&=&\left(\int f^{\eta}(x) g^{1-\eta}(x){\rm d}x\right) \int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta}(x)g^{1-\eta}(x)}}{\rm d}x\\
&=& R_{\eta}(\,f:g)\int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta}(x)g^{1-\eta}(x)}}{\rm d}x\\
&\geq&R_{\eta}(\,f:g) \int \frac{{\big(\,f(x)-g(x)\big)^2}}{\eta f(x)+(1-\eta) g(x)}{\rm d}x\\
&=&{\frac{R_{\eta}(\,f:g)}{(1-\eta)^2} \int \frac{{\big(\,f_\eta(x)-f(x)\big)^2}}{f_\eta(x)}{\rm d}x}\\
&=&\frac{R_{\eta}(\,f:g)}{(1-\eta)^2}\chi^2(\,f_\eta:f),
\end{eqnarray*}
\begin{eqnarray*}
2D_{\alpha=0}^{\psi}(\,f:g)&=&\int \frac{\big(\,f(x)-g(x)\big)^2}{h_{\eta}(x)} {\rm d}x\\
&=&\left(\int f^{\eta}(x) g^{1-\eta}(x){\rm d}x\right) \int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta}(x)g^{1-\eta}(x)}}{\rm d}x\\
&=& R_{\eta}(\,f:g)\int \frac{\big(\,f(x)-g(x)\big)^2}{{f^{\eta}(x)g^{1-\eta}(x)}}{\rm d}x\\
&\geq&R_{\eta}(\,f:g) \int \frac{{\big(\,f(x)-g(x)\big)^2}}{\eta f(x)+(1-\eta) g(x)}{\rm d}x\\
&=&{\frac{R_{\eta}(\,f:g)}{(1-\eta)^2} \int \frac{{\big(\,f_\eta(x)-f(x)\big)^2}}{f_\eta(x)}{\rm d}x}\\
&=&\frac{R_{\eta}(\,f:g)}{(1-\eta)^2}\chi^2(\,f_\eta:f),
\end{eqnarray*}as required.
5.2.  $D_{\alpha}^{\psi}$ divergence measure between two arithmetic mixture densities
$D_{\alpha}^{\psi}$ divergence measure between two arithmetic mixture densities
In this subsection, we study ![]() $D_{\alpha}^{\psi}$ divergence measure between two arithmetic mixture densities. Consider two mixture density functions
$D_{\alpha}^{\psi}$ divergence measure between two arithmetic mixture densities. Consider two mixture density functions ![]() $f_m(x)=\sum_{i=1}^{n} p_i f_i(x)$ and
$f_m(x)=\sum_{i=1}^{n} p_i f_i(x)$ and ![]() $g_m(x)=\sum_{i=1}^{n} p_i g_i(x)$. Then, we have
$g_m(x)=\sum_{i=1}^{n} p_i g_i(x)$. Then, we have
 \begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_m:g_m)&=&\frac{1+\alpha}{2}\int \frac{\big(\,f_m(x)-g_m(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x=\frac{1+\alpha}{2}\int \frac{\left(\sum_{i=1}^{n} p_i f_i(x)-\sum_{i=1}^{n} p_i g_i(x)\right)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&\frac{1+\alpha}{2}\int \frac{\left(\sum_{i=1}^{n} p_i\big(\,f_i(x)- g_i(x)\big)\right)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&\frac{1+\alpha}{2}\int\left\{\sum_{i=1}^{n} p_{i}^{2} \frac{\big(\,f_i(x)- g_i(x)\big)^2}{\psi^{1-\alpha}(x)} +2\underset{i \lt j}{\sum_{i=1}^{n}\sum_{j=1}^{n}} p_{i}p_{j}\frac{\big(\,f_i(x)- g_i(x)\big)\big(\,f_j(x)- g_j(x)\big)}{\psi^{1-\alpha}(x)} \right\} {\rm d}x\\
&=&\frac{1+\alpha}{2}\sum_{i=1}^{n}p_{i}^{2} \int \frac{\big(\,f_i(x)- g_i(x)\big)^2}{{\psi^{1-\alpha}(x)}}{\rm d}x \\
&\quad&+(1+\alpha) \underset{i \lt j}{\sum_{i=1}^{n}\sum_{j=1}^{n}} p_{i}p_{j}\int
\frac{\big(\,f_i(x)- g_i(x)\big)\big(\,f_j(x)- g_j(x)\big)}{{\psi^{1-\alpha}(x)}}{\rm d}x\\
&=&\frac{1+\alpha}{2}\sum_{i=1}^{n}p_{i}^{2} D_{\alpha}^{\psi}(\,f_i:g_i)+(1+\alpha)\underset{i \lt j}{\sum_{i=1}^{n}\sum_{j=1}^{n}} p_{i}p_{j}\int
\frac{\big(\,f_i(x)- g_i(x)\big)\big(\,f_j(x)- g_j(x)\big)}{{\psi^{1-\alpha}(x)}}{\rm d}x.
\end{eqnarray*}
\begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_m:g_m)&=&\frac{1+\alpha}{2}\int \frac{\big(\,f_m(x)-g_m(x)\big)^2}{\psi^{1-\alpha}(x)} {\rm d}x=\frac{1+\alpha}{2}\int \frac{\left(\sum_{i=1}^{n} p_i f_i(x)-\sum_{i=1}^{n} p_i g_i(x)\right)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&\frac{1+\alpha}{2}\int \frac{\left(\sum_{i=1}^{n} p_i\big(\,f_i(x)- g_i(x)\big)\right)^2}{\psi^{1-\alpha}(x)} {\rm d}x\\
&=&\frac{1+\alpha}{2}\int\left\{\sum_{i=1}^{n} p_{i}^{2} \frac{\big(\,f_i(x)- g_i(x)\big)^2}{\psi^{1-\alpha}(x)} +2\underset{i \lt j}{\sum_{i=1}^{n}\sum_{j=1}^{n}} p_{i}p_{j}\frac{\big(\,f_i(x)- g_i(x)\big)\big(\,f_j(x)- g_j(x)\big)}{\psi^{1-\alpha}(x)} \right\} {\rm d}x\\
&=&\frac{1+\alpha}{2}\sum_{i=1}^{n}p_{i}^{2} \int \frac{\big(\,f_i(x)- g_i(x)\big)^2}{{\psi^{1-\alpha}(x)}}{\rm d}x \\
&\quad&+(1+\alpha) \underset{i \lt j}{\sum_{i=1}^{n}\sum_{j=1}^{n}} p_{i}p_{j}\int
\frac{\big(\,f_i(x)- g_i(x)\big)\big(\,f_j(x)- g_j(x)\big)}{{\psi^{1-\alpha}(x)}}{\rm d}x\\
&=&\frac{1+\alpha}{2}\sum_{i=1}^{n}p_{i}^{2} D_{\alpha}^{\psi}(\,f_i:g_i)+(1+\alpha)\underset{i \lt j}{\sum_{i=1}^{n}\sum_{j=1}^{n}} p_{i}p_{j}\int
\frac{\big(\,f_i(x)- g_i(x)\big)\big(\,f_j(x)- g_j(x)\big)}{{\psi^{1-\alpha}(x)}}{\rm d}x.
\end{eqnarray*}Theorem 5.3. Let ![]() $f_1,\ldots,f_n$ be n density functions. Now, consider the probability mixing vector
$f_1,\ldots,f_n$ be n density functions. Now, consider the probability mixing vector ![]() ${\textbf{P}}=(p_1,\ldots,p_n)$ and its corresponding negation probability vector
${\textbf{P}}=(p_1,\ldots,p_n)$ and its corresponding negation probability vector
 \begin{equation*}\bar{\textbf{P}}=(\bar{p}_1,\ldots,\bar{p}_n)=\left(\frac{1-p_1}{n-1},\ldots,\frac{1-p_n}{n-1}\right).\end{equation*}
\begin{equation*}\bar{\textbf{P}}=(\bar{p}_1,\ldots,\bar{p}_n)=\left(\frac{1-p_1}{n-1},\ldots,\frac{1-p_n}{n-1}\right).\end{equation*} Then, we have the lower bound for  $D_{\alpha=0}^{\psi}$ as
$D_{\alpha=0}^{\psi}$ as
 \begin{eqnarray*}
D_{\alpha=0}^{\psi}\left(\sum_{i=1}^{n}p_i f_i:\sum_{i=1}^{n}\bar{p}_i f_i\right)\geq {\frac{1}{2} \sum_{i=1}^{n} \left(\frac{np_i-1}{n-1}\right)^2}\big(KL(\,f_i:\psi)+1\big)+L,
\end{eqnarray*}
\begin{eqnarray*}
D_{\alpha=0}^{\psi}\left(\sum_{i=1}^{n}p_i f_i:\sum_{i=1}^{n}\bar{p}_i f_i\right)\geq {\frac{1}{2} \sum_{i=1}^{n} \left(\frac{np_i-1}{n-1}\right)^2}\big(KL(\,f_i:\psi)+1\big)+L,
\end{eqnarray*}where  $L=\underset{i \lt j}{\sum_{i=1}^{n}\sum_{j=1}^{n}}\frac{(np_i-1)(np_j-1)}{(n-1)^2}\int\frac{f_i(x)f_j(x)}{\psi^2(x)}{\rm d}x.$ For more details about negation probability, see [Reference Wu, Deng and Xiong22].
$L=\underset{i \lt j}{\sum_{i=1}^{n}\sum_{j=1}^{n}}\frac{(np_i-1)(np_j-1)}{(n-1)^2}\int\frac{f_i(x)f_j(x)}{\psi^2(x)}{\rm d}x.$ For more details about negation probability, see [Reference Wu, Deng and Xiong22].
Proof. From the definition of  $D_{\alpha=0}^{\psi}$ divergence measure between mixture densities
$D_{\alpha=0}^{\psi}$ divergence measure between mixture densities ![]() $\sum_{i=1}^{n}p_i\,f_i$ and
$\sum_{i=1}^{n}p_i\,f_i$ and ![]() $\sum_{i=1}^{n}\bar{p}_i f_i$ and upon setting
$\sum_{i=1}^{n}\bar{p}_i f_i$ and upon setting
 \begin{equation*}L=\underset{i \lt j}{\sum_{i=1}^{n}\sum_{j=1}^{n}}\frac{(np_i-1)(np_j-1)}{(n-1)^2}\int\frac{f_i(x)f_j(x)}{\psi^2(x)}{\rm d}x,\end{equation*}
\begin{equation*}L=\underset{i \lt j}{\sum_{i=1}^{n}\sum_{j=1}^{n}}\frac{(np_i-1)(np_j-1)}{(n-1)^2}\int\frac{f_i(x)f_j(x)}{\psi^2(x)}{\rm d}x,\end{equation*}we find
 \begin{eqnarray*}D_{\alpha=0}^{\psi}\bigg(\sum_{i=1}^{n}p_i f_i:\sum_{i=1}^{n}\bar{p}_i f_i\bigg)&=&\frac{1}{2}\int \frac{\big(\sum_{i=1}^{n}p_i f_i(x)-\sum_{i=1}^{n}\bar{p}_i f_i(x)\big)^2}{\psi(x)}{\rm d}x\\
&=&\frac{1}{2}\sum_{i=1}^{n}{\left(\frac{np_i-1}{n-1}\right)^2} \int \frac{f_{i}^2(x){\rm d}x}{\psi(x)}{\rm d}x+L\\
&=&\frac{1}{2}\sum_{i=1}^{n}{\left(\frac{np_i-1}{n-1}\right)^2}\left(\chi^{2}(\,f_i:\psi)+1\right)+L\\
&\geq& \frac{1}{2}\sum_{i=1}^{n}{\left(\frac{np_i-1}{n-1}\right)^2}\left(KL(\,f_i:\psi)+1\right)+L,
\end{eqnarray*}
\begin{eqnarray*}D_{\alpha=0}^{\psi}\bigg(\sum_{i=1}^{n}p_i f_i:\sum_{i=1}^{n}\bar{p}_i f_i\bigg)&=&\frac{1}{2}\int \frac{\big(\sum_{i=1}^{n}p_i f_i(x)-\sum_{i=1}^{n}\bar{p}_i f_i(x)\big)^2}{\psi(x)}{\rm d}x\\
&=&\frac{1}{2}\sum_{i=1}^{n}{\left(\frac{np_i-1}{n-1}\right)^2} \int \frac{f_{i}^2(x){\rm d}x}{\psi(x)}{\rm d}x+L\\
&=&\frac{1}{2}\sum_{i=1}^{n}{\left(\frac{np_i-1}{n-1}\right)^2}\left(\chi^{2}(\,f_i:\psi)+1\right)+L\\
&\geq& \frac{1}{2}\sum_{i=1}^{n}{\left(\frac{np_i-1}{n-1}\right)^2}\left(KL(\,f_i:\psi)+1\right)+L,
\end{eqnarray*}where the last inequality follows from the inequality between Kullback–Leibler and chi-square divergence measures. This proves the required result.
6. Optimal information under  $\chi_{\alpha}^2$ divergence measure
$\chi_{\alpha}^2$ divergence measure
In this section, we first introduce ![]() $(p,\eta)$-mixture density as a generalization of arithmetic and harmonic mixture densities. Then, we examine optimal information property of
$(p,\eta)$-mixture density as a generalization of arithmetic and harmonic mixture densities. Then, we examine optimal information property of ![]() $(p,\eta)$-mixture density. To follow this, we consider optimization problem for
$(p,\eta)$-mixture density. To follow this, we consider optimization problem for ![]() $\chi_{\alpha}^2$ divergence under three types of constraints. For more details about optimal information properties of some mixture distributions (arithmetic, geometric and
$\chi_{\alpha}^2$ divergence under three types of constraints. For more details about optimal information properties of some mixture distributions (arithmetic, geometric and ![]() $\alpha-$mixture distributions), one may refer to [Reference Asadi, Ebrahimi, Kharazmi and Soofi2] and the references therein.
$\alpha-$mixture distributions), one may refer to [Reference Asadi, Ebrahimi, Kharazmi and Soofi2] and the references therein.
6.1.  $(p,\eta)$-mixture density
$(p,\eta)$-mixture density
Definition 6.1. Let f 0 and f 1 be two density functions. Then, a generalized mixture density, called the ![]() $(p,\eta)$-mixture density, is defined as
$(p,\eta)$-mixture density, is defined as
 \begin{eqnarray*}
f_{m}(x)= \frac{pf_{0}^{\eta}(x)+(1-p)f_{1}^{\eta}(x)}{pf_{0}^{\eta-1}(x)+(1-p)f_{1}^{\eta-1}(x)}\left(\int \frac{pf_{0}^{\eta}(x)+(1-p)f_{1}^{\eta}(x)}{pf_{0}^{\eta-1}(x)+(1-p)f_{1}^{\eta-1}(x)}{\rm d}x\right)^{-1}.
\end{eqnarray*}
\begin{eqnarray*}
f_{m}(x)= \frac{pf_{0}^{\eta}(x)+(1-p)f_{1}^{\eta}(x)}{pf_{0}^{\eta-1}(x)+(1-p)f_{1}^{\eta-1}(x)}\left(\int \frac{pf_{0}^{\eta}(x)+(1-p)f_{1}^{\eta}(x)}{pf_{0}^{\eta-1}(x)+(1-p)f_{1}^{\eta-1}(x)}{\rm d}x\right)^{-1}.
\end{eqnarray*} The ![]() $(p,\eta)$-mixture density provides arithmetic and harmonic mixture densities as special cases:
$(p,\eta)$-mixture density provides arithmetic and harmonic mixture densities as special cases:
(i) If p = 0, then
 $f_m(x)=f_1(x)$.
$f_m(x)=f_1(x)$.(ii) If p = 1, then
 $f_m(x)=f_0(x)$.
$f_m(x)=f_0(x)$.(iii) If η = 1, then
 $f_m(x)=pf_0(x)+(1-p)f_1(x)$ is the arithmetic mixture density.
$f_m(x)=pf_0(x)+(1-p)f_1(x)$ is the arithmetic mixture density.(iv) If η = 0, then
 $f_m(x)=\frac{{\big(\frac{p}{{f}_0(x)}+\frac{1-p}{{f}_1(x)}\big)^{-1}}}{\int \big(\frac{p}{{f}_0(x)}+\frac{1-p}{{f}_1(x)}\big)^{-1} {\rm d}x}$ is the harmonic mixture density.
$f_m(x)=\frac{{\big(\frac{p}{{f}_0(x)}+\frac{1-p}{{f}_1(x)}\big)^{-1}}}{\int \big(\frac{p}{{f}_0(x)}+\frac{1-p}{{f}_1(x)}\big)^{-1} {\rm d}x}$ is the harmonic mixture density.
6.2. Optimal information property of  $(p,\eta)$-mixture density
$(p,\eta)$-mixture density
Theorem 6.2. Let f, f 0 and f 1 be three density functions. Then, the solution to the optimization problem
 \begin{eqnarray}
\min_{{f}} \chi_{\alpha}^2({f}_0:{f}) \ \ \text{subject to}\ \chi_{\alpha}^2({f}_1:{f})=\eta, \ \int {f}(x) {\rm d}x =1
\end{eqnarray}
\begin{eqnarray}
\min_{{f}} \chi_{\alpha}^2({f}_0:{f}) \ \ \text{subject to}\ \chi_{\alpha}^2({f}_1:{f})=\eta, \ \int {f}(x) {\rm d}x =1
\end{eqnarray}is the ![]() $(p,\eta)$-mixture density with
$(p,\eta)$-mixture density with ![]() $\eta=\alpha$ and mixing parameter
$\eta=\alpha$ and mixing parameter  $p=\frac{1}{1+\lambda_0}$, and
$p=\frac{1}{1+\lambda_0}$, and ![]() $\lambda_0 \gt 0$ is the Lagrangian multiplier.
$\lambda_0 \gt 0$ is the Lagrangian multiplier.
Proof. We use the Lagrangian multiplier technique for finding the solution of the optimization problem in Eq. (6.1). Thus, we have
 \begin{eqnarray*}
L({f},\lambda_0, \lambda_1)=\frac{1+\alpha}{2}\int \frac{({f}(x)-{f}_0(x))^{2}}{{f}_{0}^{1-\alpha}(x)}{\rm d}x+\frac{1+\alpha}{2}\lambda_0 \int \frac{({f}(x)-{f}_1(x))^{2}}{{f}_{1}^{1-\alpha}(x)}{\rm d}x+\lambda_1 \int{f}(x){\rm d}x.
\end{eqnarray*}
\begin{eqnarray*}
L({f},\lambda_0, \lambda_1)=\frac{1+\alpha}{2}\int \frac{({f}(x)-{f}_0(x))^{2}}{{f}_{0}^{1-\alpha}(x)}{\rm d}x+\frac{1+\alpha}{2}\lambda_0 \int \frac{({f}(x)-{f}_1(x))^{2}}{{f}_{1}^{1-\alpha}(x)}{\rm d}x+\lambda_1 \int{f}(x){\rm d}x.
\end{eqnarray*}Now, differentiating with respect to f, we obtain
 \begin{eqnarray}
\frac{\partial}{\partial{f}} L({f},\lambda_0, \lambda_1)=(1+\alpha)\frac{{f}(x)-{f}_0(x)}{{f}_{0}^{1-\alpha}(x)}+(1+\alpha)\lambda_0\frac{{f}(x)-{f}_1(x)}{{f}_{1}^{1-\alpha}(x)}+\lambda_1.
\end{eqnarray}
\begin{eqnarray}
\frac{\partial}{\partial{f}} L({f},\lambda_0, \lambda_1)=(1+\alpha)\frac{{f}(x)-{f}_0(x)}{{f}_{0}^{1-\alpha}(x)}+(1+\alpha)\lambda_0\frac{{f}(x)-{f}_1(x)}{{f}_{1}^{1-\alpha}(x)}+\lambda_1.
\end{eqnarray}Setting Eq. (6.2) to zero, we get the optimal density function to be
 \begin{eqnarray*}
f(x)= \frac{pf_{0}^{\alpha}(x)+(1-p)f_{1}^{\alpha}(x)}{pf_{0}^{\alpha-1}(x)+(1-p)f_{1}^{\alpha-1}(x)}\left(\int \frac{pf_{0}^{\alpha}(x)+(1-p)f_{1}^{\alpha}(x)}{pf_{0}^{\alpha-1}(x)+(1-p)f_{1}^{\alpha-1}(x)}{\rm d}x\right)^{-1},
\end{eqnarray*}
\begin{eqnarray*}
f(x)= \frac{pf_{0}^{\alpha}(x)+(1-p)f_{1}^{\alpha}(x)}{pf_{0}^{\alpha-1}(x)+(1-p)f_{1}^{\alpha-1}(x)}\left(\int \frac{pf_{0}^{\alpha}(x)+(1-p)f_{1}^{\alpha}(x)}{pf_{0}^{\alpha-1}(x)+(1-p)f_{1}^{\alpha-1}(x)}{\rm d}x\right)^{-1},
\end{eqnarray*}where  $p=\frac{1}{1+\lambda_0}$, as required.
$p=\frac{1}{1+\lambda_0}$, as required.
Theorem 6.3. Let f, f 0 and f 1 be three density functions. Then, the solution to the optimization problem,
 \begin{eqnarray}
\min_{{f}} \{w \chi_{\alpha}^2({f}_0:{f})+(1-w)\chi_{\alpha}^2({f}_1:{f})\} \quad \text{subject to} \ \int{f}(x) {\rm d}x =1, \quad 0\leq w \leq 1 ,
\end{eqnarray}
\begin{eqnarray}
\min_{{f}} \{w \chi_{\alpha}^2({f}_0:{f})+(1-w)\chi_{\alpha}^2({f}_1:{f})\} \quad \text{subject to} \ \int{f}(x) {\rm d}x =1, \quad 0\leq w \leq 1 ,
\end{eqnarray}is the ![]() $(p,\eta)$-mixture density with mixing parameter p = w.
$(p,\eta)$-mixture density with mixing parameter p = w.
Proof. Making use of the Lagrangian multiplier technique in the same way as in Theorem 6.1, the required result is obtained.
Theorem 6.4. Let f, f 0 and f 1 be three density functions and  $T_\alpha(X)=\frac{{f}(X)}{{f}_{1}^{1-\alpha}(X)}$. Then, the solution to the optimization problem,
$T_\alpha(X)=\frac{{f}(X)}{{f}_{1}^{1-\alpha}(X)}$. Then, the solution to the optimization problem,
 \begin{eqnarray}
\min_{{f}} \chi_{\alpha}^2({f}_0:{f}) \quad \text{subject to}\ E_{f}(T_\alpha(X))=\eta, \quad \int{f}(x) {\rm d}x =1,
\end{eqnarray}
\begin{eqnarray}
\min_{{f}} \chi_{\alpha}^2({f}_0:{f}) \quad \text{subject to}\ E_{f}(T_\alpha(X))=\eta, \quad \int{f}(x) {\rm d}x =1,
\end{eqnarray}is the ![]() $(p,\eta)$-mixture density with mixing parameter
$(p,\eta)$-mixture density with mixing parameter  $p=\frac{1}{1+\lambda_0}$ and
$p=\frac{1}{1+\lambda_0}$ and ![]() $\lambda_0 \gt 0$ is the Lagrangian multiplier.
$\lambda_0 \gt 0$ is the Lagrangian multiplier.
Proof. Making use of the Lagrangian multiplier technique in the same way as in Theorem 6.1, the required result is obtained.
Now, we extend Theorem 6.2 to the case of n + 2 density functions.
Theorem 6.5. Let f, ![]() ${f}_0,\ldots,f_n$ be n + 2 density functions. Then, the solution to the optimization problem,
${f}_0,\ldots,f_n$ be n + 2 density functions. Then, the solution to the optimization problem,
 \begin{eqnarray}
\min_{{f}} \chi_{\alpha}^2({f}_0:{f}) \quad \text{subject to}\ \chi_{\alpha}^2({f}_i:{f})=\eta_i, i=1,\ldots,n, \quad \int {f}(x) {\rm d}x =1,
\end{eqnarray}
\begin{eqnarray}
\min_{{f}} \chi_{\alpha}^2({f}_0:{f}) \quad \text{subject to}\ \chi_{\alpha}^2({f}_i:{f})=\eta_i, i=1,\ldots,n, \quad \int {f}(x) {\rm d}x =1,
\end{eqnarray}is the extended ![]() $(p,\eta)$-mixture density with
$(p,\eta)$-mixture density with ![]() $\eta=\alpha$ and mixing parameters
$\eta=\alpha$ and mixing parameters  $p_i=\frac{\lambda_i}{1+\sum_{i=0}^{n-1}\lambda_i}$ and
$p_i=\frac{\lambda_i}{1+\sum_{i=0}^{n-1}\lambda_i}$ and ![]() $\lambda_i \gt 0$,
$\lambda_i \gt 0$, ![]() $i=0,\ldots,n$, is the Lagrangian multiplier.
$i=0,\ldots,n$, is the Lagrangian multiplier.
Proof. We use the Lagrangian multiplier technique for finding the solution to the optimization problem in Eq. (6.5). Thus, we have
 \begin{eqnarray*}
L({f},\lambda_0,\ldots, \lambda_n)&=&\frac{1+\alpha}{2}\int \frac{({f}(x)-{f}_0(x))^{2}}{{f}_{0}^{1-\alpha}(x)}{\rm d}x+\sum_{i=0}^{n-1}\frac{\lambda_i(1+\alpha)}{2}\int \frac{({f}(x)-{f}_{i+1}(x))^{2}}{{f}_{i+1}^{1-\alpha}(x)}{\rm d}x\\
&&+\lambda_{n} \int{f}(x){\rm d}x.
\end{eqnarray*}
\begin{eqnarray*}
L({f},\lambda_0,\ldots, \lambda_n)&=&\frac{1+\alpha}{2}\int \frac{({f}(x)-{f}_0(x))^{2}}{{f}_{0}^{1-\alpha}(x)}{\rm d}x+\sum_{i=0}^{n-1}\frac{\lambda_i(1+\alpha)}{2}\int \frac{({f}(x)-{f}_{i+1}(x))^{2}}{{f}_{i+1}^{1-\alpha}(x)}{\rm d}x\\
&&+\lambda_{n} \int{f}(x){\rm d}x.
\end{eqnarray*}Now, differentiating with respect to f, we obtain
 \begin{eqnarray}
\frac{\partial}{\partial{f}} L({f},\lambda_0,\ldots,\lambda_n)=(1+\alpha)\frac{{f}(x)-{f}_0}{{f}_{0}^{1-\alpha}}+(1+\alpha)\sum_{i=0}^{n-1}\lambda_i\frac{{f}(x)-{f}_{i+1}}{{f}_{i+1}^{1-\alpha}}+\lambda_n.
\end{eqnarray}
\begin{eqnarray}
\frac{\partial}{\partial{f}} L({f},\lambda_0,\ldots,\lambda_n)=(1+\alpha)\frac{{f}(x)-{f}_0}{{f}_{0}^{1-\alpha}}+(1+\alpha)\sum_{i=0}^{n-1}\lambda_i\frac{{f}(x)-{f}_{i+1}}{{f}_{i+1}^{1-\alpha}}+\lambda_n.
\end{eqnarray}Setting Eq. (6.6) to zero, we get the optimal density function to be
 \begin{eqnarray*}
f(x)=k\frac{(1-\sum_{i=1}^{n}p_i)f_{0}^{\alpha}(x)+\sum_{i=1}^{n}p_i f_{i}^{\alpha}(x)}{(1-\sum_{i=1}^{n}p_i)f_{0}^{\alpha-1}(x)+\sum_{i=1}^{n}p_i f_{i}^{\alpha-1}(x)},
\end{eqnarray*}
\begin{eqnarray*}
f(x)=k\frac{(1-\sum_{i=1}^{n}p_i)f_{0}^{\alpha}(x)+\sum_{i=1}^{n}p_i f_{i}^{\alpha}(x)}{(1-\sum_{i=1}^{n}p_i)f_{0}^{\alpha-1}(x)+\sum_{i=1}^{n}p_i f_{i}^{\alpha-1}(x)},
\end{eqnarray*}where
 \begin{equation*}k=\int \left(\frac{(1-\sum_{i=1}^{n}p_i)f_{0}^{\alpha}(x)+\sum_{i=1}^{n}p_i f_{i}^{\alpha}(x)}{(1-\sum_{i=1}^{n}p_i)f_{0}^{\alpha-1}(x)+\sum_{i=1}^{n}p_i f_{i}^{\alpha-1}(x)}\right)^{-1}{\rm d}x\end{equation*}
\begin{equation*}k=\int \left(\frac{(1-\sum_{i=1}^{n}p_i)f_{0}^{\alpha}(x)+\sum_{i=1}^{n}p_i f_{i}^{\alpha}(x)}{(1-\sum_{i=1}^{n}p_i)f_{0}^{\alpha-1}(x)+\sum_{i=1}^{n}p_i f_{i}^{\alpha-1}(x)}\right)^{-1}{\rm d}x\end{equation*}and  $p_i=\frac{\lambda_i}{1+\sum_{i=0}^{n-1}\lambda_i}$, as required.
$p_i=\frac{\lambda_i}{1+\sum_{i=0}^{n-1}\lambda_i}$, as required.
7. Relative- $\chi_{\alpha}^2$ divergence measure of mixed reliability systems
$\chi_{\alpha}^2$ divergence measure of mixed reliability systems
Consider a system with component lifetimes ![]() $X_1,\ldots,X_n$, which are independent and identically distributed (i.i.d.) with a common lifetime cumulative distribution function (c.d.f.) F and a probability density function (p.d.f.) f. Then, the system lifetime
$X_1,\ldots,X_n$, which are independent and identically distributed (i.i.d.) with a common lifetime cumulative distribution function (c.d.f.) F and a probability density function (p.d.f.) f. Then, the system lifetime ![]() $T =\phi(X_1,\ldots , X_n)$, where ϕ is referred to as the system’s structure function, is connected to signature vector
$T =\phi(X_1,\ldots , X_n)$, where ϕ is referred to as the system’s structure function, is connected to signature vector ![]() $\textbf{s}=(s_1,\ldots,s_n)$ through
$\textbf{s}=(s_1,\ldots,s_n)$ through
 \begin{equation*}s_i=P(T=X_{i:n})=\frac{n_i}{n!},~i=1,\ldots,n,\end{equation*}
\begin{equation*}s_i=P(T=X_{i:n})=\frac{n_i}{n!},~i=1,\ldots,n,\end{equation*}where ![]() $X_{1:n},\ldots,X_{n:n}$ are the order statistics of component lifetimes and ni is the number of ways that component lifetimes can be arranged such that
$X_{1:n},\ldots,X_{n:n}$ are the order statistics of component lifetimes and ni is the number of ways that component lifetimes can be arranged such that ![]() $T =\phi(X_1,\ldots, X_n)=X_{i:n}$; for more details, see [Reference Samaniego20]. Then, the reliability function of T can be expressed as a mixture of reliability functions of
$T =\phi(X_1,\ldots, X_n)=X_{i:n}$; for more details, see [Reference Samaniego20]. Then, the reliability function of T can be expressed as a mixture of reliability functions of ![]() $X_{i:n}, i=1,\ldots,n$, as
$X_{i:n}, i=1,\ldots,n$, as
 \begin{eqnarray*}
{\bar{F}_{T}(t)}=\sum_{i=1}^{n}s_{i}{\bar{F}_{i:n}(t)}.
\end{eqnarray*}
\begin{eqnarray*}
{\bar{F}_{T}(t)}=\sum_{i=1}^{n}s_{i}{\bar{F}_{i:n}(t)}.
\end{eqnarray*}Consequently, the corresponding p.d.f. of T is
 \begin{eqnarray}
{f_{T}(t)}=\sum_{i=1}^{n}s_{i}{f_{i:n}(t)},
\end{eqnarray}
\begin{eqnarray}
{f_{T}(t)}=\sum_{i=1}^{n}s_{i}{f_{i:n}(t)},
\end{eqnarray}where ![]() $f_{i:n}$ is the p.d.f. of
$f_{i:n}$ is the p.d.f. of ![]() $X_{i:n}$, given by
$X_{i:n}$, given by
 \begin{equation*}f_{{i:n}}(x)=\frac{n!}{(i-1)!(n-i)!}f(x) F^{i-1}(x)(1-F(x))^{n-i};\end{equation*}
\begin{equation*}f_{{i:n}}(x)=\frac{n!}{(i-1)!(n-i)!}f(x) F^{i-1}(x)(1-F(x))^{n-i};\end{equation*}see [Reference Arnold, Balakrishnan and Nagaraja1].
7.1.  $D_{\alpha}^{\psi}$ measure for order statistics
$D_{\alpha}^{\psi}$ measure for order statistics
Suppose ![]() $X_1,\ldots,X_n$ are i.i.d. variables from an absolutely continuous c.d.f. F and p.d.f. f, and
$X_1,\ldots,X_n$ are i.i.d. variables from an absolutely continuous c.d.f. F and p.d.f. f, and ![]() $X_{1:n},\ldots,X_{n:n}$ are the corresponding order statistics.
$X_{1:n},\ldots,X_{n:n}$ are the corresponding order statistics.
Theorem 7.1. The ![]() $ D_{\alpha}^{\psi}$ divergence measure between densities
$ D_{\alpha}^{\psi}$ divergence measure between densities ![]() $f_{i:n}$ and f is given by
$f_{i:n}$ and f is given by
 \begin{eqnarray}
D_{\alpha}^{\psi}(\,f_{i:n}:f)=\frac{1+\alpha}{2}\int_{0}^{1} \frac{f(F^{-1}(u))}{\psi^{1-\alpha}\big(F^{-1}(u)\big)}\big(\,f_U(u)- f_{U_{i:n}(u)}\big)^2{\rm d}u,
\end{eqnarray}
\begin{eqnarray}
D_{\alpha}^{\psi}(\,f_{i:n}:f)=\frac{1+\alpha}{2}\int_{0}^{1} \frac{f(F^{-1}(u))}{\psi^{1-\alpha}\big(F^{-1}(u)\big)}\big(\,f_U(u)- f_{U_{i:n}(u)}\big)^2{\rm d}u,
\end{eqnarray}where the random variables U and ![]() $U_{i:n}$ are uniform and
$U_{i:n}$ are uniform and ![]() $Beta(i, n-i+1)$ random variables on
$Beta(i, n-i+1)$ random variables on ![]() $(0,1)$ with density functions fU and
$(0,1)$ with density functions fU and ![]() $f_{U_{i:n}}$, respectively.
$f_{U_{i:n}}$, respectively.
Proof. By using the definition of ![]() $D_{\alpha}^{\psi}$ divergence measure and the transformation
$D_{\alpha}^{\psi}$ divergence measure and the transformation ![]() $u=F(x)$, we obtain
$u=F(x)$, we obtain
 \begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_{i:n}:f)&=&\frac{1+\alpha}{2}\int_{0}^{\infty}\frac{\big(\,f_{i:n}(x)-f(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&\frac{1+\alpha}{2}\int_{0}^{1} \frac{f(F^{-1}(u))}{\psi^{1-\alpha}\big(F^{-1}(u)\big)}\left(1- \frac{n!}{(i-1)!(n-i)!} u^{i-1}(1-u)^{n-i} \right)^2{\rm d}u\\
&=&\frac{1+\alpha}{2}\int_{0}^{1} \frac{f(F^{-1}(u))}{\psi^{1-\alpha}\big(F^{-1}(u)\big)}\big(\,f_U(u)- {f_{U_{i:n}}(u)}\big)^2{\rm d}u,
\end{eqnarray*}
\begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_{i:n}:f)&=&\frac{1+\alpha}{2}\int_{0}^{\infty}\frac{\big(\,f_{i:n}(x)-f(x)\big)^2}{\psi^{1-\alpha}(x)}{\rm d}x\\
&=&\frac{1+\alpha}{2}\int_{0}^{1} \frac{f(F^{-1}(u))}{\psi^{1-\alpha}\big(F^{-1}(u)\big)}\left(1- \frac{n!}{(i-1)!(n-i)!} u^{i-1}(1-u)^{n-i} \right)^2{\rm d}u\\
&=&\frac{1+\alpha}{2}\int_{0}^{1} \frac{f(F^{-1}(u))}{\psi^{1-\alpha}\big(F^{-1}(u)\big)}\big(\,f_U(u)- {f_{U_{i:n}}(u)}\big)^2{\rm d}u,
\end{eqnarray*}as required.
Corollary 7.2. From Theorem 7.1, we readily deduce the following:
(i) If
 $\psi(x)=f(x)$, then
$\psi(x)=f(x)$, then
 \begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_{i:n}:f)=\chi_{\alpha}^2(\,f_U:f_{U_{i:n}}).
\end{eqnarray*}
\begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_{i:n}:f)=\chi_{\alpha}^2(\,f_U:f_{U_{i:n}}).
\end{eqnarray*}(ii) If
 $\psi(x)=f_{i:n}(x)$, then
$\psi(x)=f_{i:n}(x)$, then
 \begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_{i:n}:f)=\chi_{\alpha}^2(\,f_{U_{i:n}}:f_U).
\end{eqnarray*}
\begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_{i:n}:f)=\chi_{\alpha}^2(\,f_{U_{i:n}}:f_U).
\end{eqnarray*}
From Corollary 7.2, it is immediately seen that under the imposed assumptions, ![]() $D_{\alpha}^{\psi}(\,f_{i:n}:f)$ divergence is free of the baseline distribution.
$D_{\alpha}^{\psi}(\,f_{i:n}:f)$ divergence is free of the baseline distribution.
Theorem 7.3. The ![]() $D_{\alpha}^{\psi}$ divergence measure between two density functions
$D_{\alpha}^{\psi}$ divergence measure between two density functions ![]() $f_{i:n}$ and
$f_{i:n}$ and ![]() $f_{j:n}$ is given by
$f_{j:n}$ is given by
 \begin{eqnarray}
D_{\alpha}^{\psi}(\,f_{i:n}:f_{j:n})=\frac{1+\alpha}{2}\int_{0}^{1} \frac{f(\,f^{-1}(u))}{\psi^{1-\alpha}\big(\,f^{-1}(u)\big)}\big(\,f_{U_{i:n}}(u)-f_{U_{j:n}}(u)\big)^2{\rm d}u.
\end{eqnarray}
\begin{eqnarray}
D_{\alpha}^{\psi}(\,f_{i:n}:f_{j:n})=\frac{1+\alpha}{2}\int_{0}^{1} \frac{f(\,f^{-1}(u))}{\psi^{1-\alpha}\big(\,f^{-1}(u)\big)}\big(\,f_{U_{i:n}}(u)-f_{U_{j:n}}(u)\big)^2{\rm d}u.
\end{eqnarray}Proof. By using the definition of ![]() $D_{\alpha}^{\psi}$ divergence measure and the transformation
$D_{\alpha}^{\psi}$ divergence measure and the transformation ![]() $u=F(x)$ in the same way as in the proof of Theorem 7.1, the required result is obtained.
$u=F(x)$ in the same way as in the proof of Theorem 7.1, the required result is obtained.
In the special case when ![]() $\psi(x)=f_{i:n}(x)$, we find that
$\psi(x)=f_{i:n}(x)$, we find that
 \begin{eqnarray}
D_{\alpha}^{\psi}(\,f_{i:n}:f_{{j:n}})=\chi_{\alpha}^{2}(\,f_{U_{i:n}}:f_{U_{j:n}}).
\end{eqnarray}
\begin{eqnarray}
D_{\alpha}^{\psi}(\,f_{i:n}:f_{{j:n}})=\chi_{\alpha}^{2}(\,f_{U_{i:n}}:f_{U_{j:n}}).
\end{eqnarray}7.2.  $D_{\alpha}^{\psi}$ measure for mixed systems
$D_{\alpha}^{\psi}$ measure for mixed systems
In this section, we examine the ![]() $D_{\alpha}^{\psi}$ divergence measure associated with mixed reliability systems.
$D_{\alpha}^{\psi}$ divergence measure associated with mixed reliability systems.
Theorem 7.4. If ![]() $\psi(x)=f_{i:n}(x)$, then the
$\psi(x)=f_{i:n}(x)$, then the ![]() $D_{\alpha}^{\psi}(\,f_T:f_{i:n})$ divergence measure is given by
$D_{\alpha}^{\psi}(\,f_T:f_{i:n})$ divergence measure is given by
 \begin{eqnarray}
D_{\alpha}^{\psi}(\,f_T:f_{i:n})={\chi_{\alpha}^2}\left(\,f_{U_{i:n}}:\sum_{i=1}^{n}s_{i}f_{U_{i:n}}\right).
\end{eqnarray}
\begin{eqnarray}
D_{\alpha}^{\psi}(\,f_T:f_{i:n})={\chi_{\alpha}^2}\left(\,f_{U_{i:n}}:\sum_{i=1}^{n}s_{i}f_{U_{i:n}}\right).
\end{eqnarray}Proof. From the assumption that ![]() $\psi(x)=f_{i:n}(x)$ and the definition of
$\psi(x)=f_{i:n}(x)$ and the definition of ![]() $D_{\alpha}^{\psi}(\,f_T:f_{i:n})$ measure, and making use of the transformation
$D_{\alpha}^{\psi}(\,f_T:f_{i:n})$ measure, and making use of the transformation ![]() $u=F(x)$, we have
$u=F(x)$, we have
 \begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_T:f_{i:n})&=& \frac{1+\alpha}{2}\int_{0}^{\infty}\frac{\big(\sum_{j=1}^{n}{\alpha_j} f_{j:n}(x)-f_{i:n}(x)\big)^2}{f_{i:n}^{1-\alpha}(x)}{\rm d}x\\
&=&\frac{1+\alpha}{2}\int_{0}^{1} \frac{\big(\sum_{j=1}^{n}s_{j}f_{U_{j:n}}(u)-f_{U_{i:n}}(u) \big)^2}{f_{U_{i:n}}^{1-\alpha}(u)}{\rm d}u\\
&=&{\chi_{\alpha}^2}\bigg(\,f_{U_{i:n}}:\sum_{i=1}^{n}s_{j}f_{U_{j:n}}\bigg),
\end{eqnarray*}
\begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_T:f_{i:n})&=& \frac{1+\alpha}{2}\int_{0}^{\infty}\frac{\big(\sum_{j=1}^{n}{\alpha_j} f_{j:n}(x)-f_{i:n}(x)\big)^2}{f_{i:n}^{1-\alpha}(x)}{\rm d}x\\
&=&\frac{1+\alpha}{2}\int_{0}^{1} \frac{\big(\sum_{j=1}^{n}s_{j}f_{U_{j:n}}(u)-f_{U_{i:n}}(u) \big)^2}{f_{U_{i:n}}^{1-\alpha}(u)}{\rm d}u\\
&=&{\chi_{\alpha}^2}\bigg(\,f_{U_{i:n}}:\sum_{i=1}^{n}s_{j}f_{U_{j:n}}\bigg),
\end{eqnarray*}as required.
Theorem 7.5. Let T 1 and T 2 be the lifetimes of two mixed systems with signatures s and ![]() $\textbf{s}^{\prime}$ consisting of n i.i.d. components having common c.d.f. F and p.d.f. f. Then, if
$\textbf{s}^{\prime}$ consisting of n i.i.d. components having common c.d.f. F and p.d.f. f. Then, if ![]() $\psi(x)=f(x)$, we have
$\psi(x)=f(x)$, we have
 \begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_{T_1}:f_{T_2})
&=&\frac{1+\alpha}{2}\int_{0}^{1} {\left(\sum_{i=1}^{n}f_{U_{i:n}}(u)\big(s_{i}-s_{i}^{\prime}\big)\right)^2}f^{\alpha}(F^{-1}(u)){\rm d}u,
\end{eqnarray*}
\begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_{T_1}:f_{T_2})
&=&\frac{1+\alpha}{2}\int_{0}^{1} {\left(\sum_{i=1}^{n}f_{U_{i:n}}(u)\big(s_{i}-s_{i}^{\prime}\big)\right)^2}f^{\alpha}(F^{-1}(u)){\rm d}u,
\end{eqnarray*}where ![]() $f_{U_{i:n}}(u)$ is the p.d.f. of a beta distribution with parameters i and
$f_{U_{i:n}}(u)$ is the p.d.f. of a beta distribution with parameters i and ![]() $n-i+1$.
$n-i+1$.
Proof. From the assumption made and use of the transformation ![]() $u=F(x)$, we have
$u=F(x)$, we have
 \begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_{T_1}:f_{T_2})&=&\frac{1+\alpha}{2}\int_{0}^{\infty} \frac{\big(\sum_{i=1}^{n}s_{i}{f_{i:n}(x)}-\sum_{i=1}^{n}s_{i}^{\prime}{f_{i:n}(x)}\big)^2}{f^{1-\alpha}(x)}{\rm d}x\\
&=&\frac{1+\alpha}{2}\int_{0}^{1} {\left(\sum_{i=1}^{n}s_{i}f_{U_{i:n}}(u)- \sum_{i=1}^{n}s_{i}^{\prime}f_{U_{i:n}}(u)\right)^2}f^{\alpha}(F^{-1}(u)){\rm d}u\\
&=&\frac{1+\alpha}{2}\int_{0}^{1} {\left(\sum_{i=1}^{n}f_{U_{i:n}}(u)\big(s_{i}-s_{i}^{\prime}\big)\right)^2}f^{\alpha}(F^{-1}(u)){\rm d}u,
\end{eqnarray*}
\begin{eqnarray*}
D_{\alpha}^{\psi}(\,f_{T_1}:f_{T_2})&=&\frac{1+\alpha}{2}\int_{0}^{\infty} \frac{\big(\sum_{i=1}^{n}s_{i}{f_{i:n}(x)}-\sum_{i=1}^{n}s_{i}^{\prime}{f_{i:n}(x)}\big)^2}{f^{1-\alpha}(x)}{\rm d}x\\
&=&\frac{1+\alpha}{2}\int_{0}^{1} {\left(\sum_{i=1}^{n}s_{i}f_{U_{i:n}}(u)- \sum_{i=1}^{n}s_{i}^{\prime}f_{U_{i:n}}(u)\right)^2}f^{\alpha}(F^{-1}(u)){\rm d}u\\
&=&\frac{1+\alpha}{2}\int_{0}^{1} {\left(\sum_{i=1}^{n}f_{U_{i:n}}(u)\big(s_{i}-s_{i}^{\prime}\big)\right)^2}f^{\alpha}(F^{-1}(u)){\rm d}u,
\end{eqnarray*}as required.
8. Application to image processing
In this section, we present an application of Jensen-![]() $\chi_{\alpha}^2$ measure in the framework of image quality assessment. For pertinent details about image quality assessment, see [Reference Gonzalez10].
$\chi_{\alpha}^2$ measure in the framework of image quality assessment. For pertinent details about image quality assessment, see [Reference Gonzalez10].
Figure 1 shows the original lake image that includes ![]() $512\times512$ cells, and the level of the color gray of each cell assumes a value in the interval
$512\times512$ cells, and the level of the color gray of each cell assumes a value in the interval ![]() $[0,1]$ (0 for black and 1 for white). It depicts the image labeled as X and three adjusted versions of it labeled as
$[0,1]$ (0 for black and 1 for white). It depicts the image labeled as X and three adjusted versions of it labeled as ![]() $Y(=X+0.3)$ (increasing brightness),
$Y(=X+0.3)$ (increasing brightness), ![]() $Z(=\sqrt{2\times X})$ (with increased contrast and gamma correction) and
$Z(=\sqrt{2\times X})$ (with increased contrast and gamma correction) and ![]() $W(=\sqrt{X})$ (gamma corrected). For pertinent details, see EBImage package in R software [Reference Oles, Pau, Smith, Sklyar and Hube19].
$W(=\sqrt{X})$ (gamma corrected). For pertinent details, see EBImage package in R software [Reference Oles, Pau, Smith, Sklyar and Hube19].

Figure 1. The original lake image and its three adjusted versions. Image X (top-left corner), Image Y (top-right corner), Image Z (bottom-left corner) and Image W (bottom-left corner).
The extracted histograms with the corresponding empirical densities for images X, Y, Z and W are plotted in Figure 2.

Figure 2. The histograms and the corresponding empirical densities for lake image (X) and its three adjusted versions (Y, Z and W).
We can see from Figures 1 and 2 that the highest degree of similarity is first related to W and then to Y, whereas Z has the highest degree of divergence from the original image X.
8.1. Nonparametric estimation of the Jensen- $\chi_{\alpha}^2$ divergence measure
$\chi_{\alpha}^2$ divergence measure
Let f 1, f 2 and ψ be probability density functions. Suppose we draw independent and identically distributed random samples from each of these distributions, obtaining samples of sizes n 1, n 2 and nψ, respectively. Denote the resulting samples by  $X_1^{(1)}, \ldots, X_{n_1}^{(1)}$ for f 1,
$X_1^{(1)}, \ldots, X_{n_1}^{(1)}$ for f 1,  $X_1^{(2)}, \ldots, X_{n_2}^{(2)}$ for f 2 and
$X_1^{(2)}, \ldots, X_{n_2}^{(2)}$ for f 2 and  $X_1^{\psi}, \ldots, X_{n_\psi}^{\psi}$ for ψ.
$X_1^{\psi}, \ldots, X_{n_\psi}^{\psi}$ for ψ.
To estimate the underlying probability density functions f 1, f 2 and ψ using kernel density estimation, we can use the following functions:
Let ![]() $\hat{f_1}(x)$ be the kernel density estimate of f 1, based on the sample
$\hat{f_1}(x)$ be the kernel density estimate of f 1, based on the sample  $X_1^{(1)}, \ldots, X_{n_1}^{(1)}$. Then, we have
$X_1^{(1)}, \ldots, X_{n_1}^{(1)}$. Then, we have
 \begin{equation*}\hat{f_1}(x) = \frac{1}{n_1h_1}\sum_{i=1}^{n}K\left(\frac{x-X_i^{(1)}}{h_1}\right).\end{equation*}
\begin{equation*}\hat{f_1}(x) = \frac{1}{n_1h_1}\sum_{i=1}^{n}K\left(\frac{x-X_i^{(1)}}{h_1}\right).\end{equation*}where ![]() $K(\cdot)$ is a kernel function, typically chosen to be a symmetric probability density function, and h 1 is a bandwidth parameter that controls the smoothness of the estimate.
$K(\cdot)$ is a kernel function, typically chosen to be a symmetric probability density function, and h 1 is a bandwidth parameter that controls the smoothness of the estimate.
Similarly, let ![]() $\hat{f_2}(x)$ be the kernel density estimate for f 2, based on the sample
$\hat{f_2}(x)$ be the kernel density estimate for f 2, based on the sample  $X_1^{(2)}, \ldots, X_{n_2}^{(2)}$. Then, we can write
$X_1^{(2)}, \ldots, X_{n_2}^{(2)}$. Then, we can write
 \begin{equation*}\hat{f_2}(x) = \frac{1}{n_2h_2}\sum_{i=1}^{n_2}K\left(\frac{x-X_i^{(2)}}{h_2}\right),\end{equation*}
\begin{equation*}\hat{f_2}(x) = \frac{1}{n_2h_2}\sum_{i=1}^{n_2}K\left(\frac{x-X_i^{(2)}}{h_2}\right),\end{equation*}where h 2 is a bandwidth parameter for the kernel density estimate of ![]() $f_2.$ Finally, let
$f_2.$ Finally, let ![]() $\hat{\psi}(x)$ be the kernel density estimate for ψ, based on the sample
$\hat{\psi}(x)$ be the kernel density estimate for ψ, based on the sample  $x_1^{\psi}, \ldots, x_{n_\psi}^{\psi}$. Then, we have
$x_1^{\psi}, \ldots, x_{n_\psi}^{\psi}$. Then, we have
 \begin{equation*}\hat{\psi}(x) = \frac{1}{n_\psi h_\psi}\sum_{i=1}^{n_\psi}K\left(\frac{x-X_i^{\psi}}{h_\psi}\right),\end{equation*}
\begin{equation*}\hat{\psi}(x) = \frac{1}{n_\psi h_\psi}\sum_{i=1}^{n_\psi}K\left(\frac{x-X_i^{\psi}}{h_\psi}\right),\end{equation*}where hψ is a bandwidth parameter for the kernel density estimate of ψ.
For more details, see [Reference Duong, Duong and Suggests8].
Using these estimates based on Gaussian kernel,  $K(u)=\frac{1}{\sqrt{2\pi}}{\rm e}^{-\frac{u^2}{2}},$ we can compute the integrated nonparametric estimate of the Jensen-
$K(u)=\frac{1}{\sqrt{2\pi}}{\rm e}^{-\frac{u^2}{2}},$ we can compute the integrated nonparametric estimate of the Jensen-![]() $\chi_{\alpha}^2$ measure, for
$\chi_{\alpha}^2$ measure, for ![]() $0 \lt p \lt 1,$ as
$0 \lt p \lt 1,$ as
 \begin{eqnarray*}
\widehat{{\cal {J}}_{\alpha}^{\psi}}\big({f}_{1},{f}_{2}; {\textbf{P}}\big)&=& p\chi_{\alpha}^{2}(\widehat{\psi}:\widehat{f_1})+(1-p){\chi_{\alpha}^{2}}(\widehat{\psi}:\widehat{f_2})-{{\chi_{\alpha}^{2}}}\left(\widehat{\psi}:p\widehat{f_1}+(1-p)\widehat{f_2}\right).
\end{eqnarray*}
\begin{eqnarray*}
\widehat{{\cal {J}}_{\alpha}^{\psi}}\big({f}_{1},{f}_{2}; {\textbf{P}}\big)&=& p\chi_{\alpha}^{2}(\widehat{\psi}:\widehat{f_1})+(1-p){\chi_{\alpha}^{2}}(\widehat{\psi}:\widehat{f_2})-{{\chi_{\alpha}^{2}}}\left(\widehat{\psi}:p\widehat{f_1}+(1-p)\widehat{f_2}\right).
\end{eqnarray*} We have computed the Jensen-![]() $\chi_{\alpha}^2$ information measure for each pair of adjusted images with respect to the original lake image, and these are presented in Table 1. The results demonstrate that the Jensen-
$\chi_{\alpha}^2$ information measure for each pair of adjusted images with respect to the original lake image, and these are presented in Table 1. The results demonstrate that the Jensen-![]() $\chi_{\alpha}^2$ divergence is an effective measure of similarity between each pair of adjusted images and the reference original image. Specifically, the Jensen-
$\chi_{\alpha}^2$ divergence is an effective measure of similarity between each pair of adjusted images and the reference original image. Specifically, the Jensen-![]() $\chi_{\alpha}^2$ divergence highlights the high degree of similarity between images Y and Z with respect to the original image (X). Furthermore, the results in Table 1 indicate that the comparison of images Z and W with respect to the reference image X results in low similarity. Therefore, the Jensen-
$\chi_{\alpha}^2$ divergence highlights the high degree of similarity between images Y and Z with respect to the original image (X). Furthermore, the results in Table 1 indicate that the comparison of images Z and W with respect to the reference image X results in low similarity. Therefore, the Jensen-![]() $\chi_{\alpha}^2$ information measure can be considered as an efficient criteria for comparing the similarity between each pair of adjusted images with respect to the reference image.
$\chi_{\alpha}^2$ information measure can be considered as an efficient criteria for comparing the similarity between each pair of adjusted images with respect to the reference image.
Table 1. The Jensen-![]() $\chi_{\alpha}^2$ divergence measure between each pair of adjusted images with respected to the original image for the choices
$\chi_{\alpha}^2$ divergence measure between each pair of adjusted images with respected to the original image for the choices ![]() $\alpha=0.5, 1.5$ and p = 0.5
$\alpha=0.5, 1.5$ and p = 0.5

9. Concluding remarks
In this paper, by considering the ![]() $\chi_{\alpha}^2$ divergence measure, we have proposed relative-
$\chi_{\alpha}^2$ divergence measure, we have proposed relative-![]() $\chi_{\alpha}^2$, Jensen-
$\chi_{\alpha}^2$, Jensen-![]() $\chi_{\alpha}^2$ and (p, w)-Jensen-
$\chi_{\alpha}^2$ and (p, w)-Jensen-![]() $\chi_{\alpha}^2$ divergence measures. We have first shown that the
$\chi_{\alpha}^2$ divergence measures. We have first shown that the ![]() $\chi_{\alpha}^2$ divergence measure has a close relationship with q-Fisher information of mixing parameter of an arithmetic mixture distribution. We have then shown that the proposed relative-
$\chi_{\alpha}^2$ divergence measure has a close relationship with q-Fisher information of mixing parameter of an arithmetic mixture distribution. We have then shown that the proposed relative-![]() $\chi_{\alpha}^2$ divergence measure includes some other well-known versions of chi-square divergence such as the usual chi-square (χ 2), generalized-χ 2 (
$\chi_{\alpha}^2$ divergence measure includes some other well-known versions of chi-square divergence such as the usual chi-square (χ 2), generalized-χ 2 (![]() $\chi_{\alpha}^{2}$), triangular and Balakrishnan–Sanghavi divergence measures all as special cases. We have shown that the Jensen-
$\chi_{\alpha}^{2}$), triangular and Balakrishnan–Sanghavi divergence measures all as special cases. We have shown that the Jensen-![]() $\chi_{\alpha}^2$ divergence is a mixture of relative-
$\chi_{\alpha}^2$ divergence is a mixture of relative-![]() $\chi_{\alpha}^2$ divergence measures. A lower bound for Jensen-
$\chi_{\alpha}^2$ divergence measures. A lower bound for Jensen-![]() $\chi_{\alpha}^2$ divergence has been obtained in terms of Jensen–Shannon entropy measure. We have also introduced (p, w)-Jensen-
$\chi_{\alpha}^2$ divergence has been obtained in terms of Jensen–Shannon entropy measure. We have also introduced (p, w)-Jensen-![]() $\chi_{\alpha}^2$ divergence measure and have then established some of its properties. Further, we have studied the relative-
$\chi_{\alpha}^2$ divergence measure and have then established some of its properties. Further, we have studied the relative-![]() $\chi_{\alpha}^2$ divergence measure of escort and arithmetic mixture densities. Next, we have introduced
$\chi_{\alpha}^2$ divergence measure of escort and arithmetic mixture densities. Next, we have introduced ![]() $(p,\eta)$-mixture density, which includes arithmetic-mixture and harmonic-mixture densities as special cases. Interestingly, we have shown that the proposed mixture density possesses optimal information under three different optimization problems associated with the
$(p,\eta)$-mixture density, which includes arithmetic-mixture and harmonic-mixture densities as special cases. Interestingly, we have shown that the proposed mixture density possesses optimal information under three different optimization problems associated with the ![]() $\chi_{\alpha}^2$ divergence measure. We have also provided a discussion about the relative-
$\chi_{\alpha}^2$ divergence measure. We have also provided a discussion about the relative-![]() $\chi_{\alpha}^2$ divergence measure of order statistics and mixed reliability systems. Finally, we have described an application of the Jensen-
$\chi_{\alpha}^2$ divergence measure of order statistics and mixed reliability systems. Finally, we have described an application of the Jensen-![]() $\chi_{\alpha}^2$ measure in image processing.
$\chi_{\alpha}^2$ measure in image processing.
In summary, in this paper, some extensions of the chi-square divergence measure such as the relative-![]() $\chi_{\alpha}^2$,
$\chi_{\alpha}^2$, ![]() $D_{\alpha}^{\psi}$, Jensen-
$D_{\alpha}^{\psi}$, Jensen-![]() $\chi_{\alpha}^2$ and (p, w)-Jensen-
$\chi_{\alpha}^2$ and (p, w)-Jensen-![]() $\chi_{\alpha}^2$ divergence measures have been proposed. Particularly, it has been shown that the relative-
$\chi_{\alpha}^2$ divergence measures have been proposed. Particularly, it has been shown that the relative-![]() $\chi_{\alpha}^2$ divergence measure includes the well-known divergence measures, such as L 2, χ 2, triangular, symmetric χ 2,
$\chi_{\alpha}^2$ divergence measure includes the well-known divergence measures, such as L 2, χ 2, triangular, symmetric χ 2, ![]() $\chi_{\alpha}^2$ and Balakrishnan–Sanghvi divergence measures, all as special cases, and provides a flexible and powerful divergence measure for comparing probability distributions in a wide rage of problems. The choice of α and the weight function
$\chi_{\alpha}^2$ and Balakrishnan–Sanghvi divergence measures, all as special cases, and provides a flexible and powerful divergence measure for comparing probability distributions in a wide rage of problems. The choice of α and the weight function ![]() $\psi(x)$ can be tailored to suit the specific characteristics and the features of the data for the models that are being compared, allowing for greater sensitivity and flexibility in the comparison process.
$\psi(x)$ can be tailored to suit the specific characteristics and the features of the data for the models that are being compared, allowing for greater sensitivity and flexibility in the comparison process.
Furthermore, the proposed Jensen-![]() $\chi_{\alpha}^2$ and (p, w)-Jensen-
$\chi_{\alpha}^2$ and (p, w)-Jensen-![]() $\chi_{\alpha}^2$ divergence measures are extensions of
$\chi_{\alpha}^2$ divergence measures are extensions of ![]() $D_{{\alpha}}^{\psi}(\,f:g)$ that are based on a convex combination. These extensions allow for the incorporation of additional divergence measures into the framework, further increasing the flexibility and applicability of the method.
$D_{{\alpha}}^{\psi}(\,f:g)$ that are based on a convex combination. These extensions allow for the incorporation of additional divergence measures into the framework, further increasing the flexibility and applicability of the method.
There are, of course, several areas of the proposed information measures that require more study with regard to its theoretical as well as experimental analysis. Additionally, with the incorporation of the idea of relative-![]() $\chi_{\alpha}^2$ divergence and Jensen-
$\chi_{\alpha}^2$ divergence and Jensen-![]() $\chi_{\alpha}^2$ divergence measures, there is an opportunity to broaden and explore the discrete and cumulative versions of the established divergence measures, utilizing the properties of convexity or concavity. It will also be of great interest to study cumulative versions of these measures, and we plan to do this in our future work. Finally, there is also a potential to extend the idea to relative Fisher information measure. We are currently working on these problems and hope to report the findings in a future paper.
$\chi_{\alpha}^2$ divergence measures, there is an opportunity to broaden and explore the discrete and cumulative versions of the established divergence measures, utilizing the properties of convexity or concavity. It will also be of great interest to study cumulative versions of these measures, and we plan to do this in our future work. Finally, there is also a potential to extend the idea to relative Fisher information measure. We are currently working on these problems and hope to report the findings in a future paper.
Acknowledgements
The authors express their sincere thanks to the Editor and the anonymous reviewers for their useful comments and suggestion on the earlier version of this manuscript, which resulted in this much improved version.
Competing interests
On behalf of all authors, the corresponding author states that there is no conflict of interest.