Hostname: page-component-5b777bbd6c-cp4x8 Total loading time: 0 Render date: 2025-06-22T15:37:32.338Z Has data issue: false hasContentIssue false
  • English
  • Français

Discriminant and integral basis of number fields defined by exponential Taylor polynomials

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  08 April 2024

Ankita Jindal  and
Sudesh K. Khanduja
Ankita Jindal
Affiliation:
Stat-Math Unit, Indian Statistical Institute Bangalore Centre, Bangalore, India (ankitajindal1203@gmail.com)
Sudesh K. Khanduja
Affiliation:
Department of Mathematical Sciences, Indian Institute of Science Education and Research Mohali, SAS Nagar, India (skhanduja@iisermohali.ac.in) Department of Mathematics, Panjab University, Chandigarh, India
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 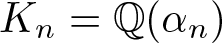$K_n=\mathbb{Q}(\alpha_n)$ be a family of algebraic number fields where 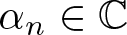$\alpha_n\in \mathbb{C}$ is a root of the nth exponential Taylor polynomial $\frac{x^n}{n!}+ \frac{x^{n-1}}{(n-1)!}+ \cdots +\frac{x^2}{2!}+\frac{x}{1!}+1$, 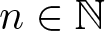$n\in \mathbb{N}$. In this paper, we give a formula for the exact power of any prime p dividing the discriminant of Kn in terms of the p-adic expansion of n. An explicit p-integral basis of Kn is also given for each prime p. These p-integral bases quickly lead to the construction of an integral basis of Kn.

Keywords

discriminantintegral basisp-integral basis

MSC classification

Primary: 11R04: Algebraic numbers; rings of algebraic integers 11R29: Class numbers, class groups, discriminants
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 2 , May 2024 , pp. 528 - 541
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Dedicated to the memory of Peter Roquette.

References

Alaca, Ş., p-Integral basis of a cubic field, Proc. Amer. Math. Soc. 126 (1998), 1949–1953.CrossRefGoogle Scholar
Alaca, Ş. and Williams, K. S., p-Integral basis of a quartic field defined by a trinomial $x^4+ax+b$, Far East J. Math. Sci. 12 (2004), 137–168.Google Scholar
Burton, D. M., Elementary Number Theory, 7th edn., (India: McGraw-Hill, 2017).Google Scholar
Borevich, Z. I. and Shafarevich, I. R., Number Theory, Academic Press, New York, 1966.Google Scholar
Cohen, S. D., Movahhedi, A. and Salinier, A., Factorisation over local fields and the irreducibility of generalised difference polynomials, Mathematika 47 (2000), 173–196.CrossRefGoogle Scholar
Coleman, R. F., On the Galois groups of the exponential Taylor polynomials, L’Enseignement Math. 33 (1987), 183–189.Google Scholar
Funakura, T., On integral bases of pure quartic fields, Math. J. Okayama Univ 26 (1984), 27–41.Google Scholar
Jakhar, A., Khanduja, S. K. and Sangwan, N., On integral basis of pure number fields, Mathematika 67 (2021), 187–195.CrossRefGoogle Scholar
Komatsu, Kenzô, Integral bases in algebraic number fields, J. Reine Angew. Math. 1975(278–279) (1975), 137–144.Google Scholar
Kaur, S. and Khanduja, S. K., Discriminant and integral basis of sextic fields defined by $x^6+ax+b$, Commun. Algebra 50 (2022), 4401–4436.CrossRefGoogle Scholar
Khanduja, S. K., A Textbook of Algebraic Number Theory, Unitext series 135, (Singapore: Springer, 2022).CrossRefGoogle Scholar
Khanduja, S. K. and Kumar, S., On prolongations of valuations via Newton polygons and liftings of polynomials, J. Pure Appl. Algebra 216 (2012), 2648–2656.CrossRefGoogle Scholar
Khanduja, S. K. and Kumar, S., A generalization of a theorem of Ore, J. Pure Appl. Algebra 218 (2014), 1206–1218.CrossRefGoogle Scholar
de Koninck, J. M. and Mercier, A., 1001 Problems in Classical Number Theory, American Mathematical Society, Providence, RI, 2007.Google Scholar
Llorente, P., Nart, E. and Vila, N., Effective determination of the decomposition of rational primes in a cubic field, Amer. Math. Soc. 87 (1983), 579–585.CrossRefGoogle Scholar
Llorente, P., Nart, E. and Vila, N., Discriminants of number fields defined by trinomials, Acta Arith. 43 (1984), 367–373.CrossRefGoogle Scholar
Llorente, P., Nart, E. and Vila, N., Decomposition of primes in number fields defined by trinomials, J. Theor. Nr. Bordx. 3 (1991), 27–41.CrossRefGoogle Scholar
Ore, Ø., Newtonsche Polygone in der Theorie der algebraischen Körper, Math. Ann. 99 (1928), 84–117.CrossRefGoogle Scholar
Schur, I., Einige Sätze über Primzahlen mit Anwendungen auf Irreduzibilitätsfragen, I, Sitzungsber. Preuss. Akad. Wiss. Berlin Phys.-Math. Kl. 14 (1929), 125–136.Google Scholar
Schur, I., Einige Sätze über Primzahlen mit Anwendungen auf Irreduzibilitätsfragen, II, Sitzungsber. Preuss. Akad. Wiss. Berlin Phys.-Math. Kl. 23 (1929), 1–24.Google Scholar
Westlund, J., On the fundamental number of the algebraic number field $k(\sqrt[p]m)$, Trans. Amer. Math. Soc. 11 (1910), 388–392.Google Scholar