Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-10T16:38:33.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Factorization of the canonical bases for higher-level Fock spaces

Part of: Lie algebras and Lie superalgebras Representation theory of groups

Published online by Cambridge University Press:  20 June 2011

Susumu Ariki ,
Nicolas Jacon  and
Cédric Lecouvey
Susumu Ariki
Affiliation:
Department of Pure and Applied Mathematics, Graduate School of Information Science and Technology, Osaka University, Toyonaka, Osaka 560-0043, Japan
Nicolas Jacon
Affiliation:
UFR Sciences et Techniques, 16 Route de Gray, 25030 Besançon, France (njacon@univ-fcomte.fr)
Cédric Lecouvey
Affiliation:
Faculté des Sciences et Techniques, Université François Rabelais, Parc de Grandmont, 37200 Tours, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

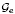The level l Fock space admits canonical bases and 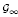. They correspond to 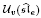and 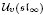-module structures. We establish that the transition matrices relating these two bases are unitriangular with coefficients in ℕ[v]. Restriction to the highest-weight modules generated by the empty l-partition then gives a natural quantization of a theorem by Geck and Rouquier on the factorization of decomposition matrices which are associated to Ariki–Koike algebras.

Keywords

Kashiwara–Lusztig canonical basisFock spacedecomposition matricescyclotomic Hecke algebras

MSC classification

Secondary: 17B37: Quantum groups (quantized enveloping algebras) and related deformations 20C08: Hecke algebras and their representations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 55 , Issue 1 , February 2012 , pp. 23 - 51
Copyright
Copyright © Edinburgh Mathematical Society 2011

References

1.Ariki, S., Representations of quantum algebras and combinatorics of Young tableaux, University Lecture Series, Volume 26 (American Mathematical Society, Providence, RI, 2002).Google Scholar
2.Ariki, S. and Koike, K., A Hecke algebra of (ℤ/rℤ)n and construction of its irreducible representations, Adv. Math. 106(2) (1994), 216–243.Google Scholar
3.Bonnafé, C. and Jacon, N., Cellular structures for Hecke algebras of type Bn, J. Alg. 321(11) (2009), 3089–3111.CrossRefGoogle Scholar
4.Brundan, J. and Kleshchev, A. S., Graded decomposition numbers for cyclotomic Hecke algebras, Adv. Math. 222 (2009), 1883–1942.CrossRefGoogle Scholar
5.Brundan, J., Kleshchev, A. S. and Wang, W., Graded Specht modules, J. Reine Angew., in press (available at http://dx.doi.org/10.1515/CRELLE.2011.033).Google Scholar
6.Deodhar, V. V., On some geometric aspects of Bruhat orderings, II, J. Alg. 111 (1987), 483–506.Google Scholar
7.Dipper, R. and Mathas, A., Morita equivalences of Ariki-Koike algebras, Math. Z. 240(3) (2002), 579–610.Google Scholar
8.Fayers, M., An LLT-type algorithm for computing higher-level canonical bases, J. Pure Appl. Alg. 214 (12) (2010), 2186–2198.CrossRefGoogle Scholar
9.Foda, O., Leclerc, B., Okado, M., Thibon, J.-Y. and Welsh, T., Branching functions of An−1(1) and Jantzen-Seitz problem for Ariki-Koike algebras, Adv. Math. 141 (1999), 322–365.Google Scholar
10.Geck, M., Representations of Hecke algebras at roots of unity, Astérisque 252(836) (1998), 33–55.Google Scholar
11.Geck, M., Modular representations of Hecke algebras, in Group representation theory (ed. Geck, M., Testerman, D. M. and Thévenaz, J.), pp. 301–353 (EPFL Press, Lausanne, 2007).Google Scholar
12.Geck, M. and Rouquier, R., Centers and simple modules for Iwahori-Hecke algebras, in Finite reductive groups, Progress in Mathematics, Volume 141, pp. 251–272 (Birkhäuser, 1997).Google Scholar
13.Graham, J. J. and Lehrer, G. I., Cellular algebras, Invent. Math. 123 (1996), 1–34.CrossRefGoogle Scholar
14.Grojnowski, I. and Haiman, M., Affine Hecke algebras and positivity of LLT and Macdonald polynomials, preprint (2007).Google Scholar
15.Halverson, T. and Ram, A., Murnaghan-Nakayama rules for characters of Iwahori-Hecke algebras of the complex reflection groups G(r, p, n), Can. J. Math. 50(1) (1998), 167–192.Google Scholar
16.Jacon, N., An algorithm for the computation of the decomposition matrices for Ariki-Koike algebras, J. Alg. 292 (2005), 100–109.CrossRefGoogle Scholar
17.Jacon, N., Crystal graphs of higher level q-deformed Fock spaces, Lusztig a-values and Ariki-Koike algebras, Alg. Representat. Theory 10(6) (2007), 565–591.CrossRefGoogle Scholar
18.Jacon, N., Constructible representations and basic sets in type Bn, preprint (2009).Google Scholar
19.Jacon, N. and Lecouvey, C., Crystal isomorphisms for irreducible highest weight -modules of higher level, Alg. Representat. Theory 13 (2009), 467–489.CrossRefGoogle Scholar
20.Jimbo, M., Misra, K. C., Miwa, T. and Okado, M., Combinatorics of representations of at q = 0, Commun. Math. Phys. 136 (1991), 543–566.CrossRefGoogle Scholar
21.Kashiwara, M., Bases cristallines des groupes quantiques, Cours Spécialisés, Tome 9 (Société Mathématique de France, Paris, 2002).Google Scholar
22.Kashiwara, M. and Tanisaki, A., Parabolic Kazhdan-Lusztig polynomials and Schubert varieties, J. Alg. 249 (2002), 306–325.CrossRefGoogle Scholar
23.Lascoux, A., Leclerc, B. and Thibon, J.-Y., Hecke algebras at roots of unity and crystal bases of quantum affine algebras, Commun. Math. Phys. 181(1) (1996), 205–263.Google Scholar
24.Leclerc, B. and Miyachi, H., Constructible characters and canonical bases. J. Alg. 277(1) (2004), 298–317.Google Scholar
25.Lecouvey, C., Parabolic Kazhdan-Lusztig polynomials, plethysm and generalized Hall-Littlewood functions for classical types, Eur. J. Combin. 30(1) (2009), 157–191.Google Scholar
26.Mathas, A., The representation theory of the Ariki-Koike and cyclotomic q-Schur algebras, in Representation theory of algebraic groups and quantum groups, Advanced Studies in Pure Mathematics, Volume 40 (2004), 261–320.Google Scholar
27.Ram, A. and Nelsen, K., Kostka-Foulkes polynomials and Macdonald spherical functions, in Surveys in Combinatorics 2003 (ed. Wensley, C.), London Mathematical Society Lecture Note Series, Volume 307, pp. 325–370 (Cambridge University Press, 2003).Google Scholar
28.Rouquier, R., q-Schur algebras and complex reflection groups. Moscow Math. J. 184(1) (2008), 119–158.Google Scholar
29.Shephard, G. C. and Todd, J. A, Finite unitary reflection groups, Can. J. Math. 6 (1954), 274–304.Google Scholar
30.Uglov, D., Canonical bases of higher-level q-deformed Fock spaces and Kazhdan-Lusztig polynomials, in Physical combinatorics, Progress in Mathematics, Volume 191, pp. 249–299 (Birkhäuser, 2000).Google Scholar
31.Yvonne, X., A conjecture for q-decomposition matrices of cyclotomic v-Schur algebras, J. Alg. 304 (2006), 419–456.Google Scholar
32.Yvonne, X., An algorithm for computing the canonical bases of higher-level q-deformed Fock spaces, J. Alg. 309 (2007), 760–785.Google Scholar
33.Yvonne, X., Base canonique d'espace de Fock de niveau supérieur, Doctoral Thesis, Université de Basse-Normandie, France (available at http://tel.archives-ouvertes.fr/tel-00137705/fr).Google Scholar