Hostname: page-component-7dd5485656-2pp2p Total loading time: 0 Render date: 2025-10-30T22:15:29.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Surjective Maps Preserving at Least One Element from the Local Spectrum

Part of: Special classes of linear operators General theory of linear operators

Published online by Cambridge University Press:  23 January 2018

Constantin Costara
Constantin Costara*
Affiliation:
Faculty of Mathematics and Informatics, Ovidius University of Constanţa, Mamaia Boul. 124, 900527 Constanţa, Romania (cdcostara@univ-ovidius.ro)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be a complex Banach space and denote by 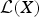${\cal L}(X)$ the Banach algebra of all bounded linear operators on X. We prove that if φ: 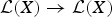${\cal L}(X) \to {\cal L}(X)$ is a linear surjective map such that for each 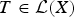$T \in {\cal L}(X)$ and x ∈ X the local spectrum of φ(T) at x and the local spectrum of T at x are either both empty or have at least one common value, then φ(T) = T for all 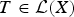$T \in {\cal L}(X)$ . If we suppose that φ always preserves the modulus of at least one element from the local spectrum, then there exists a unimodular complex constant c such that φ(T) = cT for all 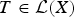$T \in {\cal L}(X)$ .

Keywords

linear preserverlocal spectrumlocal spectral radiusinner local spectral radius

MSC classification

Primary: 47B49: Transformers, preservers (operators on spaces of operators)
Secondary: 47A11: Local spectral properties

Information

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 1 , February 2018 , pp. 169 - 175
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1. Aiena, P., Fredholm and local spectral theory, with applications to multipliers (Kluwer, Dordrecht, 2004).Google Scholar
2. Aupetit, B., A primer on spectral theory (Springer, New York, 1991).Google Scholar
3. Bourhim, A. and Mashreghi, J., A survey on preservers of spectra and local spectra, Contemp. Math. 638 (2015), 45–98.Google Scholar
4. Bourhim, A. and Miller, V., Linear maps on ℳ n (ℂ) preserving the local spectral radius, Studia Math. 188 (2008), 67–75.CrossRefGoogle Scholar
5. Bourhim, A. and Ransford, T. J., Additive maps preserving local spectrum, Integr. Equ. Oper. Theory 55 (2006), 377–385.CrossRefGoogle Scholar
6. Bračič, J. and Müller, V., Local spectrum and local spectral radius of an operator at a fixed vector, Studia Math. 194 (2009), 155–162.Google Scholar
7. Brešar, M. and Šemrl, P., Linear maps preserving the spectral radius, J. Funct. Anal. 142 (1996), 360–368.Google Scholar
8. Costara, C., Automatic continuity for linear surjective maps compressing the point spectrum, Oper. Matrices. 9(2) (2015), 401–405.Google Scholar
9. González, M. and Mbekhta, M., Linear maps on ℳ n preserving the local spectrum, Linear Algebra Appl. 427 (2007), 176–182.Google Scholar
10. Jafarian, A. and Sourour, A. R., Spectrum-preserving linear maps, J. Funct. Anal. 66 (1986), 255–261.Google Scholar
11. Laursen, K. B. and Neumann, M. M., An introduction to local spectral theory (Oxford University Press, New York, 2000).Google Scholar