Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Robertson, Malcolm S.
1970.
Variational formulae for several classes of analytic functions.
Mathematische Zeitschrift,
Vol. 118,
Issue. 4,
p.
311.
Noonan, James W.
1971.
Coefficients of functions with bounded boundary rotation.
Proceedings of the American Mathematical Society,
Vol. 29,
Issue. 2,
p.
307.
Noonan, James W.
1972.
Asymptotic behavior of functions with bounded boundary rotation.
Transactions of the American Mathematical Society,
Vol. 164,
Issue. 0,
p.
397.
Pinchuk, Bernard
1973.
The Hardy class of functions of bounded boundary rotation.
Proceedings of the American Mathematical Society,
Vol. 38,
Issue. 2,
p.
355.
Leach, Ronald J.
1974.
Coefficients of Symmetric Functions of Bounded Boundary Rotation.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 6,
p.
1351.
Leach, Ronald J.
1974.
On Odd Functions of Bounded Boundary Rotation.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 3,
p.
551.
Koepf, Wolfram
1985.
Classical families of univalent functions in the Hornich space.
Monatshefte f�r Mathematik,
Vol. 100,
Issue. 2,
p.
113.
Noor, K. I.
Ul-Haq, W.
Arif, M.
and
Mustafa, S.
2009.
On Bounded Boundary and Bounded Radius Rotations.
Journal of Inequalities and Applications,
Vol. 2009,
Issue. ,
p.
1.
Noor, K. Inayat
Orhan, Halit
Mustafa, Saima
and
Bulboacă, Teodor
2009.
Generalized Alpha‐Close‐to‐Convex Functions.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2009,
Issue. 1,
Inayat Noor, Khalida
and
Hussain Bukhari, Syed Zakar
2009.
On analytic functions related with generalized Robertson functions.
Applied Mathematics and Computation,
Vol. 215,
Issue. 8,
p.
2965.
Inayat Noor, Khalida
2010.
On some subclasses ofm-fold symmetric analytic functions.
Computers & Mathematics with Applications,
Vol. 60,
Issue. 1,
p.
14.
Bhowmik, Bappaditya
2012.
On concave univalent functions.
Mathematische Nachrichten,
Vol. 285,
Issue. 5-6,
p.
606.
Polatog̃lu, Yaşar
Aydog̃an, Melike
and
Kahramaner, Yasemin
2015.
On the class of harmonic mappings which is related to the class of bounded boundary rotation.
Applied Mathematics and Computation,
Vol. 267,
Issue. ,
p.
790.
Bshouty, D.
Lyzzaik, A.
and
Sakar, F.
2017.
Harmonic mappings of bounded boundary rotation.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 3,
p.
1113.
Raza, Mohsan
and
Ul Haq, Wasim
2017.
On a subclass of Bazilevic functions.
Mathematica Slovaca,
Vol. 67,
Issue. 4,
p.
1043.
Ponnusamy, Saminathan
Sahoo, Swadesh Kumar
and
Sugawa, Toshiyuki
2019.
Hornich Operations on Functions of Bounded Boundary Rotations and Order $$\alpha $$.
Computational Methods and Function Theory,
Vol. 19,
Issue. 3,
p.
455.
Bshouty, Daoud
and
Lyzzaik, Abdallah
2019.
A Valency Criterion for Harmonic Mappings.
Computational Methods and Function Theory,
Vol. 19,
Issue. 3,
p.
433.
Prema, S.
and
Sumathi, P.
2019.
Functions of Bounded Radius Rotation Problems.
Journal of Physics: Conference Series,
Vol. 1377,
Issue. 1,
p.
012036.
Hussain, Sabir
and
Ahmad, Khalil
2020.
On strongly starlike and strongly convex functions with bounded radius and bounded boundary rotation.
Journal of Inequalities and Applications,
Vol. 2020,
Issue. 1,
Kumar, Shankey
and
Sahoo, Swadesh Kumar
2021.
Radius of convexity for integral operators involving Hornich operations.
Journal of Mathematical Analysis and Applications,
Vol. 502,
Issue. 2,
p.
125265.


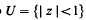 conformally onto an image domain ƒ(
conformally onto an image domain ƒ(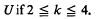 . Here we show that
. Here we show that 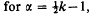 , and we give an upper bound for the valency of functions in
, and we give an upper bound for the valency of functions in 