Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-04T09:45:27.658Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Global Gaussian Lipschitz Space

Part of: Set functions and measures on spaces with additional structure Real functions Linear function spaces and their duals

Published online by Cambridge University Press:  03 January 2017

Liguang Liu  and
Peter Sjögren
Liguang Liu
Affiliation:
Department of Mathematics, School of Information, Renmin University of China, Beijing 100872, People's Republic of China (liuliguang@ruc.edu.cn)
Peter Sjögren
Affiliation:
Mathematical Sciences, University of Gothenburg and Chalmers, SE-41296 Göteborg, Sweden (peters@chalmers.se)
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that the standard Lipschitz space in Euclidean space, with exponent α ∈ (0, 1), can be characterized by means of the inequality 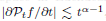, where 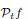is the Poisson integral of the function f. There are two cases: one can either assume that the functions in the space are bounded, or one can not make such an assumption. In the setting of the Ornstein–Uhlenbeck semigroup in ℝn, Gatto and Urbina defined a Lipschitz space by means of a similar inequality for the Ornstein–Uhlenbeck Poisson integral, considering bounded functions. In a preceding paper, the authors characterized that space by means of a Lipschitz-type continuity condition. The present paper defines a Lipschitz space in the same setting in a similar way, but now without the boundedness condition. Our main result says that this space can also be described by a continuity condition. The functions in this space turn out to have at most logarithmic growth at infinity.

Keywords

Gauss measure spaceLipschitz spaceOrnstein–Uhlenbeck Poisson kernel

MSC classification

Secondary: 26A16: Lipschitz (Hölder) classes 28C20: Set functions and measures and integrals in infinite-dimensional spaces (Wiener measure, Gaussian measure, etc.) 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 3 , August 2017 , pp. 707 - 720
Copyright
Copyright © Edinburgh Mathematical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Garrigós, G., Harzstein, S., Signes, T., Torrea, J. L. and Viviani, B., Pointwise convergence to intial data of heat and Laplace equations, Trans. Am. Math. Soc. 368(9) (2016), 6575–6600.CrossRefGoogle Scholar
2. Gatto, A. E., Pineda, E. and Urbina, W., Riesz potentials, Bessel potentials, and fractional derivatives on Besov–Lipschitz spaces for the Gaussian measure, in Recent advances in harmonic analysis and applications, Springer Proceedings in Mathematics & Statistics, Volume 25, pp. 105–130 (Springer, 2013).Google Scholar
3. Gatto, A. E. and Urbina, W., On Gaussian Lipschitz spaces and the boundedness of fractional integrals and fractional derivatives on them, Quaest. Math. 38(1) (2015), 1–25.Google Scholar
4. Liu, L. and Sjögren, P., A characterization of the Gaussian Lipschitz space and sharp estimates for the Ornstein–Uhlenbeck Poisson kernel, Rev. Mat. Iber. 32(4) (2016), 1189–1210.Google Scholar
5. Pineda, E. and Urbina, W., Some results on Gaussian Besov–Lipschitz spaces and Gaussian Triebel–Lizorkin spaces, J. Approx. Theory 161 (2009), 529–564.Google Scholar
6. Stein, E. M., Singular integrals and differentiability properties of functions (Princeton University Press, 1970).Google Scholar