Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-27T21:59:44.425Z Has data issue: false hasContentIssue false
  • English
  • Français

On weakly almost square Banach spaces

Part of: Normed linear spaces and Banach spaces; Banach lattices Linear function spaces and their duals

Published online by Cambridge University Press:  05 October 2023

José Rodríguez Open the ORCID record for José Rodríguez [Opens in a new window]  and
Abraham Rueda Zoca Open the ORCID record for Abraham Rueda Zoca [Opens in a new window]
José Rodríguez
Affiliation:
Departamento de Ingeniería y Tecnología de Computadores, Facultad de Informática, Universidad de Murcia, Espinardo (Murcia), Spain (joserr@um.es)
Abraham Rueda Zoca
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, Granada, Spain (abrahamrueda@ugr.es)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove some results on weakly almost square Banach spaces and their relatives. On the one hand, we discuss weak almost squareness in the setting of Banach function spaces. More precisely, let 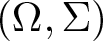$(\Omega,\Sigma)$ be a measurable space, let E be a Banach lattice and let 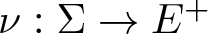$\nu:\Sigma \to E^+$ be a non-atomic countably additive measure having relatively norm compact range. Then the space 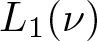$L_1(\nu)$ is weakly almost square. This result applies to some abstract Cesàro function spaces. Similar arguments show that the Lebesgue–Bochner space 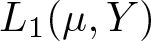$L_1(\mu,Y)$ is weakly almost square for any Banach space Y and for any non-atomic finite measure µ. On the other hand, we make some progress on the open question of whether there exists a locally almost square Banach space, which fails the diameter two property. In this line, we prove that if X is any Banach space containing a complemented isomorphic copy of c0, then for every 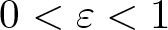$0 \lt \varepsilon \lt 1$, there exists an equivalent norm $|\cdot|$ on X satisfying the following: (i) every slice of the unit ball 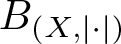$B_{(X,|\cdot|)}$ has diameter 2; (ii) 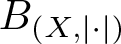$B_{(X,|\cdot|)}$ contains non-empty relatively weakly open subsets of arbitrarily small diameter and (iii) 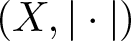$(X,|\cdot|)$ is (r, s)-SQ for all 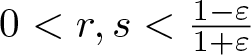$0 \lt r,s \lt \frac{1-\varepsilon}{1+\varepsilon}$.

Keywords

almost squarenesssliceweakly open setBanach function space

MSC classification

Primary: 46B04: Isometric theory of Banach spaces 46B20: Geometry and structure of normed linear spaces 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 4 , November 2023 , pp. 979 - 997
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abrahamsen, T. A., Hájek, P., Nygaard, O., Talponen, J. and Troyanski, S., Diameter 2 properties and convexity, Studia Math. 232(3) (2016), 227–242.Google Scholar
Abrahamsen, T. A., Langemets, J. and Lima, V., Almost square Banach spaces, J. Math. Anal. Appl. 434(2) (2016), 1549–1565.CrossRefGoogle Scholar
Abrahamsen, T. A., Lima, V. and Nygaard, O., Remarks on diameter 2 properties, J. Convex Anal. 20(2) (2013), 439–452.Google Scholar
Albiac, F. and Kalton, N. J., Topics in Banach space theory, Graduate Texts in Mathematics, Volume 233 (Springer, New York, 2006).Google Scholar
Argyros, S., Odell, E. and Rosenthal, H., On certain convex subsets of c0, Functional Analysis (Austin, TX, 1986–87), Lecture Notes in Mathematics, Volume 1332, (Springer, Berlin, 1988).Google Scholar
Astashkin, S. V. and Maligranda, L., Structure of Cesàro function spaces: a survey, Function Spaces X, Banach Center Publications, Volume 102, (Polish Academy of Science Institute of Mathematics, Warsaw, 2014).Google Scholar
Astashkin, S. V., Lesnik, K. and Maligranda, L., Isomorphic structure of Cesàro and Tandori spaces, Canad. J. Math. 71(3) (2019), 501–532.CrossRefGoogle Scholar
Avilés, A. and Martínez-Cervantes, G., Complete metric spaces with property (Z) are length spaces, J. Math. Anal. Appl. 473(1) (2019), 334–344.CrossRefGoogle Scholar
Avilés, A., Ciaci, S., Langemets, J., Lissitsin, A. and Zoca, A. R., Transfinite almost square Banach spaces, Studia Math. 271(1) (2023), 39–63.CrossRefGoogle Scholar
Calabuig, J. M., Lajara, S., Rodríguez, J. and Sánchez-Pérez, E. A., Compactness in L 1 of a vector measure, Studia Math. 225(3) (2014), 259–282.CrossRefGoogle Scholar
Ciaci, S., Locally almost square Banach lattices, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 117(3) (2023), .Google Scholar
Curbera, G. P., Operators into L 1 of a vector measure and applications to Banach lattices, Math. Ann. 293(2) (1992), 317–330.CrossRefGoogle Scholar
Curbera, G. P. and Ricker, W. J., Abstract Cesàro spaces: integral representations, J. Math. Anal. Appl. 441(1): (2016), 25–44.CrossRefGoogle Scholar
Curbera, G. P. and Ricker, W. J., On the Radon-Nikodym property in function spaces, Proc. Amer. Math. Soc. 145(2) (2017), 617–626.CrossRefGoogle Scholar
Curbera, G. P. and Ricker, W. J., The weak Banach-Saks property for function spaces, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 111(3) (2017), 657–671.CrossRefGoogle Scholar
Diestel, J., Sequences and series in Banach spaces, Graduate Texts in Mathematics, Volume 92 (Springer-Verlag, New York, 1984).CrossRefGoogle Scholar
Diestel, J. and Uhl, J. J.Jr., Vector measures, Mathematical Surveys, Volume 15 (American Mathematical Society, Providence, RI, 1977).CrossRefGoogle Scholar
Diestel, J., Jarchow, H. and Tonge, A., Absolutely summing operators. Cambridge Studies in Advanced Mathematics, Volume 43 (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Guerrero, J. B., López-Pérez, G. and Zoca, A. R., Big slices versus big relatively weakly open subsets in Banach spaces, J. Math. Anal. Appl. 428(2) (2015), 855–865.CrossRefGoogle Scholar
Guerrero, J. B., López-Pérez, G. and Zoca, A. R., Extreme differences between weakly open subsets and convex combinations of slices in Banach spaces, Adv. Math. 269 (2015), 56–70.CrossRefGoogle Scholar
Guerrero, J. B., López-Pérez, G. and Zoca, A. R., Some results on almost square Banach spaces, J. Math. Anal. Appl. 438(2) (2016), 1030–1040.CrossRefGoogle Scholar
Guerrero, J. B., López-Pérez, G. and Zoca, A. R., Subspaces of Banach spaces with big slices, Banach J. Math. Anal. 10(4) (2016), 771–782.CrossRefGoogle Scholar
Guerrero, J. B., López-Pérez, G. and Zoca, A. R., Diametral diameter two properties in Banach spaces, J. Convex Anal. 25(3) (2018), 817–840.Google Scholar
Haller, R., Langemets, J., Lima, V. and Nadel, R., Symmetric strong diameter two property, Mediterr. J. Math. 16(2) (2019), .CrossRefGoogle Scholar
Haller, R., Langemets, J. and Põldvere, M., On duality of diameter 2 properties, J. Convex Anal. 22(2) (2015), 465–483.Google Scholar
Haller, R., Kaasik, J. K. and Ostrak, A., The Lipschitz-free space over a length space is locally almost square but never almost square, Mediterr. J. Math. 20(1) (2023), .CrossRefGoogle Scholar
Hardtke, J.-D., Summands in locally almost square and locally octahedral spaces, Acta Comment. Univ. Tartu. Math. 22(1) (2018), 149–162.Google Scholar
Hardtke, J.-D., Locally octahedral and locally almost square Köthe–Bochner spaces. preprint, arXiv:2107.01180.Google Scholar
Kaasik, J. K. and Veeorg, T., Weakly almost square Lipschitz-free spaces, J. Math. Anal. Appl. 526(1) (2023), .CrossRefGoogle Scholar
Kluvánek, I. and Knowles, G., Vector measures and control systems, North-Holland Mathematics Studies, Notas de Matemática, No. 58, Volume 20 (North-Holland Publishing Co., Amsterdam, 1976).Google Scholar
Kubiak, D., Some geometric properties of the Cesàro function spaces, J. Convex Anal. 21(1) (2014), 189–200.Google Scholar
Langemets, J., Geometrical structure in diameter 2 Banach spaces, Diss. Math. Univ. Tartu. 99 (2015) https://dspace.ut.ee/handle/10062/47446.Google Scholar
Langemets, J., Lima, V. and Zoca, A. R., Almost square and octahedral norms in tensor products of Banach spaces, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 111(3) (2017), 841–853.CrossRefGoogle Scholar
Langemets, J. and Zoca, A. R., Octahedral norms in duals and biduals of Lipschitz-free spaces, J. Funct. Anal. 279(3) (2020), .CrossRefGoogle Scholar
Lin, P.-K., Köthe–Bochner function spaces (Birkhäuser Boston Inc., Boston, MA, 2004).CrossRefGoogle Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces. II. Function spaces, Results in Mathematics and Related Areas, Volume 97 (Springer-Verlag, Berlin, 1979).CrossRefGoogle Scholar
Nygaard, O. and Rodríguez, J., Isometric factorization of vector measures and applications to spaces of integrable functions, J. Math. Anal. Appl. 508(1) (2022), .CrossRefGoogle Scholar
Okada, S., Ricker, W. J. and Sánchez Pérez, E. A., Optimal domain and integral extension of operators. Acting in function spaces, Operator Theory: Advances and Applications, Volume 180 (Birkhäuser Verlag, Basel, 2008).CrossRefGoogle Scholar
Rodríguez, J., On non-separable L 1-spaces of a vector measure, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 111(4) (2017), 1039–1050.CrossRefGoogle Scholar
Wnuk, W., $l^{(p_n)}$ spaces with the Dunford-Pettis property, Comment. Math. Prace Mat. 30(2) (1991), 483–489.Google Scholar
Woo, J. Y. T., On modular sequence spaces, Studia Math. 48(3) (1973), 271–289.CrossRefGoogle Scholar