Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-19T18:08:58.000Z Has data issue: false hasContentIssue false
  • English
  • Français

True complexity of polynomial progressions in finite fields

Part of: Sequences and sets

Published online by Cambridge University Press:  07 June 2021

Borys Kuca
Borys Kuca*
Affiliation:
Department of Mathematics, University of Manchester, Alan Turing Building, Oxford Road, ManchesterM13 9PL, UK(borys.kuca@manchester.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

The true complexity of a polynomial progression in finite fields corresponds to the smallest-degree Gowers norm that controls the counting operator of the progression over finite fields of large characteristic. We give a conjecture that relates true complexity to algebraic relations between the terms of the progression, and we prove it for a number of progressions, including $x, x+y, x+y^{2}, x+y+y^{2}$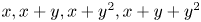 and $x, x+y, x+2y, x+y^{2}$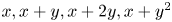. As a corollary, we prove an asymptotic for the count of certain progressions of complexity 1 in subsets of finite fields. In the process, we obtain an equidistribution result for certain polynomial progressions, analogous to the counting lemma for systems of linear forms proved by Green and Tao.

Keywords

polynomial progressionspolynomial Szemeredi theoremGowers normstrue complexity

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 3 , August 2021 , pp. 448 - 500
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergelson, V. and Leibman, A., Polynomial extensions of van der Waerden's and Szemerédi's theorems, J. Am. Math. Soc. 9 (1996), 725–753.CrossRefGoogle Scholar
Bergelson, V., Leibman, A. and Lesigne, E., Complexities of finite families of polynomials, Weyl systems, and constructions in combinatorial number theory, J. Anal. Math. 103 (2007), 47–92.CrossRefGoogle Scholar
Bourgain, J. and Chang, M.-C., Nonlinear Roth type theorems in finite fields, Israel J. Math. 221 (2017), 853–867.CrossRefGoogle Scholar
Candela, P. and Sisask, O., Convergence results for systems of linear forms on cyclic groups and periodic nilsequences, SIAM J. Discrete Math. 28 (2012), 786–810.CrossRefGoogle Scholar
Dong, D., Li, X. and Sawin, W., Improved estimates for polynomial Roth type theorems in finite fields, J. Anal. Math. 141 (2020), 689–705.CrossRefGoogle Scholar
Frantzikinakis, N., Multiple ergodic averages for three polynomials and applications, Trans. Am. Math. Soc. 360(10) (2008), 5435–5475.CrossRefGoogle Scholar
Frantzikinakis, N. and Kra, B., Polynomial averages converge to the product of integrals, Israel J. Math. 148(1) (2005), 267–276.CrossRefGoogle Scholar
Frantzikinakis, N. and Kra, B., Ergodic averages for independent polynomials and applications, J. Lond. Math. Soc. 74 (2006), 131–142.CrossRefGoogle Scholar
Gowers, W. T., A new proof of Szemerédi's theorem, Geom. Funct. Anal. 11(3) (2001), 465–588.CrossRefGoogle Scholar
Gowers, W. T., Decompositions, approximate structure, transference, and the Hahn–Banach theorem, Bull. Lond. Math. Soc 42(4) (2010), 573–606.CrossRefGoogle Scholar
Gowers, W. T. and Wolf, J., The true complexity of a system of linear equations, Proc. Lond. Math. Soc. 100(1) (2010), 155–176.CrossRefGoogle Scholar
Gowers, W. T. and Wolf, J., Linear forms and higher-degree uniformity for functions on ${\mathbb {F}}^{n}_p$, Geom. Funct. Anal. 21 (2011), 36–69.CrossRefGoogle Scholar
Gowers, W. T. and Wolf, J., Linear forms and quadratic uniformity for functions on $\mathbb {F}_p^{n}$, Mathematika 57 (2011), 215–237.CrossRefGoogle Scholar
Gowers, W. T. and Wolf, J., Linear forms and quadratic uniformity for functions on $\mathbb {Z}_N$, J. Anal. Math. 115(1) (2011), 121–186.CrossRefGoogle Scholar
Green, B., Montreal lecture notes on quadratic Fourier analysis (2007).CrossRefGoogle Scholar
Green, B. and Tao, T., An inverse theorem for the Gowers $U^{3}(G)$ norm, Proc. Edinb. Math. Soc. 51(1) (2008), 73–153.CrossRefGoogle Scholar
Green, B. and Tao, T., An arithmetic regularity lemma, an associated counting lemma, and applications, Bolyai Soc. Math. Stud. 21 (2010), 261–334.CrossRefGoogle Scholar
Green, B. and Tao, T., Linear equations in primes, Ann. Math. 171 (2010), 1753–1850.CrossRefGoogle Scholar
Green, B. and Tao, T., The quantitative behaviour of polynomial orbits on nilmanifolds, Ann. Math. 175 (2012), 465–540.CrossRefGoogle Scholar
Green, B., Tao, T. and Ziegler, T., An inverse theorem for the Gowers $U^{4}$ norm, Glasg. Math. J. 53(1) (2011), 1–50.CrossRefGoogle Scholar
Green, B., Tao, T. and Ziegler, T., An inverse theorem for the Gowers $U^{s}+1[N]$-norm, Ann. Math. 176(2) (2012), 1231–1372.10.4007/annals.2012.176.2.11CrossRefGoogle Scholar
Host, B. and Kra, B., Convergence of polynomial ergodic averages, Israel J. Math. 149(1) (2005), 1–19.CrossRefGoogle Scholar
Host, B. and Kra, B., Nonconventional ergodic averages and nilmanifolds, Ann. Math. 161(1) (2005), 397–488.CrossRefGoogle Scholar
Host, B. and Kra, B., Nilpotent structures in ergodic theory (AMS, 2018).10.1090/surv/236CrossRefGoogle Scholar
Kuca, B., Further quantitative bounds in the polynomial Szemerédi theorem over finite fields, Acta Arith. 198 (2021), 77–108.CrossRefGoogle Scholar
Leibman, A., Orbit of the diagonal in the power of a nilmanifold, Trans. Am. Math. Soc. 362(03) (2009), 1619–1658.CrossRefGoogle Scholar
Manners, F., Good bounds in certain systems of true complexity 1, Discrete Anal. 21 (2018), 40 p.Google Scholar
Peluse, S., Three-term polynomial progressions in subsets of finite fields, Israel J. Math. 228 (2018), 379–405.CrossRefGoogle Scholar
Peluse, S., On the polynomial Szemerédi theorem in finite fields, Duke Math. J. 168(5) (2019), 749–774.CrossRefGoogle Scholar
Peluse, S., Bounds for sets with no polynomial progressions, Forum Math. Pi 8(e16) (2020).CrossRefGoogle Scholar
Peluse, S. and Prendiville, S., Quantitative bounds in the non-linear Roth theorem (2019).Google Scholar
Peluse, S. and Prendiville, S., A polylogarithmic bound in the nonlinear Roth theorem, Int. Math. Res. Not. IMRN (2020), rnaa261.Google Scholar
Tao, T., A correction to “An arithmetic regularity lemma, an associated counting lemma, and applications” (2020).Google Scholar
Tao, T. and Vu, V., Additive combinatorics, Cambridge Studies in Advanced Mathematics (Cambridge University Press, 2006).CrossRefGoogle Scholar