Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Betancor, J.J.
Crescimbeni, R.
and
Torrea, J.L.
2012.
Oscillation and variation of the laguerre heat and poisson semigroups and riesz transforms.
Acta Mathematica Scientia,
Vol. 32,
Issue. 3,
p.
907.
LI, Ping
MA, Congbian
and
HOU, Youliang
2018.
The oscillation of the Poisson semigroup associated to parabolic Hermite operator.
Acta Mathematica Scientia,
Vol. 38,
Issue. 4,
p.
1214.
Chao, Zhang
and
Torrea, José L.
2021.
Boundedness of Differential Transforms for Heat Semigroups Generated by Schrödinger Operators.
Canadian Journal of Mathematics,
Vol. 73,
Issue. 3,
p.
622.
Chao, Zhang
Ma, Tao
and
Torrea, José L.
2021.
Boundedness of Differential Transforms for One-Sided Fractional Poisson-Type Operator Sequence.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 1,
p.
67.
Almeida, Víctor
and
Betancor, Jorge J.
2022.
Variation and oscillation for harmonic operators in the inverse Gaussian setting.
Communications on Pure & Applied Analysis,
Vol. 21,
Issue. 2,
p.
419.
Nader, Georges
2023.
Variation and oscillation operators associated to semigroup generated by Schrödinger operator with fractional power.
Journal of Mathematical Analysis and Applications,
Vol. 523,
Issue. 1,
p.
127000.
Lei, Hengde
Wen, Ke
and
Zhang, Chao
2023.
Boundedness of the differential transforms for the generalized Poisson operators generated by Laplacian.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 46,
Issue. 4,
Hui, Ye
Jinglan, Jia
Ping, Li
and
Yali, Xiao
2025.
The oscillation of the Poisson semigroup associated with the parabolic Laguerre operator.
SCIENTIA SINICA Mathematica,

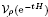 , ρ > 2, be the ρ-variation of the heat semigroup associated to the harmonic oscillator
, ρ > 2, be the ρ-variation of the heat semigroup associated to the harmonic oscillator 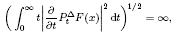
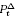 is the classical Poisson kernal in ℝ.
is the classical Poisson kernal in ℝ.