Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-14T07:24:56.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Binary quadratic forms and ray class groups

Part of: Algebraic number theory: global fields Forms and linear algebraic groups Arithmetic algebraic geometry

Published online by Cambridge University Press:  23 January 2019

Ick Sun Eum ,
Ja Kyung Koo  and
Dong Hwa Shin
Ick Sun Eum
Affiliation:
Department of Mathematics Education, Dongguk University-Gyeongju, Gyeongju-si, Gyeongsangbuk-do 38066, Republic of Korea (zandc@dongguk.ac.kr)
Ja Kyung Koo
Affiliation:
Department of Mathematical Sciences, KAIST Daejeon 34141, Republic of Korea (jkkoo@math.kaist.ac.kr)
Dong Hwa Shin
Affiliation:
Department of Mathematics, Hankuk University of Foreign Studies, Yongin-si, Gyeonggi-do 17035, Republic of Korea (dhshin@hufs.ac.kr)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be an imaginary quadratic field different from 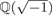$\open{Q}(\sqrt {-1})$ and 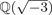$\open{Q}(\sqrt {-3})$. For a positive integer N, let KN be the ray class field of K modulo 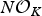$N {\cal O}_K$. By using the congruence subgroup ± Γ1(N) of SL2(ℤ), we construct an extended form class group whose operation is basically the Dirichlet composition, and explicitly show that this group is isomorphic to the Galois group Gal(KN/K). We also present an algorithm to find all distinct form classes and show how to multiply two form classes. As an application, we describe Gal(KNab/K) in terms of these extended form class groups for which KNab is the maximal abelian extension of K unramified outside prime ideals dividing 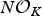$N{\cal O}_K$.

Keywords

Binary quadratic formsclass field theoryclass groupscomplex multiplication

MSC classification

Primary: 11R29: Class numbers, class groups, discriminants
Secondary: 11E16: General binary quadratic forms 11G15: Complex multiplication and moduli of abelian varieties 11R37: Class field theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 695 - 720
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Cox, D. A.. Primes of the form x 2 + ny 2: fermat, class field theory, and complex multiplication, 2nd edn. Pure and Applied Mathematics (Hoboken) (Hoboken, NJ: John Wiley & Sons, Inc., 2013).CrossRefGoogle Scholar
2Deuring, M.. Die Klassenkörper der komplexen multiplikation. Enzyklopädie der mathematischen Wissenschaften: Mit Einschluss ihrer Anwendungen, Band I 2, Heft 10, Teil II (Article I 2, 23) (Stuttgart: B.G. Teubner Verlagsgesellschaft, 1958).Google Scholar
3Hasse, H.. Neue Begründung der Komplexen Multiplikation I, II. J. für die Reine und Angewandte Math. 157 (1927), 115–139, 165 (1931), 64–88.Google Scholar
4Janusz, G. J.. Algebraic number fields, 2nd edn. Grad. Studies in Math. 7 (Providence, RI: Amer. Math. Soc., 1996).Google Scholar
5Jung, H. Y., Koo, J. K. and Shin, D. H.. Primitive and totally primitive Fricke families with applications. Results Math. 71 (2017), 841–858.CrossRefGoogle Scholar
6Koo, J. K. and Shin, D. H.. Singular values of principal moduli. J. Number Theory 133 (2013), 475–483.CrossRefGoogle Scholar
7Kubert, D. and Lang, S.. Modular units, Grundlehren der mathematischen Wissenschaften 244 (New York-Berlin: Spinger-Verlag, 1981).10.1007/978-1-4757-1741-9CrossRefGoogle Scholar
8Lang, S.. Elliptic functions, 2nd edn. With an appendix by J. Tate, Grad. Texts in Math. 112 (New York: Spinger-Verlag, 1987).CrossRefGoogle Scholar
9Lang, S.. Algebraic number theory, 2nd edn. Grad. Texts in Math. 110 (New York: Spinger-Verlag, 1994).10.1007/978-1-4612-0853-2CrossRefGoogle Scholar
10Neukirch, J.. Class field theory, Grundlehren der mathematischen Wissenschaften 280 (Berlin-Heidelberg: Springer-Verlag, 1986).CrossRefGoogle Scholar
11Ramachandra, K.. Some applications of Kronecker's limit formula. Ann. of Math. (2) 80 (1964), 104–148.CrossRefGoogle Scholar
12Serre, J.-P.. Local fields (New York: Springer-Verlag, 1979).CrossRefGoogle Scholar
13Shimura, G.. Introduction to the arithmetic theory of automorphic functions (Princeton, NJ: Iwanami Shoten and Princeton University Press, 1971).Google Scholar
14Washington, L. C.. Introduction to cyclotomic fields, 2nd edn, Grad. Texts in Math. 83 (New York: Spinger-Verlag, 1997).CrossRefGoogle Scholar