Published online by Cambridge University Press: 12 August 2020
We consider the focussing fractional periodic Korteweg–deVries (fKdV) and fractional periodic non-linear Schrödinger equations (fNLS) equations, with L2 sub-critical dispersion. In particular, this covers the case of the periodic KdV and Benjamin-Ono models. We construct two parameter family of bell-shaped travelling waves for KdV (standing waves for NLS), which are constrained minimizers of the Hamiltonian. We show in particular that for each 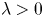 $\lambda > 0$, there is a travelling wave solution to fKdV and fNLS
$\lambda > 0$, there is a travelling wave solution to fKdV and fNLS 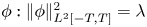 $\phi : \|\phi \|_{L^2[-T,T]}^2=\lambda $, which is non-degenerate. We also show that the waves are spectrally stable and orbitally stable, provided the Cauchy problem is locally well-posed in Hα/2[ − T, T] and a natural technical condition. This is done rigorously, without any a priori assumptions on the smoothness of the waves or the Lagrange multipliers.
$\phi : \|\phi \|_{L^2[-T,T]}^2=\lambda $, which is non-degenerate. We also show that the waves are spectrally stable and orbitally stable, provided the Cauchy problem is locally well-posed in Hα/2[ − T, T] and a natural technical condition. This is done rigorously, without any a priori assumptions on the smoothness of the waves or the Lagrange multipliers.