Using a regular Borel measure μ ⩾ 0 we derive a proper subspace 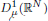of the commonly used Sobolev space D 1(ℝN ) when N ⩾ 3. The space 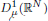resembles the standard Sobolev space H 1(Ω) when Ω is a bounded region with a compact Lipschitz boundary ∂Ω. An equivalence characterization and an example are provided that guarantee that 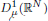is compactly embedded into L 1(RN ). In addition, as an application we prove an existence result of positive solutions to an elliptic equation in ℝN that involves the Laplace operator with the critical Sobolev nonlinearity, or with a general nonlinear term that has a subcritical and superlinear growth. We also briefly discuss the compact embedding of 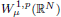to Lp (ℝN ) when N ⩾ 2 and 2 ⩽ p ⩽ N.