Hostname: page-component-7dd5485656-s6l46 Total loading time: 0 Render date: 2025-10-29T12:22:10.965Z Has data issue: false hasContentIssue false
  • English
  • Français

A criterion for compactness in Lp(ℝ) of the resolvent of the maximal general form Sturm–Liouville operator

Part of: Boundary value problems Ordinary differential operators

Published online by Cambridge University Press:  19 April 2016

N. A. Chernyavskaya  and
L. A. Shuster
N. A. Chernyavskaya
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, P.O.B. 653, Beer-Sheva 84105, Israel (nina@math.bgu.ac.il)
L. A. Shuster
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan 52900, Israel (miriam@macs.biu.ac.il)
Get access Rights & Permissions [Opens in a new window]

Extract

We consider the equation

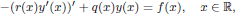
where 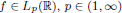and

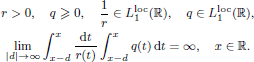
We assume that this equation is correctly solvable in Lp(ℝ). Under these assumptions, we study the problem of compactness of the resolvent 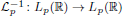of the maximal continuously invertible Sturm–Liouville operator 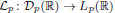. Here

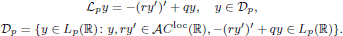
In the case p = 2, for the compact operator 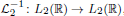, we obtain two-sided sharp-by-order estimates of the maximal eigenvalue.

Keywords

Sturm–Liouville operatorcompactness of resolventestimates of minimal eigenvalues

MSC classification

Secondary: 34B24: Sturm-Liouville theory 34L40: Particular operators (Dirac, one-dimensional Schrödinger, etc.)

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 146 , Issue 3 , June 2016 , pp. 483 - 508
Copyright
Copyright © Royal Society of Edinburgh 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable