Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-30T04:16:13.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Hardy–Littlewood–Sobolev inequality and existence of the extremal functions with extended kernel

Part of: Nonlinear integral equations Partial differential equations

Published online by Cambridge University Press:  31 October 2022

Zhao Liu
Zhao Liu*
Affiliation:
School of Mathematics and Computer Science, Jiangxi Science and Technology Normal University, Nanchang 330038, P. R. China (liuzhao@mail.bnu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the following Hardy–Littlewood–Sobolev inequality with extended kernel(0.1)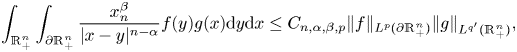

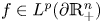\begin{equation} \int_{\mathbb{R}_+^{n}}\int_{\partial\mathbb{R}^{n}_+} \frac{x_n^{\beta}}{|x-y|^{n-\alpha}}f(y)g(x) {\rm d}y{\rm d}x\leq C_{n,\alpha,\beta,p}\|f\|_{L^{p}(\partial\mathbb{R}_+^{n})} \|g\|_{L^{q'}(\mathbb{R}_+^{n})}, \end{equation}
for any nonnegative functions $f\in L^{p}(\partial \mathbb {R}_+^{n})$, $g\in L^{q'}(\mathbb {R}_+^{n})$ 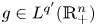and $p,\,\ q'\in (1,\,\infty )$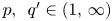, $\beta \geq 0$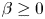, $\alpha +\beta >1$ 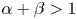such that $\frac {n-1}{n}\frac {1}{p}+\frac {1}{q'}-\frac {\alpha +\beta -1}{n}=1$.

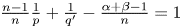We prove the existence of all extremal functions for (0.1). We show that if $f$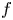 and $g$ 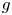are extremal functions for (0.1) then both of $f$ 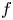and $g$ 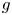are radially decreasing. Moreover, we apply the regularity lifting method to obtain the smoothness of extremal functions. Finally, we derive the sufficient and necessary condition of the existence of any nonnegative nontrivial solutions for the Euler–Lagrange equations by using Pohozaev identity.

Keywords

Existence of extremal functionsEuler–Lagrange equationsPohozaev identityHardy–Littlewood–Sobolev inequality

MSC classification

Primary: 45G15: Systems of nonlinear integral equations
Secondary: 35B40: Asymptotic behavior of solutions

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 5 , October 2023 , pp. 1683 - 1705
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Beckner, W.. Sharp Sobolev inequality on the sphere and the Moser–Trudinger inequality. Ann. Math. 138 (1993), 213–242.CrossRefGoogle Scholar
Beckner, W.. Weighted inequalities and Stein–Weiss potentials. Forum Math. 20 (2008), 587–606.CrossRefGoogle Scholar
Brascamp, H. J. and Lieb, E. H.. Best constants in Young's inequality, its converse and its generalization to more than three functions. Adv. Math. 20 (1976), 151–173.CrossRefGoogle Scholar
Brascamp, H. J., Lieb, E. H. and Luttinger, J. M.. A general rearrangement inequality for multiple integrals. J. Funct. Anal. 17 (1974), 227–237.CrossRefGoogle Scholar
Brezis, H. and Kato, T.. Remarks on the Schrödinger operator with singular complex potentials. J. Math. Pures Appl. 58 (1979), 137–151.Google Scholar
Brezis, H. and Lieb, E. H.. A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88 (1983), 486–490.CrossRefGoogle Scholar
Carleman, T.. Zur theorie de minimalflächen. Math. Z. 9 (1921), 154–160.CrossRefGoogle Scholar
Carlen, E. and Loss, M.. Extremals of functionals with competing symmetries. J. Funct. Anal. 88 (1990), 437–456.CrossRefGoogle Scholar
Chen, L., Liu, Z. and Lu, G.. Symmetry and regularity of solutions to the weighted Hardy–Sobolev type system. Adv. Nonlinear Stud. 16 (2016), 1–13.CrossRefGoogle Scholar
Chen, L., Liu, Z., Lu, G. and Tao, C.. Reverse Stein–Weiss inequalities and existence of their extremal functions. Trans. Am. Math. Soc. 370 (2018), 8429–8450.CrossRefGoogle Scholar
Chen, L., Liu, Z., Lu, G. and Tao, C.. Stein–Weiss inequalities with the fractional Poisson kernel. Rev. Mat. Iberoam. 36 (2020), 1289–1308.CrossRefGoogle Scholar
Chen, L., Lu, G. and Tao, C.. Hardy–Littlewood–Sobolev inequalities with the fractional Poisson kernel and their applications in PDEs. Acta Math. Sin. (Engl. Ser.) 35 (2019), 853–875.CrossRefGoogle Scholar
Chen, L., Lu, G. and Tao, C.. Existence of extremal functions for the Stein–Weiss inequalities on the Heisenberg group. J. Funct. Anal. 277 (2019), 1112–1138.CrossRefGoogle Scholar
Chen, S.. A new family of sharp conformally invariant integral inequalities. Int. Math. Res. Not. IMRN 5 (2014), 1205–1220.CrossRefGoogle Scholar
Chen, W. and Li, C.. The best constant in a weighted Hardy–Littlewood–Sobolev inequality. Proc. Am. Math. Soc. 136 (2008), 955–962.CrossRefGoogle Scholar
Chen, W. and Li, C.. Methods on Nonlinear Elliptic Equations, AIMS Book Series on Diff. Equ. and Dyn. Sys., Vol. 4 (USA: Springfield, 2010).Google Scholar
Chen, W., Jin, C., Li, C. and Lim, J.. Weighted Hardy–Littlewood–Sobolev inequalities and systems of integral equations. Discrete Contin. Dyn. Syst. Suppl. 35 (2019), 853–875.Google Scholar
Christ, M., Liu, H. and Zhang, A.. An Sharp Hardy–Littlewood–Sobolev inequalities on the octonionic Heisenberg group. Calc. Var. Partial Differ. Equ. 55 (2016), 11.CrossRefGoogle Scholar
Christ, M., Liu, H. and Zhang, A.. An Sharp Hardy–Littlewood–Sobolev inequalities on quaternionic Heisenberg groups. Nonlinear Anal. 130 (2016), 361–395.CrossRefGoogle Scholar
Dai, W. and Liu, Z.. Classification of positive solutions to a system of Hardy–Sobolev type equations. Acta Math. Sci. Ser. B (Engl. Ed.) 37 (2017), 1415–1436.Google Scholar
Dou, J., Guo, Q. and Zhu, M.. Subcritical approach to sharp Hardy–Littlewood–Sobolev type inequalities on the upper half space. Adv. Math. 312 (2017), 1–45.CrossRefGoogle Scholar
Dou, J. and Zhu, M.. Sharp Hardy–Littlewood–Sobolev inequality on the upper half space. Int. Math. Res. Not. IMRN 3 (2015), 651–687.CrossRefGoogle Scholar
Dou, J. and Zhu, M.. Reversed Hardy–Littlewood–Sobolev Inequality. Int. Math. Res. Not. IMRN 19 (2015), 9696–9726.CrossRefGoogle Scholar
Folland, G. B. and Stein, E. M.. Estimates for the $\partial H$ complex and analysis on the Heisenberg group. Commun. Pure Appl. Math. 27 (1974), 429–522.CrossRefGoogle Scholar
Frank, R. L. and Lieb, E. H.. Inversion positivity and the sharp Hardy–Littlewood–Sobolev inequality. Calc. Var. Partial Differ. Equ. 39 (2010), 85–99.CrossRefGoogle Scholar
Frank, R. L. and Lieb, E. H., A new rearrangement-free proof of the sharp Hardy–Littlewood–Sobolev inequality, Spectral Theory, Function Spaces and Inequalities (B. M. E. A Brown, ed.), Oper. Theory Adv. Appl. Vol. 219 (Basel: Birkh auser, 2012), 55–67.CrossRefGoogle Scholar
Frank, R. L. and Lieb, E. H.. Sharp constants in several inequalities on the Heisenberg group. Ann. Math. 176 (2012), 349–381.Google Scholar
Gao, F., Liu, H., Moroz, V. and Yang, M.. High energy positive solutions for a coupled Hartree system with Hardy–Littlewood–Sobolev critical exponents. J. Differ. Equ. 287 (2021), 329–375.CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N. S.. Elliptic Partial Differential Equations of Second Order, 2nd ed. Fundamental Principles of Mathematical Science, Vol. 224 (Berlin: Springer, 1983).Google Scholar
Gluck, M.. Subcritical approach to conformally invariant extension operators on the upper half space. J. Funct. Anal. 278 (2020), 108082.CrossRefGoogle Scholar
Gross, L.. Logarithmic Sobolev inequalities. Am. J. Math. 97 (1976), 1061–1083.CrossRefGoogle Scholar
Han, Q. and Lin, F. H., Elliptic Partial Differential Equations, Courant Lecture Notes in Mathematics, Vol. 1. New York University, Courant Institute of Mathematical Sciences (New York; American Mathematical Society, Providence, RI, 1997).Google Scholar
Hang, F., Wang, X. and Yan, X.. Sharp integral inequalities for harmonic functions. Commun. Pure Appl. Math. 61 (2008), 54–95.CrossRefGoogle Scholar
Han, X., Lu, G. and Zhu, J.. Hardy–Littlewood–Sobolev and Stein–Weiss inequalities and integral systems on the Heisenberg group. Nonlinear Anal. 75 (2012), 4296–4314.CrossRefGoogle Scholar
Han, Y. and Zhu, M.. Hardy–Littlewood–Sobolev inequalities on compact Riemannian manifolds and applications. J. Differ. Equ. 260 (2016), 1–25.CrossRefGoogle Scholar
Hardy, G. H. and Littlewood, J. E.. Some properties of fractional integrals. Math. Z. 27 (1928), 565–606.CrossRefGoogle Scholar
Hu, Y. and Liu, Z.. Classification of positive solutions for an integral system on the half space. Nonlinear Anal. 199 (2020), 1–18.CrossRefGoogle Scholar
Jerison, D. and Lee, J.. Extremals for the Sobolev inequality on the Heisenberg group and the CR Yamabe problem. J. Am. Math. Soc. 1 (1988), 1–13.CrossRefGoogle Scholar
Lieb, E. H.. Sharp constants in the Hardy–Littlewood–Sobolev and related inequalities. Ann. Math. 118 (1983), 349–374.CrossRefGoogle Scholar
Lions, P.. The concentration-compactness principle in the calculus of variations. The limit case. I. Rev. Mat. Iberoamericana 1 (1985), 145–201.CrossRefGoogle Scholar
Lions, P.. The concentration-compactness principle in the calculus of variations. The limit case. II. Rev. Mat. Iberoamericana 1 (1985), 45–121.CrossRefGoogle Scholar
Lieb, E. H. and Loss, M.. Analysis, 2nd ed, Graduate studies in Mathematics, Vol. 14 (Providence, RI: American Mathematical Society, 2001).Google Scholar
Liu, Z.. Symmetry and monotonicity of positive solutions for an integral system with negative exponents. Pacific J. Math. 300 (2019), 419–430.CrossRefGoogle Scholar
Li Remark on some conformally invariant integral equations, Y. Y.. The method of moving spheres. J. Eur. Math. Soc. 6 (2004), 153–180.Google Scholar
Lu, G. and Zhu, J.. Symmetry and regularity of extremals of an integral equation related to the Hardy–Sobolev inequality. Calc. Var. Partial Differ. Equ. 42 (2011), 563–577.CrossRefGoogle Scholar
Ma, C., Chen, W. and Li, C.. Regularity of solutions for an integral system of Wolff type. Adv. Math. 226 (2011), 2676–2699.CrossRefGoogle Scholar
Moroz, V. and Van Schaftingen, J.. Groundstates of nonlinear Choquard equations: Hardy–Littlewood–Sobolev critical exponent. Commun. Contemp. Math. 17 (2015), 1550005.CrossRefGoogle Scholar
Ngô, Q. A. and Nguyen, V. H.. Sharp reversed Hardy–Littlewood–Sobolev inequality on $\mathbb {R}^{n}$. Israel J. Math. 220 (2017), 189–223.CrossRefGoogle Scholar
Ngô, Q. A. and Nguyen, V. H.. Sharp reversed Hardy–Littlewood–Sobolev inequality on the half space $\mathbb {R}_+^{n}$. Int. Math. Res. Not. IMRN 20 (2017), 6187–6230.Google Scholar
Sobolev, S. L.. On a theorem in functional analysis (in Russian). Mat. Sb 4 (1938), 471–497.Google Scholar
Stein, E. M. and Weiss, G.. Fractional integrals on n-dimensional Euclidean space. J. Math. Mech. 7 (1958), 503–514.Google Scholar
Stein, E. M. and Weiss, G.. Introduction to Fourier Analysis on Euclidean Spaces, Princeton Mathematical Series, Vol. 32 (Princeton, NJ: Princeton University Press, 1971).Google Scholar