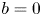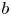1. Introduction
The 4-parameter equation
studied in [Reference Anco, da Silva and Freire1, Reference Freire and Silva15, Reference Himonas and Holliman16], is a generalization of the Camassa–Holm equation [Reference Camassa and Holm6]
and the Novikov equation [Reference Hone and Wang20, Reference Novikov25]
that admits certain scaling transformations as symmetries. The equation (1.1) has proven to be an interesting mathematical equation once it is possible to choose $a=k+2,\,b=k+1$![]() and $c=1$
and $c=1$![]() in order to transform it into a one-parameter family of equations that still unifies (1.2) and (1.3), and also admits the peaked wave solutions $u(t,\,x) = c^{1/k}e^{-|x-ct|},$
in order to transform it into a one-parameter family of equations that still unifies (1.2) and (1.3), and also admits the peaked wave solutions $u(t,\,x) = c^{1/k}e^{-|x-ct|},$![]() called peakon solutions [Reference Camassa and Holm6], where $c$
called peakon solutions [Reference Camassa and Holm6], where $c$![]() denotes the wave speed. Despite admitting an infinite number of conservation laws only when the equation is reduced to (1.2) or (1.3), it was not long before the interesting properties of (1.1) attracted attention from researchers. In terms of applied analysis, Himonas and Holliman, in the same paper [Reference Himonas and Holliman16] showed that for any positive integer $k\geq 1$
denotes the wave speed. Despite admitting an infinite number of conservation laws only when the equation is reduced to (1.2) or (1.3), it was not long before the interesting properties of (1.1) attracted attention from researchers. In terms of applied analysis, Himonas and Holliman, in the same paper [Reference Himonas and Holliman16] showed that for any positive integer $k\geq 1$![]() , $b=a+1$
, $b=a+1$![]() and $c=1$
and $c=1$![]() , the equation is Hadamard well-posed in $H^{s}(\mathbb {R})$
, the equation is Hadamard well-posed in $H^{s}(\mathbb {R})$![]() for $s>3/2$
for $s>3/2$![]() and, more recently, Barostichi, Himonas and Petronilho [Reference Barostichi, Himonas and Petronilho5] considered the choices $a=k+2,\,b=k+1$
and, more recently, Barostichi, Himonas and Petronilho [Reference Barostichi, Himonas and Petronilho5] considered the choices $a=k+2,\,b=k+1$![]() and $c=1$
and $c=1$![]() in (1.1) to extend local well-posedness to global for the resulting equation and also understand the behaviours of global analytic solutions provided that the McKean quantity $m_0=m_0(x):=(1-\partial _x^{2})u(0,\,x)$
in (1.1) to extend local well-posedness to global for the resulting equation and also understand the behaviours of global analytic solutions provided that the McKean quantity $m_0=m_0(x):=(1-\partial _x^{2})u(0,\,x)$![]() does not change sign. For a geometric interpretation of the sign persistance of the McKean quantity and its consequences, see [Reference Constantin7] and discussions in [Reference Constantin and Kolev8, Reference Kolev23].
does not change sign. For a geometric interpretation of the sign persistance of the McKean quantity and its consequences, see [Reference Constantin7] and discussions in [Reference Constantin and Kolev8, Reference Kolev23].
It is important to observe that the restriction $k\geq 1$![]() in (1.1) is due to two main reasons: firstly, the Camassa–Holm and Novikov equations are accomplished when we have two particular positive choices of $k$
in (1.1) is due to two main reasons: firstly, the Camassa–Holm and Novikov equations are accomplished when we have two particular positive choices of $k$![]() and, secondly, problems with singularity obviously arise whenever considering $k<1$
and, secondly, problems with singularity obviously arise whenever considering $k<1$![]() . Moreover, the former also explains why the constants $a,\,b,\,c$
. Moreover, the former also explains why the constants $a,\,b,\,c$![]() are taken as different than zero. However, by allowing $b=0$
are taken as different than zero. However, by allowing $b=0$![]() and $a=c=1$
and $a=c=1$![]() in (1.1), one arrives at the equation
in (1.1), one arrives at the equation
where $k$![]() will be taken as a positive integer and $m=u-u_{xx}$
will be taken as a positive integer and $m=u-u_{xx}$![]() . In the particular case where $k=1$
. In the particular case where $k=1$![]() , (1.4) is a very particular case of the $b$
, (1.4) is a very particular case of the $b$![]() -equation $m_t + bmu_x + um_x=0$
-equation $m_t + bmu_x + um_x=0$![]() considered in [Reference Degasperis, Holm and Hone10] and later shown in [Reference Dullin, Gottwald and Holm11, Reference Holm and Staley19] to have hydrodynamic applications when $b\neq -1$
considered in [Reference Degasperis, Holm and Hone10] and later shown in [Reference Dullin, Gottwald and Holm11, Reference Holm and Staley19] to have hydrodynamic applications when $b\neq -1$![]() . Moreover, it can also be obtained from Kodama transformation to describe shallow water elevation [Reference Dullin, Gottwald and Holm12]. In terms of well-posedness, we observe that in [Reference Himonas and Holliman16, Reference Yan26] the authors showed that (1.4) is well-posed for an initial value $u_0\in H^{s}(\mathbb {R}),$
. Moreover, it can also be obtained from Kodama transformation to describe shallow water elevation [Reference Dullin, Gottwald and Holm12]. In terms of well-posedness, we observe that in [Reference Himonas and Holliman16, Reference Yan26] the authors showed that (1.4) is well-posed for an initial value $u_0\in H^{s}(\mathbb {R}),$![]() where $s>3/2$
where $s>3/2$![]() .
.
It is crucial to observe, however, that although local well-posedness of (1.4) in Sobolev [Reference Himonas and Holliman16], Besov [Reference Yan26] and Gevrey [Reference Barostichi, Himonas and Petronilho3] spaces has been successfully established, not much else has been considered for $k>1$![]() . In fact, the reasons for this fact are rather simple: the case $k=1$
. In fact, the reasons for this fact are rather simple: the case $k=1$![]() in (1.4) is only known to conserve the momentum $\int _{\mathbb {R}} m(t,\,x)dx$
in (1.4) is only known to conserve the momentum $\int _{\mathbb {R}} m(t,\,x)dx$![]() for rapidly decreasing solutions, which is equivalent to saying that
for rapidly decreasing solutions, which is equivalent to saying that
is independent of time for the same sort of solution. For the generalized equation (1.4) with $k>1$![]() , the situation becomes even more drastic as no conservation laws seem to exist [Reference Anco, da Silva and Freire1], which poses a difficulty that perhaps may be impossible to overcome in the attempt to study solutions and their properties.
, the situation becomes even more drastic as no conservation laws seem to exist [Reference Anco, da Silva and Freire1], which poses a difficulty that perhaps may be impossible to overcome in the attempt to study solutions and their properties.
One of the pioneering works is [Reference da Silva and Freire9], where in the particular case of $k=1$![]() in (1.4) the authors considered global well-posedness and deduced that, also making the assumption that the McKean quantity does not change sign, in $H^{3}(\mathbb {R})$
in (1.4) the authors considered global well-posedness and deduced that, also making the assumption that the McKean quantity does not change sign, in $H^{3}(\mathbb {R})$![]() , it is possible to extend the local solutions and then the maximal time of existence is infinite. This is indeed a remarkable result once the equation (1.4) lacks the conservation of the $H^{1}(\mathbb {R})$
, it is possible to extend the local solutions and then the maximal time of existence is infinite. This is indeed a remarkable result once the equation (1.4) lacks the conservation of the $H^{1}(\mathbb {R})$![]() norm and the construction of a highly non-trivial functional was required to show that the solution could not blow up at a finite time. Following a similar direction, in [Reference Duruk Mutlubas and Freire13] the authors determined global well-posedness for the periodic case and also studied continuation of periodic solutions. For the general case $k>1$
norm and the construction of a highly non-trivial functional was required to show that the solution could not blow up at a finite time. Following a similar direction, in [Reference Duruk Mutlubas and Freire13] the authors determined global well-posedness for the periodic case and also studied continuation of periodic solutions. For the general case $k>1$![]() the authors in [Reference da Silva and Freire9] also answered some of the questions raised by Himonas and Thompson [Reference Himonas and Thompson18], giving a characterization of asymptotic behaviour or solutions based on the initial data, and a blow-up criteria has been established in [Reference Yan26]. The determination of global well-posedness for $k>1$
the authors in [Reference da Silva and Freire9] also answered some of the questions raised by Himonas and Thompson [Reference Himonas and Thompson18], giving a characterization of asymptotic behaviour or solutions based on the initial data, and a blow-up criteria has been established in [Reference Yan26]. The determination of global well-posedness for $k>1$![]() , however, is still an open problem.
, however, is still an open problem.
In this paper, we are interested in the initial value problem
where
and complementing the results found in [Reference da Silva and Freire9, Reference Duruk Mutlubas and Freire13]. We observe that (1.6)–(1.7) is nothing but the evolution formulation of the Cauchy problem of (1.4) after the inversion of the Helmholtz operator $1-\partial _x^{2}$![]() .
.
Consider the $L^{2}_x(\mathbb {R})$![]() space of square integrable functions endowed with the norm
space of square integrable functions endowed with the norm

The main function space of our interest in the present paper is the Gevrey space $G^{\sigma,s}(\mathbb {R})$![]() , where $\sigma >0$
, where $\sigma >0$![]() and $s\in \mathbb {R}$
and $s\in \mathbb {R}$![]() , of functions in $L^{2}(\mathbb {R})$
, of functions in $L^{2}(\mathbb {R})$![]() such that the norm
such that the norm

is finite, where $\hat {f}$![]() denotes the Fourier transform
denotes the Fourier transform
In the particular case where $\sigma \to 0$![]() , the space $G^{0,s}(\mathbb {R})$
, the space $G^{0,s}(\mathbb {R})$![]() becomes the usual Sobolev space $H^{s}(\mathbb {R})$
becomes the usual Sobolev space $H^{s}(\mathbb {R})$![]() . In a result known as Paley–Wiener theorem (see [Reference Katznelson22]), the Gevrey space $G^{\sigma,s}(\mathbb {R})$
. In a result known as Paley–Wiener theorem (see [Reference Katznelson22]), the Gevrey space $G^{\sigma,s}(\mathbb {R})$![]() is characterized as the restriction to the real line of functions that are analytic on a strip of width $2\sigma$
is characterized as the restriction to the real line of functions that are analytic on a strip of width $2\sigma$![]() .
.
Our main intention is to show that well-posedness of (1.6)–(1.7) goes beyond Sobolev spaces in the sense of a proof for global well-posedness in Gevrey spaces by making use of the Kato–Masuda [Reference Kato and Masuda21] machinery and certain embeddings between spaces.
Before proceeding with our main result, we state a generalization of global well-posedness in Sobolev spaces for equation (1.6)–(1.7) with $k=1$![]() . We observe that the result proven in [Reference da Silva and Freire9] covers an initial data $u_0\in H^{3}(\mathbb {R})$
. We observe that the result proven in [Reference da Silva and Freire9] covers an initial data $u_0\in H^{3}(\mathbb {R})$![]() , while here we establish the result to $u_0\in H^{s}(\mathbb {R})$
, while here we establish the result to $u_0\in H^{s}(\mathbb {R})$![]() , $s\geq 3$
, $s\geq 3$![]() , which is enough for our purposes.
, which is enough for our purposes.
Proposition 1.1 Given $u_0\in H^{s}(\mathbb {R}),$![]() $s\geq 3,$
$s\geq 3,$![]() if $m_0 \in L^{1}(\mathbb {R})$
if $m_0 \in L^{1}(\mathbb {R})$![]() does not change sign, then the unique local solution $u$
does not change sign, then the unique local solution $u$![]() for (1.6)–(1.7) with $k=1$
for (1.6)–(1.7) with $k=1$![]() exists globally in $C([0,\,\infty );H^{s}(\mathbb {R})) \cap C^{1}([0,\,\infty );H^{s-1}(\mathbb {R}))$
exists globally in $C([0,\,\infty );H^{s}(\mathbb {R})) \cap C^{1}([0,\,\infty );H^{s-1}(\mathbb {R}))$![]() .
.
With proposition 1.1 in hand, we enunciate our main result.
Theorem 1.2 Given $u_0\in G^{1,s}(\mathbb {R}),$![]() with $s>5/2,$
with $s>5/2,$![]() if $m_0(x)$
if $m_0(x)$![]() does not change sign, then the Cauchy problem of (1.6)–(1.7) with $k=1$
does not change sign, then the Cauchy problem of (1.6)–(1.7) with $k=1$![]() has a unique global analytic solution $u\in C^{\omega }([0,\,\infty )\times \mathbb {R})$
has a unique global analytic solution $u\in C^{\omega }([0,\,\infty )\times \mathbb {R})$![]() .
.
In the context of hydrodynamic applications, analyticity is a crucial ingredient to prove an intrinsic characterization of symmetric waves, see [Reference Escher and Matioc14] for more details. Here, we observe that our unique space-time analytic solutions provided by theorem 1.2 are not necessarily travelling waves, which then provides an interesting and general result.
The proof of theorem 1.2 relies on the powerful machinery of Kato and Masuda [Reference Kato and Masuda21] and embedding properties of certain spaces, see [Reference Barostichi, Himonas and Petronilho5, Reference Kato and Masuda21]. Another useful space is an adaptation of the Banach spaces proposed by Himonas and Misiolek in [Reference Himonas and Misiolek17]: for $\sigma >0$![]() and $m$
and $m$![]() is a positive integer, the set $E_{\sigma,m}(\mathbb {R})$
is a positive integer, the set $E_{\sigma,m}(\mathbb {R})$![]() of infinitely differentiable functions such that
of infinitely differentiable functions such that
is a Banach space by its own turn. In order to prove that the lifespan is infinite and the solution is analytic in both variables $t$![]() and $x$
and $x$![]() , we will make use of the auxiliary local well-posedness result.
, we will make use of the auxiliary local well-posedness result.
Proposition 1.3 Given $u_0(x)\in E_{\sigma _0,m}(\mathbb {R}),$![]() with $m\geq 3$
with $m\geq 3$![]() and for some $\sigma _0\in (0,\,1]$
and for some $\sigma _0\in (0,\,1]$![]() fixed, for
fixed, for
where

with $c_m>0$![]() depending only on $m$
depending only on $m$![]() , and for every $\sigma \in (0,\,\sigma _0),$
, and for every $\sigma \in (0,\,\sigma _0),$![]() the Cauchy problem for (1.6)–(1.7) has a unique solution $u$
the Cauchy problem for (1.6)–(1.7) has a unique solution $u$![]() that is analytic in the disc $D(0,\,T(\sigma _0-\sigma ))$
that is analytic in the disc $D(0,\,T(\sigma _0-\sigma ))$![]() with values in $E_{\sigma,m}(\mathbb {R})$
with values in $E_{\sigma,m}(\mathbb {R})$![]() . Moreover, the bound
. Moreover, the bound
holds.
The paper is organized as follows. In § 2 we establish the basic function spaces and auxiliary propositions required for the understanding and proofs of our results. In § 3, we present the proof of proposition 1.3 for any $k\in \mathbb {Z}_+$![]() , which follows from the technical estimates of § 2. After that, in § 4 we present a proof of proposition 1.1, which can also be found in [Reference da Silva and Freire9] for $s=3$
, which follows from the technical estimates of § 2. After that, in § 4 we present a proof of proposition 1.1, which can also be found in [Reference da Silva and Freire9] for $s=3$![]() . Finally, in § 5 we provide a proof for global well-posedness in $H^{\infty }(\mathbb {R})$
. Finally, in § 5 we provide a proof for global well-posedness in $H^{\infty }(\mathbb {R})$![]() and finalize with the extensive and complex proof of theorem 1.2 by making use of proposition 1.3.
and finalize with the extensive and complex proof of theorem 1.2 by making use of proposition 1.3.
2. Function spaces and auxiliary results
In this section we will enunciate the theory behind the function spaces presented in the introduction.
We start recalling that, similarly to Sobolev spaces, one interesting property of Gevrey spaces is that it is possible to continuously embed them based on the parameters $\sigma$![]() and $s$
and $s$![]() , see [Reference Barostichi, Himonas and Petronilho4]:
, see [Reference Barostichi, Himonas and Petronilho4]:
(i) If $0<\sigma '<\sigma$
 and $s\geq 0$
and $s\geq 0$ , then $\Vert \cdot \Vert _{G^{\sigma ',s}}\leq \Vert \cdot \Vert _{G^{\sigma,s}}$
, then $\Vert \cdot \Vert _{G^{\sigma ',s}}\leq \Vert \cdot \Vert _{G^{\sigma,s}}$ and $G^{\sigma,s}(\mathbb {R})\hookrightarrow G^{\sigma ',s}(\mathbb {R})$
and $G^{\sigma,s}(\mathbb {R})\hookrightarrow G^{\sigma ',s}(\mathbb {R})$ ;
;(ii) If $0< s'< s$
 and $\sigma >0$
and $\sigma >0$ , then $\Vert \cdot \Vert _{G^{\sigma,s'}}\leq \Vert \cdot \Vert _{G^{\sigma,s}}$
, then $\Vert \cdot \Vert _{G^{\sigma,s'}}\leq \Vert \cdot \Vert _{G^{\sigma,s}}$ and $G^{\sigma,s}(\mathbb {R})\hookrightarrow G^{\sigma,s'}(\mathbb {R})$
and $G^{\sigma,s}(\mathbb {R})\hookrightarrow G^{\sigma,s'}(\mathbb {R})$ .
.
Although our main result involves the use of Gevrey spaces, we will need to consider some auxiliary spaces and their embeddings. Following the work of Kato and Masuda [Reference Kato and Masuda21] about the Korteweg–de Vries equation, for $r>0$![]() fixed we define the spaces $A(r)$
fixed we define the spaces $A(r)$![]() of functions that can be analytically extended to a function on a strip of width $r$
of functions that can be analytically extended to a function on a strip of width $r$![]() , endowed with the norm
, endowed with the norm

for $s\geq 0$![]() and every $\sigma \in \mathbb {R}$
and every $\sigma \in \mathbb {R}$![]() such that $e^{\sigma }< r$
such that $e^{\sigma }< r$![]() . Observe that if $r\geq r'$
. Observe that if $r\geq r'$![]() then $f\in A(r)$
then $f\in A(r)$![]() implies that $f\in A(r')$
implies that $f\in A(r')$![]() and, therefore, $A(r)\subset A(r')$
and, therefore, $A(r)\subset A(r')$![]() .
.
For $H^{\infty }(\mathbb {R}) := \bigcap \limits _{s\geq 0}H^{s}(\mathbb {R})$![]() , we have the following sequence of embeddings (see lemma 2.3 and lemma 2.5 in [Reference Barostichi, Himonas and Petronilho4] and lemma 2.2 in [Reference Kato and Masuda21]):
, we have the following sequence of embeddings (see lemma 2.3 and lemma 2.5 in [Reference Barostichi, Himonas and Petronilho4] and lemma 2.2 in [Reference Kato and Masuda21]):
for $\sigma >0$![]() and $s\geq 0$
and $s\geq 0$![]() .
.
Similarly to Gevrey spaces, we have $E_{\sigma,m}(\mathbb {R})\hookrightarrow E_{\sigma ',m}(\mathbb {R})$![]() for $0<\sigma '<\sigma$
for $0<\sigma '<\sigma$![]() and, more importantly, $E_{\sigma,m}(\mathbb {R})$
and, more importantly, $E_{\sigma,m}(\mathbb {R})$![]() is also continuously embedded into $H^{\infty }(\mathbb {R})$
is also continuously embedded into $H^{\infty }(\mathbb {R})$![]() for all $m\geq 1$
for all $m\geq 1$![]() and $\sigma >0$
and $\sigma >0$![]() , see page 750 of [Reference Barostichi, Himonas and Petronilho5]. Moreover, it is important to emphasize that if $1\leq m\leq m'$
, see page 750 of [Reference Barostichi, Himonas and Petronilho5]. Moreover, it is important to emphasize that if $1\leq m\leq m'$![]() , then $\vert \vert \vert f\vert \vert \vert _{E_{\sigma,m}}\leq \vert \vert \vert f\vert \vert \vert _{E_{\sigma,m'}}$
, then $\vert \vert \vert f\vert \vert \vert _{E_{\sigma,m}}\leq \vert \vert \vert f\vert \vert \vert _{E_{\sigma,m'}}$![]() .
.
To be able to extend regularity of global solutions, we will need to first consider local well-posedness in $E_{\sigma _0, m}(\mathbb {R})$![]() for some $\sigma _0\in (0,\,1]$
for some $\sigma _0\in (0,\,1]$![]() and $m\geq 3$
and $m\geq 3$![]() , and for that purpose some estimates will be required. The first one we enunciate is the algebra property, which allows us to relate the norm of multiplication to the multiplication of norms.
, and for that purpose some estimates will be required. The first one we enunciate is the algebra property, which allows us to relate the norm of multiplication to the multiplication of norms.
Lemma 2.1 Algebra property
For any positive integer $m,$![]() $0<\sigma \leq 1$
$0<\sigma \leq 1$![]() and $\varphi,\,\psi \in E_{\sigma,m}(\mathbb {R}),$
and $\varphi,\,\psi \in E_{\sigma,m}(\mathbb {R}),$![]() there is a positive constant $c_m$
there is a positive constant $c_m$![]() depending only on $m$
depending only on $m$![]() such that
such that
Proof. The proof follows closely the lines of [Reference Himonas and Misiolek17].
Consider an equation of the form $m_t = F(u,\,u_x,\,u_{xx},\,u_{xxx})$![]() and let $g(x) = e^{-|x|}/2$
and let $g(x) = e^{-|x|}/2$![]() be the Green function of the equation $(1-\partial _x^{2})u = \delta (x)$
be the Green function of the equation $(1-\partial _x^{2})u = \delta (x)$![]() , where $\delta$
, where $\delta$![]() denotes de Dirac delta distribution. Then we can write the inverse of the Helmholtz operator $1-\partial _x^{2}$
denotes de Dirac delta distribution. Then we can write the inverse of the Helmholtz operator $1-\partial _x^{2}$![]() as
as
With respect to the spaces $E_{\sigma,m}(\mathbb {R})$![]() , the Helmholtz operator and its inverse have some important and useful properties that will be necessary to prove local well-posedness.
, the Helmholtz operator and its inverse have some important and useful properties that will be necessary to prove local well-posedness.
Lemma 2.2 For $0<\sigma '<\sigma \leq 1,$![]() $m\geq 1$
$m\geq 1$![]() and $\varphi \in E_{\sigma,m}(\mathbb {R}),$
and $\varphi \in E_{\sigma,m}(\mathbb {R}),$![]() then
then
Proof. The proofs of (2.4) and (2.5) follow immediately from the analogous estimates for Sobolev spaces and will be omitted, while the the proof of (2.3) requires an immediate adaptation of the proof of lemma 2.4 (page 580) of [Reference Himonas and Misiolek17].
In what follows, a function $u$![]() belongs to the space $C^{\omega }(I;X)$
belongs to the space $C^{\omega }(I;X)$![]() if it is analytic in the interval $I$
if it is analytic in the interval $I$![]() as a function of $t$
as a function of $t$![]() and $u(t,\,\cdot )$
and $u(t,\,\cdot )$![]() belongs to $X$
belongs to $X$![]() . We will be interested in $C^{\omega }(I;G^{\sigma,s}(\mathbb {R})),\, C^{\omega }(I;E_{\sigma,m}(\mathbb {R}))$
. We will be interested in $C^{\omega }(I;G^{\sigma,s}(\mathbb {R})),\, C^{\omega }(I;E_{\sigma,m}(\mathbb {R}))$![]() and $C^{\omega }(I;A(r))$
and $C^{\omega }(I;A(r))$![]() . In the case where $u\in C^{\omega }(I\times \mathbb {R})$
. In the case where $u\in C^{\omega }(I\times \mathbb {R})$![]() , then $u(t,\,x)$
, then $u(t,\,x)$![]() is analytic for $(t,\,x)\in I\times \mathbb {R}$
is analytic for $(t,\,x)\in I\times \mathbb {R}$![]() .
.
The final result of this section, called Autonomous Ovsyannikov Theorem, will be used in the next section to prove proposition 1.3. Its proof uses a very classical fixed point argument and follows closely the ideas in [Reference Barostichi, Himonas and Petronilho4, Reference Luo and Yin24], see also [Reference Baouendi and Goulaouic2].
Proposition 2.3 Autonomous Ovsyannikov Theorem
Let $X_{\delta }$![]() be a scale of decreasing Banach spaces for $0<\delta \leq 1,$
be a scale of decreasing Banach spaces for $0<\delta \leq 1,$![]() that is, $X_\delta \subset X_{\delta '},\, \Vert \cdot \Vert _{\delta '}\leq \Vert \cdot \Vert _{\delta },\, 0<\delta '<\delta \leq 1,$
that is, $X_\delta \subset X_{\delta '},\, \Vert \cdot \Vert _{\delta '}\leq \Vert \cdot \Vert _{\delta },\, 0<\delta '<\delta \leq 1,$![]() and consider the Cauchy problem
and consider the Cauchy problem

Given $\delta _0\in (0,\,1]$![]() and $u_0\in X_{\delta _0}$
and $u_0\in X_{\delta _0}$![]() , assume that $G$
, assume that $G$![]() satisfies the following conditions:
satisfies the following conditions:
(i) For $0<\delta '<\delta <\delta _0$
 , $R>0$
, $R>0$ and $a>0$
and $a>0$ , if the function $t\mapsto u(t)$
, if the function $t\mapsto u(t)$ is holomorphic on $\{t\in \mathbb {C}; 0<|t|< a(\delta _0-\delta )$
is holomorphic on $\{t\in \mathbb {C}; 0<|t|< a(\delta _0-\delta )$ with values in $X_{\delta }$
with values in $X_{\delta }$ and $\sup \limits _{t< a(\delta _0-\delta )}\Vert u-u_0\Vert _{\delta }< R$
and $\sup \limits _{t< a(\delta _0-\delta )}\Vert u-u_0\Vert _{\delta }< R$ , then the function $t\mapsto G(t,\,u(t))$
, then the function $t\mapsto G(t,\,u(t))$ is holomorphic on the same set with values in $X_{\delta '}$
is holomorphic on the same set with values in $X_{\delta '}$ .
.(ii) $G:X_{\delta }\rightarrow X_{\delta '}$
 is well defined for any $0<\delta '<\delta <\delta _0$
is well defined for any $0<\delta '<\delta <\delta _0$ and for any $R>0$
and for any $R>0$ and $u,\,v\in B(u_0,\,R)\subset X_{\delta }$
and $u,\,v\in B(u_0,\,R)\subset X_{\delta }$ , there exist positive constants $L$
, there exist positive constants $L$ and $M$
and $M$ depending only on $u_0$
depending only on $u_0$ and $R$
and $R$ such that
\[ \Vert G(u) - G(v)\Vert_{\delta'}\leq \frac{L}{\delta-\delta'}\Vert u-v\Vert_{\delta},\quad \Vert G(u_0)\Vert_{\delta}\leq \frac{M}{\delta_0-\delta}, \]
such that
\[ \Vert G(u) - G(v)\Vert_{\delta'}\leq \frac{L}{\delta-\delta'}\Vert u-v\Vert_{\delta},\quad \Vert G(u_0)\Vert_{\delta}\leq \frac{M}{\delta_0-\delta}, \]
$0<\delta <\delta _0$![]() . Then for
. Then for
the initial value problem (2.6) has a unique solution $u\in C^{\omega }([0,\,T(\delta _0-\delta )),\,X_{\delta })$![]() , for every $\delta \in (0,\,\delta _0)$
, for every $\delta \in (0,\,\delta _0)$![]() , satisfying
, satisfying
3. Local well-posedness in the Himonas–Misiolek space
In this section we want to prove proposition 1.3 by making use of Autonomous Ovsyannikov Theorem. Before doing so in the next subsections, observe that the embeddings $E_{\sigma,m}(\mathbb {R})\hookrightarrow E_{\sigma ',m}(\mathbb {R})$![]() , for $0<\sigma '<\sigma$
, for $0<\sigma '<\sigma$![]() , guarantee that the function
, guarantee that the function
taken as the right-hand side of (1.6), is a well-defined function from $E_{\sigma,m}(\mathbb {R})$![]() to $E_{\sigma ',m}(\mathbb {R})$
to $E_{\sigma ',m}(\mathbb {R})$![]() for every choice of $k$
for every choice of $k$![]() . Moreover, condition 1 for the Autonomous Ovsyannikov Theorem is trivially satisfied. Therefore, it remains to prove condition 2.
. Moreover, condition 1 for the Autonomous Ovsyannikov Theorem is trivially satisfied. Therefore, it remains to prove condition 2.
The proof of proposition 1.3 will be given in two parts. First we will separately prove the case where $k=1$![]() , and then proceed to the case $k>1$
, and then proceed to the case $k>1$![]() . We would like to point out that proposition 1.3 holds for any positive choice of the parameter $k$
. We would like to point out that proposition 1.3 holds for any positive choice of the parameter $k$![]() , which then recovers the case $b=0$
, which then recovers the case $b=0$![]() for the $b$
for the $b$![]() -equation.
-equation.
3.1 Proof for $k=1$
Consider the function $F(u)$![]() given by (1.7) with $k=1$
given by (1.7) with $k=1$![]() .
.
Proposition 3.1 Given $\sigma _0\in (0,\,1],$![]() $u_0\in E_{\sigma _0,m}(\mathbb {R}),$
$u_0\in E_{\sigma _0,m}(\mathbb {R}),$![]() with $m\geq 3,$
with $m\geq 3,$![]() and $\sigma \in (0,\,\sigma _0),$
and $\sigma \in (0,\,\sigma _0),$![]() there exists a positive constant $M$
there exists a positive constant $M$![]() that depends only on $m$
that depends only on $m$![]() and $u_0$
and $u_0$![]() such that
such that
Proof. For $u_0\in E_{\sigma _0,m}(\mathbb {R})$![]() , write
, write
Using the triangle inequality, lemma 2.2 and lemma 2.1, we obtain

where $M=2c_m \vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}^{2}$![]() , finishing the proof.
, finishing the proof.
Proposition 3.2 Let $R>0$![]() and $\sigma _0\in (0,\,1]$
and $\sigma _0\in (0,\,1]$![]() . Given $u_0\in E_{\sigma _0,m}(\mathbb {R}),$
. Given $u_0\in E_{\sigma _0,m}(\mathbb {R}),$![]() with $m\geq 3,$
with $m\geq 3,$![]() and $0<\sigma '<\sigma <\sigma _0,$
and $0<\sigma '<\sigma <\sigma _0,$![]() if $u,\,v\in E_{\sigma,m}(\mathbb {R})$
if $u,\,v\in E_{\sigma,m}(\mathbb {R})$![]() are such that
are such that
then there exists a positive constant $L$![]() that depends only on $m,$
that depends only on $m,$![]() $u_0$
$u_0$![]() and $R$
and $R$![]() such that
such that
Proof. From the triangle inequality, we have
By observing that

where in the last inequality we used the fact that $\vert \vert \vert {\partial _x(u-v)}\vert \vert \vert _{E_{{\sigma },{m-2}}}\leq \vert \vert \vert {u-v}\vert \vert \vert _{E_{{\sigma },{m}}}$![]() and an analogous estimate for $\partial _x(u+v)$
and an analogous estimate for $\partial _x(u+v)$![]() .
.
Since
we conclude that for $L = 4c_m(R + \vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}})$![]() the bound
the bound
holds for $m\geq 3$![]() and $0<\sigma '<\sigma <\sigma _0$
and $0<\sigma '<\sigma <\sigma _0$![]() , completing the proof.
, completing the proof.
We are now in conditions to finalize the proof of proposition 1.3 for $k=1$![]() . For this purpose, observe that in proposition 3.1 we have $M = 2c_m \vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}^{2},$
. For this purpose, observe that in proposition 3.1 we have $M = 2c_m \vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}^{2},$![]() while in proposition 3.2 we have $L = 4c_m (R+\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}})$
while in proposition 3.2 we have $L = 4c_m (R+\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}})$![]() for any $R>0$
for any $R>0$![]() . Letting $C = 4c_m,$
. Letting $C = 4c_m,$![]() then we can write $L = C(R+\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}})$
then we can write $L = C(R+\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}})$![]() and $M = \frac {C}{2}\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}^{2}.$
and $M = \frac {C}{2}\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}^{2}.$![]()
From propositions 3.1 and 3.2, the conditions for the Autonomous Ovsyannikov Theorem are satisfied and, therefore, for $m\geq 3$![]() and $T$
and $T$![]() given by (2.7) there exists a unique solution $u$
given by (2.7) there exists a unique solution $u$![]() to the Cauchy problem (1.6) which for every $\sigma \in (0,\,\sigma _0)$
to the Cauchy problem (1.6) which for every $\sigma \in (0,\,\sigma _0)$![]() is a holomorphic function in $D(0,\,T(\sigma _0-\sigma ))$
is a holomorphic function in $D(0,\,T(\sigma _0-\sigma ))$![]() to $E_{\sigma,m}(\mathbb {R})$
to $E_{\sigma,m}(\mathbb {R})$![]() and satisfies (2.8). Taking $R = \vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}$
and satisfies (2.8). Taking $R = \vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}$![]() yields
yields
and the proof of existence and uniqueness of proposition 1.3 is finished for $k=1$![]() .
.
3.2 Proof for $k> 1$
For the case $k>1$![]() , we will make use of the simple algebraic inequality
, we will make use of the simple algebraic inequality
Consider the function $F(u)$![]() given by (1.7). Similarly to proposition 3.1 and proposition 3.2 for the case $k=1$
given by (1.7). Similarly to proposition 3.1 and proposition 3.2 for the case $k=1$![]() , we will estimate $\vert \vert \vert {F(u_0)}\vert \vert \vert _{E_{{\sigma },{m}}}$
, we will estimate $\vert \vert \vert {F(u_0)}\vert \vert \vert _{E_{{\sigma },{m}}}$![]() and $\vert \vert \vert {F(u)-F(v)}\vert \vert \vert _{E_{{\sigma '},{m}}}$
and $\vert \vert \vert {F(u)-F(v)}\vert \vert \vert _{E_{{\sigma '},{m}}}$![]() for $m\geq 3$
for $m\geq 3$![]() and $0<\sigma '<\sigma <\sigma _0\leq 1$
and $0<\sigma '<\sigma <\sigma _0\leq 1$![]() .
.
Proposition 3.3 Given $\sigma _0\in (0,\,1],$![]() $u_0\in E_{\sigma _0,m}(\mathbb {R}),$
$u_0\in E_{\sigma _0,m}(\mathbb {R}),$![]() with $m\geq 3,$
with $m\geq 3,$![]() and $\sigma \in (0,\,\sigma _0),$
and $\sigma \in (0,\,\sigma _0),$![]() there exists a positive constant $M$
there exists a positive constant $M$![]() that depends only on $m$
that depends only on $m$![]() and $u_0$
and $u_0$![]() such that
such that
Proof. Given $u_0\in E_{\sigma _0,m}(\mathbb {R})$![]() , using (1.7) we have
, using (1.7) we have

From lemma 2.2 and the algebra property, we can write

Thus,
By letting
we finally conclude that
for $0<\sigma <\sigma _0$![]() , and the result is proven.
, and the result is proven.
Before proceeding with the next estimate, it is necessary to state a result that only requires the triangle inequality and successive applications of the algebra property.
Lemma 3.4 For $u,\,v\in E_{\sigma,m}(\mathbb {R})$![]() , with $\sigma >0$
, with $\sigma >0$![]() and $m\geq 1$
and $m\geq 1$![]() , let
, let

Then there exists a positive constant $c_m$![]() depending only on $m$
depending only on $m$![]() such that
such that
We shall now proceed with the last crucial estimate required to make use of the Autonomous Ovsyannikov Theorem and finish the proof of proposition 1.3.
Proposition 3.5 Let $R>0$![]() and $\sigma _0\in (0,\,1]$
and $\sigma _0\in (0,\,1]$![]() . Given $u_0\in E_{\sigma _0,m}(\mathbb {R}),$
. Given $u_0\in E_{\sigma _0,m}(\mathbb {R}),$![]() with $m\geq 3$
with $m\geq 3$![]() and $0<\sigma '<\sigma <\sigma _0,$
and $0<\sigma '<\sigma <\sigma _0,$![]() if $u,\,v\in E_{\sigma,m}(\mathbb {R})$
if $u,\,v\in E_{\sigma,m}(\mathbb {R})$![]() are such that
are such that
then there exists a positive constant $L$![]() that depends only on $m,$
that depends only on $m,$![]() $u_0$
$u_0$![]() and $R$
and $R$![]() such that
such that
Proof. Given $R>0$![]() , $\sigma _0\in (0,\,1]$
, $\sigma _0\in (0,\,1]$![]() and $u_0\in E_{\sigma _0,m}(\mathbb {R})$
and $u_0\in E_{\sigma _0,m}(\mathbb {R})$![]() , with $m\geq 3$
, with $m\geq 3$![]() , let $0<\sigma '<\sigma <\sigma _0$
, let $0<\sigma '<\sigma <\sigma _0$![]() . In terms (1.7), we write
. In terms (1.7), we write

Since $u^{k+1}-v^{k+1} = (u-v)f_k(u,\,v)$![]() , from lemma 2.2 and lemma 3.4 we obtain
, from lemma 2.2 and lemma 3.4 we obtain

For the second term, write
which, together with the triangle inequality, the algebra property and proposition 3.2, yield

From the proof of proposition 3.2 we know that $\vert \vert \vert {u+v}\vert \vert \vert _{E_{{\sigma },{m}}}<2 (R+\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}).$![]() Moreover, we also have
Moreover, we also have
which tells that

and
To deal with the third and last term on the right-hand side of (3.2), observe that

Thus, we can write

From the estimate (3.3) it is then obtained

Now under substitution of the respective terms in (3.2), we arrive at

Observe now that for $k>1$![]() we have $2^{k-2}<2^{k-1}$
we have $2^{k-2}<2^{k-1}$![]() , $2\leq 2^{k-1}$
, $2\leq 2^{k-1}$![]() and, from (3.1), $3+2^{k-3}<2^{k}$
and, from (3.1), $3+2^{k-3}<2^{k}$![]() . It means that the last inequality can be written as
. It means that the last inequality can be written as
where L = $C(R+\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}})^{k},$![]() with $C = 2^{k}[\tfrac {1}{k+1}+\tfrac {3k}{2}+\tfrac {k(k-1)}{2}]c_m^{k}$
with $C = 2^{k}[\tfrac {1}{k+1}+\tfrac {3k}{2}+\tfrac {k(k-1)}{2}]c_m^{k}$![]() , and the proof is finished.
, and the proof is finished.
We will now proceed with the final part of the proof of proposition 1.3. For $M = \frac {C}{2^{k}}\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}^{k+1}$![]() and $R=\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}$
and $R=\vert \vert \vert {u_0}\vert \vert \vert _{E_{{\sigma _0},{m}}}$![]() , from the Autonomous Ovsyannikov Theorem, for
, from the Autonomous Ovsyannikov Theorem, for

there exists a unique solution $u$![]() to the Cauchy problem of (1.6) which, for every $\sigma \in (0,\,\sigma _0)$
to the Cauchy problem of (1.6) which, for every $\sigma \in (0,\,\sigma _0)$![]() , is a holomorphic function in $D(0,\,T(\sigma _0-\sigma ))$
, is a holomorphic function in $D(0,\,T(\sigma _0-\sigma ))$![]() into $E_{\sigma _0,m}(\mathbb {R})$
into $E_{\sigma _0,m}(\mathbb {R})$![]() . Therefore, the proof of proposition 1.3 is complete for any positive integer $k$
. Therefore, the proof of proposition 1.3 is complete for any positive integer $k$![]() . Observe that taking $k=1$
. Observe that taking $k=1$![]() will result in the same $T$
will result in the same $T$![]() obtained last section, which shows that it indeed unifies both cases.
obtained last section, which shows that it indeed unifies both cases.
Since lemma 2.1 and a similar lemma 2.2 are still valid for Gevrey spaces $G^{\sigma,s}(\mathbb {R})$![]() , where $0<\sigma <\sigma '\leq \sigma _0\leq 1$
, where $0<\sigma <\sigma '\leq \sigma _0\leq 1$![]() and $s>1/2$
and $s>1/2$![]() , see [Reference Barostichi, Himonas and Petronilho4, Reference Luo and Yin24], a repetition of the same calculations for $\sigma _0=1$
, see [Reference Barostichi, Himonas and Petronilho4, Reference Luo and Yin24], a repetition of the same calculations for $\sigma _0=1$![]() provides an analogous result for these spaces, which will be useful and is therefore stated in the next result. For an alternative proof, see theorem 1 in [Reference Barostichi, Himonas and Petronilho3].
provides an analogous result for these spaces, which will be useful and is therefore stated in the next result. For an alternative proof, see theorem 1 in [Reference Barostichi, Himonas and Petronilho3].
Corollary 3.6 Given $u_0(x):=u(0,\,x)\in G^{1,s}(\mathbb {R}),$![]() with $s\geq 5/2,$
with $s\geq 5/2,$![]() there exists $T>0$
there exists $T>0$![]() such that for every $\sigma \in (0,\,1)$
such that for every $\sigma \in (0,\,1)$![]() the Cauchy problem for (1.6) has a unique solution $u\in C^{\omega }([0,\,T(1-\sigma )); G^{\sigma,s}(\mathbb {R}))$
the Cauchy problem for (1.6) has a unique solution $u\in C^{\omega }([0,\,T(1-\sigma )); G^{\sigma,s}(\mathbb {R}))$![]() .
.
4. Global well-posedness in Sobolev spaces
In this section we will prove proposition 1.1 and the proof will be based on the local well-posedness in Sobolev spaces, a certain estimate for the $H^{3}(\mathbb {R})$![]() norm of the local solution and the Sobolev embedding theorem. It is worth mentioning that the proof for the case $s=3$
norm of the local solution and the Sobolev embedding theorem. It is worth mentioning that the proof for the case $s=3$![]() is already proven in [Reference da Silva and Freire9] and, therefore, presented here just for the sake of completeness. Firstly we enuntiate a result due to Yan [Reference Yan26], see also Himonas and Holliman [Reference Himonas and Holliman16].
is already proven in [Reference da Silva and Freire9] and, therefore, presented here just for the sake of completeness. Firstly we enuntiate a result due to Yan [Reference Yan26], see also Himonas and Holliman [Reference Himonas and Holliman16].
Lemma 4.1 Suppose that $u_0\in H^{s}(\mathbb {R}),\, s>3/2$![]() . There exist a maximal time of existence $T>0$
. There exist a maximal time of existence $T>0$![]() and a unique solution $u\in C([0,\,T);H^{s}(\mathbb {R}))\cap C^{1}([0,\,T);H^{s-1}(\mathbb {R}))$
and a unique solution $u\in C([0,\,T);H^{s}(\mathbb {R}))\cap C^{1}([0,\,T);H^{s-1}(\mathbb {R}))$![]() of (1.6)–(1.7) with $k=1$
of (1.6)–(1.7) with $k=1$![]() . Moreover, the solution $u$
. Moreover, the solution $u$![]() satisfies the following energy estimate:
satisfies the following energy estimate:
for some positive constant $c_s$![]() . Finally, the data-to-solution map $u(0)\mapsto u(t)$
. Finally, the data-to-solution map $u(0)\mapsto u(t)$![]() is continuous.
is continuous.
Proof. For the proof of existence and uniqueness of solution, see corollary 2.1 of [Reference Yan26], while the estimate (4.1) is given by (2.29) of [Reference Himonas and Holliman16].
After having the energy estimate (4.1) guaranteed, we enunciate a result stated as part of lemma 5.1 and theorem 3.1 of da Silva and Freire [Reference da Silva and Freire9].
Lemma 4.2 Given $u_0\in H^{3}(\mathbb {R})$![]() , let $u$
, let $u$![]() be the corresponding unique solution of (1.6)–(1.7) with $k=1$
be the corresponding unique solution of (1.6)–(1.7) with $k=1$![]() .
.
(a) If there exists $\kappa >0$
 such that $u_x>-\kappa$
such that $u_x>-\kappa$ , then $\Vert u\Vert _{H^{3}}\leq e^{\kappa t/2}\Vert u_0\Vert _{H^{3}}$
, then $\Vert u\Vert _{H^{3}}\leq e^{\kappa t/2}\Vert u_0\Vert _{H^{3}}$ ;
;(b) If $m_0$
 does not change sign, then $-u_x \leq \Vert m_0\Vert _{L^{1}}$
does not change sign, then $-u_x \leq \Vert m_0\Vert _{L^{1}}$ for each $(t,\,x)\in [0.T)\times \mathbb {R}$
for each $(t,\,x)\in [0.T)\times \mathbb {R}$ .
.
As a consequence, we can extend the last lemma to and initial data in $H^{s}(\mathbb {R})$![]() for $s\geq 3$
for $s\geq 3$![]() as the following corollary states:
as the following corollary states:
Corollary 4.3 Let $u_0\in H^{s}(\mathbb {R}),\, s\geq 3,$![]() be an initial data with corresponding local solution $u$
be an initial data with corresponding local solution $u$![]() . If $m_0$
. If $m_0$![]() does not change sign, then
does not change sign, then
Proof. Since $s\geq 3,$![]() we have $H^{s}(\mathbb {R})\subset H^{3}(\mathbb {R})$
we have $H^{s}(\mathbb {R})\subset H^{3}(\mathbb {R})$![]() and $H^{s-1}(\mathbb {R})\subset H^{2}(\mathbb {R})$
and $H^{s-1}(\mathbb {R})\subset H^{2}(\mathbb {R})$![]() . Therefore, $u_0\in H^{3}(\mathbb {R})$
. Therefore, $u_0\in H^{3}(\mathbb {R})$![]() and, from lemma 4.2(b), there exists $\kappa = \Vert m_0\Vert _{L^{1}}$
and, from lemma 4.2(b), there exists $\kappa = \Vert m_0\Vert _{L^{1}}$![]() such that $-u_x < \kappa$
such that $-u_x < \kappa$![]() . The result now follows from lemma 4.2(a).
. The result now follows from lemma 4.2(a).
We are now ready to prove theorem 1.1.
Proof of proposition 1.1. For $u_0\in H^{s}(\mathbb {R}),\, s\geq 3,$![]() let $u\in C([0,\,T);H^{s}(\mathbb {R}))\cap C^{1} ([0,\,T);H^{s-1}(\mathbb {R}))$
let $u\in C([0,\,T);H^{s}(\mathbb {R}))\cap C^{1} ([0,\,T);H^{s-1}(\mathbb {R}))$![]() be the unique local solution. From lemma 4.1, the solution is such that (4.1) holds for $0\leq t< T$
be the unique local solution. From lemma 4.1, the solution is such that (4.1) holds for $0\leq t< T$![]() . From Grönwall's inequality, we have
. From Grönwall's inequality, we have
Since $m_0$![]() does not change sign, from the Sobolev embedding theorem we have
does not change sign, from the Sobolev embedding theorem we have
for $s>1/2$![]() . Taking $s=2$
. Taking $s=2$![]() and using corollary 4.3, we obtain
and using corollary 4.3, we obtain
Note that $u_0\in H^{s}(\mathbb {R})$![]() for $s\geq 3$
for $s\geq 3$![]() tells that $u_0\in H^ 3(\mathbb {R})$
tells that $u_0\in H^ 3(\mathbb {R})$![]() and then, under substitution in (4.2), the condition becomes
and then, under substitution in (4.2), the condition becomes
where $K = \kappa /2$![]() . This means that $u$
. This means that $u$![]() does not blow-up at a finite time and the solution $u$
does not blow-up at a finite time and the solution $u$![]() can be extended globally in time.
can be extended globally in time.
5. Global well-posedness and radius of spatial analyticity
In this section we prove theorem 1.2. In what follows, we will consider the initial value problem

and make use of local and global well-posedness in Sobolev spaces to extend regularity. The machinery here presented follows closely the ideas of Kato and Masuda [Reference Kato and Masuda21] and later Barostichi, Himonas and Petronilho [Reference Barostichi, Himonas and Petronilho5]. Since the proof of theorem 1.2 is extremely technical and extensive, we opt to divide the result in several propositions that together will give our desired result. The propositions that will be presented next will be proven in the next subsections. We start with a very important result regarding global well-posedness in $H^{\infty }(\mathbb {R})$![]() .
.
Proposition 5.1 If $u_0\in G^{1,s}(\mathbb {R}),$![]() $s>3/2,$
$s>3/2,$![]() and $m_0$
and $m_0$![]() does not change sign, then (5.1) has a unique solution $u\in C([0,\,\infty );H^{\infty }(\mathbb {R}))$
does not change sign, then (5.1) has a unique solution $u\in C([0,\,\infty );H^{\infty }(\mathbb {R}))$![]() .
.
Once we have the global solution established, we will extend regularity to the Kato–Masuda space. We are able to find $r_1>0$![]() such that for each fixed arbitrary time $T>0$
such that for each fixed arbitrary time $T>0$![]() the solution will belong to $A(r_1(t))$
the solution will belong to $A(r_1(t))$![]() as a space function for $t\in [0,\,T]$
as a space function for $t\in [0,\,T]$![]() . From the definition of the spaces $A(r)$
. From the definition of the spaces $A(r)$![]() , this $r_1$
, this $r_1$![]() will be the radius of spatial analyticity of the solution.
will be the radius of spatial analyticity of the solution.
Proposition 5.2 Given $u_0\in G^{1,s}(\mathbb {R})$![]() , with $s>5/2$
, with $s>5/2$![]() , suppose that $m_0$
, suppose that $m_0$![]() does not change sign and let $u\in C([0,\,\infty );H^{\infty }(\mathbb {R}))$
does not change sign and let $u\in C([0,\,\infty );H^{\infty }(\mathbb {R}))$![]() be the unique solution to the initial value problem of (5.1). Then there exists $r_1>0$
be the unique solution to the initial value problem of (5.1). Then there exists $r_1>0$![]() such that $u\in C([0,\,\infty );A(r_1))$
such that $u\in C([0,\,\infty );A(r_1))$![]() . Moreover, for every $T>0$
. Moreover, for every $T>0$![]() an explicit lower bound for the radius of spatial analyticity is given by
an explicit lower bound for the radius of spatial analyticity is given by
where $L_1=\frac {52\sqrt {2}}{7}\Vert {u_0}\Vert _{{\sigma _0},{2}}$![]() for $\sigma _0<0$
for $\sigma _0<0$![]() fixed, $L_2 = 112\mu,\, L_3 = r(0)e^{L_1}$
fixed, $L_2 = 112\mu,\, L_3 = r(0)e^{L_1}$![]() and $\mu = 1+\max \{\Vert {u}\Vert _{H^{2}};t\in [0,\,T]\}$
and $\mu = 1+\max \{\Vert {u}\Vert _{H^{2}};t\in [0,\,T]\}$![]() .
.
Proposition 5.2 says that the global solution is analytic in $x$![]() and gives a lower bound for the radius of spatial analyticity. The next step is to extend regularity to $t$
and gives a lower bound for the radius of spatial analyticity. The next step is to extend regularity to $t$![]() . Our first step towards this goal is to prove that the solution $u$
. Our first step towards this goal is to prove that the solution $u$![]() is locally analytic in time, as enunciated by the next result.
is locally analytic in time, as enunciated by the next result.
Proposition 5.3 Given $u_0\in G^{1,s}(\mathbb {R}),$![]() with $s>5/2,$
with $s>5/2,$![]() let $u\in C([0,\,\infty ); A(r_1))$
let $u\in C([0,\,\infty ); A(r_1))$![]() be the unique solution of (5.1). Then there exist $T>0$
be the unique solution of (5.1). Then there exist $T>0$![]() and $\delta (T)>0$
and $\delta (T)>0$![]() such that the unique solution $u$
such that the unique solution $u$![]() belongs to $C^{\omega }([0,\,T];A(\delta (T)))$
belongs to $C^{\omega }([0,\,T];A(\delta (T)))$![]() .
.
Once local analyticity is established, we show that the analytic lifespan is infinite.
Proposition 5.4 For the unique solution $u \in C^{\omega }([0,\,T];A(\delta (T)))$![]() , we have
, we have
Finally, to conclude our result, we use a result proved by Barostichi, Himonas and Petronilho in [Reference Barostichi, Himonas and Petronilho5] (see page 752).
Lemma 5.5 If $u\in C^{\omega }([0,\,T]; A(r(T)))$![]() for all $T>0$
for all $T>0$![]() and some $r(T)>0,$
and some $r(T)>0,$![]() then $u \in C^{\omega }([0,\,\infty )\times \mathbb {R})$
then $u \in C^{\omega }([0,\,\infty )\times \mathbb {R})$![]() .
.
Proof of theorem 1.2. The proof is now reduced to a recollection of the previous propositions. Given $u_0\in G^{1,s}(\mathbb {R})$![]() , if $m_0$
, if $m_0$![]() does not change sign, from proposition 5.1 we have a unique solution $u\in C([0,\,\infty ),\, H^{\infty }(\mathbb {R}))$
does not change sign, from proposition 5.1 we have a unique solution $u\in C([0,\,\infty ),\, H^{\infty }(\mathbb {R}))$![]() . From proposition 5.2, we guarantee the existence of $r_1>0$
. From proposition 5.2, we guarantee the existence of $r_1>0$![]() such that $u \in C([0,\,\infty ),\,A(r_1))$
such that $u \in C([0,\,\infty ),\,A(r_1))$![]() , which by proposition 5.3 belongs to $C^{\omega }([0,\,T],\,A(\delta (T)))$
, which by proposition 5.3 belongs to $C^{\omega }([0,\,T],\,A(\delta (T)))$![]() for certain $T>0$
for certain $T>0$![]() and $\delta (T)>0$
and $\delta (T)>0$![]() . Proposition 5.4 then guarantees that $u\in C^{\omega }([0,\,T],\,A(\delta (T)))$
. Proposition 5.4 then guarantees that $u\in C^{\omega }([0,\,T],\,A(\delta (T)))$![]() for every $T>0$
for every $T>0$![]() and then lemma 5.5 concludes that the solution $u$
and then lemma 5.5 concludes that the solution $u$![]() is global analytic for both variables.
is global analytic for both variables.
Moreover, we observe from proposition 5.2 that given $T>0$![]() , we have $u(t)\in A(r_1)$
, we have $u(t)\in A(r_1)$![]() for $t\in [0,\,T]$
for $t\in [0,\,T]$![]() and $r_1(t) \geq L_3e^{-L_1e^{L_2t}}$
and $r_1(t) \geq L_3e^{-L_1e^{L_2t}}$![]() . By means of the forthcoming expression (5.3) obtained in the proof of proposition 5.1 we can determine the radius of spatial analyticity as
. By means of the forthcoming expression (5.3) obtained in the proof of proposition 5.1 we can determine the radius of spatial analyticity as
where
and $\mu,\, \sigma _0$![]() are given as in proposition 5.2.
are given as in proposition 5.2.
5.1 Proof of proposition 5.1
For the proof of proposition 5.1, the only ingredients required are proposition 1.1, the embeddings $G^{1,s}(\mathbb {R})\subset H^{\infty }(\mathbb {R})$![]() and $H^{s}(\mathbb {R})\subset H^{s'}(\mathbb {R})$
and $H^{s}(\mathbb {R})\subset H^{s'}(\mathbb {R})$![]() for $s>s'$
for $s>s'$![]() , as shown next.
, as shown next.
Since $u_0\in G^{1,s}(\mathbb {R})$![]() , from the embedding $G^{1,s}(\mathbb {R})\subset H^{\infty }(\mathbb {R})$
, from the embedding $G^{1,s}(\mathbb {R})\subset H^{\infty }(\mathbb {R})$![]() the initial data belongs, in particular, to $H^{s}(\mathbb {R})$
the initial data belongs, in particular, to $H^{s}(\mathbb {R})$![]() for any $s\geq 3$
for any $s\geq 3$![]() . From theorem 1.1, there exists a unique global solution $u$
. From theorem 1.1, there exists a unique global solution $u$![]() in $C([0,\,\infty );H^{s}(\mathbb {R}))\cap C^{1}([0,\,\infty );H^{s-1}(\mathbb {R}))$
in $C([0,\,\infty );H^{s}(\mathbb {R}))\cap C^{1}([0,\,\infty );H^{s-1}(\mathbb {R}))$![]() for $s\geq 3$
for $s\geq 3$![]() , which means that $u(t,\,\cdot ) \in \bigcap \limits _{s\geq 3}H^{s}(\mathbb {R})$
, which means that $u(t,\,\cdot ) \in \bigcap \limits _{s\geq 3}H^{s}(\mathbb {R})$![]() . Now, the embedding $H^{3}(\mathbb {R})\subset H^{s'}(\mathbb {R})$
. Now, the embedding $H^{3}(\mathbb {R})\subset H^{s'}(\mathbb {R})$![]() for $s'\in [0,\,3]$
for $s'\in [0,\,3]$![]() shows that $u(t,\,\cdot )\in H^{s'}(\mathbb {R})$
shows that $u(t,\,\cdot )\in H^{s'}(\mathbb {R})$![]() and $u(t,\,\cdot )\in H^{\infty }(\mathbb {R})$
and $u(t,\,\cdot )\in H^{\infty }(\mathbb {R})$![]() , concluding the proof of proposition 5.1
, concluding the proof of proposition 5.1
5.2 Proof of proposition 5.2
This is by far the most technical and complicated result. The proof consists of bounding a certain inner product and using properties of dense spaces to find such $r_1$![]() . For $m\geq 0$
. For $m\geq 0$![]() , it will be more convenient to consider an auxiliary norm
, it will be more convenient to consider an auxiliary norm

in $A(r)$![]() and recover the usual norm (2.1) as we make $m\to \infty$
and recover the usual norm (2.1) as we make $m\to \infty$![]() . Moreover, we observe that $\Vert {u}\Vert _{{\sigma },2,m}\leq \Vert {u}\Vert _{{\sigma },{2}}$
. Moreover, we observe that $\Vert {u}\Vert _{{\sigma },2,m}\leq \Vert {u}\Vert _{{\sigma },{2}}$![]() .
.
For our initial value problem (5.1), we note that, given $m\geq 0$![]() , the function $F:H^{m+5}(\mathbb {R})\rightarrow H^{m+2}(\mathbb {R})$
, the function $F:H^{m+5}(\mathbb {R})\rightarrow H^{m+2}(\mathbb {R})$![]() is well-defined and continuous. Therefore, for $Z=H^{m+5}(\mathbb {R})$
is well-defined and continuous. Therefore, for $Z=H^{m+5}(\mathbb {R})$![]() and $X= H^{m+2}(\mathbb {R})$
and $X= H^{m+2}(\mathbb {R})$![]() the following result, which will be called Kato–Masuda Theorem, is valid, see theorem 1 in [Reference Kato and Masuda21] or theorem 4.1 in [Reference Barostichi, Himonas and Petronilho5] for more general formulations.
the following result, which will be called Kato–Masuda Theorem, is valid, see theorem 1 in [Reference Kato and Masuda21] or theorem 4.1 in [Reference Barostichi, Himonas and Petronilho5] for more general formulations.
Lemma 5.6 Kato–Masuda
Let $\{\Phi _{\sigma }:-\infty <\sigma <\bar {\sigma }\}$![]() be a family of real functions defined on an open set $O\subset Z$
be a family of real functions defined on an open set $O\subset Z$![]() for some $\bar {\sigma }\in \mathbb {R}$
for some $\bar {\sigma }\in \mathbb {R}$![]() . Suppose that $F: O \rightarrow X$
. Suppose that $F: O \rightarrow X$![]() is continuous, where $F$
is continuous, where $F$![]() is the function given by (5.1) and
is the function given by (5.1) and
(a) $D\Phi _{\cdot }(\cdot ):\mathbb {R}\times Z\rightarrow \mathcal {L}(\mathbb {R}\times X; \mathbb {R})$
 given by
\[ D\Phi_{\sigma}(v)F(v):=\langle F(v),\quad D \Phi_{\sigma}(v)\rangle \]is continuous, where $D$
given by
\[ D\Phi_{\sigma}(v)F(v):=\langle F(v),\quad D \Phi_{\sigma}(v)\rangle \]is continuous, where $D$
 denotes the Fréchet derivative;
denotes the Fréchet derivative;(b) there exists $\bar {r}>0$
 such that
\[ D\Phi_{\sigma}(v)F(v) \leq \beta(\Phi_{\sigma}(v)) + \alpha(\Phi_{\sigma}(v))\partial_{\sigma}\Phi_{\sigma}(v), \]for all $v\in O$
such that
\[ D\Phi_{\sigma}(v)F(v) \leq \beta(\Phi_{\sigma}(v)) + \alpha(\Phi_{\sigma}(v))\partial_{\sigma}\Phi_{\sigma}(v), \]for all $v\in O$
 and some nonnegative continuous real functions $\alpha (r)$
and some nonnegative continuous real functions $\alpha (r)$ and $\beta (r)$
and $\beta (r)$ well-defined for $-\infty < r<\bar {r}$
well-defined for $-\infty < r<\bar {r}$ .
.
For $T>0,$![]() let $u\in C([0,\,T];O)\cap C^{1}([0,\,T];X)$
let $u\in C([0,\,T];O)\cap C^{1}([0,\,T];X)$![]() be a solution of the initial value problem (5.1) such that there exists $b<\bar {\sigma }$
be a solution of the initial value problem (5.1) such that there exists $b<\bar {\sigma }$![]() with $\Phi _{b}(u_0)<\bar {r}$
with $\Phi _{b}(u_0)<\bar {r}$![]() . Finally, let $\rho (v)$
. Finally, let $\rho (v)$![]() be the unique solution of
be the unique solution of

Then for
where $T_1>0$![]() is the lifespan of $\rho,$
is the lifespan of $\rho,$![]() we have
we have
We observe the complexity of the Kato–Masuda Theorem and the amount of hypothesis required for the final result. It is important to mention as well that the procedure to prove our desired proposition 5.2 goes through Kato–Masuda Theorem and (5.2), see also proposition 4.1 of [Reference Barostichi, Himonas and Petronilho5].
However, one of the main issues is to establish the bound of item $(b)$![]() . Before doing so, we shall define convenient parameters and functions that will be used from now on.
. Before doing so, we shall define convenient parameters and functions that will be used from now on.
For $u\in H^{m+5}(\mathbb {R})$![]() and $m\geq 0$
and $m\geq 0$![]() , let
, let

Given $u_0\in G^{1,s}(\mathbb {R}),\, s>5/2,$![]() such that $m_0$
such that $m_0$![]() does not change sign, let $u\in C([0,\,\infty ),\,H^{\infty }(\mathbb {R}))$
does not change sign, let $u\in C([0,\,\infty ),\,H^{\infty }(\mathbb {R}))$![]() be the unique global solution of (5.1). From the embedding $G^{1,s}(\mathbb {R})\subset A(1),$
be the unique global solution of (5.1). From the embedding $G^{1,s}(\mathbb {R})\subset A(1),$![]() we have that $u_0\in A(1)$
we have that $u_0\in A(1)$![]() . Let $\sigma _0<0=: \bar {\sigma }$
. Let $\sigma _0<0=: \bar {\sigma }$![]() , which means that $e^{\sigma _0}<1$
, which means that $e^{\sigma _0}<1$![]() and, from the definition of $A(1)$
and, from the definition of $A(1)$![]() , we have $\Vert u\Vert _{\sigma _0,2}<\infty$
, we have $\Vert u\Vert _{\sigma _0,2}<\infty$![]() .
.
For the global solution $u$![]() , fix $T>0$
, fix $T>0$![]() and define $\mu = 1+\max \{\Vert {u}\Vert _{H^{2}}; t\in [0,\,T]\}$
and define $\mu = 1+\max \{\Vert {u}\Vert _{H^{2}}; t\in [0,\,T]\}$![]() and $O= \{v\in H^{m+5}(\mathbb {R}); \Vert v\Vert _{H^{2}}<\mu \}$
and $O= \{v\in H^{m+5}(\mathbb {R}); \Vert v\Vert _{H^{2}}<\mu \}$![]() . Observe that the family $\{\Psi _{\sigma,m}; -\infty < \sigma < \bar {\sigma }, m\geq 0\}$
. Observe that the family $\{\Psi _{\sigma,m}; -\infty < \sigma < \bar {\sigma }, m\geq 0\}$![]() is well-defined on $O$
is well-defined on $O$![]() and $F:O\rightarrow X$
and $F:O\rightarrow X$![]() is continuous. Moreover, for this same family item $(a)$
is continuous. Moreover, for this same family item $(a)$![]() is satisfied, see Kato and Masuda [Reference Kato and Masuda21], page 460. For item $(b)$
is satisfied, see Kato and Masuda [Reference Kato and Masuda21], page 460. For item $(b)$![]() , we will need the following result.
, we will need the following result.
Proposition 5.7 Given $u\in H^{m+5}(\mathbb {R}),\, m\geq 0,$![]() for $\sigma \in \mathbb {R}$
for $\sigma \in \mathbb {R}$![]() we have the bound
we have the bound
where $\bar {K}(p) = 224p$![]() and $\bar {\alpha }(p,\,q) = 832(1+p)q^{1/2}$
and $\bar {\alpha }(p,\,q) = 832(1+p)q^{1/2}$![]() .
.
Proof. Since $F(u) \!=\! \displaystyle {-\frac {1}{2}\partial _x[u^{2} \!+\! 3(1\!-\!\partial _x^{2})^{-1}u_x^{2}]}$![]() and $\displaystyle {\frac {1}{2}D\Vert {\partial _x^{j}u}\Vert _{H^{2}}^{2}w = \langle \partial _x^{j}w\,,\, \partial _x^{j} u\rangle _{H^{2}}},$
and $\displaystyle {\frac {1}{2}D\Vert {\partial _x^{j}u}\Vert _{H^{2}}^{2}w = \langle \partial _x^{j}w\,,\, \partial _x^{j} u\rangle _{H^{2}}},$![]() see [Reference Barostichi, Himonas and Petronilho4, Reference Kato and Masuda21], by making $w = F(u)$
see [Reference Barostichi, Himonas and Petronilho4, Reference Kato and Masuda21], by making $w = F(u)$![]() and summing over $j$
and summing over $j$![]() according to $\Phi _{\sigma,m}$
according to $\Phi _{\sigma,m}$![]() we have
we have

From the proof of lemma 4.1 in [Reference Barostichi, Himonas and Petronilho5] (equations (6.14) and (6.16) with $k=1$![]() ), we know that
), we know that

where $\bar {K_1}(p) = 32p$![]() and $\alpha _1(p,\,q) = 64(1+p)q^{1/2}$
and $\alpha _1(p,\,q) = 64(1+p)q^{1/2}$![]() , and
, and

where $\bar {K_2}(p) = 64p$![]() and $\alpha _1(p,\,q) = 256(1+p)q^{1/2}$
and $\alpha _1(p,\,q) = 256(1+p)q^{1/2}$![]() . Under substitution of the respective terms in the inequality for $D\Phi _{\sigma,m}(u)F(u)$
. Under substitution of the respective terms in the inequality for $D\Phi _{\sigma,m}(u)F(u)$![]() we obtain
we obtain
where $\bar {K}(p) = 224p$![]() and $\bar {\alpha }(p,\,q) = 832(1+p)q^{1/2}$
and $\bar {\alpha }(p,\,q) = 832(1+p)q^{1/2}$![]() .
.
Proof of proposition 5.2. To prove the proposition, we basically need to complete the details for item $(b)$![]() of the Kato–Masuda Theorem. Therefore, we need to find $\bar {r}>0$
of the Kato–Masuda Theorem. Therefore, we need to find $\bar {r}>0$![]() and continuous functions $\alpha (r)$
and continuous functions $\alpha (r)$![]() and $\beta (r)$
and $\beta (r)$![]() for $-\infty < r<\bar {r}$
for $-\infty < r<\bar {r}$![]() .
.
For $\bar {K}$![]() and $\bar {\alpha }$
and $\bar {\alpha }$![]() given in proposition 5.7, let
given in proposition 5.7, let

Observe that
(i) $\alpha (r)$
 and $\beta (r)$
and $\beta (r)$ are continuous for $r<\bar {r}$
are continuous for $r<\bar {r}$ ;
;(ii) $\rho _m(t)\leq \rho (t),$
 for $t\in [0,\,T]$
for $t\in [0,\,T]$ and $\rho _m(t)\to \rho (t)$
and $\rho _m(t)\to \rho (t)$ uniformly.
uniformly.(iii) $\bar {K}(p)= 224p$
 and $\bar {\alpha }(\bar {p},\,q) = 832(1+\bar {p})q^{1/2}$
and $\bar {\alpha }(\bar {p},\,q) = 832(1+\bar {p})q^{1/2}$ , for fixed $\bar {p}$
, for fixed $\bar {p}$ , are nondecreasing.
, are nondecreasing.
From the definition of $\mu$![]() , $\mu >\Vert u\Vert _{H^{2}}$
, $\mu >\Vert u\Vert _{H^{2}}$![]() and then from observation (iii) above, for all $v\in O$
and then from observation (iii) above, for all $v\in O$![]() , we have
, we have
The inequality of proposition 5.7 then yields
and item $(b)$![]() is finally satisfied.
is finally satisfied.
For the same $T>0$![]() , let $b:=\sigma _0<\bar {\sigma }$
, let $b:=\sigma _0<\bar {\sigma }$![]() and observe that $\rho _m(t)$
and observe that $\rho _m(t)$![]() is a solution for the Cauchy problem
is a solution for the Cauchy problem
Since
Kato–Masuda Theorem says that for
we have
for $t\in [0,\,T]$![]() . By letting $m\to \infty$
. By letting $m\to \infty$![]() , we obtain
, we obtain
and $u(t)\in A(r_1)$![]() for $r_1 = e^{\sigma (t)}\leq e^{\sigma (T)}$
for $r_1 = e^{\sigma (t)}\leq e^{\sigma (T)}$![]() for $t\in [0,\,T]$
for $t\in [0,\,T]$![]() . Once we have the expressions for $\alpha$
. Once we have the expressions for $\alpha$![]() and $\rho$
and $\rho$![]() , we can estimate the radius of spatial analyticity $\sigma (t)$
, we can estimate the radius of spatial analyticity $\sigma (t)$![]() . In fact, we have
. In fact, we have
where $A=\frac {26\sqrt {2}}{7\mu }(1+\mu )\Vert {u_0}\Vert _{{\sigma _0},{2}}$![]() and $B=112\mu$
and $B=112\mu$![]() . Observe that since $\mu \geq 1,$
. Observe that since $\mu \geq 1,$![]() we have $A\leq \frac {52\sqrt {2}}{7}\Vert {u_0}\Vert _{{\sigma _0},{2}}=:L_1$
we have $A\leq \frac {52\sqrt {2}}{7}\Vert {u_0}\Vert _{{\sigma _0},{2}}=:L_1$![]() . By letting $L_2:=B$
. By letting $L_2:=B$![]() , we have
, we have
where $L_3=r(0)e^{L_1}$![]() .
.
5.3 Proof of proposition 5.3
Given $u_0 \in G^{1,s}(\mathbb {R}),$![]() with $s>5/2$
with $s>5/2$![]() , let $u\in C([0,\,\infty );A(r_1))$
, let $u\in C([0,\,\infty );A(r_1))$![]() be the unique solution whose existence is guaranteed by proposition 5.2. For the same initial data, from corollary 3.6 there are $\tilde {T}>0$
be the unique solution whose existence is guaranteed by proposition 5.2. For the same initial data, from corollary 3.6 there are $\tilde {T}>0$![]() and a unique solution $\tilde {u}\in C^{\omega }([0,\,\tilde {T} (1-\delta );G^{\delta,s}(\mathbb {R}))$
and a unique solution $\tilde {u}\in C^{\omega }([0,\,\tilde {T} (1-\delta );G^{\delta,s}(\mathbb {R}))$![]() for $\delta \in (0,\,1)$
for $\delta \in (0,\,1)$![]() . Let $T = \frac {\tilde {T}}{2}(1-\delta )$
. Let $T = \frac {\tilde {T}}{2}(1-\delta )$![]() , that is, $\delta = \displaystyle {1-2\frac {T}{\tilde {T}} =: \delta (T)},$
, that is, $\delta = \displaystyle {1-2\frac {T}{\tilde {T}} =: \delta (T)},$![]() and $\tilde {u}\in C^{\omega }([0,\,T];G^{\delta,s}(\mathbb {R}))\subset C^{\omega }([0,\,T];A(\delta (T)))$
and $\tilde {u}\in C^{\omega }([0,\,T];G^{\delta,s}(\mathbb {R}))\subset C^{\omega }([0,\,T];A(\delta (T)))$![]() once $G^{\delta,s}(\mathbb {R}) \subset A(\delta )$
once $G^{\delta,s}(\mathbb {R}) \subset A(\delta )$![]() .
.
Since $A(r)\hookrightarrow H^{\infty }(\mathbb {R})$![]() for $r>0$
for $r>0$![]() , then $\tilde {u}\in C^{\omega }([0,\,T];H^{\infty }(\mathbb {R}))\subset C([0,\,T];H^{\infty }(\mathbb {R}))$
, then $\tilde {u}\in C^{\omega }([0,\,T];H^{\infty }(\mathbb {R}))\subset C([0,\,T];H^{\infty }(\mathbb {R}))$![]() . From the uniqueness of the solution, we know that $u=\tilde {u}$
. From the uniqueness of the solution, we know that $u=\tilde {u}$![]() for $t\in [0,\,T]$
for $t\in [0,\,T]$![]() , which means that $u\in C^{\omega }([0,\,T];A(\delta (T))),$
, which means that $u\in C^{\omega }([0,\,T];A(\delta (T))),$![]() for $T = \frac {\tilde {T}}{2}(1-\delta )$
for $T = \frac {\tilde {T}}{2}(1-\delta )$![]() and $\delta (T)>0$
and $\delta (T)>0$![]() .
.
5.4 Proof of proposition 5.4
We will make use of the following result from [Reference Barostichi, Himonas and Petronilho5] (lemma 5.1).
Lemma 5.8 Let $\delta >0$![]() and $m\geq 1$
and $m\geq 1$![]() . Then $E_{\delta,m}(\mathbb {R})$
. Then $E_{\delta,m}(\mathbb {R})$![]() is continuously embedded in $A(\delta )$
is continuously embedded in $A(\delta )$![]() . Conversely, if $f\in A(r)$
. Conversely, if $f\in A(r)$![]() for some $r>0$
for some $r>0$![]() then $f\in E_{\delta,m}(\mathbb {R})$
then $f\in E_{\delta,m}(\mathbb {R})$![]() for all $\delta < r/e$
for all $\delta < r/e$![]() .
.
Proof of proposition 5.4. We will prove the result by contradiction as we assume that $T^{\ast }<\infty$![]() . For the solution $u \in C^{\omega }([0,\,T];A(\delta (T)))\subset C([0,\,T];H^{\infty }(\mathbb {R}))$
. For the solution $u \in C^{\omega }([0,\,T];A(\delta (T)))\subset C([0,\,T];H^{\infty }(\mathbb {R}))$![]() , from the uniqueness of the global solution and the definition of $T^{\ast }$
, from the uniqueness of the global solution and the definition of $T^{\ast }$![]() it is immediate that if $T^{\ast }<\infty$
it is immediate that if $T^{\ast }<\infty$![]() , then $u(T^{\ast })$
, then $u(T^{\ast })$![]() is well-defined. Moreover, from proposition (5.2), we have $u(T^{\ast })\in A(r_1)$
is well-defined. Moreover, from proposition (5.2), we have $u(T^{\ast })\in A(r_1)$![]() .
.
Let $\delta _0<\min \{1,\, r_1/e\}$![]() and then the converse of lemma 5.8 tells that
and then the converse of lemma 5.8 tells that
for all $\delta _0>0.$![]() From proposition 1.3, there exist $\epsilon >0$
From proposition 1.3, there exist $\epsilon >0$![]() and a unique solution $\tilde {u}\in C^{\omega }([0,\,\epsilon ];E_{\delta,m}(\mathbb {R}))$
and a unique solution $\tilde {u}\in C^{\omega }([0,\,\epsilon ];E_{\delta,m}(\mathbb {R}))$![]() for $0<\delta <\delta _0$
for $0<\delta <\delta _0$![]() such that $\tilde {u}(0) = u(T^{\ast })$
such that $\tilde {u}(0) = u(T^{\ast })$![]() . On the other hand, since $E_{\delta,m}(\mathbb {R})\hookrightarrow A(\delta )\subset H^{\infty }(\mathbb {R}),$
. On the other hand, since $E_{\delta,m}(\mathbb {R})\hookrightarrow A(\delta )\subset H^{\infty }(\mathbb {R}),$![]() we have
we have
and the uniqueness of the global solution tells that $\tilde {u}(0) = u(T^{\ast })$![]() , which means that
, which means that
Let $s=T^{\ast }+t$![]() . Then $u(s) = \tilde {u}(s-T^{\ast }),$
. Then $u(s) = \tilde {u}(s-T^{\ast }),$![]() for $s\in [T^{\ast },\,T^{\ast }+\epsilon ],$
for $s\in [T^{\ast },\,T^{\ast }+\epsilon ],$![]() that is,
that is,
Based on the definition of $T^{\ast }$![]() , let $T>0$
, let $T>0$![]() be such that $T^{\ast }-\epsilon < T< T^{\ast }$
be such that $T^{\ast }-\epsilon < T< T^{\ast }$![]() and the solution $u$
and the solution $u$![]() then belongs to $C^{\omega }([0,\,T];A(\delta (T)))$
then belongs to $C^{\omega }([0,\,T];A(\delta (T)))$![]() for some $\delta (T)>0$
for some $\delta (T)>0$![]() .
.
Observe now that if $\sigma '\geq \sigma,$![]() then $A(\sigma ')\subset A(\sigma ).$
then $A(\sigma ')\subset A(\sigma ).$![]() By defining $\tilde {\delta } = \min \{\delta,\,\delta (T)\}$
By defining $\tilde {\delta } = \min \{\delta,\,\delta (T)\}$![]() , which means in particular that $\delta \geq \tilde {\delta }$
, which means in particular that $\delta \geq \tilde {\delta }$![]() and $\delta (T)\geq \tilde {\delta }$
and $\delta (T)\geq \tilde {\delta }$![]() , then
, then
which says that $T^{\ast }$![]() cannot be the supremum. As a result of the contradiction, $T^{\ast }$
cannot be the supremum. As a result of the contradiction, $T^{\ast }$![]() must be infinite and, for every $T>0$
must be infinite and, for every $T>0$![]() , there exists $r(T)>0$
, there exists $r(T)>0$![]() such that $u\in C^{\omega }([0,\,T];A(r(T)))$
such that $u\in C^{\omega }([0,\,T];A(r(T)))$![]() .
.
Acknowledgments
This work was supported by FAPESP (grant number 2019/23688-4) and the Royal Society under a Newton International Fellowship (reference number 201625). The author would also like to thank the reviewers for the suggestions that led to the improvement of this paper.