Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-05-05T10:45:01.633Z Has data issue: false hasContentIssue false
  • English
  • Français

A monotonicity result under symmetry and Morse index constraints in the plane

Part of: Partial differential equations

Published online by Cambridge University Press:  21 July 2020

Francesca Gladiali
Francesca Gladiali*
Affiliation:
Dipartimento di Chimica e Farmacia, Università di Sassari, via Piandanna 4, 07100Sassari, Italy (fgladiali@uniss.it)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper deals with solutions of semilinear elliptic equations of the type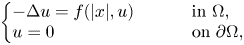

\[ \left\{\begin{array}{@{}ll} -\Delta u = f(|x|, u) \qquad & \text{ in } \Omega, \\ u= 0 & \text{ on } \partial \Omega, \end{array} \right. \]
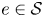where Ω is a radially symmetric domain of the plane that can be bounded or unbounded. We consider solutions u that are invariant by rotations of a certain angle θ and which have a bound on their Morse index in spaces of functions invariant by these rotations. We can prove that or u is radial, or, else, there exists a direction $e\in \mathcal {S}$ such that u is symmetric with respect to e and it is strictly monotone in the angular variable in a sector of angle θ/2. The result applies to least-energy and nodal least-energy solutions in spaces of functions invariant by rotations and produces multiplicity results.

Keywords

Semilinear elliptic equationssymmetry and monotonicity resultsbounded and unbounded domainslinearized equationfirst eigenvalue and first eigenfunctionMorse index

MSC classification

Primary: 35B06: Symmetries, invariants, etc.
Secondary: 35B07: Axially symmetric solutions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 3 , June 2021 , pp. 885 - 915
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aftalion, A. and Pacella, F.. Qualitative properties of nodal solutions of semilinear elliptic equations in radially symmetric domains. C. R. Acad. Sci. 339 (2004), 339–344.CrossRefGoogle Scholar
Amadori, A. L. and Gladiali, F.. The Hénon problem with large exponent in the disc. J. Differential Equations 268 (2020), no. 10, 5892–5944.CrossRefGoogle Scholar
Bartsch, T., Pistoia, A. and Weth, T.. N-Vortex equilibria for ideal fluids in bounded planar domains and new nodal solutions of the sinh-Poisson and the Lane–Emden–Fowler Equations. Commun. Math. Phys. 297 (2010), 653–686.CrossRefGoogle Scholar
Bartsch, T. and Weth, T.. A note on additional properties of sign changing solutions to superlinear elliptic equations. Topol. Methods Nonlinear Anal. 22 (2003), 1–14.CrossRefGoogle Scholar
Bartsch, T., Weth, T. and Willem, M.. Partial symmetry of least energy nodal solutions to some variational problems. J. Anal. Math. 96 (2005), 1–18.CrossRefGoogle Scholar
Brezis, H. and Nirenberg, L.. Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Commun. Pure Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
Chen, W. and Li, C.. Classification of solutions of some nonlinear elliptic equations. Duke Math. J. 63 (1991), 615–622.CrossRefGoogle Scholar
Coffman, C. V.. A nonlinear boundary value problem with many positive solutions. J. Differ. Equ. 54 (1984), 429–437.CrossRefGoogle Scholar
Damascelli, L. and Pacella, F.. Symmetry results for cooperative elliptic systems via linearization. SIAM J. Math. Anal. 45 (2013), 1003–1026.CrossRefGoogle Scholar
Damascelli, L., Gladiali, F. and Pacella, F.. A symmetry result for semilinear cooperative elliptic systems. Proc. Conf. Nonlinear Partial Differential Equations, AMS -Contemporary Mathematics Series, vol. 595 (2013), pp. 187–204.Google Scholar
Damascelli, L., Gladiali, F. and Pacella, F.. Symmetry results for semilinear cooperative elliptic systems in unbounded domains, Indiana Univ. Math. J. 63 (2014), 615–649.Google Scholar
D'Aprile, T.. Multiple blow-up solutions for the Liouville equation with singular data. Commun. Part. Differ. Equ. 38 (2013), 1409–1436.CrossRefGoogle Scholar
D'Aprile, T.. Sign-changing blow-up solutions for Hénon type elliptic equations with exponential nonlinearity. J. Funct. Anal. 268 (2015), 2067–2101.CrossRefGoogle Scholar
del Pino, M., Kowalczyk, M. and Musso, M.. Singular limits in Liouville-type equations. Calc. Var. Part Differ. Equ. 24 (2005), 47–81.CrossRefGoogle Scholar
Esposito, P., Grossi, M. and Pistoia, A.. On the existence of blowing-up solutions for a mean field equation. Ann. Inst. H. Poincaré Anal. Non Linéaire 22 (2005), 227–257.CrossRefGoogle Scholar
Esposito, P., Musso, M. and Pistoia, A.. Concentrating solutions for a planar elliptic problem involving nonlinearities with large exponent. J. Differ. Equ. 227 (2006), 29–68.CrossRefGoogle Scholar
Esposito, P., Musso, M. and Pistoia, A.. On the existence and profile of nodal solutions for a two-dimensional elliptic problem with large exponent in nonlinearity. Proc. London Math. Soc. 94 (2007), 497–519.CrossRefGoogle Scholar
Esposito, P., Pistoia, A. and Wei, J.. Concentrating solutions for the Hénon equation in R 2. J. d'Anal. Math. 100 (2006), 249–280.CrossRefGoogle Scholar
Gidas, B., Ni, W. M. and Nirenberg, L.. Symmetry and related properties via the maximum principle. Commun. Math. Phys. 68 (1979), 209–243.CrossRefGoogle Scholar
Gidas, B., Ni, W. M. and Nirenberg, L..Symmetry of positive solutions of nonlinear elliptic equations in ℝ N. Mathematical analysis and applications, Part A, vol. 7a. in: Adv. in Math. Suppl. Stud. (New York, London: Academic Press, 1981), pp. 369–402.Google Scholar
Gladiali, F.. A global bifurcation result for a semilinear elliptic equation. J. Math. Anal. Appl. 369 (2010), 306–311.CrossRefGoogle Scholar
Gladiali, F.. Separation of branches of O(N − 1)-invariant solutions for a semilinear elliptic equation. J. Math. Anal. Appl. 453 (2017), 159–173.CrossRefGoogle Scholar
Gladiali, F. and Grossi, M.. Singular limit of radial solutions in an annulus. Asymptot. Anal. 55 (2007), 73–83.Google Scholar
Gladiali, F., Grossi, S M.. Neves Symmetry breaking and Morse index of solutions of nonlinear elliptic problems in the plane. Commun. Contemp. Math. 18 (2016), 5CrossRefGoogle Scholar
Gladiali, F., Grossi, M., Pacella, F. and Srikanth, P. N.. Bifurcation and symmetry breaking for a class of semilinear elliptic equations in an annulus. Calc. Var. Part Differ. Equ. 40 (2011), 295–317.CrossRefGoogle Scholar
Gladiali, F. and Ianni, I.. Quasi-radial solutions for the Lane-Emden problem in the ball. NoDEA Nonlinear Differential Equations Appl. 27 (2020), no. 2, Art. 13, 61 pp.CrossRefGoogle Scholar
Gladiali, F., Pacella, F. and Weth, T.. Symmetry and nonexistence of low Morse index solutions in unbounded domains. J. Math. Pures Appl. 93 (2010), 536–558.CrossRefGoogle Scholar
Grossi, M., Grumiau, C. and Pacella, F.. Lane–Emden problems with large exponents and singular Liouville equations. J. Math. Pures Appl. 101 (2014), 735–754.CrossRefGoogle Scholar
Li, Y. Y.. Existence of many positive solutions of semilinear elliptic equations on annulus. J. Differ. Equ. 83 (1990), 348–367.CrossRefGoogle Scholar
Pacella, F.. Symmetry results for solutions of semilinear elliptic equations with convex nonlinearities. J. Funct. Anal. 192 (2002), 271–282.CrossRefGoogle Scholar
Pacella, F. and Weth, T.. Symmetry of solutions to semilinear elliptic equations via Morse index. Proc. Am. Math. Soc. 135 (2007), 1753–1762.CrossRefGoogle Scholar
Palais, R. S.. The Principle of Symmetric Criticality. Commun. Math. Phys. 69 (1979), 19–30.CrossRefGoogle Scholar
Prajapat, J. and Tarantello, G.. On a class of elliptic problems in ℝ2: symmetry and uniqueness results. Proc. Royal Soc. Edinburgh: A 131 (2001), 967–985.CrossRefGoogle Scholar
Smets, D. and Willem, M.. Partial symmetry and asymptotic behavior for some elliptic variational problems. Calc. Var. Part. Differ. Equ. 18 (2003), 57–75.CrossRefGoogle Scholar
Smets, D., Willem, M. and Su, J.. Non-radial ground states for the Hénon equation. Commun. Contemp. Math. 4 (2002), 467–480.CrossRefGoogle Scholar
Zhang, Y. B. and Yang, H. T.. Multi-peak nodal solutions for a two-dimensional elliptic problem with large exponent in weighted nonlinearity. Acta Math. Appl. Sin. 31 (2015), 261–276.CrossRefGoogle Scholar