We focus on the existence of ground state solutions to the following class of elliptic equations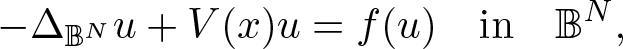

\begin{equation*}-\Delta_{\mathbb{B}^N} u+V(x)u=f(u) \quad \hbox{in} \quad \mathbb{B}^N,\end{equation*}

where 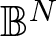$\mathbb{B}^N$ is the disc model of the Hyperbolic space and 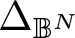$\Delta_{\mathbb{B}^N}$ denotes the Laplace–Beltrami operator with 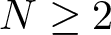$N \geq 2$, 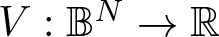$V:\mathbb{B}^N \to \mathbb{R}$ and 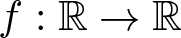$f:\mathbb{R} \to \mathbb{R}$ are continuous functions that satisfy some technical conditions. With different types of the potential V, by introducing some new tricks handling the hurdle that the Hyperbolic space is not a compact manifold, we are able to obtain at least a positive ground state solution using variational methods.

As some applications for the methods adopted above, we derive the existence of normalized solutions to the elliptic problems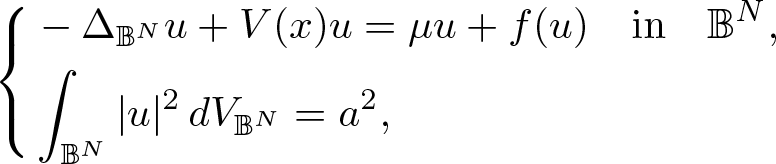

\begin{equation*}\left\{\begin{aligned}&-\Delta_{\mathbb{B}^N} u+V(x)u=\mu u+f(u) \quad \hbox{in} \quad \mathbb{B}^N,\\&\int_{\mathbb{B}^N}|u|^{2}\,dV_{{\mathbb{B}^N}}=a^{2},\end{aligned}\right.\end{equation*}

where a > 0, 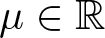$\mu\in \mathbb{R}$ is an unknown parameter that appears as a Lagrange multiplier and f is a continuous function that fulfils the L2-subcritical or L2-supercritical growth. We do believe that it seems the first results to deal with normalized solutions for the Schrödinger equations in the Hyperbolic space.