Article contents
Abstract
I present a reconstruction of the logical system of the Tractatus, which differs from classical logic in two ways. It includes an account of Wittgenstein’s “form-series” device, which suffices to express some effectively generated countably infinite disjunctions. And its attendant notion of structure is relativized to the fixed underlying universe of what is named.
There follow three results. First, the class of concepts definable in the system is closed under finitary induction. Second, if the universe of objects is countably infinite, then the property of being a tautology is 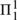 $\Pi _1^1$ -complete. But third, it is only granted the assumption of countability that the class of tautologies is
$\Pi _1^1$ -complete. But third, it is only granted the assumption of countability that the class of tautologies is 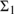 ${\Sigma _1}$ -definable in set theory.
${\Sigma _1}$ -definable in set theory.
Wittgenstein famously urges that logical relationships must show themselves in the structure of signs. He also urges that the size of the universe cannot be prejudged. The results of this paper indicate that there is no single way in which logical relationships could be held to make themselves manifest in signs, which does not prejudge the number of objects.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2017
References
BIBLIOGRAPHY
- 9
- Cited by

