There exist two notions of equivalence of behavior between states of a Labelled Markov Process (LMP): state bisimilarity and event bisimilarity. The first one can be considered as an appropriate generalization to continuous spaces of Larsen and Skou’s probabilistic bisimilarity, whereas the second one is characterized by a natural logic. C. Zhou expressed state bisimilarity as the greatest fixed point of an operator $\mathcal {O}$, and thus introduced an ordinal measure of the discrepancy between it and event bisimilarity. We call this ordinal the Zhou ordinal of 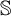$\mathbb {S}$, 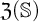$\mathfrak {Z}(\mathbb {S})$. When 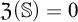$\mathfrak {Z}(\mathbb {S})=0$, 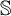$\mathbb {S}$ satisfies the Hennessy–Milner property. The second author proved the existence of an LMP 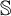$\mathbb {S}$ with 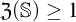$\mathfrak {Z}(\mathbb {S}) \geq 1$ and Zhou showed that there are LMPs having an infinite Zhou ordinal. In this paper we show that there are LMPs 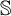$\mathbb {S}$ over separable metrizable spaces having arbitrary large countable 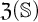$\mathfrak {Z}(\mathbb {S})$ and that it is consistent with the axioms of 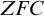$\mathit {ZFC}$ that there is such a process with an uncountable Zhou ordinal.