With the increasing availability of exome/genome sequencing data, rare variant (RV) association studies are gaining importance in human genetic research. One important test of association between a target set of RVs and a given phenotype is the sequence kernel-based association test (SKAT) (Chen et al., Reference Chen, Meigs and Dupuis2013; Ionita-Laza et al., Reference Ionita-Laza, Lee, Makarov, Buxbaum and Lin2013; Lee et al., Reference Lee, Wu and Lin2012; Lippert et al., Reference Lippert, Xiang, Horta, Widmer, Kadie, Heckerman and Listgarten2014; Listgarten et al., Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013; Svishcheva et al., Reference Svishcheva, Belonogova and Axenovich2014; Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011). SKAT is based on a random effects model, in which the effect sizes of the RVs are assumed to be drawn from a distribution with a zero mean and a variance. That the effect sizes are characterized by a single variance is a strong assumption that is made plausible by weighting of effect sizes. The required weights are typically assigned based on meta-information about the tested variants, such as allele frequency and functional predictions (Kryukov et al., Reference Kryukov, Pennacchio and Sunyaev2007; Madsen & Browning, Reference Madsen and Browning2009; Price et al., Reference Price, Kryukov, de Bakker, Purcell, Staples, Wei and Sunyaev2010; Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011), with rarer and functional variants expected to have larger effects. Allele frequency, in particular, is an important weighting factor, as the rarer the variant is, the stronger the average purifying selection coefficient (Pritchard, Reference Pritchard2001; Schork et al., Reference Schork, Murray, Frazer and Topol2009). Accordingly, the effect sizes for RVs will tend to be larger than for more common variants.
The relationship between effect size, frequency, and selection, however, rests on directional assumptions about the extent of selection on the phenotype in question and the demographic history of the population (Eyre-Walker & Keightley, Reference Eyre-Walker and Keightley2007; Price et al., Reference Price, Kryukov, de Bakker, Purcell, Staples, Wei and Sunyaev2010; Zuk et al., Reference Zuk, Schaffner, Samocha, Do, Hechter, Kathiresan, Lander and E.2014). Specifically, there are several conditions that have to hold for the frequency to be genuinely informative about the functional effect that a genetic variant has on a trait, namely: (a) the population under study has not experienced recent severe bottlenecks; (b) the selection on the trait of interest is direct; (c) strong (i.e., selection coefficient s ≥ 10-2.5); and (d) it acts uniformly across the associated genes. Yet, for the reasons detailed below, the circumstances in which these conditions are expected to hold are rather special. First, population genetics theory predicts that the frequency of deleterious variants will vary with the size of the effect the associated trait has on fitness. For instance, risk variants implicated in early-onset diseases (e.g., autism) will be mostly rare, that is, kept at low frequencies by selection pressures because of the high impact these diseases have on reproductive fitness (Manolio et al., Reference Manolio, Collins, Cox, Goldstein, Hindorff, Hunter and Visscher2009). In contrast, variants associated with a trait having a negligible effect on fitness (e.g., Alzheimer's disease) will likely escape selection and so may occur at relatively high frequencies in the population (Zuk et al., Reference Zuk, Schaffner, Samocha, Do, Hechter, Kathiresan, Lander and E.2014). Second, it should be noted that even if the trait of interest is under strong selection pressure, variants across the whole frequency spectrum may jointly contribute to disease risk, as simulation studies (Price et al., Reference Price, Kryukov, de Bakker, Purcell, Staples, Wei and Sunyaev2010) and empirical results (e.g., Cohen et al., Reference Cohen, Boerwinkle, Mosley and Hobbs2006; Teslovich et al., Reference Teslovich, Musunuru, Smith, Edmondson, Stylianou, Koseki and Willer2010) have demonstrated. Third, allele frequency distribution is expected to vary as a function of the demographic history of the population. Using population genetics simulations, Zuk et al. (Reference Zuk, Schaffner, Samocha, Do, Hechter, Kathiresan, Lander and E.2014) showed that given the same selection coefficient s, the frequency of deleterious alleles influencing a trait will depend on mutation rate and on whether the population under study has encountered recent severe bottlenecks. For example, given strong selection pressures (i.e., s > 10-2.5) acting directly on the phenotype, the median frequency of the associated alleles may vary from as high as 0.0377 in recently bottlenecked populations (e.g., Finland), to as low as 9.36E-005 in a large population with simple exponential expansion. Finally, the strength of selection is expected to vary across genes, and so will the allele frequency–functional effect relationship (Price et al., Reference Price, Kryukov, de Bakker, Purcell, Staples, Wei and Sunyaev2010; Zuk et al., Reference Zuk, Schaffner, Samocha, Do, Hechter, Kathiresan, Lander and E.2014). Genes under weak selection will harbor both common and RVs, both with functional effects, whereas functional variants within genes under strong selective constraints will mainly be rare. The examples above indicate that testing genomic regions by relying on a weighting scheme which up-weights rarer variants and puts low or zero weights on the more common ones is optimal only in specific circumstances.
Because the true weights are generally unknown and, therefore, subject to misspecification, we examined the efficiency of a data-driven weighting scheme. We propose the use of a set of theoretically defensible weighting schemes of which, we assume, the one that gives the largest test statistic is likely to capture best the allele frequency–functional effect relationship. The set of alternative weighting schemes will accommodate genomic regions where only very RVs are likely to be functional, as well as regions under weak selection pressures, harboring both rare and common variants, both (possibly) related to the risk of the disease of interest. As such, this adaptive weighting procedure renders the (arbitrary) MAF thresholding unnecessary. Family-wise error rate can be protected by using a multiple testing correction method (e.g., the Bonferroni method) or by using permutation. Using simulations, we demonstrate that the use of alternative (incorrect) weights does not inflate the type I error rate. We show the power benefits conferred by the use of such a data-driven weighting procedure in both simulated and empirical data. As both the score test (Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011) and the likelihood ratio test (LRT) (Listgarten et al., Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013) may be used in this context, and may differ in power (Zeng et al., Reference Zeng, Zhao, Liu, Liu, Zhang, Wang and Chen2014), we characterize the behavior of both tests.
Below, we first formulate the model and briefly describe the LRT and the score test. We then present and evaluate the use of a data-driven weighting scheme in simulated and empirical data. Specifically, we evaluate the efficiency of the two tests under (a) the data-driven weighting scheme, relative to their efficiency under (b) incorrect, and (c) correct weighting. Finally, we discuss the robustness of the two tests to misspecification, and the power advantages conferred by our proposed weighting procedure in SKAT.
Methods
Model Formulation
Let y be the n-dimensional vector of continuous phenotypic scores obtained in a sample of n individuals. Let X be the n×p design matrix containing covariates. Let G be the n×m matrix of genotype values, with the gij element denoting the genotype value of the individual i (i = 1. . .n) at locus j (j = 1. . .m). Genotypes are coded as additive-codominant, that is, gij = (0,1,2). The association between the phenotype and the set of m variants is modeled within the linear mixed model framework as follows:
with β t = (β1, . . ., β p ) being the p-dimensional vector of fixed effects of covariates, bt = (b 1, . . ., bm ) being the m×1 vector of regression coefficients in the regression of the phenotype on the m genetic variants within the target set, and e being the n-dimensional vector of random residuals. The random vectors b and e are assumed to be normally distributed: b ~ N(0, Iσ2 b ) and e ~ N(0, Iσ2 e ), with I being the identity matrix of appropriate dimension.
Let W be the m×m diagonal matrix containing the weights used to weigh the contribution to the test statistic of the variants in the set. The normally distributed phenotype y has expected mean E[y] = Xβ and variance–covariance matrix:
with GWGt being the weighted kernel or genetic relationship matrix. As implemented in the SKAT (Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011), the diagonal elements of the W matrix, diag(w 1. . .wm ) are related to the minor allele frequency of the j th variant by means of the beta density distribution function (dbeta), which is characterized by two shape parameters. The specification of the two shape parameters is informed by the hypothesized relationship between the j th variant effect and its minor allele frequency (MAF; see the section on Weighting below).
Tests of Variance Components
To test whether the parameter of interest σ2 b deviates significantly from zero, one can employ a LRT or a score test. The LRT is computed as two times the difference between the log-likelihoods of the null model (σ2 b constrained to equal 0) and the alternative model (σ2 b estimated freely). Parameter estimation can be performed by restricted/residual maximum likelihood:
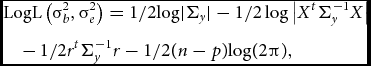 $$\begin{eqnarray}
&&{\rm{LogL}}\left(\sigma_b^2, \sigma_e^2\right) = {\rm{ 1/2log}}| {{\Sigma_y}} | - 1/2\log \big| {{X^t}\Sigma_y^{ - 1}X} \big|\nonumber\\
&&\quad -\, 1/2{r^t}\Sigma_y^{ - 1} {r - 1} /2(n - p){\rm{log(2}}\pi {\rm{),}}
\end{eqnarray}$$
$$\begin{eqnarray}
&&{\rm{LogL}}\left(\sigma_b^2, \sigma_e^2\right) = {\rm{ 1/2log}}| {{\Sigma_y}} | - 1/2\log \big| {{X^t}\Sigma_y^{ - 1}X} \big|\nonumber\\
&&\quad -\, 1/2{r^t}\Sigma_y^{ - 1} {r - 1} /2(n - p){\rm{log(2}}\pi {\rm{),}}
\end{eqnarray}$$
where
![]() $r = y - X{({X^t}\sum\nolimits_y^{ - 1} X )^ - }{X^t}\sum\nolimits_y^{ - 1} y $
with superscript ‘−’ denoting a generalized inverse (Basilevsky, Reference Basilevsky1983).
$r = y - X{({X^t}\sum\nolimits_y^{ - 1} X )^ - }{X^t}\sum\nolimits_y^{ - 1} y $
with superscript ‘−’ denoting a generalized inverse (Basilevsky, Reference Basilevsky1983).
In evaluating the statistical significance of the restricted LRT, we note the null distribution of the test statistic is a πχ2 0: (1 − π)aχ d 2 mixture of distributions, with the mixture parameter π, the scale parameter a, and the degrees of freedom d on the second component estimated using the computationally efficient permutation-based approach developed by Listgarten et al. (Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013).
The score test is computed as follows:
With its expected null distribution following a mixture of chi-square distribution and statistical significance assessed by means of the Davies exact method (Davies, Reference Davies1980).
Data Simulation
Phenotypes and genotypes in Hardy–Weinberg equilibrium were generated in samples of n = 10,000 unrelated individuals. Specifically, we simulated two m-dimensional random vectors of continuous variables representing alleles at m equidistant loci for each individual i from the sample. The vectors were drawn from a multivariate distribution with zero mean and Σ LD correlation matrix. We set Σ LD to equal an identity matrix, as we considered sets of RVs expected to be in linkage equilibrium (see e.g., Daye et al., Reference Daye, Li and Wei2012); but see the Supplementary material for results based on rare, and rare and common variants in linkage disequilibrium simulated using a coalescent model (Shlyakhter et al., Reference Shlyakhter, Sabeti and Schaffner2014). The multivariate normally distributed variables were then discretized given chosen thresholds based on the MAF at each locus. We considered, MAFs varying randomly between 0.005 and 0.05, sampled from a uniform distribution. Given the vectors of alleles, we then created the m vectors of genotypes, gij . Based on the genotypes, the n×1 vector of phenotypes, y, was generated as follows:
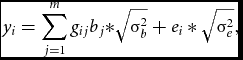 $$\begin{equation}
{y_i} = \sum\limits_{j = 1}^m {{g_{ij}}{b_j}*} \sqrt {{\rm{\sigma }}_b^2} + {e_i}*\sqrt {{\rm{\sigma }}_e^2} ,
\end{equation}$$
$$\begin{equation}
{y_i} = \sum\limits_{j = 1}^m {{g_{ij}}{b_j}*} \sqrt {{\rm{\sigma }}_b^2} + {e_i}*\sqrt {{\rm{\sigma }}_e^2} ,
\end{equation}$$
bj , the regression weight of the variant at the j th locus was computed as a function of MAFj and of its contribution to the standardized variance of the polygenic scores (Mather & Jinks, Reference Mather and Jinks1977). Namely, the regression weights varied with MAF, while their contribution to the genetic variance was equal. Simulating data in this fashion is equivalent to simulation according to dbeta (MAF, 0.5, 0.5) weights (Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011), with weights increasing with decreasing MAF. The variance σ2 b equaled 0.01 across all scenarios we considered, and σ2 e = 1 − σ b 2. The n-dimensional vector of environmental scores e was drawn from a standard normal distribution N(0, 1).
Data-Driven Search for Optimal Weights: Exploring the Misspecification Space
Because the strength and effectiveness of selection pressures vary across the genome, committing to a single weighting scheme when testing thousands of genes may only capture signal from genes under selection pressures matching the chosen weighting scheme. An optimal weighting scheme should be allowed to vary across the tested genes, to match variable selection pressures. To this end, we evaluated the efficiency of a data-driven search for optimal weights. We carried out simulations to evaluate the efficiency of the LRT and the score test under (a) the variable data-driven weighting scheme, relative to their efficiency under (b) incorrect, and (c) correct weighting.
The m-dimensional vector of weights w was computed using the beta density function, with the j th element calculated as wj = dbeta(MAF j ; a 1, a 2) given the MAF of the j th variant and the shape parameters a 1 and a 2. As described in the previous section, data were simulated according to dbeta (0.5, 0.5) weights (i.e., the true weights increase with decreasing MAF). Next, in computing the tests statistic we (mis)specified the weights as: (a) dbeta (1,1); (b) dbeta (0.5, 0.5); (c) dbeta (1,25), and (d) dbeta(1,50). The first weighting scheme pertains to the hypothesis that there is no relationship between the regression weight and the frequency of the variant (hence, the more common variants contribute on average more to variation in the phenotype). In this scenario, the association test is carried out with raw additive-codominant coding of the genotypes. The use of the second weighting scheme is equivalent to standardization of the genotypic values prior to the analysis. We considered the effect of this weighting scheme as this treatment of the genotypes is default in GCTA (Yang et al., Reference Yang, Lee, Goddard and Visscher2011) and in FaST-LMM-set (Listgarten et al., Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013). Standardization and assignment of weights dbeta (0.5, 0.5) are equivalent weighting schemes (Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011), in which the contribution to the test of rarer variants is up-weighed relative to that of the more common ones (Speed et al., Reference Speed, Hemani, Johnson and Balding2012), and hence the variants contribute on average equally to the variance in the phenotype (regardless of frequency). We also considered the effects of the third weighting scheme dbeta (1,25), as these are the default weights in SKAT (Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011). Finally, we considered the effect of a more extreme weighting scheme, dbeta (1,50), including weights that overlook common variants and favor the contribution to the test statistic of rarer ones. This weighting scheme pertains to the hypothesis that only ultra-RVs contribute to the phenotypic variance.
We performed association tests by using the set of three incorrect weighting schemes, that is, (a) dbeta (1,1), (b) dbeta (1,25), and (c) dbeta (1,50). The p value for the gene equaled the minimum Bonferroni corrected p value minPLRT (minPscore) out of the three p values obtained, given the genotypes transformed according to each of the weighting schemes enumerated above. We also report the power of the tests under each of these misspecified weighting schemes, as it is of interest to assess whether our procedure confers power gains relative to a test that uses a single (misspecified) weighting scheme (i.e., three tests vs. one test). We assessed the behavior of the two tests under the above weighting schemes by considering target regions harboring both deleterious and beneficial variants.
Evaluating the Type I Error Rates and Power
We evaluated the type I error rate by generating 1,000 datasets under the null hypothesis of no phenotypic variance explained by the variants within the target set. The type I error rate was computed as the proportion of datasets in which the tests incorrectly rejected the null hypothesis and it was evaluated given α = 0.01. We refer to Listgarten et al. (Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013) for an exhaustive evaluation of the type I error at more stringent alpha levels.
Power was assessed based on 1,000 simulated datasets, an effect size of 1% explained phenotypic variance and 7 alpha thresholds. Given the 7 alpha thresholds, power was computed using the permutation-based procedure implemented in FaST-LMM-Set (Listgarten et al., Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013). Estimation of the free parameters π, a, and d of the null distribution πχ2 0: (1 − π)aχ d 2 used 1,000 permutations. As a validity check of our simulation program, we also report the power and the type I error rates of the true (i.e., correct) model.
Software
The R-package MASS (Venables & Ripley, Reference Venables and Ripley2002) was used for data generation. Model fitting was performed in FaST-LMM-set (Listgarten et al., Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013). The software is readily available for use on Github. For the sake of comparison, we analyzed one simulated sample of 5,000 individuals by using four independent programs implementing genetic similarity/kernel-based variance component tests: the nlme R-package, the software Genome-wide Complex Trait Analysis (GCTA; Yang et al., Reference Yang, Lee, Goddard and Visscher2011), the software FaST-LMM-set (Listgarten et al., Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013), and the R-package OpenMx (Neale et al., Reference Neale, Hunter, Pritikin, Zahery, Brick, Kirkpatrick and Boker2016). The values for the LRT and the estimates for the variance component obtained by the four programs were almost identical (see Table S1 for details), indicating that these implement equivalent approaches. Having established the equivalence, the empirical analyses were conducted using the software FaST-LMM-set. Analyses were carried out on the Broad Institute Gold Compute cluster and on the Lisa cluster (https://www.surf.nl/en).
Empirical Analysis: Evaluating the Importance of Thresholding and Variable Weighting
We compared the performance of the LRT and of the score test under our proposed data-driven weighting scheme in a real dataset. For this illustration, we used the Swedish schizophrenia case-control cohort of 11,040 individuals with exome-sequencing data from blood DNA. Cases had a clinical diagnosis of schizophrenia and at least two hospitalizations as determined by expert review based on the Hospital Discharge Register (Dalman et al., Reference Dalman, Broms, Cullberg and Allebeck2002; Kristjansson et al., Reference Kristjansson, Allebeck and Wistedt1987). Controls, without a diagnosis of schizophrenia or bipolar disorder, were randomly selected from population registries. Both cases and controls are of Scandinavian ancestry, aged 18 or older (see Purcell et al. (Reference Purcell, Moran, Fromer, Ruderfer, Solovieff, Roussos and Kähler2014), and Ripke et al. (Reference Ripke, O'Dushlaine, Chambert, Moran, Kähler, Akterin and Fromer2013), for a detailed description of the sample). There were 175 individuals with unreliable samples (i.e., duplicates, ethnic outliers, or having a genotype missing rate higher than 10%) whom we removed from the analysis. This left for the analysis 4,867 cases and 6,173 controls; 6052 of these were males. Written informed consent was obtained from all participants (or legal guardian consent and subject assent). All procedures were approved by the ethical committees in Sweden and in the United States. Data are available through dbGAP.
Exome-sequencing was performed in 12 waves at the Broad Institute of MIT and Harvard. For samples in the first wave, hybrid capture was performed using the Agilent SureSelect Human All Exon Kit method. In this version, the method targets ~28 million base-pairs partitioned in ~160,000 regions. Sequencing was done using Illumina GAII instruments. For samples in the waves 2– 12, hybrid capture was done by using the newer version of the Agilent SureSelect Human All Exon v.2 Kit method, which targets ~32 million base-pairs partitioned in ~190,000 regions. Sequencing was performed using the Illumina HiSeq 2000 and HiSeq 2500 instruments. We used BWA ALN version 0.5.9 (Li & Durbin, Reference Li and Durbin2009) to align the reads to the GRCh37 human genome reference, and we applied Picard/GATK to process the sequence data and to call variants (http://broadinstitute.github.io/picard/; McKenna et al., Reference McKenna, Hanna, Banks, Sivachenko, Cibulskis, Kernytsky and Daly2010). Selected singletons were validated using Sanger sequencing (see Purcell et al. (Reference Purcell, Moran, Fromer, Ruderfer, Solovieff, Roussos and Kähler2014), for details). Variants out of Hardy–Weinberg equilibrium (p value < 5E-8) and showing excess heterozygosity, or variants showing excessive correlation (p value < 5E-8) with the covariates that could not be explained by principal components were excluded from the analysis. In addition, we excluded variants that did not pass the GATK default filters (DePristo et al., Reference DePristo, Banks, Poplin, Garimella, Maguire, Hartl and Hanna2011; Van der Auwera et al., Reference Van der Auwera, Carneiro, Hartl, Poplin, del Angel, Levy‐Moonshine and Thibault2013). There were 1,584,195 variants meeting all our quality control criteria.
For this empirical illustration, we focused on two partially overlapping sets of genes (1,435 genes) likely relevant to schizophrenia. The first set consisted of 941 genes that are part of the list identified by Samocha et al. (Reference Samocha, Robinson, Sanders, Stevens, Sabo, McGrath and Kirby2014) as highly constrained. These constrained genes were proposed as candidates in autism spectrum disorder (ASD) given their enrichment for de novo loss of function case mutations. Given evidence favoring the hypothesis that schizophrenia and ASD share genetic etiology (Fromer et al., Reference Fromer, Pocklington, Kavanagh, Williams, Dwyer, Gormley and Ruderfer2014; Schizophrenia Working Group of the Psychiatric Genomics Consortium, 2014), this set of genes is likely to be relevant also to schizophrenia. The second set consisted of 768 genes targeted by the fragile-X mental retardation protein (FMRP). This set is part of the list of genes derived by Darnell et al. (Reference Darnell, Van Driesche, Zhang, Hung, Mele, Fraser and Chi2011) from mouse brain as likely implicated in regulating synaptic plasticity. Genes targeted by FMRP were found to be enriched for de novo non-synonymous case mutations in both ASD (Iossifov et al., Reference Iossifov, Ronemus, Levy, Wang, Hakker, Rosenbaum and Leotta2012) and schizophrenia (Fromer et al., Reference Fromer, Pocklington, Kavanagh, Williams, Dwyer, Gormley and Ruderfer2014). Purcell et al. (Reference Purcell, Moran, Fromer, Ruderfer, Solovieff, Roussos and Kähler2014) also tested the FMRP set for enrichment of RVs in half of the current sample, and their analysis yielded nominally significant results.
We performed sequence-based kernel association analyses using the LRT and score tests with variable weights. The analyses were carried out using the FaST-LMM-Set software (Listgarten et al., Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013). To adjust for ancestry, we included into analysis the first two principal components explaining the largest amount of variance in the sample and reflecting the Finish and Northern/Southern Swedish ancestry (see Extended Data Figure 1 in Purcell et al. (Reference Purcell, Moran, Fromer, Ruderfer, Solovieff, Roussos and Kähler2014); see also Genovese et al. (Reference Genovese, Fromer, Stahl, Ruderfer, Chambert, Landén and Sullivan2016)). Principal components were computed from genotypes at variants shared with the 1,000 Genomes Project phase 1 dataset. To accommodate the scenario in which only RVs are likely to be functional, as well as the scenario in which the targeted region is under weak selection pressures, harboring both rare and more common variants, both (possibly) related to the risk of disease (regardless of frequency), we used three alternative weighting schemes: dbeta (1,25), dbeta (0.5, 0.5), and dbeta (1,1). The use of alternative weights obviates the need for choosing arbitrary frequency thresholds to select the target set. However, for the sake of illustration, we also report the results obtained in the analyses stratified based on allele counts thresholds (i.e., we selected variants with a minor allele count (MAC) up to 10 and a MAC up to 50). For each of the tested genes, we selected the Bonferroni corrected p value corresponding to the weighting scheme that yields the largest test statistic (i.e., the p value was adjusted for multiple hypothesis testing of 1,435 genes and three weighting schemes). An alpha of 0.05 was used as the significance threshold. For computational ease, we used a linear model (Listgarten et al., Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013). The linear LRT (and the linear score test) shows good control of the type I error rate and has performed as well as a generalized linear model in case-control samples (see Lippert et al., Reference Lippert, Xiang, Horta, Widmer, Kadie, Heckerman and Listgarten2014).

FIGURE 1 The power of the likelihood ratio test (LRT) and the score test to detect a gene harboring 50 functional variants, jointly explaining 1% of the phenotypic variance (minor allele frequency 0.5–5%). Data were simulated according to weights dbeta (0.5, 0.5). Power was evaluated in 1,000 datasets consisting of 10,000 individuals each.
Results
Type I Error
Table 1 contains the results pertaining to the type I error rates of the two tests, given correct and incorrect model specification.
TABLE 1 The Empirical 95% Confidence Intervals around the Type I Error for the Restricted Likelihood Ratio Test (LRT) and the Score Test, given data simulated under the null model of no association between the target region and the phenotype

Type I error was evaluated at alpha = 0.01. The tests were computed for five weighting schemes in each of the 1,000 simulated samples of 10,000 individuals with genotypes at 50 variants in linkage equilibrium (minor allele frequency 0.5–5%).
Both the restricted LRT and the score test yield correct type I error rates, regardless of whether the weights used are correctly specified or misspecified. The two tests show good control of the type I error rate also under our proposed Bonferroni data-driven weighting procedure. Note that these conclusions generalize to scenarios in which the target set includes common and RVs in linkage equilibrium/disequilibrium (see Table S2).
Power
Figure 1 displays the results relating to power to detect a target set of 50 functional variants (but see Figure S1 for simulation results involving a region harboring a mixture of functional and phenotypically neutral variants).
Four important conclusions follow from our simulation results. First, the restricted LRT and the score test have equal power when the weights are correctly specified. This is expected, as the two tests are asymptotically equivalent when the model is true, that is, correctly specified (e.g., Greene, Reference Greene2003). The powers of the two tests are similar when the assigned weights correspond to the true weights, that is, dbeta (0.5, 0.5).
Second, misspecification of weights always reduces power. This is shown in Figure 1 as the departure of the power under model misspecification from the power of the true model, that is, dbeta (0.5, 0.5). The exact loss in power depends on the degree of weight misspecification and on the statistical test employed. We note that the power loss is relatively small given mild misspecification of weights; for example, when the assigned weights dbeta (1,25) resemble the true weights dbeta (0.5, 0.5), as illustrated in Figure 1. However, the power may suffer dramatically with increasing misspecification. For instance, using a dbeta (1,50) weighting scheme — which acts as a frequency threshold, removing from the test the more common variants — results in a loss in power of up to ~10% and ~34% (given an alpha of 10-7), for the restricted LRT and for the score test, respectively.
Third, relative to the score test, we note that the restricted LRT is consistently more robust to weight misspecification. These results are consistent with those reported by Zeng et al. (Reference Zeng, Zhao, Liu, Liu, Zhang, Wang and Chen2014) and by Lippert et al. (Reference Lippert, Xiang, Horta, Widmer, Kadie, Heckerman and Listgarten2014), who found the LRT to be generally more powerful than the score test across their simulated settings. Although Lippert et al. did not consider the behavior of the two tests under misspecified weights, they reported the same pattern of results in real data analysis, where the LRT yielded consistently more associations than the score test. As the real weights are in all likelihood not known, the superior power of the restricted LRT in real data might be explained as well by its robustness to weight misspecification and to the inclusion of weighed neutral variation in the computation of the test statistic.
Fourth, we note that both tests benefit from the use of variable weights. The data-driven search for optimal weights confers power advantages over a model that uses misspecified weights, and maintains the power close to that afforded by a correctly specified model. It should be noted, however, that there is a price to pay in terms of power by using this data-driven weighting scheme in contrast to correct weighting (i.e., using alternative weights increases the burden of multiple testing). The two tests have equal powers with the Bonferroni corrected data-driven weighting procedure; this is due to the fact that the weights resembling the correct ones were included in the procedure (the more weights one tries, the largest the price in terms of power one has to pay). Had the procedure included weights misspecified to a greater extent, the power of the score test would have decreased relative to that of the LRT (which appears to be more robust to misspecification). As the true weights are typically unknown, conjecturing the correct ones by employing the proposed Bonferroni scheme with alternative weights and using the LRT appears to be the strategy most likely to maintain the power close to that of the true model.
Empirical Analysis: Evaluating the Importance of Thresholding and Variable Weighting
We next looked at the behavior of the score test and of the LRT (Listgarten et al., Reference Listgarten, Lippert, Kang, Xiang, Kadie and Heckerman2013) under variable weights in the empirical dataset. Tables 2 and 3 display results pertaining to the association tests in the analyses stratified based on arbitrary MAC thresholds.
TABLE 2 Results of the gene based analysis run in the Swedish sample (N = 11,040)
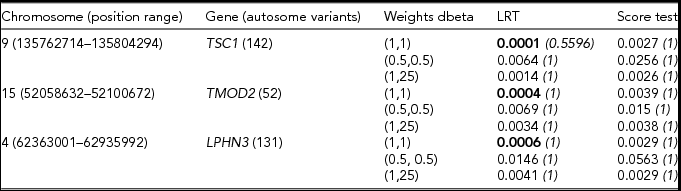
The gene-based analysis was restricted to variants with minor allele count below 10. Bonferroni corrected p values are given in italics. For each gene, the lowest p value is given in bold type.
TABLE 3 Results of the gene-based analysis run in the Swedish sample (N = 11,040)

The gene-based analysis was restricted to variants with minor allele count below 50. Bonferroni corrected p values are given in italics. For each gene, the lowest p value is given in bold type.
From Table 2, we note that the LRT appears to be more powerful than the score test. The two tests seem to agree in selecting the top association signals, as both ranked in the top three the same genes. All three weighting schemes tend to pick up nominally significant association signals. Of these, the dbeta (1,1) weighting scheme yields the lowest p value for all three genes. Similar trends in the results were observed when we restricted the analyses to variants with a MAC below 50 (see Table 3).
The use of alternative weights obviates the need of thresholding to prioritize the contribution of the variants to the test statistic (the thresholds are, however, arbitrary: variants defined as rare in one sample might feature as common in another sample). We conducted the analysis using our proposed data-driven weighting scheme, without imposing any frequency threshold. Table 4 contains the results.
TABLE 4 Results of the gene-based analysis run in the Swedish schizophrenia case-control sample (N = 11,040)

The gene-based analysis was conducted by relying on the data-driven weighting procedure, without imposing a-priori a frequency threshold. Bonferroni corrected p values are given in italics. For each gene, the lowest p value is given in bold type.
For the top three genes, Table 4 shows that the dbeta (1,1) weighting scheme appears to best capture the allele frequency–functional effect relationship. This weighting scheme yields the largest test statistic and singles out the PRRC2A and the VARS2 as significantly associated with schizophrenia disease status given our chosen alpha threshold (i.e., p value = 1.020e-06 and p value = 2.383e-06, respectively). The third top gene is the AKT3 gene (p value = 2.825e-05). All three genes belong to the Samocha et al. (Reference Samocha, Robinson, Sanders, Stevens, Sabo, McGrath and Kirby2014) list of genes under selection constraints. Had one relied on a weighting scheme that up-weights rarer variants and down-weights the more common ones, these association signals would have been missed. As these genes did not pass the significance threshold in the analyses stratified by MAC, the results suggest that arbitrary thresholding might remove from the target causal variants and in doing so might weaken the association signal. We observed similar trends in power when we simulated sets of common and rare functional variants, where — similar to a frequency threshold — the dbeta (1,25) weighting scheme discarded from the target set causal variants (see Figure S2).
Importantly, association signals in all three genes have been previously reported (e.g., Ripke et al., Reference Ripke, O'Dushlaine, Chambert, Moran, Kähler, Akterin and Fromer2013) and replicated (e.g., Aberg et al., Reference Aberg, Liu, Bukszár, McClay, Khachane, Andreassen and Gurling2013), suggesting that these results are unlikely to be false positives. Without thresholding, common variants might also be included in the analysis. In our sample, of the 43 (AKT3), 238 (PRRC2A), and 408 (VARS2) tested variants, 1, 29, and 15 variants, respectively, had a MAC greater than 50. The question remains whether the test was dominated by these common variants. We checked in our sample whether the common variants, if tested with a univariate test, do yield genome-wide significant association signals. Results showed that none of them would be detected in an ordinary genome-wide association study (GWAS) (see Tables S3–S5). Hence, either thresholding or relying on a default weighting scheme would result in missing true association signals. We elaborate on these results in the Discussion.
Discussion
We considered the issue of optimizing weighting in association studies based on the sequence kernel test. Consistent with empirical (Lippert et al., Reference Lippert, Xiang, Horta, Widmer, Kadie, Heckerman and Listgarten2014) and simulation (Zeng et al., Reference Zeng, Zhao, Liu, Liu, Zhang, Wang and Chen2014) results, we found that the LRT is generally more robust to weight misspecification, and more powerful than the score test in such a circumstance. The principal finding of this study is that using a weighting scheme that includes alternative weights is likely to boost statistical power. Our results are of interest because weight assignment is embedded within any set-based test and the true weights of the variants within the target are generally unknown.
In the literature, weighting is mostly informed by allele frequency; frequency is taken as indicative of the strength of the purifying selection coefficient (Kryukov et al., Reference Kryukov, Pennacchio and Sunyaev2007). Accordingly, rarer variants are typically being assigned larger weights/contribution to the test statistic (e.g., Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011). This relationship between effect size, frequency, and selection is not always straightforward, however, because it relies on assumptions about the extent of direct selection on the phenotype in question and the demographic history of the population (Eyre-Walker & Keightley, Reference Eyre-Walker and Keightley2007; Price et al., Reference Price, Kryukov, de Bakker, Purcell, Staples, Wei and Sunyaev2010; Zuk et al., Reference Zuk, Schaffner, Samocha, Do, Hechter, Kathiresan, Lander and E.2014). Genes under weak selection may harbor rare as well as more common variants with disruptive effects (Zuk et al., Reference Zuk, Schaffner, Samocha, Do, Hechter, Kathiresan, Lander and E.2014).
Such variants with deleterious effects, escaping selection and occurring at relatively high frequencies in the population, are plausible also under strong purifying selection, as simulation studies have demonstrated (Price et al., Reference Price, Kryukov, de Bakker, Purcell, Staples, Wei and Sunyaev2010).
Achieving maximal power when testing such regions requires adapting the weighting scheme to match the hypothesized selection types. To this end, we proposed the use of a data-driven weighting approach. Our simulation results showed, that such an approach maintains the power close to that of the true (i.e., correctly specified) model. When applied to real data, this approach allowed us to locate previously reported genes conferring risk to schizophrenia (e.g., Aberg et al., Reference Aberg, Liu, Bukszár, McClay, Khachane, Andreassen and Gurling2013; Ripke et al., Reference Ripke, O'Dushlaine, Chambert, Moran, Kähler, Akterin and Fromer2013), lending support to the conclusion that such a variable weighting approach is likely to boost statistical power. Such adaptive approaches were also recommended by Zuk et al. (Reference Zuk, Schaffner, Samocha, Do, Hechter, Kathiresan, Lander and E.2014) and Price et al. (Reference Price, Kryukov, de Bakker, Purcell, Staples, Wei and Sunyaev2010) as being optimal for gene-based tests. Deriving weights based on allele frequency is but one of the possible ways of prioritizing the contribution to the test statistic of the variants within the target set (Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011). Alternative weighting schemes that incorporate probabilities of a variant being damaging, as estimated by annotation tools such as, for example, Polyphen-2 (Adzhubei et al., Reference Adzhubei, Schmidt, Peshkin, Ramensky, Gerasimova, Bork and Sunyaev2010) or SIFT (Ng & Henikoff, Reference Ng and Henikoff2003), may also be considered.
We emphasize that our data-driven weighting approach renders thresholding unnecessary. Thresholding (either based on counts or on allele frequency) has been initially used in burden tests (e.g., Li & Leal, Reference Li and Leal2008; Madsen & Browning, Reference Madsen and Browning2009; Price et al., Reference Price, Kryukov, de Bakker, Purcell, Staples, Wei and Sunyaev2010; see also Franić et al., Reference Franić, Dolan, Broxholme, Hu, Zemojtel, Davies and Hottenga2015, for an overview on burden tests), but it has been employed also in sequence-based variance component tests (Lohmueller et al., Reference Lohmueller, Sparsø, Li, Andersson, Korneliussen, Albrechtsen and Kiil2013; Xu et al., Reference Xu, Tachmazidou, Walter, Ciampi, Zeggini and Greenwood2014) for the purpose of removing neutral variation (see, e.g., Kryukov et al., Reference Kryukov, Pennacchio and Sunyaev2007). Yet, in our empirical analysis this practice was counterproductive: imposing the (arbitrarily chosen) MAC thresholds muted the signal in genes located in regions already confirmed as associated with schizophrenia (i.e., the PRRC2A and the VARS2 genes; e.g., Aberg et al., Reference Aberg, Liu, Bukszár, McClay, Khachane, Andreassen and Gurling2013; and the AKT3 gene; e.g., Ripke et al., Reference Ripke, O'Dushlaine, Chambert, Moran, Kähler, Akterin and Fromer2013). Considering common variants along with the rare ones in sequence-based kernel association tests appears to be justified for three main reasons. First, the use of variable weighting schemes is equivalent to applying variable frequency thresholds: the weights are removing from the test or favoring the contribution to the test statistic of the variants within the target set based on their frequency. Second, only the joint signal — coming from rare and more common variants — enabled us to detect significant enrichment. That is, we note that none of these common variants would be detected in an ordinary GWAS (see Tables S3–S5). And third, importantly, with the current samples, our tests are mostly powered to locate regions under relatively weak selection pressures, and such regions are expected to harbor rare as well as common variants, both with functional effects. To locate genes under stronger selection pressures, larger samples (see Zuk et al., Reference Zuk, Schaffner, Samocha, Do, Hechter, Kathiresan, Lander and E.2014) and the inclusion of more extreme weights (i.e., weights that overlook common variants and favor rare ones) will probably be required.
The LRT and the score test had equal power under the data-driven weighting approach. Note, however, that this equivalence hinged upon the inclusion of weights that closely resemble the true ones among the alternatives. The powers of the two tests will likely diverge when the weights in the set are all badly specified; in such a circumstance, the LRT is expected to show superior power (due to its robustness to assumption violation). This is likely illustrated in the empirical analysis where the LRT has always yielded lower p values. Yet, despite these differences in power, currently the score test is the dominant association test with RVs, involving single studies and also in meta-analyses (see, e.g., Tang & Lin, Reference Tang and Lin2015). Integrating LRT into meta-analytic techniques for rare-variant association testing is desirable — to ensure maximal power of detection — and will likely boost its application.
Both in the simulations and in the empirical analysis, we chose to correct alpha by using the Bonferroni method. We chose this method for the sake of simplicity. Although one may argue that the method is slightly conservative as the tests are correlated, it is important to note that the Bonferroni corrected weighing procedure confers more power than a badly specified weighting scheme would do; p value correction for larger number of tests can be easily obtained using the p.adjust function implemented in the stats R-package. Permutation may also be used to compute the p value. However, the data-driven weighting approach based on permutations is prohibitively slow, when the number of tested variants within the target set (or the number of genes) and the sample are large. The Bonferroni correction — though easier computationally — comes at a price in terms of power: the more weighting schemes one ‘tries’, the more stringent the significance threshold correction. An algorithm for optimal search for the ‘true’ weights (e.g., Neale & Cardon, Reference Neale and Cardon1992) or limiting the choice of weights based on knowledge on theorized selection on each gene (Zuk et al., Reference Zuk, Schaffner, Samocha, Do, Hechter, Kathiresan, Lander and E.2014) would decrease the burden of multiple testing, and further increase power.
Conclusion
The score test is currently widely used in sequence-based association studies (e.g., Cruchaga et al., Reference Cruchaga, Karch, Jin, Benitez, Cai, Guerreiro and Bertelsen2014; Huyghe et al., Reference Huyghe, Jackson, Fogarty, Buchkovich, Stančáková, Stringham and Cederberg2013; Peloso et al., Reference Peloso, Auer, Bis, Voorman, Morrison, Stitziel and Fornage2014; Zhan et al., Reference Zhan, Larson, Wang, Koboldt, Sergeev, Fulton and Bragg-Gresham2013) for both its computational efficiency and power (Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011). Indeed, assuming correct specification, in some circumstances the score test is the most powerful test (Lippert et al., Reference Lippert, Xiang, Horta, Widmer, Kadie, Heckerman and Listgarten2014; Wu et al., Reference Wu, Lee, Cai, Li, Boehnke and Lin2011). However, the results provided herein showed that the LRT has the compelling qualities of being generally more robust and more powerful under weight misspecification. This is an important result given that, arguably, misspecified models are likely to be the rule rather than the exception in the weighting-based approaches.
Acknowledgments
We thank the Swedish cohort participants whose data we analyzed in this study. Camelia C. Minică and Michael C. Neale are supported by the National Institute on Drug Abuse Grant DA-018673. Jacqueline M. Vink is supported by the ERC starting grant 284167.
Supplementary Material
To view supplementary material for this article, please visit https://doi.org/10.1017/thg.2017.7.






