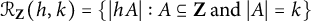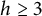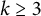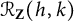1 Sums of finite sets of integers

An additive abelian semigroup is simply a nonempty set G with a commutative and associative binary operation, written additively. For every nonempty subset A of the semigroup G, the h-fold sumset of A is the set of all sums of h not necessarily distinct elements of A, that is,

$$\begin{align*}hA = \left\{a_{j_1}+\cdots + a_{j_h}: a_{j_r} \in A \text{ for all } r= 1,\ldots, h \right\}. \end{align*}$$

We define $0A = \{0\}$ . A core part of additive number theory is the study of sumsets of finite subsets of additive abelian semigroups. We define the sumset size set

$$\begin{align*}\mathcal R_G(h,k) = \left\{ |hA|: A \subseteq G \text{ and } |A| = k \right\}. \end{align*}$$

A basic problem is to understand this set.

We consider the set $ \mathcal R_{\mathbf Z}(h,k)$ of sumset sizes of finite sets of integers. The dilation of a set A by $\lambda $ is the set $ \lambda \ast A = \{\lambda a : a \in A\}$ . Sets A and B are affinely equivalent if there are numbers $\lambda \neq 0$ and $\mu $ such that

$$\begin{align*}B = \lambda\ast A + \mu = \{\lambda a + \mu: a \in A\}. \end{align*}$$

If A and B are affinely equivalent, then

$$\begin{align*}hB = h(\lambda\ast A + \mu) = \lambda \ast hA + h\mu \end{align*}$$

and so $|hB| = |hA|$ . Because sumset size is an affine invariant, we have $ \mathcal R_{\mathbf Z}(h,k) = \mathcal R_{ \mathbf N _0}(h,k)$ . It is proved in [Reference Nathanson9] that $ \mathcal R_{\mathbf Z^n}(h,k) = \mathcal R_{\mathbf Z}(h,k)$ for all positive integers n.

There are simple lower and upper bounds for $ \mathcal R_{\mathbf Z}(h,k)$ . We have

(1) $$ \begin{align} \min \mathcal R_{\mathbf Z}(h,k) = hk-h+1 \end{align} $$

and, if $ A \subseteq \mathbf Z \text { and } |A| = k $ , then $|hA| = hk-h+1$ if and only if A is an arithmetic progression of length k. Similarly, if A is a $B_h$ -set, that is, a set all of whose h-fold sums are distinct, then $|hA| = \binom {h+k-1}{h}$ and

(2) $$ \begin{align} \max \mathcal R_{\mathbf Z}(h,k) = \binom{h+k-1}{h}. \end{align} $$

Beginning with the work of Freiman [Reference Freiman3, Reference Freiman4, Reference Nathanson7], a large research literature has investigated finite sets whose sumsets are very small, that is, close to the minimum size. There is also a large research literature [Reference O’Bryant11] on sets whose sumsets are close to the maximum size.

What is surprising is the lack of attention to the full range of sumset sizes of finite sets of integers. Possibly, the only published statement related to this problem occurs in a 1983 paper by Erdős and Szemerédi [Reference Erdős and Szemerédi1] about the number of sums and products. They wrote:

Theorem 1 refines this assertion. For real numbers u and v, define the integer interval

$$\begin{align*}[u,v] = \{ n \in \mathbf Z: u \leq n \leq v\}. \end{align*}$$

Theorem 1 (Nathanson [Reference Nathanson8])

For all positive integers k,

$$\begin{align*}\mathcal R_{\mathbf Z}(2,k) = \left[ 2k-1, \binom{k+1}{2} \right]. \end{align*}$$

Moreover, for all $t \in \mathcal R_{\mathbf Z}(2,k)$ , there exists a set $A \subseteq \left [0,2^k -1 \right ]$ such that $|A| = k$ and $\left | 2A \right | = t$ .

Here are two important observations. First, the set of sumset sizes $ \mathcal R_{\mathbf Z}(2,k)$ is known exactly, and it is an integer interval: There is no “missing number” between $\min \mathcal R_{\mathbf Z}(2,k)$ and $\max \mathcal R_{\mathbf Z}(2,k)$ . Second, there is a finite, albeit exponential, upper bound on the amount of computation needed to find a set A with $|A| = k$ and $|2A| = t$ for all $t \in \mathcal R_{\mathbf Z}(2,k)$ . For all $h \geq 2$ , the set $ \mathcal R(h,k)$ is finite and so there exists an integer N such that, for all $t \in \mathcal R(h,k)$ , there is a set A with $|A| = k$ , $|hA| = t$ , and $A \subseteq [0,N]$ . Let $N(h,k)$ be the least such number. By Theorem 1, $N(2,k) < 2^k$ . For $h \geq 3$ , there is the following exponential upper bound.

Theorem 2 (Nathanson [Reference Nathanson9])

For all $h \geq 3$ and $k \geq 3$ ,

$$\begin{align*}N(h,k) < 4(4h)^{k-1}. \end{align*}$$

It would be of interest to know if, for fixed h, there is a subexponential or even polynomial upper bound for $N(h,k)$ .

We have

$$\begin{align*}\mathcal R_{\mathbf Z}(h,1) = \{1\} \operatorname{\mathrm{\quad\text{and}\quad}} \mathcal R_{\mathbf Z}(h,2) = \{h+1\} \qquad \text{for all } h \geq 1 \end{align*}$$

and

$$\begin{align*}\mathcal R_{\mathbf Z}(1,k) = \{k\} \qquad \text{for all } k \geq 1. \end{align*}$$

Theorem 1 describes $ \mathcal R_{\mathbf Z}(2,k)$ . Thus, the problem is to understand $ \mathcal R_{\mathbf Z}(h,k) $ for $h \geq 3$ and $k \geq 3$ .

Let $k = 3$ . From (1) and (2), we have

$$\begin{align*}\mathcal R_{\mathbf Z}(h,3) \subseteq \left[ 2h+1, \binom{h+2}{2}\right]. \end{align*}$$

In particular,

$$\begin{align*}\mathcal R_{\mathbf Z}(3,3) \subseteq \{7,8,9,10\}. \end{align*}$$

We have

$$ \begin{align*} 3\{0,1,2\} = [0,6] & \operatorname{\mathrm{\qquad\text{and}\qquad}} |3\{0,1,2\} | = 7 \\ 3\{0,1,3\} = [0,7] \cup \{9\} & \operatorname{\mathrm{\qquad\text{and}\qquad}} |3\{0,1,3\} | = 9 \\ 3\{0,1,4\} = [0,6] \cup \{8,9,12\} & \operatorname{\mathrm{\qquad\text{and}\qquad}} |3\{0,1,4\} | = 10 \end{align*} $$

and so

$$\begin{align*}\{7,9,10\} \subseteq \mathcal R_{\mathbf Z}(3,3). \end{align*}$$

Where is 8? A computer search failed to find a set A of integers with $|A| = 3$ and ${|3A| = 8}$ . Nathanson [Reference Nathanson8] proved that $8 \notin \mathcal R_{\mathbf Z}(3,3)$ , that is,

$$\begin{align*}\mathcal R_{\mathbf Z}(3,3) = \{7,9,10\}. \end{align*}$$

Why is there no 8 in $ \mathcal R_{\mathbf Z}(3,3)$ ? There is a proof but not a reason.

More generally, we have the following “missing number” result.

Theorem 3 (Nathanson [Reference Nathanson8])

For all $h \geq 3$ and $k \geq 3$ ,

$$\begin{align*}hk-h+2 \notin \mathcal R_{\mathbf Z}(h,k) \end{align*}$$

and so the sumset size set $ \mathcal R_{\mathbf Z}(h,k)$ is not an interval.

Theorems 1 and 3 inspire this field of research. For $h \geq 3$ and $k \geq 3$ , the sumset size set $ \mathcal R_{\mathbf Z}(h,k)$ is not the integer interval defined by its minimum and maximum values. What is it? One can generate random sets A of size k, compute their sumset size $|hA|$ , and generate subsets of the set $ \mathcal R_{\mathbf Z}(h,k)$ . From these tables, one can formulate conjectures. Observation of gaps in tables of the sumset sizes of random subsets suggested the following result, which was proved by Vincent Schinina.

Theorem 4 (Schinina [Reference Schinina14])

For all $h \geq 3$ and $k \geq 3$ ,

$$\begin{align*}[hk-h+2,hk-1] \cap \mathcal R_{\mathbf Z}(h,k) = \emptyset \end{align*}$$

and

$$\begin{align*}hk \in \mathcal R_{\mathbf Z}(h,k). \end{align*}$$

For sets of size 3, there is the following result.

Theorem 5 (Nathanson [Reference Nathanson8])

For all positive integers h,

(3) $$ \begin{align} \mathcal R_{\mathbf Z}(h,3) = \left\{ \binom{h+2}{2} - \binom{\ell}{2} : \ell \in [1,h] \right\}. \end{align} $$

Thus, the sumset sizes of 3-element sets are differences of triangular numbers. We know $ \mathcal R_{\mathbf Z}(h,3)$ , but the set $ \mathcal R_{\mathbf Z}(h,4)$ of sumset sizes of 4-element sets is still a mystery.

While the computation of the sumset sizes of random finite sets of integers generates elements of the sumset size sets $ \mathcal R_{\mathbf Z}(h,k)$ , it is useful and important to have explicit constructions of finite sets and explicit families of sumset sizes in $ \mathcal R_{\mathbf Z}(h,k)$ . In Theorems 6 and 7 and Corollaries 1–7, we construct infinite families of such sets, and, in particular, interesting elements of $ \mathcal R_{\mathbf Z}(h,4)$ .

2 Arithmetic progressions of intervals

Let $ \mathbf N _0 = \{0,1,2,3,\ldots \}$ be the set of nonnegative integers. For positive integers h and k, let

$$\begin{align*}\mathcal X_{h,k} = \left\{ (x_1,\ldots, x_k) \in \mathbf N _0^k: \sum_{j=1}^k x_j = h\right\}. \end{align*}$$

The set $ \mathcal X_{h,k}$ is invariant under permutations: For all $\sigma \in S_k$ , we have $(x_1,\ldots , x_k) \in \mathcal X_{h,k}$ if and only if $(x_{\sigma (1)},\ldots , x_{\sigma (k)}) \in \mathcal X_{h,k}$ .

Let $A = \{a_1,\ldots , a_k\} \subseteq \mathbf Z$ with $|A| = k$ and let $ \mathbf a = (a_1,\ldots , a_k) \in \mathbf Z^k$ . For $ \mathbf x = (x_1,\ldots , x_k) \in \mathcal X_{h,k}$ , we define

$$\begin{align*}\mathbf x \cdot \mathbf a = \left(x_1,\ldots, x_k) \cdot (a_1,\ldots, a_k \right) = \sum_{j=1}^k x_ja_j. \end{align*}$$

Then, $ \mathbf x \cdot \mathbf a \in hA$ and

$$\begin{align*}hA = \left\{ \mathbf x \cdot \mathbf a : \mathbf x \in \mathcal X_{h,k} \right\}. \end{align*}$$

The vector $\mathbf a$ depends on the ordering of the elements of the set A, but, because $ \mathcal X_{h,k}$ is $S_k$ -invariant, the sumset $hA$ is independent of the ordering of A.

It is straightforward to check that, for all positive integers h and k,

(4) $$ \begin{align} \mathcal X_{h,k} = \bigcup_{x_k=0}^{h} \left\{ (x_1,\ldots, x_{k-1}, x_k): (x_1,\ldots, x_{k-1}) \in \mathcal X_{h - x_k,k-1} \right\}. \end{align} $$

The following terminology is useful. Let $u_1 \leq u_2$ . We say that there is a gap between integer intervals $[u_1,v_1]$ and $[u_2,v_2]$ if there is an integer n such that

$$\begin{align*}v_1 < n < u_2. \end{align*}$$

The integer intervals $[u_1,v_1]$ and $[u_2,v_2]$ have no gap if $u_2 \leq v_1+1$ or, equivalently if $[u_1,v_1] \cup [u_2,v_2] $ is an integer interval.

Lemma 1 For all positive integers h and k,

$$\begin{align*}\mathcal I_{h,k} = \left\{ \sum_{j=2}^{k} (j-1) x_j : (x_1,\ldots, x_{k}) \in \mathcal X_{h,k} \right\} = [0, (k-1) h ]. \end{align*}$$

Proof The proof is by induction on k. For $k=1$ , we have $ \mathcal X_{h,1} = \{(h)\}$ and $ \mathcal I_{h,1} = \{0\} = [0,0]$ . For $k =2$ , we have

$$ \begin{align*} \mathcal X_{h,2} &= \left\{ (x_1,x_2) \in \mathbf N _0^2: x_1+x_2= h\right\} \\ & = \left\{ (h-x_2,x_2) \in \mathbf N _0^2: x_2 \in [0,h] \right\} \end{align*} $$

and so

$$\begin{align*}\mathcal I_{h,2} = \left\{ x_2 : (x_1,x_2) \in \mathcal X_{h,2} \right\} = [0,h]. \end{align*}$$

Let $k \geq 3$ and assume that $ \mathcal I_{h,k-1} = [0, (k-2) h ]$ for all $h \geq 1$ .

If $x_k \in [0,h-1]$ , then

$$\begin{align*}(k-1)(x_k+1) \leq (k-2)h+x_k+1. \end{align*}$$

It follows that there is no gap between the integer intervals

$$\begin{align*}\left[ (k-1)x_k, (k-2)h + x_k \right] \end{align*}$$

and

$$\begin{align*}\left[ (k-1)(x_k +1), (k-2)h + x_k + 1 \right] \end{align*}$$

and so their union is the integer interval

$$ \begin{align*} \left[ (k-1)x_k, (k-2)h + x_k + 1 \right]. \end{align*} $$

Applying relation (4), we obtain

$$ \begin{align*} \mathcal I_{h,k} & = \left\{ \sum_{j=2}^{k} (j-1) x_j : (x_1,\ldots, x_k) \in \mathcal X_{h,k} \right\} \\ & = \left\{ (k-1)x_k+ \sum_{j=2}^{k-1} (j-1) x_j : (x_1,\ldots, x_k) \in \mathcal X_{h,k} \right\} \\ & = \bigcup_{x_k=0}^h \left\{ (k-1)x_k+ \left\{ \sum_{j=2}^{k-1} (j-1) x_j : (x_1,\ldots, x_{k-1}) \in \mathcal X_{h - x_k,k-1} \right\} \right\} \\& = \bigcup_{x_k=0}^h \left\{ (k-1)x_k+ \mathcal I_{h - x_k,k-1} \right\} \\ & = \bigcup_{x_k=0}^h \left\{ (k-1)x_k+ [0, (k-2) (h - x_k) ]\right\} \\ & = \bigcup_{x_k=0}^h \left[ (k-1)x_k, (k-2)h + x_k \right]. \end{align*} $$

Because there is no gap between consecutive pairs of these $h+1$ intervals, we obtain

$$\begin{align*}\mathcal I_{h,k} = [0, (k-1)h]. \end{align*}$$

This completes the proof.

Theorem 6 Let k, a, b, and $\ell $ be positive integers with $k=a\ell $ and $a \leq b$ . Let

$$\begin{align*}P = b\ast [0,\ell -1] = \{0,b,2b,\ldots, (\ell-1)b \} \end{align*}$$

be the $\ell $ -term arithmetic progression with difference b and smallest element 0. Let A be the $\ell $ -term arithmetic progression of translates of the interval $[0, a-1 ]$ :

$$ \begin{align*} A & = P+[0,a-1] = \bigcup_{j=1}^{\ell} \left( (j-1)b + [0,a-1] \right). \end{align*} $$

Then, $|A| = k$ .

For every positive integer h, let

$$\begin{align*}Q = b\ast [0, h(\ell -1)] = \{0,b,2b,\ldots, h(\ell-1) b \} \end{align*}$$

be the $(h(\ell -1) +1)$ -term arithmetic progression with difference b and smallest element 0. The sumset $hA$ is an $(h(\ell -1) +1)$ -term arithmetic progression of translates of the interval $[0, h(a-1)]$ :

(5) $$ \begin{align} hA = Q + \left[ 0, h (a-1) \right] \end{align} $$

and

(6) $$ \begin{align} |hA| = \begin{cases} (a+ b(\ell-1) - 1)h+1 & \text{if } a \leq b \leq (a-1)h+1 \\ (a-1)(\ell-1)h^2 + (a+\ell-2)h +1 & \text{if } b \geq h(a-1) +1. \end{cases} \end{align} $$

Proof We have

$$ \begin{align*} A & = P+[0,a-1] \\ & = \bigcup_{j=1}^{\ell} [ (j-1)b, \ a -1 + (j-1)b ] \\ & = \bigcup_{j=1}^{\ell } L_j, \end{align*} $$

where $L_j$ is the integer interval

$$\begin{align*}L_j = [ (j-1)b, \ a -1 + (j-1)b ] \end{align*}$$

and $|L_j|=a$ . The inequality $a \leq b$ implies $a -1 +(j-1)b < jb$ for all $j \in [1,\ell ]$ and so the integer intervals $L_j$ are pairwise disjoint and $|A| = \sum _{j=1}^{\ell } |L_j| = a\ell = k$ .

If $ (x_1,\ldots , x_{\ell }) \in \mathcal X_{h,\ell }$ , then $\sum _{j=1}^k x_j = h$ . Applying Lemma 1 with $k=\ell $ , we have

$$ \begin{align*} hA & = h\left(\bigcup_{j=1}^{\ell } L_j \right) = \bigcup_{ \mathbf x = (x_1,\ldots, x_{\ell}) \in \mathcal X_{h,\ell} } \left(x_1 L_1 + \cdots + x_{\ell} L_{\ell} \right) \\ & = \bigcup_{ \mathbf x \in \mathcal X_{h,\ell} } \sum_{j=1}^{\ell} [ (j-1) x_j b, (a-1) x_j + (j-1) x_j b ] \\ & = \bigcup_{ \mathbf x \in \mathcal X_{h,\ell}} \left[ \sum_{j=1}^{\ell } (j-1) x_j b, \sum_{j=1}^{\ell } (a-1) x_j + \sum_{j=1}^{\ell } (j-1) x_j b \right] \\ & = \bigcup_{ \mathbf x \in \mathcal X_{h,\ell}} \left[ \sum_{j=2}^{\ell } (j-1) x_j b, h(a-1) + \sum_{j=2}^{\ell } (j-1) x_j b \right] \\ & = \bigcup_{ \mathbf x \in \mathcal X_{h,\ell}} \left( b \sum_{j=2}^{\ell } (j-1) x_j + \left[ 0, h(a-1) \right] \right) \\ & = \left\{ b \sum_{j=2}^{\ell } (j-1) x_j : \mathbf x \in \mathcal X_{h,\ell}\right\} + \left[ 0, h (a-1) \right] \\ & = b\ast \mathcal I_{h,\ell} + \left[ 0, h (a-1) \right] \\ & = b\ast [0, (\ell -1) h ] + \left[ 0, h (a-1) \right] \\ & = Q + \left[ 0, h (a-1) \right]. \end{align*} $$

This proves (5).

To obtain the sumset size formula (6), we write $hA$ as a union of intervals:

$$ \begin{align*} hA &= \bigcup_{j=0}^{ (\ell -1) h} \left[ bj, bj + h (a-1) \right]. \end{align*} $$

If $b \geq h(a-1)+1$ , then the $(\ell -1) h +1$ intervals are pairwise disjoint and

$$\begin{align*}|hA| = ((\ell -1) h +1)( (a-1)h+1). \end{align*}$$

If $a \leq b \leq h(a-1)+1$ , then there are no gaps between successive intervals and so

$$\begin{align*}hA = [0, b(\ell -1) h +(a-1)h] \end{align*}$$

and

$$\begin{align*}|hA| = (a+ b(\ell -1) -1)h +1. \end{align*}$$

This completes the proof.

The following results are immediate consequences of Theorem 6.

Corollary 1 Let h and k be positive integers. If a and $\ell $ are positive integers such that $k=a\ell $ , then the sumset size set $ \mathcal R_{\mathbf Z}(h,k)$ contains the arithmetic progression

$$\begin{align*}\left\{ (\ell -1) hb + (a -1)h +1 :b \in [a, (a-1)h+1] \right\}. \end{align*}$$

3 Sums of intervals of different lengths

Consider a finite set that is the union of two intervals of different lengths. Let a, b, and c be nonnegative integers with $a < b$ and $a \neq c$ , and let $A = [0,a] \cup [b,b+c]$ . The set A is affinely equivalent to the set

$$ \begin{align*} A' & = (-1)\ast A + b+c \\ & = [0,c] \cup [ b+c-a, b+c] \\ & = [0,a'] \cup [b', b'+c'] \end{align*} $$

with $a'=c < b+c-a = b'$ , and $c' = a$ . If $a < c$ , then $a'> c'$ . Moreover, $|A| = |A'|$ and $|hA| = |hA'|$ . Thus, it suffices to consider only the case $a>c$ .

Note that the case $a=c$ (that is, $A = [0,a] \cup [b,b+a] = \{0,b\}+[0,a]$ ) is a special case of Theorem 6.

The integer part (also called the floor) of the real number w, denoted $[w]$ , is the unique integer n such that $n \leq w < n+1$ . There should be no notational confusion between $[u,v]$ and $[w]$ .

Theorem 7 Let a, b, and c be integers with $0 \leq c < a < b$ and let

$$\begin{align*}A= [0,a] \cup [b,b+c]. \end{align*}$$

Let $h \geq 2$ and

(7) $$ \begin{align} i_0 = \left[\frac{ha-b}{a-c}\right]. \end{align} $$

If $b> ha$ , then

(8) $$ \begin{align} |hA| = (h+1)\left( 1 + \frac{h(a+c)}{2} \right). \end{align} $$

If $a < b \leq ha$ , then

(9) $$ \begin{align} |hA| & = (i_0+1) b + (h-i_0)( ha + 1) - \frac{(h+i_0+1)(h-i_0)(a-c)}{2}. \end{align} $$

Proof We have

$$ \begin{align*} hA & = \bigcup_{i=0}^h \left( (h-i) [0,a] + i[b,b+c] \right) \\ & = \bigcup_{i=0}^h [ib, (h-i)a+ i(b+c)] \\ & = \bigcup_{i=0}^h L_i, \end{align*} $$

where $L_i$ is the integer interval

$$ \begin{align*} L_i & = [ib, (h-i)a+ i(b+c) ] \\ & = [ib, ha +i(b-a+c)] \end{align*} $$

and

$$\begin{align*}\left| L_i \right| = ha + 1 - i (a-c). \end{align*}$$

Because $b \geq 1$ , the lower bounds of the intervals $L_0, L_1,\ldots , L_h$ are strictly increasing. Let $i \in [0,h-1]$ . Because $a> c$ , the intervals $L_i$ and $L_{i+1}$ are disjoint if and only if

$$\begin{align*}ha - i (a-c) + ib < (i+1)b \end{align*}$$

if and only if

(10) $$ \begin{align} \frac{ha-b}{a-c} < i \leq h-1. \end{align} $$

Let

$$\begin{align*}i_0 = \left[ \frac{ha-b}{a-c} \right]. \end{align*}$$

Thus, for $i \in [0,h-1]$ , the intervals $L_i$ and $L_{i+1}$ are disjoint if and only if

$$\begin{align*}i \in [i_0+1,h-1]. \end{align*}$$

Thus, the $h+1$ intervals $L_i$ are pairwise disjoint if and only if $i_0 \leq -1$ or, equivalently, if and only if $b> ha$ . In this case,

$$ \begin{align*} |hA| & = \left| \bigcup_{i=0}^h L_i \right| = \sum_{i=0}^h \left| L_i \right| \\ & = \sum_{i=0}^h \left( ha + 1 - i (a-c) \right) \\ & = (h+1) \left( ha + 1 \right) - \frac{h(h+1)(a-c)}{2} \\ & = (h+1)\left( 1 + \frac{h(a+c)}{2} \right). \end{align*} $$

If $b \leq ha$ or, equivalently, if $i_0 \geq 0$ , then the $h-i_0-1$ intervals $L_{i_0+2},L_{i_0+3}, \ldots , L_h$ are pairwise disjoint and $L_i \cap L_{i+1} \neq \emptyset $ for $i \in [0,i_0]$ . It follows that

$$\begin{align*}L_0^* = \bigcup_{i=0}^{i_0+1} L_i = [0, ha + (i_0+1)(b-a+c)] \end{align*}$$

and

$$\begin{align*}\left| L_0^* \right| = ha + 1 + (i_0+1)(b-a+c). \end{align*}$$

Moreover,

$$ \begin{align*} \left| \bigcup_{i=i_0+2}^h L_i \right| & = \sum_{i=i_0+2}^h |L_i | = \sum_{i=i_0+2}^h( ha + 1- i (a-c)) \\ & = (h-i_0-1)(ha + 1) - \frac{(h+i_0+2)(h-i_0-1)(a-c)}{2} \end{align*} $$

and

$$\begin{align*}L_0^* \cap \left( \bigcup_{i=i_0+2}^h L_i \right) = \left( \bigcup_{i=0}^{i_0+1} L_i \right) \cap \left( \bigcup_{i=i_0+2}^h L_i \right) = \emptyset. \end{align*}$$

We obtain

$$ \begin{align*} |hA| & = \left| \bigcup_{i=0}^h L_i \right| = \left| L_0^* \right| + \sum_{i=i_0+2}^h \left| L_i \right| \\ & = (i_0+1)(b-a+c) + (h-i_0)(ha + 1) \\ & \qquad - \frac{(h+i_0+2)(h-i_0-1)(a-c)}{2} \\ & = (i_0+1) b + (h-i_0)( ha + 1) - \frac{(h+i_0+1)(h-i_0)(a-c)}{2}. \end{align*} $$

This completes the proof.

Corollary 4 Let $h \geq 2$ and $k \geq 3$ .

If $b> h(k-2)$ , then the set $A= [0,k-2] \cup \{b\}$ satisfies

$$\begin{align*}|hA| = (h+1)\left( 1 + \frac{h(k-2)}{2} \right). \end{align*}$$

If $b \in [k-1, h(k-2)]$ , then there exist unique integers $i_0 \in [0,h-2]$ and ${r \in [0,k-3]}$ such that

$$\begin{align*}b = (h-i_0)(k-2)-r \end{align*}$$

and the set $A= [0,k-2] \cup \{b\}$ satisfies

$$\begin{align*}|hA| = (i_0+1) b + (h-i_0)( h(k-2) + 1) - \frac{(h+i_0+1)(h-i_0)(k-2)}{2}. \end{align*}$$

Corollary 5 For all $h \geq 2$ ,

$$\begin{align*}(h+1)^2 \in \mathcal R_{\mathbf Z}(h,4) \end{align*}$$

and, for all $i_0 \in [0,h-2]$ and $r \in [0,1]$ ,

$$\begin{align*}(i_0+1) (2(h-i_0) -r ) + (h-i_0)^2 \in \mathcal R_{\mathbf Z}(h,4). \end{align*}$$

Proof Apply Corollary 4 with $k=4$ . Let $A= [0,2] \cup \{b\}$ . If $b> 2h$ , then

$$\begin{align*}|hA| = (h+1)^2 \in \mathcal R_{\mathbf Z}(h,4). \end{align*}$$

If $i_0 \in [0,h-2]$ and $r \in [0,1]$ , then

$$\begin{align*}b = 2(h-i_0) -r \in [3, 2h]. \end{align*}$$

Conversely, if $b \in [3, 2h]$ , then there exist unique integers $i_0 \in [0,h-2]$ and ${r \in [0,1]}$ such that

$$\begin{align*}b = 2(h-i_0) -r. \end{align*}$$

Setting $A = [0,2] \cup \{b\}$ , we obtain

$$\begin{align*}|hA| = (i_0+1) b + (h-i_0)^2 \in \mathcal R_{\mathbf Z}(h,4). \end{align*}$$

This completes the proof.

Corollary 6 For all $h \geq 2$ and $k \geq 3$ ,

$$\begin{align*}hk \in \mathcal R_{\mathbf Z}(h,k). \end{align*}$$

Corollary 7 Let $h \geq 2$ and $k \geq 3$ . For all $i_0 \in [0,h-2]$ , the sumset size set $ \mathcal R_{\mathbf Z}(h,k)$ contains the arithmetic progression

$$\begin{align*}(i_0+1) b + (h-i_0)( h(k-2) + 1) - \frac{(h+i_0+1)(h-i_0)(k-2)}{2} \end{align*}$$

for $b \in [ (h-i_0)(k-2) - (k-3), (h-i_0)(k-2)]$ .

In particular, $ \mathcal R_{\mathbf Z}(h,k)$ contains the integer interval

$$\begin{align*}\left[ \frac{ h^2 (k - 2)}{2} + \frac{hk}{2} - k + 3 , \frac{ h^2 (k - 2)}{2} + \frac{hk}{2} \right]. \end{align*}$$

For related work on sumset sizes, see [Reference Fox, Kravitz and Zhang2, Reference Hegyvári5, Reference Kravitz6, Reference Nathanson10, Reference O’Bryant12, Reference Péringuey and de Roton13].