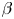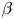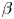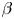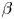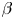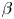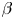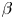1. Introduction
In magnetic fusion devices such as stellarators, zeroth-order confinement of particles and energy is obtained by constructing an equilibrium with magnetic surfaces. Magnetic islands and magnetic field line chaos can be detrimental to confinement, i.e. they can contribute to the radial transport of particle and energy (Hudson & Nakajima Reference Hudson and Nakajima2010). While it is possible to design equilibria with good magnetic surfaces in a vacuum (Cary & Kotschenreuther Reference Cary and Kotschenreuther1985; Cary & Hanson Reference Cary and Hanson1986; Pedersen et al. Reference Pedersen, Otte, Lazerson, Helander, Bozhenkov, Biedermann, Klinger, Wolf and Bosch2016), pressure-driven plasma currents, such as diamagnetic, Pfirsch–Schlüter and bootstrap currents, perturb finite pressure equilibria, and, at a sufficiently large pressure, magnetic islands and chaos emerge.
A pressure increase can also sometimes heal magnetic islands (Bhattacharjee et al. Reference Bhattacharjee, Hayashi, Hegna, Nakajima and Sato1995). While this mechanism can improve confinement locally, other islands might open elsewhere in the plasma as $\beta$![]() increases. There is thus a critical value of $\beta$
increases. There is thus a critical value of $\beta$![]() at which magnetic islands open and magnetic field line chaos emerges. This defines an equilibrium $\beta$
at which magnetic islands open and magnetic field line chaos emerges. This defines an equilibrium $\beta$![]() -limit. Note, however, that the equilibrium $\beta$
-limit. Note, however, that the equilibrium $\beta$![]() -limit is a ‘soft’ limit, since crossing it does not lead to a loss of control of the plasma. Additional input power may, however, leak through the damaged magnetic surfaces more easily (Rechester & Rosenbluth Reference Rechester and Rosenbluth1978), thereby preventing an increase of $\beta$
-limit is a ‘soft’ limit, since crossing it does not lead to a loss of control of the plasma. Additional input power may, however, leak through the damaged magnetic surfaces more easily (Rechester & Rosenbluth Reference Rechester and Rosenbluth1978), thereby preventing an increase of $\beta$![]() . Crossing the equilibrium $\beta$
. Crossing the equilibrium $\beta$![]() -limit may thus not be as concerning as crossing a stability limit (which may lead to plasma disruptions), but it still limits the overall performance of the reactor. It is consequently of crucial importance to understand these equilibrium $\beta$
-limit may thus not be as concerning as crossing a stability limit (which may lead to plasma disruptions), but it still limits the overall performance of the reactor. It is consequently of crucial importance to understand these equilibrium $\beta$![]() -limits better, especially for the operation of existing experiments and the design of new machines. Configurations where good magnetic surfaces are preserved over a large range of $\beta$
-limits better, especially for the operation of existing experiments and the design of new machines. Configurations where good magnetic surfaces are preserved over a large range of $\beta$![]() have to be sought, which will help to ultimately identify configurations with large enough equilibrium $\beta$
have to be sought, which will help to ultimately identify configurations with large enough equilibrium $\beta$![]() -limit.
-limit.
In the case of a classical stellarator, Loizu et al. (Reference Loizu, Hudson, Nührenberg, Geiger and Helander2017) proposed a model for the equilibrium $\beta$![]() -limit of a configuration with zero net toroidal current as well as one with a fixed edge rotational transform. Other studies computed high $\beta$
-limit of a configuration with zero net toroidal current as well as one with a fixed edge rotational transform. Other studies computed high $\beta$![]() equilibria in a number of experimentally relevant stellarator configurations and predicted the emergence of magnetic field line chaos at sufficiently large $\beta$
equilibria in a number of experimentally relevant stellarator configurations and predicted the emergence of magnetic field line chaos at sufficiently large $\beta$![]() – see, for example, the calculation by Suzuki, Watanabe & Sakakibara (Reference Suzuki, Watanabe and Sakakibara2020) in the Large Helical Device and Reiman et al. (Reference Reiman, Zarnstorff, Monticello, Weller and Geiger2007) in Wendelstein 7-AS (W7-AS). However, to the authors’ knowledge, no attempt has been made to analytically model the impact of the bootstrap current on the equilibrium $\beta$
– see, for example, the calculation by Suzuki, Watanabe & Sakakibara (Reference Suzuki, Watanabe and Sakakibara2020) in the Large Helical Device and Reiman et al. (Reference Reiman, Zarnstorff, Monticello, Weller and Geiger2007) in Wendelstein 7-AS (W7-AS). However, to the authors’ knowledge, no attempt has been made to analytically model the impact of the bootstrap current on the equilibrium $\beta$![]() -limit, and to determine how this critical $\beta$
-limit, and to determine how this critical $\beta$![]() depends on the device parameters.
depends on the device parameters.
We propose to extend the work of Loizu et al. (Reference Loizu, Hudson, Nührenberg, Geiger and Helander2017) to the case of a classical stellarator with bootstrap current. We use the stepped pressure equilibrium code (SPEC) to compute a large number of free-boundary equilibria at different $\beta$![]() , including the effect of bootstrap current. The code SPEC has been chosen for its speed, its capability to describe equilibria with magnetic islands and chaos, and the possibility to calculate free-boundary equilibria (Hudson et al. Reference Hudson, Loizu, Zhu, Qu, Nührenberg, Lazerson, Smiet and Hole2020) with a constrained toroidal current profile (Baillod et al. Reference Baillod, Loizu, Qu, Kumar and Graves2021). The code SPEC has been verified in stellarator geometry (Loizu, Hudson & Nührenberg Reference Loizu, Hudson and Nührenberg2016b), and its core algorithm has been improved to run faster and to be more robust (Qu et al. Reference Qu, Pfefferlé, Hudson, Baillod, Kumar, Dewar and Hole2020b). It has been successfully applied to study current sheets at rational surfaces (Loizu et al. Reference Loizu, Hudson, Bhattacharjee and Helander2015a,Reference Loizu, Hudson, Bhattacharjee, Lazerson and Helanderb; Huang et al. Reference Huang, Hudson, Loizu, Zhou and Bhattacharjee2022), ideal linear instabilities (Kumar et al. Reference Kumar, Qu, Hole, Wright, Loizu, Hudson, Baillod, Dewar and Ferraro2021, Reference Kumar, Nührenberg, Qu, Hole, Doak, Dewar, Hudson, Loizu, Aleynikova and Baillod2022), tearing mode stability (Loizu & Hudson Reference Loizu and Hudson2019) and nonlinear saturation (Loizu et al. Reference Loizu, Huang, Hudson, Baillod, Kumar and Qu2020), penetration of resonant magnetic perturbations in the ideal limit (Loizu et al. Reference Loizu, Hudson, Helander, Lazerson and Bhattacharjee2016a) and relaxation phenomena in reversed field pinches (Dennis et al. Reference Dennis, Hudson, Terranova, Franz, Dewar and Hole2013b, Reference Dennis, Hudson, Dewar and Hole2014; Qu et al. Reference Qu, Dewar, Ebrahimi, Anderson, Hudson and Hole2020a).
, including the effect of bootstrap current. The code SPEC has been chosen for its speed, its capability to describe equilibria with magnetic islands and chaos, and the possibility to calculate free-boundary equilibria (Hudson et al. Reference Hudson, Loizu, Zhu, Qu, Nührenberg, Lazerson, Smiet and Hole2020) with a constrained toroidal current profile (Baillod et al. Reference Baillod, Loizu, Qu, Kumar and Graves2021). The code SPEC has been verified in stellarator geometry (Loizu, Hudson & Nührenberg Reference Loizu, Hudson and Nührenberg2016b), and its core algorithm has been improved to run faster and to be more robust (Qu et al. Reference Qu, Pfefferlé, Hudson, Baillod, Kumar, Dewar and Hole2020b). It has been successfully applied to study current sheets at rational surfaces (Loizu et al. Reference Loizu, Hudson, Bhattacharjee and Helander2015a,Reference Loizu, Hudson, Bhattacharjee, Lazerson and Helanderb; Huang et al. Reference Huang, Hudson, Loizu, Zhou and Bhattacharjee2022), ideal linear instabilities (Kumar et al. Reference Kumar, Qu, Hole, Wright, Loizu, Hudson, Baillod, Dewar and Ferraro2021, Reference Kumar, Nührenberg, Qu, Hole, Doak, Dewar, Hudson, Loizu, Aleynikova and Baillod2022), tearing mode stability (Loizu & Hudson Reference Loizu and Hudson2019) and nonlinear saturation (Loizu et al. Reference Loizu, Huang, Hudson, Baillod, Kumar and Qu2020), penetration of resonant magnetic perturbations in the ideal limit (Loizu et al. Reference Loizu, Hudson, Helander, Lazerson and Bhattacharjee2016a) and relaxation phenomena in reversed field pinches (Dennis et al. Reference Dennis, Hudson, Terranova, Franz, Dewar and Hole2013b, Reference Dennis, Hudson, Dewar and Hole2014; Qu et al. Reference Qu, Dewar, Ebrahimi, Anderson, Hudson and Hole2020a).
To numerically identify the equilibrium $\beta$![]() -limit, Loizu et al. used a diagnostic based on the volume of chaos, i.e. the volume of plasma occupied by chaotic field lines, which were identified by measuring their fractal dimension (Meiss Reference Meiss1992). However, this approach is too pessimistic since some chaotic magnetic field lines might be able to preserve confinement (Hudson & Breslau Reference Hudson and Breslau2008). An alternative approach, proposed by Paul, Hudson & Helander (Reference Paul, Hudson and Helander2022), is to measure the effective volume of parallel diffusion. This measures the fraction of plasma volume over which the local parallel transport dominates over the perpendicular one in setting the radial transport. Contrary to the volume of chaos, this approach takes into account only sufficiently large resonances that do participate significantly to the radial transport. In this paper, we follow Paul et al. and measure the equilibrium $\beta$
-limit, Loizu et al. used a diagnostic based on the volume of chaos, i.e. the volume of plasma occupied by chaotic field lines, which were identified by measuring their fractal dimension (Meiss Reference Meiss1992). However, this approach is too pessimistic since some chaotic magnetic field lines might be able to preserve confinement (Hudson & Breslau Reference Hudson and Breslau2008). An alternative approach, proposed by Paul, Hudson & Helander (Reference Paul, Hudson and Helander2022), is to measure the effective volume of parallel diffusion. This measures the fraction of plasma volume over which the local parallel transport dominates over the perpendicular one in setting the radial transport. Contrary to the volume of chaos, this approach takes into account only sufficiently large resonances that do participate significantly to the radial transport. In this paper, we follow Paul et al. and measure the equilibrium $\beta$![]() -limit by taking the $\beta$
-limit by taking the $\beta$![]() above which the radial transport generated by damaged magnetic surfaces represents a significant fraction of the total radial transport.
above which the radial transport generated by damaged magnetic surfaces represents a significant fraction of the total radial transport.
This paper is organized as follows. In § 2, the equations solved by SPEC are recalled. In § 3, we construct free-boundary equilibria in a rotating ellipse geometry, and construct a bootstrap current model. In § 4, a new diagnostic is developed to measure the equilibrium $\beta$![]() -limit and compared with the volume of chaos. In § 5, we derive an analytical model to explain the numerically obtained equilibrium $\beta$
-limit and compared with the volume of chaos. In § 5, we derive an analytical model to explain the numerically obtained equilibrium $\beta$![]() -limit. Finally, some concluding remarks are provided in § 6.
-limit. Finally, some concluding remarks are provided in § 6.
2. The stepped-pressure equilibrium code
The code SPEC finds three-dimensional free-boundary magnetohydrodynamic (MHD) equilibria with stepped-pressure profiles. Pressure steps are supported by a finite number of nested toroidal surfaces $\mathcal {I}_l$![]() , thereby defining $N_{{\rm vol}}$
, thereby defining $N_{{\rm vol}}$![]() nested volumes $\mathcal {V}_l$
nested volumes $\mathcal {V}_l$![]() with constant pressure $p_l$
with constant pressure $p_l$![]() , with $l\in \{1,\ldots, N_{{\rm vol}}\}$
, with $l\in \{1,\ldots, N_{{\rm vol}}\}$![]() (see figure 1).
(see figure 1).

Figure 1. Sketch of a SPEC equilibrium with four volumes. The plasma boundary, $\varGamma _{{\rm PB}}=\mathcal {I}_4$![]() , is the dark grey surface and the computational boundary; $\varGamma _{{\rm CB}}$
, is the dark grey surface and the computational boundary; $\varGamma _{{\rm CB}}$![]() , is the light grey surface.
, is the light grey surface.
The magnetic field $\boldsymbol {B}$![]() in each volume is allowed to reconnect and can form magnetic islands and chaotic field lines, while the volume interfaces are constrained to be nested magnetic surfaces. The magnetic field in each volume is a force-free field described by a Taylor state (Taylor Reference Taylor1974, Reference Taylor1986),
in each volume is allowed to reconnect and can form magnetic islands and chaotic field lines, while the volume interfaces are constrained to be nested magnetic surfaces. The magnetic field in each volume is a force-free field described by a Taylor state (Taylor Reference Taylor1974, Reference Taylor1986),
with $\mu _l$![]() a constant specific to the volume $\mathcal {V}_l$
a constant specific to the volume $\mathcal {V}_l$![]() , and the solution to (2.1) depends on the geometry of the interfaces enclosing the volume $\mathcal {V}_l$
, and the solution to (2.1) depends on the geometry of the interfaces enclosing the volume $\mathcal {V}_l$![]() . The code SPEC finds the geometries of interfaces $\mathcal {I}_l$
. The code SPEC finds the geometries of interfaces $\mathcal {I}_l$![]() such that force balance is satisfied,
such that force balance is satisfied,
where $\mu _0$![]() is the vacuum permeability, $p$
is the vacuum permeability, $p$![]() is the pressure and $[[\cdot ]]_l$
is the pressure and $[[\cdot ]]_l$![]() denotes the jump across the interface $\mathcal {I}_l$
denotes the jump across the interface $\mathcal {I}_l$![]() . Equation (2.2) is the local equivalent to the more common force-balance condition $\boldsymbol {j}\times \boldsymbol {B}=\boldsymbol {\nabla } p$
. Equation (2.2) is the local equivalent to the more common force-balance condition $\boldsymbol {j}\times \boldsymbol {B}=\boldsymbol {\nabla } p$![]() .
.
The last interface defines the plasma boundary $\varGamma _{{\rm PB}}$![]() . The plasma is surrounded by a vacuum region (where $p_l=0$
. The plasma is surrounded by a vacuum region (where $p_l=0$![]() and $\mu _l=0$
and $\mu _l=0$![]() ), itself bounded by a computational boundary $\varGamma _{{\rm CB}}$
), itself bounded by a computational boundary $\varGamma _{{\rm CB}}$![]() that lies outside the plasma and inside the coils. The toroidal surface $\varGamma _{{\rm CB}}$
that lies outside the plasma and inside the coils. The toroidal surface $\varGamma _{{\rm CB}}$![]() is an otherwise arbitrary mathematical surface and not necessarily a magnetic surface, i.e. generally $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {n}\neq 0$
is an otherwise arbitrary mathematical surface and not necessarily a magnetic surface, i.e. generally $\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {n}\neq 0$![]() on $\varGamma _{{\rm CB}}$
on $\varGamma _{{\rm CB}}$![]() , with $\boldsymbol {n}$
, with $\boldsymbol {n}$![]() a vector normal to $\varGamma _{{\rm CB}}$
a vector normal to $\varGamma _{{\rm CB}}$![]() . Note that the plasma averaged $\beta$
. Note that the plasma averaged $\beta$![]() is evaluated from a SPEC equilibrium as
is evaluated from a SPEC equilibrium as

with $V$![]() the volume enclosed by $\varGamma _{{\rm PB}}$
the volume enclosed by $\varGamma _{{\rm PB}}$![]() .
.
Free-boundary equilibria are determined by providing the total current flowing through the torus hole, $I_c$![]() , the geometry of the computational boundary, and the harmonics of the vacuum field (produced by the coils) normal to the computational boundary. In addition, SPEC requires as input, in each volume, the enclosed toroidal flux $\psi _{t,l}$
, the geometry of the computational boundary, and the harmonics of the vacuum field (produced by the coils) normal to the computational boundary. In addition, SPEC requires as input, in each volume, the enclosed toroidal flux $\psi _{t,l}$![]() , the pressure $p_l$
, the pressure $p_l$![]() , the net toroidal current within the volume $I^v_{\phi,l}$
, the net toroidal current within the volume $I^v_{\phi,l}$![]() (closely related to the constant $\mu _l$
(closely related to the constant $\mu _l$![]() ), and the net toroidal current flowing at each interface $I^s_{\phi,l}$
), and the net toroidal current flowing at each interface $I^s_{\phi,l}$![]() , which is a surface current.
, which is a surface current.
Volume currents $I^v_{\phi,l}$![]() represent all externally driven currents, such as ohmic current, electron cyclotron current drive or neutral beam current drive. Surface currents $I^s_{\phi,l}$
represent all externally driven currents, such as ohmic current, electron cyclotron current drive or neutral beam current drive. Surface currents $I^s_{\phi,l}$![]() are all pressure-driven currents, such as diamagnetic, Pfirsch–Schlüter or bootstrap current, or island shielding currents. Further details about the SPEC algorithm and implementation can be found in Hudson et al. (Reference Hudson, Dewar, Hole and McGann2012, Reference Hudson, Loizu, Zhu, Qu, Nührenberg, Lazerson, Smiet and Hole2020) and Baillod et al. (Reference Baillod, Loizu, Qu, Kumar and Graves2021).
are all pressure-driven currents, such as diamagnetic, Pfirsch–Schlüter or bootstrap current, or island shielding currents. Further details about the SPEC algorithm and implementation can be found in Hudson et al. (Reference Hudson, Dewar, Hole and McGann2012, Reference Hudson, Loizu, Zhu, Qu, Nührenberg, Lazerson, Smiet and Hole2020) and Baillod et al. (Reference Baillod, Loizu, Qu, Kumar and Graves2021).
3. Rotating ellipse with bootstrap current
We study the case of a rotating ellipse (sometimes also called a classical stellarator) with an analytical bootstrap current model. While a rotating ellipse is arguably a simple geometry, it is still relevant since all stellarators without magnetic axis torsion are rotating ellipses close to the magnetic axis (Helander Reference Helander2014). An experimental instance of rotating ellipse was, for example, the Wendelstein VII-A stellarator (Grieger, Renner & Wobig Reference Grieger, Renner and Wobig1985).
We choose a computational boundary $\varGamma _{{\rm CB}}$![]() (see figure 2) using standard cylindrical coordinates $\boldsymbol {x}=R_{{\rm CB}}(\theta,\phi )\boldsymbol {\hat {e}}_R +Z_{{\rm CB}}(\theta,\phi )\boldsymbol {\hat {e}}_Z$
(see figure 2) using standard cylindrical coordinates $\boldsymbol {x}=R_{{\rm CB}}(\theta,\phi )\boldsymbol {\hat {e}}_R +Z_{{\rm CB}}(\theta,\phi )\boldsymbol {\hat {e}}_Z$![]() , with
, with
with $N_{{\rm fp}}=5$![]() the number of field periods, $R_0=10$
the number of field periods, $R_0=10$![]() m, $R_{10}=-Z_{10}=1$
m, $R_{10}=-Z_{10}=1$![]() m, $R_{11}=Z_{11}=0.25$
m, $R_{11}=Z_{11}=0.25$![]() m. The effective minor radius is $a_{\text {eff}}=\sqrt {r_{\min }r_{\max }}$
m. The effective minor radius is $a_{\text {eff}}=\sqrt {r_{\min }r_{\max }}$![]() with $r_{\min }=R_{10}-R_{11}$
with $r_{\min }=R_{10}-R_{11}$![]() and $r_{\max }=R_{10}+R_{11}$
and $r_{\max }=R_{10}+R_{11}$![]() the minor and major radii of the ellipse, respectively. We define $\epsilon _a=a_{\text {eff}}/R_0$
the minor and major radii of the ellipse, respectively. We define $\epsilon _a=a_{\text {eff}}/R_0$![]() as the inverse aspect ratio at the plasma boundary.
as the inverse aspect ratio at the plasma boundary.
We assume that a coil system exists such that $\boldsymbol {B}_c\boldsymbol {\cdot }\boldsymbol {n}=B_v\hat {\boldsymbol {e}}_z\boldsymbol {\cdot }\boldsymbol {n}$![]() on $\varGamma _{{\rm CB}}$
on $\varGamma _{{\rm CB}}$![]() , where $\boldsymbol {B}_c$
, where $\boldsymbol {B}_c$![]() is the magnetic field produced by the coils, and $B_v\hat {\boldsymbol {e}}_z$
is the magnetic field produced by the coils, and $B_v\hat {\boldsymbol {e}}_z$![]() is a constant vertical field, which is applied to keep the plasma within the computational boundary at high $\beta$
is a constant vertical field, which is applied to keep the plasma within the computational boundary at high $\beta$![]() . We set $B_v=-0.03$
. We set $B_v=-0.03$![]() T. This vertical field has little to no impact on the results presented hereafter; its only purpose is to keep the plasma within the volume defined by $\varGamma _{{\rm CB}}$
T. This vertical field has little to no impact on the results presented hereafter; its only purpose is to keep the plasma within the volume defined by $\varGamma _{{\rm CB}}$![]() . We fix the total current flowing in the torus hole to $I_c=17.1$
. We fix the total current flowing in the torus hole to $I_c=17.1$![]() MA, which determines the toroidal flux enclosed by the computational boundary, $\psi _{t,V}=1\,\text {Tm}^2$
MA, which determines the toroidal flux enclosed by the computational boundary, $\psi _{t,V}=1\,\text {Tm}^2$![]() .
.
We choose a pressure profile with a linear dependence on the toroidal flux, i.e. $p=p_0(1-\psi _t/\psi _a)$![]() , with $p_0$
, with $p_0$![]() a free parameter and $\psi _a=0.25\,\text {Tm}^2$
a free parameter and $\psi _a=0.25\,\text {Tm}^2$![]() the total toroidal flux enclosed by the plasma boundary $\varGamma _{{\rm PB}}$
the total toroidal flux enclosed by the plasma boundary $\varGamma _{{\rm PB}}$![]() . We approximate the pressure profile with seven steps of equal magnitude $[[p]]_l=p_0/N_{{\rm vol}}$
. We approximate the pressure profile with seven steps of equal magnitude $[[p]]_l=p_0/N_{{\rm vol}}$![]() . We thus define seven plasma regions, i.e. $N_{{\rm vol}}=7$
. We thus define seven plasma regions, i.e. $N_{{\rm vol}}=7$![]() , surrounded by a vacuum region. This means that $\psi _{t,l}=(l-1)\psi _a / N_{{\rm vol}}$
, surrounded by a vacuum region. This means that $\psi _{t,l}=(l-1)\psi _a / N_{{\rm vol}}$![]() and $p_l=p(\psi _{t,l})$
and $p_l=p(\psi _{t,l})$![]() . The number of volumes determines how the pressure profile is represented – more volumes means more and smaller pressure steps. As each interface is a discrete constraint on the magnetic topology, increasing the number of volumes reduces the available space for reconnection and thus the maximum size of magnetic islands and regions of magnetic field line chaos. In this paper, we are, however, interested in the onset of loss of magnetic surfaces, which is not affected by the volume available for islands to grow. Therefore, our results only depend weakly on the number of volumes (see the Appendix).
. The number of volumes determines how the pressure profile is represented – more volumes means more and smaller pressure steps. As each interface is a discrete constraint on the magnetic topology, increasing the number of volumes reduces the available space for reconnection and thus the maximum size of magnetic islands and regions of magnetic field line chaos. In this paper, we are, however, interested in the onset of loss of magnetic surfaces, which is not affected by the volume available for islands to grow. Therefore, our results only depend weakly on the number of volumes (see the Appendix).
Two current profiles have to be provided to SPEC: the profile of volume currents, $\{I^v_{\phi,l}\}$![]() , and the profile of surface currents $\{I^s_{\phi,l}\}$
, and the profile of surface currents $\{I^s_{\phi,l}\}$![]() (see § 2). Here we study the case of an equilibrium with zero externally driven currents and with bootstrap current. No externally driven currents implies, in SPEC, that there are no currents in the plasma volumes, i.e.
(see § 2). Here we study the case of an equilibrium with zero externally driven currents and with bootstrap current. No externally driven currents implies, in SPEC, that there are no currents in the plasma volumes, i.e.
The bootstrap current is a pressure-driven current, and is consequently described by a surface current at the volume's interfaces. We model it with

where $(\psi _t / \psi _a)^{1/4}\approx \sqrt {\epsilon /\epsilon _a}$![]() is related to the fraction of trapped particles, with $\epsilon$
is related to the fraction of trapped particles, with $\epsilon$![]() the inverse aspect ratio; $[[p]]_l$
the inverse aspect ratio; $[[p]]_l$![]() is a measure of the local pressure gradient; and $C$
is a measure of the local pressure gradient; and $C$![]() is a coupling constant, in $[{\rm APa}^{-1}]$
is a coupling constant, in $[{\rm APa}^{-1}]$![]() , which controls the strength of the bootstrap current in the system. A full neoclassical calculation of the bootstrap current, for example with the SFINCS code (Landreman et al. Reference Landreman, Smith, Mollén and Helander2014), would require the density and temperature profiles as inputs – and the freedom in the choice of the coupling constant $C$
, which controls the strength of the bootstrap current in the system. A full neoclassical calculation of the bootstrap current, for example with the SFINCS code (Landreman et al. Reference Landreman, Smith, Mollén and Helander2014), would require the density and temperature profiles as inputs – and the freedom in the choice of the coupling constant $C$![]() reflects the freedom in these profiles.
reflects the freedom in these profiles.
The current density associated with the current in (3.4) is

Note that if
with $\iota \hspace {-0.4em}\text {-}_v$![]() the edge rotational transform in vacuum and $B_0$
the edge rotational transform in vacuum and $B_0$![]() such that $\mu _0I_c= 2{\rm \pi} R_0 B_0$
such that $\mu _0I_c= 2{\rm \pi} R_0 B_0$![]() , (3.5) reduces to the well-known large-aspect ratio tokamak bootstrap current approximation (Helander & Sigmar Reference Helander and Sigmar2002),
, (3.5) reduces to the well-known large-aspect ratio tokamak bootstrap current approximation (Helander & Sigmar Reference Helander and Sigmar2002),
where $\psi _p$![]() is the poloidal flux, and we made the approximation ${\rm d}\psi _p/{\rm d}\psi _t=\iota \hspace {-0.4em}\text {-}\approx \iota \hspace {-0.4em}\text {-}_v$
is the poloidal flux, and we made the approximation ${\rm d}\psi _p/{\rm d}\psi _t=\iota \hspace {-0.4em}\text {-}\approx \iota \hspace {-0.4em}\text {-}_v$![]() . We normalize $C$
. We normalize $C$![]() by $C_0$
by $C_0$![]() , and define $\hat {C}\equiv C / C_0$
, and define $\hat {C}\equiv C / C_0$![]() . In the case of a large aspect ratio circular tokamak, we thus have $\hat C = 1$
. In the case of a large aspect ratio circular tokamak, we thus have $\hat C = 1$![]() , while in a stellarator with no bootstrap current, $\hat C=0$
, while in a stellarator with no bootstrap current, $\hat C=0$![]() .
.
We use the recently implemented capability of SPEC to prescribe the toroidal current profile (Baillod et al. Reference Baillod, Loizu, Qu, Kumar and Graves2021), with the profiles defined in (3.3) and (3.4). Unless stated otherwise, the Fourier resolution used in all results presented in this paper is $|n|\leq N=12$![]() , $m\leq M=12$
, $m\leq M=12$![]() , with $n$
, with $n$![]() the toroidal mode number and $m$
the toroidal mode number and $m$![]() the poloidal mode number, meaning that $2[N+M(2N+1)]+1=625$
the poloidal mode number, meaning that $2[N+M(2N+1)]+1=625$![]() Fourier modes are used to describe each interface geometry. Results presented in this paper have been checked for convergence with respect to Fourier resolution (see the Appendix).
Fourier modes are used to describe each interface geometry. Results presented in this paper have been checked for convergence with respect to Fourier resolution (see the Appendix).
In summary, we can construct free-boundary SPEC equilibria with a simple bootstrap current model and we are left with two free parameters, namely (i) $\beta$![]() which controls the total pressure in the system and (ii) $\hat {C}$
which controls the total pressure in the system and (ii) $\hat {C}$![]() , a dimensionless parameter, that controls the bootstrap current strength for a given plasma $\beta$
, a dimensionless parameter, that controls the bootstrap current strength for a given plasma $\beta$![]() .
.
3.1. Scans over $\hat {C}$ and $\beta$
and $\beta$
A scan has been performed with $\beta \in [0,2\,\%]$![]() and $\hat {C}\in [0,2.26]$
and $\hat {C}\in [0,2.26]$![]() representing $680$
representing $680$![]() SPEC calculations, each requiring approximately $24$
SPEC calculations, each requiring approximately $24$![]() CPU-hours on the MARCONI clusterFootnote 1 . Figure 3 shows some selected Poincaré sections at different values of $\beta$
CPU-hours on the MARCONI clusterFootnote 1 . Figure 3 shows some selected Poincaré sections at different values of $\beta$![]() and $\hat {C}$
and $\hat {C}$![]() , while figure 4 shows the edge rotational transform, i.e. the rotational transform on the outer side of $\varGamma _{{\rm PB}}$
, while figure 4 shows the edge rotational transform, i.e. the rotational transform on the outer side of $\varGamma _{{\rm PB}}$![]() , as a function of $\beta$
, as a function of $\beta$![]() for four different values of $\hat {C}$
for four different values of $\hat {C}$![]() .
.

Figure 3. Poincaré plot (black dots) of equilibria at toroidal angle $\phi =0$![]() and at different values of $(\beta,\hat {C})$
and at different values of $(\beta,\hat {C})$![]() : (a,c,e) $\hat {C}=0.46$
: (a,c,e) $\hat {C}=0.46$![]() ; (b,d,f) $\hat {C}=0.91$
; (b,d,f) $\hat {C}=0.91$![]() . Red lines, inner plasma volume interfaces; blue line, plasma boundary; yellow line, computational boundary.
. Red lines, inner plasma volume interfaces; blue line, plasma boundary; yellow line, computational boundary.

Figure 4. Edge rotational transform, $\iota \hspace {-0.4em}\text {-}_a$![]() , as a function of plasma average $\beta$
, as a function of plasma average $\beta$![]() , for different values of $\hat {C}$
, for different values of $\hat {C}$![]() ; stars, circles, crosses and squares are SPEC calculations while full lines are given by (5.1).
; stars, circles, crosses and squares are SPEC calculations while full lines are given by (5.1).
For small values of $\hat {C}$![]() , namely for $\hat {C} < \hat {C}_{{\rm crit}}\approx 0.59$
, namely for $\hat {C} < \hat {C}_{{\rm crit}}\approx 0.59$![]() , the edge rotational transform decreases with increasing $\beta$
, the edge rotational transform decreases with increasing $\beta$![]() and eventually reaches zero (figure 4, black stars and red dots), at which point an $m=1,\ n=0$
and eventually reaches zero (figure 4, black stars and red dots), at which point an $m=1,\ n=0$![]() island opens and forms a separatrix at the plasma boundary (see figure 3a,c,e). We will refer to this $\beta$
island opens and forms a separatrix at the plasma boundary (see figure 3a,c,e). We will refer to this $\beta$![]() -limit as the ideal equilibrium $\beta$
-limit as the ideal equilibrium $\beta$![]() -limit, denoted by $\beta _{{\rm lim}}^{{\rm ideal}}$
-limit, denoted by $\beta _{{\rm lim}}^{{\rm ideal}}$![]() , since it is well described by ideal MHD theory (see § 5.1). The value of $\beta ^{{\rm ideal}}_{{\rm lim}}$
, since it is well described by ideal MHD theory (see § 5.1). The value of $\beta ^{{\rm ideal}}_{{\rm lim}}$![]() obtained with SPEC is shown as a function of $\hat {C}$
obtained with SPEC is shown as a function of $\hat {C}$![]() in figure 5 (black triangles).
in figure 5 (black triangles).

Figure 5. Equilibrium $\beta$![]() -limit as a function of $\hat {C}$
-limit as a function of $\hat {C}$![]() : black triangles, ideal equilibrium $\beta$
: black triangles, ideal equilibrium $\beta$![]() -limit, $\beta _{{\rm lim}}^{{\rm ideal}}$
-limit, $\beta _{{\rm lim}}^{{\rm ideal}}$![]() , as obtained from SPEC; solid black line, analytical prediction for $\beta _{{\rm lim}}^{{\rm ideal}}$
, as obtained from SPEC; solid black line, analytical prediction for $\beta _{{\rm lim}}^{{\rm ideal}}$![]() from (5.6); the dashed vertical line indicates the analytical value of $\hat {C}_{{\rm crit}}$
from (5.6); the dashed vertical line indicates the analytical value of $\hat {C}_{{\rm crit}}$![]() from (5.7); red dots, values of the chaotic equilibrium $\beta$
from (5.7); red dots, values of the chaotic equilibrium $\beta$![]() -limit, $\beta _{{\rm lim}}^{{\rm chaos}}$
-limit, $\beta _{{\rm lim}}^{{\rm chaos}}$![]() , obtained from SPEC for $B_{r,{\rm crit}}/B=10^{-5}$
, obtained from SPEC for $B_{r,{\rm crit}}/B=10^{-5}$![]() ; the red area shows the range obtained from SPEC for $B_{r,{\rm crit}}/B\in [10^{-6},10^{-4}]$
; the red area shows the range obtained from SPEC for $B_{r,{\rm crit}}/B\in [10^{-6},10^{-4}]$![]() ; solid red line, analytical prediction for $\beta _{{\rm lim}}^{{\rm chaos}}$
; solid red line, analytical prediction for $\beta _{{\rm lim}}^{{\rm chaos}}$![]() obtained by solving (5.10); blue squares, SPEC values for which $\iota \hspace {-0.4em}\text {-}_a=2\iota \hspace {-0.4em}\text {-}_v$
obtained by solving (5.10); blue squares, SPEC values for which $\iota \hspace {-0.4em}\text {-}_a=2\iota \hspace {-0.4em}\text {-}_v$![]() .
.
The ideal equilibrium $\beta$![]() -limit can also be observed in tokamaks, although the underlying mechanism is different. In a tokamak, the plasma may be kept centred by applying a vertical magnetic field $B_Z$
-limit can also be observed in tokamaks, although the underlying mechanism is different. In a tokamak, the plasma may be kept centred by applying a vertical magnetic field $B_Z$![]() . As $\beta$
. As $\beta$![]() grows, $B_Z$
grows, $B_Z$![]() has to be increased, until it compensates the poloidal field $\boldsymbol {B}_p$
has to be increased, until it compensates the poloidal field $\boldsymbol {B}_p$![]() on the high field side. When this happens, the field is purely toroidal and a separatrix opens. In a stellarator, the poloidal magnetic field does not have to cancel everywhere for a separatrix to open, it merely has to be such that a field line never completes a poloidal turn. If this happens, the edge rotational transform is zero and a separatrix opens. In our calculations, the net toroidal current is constrained in the plasma volumes and at the interfaces. However, the actual dependencies of the current density on the toroidal and poloidal angle are unconstrained. Pfirsch–Schlüter and diamagnetic currents angular dependencies are the source of the poloidal magnetic field perturbation, the lowering of the edge rotational transform, and ultimately the opening of the separatrix. This is why, even in a zero net-toroidal-current stellarator ($\hat {C}=0$
on the high field side. When this happens, the field is purely toroidal and a separatrix opens. In a stellarator, the poloidal magnetic field does not have to cancel everywhere for a separatrix to open, it merely has to be such that a field line never completes a poloidal turn. If this happens, the edge rotational transform is zero and a separatrix opens. In our calculations, the net toroidal current is constrained in the plasma volumes and at the interfaces. However, the actual dependencies of the current density on the toroidal and poloidal angle are unconstrained. Pfirsch–Schlüter and diamagnetic currents angular dependencies are the source of the poloidal magnetic field perturbation, the lowering of the edge rotational transform, and ultimately the opening of the separatrix. This is why, even in a zero net-toroidal-current stellarator ($\hat {C}=0$![]() ), the edge rotational transform reaches zero.
), the edge rotational transform reaches zero.
For values of $\hat {C}>\hat {C}_{{\rm crit}}$![]() , the (now strong enough) bootstrap current is able to prevent the edge rotational transform from reaching zero for any $\beta$
, the (now strong enough) bootstrap current is able to prevent the edge rotational transform from reaching zero for any $\beta$![]() , and hence no $m=1,\ n=0$
, and hence no $m=1,\ n=0$![]() island appears anywhere (see the blue crosses and green squares in figure 4). Instead, the edge rotational transform increases until many island chains open in the plasma and in the vacuum region (figure 3b,d,f). When these islands are large enough to have a significant impact on the radial transport, the chaotic equilibrium $\beta$
island appears anywhere (see the blue crosses and green squares in figure 4). Instead, the edge rotational transform increases until many island chains open in the plasma and in the vacuum region (figure 3b,d,f). When these islands are large enough to have a significant impact on the radial transport, the chaotic equilibrium $\beta$![]() -limit is reached, denoted by $\beta _{{\rm lim}}^{{\rm chaos}}$
-limit is reached, denoted by $\beta _{{\rm lim}}^{{\rm chaos}}$![]() . Finally, for all values of $\hat {C}$
. Finally, for all values of $\hat {C}$![]() , islands start to overlap and generate large regions of chaotic field lines at sufficiently large values of $\beta$
, islands start to overlap and generate large regions of chaotic field lines at sufficiently large values of $\beta$![]() (figure 3e,f). In § 4, a diagnostic to measure the critical value of $\beta$
(figure 3e,f). In § 4, a diagnostic to measure the critical value of $\beta$![]() at which the chaotic equilibrium $\beta$
at which the chaotic equilibrium $\beta$![]() -limit is reached will be presented, and an analytical model that explain the results will be derived in § 5.2.
-limit is reached will be presented, and an analytical model that explain the results will be derived in § 5.2.
It may be argued that volume interfaces might not be able to support the pressure if islands or chaos are close by (see, for example, figure 3f) – i.e. that SPEC equilibria might not be trusted at large $\beta$![]() without further analyses. This question has been thoroughly studied in slab geometry by Qu et al. (Reference Qu, Hudson, Dewar, Loizu and Hole2021). They identified two reasons why a solution might not exist.
without further analyses. This question has been thoroughly studied in slab geometry by Qu et al. (Reference Qu, Hudson, Dewar, Loizu and Hole2021). They identified two reasons why a solution might not exist.
The first possibility is that the magnetic surface does not exist, in particular that it is fractal. In our calculations above the equilibrium $\beta$![]() -limit, large magnetic islands and chaotic regions develop close to volume interfaces. In this situation, it is indeed not known if the solution exists and additional analyses would be required, for example with convergence studies as proposed by Qu et al. (Reference Qu, Hudson, Dewar, Loizu and Hole2021). Below the equilibrium $\beta$
-limit, large magnetic islands and chaotic regions develop close to volume interfaces. In this situation, it is indeed not known if the solution exists and additional analyses would be required, for example with convergence studies as proposed by Qu et al. (Reference Qu, Hudson, Dewar, Loizu and Hole2021). Below the equilibrium $\beta$![]() -limit, however, only small islands are present. The interfaces are not perturbed by neighbouring, large magnetic islands, and it is likely that the volume interfaces are magnetic surfaces. Since we are only interested in computing the equilibrium $\beta$
-limit, however, only small islands are present. The interfaces are not perturbed by neighbouring, large magnetic islands, and it is likely that the volume interfaces are magnetic surfaces. Since we are only interested in computing the equilibrium $\beta$![]() -limit, it is sufficient to calculate equilibria below or equal to the equilibrium $\beta$
-limit, it is sufficient to calculate equilibria below or equal to the equilibrium $\beta$![]() -limit; larger $\beta$
-limit; larger $\beta$![]() equilibria are irrelevant, and thus the question of existence of interfaces is eluded. In practice, we observe that large magnetic islands and chaotic field lines get close to the volume interfaces only for equilibria with $\beta$
equilibria are irrelevant, and thus the question of existence of interfaces is eluded. In practice, we observe that large magnetic islands and chaotic field lines get close to the volume interfaces only for equilibria with $\beta$![]() sufficiently large to trust the results presented in this paper. Nevertheless, convergence studies have been performed, and results presented in this paper have been shown to be spectrally converged (see the Appendix).
sufficiently large to trust the results presented in this paper. Nevertheless, convergence studies have been performed, and results presented in this paper have been shown to be spectrally converged (see the Appendix).
The second possibility is that the pressure jump on an interface is too large and a solution to the force-balance equation (2.2) does not exist. This is a possible explanation for when SPEC does not find an interface geometry that satisfies the force balance equation (2.2). However, in our calculations, SPEC finds magnetic geometries that do satisfy force balance. This means that the pressure jump across the interfaces is small enough and a solution exists. To summarize this discussion, we can trust the SPEC solutions presented in this paper.
4. Measure of magnetic chaos and its effect on radial transport
4.1. Fractal dimension, volume of chaos
One approach to discriminate between a chaotic field line and other magnetic field line topologies is to evaluate the fractal dimension $D$![]() of the field line Poincaré section, for example using a box-counting algorithm (Meiss Reference Meiss1992). An almost binary behaviour is then observed: either a magnetic field line stays on a magnetic surface whose Poincaré section is a one-dimensional object, $D=1$
of the field line Poincaré section, for example using a box-counting algorithm (Meiss Reference Meiss1992). An almost binary behaviour is then observed: either a magnetic field line stays on a magnetic surface whose Poincaré section is a one-dimensional object, $D=1$![]() , or the magnetic field line has a fractal dimension $D>D_{{\rm crit}}$
, or the magnetic field line has a fractal dimension $D>D_{{\rm crit}}$![]() , with $1< D_{{\rm crit}}<2$
, with $1< D_{{\rm crit}}<2$![]() . In our case, we observe that $D_{{\rm crit}}=1.3$
. In our case, we observe that $D_{{\rm crit}}=1.3$![]() can be used to differentiate between magnetic surfaces and chaos. Loizu et al. (Reference Loizu, Hudson, Nührenberg, Geiger and Helander2017) proposed to evaluate the volume occupied by chaotic field lines with
can be used to differentiate between magnetic surfaces and chaos. Loizu et al. (Reference Loizu, Hudson, Nührenberg, Geiger and Helander2017) proposed to evaluate the volume occupied by chaotic field lines with

where $N_{{\rm lines}}$![]() is the number of considered field lines, $D_i$
is the number of considered field lines, $D_i$![]() is the fractal dimension of the $i$
is the fractal dimension of the $i$![]() th line, $\mathcal {H}$
th line, $\mathcal {H}$![]() is the Heaviside function, $V_{{\rm total}}$
is the Heaviside function, $V_{{\rm total}}$![]() is the total plasma volume, and $\psi _{t,i}-\psi _{t,i-1}$
is the total plasma volume, and $\psi _{t,i}-\psi _{t,i-1}$![]() measures the enclosed toroidal flux between field lines $i$
measures the enclosed toroidal flux between field lines $i$![]() and $i-1$
and $i-1$![]() .
.
The chaotic equilibrium $\beta$![]() -limit could then be defined as the $\beta$
-limit could then be defined as the $\beta$![]() above which $V_{{\rm chaos}}>0$
above which $V_{{\rm chaos}}>0$![]() . The volume of chaos, however, while very useful as a measure of the number of chaotic field lines, does not provide enough information about whether or not the radial transport is enhanced by the destruction of magnetic surfaces. In addition, the volume of chaos is sensitive to the numerical resolution of the equilibrium – the larger the number of Fourier modes, the greater the number of potential resonances in the equilibrium. Due to overlap between small islands chains generated by high-order rationals, chaos may emerge at smaller $\beta$
. The volume of chaos, however, while very useful as a measure of the number of chaotic field lines, does not provide enough information about whether or not the radial transport is enhanced by the destruction of magnetic surfaces. In addition, the volume of chaos is sensitive to the numerical resolution of the equilibrium – the larger the number of Fourier modes, the greater the number of potential resonances in the equilibrium. Due to overlap between small islands chains generated by high-order rationals, chaos may emerge at smaller $\beta$![]() as the Fourier resolution is increased. For example, in figure 6 the volume of chaos is plotted as a function of $\beta$
as the Fourier resolution is increased. For example, in figure 6 the volume of chaos is plotted as a function of $\beta$![]() for two different Fourier resolutions, $M=N=8$
for two different Fourier resolutions, $M=N=8$![]() and $M=N=10$
and $M=N=10$![]() (blue lines). We see that with this diagnostic, the measured chaotic equilibrium $\beta$
(blue lines). We see that with this diagnostic, the measured chaotic equilibrium $\beta$![]() -limit would drop from ${\sim }1.5\,\%$
-limit would drop from ${\sim }1.5\,\%$![]() to ${\sim }1\,\%$
to ${\sim }1\,\%$![]() if it were defined as the $\beta$
if it were defined as the $\beta$![]() above which $V_{{\rm chaos}}>0$
above which $V_{{\rm chaos}}>0$![]() . However, in the $M=N=10$
. However, in the $M=N=10$![]() scan, some of the chaotic field lines are formed by high-order rationals and their associated smaller islands are expected to participate weakly with the radial transport, and could potentially be ignored. An alternative diagnostic that takes into account the effect of the magnetic field lines topology on the radial transport is thus required.
scan, some of the chaotic field lines are formed by high-order rationals and their associated smaller islands are expected to participate weakly with the radial transport, and could potentially be ignored. An alternative diagnostic that takes into account the effect of the magnetic field lines topology on the radial transport is thus required.

Figure 6. Here $V_{{\rm chaos}}/V_{{\rm total}}$![]() (blue), and $f_{{\rm PD}}$
(blue), and $f_{{\rm PD}}$![]() evaluated for $B_{r,{\rm crit}}/B=10^{-5}$
evaluated for $B_{r,{\rm crit}}/B=10^{-5}$![]() (red) versus plasma averaged $\beta$
(red) versus plasma averaged $\beta$![]() , for $M=N=8$
, for $M=N=8$![]() (crosses) and $M=N=10$
(crosses) and $M=N=10$![]() (circles).
(circles).
4.2. Fraction of effective parallel diffusion
We discuss an alternative measure to the volume of chaos to determine if the destruction of magnetic surfaces significantly impacts the radial transport. Here the parallel and perpendicular direction are defined as the direction along and across the magnetic field, respectively, and the radial direction $r$![]() as the direction perpendicular to isotherms, $\boldsymbol {\nabla } T\times \boldsymbol {\nabla } r=0$
as the direction perpendicular to isotherms, $\boldsymbol {\nabla } T\times \boldsymbol {\nabla } r=0$![]() , with $T$
, with $T$![]() the temperature. In recent work, Paul et al. (Reference Paul, Hudson and Helander2022) discussed the properties of the anisotropic heat diffusion equation, $\boldsymbol {\nabla }\boldsymbol {\cdot }(\kappa _\parallel T + \kappa _\perp T)=0$
the temperature. In recent work, Paul et al. (Reference Paul, Hudson and Helander2022) discussed the properties of the anisotropic heat diffusion equation, $\boldsymbol {\nabla }\boldsymbol {\cdot }(\kappa _\parallel T + \kappa _\perp T)=0$![]() , where $\kappa _\parallel$
, where $\kappa _\parallel$![]() and $\kappa _\perp$
and $\kappa _\perp$![]() are the parallel and perpendicular heat conductivities. In particular, Paul et al. demonstrated that, under the assumption that $\boldsymbol {\kappa }$
are the parallel and perpendicular heat conductivities. In particular, Paul et al. demonstrated that, under the assumption that $\boldsymbol {\kappa }$![]() and $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\kappa }$
and $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\kappa }$![]() are analytical, isotherms are topologically constrained to be toroidal surfaces – this forbids isotherms to align with the magnetic field in regions occupied by magnetic islands and magnetic field line chaos. Here $\boldsymbol {\kappa }$
are analytical, isotherms are topologically constrained to be toroidal surfaces – this forbids isotherms to align with the magnetic field in regions occupied by magnetic islands and magnetic field line chaos. Here $\boldsymbol {\kappa }$![]() is the diffusion tensor, defined as $\boldsymbol {\kappa }=\kappa _\perp \boldsymbol {I}+(\kappa _\parallel -\kappa _\perp )\boldsymbol {B}\boldsymbol {B}/B^2$
is the diffusion tensor, defined as $\boldsymbol {\kappa }=\kappa _\perp \boldsymbol {I}+(\kappa _\parallel -\kappa _\perp )\boldsymbol {B}\boldsymbol {B}/B^2$![]() , with $\boldsymbol {I}$
, with $\boldsymbol {I}$![]() the identity tensor. Motivated by comparing the local parallel diffusion with the local perpendicular diffusion, Paul et al. introduced the volume of effective parallel diffusion, which is the volume of plasma where the parallel heat transport dominates perpendicular heat transport,
the identity tensor. Motivated by comparing the local parallel diffusion with the local perpendicular diffusion, Paul et al. introduced the volume of effective parallel diffusion, which is the volume of plasma where the parallel heat transport dominates perpendicular heat transport,
where the parallel and perpendicular gradients are defined as $\boldsymbol {\nabla }_\parallel =\boldsymbol {B}(\boldsymbol {B}\boldsymbol {\cdot }\boldsymbol {\nabla }) / B^2$![]() and $\boldsymbol {\nabla }_\perp =\boldsymbol {\nabla }-\boldsymbol {\nabla }_\parallel$
and $\boldsymbol {\nabla }_\perp =\boldsymbol {\nabla }-\boldsymbol {\nabla }_\parallel$![]() , respectively. In regions occupied by magnetic islands and magnetic field line chaos, the constraint on the isotherms topology implies that the magnetic field has a non-zero radial component, thus $\boldsymbol {\nabla }_\parallel T> 0$
, respectively. In regions occupied by magnetic islands and magnetic field line chaos, the constraint on the isotherms topology implies that the magnetic field has a non-zero radial component, thus $\boldsymbol {\nabla }_\parallel T> 0$![]() . Depending on the ratio $\kappa _\parallel / \kappa _\perp$
. Depending on the ratio $\kappa _\parallel / \kappa _\perp$![]() , the volume of effective parallel diffusion can then be greater than zero. On the contrary, in regions occupied by magnetic surfaces, isotherms largely coincide with magnetic surfaces, which means that $\boldsymbol {\nabla }_\parallel T$
, the volume of effective parallel diffusion can then be greater than zero. On the contrary, in regions occupied by magnetic surfaces, isotherms largely coincide with magnetic surfaces, which means that $\boldsymbol {\nabla }_\parallel T$![]() is negligible, and consequently the volume $\mathcal {V}_{{\rm PD}}$
is negligible, and consequently the volume $\mathcal {V}_{{\rm PD}}$![]() is zero. Leveraging these properties, we can define the chaotic equilibrium $\beta$
is zero. Leveraging these properties, we can define the chaotic equilibrium $\beta$![]() -limit as the $\beta$
-limit as the $\beta$![]() above which $V_{{\rm PD}}>0$
above which $V_{{\rm PD}}>0$![]() .
.
To determine the chaotic equilibrium $\beta$![]() -limit, it is only required to determine if $V_{{\rm PD}}$
-limit, it is only required to determine if $V_{{\rm PD}}$![]() is zero or not; its absolute value is irrelevant. We thus construct a proxy function for $V_{{\rm PD}}$
is zero or not; its absolute value is irrelevant. We thus construct a proxy function for $V_{{\rm PD}}$![]() that does not depend on the temperature profile, but only on the magnetic field. We start by noticing that the Heaviside function in (4.2) is greater than zero when $\kappa _\parallel |\boldsymbol {\nabla }_\parallel T|^2\ge \kappa _\perp |\boldsymbol {\nabla }_\perp T |^2$
that does not depend on the temperature profile, but only on the magnetic field. We start by noticing that the Heaviside function in (4.2) is greater than zero when $\kappa _\parallel |\boldsymbol {\nabla }_\parallel T|^2\ge \kappa _\perp |\boldsymbol {\nabla }_\perp T |^2$![]() . As we expect the radial magnetic field to be small in comparison with the total magnetic field, $B_r\ll B$
. As we expect the radial magnetic field to be small in comparison with the total magnetic field, $B_r\ll B$![]() , we can write $\boldsymbol {\nabla }_\parallel T\sim \boldsymbol {\nabla } T B_r /B$
, we can write $\boldsymbol {\nabla }_\parallel T\sim \boldsymbol {\nabla } T B_r /B$![]() , and $\boldsymbol {\nabla }_\perp T\sim \boldsymbol {\nabla } T$
, and $\boldsymbol {\nabla }_\perp T\sim \boldsymbol {\nabla } T$![]() . The volume of effective parallel diffusion is then greater than zero if there is a finite volume where
. The volume of effective parallel diffusion is then greater than zero if there is a finite volume where

Considering the electron heat transport as a figure of merit for the confinement properties of the equilibrium, and using the Spitzer–Härm conductivity for $\kappa _{\parallel,e}$![]() (Braginskii Reference Braginskii1965), we get
(Braginskii Reference Braginskii1965), we get

where $\log \varLambda$![]() is the Coulomb logarithm, and typically $\chi _{\perp,e}=\kappa _{\perp,e}/n_e\sim 1\,\text {m}^2\,\text {s}^{-1}$
is the Coulomb logarithm, and typically $\chi _{\perp,e}=\kappa _{\perp,e}/n_e\sim 1\,\text {m}^2\,\text {s}^{-1}$![]() . Here everything is to be expressed in SI units except $T_e$
. Here everything is to be expressed in SI units except $T_e$![]() , which is in $eV$
, which is in $eV$![]() . For temperatures and densities between $1$
. For temperatures and densities between $1$![]() to 10 keV and $10^{19}$
to 10 keV and $10^{19}$![]() to $10^{20}\,\text {m}^{-3}$
to $10^{20}\,\text {m}^{-3}$![]() , respectively, $B_{r,{\rm crit}}/B$
, respectively, $B_{r,{\rm crit}}/B$![]() ranges from $10^{-6}$
ranges from $10^{-6}$![]() to $10^{-4}$
to $10^{-4}$![]() . For example using typical values for W7-X high performance experiments (Klinger et al. Reference Klinger, Andreeva, Bozhenkov, Brandt, Burhenn, Buttenschön, Fuchert, Geiger, Grulke and Laqua2019), i.e. $n_e=4\times 10^{19}\,\text {m}^{-3}$
. For example using typical values for W7-X high performance experiments (Klinger et al. Reference Klinger, Andreeva, Bozhenkov, Brandt, Burhenn, Buttenschön, Fuchert, Geiger, Grulke and Laqua2019), i.e. $n_e=4\times 10^{19}\,\text {m}^{-3}$![]() , $T_e=5\,\text {keV}$
, $T_e=5\,\text {keV}$![]() , we obtain a critical normalized radial magnetic field of $B_{r,{\rm crit}}/B\sim 10^{-5}$
, we obtain a critical normalized radial magnetic field of $B_{r,{\rm crit}}/B\sim 10^{-5}$![]() . As a side note, we remark that the criterion (4.3) can also be derived by considering the radial heat diffusion equation for electrons, $q_r = -\kappa _{\perp,e} (\boldsymbol {\nabla }_\perp T_e)_r - \kappa _{\parallel,e} (\boldsymbol {\nabla }_\parallel T_e)_r \sim -\kappa _{\perp,e} \,{\rm d} T_e/{\rm d} r -\kappa _{\parallel,e} \,{\rm d} T_e/{\rm d} r B_r^2/B^2$
. As a side note, we remark that the criterion (4.3) can also be derived by considering the radial heat diffusion equation for electrons, $q_r = -\kappa _{\perp,e} (\boldsymbol {\nabla }_\perp T_e)_r - \kappa _{\parallel,e} (\boldsymbol {\nabla }_\parallel T_e)_r \sim -\kappa _{\perp,e} \,{\rm d} T_e/{\rm d} r -\kappa _{\parallel,e} \,{\rm d} T_e/{\rm d} r B_r^2/B^2$![]() . Magnetic islands and chaos play then an important role in setting the local heat radial transport when the second term on the right-hand side of the heat diffusion equation is larger than the first one, which occurs when $B_r^2/B^2\ge \kappa _\perp /\kappa _\parallel$
. Magnetic islands and chaos play then an important role in setting the local heat radial transport when the second term on the right-hand side of the heat diffusion equation is larger than the first one, which occurs when $B_r^2/B^2\ge \kappa _\perp /\kappa _\parallel$![]() , recovering (4.3).
, recovering (4.3).
The volume of effective parallel diffusion can thus be written using the criterion (4.3),

This measure is, however, unpractical for the purpose of this paper, as it would require us to evaluate the radial magnetic field everywhere in the plasma. Instead, the radial magnetic field is evaluated where it is expected to be the largest, i.e. on a selected number of rational surfaces. We then construct the fraction of parallel diffusion,

where $N_{{\rm res}}$![]() is the number of considered resonances, and the algorithm used to evaluate the radial magnetic field $B_r$
is the number of considered resonances, and the algorithm used to evaluate the radial magnetic field $B_r$![]() from SPEC equilibria is described in § 4.3. The fraction of effective parallel diffusion is then the fraction of resonances in the plasma that contribute to the transport, i.e. the fraction of resonances over which the diffusion due to parallel dynamics dominates. Note that $f_{{\rm PD}}\neq V_{{\rm PD}}$
from SPEC equilibria is described in § 4.3. The fraction of effective parallel diffusion is then the fraction of resonances in the plasma that contribute to the transport, i.e. the fraction of resonances over which the diffusion due to parallel dynamics dominates. Note that $f_{{\rm PD}}\neq V_{{\rm PD}}$![]() , but if $f_{{\rm PD}}=0$
, but if $f_{{\rm PD}}=0$![]() , we can expect $\mathcal {V}_{{\rm PD}}$
, we can expect $\mathcal {V}_{{\rm PD}}$![]() to be zero, and the opposite is true as well. The fraction of parallel diffusion can then be used as a proxy function to determine if the volume of parallel diffusion is zero or not. The chaotic equilibrium $\beta$
to be zero, and the opposite is true as well. The fraction of parallel diffusion can then be used as a proxy function to determine if the volume of parallel diffusion is zero or not. The chaotic equilibrium $\beta$![]() -limit, $\beta ^{{\rm chaos}}_{{\rm lim}}$
-limit, $\beta ^{{\rm chaos}}_{{\rm lim}}$![]() , is obtained by taking the value of $\beta$
, is obtained by taking the value of $\beta$![]() above which $f_{{\rm PD}}>0$
above which $f_{{\rm PD}}>0$![]() (see figure 6).
(see figure 6).
Note that this does not define an equilibrium $\beta$![]() -limit from an experimental point of view – the metric $f_{{\rm PD}}$
-limit from an experimental point of view – the metric $f_{{\rm PD}}$![]() is positive as soon as one resonance satisfies (4.3), which would, in practice, only flatten the temperature and density profiles locally. It is certainly possible to increase the plasma averaged $\beta$
is positive as soon as one resonance satisfies (4.3), which would, in practice, only flatten the temperature and density profiles locally. It is certainly possible to increase the plasma averaged $\beta$![]() further by increasing the input power. Our metric $f_{{\rm PD}}$
further by increasing the input power. Our metric $f_{{\rm PD}}$![]() , however, informs us that the effect of field line topology starts to become important and has to be taken into account in transport calculations for $\beta >\beta ^{{\rm chaos}}_{{\rm lim}}$
, however, informs us that the effect of field line topology starts to become important and has to be taken into account in transport calculations for $\beta >\beta ^{{\rm chaos}}_{{\rm lim}}$![]() . One could imagine to combine the volume of chaos given by (4.1) with the criterion given by (4.3), and only consider resonances that span a sufficiently large volume and that contribute significantly to the radial transport. This idea will not be explored in this paper, and is left for future studies.
. One could imagine to combine the volume of chaos given by (4.1) with the criterion given by (4.3), and only consider resonances that span a sufficiently large volume and that contribute significantly to the radial transport. This idea will not be explored in this paper, and is left for future studies.
In practice, the metric $f_{{\rm PD}}$![]() is greater than zero when relatively small islands in comparison with the plasma minor radius emerge (using $B_{r,{\rm crit}}/B=10^{-5}$
is greater than zero when relatively small islands in comparison with the plasma minor radius emerge (using $B_{r,{\rm crit}}/B=10^{-5}$![]() ). Thus, as long as the SPEC volumes are large enough to allow these islands to grow, the number of volumes does not affect the metric evaluation. In addition, given a sufficiently large number of volumes, the pressure profile is well resolved by the stepped-pressure approximation and thus the equilibrium does not depend strongly on the number of volumes (see the Appendix).
). Thus, as long as the SPEC volumes are large enough to allow these islands to grow, the number of volumes does not affect the metric evaluation. In addition, given a sufficiently large number of volumes, the pressure profile is well resolved by the stepped-pressure approximation and thus the equilibrium does not depend strongly on the number of volumes (see the Appendix).
4.3. Measure of the radial magnetic field
To evaluate the radial magnetic field $B_r$![]() , it is useful to construct a general set of coordinates, such as quadratic flux minimizing (QFM) surfaces (Dewar, Hudson & Price Reference Dewar, Hudson and Price1994; Hudson & Dewar Reference Hudson and Dewar1996, Reference Hudson and Dewar1998), or ghost surfaces (Hudson & Dewar Reference Hudson and Dewar2009), which have been shown to coincide with isotherms (Hudson & Breslau Reference Hudson and Breslau2008). We construct QFM surfaces using the pyoculus packageFootnote 2 . These surfaces, thereafter named $\varGamma _{mn}$
, it is useful to construct a general set of coordinates, such as quadratic flux minimizing (QFM) surfaces (Dewar, Hudson & Price Reference Dewar, Hudson and Price1994; Hudson & Dewar Reference Hudson and Dewar1996, Reference Hudson and Dewar1998), or ghost surfaces (Hudson & Dewar Reference Hudson and Dewar2009), which have been shown to coincide with isotherms (Hudson & Breslau Reference Hudson and Breslau2008). We construct QFM surfaces using the pyoculus packageFootnote 2 . These surfaces, thereafter named $\varGamma _{mn}$![]() , are smooth toroidal surfaces that pass through the X- and O- points of the island chain corresponding to the $\iota \hspace {-0.4em}\text {-}=n/m$
, are smooth toroidal surfaces that pass through the X- and O- points of the island chain corresponding to the $\iota \hspace {-0.4em}\text {-}=n/m$![]() rational resonant surface, and are constructed by finding the surfaces $\varGamma _{mn}$
rational resonant surface, and are constructed by finding the surfaces $\varGamma _{mn}$![]() minimizing the weighted quadratic flux $\int _{\varGamma _{mn}} w (\boldsymbol{B}\boldsymbol {\cdot }\boldsymbol {n})^2 \,{\rm d} S$
minimizing the weighted quadratic flux $\int _{\varGamma _{mn}} w (\boldsymbol{B}\boldsymbol {\cdot }\boldsymbol {n})^2 \,{\rm d} S$![]() , where the weight $w$
, where the weight $w$![]() is cleverly chosen such that the underlying Euler–Lagrange equation has non-singular solutions. Some examples of QFM surfaces are plotted in figure 7. The radial coordinate $r$
is cleverly chosen such that the underlying Euler–Lagrange equation has non-singular solutions. Some examples of QFM surfaces are plotted in figure 7. The radial coordinate $r$![]() is then defined as the direction perpendicular to the QFM surfaces.
is then defined as the direction perpendicular to the QFM surfaces.

Figure 7. Black, Poincaré plot with magnetic surfaces and magnetic islands; red, QFM surface $r=\text {const}$![]() . The coordinate $s$
. The coordinate $s$![]() is a radial-like coordinate.
is a radial-like coordinate.
We can now measure the radial component of the magnetic field at each resonant surface $\iota \hspace {-0.4em}\text {-}=n/m$![]() . We start by identifying all potential resonances $(m,n)\in \mathbb {N}$
. We start by identifying all potential resonances $(m,n)\in \mathbb {N}$![]() in each volume $\mathcal {V}_l$
in each volume $\mathcal {V}_l$![]() within the plasma boundary, such that (i) $n/m$
within the plasma boundary, such that (i) $n/m$![]() is within the rotational transform extrema in the volume, and (ii) $n$
is within the rotational transform extrema in the volume, and (ii) $n$![]() is a multiple of the number of field periods. We construct QFM surfaces $\varGamma _{mn}$
is a multiple of the number of field periods. We construct QFM surfaces $\varGamma _{mn}$![]() for each of the identified resonances $\iota \hspace {-0.4em}\text {-}=n/m$
for each of the identified resonances $\iota \hspace {-0.4em}\text {-}=n/m$![]() . The magnetic field perpendicular to the QFM surface, $B_r$
. The magnetic field perpendicular to the QFM surface, $B_r$![]() , is obtained by projecting the magnetic field on their normal direction, and the magnetic field resonant harmonic, $B_{r,mn}$
, is obtained by projecting the magnetic field on their normal direction, and the magnetic field resonant harmonic, $B_{r,mn}$![]() is obtained after a standard Fourier transform of $B_r$
is obtained after a standard Fourier transform of $B_r$![]() . Here, the poloidal angle is the straight-field line angle of the magnetic field tangential to the QFM surface. The Fourier spectrum of $B_r$
. Here, the poloidal angle is the straight-field line angle of the magnetic field tangential to the QFM surface. The Fourier spectrum of $B_r$![]() is largely dominated by the $(m,n)$
is largely dominated by the $(m,n)$![]() harmonic – it has been verified that $B_{r,mn}$
harmonic – it has been verified that $B_{r,mn}$![]() is at least twice as large as the other Fourier harmonics of the radial magnetic field. We can thus assume $B_r\approx B_{r,mn}$
is at least twice as large as the other Fourier harmonics of the radial magnetic field. We can thus assume $B_r\approx B_{r,mn}$![]() to filter out numerical noise that may be generated by the QFM surface construction.
to filter out numerical noise that may be generated by the QFM surface construction.
Only resonances with large radial magnetic field will significantly participate to the radial transport. Since the magnetic field harmonics $B_{mn}$![]() are expected to decrease exponentially with the square of their mode numbers $m$
are expected to decrease exponentially with the square of their mode numbers $m$![]() and $n$
and $n$![]() , i.e. $B_{mn}\sim \exp (-m^2-n^2)$
, i.e. $B_{mn}\sim \exp (-m^2-n^2)$![]() , we can discard resonances with large poloidal and toroidal mode number and study only harmonics with mode number smaller than a given resolution, $m\leq M_{{\rm res}}$
, we can discard resonances with large poloidal and toroidal mode number and study only harmonics with mode number smaller than a given resolution, $m\leq M_{{\rm res}}$![]() and $n\leq N_{{\rm res}}$
and $n\leq N_{{\rm res}}$![]() . In this paper, we set $M_{{\rm res}}=25$
. In this paper, we set $M_{{\rm res}}=25$![]() and $N_{{\rm res}}=10$
and $N_{{\rm res}}=10$![]() .
.
With the definition of the chaotic equilibrium $\beta$![]() -limit from the fraction of effective parallel diffusion (4.6), only resonances with large radial magnetic field component matter; increasing the Fourier resolution of the equilibrium only introduces resonances with small radial magnetic field components, and thus has only a small impact on the value of $f_{{\rm PD}}$
-limit from the fraction of effective parallel diffusion (4.6), only resonances with large radial magnetic field component matter; increasing the Fourier resolution of the equilibrium only introduces resonances with small radial magnetic field components, and thus has only a small impact on the value of $f_{{\rm PD}}$![]() – see for example the comparison between two $\beta$
– see for example the comparison between two $\beta$![]() -scans with resolution $M=N=8$
-scans with resolution $M=N=8$![]() and $M=N=10$
and $M=N=10$![]() in figure 6 (red curves), and the chaotic equilibrium $\beta$
in figure 6 (red curves), and the chaotic equilibrium $\beta$![]() -limit convergence study in the Appendix. Indeed, the critical $\beta$
-limit convergence study in the Appendix. Indeed, the critical $\beta$![]() at which $f_{{\rm PD}}$
at which $f_{{\rm PD}}$![]() becomes larger than zero, namely $\beta _{{\rm lim}}^{{\rm chaos}}$
becomes larger than zero, namely $\beta _{{\rm lim}}^{{\rm chaos}}$![]() , becomes quite insensitive to the Fourier resolution for sufficiently large values of $M$
, becomes quite insensitive to the Fourier resolution for sufficiently large values of $M$![]() and $N$
and $N$![]() , as the ones used for this paper ($M=N=12$
, as the ones used for this paper ($M=N=12$![]() ). In that sense, this new diagnostic is more robust than the diagnostic based on the volume of chaos.
). In that sense, this new diagnostic is more robust than the diagnostic based on the volume of chaos.
The chaotic equilibrium $\beta$![]() -limit obtained using the metric $f_{{\rm PD}}$
-limit obtained using the metric $f_{{\rm PD}}$![]() defined in (4.6) is plotted in figure 5 with a red shaded area, spanning the range of $\beta _{{\rm lim}}^{{\rm chaos}}$
defined in (4.6) is plotted in figure 5 with a red shaded area, spanning the range of $\beta _{{\rm lim}}^{{\rm chaos}}$![]() obtained when varying $B_{r,{\rm crit}}/B$
obtained when varying $B_{r,{\rm crit}}/B$![]() from $10^{-6}$
from $10^{-6}$![]() to $10^{-4}$
to $10^{-4}$![]() . The value of $\beta ^{{\rm chaos}}_{{\rm lim}}$
. The value of $\beta ^{{\rm chaos}}_{{\rm lim}}$![]() obtained for $B_{r,{\rm crit}}/B = 10^{-5}$
obtained for $B_{r,{\rm crit}}/B = 10^{-5}$![]() is shown with red dots. We observe that the largest $\beta$
is shown with red dots. We observe that the largest $\beta$![]() -limit occurs at $\hat {C}\approx 0.75$
-limit occurs at $\hat {C}\approx 0.75$![]() . A small, but non-zero bootstrap current thus increases the equilibrium $\beta$
. A small, but non-zero bootstrap current thus increases the equilibrium $\beta$![]() -limit with respect to a classical stellarator without any net toroidal current ($\hat {C}=0$
-limit with respect to a classical stellarator without any net toroidal current ($\hat {C}=0$![]() ), and is thus beneficial.
), and is thus beneficial.
5. Analytical prediction for the equilibrium $\beta$ -limits
-limits
We now derive an analytical model that predicts both the ideal and chaotic equilibrium $\beta$![]() -limits. We make use of high-$\beta$
-limits. We make use of high-$\beta$![]() stellarator expansion theories derived by Wakatani (Reference Wakatani1998) and Freidberg (Reference Freidberg2014) to describe how the rotational transform at the plasma edge $\iota \!\!\text {-}_a$
stellarator expansion theories derived by Wakatani (Reference Wakatani1998) and Freidberg (Reference Freidberg2014) to describe how the rotational transform at the plasma edge $\iota \!\!\text {-}_a$![]() evolves with $\beta$
evolves with $\beta$![]() , taking into account the effect of the bootstrap current as well. Once a formula for $\iota \hspace {-0.4em}\text {-}_a(\beta )$
, taking into account the effect of the bootstrap current as well. Once a formula for $\iota \hspace {-0.4em}\text {-}_a(\beta )$![]() has been derived, we can find whether an ideal $\beta$
has been derived, we can find whether an ideal $\beta$![]() -limit is reached by solving $\iota \hspace {-0.4em}\text {-}_a(\beta )=0$
-limit is reached by solving $\iota \hspace {-0.4em}\text {-}_a(\beta )=0$![]() . When no solution is possible, a chaotic $\beta$
. When no solution is possible, a chaotic $\beta$![]() -limit may also be estimated by assuming that the edge iota is modified by order one with respect to the vacuum rotational transform, $\iota \hspace {-0.4em}\text {-}_a(\beta )-\iota \hspace {-0.4em}\text {-}_a(0) \sim \iota \hspace {-0.4em}\text {-}_a(0)$
-limit may also be estimated by assuming that the edge iota is modified by order one with respect to the vacuum rotational transform, $\iota \hspace {-0.4em}\text {-}_a(\beta )-\iota \hspace {-0.4em}\text {-}_a(0) \sim \iota \hspace {-0.4em}\text {-}_a(0)$![]() , at which point it is likely that many resonances exist.
, at which point it is likely that many resonances exist.
Assuming that (i) $\epsilon \ll 1$![]() , $\delta =|\boldsymbol {B}_p|/B_\phi \sim \epsilon ^{3/4}$
, $\delta =|\boldsymbol {B}_p|/B_\phi \sim \epsilon ^{3/4}$![]() with $\boldsymbol {B}_p$
with $\boldsymbol {B}_p$![]() the poloidal magnetic field, $\beta \sim \epsilon$
the poloidal magnetic field, $\beta \sim \epsilon$![]() and $N_{{\rm fp}}\sim \epsilon ^{-1/2}$
and $N_{{\rm fp}}\sim \epsilon ^{-1/2}$![]() , that (ii) magnetic surfaces are circular, and (iii) considering Solove'v profiles for the pressure ${\rm d} p/{\rm d}\psi _p=\text {const}$
, that (ii) magnetic surfaces are circular, and (iii) considering Solove'v profiles for the pressure ${\rm d} p/{\rm d}\psi _p=\text {const}$![]() , and the surface averaged toroidal current density $\langle j_\phi \rangle =\text {const}$
, and the surface averaged toroidal current density $\langle j_\phi \rangle =\text {const}$![]() , one can derive (Wakatani Reference Wakatani1998; Freidberg Reference Freidberg2014) an analytical model for the edge rotational transform,
, one can derive (Wakatani Reference Wakatani1998; Freidberg Reference Freidberg2014) an analytical model for the edge rotational transform,
where $I_\phi$![]() is the net toroidal current enclosed by the plasma and $\iota \hspace {-0.4em}\text {-}_v$
is the net toroidal current enclosed by the plasma and $\iota \hspace {-0.4em}\text {-}_v$![]() is the edge rotational transform in a vacuum.
is the edge rotational transform in a vacuum.
The bootstrap current model we employed in our equilibrium calculations (3.4) implies a linear relation between the net toroidal current in the system and the plasma $\beta$![]() , thus
, thus
where $\sigma$![]() is a proportionality constant. It can be related to $C$
is a proportionality constant. It can be related to $C$![]() by integrating (3.5) to compute $I_\phi$
by integrating (3.5) to compute $I_\phi$![]() in (5.3), leading to
in (5.3), leading to
Combining (5.1)–(5.5), analytical expressions of the edge rotational transform as a function of $\beta$![]() for different values of $\hat {C}$
for different values of $\hat {C}$![]() can be obtained. Figure 4 compares the analytical curves with results obtained with SPEC. We observe reasonable agreement especially at low $\beta$
can be obtained. Figure 4 compares the analytical curves with results obtained with SPEC. We observe reasonable agreement especially at low $\beta$![]() . As $\beta$
. As $\beta$![]() increases, however, (5.1) consistently underestimates the actual value of the rotational transform found by SPEC. Thus, even though the equilibrium constructed in § 3 does not exactly satisfy the assumptions used to derive (5.1), the assumptions are reasonable enough to use this analytical model to understand our numerical results. Equation (5.1) provides indeed an analytical (nonlinear) relation for $\iota \hspace {-0.4em}\text {-}_a(\beta )$
increases, however, (5.1) consistently underestimates the actual value of the rotational transform found by SPEC. Thus, even though the equilibrium constructed in § 3 does not exactly satisfy the assumptions used to derive (5.1), the assumptions are reasonable enough to use this analytical model to understand our numerical results. Equation (5.1) provides indeed an analytical (nonlinear) relation for $\iota \hspace {-0.4em}\text {-}_a(\beta )$![]() which can be used to predict both the ideal and chaotic $\beta$
which can be used to predict both the ideal and chaotic $\beta$![]() -limits, as described in the following subsections.
-limits, as described in the following subsections.
5.1. Ideal equilibrium $\beta$ -limit
-limit
The solution to the relation $\iota \hspace {-0.4em}\text {-}_a(\beta ^{{\rm ideal}}_{{\rm lim}})=0$![]() is given by
is given by
which is real for $\sigma <(4\iota \hspace {-0.4em}\text {-}_v\epsilon _a)^{-1}$![]() , or
, or
Note the limit
retrieving the result from Freidberg (Reference Freidberg2014) and Loizu et al. (Reference Loizu, Hudson, Nührenberg, Geiger and Helander2017) for a zero-net-current stellarator ($\hat C=0$![]() ).
).
The curve $\beta ^{{\rm ideal}}_{{\rm lim}}(\hat {C})$![]() is plotted in figure 5 with a black line. We observe that as $\hat {C}$
is plotted in figure 5 with a black line. We observe that as $\hat {C}$![]() increases, the ideal equilibrium $\beta$
increases, the ideal equilibrium $\beta$![]() -limit increases. Comparison with data points measured from SPEC equilibria (red triangles) shows good agreement, especially for weaker bootstrap current ($\hat C<0.5$
-limit increases. Comparison with data points measured from SPEC equilibria (red triangles) shows good agreement, especially for weaker bootstrap current ($\hat C<0.5$![]() ). The analytical value of $\hat {C}_{{\rm crit}}\approx 0.48$
). The analytical value of $\hat {C}_{{\rm crit}}\approx 0.48$![]() is reasonably close to the one obtained with SPEC (smaller by approximately $18\,\%$
is reasonably close to the one obtained with SPEC (smaller by approximately $18\,\%$![]() ).
).
5.2. Chaotic equilibrium $\beta$ -limit
-limit
For larger values of $\hat C$![]() , i.e. $\hat {C}>\hat {C}_{{\rm crit}}$
, i.e. $\hat {C}>\hat {C}_{{\rm crit}}$![]() , the chaotic equilibrium $\beta$
, the chaotic equilibrium $\beta$![]() -limit is due to the emergence of chaos and its effectiveness in increasing the transport, thus estimating the chaotic equilibrium $\beta$
-limit is due to the emergence of chaos and its effectiveness in increasing the transport, thus estimating the chaotic equilibrium $\beta$![]() -limit with (5.1) is not trivial – it is not known, a priori, which resonance will participate to the radial transport first. However, it is reasonable to assume that when the bootstrap current modifies the edge rotational transform by order one with respect to $\iota \hspace {-0.4em}\text {-}_v$
-limit with (5.1) is not trivial – it is not known, a priori, which resonance will participate to the radial transport first. However, it is reasonable to assume that when the bootstrap current modifies the edge rotational transform by order one with respect to $\iota \hspace {-0.4em}\text {-}_v$![]() , i.e.
, i.e.
magnetic islands and chaos are expected to appear. The values of $\beta$![]() computed with SPEC at which the condition (5.9) is satisfied are plotted with brown squares in figure 5. We observe good agreement with the chaotic equilibrium $\beta$
computed with SPEC at which the condition (5.9) is satisfied are plotted with brown squares in figure 5. We observe good agreement with the chaotic equilibrium $\beta$![]() -limit (blue dots) for $\hat {C}>1$
-limit (blue dots) for $\hat {C}>1$![]() .
.
We can also directly solve (5.9) using (5.1). We obtain a fourth-order polynomial equation for $\beta$![]() ,
,
The real, positive root of (5.10) is plotted with a red line in figure 5. Direct comparison with the numerical data (blue squares) shows that (5.10) consistently underestimates the values of $\beta$![]() that satisfy (5.9); this is a direct consequence of the underestimate of $\iota \hspace {-0.4em}\text {-}_a$
that satisfy (5.9); this is a direct consequence of the underestimate of $\iota \hspace {-0.4em}\text {-}_a$![]() by the analytical model (figure 4). The general dependence on $\hat {C}$
by the analytical model (figure 4). The general dependence on $\hat {C}$![]() is, however, recovered, capturing the chaotic equilibrium $\beta$
is, however, recovered, capturing the chaotic equilibrium $\beta$![]() -limit trend (red dots in figure 5) observed numerically for values of $\hat {C}>1$
-limit trend (red dots in figure 5) observed numerically for values of $\hat {C}>1$![]() . We remark that there are no free parameters in this analytical model. For $\hat {C}_{critical}<\hat {C}<1$
. We remark that there are no free parameters in this analytical model. For $\hat {C}_{critical}<\hat {C}<1$![]() , the analytical model (5.10) overestimates greatly the chaotic equilibrium $\beta$
, the analytical model (5.10) overestimates greatly the chaotic equilibrium $\beta$![]() -limit obtained with SPEC. In this transition region, the edge rotational transform depends weakly on $\beta$
-limit obtained with SPEC. In this transition region, the edge rotational transform depends weakly on $\beta$![]() for $\beta \lesssim 1$
for $\beta \lesssim 1$![]() (see, for example, the blue crosses in figure 4). As a consequence, the solution to (5.9) is large, and is therefore a bad estimate for the chaotic equilibrium $\beta$
(see, for example, the blue crosses in figure 4). As a consequence, the solution to (5.9) is large, and is therefore a bad estimate for the chaotic equilibrium $\beta$![]() -limit. A more refined model would be required to better reproduce the results.
-limit. A more refined model would be required to better reproduce the results.
5.3. Dependence on design parameters
The edge rotational transform in a vacuum is approximately equal to the rotational transform on axis (low shear configuration), and can be estimated by a zeroth-order near axis expansion (Helander Reference Helander2014; Loizu et al. Reference Loizu, Hudson, Nührenberg, Geiger and Helander2017),
For low values of $\hat {C}$![]() , the ideal equilibrium $\beta$
, the ideal equilibrium $\beta$![]() -limit grows with the vacuum rotational transform (see (5.8)). For example, increasing the number of field periods increases $\iota \hspace {-0.4em}\text {-}_v$
-limit grows with the vacuum rotational transform (see (5.8)). For example, increasing the number of field periods increases $\iota \hspace {-0.4em}\text {-}_v$![]() , thus also the equilibrium $\beta$
, thus also the equilibrium $\beta$![]() -limit, as shown in figure 8. These results were corroborated by SPEC calculations with $N_{{\rm fp}}=2$
-limit, as shown in figure 8. These results were corroborated by SPEC calculations with $N_{{\rm fp}}=2$![]() , while calculations with $N_{{\rm fp}}=10$
, while calculations with $N_{{\rm fp}}=10$![]() were difficult to achieve due to SPEC numerical fragility issues.
were difficult to achieve due to SPEC numerical fragility issues.

Figure 8. Analytical predictions of the equilibrium $\beta$![]() -limit for different numbers of field period $N_{{\rm fp}}$
-limit for different numbers of field period $N_{{\rm fp}}$![]() : full lines, ideal and chaotic equilibrium $\beta$
: full lines, ideal and chaotic equilibrium $\beta$![]() -limits as predicted by (5.6) and (5.10), respectively; triangles and dots, ideal and chaotic equilibrium $\beta$
-limits as predicted by (5.6) and (5.10), respectively; triangles and dots, ideal and chaotic equilibrium $\beta$![]() -limits as obtained by SPEC, respectively.
-limits as obtained by SPEC, respectively.
More generally, any mechanism that increases the rotational transform in a vacuum will increase the ideal and chaotic equilibrium $\beta$![]() -limits. An increase in rotational transform can be achieved by either increasing the number of field periods, increasing the ellipse eccentricity (i.e. increasing the harmonic $R_{11}=Z_{11}$
-limits. An increase in rotational transform can be achieved by either increasing the number of field periods, increasing the ellipse eccentricity (i.e. increasing the harmonic $R_{11}=Z_{11}$![]() ) or adding some torsion to the magnetic axis. Magnetic axis torsion can, however, have a strong impact on the computed equilibrium, and additional studies would be required to see if it affects the conclusions of this paper.
) or adding some torsion to the magnetic axis. Magnetic axis torsion can, however, have a strong impact on the computed equilibrium, and additional studies would be required to see if it affects the conclusions of this paper.
Equation (5.7) gives $\hat {C}_{{\rm crit}}=0.48$![]() , i.e. the equilibrium $\beta$
, i.e. the equilibrium $\beta$![]() -limit is maximized for a bootstrap current that has half the strength of the bootstrap current in an equivalent circular tokamak. Interestingly, if we approximate the total toroidal flux in the plasma as $\psi _a\approx {\rm \pi}a_{{\rm eff}}^2 B_0$
-limit is maximized for a bootstrap current that has half the strength of the bootstrap current in an equivalent circular tokamak. Interestingly, if we approximate the total toroidal flux in the plasma as $\psi _a\approx {\rm \pi}a_{{\rm eff}}^2 B_0$![]() , with $B_0$
, with $B_0$![]() the modulus of the magnetic field on axis, we get $\hat {C}_{{\rm crit}}=5{\rm \pi} \sqrt {\epsilon _a}/8$
the modulus of the magnetic field on axis, we get $\hat {C}_{{\rm crit}}=5{\rm \pi} \sqrt {\epsilon _a}/8$![]() , which only depends on the inverse aspect ratio.
, which only depends on the inverse aspect ratio.
6. Conclusion
The SPEC code has been used to perform a large number of free-boundary stellarator equilibrium calculations including bootstrap current that allowed us to completely characterize classical stellarators in terms of their equilibrium $\beta$![]() -limit. For configurations with low bootstrap current ($\hat {C}<\hat {C}_{{\rm crit}}$
-limit. For configurations with low bootstrap current ($\hat {C}<\hat {C}_{{\rm crit}}$![]() ), an ideal equilibrium $\beta$
), an ideal equilibrium $\beta$![]() -limit has been identified, where a central $(m,n)=(1,0)$
-limit has been identified, where a central $(m,n)=(1,0)$![]() island appears. Stronger bootstrap current ($\hat {C}>\hat {C}_{{\rm crit}}$
island appears. Stronger bootstrap current ($\hat {C}>\hat {C}_{{\rm crit}}$![]() ) prevents this central island from opening. Instead, a chaotic equilibrium $\beta$
) prevents this central island from opening. Instead, a chaotic equilibrium $\beta$![]() -limit is reached, where the radial heat transport generated by pressure-induced magnetic islands and magnetic field line chaos competes with turbulence. We have implemented a proxy function to determine if the effective volume of parallel diffusion proposed by Paul et al. (Reference Paul, Hudson and Helander2022) is greater than zero, thereby assessing the impact of the field line topology on radial transport and deducing the equilibrium $\beta$
-limit is reached, where the radial heat transport generated by pressure-induced magnetic islands and magnetic field line chaos competes with turbulence. We have implemented a proxy function to determine if the effective volume of parallel diffusion proposed by Paul et al. (Reference Paul, Hudson and Helander2022) is greater than zero, thereby assessing the impact of the field line topology on radial transport and deducing the equilibrium $\beta$![]() -limit from SPEC equilibrium calculations.
-limit from SPEC equilibrium calculations.
An analytical model showed good agreement with the ideal equilibrium $\beta$![]() -limit obtained numerically for weak bootstrap current. The general trend for the chaotic equilibrium $\beta$
-limit obtained numerically for weak bootstrap current. The general trend for the chaotic equilibrium $\beta$![]() -limit could also be extracted for stronger bootstrap current, up to $\hat {C}\sim 2$
-limit could also be extracted for stronger bootstrap current, up to $\hat {C}\sim 2$![]() . Analytical insights provided ways to predict the effect of design parameters on the equilibrium $\beta$
. Analytical insights provided ways to predict the effect of design parameters on the equilibrium $\beta$![]() -limit; for example, the ideal $\beta$
-limit; for example, the ideal $\beta$![]() -limit has been shown to increase with $\hat {C}$
-limit has been shown to increase with $\hat {C}$![]() , while the chaotic equilibrium $\beta$
, while the chaotic equilibrium $\beta$![]() -limit decreases with $\hat {C}$
-limit decreases with $\hat {C}$![]() , thereby showing a peak equilibrium $\beta$
, thereby showing a peak equilibrium $\beta$![]() -limit around $\hat {C}_{{\rm crit}}$
-limit around $\hat {C}_{{\rm crit}}$![]() . The critical value of $\hat {C}_{{\rm crit}}$
. The critical value of $\hat {C}_{{\rm crit}}$![]() depends only on the inverse aspect ratio, under reasonable assumptions.
depends only on the inverse aspect ratio, under reasonable assumptions.
To improve the equilibrium $\beta$![]() -limit of stellarators, optimization of different parameters can be performed. For example, Landreman, Medasani & Zhu (Reference Landreman, Medasani and Zhu2021b) recently coupled SPEC with the simsopt framework (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021a) to perform optimization for good magnetic surfaces at the same time as quasisymmetry in a vacuum, and Baillod et al. (Reference Baillod, Loizu, Graves and Landreman2022) showed that good magnetic surfaces can be recovered in finite $\beta$
-limit of stellarators, optimization of different parameters can be performed. For example, Landreman, Medasani & Zhu (Reference Landreman, Medasani and Zhu2021b) recently coupled SPEC with the simsopt framework (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021a) to perform optimization for good magnetic surfaces at the same time as quasisymmetry in a vacuum, and Baillod et al. (Reference Baillod, Loizu, Graves and Landreman2022) showed that good magnetic surfaces can be recovered in finite $\beta$![]() , finite current equilibria by modifying either the plasma boundary, the coils, or by injecting a toroidal current in the plasma. Applying the same recipe to a sequence of equilibria with increasing $\beta$
, finite current equilibria by modifying either the plasma boundary, the coils, or by injecting a toroidal current in the plasma. Applying the same recipe to a sequence of equilibria with increasing $\beta$![]() , one can optimize a stellarator configuration for larger equilibrium $\beta$
, one can optimize a stellarator configuration for larger equilibrium $\beta$![]() -limit. Note, however, that the fraction $f_{{\rm PD}}$
-limit. Note, however, that the fraction $f_{{\rm PD}}$![]() is generally not a smooth function of the equilibrium and might not be a good target function for optimization. Another smooth function should be developed from the radial magnetic field component $B_{r}$
is generally not a smooth function of the equilibrium and might not be a good target function for optimization. Another smooth function should be developed from the radial magnetic field component $B_{r}$![]() if one desires to minimize the impact of field line topology on radial transport.
if one desires to minimize the impact of field line topology on radial transport.
Future studies will focus on more exotic stellarator geometries, for example configurations optimized for quasisymmetry or quasi-isodynamicity, and include self-consistent bootstrap currents, as proposed by Landreman, Buller & Drevlak (Reference Landreman, Buller and Drevlak2022). Finally, one could use the SPEC code to evaluate the stability limit for different values of $\hat C$![]() , using the methods developed by Kumar et al. (Reference Kumar, Qu, Hole, Wright, Loizu, Hudson, Baillod, Dewar and Ferraro2021, Reference Kumar, Nührenberg, Qu, Hole, Doak, Dewar, Hudson, Loizu, Aleynikova and Baillod2022). This would provide useful information on the dependence of the stability limit on the parameter $\hat C$
, using the methods developed by Kumar et al. (Reference Kumar, Qu, Hole, Wright, Loizu, Hudson, Baillod, Dewar and Ferraro2021, Reference Kumar, Nührenberg, Qu, Hole, Doak, Dewar, Hudson, Loizu, Aleynikova and Baillod2022). This would provide useful information on the dependence of the stability limit on the parameter $\hat C$![]() , and allow comparison with the equilibrium $\beta$
, and allow comparison with the equilibrium $\beta$![]() -limit.
-limit.
Acknowledgements
The authors thank P. Helander, S.R. Hudson, C. Zhu, J. Schilling, J. Cazabonne and E. Balkovic for useful discussions. This work was supported in part by the Swiss National Science Foundation.
Editor P. Helander thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, via the Euratom Research and Training Programme (grant agreement no. 101052200 – EUROfusion) and funded by the Swiss State Secretariat for Education, Research and Innovation (SERI). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union, the European Commission or SERI. Neither the European Union nor the European Commission nor SERI can be held responsible for them. This research was supported by a grant from the Simons Foundation (1013657, J.L.).
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Declaration of interests
The authors report no conflict of interest.
Appendix. Convergence on numerical resolution and number of volumes
The chaotic equilibrium $\beta$![]() -limit, as obtained by SPEC for $B_{r,{\rm crit}}/B_0=10^{-6}$
-limit, as obtained by SPEC for $B_{r,{\rm crit}}/B_0=10^{-6}$![]() , and $\hat {C}=1.37$
, and $\hat {C}=1.37$![]() , is plotted on figure 9 as a function of the equilibrium Fourier resolution. Convergence towards a value close to the analytical prediction is observed. The resolution used to compute the results presented in this paper, i.e. $M_{{\rm pol}}=N_{{\rm tor}}=12$
, is plotted on figure 9 as a function of the equilibrium Fourier resolution. Convergence towards a value close to the analytical prediction is observed. The resolution used to compute the results presented in this paper, i.e. $M_{{\rm pol}}=N_{{\rm tor}}=12$![]() , seems large enough so that the relative variations obtained by further increasing the Fourier resolution become small, of the order of $3\,\%$
, seems large enough so that the relative variations obtained by further increasing the Fourier resolution become small, of the order of $3\,\%$![]() .
.

Figure 9. Chaotic equilibrium $\beta$![]() -limit, as obtained by SPEC for $B_{r,{\rm crit}}/B_0=10^{-6}$
-limit, as obtained by SPEC for $B_{r,{\rm crit}}/B_0=10^{-6}$![]() , and $\hat {C}=1.37$
, and $\hat {C}=1.37$![]() as a function of the equilibrium Fourier resolution. The black, dashed line is the analytical prediction obtained by solving (5.10).
as a function of the equilibrium Fourier resolution. The black, dashed line is the analytical prediction obtained by solving (5.10).
We now discuss the dependence of the ideal and the chaotic equilibrium $\beta$![]() -limit dependence on the number of volumes $N_{{\rm vol}}$
-limit dependence on the number of volumes $N_{{\rm vol}}$![]() . Keeping the same coil shapes and currents, we approximate the pressure profile $p=p_0(1-\psi _t/\psi _a)$
. Keeping the same coil shapes and currents, we approximate the pressure profile $p=p_0(1-\psi _t/\psi _a)$![]() with different numbers of interfaces supporting an equal pressure step, $[[p]]_l = p_0 / N_{{\rm vol}}$
with different numbers of interfaces supporting an equal pressure step, $[[p]]_l = p_0 / N_{{\rm vol}}$![]() . We set $I^v_{\phi,l}=0$
. We set $I^v_{\phi,l}=0$![]() and $I^s_{\phi,l}$
and $I^s_{\phi,l}$![]() following the bootstrap current model described in (3.4). A large range of $\beta$
following the bootstrap current model described in (3.4). A large range of $\beta$![]() is scanned for $\hat {C}=0.46<\hat {C}_{{\rm crit}}$
is scanned for $\hat {C}=0.46<\hat {C}_{{\rm crit}}$![]() and $\hat {C}=1.37>\hat {C}_{{\rm crit}}$
and $\hat {C}=1.37>\hat {C}_{{\rm crit}}$![]() , and for $N_{{\rm vol}}=\{2,4,6,8,10,12\}$
, and for $N_{{\rm vol}}=\{2,4,6,8,10,12\}$![]() . The corresponding ideal and chaotic equilibrium $\beta$
. The corresponding ideal and chaotic equilibrium $\beta$![]() -limits obtained from SPEC are shown on figure 10.
-limits obtained from SPEC are shown on figure 10.

Figure 10. Dependence of the equilibrium $\beta$![]() -limit on the number of volumes $N_{{\rm vol}}$
-limit on the number of volumes $N_{{\rm vol}}$![]() : black, ideal equilibrium $\beta$
: black, ideal equilibrium $\beta$![]() -limit, obtained for $\hat {C}=0.45$
-limit, obtained for $\hat {C}=0.45$![]() ; red, chaotic equilibrium $\beta$
; red, chaotic equilibrium $\beta$![]() -limit, obtained for $\hat {C}=1.37$
-limit, obtained for $\hat {C}=1.37$![]() ; full lines, equilibrium $\beta$
; full lines, equilibrium $\beta$![]() -limit, as obtained with SPEC; dashed line, analytical prediction, as obtained with the HBS theory.
-limit, as obtained with SPEC; dashed line, analytical prediction, as obtained with the HBS theory.
For $\hat {C}=0.45$![]() , an ideal equilibrium $\beta$
, an ideal equilibrium $\beta$![]() -limit is found, that grows with the number of volumes, asymptotically approaching the analytical prediction as obtained by (5.6). This is expected, as ideal MHD is recovered as the number of volumes approaches infinity (Dennis et al. Reference Dennis, Hudson, Dewar and Hole2013a). Interestingly, we observe variations of the chaotic equilibrium $\beta$
-limit is found, that grows with the number of volumes, asymptotically approaching the analytical prediction as obtained by (5.6). This is expected, as ideal MHD is recovered as the number of volumes approaches infinity (Dennis et al. Reference Dennis, Hudson, Dewar and Hole2013a). Interestingly, we observe variations of the chaotic equilibrium $\beta$![]() -limit of the order of $30\,\%$
-limit of the order of $30\,\%$![]() as the number of volumes is changed, clearly within the range of values covered when $B_{r,{\rm crit}}$
as the number of volumes is changed, clearly within the range of values covered when $B_{r,{\rm crit}}$![]() is varied. The dependence of the chaotic equilibrium $\beta$
is varied. The dependence of the chaotic equilibrium $\beta$![]() -limit is thus negligible in comparison with its dependence on $B_{r,{\rm crit}}$
-limit is thus negligible in comparison with its dependence on $B_{r,{\rm crit}}$![]() , i.e. on the plasma temperature and densities. We conclude that the stepped-pressure assumption made by the SPEC model has few to no consequences on the physical results presented in this paper.
, i.e. on the plasma temperature and densities. We conclude that the stepped-pressure assumption made by the SPEC model has few to no consequences on the physical results presented in this paper.