1. Introduction
The Hodge conjecture is major open problem in Complex Algebraic Geometry that has been puzzling mathematician for decades now. The modern statement is the following: Let X be smooth complex projective variety, then the (rational) cycle class map is surjective:
$$ {cl}_{\otimes \mathrm{\mathbb{Q}}}:{CH}^p(X)\otimes \mathrm{\mathbb{Q}}\to {H}^{p,p}\cap {H}^{2p}\left(X,\mathrm{\mathbb{Q}}\right), $$ where 
$ {cl}_{\otimes \mathrm{\mathbb{Q}}}\left(\sum {a}_i{X}_i\right)=\sum {a}_i\left[{X}_i\right] $, 
$ {a}_i\hskip0.5em \in \hskip0.5em \mathrm{\mathbb{Q}} $, and 
$ \left[{X}_i\right] $ is the class of the subvariety Xi.
The case p = 1 is the only case that it is known to hold in general, which follows from Lefschetz’s theorem on (1,1)-classes. Special cases have emerged during the years, but all of them were specific for certain classes of varieties, for example, abelian varieties of prime dimension, unirational and uniruled fourfolds, and hypersurfaces of degree less than 6. For a summary of known cases before 2000, see Lewis (Reference Lewis1999), and for more recent approaches, see Arapura (Reference Arapura2019), Bergeron et al. (Reference Bergeron, Millson and Moeglin2016), and Markman (Reference Markman2021).
Using hard Lefschetz theorem, Lefschetz hyperplane theorem, and some Hilbert scheme arguments, we can reduce the Hodge conjecture to the case of an even dimensional (>2) variety and primitive middle cohomology classes.
Shioda (Reference Shioda1979) gave an interesting characterization of the Hodge conjecture for Fermat varieties, which we now review.
2. Shioda’s work
Let 
$ {X}_m^n\hskip0.5em \in \hskip0.5em {\mathrm{\mathbb{P}}}^{n+1} $ denote the Fermat variety of dimension n and degree m, that is, the solution to the equation:
$$ {x}_0^m+{x}_1^m+\dots +{x}_{n+1}^m=0, $$ and 
$ {\mu}_m $ the group of mth roots of unity. Let 
$ {G}_m^n $ be quotient of the group 
by the subgroup of diagonal elements.
The group 
$ {G}_m^n $ acts naturally on 
$ {X}_m^n $ by coordinatewise multiplication; moreover, the character group 
$ {\hat{G}}_m^n $ of 
$ {G}_m^n $ can be identified with the group:
$$ {\hat{G}}_m^n=\left\{\left({a}_0,\dots, {a}_{n+1}\right)|{a}_i\hskip0.5em \in \hskip0.5em {\mathrm{\mathbb{Z}}}_m,{a}_0+\dots +{a}_{n+1}=0\right\} $$via 
$ \left({\zeta}_0,\dots, {\zeta}_{n+1}\right)\mapsto {\zeta}_0^{a_0}\dots {\zeta}_{n+1}^{a_{n+1}} $, where 
$ \left({\zeta}_0,\dots, {\zeta}_{n+1}\right)\hskip0.5em \in \hskip0.5em {G}_m^n. $
By the previous section, in order to prove the Hodge conjecture, it is enough to prove it for primitive classes; therefore, in this paper, we will focus on primitive cohomology 
$ {H}_{prim}^i\left({X}_m^n,\mathrm{\mathbb{C}}\right):= \ker \left(\smile {H}^{n-i+1}\right) $, where H is a hyperplane class. The action of 
$ {G}_m^n $ into the primitive cohomology and makes 
$ {H}_{prim}^i\left({X}_m^n,\mathrm{\mathbb{Q}}\right) $ and 
$ {H}_{prim}^i\left({X}_m^n,\mathrm{\mathbb{C}}\right) $ 
$ {G}_m^n $-modules. For 
$ \alpha \hskip0.5em \in \hskip0.5em {\hat{G}}_m^n $, we set:
$$ V\left(\alpha \right)=\left\{\xi \hskip0.5em \in \hskip0.5em {H}_{prim}^n\left({X}_m^n,\mathrm{\mathbb{C}}\right)|{g}^{\ast}\left(\xi \right)=\alpha (g)\xi \hskip0.5em \mathrm{for}\hskip0.5em \mathrm{all}\hskip0.5em g\hskip0.5em \in \hskip0.5em {G}_m^n\right\}. $$Before stating the characterization of Hodge classes, we need a few notations. Let
$$ {\mathfrak{U}}_m^n:= \left\{\alpha =\left({a}_0,\dots, {a}_{n+1}\right)\hskip0.5em \in \hskip0.5em {\hat{G}}_m^n|{a}_i\ne 0\hskip0.5em \mathrm{for}\hskip0.5em \mathrm{all}\hskip0.5em i\right\}. $$ For 
$ \alpha \hskip0.5em \in \hskip0.5em {\mathfrak{U}}_m^n, $ we set 
$ \mid \alpha \mid ={\sum}_i\frac{<{a}_i>}{m} $, where < ai > is the representative of 
$ {a}_i\hskip0.5em \in \hskip0.5em {\mathrm{\mathbb{Z}}}_m $ between 1 and m − 1. Suppose n = 2p: then, we set
$$ {\mathfrak{B}}_m^n:= \left\{\alpha \hskip0.5em \in \hskip0.5em {\mathfrak{U}}_m^n\Big\Vert t\alpha |=p+1\hskip0.5em \mathrm{for}\hskip0.5em \mathrm{all}\hskip0.5em t\hskip0.5em \in \hskip0.5em {\mathrm{\mathbb{Z}}}_m^{\ast}\right\}. $$Theorem 2.1 (Ran, Reference Ran1980; Shioda, Reference Shioda1979). Let 
$ {Hdg}^p:= {H}^{p,p}\cap {H}_{prim}^{2p}\left(X,\mathrm{\mathbb{Q}}\right) $ be the group of primitive Hodge cycles. Then:
(a)
$ \dim V\left(\alpha \right)=0 $ or $ 1 $, and $ V\left(\alpha \right)\ne 0\Leftarrow \alpha \hskip0.5em \in \hskip0.5em {\mathfrak{U}}_m^n, $(b)
$ {Hdg}^p={\oplus}_{\alpha \hskip0.5em \in \hskip0.5em {\mathfrak{B}}_m^n}V\left(\alpha \right). $
Now, let 
$ C\left({X}_m^n\right) $ denote the subspace of 
$ {Hdg}^p $ which are classes of algebraic cycles. Then, 
$ C\left({X}_m^n\right) $ is a 
$ {G}_m^n $-submodule, and by the theorem above, there is a subset 
$ {\mathrm{\mathfrak{C}}}_m^n\subseteq {\mathfrak{B}}_m^n $ such that:
$$ C\left({X}_m^n\right)=\underset{\alpha \hskip0.5em \in \hskip0.5em {\mathrm{\mathfrak{C}}}_m^n}{\oplus }V\left(\alpha \right) $$the Hodge conjecture can then be stated as follows.
Conjecture 1 (Hodge conjecture). For all n,m, we have 
$ {\mathrm{\mathfrak{C}}}_m^n={\mathfrak{B}}_m^n. $
By the discussion in the previous section, this is true for 
$ n\hskip0.5em \le \hskip0.5em 2 $ and all m. The idea to prove this equality for Fermat varieties it to use the fact that 
$ {X}_m^n $ “contains” disjoint unions of 
$ {X}_m^k $ with k < n; we then blow those subvarieties up to find a relation between the cohomologies and to inductively construct algebraic cycles in 
$ {X}_m^n $. More precisely, we have:
Theorem 2.2 (Shioda, Reference Shioda1979). Let 
$ n=r+s $ with 
$ r,s\hskip0.5em \ge 1 $. Consider the map 
$ h:{G}_m^r\times {G}_m^s\to {G}_m^n, $ which sends 
$ \left(\left[{\zeta}_0,\dots, {\zeta}_r,1\right],\left[{\zeta}_0^{\prime },\dots, {\zeta}_s^{\prime },1\right]\right) $ to 
$ \left(\left[{\zeta}_0,\dots, {\zeta}_r,{\zeta}_0^{\prime },\dots, {\zeta}_s^{\prime}\right]\right) $, and set 
$ {\mu}_m:= \ker (h) $. Then, there is an isomorphism
$ f:{\left[{H}_{prim}^r\left({X}_m^r,\mathrm{\mathbb{C}}\right)\otimes {H}_{prim}^s\left({X}_m^s,\mathrm{\mathbb{C}}\right)\right]}^{\mu_m}\oplus {H}_{prim}^{r-1}\left({X}_m^{r-1},\mathrm{\mathbb{C}}\right)\otimes {H}_{prim}^{s-1}\left({X}_m^{s-1},\mathrm{\mathbb{C}}\right)\hskip0.5em \overset{\sim }{\to}\hskip1em {H}_{prim}^n\left({X}_m^n,\mathrm{\mathbb{C}}\right) $with the following properties:
(a) f is
$ {G}_m^n $-equivariant.(b) f is a morphism of Hodge structures of type (1,1) on the first summand and of type (1,1) on the second.
(c) If n = 2p, then f preserves algebraic cycles; moreover, if
$ {Z}_1\otimes {Z}_2\hskip0.5em \in \hskip0.5em {H}_{prim}^{r-1}\left({X}_m^{r-1},\mathrm{\mathbb{C}}\right)\otimes {H}_{prim}^{s-1}\left({X}_m^{s-1},\mathrm{\mathbb{C}}\right), $then
$ f\left({Z}_1\otimes {Z}_2\right)={mZ}_1\wedge {Z}_2 $, where $ {Z}_1\wedge {Z}_2 $ is the algebraic cycle obtained by joining Z 1 and Z 2 by lines on $ {X}_m^n $, when Z 1, Z 2 are viewed as cycles in $ {X}_m^n. $
In light of this theorem, we introduce the following notation:
$$ {\mathfrak{U}}_m^{r,s}=\left\{\left(\beta, \gamma \right)\kern0.5em \in \kern0.5em {\mathfrak{U}}_m^r\times {\mathfrak{U}}_m^s\kern0.5em |\beta =\left({b}_0,\dots, {b}_{r+1}\right),\kern0.5em \gamma =\left({c}_0,\dots, {c}_{s+1}\right),\text{
and
}{b}_{r+1}+{c}_{s+1}=0\right\}. $$ For 
$ \left(\beta, \gamma \right)\hskip0.5em \in \hskip0.5em {\mathfrak{U}}_m^{r,s} $, we define:
$$ \beta \#\gamma =\left({b}_0,\dots, {b}_r,{c}_0,\dots, {c}_s\right)\hskip0.5em \in \hskip0.5em {\mathfrak{U}}_m^{r+s}, $$ and for 
$ {\beta}^{\prime }=\left({b}_0,\dots, {b}_r\right)\hskip0.5em \in \hskip0.5em {\mathfrak{U}}_m^{r-1} $ and 
$ {\gamma}^{\prime }=\left({c}_0,\dots, {c}_s\right)\hskip0.5em \in \hskip0.5em {\mathfrak{U}}_m^{s-1} $, we set:
$$ {\beta}^{\prime}\ast {\gamma}^{\prime }=\left({b}_0,\dots, {b}_r,{c}_0,\dots, {c}_s\right)\hskip0.5em \in \hskip0.5em {\mathfrak{U}}_m^{r+s}. $$Then, we have a bijection
$$ {\mathfrak{U}}_m^{r,s}\coprod \left({\mathfrak{U}}_m^{r-1}\times {\mathfrak{U}}_m^{s-1}\right)\leftrightarrow {\mathfrak{U}}_m^{r+s}. $$Using the theorem above, we have:
$$ {\displaystyle \begin{array}{c}V\left(\beta \#\gamma \right)=f\left(V\left(\beta \right)\otimes V\left(\gamma \right)\right),\\ {}V\left({\beta}^{\prime}\ast {\gamma}^{\prime}\right)=f\left(V\left({\beta}^{\prime}\right)\otimes V\left({\gamma}^{\prime}\right)\right).\end{array}} $$Corollary 2.3. Suppose 
$ n=2p=r+s $, where 
$ r,s\hskip0.5em \ge 1 $.
(a) If r, s are odd and
$ \left({\beta}^{\prime },{\gamma}^{\prime}\right)\hskip0.5em \in \hskip0.5em {\mathrm{\mathfrak{C}}}_m^{r-1}\times {\mathrm{\mathfrak{C}}}_m^{s-1} $, then $ {\beta}^{\prime}\ast {\gamma}^{\prime}\hskip0.5em \in \hskip0.5em {\mathrm{\mathfrak{C}}}_m^n. $(b) If r, s are even and
$ \left(\beta, \gamma \right)\hskip0.5em \in \hskip0.5em \left({\mathrm{\mathfrak{C}}}_m^r\times {\mathrm{\mathfrak{C}}}_m^s\right)\cap {\mathfrak{U}}_m^{r,s} $, then $ \beta \#\gamma \hskip0.5em \in \hskip0.5em {\mathrm{\mathfrak{C}}}_m^n. $
By the above corollary, the Hodge conjecture can be proved inductively for the Fermat 
$ {X}_m^n $ if the following conditions are true for every 
$ \alpha \hskip0.5em \in \hskip0.5em {\mathfrak{B}}_m^n $:
(P1) 
$ \alpha \sim {\beta}^{\prime}\ast {\gamma}^{\prime } $ for some 
$ \left({\beta}^{\prime },{\gamma}^{\prime}\right)\hskip0.5em \in \hskip0.5em {\mathfrak{B}}_m^{r-1}\times {\mathfrak{B}}_m^{s-1}\left(r,s\mathrm{odd}\right), $
(P2) 
$ \alpha \sim \beta \#\gamma $ for some 
$ \left(\beta, \gamma \right)\kern0.5em \in \kern0.5em \left({\mathfrak{B}}_m^r\times {\mathfrak{B}}_m^s\right)\cap {\mathfrak{U}}_m^{r,s}\left(r,s\kern0.5em \mathrm{even}\text{
and
positive}\right), $
where ∼ means equality up to permutation between factors.
In order to make these conditions more explicit, we introduce the additive semigroup Mm of nonnegative solutions 
$ \left({x}_1,\dots, {x}_{m-1};y\right) $ with y > 0, to the following system of linear equations:
$$ \sum \limits_{i=1}^{m-1}< ti>{x}_i= my\hskip0.5em \mathrm{for}\hskip0.5em \mathrm{all}\hskip0.5em t\hskip0.5em \in \hskip0.5em {\mathrm{\mathbb{Z}}}_m^{\ast }. $$Furthermore, define Mm(y) as those solutions, where y is fixed. Note that by Gordan’s lemma, Mm is finitely generated.
Definition 2.4. An element 
$ a\hskip0.5em \in \hskip0.5em {M}_m $ is called decomposable if a = c + d for some 
$ c,d\hskip0.5em \in \hskip0.5em {M}_m $; otherwise, it is called indecomposable. An element b is called quasi-decomposable if a + b = c + d for some 
$ a\hskip0.5em \in \hskip0.5em {M}_m(1) $ and 
$ c,d\hskip0.5em \in \hskip0.5em {M}_m $ with 
$ c,d\ne b. $
With this notation, we can identify elements of 
$ {\mathfrak{B}}_m^n $ with elements of Mm using the map:
$$ \left\{\right\}:\alpha =\left({a}_0,\dots, {a}_{n+1}\right)\hskip0.5em \in \hskip0.5em {\mathfrak{B}}_m^n\mapsto \left\{\alpha \right\}=\left({x}_1\left(\alpha \right),\dots, {x}_{m-1}\left(\alpha \right),\frac{n}{2}+1\right)\hskip0.5em \in \hskip0.5em {M}_m\left(\frac{n}{2}+1\right), $$ where 
$ {x}_k\left(\alpha \right) $ is the number of i’s such that <ai > =k.
Note that 
$ \alpha $ satisfies 
$ (P1) $ above if and only if 
$ \left\{\alpha \right\} $ is decomposable. If 
$ \alpha $ satisfies 
$ (P2) $, then 
$ \left\{\alpha \right\} $ is quasi-decomposable. Conversely, if the latter is true, then 
$ \alpha $ satisfies 
$ (P1) $ or 
$ (P2) $. So it makes sense to introduce the following conditions:
- $ \left({P}_m^n\right) $ Every indecomposable element of Mm(y) with $ 3\hskip0.5em \le \hskip0.5em y\hskip0.5em \le \hskip0.5em \frac{n}{2}+1 $, if any, is quasi-decomposable.
(Pm) Every indecomposable element of Mm(y) with
$ y\hskip0.5em \ge \hskip0.5em 3 $ is quasi-decomposable.
By the results above, we conclude:
Theorem 2.5 (Shioda, Reference Shioda1979). If condition (Pm) is satisfied, then the Hodge conjecture is true for 
$ {X}_m^n $, for any n. If ( 
$ {P}_m^n $) is satisfied, then the Hodge conjecture is true for 
$ {X}_m^n. $
For m prime or m = 4, Mm is generated by 
$ {M}_m(1) $, which gives:
Theorem 2.6 (Ran, Reference Ran1980; Shioda, Reference Shioda1979). If m is prime or m = 4, the Hodge conjecture is true for 
$ {X}_m^n $, for all n. Shioda manually verified condition (Pm) for m ≤ 20 and concluded:
Theorem 2.7 (Shioda, Reference Shioda1979). If m ≤ 20, the Hodge conjecture is true for 
$ {X}_m^n $, for all n.
Starting at m = 21, the number of indecomposables and the length of elements of Mm are very large, so it is hard to verify (Pm) by hand for unknown cases, unless 
$ m={p}^2 $ is a square of a prime. In the latter case, condition (Pm) is not always true; it is false for 
$ m=25 $, for example. However, Aoki (Reference Aoki1987) explicitly constructed the algebraic cycles that generate each 
$ V\left(\alpha \right) $; such cycles are called standard cycles.
Theorem 2.8 (Aoki, Reference Aoki1987). If m = p 2, the Hodge conjecture is true for 
$ {X}_m^n $, for all n, even though condition (Pm) may be false.
3. New cases of the Hodge conjecture
A natural question is whether or not the Hodge conjecture can always be proved using condition (Pm). As described above, there are false negatives, that is, (Pm) is false, but the Hodge conjecture is still true. This is due to the fact that there are cycles not coming from the induced structure (see Aoki, Reference Aoki1987).
The next obvious question is then for which values of m, if any, the condition (Pm) is false, besides m = p 2. In such cases, one expects (if one believes the Hodge conjecture) that there are cycles, not of standard type as in Aoki (Reference Aoki1987), such that they too do not come from the induced structure. Alternatively, they are candidates for a counterexample to the Hodge conjecture.
We used SAGE math to answer that question by investigating when condition (Pm) is true. All the code used in this section can be found in the Appendix.
In the case of Fermat fourfolds, we computed, first, all the indecomposable elements with length 3, because the (2,2) cycles have length exactly 3. So the idea was to find values of m for which there were none of them.
Proposition 3.1. If m ≤ 100 is an integer coprime to 6, then the Hodge conjecture is true for all Fermat fourfolds 
$ {X}_m^4 $.
This is a strong evidence that the Hodge conjecture should be true for fourfolds 
$ {X}_m^4 $ where m is coprime to 6. It suggests the structure of 
$ {\mathfrak{B}}_m^4 $, namely, if 
$ 3\mid m $, then there are indecomposables elements of length 3 (see Proposition 3.4 below).
The following corollary is immediate by Shioda (Reference Shioda1979).
Corollary 3.2. If 
$ {m}_i\hskip0.5em \le \hskip0.5em 100 $ are integers coprime to 6, then the Hodge conjecture is true for arbitrary products of Fermat fourfolds 
$ {X}_{m_1}^4\times \dots \times {X}_{m_k}^4 $.
We slightly extended Shioda’s work by verifying condition (Pm) for 
$ m=21,27 $. A computational proof can be found in the Appendix.
Theorem 3.3. The Hodge conjecture is true for Fermats 
$ {X}_{21}^n $ and 
$ {X}_{27}^n $, for all n.
An interesting case is m = 33, where condition (Pm) is false, because we have explicitly found a Hodge class that is not quasi-decomposable and is not of standard type either.
Proposition 3.4. Condition P 33 is false. More precisely, the following cycle
$$ \left(0,0,0,0,0,0,1,0,0,1,0,0,1,0,0,0,0,0,1,0,0,1,0,0,0,0,0,1,0,0,0,0,3\right) $$ supported on 
$ {X}_{33}^4 $ is not quasi-decomposable in M 33.
This proposition confirms that starting at n = 4, there are cycles not coming from the induced structure. Therefore, we cannot prove the Hodge conjecture only using this approach. One thing that can be done is to find explicitly the algebraic cycles whose class project nontrivially to 
$ V\left(\alpha \right) $ for each 
$ \alpha \hskip0.5em \in \hskip0.5em {\mathfrak{B}}_m^n $ (see Aoki, Reference Aoki1987).
In the particular case where m = 3d and 
$ 3\nmid d $, as above, we have a candidate. Consider the following elementary symmetric polynomials in x
$ =\left({x}_0,\dots, {x}_5\right) $:
$$ {\displaystyle \begin{array}{l}{p}_1\left(\mathrm{x}\right):= {x}_0+{x}_1+{x}_2+{x}_3+{x}_4+{x}_5,\\ {}{p}_2\left(\mathrm{x}\right):= {x}_0{x}_1+{x}_0{x}_2+\dots +{x}_4{x}_5,\\ {}{p}_3\left(\mathrm{x}\right):= {x}_0{x}_1{x}_2+\dots +{x}_3{x}_4{x}_5.\end{array}} $$Recall the Newton identity:
$$ {x}_0^3+{x}_1^3+{x}_2^3+{x}_3^3+{x}_4^3+{x}_5^3={p}_1{\left(\mathrm{x}\right)}^3-3{p}_1\left(\mathrm{x}\right){p}_2\left(\mathrm{x}\right)+3{p}_3\left(\mathrm{x}\right). $$ Set 
$ {\mathrm{x}}^d=\left({x}_0^d,\dots, {x}_5^d\right) $, then:
$$ {x}_0^m+{x}_1^m+{x}_2^m+{x}_3^m+{x}_4^m+{x}_5^m={p}_1{\left({x}^d\right)}^3-3{p}_1\left({x}^d\right){p}_2\left({x}^d\right)+3{p}_3\left({x}^d\right). $$ Let W denote the following variety in 
$ {\mathrm{\mathbb{P}}}^5 $:
$$ {p}_1\left({\mathrm{x}}^d\right)={p}_2\left({\mathrm{x}}^d\right)={p}_3\left({\mathrm{x}}^d\right)=0. $$ By construction, 
$ W\subseteq {X}_m^4 $ is a subvariety of codimension 2, so 
$ \left[W\right]\hskip0.5em \in \hskip0.5em {Hdg}^2\left({X}_m^4\right). $
Question 1. Can 
$ \left[W\right] $ project nontrivially in 
$ V\left(\alpha \right) $ for every 
$ \alpha \hskip0.5em \in \hskip0.5em {\mathfrak{B}}_m^4 $ which is not quasi-decomposable and not of standard type?
If the answer is yes, then we would have a positive answer to the Hodge conjecture in this case.
We know by Gordan’s lemma that the number of indecomposable elements is finite. Given 
$ m\hskip0.5em \in \hskip0.5em {\mathrm{\mathbb{Z}}}_{+} $, in order to prove the Hodge conjecture for 
$ {X}_m^n $ and any n, it is enough to prove for all 
$ {X}_m^n,n\hskip0.5em \le \hskip0.5em {n}^{\prime } $, where 
$ {n}^{\prime }=2\left({m}^{\prime }-1\right) $ and 
$ {m}^{\prime } $ is the largest length of all the indecomposable elements in Mm.
Let 
$ {\mathrm{\mathcal{I}}}_m $ be set of indecomposable elements of Mm. Define 
$ \phi :{\mathrm{\mathbb{Z}}}_{+}\to {\mathrm{\mathbb{Z}}}_{+} $ by the rule
$$ \phi (m)=\left\{\max y\hskip0.5em |\hskip0.5em \left({x}_1,\dots {x}_{m-1},y\right)\hskip0.5em \in \hskip0.5em {\mathrm{\mathcal{I}}}_m\right\}. $$We have the following:
Proposition 3.5. If the Hodge conjecture is true for 
$ {X}_m^n $, for all 
$ n\hskip0.5em \le \hskip0.5em 2\left(\phi (m)-1\right) $, then it is true for 
$ {X}_m^n $ and any n.
Proof. The Hodge classes in 
$ {X}_m^n $ are parametrized by 
$ {\mathrm{\mathcal{B}}}_m^n $, which can be viewed inside Mm as elements of length 
$ \frac{n}{2}+1 $. Since the indecomposables generate Mm, it is enough that those be classes of algebraic cycles. But that is the case if the Hodge conjecture is true when 
$ \frac{n}{2}+1\hskip0.5em \le \hskip0.5em \phi (m) $, by definition of ɸ(m).
Therefore, for Fermat varieties of degree m, we do not need to check the Hodge conjecture in every dimension. It is enough to prove the result for dimension up to 2(ɸ(m)–1).
Clearly then, it is desirable to find an expression for the function ɸ(m). For m prime or m = 4, we know already that ɸ(m) = 1. Furthermore, by Aoki (Reference Aoki1987), we know that for p > 2 prime, 
$ \phi \left({p}^2\right)=\frac{p+1}{2} $. Here is a table with the a few values of ɸ(m):
Based on the values above and the ones already computed, we believe the following is true.
Conjecture 2. For p > 2 prime, we have 
$ \phi \left({p}^k\right)=\frac{p^{k-1}+1}{2} $, and 
$ \phi \left({2}^l\right)={2}^{l-2}+1 $, for l > 2.
Computing ɸ(m) for m < 48 gives the following:
For m < 48, computations become more time-consuming, and specially if m has a lot of prime powers in its prime decomposition. But the results obtained here give us a glimpse about the structure of Mm and, consequently, the Hodge conjecture in the case of Fermat varieties.
Acknowledgment
I would like to thank Prof. Matt Kerr for helpful discussions during the preparation of this work.
Data availability statement
The author confirms that the data supporting the findings of this study are available within the article [and/or its supplementary materials].
Conflicts of interest
The author declares none.
Funding information
This research received no specific grant from any funding agency, commercial, or not-for-profit sectors.
Appendix: A code implementation of Shioda’s approach
The following SAGE code, for a fixed m > 1, checks whether or not every indecomposable element is quasi-decomposable. If such condition is true, then the Hodge conjecture holds for 
$ {X}_m^n $.
Open access
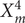
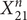
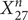
Comments
Comments to the Author: This paper provides an excellent overview of what is known about the Hodge conjecture for Fermat hypersurfaces. Additionally, new cases of the Hodge conjecture are obtained experimentally for those Fermat hypersurfaces where the inductive structure of the Fermat variety in question fails to supply all of the algebraic cycles. There are very minor spelling corrections that the author can easily detect using spell-check.