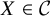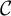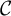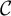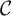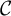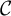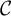1 Introduction
We assume the reader is familiar with tensor categories; many of the definitions omitted below can be found in [Reference Etingof, Gelaki, Nikshych and OstrikEGNO15]. Let
![]() $\mathbb {k}$
be a field, and let
$\mathbb {k}$
be a field, and let
![]() $\mathcal {C}$
be a Cauchy completeFootnote 1
$\mathcal {C}$
be a Cauchy completeFootnote 1
![]() $\mathbb {k}$
-linear braided monoidal category with finite-dimensional morphism spaces and
$\mathbb {k}$
-linear braided monoidal category with finite-dimensional morphism spaces and ![]() . We say that an indecomposable
. We say that an indecomposable
![]() $X\in \mathcal {C}$
is non-negligible if there exists
$X\in \mathcal {C}$
is non-negligible if there exists
![]() $Y\in \mathcal {C}$
such that
$Y\in \mathcal {C}$
such that ![]() is a direct summand in
is a direct summand in
![]() $Y\otimes X$
.Footnote 2 We say that X has moderate growth if there exists
$Y\otimes X$
.Footnote 2 We say that X has moderate growth if there exists
![]() $n\in \Bbb N$
such that
$n\in \Bbb N$
such that
![]() $\dim \operatorname {\mathrm {End}}(X^{\otimes n})<n!$
.Footnote 3 Our main result, proved in §2.2, is:
$\dim \operatorname {\mathrm {End}}(X^{\otimes n})<n!$
.Footnote 3 Our main result, proved in §2.2, is:
Theorem 1.1. Every non-negligible object of moderate growth in
![]() $\mathcal {C}$
is rigid.
$\mathcal {C}$
is rigid.
We say
![]() $\mathcal {C}$
has moderate growth if all indecomposable
$\mathcal {C}$
has moderate growth if all indecomposable
![]() $X\in \mathcal {C}$
have moderate growth. Thus we get:
$X\in \mathcal {C}$
have moderate growth. Thus we get:
Corollary 1.2. If
![]() $\mathcal {C}$
has moderate growth, then every non-negligible
$\mathcal {C}$
has moderate growth, then every non-negligible
![]() $X\in \mathcal {C}$
is rigid.
$X\in \mathcal {C}$
is rigid.
Recall from [Reference Boyarchenko and DrinfeldBD13] that an r-category is a monoidal category
![]() $\mathcal {C}$
such that for every
$\mathcal {C}$
such that for every
![]() $X\in \mathcal {C}$
, the functor
$X\in \mathcal {C}$
, the functor ![]() is representable by some object
is representable by some object
![]() $X^*$
, and the functor
$X^*$
, and the functor
![]() $*:\mathcal {C}\to \mathcal {C}^{\mathrm {mop}}$
(monoidal and arrow opposite) is an equivalence. Note that r-categories are particular examples of Grothendieck-Verdier categories, also known as
$*:\mathcal {C}\to \mathcal {C}^{\mathrm {mop}}$
(monoidal and arrow opposite) is an equivalence. Note that r-categories are particular examples of Grothendieck-Verdier categories, also known as
![]() $*$
-autonomous categories [Reference BarrBar79]. Up to taking opposites, this is exactly the notion of weak rigidity in [Reference Bakalov and KirillovBK01, Def. 5.3.4].Footnote 4 Clearly, in a semisimple braided r-category with simple
$*$
-autonomous categories [Reference BarrBar79]. Up to taking opposites, this is exactly the notion of weak rigidity in [Reference Bakalov and KirillovBK01, Def. 5.3.4].Footnote 4 Clearly, in a semisimple braided r-category with simple ![]() , every simple object is non-negligible.Footnote 5 Thus we obtain:
, every simple object is non-negligible.Footnote 5 Thus we obtain:
Corollary 1.3. Every semisimple braided r-category of moderate growth is rigid.Footnote 6
There are several applications of our results. The first is a simplification of the proof that the representation categories of certain vertex operator algebras (VOAs) are rigid [Reference HuangHua05, Hua08b, Hua08a]. Indeed, before the proof of rigidity in [Reference HuangHua08a, §3], the main assumptions on the VOA V already imply that
![]() $\mathsf {Rep}(V)$
is a finite semisimple braided r-category, and thus our Corollary 1.3 directly applies.
$\mathsf {Rep}(V)$
is a finite semisimple braided r-category, and thus our Corollary 1.3 directly applies.
Second, given a finite splitFootnote 7 semisimple category
![]() $\mathcal {C}$
, the data of a
$\mathcal {C}$
, the data of a
![]() $\mathcal {C}$
-modular functor is essentially equivalentFootnote 8 to the data of nondegenerate weak ribbon structure on
$\mathcal {C}$
-modular functor is essentially equivalentFootnote 8 to the data of nondegenerate weak ribbon structure on
![]() $\mathcal {C}$
[Reference Bakalov and KirillovBK01, Def. 5.3.5, Thm. 5.7.10], which implies that
$\mathcal {C}$
[Reference Bakalov and KirillovBK01, Def. 5.3.5, Thm. 5.7.10], which implies that
![]() $\mathcal {C}$
is a finite split semisimple braided r-category with simple
$\mathcal {C}$
is a finite split semisimple braided r-category with simple ![]() . It was left open in [Reference Bakalov and KirillovBK01, Rem. 5.3.7] whether every such
. It was left open in [Reference Bakalov and KirillovBK01, Rem. 5.3.7] whether every such
![]() $\mathcal {C}$
is a modular fusion category, hinging on whether weak rigidity implies rigidity. Since finite semisimple monoidal categories have moderate growth, we answer this question affirmatively:
$\mathcal {C}$
is a modular fusion category, hinging on whether weak rigidity implies rigidity. Since finite semisimple monoidal categories have moderate growth, we answer this question affirmatively:
Corollary 1.4. Given a finite split semisimple category
![]() $\mathcal {C}$
, the data of a
$\mathcal {C}$
, the data of a
![]() $\mathcal {C}$
-modular functor in the sense of [Reference Bakalov and KirillovBK01] is essentially equivalent
8
to a modular fusion category structure on
$\mathcal {C}$
-modular functor in the sense of [Reference Bakalov and KirillovBK01] is essentially equivalent
8
to a modular fusion category structure on
![]() $\mathcal {C}$
.Footnote 9
$\mathcal {C}$
.Footnote 9
A third application concerns semisimplification; here, we assume that
![]() $\mathbb {k}$
is algebraically closed.Footnote 10 For rigid
$\mathbb {k}$
is algebraically closed.Footnote 10 For rigid
![]() $X\in \mathcal {C}$
, let
$X\in \mathcal {C}$
, let
![]() $\operatorname {\mathrm {Tr}}_X$
denote the quantum trace constructed from the Drinfeld isomorphism (see (2.3) below). We first show that X is non-negligible iff
$\operatorname {\mathrm {Tr}}_X$
denote the quantum trace constructed from the Drinfeld isomorphism (see (2.3) below). We first show that X is non-negligible iff
![]() $\operatorname {\mathrm {Tr}}_X\ne 0$
, which is the traditional definition of non-negligibility. In particular, direct sums of negligible objects form a thick tensor ideal
$\operatorname {\mathrm {Tr}}_X\ne 0$
, which is the traditional definition of non-negligibility. In particular, direct sums of negligible objects form a thick tensor ideal
![]() $\mathcal I\subset \mathcal {C}$
: if
$\mathcal I\subset \mathcal {C}$
: if
![]() $X\in \mathcal {C}$
and
$X\in \mathcal {C}$
and
![]() $Z\in \mathcal I$
then
$Z\in \mathcal I$
then
![]() $X\otimes Z\in \mathcal I$
. Hence we can define the Green ring
$X\otimes Z\in \mathcal I$
. Hence we can define the Green ring
![]() $K(\mathcal {C}):=\mathrm {Green}(\mathcal {C}/\mathcal I)$
whose
$K(\mathcal {C}):=\mathrm {Green}(\mathcal {C}/\mathcal I)$
whose
![]() $\Bbb Z_+$
-basis is formed by the isomorphism classes of non-negligible objects of
$\Bbb Z_+$
-basis is formed by the isomorphism classes of non-negligible objects of
![]() $\mathcal {C}$
and multiplication is defined by the tensor product.
$\mathcal {C}$
and multiplication is defined by the tensor product.
Next, the proof of Theorem 1.1 can be adapted (see §2.4) to establish the following characterization of the nilradical
![]() $R(X)\subset \operatorname {\mathrm {End}}(X)$
for non-negligible
$R(X)\subset \operatorname {\mathrm {End}}(X)$
for non-negligible
![]() $X\in \mathcal {C}$
of moderate growth:Footnote 11
$X\in \mathcal {C}$
of moderate growth:Footnote 11
Corollary 1.5. If X is non-negligible of moderate growth (hence rigid by Theorem 1.1), then
![]() $R(X)=ker ( { {Tr}}_X)$
. In other words, the quantum trace of every nilpotent endomorphism of X is zero, but
$R(X)=ker ( { {Tr}}_X)$
. In other words, the quantum trace of every nilpotent endomorphism of X is zero, but
![]() $ { {Tr}}_X( { {id}}_X)\ne 0$
.
$ { {Tr}}_X( { {id}}_X)\ne 0$
.
We also have the following standard lemma, proved in §2.5.
Lemma 1.6. If
![]() $\mathcal {C}$
is rigid and the quantum trace of a nilpotent endomorphism of each non-negligible object of
$\mathcal {C}$
is rigid and the quantum trace of a nilpotent endomorphism of each non-negligible object of
![]() $\mathcal {C}$
is zero, then this is so for any object of
$\mathcal {C}$
is zero, then this is so for any object of
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Thus, if
![]() $\mathcal {C}$
has moderate growth, then Corollary 1.5 enables the semisimplification procedure of [Reference Etingof and OstrikEO22, Thm. 2.6]Footnote 12 to obtain a semisimple braided tensor category
$\mathcal {C}$
has moderate growth, then Corollary 1.5 enables the semisimplification procedure of [Reference Etingof and OstrikEO22, Thm. 2.6]Footnote 12 to obtain a semisimple braided tensor category
![]() $\overline {\mathcal {C}}$
of moderate growth. We get:
$\overline {\mathcal {C}}$
of moderate growth. We get:
Corollary 1.7. If
![]() $\mathcal {C}$
has moderate growth, then
$\mathcal {C}$
has moderate growth, then
![]() $\mathcal {C}$
admits a semisimplification
$\mathcal {C}$
admits a semisimplification
![]() $\overline {\mathcal {C}}$
, a semisimple braided tensor category of moderate growth whose Grothendieck ring is
$\overline {\mathcal {C}}$
, a semisimple braided tensor category of moderate growth whose Grothendieck ring is
![]() $K(\mathcal {C})$
.
$K(\mathcal {C})$
.
In particular, applying the main results of [Reference DeligneDel02] in characteristic zero and of [Reference Coulembier, Etingof and OstrikCEO23] in positive characteristic, we obtain:
Corollary 1.8. If
![]() $\mathcal {C}$
is symmetric, then the category
$\mathcal {C}$
is symmetric, then the category
![]() $\overline {\mathcal {C}}$
from Corollary 1.7 admits a fiber functor to
$\overline {\mathcal {C}}$
from Corollary 1.7 admits a fiber functor to
![]() $\operatorname {SuperVect}$
in characteristic zero and to the Verlinde category
$\operatorname {SuperVect}$
in characteristic zero and to the Verlinde category
![]() $\operatorname {Ver}_p$
in positive characteristic, and thus is equivalent to the representation category of a linearly reductive affine group scheme in
$\operatorname {Ver}_p$
in positive characteristic, and thus is equivalent to the representation category of a linearly reductive affine group scheme in
![]() $ {SuperVect}$
, respectively
$ {SuperVect}$
, respectively
![]() $ {Ver}_p$
.
$ {Ver}_p$
.
In characteristic zero, such semisimple symmetric categories are just representation categories of pro-reductive groups, and for characteristics
![]() $2,3$
, they are representation categories of linearly reductive group schemes classified by Nagata’s theorem, see [Reference Coulembier, Etingof and OstrikCEO23, Section 8] (up to a super-twist of the symmetric structure outside characteristic
$2,3$
, they are representation categories of linearly reductive group schemes classified by Nagata’s theorem, see [Reference Coulembier, Etingof and OstrikCEO23, Section 8] (up to a super-twist of the symmetric structure outside characteristic
![]() $2$
). In positive characteristics
$2$
). In positive characteristics
![]() $p\ge 5$
, there is a conjectural classification of them [Reference Coulembier, Etingof and OstrikCEO24, Conjecture 4.1]. Thus the
$p\ge 5$
, there is a conjectural classification of them [Reference Coulembier, Etingof and OstrikCEO24, Conjecture 4.1]. Thus the
![]() $\mathbb {Z}_+$
-ring spanned by non-negligible summands in
$\mathbb {Z}_+$
-ring spanned by non-negligible summands in
![]() $X^{*\otimes m}\otimes X^{\otimes n}$
, where X is a non-negligible (hence rigid) object of any symmetric category
$X^{*\otimes m}\otimes X^{\otimes n}$
, where X is a non-negligible (hence rigid) object of any symmetric category
![]() $\mathcal {C}$
of moderate growth, is very strongly constrained.
$\mathcal {C}$
of moderate growth, is very strongly constrained.
As a fourth application, in §4, we apply our results to braided r-categories which are not necessarily semisimple. Such categories arise in logarithmic conformal field theory. The results in this section allow us to significantly simplify a number of arguments in [Reference Kazhdan and LusztigKL94].
2 Proofs
2.1 Auxiliary lemmas
Let
![]() $\mathcal {C}$
be as in the last section. By convention, we suppress all associators and unitors. Let
$\mathcal {C}$
be as in the last section. By convention, we suppress all associators and unitors. Let
![]() $X\in \mathcal {C}$
be non-negligible, that is, there is an indecomposable
$X\in \mathcal {C}$
be non-negligible, that is, there is an indecomposable
![]() $Y\in \mathcal {C}$
such that
$Y\in \mathcal {C}$
such that ![]() is a direct summand of
is a direct summand of
![]() $Y\otimes X\cong X\otimes Y$
. We denote X by an upwards oriented strand and Y by a downwards oriented strand. We begin with a well-known observation.
$Y\otimes X\cong X\otimes Y$
. We denote X by an upwards oriented strand and Y by a downwards oriented strand. We begin with a well-known observation.
Lemma 2.1. If ![]() and
and ![]() are such that
are such that  is invertible, then
is invertible, then
![]() $X,Y$
are rigid with
$X,Y$
are rigid with
![]() ${}^*X\cong Y\cong X^*$
.
${}^*X\cong Y\cong X^*$
.
Proof. By rescaling, we may assume
![]() $z=\operatorname {\mathrm {id}}_{X}$
. Then
$z=\operatorname {\mathrm {id}}_{X}$
. Then  is a subdiagram of
is a subdiagram of
![]() $z^2=z=\operatorname {\mathrm {id}}_X$
, which implies
$z^2=z=\operatorname {\mathrm {id}}_X$
, which implies
![]() $z'\neq 0$
. Since
$z'\neq 0$
. Since
![]() $z^{\prime 2}=z'$
,
$z^{\prime 2}=z'$
,
![]() $z'=\operatorname {\mathrm {id}}_Y$
as Y is indecomposable. Using the braiding,
$z'=\operatorname {\mathrm {id}}_Y$
as Y is indecomposable. Using the braiding,

Thus X is rigid with
![]() ${}^*X\cong Y\cong X^*$
.
${}^*X\cong Y\cong X^*$
.
For
![]() $W,Z\in \mathcal {C}$
, a morphism
$W,Z\in \mathcal {C}$
, a morphism
![]() $r: W\to Z$
is called a retraction or a split surjection if it admits a splitting
$r: W\to Z$
is called a retraction or a split surjection if it admits a splitting
![]() $s: Z\to W$
such that
$s: Z\to W$
such that
![]() $rs = \operatorname {\mathrm {id}}_Z$
. Clearly, the existence of a retraction
$rs = \operatorname {\mathrm {id}}_Z$
. Clearly, the existence of a retraction
![]() $r:W\to Z$
is equivalent to Z being a direct summand of W. Thus there exists a retraction
$r:W\to Z$
is equivalent to Z being a direct summand of W. Thus there exists a retraction ![]() . Next, we carefully choose one via the following lemma.
. Next, we carefully choose one via the following lemma.
Lemma 2.2. Let Z be any object containing ![]() as a direct summand, and
as a direct summand, and
![]() $N\subset {{End}}(Z)$
a nilpotent subspace, that is,
$N\subset {{End}}(Z)$
a nilpotent subspace, that is,
![]() $N^n=0$
for some n. There exists a retraction
$N^n=0$
for some n. There exists a retraction ![]() such that for any
such that for any ![]() , we have
, we have
![]() $rNa=0$
.
$rNa=0$
.
Proof. Let
![]() $k\in \mathbb {N}$
be minimal for which there is a retraction
$k\in \mathbb {N}$
be minimal for which there is a retraction ![]() such that for any
such that for any ![]() ,
,
![]() $rN^k a=0$
. (Since
$rN^k a=0$
. (Since
![]() $N^n=0$
, such a
$N^n=0$
, such a
![]() $k\leq n$
exists.) Suppose for contradiction that
$k\leq n$
exists.) Suppose for contradiction that
![]() $k\ge 2$
. Then there are
$k\ge 2$
. Then there are ![]() ,
,
![]() $x\in N$
, and
$x\in N$
, and
![]() $y\in N^{k-2}$
such that
$y\in N^{k-2}$
such that
![]() $rxya_0=1$
. Thus
$rxya_0=1$
. Thus
![]() $r':=rx$
is also a retraction, and for every
$r':=rx$
is also a retraction, and for every ![]() we have
we have
![]() $r'N^{k-1}a\subseteq rN^ka=0$
, contradicting the minimality of k. Thus
$r'N^{k-1}a\subseteq rN^ka=0$
, contradicting the minimality of k. Thus
![]() $k=1$
.
$k=1$
.
Let
![]() $R(X)\subset \operatorname {\mathrm {End}}(X)$
be the nilradical, and choose a retraction
$R(X)\subset \operatorname {\mathrm {End}}(X)$
be the nilradical, and choose a retraction ![]() and splitting
and splitting ![]() satisfying Lemma 2.2 for
satisfying Lemma 2.2 for
![]() $Z=X\otimes Y$
and
$Z=X\otimes Y$
and
![]() $N:=R(X)\otimes \operatorname {\mathrm {id}}_Y\subset \operatorname {\mathrm {End}}(X\otimes Y)$
. We prove the contrapositive of Theorem 1.1, that is, if X is not rigid, then
$N:=R(X)\otimes \operatorname {\mathrm {id}}_Y\subset \operatorname {\mathrm {End}}(X\otimes Y)$
. We prove the contrapositive of Theorem 1.1, that is, if X is not rigid, then
![]() $\dim \operatorname {\mathrm {End}}(X^{\otimes n})\ge n!$
for all
$\dim \operatorname {\mathrm {End}}(X^{\otimes n})\ge n!$
for all
![]() $n\in \Bbb N$
. Using the braiding, we get a retraction
$n\in \Bbb N$
. Using the braiding, we get a retraction ![]() with a splitting:
with a splitting:

Observe that if any of the following morphisms is invertible, then after redefining ![]() , X is rigid with
, X is rigid with
![]() ${}^*X\cong Y\cong X^*$
by Lemma 2.1.
${}^*X\cong Y\cong X^*$
by Lemma 2.1.

Recall that since X is indecomposable, the finite-dimensional algebra
![]() $\operatorname {\mathrm {End}}(X)$
is local, hence every element of
$\operatorname {\mathrm {End}}(X)$
is local, hence every element of
![]() $\operatorname {\mathrm {End}}(X)$
is either invertible or nilpotent [Reference Assem, Simson and SkowrońskiASS06, Cor. 4.8(b)]. We may thus assume that the morphisms in (2.1) are all nilpotent, that is, lie in
$\operatorname {\mathrm {End}}(X)$
is either invertible or nilpotent [Reference Assem, Simson and SkowrońskiASS06, Cor. 4.8(b)]. We may thus assume that the morphisms in (2.1) are all nilpotent, that is, lie in
![]() $R(X)$
.
$R(X)$
.
Now consider the n-strand braid group

Given an element of
![]() $B_n$
, we number its strands from left to right on the bottom; for example,
$B_n$
, we number its strands from left to right on the bottom; for example,
![]() $\sigma _i$
swaps the i-th and
$\sigma _i$
swaps the i-th and
![]() $i+1$
-th strands. The standard set embedding of
$i+1$
-th strands. The standard set embedding of
![]() $S_n$
into
$S_n$
into
![]() $B_n$
is given by taking a reduced word
$B_n$
is given by taking a reduced word
![]() $w\in S_n$
and writing the same word in
$w\in S_n$
and writing the same word in
![]() $B_n$
. In braid diagrams, these are the elements that can be written in the following form:
$B_n$
. In braid diagrams, these are the elements that can be written in the following form:
-
• any two distinct strands cross at most once, and
-
• if the i-th and j-th strands cross with
 $i<j$
, then the i-th strand passes over the j-th strand.
$i<j$
, then the i-th strand passes over the j-th strand.
Every element of
![]() $S_n\subset B_n$
can be written uniquely as
$S_n\subset B_n$
can be written uniquely as
![]() $w_{n-1}w_{n-2}\cdots w_2w_1$
where for each index
$w_{n-1}w_{n-2}\cdots w_2w_1$
where for each index
![]() $1\leq j\leq n-1$
, denoting multiple strands by thick colored strands,
$1\leq j\leq n-1$
, denoting multiple strands by thick colored strands,

We identify
![]() $B_n,S_n$
with their respective images in
$B_n,S_n$
with their respective images in
![]() $B_{n+1},S_{n+1}$
under adding a strand to the right.
$B_{n+1},S_{n+1}$
under adding a strand to the right.
Lemma 2.3. Suppose
![]() $s,t\in S_n$
are distinct. There are
$s,t\in S_n$
are distinct. There are
![]() $u,v\in B_{n-1}\subset B_n$
such that
$u,v\in B_{n-1}\subset B_n$
such that
![]() $s^{-1}t = u\sigma _{n-1}^{j} v$
in
$s^{-1}t = u\sigma _{n-1}^{j} v$
in
![]() $B_n$
, where
$B_n$
, where
![]() $j\in \{-1,0,+1\}$
. (However,
$j\in \{-1,0,+1\}$
. (However,
![]() $u,v\notin S_{n-1}$
necessarily.)
$u,v\notin S_{n-1}$
necessarily.)
Proof. If
![]() $s^{-1}t\in B_{n-1}$
, we are finished. Otherwise, since the n-th strands of
$s^{-1}t\in B_{n-1}$
, we are finished. Otherwise, since the n-th strands of
![]() $s,t$
pass behind all other strands, there are
$s,t$
pass behind all other strands, there are
![]() $s',t'\in S_{n-1}$
such that
$s',t'\in S_{n-1}$
such that
![]() $s= \sigma _i \sigma _{i+1}\cdots \sigma _{n-1}s'$
and
$s= \sigma _i \sigma _{i+1}\cdots \sigma _{n-1}s'$
and
![]() $t= \sigma _j \sigma _{j+1}\cdots \sigma _{n-1}t'$
with
$t= \sigma _j \sigma _{j+1}\cdots \sigma _{n-1}t'$
with
![]() $i\neq j$
. Without loss of generality, we may assume
$i\neq j$
. Without loss of generality, we may assume
![]() $s=\sigma _i \sigma _{i+1}\cdots \sigma _{n-1}$
and
$s=\sigma _i \sigma _{i+1}\cdots \sigma _{n-1}$
and
![]() $t=\sigma _j \sigma _{j+1}\cdots \sigma _{n-1}$
with
$t=\sigma _j \sigma _{j+1}\cdots \sigma _{n-1}$
with
![]() $i<j$
. The result now follows by inspection; representing multiple strands by thick lines, we see
$i<j$
. The result now follows by inspection; representing multiple strands by thick lines, we see

2.2 Proof of Theorem 1.1
As above, we assume the morphisms in (2.1) are nilpotent, that is, lie in the nilradical
![]() $R(X)\subset \operatorname {\mathrm {End}}(X)$
. For
$R(X)\subset \operatorname {\mathrm {End}}(X)$
. For
![]() $t\in S_n$
, let
$t\in S_n$
, let
![]() $f_t\in \operatorname {\mathrm {End}}(X^{\otimes n})$
denote the corresponding morphism. We claim that the set
$f_t\in \operatorname {\mathrm {End}}(X^{\otimes n})$
denote the corresponding morphism. We claim that the set ![]() is linearly independent, which implies the result.
is linearly independent, which implies the result.
Consider the bilinear form ![]() given by
given by

For
![]() $s,t\in S_n$
, we claim that
$s,t\in S_n$
, we claim that
![]() $ \Phi (f_s^{-1},f_t) = \delta _{s,t}$
, which immediately implies that
$ \Phi (f_s^{-1},f_t) = \delta _{s,t}$
, which immediately implies that ![]() is linearly independent:
is linearly independent:
 $$\begin{align*}0 = \sum_{t\in S_n} \lambda_t f_t \qquad\Longrightarrow\qquad 0 = \Phi\left( f_s^{-1}, \sum_{t\in S_n} \lambda_t f_t \right ) = \sum_{t\in S_n} \lambda_t \delta_{s,t} = \lambda_s \qquad \forall s\in S_n. \end{align*}$$
$$\begin{align*}0 = \sum_{t\in S_n} \lambda_t f_t \qquad\Longrightarrow\qquad 0 = \Phi\left( f_s^{-1}, \sum_{t\in S_n} \lambda_t f_t \right ) = \sum_{t\in S_n} \lambda_t \delta_{s,t} = \lambda_s \qquad \forall s\in S_n. \end{align*}$$
Clearly
![]() $\Phi (f_s^{-1}, f_s) = 1$
by construction. If
$\Phi (f_s^{-1}, f_s) = 1$
by construction. If
![]() $s\neq t$
, then writing
$s\neq t$
, then writing
![]() $s=v_{n-1}\cdots v_{1}$
and
$s=v_{n-1}\cdots v_{1}$
and
![]() $t=w_{n-1}\cdots w_{1}$
as in (2.2), pick k maximal such that
$t=w_{n-1}\cdots w_{1}$
as in (2.2), pick k maximal such that
![]() $w_k\neq v_k$
. Then
$w_k\neq v_k$
. Then
![]() $s^{-1}t$
lies in the image of
$s^{-1}t$
lies in the image of
![]() $S_k$
included into
$S_k$
included into
![]() $S_n$
, but the k-th lower boundary point of
$S_n$
, but the k-th lower boundary point of
![]() $s^{-1}t$
does not connect to the k-th upper boundary point. By Lemma 2.3, there are
$s^{-1}t$
does not connect to the k-th upper boundary point. By Lemma 2.3, there are
![]() $u,v\in B_{k-1}\subset B_n$
such that
$u,v\in B_{k-1}\subset B_n$
such that
![]() $s^{-1}t=u\sigma _{k-1}^{\pm 1}v$
. Then
$s^{-1}t=u\sigma _{k-1}^{\pm 1}v$
. Then ![]() has
has
![]() $n-k$
closed loops which can be removed, but the k-th strand performs a self-crossing of the form
$n-k$
closed loops which can be removed, but the k-th strand performs a self-crossing of the form

which lie in
![]() $R(X)$
by assumption. By naturality of the braiding, there is an
$R(X)$
by assumption. By naturality of the braiding, there is an ![]() such that
such that

Remark 2.4. If
![]() $\mathcal {C}$
is semisimple then
$\mathcal {C}$
is semisimple then
![]() $R(X)=0$
, so Lemma 2.2 is not needed and the proof simplifies.
$R(X)=0$
, so Lemma 2.2 is not needed and the proof simplifies.
2.3 Non-negligible rigid objects
Let
![]() $\mathbb {k}$
be algebraically closed. It is well known that when
$\mathbb {k}$
be algebraically closed. It is well known that when
![]() $\mathcal {C}$
is braided and
$\mathcal {C}$
is braided and
![]() $X\in \mathcal {C}$
is rigid, we have a distinguished quantum trace
$X\in \mathcal {C}$
is rigid, we have a distinguished quantum trace ![]() using the Drinfeld isomorphism
using the Drinfeld isomorphism
![]() $u_X: X\to X^{**}$
:
$u_X: X\to X^{**}$
:

It is straightforward to verify that
![]() $\operatorname {\mathrm {Tr}}_X(fg)=\operatorname {\mathrm {Tr}}_X(gf)$
for all
$\operatorname {\mathrm {Tr}}_X(fg)=\operatorname {\mathrm {Tr}}_X(gf)$
for all
![]() $f,g\in \operatorname {\mathrm {End}}(X)$
.
$f,g\in \operatorname {\mathrm {End}}(X)$
.
Lemma 2.5.
-
(i) If X is rigid, then X is non-negligible if and only if there is an
 $f\in \operatorname {\mathrm {End}}(X)$
such that
$f\in \operatorname {\mathrm {End}}(X)$
such that
 $\operatorname {\mathrm {Tr}}_X(f)$
is nonzero. In this case one may take
$\operatorname {\mathrm {Tr}}_X(f)$
is nonzero. In this case one may take
 $Y=X^*$
for the witness of non-negligibility of X.
$Y=X^*$
for the witness of non-negligibility of X. -
(ii) If X is rigid indecomposable and
 $\mathrm {ker}(\operatorname {\mathrm {Tr}}_X)=R(X)$
(i.e., the trace of a nilpotent endomorphism of X is zero), and if Y is indecomposable such that
$\mathrm {ker}(\operatorname {\mathrm {Tr}}_X)=R(X)$
(i.e., the trace of a nilpotent endomorphism of X is zero), and if Y is indecomposable such that
 $Y\otimes X$
contains
$Y\otimes X$
contains  as a direct summand, then
as a direct summand, then
 $Y\cong X^*$
.
$Y\cong X^*$
.
Proof. (i) If such an f exists, we can take
![]() $Y=X^*$
,
$Y=X^*$
,
![]() $r:= \operatorname {\mathrm {ev}}_{X^{*}} (u_X f \otimes \operatorname {\mathrm {id}}_{X^*})$
and
$r:= \operatorname {\mathrm {ev}}_{X^{*}} (u_X f \otimes \operatorname {\mathrm {id}}_{X^*})$
and
![]() $s:= \operatorname {\mathrm {Tr}}_X(f)^{-1} \operatorname {\mathrm {coev}}_X$
so that
$s:= \operatorname {\mathrm {Tr}}_X(f)^{-1} \operatorname {\mathrm {coev}}_X$
so that
![]() $rs=1$
, and thus X is non-negligible. Conversely, if
$rs=1$
, and thus X is non-negligible. Conversely, if ![]() is a retraction with splitting
is a retraction with splitting ![]() , then set
, then set

(ii) If ![]() is a retraction with splitting
is a retraction with splitting ![]() , then the f from (2.4) above is invertible as
, then the f from (2.4) above is invertible as
![]() $\operatorname {\mathrm {Tr}}_X(f)=1$
,
$\operatorname {\mathrm {Tr}}_X(f)=1$
,
![]() $\ker (\operatorname {\mathrm {Tr}}_X)=R(X)$
, and X is indecomposable. Dualizing, we see that
$\ker (\operatorname {\mathrm {Tr}}_X)=R(X)$
, and X is indecomposable. Dualizing, we see that
![]() $f^*: X^*\to X^*$
is an isomorphism. But
$f^*: X^*\to X^*$
is an isomorphism. But
![]() $f^*$
can be written as
$f^*$
can be written as
![]() $g\circ h$
, where
$g\circ h$
, where

This implies that g is a retraction with splitting
![]() $h\circ (f^*)^{-1}$
, so h identifies
$h\circ (f^*)^{-1}$
, so h identifies
![]() $X^*$
with a direct summand of Y. Since Y is indecomposable, it follows that h is an isomorphism.
$X^*$
with a direct summand of Y. Since Y is indecomposable, it follows that h is an isomorphism.
2.4 Proof of Corollary 1.5
When X is rigid and non-negligible, then
![]() $\operatorname {\mathrm {Tr}}_X: \operatorname {\mathrm {End}}(X)\to \mathbb {k}$
is nonzero by Lemma 2.5. Since
$\operatorname {\mathrm {Tr}}_X: \operatorname {\mathrm {End}}(X)\to \mathbb {k}$
is nonzero by Lemma 2.5. Since
![]() $\dim \operatorname {\mathrm {End}}(X)<\infty $
and
$\dim \operatorname {\mathrm {End}}(X)<\infty $
and
![]() $R(X)$
is a maximal ideal as X is indecomposable, it suffices to prove that when X is rigid, non-negligible, and
$R(X)$
is a maximal ideal as X is indecomposable, it suffices to prove that when X is rigid, non-negligible, and
![]() $\dim \operatorname {\mathrm {End}}(X^{\otimes n})<n!$
for some n, then
$\dim \operatorname {\mathrm {End}}(X^{\otimes n})<n!$
for some n, then
![]() $R(X)\subseteq \ker (\operatorname {\mathrm {Tr}}_X)$
. To do so, we show that if X is rigid and non-negligible and there is a nilpotent
$R(X)\subseteq \ker (\operatorname {\mathrm {Tr}}_X)$
. To do so, we show that if X is rigid and non-negligible and there is a nilpotent
![]() $f\in R(X)$
with
$f\in R(X)$
with
![]() $\operatorname {\mathrm {Tr}}_X(f)\neq 0$
, then
$\operatorname {\mathrm {Tr}}_X(f)\neq 0$
, then
![]() $\dim \operatorname {\mathrm {End}}(X^{\otimes n})\ge n!$
for all n.
$\dim \operatorname {\mathrm {End}}(X^{\otimes n})\ge n!$
for all n.
First, we mimic the proof of Lemma 2.2. Set
![]() $Y=X^*$
,
$Y=X^*$
,
![]() $r:= \operatorname {\mathrm {ev}}_{X^{*}}(u_X\otimes \operatorname {\mathrm {id}}_{X^*})$
and
$r:= \operatorname {\mathrm {ev}}_{X^{*}}(u_X\otimes \operatorname {\mathrm {id}}_{X^*})$
and
![]() $N:=R(X)\otimes \operatorname {\mathrm {id}}_{X^*}$
. Let
$N:=R(X)\otimes \operatorname {\mathrm {id}}_{X^*}$
. Let
![]() $k\in \mathbb {N}$
be minimal such that
$k\in \mathbb {N}$
be minimal such that
![]() $rN^ka= 0$
for all
$rN^ka= 0$
for all ![]() . Since
. Since
![]() $\operatorname {\mathrm {Tr}}_X(f)\neq 0$
, taking
$\operatorname {\mathrm {Tr}}_X(f)\neq 0$
, taking
![]() $a=\operatorname {\mathrm {coev}}_X$
shows that
$a=\operatorname {\mathrm {coev}}_X$
shows that
![]() $k\geq 2$
. Pick
$k\geq 2$
. Pick
![]() $g\in R(X)^{k-1}$
and
$g\in R(X)^{k-1}$
and ![]() so that
so that
![]() $r(g\otimes \operatorname {\mathrm {id}}_{X^*})s_0=1$
. Setting
$r(g\otimes \operatorname {\mathrm {id}}_{X^*})s_0=1$
. Setting
![]() $r_0:= r(g\otimes \operatorname {\mathrm {id}}_{X^*})$
, we have
$r_0:= r(g\otimes \operatorname {\mathrm {id}}_{X^*})$
, we have
![]() $r_0s_0=1$
and
$r_0s_0=1$
and
![]() $r_0Ns_0=0$
. Observe that
$r_0Ns_0=0$
. Observe that

both lie in
![]() $R(X)$
as they contain
$R(X)$
as they contain
![]() $g\in R(X)^{k-1}\subset R(X)$
. Now by mimicking the proof of Theorem 1.1, we can use
$g\in R(X)^{k-1}\subset R(X)$
. Now by mimicking the proof of Theorem 1.1, we can use
![]() $r_0,s_0$
in place of the cap/cup to see that
$r_0,s_0$
in place of the cap/cup to see that
![]() $\dim \operatorname {\mathrm {End}}(X^{\otimes n})\ge n!$
for all n.
$\dim \operatorname {\mathrm {End}}(X^{\otimes n})\ge n!$
for all n.
2.5 Proof of Lemma 1.6
Suppose
 $$ \begin{align*}Z=\bigoplus_{i=1}^r V_i\otimes X_i, \end{align*} $$
$$ \begin{align*}Z=\bigoplus_{i=1}^r V_i\otimes X_i, \end{align*} $$
where
![]() $X_i$
are pairwise nonisomorphic indecomposable objects of
$X_i$
are pairwise nonisomorphic indecomposable objects of
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $V_i$
are finite-dimensional vector spaces. Then the nilradical
$V_i$
are finite-dimensional vector spaces. Then the nilradical
![]() $R(Z)$
of
$R(Z)$
of
![]() $\operatorname {\mathrm {End}}(Z)$
has the form
$\operatorname {\mathrm {End}}(Z)$
has the form
 $$ \begin{align*}R(Z)=\bigoplus_{i=1}^r \operatorname{\mathrm{End}}(V_i)\otimes R(X_i) \oplus \bigoplus_{i\ne j}\operatorname{\mathrm{Hom}}(V_i,V_j)\otimes \operatorname{\mathrm{Hom}}(X_i,X_j). \end{align*} $$
$$ \begin{align*}R(Z)=\bigoplus_{i=1}^r \operatorname{\mathrm{End}}(V_i)\otimes R(X_i) \oplus \bigoplus_{i\ne j}\operatorname{\mathrm{Hom}}(V_i,V_j)\otimes \operatorname{\mathrm{Hom}}(X_i,X_j). \end{align*} $$
So
![]() $\operatorname {\mathrm {Tr}}_Z$
vanishes on
$\operatorname {\mathrm {Tr}}_Z$
vanishes on
![]() $R(Z)$
, and on the quotient
$R(Z)$
, and on the quotient
 $$ \begin{align*}\operatorname{\mathrm{End}}(Z)/R(Z)\cong \bigoplus_{i=1}^r \operatorname{\mathrm{End}}(V_i) \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{End}}(Z)/R(Z)\cong \bigoplus_{i=1}^r \operatorname{\mathrm{End}}(V_i) \end{align*} $$
induces the linear functional
![]() $T(f_1,\cdots ,f_r):=\sum _{i=1}^r c_i\operatorname {\mathrm {Tr}}_{\operatorname {\mathrm {End}}(V_i)}(f_i)$
, where
$T(f_1,\cdots ,f_r):=\sum _{i=1}^r c_i\operatorname {\mathrm {Tr}}_{\operatorname {\mathrm {End}}(V_i)}(f_i)$
, where
![]() $c_i:=\operatorname {\mathrm {Tr}}_{X_i}(\mathrm {id}_{X_i})$
. If
$c_i:=\operatorname {\mathrm {Tr}}_{X_i}(\mathrm {id}_{X_i})$
. If
![]() $f: Z\to Z$
is a nilpotent endomorphism, then its image
$f: Z\to Z$
is a nilpotent endomorphism, then its image
![]() $(f_1,\dots , f_r)\in \operatorname {\mathrm {End}}(Z)/R(Z)$
satisfies that
$(f_1,\dots , f_r)\in \operatorname {\mathrm {End}}(Z)/R(Z)$
satisfies that
![]() $f_i\in \operatorname {\mathrm {End}}(V_i)$
is nilpotent for each i, and thus
$f_i\in \operatorname {\mathrm {End}}(V_i)$
is nilpotent for each i, and thus
![]() $\operatorname {\mathrm {Tr}}_{\operatorname {\mathrm {End}}(V_i)}(f_i)=0$
for each i. We conclude that
$\operatorname {\mathrm {Tr}}_{\operatorname {\mathrm {End}}(V_i)}(f_i)=0$
for each i. We conclude that
![]() $\operatorname {\mathrm {Tr}}_Z(f)=T(f_1,\cdots ,f_r)=0$
.
$\operatorname {\mathrm {Tr}}_Z(f)=T(f_1,\cdots ,f_r)=0$
.
3 Remarks
3.1 The linearized category of crystals
The assumption that
![]() $\mathcal {C}$
is braided in Theorem 1.1 cannot be removed. A counterexample is the
$\mathcal {C}$
is braided in Theorem 1.1 cannot be removed. A counterexample is the
![]() $\Bbb C$
-linearization
$\Bbb C$
-linearization
![]() $\mathrm {Crys}(G)$
of the category of crystals for the quantum group
$\mathrm {Crys}(G)$
of the category of crystals for the quantum group
![]() $G_q$
attached to a simply connected simple complex group G [Reference Henriques and KamnitzerHK06], which is a semisimple category of moderate growth but is not braided, nor rigid (only weakly rigid). This category is a limit when
$G_q$
attached to a simply connected simple complex group G [Reference Henriques and KamnitzerHK06], which is a semisimple category of moderate growth but is not braided, nor rigid (only weakly rigid). This category is a limit when
![]() $q\to 0$
of the braided, rigid categories
$q\to 0$
of the braided, rigid categories
![]() $\mathsf {Rep}(G_q)$
with the same Grothendieck ring, but the braiding and rigidity are destroyed in the limit; in fact, the only rigid objects in
$\mathsf {Rep}(G_q)$
with the same Grothendieck ring, but the braiding and rigidity are destroyed in the limit; in fact, the only rigid objects in
![]() $\mathrm {Crys}(G)$
are multiples of
$\mathrm {Crys}(G)$
are multiples of ![]() . Indeed, in
. Indeed, in
![]() $\mathsf {Rep}(G_q)$
, if
$\mathsf {Rep}(G_q)$
, if
![]() $V_\lambda $
is the irreducible representation with highest weight
$V_\lambda $
is the irreducible representation with highest weight
![]() $\lambda $
and
$\lambda $
and
![]() $f: V_\lambda \to V_\lambda ^{**}$
is an isomorphism, then
$f: V_\lambda \to V_\lambda ^{**}$
is an isomorphism, then
![]() $\operatorname {\mathrm {Tr}}(f)\operatorname {\mathrm {Tr}}((f^*)^{-1})=(\dim _q V_\lambda )^2$
, which goes to infinity as
$\operatorname {\mathrm {Tr}}(f)\operatorname {\mathrm {Tr}}((f^*)^{-1})=(\dim _q V_\lambda )^2$
, which goes to infinity as
![]() $q\to 0$
for any
$q\to 0$
for any
![]() $\lambda \ne 0$
, as do those eigenvalues of the squared braiding on
$\lambda \ne 0$
, as do those eigenvalues of the squared braiding on
![]() $V_\lambda \otimes V_\mu $
which are negative powers of q. The category
$V_\lambda \otimes V_\mu $
which are negative powers of q. The category
![]() $\mathrm {Crys}(G)$
is, however, a coboundary category [Reference Henriques and KamnitzerHK06]: it carries a symmetric commutor (a natural isomorphism
$\mathrm {Crys}(G)$
is, however, a coboundary category [Reference Henriques and KamnitzerHK06]: it carries a symmetric commutor (a natural isomorphism
![]() $\sigma _{X,Y}:X\otimes Y\to Y\otimes X$
) satisfying the Reidemeister move R2, but not R3. This shows that the move R3 plays a crucial role in the proof of Theorem 1.1.
$\sigma _{X,Y}:X\otimes Y\to Y\otimes X$
) satisfying the Reidemeister move R2, but not R3. This shows that the move R3 plays a crucial role in the proof of Theorem 1.1.
To make things concrete, let us restrict to the case
![]() $G=SL(2)$
. In this case,
$G=SL(2)$
. In this case,
![]() $\mathrm {Crys}(G)$
can be realized as the asymptotic Temperley-Lieb-Jones category
$\mathrm {Crys}(G)$
can be realized as the asymptotic Temperley-Lieb-Jones category
![]() $TLJ(\infty )$
. Namely, recall that the usual Temperley-Lieb-Jones category
$TLJ(\infty )$
. Namely, recall that the usual Temperley-Lieb-Jones category
![]() $TLJ(\delta )$
is defined so that the circle evaluates to
$TLJ(\delta )$
is defined so that the circle evaluates to
![]() $\delta $
, while the zig-zag evaluates to
$\delta $
, while the zig-zag evaluates to
![]() $1$
(namely,
$1$
(namely,
![]() $TLJ(\delta )=\mathsf {Rep}(SL(2)_q)$
where
$TLJ(\delta )=\mathsf {Rep}(SL(2)_q)$
where
![]() $\delta =-q-q^{-1}$
). By renormalizing the diagrams, we may arrange that the circle evaluates to
$\delta =-q-q^{-1}$
). By renormalizing the diagrams, we may arrange that the circle evaluates to
![]() $1$
, while the zig-zag evaluates to
$1$
, while the zig-zag evaluates to
![]() $\delta ^{-1}$
. This allows us to specialize
$\delta ^{-1}$
. This allows us to specialize
![]() $TLJ(\delta )$
at
$TLJ(\delta )$
at
![]() $\delta =\infty $
(i.e.,
$\delta =\infty $
(i.e.,
![]() $\delta ^{-1}=0$
), which yields a semisimple category
$\delta ^{-1}=0$
), which yields a semisimple category
![]() $TLJ(\infty )$
with Grothendieck ring the representation ring of
$TLJ(\infty )$
with Grothendieck ring the representation ring of
![]() $SL(2)$
where the circle evaluates to
$SL(2)$
where the circle evaluates to
![]() $1$
while the zig-zag evaluates to
$1$
while the zig-zag evaluates to
![]() $0$
(see [Reference VirkVir, §3]), which is not braided, nor rigid (although is weakly rigid). Namely,
$0$
(see [Reference VirkVir, §3]), which is not braided, nor rigid (although is weakly rigid). Namely,
![]() $\operatorname {\mathrm {Hom}}([n],[m])$
in
$\operatorname {\mathrm {Hom}}([n],[m])$
in
![]() $TLJ(\infty )$
has the usual basis of Temperley-Lieb-Jones diagrams with n inputs and m outputs and composition given by concatenation of diagrams and removing the circles, but when the concatenation contains a zig-zag, instead of straightening it, the composition is declared to be zero.
$TLJ(\infty )$
has the usual basis of Temperley-Lieb-Jones diagrams with n inputs and m outputs and composition given by concatenation of diagrams and removing the circles, but when the concatenation contains a zig-zag, instead of straightening it, the composition is declared to be zero.
The endomorphism algebra of the object
![]() $[n]$
in
$[n]$
in
![]() $TLJ(\infty )$
is thus the asymptotic Temperley-Lieb-Jones algebra
$TLJ(\infty )$
is thus the asymptotic Temperley-Lieb-Jones algebra
![]() $TLJ_n(\infty )$
spanned by diagrams with n inputs and n outputs (no longer generated by the usual generators
$TLJ_n(\infty )$
spanned by diagrams with n inputs and n outputs (no longer generated by the usual generators
![]() $e_i$
if
$e_i$
if
![]() $n\ge 3$
, however). We obtain a quick proof that
$n\ge 3$
, however). We obtain a quick proof that
![]() $TLJ_n(\infty )$
and hence the category
$TLJ_n(\infty )$
and hence the category
![]() $TLJ(\infty )$
are semisimple by defining a filtrationFootnote 13 on
$TLJ(\infty )$
are semisimple by defining a filtrationFootnote 13 on
![]() $TLJ_n(\infty )$
in which the degree of a diagram u is its number of cups.
$TLJ_n(\infty )$
in which the degree of a diagram u is its number of cups.
We can even identify
![]() $TLJ_n(\infty )$
as a multimatrix algebra by observing that the Jones-Wenzl idempotents exist and are nonzero for all
$TLJ_n(\infty )$
as a multimatrix algebra by observing that the Jones-Wenzl idempotents exist and are nonzero for all
![]() $n\in \mathbb {N}$
. Indeed, the usual Jones-Wenzl recurrence relation [Reference WenzlWen87] simplifies greatly as zig-zags are zero:
$n\in \mathbb {N}$
. Indeed, the usual Jones-Wenzl recurrence relation [Reference WenzlWen87] simplifies greatly as zig-zags are zero:
One can also check via this recurrence relation that
![]() $JW_n$
is the linear combination of all projections p with no nested cups/caps where the coefficient of p is
$JW_n$
is the linear combination of all projections p with no nested cups/caps where the coefficient of p is
![]() $(-1)^{\#\text { caps in }p}$
. Matrix units for the summands of
$(-1)^{\#\text { caps in }p}$
. Matrix units for the summands of
![]() $TLJ_n(\infty )$
are then obtained by cabling the ‘waists’ of basis elements by the appropriate Jones-Wenzl idempotents. It then follows that
$TLJ_n(\infty )$
are then obtained by cabling the ‘waists’ of basis elements by the appropriate Jones-Wenzl idempotents. It then follows that
![]() $TLJ_n(\infty )$
is a multimatrix algebra, as diagrams whose through strings are cabled by different Jones-Wenzl idempotents are orthogonal.Footnote 14
$TLJ_n(\infty )$
is a multimatrix algebra, as diagrams whose through strings are cabled by different Jones-Wenzl idempotents are orthogonal.Footnote 14
All these counterexamples have infinitely many simple objects, however. This gives rise to the following question, which is open even for weakly rigid categorifications of based rings (with duality).
Question 3.1. Can Corollary 1.3 be generalized to finite semisimple weakly rigid categories (not necessarily braided)?
Remark 3.2. The answer to Question 3.1 is “yes” when
![]() $\mathcal {C}$
is a semisimple (not necessarily braided) full monoidal subcategory of endomorphisms of an infinite von Neumann factor which is weakly rigid when
$\mathcal {C}$
is a semisimple (not necessarily braided) full monoidal subcategory of endomorphisms of an infinite von Neumann factor which is weakly rigid when
![]() $*:\mathcal {C}\to \mathcal {C}^{\mathrm {mop}}$
is taking conjugates (so that
$*:\mathcal {C}\to \mathcal {C}^{\mathrm {mop}}$
is taking conjugates (so that
![]() $*\circ *\cong \operatorname {\mathrm {id}}_{\mathcal {C}}$
). Indeed, rigidity follows by [Reference LongoLon90, Thm. 4.1]; see also [Reference Bartels, Douglas and HenriquesBDH14, Prop. 7.17] for bimodules over a von Neumann factor.
$*\circ *\cong \operatorname {\mathrm {id}}_{\mathcal {C}}$
). Indeed, rigidity follows by [Reference LongoLon90, Thm. 4.1]; see also [Reference Bartels, Douglas and HenriquesBDH14, Prop. 7.17] for bimodules over a von Neumann factor.
3.2 Rigidity for small growth dimension in nonbraided categories
For a positive element Z of a based ring A as in [Reference Etingof, Gelaki, Nikshych and OstrikEGNO15, Def. 3.1.3], define the growth dimension
![]() $\operatorname {\mathrm {gd}}(Z)$
to be
$\operatorname {\mathrm {gd}}(Z)$
to be
(see [Reference Coulembier, Etingof and OstrikCEO23, Def. 4.1]), where the length of a positive element is the sum of its coefficients.Footnote 15 For example, for A the character ring of a complex reductive group G,
![]() $\operatorname {\mathrm {gd}}(Z)$
is the usual dimension of the representation Z, and if A is finite, then
$\operatorname {\mathrm {gd}}(Z)$
is the usual dimension of the representation Z, and if A is finite, then
![]() $\operatorname {\mathrm {gd}}(Z)$
coincides with the Frobenius-Perron dimension
$\operatorname {\mathrm {gd}}(Z)$
coincides with the Frobenius-Perron dimension
![]() $\operatorname {\mathrm {FPdim}}(Z)$
.
$\operatorname {\mathrm {FPdim}}(Z)$
.
Proposition 3.3. Let
![]() $X,Y$
be simple objects of a split semisimple weakly rigid category
$X,Y$
be simple objects of a split semisimple weakly rigid category
![]() $\mathcal {C}$
over
$\mathcal {C}$
over
![]() $\mathbb {k}$
such that
$\mathbb {k}$
such that ![]() is a direct summand in
is a direct summand in
![]() $Y\otimes X$
(and thus in
$Y\otimes X$
(and thus in
![]() $X\otimes Y$
). If
$X\otimes Y$
). If
![]() $ { {gd}}(Y\otimes X)<\textit{4}$
then X is rigid and
$ { {gd}}(Y\otimes X)<\textit{4}$
then X is rigid and
![]() $Y\cong X^*$
.
$Y\cong X^*$
.
Proof. Fix a retraction (cap) ![]() and splitting (cup)
and splitting (cup) ![]() such that
such that
![]() $r_+s_+=1$
and similarly
$r_+s_+=1$
and similarly ![]() and
and ![]() such that
such that
![]() $r_-s_-=1$
. We therefore have the zig-zags
$r_-s_-=1$
. We therefore have the zig-zags
Moreover,
![]() $z_1^2=z_1z_2=z_2^2$
, so
$z_1^2=z_1z_2=z_2^2$
, so
![]() $z_1=z_2=:z$
, and similarly
$z_1=z_2=:z$
, and similarly
![]() $z_3=z_4=:z_*$
.Footnote 16
$z_3=z_4=:z_*$
.Footnote 16
For a noncrossing matching u on the word
![]() $(YX)^n$
, let
$(YX)^n$
, let
![]() $D(u)$
be the number of
$D(u)$
be the number of
![]() $YX$
-matchings in u (so the number of
$YX$
-matchings in u (so the number of
![]() $XY$
-matchings is
$XY$
-matchings is
![]() $n-D(u)$
). Consider the pairing
$n-D(u)$
). Consider the pairing
given by
![]() $\Phi (f,g)=f\circ g$
. For every non-crossing matching u of
$\Phi (f,g)=f\circ g$
. For every non-crossing matching u of
![]() $[1,2n]$
we have elements
$[1,2n]$
we have elements ![]() defined using
defined using
![]() $r_+,r_-$
and
$r_+,r_-$
and ![]() defined using
defined using
![]() $s_+,s_-$
. It is easy to see that for any two noncrossing matchings
$s_+,s_-$
. It is easy to see that for any two noncrossing matchings
![]() $u,v$
, we have
$u,v$
, we have
where
![]() $a(u,v)-b(u,v)=D(u)-D(v)$
,
$a(u,v)-b(u,v)=D(u)-D(v)$
,
![]() $a(u,v)+b(u,v)>0$
if
$a(u,v)+b(u,v)>0$
if
![]() $u\ne v$
, and
$u\ne v$
, and
![]() $\Phi (f_u,g_u)=1$
. Thus if
$\Phi (f_u,g_u)=1$
. Thus if
![]() $z=0$
or
$z=0$
or
![]() $z_*=0$
, then the matrix
$z_*=0$
, then the matrix
![]() $[\Phi (f_u,g_v)]$
is upper or lower triangular in any ordering compatible with the D-grading, with
$[\Phi (f_u,g_v)]$
is upper or lower triangular in any ordering compatible with the D-grading, with
![]() $1$
on the diagonal, hence nondegenerate. It then follows that
$1$
on the diagonal, hence nondegenerate. It then follows that
![]() $\lbrace g_u\rbrace $
are linearly independent. Since the number of noncrossing matchings is
$\lbrace g_u\rbrace $
are linearly independent. Since the number of noncrossing matchings is
![]() $C_n$
(the n-th Catalan number), this implies that
$C_n$
(the n-th Catalan number), this implies that
Since
![]() $\lim _{n\to \infty }C_n^{\frac {1}{n}}=4$
, it follows that
$\lim _{n\to \infty }C_n^{\frac {1}{n}}=4$
, it follows that
![]() $\operatorname {\mathrm {gd}}(Y\otimes X)\ge 4$
. Thus if
$\operatorname {\mathrm {gd}}(Y\otimes X)\ge 4$
. Thus if
![]() $\operatorname {\mathrm {gd}}(Y\otimes X)<4$
then
$\operatorname {\mathrm {gd}}(Y\otimes X)<4$
then
![]() $z,z_*\ne 0$
, implying that X is rigid and
$z,z_*\ne 0$
, implying that X is rigid and
![]() $Y\cong X^*$
.
$Y\cong X^*$
.
Remark 3.4. Note that the bound in Proposition 3.3 is sharp: for the crystal
![]() $X\in \mathrm {Crys}(SL_2)$
of the two-dimensional representation,
$X\in \mathrm {Crys}(SL_2)$
of the two-dimensional representation,
![]() $Y=X$
and
$Y=X$
and
![]() $\operatorname {\mathrm {gd}}(X)=2$
, so
$\operatorname {\mathrm {gd}}(X)=2$
, so
![]() $\operatorname {\mathrm {gd}}(Y\otimes X)=4$
, but X is not rigid.
$\operatorname {\mathrm {gd}}(Y\otimes X)=4$
, but X is not rigid.
Moreover, if
![]() $\mathrm {gd}(Y\otimes X)=4$
, it is possible that exactly one of
$\mathrm {gd}(Y\otimes X)=4$
, it is possible that exactly one of
![]() $z,z_*$
is zero. Namely, we may consider the universal pivotal category defined in [Reference Coulembier and EtingofCE24, §3.2] which in our notation would be natural to denote
$z,z_*$
is zero. Namely, we may consider the universal pivotal category defined in [Reference Coulembier and EtingofCE24, §3.2] which in our notation would be natural to denote
![]() $TLJ(\delta _1,\delta _2)$
. Its morphisms are oriented Temperley-Lieb-Jones diagrams, with counterclockwise circles evaluated to
$TLJ(\delta _1,\delta _2)$
. Its morphisms are oriented Temperley-Lieb-Jones diagrams, with counterclockwise circles evaluated to
![]() $\delta _1$
and clockwise circles to
$\delta _1$
and clockwise circles to
![]() $\delta _2$
. We can renormalize the diagrams so that both circles evaluate to
$\delta _2$
. We can renormalize the diagrams so that both circles evaluate to
![]() $1$
while
$1$
while
![]() $z=\delta _1^{-1}$
,
$z=\delta _1^{-1}$
,
![]() $z_*=\delta _2^{-1}$
. Now we can take
$z_*=\delta _2^{-1}$
. Now we can take
![]() $\delta _1$
or
$\delta _1$
or
![]() $\delta _2$
to
$\delta _2$
to
![]() $\infty $
to get categories
$\infty $
to get categories
![]() $TLJ(\infty ,\delta _2)$
,
$TLJ(\infty ,\delta _2)$
,
![]() $TLJ(\delta _1,\infty )$
where
$TLJ(\delta _1,\infty )$
where
![]() $z=0,z_*\ne 0$
, respectively
$z=0,z_*\ne 0$
, respectively
![]() $z\ne 0,z_*= 0$
.
$z\ne 0,z_*= 0$
.
Note that the category
![]() $TLJ(\delta ,\infty )$
(and likewise
$TLJ(\delta ,\infty )$
(and likewise
![]() $TLJ(\infty ,\delta )$
) is semisimple for
$TLJ(\infty ,\delta )$
) is semisimple for
![]() $\delta \ne 0$
. Indeed, the endomorphism algebra of a word W in
$\delta \ne 0$
. Indeed, the endomorphism algebra of a word W in
![]() $X,Y$
in
$X,Y$
in
![]() $TLJ(\delta ,\infty )$
is the asymptotic lopsided Temperley-Lieb-Jones algebra
$TLJ(\delta ,\infty )$
is the asymptotic lopsided Temperley-Lieb-Jones algebra
![]() $TLJ_W(\delta ,\infty )$
in which both circles evaluate to
$TLJ_W(\delta ,\infty )$
in which both circles evaluate to
![]() $1$
,
$1$
,
![]() $z=\delta ^{-1}$
and
$z=\delta ^{-1}$
and
![]() $z_*=0$
. Define a filtration on this algebra in which the degree of a diagram u is the number of
$z_*=0$
. Define a filtration on this algebra in which the degree of a diagram u is the number of ![]() minus the number of
minus the number of ![]() in u. It is easy to check that this indeed defines a filtration, and the associated graded algebra
in u. It is easy to check that this indeed defines a filtration, and the associated graded algebra
![]() $\mathrm {gr}(TLJ_W(\delta ,\infty ))\cong TLJ_W(\infty ,\infty )$
, where
$\mathrm {gr}(TLJ_W(\delta ,\infty ))\cong TLJ_W(\infty ,\infty )$
, where
![]() $z=0=z_*$
.
$z=0=z_*$
.
Thus, it suffices to show that
![]() $TLJ_W(\infty ,\infty )$
is semisimple; we argue similarly to §3.1. Define the degree of a diagram u in
$TLJ_W(\infty ,\infty )$
is semisimple; we argue similarly to §3.1. Define the degree of a diagram u in
![]() $TLJ_W(\infty ,\infty )$
as its number of cups. Then
$TLJ_W(\infty ,\infty )$
as its number of cups. Then
![]() $I_k/I_{k+1}$
is a direct sum of matrix algebras indexed over subwords of W which can be obtained by successively removing instances of
$I_k/I_{k+1}$
is a direct sum of matrix algebras indexed over subwords of W which can be obtained by successively removing instances of
![]() $XY$
or
$XY$
or
![]() $YX$
from W. (These subwords are the words which are retractions of W via
$YX$
from W. (These subwords are the words which are retractions of W via
![]() $r_\pm $
.)
$r_\pm $
.)
3.3 Categories of nonmoderate growth
The assumption that X has moderate growth in Theorem 1.1 cannot be removed, even for symmetric categories. A counterexample is the symmetric oriented Brauer category
![]() $OB(\infty )$
, which is the limit as
$OB(\infty )$
, which is the limit as
![]() $t\to \infty $
of the oriented Brauer categories
$t\to \infty $
of the oriented Brauer categories
![]() $OB(t)$
, also known as the Deligne categories
$OB(t)$
, also known as the Deligne categories
![]() $\mathsf {Rep}(GL_t)$
,
$\mathsf {Rep}(GL_t)$
,
![]() $t\in \Bbb C$
[Reference Etingof, Gelaki, Nikshych and OstrikEGNO15, §9.12]. Namely, recall that
$t\in \Bbb C$
[Reference Etingof, Gelaki, Nikshych and OstrikEGNO15, §9.12]. Namely, recall that
![]() $OB(t)$
has objects
$OB(t)$
has objects
![]() $[n,m]$
for
$[n,m]$
for
![]() $n,m\in \mathbb {N}$
, and
$n,m\in \mathbb {N}$
, and
![]() $\operatorname {\mathrm {Hom}}([n_1,m_1],[n_2,m_2])$
is spanned by appropriate walled Brauer diagrams, with composition given by concatenation of diagrams, so that the circle evaluates to t. Similar to the construction of
$\operatorname {\mathrm {Hom}}([n_1,m_1],[n_2,m_2])$
is spanned by appropriate walled Brauer diagrams, with composition given by concatenation of diagrams, so that the circle evaluates to t. Similar to the construction of
![]() $TLJ(\infty )$
in §3.1, we may renormalize these diagrams by suitable powers of t so that the circle evaluates to
$TLJ(\infty )$
in §3.1, we may renormalize these diagrams by suitable powers of t so that the circle evaluates to
![]() $1$
, but the zig-zags are
$1$
, but the zig-zags are
![]() $t^{-1}$
. This allows us to evaluate at
$t^{-1}$
. This allows us to evaluate at
![]() $t=\infty $
(i.e.,
$t=\infty $
(i.e.,
![]() $t^{-1}=0$
) and, upon Cauchy completion, obtain a symmetric category
$t^{-1}=0$
) and, upon Cauchy completion, obtain a symmetric category
![]() $OB(\infty )$
. In this category, diagrams are composed by concatenation and removing circles, but if the concatenated diagram contains a zig-zag, the composition is declared to be zero.
$OB(\infty )$
. In this category, diagrams are composed by concatenation and removing circles, but if the concatenated diagram contains a zig-zag, the composition is declared to be zero.
For example,
![]() $\operatorname {\mathrm {End}}([n,m])$
is the asymptotic walled Brauer algebra
$\operatorname {\mathrm {End}}([n,m])$
is the asymptotic walled Brauer algebra
![]() $W_{n,m}(\infty )$
obtained by the above limiting procedure from the usual walled Brauer algebra
$W_{n,m}(\infty )$
obtained by the above limiting procedure from the usual walled Brauer algebra
![]() $W_{n,m}(t)$
. This algebra has the usual basis of walled Brauer diagrams with n inputs and n outputs to the left of the wall and m inputs and m outputs to the right of the wall. As in §3.1, we can define a filtration on
$W_{n,m}(t)$
. This algebra has the usual basis of walled Brauer diagrams with n inputs and n outputs to the left of the wall and m inputs and m outputs to the right of the wall. As in §3.1, we can define a filtration on
![]() $W_{n,m}(\infty )$
in which the degree of a diagram u is its number of cups, and the associated graded algebra
$W_{n,m}(\infty )$
in which the degree of a diagram u is its number of cups, and the associated graded algebra
![]() $\operatorname {\mathrm {gr}}(W_{n,m}(\infty ))=\bigoplus _k I_k/I_{k+1}$
is manifestly semisimple with k-th summand
$\operatorname {\mathrm {gr}}(W_{n,m}(\infty ))=\bigoplus _k I_k/I_{k+1}$
is manifestly semisimple with k-th summand
 $$\begin{align*}I_k/I_{k+1} \cong \mathbb{C}[S_{n-k}]\otimes \mathbb{C}[S_{m-k}]\otimes \operatorname{Mat}\left(\frac{n!m!}{(n-k)!(m-k)!k!}\right). \end{align*}$$
$$\begin{align*}I_k/I_{k+1} \cong \mathbb{C}[S_{n-k}]\otimes \mathbb{C}[S_{m-k}]\otimes \operatorname{Mat}\left(\frac{n!m!}{(n-k)!(m-k)!k!}\right). \end{align*}$$
This implies that
![]() $W_{n,m}(\infty )$
and thus the category
$W_{n,m}(\infty )$
and thus the category
![]() $OB(\infty )$
are semisimple, with simples
$OB(\infty )$
are semisimple, with simples
![]() $X_{\lambda ,\mu }$
labeled by pairs of partitions, and the same fusion rules as in
$X_{\lambda ,\mu }$
labeled by pairs of partitions, and the same fusion rules as in
![]() $OB(t)$
. However, the only rigid objects in this category are multiples of
$OB(t)$
. However, the only rigid objects in this category are multiples of ![]() : the dimension
: the dimension
![]() $\dim V_{\lambda ,\mu }(t)$
in
$\dim V_{\lambda ,\mu }(t)$
in
![]() $OB(t)$
is a nonconstant polynomial of t, hence goes to infinity as
$OB(t)$
is a nonconstant polynomial of t, hence goes to infinity as
![]() $t\to \infty $
. Unsurprisingly, these are also the only objects in this category that have moderate growth.
$t\to \infty $
. Unsurprisingly, these are also the only objects in this category that have moderate growth.
One can also perform the same limiting procedure to the unoriented Brauer category
![]() $UB(t)=\mathsf {Rep}(O_t)$
([Reference Etingof, Gelaki, Nikshych and OstrikEGNO15, §9.12]), getting a semisimple category
$UB(t)=\mathsf {Rep}(O_t)$
([Reference Etingof, Gelaki, Nikshych and OstrikEGNO15, §9.12]), getting a semisimple category
![]() $UB(\infty )$
which is likewise a counterexample to Theorem 1.1 without moderate growth.
$UB(\infty )$
which is likewise a counterexample to Theorem 1.1 without moderate growth.
3.4 Categories with nilpotent endomorphisms of nonzero trace
The moderate growth assumption in Corollary 1.5 cannot be removed, even for symmetric categories, as was first observed by Deligne [Reference DeligneDel07, §5.8]. Namely, there exist symmetric categories (of nonmoderate growth) in which the trace of a nilpotent endomorphism of an object can be nonzero. A nice example is the oriented Brauer category
![]() $OB(t)$
over a field
$OB(t)$
over a field
![]() $\mathbb {k}$
of characteristic
$\mathbb {k}$
of characteristic
![]() $2$
, where
$2$
, where
![]() $t\in \mathbb {k}$
is not equal to
$t\in \mathbb {k}$
is not equal to
![]() $0$
or
$0$
or
![]() $1$
. Then we can take
$1$
. Then we can take
![]() $V:=[1,0]$
,
$V:=[1,0]$
,
![]() $X=V^{\otimes 2}=[2,0]$
and
$X=V^{\otimes 2}=[2,0]$
and
![]() $z=1-s\in \operatorname {\mathrm {End}}(X)$
where s is the swap
$z=1-s\in \operatorname {\mathrm {End}}(X)$
where s is the swap
![]() $V^{\otimes 2}\to V^{\otimes 2}$
. Then
$V^{\otimes 2}\to V^{\otimes 2}$
. Then
![]() $z^2=0$
but
$z^2=0$
but
![]() $\operatorname {\mathrm {Tr}}(z)=\operatorname {\mathrm {Tr}}(1)-\operatorname {\mathrm {Tr}}(s)=t^2-t\ne 0$
. Many other examples of categories containing nilpotent endomorphisms with nonzero trace appear in [Reference Khovanov, Ostrik and KononovKOK22]. Of course, such a symmetric category cannot have monoidal functors to abelian symmetric tensor categories, since in the latter the trace of any nilpotent endomorphism z must be zero (as z is strictly upper triangular in the filtration by kernels of its powers).
$\operatorname {\mathrm {Tr}}(z)=\operatorname {\mathrm {Tr}}(1)-\operatorname {\mathrm {Tr}}(s)=t^2-t\ne 0$
. Many other examples of categories containing nilpotent endomorphisms with nonzero trace appear in [Reference Khovanov, Ostrik and KononovKOK22]. Of course, such a symmetric category cannot have monoidal functors to abelian symmetric tensor categories, since in the latter the trace of any nilpotent endomorphism z must be zero (as z is strictly upper triangular in the filtration by kernels of its powers).
4 Rigidity in braided r-categories
This section is inspired by the paper [Reference Kazhdan and LusztigKL94]. Its goal is to apply our results to braided r-categories that are not necessarily semisimple. Such categories arise in logarithmic conformal field theory [Reference Allen, Lentner, Schweigert and WoodALSW25]. In particular, this allows us to significantly simplify a number of arguments in [Reference Kazhdan and LusztigKL94].
4.1 2-out-of-3 rigidity
Let
![]() $\mathcal {C}$
be a braided monoidal category. Recall that if
$\mathcal {C}$
be a braided monoidal category. Recall that if
![]() $X\in \mathcal {C}$
is rigid then so is
$X\in \mathcal {C}$
is rigid then so is
![]() $X^*\cong {}^*X$
.
$X^*\cong {}^*X$
.
Assume in addition that
![]() $\mathcal {C}$
is abelian and artinian with right exact tensor product, so that
$\mathcal {C}$
is abelian and artinian with right exact tensor product, so that
![]() $\operatorname {\mathrm {Tor}}(X,Y)$
is well defined for every
$\operatorname {\mathrm {Tor}}(X,Y)$
is well defined for every
![]() $X,Y\in \mathcal {C}$
, possibly as a pro-object.Footnote 17 An object
$X,Y\in \mathcal {C}$
, possibly as a pro-object.Footnote 17 An object
![]() $X\in \mathcal {C}$
is called flat if the functor
$X\in \mathcal {C}$
is called flat if the functor
![]() $X\otimes -$
is exact.
$X\otimes -$
is exact.
Lemma 4.1 (c.f. [Reference Kazhdan and LusztigKL94, Cor. 1, p. 441])
Every rigid object in
![]() $\mathcal {C}$
is flat.
$\mathcal {C}$
is flat.
Proof. Although this follows formally from the adjunctions
![]() $X^* \otimes - \dashv X \otimes - \dashv {}^*X\otimes -$
, we provide a direct proof for convenience and simplicity. We show that if a morphism
$X^* \otimes - \dashv X \otimes - \dashv {}^*X\otimes -$
, we provide a direct proof for convenience and simplicity. We show that if a morphism
![]() $f: Y\to Z$
is a monomorphism, then so is the morphism
$f: Y\to Z$
is a monomorphism, then so is the morphism
![]() $\operatorname {\mathrm {id}}_X\otimes f: X\otimes Y\to X\otimes Z$
, that is, that for every object
$\operatorname {\mathrm {id}}_X\otimes f: X\otimes Y\to X\otimes Z$
, that is, that for every object
![]() $T\in \mathcal {C}$
, the associated linear map
$T\in \mathcal {C}$
, the associated linear map
![]() $f_{T,X}:\operatorname {\mathrm {Hom}}(T,X\otimes Y)\to \operatorname {\mathrm {Hom}}(T,X\otimes Z)$
is injective. Since X is rigid, this map can be viewed as the pullback map
$f_{T,X}:\operatorname {\mathrm {Hom}}(T,X\otimes Y)\to \operatorname {\mathrm {Hom}}(T,X\otimes Z)$
is injective. Since X is rigid, this map can be viewed as the pullback map
![]() $\widetilde f_{T,X}: \operatorname {\mathrm {Hom}}(X^*\otimes T,Y)\to \operatorname {\mathrm {Hom}}(X^*\otimes T,Z)$
, which is obviously injective.
$\widetilde f_{T,X}: \operatorname {\mathrm {Hom}}(X^*\otimes T,Y)\to \operatorname {\mathrm {Hom}}(X^*\otimes T,Z)$
, which is obviously injective.
Lemma 4.2. Consider a short exact sequence in
![]() $\mathcal {C}$
of the form
$\mathcal {C}$
of the form
![]() $ 0\to Y\xrightarrow {i} Z\xrightarrow {p} X\to 0 $
. Then:
$ 0\to Y\xrightarrow {i} Z\xrightarrow {p} X\to 0 $
. Then:
-
(i) If
 $X,Y$
are rigid then Z is rigid.
$X,Y$
are rigid then Z is rigid. -
(ii) If
 $Z,X$
are rigid then Y is rigid.
$Z,X$
are rigid then Y is rigid. -
(iii) If
 $Y,Z$
are rigid and the natural morphism
$Y,Z$
are rigid and the natural morphism
 $i^*:Z^*\to Y^*$
is an epimorphism, then X is rigid.
$i^*:Z^*\to Y^*$
is an epimorphism, then X is rigid.
Proof. (i) Since
![]() $X,Y$
are rigid, by Lemma 4.1 they are flat. Using the long exact sequence of Tor groups, we see that Z is flat as well. Also Z represents an element
$X,Y$
are rigid, by Lemma 4.1 they are flat. Using the long exact sequence of Tor groups, we see that Z is flat as well. Also Z represents an element
Let
![]() $Z^\vee $
be the extension of
$Z^\vee $
be the extension of
![]() $Y^*$
by
$Y^*$
by
![]() $X^*$
defined by the element
$X^*$
defined by the element
![]() $-\alpha $
, so it is also flat. Since
$-\alpha $
, so it is also flat. Since
![]() $X,Y,Z,X^*,Y^*,Z^\vee $
are flat, we see that the object
$X,Y,Z,X^*,Y^*,Z^\vee $
are flat, we see that the object
![]() $Z\otimes Z^\vee $
has a three-step filtration with successive quotients
$Z\otimes Z^\vee $
has a three-step filtration with successive quotients
![]() $Y\otimes X^*,X\otimes X^*\oplus Y\otimes Y^*,X\otimes Y^*$
, meaning that we have subobjects
$Y\otimes X^*,X\otimes X^*\oplus Y\otimes Y^*,X\otimes Y^*$
, meaning that we have subobjects
with
![]() $F_2/F_1\cong X\otimes X^*\oplus Y\otimes Y^*$
and
$F_2/F_1\cong X\otimes X^*\oplus Y\otimes Y^*$
and
![]() $F_3/F_2\cong X\otimes Y^*$
. By construction of
$F_3/F_2\cong X\otimes Y^*$
. By construction of
![]() $Z^\vee $
, the morphism
$Z^\vee $
, the morphism ![]() lifts to a morphism
lifts to a morphism ![]() , hence to a morphism
, hence to a morphism ![]() , which we denote by
, which we denote by
![]() $\operatorname {\mathrm {coev}}_Z$
. To see this, one looks at the exact sequence
$\operatorname {\mathrm {coev}}_Z$
. To see this, one looks at the exact sequence
and computes that the pullback in ![]() of its class in
of its class in
![]() $\operatorname {\mathrm {Ext}}^1(X\otimes X^*\oplus Y\otimes Y^*, Y\otimes X^*)$
is trivial since we used
$\operatorname {\mathrm {Ext}}^1(X\otimes X^*\oplus Y\otimes Y^*, Y\otimes X^*)$
is trivial since we used
![]() $-\alpha $
to define
$-\alpha $
to define
![]() $Z^\vee $
, whence our lift
$Z^\vee $
, whence our lift ![]() exists. We remark that writing
exists. We remark that writing
![]() $i^\vee : Z^\vee \to Y^*$
and
$i^\vee : Z^\vee \to Y^*$
and
![]() $p^\vee :X^*\to Z^\vee $
, the following diagram commutes.
$p^\vee :X^*\to Z^\vee $
, the following diagram commutes.

This can be seen by analyzing the other faces of the following larger diagram.

By a dual argument, we can analyze
![]() $Z^\vee \otimes Z$
by a three-step filtration with successive quotients
$Z^\vee \otimes Z$
by a three-step filtration with successive quotients
![]() $X^*\otimes Y, X^*\otimes X\oplus Y^*\otimes Y,Y^*\otimes X$
given by
$X^*\otimes Y, X^*\otimes X\oplus Y^*\otimes Y,Y^*\otimes X$
given by
to construct an evaluation map ![]() . One looks at the exact sequence
. One looks at the exact sequence
By reasoning dually as before, the morphism ![]() extends to a morphism
extends to a morphism ![]() , hence to a morphism
, hence to a morphism ![]() , which we denote by
, which we denote by
![]() $\operatorname {\mathrm {ev}}_Z$
. By similar reasoning,
$\operatorname {\mathrm {ev}}_Z$
. By similar reasoning,
![]() $\operatorname {\mathrm {ev}}_Z$
makes the following diagram commute.
$\operatorname {\mathrm {ev}}_Z$
makes the following diagram commute.

Now one verifies that both
![]() $\operatorname {\mathrm {ev}}_Z,\operatorname {\mathrm {coev}}_Z$
make the following diagram commute.
$\operatorname {\mathrm {ev}}_Z,\operatorname {\mathrm {coev}}_Z$
make the following diagram commute.

Looking at the outside rectangle above and the zig-zag
![]() $z:Z\to Z$
in the middle, since the zig-zags for
$z:Z\to Z$
in the middle, since the zig-zags for
![]() $X,Y$
are both identities, our short exact sequence fits in the following commutative diagram.
$X,Y$
are both identities, our short exact sequence fits in the following commutative diagram.

Since
![]() $\mathcal {C}$
is abelian, z is an isomorphism by the Short Five Lemma. We may thus renormalize one of
$\mathcal {C}$
is abelian, z is an isomorphism by the Short Five Lemma. We may thus renormalize one of
![]() $\operatorname {\mathrm {ev}}_Z,\operatorname {\mathrm {coev}}_Z$
so that the zig-zag axiom holds on the nose. One then uses a similar diagram to check that the zig-zag for
$\operatorname {\mathrm {ev}}_Z,\operatorname {\mathrm {coev}}_Z$
so that the zig-zag axiom holds on the nose. One then uses a similar diagram to check that the zig-zag for
![]() $Z^\vee $
, which is an idempotent,Footnote 18 is also invertible, and is thus the identity.
$Z^\vee $
, which is an idempotent,Footnote 18 is also invertible, and is thus the identity.
(ii) We have an epimorphism
![]() $p: Z\to X$
whose kernel is Y. We have
$p: Z\to X$
whose kernel is Y. We have
and we write
![]() $p^*:X^*\to Z^*$
for the corresponding morphism.Footnote 19 Denote by
$p^*:X^*\to Z^*$
for the corresponding morphism.Footnote 19 Denote by
![]() $Y^\vee $
the cokernel of
$Y^\vee $
the cokernel of
![]() $p^*$
. We have a morphism
$p^*$
. We have a morphism ![]() , where
, where
![]() $\pi : Z^*\to Y^\vee $
is the projection.
$\pi : Z^*\to Y^\vee $
is the projection.
Since X is rigid, it is flat by Lemma 4.1, so
![]() $\mathrm {Tor}^1(X,Y^\vee )=0$
. Hence we have a short exact sequence
$\mathrm {Tor}^1(X,Y^\vee )=0$
. Hence we have a short exact sequence
(cf. [Reference Kazhdan and LusztigKL94, Lem. 4.6]). The morphism
![]() $(p\otimes \operatorname {\mathrm {id}}_{Y^\vee })\circ (\operatorname {\mathrm {id}}_Z\otimes \pi )\circ \operatorname {\mathrm {coev}}_Z$
is the morphism
$(p\otimes \operatorname {\mathrm {id}}_{Y^\vee })\circ (\operatorname {\mathrm {id}}_Z\otimes \pi )\circ \operatorname {\mathrm {coev}}_Z$
is the morphism ![]() corresponding to the composition
corresponding to the composition
![]() $X^*\to Z^*\to Y^\vee $
, which is zero by definition of
$X^*\to Z^*\to Y^\vee $
, which is zero by definition of
![]() $Y^\vee $
. Thus the morphism
$Y^\vee $
. Thus the morphism
![]() $(\operatorname {\mathrm {id}}_Z\otimes \pi )\circ \operatorname {\mathrm {coev}}_Z$
lands in
$(\operatorname {\mathrm {id}}_Z\otimes \pi )\circ \operatorname {\mathrm {coev}}_Z$
lands in
![]() $Y\otimes Y^\vee $
, and we denote this morphism by
$Y\otimes Y^\vee $
, and we denote this morphism by
![]() $\operatorname {\mathrm {coev}}_Y$
.
$\operatorname {\mathrm {coev}}_Y$
.
Similarly, consider the morphism ![]() . It pulls back to a morphism
. It pulls back to a morphism ![]() . Moreover, since the pullback of this morphism to
. Moreover, since the pullback of this morphism to
![]() $X^*\otimes Y$
is zero (as it corresponds to the composition
$X^*\otimes Y$
is zero (as it corresponds to the composition
![]() $Y\to Z\to X$
) and since we have an exact sequence
$Y\to Z\to X$
) and since we have an exact sequence
![]() $X^*\otimes Y\to Z^*\otimes Y\to Y^\vee \otimes Y\to 0$
, the morphism
$X^*\otimes Y\to Z^*\otimes Y\to Y^\vee \otimes Y\to 0$
, the morphism
![]() $\operatorname {\mathrm {ev}}_Z\circ (\operatorname {\mathrm {id}}_{Z^*}\otimes i)$
is the pullback of a unique morphism
$\operatorname {\mathrm {ev}}_Z\circ (\operatorname {\mathrm {id}}_{Z^*}\otimes i)$
is the pullback of a unique morphism ![]() , which we denote
, which we denote
![]() $\operatorname {\mathrm {ev}}_Y$
. Now diagram chasing shows that the morphisms
$\operatorname {\mathrm {ev}}_Y$
. Now diagram chasing shows that the morphisms
![]() $\operatorname {\mathrm {ev}}_Y,\operatorname {\mathrm {coev}}_Y$
equip
$\operatorname {\mathrm {ev}}_Y,\operatorname {\mathrm {coev}}_Y$
equip
![]() $Y^\vee $
with the structure of the left dual
$Y^\vee $
with the structure of the left dual
![]() $Y^*$
of Y, as desired.
$Y^*$
of Y, as desired.
(iii) We have a monomorphism
![]() $i: Y\to Z$
which by assumption gives rise to an epimorphism
$i: Y\to Z$
which by assumption gives rise to an epimorphism
![]() $i^*: Z^*\to Y^*$
, and we may define
$i^*: Z^*\to Y^*$
, and we may define
![]() $X^\vee $
to be the kernel of
$X^\vee $
to be the kernel of
![]() $i^*$
, so that we have a short exact sequence
$i^*$
, so that we have a short exact sequence
Since
![]() $Y^*$
is flat,
$Y^*$
is flat,
![]() $\mathrm {Tor}^1(X,Y^*)=0$
, so we obtain a short exact sequence
$\mathrm {Tor}^1(X,Y^*)=0$
, so we obtain a short exact sequence
We have a morphism ![]() where
where
![]() $p: Z\to X$
is the projection. We have
$p: Z\to X$
is the projection. We have
![]() $(\operatorname {\mathrm {id}}_X\otimes i^*)\circ (p\otimes \operatorname {\mathrm {id}}_{Z^*})\circ \operatorname {\mathrm {coev}}_Z=0$
, so the morphism
$(\operatorname {\mathrm {id}}_X\otimes i^*)\circ (p\otimes \operatorname {\mathrm {id}}_{Z^*})\circ \operatorname {\mathrm {coev}}_Z=0$
, so the morphism
![]() $(p\otimes \operatorname {\mathrm {id}}_{Z^*})\circ \operatorname {\mathrm {coev}}_Z$
lands in the kernel of the morphism
$(p\otimes \operatorname {\mathrm {id}}_{Z^*})\circ \operatorname {\mathrm {coev}}_Z$
lands in the kernel of the morphism
![]() $\operatorname {\mathrm {id}}_X\otimes i^*: X\otimes Z^*\to X\otimes Y^*$
. Thus
$\operatorname {\mathrm {id}}_X\otimes i^*: X\otimes Z^*\to X\otimes Y^*$
. Thus
![]() $(p\otimes \operatorname {\mathrm {id}}_{Z^*})\circ \operatorname {\mathrm {coev}}_Z$
lands in
$(p\otimes \operatorname {\mathrm {id}}_{Z^*})\circ \operatorname {\mathrm {coev}}_Z$
lands in
![]() $X\otimes X^\vee $
, and we denote this morphism by
$X\otimes X^\vee $
, and we denote this morphism by
![]() $\operatorname {\mathrm {coev}}_X$
.
$\operatorname {\mathrm {coev}}_X$
.
Similarly, we have a morphism ![]() , where
, where
![]() $\iota : X^\vee \hookrightarrow Z^*$
is the inclusion, and its pullback to a morphism
$\iota : X^\vee \hookrightarrow Z^*$
is the inclusion, and its pullback to a morphism ![]() corresponds to the morphism
corresponds to the morphism
![]() $X^\vee \to Y^*$
, which is zero by definition of
$X^\vee \to Y^*$
, which is zero by definition of
![]() $X^\vee $
. But we have an exact sequence
$X^\vee $
. But we have an exact sequence
so
![]() $\operatorname {\mathrm {ev}}_Z\circ (\iota \otimes \operatorname {\mathrm {id}}_Z)$
is the pullback of the unique morphism
$\operatorname {\mathrm {ev}}_Z\circ (\iota \otimes \operatorname {\mathrm {id}}_Z)$
is the pullback of the unique morphism ![]() , which we denote by
, which we denote by
![]() $\operatorname {\mathrm {ev}}_X$
. Now diagram chasing shows that the morphisms
$\operatorname {\mathrm {ev}}_X$
. Now diagram chasing shows that the morphisms
![]() $\operatorname {\mathrm {ev}}_X,\operatorname {\mathrm {coev}}_X$
equip
$\operatorname {\mathrm {ev}}_X,\operatorname {\mathrm {coev}}_X$
equip
![]() $X^\vee $
with the structure of the left dual
$X^\vee $
with the structure of the left dual
![]() $X^*$
of X, as desired.
$X^*$
of X, as desired.
Remark 4.3. In Lemma 4.2(iii), the assumption that the morphism
![]() $i^*:Z^*\to Y^*$
is an epimorphism cannot be dropped. For example, let
$i^*:Z^*\to Y^*$
is an epimorphism cannot be dropped. For example, let
![]() $\mathcal {C}$
be the category of
$\mathcal {C}$
be the category of
![]() $\mathbb {k}[x]$
-modules and
$\mathbb {k}[x]$
-modules and
![]() $X=\mathbb {k}$
,
$X=\mathbb {k}$
,
![]() $Y=Z=\mathbb {k}[x]$
. Then the morphism
$Y=Z=\mathbb {k}[x]$
. Then the morphism
![]() $i: Y\to Z$
is the multiplication map
$i: Y\to Z$
is the multiplication map
![]() $x: \mathbb {k}[x]\to \mathbb {k}[x]$
, so the dual morphism
$x: \mathbb {k}[x]\to \mathbb {k}[x]$
, so the dual morphism
![]() $i^*: Z^*\to Y^*$
is the same, hence not an epimorphism. In this case X is not rigid, even though
$i^*: Z^*\to Y^*$
is the same, hence not an epimorphism. In this case X is not rigid, even though
![]() $Y,Z$
are.
$Y,Z$
are.
See Remark 4.13 below for another example pointed out by Robert McRae in which
![]() $\mathcal {C}$
is artinian.
$\mathcal {C}$
is artinian.
Remark 4.4. A similar result to Lemma 4.2(i) was proved in [Reference Creutzig, McRae and YangCMY21] for ribbon r-categories, but stated in the language of VOA tensor categories. However, their result holds in the more general setting of abelian r-categories; see [Reference Creutzig, McRae, Shimizu and YadavCMSY, Thm. 3.13]. The interested reader may also extend our Lemma 4.2 beyond the braided case taking more care about left versus right duals. (We only used the braiding to check only one kind of duals.)
Defintion 4.5. We say that
![]() $\mathcal {C}$
is 2-out-of-3 rigid if in every short exact sequence in
$\mathcal {C}$
is 2-out-of-3 rigid if in every short exact sequence in
![]() $\mathcal {C}$
, if any two of its members are rigid then so is the third.
$\mathcal {C}$
, if any two of its members are rigid then so is the third.
The following corollary follows immediately from Lemma 4.2.
Corollary 4.6. Suppose that in
![]() $\mathcal {C}$
, for any monomorphism
$\mathcal {C}$
, for any monomorphism
![]() $Y\to Z$
between rigid objects, the dual morphism
$Y\to Z$
between rigid objects, the dual morphism
![]() $Z^*\to Y^*$
is an epimorphism. Then
$Z^*\to Y^*$
is an epimorphism. Then
![]() $\mathcal {C}$
is 2-out-of-3 rigid.
$\mathcal {C}$
is 2-out-of-3 rigid.
Corollary 4.7 (cf. [Reference Kazhdan and LusztigKL94, Prop. A.2, p. 444])
Let
![]() $\mathcal {C}$
be a braided artinian abelian r-category.Footnote 20 Then
$\mathcal {C}$
be a braided artinian abelian r-category.Footnote 20 Then
![]() $\mathcal {C}$
is 2-out-of-3 rigid.
$\mathcal {C}$
is 2-out-of-3 rigid.
Proof. It is well known that an abelian r-category admits internal homs [Reference Boyarchenko and DrinfeldBD13], so its tensor product is right exact. Since the dualization functor
![]() $X\to X^\vee $
is an antiequivalence and
$X\to X^\vee $
is an antiequivalence and
![]() $X^\vee \cong X^*$
when X is rigid, the assumption of Lemma 4.2(iii) holds. Thus the result follows from Lemma 4.2.
$X^\vee \cong X^*$
when X is rigid, the assumption of Lemma 4.2(iii) holds. Thus the result follows from Lemma 4.2.
4.2 Recursive filtrations
Let
![]() $\mathbb {k}$
be an algebraically closed field.
$\mathbb {k}$
be an algebraically closed field.
Defintion 4.8 [Reference Kazhdan and LusztigKL94, Def. A.6]
A semirigid monoidal category over
![]() $\mathbb {k}$
is an abelian r-category over
$\mathbb {k}$
is an abelian r-category over
![]() $\mathbb {k}$
with objects of finite length and simple
$\mathbb {k}$
with objects of finite length and simple ![]() .
.
Note that in such a category, ![]() so
so
Hence
![]() $\operatorname {\mathrm {Hom}}(X,Y)$
is finite dimensional, so
$\operatorname {\mathrm {Hom}}(X,Y)$
is finite dimensional, so
![]() $\mathcal {C}$
is artinian and
$\mathcal {C}$
is artinian and ![]() .
.
Defintion 4.9. Let
![]() $\mathcal {C}$
be an artinian monoidal category over
$\mathcal {C}$
be an artinian monoidal category over
![]() $\mathbb {k}$
with the set
$\mathbb {k}$
with the set
![]() $\operatorname {\mathrm {Irr}}(\mathcal {C})$
of isomorphism classes of simple (=irreducible) objects. A recursive filtration on
$\operatorname {\mathrm {Irr}}(\mathcal {C})$
of isomorphism classes of simple (=irreducible) objects. A recursive filtration on
![]() $\operatorname {\mathrm {Irr}}(\mathcal {C})$
relative to a subset
$\operatorname {\mathrm {Irr}}(\mathcal {C})$
relative to a subset
![]() $S\subset \operatorname {\mathrm {Irr}}(\mathcal {C})$
is an increasing exhaustive filtration of
$S\subset \operatorname {\mathrm {Irr}}(\mathcal {C})$
is an increasing exhaustive filtration of
![]() $\operatorname {\mathrm {Irr}}(\mathcal {C})$
by subsets
$\operatorname {\mathrm {Irr}}(\mathcal {C})$
by subsets
![]() $\operatorname {\mathrm {Irr}}_n(\mathcal {C})$
,
$\operatorname {\mathrm {Irr}}_n(\mathcal {C})$
,
![]() $n\in \Bbb Z_{\ge 0}$
such that for every
$n\in \Bbb Z_{\ge 0}$
such that for every
![]() $n\ge 0$
and
$n\ge 0$
and
![]() $X\in \operatorname {\mathrm {Irr}}_{n}(\mathcal {C})$
, there exist
$X\in \operatorname {\mathrm {Irr}}_{n}(\mathcal {C})$
, there exist
![]() $X_1,\cdots ,X_m\in \mathcal {C}$
with composition factors in S for which the composition series of
$X_1,\cdots ,X_m\in \mathcal {C}$
with composition factors in S for which the composition series of
![]() $X_1\otimes \cdots \otimes X_m$
consists of a single copy of X and elements of
$X_1\otimes \cdots \otimes X_m$
consists of a single copy of X and elements of
![]() $\operatorname {\mathrm {Irr}}_{n-1}(\mathcal {C})$
, where by convention,
$\operatorname {\mathrm {Irr}}_{n-1}(\mathcal {C})$
, where by convention,
![]() $\operatorname {\mathrm {Irr}}_{-1}(\mathcal {C}):=\emptyset $
. Note that we may have
$\operatorname {\mathrm {Irr}}_{-1}(\mathcal {C}):=\emptyset $
. Note that we may have
![]() $m=0$
giving the tensor product of the empty set of objects, which is
$m=0$
giving the tensor product of the empty set of objects, which is ![]() by definition.
by definition.
Proposition 4.10. Suppose
![]() $\mathcal {C}$
is 2-out-of-3 rigid and
$\mathcal {C}$
is 2-out-of-3 rigid and
![]() $\operatorname {\mathrm {Irr}}(\mathcal {C})$
admits a recursive filtration relative to S. If S consists of rigid objects then
$\operatorname {\mathrm {Irr}}(\mathcal {C})$
admits a recursive filtration relative to S. If S consists of rigid objects then
![]() $\mathcal {C}$
is rigid.
$\mathcal {C}$
is rigid.
Proof. It suffices to show that all simple objects in
![]() $\mathcal {C}$
are rigid. To this end, it suffices to show that for all n, all
$\mathcal {C}$
are rigid. To this end, it suffices to show that for all n, all
![]() $X\in \operatorname {\mathrm {Irr}}_n(\mathcal {C})$
are rigid. We induct on n. The base case is trivial. To pass from n to
$X\in \operatorname {\mathrm {Irr}}_n(\mathcal {C})$
are rigid. We induct on n. The base case is trivial. To pass from n to
![]() $n+1$
, let
$n+1$
, let
![]() $X\in \operatorname {\mathrm {Irr}}_{n+1}(\mathcal {C})$
and let
$X\in \operatorname {\mathrm {Irr}}_{n+1}(\mathcal {C})$
and let
![]() $X_1,\cdots ,X_m\in \mathcal {C}$
be objects with composition factors in S such that the composition series of
$X_1,\cdots ,X_m\in \mathcal {C}$
be objects with composition factors in S such that the composition series of
![]() $X_1\otimes \cdots \otimes X_m$
consists of a single copy of X and objects in
$X_1\otimes \cdots \otimes X_m$
consists of a single copy of X and objects in
![]() $\operatorname {\mathrm {Irr}}_n(\mathcal {C})$
. So there is a three-step filtration of
$\operatorname {\mathrm {Irr}}_n(\mathcal {C})$
. So there is a three-step filtration of
![]() $X_1\otimes \cdots \otimes X_m$
with terms
$X_1\otimes \cdots \otimes X_m$
with terms
![]() $Z,X,Y$
, where all composition factors of Z and Y are in
$Z,X,Y$
, where all composition factors of Z and Y are in
![]() $\operatorname {\mathrm {Irr}}_n(\mathcal {C})$
. Let T be the kernel of the morphism
$\operatorname {\mathrm {Irr}}_n(\mathcal {C})$
. Let T be the kernel of the morphism
![]() $X_1\otimes \cdots \otimes X_m\to Y$
, so we have a short exact sequence
$X_1\otimes \cdots \otimes X_m\to Y$
, so we have a short exact sequence
Since
![]() $X_i$
and (by the induction assumption)
$X_i$
and (by the induction assumption)
![]() $Y,Z$
have rigid composition factors, they are rigid by the 2-out-of-3 property. Hence
$Y,Z$
have rigid composition factors, they are rigid by the 2-out-of-3 property. Hence
![]() $X_1\otimes \cdots \otimes X_m$
is rigid. Thus T is rigid by the 2-out-of-3 property. But we also have a short exact sequence
$X_1\otimes \cdots \otimes X_m$
is rigid. Thus T is rigid by the 2-out-of-3 property. But we also have a short exact sequence
Since
![]() $Z,T$
are rigid, we conclude by the 2-out-of-3 property that X is rigid, as needed.
$Z,T$
are rigid, we conclude by the 2-out-of-3 property that X is rigid, as needed.
Combining Proposition 4.10 with our main result Theorem 1.1, we thus obtain:
Theorem 4.11. Let
![]() $\mathcal {C}$
be a braided semirigid category of moderate growth such that
$\mathcal {C}$
be a braided semirigid category of moderate growth such that
![]() $\operatorname {\mathrm {Irr}}(\mathcal {C})$
has a recursive filtration with respect to a subset
$\operatorname {\mathrm {Irr}}(\mathcal {C})$
has a recursive filtration with respect to a subset
![]() $S\subset \operatorname {\mathrm {Irr}}(\mathcal {C})$
consisting of non-negligible objects. Then
$S\subset \operatorname {\mathrm {Irr}}(\mathcal {C})$
consisting of non-negligible objects. Then
![]() $\mathcal {C}$
is rigid.
$\mathcal {C}$
is rigid.
4.3 Application: rigidity of the Kazhdan-Lusztig category at negative rational levels
An example of application of Theorem 4.11 is a simplification of the proof of rigidity of the category
![]() $\mathcal O_\kappa $
in [Reference Kazhdan and LusztigKL94]. Namely, let
$\mathcal O_\kappa $
in [Reference Kazhdan and LusztigKL94]. Namely, let
![]() $\kappa \in \Bbb Q_{<0}$
,
$\kappa \in \Bbb Q_{<0}$
,
![]() $\mathfrak {g}$
be a simply laced simple finite-dimensional complex Lie algebra, and
$\mathfrak {g}$
be a simply laced simple finite-dimensional complex Lie algebra, and
![]() $\mathcal O_\kappa $
be the Kazhdan-Lusztig category of
$\mathcal O_\kappa $
be the Kazhdan-Lusztig category of
![]() $\mathfrak {g}[[t]]$
-integrable finitely generated representations of the affine Lie algebra
$\mathfrak {g}[[t]]$
-integrable finitely generated representations of the affine Lie algebra
![]() $\widehat {\mathfrak {g}}$
at level
$\widehat {\mathfrak {g}}$
at level
![]() $\kappa -h^\vee $
, where
$\kappa -h^\vee $
, where
![]() $h^\vee $
is the dual Coxeter number of
$h^\vee $
is the dual Coxeter number of
![]() $\mathfrak {g}$
. In [Reference Kazhdan and LusztigKL94, Prop 31.2, p. 410] it is proved that
$\mathfrak {g}$
. In [Reference Kazhdan and LusztigKL94, Prop 31.2, p. 410] it is proved that
![]() $\mathcal O_\kappa $
is a braided, semirigid category, with
$\mathcal O_\kappa $
is a braided, semirigid category, with
![]() $\operatorname {\mathrm {Irr}}(\mathcal {C})=P_+$
, the set of dominant integral weights, and it is easy to see that it has moderate growth. Let
$\operatorname {\mathrm {Irr}}(\mathcal {C})=P_+$
, the set of dominant integral weights, and it is easy to see that it has moderate growth. Let
![]() $S:=\lbrace \omega _1,\cdots ,\omega _r\rbrace $
be the fundamental weights for
$S:=\lbrace \omega _1,\cdots ,\omega _r\rbrace $
be the fundamental weights for
![]() $\mathfrak {g}$
, let
$\mathfrak {g}$
, let
![]() $\rho =\sum _i \omega _i$
, and let
$\rho =\sum _i \omega _i$
, and let
![]() $\operatorname {\mathrm {Irr}}_n(\mathcal {C})$
be the set of weights
$\operatorname {\mathrm {Irr}}_n(\mathcal {C})$
be the set of weights
![]() $\lambda \in P_+$
with
$\lambda \in P_+$
with
![]() $(\lambda ,\rho )\le n$
. Assume that
$(\lambda ,\rho )\le n$
. Assume that
![]() $\kappa $
is such that the Weyl module
$\kappa $
is such that the Weyl module
![]() $V_\lambda ^\kappa $
over
$V_\lambda ^\kappa $
over
![]() $\widehat {\mathfrak {g}}$
is irreducible, and its quantum dimension
$\widehat {\mathfrak {g}}$
is irreducible, and its quantum dimension
![]() $d_\lambda (q):=\prod _{\alpha>0} \frac {[(\omega _i+\rho ,\alpha )]_q}{[(\rho ,\alpha _i)]_q}$
is nonzero at
$d_\lambda (q):=\prod _{\alpha>0} \frac {[(\omega _i+\rho ,\alpha )]_q}{[(\rho ,\alpha _i)]_q}$
is nonzero at
![]() $q=e^{\pi i/\kappa }$
(this rules out an explicit finite set of numerators for
$q=e^{\pi i/\kappa }$
(this rules out an explicit finite set of numerators for
![]() $\kappa $
, cf. [Reference Kazhdan and LusztigKL94, p. 413]). Then, as shown in [Reference Kazhdan and LusztigKL94] (see p. 413),
$\kappa $
, cf. [Reference Kazhdan and LusztigKL94, p. 413]). Then, as shown in [Reference Kazhdan and LusztigKL94] (see p. 413),
![]() $V_{\omega _i}^\kappa \otimes V_{\omega _{i^*}}^\kappa $
contains
$V_{\omega _i}^\kappa \otimes V_{\omega _{i^*}}^\kappa $
contains ![]() as a direct summand, so the
as a direct summand, so the
![]() $V_{\omega _i}^\kappa $
are non-negligible. If
$V_{\omega _i}^\kappa $
are non-negligible. If
![]() $\lambda =\sum _i n_i\omega _i$
,
$\lambda =\sum _i n_i\omega _i$
,
![]() $n=\sum _i n_i$
, and
$n=\sum _i n_i$
, and
![]() $L_\lambda ^\kappa \in \mathcal O_\kappa $
is the simple module with highest weight
$L_\lambda ^\kappa \in \mathcal O_\kappa $
is the simple module with highest weight
![]() $\lambda $
, then the composition series of
$\lambda $
, then the composition series of
![]() $\bigotimes _i (V_{\omega _i}^\kappa )^{\otimes n_i}$
consists of
$\bigotimes _i (V_{\omega _i}^\kappa )^{\otimes n_i}$
consists of
![]() $L_\lambda ^\kappa $
and elements of
$L_\lambda ^\kappa $
and elements of
![]() $\operatorname {\mathrm {Irr}}_{n-1}(\mathcal {C})$
, so
$\operatorname {\mathrm {Irr}}_{n-1}(\mathcal {C})$
, so
![]() $\mathcal {C}$
admits a recursive filtration relative to S. Thus applying Theorem 4.11, we get that
$\mathcal {C}$
admits a recursive filtration relative to S. Thus applying Theorem 4.11, we get that
![]() $\mathcal O_\kappa $
is rigid, which is [Reference Kazhdan and LusztigKL94, Thm. 32.1, p. 419]. This allows us to avoid quite a few technicalities in the proof of this theorem.
$\mathcal O_\kappa $
is rigid, which is [Reference Kazhdan and LusztigKL94, Thm. 32.1, p. 419]. This allows us to avoid quite a few technicalities in the proof of this theorem.
Remark 4.12. Conjecture A.1 in [Reference Kazhdan and LusztigKL94, p. 477] states that in a semirigid category, if
![]() $X\otimes Y$
is rigid then so are
$X\otimes Y$
is rigid then so are
![]() $X,Y$
. We note that for braided semirigid categories (which is the setting needed in [Reference Kazhdan and LusztigKL94]) this immediately follows from [Reference Boyarchenko and DrinfeldBD13, Cor. 3.5].
$X,Y$
. We note that for braided semirigid categories (which is the setting needed in [Reference Kazhdan and LusztigKL94]) this immediately follows from [Reference Boyarchenko and DrinfeldBD13, Cor. 3.5].
Remark 4.13. We thank Robert McRae for an email exchange providing the following additional example showing the assumption that
![]() $i^*$
is an epimorphism in Lemma 4.2(iii) cannot be dropped. His example comes from Grothendieck-Verdier categories which are not r-categories, and is artinian, whereas the example in Remark 4.3 above is not.
$i^*$
is an epimorphism in Lemma 4.2(iii) cannot be dropped. His example comes from Grothendieck-Verdier categories which are not r-categories, and is artinian, whereas the example in Remark 4.3 above is not.
The Weyl modules
![]() $V_n=V^{p/q}_{n\omega _1}$
for affine
$V_n=V^{p/q}_{n\omega _1}$
for affine
![]() $\mathfrak {sl}_2$
obtained by parabolic induction from the
$\mathfrak {sl}_2$
obtained by parabolic induction from the
![]() $(n+1)$
-dimensional simple
$(n+1)$
-dimensional simple
![]() $\mathfrak {sl}_2$
-module, at level
$\mathfrak {sl}_2$
-module, at level
![]() $k = -2 + p/q$
where
$k = -2 + p/q$
where
![]() $p,q$
are relatively prime positive integers, give an exact sequence
$p,q$
are relatively prime positive integers, give an exact sequence
Here,
![]() $V_{p-1}$
is the analogue of the Steinberg representation for quantum
$V_{p-1}$
is the analogue of the Steinberg representation for quantum
![]() $\mathfrak {sl}_2$
, or for
$\mathfrak {sl}_2$
, or for
![]() $sl_2$
in positive characteristic. In this case,
$sl_2$
in positive characteristic. In this case,
![]() $V_{p-2}$
and
$V_{p-2}$
and
![]() $V_1\otimes V_{p-1}$
are rigid, but
$V_1\otimes V_{p-1}$
are rigid, but
![]() $V_p$
is not. Although the Grothendieck-Verdier dual of the inclusion
$V_p$
is not. Although the Grothendieck-Verdier dual of the inclusion
![]() $V_{p-2} \to V_1\otimes V_{p-1}$
is surjective, the rigid dual of
$V_{p-2} \to V_1\otimes V_{p-1}$
is surjective, the rigid dual of
![]() $V_{p-2}$
is not the same as its Grothendieck-Verdier dual, so the rigid dual of the inclusion
$V_{p-2}$
is not the same as its Grothendieck-Verdier dual, so the rigid dual of the inclusion
![]() $V_{p-2} \to V_1\otimes V_{p-1}$
cannot be surjective.
$V_{p-2} \to V_1\otimes V_{p-1}$
cannot be surjective.
Acknowledgments
This collaboration started at the 2024 Annual Meeting of the Simons Collaboration on Global Categorical Symmetries. Pavel Etingof is grateful to Yi-Zhi Huang for a discussion at MIT in Fall 2021 which motivated him to think about the problem solved in this paper. The authors would like to thank Kevin Coulembier, Thomas Creutzig, André Henriques, Corey Jones, Robert McRae, Victor Ostrik, Emily Peters, Kenichi Shimizu, and Harshit Yadav for helpful conversations. We thank Victor Ostrik for suggesting that our results should simplify results in [Reference Kazhdan and LusztigKL94], leading to §4. Finally, we thank an anonymous referee for supplying the example of an r-category that is not weakly rigid in Footnote 4.
Competing interests
The authors have no competing interest to declare.
Funding statement
Pavel Etingof was supported by NSF grant DMS-2001318 and David Penneys was supported by NSF grant DMS-2154389.
Data availability statement
Not applicable
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the US.
Author contributions
Both PE and DP proved results and drafted the manuscript for publication

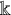
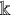
 . We call an indecomposable object
. We call an indecomposable object 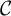
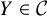
 is a direct summand of
is a direct summand of