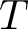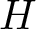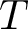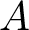1. Introduction
Perturbation theory of linear operator has a long history. Vast parts of the literature are dedicated to the perturbation theory of selfadjoint linear operators where the perturbation is symmetric and small in some sense with respect to the unperturbed operator, see for instance the classic monograph [Reference Kato13].
Recently, however, there is growing interest in the spectral theory of non-selfadjoint operators. Such operators may be used to model open physical systems where certain quantities are not conserved. For instance, in [Reference Hussein, Krejčiřík and Siegl12, Reference Rivière and Royer19], the Laplace operator on a quantum graph with non-selfadjoint boundary conditions is studied. Here the unperturbed operator is not selfadjoint and not even similar to a selfadjoint operator. Perturbations of non-selfadjoint operators have been studied for example in the influential books by Gohberg and Krein [Reference Gohberg and Kreın10], by Dunford and Schwartz [Reference Dunford and Schwartz7] and by Markus [Reference Markus17]. The case of a normal discrete operator with a ![]() $p$-subordinate perturbation was studied by Markus and Matsaev ([Reference Markus and Matsaev18], [Reference Markus17, Theorem 6.12]). Wyss [Reference Wyss24] could extend their results by allowing for weaker hypotheses on the asymptotic behaviour of eigenvalues of the normal discrete operator. Shkalikov also studied
$p$-subordinate perturbation was studied by Markus and Matsaev ([Reference Markus and Matsaev18], [Reference Markus17, Theorem 6.12]). Wyss [Reference Wyss24] could extend their results by allowing for weaker hypotheses on the asymptotic behaviour of eigenvalues of the normal discrete operator. Shkalikov also studied ![]() $p$-subordinate perturbations of normal operators in [Reference Shkalikov21] where he considered other kinds of perturbations, for example relatively bounded perturbations with relative bound equal to zero.
$p$-subordinate perturbations of normal operators in [Reference Shkalikov21] where he considered other kinds of perturbations, for example relatively bounded perturbations with relative bound equal to zero.
Analytic bounds for the spectrum of non-selfadjoint operators are valuable because it is in general difficult to obtain good numerical bounds. In this paper, we will study the spectra of perturbations of normal operators where the perturbation is either relatively bounded or ![]() $p$-subordinate.
$p$-subordinate.
Definition 1.1. Let ![]() $T$ and
$T$ and ![]() $A$ be linear operators on a Banach space. We say that
$A$ be linear operators on a Banach space. We say that ![]() $A$ is
$A$ is ![]() $T$-bounded or relatively bounded with respect to
$T$-bounded or relatively bounded with respect to ![]() $T$ if
$T$ if ![]() $\mathcal{D}(T)\subseteq \mathcal{D}(A)$ and if there exist
$\mathcal{D}(T)\subseteq \mathcal{D}(A)$ and if there exist ![]() $a,b\geq 0$ such that
$a,b\geq 0$ such that
The infimum ![]() $\delta_A$ of all
$\delta_A$ of all ![]() $b\geq 0$ such that (1.1) is satisfied for some
$b\geq 0$ such that (1.1) is satisfied for some ![]() $a\geq 0$ is called the
$a\geq 0$ is called the ![]() $T$-bound of
$T$-bound of ![]() $A$.
$A$.
Definition 1.2. Let ![]() $T$ and
$T$ and ![]() $A$ be linear operators on a Banach space. We say that
$A$ be linear operators on a Banach space. We say that ![]() $A$ is
$A$ is ![]() $p$-subordinate to
$p$-subordinate to ![]() $T$ for some
$T$ for some ![]() $p\in [0,1]$ if
$p\in [0,1]$ if ![]() $\mathcal{D}(T)\subseteq \mathcal{D}(A)$ and if there exists
$\mathcal{D}(T)\subseteq \mathcal{D}(A)$ and if there exists ![]() $c\geq 0$ such that
$c\geq 0$ such that
The infimum over all constants ![]() $c\geq 0$ such that (1.2) holds is called the
$c\geq 0$ such that (1.2) holds is called the ![]() $p$-subordination bound of
$p$-subordination bound of ![]() $A$ to
$A$ to ![]() $T$.
$T$.
Remark 1.3. If ![]() $A$ is
$A$ is ![]() $p$-subordinate to
$p$-subordinate to ![]() $T$ with
$T$ with ![]() $p \lt 1$, then
$p \lt 1$, then ![]() $A$ is
$A$ is ![]() $T$-bounded with
$T$-bounded with ![]() $T$-bound zero; if in addition
$T$-bound zero; if in addition ![]() $0\in \rho(T)$ and
$0\in \rho(T)$ and ![]() $q \gt p$, then
$q \gt p$, then ![]() $A$ is
$A$ is ![]() $q$-subordinate to
$q$-subordinate to ![]() $T$ (see, e.g., [Reference Krasnosel’skiı, Zabreıko, Pustylʼnik and Sobolevskiı14, Theorem 12.3]).
$T$ (see, e.g., [Reference Krasnosel’skiı, Zabreıko, Pustylʼnik and Sobolevskiı14, Theorem 12.3]).
Cuenin and Tretter studied in [Reference Cuenin and Tretter5] the case when the unperturbed operator ![]() $T$ is selfadjoint and the additive perturbation
$T$ is selfadjoint and the additive perturbation ![]() $A$ is
$A$ is ![]() $T$-bounded with relative bound less than 1. The perturbation is not assumed to be symmetric so that
$T$-bounded with relative bound less than 1. The perturbation is not assumed to be symmetric so that ![]() $T+A$ is in general not selfadjoint or even symmetric. The authors give sufficient conditions for gaps in the spectrum of
$T+A$ is in general not selfadjoint or even symmetric. The authors give sufficient conditions for gaps in the spectrum of ![]() $T$ to remain open under the perturbation. They show the following localisation of the spectrum between two hyperbolas.
$T$ to remain open under the perturbation. They show the following localisation of the spectrum between two hyperbolas.
Theorem A (see Theorem 2.1 in [Reference Cuenin and Tretter5])
Let ![]() $T$ be a selfadjoint operator on a Hilbert space
$T$ be a selfadjoint operator on a Hilbert space ![]() $H$ and let
$H$ and let ![]() $A$ be
$A$ be ![]() $T$-bounded with
$T$-bounded with ![]() $T$-bound
$T$-bound ![]() $ \lt 1$ and let
$ \lt 1$ and let ![]() $a,b \geq 0$,
$a,b \geq 0$, ![]() $b \lt 1$, as in (1.1). Then the following is true:
$b \lt 1$, as in (1.1). Then the following is true:
(i) The spectrum of
 $T+A$ lies between two hyperbolas, more precisely,
$T+A$ lies between two hyperbolas, more precisely,
 \begin{align*}
\left\{z\in\mathbb{C}: |\operatorname{Im} z|^2 \gt \frac{a^2+b^2|\operatorname{Re} z|^2}{1-b^2}\right\} \subseteq \rho(T+A).
\end{align*}
\begin{align*}
\left\{z\in\mathbb{C}: |\operatorname{Im} z|^2 \gt \frac{a^2+b^2|\operatorname{Re} z|^2}{1-b^2}\right\} \subseteq \rho(T+A).
\end{align*}(ii) If
 $T$ has a spectral gap
$T$ has a spectral gap  $(\alpha_{T},\beta_{T})\subset \mathbb{R}$, i.e.
$(\alpha_{T},\beta_{T})\subset \mathbb{R}$, i.e.  $\sigma(T)\cap (\alpha_{T},\beta_{T})=\emptyset$, then
$\sigma(T)\cap (\alpha_{T},\beta_{T})=\emptyset$, then
 \begin{align*}
\{z\in\mathbb{C}: \alpha_{T+A} \lt \operatorname{Re} z \lt \beta_{T+A}\} \subseteq \rho(T+A)
\end{align*}
\begin{align*}
\{z\in\mathbb{C}: \alpha_{T+A} \lt \operatorname{Re} z \lt \beta_{T+A}\} \subseteq \rho(T+A)
\end{align*}where
 $\alpha_{T+A}:=\alpha_{T}+\sqrt{a^2+b^2\alpha_{T}^2}\,,\ \beta_{T+A}:= \beta_T -\sqrt{a^2+b^2\beta_{T}^2}$.
$\alpha_{T+A}:=\alpha_{T}+\sqrt{a^2+b^2\alpha_{T}^2}\,,\ \beta_{T+A}:= \beta_T -\sqrt{a^2+b^2\beta_{T}^2}$.(iii) If
 $T$ has an essential spectral gap
$T$ has an essential spectral gap  $(\alpha_{T},\beta_{T})\subset \mathbb{R}$, i.e.
$(\alpha_{T},\beta_{T})\subset \mathbb{R}$, i.e.  $\sigma_{\mathrm{ess} }(T)\cap (\alpha_{T},\beta_{T})=\emptyset$ with
$\sigma_{\mathrm{ess} }(T)\cap (\alpha_{T},\beta_{T})=\emptyset$ with  $\alpha_{T},\beta_{T}\in \sigma_{\mathrm{ess} }(T)$, and
$\alpha_{T},\beta_{T}\in \sigma_{\mathrm{ess} }(T)$, and  $\alpha_{T+A} \le \beta_{T+A}$ holds, then the set
$\alpha_{T+A} \le \beta_{T+A}$ holds, then the set
 \begin{equation*}\sigma(T+A)\cap \{z\in\mathbb{C}: \alpha_{T+A} \lt \operatorname{Re} z \lt \beta_{T+A}\}\end{equation*}
\begin{equation*}\sigma(T+A)\cap \{z\in\mathbb{C}: \alpha_{T+A} \lt \operatorname{Re} z \lt \beta_{T+A}\}\end{equation*}consists of at most countably many isolated eigenvalues of finite algebraic multiplicity which may accumulate at most at the points
 $\alpha_{T+A}$ and
$\alpha_{T+A}$ and  $\beta_{T+A}$.
$\beta_{T+A}$.
Moreover, the following estimate for the norm of the resolvent operator is proved.
Theorem B ([Reference Cuenin and Tretter5], Proposition 2.8)
Let ![]() $T$ be a selfadjoint operator in a Hilbert space
$T$ be a selfadjoint operator in a Hilbert space ![]() $H$, let
$H$, let ![]() $A$ be
$A$ be ![]() $T$-bounded with
$T$-bounded with ![]() $T$-bound
$T$-bound ![]() $ \lt 1$ and let
$ \lt 1$ and let ![]() $a,b \geq 0$,
$a,b \geq 0$, ![]() $b \lt 1$, as in (1.1). Then the following statements hold:
$b \lt 1$, as in (1.1). Then the following statements hold:
(i) For
 $z\in \mathbb{C}$ such that
$z\in \mathbb{C}$ such that  $|\operatorname{Im} z|^2 \gt \frac{a^2+b^2|\operatorname{Re} z|^2}{1-b^2}$, we have that
(1.3)
$|\operatorname{Im} z|^2 \gt \frac{a^2+b^2|\operatorname{Re} z|^2}{1-b^2}$, we have that
(1.3) \begin{equation}
\|(T+A-z)^{-1}\|\leq \frac{1}{|\operatorname{Im} z|-\sqrt{a^2+b^2|z|^2}}.
\end{equation}
\begin{equation}
\|(T+A-z)^{-1}\|\leq \frac{1}{|\operatorname{Im} z|-\sqrt{a^2+b^2|z|^2}}.
\end{equation}(ii) If
 $(\alpha_T,\beta_T)$ is a spectral gap of
$(\alpha_T,\beta_T)$ is a spectral gap of  $T$ then for
$T$ then for  $z\in \mathbb{C}$ such that
$z\in \mathbb{C}$ such that  $\alpha_{T+A} \lt \operatorname{Re} z \lt \beta_{T+A}$ with
$\alpha_{T+A} \lt \operatorname{Re} z \lt \beta_{T+A}$ with  $\alpha_{T+A}$ and
$\alpha_{T+A}$ and  $\beta_{T+A}$ as in Theorem A, we have that
(1.4)
$\beta_{T+A}$ as in Theorem A, we have that
(1.4) \begin{align}
\|(T+A-z)^{-1}\|
\leq
\frac{
\left( \sqrt{\min\{\operatorname{Re} z-\alpha_T,\beta_T-\operatorname{Re} z\}^2+(\operatorname{Im} z)^2} \right)^{-1}}{1-\max\left\{b,~\frac{\sqrt{a^2+b^2\alpha_T^2}}{\mu-\alpha_T},~\frac{\sqrt{a^2+b^2\beta_T^2}}{\beta_T-\mu}\right\}}.
\end{align}
\begin{align}
\|(T+A-z)^{-1}\|
\leq
\frac{
\left( \sqrt{\min\{\operatorname{Re} z-\alpha_T,\beta_T-\operatorname{Re} z\}^2+(\operatorname{Im} z)^2} \right)^{-1}}{1-\max\left\{b,~\frac{\sqrt{a^2+b^2\alpha_T^2}}{\mu-\alpha_T},~\frac{\sqrt{a^2+b^2\beta_T^2}}{\beta_T-\mu}\right\}}.
\end{align}
The case of infinitely many gaps in the spectrum is also considered.
In the present work, however, we assume that the unperturbed operator is only normal instead of selfadjoint which makes the situation more complicated and appropriate conditions on its spectrum have to be identified that allow us to establish perturbational results about its spectrum. In Proposition 3.1 we assume that ![]() $T$ is normal and that the imaginary part of the spectrum of
$T$ is normal and that the imaginary part of the spectrum of ![]() $T$ is bounded. Then the spectrum of
$T$ is bounded. Then the spectrum of ![]() $T+A$ is contained in the region between two hyperbolas which are shifted away from the real axis. If in addition we assume that the resolvent set of
$T+A$ is contained in the region between two hyperbolas which are shifted away from the real axis. If in addition we assume that the resolvent set of ![]() $T$ contains a strip parallel to the imaginary axis, we can provide a condition under which the resolvent set of
$T$ contains a strip parallel to the imaginary axis, we can provide a condition under which the resolvent set of ![]() $T+A$ still contains a (possibly smaller) strip and we give estimates for
$T+A$ still contains a (possibly smaller) strip and we give estimates for ![]() $\|(T+A-z)^{-1}\|$ for
$\|(T+A-z)^{-1}\|$ for ![]() $z$ in that strip, see Theorem 3.4. If the bound on the imaginary part of the spectrum of
$z$ in that strip, see Theorem 3.4. If the bound on the imaginary part of the spectrum of ![]() $T$ is 0, we recover and in fact improve the spectral inclusion from Theorem A and the estimate for the resolvent operator, see (3.4). If the real part of the spectrum of
$T$ is 0, we recover and in fact improve the spectral inclusion from Theorem A and the estimate for the resolvent operator, see (3.4). If the real part of the spectrum of ![]() $T$ is lower bounded, then we show in Corollary 3.6 that the real part of the spectrum of
$T$ is lower bounded, then we show in Corollary 3.6 that the real part of the spectrum of ![]() $T+A$ remains lower bounded, which is a generalisation of Corollary 2.4 in [Reference Cuenin and Tretter5].
$T+A$ remains lower bounded, which is a generalisation of Corollary 2.4 in [Reference Cuenin and Tretter5].
We can even allow for normal operators with unbounded imaginary part of the spectrum. We show in Theorem 4.6 that if the spectrum of the normal operator ![]() $T$ is contained in two sectors symmetric around the real axis, then the spectrum of
$T$ is contained in two sectors symmetric around the real axis, then the spectrum of ![]() $T+A$ is contained in two possibly bigger sectors and some neighbourhood of
$T+A$ is contained in two possibly bigger sectors and some neighbourhood of ![]() $0$ if the perturbation
$0$ if the perturbation ![]() $A$ is small enough. More precisely, the exterior of certain shifted and rotated hyperbolas is contained in the resolvent set of
$A$ is small enough. More precisely, the exterior of certain shifted and rotated hyperbolas is contained in the resolvent set of ![]() $T+A$. If we set the opening angles of the sectors equal to
$T+A$. If we set the opening angles of the sectors equal to ![]() $0$, we again recover and improve the results from Theorem A. We can also show that a spectral free strip
$0$, we again recover and improve the results from Theorem A. We can also show that a spectral free strip
of the unperturbed operator leads to a possibly smaller spectral free strip of ![]() $T+A$ if the perturbation is small enough. That the strips under consideration are parallel to the real or the imaginary axis is a choice of convenience. Clearly, if
$T+A$ if the perturbation is small enough. That the strips under consideration are parallel to the real or the imaginary axis is a choice of convenience. Clearly, if ![]() $T$ is normal, then so is
$T$ is normal, then so is ![]() $e^{\mathrm{i}\phi}T$ for any
$e^{\mathrm{i}\phi}T$ for any ![]() $\phi \in\mathbb{R}$ and we could as well consider other infinite strips which are not necessarily parallel to the real or imaginary axis.
$\phi \in\mathbb{R}$ and we could as well consider other infinite strips which are not necessarily parallel to the real or imaginary axis.
The paper is organised as follows. In ![]() $\S$ 2, we use a Neumann series argument and the spectral theorem to establish a basic criterion for
$\S$ 2, we use a Neumann series argument and the spectral theorem to establish a basic criterion for ![]() $z$ to belong to
$z$ to belong to ![]() $\rho(T+A)$ and we give estimates for
$\rho(T+A)$ and we give estimates for ![]() $\|(T+A-z)^{-1}\|$ for such
$\|(T+A-z)^{-1}\|$ for such ![]() $z$. An important ingredient here is that
$z$. An important ingredient here is that ![]() $\Arrowvert(T-z)^{-1}\Arrowvert=\operatorname{dist}(z,\sigma(T))^{-1}$ for all
$\Arrowvert(T-z)^{-1}\Arrowvert=\operatorname{dist}(z,\sigma(T))^{-1}$ for all ![]() $z\in\rho(T)$, since
$z\in\rho(T)$, since ![]() $T$ is a normal operator. Moreover we prove a perturbation theorem for the essential spectrum of normal operators. In
$T$ is a normal operator. Moreover we prove a perturbation theorem for the essential spectrum of normal operators. In ![]() $\S$ 3, we consider normal operators whose imaginary part is bounded. Under a relatively bounded perturbation, the imaginary part of the spectrum may become unbounded but it is contained in the region between two shifted hyperbolas. Theorem 3.4 shows that a spectral free strip of
$\S$ 3, we consider normal operators whose imaginary part is bounded. Under a relatively bounded perturbation, the imaginary part of the spectrum may become unbounded but it is contained in the region between two shifted hyperbolas. Theorem 3.4 shows that a spectral free strip of ![]() $T$ may give rise to a spectral free strip of
$T$ may give rise to a spectral free strip of ![]() $T+A$ if the perturbation
$T+A$ if the perturbation ![]() $A$ is small enough. In
$A$ is small enough. In ![]() $\S$ 4, we investigate normal (bi)sectorial-like operators. Our main theorem, Theorem 4.6, shows that the spectrum of
$\S$ 4, we investigate normal (bi)sectorial-like operators. Our main theorem, Theorem 4.6, shows that the spectrum of ![]() $T+A$ away from 0 is contained in two sectors if the relative bound of
$T+A$ away from 0 is contained in two sectors if the relative bound of ![]() $A$ is small enough. The amount by which the opening angle of the new sector increases depends on the
$A$ is small enough. The amount by which the opening angle of the new sector increases depends on the ![]() $T$-bound of
$T$-bound of ![]() $A$. Moreover, we give sufficient conditions for a spectral free strip around the imaginary axis to remain open.
$A$. Moreover, we give sufficient conditions for a spectral free strip around the imaginary axis to remain open.
The special case when the spectrum of ![]() $T$ is contained in only one sector has implications for semigroup generator properties of
$T$ is contained in only one sector has implications for semigroup generator properties of ![]() $T_A$ which will be dealt with in more detail in a forthcoming paper. In
$T_A$ which will be dealt with in more detail in a forthcoming paper. In ![]() $\S$ 5 we apply our method to several other situations. Most notably we study the case when infinitely many strips parallel to the imaginary axis belong to the resolvent set of
$\S$ 5 we apply our method to several other situations. Most notably we study the case when infinitely many strips parallel to the imaginary axis belong to the resolvent set of ![]() $T$, see Theorems 5.4 and 5.5. In
$T$, see Theorems 5.4 and 5.5. In ![]() $\S$ 6, we consider
$\S$ 6, we consider ![]() $p$-subordinate perturbations. In this case, we can prove spectral enclosures even if the spectrum of
$p$-subordinate perturbations. In this case, we can prove spectral enclosures even if the spectrum of ![]() $T$ is bounded only by parabolas as opposed to by linear functions in the sectorial case. § 7 contains applications to a non-selfadjoint quantum graph and to a first order system of differential equations. Several estimates that are used throughout this work are collected in Appendix A.
$T$ is bounded only by parabolas as opposed to by linear functions in the sectorial case. § 7 contains applications to a non-selfadjoint quantum graph and to a first order system of differential equations. Several estimates that are used throughout this work are collected in Appendix A.
2. Perturbation of normal operators
In this section, we will establish our notation and provide some basic facts on normal operators. The main result in this section is Proposition 2.1 on which most of our results are based. Recall that a closed densely defined operator ![]() $T$ on a Hilbert space
$T$ on a Hilbert space ![]() $H$ is called normal if
$H$ is called normal if ![]() $TT^* = T^*T$. Note that for a normal operator
$TT^* = T^*T$. Note that for a normal operator ![]() $\mathcal{D}(T)= \mathcal{D}(T^*)$ and
$\mathcal{D}(T)= \mathcal{D}(T^*)$ and ![]() $\|Tx\| = \|T^*x\|$ for all
$\|Tx\| = \|T^*x\|$ for all ![]() $x\in\mathcal{D}(T)$. As for selfadjoint operators, there is a spectral theorem for normal operators: There exists a unique projection valued measure
$x\in\mathcal{D}(T)$. As for selfadjoint operators, there is a spectral theorem for normal operators: There exists a unique projection valued measure ![]() $E$ supported on the spectrum
$E$ supported on the spectrum ![]() $\sigma(T)$ of
$\sigma(T)$ of ![]() $T$ such that
$T$ such that
 \begin{equation*}
T = \int_{\sigma(T)} \lambda\, \mathrm d E(\lambda),
\end{equation*}
\begin{equation*}
T = \int_{\sigma(T)} \lambda\, \mathrm d E(\lambda),
\end{equation*}see for instance, [Reference Schmüdgen20] or [Reference van Neerven23]. An important consequence which we will use frequently is that
 \begin{equation*}
\| (T-\lambda)^{-1} \| = \frac{1}{\operatorname{dist}(\lambda, \sigma(T))} .
\end{equation*}
\begin{equation*}
\| (T-\lambda)^{-1} \| = \frac{1}{\operatorname{dist}(\lambda, \sigma(T))} .
\end{equation*} In this work, the operators ![]() $T$ and
$T$ and ![]() $A$ and the constants
$A$ and the constants ![]() $a,b, c$ will always satisfy one of the following assumptions.
$a,b, c$ will always satisfy one of the following assumptions.
Assumption 1. ![]() $T$ is a closed normal operator on a Hilbert space
$T$ is a closed normal operator on a Hilbert space ![]() $H$ and
$H$ and ![]() $A$ is
$A$ is ![]() $T$-bounded with
$T$-bounded with ![]() $T$-bound
$T$-bound ![]() $\delta_A \lt 1$ and the constants
$\delta_A \lt 1$ and the constants ![]() $a\ge 0$ and
$a\ge 0$ and ![]() $0\le b \leq \delta_A$ satisfy (1.1).
$0\le b \leq \delta_A$ satisfy (1.1).
Assumption 2. ![]() $T$ is a closed normal operator on a Hilbert space
$T$ is a closed normal operator on a Hilbert space ![]() $H$ and
$H$ and ![]() $A$ is
$A$ is ![]() $p$-subordinate to
$p$-subordinate to ![]() $T$ for some
$T$ for some ![]() $p\in [0,1]$ and the constant
$p\in [0,1]$ and the constant ![]() $c \gt 0$ satisfies (1.2).
$c \gt 0$ satisfies (1.2).
Note that under either of the assumptions the perturbed operator ![]() $T+A$ is closed and that Assumption 2 is stronger than Assumption 1 by Remark 1.3.
$T+A$ is closed and that Assumption 2 is stronger than Assumption 1 by Remark 1.3.
Recall that the resolvent set ![]() $\rho(T)$ of a closed linear operator consists of all
$\rho(T)$ of a closed linear operator consists of all ![]() $z\in\mathbb{C}$ such that
$z\in\mathbb{C}$ such that ![]() $T-z$ is bijective. In this case, the resolvent operator
$T-z$ is bijective. In this case, the resolvent operator ![]() $(T-z)^{-1}$ is bounded. Much of perturbation theory is based on the well-known fact that
$(T-z)^{-1}$ is bounded. Much of perturbation theory is based on the well-known fact that ![]() $I + S$ is bijective and
$I + S$ is bijective and  $\|(I+S)^{-1}\|\le \frac{1}{1-\|S\|}$ if
$\|(I+S)^{-1}\|\le \frac{1}{1-\|S\|}$ if ![]() $S$ is a bounded linear operator with
$S$ is a bounded linear operator with ![]() $\|S\| \lt 1$. This allows us to prove the next Proposition which is fundamental for most of our results.
$\|S\| \lt 1$. This allows us to prove the next Proposition which is fundamental for most of our results.
Proposition 2.1. Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1. Then for every
$A$ be as in Assumption 1. Then for every ![]() $z \in \rho(T)$ the following holds.
$z \in \rho(T)$ the following holds.
(i) If
 $\displaystyle \|A(T-z)^{-1}\| \lt 1$, then
$\displaystyle \|A(T-z)^{-1}\| \lt 1$, then  $T+A-z$ is invertible and
$T+A-z$ is invertible and
 \begin{equation*}
\| (T+A-z)^{-1} \| \le \frac{\| (T-z)^{-1} \| }{1 - \| A(T-z)^{-1} \|}.
\end{equation*}
\begin{equation*}
\| (T+A-z)^{-1} \| \le \frac{\| (T-z)^{-1} \| }{1 - \| A(T-z)^{-1} \|}.
\end{equation*}(ii)
 $\displaystyle \|A(T-z)^{-1}\|\leq \sup_{t\in\sigma(T)} \frac{\sqrt{a^2+b^2|t|^2}}{|t-z|}.$
$\displaystyle \|A(T-z)^{-1}\|\leq \sup_{t\in\sigma(T)} \frac{\sqrt{a^2+b^2|t|^2}}{|t-z|}.$(iii) If
 $\displaystyle \sup_{t\in\sigma(T)} \frac{\sqrt{a^2+b^2|t|^2}}{|t-z|} \lt 1$, then
$\displaystyle \sup_{t\in\sigma(T)} \frac{\sqrt{a^2+b^2|t|^2}}{|t-z|} \lt 1$, then  $T+A-z$ is invertible and
$T+A-z$ is invertible and
 \begin{equation*}
\| (T+A-z)^{-1} \| \le \frac{\| (T-z)^{-1} \| }{1 - \| A(T-z)^{-1} \|}
\le \frac{1}{\operatorname{dist}(z, \sigma(T))} \frac{1}{1 - \sup_{t\in\sigma(T)} \frac{\sqrt{a^2+b^2|t|^2}}{|t-z|}} .
\end{equation*}
\begin{equation*}
\| (T+A-z)^{-1} \| \le \frac{\| (T-z)^{-1} \| }{1 - \| A(T-z)^{-1} \|}
\le \frac{1}{\operatorname{dist}(z, \sigma(T))} \frac{1}{1 - \sup_{t\in\sigma(T)} \frac{\sqrt{a^2+b^2|t|^2}}{|t-z|}} .
\end{equation*}
Proof. (i) is well known and follows from the Neumann series for the resolvent: If ![]() $z\in\rho(T)$, we can write
$z\in\rho(T)$, we can write ![]() $T+A-z = (I + A (T-z)^{-1})(T-z)$. Therefore, if
$T+A-z = (I + A (T-z)^{-1})(T-z)$. Therefore, if ![]() $\| A (T-z)^{-1}\| \lt 1$, then
$\| A (T-z)^{-1}\| \lt 1$, then ![]() $T+A-z$ is invertible with inverse
$T+A-z$ is invertible with inverse
 \begin{equation*}
(T+A-z)^{-1} = (T-z)^{-1} \sum_{n=0}^\infty (-A (T-z)^{-1})^n,
\end{equation*}
\begin{equation*}
(T+A-z)^{-1} = (T-z)^{-1} \sum_{n=0}^\infty (-A (T-z)^{-1})^n,
\end{equation*}and
 \begin{equation*}\Arrowvert(T+A-z)^{-1}\Arrowvert\leq\Arrowvert(T-z)^{-1}\Arrowvert\sum_{n=0}^\infty\Arrowvert A(T-z)^{-1}\Arrowvert^n=\frac{\Arrowvert(T-z)^{-1}\Arrowvert}{1-\Arrowvert A(T-z)^{-1}\Arrowvert}.\end{equation*}
\begin{equation*}\Arrowvert(T+A-z)^{-1}\Arrowvert\leq\Arrowvert(T-z)^{-1}\Arrowvert\sum_{n=0}^\infty\Arrowvert A(T-z)^{-1}\Arrowvert^n=\frac{\Arrowvert(T-z)^{-1}\Arrowvert}{1-\Arrowvert A(T-z)^{-1}\Arrowvert}.\end{equation*} (ii) Since ![]() $T$ is normal, we have
$T$ is normal, we have ![]() $\||T|x\| = \|Tx\|$ for all
$\||T|x\| = \|Tx\|$ for all ![]() $x\in \mathcal{D}(T) = \mathcal{D}(|T|)$ where
$x\in \mathcal{D}(T) = \mathcal{D}(|T|)$ where ![]() $|T| := (T^*T)^{1/2}$. Using that
$|T| := (T^*T)^{1/2}$. Using that ![]() $A$ is
$A$ is ![]() $T$-bounded, we obtain from (1.1) for all
$T$-bounded, we obtain from (1.1) for all ![]() $x\in \mathcal{D}(|T|^2)$ and
$x\in \mathcal{D}(|T|^2)$ and ![]() $z\in\rho(T)$ that
$z\in\rho(T)$ that
 \begin{align*}
\|Ax\|^2&\leq a^2\|x\|^2 +b^2\||T|x\|^2
=a^2\langle x,\, x\rangle +b^2\langle |T|x,\, |T|x\rangle
\\
&= \langle (a^2+b^2|T|^2)x,\, x\rangle
\\
&=\|\sqrt{a^2+b^2|T|^2}\, x\|^2.
\end{align*}
\begin{align*}
\|Ax\|^2&\leq a^2\|x\|^2 +b^2\||T|x\|^2
=a^2\langle x,\, x\rangle +b^2\langle |T|x,\, |T|x\rangle
\\
&= \langle (a^2+b^2|T|^2)x,\, x\rangle
\\
&=\|\sqrt{a^2+b^2|T|^2}\, x\|^2.
\end{align*} Therefore, for all ![]() $x\in\mathcal{D}(T)$ with
$x\in\mathcal{D}(T)$ with ![]() $\|x\|=1$,
$\|x\|=1$,
 \begin{equation}\Arrowvert A(T-z)^{-1}x\Arrowvert\leq\Arrowvert\sqrt{a^2+b^2\vert T\vert^2}\, (T-z)^{-1}x\Arrowvert\leq\sup_{t\in\sigma(T)}\frac{\sqrt{a^2+b^2\vert t\vert^2}}{\vert t-z\vert}.\end{equation}
\begin{equation}\Arrowvert A(T-z)^{-1}x\Arrowvert\leq\Arrowvert\sqrt{a^2+b^2\vert T\vert^2}\, (T-z)^{-1}x\Arrowvert\leq\sup_{t\in\sigma(T)}\frac{\sqrt{a^2+b^2\vert t\vert^2}}{\vert t-z\vert}.\end{equation} In the last step we used that, by the spectral theorem for normal operators, ![]() $\|g(T)x \| \le \sup_{t\in\sigma(T)} |g(t)| \|x\|$ for every bounded continuous function
$\|g(T)x \| \le \sup_{t\in\sigma(T)} |g(t)| \|x\|$ for every bounded continuous function ![]() $g$. In our case,
$g$. In our case, ![]() $g(t) = \sqrt{a^2+b^2t \overline t}\,(t-z)^{-1}$. Since
$g(t) = \sqrt{a^2+b^2t \overline t}\,(t-z)^{-1}$. Since ![]() $A(T-z)^{-1}$ is bounded on the dense subset
$A(T-z)^{-1}$ is bounded on the dense subset ![]() $\mathcal{D}(T)$, it extends uniquely to a bounded operator on
$\mathcal{D}(T)$, it extends uniquely to a bounded operator on ![]() $H$ and (2.1) holds for all
$H$ and (2.1) holds for all ![]() $x\in H$.
$x\in H$.
(iii) follows from (i) and (ii).
The proposition shows that in order to establish ![]() $z\in\rho(T+A)$ for a given
$z\in\rho(T+A)$ for a given ![]() $z\in\rho(T)$, it is crucial to find good estimates for
$z\in\rho(T)$, it is crucial to find good estimates for ![]() $\operatorname{dist}(z, \sigma(T))$ and for the supremum of the function
$\operatorname{dist}(z, \sigma(T))$ and for the supremum of the function
 \begin{equation}
H_z(t) := \frac{a^2 + b^2|t|^2 }{|t-z|^2},
\end{equation}
\begin{equation}
H_z(t) := \frac{a^2 + b^2|t|^2 }{|t-z|^2},
\end{equation} where the supremum is taken over ![]() $t\in\sigma(T)$. We show in Lemma A.1 that for fixed
$t\in\sigma(T)$. We show in Lemma A.1 that for fixed ![]() $z$, the function
$z$, the function ![]() $H_z$ has no local maximum in open subsets of
$H_z$ has no local maximum in open subsets of ![]() $\mathbb{C}\setminus\{z\}$. Therefore it suffices to take the supremum over the boundary of
$\mathbb{C}\setminus\{z\}$. Therefore it suffices to take the supremum over the boundary of ![]() $\sigma(T)$ or any set containing
$\sigma(T)$ or any set containing ![]() $\sigma(T)$ which may include the point at infinity. In Appendix A, we give bounds for
$\sigma(T)$ which may include the point at infinity. In Appendix A, we give bounds for ![]() $\sup_{t\in U} H_z(t)$ for various sets
$\sup_{t\in U} H_z(t)$ for various sets ![]() $U$ which then lead to the characterisation of regions contained in the resolvent set of
$U$ which then lead to the characterisation of regions contained in the resolvent set of ![]() $T+A$.
$T+A$.
We finish this section with the following theorem about the essential spectrumFootnote 1 which for a closed operator ![]() $S$ is defined in [Reference Gohberg, Goldberg and Kaashoek11, Sec. XVII.2] as
$S$ is defined in [Reference Gohberg, Goldberg and Kaashoek11, Sec. XVII.2] as
If ![]() $U$ is an open connected set in
$U$ is an open connected set in ![]() $\mathbb{C}\setminus\sigma_{\mathrm{ess} }(S)$ which contains at least one point from
$\mathbb{C}\setminus\sigma_{\mathrm{ess} }(S)$ which contains at least one point from ![]() $\rho(S)$, then
$\rho(S)$, then ![]() $\sigma(S)\cap U$ consists of at most countably many eigenvalues of
$\sigma(S)\cap U$ consists of at most countably many eigenvalues of ![]() $S$ of finite type which cannot accumulate in
$S$ of finite type which cannot accumulate in ![]() $U$, see [Reference Gohberg, Goldberg and Kaashoek11, Chapter XVII, Theorem 2.1].
$U$, see [Reference Gohberg, Goldberg and Kaashoek11, Chapter XVII, Theorem 2.1].
Theorem 2.2 Let ![]() $T$ and
$T$ and ![]() $A$ and the constants
$A$ and the constants ![]() $a,b$ be as in Assumption 1. Assume that there exists a subspace
$a,b$ be as in Assumption 1. Assume that there exists a subspace  $\widetilde H\subseteq \mathcal{D}(T)$ such that
$\widetilde H\subseteq \mathcal{D}(T)$ such that ![]() $\dim \widetilde H \lt \infty$,
$\dim \widetilde H \lt \infty$,  $\mathcal{D}(T) = \widetilde H \oplus \mathcal{D}_2$ where
$\mathcal{D}(T) = \widetilde H \oplus \mathcal{D}_2$ where  $\mathcal{D}_2 = \mathcal{D}(T) \cap \widetilde H^\perp$ and
$\mathcal{D}_2 = \mathcal{D}(T) \cap \widetilde H^\perp$ and ![]() $\widetilde H$ and
$\widetilde H$ and ![]() $\mathcal{D}_2$ are
$\mathcal{D}_2$ are ![]() $T$-invariant so that we can write
$T$-invariant so that we can write ![]() $T = T_1\oplus T_2$ where
$T = T_1\oplus T_2$ where ![]() $T_1$ is defined on
$T_1$ is defined on ![]() $\widetilde H$ and
$\widetilde H$ and ![]() $T_2$ on
$T_2$ on ![]() $\mathcal{D}_2 \subseteq \widetilde H^\perp$. Let
$\mathcal{D}_2 \subseteq \widetilde H^\perp$. Let ![]() $P_1$ and
$P_1$ and ![]() $P_2$ be the orthogonal projections onto
$P_2$ be the orthogonal projections onto ![]() $\widetilde H$ and
$\widetilde H$ and ![]() $\widetilde H^\perp$ respectively. Then
$\widetilde H^\perp$ respectively. Then  $A_{22} := P_2 A|_{\mathcal{D}(T)\cap\widetilde H^\perp}$, viewed as an operator on
$A_{22} := P_2 A|_{\mathcal{D}(T)\cap\widetilde H^\perp}$, viewed as an operator on ![]() $\widetilde H^\perp$, is
$\widetilde H^\perp$, is ![]() $T_2$-bounded with the same constants
$T_2$-bounded with the same constants ![]() $a,b$ and
$a,b$ and
In any open connected subset of ![]() $\mathbb{C}\setminus\sigma_{\mathrm{ess} }(T+A)$ which contains at least one point from the resolvent set of
$\mathbb{C}\setminus\sigma_{\mathrm{ess} }(T+A)$ which contains at least one point from the resolvent set of ![]() $T+A$, there are at most countably many eigenvalues of
$T+A$, there are at most countably many eigenvalues of ![]() $T+A$ and they may accumulate only at its boundary.
$T+A$ and they may accumulate only at its boundary.
Proof. Since ![]() $\mathcal{D}(T)\subseteq \mathcal{D}(A)$, we can write
$\mathcal{D}(T)\subseteq \mathcal{D}(A)$, we can write  $\mathcal{D}(T+A)=\mathcal{D}(T_1)\oplus \mathcal{D}(T_2) = \widetilde H \oplus \mathcal{D}_2$ and, if we define
$\mathcal{D}(T+A)=\mathcal{D}(T_1)\oplus \mathcal{D}(T_2) = \widetilde H \oplus \mathcal{D}_2$ and, if we define
 \begin{equation*}
A_{j1}:=P_j A|_{\mathcal{D}(T)\cap \widetilde H},\quad
A_{j2}:=P_j A|_{\mathcal{D}(T)\cap \widetilde H^\perp},
\qquad j=1,2,
\end{equation*}
\begin{equation*}
A_{j1}:=P_j A|_{\mathcal{D}(T)\cap \widetilde H},\quad
A_{j2}:=P_j A|_{\mathcal{D}(T)\cap \widetilde H^\perp},
\qquad j=1,2,
\end{equation*} we can represent both ![]() $T$ and
$T$ and ![]() $T+A$ as block operator matrices
$T+A$ as block operator matrices
 \begin{align*}
T =
\begin{pmatrix} T_1 & 0 \\ 0 & T_2
\end{pmatrix}
: \mathcal{D}(T_1)\oplus \mathcal{D}(T_2) \subseteq H \longrightarrow \widetilde H \oplus \widetilde H^\perp,
\end{align*}
\begin{align*}
T =
\begin{pmatrix} T_1 & 0 \\ 0 & T_2
\end{pmatrix}
: \mathcal{D}(T_1)\oplus \mathcal{D}(T_2) \subseteq H \longrightarrow \widetilde H \oplus \widetilde H^\perp,
\end{align*}and
 \begin{align*}
T + A =
\begin{pmatrix} T_1 + A_{11} & A_{12} \\ A_{21} & T_2 + A_{22}
\end{pmatrix}
: \mathcal{D}(T_1)\oplus \mathcal{D}(T_2) \subseteq H \longrightarrow \widetilde H \oplus \widetilde H^\perp.
\end{align*}
\begin{align*}
T + A =
\begin{pmatrix} T_1 + A_{11} & A_{12} \\ A_{21} & T_2 + A_{22}
\end{pmatrix}
: \mathcal{D}(T_1)\oplus \mathcal{D}(T_2) \subseteq H \longrightarrow \widetilde H \oplus \widetilde H^\perp.
\end{align*}We decompose the sum as
 \begin{equation*}
T+A=\mathcal{T}+\mathcal{A}
\qquad\text{with }\quad
\mathcal{T}:=
\begin{pmatrix} T_1 & 0 \\ 0 & T_2+A_{22}
\end{pmatrix},
\quad
\mathcal{A}:=
\begin{pmatrix} A_{11} & A_{12} \\ A_{21} & 0
\end{pmatrix}.
\end{equation*}
\begin{equation*}
T+A=\mathcal{T}+\mathcal{A}
\qquad\text{with }\quad
\mathcal{T}:=
\begin{pmatrix} T_1 & 0 \\ 0 & T_2+A_{22}
\end{pmatrix},
\quad
\mathcal{A}:=
\begin{pmatrix} A_{11} & A_{12} \\ A_{21} & 0
\end{pmatrix}.
\end{equation*} Note that for ![]() $j=1, 2$ and
$j=1, 2$ and ![]() $x\in\mathcal{D}(T_j)$ we have that
$x\in\mathcal{D}(T_j)$ we have that
 \begin{equation*}
\|A_{j1}x\|^2 + \|A_{j2}x\|^2
= \|Ax\|^2
\le a^2 \|x\|^2 + b^2 \|Tx\|^2
= a^2 \|x\|^2 + b^2 \|T_jx\|^2,
\end{equation*}
\begin{equation*}
\|A_{j1}x\|^2 + \|A_{j2}x\|^2
= \|Ax\|^2
\le a^2 \|x\|^2 + b^2 \|Tx\|^2
= a^2 \|x\|^2 + b^2 \|T_jx\|^2,
\end{equation*} hence ![]() $A_{j\ell}$ is
$A_{j\ell}$ is ![]() $T_j$-bounded with relative bound less or equal to the
$T_j$-bounded with relative bound less or equal to the ![]() $T$-bound of
$T$-bound of ![]() $A$. Since
$A$. Since ![]() $\widetilde H$ is finite dimensional, an easy calculation shows that
$\widetilde H$ is finite dimensional, an easy calculation shows that ![]() $\mathcal{A}$ is
$\mathcal{A}$ is ![]() $\mathcal{T}$-compact. Thus, by [Reference Gohberg, Goldberg and Kaashoek11, Chapter XVII, Theorem 4.3],
$\mathcal{T}$-compact. Thus, by [Reference Gohberg, Goldberg and Kaashoek11, Chapter XVII, Theorem 4.3],
Observe that for ![]() $\lambda \in \mathbb{C}$
$\lambda \in \mathbb{C}$
 \begin{align*}
\ker(\mathcal{T}-\lambda)
& =\ker(T_1-\lambda)\oplus \ker(T_2+A_{22} - \lambda),
\\
\operatorname{Ran}(\mathcal{T}-\lambda)
& =\operatorname{Ran}(T_1-\lambda)\oplus \operatorname{Ran}(T_2+A_{22} - \lambda).
\end{align*}
\begin{align*}
\ker(\mathcal{T}-\lambda)
& =\ker(T_1-\lambda)\oplus \ker(T_2+A_{22} - \lambda),
\\
\operatorname{Ran}(\mathcal{T}-\lambda)
& =\operatorname{Ran}(T_1-\lambda)\oplus \operatorname{Ran}(T_2+A_{22} - \lambda).
\end{align*} Since ![]() $\ker(T_1-\lambda)$ and
$\ker(T_1-\lambda)$ and ![]() $\operatorname{Ran}(T_1-\lambda)$ are finite dimensional, we have that
$\operatorname{Ran}(T_1-\lambda)$ are finite dimensional, we have that
 \begin{align*}
\dim(\ker(\mathcal{T}-\lambda)) \lt \infty
& \quad \Longleftrightarrow \quad
\dim(\ker(T_2+A_{22}-\lambda)) \lt \infty,
\\
\operatorname{codim}(\operatorname{Ran}(\mathcal{T}-\lambda)) \lt \infty
& \quad\Longleftrightarrow\quad
\operatorname{codim}(\operatorname{Ran}(T_2+A_{22}-\lambda)) \lt \infty,
\end{align*}
\begin{align*}
\dim(\ker(\mathcal{T}-\lambda)) \lt \infty
& \quad \Longleftrightarrow \quad
\dim(\ker(T_2+A_{22}-\lambda)) \lt \infty,
\\
\operatorname{codim}(\operatorname{Ran}(\mathcal{T}-\lambda)) \lt \infty
& \quad\Longleftrightarrow\quad
\operatorname{codim}(\operatorname{Ran}(T_2+A_{22}-\lambda)) \lt \infty,
\end{align*}and therefore
which together with (2.4) shows (2.3). The claim about nonaccumulation of the spectrum follows from [Reference Gohberg, Goldberg and Kaashoek11, Chapter XVII, Theorem 2.1].
Let us remark that we need to assume conditions on ![]() $\sigma(T)$ in order to be able to control
$\sigma(T)$ in order to be able to control ![]() $\sigma(T+A)$. For instance, the condition (1.5) in general will not be enough to guarantee that a spectral gap remains open under a perturbation even in the case of an arbitrarily large gap and a
$\sigma(T+A)$. For instance, the condition (1.5) in general will not be enough to guarantee that a spectral gap remains open under a perturbation even in the case of an arbitrarily large gap and a ![]() $p$-subordinate perturbation.
$p$-subordinate perturbation.
Example 2.3. Let ![]() $H=L^2(\mathbb{R};\mathbb{C})\oplus L^2(\mathbb{R};\mathbb{C})$. For
$H=L^2(\mathbb{R};\mathbb{C})\oplus L^2(\mathbb{R};\mathbb{C})$. For ![]() $k \gt 0$ we define the operator
$k \gt 0$ we define the operator ![]() $T$ by
$T$ by
 \begin{equation*}
\mathcal{D}(T):= \left\{
\begin{pmatrix}
f \\ g
\end{pmatrix}
\in L^2(\mathbb{R};\mathbb{C})\oplus L^2(\mathbb{R};\mathbb{C}): xf(x),~xg(x)\in L^2(\mathbb{R};\mathbb{C}) \right\}
\end{equation*}
\begin{equation*}
\mathcal{D}(T):= \left\{
\begin{pmatrix}
f \\ g
\end{pmatrix}
\in L^2(\mathbb{R};\mathbb{C})\oplus L^2(\mathbb{R};\mathbb{C}): xf(x),~xg(x)\in L^2(\mathbb{R};\mathbb{C}) \right\}
\end{equation*}and
 \begin{equation*}
T \begin{pmatrix} f \\ g
\end{pmatrix}
:=
\begin{pmatrix}
\mathcal{M}_{k+\mathrm{i} x} & 0 \\
0 & \mathcal{M}_{-k+\mathrm{i} x}
\end{pmatrix}
\begin{pmatrix} f \\ g
\end{pmatrix}
=
\begin{pmatrix} (k+\mathrm{i} x)f\\ (-k+\mathrm{i} x)g
\end{pmatrix},
\qquad
\begin{pmatrix} f \\ g
\end{pmatrix} \in \mathcal{D}(T).
\end{equation*}
\begin{equation*}
T \begin{pmatrix} f \\ g
\end{pmatrix}
:=
\begin{pmatrix}
\mathcal{M}_{k+\mathrm{i} x} & 0 \\
0 & \mathcal{M}_{-k+\mathrm{i} x}
\end{pmatrix}
\begin{pmatrix} f \\ g
\end{pmatrix}
=
\begin{pmatrix} (k+\mathrm{i} x)f\\ (-k+\mathrm{i} x)g
\end{pmatrix},
\qquad
\begin{pmatrix} f \\ g
\end{pmatrix} \in \mathcal{D}(T).
\end{equation*} It is clear that ![]() $T$ is a normal operator with spectrum
$T$ is a normal operator with spectrum
In particular, ![]() $T$ has a spectral free strip
$T$ has a spectral free strip
Consider the operator ![]() $A$ defined by
$A$ defined by
 \begin{equation*}A\begin{pmatrix}f\\g\end{pmatrix}:=\begin{pmatrix}{\mathcal M}_{-\sqrt{\vert x\vert}}&0\\0& {\mathcal M}_{\sqrt{\vert x\vert}}\end{pmatrix}\begin{pmatrix}f\\g\end{pmatrix}=\begin{pmatrix}-{\sqrt{\vert x\vert}}f\\\sqrt{\vert x\vert}g\end{pmatrix},\qquad\begin{pmatrix}f\\g\end{pmatrix}\in\mathcal D(A):=\mathcal D(T).\end{equation*}
\begin{equation*}A\begin{pmatrix}f\\g\end{pmatrix}:=\begin{pmatrix}{\mathcal M}_{-\sqrt{\vert x\vert}}&0\\0& {\mathcal M}_{\sqrt{\vert x\vert}}\end{pmatrix}\begin{pmatrix}f\\g\end{pmatrix}=\begin{pmatrix}-{\sqrt{\vert x\vert}}f\\\sqrt{\vert x\vert}g\end{pmatrix},\qquad\begin{pmatrix}f\\g\end{pmatrix}\in\mathcal D(A):=\mathcal D(T).\end{equation*} It is easy to see that ![]() $A$ is
$A$ is ![]() $p$-subordinate to
$p$-subordinate to ![]() $T$ for
$T$ for  $p=\frac{1}{2}$, in particular
$p=\frac{1}{2}$, in particular ![]() $A$ is also
$A$ is also ![]() $T$-bounded with relative bound
$T$-bounded with relative bound ![]() $0$. However, the spectrum of
$0$. However, the spectrum of ![]() $T+A$ is
$T+A$ is
 \begin{equation*}
\sigma(T+A)
=\left\{k-\sqrt{|x|} + \mathrm{i} x : x\in \mathbb{R}\right\}\cup\left\{-k+\sqrt{|x|} + \mathrm{i} x : x\in \mathbb{R}\right\},
\end{equation*}
\begin{equation*}
\sigma(T+A)
=\left\{k-\sqrt{|x|} + \mathrm{i} x : x\in \mathbb{R}\right\}\cup\left\{-k+\sqrt{|x|} + \mathrm{i} x : x\in \mathbb{R}\right\},
\end{equation*} hence ![]() $T+A$ does not have any spectral free strip.
$T+A$ does not have any spectral free strip.
3. Normal operators with bounded imaginary part
Except for Proposition 3.1 we will always assume in this section that the imaginary part of the spectrum of the normal operator ![]() $T$ is bounded.
$T$ is bounded.
For ![]() $\gamma\in\mathbb{R}$ we define the sets
$\gamma\in\mathbb{R}$ we define the sets
 \begin{align}
\mathrm{Hyp}_{\gamma} &=
\left\{z\in\mathbb{C} \ :\
a^2 + b^2\gamma^2 + \frac{b^2(\operatorname{Re} z)^2 }{1-b^2} \lt ( \operatorname{Im} z )^2,\
\operatorname{Im} z \gt 0
\right\}.
\end{align}
\begin{align}
\mathrm{Hyp}_{\gamma} &=
\left\{z\in\mathbb{C} \ :\
a^2 + b^2\gamma^2 + \frac{b^2(\operatorname{Re} z)^2 }{1-b^2} \lt ( \operatorname{Im} z )^2,\
\operatorname{Im} z \gt 0
\right\}.
\end{align} ![]() $\mathrm{Hyp}_{\gamma}$ is the set of all points above the hyperbola in the complex plane which passes through
$\mathrm{Hyp}_{\gamma}$ is the set of all points above the hyperbola in the complex plane which passes through ![]() $\mathrm{i} \sqrt{a^2 + b^2\gamma^2 }$ and has the asymptotes
$\mathrm{i} \sqrt{a^2 + b^2\gamma^2 }$ and has the asymptotes  $\operatorname{Im} z = \pm \frac{b}{\sqrt{1-b^2}} \operatorname{Re} z$ for
$\operatorname{Im} z = \pm \frac{b}{\sqrt{1-b^2}} \operatorname{Re} z$ for ![]() $\operatorname{Re} z \to\pm \infty$.
$\operatorname{Re} z \to\pm \infty$.
For ![]() $\mu, \nu, \gamma\in\mathbb{R}$, let us define, as in Lemma A.4,
$\mu, \nu, \gamma\in\mathbb{R}$, let us define, as in Lemma A.4,
 \begin{align}
M(\mu, \nu, \gamma)
&:= \sup_{\tau\in\mathbb{R}} H_{\mu + \mathrm{i}\nu}(\tau + \mathrm{i} \gamma)\cr
&=
(2(\nu-\gamma)^2)^{-1}\bigg(
a^2 + b^2 \Big(\mu^2 + \gamma^2 + (\gamma - \nu)^2 \Big) \cr
&\quad \quad +\sqrt{
\big[ -a^2 + b^2 (\mu^2 - \gamma^2 + (\gamma - \nu)^2 )]^2
+ 4 \mu^2b^2( a^2 + b^2\gamma^2 ) }
\bigg)
\end{align}
\begin{align}
M(\mu, \nu, \gamma)
&:= \sup_{\tau\in\mathbb{R}} H_{\mu + \mathrm{i}\nu}(\tau + \mathrm{i} \gamma)\cr
&=
(2(\nu-\gamma)^2)^{-1}\bigg(
a^2 + b^2 \Big(\mu^2 + \gamma^2 + (\gamma - \nu)^2 \Big) \cr
&\quad \quad +\sqrt{
\big[ -a^2 + b^2 (\mu^2 - \gamma^2 + (\gamma - \nu)^2 )]^2
+ 4 \mu^2b^2( a^2 + b^2\gamma^2 ) }
\bigg)
\end{align}where the last equality is shown in Lemma A.3(i).
Proposition 3.1. Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1. Moreover, we assume that
$A$ be as in Assumption 1. Moreover, we assume that ![]() $\operatorname{Im}\sigma(T)\le \gamma$ for some
$\operatorname{Im}\sigma(T)\le \gamma$ for some ![]() $\gamma\in\mathbb{R}$. Then
$\gamma\in\mathbb{R}$. Then
For ![]() $z\in \mathrm{i} \gamma + \mathrm{Hyp}_\gamma$ we have the resolvent estimate
$z\in \mathrm{i} \gamma + \mathrm{Hyp}_\gamma$ we have the resolvent estimate
 \begin{equation}
\|(T+A-z)^{-1}\|
\leq \frac{1}{\operatorname{Im} z -\gamma - (\operatorname{Im} z -\gamma)\sqrt{M(\operatorname{Re} z,\, \operatorname{Im} z,\, \gamma)} }.
\end{equation}
\begin{equation}
\|(T+A-z)^{-1}\|
\leq \frac{1}{\operatorname{Im} z -\gamma - (\operatorname{Im} z -\gamma)\sqrt{M(\operatorname{Re} z,\, \operatorname{Im} z,\, \gamma)} }.
\end{equation}Proof. Let ![]() $z=\mu + \mathrm{i}\nu\in\mathbb{C}$ with
$z=\mu + \mathrm{i}\nu\in\mathbb{C}$ with ![]() $\nu \gt \gamma$. Then
$\nu \gt \gamma$. Then ![]() $z\in\rho(T)$ and it belongs to
$z\in\rho(T)$ and it belongs to ![]() $\rho(T+A)$ if
$\rho(T+A)$ if ![]() $\sup_{\operatorname{Im} t \le \gamma} H_z(t) \lt 1$. By Lemma A.1,
$\sup_{\operatorname{Im} t \le \gamma} H_z(t) \lt 1$. By Lemma A.1, ![]() $H_z$ has no local extrema, so we obtain
$H_z$ has no local extrema, so we obtain
 \begin{equation}
\sup_{\operatorname{Im} t \le \gamma} H_z(t)
= \sup_{\operatorname{Im} t = \gamma} H_z(t).
\end{equation}
\begin{equation}
\sup_{\operatorname{Im} t \le \gamma} H_z(t)
= \sup_{\operatorname{Im} t = \gamma} H_z(t).
\end{equation} By Lemma A.3, ![]() $\sup_{\operatorname{Im} t = \gamma} H_z(t) \lt 1$ for
$\sup_{\operatorname{Im} t = \gamma} H_z(t) \lt 1$ for ![]() $\operatorname{Im} z \gt \gamma$ if and only if
$\operatorname{Im} z \gt \gamma$ if and only if
 \begin{equation*}
a^2 + b^2\gamma^2 + \frac{b^2\mu^2}{1-b^2} \lt (\operatorname{Im} z -\gamma)^2,
\end{equation*}
\begin{equation*}
a^2 + b^2\gamma^2 + \frac{b^2\mu^2}{1-b^2} \lt (\operatorname{Im} z -\gamma)^2,
\end{equation*} which is true if and only if ![]() $z\in\mathrm{i}\gamma + \mathrm{Hyp}_\gamma$. The resolvent estimate (3.4) follows from Proposition 2.1(iii) together with (A.3) and
$z\in\mathrm{i}\gamma + \mathrm{Hyp}_\gamma$. The resolvent estimate (3.4) follows from Proposition 2.1(iii) together with (A.3) and  $\|(T-z)^{-1}\| = \frac{1}{\operatorname{dist}(z,\sigma(T))}\leq \frac{1}{\operatorname{Im} z -\gamma}$.
$\|(T-z)^{-1}\| = \frac{1}{\operatorname{dist}(z,\sigma(T))}\leq \frac{1}{\operatorname{Im} z -\gamma}$.
For the rest of this section, we assume that the imaginary part of the spectrum of ![]() $T$ is bounded. Our next proposition shows that in this case the spectrum of the perturbed operator
$T$ is bounded. Our next proposition shows that in this case the spectrum of the perturbed operator ![]() $T+A$ is confined between two shifted hyperbolas whose asymptotic slopes
$T+A$ is confined between two shifted hyperbolas whose asymptotic slopes  $\pm \frac{b}{\sqrt{1-b^2}}$ depend only on the
$\pm \frac{b}{\sqrt{1-b^2}}$ depend only on the ![]() $T$-bound of
$T$-bound of ![]() $A$, while the amount of the shift depends also on the bound for the imaginary part of
$A$, while the amount of the shift depends also on the bound for the imaginary part of ![]() $\sigma(T)$. Note that if
$\sigma(T)$. Note that if ![]() $\gamma_1 = \gamma_2 =0$ in the Proposition below, then our spectral inclusion improves the one for selfadjoint operators proved in [Reference Cuenin and Tretter5, Theorem 2.1].
$\gamma_1 = \gamma_2 =0$ in the Proposition below, then our spectral inclusion improves the one for selfadjoint operators proved in [Reference Cuenin and Tretter5, Theorem 2.1].
Proposition 3.2. Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1. If
$A$ be as in Assumption 1. If
for some ![]() $\gamma_1 \leq \gamma_2$, then
$\gamma_1 \leq \gamma_2$, then
and for all ![]() $z$ in the set on the left hand side of (3.7) we have the resolvent estimate (3.4) with
$z$ in the set on the left hand side of (3.7) we have the resolvent estimate (3.4) with ![]() $\gamma = \gamma_1$ if
$\gamma = \gamma_1$ if ![]() $\operatorname{Im} z \lt \gamma_1$ and
$\operatorname{Im} z \lt \gamma_1$ and ![]() $\gamma = \gamma_2$ if
$\gamma = \gamma_2$ if ![]() $\operatorname{Im} z \gt \gamma_2$, see Figure 1.
$\operatorname{Im} z \gt \gamma_2$, see Figure 1.

Figure 1. Spectral inclusion from Proposition 3.2 and Theorem 3.4. The left graphic shows the location of the spectrum of ![]() $T$, the gray area in the graphics on the right shows the spectral enclosure of
$T$, the gray area in the graphics on the right shows the spectral enclosure of ![]() $T+A$ proved in Proposition 3.2 and Theorem 3.4. In the upper row we have
$T+A$ proved in Proposition 3.2 and Theorem 3.4. In the upper row we have ![]() $\gamma_1 = -\gamma_2$, in the lower row
$\gamma_1 = -\gamma_2$, in the lower row ![]() $0 \lt \gamma_1 \lt \gamma_2$. The upper red dashed line is the boundary of
$0 \lt \gamma_1 \lt \gamma_2$. The upper red dashed line is the boundary of ![]() $\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\gamma_2}$, the lower red dashed line is the boundary of
$\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\gamma_2}$, the lower red dashed line is the boundary of ![]() $\mathrm{i}\gamma_1 - \mathrm{Hyp}_{\gamma_1}$. The green dotted lines are their asymptotes.
$\mathrm{i}\gamma_1 - \mathrm{Hyp}_{\gamma_1}$. The green dotted lines are their asymptotes.
Proof. This is an immediate consequence of Lemma A.4(i). The resolvent estimate follows as in the previous proposition.
Remark 3.3. In the special case ![]() $\gamma=0$, the denominator of the resolent estimate (3.4) is, with
$\gamma=0$, the denominator of the resolent estimate (3.4) is, with ![]() $\mu=\operatorname{Re} z$ and
$\mu=\operatorname{Re} z$ and ![]() $\nu = |\operatorname{Im} z|$,
$\nu = |\operatorname{Im} z|$,
 \begin{align*}
\nu -\nu \sqrt{M(\mu,\, \nu, 0)}
&= \nu - \frac{1}{\sqrt 2} \sqrt{a^2 + b^2|z|^2 + \sqrt{(-a^2+b^2|z|^2)^2 + 4\mu^2 a^2 b^2 }}
\\
&= \nu - \frac{1}{\sqrt 2} \sqrt{a^2 + b^2|z|^2 + \sqrt{(a^2+b^2|z|^2)^2 - 4\nu^2 a^2 b^2 }}
\\
&\ge \nu - \sqrt{a^2 + b^2|z|^2 }
\end{align*}
\begin{align*}
\nu -\nu \sqrt{M(\mu,\, \nu, 0)}
&= \nu - \frac{1}{\sqrt 2} \sqrt{a^2 + b^2|z|^2 + \sqrt{(-a^2+b^2|z|^2)^2 + 4\mu^2 a^2 b^2 }}
\\
&= \nu - \frac{1}{\sqrt 2} \sqrt{a^2 + b^2|z|^2 + \sqrt{(a^2+b^2|z|^2)^2 - 4\nu^2 a^2 b^2 }}
\\
&\ge \nu - \sqrt{a^2 + b^2|z|^2 }
\end{align*}which is the denominator of the resolvent estimate in (1.3). Therefore our estimate improves (1.3).
Next we show that if the imaginary part of the spectrum of ![]() $T$ is bounded, then a gap in the spectrum of
$T$ is bounded, then a gap in the spectrum of ![]() $T$ remains open if the perturbation is small enough.
$T$ remains open if the perturbation is small enough.
Theorem 3.4 Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1. As in Proposition 3.2 we assume that there exist
$A$ be as in Assumption 1. As in Proposition 3.2 we assume that there exist ![]() $\gamma_1\leq\gamma_2\in\mathbb{R}$ such that
$\gamma_1\leq\gamma_2\in\mathbb{R}$ such that ![]() $\sigma(T)\subseteq \mathbb{R} + \mathrm{i}[\gamma_1, \gamma_2]$. In addition, we assume that
$\sigma(T)\subseteq \mathbb{R} + \mathrm{i}[\gamma_1, \gamma_2]$. In addition, we assume that ![]() $T$ has a spectral free strip
$T$ has a spectral free strip
Set ![]() $\widetilde \gamma := \max\{|\gamma_1|, |\gamma_2|\}$ and
$\widetilde \gamma := \max\{|\gamma_1|, |\gamma_2|\}$ and
 \begin{align}
\alpha'_{T+A}:=\alpha_{T}+\sqrt{a^2+b^2\widetilde \gamma^2+b^2\alpha_{T}^2}\, ,\qquad
\beta'_{T+A}:= \beta_T -\sqrt{a^2+b^2\widetilde \gamma^2+b^2\beta_{T}^2}\, .
\end{align}
\begin{align}
\alpha'_{T+A}:=\alpha_{T}+\sqrt{a^2+b^2\widetilde \gamma^2+b^2\alpha_{T}^2}\, ,\qquad
\beta'_{T+A}:= \beta_T -\sqrt{a^2+b^2\widetilde \gamma^2+b^2\beta_{T}^2}\, .
\end{align} If ![]() $\alpha_{T+A}' \lt \beta_{T+A}'$, then
$\alpha_{T+A}' \lt \beta_{T+A}'$, then ![]() $T+A$ has a spectral free strip
$T+A$ has a spectral free strip
See Figure 1. Moreover, if ![]() $\alpha_{T+A}' \le \operatorname{Re} z \le \beta_{T+A}'$, then
$\alpha_{T+A}' \le \operatorname{Re} z \le \beta_{T+A}'$, then
 \begin{align}
& \|(T+A-z)^{-1}\|\cr
&\quad \leq \frac{\left(\sqrt{(\min\{\operatorname{Re} z-\alpha_T,\beta_T-\operatorname{Re} z\})^2+
(\min\{0, \gamma_2-\operatorname{Im} z, \operatorname{Im} z - \gamma_1 \})^2}\right)^{-1}}
{1-\max\left\{
b,\ \frac{\sqrt{a^2+b^2\widetilde \gamma^2+b^2\alpha_T^2}}{\operatorname{Re} z-\alpha_T},\ \frac{\sqrt{a^2+b^2\widetilde \gamma^2+b^2\beta_T^2}}{\beta_T-\operatorname{Re} z}\right\}}.\cr
\end{align}
\begin{align}
& \|(T+A-z)^{-1}\|\cr
&\quad \leq \frac{\left(\sqrt{(\min\{\operatorname{Re} z-\alpha_T,\beta_T-\operatorname{Re} z\})^2+
(\min\{0, \gamma_2-\operatorname{Im} z, \operatorname{Im} z - \gamma_1 \})^2}\right)^{-1}}
{1-\max\left\{
b,\ \frac{\sqrt{a^2+b^2\widetilde \gamma^2+b^2\alpha_T^2}}{\operatorname{Re} z-\alpha_T},\ \frac{\sqrt{a^2+b^2\widetilde \gamma^2+b^2\beta_T^2}}{\beta_T-\operatorname{Re} z}\right\}}.\cr
\end{align}Proof. Let ![]() $z=\mu + \mathrm{i}\nu$ with
$z=\mu + \mathrm{i}\nu$ with ![]() $\mu \in (\alpha_{T},\beta_{T})$ and
$\mu \in (\alpha_{T},\beta_{T})$ and ![]() $\nu \in\mathbb{R}\setminus [\gamma_1, \gamma_2]$. Then
$\nu \in\mathbb{R}\setminus [\gamma_1, \gamma_2]$. Then
 \begin{align}
\sup_{t\in\sigma(T)}
\frac{a^2+b^2|t|^2}{|t-z|^2}
&\le
\sup_{\sigma\in \{\gamma_1, \gamma_2\}\; }
\sup_{t\in(\mathbb{R}\setminus(\alpha_T, \beta_T)) + \mathrm{i}\sigma}
\frac{a^2+b^2|t|^2}{|t-z|^2}\cr
&\le
\sup_{\sigma\in \{\gamma_1, \gamma_2\} }
\sup_{\tau\in \mathbb{R}\setminus(\alpha_T, \beta_T)}
\frac{a^2+b^2(\tau^2+\sigma^2)}{(\tau-\mu)^2}\cr
&= \sup_{\tau\in \mathbb{R}\setminus(\alpha_T, \beta_T)}
\frac{a^2 + b^2\widetilde \gamma^2 + b^2 \tau^2}{(\tau-\mu)^2}\cr
& \leq \max\left\{b^2,~\frac{{a^2+b^2\widetilde \gamma^2+b^2\alpha_T^2}}{(\mu-\alpha_T)^2},~\frac{{a^2+b^2\widetilde \gamma^2+b^2\beta_T^2}}{(\beta_T-\mu)^2} \right\}
\end{align}
\begin{align}
\sup_{t\in\sigma(T)}
\frac{a^2+b^2|t|^2}{|t-z|^2}
&\le
\sup_{\sigma\in \{\gamma_1, \gamma_2\}\; }
\sup_{t\in(\mathbb{R}\setminus(\alpha_T, \beta_T)) + \mathrm{i}\sigma}
\frac{a^2+b^2|t|^2}{|t-z|^2}\cr
&\le
\sup_{\sigma\in \{\gamma_1, \gamma_2\} }
\sup_{\tau\in \mathbb{R}\setminus(\alpha_T, \beta_T)}
\frac{a^2+b^2(\tau^2+\sigma^2)}{(\tau-\mu)^2}\cr
&= \sup_{\tau\in \mathbb{R}\setminus(\alpha_T, \beta_T)}
\frac{a^2 + b^2\widetilde \gamma^2 + b^2 \tau^2}{(\tau-\mu)^2}\cr
& \leq \max\left\{b^2,~\frac{{a^2+b^2\widetilde \gamma^2+b^2\alpha_T^2}}{(\mu-\alpha_T)^2},~\frac{{a^2+b^2\widetilde \gamma^2+b^2\beta_T^2}}{(\beta_T-\mu)^2} \right\}
\end{align} where the last inequality follows from Lemma A.6 with ![]() $a^2+b^2\widetilde \gamma^2$ instead of
$a^2+b^2\widetilde \gamma^2$ instead of ![]() $a^2$. Note that the expression in (3.11) is less than 1 if
$a^2$. Note that the expression in (3.11) is less than 1 if ![]() $\alpha_{T+A}' \lt \operatorname{Re} z = \mu \lt \beta_{T+A}'$. Therefore (3.9) follows from Proposition 2.1(iii).
$\alpha_{T+A}' \lt \operatorname{Re} z = \mu \lt \beta_{T+A}'$. Therefore (3.9) follows from Proposition 2.1(iii).
The resolvent estimate (3.10) follows again from Proposition 2.1(iii) together with (3.11) and
 \begin{align*}
\operatorname{dist}(z, \sigma(T)) \ge \sqrt{(\min\{\operatorname{Re} z-\alpha_T,\beta_T-\operatorname{Re} z\})^2+(\min\{0, \gamma_2-\operatorname{Im} z, \operatorname{Im} z - \gamma_1 \})^2}. \\[-40pt]
\end{align*}
\begin{align*}
\operatorname{dist}(z, \sigma(T)) \ge \sqrt{(\min\{\operatorname{Re} z-\alpha_T,\beta_T-\operatorname{Re} z\})^2+(\min\{0, \gamma_2-\operatorname{Im} z, \operatorname{Im} z - \gamma_1 \})^2}. \\[-40pt]
\end{align*}In Theorem 3.8 below we extend Theorem 3.4 and allow for finitely many eigenvalues outside the strip. We will also prove a stability result for the total algebraic multiplicity of these eigenvalues.
Remark 3.5. In the special case when ![]() $\gamma_2 = -\gamma_1 =: \gamma$, our formulas simplify slightly. Proposition 3.2 yields that
$\gamma_2 = -\gamma_1 =: \gamma$, our formulas simplify slightly. Proposition 3.2 yields that
 \begin{equation}\begin{aligned}
( -\mathrm{i}\gamma&-\mathrm{Hyp}_{\gamma} )
\cup ( \mathrm{i}\gamma+\mathrm{Hyp}_{\gamma} )
\\[1ex]
&\left\{z\in\mathbb{C}:
a^2 + b^2 \gamma^2 + \frac{b^2 (\operatorname{Re} z)^2 }{1-b^2} \lt \left(|\operatorname{Im} z|-\gamma\right)^2,\
|\operatorname{Im} z| \gt \gamma
\right\}
\subseteq \rho(T+A)
\end{aligned}
\end{equation}
\begin{equation}\begin{aligned}
( -\mathrm{i}\gamma&-\mathrm{Hyp}_{\gamma} )
\cup ( \mathrm{i}\gamma+\mathrm{Hyp}_{\gamma} )
\\[1ex]
&\left\{z\in\mathbb{C}:
a^2 + b^2 \gamma^2 + \frac{b^2 (\operatorname{Re} z)^2 }{1-b^2} \lt \left(|\operatorname{Im} z|-\gamma\right)^2,\
|\operatorname{Im} z| \gt \gamma
\right\}
\subseteq \rho(T+A)
\end{aligned}
\end{equation} and for all ![]() $z$ in the set on the left hand side of (3.12) we have the resolvent estimate
$z$ in the set on the left hand side of (3.12) we have the resolvent estimate
 \begin{align}
\|(T+A-z)^{-1}\|
\leq \frac{1}{|\operatorname{Im} z| -\gamma - (|\operatorname{Im} z| -\gamma)\sqrt{M(\operatorname{Re} z,\, |\operatorname{Im} z|,\, \gamma)} }.
\end{align}
\begin{align}
\|(T+A-z)^{-1}\|
\leq \frac{1}{|\operatorname{Im} z| -\gamma - (|\operatorname{Im} z| -\gamma)\sqrt{M(\operatorname{Re} z,\, |\operatorname{Im} z|,\, \gamma)} }.
\end{align} If in addition ![]() $(\alpha_{T},\beta_{T})+\mathrm{i} \mathbb{R} \subseteq\rho(T)$ and
$(\alpha_{T},\beta_{T})+\mathrm{i} \mathbb{R} \subseteq\rho(T)$ and ![]() $\alpha'_{T+A} \lt \beta'_{T+A}$ (with
$\alpha'_{T+A} \lt \beta'_{T+A}$ (with ![]() $\gamma$ instead of
$\gamma$ instead of ![]() $\widetilde \gamma$), then
$\widetilde \gamma$), then ![]() $T+A$ has a spectral free strip
$T+A$ has a spectral free strip
and for ![]() $\alpha_{T+A}' \lt \operatorname{Re} z \lt \beta_{T+A}'$ we have the resolvent estimate
$\alpha_{T+A}' \lt \operatorname{Re} z \lt \beta_{T+A}'$ we have the resolvent estimate
 \begin{equation}
\|(T+A-z)^{-1}\|
\leq \frac{\left(\sqrt{(\min\{\operatorname{Re} z-\alpha_T,\beta_T-\operatorname{Re} z\})^2+
(\min\{0, \gamma-|\operatorname{Im} z|\})^2}\right)^{-1}}
{1-\max\left\{
b,\ \frac{\sqrt{a^2+b^2\gamma^2+b^2\alpha_T^2}}{\operatorname{Re} z-\alpha_T},\ \frac{\sqrt{a^2+b^2\gamma^2+b^2\beta_T^2}}{\beta_T-\operatorname{Re} z}\right\}}.
\end{equation}
\begin{equation}
\|(T+A-z)^{-1}\|
\leq \frac{\left(\sqrt{(\min\{\operatorname{Re} z-\alpha_T,\beta_T-\operatorname{Re} z\})^2+
(\min\{0, \gamma-|\operatorname{Im} z|\})^2}\right)^{-1}}
{1-\max\left\{
b,\ \frac{\sqrt{a^2+b^2\gamma^2+b^2\alpha_T^2}}{\operatorname{Re} z-\alpha_T},\ \frac{\sqrt{a^2+b^2\gamma^2+b^2\beta_T^2}}{\beta_T-\operatorname{Re} z}\right\}}.
\end{equation} Note that for ![]() $\gamma=0$, the estimate (3.13) improves (1.3) and and (3.15) coincides with (1.4).
$\gamma=0$, the estimate (3.13) improves (1.3) and and (3.15) coincides with (1.4).
If the spectrum of ![]() $T$ is bounded from below, then we can choose
$T$ is bounded from below, then we can choose ![]() $\alpha_T$ in Theorem 3.4 arbitrarily small and the spectrum of
$\alpha_T$ in Theorem 3.4 arbitrarily small and the spectrum of ![]() $T+A$ is also bounded from below as the following corollary shows.
$T+A$ is also bounded from below as the following corollary shows.
Corollary 3.6. Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1. As in Proposition 3.2, we assume that
$A$ be as in Assumption 1. As in Proposition 3.2, we assume that ![]() $\sigma(T)\subseteq \mathbb{R} + \mathrm{i} [\gamma_1,\gamma_2]$ for
$\sigma(T)\subseteq \mathbb{R} + \mathrm{i} [\gamma_1,\gamma_2]$ for ![]() $\gamma_1\le\gamma_2\in\mathbb{R}$ and we set
$\gamma_1\le\gamma_2\in\mathbb{R}$ and we set ![]() $\widetilde \gamma := \max\{|\gamma_1|, |\gamma_2|\}$.
$\widetilde \gamma := \max\{|\gamma_1|, |\gamma_2|\}$.
(i) If
 $\operatorname{Re}\sigma(T) \ge \beta_{T}$ for some
$\operatorname{Re}\sigma(T) \ge \beta_{T}$ for some  $\beta_T\in\mathbb{R}$, then
$\beta_T\in\mathbb{R}$, then
 \begin{align*}
\operatorname{Re} \sigma(T+A)\ge
\beta'_{T+A}:= \beta_T -\sqrt{a^2+b^2\widetilde \gamma^2+b^2\beta_{T}^2}\, .
\end{align*}
\begin{align*}
\operatorname{Re} \sigma(T+A)\ge
\beta'_{T+A}:= \beta_T -\sqrt{a^2+b^2\widetilde \gamma^2+b^2\beta_{T}^2}\, .
\end{align*}(ii) If
 $\operatorname{Re}\sigma(T) \le \alpha_{T}$ for some
$\operatorname{Re}\sigma(T) \le \alpha_{T}$ for some  $\alpha_T\in\mathbb{R}$, then
$\alpha_T\in\mathbb{R}$, then
 \begin{align*}
\operatorname{Re} \sigma(T+A)\le
\alpha'_{T+A}:= \alpha_T + \sqrt{a^2+b^2\widetilde \gamma^2+b^2\alpha_{T}^2}\, .
\end{align*}
\begin{align*}
\operatorname{Re} \sigma(T+A)\le
\alpha'_{T+A}:= \alpha_T + \sqrt{a^2+b^2\widetilde \gamma^2+b^2\alpha_{T}^2}\, .
\end{align*}
Proof. We proof only (i). Let ![]() $\beta_{T+A}'$ be as in (3.8). Since the spectrum of
$\beta_{T+A}'$ be as in (3.8). Since the spectrum of ![]() $T$ is bounded from below, we can choose
$T$ is bounded from below, we can choose ![]() $\alpha_T$, and hence also
$\alpha_T$, and hence also ![]() $\alpha_{T+A}'$ from (3.8) arbitrarily small because
$\alpha_{T+A}'$ from (3.8) arbitrarily small because ![]() $0\le b \lt 1$ and therefore
$0\le b \lt 1$ and therefore
 \begin{equation*}
\alpha_{T+A}'
= \alpha_T+\sqrt{a^2+b^2\widetilde \gamma^2+b^2\alpha_{T}^2}
\ \longrightarrow -\infty
\quad\text{for }\
\alpha_T\to -\infty.
\end{equation*}
\begin{equation*}
\alpha_{T+A}'
= \alpha_T+\sqrt{a^2+b^2\widetilde \gamma^2+b^2\alpha_{T}^2}
\ \longrightarrow -\infty
\quad\text{for }\
\alpha_T\to -\infty.
\end{equation*}Hence (3.9) shows that
Under the conditions from Corollary 3.6(ii), the spectrum of ![]() $T+A$ is contained in a sector. In fact, if
$T+A$ is contained in a sector. In fact, if  $\phi_b = \arctan( \frac{b}{\sqrt{1-b^2}})$, we can find an
$\phi_b = \arctan( \frac{b}{\sqrt{1-b^2}})$, we can find an ![]() $\omega\in\mathbb{R}$ such that
$\omega\in\mathbb{R}$ such that ![]() $\sigma(T+A)\subseteq -S_{\phi_b}(\omega)$. It is even true that
$\sigma(T+A)\subseteq -S_{\phi_b}(\omega)$. It is even true that ![]() $T+A-\omega$ is sectorial and therefore generates an analytic semigroup. Semigroup generator properties of
$T+A-\omega$ is sectorial and therefore generates an analytic semigroup. Semigroup generator properties of ![]() $T+A$ will be discussed in a forthcoming work.
$T+A$ will be discussed in a forthcoming work.
The last two theorems in this section give a perturbation result for the essential spectrum and a stability result for the total algebraic multiplicity of eigenvalues in a gap of the essential spectrum.
Theorem 3.7 Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1. For
$A$ be as in Assumption 1. For ![]() $\alpha \lt \beta$ and
$\alpha \lt \beta$ and ![]() $\gamma_1 \le \gamma_2$ we define the gapped strip
$\gamma_1 \le \gamma_2$ we define the gapped strip ![]() $\mathrm{Str} = \{z\in\mathbb{C} : \operatorname{Re} z \in \mathbb{R}\setminus (\alpha, \beta),\ \gamma_1 \le \operatorname{Im} z \le \gamma_2 \}$. Assume that
$\mathrm{Str} = \{z\in\mathbb{C} : \operatorname{Re} z \in \mathbb{R}\setminus (\alpha, \beta),\ \gamma_1 \le \operatorname{Im} z \le \gamma_2 \}$. Assume that ![]() $\sigma_{\mathrm{ess} }(T)\subseteq \mathrm{Str}$ and
$\sigma_{\mathrm{ess} }(T)\subseteq \mathrm{Str}$ and ![]() $\sigma(T) = \sigma_{\mathrm{ess} }(T) \cup \Sigma$ where
$\sigma(T) = \sigma_{\mathrm{ess} }(T) \cup \Sigma$ where ![]() $\Sigma \subseteq\mathbb{C}\setminus\mathrm{Str}$ is a bounded countable set which may accumulate at most at the boundary of
$\Sigma \subseteq\mathbb{C}\setminus\mathrm{Str}$ is a bounded countable set which may accumulate at most at the boundary of ![]() $\sigma_{\mathrm{ess} }(T)$ Let
$\sigma_{\mathrm{ess} }(T)$ Let ![]() $\alpha'_{T+A}$ and
$\alpha'_{T+A}$ and ![]() $\beta'_{T+A}$ as in (3.8) and set
$\beta'_{T+A}$ as in (3.8) and set ![]() $\widetilde \gamma = \max\{|\gamma_1|,\, |\gamma_2|\}$. If
$\widetilde \gamma = \max\{|\gamma_1|,\, |\gamma_2|\}$. If ![]() $\alpha_{T+A}' \lt \beta_{T+A}'$ then
$\alpha_{T+A}' \lt \beta_{T+A}'$ then
 \begin{align}
\begin{aligned}
\{z\in \mathbb{C}: \alpha'_{T+A} \lt \operatorname{Re} z \lt \beta'_{T+A}\}
\cup
(\mathrm{i}\gamma_1 - \mathrm{Hyp}_{\widetilde \gamma}) \cup (\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\widetilde \gamma})
\subseteq \mathbb{C}\setminus\sigma_{\mathrm{ess} }(T+A)
\end{aligned}
\end{align}
\begin{align}
\begin{aligned}
\{z\in \mathbb{C}: \alpha'_{T+A} \lt \operatorname{Re} z \lt \beta'_{T+A}\}
\cup
(\mathrm{i}\gamma_1 - \mathrm{Hyp}_{\widetilde \gamma}) \cup (\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\widetilde \gamma})
\subseteq \mathbb{C}\setminus\sigma_{\mathrm{ess} }(T+A)
\end{aligned}
\end{align}and the set on the left hand side consists of at most countably many isolated eigenvalues of finite algebraic multiplicity which may accumulate only at its boundary.
Proof. For ![]() $n\in\mathbb{N}$ define the sets
$n\in\mathbb{N}$ define the sets
 \begin{equation*}
S_n := \left\{z\in\mathbb{C} : \alpha+\frac{1}{n} \le \operatorname{Re} z \le \beta-\frac{1}{n},\ \gamma_1 - \frac{1}{n} \le \operatorname{Im} z \le \gamma_2 + \frac{1}{n} \right\}
\end{equation*}
\begin{equation*}
S_n := \left\{z\in\mathbb{C} : \alpha+\frac{1}{n} \le \operatorname{Re} z \le \beta-\frac{1}{n},\ \gamma_1 - \frac{1}{n} \le \operatorname{Im} z \le \gamma_2 + \frac{1}{n} \right\}
\end{equation*} and ![]() $U_n := \mathbb{C}\setminus S_n$. Then
$U_n := \mathbb{C}\setminus S_n$. Then ![]() $\sigma_{\mathrm{ess} }(T)\subseteq S_n$ for every
$\sigma_{\mathrm{ess} }(T)\subseteq S_n$ for every ![]() $n\in\mathbb{N}$ and
$n\in\mathbb{N}$ and ![]() $U_n\cap \sigma(T)$ is finite and contains only finite eigenvalues of finite multiplicity. Let
$U_n\cap \sigma(T)$ is finite and contains only finite eigenvalues of finite multiplicity. Let ![]() $P_1$ be the spectral projection of
$P_1$ be the spectral projection of ![]() $T$ for the set
$T$ for the set ![]() $U_n$ and set
$U_n$ and set  $\widetilde H_n := \operatorname{Ran}(P_1) = \bigoplus_{\lambda\in U_n\cap \sigma(T)} \ker(T-\lambda)$. Set
$\widetilde H_n := \operatorname{Ran}(P_1) = \bigoplus_{\lambda\in U_n\cap \sigma(T)} \ker(T-\lambda)$. Set  $\mathcal{D}_2 = \mathcal{D}(T)\cap \widetilde H_n^\perp$. Then
$\mathcal{D}_2 = \mathcal{D}(T)\cap \widetilde H_n^\perp$. Then ![]() $\dim \widetilde H_n \lt \infty$,
$\dim \widetilde H_n \lt \infty$,  $\mathcal{D}(T) = \widetilde H_n \oplus \mathcal{D}_2$ and both
$\mathcal{D}(T) = \widetilde H_n \oplus \mathcal{D}_2$ and both ![]() $\widetilde H_n$ and
$\widetilde H_n$ and  $\widetilde H_n^\perp$ are
$\widetilde H_n^\perp$ are ![]() $T$-invariant, see [Reference Schmüdgen20, pag. 83]). Let us define
$T$-invariant, see [Reference Schmüdgen20, pag. 83]). Let us define  $T_j^{(n)}$ and
$T_j^{(n)}$ and  $A_{ij}^{(n)}$ as in Theorem 2.2. Then
$A_{ij}^{(n)}$ as in Theorem 2.2. Then  $A_{22}^{(n)}$ is
$A_{22}^{(n)}$ is  $T_2^{(n)}$-bounded with the same constants
$T_2^{(n)}$-bounded with the same constants ![]() $a,b$ that work for
$a,b$ that work for ![]() $T$ and
$T$ and ![]() $A$ and, by the spectral theorem,
$A$ and, by the spectral theorem,  $\sigma(T_2^{(n)})\subseteq S_n$. If we apply Proposition 3.2 to
$\sigma(T_2^{(n)})\subseteq S_n$. If we apply Proposition 3.2 to  $T_2^{(n)}$ and
$T_2^{(n)}$ and  $A_{22}^{(n)}$, we obtain that
$A_{22}^{(n)}$, we obtain that
 \begin{align*}
F_n & :=
\textstyle
(\mathrm{i}(\gamma_1 - \frac{1}{n} ) - \mathrm{Hyp}_{\widetilde \gamma + \frac{1}{n} }) \cup
(\mathrm{i}(\gamma_2 + \frac{1}{n} ) + \mathrm{Hyp}_{\widetilde \gamma + \frac{1}{n} })
\subseteq \rho(T_2^{(n)} + A_{22}^{(n)}).
\end{align*}
\begin{align*}
F_n & :=
\textstyle
(\mathrm{i}(\gamma_1 - \frac{1}{n} ) - \mathrm{Hyp}_{\widetilde \gamma + \frac{1}{n} }) \cup
(\mathrm{i}(\gamma_2 + \frac{1}{n} ) + \mathrm{Hyp}_{\widetilde \gamma + \frac{1}{n} })
\subseteq \rho(T_2^{(n)} + A_{22}^{(n)}).
\end{align*} Moreover, Theorem 3.4 applied to  $T_2^{(n)}$ and
$T_2^{(n)}$ and  $A_{22}^{(n)}$ shows that
$A_{22}^{(n)}$ shows that
 \begin{align*}
G_n := \left\{z\in\mathbb{C} : \alpha_{n}' \lt \operatorname{Re} z \lt \beta_{n}' \right\}
\subseteq \rho(T_2^{(n)} + A_{22}^{(n)}),
\end{align*}
\begin{align*}
G_n := \left\{z\in\mathbb{C} : \alpha_{n}' \lt \operatorname{Re} z \lt \beta_{n}' \right\}
\subseteq \rho(T_2^{(n)} + A_{22}^{(n)}),
\end{align*}where
 \begin{align*}
\alpha_{n}' & := \alpha + \frac{1}{n} + \sqrt{\textstyle a^2 + b^2(\widetilde \gamma+\frac{1}{n})^2 + b^2 (\alpha + \frac{1}{n})^2},
\\
\beta_{n}' & := \beta - \frac{1}{n} + \sqrt{\textstyle a^2 + b^2(\widetilde \gamma+\frac{1}{n})^2 + b^2 (\beta - \frac{1}{n})^2}.
\end{align*}
\begin{align*}
\alpha_{n}' & := \alpha + \frac{1}{n} + \sqrt{\textstyle a^2 + b^2(\widetilde \gamma+\frac{1}{n})^2 + b^2 (\alpha + \frac{1}{n})^2},
\\
\beta_{n}' & := \beta - \frac{1}{n} + \sqrt{\textstyle a^2 + b^2(\widetilde \gamma+\frac{1}{n})^2 + b^2 (\beta - \frac{1}{n})^2}.
\end{align*} In summary,  $\sigma_{\mathrm{ess} }(T_2^{(n)}+A_{22}^{(n)}) \subseteq \sigma(T_2^{(n)}+A_{22}^{(n)})\subseteq \mathbb{C}\setminus (F_n\cup G_n)$. Since by Theorem 2.2 the essential spectra of
$\sigma_{\mathrm{ess} }(T_2^{(n)}+A_{22}^{(n)}) \subseteq \sigma(T_2^{(n)}+A_{22}^{(n)})\subseteq \mathbb{C}\setminus (F_n\cup G_n)$. Since by Theorem 2.2 the essential spectra of ![]() $T+A$ and
$T+A$ and  $T_2^{(n)} + A_{22}^{(n)}$ coincide for every
$T_2^{(n)} + A_{22}^{(n)}$ coincide for every ![]() $n\in\mathbb{N}$, we obtain that
$n\in\mathbb{N}$, we obtain that
 \begin{equation*}
\sigma_{\mathrm{ess} }(T+A) \subseteq \bigcap_{n\in\mathbb{N}} \mathbb{C}\setminus (F_n\cup G_n).
\end{equation*}
\begin{equation*}
\sigma_{\mathrm{ess} }(T+A) \subseteq \bigcap_{n\in\mathbb{N}} \mathbb{C}\setminus (F_n\cup G_n).
\end{equation*} Since ![]() $\bigcup_{n\in\mathbb{N}} (F_n\cup G_n)$ is equal to the right hand side of (3.16), that inclusion is proved. The claim about nonaccumulation of the spectrum follows from [Reference Gohberg, Goldberg and Kaashoek11, Chapter XVII, Theorem 2.1] because by Proposition 3.2 the exterior of certain hyperbolas belongs to the resolvent set of
$\bigcup_{n\in\mathbb{N}} (F_n\cup G_n)$ is equal to the right hand side of (3.16), that inclusion is proved. The claim about nonaccumulation of the spectrum follows from [Reference Gohberg, Goldberg and Kaashoek11, Chapter XVII, Theorem 2.1] because by Proposition 3.2 the exterior of certain hyperbolas belongs to the resolvent set of ![]() $T+A$, hence the complement of the left hand side of (3.16) contains points in the resolvent set of
$T+A$, hence the complement of the left hand side of (3.16) contains points in the resolvent set of ![]() $T+A$.
$T+A$.
The situation in our next theorem is similar to that in Theorem 3.4 but here we allow for additional finitely many eigenvalues.
Theorem 3.8 Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1. For
$A$ be as in Assumption 1. For ![]() $\alpha \lt \beta$ and
$\alpha \lt \beta$ and ![]() $\gamma_1 \le \gamma_2$ we define the gapped strip
$\gamma_1 \le \gamma_2$ we define the gapped strip ![]() $\mathrm{Str} = \{z\in\mathbb{C} : \operatorname{Re} z \in \mathbb{R}\setminus (\alpha, \beta),\ \gamma_1 \le \operatorname{Im} z \le \gamma_2 \}$. Assume that
$\mathrm{Str} = \{z\in\mathbb{C} : \operatorname{Re} z \in \mathbb{R}\setminus (\alpha, \beta),\ \gamma_1 \le \operatorname{Im} z \le \gamma_2 \}$. Assume that ![]() $\sigma(T) = \Sigma_0 \cup \Sigma_1$ where
$\sigma(T) = \Sigma_0 \cup \Sigma_1$ where ![]() $\Sigma_0 \subseteq \mathrm{Str}$ and
$\Sigma_0 \subseteq \mathrm{Str}$ and ![]() $\Sigma_1 = \{\lambda_1,\,\dots,\, \lambda_N\}$ is a finite set of eigenvalues of
$\Sigma_1 = \{\lambda_1,\,\dots,\, \lambda_N\}$ is a finite set of eigenvalues of ![]() $T$, each of finite multiplicity, which satisfies
$T$, each of finite multiplicity, which satisfies ![]() $\Sigma_0 \cap \mathrm{Str} = \emptyset$. Set
$\Sigma_0 \cap \mathrm{Str} = \emptyset$. Set ![]() $\widetilde \gamma = \max\{|\gamma_1|,\, |\gamma_2|\}$ and let
$\widetilde \gamma = \max\{|\gamma_1|,\, |\gamma_2|\}$ and let ![]() $\alpha'_{T+A}$ and
$\alpha'_{T+A}$ and ![]() $\beta'_{T+A}$ as in (3.8). Moreover, for each
$\beta'_{T+A}$ as in (3.8). Moreover, for each ![]() $j=1,\dots,N$ we define
$j=1,\dots,N$ we define  $r_j = \sqrt{a^2 + b^2 |\lambda_j|^2}$.
$r_j = \sqrt{a^2 + b^2 |\lambda_j|^2}$.
(i) For the resolvent set of
 $T+A$ we have that
(3.17)
$T+A$ we have that
(3.17) \begin{align}
&\Big(
\{z\in \mathbb{C}: \alpha'_{T+A} \le \operatorname{Re} z \le \beta'_{T+A}\}
\cup
(\mathrm{i}\gamma_1 - \mathrm{Hyp}_{\gamma_1})
\cup (\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\gamma_2})
\Big) \setminus \cr
&\quad
\bigcup_{j=1}^N K_{r_j}(\lambda_j)
\subseteq \rho(T+A)
\end{align}
\begin{align}
&\Big(
\{z\in \mathbb{C}: \alpha'_{T+A} \le \operatorname{Re} z \le \beta'_{T+A}\}
\cup
(\mathrm{i}\gamma_1 - \mathrm{Hyp}_{\gamma_1})
\cup (\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\gamma_2})
\Big) \setminus \cr
&\quad
\bigcup_{j=1}^N K_{r_j}(\lambda_j)
\subseteq \rho(T+A)
\end{align}where
 $K_{r_j}(\lambda_j)$ is the closed disk of radius
$K_{r_j}(\lambda_j)$ is the closed disk of radius  $r_j$ centred in
$r_j$ centred in  $\lambda_j$.
$\lambda_j$.(ii) If there exists
 $k\in\{1,\,\dots,\, N\}$ and
$k\in\{1,\,\dots,\, N\}$ and  $\epsilon \gt 0$ such that
$\epsilon \gt 0$ such that  $K_{r_k+2\epsilon}(\lambda_k)$ is contained in the set
(3.18)
$K_{r_k+2\epsilon}(\lambda_k)$ is contained in the set
(3.18) \begin{equation}\begin{aligned}
\Big(
\{z\in \mathbb{C}: \alpha'_{T+A} \le \operatorname{Re} z \le \beta'_{T+A}\}
\cup
(\mathrm{i}\gamma_1 - \mathrm{Hyp}_{\gamma_1}) \cup (\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\gamma_1})
\Big)
\setminus \bigcup_{\substack{j=1\\ j\neq k}}^N K_{r_j}(\lambda_j),
\end{aligned}
\end{equation}
\begin{equation}\begin{aligned}
\Big(
\{z\in \mathbb{C}: \alpha'_{T+A} \le \operatorname{Re} z \le \beta'_{T+A}\}
\cup
(\mathrm{i}\gamma_1 - \mathrm{Hyp}_{\gamma_1}) \cup (\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\gamma_1})
\Big)
\setminus \bigcup_{\substack{j=1\\ j\neq k}}^N K_{r_j}(\lambda_j),
\end{aligned}
\end{equation}then
 $\sigma(T+A)\cap K_{r_k}(\lambda_k)$ consists of finitely many eigenvalues and their total algebraic multiplicity is equal to the multiplicity of
$\sigma(T+A)\cap K_{r_k}(\lambda_k)$ consists of finitely many eigenvalues and their total algebraic multiplicity is equal to the multiplicity of  $\lambda_k$ as eigenvalue of
$\lambda_k$ as eigenvalue of  $T$.
$T$.(iii) If there exists
 $\epsilon \gt 0$ such that for all
$\epsilon \gt 0$ such that for all  $k\in\{1,\,\dots,\, N\}$ the closed disk
$k\in\{1,\,\dots,\, N\}$ the closed disk  $K_{r_k+2\epsilon}(\lambda_k)$ is contained in the set in (3.18), then
$K_{r_k+2\epsilon}(\lambda_k)$ is contained in the set in (3.18), then  $\sigma(T+A)\cap \left( \bigcup_{j=1}^N K_{r_j}(\lambda_j) \right)$ consists of finitely many eigenvalues and their total algebraic multiplicity is equal to the total multiplicity of
$\sigma(T+A)\cap \left( \bigcup_{j=1}^N K_{r_j}(\lambda_j) \right)$ consists of finitely many eigenvalues and their total algebraic multiplicity is equal to the total multiplicity of  $\lambda_1,\, \dots,\, \lambda_N$ as eigenvalues of
$\lambda_1,\, \dots,\, \lambda_N$ as eigenvalues of  $T$.
$T$.
Proof. In order to prove (i), we start with ![]() $z\in\rho(T)$. As in the proofs of Proposition 3.2 and Theorem 3.4, we have to show that
$z\in\rho(T)$. As in the proofs of Proposition 3.2 and Theorem 3.4, we have to show that ![]() $\sup_{t\in\sigma(T)} H_z(t) \lt 1$ for
$\sup_{t\in\sigma(T)} H_z(t) \lt 1$ for ![]() $z$ in the set on the left side of (3.17). Note that
$z$ in the set on the left side of (3.17). Note that
 \begin{equation*}
\sup_{t\in\sigma(T)} H_z(t)
= \max\left\{\sup_{t\in\Sigma_0} H_z(t),\ \sup_{t\in\Sigma_1} H_z(t) \right\}
\le \max\left\{\sup_{t\in\mathrm{Str}} H_z(t),\ \sup_{t\in\Sigma_1} H_z(t) \right\}.
\end{equation*}
\begin{equation*}
\sup_{t\in\sigma(T)} H_z(t)
= \max\left\{\sup_{t\in\Sigma_0} H_z(t),\ \sup_{t\in\Sigma_1} H_z(t) \right\}
\le \max\left\{\sup_{t\in\mathrm{Str}} H_z(t),\ \sup_{t\in\Sigma_1} H_z(t) \right\}.
\end{equation*} By Proposition 3.2 and Theorem 3.4 we know that ![]() $\sup_{t\in\mathrm{Str}} H_z(t) \lt 1$ if
$\sup_{t\in\mathrm{Str}} H_z(t) \lt 1$ if ![]() $z$ belongs to the union of the first three sets on the left hand side in (3.17). Moreover,
$z$ belongs to the union of the first three sets on the left hand side in (3.17). Moreover,
 \begin{equation*}
\sup_{t\in\Sigma_1} H_z(t)
= \max_{j=1}^N H_z(\lambda_j)
= \max_{j=1}^N \frac{a^2 + b^2 |\lambda_j|^2}{|\lambda_j - z |^2 }
\end{equation*}
\begin{equation*}
\sup_{t\in\Sigma_1} H_z(t)
= \max_{j=1}^N H_z(\lambda_j)
= \max_{j=1}^N \frac{a^2 + b^2 |\lambda_j|^2}{|\lambda_j - z |^2 }
\end{equation*} which is smaller than ![]() $1$ if
$1$ if ![]() $z$ is outside
$z$ is outside  $\bigcup_{j=1}^N K_{r_j}(\lambda_j)$.
$\bigcup_{j=1}^N K_{r_j}(\lambda_j)$.
We proceed to prove (ii). For ![]() $s\in [0,1]$ define
$s\in [0,1]$ define ![]() $A_s := sA$. Then all
$A_s := sA$. Then all ![]() $A_s$ are
$A_s$ are ![]() $T$-bounded and if
$T$-bounded and if ![]() $a,b$ are the constants from (1.1), then we have the corresponding inequality for
$a,b$ are the constants from (1.1), then we have the corresponding inequality for ![]() $A_s$ if we use
$A_s$ if we use ![]() $a_s:=\sqrt{s}a$ and
$a_s:=\sqrt{s}a$ and ![]() $b_s:=\sqrt{s}b$ instead of
$b_s:=\sqrt{s}b$ instead of ![]() $a$ and
$a$ and ![]() $b$. Note that the numbers
$b$. Note that the numbers ![]() $\alpha'_{T+A_s}, \beta'_{T+A_s}$ and
$\alpha'_{T+A_s}, \beta'_{T+A_s}$ and  $r_{j,s} := \sqrt{a_s^2 + b_s^2|\lambda_j|^2}$ are non-decreasing in
$r_{j,s} := \sqrt{a_s^2 + b_s^2|\lambda_j|^2}$ are non-decreasing in ![]() $s$. In particular we have (3.17) for all
$s$. In particular we have (3.17) for all ![]() $A_s$ with the corresponding
$A_s$ with the corresponding ![]() $\alpha'_{T+A_s}, \beta'_{T+A_s}$. Therefore, if for the moment we denote the set (3.18) by
$\alpha'_{T+A_s}, \beta'_{T+A_s}$. Therefore, if for the moment we denote the set (3.18) by ![]() $U(A)$, we have that
$U(A)$, we have that ![]() $U(sA)\supset U(s'A)$ for all
$U(sA)\supset U(s'A)$ for all ![]() $0\le s \le s' \le 1$ and for any
$0\le s \le s' \le 1$ and for any ![]() $s,s'\in [0,1]$ we have that
$s,s'\in [0,1]$ we have that ![]() $K_{r_{k,s}+2\epsilon} \subseteq U(s'A)$. Therefore we can define the Riesz projections
$K_{r_{k,s}+2\epsilon} \subseteq U(s'A)$. Therefore we can define the Riesz projections
 \begin{equation}
P_s := \frac{1}{2\pi \mathrm{i}} \int_{\partial K_{r_k+\epsilon}(\lambda_k)} (T+A_s-\lambda)^{-1}\,\mathrm d\lambda,
\qquad s\in[0,1].
\end{equation}
\begin{equation}
P_s := \frac{1}{2\pi \mathrm{i}} \int_{\partial K_{r_k+\epsilon}(\lambda_k)} (T+A_s-\lambda)^{-1}\,\mathrm d\lambda,
\qquad s\in[0,1].
\end{equation} The dimension of the range of ![]() $P_s$ is equal to the total algebraic multiplicity of the eigenvalues of
$P_s$ is equal to the total algebraic multiplicity of the eigenvalues of ![]() $A_s$ contained in
$A_s$ contained in ![]() $B_{r_k+\epsilon}(\lambda_k)$, hence in
$B_{r_k+\epsilon}(\lambda_k)$, hence in ![]() $K_{r_k}(\lambda_k)$. So we have to show that
$K_{r_k}(\lambda_k)$. So we have to show that ![]() $\dim\operatorname{Ran} P_0 = \dim\operatorname{Ran} P_1$. To this end, observe that for
$\dim\operatorname{Ran} P_0 = \dim\operatorname{Ran} P_1$. To this end, observe that for ![]() $\lambda\in\partial K_{r_k+\epsilon}(\lambda_k)$
$\lambda\in\partial K_{r_k+\epsilon}(\lambda_k)$
 \begin{equation*}
(T+A_s-\lambda)^{-1}
= (T-\lambda)^{-1} \sum_{n=0}^\infty s^n(-A(T-\lambda)^{-1})^n
\end{equation*}
\begin{equation*}
(T+A_s-\lambda)^{-1}
= (T-\lambda)^{-1} \sum_{n=0}^\infty s^n(-A(T-\lambda)^{-1})^n
\end{equation*} which is continuous in ![]() $s$, uniformly with respect to
$s$, uniformly with respect to ![]() $\lambda$. Therefore
$\lambda$. Therefore ![]() $P_s$ is continuous in
$P_s$ is continuous in ![]() $s$, hence
$s$, hence ![]() $\dim\operatorname{Ran} P_s$ is constant in
$\dim\operatorname{Ran} P_s$ is constant in ![]() $s$ by [Reference Kato13, Ch.I, Lemma 4.10].
$s$ by [Reference Kato13, Ch.I, Lemma 4.10].
The claim in (iii) follows as in (ii) if we replace the contour of integration in (3.19) by  $\Gamma = \bigcup_{j=1}^N \partial K_{r_j+\epsilon}(\lambda_j)$.
$\Gamma = \bigcup_{j=1}^N \partial K_{r_j+\epsilon}(\lambda_j)$.
As a corollary, we obtain a generalization of [Reference Cuenin and Tretter5, Theorem 2.12].
Corollary 3.9. Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1. For
$A$ be as in Assumption 1. For ![]() $\alpha \lt \beta$ and
$\alpha \lt \beta$ and ![]() $\gamma_1 \le \gamma_2$ we define the gapped strip
$\gamma_1 \le \gamma_2$ we define the gapped strip ![]() $\mathrm{Str} = \{z\in\mathbb{C} : \operatorname{Re} z \in \mathbb{R}\setminus (\alpha, \beta),\ \gamma_1 \le \operatorname{Im} z \le \gamma_2 \}$. Assume that
$\mathrm{Str} = \{z\in\mathbb{C} : \operatorname{Re} z \in \mathbb{R}\setminus (\alpha, \beta),\ \gamma_1 \le \operatorname{Im} z \le \gamma_2 \}$. Assume that ![]() $\sigma(T) = \Sigma_0 \cup \Sigma_1$ where
$\sigma(T) = \Sigma_0 \cup \Sigma_1$ where ![]() $\Sigma_0 \subseteq \mathrm{Str}$ and
$\Sigma_0 \subseteq \mathrm{Str}$ and ![]() $\Sigma_1 = \{\lambda_1,\,\dots,\, \lambda_N\}$ is a finite set of eigenvalues counted with multiplicity that satisfies
$\Sigma_1 = \{\lambda_1,\,\dots,\, \lambda_N\}$ is a finite set of eigenvalues counted with multiplicity that satisfies ![]() $\Sigma_0 \cap \mathrm{Str} = \emptyset$ and
$\Sigma_0 \cap \mathrm{Str} = \emptyset$ and ![]() $\gamma_1 \lt \operatorname{Im}\lambda_j \lt \gamma_2$ for
$\gamma_1 \lt \operatorname{Im}\lambda_j \lt \gamma_2$ for ![]() $j=1,\dots, N$. Without restriction we may assume that
$j=1,\dots, N$. Without restriction we may assume that ![]() $\operatorname{Re} \lambda_1 \le \operatorname{Re}\lambda_2 \le \dots \le \operatorname{Re} \lambda_N$. Set
$\operatorname{Re} \lambda_1 \le \operatorname{Re}\lambda_2 \le \dots \le \operatorname{Re} \lambda_N$. Set ![]() $\widetilde \gamma = \max\{|\gamma_1|,\, |\gamma_2|\}$ and, as in (3.8), let
$\widetilde \gamma = \max\{|\gamma_1|,\, |\gamma_2|\}$ and, as in (3.8), let
 \begin{equation*}
\alpha'_{T+A}:=\alpha_{T}+\sqrt{a^2+b^2\widetilde \gamma^2+b^2\alpha_{T}^2},\qquad
\beta'_{T+A}:= \beta_T -\sqrt{a^2+b^2\widetilde \gamma^2+b^2\beta_{T}^2}.
\end{equation*}
\begin{equation*}
\alpha'_{T+A}:=\alpha_{T}+\sqrt{a^2+b^2\widetilde \gamma^2+b^2\alpha_{T}^2},\qquad
\beta'_{T+A}:= \beta_T -\sqrt{a^2+b^2\widetilde \gamma^2+b^2\beta_{T}^2}.
\end{equation*}Moreover, we set
 \begin{equation*}
R_1 := \operatorname{Re} \lambda_1 - \sqrt{a^2+b^2\widetilde \gamma^2+b^2(\operatorname{Re} \lambda_1)^2},\qquad
R_N := \operatorname{Re}\lambda_N + \sqrt{a^2+b^2\widetilde \gamma^2+b^2(\operatorname{Re}\lambda_N)^2}.
\end{equation*}
\begin{equation*}
R_1 := \operatorname{Re} \lambda_1 - \sqrt{a^2+b^2\widetilde \gamma^2+b^2(\operatorname{Re} \lambda_1)^2},\qquad
R_N := \operatorname{Re}\lambda_N + \sqrt{a^2+b^2\widetilde \gamma^2+b^2(\operatorname{Re}\lambda_N)^2}.
\end{equation*} If ![]() $\alpha'_{T+A} \lt R_1$ and
$\alpha'_{T+A} \lt R_1$ and ![]() $R_N \lt \beta'_{T+A}$, then for any
$R_N \lt \beta'_{T+A}$, then for any  $\widetilde R_1\in (\alpha'_{T+A},\, R_1)$,
$\widetilde R_1\in (\alpha'_{T+A},\, R_1)$,  $\widetilde R_2\in (R_N, \, \beta'_{T+A})$ and large enough
$\widetilde R_2\in (R_N, \, \beta'_{T+A})$ and large enough ![]() $\eta$ the rectangular curve with corners
$\eta$ the rectangular curve with corners  $\widetilde R_1\pm\mathrm{i}\eta$ and
$\widetilde R_1\pm\mathrm{i}\eta$ and  $\widetilde R_2\pm\mathrm{i}\eta$ belongs to
$\widetilde R_2\pm\mathrm{i}\eta$ belongs to ![]() $\rho (T+sA)$ for any
$\rho (T+sA)$ for any ![]() $s\in [0,1]$, its interior contains only eigenvalues of
$s\in [0,1]$, its interior contains only eigenvalues of ![]() $T+A$ and their total algebraic multiplicity is equal to
$T+A$ and their total algebraic multiplicity is equal to ![]() $N$.
$N$.
Proof. As in the proof of (iii) in Theorem 3.8 it can be shown that the vertical parts of ![]() $\Gamma$ belong to
$\Gamma$ belong to ![]() $\rho(T+sA)$ for all
$\rho(T+sA)$ for all ![]() $s\in [0,1]$ by Theorem 3.4, applied to the spectral gaps
$s\in [0,1]$ by Theorem 3.4, applied to the spectral gaps ![]() $\{\alpha \lt \operatorname{Re} z \lt \operatorname{Re}\lambda_1\}$ and
$\{\alpha \lt \operatorname{Re} z \lt \operatorname{Re}\lambda_1\}$ and ![]() $\{\operatorname{Re}\lambda_N \lt \operatorname{Re} z \lt \beta\}$. The same is true for the horizontal lines from
$\{\operatorname{Re}\lambda_N \lt \operatorname{Re} z \lt \beta\}$. The same is true for the horizontal lines from  $\widetilde R_1\pm\mathrm{i}\eta$ if we choose
$\widetilde R_1\pm\mathrm{i}\eta$ if we choose ![]() $\eta$ large enough such that they lie in
$\eta$ large enough such that they lie in ![]() $\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\widetilde \gamma}$ and
$\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\widetilde \gamma}$ and ![]() $\mathrm{i}\gamma_1 - \mathrm{Hyp}_{\widetilde \gamma}$ respectively. Now the same continuity argument shows that the rank of the Riesz projections in (3.19) with contour
$\mathrm{i}\gamma_1 - \mathrm{Hyp}_{\widetilde \gamma}$ respectively. Now the same continuity argument shows that the rank of the Riesz projections in (3.19) with contour ![]() $\Gamma$ is constant in
$\Gamma$ is constant in ![]() $s$.
$s$.
4. Bisectorial and sectorial operators
We will denote the closed sector of angle ![]() $\theta$ and centred at
$\theta$ and centred at ![]() $\lambda \in \mathbb{R}$ by
$\lambda \in \mathbb{R}$ by
For ![]() $\alpha, \beta$, with
$\alpha, \beta$, with ![]() $\alpha\leq \beta$ we define, see Figure 2,
$\alpha\leq \beta$ we define, see Figure 2,

Figure 2. The set ![]() $\Omega(\alpha,\beta,\theta)=S_\theta(\beta)\cup-S_\theta(-\alpha)$.
$\Omega(\alpha,\beta,\theta)=S_\theta(\beta)\cup-S_\theta(-\alpha)$.
Definition 4.1. An operator ![]() $T$ on a Hilbert space
$T$ on a Hilbert space ![]() $H$ is called sectorial if
$H$ is called sectorial if ![]() $\sigma(T)\subseteq -S_{\theta}(0)$ for some
$\sigma(T)\subseteq -S_{\theta}(0)$ for some ![]() $\theta\in [0,\pi)$ and if for every
$\theta\in [0,\pi)$ and if for every ![]() $\theta' \in (\theta, \pi)$ there exists a constant
$\theta' \in (\theta, \pi)$ there exists a constant ![]() $M\ge 0$ such that
$M\ge 0$ such that  $\|(T-z)^{-1}\| \le \frac{M}{|z|}$ for all
$\|(T-z)^{-1}\| \le \frac{M}{|z|}$ for all ![]() $z\in\mathbb{C}\setminus (-S_{\theta'}(0))$. An operator
$z\in\mathbb{C}\setminus (-S_{\theta'}(0))$. An operator ![]() $T$ is called quasi-sectorial if there exists some
$T$ is called quasi-sectorial if there exists some ![]() $c \in\mathbb{R}$ such that
$c \in\mathbb{R}$ such that ![]() $T+c I$ is sectorial.
$T+c I$ is sectorial.
We call the operator ![]() $T$ bisectorial if
$T$ bisectorial if ![]() $\sigma(T)\subseteq \Omega(0,0,\theta)$ for some
$\sigma(T)\subseteq \Omega(0,0,\theta)$ for some ![]() $\theta \in [0,\pi)$ and if for every
$\theta \in [0,\pi)$ and if for every ![]() $\theta' \in (\theta, \pi)$ there exists a constant
$\theta' \in (\theta, \pi)$ there exists a constant ![]() $M\ge 0$ such that
$M\ge 0$ such that  $\|(T-z)^{-1}\| \le \frac{M}{|z|}$ for all
$\|(T-z)^{-1}\| \le \frac{M}{|z|}$ for all ![]() $z\in\mathbb{C}\setminus \Omega(0, 0, \theta')$.
$z\in\mathbb{C}\setminus \Omega(0, 0, \theta')$.
Since ![]() $\|(T-z)^{-1}\| = \operatorname{dist}(z,\sigma(T))$ for all
$\|(T-z)^{-1}\| = \operatorname{dist}(z,\sigma(T))$ for all ![]() $z\in\rho(T)$ if
$z\in\rho(T)$ if ![]() $T$ is a normal operator, we obtain the following lemma.
$T$ is a normal operator, we obtain the following lemma.
Lemma 4.2. Let ![]() $T$ be a closed normal operator on a Hilbert space
$T$ be a closed normal operator on a Hilbert space ![]() $H$.
$H$.
(i) If
 $\sigma(T)\subseteq \Omega(\alpha_T, \beta_T, \theta)$, then, for any
$\sigma(T)\subseteq \Omega(\alpha_T, \beta_T, \theta)$, then, for any  $c\in(\alpha_T,\beta_T)$, the operator
$c\in(\alpha_T,\beta_T)$, the operator  $T -cI$ is bisectorial with a possibly larger angle
$T -cI$ is bisectorial with a possibly larger angle  $\theta' \gt \theta$.
$\theta' \gt \theta$.(ii) If there exists
 $\mu, M \in\mathbb{R}$ such that
$\mu, M \in\mathbb{R}$ such that  $(\mu+\mathrm i\mathbb{R})\setminus\{0\}\subseteq\rho(T)$ and
$(\mu+\mathrm i\mathbb{R})\setminus\{0\}\subseteq\rho(T)$ and  $\| (T-\mu-\mathrm{i}\nu)^{-1}\| \le \frac{M}{|\nu|}$ for all
$\| (T-\mu-\mathrm{i}\nu)^{-1}\| \le \frac{M}{|\nu|}$ for all  $\nu\in\mathbb{R}\setminus\{0\}$, then
$\nu\in\mathbb{R}\setminus\{0\}$, then  $T$ is bisectorial.
$T$ is bisectorial.
In our first theorem, we will show that the spectrum of ![]() $T+A$ is contained in a set of the form (4.1) if
$T+A$ is contained in a set of the form (4.1) if ![]() $T$ is a normal bisectorial operator and
$T$ is a normal bisectorial operator and ![]() $A$ is a sufficiently small perturbation. We saw in
$A$ is a sufficiently small perturbation. We saw in ![]() $\S$ 3 that the guaranteed bounds for the spectrum of
$\S$ 3 that the guaranteed bounds for the spectrum of ![]() $T+A$ bend away from the boundary of
$T+A$ bend away from the boundary of ![]() $\sigma(T)$ by the angle
$\sigma(T)$ by the angle  $\arctan \frac{b}{\sqrt{1-b^2}}$. Therefore, if
$\arctan \frac{b}{\sqrt{1-b^2}}$. Therefore, if ![]() $\sigma(T)$ is contained in some
$\sigma(T)$ is contained in some ![]() $\Omega(\alpha,\beta,\theta)$ and if we want a half-plane or at least a strip to be contained in
$\Omega(\alpha,\beta,\theta)$ and if we want a half-plane or at least a strip to be contained in ![]() $\rho(T+A)$, then it is reasonable to assume that the constant
$\rho(T+A)$, then it is reasonable to assume that the constant ![]() $b$ should satisfy
$b$ should satisfy ![]() $b \lt \cos\theta$ in order to guarantee that
$b \lt \cos\theta$ in order to guarantee that  $\theta + \arctan \frac{b}{\sqrt{1-b^2}} \lt \pi/2$.
$\theta + \arctan \frac{b}{\sqrt{1-b^2}} \lt \pi/2$.
In the following we will need the set
 \begin{equation}{\widetilde{\mathrm{Hyp}}}_\gamma=\left\{z\in\mathbb{C}\;:\;\frac{a^2+b^2\gamma^2}{1-b^2}+\frac{b^2}{1-b^2}\,(\operatorname{Re}z)^2 \gt (\operatorname{Im}z)^2,\;\operatorname{Im}z \gt 0\right\},\end{equation}
\begin{equation}{\widetilde{\mathrm{Hyp}}}_\gamma=\left\{z\in\mathbb{C}\;:\;\frac{a^2+b^2\gamma^2}{1-b^2}+\frac{b^2}{1-b^2}\,(\operatorname{Re}z)^2 \gt (\operatorname{Im}z)^2,\;\operatorname{Im}z \gt 0\right\},\end{equation} and, for ![]() $\delta \in\mathbb{R}$,
$\delta \in\mathbb{R}$,
 \begin{equation*}
\mathrm{e}^{\mathrm{i}\phi}( \delta + \widetilde{\mathrm{Hyp}}_\gamma)
=
\left\{z\in\mathbb{C} \,:\,
\begin{aligned}
& a^2 + b^2\gamma^2 + \frac{b^2 (\operatorname{Re} (\mathrm{e}^{-\mathrm{i}\phi}(z-\delta)) )^2 }{1-b^2} \lt (\operatorname{Im} (\mathrm{e}^{-\mathrm{i}\phi} (z - \delta)) )^2,
\\
& \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\phi} (z - \delta)) \gt 0
\end{aligned}
\right\},
\end{equation*}
\begin{equation*}
\mathrm{e}^{\mathrm{i}\phi}( \delta + \widetilde{\mathrm{Hyp}}_\gamma)
=
\left\{z\in\mathbb{C} \,:\,
\begin{aligned}
& a^2 + b^2\gamma^2 + \frac{b^2 (\operatorname{Re} (\mathrm{e}^{-\mathrm{i}\phi}(z-\delta)) )^2 }{1-b^2} \lt (\operatorname{Im} (\mathrm{e}^{-\mathrm{i}\phi} (z - \delta)) )^2,
\\
& \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\phi} (z - \delta)) \gt 0
\end{aligned}
\right\},
\end{equation*} which is the region above a hyperbola shifted by ![]() $\delta$ and then rotated by
$\delta$ and then rotated by ![]() $\phi$, see Figure 3.
$\phi$, see Figure 3.

Figure 3. Illustration for the proof of Theorem 4.6 and Lemma A.3 (ii). In (a), the lightblue half-plane is the plane ![]() $P$ above which the estimate (A.6) holds. The white regions in (b) and (d) correspond to the sets
$P$ above which the estimate (A.6) holds. The white regions in (b) and (d) correspond to the sets  $\beta_T + \mathrm{e}^{\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_{\beta_T}$ and
$\beta_T + \mathrm{e}^{\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_{\beta_T}$ and  $\beta_T - \mathrm{e}^{-\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_{\beta_T}$, respectively. There,
$\beta_T - \mathrm{e}^{-\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_{\beta_T}$, respectively. There, ![]() $\sup_{t\in\partial(S_{\theta}(\beta_T))} H_z(t) \lt 1$ holds. The red dashed lines indicate the asymptotes of the hyperbola. If we combine the guaranteed regions for the resolvent set from (b) and (d), we find that the spectrum of
$\sup_{t\in\partial(S_{\theta}(\beta_T))} H_z(t) \lt 1$ holds. The red dashed lines indicate the asymptotes of the hyperbola. If we combine the guaranteed regions for the resolvent set from (b) and (d), we find that the spectrum of ![]() $T+A$ must be contained in the grey area in (e). The vertical blue line in (e) and (f) is the lower bound
$T+A$ must be contained in the grey area in (e). The vertical blue line in (e) and (f) is the lower bound ![]() $\beta_{T+A}$ for the real part of the spectrum of
$\beta_{T+A}$ for the real part of the spectrum of ![]() $T+A$ in the case
$T+A$ in the case ![]() $b \lt \cos\theta$, so
$b \lt \cos\theta$, so ![]() $\sigma(T+A)$ is contained in the grey area to its right. The graphic in (f) shows the spectral inclusion for a larger angle
$\sigma(T+A)$ is contained in the grey area to its right. The graphic in (f) shows the spectral inclusion for a larger angle ![]() $\theta$.
$\theta$.
Let  $\phi_b=\arctan \frac{b}{\sqrt{1-b^2}}$. Then the asymptotes of the hyperbola
$\phi_b=\arctan \frac{b}{\sqrt{1-b^2}}$. Then the asymptotes of the hyperbola  $\mathrm{e}^{\mathrm{i}\phi}( \delta + \mathrm{Hyp}_\gamma)$ are
$\mathrm{e}^{\mathrm{i}\phi}( \delta + \mathrm{Hyp}_\gamma)$ are
 \begin{align*}
\operatorname{Im} z &= (\operatorname{Re} z - \delta)\tan(\phi + \phi_b) \text{for }\operatorname{Re} z \to\infty,\\
\operatorname{Im} z &= (\operatorname{Re} z - \delta)\tan(\phi - \phi_b) \text{for }\operatorname{Re} z \to -\infty.
\end{align*}
\begin{align*}
\operatorname{Im} z &= (\operatorname{Re} z - \delta)\tan(\phi + \phi_b) \text{for }\operatorname{Re} z \to\infty,\\
\operatorname{Im} z &= (\operatorname{Re} z - \delta)\tan(\phi - \phi_b) \text{for }\operatorname{Re} z \to -\infty.
\end{align*} If ![]() $b \lt \cos\theta$, we define
$b \lt \cos\theta$, we define
 \begin{align}
\alpha_{T+A}:=\alpha_{T}+\frac{\sqrt{a^2+b^2\alpha_{T}^2}}{\sqrt{1-b^2\tan^2\theta}},
\qquad
\beta_{T+A}:= \beta_T-\frac{\sqrt{a^2+b^2\beta_{T}^2}}{\sqrt{1-b^2\tan^2\theta}}.
\end{align}
\begin{align}
\alpha_{T+A}:=\alpha_{T}+\frac{\sqrt{a^2+b^2\alpha_{T}^2}}{\sqrt{1-b^2\tan^2\theta}},
\qquad
\beta_{T+A}:= \beta_T-\frac{\sqrt{a^2+b^2\beta_{T}^2}}{\sqrt{1-b^2\tan^2\theta}}.
\end{align} Let us first generalise Corollary 3.6 to the case when ![]() $-T$ is quasi-sectorial.
$-T$ is quasi-sectorial.
Theorem 4.3 Let ![]() $T$ and
$T$ and ![]() $A$ and the constants
$A$ and the constants ![]() $a,b$ be as in Assumption 1 and assume that
$a,b$ be as in Assumption 1 and assume that
for some ![]() $\theta\in[0,\pi/2)$. Then
$\theta\in[0,\pi/2)$. Then
 \begin{align}
\mathrm{e}^{\mathrm{i}\theta}(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\subseteq \rho(T+A).
\end{align}
\begin{align}
\mathrm{e}^{\mathrm{i}\theta}(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\subseteq \rho(T+A).
\end{align} If in addition ![]() $b \lt \cos\theta$ holds, then the real part of
$b \lt \cos\theta$ holds, then the real part of ![]() $\sigma(T+A)$ is lower bounded by
$\sigma(T+A)$ is lower bounded by ![]() $\beta_{T+A}$ and we even have
$\beta_{T+A}$ and we even have
 \begin{align}
\{z\in\mathbb{C} : \operatorname{Re} z \lt \beta_{T+A}\}
\cup
\mathrm{e}^{\mathrm{i}\theta}(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\subseteq \rho(T+A),
\end{align}
\begin{align}
\{z\in\mathbb{C} : \operatorname{Re} z \lt \beta_{T+A}\}
\cup
\mathrm{e}^{\mathrm{i}\theta}(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\subseteq \rho(T+A),
\end{align}Remark 4.4. The analogous inclusions for the case when ![]() $\sigma(T)\subseteq -S_{\theta}(-\alpha_T)$ are:
$\sigma(T)\subseteq -S_{\theta}(-\alpha_T)$ are:
 \begin{align}
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\subseteq \rho(T+A).
\end{align}
\begin{align}
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\subseteq \rho(T+A).
\end{align} Moreover, if ![]() $b \lt \cos\theta$, then the real part of
$b \lt \cos\theta$, then the real part of ![]() $\sigma(T+A)$ is upper bounded by
$\sigma(T+A)$ is upper bounded by ![]() $\alpha_{T+A}$ and we obtain the stronger result
$\alpha_{T+A}$ and we obtain the stronger result
 \begin{align}
\{z\in\mathbb{C} : \operatorname{Re} z \gt \alpha_{T+A}\}
\cup
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\subseteq \rho(T+A).
\end{align}
\begin{align}
\{z\in\mathbb{C} : \operatorname{Re} z \gt \alpha_{T+A}\}
\cup
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\subseteq \rho(T+A).
\end{align}Remark 4.5. If (4.5) holds, then clearly there exists ![]() $\omega\in\mathbb{R}$ such that
$\omega\in\mathbb{R}$ such that ![]() $\sigma(T+A) \subseteq S_{\theta+\phi_b}(\omega)$.
$\sigma(T+A) \subseteq S_{\theta+\phi_b}(\omega)$.
Proof of Theorem 4.3
Let ![]() $z = \mu + \mathrm{i}\nu \in\mathbb{C}\setminus S_{\theta}(\beta_T)$ and define the function
$z = \mu + \mathrm{i}\nu \in\mathbb{C}\setminus S_{\theta}(\beta_T)$ and define the function ![]() $H_z$ as in (2.2). Note that
$H_z$ as in (2.2). Note that
 \begin{align*}
\sup_{t\in \sigma(T)} H_z(t)
\le
\sup_{t\in S_{\theta}(\beta_T)}
H_z(t),
\end{align*}
\begin{align*}
\sup_{t\in \sigma(T)} H_z(t)
\le
\sup_{t\in S_{\theta}(\beta_T)}
H_z(t),
\end{align*}and the right hand side was calculated in (A.6). Therefore we obtain the inclusion (4.4) from Lemma A.4(ii).
Now let us assume that ![]() $\mu = \operatorname{Re} z \lt \beta_T$. Then (A.12) shows that
$\mu = \operatorname{Re} z \lt \beta_T$. Then (A.12) shows that
 \begin{align}
\sup_{t\in \partial S_{\theta}(\beta_T)} H_z(t) \le \max\left\{b^2,\ \frac{a^2+b^2\beta_T^2}{(\beta_T-\mu)^2} \right\} + b^2\tan^2\theta.
\end{align}
\begin{align}
\sup_{t\in \partial S_{\theta}(\beta_T)} H_z(t) \le \max\left\{b^2,\ \frac{a^2+b^2\beta_T^2}{(\beta_T-\mu)^2} \right\} + b^2\tan^2\theta.
\end{align} Under the additional assumption ![]() $\beta \lt \cos\theta$ we have that
$\beta \lt \cos\theta$ we have that ![]() $b^2(1+\tan^2\theta) \lt 1$. So the right hand side in (4.8) is smaller than 1 if
$b^2(1+\tan^2\theta) \lt 1$. So the right hand side in (4.8) is smaller than 1 if  $\frac{{a^2+b^2\beta_T^2}}{(\beta_T-\mu)^2}+b^2\tan^2\theta \lt 1$. This is the case if and only if
$\frac{{a^2+b^2\beta_T^2}}{(\beta_T-\mu)^2}+b^2\tan^2\theta \lt 1$. This is the case if and only if  $\mu \lt \beta_T - \frac{\sqrt{a^2+b^2\beta_T^2}}{1-b^2\tan^2\theta} = \beta_{T+A}$. It follows that
$\mu \lt \beta_T - \frac{\sqrt{a^2+b^2\beta_T^2}}{1-b^2\tan^2\theta} = \beta_{T+A}$. It follows that ![]() $\{z\in\mathbb{C} : \operatorname{Re} z \lt \beta_{T+A} \}\subseteq\rho(T+A)$ and (4.5) is proved.
$\{z\in\mathbb{C} : \operatorname{Re} z \lt \beta_{T+A} \}\subseteq\rho(T+A)$ and (4.5) is proved.
Theorem 4.6 Let ![]() $T$ and
$T$ and ![]() $A$ and the constants
$A$ and the constants ![]() $a,b$ be as in Assumption 1 and assume that there are
$a,b$ be as in Assumption 1 and assume that there are ![]() $\alpha_T \lt \beta_T$ and
$\alpha_T \lt \beta_T$ and ![]() $\theta\in [0, \pi/2)$ such that
$\theta\in [0, \pi/2)$ such that
Then
 \begin{equation}\begin{aligned}
\Big(
\mathrm{e}^{\mathrm{i}\theta}(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\Big)
\cap
\Big(
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\Big)
\\
\subseteq \rho(T+A).
\end{aligned}
\end{equation}
\begin{equation}\begin{aligned}
\Big(
\mathrm{e}^{\mathrm{i}\theta}(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\Big)
\cap
\Big(
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\Big)
\\
\subseteq \rho(T+A).
\end{aligned}
\end{equation} If ![]() $b \lt \cos\theta$, then we have in addition
$b \lt \cos\theta$, then we have in addition
where ![]() $\alpha_{T+A}$ and
$\alpha_{T+A}$ and ![]() $\beta_{T+A}$ are defined in (4.3). See Figure 4.
$\beta_{T+A}$ are defined in (4.3). See Figure 4.

Figure 4. Illustration of the spectral inclusion from Theorem 4.6 for different angles ![]() $\theta$. The blue sectors
$\theta$. The blue sectors ![]() $\Omega(\alpha_T, \beta_T, \theta)$ contain the spectrum of
$\Omega(\alpha_T, \beta_T, \theta)$ contain the spectrum of ![]() $T$ and the spectrum of
$T$ and the spectrum of ![]() $T+A$ is contained in the grey area.
$T+A$ is contained in the grey area.
Proof. Let ![]() $z = \mu + \mathrm{i}\nu \in\mathbb{C}\setminus\Omega(\alpha_T, \beta_T, \theta)$ and define the function
$z = \mu + \mathrm{i}\nu \in\mathbb{C}\setminus\Omega(\alpha_T, \beta_T, \theta)$ and define the function ![]() $H_z$ as in (2.2). Proposition 2.1(iii) shows that
$H_z$ as in (2.2). Proposition 2.1(iii) shows that ![]() $z\in\rho(T+A)$ if
$z\in\rho(T+A)$ if ![]() $\sup_{\sigma(T)} H_z(t) \lt 1$. Observe that
$\sup_{\sigma(T)} H_z(t) \lt 1$. Observe that
 \begin{align}
\sup_{t\in \sigma(T)} H_z(t)
\le \max\left\{\sup_{t\in -S_{\theta}(-\alpha_T)} H_z(t),\
\sup_{t\in S_{\theta}(\beta_T)} H_z(t) \right\}.
\end{align}
\begin{align}
\sup_{t\in \sigma(T)} H_z(t)
\le \max\left\{\sup_{t\in -S_{\theta}(-\alpha_T)} H_z(t),\
\sup_{t\in S_{\theta}(\beta_T)} H_z(t) \right\}.
\end{align} From the proof of Theorem 4.3, we know that ![]() $\sup_{t\in S_{\theta}(\alpha_T)} H_z(t) \lt 1$ if
$\sup_{t\in S_{\theta}(\alpha_T)} H_z(t) \lt 1$ if ![]() $z$ belongs to the left hand side of (4.4) and that
$z$ belongs to the left hand side of (4.4) and that ![]() $\sup_{t\in -S_{\theta}(-\alpha_T)} H_z(t) \lt 1$ if
$\sup_{t\in -S_{\theta}(-\alpha_T)} H_z(t) \lt 1$ if ![]() $z$ belongs to the left hand side of (4.6). Therefore the right hand side of (4.11) is less than 1 if
$z$ belongs to the left hand side of (4.6). Therefore the right hand side of (4.11) is less than 1 if ![]() $z$ belongs to both sets which proves (4.9).
$z$ belongs to both sets which proves (4.9).
If ![]() $b \lt \cos\theta$, then the proofs of (4.5) and (4.7) show that the right hand side of (4.11) is less than 1 if
$b \lt \cos\theta$, then the proofs of (4.5) and (4.7) show that the right hand side of (4.11) is less than 1 if ![]() $\alpha_{T+A} \lt \operatorname{Re} z \lt \beta_{T+A}$. Hence (4.10) holds.
$\alpha_{T+A} \lt \operatorname{Re} z \lt \beta_{T+A}$. Hence (4.10) holds.
The proof of Theorem 4.6 leads to estimates for the norm of the resolvent of ![]() $T+A$.
$T+A$.
Corollary 4.7. Let ![]() $T$ and
$T$ and ![]() $A$ be as in Theorem 4.6 with
$A$ be as in Theorem 4.6 with ![]() $\alpha_{T+A}$ and
$\alpha_{T+A}$ and ![]() $\beta_{T+A}$ as in (4.3). Then, for
$\beta_{T+A}$ as in (4.3). Then, for ![]() $z\in \mathbb{C}$ with
$z\in \mathbb{C}$ with ![]() $\alpha_{T+A} \lt \operatorname{Re} z \lt \beta_{T+A}$, we have that
$\alpha_{T+A} \lt \operatorname{Re} z \lt \beta_{T+A}$, we have that
 \begin{align*}
&\|(T+A-z)^{-1}\|\\
&\leq \frac{1}{\operatorname{dist}(z,\Omega(\alpha_T, \beta_T, \theta))}
\frac{1}{1- \sqrt{b^2\tan^2\theta + \max\left\{
b^2,\ \frac{{a^2+b^2\beta_T^2}}{(\beta_T-\operatorname{Re} z)^2},\ \frac{{a^2+b^2\alpha_T^2}}{(\operatorname{Re} z-\alpha_T)^2}
\right\}} }.
\end{align*}
\begin{align*}
&\|(T+A-z)^{-1}\|\\
&\leq \frac{1}{\operatorname{dist}(z,\Omega(\alpha_T, \beta_T, \theta))}
\frac{1}{1- \sqrt{b^2\tan^2\theta + \max\left\{
b^2,\ \frac{{a^2+b^2\beta_T^2}}{(\beta_T-\operatorname{Re} z)^2},\ \frac{{a^2+b^2\alpha_T^2}}{(\operatorname{Re} z-\alpha_T)^2}
\right\}} }.
\end{align*}Proof. Let ![]() $z= \mu + \mathrm{i}\nu$ with
$z= \mu + \mathrm{i}\nu$ with ![]() $\alpha_{T+A} \lt \mu \lt \beta_{T+A}$. Then, by (4.8) and the analogous estimate for
$\alpha_{T+A} \lt \mu \lt \beta_{T+A}$. Then, by (4.8) and the analogous estimate for ![]() $-S_{\theta}(-\alpha)$, we obtain
$-S_{\theta}(-\alpha)$, we obtain
 \begin{equation}
\sup_{t\in\sigma(T)} H_z(t)
\le
\max\left\{b^2,\ \frac{{a^2+b^2\beta_T^2}}{(\beta_T-\operatorname{Re} z)^2},\ \frac{{a^2+b^2\alpha_T^2}}{(\operatorname{Re} z-\alpha_T)^2} \right\}
+ b^2\tan^2\theta.
\end{equation}
\begin{equation}
\sup_{t\in\sigma(T)} H_z(t)
\le
\max\left\{b^2,\ \frac{{a^2+b^2\beta_T^2}}{(\beta_T-\operatorname{Re} z)^2},\ \frac{{a^2+b^2\alpha_T^2}}{(\operatorname{Re} z-\alpha_T)^2} \right\}
+ b^2\tan^2\theta.
\end{equation}Note that
 \begin{align}
\|(T-z)^{-1}\|
&\leq \frac{1}{\operatorname{dist}(z,\sigma(T))}
\leq \frac{1}{\operatorname{dist}(z,\Omega(\alpha_T,\beta_T,\theta))}.
\end{align}
\begin{align}
\|(T-z)^{-1}\|
&\leq \frac{1}{\operatorname{dist}(z,\sigma(T))}
\leq \frac{1}{\operatorname{dist}(z,\Omega(\alpha_T,\beta_T,\theta))}.
\end{align}Now the resolvent estimate follows from Proposition 2.1(iii), (4.12) and (4.13).
There are various ways to estimate (4.13). The most straight forward is
 \begin{align*}
\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \frac{1}{\operatorname{dist}(z,\Omega(\alpha_T,\beta_T,\theta))}
\le
\frac{1}{{\min\{\operatorname{Re} z-\alpha_T,\beta_T-\operatorname{Re} z\}} }.
\end{align*}
\begin{align*}
\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \frac{1}{\operatorname{dist}(z,\Omega(\alpha_T,\beta_T,\theta))}
\le
\frac{1}{{\min\{\operatorname{Re} z-\alpha_T,\beta_T-\operatorname{Re} z\}} }.
\end{align*} We can also use (A.6) and (A.8) with ![]() $b=0$ and
$b=0$ and ![]() $a=1$. Then we obtain for
$a=1$. Then we obtain for ![]() $\operatorname{Im} z \gt 0$ that
$\operatorname{Im} z \gt 0$ that
 \begin{align*}
\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \frac{1}{\operatorname{dist}(z,\Omega(\alpha_T,\beta_T,\theta))}
\le
\frac{1}{{\min\{|\operatorname{Im}(\mathrm{e}^{-\mathrm{i}\theta}(z-\beta_T) )|,\ |\operatorname{Im}(\mathrm{e}^{\mathrm{i}\theta}(z-\alpha_T) )| \}} }
\end{align*}
\begin{align*}
\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \frac{1}{\operatorname{dist}(z,\Omega(\alpha_T,\beta_T,\theta))}
\le
\frac{1}{{\min\{|\operatorname{Im}(\mathrm{e}^{-\mathrm{i}\theta}(z-\beta_T) )|,\ |\operatorname{Im}(\mathrm{e}^{\mathrm{i}\theta}(z-\alpha_T) )| \}} }
\end{align*} which gives a decay of order ![]() $(\operatorname{Im} z)^{-1}$ for
$(\operatorname{Im} z)^{-1}$ for ![]() $\operatorname{Im}(z)\to\pm\infty$.
$\operatorname{Im}(z)\to\pm\infty$.
The next proposition combines the results from Theorem 4.6 and Proposition 3.2. Of course, an analogous result can be formulated for a strip that is not symmetric to the real axis.
Proposition 4.8. Let ![]() $T$ and
$T$ and ![]() $A$ and the constants
$A$ and the constants ![]() $a,b$ be as in Assumption 1. Assume that there are
$a,b$ be as in Assumption 1. Assume that there are ![]() $\alpha_T \lt \beta_T$ and
$\alpha_T \lt \beta_T$ and ![]() $\theta\in [0, \pi/2)$ such that
$\theta\in [0, \pi/2)$ such that ![]() $b \lt \cos\theta$ and that
$b \lt \cos\theta$ and that
Let ![]() $\alpha_{T+A}$ and
$\alpha_{T+A}$ and ![]() $\beta_{T+A}$ as in (4.3) and
$\beta_{T+A}$ as in (4.3) and ![]() $\mathrm{Hyp}_{\gamma}$ and
$\mathrm{Hyp}_{\gamma}$ and  $\widetilde{\mathrm{Hyp}}_{\gamma}$ as in (3.1) and (4.2). Then
$\widetilde{\mathrm{Hyp}}_{\gamma}$ as in (3.1) and (4.2). Then
 \begin{equation*}\begin{aligned}
\Big(
\mathrm{e}^{\mathrm{i}\theta}(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\Big)
\cap
\Big(
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\Big)
\\
\cap
\Big(
(\mathrm{i}\gamma + \mathrm{Hyp}_{\gamma_T})
\cup
(-\mathrm{i}\gamma - \mathrm{Hyp}_{\gamma_T})
\Big)
\subseteq \rho(T+A),
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}
\Big(
\mathrm{e}^{\mathrm{i}\theta}(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\Big)
\cap
\Big(
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\Big)
\\
\cap
\Big(
(\mathrm{i}\gamma + \mathrm{Hyp}_{\gamma_T})
\cup
(-\mathrm{i}\gamma - \mathrm{Hyp}_{\gamma_T})
\Big)
\subseteq \rho(T+A),
\end{aligned}
\end{equation*}see Figure 5.

Figure 5. Localisation of the spectrum of ![]() $T+A$ in the case of Proposition 4.8 when
$T+A$ in the case of Proposition 4.8 when ![]() $A$ is
$A$ is ![]() $T$-bounded and the spectrum of
$T$-bounded and the spectrum of ![]() $T$ is contained in
$T$ is contained in ![]() $\Omega(\alpha_T,\beta_T,\theta)\cup ( \mathbb{R} + \mathrm{i} [-\gamma_T,\gamma_T]$. The dashed lines in the left picture indicate the boundaries of
$\Omega(\alpha_T,\beta_T,\theta)\cup ( \mathbb{R} + \mathrm{i} [-\gamma_T,\gamma_T]$. The dashed lines in the left picture indicate the boundaries of ![]() $\Omega(\alpha_T,\beta_T,\theta)$. In the picture on the right, the grey area indicate the area that we get from Theorem 4.6. The green area shows the contribution from the strip
$\Omega(\alpha_T,\beta_T,\theta)$. In the picture on the right, the grey area indicate the area that we get from Theorem 4.6. The green area shows the contribution from the strip ![]() $\mathbb{R}+\mathrm{i}[-\gamma_T,\gamma_t]$. Therefore the spectrum of
$\mathbb{R}+\mathrm{i}[-\gamma_T,\gamma_t]$. Therefore the spectrum of ![]() $T+A$ is contained in the union of the colourekd areas.
$T+A$ is contained in the union of the colourekd areas.
Proof. The proof is analogous to that of Theorem 4.6. We define the function ![]() $H_z$ as in (2.2). In order to localise
$H_z$ as in (2.2). In order to localise ![]() $\rho(T+A)$ we need to find those
$\rho(T+A)$ we need to find those ![]() $z\in\mathbb{C}$ for which
$z\in\mathbb{C}$ for which ![]() $\sup_{t\in\sigma(T)} H_z(t) \lt 1$. As before, we use the estimate
$\sup_{t\in\sigma(T)} H_z(t) \lt 1$. As before, we use the estimate
 \begin{align*}
\sup_{t\in\sigma(T)} H_z(t)
& \le \sup \left\{H_z(t) :
t\in \Omega(\alpha_T,\beta_T, \theta) \cup (\mathbb{R} + \mathrm{i} [-\gamma_T,\gamma_T]) \right\}
\\
& \le \max\left\{
\sup_{t\in \Omega(\alpha_T,\beta_T, \theta)} H_z(t),\
\sup_{t\in \mathbb{R} + \mathrm{i} [-\gamma_T,\gamma_T]} H_z(t)
\right\}.
\end{align*}
\begin{align*}
\sup_{t\in\sigma(T)} H_z(t)
& \le \sup \left\{H_z(t) :
t\in \Omega(\alpha_T,\beta_T, \theta) \cup (\mathbb{R} + \mathrm{i} [-\gamma_T,\gamma_T]) \right\}
\\
& \le \max\left\{
\sup_{t\in \Omega(\alpha_T,\beta_T, \theta)} H_z(t),\
\sup_{t\in \mathbb{R} + \mathrm{i} [-\gamma_T,\gamma_T]} H_z(t)
\right\}.
\end{align*} We know from the proof of Theorem 4.6 that  $\sup\limits_{t\in \Omega(\alpha_T,\beta_T, \theta)} H_z(t) \lt 1$ if
$\sup\limits_{t\in \Omega(\alpha_T,\beta_T, \theta)} H_z(t) \lt 1$ if  $z\in
\Big(
\mathrm{e}^{\mathrm{i}\theta}(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\Big)
\cap
\Big(
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\Big)$ while
$z\in
\Big(
\mathrm{e}^{\mathrm{i}\theta}(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\Big)
\cap
\Big(
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\Big)$ while  $\sup\limits_{t\in \mathbb{R} + \mathrm{i} [-\gamma_T,\gamma_T]} H_z(t) \lt 1$ if
$\sup\limits_{t\in \mathbb{R} + \mathrm{i} [-\gamma_T,\gamma_T]} H_z(t) \lt 1$ if ![]() $z\in (\mathrm{i}\gamma + \mathrm{Hyp}_{\gamma_T}) \cup (-\mathrm{i}\gamma - \mathrm{Hyp}_{\gamma_T})$ by the proof of Proposition 3.2.
$z\in (\mathrm{i}\gamma + \mathrm{Hyp}_{\gamma_T}) \cup (-\mathrm{i}\gamma - \mathrm{Hyp}_{\gamma_T})$ by the proof of Proposition 3.2.
We finish this section with the following theorem for essential spectral gaps.
Theorem 4.9 Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1. Assume that there exist
$A$ be as in Assumption 1. Assume that there exist ![]() $\alpha \lt \beta$ and
$\alpha \lt \beta$ and ![]() $\theta\in [0,\pi/2)$ such that
$\theta\in [0,\pi/2)$ such that ![]() $\sigma_{\mathrm{ess} }(T)\subseteq \Omega(\alpha,\beta,\theta)$ and
$\sigma_{\mathrm{ess} }(T)\subseteq \Omega(\alpha,\beta,\theta)$ and ![]() $\sigma(T) = \sigma_{\mathrm{ess} }(T) \cup \Sigma$ where
$\sigma(T) = \sigma_{\mathrm{ess} }(T) \cup \Sigma$ where ![]() $\Sigma\subseteq \mathbb{C}\setminus\Omega(\alpha, \beta, \theta)$ is a bounded countable set which may accumulate at most at the boundary of
$\Sigma\subseteq \mathbb{C}\setminus\Omega(\alpha, \beta, \theta)$ is a bounded countable set which may accumulate at most at the boundary of ![]() $\sigma_{\mathrm{ess} }(T)$. Let
$\sigma_{\mathrm{ess} }(T)$. Let ![]() $\alpha_{T+A}$ and
$\alpha_{T+A}$ and ![]() $\beta_{T+A}$ as in (4.3). If
$\beta_{T+A}$ as in (4.3). If ![]() $\alpha_{T+A} \lt \beta_{T+A}$ then
$\alpha_{T+A} \lt \beta_{T+A}$ then
 \begin{equation*}\begin{aligned}
\Big(
\mathrm{e}^{\mathrm{i}\theta}&(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\cup \{\operatorname{Re} z \lt \beta_{T+A} \}
\Big)
\\
&\cap
\Big(
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\cup \{\operatorname{Re} z \gt \alpha_{T+A} \}
\Big)
\subseteq \mathbb{C}\setminus\sigma_{\mathrm{ess} }(T+A).
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}
\Big(
\mathrm{e}^{\mathrm{i}\theta}&(\beta_T + \widetilde{\mathrm{Hyp}}_{\beta_T}) \cup \mathrm{e}^{-\mathrm{i}\theta}(\beta_T - \widetilde{\mathrm{Hyp}}_{\beta_T})
\cup \{\operatorname{Re} z \lt \beta_{T+A} \}
\Big)
\\
&\cap
\Big(
\mathrm{e}^{-\mathrm{i}\theta}(\alpha_T + \widetilde{\mathrm{Hyp}}_{\alpha_T}) \cup \mathrm{e}^{\mathrm{i}\theta}(\alpha_T - \widetilde{\mathrm{Hyp}}_{\alpha_T})
\cup \{\operatorname{Re} z \gt \alpha_{T+A} \}
\Big)
\subseteq \mathbb{C}\setminus\sigma_{\mathrm{ess} }(T+A).
\end{aligned}
\end{equation*}and the set on the left hand side consists of at most countably many isolated eigenvalues of finite algebraic multiplicity which may accumulate only at its boundary.
Proof. The proof is analogous to that of Theorem 3.7 if we use for instance the sets  $S_n = \Omega(\alpha+\frac{1}{n}, \beta-\frac{1}{n}, \theta)$.
$S_n = \Omega(\alpha+\frac{1}{n}, \beta-\frac{1}{n}, \theta)$.
Clearly, a theorem analogous to Theorem 3.8 about the multiplicity of isolated eigenvalues can be proved. We omit details.
In the proofs of Theorem 4.3, Theorem 4.6, Corollary 4.7, Proposition 4.8 we used the estimates (A.6) and (A.8) from Lemma A.4. If we use the alternative estimates (A.6’) and (A.8’) from Lemma A.5 then we obtain slightly different spectral inclusions for ![]() $T+A$. For details see Appendix B.
$T+A$. For details see Appendix B.
5. Other spectral inclusions
Using the techniques from ![]() $\S$ 3 and
$\S$ 3 and ![]() $\S$ 4 we can prove a variety of results for the location of the spectra of perturbed normal operators. We only sketch some of their proofs.
$\S$ 4 we can prove a variety of results for the location of the spectra of perturbed normal operators. We only sketch some of their proofs.
Proposition 5.1. Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1 and assume that there are constants
$A$ be as in Assumption 1 and assume that there are constants ![]() $\gamma_1 \lt \gamma_2$ such that
$\gamma_1 \lt \gamma_2$ such that
Then
 \begin{align*}
&(\gamma_1 + \mathrm{i}\mathrm{Hyp}_{\gamma_1}) \cap (\gamma_2 - \mathrm{i}\mathrm{Hyp}_{\gamma_2}) \\
&= \left\{\gamma_1 + \sqrt{a^2 + b^2\gamma_1^2 + \frac{b^2}{1-b^2} (\operatorname{Im} z)^2} \lt \operatorname{Re} z \lt \gamma_2 - \sqrt{a^2 + b^2\gamma_2^2 + \frac{b^2}{1-b^2} (\operatorname{Im} z)^2}
\right\} \\
&\subseteq \rho(T+A).
\end{align*}
\begin{align*}
&(\gamma_1 + \mathrm{i}\mathrm{Hyp}_{\gamma_1}) \cap (\gamma_2 - \mathrm{i}\mathrm{Hyp}_{\gamma_2}) \\
&= \left\{\gamma_1 + \sqrt{a^2 + b^2\gamma_1^2 + \frac{b^2}{1-b^2} (\operatorname{Im} z)^2} \lt \operatorname{Re} z \lt \gamma_2 - \sqrt{a^2 + b^2\gamma_2^2 + \frac{b^2}{1-b^2} (\operatorname{Im} z)^2}
\right\} \\
&\subseteq \rho(T+A).
\end{align*}Proof. We write ![]() $\sigma(T) \subseteq \{\operatorname{Re} z \le \gamma_1 \} \cup \{\operatorname{Re} z \ge \gamma_2 \}$. We know that a sufficient condition for
$\sigma(T) \subseteq \{\operatorname{Re} z \le \gamma_1 \} \cup \{\operatorname{Re} z \ge \gamma_2 \}$. We know that a sufficient condition for ![]() $z\in \rho(T+A)$ is that
$z\in \rho(T+A)$ is that ![]() $\sup_{t\in\partial M} H_z(t) \lt 1$ for
$\sup_{t\in\partial M} H_z(t) \lt 1$ for ![]() $M = \{\operatorname{Re} z \le \gamma_2 \}$ and
$M = \{\operatorname{Re} z \le \gamma_2 \}$ and ![]() $M = \{\operatorname{Re} z \ge \gamma_1 \}$. The claim then follows as in Proposition 3.1. See Figure 6.
$M = \{\operatorname{Re} z \ge \gamma_1 \}$. The claim then follows as in Proposition 3.1. See Figure 6.

Figure 6. Illustration of Proposition 5.1 when ![]() $\sigma(T)\subseteq \mathbb{C}\setminus \{\gamma_{1}\le \operatorname{Re}(z) \le \gamma_{2} \}$. In the upper row we have the special case
$\sigma(T)\subseteq \mathbb{C}\setminus \{\gamma_{1}\le \operatorname{Re}(z) \le \gamma_{2} \}$. In the upper row we have the special case ![]() $\gamma_1 = -\gamma_2$. The dashed red lines show the boundaries of the corresponding hyperbolas. The spectrum of
$\gamma_1 = -\gamma_2$. The dashed red lines show the boundaries of the corresponding hyperbolas. The spectrum of ![]() $T+A$ is contained in coloured regions.
$T+A$ is contained in coloured regions.
Proposition 5.2. Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1 and assume that there are constants
$A$ be as in Assumption 1 and assume that there are constants ![]() $\gamma_j$ and
$\gamma_j$ and ![]() $\eta_j$
$\eta_j$ ![]() $(j=1, 2)$ such that
$(j=1, 2)$ such that
Then
Proof. We write ![]() $\sigma(T)$ as union of the half-planes
$\sigma(T)$ as union of the half-planes ![]() $\{\operatorname{Im} z \ge \eta_2 \},\, \{\operatorname{Im} z \le \eta_2 \},\, \{\operatorname{Re} z \le \gamma_1 \}$ and
$\{\operatorname{Im} z \ge \eta_2 \},\, \{\operatorname{Im} z \le \eta_2 \},\, \{\operatorname{Re} z \le \gamma_1 \}$ and ![]() $\{\operatorname{Re} z \ge \gamma_2 \}$. A sufficient condition for
$\{\operatorname{Re} z \ge \gamma_2 \}$. A sufficient condition for ![]() $z\in \rho(T+A)$ is that
$z\in \rho(T+A)$ is that ![]() $\sup_{t\in\partial M} H_z(t) \lt 1$ for all of the four half-planes
$\sup_{t\in\partial M} H_z(t) \lt 1$ for all of the four half-planes ![]() $M$. The claim then follows as in Proposition 3.1. See Figure 7.
$M$. The claim then follows as in Proposition 3.1. See Figure 7.

Figure 7. Illustration of Proposition 5.2 when ![]() $\sigma(T)\subseteq \mathbb{C}\setminus \{\gamma_{1}\le \operatorname{Re}(z) \le \gamma_{2},\ \eta_{1} \le \operatorname{Im}(z) \le \eta_{2} \}$. In the upper row we have the special case
$\sigma(T)\subseteq \mathbb{C}\setminus \{\gamma_{1}\le \operatorname{Re}(z) \le \gamma_{2},\ \eta_{1} \le \operatorname{Im}(z) \le \eta_{2} \}$. In the upper row we have the special case ![]() $\gamma_1 = -\gamma_2, \eta_1 = -\eta_2$. The dashed red lines show the boundaries of the corresponding hyperbolas. The white area is contained in
$\gamma_1 = -\gamma_2, \eta_1 = -\eta_2$. The dashed red lines show the boundaries of the corresponding hyperbolas. The white area is contained in ![]() $\rho(T+A)$.
$\rho(T+A)$.
Proposition 5.3. Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1 and assume that there is a constant
$A$ be as in Assumption 1 and assume that there is a constant ![]() $R \gt 0$ such that
$R \gt 0$ such that
If ![]() $r := R - \sqrt{a^2 + b^2 R^2} \gt 0$, then
$r := R - \sqrt{a^2 + b^2 R^2} \gt 0$, then ![]() $B_r(0)\subseteq\rho(T+A)$.
$B_r(0)\subseteq\rho(T+A)$.
Proof. Again we will use that ![]() $\sup_{t\in\sigma(T)} H_z(t) \lt 1$ is a sufficient condition for
$\sup_{t\in\sigma(T)} H_z(t) \lt 1$ is a sufficient condition for ![]() $z\in \rho(T+A)$. We estimate
$z\in \rho(T+A)$. We estimate
 \begin{equation*}
\sup_{t\in\sigma(T)} H_z(t)
\le \sup_{|t|\ge R} H_z(t)
= \max\left\{b^2, \sup_{|t|= R} H_z(t) \right\}.
\end{equation*}
\begin{equation*}
\sup_{t\in\sigma(T)} H_z(t)
\le \sup_{|t|\ge R} H_z(t)
= \max\left\{b^2, \sup_{|t|= R} H_z(t) \right\}.
\end{equation*} Note that  $\sup_{|t|= R} H_z(t)
= \sup_{|t|= R} \frac{a^2 + b^2|t|^2}{|z-t|^2}
= \sup_{|t|= R} \frac{a^2 + b^2R^2}{|z-t|^2}$. Clearly, the supremum is attained when
$\sup_{|t|= R} H_z(t)
= \sup_{|t|= R} \frac{a^2 + b^2|t|^2}{|z-t|^2}
= \sup_{|t|= R} \frac{a^2 + b^2R^2}{|z-t|^2}$. Clearly, the supremum is attained when ![]() $\arg t = \arg z$, so
$\arg t = \arg z$, so  $\sup_{|t|= R} H_z(t)
= \frac{a^2 + b^2R^2}{(R - |z|)^2}$. This is smaller than 1 if and only if
$\sup_{|t|= R} H_z(t)
= \frac{a^2 + b^2R^2}{(R - |z|)^2}$. This is smaller than 1 if and only if ![]() $|z| \lt R - \sqrt{a^2 + b^2 R^2} =: r$. Therefore, such
$|z| \lt R - \sqrt{a^2 + b^2 R^2} =: r$. Therefore, such ![]() $z$ belong to
$z$ belong to ![]() $\rho(T+A)$ by Proposition 2.1. See Figure 8.
$\rho(T+A)$ by Proposition 2.1. See Figure 8.

Figure 8. Illustration of Proposition 5.3. If ![]() $\sigma(T)\subseteq \mathbb{C}\setminus \{|z| \lt R\}$, then
$\sigma(T)\subseteq \mathbb{C}\setminus \{|z| \lt R\}$, then ![]() $\sigma(T+A)\subseteq \mathbb{C}\setminus \{|z| \lt r\}$ with
$\sigma(T+A)\subseteq \mathbb{C}\setminus \{|z| \lt r\}$ with ![]() $r = R - \sqrt{a^2 + b^2 R^2}$.
$r = R - \sqrt{a^2 + b^2 R^2}$.
In Figure 9 we show the spectral enclosures that can be obtained as in Theorem 4.6 when the sectors have different angles. Figure 10 shows the spectral enclosures if we have more than two sectors. In Figure 10, all sectors have the same angle and the same distance from the origin, however it is not difficult to adapt the method of the proof of Theorem 4.6 to situations with different angles or different distances from the origin.

Figure 9. Spectral inclusion for ![]() $T+A$ if
$T+A$ if ![]() $\sigma(T)\subseteq-S_{\theta_\alpha}(-\alpha)\cup S_{\theta_\beta}(\beta)$ with
$\sigma(T)\subseteq-S_{\theta_\alpha}(-\alpha)\cup S_{\theta_\beta}(\beta)$ with ![]() $\theta_\alpha\neq \theta_\beta$.
$\theta_\alpha\neq \theta_\beta$.

Figure 10. Spectral inclusion for ![]() $T+A$ if the
$T+A$ if the ![]() $\sigma(T)$ is contained in several sectors symmetrically distributed around
$\sigma(T)$ is contained in several sectors symmetrically distributed around ![]() $0$.
$0$.
5.1 Infinitely many gaps
In this subsection, we apply the results from ![]() $\S$ 3 to normal operators with infinitely many spectral gaps along the real axis. First we consider the case when the imaginary part of the spectrum of
$\S$ 3 to normal operators with infinitely many spectral gaps along the real axis. First we consider the case when the imaginary part of the spectrum of ![]() $T$ is bounded. The next theorem can be considered a generalisation of Theorem 3.4 to the case of infinitely many spectral free strips.
$T$ is bounded. The next theorem can be considered a generalisation of Theorem 3.4 to the case of infinitely many spectral free strips.
Theorem 5.4 Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1. As in Proposition 3.2 we assume that
$A$ be as in Assumption 1. As in Proposition 3.2 we assume that ![]() $\sigma(T)\subseteq \{z\in\mathbb{C}: \gamma_1\le \operatorname{Im} z \le \gamma_2\}$ for some
$\sigma(T)\subseteq \{z\in\mathbb{C}: \gamma_1\le \operatorname{Im} z \le \gamma_2\}$ for some ![]() $\gamma_1 \leq \gamma_2$. Let us set
$\gamma_1 \leq \gamma_2$. Let us set ![]() $\widetilde \gamma = \max\{|\gamma_1|,\, |\gamma_2|\}$. Assume in addition that there are unbounded sequences
$\widetilde \gamma = \max\{|\gamma_1|,\, |\gamma_2|\}$. Assume in addition that there are unbounded sequences ![]() $(\alpha_n)_n$ and
$(\alpha_n)_n$ and ![]() $(\beta_n)_n$ such that
$(\beta_n)_n$ such that ![]() $\alpha_n \lt \beta_n \le \alpha_{n+1}$ and
$\alpha_n \lt \beta_n \le \alpha_{n+1}$ and ![]() $\{z\in\mathbb{C} : \alpha_n \lt \operatorname{Re} z \lt \beta_n\}\subseteq\rho(T)$ for every
$\{z\in\mathbb{C} : \alpha_n \lt \operatorname{Re} z \lt \beta_n\}\subseteq\rho(T)$ for every ![]() $n$.
$n$.
(i) The resolvent set of the operator
 $T+A$ contains infinitely many strips parallel to the imaginary axis if
(5.1)
$T+A$ contains infinitely many strips parallel to the imaginary axis if
(5.1) \begin{equation}
\liminf_{n\to\infty}
\frac{\sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\alpha_n^2} + \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\beta_n^2} }{\beta_n-\alpha_n } \lt 1.
\end{equation}
\begin{equation}
\liminf_{n\to\infty}
\frac{\sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\alpha_n^2} + \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\beta_n^2} }{\beta_n-\alpha_n } \lt 1.
\end{equation}If
 $b=0$, then inequality (5.1) holds if and only if
$b=0$, then inequality (5.1) holds if and only if  $\limsup \beta_n - \alpha_n \gt 2a$; if
$\limsup \beta_n - \alpha_n \gt 2a$; if  $0 \lt b \lt 1$, then it holds if and only if
(5.2)
$0 \lt b \lt 1$, then it holds if and only if
(5.2) \begin{equation}
\limsup_{n\to\infty} \frac{\beta_n}{\alpha_n} \gt \frac{1+b}{1-b}.
\end{equation}
\begin{equation}
\limsup_{n\to\infty} \frac{\beta_n}{\alpha_n} \gt \frac{1+b}{1-b}.
\end{equation}(ii) At most finitely many spectral gaps of
 $T$ close if
(5.3)
$T$ close if
(5.3) \begin{equation}
\limsup_{n\to\infty}
\frac{\sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\alpha_n^2} + \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\beta_n^2} }{\beta_n-\alpha_n } \lt 1.
\end{equation}
\begin{equation}
\limsup_{n\to\infty}
\frac{\sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\alpha_n^2} + \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\beta_n^2} }{\beta_n-\alpha_n } \lt 1.
\end{equation}If
 $b=0$, then inequality (5.3) holds if and only if
$b=0$, then inequality (5.3) holds if and only if  $\liminf \beta_n - \alpha_n \gt 2a$; if
$\liminf \beta_n - \alpha_n \gt 2a$; if  $0 \lt b \lt 1$, then it holds if and only if
(5.4)
$0 \lt b \lt 1$, then it holds if and only if
(5.4) \begin{equation}
\liminf_{n\to\infty} \frac{\beta_n}{\alpha_n} \gt \frac{1+b}{1-b}.
\end{equation}
\begin{equation}
\liminf_{n\to\infty} \frac{\beta_n}{\alpha_n} \gt \frac{1+b}{1-b}.
\end{equation}
The theorem can easily be modified to the situation when ![]() $\alpha_n \lt \beta_n \le \alpha_{n+1}$ for
$\alpha_n \lt \beta_n \le \alpha_{n+1}$ for ![]() $n\in\mathbb{Z}$ or for
$n\in\mathbb{Z}$ or for ![]() $n\in -\mathbb{N}$.
$n\in -\mathbb{N}$.
Proof. Let  $\alpha_n' = \alpha_n + \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\alpha_n^2}$ and
$\alpha_n' = \alpha_n + \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\alpha_n^2}$ and  $\beta_n' = \beta_n - \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\beta_n^2}$. Theorem 3.4 guarantees that
$\beta_n' = \beta_n - \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\beta_n^2}$. Theorem 3.4 guarantees that ![]() $\{\alpha_n' \lt \operatorname{Re} z \lt \beta_n'\}\subseteq \rho(T+A)$. This strip is not empty if and only if
$\{\alpha_n' \lt \operatorname{Re} z \lt \beta_n'\}\subseteq \rho(T+A)$. This strip is not empty if and only if ![]() $\beta_n' \gt \alpha_n'$. This is the case if and only if
$\beta_n' \gt \alpha_n'$. This is the case if and only if
 \begin{align*}
\frac{\sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\alpha_n^2} + \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\beta_n^2} }{\beta_n-\alpha_n } \lt 1.
\end{align*}
\begin{align*}
\frac{\sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\alpha_n^2} + \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\beta_n^2} }{\beta_n-\alpha_n } \lt 1.
\end{align*}Therefore the first part of (i) and (ii) follows.
If ![]() $b=0$, then
$b=0$, then ![]() $\beta_n' \lt \alpha_n'$ if and only if
$\beta_n' \lt \alpha_n'$ if and only if ![]() $\beta_n-\alpha_n \gt 2a$. Therefore infinitely many spectral gaps remain if
$\beta_n-\alpha_n \gt 2a$. Therefore infinitely many spectral gaps remain if ![]() $\limsup_{n\to\infty} \beta_n-\alpha_n \gt 2a$ and at most finitely many gaps close if
$\limsup_{n\to\infty} \beta_n-\alpha_n \gt 2a$ and at most finitely many gaps close if ![]() $\liminf_{n\to\infty} \beta_n-\alpha_n \gt 2a$.
$\liminf_{n\to\infty} \beta_n-\alpha_n \gt 2a$.
Now let us assume that ![]() $b \gt 0$ and set
$b \gt 0$ and set  $L := \limsup_{n\to\infty} \frac{\beta_n}{\alpha_n}$. Note that
$L := \limsup_{n\to\infty} \frac{\beta_n}{\alpha_n}$. Note that ![]() $L\ge 1$. Then
$L\ge 1$. Then
 \begin{align*}
& \liminf_{n\to\infty}
\frac{\sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\alpha_n^2}
+ \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\beta_n^2} }{\beta_n-\alpha_n } \cr
&\quad = \liminf_{n\to\infty}
\frac{\sqrt{(a^2 + b^2 \widetilde \gamma^2)/\alpha_n^2 + b^2}
+ \sqrt{(a^2 + b^2 \widetilde \gamma^2)/\alpha_n^2 + b^2 \beta_n^2/\alpha_n^2} }{\frac{\beta_n}{\alpha_n} - 1 }
\cr
&\quad = \liminf_{n\to\infty}
\frac{b (\frac{\beta_n}{\alpha_n} + 1) }{\frac{\beta_n}{\alpha_n} - 1 }
= b \liminf_{n\to\infty}
\left( 1 + \frac{2 }{\frac{\beta_n}{\alpha_n} - 1 } \right)
= b\left( 1 + \frac{2 }{L - 1 } \right)
= \frac{ b( L+1) }{L - 1 }
\end{align*}
\begin{align*}
& \liminf_{n\to\infty}
\frac{\sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\alpha_n^2}
+ \sqrt{a^2 + b^2 \widetilde \gamma^2 + b^2\beta_n^2} }{\beta_n-\alpha_n } \cr
&\quad = \liminf_{n\to\infty}
\frac{\sqrt{(a^2 + b^2 \widetilde \gamma^2)/\alpha_n^2 + b^2}
+ \sqrt{(a^2 + b^2 \widetilde \gamma^2)/\alpha_n^2 + b^2 \beta_n^2/\alpha_n^2} }{\frac{\beta_n}{\alpha_n} - 1 }
\cr
&\quad = \liminf_{n\to\infty}
\frac{b (\frac{\beta_n}{\alpha_n} + 1) }{\frac{\beta_n}{\alpha_n} - 1 }
= b \liminf_{n\to\infty}
\left( 1 + \frac{2 }{\frac{\beta_n}{\alpha_n} - 1 } \right)
= b\left( 1 + \frac{2 }{L - 1 } \right)
= \frac{ b( L+1) }{L - 1 }
\end{align*} with the convention that the latter is ![]() $\infty$ if
$\infty$ if ![]() $L=1$. This is smaller than 1 if and only if (5.2) holds hence (i) is proved. The calculation for (ii) is analogous.
$L=1$. This is smaller than 1 if and only if (5.2) holds hence (i) is proved. The calculation for (ii) is analogous.
If in Theorem 5.4, we drop the assumption that the imaginary part of the spectrum of ![]() $T$ is bounded, we cannot expect that the resolvent set of
$T$ is bounded, we cannot expect that the resolvent set of ![]() $T+A$ contains any strip. The case of one such spectral free strip is dealt with in Proposition 5.1. There we saw that the area between two hyperbolas, which bend towards each other, is contained in the resolvent set of
$T+A$ contains any strip. The case of one such spectral free strip is dealt with in Proposition 5.1. There we saw that the area between two hyperbolas, which bend towards each other, is contained in the resolvent set of ![]() $T+A$. Although they touch for
$T+A$. Although they touch for ![]() $|\operatorname{Im} z|$ large enough, a neighbourhood of a real interval is contained in the resolvent set of
$|\operatorname{Im} z|$ large enough, a neighbourhood of a real interval is contained in the resolvent set of ![]() $T+A$. For infinitely many such strips, we obtain the following theorem.
$T+A$. For infinitely many such strips, we obtain the following theorem.
Theorem 5.5 Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 1 and assume that
$A$ be as in Assumption 1 and assume that  $b \lt \frac{1}{\sqrt{5}}$ where
$b \lt \frac{1}{\sqrt{5}}$ where ![]() $b$ is as in (1.1). In addition we assume that there are unbounded sequences
$b$ is as in (1.1). In addition we assume that there are unbounded sequences ![]() $(\alpha_n)_n$ and
$(\alpha_n)_n$ and ![]() $(\beta_n)_n$ such that
$(\beta_n)_n$ such that ![]() $\alpha_n \lt \beta_n \le \alpha_{n+1}$ and
$\alpha_n \lt \beta_n \le \alpha_{n+1}$ and ![]() $\{z\in\mathbb{C} : \alpha_n \lt \operatorname{Re} z \lt \beta_n\}\subseteq\rho(T)$ for every
$\{z\in\mathbb{C} : \alpha_n \lt \operatorname{Re} z \lt \beta_n\}\subseteq\rho(T)$ for every ![]() $n$.
$n$.
(i) The resolvent set of the operator
 $T+A$ contains infinitely many rectangular regions around real intervals if
(5.5)
$T+A$ contains infinitely many rectangular regions around real intervals if
(5.5) \begin{equation}
\liminf_{n\to\infty}
\frac{2\sqrt{\frac{a^2 + b^2\beta_n^2 }{1-b^2}} }{\beta_n-\alpha_n } \lt 1.
\end{equation}
\begin{equation}
\liminf_{n\to\infty}
\frac{2\sqrt{\frac{a^2 + b^2\beta_n^2 }{1-b^2}} }{\beta_n-\alpha_n } \lt 1.
\end{equation}If
 $b=0$, then inequality (5.5) holds if and only if
$b=0$, then inequality (5.5) holds if and only if  $\limsup \beta_n - \alpha_n \gt 2a$; if
$\limsup \beta_n - \alpha_n \gt 2a$; if  $0 \lt b \lt \frac{1}{\sqrt 5} $, then it holds if and only if
(5.6)
$0 \lt b \lt \frac{1}{\sqrt 5} $, then it holds if and only if
(5.6) \begin{equation}
\limsup_{n\to\infty} \frac{\beta_n}{\alpha_n} \gt 1 + \frac{2b }{\sqrt{1-b^2} - 2b}.
\end{equation}
\begin{equation}
\limsup_{n\to\infty} \frac{\beta_n}{\alpha_n} \gt 1 + \frac{2b }{\sqrt{1-b^2} - 2b}.
\end{equation}(ii) At most finitely many spectral gaps of
 $T$ disappear completely if
(5.7)
$T$ disappear completely if
(5.7) \begin{equation}
\limsup_{n\to\infty}
\frac{2\sqrt{\frac{a^2 + b^2\beta_n^2 }{1-b^2}} }{\beta_n-\alpha_n } \lt 1.
\end{equation}
\begin{equation}
\limsup_{n\to\infty}
\frac{2\sqrt{\frac{a^2 + b^2\beta_n^2 }{1-b^2}} }{\beta_n-\alpha_n } \lt 1.
\end{equation}If
 $b=0$, then inequality (5.7) holds if and only if
$b=0$, then inequality (5.7) holds if and only if  $\liminf \beta_n - \alpha_n \gt 2a$; if
$\liminf \beta_n - \alpha_n \gt 2a$; if  $0 \lt b \lt \frac{1}{\sqrt 5} $, then it holds if and only if
(5.8)
$0 \lt b \lt \frac{1}{\sqrt 5} $, then it holds if and only if
(5.8) \begin{equation}
\liminf_{n\to\infty} \frac{\beta_n}{\alpha_n} \gt 1 + \frac{2b }{\sqrt{1-b^2} - 2b}.
\end{equation}
\begin{equation}
\liminf_{n\to\infty} \frac{\beta_n}{\alpha_n} \gt 1 + \frac{2b }{\sqrt{1-b^2} - 2b}.
\end{equation}
See Figure 11.

Figure 11. Illustration of Theorem 5.5 when ![]() $\sigma(T)\subseteq \bigcup_{n\in\mathbb{N}} \{\beta_{n}\le \operatorname{Re}(z) \le \alpha_{n+1} \}$. The blue areas contain the spectrum of
$\sigma(T)\subseteq \bigcup_{n\in\mathbb{N}} \{\beta_{n}\le \operatorname{Re}(z) \le \alpha_{n+1} \}$. The blue areas contain the spectrum of ![]() $T$, the shaded areas are enclosures for the spectrum of
$T$, the shaded areas are enclosures for the spectrum of ![]() $T+A$.
$T+A$.
The theorem can easily be modified to the situation when ![]() $\alpha_n \lt \beta_n \le \alpha_{n+1}$ for
$\alpha_n \lt \beta_n \le \alpha_{n+1}$ for ![]() $n\in\mathbb{Z}$ or for
$n\in\mathbb{Z}$ or for ![]() $n\in -\mathbb{N}$.
$n\in -\mathbb{N}$.
Proof. Let  $\alpha_n' = \alpha_n + \sqrt{\frac{a^2 + b^2\beta_n^2 }{1-b^2}}$,
$\alpha_n' = \alpha_n + \sqrt{\frac{a^2 + b^2\beta_n^2 }{1-b^2}}$,  $\beta_n' = \beta_n - \sqrt{\frac{a^2 + b^2\beta_n^2 }{1-b^2}}$ and
$\beta_n' = \beta_n - \sqrt{\frac{a^2 + b^2\beta_n^2 }{1-b^2}}$ and
 \begin{align*}
I_n &:=
\left\{x\in\mathbb{R} :
\alpha_n + \sqrt{\frac{a^2 + b^2\beta_n^2}{1-b^2} + \frac{b^2}{1-b^2} (\operatorname{Im} z)^2} \lt x \lt \beta_n \right.\cr
&\qquad\qquad\qquad\qquad\qquad \left.- \sqrt{\frac{a^2 + b^2\beta_n^2}{1-b^2} + \frac{b^2}{1-b^2} (\operatorname{Im} z)^2}
\right\}.
\end{align*}
\begin{align*}
I_n &:=
\left\{x\in\mathbb{R} :
\alpha_n + \sqrt{\frac{a^2 + b^2\beta_n^2}{1-b^2} + \frac{b^2}{1-b^2} (\operatorname{Im} z)^2} \lt x \lt \beta_n \right.\cr
&\qquad\qquad\qquad\qquad\qquad \left.- \sqrt{\frac{a^2 + b^2\beta_n^2}{1-b^2} + \frac{b^2}{1-b^2} (\operatorname{Im} z)^2}
\right\}.
\end{align*} Note that for ![]() $n$ large enough,
$n$ large enough, ![]() $0\; \lt \;\alpha_n\; \lt \;\beta_n$, therefore Proposition 5.1 guarantees that an open complex neighourhood of
$0\; \lt \;\alpha_n\; \lt \;\beta_n$, therefore Proposition 5.1 guarantees that an open complex neighourhood of ![]() $I_n$ is contained in
$I_n$ is contained in ![]() $\rho(T+A)$ for every
$\rho(T+A)$ for every ![]() $n$. Clearly,
$n$. Clearly, ![]() $I_n$ is nonempty if and only if
$I_n$ is nonempty if and only if ![]() $\alpha_n' \lt \beta_n'$ and in this case, for every
$\alpha_n' \lt \beta_n'$ and in this case, for every ![]() $\alpha_n' \lt \alpha_n'' \lt \beta_n'' \lt \beta_n'$ we can find
$\alpha_n' \lt \alpha_n'' \lt \beta_n'' \lt \beta_n'$ we can find ![]() $\epsilon_n \gt 0$ such that
$\epsilon_n \gt 0$ such that ![]() $\{z\in\mathbb{C} : \alpha_n'' \lt \operatorname{Re} z \lt \beta_n'',\ -\epsilon_n \lt \operatorname{Im} z \lt \epsilon_n \}\subseteq\rho(T+A)$. It remains to check for how many
$\{z\in\mathbb{C} : \alpha_n'' \lt \operatorname{Re} z \lt \beta_n'',\ -\epsilon_n \lt \operatorname{Im} z \lt \epsilon_n \}\subseteq\rho(T+A)$. It remains to check for how many ![]() $n$ the inequality
$n$ the inequality ![]() $\alpha_n' \lt \beta_n'$ holds. This can be done as in Theorem 5.4. For the proof that (5.5) and (5.6) are equivalent, we set
$\alpha_n' \lt \beta_n'$ holds. This can be done as in Theorem 5.4. For the proof that (5.5) and (5.6) are equivalent, we set  $L := \limsup_{n\to\infty} \frac{\beta_n}{\alpha_n}$. Note that
$L := \limsup_{n\to\infty} \frac{\beta_n}{\alpha_n}$. Note that ![]() $L\ge 1$. If
$L\ge 1$. If ![]() $b=0$, then (5.5) is equivalent to
$b=0$, then (5.5) is equivalent to ![]() $\limsup (\beta_n - \alpha_n) \gt 2a$. If
$\limsup (\beta_n - \alpha_n) \gt 2a$. If  $0 \lt b \lt \frac{1}{\sqrt{2}}$, then
$0 \lt b \lt \frac{1}{\sqrt{2}}$, then
 \begin{align*}
\liminf_{n\to\infty}
\frac{2 \sqrt{\frac{a^2 + b^2\beta_n^2 }{1-b^2}} }{\beta_n-\alpha_n }
&= \liminf_{n\to\infty} \frac{2 \sqrt{a^2 + b^2\beta_n^2 } }{\sqrt{1-b^2} (\beta_n-\alpha_n) }
= \liminf_{n\to\infty} \frac{2 \sqrt{a^2/\alpha_n^2 + b^2\beta_n^2/\alpha_n^2 } }{\sqrt{1-b^2} (\beta_n/\alpha_n - 1) }
\\
&= \liminf_{n\to\infty} \frac{b }{\sqrt{1-b^2} } \cdot \frac{2\beta_n/\alpha_n }{\beta_n/\alpha_n - 1 }
= \frac{b }{\sqrt{1-b^2} } \cdot \frac{2L }{L - 1 } .
\end{align*}
\begin{align*}
\liminf_{n\to\infty}
\frac{2 \sqrt{\frac{a^2 + b^2\beta_n^2 }{1-b^2}} }{\beta_n-\alpha_n }
&= \liminf_{n\to\infty} \frac{2 \sqrt{a^2 + b^2\beta_n^2 } }{\sqrt{1-b^2} (\beta_n-\alpha_n) }
= \liminf_{n\to\infty} \frac{2 \sqrt{a^2/\alpha_n^2 + b^2\beta_n^2/\alpha_n^2 } }{\sqrt{1-b^2} (\beta_n/\alpha_n - 1) }
\\
&= \liminf_{n\to\infty} \frac{b }{\sqrt{1-b^2} } \cdot \frac{2\beta_n/\alpha_n }{\beta_n/\alpha_n - 1 }
= \frac{b }{\sqrt{1-b^2} } \cdot \frac{2L }{L - 1 } .
\end{align*} Note that this is smaller than 1 if and only if ![]() $L( \sqrt{1-b^2} - 2b) \gt \sqrt{1-b^2}$. By assumption,
$L( \sqrt{1-b^2} - 2b) \gt \sqrt{1-b^2}$. By assumption,  $b \lt \frac{1}{\sqrt{5}}$, so the term in brackets on the left hand side is positive and we have that (5.5) holds if and only if (5.6) holds. The equivalence of (5.7) and (5.8) is shown analogously.
$b \lt \frac{1}{\sqrt{5}}$, so the term in brackets on the left hand side is positive and we have that (5.5) holds if and only if (5.6) holds. The equivalence of (5.7) and (5.8) is shown analogously.
Observe that in Theorem 5.4 we assumed that the imaginary part of ![]() $\sigma(T)\cap \{\operatorname{Re} z \ge \alpha_1\}$ is bounded whereas in Theorem 5.5 we had no such assumption. As an intermediate situation we could assume that the “height” of the boxes that contain the spectrum of
$\sigma(T)\cap \{\operatorname{Re} z \ge \alpha_1\}$ is bounded whereas in Theorem 5.5 we had no such assumption. As an intermediate situation we could assume that the “height” of the boxes that contain the spectrum of ![]() $T$ is increasing linearly. For instance, if
$T$ is increasing linearly. For instance, if
 \begin{equation*}
\sigma(T) \subseteq \bigcup_{n\in\mathbb{Z}} \{\alpha_n \lt \operatorname{Re} z \lt \beta_{n}\} \cap (-S_{\theta}(0)\cup S_{\theta}(0)),
\end{equation*}
\begin{equation*}
\sigma(T) \subseteq \bigcup_{n\in\mathbb{Z}} \{\alpha_n \lt \operatorname{Re} z \lt \beta_{n}\} \cap (-S_{\theta}(0)\cup S_{\theta}(0)),
\end{equation*}then we can combine the results from Theorem 5.4 with those from Theorem 4.6 to obtain spectral inclusions.
6.  $p$-subordinate perturbations
$p$-subordinate perturbations
In this section, we consider ![]() $p$-subordinate perturbations of a normal operator
$p$-subordinate perturbations of a normal operator ![]() $T$. In our first theorem we assume that
$T$. In our first theorem we assume that ![]() $T$ has spectrum as in Theorem 3.4, but the perturbation
$T$ has spectrum as in Theorem 3.4, but the perturbation ![]() $A$ is now assumed to be
$A$ is now assumed to be ![]() $p$-subordinate.
$p$-subordinate.
Theorem 6.1 Let ![]() $T$ and
$T$ and ![]() $A$ be as in Assumption 2. That is,
$A$ be as in Assumption 2. That is, ![]() $T$ is a normal operator in a Hilbert space
$T$ is a normal operator in a Hilbert space ![]() $H$,
$H$, ![]() $A$ is
$A$ is ![]() $p$-subordinate to
$p$-subordinate to ![]() $T$ with
$T$ with ![]() $0\leq p\leq 1$ and
$0\leq p\leq 1$ and ![]() $c \geq 0$ as in (1.2). We assume that there exist
$c \geq 0$ as in (1.2). We assume that there exist ![]() $\alpha_T \lt \beta_T$ such that
$\alpha_T \lt \beta_T$ such that ![]() $(\alpha_{T},\beta_{T})+\mathrm{i}\mathbb{R} \subseteq \rho(T)$ and that
$(\alpha_{T},\beta_{T})+\mathrm{i}\mathbb{R} \subseteq \rho(T)$ and that ![]() $\operatorname{Im}\sigma(T)\subseteq [-\gamma_T,\gamma_T]$ for some
$\operatorname{Im}\sigma(T)\subseteq [-\gamma_T,\gamma_T]$ for some ![]() $\gamma_T\geq 0$. If
$\gamma_T\geq 0$. If
then the resolvent set of ![]() $T+A$ contains a strip parallel to the imaginary axis; more precisely,
$T+A$ contains a strip parallel to the imaginary axis; more precisely,
 \begin{align}
\{z\in\mathbb{C}: \alpha'_{T,p} \lt \operatorname{Re} z \lt \beta'_{T,p} \} \subseteq \rho(T+A)
\end{align}
\begin{align}
\{z\in\mathbb{C}: \alpha'_{T,p} \lt \operatorname{Re} z \lt \beta'_{T,p} \} \subseteq \rho(T+A)
\end{align}with
 \begin{align}
\alpha'_{T,p}:=\alpha_{T}+c\cdot\max\left\{|\alpha_T+\mathrm{i}\gamma_T|^p,|\beta_T+\mathrm{i}\gamma_T|^p\right\},
\end{align}
\begin{align}
\alpha'_{T,p}:=\alpha_{T}+c\cdot\max\left\{|\alpha_T+\mathrm{i}\gamma_T|^p,|\beta_T+\mathrm{i}\gamma_T|^p\right\},
\end{align} \begin{align}
\beta'_{T,p}:= \beta_T -c\cdot\max\left\{|\alpha_T+\mathrm{i}\gamma_T|^p,|\beta_T+\mathrm{i}\gamma_T|^p\right\}.
\end{align}
\begin{align}
\beta'_{T,p}:= \beta_T -c\cdot\max\left\{|\alpha_T+\mathrm{i}\gamma_T|^p,|\beta_T+\mathrm{i}\gamma_T|^p\right\}.
\end{align}Proof. Let ![]() $z\in \mathbb{C}$ with
$z\in \mathbb{C}$ with ![]() $ \alpha_{T} \lt \operatorname{Re} z \lt \beta_{T}$. We set
$ \alpha_{T} \lt \operatorname{Re} z \lt \beta_{T}$. We set ![]() $\mu = \operatorname{Re} z$ and
$\mu = \operatorname{Re} z$ and ![]() $\nu=\operatorname{Im} z$. Then
$\nu=\operatorname{Im} z$. Then ![]() $z\in \rho(T)$ and
$z\in \rho(T)$ and
 \begin{equation*}
\|(T-z)^{-1}\|=\frac{1}{\operatorname{dist} (z,\sigma (T))}\leq \max\left\{\frac{1}{\mu-\alpha_T}, \frac{1}{\beta_T-\mu}\right\}.
\end{equation*}
\begin{equation*}
\|(T-z)^{-1}\|=\frac{1}{\operatorname{dist} (z,\sigma (T))}\leq \max\left\{\frac{1}{\mu-\alpha_T}, \frac{1}{\beta_T-\mu}\right\}.
\end{equation*} If we set ![]() $\tau =\operatorname{Re} t$ and
$\tau =\operatorname{Re} t$ and ![]() $\sigma = \operatorname{Im} t$ for
$\sigma = \operatorname{Im} t$ for ![]() $t\in\sigma(T)$, then we obtain
$t\in\sigma(T)$, then we obtain
 \begin{align*}
\|T(T-z)^{-1}\|^2
&= \sup_{t\in\sigma(T)} \frac{|t|^2}{|t-z|^2}
=\sup_{\tau + \mathrm{i}\sigma \in\sigma(T)} \frac{\tau^2+\sigma^2}{(\tau-\mu)^2+(\sigma-\nu)^2}
\leq \sup_{\tau + \mathrm{i}\sigma \in\sigma(T)} \frac{\tau^2+\gamma_T^2}{(\tau-\mu)^2}
\\
& \le \sup_{\tau\in\mathbb{R}\setminus\ (\alpha_T,\beta_T)} \frac{\tau^2+\gamma_T^2}{(\tau-\mu)^2}
= \max \left\{\frac{\alpha_T^2+\gamma_T^2}{(\alpha_T-\mu)^2},\, \frac{\beta_T^2+\gamma_T^2}{(\beta_T-\mu)^2} \right\}
\end{align*}
\begin{align*}
\|T(T-z)^{-1}\|^2
&= \sup_{t\in\sigma(T)} \frac{|t|^2}{|t-z|^2}
=\sup_{\tau + \mathrm{i}\sigma \in\sigma(T)} \frac{\tau^2+\sigma^2}{(\tau-\mu)^2+(\sigma-\nu)^2}
\leq \sup_{\tau + \mathrm{i}\sigma \in\sigma(T)} \frac{\tau^2+\gamma_T^2}{(\tau-\mu)^2}
\\
& \le \sup_{\tau\in\mathbb{R}\setminus\ (\alpha_T,\beta_T)} \frac{\tau^2+\gamma_T^2}{(\tau-\mu)^2}
= \max \left\{\frac{\alpha_T^2+\gamma_T^2}{(\alpha_T-\mu)^2},\, \frac{\beta_T^2+\gamma_T^2}{(\beta_T-\mu)^2} \right\}
\end{align*} where the last equality is a straightforward calculation. Therefore, if ![]() $\alpha_{T,p}' \lt \operatorname{Re} z \lt \beta_{T,p}'$, then
$\alpha_{T,p}' \lt \operatorname{Re} z \lt \beta_{T,p}'$, then
 \begin{align*}
\|A(T-z)^{-1}\|&\leq c\|(T-z)^{-1}\|^{1-p}\|T(T-z)^{-1}\|^{p}\\
&\leq c\cdot
\max\left\{\frac{1}{(\mu-\alpha_T)^{1-p}}, \frac{1}{(\beta_T-\mu)^{1-p}}\right\}
\max\left\{\frac{|\alpha_T+\mathrm{i}\gamma_T|^p}{(\mu-\alpha_T)^p},\ \frac{|\beta_T+\mathrm{i}\gamma_T|^p}{(\beta_T-\mu)^p} \right\}
\\
&\leq c\cdot
\max\left\{\frac{1}{\mu-\alpha_T}, \frac{1}{\beta_T-\mu}\right\}
\max\left\{|\alpha_T+\mathrm{i}\gamma_T|^p,\ |\beta_T+\mathrm{i}\gamma_T|^p \right\}
\\
& \lt c\cdot
\max\left\{\frac{1}{\alpha_{T,p}'-\alpha_T}, \frac{1}{\beta_T-\beta_{T,p}'}\right\}
\max\left\{|\alpha_T+\mathrm{i}\gamma_T|^p,\ |\beta_T+\mathrm{i}\gamma_T|^p \right\}
= 1
\end{align*}
\begin{align*}
\|A(T-z)^{-1}\|&\leq c\|(T-z)^{-1}\|^{1-p}\|T(T-z)^{-1}\|^{p}\\
&\leq c\cdot
\max\left\{\frac{1}{(\mu-\alpha_T)^{1-p}}, \frac{1}{(\beta_T-\mu)^{1-p}}\right\}
\max\left\{\frac{|\alpha_T+\mathrm{i}\gamma_T|^p}{(\mu-\alpha_T)^p},\ \frac{|\beta_T+\mathrm{i}\gamma_T|^p}{(\beta_T-\mu)^p} \right\}
\\
&\leq c\cdot
\max\left\{\frac{1}{\mu-\alpha_T}, \frac{1}{\beta_T-\mu}\right\}
\max\left\{|\alpha_T+\mathrm{i}\gamma_T|^p,\ |\beta_T+\mathrm{i}\gamma_T|^p \right\}
\\
& \lt c\cdot
\max\left\{\frac{1}{\alpha_{T,p}'-\alpha_T}, \frac{1}{\beta_T-\beta_{T,p}'}\right\}
\max\left\{|\alpha_T+\mathrm{i}\gamma_T|^p,\ |\beta_T+\mathrm{i}\gamma_T|^p \right\}
= 1
\end{align*}The theorem can be generalised to the case of a (bi)sectorial normal operator which will be discussed in detail elsewhere.
For ![]() $\lambda\in \mathbb{R}$ we define the set, see Figure 12,
$\lambda\in \mathbb{R}$ we define the set, see Figure 12,
 \begin{equation*}
\Pi(\lambda) := \left\{z\in \mathbb{C}: \operatorname{Re} z \geq \lambda, \ | \operatorname{Im} z | \leq (\operatorname{Re} z - \lambda)^2 \right\}.
\end{equation*}
\begin{equation*}
\Pi(\lambda) := \left\{z\in \mathbb{C}: \operatorname{Re} z \geq \lambda, \ | \operatorname{Im} z | \leq (\operatorname{Re} z - \lambda)^2 \right\}.
\end{equation*}Proposition 6.2. Let ![]() $T$ be a normal operator in a Hilbert space
$T$ be a normal operator in a Hilbert space ![]() $H$ with
$H$ with
for some ![]() $\alpha_T \lt \beta_T$. Let
$\alpha_T \lt \beta_T$. Let ![]() $A$ be
$A$ be ![]() $p$-subordinate to
$p$-subordinate to ![]() $T$ for some
$T$ for some ![]() $0\leq p \lt 1/2$ and let
$0\leq p \lt 1/2$ and let ![]() $c \gt 0$ such that (1.2) holds. Let
$c \gt 0$ such that (1.2) holds. Let ![]() $\zeta_T:= \max\{|\beta_T|,|\alpha_T|\}$ and let
$\zeta_T:= \max\{|\beta_T|,|\alpha_T|\}$ and let ![]() $\nu_0\geq 1/2$ such that
$\nu_0\geq 1/2$ such that
 \begin{equation*}\frac{c\left(\sqrt{\widehat{\nu}-\frac{1}{4}}+\sqrt{\zeta_T^2+\widehat{\nu}^2}\right)^p}{\sqrt{\widehat{\nu}-\frac{1}{4}} } \lt 1~~~ \mbox{for } \widehat{\nu} \gt \nu_0.\end{equation*}
\begin{equation*}\frac{c\left(\sqrt{\widehat{\nu}-\frac{1}{4}}+\sqrt{\zeta_T^2+\widehat{\nu}^2}\right)^p}{\sqrt{\widehat{\nu}-\frac{1}{4}} } \lt 1~~~ \mbox{for } \widehat{\nu} \gt \nu_0.\end{equation*} If there exists ![]() $M \gt 0$ such that
$M \gt 0$ such that
 \begin{align}
\frac{c\left(M+\sqrt{\zeta_T^2+\nu_0^2}\right)^p}{M} \lt 1 ~\mbox{and }~ 2M \lt \beta_{T}-\alpha_{T},
\end{align}
\begin{align}
\frac{c\left(M+\sqrt{\zeta_T^2+\nu_0^2}\right)^p}{M} \lt 1 ~\mbox{and }~ 2M \lt \beta_{T}-\alpha_{T},
\end{align} then the resolvent set of ![]() $T+A$ contains a strip parallel to the imaginary axis; more precisely,
$T+A$ contains a strip parallel to the imaginary axis; more precisely,
 \begin{align}
\{z\in\mathbb{C}: \alpha_{T+A}^{(p)} \lt \operatorname{Re} z \lt \beta_{T+A}^{(p)}\} \subseteq \rho(T+A)
\end{align}
\begin{align}
\{z\in\mathbb{C}: \alpha_{T+A}^{(p)} \lt \operatorname{Re} z \lt \beta_{T+A}^{(p)}\} \subseteq \rho(T+A)
\end{align}with
 \begin{align}
\alpha_{T+A}^{(p)}:=\alpha_{T}+M,~~~~ \beta_{T+A}^{(p)}:= \beta_T-M.
\end{align}
\begin{align}
\alpha_{T+A}^{(p)}:=\alpha_{T}+M,~~~~ \beta_{T+A}^{(p)}:= \beta_T-M.
\end{align}Proof. Let ![]() $z\in \rho(T)$ with
$z\in \rho(T)$ with ![]() $\mu=\operatorname{Re} z$ and
$\mu=\operatorname{Re} z$ and ![]() $\nu=\operatorname{Im} z$ and let
$\nu=\operatorname{Im} z$ and let ![]() $d(z) :=\operatorname{dist}(z,\sigma(T)$. Since
$d(z) :=\operatorname{dist}(z,\sigma(T)$. Since ![]() $T$ is normal, we have that
$T$ is normal, we have that
 \begin{equation*}
\|(T-z)^{-1}\| = \frac{1}{d(z)},
\qquad
\|T(T-z)^{-1}\| = \|I+z(T-z)^{-1}\| \leq 1+\frac{|z|}{d(z)}.
\end{equation*}
\begin{equation*}
\|(T-z)^{-1}\| = \frac{1}{d(z)},
\qquad
\|T(T-z)^{-1}\| = \|I+z(T-z)^{-1}\| \leq 1+\frac{|z|}{d(z)}.
\end{equation*}Together with
we obtain for  $\alpha_{T+A}^{(p)} \lt \operatorname{Re} z \lt \beta_{T+A}^{(p)}$
$\alpha_{T+A}^{(p)} \lt \operatorname{Re} z \lt \beta_{T+A}^{(p)}$
 \begin{equation*}\begin{aligned}
\|A(T-z)^{-1}\|
\leq c\|(T-z)^{-1}\|^{1-p}\|T(T-z)^{-1}\|^{p}
\leq c\frac{1}{d(z)^{1-p}} \left(1+\frac{|z|}{d(z)}\right)^p \\
\leq
\begin{cases}
\frac{c\left(1+\frac{|z|}{\sqrt{\min\{\mu-\alpha_T, \beta_T-\mu\}^2+\nu^2}}\right)^p}{\left(\sqrt{\min\{\mu-\alpha_T, \beta_T-\mu\}^2+\nu^2}\right)^{1-p}},
&\text{if } |\nu| \leq 1/2,
\\[4ex]
\frac{c\left(1+\frac{|z|}{\sqrt{\min\{\mu-\alpha_T, \beta_T-\mu\}^2+|\nu|-\frac{1}{4}} }\right)^p}{\left(\sqrt{\min\{\mu-\alpha_T, \beta_T-\mu\}^2+|\nu|-\frac{1}{4}}\right)^{1-p}},
&\text{if } |\nu| \gt 1/2
\end{cases}
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}
\|A(T-z)^{-1}\|
\leq c\|(T-z)^{-1}\|^{1-p}\|T(T-z)^{-1}\|^{p}
\leq c\frac{1}{d(z)^{1-p}} \left(1+\frac{|z|}{d(z)}\right)^p \\
\leq
\begin{cases}
\frac{c\left(1+\frac{|z|}{\sqrt{\min\{\mu-\alpha_T, \beta_T-\mu\}^2+\nu^2}}\right)^p}{\left(\sqrt{\min\{\mu-\alpha_T, \beta_T-\mu\}^2+\nu^2}\right)^{1-p}},
&\text{if } |\nu| \leq 1/2,
\\[4ex]
\frac{c\left(1+\frac{|z|}{\sqrt{\min\{\mu-\alpha_T, \beta_T-\mu\}^2+|\nu|-\frac{1}{4}} }\right)^p}{\left(\sqrt{\min\{\mu-\alpha_T, \beta_T-\mu\}^2+|\nu|-\frac{1}{4}}\right)^{1-p}},
&\text{if } |\nu| \gt 1/2
\end{cases}
\end{aligned}
\end{equation*} where in the last step we used Lemma A.8. If ![]() $|\nu|\leq \nu_0$, then
$|\nu|\leq \nu_0$, then
 \begin{align*}
\|A(T-z)^{-1}\|&\leq c\left(1+\frac{|z|}{\min\{\mu-\alpha_T, \beta_T-\mu\}}\right)^p\frac{1}{\left(\min\{\mu-\alpha_T, \beta_T-\mu\}\right)^{1-p}}\\
&\leq c\left(1+\frac{\sqrt{\zeta_T^2+\nu_0^2}}{M}\right)^p\frac{1}{M^{1-p}}=\frac{c\left(M+\sqrt{\zeta_T^2+\nu_0^2}\right)^p}{M} \lt 1
\end{align*}
\begin{align*}
\|A(T-z)^{-1}\|&\leq c\left(1+\frac{|z|}{\min\{\mu-\alpha_T, \beta_T-\mu\}}\right)^p\frac{1}{\left(\min\{\mu-\alpha_T, \beta_T-\mu\}\right)^{1-p}}\\
&\leq c\left(1+\frac{\sqrt{\zeta_T^2+\nu_0^2}}{M}\right)^p\frac{1}{M^{1-p}}=\frac{c\left(M+\sqrt{\zeta_T^2+\nu_0^2}\right)^p}{M} \lt 1
\end{align*} whereas if ![]() $|\nu| \gt \nu_0\geq 1/2$, then
$|\nu| \gt \nu_0\geq 1/2$, then
 \begin{align*}
\|A(T-z)^{-1}\|&\leq c\left(1+\frac{|z|}{\sqrt{|\nu|-\frac{1}{4}} }\right)^p\frac{1}{\left(\sqrt{|\nu|-\frac{1}{4}}\right)^{1-p}}= \frac{c\left(\sqrt{|\nu|-\frac{1}{4}}+|z|\right)^p}{\sqrt{|\nu|-\frac{1}{4}} }\\
&\leq \frac{c\left(\sqrt{|\nu|-\frac{1}{4}}+\sqrt{\zeta_T^2+\nu^2}\right)^p}{\sqrt{|\nu|-\frac{1}{4}} } \lt 1
\end{align*}
\begin{align*}
\|A(T-z)^{-1}\|&\leq c\left(1+\frac{|z|}{\sqrt{|\nu|-\frac{1}{4}} }\right)^p\frac{1}{\left(\sqrt{|\nu|-\frac{1}{4}}\right)^{1-p}}= \frac{c\left(\sqrt{|\nu|-\frac{1}{4}}+|z|\right)^p}{\sqrt{|\nu|-\frac{1}{4}} }\\
&\leq \frac{c\left(\sqrt{|\nu|-\frac{1}{4}}+\sqrt{\zeta_T^2+\nu^2}\right)^p}{\sqrt{|\nu|-\frac{1}{4}} } \lt 1
\end{align*} by (6.5). We conclude that, in any case, ![]() $T+A-z$ is bijective and so
$T+A-z$ is bijective and so ![]() $z\in \rho(T+A)$.
$z\in \rho(T+A)$.

Figure 12. The set ![]() $\Pi (\lambda) = \left\{z\in \mathbb{C}: \operatorname{Re} z \geq \lambda, \ | \operatorname{Im} z | \leq (\operatorname{Re} z - \lambda)^2 \right\}$.
$\Pi (\lambda) = \left\{z\in \mathbb{C}: \operatorname{Re} z \geq \lambda, \ | \operatorname{Im} z | \leq (\operatorname{Re} z - \lambda)^2 \right\}$.
7. Applications
7.1. Schrödinger operators on a non-selfadjoint quantum star graph
In this last section, we apply some of the above results to a non-selfadjoint Schrödinger operator on a quantum star graph ![]() $\Gamma$ with a non-selfadjoint Robin condition at the central vertex and Dirichlet boundary conditions on the set of outer vertices. Set
$\Gamma$ with a non-selfadjoint Robin condition at the central vertex and Dirichlet boundary conditions on the set of outer vertices. Set ![]() $\mathcal{J}=\{1,2,\ldots,n\}$. Our Hilbert space is
$\mathcal{J}=\{1,2,\ldots,n\}$. Our Hilbert space is  $\mathcal{H}=\bigoplus_{j=1}^n L^2(0,a_j; \mathbb{C})$, with
$\mathcal{H}=\bigoplus_{j=1}^n L^2(0,a_j; \mathbb{C})$, with ![]() $a_j \gt 0$ for
$a_j \gt 0$ for ![]() $j=1,\ldots,n$, and for
$j=1,\ldots,n$, and for ![]() $c\in \mathbb{C}\cup \{\infty\}$, we define the operator
$c\in \mathbb{C}\cup \{\infty\}$, we define the operator ![]() $L_c$ by
$L_c$ by
 \begin{equation*}
D(L_c):= \left\{\psi=(\psi_j)_{j=1}^n\in \bigoplus_{j=1}^n H^2(0,a_j;\mathbb{C}):
\begin{array}{ll}
\psi_j(a_j)=0,\qquad &j \in \mathcal{J}\\
\psi_j(0)=\psi_i(0),\qquad &i,j\in\mathcal{J}\\
\sum_{j\in\mathcal{J}} \big(\psi_j(0)+ c\psi_j'(0)\big)=0
\end{array}
\right\}
\end{equation*}
\begin{equation*}
D(L_c):= \left\{\psi=(\psi_j)_{j=1}^n\in \bigoplus_{j=1}^n H^2(0,a_j;\mathbb{C}):
\begin{array}{ll}
\psi_j(a_j)=0,\qquad &j \in \mathcal{J}\\
\psi_j(0)=\psi_i(0),\qquad &i,j\in\mathcal{J}\\
\sum_{j\in\mathcal{J}} \big(\psi_j(0)+ c\psi_j'(0)\big)=0
\end{array}
\right\}
\end{equation*}and
 \begin{equation}
L_c\psi:=L_c(\psi_j)_{j=1}^n=(-\psi_j'')_{j=1}^n,\qquad\psi\in D(L_c).
\end{equation}
\begin{equation}
L_c\psi:=L_c(\psi_j)_{j=1}^n=(-\psi_j'')_{j=1}^n,\qquad\psi\in D(L_c).
\end{equation} If ![]() $c=\infty$, the conditions at the central vertex are understood as Neumann-Kirchhoff conditions
$c=\infty$, the conditions at the central vertex are understood as Neumann-Kirchhoff conditions
 \begin{equation*}
\sum_{j\in\mathcal{J}} \psi_j'(0)=0
\quad\text{and}\quad
\psi_j(0)=\psi_i(0)\ \text{for all }\ i,j\in\mathcal{J}.
\end{equation*}
\begin{equation*}
\sum_{j\in\mathcal{J}} \psi_j'(0)=0
\quad\text{and}\quad
\psi_j(0)=\psi_i(0)\ \text{for all }\ i,j\in\mathcal{J}.
\end{equation*}
Figure 13. Quantum star graph with Robin condition at the central vertex.
In the next proposition we collect some well-known properties of ![]() $L_c$.
$L_c$.
(i)
 $L_c$ is selfadjoint if and only if
$L_c$ is selfadjoint if and only if  $c\in \mathbb{R}\cup \{\infty\}$.
$c\in \mathbb{R}\cup \{\infty\}$.(ii)
 $L_c$ is m-sectorial for all
$L_c$ is m-sectorial for all  $c\in \mathbb{C} $, i.e.
$c\in \mathbb{C} $, i.e.  $L_c$ is closed, its spectrum is contained in a closed sector symmetric to the real axis, and its numerical range is also contained in this sector.
$L_c$ is closed, its spectrum is contained in a closed sector symmetric to the real axis, and its numerical range is also contained in this sector.(iii)
 $L_c$ has purely discrete spectrum for all
$L_c$ has purely discrete spectrum for all  $c\in \mathbb{C} \cup \{\infty\}$.
$c\in \mathbb{C} \cup \{\infty\}$.(iv)
 $L_c$ has a Riesz basis of generalised eigenfunctions, for all
$L_c$ has a Riesz basis of generalised eigenfunctions, for all  $c\in \mathbb{C}$.
$c\in \mathbb{C}$.
For property (i) we refer to [Reference Berkolaiko and Kuchment2, Theorem 1.4.4]. The proof of (ii) is contained in [Reference Rivière and Royer19, Proposition 2.1]. The properties (iii) and (iv) are consequences of [Reference Hussein, Krejčiřík and Siegl12, Theorem 5.1].
Here we study perturbations of the form
where ![]() $V\in \mathcal{H}$ and
$V\in \mathcal{H}$ and ![]() $\mathcal{M}_V$ is the operator of multiplication defined by
$\mathcal{M}_V$ is the operator of multiplication defined by ![]() $V$. Our goal is to determine conditions on
$V$. Our goal is to determine conditions on ![]() $V$ that ensure that the gaps in the spectrum of
$V$ that ensure that the gaps in the spectrum of ![]() $L_c$ result in gaps in the spectrum of
$L_c$ result in gaps in the spectrum of ![]() $S_c$. For
$S_c$. For ![]() $c\in\mathbb{C}\cup\{\infty\}$ we denote the eigenvalues of
$c\in\mathbb{C}\cup\{\infty\}$ we denote the eigenvalues of ![]() $L_c$ by
$L_c$ by ![]() $\lambda_m(c)$,
$\lambda_m(c)$, ![]() $m\in \mathbb{N}$, repeated according to their algebraic multiplicities and ordered such that
$m\in \mathbb{N}$, repeated according to their algebraic multiplicities and ordered such that
Rivière and Royer proved the following spectral properties of ![]() $L_c$.
$L_c$.
Proposition 7.2. ([Reference Rivière and Royer19], Proposition 2.5)
For ![]() $c\in\mathbb{C}$, there exists
$c\in\mathbb{C}$, there exists ![]() $\gamma_c\geq 0$ such that
$\gamma_c\geq 0$ such that
Moreover,
 \begin{equation*}
\lim_{R\rightarrow\infty}\sup_{\operatorname{Re}(\lambda_{m}(c))\geq R} |\operatorname{Im} (\lambda_m(c))|
\leq \frac{2n|\operatorname{Im} (c^{-1})|}{|\Gamma|},
\end{equation*}
\begin{equation*}
\lim_{R\rightarrow\infty}\sup_{\operatorname{Re}(\lambda_{m}(c))\geq R} |\operatorname{Im} (\lambda_m(c))|
\leq \frac{2n|\operatorname{Im} (c^{-1})|}{|\Gamma|},
\end{equation*} where  $|\Gamma|:= \sum_{j=1}^n a_j$ is the total length of the graph.
$|\Gamma|:= \sum_{j=1}^n a_j$ is the total length of the graph.
Definition 7.3. We say that the lengths ![]() $a_1,a_2,\ldots,a_n$ are incommensurable over
$a_1,a_2,\ldots,a_n$ are incommensurable over ![]() $\{-1,0,1\}$ if only a trivial linear combination of
$\{-1,0,1\}$ if only a trivial linear combination of ![]() $a_1,a_2,\ldots,a_n$ with these coefficients vanishes.
$a_1,a_2,\ldots,a_n$ with these coefficients vanishes.
Proposition 7.4. ([Reference Rivière and Royer19], Proposition 1.1 and Lemma 2.7)
For all ![]() $c\in \mathbb{C}$ the geometric and algebraic multiplicity of the eigenvalue
$c\in \mathbb{C}$ the geometric and algebraic multiplicity of the eigenvalue ![]() $\lambda_{m}(c)$ are equal, for all
$\lambda_{m}(c)$ are equal, for all ![]() $m\in \mathbb{N}$. Moreover, if
$m\in \mathbb{N}$. Moreover, if ![]() $\{a_j\}_{j=1}^n$ are incommensurable over
$\{a_j\}_{j=1}^n$ are incommensurable over ![]() $\{-1,-0, 1\}$ then the multiplicity of each eigenvalue of
$\{-1,-0, 1\}$ then the multiplicity of each eigenvalue of ![]() $L_c$ is 1.
$L_c$ is 1.
Corollary 7.5. If ![]() $c\in \mathbb{C}\setminus \mathbb{R}$, then
$c\in \mathbb{C}\setminus \mathbb{R}$, then ![]() $L_c$ is similar to a non-selfadjoint normal operator.
$L_c$ is similar to a non-selfadjoint normal operator.
Proof. The claim follows from Proposition 7.1(iv), Proposition 7.4 and [Reference Dunford and Schwartz7, Chapter XV, Theorem 6.4].
The next lemma shows that ![]() $L^q$ integrability of
$L^q$ integrability of ![]() $V$ ensures its
$V$ ensures its ![]() $p$-subordination to
$p$-subordination to ![]() $L_{c}$ with
$L_{c}$ with  $p=\frac{1}{q}$.
$p=\frac{1}{q}$.
Lemma 7.6. Let  $c_\Gamma := n \left( \sum_{n\in\mathcal J} \frac{1}{a_j} \right)^{-1}$ and
$c_\Gamma := n \left( \sum_{n\in\mathcal J} \frac{1}{a_j} \right)^{-1}$ and ![]() $c\in \mathbb{C}\setminus \{c_\Gamma\}$. If
$c\in \mathbb{C}\setminus \{c_\Gamma\}$. If  $V=(V_j)_{j=1}^n\in L^q(\Gamma):=\bigoplus_{j=1}^n L^q(0,a_j; \mathbb{C})$ for some
$V=(V_j)_{j=1}^n\in L^q(\Gamma):=\bigoplus_{j=1}^n L^q(0,a_j; \mathbb{C})$ for some ![]() $q\geq 2$, then there exists a constant
$q\geq 2$, then there exists a constant ![]() $C \gt 0$ which depends only on
$C \gt 0$ which depends only on ![]() $c$,
$c$, ![]() $q$ and
$q$ and ![]() $\{a_j\}_{j=1}^n$, such that
$\{a_j\}_{j=1}^n$, such that
 \begin{equation*}
\|V u\|_{L^2(\Gamma)}\leq C\|V\|_{L^q(\Gamma)}\|u\|_{L^2(\Gamma)}^{1-\frac{1}{q}}\|L_{c}u\|_{L^2(\Gamma)}^{\frac{1}{q}},
\qquad
u\in D(L_c).
\end{equation*}
\begin{equation*}
\|V u\|_{L^2(\Gamma)}\leq C\|V\|_{L^q(\Gamma)}\|u\|_{L^2(\Gamma)}^{1-\frac{1}{q}}\|L_{c}u\|_{L^2(\Gamma)}^{\frac{1}{q}},
\qquad
u\in D(L_c).
\end{equation*}Proof. First we show that ![]() $0\in \rho(L_c)$. Assume for the sake of a contradiction that
$0\in \rho(L_c)$. Assume for the sake of a contradiction that ![]() $0\in \sigma(L_c)$. Then
$0\in \sigma(L_c)$. Then ![]() $0$ is an eigenvalue of
$0$ is an eigenvalue of ![]() $L_c$ and we can pick
$L_c$ and we can pick ![]() $\psi := (\psi_j)_{j=1}^n\in \mathcal{D}(L_c)$ with
$\psi := (\psi_j)_{j=1}^n\in \mathcal{D}(L_c)$ with ![]() $L_c\psi =0$. Hence for
$L_c\psi =0$. Hence for ![]() $j=1,\,\dots,\, n$ there exist
$j=1,\,\dots,\, n$ there exist ![]() $A_j, B_j$ such that
$A_j, B_j$ such that
By the continuity of ![]() $\psi$ at the central vertex, we obtain that
$\psi$ at the central vertex, we obtain that ![]() $A_j= A_1$ for all
$A_j= A_1$ for all ![]() $j$. The Dirichlet conditions at the outer vertices imply that
$j$. The Dirichlet conditions at the outer vertices imply that  $B_j = -\frac{A_j}{a_j} = -\frac{A_1}{a_j}$. Therefore it follows that
$B_j = -\frac{A_j}{a_j} = -\frac{A_1}{a_j}$. Therefore it follows that  $0 = nA_1 + c\sum_{j=1}^n B_j = nA_1 (1 - c\sum_{j=1}^n \frac{1}{a_j}) = nA_1 (1 - \frac{c}{c_\Gamma})$. Since
$0 = nA_1 + c\sum_{j=1}^n B_j = nA_1 (1 - c\sum_{j=1}^n \frac{1}{a_j}) = nA_1 (1 - \frac{c}{c_\Gamma})$. Since ![]() $c\neq c_\Gamma$, we must have
$c\neq c_\Gamma$, we must have ![]() $A_1=0$ and consequently
$A_1=0$ and consequently ![]() $\psi=0$.
$\psi=0$.
For every  $u=(u_j)_{j=1}^n\in D(L_c)\subseteq\bigoplus_{j=1}^n H^2(0,a_j;\mathbb{C})$ we have, by [Reference Engel, Nagel, Brendle, Campiti, Hahn, Metafune, Nickel, Pallara, Perazzoli, Rhandi, Romanelli and Schnaubelt9,
Chapter III, Example 2.2]),
$u=(u_j)_{j=1}^n\in D(L_c)\subseteq\bigoplus_{j=1}^n H^2(0,a_j;\mathbb{C})$ we have, by [Reference Engel, Nagel, Brendle, Campiti, Hahn, Metafune, Nickel, Pallara, Perazzoli, Rhandi, Romanelli and Schnaubelt9,
Chapter III, Example 2.2]),
 \begin{align*}
\|u_j'\|_{L^2(0,a_j)}\leq 3\|u_j\|_{L^2(0,a_j)}+3\|u_j''\|_{L^2(0,a_j)}.
\end{align*}
\begin{align*}
\|u_j'\|_{L^2(0,a_j)}\leq 3\|u_j\|_{L^2(0,a_j)}+3\|u_j''\|_{L^2(0,a_j)}.
\end{align*} The Gagliardo-Nirenberg inequality, see for instance [Reference Brezis4], shows that for each ![]() $j=1,2,\ldots, n$ there exists
$j=1,2,\ldots, n$ there exists ![]() $d_j \gt 0$ such that
$d_j \gt 0$ such that
 \begin{equation*}
\|u_j\|_{L^r(0,a_j)}\leq d_j \|u_j\|_{L^2(0,a_j)}^{1-\frac{1}{q}}\|u_j\|_{H^1(0,a_j)}^{\frac{1}{q}},
\end{equation*}
\begin{equation*}
\|u_j\|_{L^r(0,a_j)}\leq d_j \|u_j\|_{L^2(0,a_j)}^{1-\frac{1}{q}}\|u_j\|_{H^1(0,a_j)}^{\frac{1}{q}},
\end{equation*}where
 \begin{equation*}
\frac{1}{r}+\frac{1}{q}=\frac{1}{2}
\end{equation*}
\begin{equation*}
\frac{1}{r}+\frac{1}{q}=\frac{1}{2}
\end{equation*}and from Hölder’s inequality we infer that
Therefore, combining these three inequalities, we can find constants ![]() $d, C \gt 0$ such that
$d, C \gt 0$ such that
 \begin{align*}
\|Vu\|_{L^2(\Gamma)}&= \sum_{j=1}^n \|V_ju_j\|_{L^2(0,a_j)} \leq\sum_{j=1}^n \|V_j\|_{L^q(0,a_j)}\|u_j\|_{L^r(0,a_j)} \\
&\leq \sum_{j=1}^n d_j\|V_j\|_{L^q(0,a_j)} \|u_j\|_{L^2(0,a_j)}^{1-\frac{1}{q}}\|u_j\|_{H^1(0,a_j)}^{\frac{1}{q}}\\
&\leq \sum_{j=1}^n d_j\|V_j\|_{L^q(0,a_j)} \|u_j\|_{L^2(0,a_j)}^{1-\frac{1}{q}}\left(4\|u_j\|_{L^2(0,a_j)}+3\|u_j''\|_{L^2(0,a_j)}\right)^{\frac{1}{q}} \\
&\leq n d \max_{1\leq j\leq n}\|V_j\|_{L^q(0,a_j)} \left(\max_{1\leq j\leq n}\|u_j\|_{L^2(0,a_j)}\right)^{1-\frac{1}{q}}\\
&\quad \times \left(4\max_{1\leq j\leq n}\|u_j\|_{L^2(0,a_j)}+3\max_{1\leq j\leq n}\|u_j''\|_{L^2(0,a_j)}\right)^{\frac{1}{q}} \\
&\leq n d \|V\|_{L^q(\Gamma)}\|u\|_{L^2(\Gamma)}^{1-\frac{1}{q}}\left(4\|u\|_{L^2(\Gamma)}+3\|L_cu\|_{L^2(\Gamma)}\right)^{\frac{1}{q}}\\
&\leq n d \|V\|_{L^q(\Gamma)}\|u\|_{L^2(\Gamma)}^{1-\frac{1}{q}}\left(3+4\|L_c^{-1}\|\right)^{\frac{1}{q}}\|L_cu\|_{L^2(\Gamma)}^{\frac{1}{q}} \\
&\leq C\|V\|_{L^q(\Gamma)}\|u\|_{L^2(\Gamma)}^{1-\frac{1}{q}}\|L_{c}u\|_{L^2(\Gamma)}^{\frac{1}{q}}.
\end{align*}
\begin{align*}
\|Vu\|_{L^2(\Gamma)}&= \sum_{j=1}^n \|V_ju_j\|_{L^2(0,a_j)} \leq\sum_{j=1}^n \|V_j\|_{L^q(0,a_j)}\|u_j\|_{L^r(0,a_j)} \\
&\leq \sum_{j=1}^n d_j\|V_j\|_{L^q(0,a_j)} \|u_j\|_{L^2(0,a_j)}^{1-\frac{1}{q}}\|u_j\|_{H^1(0,a_j)}^{\frac{1}{q}}\\
&\leq \sum_{j=1}^n d_j\|V_j\|_{L^q(0,a_j)} \|u_j\|_{L^2(0,a_j)}^{1-\frac{1}{q}}\left(4\|u_j\|_{L^2(0,a_j)}+3\|u_j''\|_{L^2(0,a_j)}\right)^{\frac{1}{q}} \\
&\leq n d \max_{1\leq j\leq n}\|V_j\|_{L^q(0,a_j)} \left(\max_{1\leq j\leq n}\|u_j\|_{L^2(0,a_j)}\right)^{1-\frac{1}{q}}\\
&\quad \times \left(4\max_{1\leq j\leq n}\|u_j\|_{L^2(0,a_j)}+3\max_{1\leq j\leq n}\|u_j''\|_{L^2(0,a_j)}\right)^{\frac{1}{q}} \\
&\leq n d \|V\|_{L^q(\Gamma)}\|u\|_{L^2(\Gamma)}^{1-\frac{1}{q}}\left(4\|u\|_{L^2(\Gamma)}+3\|L_cu\|_{L^2(\Gamma)}\right)^{\frac{1}{q}}\\
&\leq n d \|V\|_{L^q(\Gamma)}\|u\|_{L^2(\Gamma)}^{1-\frac{1}{q}}\left(3+4\|L_c^{-1}\|\right)^{\frac{1}{q}}\|L_cu\|_{L^2(\Gamma)}^{\frac{1}{q}} \\
&\leq C\|V\|_{L^q(\Gamma)}\|u\|_{L^2(\Gamma)}^{1-\frac{1}{q}}\|L_{c}u\|_{L^2(\Gamma)}^{\frac{1}{q}}.
\end{align*} By Corollary 7.5, for every ![]() $c\in\mathbb{C}\cup\{\infty\}$ there exists a normal operator
$c\in\mathbb{C}\cup\{\infty\}$ there exists a normal operator ![]() $T_c$ on
$T_c$ on ![]() $\mathcal{H}$ and an isomorphism
$\mathcal{H}$ and an isomorphism ![]() $J_c\in B(\mathcal{H})$ such that
$J_c\in B(\mathcal{H})$ such that
Note that ![]() $T_c$ and
$T_c$ and ![]() $L_c$ have the same spectra. Set
$L_c$ have the same spectra. Set ![]() $A_{V}:= J_c\mathcal{M}_{V}J_c^{-1}$ and
$A_{V}:= J_c\mathcal{M}_{V}J_c^{-1}$ and ![]() $\kappa_c:= \|J_c\|\|J_c^{-1}\|$. If
$\kappa_c:= \|J_c\|\|J_c^{-1}\|$. If ![]() $V\in L^q(\Gamma)$, then the above lemma shows that
$V\in L^q(\Gamma)$, then the above lemma shows that ![]() $A_V$ is
$A_V$ is ![]() $\frac{1}{q}$-subordinate to
$\frac{1}{q}$-subordinate to ![]() $T_c$ and that
$T_c$ and that
 \begin{align}
\|A_V w\|_{L^2(\Gamma)}
\leq \kappa_cC\|V\|_{L^q(\Gamma)}\|w\|_{L^2(\Gamma)}^{1-\frac{1}{q}}\|T_{c}w\|_{L^2(\Gamma)}^{\frac{1}{q}},
\end{align}
\begin{align}
\|A_V w\|_{L^2(\Gamma)}
\leq \kappa_cC\|V\|_{L^q(\Gamma)}\|w\|_{L^2(\Gamma)}^{1-\frac{1}{q}}\|T_{c}w\|_{L^2(\Gamma)}^{\frac{1}{q}},
\end{align} for all ![]() $w\in D(T_c)$. The Weyl law proved by Rivière and Royer in [Reference Rivière and Royer19, Proposition 1.2] shows that
$w\in D(T_c)$. The Weyl law proved by Rivière and Royer in [Reference Rivière and Royer19, Proposition 1.2] shows that
 \begin{equation*}\operatorname{Re}(\lambda_m(c))= \frac{\pi^2}{|\Gamma|^2}m^2+O(m) \text{as } m\rightarrow \infty\end{equation*}
\begin{equation*}\operatorname{Re}(\lambda_m(c))= \frac{\pi^2}{|\Gamma|^2}m^2+O(m) \text{as } m\rightarrow \infty\end{equation*}and
This implies that, for ![]() $m\in \mathbb{N}$ such that
$m\in \mathbb{N}$ such that ![]() $\operatorname{Re}(\lambda_{m}(c))\neq \operatorname{Re}(\lambda_{m+1}(c))$,
$\operatorname{Re}(\lambda_{m}(c))\neq \operatorname{Re}(\lambda_{m+1}(c))$,
 \begin{equation*}
\frac{\max\{|\operatorname{Re}(\lambda_{m}(c))+\mathrm{i}\gamma_c|^{\frac{1}{q}},|\operatorname{Re}(\lambda_{m+1}(c))+\mathrm{i}\gamma_c|^{\frac{1}{q}}\} }{\operatorname{Re}(\lambda_{m+1}(c))-\operatorname{Re}(\lambda_{m}(c)) }
\longrightarrow 0
\quad\text{for } m\to\infty.
\end{equation*}
\begin{equation*}
\frac{\max\{|\operatorname{Re}(\lambda_{m}(c))+\mathrm{i}\gamma_c|^{\frac{1}{q}},|\operatorname{Re}(\lambda_{m+1}(c))+\mathrm{i}\gamma_c|^{\frac{1}{q}}\} }{\operatorname{Re}(\lambda_{m+1}(c))-\operatorname{Re}(\lambda_{m}(c)) }
\longrightarrow 0
\quad\text{for } m\to\infty.
\end{equation*} Therefore, Hypothesis (6.1) is satisfied for ![]() $T_c$ and
$T_c$ and ![]() $A_V$ for large enough
$A_V$ for large enough ![]() $m$ and hence Theorem 6.1 leads to the following theorem.
$m$ and hence Theorem 6.1 leads to the following theorem.
Theorem 7.7 Let ![]() $L_c$ and
$L_c$ and ![]() $S_c$ be as in (7.1) and (7.2), respectively, for some
$S_c$ be as in (7.1) and (7.2), respectively, for some ![]() $c\in \mathbb{C}\setminus \{c_\Gamma\}$ and
$c\in \mathbb{C}\setminus \{c_\Gamma\}$ and ![]() $V\in L^q(\Gamma)$ with
$V\in L^q(\Gamma)$ with ![]() $q \gt 2$. Then at most finitely many of the vertical spectral free strips of
$q \gt 2$. Then at most finitely many of the vertical spectral free strips of ![]() $L_c$ close under perturbation by
$L_c$ close under perturbation by ![]() $V$.
$V$.
Remark 7.8. By Proposition 3.2 and 3.6, we have that, for all ![]() $\theta\in (0,\pi/2]$, there is
$\theta\in (0,\pi/2]$, there is ![]() $\beta\in \mathbb{R}$ such that
$\beta\in \mathbb{R}$ such that ![]() $\sigma(L_c+\mathcal{M}_V)\subseteq S_{\theta}(\beta)$.
$\sigma(L_c+\mathcal{M}_V)\subseteq S_{\theta}(\beta)$.
Remark 7.9. We can also admit more general perturbations. Consider the operator ![]() $\mathcal{A}$ defined by
$\mathcal{A}$ defined by
and
 \begin{equation*}\mathcal{A}\psi(x):= \zeta(x)\frac{d}{dx}\psi(x)+V(x)\psi(x),~~~~\psi(x)\in D(L_c)\end{equation*}
\begin{equation*}\mathcal{A}\psi(x):= \zeta(x)\frac{d}{dx}\psi(x)+V(x)\psi(x),~~~~\psi(x)\in D(L_c)\end{equation*} with ![]() $\zeta, V\in L^{2}(\Gamma)$. Then the following is true.
$\zeta, V\in L^{2}(\Gamma)$. Then the following is true.
• If
 $\zeta\in L^{\infty}(\Gamma)$ then
$\zeta\in L^{\infty}(\Gamma)$ then  $J_{c}\mathcal{A}J^{-1}_c$ is
$J_{c}\mathcal{A}J^{-1}_c$ is  $\frac{1}{2}$-subordinate to
$\frac{1}{2}$-subordinate to  $T_{c}$.
$T_{c}$.• If
 $\zeta\in L^{2}(\Gamma)$ then
$\zeta\in L^{2}(\Gamma)$ then  $J_{c}\mathcal{A}J^{-1}_c$is
$J_{c}\mathcal{A}J^{-1}_c$is  $T_{c}$-bounded.
$T_{c}$-bounded.
7.2. Perturbations of normal operators generated by first order systems
We consider the following first order system of ODEs
 \begin{equation*}
\mathcal{L}y:= \mathcal{L}(B,Q)y:= -\mathrm{i} B y'+Q(x)y=\lambda y,\qquad y
=
\begin{pmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{pmatrix}
\end{equation*}
\begin{equation*}
\mathcal{L}y:= \mathcal{L}(B,Q)y:= -\mathrm{i} B y'+Q(x)y=\lambda y,\qquad y
=
\begin{pmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{pmatrix}
\end{equation*}with
 \begin{equation*}
B:=\operatorname{diag}(b_1,b_2,\ldots, b_n)\in \mathbb{C}^{n\times n} \quad\text{and}\quad Q:= \left(q_{jk}\right)_{j,k=1}^n\in L^1([0,1]; \mathbb{C}^{n\times n}).
\end{equation*}
\begin{equation*}
B:=\operatorname{diag}(b_1,b_2,\ldots, b_n)\in \mathbb{C}^{n\times n} \quad\text{and}\quad Q:= \left(q_{jk}\right)_{j,k=1}^n\in L^1([0,1]; \mathbb{C}^{n\times n}).
\end{equation*} We associate to ![]() $\mathcal{L}$ the maximal operator
$\mathcal{L}$ the maximal operator ![]() $L_{\max}:= L_{\max}(B,Q)$ acting in
$L_{\max}:= L_{\max}(B,Q)$ acting in ![]() $ L^2([0,1]; \mathbb{C}^{n})$ on the domain
$ L^2([0,1]; \mathbb{C}^{n})$ on the domain
 \begin{equation*}D(L_{\max}):=\left\{y\in AC([0,1]; \mathbb{C}^{n}): \mathcal{L}y \in L^2([0,1]; \mathbb{C}^{n}) \right\}\end{equation*}
\begin{equation*}D(L_{\max}):=\left\{y\in AC([0,1]; \mathbb{C}^{n}): \mathcal{L}y \in L^2([0,1]; \mathbb{C}^{n}) \right\}\end{equation*}and with action
The minimal operator ![]() $L_{\min}:= L_{\min}(B,Q)$ is defined by
$L_{\min}:= L_{\min}(B,Q)$ is defined by
and
Let us first consider the case when ![]() $Q=0$. The next proposition describes the situation when the operators on the different vertices are decoupled and satisfy so-called quasi-periodic boundary conditions on each edge. We omit the proof.
$Q=0$. The next proposition describes the situation when the operators on the different vertices are decoupled and satisfy so-called quasi-periodic boundary conditions on each edge. We omit the proof.
Proposition 7.10. Let ![]() $D:=\operatorname{diag}(d_1,d_2,\ldots, d_n)\in \mathbb{C}^{n\times n} $ and consider the operator
$D:=\operatorname{diag}(d_1,d_2,\ldots, d_n)\in \mathbb{C}^{n\times n} $ and consider the operator ![]() $L_{D}(B,0)$ defined by
$L_{D}(B,0)$ defined by
and
Then the following is true.
(i) If
 $|d_i|=1$ for all
$|d_i|=1$ for all  $i=1,\ldots,n$, then
$i=1,\ldots,n$, then  $L_D(B,0)$ is normal.
$L_D(B,0)$ is normal.(ii) If
 $|d_i|=1$ and
$|d_i|=1$ and  $b_i\in \mathbb{C}\setminus \{0\}$ for all
$b_i\in \mathbb{C}\setminus \{0\}$ for all  $i=1,\ldots,n$, then
$i=1,\ldots,n$, then  $L_D(B,0)$ is normal and discrete.
$L_D(B,0)$ is normal and discrete.(iii) If
 $|d_i|=1$ and
$|d_i|=1$ and  $b_i\in \mathbb{R}\setminus \{0\}$ for all
$b_i\in \mathbb{R}\setminus \{0\}$ for all  $i=1,\ldots,n$, then
$i=1,\ldots,n$, then  $L_D(B,0)$ is selfadjoint and discrete.
$L_D(B,0)$ is selfadjoint and discrete.
Now we consider the following more general boundary conditions
where we always assume that ![]() $\operatorname{rank}(C~D) = n$. We define the operator
$\operatorname{rank}(C~D) = n$. We define the operator ![]() $L_{C,D}(B,Q)$ as restriction of
$L_{C,D}(B,Q)$ as restriction of ![]() $L_{\max}$ to the domain
$L_{\max}$ to the domain
This class of operators has appeared in numerous papers (see e.g. [Reference Birkhoff and Langer3], [Reference Malamud and Oridoroga16], [Reference Lunyov and Malamud15] and [Reference Agibalova, Lunyov, Malamud and Oridoroga1]). For instance, Lunyov and Malamud found in [Reference Lunyov and Malamud15, Lemma 5.1] all normal realizations ![]() $L_{C,D}(B,0)$ of the minimal operator
$L_{C,D}(B,0)$ of the minimal operator ![]() $L_{\min}(B,0)$ under so-called regular boundary conditions (see [Reference Birkhoff and Langer3, pag. 89] or [Reference Agibalova, Lunyov, Malamud and Oridoroga1, Definition 5.1]). Later, Agibalova, Lunyov, Malamud and Oridoroga in [Reference Agibalova, Lunyov, Malamud and Oridoroga1, Lemma 4.4] characterized these normal extensions for the case
$L_{\min}(B,0)$ under so-called regular boundary conditions (see [Reference Birkhoff and Langer3, pag. 89] or [Reference Agibalova, Lunyov, Malamud and Oridoroga1, Definition 5.1]). Later, Agibalova, Lunyov, Malamud and Oridoroga in [Reference Agibalova, Lunyov, Malamud and Oridoroga1, Lemma 4.4] characterized these normal extensions for the case ![]() $n=2$.
$n=2$.
Proposition 7.11. ([Reference Lunyov and Malamud15], Lemma 5.1)
Let ![]() $B$ be a nonsingular diagonal
$B$ be a nonsingular diagonal ![]() $n \times n$ matrix with complex entries and let
$n \times n$ matrix with complex entries and let ![]() $C, D\in \mathbb{C}^{n\times n}$ such that the boundary conditions given in (7.6) are regular. Then the operator
$C, D\in \mathbb{C}^{n\times n}$ such that the boundary conditions given in (7.6) are regular. Then the operator ![]() $L_{C,D}(B,0)$ is normal if and only if
$L_{C,D}(B,0)$ is normal if and only if
Proposition 7.12. ([Reference Agibalova, Lunyov, Malamud and Oridoroga1], Lemma 4.4)
Let ![]() $n=2$,
$n=2$, ![]() $C, D\in \mathbb{C}^{2\times 2}$ such that
$C, D\in \mathbb{C}^{2\times 2}$ such that ![]() $\operatorname{rank}(C~D) = 2$ and
$\operatorname{rank}(C~D) = 2$ and ![]() $b_1b_2^{-1}\notin \mathbb{R}$. Then the operator
$b_1b_2^{-1}\notin \mathbb{R}$. Then the operator ![]() $L_{C,D}(B,0)$ is normal if and only if
$L_{C,D}(B,0)$ is normal if and only if
Remark 7.13. The operator ![]() $L_{C,D}(B,0)$ is normal if and only if there exist
$L_{C,D}(B,0)$ is normal if and only if there exist ![]() $d_1,d_2\in \mathbb{C}$ with
$d_1,d_2\in \mathbb{C}$ with ![]() $|d_1|=|d_2|=1$ such that
$|d_1|=|d_2|=1$ such that ![]() $L_{C,D}(B,0)=L_{D'}(B,0)$ with
$L_{C,D}(B,0)=L_{D'}(B,0)$ with ![]() $D'=\operatorname{diag}(d_1,d_2)$.
$D'=\operatorname{diag}(d_1,d_2)$.
Now we focus on the case ![]() $n=2$. Our goal is to obtain spectral inclusions for the operator
$n=2$. Our goal is to obtain spectral inclusions for the operator ![]() $L_D(B,Q)$ with
$L_D(B,Q)$ with ![]() $B=\operatorname{diag}(b_1,b_2)$ and
$B=\operatorname{diag}(b_1,b_2)$ and ![]() $D=\operatorname{diag}(d_1,d_2)$. The next lemma shows that
$D=\operatorname{diag}(d_1,d_2)$. The next lemma shows that ![]() $L^q$ integrability of
$L^q$ integrability of ![]() $Q$ with
$Q$ with ![]() $q\geq 2$ ensures that its corresponding operator of multiplication is
$q\geq 2$ ensures that its corresponding operator of multiplication is ![]() $L_D(B,0)$-bounded with
$L_D(B,0)$-bounded with ![]() $L_D(B,0)$-bound equal to zero.
$L_D(B,0)$-bound equal to zero.
Lemma 7.14. Let ![]() $Q\in L^q([0,1]; \mathbb{C}^{2\times 2})$ for some
$Q\in L^q([0,1]; \mathbb{C}^{2\times 2})$ for some ![]() $q \ge 2$. As before, let
$q \ge 2$. As before, let ![]() $B=\operatorname{diag}(b_1,b_2)$ and
$B=\operatorname{diag}(b_1,b_2)$ and ![]() $D=\operatorname{diag}(d_1,d_2)$ with
$D=\operatorname{diag}(d_1,d_2)$ with ![]() $b_1,b_2\neq 0$,
$b_1,b_2\neq 0$, ![]() $d_1,d_2\in \mathbb{C}\setminus\{0,1\}$. Then
$d_1,d_2\in \mathbb{C}\setminus\{0,1\}$. Then ![]() $\mathcal{M}_{Q}$, the operator of multiplication defined by
$\mathcal{M}_{Q}$, the operator of multiplication defined by ![]() $Q$, is
$Q$, is ![]() $q$-subordinate to
$q$-subordinate to ![]() $L_D(B,0)$, in particular it has
$L_D(B,0)$, in particular it has ![]() $L_D(B,0)$-bound equal to zero.
$L_D(B,0)$-bound equal to zero.
Proof. Let  $ y=\begin{pmatrix}
y_1 \\ y_2
\end{pmatrix} \in D(L_{D}(B,0))$ Then
$ y=\begin{pmatrix}
y_1 \\ y_2
\end{pmatrix} \in D(L_{D}(B,0))$ Then ![]() $y_1,y_2\in H^1(0,1)$ and
$y_1,y_2\in H^1(0,1)$ and
and ![]() $L_D(B,0)$ can be written as the direct sum
$L_D(B,0)$ can be written as the direct sum ![]() $L_D(B,0) = b_1 L_{d_1}\oplus b_2 L_{d_2}$. Note that the condition
$L_D(B,0) = b_1 L_{d_1}\oplus b_2 L_{d_2}$. Note that the condition ![]() $d_1, d_2 \notin \{0,1\}$ guarantees that
$d_1, d_2 \notin \{0,1\}$ guarantees that ![]() $L_{d_1}$ and
$L_{d_1}$ and ![]() $L_{d_2}$ are boundedly invertible. The Gagliardo-Nirenberg inequality shows that there exists a constant
$L_{d_2}$ are boundedly invertible. The Gagliardo-Nirenberg inequality shows that there exists a constant ![]() $c_q \gt 0$ such that for
$c_q \gt 0$ such that for ![]() $j=1,2$
$j=1,2$
 \begin{equation*}
\|y_j\|_{L^r(0,1)}\leq c_q \|y_j\|_{L^2(0,1)}^{1-\frac{1}{q}}\|y_j\|_{H^1(0,1)}^{\frac{1}{q}},
\end{equation*}
\begin{equation*}
\|y_j\|_{L^r(0,1)}\leq c_q \|y_j\|_{L^2(0,1)}^{1-\frac{1}{q}}\|y_j\|_{H^1(0,1)}^{\frac{1}{q}},
\end{equation*}where
 \begin{equation*}
\frac{1}{r}+\frac{1}{q}=\frac{1}{2}
\end{equation*}
\begin{equation*}
\frac{1}{r}+\frac{1}{q}=\frac{1}{2}
\end{equation*} and from Hölder’s inequality we infer that, for any ![]() $\tilde q\in L^q(0,1)$,
$\tilde q\in L^q(0,1)$,
Therefore, combining these two inequalities, we can find constants ![]() $C_j \gt 0$ such that
$C_j \gt 0$ such that
 \begin{align*}
\|\tilde q y_j\|_{L^2(0,1)}
& \leq \|\tilde q\|_{L^q(0,1)}\|y_j\|_{L^r(0,1)}
\leq c_q \|\tilde q\|_{L^q(0,1)}\|y_j\|_{L^2(0,1)}^{1-\frac{1}{q}}\|y_j\|_{H^1(0,1)}^{\frac{1}{q}} \\
&= c_q \|\tilde q\|_{L^q(0,1)}\|y_j\|_{L^2(0,1)}^{1-\frac{1}{q}}
\left(\|y_j\|_{L^2(0,1)}+\|y_j'\|_{L^2(0,1)}\right)^{\frac{1}{q}}
\\
&\leq c_q \|\tilde q\|_{L^q(0,1)}\|y_j\|_{L^2(0,1)}^{1-\frac{1}{q}}
\left(1+\|(L_{d_j})^{-1}\|\right)^{\frac{1}{q}}\|L_{d_j}y_j\|_{L^2(0,1)}^{\frac{1}{q}}
\\
&= C_j\|\tilde q\|_{L^q(0,1)}\|y_j\|_{L^2(0,1)}^{1-\frac{1}{q}}
\|L_{d_j}y_j\|_{L^2(0,1)}^{\frac{1}{q}}.
\end{align*}
\begin{align*}
\|\tilde q y_j\|_{L^2(0,1)}
& \leq \|\tilde q\|_{L^q(0,1)}\|y_j\|_{L^r(0,1)}
\leq c_q \|\tilde q\|_{L^q(0,1)}\|y_j\|_{L^2(0,1)}^{1-\frac{1}{q}}\|y_j\|_{H^1(0,1)}^{\frac{1}{q}} \\
&= c_q \|\tilde q\|_{L^q(0,1)}\|y_j\|_{L^2(0,1)}^{1-\frac{1}{q}}
\left(\|y_j\|_{L^2(0,1)}+\|y_j'\|_{L^2(0,1)}\right)^{\frac{1}{q}}
\\
&\leq c_q \|\tilde q\|_{L^q(0,1)}\|y_j\|_{L^2(0,1)}^{1-\frac{1}{q}}
\left(1+\|(L_{d_j})^{-1}\|\right)^{\frac{1}{q}}\|L_{d_j}y_j\|_{L^2(0,1)}^{\frac{1}{q}}
\\
&= C_j\|\tilde q\|_{L^q(0,1)}\|y_j\|_{L^2(0,1)}^{1-\frac{1}{q}}
\|L_{d_j}y_j\|_{L^2(0,1)}^{\frac{1}{q}}.
\end{align*} Consequently, there is a constant ![]() $C_0 \gt 0$ such that
$C_0 \gt 0$ such that
 \begin{align*}
\|Qy\|_{L^2(0,1)}^2
&= \| q_{11} y_1 + q_{12} y_2 \|_{L^2(0,1)}^2 + \| q_{21} y_1 + q_{22} y_2 \|_{L^2(0,1)}^2
\\
& \le 2\left\{\| q_{11} y_1 \|_{L^2(0,1)}^2 + \|q_{12} y_2 \|_{L^2(0,1)}^2 + \| q_{21} y_1 \|_{L^2(0,1)}^2 + \|q_{22} y_2 \|_{L^2(0,1)}^2
\right\}
\\
&\le
C_0\, \|Q\|_{L^q(0,1)}^2
\sum_{j=1}^2
\|y_j\|_{L^2(0,1)}^{2(1-\frac{1}{q})} \|L_{d_j}(1,0)y_j\|_{L^2(0,1)}^{\frac{2}{q}}
\\
&\le
C_0\, \|Q\|_{L^q(0,1)}^2
\bigg( \sum_{j=1}^2 \|y_j\|_{L^2(0,1)}^2 \bigg)^{1-\frac{1}{q}}
\bigg( \sum_{j=1}^2 \|L_{d_j}(1,0)y_j\|_{L^2(0,1)}^2 \bigg)^{\frac{1}{q}}
\\
& =
C_0\, \left(
\|Q\|_{L^q(0,1)}
\|y\|_{L^2(0,1)}^{1-\frac{1}{q}}
\|L_{D}(1,0)y\|_{L^2(0,1)}^{\frac{1}{q}}
\right)^2.\\[-40pt]
\end{align*}
\begin{align*}
\|Qy\|_{L^2(0,1)}^2
&= \| q_{11} y_1 + q_{12} y_2 \|_{L^2(0,1)}^2 + \| q_{21} y_1 + q_{22} y_2 \|_{L^2(0,1)}^2
\\
& \le 2\left\{\| q_{11} y_1 \|_{L^2(0,1)}^2 + \|q_{12} y_2 \|_{L^2(0,1)}^2 + \| q_{21} y_1 \|_{L^2(0,1)}^2 + \|q_{22} y_2 \|_{L^2(0,1)}^2
\right\}
\\
&\le
C_0\, \|Q\|_{L^q(0,1)}^2
\sum_{j=1}^2
\|y_j\|_{L^2(0,1)}^{2(1-\frac{1}{q})} \|L_{d_j}(1,0)y_j\|_{L^2(0,1)}^{\frac{2}{q}}
\\
&\le
C_0\, \|Q\|_{L^q(0,1)}^2
\bigg( \sum_{j=1}^2 \|y_j\|_{L^2(0,1)}^2 \bigg)^{1-\frac{1}{q}}
\bigg( \sum_{j=1}^2 \|L_{d_j}(1,0)y_j\|_{L^2(0,1)}^2 \bigg)^{\frac{1}{q}}
\\
& =
C_0\, \left(
\|Q\|_{L^q(0,1)}
\|y\|_{L^2(0,1)}^{1-\frac{1}{q}}
\|L_{D}(1,0)y\|_{L^2(0,1)}^{\frac{1}{q}}
\right)^2.\\[-40pt]
\end{align*}Remark 7.15. Let ![]() $\epsilon \gt 0$ and
$\epsilon \gt 0$ and ![]() $y\in D( L_{D}(B,0))$, then
$y\in D( L_{D}(B,0))$, then
where
 \begin{align*}
a'_{\epsilon} := 2\left(1-\frac{1}{q}\right) \epsilon^{\frac{q}{1-q}}C_0
\max_{i,j=1}^2 \|q_{ij}\|_{L^q(0,1)} \quad\text{and }\quad
b'_{\epsilon} := \frac{2}{q}\, {\epsilon^{q}}C_0
\max_{i,j=1}^2 \|q_{ij}\|_{L^q(0,1)}.
\end{align*}
\begin{align*}
a'_{\epsilon} := 2\left(1-\frac{1}{q}\right) \epsilon^{\frac{q}{1-q}}C_0
\max_{i,j=1}^2 \|q_{ij}\|_{L^q(0,1)} \quad\text{and }\quad
b'_{\epsilon} := \frac{2}{q}\, {\epsilon^{q}}C_0
\max_{i,j=1}^2 \|q_{ij}\|_{L^q(0,1)}.
\end{align*}Proposition 7.16. Let ![]() $Q\in L^q([0,1]; \mathbb{C}^{2\times 2})$,
$Q\in L^q([0,1]; \mathbb{C}^{2\times 2})$, ![]() $b_1,b_2\neq 0$,
$b_1,b_2\neq 0$, ![]() $d_1,d_2\in \mathbb{C}\setminus\{1\}$ with
$d_1,d_2\in \mathbb{C}\setminus\{1\}$ with ![]() $|d_1|=|d_2|=1$ and
$|d_1|=|d_2|=1$ and ![]() $q\geq 2$. If
$q\geq 2$. If ![]() $B:=\operatorname{diag}(b_1,b_2)$ and
$B:=\operatorname{diag}(b_1,b_2)$ and ![]() $D:=\operatorname{diag}(d_1,d_2)$ then the operator
$D:=\operatorname{diag}(d_1,d_2)$ then the operator ![]() $L_{D}(B,Q)$ has compact resolvent. Moreover, if
$L_{D}(B,Q)$ has compact resolvent. Moreover, if  $ \theta_{\mathfrak s}:= \frac{1}{2}\left|\arg\left(\frac{\mathfrak s b_2}{b_1}\right)\right| $, with
$ \theta_{\mathfrak s}:= \frac{1}{2}\left|\arg\left(\frac{\mathfrak s b_2}{b_1}\right)\right| $, with ![]() $\mathfrak s = \pm 1$, then for all
$\mathfrak s = \pm 1$, then for all ![]() $\epsilon \gt 0$, there exists
$\epsilon \gt 0$, there exists ![]() $r_\epsilon \gt 0$ such that
$r_\epsilon \gt 0$ such that
for some ![]() $\varphi_{\mathfrak s} \in[0,2\pi)$ and
$\varphi_{\mathfrak s} \in[0,2\pi)$ and ![]() $K_{r_\epsilon}(0)$ is the closed disk of radius
$K_{r_\epsilon}(0)$ is the closed disk of radius ![]() $r_\epsilon$ centred in
$r_\epsilon$ centred in ![]() $0$.
$0$.
Proof. Let ![]() $\varphi_{\mathfrak s}\in [0,2\pi) $ such that
$\varphi_{\mathfrak s}\in [0,2\pi) $ such that
The spectral inclusion (7.7) follows from Proposition 4.8. Moreover, if ![]() $T:= \mathrm{e}^{\mathrm{i}\varphi_{\mathfrak s}} L_D(B,0)$ we have that
$T:= \mathrm{e}^{\mathrm{i}\varphi_{\mathfrak s}} L_D(B,0)$ we have that ![]() $\sup_{t\in\sigma(T)} H_z(t) \lt 1$, for
$\sup_{t\in\sigma(T)} H_z(t) \lt 1$, for ![]() $z\in {K_{r_\epsilon}(0)}\cup S_{\theta_{\mathfrak s}+\epsilon}(0)\cup -S_{\theta_{\mathfrak s}+\epsilon}(0) $, where
$z\in {K_{r_\epsilon}(0)}\cup S_{\theta_{\mathfrak s}+\epsilon}(0)\cup -S_{\theta_{\mathfrak s}+\epsilon}(0) $, where ![]() $H_z$ is as in (2.2). So, by Proposition 2.1(iii) we have that
$H_z$ is as in (2.2). So, by Proposition 2.1(iii) we have that
 \begin{equation*}
( L_D(B,Q)-w)^{-1}=( L_D(B,0)-w)^{-1} \sum_{n=0}^\infty (-\mathcal{M}_{Q} (L_D(B,Q)-w)^{-1})^n,
\end{equation*}
\begin{equation*}
( L_D(B,Q)-w)^{-1}=( L_D(B,0)-w)^{-1} \sum_{n=0}^\infty (-\mathcal{M}_{Q} (L_D(B,Q)-w)^{-1})^n,
\end{equation*} for ![]() $w\notin\mathrm{e}^{-\mathrm{i}\varphi_{\mathfrak s}}\left( {K_{r_\epsilon}(0)}\cup S_{\theta_{\mathfrak s}+\epsilon}(0)\cup -S_{\theta_{\mathfrak s}+\epsilon}(0)\right)$. Since
$w\notin\mathrm{e}^{-\mathrm{i}\varphi_{\mathfrak s}}\left( {K_{r_\epsilon}(0)}\cup S_{\theta_{\mathfrak s}+\epsilon}(0)\cup -S_{\theta_{\mathfrak s}+\epsilon}(0)\right)$. Since ![]() $L_{D}(B,0)$ is a discrete normal operator, we conclude that
$L_{D}(B,0)$ is a discrete normal operator, we conclude that ![]() $L_{D}(B,Q)$ has compact resolvent.
$L_{D}(B,Q)$ has compact resolvent.
Remark 7.17. Resolvent estimates for ![]() $L_{D}(B,Q)$ will be given in a forthcoming work. For instance, we will prove that, even if
$L_{D}(B,Q)$ will be given in a forthcoming work. For instance, we will prove that, even if ![]() $|d_1|,|d_2|\neq 1$, this operator is bisectorial for some angle
$|d_1|,|d_2|\neq 1$, this operator is bisectorial for some angle ![]() $\phi\in [0, \pi/2)$ and radius
$\phi\in [0, \pi/2)$ and radius ![]() $r\geq 0$, see [Reference Tretter and Wyss22, Definition 2.7] .
$r\geq 0$, see [Reference Tretter and Wyss22, Definition 2.7] .
Acknowledgements
The authors thank Lyonell Boulton for fruitful discussions. They are grateful to the referee for suggesting improvements of the bounds in Lemma A.3 and Lemma A.5.
Appendix A. Estimates in the complex plane
In this section, we prove some technical estimates for functions in the complex plane that are used in ![]() $\S$ 3 and
$\S$ 3 and ![]() $\S$ 4.
$\S$ 4.
Lemma A.1. For ![]() $a,b\ge0$ and
$a,b\ge0$ and ![]() $z\in\mathbb{C}$ fixed, the function
$z\in\mathbb{C}$ fixed, the function
 \begin{equation*}
H_z:\mathbb{C}\setminus\{z\}\to\mathbb{C},
\qquad
H_z(t) = \frac{a^2 + b^2 |t|^2}{|t-z|^2}
\end{equation*}
\begin{equation*}
H_z:\mathbb{C}\setminus\{z\}\to\mathbb{C},
\qquad
H_z(t) = \frac{a^2 + b^2 |t|^2}{|t-z|^2}
\end{equation*}does not have any local maximum and
 \begin{equation*}
\lim_{|t|\to\infty }H_z(t) = b^2.
\end{equation*}
\begin{equation*}
\lim_{|t|\to\infty }H_z(t) = b^2.
\end{equation*} Consequently, for every set ![]() $U\subseteq\mathbb{C}$ with unbounded boundary
$U\subseteq\mathbb{C}$ with unbounded boundary ![]() $\partial U$, we have that
$\partial U$, we have that
 \begin{equation*}
\sup_{t\in U} H_z(t) = \sup_{t\in \partial U} H_z(t).
\end{equation*}
\begin{equation*}
\sup_{t\in U} H_z(t) = \sup_{t\in \partial U} H_z(t).
\end{equation*} If ![]() $U$ is unbounded but
$U$ is unbounded but ![]() $\partial U$ is bounded, then
$\partial U$ is bounded, then
 \begin{equation*}
\sup_{t\in U} H_z(t) = \max\{b^2, \sup_{t\in \partial U} H_z(t) \}.
\end{equation*}
\begin{equation*}
\sup_{t\in U} H_z(t) = \max\{b^2, \sup_{t\in \partial U} H_z(t) \}.
\end{equation*}Proof. The cases when ![]() $z=0$ or
$z=0$ or ![]() $b=0$ are clear. So let us now assume that
$b=0$ are clear. So let us now assume that ![]() $b \gt 0$ and
$b \gt 0$ and ![]() $z\neq 0$. Let us restrict
$z\neq 0$. Let us restrict ![]() $H_z$ to
$H_z$ to ![]() $t\in\mathbb{C}$ with
$t\in\mathbb{C}$ with ![]() $t = rz$ for
$t = rz$ for ![]() $r\in\mathbb{R}\setminus\{1\}$. Then
$r\in\mathbb{R}\setminus\{1\}$. Then
 \begin{equation*}
f(r) := H_z(r z) = \frac{a^2 + b^2 r^2|z|^2 }{|z|^2(r-1)^2}
= b^2 + \frac{a^2 + |z|^2b^2}{|z|^2(r-1)^2} + \frac{2b^2}{r-1} .
\end{equation*}
\begin{equation*}
f(r) := H_z(r z) = \frac{a^2 + b^2 r^2|z|^2 }{|z|^2(r-1)^2}
= b^2 + \frac{a^2 + |z|^2b^2}{|z|^2(r-1)^2} + \frac{2b^2}{r-1} .
\end{equation*} It is easy to see that ![]() $f$ has only one local extremum; it is a global minimum and it is attained at
$f$ has only one local extremum; it is a global minimum and it is attained at  $r_0 = -\frac{a^2}{b^2 |z|^2}$ and
$r_0 = -\frac{a^2}{b^2 |z|^2}$ and  $f(r_0) = \frac{b^2 a^2}{b^2|z|^2 + a^2} \lt b^2$. Therefore
$f(r_0) = \frac{b^2 a^2}{b^2|z|^2 + a^2} \lt b^2$. Therefore ![]() $H_z$ cannot have a local maximum in any
$H_z$ cannot have a local maximum in any ![]() $t\in\mathbb{C}\setminus\{z\}$ with
$t\in\mathbb{C}\setminus\{z\}$ with ![]() $\arg t = \arg(\pm z)$. If
$\arg t = \arg(\pm z)$. If ![]() $\arg t\neq \arg \pm z$, then we write
$\arg t\neq \arg \pm z$, then we write ![]() $t= z + R\mathrm{e}^{\mathrm{i}\phi}$ with
$t= z + R\mathrm{e}^{\mathrm{i}\phi}$ with ![]() $R=|t-z|$ and appropriate
$R=|t-z|$ and appropriate ![]() $\phi\in\mathbb{R}$. Then
$\phi\in\mathbb{R}$. Then  $H_z(z + R\mathrm{e}^{\mathrm{i}(\phi+h)}) = \frac{a^2 + b^2|z + R\mathrm{e}^{\mathrm{i}(\phi+h)}|^2}{R^2}$ is strictly monotonic in
$H_z(z + R\mathrm{e}^{\mathrm{i}(\phi+h)}) = \frac{a^2 + b^2|z + R\mathrm{e}^{\mathrm{i}(\phi+h)}|^2}{R^2}$ is strictly monotonic in ![]() $h$ for
$h$ for ![]() $h\in\mathbb{R}$ in a small enough neighbourhood of zero, see Figure A1. Therefore
$h\in\mathbb{R}$ in a small enough neighbourhood of zero, see Figure A1. Therefore ![]() $H_z$ cannot have a local extremum in
$H_z$ cannot have a local extremum in ![]() $t$.
$t$.

Figure A1. Illustration for the proof of Lemma A.1. If ![]() $h\in\mathbb{R}$, then
$h\in\mathbb{R}$, then ![]() $t' = z+ R\mathrm{e}^{\mathrm{i}(\phi+h)}$ varies on the red circle leaving
$t' = z+ R\mathrm{e}^{\mathrm{i}(\phi+h)}$ varies on the red circle leaving ![]() $|z-t'|$ constant while
$|z-t'|$ constant while ![]() $|t'|$ is strictly monotonic for
$|t'|$ is strictly monotonic for ![]() $h$ in a neighbourhood of
$h$ in a neighbourhood of ![]() $0$.
$0$.
In the special case ![]() $a=0$ and
$a=0$ and ![]() $b=1$, we have the following estimates for
$b=1$, we have the following estimates for ![]() $H_z$ on lines paralell to the real line.
$H_z$ on lines paralell to the real line.
Remark A.2. Let ![]() $w\in\mathbb{C}\setminus\mathbb{R}$ and
$w\in\mathbb{C}\setminus\mathbb{R}$ and ![]() $\gamma\in\mathbb{R}\setminus\{\operatorname{Im} w\}$. Then
$\gamma\in\mathbb{R}\setminus\{\operatorname{Im} w\}$. Then
 \begin{align}
\sup_{\tau\in \mathbb{R}}\frac{|\tau|}{|\tau-w|} &= \frac{|w|}{|\operatorname{Im} w|}
\end{align}
\begin{align}
\sup_{\tau\in \mathbb{R}}\frac{|\tau|}{|\tau-w|} &= \frac{|w|}{|\operatorname{Im} w|}
\end{align}and
 \begin{align}
\sup_{t\in \mathbb{R} + \mathrm{i}\gamma }\frac{|t|^2}{|t-w|^2}
& \le 1 + \frac{(\operatorname{Re} w)^2}{(\gamma - \operatorname{Im} w)^2 } + \frac{\gamma^2}{( \gamma- \operatorname{Im} w )^2} .
\end{align}
\begin{align}
\sup_{t\in \mathbb{R} + \mathrm{i}\gamma }\frac{|t|^2}{|t-w|^2}
& \le 1 + \frac{(\operatorname{Re} w)^2}{(\gamma - \operatorname{Im} w)^2 } + \frac{\gamma^2}{( \gamma- \operatorname{Im} w )^2} .
\end{align}Proof. In fact, if ![]() $\operatorname{Re} w \neq 0$, then the supremum in (A.1) is a maximum and it is attained at
$\operatorname{Re} w \neq 0$, then the supremum in (A.1) is a maximum and it is attained at  $\tau = \frac{|z|^2}{\mu}$. If
$\tau = \frac{|z|^2}{\mu}$. If ![]() $\operatorname{Re} w = 0$, then the function on the left hand side has no maximum and
$\operatorname{Re} w = 0$, then the function on the left hand side has no maximum and  $\sup_{\tau\in \mathbb{R}}\frac{|\tau|}{|\tau-w|}= \operatorname{Im}_{|\tau|\to\infty}\frac{|\tau|}{|\tau-w|} = 1 = \frac{|w|}{|\operatorname{Im} w|}$.
$\sup_{\tau\in \mathbb{R}}\frac{|\tau|}{|\tau-w|}= \operatorname{Im}_{|\tau|\to\infty}\frac{|\tau|}{|\tau-w|} = 1 = \frac{|w|}{|\operatorname{Im} w|}$.
For the proof of (A.2) observe that
 \begin{align*}
\sup_{t\in \mathbb{R} + \mathrm{i}\gamma }\frac{|t|^2}{|t-w|^2}
& = \sup_{\tau\in \mathbb{R}}\frac{|\tau + \mathrm{i}\gamma|^2}{|\tau + \mathrm{i}\gamma-w|^2}
= \sup_{\tau\in \mathbb{R}} \frac{\tau^2}{|\tau + \mathrm{i}\gamma-w|^2} + \frac{\gamma^2}{|\tau + \mathrm{i}\gamma-w|^2}
\\
& \le \frac{|\mathrm{i}\gamma - w|^2}{(\operatorname{Im}(\mathrm{i}\gamma-w))^2 } + \frac{\gamma^2}{( \operatorname{Im}( \mathrm{i}\gamma-w ) )^2}
\end{align*}
\begin{align*}
\sup_{t\in \mathbb{R} + \mathrm{i}\gamma }\frac{|t|^2}{|t-w|^2}
& = \sup_{\tau\in \mathbb{R}}\frac{|\tau + \mathrm{i}\gamma|^2}{|\tau + \mathrm{i}\gamma-w|^2}
= \sup_{\tau\in \mathbb{R}} \frac{\tau^2}{|\tau + \mathrm{i}\gamma-w|^2} + \frac{\gamma^2}{|\tau + \mathrm{i}\gamma-w|^2}
\\
& \le \frac{|\mathrm{i}\gamma - w|^2}{(\operatorname{Im}(\mathrm{i}\gamma-w))^2 } + \frac{\gamma^2}{( \operatorname{Im}( \mathrm{i}\gamma-w ) )^2}
\end{align*} where we used (A.1) to estimate the first term. The second term clearly attains its maximum when ![]() $\tau = \operatorname{Re} w$. The claim follows if we observe that
$\tau = \operatorname{Re} w$. The claim follows if we observe that  $\frac{|\mathrm{i}\gamma - w|^2}{(\operatorname{Im}(\mathrm{i}\gamma-w))^2 } = 1 + \frac{(\operatorname{Re} w)^2}{(\operatorname{Im}(\mathrm{i}\gamma-w))^2 }$.
$\frac{|\mathrm{i}\gamma - w|^2}{(\operatorname{Im}(\mathrm{i}\gamma-w))^2 } = 1 + \frac{(\operatorname{Re} w)^2}{(\operatorname{Im}(\mathrm{i}\gamma-w))^2 }$.
In our next lemma we find the supremum of ![]() $H_z$ when restricted to a line parallel to the real axis and we show when the supremum is less than 1.
$H_z$ when restricted to a line parallel to the real axis and we show when the supremum is less than 1.
Lemma A.3. Let ![]() $a,b\ge 0$. Let
$a,b\ge 0$. Let  $H_z(t) = \frac{a^2 + b^2 |t|^2}{|t-z|^2 } $ be the function from Lemma A.1.
$H_z(t) = \frac{a^2 + b^2 |t|^2}{|t-z|^2 } $ be the function from Lemma A.1.
(i) Let
 $\gamma\in\mathbb{R}$ and let
$\gamma\in\mathbb{R}$ and let  $L = \{\tau + \mathrm{i} \gamma : \tau\in\mathbb{R}\}$. Then for
$L = \{\tau + \mathrm{i} \gamma : \tau\in\mathbb{R}\}$. Then for  $z \in\mathbb{C}\setminus L$ we have that
(A.3)
$z \in\mathbb{C}\setminus L$ we have that
(A.3) \begin{equation}\begin{aligned}
\sup_{t\in L} H_z(t)
=
\big( 2 (\nu-\gamma)^2 \big)^{-1}
\bigg(
a^2 + b^2 (\mu^2 + \gamma^2 + (\gamma - \nu)^2 )
\\
+\sqrt{
\big[ -a^2 + b^2 (\mu^2- \gamma^2 + (\gamma - \nu)^2 )]^2
+ 4 \mu^2b^2( a^2 + b^2\gamma^2 ) }
\bigg)
\end{aligned}
\end{equation}
\begin{equation}\begin{aligned}
\sup_{t\in L} H_z(t)
=
\big( 2 (\nu-\gamma)^2 \big)^{-1}
\bigg(
a^2 + b^2 (\mu^2 + \gamma^2 + (\gamma - \nu)^2 )
\\
+\sqrt{
\big[ -a^2 + b^2 (\mu^2- \gamma^2 + (\gamma - \nu)^2 )]^2
+ 4 \mu^2b^2( a^2 + b^2\gamma^2 ) }
\bigg)
\end{aligned}
\end{equation}with
 $\mu = \operatorname{Re}(z)$ and
$\mu = \operatorname{Re}(z)$ and  $\nu = \operatorname{Im}(z)$. The supremum is attained except when
$\nu = \operatorname{Im}(z)$. The supremum is attained except when  $\mu=0$ and
$\mu=0$ and  $a^2-b^2(\nu^2-2\nu\gamma) \lt 0$ in which case
$a^2-b^2(\nu^2-2\nu\gamma) \lt 0$ in which case  $H_z(t) \lt \lim_{\tau\to \pm\infty} H_z(\tau + \mathrm{i}\gamma) = b^2 $ for all
$H_z(t) \lt \lim_{\tau\to \pm\infty} H_z(\tau + \mathrm{i}\gamma) = b^2 $ for all  $\tau\in\mathbb{R}$.
$\tau\in\mathbb{R}$.(ii) We have that
 \begin{align*}
\sup_{t\in L} H_z(t) \lt 1
&\quad\iff\quad
a^2 + b^2\gamma^2 + \frac{b^2(\operatorname{Re} z)^2}{1-b^2} \lt (\gamma - (\operatorname{Im} z))^2\\
& \quad\iff\quad
z\in \mathrm{i}\gamma + \mathrm{Hyp}_{\gamma}.
\end{align*}
\begin{align*}
\sup_{t\in L} H_z(t) \lt 1
&\quad\iff\quad
a^2 + b^2\gamma^2 + \frac{b^2(\operatorname{Re} z)^2}{1-b^2} \lt (\gamma - (\operatorname{Im} z))^2\\
& \quad\iff\quad
z\in \mathrm{i}\gamma + \mathrm{Hyp}_{\gamma}.
\end{align*}
Proof. If ![]() $\mu = \operatorname{Re}(z) = 0$, then
$\mu = \operatorname{Re}(z) = 0$, then
 \begin{align*}
H_z(t)
&= \frac{a^2 + b^2 \gamma^2 + b^2\tau^2 }{\tau^2 + (\gamma - \nu)^2}
= b^2 + \frac{a^2 - b^2 (\nu^2 - 2\nu \gamma) }{\tau^2 + (\gamma - \nu)^2} .
\end{align*}
\begin{align*}
H_z(t)
&= \frac{a^2 + b^2 \gamma^2 + b^2\tau^2 }{\tau^2 + (\gamma - \nu)^2}
= b^2 + \frac{a^2 - b^2 (\nu^2 - 2\nu \gamma) }{\tau^2 + (\gamma - \nu)^2} .
\end{align*} If ![]() $a^2 - b^2 (\nu^2 - 2\nu \gamma) \lt 0$, then
$a^2 - b^2 (\nu^2 - 2\nu \gamma) \lt 0$, then ![]() $H_z(t) \lt \sup_{\tau\to\pm\infty} H_z(\tau+\mathrm{i}\gamma) = b^2$. If
$H_z(t) \lt \sup_{\tau\to\pm\infty} H_z(\tau+\mathrm{i}\gamma) = b^2$. If ![]() $a^2 - b^2 (\nu^2 - 2\nu \gamma) \ge 0$, then
$a^2 - b^2 (\nu^2 - 2\nu \gamma) \ge 0$, then ![]() $H_z$ has its maximum when
$H_z$ has its maximum when ![]() $\tau =0$ and
$\tau =0$ and  $\sup_{t\in L} H_z(t) = H_z(\mathrm{i}\gamma) = \frac{a^2 + b^2\gamma^2 }{(\gamma-\nu)^2}$. So in both cases, (A.3) holds.
$\sup_{t\in L} H_z(t) = H_z(\mathrm{i}\gamma) = \frac{a^2 + b^2\gamma^2 }{(\gamma-\nu)^2}$. So in both cases, (A.3) holds.
Now assume that ![]() $\mu \neq 0$ and set
$\mu \neq 0$ and set ![]() $F(\tau) := H_{z}(\tau + \mathrm{i}\gamma)$. If
$F(\tau) := H_{z}(\tau + \mathrm{i}\gamma)$. If ![]() $a=b=0$, then the claim is clear. Otherwise, it is easy to check that
$a=b=0$, then the claim is clear. Otherwise, it is easy to check that ![]() $F$ has the two different critical points
$F$ has the two different critical points
 \begin{align*}
\tau_\pm =
(2\mu b^2)^{-1}\bigg(
& -a^2 + b^2 \Big(\mu^2- \gamma^2 + (\gamma - \nu)^2 \Big)
\\
& \qquad \pm \sqrt{
\big[ -a^2 + b^2 (\mu^2- \gamma^2 + (\gamma - \nu)^2 ) ]^2 + 4 \mu^2b^2( a^2 + b^2\gamma^2 ) }
\bigg).
\end{align*}
\begin{align*}
\tau_\pm =
(2\mu b^2)^{-1}\bigg(
& -a^2 + b^2 \Big(\mu^2- \gamma^2 + (\gamma - \nu)^2 \Big)
\\
& \qquad \pm \sqrt{
\big[ -a^2 + b^2 (\mu^2- \gamma^2 + (\gamma - \nu)^2 ) ]^2 + 4 \mu^2b^2( a^2 + b^2\gamma^2 ) }
\bigg).
\end{align*} Since ![]() $F$ is continuous and tends to
$F$ is continuous and tends to ![]() $b^2$ for
$b^2$ for ![]() $\tau\to\pm\infty$, it must have a global maximum. It can be shown that the maximum is
$\tau\to\pm\infty$, it must have a global maximum. It can be shown that the maximum is
 \begin{align}
\begin{aligned}
M(\mu,\nu,\gamma)
&:= F(\tau_-)
= \Big(2(\nu-\gamma)^2\Big)^{-1}\bigg(
a^2 + b^2 \Big(\mu^2 + \gamma^2 + (\gamma - \nu)^2 \Big)
\\
& \quad +\sqrt{
\big[ -a^2 + b^2 (\mu^2 - \gamma^2 + (\gamma - \nu)^2 )]^2
+ 4 \mu^2b^2( a^2 + b^2\gamma^2 ) }
\bigg)
\end{aligned}
\end{align}
\begin{align}
\begin{aligned}
M(\mu,\nu,\gamma)
&:= F(\tau_-)
= \Big(2(\nu-\gamma)^2\Big)^{-1}\bigg(
a^2 + b^2 \Big(\mu^2 + \gamma^2 + (\gamma - \nu)^2 \Big)
\\
& \quad +\sqrt{
\big[ -a^2 + b^2 (\mu^2 - \gamma^2 + (\gamma - \nu)^2 )]^2
+ 4 \mu^2b^2( a^2 + b^2\gamma^2 ) }
\bigg)
\end{aligned}
\end{align}which concludes the proof of (A.3). The claim in (ii) follows from (A.3) by a straightforward calculation.
Next, we give bounds for the supremum of ![]() $H_z$ when restricted to a strip around the real axis or a sectors centred in
$H_z$ when restricted to a strip around the real axis or a sectors centred in ![]() $0$. They are used in Proposition 3.2, Proposition 4.8 and Theorem 4.6 respectively. Recall that for
$0$. They are used in Proposition 3.2, Proposition 4.8 and Theorem 4.6 respectively. Recall that for ![]() $\beta\in\mathbb{R}$ and
$\beta\in\mathbb{R}$ and ![]() $\theta\in [0, \pi/2)$ we define the closed sector
$\theta\in [0, \pi/2)$ we define the closed sector ![]() $S_{\theta}(\beta) = \{z\in\mathbb{C} : |\arg(z-\beta)| \le \theta \} \cup \{\beta\}$.
$S_{\theta}(\beta) = \{z\in\mathbb{C} : |\arg(z-\beta)| \le \theta \} \cup \{\beta\}$.
Lemma A.4. Let ![]() $a,b\ge 0$. Let
$a,b\ge 0$. Let  $H_z(t) = \frac{a^2 + b^2 |t|^2}{|t-z|^2 } $ be the function from Lemma A.1 and let us denote the right hand side of (A.4) by
$H_z(t) = \frac{a^2 + b^2 |t|^2}{|t-z|^2 } $ be the function from Lemma A.1 and let us denote the right hand side of (A.4) by ![]() $M(\mu, \nu, \gamma)$.
$M(\mu, \nu, \gamma)$.
(i) Let
 $\gamma_1 \lt \gamma_2$ and let
$\gamma_1 \lt \gamma_2$ and let  $\mathrm{Str}_{\gamma_1,\gamma_2}
= \{\tau + \mathrm{i} \sigma : \tau\in\mathbb{R},\, \gamma_1 \le \sigma\le \gamma_2\}$ be the strip parallel to the real axis. Then for
$\mathrm{Str}_{\gamma_1,\gamma_2}
= \{\tau + \mathrm{i} \sigma : \tau\in\mathbb{R},\, \gamma_1 \le \sigma\le \gamma_2\}$ be the strip parallel to the real axis. Then for  $z\in\mathbb{C}\setminus \mathrm{Str}_{\gamma_1,\gamma_2}$ we have that
(A.5)
$z\in\mathbb{C}\setminus \mathrm{Str}_{\gamma_1,\gamma_2}$ we have that
(A.5) \begin{equation}
\sup_{t\in \mathrm{Str}_{\gamma_1,\gamma_2}} H_z(t)
=
\begin{cases}
M(\mu, \nu, \gamma_1)\qquad & \text{if }\ \nu \lt \gamma_1, \\
M(\mu, \nu, \gamma_2)\qquad & \text{if }\ \nu \gt \gamma_2,
\end{cases}
\end{equation}
\begin{equation}
\sup_{t\in \mathrm{Str}_{\gamma_1,\gamma_2}} H_z(t)
=
\begin{cases}
M(\mu, \nu, \gamma_1)\qquad & \text{if }\ \nu \lt \gamma_1, \\
M(\mu, \nu, \gamma_2)\qquad & \text{if }\ \nu \gt \gamma_2,
\end{cases}
\end{equation}and
 \begin{align*}
\sup_{t\in \mathrm{Str}_{\gamma_1,\gamma_2}} H_z(t) \lt 1
& \quad \iff\quad
a^2 + b^2\gamma_j^2 + \frac{b^2\mu^2}{1-b^2 } \lt (\gamma_j-\nu)^2\\
&\qquad\qquad\qquad\qquad \text{where }\
\begin{cases}
j = 1\ &\text{if }\ \nu \lt \gamma_1,
\\
j = 2\ &\text{if }\ \nu \gt \gamma_2,
\end{cases}
\\
& \quad \iff\quad
z\in -( -\mathrm{i}\gamma_1 + \mathrm{Hyp}_{-\gamma_1}) \cup (\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\gamma_2} ).
\end{align*}
\begin{align*}
\sup_{t\in \mathrm{Str}_{\gamma_1,\gamma_2}} H_z(t) \lt 1
& \quad \iff\quad
a^2 + b^2\gamma_j^2 + \frac{b^2\mu^2}{1-b^2 } \lt (\gamma_j-\nu)^2\\
&\qquad\qquad\qquad\qquad \text{where }\
\begin{cases}
j = 1\ &\text{if }\ \nu \lt \gamma_1,
\\
j = 2\ &\text{if }\ \nu \gt \gamma_2,
\end{cases}
\\
& \quad \iff\quad
z\in -( -\mathrm{i}\gamma_1 + \mathrm{Hyp}_{-\gamma_1}) \cup (\mathrm{i}\gamma_2 + \mathrm{Hyp}_{\gamma_2} ).
\end{align*}(ii) Let
 $\theta\in [0, \pi/2)$,
$\theta\in [0, \pi/2)$,  $\beta\in\mathbb{R}$ and let
$\beta\in\mathbb{R}$ and let  $z\in \mathbb{C} \setminus S_{\theta}(\beta)$. Then either
$z\in \mathbb{C} \setminus S_{\theta}(\beta)$. Then either  $\arg(z-\beta)\in (\theta, \theta+\pi)$ or
$\arg(z-\beta)\in (\theta, \theta+\pi)$ or  $\arg(z-\beta)\in (-\theta-\pi, -\theta)$ and
(A.6)
$\arg(z-\beta)\in (-\theta-\pi, -\theta)$ and
(A.6) \begin{align}
&\sup_{t\in S_{\theta}(\beta)} H_z(t)
\cr
&\le b^2 +
\begin{cases}
b^2\, \frac{(\operatorname{Re}( \mathrm{e}^{-\mathrm{i}\theta}(z-\beta)) )^2 }{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} (z-\beta)) )^2 }
+ \frac{a^2 + b^2\beta^2}{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} (z-\beta)) )^2 }
&\qquad \text{if } \arg(z-\beta)\in(\theta, \theta+\pi),
\\[1ex]
b^2\, \frac{(\operatorname{Re}( \mathrm{e}^{\mathrm{i}\theta}(z-\beta)) )^2 }{( \operatorname{Im} (\mathrm{e}^{\mathrm{i}\theta} (z-\beta)) )^2 }
+ \frac{a^2 + b^2\beta^2}{( \operatorname{Im} (\mathrm{e}^{\mathrm{i}\theta} (z-\beta)) )^2 }
&\qquad \text{if } \arg(z-\beta)\in(-\theta-\pi, -\theta).
\end{cases}\cr
\end{align}
\begin{align}
&\sup_{t\in S_{\theta}(\beta)} H_z(t)
\cr
&\le b^2 +
\begin{cases}
b^2\, \frac{(\operatorname{Re}( \mathrm{e}^{-\mathrm{i}\theta}(z-\beta)) )^2 }{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} (z-\beta)) )^2 }
+ \frac{a^2 + b^2\beta^2}{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} (z-\beta)) )^2 }
&\qquad \text{if } \arg(z-\beta)\in(\theta, \theta+\pi),
\\[1ex]
b^2\, \frac{(\operatorname{Re}( \mathrm{e}^{\mathrm{i}\theta}(z-\beta)) )^2 }{( \operatorname{Im} (\mathrm{e}^{\mathrm{i}\theta} (z-\beta)) )^2 }
+ \frac{a^2 + b^2\beta^2}{( \operatorname{Im} (\mathrm{e}^{\mathrm{i}\theta} (z-\beta)) )^2 }
&\qquad \text{if } \arg(z-\beta)\in(-\theta-\pi, -\theta).
\end{cases}\cr
\end{align}Moreover,
 \begin{equation*}
z\in
\big(\beta + \mathrm{e}^{\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_\beta \big)
\cup
\big(\beta + \mathrm{e}^{-\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_\beta \big)
\quad\implies\quad
\sup_{t\in S_{\theta}(\beta)} H_z(t) \lt 1
\end{equation*}
\begin{equation*}
z\in
\big(\beta + \mathrm{e}^{\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_\beta \big)
\cup
\big(\beta + \mathrm{e}^{-\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_\beta \big)
\quad\implies\quad
\sup_{t\in S_{\theta}(\beta)} H_z(t) \lt 1
\end{equation*}where
(A.7) \begin{equation}
\widetilde{\mathrm{Hyp}}_\beta
= \left\{x+\mathrm{i} y \ :\ \frac{a^2 + b^2\beta^2}{1-b^2} + \frac{b^2}{1-b^2}\, x^2 \gt y^2,\ y \gt 0 \right\}.
\end{equation}
\begin{equation}
\widetilde{\mathrm{Hyp}}_\beta
= \left\{x+\mathrm{i} y \ :\ \frac{a^2 + b^2\beta^2}{1-b^2} + \frac{b^2}{1-b^2}\, x^2 \gt y^2,\ y \gt 0 \right\}.
\end{equation}(iii) Let
 $\theta\in [0, \pi/2)$,
$\theta\in [0, \pi/2)$,  $\alpha\in\mathbb{R}$ and let
$\alpha\in\mathbb{R}$ and let  $z\in \mathbb{C} \setminus -S_{\theta}(-\alpha)$. Then either
$z\in \mathbb{C} \setminus -S_{\theta}(-\alpha)$. Then either  $\arg(z-\alpha)\in (-\theta, -\theta+\pi)$ or
$\arg(z-\alpha)\in (-\theta, -\theta+\pi)$ or  $\arg(z-\alpha)\in (\theta-\pi, \theta)$ and
(A.8)
$\arg(z-\alpha)\in (\theta-\pi, \theta)$ and
(A.8) \begin{align}
&\sup_{t\in -S_{\theta}(-\alpha)} H_z(t)
\le b^2 +\cr
&\begin{cases}
b^2\, \frac{(\operatorname{Re}( \mathrm{e}^{\mathrm{i}\theta}(z-\alpha)) )^2 }{( \operatorname{Im} (\mathrm{e}^{\mathrm{i}\theta} (z-\alpha)) )^2 }
+ \frac{a^2 + b^2\alpha^2}{( \operatorname{Im} (\mathrm{e}^{\mathrm{i}\theta} (z-\alpha)) )^2 }
&\qquad \text{if } \arg(z-\alpha)\in(-\theta, -\theta+\pi),
\\[2ex]
b^2\, \frac{(\operatorname{Re}( \mathrm{e}^{-\mathrm{i}\theta}(z-\alpha)) )^2 }{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} (z-\alpha)) )^2 }
+ \frac{a^2 + b^2\alpha^2}{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} (z-\alpha)) )^2 }
&\qquad \text{if } \arg(z-\alpha)\in(\theta, \theta+\pi).
\end{cases}\cr
\end{align}
\begin{align}
&\sup_{t\in -S_{\theta}(-\alpha)} H_z(t)
\le b^2 +\cr
&\begin{cases}
b^2\, \frac{(\operatorname{Re}( \mathrm{e}^{\mathrm{i}\theta}(z-\alpha)) )^2 }{( \operatorname{Im} (\mathrm{e}^{\mathrm{i}\theta} (z-\alpha)) )^2 }
+ \frac{a^2 + b^2\alpha^2}{( \operatorname{Im} (\mathrm{e}^{\mathrm{i}\theta} (z-\alpha)) )^2 }
&\qquad \text{if } \arg(z-\alpha)\in(-\theta, -\theta+\pi),
\\[2ex]
b^2\, \frac{(\operatorname{Re}( \mathrm{e}^{-\mathrm{i}\theta}(z-\alpha)) )^2 }{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} (z-\alpha)) )^2 }
+ \frac{a^2 + b^2\alpha^2}{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} (z-\alpha)) )^2 }
&\qquad \text{if } \arg(z-\alpha)\in(\theta, \theta+\pi).
\end{cases}\cr
\end{align}Moreover,
 \begin{equation*}
z\in
\big(\alpha + \mathrm{e}^{-\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_\alpha \big)
\cup
\big(\alpha + \mathrm{e}^{\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_\alpha \big)
\quad\implies\quad
\sup_{t\in S_{\theta}(\beta)} H_z(t) \lt 1.
\end{equation*}
\begin{equation*}
z\in
\big(\alpha + \mathrm{e}^{-\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_\alpha \big)
\cup
\big(\alpha + \mathrm{e}^{\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_\alpha \big)
\quad\implies\quad
\sup_{t\in S_{\theta}(\beta)} H_z(t) \lt 1.
\end{equation*}
Proof. We know from Lemma A.1 that the supremum of ![]() $H_z$ on the given sets is equal to its supremum on their respective boundaries. Therefore, in (A.5) – (A.8) we can replace the supremum by the supremum over the boundary of the respective sets. Let
$H_z$ on the given sets is equal to its supremum on their respective boundaries. Therefore, in (A.5) – (A.8) we can replace the supremum by the supremum over the boundary of the respective sets. Let ![]() $\mu = \operatorname{Re} z$ and
$\mu = \operatorname{Re} z$ and ![]() $\nu = \operatorname{Im} z$.
$\nu = \operatorname{Im} z$.
(i) The claim follows directly from Lemma A.3 if we note that ![]() $M(\mu,\nu,\gamma)$ is decreasing in
$M(\mu,\nu,\gamma)$ is decreasing in ![]() $(\nu-\gamma)^2$ if
$(\nu-\gamma)^2$ if ![]() $\mu$ and
$\mu$ and ![]() $\gamma$ are fixed.
$\gamma$ are fixed.
(ii) Suppose that ![]() $\arg(z-\beta)\in(\theta,\theta+\pi)$. Then
$\arg(z-\beta)\in(\theta,\theta+\pi)$. Then ![]() $H_z$ is well defined in the half-plane
$H_z$ is well defined in the half-plane ![]() $P = \beta + \mathrm{e}^{\mathrm{i}\theta} \{\zeta \in\mathbb{C} : \operatorname{Im} \zeta \le 0\}$ and
$P = \beta + \mathrm{e}^{\mathrm{i}\theta} \{\zeta \in\mathbb{C} : \operatorname{Im} \zeta \le 0\}$ and ![]() $S_{\theta}(\beta)\subseteq P$. See Figure 3. Therefore
$S_{\theta}(\beta)\subseteq P$. See Figure 3. Therefore
 \begin{align*}
\sup_{t\in S_{\theta}(\beta) } H_z(t)
& \le \sup_{t\in P } H_z(t)
= \sup_{t\in \partial P } H_z(t)
= \sup_{r\in\mathbb{R} } H_z(\beta + r\mathrm{e}^{\mathrm{i}\theta})
\end{align*}
\begin{align*}
\sup_{t\in S_{\theta}(\beta) } H_z(t)
& \le \sup_{t\in P } H_z(t)
= \sup_{t\in \partial P } H_z(t)
= \sup_{r\in\mathbb{R} } H_z(\beta + r\mathrm{e}^{\mathrm{i}\theta})
\end{align*} \begin{align*}
& = \sup_{r\in\mathbb{R} } \frac{a^2 + b^2|\beta + r\mathrm{e}^{\mathrm{i}\theta}|^2 }{| \beta + r\mathrm{e}^{\mathrm{i}\theta} - z |^2 }
= \sup_{r\in\mathbb{R} } \frac{a^2 + b^2 | r + \mathrm{e}^{-\mathrm{i}\theta}\beta |^2 }{| r - \mathrm{e}^{-\mathrm{i}\theta} ( z - \beta) |^2 }
\end{align*}
\begin{align*}
& = \sup_{r\in\mathbb{R} } \frac{a^2 + b^2|\beta + r\mathrm{e}^{\mathrm{i}\theta}|^2 }{| \beta + r\mathrm{e}^{\mathrm{i}\theta} - z |^2 }
= \sup_{r\in\mathbb{R} } \frac{a^2 + b^2 | r + \mathrm{e}^{-\mathrm{i}\theta}\beta |^2 }{| r - \mathrm{e}^{-\mathrm{i}\theta} ( z - \beta) |^2 }
\end{align*} \begin{align*}
& \hspace{-22pt} \le \sup_{r\in\mathbb{R} }
\frac{b^2 |r|^2 }{| r - \mathrm{e}^{-\mathrm{i}\theta} ( z - \beta ) |^2 }
+ \frac{a^2 + b^2 \beta^2 }{| r - \mathrm{e}^{-\mathrm{i}\theta} ( z - \beta ) |^2 }
\end{align*}
\begin{align*}
& \hspace{-22pt} \le \sup_{r\in\mathbb{R} }
\frac{b^2 |r|^2 }{| r - \mathrm{e}^{-\mathrm{i}\theta} ( z - \beta ) |^2 }
+ \frac{a^2 + b^2 \beta^2 }{| r - \mathrm{e}^{-\mathrm{i}\theta} ( z - \beta ) |^2 }
\end{align*} \begin{align}
& \le b^2 + b^2\, \frac{(\operatorname{Re}( \mathrm{e}^{-\mathrm{i}\theta}(z-\beta)) )^2 }{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} ( z - \beta )) )^2 }
+ \frac{a^2 + b^2\beta^2}{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} ( z - \beta )) )^2 }
\end{align}
\begin{align}
& \le b^2 + b^2\, \frac{(\operatorname{Re}( \mathrm{e}^{-\mathrm{i}\theta}(z-\beta)) )^2 }{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} ( z - \beta )) )^2 }
+ \frac{a^2 + b^2\beta^2}{( \operatorname{Im} (\mathrm{e}^{-\mathrm{i}\theta} ( z - \beta )) )^2 }
\end{align} where in the last inequality we used (A.1) to bound the first term and ![]() $|r+\mathrm{e}^{-\mathrm{i}\theta}(z-\beta)| \ge |\operatorname{Im} (r+\mathrm{e}^{-\mathrm{i}\theta}(z-\beta))|$ to bound the second term. This shows the first line in (A.6). Therefore,
$|r+\mathrm{e}^{-\mathrm{i}\theta}(z-\beta)| \ge |\operatorname{Im} (r+\mathrm{e}^{-\mathrm{i}\theta}(z-\beta))|$ to bound the second term. This shows the first line in (A.6). Therefore, ![]() $\sup_{t\in S_{\theta}(\beta) } H_z(t) \lt 1$ if
$\sup_{t\in S_{\theta}(\beta) } H_z(t) \lt 1$ if
 \begin{equation*}
\mathrm{e}^{\mathrm{i}\theta}(z-\beta)\in \widetilde{\mathrm{Hyp}}_\beta
= \left\{x+\mathrm{i} y \ :\ \frac{a^2 + b^2\beta^2}{1-b^2} + \frac{b^2}{1-b^2}\, x^2 \gt y^2,\ y \gt 0 \right\},
\end{equation*}
\begin{equation*}
\mathrm{e}^{\mathrm{i}\theta}(z-\beta)\in \widetilde{\mathrm{Hyp}}_\beta
= \left\{x+\mathrm{i} y \ :\ \frac{a^2 + b^2\beta^2}{1-b^2} + \frac{b^2}{1-b^2}\, x^2 \gt y^2,\ y \gt 0 \right\},
\end{equation*} that is, if  $z\in \beta + \mathrm{e}^{-\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_\beta$.
$z\in \beta + \mathrm{e}^{-\mathrm{i}\theta}\widetilde{\mathrm{Hyp}}_\beta$.
If ![]() $\arg(z-\beta)\in(-\theta-\pi, -\theta)$, then
$\arg(z-\beta)\in(-\theta-\pi, -\theta)$, then ![]() $H_z$ is well defined in the half-plane
$H_z$ is well defined in the half-plane ![]() $Q = \beta + \mathrm{e}^{-\mathrm{i}\theta} \{\zeta\in\mathbb{C} : \operatorname{Im} \zeta \ge 0\}$ and
$Q = \beta + \mathrm{e}^{-\mathrm{i}\theta} \{\zeta\in\mathbb{C} : \operatorname{Im} \zeta \ge 0\}$ and ![]() $S_{\theta}(\beta)\subseteq Q$ and an analogous calculation shows the second line in (A.6).
$S_{\theta}(\beta)\subseteq Q$ and an analogous calculation shows the second line in (A.6).
(iii) Note that
 \begin{align*}
\sup_{t\in-S_{\theta}(-\alpha)} \frac{|t|^2}{|t-z|^2}
= \sup_{t\in-S_{\theta}(-\alpha)} \frac{|-t|^2}{|-t+z|^2}
= \sup_{t\in S_{\theta}(\alpha)} \frac{|t|^2}{|t+z|^2} .
\end{align*}
\begin{align*}
\sup_{t\in-S_{\theta}(-\alpha)} \frac{|t|^2}{|t-z|^2}
= \sup_{t\in-S_{\theta}(-\alpha)} \frac{|-t|^2}{|-t+z|^2}
= \sup_{t\in S_{\theta}(\alpha)} \frac{|t|^2}{|t+z|^2} .
\end{align*} Now the claim follows from (ii) applied to ![]() $\beta = -\alpha$ and
$\beta = -\alpha$ and ![]() $-z$ instead of
$-z$ instead of ![]() $z$.
$z$.
The next lemma provides alternative estimates for ![]() $H_z$. Instead of the half-plane
$H_z$. Instead of the half-plane ![]() $P= \beta + \mathrm{e}^{\mathrm{i}\theta} \{\zeta\in\mathbb{C}: \operatorname{Im} \zeta \le 0 \}$ from the proof of Lemma A.4(ii), we use the half-plane
$P= \beta + \mathrm{e}^{\mathrm{i}\theta} \{\zeta\in\mathbb{C}: \operatorname{Im} \zeta \le 0 \}$ from the proof of Lemma A.4(ii), we use the half-plane ![]() $P' = \mathrm{e}^{\mathrm{i}\theta} \{ \zeta\in\mathbb{C}: \operatorname{Im} \zeta \le \beta\sin\theta \}$.
$P' = \mathrm{e}^{\mathrm{i}\theta} \{ \zeta\in\mathbb{C}: \operatorname{Im} \zeta \le \beta\sin\theta \}$.
Lemma A.5. Let ![]() $a,b\ge 0$. Let
$a,b\ge 0$. Let  $H_z(t) = \frac{a^2 + b^2 |t|^2}{|t-z|^2 } $ be the function from Lemma A.1.
$H_z(t) = \frac{a^2 + b^2 |t|^2}{|t-z|^2 } $ be the function from Lemma A.1.
(i) Let
 $\theta \in [0,\pi/2)$,
$\theta \in [0,\pi/2)$,  $\beta\in\mathbb{R}$ and let
$\beta\in\mathbb{R}$ and let  $z\in \mathbb{C} \setminus S_{\theta}(\beta)$. Then
(A.6’)
$z\in \mathbb{C} \setminus S_{\theta}(\beta)$. Then
(A.6’) \begin{align}
\sup_{t\in S_{\theta}(\beta)} H_z(t)
\le
\begin{cases}
M(\operatorname{Re}(\mathrm{e}^{-\mathrm{i}\theta}z),\, \operatorname{Im}(\mathrm{e}^{-\mathrm{i}\theta}z),\, \beta\sin\theta)
& \text{if } \arg(z-\beta)\in(\theta, \theta+\pi),
\\[2ex]
M(\operatorname{Re}(\mathrm{e}^{\mathrm{i}\theta}z),\, \operatorname{Im}(\mathrm{e}^{\mathrm{i}\theta}z),\, -\beta\sin\theta)
& \text{if } \arg(z-\beta)\in(-\pi-\theta, -\theta).
\end{cases}
\end{align}
\begin{align}
\sup_{t\in S_{\theta}(\beta)} H_z(t)
\le
\begin{cases}
M(\operatorname{Re}(\mathrm{e}^{-\mathrm{i}\theta}z),\, \operatorname{Im}(\mathrm{e}^{-\mathrm{i}\theta}z),\, \beta\sin\theta)
& \text{if } \arg(z-\beta)\in(\theta, \theta+\pi),
\\[2ex]
M(\operatorname{Re}(\mathrm{e}^{\mathrm{i}\theta}z),\, \operatorname{Im}(\mathrm{e}^{\mathrm{i}\theta}z),\, -\beta\sin\theta)
& \text{if } \arg(z-\beta)\in(-\pi-\theta, -\theta).
\end{cases}
\end{align}Moreover,
 \begin{equation*}
z \in
\mathrm{e}^{\mathrm{i}\theta} \big( -\mathrm{i}\beta\sin\theta + \mathrm{Hyp}_{-\beta\sin\theta} \big)
\cup
\mathrm{e}^{-\mathrm{i}\theta} \big( -\mathrm{i}\beta\sin\theta - \mathrm{Hyp}_{\beta\sin\theta} \big)
\,\implies\,
\sup_{t\in S_{\theta}(\beta)} H_z(t) \lt 1
\end{equation*}
\begin{equation*}
z \in
\mathrm{e}^{\mathrm{i}\theta} \big( -\mathrm{i}\beta\sin\theta + \mathrm{Hyp}_{-\beta\sin\theta} \big)
\cup
\mathrm{e}^{-\mathrm{i}\theta} \big( -\mathrm{i}\beta\sin\theta - \mathrm{Hyp}_{\beta\sin\theta} \big)
\,\implies\,
\sup_{t\in S_{\theta}(\beta)} H_z(t) \lt 1
\end{equation*}with
 $\mathrm{Hyp}_\gamma$ defined in (3.1).
$\mathrm{Hyp}_\gamma$ defined in (3.1).(ii) Let
 $\theta \in [0,\pi/2)$,
$\theta \in [0,\pi/2)$,  $\alpha\in\mathbb{R}$ and let
$\alpha\in\mathbb{R}$ and let  $z\in \mathbb{C} \setminus -S_{\theta}(-\alpha)$. Then
(A.8’)
$z\in \mathbb{C} \setminus -S_{\theta}(-\alpha)$. Then
(A.8’) \begin{align}
&\sup_{t\in -S_{\theta}(-\alpha)} H_z(t)\cr
&\le
\begin{cases}
M(\operatorname{Re}(\mathrm{e}^{\mathrm{i}\theta}z),\, \operatorname{Im}(\mathrm{e}^{\mathrm{i}\theta}z),\, \alpha\sin\theta)
& \text{if } \arg(z-\alpha)\in(\theta, \theta+\pi).
\\[2ex]
M(\operatorname{Re}(\mathrm{e}^{-\mathrm{i}\theta}z),\, \operatorname{Im}(\mathrm{e}^{-\mathrm{i}\theta}z),\, -\alpha\sin\theta)
& \text{if } \arg(z-\alpha)\in(-\theta, -\theta+\pi).
\end{cases}\cr
\end{align}
\begin{align}
&\sup_{t\in -S_{\theta}(-\alpha)} H_z(t)\cr
&\le
\begin{cases}
M(\operatorname{Re}(\mathrm{e}^{\mathrm{i}\theta}z),\, \operatorname{Im}(\mathrm{e}^{\mathrm{i}\theta}z),\, \alpha\sin\theta)
& \text{if } \arg(z-\alpha)\in(\theta, \theta+\pi).
\\[2ex]
M(\operatorname{Re}(\mathrm{e}^{-\mathrm{i}\theta}z),\, \operatorname{Im}(\mathrm{e}^{-\mathrm{i}\theta}z),\, -\alpha\sin\theta)
& \text{if } \arg(z-\alpha)\in(-\theta, -\theta+\pi).
\end{cases}\cr
\end{align}Moreover,
 \begin{equation*}
z\in
\mathrm{e}^{-\mathrm{i}\theta}\big(\mathrm{i}\alpha\sin\theta + \mathrm{Hyp}_{\mathrm{i}\alpha\sin\theta} \big)
\cup
\mathrm{e}^{\mathrm{i}\theta}\big(\mathrm{i}\alpha\sin\theta - \mathrm{Hyp}_{-\mathrm{i}\alpha\sin\theta} \big)
\, \implies\,
\sup_{t\in -S_{\theta}(-\alpha)} H_z(t) \lt 1.
\end{equation*}
\begin{equation*}
z\in
\mathrm{e}^{-\mathrm{i}\theta}\big(\mathrm{i}\alpha\sin\theta + \mathrm{Hyp}_{\mathrm{i}\alpha\sin\theta} \big)
\cup
\mathrm{e}^{\mathrm{i}\theta}\big(\mathrm{i}\alpha\sin\theta - \mathrm{Hyp}_{-\mathrm{i}\alpha\sin\theta} \big)
\, \implies\,
\sup_{t\in -S_{\theta}(-\alpha)} H_z(t) \lt 1.
\end{equation*}
Proof. We only show (A.6’). Its proof is similar to the one of (A.6).
Suppose that ![]() $\arg(z-\beta)\in(\theta,\theta+\pi)$. Then
$\arg(z-\beta)\in(\theta,\theta+\pi)$. Then ![]() $H_z$ is well defined in the half-plane
$H_z$ is well defined in the half-plane ![]() $P' = \mathrm{e}^{\mathrm{i}\theta} \{\zeta\in\mathbb{C} : \operatorname{Im} \zeta \le -\beta\sin\theta\}$ and
$P' = \mathrm{e}^{\mathrm{i}\theta} \{\zeta\in\mathbb{C} : \operatorname{Im} \zeta \le -\beta\sin\theta\}$ and ![]() $S_{\theta}(\beta)\subseteq P'$. Note that
$S_{\theta}(\beta)\subseteq P'$. Note that ![]() $\partial P' = \{\mathrm{e}^{\mathrm{i}\theta}(\tau - \mathrm{i}\beta\sin\theta) : \tau\in\mathbb{R} \}$ and for
$\partial P' = \{\mathrm{e}^{\mathrm{i}\theta}(\tau - \mathrm{i}\beta\sin\theta) : \tau\in\mathbb{R} \}$ and for ![]() $\tau\in\mathbb{R}$ we have
$\tau\in\mathbb{R}$ we have
 \begin{align*}
H_z(\mathrm{e}^{\mathrm{i}\theta}(\tau-\mathrm{i}\beta\sin\theta))
& = \frac{a^2 + b^2 | \mathrm{e}^{\mathrm{i}\theta} (\tau - \mathrm{i}\beta\sin\theta) |^2 }{| \mathrm{e}^{\mathrm{i}\theta}( \tau - \mathrm{i}\beta\sin\theta) - z |^2 }
= \frac{a^2 + b^2 | \tau - \mathrm{i}\beta\sin\theta|^2 }{| \tau - \mathrm{i}\beta\sin\theta - \mathrm{e}^{-\mathrm{i}\theta} z |^2 }
\\
& = H_{\mathrm{e}^{-\mathrm{i}\theta}z } (\tau-\mathrm{i}\beta\sin\theta).
\end{align*}
\begin{align*}
H_z(\mathrm{e}^{\mathrm{i}\theta}(\tau-\mathrm{i}\beta\sin\theta))
& = \frac{a^2 + b^2 | \mathrm{e}^{\mathrm{i}\theta} (\tau - \mathrm{i}\beta\sin\theta) |^2 }{| \mathrm{e}^{\mathrm{i}\theta}( \tau - \mathrm{i}\beta\sin\theta) - z |^2 }
= \frac{a^2 + b^2 | \tau - \mathrm{i}\beta\sin\theta|^2 }{| \tau - \mathrm{i}\beta\sin\theta - \mathrm{e}^{-\mathrm{i}\theta} z |^2 }
\\
& = H_{\mathrm{e}^{-\mathrm{i}\theta}z } (\tau-\mathrm{i}\beta\sin\theta).
\end{align*}Therefore,
 \begin{align*}
\sup_{t\in S_{\theta}(\beta) } H_z(t)
& \le \sup_{t\in P' } H_z(t)
= \sup_{t\in \partial P' } H_z(t)
= \sup_{\tau\in\mathbb{R} } H_z(\mathrm{e}^{\mathrm{i}\theta}(\tau-\mathrm{i}\beta\sin\theta))
\\
& = \sup_{\tau\in\mathbb{R} } H_{\mathrm{e}^{-\mathrm{i}\theta}z } (\tau-\mathrm{i}\beta\sin\theta)
= M(\operatorname{Re}(\mathrm{e}^{-\mathrm{i}\theta}z),\, \operatorname{Im}(\mathrm{e}^{-\mathrm{i}\theta}z),\, -\beta\sin\theta).
\end{align*}
\begin{align*}
\sup_{t\in S_{\theta}(\beta) } H_z(t)
& \le \sup_{t\in P' } H_z(t)
= \sup_{t\in \partial P' } H_z(t)
= \sup_{\tau\in\mathbb{R} } H_z(\mathrm{e}^{\mathrm{i}\theta}(\tau-\mathrm{i}\beta\sin\theta))
\\
& = \sup_{\tau\in\mathbb{R} } H_{\mathrm{e}^{-\mathrm{i}\theta}z } (\tau-\mathrm{i}\beta\sin\theta)
= M(\operatorname{Re}(\mathrm{e}^{-\mathrm{i}\theta}z),\, \operatorname{Im}(\mathrm{e}^{-\mathrm{i}\theta}z),\, -\beta\sin\theta).
\end{align*} By Lemma A.3(ii), the right hand side is smaller than 1 if and only if  $\mathrm{e}^{-\mathrm{i}\theta}z \in -\mathrm{i}\beta\sin\theta + \mathrm{Hyp}_{-\beta\sin\theta}$, that is, if and only if
$\mathrm{e}^{-\mathrm{i}\theta}z \in -\mathrm{i}\beta\sin\theta + \mathrm{Hyp}_{-\beta\sin\theta}$, that is, if and only if  $z \in \mathrm{e}^{\mathrm{i}\theta} \big( -\mathrm{i}\beta\sin\theta + \mathrm{Hyp}_{-\beta\sin\theta} \big)$. See Figure B1. If
$z \in \mathrm{e}^{\mathrm{i}\theta} \big( -\mathrm{i}\beta\sin\theta + \mathrm{Hyp}_{-\beta\sin\theta} \big)$. See Figure B1. If ![]() $\arg(z-\beta)\in(-\theta-\pi, -\theta)$, then
$\arg(z-\beta)\in(-\theta-\pi, -\theta)$, then ![]() $H_z$ is well defined in the half-plane
$H_z$ is well defined in the half-plane ![]() $Q' = \mathrm{e}^{-\mathrm{i}\theta} \{\zeta\in\mathbb{C} : \operatorname{Im} \zeta \ge \beta\sin\theta\}$ and
$Q' = \mathrm{e}^{-\mathrm{i}\theta} \{\zeta\in\mathbb{C} : \operatorname{Im} \zeta \ge \beta\sin\theta\}$ and ![]() $S_{\theta}(\beta)\subseteq Q'$ and we can use an analogous calculation to estimate
$S_{\theta}(\beta)\subseteq Q'$ and we can use an analogous calculation to estimate ![]() $H_z(t)$ for such
$H_z(t)$ for such ![]() $z$. The proof for the sector
$z$. The proof for the sector ![]() $-S_{\theta}(-\alpha)$ is similar.
$-S_{\theta}(-\alpha)$ is similar.
The situation in the next lemma is as in Lemma A.3 (i) but for the special case when ![]() $\operatorname{Im}(z) =0$.
$\operatorname{Im}(z) =0$.
Lemma A.6. Let ![]() $a,b\ge 0$ and
$a,b\ge 0$ and ![]() $\mu \gt 0$. Let
$\mu \gt 0$. Let  $H_z(t) = \frac{a^2 + b^2 |t|^2}{|t-z|^2 } $ be the function from Lemma A.1.
$H_z(t) = \frac{a^2 + b^2 |t|^2}{|t-z|^2 } $ be the function from Lemma A.1.
(i) For all
 $x \in\mathbb{R}\setminus\{\mu\}$,
(A.10)
$x \in\mathbb{R}\setminus\{\mu\}$,
(A.10) \begin{equation}
\sup_{t\in x+\mathrm{i}\mathbb{R}} H_\mu(t)
=\max\left\{b^2,\ \frac{a^2+b^2 x^2 }{(\mu- x)^2} \right\}.
\end{equation}
\begin{equation}
\sup_{t\in x+\mathrm{i}\mathbb{R}} H_\mu(t)
=\max\left\{b^2,\ \frac{a^2+b^2 x^2 }{(\mu- x)^2} \right\}.
\end{equation}(ii) Let
 $\alpha, \beta \in \mathbb{R}$ with
$\alpha, \beta \in \mathbb{R}$ with  $\alpha \lt \beta$ and let
$\alpha \lt \beta$ and let  $a, b\geq 0$. Then, for all
$a, b\geq 0$. Then, for all  $\mu\in (\alpha, \beta)$,
(A.11)
$\mu\in (\alpha, \beta)$,
(A.11) \begin{equation}
\sup_{t\in\mathbb{C}\setminus\big((\alpha,\beta)+\mathrm{i} \mathbb{R}\big)} H_\mu(t)
=\max\left\{b^2,\ \frac{a^2+b^2\alpha^2 }{(\mu-\alpha)^2},\ \frac{a^2+b^2\beta^2}{(\beta-\mu)^2}\right\}.
\end{equation}
\begin{equation}
\sup_{t\in\mathbb{C}\setminus\big((\alpha,\beta)+\mathrm{i} \mathbb{R}\big)} H_\mu(t)
=\max\left\{b^2,\ \frac{a^2+b^2\alpha^2 }{(\mu-\alpha)^2},\ \frac{a^2+b^2\beta^2}{(\beta-\mu)^2}\right\}.
\end{equation}
Proof. For ![]() $t=x + \mathrm{i}\sigma$ we obtain
$t=x + \mathrm{i}\sigma$ we obtain
 \begin{equation*}
H_\mu(t)
= H_\mu(x + \mathrm{i}\sigma)
= \frac{a^2 + b^2 x^2 + b^2 \sigma^2 }{(x-\mu)^2 + \sigma^2}
= b^2 + \frac{a^2 + b^2 [ x^2 - (x-\mu)^2] }{(x-\mu)^2 + \sigma^2}.
\end{equation*}
\begin{equation*}
H_\mu(t)
= H_\mu(x + \mathrm{i}\sigma)
= \frac{a^2 + b^2 x^2 + b^2 \sigma^2 }{(x-\mu)^2 + \sigma^2}
= b^2 + \frac{a^2 + b^2 [ x^2 - (x-\mu)^2] }{(x-\mu)^2 + \sigma^2}.
\end{equation*} If ![]() $a^2 + b^2 [ x^2 - (x-\mu)^2] \ge 0$, then the function has a global maximum when
$a^2 + b^2 [ x^2 - (x-\mu)^2] \ge 0$, then the function has a global maximum when ![]() $\sigma=0$, that is in
$\sigma=0$, that is in ![]() $t = x$; otherwise it has no global maximum and its supremum is
$t = x$; otherwise it has no global maximum and its supremum is ![]() $b^2$ which proves (A.10). Note that
$b^2$ which proves (A.10). Note that ![]() $H_\mu$ has no local maxima by Lemma A.1.
$H_\mu$ has no local maxima by Lemma A.1.
 \begin{equation*}
\sup_{t\in\mathbb{C}\setminus\big((\alpha,\beta)+\mathrm{i} \mathbb{R}\big)}\frac{a^2+b^2|t|^2 }{|t-\mu|^2 }
= \sup_{t\in\{\alpha, \beta\} +\mathrm{i} \mathbb{R}} H_\mu(t)
= \max_{x \in \{\alpha, \beta\} } \sup_{\sigma\in\mathbb{R}} H_\mu( x + \mathrm{i}\sigma).
\end{equation*}
\begin{equation*}
\sup_{t\in\mathbb{C}\setminus\big((\alpha,\beta)+\mathrm{i} \mathbb{R}\big)}\frac{a^2+b^2|t|^2 }{|t-\mu|^2 }
= \sup_{t\in\{\alpha, \beta\} +\mathrm{i} \mathbb{R}} H_\mu(t)
= \max_{x \in \{\alpha, \beta\} } \sup_{\sigma\in\mathbb{R}} H_\mu( x + \mathrm{i}\sigma).
\end{equation*}
Figure B1. Illustration for the proof of Lemma A.5 and the corresponding boundaries for the spectrum of ![]() $T+A$ from Theorem 4.6. In (a), the lightblue half-plane is the plane
$T+A$ from Theorem 4.6. In (a), the lightblue half-plane is the plane ![]() $P'$ above which the estimate (A.6’) for
$P'$ above which the estimate (A.6’) for ![]() $\arg(z-\beta)\in(\theta, \theta+\pi)$ holds. The white regions in (b) and (d) correspond to the sets
$\arg(z-\beta)\in(\theta, \theta+\pi)$ holds. The white regions in (b) and (d) correspond to the sets  $\mathrm{e}^{\mathrm{i}\theta}(\beta_T\sin\theta + \mathrm{Hyp}_{\beta_T\sin\theta})$ and
$\mathrm{e}^{\mathrm{i}\theta}(\beta_T\sin\theta + \mathrm{Hyp}_{\beta_T\sin\theta})$ and  $\mathrm{e}^{-\mathrm{i}\theta}(-\beta_T\sin\theta - \mathrm{Hyp}_{\beta_T\sin\theta})$ respectively. There,
$\mathrm{e}^{-\mathrm{i}\theta}(-\beta_T\sin\theta - \mathrm{Hyp}_{\beta_T\sin\theta})$ respectively. There, ![]() $\sup_{t\in\partial(S_{\theta}(\beta_T))} H_z(t) \lt 1$ holds. Therefore, the spectrum of
$\sup_{t\in\partial(S_{\theta}(\beta_T))} H_z(t) \lt 1$ holds. Therefore, the spectrum of ![]() $T+A$ must be contained in the grey area in (e). The graphic in (f) shows the spectral inclusion for a larger angle
$T+A$ must be contained in the grey area in (e). The graphic in (f) shows the spectral inclusion for a larger angle ![]() $\theta$. The vertical blue line in (e) and (f) is the lower bound
$\theta$. The vertical blue line in (e) and (f) is the lower bound ![]() $\beta_{T+A}$ for the real part of the spectrum of
$\beta_{T+A}$ for the real part of the spectrum of ![]() $T+A$ in the case
$T+A$ in the case ![]() $b \lt \cos\theta$, so
$b \lt \cos\theta$, so ![]() $\sigma(T+A)$ is contained in the grey area to its right.
$\sigma(T+A)$ is contained in the grey area to its right.
The next lemma is used in Theorem 4.6.
Lemma A.7. Let ![]() $\alpha \lt \beta$ and
$\alpha \lt \beta$ and  $\theta\in \left[0, \frac{\pi}{2}\right)$. Then, for all
$\theta\in \left[0, \frac{\pi}{2}\right)$. Then, for all ![]() $z\in \mathbb{C}$ we obtain
$z\in \mathbb{C}$ we obtain
 \begin{align}
\sup_{t\in S_{\theta}(\beta)} H_z(t)
\le
\max\left\{b^2,\ \frac{{a^2+b^2\beta^2}}{(\beta- \operatorname{Re} z)^2} \right\} + \tan^2\theta
\qquad
&\text{if } \operatorname{Re} z \lt \beta,
\end{align}
\begin{align}
\sup_{t\in S_{\theta}(\beta)} H_z(t)
\le
\max\left\{b^2,\ \frac{{a^2+b^2\beta^2}}{(\beta- \operatorname{Re} z)^2} \right\} + \tan^2\theta
\qquad
&\text{if } \operatorname{Re} z \lt \beta,
\end{align} \begin{align}
\sup_{t\in -S_{\theta}(\alpha)} H_z(t)
\le
\max\left\{b^2,\ \frac{{a^2+b^2\alpha^2}}{( \operatorname{Re} z-\alpha)^2} \right\} + \tan^2\theta
\qquad
&\text{if } \operatorname{Re} z \gt \alpha.
\end{align}
\begin{align}
\sup_{t\in -S_{\theta}(\alpha)} H_z(t)
\le
\max\left\{b^2,\ \frac{{a^2+b^2\alpha^2}}{( \operatorname{Re} z-\alpha)^2} \right\} + \tan^2\theta
\qquad
&\text{if } \operatorname{Re} z \gt \alpha.
\end{align}Proof. We only prove (A.12). Let us write ![]() $z = \mu + \mathrm{i} \nu$ and
$z = \mu + \mathrm{i} \nu$ and ![]() $t = \tau + \mathrm{i} \sigma$. Observe that
$t = \tau + \mathrm{i} \sigma$. Observe that
 \begin{align*}
H_z(t)
&= \frac{a^2+b^2|t|^2}{|t-z|^2}
= \frac{a^2+b^2|t-\mathrm{i}\nu|^2}{|t-z|^2}
+ \frac{b^2((\sigma^2 - (\sigma-\nu)^2}{|t-z|^2 }
\\
&= H_{\mu}(\tau + \mathrm{i}(\sigma-\nu)) + b^2\frac{\sigma^2-(\sigma-\nu)^2}{|t-z|^2}
\\
&= H_{\mu}(t - \mathrm{i}\nu) + b^2\frac{\sigma^2-(\sigma-\nu)^2}{|t-z|^2}.
\end{align*}
\begin{align*}
H_z(t)
&= \frac{a^2+b^2|t|^2}{|t-z|^2}
= \frac{a^2+b^2|t-\mathrm{i}\nu|^2}{|t-z|^2}
+ \frac{b^2((\sigma^2 - (\sigma-\nu)^2}{|t-z|^2 }
\\
&= H_{\mu}(\tau + \mathrm{i}(\sigma-\nu)) + b^2\frac{\sigma^2-(\sigma-\nu)^2}{|t-z|^2}
\\
&= H_{\mu}(t - \mathrm{i}\nu) + b^2\frac{\sigma^2-(\sigma-\nu)^2}{|t-z|^2}.
\end{align*}Therefore Lemma A.1 implies that
 \begin{align*}
\sup_{t\in S_{\theta}(\beta)} H_z(t)
= \sup_{t\in \partial S_{\theta}(\beta)} H_z(t)
\le \sup_{t\in \partial S_{\theta}(\beta)} H_{\mu}(t - \mathrm{i}\nu)
+ \sup_{t\in \partial S_{\theta}(\beta)} b^2\frac{\sigma^2-(\sigma-\nu)^2}{|t-z|^2}.
\end{align*}
\begin{align*}
\sup_{t\in S_{\theta}(\beta)} H_z(t)
= \sup_{t\in \partial S_{\theta}(\beta)} H_z(t)
\le \sup_{t\in \partial S_{\theta}(\beta)} H_{\mu}(t - \mathrm{i}\nu)
+ \sup_{t\in \partial S_{\theta}(\beta)} b^2\frac{\sigma^2-(\sigma-\nu)^2}{|t-z|^2}.
\end{align*}For the first term we obtain
 \begin{align*}
\sup_{t\in \partial S_{\theta}(\beta)} H_{\mu}(t - \mathrm{i}\nu)
& \le \sup_{\operatorname{Re} t \ge \beta} H_{\mu}(t - \mathrm{i}\nu)
= \sup_{\operatorname{Re} t = \beta} H_{\mu}(t)
\le \max\left\{b^2,\ \frac{{a^2+b^2\beta^2}}{(\beta-\mu)^2} \right\}
\end{align*}
\begin{align*}
\sup_{t\in \partial S_{\theta}(\beta)} H_{\mu}(t - \mathrm{i}\nu)
& \le \sup_{\operatorname{Re} t \ge \beta} H_{\mu}(t - \mathrm{i}\nu)
= \sup_{\operatorname{Re} t = \beta} H_{\mu}(t)
\le \max\left\{b^2,\ \frac{{a^2+b^2\beta^2}}{(\beta-\mu)^2} \right\}
\end{align*} by (A.10). For the second term, we use that ![]() $t = \tau + \mathrm{i}\sigma = (\beta + |\sigma|\cot\theta) + \mathrm{i}\sigma$,
$t = \tau + \mathrm{i}\sigma = (\beta + |\sigma|\cot\theta) + \mathrm{i}\sigma$, ![]() $\sigma\in \mathbb{R}$, on
$\sigma\in \mathbb{R}$, on ![]() $\partial S_{\theta}(\beta)$. Therefore we obtain
$\partial S_{\theta}(\beta)$. Therefore we obtain
 \begin{align*}
\sup_{t\in \partial S_{\theta}(\beta)} b^2\frac{\sigma^2-(\sigma-\nu)^2}{|t-z|^2}
& = b^2 \sup_{\sigma\in \mathbb{R}} \frac{\sigma^2-(\sigma-\nu)^2}{(\beta-\mu + |\sigma|\cot\theta)^2 + (\nu-\sigma)^2}\\
& \le b^2 \sup_{\sigma\in \mathbb{R}} \frac{\sigma^2}{(\beta-\mu + |\sigma|\cot\theta)^2}
\le b^2 \tan^2\theta.
\end{align*}
\begin{align*}
\sup_{t\in \partial S_{\theta}(\beta)} b^2\frac{\sigma^2-(\sigma-\nu)^2}{|t-z|^2}
& = b^2 \sup_{\sigma\in \mathbb{R}} \frac{\sigma^2-(\sigma-\nu)^2}{(\beta-\mu + |\sigma|\cot\theta)^2 + (\nu-\sigma)^2}\\
& \le b^2 \sup_{\sigma\in \mathbb{R}} \frac{\sigma^2}{(\beta-\mu + |\sigma|\cot\theta)^2}
\le b^2 \tan^2\theta.
\end{align*} In the last step we used that ![]() $\beta-\mu = \beta-\operatorname{Re} z \gt 0$.
$\beta-\mu = \beta-\operatorname{Re} z \gt 0$.
The next lemma is used in Proposition 6.2. Recall that ![]() $\Pi(\beta) = \{z\in\mathbb{C} : \operatorname{Re} z \gt \beta,\, |\operatorname{Im} (z)| \le (\operatorname{Re} z - \beta)^2 \}$.
$\Pi(\beta) = \{z\in\mathbb{C} : \operatorname{Re} z \gt \beta,\, |\operatorname{Im} (z)| \le (\operatorname{Re} z - \beta)^2 \}$.
Lemma A.8. Let ![]() $\alpha, \beta\in\mathbb{R}$ and
$\alpha, \beta\in\mathbb{R}$ and ![]() $z\in\mathbb{C}$. Then
$z\in\mathbb{C}$. Then
 \begin{align}
\operatorname{dist}(z,\Pi(\beta)) &\ge
\begin{cases}
\sqrt{(\beta- \operatorname{Re} z)^2 + (\operatorname{Im} z)^2},\quad & |\operatorname{Im} z|\le \frac{1}{2}, \\
\sqrt{(\beta- \operatorname{Re} z)^2 + |\operatorname{Im} z| - \frac{1}{4}},\quad & |\operatorname{Im} z| \gt \frac{1}{2},
\end{cases}
\qquad\text{if } \operatorname{Re} z \lt \beta,
\end{align}
\begin{align}
\operatorname{dist}(z,\Pi(\beta)) &\ge
\begin{cases}
\sqrt{(\beta- \operatorname{Re} z)^2 + (\operatorname{Im} z)^2},\quad & |\operatorname{Im} z|\le \frac{1}{2}, \\
\sqrt{(\beta- \operatorname{Re} z)^2 + |\operatorname{Im} z| - \frac{1}{4}},\quad & |\operatorname{Im} z| \gt \frac{1}{2},
\end{cases}
\qquad\text{if } \operatorname{Re} z \lt \beta,
\end{align} \begin{align}
[2ex]
\operatorname{dist}(z,-\Pi(-\alpha)) &\ge
\begin{cases}
\sqrt{(\alpha- \operatorname{Re} z)^2 + (\operatorname{Im} z)^2},\quad & |\operatorname{Im} z|\le \frac{1}{2}, \\
\sqrt{(\alpha- \operatorname{Re} z)^2 + |\operatorname{Im} z| - \frac{1}{4}},\quad & |\operatorname{Im} z| \gt \frac{1}{2}.
\end{cases}
\qquad\text{if } \operatorname{Re} z \gt \alpha.
\end{align}
\begin{align}
[2ex]
\operatorname{dist}(z,-\Pi(-\alpha)) &\ge
\begin{cases}
\sqrt{(\alpha- \operatorname{Re} z)^2 + (\operatorname{Im} z)^2},\quad & |\operatorname{Im} z|\le \frac{1}{2}, \\
\sqrt{(\alpha- \operatorname{Re} z)^2 + |\operatorname{Im} z| - \frac{1}{4}},\quad & |\operatorname{Im} z| \gt \frac{1}{2}.
\end{cases}
\qquad\text{if } \operatorname{Re} z \gt \alpha.
\end{align}Proof. It suffices to show (A.14) because ![]() $\operatorname{dist}(z,-\Pi(-\alpha)) = \operatorname{dist}(-z,\Pi(\alpha))$. Let
$\operatorname{dist}(z,-\Pi(-\alpha)) = \operatorname{dist}(-z,\Pi(\alpha))$. Let ![]() $z = \mu + \mathrm{i} \nu\in\mathbb{C}$ and assume
$z = \mu + \mathrm{i} \nu\in\mathbb{C}$ and assume ![]() $\operatorname{Re} z \lt \beta$. For
$\operatorname{Re} z \lt \beta$. For ![]() $t= \tau + \mathrm{i}\sigma \in \Pi(\beta)$ we define
$t= \tau + \mathrm{i}\sigma \in \Pi(\beta)$ we define
Clearly, ![]() $\delta$ has no critical points in the interior of
$\delta$ has no critical points in the interior of ![]() $\Pi(\beta)$, hence
$\Pi(\beta)$, hence
 \begin{equation*}
\inf_{t\in \Pi(\beta) }\delta_z(t) = \inf_{t\in \partial(\Pi(\beta)) }\delta_z(t).
\end{equation*}
\begin{equation*}
\inf_{t\in \Pi(\beta) }\delta_z(t) = \inf_{t\in \partial(\Pi(\beta)) }\delta_z(t).
\end{equation*} Note that the infimum is in fact a minimum. Let ![]() $t = \tau + \mathrm{i} \sigma \in\Pi(\beta)$. Hence
$t = \tau + \mathrm{i} \sigma \in\Pi(\beta)$. Hence ![]() $\sigma = \pm (\tau - \beta)^2$. Let us first assume that
$\sigma = \pm (\tau - \beta)^2$. Let us first assume that ![]() $\sigma = (\tau-\beta)^2$. Then
$\sigma = (\tau-\beta)^2$. Then
If ![]() $\nu \leq 0$, then
$\nu \leq 0$, then
If ![]() $\nu \geq 0$, let
$\nu \geq 0$, let ![]() $\Delta(\tau):=(\tau-\mu)^2-(\tau-\beta)^2$. Then
$\Delta(\tau):=(\tau-\mu)^2-(\tau-\beta)^2$. Then
 \begin{align*}
\delta_z(t)
&= \left[(\tau-\beta)^2+\frac{1-2\nu}{2}\right]^2+\nu^2-\left(\frac{1-2\nu}{2}\right)^2+\Delta(\tau).
\end{align*}
\begin{align*}
\delta_z(t)
&= \left[(\tau-\beta)^2+\frac{1-2\nu}{2}\right]^2+\nu^2-\left(\frac{1-2\nu}{2}\right)^2+\Delta(\tau).
\end{align*} Suppose that ![]() $\nu\leq 1/2$, so that
$\nu\leq 1/2$, so that ![]() $1-2\nu \geq 0$. Then
$1-2\nu \geq 0$. Then
 \begin{equation*}\delta_z(t)\geq \left(\frac{1-2\nu}{2}\right)^2+\nu^2-\left(\frac{1-2\nu}{2}\right)^2+\Delta(\tau)= \nu^2+\Delta(\tau). \end{equation*}
\begin{equation*}\delta_z(t)\geq \left(\frac{1-2\nu}{2}\right)^2+\nu^2-\left(\frac{1-2\nu}{2}\right)^2+\Delta(\tau)= \nu^2+\Delta(\tau). \end{equation*} If ![]() $\nu \gt 1/2$, we have that
$\nu \gt 1/2$, we have that
 \begin{equation*}\delta_z(t)\geq \nu^2-\left(\frac{1-2\nu}{2}\right)^2+\Delta(\tau)= \nu-\frac{1}{4}+\Delta(\tau).\end{equation*}
\begin{equation*}\delta_z(t)\geq \nu^2-\left(\frac{1-2\nu}{2}\right)^2+\Delta(\tau)= \nu-\frac{1}{4}+\Delta(\tau).\end{equation*}Note that
Therefore
 \begin{align}
\delta_z(t)\geq
\begin{cases}
(\beta-\mu)^2+\nu^2,&\text{if } \nu \leq 1/2, \\
(\beta-\mu)^2+ \nu-\frac{1}{4},&\text{if } \nu \gt 1/2.
\end{cases}
\qquad\text{if } \operatorname{Im} t = (\operatorname{Re} t -\beta)^2.
\end{align}
\begin{align}
\delta_z(t)\geq
\begin{cases}
(\beta-\mu)^2+\nu^2,&\text{if } \nu \leq 1/2, \\
(\beta-\mu)^2+ \nu-\frac{1}{4},&\text{if } \nu \gt 1/2.
\end{cases}
\qquad\text{if } \operatorname{Im} t = (\operatorname{Re} t -\beta)^2.
\end{align} Since ![]() $\delta_z(t) = \delta_{\overline z}(\overline t)$, we obtain
$\delta_z(t) = \delta_{\overline z}(\overline t)$, we obtain
 \begin{align}
\delta_z(t)\geq
\begin{cases}
(\beta-\mu)^2 + \nu^2,&\text{if } \nu \geq -1/2, \\
(\beta-\mu)^2 - \nu-\frac{1}{4},&\text{if } \nu \lt 1/2.
\end{cases}
\qquad\text{if } \operatorname{Im} t = -(\operatorname{Re} t -\beta)^2.
\end{align}
\begin{align}
\delta_z(t)\geq
\begin{cases}
(\beta-\mu)^2 + \nu^2,&\text{if } \nu \geq -1/2, \\
(\beta-\mu)^2 - \nu-\frac{1}{4},&\text{if } \nu \lt 1/2.
\end{cases}
\qquad\text{if } \operatorname{Im} t = -(\operatorname{Re} t -\beta)^2.
\end{align}
Since the right hand sides of (A.16) and (A.17) are independent of ![]() $t$, the claim follows.
$t$, the claim follows.
Appendix B. Alternative bounds for the resolvent set of  $T+A$ for sectorial operators
$T+A$ for sectorial operators  $T$
$T$
In the proofs of Theorem 4.3, Theorem 4.6, Corollary 4.7, Proposition 4.8 we used the estimates (A.6) and (A.8) from Lemma A.4 which resulted in sets of the form  $\mathrm{e}^{\mathrm{i}\theta}(\beta+\mathrm{Hyp}_\beta)$. If we use the estimates (A.6’) and (A.8’) from Lemma A.5 then (4.4) becomes
$\mathrm{e}^{\mathrm{i}\theta}(\beta+\mathrm{Hyp}_\beta)$. If we use the estimates (A.6’) and (A.8’) from Lemma A.5 then (4.4) becomes
 \begin{align}
\mathrm{e}^{\mathrm{i}\theta} \big( -\mathrm{i}\beta\sin\theta + \mathrm{Hyp}_{\beta\sin\theta} \big)
\cup
\mathrm{e}^{-\mathrm{i}\theta} \big( \mathrm{i}\beta\sin\theta + \mathrm{Hyp}_{-\beta\sin\theta} \big)
\subseteq \rho(T+A).
\end{align}
\begin{align}
\mathrm{e}^{\mathrm{i}\theta} \big( -\mathrm{i}\beta\sin\theta + \mathrm{Hyp}_{\beta\sin\theta} \big)
\cup
\mathrm{e}^{-\mathrm{i}\theta} \big( \mathrm{i}\beta\sin\theta + \mathrm{Hyp}_{-\beta\sin\theta} \big)
\subseteq \rho(T+A).
\end{align}Under the conditions of Theorem 4.6
 \begin{equation*}\begin{aligned}
\Big(
\mathrm{e}^{\mathrm{i}\theta}(-\mathrm{i}\beta_T\sin\theta +\mathrm{Hyp}_{-\beta_T\sin\theta})
\cup \mathrm{e}^{-\mathrm{i}\theta}(-\mathrm{i}\beta_T\sin\theta -\mathrm{Hyp}_{\beta_T\sin\theta}
\cup \{\operatorname{Re} z \lt \beta_{T+A} \}
\Big)
\\
\cap
\Big(
\mathrm{e}^{-\mathrm{i}\theta}(\mathrm{i}\alpha_T\sin\theta +\mathrm{Hyp}_{\alpha_T\sin\theta})
\cup \mathrm{e}^{\mathrm{i}\theta}(\mathrm{i}\alpha_T\sin\theta -\mathrm{Hyp}_{-\alpha_T\sin\theta})
\cup \{\operatorname{Re} z \gt \alpha_{T+A} \}
\Big)
\\
\subseteq \rho(T+A).
\end{aligned}
\end{equation*}
\begin{equation*}\begin{aligned}
\Big(
\mathrm{e}^{\mathrm{i}\theta}(-\mathrm{i}\beta_T\sin\theta +\mathrm{Hyp}_{-\beta_T\sin\theta})
\cup \mathrm{e}^{-\mathrm{i}\theta}(-\mathrm{i}\beta_T\sin\theta -\mathrm{Hyp}_{\beta_T\sin\theta}
\cup \{\operatorname{Re} z \lt \beta_{T+A} \}
\Big)
\\
\cap
\Big(
\mathrm{e}^{-\mathrm{i}\theta}(\mathrm{i}\alpha_T\sin\theta +\mathrm{Hyp}_{\alpha_T\sin\theta})
\cup \mathrm{e}^{\mathrm{i}\theta}(\mathrm{i}\alpha_T\sin\theta -\mathrm{Hyp}_{-\alpha_T\sin\theta})
\cup \{\operatorname{Re} z \gt \alpha_{T+A} \}
\Big)
\\
\subseteq \rho(T+A).
\end{aligned}
\end{equation*}Similarly, the estimates for the spectral inclusions in the proofs of Theorem 4.3, Corollary 4.7, Proposition 4.8 can be modified. The hyperbolas that provide the spectral inclusions have the same asymptotic slopes with either of the estimates from Lemma A.4 or Lemma A.5 but they are shifted differently, thus leading to different spectral inclusions. See Figure B2.

Figure B2. Comparison of the estimates for the spectral enclosure obtained with the estimates from Lemma A.4 and Lemma A.5. The blue area is ![]() $S_{\theta}(\beta_T)$ for the angles
$S_{\theta}(\beta_T)$ for the angles ![]() $\theta=30^\circ$ and
$\theta=30^\circ$ and ![]() $\theta=10^\circ$ and
$\theta=10^\circ$ and ![]() $\beta_T=5$,
$\beta_T=5$, ![]() $\beta_T=2$ and
$\beta_T=2$ and ![]() $\beta_T=-2$. The vertical blue line is the lower bound
$\beta_T=-2$. The vertical blue line is the lower bound ![]() $\beta_{T+A}$ for the real part of the spectrum of
$\beta_{T+A}$ for the real part of the spectrum of ![]() $T+A$, so only the region to its right is of interest. The green area shows the enclosure for
$T+A$, so only the region to its right is of interest. The green area shows the enclosure for ![]() $\sigma(T+A)$ which corresponds to the estimates from Lemma A.4 that we used throughout this work. The red area shows the enclosure for
$\sigma(T+A)$ which corresponds to the estimates from Lemma A.4 that we used throughout this work. The red area shows the enclosure for ![]() $\sigma(T+A)$ which corresponds to the estimates from Lemma A.5. For large
$\sigma(T+A)$ which corresponds to the estimates from Lemma A.5. For large ![]() $|z|$ the green hyperbolas provide better estimates if
$|z|$ the green hyperbolas provide better estimates if ![]() $\beta_T \gt 0$ than those given by the red ones. If
$\beta_T \gt 0$ than those given by the red ones. If ![]() $\beta_T \lt 0$ the converse is true.
$\beta_T \lt 0$ the converse is true.