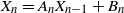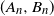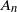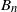1. Introduction
1.1. Stochastic gradient descent
Consider the following learning problem: For
$d, p \ge 1$
, let
$\mathcal{H}$
and
$\mathcal{Z}$
be subsets of
${\mathbb{R}}^{d}$
and
${\mathbb{R}}^{p}$
, respectively. We consider
$\mathcal{H}$
to be a set of parameters and
$\mathcal{Z}$
the domain of the observable data. Let
$\ell \colon \mathcal{H} \times \mathcal{Z} \to [0, \infty)$
be a measurable function, called the loss function. The aim is to minimize the risk function
$L_\mathcal{D}(x)\,:\!=\, \mathbb{E} \ell(x,Z)$
, where Z is a random variable on
$\mathcal{Z}$
that is assumed to generate the data, and the law
$\mathcal{D}$
of Z is unknown.
Upon observing a sample
$S=(z_1, \ldots, z_m)$
of realizations of Z, we can define the empirical risk function by
\begin{align*}L_S(x) \,:\!=\, \frac{1}{m}\sum_{i=1}^m \ell(x,z_i).\end{align*}
If
$\mathcal{H}$
is convex and
$\ell$
is differentiable on
$\mathcal{H}$
, we can employ the gradient descent algorithm in order to minimize
$L_S$
: Starting with
$x_0 \in \mathcal{H}$
, we recursively define, for
$n \in \mathbb{N}$
,
\begin{align*}x_n = x_{n-1} - \eta_n\nabla L_S(x_{n-1}) = x_{n-1} - \eta_n\Bigg(\frac1m\sum_{i=1}^m\nabla\ell(x_{n-1},z_i)\Bigg)\end{align*}
with parameter
$\eta_n>0$
, called the step size or learning rate, which may vary with time. The parameter
$\eta_n$
has to be chosen sufficiently small that the first-order approximation of the function about
$x_{n-1}$
by its gradient is good enough; see, e.g., [Reference Murphy17, Section 8.4.3] for a discussion.
In stochastic gradient descent (see, e.g., [Reference Shalev-Shwartz and Ben-David18, Chapter 14]), the idea is to use at each step only a random subsample
$(z_{i,n})_{1 \le i \le b}$
of size b of the observations to calculate the gradient:
\begin{equation} x_n = x_{n-1} - \frac{\eta_n}{b}\sum_{i=1}^b \nabla \ell(x_{n-1},z_{i,n}) \,=\!:\, x_{n-1} - g_n.\end{equation}
By choosing the subsample at random, the gradient term
$g_n$
becomes a random variable. If, in each step, a new sample is drawn independently of the previous samples, then the successive gradient terms
$(g_n)_{n \ge 1}$
are independent as well. However, the
$(g_n)_{n \ge 1}$
are not identically distributed, since the gradients are evaluated at different points
$x_{n-1}$
in each step.
To analyze the algorithm, it is of prime interest to study the random distance between
$x_n$
and local minima of
$L_S$
. To show how this relates to stochastic recursions, we focus now on the particular setting (more general settings will be considered in Section 3.4) of a quadratic loss function with constant step size, as considered in [Reference Gürbüzbalaban, Simsekli and Zhu12]: The parameter set is
$\mathcal{H}={\mathbb{R}}^d$
, the observed data
$z \in\mathcal{Z}={\mathbb{R}}^d \times {\mathbb{R}}$
, and with
$z=(a,y)$
the loss function is given by
\begin{align*} \ell(x,a,y) = \frac12 (a^\top x-y)^2.\end{align*}
This corresponds to the setting of linear regression where
$y \in {\mathbb{R}}$
would be the target variable and a the vector of explanatory variables;
$L_S(x)$
is then equal to the mean squared error.
In this setting, the function
$L_S(x)$
has a unique global minimum
$x_*$
, and we can expand the gradient of
$\ell$
around
$x_*$
:
$\nabla\ell(x,a,y) = a(a^\top x-y) = -ya + (aa^\top)x_* + (aa^\top)(x-x_*)$
. Note that a and x are d-dimensional column vectors,
$a^\top$
is a row vector,
$aa^\top$
is the
$(d \times d)$
rank-one projection matrix onto a. Using this in (1.1), we obtain, for the distance
$x_n-x_*$
,
\begin{equation*} x_n - x_* = x_{n-1} - x_* - \frac{\eta}{b}\sum_{i=1}^b\big(a_ia_i^\top\big)(x_{n-1}-x_*) + \frac{\eta}{b}\sum_{i=1}^b\big(y_ia_i - \big(a_ia_i^\top\big)x_*\big).\end{equation*}
Let I be the
$d\times d$
identity matrix. Writing
\begin{equation} X_n \,:\!=\, x_n-x_*, \qquad A_n \,:\!=\, \Bigg(\mathrm{I} - \frac{\eta}{b} \sum_{i=1}^b a_i a_i^\top\Bigg), \qquad B_n \,:\!=\, \frac{\eta}{b} \sum_{i=1}^b\big(y_ia_i - \big(a_ia_i^\top\big)x_*\big),\end{equation}
we see that
$X_n$
satisfies an affine stochastic recursion
\begin{equation} X_n = A_n X_{n-1} + B_n,\end{equation}
with
$(A_n,B_n)$
now being an independent and identically distributed (i.i.d.) sequence of random matrices and vectors.
1.2. Summary of results
It is known ([Reference Alsmeyer and Mentemeier1, Reference Guivarc’h and Le Page10, Reference Kesten15]; see also [Reference Buraczewski, Damek and Mikosch5]) that under mild assumptions, stationary solutions to such recursive equations will exhibit heavy tails even if the law of
$a_i$
has all the moments. This means that there is a substantial probability that iterations of the stochastic gradient descent go far away from the minimum, due to the randomness.
Here, a random variable X is a stationary solution to (1.3) if X has the same law as
$A_1X+B_1$
, and X is independent of
$(A_1,B_1)$
. The main condition for the existence (and uniqueness) of such a stationary solution is that the top Lyapunov exponent is negative; see below for details. We say that (the law of) X has Pareto tails with tail index
$\alpha$
if there is
$c>0$
such that
$\lim_{t\to \infty}{t^\alpha} {\mathbb{P}}(|X|>t)=c$
. This is a particular instance of heavy-tail behavior. Intriguing questions are: How is the tail behavior affected by the subsample size b, the step size
$\eta$
, or the distribution generating
$(a_i,y_i)$
? What can be said about the law or the moments of finite iterations
$X_n$
?
In [Reference Gürbüzbalaban, Simsekli and Zhu12], these questions have been studied under a density assumption on the law of
$a_i$
, and relevant results have been proved when
$a_i\sim \mathcal{N}(0,\sigma ^2I_d)$
is standard normal. However, the proof of the heavy-tail behavior of X in [Reference Gürbüzbalaban, Simsekli and Zhu12] is based on a theorem of Alsmeyer and Mentemeier [Reference Alsmeyer and Mentemeier1] that cannot be used since the matrix A does not have density on
${\mathbb{R}} ^{d^2}$
. Namely, in [Reference Gürbüzbalaban, Simsekli and Zhu12, Theorem 2], M does not have a Lebesgue density on
${\mathbb{R}}^{d^2}$
that is positive in a neighborhood of the identity matrix I since the law of M is concentrated on symmetric matrices, which constitute a
$d(d+1)/2$
-dimensional subspace of
$d^2$
-Lebesgue measure 0. In fact, of all the existing results [Reference Alsmeyer and Mentemeier1, Reference Buraczewski, Damek, Guivarc’h, Hulanicki and Urban4, Reference Guivarc’h and Le Page10, Reference Kesten15] implying the heavy-tail behavior of X, only the one in [Reference Guivarc’h and Le Page10] is applicable here. We need to employ the theory of irreducible-proximal (i-p) matrices from [Reference Guivarc’h and Le Page10], which is the right framework for the problem and at the same time allows us to go beyond the setting of [Reference Gürbüzbalaban, Simsekli and Zhu12]: we neither require a Gaussian density nor the particular form of A as in (1.2). Further, it will allow us to include the case of cyclic varying stepsizes, see Section 3.4. Under conditions of i-p, the tail behavior of X is described in Theorem 3.1, which we quote from [Reference Guivarc’h and Le Page10].
In particular, we may consider settings where
$A_n = \mathrm{I} - ({\eta}/{b}) \sum_{i=1}^b H_{i,n}$
for i.i.d. random symmetric
$d \times d$
matrices
$H_{i,n}$
. On one hand, this corresponds to a loss function
$\ell(x,H)=x^{\top} H x$
that is a random quadratic form; on the other hand, this is motivated by the observation (cf. [Reference Gürbüzbalaban, Simsekli and Zhu12, Reference Hodgkinson and Mahoney14]) that for a twice-differentiable loss function
$\ell$
, we may perform a Taylor expansion of the gradient about
$x_*$
to obtain
\begin{equation*} x_n - x_* \approx \Bigg(\mathrm{I} - \frac{\eta}{b}\sum_{i=1}^b H_\ell(x_*,z_{i,n})\Bigg)(x_{n-1} - x_*) - \frac{\eta}{b}\sum_{i=1}^b\nabla\ell(x_*,z_{i,n}), \end{equation*}
where
$H_\ell$
denotes the Hessian of
$\ell$
. However, we have to keep in mind that such an approximation is in general valid only for
$x_n$
close to
$x_*$
.
In the setting of i-p, we are able to prove that
$\mathbb{E} |X_n|^{\alpha}$
grows linearly with n, see Theorem 3.2, which considerably improves the result of [Reference Gürbüzbalaban, Simsekli and Zhu12, Proposition 10] (which gives only a polynomial bound).
The main issue is how the tail index
$\alpha$
depends on
$\eta$
and b. For that, we need a tractable expression for the value of
$\alpha$
as well as for the top Lyapunov exponent. It turns out that invariance of the law of A under rotations does the job and this, besides i-p, is the second vital ingredient for the right framework. This includes the Gaussian case studied in [Reference Gürbüzbalaban, Simsekli and Zhu12], and particular calculations suitable for the Gaussian case are no longer indispensable. We derive a simple formula for the Lyapunov exponent and an appropriate moment-generating function in Lemma 3.4, which allows us to completely describe the behavior of
$\alpha$
as a function of
$\eta$
and b, see Theorem 3.5.
Finally, we turn to the question of the finiteness of
$\mathbb{E} \det(A)^{-\varepsilon}$
for some
$\varepsilon>0$
, which is required as an assumption Theorem 3.1. Unless
$\det A$
is bounded away from zero, this cannot be claimed in general. Indeed, there are gaps in [Reference Gürbüzbalaban, Simsekli and Zhu12]: In [Reference Gürbüzbalaban, Simsekli and Zhu13, Lemma 20], the inequality D.18,
$\log({1}/({1-x}))\le 2x$
, is wrong for x close to 1. We show that a simple sufficient condition for the integrability of
$\det(A)^{-\varepsilon}$
is the existence of a density of the law of A with some weak decay properties (see Section 7), which is also natural from the point of view of applications. The proof is given in Section 7. The problem is interesting in itself and, as far as we know, has not previously been approached in the context of multivariate stochastic recursions. Finally, the existence of a density considerably simplifies the assumptions in Lemma 3.4 and Theorem 3.5.
We introduce all relevant notation, descriptions of the models, and assumptions in Section 2, in order to state our main results in Section 3, accompanied by a list of examples to which our findings apply. The proofs are deferred to the subsequent sections.
2. Assumptions, notations, and preliminaries
We assume that all random variables are defined on a generic probability space
$(\Omega, \mathcal F, {\mathbb{P}})$
. Let
$d \ge 1$
. Equip
${\mathbb{R}}^d$
with the Euclidean norm
$|\cdot |$
, and let
$\|\cdot \|$
be the corresponding operator norm for matrices. In addition, for a
$d \times d$
matrix g,
$\|g \|_{\mathrm{F}}\,:\!=\, \big(\sum_{1\le i,j\le d}g_{ij}^2\big)^{1/2}$
denotes the Frobenius norm. We write
${\mathrm{Sym}(d,\mathbb{R})}$
for the set of symmetric
$d \times d$
matrices,
$\mathrm{GL}(d,\mathbb{R})$
for the group of invertible
$d \times d$
matrices over
${\mathbb{R}}$
, and O(d) for its subgroup of orthogonal matrices. The identity matrix is denoted by I. Write
$S\,:\!=\,S^{d-1}$
for the unit sphere in
${\mathbb{R}}^d$
with respect to
$|\cdot |$
. For
$x \in S$
and
$g \in \mathrm{GL}(d,\mathbb{R})$
, define the action of g on x by
\begin{equation} g \cdot x\,:\!=\, \frac{gx}{|gx |} \in S.\end{equation}
We fix an orthonormal basis
$e_1, \ldots, e_d$
of
${\mathbb{R}}^d$
. We write
$\mathcal{C}(S)$
for the set of continuous functions on S, equipped with the norm
$\|\ f \|=\max \{|\ f(x)| \colon x \in S\}$
. The uniform measure
$\sigma $
on S is defined by
\begin{equation} \int_Sf(y)\,\mathrm{d}\sigma(y) \,:\!=\, \int_{O(d)}f(o\cdot e_1)\,\mathrm{d}o \quad \text{for all }f \in \mathcal{C}(S),\end{equation}
where
$\mathrm{d}o$
is the Haar measure on O(d) normalized to have mass 1. For
$g \in \mathrm{GL}(d,\mathbb{R})$
we introduce the quantity
\begin{equation} N(g)\,:\!=\,\max\{\|g \|,\|g^{-1} \|\}.\end{equation}
For an interval
$I \subset {\mathbb{R}}$
, the set of continuously differentiable functions on I is denoted
$\mathcal{C}^{1}(I)$
. For a random variable X, we denote by
${\mathrm{supp}}(X)$
its support, i.e. the smallest closed subset E of its range with
${\mathbb{P}}(X \in E)=1$
. We also use this notation for measures, where the support is the smallest closed set of full measure.
2.1. Stochastic recurrence equations
Given a sequence of i.i.d. copies
$(A_n,B_n)_{n \ge 1}$
of a random pair
$(A,B) \in \mathrm{GL}(d,\mathbb{R}) \times \mathbb{R}^d$
, which are also independent of the random vector
$X_0 \in {\mathbb{R}}^d$
, we consider the sequence of random d-vectors
$(X_n)_{n \ge 1}$
defined by the affine stochastic recurrence equation
\begin{equation} X_n = A_n X_{n-1} + B_n, \quad n \ge 1.\end{equation}
The study of equation (2.4) goes back to [Reference Kesten15]; see [Reference Buraczewski, Damek and Mikosch5] for a comprehensive account. Let
$\Pi_n \,:\!=\, \prod_{i=1}^n A_i$
and write
$\log^+ x\,:\!=\,\max\{0, \log x\}$
. Assume
$\mathbb{E} \log^+ \|A \| < \infty$
,
$\mathbb{E} \log^+ |B |<\infty$
, and that the top Lyapunov exponent
\begin{equation*} \gamma \,:\!=\, \lim_{n\to\infty}\frac{1}{n}\log\|\Pi_n \| \quad \text{almost surely (a.s.)}\end{equation*}
is negative. Then there exist a unique stationary distribution for the Markov chain defined by (2.4) and its law is given by the then almost surely convergent series
see [Reference Buraczewski, Damek and Mikosch5, Theorem 4.1.4]. Indeed, let us write
\begin{align*}R^{(1)} \,:\!=\, \lim_{n\to\infty}R_n^{(1)} \,:\!=\, \lim_{n\to\infty}\sum_{j=1}^n A_2\cdots A_{j}B_{j+1},\end{align*}
i.e. we shift all the indices by 1. Then
$R_n \overset{\textrm{D}}{=} R_n^{(1)}$
,
$R \overset{\textrm{D}}{=} R^{(1)}$
, and
$R_{n+1}=A_1 R_n^{(1)} +B_1$
. Hence, upon taking limits
$n\to \infty$
, we see that R satisfies the distributional equation
\begin{equation} R \overset{\textrm{D}}{=} A R + B,\end{equation}
where A, B are independent of R. Let
$I_k\,:\!=\, \{s \ge 0 \colon \mathbb{E}\|A \|^s < \infty\}$
and
$s_0\,:\!=\,\sup I_k$
. For any
$s \in I_k$
, define the quantity
$k(s) \,:\!=\, \lim_{n\to\infty}(\mathbb{E}{\|A_n\cdots A_1 \|^s})^{{1}/{n}}$
. Considering (2.5), a simple calculation gives that
$k(s)<1$
together with
$\mathbb{E} |B |^s<\infty$
implies
$\mathbb{E} |R |^s < \infty$
(see also [Reference Buraczewski, Damek and Mikosch5, Remark 4.4.3]).
2.2. The setup:
$\boldsymbol{A} = \mathrm{\textbf{I}} - \xi \boldsymbol{H}$
for
$\boldsymbol{H} \in {\mathrm{\textbf{Sym}}(\boldsymbol{d},\mathbb{R})}$
Motivated by the application to stochastic gradient descent, we want to study matrices A of the form
$A=\mathrm{I}-\xi H$
, where
$\xi >0$
and H is a random symmetric matrix. More specifically, we want to consider the following two models, both for
$b \in \mathbb{N}$
and
$\eta>0$
. Firstly, a setup where B is arbitrary and A is composed from random symmetric matrices. Given a tuple
$(H_i)_{1\le i \le b}$
of i.i.d. random symmetric
$d \times d$
matrices, let
\begin{align*} &\qquad\qquad A = \mathrm{I} - \frac{\eta}{b}\sum_{i=1}^b H_i, \qquad \qquad \quad B \text{ a random vector in } {\mathbb{R}}^d. \end{align*}
Secondly, we consider a setup where A is composed from rank-one projections and B is a weighted sum of the corresponding eigenvectors:
\begin{align*} \\&\qquad\qquad A = \mathrm{I} - \frac{\eta}{b}\sum_{i=1}^b a_i a_i^{\top}, \qquad\qquad B = \frac{\eta}{b} \sum_{i=1}^b a_i y_i,\end{align*}
where
$(a_i,y_i)$
are i.i.d. pairs in
${\mathbb{R}}^d \times {\mathbb{R}}$
. Of course, model (Symm) contains model (Rank1) as a particular case. In what follows, we study a general model wherever possible, and only restrict to the particular case (that still covers [Reference Gürbüzbalaban, Simsekli and Zhu12] completely) when this is necessary to obtain more precise results.
2.3. Geometric assumptions
Let
$\mu_A$
be the law of A, and let
$G_A$
denote the closed semigroup generated by
${\mathrm{supp}}(\mu_A)$
. It will be required that
$G_A \subset GL(d,{\mathbb{R}})$
, i.e. the matrix A is invertible with probability 1. This is satisfied, e.g., when
$\mu_A$
has a density with respect to Lebesgue measure on the set of symmetric matrices: the set of matrices with determinant 0 is of lower dimension.
Here and below, a matrix is called proximal if it has a unique largest eigenvalue (with respect to the absolute value) and the corresponding eigenspace is one-dimensional. We say that
$\mu_A$
satisfies an irreducible-proximal (i-p) condition if the following hold:
-
(i) Irreducibility condition: There exists no finite union
$\mathcal{W}=\bigcup_{i=1}^n W_i$
of proper subspaces
$W_i \subsetneq \mathbb{R}^d$
that is
$G_A$
-invariant. -
(ii) Proximality condition:
$G_A$
contains a proximal matrix.
The irreducibility condition does not exclude a setting where
$G_A$
leaves invariant a cone (e.g. if all matrices are nonnegative in addition), see [Reference Guivarc’h and Le Page10, Proposition 2.14]. Since this setting is not relevant to the applications that we have in mind, we will exclude it and consider the following assumption in all of the subsequent results:
\begin{equation} \quad\,\,\, G_A \subset GL(d,{\mathbb{R}}),\ \mu_A \text{ satisfies (i-p), and there is no $G_A$-invariant cone}.\end{equation}
For some results, we will require more specific assumptions. We say that
$\mu_A$
is invariant under rotations if, for every
$o\in O(d)$
,
$o Ho^\top$
has the same distribution law as H. We will make use of the following condition:
\begin{align} G_A \subset GL(d,{\mathbb{R}}),\ \mu_A \text{is invariant under rotations, and } G_A \text{ contains a proximal matrix.}\end{align}
Remark 2.1. If a random vector
$a\in {\mathbb{R}} ^d$
has the property that, for every
$o \in O(d)$
, oa has the same law as a, then we call (the law of) a rotationally invariant as well. This is justified by the observation that then the law of
$H\,:\!=\,aa^\top$
is invariant under rotations.
We will sometimes assume a Gaussian distribution for the
$a_i$
:
\begin{equation} \quad A, B \text{ are of the form (Rank1)}, a_i \sim \mathcal{N}(0,\mathrm{I}) \text{ and independent of } y_i \sim \mathcal{N}(0,1).\end{equation}
Remark 2.2. The independence between
$a_i$
and
$y_i$
is not essential (and unrealistic for structured data). It suffices to assume, as in (Rank1) that
$(a_i,y_i)$
are i.i.d. pairs for
$1 \le i \le b$
, with the marginals being standard Gaussian, and then to assume in addition that
${\mathbb{P}}(Ax+B=x)<1$
holds for all
$x \in {\mathbb{R}}^d$
. See the proof of Corollary 3.1 for further information.
Note that (Rank1Gauss) is assumed throughout in [Reference Gürbüzbalaban, Simsekli and Zhu12]; we will show that indeed all their results hold at least under (rotinv-p), and some already under (i-p-nc).
2.4. Density
As has already been mentioned, to study
$\alpha$
as a function of
$\eta$
and b, finiteness of
$\mathbb{E} \log N(A)$
or
$\mathbb{E} N(A)^\varepsilon$
for some
$\varepsilon>0$
is needed. This means, in particular, that we require finiteness of small (or logarithmic) moments of
$\|A^{-1} \|$
– see (2.3). Such a property is difficult to check in general (unless
$\det A$
is bounded away from zero). However, it holds when the law of A has density, see Theorem 3.6 and Section 7. This is why we provide two sufficient conditions, formulated in terms of densities. The first one is for the model (Symm) where
$A=I-\xi H\,:\!=\,I-({\eta}/{b})\sum_{i=1}^b H_i$
:
The law of H has a density f with respect to Lebesgue measure on
$\text{Sym(d},\mathbb{R})$
that satisfies
\begin{align} f(g) \leq C(1+\|g \|_{\mathrm{F}}^2)^{-D} \qquad \text{for some } D > \frac{d(d+1)}{4}. \end{align}
The second one is for the model (Rank1):
The law of
$a_1, \ldots, a_b\ \textrm{on}\ {\mathbb{R}}^{db}$
has a joint density f that satisfies
\begin{align} f(a_1, \ldots,a_b) \leq C\Bigg(1+\sum_i^b|a_i|^2\Bigg)^{-D} \quad \text{for some } D > \frac{db}{2}. \end{align}
Under (Decay:Symm) or (Decay:Rank1), small moments of
$\| A^{-1}\| $
are finite, which simplifies the assumptions in Lemma 3.4 and Theorem 3.5. The latter is essential from the point of view of applications.
2.5. Preliminaries
For
$s \in I_k$
, we define the operators
$P^s$
and
$P^s_*$
in
$\mathcal{C}(S)$
as follows: For any
$f \in \mathcal{C}(S)$
,
\begin{equation} P^s f(x) \,:\!=\, \mathbb{E}|Ax |^s f(A \cdot x), \qquad P^s_{*}\, {f(x)} \,:\!=\, \mathbb{E}|A^{\top}x |^s f(A^\top \cdot x) .\end{equation}
Properties of both operators will be important in our results.
Proposition 2.1. Assume that
$\mu_A$
satisfies (i-p-nc) and let
$s \in I_k$
. Then the following hold. The spectral radii
$\rho(P^s)$
and
$\rho(P^s_*)$
both equal k(s), and there is a unique probability measure
$\nu_{s}$
on S and a unique function
$r_{s} \in \mathcal{C}({S})$
satisfying
$\int r_{s}(x)\,\nu_{s}(\mathrm{d} x)=1$
,
$P^s r_{s} = k(s)r_{s}$
, and
$P^s\nu_{s} = k(s)\nu_{s}$
. Further, the function
$r_{s}$
is strictly positive.
Also, there is a unique probability measure
${\nu^*_{s}}$
satisfying
$P^s_* {\nu^*_{s}} = k(s) {\nu^*_{s}}$
and neither
${\mathrm{supp}}(\nu_{s})$
nor
${\mathrm{supp}}({\nu^*_{s}})$
are concentrated on any hyperplane. There is a
$c>0$
such that
$r_{s}(x) = c\int_S|\langle x,y \rangle |^s\,{\nu^*_{s}}(\mathrm{d} y)$
. The function
$s \mapsto k(s)$
is log-convex on
$I_k$
, hence continuous on
$\mathrm{int}(I_k)$
with left and right derivatives, and there is a constant
$C_s$
such that, for all
$n \in \mathbb{N}$
,
$\mathbb{E} \|\Pi_n \|^s \le C_sk(s)^n$
.
Source. A combination of [Reference Guivarc’h and Le Page10, Theorem 2.6] and [Reference Guivarc’h and Le Page10, Theorem 2.16], where (i-p-nc) corresponds to Case I. The results concerning the supports as well as the bound for k(s) are proved in [Reference Guivarc’h and Le Page10, Lemma 2.8].
Proposition 2.2. ([Reference Guivarc’h and Le Page10, Theorem 3.10].) Assume (i-p-nc), and that
$\mathbb{E}(1+\|A\|^s)\log N(A)<\infty$
for some
$s>0$
. Then k is continuously differentiable on [
$0$
,s] with
$k'(0)=\gamma$
.
Remark 2.3. Hence, a sufficient condition for
$\gamma <0$
is
$\mathbb{E} \|A_1 \|<1$
(together with
$\mathbb{E} (1+\|A \|) \log N(A)<\infty$
): Observing that
$k(0)=1$
and
$k(1)\le \mathbb{E} \|A_1 \|<1$
by the submultiplicativity of the norm, the convexity of k (see Proposition 2.1) implies that
$k'(0)=\gamma<0$
.
3. Main results
In this section we state our main results, the proofs of which are deferred to the subsequent sections. We formulate all the results with the minimal set of assumptions required; note that these assumptions are in particular satisfied for model (Rank1Gauss).
3.1. Heavy-tail properties
For completeness, we start by quoting the fundamental result about the tail behavior of R from [Reference Guivarc’h and Le Page10] and adapt it to our notation.
Theorem 3.1. ([Reference Guivarc’h and Le Page10, Theorem 5.2].) Assume (i-p-nc),
$\gamma <0$
, and
${\mathbb{P}}(Ax+B=x)<1$
for all
$x \in {\mathbb{R}}^d$
. Assume further that there is an
$\alpha\in\mathrm{int}(I_k)$
with
$k(\alpha)=1$
,
$\mathbb{E}|B|^{\alpha + \varepsilon} < \infty$
, and
$\mathbb{E} \|A \|^{\alpha}N(A)^\varepsilon < \infty$
for some
$\varepsilon>0$
. Then there is a
$C>0$
such that
\begin{align*}\lim_{t\to\infty}t^\alpha{\mathbb{P}}\bigg(|R|>t,\frac{R}{|R|}\in\cdot\bigg) = C\,\nu_\alpha(\!\cdot\!).\end{align*}
Remark 3.1. This fundamental result gives, inter alia, that R is in the domain of attraction of a multivariate
$\alpha$
-stable law if
$\alpha \in (0,2)$
. In fact, even more can be said about sums of the iterations. Write
$S_n\,:\!=\,\sum_{k=1}^n R_k$
and let
$ m_R\,:\!=\,\mathbb{E} R$
if
$\alpha>1$
(then this expectation is finite). It is shown in [Reference Gao, Guivarc’h and Le Page7, Theorem 1.1] that, under the assumptions of Theorem 3.1, the following holds. If
$\alpha>2$
, then
$(S_n-n m_R)/{\sqrt{n}}$
converges in law to a multivariate normal distribution. If
$\alpha=2$
, then
$(S_n-n m_R)/{\sqrt{n \log n}}$
converges in law to a multivariate normal distribution. If
$\alpha \in (0,1) \cup (1,2)$
, let
$t_n\,:\!=\,n^{-1/\alpha}$
and
$d_n= n t_n m_R \mathbf{1}_{\{\alpha > 1\}}$
. Then
$(t_n S_n - d_n)$
converges in law to a multivariate
$\alpha$
-stable distribution. In all cases, the limit laws are fully nondegenerate.
Theorem 3.1 gives, in particular, that
$|R|$
has Pareto-like tails, hence
$\mathbb{E} |R|^\alpha=\infty$
. Our first result shows that
$\mathbb{E} |R_n|^\alpha$
is of order n precisely.
Theorem 3.2. Assume (i-p-nc),
$\gamma <0$
,
${\mathbb{P}}(Ax+B=x)<1$
for all
$x\in{\mathbb{R}}^d$
, and that there exists
$\alpha\in I_k$
with
$k(\alpha)=1$
and
$\mathbb{E}|B|^\alpha<\infty$
. Then
\begin{equation} \limsup \frac{1}{n}\mathbb{E} |R_{n}|^{\alpha}<\infty, \qquad \liminf \frac{1}{n}\mathbb{E} |R_{n}|^{\alpha}>0.\end{equation}
Remark 3.2. Our result improves [Reference Gürbüzbalaban, Simsekli and Zhu12, Proposition 10], where it was shown that
$\mathbb{E} |R_n|$
is at most of order
$n^\alpha$
. Analogous results were obtained in [Reference Buraczewski, Damek and Zienkiewicz6] for the stochastic recursion (1.3) in the one-dimensional case, as well as for a multidimensional case with
$A_n$
being similarity matrices, i.e. products of orthogonal matrices and dilations.
While Theorem 3.1 is concerned with the tail behavior of the stationary distribution R, our next theorem gives an upper bound on the tails of finite iterations.
Theorem 3.3. Assume (i-p-nc),
$\gamma <0$
, and that there is an
$\alpha \in I_k$
with
$k(\alpha)=1$
. Assume further that there is an
$\varepsilon>0$
such that
$k(\alpha+\varepsilon)<\infty$
and
$\mathbb{E}|B|^{\alpha+\varepsilon}<\infty$
. Then, for each
$n \in \mathbb{N}$
, there is a constant
$C_n$
such that, for all
$t>0$
,
${\mathbb{P}}(|R_n | > t) \le C_n t^{-(\alpha + \varepsilon)}$
.
Note that the constant
$C_n$
changes with n, but is independent of t. This shows that, for any fixed n, the tails of
$R_n$
are of (substantially) smaller order than the tails of the limit R.
Theorem 3.1 states that the directional behavior of large values of R is governed by
$\nu_\alpha$
, which is given by Proposition 2.1 in an abstract way: as the invariant measure of the operator
$P^\alpha$
. The next theorem allows us to obtain a simple expression for both
$\nu_\alpha$
and the top Lyapunov exponent, under assumption (rotinv-p).
Theorem 3.4 Assume (rotinv-p). Then, for all
$s \in I_k$
,
$k(s)= \mathbb{E} | (I-\xi H)e_1| ^s$
and
$\nu_{s}$
is the uniform measure on S. If, in addition,
$\mathbb{E}(1+\|A\|^s)\log N(A)<\infty$
holds for some
$s>0$
, then the top Lyapunov exponent
$\gamma$
is
\begin{equation} \gamma=k'(0)=\mathbb{E} \log | (I-\xi H)e_1| . \end{equation}
Remark 3.3. Our result strengthens [Reference Gürbüzbalaban, Simsekli and Zhu12, Theorem 3], where the formulae for k(s) and
$\gamma$
were proved for the (Rank1Gauss) model. (3.2) holds, in particular, under (Decay:Symm).
Remark 3.4. Note that if
$\|I-\xi H \| < 1$
a.s., then
$k(s)<1$
for all
$s>0$
, and
${\mathbb{P}}(|R|>t)=o(t^s)$
for all
$s>0$
, i.e. Pareto tails can occur only if
${\mathbb{P}}(\|I-\xi H \|>1)>0$
.
3.2. How does the tail index depend on
$\xi$
?
For
$A=I-\xi H$
and the corresponding R, we intend to determine how the tail index of R depends on
$\xi$
, assuming model (rotinv-p). For this model, Theorem 3.4 provides us with the formulae
$k(s)=\mathbb{E} | (I-\xi H)e_1| ^s\,=\!:\,h(\xi,s)$
and
$\gamma =\mathbb{E} \log|(I-\xi H)e_1|$
. We introduce the function h here to highlight the dependence on both
$\xi$
and s, and to remind the reader that it is equal to the spectral radius k(s) only for this particular model. By Theorem 3.1, the tail index
$\alpha (\xi ) $
of R corresponding to
$\xi $
satisfies
\begin{equation} h(\xi, \alpha (\xi))=1 .\end{equation}
For fixed
$\xi>0$
, h is convex as a function of s (see Proposition 2.1), with
$h(0)=1$
. Thus,
$\gamma=({\partial h}/{\partial s})'(\xi,0)<0$
is a necessary condition for the existence of
$\alpha>0$
with
$h(\xi,\alpha)=1$
.
A simple calculation shows that
$\gamma \to \infty$
when
$\xi \to \infty$
, so (3.3) may happen only for
$\xi$
from a bounded set. However, for an arbitrary law of H it is difficult to determine the set
$U\,:\!=\,\{\xi\colon\mathbb{E}\log|(I-\xi H)e_1|<0\}=\{\xi\colon\gamma(\xi)<0\}$
directly. Therefore, we will provide sufficient conditions for
$U \neq \emptyset$
.
Theorem 3.5. Consider
$A=\mathrm{I} - \xi H$
with variable
$\xi>0$
. Assume (rotinv-p), and that
${\mathrm{supp}}(H)$
is unbounded. Assume
$s_0=\infty$
, and that
\begin{equation} \mathbb{E}\langle He_1,e_1\rangle>0 \quad and \quad \mathbb{E}|\langle He_2,e_1\rangle|^{-\delta} < \infty \ for\ every\ \delta\ \in (0,1). \end{equation}
Then the following hold:
-
(i) There is a unique
$\xi _1>0$
such that
$h(\xi _1,1)=1$
and, for every
$\xi \in (0,\xi_1)$
, there is a unique
$\alpha =\alpha (\xi )>1$
such that
$h(\xi, \alpha (\xi))=1$
. In particular,
$\mathbb{E}\log|(I-\xi H)e_1|<0$
for all
$\xi \in (0,\xi _1]$
and the set U is nonempty. -
(ii) The function
$\xi \mapsto \alpha (\xi)$
is strictly decreasing and in
$\mathcal{C}^{1}((0,\xi_1))$
, with
$\lim _{\xi \to 0^+}\alpha (\xi )=\infty$
and
$\lim _{\xi \to \xi ^-_1}\alpha (\xi )=1$
. -
(iii) For
$\xi \in U$
with
$\xi >\xi _1$
,
$\alpha(\xi )<1$
.
The conditions of Theorem 3.5 are satisfied in particular if we impose a density assumption. Suppose that H is positive definite a.s., and (Decay:Symm) holds. Then, by Theorem 3.6, condition (3.4) is satisfied, and we have the following corollary.
Corollary 3.1. Assume (rotinv-p), (Decay:Symm), that H is positive definite a.s.,
${\mathrm{supp}}(H)$
is unbounded, and
$s_0=\infty$
. Then the tail index
$\alpha$
is strictly decreasing in the step size
$\eta$
and strictly increasing in the batch size b, provided that
$\alpha>1$
.
In particular, our result generalizes [Reference Gürbüzbalaban, Simsekli and Zhu12, Theorem 3] (which covers (Rank1Gauss) only).
Remark 3.5. The assumption
$\mathbb{E} \langle He_1,e_1\rangle >0$
will imply that
$U \neq \emptyset$
, while the second assumption in (3.4) is used to ensure that
$h\in C^1((0,\infty )\times(1,\infty ))$
, which we need to employ the implicit function theorem to study properties of
$\xi \mapsto \alpha(\xi)$
. Note that
$\mathbb{E} \langle He_1,e_1\rangle >0$
is automatically satisfied in the (Rank1) case.
For
$\xi \in U$
with
$\xi > \xi_1$
, there still exists a unique
$\alpha(\xi)$
which then satisfies
$\alpha(\xi)<1$
. However, we are not able to prove the
$\mathcal{C}^1$
regularity of
$h(\xi,s)$
when
$s<1$
since
$\partial h/\partial \xi$
does not exist when
$\xi$
satisfies
$\det(I-\xi H)=0$
; see the proof of Lemma 5.2 for details.
The behavior of h for different values of the batch size b and step size
$\eta$
is shown in Figures 1 and 2 respectively.
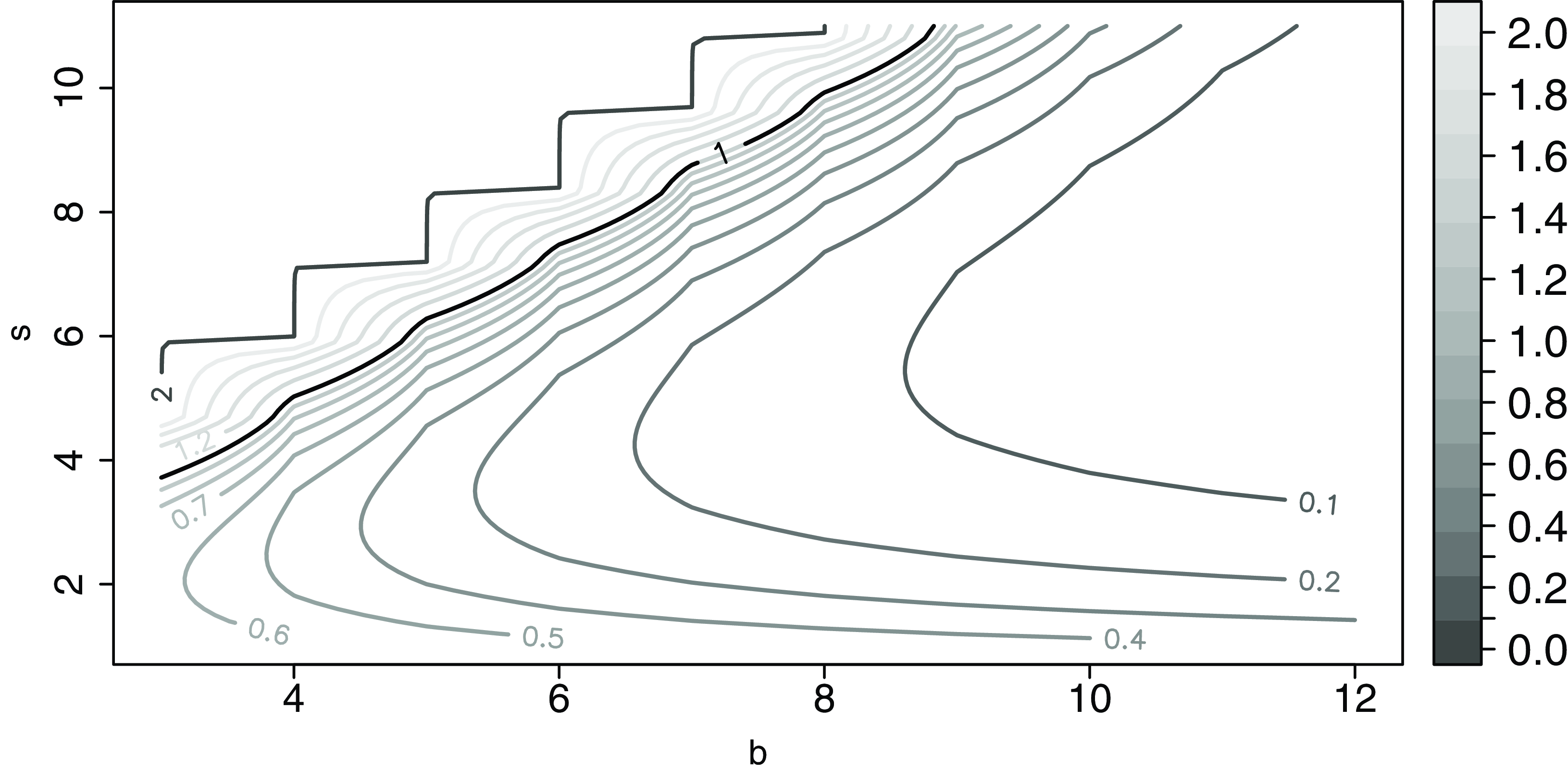
Figure 1. Contour plot of h as a function of b and s for model (Rank1Gauss) with
$d=2$
and
$\eta=0.75$
. The black line is the contour of
$k\equiv1$
. The values of h have been cut at level 2 for better visualization.
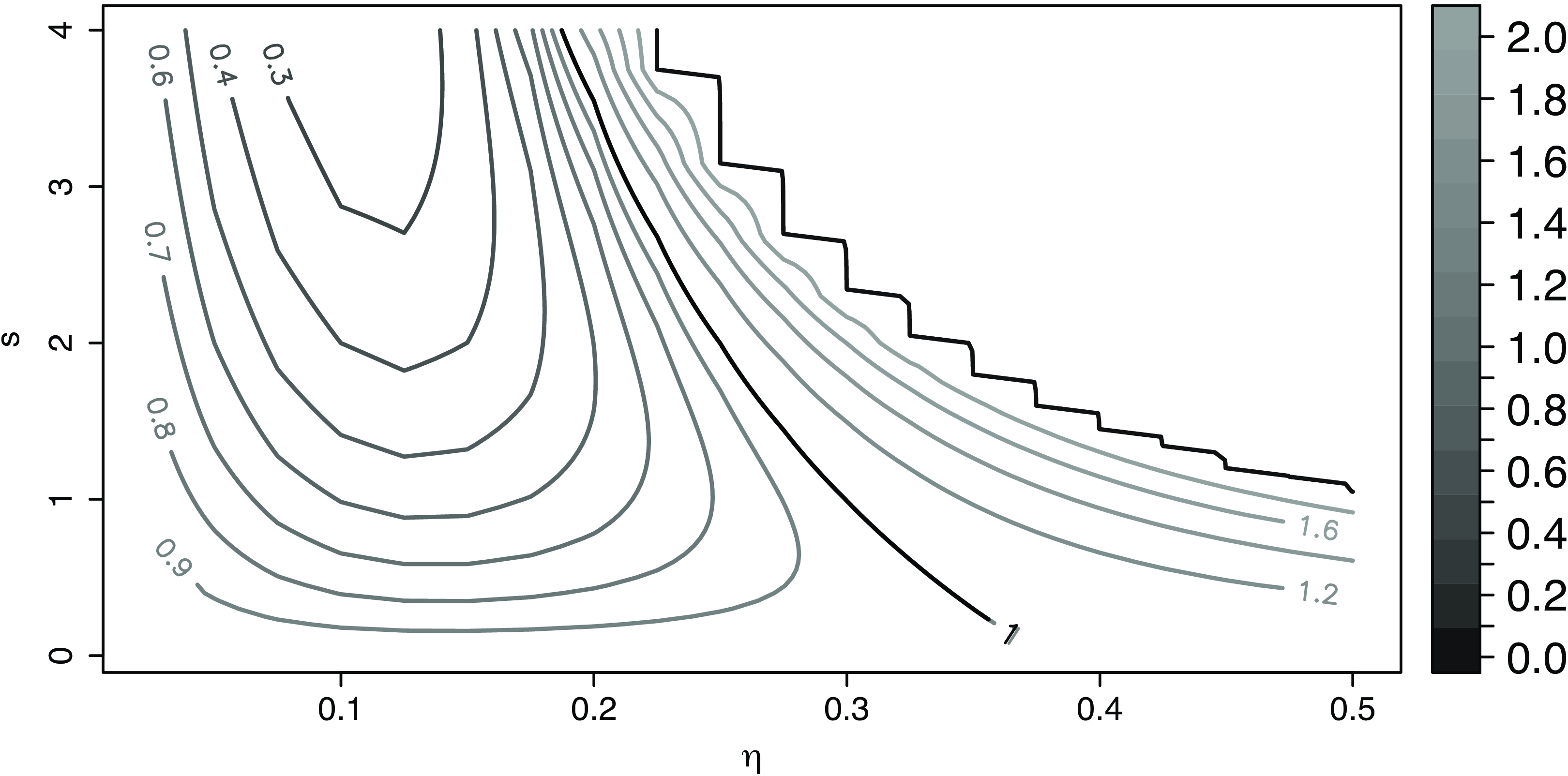
Figure 2. Contour plot of h as a function of
$\eta$
and s for model (Rank1Gauss) with
$d=2$
and
$b=5$
. The black line is the contour of
$k\equiv1$
. The values of h have been cut at level 2 for better visualization.
3.3. Checking the assumptions – the model (Rank1Gauss)
The following results confirm the hierarchy of our assumptions.
Lemma 3.1. Concerning the conditions imposed for the various models considered, we have the following implications:
Moreover, if we consider model (Rank1) with i.i.d.
$a_i$
,
$1 \le i \le b$
, such that the law of
$a_i$
is rotationally invariant with
${\mathrm{supp}}(a_i)={\mathbb{R}}^d$
, then (rotinv-p) is satisfied as well.
Our next result is concerned with the density of the law of
$H=\sum_{i=1}^b a_ia_i^\top$
in the (Rank1Gauss) model. The entries of
$g\in {\mathrm{Sym}(d,\mathbb{R})}$
will be denoted
$g_{ij}$
, i.e.
$g=(g_{ij})$
, where
$g_{ij}=g_{ji}$
. We identify
${\mathrm{Sym}(d,\mathbb{R})}$
with
${\mathbb{R}}^{d(d+1)/2}$
. Observe that then the Frobenius norm of g is bounded by the Euclidean norm of the corresponding vector x of
${\mathbb{R}}^{d(d+1)/2}$
, which contains the diagonal and upper diagonal entries of g:
$\|g \|_{\mathrm{F}} \le 2 |x |$
.
Lemma 3.2. Assume (Rank1Gauss). If
$b > d+1$
, then
$H=\sum_{i=1}^b a_ia_i^\top$
has a density f with respect to Lebesgue measure on
${\mathbb{R}}^{d(d+1)/2}$
that satisfies
$f(x)\leq C(1+|x |^2)^{-D}$
for all
$D>0$
and some constant
$C=C(D)$
depending only on D.
In particular, it is possible to choose
$D>{d(d+1)}/{4}$
in Lemma 3.2 so that the condition (Decay:Symm) is satisfied. The next result gives that the decay assumptions are sufficient for the existence of negative moments, which are required in the previous theorems. Its proof is contained in Section 7.
Theorem 3.6. Consider model (Symm) with (Decay:Symm) or model (Rank1) with (Decay:Rank1). Then, for every
$0\leq \delta < 1/ 2$
and
$\xi$
,
\begin{equation} \mathbb{E} |\det A|^{-\delta } <\infty, \end{equation}
and for every
$s<s_0$
,
$\mathbb{E} (1+\|A \|^s) N(A)^\varepsilon<\infty$
for some
$\varepsilon>0$
. Further, for every
$0 < \delta < 1$
,
$\mathbb{E}|\langle He_2,e_1\rangle|^{-\delta}<\infty$
.
3.4. Examples
3.4.1. Linear regression with Gaussian data distribution and constant step size.
This is the model (Rank1Gauss) studied in [Reference Gürbüzbalaban, Simsekli and Zhu12] and discussed in the introduction. All results are valid for this particular model.
Corollary 3.2. Assume (Rank1Gauss) with
$b>d+1$
, i.e.
\begin{align*}A = \mathrm{I} - \frac{\eta}{b}\sum_{i=1}^ba_ia_i^{\top}, \qquad B = \frac{\eta}{b}\sum_{i=1}^ba_iy_i,\end{align*}
where
$a_i$
,
$1 \le i \le b$
are i.i.d. standard Gaussian random vectors in
${\mathbb{R}}^d$
, independent of
$y_i$
. Then the assertions of Theorems 3.1, 3.2, 3.3, 3.4, and 3.5 hold. The tail index
$\alpha$
is strictly decreasing in the step size
$\eta$
and strictly increasing in the batch size b, provided that
$\alpha>1$
.
3.4.2. Linear regression with continuous data distribution and i.i.d. step size.
We may easily go beyond the previous example and consider model (Rank1) with an arbitrary (continuous) distribution for
$a_i$
that is rotationally invariant (cf. Remark 2.1) with
${\mathrm{supp}}(a_i)={\mathbb{R}}^d$
and satisfies (Decay:Rank1). This is satisfied, for example, if
$a_i$
are i.i.d. (as assumed in (Rank1)). with generic copy a such that the density of the law of a is bounded, depends only on
$|a|$
, and is of order
$o(|a|^{-db})$
as
$|a|\to \infty$
.
In addition, similar to [Reference Gürbüzbalaban, Hu, Simsekli and Zhu11, Theorem 11], we may allow for i.i.d. random step sizes, meaning that
$\eta_n$
is a sequence of i.i.d. positive random variables with generic copy
$\eta$
.
Corollary 3.3. Assume (Rank1) with random i.i.d. step sizes taking values in a compact interval
$J\subset (0,\infty)$
, i.e.
\begin{align*}A =\mathrm{I} - \frac{\eta}{b}\sum_{i=1}^ba_ia_i^{\top}, \qquad B = \frac{\eta}{b}\sum_{i=1}^ba_iy_i,\end{align*}
where
$(a_i,y_i)$
,
$1 \le i \le b$
, are i.i.d. and the distribution of
$a_i$
is an arbitrary continuous distribution that is rotationally invariant with
${\mathrm{supp}}(a_i)={\mathbb{R}}^d$
and satisfies (Decay:Rank1). Further,
$\eta$
is a random variable taking values in J that is independent of
$(a_i,b_i)$
,
$1 \le i \le b$
. Assume that
${\mathbb{P}}(Ax+B=x)<1$
is satisfied. Then the assertions of Theorems 3.1, 3.2, 3.3, 3.4, and 3.5 hold. The tail index
$\alpha$
is strictly increasing in the batch size b, provided that
$\alpha>1$
.
Proof. We have to check that the introduction of the random step size does not affect the validity of the assumptions. This is obvious for the rotation invariance, since
$\eta$
is scalar. Concerning condition (Decay:Rank1), consider the case where
$\eta$
has a density h on the interval
$J=[j_1,j_2]$
. Given that (Decay:Rank1) holds for the joint density f of
$(a_1, \ldots, a_b)$
, then by standard calculations (see, e.g., [Reference Grimmett and Stirzaker9, Example 4.7.6]) the joint density g of
$(\eta a_1, \ldots, \eta a_b)$
satisfies
\begin{align*} g(y_1,\ldots,y_d) & = \int_Jf(y_1/x,\ldots,y_b/x)h(x)\frac{1}{x^{bd}}\,\mathrm{d} x \\[5pt] & \le \int_JC\Bigg(1+\sum_{i=1}^b\frac1{x^2}|y_i|^2\Bigg)^{-D}h(x)\frac{1}{x^{bd}}\,\mathrm{d} x \\[5pt] & \le C\Bigg(1+\frac{1}{j_2^2}\sum_{i=1}^b|y_i|^2\Bigg)^{-D}\frac{1}{j_1^{bd}} \le C'\Bigg(1+\sum_{i=1}^b|y_i|^2\Bigg)^{-D}. \end{align*}
In the penultimate step we have used that in the integral,
$0 < j_1\le x \le j_2$
; in the last step we included these factors in the constant.
Remark 3.6. (Linear regression with a finite set of data points.) If
$a_i$
takes only finitely many different values, i.e.
${\mathrm{supp}}(a_i)=\{v_1,\ldots,v_m\}$
, then the irreducibility condition of (i-p-nc) is violated: the union of the one-dimensional subspaces
$W_j=\mathrm{span}(v_j)$
is
$G_A$
invariant. This is why this setting is outside the scope of our paper, but we believe that similar results hold when applying Markov renewal theory with finite state space – for example, the operator
$P^\alpha$
would become a (finite-dimensional) transition matrix.
Still, there are simple settings where A takes only two distinct values and condition (i-p-nc) is satisfied; namely, if
$d=2$
,
${\mathrm{supp}}(A)$
contains an irrational rotation, and a proximal matrix; see [Reference Bougerol and Lacroix3, Proposition 2.5] for further information.
3.4.3. Quadratic loss function with cyclic step size.
Note that we cannot cover general time-dependent learning rates because then we would lose the i.i.d. property of the sequence
$(A_i)_{i \ge 1}$
. However, our setup allows us to study the effect of cyclic step sizes, as introduced in [Reference Smith19]; see also [Reference Smith20], as well as [Reference Gürbüzbalaban, Hu, Simsekli and Zhu11, Theorem 5] for a recent related treatment.
Here,
$\eta_n$
takes values from a finite set
$\{c_1, \ldots, c_m\}$
in a cyclic way:
$\eta_n = c_j$
if and only if m divides
$(n-j)$
. Then
$A_i$
,
$1 \le i \le n$
, are no longer i.i.d., but their m-fold products (covering one cycle of step sizes) are. It is well known (cf. [Reference Vervaat22, Lemma 1.2]) that R satisfies (2.6) if and only if
\begin{equation} R \overset{\textrm{D}}{=} \Pi_m R + B^{(m)},\end{equation}
where R is independent of
$(A_1,B_1, \ldots, A_m, B_m)$
and
$B^{(m)}=\sum_{j=1}^m\Pi_{j-1}B_j$
. Hence, we may analyze (3.6) instead of (2.6). Note that the (Rank1) structure is not preserved when going from A to
$\Pi_m$
, but property (rotinv-p) remains valid for
$\Pi_m$
, if it holds for A. This is why we cannot recover all the results in this setting, and also why we consider directly here the more general model (Symm) that corresponds to a quadratic loss function
$\ell(x,H)=x^\top H x$
, where the symmetric matrix H takes the role of the data Z. Recall that this includes (Rank1) as a particular case.
Corollary 3.4 Assume (Symm) with cyclic step sizes
$\{c_1, \ldots, c_m\}$
, i.e.
\begin{align*}A_n = \mathrm{I} - \frac{\eta_n}{b}\sum_{i =1}^bH_{i,n},\end{align*}
with
$\eta_n=c_j$
if and only if m divides
$(n-j)$
and where
$H_{i,n}$
,
$1 \le i \le b$
,
$n \ge 1$
, are i.i.d. random symmetric matrices with unbounded support such that (rotinv-p) and (Decay:Symm) hold. Then the assertions of Theorems 3.1 and 3.2 hold. Further, Theorem 3.3 holds with
$R_n$
replaced by
$R_{nm}$
, and Theorem 3.4 holds upon replacing
$I-\xi H$
by
$\Pi_m$
.
Proof. By assumption, each random matrix
$A_1,\ldots,A_m$
satisfies both (rotinv-p) and (Decay:Symm). Then, for any
$o \in O(d)$
,
$oA_1 \cdots A_m o^{\top} = oA_1o^{\top} \cdots o A_m o^{\top} \overset{\textrm{D}}{=} A_1 \cdots A_m$
, using the rotation invariance and independence of
$A_1, \ldots A_m$
. Thus,
$\Pi_m$
satisfies (rotinv-p) as well – the product of proximal matrices is again a proximal matrix. The assumption (Decay:Symm) is used to infer from Theorem 3.6 that
$\mathbb{E} |\det(A_i)|^{-\delta}< \infty$
for each
$1 \le i \le m$
and some suitable
$\delta>0$
. Again using independence and the multiplicativity of the determinant, it follows that
\begin{align*}\mathbb{E}|\det(\Pi_m)|^{-\delta} = \prod_{i=1}^m\mathbb{E}|\det(A_i)|^{-\delta}<\infty.\end{align*}
From this, it also follows that
$\mathbb{E}(1+\|\Pi_m \|^s)N(\Pi_m)^\varepsilon<\infty$
for some
$\varepsilon >0$
and all
$s<s_0$
; see Step 2 in the proof of Theorem 3.6 for details of how this is deduced from the finiteness of the determinant.
We have thus shown that
$\Pi_m$
satisfies the assumptions of Theorems (3.1)–(3.4).
3.5. Related works and discussion
There is a large body of work on stochastic gradient descent. For a gentle introduction from a mathematical point of view, we recommend [Reference Murphy17, Reference Shalev-Shwartz and Ben-David18].
Our approach, to analyze heavy-tail properties of stochastic gradient descent by means of stochastic recurrence equations, was motivated by [Reference Gürbüzbalaban, Simsekli and Zhu12, Reference Hodgkinson and Mahoney14]; see also references therein, for example [Reference Mandt, Hoffman and Blei16] for an early contribution relating stochastic gradient descent to Markov processes. As mentioned in the examples above, this approach is limited by the fact that
$\lim_{n \to \infty} \eta_n \to 0$
is excluded, for this would violate the assumption that the matrices
$A_n$
are i.i.d. Still, we are able to study cyclic step sizes as proposed in [Reference Smith19] and analyzed recently in [Reference Gürbüzbalaban, Hu, Simsekli and Zhu11]. In addition, for the setting of piecewise constant step sizes (cf., e.g., [Reference Murphy17, Section 8.4.3]), our findings show that (over the time where the step size is constant) the approximation error behaves qualitatively as a random quantity with a heavy-tailed limit.
Hence, our results provide a qualitative analysis and a rigorous mathematical treatment of the origin of heavy-tail phenomena in stochastic gradient descent, the heavy-tail feature that is employed in many recent works on stochastic gradient descent; see [Reference Blanchet, Mijatović and Yang2, Reference Wang, Gurbuzbalaban, Zhu, Simsekli and Erdogdu23] and references therein.
4. Finite iterations: Proofs of Theorems 3.2 and 3.3
We start by proving (3.1), i.e. that
$\mathbb{E} |R_n |$
is of precise order n as
$n \to \infty$
.
Proof of Theorem
3.2. By Proposition 2.1, for any
$x\in {\mathbb{R}} ^d$
,
\begin{align*}r_{\alpha}\bigg(\frac{x}{|x|}\bigg)|x|^\alpha = c\int_S|\langle x,y \rangle |^{\alpha}\,\nu^*_{\alpha}(\mathrm{d} y).\end{align*}
Substituting
$x=R _n$
and taking expectations on both sides, we have
\begin{equation*} \mathbb{E} r_{\alpha}\bigg(\frac{R_n}{|R_n|}\bigg)|R_n|^\alpha = c\int_S\mathbb{E}|\langle y,R_n \rangle |^{\alpha}\,\nu^*_{\alpha}(\mathrm{d} y) \,=\!:\, b_n. \end{equation*}
Step 1. We shall prove that
$\lim_{n \to \infty}({b_n}/{n})=C$
, where
\begin{align*}C = \int_S\mathbb{E}[|\langle y,A_1R^{(1)}+B_1 \rangle |^{\alpha}-|\langle y,A_1R^{(1)} \rangle |^{\alpha}]\,\nu^*_{\alpha}(\mathrm{d} y).\end{align*}
Since
$R_n^{(1)}$
has the same law as
$R_n$
, we may write
\begin{equation*} b_n = \mathbb{E} r_{\alpha}\bigg(\frac{R_n^{(1)}}{|R_n^{(1)}|}\bigg)|R_n^{(1)}|^\alpha . \end{equation*}
Recall from (2.7) the definition of the operator
$P^{\alpha}$
and the definition of
$g \cdot x$
from (2.1). Using that
$r_{\alpha}$
is an eigenfunction of
$P^{\alpha}$
with eigenvalue 1 (see Proposition 2.1), we may replace
$r_\alpha$
by
$P^\alpha r_\alpha$
in the above equation for
$b_n$
and subsequently employ the definition of
$P^\alpha$
to deduce that
\begin{align*} b_n & = \mathbb{E}\bigg[P^{\alpha}(r_{\alpha})\bigg(\frac{R_n^{(1)}}{|R_n^{(1)}|}\bigg)|R_n^{(1)}|^\alpha\bigg] \\[3pt] & = \mathbb{E}\bigg[r_{\alpha}\bigg(A_1\cdot\frac{R_n^{(1)}}{|R_n^{(1)}|}\bigg) \bigg|A_1\frac{R_n^{(1)}}{|R_n^{(1)}|}\bigg|^{\alpha}|R_n^{(1)}|^\alpha\bigg] \\[3pt] & = \mathbb{E}\bigg[r_{\alpha}\bigg(A_1\cdot\frac{R_n^{(1)}}{|R_n^{(1)}|}\bigg)|A_1R_n^{(1)}|^\alpha\bigg] \\[3pt] & = \mathbb{E} c\int_S\bigg|\bigg\langle{y,A_1\frac{R_n^{(1)}}{|R_n^{(1)}|}}\bigg\rangle\bigg|^{\alpha} |A_1R_n^{(1)}|^\alpha\,\nu^*_{\alpha}(\mathrm{d} y) = c\int_S\mathbb{E}|\langle y,A_1R_n^{(1)} \rangle |^{\alpha}\,\nu^*_{\alpha}(\mathrm{d} y). \end{align*}
We used Proposition 2.1 in the second-to-last step and Fubini in the last line to change integral and expectation. Using that
$R_{n+1}=A_1R_n^{(1)}+B_1$
a.s., we obtain for
$b_{n+1}$
the expression
\begin{equation*} b_{n+1} = c\int_S\mathbb{E}|\langle y,A_1R_n^{(1)}+B \rangle |^{\alpha}\,\nu^*_{\alpha}(\mathrm{d} y), \end{equation*}
and consequently
\begin{equation} b_{n+1} - b_n = \int_S\mathbb{E}[|\langle y,A_1R_n^{(1)}+B_1 \rangle |^{\alpha} - |\langle y,A_1R_n^{(1)} \rangle |^{\alpha}]\,\nu^*_{\alpha}(\mathrm{d} y). \end{equation}
If we are allowed to take the limit inside the expectation, then it immediately follows that
$\lim_{n\to\infty}b_{n+1}-b_n=C$
and, using a telescoping sum, we also have the desired result
$\lim _{n\to\infty}({b_n}/{n})=C$
.
Hence, we have to come up with a uniform bound for the term inside the expectation. In the case
$\alpha \leq 1$
,
\begin{equation*} \big||\langle y,A_1R_n^{(1)}+B_1 \rangle |^{\alpha}-|\langle y,A_1R_n^{(1)} \rangle |^{\alpha}\big| \leq \big|\langle y,A_1R_n^{(1)}+B_1 \rangle-\langle y,A_1R_n^{(1)} \rangle\big|^{\alpha} \leq |\langle y,B_1 \rangle|^{\alpha} \end{equation*}
and
$\int_S\mathbb{E}|\langle y,B_1 \rangle|^{\alpha}\,\nu_\alpha^*(\mathrm{d} x) \le \mathbb{E}|B_1|^\alpha < \infty$
.
In the case
$\alpha > 1$
, we use the inequality
$||a|^{\alpha}-|b|^{\alpha}| \leq \alpha |a-b|\max\{|a|^{\alpha-1},|b|^{\alpha-1}\}$
to infer that
\begin{align*} & \big||\langle y,A_1R_n^{(1)} +B_1 \rangle |^{\alpha} -|\langle y,A_1R_n^{(1)} \rangle |^{\alpha}\big| \\[3pt] & \qquad \leq \alpha|\langle y,B_1 \rangle|\max\{|\langle y,A_1R_n^{(1)}+B_1 \rangle |^{\alpha-1}, |\langle y,A_1R_n^{(1)} \rangle |^{\alpha-1}\} \\[3pt] & \qquad \leq \alpha 2^\alpha|B_1|(|A_1R_n^{(1)}|^{\alpha-1}+|B_1|^{\alpha -1}) \\[3pt] & \qquad \leq \alpha 2^\alpha(|B_1|^{\alpha}+|B_1|\|A_1\|^{\alpha-1}|R_n^{(1)}|^{\alpha-1}). \end{align*}
Observe that
$|B_1|\|A_1\|^{\alpha-1}$
and
$|R_n^{(1)}|^{\alpha-1}$
are independent, and
\begin{equation*} \mathbb{E}|B_1|\|A_1\|^{\alpha-1} \leq (\mathbb{E}|B_1|^{\alpha})^{1/\alpha}(\mathbb{E}\|A_1\|^{\alpha})^{(\alpha-1)/\alpha}<\infty. \end{equation*}
So it remains to dominate
$|R_n^{(1)}|^{\alpha-1}$
independently of n by an integrable function. We have
$|R_n| \leq \sum_{i=1}^{\infty}\|\Pi_{i-1}\||B_i|$
. Hence, for
$\alpha -1 \leq 1$
,
\begin{equation} |R_n|^{\alpha-1} \leq \sum_{i=1}^{\infty}\|A_1\cdots A_{i-1}\|^{\alpha-1}|B_i|^{\alpha-1}. \end{equation}
Since k is log-convex (see Proposition 2.1), there is
$\rho <1 $
such that
$\mathbb{E}\|\Pi_{i-1}\|^{\alpha-1} \leq c\rho^n$
and so the right-hand side of 4.2 is integrable. If
$\alpha >2$
then by the Minkowski inequality we have
\begin{align*} \Bigg(\mathbb{E}\Bigg[\sum_{i=1}^{\infty}\|\Pi_{i-1}\||B_i|\Bigg]^{\alpha-1}\Bigg)^{1/(\alpha-1)} & \le \sum_{i=1}^{\infty}(\mathbb{E}\|\Pi_{i-1}\|^{\alpha-1}\mathbb{E}|B_i|^{\alpha-1})^{1(\alpha-1)} \\ & \le \sum_{i=1}^{\infty}\rho^{(i-1)/(\alpha-1)}(\mathbb{E}|B_1|^{\alpha-1})^{1/(\alpha-1)}<\infty . \end{align*}
This shows that we may use the Lebesgue dominated convergence theorem in (4.1) to infer that
$\lim_{n\to\infty}({b_n}/{n})=C$
.
Step 2. To obtain the announced results for
$\mathbb{E} |R_n|^\alpha$
(without the eigenfunction
$r_\alpha$
), observe that
$b_n\leq c\mathbb{E} |R_n|^{\alpha}$
. From this, the lower bound follows. We shall prove that the inverse inequality also holds, i.e. there is a
$c_1$
such that
$c_1\mathbb{E}|R_n|^{\alpha} \leq \int_{S}\mathbb{E}|\langle y,R_n \rangle |^{\alpha}\,\nu^*_{\alpha}(\mathrm{d} y)$
. Indeed, the function
\begin{equation*} S \ni x \mapsto \int_S|\langle y,x \rangle |^{\alpha}\,\nu^*_{\alpha}(\mathrm{d} y) \end{equation*}
is continuous and attains its minimum
$c_1$
on S. Suppose that
$c_1=0$
. Then there is
$x_1\in S$
such that
$|\langle y,x_1 \rangle |^{\alpha}=0$
on the support of
$\nu^*_{\alpha}$
, i.e.
$\mathrm{supp}\,\nu^*_{\alpha}$
is contained in a hyperplane orthogonal to
$x_1$
, which is impossible by Proposition 2.1. Therefore,
\begin{equation*} \int_{S}|\langle y,R_n|R_n|^{-1} \rangle |^{\alpha}\,\nu^*_{\alpha}(\mathrm{d} y) \geq c_1 \quad \text{if } R_n\neq 0, \end{equation*}
and thus
$\mathbb{E}\int_{S}|\langle y,R_n \rangle |^{\alpha}\,\nu^*_{\alpha}(\mathrm{d} y) \geq c_1\mathbb{E}|R_n|^{\alpha}$
.
We continue with the proof of Theorem 3.3 that provides an upper bound for the tails of finite iterations
$R_n$
.
Proof of Theorem
3.3. Using a union bound, the summability of
${1}/{k^2}$
, and the Markov inequality, we have
\begin{align*} {\mathbb{P}}(R_n > t) & \le \sum_{m=1}^n{\mathbb{P}}\bigg(\|\Pi_{m-1} \||B_m| > \frac{6t}{\pi^2m^2}\bigg) \\ & \le \sum_{m=1}^n\mathbb{E}\|\Pi_{m-1} \|^{\alpha+\varepsilon}\mathbb{E}|B_m|^{\alpha+\varepsilon} \cdot \frac{(\pi^2m^2)^{\alpha+\varepsilon}}{(6t)^{\alpha+\varepsilon}} \\ & \le \sum_{m=1}^nC \cdot k(\alpha+\varepsilon)^{m-1} \mathbb{E}|B_m|^{\alpha+\varepsilon}\frac{(\pi^2m^2)^{\alpha+\varepsilon}}{(6t)^{\alpha+\varepsilon}} \\ & \le nC \cdot k(\alpha+\varepsilon)^{n-1}\mathbb{E}|B_1|^{\alpha+\varepsilon}\frac{(\pi^2n^2)^{\alpha+\varepsilon}}{6^{\alpha+\varepsilon}} \cdot t^{-(\alpha+\varepsilon)} \,=\!:\, C_nt^{-(\alpha+\varepsilon)}, \end{align*}
where we have further used that
$\mathbb{E} \|\Pi_m \|^s \le C_sk(s)^m$
for each
$m \in \mathbb{N}$
and
$k(\alpha+\varepsilon)>1$
due to the convexity of k.
5. Evaluation of tail index and stationary measure: Proofs of Theorems 3.4 and 3.5
5.1. Identification and differentiability of
$\boldsymbol{k}(\boldsymbol{s})=\mathbb{E} | (\boldsymbol{I}-\xi \boldsymbol{H})\boldsymbol{e}_1| ^{\boldsymbol{s}}$
We start by proving Theorem 3.4, which identifies
$\nu_{s}$
as the uniform measure on S and provides a tractable formula for k(s) under the assumption of rotational invariance.
Proof of Theorem
3.4. Let
$\xi = \eta / b$
. For
$y \in S$
, let o be an orthogonal matrix such that
$y=o e_1$
. For any
$f \in \mathcal{C}(S)$
,
\begin{align} P^sf(y) = P^s f(ke_1) & = \mathbb{E} f((I-\xi H)\cdot (o e_1))| (I-\xi H)(o e_1)|^s \notag \\ & = \mathbb{E} f(o(I-\xi o^{-1}Ho)\cdot e_1)| o(I-\xi o^{-1}Ho)e_1|^s \notag \\ & = \mathbb{E} f(o(I-\xi H)\cdot e_1)| (I-\xi H)e_1|^s \end{align}
because
$o^{-1}Ho$
has the same law as H and o preserves the norm. Using this for
$f \in \mathcal{C}(S)$
with
$\|\ f \|=1$
, we obtain
$|P^sf(y)| \le \mathbb{E}\|\ f \||(I-\xi H)e_1|^s \le \mathbb{E}|(I-\xi H)e_1|^s$
. In particular, the spectral radius of
$P^s$
is bounded by
$\mathbb{E}|(I-\xi H)e_1 |^s$
and thus, by Proposition 2.1,
$k(s)\le \mathbb{E} |(I-\xi H)e_1 |^s$
. Using the representation (2.2) of the uniform measure on S together with (5.1), we further obtain that
\begin{align*} \int_SP^sf(y)\,\sigma(\mathrm{d} y) = \int_{O(d)}P^sf(o e_1)\,\mathrm{d}o & = \int_{O(d)}\mathbb{E} f(o(I-\xi H)\cdot e_1)|(I-\xi H)e_1|^s\,\mathrm{d}o \\ & = \mathbb{E}\bigg[|(I-\xi H)e_1|^s \cdot \int_{O(d)}f(o(I-\xi H)\cdot e_1)\,\mathrm{d}o\bigg] . \end{align*}
Here, we have used the Fubini theorem in the last step. Inside the integral, H is a fixed matrix and we may write
$(I-\xi H) \cdot e_1\,=\!:\,ae_1$
for some orthogonal matrix a. Then using the invariance properties of the Haar measure on O(d), we deduce that
\begin{equation*} \int_{O(d)}f(o(I-\xi H)\cdot e_1)\,\mathrm{d}o = \int_{O(d)}f(o a\cdot e_1)\,\mathrm{d}o = \int_{O(d)}f(o\cdot e_1)\,\mathrm{d}o . \end{equation*}
Therefore,
\begin{equation*} \int_S P^sf(y)\,\sigma(\mathrm{d} y) = \bigg(\int_Sf(y)\,\sigma(\mathrm{d} y)\bigg)\mathbb{E}|(I-\xi H)e_1|^s, \end{equation*}
and hence
$\sigma$
is an eigenmeasure of
$P^s$
with eigenvalue
$\mathbb{E}|(I-\xi H)e_1|^s$
. Since the latter one is also the upper bound on the spectral radius and on k(s), we infer that we have indeed found the dominating eigenvalue and the corresponding eigenmeasure. Thus, due to the uniqueness results of Proposition 2.1,
$\nu_s=\sigma$
and
$k(s)=\mathbb{E}|(I-\xi H)e_1|^s$
.
The formula for the Lyapunov exponent then follows from Proposition 2.2.
Propositions 2.1 and 2.2 provide general results about the differentiability of k as a function of s. We now focus on the particular instance of (rotinv-p), where
$k(s)=\mathbb{E}|(I-\xi H)e_1|^s$
$=\!:\,h(\xi,s)$
, and prove that
$h(\xi,s)$
is
$\mathcal{C}^1$
.
Lemma 5.1. Assume (rotinv-p), and that
$\mathbb{E}|\langle He_2,e_1\rangle|^{-\delta}<\infty$
for some
$\delta>0$
. Then
\begin{equation*} \frac{\partial h}{\partial s}= \mathbb{E} | (I-\xi H)e_1| ^s\log | (I-\xi H)e_1| \end{equation*}
exists and is continuous on
$(0,\infty )\times [0,s_0)$
with
$({\partial h}/{\partial s})(\xi ,0)= \mathbb{E} \log | (I-\xi H)e_1| $
.
Proof. Fix
$\xi>0$
and let
$s \in [0,s_0)$
. By the mean value theorem there is
$\theta \in (0,1)$
such that
\begin{align*} \frac{h(\xi,s+v)-h(\xi,s)}{v} & = \frac{1}{v}\mathbb{E}[|(I-\xi H)e_1 |^{s+v} - |(I-\xi H)e_1 |^s] \\ & = \mathbb{E}[|(I-\xi H)e_1 |^{s+\theta v}\log|(I-\xi H)e_1 |]. \end{align*}
Thus, the asserted differentiability follows by the Lebesgue dominated convergence theorem once we can provide a bound for the right-hand side that is uniform in
$\theta$
.
Observe that for any small
$\varepsilon >0$
,
$|\log x| < |x|^\varepsilon$
for
$x>1$
and
$|\log x| \le |x|^{-\varepsilon}$
for
$0 < x < 1$
; hence,
\begin{align*} & \mathbb{E}|(I-\xi H)e_1 |^s\log|(I-\xi H)e_1 | \\ & \qquad \le \mathbb{E}|(I-\xi H)e_1 |^{s+\varepsilon}\mathbf{1}_{\{|(I-\xi H)e_1 |\ge1\}} + \mathbb{E}|(I-\xi H)e_1 |^{s-\varepsilon}\mathbf{1}_{\{|(I-\xi H)e_1 | < 1\}} \,=\!:\, T_1+ T_2. \end{align*}
The first term,
$T_1$
, is finite as long as
$s+\varepsilon < s_0$
. For
$T_2$
, we only need to consider the case where
$s-\varepsilon <0$
. We use that
\begin{equation*} |(I-\xi H)e_1 | = \Bigg((1-\xi\langle He_1,e_1\rangle)^2 + \xi^2\sum_{j=2}^d\langle He_j,e_1\rangle^2\Bigg)^{1 / 2} \geq \xi|\langle He_j,e_1\rangle|. \end{equation*}
Therefore, if
$|\langle He_j,e_1\rangle|^{-\varepsilon}$
is integrable for all j, then
$T_2$
is finite for any
$\xi$
. Observe that, by (rotinv-p), for any function f and
$o \in O(d)$
chosen such that
$o e_2=e_j$
,
$o e_1=e_i$
(
$j\neq i$
),
\begin{equation*} \mathbb{E} f(\langle He_j,e_i\rangle) = \mathbb{E} f(\langle Ho e_2,o e_1\rangle) = \mathbb{E} f(\langle o^\top Ho e_2,e_1\rangle) = \mathbb{E} f(\langle He_2,e_1\rangle ). \end{equation*}
Therefore, integrability of a matrix coefficient
$|\langle He_j,e_i\rangle|^{\varepsilon}$
,
$j\neq i$
, is equivalent to integrability of
$|\langle He_2,e_1\rangle |^{-\varepsilon}$
.
The existence of
${\partial h}/{\partial \xi}$
is a little bit more complicated, in particular for
$1<s<2$
, and it is not well clarified in [Reference Gürbüzbalaban, Simsekli and Zhu13]. We have the following lemma.
Lemma 5.2. Suppose
$s_0> 2$
. Then
${\partial h}/{\partial \xi}$
exists and is continuous on
$(0,\infty)\times[2,s_0)$
with
\begin{equation} \frac{\partial h}{\partial \xi}(0,s)=-s\mathbb{E} \langle He_1,e_1\rangle . \end{equation}
If, in addition,
$\mathbb{E}|\langle He_2,e_1\rangle|^{-\delta}<\infty$
holds for every
$0 < \delta < 1$
, then
${\partial h}/{\partial \xi}$
exists and is continuous on
$(0,\infty)\times(1,s_0)$
.
Proof. Let
$g(\xi) = \langle(I-\xi H)e_1,(I-\xi H)e_1\rangle$
. By the mean value theorem, for some
$\theta \in (0,1)$
,
\begin{equation*} \frac{h(\xi+v,s) - h(\xi,s)}{v} = \frac{1}{v}\mathbb{E}(g(\xi+v)^{s/2} - g(\xi)^{s/2}) = \frac{s}{2}\mathbb{E} g(\xi+\theta v)^{s/2-1}g'(\xi+\theta v). \end{equation*}
Suppose we were able to dominate
$g(\xi+\theta v)^{s/2-1}g'(\xi+\theta v)$
independently of
$\theta v$
by an integrable function. Then, by the Lebesgue dominated convergence theorem,
\begin{equation} \frac{\partial h}{\partial \xi} = s\mathbb{E}|(I-\xi H)e_1|^{s-2}(-\langle He_1,e_1\rangle+\xi\langle He_1,He_1\rangle). \end{equation}
For the case where
$s\ge2$
, the right-hand side is dominated by
$C(\xi)\|H\|^s$
and so is finite.
$C(\xi)\|H\|^s$
is also in the right domination in the Lebesgue dominated convergence theorem. In particular, (5.2) holds.
For the case where
$1<s<2$
, observe that
$|g'(\xi +\theta v)|\leq C(\xi)(1+\| H\|^2)$
and
\begin{align*} g(\xi+\theta v)^{s/2-1} & = |(I-(\xi+\theta v)H)e_1|^{s-2} \\ & = \Bigg((1-(\xi+\theta v)\langle He_1,e_1\rangle)^2 + (\xi+\theta v)^2\sum_{j=2}^d\langle He_j,e_1\rangle^2\Bigg)^{(s-2)/2} \end{align*}
with
$-1<s-2<0$
. As before,
$g(\xi+\theta h)^{s/2-1} \leq (\xi/2)^{s-2}|\langle He_j,e_1\rangle|^{s-2}$
for sufficiently small
$\theta v$
. Similar to the proof of Lemma 5.1, integrability of
$|\langle He_j,e_i\rangle|^{-\delta}$
for some positive
$\delta$
is equivalent to integrability of
$|\langle He_2,e_1\rangle|^{-\delta}$
. Therefore, we may apply the Lebesgue dominated convergence theorem and we obtain (5.3) for
$\xi >0$
.
Remark 5.1. It follows from the proof that if
$\mathbb{E}|\langle He_2,e_1\rangle|^{-\delta}<\infty$
for
$\delta\leq\delta_0<1$
then
$h\in\mathcal{C}^1((0,\infty)\times(2-\delta_0,s_0))$
.
5.2. The shape of the tail index function
$\alpha (\xi)$
: Proof of Theorem 3.5
Now, using the differentiability of h, we study the dependence of the tail index on
$\xi$
.
Proof of Theorem
3.5. Using
$s_0=\infty$
and the assumption that
${\mathrm{supp}}(H)$
is unbounded, a simple calculation shows that, for every fixed
$\xi \in U$
,
$\lim_{s \to \infty} h(\xi,s)=\infty$
. By Proposition 2.1, for fixed
$\xi$
,
$s\mapsto h(\xi,s)$
is strictly convex; hence, for every
$\xi \in U$
there is a unique
$\alpha(\xi)>0$
with
$h(\xi, \alpha(\xi))=1$
.
Step 1. Observe, that for every
$s>1$
,
$h(\cdot,s)$
is a strictly convex function of
$\xi$
. Moreover,
$h(0,s)=1$
and, by (5.2) and (3.4), for
$s\geq 2$
,
$({\partial h}/{\partial \xi})(0,s)<0$
. Hence, for each s, there is a unique
$\xi>0$
such that
$h(\xi,s)=1$
. Therefore, the set
$\tilde{\kern-2pt U} = \{\xi\colon\text{there exists}\ \alpha>1$
such that
$h(\xi,\alpha)=1\}$
is not empty, and the mapping
$\xi\to\alpha(\xi)$
is one-to-one on
$\tilde{\kern-2pt U}$
.
Let us prove that
$\tilde{\kern-2pt U}$
is open. Let
$\xi_*\in U$
and
$h(\xi_*,\alpha_*)=1$
. Given
$\xi$
,
$h(\xi,\cdot)$
is a strictly convex
$C^1$
function of s, and
$h(\xi,0)=1$
. Therefore,
$({\partial h}/{\partial s})(\xi_*,\alpha_*)>0$
and the same holds in a neighborhood of
$(\xi_*,\alpha_*)$
. Moreover, there is
$\varepsilon_0>0$
such that
$h(\xi_*,\alpha_*-\varepsilon_0)<1$
,
$h(\xi_*,\alpha_*+\varepsilon_0)>1$
, and
$\alpha_*-\varepsilon_0>1$
. Let
$\eta_0>0$
be such that, for
$0 < \eta < \eta_0$
,
$h(\xi_*\pm\eta,\alpha_*-\varepsilon_0)<1$
,
$h(\xi_*\pm\eta,\alpha_*+\varepsilon _0)>1$
, and
$({\partial h}/{\partial s})(\xi_*\pm\eta,\alpha_*\pm\varepsilon)>0$
for
$0\leq\eta < \eta_0$
,
$0\leq\varepsilon < \varepsilon_0$
. This proves that, for such
$\eta$
, we have
$\alpha(\xi_*\pm\eta)>1$
and so
$(\xi_*-\eta_0,\xi_*+\eta_0)\subset\tilde U$
.
Step 2. Now we shall prove that
Being an open set,
$\tilde{\kern-2pt U}$
could possibly be a sum of disjoint open intervals. Let
$I\,:\!=\,(\xi',\xi'')$
be an interval with
$I \subset U$
, and every open connected interval containing I is not a subset of U, i.e. I is maximal. Let
$\xi _*\in I$
. Then, by the strict convexity of both
$h(\xi,\cdot)$
and
$h(\cdot,s)$
, we have
$({\partial h}/{\partial \xi})(\xi_*,\alpha_*)$
,
$({\partial h}/{\partial s})(\xi_*,\alpha_*)>0$
. Hence, by the implicit function theorem,
$\alpha(\xi)$
is a
$C^1$
function on
$(\xi',\xi'')$
and
$\alpha'(\xi)<0$
for
$\xi\in(\xi',\xi'')$
. This proves the first part of assertion (3.5) (except for the identification
$I=(0,\xi)$
).
Step 3. Both
$\lim_{\xi\to(\xi'')^-}\alpha(\xi)$
and
$\lim_{\xi\to(\xi')^+}\alpha(\xi)$
exist, with the latter possibly unbounded. Suppose that
$\alpha_1=\lim_{\xi\to(\xi'')^-}\alpha(\xi)>1$
. Then
$h(\xi'',\alpha_1) = \lim_{\xi\to(\xi'')^-}h(\xi,\alpha(\xi))=1$
, which shows that
$\xi''\in\tilde U$
and
$(\xi',\xi'')$
is not maximal. This proves the existence of
$\xi_1$
.
Suppose that
$\alpha_1=\lim_{\xi\to(\xi')^+}\alpha(\xi)$
is finite. Then
$h(\xi',\alpha_1)=\lim_{\xi\to(\xi')^+}h(\xi,\alpha(\xi))=1$
, which shows that either
$\xi'=0$
or
$\xi'\in U$
, and thus
$(\xi',\xi'')$
is not maximal.
Therefore,
$\lim_{\xi\to(\xi')^+}\alpha(\xi)=\infty$
or
$\xi'=0$
. Let us prove that in fact
$\xi'=0$
and
$\lim_{\xi\to0^+}\alpha(\xi)=\infty$
. Suppose that
$\xi'>0$
. The range of
$\alpha(\xi)$
on
$(\xi',\xi'')$
is
$(1,\infty)$
and so, by the strict convexity of
$h(\cdot,s')$
for given
$s'>1$
, there is
$0 < \xi_* < \xi'$
such that
$h(\xi_*,s')<1$
. On the other hand,
$\lim_{s\to\infty}h(\xi_*,s)=\infty$
and so there is
$s_*>s'$
such that
$h(\xi_*,s_*)=1$
. But, for
$s^*$
there is also
$\xi > \xi'$
such that
$h(\xi,s_*)=1$
, which is not possible by the strict convexity of
$h(\cdot,s_*)$
. This proves (5.4), and hence assertion (3.5).
Similarly,
$\lim_{\xi\to0^+}\alpha(\xi)$
cannot be finite. Indeed, suppose that
$\alpha_1=\lim_{\xi\to0^+}\alpha(\xi)<\infty$
. Then, by (3.4), for every
$s>\max(\alpha_1,2)$
there is
$\xi$
close to 0 such that
$h(\xi,s)<1$
. At the same time, there is
$s<\alpha_1$
such that
$h(\xi,s)=1$
. Since
$k(\xi,\cdot)$
is strictly convex, we get a contradiction.
Finally, by the strict convexity of
$h(\cdot,s)$
for
$s>1$
,
$\alpha(\xi)$
must be strictly smaller than 1 as far as
$\xi>\xi_1$
.
Remark 5.2. By (5.2), the assumption
$\mathbb{E}\langle He_1,e_1\rangle < 0$
is equivalent to U being not empty and
$\sup\{s(\xi)\colon\xi\in U\}>2$
. Suppose, however, we know only that
$\sup\{s(\xi)\colon\xi\in U\}>1$
. Then the same argument as in the proof allows us to conclude that s is strictly decreasing on an interval
$(0,\xi_1)$
,
$h(\xi_1,1)=1$
, but this time
$ \lim_{\xi\to0^+}s(\xi)$
may possibly be finite.
6. Specific models
6.1. Hierarchy of assumptions
Proof of Lemma
3.1. We start by proving the first implication. By assumption,
$a_i$
have a d-dimensional standard Gaussian distribution, hence
$o a_i$
has the same law as
$a_i$
for any
$o \in O(d)$
. Thus (cf. Remark 2.1), each
$H_i$
is invariant under rotations. Further,
\begin{align*} o Ao^{\top} = o\Bigg(\mathrm{I} - \frac{\eta}{b}\sum_{i=1}^b H_i\Bigg)o^{\top} = \mathrm{I} - \frac{\eta}{b}\sum_{i=1}^bo H_io^{\top} \overset{\textrm{D}}{=} \mathrm{I} - \frac{\eta}{b}\sum_{i=1}^b H_i, \end{align*}
where we have used that the
$H_i$
are i.i.d. and that o is deterministic to replace each summand
$o H_io^\top$
by the random variable
$H_i$
, which is the same in law only. This proves the first part of (rotinv-p). In order to show that
$G_A$
contains a proximal matrix, note that
${\mathrm{supp}}(a_i) = {\mathbb{R}}^d$
. Let
$v \in {\mathbb{R}}^d$
be such that
$|v |^2 > {2b}/{\eta}$
. Then
$(v,0,0,\ldots,0) \in \mathrm{supp}((a_1, \ldots, a_b))$
, hence
$\mathrm{I} - ({\eta}/{b})vv^\top\in G_A$
and v is an eigenvector with corresponding eigenvalue
$1-({\eta}/{b})|v |^2 < -1$
. Its eigenspace is one-dimensional: any
$y \in {\mathbb{R}}^d$
that is orthogonal to v is just mapped to itself (eigenvalue 1).
Note that we have used here only the facts that the law of
$a_i$
is rotationally invariant, and that
${\mathrm{supp}}(a_i)={\mathbb{R}}^d$
; hence, the final assertion of the lemma holds.
Considering the second implication, it is proved in [Reference Bougerol and Lacroix3, Proposition IV.2.5] (applied with
$p=1$
) that (rotinv-p) implies condition (i-p-nc). By [Reference Guivarc’h and Le Page10, Proposition 2.14], there is either no
$G_A$
-invariant cone, or there is a minimal
$G_A$
-invariant subset M of S that generates a proper
$G_A$
-invariant cone C. Using the rotation invariance, we can deduce from
$G_A \cdot M \subset M\subset C$
that
$o^{-1}G_A o \cdot M \subset M\subset C$
, and hence
$G_A o \cdot M \subset o M \subset o C$
for all
$o \in O(d)$
. Consequently,
$G_A \cdot (o M \cap M) \subset (o M \cap M)$
, and since O(d) acts transitively on S, there is an o such that
$M \nsubseteq o M$
. Hence,
$o M \cap M$
is
$G_A$
-invariant and strictly smaller than M; which contradicts the minimality of M.
6.2. The Gaussian model
Proof of Lemma
3.2. Let us write
$a_{i,k}$
,
$1 \le i \le b$
,
$1 \le k \le d$
, for the kth component of the ith vector
$a_i$
, and note that
$(a_{i,k})_{i,k}$
are i.i.d. standard Gaussian random variables.
Step 1. Recalling that
\begin{align*} a_ia_i^\top = \begin{pmatrix} a_{i,1}^2 &\quad a_{i,1}a_{i,2} &\quad a_{i,1}a_{i,3} &\quad \ldots &\quad a_{i,1}a_{i,d} \\[2pt] &\quad a_{i,2}^2 &\quad a_{i,2} a_{i,3} &\quad \ldots &\quad a_{i,2}a_{i,d} \\[2pt] &\quad &\quad a_{i,3}^2 &\quad \ldots &\quad a_{i,3}a_{i,d} \\[2pt] &\quad &\quad &\quad \ddots &\quad\vdots \\[2pt] &\quad &\quad &\quad &\quad a_{i,d}^2 \end{pmatrix}, \end{align*}
we obtain, for
$H=\sum_{i=1}^b a_i a_i^\top$
, that
$H_{\ell,\ell} = \sum_{i=1}^ba_{i,\ell}^2$
,
$H_{\ell,k} = \sum_{i=1}^ba_{i,\ell}a_{i,k}$
. Introducing the b-dimensional vectors
$x_k=(x_{k,i})_{i=1}^b$
,
$1 \le k \le d$
, by setting
$x_{k,i}=a_{i,k}$
we see that
$H_{\ell,\ell} = |x_{\ell} |^2$
,
$H_{\ell,k} = \sum_{i=1}^b\langle x_\ell,x_k \rangle$
. Note that
$x_k$
,
$1 \le k \le d$
, are i.i.d. b-dimensional standard Gaussian vectors. Hence,
$Z_\ell^2\,:\!=\,H_{\ell,\ell}$
,
$1 \le \ell \le d$
, are i.i.d. random variables with a
$\chi^2(b)$
distribution, and
$Y_\ell \,:\!=\, {x_\ell}/{|x_\ell |}$
has the uniform distribution on
$S^{b-1}$
, due to the radial symmetry of the b-dimensional Gaussian distribution. Moreover,
$Y_{\ell}$
is independent of
$H_\ell$
, so that we have that all the random variables
$Z_{1}, \ldots, Z_{d}, Y_{1}, \ldots, Y_d$
are independent, and
\begin{align*} H = \begin{pmatrix} Z_1^2 &\quad Z_1Z_2 \langle Y_1,Y_2 \rangle &\quad Z_1Z_3 \langle Y_1,Y_3 \rangle &\quad \ldots &\quad Z_1Z_d \langle Y_1,Y_d \rangle \\[4pt] &\quad Z_2^2 &\quad Z_2Z_3 \langle Y_2,Y_3 \rangle &\quad \ldots &\quad Z_2Z_d \langle Y_2,Y_d \rangle \\[4pt] &\quad &\quad Z_3^2 &\quad \ldots &\quad Z_3Z_d \langle Y_3,Y_d \rangle \\[4pt] &\quad &\quad &\quad \ddots &\quad\vdots \\[4pt] &\quad &\quad &\quad &\quad Z_d^2 \end{pmatrix}. \end{align*}
The density of each
$Z_\ell^2$
is given by the
$\chi^2(b)$
density:
\begin{align*}f_Z(z)=\frac{1}{2^{b/2}\Gamma(b/2)}z^{b/2-1}\mathrm{e}^{-z/2}, \quad z>0.\end{align*}
Step 2. We may then condition on
$Z_1^2, \ldots, Z_d^2$
, and analyze the joint density of the
$d(d-1)$
inner products
$U_{\ell ,k}\,:\!=\,\langle Y_\ell, Y_k \rangle$
,
$1 \le \ell < k \le d$
. This has been done in the proof of [Reference Stam21, Theorem 4]. Since
$Y_\ell$
,
$1 \le \ell \le d$
, are independent random vectors that have the uniform distribution on
$S^{b-1}$
, the assumptions of that theorem are satsified. In the proof, a recursive formula for the joint density
$p(u_{1,2}, \ldots, u_{d-1,d})$
of
$\sqrt{b}\cdot U_{\ell ,k}$
,
$1 \le \ell < k \le d$
, is obtained, which is continuous and positive (due to the assumption
$b>d+1$
) on
$(-\sqrt{b},\sqrt{b})^{d(d-1)/2}$
, and zero outside. For ease of reference, we quote the formula obtained there. Write
$p^{(b)}_d$
for the joint density of the inner products of d random unit vectors in b-dimensional space. Then, for
$d=2$
,
$b>3$
,
\begin{align*}p^{(b)}_2(u) = \frac{\pi^{-1/2}\Gamma({b}/2)}{\Gamma(({b-1})/{2})}(1-u^2)^{({b-3})/{2}}\end{align*}
and, recursively, for
$b>d+1$
,
\begin{multline*} p_{d}^{(b)}(u_{1,2}, \ldots, u_{d-1,d}) \\ = (b\pi)^{-(d-1)/2}\bigg(\frac{\Gamma({b}/{2})}{\Gamma(({b-1})/{2})}\bigg)^{d-1} \prod_{i=2}^d\bigg(1-\frac{u_{1,i}^2}{b}\bigg)^{(b-d-1)/2}p_{d-1}^{(b-1)}(w_{2,3}, \ldots, w_{r-1,r}), \end{multline*}
where
\begin{align*} w_{\ell,k} = \frac{u_{i,j}-b^{-1/2}u_{1,i}u_{1,j}}{(1-b^{-1}u_{1,i}^2)^{1/2}(1-b^{-1}u_{1,j}^2)^{1/2}}, \quad 2 \le \ell < k \le d. \end{align*}
We obtain that
$H_{\ell, \ell}=Z_\ell^2$
and
$H_{\ell,k}=Z_\ell Z_k U_{\ell,k}$
, where the vector
\begin{align*}\big(Z_1^2, \ldots, Z_d^2, \sqrt{b}U_{1,2}, \ldots \sqrt{b}U_{d-1,d}\big)\end{align*}
has a density g with respect to Lebesgue measure on
${\mathbb{R}}^{d(d+1)/2}$
given by
\begin{align*} g(z_1,\ldots,z_d,u_{1,2},\ldots,u_{d-1,d}) = Cp^{(b)}_d(u_{1,2},\ldots,u_{d-1,d})\prod_{\ell=1}^dz_\ell^{b/2-1}\mathrm{e}^{-z_\ell/2}. \end{align*}
Step 3. A density of
$(Z_iZ_j U_{i,j})$
is then obtained by first considering the conditional density of
$\sqrt{z_iz_j} U_{i,j}$
for fixed
$Z_i^2=z_i$
,
$Z_j^2=z_j$
, which is obtained from
$p(\ldots,u_{i,j},\ldots)$
by the change of measure
$\widetilde{u}_{i,j}=({\sqrt{z_i z_j}}/{\sqrt{b}})u_{i,j}$
, hence
$\mathrm{d} u_{i,j}$
becomes
$({\sqrt{b}}/{\sqrt{z_i z_j}})\,\mathrm{d} u_{i,j}$
. We thus finally obtain that the entries
$(H_{\ell,k})_{1 \le \ell \le k \le d}$
have the density
\begin{align*} f(y) & = C \cdot b^{d(d-1)/4} \cdot p^{(b)}_d\bigg(\frac{\sqrt{b}}{\sqrt{y_{1,1}y_{2,2}}}y_{1,2}, \ldots, \frac{\sqrt{b}}{\sqrt{y_{d-1,d-1}y_{d,d}}}y_{1,2}y_{d-1,d}\bigg) \\ & \quad \times \prod_{\ell=1}^d y_{\ell,\ell}^{(b-d+1)/2-1}\mathrm{e}^{-y_{\ell,\ell}/2}, \end{align*}
where
$y=(y_{\ell,k})_{1 \le \ell \le k \le d}$
. Due to the Cauchy–Schwartz inequality, the off-diagonal entries of a positive semi-definite matrix (as H is), are always bounded by the square root of the product of the corresponding diagonal entries, i.e.
$y_{\ell,k} \le \sqrt{y_{\ell,\ell} y_{k,k}}$
. This gives
$|y |^2 \le \big(\sum_{\ell=1}^d y_{\ell,\ell}^2\big)^2$
. Since
$p_d^{(b)}$
is bounded, we finally obtain (due to the exponential term) that
$f(y)\leq C(1+|y |^2)^{-D}$
for any
$D>0$
.
Proof of Corollary 3.2. We start by noting that
\begin{align*}Ax + B = x \Leftrightarrow x = (\mathrm{I}-A)^{-1}B = \Bigg(\sum_{i=1}^ba_ia_i^\top\Bigg)^{-1}\sum_{i=1}^ba_iy_i.\end{align*}
Since the
$y_i$
are independent of the
$a_i$
, this identity cannot hold
${\mathbb{P}}$
-a.s. for a fixed
$x \in {\mathbb{R}}^d$
, hence
${\mathbb{P}}(Ax+B=x)<1$
for all
$x \in {\mathbb{R}}^d$
. By Lemma 3.1, (Rank1Gauss) implies (rotinv-p) and (i-p-nc). By Lemma 3.2, condition (Decay:Symm) is fulfilled and hence Theorem 3.6 applies and asserts that the moment conditions of all theorems are satisfied. Finally,
$H=({\eta}/{b})\sum_{i=1}^b a_ia_i^\top$
is positive semi-definite and nontrivial, hence
$\mathbb{E} \langle He_1, e_1 \rangle>0$
holds as well. Thus, all the assumptions of the theorems are satisfied.
The dependence of
$\alpha$
on
$\eta$
is a direct consequence of Theorem 3.2. Note that the dependence on b does not follow from that theorem, since changing b also changes the law of H. Instead, this follows as in [Reference Gürbüzbalaban, Simsekli and Zhu13, C.3, part (II)]. Note that the argument given there remains valid under (rotinv-p).
7. Integrability of
$\| \boldsymbol{A}^{-1}\|^{\delta } $
In this section we study the integrability of N(A), in particular of moments of
$\|A^{-1} \|$
or, similarly, negative moments of
$\det(A)$
. The approach taken here is applicable to general classes of matrices and relies on the following general result about the integrability of polynomials.
Theorem 7.1. Let
$W(x_1,\ldots,x_m)$
be a polynomial on
${\mathbb{R}}^m$
such that the maximal degree of
$x_i$
in W is at most 2 for every i, and W is not identically zero. Let f be a nonnegative function of
${\mathbb{R}}^m$
such that
$f(x)\leq C(1+| x| ^2)^{-D}$
for
$D>m/2$
. Then, for every
$\varepsilon <\frac12$
,
\begin{equation} \int _{{\mathbb{R}} ^m}|W(x)|^{-\varepsilon }f(x)\, \mathrm{d} x<\infty. \end{equation}
If the maximal degree of
$x_i$
in W is at most 1 for all i, then (7.1) holds for every
$\varepsilon<1$
.
Proof. We use induction with respect to the number of variables m. To do so, we write
$x=(x_1,\bar x)\in{\mathbb{R}}^m$
, where
$x_1 \in {\mathbb{R}}$
and
$\bar x \in {\mathbb{R}}^{m-1}$
. We only provide the induction step, since the proof for
$m=1$
is along the same lines (omitting dependence on
$\bar{x}$
in all calculations). To wit, we are going to prove that
\begin{equation} \int_{{\mathbb{R}}^m}|W(x)|^{-\varepsilon}f(x)\,\mathrm{d} x \le C'\int_{{\mathbb{R}}^{m-1}}|P(\bar{x})|^{-\varepsilon}\bar{f}(\bar x)\, \mathrm{d}\bar x \end{equation}
for a constant C
′, a polynomial P with the same properties as W, and a nonnegative function
$\bar{f}$
that satisfies
$\bar{f}(\bar x) \le C'' (1 + |x |^2){-D'}$
for
$D'=D-\frac12>{(m-1)/2}$
.
Step 1. Fix
$\varepsilon \in \big(0,\tfrac12\big)$
. Let
$x=(x_1,\bar x)\in {\mathbb{R}} ^m$
for a variable
$x_1 \in {\mathbb{R}}$
that appears in W [in the case that W does not depend on
$x_1$
, then (7.3) holds automatically with
$C(\varepsilon)=1$
and
$P(\bar x)=W(\bar x)$
]. Then we may write
$W(x)=P(\bar x)x_1^2+P_1(\bar x)x_1+P_0(\bar x)$
or
$W(x)=P(\bar x)x_1+P_0(\bar x)$
with P not being identically zero and satisfying the induction assumption. We will prove (7.2) with this P. More precisely, we will show the inequality on the set
$\{\bar{x}\in{\mathbb{R}}^{m-1}\colon P(\bar x)\neq0\}$
and use the fact that its complement has
$(m-1)$
-Lebesgue measure zero (this is true for any polynomial that is not identically zero).
We employ [Reference Greenblatt8, Lemma 2.3], which gives that there is a constant
$C(\varepsilon)$
such that, for every
$n \in \mathbb{N}$
,
\begin{equation} \int_n^{n+1}|W(x_1,\bar x)|^{-\varepsilon}\,\mathrm{d} x_1 \leq C(\varepsilon)|P(\bar x)|^{-\varepsilon} \end{equation}
as long as
$P(\bar x)\neq 0$
– note that we may exclude the case
$P(\bar x)= 0$
by the above discussion. For
$p>0$
such that
$p\varepsilon <\frac12$
we have, by an application of Hölder’s inequality,
\begin{align*} \int_{{\mathbb{R}}}|W(x_1,\bar x)|^{-\varepsilon}f(x_1,\bar x)\,\mathrm{d} x_1 & = \sum_{n=-\infty}^{\infty}\int_n^{n+1}|W(x_1,\bar x)|^{-\varepsilon}f(x_1,\bar x)\,\mathrm{d} x_1 \\ & \leq \sum_{n=-\infty}^{\infty}\bigg(\int_n^{n+1}|W(x_1,\bar x)|^{-p\varepsilon}\bigg)^{1/p} \bigg(\int_n^{n+1}f(x_1,\bar x)^q\,\mathrm{d} x_1\bigg)^{1/q} \\ & \leq C(\varepsilon p)^{1/p}|P(\bar x)|^{-\varepsilon}\sum_{n=-\infty}^{\infty}\bigg(\int_n^{n+1}f(x_1,\bar x)^q\,\mathrm{d} x_1\bigg)^{1/q}, \end{align*}
with
$q={p}/({p-1})$
.
Step 2. It remains to prove that
\begin{equation*} \bar f(\bar x) = \sum_{n=-\infty}^{\infty}\bigg(\int_n^{n+1}f(x_1,\bar x)^q\,\mathrm{d} x_1\bigg)^{1/q} \leq C(1+|\bar x|^2)^{-D_1}, \quad D_1>\frac{m-1}{2}. \end{equation*}
Changing variables to
$x_1=\sqrt{1+| \bar x| ^2}u$
, we have
\begin{align*} \int_n^{n+1}f(x_1,\bar x)^q\,\mathrm{d} x_1 & \leq C\int_n^{n+1}\big(1+x_1^2+|x|^2\big)^{-Dq}\,\mathrm{d} x_1 \\ & = C\big(1+|\bar x|^2\big)^{-Dq+1/2}\int_{n/\sqrt{1+|\bar x|^2}}^{(n+1)/\sqrt{1+|\bar x|^2}}\big(1+u^2\big)^{-Dq}\,\mathrm{d} u \\ & \leq C\big(1+|\bar x|^2\big)^{-Dq}\big(1+n^2(1+|\bar x|^2)^{-1}\big)^{-Dq}. \end{align*}
Hence,
\begin{align*} \bar f(\bar x) & = \sum_{n=-\infty}^{\infty}\bigg(\int_n^{n+1}f(x_1,\bar x)^q\,\mathrm{d} x_1\bigg)^{1/q} \\ & \leq C(1+|\bar x|^2)^{-D}\sum_{n=-\infty}^{\infty}(1+n^2(1+|\bar x|^2)^{-1})^{-D} \\ & \leq C(1+|\bar x|^2)^{-D}\bigg(1+\sqrt{1+|\bar x|^2}\int_{-\infty}^{\infty}(1+u^2)^{-D}\,\mathrm{d} u\bigg) \\ & \leq C(1+|\bar x|^2)^{-D+1/2} \end{align*}
and
$D-\frac12>({m-1})/{2}$
. This concludes the proof of (7.1).
Step 3. It remains to prove the final assertion of the theorem. If
$W(x)=P(\bar x)x_1+P_0(\bar x)$
, the induction step is a simple change of variables and it holds for any
$\varepsilon <1$
. Indeed, for
$\varepsilon p<1$
we have
\begin{align*} & \int_{{\mathbb{R}}}|W(x_1,\bar x)|^{-\varepsilon}f(x_1,\bar x)\,\mathrm{d} x_1 \\ & \leq \bigg(\int_{\{x_1:|W(x_1,\bar x)|\leq 1\}}|P(\bar x)x_1+P_0(\bar x)|^{-p\varepsilon}\bigg)^{1/p} \bigg(\int_{{\mathbb{R}}}f(x_1,\bar x)^q\,\mathrm{d} x_1\bigg)^{1/q} + \int_{{\mathbb{R}}}f(x_1,\bar x)\,\mathrm{d} x_1 \\ & \leq C|P(\bar x)|^{-1/p}\bigg(\int_{{\mathbb{R}}}f(x_1,\bar x)^q\,\mathrm{d} x_1\bigg)^{1/q} + \int_{{\mathbb{R}}}f(x_1,\bar x)\,\mathrm{d} x_1, \end{align*}
and from here we can proceed as in Step 2.
Proof of Theorem 3.6. As discussed before, the proof will rely on several applications of Theorem 7.1 together with the assumed decay properties.
Step 1. We consider the determinant
$\det A=\det(I-\xi H)$
as a polynomial in the (random) entries of H. Note that these entries have a joint density due to assumption (Decay:Symm) or (Decay:Rank1), respectively. In particular, the determinant is a polynomial in
$d(d+1)$
variables (case (Symm)) or in db variables (case (Rank1)). The constant term in
$\det A$
is 1 so the polynomial
$\det A$
is not identically zero. Each summand of the determinant is a product of different entries, hence the maximal degree of any variable in it is less than or equal to two – it can be two because off-diagonal entries appear twice due to symmetry.
We may thus apply Theorem 7.1 with
$W=\det A$
, observing that (Decay:Symm) and (Decay:Rank1) guarantee the required properties of f. We thus obtain (3.5).
Step 2. First note that
$\mathbb{E}(1+\|A \|^s)N(A)^\varepsilon \le \mathbb{E}\|A \|^\varepsilon + \mathbb{E}\|A^{-1} \|^\varepsilon + \mathbb{E}\|A \|^{s+\varepsilon} + \mathbb{E}\|A \|^s\|A^{-1} \|^\varepsilon$
. For the last term, we use Hölder’s inequality with
$p>1$
chosen such that
$ps < s_0$
to obtain
\begin{align*}\mathbb{E}\|A \|^s\|A^{-1} \|^\varepsilon \le (\mathbb{E}\|A \|^{sp})^{1/p}(\mathbb{E}\|A^{-1} \|^{q\varepsilon})^{1/q}\end{align*}
with
$q={p}/({p-1})$
. Hence, if we can show that
$\mathbb{E}\|A^{-1} \|^\delta < \infty$
for some
$\delta>0$
, then we may choose
$\varepsilon = {\delta}/{q}<\delta$
and obtain the finiteness of
$\mathbb{E}(1+\|A \|^s)N(A)^\varepsilon$
. To prove the finiteness of
$\mathbb{E}\|A^{-1} \|^\delta$
, we compare the norm with the determinant, as follows. For any
$x \in S$
,
\begin{equation*} | Ax| \geq |\lambda _1|=\frac{|\det A |}{|\lambda _2\cdots \lambda _d|}, \end{equation*}
where
$\lambda_1,\ldots,\lambda_d$
denote the eigenvalues of A,
$|\lambda_1|\leq \cdots \leq |\lambda_d|\le \|A \|$
. Hence,
\begin{equation*} \|A^{-1} \| = (\operatorname{inf}_{x\in{S}}|Ax |)^{-1} = \sup_{x\in{S}}|Ax|^{-1} \leq \|A\|^{d-1}|\det A|^{-1}. \end{equation*}
Therefore, using the Cauchy–Schwartz inequality,
\begin{equation*} \mathbb{E}\|A^{-1}\|^{\delta} \leq \mathbb{E}\|A\|^{(d-1)\delta}|\det A|^{-\delta} \leq (\mathbb{E}\|A\|^{2(d-1)\delta})^{1/2}(\mathbb{E}|\det A|^{-2\delta})^{1/2}. \end{equation*}
This gives the desired finiteness of
$\mathbb{E} \|A^{-1} \|^\delta$
with some
$\delta < \frac14$
, using the finiteness of
$\mathbb{E} |\det A|^{-2\delta}$
that was proved in the first step.
Step 3. In order to show that
$\mathbb{E} |\langle H e_2, e_1\rangle |^{-\delta}<\infty$
for all
$\delta \in (0,1)$
, we observe that
$\langle H e_2, e_1\rangle = x_{12}$
for model (Symm) or
$\langle H e_2, e_1\rangle = \sum _{i=1}^ba_{i,1}a_{i,2}$
for model (Rank1). In particular, it is a polynomial with the maximal degree of any variable being one in both cases. Hence, the second part of Theorem 7.1 applies and yields the desired result.
Funding information
Ewa Damek was supported by NCN grant 2019/33/B/ST1/00207. Sebastian Mentemeier was supported by DFG grant ME 4473/2-1.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
Open access
