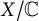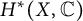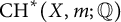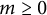1 Introduction
Let
$X/{\mathbb C}$
be a smooth projective variety of dimension n. Associated with X are the Chow groups
${\mathrm {CH}}^r(X) = {\mathrm {CH}}_{n-r}(X)$
of algebraic cycles on X of codimension r (resp. dimension
$n-r$
), modulo rational equivalence. Historically, there are two cycle class maps, namely the fundamental cycle class map
$[\ ]:{\mathrm {CH}}^r(X) \to H^{2r}(X,{\mathbb Z})$
and the Abel–Jacobi map on
${\mathrm {CH}}_{\hom }^r(X) = \ker [\ ]$
, the latter being a certain membrane integral generalizing the classical elliptic integral. It was once thought that
${\mathrm {CH}}^r(X)$
could be characterized by these two aforementioned maps. However, that myth was debunked by the seminal works of Mumford [Reference Mumford11] and Griffiths [Reference Griffiths3], where both the kernel and image of the Abel–Jacobi map are very complicated in general. These seminal works resulted in a turning point in the subject of algebraic cycles. One point of view is that there should be higher cycle class maps “explaining” the kernel of the previous map, giving rise to a descending filtration on
${\mathrm {CH}}^r(X,{\mathbb Q}) := {\mathrm {CH}}^r(X)\otimes {\mathbb Q}$
,Footnote
1
an idea which originally goes back to Bloch. Such a filtration can be seen as a measure of the “complexity” of Chow groups. Subsequent to this was Beilinson’s fortification, that the graded pieces of such a filtration should be described in terms of extension datum involving a conjectural category
${\mathcal M}{\mathcal M}({\mathbb C})$
of mixed motives. Moving toward the latter part of the twentieth century, we have the higher Chow groups
${\mathrm {CH}}^r(W/k,m)$
invented by Bloch [Reference Bloch2] (see Definition 1.3), where W is quasi-projective over a field k, the case
$m=0$
recovers the original Chow groups. As in the case
$m=0$
, one conjectures that there should be a descending filtration
$$\begin{align*}{\mathrm{CH}}^r(X/{\mathbb C},m;{\mathbb Q}) = F^0\supset F^1\supset \cdots, \end{align*}$$
whose graded pieces
$Gr_F^{\nu }$
can be described in terms of extension datum. Of course, this was formulated for smooth projective X over a field k. A generalization of Beilinson’s formula is then
$$\begin{align*}Gr^{\nu}_F{\mathrm{CH}}^r(X/k,m;{\mathbb Q}) \simeq {\mathrm{Ext}}^{\nu}_{{\mathcal M}{\mathcal M}(k)}({\text{Sp}}(k),h^{2r-m-\nu}(X)(r)), \end{align*}$$
where Beilinson’s formulation involved the case
$m=0$
and where conjecturally speaking,
$h^{\bullet }(-)(r)$
is motivic cohomology. It is then reasonably clear that the existence of such a filtration (called the conjectural Bloch–Beilinson filtration) is pivotable with regard to issues of complexity. With this in mind, we begin with the following.
Definition 1.1 Let
$X/{\mathbb C}$
be a smooth projective variety, with Hodge cohomology
$H^*(X,{\mathbb C}) = \oplus _{p,q}H^{p,q}(X)$
. We defineFootnote
2
$$\begin{align*}\mathrm{Level}(H^*(X,{\mathbb C})) = \max\{p-q \ |\ H^{p,q}(X)\ne 0\}. \end{align*}$$
$$\begin{align*}\mathrm{Level}({\mathrm{CH}}^*(X,m;{\mathbb Q})) = {\max}_r\big\{\mathrm{Level}({\mathrm{CH}}^r(X,m{;\mathbb Q})) \big\}, \end{align*}$$
where
$\mathrm {Level}({\mathrm {CH}}^r(X,m;{\mathbb Q})) = 0$
for
$r<m$
, otherwise for
$r\geq m$
,
$\mathrm {Level} ({\mathrm { CH}}^r(X,m;{\mathbb Q})) =$
$$\begin{align*}\mathrm{min}\big\{\mu\geq 0 \ \big|\ {\mathrm{CH}}^r(X,m;{\mathbb Q}) \to {\mathrm{CH}}^r(X\backslash Y,m;{\mathbb Q})) \ \mathrm{is\ zero,} \end{align*}$$
$$\begin{align*}Y\hookrightarrow X \ \mathrm{closed,\ codim}_XY= r-\mu-m\big\}. \end{align*}$$
TheFootnote 3 expected relationship between these invariants is the following conjecture.
Conjecture 1.2 For all
$m\geq 0$
,
$$\begin{align*}\mathrm{Level}(H^*(X,{\mathbb C})) = \mathrm{Level}({\mathrm{CH}}^*(X,m;{\mathbb Q})). \end{align*}$$
Based on conjectural assumptions, an outline of a proof of Conjecture 1.2 in the case where
$m=0$
appeared in [Reference Lewis8, Corollary 15.64]. In this paper, we provide the full details for all
$m\geq 0$
; the case
$m>0$
requires some new ingredients which should be of interest to the reader. Finally, we exhibit a class of examples involving complete intersections, based on new ideas from [Reference Lewis and Shtayat10].
Before stating our main result, it is important to include some background. We will assume the (Grothendieck amended) general Hodge conjecture (GHC), which is discussed in [Reference Lewis8, Chapter 7]. We will also assume that the reader is familiar with the category of
${\mathbb Q}$
mixed Hodge structures
${\mathrm {MHS}}$
, as well as a description of the Abel–Jacobi map in terms of extension classes of MHS. Again, all of this appears in Lewis (op. cit.) as well as in [Reference Lewis9, Definition 3.11]; however, the latter (viz., extension classes) is explicitly described in [Reference Kerr, Lewis and Müller-Stach6]. Let
${\mathbb A} \subseteq {\mathbb R}$
be a subring. The Tate twist is given by
${\mathbb A}(r) = (2\pi {\text {i}})^r\cdot {\mathbb A}$
. It is a mixed Hodge structure of pure weight
$-2r$
and Hodge type
$(-r,-r)$
.
$H^{\bullet }(X,{\mathbb A})$
represents Betti cohomology and
$H^{\bullet }(X,{\mathbb A}(r)) := H^{\bullet }(X,{\mathbb A})\otimes {\mathbb A}(r)$
. For our purposes, we only need real Deligne cohomology in one instance, namely
$H_{\mathcal D}^m(X,{\mathbb R}(m)) \simeq H^{m-1}(X,{\mathbb R}(m-1))$
. We only need the following abridged definition of Bloch’s higher Chow groups. Let
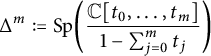$$\begin{align*}\Delta^m := {\text{Sp}}\biggl(\frac{{\mathbb C}[t_0,\ldots,t_m]}{1-\sum_{j=0}^mt_j}\biggr) \end{align*}$$
be the standard m-simplex. Furthermore, let
$z^r(X,m)$
be the codimension r cycles in
$X\times \Delta ^m$
which meet all faces defined by
$\{t_{i_1}=0,\ldots ,t_{i_q}=0,\ q< n\}$
properly. Associated with
$z^r(X,m)$
are ith face maps
$\partial _i : z^r(X,m)\to z^r(X,m-1)$
,
$i=0,\ldots ,m$
, defined by
$t_i=0$
. One then has the boundary operator
$\partial = \sum _{i=0}^m(-1)^i\partial _i : z^r(X,m) \to z^r(X,m-1)$
satisfying
$\partial ^2=0$
.
Definition 1.3
${\mathrm {CH}}^r(X,m) = H^{\partial }_m(z^r(X,\bullet ))$
.
As in the case
$m=0$
, there is a cycle class map
$[\ ]: {\mathrm {CH}}^r(X,m) \to H^{2r-m}(X,{\mathbb Z}(r))$
with torsion image for
$m>0$
(due to a Hodge theoretic argument). We put
${\mathrm {CH}}^r(X,m;{\mathbb Q}) = {\mathrm {CH}}^r(X,m)\otimes {\mathbb Q}$
. It is clear that
${\mathrm {CH}}^r_{\hom }(X,m;{\mathbb Q}) = {\mathrm {CH}}^r(X,m;{\mathbb Q})$
for
$m>0$
.
Our main result is the following theorem.
Theorem 1.4 Assume that:
$\bullet _1$
The GHC holds.
$\bullet _2$
For any smooth projective variety Y defined over
$\overline {{\mathbb Q}}$
, the Abel–Jacobi map
$$\begin{align*}\Phi_{r,m}: {\mathrm{CH}}^r_{\hom}(Y/\overline{{\mathbb Q}},m;{\mathbb Q}) \to {\mathrm{Ext}}^1_{{\mathrm{MHS}}}({\mathbb Q}(0),H^{2r-m-1}(Y({\mathbb C}),{\mathbb Q}(r))) \end{align*}$$
is injective.
$\bullet _3$
Either
$m\leq 2$
, or for a given
$m\geq 3$
, there exists a smooth projective variety
$B/{\mathbb C}$
of dimension
$m-1$
and a class
$\gamma \in H^{m-1}(B,{\mathbb R}(m-1))$
with (Hodge component)
$\gamma ^{m-1,0}\ne 0$
in the image of the real regulator map
$r_{\mathcal D}: {\mathrm {CH}}^m(B,{\mathbb Q}(m))\otimes {\mathbb R} \to H_{\mathcal D}^m(B,{\mathbb R}(m)) \simeq H^{m-1}(B,{\mathbb R}(m-1))$
.
Then, for any smooth projective
$X/{\mathbb C}$
,
$$\begin{align*}\mathrm{Level}(H^*(X,{\mathbb C})) = \mathrm{Level}({\mathrm{CH}}^*(X,m;{\mathbb Q})). \end{align*}$$
2 More background
(i) To re-iterate and unless otherwise stated, we assume that
$X/{\mathbb C}$
is a smooth projective variety of dimension n.
(ii) A full explanation of the Hodge conjecture, the GHC, and the hard Lefschetz conjecture appear in [Reference Lewis8, Chapters 7 and 15]. For the reader with pressing obligations, here is an abridged description. Corresponding to a projective embedding
$X \subset {\mathbb P}^N$
is a hyperplane class
$H_X$
and corresponding operator
$L_X = H_X\smile : H^{\bullet }(X,{\mathbb Q})\to H^{\bullet +2}(X,{\mathbb Q})$
. Iterating this is the hard Lefschetz theorem: for
$i\leq n$
,
$L_X^{n-i} : H^i(X,{\mathbb Q}) \to H^{2n-i}(X,{\mathbb Q})$
is an isomorphism. The hard Lefschetz conjecture states that the inverse map
$H^{2n-i}(X,{\mathbb Q}) \to H^i(X,{\mathbb Q})$
is algebraic cycle induced. For a complete clarification of cycle induced, the reader can consult [Reference Lewis8, Chapter 7]. The reader may find it helpful to know that the Hodge conjecture implies the hard Lefschetz conjecture [Reference Lewis8, Chapter 15].
(iii)
$\{N^pH^i(X,{\mathbb Q})\}_{p\geq 0}$
is the coniveau filtration as defined in [Reference Lewis8, Chapter 7]. Succinctly,
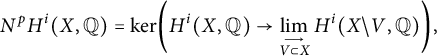$$\begin{align*}N^pH^i(X,{\mathbb Q}) = \ker\biggl(H^i(X,{\mathbb Q}) \to \lim_{{\buildrel \longrightarrow\over {V\subset X}}}H^i(X{\backslash} V,{\mathbb Q})\biggr), \end{align*}$$
as V runs through all codimension
$\geq p$
closed algebraic subsets of X. This can be compared to another filtration,
$$\begin{align*}F^p_HH^i(X,{\mathbb Q}) = \mathrm{maximal\ Hodge\ structure\ contained\ in} \ F^pH^i(X,{\mathbb C})\cap H^i(X,{\mathbb Q}). \end{align*}$$
Indeed, one knows that
$N^pH^i(X,{\mathbb Q})\subseteq F^p_HH^i(X,{\mathbb Q})$
and the GHC states that the inclusion is an equality (op. cit.).
(iv) Given a family of varieties
$\{X_t\}_{t\in S}$
, where S is a base variety, a general member of this family refers to an
$X_t$
,
$t\in U$
, where
$U\subset S$
is a nonempty Zariski open subset, determined by certain “generic” properties, such as
$X_t$
nonsingular.
3 Proof of Theorem 1.4
We introduce our first key ingredient.
Theorem 3.1 [Reference Lewis7]
Let X be a projective algebraic manifold. Assume the following:
(i) The hard Lefschetz conjecture holds.
(ii) Either
$m\leq 2$
, or for a given
$m\geq 3$
, there exists a projective algebraic manifold B of dimension
$m-1$
and a class
$\gamma \in H^{m-1}(B,{\mathbb R}(m-1))$
with
$\gamma ^{m-1,0}\ne 0$
in the image of the regulator map
$r_{\mathcal D}: {\mathrm {CH}}^m(B,m;{\mathbb Q}) \otimes {\mathbb R} \to H_{\mathcal D}^m(B,{\mathbb R}(m)) \simeq H^{m-1}(B,{\mathbb R}(m-1))$
. Then,
$$\begin{align*}\mathrm{Level}\big(N^{r-\mu}H^{2r-\mu-m}(X,{\mathbb Q})\big) = \mu -m \Rightarrow \mathrm{Level}\big({\mathrm{CH}}^r(X,m;{\mathbb Q})\big)\geq \mu -m. \end{align*}$$
Corollary 3.2 Let us assume the GHC and Theorem 3.1 . Then,
$$\begin{align*}\mathrm{Level}(H^*(X,{\mathbb C})) \leq \mathrm{Level}({\mathrm{CH}}^*(X,m;{\mathbb Q})). \end{align*}$$
Proof Let
$\ell = \mathrm {Level}(H^*(X,{\mathbb C}))$
. Then, for some i, we have
$$\begin{align*}\mathrm{Level}(H^i(X,{\mathbb C})) = \ell = q-p,\ \mathrm{where}\ p+q=i,\ q \geq p,\ F^pH^i(X,{\mathbb C}) = H^i(X,{\mathbb C}). \end{align*}$$
Now, for fixed
$m\geq 0$
, we need only find
$(r,\mu )$
such that
$2r-\mu -m = i$
and
$p=r-\mu $
. Solving for
$(r,\mu )$
gives
$r= i+m-p$
and
$\mu = r -p = \ell +m$
. By Theorem 3.1, it follows that
$\mathrm {Level}({\mathrm {CH}}^*(X,m;{\mathbb Q})) \geq \ell $
and we are done.
Next, let
$V/\overline {{\mathbb Q}}$
be a smooth quasi-projective variety defined over
$\overline {{\mathbb Q}}$
. Based on a Bloch–Beilinson conjecture assumption in the case
$m=0$
, it is conjectured in [Reference Kerr and Lewis5] that:
Conjecture 3.3 The Abel–Jacobi map
$$\begin{align*}\Phi_{r,m} : {\mathrm{CH}}_{\hom}^r(V/\overline{{\mathbb Q}},m;{\mathbb Q}) \to {\mathrm{Ext}}^1_{{\mathrm{MHS}}}({\mathbb Q}(0),H^{2r-m-1}(V/{\mathbb C},{\mathbb Q}(r))) \end{align*}$$
is injective.
Remark 3.4 One can show [Reference Kerr and Lewis5] using a weight filtered spectral sequence together with the Hodge conjecture, that one need to only verify Conjecture 3.3 for smooth projective
$V/\overline {{\mathbb Q}}$
.
Now we need to establish the reverse inequality, viz.,
Theorem 3.5 Let us assume the GHC and Conjecture
3.3
. Then, for any integer
$m\geq 0$
,
$$\begin{align*}\mathrm{Level}(H^*(X,{\mathbb C})) \geq \mathrm{Level}({\mathrm{CH}}^*(X,m;{\mathbb Q})). \end{align*}$$
Proof Using [Reference Asakura1] together with the GHC and Conjecture 3.3, there is for any smooth projective variety
$X/{\mathbb C}$
a descending filtration
$\{F^{\nu }{\mathrm {CH}}^r(X,m;{\mathbb Q})\}_{\nu =0}^r$
with:
$\bullet _0\ F^0 = {\mathrm {CH}}^r(X,m;{\mathbb Q})$
.
$\bullet _1\ F^1 = {\mathrm {CH}}^r_{\hom }(X,m;{\mathbb Q})$
for
$m=0$
,
$F^0=F^1 = {\mathrm {CH}}^r_{\hom }(X,m;{\mathbb Q})$
for
$m\geq 1$
.
$\bullet _2\ F^2\subseteq \ker \Phi _{r,m}: {\mathrm {CH}}^r_{\hom }(X/{\mathbb C},m;{\mathbb Q}) \to {\mathrm {Ext}}^1_{{\mathrm { MHS}}}({\mathbb Q}(0),H^{2r-m-1}(X,{\mathbb Q}(r)))$
.
$\bullet _3\ F^{\nu _1}{\mathrm {CH}}^{r_1}(X,m_1;{\mathbb Q}) \smile F^{\nu _2}{\mathrm {CH}}^{r_2}(X,m_2;{\mathbb Q}) \subset F^{\nu _1+\nu _2}{\mathrm {CH}}^{r_1+r_2}(X,m_1+m_2;{\mathbb Q})$
.Footnote
4
$\bullet _4\ \{F^{\nu }\}_{\nu \geq 0}$
is functorial with respect to correspondences between smooth projective varieties.
$\bullet _5$
Factorization through the Grothendieck motive: Namely, if
$$\begin{align*}[\Delta_X] = \bigoplus_{p+q=2n}[\Delta_X(p,q)]\in H^{2n}(X\times X,{\mathbb Q}) \end{align*}$$
is the Künneth decomposition with
$[\Delta _X(p,q)]\in H^p(X,{\mathbb Q})\otimes H^q(X,{\mathbb Q})$
algebraic, then
$[\Delta _X(p,q)]$
acts on the graded pieces
$Gr_F^{\nu }{\mathrm {CH}}^r(X,m;{\mathbb Q})$
and in particular
$$\begin{align*}[\Delta_X(2n-2r+\nu+m,2r-\nu-m)]_*Gr_F^k{\mathrm{CH}}^r(X,m;{\mathbb Q}) = \delta_{\nu,k}\cdot\mathrm{Id}. \end{align*}$$
[Explanation. Any correspondence induced by
$Z\in {\mathrm {CH}}^{\bullet }(X\times X;{\mathbb Q})$
on
$Gr_F^{\nu }{\mathrm {CH}}^r(X.m;{\mathbb Q})$
depends only on the cohomology class
$[Z]\in H^{2\bullet }(X\times X,{\mathbb Q})$
. This is immediate from the previous
$\bullet $
’s.]
$\bullet _6\ F^{r+1} = 0$
.
Note that if we view
${\mathrm {CH}}^n(X\times X;{\mathbb Q})$
as the ring of correspondences on X, under composition, then by the above
$\bullet $
’s,
$F^1{\mathrm {CH}}^n(X\times X;{\mathbb Q})$
is a nilpotent two-sided ideal of
${\mathrm {CH}}^n(X\times X;{\mathbb Q})$
. One has a Künneth decomposition of idempotents:
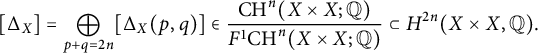$$\begin{align*}[\Delta_X] = \bigoplus_{p+q=2n}[\Delta_X(p,q)]\in\frac{{\mathrm{CH}}^n(X\times X;{\mathbb Q})}{F^1{\mathrm{CH}}^n(X\times X;{\mathbb Q})} \subset H^{2n}(X\times X,{\mathbb Q}). \end{align*}$$
As Beilinson observed, such a decomposition lifts to an idempotent decomposition
$$\begin{align*}\Delta_X = \bigoplus_{p+q=2n}\Delta_X(p,q)\in {\mathrm{CH}}^n(X\times X;{\mathbb Q}), \end{align*}$$
called a Chow–Künneth decomposition in the sense of [Reference Murre12]. Let
$\ell = \mathrm {Level}(H^*(X,{\mathbb C}))$
. One can easily argue that
$\ell \leq n$
. Note that
$$\begin{align*}{\mathrm{CH}}^r(X,m;{\mathbb Q}) = \bigoplus_{p+q=2n}\Delta_X(p,q)_*{\mathrm{CH}}^r(X,m;{\mathbb Q}). \end{align*}$$
It will suffice, via Proposition 3.6, to determine the level of
$\Delta _X(p,q)_*{\mathrm {CH}}^r(X,m;{\mathbb Q})$
, for a fixed algebraic cohomological representative
$\Delta _X(p,q)$
of
$[\Delta _X(p,q)]$
.
Case
$p\leq \ell $
. Then
$q = 2n-p \geq n$
. By the hard Lefschetz theorem,
$H^q(X,{\mathbb Q}) = L_X^{n-p}H^{p}(X,{\mathbb Q})$
; hence, we may assume that the support
$|\Delta _X(p,q)| \subset X \times V$
, where codim
$_XV = n-p$
. It follows that
$$\begin{align*}\mathrm{Level}(\Delta_X(p,q)_*{\mathrm{CH}}^r(X,m;{\mathbb Q})) \leq (r-n-m)+p \leq p \leq \ell, \end{align*}$$
where by dimension reasons alone we use the fact that
${\mathrm {CH}}^{r> n+m}(X,m) = 0$
.
Case
$\ell < p\leq n$
. Thus,
$p = \ell + k$
, where
$k\geq 1$
. Note that Level
$(H^p(X,{\mathbb Q})) =: \ell '\leq \ell $
. Replacing
$\ell $
by
$\ell '$
, we can write
$p=\ell '+k$
. From Hodge theory, k has to be even. Specifically,
$\ell ' = p-2M$
, where M is maximal subject to
$F^M\cap H^p(X) = H^p(X)$
. Thus,
$k=2M$
. It follows that
$H^p(X,{\mathbb Q}) = F^{k/2}\cap H^p(X,{\mathbb Q}) = N^{k/2}H^p(X,{\mathbb Q})$
, where the latter equality is due to the GHC. Thus, we can assume that
$|\Delta _X(p,q)| \subset Y \times V$
, where codim
$_XV = n-p + k/2$
and codim
$_XY = k/2$
. However,
${\mathrm {CH}}^r(Y,m;{\mathbb Q}) = 0$
for
$r> n-k/2 + m$
. Accordingly,
$r \leq (n- k/2)+m$
. Thus,
$\mu \leq p-k = \ell '\leq \ell $
.
Case
$p>n$
. Thus,
$q < n$
and again by hard Lefschetz
$L_X^{n-q}H^q(X,{\mathbb Q}) = H^p(X,{\mathbb Q})$
. Let us first assume that
$q\leq \ell \leq n$
. Then
$|\Delta _X(p,q)| \subset V\times X$
, where codim
$_XV = n-q$
. However,
${\mathrm {CH}}^r(V,m;{\mathbb Q}) = 0$
for
$r>q+m$
. Thus, we can assume that
$r\leq q+m$
. We already know that from the definition of level,
$r-\mu -m\geq 0$
; hence,
$$\begin{align*}\mu \leq r-m \leq (q+m)-m = q\leq \ell. \end{align*}$$
Finally, we now assume that
$\ell < q < n$
. Thus, by the GHC,
$$\begin{align*}H^q(X,{\mathbb Q}) = N^{k/2}H^q(X,{\mathbb Q}), \end{align*}$$
where as in the previous case we have
$k> 0$
is an even integer. Thus,
$$\begin{align*}|\Delta_X(p,q)| \subset V \times Y, \end{align*}$$
where codim
$_XV = n-q + k/2$
(because
$L_X^{n-q}H^q(X,{\mathbb Q}) = H^p(X,{\mathbb Q})$
) and codim
$_XY = k/2$
. Thus,
${\mathrm {CH}}^r(V,m;{\mathbb Q}) = 0$
for
$r>q+m-k/2$
. Therefore, we can assume that
$r\leq q+m-k/2$
. From the definition of level, we have
$k/2\leq r-\mu -m$
. Hence,
$$\begin{align*}\mu \leq r-m-k/2 \leq q- k = \ell.\\[-34pt] \end{align*}$$
Now for the details on how to reduce to the graded pieces
$Gr_F^{\bullet }{\mathrm {CH}}^r(X,m;{\mathbb Q})$
. What we have is the following. Consider another Künneth decomposition
$$\begin{align*}[\Delta] = \bigoplus_{p+q=2n}[\Delta(p,q)'], \end{align*}$$
where
$\Delta (p,q)'$
are algebraic. Thus,
$$\begin{align*}\Delta' := \oplus_{p+q=2n}\Delta(p,q)' \sim_{\hom} \Delta. \end{align*}$$
We are reduced to the following proposition.
Proposition 3.6 Let
$\Xi \in {\mathrm {CH}}^n_{\hom }(X\times X;{\mathbb Q})$
. Then,
$$\begin{align*}\mathrm{Level}\big(\Xi_*{\mathrm{CH}}^r(X,m;{\mathbb Q})\big) \leq \ell. \end{align*}$$
Restatement. For any cycle
$\xi \in {\mathrm {CH}}^n(X\times X;{\mathbb Q})$
, the statement Level
$(\xi _*{\mathrm {CH}}^{\bullet }(X, m;{\mathbb Q})) \leq \ell $
depends only on the cohomology class of
$\xi $
.
Proof Let
$F^{\nu } := F^{\nu }{\mathrm {CH}}^r(X,m;{\mathbb Q})$
. Note that
$F^r = Gr_F^r{\mathrm {CH}}^r(X,m;{\mathbb Q})$
. Since
${\mathrm {CH}}^n_{\hom }(X\times X;{\mathbb Q}) = F^1{\mathrm {CH}}^n(X\times X;{\mathbb Q})$
, then
$\Xi _*F^r = 0$
. Consider the short exact sequence
$$\begin{align*}0\to F^r \to F^{r-1}\to Gr_F^{r-1} \to 0. \end{align*}$$
Then
$\Xi _*F^{r-1}\mapsto 0\in Gr_F^{r-1}$
; hence,
$\Xi _*F^{r-1} \subset F^r$
, where we know that Level
$(F^r) \leq \ell $
. Proceeding by downward induction, consider the short exact sequence
$$\begin{align*}0\to F^{\nu}\to F^{\nu-1}\to Gr_F^{\nu}\to 0. \end{align*}$$
By induction, Level
$(F^{\nu }) \leq \ell $
and
$\Xi _*F^{\nu -1} \mapsto 0\in Gr_F^{\nu -1}$
. Thus, Level
$(\Xi _*F^{\nu -1}) \leq \ell $
, and this completes the induction step.
4 An explicit example
Let
$X/{\mathbb C}\subset \mathbb {P}^{n+r}$
be a general complete intersection of multidegree
$(d_1,\ldots ,d_r)$
, let
$\Omega _X(k) := \{{\mathbb P}^k$
’s
$\subset X\}$
be its Fano variety of k-planes, and suppose
$X=Z\cap \mathbb {P}^{n+r}$
, where
$Z\subset \mathbb {P}^{n+r+1}$
is a general complete intersection of multidegree
$(d_1,\ldots ,d_r)$
. The geometric properties of such complete intersections are explored elsewhere ([Reference Lewis and Shtayat10], [Reference Lewis8, Chapter 13]). In particular,
$\Omega _X(k)$
is smooth. Set
$\delta := (k+1)(n+r-k)-\sum _{j=1}^r \binom {d_j+k}{k}$
,
$l=k(n+1+r-k)+r-\sum _{j=1}^r \binom {d_j+k}{k}$
and assume
$\delta \geq n- 2k\geq 0$
. Observe that
$\delta = n-2k + l$
. Indeed,
$\delta = \dim \Omega _X(k)$
and through a generic point of Z passes an l-dimensional family of
${\mathbb P}^k$
’s. Let
$\Omega _Z$
be the subvariety of
$\Omega _Z(k)$
obtained by the intersection of l general hyperplane sections. By Bertini’s theorem, and a dimension count,
$\Omega _Z$
is smooth and irreducible of dimension
$n+1-k$
. If we set
$\Omega _X=\Omega _Z\cap \Omega _X(k)$
, then
$\Omega _X$
is smooth of pure dimension
$n-2k$
. There is the following diagram [Reference Lewis and Shtayat10]:
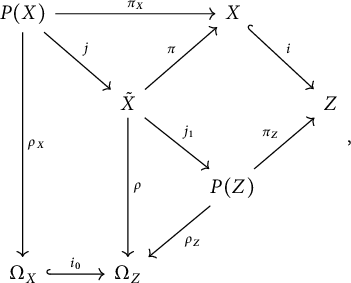
where
$P(X)$
and
$P(Z)$
are
${\mathbb P}^k$
-bundles,
$\tilde {X}=\pi ^{-1}_Z(X)$
, and all the maps depicted are natural projections, except
$i_0,i,j$
which are inclusions.
Proposition 4.1 [Reference Lewis8, Corollary 13.42]
Assume that
$\delta \geq n-2k\geq 0$
. Then the cylinder homomorphism
$$ \begin{align*}\Phi_* := \pi_{X,*}\circ \rho_X^*:H^{n-2k}(\Omega_X,\mathbb{Q})\to H^n(X,\mathbb{Q})\end{align*} $$
is surjective.
Set
$Y=\pi _X(P(X))$
. Then
$Y\subset X$
is a subvariety of codimension k. We conclude the following.
Corollary 4.2 The natural map
$H_n(Y,\mathbb {Q})\to H_n(X,\mathbb {Q})$
is surjective. Hence, cycles on X are supported on a subvariety of codimension k.
This corollary gives an instance of the GHC.
Corollary 4.3
$$\begin{align*}F^k\cap H^n(X,{\mathbb Q}) = H^n(X,{\mathbb Q}) = N^kH^n(X,{\mathbb Q}). \end{align*}$$
Next, let us write
$X = V(F_1,\ldots ,F_r)\subset {\mathbb P}^{n+r}$
, for generic choice of
$\{F_1,\ldots ,F_r\}$
, and
$W = V(F_1,\ldots ,F_{r-1}) \subset {\mathbb P}^{n+r}$
, with inclusion
$j:X \hookrightarrow W$
.
Theorem 4.4 [Reference Lewis and Shtayat10]
Assume that
$\delta \geq n-2k\geq 0$
. Then the cylinder map
$$\begin{align*}\Phi_{X,*} : {\mathrm{CH}}^{r-k}(\Omega_X,m;{\mathbb Q}) \to {\mathrm{CH}}^r(X,m;{\mathbb Q})/j^*{\mathrm{CH}}^r(W,m;{\mathbb Q}) \end{align*}$$
is surjective.
Now, observe that
$r> n+m-k \Rightarrow r-k > n-2k+m = \dim \Omega _X + m$
; hence,
${\mathrm {CH}}^{r-k}(\Omega _X,m;{\mathbb Q}) = 0$
by dimension reasons alone. Thus, we can assume that
$r\leq n+m-k$
. Choose k such that Level
$(H^{*}(X,{\mathbb Q})) = n-2k$
and assume that
$\delta \geq n-2k$
. Furthermore, put
$$\begin{align*}\nu := \mathrm{Level}\big({\mathrm{CH}}^r(X,m;{\mathbb Q})/j^*{\mathrm{CH}}^r(W,m;{\mathbb Q})\big). \end{align*}$$
By definition of
$\nu $
, observe that
$\nu \leq r - \mathrm {codim}_XY -m = r-k-m$
. However,
$r\leq n+m-k$
, and hence
$\nu \leq n-2k$
. Finally, W is of a lower order (viz., multidegree) than X and one can argue via an inductive argument, that Level
$(j^*{\mathrm {CH}}^r(W,m;{\mathbb Q})) \leq n-2k$
. From Corollaries 3.2 and 4.3 and Theorem 3.1, we deduce the following corollary.
Corollary 4.5 If X is a general complete intersection satisfying
$\delta \geq n-2k\geq 0$
, where
$k\geq 0$
is given such that Level
$(H^*(X,{\mathbb Q})) = n-2k$
, then
$$ \begin{align*}\mathrm{Level}(H^*(X,{\mathbb C})) \geq \mathrm{Level}({\mathrm{CH}}^*(X,m;{\mathbb Q})),\end{align*} $$
and we have an equality in the case
$m<3$
.
Proof The only remaining issue involves replacing the assumption in Theorem 3.1(i) by Proposition 4.1. The details of this can be found in [Reference Lewis7, Section 5].
Acknowledgment
We are very grateful to the referees for pointing out the need for improvements to our original paper.
Open access
