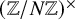1 Introduction
1.1 Context and quantum computing results
Public key cryptography has become a crucial element of our global digital communication infrastructure. Notable examples include the Diffie-Hellman key exchange [Reference Diffie and Hellman6] and the RSA (Rivest-Shamir-Adleman) cryptosystem [Reference Rivest, Shamir and Adleman19], which rely on the difficulty of finding discrete logarithms and factoring large numbers, respectively.
However, in 1994, Peter Shor [Reference Peter20] developed an algorithm capable of efficiently solving these problems using a quantum computer.
Theorem (ShorFootnote 1 ).
There is a quantum circuit having
![]() $O(n^{2} \log n)$
quantum gates and
$O(n^{2} \log n)$
quantum gates and
![]() $O(n \log n)$
qubits with the following property. There is a classical randomised polynomial-time algorithm that solves the factoring problem
$O(n \log n)$
qubits with the following property. There is a classical randomised polynomial-time algorithm that solves the factoring problem
 $$ \begin{align*} & \mathbf{Input: }\text{ a composite integer } N \leq 2^n \\ & \mathbf{Output: }\text{ a nontrivial divisor of } N \end{align*} $$
$$ \begin{align*} & \mathbf{Input: }\text{ a composite integer } N \leq 2^n \\ & \mathbf{Output: }\text{ a nontrivial divisor of } N \end{align*} $$
using
![]() $O(1)$
calls to this quantum circuit, and succeeds with probability
$O(1)$
calls to this quantum circuit, and succeeds with probability
![]() $\Theta (1)$
.
$\Theta (1)$
.
Shor’s original article [Reference Peter20] also includes a similar algorithm to solve the discrete logarithm problem. This advancement prompted the development of postquantum cryptography, such as lattice-based cryptography, to ensure the security of our communications in the face of potential quantum computing breakthroughs [Reference Bernstein, Buchmann and Dahmen4].
Recently, Regev [Reference Regev18] devised a multidimensional variant of Shor’s factoring algorithm that reduces the size of the quantum circuit, that is, the number of quantum gates, to
![]() $O(n^{3/2}\log n)$
. A distinctive feature of Regev’s algorithm is that the quantum circuit must be called
$O(n^{3/2}\log n)$
. A distinctive feature of Regev’s algorithm is that the quantum circuit must be called
![]() $O(\sqrt {n})$
times, rather than a constant number of times for Shor’s algorithm. This is not considered to be a serious drawback as the various complexity parameters of the quantum circuit are far more relevant metrics in quantum computing.
$O(\sqrt {n})$
times, rather than a constant number of times for Shor’s algorithm. This is not considered to be a serious drawback as the various complexity parameters of the quantum circuit are far more relevant metrics in quantum computing.
However, this remarkable work of Regev initially came with two main limitations.
First, the original version of Regev’s algorithm requires
![]() $O(n^{3/2})$
qubits – many more than Shor’s algorithm. The reason for this ultimately lies in the difficulty of performing classical computations on quantum computers in a space-efficient manner, due to the need for any quantum computation to be reversible. In a subsequent paper, Ragavan and Vaikuntanathan [Reference Ragavan and Vaikuntanathan17] improved Regev’s algorithm to use only
$O(n^{3/2})$
qubits – many more than Shor’s algorithm. The reason for this ultimately lies in the difficulty of performing classical computations on quantum computers in a space-efficient manner, due to the need for any quantum computation to be reversible. In a subsequent paper, Ragavan and Vaikuntanathan [Reference Ragavan and Vaikuntanathan17] improved Regev’s algorithm to use only
![]() $O(n\log n)$
qubits, while maintaining the circuit size at
$O(n\log n)$
qubits, while maintaining the circuit size at
![]() $O(n^{3/2}\log n)$
quantum gates. This work, inspired by ideas of Kalinski [Reference Kaliski13], essentially matches the space cost of Shor’s algorithm.
$O(n^{3/2}\log n)$
quantum gates. This work, inspired by ideas of Kalinski [Reference Kaliski13], essentially matches the space cost of Shor’s algorithm.
The second issue, which we address in this paper, is that Regev’s algorithm [Reference Regev18] does not have theoretical guarantees, unlike Shor’s algorithm. The correctness of Regev’s algorithm is based on an ad hoc number-theoretic conjecture which we describe below. This unproven assumption cannot be avoided as it lies at the core of Regev’s improvement on the circuit size. The variant of Ragavan and Vaikuntanathan [Reference Ragavan and Vaikuntanathan17] also crucially relies on this conjecture.
In this paper, we prove a version of Regev’s conjecture. This allows us to unconditionally prove the correctness of (slightly modified versions of) the algorithms of Regev [Reference Regev18] and Ragavan and Vaikuntanathan [Reference Ragavan and Vaikuntanathan17]. More precisely, we obtain the following algorithmic result.
Theorem 1.1. There is a quantum circuit having
![]() $O(n^{3/2} \log ^3 n)$
quantum gates and
$O(n^{3/2} \log ^3 n)$
quantum gates and
![]() $O(n \log ^3 n)$
qubits with the following property. There is a classical randomised polynomial-time algorithm that solves the factoring problem
$O(n \log ^3 n)$
qubits with the following property. There is a classical randomised polynomial-time algorithm that solves the factoring problem
 $$ \begin{align*} & \mathbf{Input: }\text{ a composite integer } N \leq 2^n \\ & \mathbf{Output: }\text{ a nontrivial divisor of } N \end{align*} $$
$$ \begin{align*} & \mathbf{Input: }\text{ a composite integer } N \leq 2^n \\ & \mathbf{Output: }\text{ a nontrivial divisor of } N \end{align*} $$
using
![]() $O(\sqrt {n})$
calls to this quantum circuit, and succeeds with probability
$O(\sqrt {n})$
calls to this quantum circuit, and succeeds with probability
![]() $\Theta (1)$
.
$\Theta (1)$
.
This unconditionally establishes the results in [Reference Ragavan and Vaikuntanathan17, Reference Regev18] up to logarithmic factors.
Regev’s algorithm was adapted by Ekerå and Gärtner [Reference Ekerå and Gärtner7] to the discrete logarithm problem. Their paper [Reference Ekerå and Gärtner7] also uses the space-saving arithmetic of Ragavan and Vaikuntanathan [Reference Ragavan and Vaikuntanathan17] to obtain a quantum circuit with
![]() $O(n^{3/2}\log n)$
gates and
$O(n^{3/2}\log n)$
gates and
![]() $O(n\log n)$
qubits for computing discrete logarithms.
$O(n\log n)$
qubits for computing discrete logarithms.
Once more, the correctness of the algorithm by Ekerå and Gärtner [Reference Ekerå and Gärtner7] relies on an unproven hypothesis, which can be viewed as a stronger form of Regev’s conjecture. Our methods also apply to this stronger statement (again, with minor technical adjustments). Thus, we get an analogue of Theorem 1.1 for the discrete logarithm problem, that is, an unconditional proof of the results in [Reference Ekerå and Gärtner7] up to logarithmic factors.
Theorem 1.2. There is a quantum circuit having
![]() $O(n^{3/2} \log ^3 n)$
quantum gates and
$O(n^{3/2} \log ^3 n)$
quantum gates and
![]() $O(n \log ^3 n)$
qubits with the following property. There is a classical randomised polynomial-time algorithm that solves the discrete logarithm problem
$O(n \log ^3 n)$
qubits with the following property. There is a classical randomised polynomial-time algorithm that solves the discrete logarithm problem
 $$ \begin{align*} & \mathbf{Input: }\text{ an integer } N \leq 2^n \text{ and elements } g,y \in (\mathbb{Z}/N\mathbb{Z})^{\times} \text{ such that } y\in \left\langle g\right\rangle \\ & \mathbf{Output: }\text{ an integer } x \text{ such that } g^x \equiv y \quad\pmod{N} \end{align*} $$
$$ \begin{align*} & \mathbf{Input: }\text{ an integer } N \leq 2^n \text{ and elements } g,y \in (\mathbb{Z}/N\mathbb{Z})^{\times} \text{ such that } y\in \left\langle g\right\rangle \\ & \mathbf{Output: }\text{ an integer } x \text{ such that } g^x \equiv y \quad\pmod{N} \end{align*} $$
using
![]() $O(\sqrt {n})$
calls to this quantum circuit, and succeeds with probability
$O(\sqrt {n})$
calls to this quantum circuit, and succeeds with probability
![]() $\Theta (1)$
.
$\Theta (1)$
.
Moreover, the slight technical modifications that we need to introduce to make all these quantum algorithms unconditional are compatible with the error-correction results of [Reference Ekerå and Gärtner7, Reference Ragavan and Vaikuntanathan17]. Finally, our results extend to further variants of Regev’s algorithm, such as computing discrete logarithms or multiplicative orders modulo N for several elements simultaneously (see [Reference Ekerå and Gärtner7]).
1.2 An overview of Regev’s algorithm
Let us start by recalling the basic idea behind Shor’s factoring algorithm [Reference Peter20].
Let N be the integer to be factored, which can be assumed to be odd and with at least two distinct prime factors. Shor proved that there is an efficient quantum algorithm to find the multiplicative order of any invertible element modulo N. With this in hand, factoring N is straightforward. The first step is to pick an integer
![]() $1 < a < N$
uniformly at random. If
$1 < a < N$
uniformly at random. If
![]() $\gcd (a,N)>1$
, the factoring task is trivial. Otherwise, with probability at least
$\gcd (a,N)>1$
, the factoring task is trivial. Otherwise, with probability at least
![]() $1/2$
, the order of a modulo N, denoted r, is even and satisfies
$1/2$
, the order of a modulo N, denoted r, is even and satisfies
![]() $a^{r/2}\not \equiv \pm 1$
(i.e.,
$a^{r/2}\not \equiv \pm 1$
(i.e.,
![]() $a^{r/2}$
is a nontrivial square root of
$a^{r/2}$
is a nontrivial square root of
![]() $1$
modulo N). Whenever this is the case, we get a nontrivial divisor of N, namely
$1$
modulo N). Whenever this is the case, we get a nontrivial divisor of N, namely
![]() $\gcd (N, a^{r/2}-1)$
.
$\gcd (N, a^{r/2}-1)$
.
The reason that Shor’s algorithm uses
![]() $O(n^2\log n)$
quantum gates, where
$O(n^2\log n)$
quantum gates, where
![]() $n := \lceil \log _2 N\rceil $
, comes from the part of the quantum circuit that performs modular exponentiation. Consider the task of computing a power
$n := \lceil \log _2 N\rceil $
, comes from the part of the quantum circuit that performs modular exponentiation. Consider the task of computing a power
![]() $a^M\,(\mathrm {mod}\, N)$
on a classical computer, where
$a^M\,(\mathrm {mod}\, N)$
on a classical computer, where
![]() $1<a<N-1$
and
$1<a<N-1$
and
![]() $M \leq N$
. This computation can be performed efficiently using the well-known square-and-multiply method, which involves
$M \leq N$
. This computation can be performed efficiently using the well-known square-and-multiply method, which involves
![]() $O(\log M)$
multiplications of two integers modulo N. Since two n-bit integers can be multiplied in time
$O(\log M)$
multiplications of two integers modulo N. Since two n-bit integers can be multiplied in time
![]() $O(n\log n)$
by [Reference Harvey and van der Hoeven10], the complexity of this modular exponentiation problem is thus
$O(n\log n)$
by [Reference Harvey and van der Hoeven10], the complexity of this modular exponentiation problem is thus
![]() $O(n^2\log n)$
.Footnote
2
For Shor’s algorithm, a similar modular exponentiation needs to be performed quantumly, which requires
$O(n^2\log n)$
.Footnote
2
For Shor’s algorithm, a similar modular exponentiation needs to be performed quantumly, which requires
![]() $O(n^2\log n)$
quantum gates.
$O(n^2\log n)$
quantum gates.
Regev’s improvement of Shor’s algorithm is made possible by combining two key ideas.
The first idea in Regev’s algorithm is to work in higher-dimensional space and replace the random parameter a by several integers
![]() $b_1, \ldots , b_d$
(chosen in a specific way, as we explain below). Eventually, the optimal choice of dimension turns out to be
$b_1, \ldots , b_d$
(chosen in a specific way, as we explain below). Eventually, the optimal choice of dimension turns out to be
![]() ${d \asymp \sqrt {\log N}}$
. Similarly to Shor’s algorithm, the problem of factoring N easily reduces to the task of finding a vector
${d \asymp \sqrt {\log N}}$
. Similarly to Shor’s algorithm, the problem of factoring N easily reduces to the task of finding a vector
![]() $(e_1, \ldots , e_d) \in \mathbb {Z}^d$
such that
$(e_1, \ldots , e_d) \in \mathbb {Z}^d$
such that
![]() $\prod _{i=1}^d b_i^{e_i}$
is a nontrivial square root of
$\prod _{i=1}^d b_i^{e_i}$
is a nontrivial square root of
![]() $1$
modulo N.
$1$
modulo N.
Using additional tools such as the LLL lattice reduction algorithm, Regev [Reference Regev18] generalised Shor’s quantum algorithm to efficiently find all such vectors
![]() $(e_1, \ldots , e_d)$
in a ball of radius
$(e_1, \ldots , e_d)$
in a ball of radius
![]() $N^{O(1/d)}$
centred at the origin.
$N^{O(1/d)}$
centred at the origin.
Regev’s algorithm only succeeds if there indeed exists a vector
![]() $v = (e_1, \ldots , e_d) \in \mathbb {Z}^d$
such that
$v = (e_1, \ldots , e_d) \in \mathbb {Z}^d$
such that
-
(i)
 $\left \|v\right \|_2 \leq N^{O(1/d)}$
, and
$\left \|v\right \|_2 \leq N^{O(1/d)}$
, and -
(ii)
 $\prod _{i=1}^d b_i^{e_i}$
is a nontrivial square root of
$\prod _{i=1}^d b_i^{e_i}$
is a nontrivial square root of
 $1$
modulo N.
$1$
modulo N.
If the parameters
![]() $b_1, \ldots , b_d$
are ‘sufficiently multiplicatively independent’ modulo N, one might heuristically expect the existence of a vector
$b_1, \ldots , b_d$
are ‘sufficiently multiplicatively independent’ modulo N, one might heuristically expect the existence of a vector
![]() $v = (e_1, \ldots , e_d)$
satisfying Item i and Item ii. This is, roughly speaking, what Regev needs to assume. To state his conjecture properly, it remains to specify how the parameters
$v = (e_1, \ldots , e_d)$
satisfying Item i and Item ii. This is, roughly speaking, what Regev needs to assume. To state his conjecture properly, it remains to specify how the parameters
![]() $b_1, \ldots , b_d$
are chosen. This is a crucial point, as the idea of working in dimension d does not, on its own, offer any advantage over Shor’s algorithm.
$b_1, \ldots , b_d$
are chosen. This is a crucial point, as the idea of working in dimension d does not, on its own, offer any advantage over Shor’s algorithm.
The second key insight of Regev is to choose
![]() $b_1, \ldots , b_d$
to be very small compared to N. We mentioned that the most costly part of Shor’s quantum circuit lies in the modular exponentiation step. Similarly, the number of gates of Regev’s circuit is dominated by the cost of computing an expression of the form
$b_1, \ldots , b_d$
to be very small compared to N. We mentioned that the most costly part of Shor’s quantum circuit lies in the modular exponentiation step. Similarly, the number of gates of Regev’s circuit is dominated by the cost of computing an expression of the form
 $$ \begin{align} \prod_{i=1}^d b_i^{M_i}\quad (\mathrm{mod}\, N) \end{align} $$
$$ \begin{align} \prod_{i=1}^d b_i^{M_i}\quad (\mathrm{mod}\, N) \end{align} $$
in the quantum setting, where the exponents
![]() $M_1, \ldots , M_d$
are
$M_1, \ldots , M_d$
are
![]() $\leq N^{O(1/d)}$
. Regev observed that (1) can be computed classically in time
$\leq N^{O(1/d)}$
. Regev observed that (1) can be computed classically in time
![]() $O(n^{3/2} \log n)$
if
$O(n^{3/2} \log n)$
if
![]() $|b_i| \leq (\log N)^{O(1)}$
for all i (for
$|b_i| \leq (\log N)^{O(1)}$
for all i (for
![]() $d \asymp \sqrt {n} \asymp \sqrt {\log N}$
). This can be achieved by cleverly ordering the intermediate multiplications so that most of them involve integers with much fewer than n bits. This classical procedure can then be turned into a quantum version that uses
$d \asymp \sqrt {n} \asymp \sqrt {\log N}$
). This can be achieved by cleverly ordering the intermediate multiplications so that most of them involve integers with much fewer than n bits. This classical procedure can then be turned into a quantum version that uses
![]() $O(n^{3/2}\log n)$
gates.
$O(n^{3/2}\log n)$
gates.
Shor’s algorithm corresponds to the
![]() $d=1$
case of Regev’s algorithm where the parameter
$d=1$
case of Regev’s algorithm where the parameter
![]() $b_1$
is an element of
$b_1$
is an element of
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
chosen uniformly at random. In this case, simple considerations from elementary number theory immediately imply the existence of an integer
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
chosen uniformly at random. In this case, simple considerations from elementary number theory immediately imply the existence of an integer
![]() $e_1$
satisfying Item i and Item ii with probability
$e_1$
satisfying Item i and Item ii with probability
![]() $\gg 1$
. This would hold more generally for
$\gg 1$
. This would hold more generally for
![]() $d\geq 1$
if
$d\geq 1$
if
![]() $b_1, \ldots , b_d$
were independent, uniformly distributed random elements of
$b_1, \ldots , b_d$
were independent, uniformly distributed random elements of
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
. However, for Regev’s algorithm, the
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
. However, for Regev’s algorithm, the
![]() $b_i$
’s are far from uniformly distributed in
$b_i$
’s are far from uniformly distributed in
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
as they are constrained to lie in a very small subset of
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
as they are constrained to lie in a very small subset of
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
.
1.3 The number-theoretic conjecture behind Regev’s algorithm
Regev’s algorithm [Reference Regev18] and its space-efficient variant [Reference Ragavan and Vaikuntanathan17] crucially rely on the possibility of choosing very small integers
![]() $b_1, \ldots , b_d$
such that
$b_1, \ldots , b_d$
such that
![]() $\prod _{i=1}^d b_i^{e_i}$
is a nontrivial square root of
$\prod _{i=1}^d b_i^{e_i}$
is a nontrivial square root of
![]() $1$
modulo N for some
$1$
modulo N for some
![]() $e_1, \ldots , e_d$
with
$e_1, \ldots , e_d$
with
![]() $|e_i| \leq N^{O(1/d)}$
. We remind the reader that
$|e_i| \leq N^{O(1/d)}$
. We remind the reader that
![]() $n \asymp \log N$
and
$n \asymp \log N$
and
![]() $d \asymp \sqrt {n}$
.
$d \asymp \sqrt {n}$
.
The least restrictive boundFootnote
3
on the
![]() $b_i$
’s that still allows for a quantum circuit with
$b_i$
’s that still allows for a quantum circuit with
![]() $\tilde {O}(n^{3/2})$
gates is to have
$\tilde {O}(n^{3/2})$
gates is to have
![]() $|b_i| \leq \exp (\tilde {O}(d))$
, where the
$|b_i| \leq \exp (\tilde {O}(d))$
, where the
![]() $\tilde {O}(\cdot )$
notation possibly hides a factor
$\tilde {O}(\cdot )$
notation possibly hides a factor
![]() $(\log n)^{O(1)}$
. Moreover, it is natural to set the
$(\log n)^{O(1)}$
. Moreover, it is natural to set the
![]() $b_i$
’s to be prime numbers (as in [Reference Ekerå and Gärtner7, Reference Ragavan and Vaikuntanathan17, Reference Regev18]) in order to avoid obvious multiplicative relations between them.
$b_i$
’s to be prime numbers (as in [Reference Ekerå and Gärtner7, Reference Ragavan and Vaikuntanathan17, Reference Regev18]) in order to avoid obvious multiplicative relations between them.
In this paper, we choose
![]() $b_1, \ldots , b_d$
to be independent random prime numbers less than
$b_1, \ldots , b_d$
to be independent random prime numbers less than
![]() $d^{10^3d}$
. With these parameters, we can now state a version of Regev’s conjectureFootnote
4
that follows from our results.
$d^{10^3d}$
. With these parameters, we can now state a version of Regev’s conjectureFootnote
4
that follows from our results.
Corollary 1.4. Let
![]() $N>2$
be an integer. Let
$N>2$
be an integer. Let
![]() $d := \lceil \!\sqrt {\log N} \rceil $
and
$d := \lceil \!\sqrt {\log N} \rceil $
and
![]() $X := d^{10^3d}$
.
$X := d^{10^3d}$
.
Let
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes
![]() $\leq X$
not dividing N.
$\leq X$
not dividing N.
Then, with high probability, every
![]() $x \in \left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
can be expressed as
$x \in \left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
can be expressed as
 $$ \begin{align*} x \equiv \prod_{i=1}^d {\mathbf{b}}_i^{e_i} \quad\pmod{N} \end{align*} $$
$$ \begin{align*} x \equiv \prod_{i=1}^d {\mathbf{b}}_i^{e_i} \quad\pmod{N} \end{align*} $$
for some integers
![]() $e_i$
with
$e_i$
with
![]() $|e_i|\leq e^{O(d)}$
for all
$|e_i|\leq e^{O(d)}$
for all
![]() $1\leq i\leq d$
.
$1\leq i\leq d$
.
The analogue of Regev’s algorithm for the discrete logarithm problem, proposed by Ekerå and Gärtner [Reference Ekerå and Gärtner7], relies on a stronger version of Regev’s conjecture. It concerns the geometry of a certain lattice
![]() $\mathcal {L}$
which encodes all multiplicative dependencies between the
$\mathcal {L}$
which encodes all multiplicative dependencies between the
![]() ${\mathbf {b}}_i$
’s (modulo N). We prove the following version of it.Footnote
5
${\mathbf {b}}_i$
’s (modulo N). We prove the following version of it.Footnote
5
Corollary 1.5. Let
![]() $N>2$
be an integer. Let
$N>2$
be an integer. Let
![]() $d := \lceil \!\sqrt {\log N} \rceil $
and
$d := \lceil \!\sqrt {\log N} \rceil $
and
![]() $X := d^{10^3d}$
.
$X := d^{10^3d}$
.
Let
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes
![]() $\leq X$
not dividing N.
$\leq X$
not dividing N.
Let
![]() $\mathcal {L}$
be the random lattice defined by
$\mathcal {L}$
be the random lattice defined by
 $$ \begin{align} \mathcal{L} := \Big\{ (e_1, \ldots, e_d) \in \mathbb{Z}^d \ : \ \prod_{i=1}^d {\mathbf{b}}_i^{e_i} \equiv 1 \quad\pmod{N} \Big\}. \end{align} $$
$$ \begin{align} \mathcal{L} := \Big\{ (e_1, \ldots, e_d) \in \mathbb{Z}^d \ : \ \prod_{i=1}^d {\mathbf{b}}_i^{e_i} \equiv 1 \quad\pmod{N} \Big\}. \end{align} $$
Then, with high probability, this lattice
![]() $\mathcal {L}$
has a basis consisting of vectors of Euclidean norm
$\mathcal {L}$
has a basis consisting of vectors of Euclidean norm
![]() $\leq e^{O(d)}$
.
$\leq e^{O(d)}$
.
The main technical result of this paper is Theorem 3.18, of which Corollary 1.5 is a special case. In turn, Corollary 1.4 is a direct consequence of Corollary 1.5.
1.4 Subgroup obstructions
Let N, d and
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be as in Corollary 1.4. This corollary shows that, with high probability, every element x in the subgroup generated by
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be as in Corollary 1.4. This corollary shows that, with high probability, every element x in the subgroup generated by
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
can be written as a short product of these
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
can be written as a short product of these
![]() ${\mathbf {b}}_i$
modulo N. To obtain the full strength of Regev’s assumption [Reference Ragavan and Vaikuntanathan17, Conjecture 1], it would be necessary to show that this subgroup
${\mathbf {b}}_i$
modulo N. To obtain the full strength of Regev’s assumption [Reference Ragavan and Vaikuntanathan17, Conjecture 1], it would be necessary to show that this subgroup
![]() $\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
contains a nontrivial square root of
$\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
contains a nontrivial square root of
![]() $1$
modulo N.
$1$
modulo N.
Unfortunately, it is not possible to prove this in full generality without considerable advances on the well-known least quadratic nonresidue problem in number theory. For any prime number p, write
![]() $n(p)$
for the smallest positive integer a which is a quadratic nonresidue (i.e., not a square) modulo p. The best known asymptotic upper bound for
$n(p)$
for the smallest positive integer a which is a quadratic nonresidue (i.e., not a square) modulo p. The best known asymptotic upper bound for
![]() $n(p)$
is Burgess’s classical result [Reference Burgess5] that
$n(p)$
is Burgess’s classical result [Reference Burgess5] that
For simplicity, suppose that the integer N to be factored is a product of two equally sized primes
![]() ${p_1, p_2\equiv 3 \ \pmod {4}}$
. Recall that, for Regev’s algorithm, the parameters
${p_1, p_2\equiv 3 \ \pmod {4}}$
. Recall that, for Regev’s algorithm, the parameters
![]() ${\mathbf {b}}_i$
are chosen to be less than
${\mathbf {b}}_i$
are chosen to be less than
![]() $\exp (\tilde {O}(d))$
. With current techniques, we cannot rule out the possibility that both
$\exp (\tilde {O}(d))$
. With current techniques, we cannot rule out the possibility that both
![]() $n(p_1)$
and
$n(p_1)$
and
![]() $n(p_2)$
are larger than this threshold. If this is the case, all
$n(p_2)$
are larger than this threshold. If this is the case, all
![]() ${\mathbf {b}}_i$
will be quadratic residues modulo both
${\mathbf {b}}_i$
will be quadratic residues modulo both
![]() $p_1$
and
$p_1$
and
![]() $p_2$
, which implies that
$p_2$
, which implies that
![]() $\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
is contained in the subgroup of squares modulo N. In particular, since
$\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
is contained in the subgroup of squares modulo N. In particular, since
![]() $p_1, p_2\equiv 3 \ \pmod {4}$
, the subgroup
$p_1, p_2\equiv 3 \ \pmod {4}$
, the subgroup
![]() $\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
does not contain any nontrivial square roots of
$\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
does not contain any nontrivial square roots of
![]() $1$
modulo N.
$1$
modulo N.
This issue can be approached from several perspectives.
-
1. Assuming the Generalised Riemann Hypothesis, Ankeny proved the much stronger bound
 $n(p) \ll (\log p)^2$
[Reference Ankeny2]. This suggests that quadratic residues may no longer be an obstruction in this case, and indeed, under GRH, it is straightforward to show that
$n(p) \ll (\log p)^2$
[Reference Ankeny2]. This suggests that quadratic residues may no longer be an obstruction in this case, and indeed, under GRH, it is straightforward to show that
 $\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
contains a nontrivial square root of
$\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
contains a nontrivial square root of
 $1$
modulo N with high probability. Assuming GRH would also considerably simplify the proof of Theorem 3.18 and remove a logarithmic factor for the gate and qubit costs in Theorems 1.1 and 1.2. However, in this paper we seek fully unconditional results.
$1$
modulo N with high probability. Assuming GRH would also considerably simplify the proof of Theorem 3.18 and remove a logarithmic factor for the gate and qubit costs in Theorems 1.1 and 1.2. However, in this paper we seek fully unconditional results. -
2. It is possible to prove the following partial result unconditionally: for almost all odd N with at least two distinct prime factors, the subgroup
 $\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
contains a nontrivial square root of
$\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
contains a nontrivial square root of
 $1$
modulo N with high probability (with
$1$
modulo N with high probability (with
 $d = d(N)$
and
$d = d(N)$
and
 ${\mathbf {b}}_i = {\mathbf {b}}_i(N)$
as in Corollary 1.4). By Corollary 1.4, this implies that Regev’s original algorithm (with these parameters
${\mathbf {b}}_i = {\mathbf {b}}_i(N)$
as in Corollary 1.4). By Corollary 1.4, this implies that Regev’s original algorithm (with these parameters
 ${\mathbf {b}}_i$
) finds a nontrivial divisor of N with high probability, for almost all N. More precisely, the set
${\mathbf {b}}_i$
) finds a nontrivial divisor of N with high probability, for almost all N. More precisely, the set
 $E\subset \mathbb {N}$
of exceptional values of N for which the above does not hold can be shown to satisfy for
$E\subset \mathbb {N}$
of exceptional values of N for which the above does not hold can be shown to satisfy for $$ \begin{align*} \left|E \cap [1, x]\right| \leq \exp\!\big((\log x)^{1/2+o(1)}\big) \end{align*} $$
$$ \begin{align*} \left|E \cap [1, x]\right| \leq \exp\!\big((\log x)^{1/2+o(1)}\big) \end{align*} $$
 $x\geq 1$
. This partial result can be proved using character sums, the Landau-Page theorem [Reference Montgomery and Vaughan15, Corollary 11.10] and a grand zero-density estimate [Reference Jutila11, Theorem 1 (1.8)], by means of a case analysis depending on the prime factorisation of N.
$x\geq 1$
. This partial result can be proved using character sums, the Landau-Page theorem [Reference Montgomery and Vaughan15, Corollary 11.10] and a grand zero-density estimate [Reference Jutila11, Theorem 1 (1.8)], by means of a case analysis depending on the prime factorisation of N.
-
3. In the present work, we follow a different approach to obtain a completely unconditional result that applies to all N, by slightly modifying the algorithm itself. While the key to the efficiency of Regev’s algorithm is that the
 ${\mathbf {b}}_i$
’s are small, one can tolerate a bounded number of large
${\mathbf {b}}_i$
’s are small, one can tolerate a bounded number of large
 ${\mathbf {b}}_i$
’s.Footnote
6
We use this extra flexibility to overcome the subgroup obstructions. The simplest way to proceed is to allow for one of the parameters, say
${\mathbf {b}}_i$
’s.Footnote
6
We use this extra flexibility to overcome the subgroup obstructions. The simplest way to proceed is to allow for one of the parameters, say
 ${\mathbf {b}}_1$
, to be uniformly distributed in
${\mathbf {b}}_1$
, to be uniformly distributed in
 $(\mathbb {Z}/N\mathbb {Z})^{\times }$
. As with Shor’s algorithm, this ensures that the subgroup
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
. As with Shor’s algorithm, this ensures that the subgroup
 $\left \langle {\mathbf {b}}_1\right \rangle $
, and hence also
$\left \langle {\mathbf {b}}_1\right \rangle $
, and hence also
 $\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
, contains a nontrivial square root of
$\left \langle {\mathbf {b}}_1, \ldots , {\mathbf {b}}_d\right \rangle $
, contains a nontrivial square root of
 $1$
with probability
$1$
with probability
 $\gg 1$
.
$\gg 1$
.
Remark 1.6. In his paper [Reference Regev18], Regev proposed to select the parameters
![]() $b_1, \ldots , b_d$
deterministically, for example by setting
$b_1, \ldots , b_d$
deterministically, for example by setting
![]() $b_i$
to be the i-th smallest prime for
$b_i$
to be the i-th smallest prime for
![]() $1\leq i\leq d$
. While such a deterministic choice of parameters is likely to work for almost all N, this seems to be very difficult to prove.
$1\leq i\leq d$
. While such a deterministic choice of parameters is likely to work for almost all N, this seems to be very difficult to prove.
Remark 1.7. In this paper, the parameters
![]() ${\mathbf {b}}_i$
are chosen to be random primes (not dividing N) under a certain threshold X. Another natural choice would have been to let
${\mathbf {b}}_i$
are chosen to be random primes (not dividing N) under a certain threshold X. Another natural choice would have been to let
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables uniformly distributed in the set of all integers
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables uniformly distributed in the set of all integers
![]() $\leq X$
coprime to N. The proofs in this paper would carry over to this framework if an analogue of Proposition 3.9 for short character sums
$\leq X$
coprime to N. The proofs in this paper would carry over to this framework if an analogue of Proposition 3.9 for short character sums
![]() $\sum _{n\leq x} \chi (n)$
were available. Assuming the Generalised Riemann Hypothesis, the work of Granville and Soundararajan [Reference Granville and Soundararajan9, Theorem 2] gives a bound of the required strength. However, this approach does not seem sufficient to obtain an unconditional result (the bounds in [Reference Granville and Soundararajan9] become too weak when
$\sum _{n\leq x} \chi (n)$
were available. Assuming the Generalised Riemann Hypothesis, the work of Granville and Soundararajan [Reference Granville and Soundararajan9, Theorem 2] gives a bound of the required strength. However, this approach does not seem sufficient to obtain an unconditional result (the bounds in [Reference Granville and Soundararajan9] become too weak when
![]() $L(s, \chi )$
has zeroes close to the line
$L(s, \chi )$
has zeroes close to the line
![]() $\Re s = 1$
).
$\Re s = 1$
).
1.5 Structure of the paper
We begin in Section 2 with a proof of a simple special case of our main theorem. This is intended to illustrate our overall strategy and motivate the need for the more technical approach required in the general case. The purpose of this section is to build intuition; it is not formally required for the main argument.
Our main technical result is Theorem 3.18, which shows that lattices
![]() $\mathcal {L}$
similar to that in Corollary 1.5 have a basis of short vectors with high probability. Using simple geometry of numbers (see Section 3.4), we reduce this problem to estimating the number of lattice points in balls of growing radii. Unfortunately, we are unable to obtain a suitable lattice point count for
$\mathcal {L}$
similar to that in Corollary 1.5 have a basis of short vectors with high probability. Using simple geometry of numbers (see Section 3.4), we reduce this problem to estimating the number of lattice points in balls of growing radii. Unfortunately, we are unable to obtain a suitable lattice point count for
![]() $\mathcal {L}$
directly. We resolve this by considering a different lattice
$\mathcal {L}$
directly. We resolve this by considering a different lattice
![]() $\mathcal {L}_M$
from the start of the argument (using the lemmas in Section 3.1). In Section 3.2, we expand the lattice point count for
$\mathcal {L}_M$
from the start of the argument (using the lemmas in Section 3.1). In Section 3.2, we expand the lattice point count for
![]() $\mathcal {L}_M$
in terms of Dirichlet characters modulo N. This produces a main term, which can be estimated precisely, and an error term. The heart of the proof lies in using a zero-density estimate for Dirichlet characters modulo N to bound this error term unconditionally. Finally, we prove our quantum algorithmic applications (Theorems 1.1 and 1.2) in Section 4.
$\mathcal {L}_M$
in terms of Dirichlet characters modulo N. This produces a main term, which can be estimated precisely, and an error term. The heart of the proof lies in using a zero-density estimate for Dirichlet characters modulo N to bound this error term unconditionally. Finally, we prove our quantum algorithmic applications (Theorems 1.1 and 1.2) in Section 4.
1.6 Notation
We write
![]() $f\ll g$
or
$f\ll g$
or
![]() $f = O(g)$
if
$f = O(g)$
if
![]() $|f| \leq Cg$
for some absolute constant
$|f| \leq Cg$
for some absolute constant
![]() $C>0$
. If instead, C depends on a parameter
$C>0$
. If instead, C depends on a parameter
![]() $\theta $
, we write
$\theta $
, we write
![]() $f \ll _{\theta } g$
or
$f \ll _{\theta } g$
or
![]() $f = O_{\theta }(g)$
. The notation
$f = O_{\theta }(g)$
. The notation
![]() $f\asymp g$
or
$f\asymp g$
or
![]() $f = \Theta (g)$
means that
$f = \Theta (g)$
means that
![]() $f\ll g$
and
$f\ll g$
and
![]() $g\ll f$
.
$g\ll f$
.
A character of a finite abelian group G is a homomorphism
![]() $\chi : G\to \mathbb {C}^{\times }$
. The order of
$\chi : G\to \mathbb {C}^{\times }$
. The order of
![]() $\chi $
, denoted by
$\chi $
, denoted by
![]() $\mathrm {ord}(\chi )$
, is the least positive integer n such that
$\mathrm {ord}(\chi )$
, is the least positive integer n such that
![]() $\chi ^n$
is the trivial character
$\chi ^n$
is the trivial character
![]() $1$
. The group of all characters of G is denoted by
$1$
. The group of all characters of G is denoted by
![]() $\widehat {G}$
. If
$\widehat {G}$
. If
![]() $g_1, \dots , g_k\in G$
, we write
$g_1, \dots , g_k\in G$
, we write
![]() $\left \langle g_1, \ldots , g_k\right \rangle $
for the subgroup of G generated by these elements.
$\left \langle g_1, \ldots , g_k\right \rangle $
for the subgroup of G generated by these elements.
A nontrivial square root of
![]() $1$
modulo N is an element
$1$
modulo N is an element
![]() $a\in (\mathbb {Z}/N\mathbb {Z})^{\times }$
such that
$a\in (\mathbb {Z}/N\mathbb {Z})^{\times }$
such that
![]() $a^2 \equiv 1\ \pmod N$
and
$a^2 \equiv 1\ \pmod N$
and
![]() $a\not \equiv \pm 1 \ \pmod N$
. Euler’s totient function and the prime counting function are denoted by
$a\not \equiv \pm 1 \ \pmod N$
. Euler’s totient function and the prime counting function are denoted by
![]() $\varphi $
and
$\varphi $
and
![]() $\pi $
, respectively. We use the notation
$\pi $
, respectively. We use the notation
![]() $\left \|\cdot \right \|_2$
for the Euclidean norm. We write
$\left \|\cdot \right \|_2$
for the Euclidean norm. We write
![]() $\log $
for the natural logarithm and
$\log $
for the natural logarithm and
![]() $\log _2$
for the logarithm in base
$\log _2$
for the logarithm in base
![]() $2$
.
$2$
.
Random variables are typically written in bold font, such as
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
. A statement will be said to occur with high probability if it holds with probability tending to
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
. A statement will be said to occur with high probability if it holds with probability tending to
![]() $1$
as
$1$
as
![]() $N\to \infty $
.
$N\to \infty $
.
We refer the reader to [Reference Nielsen and Chuang16] for a detailed textbook on quantum computing, and [Reference Bernstein, Buchmann and Dahmen4, Chapter 2] for a brief overview.
2 An illustrative special case
In this section, we prove a weak version of our main theorem in a simplified setting. This special case can be used to obtain an unconditional factoring algorithm for integers N of a special form: RSA moduli that are products of two ‘safe primes’.Footnote 7
Definition 2.1 (RSA moduli with safe primes).
Let
![]() $\mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
be the set of integers N of the form
$\mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
be the set of integers N of the form
![]() $N = P\cdot Q$
, where
$N = P\cdot Q$
, where
![]() $P,Q\geq N^{1/4}$
are distinct primes such that
$P,Q\geq N^{1/4}$
are distinct primes such that
![]() $(P-1)/2$
and
$(P-1)/2$
and
![]() $(Q-1)/2$
are also prime.
$(Q-1)/2$
are also prime.
For
![]() $N\in \mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
, the multiplicative group
$N\in \mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
, the multiplicative group
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
has a very convenient structure, allowing us to give a relatively short proof of the following proposition.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
has a very convenient structure, allowing us to give a relatively short proof of the following proposition.
Proposition 2.2. Let
![]() $N\in \mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
be a sufficiently large integer. Let
$N\in \mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
be a sufficiently large integer. Let
![]() $d := \lceil \!\sqrt {\log N} \rceil $
and
$d := \lceil \!\sqrt {\log N} \rceil $
and
![]() $X := d^{d}$
.
$X := d^{d}$
.
Let
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes less than X. Let
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes less than X. Let
![]() ${\mathbf {b}}_0$
be a random variable uniformly distributed in
${\mathbf {b}}_0$
be a random variable uniformly distributed in
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
, independent from the
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
, independent from the
![]() ${\mathbf {b}}_i$
’s.
${\mathbf {b}}_i$
’s.
Let
![]() $x\in (\mathbb {Z}/N\mathbb {Z})^{\times }$
. Then, with probability
$x\in (\mathbb {Z}/N\mathbb {Z})^{\times }$
. Then, with probability
![]() $\gg 1$
, there are integers
$\gg 1$
, there are integers
![]() $0\leq e_0, \ldots , e_d\leq e^{O(d)}$
such that
$0\leq e_0, \ldots , e_d\leq e^{O(d)}$
such that
 $$ \begin{align*} \prod_{i=0}^d {\mathbf{b}}_i^{e_i} \equiv x \quad\pmod{N}. \end{align*} $$
$$ \begin{align*} \prod_{i=0}^d {\mathbf{b}}_i^{e_i} \equiv x \quad\pmod{N}. \end{align*} $$
Applying Proposition 2.2 (with x being a nontrivial square root of
![]() $1$
modulo N) shows that Regev’s factoring algorithm, with random parameters
$1$
modulo N) shows that Regev’s factoring algorithm, with random parameters
![]() ${\mathbf {b}}_0, \ldots , {\mathbf {b}}_d$
as in that propositionFootnote
8
, admits an unconditional proof of correctness for integers
${\mathbf {b}}_0, \ldots , {\mathbf {b}}_d$
as in that propositionFootnote
8
, admits an unconditional proof of correctness for integers
![]() $N\in \mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
.
$N\in \mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
.
It should be noted that Theorem 3.18 not only removes the restriction
![]() $N\in \mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
, it also provides a stronger geometric conclusion required for applications to the discrete logarithm problem.
$N\in \mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
, it also provides a stronger geometric conclusion required for applications to the discrete logarithm problem.
Notation 2.3. For the rest of this section, we fix N, d, X,
![]() ${\mathbf {b}}_0, \ldots , {\mathbf {b}}_d$
and x as in the statement of Proposition 2.2. In particular,
${\mathbf {b}}_0, \ldots , {\mathbf {b}}_d$
and x as in the statement of Proposition 2.2. In particular,
![]() $N\in \mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
is assumed to be sufficiently large. Moreover, there are primes P, Q,
$N\in \mathcal {M}_{\scriptscriptstyle {\mathrm {RSA}}}$
is assumed to be sufficiently large. Moreover, there are primes P, Q,
![]() $P'$
and
$P'$
and
![]() $Q'$
such that
$Q'$
such that
![]() $N = P\cdot Q$
,
$N = P\cdot Q$
,
![]() $P = 2P'+1$
and
$P = 2P'+1$
and
![]() $Q = 2Q'+1$
. Hence,
$Q = 2Q'+1$
. Hence,
To prove Proposition 2.2, we require the following lemma from analytic number theory, that ultimately relies on a zero-density estimate for Dirichlet L-functions.
Lemma 2.4. For every
![]() $j\geq 0$
, the number of characters
$j\geq 0$
, the number of characters
![]() $\psi \in \widehat {G}$
such that
$\psi \in \widehat {G}$
such that
is at most
![]() $e^{O(d)}N^{O(j/\log X)}$
. Here,
$e^{O(d)}N^{O(j/\log X)}$
. Here,
![]() ${\mathbb {E}}_{p\leq X}$
denotes the average over primes
${\mathbb {E}}_{p\leq X}$
denotes the average over primes
![]() $p\leq X$
.
$p\leq X$
.
We omit the proof of Lemma 2.4, as it is somewhat tangential to the aim of this explanatory section.Footnote 9
Proof of Proposition 2.2.
Let
![]() $H = \lfloor e^{Cd} \rfloor $
, where C is a large absolute constant to be chosen later.
$H = \lfloor e^{Cd} \rfloor $
, where C is a large absolute constant to be chosen later.
We will show that, with probability
![]() $\gg 1$
, there exist integers
$\gg 1$
, there exist integers
![]() $0\leq h_1, \ldots , h_d < H$
such that
$0\leq h_1, \ldots , h_d < H$
such that
which clearly implies the desired conclusion. By orthogonality of characters modulo N, we have
 $$ \begin{align} \sum_{0\leq h_1, \ldots, h_d < H} \mathbf{1}_{{\mathbf{b}}_0 {\mathbf{b}}_1^{h_1}\cdots {\mathbf{b}}_d^{h_d} \equiv x \,(\mathrm{mod}\, N)} = \frac{1}{\varphi(N)} \sum_{\chi \in \widehat{G}} \chi({\mathbf{b}}_0x^{-1}) \prod_{i=1}^d \sum_{0\leq h < H} \chi^{h}({\mathbf{b}}_i). \end{align} $$
$$ \begin{align} \sum_{0\leq h_1, \ldots, h_d < H} \mathbf{1}_{{\mathbf{b}}_0 {\mathbf{b}}_1^{h_1}\cdots {\mathbf{b}}_d^{h_d} \equiv x \,(\mathrm{mod}\, N)} = \frac{1}{\varphi(N)} \sum_{\chi \in \widehat{G}} \chi({\mathbf{b}}_0x^{-1}) \prod_{i=1}^d \sum_{0\leq h < H} \chi^{h}({\mathbf{b}}_i). \end{align} $$
Let
![]() $\chi _0$
be the trivial character and
$\chi _0$
be the trivial character and
![]() $\chi _1, \chi _2, \chi _3$
be the three characters of order
$\chi _1, \chi _2, \chi _3$
be the three characters of order
![]() $2$
in
$2$
in
![]() $\widehat {G}$
. Each of these four characters
$\widehat {G}$
. Each of these four characters
![]() $\chi _j$
satisfies
$\chi _j$
satisfies
![]() $\chi _j({\mathbf {b}}_i)\in \{\pm 1\}$
for all i, so the term
$\chi _j({\mathbf {b}}_i)\in \{\pm 1\}$
for all i, so the term
![]() $\sum _{0\leq h < H} \chi _j^{h}({\mathbf {b}}_i)$
is either equal to H or lies in
$\sum _{0\leq h < H} \chi _j^{h}({\mathbf {b}}_i)$
is either equal to H or lies in
![]() $\{0,1\}$
. Hence, the contribution of these four characters to (4) is
$\{0,1\}$
. Hence, the contribution of these four characters to (4) is
 $$ \begin{align} \frac{H^d}{\varphi(N)} + \frac{1}{\varphi(N)} \sum_{j=1}^3 \chi_j({\mathbf{b}}_0x^{-1})\, C_j({\mathbf{b}}_1,\ldots, {\mathbf{b}}_d). \end{align} $$
$$ \begin{align} \frac{H^d}{\varphi(N)} + \frac{1}{\varphi(N)} \sum_{j=1}^3 \chi_j({\mathbf{b}}_0x^{-1})\, C_j({\mathbf{b}}_1,\ldots, {\mathbf{b}}_d). \end{align} $$
for some quantities
![]() $C_j({\mathbf {b}}_1,\ldots , {\mathbf {b}}_d)\geq 0$
. Since
$C_j({\mathbf {b}}_1,\ldots , {\mathbf {b}}_d)\geq 0$
. Since
![]() ${\mathbf {b}}_0$
is uniformly distributed in G, by (3) we have
${\mathbf {b}}_0$
is uniformly distributed in G, by (3) we have
as this is the probability that
![]() ${\mathbf {b}}_0x^{-1}$
lies in the subgroup of squares modulo N, which has index
${\mathbf {b}}_0x^{-1}$
lies in the subgroup of squares modulo N, which has index
![]() $4$
in G. Therefore, with probability
$4$
in G. Therefore, with probability
![]() $\geq 1/4$
, the expression (5) is bounded below by
$\geq 1/4$
, the expression (5) is bounded below by
![]() $H^d/\varphi (N)$
.
$H^d/\varphi (N)$
.
As a result, Proposition 2.2 reduces to showing that the contribution of the remaining characters
![]() $\chi \in \widehat {G}\setminus \{\chi _0,\chi _1,\chi _2,\chi _3\}$
to (4) is, with high probability, at most
$\chi \in \widehat {G}\setminus \{\chi _0,\chi _1,\chi _2,\chi _3\}$
to (4) is, with high probability, at most
![]() $H^d/(2\varphi (N))$
in absolute value. By Chebyshev’s inequality, it suffices to prove that
$H^d/(2\varphi (N))$
in absolute value. By Chebyshev’s inequality, it suffices to prove that
where
![]() $\mathbf {z}$
is the random variable defined by
$\mathbf {z}$
is the random variable defined by
 $$ \begin{align*} \mathbf{z} := \sum_{\substack{\chi\in \widehat{G} \\ \mathrm{ord}(\chi)> 2}} \Bigg\lvert \prod_{i=1}^d \sum_{0\leq h < H} \chi^{h}({\mathbf{b}}_i)\Bigg\rvert. \end{align*} $$
$$ \begin{align*} \mathbf{z} := \sum_{\substack{\chi\in \widehat{G} \\ \mathrm{ord}(\chi)> 2}} \Bigg\lvert \prod_{i=1}^d \sum_{0\leq h < H} \chi^{h}({\mathbf{b}}_i)\Bigg\rvert. \end{align*} $$
By the triangle inequality for the
![]() $L^2$
-norm and the definition of the random variables
$L^2$
-norm and the definition of the random variables
![]() ${\mathbf {b}}_i$
, we have
${\mathbf {b}}_i$
, we have
 $$ \begin{align*} {\mathbb{E}}\!\big[\left|\mathbf{z}\right|{}^2\big]^{1/2} \leq \sum_{\substack{\chi\in \widehat{G} \\ \mathrm{ord}(\chi)> 2}} \Bigg( {\mathbb{E}}\Bigg[ \bigg\lvert \prod_{i=1}^d \sum_{0\leq h < H} \chi^{h}({\mathbf{b}}_i)\bigg\rvert^2\Bigg]\Bigg)^{1/2} = \sum_{\substack{\chi\in \widehat{G} \\ \mathrm{ord}(\chi)> 2}} \Bigg( \mathop{\mathbb{E}}\limits_{p\leq X} \bigg\lvert \! \sum_{0\leq h < H} \chi^h(p) \bigg\rvert^2 \Bigg)^{d/2}. \end{align*} $$
$$ \begin{align*} {\mathbb{E}}\!\big[\left|\mathbf{z}\right|{}^2\big]^{1/2} \leq \sum_{\substack{\chi\in \widehat{G} \\ \mathrm{ord}(\chi)> 2}} \Bigg( {\mathbb{E}}\Bigg[ \bigg\lvert \prod_{i=1}^d \sum_{0\leq h < H} \chi^{h}({\mathbf{b}}_i)\bigg\rvert^2\Bigg]\Bigg)^{1/2} = \sum_{\substack{\chi\in \widehat{G} \\ \mathrm{ord}(\chi)> 2}} \Bigg( \mathop{\mathbb{E}}\limits_{p\leq X} \bigg\lvert \! \sum_{0\leq h < H} \chi^h(p) \bigg\rvert^2 \Bigg)^{d/2}. \end{align*} $$
Expanding the square and exchanging the order of summation, we obtain
 $$ \begin{align*} \mathop{\mathbb{E}}\limits_{p\leq X} \bigg\lvert\!\sum_{0\leq h < H} \chi^h(p) \bigg\rvert^2 \leq \sum_{0\leq h_1,h_2 < H}\, \left|\mathop{\mathbb{E}}\limits_{p\leq X} \chi^{h_1 - h_2}(p)\right| \leq H \sum_{|h| < H} \, \left|\mathop{\mathbb{E}}\limits_{p\leq X} \chi^{h}(p)\right|. \end{align*} $$
$$ \begin{align*} \mathop{\mathbb{E}}\limits_{p\leq X} \bigg\lvert\!\sum_{0\leq h < H} \chi^h(p) \bigg\rvert^2 \leq \sum_{0\leq h_1,h_2 < H}\, \left|\mathop{\mathbb{E}}\limits_{p\leq X} \chi^{h_1 - h_2}(p)\right| \leq H \sum_{|h| < H} \, \left|\mathop{\mathbb{E}}\limits_{p\leq X} \chi^{h}(p)\right|. \end{align*} $$
Therefore,
 $$ \begin{align} {\mathbb{E}}\!\big[\left|\mathbf{z}\right|{}^2\big]^{1/2} \leq H^{d/2} \sum_{\substack{\chi\in \widehat{G} \\ \mathrm{ord}(\chi)> 2}} \Bigg( \sum_{|h| < H} \left|\mathop{\mathbb{E}}\limits_{p\leq X} \chi^{h}(p)\right| \Bigg)^{d/2}. \end{align} $$
$$ \begin{align} {\mathbb{E}}\!\big[\left|\mathbf{z}\right|{}^2\big]^{1/2} \leq H^{d/2} \sum_{\substack{\chi\in \widehat{G} \\ \mathrm{ord}(\chi)> 2}} \Bigg( \sum_{|h| < H} \left|\mathop{\mathbb{E}}\limits_{p\leq X} \chi^{h}(p)\right| \Bigg)^{d/2}. \end{align} $$
To estimate the right-hand side of (7), we partition the set of characters as follows. For
![]() $j\geq 0$
, let
$j\geq 0$
, let
Notice that, by (3) and Definition 2.1, every character
![]() $\chi $
of order greater than
$\chi $
of order greater than
![]() $2$
has order at least
$2$
has order at least
![]() $\min (P', Q') \gg N^{1/4}$
. Hence, provided N is sufficiently large, for any
$\min (P', Q') \gg N^{1/4}$
. Hence, provided N is sufficiently large, for any
![]() $\chi $
of order greater than
$\chi $
of order greater than
![]() $2$
, the characters
$2$
, the characters
![]() $\chi ^h$
for
$\chi ^h$
for
![]() $0<|h|<H$
are all distinct. In addition, for any fixed
$0<|h|<H$
are all distinct. In addition, for any fixed
![]() $\psi \in \widehat {G}\setminus \{\chi _0,\chi _1,\chi _2,\chi _3\}$
and
$\psi \in \widehat {G}\setminus \{\chi _0,\chi _1,\chi _2,\chi _3\}$
and
![]() $0<|h|<H$
, there are at most four characters
$0<|h|<H$
, there are at most four characters
![]() $\chi $
such that
$\chi $
such that
![]() $\chi ^h = \psi $
. By Lemma 2.4, these observations imply that
$\chi ^h = \psi $
. By Lemma 2.4, these observations imply that
for all
![]() $j\geq 0$
.Footnote
10
$j\geq 0$
.Footnote
10
Let
![]() $j\geq 0$
and let
$j\geq 0$
and let
![]() $\chi \in E_j$
. By Lemma 2.4, there are at most
$\chi \in E_j$
. By Lemma 2.4, there are at most
![]() $e^{O(d)}$
integers
$e^{O(d)}$
integers
![]() $0\leq |h|<H$
such that
$0\leq |h|<H$
such that
![]() $\left |{\mathbb {E}}_{p\leq X} \chi ^{h}(p)\right |> d^{-2}$
. By definition of
$\left |{\mathbb {E}}_{p\leq X} \chi ^{h}(p)\right |> d^{-2}$
. By definition of
![]() $E_j$
, all other integers
$E_j$
, all other integers
![]() $0<|h|<H$
satisfy
$0<|h|<H$
satisfy
 $$ \begin{align*} \left|\mathop{\mathbb{E}}\limits_{p\leq X} \chi^{h}(p)\right| \leq \min(d^{-2}, e^{-j}). \end{align*} $$
$$ \begin{align*} \left|\mathop{\mathbb{E}}\limits_{p\leq X} \chi^{h}(p)\right| \leq \min(d^{-2}, e^{-j}). \end{align*} $$
Hence,
 $$ \begin{align*} \Bigg( \sum_{|h| < H} \left|\mathop{\mathbb{E}}\limits_{p\leq X} \chi^{h}(p)\right| \Bigg)^{d/2} \!\leq \big(e^{O(d)} + 2H \min(d^{-2}, e^{-j})\big)^{d/2} \leq e^{O(d^2)} + e^{O(d)}H^{d/2} \min(d^{-d}, e^{-jd/2}). \end{align*} $$
$$ \begin{align*} \Bigg( \sum_{|h| < H} \left|\mathop{\mathbb{E}}\limits_{p\leq X} \chi^{h}(p)\right| \Bigg)^{d/2} \!\leq \big(e^{O(d)} + 2H \min(d^{-2}, e^{-j})\big)^{d/2} \leq e^{O(d^2)} + e^{O(d)}H^{d/2} \min(d^{-d}, e^{-jd/2}). \end{align*} $$
Summing this over all
![]() $\chi \in E_j$
and
$\chi \in E_j$
and
![]() $j\geq 0$
, we can bound (7) by
$j\geq 0$
, we can bound (7) by
 $$ \begin{align*} {\mathbb{E}}\!\big[\left|\mathbf{z}\right|{}^2\big]^{1/2} \leq e^{O(d^2)}\phi(N)H^{d/2} + e^{O(d)}H^d \sum_{j\geq 0} \left|E_j\right| \min(d^{-d}, e^{-jd/2}). \end{align*} $$
$$ \begin{align*} {\mathbb{E}}\!\big[\left|\mathbf{z}\right|{}^2\big]^{1/2} \leq e^{O(d^2)}\phi(N)H^{d/2} + e^{O(d)}H^d \sum_{j\geq 0} \left|E_j\right| \min(d^{-d}, e^{-jd/2}). \end{align*} $$
Note that
![]() $\varphi (N)\leq N\leq e^{d^2}$
. Bounding
$\varphi (N)\leq N\leq e^{d^2}$
. Bounding
![]() $\left |E_j\right |$
using (8) and summing the resulting geometric series (using that N is sufficiently large), we obtain
$\left |E_j\right |$
using (8) and summing the resulting geometric series (using that N is sufficiently large), we obtain
Recalling that
![]() $H = \lfloor e^{Cd} \rfloor $
we see that, if C is a sufficiently large absolute constant, the right-hand side is
$H = \lfloor e^{Cd} \rfloor $
we see that, if C is a sufficiently large absolute constant, the right-hand side is
![]() $o(H^d)$
as
$o(H^d)$
as
![]() $N\to \infty $
. This establishes (6) and concludes the proof of Proposition 2.2.
$N\to \infty $
. This establishes (6) and concludes the proof of Proposition 2.2.
Remark 2.5. For Theorem 3.18, we obtain (with high probability) an asymptotic formula for quantities similar to (4), which is then combined with techniques from geometry of numbers to prove the existence of a short lattice basis.
This requires a more careful analysis of the small-order characters, which may be more numerous than in the special case treated above. Moreover, the analysis of large-order characters is much more delicate, as an exceptional character
![]() $\psi $
(in the sense of Lemma 2.4) may have more representations of the form
$\psi $
(in the sense of Lemma 2.4) may have more representations of the form
![]() $\psi = \chi ^h$
(for some
$\psi = \chi ^h$
(for some
![]() $\chi \in \widehat {G}$
and
$\chi \in \widehat {G}$
and
![]() $|h|<H$
) than the previous argument can handle. This issue is resolved by performing Fourier analysis on a well-chosen subgroup of
$|h|<H$
) than the previous argument can handle. This issue is resolved by performing Fourier analysis on a well-chosen subgroup of
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
, introduced in Section 3.1.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
, introduced in Section 3.1.
3 Proof of the existence of a short lattice basis
3.1 Restricting to a convenient subgroup of
 $\widehat {(\mathbb {Z}/N\mathbb {Z})^{\times }}$
$\widehat {(\mathbb {Z}/N\mathbb {Z})^{\times }}$
The goal of this preliminary section is to define a subgroup of the character group of
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
that does not have too many elements of small order. This will be crucial for Section 3.3, to reduce the influence of potential counterexamples to the Generalised Riemann Hypothesis. For example, we need to avoid having many characters
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
that does not have too many elements of small order. This will be crucial for Section 3.3, to reduce the influence of potential counterexamples to the Generalised Riemann Hypothesis. For example, we need to avoid having many characters
![]() $\chi _1, \ldots , \chi _k$
modulo N such that
$\chi _1, \ldots , \chi _k$
modulo N such that
![]() $\chi _i^2 = \psi $
for all i, where
$\chi _i^2 = \psi $
for all i, where
![]() $\psi $
is an exceptional character (in the sense that
$\psi $
is an exceptional character (in the sense that
![]() $L(s, \psi )$
has a zero very close to the line
$L(s, \psi )$
has a zero very close to the line
![]() $\Re s = 1$
). The definition of the suitable subgroup depends on the precise structure of
$\Re s = 1$
). The definition of the suitable subgroup depends on the precise structure of
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
.
Notation 3.1. If G is a finite abelian group (written multiplicatively) and
![]() $M\geq 1$
, we write
$M\geq 1$
, we write
![]() $G^M := \{x^M : x\in G\}$
for the subgroup of Mth powers in G.Footnote
11
$G^M := \{x^M : x\in G\}$
for the subgroup of Mth powers in G.Footnote
11
Lemma 3.2. Let G be a finite abelian group (written multiplicatively) and
![]() $M\geq 1$
. There is an isomorphism
$M\geq 1$
. There is an isomorphism
such that, for any
![]() $\chi \in \widehat {G^M}$
,
$\chi \in \widehat {G^M}$
,
![]() $\iota (\chi ) = \widetilde {\chi }^M$
where
$\iota (\chi ) = \widetilde {\chi }^M$
where
![]() $\widetilde {\chi }\in \widehat {G}$
is an arbitrary extension of
$\widetilde {\chi }\in \widehat {G}$
is an arbitrary extension of
![]() $\chi $
to G.
$\chi $
to G.
Proof. Pontryagin duality for finite abelian groups is an equivalence of categories, and therefore an exact functor. In simple terms, this implies that injections turn into surjections when switching to the dual, and vice versa. Hence, the Mth power map
![]() $G \twoheadrightarrow G^M$
,
$G \twoheadrightarrow G^M$
,
![]() $g\mapsto g^M$
, induces an injection
$g\mapsto g^M$
, induces an injection ![]() defined by
defined by
for every
![]() $\chi \in \widehat {G^M}$
and
$\chi \in \widehat {G^M}$
and
![]() $g\in G$
. Moreover, the restriction map
$g\in G$
. Moreover, the restriction map
![]() $\widehat {G} \to \widehat {G^M}$
is surjective, using exactness of Pontryagin duality again. Thus, every
$\widehat {G} \to \widehat {G^M}$
is surjective, using exactness of Pontryagin duality again. Thus, every
![]() $\chi \in \widehat {G^M}$
can be extended to a character
$\chi \in \widehat {G^M}$
can be extended to a character
![]() $\widetilde {\chi }$
on G, and
$\widetilde {\chi }$
on G, and
This implies that the image of
![]() $\iota $
is contained in
$\iota $
is contained in
![]() $\widehat {G}^M$
. Since
$\widehat {G}^M$
. Since
![]() $\big \lvert \widehat {G^M}\big \rvert = \big \lvert {G^M}\big \rvert = \big \lvert \widehat {G}^M\big \rvert $
, the lemma follows.
$\big \lvert \widehat {G^M}\big \rvert = \big \lvert {G^M}\big \rvert = \big \lvert \widehat {G}^M\big \rvert $
, the lemma follows.
Definition 3.3. Let
![]() $N \geq 1$
. For every
$N \geq 1$
. For every
![]() $h\geq 1$
we define
$h\geq 1$
we define
 $$ \begin{align*} K(h) := \frac{\left|(\mathbb{Z}/N\mathbb{Z})^{\times}\right|}{\left|((\mathbb{Z}/N\mathbb{Z})^{\times})^{h}\right|}. \end{align*} $$
$$ \begin{align*} K(h) := \frac{\left|(\mathbb{Z}/N\mathbb{Z})^{\times}\right|}{\left|((\mathbb{Z}/N\mathbb{Z})^{\times})^{h}\right|}. \end{align*} $$
In other words,
![]() $K(h)$
is the size of the kernel of the hth power map in
$K(h)$
is the size of the kernel of the hth power map in
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
.
Lemma 3.4. Let
![]() $N>2$
be an integer and
$N>2$
be an integer and
![]() $d := \lceil \! \sqrt {\log N} \rceil $
.
$d := \lceil \! \sqrt {\log N} \rceil $
.
For every prime p, define
![]() $m_p$
to be the largest non-negative integer such that
$m_p$
to be the largest non-negative integer such that
Let
![]() ${M_*} = {M_*}(N) := \prod _{p} p^{m_p}$
. Then the following holds.
${M_*} = {M_*}(N) := \prod _{p} p^{m_p}$
. Then the following holds.
-
1. We have
 ${M_*} \leq e^{10d}$
.
${M_*} \leq e^{10d}$
. -
2. For every
 $h\geq 1$
, we have
$h\geq 1$
, we have
 $K({M_*} h)/K({M_*})\leq h^{d/10}$
.
$K({M_*} h)/K({M_*})\leq h^{d/10}$
.
Proof.
-
1. For every prime p, since
 $K(p^{m_p})$
is a power of p dividing
$K(p^{m_p})$
is a power of p dividing
 $\left |(\mathbb {Z}/N\mathbb {Z})^{\times }\right | = \phi (N)$
, we have
$\left |(\mathbb {Z}/N\mathbb {Z})^{\times }\right | = \phi (N)$
, we have  $$ \begin{align*} \prod_{p} K(p^{m_p}) \mid \phi(N). \end{align*} $$
$$ \begin{align*} \prod_{p} K(p^{m_p}) \mid \phi(N). \end{align*} $$
By definition of
 $m_p$
, we know that
$m_p$
, we know that
 $K(p^{m_p}) \geq p^{d m_p/10}$
for every p, and thus
$K(p^{m_p}) \geq p^{d m_p/10}$
for every p, and thus  $$ \begin{align*} {M_*}^{d/10} = \prod_p p^{dm_p/10} \leq \prod_{p} K(p^{m_p}) \leq \phi(N) \leq N. \end{align*} $$
$$ \begin{align*} {M_*}^{d/10} = \prod_p p^{dm_p/10} \leq \prod_{p} K(p^{m_p}) \leq \phi(N) \leq N. \end{align*} $$
Recalling that
 $d = \lceil \! \sqrt {\log N} \rceil $
, it follows that
$d = \lceil \! \sqrt {\log N} \rceil $
, it follows that
 ${M_*} \leq e^{10d}$
.
${M_*} \leq e^{10d}$
. -
2. In any finite abelian group (written multiplicatively) and for any coprime integers a and b, there is an isomorphism
 $$ \begin{align*} \ker\!\big(g\mapsto g^{a}\big) \times \ker\!\big(g\mapsto g^{b}\big) \cong \ker\!\big(g\mapsto g^{ab}\big). \end{align*} $$
$$ \begin{align*} \ker\!\big(g\mapsto g^{a}\big) \times \ker\!\big(g\mapsto g^{b}\big) \cong \ker\!\big(g\mapsto g^{ab}\big). \end{align*} $$
Thus, if
 $h = \prod _{p} p^{e_p}$
is the prime factorisation of h, we see that
$h = \prod _{p} p^{e_p}$
is the prime factorisation of h, we see that
 $K({M_*}) = \prod _p K(p^{m_p})$
and
$K({M_*}) = \prod _p K(p^{m_p})$
and
 $K({M_*} h) = \prod _{p} K(p^{m_p+e_p})$
, where all products are finite. Whenever
$K({M_*} h) = \prod _{p} K(p^{m_p+e_p})$
, where all products are finite. Whenever
 $e_p\geq 1$
, we have
$e_p\geq 1$
, we have  $$ \begin{align*} K(p^{m_p+e_p}) < p^{d(m_p+e_p)/10},\quad K(p^{m_p}) \geq p^{dm_p/10} \end{align*} $$
$$ \begin{align*} K(p^{m_p+e_p}) < p^{d(m_p+e_p)/10},\quad K(p^{m_p}) \geq p^{dm_p/10} \end{align*} $$
by definition of
 $m_p$
. Thus
$m_p$
. Thus
 ${K(p^{m_p+e_p})}/{K(p^{m_p})} \leq p^{de_p/10}$
, and this last inequality also holds when
${K(p^{m_p+e_p})}/{K(p^{m_p})} \leq p^{de_p/10}$
, and this last inequality also holds when
 $e_p = 0$
. We conclude that
$e_p = 0$
. We conclude that  $$ \begin{align*} \frac{K({M_*} h)}{K({M_*})} = \prod_p \frac{K(p^{m_p+e_p})}{K(p^{m_p})} \leq \prod_p p^{de_p/10} = h^{d/10}. \end{align*} $$
$$ \begin{align*} \frac{K({M_*} h)}{K({M_*})} = \prod_p \frac{K(p^{m_p+e_p})}{K(p^{m_p})} \leq \prod_p p^{de_p/10} = h^{d/10}. \end{align*} $$
as claimed.
Lemma 3.5. Let
![]() $N> 2$
,
$N> 2$
,
![]() $d := \lceil \! \sqrt {\log N} \rceil $
,
$d := \lceil \! \sqrt {\log N} \rceil $
,
![]() $G := (\mathbb {Z}/N\mathbb {Z})^{\times }$
and let
$G := (\mathbb {Z}/N\mathbb {Z})^{\times }$
and let
![]() ${M_*}\geq 1$
be the integer defined in the statement of Lemma 3.4.
${M_*}\geq 1$
be the integer defined in the statement of Lemma 3.4.
Let
![]() $h\geq 1$
. Let
$h\geq 1$
. Let
![]() $\chi _1, \ldots , \chi _n \in \widehat {G^{M_*}}$
be distinct characters such that
$\chi _1, \ldots , \chi _n \in \widehat {G^{M_*}}$
be distinct characters such that
Then
![]() $n \leq h^{d/10}$
.
$n \leq h^{d/10}$
.
Proof. Let
![]() $f_h : G^{M_*} \to G^{M_*}$
be the hth power map,
$f_h : G^{M_*} \to G^{M_*}$
be the hth power map,
![]() $f(\chi ) := \chi ^h$
. By assumption, the n distinct characters
$f(\chi ) := \chi ^h$
. By assumption, the n distinct characters
![]() $\chi _1\chi _n^{-1}, \chi _2\chi _n^{-1}, \ldots , \chi _n\chi _n^{-1}$
lie in the kernel of f. Hence,
$\chi _1\chi _n^{-1}, \chi _2\chi _n^{-1}, \ldots , \chi _n\chi _n^{-1}$
lie in the kernel of f. Hence,
 $$ \begin{align*} n \leq \big\lvert \!\ker(f)\big\rvert = \frac{|G^{M_*}|}{|(G^{M_*})^h|} = \frac{|((\mathbb{Z}/N\mathbb{Z})^{\times})^{M_*}|}{|((\mathbb{Z}/N\mathbb{Z})^{\times})^{{M_*} h}|} = \frac{K({M_*} h)}{K({M_*})}, \end{align*} $$
$$ \begin{align*} n \leq \big\lvert \!\ker(f)\big\rvert = \frac{|G^{M_*}|}{|(G^{M_*})^h|} = \frac{|((\mathbb{Z}/N\mathbb{Z})^{\times})^{M_*}|}{|((\mathbb{Z}/N\mathbb{Z})^{\times})^{{M_*} h}|} = \frac{K({M_*} h)}{K({M_*})}, \end{align*} $$
which is
![]() $\leq h^{d/10}$
by Lemma 3.4.
$\leq h^{d/10}$
by Lemma 3.4.
3.2 Lattice point counting via characters
To prove Theorem 3.18, we will need to study the following quantities.
Definition 3.6. Let
![]() $N\geq 1$
,
$N\geq 1$
,
![]() $G = (\mathbb {Z}/N\mathbb {Z})^{\times }$
and
$G = (\mathbb {Z}/N\mathbb {Z})^{\times }$
and
![]() $\chi \in \widehat {G}$
. For all
$\chi \in \widehat {G}$
. For all
![]() $d\geq 1$
and
$d\geq 1$
and
![]() $b_1, \ldots , b_d\in G$
, we define the quantity
$b_1, \ldots , b_d\in G$
, we define the quantity
 $$ \begin{align*} F_{\chi,H}(b_1, \ldots, b_d) := \prod_{i=1}^d \sum_{|h|\leq H} \chi^h(b_i). \end{align*} $$
$$ \begin{align*} F_{\chi,H}(b_1, \ldots, b_d) := \prod_{i=1}^d \sum_{|h|\leq H} \chi^h(b_i). \end{align*} $$
The following lemma relates these expressions to a lattice point counting problem.
Lemma 3.7. Let
![]() $N,M,d,H \geq 1$
be integers. Let
$N,M,d,H \geq 1$
be integers. Let
![]() $b_1, \ldots , b_d\in G := (\mathbb {Z}/N\mathbb {Z})^{\times }$
. The number of vectors
$b_1, \ldots , b_d\in G := (\mathbb {Z}/N\mathbb {Z})^{\times }$
. The number of vectors
![]() $(e_1, \ldots , e_d)\in \mathbb {Z}^d \cap [-H,H]^d$
such that
$(e_1, \ldots , e_d)\in \mathbb {Z}^d \cap [-H,H]^d$
such that
 $$ \begin{align*} \prod_{i=1}^d b_i^{Me_i} \equiv 1 \quad\pmod N \end{align*} $$
$$ \begin{align*} \prod_{i=1}^d b_i^{Me_i} \equiv 1 \quad\pmod N \end{align*} $$
is equal to
 $$ \begin{align} \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \sum_{\chi \in \widehat{G}^M} F_{\chi,H}(b_1, \ldots, b_d). \end{align} $$
$$ \begin{align} \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \sum_{\chi \in \widehat{G}^M} F_{\chi,H}(b_1, \ldots, b_d). \end{align} $$
Proof. By orthogonality of characters in the abelian group
![]() $G^M$
, we have
$G^M$
, we have
 $$ \begin{align*} \mathbf{1}_{\prod_i b_i^{Me_i} \equiv 1 \,(\mathrm{mod}\, N)} = \frac{1}{\big\lvert \widehat{G^M}\big\rvert} \sum_{\psi \in \widehat{G^M}} \psi \left(\prod_{i=1}^d b_i^{Me_i}\right) = \frac{1}{\big\lvert \widehat{G^M}\big\rvert} \sum_{\psi \in \widehat{G^M}} \prod_{i=1}^d \psi \big( b_i^{Me_i}\big). \end{align*} $$
$$ \begin{align*} \mathbf{1}_{\prod_i b_i^{Me_i} \equiv 1 \,(\mathrm{mod}\, N)} = \frac{1}{\big\lvert \widehat{G^M}\big\rvert} \sum_{\psi \in \widehat{G^M}} \psi \left(\prod_{i=1}^d b_i^{Me_i}\right) = \frac{1}{\big\lvert \widehat{G^M}\big\rvert} \sum_{\psi \in \widehat{G^M}} \prod_{i=1}^d \psi \big( b_i^{Me_i}\big). \end{align*} $$
Observe that
![]() $\psi \big ( b_i^{Me_i}\big ) = \iota (\psi ) (b_i^{e_i})$
, where
$\psi \big ( b_i^{Me_i}\big ) = \iota (\psi ) (b_i^{e_i})$
, where
![]() $\iota $
is the isomorphism
$\iota $
is the isomorphism
![]() $\widehat {G^M} \xrightarrow {\sim } \widehat {G}^M$
defined in Lemma 3.2. We may thus rewrite this equality as
$\widehat {G^M} \xrightarrow {\sim } \widehat {G}^M$
defined in Lemma 3.2. We may thus rewrite this equality as
 $$ \begin{align*} \mathbf{1}_{\prod_i b_i^{Me_i} \equiv 1 \,(\mathrm{mod}\, N)} = \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \sum_{\chi \in \widehat{G}^M} \prod_{i=1}^d \chi \big( b_i^{e_i}\big). \end{align*} $$
$$ \begin{align*} \mathbf{1}_{\prod_i b_i^{Me_i} \equiv 1 \,(\mathrm{mod}\, N)} = \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \sum_{\chi \in \widehat{G}^M} \prod_{i=1}^d \chi \big( b_i^{e_i}\big). \end{align*} $$
Therefore, the number of vectors
![]() $(e_1, \ldots , e_d)\in \mathbb {Z}^d \cap [-H,H]^d$
such that
$(e_1, \ldots , e_d)\in \mathbb {Z}^d \cap [-H,H]^d$
such that
![]() $\prod _{i=1}^d b_i^{Me_i} \equiv 1 \ \pmod N$
is
$\prod _{i=1}^d b_i^{Me_i} \equiv 1 \ \pmod N$
is
 $$ \begin{align*} \sum_{\substack{(e_1, \ldots, e_d)\in \mathbb{Z}^d \\ \max_i |e_i|\leq H}} \mathbf{1}_{\prod_i {\mathbf{b}}_i^{Me_i} \equiv 1~(N)} = \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \sum_{\chi \in \widehat{G}^M} \sum_{\substack{(e_1, \ldots, e_d)\in \mathbb{Z}^d \\ \max_i |e_i|\leq H}} \prod_{i=1}^d \chi^{e_i} (b_i) = \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \sum_{\chi \in \widehat{G}^M} F_{\chi,H}(b_1, \ldots, b_d) \end{align*} $$
$$ \begin{align*} \sum_{\substack{(e_1, \ldots, e_d)\in \mathbb{Z}^d \\ \max_i |e_i|\leq H}} \mathbf{1}_{\prod_i {\mathbf{b}}_i^{Me_i} \equiv 1~(N)} = \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \sum_{\chi \in \widehat{G}^M} \sum_{\substack{(e_1, \ldots, e_d)\in \mathbb{Z}^d \\ \max_i |e_i|\leq H}} \prod_{i=1}^d \chi^{e_i} (b_i) = \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \sum_{\chi \in \widehat{G}^M} F_{\chi,H}(b_1, \ldots, b_d) \end{align*} $$
as claimed.
It is fairly straightforward to estimate
![]() $F_{\chi ,H}(b_1, \ldots , b_d)$
when
$F_{\chi ,H}(b_1, \ldots , b_d)$
when
![]() $\chi $
is a character of small order in
$\chi $
is a character of small order in
![]() $\widehat {G}$
. The contribution of these small-order characters gives the expected main term for (9).
$\widehat {G}$
. The contribution of these small-order characters gives the expected main term for (9).
Lemma 3.8 (Main term).
Let
![]() $N,M,d \geq 1$
be integers. Let
$N,M,d \geq 1$
be integers. Let
![]() $b_1, \ldots , b_d\in G := (\mathbb {Z}/N\mathbb {Z})^{\times }$
. Uniformly for all integers
$b_1, \ldots , b_d\in G := (\mathbb {Z}/N\mathbb {Z})^{\times }$
. Uniformly for all integers
![]() $H\geq e^{31d}$
, we have
$H\geq e^{31d}$
, we have
 $$ \begin{align} \frac{1}{\big\lvert \widehat{G}^M\big\rvert}\sum_{\chi \in \widehat{G}^M} F_{\chi,H}(\underline{b}) = \left(1 + O\left(\frac{e^{31d}}{H}\right)\right) \frac{ (2H+1)^{d} }{ \big\lvert\left\langle b_1^M, \ldots, b_d^M\right\rangle\big\rvert } + \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \!\!\!\!\sum_{\substack{\chi \in \widehat{G}^M\\ \mathrm{ord}(\chi) \geq e^{10d}}} \!\!\!\! \left|F_{\chi,H}(\underline{b})\right|, \end{align} $$
$$ \begin{align} \frac{1}{\big\lvert \widehat{G}^M\big\rvert}\sum_{\chi \in \widehat{G}^M} F_{\chi,H}(\underline{b}) = \left(1 + O\left(\frac{e^{31d}}{H}\right)\right) \frac{ (2H+1)^{d} }{ \big\lvert\left\langle b_1^M, \ldots, b_d^M\right\rangle\big\rvert } + \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \!\!\!\!\sum_{\substack{\chi \in \widehat{G}^M\\ \mathrm{ord}(\chi) \geq e^{10d}}} \!\!\!\! \left|F_{\chi,H}(\underline{b})\right|, \end{align} $$
where
![]() $F_{\chi ,H}(\underline {b})$
is short for
$F_{\chi ,H}(\underline {b})$
is short for
![]() $F_{\chi ,H}(b_1, \ldots , b_d)$
.
$F_{\chi ,H}(b_1, \ldots , b_d)$
.
Proof. Define
Observe that
 $$ \begin{align} \big\lvert \left\langle b_1, \ldots, b_d\right\rangle^{\perp} \cap \widehat{G}^M \big\rvert = \big\lvert \big\{\chi\in \widehat{G^M} \ :\ \forall i\in [d], \,\chi\big(b_i^M\big)=1 \big\}\big\rvert = \frac{\big\lvert {G^M}\big\rvert}{\big\lvert\left\langle b_1^M, \ldots, b_d^M\right\rangle\big\rvert} \end{align} $$
$$ \begin{align} \big\lvert \left\langle b_1, \ldots, b_d\right\rangle^{\perp} \cap \widehat{G}^M \big\rvert = \big\lvert \big\{\chi\in \widehat{G^M} \ :\ \forall i\in [d], \,\chi\big(b_i^M\big)=1 \big\}\big\rvert = \frac{\big\lvert {G^M}\big\rvert}{\big\lvert\left\langle b_1^M, \ldots, b_d^M\right\rangle\big\rvert} \end{align} $$
where the first equality follows from Lemma 3.2 and the second from the canonical isomorphism
![]() $H_1^{\perp } \cong \widehat {G_1/H_1}$
for any subgroup
$H_1^{\perp } \cong \widehat {G_1/H_1}$
for any subgroup
![]() $H_1$
of a finite abelian group
$H_1$
of a finite abelian group
![]() $G_1$
.
$G_1$
.
Clearly, if
![]() $\chi \in \left \langle b_1, \ldots , b_d\right \rangle ^{\perp }\cap \widehat {G}^M$
, we have
$\chi \in \left \langle b_1, \ldots , b_d\right \rangle ^{\perp }\cap \widehat {G}^M$
, we have
![]() $F_{\chi ,H}(\underline {b}) = (2H+1)^d$
. Hence, by (11), those characters contribute
$F_{\chi ,H}(\underline {b}) = (2H+1)^d$
. Hence, by (11), those characters contribute
 $$ \begin{align*} \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \sum_{\chi \in \left\langle b_1, \ldots, b_d\right\rangle^{\perp} \cap \widehat{G}^M} F_{\chi,H}(\underline{b}) = \frac{(2H+1)^d}{\big\lvert\left\langle b_1^M, \ldots, b_d^M\right\rangle\big\rvert} \end{align*} $$
$$ \begin{align*} \frac{1}{\big\lvert \widehat{G}^M\big\rvert} \sum_{\chi \in \left\langle b_1, \ldots, b_d\right\rangle^{\perp} \cap \widehat{G}^M} F_{\chi,H}(\underline{b}) = \frac{(2H+1)^d}{\big\lvert\left\langle b_1^M, \ldots, b_d^M\right\rangle\big\rvert} \end{align*} $$
to the sum (10).
For any character
![]() $\chi \in \widehat {G}^{M}\setminus \left \langle b_1, \ldots , b_d\right \rangle ^{\perp }$
of order
$\chi \in \widehat {G}^{M}\setminus \left \langle b_1, \ldots , b_d\right \rangle ^{\perp }$
of order
![]() $\leq e^{10d}$
, and any
$\leq e^{10d}$
, and any
![]() $i\in [d]$
such that
$i\in [d]$
such that
![]() $\chi (b_i) \neq 1$
, we can bound
$\chi (b_i) \neq 1$
, we can bound
 $$ \begin{align*} \left|\sum_{|h| \leq H} \chi(b_i)^h\right| \leq \mathrm{ord}(\chi) \leq e^{10d} \end{align*} $$
$$ \begin{align*} \left|\sum_{|h| \leq H} \chi(b_i)^h\right| \leq \mathrm{ord}(\chi) \leq e^{10d} \end{align*} $$
by the geometric series formula. Thus, defining
we have
Consequently,
 $$ \begin{align} \sum_{\substack{\chi \in \widehat{G}^{M}\setminus \left\langle b_1, \ldots, b_d\right\rangle^{\perp}\\ \mathrm{ord}(\chi) \leq e^{10d}}} \left|F_{\chi,H}(\underline{b})\right| \ll \sum_{\substack{I \subset [d]\\ I\neq \emptyset}} e^{10d\left|I\right|} (2H+1)^{d - \left|I\right|} \sum_{\substack{\chi \in \widehat{G}^M\\ \mathrm{ord}(\chi) \leq e^{10d}\\ I_{\chi} = I}} 1. \end{align} $$
$$ \begin{align} \sum_{\substack{\chi \in \widehat{G}^{M}\setminus \left\langle b_1, \ldots, b_d\right\rangle^{\perp}\\ \mathrm{ord}(\chi) \leq e^{10d}}} \left|F_{\chi,H}(\underline{b})\right| \ll \sum_{\substack{I \subset [d]\\ I\neq \emptyset}} e^{10d\left|I\right|} (2H+1)^{d - \left|I\right|} \sum_{\substack{\chi \in \widehat{G}^M\\ \mathrm{ord}(\chi) \leq e^{10d}\\ I_{\chi} = I}} 1. \end{align} $$
Fix some nonempty set
![]() $I \subset [d]$
and complex numbers
$I \subset [d]$
and complex numbers
![]() $(z_i)_{i\in I}$
. Let
$(z_i)_{i\in I}$
. Let
![]() $C_{I, (z_i)}$
be the set of all characters
$C_{I, (z_i)}$
be the set of all characters
![]() $\chi \in \widehat {G}^M$
such that
$\chi \in \widehat {G}^M$
such that
 $$ \begin{align*} \chi(b_i) = \begin{cases} z_i & \text{if }i\in I \\ 1 & \text{if }i\in [d]\setminus I. \end{cases} \end{align*} $$
$$ \begin{align*} \chi(b_i) = \begin{cases} z_i & \text{if }i\in I \\ 1 & \text{if }i\in [d]\setminus I. \end{cases} \end{align*} $$
Note that
![]() $C_{I, (z_i)}$
is either the empty set, or a coset of
$C_{I, (z_i)}$
is either the empty set, or a coset of
![]() $\left \langle b_1, \ldots , b_d\right \rangle ^{\perp } \cap \widehat {G}^M$
in
$\left \langle b_1, \ldots , b_d\right \rangle ^{\perp } \cap \widehat {G}^M$
in
![]() $\widehat {G}^M$
. Moreover, if
$\widehat {G}^M$
. Moreover, if
![]() $\chi $
has order at most
$\chi $
has order at most
![]() $e^{10d}$
, this set
$e^{10d}$
, this set
![]() $C_{I, (z_i)}$
can only be nonempty if all
$C_{I, (z_i)}$
can only be nonempty if all
![]() $z_i$
are roots of unity of order
$z_i$
are roots of unity of order
![]() $\leq e^{10d}$
, and there are
$\leq e^{10d}$
, and there are
![]() $\leq e^{20d}$
such roots of unity. We conclude that
$\leq e^{20d}$
such roots of unity. We conclude that
 $$ \begin{align*} \sum_{\substack{\chi \in \widehat{G}^M\\ \mathrm{ord}(\chi) \leq e^{10d}\\ I_{\chi} = I}} 1 \leq \sum_{(z_i)_{i\in I}} \left|C_{I, (z_i)}\right|\leq e^{20d|I|} \big\lvert \left\langle b_1, \ldots, b_d\right\rangle^{\perp} \cap \widehat{G}^M \big\rvert. \end{align*} $$
$$ \begin{align*} \sum_{\substack{\chi \in \widehat{G}^M\\ \mathrm{ord}(\chi) \leq e^{10d}\\ I_{\chi} = I}} 1 \leq \sum_{(z_i)_{i\in I}} \left|C_{I, (z_i)}\right|\leq e^{20d|I|} \big\lvert \left\langle b_1, \ldots, b_d\right\rangle^{\perp} \cap \widehat{G}^M \big\rvert. \end{align*} $$
Thus, we can bound the right-hand side of (12) by
 $$ \begin{align*} \ll (2H+1)^{d} \big\lvert \left\langle b_1, \ldots, b_d\right\rangle^{\perp} \cap \widehat{G}^M \big\rvert \sum_{\substack{I \subset [d]\\ I\neq \emptyset}} \big(e^{30d} H^{-1}\big)^{\left|I\right|} \ll (2H+1)^{d} \big\lvert \left\langle b_1, \ldots, b_d\right\rangle^{\perp} \cap \widehat{G}^M \big\rvert 2^{d}e^{30d}H^{-1} \end{align*} $$
$$ \begin{align*} \ll (2H+1)^{d} \big\lvert \left\langle b_1, \ldots, b_d\right\rangle^{\perp} \cap \widehat{G}^M \big\rvert \sum_{\substack{I \subset [d]\\ I\neq \emptyset}} \big(e^{30d} H^{-1}\big)^{\left|I\right|} \ll (2H+1)^{d} \big\lvert \left\langle b_1, \ldots, b_d\right\rangle^{\perp} \cap \widehat{G}^M \big\rvert 2^{d}e^{30d}H^{-1} \end{align*} $$
where we used that
![]() $H\geq e^{30d}$
in the last step. By (11), this means that
$H\geq e^{30d}$
in the last step. By (11), this means that
 $$ \begin{align*} \frac{1}{\big\lvert \widehat{G}^M\big\rvert}\sum_{\substack{\chi \in \widehat{G}^{M}\setminus \left\langle b_1, \ldots, b_d\right\rangle^{\perp}\\ \mathrm{ord}(\chi) \leq e^{10d}}} \left|F_{\chi,H}(\underline{b})\right|\ll e^{31d}H^{-1} \frac{(2H+1)^d}{\big\lvert\left\langle b_1^M, \ldots, b_d^M\right\rangle\big\rvert}, \end{align*} $$
$$ \begin{align*} \frac{1}{\big\lvert \widehat{G}^M\big\rvert}\sum_{\substack{\chi \in \widehat{G}^{M}\setminus \left\langle b_1, \ldots, b_d\right\rangle^{\perp}\\ \mathrm{ord}(\chi) \leq e^{10d}}} \left|F_{\chi,H}(\underline{b})\right|\ll e^{31d}H^{-1} \frac{(2H+1)^d}{\big\lvert\left\langle b_1^M, \ldots, b_d^M\right\rangle\big\rvert}, \end{align*} $$
which completes the proof.
3.3 Bounding the contribution of large-order characters
In this section, we bound the error term coming from large-order characters, on average over primes
![]() $b_1, \ldots , b_d$
in a short interval.
$b_1, \ldots , b_d$
in a short interval.
We will need the following ingredients from classical analytic number theory.
Proposition 3.9 (Character sums over primes).
Let
![]() $1/2 \leq \alpha \leq 1$
. Let
$1/2 \leq \alpha \leq 1$
. Let
![]() $q, x\geq 2$
. Let
$q, x\geq 2$
. Let
![]() $\chi $
be a nonprincipal character modulo q whose Dirichlet L-function
$\chi $
be a nonprincipal character modulo q whose Dirichlet L-function
![]() $L(s, \chi )$
has no zero in the rectangle
$L(s, \chi )$
has no zero in the rectangle
Then
 $$ \begin{align*} \frac{1}{\pi(x)} \sum_{p\leq x} \chi(p) \ll x^{-(1-\alpha)} \log^3 (qx). \end{align*} $$
$$ \begin{align*} \frac{1}{\pi(x)} \sum_{p\leq x} \chi(p) \ll x^{-(1-\alpha)} \log^3 (qx). \end{align*} $$
Proposition 3.9 is a standard consequence of the explicit formula for
![]() $L(s, \chi )$
and is proved in Appendix A. The logarithmic factors can be somewhat improved, but such refinements are irrelevant here.
$L(s, \chi )$
and is proved in Appendix A. The logarithmic factors can be somewhat improved, but such refinements are irrelevant here.
The Generalised Riemann Hypothesis is the claim that, for every Dirichlet character
![]() $\chi $
,
$\chi $
,
![]() $L(s, \chi )$
has no zero
$L(s, \chi )$
has no zero
![]() $\rho $
with
$\rho $
with
![]() $\frac {1}{2} < \Re \rho < 1$
. Assuming GRH, Proposition 3.9 thus implies almost square-root cancellation for character sums over primes. Proposition 3.10 will serve as an unconditional substitute for GRH.
$\frac {1}{2} < \Re \rho < 1$
. Assuming GRH, Proposition 3.9 thus implies almost square-root cancellation for character sums over primes. Proposition 3.10 will serve as an unconditional substitute for GRH.
Proposition 3.10 (Zero-density estimate for a fixed modulus).
Uniformly for
![]() $\tfrac 45 \leq \alpha \leq 1$
and
$\tfrac 45 \leq \alpha \leq 1$
and
![]() $q, T\geq 1$
, we have
$q, T\geq 1$
, we have
 $$ \begin{align*} \sum_{\substack{\chi \,(\mathrm{mod}\, q)}} \mathcal{N}(\alpha, T, \chi) \ll_{\varepsilon} (qT)^{(2+\varepsilon)(1-\alpha)}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{\chi \,(\mathrm{mod}\, q)}} \mathcal{N}(\alpha, T, \chi) \ll_{\varepsilon} (qT)^{(2+\varepsilon)(1-\alpha)}. \end{align*} $$
where
![]() $\mathcal {N}(\alpha , T, \chi )$
denotes the number of zeros (with multiplicity) of
$\mathcal {N}(\alpha , T, \chi )$
denotes the number of zeros (with multiplicity) of
![]() $L(s, \chi )$
in the rectangle
$L(s, \chi )$
in the rectangle
Proof. This is [Reference Jutila11, Theorem 1 (1.7)].
Our goal is to control the total contribution of all large-order characters in (10). We will do so in Proposition 3.14 (restricting to a suitable sugbroup of
![]() $\widehat {G}$
). We first prove the following
$\widehat {G}$
). We first prove the following
![]() $L^2$
bound for a single large-order character.
$L^2$
bound for a single large-order character.
Lemma 3.11. Let
![]() $N> 2$
be an integer and let
$N> 2$
be an integer and let
![]() $G = (\mathbb {Z}/N\mathbb {Z})^{\times }$
. Let
$G = (\mathbb {Z}/N\mathbb {Z})^{\times }$
. Let
![]() $d = \lceil \sqrt {\log N} \rceil $
and
$d = \lceil \sqrt {\log N} \rceil $
and
![]() $X = d^{10^3 d}$
.
$X = d^{10^3 d}$
.
Let
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes less than X not dividing N. Let
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes less than X not dividing N. Let
![]() $\chi \in \widehat {G}$
be a character of order
$\chi \in \widehat {G}$
be a character of order
![]() $\geq e^{10d}$
. Then, for every
$\geq e^{10d}$
. Then, for every
![]() $H\geq e^{10d}$
,
$H\geq e^{10d}$
,
Proof. By Proposition 3.10 (the zero-density estimate), the number of Dirichlet characters modulo N whose associated L-function has a zero in the region
 $$ \begin{align} \left\{s\in \mathbb{C}\ : \ {1-\frac{1}{10d}}< \Re{s} \leq 1,\ \left|\Im{s}\right| \leq {X}\right\} \end{align} $$
$$ \begin{align} \left\{s\in \mathbb{C}\ : \ {1-\frac{1}{10d}}< \Re{s} \leq 1,\ \left|\Im{s}\right| \leq {X}\right\} \end{align} $$
is bounded by
If a nonprincipal character
![]() $\psi $
modulo N has no zero in the region (13), then by Proposition 3.9 we have
$\psi $
modulo N has no zero in the region (13), then by Proposition 3.9 we have
We now expand
![]() $\mathbb {E}\left [ |F_{\chi ,H}({\mathbf {b}}_1, \ldots , {\mathbf {b}}_d)|^2 \right ]$
as
$\mathbb {E}\left [ |F_{\chi ,H}({\mathbf {b}}_1, \ldots , {\mathbf {b}}_d)|^2 \right ]$
as
 $$ \begin{align*} \mathbb{E}\left[ \bigg\lvert \prod_{i=1}^d \sum_{|h|\leq H} \chi^h({\mathbf{b}}_i) \bigg\rvert^2 \right] & = \prod_{i=1}^d \mathbb{E}\left[\bigg\lvert\sum_{|h|\leq H} \chi^h({\mathbf{b}}_i)\bigg\rvert^2 \right] \\ & = \Bigg(\sum_{|h_1|\leq H} \sum_{|h_2|\leq H} \mathbb{E}\left[\chi^{h_1-h_2}({\mathbf{b}}_1)\right]\Bigg)^d \\ & \leq (2H+1)^d \Bigg(\sum_{|h|\leq 2H} \left|\mathbb{E}\left[\chi^h({\mathbf{b}}_1)\right]\right|\Bigg)^d. \end{align*} $$
$$ \begin{align*} \mathbb{E}\left[ \bigg\lvert \prod_{i=1}^d \sum_{|h|\leq H} \chi^h({\mathbf{b}}_i) \bigg\rvert^2 \right] & = \prod_{i=1}^d \mathbb{E}\left[\bigg\lvert\sum_{|h|\leq H} \chi^h({\mathbf{b}}_i)\bigg\rvert^2 \right] \\ & = \Bigg(\sum_{|h_1|\leq H} \sum_{|h_2|\leq H} \mathbb{E}\left[\chi^{h_1-h_2}({\mathbf{b}}_1)\right]\Bigg)^d \\ & \leq (2H+1)^d \Bigg(\sum_{|h|\leq 2H} \left|\mathbb{E}\left[\chi^h({\mathbf{b}}_1)\right]\right|\Bigg)^d. \end{align*} $$
We can use (15) to bound the term
![]() $\mathbb {E}\left [\chi ^h({\mathbf {b}}_1)\right ]$
, unless
$\mathbb {E}\left [\chi ^h({\mathbf {b}}_1)\right ]$
, unless
![]() $\chi ^h$
is principal or
$\chi ^h$
is principal or
![]() $L(s, \chi ^h)$
has a zero in the region (13). By (14), the number of values of h with
$L(s, \chi ^h)$
has a zero in the region (13). By (14), the number of values of h with
![]() $|h|\leq 2H$
for which one of these two situations occurs is
$|h|\leq 2H$
for which one of these two situations occurs is
 $$ \begin{align*} \ll \left(1+\frac{H}{\mathrm{ord}(\chi)}\right) e^{d} \ll e^{-10d} e^{d}H \ll e^{-d}H. \end{align*} $$
$$ \begin{align*} \ll \left(1+\frac{H}{\mathrm{ord}(\chi)}\right) e^{d} \ll e^{-10d} e^{d}H \ll e^{-d}H. \end{align*} $$
By (15), we deduce that, for all but
![]() $O(e^{-d}H)$
values of
$O(e^{-d}H)$
values of
![]() $|h|\leq 2H$
, the bound
$|h|\leq 2H$
, the bound
![]() $\mathbb {E}\left [\chi ^h({\mathbf {b}}_1)\right ]\ll d^{-94}$
holds. Hence
$\mathbb {E}\left [\chi ^h({\mathbf {b}}_1)\right ]\ll d^{-94}$
holds. Hence
as desired.
Lemma 3.11 applies to all characters
![]() $\chi $
of order at least
$\chi $
of order at least
![]() $e^{10d}$
, but gives a relatively weak upper bound. In Lemma 3.13, we will prove that a stronger bound can be obtained if a small set of exceptions is allowed. We begin by describing the exceptional characters in the following lemma.
$e^{10d}$
, but gives a relatively weak upper bound. In Lemma 3.13, we will prove that a stronger bound can be obtained if a small set of exceptions is allowed. We begin by describing the exceptional characters in the following lemma.
Lemma 3.12. There is some absolute constant
![]() $t_0\geq 1$
such that the following holds.
$t_0\geq 1$
such that the following holds.
Let
![]() $N,G,d,X$
and
$N,G,d,X$
and
![]() ${\mathbf {b}}_i$
be as in Lemma 3.11. Let
${\mathbf {b}}_i$
be as in Lemma 3.11. Let
![]() $H\geq e^{10d}$
.
$H\geq e^{10d}$
.
Let
![]() $\chi \in \widehat {G}$
be a character of order
$\chi \in \widehat {G}$
be a character of order
![]() $\geq e^{10d}$
such that
$\geq e^{10d}$
such that
for some t with
![]() $t_0 \leq t\leq 2d$
.
$t_0 \leq t\leq 2d$
.
Then there are integers
![]() $-2H \leq h_1, h_2\leq 2H$
with
$-2H \leq h_1, h_2\leq 2H$
with
![]() $0 < h_2-h_1 \leq e^{3t}$
such that both
$0 < h_2-h_1 \leq e^{3t}$
such that both
![]() $L(s, \chi ^{h_1})$
and
$L(s, \chi ^{h_1})$
and
![]() $L(s, \chi ^{h_2})$
have a zero in the region
$L(s, \chi ^{h_2})$
have a zero in the region
Proof. As in the proof of Lemma 3.11, we have
 $$ \begin{align} \mathbb{E}\left[ |F_{\chi,H}({\mathbf{b}}_1, \ldots, {\mathbf{b}}_d)|^2 \right] = \mathbb{E}\left[ \bigg\lvert \prod_{i=1}^d \sum_{|h|\leq H} \chi^h({\mathbf{b}}_i) \bigg\rvert^2 \right] \leq (2H+1)^d \Bigg(\sum_{|h|\leq 2H} \left|\mathbb{E}\left[\chi^h({\mathbf{b}}_1)\right]\right|\Bigg)^d. \end{align} $$
$$ \begin{align} \mathbb{E}\left[ |F_{\chi,H}({\mathbf{b}}_1, \ldots, {\mathbf{b}}_d)|^2 \right] = \mathbb{E}\left[ \bigg\lvert \prod_{i=1}^d \sum_{|h|\leq H} \chi^h({\mathbf{b}}_i) \bigg\rvert^2 \right] \leq (2H+1)^d \Bigg(\sum_{|h|\leq 2H} \left|\mathbb{E}\left[\chi^h({\mathbf{b}}_1)\right]\right|\Bigg)^d. \end{align} $$
Let
![]() $I_1$
be the set of all
$I_1$
be the set of all
![]() $-2H\leq h\leq 2H$
such that
$-2H\leq h\leq 2H$
such that
![]() $\chi ^h$
is principal. Since
$\chi ^h$
is principal. Since
![]() $\chi $
has order
$\chi $
has order
![]() $\geq e^{10d}$
, we have
$\geq e^{10d}$
, we have
Let
![]() $I_2$
be the set of all
$I_2$
be the set of all
![]() $-2H\leq h\leq 2H$
such that
$-2H\leq h\leq 2H$
such that
![]() $L(s, \chi ^h)$
has a zero in the region (16). By contradiction, suppose that the conclusion of Lemma 3.12 does not hold. Then any sub-interval of
$L(s, \chi ^h)$
has a zero in the region (16). By contradiction, suppose that the conclusion of Lemma 3.12 does not hold. Then any sub-interval of
![]() $[-2H, 2H]$
of length
$[-2H, 2H]$
of length
![]() $e^{3t}$
contains at most one element of
$e^{3t}$
contains at most one element of
![]() $I_2$
. This implies that
$I_2$
. This implies that
Moreover, for any integer
![]() $h\in [-2H, 2H]\setminus (I_1\cup I_2)$
, the character
$h\in [-2H, 2H]\setminus (I_1\cup I_2)$
, the character
![]() $\chi ^h$
is nonprincipal and has no zero in the region (16), which by Proposition 3.9 implies that
$\chi ^h$
is nonprincipal and has no zero in the region (16), which by Proposition 3.9 implies that
Therefore, we can bound
Hence, by (17) we get
which contradicts the assumption in the statement if
![]() $t_0$
is chosen to be sufficiently large.
$t_0$
is chosen to be sufficiently large.
We wish to use a zero-density estimate again to show that there are few characters satisfying the conclusion of Lemma 3.12. For this step to work, we need to restrict to the subgroup
![]() $\widehat {G}^{{M_*}}$
of the full character group
$\widehat {G}^{{M_*}}$
of the full character group
![]() $\widehat {G}$
, where
$\widehat {G}$
, where
![]() ${M_*}$
is the integer defined in Lemma 3.4.
${M_*}$
is the integer defined in Lemma 3.4.
Lemma 3.13. Let
![]() $t_0\geq 1$
be the constant from Lemma 3.12. Let
$t_0\geq 1$
be the constant from Lemma 3.12. Let
![]() $N,G,d,X$
and
$N,G,d,X$
and
![]() ${\mathbf {b}}_i$
be as in Lemma 3.11. Let
${\mathbf {b}}_i$
be as in Lemma 3.11. Let
![]() $H\geq e^{10d}$
and let
$H\geq e^{10d}$
and let
![]() ${M_*}\geq 1$
be the integer defined in Lemma 3.4.
${M_*}\geq 1$
be the integer defined in Lemma 3.4.
For every
![]() $t\geq t_0$
,
$t\geq t_0$
,
Proof. If
![]() $t\geq 2d$
, the bound (18) is trivially satisfied as the right-hand side is
$t\geq 2d$
, the bound (18) is trivially satisfied as the right-hand side is
![]() $\gg N$
. We may thus assume that
$\gg N$
. We may thus assume that
![]() ${t_0 \leq t\leq 2d}$
, in which case Lemma 3.12 applies.
${t_0 \leq t\leq 2d}$
, in which case Lemma 3.12 applies.
Let
![]() $E_t$
be the set of all characters
$E_t$
be the set of all characters
![]() $\psi $
modulo N such that
$\psi $
modulo N such that
![]() $L(s, \psi )$
has a zero in the rectangle defined in (16). By Proposition 3.10, this set
$L(s, \psi )$
has a zero in the rectangle defined in (16). By Proposition 3.10, this set
![]() $E_t$
has size
$E_t$
has size
For every
![]() $\chi \in \widehat {G}$
of order
$\chi \in \widehat {G}$
of order
![]() $\geq e^{10d}$
, if
$\geq e^{10d}$
, if
![]() $\mathbb {E}\left [ |F_{\chi ,H}({\mathbf {b}}_1, \ldots , {\mathbf {b}}_d)|^2 \right ]> e^{-2td} H^{2d}$
then by Lemma 3.12 we can write
$\mathbb {E}\left [ |F_{\chi ,H}({\mathbf {b}}_1, \ldots , {\mathbf {b}}_d)|^2 \right ]> e^{-2td} H^{2d}$
then by Lemma 3.12 we can write
for some integer
![]() $0< h < e^{3t}$
and some characters
$0< h < e^{3t}$
and some characters
![]() $\psi _1, \psi _2\in E_t$
. Hence, the left-hand side of (18) is
$\psi _1, \psi _2\in E_t$
. Hence, the left-hand side of (18) is
 $$ \begin{align} \leq \sum_{\psi_1,\psi_2\in E_t} \sum_{0 < h < e^{3t}} \left|\big\{ \chi\in \widehat{G}^M \ : \ \chi^h = \psi_1\overline{\psi_2}\big\}\right|. \end{align} $$
$$ \begin{align} \leq \sum_{\psi_1,\psi_2\in E_t} \sum_{0 < h < e^{3t}} \left|\big\{ \chi\in \widehat{G}^M \ : \ \chi^h = \psi_1\overline{\psi_2}\big\}\right|. \end{align} $$
Since
![]() $\widehat {G}^{{M_*}}$
and
$\widehat {G}^{{M_*}}$
and
![]() $\widehat {G^{M_*}}$
are isomorphic, Lemma 3.5 implies that
$\widehat {G^{M_*}}$
are isomorphic, Lemma 3.5 implies that
Inserting Eqs. (19) and(21) into (20), we conclude that the left-hand side of (18) is
as claimed.
Combining the previous lemmas, we obtain a suitable bound for the sum of second moments of
![]() $F_{\chi ,H}({\mathbf {b}}_1, \ldots , {\mathbf {b}}_d)$
over all large-order characters in
$F_{\chi ,H}({\mathbf {b}}_1, \ldots , {\mathbf {b}}_d)$
over all large-order characters in
![]() $\widehat {G}^{{M_*}}$
.
$\widehat {G}^{{M_*}}$
.
Proposition 3.14 (Large-order characters).
Let
![]() $N,G,d,X$
and
$N,G,d,X$
and
![]() ${\mathbf {b}}_i$
be as in Lemma 3.11. Let
${\mathbf {b}}_i$
be as in Lemma 3.11. Let
![]() ${M_*}\geq 1$
be the integer defined in Lemma 3.4. For
${M_*}\geq 1$
be the integer defined in Lemma 3.4. For
![]() $H\geq e^{10d}$
, we have
$H\geq e^{10d}$
, we have
 $$ \begin{align*} \sum_{\substack{\chi\in \widehat{G}^{{M_*}}\\ \mathrm{ord}(\chi) \geq e^{10d}}} \mathbb{E}\left[ |F_{\chi,H}({\mathbf{b}}_1, \ldots, {\mathbf{b}}_d)|^2\right]^{1/2} \ll d^{-2d} H^d. \end{align*} $$
$$ \begin{align*} \sum_{\substack{\chi\in \widehat{G}^{{M_*}}\\ \mathrm{ord}(\chi) \geq e^{10d}}} \mathbb{E}\left[ |F_{\chi,H}({\mathbf{b}}_1, \ldots, {\mathbf{b}}_d)|^2\right]^{1/2} \ll d^{-2d} H^d. \end{align*} $$
Proof. By Lemma 3.11, we know that
![]() $\mathbb {E}\left [ |F_{\chi ,H}(\underline {{\mathbf {b}}})|^2\right ]^{1/2} \leq C d^{-5d} H^d$
for all characters
$\mathbb {E}\left [ |F_{\chi ,H}(\underline {{\mathbf {b}}})|^2\right ]^{1/2} \leq C d^{-5d} H^d$
for all characters
![]() $\chi \in \widehat {G}$
of order
$\chi \in \widehat {G}$
of order
![]() $\geq e^{10d}$
, where
$\geq e^{10d}$
, where
![]() $C>0$
is an absolute constant (as before,
$C>0$
is an absolute constant (as before,
![]() $\underline {{\mathbf {b}}}$
stands for
$\underline {{\mathbf {b}}}$
stands for
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
). Therefore,
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
). Therefore,
 $$ \begin{align*} \sum_{\substack{\chi\in \widehat{G}^{{M_*}}\\ \mathrm{ord}(\chi) \geq e^{10d}}} \mathbb{E}\left[ |F_{\chi,H}(\underline{{\mathbf{b}}})|^2\right]^{1/2} \leq \sum_{m = m_0}^{+\infty}\sum_{\substack{\chi\in \widehat{G}^{{M_*}}\\ \mathrm{ord}(\chi) \geq e^{10d}}} e^{-m+1}H^d \mathbf{1}_{e^{-m} < \mathbb{E}\left[ |F_{\chi,H}(\underline{{\mathbf{b}}})|^2\right]^{1/2} H^{-d} \leq e^{-m+1}}(\chi) \end{align*} $$
$$ \begin{align*} \sum_{\substack{\chi\in \widehat{G}^{{M_*}}\\ \mathrm{ord}(\chi) \geq e^{10d}}} \mathbb{E}\left[ |F_{\chi,H}(\underline{{\mathbf{b}}})|^2\right]^{1/2} \leq \sum_{m = m_0}^{+\infty}\sum_{\substack{\chi\in \widehat{G}^{{M_*}}\\ \mathrm{ord}(\chi) \geq e^{10d}}} e^{-m+1}H^d \mathbf{1}_{e^{-m} < \mathbb{E}\left[ |F_{\chi,H}(\underline{{\mathbf{b}}})|^2\right]^{1/2} H^{-d} \leq e^{-m+1}}(\chi) \end{align*} $$
where
![]() $m_0 := \lfloor 5d\log d - \log C + 1\rfloor $
. We may assume that
$m_0 := \lfloor 5d\log d - \log C + 1\rfloor $
. We may assume that
![]() $m_0 \geq \max (t_0d, 4d\log d)$
, since otherwise
$m_0 \geq \max (t_0d, 4d\log d)$
, since otherwise
![]() $d\ll 1$
and Proposition 3.14 is trivially satisfied (given that
$d\ll 1$
and Proposition 3.14 is trivially satisfied (given that
![]() $|\widehat {G}^{M_*}| \leq N \ll 1$
when
$|\widehat {G}^{M_*}| \leq N \ll 1$
when
![]() $d\ll 1$
).
$d\ll 1$
).
Applying Lemma 3.13 with
![]() $t := m/d$
, we obtain that for every
$t := m/d$
, we obtain that for every
![]() $m \geq t_0d$
,
$m \geq t_0d$
,
Therefore,
 $$ \begin{align*} \sum_{\substack{\chi\in \widehat{G}^{M_*}\\ \mathrm{ord}(\chi) \geq e^{10d}}} \mathbb{E}\left[ |F_{\chi,H}(\underline{{\mathbf{b}}})|^2\right]^{1/2} \ll \sum_{m = m_0}^{+\infty} e^{m/2} e^{-m+1} H^d \ll e^{-m_0/2} H^d \end{align*} $$
$$ \begin{align*} \sum_{\substack{\chi\in \widehat{G}^{M_*}\\ \mathrm{ord}(\chi) \geq e^{10d}}} \mathbb{E}\left[ |F_{\chi,H}(\underline{{\mathbf{b}}})|^2\right]^{1/2} \ll \sum_{m = m_0}^{+\infty} e^{m/2} e^{-m+1} H^d \ll e^{-m_0/2} H^d \end{align*} $$
which is
![]() $O(d^{-2d} H^d)$
as
$O(d^{-2d} H^d)$
as
![]() $m_0 \geq 4d\log d$
.
$m_0 \geq 4d\log d$
.
3.4 Geometry of numbers
In this section, we show how to pass from good estimates on the number of lattice points in certain regions to the existence of a short basis for the lattice.
Lemma 3.15. Let
![]() $L\geq 1$
be an integer. Cover the cube
$L\geq 1$
be an integer. Cover the cube
![]() $[-L,L]^d$
by
$[-L,L]^d$
by
![]() $(2L)^d$
cubes of side length
$(2L)^d$
cubes of side length
![]() $1$
in the obvious way. Label these unit cubes
$1$
in the obvious way. Label these unit cubes
![]() $C_1, \ldots , C_{(2L)^d}$
(in any order). Let
$C_1, \ldots , C_{(2L)^d}$
(in any order). Let
![]() $V\subset \mathbb {R}^d$
be a hyperplane through the origin. Then the number of unit cubes
$V\subset \mathbb {R}^d$
be a hyperplane through the origin. Then the number of unit cubes
![]() $C_i$
intersecting V is at most
$C_i$
intersecting V is at most
![]() $(d+1) (2L)^{d-1}$
.
$(d+1) (2L)^{d-1}$
.
Proof. Let
![]() $e_1, \ldots , e_d$
be the standard basis for
$e_1, \ldots , e_d$
be the standard basis for
![]() $\mathbb {R}^d$
. Let
$\mathbb {R}^d$
. Let
![]() $v\in \mathbb {R}^d$
be a unit vector orthogonal to V. Without loss of generality, since
$v\in \mathbb {R}^d$
be a unit vector orthogonal to V. Without loss of generality, since
![]() $\left \|v\right \|_2 = 1$
, we may assume that
$\left \|v\right \|_2 = 1$
, we may assume that
![]() $\left \langle v, e_1\right \rangle \geq 1/\sqrt {d}$
.
$\left \langle v, e_1\right \rangle \geq 1/\sqrt {d}$
.
Suppose that V intersects two unit cubes
![]() $C_i$
and
$C_i$
and
![]() $C_j$
where
$C_j$
where
![]() $C_i = C_j + ke_1$
for some integer
$C_i = C_j + ke_1$
for some integer
![]() $k \geq 0$
. Then, there is some
$k \geq 0$
. Then, there is some
![]() $p\in C_i$
and some
$p\in C_i$
and some
![]() $w\in \mathbb {R}^d$
with
$w\in \mathbb {R}^d$
with
![]() $\left \|w\right \|_{\infty } \leq 1$
such that
$\left \|w\right \|_{\infty } \leq 1$
such that
![]() $p\in V$
and
$p\in V$
and
![]() $p+ke_1+w\in V$
. Therefore,
$p+ke_1+w\in V$
. Therefore,
![]() $ke_1+w \in V$
and thus
$ke_1+w \in V$
and thus
![]() $\left \langle ke_1+w,v\right \rangle = 0$
. Noting that
$\left \langle ke_1+w,v\right \rangle = 0$
. Noting that
we deduce that
![]() $k\leq d$
.
$k\leq d$
.
We have thus proved that, for any cube
![]() $C_i$
, there are at most
$C_i$
, there are at most
![]() $d+1$
cubes of the form
$d+1$
cubes of the form
![]() $C_i+ke_1$
for some
$C_i+ke_1$
for some
![]() $k\in \mathbb {Z}$
which intersect V. The lemma follows.
$k\in \mathbb {Z}$
which intersect V. The lemma follows.
The next lemma allows us to convert information about the number of lattice points in cubes into the existence of short linearly independent lattice vectors.
Lemma 3.16. Let
![]() $d \geq 1$
. Let
$d \geq 1$
. Let
![]() $\Lambda \subset \mathbb {R}^d$
be a full-rank lattice. Let
$\Lambda \subset \mathbb {R}^d$
be a full-rank lattice. Let
![]() $2\leq H_0 < H_1$
be real numbers such that
$2\leq H_0 < H_1$
be real numbers such that
![]() $H_1/H_0$
is an integer. Suppose that, for
$H_1/H_0$
is an integer. Suppose that, for
![]() $i\in \{0, 1\}$
,
$i\in \{0, 1\}$
,
 $$ \begin{align} \left|\Lambda \cap [-H_i, H_i]^d\right| = \theta_i \frac{(2H_i+1)^d}{\operatorname{vol}(\mathbb{R}^d/\Lambda)} \end{align} $$
$$ \begin{align} \left|\Lambda \cap [-H_i, H_i]^d\right| = \theta_i \frac{(2H_i+1)^d}{\operatorname{vol}(\mathbb{R}^d/\Lambda)} \end{align} $$
where
![]() $\theta _0, \theta _1>0$
satisfy
$\theta _0, \theta _1>0$
satisfy
![]() $\frac {H_1}{H_0}> \frac {\theta _0}{\theta _1} d \big (\tfrac {5}{2}\big )^d$
. Then
$\frac {H_1}{H_0}> \frac {\theta _0}{\theta _1} d \big (\tfrac {5}{2}\big )^d$
. Then
![]() $\Lambda \cap [-H_1, H_1]^d$
contains d linearly independent vectors.
$\Lambda \cap [-H_1, H_1]^d$
contains d linearly independent vectors.
Proof. By contradiction, suppose that there exists a linear hyperplane V containing all the points
![]() $v\in \Lambda \cap [-H_1, H_1]^d$
.
$v\in \Lambda \cap [-H_1, H_1]^d$
.
Let
![]() $L = H_1/H_0$
. The large cube
$L = H_1/H_0$
. The large cube
![]() $[-H_1, H_1]^d$
can be covered by
$[-H_1, H_1]^d$
can be covered by
![]() $(2L)^d$
axis-parallel cubes of side length
$(2L)^d$
axis-parallel cubes of side length
![]() $H_0$
in the natural way. By Lemma 3.15, we can bound
$H_0$
in the natural way. By Lemma 3.15, we can bound
where the supremum runs over all (not necessarily centred) axis-parallel cubes
![]() $C\subset \mathbb {R}^d$
of side length
$C\subset \mathbb {R}^d$
of side length
![]() $H_0$
. If C is such a cube and
$H_0$
. If C is such a cube and
![]() $v\in \Lambda \cap C$
, then
$v\in \Lambda \cap C$
, then
![]() $C \subset v + [-H_0, H_0]^d$
, which implies that
$C \subset v + [-H_0, H_0]^d$
, which implies that
Thus,
Plugging in our lattice point estimate (22), we get
Using
![]() $2H_1+1 \geq 2LH_0$
and
$2H_1+1 \geq 2LH_0$
and
![]() $d+1 \leq 2d$
, this implies that
$d+1 \leq 2d$
, this implies that
![]() $L \leq \frac {\theta _0}{\theta _1} d \big (2+\frac {1}{H_0}\big )^d$
, contradicting the inequality in the statement of the lemma.
$L \leq \frac {\theta _0}{\theta _1} d \big (2+\frac {1}{H_0}\big )^d$
, contradicting the inequality in the statement of the lemma.
The linearly independent vectors given by Lemma 3.16 can be upgraded to a genuine basis for
![]() $\Lambda $
by standard geometry of numbers, namely Mahler’s theorem. We state this fact in a slightly more general situation.
$\Lambda $
by standard geometry of numbers, namely Mahler’s theorem. We state this fact in a slightly more general situation.
Lemma 3.17. Let
![]() $d\geq 1$
. Let
$d\geq 1$
. Let
![]() $\Lambda _1, \Lambda _2 \subset \mathbb {R}^d$
be full-rank lattices such that
$\Lambda _1, \Lambda _2 \subset \mathbb {R}^d$
be full-rank lattices such that
![]() $M \Lambda _1 \subset \Lambda _2$
for some integer
$M \Lambda _1 \subset \Lambda _2$
for some integer
![]() $M\geq 1$
. Suppose that
$M\geq 1$
. Suppose that
![]() $\Lambda _1$
contains d linearly independent vectors in
$\Lambda _1$
contains d linearly independent vectors in
![]() $[-H, H]^d$
for some
$[-H, H]^d$
for some
![]() $H>0$
. Then,
$H>0$
. Then,
![]() $\Lambda _2$
admits a basis where each basis vector has Euclidean norm
$\Lambda _2$
admits a basis where each basis vector has Euclidean norm
![]() $\leq d^{3/2}MH$
.
$\leq d^{3/2}MH$
.
Proof. By assumption, there are linearly independent vectors
![]() $v_1, \ldots , v_d \in \Lambda _1 \cap [-H, H]^d$
. Then
$v_1, \ldots , v_d \in \Lambda _1 \cap [-H, H]^d$
. Then
![]() $Mv_1, \ldots , Mv_d$
are linearly independent vectors of
$Mv_1, \ldots , Mv_d$
are linearly independent vectors of
![]() $\Lambda _2$
such that
$\Lambda _2$
such that
![]() $\max _{i\in [d]} \left \|Mv_i\right \|_2 \leq \sqrt {d} MH$
.
$\max _{i\in [d]} \left \|Mv_i\right \|_2 \leq \sqrt {d} MH$
.
Let
![]() $B\subset \mathbb {R}^d$
be the unit ball for the Euclidean norm. Let
$B\subset \mathbb {R}^d$
be the unit ball for the Euclidean norm. Let
![]() ${0 < \lambda _1 \leq \cdots \leq \lambda _d}$
be the successive minimaFootnote
12
of B with respect to
${0 < \lambda _1 \leq \cdots \leq \lambda _d}$
be the successive minimaFootnote
12
of B with respect to
![]() $\Lambda _2$
. Since
$\Lambda _2$
. Since
![]() $Mv_1, \ldots , Mv_d \in \Lambda _2$
are linearly independent, we deduce from the above that
$Mv_1, \ldots , Mv_d \in \Lambda _2$
are linearly independent, we deduce from the above that
![]() $\lambda _d \leq \sqrt {d} MH$
.
$\lambda _d \leq \sqrt {d} MH$
.
By Mahler’s theorem (see [Reference Tao and Vu22, Theorem 3.34]), we conclude that
![]() $\Lambda _2$
admits a basis of vectors of Euclidean norm at most
$\Lambda _2$
admits a basis of vectors of Euclidean norm at most
![]() $d \lambda _d \leq d^{3/2}MH$
, which is what we needed to show.
$d \lambda _d \leq d^{3/2}MH$
, which is what we needed to show.
3.5 Short basis vectors
We can now prove our main technical result, which may be of independent interest.
Theorem 3.18. Let
![]() $N>2$
be an integer. Let
$N>2$
be an integer. Let
![]() $d := \lceil \!\sqrt {\log N} \rceil $
and
$d := \lceil \!\sqrt {\log N} \rceil $
and
![]() $X := d^{10^3d}$
.
$X := d^{10^3d}$
.
Let
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes
![]() $\leq X$
not dividing N. Let
$\leq X$
not dividing N. Let
![]() $r\geq 0$
and let
$r\geq 0$
and let
![]() $\mathbf {x}_1, \ldots , \mathbf {x}_r$
be arbitraryFootnote
13
random variables taking values in
$\mathbf {x}_1, \ldots , \mathbf {x}_r$
be arbitraryFootnote
13
random variables taking values in
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
.
Then, with probability
![]() $1 +O\big (d^{-d}\big )$
, the lattice
$1 +O\big (d^{-d}\big )$
, the lattice
 $$ \begin{align*} \mathcal{L} := \Big\{ (e_1, \ldots, e_d, f_1, \ldots, f_r) \in \mathbb{Z}^{d+r} \ : \ \prod_{i=1}^d {\mathbf{b}}_i^{e_i} \prod_{i=1}^r \mathbf{x}_i^{f_i} \equiv 1 \quad\pmod{N} \Big\} \end{align*} $$
$$ \begin{align*} \mathcal{L} := \Big\{ (e_1, \ldots, e_d, f_1, \ldots, f_r) \in \mathbb{Z}^{d+r} \ : \ \prod_{i=1}^d {\mathbf{b}}_i^{e_i} \prod_{i=1}^r \mathbf{x}_i^{f_i} \equiv 1 \quad\pmod{N} \Big\} \end{align*} $$
has a basis consisting of vectors of Euclidean norm
![]() $\ll e^{42(d+r)}$
.
$\ll e^{42(d+r)}$
.
Remark 3.19. The constant
![]() $42$
in the exponent is by no means the limit our techniques. For example, using smooth cutoffs in Definition 3.6 would significantly reduce the error term in Lemma 3.8 and hence lower this constant. We have not performed such optimisations to keep the paper as simple as possible.
$42$
in the exponent is by no means the limit our techniques. For example, using smooth cutoffs in Definition 3.6 would significantly reduce the error term in Lemma 3.8 and hence lower this constant. We have not performed such optimisations to keep the paper as simple as possible.
Proof of Theorem 3.18.
Let
![]() $M := {M_*}(N)$
be the integer defined in Lemma 3.4. We introduce the auxiliary lattice
$M := {M_*}(N)$
be the integer defined in Lemma 3.4. We introduce the auxiliary lattice
 $$ \begin{align*} \mathcal{L}_{M} := \Big\{ (e_1, \ldots, e_d, f_1, \ldots, f_r) \in \mathbb{Z}^{d+r} \ : \ \prod_{i=1}^d {\mathbf{b}}_i^{M e_i} \prod_{i=1}^r \mathbf{x}_i^{M f_i} \equiv 1 \quad\pmod{N} \Big\}. \end{align*} $$
$$ \begin{align*} \mathcal{L}_{M} := \Big\{ (e_1, \ldots, e_d, f_1, \ldots, f_r) \in \mathbb{Z}^{d+r} \ : \ \prod_{i=1}^d {\mathbf{b}}_i^{M e_i} \prod_{i=1}^r \mathbf{x}_i^{M f_i} \equiv 1 \quad\pmod{N} \Big\}. \end{align*} $$
By Lemmas 3.7 and 3.8, we have the lattice point estimate
 $$ \begin{align} \left|\mathcal{L}_{M} \cap [-H, H]^{d+r}\right| = \frac{ \left(1 + O\left({e^{31(d+r)}}{H^{-1}}\right)\right) (2H+1)^{d+r} }{ \big\lvert\left\langle {\mathbf{b}}_1^{M}, \ldots, {\mathbf{b}}_d^{M}, \mathbf{x}_1^{M}, \ldots, \mathbf{x}_r^M \right\rangle\big\rvert } + \frac{1}{\big\lvert \widehat{G}^{M}\big\rvert} \!\!\!\!\sum_{\substack{\chi \in \widehat{G}^M\\ \mathrm{ord}(\chi) \geq e^{10d}}} \!\!\!\! \left|F_{\chi,H}(\underline{{\mathbf{b}}}, \underline{\mathbf{x}})\right| \end{align} $$
$$ \begin{align} \left|\mathcal{L}_{M} \cap [-H, H]^{d+r}\right| = \frac{ \left(1 + O\left({e^{31(d+r)}}{H^{-1}}\right)\right) (2H+1)^{d+r} }{ \big\lvert\left\langle {\mathbf{b}}_1^{M}, \ldots, {\mathbf{b}}_d^{M}, \mathbf{x}_1^{M}, \ldots, \mathbf{x}_r^M \right\rangle\big\rvert } + \frac{1}{\big\lvert \widehat{G}^{M}\big\rvert} \!\!\!\!\sum_{\substack{\chi \in \widehat{G}^M\\ \mathrm{ord}(\chi) \geq e^{10d}}} \!\!\!\! \left|F_{\chi,H}(\underline{{\mathbf{b}}}, \underline{\mathbf{x}})\right| \end{align} $$
for every integer
![]() $H\geq e^{31(d+r)}$
, where
$H\geq e^{31(d+r)}$
, where
 $$ \begin{align*} F_{\chi,H}(\underline{{\mathbf{b}}}, \underline{\mathbf{x}}) := F_{\chi, H}({\mathbf{b}}_1, \ldots, {\mathbf{b}}_d, \mathbf{x}_1, \ldots, \mathbf{x}_r) = \Bigg(\prod_{i=1}^d \sum_{|h|\leq H} \chi^h({\mathbf{b}}_i)\Bigg) \Bigg(\prod_{i=1}^r \sum_{|h|\leq H} \chi^h(\mathbf{x}_i)\Bigg). \end{align*} $$
$$ \begin{align*} F_{\chi,H}(\underline{{\mathbf{b}}}, \underline{\mathbf{x}}) := F_{\chi, H}({\mathbf{b}}_1, \ldots, {\mathbf{b}}_d, \mathbf{x}_1, \ldots, \mathbf{x}_r) = \Bigg(\prod_{i=1}^d \sum_{|h|\leq H} \chi^h({\mathbf{b}}_i)\Bigg) \Bigg(\prod_{i=1}^r \sum_{|h|\leq H} \chi^h(\mathbf{x}_i)\Bigg). \end{align*} $$
Since the
![]() $\mathbf {x}_i$
have unknown distributions, we will use the trivial bound
$\mathbf {x}_i$
have unknown distributions, we will use the trivial bound
Applying Proposition 3.14, we deduce that, for all
![]() $H\geq e^{10d}$
,
$H\geq e^{10d}$
,
 $$ \begin{align*} \sum_{\substack{\chi\in \widehat{G}^{{M_*}}\\ \mathrm{ord}(\chi) \geq e^{10d}}} \mathbb{E}\left[ |F_{\chi,H}(\underline{{\mathbf{b}}}, \underline{\mathbf{x}})|^2\right]^{1/2} \ll d^{-2d} (2H+1)^{d+r}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{\chi\in \widehat{G}^{{M_*}}\\ \mathrm{ord}(\chi) \geq e^{10d}}} \mathbb{E}\left[ |F_{\chi,H}(\underline{{\mathbf{b}}}, \underline{\mathbf{x}})|^2\right]^{1/2} \ll d^{-2d} (2H+1)^{d+r}. \end{align*} $$
By the
![]() $L^2$
triangle inequality and Chebyshev’s inequality, this implies that, for fixed
$L^2$
triangle inequality and Chebyshev’s inequality, this implies that, for fixed
![]() $H\geq e^{10d}$
,
$H\geq e^{10d}$
,
 $$ \begin{align} \mathbb{P}\bigg({\sum_{\substack{\chi \in \widehat{G}^M\\ \mathrm{ord}(\chi) \geq e^{10d}}} \!\!\!\! \left|F_{\chi,H}(\underline{{\mathbf{b}}}, \underline{\mathbf{x}})\right|}> d^{-d}(2H+1)^{d+r}\bigg) \ll d^{-2d}. \end{align} $$
$$ \begin{align} \mathbb{P}\bigg({\sum_{\substack{\chi \in \widehat{G}^M\\ \mathrm{ord}(\chi) \geq e^{10d}}} \!\!\!\! \left|F_{\chi,H}(\underline{{\mathbf{b}}}, \underline{\mathbf{x}})\right|}> d^{-d}(2H+1)^{d+r}\bigg) \ll d^{-2d}. \end{align} $$
Let
![]() $H_0 := d \lceil e^{31(d+r)}\rceil $
and
$H_0 := d \lceil e^{31(d+r)}\rceil $
and
![]() $H_1 := \lceil d (d+r) (5/2)^{d+r}\rceil H_0$
. We apply Eqs. (23) and (24) twice, once with
$H_1 := \lceil d (d+r) (5/2)^{d+r}\rceil H_0$
. We apply Eqs. (23) and (24) twice, once with
![]() $H = H_0$
and once with
$H = H_0$
and once with
![]() $H = H_1$
to obtain the following: with probability
$H = H_1$
to obtain the following: with probability
![]() ${1+O\big (d^{-d}\big )}$
, the two estimates
${1+O\big (d^{-d}\big )}$
, the two estimates
 $$ \begin{align*} \left|\mathcal{L}_{M} \cap [-H_0, H_0]^{d+r}\right| = \left(1 + O(1/d)\right) \frac{(2H_0+1)^{d+r}}{ \big\lvert\left\langle {\mathbf{b}}_1^{M}, \ldots, {\mathbf{b}}_d^{M}, \mathbf{x}_1^{M}, \ldots, \mathbf{x}_r^M \right\rangle\big\rvert} \end{align*} $$
$$ \begin{align*} \left|\mathcal{L}_{M} \cap [-H_0, H_0]^{d+r}\right| = \left(1 + O(1/d)\right) \frac{(2H_0+1)^{d+r}}{ \big\lvert\left\langle {\mathbf{b}}_1^{M}, \ldots, {\mathbf{b}}_d^{M}, \mathbf{x}_1^{M}, \ldots, \mathbf{x}_r^M \right\rangle\big\rvert} \end{align*} $$
and
 $$ \begin{align*} \left|\mathcal{L}_{M} \cap [-H_1, H_1]^{d+r}\right| = \left(1 + O(1/d)\right) \frac{(2H_1+1)^{d+r}}{ \big\lvert\left\langle {\mathbf{b}}_1^{M}, \ldots, {\mathbf{b}}_d^{M}, \mathbf{x}_1^{M}, \ldots, \mathbf{x}_r^M \right\rangle\big\rvert} \end{align*} $$
$$ \begin{align*} \left|\mathcal{L}_{M} \cap [-H_1, H_1]^{d+r}\right| = \left(1 + O(1/d)\right) \frac{(2H_1+1)^{d+r}}{ \big\lvert\left\langle {\mathbf{b}}_1^{M}, \ldots, {\mathbf{b}}_d^{M}, \mathbf{x}_1^{M}, \ldots, \mathbf{x}_r^M \right\rangle\big\rvert} \end{align*} $$
simultaneously hold.
We now apply Lemma 3.16. By our choice of
![]() $H_0$
and
$H_0$
and
![]() $H_1$
, the inequality in the statement is satisfied provided that d is sufficiently large. We can assume that d is large enough as, for
$H_1$
, the inequality in the statement is satisfied provided that d is sufficiently large. We can assume that d is large enough as, for
![]() $d\ll 1$
, we have
$d\ll 1$
, we have
![]() $N \ll 1$
and Theorem 3.18 is trivially true. Thus, Lemma 3.16 implies that
$N \ll 1$
and Theorem 3.18 is trivially true. Thus, Lemma 3.16 implies that
![]() ${\mathcal {L}_M \cap [-H_1, H_1]^{d+r}}$
contains
${\mathcal {L}_M \cap [-H_1, H_1]^{d+r}}$
contains
![]() $d+r$
linearly independent vectors, with probability
$d+r$
linearly independent vectors, with probability
![]() ${1+O\big (d^{-d}\big )}$
. By Lemma 3.17, since
${1+O\big (d^{-d}\big )}$
. By Lemma 3.17, since
![]() $M\mathcal {L} \subset \mathcal {L}_M$
, we conclude that, with probability
$M\mathcal {L} \subset \mathcal {L}_M$
, we conclude that, with probability
![]() ${1+O\big (d^{-d}\big )}$
,
${1+O\big (d^{-d}\big )}$
,
![]() $\mathcal {L}$
admits a basis of vectors of Euclidean norm at most
$\mathcal {L}$
admits a basis of vectors of Euclidean norm at most
using the bound
![]() $M \leq e^{10d}$
given by Lemma 3.4. This completes the proof.
$M \leq e^{10d}$
given by Lemma 3.4. This completes the proof.
4 Applications to quantum computing
In this section, we prove the correctness of efficient quantum algorithms for factoring and for the discrete logarithm problem by applying our version of Regev’s number-theoretic conjecture, Theorem 3.18.
4.1 Preparatory lemmas
Lemma 4.1. Let
![]() $N, d, m \geq 2$
be integers. There is a classical algorithm that, given integers
$N, d, m \geq 2$
be integers. There is a classical algorithm that, given integers
![]() ${0\leq a_1, \ldots , a_d\leq 2^{m}}$
and exponents
${0\leq a_1, \ldots , a_d\leq 2^{m}}$
and exponents
![]() $t_1, \ldots , t_d \in \{0, 1\}$
, computes the product
$t_1, \ldots , t_d \in \{0, 1\}$
, computes the product
 $$ \begin{align*} \prod_{i=1}^d a_i^{t_i} \,(\mathrm{mod}\, N) \end{align*} $$
$$ \begin{align*} \prod_{i=1}^d a_i^{t_i} \,(\mathrm{mod}\, N) \end{align*} $$
in time
![]() $O\big (md (\log d) \log (md)\big )$
.
$O\big (md (\log d) \log (md)\big )$
.
Proof. This is similar to [Reference Regev18, p5] or [Reference Ragavan and Vaikuntanathan17, Lemma 12] but for general values of m. Without loss of generality, assume that d is a power of
![]() $2$
, say
$2$
, say
![]() $d = 2^l$
. We proceed to compute this product in a binary tree fashion. Let
$d = 2^l$
. We proceed to compute this product in a binary tree fashion. Let
![]() $T(k)$
be the complexity of multiplying any k of these numbers
$T(k)$
be the complexity of multiplying any k of these numbers
![]() $a_i^{t_i}$
modulo N. Note that
$a_i^{t_i}$
modulo N. Note that
![]() $T(2k) \leq 2T(k) + O(M(mk))$
where
$T(2k) \leq 2T(k) + O(M(mk))$
where
![]() $M(x)$
is the time needed to multiply two integers having at most x bits. By the work of Harvey and van der Hoeven [Reference Harvey and van der Hoeven10], it is known that
$M(x)$
is the time needed to multiply two integers having at most x bits. By the work of Harvey and van der Hoeven [Reference Harvey and van der Hoeven10], it is known that
![]() $M(x) = O(x\log x)$
, which leads to the bound
$M(x) = O(x\log x)$
, which leads to the bound
 $$ \begin{align*} T(d) \ll \sum_{j=0}^{l} 2^j M(md/2^{j+1}) \ll \sum_{j=0}^{l} md \log(md/2^{j+1}) \ll md (\log d) \log(md). \end{align*} $$
$$ \begin{align*} T(d) \ll \sum_{j=0}^{l} 2^j M(md/2^{j+1}) \ll \sum_{j=0}^{l} md \log(md/2^{j+1}) \ll md (\log d) \log(md). \end{align*} $$
as claimed.
We can turn this into a quantum circuit with the following well-known fact.
Lemma 4.2. Any classical circuit can be ‘compiled’ into a reversible quantum circuit that carries out the same computations, with the number of gates and qubits used being proportional to the size of the classical circuit.
Proof. This well-known fact is explained in Section A.1 of the full version of [Reference Ragavan and Vaikuntanathan17].
Lemma 4.3. Let N be a sufficiently large integer. Let
![]() $d := \lceil \! \sqrt {\log N}\rceil $
and
$d := \lceil \! \sqrt {\log N}\rceil $
and
![]() $X = d^{10^3d}$
. Let
$X = d^{10^3d}$
. Let
![]() $k = d^4$
.
$k = d^4$
.
Let
![]() $\mathbf {n}_1, \ldots , \mathbf {n}_k$
be i.i.d. random variables uniformly distributed in
$\mathbf {n}_1, \ldots , \mathbf {n}_k$
be i.i.d. random variables uniformly distributed in
![]() $\{1, \ldots , X\}$
. Then, the probability that at least d of these
$\{1, \ldots , X\}$
. Then, the probability that at least d of these
![]() $\mathbf {n}_i$
are prime numbers not dividing N is
$\mathbf {n}_i$
are prime numbers not dividing N is
![]() $1 +O(1/N)$
.
$1 +O(1/N)$
.
Proof. Since N has
![]() $\ll \log N$
prime factors, and since the number of primes
$\ll \log N$
prime factors, and since the number of primes
![]() $\leq X$
is
$\leq X$
is
![]() $\gg X/\log X$
, we have
$\gg X/\log X$
, we have
for some absolute constant
![]() $c>0$
. Thus, if
$c>0$
. Thus, if
![]() $E_i$
is the event that
$E_i$
is the event that
![]() $\mathbf {n}_i$
is not prime or divides N, then by the union bound and independence,
$\mathbf {n}_i$
is not prime or divides N, then by the union bound and independence,
 $$ \begin{align*} \mathbb{P} \bigg(\bigcup_{\substack{I \subset [k]\\ |I|> k-d}} \bigcap_{i\in I} E_i\bigg) \leq \sum_{l< d} \binom{k}{l} \left(1-\frac{c}{\log X}\right)^{k-l} \leq dk^d e^{-c(k-d)/\log X} \ll e^{-d^2} \end{align*} $$
$$ \begin{align*} \mathbb{P} \bigg(\bigcup_{\substack{I \subset [k]\\ |I|> k-d}} \bigcap_{i\in I} E_i\bigg) \leq \sum_{l< d} \binom{k}{l} \left(1-\frac{c}{\log X}\right)^{k-l} \leq dk^d e^{-c(k-d)/\log X} \ll e^{-d^2} \end{align*} $$
as needed.
4.2 The discrete logarithm problem
We now prove Theorem 1.2. For convenience, we restate it here.
Theorem 1.2. There is a quantum circuit having
![]() $O(n^{3/2} \log ^3 n)$
quantum gates and
$O(n^{3/2} \log ^3 n)$
quantum gates and
![]() $O(n \log ^3 n)$
qubits with the following property. There is a classical randomised polynomial-time algorithm that solves the discrete logarithm problem
$O(n \log ^3 n)$
qubits with the following property. There is a classical randomised polynomial-time algorithm that solves the discrete logarithm problem
 $$ \begin{align*} & \mathbf{Input: }\text{ an integer } N \leq 2^n \text{ and elements } g,y \in (\mathbb{Z}/N\mathbb{Z})^{\times} \text{ such that } y\in \left\langle g\right\rangle \\ & \mathbf{Output: }\text{ an integer } x \text{ such that } g^x \equiv y \quad\pmod{N} \end{align*} $$
$$ \begin{align*} & \mathbf{Input: }\text{ an integer } N \leq 2^n \text{ and elements } g,y \in (\mathbb{Z}/N\mathbb{Z})^{\times} \text{ such that } y\in \left\langle g\right\rangle \\ & \mathbf{Output: }\text{ an integer } x \text{ such that } g^x \equiv y \quad\pmod{N} \end{align*} $$
using
![]() $O(\sqrt {n})$
calls to this quantum circuit, and succeeds with probability
$O(\sqrt {n})$
calls to this quantum circuit, and succeeds with probability
![]() $\Theta (1)$
.
$\Theta (1)$
.
Proof of Theorem 1.2.
Suppose we are given an integer
![]() $N>2$
and elements
$N>2$
and elements
![]() $g,y\in (\mathbb {Z}/N\mathbb {Z})^{\times }$
such that y lies in the subgroup generated by g in
$g,y\in (\mathbb {Z}/N\mathbb {Z})^{\times }$
such that y lies in the subgroup generated by g in
![]() $ (\mathbb {Z}/N\mathbb {Z})^{\times }$
. Let
$ (\mathbb {Z}/N\mathbb {Z})^{\times }$
. Let
![]() $d := \lceil \!\sqrt {\log N} \rceil $
and
$d := \lceil \!\sqrt {\log N} \rceil $
and
![]() $X := d^{10^3d}$
. Let
$X := d^{10^3d}$
. Let
![]() ${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes
${\mathbf {b}}_1, \ldots , {\mathbf {b}}_d$
be i.i.d. random variables, each uniformly distributed in the set of primes
![]() $\leq X$
not dividing N.
$\leq X$
not dividing N.
Consider the random lattice
 $$ \begin{align*} \mathcal{L}_{\underline{{\mathbf{b}}},g,y} := \Big\{(e_1, \ldots, e_d, f_1, f_2) \in \mathbb{Z}^{d+2} \ : \ \Bigg(\prod_{i=1}^d {\mathbf{b}}_i^{e_i}\Bigg) g^{f_1} y^{f_2} \equiv 1 \quad\pmod{N}\Big\}. \end{align*} $$
$$ \begin{align*} \mathcal{L}_{\underline{{\mathbf{b}}},g,y} := \Big\{(e_1, \ldots, e_d, f_1, f_2) \in \mathbb{Z}^{d+2} \ : \ \Bigg(\prod_{i=1}^d {\mathbf{b}}_i^{e_i}\Bigg) g^{f_1} y^{f_2} \equiv 1 \quad\pmod{N}\Big\}. \end{align*} $$
By Theorem 3.18, with probability
![]() $1 +O(d^{-d})$
, this lattice has a basis consisting of vectors of Euclidean norm
$1 +O(d^{-d})$
, this lattice has a basis consisting of vectors of Euclidean norm
![]() $\ll e^{42d}$
.
$\ll e^{42d}$
.
Computing the discrete logarithm of y with respect to the base g reduces (with a polynomial-time classical algorithm) to computing a short basis for
![]() $\mathcal {L}_{\underline {{\mathbf {b}}},g,y}$
. To see why this is the case, suppose that we managed to compute a basis
$\mathcal {L}_{\underline {{\mathbf {b}}},g,y}$
. To see why this is the case, suppose that we managed to compute a basis
![]() $v_1, \ldots , v_{d+2}$
for
$v_1, \ldots , v_{d+2}$
for
![]() $\mathcal {L}_{\underline {{\mathbf {b}}},g,y}$
with
$\mathcal {L}_{\underline {{\mathbf {b}}},g,y}$
with
![]() $\max _i \left \|v_i\right \|_2 \ll e^{42d}$
. It is then easy to find a vector in
$\max _i \left \|v_i\right \|_2 \ll e^{42d}$
. It is then easy to find a vector in
![]() $\mathcal {L}_{\underline {{\mathbf {b}}},g,y}$
of the form
$\mathcal {L}_{\underline {{\mathbf {b}}},g,y}$
of the form
![]() $(0, \ldots , 0, x, 1)$
for some integer x (note that such a vector exists since we assume that
$(0, \ldots , 0, x, 1)$
for some integer x (note that such a vector exists since we assume that
![]() $y\in \left \langle g\right \rangle $
). Indeed, this amounts to solving a linear system with integer coefficients. The complexity of solving an integer linear system is polynomial in the dimensions of the matrix and the number of bits of the coefficients, which are both
$y\in \left \langle g\right \rangle $
). Indeed, this amounts to solving a linear system with integer coefficients. The complexity of solving an integer linear system is polynomial in the dimensions of the matrix and the number of bits of the coefficients, which are both
![]() $O(d)$
since
$O(d)$
since
![]() $\max _i \left \|v_i\right \|_2 \ll e^{42d}$
(see [Reference Bareiss3]). This yields an integer x such that
$\max _i \left \|v_i\right \|_2 \ll e^{42d}$
(see [Reference Bareiss3]). This yields an integer x such that
![]() $g^x \equiv y \ \pmod {N}$
.
$g^x \equiv y \ \pmod {N}$
.
The algorithm for solving the discrete logarithm problem thus proceeds as follows.
-
1. Generate d primes
 $b_1, \ldots , b_d$
independently and uniformly at random in the set of primes
$b_1, \ldots , b_d$
independently and uniformly at random in the set of primes
 $\leq X$
not dividing N. To do this, it suffices to generate
$\leq X$
not dividing N. To do this, it suffices to generate
 $d^4$
independent random integers
$d^4$
independent random integers
 $\leq X$
. By Lemma 4.3, the required conditions will be satisfied for at least d of those with probability
$\leq X$
. By Lemma 4.3, the required conditions will be satisfied for at least d of those with probability
 $1+O(1/N)$
. This first step takes polynomial time on a classical computer using the AKS primality test [Reference Agrawal, Kayal and Saxena1].
$1+O(1/N)$
. This first step takes polynomial time on a classical computer using the AKS primality test [Reference Agrawal, Kayal and Saxena1]. -
2. Use the procedure described by Ekerå and Gärtner [Reference Ekerå and Gärtner7] to obtain a basis for the lattice
 $\mathcal {L}_{\underline {b},g,y}$
. This involves making
$\mathcal {L}_{\underline {b},g,y}$
. This involves making
 $O(d)$
calls to a quantum circuit, followed by polynomial-time classical postprocessing. This step is now guaranteed to succeed with probability
$O(d)$
calls to a quantum circuit, followed by polynomial-time classical postprocessing. This step is now guaranteed to succeed with probability
 $\Theta (1)$
, using the fact that
$\Theta (1)$
, using the fact that
 $\mathcal {L}_{\underline {b},g,y}$
has a basis of vectors of Euclidean norm
$\mathcal {L}_{\underline {b},g,y}$
has a basis of vectors of Euclidean norm
 $\ll e^{42d}$
with probability
$\ll e^{42d}$
with probability
 $1 +O(d^{-d})$
(Theorem 3.18).
$1 +O(d^{-d})$
(Theorem 3.18). -
3. Compute the discrete logarithm of y in classical polynomial time using this basis, as explained above.
It remains to analyse the gate and space costs of the quantum part of this algorithm.
The only modification needed to the analysis of the quantum circuit in [Reference Ekerå and Gärtner7] comes from the fact that
![]() $b_1, \ldots , b_d$
are not quite as small as in [Reference Ekerå and Gärtner7]. In [Reference Ekerå and Gärtner7] (and more generally in [Reference Ragavan and Vaikuntanathan17, Reference Regev18]), the primes
$b_1, \ldots , b_d$
are not quite as small as in [Reference Ekerå and Gärtner7]. In [Reference Ekerå and Gärtner7] (and more generally in [Reference Ragavan and Vaikuntanathan17, Reference Regev18]), the primes
![]() $b_i$
are assumed to have
$b_i$
are assumed to have
![]() $O(\log d)$
bits. In the present situation, we instead have the bound
$O(\log d)$
bits. In the present situation, we instead have the bound
![]() $b_i\leq X = d^{10^3d}$
, that is, each
$b_i\leq X = d^{10^3d}$
, that is, each
![]() $b_i$
has
$b_i$
has
![]() $O(d\log d)$
bits.
$O(d\log d)$
bits.
The only place in [Reference Ekerå and Gärtner7] where the assumption on the size of the
![]() $b_i$
’s is used is in [Reference Ekerå and Gärtner7, Lemma 3]. In turn, the only point in the proof of [Reference Ekerå and Gärtner7, Lemma 3] where this assumption is needed is when [Reference Ragavan and Vaikuntanathan17, Lemma 5] is invoked (as a black box). The proof of [Reference Ragavan and Vaikuntanathan17, Lemma 5] is given in [Reference Ragavan and Vaikuntanathan17, Section 5], and the size assumption on the
$b_i$
’s is used is in [Reference Ekerå and Gärtner7, Lemma 3]. In turn, the only point in the proof of [Reference Ekerå and Gärtner7, Lemma 3] where this assumption is needed is when [Reference Ragavan and Vaikuntanathan17, Lemma 5] is invoked (as a black box). The proof of [Reference Ragavan and Vaikuntanathan17, Lemma 5] is given in [Reference Ragavan and Vaikuntanathan17, Section 5], and the size assumption on the
![]() $b_i$
’s only comes up in [Reference Ragavan and Vaikuntanathan17, Lemma 12].
$b_i$
’s only comes up in [Reference Ragavan and Vaikuntanathan17, Lemma 12].
The result [Reference Ragavan and Vaikuntanathan17, Lemma 12] essentiallyFootnote
14
states that there is a quantum circuit using
![]() $O(d \log ^3d)$
gates and
$O(d \log ^3d)$
gates and
![]() $O(d \log ^3d)$
qubits to perform the computation of
$O(d \log ^3d)$
qubits to perform the computation of
![]() $\prod _{i=1}^d a_i^{t_i}$
where
$\prod _{i=1}^d a_i^{t_i}$
where
![]() $t_i\in \{0, 1\}$
and
$t_i\in \{0, 1\}$
and
![]() $a_i$
are integers on
$a_i$
are integers on
![]() $O(\log d)$
bits. This is a special case of Lemma 4.1 (used together with Lemma 4.2) applied with
$O(\log d)$
bits. This is a special case of Lemma 4.1 (used together with Lemma 4.2) applied with
![]() $m = O(\log d)$
. In our case, we just apply Lemma 4.1 with
$m = O(\log d)$
. In our case, we just apply Lemma 4.1 with
![]() $m = O(d\log d)$
, together with Lemma 4.2 to convert the classical circuit into a quantum one. This yields a quantum circuit having
$m = O(d\log d)$
, together with Lemma 4.2 to convert the classical circuit into a quantum one. This yields a quantum circuit having
![]() $O(d^2\log ^3 d)$
gates and
$O(d^2\log ^3 d)$
gates and
![]() $O(d^2\log ^3 d)$
qubits to compute
$O(d^2\log ^3 d)$
qubits to compute
![]() $\prod _{i=1}^d b_i^{t_i}$
.
$\prod _{i=1}^d b_i^{t_i}$
.
The number of gates of the quantum circuit [Reference Ragavan and Vaikuntanathan17, Lemma 5] is
(because [Reference Ragavan and Vaikuntanathan17, Lemma 12] is used
![]() $O(d)$
times, see [Reference Ragavan and Vaikuntanathan17, Algorithm 5.2] and the surrounding explanations). Note that this is the same as for Regev’s algorithm (see [Reference Regev18, p5]). In our case, the number of gates is
$O(d)$
times, see [Reference Ragavan and Vaikuntanathan17, Algorithm 5.2] and the surrounding explanations). Note that this is the same as for Regev’s algorithm (see [Reference Regev18, p5]). In our case, the number of gates is
The space optimisations of Ragavan and Vaikuntanathan keep the total number of qubits for their circuit [Reference Ragavan and Vaikuntanathan17, Lemma 5] under
due to the way the qubits are used and restored in the main loop of [Reference Ragavan and Vaikuntanathan17, Algorithm 5.2]. In our situation, the number of qubits is
In summary, our final quantum circuit has
![]() $O(n^{3/2}\log ^3 n)$
gates and
$O(n^{3/2}\log ^3 n)$
gates and
![]() $O(n \log ^3 n)$
qubits. As noted in [Reference Ekerå and Gärtner7], the fact that the two elements g and y are not small (g and y can be as large as N, as opposed to the
$O(n \log ^3 n)$
qubits. As noted in [Reference Ekerå and Gärtner7], the fact that the two elements g and y are not small (g and y can be as large as N, as opposed to the
![]() $b_i$
’s) does not affect these complexity bounds.
$b_i$
’s) does not affect these complexity bounds.
Remark 4.4. In the proof of Theorem 1.2, we used the naive Lemma 4.2 to convert a classical circuit into a quantum one. As mentioned in Remark 1.3, it is possible to save a factor of
![]() $\log n$
in the space cost for Theorems 1.1 and 1.2 by reusing certain qubits when performing the quantum computation corresponding to Lemma 4.1.
$\log n$
in the space cost for Theorems 1.1 and 1.2 by reusing certain qubits when performing the quantum computation corresponding to Lemma 4.1.
4.3 Factoring integers
In this section, we prove Theorem 1.1.
Lemma 4.5. Let
![]() $N>1$
be an odd integer with at least two distinct prime factors. Let
$N>1$
be an odd integer with at least two distinct prime factors. Let
![]() $\mathbf {x}$
be a random variable, uniformly distributed in
$\mathbf {x}$
be a random variable, uniformly distributed in
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
. Then
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
. Then
![]() $\left \langle \mathbf {x}\right \rangle $
contains a nontrivial square root of
$\left \langle \mathbf {x}\right \rangle $
contains a nontrivial square root of
![]() $1$
modulo N with probability
$1$
modulo N with probability
![]() $\geq 1/2$
.
$\geq 1/2$
.
Proof. This elementary number-theoretic fact is well-known – it was already needed for Shor’s algorithm [Reference Peter20]. See [Reference Nielsen and Chuang16, Appendix A4.3] for a detailed proof.
Theorem 1.1. There is a quantum circuit having
![]() $O(n^{3/2} \log ^3 n)$
quantum gates and
$O(n^{3/2} \log ^3 n)$
quantum gates and
![]() $O(n \log ^3 n)$
qubits with the following property. There is a classical randomised polynomial-time algorithm that solves the factoring problem
$O(n \log ^3 n)$
qubits with the following property. There is a classical randomised polynomial-time algorithm that solves the factoring problem
 $$ \begin{align*} & \mathbf{Input: }\text{ a composite integer } N \leq 2^n \\ & \mathbf{Output: }\text{ a nontrivial divisor of } N \end{align*} $$
$$ \begin{align*} & \mathbf{Input: }\text{ a composite integer } N \leq 2^n \\ & \mathbf{Output: }\text{ a nontrivial divisor of } N \end{align*} $$
using
![]() $O(\sqrt {n})$
calls to this quantum circuit, and succeeds with probability
$O(\sqrt {n})$
calls to this quantum circuit, and succeeds with probability
![]() $\Theta (1)$
.
$\Theta (1)$
.
Proof of Theorem 1.1.
We can assume that N is odd and not a perfect prime power, as otherwise it is easy to factor N in polynomial time with a classical computer (see [Reference Nielsen and Chuang16, Exercise 5.17]).
Let
![]() $d := \lceil \!\sqrt {\log N} \rceil $
and
$d := \lceil \!\sqrt {\log N} \rceil $
and
![]() $X := d^{10^3d}$
. The probabilistic algorithm to find a nontrivial divisor of N goes as follows.
$X := d^{10^3d}$
. The probabilistic algorithm to find a nontrivial divisor of N goes as follows.
-
1. Generate d primes
 $b_1, \ldots , b_d$
independently and uniformly at random in the set of primes
$b_1, \ldots , b_d$
independently and uniformly at random in the set of primes
 $\leq X$
not dividing N. Sample another integer x uniformly chosen in
$\leq X$
not dividing N. Sample another integer x uniformly chosen in
 $(\mathbb {Z}/N\mathbb {Z})^{\times }$
. As in the proof of Theorem 1.2, this can be done classically in polynomial time with probability
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
. As in the proof of Theorem 1.2, this can be done classically in polynomial time with probability
 $1+O(1/N)$
.
$1+O(1/N)$
. -
2. Use the algorithm of Ekerå and Gärtner [Reference Ekerå and Gärtner7] to obtain a basis for the lattice
This involves making $$ \begin{align*} \mathcal{L}_{\underline{b},x} := \Big\{(e_1, \ldots, e_d, f) \in \mathbb{Z}^{d+1} \ : \ \Bigg(\prod_{i=1}^d b_i^{e_i}\Bigg) x^f \equiv 1 \quad\pmod{N}\Big\}. \end{align*} $$
$$ \begin{align*} \mathcal{L}_{\underline{b},x} := \Big\{(e_1, \ldots, e_d, f) \in \mathbb{Z}^{d+1} \ : \ \Bigg(\prod_{i=1}^d b_i^{e_i}\Bigg) x^f \equiv 1 \quad\pmod{N}\Big\}. \end{align*} $$
 $O(d)$
calls to a quantum circuit, followed by polynomial-time classical postprocessing. By Theorem 3.18,
$O(d)$
calls to a quantum circuit, followed by polynomial-time classical postprocessing. By Theorem 3.18,
 $\mathcal {L}_{\underline {b},x}$
has a basis of vectors of Euclidean norm
$\mathcal {L}_{\underline {b},x}$
has a basis of vectors of Euclidean norm
 $\ll e^{42d}$
with probability
$\ll e^{42d}$
with probability
 $1 +O(d^{-d})$
, which means that this step is guaranteed to succeed with probability
$1 +O(d^{-d})$
, which means that this step is guaranteed to succeed with probability
 $\Theta (1)$
.
$\Theta (1)$
.
-
3. Using the short basis for
 $\mathcal {L}_{\underline {b},x}$
computed in the previous step, find the vector of the form
$\mathcal {L}_{\underline {b},x}$
computed in the previous step, find the vector of the form
 $(0, \ldots , 0, r)$
in
$(0, \ldots , 0, r)$
in
 $\mathcal {L}_{\underline {b},x}$
with
$\mathcal {L}_{\underline {b},x}$
with
 $r\geq 1$
as small as possible. This involves solving a linear system with integer coefficients, which can be done efficiently as in the proof of Theorem 1.2. This integer r is the order of x in
$r\geq 1$
as small as possible. This involves solving a linear system with integer coefficients, which can be done efficiently as in the proof of Theorem 1.2. This integer r is the order of x in
 $(\mathbb {Z}/N\mathbb {Z})^{\times }$
. By Lemma 4.5, with probability
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
. By Lemma 4.5, with probability
 $\geq 1/2$
, this order r will be even and the element
$\geq 1/2$
, this order r will be even and the element
 $x^{r/2}$
will be a nontrivial square root of
$x^{r/2}$
will be a nontrivial square root of
 $1$
modulo N. Hence, N divides the product
$1$
modulo N. Hence, N divides the product
 $(x^{r/2}-1)(x^{r/2}+1)$
but neither term individually, which implies that
$(x^{r/2}-1)(x^{r/2}+1)$
but neither term individually, which implies that
 $\gcd (N,\, x^{r/2}-1 \!\!\mod {N})$
is a nontrivial divisor of N.
$\gcd (N,\, x^{r/2}-1 \!\!\mod {N})$
is a nontrivial divisor of N.
The analysis of this algorithm is identical to the corresponding part of the proof of Theorem 1.2.
A Bounds for character sums over primes
In this appendix, we prove Proposition 3.9. We start by stating the truncated explicit formula for
![]() $L(s, \chi )$
.
$L(s, \chi )$
.
Lemma A.1. Let
![]() $q\geq 2$
. Let
$q\geq 2$
. Let
![]() $\chi $
be a nonprincipal Dirichlet character modulo q. For
$\chi $
be a nonprincipal Dirichlet character modulo q. For
![]() $x\geq T\geq 2$
, we have
$x\geq T\geq 2$
, we have
 $$ \begin{align*} \sum_{n\leq x} \chi(n) \Lambda(n) = -\sum_{\substack{\rho = \beta+i\gamma\\ \left|\gamma\right| \leq T}} \frac{x^{\rho}-1}{\rho} + O\left(\frac{x \log^2(xq)}{T}\right) \end{align*} $$
$$ \begin{align*} \sum_{n\leq x} \chi(n) \Lambda(n) = -\sum_{\substack{\rho = \beta+i\gamma\\ \left|\gamma\right| \leq T}} \frac{x^{\rho}-1}{\rho} + O\left(\frac{x \log^2(xq)}{T}\right) \end{align*} $$
where the sum runs over all nontrivial zeros
![]() $\rho $
of
$\rho $
of
![]() $L(s, \chi )$
with multiplicity.
$L(s, \chi )$
with multiplicity.
Proof. This is [Reference Koukoulopoulos14, Theorem 11.3].
We will also need the following standard bound for the number of zeros of
![]() $L(s, \chi )$
in the critical strip at some height t.
$L(s, \chi )$
in the critical strip at some height t.
Lemma A.2. Let
![]() $q\geq 1$
and let
$q\geq 1$
and let
![]() $\chi $
be a Dirichlet character modulo q. Let
$\chi $
be a Dirichlet character modulo q. Let
![]() $t\in \mathbb {R}$
. The number of zeros
$t\in \mathbb {R}$
. The number of zeros
![]() $\rho = \beta + i \gamma $
of
$\rho = \beta + i \gamma $
of
![]() $L(s, \chi )$
in the rectangle
$L(s, \chi )$
in the rectangle
![]() $0\leq \beta \leq 1$
,
$0\leq \beta \leq 1$
,
![]() $t\leq \gamma \leq t+1$
is
$t\leq \gamma \leq t+1$
is
![]() $\ll \log (q(|t|+2))$
, where zeros are counted with multiplicity.
$\ll \log (q(|t|+2))$
, where zeros are counted with multiplicity.
Proof. This is [Reference Montgomery and Vaughan15, Theorem 10.17].
Proof of Proposition 3.9.
By Lemmas A.1 and A.2, choosing
![]() $T = x^{1-\alpha } - 1$
, we have
$T = x^{1-\alpha } - 1$
, we have
 $$ \begin{align*} \sum_{n\leq x} \chi(n) \Lambda(n) \ll \log(qx) \sum_{\substack{t\in \mathbb{Z}\\ |t| \leq x^{1-\alpha}-1}} \max_{\substack{\rho = \beta+i\gamma\\ \left|\gamma - t\right| \leq 1/2}} \left|\frac{x^{\rho}-1}{\rho}\right| + x^{\alpha}\log^2(qx), \end{align*} $$
$$ \begin{align*} \sum_{n\leq x} \chi(n) \Lambda(n) \ll \log(qx) \sum_{\substack{t\in \mathbb{Z}\\ |t| \leq x^{1-\alpha}-1}} \max_{\substack{\rho = \beta+i\gamma\\ \left|\gamma - t\right| \leq 1/2}} \left|\frac{x^{\rho}-1}{\rho}\right| + x^{\alpha}\log^2(qx), \end{align*} $$
where the maximum is over all zeros of
![]() $L(s, \chi )$
in the specified region. Since
$L(s, \chi )$
in the specified region. Since
![]() $\left |x^\rho \right |\leq x^{\alpha }$
for all zeros
$\left |x^\rho \right |\leq x^{\alpha }$
for all zeros
![]() $\rho = \beta + i\gamma $
with imaginary part
$\rho = \beta + i\gamma $
with imaginary part
![]() $|\gamma |\leq x^{1-\alpha }$
by our zero-free rectangle assumption, we can bound
$|\gamma |\leq x^{1-\alpha }$
by our zero-free rectangle assumption, we can bound
 $$ \begin{align*} \left|\frac{x^{\rho}-1}{\rho}\right| \ll \frac{x^{\alpha}}{1+|\gamma|} \end{align*} $$
$$ \begin{align*} \left|\frac{x^{\rho}-1}{\rho}\right| \ll \frac{x^{\alpha}}{1+|\gamma|} \end{align*} $$
(using for example that
![]() $\frac {x^{\rho }-1}{\rho } = \int _1^x t^{\rho -1} dt$
for
$\frac {x^{\rho }-1}{\rho } = \int _1^x t^{\rho -1} dt$
for
![]() $|\gamma |<1$
). Thus, we obtain
$|\gamma |<1$
). Thus, we obtain
 $$ \begin{align*} \sum_{n\leq x} \chi(n) \Lambda(n) \ll \log(qx) x^{\alpha} \sum_{|t|\leq x} \frac{1}{1+|t|}+ x^{\alpha}\log^2(qx)\ll x^{\alpha} \log^2(qx). \end{align*} $$
$$ \begin{align*} \sum_{n\leq x} \chi(n) \Lambda(n) \ll \log(qx) x^{\alpha} \sum_{|t|\leq x} \frac{1}{1+|t|}+ x^{\alpha}\log^2(qx)\ll x^{\alpha} \log^2(qx). \end{align*} $$
Discarding perfect prime powers, which contribute
![]() $O(x^{1/2}\log x)$
, and using partial summation, we get
$O(x^{1/2}\log x)$
, and using partial summation, we get
 $$ \begin{align*} \sum_{p\leq x} \chi(p) \ll \frac{x^{\alpha} \log^2(qx)}{(1-\alpha)\log x}. \end{align*} $$
$$ \begin{align*} \sum_{p\leq x} \chi(p) \ll \frac{x^{\alpha} \log^2(qx)}{(1-\alpha)\log x}. \end{align*} $$
We may assume that
![]() $1-\alpha \geq \frac {1}{\log x}$
, as otherwise Proposition 3.9 is trivial. If this is the case, we conclude that
$1-\alpha \geq \frac {1}{\log x}$
, as otherwise Proposition 3.9 is trivial. If this is the case, we conclude that
 $$ \begin{align*} \frac{1}{\pi(x)} \sum_{p\leq x} \chi(p) \ll \frac{x^{\alpha} \log^2(qx)}{\pi(x)} \ll x^{-(1-\alpha)} \log^3 (qx) \end{align*} $$
$$ \begin{align*} \frac{1}{\pi(x)} \sum_{p\leq x} \chi(p) \ll \frac{x^{\alpha} \log^2(qx)}{\pi(x)} \ll x^{-(1-\alpha)} \log^3 (qx) \end{align*} $$
as claimed.
Acknowledgments
I am indebted to my advisors, Ben Green and James Maynard, for their invaluable advice and support. I also wish to thank Seyoon Ragavan for his kind explanations, and in particular for showing me that the upper bound for the parameters in Regev’s algorithm could be relaxed considerably.
Competing interest
The author has no competing interest to declare.
Financial support
The author is supported by the Mathematical Institute of the University of Oxford, by a Saven European Scholarship and by a Jane Street Graduate Research Fellowship.