1. Introduction
First-order homogenization does not exist. The non-existence has its roots in two types of boundary effects. The first one arises when the domain is not a disjoint union of suitable rescaled copies of the periodicity cell (see [Reference Braides and Truskinovsky14, Example 1.12]). The second comes from the oscillatory nature of correctors in the homogenization theory (see [Reference Allaire and Amar2, Equation (2.12)]). Nevertheless, in this manuscript, we will provide a first-order ![]() $\Gamma$-convergence result for quadratic energies under suitable assumptions that allow us to ‘forget’ about the boundary. In particular, the scaling and the principal part of the energy in the bulk will be identified.
$\Gamma$-convergence result for quadratic energies under suitable assumptions that allow us to ‘forget’ about the boundary. In particular, the scaling and the principal part of the energy in the bulk will be identified.
Nowadays, homogenization is a very well-established mathematical theory describing how the microstructure affects the overall behaviour of a material (see, e.g., [Reference Berlyand and Rybalko9, Reference Braides and Defranceschi13]). The mathematical literature on the topic is too vast for an exhaustive list, and thus we limit ourselves to mention here some examples where it has been successfully applied: from thin structures (see, for instance, [Reference Balazi, Allaire and Omnes7, Reference Bouchitté and Fragalà10, Reference Braides and D’Elia12, Reference Zhikov and Pyatnitskii35]), to phase separation (see, for instance, [Reference Cristoferi, Fonseca and Ganedi17–Reference Cristoferi, Fonseca, Hagerty and Popovici19]), and from micromagnetism (see [Reference Alouges and Di Fratta3, Reference Christowiak and Kreisbeck16, Reference Davoli and D’Elia21, Reference Davoli and Di Fratta22]) to supremal functionals (see [Reference Briani, Prinari and Garroni15, Reference D’Elia, Eleuteri and Zappale20]). The investigation of boundary layers in homogenization is vast and here we mention only some contributions relevant for our analysis. Such an investigation is of great importance in spectral problems: in [Reference Moskow and Vogelius30], results for first-order corrections in periodic media have been proved, and in [Reference Santosa and Vogelius33], the interaction between periodic microstructure and the domain boundary has been investigated, providing also explicit examples of boundary effects. A quantitative boundary-layer analysis has been performed in [Reference Kenig, Lin and Shen26] which provides asymptotic expansions of Green and Neumann functions as well as in [Reference Shen and Zhuge34] where a ![]() $L^2$ convergence rate and a regularity estimate for homogenize boundary data for Neumann problems have been proved. A detailed asymptotic analysis of boundary-layer tail in half-space has been carried out in [Reference Prange32], which can be thought of as a complement of the contribution [Reference Allaire and Amar2]. Furthermore, we also mention the contribution [Reference Feldman and Kim23] where continuity and discontinuity properties of boundary-layer analysis have been addressed. Finally, in [Reference Alouges and Di Fratta4], the authors introduced an alternative notion of two-scale convergence based on cell averaging, illustrating its advantages in dealing with classical linear elliptic homogenization problems as well as first-order boundary corrector results.
$L^2$ convergence rate and a regularity estimate for homogenize boundary data for Neumann problems have been proved. A detailed asymptotic analysis of boundary-layer tail in half-space has been carried out in [Reference Prange32], which can be thought of as a complement of the contribution [Reference Allaire and Amar2]. Furthermore, we also mention the contribution [Reference Feldman and Kim23] where continuity and discontinuity properties of boundary-layer analysis have been addressed. Finally, in [Reference Alouges and Di Fratta4], the authors introduced an alternative notion of two-scale convergence based on cell averaging, illustrating its advantages in dealing with classical linear elliptic homogenization problems as well as first-order boundary corrector results.
The prototype of energies used in the homogenization theory is given by a family of functionals ![]() $\mathcal F_\varepsilon: L^p(\Omega; \mathbb{R}^M)\to \mathbb{R}\cup\{+\infty\}$, for
$\mathcal F_\varepsilon: L^p(\Omega; \mathbb{R}^M)\to \mathbb{R}\cup\{+\infty\}$, for ![]() $p\in(1,\infty)$, with
$p\in(1,\infty)$, with ![]() $\varepsilon \gt 0$ being the length scale characterizing the fine structure, of the form
$\varepsilon \gt 0$ being the length scale characterizing the fine structure, of the form
 \begin{equation*}
\notag
\mathcal F_\varepsilon(u):=
\begin{cases}
\int_\Omega W\left({x\over \varepsilon}, \nabla u(x)\right)\,\mathrm{d}x & \mbox{if } u\in W^{1,p}_0(\Omega; \mathbb{R}^M),\\
+\infty & \mbox{else}.
\end{cases}
\end{equation*}
\begin{equation*}
\notag
\mathcal F_\varepsilon(u):=
\begin{cases}
\int_\Omega W\left({x\over \varepsilon}, \nabla u(x)\right)\,\mathrm{d}x & \mbox{if } u\in W^{1,p}_0(\Omega; \mathbb{R}^M),\\
+\infty & \mbox{else}.
\end{cases}
\end{equation*} The first variable of the energy density ![]() $W$ accounts for the presence of a periodic microstructure, which is reflected in requiring that
$W$ accounts for the presence of a periodic microstructure, which is reflected in requiring that ![]() $W(\cdot, \xi)$ is a periodic function. The variational investigation of the periodic homogenization goes back to the end of Seventies. In [Reference Marcellini28], the limiting functional
$W(\cdot, \xi)$ is a periodic function. The variational investigation of the periodic homogenization goes back to the end of Seventies. In [Reference Marcellini28], the limiting functional ![]() $\mathcal F_{{\rm hom}}$ of
$\mathcal F_{{\rm hom}}$ of ![]() $\mathcal F_\varepsilon$ has been fully characterized in the scalar case, i.e.,
$\mathcal F_\varepsilon$ has been fully characterized in the scalar case, i.e., ![]() $M=1$, and under the assumptions of convexity and of
$M=1$, and under the assumptions of convexity and of ![]() $p$-growth of
$p$-growth of ![]() $W(x, \cdot)$. The
$W(x, \cdot)$. The ![]() $\Gamma$-limit
$\Gamma$-limit ![]() $F_{{\rm hom}}: L^p(\Omega)\to \mathbb{R}\cup\{+\infty\}$ is given by
$F_{{\rm hom}}: L^p(\Omega)\to \mathbb{R}\cup\{+\infty\}$ is given by
 \begin{equation}
\mathcal F_{{\rm hom}}(u):=
\begin{cases}
\int_\Omega W_{{\rm hom}}\left(\nabla u(x)\right)\,\mathrm{d}x & \mbox{if } u\in W^{1,p}_0(\Omega),\\
+\infty & \mbox{else},
\end{cases}
\end{equation}
\begin{equation}
\mathcal F_{{\rm hom}}(u):=
\begin{cases}
\int_\Omega W_{{\rm hom}}\left(\nabla u(x)\right)\,\mathrm{d}x & \mbox{if } u\in W^{1,p}_0(\Omega),\\
+\infty & \mbox{else},
\end{cases}
\end{equation} with the effective energy density ![]() $W_{{\rm hom}}:\mathbb{R}^N\to \mathbb{R}$ being characterized through the so-called cell formula
$W_{{\rm hom}}:\mathbb{R}^N\to \mathbb{R}$ being characterized through the so-called cell formula
 \begin{equation}
W_{{\rm hom}}(\xi):= \inf\left\{\int_{[0,1)^N} W(y, \xi+\nabla u(x)): u\in W_0^{1,p}([0,1)^N) \right\}.
\end{equation}
\begin{equation}
W_{{\rm hom}}(\xi):= \inf\left\{\int_{[0,1)^N} W(y, \xi+\nabla u(x)): u\in W_0^{1,p}([0,1)^N) \right\}.
\end{equation} Removing the assumption of convexity and in the vectorial framework, the analysis of the ![]() $\Gamma$-limit has been carried out independently in [Reference Braides11] and [Reference Müller27]. In this case, the limiting energy
$\Gamma$-limit has been carried out independently in [Reference Braides11] and [Reference Müller27]. In this case, the limiting energy ![]() $\mathcal F_{{\rm hom}}: L^p(\Omega; \mathbb{R}^M)\to \mathbb{R}\cup\{+\infty\}$ is again of the form (1.1) but the homogenized energy density
$\mathcal F_{{\rm hom}}: L^p(\Omega; \mathbb{R}^M)\to \mathbb{R}\cup\{+\infty\}$ is again of the form (1.1) but the homogenized energy density ![]() $W_{{\rm hom}}:\mathbb{R}^{M\times N}\to \mathbb{R}$ is characterized by the asymptotic cell formula
$W_{{\rm hom}}:\mathbb{R}^{M\times N}\to \mathbb{R}$ is characterized by the asymptotic cell formula
 \begin{equation}
W_{{\rm hom}}(\Xi):= \lim_{k\to\infty}{1\over k^N}\inf\left\{\int_{[0,k)^N} W(y, \Xi+\nabla u(x)): u\in W_0^{1,p}([0,k)^N; \mathbb{R}^M) \right\}.
\end{equation}
\begin{equation}
W_{{\rm hom}}(\Xi):= \lim_{k\to\infty}{1\over k^N}\inf\left\{\int_{[0,k)^N} W(y, \Xi+\nabla u(x)): u\in W_0^{1,p}([0,k)^N; \mathbb{R}^M) \right\}.
\end{equation} It is worth noticing that in the scalar setting and assuming the convexity of ![]() $W$ in the second variable, formula (1.3) turns into (1.2) (see [Reference Müller27, Lemma 4.1]).
$W$ in the second variable, formula (1.3) turns into (1.2) (see [Reference Müller27, Lemma 4.1]).
The aim of the present paper is to undertake a first-order analysis of a suitable version of the functional ![]() $\mathcal F_\varepsilon$ via
$\mathcal F_\varepsilon$ via ![]() $\Gamma$-convergence. We focus on quadratic energies
$\Gamma$-convergence. We focus on quadratic energies ![]() $F_\varepsilon: L^2(\Omega)\to \mathbb{R}\cup\{+\infty\}$ of the form
$F_\varepsilon: L^2(\Omega)\to \mathbb{R}\cup\{+\infty\}$ of the form
 \begin{equation*}
\notag
F_\varepsilon(u):=
\begin{cases}
\int_\Omega A\left({x\over \varepsilon}\right)\nabla u(x)\cdot \nabla u(x)\,\mathrm{d}x - \int_\Omega f(x)u(x)\,\mathrm{d}x &\mbox{if } u\in H^1_0(\Omega),\\
+\infty & \mbox{else},
\end{cases}
\end{equation*}
\begin{equation*}
\notag
F_\varepsilon(u):=
\begin{cases}
\int_\Omega A\left({x\over \varepsilon}\right)\nabla u(x)\cdot \nabla u(x)\,\mathrm{d}x - \int_\Omega f(x)u(x)\,\mathrm{d}x &\mbox{if } u\in H^1_0(\Omega),\\
+\infty & \mbox{else},
\end{cases}
\end{equation*} where ![]() $\Omega\subset\mathbb{R}^N$ is a bounded open set,
$\Omega\subset\mathbb{R}^N$ is a bounded open set, ![]() $f\in L^2(\Omega)$ and
$f\in L^2(\Omega)$ and ![]() $A:\Omega\to\mathbb{R}^{N\times N}$ is a matrix-valued function in
$A:\Omega\to\mathbb{R}^{N\times N}$ is a matrix-valued function in ![]() $L^\infty$ that is
$L^\infty$ that is ![]() $[0,1)^N$-periodic, symmetric and with lower and upper quadratic bounds.
$[0,1)^N$-periodic, symmetric and with lower and upper quadratic bounds.
To identify the contribution of the bulk in the first-order limit, we restrict the admissible class for the source term ![]() $f$ (see Section 2.2 for further details). This allows us to get rid of both types of boundary effect.
$f$ (see Section 2.2 for further details). This allows us to get rid of both types of boundary effect.
Using the asymptotic expansion of functionals given in [Reference Anzellotti and Baldo5] in terms of ![]() $\Gamma$-convergence, we consider the functionals
$\Gamma$-convergence, we consider the functionals ![]() $F_{\varepsilon}^1: L^2(\Omega)\to \mathbb{R}\cup\{+\infty\}$ defined as
$F_{\varepsilon}^1: L^2(\Omega)\to \mathbb{R}\cup\{+\infty\}$ defined as
 \begin{equation*}
\notag
F_{\varepsilon}^1 (u):= {F_{\varepsilon}(u) - \min_{H^1_0(\Omega)} F_{{\rm hom}} \over \varepsilon}.
\end{equation*}
\begin{equation*}
\notag
F_{\varepsilon}^1 (u):= {F_{\varepsilon}(u) - \min_{H^1_0(\Omega)} F_{{\rm hom}} \over \varepsilon}.
\end{equation*} The principal result of the present manuscript is the identification of the scale ![]() $\varepsilon$ above as well as the
$\varepsilon$ above as well as the ![]() $\Gamma$-limit of
$\Gamma$-limit of ![]() $F_{\varepsilon}^1$ (see Theorem 2.7). The main novelty lies in the use of the dual correspondence between quadratic functionals and PDEs. To the best of the authors’ knowledge, this is the first time that these two theories are combined to get a variational result.
$F_{\varepsilon}^1$ (see Theorem 2.7). The main novelty lies in the use of the dual correspondence between quadratic functionals and PDEs. To the best of the authors’ knowledge, this is the first time that these two theories are combined to get a variational result.
We briefly outline the strategy we employ. The unique minimizer of ![]() $F_{\varepsilon}$ turns out to be the unique solution of the following elliptic problem with Dirichlet boundary conditions
$F_{\varepsilon}$ turns out to be the unique solution of the following elliptic problem with Dirichlet boundary conditions
 \begin{equation*}
\left\{
\begin{aligned}
-{\rm div}\left(A\left({x\over\varepsilon}\right)\nabla u_\varepsilon(x)\right)&=f(x) && \mbox{in } \Omega,\\
u_\varepsilon(x)&=0 && \mbox{on } \partial\Omega.
\end{aligned}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{aligned}
-{\rm div}\left(A\left({x\over\varepsilon}\right)\nabla u_\varepsilon(x)\right)&=f(x) && \mbox{in } \Omega,\\
u_\varepsilon(x)&=0 && \mbox{on } \partial\Omega.
\end{aligned}
\right.
\end{equation*} The investigation of such an elliptic problem has been broadly carried out by many authors, [Reference Allaire1, Reference Bensoussan, Lions and Papanicolaou8, Reference Jikov, Kozlov and Oleinik25] to name a few (see [Reference Berlyand and Rybalko9] for an extensive review on the topic). To get a homogenized equation, the classical strategy relies on the two-scale expansion developed in [Reference Allaire1, Reference Nguetseng31] of the solution ![]() $u_\varepsilon$:
$u_\varepsilon$:
 \begin{equation}
u_\varepsilon(x)= u_0(x) + \varepsilon u_1\left(x, {x\over\varepsilon}\right) + \dots,
\end{equation}
\begin{equation}
u_\varepsilon(x)= u_0(x) + \varepsilon u_1\left(x, {x\over\varepsilon}\right) + \dots,
\end{equation} where ![]() $u_0$ is the solution of the homogenized equation given by
$u_0$ is the solution of the homogenized equation given by
 \begin{equation*}
\left\{
\begin{aligned}
-{\rm div}\left(A_{\rm hom}\nabla u_0(x)\right)&=f(x) && \mbox{in } \Omega,\\
u_0(x)&=0 && \mbox{on } \partial\Omega,
\end{aligned}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{aligned}
-{\rm div}\left(A_{\rm hom}\nabla u_0(x)\right)&=f(x) && \mbox{in } \Omega,\\
u_0(x)&=0 && \mbox{on } \partial\Omega,
\end{aligned}
\right.
\end{equation*} where ![]() $A_{{\rm hom}}$ is defined through the cell formula (1.2) with
$A_{{\rm hom}}$ is defined through the cell formula (1.2) with ![]() $W(y, \xi+\nabla u)= A(y)(\xi+\nabla u(x))\cdot(\xi+\nabla u(x))$. Moreover, the function
$W(y, \xi+\nabla u)= A(y)(\xi+\nabla u(x))\cdot(\xi+\nabla u(x))$. Moreover, the function ![]() $u_1$ is defined through the first-order correctors (see Section 3 for the precise definition). One would be tempted to use the ansatz (1.4) in the variational analysis for the functional
$u_1$ is defined through the first-order correctors (see Section 3 for the precise definition). One would be tempted to use the ansatz (1.4) in the variational analysis for the functional ![]() $F_\varepsilon^1$ to deduce the limiting energy. However, this idea does not work out. The reason is that the following estimate
$F_\varepsilon^1$ to deduce the limiting energy. However, this idea does not work out. The reason is that the following estimate
 \begin{equation*}
\left\| u_\varepsilon - u_0 - \varepsilon u_1\left(\cdot, {\cdot\over\varepsilon}\right) \right\|_{H^1(\Omega)}\leq C\sqrt{\varepsilon}
\end{equation*}
\begin{equation*}
\left\| u_\varepsilon - u_0 - \varepsilon u_1\left(\cdot, {\cdot\over\varepsilon}\right) \right\|_{H^1(\Omega)}\leq C\sqrt{\varepsilon}
\end{equation*} turns out to be sharp (see, e.g., [Reference Bensoussan, Lions and Papanicolaou8]). This surprising result suggests the presence of another phenomenon, known as boundary layers. They are further first-order corrections needed to match the boundary conditions (see [Reference Allaire and Amar2, Reference Armstrong, Kuusi, Mourrat and Prange6, Reference Gérard-Varet and Masmoudi24]). Due to the high oscillatory nature of these functions, their energy contribution is not clearly quantifiable with respect to the parameter ![]() $\varepsilon$. This is what we have referred to as the second type of boundary effect. In order to avoid this high oscillatory behaviour at the boundary, we essentially consider the case where the function
$\varepsilon$. This is what we have referred to as the second type of boundary effect. In order to avoid this high oscillatory behaviour at the boundary, we essentially consider the case where the function ![]() $u_\varepsilon$ is compactly supported in
$u_\varepsilon$ is compactly supported in ![]() $\Omega$ by requiring the source term
$\Omega$ by requiring the source term ![]() $f$ to be in a specific class (see Assumption (H4) in Section 2.2). This enables us to get the first-order
$f$ to be in a specific class (see Assumption (H4) in Section 2.2). This enables us to get the first-order ![]() $\Gamma$-limit by using the ansatz in (1.4) together with a refinement of the classical Riemann–Lebesgue lemma (see Proposition 4.6).
$\Gamma$-limit by using the ansatz in (1.4) together with a refinement of the classical Riemann–Lebesgue lemma (see Proposition 4.6).
Finally, we show that the first-order ![]() $\Gamma$-convergence analysis is not needed when the functional
$\Gamma$-convergence analysis is not needed when the functional ![]() $F_\varepsilon$ only depends on the function
$F_\varepsilon$ only depends on the function ![]() $u$ and not on its gradient
$u$ and not on its gradient ![]() $\nabla u$ (see Theorem 2.14). Indeed, in such a case, we have that the value of the minimum of the functional
$\nabla u$ (see Theorem 2.14). Indeed, in such a case, we have that the value of the minimum of the functional ![]() $F_\varepsilon$ is the same as the one of
$F_\varepsilon$ is the same as the one of ![]() $F_{\rm hom}$. This implies that the expansion by
$F_{\rm hom}$. This implies that the expansion by ![]() $\Gamma$-convergence does not provide additional information on the minimizers of the functional
$\Gamma$-convergence does not provide additional information on the minimizers of the functional ![]() $F_\varepsilon$.
$F_\varepsilon$.
The paper is organized as follows. In Section 2, we specify the set-up of the problem. The preliminaries and the technical results are given in Sections 3 and 4, respectively. We then turn to the proofs of the main result: in Section 5, we provide the compactness, while Sections 6 and 7 are devoted to the lower and upper bound, respectively. Finally, Section 8 is devoted to the proof of the first-order homogenization for functionals in ![]() $L^p$, for
$L^p$, for ![]() $p\in(1,\infty)$.
$p\in(1,\infty)$.
2. Set-up of the problem and main result
2.1. Basic notation
Here, we collect the basic notation we are going to use throughout the manuscript. Let ![]() $Y\subset\mathbb{R}^N$ be a periodicity cell, namely
$Y\subset\mathbb{R}^N$ be a periodicity cell, namely
 \begin{equation*}
Y = \left\{\, \sum_{i=1}^N \lambda_i v_i \,:\, 0 \lt \lambda_i \lt 1\right\},
\end{equation*}
\begin{equation*}
Y = \left\{\, \sum_{i=1}^N \lambda_i v_i \,:\, 0 \lt \lambda_i \lt 1\right\},
\end{equation*} where ![]() $v_1,\dots,v_N$ is a basis of
$v_1,\dots,v_N$ is a basis of ![]() $\mathbb{R}^N$. Without loss of generality, up to a translation, we can even assume that
$\mathbb{R}^N$. Without loss of generality, up to a translation, we can even assume that ![]() $Y$ has its barycentre at the origin. This assumption is just to simplify the writing of the main result.
$Y$ has its barycentre at the origin. This assumption is just to simplify the writing of the main result.
The space 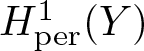 $H^1_{{\rm per}}(Y)$ is the subset of
$H^1_{{\rm per}}(Y)$ is the subset of ![]() $H^1(Y)$ of functions with periodic boundary conditions. More precisely,
$H^1(Y)$ of functions with periodic boundary conditions. More precisely, ![]() $u\in H^1(Y)$ if and only if the function
$u\in H^1(Y)$ if and only if the function ![]() $\widetilde{u}: \mathbb{R}^N\to\mathbb{R}$ defined as
$\widetilde{u}: \mathbb{R}^N\to\mathbb{R}$ defined as ![]() $\widetilde{u}(y):= u(\widetilde{y})$ belongs to
$\widetilde{u}(y):= u(\widetilde{y})$ belongs to ![]() $H^1_{\mathrm{loc}}(\mathbb{R}^N)$, where
$H^1_{\mathrm{loc}}(\mathbb{R}^N)$, where
 \begin{equation*}
y=\sum_{i=1}^N \lambda_i v_i,\quad\quad\quad
\widetilde{y}:=\sum_{i=1}^N \{\lambda_i\} v_i,
\end{equation*}
\begin{equation*}
y=\sum_{i=1}^N \lambda_i v_i,\quad\quad\quad
\widetilde{y}:=\sum_{i=1}^N \{\lambda_i\} v_i,
\end{equation*} and ![]() $\{\lambda_i\}:= \lambda_i - \lfloor \lambda_i \rfloor$.
$\{\lambda_i\}:= \lambda_i - \lfloor \lambda_i \rfloor$.
Given a function ![]() $f$, the notation
$f$, the notation ![]() $f^\varepsilon$ stands for
$f^\varepsilon$ stands for ![]() $f^\varepsilon(x):= f(x/\varepsilon)$. Moreover, we denote by
$f^\varepsilon(x):= f(x/\varepsilon)$. Moreover, we denote by ![]() $\partial_i$ the
$\partial_i$ the ![]() $i^{th}$ partial derivative operator with respect to the variable
$i^{th}$ partial derivative operator with respect to the variable ![]() $x$, and by
$x$, and by ![]() $\partial_{y_i}$ the
$\partial_{y_i}$ the ![]() $i^{th}$ partial derivative operator with respect to the variable
$i^{th}$ partial derivative operator with respect to the variable ![]() $y$. In particular, we have that
$y$. In particular, we have that
 \begin{equation*}
\partial_i f^\varepsilon(x) = \frac{1}{\varepsilon} \partial_{y_i}f^\varepsilon(x).
\end{equation*}
\begin{equation*}
\partial_i f^\varepsilon(x) = \frac{1}{\varepsilon} \partial_{y_i}f^\varepsilon(x).
\end{equation*} Finally, the symbol ![]() $\langle\cdot\rangle_Y$ denotes the average over
$\langle\cdot\rangle_Y$ denotes the average over ![]() $Y$, i.e.,
$Y$, i.e.,
 \begin{equation*}
\langle f\rangle_Y:= {1\over |Y|}\int_Y f(y)\,\mathrm{d} y,
\end{equation*}
\begin{equation*}
\langle f\rangle_Y:= {1\over |Y|}\int_Y f(y)\,\mathrm{d} y,
\end{equation*} with ![]() $|Y|$ being the
$|Y|$ being the ![]() $N$-dimensional Lebesgue measure of
$N$-dimensional Lebesgue measure of ![]() $Y$.
$Y$.
2.2. Main result
Let ![]() $\Omega\subset\mathbb{R}^N$ be an open, bounded set, and let
$\Omega\subset\mathbb{R}^N$ be an open, bounded set, and let ![]() $f\in L^2(\Omega)$. Let
$f\in L^2(\Omega)$. Let ![]() $A:\mathbb{R}^N\to\mathbb{R}^{N\times N}$ be a matrix-valued function in
$A:\mathbb{R}^N\to\mathbb{R}^{N\times N}$ be a matrix-valued function in ![]() $L^\infty$ such that
$L^\infty$ such that
(H1)
 $A$ is
$A$ is  $Y$-periodic;
$Y$-periodic;(H2)
 $A$ is symmetric, i.e.,
$A$ is symmetric, i.e.,  $a_{ij}(y)=a_{ji}(y)$;
$a_{ij}(y)=a_{ji}(y)$;(H3) there exist two positive constants
 $\alpha, \beta$ such that
$\alpha, \beta$ such that
 \begin{equation*}
\notag
\alpha|\xi|^2\leq A(y)\xi\cdot\xi\leq \beta |\xi|^2,
\end{equation*}
\begin{equation*}
\notag
\alpha|\xi|^2\leq A(y)\xi\cdot\xi\leq \beta |\xi|^2,
\end{equation*}for all
 $\xi\in\mathbb{R}^N$.
$\xi\in\mathbb{R}^N$.
For ![]() $\varepsilon \gt 0$, let
$\varepsilon \gt 0$, let ![]() $F_{\varepsilon}: L^2(\Omega)\to \mathbb{R}\cup \{+\infty\}$ be the functional defined as
$F_{\varepsilon}: L^2(\Omega)\to \mathbb{R}\cup \{+\infty\}$ be the functional defined as
 \begin{equation*}
\notag
F_{\varepsilon}(u):= \int_\Omega A^{\varepsilon}\left(x\right) \nabla u(x)\cdot\nabla u(x) \,\mathrm{d}x
- \int_\Omega f(x) u(x)\,\mathrm{d}x,
\end{equation*}
\begin{equation*}
\notag
F_{\varepsilon}(u):= \int_\Omega A^{\varepsilon}\left(x\right) \nabla u(x)\cdot\nabla u(x) \,\mathrm{d}x
- \int_\Omega f(x) u(x)\,\mathrm{d}x,
\end{equation*} if ![]() $u\in H^1_0(\Omega)$, and as
$u\in H^1_0(\Omega)$, and as ![]() $F_{\varepsilon}(u):=+\infty$ otherwise in
$F_{\varepsilon}(u):=+\infty$ otherwise in ![]() $L^2(\Omega)$.
$L^2(\Omega)$.
Under Assumptions (H1)–(H3), we know (see, for instance, [Reference Marcellini28], [Reference Müller27, Theorem 1.3], or [Reference Maso29, Corollary 24.5]) that ![]() $\{F_{\varepsilon}\}_\varepsilon$
$\{F_{\varepsilon}\}_\varepsilon$ ![]() $\Gamma$-converges with respect to the weak topology of
$\Gamma$-converges with respect to the weak topology of ![]() $H^1(\Omega)$, or equivalently the strong topology of
$H^1(\Omega)$, or equivalently the strong topology of ![]() $L^2(\Omega)$, to the effective functional
$L^2(\Omega)$, to the effective functional ![]() $F^0_{\rm hom}: L^2(\Omega)\to\mathbb{R}\cup\{+\infty\}$ given by
$F^0_{\rm hom}: L^2(\Omega)\to\mathbb{R}\cup\{+\infty\}$ given by
 \begin{equation*}
\notag
F^0_{\rm hom}(u):= \int_{\Omega} A_{{\rm hom}}\nabla u(x)\cdot\nabla u(x) \,\mathrm{d}x
- \int_\Omega f(x) u(x)\,\mathrm{d}x,
\end{equation*}
\begin{equation*}
\notag
F^0_{\rm hom}(u):= \int_{\Omega} A_{{\rm hom}}\nabla u(x)\cdot\nabla u(x) \,\mathrm{d}x
- \int_\Omega f(x) u(x)\,\mathrm{d}x,
\end{equation*} if ![]() $u\in H^1_0(\Omega)$, and by
$u\in H^1_0(\Omega)$, and by ![]() $F^0_{\rm hom}(u):=+\infty$ otherwise in
$F^0_{\rm hom}(u):=+\infty$ otherwise in ![]() $L^2(\Omega)$. Here, the effective matrix
$L^2(\Omega)$. Here, the effective matrix ![]() $A_{{\rm hom}}$ is a constant matrix given by the cell-formula
$A_{{\rm hom}}$ is a constant matrix given by the cell-formula
 \begin{equation}
A_{{\rm hom}}\xi\cdot\xi := \inf\Big\{\int_{Y} A(y) (\xi + \nabla \varphi(y))\cdot(\xi+ \nabla \varphi(y)) \,\mathrm{d} y : \varphi \in H^1_{{\rm per}}(Y)\Big\}.
\end{equation}
\begin{equation}
A_{{\rm hom}}\xi\cdot\xi := \inf\Big\{\int_{Y} A(y) (\xi + \nabla \varphi(y))\cdot(\xi+ \nabla \varphi(y)) \,\mathrm{d} y : \varphi \in H^1_{{\rm per}}(Y)\Big\}.
\end{equation} We refer to this ![]() $\Gamma$-convergence result as the zeroth-order term in the expansion by
$\Gamma$-convergence result as the zeroth-order term in the expansion by ![]() $\Gamma$-convergence of
$\Gamma$-convergence of ![]() $F_\varepsilon$. For our analysis, we need to recall the following. Using the fact that the functional in (2.1) is quadratic, for each
$F_\varepsilon$. For our analysis, we need to recall the following. Using the fact that the functional in (2.1) is quadratic, for each ![]() $\xi\in\mathbb{R}^N$, the minimization problem defining
$\xi\in\mathbb{R}^N$, the minimization problem defining ![]() $A_{{\rm hom}}\xi\cdot\xi$ has a unique solution (up to an additive constant), denoted by
$A_{{\rm hom}}\xi\cdot\xi$ has a unique solution (up to an additive constant), denoted by ![]() $\psi_\xi$.
$\psi_\xi$.
Definition 2.1. Let ![]() $e_1,\dots,e_N$ be the standard orthonormal basis of
$e_1,\dots,e_N$ be the standard orthonormal basis of ![]() $\mathbb{R}^N$. For each
$\mathbb{R}^N$. For each ![]() $i=1,\dots,N$, let
$i=1,\dots,N$, let 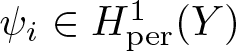 $\psi_i\in H^1_{{\rm per}}(Y)$ be the unique solution to
$\psi_i\in H^1_{{\rm per}}(Y)$ be the unique solution to
 \begin{equation*}
\inf\left\{\int_{Y} A(y) (e_i + \nabla \varphi(y))\cdot(e_i+ \nabla \varphi(y)) \,\mathrm{d} y : \varphi \in H^1_{{\rm per}}(Y),\,\, \int_Y \varphi(y)\,\mathrm{d} y =0 \right\}.
\end{equation*}
\begin{equation*}
\inf\left\{\int_{Y} A(y) (e_i + \nabla \varphi(y))\cdot(e_i+ \nabla \varphi(y)) \,\mathrm{d} y : \varphi \in H^1_{{\rm per}}(Y),\,\, \int_Y \varphi(y)\,\mathrm{d} y =0 \right\}.
\end{equation*} The function ![]() $\psi_i$ is called the first-order corrector for
$\psi_i$ is called the first-order corrector for ![]() $A$ associated with the vector
$A$ associated with the vector ![]() $e_i$.
$e_i$.
Remark 2.2. It turns out that the map ![]() $\xi\mapsto \psi_\xi$ is linear (see [Reference Maso29, Example 25.5]). Namely,
$\xi\mapsto \psi_\xi$ is linear (see [Reference Maso29, Example 25.5]). Namely,
 \begin{equation*}
\psi_\xi = \sum_{i=1}^N \psi_i \xi_i,
\end{equation*}
\begin{equation*}
\psi_\xi = \sum_{i=1}^N \psi_i \xi_i,
\end{equation*} where ![]() $\xi=(\xi_1,\dots,\xi_N)$. Therefore, the knowledge of the first-order correctors for
$\xi=(\xi_1,\dots,\xi_N)$. Therefore, the knowledge of the first-order correctors for ![]() $A$ is sufficient to obtain
$A$ is sufficient to obtain ![]() $A_{{\rm hom}}$.
$A_{{\rm hom}}$.
The goal of this paper is to develop further the expansion by ![]() $\Gamma$-convergence of
$\Gamma$-convergence of ![]() $F_\varepsilon$ (see [Reference Anzellotti and Baldo5] for further details). As explained in the Introduction, there are two issues with boundary effects in obtaining such a result. Thus, in order to carry out our analysis, we need to assume the following
$F_\varepsilon$ (see [Reference Anzellotti and Baldo5] for further details). As explained in the Introduction, there are two issues with boundary effects in obtaining such a result. Thus, in order to carry out our analysis, we need to assume the following
(H4) It holds that
 \begin{equation*}
f = -\mathrm{div}(A_{{\rm hom}}\nabla g),
\end{equation*}
\begin{equation*}
f = -\mathrm{div}(A_{{\rm hom}}\nabla g),
\end{equation*}for some
 $g\in C^\infty_c(Y)$.
$g\in C^\infty_c(Y)$.
Assumption (H4) is in order to ensure that the solution ![]() $u_0^{\min}$ has compact support in
$u_0^{\min}$ has compact support in ![]() $\Omega$. This allows us to avoid using boundary layers, which have two main issues: they do not have a variational definition, and their contribution to the energy is not clearly quantifiable in terms of the parameter
$\Omega$. This allows us to avoid using boundary layers, which have two main issues: they do not have a variational definition, and their contribution to the energy is not clearly quantifiable in terms of the parameter ![]() $\varepsilon$, which prevents us from getting an order of the energy.
$\varepsilon$, which prevents us from getting an order of the energy.
We are now in position to write the asymptotic expansion through ![]() $\Gamma$-convergence we will study.
$\Gamma$-convergence we will study.
Definition 2.3. Let ![]() $\{\varepsilon_n\}_n$ be an infinitesimal sequence. For
$\{\varepsilon_n\}_n$ be an infinitesimal sequence. For ![]() $n\in\mathbb{N}\setminus\{0\}$, we define the functional
$n\in\mathbb{N}\setminus\{0\}$, we define the functional ![]() $F_n^1: L^2(\Omega)\to \mathbb{R}\cup\{+\infty\}$ as
$F_n^1: L^2(\Omega)\to \mathbb{R}\cup\{+\infty\}$ as
 \begin{equation}
F_n^1 (u):= {F_{n}(u) - \min_{H^1_0(\Omega)}F^0_{{\rm hom}} \over \varepsilon_n}.
\end{equation}
\begin{equation}
F_n^1 (u):= {F_{n}(u) - \min_{H^1_0(\Omega)}F^0_{{\rm hom}} \over \varepsilon_n}.
\end{equation}Remark 2.4. Note that, using standard estimates (see the proof of Proposition 5.1), it is possible to prove that, for each ![]() $n\in\mathbb N\setminus\{0\}$, the minimization problem
$n\in\mathbb N\setminus\{0\}$, the minimization problem
 \begin{equation*}
\min_{u\in H^1_0(\Omega)} F_n(u)
\end{equation*}
\begin{equation*}
\min_{u\in H^1_0(\Omega)} F_n(u)
\end{equation*} admits a unique solution ![]() $u^{\rm min}_n\in H^1(\Omega)$. In a similar way, it is possible to prove that the minimization problem
$u^{\rm min}_n\in H^1(\Omega)$. In a similar way, it is possible to prove that the minimization problem
 \begin{equation*}
\min_{u\in H^1_0(\Omega)} F^0_{\rm hom}(u)
\end{equation*}
\begin{equation*}
\min_{u\in H^1_0(\Omega)} F^0_{\rm hom}(u)
\end{equation*} admits a unique minimizer ![]() $u^{\rm min}_0\in H^1(\Omega)$. In particular, we have that
$u^{\rm min}_0\in H^1(\Omega)$. In particular, we have that
 \begin{equation*}
F_{n}^1 (u) = {F_{n}(u) - F^0_{{\rm hom}}(u^{\rm min}_0) \over \varepsilon_n}.
\end{equation*}
\begin{equation*}
F_{n}^1 (u) = {F_{n}(u) - F^0_{{\rm hom}}(u^{\rm min}_0) \over \varepsilon_n}.
\end{equation*} Moreover, the ![]() $\Gamma$-convergence of
$\Gamma$-convergence of ![]() $F_{n}$ to
$F_{n}$ to ![]() $F^0_{\rm hom}$ together with the compactness of
$F^0_{\rm hom}$ together with the compactness of ![]() $\{u^{\rm min}_n\}_{n}$ yields that
$\{u^{\rm min}_n\}_{n}$ yields that ![]() $u^{\rm min}_n\to u^{\rm min}_0$ in
$u^{\rm min}_n\to u^{\rm min}_0$ in ![]() $L^2(\Omega)$ as
$L^2(\Omega)$ as ![]() $n\to\infty$.
$n\to\infty$.
Remark 2.5. Note that assumption (H4) implies that ![]() $u^{\min}_0=g$. In particular,
$u^{\min}_0=g$. In particular, ![]() $u^{\min}_0\in C^\infty_c(\Omega)$.
$u^{\min}_0\in C^\infty_c(\Omega)$.
Our goal is to study the ![]() $\Gamma$-limit of the family of functionals
$\Gamma$-limit of the family of functionals ![]() $\{F_n^1\}_{n}$. To this end, we introduce the candidate limiting functional.
$\{F_n^1\}_{n}$. To this end, we introduce the candidate limiting functional.
Definition 2.6. Define the functional ![]() $F^1_{{\rm hom}}: L^2(\Omega)\to \mathbb{R}\cup\{+\infty\}$ as
$F^1_{{\rm hom}}: L^2(\Omega)\to \mathbb{R}\cup\{+\infty\}$ as
 \begin{align}
F^1_{{\rm hom}}(u)&:=
\sum_{i,j=1}^N \int_\Omega
\nabla(\partial_i u^{\rm min}_0\partial_j u^{\rm min}_0)(x)\,\mathrm{d}x
\cdot\left\langle y \left[ a_{ij}
+ 2A e_j \cdot \nabla \psi_i
+ A \nabla \psi_i \cdot \nabla \psi_j \right]\right\rangle_Y \nonumber \\
&\quad+2 \sum_{i=1}^N \int_\Omega \langle \psi_i A\rangle_Y \nabla u^{\rm min}_0(x)\cdot \partial_i\nabla u^{\rm min}_0(x)\,\mathrm{d}x \nonumber \\
&\quad+ 2 \sum_{j=1}^N\sum_{i=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \langle \psi_i A\nabla_y\psi_j \rangle_Y \cdot \partial_i \nabla u^{\rm min}_0(x) \,\mathrm{d}x,
\end{align}
\begin{align}
F^1_{{\rm hom}}(u)&:=
\sum_{i,j=1}^N \int_\Omega
\nabla(\partial_i u^{\rm min}_0\partial_j u^{\rm min}_0)(x)\,\mathrm{d}x
\cdot\left\langle y \left[ a_{ij}
+ 2A e_j \cdot \nabla \psi_i
+ A \nabla \psi_i \cdot \nabla \psi_j \right]\right\rangle_Y \nonumber \\
&\quad+2 \sum_{i=1}^N \int_\Omega \langle \psi_i A\rangle_Y \nabla u^{\rm min}_0(x)\cdot \partial_i\nabla u^{\rm min}_0(x)\,\mathrm{d}x \nonumber \\
&\quad+ 2 \sum_{j=1}^N\sum_{i=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \langle \psi_i A\nabla_y\psi_j \rangle_Y \cdot \partial_i \nabla u^{\rm min}_0(x) \,\mathrm{d}x,
\end{align} if ![]() $u=u^{\min}_0$, and
$u=u^{\min}_0$, and ![]() $+\infty$ else in
$+\infty$ else in ![]() $L^2(\Omega)$. Here,
$L^2(\Omega)$. Here, ![]() $\psi_i$ are the first-order correctors defined in Definition 2.1.
$\psi_i$ are the first-order correctors defined in Definition 2.1.
We now state the main result of the present paper.
Theorem 2.7. Let ![]() $F_n^1$ and
$F_n^1$ and ![]() $F_{{\rm hom}}^1$ be the functionals given by (2.2) and (2.3), respectively. Assume that Assumptions (H1)-(H4) hold. Then, we have the following:
$F_{{\rm hom}}^1$ be the functionals given by (2.2) and (2.3), respectively. Assume that Assumptions (H1)-(H4) hold. Then, we have the following:
(i) Let
 $\{u_n\}_{n}$ be a sequence in
$\{u_n\}_{n}$ be a sequence in  $H^1(\Omega)$ such that
$H^1(\Omega)$ such that  $\sup_{n} F^1_n(u_n) \lt \infty$. Then,
$\sup_{n} F^1_n(u_n) \lt \infty$. Then,  $\{u_n\}_n$ converges in
$\{u_n\}_n$ converges in  $L^2(\Omega)$ to
$L^2(\Omega)$ to  $u^{\rm min}_0$, where
$u^{\rm min}_0$, where  $u^{\rm min}_0$ is the unique minimizer of
$u^{\rm min}_0$ is the unique minimizer of  $F_{{\rm hom}}^0$.
$F_{{\rm hom}}^0$.(ii) The sequence
 $\{F_n^1\}_{n}$
$\{F_n^1\}_{n}$  $\Gamma$-converges with respect to
$\Gamma$-converges with respect to  $L^2(\Omega)$ topology to
$L^2(\Omega)$ topology to  $F_{{\rm hom}}^1$.
$F_{{\rm hom}}^1$.
Remark 2.8. It is worth noticing that the (constant) functional ![]() $F^1_{{\rm hom}}$ does not depend on the source
$F^1_{{\rm hom}}$ does not depend on the source ![]() $f$.
$f$.
Remark 2.9. For an interpretation of the functional ![]() $F_{{\rm hom}}^1$, we refer to Remark 7.2.
$F_{{\rm hom}}^1$, we refer to Remark 7.2.
We show that the analogous first-order ![]() $\Gamma$-expansion is trivial in the case of functionals defined on
$\Gamma$-expansion is trivial in the case of functionals defined on ![]() $L^p$. We are able to prove this statement in a more general setting than that considered above. Fix
$L^p$. We are able to prove this statement in a more general setting than that considered above. Fix ![]() $p\in(1,\infty)$ and
$p\in(1,\infty)$ and ![]() $M\geq1$. Let
$M\geq1$. Let ![]() $V:\Omega\times\mathbb{R}^M\to\mathbb{R}$ be a Carathéodory function such that
$V:\Omega\times\mathbb{R}^M\to\mathbb{R}$ be a Carathéodory function such that
(A1) For each
 $z\in\mathbb{R}^M$, the function
$z\in\mathbb{R}^M$, the function  $x\mapsto V(x,z)$ is
$x\mapsto V(x,z)$ is  $Y$-periodic;
$Y$-periodic;(A2) There exists
 $0 \lt c_1 \lt c_2 \lt +\infty$ such that
$0 \lt c_1 \lt c_2 \lt +\infty$ such that
 \begin{equation*}
c_1(|z|^p-1) \leq V(x,z)\leq c_2(|z|^p+1),
\end{equation*}
\begin{equation*}
c_1(|z|^p-1) \leq V(x,z)\leq c_2(|z|^p+1),
\end{equation*}for all
 $x\in\Omega$ and
$x\in\Omega$ and  $z\in\mathbb{R}^M$.
$z\in\mathbb{R}^M$.
Note that in this case, the source term would only be a part of the function ![]() $V$. That is why there is no analogue of assumption (H4).
$V$. That is why there is no analogue of assumption (H4).
Definition 2.10. For ![]() $n\in\mathbb{N}\setminus\{0\}$, define
$n\in\mathbb{N}\setminus\{0\}$, define ![]() $G_n: L^p(\Omega;\mathbb{R}^M)\to\mathbb{R}\cup\{+\infty\}$ as
$G_n: L^p(\Omega;\mathbb{R}^M)\to\mathbb{R}\cup\{+\infty\}$ as
 \begin{equation*}
G_n(u) := \int_\Omega V\left( \frac{x}{\varepsilon_n}, u(x) \right)\,\mathrm{d}x.
\end{equation*}
\begin{equation*}
G_n(u) := \int_\Omega V\left( \frac{x}{\varepsilon_n}, u(x) \right)\,\mathrm{d}x.
\end{equation*}Remark 2.11. Note that there is no loss of generality in assuming the function ![]() $V$ to be convex in the second variable. Indeed, the relaxation of
$V$ to be convex in the second variable. Indeed, the relaxation of ![]() $G_n$ with respect to the weak-
$G_n$ with respect to the weak-![]() $L^p(\Omega)$ topology is given by
$L^p(\Omega)$ topology is given by
 \begin{equation*}
\overline{G_n}(u) = \int_\Omega V^c\left( \frac{x}{\varepsilon_n}, u(x) \right)\,\mathrm{d}x
\end{equation*}
\begin{equation*}
\overline{G_n}(u) = \int_\Omega V^c\left( \frac{x}{\varepsilon_n}, u(x) \right)\,\mathrm{d}x
\end{equation*} where ![]() $V^c$ denotes the convex envelope of the function
$V^c$ denotes the convex envelope of the function ![]() $V$ in the second variable.
$V$ in the second variable.
We now introduce the homogenized functional.
Definition 2.12. For ![]() $z\in\mathbb{R}^M$, let
$z\in\mathbb{R}^M$, let
 \begin{equation*}
V_{\rm hom}(z):= \inf\left\{\frac{1}{|Y|} \int_Y V^c(y,z + \varphi(y))\,\mathrm{d} y \,: \, \varphi\in L^p(Y;\mathbb{R}^M),\, \int_Y \varphi(y)\,\mathrm{d} y = 0 \right\}.
\end{equation*}
\begin{equation*}
V_{\rm hom}(z):= \inf\left\{\frac{1}{|Y|} \int_Y V^c(y,z + \varphi(y))\,\mathrm{d} y \,: \, \varphi\in L^p(Y;\mathbb{R}^M),\, \int_Y \varphi(y)\,\mathrm{d} y = 0 \right\}.
\end{equation*} Define the functional ![]() $G_{\rm hom}: L^p(\Omega;\mathbb{R}^M)\to\mathbb{R}\cup\{+\infty\}$ as
$G_{\rm hom}: L^p(\Omega;\mathbb{R}^M)\to\mathbb{R}\cup\{+\infty\}$ as
 \begin{equation*}
G_{\rm hom} := \int_\Omega V_{\rm hom} (u(x))\,\mathrm{d}x.
\end{equation*}
\begin{equation*}
G_{\rm hom} := \int_\Omega V_{\rm hom} (u(x))\,\mathrm{d}x.
\end{equation*}Using the same arguments as in the proof of [Reference Cristoferi, Fonseca and Ganedi17, Theorem 3.3], we get the following.
Lemma 2.13. Assume that Assumptions (A1)-(A2) hold. Then, ![]() $G_n\to G_{{\rm hom}}$ with respect to the weak-
$G_n\to G_{{\rm hom}}$ with respect to the weak-![]() $L^p(\Omega)$ topology.
$L^p(\Omega)$ topology.
Next result justifies our claim that the ![]() $\Gamma$-expansion is trivial in such a case.
$\Gamma$-expansion is trivial in such a case.
Theorem 2.14. Assume that Assumptions (A1)-(A2), as well as (H4) hold and that, for all ![]() $y\in Y$, the function
$y\in Y$, the function ![]() $u\mapsto V(y,u)$ is strictly convex. Let
$u\mapsto V(y,u)$ is strictly convex. Let ![]() $m\in\mathbb{R}^M$. Then,
$m\in\mathbb{R}^M$. Then,
 \begin{align*}
&\min\left\{G_n(v) : v\in L^p(\Omega;\mathbb{R}^M),\, \int_\Omega u(x)\,\mathrm{d}x =m \right\} \\ &
=
\min\left\{G_{{\rm hom}}(v) : v\in L^p(\Omega;\mathbb{R}^M),\, \int_\Omega u(x)\,\mathrm{d}x =m \right\},
\end{align*}
\begin{align*}
&\min\left\{G_n(v) : v\in L^p(\Omega;\mathbb{R}^M),\, \int_\Omega u(x)\,\mathrm{d}x =m \right\} \\ &
=
\min\left\{G_{{\rm hom}}(v) : v\in L^p(\Omega;\mathbb{R}^M),\, \int_\Omega u(x)\,\mathrm{d}x =m \right\},
\end{align*} for all ![]() $n\in\mathbb{N}\setminus\{0\}$.
$n\in\mathbb{N}\setminus\{0\}$.
Remark 2.15. The assumption of strict convexity is needed only to simplify the strategy of the proof, since we need to invert the relation
Strict convexity gives us a unique inverse, while with convexity alone, we would have to get a slightly more involved argument. Since this result is to show that for these functionals there is no need for a first order ![]() $\Gamma$-expansion, we decided to use this extra technical assumption.
$\Gamma$-expansion, we decided to use this extra technical assumption.
Remark 2.16. Note that, in this case, boundary conditions are not natural. This is why we consider a mass constraint instead.
3. Preliminaries
3.1. Recall of homogenization
We recall the foundations of the homogenization theory for elliptic equations. Even if this theory is classical by now, we revisit it since we will use a slightly different definition of the correctors than that in [Reference Allaire and Amar2, Reference Bensoussan, Lions and Papanicolaou8].
Let ![]() $\Omega$ be a bounded and open subset of
$\Omega$ be a bounded and open subset of ![]() $\mathbb{R}^N$. Let
$\mathbb{R}^N$. Let ![]() $A$ be the matrix-valued function satisfying Assumptions (H1)-(H3). For a given
$A$ be the matrix-valued function satisfying Assumptions (H1)-(H3). For a given ![]() $f\in L^2(\Omega)$, we consider the following equation
$f\in L^2(\Omega)$, we consider the following equation
 \begin{equation}
\left\{
\begin{aligned}
-{\rm div}(A^\varepsilon(x)\nabla u_\varepsilon(x))
&= f(x) && \mbox{in }\Omega,\\
u_\varepsilon(x)&=0 && \mbox{on } \partial\Omega.
\end{aligned}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{aligned}
-{\rm div}(A^\varepsilon(x)\nabla u_\varepsilon(x))
&= f(x) && \mbox{in }\Omega,\\
u_\varepsilon(x)&=0 && \mbox{on } \partial\Omega.
\end{aligned}
\right.
\end{equation} It is well-known that this problem admits a unique solution in ![]() $H^1_0(\Omega)$ (see, e.g., [Reference Bensoussan, Lions and Papanicolaou8]). To carry out a homogenization procedure, the solution
$H^1_0(\Omega)$ (see, e.g., [Reference Bensoussan, Lions and Papanicolaou8]). To carry out a homogenization procedure, the solution ![]() $u_\varepsilon$ is assumed to have the following two-scale expansion
$u_\varepsilon$ is assumed to have the following two-scale expansion
 \begin{equation*}
u_\varepsilon(x) = u_0\left(x, {x\over \varepsilon}\right) + \varepsilon u_1\left(x, {x\over \varepsilon}\right) + \varepsilon^2u_2\left(x, {x\over \varepsilon}\right) + \dots,
\end{equation*}
\begin{equation*}
u_\varepsilon(x) = u_0\left(x, {x\over \varepsilon}\right) + \varepsilon u_1\left(x, {x\over \varepsilon}\right) + \varepsilon^2u_2\left(x, {x\over \varepsilon}\right) + \dots,
\end{equation*} where each ![]() $u_i$ is
$u_i$ is ![]() $Y$-periodic with respect to the fast variable
$Y$-periodic with respect to the fast variable ![]() $y={x\over\varepsilon}$. The variables
$y={x\over\varepsilon}$. The variables ![]() $x$ and
$x$ and ![]() $y$ are treated as independent. Plugging such an expansion into (3.1) and identifying powers of
$y$ are treated as independent. Plugging such an expansion into (3.1) and identifying powers of ![]() $\varepsilon$, we get a cascade of equations. Here, we only care about the second-order expansion. Therefore, setting
$\varepsilon$, we get a cascade of equations. Here, we only care about the second-order expansion. Therefore, setting ![]() $\mathcal{A}_\varepsilon \varphi(x):= -{\rm div}(A^\varepsilon(x)\nabla \varphi(x))$, we deduce that
$\mathcal{A}_\varepsilon \varphi(x):= -{\rm div}(A^\varepsilon(x)\nabla \varphi(x))$, we deduce that
where
 \begin{align*}
\mathcal{A}_0 &:= -\sum_{i=1}^N{\partial_ {y_i}}\left(\sum_{j=1}^N a_{ij}(y){\partial_{y_j}}\right),\notag\\
\mathcal{A}_1 &:= -\sum_{i=1}^N{\partial_{y_i}}\left(\sum_{j=1}^N a_{ij}(y){\partial_j}\right) - \sum_{i=1}^N{\partial_i}\left(\sum_{j=1}^N a_{ij}(y){\partial_{y_j}}\right),\notag\\
\mathcal{A}_2 &:= -\sum_{i=1}^N{\partial_i}\left(\sum_{j=1}^N a_{ij}(y){\partial_j}\right)\notag.
\end{align*}
\begin{align*}
\mathcal{A}_0 &:= -\sum_{i=1}^N{\partial_ {y_i}}\left(\sum_{j=1}^N a_{ij}(y){\partial_{y_j}}\right),\notag\\
\mathcal{A}_1 &:= -\sum_{i=1}^N{\partial_{y_i}}\left(\sum_{j=1}^N a_{ij}(y){\partial_j}\right) - \sum_{i=1}^N{\partial_i}\left(\sum_{j=1}^N a_{ij}(y){\partial_{y_j}}\right),\notag\\
\mathcal{A}_2 &:= -\sum_{i=1}^N{\partial_i}\left(\sum_{j=1}^N a_{ij}(y){\partial_j}\right)\notag.
\end{align*} Using (3.1), matching powers of ![]() $\varepsilon$ up to second order gives us the following equations
$\varepsilon$ up to second order gives us the following equations
From (3.2), it follows that ![]() $u_0(x,y)\equiv u_0(x)$. The solution
$u_0(x,y)\equiv u_0(x)$. The solution ![]() $u_1$ to (3.3) is given by
$u_1$ to (3.3) is given by
 \begin{equation}
u_1\left(x, {x\over \varepsilon}\right)= \sum_{j=1}^N \psi_j^{\varepsilon}\left(x\right) {\partial_j}u_0(x) + \widetilde{u}_1(x),
\end{equation}
\begin{equation}
u_1\left(x, {x\over \varepsilon}\right)= \sum_{j=1}^N \psi_j^{\varepsilon}\left(x\right) {\partial_j}u_0(x) + \widetilde{u}_1(x),
\end{equation} where, for ![]() $j=1,\dots, N$,
$j=1,\dots, N$, ![]() $\psi_j$ is the unique solution in
$\psi_j$ is the unique solution in  $H^1_{\rm per}(Y)$ to the problem
$H^1_{\rm per}(Y)$ to the problem
 \begin{equation}
\begin{cases}
\mathcal{A}_0 \psi_j(y)= \sum_{i=1}^N\partial_{y_i} a_{ij}(y) & \mbox{in } Y,\\
\int_Y \psi_j(y)\,\mathrm{d} y=0, \\
y\mapsto \psi_j(y) &Y\mbox{-periodic}.
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
\mathcal{A}_0 \psi_j(y)= \sum_{i=1}^N\partial_{y_i} a_{ij}(y) & \mbox{in } Y,\\
\int_Y \psi_j(y)\,\mathrm{d} y=0, \\
y\mapsto \psi_j(y) &Y\mbox{-periodic}.
\end{cases}
\end{equation} Namely, for ![]() $j=1,\dots, N$, the function
$j=1,\dots, N$, the function ![]() $\psi_j$ are the first-order corrector defined in Definition 2.1. The solution to equation (3.4) is given by
$\psi_j$ are the first-order corrector defined in Definition 2.1. The solution to equation (3.4) is given by
 \begin{equation}
u_2\left(x, {x\over \varepsilon} \right) = \sum_{i,j=1}^N\chi^{\varepsilon}_{ij}\left(x\right) {\partial^2_{ij}} u_0(x)
+\sum_{j=1}^N \psi_j^{\varepsilon}\left(x\right) {\partial_j}\widetilde{u}_1(x)+ \widetilde{u}_2(x),
\end{equation}
\begin{equation}
u_2\left(x, {x\over \varepsilon} \right) = \sum_{i,j=1}^N\chi^{\varepsilon}_{ij}\left(x\right) {\partial^2_{ij}} u_0(x)
+\sum_{j=1}^N \psi_j^{\varepsilon}\left(x\right) {\partial_j}\widetilde{u}_1(x)+ \widetilde{u}_2(x),
\end{equation} where for all ![]() $i,j=1,\dots, n$, the second-order corrector
$i,j=1,\dots, n$, the second-order corrector 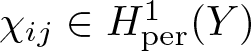 $\chi_{ij}\in H^1_{{\rm per}}(Y)$ satisfies the following auxiliary problem
$\chi_{ij}\in H^1_{{\rm per}}(Y)$ satisfies the following auxiliary problem
 \begin{equation}
\begin{cases}
\mathcal{A}_0 \chi_{ij}(y) = b_{ij}(y)-\int_Y b_{ij}(y)\,\mathrm{d} y &\mbox{in } Y,\\
\int_Y \chi_{ij}(y)\,\mathrm{d} y=0,\\
y\mapsto \chi_{ij}(y)&Y\mbox{-periodic},
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
\mathcal{A}_0 \chi_{ij}(y) = b_{ij}(y)-\int_Y b_{ij}(y)\,\mathrm{d} y &\mbox{in } Y,\\
\int_Y \chi_{ij}(y)\,\mathrm{d} y=0,\\
y\mapsto \chi_{ij}(y)&Y\mbox{-periodic},
\end{cases}
\end{equation}with
 \begin{equation}
b_{ij}(y):= a_{ij}(y) +\sum_{k=1}^N a_{ik}(y){\partial_{y_k} \psi_j}(y) + \sum_{k=1}^N{\partial_{y_k}}(a_{ki}\psi_j)(y).
\end{equation}
\begin{equation}
b_{ij}(y):= a_{ij}(y) +\sum_{k=1}^N a_{ik}(y){\partial_{y_k} \psi_j}(y) + \sum_{k=1}^N{\partial_{y_k}}(a_{ki}\psi_j)(y).
\end{equation} It is worth recalling that the function ![]() $\widetilde{u}_1$ in (3.6) can be taken identically equal to zero if one is only interested in the first-order expansion of
$\widetilde{u}_1$ in (3.6) can be taken identically equal to zero if one is only interested in the first-order expansion of ![]() $u_\varepsilon$. Otherwise,
$u_\varepsilon$. Otherwise, ![]() $\widetilde{u}_1$ is determined by the compatibility condition of equation (3.5), namely,
$\widetilde{u}_1$ is determined by the compatibility condition of equation (3.5), namely,
 \begin{equation}
{\rm div}(A_{{\rm hom}}\nabla \widetilde{u}_1(x))= -\sum_{i,j,k=1}^N c_{ijk}{\partial^3_{ijk} u_0^{\min}}(x),
\end{equation}
\begin{equation}
{\rm div}(A_{{\rm hom}}\nabla \widetilde{u}_1(x))= -\sum_{i,j,k=1}^N c_{ijk}{\partial^3_{ijk} u_0^{\min}}(x),
\end{equation} where ![]() $A_{{\rm hom}}$ is the homogenized matrix defined by (2.1) and for
$A_{{\rm hom}}$ is the homogenized matrix defined by (2.1) and for ![]() $i,j,k=1,\dots,N$, the constant
$i,j,k=1,\dots,N$, the constant ![]() $c_{ijk}$ is defined as
$c_{ijk}$ is defined as
 \begin{equation}
c_{ijk}:= \left\langle \sum_{l=1}^N a_{kl}{\partial_{y_l} \chi_{ij}} + a_{ij}\psi_k \right\rangle_Y.
\end{equation}
\begin{equation}
c_{ijk}:= \left\langle \sum_{l=1}^N a_{kl}{\partial_{y_l} \chi_{ij}} + a_{ij}\psi_k \right\rangle_Y.
\end{equation} Since in the present paper, we are interested in expanding ![]() $u_\varepsilon$ up to the second-order, the function
$u_\varepsilon$ up to the second-order, the function ![]() $\widetilde{u}_2$ in (3.8) can be taken identically equal to zero.
$\widetilde{u}_2$ in (3.8) can be taken identically equal to zero.
Remark 3.1. In the following, we will use the above theory for the function ![]() $u_0^{\min}$ in place of
$u_0^{\min}$ in place of ![]() $u_0$.
$u_0$.
3.2. Periodic functions
We collect some useful properties of the space  $L^2_{{\rm per}}(Y; \mathbb{R}^N)$ of the periodic functions (see [Reference Jikov, Kozlov and Oleinik25, Chapter 1] for further details).
$L^2_{{\rm per}}(Y; \mathbb{R}^N)$ of the periodic functions (see [Reference Jikov, Kozlov and Oleinik25, Chapter 1] for further details).
The space ![]() $L^2_{\rm sol}(Y)$ of solenoidal periodic functions is defined as
$L^2_{\rm sol}(Y)$ of solenoidal periodic functions is defined as
 \begin{equation*}
L^2_{\rm sol}(Y):=\{f\in L^2_{{\rm per}}(Y; \mathbb{R}^N)\; : \; \hbox{div}f=0\hbox{in } \mathbb{R}^N \},
\end{equation*}
\begin{equation*}
L^2_{\rm sol}(Y):=\{f\in L^2_{{\rm per}}(Y; \mathbb{R}^N)\; : \; \hbox{div}f=0\hbox{in } \mathbb{R}^N \},
\end{equation*} where the equality ![]() $\hbox{div}f=0$ is to be intended in distributional sense, i.e.,
$\hbox{div}f=0$ is to be intended in distributional sense, i.e.,
 \begin{equation*}
\int_{\mathbb{R}^N} f(x)\cdot \nabla \varphi(x)\; dx=0, \;\;\;\hbox{for any } \varphi \in C^\infty_c(\mathbb{R}^N).
\end{equation*}
\begin{equation*}
\int_{\mathbb{R}^N} f(x)\cdot \nabla \varphi(x)\; dx=0, \;\;\;\hbox{for any } \varphi \in C^\infty_c(\mathbb{R}^N).
\end{equation*} The space ![]() $L^2_{\rm sol}(Y)$ turns out to be a closed subspace of
$L^2_{\rm sol}(Y)$ turns out to be a closed subspace of ![]() $L^2(Y; \mathbb{R}^N)$. Setting
$L^2(Y; \mathbb{R}^N)$. Setting
 \begin{equation*}
\notag
\mathcal V^2_{\rm pot}(Y):= \{\nabla u\;: u\in H^1_{{\rm per}}(Y; \mathbb{R}^N)\},
\end{equation*}
\begin{equation*}
\notag
\mathcal V^2_{\rm pot}(Y):= \{\nabla u\;: u\in H^1_{{\rm per}}(Y; \mathbb{R}^N)\},
\end{equation*}we immediately deduce the following orthogonal representation
 \begin{equation*}
\notag
L^2_{{\rm per}}(Y; \mathbb{R}^N) = L^2_{\rm sol}(Y) \oplus \mathcal V^2_{\rm pot}(Y).
\end{equation*}
\begin{equation*}
\notag
L^2_{{\rm per}}(Y; \mathbb{R}^N) = L^2_{\rm sol}(Y) \oplus \mathcal V^2_{\rm pot}(Y).
\end{equation*}The next proposition provides a representation of solenoidal functions, which will be a key tool in Proposition 4.8.
Proposition 3.2. Let ![]() $f\in L^2_{\rm sol}(Y)$. Then,
$f\in L^2_{\rm sol}(Y)$. Then, ![]() $f=(f_1, \dots, f_N)$ can be represented in the form
$f=(f_1, \dots, f_N)$ can be represented in the form
 \begin{equation*}
\notag
f_j(x)= \langle f_j\rangle_Y +\sum_{i=1}^N {\partial_i} \alpha_{ij}(x),\;\;\;\hbox{for all } j=1,\dots, N,
\end{equation*}
\begin{equation*}
\notag
f_j(x)= \langle f_j\rangle_Y +\sum_{i=1}^N {\partial_i} \alpha_{ij}(x),\;\;\;\hbox{for all } j=1,\dots, N,
\end{equation*} where ![]() $\alpha_{ij}\in H^1(Y)$ is such that
$\alpha_{ij}\in H^1(Y)$ is such that ![]() $\alpha_{ij}=-\alpha_{ji}$ and
$\alpha_{ij}=-\alpha_{ji}$ and ![]() $\langle \alpha_{ij}\rangle_Y=0$, for all
$\langle \alpha_{ij}\rangle_Y=0$, for all ![]() $i,j=1, \dots, N$.
$i,j=1, \dots, N$.
Proof. Without loss of generality, we can assume that ![]() $Y=[0, 2\pi)^N$. Using the Fourier series of
$Y=[0, 2\pi)^N$. Using the Fourier series of ![]() $f$, we have that
$f$, we have that
 \begin{equation*}
\notag
f=\langle f \rangle_Y + \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}} f^k e^{\mathrm{i}k\cdot x},
\end{equation*}
\begin{equation*}
\notag
f=\langle f \rangle_Y + \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}} f^k e^{\mathrm{i}k\cdot x},
\end{equation*} where ![]() $f^k$ is the Fourier coefficient of
$f^k$ is the Fourier coefficient of ![]() $f$. We claim that
$f$. We claim that ![]() $f^k\cdot k=0$, for each
$f^k\cdot k=0$, for each ![]() $k\in\mathbb{Z}^N$. Indeed, for fixed
$k\in\mathbb{Z}^N$. Indeed, for fixed ![]() $k\in \mathbb{Z}^N\setminus\{0\}$, we can decompose
$k\in \mathbb{Z}^N\setminus\{0\}$, we can decompose ![]() $f^k$ as
$f^k$ as ![]() $f^k = C_1^k k + C_2^k v$, for some constants
$f^k = C_1^k k + C_2^k v$, for some constants ![]() $C_1^k, C_2^k$ and
$C_1^k, C_2^k$ and ![]() $v\in ({\rm span}(k))^{\perp}$. Therefore,
$v\in ({\rm span}(k))^{\perp}$. Therefore,
 \begin{equation*}
\notag
f=\langle f\rangle_Y + \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}}C_1^k ke^{\mathrm{i}k\cdot x} + \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}}C_2^k v e^{\mathrm{i}k\cdot x}.
\end{equation*}
\begin{equation*}
\notag
f=\langle f\rangle_Y + \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}}C_1^k ke^{\mathrm{i}k\cdot x} + \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}}C_2^k v e^{\mathrm{i}k\cdot x}.
\end{equation*} Noticing that 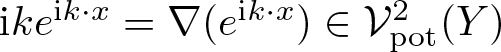 $\mathrm{i} ke^{\mathrm{i}k\cdot x}=\nabla(e^{\mathrm{i}k\cdot x}) \in \mathcal V^2_{\rm pot}(Y)$ and since by assumption, we know that
$\mathrm{i} ke^{\mathrm{i}k\cdot x}=\nabla(e^{\mathrm{i}k\cdot x}) \in \mathcal V^2_{\rm pot}(Y)$ and since by assumption, we know that ![]() $f\in L^2_{\rm sol}(Y)$, we obtain that
$f\in L^2_{\rm sol}(Y)$, we obtain that ![]() $C_1^k=0$, for any
$C_1^k=0$, for any ![]() $k\in\mathbb{Z}^N\setminus\{0\}$. This leads us to conclude that
$k\in\mathbb{Z}^N\setminus\{0\}$. This leads us to conclude that ![]() $f^k\cdot k=0$, and that
$f^k\cdot k=0$, and that ![]() $C_2^k v = f^k$.
$C_2^k v = f^k$.
Therefore,
 \begin{equation*}
f^k = f^k - \frac{f^k\cdot k}{|k|^2}k,
\end{equation*}
\begin{equation*}
f^k = f^k - \frac{f^k\cdot k}{|k|^2}k,
\end{equation*}which writes, component-wise, as
 \begin{equation*}
f_j^k = \sum_{i=1}^N\ g_{ij}^k k_i, \;\;\;\hbox{with }\,\,\,\,\, g_{ij}:={f_j^k k_i- f_i^k k_j \over |k|^2}.
\end{equation*}
\begin{equation*}
f_j^k = \sum_{i=1}^N\ g_{ij}^k k_i, \;\;\;\hbox{with }\,\,\,\,\, g_{ij}:={f_j^k k_i- f_i^k k_j \over |k|^2}.
\end{equation*} Therefore, for each ![]() $j=1,\dots, N$, we get that
$j=1,\dots, N$, we get that
 \begin{align*}
f_j &= \langle f_j \rangle_Y + \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}} f^k_j e^{\mathrm{i}k\cdot x}
= \langle f_j \rangle_Y + \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}} \sum_{i=1}^N\ g_{ij}^k k_i e^{\mathrm{i}k\cdot x}\\&
= \langle f_j \rangle_Y + \sum_{i=1}^N \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}} \ g_{ij}^k k_i e^{\mathrm{i}k\cdot x}.
\end{align*}
\begin{align*}
f_j &= \langle f_j \rangle_Y + \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}} f^k_j e^{\mathrm{i}k\cdot x}
= \langle f_j \rangle_Y + \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}} \sum_{i=1}^N\ g_{ij}^k k_i e^{\mathrm{i}k\cdot x}\\&
= \langle f_j \rangle_Y + \sum_{i=1}^N \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}} \ g_{ij}^k k_i e^{\mathrm{i}k\cdot x}.
\end{align*}Thus, by defining
 \begin{equation*}
\notag
\alpha_{ij}(x) := -\mathrm{i} \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}} g_{ij}^k e^{\mathrm{i}k\cdot x},
\end{equation*}
\begin{equation*}
\notag
\alpha_{ij}(x) := -\mathrm{i} \sum_{\substack{k\in\mathbb{Z}^N\\k\neq 0}} g_{ij}^k e^{\mathrm{i}k\cdot x},
\end{equation*}we get the desired result.
4. Technical lemmata
4.1. First-order Riemann–Lebesgue lemma
We prove a quantitative version of the Riemann–Lebesgue lemma. Since we will use this latter result several times, we recall it here for the reader’s convenience.
Lemma 4.1. (Riemann–Lebesgue lemma)
Let ![]() $p\in[1,\infty]$, and let
$p\in[1,\infty]$, and let ![]() $\Omega\subset\mathbb{R}^N$ be an open bounded set. Let
$\Omega\subset\mathbb{R}^N$ be an open bounded set. Let ![]() $\{\varepsilon_n\}_{n}$ be an infinitesimal sequence. Let
$\{\varepsilon_n\}_{n}$ be an infinitesimal sequence. Let ![]() $g\in L^p(\mathbb{R}^N)$ be an
$g\in L^p(\mathbb{R}^N)$ be an ![]() $Y$-periodic function. Then,
$Y$-periodic function. Then,
 \begin{equation*}
\lim_{n\to\infty}\int_\Omega g\left(\frac{x}{\varepsilon_n}\right)\varphi(x)\, dx
= \langle g \rangle_Y \int_\Omega \varphi(x)\, dx,
\end{equation*}
\begin{equation*}
\lim_{n\to\infty}\int_\Omega g\left(\frac{x}{\varepsilon_n}\right)\varphi(x)\, dx
= \langle g \rangle_Y \int_\Omega \varphi(x)\, dx,
\end{equation*} for all ![]() $\varphi\in L^{p'}(\Omega)$, with
$\varphi\in L^{p'}(\Omega)$, with 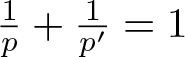 $\tfrac{1}{p}+\tfrac{1}{p'}=1$ if
$\tfrac{1}{p}+\tfrac{1}{p'}=1$ if ![]() $p \lt \infty$, and
$p \lt \infty$, and ![]() $p':= 1$ if
$p':= 1$ if ![]() $p=\infty$.
$p=\infty$.
We will present two versions of the refined result, which will require more stringent assumptions on the test functions ![]() $\varphi$. We start by assuming our test function
$\varphi$. We start by assuming our test function ![]() $\varphi$ to belong to
$\varphi$ to belong to ![]() $C^2(\Omega)\cap L^1(\Omega)$. This will require us to also impose geometric requirement on
$C^2(\Omega)\cap L^1(\Omega)$. This will require us to also impose geometric requirement on ![]() $\Omega$ and on the infinitesimal sequence.
$\Omega$ and on the infinitesimal sequence.
Proposition 4.2. (First-order Riemann–Lebesgue lemma)
Let ![]() $p\in[1,\infty]$, and let
$p\in[1,\infty]$, and let ![]() $g\in L^p_{\mathrm{loc}}(\mathbb{R}^N)$ be an
$g\in L^p_{\mathrm{loc}}(\mathbb{R}^N)$ be an ![]() $Y$-periodic function. Let
$Y$-periodic function. Let ![]() $\Omega\subset\mathbb{R}^N$ be an open bounded set such that, up to a set of Lebesgue measure zero, can be written as
$\Omega\subset\mathbb{R}^N$ be an open bounded set such that, up to a set of Lebesgue measure zero, can be written as
 \begin{equation}
\Omega = \bigcup_{i=1}^k (x_i + Y),\quad x_i\in \mathbb{Z}^N,\quad\quad
(x_i+Y)\cap(x_j+Y)=\emptyset\, \text{if }\, i\neq j.
\end{equation}
\begin{equation}
\Omega = \bigcup_{i=1}^k (x_i + Y),\quad x_i\in \mathbb{Z}^N,\quad\quad
(x_i+Y)\cap(x_j+Y)=\emptyset\, \text{if }\, i\neq j.
\end{equation}Then,
 \begin{align*}
&\lim_{n\to\infty} n\left[ \int_\Omega g(nx)\varphi(x)\, dx
- \langle g \rangle_Y \int_\Omega \varphi(x)\, dx \right] = \int_\Omega \nabla \varphi(x) \,\mathrm{d}x \cdot
\left[ \langle y g \rangle_Y - \langle y \rangle_Y\, \langle g\rangle_Y \right],
\end{align*}
\begin{align*}
&\lim_{n\to\infty} n\left[ \int_\Omega g(nx)\varphi(x)\, dx
- \langle g \rangle_Y \int_\Omega \varphi(x)\, dx \right] = \int_\Omega \nabla \varphi(x) \,\mathrm{d}x \cdot
\left[ \langle y g \rangle_Y - \langle y \rangle_Y\, \langle g\rangle_Y \right],
\end{align*} for all ![]() $\varphi\in C^2(\Omega)\cap L^1(\Omega)$.
$\varphi\in C^2(\Omega)\cap L^1(\Omega)$.
Proof. Let ![]() $\{z_i\}_{i}$ be an enumeration of
$\{z_i\}_{i}$ be an enumeration of ![]() $\mathbb{Z}^N$. For each
$\mathbb{Z}^N$. For each ![]() $n\in\mathbb{N}\setminus\{0\}$, let
$n\in\mathbb{N}\setminus\{0\}$, let
 \begin{equation*}
I_n:= \left\{i\in\mathbb{N} : \frac{1}{n} (z_i + Y)\subset \Omega \right\}.
\end{equation*}
\begin{equation*}
I_n:= \left\{i\in\mathbb{N} : \frac{1}{n} (z_i + Y)\subset \Omega \right\}.
\end{equation*}Note that, by (4.1), we get that (up to a set of Lebesgue measure zero)
 \begin{equation*}
\Omega = \bigcup_{i\in I_n} Y^n_i,
\quad \quad \quad Y^n_i:= \frac{1}{n}(z_i + Y),
\end{equation*}
\begin{equation*}
\Omega = \bigcup_{i\in I_n} Y^n_i,
\quad \quad \quad Y^n_i:= \frac{1}{n}(z_i + Y),
\end{equation*} where the sets ![]() $Y_i^n$ are pairwise disjoint. Thus,
$Y_i^n$ are pairwise disjoint. Thus,
 \begin{align*}
&\int_\Omega g(nx)\varphi(x)\, dx
- \frac{1}{|Y|}\int_Y g(y)\, dy \, \int_\Omega \varphi(x)\, dx \\
&\quad =\sum_{i\in I_n}\left[ \int_{Y^n_i} g(nx)\varphi(x)\, dx
- \frac{1}{|Y|}\int_Y g(y)\, dy \, \int_{Y^n_i} \varphi(x)\, dx \right].
\end{align*}
\begin{align*}
&\int_\Omega g(nx)\varphi(x)\, dx
- \frac{1}{|Y|}\int_Y g(y)\, dy \, \int_\Omega \varphi(x)\, dx \\
&\quad =\sum_{i\in I_n}\left[ \int_{Y^n_i} g(nx)\varphi(x)\, dx
- \frac{1}{|Y|}\int_Y g(y)\, dy \, \int_{Y^n_i} \varphi(x)\, dx \right].
\end{align*} Then, using the change of variable ![]() $x = z_i + y/n$ in every set
$x = z_i + y/n$ in every set ![]() $Y^n_i$, and recalling that, by periodicity of
$Y^n_i$, and recalling that, by periodicity of ![]() $g$, we have that
$g$, we have that ![]() $g(z_i + y) = g(y)$ for all
$g(z_i + y) = g(y)$ for all ![]() $z_i\in\mathbb{Z}^N$, we obtain
$z_i\in\mathbb{Z}^N$, we obtain
 \begin{align*}
\int_\Omega & g(nx)\varphi(x)\, dx
- \frac{1}{|Y|}\int_Y g(y)\, dy \, \int_\Omega \varphi(x)\, dx \\
&\quad =\sum_{i\in I_n} \frac{1}{n^N }\left[ \int_Y g(y)\varphi\left(\frac{z_i + y}{n}\right)\, dy
- \frac{1}{|Y|}\int_Y \varphi\left(\frac{z_i + y}{n}\right)\, dy \, \int_Y g(y)\, dy \right] \\
&\quad =\sum_{i\in I_n} \frac{1}{n^N} \left[ \int_Y g(y)
\left[\varphi\left(\frac{z_i + y}{n}\right) - \varphi\left(\frac{z_i}{n}\right) \right]\,\right. \\ & \qquad \left.dy
- \frac{1}{|Y|}\int_Y \left[\varphi\left(\frac{z_i + y}{n}\right) - \varphi\left(\frac{z_i}{n}\right) \right]\, dy \, \int_Y g(y)\, dy \right].
\end{align*}
\begin{align*}
\int_\Omega & g(nx)\varphi(x)\, dx
- \frac{1}{|Y|}\int_Y g(y)\, dy \, \int_\Omega \varphi(x)\, dx \\
&\quad =\sum_{i\in I_n} \frac{1}{n^N }\left[ \int_Y g(y)\varphi\left(\frac{z_i + y}{n}\right)\, dy
- \frac{1}{|Y|}\int_Y \varphi\left(\frac{z_i + y}{n}\right)\, dy \, \int_Y g(y)\, dy \right] \\
&\quad =\sum_{i\in I_n} \frac{1}{n^N} \left[ \int_Y g(y)
\left[\varphi\left(\frac{z_i + y}{n}\right) - \varphi\left(\frac{z_i}{n}\right) \right]\,\right. \\ & \qquad \left.dy
- \frac{1}{|Y|}\int_Y \left[\varphi\left(\frac{z_i + y}{n}\right) - \varphi\left(\frac{z_i}{n}\right) \right]\, dy \, \int_Y g(y)\, dy \right].
\end{align*} We now use a second-order Taylor expansion for ![]() $\varphi$ to write
$\varphi$ to write
 \begin{equation*}
\varphi\left(\frac{z_i + y}{n}\right) - \varphi\left(\frac{z_i}{n}\right)
= \frac{1}{n} \nabla \varphi\left(\frac{z_i}{n}\right)\cdot y
+ \frac{1}{2n^2} H\varphi\left(\frac{z_i}{n}\right)[y,y]
+ o\left(\frac{1}{n^2}\right),
\end{equation*}
\begin{equation*}
\varphi\left(\frac{z_i + y}{n}\right) - \varphi\left(\frac{z_i}{n}\right)
= \frac{1}{n} \nabla \varphi\left(\frac{z_i}{n}\right)\cdot y
+ \frac{1}{2n^2} H\varphi\left(\frac{z_i}{n}\right)[y,y]
+ o\left(\frac{1}{n^2}\right),
\end{equation*} where ![]() $H\varphi(x)$ denotes the Hessian matrix of
$H\varphi(x)$ denotes the Hessian matrix of ![]() $\varphi$ at
$\varphi$ at ![]() $x$. Thus, we get that
$x$. Thus, we get that
 \begin{align*}
&\int_\Omega g(nx)\varphi(x)\, dx
- \frac{1}{|Y|}\int_Y g(y)\, dy \, \int_Y \varphi(x)\, dx \\
& = \frac{1}{n} \sum_{i\in I_n} \frac{1}{n^N} \nabla \varphi\left(\frac{z_i}{n}\right)
\cdot \left[ \int_Y g(y)y\, dy - \frac{1}{|Y|}\int_Y y\, dy\, \int_Y g(y)\, dy \right]
+O\left(\frac{1}{n^2}\right) \\
& = \frac{1}{n} \sum_{i\in I_n} \frac{|Y|}{n^N} \nabla \varphi\left(\frac{z_i}{n}\right)
\cdot \left[ \langle y g \rangle_Y - \langle y \rangle_Y\, \langle g\rangle_Y \right]
+O\left(\frac{1}{n^2}\right).
\end{align*}
\begin{align*}
&\int_\Omega g(nx)\varphi(x)\, dx
- \frac{1}{|Y|}\int_Y g(y)\, dy \, \int_Y \varphi(x)\, dx \\
& = \frac{1}{n} \sum_{i\in I_n} \frac{1}{n^N} \nabla \varphi\left(\frac{z_i}{n}\right)
\cdot \left[ \int_Y g(y)y\, dy - \frac{1}{|Y|}\int_Y y\, dy\, \int_Y g(y)\, dy \right]
+O\left(\frac{1}{n^2}\right) \\
& = \frac{1}{n} \sum_{i\in I_n} \frac{|Y|}{n^N} \nabla \varphi\left(\frac{z_i}{n}\right)
\cdot \left[ \langle y g \rangle_Y - \langle y \rangle_Y\, \langle g\rangle_Y \right]
+O\left(\frac{1}{n^2}\right).
\end{align*} Now, since by assumption ![]() $\varphi\in C^0(\Omega)\cap L^1(\Omega)$, we have that
$\varphi\in C^0(\Omega)\cap L^1(\Omega)$, we have that
 \begin{equation*}
\lim_{n\to\infty} \sum_{i\in I_n}\frac{|Y|}{n^N} \nabla \varphi\left(\frac{z_i}{n}\right)
= \int_\Omega |\nabla \varphi(x)| dx.
\end{equation*}
\begin{equation*}
\lim_{n\to\infty} \sum_{i\in I_n}\frac{|Y|}{n^N} \nabla \varphi\left(\frac{z_i}{n}\right)
= \int_\Omega |\nabla \varphi(x)| dx.
\end{equation*}This concludes the proof of the result.
Remark 4.3. Note that the above result is invariant under translation of the periodicity grid and of the function ![]() $g$. In particular, there is no loss of generality in assuming that
$g$. In particular, there is no loss of generality in assuming that ![]() $\langle y\rangle_Y=0$, namely that the barycentre of the periodicity cell is at the origin. Therefore, assuming without loss of generality that
$\langle y\rangle_Y=0$, namely that the barycentre of the periodicity cell is at the origin. Therefore, assuming without loss of generality that ![]() $\langle y \rangle_Y=0$, the above result yields
$\langle y \rangle_Y=0$, the above result yields
 \begin{align*}
&\lim_{n\to\infty} n\left[ \int_\Omega g(nx)\varphi(x)\, dx
- \langle g \rangle_Y \int_\Omega \varphi(x)\, dx \right] = \int_\Omega \nabla \varphi(x) \,\mathrm{d}x \cdot \langle y g \rangle_Y,
\end{align*}
\begin{align*}
&\lim_{n\to\infty} n\left[ \int_\Omega g(nx)\varphi(x)\, dx
- \langle g \rangle_Y \int_\Omega \varphi(x)\, dx \right] = \int_\Omega \nabla \varphi(x) \,\mathrm{d}x \cdot \langle y g \rangle_Y,
\end{align*} for all ![]() $\varphi\in C^2(\Omega)\cap L^1(\Omega)$. Note that
$\varphi\in C^2(\Omega)\cap L^1(\Omega)$. Note that ![]() $\langle y g \rangle_Y$ is the barycentre of the periodicity cell
$\langle y g \rangle_Y$ is the barycentre of the periodicity cell ![]() $Y$ with respect to the density
$Y$ with respect to the density ![]() $g$.
$g$.
Remark 4.4. In particular, the above result implies that
 \begin{equation*}
\lim_{n\to\infty} n\left[ \int_\Omega g(nx)\varphi(x)\, dx
- \langle g\rangle_Y \, \int_\Omega \varphi(x)\, dx \right] =0,
\end{equation*}
\begin{equation*}
\lim_{n\to\infty} n\left[ \int_\Omega g(nx)\varphi(x)\, dx
- \langle g\rangle_Y \, \int_\Omega \varphi(x)\, dx \right] =0,
\end{equation*} for all ![]() $Y$-periodic function
$Y$-periodic function ![]() $\varphi\in C^2(\mathbb{R}^N)$.
$\varphi\in C^2(\mathbb{R}^N)$.
Remark 4.5. The reason why we require strong assumptions on the geometry of the set ![]() $\Omega$ is because we need to avoid having boundary effects. Indeed, the estimate of these latter will be, in general, not possible.
$\Omega$ is because we need to avoid having boundary effects. Indeed, the estimate of these latter will be, in general, not possible.
We now present the version of the first-order Riemann–Lebesgue lemma that we will use in the proof of our main result (Theorem 2.7). Thanks to Assumption (H4), we will only need to consider functions ![]() $\varphi\in C^2(\Omega)\cap C_c(\Omega)$. This assumption allows us to consider a general infinitesimal sequence
$\varphi\in C^2(\Omega)\cap C_c(\Omega)$. This assumption allows us to consider a general infinitesimal sequence ![]() $(\varepsilon_n)_n$, and a general open set
$(\varepsilon_n)_n$, and a general open set ![]() $\Omega\subset\mathbb{R}^N$.
$\Omega\subset\mathbb{R}^N$.
Proposition 4.6. (First-order Riemann–Lebesgue lemma - test functions with compact support)
Let ![]() $p\in[1,\infty]$, and let
$p\in[1,\infty]$, and let ![]() $g\in L^p_{\mathrm{loc}}(\mathbb{R}^N)$ be an
$g\in L^p_{\mathrm{loc}}(\mathbb{R}^N)$ be an ![]() $Y$-periodic function. Let
$Y$-periodic function. Let ![]() $\Omega\subset\mathbb{R}^N$ be an open set, and let
$\Omega\subset\mathbb{R}^N$ be an open set, and let ![]() $\{\varepsilon_n\}_n$ be an infinitesimal sequence. Then,
$\{\varepsilon_n\}_n$ be an infinitesimal sequence. Then,
 \begin{align*}
&\lim_{n\to\infty} \frac{1}{\varepsilon_n}\left[ \int_\Omega g\left(\frac{x}{\varepsilon_n}\right)\varphi(x)\, dx
- \langle g \rangle_Y \int_\Omega \varphi(x)\, dx \right] \\&\quad = \int_\Omega \nabla \varphi(x) \,\mathrm{d}x \cdot
\left[ \langle y g \rangle_Y - \langle y \rangle_Y\, \langle g\rangle_Y \right],
\end{align*}
\begin{align*}
&\lim_{n\to\infty} \frac{1}{\varepsilon_n}\left[ \int_\Omega g\left(\frac{x}{\varepsilon_n}\right)\varphi(x)\, dx
- \langle g \rangle_Y \int_\Omega \varphi(x)\, dx \right] \\&\quad = \int_\Omega \nabla \varphi(x) \,\mathrm{d}x \cdot
\left[ \langle y g \rangle_Y - \langle y \rangle_Y\, \langle g\rangle_Y \right],
\end{align*} for all ![]() $\varphi\in C^2(\Omega)\cap C_c(\Omega)$.
$\varphi\in C^2(\Omega)\cap C_c(\Omega)$.
Proof. Let ![]() $\varphi\in C^2(\Omega)\cap C_c(\Omega)$. Let
$\varphi\in C^2(\Omega)\cap C_c(\Omega)$. Let ![]() $\{z_i\}_{i}$ be an enumeration of
$\{z_i\}_{i}$ be an enumeration of ![]() $\mathbb{Z}^N$. Let
$\mathbb{Z}^N$. Let ![]() $\bar{n}\in\mathbb{N}$ be such that, for all
$\bar{n}\in\mathbb{N}$ be such that, for all ![]() $n\geq\bar{n}$, there exists
$n\geq\bar{n}$, there exists ![]() $I_n\subset\mathbb{N}$ for which
$I_n\subset\mathbb{N}$ for which
 \begin{equation}
\mathrm{supp}(\varphi) \subset \bigcup_{i\in I_n} \varepsilon_n(z_i + Y) \subset \Omega.
\end{equation}
\begin{equation}
\mathrm{supp}(\varphi) \subset \bigcup_{i\in I_n} \varepsilon_n(z_i + Y) \subset \Omega.
\end{equation} where ![]() $\mathrm{supp}(\varphi)$ denotes the support of
$\mathrm{supp}(\varphi)$ denotes the support of ![]() $\varphi$. Then, by using the same argument as that employed in the proof of Proposition 4.2, we obtain
$\varphi$. Then, by using the same argument as that employed in the proof of Proposition 4.2, we obtain
 \begin{align*}
&\int_\Omega g\left(\frac{x}{\varepsilon_n}\right)\varphi(x)\, dx
- \frac{1}{|Y|}\int_Y g(y)\, dy \, \int_Y \varphi(x)\, dx \\
&\quad = \varepsilon_n\sum_{i\in I_n} \varepsilon_n^N \nabla \varphi\left(\frac{z_i}{n}\right)
\cdot \left[ \int_Y g(y)y\, dy - \frac{1}{|Y|}\int_Y y\, dy\, \int_Y g(y)\, dy \right]
+O\left(\varepsilon_n^2\right) \\
&\quad = \varepsilon_n \sum_{i\in I_n} |Y|\varepsilon_n^N \nabla \varphi\left(\frac{z_i}{n}\right)
\cdot \left[ \langle y g \rangle_Y - \langle y \rangle_Y\, \langle g\rangle_Y \right]
+O\left(\varepsilon_n^2\right).
\end{align*}
\begin{align*}
&\int_\Omega g\left(\frac{x}{\varepsilon_n}\right)\varphi(x)\, dx
- \frac{1}{|Y|}\int_Y g(y)\, dy \, \int_Y \varphi(x)\, dx \\
&\quad = \varepsilon_n\sum_{i\in I_n} \varepsilon_n^N \nabla \varphi\left(\frac{z_i}{n}\right)
\cdot \left[ \int_Y g(y)y\, dy - \frac{1}{|Y|}\int_Y y\, dy\, \int_Y g(y)\, dy \right]
+O\left(\varepsilon_n^2\right) \\
&\quad = \varepsilon_n \sum_{i\in I_n} |Y|\varepsilon_n^N \nabla \varphi\left(\frac{z_i}{n}\right)
\cdot \left[ \langle y g \rangle_Y - \langle y \rangle_Y\, \langle g\rangle_Y \right]
+O\left(\varepsilon_n^2\right).
\end{align*}Using (4.2), we get that
 \begin{equation*}
\lim_{n\to\infty}\sum_{i\in I_n} |Y|\varepsilon_n^N \nabla \varphi\left(\frac{z_i}{n}\right) = \int_\Omega |\nabla\varphi(x)|dx.
\end{equation*}
\begin{equation*}
\lim_{n\to\infty}\sum_{i\in I_n} |Y|\varepsilon_n^N \nabla \varphi\left(\frac{z_i}{n}\right) = \int_\Omega |\nabla\varphi(x)|dx.
\end{equation*}This gives the desired result.
Finally, we present the version of the first-order Riemann–Lebesgue lemma in the nonlinear case.
Proposition 4.7. Let ![]() $V:\mathbb{R}^N\times\mathbb{R}\to\mathbb{R}$ be a function such that
$V:\mathbb{R}^N\times\mathbb{R}\to\mathbb{R}$ be a function such that
(i) For all
 $p\in\mathbb{R}$, the function
$p\in\mathbb{R}$, the function  $x\mapsto V(x,p)$ is
$x\mapsto V(x,p)$ is  $Y$-periodic;
$Y$-periodic;(ii) For all
 $x\in\mathbb{R}^N$, the function
$x\in\mathbb{R}^N$, the function  $p\mapsto V(x,p)$ is of class
$p\mapsto V(x,p)$ is of class  $C^2$;
$C^2$;(iii) The function
 \begin{equation*}
t\mapsto \int_Y \partial_p V(y,t) \, dy,\quad\quad\quad
\end{equation*}
\begin{equation*}
t\mapsto \int_Y \partial_p V(y,t) \, dy,\quad\quad\quad
\end{equation*}is Riemann integrable, where
 $\partial_p V$ denotes the partial derivative of
$\partial_p V$ denotes the partial derivative of  $V$ with respect to the second variable.
$V$ with respect to the second variable.
Let ![]() $\{\varepsilon_n\}_n$ be an infinitesimal sequence. Then, the following holds
$\{\varepsilon_n\}_n$ be an infinitesimal sequence. Then, the following holds
 \begin{align*}
&\lim_{n\to\infty} \frac{1}{\varepsilon_n}\left[ \int_\Omega V\left(\frac{x}{\varepsilon_n},\varphi(x)\right)\, dx
- \frac{1}{|Y|}\int_\Omega \int_Y V(t, \varphi(x) \, dt \, dx \right] \\
&\quad= \int_\Omega \nabla \varphi(x) \cdot \left[
\frac{1}{|Y|} \int_Y \partial_p V(y,\varphi(x)) y \, dy
- \frac{1}{|Y|^2} \int_Y\int_Y \partial_p V(t,\varphi(x)) y \, dt \, dy
\right] dx,
\end{align*}
\begin{align*}
&\lim_{n\to\infty} \frac{1}{\varepsilon_n}\left[ \int_\Omega V\left(\frac{x}{\varepsilon_n},\varphi(x)\right)\, dx
- \frac{1}{|Y|}\int_\Omega \int_Y V(t, \varphi(x) \, dt \, dx \right] \\
&\quad= \int_\Omega \nabla \varphi(x) \cdot \left[
\frac{1}{|Y|} \int_Y \partial_p V(y,\varphi(x)) y \, dy
- \frac{1}{|Y|^2} \int_Y\int_Y \partial_p V(t,\varphi(x)) y \, dt \, dy
\right] dx,
\end{align*} for all ![]() $\varphi\in C^2(\Omega)\cap L^1(\Omega)$, provided either one of the following assumptions is in force:
$\varphi\in C^2(\Omega)\cap L^1(\Omega)$, provided either one of the following assumptions is in force:
(a) For each
 $n\in\mathbb{N}\setminus\{0\}$,
$n\in\mathbb{N}\setminus\{0\}$,  $\varepsilon_n=1/n$, and assumption (4.1) holds;
$\varepsilon_n=1/n$, and assumption (4.1) holds;(b) The function
 $\varphi$ has compact support in
$\varphi$ has compact support in  $\Omega$.
$\Omega$.
The argument to prove the nonlinear version of the first-order Riemann–Lebesgue lemma follows a similar strategy to the one used in the proof of the two results above, and therefore it will be omitted.
4.2. Estimates
In this section, we prove the fundamental estimate that allows us to consider the ‘surrogate’ sequence given by the expansion with first and second-order correctors in place of the minimizer ![]() $u^{min}_\varepsilon$. Note that while
$u^{min}_\varepsilon$. Note that while ![]() $u_\varepsilon$ only approximates the formal expansion
$u_\varepsilon$ only approximates the formal expansion ![]() $u_0+\varepsilon u_1$ to an order of
$u_0+\varepsilon u_1$ to an order of ![]() $O(\sqrt{\varepsilon})$ in the
$O(\sqrt{\varepsilon})$ in the ![]() $H^1$ norm, we now show that the higher-order expansion
$H^1$ norm, we now show that the higher-order expansion ![]() $u_{\varepsilon}^{(2)}$ satisfies the underlying PDE to a much higher order,
$u_{\varepsilon}^{(2)}$ satisfies the underlying PDE to a much higher order, ![]() $O(\varepsilon^2)$, in the
$O(\varepsilon^2)$, in the ![]() $H^{-1}$ norm. This refined approximation in the dual space is the key to overcoming the
$H^{-1}$ norm. This refined approximation in the dual space is the key to overcoming the ![]() $H^1$-based limitations in the variational analysis. Recall that
$H^1$-based limitations in the variational analysis. Recall that ![]() $u_0^{\min}\in C^\infty_c(\Omega)$ (see Remark 2.5).
$u_0^{\min}\in C^\infty_c(\Omega)$ (see Remark 2.5).
Proposition 4.8. Assume that Assumption (H4) holds. Let ![]() $u^{(2)}_\varepsilon$ be the function defined as
$u^{(2)}_\varepsilon$ be the function defined as
with ![]() $u_1$ and
$u_1$ and ![]() $u_2$ being defined as in (3.6) and (3.8), respectively. Then, it holds that
$u_2$ being defined as in (3.6) and (3.8), respectively. Then, it holds that
 \begin{equation*}
\notag
\|{\rm div}(A^\varepsilon \nabla u^{(2)}_\varepsilon)-{\rm div}(A^{{\rm hom}} \nabla u^{\rm min}_0) \|_{H^{-1}(\Omega)}\leq C \varepsilon^2,
\end{equation*}
\begin{equation*}
\notag
\|{\rm div}(A^\varepsilon \nabla u^{(2)}_\varepsilon)-{\rm div}(A^{{\rm hom}} \nabla u^{\rm min}_0) \|_{H^{-1}(\Omega)}\leq C \varepsilon^2,
\end{equation*} for some ![]() $C \lt +\infty$.
$C \lt +\infty$.
Proof. Recall that ![]() $\widetilde{u}_2\equiv 0$ since we are only interested in the asymptotic expansion up to the second-order. Note that
$\widetilde{u}_2\equiv 0$ since we are only interested in the asymptotic expansion up to the second-order. Note that
 \begin{equation*}
\notag
{\rm div}(A^\varepsilon(x) \nabla u^{(2)}(x)_\varepsilon-A^{{\rm hom}} \nabla u^{\rm min}_0(x)) \!=\! \sum_{i=1}^N \partial_i\left( (A^\varepsilon(x)\nabla u^{(2)}_\varepsilon(x)\!-\! A^{{\rm hom}}\nabla u^{\rm min}_0(x))_i\right),
\end{equation*}
\begin{equation*}
\notag
{\rm div}(A^\varepsilon(x) \nabla u^{(2)}(x)_\varepsilon-A^{{\rm hom}} \nabla u^{\rm min}_0(x)) \!=\! \sum_{i=1}^N \partial_i\left( (A^\varepsilon(x)\nabla u^{(2)}_\varepsilon(x)\!-\! A^{{\rm hom}}\nabla u^{\rm min}_0(x))_i\right),
\end{equation*} where, for ![]() $i=1,\dots, N$, the
$i=1,\dots, N$, the ![]() $i$-th component
$i$-th component 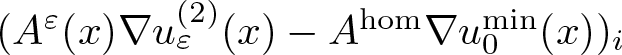 $(A^\varepsilon(x)\nabla u^{(2)}_\varepsilon(x)- A^{{\rm hom}}\nabla u^{\rm min}_0(x))_i$ is given by
$(A^\varepsilon(x)\nabla u^{(2)}_\varepsilon(x)- A^{{\rm hom}}\nabla u^{\rm min}_0(x))_i$ is given by
 \begin{equation}
(A^\varepsilon(x)\nabla u^{(2)}_\varepsilon(x)- A^{{\rm hom}}\nabla u^{\rm min}_0(x))_i= P_{i, \varepsilon}(x)+ \varepsilon Q_{i, \varepsilon}(x)+ \varepsilon^2R_{i,\varepsilon}(x),
\end{equation}
\begin{equation}
(A^\varepsilon(x)\nabla u^{(2)}_\varepsilon(x)- A^{{\rm hom}}\nabla u^{\rm min}_0(x))_i= P_{i, \varepsilon}(x)+ \varepsilon Q_{i, \varepsilon}(x)+ \varepsilon^2R_{i,\varepsilon}(x),
\end{equation}with
 \begin{align}
P_{i, \varepsilon}(x) &:= \sum_{j=1}^N a^\varepsilon_{ij}(x) \partial_j u^{\rm min}_0(x) \!+\! \sum_{j,k=1}^N a_{ik}^\varepsilon(x)\partial_{y_k}\psi^\varepsilon_j(x)\partial_j u^{\rm min}_0 (x)\!-\!
\sum_{j=1}^N a_{ij}^{{\rm hom}}\partial_j u^{\rm min}_0(x),\nonumber\\
Q_{i, \varepsilon}(x)&:= \sum_{j,k=1}^N \psi^\varepsilon_j(x) a^\varepsilon_{ik}(x)\partial^2_{kj} u^{\rm min}_0(x) \!+\! \sum_{k,j,l=1}^N a_{il}^\varepsilon(x) \partial_{y_l}\chi^{\varepsilon}_{kj}(x)\partial^2_{kj}u^{\rm min}_0(x)\nonumber\\
&\quad + \sum_{j=1}^N a_{ij}^\varepsilon(x)\partial_j\widetilde{u}_1(x) + \sum_{j,k=1}^N a_{ik}^\varepsilon(x)\partial_{y_k}\psi^\varepsilon_j(x)\partial_j\widetilde{u}_1(x),\nonumber\\
R_{i, \varepsilon}(x)&:= \sum_{k,j,l=1}^N \chi_{kj}^\varepsilon(x) a_{il}^\varepsilon(x)\partial^3_{lkj}u^{\rm min}_0(x) + \sum_{j,k=1}^N \psi_j^\varepsilon(x) a^{\varepsilon}_{ik}(x)\partial^2_{kj}\widetilde{u}_1(x) .
\end{align}
\begin{align}
P_{i, \varepsilon}(x) &:= \sum_{j=1}^N a^\varepsilon_{ij}(x) \partial_j u^{\rm min}_0(x) \!+\! \sum_{j,k=1}^N a_{ik}^\varepsilon(x)\partial_{y_k}\psi^\varepsilon_j(x)\partial_j u^{\rm min}_0 (x)\!-\!
\sum_{j=1}^N a_{ij}^{{\rm hom}}\partial_j u^{\rm min}_0(x),\nonumber\\
Q_{i, \varepsilon}(x)&:= \sum_{j,k=1}^N \psi^\varepsilon_j(x) a^\varepsilon_{ik}(x)\partial^2_{kj} u^{\rm min}_0(x) \!+\! \sum_{k,j,l=1}^N a_{il}^\varepsilon(x) \partial_{y_l}\chi^{\varepsilon}_{kj}(x)\partial^2_{kj}u^{\rm min}_0(x)\nonumber\\
&\quad + \sum_{j=1}^N a_{ij}^\varepsilon(x)\partial_j\widetilde{u}_1(x) + \sum_{j,k=1}^N a_{ik}^\varepsilon(x)\partial_{y_k}\psi^\varepsilon_j(x)\partial_j\widetilde{u}_1(x),\nonumber\\
R_{i, \varepsilon}(x)&:= \sum_{k,j,l=1}^N \chi_{kj}^\varepsilon(x) a_{il}^\varepsilon(x)\partial^3_{lkj}u^{\rm min}_0(x) + \sum_{j,k=1}^N \psi_j^\varepsilon(x) a^{\varepsilon}_{ik}(x)\partial^2_{kj}\widetilde{u}_1(x) .
\end{align} We now estimate the above terms, starting from ![]() $P_{i, \varepsilon}(x)$. Note that
$P_{i, \varepsilon}(x)$. Note that ![]() $P_{i, \varepsilon}(x)$ rewrites as
$P_{i, \varepsilon}(x)$ rewrites as
 \begin{equation*}
\notag
P_{i, \varepsilon}(x) = \sum_{j=1}^N g_i^{j, \varepsilon}(x) \partial_j u^{\rm min}_0(x), \;\;\; \mbox{for all } i=1,\dots, N,
\end{equation*}
\begin{equation*}
\notag
P_{i, \varepsilon}(x) = \sum_{j=1}^N g_i^{j, \varepsilon}(x) \partial_j u^{\rm min}_0(x), \;\;\; \mbox{for all } i=1,\dots, N,
\end{equation*} where ![]() $g_i^j$ is defined as
$g_i^j$ is defined as
 \begin{align*}
\notag
g_i^j(y) := a_{ij}(y)+ \sum_{k=1}^Na_{ik}(y)\partial_{y_k}\psi_{j}(y) -a_{ij}^{{\rm hom}}, \;\;\; \hbox{for all } i, j=1,\cdots, N.
\end{align*}
\begin{align*}
\notag
g_i^j(y) := a_{ij}(y)+ \sum_{k=1}^Na_{ik}(y)\partial_{y_k}\psi_{j}(y) -a_{ij}^{{\rm hom}}, \;\;\; \hbox{for all } i, j=1,\cdots, N.
\end{align*} For fixed ![]() $j=1,\dots, N$, set
$j=1,\dots, N$, set ![]() $G^j:=(g_i^1,\dots, g_i^N)$. We have that
$G^j:=(g_i^1,\dots, g_i^N)$. We have that ![]() $G^j\in L^2_{\rm sol}(Y)$. Indeed, thanks to problem (3.7) satisfied by
$G^j\in L^2_{\rm sol}(Y)$. Indeed, thanks to problem (3.7) satisfied by ![]() $\psi_j$, it follows that
$\psi_j$, it follows that
 \begin{equation*}
\notag
\mbox{div } G^j(y)= \sum_{i=1}^N \partial_{y_i} g_{i}^j(y)=0.
\end{equation*}
\begin{equation*}
\notag
\mbox{div } G^j(y)= \sum_{i=1}^N \partial_{y_i} g_{i}^j(y)=0.
\end{equation*} Therefore, by applying Proposition 3.2, the components of ![]() $G^j$ are represented by
$G^j$ are represented by
 \begin{equation}
g_i^j(y) = \sum_{k=1}^N \partial_{y_k}\alpha^j_{ik}(y).
\end{equation}
\begin{equation}
g_i^j(y) = \sum_{k=1}^N \partial_{y_k}\alpha^j_{ik}(y).
\end{equation} Note that 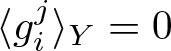 $\langle g_i^j\rangle_Y=0$, since
$\langle g_i^j\rangle_Y=0$, since
 \begin{equation}
a_{ij}^{{\rm hom}}= \left\langle a_{ij}(y)+ \sum_{k=1}^Na_{ik}(y)\partial_{y_k}\psi_{j}(y) \right\rangle_Y.
\end{equation}
\begin{equation}
a_{ij}^{{\rm hom}}= \left\langle a_{ij}(y)+ \sum_{k=1}^Na_{ik}(y)\partial_{y_k}\psi_{j}(y) \right\rangle_Y.
\end{equation}Using the representation (4.6) as well as the Leibniz rule, we get that
 \begin{align*}
P_{i, \varepsilon}(x) &= \sum_{j,k=1}^N \partial_{y_k} \alpha_{ik}^{j, \varepsilon}(x)\partial_ju^{\rm min}_0(x) \notag\\
&\quad= \varepsilon\left(\sum_{j,k=1}^N \partial_{k}(\alpha_{ik}^{j,\varepsilon}\partial_ju^{\rm min}_0)(x) - \sum_{j,k=1}^N \alpha_{ik}^{j, \varepsilon}(x)\partial^2_{kj}u^{\rm min}_0(x) \right).\notag
\end{align*}
\begin{align*}
P_{i, \varepsilon}(x) &= \sum_{j,k=1}^N \partial_{y_k} \alpha_{ik}^{j, \varepsilon}(x)\partial_ju^{\rm min}_0(x) \notag\\
&\quad= \varepsilon\left(\sum_{j,k=1}^N \partial_{k}(\alpha_{ik}^{j,\varepsilon}\partial_ju^{\rm min}_0)(x) - \sum_{j,k=1}^N \alpha_{ik}^{j, \varepsilon}(x)\partial^2_{kj}u^{\rm min}_0(x) \right).\notag
\end{align*}Hence, (4.4) turns into
 \begin{align}
&(A^\varepsilon(x)\nabla u^{(2)}_\varepsilon(x)- A^{{\rm hom}}\nabla u^{\rm min}_0(x))_i \nonumber \\&\quad = \varepsilon\left( \sum_{j,k=1}^N \partial_{k}(\alpha_{ik}^{j,\varepsilon}\partial_ju^{\rm min}_0)(x) + \widetilde{Q}_{i,\varepsilon}(x)\right)+ \varepsilon^2R_{i,\varepsilon}(x),
\end{align}
\begin{align}
&(A^\varepsilon(x)\nabla u^{(2)}_\varepsilon(x)- A^{{\rm hom}}\nabla u^{\rm min}_0(x))_i \nonumber \\&\quad = \varepsilon\left( \sum_{j,k=1}^N \partial_{k}(\alpha_{ik}^{j,\varepsilon}\partial_ju^{\rm min}_0)(x) + \widetilde{Q}_{i,\varepsilon}(x)\right)+ \varepsilon^2R_{i,\varepsilon}(x),
\end{align}where
 \begin{equation*}
\notag
\widetilde{Q}_{i,\varepsilon}(x) := Q_{i,\varepsilon}(x)- \sum_{j,k=1}^N \alpha_{ik}^{j, \varepsilon}(x)\partial^2_{kj}u^{\rm min}_0(x),
\end{equation*}
\begin{equation*}
\notag
\widetilde{Q}_{i,\varepsilon}(x) := Q_{i,\varepsilon}(x)- \sum_{j,k=1}^N \alpha_{ik}^{j, \varepsilon}(x)\partial^2_{kj}u^{\rm min}_0(x),
\end{equation*} with ![]() $Q_{i,\varepsilon}$ being defined as in (4.5). We now estimate
$Q_{i,\varepsilon}$ being defined as in (4.5). We now estimate 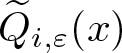 $\widetilde{Q}_{i,\varepsilon}(x)$. As for
$\widetilde{Q}_{i,\varepsilon}(x)$. As for ![]() $P_{i,\varepsilon}$,
$P_{i,\varepsilon}$, 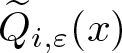 $\widetilde{Q}_{i,\varepsilon}(x)$ can be rewritten as
$\widetilde{Q}_{i,\varepsilon}(x)$ can be rewritten as
 \begin{equation}
\widetilde{Q}_{i,\varepsilon}(x)= \sum_{j,k=1}^N h_i^{jk, \varepsilon}(x)\partial_{kj}^2u^{\rm min}_0(x) +\sum_{j=1}^N t_i^{j,\varepsilon}(x)\partial_j\widetilde{u}_1(x), \;\;\; \hbox{for all } i=1,\dots, N,
\end{equation}
\begin{equation}
\widetilde{Q}_{i,\varepsilon}(x)= \sum_{j,k=1}^N h_i^{jk, \varepsilon}(x)\partial_{kj}^2u^{\rm min}_0(x) +\sum_{j=1}^N t_i^{j,\varepsilon}(x)\partial_j\widetilde{u}_1(x), \;\;\; \hbox{for all } i=1,\dots, N,
\end{equation} where for any fixed ![]() $j,k=1,\dots, N$, the functions
$j,k=1,\dots, N$, the functions 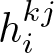 $h^{kj}_i$ and
$h^{kj}_i$ and ![]() $t^j_i$ are defined as
$t^j_i$ are defined as
 \begin{equation}
h_i^{kj} (y):= \psi_j(y) a_{ik}(y) + \sum_{l=1}^N a_{il}(y) \partial_{y_l}\chi_{kj}(y) -\alpha_{ik}^j(y),
\end{equation}
\begin{equation}
h_i^{kj} (y):= \psi_j(y) a_{ik}(y) + \sum_{l=1}^N a_{il}(y) \partial_{y_l}\chi_{kj}(y) -\alpha_{ik}^j(y),
\end{equation} \begin{equation}
t_i^j(y):= a_{ij}(y) +\sum_{k=1}^N a_{ik}(y) \partial_{y_k}\psi_j(y).
\end{equation}
\begin{equation}
t_i^j(y):= a_{ij}(y) +\sum_{k=1}^N a_{ik}(y) \partial_{y_k}\psi_j(y).
\end{equation} We claim that 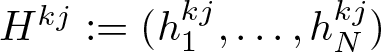 $H^{kj}:= (h_1^{kj}, \dots, h_N^{kj})$ as well as
$H^{kj}:= (h_1^{kj}, \dots, h_N^{kj})$ as well as 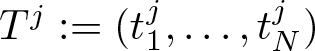 $T^j:= (t_1^j, \dots, t_N^j)$ belong to
$T^j:= (t_1^j, \dots, t_N^j)$ belong to ![]() $L^2_{\rm sol}(Y)$. Indeed, bearing in mind that
$L^2_{\rm sol}(Y)$. Indeed, bearing in mind that ![]() $\chi_{kj}^\varepsilon$ is the solution to (3.9) together with the fact that
$\chi_{kj}^\varepsilon$ is the solution to (3.9) together with the fact that
 \begin{equation*}\sum_{i=1}^N\partial_{y_i}(-\alpha_{ik}^j)=\sum_{i=1}^N\partial_{y_i}(\alpha_{ki}^j) = g_k^j,\end{equation*}
\begin{equation*}\sum_{i=1}^N\partial_{y_i}(-\alpha_{ik}^j)=\sum_{i=1}^N\partial_{y_i}(\alpha_{ki}^j) = g_k^j,\end{equation*} we deduce that for fixed ![]() $j,k=1,\dots, N$,
$j,k=1,\dots, N$,
 \begin{align*}
{\rm div}(H^{kj}) &= \sum_{i=1}^N \partial_{y_i} h_i^{kj}(y)\\&= \sum_{i=1}^N\partial_{y_i}(\psi_j^\varepsilon a_{ik}^\varepsilon)(y) +\sum_{i=1}^N\partial_{y_i}\left(\sum_{l=1}^N a_{il}\partial_l\chi_{kj}\right)(y) +\sum_{i=1}^N \partial_{y_i}(-\alpha_{ik}^j)(y) \notag\\
&=\sum_{i=1}^N \partial_{y_i}(\psi_j(y) a_{ik}(y)) -b_{kj}(y)+\int_Y b_{kj}dy + g_k^j(y) =0, \notag
\end{align*}
\begin{align*}
{\rm div}(H^{kj}) &= \sum_{i=1}^N \partial_{y_i} h_i^{kj}(y)\\&= \sum_{i=1}^N\partial_{y_i}(\psi_j^\varepsilon a_{ik}^\varepsilon)(y) +\sum_{i=1}^N\partial_{y_i}\left(\sum_{l=1}^N a_{il}\partial_l\chi_{kj}\right)(y) +\sum_{i=1}^N \partial_{y_i}(-\alpha_{ik}^j)(y) \notag\\
&=\sum_{i=1}^N \partial_{y_i}(\psi_j(y) a_{ik}(y)) -b_{kj}(y)+\int_Y b_{kj}dy + g_k^j(y) =0, \notag
\end{align*} where we have used the equality 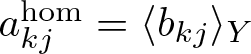 $a_{kj}^{{\rm hom}}=\langle b_{kj}\rangle_Y$ (cf. (3.10) and (4.7)). Likewise, since
$a_{kj}^{{\rm hom}}=\langle b_{kj}\rangle_Y$ (cf. (3.10) and (4.7)). Likewise, since ![]() $\psi_j$ is the solution to (3.7), we immediately conclude that
$\psi_j$ is the solution to (3.7), we immediately conclude that
 \begin{equation*}
\notag
{\rm div}(T^j) = \sum_{i=1}^N \partial_{y_i} t_i^j (y)=\sum_{i=1}^N\partial_{y_i}\left(a_{ij}(y) +\sum_{k=1}^N a_{ik}(y)\partial_{y_k}\psi_j(y)\right) =0.
\end{equation*}
\begin{equation*}
\notag
{\rm div}(T^j) = \sum_{i=1}^N \partial_{y_i} t_i^j (y)=\sum_{i=1}^N\partial_{y_i}\left(a_{ij}(y) +\sum_{k=1}^N a_{ik}(y)\partial_{y_k}\psi_j(y)\right) =0.
\end{equation*} Therefore, applying Proposition 3.2, it follows that the components of ![]() $H^{kj}$ and
$H^{kj}$ and ![]() $T^j$ are represented by
$T^j$ are represented by
 \begin{align*}\notag
h_i^{kj}(y)= \langle h_i^{kj}\rangle_Y+ \sum_{l=1}^N \partial_{y_l} \beta_{il}^{kj}(y)\;\;\;\hbox{and}\;\;\;
t_i^j(y)= \langle t_i^{j}\rangle_Y+\sum_{k=1}^N \partial_{y_k}\gamma_{ik}^j(y),
\end{align*}
\begin{align*}\notag
h_i^{kj}(y)= \langle h_i^{kj}\rangle_Y+ \sum_{l=1}^N \partial_{y_l} \beta_{il}^{kj}(y)\;\;\;\hbox{and}\;\;\;
t_i^j(y)= \langle t_i^{j}\rangle_Y+\sum_{k=1}^N \partial_{y_k}\gamma_{ik}^j(y),
\end{align*} for all ![]() $i=1,\dots, N$. This implies that
$i=1,\dots, N$. This implies that
 \begin{align*}
\widetilde{Q}_{i,\varepsilon}(x) &= \sum_{j,k=1}^N \langle h_i^{kj}\rangle_Y\partial^2_{kj}u_0^{\min}(x)+ \sum_{j,k,l=1}^N \partial_{y_l} \beta_{il}^{kj,\varepsilon}(x)\partial^2_{kj}u_0^{\min}(x) \notag\\
&\quad+ \sum_{j=1}^N\langle t_i^{j}\rangle_Y\partial_j\widetilde{u}_1(x)+\sum_{j,k=1}^N \sum_{k=1}^N \partial_{y_k}\gamma_{ik}^{j, \varepsilon}(x)
\partial_j\widetilde{u}_1(x)\notag\\
& =\sum_{j,k=1}^N \langle h_i^{kj}\rangle_Y\partial^2_{kj}u_0^{\min}(x)+ \sum_{j=1}^N\langle t_i^{j}\rangle_Y\partial_j\widetilde{u}_1(x) \notag\\
&\quad +\varepsilon\biggl( \sum_{j,k,l=1}^N \partial_l(\beta_{il}^{kj, \varepsilon}\partial_{kj}^2u^{\rm min}_0)(x)- \sum_{j,k,l=1}^N \beta_{il}^{kj,\varepsilon}(x)\partial_{lkj}^3u^{\rm min}_0(x)\notag\\
&\quad+ \sum_{j,k=1}^N\partial_i(\gamma_{ik}^{j,\varepsilon}\partial_j\widetilde{u}_1)(x) -\sum_{j,k=1}^N\gamma_{ik}^{j,\varepsilon}(x)\partial^2_{kj}\widetilde{u}_1)(x) \biggr)\notag
\end{align*}
\begin{align*}
\widetilde{Q}_{i,\varepsilon}(x) &= \sum_{j,k=1}^N \langle h_i^{kj}\rangle_Y\partial^2_{kj}u_0^{\min}(x)+ \sum_{j,k,l=1}^N \partial_{y_l} \beta_{il}^{kj,\varepsilon}(x)\partial^2_{kj}u_0^{\min}(x) \notag\\
&\quad+ \sum_{j=1}^N\langle t_i^{j}\rangle_Y\partial_j\widetilde{u}_1(x)+\sum_{j,k=1}^N \sum_{k=1}^N \partial_{y_k}\gamma_{ik}^{j, \varepsilon}(x)
\partial_j\widetilde{u}_1(x)\notag\\
& =\sum_{j,k=1}^N \langle h_i^{kj}\rangle_Y\partial^2_{kj}u_0^{\min}(x)+ \sum_{j=1}^N\langle t_i^{j}\rangle_Y\partial_j\widetilde{u}_1(x) \notag\\
&\quad +\varepsilon\biggl( \sum_{j,k,l=1}^N \partial_l(\beta_{il}^{kj, \varepsilon}\partial_{kj}^2u^{\rm min}_0)(x)- \sum_{j,k,l=1}^N \beta_{il}^{kj,\varepsilon}(x)\partial_{lkj}^3u^{\rm min}_0(x)\notag\\
&\quad+ \sum_{j,k=1}^N\partial_i(\gamma_{ik}^{j,\varepsilon}\partial_j\widetilde{u}_1)(x) -\sum_{j,k=1}^N\gamma_{ik}^{j,\varepsilon}(x)\partial^2_{kj}\widetilde{u}_1)(x) \biggr)\notag
\end{align*}From (4.4) together with (4.8), we conclude that
 \begin{align*}
&(A^\varepsilon(x)\nabla u^{(2)}_\varepsilon(x)- A^{{\rm hom}}\nabla u^{\rm min}_0(x))_i \\& = \varepsilon\left( \sum_{j,k=1}^N \partial_{k}(\alpha_{ik}^{j,\varepsilon}\partial_ju^{\rm min}_0)(x)+\sum_{j,k=1}^N \langle h_i^{kj}\rangle_Y\partial^2_{kj}u_0^{\min}(x)+ \sum_{j=1}^N\langle t_i^{j}\rangle_Y\partial_j\widetilde{u}_1(x)\right)\notag\\
&\quad + \varepsilon^2\left( \sum_{j,k,l=1}^N \partial_l(\beta_{il}^{kj, \varepsilon}\partial_{kj}^2u^{\rm min}_0)(x)+ \sum_{j,k=1}^N\partial_i(\gamma_{ik}^{j,\varepsilon}\partial_j\widetilde{u}_1)(x) + \widetilde{R}_{i,\varepsilon}(x) \right),\notag
\end{align*}
\begin{align*}
&(A^\varepsilon(x)\nabla u^{(2)}_\varepsilon(x)- A^{{\rm hom}}\nabla u^{\rm min}_0(x))_i \\& = \varepsilon\left( \sum_{j,k=1}^N \partial_{k}(\alpha_{ik}^{j,\varepsilon}\partial_ju^{\rm min}_0)(x)+\sum_{j,k=1}^N \langle h_i^{kj}\rangle_Y\partial^2_{kj}u_0^{\min}(x)+ \sum_{j=1}^N\langle t_i^{j}\rangle_Y\partial_j\widetilde{u}_1(x)\right)\notag\\
&\quad + \varepsilon^2\left( \sum_{j,k,l=1}^N \partial_l(\beta_{il}^{kj, \varepsilon}\partial_{kj}^2u^{\rm min}_0)(x)+ \sum_{j,k=1}^N\partial_i(\gamma_{ik}^{j,\varepsilon}\partial_j\widetilde{u}_1)(x) + \widetilde{R}_{i,\varepsilon}(x) \right),\notag
\end{align*} where 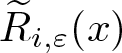 $\widetilde{R}_{i,\varepsilon}(x)$ is defined as
$\widetilde{R}_{i,\varepsilon}(x)$ is defined as
 \begin{align*}
\widetilde{R}_{i,\varepsilon}(x)&:= R_{i,\varepsilon}(x) - \sum_{j,k,l=1}^N \beta_{il}^{kj,\varepsilon}(x)\partial_{lkj}^3u^{\rm min}_0(x)-\sum_{j,k=1}^N\gamma_{ik}^{j,\varepsilon}(x)\partial^2_{kj}\widetilde{u}_1(x). \notag
\end{align*}
\begin{align*}
\widetilde{R}_{i,\varepsilon}(x)&:= R_{i,\varepsilon}(x) - \sum_{j,k,l=1}^N \beta_{il}^{kj,\varepsilon}(x)\partial_{lkj}^3u^{\rm min}_0(x)-\sum_{j,k=1}^N\gamma_{ik}^{j,\varepsilon}(x)\partial^2_{kj}\widetilde{u}_1(x). \notag
\end{align*} Noticing that 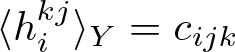 $\langle h_i^{kj}\rangle_Y= c_{ijk}$ (cf. (3.12) and (4.10)) and
$\langle h_i^{kj}\rangle_Y= c_{ijk}$ (cf. (3.12) and (4.10)) and  $\langle t_i^{j}\rangle_Y= a_{ij}^{{\rm hom}}$ (cf. (4.7) and (4.11)) as well as bearing in mind problem (3.11), we obtain that
$\langle t_i^{j}\rangle_Y= a_{ij}^{{\rm hom}}$ (cf. (4.7) and (4.11)) as well as bearing in mind problem (3.11), we obtain that
 \begin{align*}
\notag
\sum_{i=1}^N \partial_i\left(\sum_{j,k=1}^N \langle h_i^{kj}\rangle_Y\partial^2_{kj}u_0^{\min}(x)+ \sum_{j=1}^N\langle t_i^{j}\rangle_Y\partial_j\widetilde{u}_1(x) \right)=0.
\end{align*}
\begin{align*}
\notag
\sum_{i=1}^N \partial_i\left(\sum_{j,k=1}^N \langle h_i^{kj}\rangle_Y\partial^2_{kj}u_0^{\min}(x)+ \sum_{j=1}^N\langle t_i^{j}\rangle_Y\partial_j\widetilde{u}_1(x) \right)=0.
\end{align*} Moreover, since 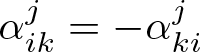 $\alpha_{ik}^j=-\alpha_{ki}^j$, it follows that
$\alpha_{ik}^j=-\alpha_{ki}^j$, it follows that
 \begin{equation*}
\notag
\sum_{i=1}^N\partial_i\left(\sum_{j,k=1}^N \partial_{k}(\alpha_{ik}^{j,\varepsilon}\partial_ju^{\rm min}_0)(x)
\right)=0.
\end{equation*}
\begin{equation*}
\notag
\sum_{i=1}^N\partial_i\left(\sum_{j,k=1}^N \partial_{k}(\alpha_{ik}^{j,\varepsilon}\partial_ju^{\rm min}_0)(x)
\right)=0.
\end{equation*} Likewise, since 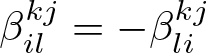 $\beta_{il}^{kj} = - \beta_{li}^{kj}$ and
$\beta_{il}^{kj} = - \beta_{li}^{kj}$ and 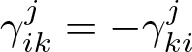 $\gamma_{ik}^{j}=-\gamma_{ki}^{j}$,
$\gamma_{ik}^{j}=-\gamma_{ki}^{j}$,
 \begin{equation*}
\notag
\sum_{i=1}^N\partial_i\left(
\sum_{j,k,l=1}^N \partial_l(\beta_{il}^{kj, \varepsilon}\partial_{kj}^2u^{\rm min}_0)(x)\right)= \sum_{i=1}^N\partial_i\left(\sum_{j,k=1}^N\partial_i(\gamma_{ik}^{j,\varepsilon}\partial_j\widetilde{u}_1)(x)\right)=0.
\end{equation*}
\begin{equation*}
\notag
\sum_{i=1}^N\partial_i\left(
\sum_{j,k,l=1}^N \partial_l(\beta_{il}^{kj, \varepsilon}\partial_{kj}^2u^{\rm min}_0)(x)\right)= \sum_{i=1}^N\partial_i\left(\sum_{j,k=1}^N\partial_i(\gamma_{ik}^{j,\varepsilon}\partial_j\widetilde{u}_1)(x)\right)=0.
\end{equation*}Therefore,
 \begin{equation*}
\notag
{\rm div}(A^\varepsilon(x) \nabla u^{(2)}(x)_\varepsilon-A^{{\rm hom}} \nabla u^{\rm min}_0(x)) = \varepsilon^2 {\rm div}(\widetilde{R}_\varepsilon(x)),
\end{equation*}
\begin{equation*}
\notag
{\rm div}(A^\varepsilon(x) \nabla u^{(2)}(x)_\varepsilon-A^{{\rm hom}} \nabla u^{\rm min}_0(x)) = \varepsilon^2 {\rm div}(\widetilde{R}_\varepsilon(x)),
\end{equation*} with 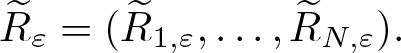 $\widetilde{R}_\varepsilon=(\widetilde{R}_{1,\varepsilon}, \dots, \widetilde{R}_{N,\varepsilon}).$ Now,
$\widetilde{R}_\varepsilon=(\widetilde{R}_{1,\varepsilon}, \dots, \widetilde{R}_{N,\varepsilon}).$ Now,
 \begin{equation*}
\notag
\|{\rm div}(A^\varepsilon \nabla u^{(2)}_\varepsilon-A^{{\rm hom}} \nabla u^{\rm min}_0) \|_{H^{-1}(\Omega)} = \|{\rm div}\widetilde{R}_\varepsilon\|_{H^{-1}(\Omega)} \leq \|\widetilde{R}_\varepsilon\|_{L^{2}(\Omega)} \leq C \varepsilon^2,
\end{equation*}
\begin{equation*}
\notag
\|{\rm div}(A^\varepsilon \nabla u^{(2)}_\varepsilon-A^{{\rm hom}} \nabla u^{\rm min}_0) \|_{H^{-1}(\Omega)} = \|{\rm div}\widetilde{R}_\varepsilon\|_{H^{-1}(\Omega)} \leq \|\widetilde{R}_\varepsilon\|_{L^{2}(\Omega)} \leq C \varepsilon^2,
\end{equation*}which concludes the proof.
5. Compactness result in Theorem 2.7
In this section, we are going to prove a compactness result stated in Theorem 2.7(i).
Proposition 5.1. Let ![]() $\{\varepsilon_n\}_{n}$ be a sequence such that
$\{\varepsilon_n\}_{n}$ be a sequence such that ![]() $\varepsilon_n\to 0$ as
$\varepsilon_n\to 0$ as ![]() $n\to\infty$. Suppose that Assumptions (H1)-(H3) hold. If
$n\to\infty$. Suppose that Assumptions (H1)-(H3) hold. If ![]() $\{u_n\}_{n}\subset H^1(\Omega)$ is a sequence such that
$\{u_n\}_{n}\subset H^1(\Omega)$ is a sequence such that
 \begin{equation*}
\notag
\sup_{n} F^1_n(u_n) \lt \infty,
\end{equation*}
\begin{equation*}
\notag
\sup_{n} F^1_n(u_n) \lt \infty,
\end{equation*} then, ![]() $\{u_n\}_{n}$ converges to
$\{u_n\}_{n}$ converges to ![]() $u^{\rm min}_0\in H^1(\Omega)$ weakly in
$u^{\rm min}_0\in H^1(\Omega)$ weakly in ![]() $H^1(\Omega)$.
$H^1(\Omega)$.
Proof. First, recall that thanks to Assumption (H3), the homogenized matrix ![]() $A_{{\rm hom}}$ satisfies the same growth conditions with the same constants, i.e.,
$A_{{\rm hom}}$ satisfies the same growth conditions with the same constants, i.e.,
for all ![]() $\xi\in\mathbb{R}^N$. Let
$\xi\in\mathbb{R}^N$. Let ![]() $\lambda \gt 0$ that will be fixed later. Note that
$\lambda \gt 0$ that will be fixed later. Note that
 \begin{equation}
-ab \geq -\frac{a^2}{2\lambda^2} - \frac{\lambda^2}{2}b^2,
\end{equation}
\begin{equation}
-ab \geq -\frac{a^2}{2\lambda^2} - \frac{\lambda^2}{2}b^2,
\end{equation} for all ![]() $a,b\geq 0$. Let
$a,b\geq 0$. Let ![]() $C_\Omega \gt 0$ be the Poincaré constant of
$C_\Omega \gt 0$ be the Poincaré constant of ![]() $\Omega$, i.e., such that,
$\Omega$, i.e., such that,
for all ![]() $v\in H^1_0(\Omega)$. Recall that if
$v\in H^1_0(\Omega)$. Recall that if ![]() $u\in L^2(\Omega)$ is such that
$u\in L^2(\Omega)$ is such that ![]() $F_{n}(u) \lt +\infty$, then
$F_{n}(u) \lt +\infty$, then ![]() $u\in H^1_0(\Omega)$. By using (H3), (5.1) and (5.2), we get
$u\in H^1_0(\Omega)$. By using (H3), (5.1) and (5.2), we get
 \begin{align*}
F_n(u)
&\geq \alpha\|\nabla u\|^2_{L^2(\Omega;\mathbb{R}^N)}
- \frac{\lambda^2}{2}\|u\|^2_{L^2(\Omega)}
-\frac{1}{2\lambda^2}\|f\|^2_{L^2(\Omega)} \\
&\geq \left(\alpha - \frac{\lambda^2}{2} C_\Omega^2 \right)
\|\nabla u\|^2_{L^2(\Omega;\mathbb{R}^N)}
-\frac{1}{2\lambda^2}\|f\|^2_{L^2(\Omega)}.
\end{align*}
\begin{align*}
F_n(u)
&\geq \alpha\|\nabla u\|^2_{L^2(\Omega;\mathbb{R}^N)}
- \frac{\lambda^2}{2}\|u\|^2_{L^2(\Omega)}
-\frac{1}{2\lambda^2}\|f\|^2_{L^2(\Omega)} \\
&\geq \left(\alpha - \frac{\lambda^2}{2} C_\Omega^2 \right)
\|\nabla u\|^2_{L^2(\Omega;\mathbb{R}^N)}
-\frac{1}{2\lambda^2}\|f\|^2_{L^2(\Omega)}.
\end{align*}Namely,
 \begin{equation*}
\left(\alpha - \frac{\lambda^2}{2} C_\Omega^2 \right)
\|\nabla u\|^2_{L^2(\Omega;\mathbb{R}^N)} \leq F_n(u).
\end{equation*}
\begin{equation*}
\left(\alpha - \frac{\lambda^2}{2} C_\Omega^2 \right)
\|\nabla u\|^2_{L^2(\Omega;\mathbb{R}^N)} \leq F_n(u).
\end{equation*}Choosing
 \begin{equation*}
\lambda \in \left(0, \frac{\sqrt{2\alpha}}{C_\Omega} \right),
\end{equation*}
\begin{equation*}
\lambda \in \left(0, \frac{\sqrt{2\alpha}}{C_\Omega} \right),
\end{equation*}yields that
 \begin{equation*}
\|\nabla u\|_{L^2(\Omega;\mathbb{R}^N)} \leq C ( F_n(u) + 1)
\leq C(F^1_n(u) + 1),
\end{equation*}
\begin{equation*}
\|\nabla u\|_{L^2(\Omega;\mathbb{R}^N)} \leq C ( F_n(u) + 1)
\leq C(F^1_n(u) + 1),
\end{equation*} where the constant ![]() $C \gt 0$ changes all the times. Since
$C \gt 0$ changes all the times. Since ![]() $u\in H^1_0(\Omega)$, using the Poincaré inequality again, we get that
$u\in H^1_0(\Omega)$, using the Poincaré inequality again, we get that
 \begin{equation*}
\|u\|_{H^1(\Omega)} \lt C(F^1_n(u) + 1).
\end{equation*}
\begin{equation*}
\|u\|_{H^1(\Omega)} \lt C(F^1_n(u) + 1).
\end{equation*} Therefore, if ![]() $\{u_n\}_{n\in\mathbb{N}}\subset L^2(\Omega)$ is such that
$\{u_n\}_{n\in\mathbb{N}}\subset L^2(\Omega)$ is such that
 \begin{equation*}
\sup_{n\in\mathbb{N}} F_n^1(u_n) \lt +\infty,
\end{equation*}
\begin{equation*}
\sup_{n\in\mathbb{N}} F_n^1(u_n) \lt +\infty,
\end{equation*} then, there exists a subsequence ![]() $\{u_{n_k}\}_{k\in\mathbb{N}}$ such that
$\{u_{n_k}\}_{k\in\mathbb{N}}$ such that ![]() $u_{n_k}\rightharpoonup v$ weakly in
$u_{n_k}\rightharpoonup v$ weakly in ![]() $H^1(\Omega)$, for some
$H^1(\Omega)$, for some ![]() $v\in H^1(\Omega)$.
$v\in H^1(\Omega)$.
We now prove that ![]() $v=u^{\rm min}_0$. Assume by contradiction that
$v=u^{\rm min}_0$. Assume by contradiction that ![]() $v\neq u^{\rm min}_0$. Since the minimizer
$v\neq u^{\rm min}_0$. Since the minimizer ![]() $u^{\rm min}_0$ is unique, it follows that
$u^{\rm min}_0$ is unique, it follows that
 \begin{equation*}
\liminf_{k\to\infty} F_{n_k}(u_{n_k}) \geq F_{\rm hom}^0(v) \gt F_{\rm hom}^0(u^{\rm min}_0).
\end{equation*}
\begin{equation*}
\liminf_{k\to\infty} F_{n_k}(u_{n_k}) \geq F_{\rm hom}^0(v) \gt F_{\rm hom}^0(u^{\rm min}_0).
\end{equation*}Thus,
 \begin{equation*}
\lim_{k\to\infty} F^1_{n_k}(u_{n_k})
=\lim_{k\to\infty} \frac{F_{n_k}(u_{n_k}) - F_{\rm hom}^0(u^{\rm min}_0)}{\varepsilon_{n_k}} = +\infty.
\end{equation*}
\begin{equation*}
\lim_{k\to\infty} F^1_{n_k}(u_{n_k})
=\lim_{k\to\infty} \frac{F_{n_k}(u_{n_k}) - F_{\rm hom}^0(u^{\rm min}_0)}{\varepsilon_{n_k}} = +\infty.
\end{equation*}This gives the desired contradiction. Since the limit is unique, we also get that the full sequence converges.
Remark 5.2. Note that, in order to get compactness, we do not need to have Assumptions (H4) in force.
6. The liminf inequality for Theorem 2.7
In this section, we prove the lower bound of Theorem 2.7 (ii).
Proposition 6.1. Assume that Assumptions (H1)-(H4) hold. Then, for any sequence ![]() $\{u_n\}_{n}\subset L^2(\Omega)$ converging to
$\{u_n\}_{n}\subset L^2(\Omega)$ converging to ![]() $u^{\rm min}_0$ with respect to
$u^{\rm min}_0$ with respect to ![]() $L^2(\Omega)$ it holds that
$L^2(\Omega)$ it holds that
 \begin{equation*}
\notag
\liminf_{n\to \infty}F_n^1(u_n) \geq F_{{\rm hom}}^1(u^{\rm min}_0).
\end{equation*}
\begin{equation*}
\notag
\liminf_{n\to \infty}F_n^1(u_n) \geq F_{{\rm hom}}^1(u^{\rm min}_0).
\end{equation*}Proof. Without loss of generality, we can assume that
 \begin{equation*}
\liminf_{n\to\infty} F^1_n(u_n) \lt \infty.
\end{equation*}
\begin{equation*}
\liminf_{n\to\infty} F^1_n(u_n) \lt \infty.
\end{equation*} Let ![]() $u^{(2)}_n$ be the function defined in (4.3). Then, it holds that
$u^{(2)}_n$ be the function defined in (4.3). Then, it holds that
 \begin{align*}
\liminf_{n\to\infty} F^{1}_n (u_n)
&= \liminf_{n\to\infty} {F_n (u_n) - F^{0}_{{\rm hom}} (u^{\rm min}_0)\over \varepsilon_n}\notag\\
&\geq \liminf_{n\to\infty} {F_n (u^{\rm min}_n) - F^{0}_{{\rm hom}} (u^{\rm min}_0) \over\varepsilon_n}\notag\\
&\geq \liminf_{n\to\infty} {F_n (u^{\rm min}_n) - F_n (u^{(2)}_n) \over\varepsilon_n}
+ \liminf_{n\to\infty}{ F_n (u^{(2)}_n) - F^{0}_{{\rm hom}} (u^{\rm min}_0) \over \varepsilon_n}\notag\\
& = \liminf_{n\to\infty} I^1_n + \liminf_{n\to\infty} I_n^2
+ \liminf_{n\to\infty} I_n^3,
\end{align*}
\begin{align*}
\liminf_{n\to\infty} F^{1}_n (u_n)
&= \liminf_{n\to\infty} {F_n (u_n) - F^{0}_{{\rm hom}} (u^{\rm min}_0)\over \varepsilon_n}\notag\\
&\geq \liminf_{n\to\infty} {F_n (u^{\rm min}_n) - F^{0}_{{\rm hom}} (u^{\rm min}_0) \over\varepsilon_n}\notag\\
&\geq \liminf_{n\to\infty} {F_n (u^{\rm min}_n) - F_n (u^{(2)}_n) \over\varepsilon_n}
+ \liminf_{n\to\infty}{ F_n (u^{(2)}_n) - F^{0}_{{\rm hom}} (u^{\rm min}_0) \over \varepsilon_n}\notag\\
& = \liminf_{n\to\infty} I^1_n + \liminf_{n\to\infty} I_n^2
+ \liminf_{n\to\infty} I_n^3,
\end{align*}where
 \begin{equation*}
I^1_n:= { F_n (u^{\rm min}_n) - F_n (u^{(2)}_n) \over \varepsilon_n},
\end{equation*}
\begin{equation*}
I^1_n:= { F_n (u^{\rm min}_n) - F_n (u^{(2)}_n) \over \varepsilon_n},
\end{equation*} \begin{equation*}
I^2_n:= \frac{1}{\varepsilon_n} \left[ \int_\Omega A^{\varepsilon_n}(x) \nabla u^{(2)}_n (x) \cdot \nabla u^{(2)}_n(x) \,\mathrm{d}x
- \int_\Omega A_{{\rm hom}} u^{\rm min}_0(x)\cdot u^{\rm min}_0(x) \,\mathrm{d}x \right],
\end{equation*}
\begin{equation*}
I^2_n:= \frac{1}{\varepsilon_n} \left[ \int_\Omega A^{\varepsilon_n}(x) \nabla u^{(2)}_n (x) \cdot \nabla u^{(2)}_n(x) \,\mathrm{d}x
- \int_\Omega A_{{\rm hom}} u^{\rm min}_0(x)\cdot u^{\rm min}_0(x) \,\mathrm{d}x \right],
\end{equation*}and
 \begin{equation*}
I^3_n:= \frac{1}{\varepsilon_n} \int_\Omega f(x)(u^{(2)}_n(x) - u^{\rm min}_0(x)) \,\mathrm{d}x.
\end{equation*}
\begin{equation*}
I^3_n:= \frac{1}{\varepsilon_n} \int_\Omega f(x)(u^{(2)}_n(x) - u^{\rm min}_0(x)) \,\mathrm{d}x.
\end{equation*}We now claim that
 \begin{equation*}
\lim_{n\to\infty}I^1_n =0,
\end{equation*}
\begin{equation*}
\lim_{n\to\infty}I^1_n =0,
\end{equation*}and that
 \begin{equation*}
\lim_{n\to\infty}(I^2_n + I^3_n ) =F_{{\rm hom}}^1(u^{\rm min}_0).
\end{equation*}
\begin{equation*}
\lim_{n\to\infty}(I^2_n + I^3_n ) =F_{{\rm hom}}^1(u^{\rm min}_0).
\end{equation*}These will give the desired result.
Step 1: limit of ![]() $I^1_n$. We have that
$I^1_n$. We have that
 \begin{align*}
I^1_n &= \frac{1}{\varepsilon_n} \left[ \int_\Omega A^{\varepsilon_n}(x) \nabla u^{(2)}_n (x)\cdot \nabla u^{(2)}_n (x)\,\mathrm{d}x
- \int_\Omega A^{\varepsilon_n} (x)\nabla u^{\rm min}_n (x)\cdot \nabla u^{\rm min}_n (x)\,\mathrm{d}x \right] \\
&\quad- \frac{1}{\varepsilon_n} \int_\Omega f (x)(u^{(2)}_n(x) - u^{\rm min}_n(x)) \,\mathrm{d}x.
\end{align*}
\begin{align*}
I^1_n &= \frac{1}{\varepsilon_n} \left[ \int_\Omega A^{\varepsilon_n}(x) \nabla u^{(2)}_n (x)\cdot \nabla u^{(2)}_n (x)\,\mathrm{d}x
- \int_\Omega A^{\varepsilon_n} (x)\nabla u^{\rm min}_n (x)\cdot \nabla u^{\rm min}_n (x)\,\mathrm{d}x \right] \\
&\quad- \frac{1}{\varepsilon_n} \int_\Omega f (x)(u^{(2)}_n(x) - u^{\rm min}_n(x)) \,\mathrm{d}x.
\end{align*} Writing 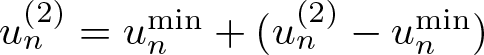 $u^{(2)}_n = u^{\rm min}_n + (u^{(2)}_n-u^{\rm min}_n)$ gives
$u^{(2)}_n = u^{\rm min}_n + (u^{(2)}_n-u^{\rm min}_n)$ gives
 \begin{align}
&\frac{1}{\varepsilon_n} \left| \int_\Omega A^{\varepsilon_n}(x) \nabla u^{(2)}_n(x) \cdot \nabla u^{(2)}_n(x) \,\mathrm{d}x
- \int_\Omega A^{\varepsilon_n}(x) \nabla u^{\rm min}_n(x) \cdot \nabla u^{\rm min}_n(x) \,\mathrm{d}x \right| \nonumber \\
&=\frac{1}{\varepsilon_n} \Bigl| \int_\Omega A^{\varepsilon_n}(x) \nabla (u^{(2)}_n-u^{\rm min}_n)(x)
\cdot \nabla (u^{(2)}_n-u^{\rm min}_n)(x) \,\mathrm{d}x \nonumber \\
&+\frac{2}{\varepsilon_n} \int_\Omega A^{\varepsilon_n} (x)\nabla (u^{(2)}_n-u^{\rm min}_n)(x)
\cdot \nabla u^{(2)}_n(x) \,\mathrm{d}x \Bigr| \nonumber \\
&\leq \frac{1}{\varepsilon_n} \left\| \mathrm{div}\left( A^{\varepsilon_n} \nabla (u^{(2)}_n-u^{\rm min}_n) \right) \right\|_{H^{-1}(\Omega)}
\left( \| u^{(2)}_n-u^{\rm min}_n \|_{H^1_0(\Omega)}
+ 2\| u^{(2)}_n \|_{H^1_0(\Omega)} \right) \nonumber\\
&\leq \varepsilon_n\left( \| u^{\rm min}_n \|_{H^1_0(\Omega)} + 3\| u^{(2)}_n \|_{H^1_0(\Omega)} \right),\end{align}
\begin{align}
&\frac{1}{\varepsilon_n} \left| \int_\Omega A^{\varepsilon_n}(x) \nabla u^{(2)}_n(x) \cdot \nabla u^{(2)}_n(x) \,\mathrm{d}x
- \int_\Omega A^{\varepsilon_n}(x) \nabla u^{\rm min}_n(x) \cdot \nabla u^{\rm min}_n(x) \,\mathrm{d}x \right| \nonumber \\
&=\frac{1}{\varepsilon_n} \Bigl| \int_\Omega A^{\varepsilon_n}(x) \nabla (u^{(2)}_n-u^{\rm min}_n)(x)
\cdot \nabla (u^{(2)}_n-u^{\rm min}_n)(x) \,\mathrm{d}x \nonumber \\
&+\frac{2}{\varepsilon_n} \int_\Omega A^{\varepsilon_n} (x)\nabla (u^{(2)}_n-u^{\rm min}_n)(x)
\cdot \nabla u^{(2)}_n(x) \,\mathrm{d}x \Bigr| \nonumber \\
&\leq \frac{1}{\varepsilon_n} \left\| \mathrm{div}\left( A^{\varepsilon_n} \nabla (u^{(2)}_n-u^{\rm min}_n) \right) \right\|_{H^{-1}(\Omega)}
\left( \| u^{(2)}_n-u^{\rm min}_n \|_{H^1_0(\Omega)}
+ 2\| u^{(2)}_n \|_{H^1_0(\Omega)} \right) \nonumber\\
&\leq \varepsilon_n\left( \| u^{\rm min}_n \|_{H^1_0(\Omega)} + 3\| u^{(2)}_n \|_{H^1_0(\Omega)} \right),\end{align} where the last step follows from Proposition 4.8. Note that from (H3), together with the fact that 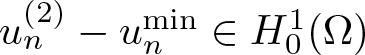 $u^{(2)}_n - u^{\rm min}_n \in H^1_0(\Omega)$, it holds that
$u^{(2)}_n - u^{\rm min}_n \in H^1_0(\Omega)$, it holds that
 \begin{align*}
&\alpha \| \nabla (u^{(2)}_n - u^{\rm min}_n) \|^2_{L^2(\Omega)} \\
&\leq
\int_\Omega A^{\varepsilon_n} (x) \nabla (u^{(2)}_n - u^{\rm min}_n)(x)\cdot \nabla (u^{(2)}_n - u^{\rm min}_n)(x)\,\mathrm{d}x \\
&\leq \sup_{\varphi\in H^1_0(\Omega)}\int_\Omega A^{\varepsilon_n}(x) \nabla (u^{(2)}_n - u^{\rm min}_n)(x)\cdot \nabla \varphi(x)\,\mathrm{d}x \\
&=\left\| \mathrm{div}\left( A^{\varepsilon_n} \nabla (u^{(2)}_n-u^{\rm min}_n) \right) \right\|_{H^{-1}(\Omega)} \| u^{(2)}_n - u^{\rm min}_n \|_{H^1_0(\Omega)}\\
&\leq(1+C_\Omega)\left\| \mathrm{div}\left( A^{\varepsilon_n} \nabla (u^{(2)}_n-u^{\rm min}_n) \right) \right\|_{H^{-1}(\Omega)} \| \nabla (u^{(2)}_n - u^{\rm min}_n) \|_{L^2(\Omega)}.
\end{align*}
\begin{align*}
&\alpha \| \nabla (u^{(2)}_n - u^{\rm min}_n) \|^2_{L^2(\Omega)} \\
&\leq
\int_\Omega A^{\varepsilon_n} (x) \nabla (u^{(2)}_n - u^{\rm min}_n)(x)\cdot \nabla (u^{(2)}_n - u^{\rm min}_n)(x)\,\mathrm{d}x \\
&\leq \sup_{\varphi\in H^1_0(\Omega)}\int_\Omega A^{\varepsilon_n}(x) \nabla (u^{(2)}_n - u^{\rm min}_n)(x)\cdot \nabla \varphi(x)\,\mathrm{d}x \\
&=\left\| \mathrm{div}\left( A^{\varepsilon_n} \nabla (u^{(2)}_n-u^{\rm min}_n) \right) \right\|_{H^{-1}(\Omega)} \| u^{(2)}_n - u^{\rm min}_n \|_{H^1_0(\Omega)}\\
&\leq(1+C_\Omega)\left\| \mathrm{div}\left( A^{\varepsilon_n} \nabla (u^{(2)}_n-u^{\rm min}_n) \right) \right\|_{H^{-1}(\Omega)} \| \nabla (u^{(2)}_n - u^{\rm min}_n) \|_{L^2(\Omega)}.
\end{align*} Therefore, calling ![]() $C_\Omega$ the Poincaré constant of
$C_\Omega$ the Poincaré constant of ![]() $\Omega$, we obtain that
$\Omega$, we obtain that
 \begin{align}
&\left|\frac{1}{\varepsilon_n} \int_\Omega f(x) (u^{(2)}_n(x) - u^{\rm min}_n(x)) \,\mathrm{d}x \right| \nonumber \\
& \leq \frac{1}{\varepsilon_n} \| f\|_{L^2(\Omega)} \| u^{(2)}_n - u^{\rm min}_n \|_{L^2(\Omega)} \nonumber \\
&\leq \frac{C_\Omega}{\varepsilon_n} \| f\|_{L^2(\Omega)} \| \nabla (u^{(2)}_n - u^{\rm min}_n) \|_{L^2(\Omega)}
\nonumber \\
&\leq \frac{(1+C_\Omega)C_\Omega}{\alpha\varepsilon_n} \| f\|_{L^2(\Omega)}
\left\| \mathrm{div}\left( A^{\varepsilon_n} \nabla (u^{(2)}_n-u^{\rm min}_n) \right) \right\|_{H^{-1}(\Omega)} \nonumber \\
&\leq \frac{(1+C_\Omega)C_\Omega}{\alpha} \| f\|_{L^2(\Omega)} \varepsilon_n,\end{align}
\begin{align}
&\left|\frac{1}{\varepsilon_n} \int_\Omega f(x) (u^{(2)}_n(x) - u^{\rm min}_n(x)) \,\mathrm{d}x \right| \nonumber \\
& \leq \frac{1}{\varepsilon_n} \| f\|_{L^2(\Omega)} \| u^{(2)}_n - u^{\rm min}_n \|_{L^2(\Omega)} \nonumber \\
&\leq \frac{C_\Omega}{\varepsilon_n} \| f\|_{L^2(\Omega)} \| \nabla (u^{(2)}_n - u^{\rm min}_n) \|_{L^2(\Omega)}
\nonumber \\
&\leq \frac{(1+C_\Omega)C_\Omega}{\alpha\varepsilon_n} \| f\|_{L^2(\Omega)}
\left\| \mathrm{div}\left( A^{\varepsilon_n} \nabla (u^{(2)}_n-u^{\rm min}_n) \right) \right\|_{H^{-1}(\Omega)} \nonumber \\
&\leq \frac{(1+C_\Omega)C_\Omega}{\alpha} \| f\|_{L^2(\Omega)} \varepsilon_n,\end{align}where the last step follows by Proposition 4.8. Since
 \begin{equation*}
\sup_{n} \left( \| u^{\rm min}_n \|_{H^1_0(\Omega)} + 3\| u^{(2)}_n \|_{H^1_0(\Omega)} \right) \lt \infty,
\end{equation*}
\begin{equation*}
\sup_{n} \left( \| u^{\rm min}_n \|_{H^1_0(\Omega)} + 3\| u^{(2)}_n \|_{H^1_0(\Omega)} \right) \lt \infty,
\end{equation*}from (6.1) and (6.2), we get the desired result.
Step 2: limit of ![]() $I^2_n$. Note that
$I^2_n$. Note that
 \begin{align*}
\nabla u^{(2)}_{\varepsilon_n}(x) &= \nabla \left( u^{\rm min}_0(x) + {\varepsilon_n}\sum_{i=1}^{N}\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x) + {\varepsilon_n}^2\sum_{r,s=1}^{N} \chi_{rs}^{\varepsilon_n}(x)\partial^2_{rs} u^{\rm min}_0(x)\right.\\& \left.- {\varepsilon_n}^2\sum_{l=1}^N \psi_l^{\varepsilon_n}(x) \partial_l \widetilde{u}_1(x) \right) \notag\\
&= \nabla u^{\rm min}_0(x) +\sum_{i=1}^{n} \nabla_y\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x)\notag\\
&\quad +{\varepsilon_n}\left[\sum_{i=1}^{N} \psi_i^{\varepsilon_n}(x)\nabla (\partial_i u^{\rm min}_0(x)) + \sum_{r,s=1}^{N} \nabla_y(\chi^{\varepsilon_n}_{rs}(x))\partial^2_{rs}u^{\rm min}_0(x)\right.\\ & \qquad \left.- \sum_{l=1}^{N} \nabla_y(\psi^{\varepsilon_n}_l(x))\partial_l\widetilde{u}_1(x) \right] +O(\varepsilon_n).
\end{align*}
\begin{align*}
\nabla u^{(2)}_{\varepsilon_n}(x) &= \nabla \left( u^{\rm min}_0(x) + {\varepsilon_n}\sum_{i=1}^{N}\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x) + {\varepsilon_n}^2\sum_{r,s=1}^{N} \chi_{rs}^{\varepsilon_n}(x)\partial^2_{rs} u^{\rm min}_0(x)\right.\\& \left.- {\varepsilon_n}^2\sum_{l=1}^N \psi_l^{\varepsilon_n}(x) \partial_l \widetilde{u}_1(x) \right) \notag\\
&= \nabla u^{\rm min}_0(x) +\sum_{i=1}^{n} \nabla_y\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x)\notag\\
&\quad +{\varepsilon_n}\left[\sum_{i=1}^{N} \psi_i^{\varepsilon_n}(x)\nabla (\partial_i u^{\rm min}_0(x)) + \sum_{r,s=1}^{N} \nabla_y(\chi^{\varepsilon_n}_{rs}(x))\partial^2_{rs}u^{\rm min}_0(x)\right.\\ & \qquad \left.- \sum_{l=1}^{N} \nabla_y(\psi^{\varepsilon_n}_l(x))\partial_l\widetilde{u}_1(x) \right] +O(\varepsilon_n).
\end{align*}Therefore,
 \begin{align*}
\notag
\int_\Omega A^{\varepsilon_n}(x) \nabla u^{(2)}_{\varepsilon_n}(x)\cdot \nabla u^{(2)}_{\varepsilon_n}(x) \,\mathrm{d}x
= H_n + \varepsilon_n G_n + o(\varepsilon_n),
\end{align*}
\begin{align*}
\notag
\int_\Omega A^{\varepsilon_n}(x) \nabla u^{(2)}_{\varepsilon_n}(x)\cdot \nabla u^{(2)}_{\varepsilon_n}(x) \,\mathrm{d}x
= H_n + \varepsilon_n G_n + o(\varepsilon_n),
\end{align*} where ![]() $H_{\varepsilon_n}$ and
$H_{\varepsilon_n}$ and ![]() $G_{\varepsilon_n}$ are defined as
$G_{\varepsilon_n}$ are defined as
 \begin{align}
H_n&:= \!\int_\Omega A^{\varepsilon_n}(x) \left(\nabla u^{\rm min}_0(x) +\sum_{i=1}^{N} \nabla_y(\psi_i^{\varepsilon_n}(x))\partial_i u^{\rm min}_0(x) \right) \cdot \nonumber \\
&\cdot\left(\nabla u^{\rm min}_0(x) +\sum_{i=1}^{n} \nabla_y(\psi_i^{\varepsilon_n}(x))\partial_i u^{\rm min}_0(x) \right)\,\mathrm{d}x,\end{align}
\begin{align}
H_n&:= \!\int_\Omega A^{\varepsilon_n}(x) \left(\nabla u^{\rm min}_0(x) +\sum_{i=1}^{N} \nabla_y(\psi_i^{\varepsilon_n}(x))\partial_i u^{\rm min}_0(x) \right) \cdot \nonumber \\
&\cdot\left(\nabla u^{\rm min}_0(x) +\sum_{i=1}^{n} \nabla_y(\psi_i^{\varepsilon_n}(x))\partial_i u^{\rm min}_0(x) \right)\,\mathrm{d}x,\end{align}and
 \begin{align*}
G_n&\!:=\! 2\int_\Omega A^{\varepsilon_n}(x) \biggl(\nabla u^{\rm min}_0(x) \!+\!\sum_{i=1}^{N} \nabla_y(\psi_i^{\varepsilon_n}(x))\partial_i u^{\rm min}_0(x) \biggr) \!\cdot\! \biggl( \sum_{i=1}^{N} \psi_i^{\varepsilon_n}(x)\nabla (\partial_i u^{\rm min}_0(x))\notag\\
&\quad \quad \quad \quad \quad + \sum_{r,s=1}^{N} \nabla_y(\chi^{\varepsilon_n}_{rs}(x))\partial^2_{rs}u^{\rm min}_0(x)
- \sum_{l=1}^{N} \nabla_y(\psi^{\varepsilon_n}_l(x))\partial_l\widetilde{u}_1(x) \biggr)\,\mathrm{d}x,
\end{align*}
\begin{align*}
G_n&\!:=\! 2\int_\Omega A^{\varepsilon_n}(x) \biggl(\nabla u^{\rm min}_0(x) \!+\!\sum_{i=1}^{N} \nabla_y(\psi_i^{\varepsilon_n}(x))\partial_i u^{\rm min}_0(x) \biggr) \!\cdot\! \biggl( \sum_{i=1}^{N} \psi_i^{\varepsilon_n}(x)\nabla (\partial_i u^{\rm min}_0(x))\notag\\
&\quad \quad \quad \quad \quad + \sum_{r,s=1}^{N} \nabla_y(\chi^{\varepsilon_n}_{rs}(x))\partial^2_{rs}u^{\rm min}_0(x)
- \sum_{l=1}^{N} \nabla_y(\psi^{\varepsilon_n}_l(x))\partial_l\widetilde{u}_1(x) \biggr)\,\mathrm{d}x,
\end{align*}respectively.
Step 2.1: asymptotic behaviour of ![]() $H_n$. Using Proposition 4.6, and recalling that we are assuming the barycentre of
$H_n$. Using Proposition 4.6, and recalling that we are assuming the barycentre of ![]() $Y$ to be at the origin, we get that
$Y$ to be at the origin, we get that
 \begin{align}
&\int_\Omega A^{\varepsilon_n}(x) \nabla u^{\rm min}_0(x) \cdot \nabla u^{\rm min}_0(x) \,\mathrm{d}x \nonumber \\
&\quad= \sum_{i,j=1}^N \int_\Omega a_{ij}^{\varepsilon_n}(x) \partial_i u^{\rm min}_0(x)\partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\quad=\sum_{i,j=1}^N \langle a_{ij}\rangle_Y\,\int_\Omega \partial_i u^{\rm min}_0(x)\partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\qquad+\varepsilon_n \sum_{i,j=1}^N \int_\Omega \nabla(\partial_i u^{\rm min}_0\partial_j u^{\rm min}_0)(x)\,\mathrm{d}x
\cdot \langle y a_{ij} \rangle_Y
+o(\varepsilon_n).\end{align}
\begin{align}
&\int_\Omega A^{\varepsilon_n}(x) \nabla u^{\rm min}_0(x) \cdot \nabla u^{\rm min}_0(x) \,\mathrm{d}x \nonumber \\
&\quad= \sum_{i,j=1}^N \int_\Omega a_{ij}^{\varepsilon_n}(x) \partial_i u^{\rm min}_0(x)\partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\quad=\sum_{i,j=1}^N \langle a_{ij}\rangle_Y\,\int_\Omega \partial_i u^{\rm min}_0(x)\partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\qquad+\varepsilon_n \sum_{i,j=1}^N \int_\Omega \nabla(\partial_i u^{\rm min}_0\partial_j u^{\rm min}_0)(x)\,\mathrm{d}x
\cdot \langle y a_{ij} \rangle_Y
+o(\varepsilon_n).\end{align}Moreover,
 \begin{align}
&\int_\Omega A^{\varepsilon_n}(x) \left( \sum_{i=1}^{N} \nabla_y(\psi_i^{\varepsilon_n}(x))\partial_i u^{\rm min}_0(x) \right) \cdot \nabla u^{\rm min}_0(x) \,\mathrm{d}x \nonumber \\
&\quad= \sum_{i,j,s=1}^N \int_\Omega a_{js}^{\varepsilon_n}(x) \partial_{y_s} \psi_i^{\varepsilon_n}(x)
\partial_i u^{\rm min}_0(x) \partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\quad=\sum_{i,j,s=1}^N \langle a_{js} \partial_{y_s} \psi_i\rangle_Y\,
\int_\Omega \partial_i u^{\rm min}_0(x)\partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\qquad+\varepsilon_n \sum_{i,j,s=1}^N \int_\Omega \nabla(\partial_i u^{\rm min}_0\partial_j u^{\rm min}_0)(x)\,\mathrm{d}x
\cdot \langle y a_{js}\partial_{y_s} \psi_i\rangle_Y
+o(\varepsilon_n).\end{align}
\begin{align}
&\int_\Omega A^{\varepsilon_n}(x) \left( \sum_{i=1}^{N} \nabla_y(\psi_i^{\varepsilon_n}(x))\partial_i u^{\rm min}_0(x) \right) \cdot \nabla u^{\rm min}_0(x) \,\mathrm{d}x \nonumber \\
&\quad= \sum_{i,j,s=1}^N \int_\Omega a_{js}^{\varepsilon_n}(x) \partial_{y_s} \psi_i^{\varepsilon_n}(x)
\partial_i u^{\rm min}_0(x) \partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\quad=\sum_{i,j,s=1}^N \langle a_{js} \partial_{y_s} \psi_i\rangle_Y\,
\int_\Omega \partial_i u^{\rm min}_0(x)\partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\qquad+\varepsilon_n \sum_{i,j,s=1}^N \int_\Omega \nabla(\partial_i u^{\rm min}_0\partial_j u^{\rm min}_0)(x)\,\mathrm{d}x
\cdot \langle y a_{js}\partial_{y_s} \psi_i\rangle_Y
+o(\varepsilon_n).\end{align}Finally,
 \begin{align}
&\int_\Omega A^{\varepsilon_n}(x) \left( \sum_{i=1}^{N} \nabla_y(\psi_i^{\varepsilon_n}(x))\partial_i u^{\rm min}_0(x) \right) \cdot \left( \sum_{j=1}^{N} \nabla_y(\psi_j^{\varepsilon_n}(x))\partial_j u^{\rm min}_0(x) \right) \,\mathrm{d}x \nonumber \\
&\quad= \sum_{i,j,r,s=1}^N \int_\Omega a_{rs}^{\varepsilon_n}(x) \partial_{y_s} \psi_i^{\varepsilon_n}(x)
\partial_i u^{\rm min}_0(x) \partial_{y_r} \psi_j^{\varepsilon_n}(x)
\partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\quad=\sum_{i,j,r,s=1}^N \langle a_{rs}\partial_{y_s} \psi_i
\partial_{y_r} \psi_j\rangle_Y\,
\int_\Omega \partial_i u^{\rm min}_0(x)\partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\qquad+\varepsilon_n \sum_{i,j,r,s=1}^N \int_\Omega \nabla(\partial_i u^{\rm min}_0\partial_j u^{\rm min}_0)(x)\,\mathrm{d}x
\cdot \langle y a_{rs}\partial_{y_s} \psi_i\partial_{y_r} \psi_j\rangle_Y
+o(\varepsilon_n).\end{align}
\begin{align}
&\int_\Omega A^{\varepsilon_n}(x) \left( \sum_{i=1}^{N} \nabla_y(\psi_i^{\varepsilon_n}(x))\partial_i u^{\rm min}_0(x) \right) \cdot \left( \sum_{j=1}^{N} \nabla_y(\psi_j^{\varepsilon_n}(x))\partial_j u^{\rm min}_0(x) \right) \,\mathrm{d}x \nonumber \\
&\quad= \sum_{i,j,r,s=1}^N \int_\Omega a_{rs}^{\varepsilon_n}(x) \partial_{y_s} \psi_i^{\varepsilon_n}(x)
\partial_i u^{\rm min}_0(x) \partial_{y_r} \psi_j^{\varepsilon_n}(x)
\partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\quad=\sum_{i,j,r,s=1}^N \langle a_{rs}\partial_{y_s} \psi_i
\partial_{y_r} \psi_j\rangle_Y\,
\int_\Omega \partial_i u^{\rm min}_0(x)\partial_j u^{\rm min}_0(x)\,\mathrm{d}x
\nonumber \\
&\qquad+\varepsilon_n \sum_{i,j,r,s=1}^N \int_\Omega \nabla(\partial_i u^{\rm min}_0\partial_j u^{\rm min}_0)(x)\,\mathrm{d}x
\cdot \langle y a_{rs}\partial_{y_s} \psi_i\partial_{y_r} \psi_j\rangle_Y
+o(\varepsilon_n).\end{align} Therefore, from (6.4), (6.5), (6.6), and the definition of ![]() $A_{{\rm hom}}$ (see (2.1)) we obtain that
$A_{{\rm hom}}$ (see (2.1)) we obtain that
 \begin{align}
H_n &= \int_\Omega A_{{\rm hom}} \nabla u^{\rm min}_0(x)\cdot \nabla u^{\rm min}_0(x) \,\mathrm{d}x
\nonumber \\
&\quad+ \varepsilon_n \sum_{i,j=1}^N \int_\Omega
\nabla(\partial_i u^{\rm min}_0\partial_j u^{\rm min}_0)(x)\,\mathrm{d}x
\cdot\left\langle y \left[ a_{ij}
+ 2A e_j \cdot \nabla \psi_i
+ A \nabla \psi_i \cdot \nabla \psi_j \right]\right\rangle_Y\nonumber \\
&\quad+o(\varepsilon_n).\end{align}
\begin{align}
H_n &= \int_\Omega A_{{\rm hom}} \nabla u^{\rm min}_0(x)\cdot \nabla u^{\rm min}_0(x) \,\mathrm{d}x
\nonumber \\
&\quad+ \varepsilon_n \sum_{i,j=1}^N \int_\Omega
\nabla(\partial_i u^{\rm min}_0\partial_j u^{\rm min}_0)(x)\,\mathrm{d}x
\cdot\left\langle y \left[ a_{ij}
+ 2A e_j \cdot \nabla \psi_i
+ A \nabla \psi_i \cdot \nabla \psi_j \right]\right\rangle_Y\nonumber \\
&\quad+o(\varepsilon_n).\end{align} Step 2.2: limit of ![]() $G_n$. To make the computations more clear, we split
$G_n$. To make the computations more clear, we split ![]() $G_{n} (u^{\rm min}_n):= G_{n} (u^{\rm min}_0, \widetilde{u}_1)$ as follows
$G_{n} (u^{\rm min}_n):= G_{n} (u^{\rm min}_0, \widetilde{u}_1)$ as follows
 \begin{align*}
G_{n} (u^{\rm min}_0, \widetilde{u}_1) &:= G^1_{n} (u^{\rm min}_0, \widetilde{u}_1) + G^2_{n} (u^{\rm min}_0, \widetilde{u}_1) + G^3_{n} (u^{\rm min}_0, \widetilde{u}_1) + G^4_{n} (u^{\rm min}_0, \widetilde{u}_1) \notag\\
&\quad + G^5_{n} (u^{\rm min}_0, \widetilde{u}_1) + G^6_{n} (u^{\rm min}_0, \widetilde{u}_1),
\end{align*}
\begin{align*}
G_{n} (u^{\rm min}_0, \widetilde{u}_1) &:= G^1_{n} (u^{\rm min}_0, \widetilde{u}_1) + G^2_{n} (u^{\rm min}_0, \widetilde{u}_1) + G^3_{n} (u^{\rm min}_0, \widetilde{u}_1) + G^4_{n} (u^{\rm min}_0, \widetilde{u}_1) \notag\\
&\quad + G^5_{n} (u^{\rm min}_0, \widetilde{u}_1) + G^6_{n} (u^{\rm min}_0, \widetilde{u}_1),
\end{align*} where the functionals ![]() $G^i_{n} (u^{\rm min}_0, \widetilde{u}_1)$, for
$G^i_{n} (u^{\rm min}_0, \widetilde{u}_1)$, for ![]() $i=1,\dots,6$ are given by
$i=1,\dots,6$ are given by
 \begin{align}
G^1_{n} (u^{\rm min}_0, \widetilde{u}_1) &:= 2\int_\Omega A^{\varepsilon_n}(x) \nabla u^{\rm min}_0(x)\cdot \sum_{i=1}^{N}\psi_i^{\varepsilon_n}(x)\nabla (\partial_i u^{\rm min}_0(x))\,\mathrm{d}x,\nonumber\\
G^2_{n} (u^{\rm min}_0, \widetilde{u}_1)&:= 2\int_\Omega A^{\varepsilon_n}(x) \nabla u^{\rm min}_0(x)\cdot \sum_{r,s=1}^{N}\nabla_y(\chi_{rs}^{\varepsilon_n}(x))\partial^2_{rs} u^{\rm min}_0(x)\,\mathrm{d}x,\nonumber\\
G^3_{n} (u^{\rm min}_0, \widetilde{u}_1)&:= -2\int_\Omega A^{\varepsilon_n}(x) \nabla u^{\rm min}_0(x)\cdot \sum_{l=1}^{N}\nabla_y(\psi_l^{\varepsilon_n}(x))\partial_l \widetilde{u}_1(x)\,\mathrm{d}x,
\end{align}
\begin{align}
G^1_{n} (u^{\rm min}_0, \widetilde{u}_1) &:= 2\int_\Omega A^{\varepsilon_n}(x) \nabla u^{\rm min}_0(x)\cdot \sum_{i=1}^{N}\psi_i^{\varepsilon_n}(x)\nabla (\partial_i u^{\rm min}_0(x))\,\mathrm{d}x,\nonumber\\
G^2_{n} (u^{\rm min}_0, \widetilde{u}_1)&:= 2\int_\Omega A^{\varepsilon_n}(x) \nabla u^{\rm min}_0(x)\cdot \sum_{r,s=1}^{N}\nabla_y(\chi_{rs}^{\varepsilon_n}(x))\partial^2_{rs} u^{\rm min}_0(x)\,\mathrm{d}x,\nonumber\\
G^3_{n} (u^{\rm min}_0, \widetilde{u}_1)&:= -2\int_\Omega A^{\varepsilon_n}(x) \nabla u^{\rm min}_0(x)\cdot \sum_{l=1}^{N}\nabla_y(\psi_l^{\varepsilon_n}(x))\partial_l \widetilde{u}_1(x)\,\mathrm{d}x,
\end{align} \begin{align}
G^4_{n} (u^{\rm min}_0, \widetilde{u}_1)&:= 2\int_\Omega A^{\varepsilon_n}(x) \sum_{j=1}^{N} \nabla_y(\psi_j^{\varepsilon_n}(x))\partial_j u^{\rm min}_0(x)\cdot\sum_{i=1}^{N}\psi_i^{\varepsilon_n}(x)\nabla (\partial_i u^{\rm min}_0)\,\mathrm{d}x,\nonumber\\
G^5_{n} (u^{\rm min}_0, \widetilde{u}_1)&:= 2\int_\Omega A^{\varepsilon_n}(x) \sum_{j=1}^{N}\nabla_y(\psi_j^{\varepsilon_n}(x)) \partial_j u^{\rm min}_0(x)\cdot \sum_{r,s=1}^{N}\nabla_y(\chi_{rs}^{\varepsilon_n}(x))\partial^2_{rs} u^{\rm min}_0(x)\,\mathrm{d}x,\nonumber\\
G^6_{n} (u^{\rm min}_0, \widetilde{u}_1)&:= -2\int_\Omega A^{\varepsilon_n}(x) \sum_{j=1}^{N}\nabla(\psi_j^{\varepsilon_n}(x)) \partial_j u^{\rm min}_0(x)\cdot \sum_{l=1}^{N} \nabla_y(\psi_l^{\varepsilon_n}(x))\partial_l \widetilde{u}_1(x)\,\mathrm{d}x.
\end{align}
\begin{align}
G^4_{n} (u^{\rm min}_0, \widetilde{u}_1)&:= 2\int_\Omega A^{\varepsilon_n}(x) \sum_{j=1}^{N} \nabla_y(\psi_j^{\varepsilon_n}(x))\partial_j u^{\rm min}_0(x)\cdot\sum_{i=1}^{N}\psi_i^{\varepsilon_n}(x)\nabla (\partial_i u^{\rm min}_0)\,\mathrm{d}x,\nonumber\\
G^5_{n} (u^{\rm min}_0, \widetilde{u}_1)&:= 2\int_\Omega A^{\varepsilon_n}(x) \sum_{j=1}^{N}\nabla_y(\psi_j^{\varepsilon_n}(x)) \partial_j u^{\rm min}_0(x)\cdot \sum_{r,s=1}^{N}\nabla_y(\chi_{rs}^{\varepsilon_n}(x))\partial^2_{rs} u^{\rm min}_0(x)\,\mathrm{d}x,\nonumber\\
G^6_{n} (u^{\rm min}_0, \widetilde{u}_1)&:= -2\int_\Omega A^{\varepsilon_n}(x) \sum_{j=1}^{N}\nabla(\psi_j^{\varepsilon_n}(x)) \partial_j u^{\rm min}_0(x)\cdot \sum_{l=1}^{N} \nabla_y(\psi_l^{\varepsilon_n}(x))\partial_l \widetilde{u}_1(x)\,\mathrm{d}x.
\end{align}We will prove that
 \begin{equation*}
\lim_{n\to \infty} G_{n} (u^{\rm min}_0, \widetilde{u}_1) = \lim_{n\to \infty} G^1_{n} (u^{\rm min}_0, \widetilde{u}_1) + \lim_{n\to \infty} G^4_{n} (u^{\rm min}_0, \widetilde{u}_1),
\end{equation*}
\begin{equation*}
\lim_{n\to \infty} G_{n} (u^{\rm min}_0, \widetilde{u}_1) = \lim_{n\to \infty} G^1_{n} (u^{\rm min}_0, \widetilde{u}_1) + \lim_{n\to \infty} G^4_{n} (u^{\rm min}_0, \widetilde{u}_1),
\end{equation*}and we will compute explicitly the two limits on the right-hand side.
Now, we separately compute the limit as ![]() $n\to \infty$ of each functionals
$n\to \infty$ of each functionals ![]() $G^i_{n}$. Using the Riemann–Lebesgue lemma (see Lemma 4.1), we get
$G^i_{n}$. Using the Riemann–Lebesgue lemma (see Lemma 4.1), we get
 \begin{align}
\lim_{n\to \infty} G^1_{n} (u^{\rm min}_0, \widetilde{u}_1) &= 2\lim_{n\to \infty} \sum_{i=1}^N \int_\Omega \psi_i^{\varepsilon_n}(x) A^{\varepsilon_n}(x) \nabla u^{\rm min}_0(x)\cdot \partial_i\nabla u^{\rm min}_0(x)\,\mathrm{d}x\nonumber\\
&= 2 \sum_{i=1}^N \int_\Omega \langle \psi_i A\rangle_Y \nabla u^{\rm min}_0(x)\cdot \partial_i\nabla u^{\rm min}_0(x)\,\mathrm{d}x.\end{align}
\begin{align}
\lim_{n\to \infty} G^1_{n} (u^{\rm min}_0, \widetilde{u}_1) &= 2\lim_{n\to \infty} \sum_{i=1}^N \int_\Omega \psi_i^{\varepsilon_n}(x) A^{\varepsilon_n}(x) \nabla u^{\rm min}_0(x)\cdot \partial_i\nabla u^{\rm min}_0(x)\,\mathrm{d}x\nonumber\\
&= 2 \sum_{i=1}^N \int_\Omega \langle \psi_i A\rangle_Y \nabla u^{\rm min}_0(x)\cdot \partial_i\nabla u^{\rm min}_0(x)\,\mathrm{d}x.\end{align} Regarding the second functional ![]() $G^2_{n}$, we obtain that
$G^2_{n}$, we obtain that
 \begin{align}
&\lim_{n\to \infty} G^2_{n} (u^{\rm min}_0, \widetilde{u}_1)\nonumber \\
&\quad = 2\lim_{n\to \infty} \sum_{r,s =1}^N \int_{\Omega} \nabla u^{\rm min}_0(x)\cdot A^{\varepsilon_n}(x)\nabla_y(\chi^{\varepsilon_n}_{rs}(x))\partial^2_{rs} u^{\rm min}_0(x)\,\mathrm{d}x \nonumber\\
&\quad= 2\lim_{n\to \infty} \sum_{r,s =1}^N \sum_{j =1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \left(\nabla_y(\chi^{\varepsilon_n}_{rs}(x))\cdot A^{\varepsilon_n}(x)e_j\right)\partial^2_{rs} u^{\rm min}_0(x)\,\mathrm{d}x \nonumber\\
&\quad= 2\sum_{r,s =1}^N \sum_{j =1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \langle Ae_j\cdot\nabla\chi_{rs}\rangle_Y\partial^2_{rs} u^{\rm min}_0(x)\,\mathrm{d}x.
\end{align}
\begin{align}
&\lim_{n\to \infty} G^2_{n} (u^{\rm min}_0, \widetilde{u}_1)\nonumber \\
&\quad = 2\lim_{n\to \infty} \sum_{r,s =1}^N \int_{\Omega} \nabla u^{\rm min}_0(x)\cdot A^{\varepsilon_n}(x)\nabla_y(\chi^{\varepsilon_n}_{rs}(x))\partial^2_{rs} u^{\rm min}_0(x)\,\mathrm{d}x \nonumber\\
&\quad= 2\lim_{n\to \infty} \sum_{r,s =1}^N \sum_{j =1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \left(\nabla_y(\chi^{\varepsilon_n}_{rs}(x))\cdot A^{\varepsilon_n}(x)e_j\right)\partial^2_{rs} u^{\rm min}_0(x)\,\mathrm{d}x \nonumber\\
&\quad= 2\sum_{r,s =1}^N \sum_{j =1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \langle Ae_j\cdot\nabla\chi_{rs}\rangle_Y\partial^2_{rs} u^{\rm min}_0(x)\,\mathrm{d}x.
\end{align} Here, we have exploited the symmetry of the matrix ![]() $A$ to deduce that
$A$ to deduce that
 \begin{align*}
\nabla u^{\rm min}_0(x)\cdot A^{\varepsilon_n}(x) \nabla_y(\chi^{\varepsilon_n}_{rs}(x))
&= \sum_{j=1}^N \partial_ju^{\rm min}_0(x) \left( A^{\varepsilon_n}(x) \nabla_y\chi^{\varepsilon_n}_{rs}(x)\right)_j\notag\\
&= \sum_{j=1}^N \partial_ju^{\rm min}_0(x) \left( A^{\varepsilon_n}(x) \nabla_y\chi^{\varepsilon_n}_{rs}(x)\cdot e_j\right)\notag\\
&= \sum_{j=1}^N \partial_ju^{\rm min}_0(x) \left( \nabla_y\chi^{\varepsilon_n}_{rs}(x)\cdot A^{\varepsilon_n}(x) e_j\right).\notag
\end{align*}
\begin{align*}
\nabla u^{\rm min}_0(x)\cdot A^{\varepsilon_n}(x) \nabla_y(\chi^{\varepsilon_n}_{rs}(x))
&= \sum_{j=1}^N \partial_ju^{\rm min}_0(x) \left( A^{\varepsilon_n}(x) \nabla_y\chi^{\varepsilon_n}_{rs}(x)\right)_j\notag\\
&= \sum_{j=1}^N \partial_ju^{\rm min}_0(x) \left( A^{\varepsilon_n}(x) \nabla_y\chi^{\varepsilon_n}_{rs}(x)\cdot e_j\right)\notag\\
&= \sum_{j=1}^N \partial_ju^{\rm min}_0(x) \left( \nabla_y\chi^{\varepsilon_n}_{rs}(x)\cdot A^{\varepsilon_n}(x) e_j\right).\notag
\end{align*} Similarly for ![]() $G^3_{n}$, it follows that
$G^3_{n}$, it follows that
 \begin{align}
\lim_{n\to \infty} G^3_{n} (u^{\rm min}_0, \widetilde{u}_1)
&= -2\lim_{n\to \infty} \sum_{l=1}^N \int_{\Omega} \nabla u^{\rm min}_0(x)\cdot A^{\varepsilon_n}(x) \nabla_y(\psi^{\varepsilon_n}_l(x))\partial_l\widetilde{u}_1(x)\,\mathrm{d}x \nonumber\\
&=-2\lim_{n\to \infty} \sum_{l=1}^N\sum_{j=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \nonumber\\
&\qquad \cdot [A^{\varepsilon_n}(x)e_j\cdot \nabla_y(\psi^{\varepsilon_n}_l(x))] \partial_l\widetilde{u}_1(x)\,\mathrm{d}x \nonumber\\
&= -2 \sum_{l=1}^N \sum_{j=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x)
\langle Ae_j\cdot\nabla_y\psi_l\rangle_Y \partial_l\widetilde{u}_1(x)\,\mathrm{d}x.
\end{align}
\begin{align}
\lim_{n\to \infty} G^3_{n} (u^{\rm min}_0, \widetilde{u}_1)
&= -2\lim_{n\to \infty} \sum_{l=1}^N \int_{\Omega} \nabla u^{\rm min}_0(x)\cdot A^{\varepsilon_n}(x) \nabla_y(\psi^{\varepsilon_n}_l(x))\partial_l\widetilde{u}_1(x)\,\mathrm{d}x \nonumber\\
&=-2\lim_{n\to \infty} \sum_{l=1}^N\sum_{j=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \nonumber\\
&\qquad \cdot [A^{\varepsilon_n}(x)e_j\cdot \nabla_y(\psi^{\varepsilon_n}_l(x))] \partial_l\widetilde{u}_1(x)\,\mathrm{d}x \nonumber\\
&= -2 \sum_{l=1}^N \sum_{j=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x)
\langle Ae_j\cdot\nabla_y\psi_l\rangle_Y \partial_l\widetilde{u}_1(x)\,\mathrm{d}x.
\end{align} The limit ![]() $G^4_{n} (u^{\rm min}_0, \widetilde{u}_1)$ as
$G^4_{n} (u^{\rm min}_0, \widetilde{u}_1)$ as ![]() $n\to\infty$ reads as follows
$n\to\infty$ reads as follows
 \begin{align}
\lim_{n\to \infty} G^4_{n} (u^{\rm min}_0, \widetilde{u}_1)
&= 2\lim_{n\to \infty} \sum_{j=1}^N\sum_{i=1}^N \int_\Omega \partial_j u^{\rm min}_0(x)\psi_i^{\varepsilon_n}(x) A^{\varepsilon_n}(x) \nonumber\\& \nabla_y(\psi^{\varepsilon_n}_j(x))\cdot\partial_i(\nabla u^{\rm min}_0(x))\,\mathrm{d}x\nonumber\\
&= 2 \sum_{j=1}^N\sum_{i=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x)\langle \psi_i A\nabla_y \psi_j \rangle_Y \cdot \partial_i (\nabla u^{\rm min}_0(x))\,\mathrm{d}x.\end{align}
\begin{align}
\lim_{n\to \infty} G^4_{n} (u^{\rm min}_0, \widetilde{u}_1)
&= 2\lim_{n\to \infty} \sum_{j=1}^N\sum_{i=1}^N \int_\Omega \partial_j u^{\rm min}_0(x)\psi_i^{\varepsilon_n}(x) A^{\varepsilon_n}(x) \nonumber\\& \nabla_y(\psi^{\varepsilon_n}_j(x))\cdot\partial_i(\nabla u^{\rm min}_0(x))\,\mathrm{d}x\nonumber\\
&= 2 \sum_{j=1}^N\sum_{i=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x)\langle \psi_i A\nabla_y \psi_j \rangle_Y \cdot \partial_i (\nabla u^{\rm min}_0(x))\,\mathrm{d}x.\end{align} For ![]() $G^5_{n}$, it follows that
$G^5_{n}$, it follows that
 \begin{align*}
\lim_{n\to \infty} G^5_{n} (u^{\rm min}_0, \widetilde{u}_1) &= 2\lim_{n\to \infty} \sum_{j=1}^N\sum_{r,s=1}^N \int_\Omega \partial_j u^{\rm min}_0(x) A^{\varepsilon_n}(x) \\& \nabla_y(\psi_j^{\varepsilon_n}(x))\cdot \nabla_y(\chi_{rs}^{\varepsilon_n}(x)) \partial_{rs}^2 u^{\rm min}_0(x)\,\mathrm{d}x\notag\\
&= 2 \sum_{j=1}^N\sum_{r,s=1}^N \int_\Omega \partial_j u^{\rm min}_0(x)\langle A \nabla_y\psi_j\cdot \nabla_y\chi_{rs}\rangle_Y \partial_{rs}^2 u^{\rm min}_0(x)\,\mathrm{d}x.
\end{align*}
\begin{align*}
\lim_{n\to \infty} G^5_{n} (u^{\rm min}_0, \widetilde{u}_1) &= 2\lim_{n\to \infty} \sum_{j=1}^N\sum_{r,s=1}^N \int_\Omega \partial_j u^{\rm min}_0(x) A^{\varepsilon_n}(x) \\& \nabla_y(\psi_j^{\varepsilon_n}(x))\cdot \nabla_y(\chi_{rs}^{\varepsilon_n}(x)) \partial_{rs}^2 u^{\rm min}_0(x)\,\mathrm{d}x\notag\\
&= 2 \sum_{j=1}^N\sum_{r,s=1}^N \int_\Omega \partial_j u^{\rm min}_0(x)\langle A \nabla_y\psi_j\cdot \nabla_y\chi_{rs}\rangle_Y \partial_{rs}^2 u^{\rm min}_0(x)\,\mathrm{d}x.
\end{align*} The variational formulation of the problem of the corrector ![]() $\psi_j$ (see (3.7)) with
$\psi_j$ (see (3.7)) with ![]() $\chi_{rs}$ as a test function yields
$\chi_{rs}$ as a test function yields
 \begin{align*}
\langle A \nabla_y(\psi_j)\cdot \nabla_y(\chi_{rs}) \rangle_Y
&= \int_Y A(y)\nabla_y\psi_j(y)\cdot \nabla_y \chi_{rs}(y)\,\mathrm{d} y\\& = -\int_Y A(y)e_j\cdot \nabla_y\chi_{rs}(y)\,\mathrm{d} y
= -\langle A e_j\cdot \nabla_y\chi_{rs} \rangle_Y.\notag
\end{align*}
\begin{align*}
\langle A \nabla_y(\psi_j)\cdot \nabla_y(\chi_{rs}) \rangle_Y
&= \int_Y A(y)\nabla_y\psi_j(y)\cdot \nabla_y \chi_{rs}(y)\,\mathrm{d} y\\& = -\int_Y A(y)e_j\cdot \nabla_y\chi_{rs}(y)\,\mathrm{d} y
= -\langle A e_j\cdot \nabla_y\chi_{rs} \rangle_Y.\notag
\end{align*}This implies that
 \begin{equation}
\lim_{n\to \infty} G^5_{n} (u^{\rm min}_0, \widetilde{u}_1)
=- 2 \sum_{j=1}^N\sum_{r,s=1}^N \int_\Omega \partial_j u^{\rm min}_0(x)\langle A e_j\cdot \nabla_y\chi_{rs} \rangle_Y \partial_{rs}^2 u^{\rm min}_0(x)\,\mathrm{d}x.
\end{equation}
\begin{equation}
\lim_{n\to \infty} G^5_{n} (u^{\rm min}_0, \widetilde{u}_1)
=- 2 \sum_{j=1}^N\sum_{r,s=1}^N \int_\Omega \partial_j u^{\rm min}_0(x)\langle A e_j\cdot \nabla_y\chi_{rs} \rangle_Y \partial_{rs}^2 u^{\rm min}_0(x)\,\mathrm{d}x.
\end{equation} Finally, the limit of ![]() $G^6_{n}$ as
$G^6_{n}$ as ![]() $n \to \infty$ is
$n \to \infty$ is
 \begin{align*}
\lim_{n\to \infty} G^6_{n} (u^{\rm min}_0, \widetilde{u}_1) &= -2\lim_{n\to \infty} \sum_{j=1}^N\sum_{l=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) A^{\varepsilon_n}(x) \nabla_y(\psi_j^{\varepsilon_n}(x)) \\& \cdot \nabla_y(\psi_l^{\varepsilon_n}(x))\partial_l \widetilde{u}_1(x)\,\mathrm{d}x\notag\\
&=-2 \sum_{j=1}^N\sum_{l=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \langle A \nabla_y\psi_j\cdot \nabla_y\psi_l \rangle_Y\partial_l \widetilde{u}_1(x)\,\mathrm{d}x.\notag
\end{align*}
\begin{align*}
\lim_{n\to \infty} G^6_{n} (u^{\rm min}_0, \widetilde{u}_1) &= -2\lim_{n\to \infty} \sum_{j=1}^N\sum_{l=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) A^{\varepsilon_n}(x) \nabla_y(\psi_j^{\varepsilon_n}(x)) \\& \cdot \nabla_y(\psi_l^{\varepsilon_n}(x))\partial_l \widetilde{u}_1(x)\,\mathrm{d}x\notag\\
&=-2 \sum_{j=1}^N\sum_{l=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \langle A \nabla_y\psi_j\cdot \nabla_y\psi_l \rangle_Y\partial_l \widetilde{u}_1(x)\,\mathrm{d}x.\notag
\end{align*} Using again the variational formulation of the problem of the corrector ![]() $\psi_j$ (see (3.7)), choosing as test function
$\psi_j$ (see (3.7)), choosing as test function ![]() $\psi_l$, yields to
$\psi_l$, yields to
Thanks to this equality, it follows that
 \begin{equation}
\lim_{n\to \infty} G^6_{n} (u^{\rm min}_0, \widetilde{u}_1) = 2 \sum_{j=1}^N\sum_{l=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \langle A e_j\cdot \nabla_y\psi_l \rangle_Y\partial_l \widetilde{u}_1(x)\,\mathrm{d}x.
\end{equation}
\begin{equation}
\lim_{n\to \infty} G^6_{n} (u^{\rm min}_0, \widetilde{u}_1) = 2 \sum_{j=1}^N\sum_{l=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \langle A e_j\cdot \nabla_y\psi_l \rangle_Y\partial_l \widetilde{u}_1(x)\,\mathrm{d}x.
\end{equation}Gathering formulas (6.10)-(6.15) and noting that (6.11) and (6.14) as well as (6.12) and (6.15) cancel out, we deduce that
 \begin{align}
&\lim_{n\to \infty} G_{n} (u^{\rm min}_0, \widetilde{u}_1) = \lim_{n\to \infty} G^1_{n} (u^{\rm min}_0, \widetilde{u}_1) + \lim_{n\to \infty} G^4_{n} (u^{\rm min}_0, \widetilde{u}_1)\nonumber\\
&\quad= 2 \sum_{i=1}^N \int_\Omega \langle \psi_i A\rangle_Y \nabla u^{\rm min}_0(x)\cdot \partial_i(u^{\rm min}_0(x))\,\mathrm{d}x \nonumber\\
&\qquad + 2 \sum_{j=1}^N\sum_{i=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \langle \psi_i A\nabla_y\psi_j \rangle_Y \cdot \partial_i (\nabla u^{\rm min}_0(x)) \,\mathrm{d}x.\end{align}
\begin{align}
&\lim_{n\to \infty} G_{n} (u^{\rm min}_0, \widetilde{u}_1) = \lim_{n\to \infty} G^1_{n} (u^{\rm min}_0, \widetilde{u}_1) + \lim_{n\to \infty} G^4_{n} (u^{\rm min}_0, \widetilde{u}_1)\nonumber\\
&\quad= 2 \sum_{i=1}^N \int_\Omega \langle \psi_i A\rangle_Y \nabla u^{\rm min}_0(x)\cdot \partial_i(u^{\rm min}_0(x))\,\mathrm{d}x \nonumber\\
&\qquad + 2 \sum_{j=1}^N\sum_{i=1}^N \int_{\Omega} \partial_j u^{\rm min}_0(x) \langle \psi_i A\nabla_y\psi_j \rangle_Y \cdot \partial_i (\nabla u^{\rm min}_0(x)) \,\mathrm{d}x.\end{align} Step 3: limit of ![]() $I^3_n$. A direct computation shows that
$I^3_n$. A direct computation shows that
 \begin{align}
\lim_{n\to\infty} {1\over \varepsilon_n}\int_\Omega f(x)(u^{(2)}_n(x) - u_0^{\min}(x))\,\mathrm{d}x &= \lim_{n\to\infty} \sum_{j=1}^N\int_\Omega f(x) \psi_j^{\varepsilon_n}(x) \partial_ju_0^{\min}(x)\,\mathrm{d}x \nonumber\\
&= \sum_{j=1}^N \langle \psi_j \rangle_Y \int_\Omega f(x) \partial_j u_0^{\min}(x)\,\mathrm{d}x =0,\end{align}
\begin{align}
\lim_{n\to\infty} {1\over \varepsilon_n}\int_\Omega f(x)(u^{(2)}_n(x) - u_0^{\min}(x))\,\mathrm{d}x &= \lim_{n\to\infty} \sum_{j=1}^N\int_\Omega f(x) \psi_j^{\varepsilon_n}(x) \partial_ju_0^{\min}(x)\,\mathrm{d}x \nonumber\\
&= \sum_{j=1}^N \langle \psi_j \rangle_Y \int_\Omega f(x) \partial_j u_0^{\min}(x)\,\mathrm{d}x =0,\end{align} since the correctors ![]() $\psi_j$ are with zero average.
$\psi_j$ are with zero average.
7. The limsup inequality for Theorem 2.7
In this section, we prove the upper bound of Theorem 2.7 (ii).
Proposition 7.1. Assume Assumptions (H1)-(H4) hold. Then, there exists a sequence ![]() $\{u_n\}_{n}\subset H^1_0(\Omega)$ converging to
$\{u_n\}_{n}\subset H^1_0(\Omega)$ converging to ![]() $u^{\rm min}_0$ weakly in
$u^{\rm min}_0$ weakly in ![]() $H^1(\Omega)$ such that
$H^1(\Omega)$ such that
 \begin{equation*}
\lim_{n\to\infty} F^1_n(u_n) = F^1_{{\rm hom}}(u^{\rm min}_0).
\end{equation*}
\begin{equation*}
\lim_{n\to\infty} F^1_n(u_n) = F^1_{{\rm hom}}(u^{\rm min}_0).
\end{equation*}Proof. For ![]() $n\in\mathbb{N}$, we define the function
$n\in\mathbb{N}$, we define the function ![]() $u_n :H^1(\Omega)$ as
$u_n :H^1(\Omega)$ as
 \begin{equation}
u_n(x):= u^{\rm min}_0(x) + \varepsilon_n\sum_{i=1}^{N}\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x).
\end{equation}
\begin{equation}
u_n(x):= u^{\rm min}_0(x) + \varepsilon_n\sum_{i=1}^{N}\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x).
\end{equation} We claim that ![]() $\{u_n\}_n$ is the required recovery sequence.
$\{u_n\}_n$ is the required recovery sequence.
First of all, we prove that ![]() $\{u_n\}_n$ converges to
$\{u_n\}_n$ converges to ![]() $u^{\rm min}_0$ weakly in
$u^{\rm min}_0$ weakly in ![]() $H^1(\Omega)$. Indeed,
$H^1(\Omega)$. Indeed,
 \begin{equation*}
\| u_n - u^{\rm min}_0 \|_{L^2(\Omega)} \leq \varepsilon_n\sum_{i=1}^{N} \|\psi_i^{\varepsilon_n}\partial_i u^{\rm min}_0\|_{L^2(\Omega)} \leq C\varepsilon_n\sum_{i=1}^{N} \|\psi_i^{\varepsilon_n}\partial_i \|_{L^2(\Omega)},
\end{equation*}
\begin{equation*}
\| u_n - u^{\rm min}_0 \|_{L^2(\Omega)} \leq \varepsilon_n\sum_{i=1}^{N} \|\psi_i^{\varepsilon_n}\partial_i u^{\rm min}_0\|_{L^2(\Omega)} \leq C\varepsilon_n\sum_{i=1}^{N} \|\psi_i^{\varepsilon_n}\partial_i \|_{L^2(\Omega)},
\end{equation*} where the last step follow from the fact that, thanks to (H4), ![]() $u^{\rm min}_0$ ha compact support in
$u^{\rm min}_0$ ha compact support in ![]() $\Omega$, and hence it is bounded. Thus,
$\Omega$, and hence it is bounded. Thus,
 \begin{equation*}
\lim_{n\to\infty} \| u_n - u^{\rm min}_0 \|_{L^2(\Omega)} =0.
\end{equation*}
\begin{equation*}
\lim_{n\to\infty} \| u_n - u^{\rm min}_0 \|_{L^2(\Omega)} =0.
\end{equation*}Moreover,
 \begin{equation*}
\nabla u_n(x) = \nabla u^{\rm min}_0(x)
+ \sum_{i=1}^{N}\nabla_y\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x)
+ \sum_{i=1}^{N}\psi_i^{\varepsilon_n}(x) \nabla(\partial_i u^{\rm min}_0(x)).
\end{equation*}
\begin{equation*}
\nabla u_n(x) = \nabla u^{\rm min}_0(x)
+ \sum_{i=1}^{N}\nabla_y\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x)
+ \sum_{i=1}^{N}\psi_i^{\varepsilon_n}(x) \nabla(\partial_i u^{\rm min}_0(x)).
\end{equation*}Therefore, using the Riemann–Lebesgue lemma (see Lemma 4.1), we have that
 \begin{align*}
\lim_{n\to\infty} \int_\Omega \nabla u_n(x)\cdot \varphi(x) \, dx
&= \int_\Omega u^{\rm min}_0(x)\cdot \varphi\, dx \\
&+ \sum_{i=1}^{N} \frac{1}{|Y|}\int_Y \nabla\psi_i(y) \, dy \cdot
\int_\Omega\partial_i u^{\rm min}_0(x) \varphi(x)\, dx \\
&+ \sum_{i=1}^{N}\frac{1}{|Y|}\int_Y\psi_i(y)\, dy
\int_\Omega \nabla\partial_i u^{\rm min}_0(x)\cdot \varphi(x)\, dx,
\end{align*}
\begin{align*}
\lim_{n\to\infty} \int_\Omega \nabla u_n(x)\cdot \varphi(x) \, dx
&= \int_\Omega u^{\rm min}_0(x)\cdot \varphi\, dx \\
&+ \sum_{i=1}^{N} \frac{1}{|Y|}\int_Y \nabla\psi_i(y) \, dy \cdot
\int_\Omega\partial_i u^{\rm min}_0(x) \varphi(x)\, dx \\
&+ \sum_{i=1}^{N}\frac{1}{|Y|}\int_Y\psi_i(y)\, dy
\int_\Omega \nabla\partial_i u^{\rm min}_0(x)\cdot \varphi(x)\, dx,
\end{align*} for all ![]() $\varphi\in L^2(\Omega;\mathbb{R}^N)$. Note that, using the properties of the correctors, we have that
$\varphi\in L^2(\Omega;\mathbb{R}^N)$. Note that, using the properties of the correctors, we have that
 \begin{equation*}
\int_Y \nabla\psi_i(y) \, dy = 0,\quad\quad\quad
\int_Y\psi_i(y)\, dy = 0,
\end{equation*}
\begin{equation*}
\int_Y \nabla\psi_i(y) \, dy = 0,\quad\quad\quad
\int_Y\psi_i(y)\, dy = 0,
\end{equation*} for all ![]() $i=1,\dots,N$.
$i=1,\dots,N$.
We now prove the convergence of the energy, namely that
 \begin{equation*}
\lim_{n\to\infty} F^1_n(u_n) = F^1_{{\rm hom}}(u^{\rm min}_0).
\end{equation*}
\begin{equation*}
\lim_{n\to\infty} F^1_n(u_n) = F^1_{{\rm hom}}(u^{\rm min}_0).
\end{equation*}Note that
 \begin{equation*}
F^1_n(u_n) = H_n + G_n^1 + G_n^4 + \int_\Omega f(x)u^{\rm min}_0(x)\, dx
+ \sum_{j=1}^N \int_\Omega f(x)\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x) \, dx,
\end{equation*}
\begin{equation*}
F^1_n(u_n) = H_n + G_n^1 + G_n^4 + \int_\Omega f(x)u^{\rm min}_0(x)\, dx
+ \sum_{j=1}^N \int_\Omega f(x)\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x) \, dx,
\end{equation*} where ![]() $H_n$,
$H_n$, ![]() $G_n^1$ and,
$G_n^1$ and, ![]() $G_n^4$ are defined in (6.3), (6.8), and (6.9), respectively. Thus, using (6.7), (6.10), (6.13), and the fact that
$G_n^4$ are defined in (6.3), (6.8), and (6.9), respectively. Thus, using (6.7), (6.10), (6.13), and the fact that ![]() $f, \psi_i, u^{\rm min}_0\in L^2(Q)$ for all
$f, \psi_i, u^{\rm min}_0\in L^2(Q)$ for all ![]() $i=1,\dots,N$, we obtain that
$i=1,\dots,N$, we obtain that
 \begin{align*}
&\lim_{n\to\infty} F^1_n(u_n) = \lim_{n\to\infty} H_n
+ \lim_{n\to\infty} G_n^1
+ \lim_{n\to\infty} G_n^4
\\&+ \lim_{n\to\infty} \sum_{j=1}^N \int_\Omega f(x)\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x) \, dx
= F^1_{{\rm hom}}(u^{\rm min}_0).
\end{align*}
\begin{align*}
&\lim_{n\to\infty} F^1_n(u_n) = \lim_{n\to\infty} H_n
+ \lim_{n\to\infty} G_n^1
+ \lim_{n\to\infty} G_n^4
\\&+ \lim_{n\to\infty} \sum_{j=1}^N \int_\Omega f(x)\psi_i^{\varepsilon_n}(x)\partial_i u^{\rm min}_0(x) \, dx
= F^1_{{\rm hom}}(u^{\rm min}_0).
\end{align*}This yields the desired convergence of the energy.
Remark 7.2. We would like to emphasize that the proof of the limsup inequality provides an interpretation of the functional ![]() $F_{{\rm hom}}^1$. Indeed, since it is obtained as the limit of the energy
$F_{{\rm hom}}^1$. Indeed, since it is obtained as the limit of the energy ![]() $F^1_n$ computed at the function defined in (7.1), it can be thought of as an estimate of the error at order
$F^1_n$ computed at the function defined in (7.1), it can be thought of as an estimate of the error at order ![]() $\varepsilon_n$ between
$\varepsilon_n$ between ![]() $F_{{\rm hom}}^0(u^0_{\min})$ and the energy
$F_{{\rm hom}}^0(u^0_{\min})$ and the energy ![]() $F_n$ computed at its first-order approximant.
$F_n$ computed at its first-order approximant.
8. Proof of Theorem 2.14
This section is devoted to the proof of Theorem 2.14. We first illustrate the idea of the proof by considering the special case
where ![]() $a:\mathbb{R}^N\to\mathbb{R}$ is an
$a:\mathbb{R}^N\to\mathbb{R}$ is an ![]() $Y$-periodic function such that
$Y$-periodic function such that ![]() $0 \lt c_1\leq a(c)\leq c_2 \lt +\infty$ for all
$0 \lt c_1\leq a(c)\leq c_2 \lt +\infty$ for all ![]() $x\in Y$. Then, it holds that
$x\in Y$. Then, it holds that
 \begin{equation*}
V_{{\rm hom}}(p) = \min\left\{\int_Y a(y)|p+\varphi(y)|^2\,\mathrm{d}y \,:\, \varphi\in L^2(Y),\, \int_Y\varphi(y)\,\mathrm{d}y=0 \right\}.
\end{equation*}
\begin{equation*}
V_{{\rm hom}}(p) = \min\left\{\int_Y a(y)|p+\varphi(y)|^2\,\mathrm{d}y \,:\, \varphi\in L^2(Y),\, \int_Y\varphi(y)\,\mathrm{d}y=0 \right\}.
\end{equation*} This minimization problem admits a solution that we can compute explicitly. Indeed, the Euler-Lagrange equation gives the existence of a constant ![]() $c(p)\in\mathbb{R}$ such that
$c(p)\in\mathbb{R}$ such that
for almost every ![]() $y\in Y$. Recalling that
$y\in Y$. Recalling that ![]() $a(y) \gt 0$, we obtain
$a(y) \gt 0$, we obtain
 \begin{equation*}
\varphi(y) = \frac{c(p)}{2a(y)} - p.
\end{equation*}
\begin{equation*}
\varphi(y) = \frac{c(p)}{2a(y)} - p.
\end{equation*} Moreover, the constant ![]() $c(p)$ can be computed by the zero average requirement for
$c(p)$ can be computed by the zero average requirement for ![]() $\varphi$:
$\varphi$:
 \begin{equation*}
c(p) = 2p \left( \int_Y \frac{1}{a(y)}\,\mathrm{d}y \right)^{-1}.
\end{equation*}
\begin{equation*}
c(p) = 2p \left( \int_Y \frac{1}{a(y)}\,\mathrm{d}y \right)^{-1}.
\end{equation*}Thus,
 \begin{equation*}
V_{{\rm hom}}(p) = p^2 \left( \int_Y \frac{1}{a(y)}\,\mathrm{d}y \right)^{-1},
\end{equation*}
\begin{equation*}
V_{{\rm hom}}(p) = p^2 \left( \int_Y \frac{1}{a(y)}\,\mathrm{d}y \right)^{-1},
\end{equation*}which yields
 \begin{equation*}
G_{\rm hom}(v) = \int_\Omega v^2(x)\,\mathrm{d}x\, \left( \int_Y \frac{1}{a(y)}\,\mathrm{d}y \right)^{-1},
\end{equation*}
\begin{equation*}
G_{\rm hom}(v) = \int_\Omega v^2(x)\,\mathrm{d}x\, \left( \int_Y \frac{1}{a(y)}\,\mathrm{d}y \right)^{-1},
\end{equation*} for all ![]() $v\in L^2(\Omega)$.
$v\in L^2(\Omega)$.
Fix ![]() $m\in\mathbb{R}$. We now consider the solution
$m\in\mathbb{R}$. We now consider the solution ![]() $v^{\min}_0\in L^2(\Omega)$ to the minimization problem
$v^{\min}_0\in L^2(\Omega)$ to the minimization problem
 \begin{equation*}
\min\left\{G_{\rm hom}(v) \,:\, v\in L^2(\Omega),\, \int_\Omega v(x)\,\mathrm{d}x = m \right\}.
\end{equation*}
\begin{equation*}
\min\left\{G_{\rm hom}(v) \,:\, v\in L^2(\Omega),\, \int_\Omega v(x)\,\mathrm{d}x = m \right\}.
\end{equation*} The Euler-Lagrange equation gives the existence of a constant ![]() $c\in\mathbb{R}$ such that
$c\in\mathbb{R}$ such that
 \begin{equation*}
2v^{\min}_0(x) \left( \int_Y \frac{1}{a(y)}\,\mathrm{d}y \right)^{-1} = c,
\end{equation*}
\begin{equation*}
2v^{\min}_0(x) \left( \int_Y \frac{1}{a(y)}\,\mathrm{d}y \right)^{-1} = c,
\end{equation*} for almost every ![]() $x\in\Omega$. Thus,
$x\in\Omega$. Thus, ![]() $v^{\min}_0$ is constant. The mass constraint gives that
$v^{\min}_0$ is constant. The mass constraint gives that
 \begin{equation*}
v^{\min}_0(x) = \frac{m}{|\Omega|},
\end{equation*}
\begin{equation*}
v^{\min}_0(x) = \frac{m}{|\Omega|},
\end{equation*} for all ![]() $x\in\Omega$, which yields
$x\in\Omega$, which yields
 \begin{align}
G_{\rm hom}(v^{\min}_0) = {m^2\over |\Omega|}\left( \int_Y \frac{1}{a(y)}\,\mathrm{d}y \right)^{-1}.\nonumber\\
\end{align}
\begin{align}
G_{\rm hom}(v^{\min}_0) = {m^2\over |\Omega|}\left( \int_Y \frac{1}{a(y)}\,\mathrm{d}y \right)^{-1}.\nonumber\\
\end{align} In a similar way, we can obtain the solution ![]() $v^{\min}_n$ to the minimization problem
$v^{\min}_n$ to the minimization problem
 \begin{equation*}
\min\left\{G_{\varepsilon_n}(v) \,:\, v\in L^2(\Omega),\, \int_\Omega v(x)\,\mathrm{d}x = m \right\}.
\end{equation*}
\begin{equation*}
\min\left\{G_{\varepsilon_n}(v) \,:\, v\in L^2(\Omega),\, \int_\Omega v(x)\,\mathrm{d}x = m \right\}.
\end{equation*}This gives
 \begin{equation*}
v^{\min}_n(x) = \frac{c_n}{2a^{\varepsilon_n}\left(x\right)},
\end{equation*}
\begin{equation*}
v^{\min}_n(x) = \frac{c_n}{2a^{\varepsilon_n}\left(x\right)},
\end{equation*}where
 \begin{equation*}
c_n:= 2m\left( \int_\Omega \frac{1}{a^{\varepsilon_n}\left(x\right)}\,\mathrm{d}x \right)^{-1}.
\end{equation*}
\begin{equation*}
c_n:= 2m\left( \int_\Omega \frac{1}{a^{\varepsilon_n}\left(x\right)}\,\mathrm{d}x \right)^{-1}.
\end{equation*}Thus,
 \begin{equation}
G_n(v^{\min}_n) = m^2 \left( \int_\Omega \frac{1}{a^{\varepsilon_n}\left(x\right)}\,\mathrm{d}x \right)^{-1}.
\end{equation}
\begin{equation}
G_n(v^{\min}_n) = m^2 \left( \int_\Omega \frac{1}{a^{\varepsilon_n}\left(x\right)}\,\mathrm{d}x \right)^{-1}.
\end{equation} Note that thanks to our assumptions on ![]() $\Omega$ and
$\Omega$ and ![]() $\varepsilon_n$, we get
$\varepsilon_n$, we get
 \begin{equation*}
\int_\Omega \frac{1}{a^{\varepsilon_n}\left(x\right)}\,\mathrm{d}x
= |\Omega| \int_Y \frac{1}{a(y)} \,\mathrm{d}y.
\end{equation*}
\begin{equation*}
\int_\Omega \frac{1}{a^{\varepsilon_n}\left(x\right)}\,\mathrm{d}x
= |\Omega| \int_Y \frac{1}{a(y)} \,\mathrm{d}y.
\end{equation*}Therefore, from (8.1) and (8.2), we conclude that
for all ![]() $n\in\mathbb{N}\setminus\{0\}$, as desired.
$n\in\mathbb{N}\setminus\{0\}$, as desired.
In the general case, we use a similar argument to the one implemented above. We first consider the homogenized energy density
 \begin{equation*}
V_{{\rm hom}}(p) = \min\left\{\int_Y V(y,p+\varphi(y))\,\mathrm{d}y \,:\, \varphi\in L^2(Y),\, \int_Y\varphi(y)\,\mathrm{d}y=0 \right\}.
\end{equation*}
\begin{equation*}
V_{{\rm hom}}(p) = \min\left\{\int_Y V(y,p+\varphi(y))\,\mathrm{d}y \,:\, \varphi\in L^2(Y),\, \int_Y\varphi(y)\,\mathrm{d}y=0 \right\}.
\end{equation*} Since we are assuming ![]() $p\mapsto V(y,p)$ to be strictly convex, for each
$p\mapsto V(y,p)$ to be strictly convex, for each ![]() $y\in Y$ we denote by
$y\in Y$ we denote by ![]() $\partial_p V^{-1}(y):\mathbb{R}\to\mathbb{R}$ the inverse of the map
$\partial_p V^{-1}(y):\mathbb{R}\to\mathbb{R}$ the inverse of the map ![]() $\partial_p V(y, \cdot)$, and we use the notation
$\partial_p V(y, \cdot)$, and we use the notation 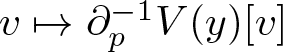 $v\mapsto \partial_p^{-1}V(y)[v]$ to avoid the use of too many round parenthesis. We get that the optimal perturbation
$v\mapsto \partial_p^{-1}V(y)[v]$ to avoid the use of too many round parenthesis. We get that the optimal perturbation ![]() $\varphi$ satisfies
$\varphi$ satisfies
 \begin{equation*}
\varphi(y) = \partial_p^{-1}V(y)[c(p)] - p,
\end{equation*}
\begin{equation*}
\varphi(y) = \partial_p^{-1}V(y)[c(p)] - p,
\end{equation*} for some ![]() $c(p)\in\mathbb{R}$, which can be computed by using the zero average constrained
$c(p)\in\mathbb{R}$, which can be computed by using the zero average constrained
 \begin{equation*}
p=\int_Y \partial_p^{-1}V(y)[c(p)]\,\mathrm{d}y.
\end{equation*}
\begin{equation*}
p=\int_Y \partial_p^{-1}V(y)[c(p)]\,\mathrm{d}y.
\end{equation*} If we now consider the solution ![]() $v^{\min}_0\in L^2(\Omega)$ to the minimization problem
$v^{\min}_0\in L^2(\Omega)$ to the minimization problem
 \begin{equation*}
\min\left\{G_{\rm hom}(v) \,:\, v\in L^2(\Omega),\, \int_\Omega v(x)\,\mathrm{d}x = m \right\},
\end{equation*}
\begin{equation*}
\min\left\{G_{\rm hom}(v) \,:\, v\in L^2(\Omega),\, \int_\Omega v(x)\,\mathrm{d}x = m \right\},
\end{equation*}we get that
 \begin{equation*}
v^{\min}_0 = \frac{m}{|\Omega|}.
\end{equation*}
\begin{equation*}
v^{\min}_0 = \frac{m}{|\Omega|}.
\end{equation*}In particular,
 \begin{equation*}
G_{{\rm hom}}(v^{\min}_0) = |\Omega|\int_Y V\left(y,\partial^{-1}_pV(y)\left[c\left( \frac{m}{|\Omega|} \right)\right]\right) \,\mathrm{d}y.\\
\end{equation*}
\begin{equation*}
G_{{\rm hom}}(v^{\min}_0) = |\Omega|\int_Y V\left(y,\partial^{-1}_pV(y)\left[c\left( \frac{m}{|\Omega|} \right)\right]\right) \,\mathrm{d}y.\\
\end{equation*} If we now consider the solution ![]() $v^{\min}_n$ to the minimization problem
$v^{\min}_n$ to the minimization problem
 \begin{equation*}
\min\left\{G_{n}(v) \,:\, v\in L^2(\Omega),\, \int_\Omega v(x)\,\mathrm{d}x = m \right\},
\end{equation*}
\begin{equation*}
\min\left\{G_{n}(v) \,:\, v\in L^2(\Omega),\, \int_\Omega v(x)\,\mathrm{d}x = m \right\},
\end{equation*}we get that
 \begin{equation*}
\partial_pV\left( \frac{x}{\varepsilon_n}, v^{\min}_n(x) \right)=c_n,
\end{equation*}
\begin{equation*}
\partial_pV\left( \frac{x}{\varepsilon_n}, v^{\min}_n(x) \right)=c_n,
\end{equation*}where, using the mass constraint,
 \begin{equation*}
m = \int_\Omega \partial_p^{-1}V\left(\frac{x}{\varepsilon_n}\right)[c_n]\,\mathrm{d}x
=|\Omega| \int_Y \partial_p^{-1}V(y)[c_n]\,\mathrm{d}y.
\end{equation*}
\begin{equation*}
m = \int_\Omega \partial_p^{-1}V\left(\frac{x}{\varepsilon_n}\right)[c_n]\,\mathrm{d}x
=|\Omega| \int_Y \partial_p^{-1}V(y)[c_n]\,\mathrm{d}y.
\end{equation*}This gives that
 \begin{equation*}
G_{n}(v^{\min}_n)
= \int_\Omega V\left( \frac{x}{\varepsilon_n}, \partial^{-1}_pV\left(\frac{x}{\varepsilon_n}\right)[c_n] \right)\,\mathrm{d}x
=|\Omega| \int_Y V\left( y, \partial^{-1}_pV\left(y\right)[c_n] \right)\,\mathrm{d}y.
\end{equation*}
\begin{equation*}
G_{n}(v^{\min}_n)
= \int_\Omega V\left( \frac{x}{\varepsilon_n}, \partial^{-1}_pV\left(\frac{x}{\varepsilon_n}\right)[c_n] \right)\,\mathrm{d}x
=|\Omega| \int_Y V\left( y, \partial^{-1}_pV\left(y\right)[c_n] \right)\,\mathrm{d}y.
\end{equation*}It is possible to choose
 \begin{equation*}
c_n = \frac{m}{|\Omega|},
\end{equation*}
\begin{equation*}
c_n = \frac{m}{|\Omega|},
\end{equation*} which gives ![]() $G_{n}(v^{\min}_n) = G_{{\rm hom}}(v^{\min}_0)$ for all
$G_{n}(v^{\min}_n) = G_{{\rm hom}}(v^{\min}_0)$ for all ![]() $n\in\mathbb{N}\setminus\{0\}$ as desired.
$n\in\mathbb{N}\setminus\{0\}$ as desired.
Acknowledgements
We would like to thank George Allaire for useful conversations about the subject. Moreover, we would like to thank the anonymous referee for insightful comments that improved the exposition of the manuscript. The authors would like to thank CIRM Luminy for its hospitality during the Research in Residence. RC was partially supported under NWO-OCENW.M.21.336, MATHEMAMI - Mathematical Analysis of phase Transitions in HEterogeneous MAterials with Materials Inclusions. LD was funded in whole or in part by the Austrian Science Fund (FWF) projects 10.55776/ESP1887024 and 10.55776/Y1292.



