Hostname: page-component-76d6cb85b7-8p85h Total loading time: 0 Render date: 2026-07-15T19:17:38.501Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERALIZED BIRTHDAY PROBLEMS IN THE LARGE-DEVIATIONS REGIME

Published online by Cambridge University Press:  13 December 2013

M. Mandjes  and
Eurandom
M. Mandjes
Affiliation:
Center for Mathematics and Computer Science Amsterdam, The Netherlands E-mail: M.R.H.Mandjes@uva.nl
Eurandom
Affiliation:
Center for Mathematics and Computer Science, Amsterdam, The Netherlands; EURANDOM, Eindhoven University of Technology, Eindhoven, The Netherlands
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers generalized birthday problems, in which there are d classes of possible outcomes. A fraction fi of the N possible outcomes has probability αi/N, where 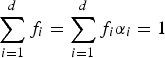$\sum_{i=1}^{d} f_{i} =\sum_{i=1}^{d} f_{i}\alpha_{i}=1$. Sampling k times (with replacements), the objective is to determine (or approximate) the probability that all outcomes are different, the so-called uniqueness probability (or: no-coincidence probability). Although it is trivial to explicitly characterize this probability for the case d=1, the situation with multiple classes is substantially harder to analyze.

Parameterizing k≡ aN, it turns out that the uniqueness probability decays essentially exponentially in N, where the associated decay rate ζ follows from a variational problem. Only for small d this can be solved in closed form. Assuming αi is of the form 1+φiɛ, the decay rate ζ can be written as a power series in ɛ; we demonstrate how to compute the corresponding coefficients explicitly. Also, a logarithmically efficient simulation procedure is proposed. The paper concludes with a series of numerical experiments, showing that (i) the proposed simulation approach is fast and accurate, (ii) assuming all outcomes equally likely would lead to estimates for the uniqueness probability that can be orders of magnitude off, and (iii) the power-series based approximations work remarkably well.

Information

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 28 , Issue 1 , January 2014 , pp. 83 - 99
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1.Asmussen, S. & Glynn, P. (2007). Stochastic Simulation: Algorithms and Analysis. NY: Springer-Verlag.CrossRefGoogle Scholar
2.Camarri, M. & Pitman, J. (2000). Limit distributions and random trees derived from the birthday problem with unequal probabilities. Electronic Journal of Probability 5: 1–18.Google Scholar
3.Diaconis, P. & Mosteller, F. (1989). Methods for studying coincidences. Journal of the American Statistical Association 84: 853–861.Google Scholar
4.Durrett, R. (1995). Probability: Theory & Examples. Wadsworth-Brooks/Cole, CA: Pacific Grove.Google Scholar
5.Feller, W. (1968). An Introduction to Probability Theory and its Applications, Vol. 1, 3rd ednNY: Wiley.Google Scholar
6.Gail, M., Weiss, G., Mantel, N. & O'Brien, S. (1979). A solution to the generalized birthday problem with application to allozyme screening for cell culture contamination. Journal of Applied Probability 16: 242–251.Google Scholar
7.Henze, N. (1998). A Poisson limit law for a generalized birthday problem. Statistics and Probability Letters 39: 333–336.Google Scholar
8.Holst, L. (1986). On birthday, collectors’, occupancy and other classical urn problems. International Statistical Review 54: 15–27.CrossRefGoogle Scholar
9.Joag-Dev, K. & Proschan, F. (1992). The birthday problem with unlike probabilities. American Mathematical Monthly 99: 10–12.CrossRefGoogle Scholar
10.Juneja, S. & Mandjes, M.Overlap problems on the circle. Journal of Applied Probability to appear.Google Scholar
11.Klotz, J. (1979). The birthday problem with unequal probabilities. Technical Report, No. 59, Department of Statistics, University of Wisconsin.Google Scholar
12.Koot, M., van't Noordende, G., Mandjes, M. & de Laat, C. (2013). A probabilistic perspective on re-identifiability. Mathematical Population Studies, 20: 155–171.Google Scholar
13.Koot, M. & Mandjes, M. (2012). The analysis of singletons in generalized birthday problems. Probability in the Engineering and Informational Sciences 26: 245–262.CrossRefGoogle Scholar
14.Mase, S. (1992). Approximations to the birthday problem with unequal occurrence probabilities and their application to the surname problem in Japan. Annals of the Institute of Statistical Mathematics 44: 479–499.Google Scholar
15.McKinney, E. (1966). Generalized birthday problem. American Mathematical Monthly 73: 385–387.CrossRefGoogle Scholar
16.von Mises, R. (1938). Über Aufteilungs- und Besetzungswahrscheinlichkeiten. Revue de la Faculté des Sciences de L'Université d'Istanbul 4: 145–163.Google Scholar
17.Nunnikhoven, T. (1992). A birthday problem solution for non-uniform birth frequencies. The American Statistician 46: 270–274.Google Scholar
18.Rust, P. (1976). The effect of leap years and seasonal trends on the birthday problem. The American Statistician 30: 197–198.Google Scholar
19.Wagner, D. (2002). A generalized birthday problem. In: Proc. Crypto 2002 Lecture Notes in Computer Science Vol. 2442, NY: Springer-Verlag, pp. 288–303.Google Scholar