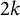1 Introduction
This article concerns the shifted moments of the Riemann zeta function
where
![]() $T \ge 1$
and
$T \ge 1$
and
![]() $\alpha _1:=\alpha _1(T), \alpha _2 :=\alpha _2(T)$
are real-valued functions satisfying
$\alpha _1:=\alpha _1(T), \alpha _2 :=\alpha _2(T)$
are real-valued functions satisfying
These are generalizations of the
![]() $2k$
th moments of the Riemann zeta function
$2k$
th moments of the Riemann zeta function
since
![]() $ I_k(T) = I_k( T, 0,0 )$
. The theory of the moments of the Riemann zeta function is an important topic in analytic number theory (see the classic books [Reference Ivić8, Reference Motohashi12, Reference Ramachandra18, Reference Titchmarsh24]). Unconditionally, Heap and Soundararajan [Reference Heap and Soundararajan6] (for
$ I_k(T) = I_k( T, 0,0 )$
. The theory of the moments of the Riemann zeta function is an important topic in analytic number theory (see the classic books [Reference Ivić8, Reference Motohashi12, Reference Ramachandra18, Reference Titchmarsh24]). Unconditionally, Heap and Soundararajan [Reference Heap and Soundararajan6] (for
![]() $0<k<1$
) and Radziwiłł and Soundararajan [Reference Radziwiłł and Soundararajan17] (for
$0<k<1$
) and Radziwiłł and Soundararajan [Reference Radziwiłł and Soundararajan17] (for
![]() $k\ge 1$
) proved that
$k\ge 1$
) proved that
Assuming the Riemann hypothesis, Harper [Reference Harper5] showed that for any
![]() $k \ge 0$
,
$k \ge 0$
,
Harper’s argument builds on the work of Soundararajan [Reference Soundararajan21], who showed that under the Riemann hypothesis, for any
![]() $\varepsilon>0$
, one has
$\varepsilon>0$
, one has
Based on a random matrix model, Keating and Snaith [Reference Keating and Snaith9] conjectured that for
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
for a precise constant
![]() $C_k$
. By the classical works of Hardy and Littlewood [Reference Hardy and Littlewood4] and Ingham [Reference Ingham7], the asymptotic (1.4) is known, unconditionally, for
$C_k$
. By the classical works of Hardy and Littlewood [Reference Hardy and Littlewood4] and Ingham [Reference Ingham7], the asymptotic (1.4) is known, unconditionally, for
![]() $k=1,2$
. Recently, the first author [Reference Ng14] showed that a certain conjecture for ternary additive divisor sums implies the validity of (1.4) for
$k=1,2$
. Recently, the first author [Reference Ng14] showed that a certain conjecture for ternary additive divisor sums implies the validity of (1.4) for
![]() $k=3$
. In [Reference Ng, Shen and Wong15], the authors have shown that the Riemann hypothesis and a certain conjecture for quaternary additive divisor sums imply that (1.4) is true in the case
$k=3$
. In [Reference Ng, Shen and Wong15], the authors have shown that the Riemann hypothesis and a certain conjecture for quaternary additive divisor sums imply that (1.4) is true in the case
![]() $k=4$
. This work [Reference Ng, Shen and Wong15] crucially uses the bounds for the shifted moments of the zeta function established in Theorem 1.3.
$k=4$
. This work [Reference Ng, Shen and Wong15] crucially uses the bounds for the shifted moments of the zeta function established in Theorem 1.3.
In [Reference Chandee1], the more general shifted moments
where
![]() $\mathbf {k} = (k_1, \ldots , k_m) \in (\mathbb {R}_{> 0})^m$
and
$\mathbf {k} = (k_1, \ldots , k_m) \in (\mathbb {R}_{> 0})^m$
and
![]() $\mathbf {\alpha }= (\alpha _1, \ldots , \alpha _m) \in \mathbb {R}^m$
, were introduced. Chandee [Reference Chandee1, Theorems 1.1 and 1.2] proved the following upper and lower bounds for
$\mathbf {\alpha }= (\alpha _1, \ldots , \alpha _m) \in \mathbb {R}^m$
, were introduced. Chandee [Reference Chandee1, Theorems 1.1 and 1.2] proved the following upper and lower bounds for
![]() $ M_{\mathbf {k}}(T, \mathbf {\alpha })$
.
$ M_{\mathbf {k}}(T, \mathbf {\alpha })$
.
Theorem 1.1 (Chandee)
Let
![]() $k_i$
be positive real numbers. Let
$k_i$
be positive real numbers. Let
![]() $\alpha _i=\alpha _i(T)$
be real-valued functions of T such that
$\alpha _i=\alpha _i(T)$
be real-valued functions of T such that
![]() $\alpha _i =o(T)$
. Assume that
$\alpha _i =o(T)$
. Assume that
![]() $\lim _{T\rightarrow \infty } \alpha _i\log T$
and
$\lim _{T\rightarrow \infty } \alpha _i\log T$
and
![]() $\lim _{T\rightarrow \infty } (\alpha _i-\alpha _j)\log T$
exist or equal
$\lim _{T\rightarrow \infty } (\alpha _i-\alpha _j)\log T$
exist or equal
![]() $\pm \infty $
. Assume that for
$\pm \infty $
. Assume that for
![]() $i\neq j$
,
$i\neq j$
,
![]() $\alpha _i\neq \alpha _j$
and
$\alpha _i\neq \alpha _j$
and
![]() $\alpha _i-\alpha _j =O(1)$
. Then the Riemann hypothesis implies that for T sufficiently large, one has
$\alpha _i-\alpha _j =O(1)$
. Then the Riemann hypothesis implies that for T sufficiently large, one has
 $$ \begin{align} M_{\mathbf{k}}(T, \mathbf{\alpha})\ll_{\mathbf{k},\varepsilon} T(\log T)^{k_1^2 + \cdots +k_m^2 +\varepsilon} \prod_{i<j} \left( \min\left\{\frac{1}{|\alpha_i-\alpha_j|}, \log T \right\}\right)^{2k_ik_j}. \end{align} $$
$$ \begin{align} M_{\mathbf{k}}(T, \mathbf{\alpha})\ll_{\mathbf{k},\varepsilon} T(\log T)^{k_1^2 + \cdots +k_m^2 +\varepsilon} \prod_{i<j} \left( \min\left\{\frac{1}{|\alpha_i-\alpha_j|}, \log T \right\}\right)^{2k_ik_j}. \end{align} $$
Furthermore, if
![]() $k_i$
are positive integers, then for T sufficiently large, unconditionally, one has
$k_i$
are positive integers, then for T sufficiently large, unconditionally, one has
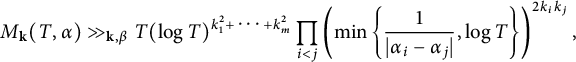 $$ \begin{align*}M_{\mathbf{k}}(T, \mathbf{\alpha})\gg_{\mathbf{k}, \beta} T(\log T)^{k_1^2 + \cdots +k_m^2 } \prod_{i<j} \left( \min\left\{\frac{1}{|\alpha_i-\alpha_j|}, \log T \right\}\right)^{2k_ik_j}, \end{align*} $$
$$ \begin{align*}M_{\mathbf{k}}(T, \mathbf{\alpha})\gg_{\mathbf{k}, \beta} T(\log T)^{k_1^2 + \cdots +k_m^2 } \prod_{i<j} \left( \min\left\{\frac{1}{|\alpha_i-\alpha_j|}, \log T \right\}\right)^{2k_ik_j}, \end{align*} $$
where
For the upper bound, Chandee used the techniques of Soundararajan [Reference Soundararajan21]; for the lower bound, Chandee’s argument is based on the work of Rudnick and Soundararajan [Reference Rudnick and Soundararajan19]. It should be noted that there is an omission in Chandee’s theorem statement of the upper bound (1.6). There should also be the additional condition
BasedFootnote 1 on Keating and Snaith’s random matrix model [Reference Keating and Snaith9], Chandee [Reference Chandee1, Conjecture 1.2] made the following conjecture on shifted moments that generalized a conjecture of Kösters [Reference Kösters11] as follows.
Conjecture 1.2 (Chandee)
Let
![]() $k \in \mathbb {N}$
, and let
$k \in \mathbb {N}$
, and let
![]() $\mathbf {\alpha }= (\alpha _1, \alpha _2)$
be as in Theorem 1.1. Then one has
$\mathbf {\alpha }= (\alpha _1, \alpha _2)$
be as in Theorem 1.1. Then one has
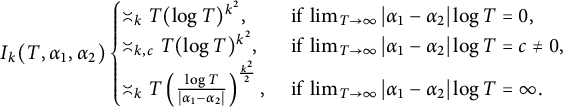 $$ \begin{align*} I_k( T, \alpha_1 , \alpha_2) \begin{cases} \asymp_k T (\log T)^{k^2}, & \text{ if } \lim_{T \to \infty} |\alpha_1- \alpha_2| \log T = 0, \\ \asymp_{k,c} T (\log T)^{k^2}, & \text{ if } \lim_{T \to \infty} |\alpha_1- \alpha_2| \log T = c \ne 0, \\ \asymp_k T \left(\frac{ \log T}{|\alpha_1- \alpha_2|}\right)^{\frac{k^2}{2}}, & \text{ if } \lim_{T \to \infty} |\alpha_1- \alpha_2| \log T = \infty. \end{cases} \end{align*} $$
$$ \begin{align*} I_k( T, \alpha_1 , \alpha_2) \begin{cases} \asymp_k T (\log T)^{k^2}, & \text{ if } \lim_{T \to \infty} |\alpha_1- \alpha_2| \log T = 0, \\ \asymp_{k,c} T (\log T)^{k^2}, & \text{ if } \lim_{T \to \infty} |\alpha_1- \alpha_2| \log T = c \ne 0, \\ \asymp_k T \left(\frac{ \log T}{|\alpha_1- \alpha_2|}\right)^{\frac{k^2}{2}}, & \text{ if } \lim_{T \to \infty} |\alpha_1- \alpha_2| \log T = \infty. \end{cases} \end{align*} $$
Note that for any positive real k,
![]() $M_{\mathbf {k}}(T, \mathbf {\alpha }) = I_{k}( T, \alpha _1 , \alpha _2)$
for
$M_{\mathbf {k}}(T, \mathbf {\alpha }) = I_{k}( T, \alpha _1 , \alpha _2)$
for
![]() $\mathbf {k} =(\tfrac {k}{2},\tfrac {k}{2})$
and
$\mathbf {k} =(\tfrac {k}{2},\tfrac {k}{2})$
and
![]() $\mathbf {\alpha }= (\alpha _1, \alpha _2)$
. Therefore, Theorem 1.1 of Chandee has established the conjectured lower bound for
$\mathbf {\alpha }= (\alpha _1, \alpha _2)$
. Therefore, Theorem 1.1 of Chandee has established the conjectured lower bound for
![]() $I_k( T, \alpha _1 , \alpha _2)$
. It remains to prove the sharp upper bound for
$I_k( T, \alpha _1 , \alpha _2)$
. It remains to prove the sharp upper bound for
![]() $I_k( T, \alpha _1 , \alpha _2)$
in order to establish Conjecture 1.2. In this article, assuming the Riemann hypothesis, we establish Chandee’s conjecture by proving the following theorem.
$I_k( T, \alpha _1 , \alpha _2)$
in order to establish Conjecture 1.2. In this article, assuming the Riemann hypothesis, we establish Chandee’s conjecture by proving the following theorem.
Theorem 1.3 Let
![]() $k\ge 1$
be real. Let
$k\ge 1$
be real. Let
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _2$
be real-valued functions
$\alpha _2$
be real-valued functions
![]() $\alpha _i=\alpha _i(T)$
of T which satisfy the bound (1.1) and
$\alpha _i=\alpha _i(T)$
of T which satisfy the bound (1.1) and
Then the Riemann hypothesis implies that for T sufficiently large, we have
where
![]() $\mathcal {F}(T,\alpha _1,\alpha _2)$
is defined by
$\mathcal {F}(T,\alpha _1,\alpha _2)$
is defined by
 $$ \begin{align} \mathcal{F}(T, \alpha_1,\alpha_2) := \begin{cases} \min\left\{\frac{1}{|\alpha_1-\alpha_2|}, \log T \right\}, & \text{ if }|\alpha_1-\alpha_2|\le \frac{1}{100}, \\ \log(2+ |\alpha_1-\alpha_2|)\,, & \text{ if} |\alpha_1-\alpha_2|> \frac{1}{100}. \end{cases} \end{align} $$
$$ \begin{align} \mathcal{F}(T, \alpha_1,\alpha_2) := \begin{cases} \min\left\{\frac{1}{|\alpha_1-\alpha_2|}, \log T \right\}, & \text{ if }|\alpha_1-\alpha_2|\le \frac{1}{100}, \\ \log(2+ |\alpha_1-\alpha_2|)\,, & \text{ if} |\alpha_1-\alpha_2|> \frac{1}{100}. \end{cases} \end{align} $$
We establish this result by following the breakthrough work of Harper [Reference Harper5].
Remarks
-
(1) This result contains Harper’s bound (1.2) as a special case by setting
 $\alpha _1=\alpha _2=0$
.
$\alpha _1=\alpha _2=0$
. -
(2) Soundararajan’s method [Reference Soundararajan21] can be easily adapted to the case of shifted moments as in [Reference Chandee1] as it has a natural additive structure. On the other hand, it is not obvious how to adapt Harper’s method to the case of shifted moments. When there are two shifts, the argument works by a stroke of luck since we can take advantage of the identity
(1.10)in (3.7). Harper’s method is of certain “multiplicative nature” which allows us to apply Lemmas 2.2 and 2.3 directly. The above trigonometric identity introduces an extra “rotation” into Harper’s method. Our main contribution is to show that such an extra rotation can be handled so that Harper’s argument still works (see, for instance, our equations (4.7) and (4.12)). It is not clear how to extend the result to three shifts as there seems to be no good trigonometric identity for $$ \begin{align} \cos(\theta_1) + \cos(\theta_2) = 2 \cos \left( \frac{\theta_1+\theta_2}{2} \right) \cos \left( \frac{\theta_1-\theta_2}{2} \right) \end{align} $$
$$ \begin{align} \cos(\theta_1) + \cos(\theta_2) = 2 \cos \left( \frac{\theta_1+\theta_2}{2} \right) \cos \left( \frac{\theta_1-\theta_2}{2} \right) \end{align} $$
 $ \cos (\theta _1) + \cos (\theta _2) + \cos (\theta _3)$
. Similarly, if one wants to extend the result to
$ \cos (\theta _1) + \cos (\theta _2) + \cos (\theta _3)$
. Similarly, if one wants to extend the result to
 $M_{\mathbf {k}}(T, \mathbf {\alpha })$
where the components of
$M_{\mathbf {k}}(T, \mathbf {\alpha })$
where the components of
 $\mathbf {k} = (k_1, \ldots , k_m)$
are not necessarily equal and
$\mathbf {k} = (k_1, \ldots , k_m)$
are not necessarily equal and
 $m \ge 2$
, one encounters the same issue. Despite this, it is highly desirable to obtain sharp bounds for
$m \ge 2$
, one encounters the same issue. Despite this, it is highly desirable to obtain sharp bounds for
 $M_{\mathbf {k}}(T, \mathbf {\alpha })$
in the general case. Recently, bounds for shifted moments of L-functions have been used in establishing asymptotics for certain moments of L-functions (see [Reference Shen20, Reference Soundararajan and Young22]), and it is possible that sharp bounds for
$M_{\mathbf {k}}(T, \mathbf {\alpha })$
in the general case. Recently, bounds for shifted moments of L-functions have been used in establishing asymptotics for certain moments of L-functions (see [Reference Shen20, Reference Soundararajan and Young22]), and it is possible that sharp bounds for
 $M_{\mathbf {k}}(T, \mathbf {\alpha })$
could be used in similar contexts.
$M_{\mathbf {k}}(T, \mathbf {\alpha })$
could be used in similar contexts.
-
(3) This theorem improves the upper bound portion of Theorem 1.1 in the case that
 $k_1=k_2=k$
. Note that there is no restriction on k as in (1.7), and we do not have the strict condition
$k_1=k_2=k$
. Note that there is no restriction on k as in (1.7), and we do not have the strict condition
 $|\alpha _1-\alpha _2| \ll 1$
. Note that we apply Lemma 2.4 instead of [Reference Chandee1, Lemma 3.5, p. 556].
$|\alpha _1-\alpha _2| \ll 1$
. Note that we apply Lemma 2.4 instead of [Reference Chandee1, Lemma 3.5, p. 556]. -
(4) In applications to moment problems, it is crucial to have bounds for shifted moments when the shifts can be far apart. In our application to
 $I_4(T)$
[Reference Ng, Shen and Wong15], we require a bound for
$I_4(T)$
[Reference Ng, Shen and Wong15], we require a bound for
 $I_k( T, \alpha _1 , \alpha _2)$
when
$I_k( T, \alpha _1 , \alpha _2)$
when
 $|\alpha _1 -\alpha _2| \le \sqrt {T}$
.
$|\alpha _1 -\alpha _2| \le \sqrt {T}$
. -
(5) In this article, we also fill in a gap in Harper’s argument. In the proof of his Lemma 3, he provides a sketch, mentioning it is very similar to his Lemma 1. However, when one tries to follow his argument, one encounters integrals of the shape
 $\int \prod _{p} \cos (t \log p) \prod _{q} \cos (2t \log q) \, dt$
. Consequently, one may not invoke Proposition 2 in his article. To address this issue, we established Lemma 2.3, which is required in the proof of his Lemma 3 and is also used in our Lemma 3.3.
$\int \prod _{p} \cos (t \log p) \prod _{q} \cos (2t \log q) \, dt$
. Consequently, one may not invoke Proposition 2 in his article. To address this issue, we established Lemma 2.3, which is required in the proof of his Lemma 3 and is also used in our Lemma 3.3. -
(6) In this theorem and throughout this article, whenever we write “sufficiently large T,” we mean that there exists
 $T_0:= T_0(k)$
a positive parameter depending on k such that
$T_0:= T_0(k)$
a positive parameter depending on k such that
 $T \ge T_0$
.
$T \ge T_0$
.
Remark added on September 8, 2023. Recently, Curran [Reference Curran2] extended Theorem 1.3 to the general shifted moments
![]() $M_{\mathbf {k}}(T, \mathbf {\alpha })$
, defined in (1.5), and analyzed the case that the differences
$M_{\mathbf {k}}(T, \mathbf {\alpha })$
, defined in (1.5), and analyzed the case that the differences
![]() $|\alpha _i-\alpha _j|$
are unbounded. Also, under the generalized Riemann hypothesis (for Dirichlet L-functions), Szabó [Reference Szabó23] proved a sharp upper bound on moments of shifted Dirichlet L-functions, which improves the previous work of Munsch [Reference Munsch13].
$|\alpha _i-\alpha _j|$
are unbounded. Also, under the generalized Riemann hypothesis (for Dirichlet L-functions), Szabó [Reference Szabó23] proved a sharp upper bound on moments of shifted Dirichlet L-functions, which improves the previous work of Munsch [Reference Munsch13].
Conventions and notation. In this article, given two functions
![]() $f(x)$
and
$f(x)$
and
![]() $g(x)$
, we shall interchangeably use the notation
$g(x)$
, we shall interchangeably use the notation
![]() $f(x)=O(g(x))$
,
$f(x)=O(g(x))$
,
![]() $f(x) \ll g(x)$
, and
$f(x) \ll g(x)$
, and
![]() $g(x) \gg f(x)$
to mean that there is
$g(x) \gg f(x)$
to mean that there is
![]() $M>0$
such that
$M>0$
such that
![]() $|f(x)| \le M |g(x)|$
for sufficiently large x. Given fixed parameters
$|f(x)| \le M |g(x)|$
for sufficiently large x. Given fixed parameters
![]() $\ell _1, \ldots , \ell _r$
, the notation
$\ell _1, \ldots , \ell _r$
, the notation
![]() $f(x) \ll _{\ell _1, \ldots , \ell _r} g(x)$
means that the
$f(x) \ll _{\ell _1, \ldots , \ell _r} g(x)$
means that the
![]() $|f(x)| \le M g(x)$
where
$|f(x)| \le M g(x)$
where
![]() $M=M(\ell _1, \ldots , \ell _r)$
depends on the parameters
$M=M(\ell _1, \ldots , \ell _r)$
depends on the parameters
![]() $\ell _1, \ldots , \ell _r$
. The letter p will always denote a prime number. In addition,
$\ell _1, \ldots , \ell _r$
. The letter p will always denote a prime number. In addition,
![]() $p_i$
,
$p_i$
,
![]() $p_{i}'$
,
$p_{i}'$
,
![]() $\mathfrak {p}_i$
,
$\mathfrak {p}_i$
,
![]() $q_i$
, and
$q_i$
, and
![]() $\mathfrak {q}_i$
with
$\mathfrak {q}_i$
with
![]() $i \in \mathbb {N}$
shall denote prime numbers.
$i \in \mathbb {N}$
shall denote prime numbers.
2 Some tools
We shall require the following tools, which are fundamental for the argument. First, by a minor modification of the main Proposition of [Reference Soundararajan21] (see also [Reference Harper5, Proposition 1]), we have the following proposition providing an upper bound for the Riemann zeta function.
Proposition 2.1 Assume that the Riemann hypothesis holds. Let
![]() $\lambda _0=0.491\cdots $
denote the unique positive solution of
$\lambda _0=0.491\cdots $
denote the unique positive solution of
![]() $e^{-\lambda _0}=\lambda _0 + \lambda _0^2/2$
. Let T be large. Then, for
$e^{-\lambda _0}=\lambda _0 + \lambda _0^2/2$
. Let T be large. Then, for
![]() $\lambda \ge \lambda _0$
,
$\lambda \ge \lambda _0$
,
![]() $2\le x\le T^2$
, and
$2\le x\le T^2$
, and
![]() $t\in [c_1T, c_2T]$
, where
$t\in [c_1T, c_2T]$
, where
![]() $0 < c_1 < c_2$
, one has
$0 < c_1 < c_2$
, one has
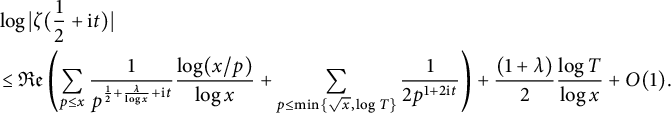 $$ \begin{align*} &\log|\zeta(\frac{1}{2} +\mathrm{i} t)|\\ &\le {\mathfrak{Re}}\left(\sum_{ p\le x}\frac{1}{p^{\frac{1}{2}+\frac{\lambda}{ \log x}+\mathrm{i} t } }\frac{\log(x/p)}{\log x } + \sum_{p\le\min\{\sqrt{x},\log T\} }\frac{1}{2p^{1+2 \mathrm{i} t}} \right) + \frac{(1+\lambda)}{2}\frac{\log T}{\log x} +O(1). \end{align*} $$
$$ \begin{align*} &\log|\zeta(\frac{1}{2} +\mathrm{i} t)|\\ &\le {\mathfrak{Re}}\left(\sum_{ p\le x}\frac{1}{p^{\frac{1}{2}+\frac{\lambda}{ \log x}+\mathrm{i} t } }\frac{\log(x/p)}{\log x } + \sum_{p\le\min\{\sqrt{x},\log T\} }\frac{1}{2p^{1+2 \mathrm{i} t}} \right) + \frac{(1+\lambda)}{2}\frac{\log T}{\log x} +O(1). \end{align*} $$
Also, we have the following variant of [Reference Radziwiłł16, Lemma 4], which Harper formulates in [Reference Harper5, Proposition 2].
Lemma 2.2 Let
![]() $n=p_1^{a_1}\cdots p_r^{a_r}$
, where
$n=p_1^{a_1}\cdots p_r^{a_r}$
, where
![]() $p_i$
are distinct primes, and
$p_i$
are distinct primes, and
![]() $a_i\in \Bbb {N}$
. Then, for T large, one has
$a_i\in \Bbb {N}$
. Then, for T large, one has
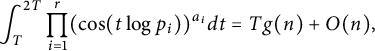 $$ \begin{align*}\int_T^{2T} \prod_{i=1}^r (\cos(t\log p_i))^{a_i} dt =Tg(n) +O(n), \end{align*} $$
$$ \begin{align*}\int_T^{2T} \prod_{i=1}^r (\cos(t\log p_i))^{a_i} dt =Tg(n) +O(n), \end{align*} $$
where the implied constant is absolute, and
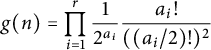 $$ \begin{align*}g(n)=\prod_{i=1}^r \frac{1}{2^{a_i}} \frac{a_i !}{((a_i/2)!)^2} \end{align*} $$
$$ \begin{align*}g(n)=\prod_{i=1}^r \frac{1}{2^{a_i}} \frac{a_i !}{((a_i/2)!)^2} \end{align*} $$
if every
![]() $a_i$
is even, and
$a_i$
is even, and
![]() $g(n)=0$
otherwise. Consequently, for T large and any real number
$g(n)=0$
otherwise. Consequently, for T large and any real number
![]() $\gamma $
, we have
$\gamma $
, we have
 $$ \begin{align*}\int_T^{2T} \prod_{i=1}^r (\cos( (t+\gamma)\log p_i))^{a_i} dt =(T+\gamma)g(n) +O(|\gamma|) + O(n), \end{align*} $$
$$ \begin{align*}\int_T^{2T} \prod_{i=1}^r (\cos( (t+\gamma)\log p_i))^{a_i} dt =(T+\gamma)g(n) +O(|\gamma|) + O(n), \end{align*} $$
where the implied constants are absolute.
Moreover, we shall require the following further variant of [Reference Radziwiłł16, Lemma 4] of Radziwiłł.
Lemma 2.3 Let
![]() $n=p_1^{a_1}\cdots p_r^{a_r} p_{r+1}^{a_{r+1}}\cdots p_{s}^{a_{s}} $
, where
$n=p_1^{a_1}\cdots p_r^{a_r} p_{r+1}^{a_{r+1}}\cdots p_{s}^{a_{s}} $
, where
![]() $p_i$
are distinct primes, and
$p_i$
are distinct primes, and
![]() $a_i\in \Bbb {N}$
. Then we have
$a_i\in \Bbb {N}$
. Then we have
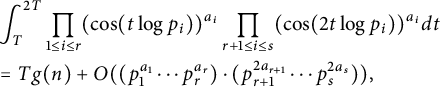 $$ \begin{align*} &\int_T^{2T} \prod_{ 1\le i\le r}(\cos(t\log p_i))^{a_i} \prod_{ r+1\le i\le s}(\cos(2t\log p_i))^{a_i} dt\\ & =Tg(n) + O(( p_1^{a_1}\cdots p_r^{a_r})\cdot ( p_{r+1}^{2a_{r+1} }\cdots p_{s}^{2a_{s}})), \end{align*} $$
$$ \begin{align*} &\int_T^{2T} \prod_{ 1\le i\le r}(\cos(t\log p_i))^{a_i} \prod_{ r+1\le i\le s}(\cos(2t\log p_i))^{a_i} dt\\ & =Tg(n) + O(( p_1^{a_1}\cdots p_r^{a_r})\cdot ( p_{r+1}^{2a_{r+1} }\cdots p_{s}^{2a_{s}})), \end{align*} $$
where the implied constant is absolute. Consequently, for any real
![]() $\gamma $
, we have
$\gamma $
, we have
 $$ \begin{align*} &\int_T^{2T} \prod_{i=1}^r (\cos( (t+\gamma)\log p_i))^{a_i} \prod_{ r+1\le i\le s}(\cos(2(t+\gamma)\log p_i))^{a_i} dt \\ &=(T+\gamma)g(n) +O(|\gamma|) + O( (p_1^{a_1}\cdots p_r^{a_r}) \cdot (p_{r+1}^{2a_{r+1}} \cdots p_{s}^{2a_{s}})), \end{align*} $$
$$ \begin{align*} &\int_T^{2T} \prod_{i=1}^r (\cos( (t+\gamma)\log p_i))^{a_i} \prod_{ r+1\le i\le s}(\cos(2(t+\gamma)\log p_i))^{a_i} dt \\ &=(T+\gamma)g(n) +O(|\gamma|) + O( (p_1^{a_1}\cdots p_r^{a_r}) \cdot (p_{r+1}^{2a_{r+1}} \cdots p_{s}^{2a_{s}})), \end{align*} $$
where the implied constants are absolute.
Proof Following Radziwiłł [Reference Radziwiłł16, Proof of Lemma 4], for
![]() $c\in \Bbb {N}$
, we can write
$c\in \Bbb {N}$
, we can write
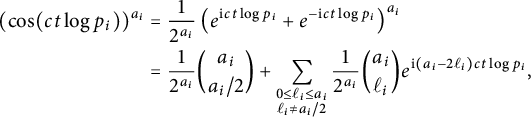 $$ \begin{align*} (\cos(c t \log p_i))^{a_i} & = \frac{1}{2^{a_i}}\left(e^{\mathrm{i} ct\log p_i} + e^{-\mathrm{i} ct\log p_i} \right)^{a_i} \\ &= \frac{1}{2^{a_i}} {a_i \choose a_i/2} +\sum_{\substack{ 0\le \ell_i \le a_i \\ \ell_i\neq a_i/2 }} \frac{1}{2^{a_i}} {a_i \choose \ell_i} e^{\mathrm{i} (a_i -2\ell_i) ct\log p_i}, \end{align*} $$
$$ \begin{align*} (\cos(c t \log p_i))^{a_i} & = \frac{1}{2^{a_i}}\left(e^{\mathrm{i} ct\log p_i} + e^{-\mathrm{i} ct\log p_i} \right)^{a_i} \\ &= \frac{1}{2^{a_i}} {a_i \choose a_i/2} +\sum_{\substack{ 0\le \ell_i \le a_i \\ \ell_i\neq a_i/2 }} \frac{1}{2^{a_i}} {a_i \choose \ell_i} e^{\mathrm{i} (a_i -2\ell_i) ct\log p_i}, \end{align*} $$
where
![]() ${a_i \choose a_i/2}=0$
if
${a_i \choose a_i/2}=0$
if
![]() $a_i/2$
is not a positive integer. Hence, setting
$a_i/2$
is not a positive integer. Hence, setting
![]() $c_i=1$
for
$c_i=1$
for
![]() $1\le i\le r$
and
$1\le i\le r$
and
![]() $c_i=2$
for
$c_i=2$
for
![]() $r+1\le i\le s$
, we obtain
$r+1\le i\le s$
, we obtain
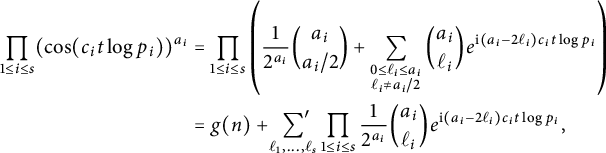 $$ \begin{align*} \prod_{ 1\le i\le s}(\cos(c_i t\log p_i))^{a_i} &= \prod_{ 1\le i\le s}\left( \frac{1}{2^{a_i}} {a_i \choose a_i/2} +\sum_{\substack{ 0\le \ell_i \le a_i \\ \ell_i\neq a_i/2 }} {a_i \choose \ell_i} e^{\mathrm{i} (a_i -2\ell_i) c_it\log p_i} \right)\\ &= g(n) + \sideset{}{'}\sum_{\ell_1,\ldots,\ell_s} \prod_{ 1\le i\le s} \frac{1}{2^{a_i}}{a_i \choose \ell_i} e^{\mathrm{i} (a_i -2\ell_i) c_it\log p_i}, \end{align*} $$
$$ \begin{align*} \prod_{ 1\le i\le s}(\cos(c_i t\log p_i))^{a_i} &= \prod_{ 1\le i\le s}\left( \frac{1}{2^{a_i}} {a_i \choose a_i/2} +\sum_{\substack{ 0\le \ell_i \le a_i \\ \ell_i\neq a_i/2 }} {a_i \choose \ell_i} e^{\mathrm{i} (a_i -2\ell_i) c_it\log p_i} \right)\\ &= g(n) + \sideset{}{'}\sum_{\ell_1,\ldots,\ell_s} \prod_{ 1\le i\le s} \frac{1}{2^{a_i}}{a_i \choose \ell_i} e^{\mathrm{i} (a_i -2\ell_i) c_it\log p_i}, \end{align*} $$
where the primed sum is over
![]() $(\ell _1,\ldots ,\ell _s)\neq (\frac {a_1}{2},\ldots ,\frac {a_s}{2})$
such that
$(\ell _1,\ldots ,\ell _s)\neq (\frac {a_1}{2},\ldots ,\frac {a_s}{2})$
such that
![]() $0\le \ell _j\le a_j$
for every
$0\le \ell _j\le a_j$
for every
![]() $1\le j\le s$
. Thus, we deduce
$1\le j\le s$
. Thus, we deduce
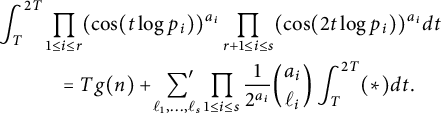 $$ \begin{align}\begin{aligned} &\int_T^{2T} \prod_{ 1\le i\le r}(\cos(t\log p_i))^{a_i} \prod_{ r+1\le i\le s}(\cos(2t\log p_i))^{a_i} dt\\&\quad\qquad=Tg(n) + \sideset{}{'}\sum_{\ell_1,\ldots,\ell_s} \prod_{ 1\le i\le s} \frac{1}{2^{a_i}}{a_i \choose \ell_i} \int_T^{2T} (*) dt.\end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} &\int_T^{2T} \prod_{ 1\le i\le r}(\cos(t\log p_i))^{a_i} \prod_{ r+1\le i\le s}(\cos(2t\log p_i))^{a_i} dt\\&\quad\qquad=Tg(n) + \sideset{}{'}\sum_{\ell_1,\ldots,\ell_s} \prod_{ 1\le i\le s} \frac{1}{2^{a_i}}{a_i \choose \ell_i} \int_T^{2T} (*) dt.\end{aligned} \end{align} $$
The integrand
![]() $(*)$
is
$(*)$
is
where
![]() $b_i =a_i -2\ell _i$
. (Note that, as later,
$b_i =a_i -2\ell _i$
. (Note that, as later,
![]() $b_1,\ldots ,b_s$
cannot be all zero, and
$b_1,\ldots ,b_s$
cannot be all zero, and
![]() $|b_i|\le a_i$
.) We then see
$|b_i|\le a_i$
.) We then see
 $$ \begin{align*}\left|\int_T^{2T} (*) dt\right|\le \frac{2}{|b_1\log p_1 +\cdots + b_r\log p_r + 2b_{r+1}\log p_{r+1} +\cdots + 2b_s\log p_s | }. \end{align*} $$
$$ \begin{align*}\left|\int_T^{2T} (*) dt\right|\le \frac{2}{|b_1\log p_1 +\cdots + b_r\log p_r + 2b_{r+1}\log p_{r+1} +\cdots + 2b_s\log p_s | }. \end{align*} $$
(Note that the denominator is nonzero since
![]() $(b_1,\ldots ,b_s)\neq (0,\ldots ,0)$
and
$(b_1,\ldots ,b_s)\neq (0,\ldots ,0)$
and
![]() $p_1,\ldots , p_s$
are distinct.) Grouping together those terms with
$p_1,\ldots , p_s$
are distinct.) Grouping together those terms with
![]() $b_i> 0$
and
$b_i> 0$
and
![]() $b_i < 0$
, respectively, we can write
$b_i < 0$
, respectively, we can write
where
![]() $M\neq N$
are positive integers. Without loss of generality, we may assume
$M\neq N$
are positive integers. Without loss of generality, we may assume
![]() $M>N$
and obtain
$M>N$
and obtain
![]() $|\log (M/N)| = \log (M/N)$
, which is
$|\log (M/N)| = \log (M/N)$
, which is
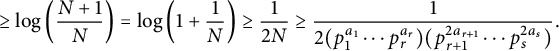 $$ \begin{align*}\ge \log\left(\frac{N+1}{N} \right) =\log\left( 1+ \frac{1}{N} \right) \ge \frac{1}{2N} \ge \frac{1}{2 (p_1^{a_1}\cdots p_r^{a_r})( p_{r+1}^{2a_{r+1}}\cdots p_{s}^{2a_{s}})}. \end{align*} $$
$$ \begin{align*}\ge \log\left(\frac{N+1}{N} \right) =\log\left( 1+ \frac{1}{N} \right) \ge \frac{1}{2N} \ge \frac{1}{2 (p_1^{a_1}\cdots p_r^{a_r})( p_{r+1}^{2a_{r+1}}\cdots p_{s}^{2a_{s}})}. \end{align*} $$
Therefore, the primed sum in (2.1) is
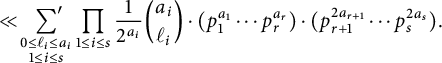 $$ \begin{align*}\ll \sideset{}{'}\sum_{\substack{ 0\le \ell_i \le a_i\\ 1\le i\le s}} \prod_{ 1\le i\le s} \frac{1}{2^{a_i}}{a_i \choose \ell_i} \cdot ( p_1^{a_1}\cdots p_r^{a_r} ) \cdot ( p_{r+1}^{2a_{r+1}}\cdots p_{s}^{2a_{s}}). \end{align*} $$
$$ \begin{align*}\ll \sideset{}{'}\sum_{\substack{ 0\le \ell_i \le a_i\\ 1\le i\le s}} \prod_{ 1\le i\le s} \frac{1}{2^{a_i}}{a_i \choose \ell_i} \cdot ( p_1^{a_1}\cdots p_r^{a_r} ) \cdot ( p_{r+1}^{2a_{r+1}}\cdots p_{s}^{2a_{s}}). \end{align*} $$
Finally, observing that
we complete the proof.
Lastly, we recall the following variant of Mertens’ estimate (see, e.g., [Reference Granville and Soundararajan3, p. 57] or [Reference Munsch13, Lemma 2.9]).
Lemma 2.4 Let a and
![]() $z\ge 1$
be real numbers. Then one has
$z\ge 1$
be real numbers. Then one has
 $$ \begin{align} \sum_{p\le z} \frac{\cos(a \log p)}{p} \begin{cases} = \log \left( \min \left\{\frac{1}{|a|}, \log z \right\} \right) +O(1), & \text{ if }|a|\le \frac{1}{100}, \\ \le \log\log(2+ |a|) +O(1), & \text{ if }|a|>\frac{1}{100}, \end{cases} \end{align} $$
$$ \begin{align} \sum_{p\le z} \frac{\cos(a \log p)}{p} \begin{cases} = \log \left( \min \left\{\frac{1}{|a|}, \log z \right\} \right) +O(1), & \text{ if }|a|\le \frac{1}{100}, \\ \le \log\log(2+ |a|) +O(1), & \text{ if }|a|>\frac{1}{100}, \end{cases} \end{align} $$
where the implied constants are absolute.
3 Setup and outline of the proof of Theorem 1.3
The goal of this section is to prove Theorem 1.3. To do so, we follow closely Harper [Reference Harper5]. We let
![]() $\beta _0 =0$
and
$\beta _0 =0$
and
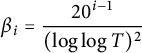 $$ \begin{align*}\beta_i = \frac{20^{i-1}}{(\log\log T)^2} \end{align*} $$
$$ \begin{align*}\beta_i = \frac{20^{i-1}}{(\log\log T)^2} \end{align*} $$
for every integer
![]() $i\ge 1$
. Define
$i\ge 1$
. Define
![]() $\mathcal {I}= \mathcal {I}_{k,T} =1+\max \{i\mid \beta _i\le e^{-1000k}\}.$
For
$\mathcal {I}= \mathcal {I}_{k,T} =1+\max \{i\mid \beta _i\le e^{-1000k}\}.$
For
![]() $1\le i\le j \le \mathcal {I}$
, we set
$1\le i\le j \le \mathcal {I}$
, we set
 $$ \begin{align} G_{i,j}(t)=G_{i,j,T,\alpha_1,\alpha_2}(t)= \sum_{T^{\beta_{i-1}}< p\le T^{\beta_{i}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_j \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_j}/p)}{\log T^{\beta_j} }. \end{align} $$
$$ \begin{align} G_{i,j}(t)=G_{i,j,T,\alpha_1,\alpha_2}(t)= \sum_{T^{\beta_{i-1}}< p\le T^{\beta_{i}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_j \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_j}/p)}{\log T^{\beta_j} }. \end{align} $$
For
![]() $1\le i\le \mathcal {I}$
, we set
$1\le i\le \mathcal {I}$
, we set
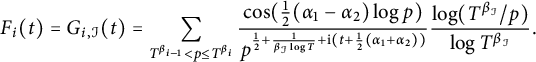 $$ \begin{align} F_i(t) =G_{i,\mathcal{I}}(t)= \sum_{T^{\beta_{i-1}}< p\le T^{\beta_{i}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} }. \end{align} $$
$$ \begin{align} F_i(t) =G_{i,\mathcal{I}}(t)= \sum_{T^{\beta_{i-1}}< p\le T^{\beta_{i}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} }. \end{align} $$
We define
For
![]() $1\le j\le \mathcal {I}-1$
, we let
$1\le j\le \mathcal {I}-1$
, we let
![]() $\mathcal {S}(j) = \mathcal {S}_{k,T,\alpha _1,\alpha _2}(j)$
stand for the set
$\mathcal {S}(j) = \mathcal {S}_{k,T,\alpha _1,\alpha _2}(j)$
stand for the set
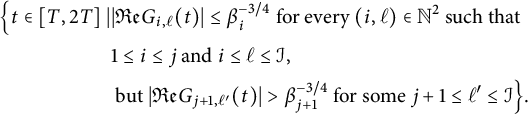 $$ \begin{align*} \Big\{ t\in [T, 2T] \mid & |{\mathfrak{Re}} G_{i,\ell}(t)|\le \beta_i^{-3/4} \text{ for every } (i,\ell) \in \mathbb{N}^2 \text{ such that }\\ & 1\le i\le j \text{ and } i\le \ell \le \mathcal{I}, \\ & \text{ but } |{\mathfrak{Re}} G_{j+1,\ell'}(t)|> \beta_{j+1}^{-3/4} \text{ for some } j+1\le \ell' \le \mathcal{I}\Big\}. \end{align*} $$
$$ \begin{align*} \Big\{ t\in [T, 2T] \mid & |{\mathfrak{Re}} G_{i,\ell}(t)|\le \beta_i^{-3/4} \text{ for every } (i,\ell) \in \mathbb{N}^2 \text{ such that }\\ & 1\le i\le j \text{ and } i\le \ell \le \mathcal{I}, \\ & \text{ but } |{\mathfrak{Re}} G_{j+1,\ell'}(t)|> \beta_{j+1}^{-3/4} \text{ for some } j+1\le \ell' \le \mathcal{I}\Big\}. \end{align*} $$
Finally, we define
Note that
![]() $\beta _{j+1}\le \beta _{ \mathcal {I}} \le 20 e^{-1000k}$
for any
$\beta _{j+1}\le \beta _{ \mathcal {I}} \le 20 e^{-1000k}$
for any
![]() $1\le j \le \mathcal {I}-1$
.
$1\le j \le \mathcal {I}-1$
.
Observe
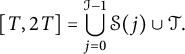 $$ \begin{align} [T,2T] = \bigcup_{j=0}^{\mathcal{I}-1} \mathcal{S}(j) \cup \mathcal{T}. \end{align} $$
$$ \begin{align} [T,2T] = \bigcup_{j=0}^{\mathcal{I}-1} \mathcal{S}(j) \cup \mathcal{T}. \end{align} $$
In order to prove Theorem 1.3, we shall establish
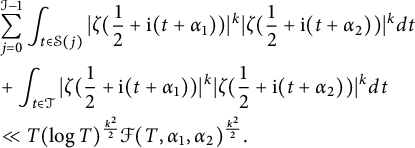 $$ \begin{align} & \sum_{j=0}^{\mathcal{I}-1} \int_{t\in \mathcal{S}(j) } |\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_2))|^k dt\nonumber\\ &+ \int_{t\in\mathcal{T} } |\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_1))|^k|\zeta(\frac{1}{2} +\mathrm{i} (t+\alpha_2))|^k dt\\ &\ll T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1, \alpha_2)^{\frac{k^2}{2}}.\nonumber \end{align} $$
$$ \begin{align} & \sum_{j=0}^{\mathcal{I}-1} \int_{t\in \mathcal{S}(j) } |\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_2))|^k dt\nonumber\\ &+ \int_{t\in\mathcal{T} } |\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_1))|^k|\zeta(\frac{1}{2} +\mathrm{i} (t+\alpha_2))|^k dt\\ &\ll T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1, \alpha_2)^{\frac{k^2}{2}}.\nonumber \end{align} $$
Applying Proposition 2.1 with
![]() $\lambda =1$
, for sufficiently large T,
$\lambda =1$
, for sufficiently large T,
![]() $2\le x\le T^2$
, and
$2\le x\le T^2$
, and
![]() $t\in [T,2T]$
, we have
$t\in [T,2T]$
, we have
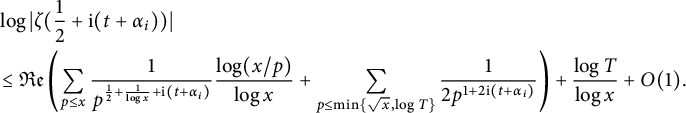 $$ \begin{align} &\log|\zeta(\frac{1}{2}+\mathrm{i} (t +\alpha_i))| \nonumber\\ &\le {\mathfrak{Re}}\left(\sum_{ p\le x}\frac{1}{p^{\frac{1}{2}+\frac{1}{ \log x}+\mathrm{i} (t +\alpha_i)} }\frac{\log(x/p)}{\log x } + \sum_{p\le\min\{\sqrt{x},\log T\} }\frac{1}{2p^{1+2 \mathrm{i} (t +\alpha_i)}} \right) +\frac{\log T}{\log x} +O(1).\nonumber\\ \end{align} $$
$$ \begin{align} &\log|\zeta(\frac{1}{2}+\mathrm{i} (t +\alpha_i))| \nonumber\\ &\le {\mathfrak{Re}}\left(\sum_{ p\le x}\frac{1}{p^{\frac{1}{2}+\frac{1}{ \log x}+\mathrm{i} (t +\alpha_i)} }\frac{\log(x/p)}{\log x } + \sum_{p\le\min\{\sqrt{x},\log T\} }\frac{1}{2p^{1+2 \mathrm{i} (t +\alpha_i)}} \right) +\frac{\log T}{\log x} +O(1).\nonumber\\ \end{align} $$
We further note that the “main term” for the upper bound of
![]() $\log ( |\zeta (\frac {1}{2}+\mathrm {i}(t+\alpha _1))|^k|\zeta (\frac {1}{2}+\mathrm {i} (t+\alpha _2))|^k )$
derived from (3.6) is
$\log ( |\zeta (\frac {1}{2}+\mathrm {i}(t+\alpha _1))|^k|\zeta (\frac {1}{2}+\mathrm {i} (t+\alpha _2))|^k )$
derived from (3.6) is
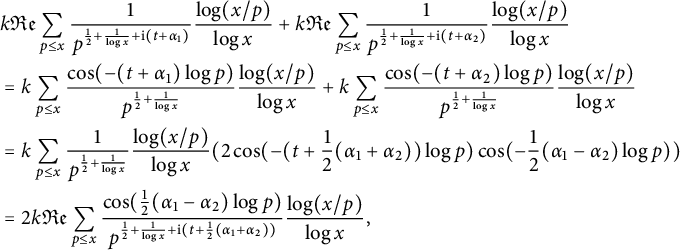 $$ \begin{align} &k{\mathfrak{Re}} \sum_{ p\le x}\frac{1}{p^{\frac{1}{2}+\frac{1}{ \log x}+\mathrm{i} (t+\alpha_1) } }\frac{\log(x/p)}{\log x } +k{\mathfrak{Re}}\sum_{ p\le x}\frac{1}{p^{\frac{1}{2}+\frac{1}{ \log x}+\mathrm{i} (t+\alpha_2) } }\frac{\log(x/p)}{\log x } \nonumber\\ &=k \sum_{ p\le x}\frac{\cos(-(t+\alpha_1)\log p)}{p^{\frac{1}{2}+\frac{1}{ \log x}} }\frac{\log(x/p)}{\log x } +k \sum_{ p\le x}\frac{\cos(-(t+\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{ \log x} } }\frac{\log(x/p)}{\log x }\nonumber\\ &=k \sum_{ p\le x}\frac{1}{p^{\frac{1}{2}+\frac{1}{ \log x} } }\frac{\log(x/p)}{\log x } (2\cos(-(t+\frac{1}{2}(\alpha_1+\alpha_2))\log p) \cos(-\frac{1}{2}(\alpha_1-\alpha_2)\log p) )\nonumber\\ &=2k {\mathfrak{Re}} \sum_{ p\le x}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{ \log x}+\mathrm{i}(t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(x/p)}{\log x }, \nonumber\\\end{align} $$
$$ \begin{align} &k{\mathfrak{Re}} \sum_{ p\le x}\frac{1}{p^{\frac{1}{2}+\frac{1}{ \log x}+\mathrm{i} (t+\alpha_1) } }\frac{\log(x/p)}{\log x } +k{\mathfrak{Re}}\sum_{ p\le x}\frac{1}{p^{\frac{1}{2}+\frac{1}{ \log x}+\mathrm{i} (t+\alpha_2) } }\frac{\log(x/p)}{\log x } \nonumber\\ &=k \sum_{ p\le x}\frac{\cos(-(t+\alpha_1)\log p)}{p^{\frac{1}{2}+\frac{1}{ \log x}} }\frac{\log(x/p)}{\log x } +k \sum_{ p\le x}\frac{\cos(-(t+\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{ \log x} } }\frac{\log(x/p)}{\log x }\nonumber\\ &=k \sum_{ p\le x}\frac{1}{p^{\frac{1}{2}+\frac{1}{ \log x} } }\frac{\log(x/p)}{\log x } (2\cos(-(t+\frac{1}{2}(\alpha_1+\alpha_2))\log p) \cos(-\frac{1}{2}(\alpha_1-\alpha_2)\log p) )\nonumber\\ &=2k {\mathfrak{Re}} \sum_{ p\le x}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{ \log x}+\mathrm{i}(t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(x/p)}{\log x }, \nonumber\\\end{align} $$
where we have made use of the trigonometric identity (1.10). Arguing similarly for the second sum in (3.6), we arrive at
 $$ \begin{align} & \log( |\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_2))|^k ) \nonumber\\ & \le 2k {\mathfrak{Re}}\left(\sum_{ p\le x}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{ \log x}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(x/p)}{\log x } + \sum_{p\le\min\{\sqrt{x},\log T\} }\!\frac{\cos((\alpha_1-\alpha_2)\log p)}{2p^{1+ \mathrm{i} (2t+(\alpha_1+\alpha_2)) }} \!\right) \nonumber\\ & +\frac{2k\log T}{\log x} +O(k).\nonumber\\ \end{align} $$
$$ \begin{align} & \log( |\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_2))|^k ) \nonumber\\ & \le 2k {\mathfrak{Re}}\left(\sum_{ p\le x}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{ \log x}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(x/p)}{\log x } + \sum_{p\le\min\{\sqrt{x},\log T\} }\!\frac{\cos((\alpha_1-\alpha_2)\log p)}{2p^{1+ \mathrm{i} (2t+(\alpha_1+\alpha_2)) }} \!\right) \nonumber\\ & +\frac{2k\log T}{\log x} +O(k).\nonumber\\ \end{align} $$
Theorem 1.3 will be deduced from the following three lemmas.
Lemma 3.1 In the notation and assumption as above and Theorem 1.3, for any sufficiently large T, we have
 $$ \begin{align*} &\int_{t\in \mathcal{T}} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \\ &\ll_k T (\log T)^{\frac{k^2}{2}} \left(\mathcal{F}(T,\alpha_1,\alpha_2) \right)^{\frac{k^2}{2}}, \end{align*} $$
$$ \begin{align*} &\int_{t\in \mathcal{T}} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \\ &\ll_k T (\log T)^{\frac{k^2}{2}} \left(\mathcal{F}(T,\alpha_1,\alpha_2) \right)^{\frac{k^2}{2}}, \end{align*} $$
where
![]() $\mathcal {F}(T,\alpha _1,\alpha _2) $
is defined in (1.9).
$\mathcal {F}(T,\alpha _1,\alpha _2) $
is defined in (1.9).
Lemma 3.2 In the notation and assumption as above, we have
In addition, for
![]() $ 1 \le j \le \mathcal {I}-1$
, we have
$ 1 \le j \le \mathcal {I}-1$
, we have
 $$ \begin{align*} &\int_{t\in \mathcal{S}(j)} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{j}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } \right)dt \\ &\ll_k T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}} \exp \left( - \frac{\log(1/\beta_j)}{21 \beta_{j+1}}\right). \end{align*} $$
$$ \begin{align*} &\int_{t\in \mathcal{S}(j)} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{j}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } \right)dt \\ &\ll_k T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}} \exp \left( - \frac{\log(1/\beta_j)}{21 \beta_{j+1}}\right). \end{align*} $$
We shall remark that although Lemma 3.1 and the second part of Lemma 3.2 are not used directly in the proof of Theorem 1.3, they will be required for the proof of the following lemma (see, for instance, the argument leading to (6.11)).
Lemma 3.3 In the notation and assumption as above, we have
 $$ \begin{align} & \int_{t\in \mathcal{T}} \exp \left( 2k {\mathfrak{Re}} \left( \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } + \sum_{p\le \log T }\frac{\cos((\alpha_1-\alpha_2)\log p)}{ 2p^{1+ \mathrm{i} (2t+(\alpha_1+\alpha_2))}} \right) \right) dt \nonumber\\ & \ll_k T (\log T)^{\frac{k^2}{2}} \left(\mathcal{F}(T,\alpha_1,\alpha_2) \right)^{\frac{k^2}{2}},\nonumber\\ \end{align} $$
$$ \begin{align} & \int_{t\in \mathcal{T}} \exp \left( 2k {\mathfrak{Re}} \left( \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } + \sum_{p\le \log T }\frac{\cos((\alpha_1-\alpha_2)\log p)}{ 2p^{1+ \mathrm{i} (2t+(\alpha_1+\alpha_2))}} \right) \right) dt \nonumber\\ & \ll_k T (\log T)^{\frac{k^2}{2}} \left(\mathcal{F}(T,\alpha_1,\alpha_2) \right)^{\frac{k^2}{2}},\nonumber\\ \end{align} $$
and for
![]() $1\le j\le \mathcal {I}-1$
, we have
$1\le j\le \mathcal {I}-1$
, we have
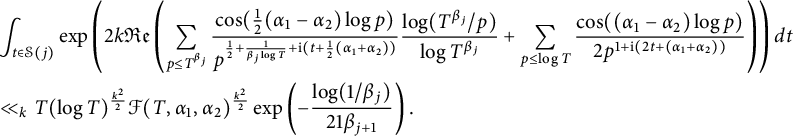 $$ \begin{align} & \int_{t\in \mathcal{S}(j)} \exp \left( 2k {\mathfrak{Re}} \left(\sum_{ p\le T^{\beta_{j}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } + \sum_{p\le \log T }\frac{\cos((\alpha_1-\alpha_2)\log p)}{ 2p^{1+ \mathrm{i} (2t+(\alpha_1+\alpha_2))}} \right) \right) dt \nonumber\\ & \ll_k T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}} \exp \left( - \frac{\log(1/\beta_j)}{21 \beta_{j+1}}\right).\nonumber\\ \end{align} $$
$$ \begin{align} & \int_{t\in \mathcal{S}(j)} \exp \left( 2k {\mathfrak{Re}} \left(\sum_{ p\le T^{\beta_{j}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } + \sum_{p\le \log T }\frac{\cos((\alpha_1-\alpha_2)\log p)}{ 2p^{1+ \mathrm{i} (2t+(\alpha_1+\alpha_2))}} \right) \right) dt \nonumber\\ & \ll_k T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}} \exp \left( - \frac{\log(1/\beta_j)}{21 \beta_{j+1}}\right).\nonumber\\ \end{align} $$
Now, we are ready to prove Theorem 1.3.
Proof of Theorem 1.3
We must show that inequality (3.5) holds. It suffices to show that each of the two terms on the left-hand side of (3.5) is
![]() $\ll T (\log T)^{\frac {k^2}{2}} \mathcal {F}(T,\alpha _1, \alpha _2)^{\frac {k^2}{2}}$
. By (3.8), we know that
$\ll T (\log T)^{\frac {k^2}{2}} \mathcal {F}(T,\alpha _1, \alpha _2)^{\frac {k^2}{2}}$
. By (3.8), we know that
![]() $\log ( |\zeta (\frac {1}{2}+\mathrm {i} (t+\alpha _1))|^k|\zeta (\frac {1}{2}+\mathrm {i}(t+\alpha _2))|^k )$
is at most
$\log ( |\zeta (\frac {1}{2}+\mathrm {i} (t+\alpha _1))|^k|\zeta (\frac {1}{2}+\mathrm {i}(t+\alpha _2))|^k )$
is at most
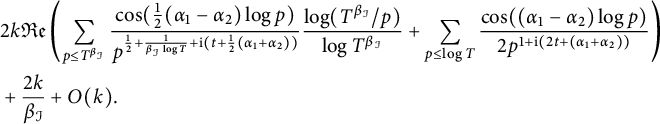 $$ \begin{align*} &2k {\mathfrak{Re}}\left( \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } + \sum_{p\le \log T }\frac{\cos((\alpha_1-\alpha_2)\log p)}{2p^{1+ \mathrm{i}( 2t+(\alpha_1+\alpha_2))}} \right)\\ & + \frac{2k}{\beta_{\mathcal{I}}} +O(k). \end{align*} $$
$$ \begin{align*} &2k {\mathfrak{Re}}\left( \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } + \sum_{p\le \log T }\frac{\cos((\alpha_1-\alpha_2)\log p)}{2p^{1+ \mathrm{i}( 2t+(\alpha_1+\alpha_2))}} \right)\\ & + \frac{2k}{\beta_{\mathcal{I}}} +O(k). \end{align*} $$
Hence, (3.9) of Lemma 3.3 implies
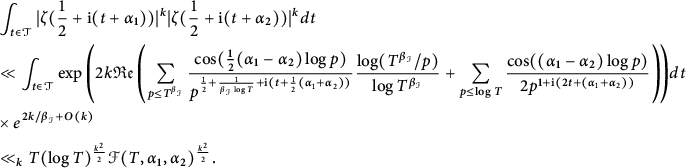 $$\begin{align} & \int_{t\in\mathcal{T} } |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_2))|^k dt \nonumber\\ &\ll \int_{t\in \mathcal{T}} \exp\left( 2k {\mathfrak{Re}}\left(\sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } + \sum_{p\le \log T }\frac{\cos((\alpha_1-\alpha_2)\log p)}{2p^{1+ \mathrm{i}(2 t+(\alpha_1+\alpha_2))}} \right) \!\right) \!dt \nonumber\\ &\times e^{2k/\beta_{\mathcal{I}} +O(k)} \nonumber\\ &\ll_k T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}. \end{align} $$
$$\begin{align} & \int_{t\in\mathcal{T} } |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_2))|^k dt \nonumber\\ &\ll \int_{t\in \mathcal{T}} \exp\left( 2k {\mathfrak{Re}}\left(\sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } + \sum_{p\le \log T }\frac{\cos((\alpha_1-\alpha_2)\log p)}{2p^{1+ \mathrm{i}(2 t+(\alpha_1+\alpha_2))}} \right) \!\right) \!dt \nonumber\\ &\times e^{2k/\beta_{\mathcal{I}} +O(k)} \nonumber\\ &\ll_k T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}. \end{align} $$
Here, we have used the fact that
![]() $e^{2k / \beta _{\mathcal {I}}}\ll _k 1$
as
$e^{2k / \beta _{\mathcal {I}}}\ll _k 1$
as
![]() $\beta _{\mathcal {I}} \geq e^{-1000k}$
by the definition of
$\beta _{\mathcal {I}} \geq e^{-1000k}$
by the definition of
![]() $\mathcal {I}$
. Similarly, for
$\mathcal {I}$
. Similarly, for
![]() $1\le j \le \mathcal {I}-1$
, we can bound
$1\le j \le \mathcal {I}-1$
, we can bound
![]() $\log ( |\zeta (\frac {1}{2}+\mathrm {i} (t+\alpha _1))|^k|\zeta (\frac {1}{2}+\mathrm {i}(t+\alpha _2))|^k )$
above by
$\log ( |\zeta (\frac {1}{2}+\mathrm {i} (t+\alpha _1))|^k|\zeta (\frac {1}{2}+\mathrm {i}(t+\alpha _2))|^k )$
above by
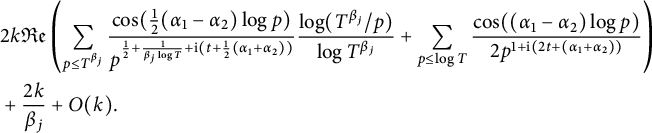 $$ \begin{align*} &2k {\mathfrak{Re}}\left(\sum_{ p\le T^{\beta_{j}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } + \sum_{p\le \log T }\frac{\cos((\alpha_1-\alpha_2)\log p)}{2p^{1+\mathrm{i}(2 t+(\alpha_1+\alpha_2))}} \right) \\ &+ \frac{2k}{\beta_{j}} +O(k). \end{align*} $$
$$ \begin{align*} &2k {\mathfrak{Re}}\left(\sum_{ p\le T^{\beta_{j}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } + \sum_{p\le \log T }\frac{\cos((\alpha_1-\alpha_2)\log p)}{2p^{1+\mathrm{i}(2 t+(\alpha_1+\alpha_2))}} \right) \\ &+ \frac{2k}{\beta_{j}} +O(k). \end{align*} $$
It then follows from Lemma 3.3 that
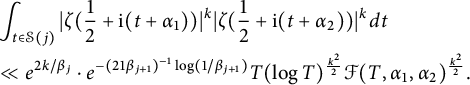 $$ \begin{align*} & \int_{t\in\mathcal{S}(j) }|\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_2))|^k dt \\ & \ll e^{2k/\beta_j}\cdot e^{- (21 \beta_{j+1})^{-1} \log(1/\beta_{j+1})} T (\log T)^{\frac{k^2}{2}}\mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}. \end{align*} $$
$$ \begin{align*} & \int_{t\in\mathcal{S}(j) }|\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_2))|^k dt \\ & \ll e^{2k/\beta_j}\cdot e^{- (21 \beta_{j+1})^{-1} \log(1/\beta_{j+1})} T (\log T)^{\frac{k^2}{2}}\mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}. \end{align*} $$
Since
![]() $20\beta _j= \beta _{j+1}\le \beta _{\mathcal {I}}\le 20 e^{-1000k}$
,
$20\beta _j= \beta _{j+1}\le \beta _{\mathcal {I}}\le 20 e^{-1000k}$
,
![]() $\log (1/\beta _{j+1})\ge 900k$
, and so
$\log (1/\beta _{j+1})\ge 900k$
, and so
Observe that
![]() $\mathcal {I} \le \frac {2}{\log 20}\log \log \log T$
and
$\mathcal {I} \le \frac {2}{\log 20}\log \log \log T$
and
 $$ \begin{align}\begin{aligned} \sum_{j=1}^{\mathcal{I}-1} e^{-0.1k/\beta_j} & = \sum_{j=1}^{\mathcal{I}-1} e^{-2k(\log\log T)^2/ 20^j}\\& \le e^{-2k(\log\log T)^2}+ \int_{1}^{\frac{2}{(\log 20)}\log\log\log T} e^{-2k(\log\log T)^2/ 20^x} dx.\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \sum_{j=1}^{\mathcal{I}-1} e^{-0.1k/\beta_j} & = \sum_{j=1}^{\mathcal{I}-1} e^{-2k(\log\log T)^2/ 20^j}\\& \le e^{-2k(\log\log T)^2}+ \int_{1}^{\frac{2}{(\log 20)}\log\log\log T} e^{-2k(\log\log T)^2/ 20^x} dx.\end{aligned}\end{align} $$
By the change of variables
![]() $20^{-x} =u$
(with
$20^{-x} =u$
(with
![]() $dx = \frac {-1}{\log 20} \frac {du}{u} $
), we see that the integral above equals
$dx = \frac {-1}{\log 20} \frac {du}{u} $
), we see that the integral above equals
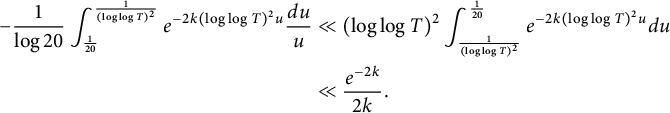 $$ \begin{align} -\frac{1}{\log 20}\int_{\frac{1}{20}}^{ \frac{1}{(\log\log T)^2}} e^{-2k(\log\log T)^2 u} \frac{du}{u} & \ll (\log\log T)^2 \int_{ \frac{1}{(\log\log T)^2}}^{\frac{1}{20}} e^{-2k(\log\log T)^2 u} du \nonumber\\ & \ll \frac{e^{-2k}}{2k}. \end{align} $$
$$ \begin{align} -\frac{1}{\log 20}\int_{\frac{1}{20}}^{ \frac{1}{(\log\log T)^2}} e^{-2k(\log\log T)^2 u} \frac{du}{u} & \ll (\log\log T)^2 \int_{ \frac{1}{(\log\log T)^2}}^{\frac{1}{20}} e^{-2k(\log\log T)^2 u} du \nonumber\\ & \ll \frac{e^{-2k}}{2k}. \end{align} $$
Combining (3.12) and (3.13), we arrive at
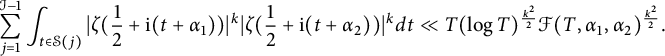 $$ \begin{align} \sum_{j=1}^{\mathcal{I}-1} \int_{t\in\mathcal{S}(j) } |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_2))|^k dt \ll T (\log T)^{\frac{k^2}{2}}\mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}. \end{align} $$
$$ \begin{align} \sum_{j=1}^{\mathcal{I}-1} \int_{t\in\mathcal{S}(j) } |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_2))|^k dt \ll T (\log T)^{\frac{k^2}{2}}\mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}. \end{align} $$
For
![]() $j=0$
, by the Cauchy–Schwarz inequality, we have
$j=0$
, by the Cauchy–Schwarz inequality, we have
 $$ \begin{align} &\int_{t\in\mathcal{S}(0) } |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_2))|^k dt \nonumber\\ &\le \operatorname{\mathrm{meas}}(\mathcal{S}(0))^{\frac{1}{2}} \left( \int_T^{2T} |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^{2k}|\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_2))|^{2k} dt \right)^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} &\int_{t\in\mathcal{S}(0) } |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_2))|^k dt \nonumber\\ &\le \operatorname{\mathrm{meas}}(\mathcal{S}(0))^{\frac{1}{2}} \left( \int_T^{2T} |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^{2k}|\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_2))|^{2k} dt \right)^{\frac{1}{2}}. \end{align} $$
Using the Cauchy–Schwarz inequality again and the upper bound (1.3) with
![]() $\varepsilon =1$
, we see
$\varepsilon =1$
, we see
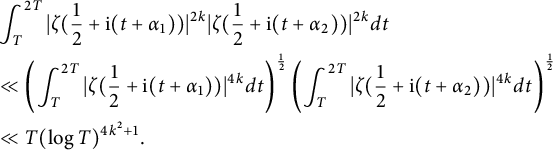 $$ \begin{align*} &\int_T^{2T} |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^{2k}|\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_2))|^{2k} dt \\ &\ll \left( \int_T^{2T} |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^{4 k} dt \right)^{\frac{1}{2}} \left( \int_T^{2T} |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_2))|^{4k} dt \right)^{\frac{1}{2}}\\ & \ll T (\log T)^{4k^2 + 1}. \end{align*} $$
$$ \begin{align*} &\int_T^{2T} |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^{2k}|\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_2))|^{2k} dt \\ &\ll \left( \int_T^{2T} |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^{4 k} dt \right)^{\frac{1}{2}} \left( \int_T^{2T} |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_2))|^{4k} dt \right)^{\frac{1}{2}}\\ & \ll T (\log T)^{4k^2 + 1}. \end{align*} $$
This, combined with (3.15) and Lemma 3.2, gives
 $$ \begin{align} &\int_{t\in\mathcal{S}(0) } |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_2))|^k dt \nonumber\\ &\ll \sqrt{T}e^{-(\log\log T)^2/20}\cdot \sqrt{T} (\log T)^{2k^2+\frac{1}{2}}\\ &\ll T.\nonumber \end{align} $$
$$ \begin{align} &\int_{t\in\mathcal{S}(0) } |\zeta(\frac{1}{2}+\mathrm{i} (t+\alpha_1))|^k|\zeta(\frac{1}{2}+\mathrm{i}(t+\alpha_2))|^k dt \nonumber\\ &\ll \sqrt{T}e^{-(\log\log T)^2/20}\cdot \sqrt{T} (\log T)^{2k^2+\frac{1}{2}}\\ &\ll T.\nonumber \end{align} $$
Therefore, by combining inequalities (3.11), (3.14), and (3.16), we establish (3.5), which together with (3.4) yields
Recall that under the Riemann hypothesis,
![]() $|\zeta (\frac {1}{2}+i t)| \ll (1+|t|)^\varepsilon $
(see [Reference Soundararajan21, Corollary C]). Hence,
$|\zeta (\frac {1}{2}+i t)| \ll (1+|t|)^\varepsilon $
(see [Reference Soundararajan21, Corollary C]). Hence,
Now, let
![]() $\log _2$
denote the base 2 logarithm, and let
$\log _2$
denote the base 2 logarithm, and let
![]() $j=j(T)$
be the smallest integer such that
$j=j(T)$
be the smallest integer such that
![]() $j\ge \log _2 \sqrt {T}$
. Plugging the values
$j\ge \log _2 \sqrt {T}$
. Plugging the values
![]() $T/2, \ldots , T/2^j$
into (3.17), we obtain
$T/2, \ldots , T/2^j$
into (3.17), we obtain
 $$ \begin{align*} I_k( T, \alpha_1 , \alpha_2) - I_k( T/2^j, \alpha_1 , \alpha_2)&\ll (T/2 + \cdots + T/2^j ) \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}\\ & \le T \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}. \end{align*} $$
$$ \begin{align*} I_k( T, \alpha_1 , \alpha_2) - I_k( T/2^j, \alpha_1 , \alpha_2)&\ll (T/2 + \cdots + T/2^j ) \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}\\ & \le T \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}. \end{align*} $$
This, together with (3.18), completes the proof of Theorem 1.3.
4 Proof of Lemma 3.1
Observe that
 $$ \begin{align} \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } = \sum_{ i=1}^{\mathcal{I}} F_i(t), \end{align} $$
$$ \begin{align} \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } = \sum_{ i=1}^{\mathcal{I}} F_i(t), \end{align} $$
where
![]() $F_i$
is defined by (3.2). By (4.1), we have
$F_i$
is defined by (3.2). By (4.1), we have
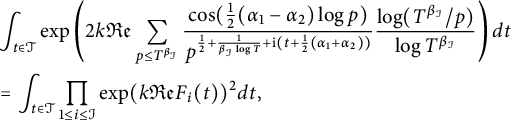 $$ \begin{align} &\int_{t\in \mathcal{T}} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \\ &= \int_{t\in \mathcal{T}} \prod_{1\le i \le \mathcal{I}} \exp( k{\mathfrak{Re}} F_i(t) )^2 dt,\nonumber \end{align} $$
$$ \begin{align} &\int_{t\in \mathcal{T}} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \\ &= \int_{t\in \mathcal{T}} \prod_{1\le i \le \mathcal{I}} \exp( k{\mathfrak{Re}} F_i(t) )^2 dt,\nonumber \end{align} $$
where we recall that
![]() $\mathcal {T}$
is defined in (3.3). To proceed, we need the following lemma, which establishes that each factor
$\mathcal {T}$
is defined in (3.3). To proceed, we need the following lemma, which establishes that each factor
![]() $\exp (k {\mathfrak {Re}} F_i(t))$
can be replaced by a Taylor polynomial of length
$\exp (k {\mathfrak {Re}} F_i(t))$
can be replaced by a Taylor polynomial of length
![]() $100k \beta _{i}^{-3/4}$
.
$100k \beta _{i}^{-3/4}$
.
Lemma 4.1 If
![]() $t\in \mathcal {T}$
, we have
$t\in \mathcal {T}$
, we have
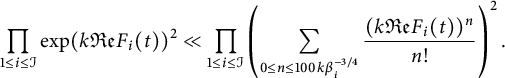 $$ \begin{align*} \prod_{1\le i \le \mathcal{I}} \exp( k{\mathfrak{Re}} F_i(t) )^2 \ll \prod_{1\le i \le \mathcal{I}}\left(\sum_{0\le n \le 100k \beta_i^{-3/4}} \frac{(k {\mathfrak{Re}} F_i(t) )^n}{n!} \right)^2. \end{align*} $$
$$ \begin{align*} \prod_{1\le i \le \mathcal{I}} \exp( k{\mathfrak{Re}} F_i(t) )^2 \ll \prod_{1\le i \le \mathcal{I}}\left(\sum_{0\le n \le 100k \beta_i^{-3/4}} \frac{(k {\mathfrak{Re}} F_i(t) )^n}{n!} \right)^2. \end{align*} $$
Proof We shall follow the argument used in [Reference Kirila10, Lemma 5.2, pp. 484–486]. We begin by recalling that for any
![]() $x\in \Bbb {R}$
and positive integer
$x\in \Bbb {R}$
and positive integer
![]() $N\in \Bbb {N}$
, Taylor’s theorem (with explicit remainder in the Lagrange form) asserts that there exists
$N\in \Bbb {N}$
, Taylor’s theorem (with explicit remainder in the Lagrange form) asserts that there exists
![]() $\xi $
between
$\xi $
between
![]() $0$
and x such that
$0$
and x such that
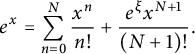 $$\begin{align*}e^x = \sum_{n=0}^N \frac{x^n}{n!} + \frac{e^\xi x^{N+1}}{(N+1)!}. \end{align*}$$
$$\begin{align*}e^x = \sum_{n=0}^N \frac{x^n}{n!} + \frac{e^\xi x^{N+1}}{(N+1)!}. \end{align*}$$
Thus, we derive
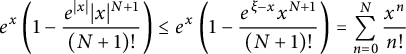 $$ \begin{align} e^x \left( 1 - \frac{e^{|x|} |x|^{N+1}}{(N+1)!}\right) \le e^{x} \left( 1 - \frac{e^{\xi-x} x^{N+1}}{(N+1)!}\right) =\sum_{n=0}^N \frac{x^n}{n!} \end{align} $$
$$ \begin{align} e^x \left( 1 - \frac{e^{|x|} |x|^{N+1}}{(N+1)!}\right) \le e^{x} \left( 1 - \frac{e^{\xi-x} x^{N+1}}{(N+1)!}\right) =\sum_{n=0}^N \frac{x^n}{n!} \end{align} $$
as
![]() $\xi -x \le |\xi -x | \le |0 -x| = |x|$
, which follows from the fact that
$\xi -x \le |\xi -x | \le |0 -x| = |x|$
, which follows from the fact that
![]() $\xi $
is closer (than
$\xi $
is closer (than
![]() $0$
) to x.
$0$
) to x.
Note that when
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $1 \leq i \leq \mathcal {I}$
,
$1 \leq i \leq \mathcal {I}$
,
![]() $\beta _i \le \beta _{\mathcal {I}}\le 20 e^{-1000k}$
, which gives
$\beta _i \le \beta _{\mathcal {I}}\le 20 e^{-1000k}$
, which gives
![]() $\beta _i^{-3/4} \geq 1$
for
$\beta _i^{-3/4} \geq 1$
for
![]() $1 \leq i \leq \mathcal {I}$
. Hence, taking
$1 \leq i \leq \mathcal {I}$
. Hence, taking
![]() $x = k {\mathfrak {Re}} F_i(t) $
and
$x = k {\mathfrak {Re}} F_i(t) $
and
![]() $N= [100k \beta _i^{-3/4}]$
in (4.3), we obtain
$N= [100k \beta _i^{-3/4}]$
in (4.3), we obtain
 $$ \begin{align} e^{k {\mathfrak{Re}} F_i(t)} \left( 1 - \frac{e^{|k {\mathfrak{Re}} F_i(t)|} |k {\mathfrak{Re}} F_i(t)|^{[100k \beta_i^{-3/4}]+1}}{([100k \beta_i^{-3/4}]+1)!}\right) \leq \sum_{n=0}^{[100k \beta_i^{-3/4}]} \frac{(k {\mathfrak{Re}} F_i(t))^n}{n!}. \end{align} $$
$$ \begin{align} e^{k {\mathfrak{Re}} F_i(t)} \left( 1 - \frac{e^{|k {\mathfrak{Re}} F_i(t)|} |k {\mathfrak{Re}} F_i(t)|^{[100k \beta_i^{-3/4}]+1}}{([100k \beta_i^{-3/4}]+1)!}\right) \leq \sum_{n=0}^{[100k \beta_i^{-3/4}]} \frac{(k {\mathfrak{Re}} F_i(t))^n}{n!}. \end{align} $$
Using the fact
![]() $n! \geq \left ( \frac {n}{e}\right )^n$
, we see
$n! \geq \left ( \frac {n}{e}\right )^n$
, we see
 $$ \begin{align*} \frac{e^{|k {\mathfrak{Re}} F_i(t)|} |k {\mathfrak{Re}} F_i(t)|^{[100k \beta_i^{-3/4}]+1}}{([100k \beta_i^{-3/4}]+1)!} &\leq \frac{e^{|k {\mathfrak{Re}} F_i(t)|} |k {\mathfrak{Re}} F_i(t)|^{[100k \beta_i^{-3/4}]+1} e^{[100k \beta_i^{-3/4}]+1}}{([100k \beta_i^{-3/4}]+1)^{[100k \beta_i^{-3/4}]+1}}. \end{align*} $$
$$ \begin{align*} \frac{e^{|k {\mathfrak{Re}} F_i(t)|} |k {\mathfrak{Re}} F_i(t)|^{[100k \beta_i^{-3/4}]+1}}{([100k \beta_i^{-3/4}]+1)!} &\leq \frac{e^{|k {\mathfrak{Re}} F_i(t)|} |k {\mathfrak{Re}} F_i(t)|^{[100k \beta_i^{-3/4}]+1} e^{[100k \beta_i^{-3/4}]+1}}{([100k \beta_i^{-3/4}]+1)^{[100k \beta_i^{-3/4}]+1}}. \end{align*} $$
As
![]() $|{\mathfrak {Re}} F_i(t)| \leq \beta _i^{-3/4}$
for
$|{\mathfrak {Re}} F_i(t)| \leq \beta _i^{-3/4}$
for
![]() $t\in \mathcal {T}$
, the right of the above expression is at most
$t\in \mathcal {T}$
, the right of the above expression is at most
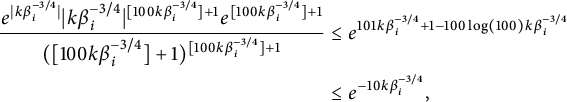 $$ \begin{align*} \frac{e^{|k \beta_i^{-3/4}|} |k \beta_i^{-3/4}|^{[100k \beta_i^{-3/4}]+1} e^{[100k \beta_i^{-3/4}]+1}}{([100k \beta_i^{-3/4}]+1)^{[100k \beta_i^{-3/4}]+1}} &\leq e^{101k \beta_i^{-3/4}+1- 100 \log (100) k\beta_i^{-3/4}}\\ & \leq e^{-10 k\beta_i^{-3/4}}, \end{align*} $$
$$ \begin{align*} \frac{e^{|k \beta_i^{-3/4}|} |k \beta_i^{-3/4}|^{[100k \beta_i^{-3/4}]+1} e^{[100k \beta_i^{-3/4}]+1}}{([100k \beta_i^{-3/4}]+1)^{[100k \beta_i^{-3/4}]+1}} &\leq e^{101k \beta_i^{-3/4}+1- 100 \log (100) k\beta_i^{-3/4}}\\ & \leq e^{-10 k\beta_i^{-3/4}}, \end{align*} $$
which implies
 $$ \begin{align*} 1 - \frac{e^{|k {\mathfrak{Re}} F_i(t)|} |k {\mathfrak{Re}} F_i(t)|^{[100k \beta_i^{-3/4}]+1}}{([100k \beta_i^{-3/4}]+1)!} \geq 1- e^{-10 k\beta_i^{-3/4}} \geq e^{-\frac{1}{10k}\beta_i^{3/4 }} (\geq 0), \end{align*} $$
$$ \begin{align*} 1 - \frac{e^{|k {\mathfrak{Re}} F_i(t)|} |k {\mathfrak{Re}} F_i(t)|^{[100k \beta_i^{-3/4}]+1}}{([100k \beta_i^{-3/4}]+1)!} \geq 1- e^{-10 k\beta_i^{-3/4}} \geq e^{-\frac{1}{10k}\beta_i^{3/4 }} (\geq 0), \end{align*} $$
where the (second) last inequality follows from the fact that
![]() $1-e^{-x} \geq e^{-1/x}$
for
$1-e^{-x} \geq e^{-1/x}$
for
![]() $x>0$
. Inserting this into (4.4), we then deduce
$x>0$
. Inserting this into (4.4), we then deduce
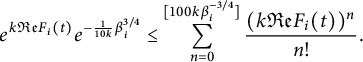 $$ \begin{align} e^{k {\mathfrak{Re}} F_i(t)} e^{-\frac{1}{10k}\beta_i^{3/4}} \leq \sum_{n=0}^{[100k \beta_i^{-3/4}]} \frac{(k {\mathfrak{Re}} F_i(t))^n}{n!}. \end{align} $$
$$ \begin{align} e^{k {\mathfrak{Re}} F_i(t)} e^{-\frac{1}{10k}\beta_i^{3/4}} \leq \sum_{n=0}^{[100k \beta_i^{-3/4}]} \frac{(k {\mathfrak{Re}} F_i(t))^n}{n!}. \end{align} $$
Note that
![]() $\prod _{i=1}^{\mathcal {I}}e^{-\frac {1}{10k}\beta _i^{3/4}} $
equals
$\prod _{i=1}^{\mathcal {I}}e^{-\frac {1}{10k}\beta _i^{3/4}} $
equals
which, together with (4.5), completes the proof of the lemma.
It follows from Lemma 4.1 that
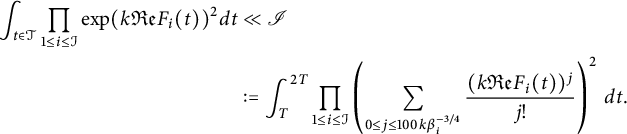 $$ \begin{align} \int_{t\in \mathcal{T}} \prod_{1\le i \le \mathcal{I}} \exp( k{\mathfrak{Re}} F_i(t) )^2 dt & \ll \mathscr{I} \nonumber\\ & := \int_T^{2T} \prod_{1\le i \le \mathcal{I}}\left(\sum_{0\le j \le 100k \beta_i^{-3/4}} \frac{(k {\mathfrak{Re}} F_i(t) )^j}{j!} \right)^2\, dt. \end{align} $$
$$ \begin{align} \int_{t\in \mathcal{T}} \prod_{1\le i \le \mathcal{I}} \exp( k{\mathfrak{Re}} F_i(t) )^2 dt & \ll \mathscr{I} \nonumber\\ & := \int_T^{2T} \prod_{1\le i \le \mathcal{I}}\left(\sum_{0\le j \le 100k \beta_i^{-3/4}} \frac{(k {\mathfrak{Re}} F_i(t) )^j}{j!} \right)^2\, dt. \end{align} $$
In order to simplify the presentation, we set
Expanding out all of the jth powers and opening the square, we see that
 $$ \begin{align} \mathscr{I} & = \sum_{\tilde{j}, \tilde{\ell}} \prod_{1\le i \le \mathcal{I}} \frac{k^{j_i}}{j_i !}\frac{k^{\ell_i}}{\ell_i !} \sum_{\tilde{p}, \tilde{q}} C(\tilde{p}, \tilde{q}) \nonumber\\ & \times \int_T^{2T}\prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos((t+\gamma^+)\log p(i,r) )\cos((t+\gamma^+)\log q(i,s) ) dt\\ & \times \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos(\gamma^-\log p(i,r) )\cos(\gamma^-\log q(i,s) ),\nonumber \end{align} $$
$$ \begin{align} \mathscr{I} & = \sum_{\tilde{j}, \tilde{\ell}} \prod_{1\le i \le \mathcal{I}} \frac{k^{j_i}}{j_i !}\frac{k^{\ell_i}}{\ell_i !} \sum_{\tilde{p}, \tilde{q}} C(\tilde{p}, \tilde{q}) \nonumber\\ & \times \int_T^{2T}\prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos((t+\gamma^+)\log p(i,r) )\cos((t+\gamma^+)\log q(i,s) ) dt\\ & \times \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos(\gamma^-\log p(i,r) )\cos(\gamma^-\log q(i,s) ),\nonumber \end{align} $$
where the first sum is over all
the second sum is over
 $$ \begin{align*} \tilde{p} & =( p(1,1),\ldots, p(1,j_1), p(2,1),\ldots,p(2,j_2),\ldots, p(\mathcal{I},j_{\mathcal{I}} )) \text{ and } \\ \tilde{q} & =( q(1,1),\ldots, q(1,\ell_1), q(2,1),\ldots,q(2,{\ell}_2),\ldots, q(\mathcal{I},{\ell}_{\mathcal{I}} )) \end{align*} $$
$$ \begin{align*} \tilde{p} & =( p(1,1),\ldots, p(1,j_1), p(2,1),\ldots,p(2,j_2),\ldots, p(\mathcal{I},j_{\mathcal{I}} )) \text{ and } \\ \tilde{q} & =( q(1,1),\ldots, q(1,\ell_1), q(2,1),\ldots,q(2,{\ell}_2),\ldots, q(\mathcal{I},{\ell}_{\mathcal{I}} )) \end{align*} $$
whose components are primes which satisfy
for any
![]() $1\le i\le \mathcal {I}$
, and
$1\le i\le \mathcal {I}$
, and
 $$ \begin{align}\begin{aligned} &C(\tilde{p}, \tilde{q})\\&\quad= \prod_{1\le i \le \mathcal{I}}\prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}}\frac{1}{p(i,r)^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T} } }\frac{\log(T^{\beta_{\mathcal{I}}}/p(i,r))}{\log T^{\beta_{\mathcal{I}}} } \frac{1}{q(i,s)^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T} } }\frac{\log(T^{\beta_{\mathcal{I}}}/q(i,s))}{\log T^{\beta_{\mathcal{I}}} }.\end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} &C(\tilde{p}, \tilde{q})\\&\quad= \prod_{1\le i \le \mathcal{I}}\prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}}\frac{1}{p(i,r)^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T} } }\frac{\log(T^{\beta_{\mathcal{I}}}/p(i,r))}{\log T^{\beta_{\mathcal{I}}} } \frac{1}{q(i,s)^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T} } }\frac{\log(T^{\beta_{\mathcal{I}}}/q(i,s))}{\log T^{\beta_{\mathcal{I}}} }.\end{aligned} \end{align} $$
Following the argument in [Reference Harper5, p. 10] (see the third displayed equation there), we have
 $$ \begin{align} \prod_{1\le i \le \mathcal{I}}\prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r)q(i,s) \le T^{0.1}. \end{align} $$
$$ \begin{align} \prod_{1\le i \le \mathcal{I}}\prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r)q(i,s) \le T^{0.1}. \end{align} $$
By Lemma 2.1 and (4.9), it follows that
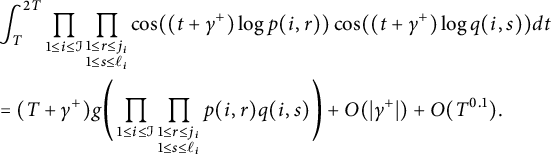 $$ \begin{align} & \int_T^{2T}\prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos((t+\gamma^+)\log p(i,r) )\cos((t+\gamma^+)\log q(i,s) ) dt \nonumber\\ & = (T+\gamma^+) g\Bigg( \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r) q(i,s) \Bigg) + O(|\gamma^+|) +O(T^{0.1}). \end{align} $$
$$ \begin{align} & \int_T^{2T}\prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos((t+\gamma^+)\log p(i,r) )\cos((t+\gamma^+)\log q(i,s) ) dt \nonumber\\ & = (T+\gamma^+) g\Bigg( \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r) q(i,s) \Bigg) + O(|\gamma^+|) +O(T^{0.1}). \end{align} $$
Observe that
 $$ \begin{align} C(\tilde{p}, \tilde{q})\le D(\tilde{p}, \tilde{q}):= \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \frac{1}{\sqrt{p(i,r)}}\frac{1}{\sqrt{ q(i,s) }}. \end{align} $$
$$ \begin{align} C(\tilde{p}, \tilde{q})\le D(\tilde{p}, \tilde{q}):= \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \frac{1}{\sqrt{p(i,r)}}\frac{1}{\sqrt{ q(i,s) }}. \end{align} $$
By (4.10), (4.11), and the bound
![]() $|\cos x|\le 1$
for real x, it follows that (4.7) equals
$|\cos x|\le 1$
for real x, it follows that (4.7) equals
 $$ \begin{align} \mathscr{I} & =(T+\gamma^+) \sum_{\tilde{j}, \tilde{\ell}} \prod_{1\le i \le \mathcal{I}} \frac{k^{j_i}}{j_i !}\frac{k^{\ell_i}}{\ell_i !} \sum_{\tilde{p}, \tilde{q}} C(\tilde{p}, \tilde{q}) g\Bigg( \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r) q(i,s) \Bigg) \nonumber\\ & \times \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos(\gamma^-\log p(i,r) )\cos(\gamma^-\log q(i,s) ) \\ &+O\left( (|\gamma^+|+T^{0.1}) \sum_{\tilde{j}, \tilde{\ell}} \prod_{1\le i \le \mathcal{I}} \frac{k^{j_i}}{j_i !}\frac{k^{\ell_i}}{\ell_i !} \sum_{\tilde{p}, \tilde{q}} D(\tilde{p}, \tilde{q}) \right).\nonumber \end{align} $$
$$ \begin{align} \mathscr{I} & =(T+\gamma^+) \sum_{\tilde{j}, \tilde{\ell}} \prod_{1\le i \le \mathcal{I}} \frac{k^{j_i}}{j_i !}\frac{k^{\ell_i}}{\ell_i !} \sum_{\tilde{p}, \tilde{q}} C(\tilde{p}, \tilde{q}) g\Bigg( \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r) q(i,s) \Bigg) \nonumber\\ & \times \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos(\gamma^-\log p(i,r) )\cos(\gamma^-\log q(i,s) ) \\ &+O\left( (|\gamma^+|+T^{0.1}) \sum_{\tilde{j}, \tilde{\ell}} \prod_{1\le i \le \mathcal{I}} \frac{k^{j_i}}{j_i !}\frac{k^{\ell_i}}{\ell_i !} \sum_{\tilde{p}, \tilde{q}} D(\tilde{p}, \tilde{q}) \right).\nonumber \end{align} $$
By the argument of Harper [Reference Harper5, p. 10], it can be shown that the big-O term above is at most
![]() $(|\gamma ^+|+T^{0.1}) T^{0.1}(\log \log T)^{2k}$
.
$(|\gamma ^+|+T^{0.1}) T^{0.1}(\log \log T)^{2k}$
.
The inner summand in (4.12) is
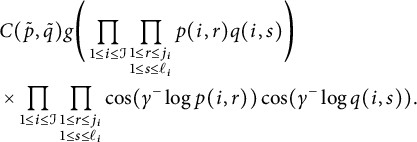 $$ \begin{align*} & C(\tilde{p}, \tilde{q}) g\Bigg( \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r) q(i,s) \Bigg)\\ & \times \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos(\gamma^-\log p(i,r) )\cos(\gamma^-\log q(i,s) ). \end{align*} $$
$$ \begin{align*} & C(\tilde{p}, \tilde{q}) g\Bigg( \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r) q(i,s) \Bigg)\\ & \times \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos(\gamma^-\log p(i,r) )\cos(\gamma^-\log q(i,s) ). \end{align*} $$
Since g is supported on squares, this expression is nonzero if and only if
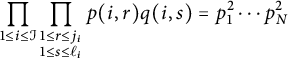 $$ \begin{align*}\prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r) q(i,s)=p_{1}^2 \cdots p_{N}^2\end{align*} $$
$$ \begin{align*}\prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r) q(i,s)=p_{1}^2 \cdots p_{N}^2\end{align*} $$
for some
![]() $N \in \mathbb {N}$
. In this case, we have
$N \in \mathbb {N}$
. In this case, we have
 $$ \begin{align} & \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos(\gamma^-\log p(i,r) )\cos(\gamma^-\log q(i,s) ) \nonumber\\ & =\cos^2(\gamma^-\log p_1) \cdots \cos^2(\gamma^- \log p_N)\\ & \ge 0.\nonumber \end{align} $$
$$ \begin{align} & \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} \cos(\gamma^-\log p(i,r) )\cos(\gamma^-\log q(i,s) ) \nonumber\\ & =\cos^2(\gamma^-\log p_1) \cdots \cos^2(\gamma^- \log p_N)\\ & \ge 0.\nonumber \end{align} $$
By (4.7) and (4.11)–(4.13), we deduce that
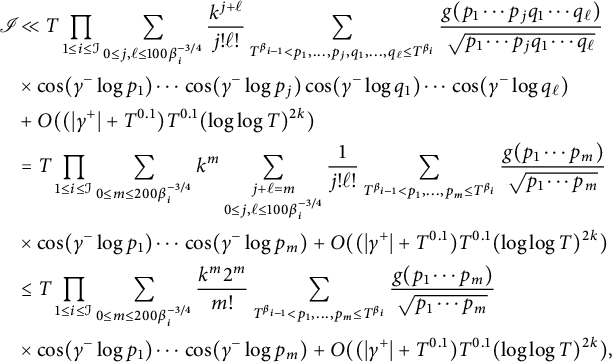 $$ \begin{align*} \mathscr{I} &\ll T \prod_{1\le i \le \mathcal{I}} \sum_{0\le j,\ell \le 100 \beta_i^{-3/4} }\frac{k^{j+\ell}}{j!\ell!} \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_j,q_1,\ldots, q_{\ell} \le T^{\beta_{i}}} \frac{g(p_1\cdots p_jq_1\cdots q_{\ell})}{\sqrt{p_1\cdots p_jq_1\cdots q_{\ell}}}\\ &\times \cos(\gamma^- \log p_1) \cdots \cos(\gamma^-\log p_j) \cos(\gamma^- \log q_1 )\cdots \cos(\gamma^- \log q_{\ell}) \\ &+ O( (|\gamma^+|+T^{0.1}) T^{0.1} (\log \log T)^{2k})\\ &= T \prod_{1\le i \le \mathcal{I}} \sum_{0\le m \le 200 \beta_i^{-3/4} } k^m \sum_{\substack{ j+\ell=m \\ 0\le j,\ell \le 100 \beta_i^{-3/4} }}\frac{1}{j!\ell!} \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_m \le T^{\beta_{i}}} \frac{g(p_1\cdots p_m)}{\sqrt{p_1\cdots p_m}}\\ &\times \cos(\gamma^- \log p_1) \cdots \cos(\gamma^- \log p_m) +O( (|\gamma^+|+T^{0.1}) T^{0.1} (\log \log T)^{2k})\\ &\le T \prod_{1\le i \le \mathcal{I}} \sum_{0\le m \le 200 \beta_i^{-3/4} } \frac{k^m 2^m}{m!} \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_m \le T^{\beta_{i}}} \frac{g(p_1\cdots p_m)}{\sqrt{p_1\cdots p_m}} \\ &\times \cos(\gamma^- \log p_1) \cdots \cos(\gamma^- \log p_m) +O( (|\gamma^+|+T^{0.1}) T^{0.1} (\log \log T)^{2k}), \end{align*} $$
$$ \begin{align*} \mathscr{I} &\ll T \prod_{1\le i \le \mathcal{I}} \sum_{0\le j,\ell \le 100 \beta_i^{-3/4} }\frac{k^{j+\ell}}{j!\ell!} \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_j,q_1,\ldots, q_{\ell} \le T^{\beta_{i}}} \frac{g(p_1\cdots p_jq_1\cdots q_{\ell})}{\sqrt{p_1\cdots p_jq_1\cdots q_{\ell}}}\\ &\times \cos(\gamma^- \log p_1) \cdots \cos(\gamma^-\log p_j) \cos(\gamma^- \log q_1 )\cdots \cos(\gamma^- \log q_{\ell}) \\ &+ O( (|\gamma^+|+T^{0.1}) T^{0.1} (\log \log T)^{2k})\\ &= T \prod_{1\le i \le \mathcal{I}} \sum_{0\le m \le 200 \beta_i^{-3/4} } k^m \sum_{\substack{ j+\ell=m \\ 0\le j,\ell \le 100 \beta_i^{-3/4} }}\frac{1}{j!\ell!} \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_m \le T^{\beta_{i}}} \frac{g(p_1\cdots p_m)}{\sqrt{p_1\cdots p_m}}\\ &\times \cos(\gamma^- \log p_1) \cdots \cos(\gamma^- \log p_m) +O( (|\gamma^+|+T^{0.1}) T^{0.1} (\log \log T)^{2k})\\ &\le T \prod_{1\le i \le \mathcal{I}} \sum_{0\le m \le 200 \beta_i^{-3/4} } \frac{k^m 2^m}{m!} \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_m \le T^{\beta_{i}}} \frac{g(p_1\cdots p_m)}{\sqrt{p_1\cdots p_m}} \\ &\times \cos(\gamma^- \log p_1) \cdots \cos(\gamma^- \log p_m) +O( (|\gamma^+|+T^{0.1}) T^{0.1} (\log \log T)^{2k}), \end{align*} $$
where the last inequality makes use of the nonnegativity of the inner summand. Since g is supported on squares, we must have that m is even, say
![]() $m=2n$
with
$m=2n$
with
![]() $n \ge 0$
. By relabeling the prime variables as
$n \ge 0$
. By relabeling the prime variables as
![]() $q_1, \ldots , q_{2n}$
, we see that
$q_1, \ldots , q_{2n}$
, we see that
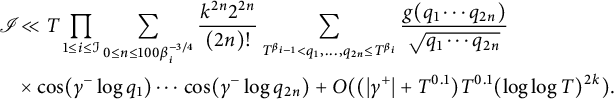 $$ \begin{align} \mathscr{I} & \ll T \prod_{1\le i \le \mathcal{I}} \sum_{0\le n \le 100 \beta_i^{-3/4} } \frac{k^{2n} 2^{2n}}{(2n)!} \sum_{T^{\beta_{i-1}}< q_1,\ldots,q_{2n} \le T^{\beta_{i}}} \frac{g(q_1\cdots q_{2n})}{\sqrt{q_1\cdots q_{2n}}} \\ &\times\cos(\gamma^- \log q_1) \cdots \cos(\gamma^- \log q_{2n}) +O( (|\gamma^+|+T^{0.1}) T^{0.1} (\log \log T)^{2k}). \nonumber \end{align} $$
$$ \begin{align} \mathscr{I} & \ll T \prod_{1\le i \le \mathcal{I}} \sum_{0\le n \le 100 \beta_i^{-3/4} } \frac{k^{2n} 2^{2n}}{(2n)!} \sum_{T^{\beta_{i-1}}< q_1,\ldots,q_{2n} \le T^{\beta_{i}}} \frac{g(q_1\cdots q_{2n})}{\sqrt{q_1\cdots q_{2n}}} \\ &\times\cos(\gamma^- \log q_1) \cdots \cos(\gamma^- \log q_{2n}) +O( (|\gamma^+|+T^{0.1}) T^{0.1} (\log \log T)^{2k}). \nonumber \end{align} $$
Next, we observe that
![]() $q_1 \cdots q_{2n}$
is a square if and only if it equals
$q_1 \cdots q_{2n}$
is a square if and only if it equals
![]() $p_{1}^2 \cdots p_{n}^2$
for some primes
$p_{1}^2 \cdots p_{n}^2$
for some primes
![]() $p_u \in [T^{\beta {i-1}}, T^{\beta _i}]$
with
$p_u \in [T^{\beta {i-1}}, T^{\beta _i}]$
with
![]() $1 \le u \le n$
. Grouping terms according to
$1 \le u \le n$
. Grouping terms according to
![]() $q_1 \cdots q_{2n} =p_{1}^2 \cdots p_{n}^2 $
gives
$q_1 \cdots q_{2n} =p_{1}^2 \cdots p_{n}^2 $
gives
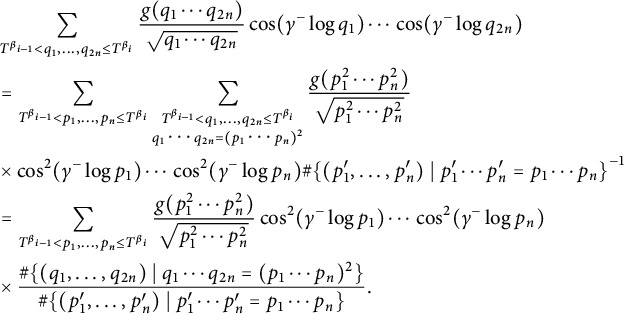 $$ \begin{align} &\sum_{T^{\beta_{i-1}}< q_1,\ldots,q_{2n} \le T^{\beta_{i}}} \frac{g(q_1\cdots q_{2n})}{\sqrt{q_1\cdots q_{2n}}} \cos(\gamma^- \log q_1) \cdots \cos(\gamma^- \log q_{2n}) \nonumber\\ &= \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_{n} \le T^{\beta_{i}}} \sum_{\substack{T^{\beta_{i-1}}< q_1,\ldots,q_{2n} \le T^{\beta_{i}} \\ q_1\cdots q_{2n} = (p_1\cdots p_{n})^2}} \frac{g(p_1^2\cdots p_{n}^2)}{\sqrt{p_1^2\cdots p_{n}^2}} \nonumber\\ &\times \cos^2(\gamma^- \log p_1) \cdots \cos^2(\gamma^- \log p_{n}){\#\{ (p_1',\ldots, p_{n}')\mid p_1'\cdots p_{n}'=p_1\cdots p_{n} \}}^{-1} \nonumber\\ &= \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_{n} \le T^{\beta_{i}}} \frac{g(p_1^2\cdots p_{n}^2)}{\sqrt{p_1^2\cdots p_{n}^2}} \cos^2(\gamma^- \log p_1) \cdots \cos^2(\gamma^- \log p_{n}) \nonumber\\ &\times \frac{ {\#\{ (q_1,\ldots, q_{2n})\mid q_1\cdots q_{2n}=(p_1 \cdots p_{n})^2 \}} }{ {\#\{ (p_1', \ldots , p_{n}')\mid p_1'\cdots p_{n}'=p_1\cdots p_{n} \}} }. \end{align} $$
$$ \begin{align} &\sum_{T^{\beta_{i-1}}< q_1,\ldots,q_{2n} \le T^{\beta_{i}}} \frac{g(q_1\cdots q_{2n})}{\sqrt{q_1\cdots q_{2n}}} \cos(\gamma^- \log q_1) \cdots \cos(\gamma^- \log q_{2n}) \nonumber\\ &= \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_{n} \le T^{\beta_{i}}} \sum_{\substack{T^{\beta_{i-1}}< q_1,\ldots,q_{2n} \le T^{\beta_{i}} \\ q_1\cdots q_{2n} = (p_1\cdots p_{n})^2}} \frac{g(p_1^2\cdots p_{n}^2)}{\sqrt{p_1^2\cdots p_{n}^2}} \nonumber\\ &\times \cos^2(\gamma^- \log p_1) \cdots \cos^2(\gamma^- \log p_{n}){\#\{ (p_1',\ldots, p_{n}')\mid p_1'\cdots p_{n}'=p_1\cdots p_{n} \}}^{-1} \nonumber\\ &= \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_{n} \le T^{\beta_{i}}} \frac{g(p_1^2\cdots p_{n}^2)}{\sqrt{p_1^2\cdots p_{n}^2}} \cos^2(\gamma^- \log p_1) \cdots \cos^2(\gamma^- \log p_{n}) \nonumber\\ &\times \frac{ {\#\{ (q_1,\ldots, q_{2n})\mid q_1\cdots q_{2n}=(p_1 \cdots p_{n})^2 \}} }{ {\#\{ (p_1', \ldots , p_{n}')\mid p_1'\cdots p_{n}'=p_1\cdots p_{n} \}} }. \end{align} $$
In the above, the factor
![]() ${\#\{ (p_1',\ldots , p_{n}')\mid p_1'\cdots p_{n}'=p_1\cdots p_{n} \}}^{-1}$
accounts for possible repetitions when counting squares
${\#\{ (p_1',\ldots , p_{n}')\mid p_1'\cdots p_{n}'=p_1\cdots p_{n} \}}^{-1}$
accounts for possible repetitions when counting squares
![]() $p_1^2 \cdots p_n^2$
. With this observation, we see that the first term on the right of (4.14) equals
$p_1^2 \cdots p_n^2$
. With this observation, we see that the first term on the right of (4.14) equals
 $$ \begin{align} & T \prod_{1\le i \le \mathcal{I}} \sum_{0\le n \le 100 \beta_i^{-3/4}} \frac{(2k)^{2n}}{(2n)!} \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_n \le T^{\beta_{i}}} \frac{g(p^2_1\cdots p^2_n)}{p_1\cdots p_n} \\ &\times \frac{\#\{(q_1\ldots q_{2n})\mid q_1\cdots q_{2n}=p_1^2\cdots p^2_{n} \}}{\#\{ (q_1\ldots q_{n})\mid q_1\cdots q_{n}=p_1\cdots p_{n} \}}\cos^2(\gamma^- \log p_1) \cdots \cos^2(\gamma^- \log p_n), \nonumber \end{align} $$
$$ \begin{align} & T \prod_{1\le i \le \mathcal{I}} \sum_{0\le n \le 100 \beta_i^{-3/4}} \frac{(2k)^{2n}}{(2n)!} \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_n \le T^{\beta_{i}}} \frac{g(p^2_1\cdots p^2_n)}{p_1\cdots p_n} \\ &\times \frac{\#\{(q_1\ldots q_{2n})\mid q_1\cdots q_{2n}=p_1^2\cdots p^2_{n} \}}{\#\{ (q_1\ldots q_{n})\mid q_1\cdots q_{n}=p_1\cdots p_{n} \}}\cos^2(\gamma^- \log p_1) \cdots \cos^2(\gamma^- \log p_n), \nonumber \end{align} $$
where each
![]() $q_i$
again denotes a prime in
$q_i$
again denotes a prime in
![]() $(T^{\beta _{i-1}},T^{\beta _{i}}]$
.
$(T^{\beta _{i-1}},T^{\beta _{i}}]$
.
By [Reference Harper5, equation (4.2)], we know
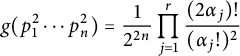 $$ \begin{align} g(p^2_1\cdots p^2_n) =\frac{1}{2^{2n}} \prod_{j=1}^r\frac{ (2\alpha_j)!}{(\alpha_j!)^2} \end{align} $$
$$ \begin{align} g(p^2_1\cdots p^2_n) =\frac{1}{2^{2n}} \prod_{j=1}^r\frac{ (2\alpha_j)!}{(\alpha_j!)^2} \end{align} $$
and
 $$ \begin{align} \frac{\#\{(q_1\ldots q_{2n})\mid q_1\cdots q_{2n}=p_1^2\cdots p^2_{n} \}}{\#\{ (q_1\ldots q_{n})\mid q_1\cdots q_{n}=p_1\cdots p_{n} \}} =\frac{(2n)!}{\prod_{j=1}^r(2\alpha_j)! } \left(\frac{n!}{\prod_{j=1}^r\alpha_j! } \right)^{-1} \end{align} $$
$$ \begin{align} \frac{\#\{(q_1\ldots q_{2n})\mid q_1\cdots q_{2n}=p_1^2\cdots p^2_{n} \}}{\#\{ (q_1\ldots q_{n})\mid q_1\cdots q_{n}=p_1\cdots p_{n} \}} =\frac{(2n)!}{\prod_{j=1}^r(2\alpha_j)! } \left(\frac{n!}{\prod_{j=1}^r\alpha_j! } \right)^{-1} \end{align} $$
whenever
![]() $p_1\cdots p_{n}$
is a product of r distinct primes with multiplicities
$p_1\cdots p_{n}$
is a product of r distinct primes with multiplicities
![]() $\alpha _1,\ldots ,\alpha _r$
(in particular,
$\alpha _1,\ldots ,\alpha _r$
(in particular,
![]() $\alpha _1+\cdots +\alpha _r=n$
). Therefore, the expression (4.16) is equal to
$\alpha _1+\cdots +\alpha _r=n$
). Therefore, the expression (4.16) is equal to
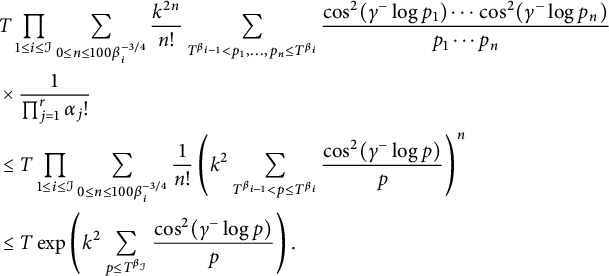 $$ \begin{align*} & T \prod_{1\le i \le \mathcal{I}} \sum_{0\le n \le 100 \beta_i^{-3/4}} \frac{k^{2n}}{n!} \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_n \le T^{\beta_{i}}} \frac{\cos^2(\gamma^- \log p_1) \cdots \cos^2(\gamma^- \log p_n)}{p_1\cdots p_n} \\ &\times\frac{1}{\prod_{j=1}^r \alpha_j {!}}\\ &\le T \prod_{1\le i \le \mathcal{I}} \sum_{0\le n \le 100 \beta_i^{-3/4}} \frac{1}{n!} \left(k^2 \sum_{T^{\beta_{i-1}}< {p} \le T^{\beta_{i}}} \frac{\cos^2(\gamma^- \log p)}{p} \right)^n\\ &\le T\exp\left( k^2 \sum_{p\le T^{\beta_{\mathcal{I}}}} \frac{\cos^2(\gamma^- \log p)}{p} \right). \end{align*} $$
$$ \begin{align*} & T \prod_{1\le i \le \mathcal{I}} \sum_{0\le n \le 100 \beta_i^{-3/4}} \frac{k^{2n}}{n!} \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_n \le T^{\beta_{i}}} \frac{\cos^2(\gamma^- \log p_1) \cdots \cos^2(\gamma^- \log p_n)}{p_1\cdots p_n} \\ &\times\frac{1}{\prod_{j=1}^r \alpha_j {!}}\\ &\le T \prod_{1\le i \le \mathcal{I}} \sum_{0\le n \le 100 \beta_i^{-3/4}} \frac{1}{n!} \left(k^2 \sum_{T^{\beta_{i-1}}< {p} \le T^{\beta_{i}}} \frac{\cos^2(\gamma^- \log p)}{p} \right)^n\\ &\le T\exp\left( k^2 \sum_{p\le T^{\beta_{\mathcal{I}}}} \frac{\cos^2(\gamma^- \log p)}{p} \right). \end{align*} $$
Hence, we arrive at
 $$ \begin{align} \mathscr{I} \ll T\exp\left( k^2 \sum_{p\le T^{\beta_{\mathcal{I}}}} \frac{\cos^2(\frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} \right) + (|\gamma^+|+T^{0.1}) T^{0.1} (\log \log T)^{2k}. \end{align} $$
$$ \begin{align} \mathscr{I} \ll T\exp\left( k^2 \sum_{p\le T^{\beta_{\mathcal{I}}}} \frac{\cos^2(\frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} \right) + (|\gamma^+|+T^{0.1}) T^{0.1} (\log \log T)^{2k}. \end{align} $$
Since
![]() $\beta _{\mathcal {I}} < 1$
and
$\beta _{\mathcal {I}} < 1$
and
![]() $\cos ^2(\theta ) = \frac {1}{2}(1+\cos (2 \theta ))$
, from (2.2), it follows that
$\cos ^2(\theta ) = \frac {1}{2}(1+\cos (2 \theta ))$
, from (2.2), it follows that
 $$ \begin{align} \sum_{p\le T^{\beta_{\mathcal{I}}}} \frac{\cos^2( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} &\le \sum_{p\le T} \frac{\cos^2( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} \nonumber\\ & =\frac{1}{2}\sum_{p\le T} \frac{1}{p} +\frac{1}{2}\sum_{p\le T} \frac{\cos((\alpha_1-\alpha_2) \log p)}{p}\\ & \le \frac{1}{2} \log\log T +\frac{1}{2}\log(\mathcal{F}(T,\alpha_1,\alpha_2)) +O(1), \nonumber \end{align} $$
$$ \begin{align} \sum_{p\le T^{\beta_{\mathcal{I}}}} \frac{\cos^2( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} &\le \sum_{p\le T} \frac{\cos^2( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} \nonumber\\ & =\frac{1}{2}\sum_{p\le T} \frac{1}{p} +\frac{1}{2}\sum_{p\le T} \frac{\cos((\alpha_1-\alpha_2) \log p)}{p}\\ & \le \frac{1}{2} \log\log T +\frac{1}{2}\log(\mathcal{F}(T,\alpha_1,\alpha_2)) +O(1), \nonumber \end{align} $$
where
![]() $\mathcal {F}(T,\alpha _1,\alpha _2)$
is defined in (1.9). Therefore, by (1.8), (4.19), and (4.20),
$\mathcal {F}(T,\alpha _1,\alpha _2)$
is defined in (1.9). Therefore, by (1.8), (4.19), and (4.20),
This combined with (4.2) and (4.6) completes the proof of Lemma 3.1.
5 Proof of Lemma 3.2
In this section, we shall prove Lemma 3.2. To begin, we first observe that
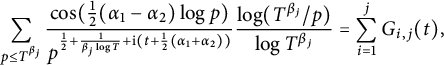 $$ \begin{align*} \sum_{ p\le T^{\beta_{j}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } = \sum_{ i=1}^{j}G_{i,j}(t), \end{align*} $$
$$ \begin{align*} \sum_{ p\le T^{\beta_{j}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } = \sum_{ i=1}^{j}G_{i,j}(t), \end{align*} $$
where
![]() $G_{i,j}(t)$
is defined as in (3.1). This gives
$G_{i,j}(t)$
is defined as in (3.1). This gives
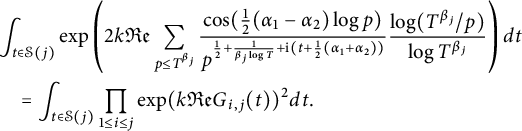 $$ \begin{align*} &\int_{t\in \mathcal{S}(j)} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{j}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } \right)dt \\ & \quad = \int_{t\in \mathcal{S}(j)} \prod_{1 \leq i \leq j} \exp ( k {\mathfrak{Re}} G_{i,j} (t))^2 dt. \end{align*} $$
$$ \begin{align*} &\int_{t\in \mathcal{S}(j)} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{j}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } \right)dt \\ & \quad = \int_{t\in \mathcal{S}(j)} \prod_{1 \leq i \leq j} \exp ( k {\mathfrak{Re}} G_{i,j} (t))^2 dt. \end{align*} $$
Similar to the proof of Lemma 3.1, we shall require the following lemma.
Lemma 5.1 If
![]() $t\in \mathcal {S}(j)$
with
$t\in \mathcal {S}(j)$
with
![]() $1 \leq j \leq \mathcal {I}-1$
, we have
$1 \leq j \leq \mathcal {I}-1$
, we have
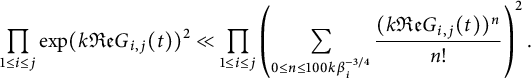 $$ \begin{align*} \prod_{1 \leq i \leq j}\exp ( k {\mathfrak{Re}} G_{i,j} (t))^2 \ll \prod_{1\le i \le j}\left(\sum_{0\le n \le 100k \beta_i^{-3/4}} \frac{(k {\mathfrak{Re}} G_{i,j}(t) )^n}{n!} \right)^2. \end{align*} $$
$$ \begin{align*} \prod_{1 \leq i \leq j}\exp ( k {\mathfrak{Re}} G_{i,j} (t))^2 \ll \prod_{1\le i \le j}\left(\sum_{0\le n \le 100k \beta_i^{-3/4}} \frac{(k {\mathfrak{Re}} G_{i,j}(t) )^n}{n!} \right)^2. \end{align*} $$
Proof It can be proved by repeating the argument for Lemma 4.1 while using
![]() $|{\mathfrak {Re}} G_{i,j}(t) |\leq \beta _i^{-3/4}$
when
$|{\mathfrak {Re}} G_{i,j}(t) |\leq \beta _i^{-3/4}$
when
![]() $t \in \mathcal {S}(j)$
(instead of
$t \in \mathcal {S}(j)$
(instead of
![]() $|{\mathfrak {Re}} F_i(t)| \leq \beta _i^{-3/4}$
) and the fact that
$|{\mathfrak {Re}} F_i(t)| \leq \beta _i^{-3/4}$
) and the fact that
![]() $\prod _{i=1}^j e^{-\frac {1}{10k} \beta _i^{3/4}} \geq \prod _{i=1}^{\mathcal {I}}e^{-\frac {1}{10k} \beta _i^{3/4}}$
.
$\prod _{i=1}^j e^{-\frac {1}{10k} \beta _i^{3/4}} \geq \prod _{i=1}^{\mathcal {I}}e^{-\frac {1}{10k} \beta _i^{3/4}}$
.
Now, setting
by Lemma 5.1, we see

where ![]() is the indicator function of
is the indicator function of
![]() $A_{j,\ell }$
.Footnote
2
By the definition of
$A_{j,\ell }$
.Footnote
2
By the definition of
![]() $A_{j,\ell }$
, we know
$A_{j,\ell }$
, we know
for any positive integer M. From this point on, we set
It then follows that the last integral in (5.1) is
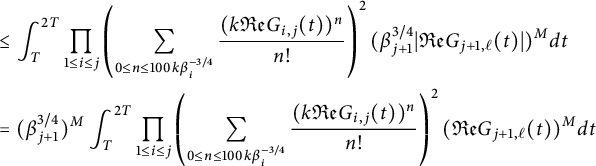 $$ \begin{align} &\le \int_{T}^{2T} \prod_{1\le i \le j}\left(\sum_{0\le n \le 100k \beta_i^{-3/4}} \frac{(k {\mathfrak{Re}} G_{i,j}(t) )^n}{n!} \right)^2 (\beta_{j+1}^{3/4} |{\mathfrak{Re}} G_{j+1,\ell}(t) |)^{M} dt\\ &= (\beta_{j+1}^{3/4})^{M} \int_{T}^{2T} \prod_{1\le i \le j} \left( \sum_{0\le n \le 100k \beta_{i}^{-3/4}} \frac{(k{\mathfrak{Re}} G_{i,j}(t))^n}{n!} \right)^2 ({\mathfrak{Re}} G_{j+1,\ell}(t) )^{M} dt \nonumber \end{align} $$
$$ \begin{align} &\le \int_{T}^{2T} \prod_{1\le i \le j}\left(\sum_{0\le n \le 100k \beta_i^{-3/4}} \frac{(k {\mathfrak{Re}} G_{i,j}(t) )^n}{n!} \right)^2 (\beta_{j+1}^{3/4} |{\mathfrak{Re}} G_{j+1,\ell}(t) |)^{M} dt\\ &= (\beta_{j+1}^{3/4})^{M} \int_{T}^{2T} \prod_{1\le i \le j} \left( \sum_{0\le n \le 100k \beta_{i}^{-3/4}} \frac{(k{\mathfrak{Re}} G_{i,j}(t))^n}{n!} \right)^2 ({\mathfrak{Re}} G_{j+1,\ell}(t) )^{M} dt \nonumber \end{align} $$
as M is even. We shall write the last expression as
![]() $(\beta _{j+1}^{3/4})^{M} S$
where
$(\beta _{j+1}^{3/4})^{M} S$
where
 $$ \begin{align*} S & := \sum_{m_1, n_1=0}^{L_1} \cdots \sum_{m_j,n_j=0}^{L_j} \frac{k^{m_1+n_1+ \cdots +m_j+n_j}}{(m_1)! (n_1)! \cdots (m_j)! (n_j)!} \\ &\quad\times \int_{T}^{2T} ({\mathfrak{Re}} G_{j+1,\ell}(t) )^{M} \prod_{i=1}^{j} ({\mathfrak{Re}} G_{i,j}(t))^{m_i+n_i} dt, \end{align*} $$
$$ \begin{align*} S & := \sum_{m_1, n_1=0}^{L_1} \cdots \sum_{m_j,n_j=0}^{L_j} \frac{k^{m_1+n_1+ \cdots +m_j+n_j}}{(m_1)! (n_1)! \cdots (m_j)! (n_j)!} \\ &\quad\times \int_{T}^{2T} ({\mathfrak{Re}} G_{j+1,\ell}(t) )^{M} \prod_{i=1}^{j} ({\mathfrak{Re}} G_{i,j}(t))^{m_i+n_i} dt, \end{align*} $$
and
![]() $L_i := 100k \beta _{i}^{-3/4}$
for
$L_i := 100k \beta _{i}^{-3/4}$
for
![]() $1 \le i \le j$
. Recalling the definition (3.1) of
$1 \le i \le j$
. Recalling the definition (3.1) of
![]() $G_{i,j}(t)$
and the fact that
$G_{i,j}(t)$
and the fact that
![]() ${\mathfrak {Re}} p^{-\mathrm {i} (t+\frac {1}{2}(\alpha _1+\alpha _2)) } = \cos ((t+ \gamma ^{+}) \log p) $
, we have
${\mathfrak {Re}} p^{-\mathrm {i} (t+\frac {1}{2}(\alpha _1+\alpha _2)) } = \cos ((t+ \gamma ^{+}) \log p) $
, we have
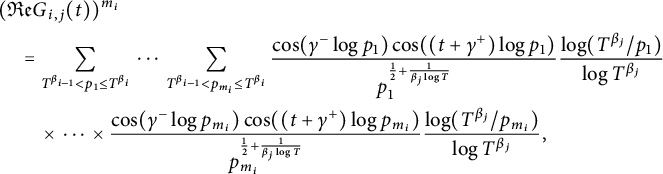 $$ \begin{align*} & ({\mathfrak{Re}} G_{i,j}(t) )^{m_i}\\ &\quad = \sum_{T^{\beta_{i-1}} < p_1 \le T^{\beta_i}} \cdots \sum_{T^{\beta_{i-1}} < p_{m_i} \le T^{\beta_i}} \frac{\cos(\gamma^{-} \log p_1) \cos((t+ \gamma^{+}) \log p_1)}{p_{1}^{\frac{1}{2} + \frac{1}{\beta_j \log T}}} \frac{ \log(T^{\beta_j}/p_1)}{\log T^{\beta_j}} \\ & \qquad\times \cdots \times \frac{\cos(\gamma^{-} \log p_{m_i}) \cos((t+ \gamma^{+}) \log p_{m_i})}{p_{m_i}^{\frac{1}{2} + \frac{1}{\beta_j \log T}}} \frac{ \log(T^{\beta_j}/p_{m_i})}{\log T^{\beta_j}}, \end{align*} $$
$$ \begin{align*} & ({\mathfrak{Re}} G_{i,j}(t) )^{m_i}\\ &\quad = \sum_{T^{\beta_{i-1}} < p_1 \le T^{\beta_i}} \cdots \sum_{T^{\beta_{i-1}} < p_{m_i} \le T^{\beta_i}} \frac{\cos(\gamma^{-} \log p_1) \cos((t+ \gamma^{+}) \log p_1)}{p_{1}^{\frac{1}{2} + \frac{1}{\beta_j \log T}}} \frac{ \log(T^{\beta_j}/p_1)}{\log T^{\beta_j}} \\ & \qquad\times \cdots \times \frac{\cos(\gamma^{-} \log p_{m_i}) \cos((t+ \gamma^{+}) \log p_{m_i})}{p_{m_i}^{\frac{1}{2} + \frac{1}{\beta_j \log T}}} \frac{ \log(T^{\beta_j}/p_{m_i})}{\log T^{\beta_j}}, \end{align*} $$
and
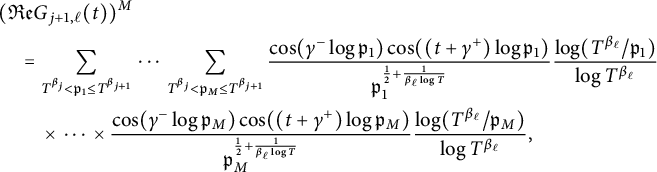 $$ \begin{align*} & ({\mathfrak{Re}} G_{j+1,\ell}(t) )^{M} \\ & \quad = \sum_{T^{\beta_{j}} < \mathfrak{p}_1 \le T^{\beta_{j+1}}} \cdots \sum_{T^{\beta_{j}} < \mathfrak{p}_{M} \le T^{\beta_{j+1}}} \frac{\cos(\gamma^{-} \log \mathfrak{p}_1) \cos((t+ \gamma^{+}) \log \mathfrak{p}_1)}{\mathfrak{p}_{1}^{\frac{1}{2} + \frac{1}{\beta_{ { \ell} } \log T}}} \frac{ \log(T^{\beta_{ { \ell} }}/\mathfrak{p}_1)}{\log T^{\beta_{ { \ell} }}} \\ & \qquad\times \cdots \times \frac{\cos(\gamma^{-} \log \mathfrak{p}_{M}) \cos((t+ \gamma^{+}) \log \mathfrak{p}_{M})}{\mathfrak{p}_{M}^{\frac{1}{2} + \frac{1}{\beta_{ { \ell} } \log T}}} \frac{ \log(T^{\beta_{ { \ell} }}/\mathfrak{p}_{M})}{\log T^{\beta_{ { \ell} }}}, \end{align*} $$
$$ \begin{align*} & ({\mathfrak{Re}} G_{j+1,\ell}(t) )^{M} \\ & \quad = \sum_{T^{\beta_{j}} < \mathfrak{p}_1 \le T^{\beta_{j+1}}} \cdots \sum_{T^{\beta_{j}} < \mathfrak{p}_{M} \le T^{\beta_{j+1}}} \frac{\cos(\gamma^{-} \log \mathfrak{p}_1) \cos((t+ \gamma^{+}) \log \mathfrak{p}_1)}{\mathfrak{p}_{1}^{\frac{1}{2} + \frac{1}{\beta_{ { \ell} } \log T}}} \frac{ \log(T^{\beta_{ { \ell} }}/\mathfrak{p}_1)}{\log T^{\beta_{ { \ell} }}} \\ & \qquad\times \cdots \times \frac{\cos(\gamma^{-} \log \mathfrak{p}_{M}) \cos((t+ \gamma^{+}) \log \mathfrak{p}_{M})}{\mathfrak{p}_{M}^{\frac{1}{2} + \frac{1}{\beta_{ { \ell} } \log T}}} \frac{ \log(T^{\beta_{ { \ell} }}/\mathfrak{p}_{M})}{\log T^{\beta_{ { \ell} }}}, \end{align*} $$
where we are using
![]() $\mathfrak {p}_u$
, for
$\mathfrak {p}_u$
, for
![]() $1 \le u \le M$
, to denote a prime variable. It follows that
$1 \le u \le M$
, to denote a prime variable. It follows that
 $$ \begin{align} S& = \sum_{\tilde{m}, \tilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} C_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} C_3( \tilde{\mathfrak{p}}) \nonumber\\ & \quad\times\int_{T}^{2T} \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos((t+\gamma^{+}) \log p(i,r)) \cos((t+\gamma^{+}) \log q(i,s)) \\ &\quad\times \prod_{u=1}^{M} \cos((t+ \gamma^{+}) \log \mathfrak{p}_u) dt \nonumber\\ &\quad \times \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos( \gamma^{-} \log p(i,r)) \cos(\gamma^{-} \log q(i,s)) \prod_{u=1}^{M} \cos(\gamma^{-} \log \mathfrak{p}_u), \nonumber \end{align} $$
$$ \begin{align} S& = \sum_{\tilde{m}, \tilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} C_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} C_3( \tilde{\mathfrak{p}}) \nonumber\\ & \quad\times\int_{T}^{2T} \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos((t+\gamma^{+}) \log p(i,r)) \cos((t+\gamma^{+}) \log q(i,s)) \\ &\quad\times \prod_{u=1}^{M} \cos((t+ \gamma^{+}) \log \mathfrak{p}_u) dt \nonumber\\ &\quad \times \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos( \gamma^{-} \log p(i,r)) \cos(\gamma^{-} \log q(i,s)) \prod_{u=1}^{M} \cos(\gamma^{-} \log \mathfrak{p}_u), \nonumber \end{align} $$
where
![]() $ \widetilde {m} = (m_1, \ldots , m_j), \, \widetilde {n} = (n_1, \ldots , n_j), \text { with } 0 \le m_i,n_i \le L_i =100k \beta _{i}^{-3/4}, $
and
$ \widetilde {m} = (m_1, \ldots , m_j), \, \widetilde {n} = (n_1, \ldots , n_j), \text { with } 0 \le m_i,n_i \le L_i =100k \beta _{i}^{-3/4}, $
and
![]() $ \tilde {p}$
,
$ \tilde {p}$
,
![]() $\tilde {q}$
, and
$\tilde {q}$
, and
![]() $\tilde {\frak p}$
are tuples:
$\tilde {\frak p}$
are tuples:
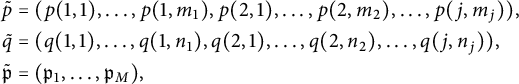 $$ \begin{align*} \tilde{p} &=( p(1,1),\ldots, p(1,m_1), p(2,1),\ldots,p(2,m_2),\ldots, p(j,m_{j} )), \\ \tilde{q} & =( q(1,1),\ldots, q(1,n_1), q(2,1),\ldots,q(2,n_2),\ldots, q(j,n_{j} )), \\ \tilde{\frak p} & = ( \mathfrak{p}_1, \ldots, \mathfrak{p}_M), \end{align*} $$
$$ \begin{align*} \tilde{p} &=( p(1,1),\ldots, p(1,m_1), p(2,1),\ldots,p(2,m_2),\ldots, p(j,m_{j} )), \\ \tilde{q} & =( q(1,1),\ldots, q(1,n_1), q(2,1),\ldots,q(2,n_2),\ldots, q(j,n_{j} )), \\ \tilde{\frak p} & = ( \mathfrak{p}_1, \ldots, \mathfrak{p}_M), \end{align*} $$
whose components satisfy
Here, we also used the notation
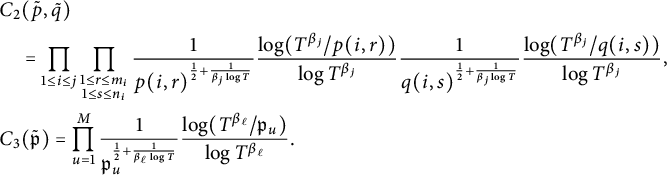 $$ \begin{align*} & C_2 (\tilde{p},\tilde{q})\\&\quad = \prod_{1\le i \le j}\prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}}\frac{1}{p(i,r)^{\frac{1}{2}+\frac{1}{\beta_{j} \log T} } }\frac{\log(T^{\beta_{j}}/p(i,r))}{\log T^{\beta_{j}} } \frac{1}{q(i,s)^{\frac{1}{2}+\frac{1}{\beta_{j} \log T} } }\frac{\log(T^{\beta_{j}}/q(i,s))}{\log T^{\beta_{j}} }, \\& C_3(\tilde{\mathfrak{p}}) = \prod_{u=1}^{M} \frac{1}{\mathfrak{p}_{u}^{\frac{1}{2} + \frac{1}{\beta_{ {\ell} }\log T}}} \frac{ \log(T^{\beta_{ { \ell} }}/\mathfrak{p}_u)}{\log T^{\beta_{ { \ell} }}}. \end{align*} $$
$$ \begin{align*} & C_2 (\tilde{p},\tilde{q})\\&\quad = \prod_{1\le i \le j}\prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}}\frac{1}{p(i,r)^{\frac{1}{2}+\frac{1}{\beta_{j} \log T} } }\frac{\log(T^{\beta_{j}}/p(i,r))}{\log T^{\beta_{j}} } \frac{1}{q(i,s)^{\frac{1}{2}+\frac{1}{\beta_{j} \log T} } }\frac{\log(T^{\beta_{j}}/q(i,s))}{\log T^{\beta_{j}} }, \\& C_3(\tilde{\mathfrak{p}}) = \prod_{u=1}^{M} \frac{1}{\mathfrak{p}_{u}^{\frac{1}{2} + \frac{1}{\beta_{ {\ell} }\log T}}} \frac{ \log(T^{\beta_{ { \ell} }}/\mathfrak{p}_u)}{\log T^{\beta_{ { \ell} }}}. \end{align*} $$
Observe that similar to (4.9), by (5.5), we have
 $$ \begin{align} \prod_{1\le i \le j}\prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r)q(i,s) \le T^{0.1} \text{ and } \prod_{u=1}^{M} \mathfrak{p}_u \le (T^{\beta_{j+1}})^M \le T^{0.2}. \end{align} $$
$$ \begin{align} \prod_{1\le i \le j}\prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r)q(i,s) \le T^{0.1} \text{ and } \prod_{u=1}^{M} \mathfrak{p}_u \le (T^{\beta_{j+1}})^M \le T^{0.2}. \end{align} $$
Thus, by Lemma 2.1 and (5.6), it follows that
 $$ \begin{align} & \int_T^{2T}\prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} \cos((t+\gamma^+)\log p(i,r) )\cos((t+\gamma^+)\log q(i,s) ) \nonumber\\ &\qquad \times \prod_{u=1}^{M} \cos((t+ \gamma^{+}) \log \mathfrak{p}_u) dt \\ & \quad = (T+\gamma^+) g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) + O(|\gamma^+|) +O(T^{0.3}).\nonumber \end{align} $$
$$ \begin{align} & \int_T^{2T}\prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} \cos((t+\gamma^+)\log p(i,r) )\cos((t+\gamma^+)\log q(i,s) ) \nonumber\\ &\qquad \times \prod_{u=1}^{M} \cos((t+ \gamma^{+}) \log \mathfrak{p}_u) dt \\ & \quad = (T+\gamma^+) g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) + O(|\gamma^+|) +O(T^{0.3}).\nonumber \end{align} $$
Using (5.7) in (5.4), we find that
 $$ \begin{align} S &=\sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} C_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} C_3(\tilde{\mathfrak{p}}) \nonumber \\ & \quad\times \Bigg( (T+\gamma^+) g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) + O(|\gamma^+|+T^{0.3}) \Bigg) \\ & \quad\times \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos( \gamma^{-} \log p(i,r)) \cos(\gamma^{-} \log q(i,s)) \prod_{u=1}^{M} \cos(\gamma^{-} \log \mathfrak{p}_u) .\nonumber \end{align} $$
$$ \begin{align} S &=\sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} C_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} C_3(\tilde{\mathfrak{p}}) \nonumber \\ & \quad\times \Bigg( (T+\gamma^+) g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) + O(|\gamma^+|+T^{0.3}) \Bigg) \\ & \quad\times \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos( \gamma^{-} \log p(i,r)) \cos(\gamma^{-} \log q(i,s)) \prod_{u=1}^{M} \cos(\gamma^{-} \log \mathfrak{p}_u) .\nonumber \end{align} $$
Observe that
where
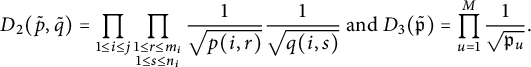 $$ \begin{align*} D_2(\tilde{p},\tilde{q}) = \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} \frac{1}{\sqrt{p(i,r)}}\frac{1}{\sqrt{ q(i,s) }} \text{ and } D_3(\tilde{\mathfrak{p}})=\prod_{u=1}^{M} \frac{1}{ \sqrt{ \mathfrak{p}_{u}} }. \end{align*} $$
$$ \begin{align*} D_2(\tilde{p},\tilde{q}) = \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} \frac{1}{\sqrt{p(i,r)}}\frac{1}{\sqrt{ q(i,s) }} \text{ and } D_3(\tilde{\mathfrak{p}})=\prod_{u=1}^{M} \frac{1}{ \sqrt{ \mathfrak{p}_{u}} }. \end{align*} $$
Therefore, we obtain
 $$ \begin{align} S &= \sum_{\tilde{m}, \tilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} C_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} C_3(\tilde{\mathfrak{p}}) \nonumber\\&\quad \times (T+\gamma^+) g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) \\&\quad \times \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos( \gamma^{-} \log p(i,r)) \cos(\gamma^{-} \log q(i,s)) \prod_{u=1}^{M} \cos(\gamma^{-} \log \mathfrak{p}_u) \nonumber\\&\quad + \mathcal{E},\nonumber \end{align} $$
$$ \begin{align} S &= \sum_{\tilde{m}, \tilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} C_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} C_3(\tilde{\mathfrak{p}}) \nonumber\\&\quad \times (T+\gamma^+) g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) \\&\quad \times \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos( \gamma^{-} \log p(i,r)) \cos(\gamma^{-} \log q(i,s)) \prod_{u=1}^{M} \cos(\gamma^{-} \log \mathfrak{p}_u) \nonumber\\&\quad + \mathcal{E},\nonumber \end{align} $$
where the error term
![]() $\mathcal {E}$
, contributed by the big-O term in (5.8), satisfies
$\mathcal {E}$
, contributed by the big-O term in (5.8), satisfies
 $$ \begin{align*} \mathcal{E} \ll \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} D_3(\tilde{\mathfrak{p}}) ( |\gamma^+|+T^{0.3}) ). \end{align*} $$
$$ \begin{align*} \mathcal{E} \ll \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} D_3(\tilde{\mathfrak{p}}) ( |\gamma^+|+T^{0.3}) ). \end{align*} $$
Note that
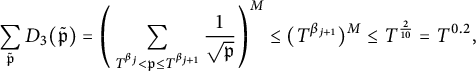 $$\begin{align*}\sum_{\tilde{\mathfrak{p}}} D_3(\tilde{\mathfrak{p}}) = \Bigg( \sum_{T^{\beta_{j}} < \mathfrak{p} \le T^{\beta_{j+1}}} \frac{1}{\sqrt{\mathfrak{p} }} \Bigg)^M \le (T^{\beta_{j+1}})^M \le T^{\frac{2}{10}} = T^{0.2}, \end{align*}$$
$$\begin{align*}\sum_{\tilde{\mathfrak{p}}} D_3(\tilde{\mathfrak{p}}) = \Bigg( \sum_{T^{\beta_{j}} < \mathfrak{p} \le T^{\beta_{j+1}}} \frac{1}{\sqrt{\mathfrak{p} }} \Bigg)^M \le (T^{\beta_{j+1}})^M \le T^{\frac{2}{10}} = T^{0.2}, \end{align*}$$
where we used the definition (5.2). Hence, we have
 $$ \begin{align} \mathcal{E} \ll ( |\gamma^+|+T^{0.3}) T^{0.2} \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}). \end{align} $$
$$ \begin{align} \mathcal{E} \ll ( |\gamma^+|+T^{0.3}) T^{0.2} \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}). \end{align} $$
Observe that
 $$ \begin{align*} \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}) = \prod_{i=1}^{j} \Bigg( \sum_{0 \le m \le 100 k \beta_{i}^{ -3/4} } \frac{k^m}{m!} \Bigg( \sum_{T^{\beta_{i-1}} < p \le T^{\beta_i}} \frac{1}{\sqrt{p}} \Bigg)^m \Bigg)^2. \end{align*} $$
$$ \begin{align*} \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}) = \prod_{i=1}^{j} \Bigg( \sum_{0 \le m \le 100 k \beta_{i}^{ -3/4} } \frac{k^m}{m!} \Bigg( \sum_{T^{\beta_{i-1}} < p \le T^{\beta_i}} \frac{1}{\sqrt{p}} \Bigg)^m \Bigg)^2. \end{align*} $$
The inner sum on the right satisfies
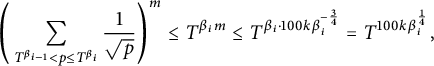 $$ \begin{align*} \Bigg( \sum_{T^{\beta_{i-1}} < p \le T^{\beta_i}} \frac{1}{\sqrt{p}} \Bigg)^{m} \le T^{\beta_i m} \le T^{\beta_i \cdot 100 k \beta_{i}^{-\frac{3}{4}}} = T^{100 k \beta_{i}^{\frac{1}{4}} }, \end{align*} $$
$$ \begin{align*} \Bigg( \sum_{T^{\beta_{i-1}} < p \le T^{\beta_i}} \frac{1}{\sqrt{p}} \Bigg)^{m} \le T^{\beta_i m} \le T^{\beta_i \cdot 100 k \beta_{i}^{-\frac{3}{4}}} = T^{100 k \beta_{i}^{\frac{1}{4}} }, \end{align*} $$
and thus
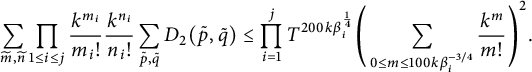 $$ \begin{align*} \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}) \le \prod_{i=1}^{j} T^{200 k \beta_{i}^{\frac{1}{4}} } \Bigg( \sum_{0 \le m \le 100 k \beta_{i}^{- 3/4}} \frac{k^m}{m!} \Bigg)^2. \end{align*} $$
$$ \begin{align*} \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}) \le \prod_{i=1}^{j} T^{200 k \beta_{i}^{\frac{1}{4}} } \Bigg( \sum_{0 \le m \le 100 k \beta_{i}^{- 3/4}} \frac{k^m}{m!} \Bigg)^2. \end{align*} $$
Since
![]() $ \prod _{i=1}^{j} T^{200 k \beta _{i}^{\frac {1}{4}} } \le T^{400 k \beta _{j}^{\frac {1}{4}}} \le T^{0.1}$
, we then obtain
$ \prod _{i=1}^{j} T^{200 k \beta _{i}^{\frac {1}{4}} } \le T^{400 k \beta _{j}^{\frac {1}{4}}} \le T^{0.1}$
, we then obtain
 $$ \begin{align*} \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}) & \le T^{0.1} \prod_{i=1}^{j} e^{2k} = T^{0.1} e^{2jk} \le T^{0.1} e^{2k \cdot \frac{2}{\log 20} \log \log \log T} , \end{align*} $$
$$ \begin{align*} \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}) & \le T^{0.1} \prod_{i=1}^{j} e^{2k} = T^{0.1} e^{2jk} \le T^{0.1} e^{2k \cdot \frac{2}{\log 20} \log \log \log T} , \end{align*} $$
which is
![]() $\le T^{0.1} (\log \log T)^{2k} $
. Here, we use the facts
$\le T^{0.1} (\log \log T)^{2k} $
. Here, we use the facts
![]() $j \le \mathcal {I}-1 \le \frac {2}{\log 20}\log \log \log T$
and
$j \le \mathcal {I}-1 \le \frac {2}{\log 20}\log \log \log T$
and
![]() $\frac {2}{\log 20} = 0.66 \ldots $
. Inserting this last bound in (5.10) yields
$\frac {2}{\log 20} = 0.66 \ldots $
. Inserting this last bound in (5.10) yields
Combining (5.9) and (5.11), we have
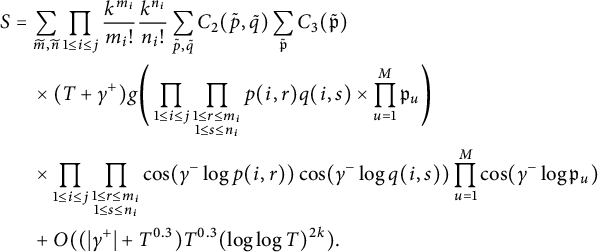 $$ \begin{align*} S & = \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} C_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} C_3(\tilde{\mathfrak{p}}) \\&\quad \times (T+\gamma^+) g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) \\&\quad \times \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos( \gamma^{-} \log p(i,r)) \cos(\gamma^{-} \log q(i,s)) \prod_{u=1}^{M} \cos(\gamma^{-} \log \mathfrak{p}_u)\\&\quad + O(( |\gamma^+|+T^{0.3}) T^{0.3} (\log \log T)^{2k}). \end{align*} $$
$$ \begin{align*} S & = \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} C_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} C_3(\tilde{\mathfrak{p}}) \\&\quad \times (T+\gamma^+) g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) \\&\quad \times \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos( \gamma^{-} \log p(i,r)) \cos(\gamma^{-} \log q(i,s)) \prod_{u=1}^{M} \cos(\gamma^{-} \log \mathfrak{p}_u)\\&\quad + O(( |\gamma^+|+T^{0.3}) T^{0.3} (\log \log T)^{2k}). \end{align*} $$
Note that
![]() $|\gamma ^{+}| \le T$
and the main term is nonnegative since g is supported on squares, following an argument similar to that establishing (4.13). Therefore, we arrive at
$|\gamma ^{+}| \le T$
and the main term is nonnegative since g is supported on squares, following an argument similar to that establishing (4.13). Therefore, we arrive at
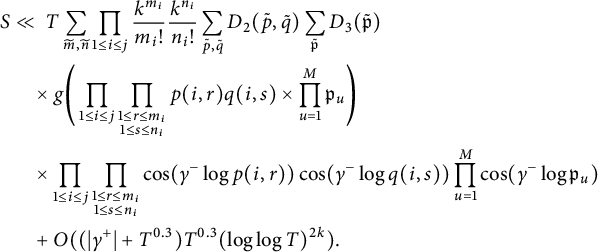 $$ \begin{align} S & \ll \ T \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} D_3(\tilde{\mathfrak{p}}) \nonumber\\&\quad \times g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) \\&\quad \times \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos( \gamma^{-} \log p(i,r)) \cos(\gamma^{-} \log q(i,s)) \prod_{u=1}^{M} \cos(\gamma^- \log \mathfrak{p}_u) \nonumber\\&\quad + O(( |\gamma^+|+T^{0.3}) T^{0.3} (\log \log T)^{2k}).\nonumber \end{align} $$
$$ \begin{align} S & \ll \ T \sum_{\widetilde{m}, \widetilde{n}} \prod_{1 \le i \le j} \frac{k^{m_i}}{m_i !} \frac{k^{n_i}}{n_i !} \sum_{\tilde{p}, \tilde{q}} D_2 (\tilde{p},\tilde{q}) \sum_{\tilde{\mathfrak{p}}} D_3(\tilde{\mathfrak{p}}) \nonumber\\&\quad \times g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) \\&\quad \times \prod_{1 \le i \le j} \prod_{\substack{ 1 \le r \le m_i \\ 1 \le s \le n_i}} \cos( \gamma^{-} \log p(i,r)) \cos(\gamma^{-} \log q(i,s)) \prod_{u=1}^{M} \cos(\gamma^- \log \mathfrak{p}_u) \nonumber\\&\quad + O(( |\gamma^+|+T^{0.3}) T^{0.3} (\log \log T)^{2k}).\nonumber \end{align} $$
Since the two integers within g are co-prime and g is multiplicative, we have
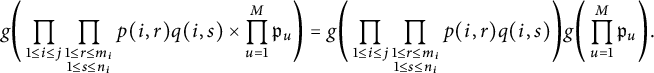 $$\begin{align*}g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) = g \Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \Bigg) g \Bigg( \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg). \end{align*}$$
$$\begin{align*}g\Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \times \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg) = g \Bigg( \prod_{1\le i \le j} \prod_{\substack{1\le r \le m_i \\ 1\le s \le n_i}} p(i,r) q(i,s) \Bigg) g \Bigg( \prod_{u=1}^{M} \mathfrak{p}_{u} \Bigg). \end{align*}$$
This, together with (5.12), implies
 $$ \begin{align} S & \ll T \prod_{1\le i \le j} \sum_{0\le m \le 200k \beta_i^{-3/4} } \frac{k^m 2^m}{m!} \nonumber\\&\quad \times \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_m \le T^{\beta_{i}}} \frac{g(p_1\cdots p_m)}{\sqrt{p_1\cdots p_m}} \cos(\gamma^- \log p_1) \cdots \cos(\gamma^- \log p_m) \\&\quad \times \sum_{T^{\beta_{j}}< \mathfrak{p}_1,\ldots,\mathfrak{p}_M \le T^{\beta_{j+1}}} \frac{g(\mathfrak{p}_1\cdots \mathfrak{p}_M)}{\sqrt{\mathfrak{p}_1\cdots \mathfrak{p}_M}} \cos(\gamma^- \log \mathfrak{p}_1) \cdots \cos(\gamma^- \log \mathfrak{p}_M) \nonumber\\&\quad +O( (|\gamma^+|+T^{0.3}) T^{0.3} (\log \log T)^{2k}).\nonumber \end{align} $$
$$ \begin{align} S & \ll T \prod_{1\le i \le j} \sum_{0\le m \le 200k \beta_i^{-3/4} } \frac{k^m 2^m}{m!} \nonumber\\&\quad \times \sum_{T^{\beta_{i-1}}< p_1,\ldots,p_m \le T^{\beta_{i}}} \frac{g(p_1\cdots p_m)}{\sqrt{p_1\cdots p_m}} \cos(\gamma^- \log p_1) \cdots \cos(\gamma^- \log p_m) \\&\quad \times \sum_{T^{\beta_{j}}< \mathfrak{p}_1,\ldots,\mathfrak{p}_M \le T^{\beta_{j+1}}} \frac{g(\mathfrak{p}_1\cdots \mathfrak{p}_M)}{\sqrt{\mathfrak{p}_1\cdots \mathfrak{p}_M}} \cos(\gamma^- \log \mathfrak{p}_1) \cdots \cos(\gamma^- \log \mathfrak{p}_M) \nonumber\\&\quad +O( (|\gamma^+|+T^{0.3}) T^{0.3} (\log \log T)^{2k}).\nonumber \end{align} $$
Since g is supported on squares, by an argument similar to that leading from (4.14) to (4.19), we find that the previous expression is bounded by
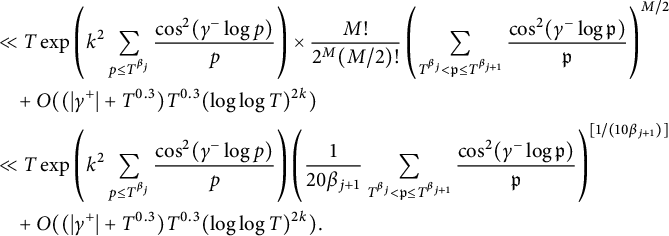 $$ \begin{align} &\ll T \exp\left( k^2 \sum_{p\le T^{\beta_{j}}} \frac{\cos^2(\gamma^- \log p)}{p} \right) \times \frac{M!}{2^M (M/2)!} \left( \sum_{T^{\beta_j} < \mathfrak{p}\le T^{\beta_{j+1}}} \frac{\cos^2(\gamma^- \log \mathfrak{p})}{\mathfrak{p}} \right)^{M/2} \nonumber\\&\quad +O( (|\gamma^+|+T^{0.3}) T^{0.3} (\log \log T)^{2k}) \nonumber\\&\ll T \exp\left( k^2 \sum_{p\le T^{\beta_{j}}} \frac{\cos^2(\gamma^- \log p)}{p} \right) \left( \frac{1}{20 \beta_{j+1}} \sum_{T^{\beta_j} < \mathfrak{p}\le T^{\beta_{j+1}}} \frac{\cos^2(\gamma^- \log \mathfrak{p})}{\mathfrak{p}} \right)^{[1/(10\beta_{j+1})]}\nonumber\\&\quad +O( (|\gamma^+|+T^{0.3}) T^{0.3} (\log \log T)^{2k}).\nonumber\\ \end{align} $$
$$ \begin{align} &\ll T \exp\left( k^2 \sum_{p\le T^{\beta_{j}}} \frac{\cos^2(\gamma^- \log p)}{p} \right) \times \frac{M!}{2^M (M/2)!} \left( \sum_{T^{\beta_j} < \mathfrak{p}\le T^{\beta_{j+1}}} \frac{\cos^2(\gamma^- \log \mathfrak{p})}{\mathfrak{p}} \right)^{M/2} \nonumber\\&\quad +O( (|\gamma^+|+T^{0.3}) T^{0.3} (\log \log T)^{2k}) \nonumber\\&\ll T \exp\left( k^2 \sum_{p\le T^{\beta_{j}}} \frac{\cos^2(\gamma^- \log p)}{p} \right) \left( \frac{1}{20 \beta_{j+1}} \sum_{T^{\beta_j} < \mathfrak{p}\le T^{\beta_{j+1}}} \frac{\cos^2(\gamma^- \log \mathfrak{p})}{\mathfrak{p}} \right)^{[1/(10\beta_{j+1})]}\nonumber\\&\quad +O( (|\gamma^+|+T^{0.3}) T^{0.3} (\log \log T)^{2k}).\nonumber\\ \end{align} $$
Indeed, the first exponential factor in (5.14) is derived by using the same argument from (4.14) to (4.19) while replacing
![]() $\mathcal {I}$
by j; the second parentheses follow from (4.15), (4.17), and (4.18) with
$\mathcal {I}$
by j; the second parentheses follow from (4.15), (4.17), and (4.18) with
![]() $n= \frac {M}{2}$
. In addition, the last estimate is due to the following application of Stirling’s approximation:
$n= \frac {M}{2}$
. In addition, the last estimate is due to the following application of Stirling’s approximation:
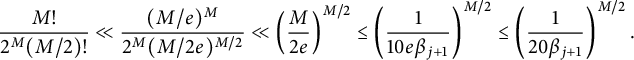 $$ \begin{align*} \frac{M!}{2^M (M/2)!}\ll \frac{(M/e)^M}{2^M (M/2e)^{M/2}} \ll \left(\frac{M}{2e}\right)^{M/2} \leq \left(\frac{1}{10e \beta_{j+1}} \right)^{M/2}\leq \left(\frac{1}{20 \beta_{j+1}} \right)^{M/2}. \end{align*} $$
$$ \begin{align*} \frac{M!}{2^M (M/2)!}\ll \frac{(M/e)^M}{2^M (M/2e)^{M/2}} \ll \left(\frac{M}{2e}\right)^{M/2} \leq \left(\frac{1}{10e \beta_{j+1}} \right)^{M/2}\leq \left(\frac{1}{20 \beta_{j+1}} \right)^{M/2}. \end{align*} $$
Hence, by (5.1), (5.3), (5.13), and (5.14), we arrive at
 $$ \begin{align} &\int_{t\in \mathcal{S}(j)} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{j}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } \right)dt \nonumber\\&\quad \ll_k (\mathcal{I}-j) T \exp\left( k^2 \sum_{p\le T^{\beta_{j}}} \frac{\cos^2( \gamma^- \log p)}{p} \right) \\&\qquad \times \left( \frac{\beta_{j+1}^{1/2}}{20} \sum_{T^{\beta_j} < p\le T^{\beta_{j+1}}} \frac{\cos^2( \gamma^- \log p)}{p} \right)^{[1/(10\beta_{j+1})]}\nonumber\\&\qquad +(\mathcal{I}-j) ( (|\gamma^+|+T^{0.3}) T^{0.3}) (\log \log T)^{2k},\nonumber \end{align} $$
$$ \begin{align} &\int_{t\in \mathcal{S}(j)} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{j}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{j} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{j}}/p)}{\log T^{\beta_{j}} } \right)dt \nonumber\\&\quad \ll_k (\mathcal{I}-j) T \exp\left( k^2 \sum_{p\le T^{\beta_{j}}} \frac{\cos^2( \gamma^- \log p)}{p} \right) \\&\qquad \times \left( \frac{\beta_{j+1}^{1/2}}{20} \sum_{T^{\beta_j} < p\le T^{\beta_{j+1}}} \frac{\cos^2( \gamma^- \log p)}{p} \right)^{[1/(10\beta_{j+1})]}\nonumber\\&\qquad +(\mathcal{I}-j) ( (|\gamma^+|+T^{0.3}) T^{0.3}) (\log \log T)^{2k},\nonumber \end{align} $$
where
![]() $\gamma ^- = \frac {1}{2}(\alpha _1-\alpha _2)$
. Recall that
$\gamma ^- = \frac {1}{2}(\alpha _1-\alpha _2)$
. Recall that
![]() $\mathcal {I}\le \log \log \log T$
,
$\mathcal {I}\le \log \log \log T$
,
![]() $\beta _0=0$
,
$\beta _0=0$
,
![]() $\beta _1=\frac {1}{(\log \log T)^2}$
, and
$\beta _1=\frac {1}{(\log \log T)^2}$
, and
 $$ \begin{align*}\sum_{p\le T^{\beta_1}} \frac{1}{p} \le \log\log T. \end{align*} $$
$$ \begin{align*}\sum_{p\le T^{\beta_1}} \frac{1}{p} \le \log\log T. \end{align*} $$
Observe that for
![]() $j=0$
, the left of (5.15) is
$j=0$
, the left of (5.15) is
![]() $\operatorname {\mathrm {meas}}(\mathcal {S}(0))$
. Therefore, by using the trivial bound
$\operatorname {\mathrm {meas}}(\mathcal {S}(0))$
. Therefore, by using the trivial bound
![]() $\cos ^2(\frac {1}{2}(\alpha _1-\alpha _2) \log p)\le 1$
and the assumption
$\cos ^2(\frac {1}{2}(\alpha _1-\alpha _2) \log p)\le 1$
and the assumption
![]() $|\gamma ^+|=|\frac {\alpha _1+\alpha _2}{2}|\ll T^{0.6}$
, we derive
$|\gamma ^+|=|\frac {\alpha _1+\alpha _2}{2}|\ll T^{0.6}$
, we derive
![]() $\operatorname {\mathrm {meas}}(\mathcal {S}(0)) \ll Te^{-(\log \log T)^2/10}$
.
$\operatorname {\mathrm {meas}}(\mathcal {S}(0)) \ll Te^{-(\log \log T)^2/10}$
.
For
![]() $1\le j\le \mathcal {I}-1$
, we have
$1\le j\le \mathcal {I}-1$
, we have
![]() $\mathcal {I}-j \le \frac {\log (1/\beta _j)}{\log 20}$
and
$\mathcal {I}-j \le \frac {\log (1/\beta _j)}{\log 20}$
and
 $$ \begin{align*}\sum_{T^{\beta_j} < p\le T^{\beta_{j+1}}} \frac{\cos^2( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} \le \sum_{T^{\beta_j} < p\le T^{\beta_{j+1}}} \frac{1}{p} = \log \beta_{j+1} -\log \beta_{j} +o(1) \le 10. \end{align*} $$
$$ \begin{align*}\sum_{T^{\beta_j} < p\le T^{\beta_{j+1}}} \frac{\cos^2( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} \le \sum_{T^{\beta_j} < p\le T^{\beta_{j+1}}} \frac{1}{p} = \log \beta_{j+1} -\log \beta_{j} +o(1) \le 10. \end{align*} $$
Also, we know
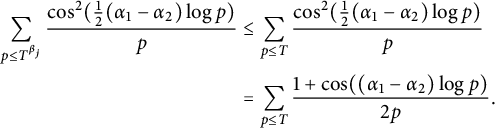 $$ \begin{align*} \sum_{p\le T^{\beta_{j}}} \frac{\cos^2( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} & \leq \sum_{p\le T} \frac{\cos^2( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} \\& = \sum_{p\le T} \frac{1+ \cos((\alpha_1-\alpha_2) \log p)}{2p}. \end{align*} $$
$$ \begin{align*} \sum_{p\le T^{\beta_{j}}} \frac{\cos^2( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} & \leq \sum_{p\le T} \frac{\cos^2( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p} \\& = \sum_{p\le T} \frac{1+ \cos((\alpha_1-\alpha_2) \log p)}{2p}. \end{align*} $$
By the above two bounds, (2.2), and the assumption
![]() $|\gamma ^+|\ll T^{0.6}$
, we see that the left of (5.15) is
$|\gamma ^+|\ll T^{0.6}$
, we see that the left of (5.15) is
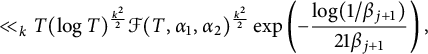 $$ \begin{align*}\ll_k T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}} \exp \left(- \frac{\log(1/\beta_{j+1})}{21 \beta_{j+1}}\right), \end{align*} $$
$$ \begin{align*}\ll_k T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}} \exp \left(- \frac{\log(1/\beta_{j+1})}{21 \beta_{j+1}}\right), \end{align*} $$
as desired.
6 Proof of Lemma 3.3
The proof of Lemma 3.3 is similar to the proofs of Lemmas 3.1 and 3.2. One key difference is that we need to invoke Lemma 2.2 in place of Lemma 2.1. In this section, we shall establish the estimate (3.9). As the proof of (3.10) is similar, the details shall be omitted. The integral in (3.9) shall be denoted
![]() $\int _{\mathcal {T}} \exp (\varphi (t)) \, dt$
where
$\int _{\mathcal {T}} \exp (\varphi (t)) \, dt$
where
![]() $\exp (\varphi (t)) $
is the integrand in (3.9). First, we decompose this integrand in terms of integer parameters m satisfying
$\exp (\varphi (t)) $
is the integrand in (3.9). First, we decompose this integrand in terms of integer parameters m satisfying
![]() $0 \le m \le \frac {\log \log T}{\log 2}$
. For each such m, we define
$0 \le m \le \frac {\log \log T}{\log 2}$
. For each such m, we define
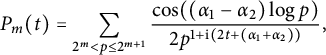 $$ \begin{align*} P_m(t) = \sum_{2^m< p\le 2^{m+1}} \frac{\cos( (\alpha_1-\alpha_2)\log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}}, \end{align*} $$
$$ \begin{align*} P_m(t) = \sum_{2^m< p\le 2^{m+1}} \frac{\cos( (\alpha_1-\alpha_2)\log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}}, \end{align*} $$
and the set
 $$ \begin{align} \mathcal{P}(m) := \Big\{ t\in [T, 2T] \mid &|{\mathfrak{Re}} P_m(t)|> 2^{-m/10}, \nonumber\\ & \text{ but } |{\mathfrak{Re}} P_n(t)|\le 2^{-n/10} \text{ for every } m+1\le n \le \frac{\log\log T}{\log 2}\Big\}. \end{align} $$
$$ \begin{align} \mathcal{P}(m) := \Big\{ t\in [T, 2T] \mid &|{\mathfrak{Re}} P_m(t)|> 2^{-m/10}, \nonumber\\ & \text{ but } |{\mathfrak{Re}} P_n(t)|\le 2^{-n/10} \text{ for every } m+1\le n \le \frac{\log\log T}{\log 2}\Big\}. \end{align} $$
Observe that
 $$ \begin{align} \sum_{p\le \log T }\frac{\cos( (\alpha_1-\alpha_2) \log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}} = \sum_{0 \le m \le \frac{\log \log T}{\log 2}} P_m(t) +O(1), \end{align} $$
$$ \begin{align} \sum_{p\le \log T }\frac{\cos( (\alpha_1-\alpha_2) \log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}} = \sum_{0 \le m \le \frac{\log \log T}{\log 2}} P_m(t) +O(1), \end{align} $$
where the error term follows from Mertens’ estimate (Lemma 2.3 with
![]() $a=0$
) as
$a=0$
) as
 $$ \begin{align*}\sum_{\log T< p\le 2\log T } \frac{1}{p} = \log\log(2\log T) - \log\log\log T + O(1) = \log \frac{\log(2\log T)}{\log\log T} + O(1) , \end{align*} $$
$$ \begin{align*}\sum_{\log T< p\le 2\log T } \frac{1}{p} = \log\log(2\log T) - \log\log\log T + O(1) = \log \frac{\log(2\log T)}{\log\log T} + O(1) , \end{align*} $$
which is
![]() $\ll 1$
. We now have the decomposition
$\ll 1$
. We now have the decomposition
 $$ \begin{align} & \int_{\mathcal{T}} \exp( \varphi(t))) dt \nonumber\\ & \quad = \sum_{0 \le m \le \frac{\log \log T}{\log 2}} \int_{\mathcal{T} \cap \mathcal{P}(m)} \exp( \varphi(t))) \, dt + \int_{\mathcal{T} \cap \left( \bigcap_{m} \mathcal{P}(m)^c \right)} \exp( \varphi(t))) dt. \end{align} $$
$$ \begin{align} & \int_{\mathcal{T}} \exp( \varphi(t))) dt \nonumber\\ & \quad = \sum_{0 \le m \le \frac{\log \log T}{\log 2}} \int_{\mathcal{T} \cap \mathcal{P}(m)} \exp( \varphi(t))) \, dt + \int_{\mathcal{T} \cap \left( \bigcap_{m} \mathcal{P}(m)^c \right)} \exp( \varphi(t))) dt. \end{align} $$
In order to establish (3.9), we shall bound each of the integrals on the right side of (6.3).
If t does not belong to any
![]() $\mathcal {P}(m)$
, then
$\mathcal {P}(m)$
, then
![]() $|{\mathfrak {Re}} P_n(t)|\le 2^{-n/10}$
for all
$|{\mathfrak {Re}} P_n(t)|\le 2^{-n/10}$
for all
![]() $n\le \frac {\log \log T}{\log 2}$
. (Indeed, for those t belonging to none of
$n\le \frac {\log \log T}{\log 2}$
. (Indeed, for those t belonging to none of
![]() $\mathcal {P}(m)$
,
$\mathcal {P}(m)$
,
![]() $0\le m\le \frac {\log \log T}{\log 2}$
, if
$0\le m\le \frac {\log \log T}{\log 2}$
, if
![]() $|{\mathfrak {Re}} P_m(t)|> 2^{-m/10}$
for some
$|{\mathfrak {Re}} P_m(t)|> 2^{-m/10}$
for some
![]() $0 \leq m \le \frac {\log \log T}{\log 2}$
, then
$0 \leq m \le \frac {\log \log T}{\log 2}$
, then
![]() $|{\mathfrak {Re}} P_L(t)|> 2^{-L/10}$
for some
$|{\mathfrak {Re}} P_L(t)|> 2^{-L/10}$
for some
![]() $m+1\le L\le \frac {\log \log T}{\log 2}$
as
$m+1\le L\le \frac {\log \log T}{\log 2}$
as
![]() $t\notin \mathcal {P}(m)$
. Choosing L to be maximal, we then have
$t\notin \mathcal {P}(m)$
. Choosing L to be maximal, we then have
![]() $|{\mathfrak {Re}} P_n(t)|\le 2^{-n/10}$
for every
$|{\mathfrak {Re}} P_n(t)|\le 2^{-n/10}$
for every
![]() $L+1\le n \le \frac {\log \log T}{\log 2}$
, which means
$L+1\le n \le \frac {\log \log T}{\log 2}$
, which means
![]() $t\in \mathcal {P}(L)$
, a contradiction.) For such an instance,
$t\in \mathcal {P}(L)$
, a contradiction.) For such an instance,
![]() ${\mathfrak {Re}} \sum _{p\le \log T }\frac {\cos ( (\alpha _1-\alpha _2)\log p)}{2p^{1+ \mathrm {i} (2t+ (\alpha _1+\alpha _2) )}} =O(1)$
. Hence, the contribution of such t to the integral
${\mathfrak {Re}} \sum _{p\le \log T }\frac {\cos ( (\alpha _1-\alpha _2)\log p)}{2p^{1+ \mathrm {i} (2t+ (\alpha _1+\alpha _2) )}} =O(1)$
. Hence, the contribution of such t to the integral
![]() $\int _{\mathcal {T}}$
can be bounded by using Lemma 3.1. That is,
$\int _{\mathcal {T}}$
can be bounded by using Lemma 3.1. That is,
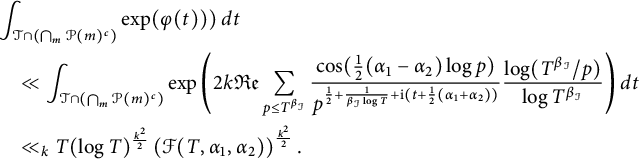 $$ \begin{align} \kern30pt & \int_{\mathcal{T} \cap \left( \bigcap_{m} \mathcal{P}(m)^c \right)} \exp( \varphi(t))) \, dt \nonumber\\&\quad \ll \int_{\mathcal{T} \cap \left( \bigcap_{m} \mathcal{P}(m)^c \right)} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \\&\quad \ll_k T (\log T)^{\frac{k^2}{2}} \left(\mathcal{F}(T,\alpha_1,\alpha_2) \right)^{\frac{k^2}{2}}. \nonumber \end{align} $$
$$ \begin{align} \kern30pt & \int_{\mathcal{T} \cap \left( \bigcap_{m} \mathcal{P}(m)^c \right)} \exp( \varphi(t))) \, dt \nonumber\\&\quad \ll \int_{\mathcal{T} \cap \left( \bigcap_{m} \mathcal{P}(m)^c \right)} \exp \left( 2k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \\&\quad \ll_k T (\log T)^{\frac{k^2}{2}} \left(\mathcal{F}(T,\alpha_1,\alpha_2) \right)^{\frac{k^2}{2}}. \nonumber \end{align} $$
It remains to estimate the contribution from
![]() $t\in \mathcal {T} \cap \mathcal {P}(m)$
, with
$t\in \mathcal {T} \cap \mathcal {P}(m)$
, with
![]() $0 \le m \le \frac {\log \log T}{\log 2}$
, to
$0 \le m \le \frac {\log \log T}{\log 2}$
, to
![]() $\int _{\mathcal {T}}$
(more precisely, the first integral on the right of (6.3)). To do so, we first consider the case that
$\int _{\mathcal {T}}$
(more precisely, the first integral on the right of (6.3)). To do so, we first consider the case that
![]() $0\le m\le \frac {2\log \log \log T}{\log 2}$
. In this case, we have
$0\le m\le \frac {2\log \log \log T}{\log 2}$
. In this case, we have
 $$ \begin{align*} & \left|{\mathfrak{Re}} \sum_{p\le \log T }\frac{\cos( (\alpha_1-\alpha_2) \log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}} \right| \\&\quad \leq \sum_{0\leq n \leq \frac{\log \log T}{\log 2}} | {\mathfrak{Re}} P_n(t)| + O(1) \\&\quad \leq \sum_{0\leq n \leq m} |{\mathfrak{Re}} P_n(t) | + \sum_{m+1 \leq n \leq \frac{\log \log T}{\log 2}} | {\mathfrak{Re}} P_n(t) | + O(1)\\&\quad \leq \sum_{ p\le 2^{m+1}} \frac{1}{2p} + \sum_{m + 1 \leq n \leq \frac{\log \log T}{\log 2}} \frac{1}{2^{n/10}} + O(1), \end{align*} $$
$$ \begin{align*} & \left|{\mathfrak{Re}} \sum_{p\le \log T }\frac{\cos( (\alpha_1-\alpha_2) \log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}} \right| \\&\quad \leq \sum_{0\leq n \leq \frac{\log \log T}{\log 2}} | {\mathfrak{Re}} P_n(t)| + O(1) \\&\quad \leq \sum_{0\leq n \leq m} |{\mathfrak{Re}} P_n(t) | + \sum_{m+1 \leq n \leq \frac{\log \log T}{\log 2}} | {\mathfrak{Re}} P_n(t) | + O(1)\\&\quad \leq \sum_{ p\le 2^{m+1}} \frac{1}{2p} + \sum_{m + 1 \leq n \leq \frac{\log \log T}{\log 2}} \frac{1}{2^{n/10}} + O(1), \end{align*} $$
where the first
![]() $O(1)$
is due to (6.2), and the last inequality makes use of the definition of
$O(1)$
is due to (6.2), and the last inequality makes use of the definition of
![]() $\mathcal {P}(m)$
in (6.1). Therefore, we deduce
$\mathcal {P}(m)$
in (6.1). Therefore, we deduce
 $$ \begin{align*} &\left| {\mathfrak{Re}}\left( \sum_{ p\le 2^{m+1}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } + \sum_{p\le \log T }\frac{\cos( (\alpha_1-\alpha_2) \log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}} \right) \right| \\&\quad \le \sum_{ p\le 2^{m+1}}\frac{1}{\sqrt{p}} + \sum_{ p\le 2^{m+1}}\frac{1}{2p} +\sum_{m+1\le n \le \frac{\log\log T}{\log 2}} \frac{1}{2^{n/10}} + O(1)\\&\quad \ll 2^{m/2}. \end{align*} $$
$$ \begin{align*} &\left| {\mathfrak{Re}}\left( \sum_{ p\le 2^{m+1}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } + \sum_{p\le \log T }\frac{\cos( (\alpha_1-\alpha_2) \log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}} \right) \right| \\&\quad \le \sum_{ p\le 2^{m+1}}\frac{1}{\sqrt{p}} + \sum_{ p\le 2^{m+1}}\frac{1}{2p} +\sum_{m+1\le n \le \frac{\log\log T}{\log 2}} \frac{1}{2^{n/10}} + O(1)\\&\quad \ll 2^{m/2}. \end{align*} $$
Thus, we derive
 $$ \begin{align} & \int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 2k {\mathfrak{Re}} \left( \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } + \sum_{p\le \log T }\frac{\cos( (\alpha_1-\alpha_2) \log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}} \right) \right)dt \nonumber\\&\quad \le e^{O(k2^{m/2})} \int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 2k {\mathfrak{Re}}\sum_{2^{m+1}< p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \nonumber\\&\quad \le e^{O(k2^{m/2})} \int_{t\in \mathcal{T}} \exp \left( 2k {\mathfrak{Re}}\sum_{2^{m+1}< p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right) \nonumber\\&\quad \times (2^{m/10} {\mathfrak{Re}} P_m(t))^{2[2^{3m/4}]}dt.\nonumber \\ \end{align} $$
$$ \begin{align} & \int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 2k {\mathfrak{Re}} \left( \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } + \sum_{p\le \log T }\frac{\cos( (\alpha_1-\alpha_2) \log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}} \right) \right)dt \nonumber\\&\quad \le e^{O(k2^{m/2})} \int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 2k {\mathfrak{Re}}\sum_{2^{m+1}< p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \nonumber\\&\quad \le e^{O(k2^{m/2})} \int_{t\in \mathcal{T}} \exp \left( 2k {\mathfrak{Re}}\sum_{2^{m+1}< p\le T^{\beta_{\mathcal{I}}}}\frac{\cos(\frac{1}{2}(\alpha_1-\alpha_2)\log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+\frac{1}{2}(\alpha_1+\alpha_2)) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right) \nonumber\\&\quad \times (2^{m/10} {\mathfrak{Re}} P_m(t))^{2[2^{3m/4}]}dt.\nonumber \\ \end{align} $$
(Here, we used the identity
![]() $|{\mathfrak {Re}} P_m(t)|^{2[2^{3m/4}]} = ({\mathfrak {Re}} P_m(t))^{2[2^{3m/4}]}$
as
$|{\mathfrak {Re}} P_m(t)|^{2[2^{3m/4}]} = ({\mathfrak {Re}} P_m(t))^{2[2^{3m/4}]}$
as
![]() $2[2^{3m/4}]$
is an even integer.) Let
$2[2^{3m/4}]$
is an even integer.) Let
![]() $N =2[2^{3m/4}] $
. To proceed further, we require the following variant of Lemma 4.1.
$N =2[2^{3m/4}] $
. To proceed further, we require the following variant of Lemma 4.1.
Lemma 6.1 Assume
![]() $0\le m\le \frac {2\log \log \log T}{\log 2}$
. If
$0\le m\le \frac {2\log \log \log T}{\log 2}$
. If
![]() $t\in \mathcal {T}$
, we have
$t\in \mathcal {T}$
, we have
 $$ \begin{align*} \prod_{1\le i \le \mathcal{I}} \exp( k{\mathfrak{Re}} \tilde{F}_i(t) )^2 \ll \prod_{1\le i \le \mathcal{I}}\left(\sum_{0\le n \le 100k \beta_i^{-3/4}} \frac{(k {\mathfrak{Re}} \tilde{F}_i(t) )^n}{n!} \right)^2, \end{align*} $$
$$ \begin{align*} \prod_{1\le i \le \mathcal{I}} \exp( k{\mathfrak{Re}} \tilde{F}_i(t) )^2 \ll \prod_{1\le i \le \mathcal{I}}\left(\sum_{0\le n \le 100k \beta_i^{-3/4}} \frac{(k {\mathfrak{Re}} \tilde{F}_i(t) )^n}{n!} \right)^2, \end{align*} $$
where
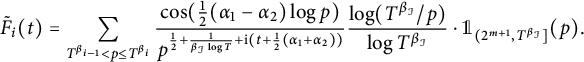
Proof We first claim that if
![]() $T^{\beta _{r-1}}<2^{m+1} \leq T^{\beta _{r}}$
for some
$T^{\beta _{r-1}}<2^{m+1} \leq T^{\beta _{r}}$
for some
![]() $1\leq r \leq \mathcal {I}$
, then
$1\leq r \leq \mathcal {I}$
, then
![]() $r=1$
. Indeed, we would otherwise have
$r=1$
. Indeed, we would otherwise have
![]() $2^{m+1}> T^{\beta _{1}} = T^{\frac {1}{(\log \log T)^2}}$
, which contradicts the assumption
$2^{m+1}> T^{\beta _{1}} = T^{\frac {1}{(\log \log T)^2}}$
, which contradicts the assumption
![]() $0\le m\le \frac {2\log \log \log T}{\log 2}$
. Consequently, when
$0\le m\le \frac {2\log \log \log T}{\log 2}$
. Consequently, when
![]() $i\geq 2$
, we know
$i\geq 2$
, we know
![]() $|{\mathfrak {Re}} \tilde {F}_i(t)| = |{\mathfrak {Re}} F_i(t)| \leq \beta _i^{-3/4}$
for
$|{\mathfrak {Re}} \tilde {F}_i(t)| = |{\mathfrak {Re}} F_i(t)| \leq \beta _i^{-3/4}$
for
![]() $t\in \mathcal {T}$
. On the other hand, for
$t\in \mathcal {T}$
. On the other hand, for
![]() $i=1$
, we can write
$i=1$
, we can write

Observe that
![]() $2^{m/2} \leq \log \log T$
as
$2^{m/2} \leq \log \log T$
as
![]() $0\le m\le \frac {2\log \log \log T}{\log 2}$
, and recall
$0\le m\le \frac {2\log \log \log T}{\log 2}$
, and recall
![]() $|{\mathfrak {Re}} F_1(t) | \leq \beta _1^{-3/4} = (\log \log T)^{3/2}$
for
$|{\mathfrak {Re}} F_1(t) | \leq \beta _1^{-3/4} = (\log \log T)^{3/2}$
for
![]() $t\in \mathcal {T}$
. It then follows that
$t\in \mathcal {T}$
. It then follows that
![]() $|{\mathfrak {Re}} \tilde {F}_1(t)| \leq 1.01\beta _1^{-3/4}$
(for all T sufficiently large). Therefore, we can establish the desired upper bound by a slight modification of the proof of Lemma 4.1 while using
$|{\mathfrak {Re}} \tilde {F}_1(t)| \leq 1.01\beta _1^{-3/4}$
(for all T sufficiently large). Therefore, we can establish the desired upper bound by a slight modification of the proof of Lemma 4.1 while using
![]() $|{\mathfrak {Re}} \tilde {F}_i(t)| \leq 1.01\beta _i^{-3/4}$
for
$|{\mathfrak {Re}} \tilde {F}_i(t)| \leq 1.01\beta _i^{-3/4}$
for
![]() $t\in \mathcal {T}$
and
$t\in \mathcal {T}$
and
![]() $1\leq i \leq \mathcal {I}$
(in the place of
$1\leq i \leq \mathcal {I}$
(in the place of
![]() $|{\mathfrak {Re}} F_i(t)| \leq \beta _i^{-3/4}$
).
$|{\mathfrak {Re}} F_i(t)| \leq \beta _i^{-3/4}$
).
Writing
 $$ \begin{align*}{\mathfrak{Re}} P_m(t) = \sum_{2^m< \mathfrak{q}\le 2^{m+1}} \frac{ \cos((2t+(\alpha_1+\alpha_2)) \log \mathfrak{q} ) \cos( (\alpha_1-\alpha_2)\log \mathfrak{q}) }{2\mathfrak{q}}, \end{align*} $$
$$ \begin{align*}{\mathfrak{Re}} P_m(t) = \sum_{2^m< \mathfrak{q}\le 2^{m+1}} \frac{ \cos((2t+(\alpha_1+\alpha_2)) \log \mathfrak{q} ) \cos( (\alpha_1-\alpha_2)\log \mathfrak{q}) }{2\mathfrak{q}}, \end{align*} $$
by Lemma 6.1, we derive

where
![]() $\tilde {j}=(j_1,\ldots ,j_{\mathcal {I}}), \, \tilde {\ell }=(\ell _1,\ldots ,\ell _{\mathcal {I}})$
, with
$\tilde {j}=(j_1,\ldots ,j_{\mathcal {I}}), \, \tilde {\ell }=(\ell _1,\ldots ,\ell _{\mathcal {I}})$
, with
![]() $0 \le j_i,\ell _i \le 100k \beta _i^{-3/4}$
, and
$0 \le j_i,\ell _i \le 100k \beta _i^{-3/4}$
, and
![]() $ \tilde {p}$
,
$ \tilde {p}$
,
![]() $\tilde {q}$
, and
$\tilde {q}$
, and
![]() $\tilde {\mathfrak {q}}$
are tuples:
$\tilde {\mathfrak {q}}$
are tuples:
 $$ \begin{align*} \tilde{p} & =( p(1,1),\ldots, p(1,j_1), p(2,1),\ldots,p(2,j_2),\ldots, p(\mathcal{I},j_{\mathcal{I}} )), \\ \tilde{q} & =( q(1,1),\ldots, q(1,\ell_1), q(2,1),\ldots,q(2,{\ell}_2),\ldots, q(\mathcal{I},{\ell}_{\mathcal{I}} )),\\ \tilde{\mathfrak{q}} & = ( \mathfrak{q}_1, \ldots, \mathfrak{q}_M) \end{align*} $$
$$ \begin{align*} \tilde{p} & =( p(1,1),\ldots, p(1,j_1), p(2,1),\ldots,p(2,j_2),\ldots, p(\mathcal{I},j_{\mathcal{I}} )), \\ \tilde{q} & =( q(1,1),\ldots, q(1,\ell_1), q(2,1),\ldots,q(2,{\ell}_2),\ldots, q(\mathcal{I},{\ell}_{\mathcal{I}} )),\\ \tilde{\mathfrak{q}} & = ( \mathfrak{q}_1, \ldots, \mathfrak{q}_M) \end{align*} $$
whose components are primes which satisfy
Here,
![]() $C(\tilde {p}, \tilde {q})$
is defined as in (4.8), and
$C(\tilde {p}, \tilde {q})$
is defined as in (4.8), and
 $$ \begin{align*} C_4(\tilde{\mathfrak{q}}) = \prod_{v=1}^{N} \frac{1}{2\mathfrak{q}_{v}}. \end{align*} $$
$$ \begin{align*} C_4(\tilde{\mathfrak{q}}) = \prod_{v=1}^{N} \frac{1}{2\mathfrak{q}_{v}}. \end{align*} $$
Applying Lemma 2.2, we see that the last integral in (6.6) is
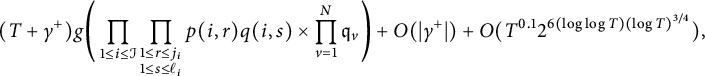 $$ \begin{align*}(T+\gamma^+) g\Bigg( \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r) q(i,s) \times\prod_{v=1}^{N} \mathfrak{q}_v \Bigg) + O(|\gamma^+|) +O(T^{0.1} 2^{6 (\log\log T) (\log T)^{3/4}}), \end{align*} $$
$$ \begin{align*}(T+\gamma^+) g\Bigg( \prod_{1\le i \le \mathcal{I}} \prod_{\substack{1\le r \le j_i \\ 1\le s \le \ell_i}} p(i,r) q(i,s) \times\prod_{v=1}^{N} \mathfrak{q}_v \Bigg) + O(|\gamma^+|) +O(T^{0.1} 2^{6 (\log\log T) (\log T)^{3/4}}), \end{align*} $$
where the last big-O term is due to the bounds (4.9) and
by
![]() $2^m< \mathfrak {q}_1,\ldots ,\mathfrak {q}_{N} \le 2^{m+1}$
and
$2^m< \mathfrak {q}_1,\ldots ,\mathfrak {q}_{N} \le 2^{m+1}$
and
![]() $2^{m}\le \log T$
. Thus, we derive
$2^{m}\le \log T$
. Thus, we derive

(Here, we used the fact that none of
![]() $p(i,r)$
and
$p(i,r)$
and
![]() $q(i,s)$
, appearing in g, equals
$q(i,s)$
, appearing in g, equals
![]() $\mathfrak {q}_v$
for any v. It is because of the factor
$\mathfrak {q}_v$
for any v. It is because of the factor ![]() , which forces
, which forces
![]() $p(i,r),q(i,s)> 2^{m+1} \ge \mathfrak {q}_v$
.) From an argument similar to the one below (4.11), it follows that the contribution of the big-O term on the right of (6.7) to
$p(i,r),q(i,s)> 2^{m+1} \ge \mathfrak {q}_v$
.) From an argument similar to the one below (4.11), it follows that the contribution of the big-O term on the right of (6.7) to
![]() $\tilde {\mathscr {I} }$
is
$\tilde {\mathscr {I} }$
is
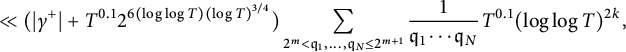 $$ \begin{align*}\ll(|\gamma^+| + T^{0.1 }2^{6 (\log\log T) (\log T)^{3/4}} ) \sum_{2^m< \mathfrak{q}_1,\ldots,\mathfrak{q}_{N} \le 2^{m+1}} \frac{1}{\mathfrak{q}_1\cdots \mathfrak{q}_{N}} T^{0.1}(\log\log T)^{2k}, \end{align*} $$
$$ \begin{align*}\ll(|\gamma^+| + T^{0.1 }2^{6 (\log\log T) (\log T)^{3/4}} ) \sum_{2^m< \mathfrak{q}_1,\ldots,\mathfrak{q}_{N} \le 2^{m+1}} \frac{1}{\mathfrak{q}_1\cdots \mathfrak{q}_{N}} T^{0.1}(\log\log T)^{2k}, \end{align*} $$
which is
![]() $\ll (|\gamma ^+| +T^{0.1+o(1)}) T^{0.1} (\log \log T)^{2k}$
as the sum above is equal to
$\ll (|\gamma ^+| +T^{0.1+o(1)}) T^{0.1} (\log \log T)^{2k}$
as the sum above is equal to
 $$ \begin{align*}\left( \sum_{2^m < \mathfrak{q}\le 2^{m+1}} \frac{1}{\mathfrak{q}} \right)^{N} \le \left( (2^{m+1} -2^m) \frac{1}{2^m} \right)^{N} =1. \end{align*} $$
$$ \begin{align*}\left( \sum_{2^m < \mathfrak{q}\le 2^{m+1}} \frac{1}{\mathfrak{q}} \right)^{N} \le \left( (2^{m+1} -2^m) \frac{1}{2^m} \right)^{N} =1. \end{align*} $$
Now, arguing as in the proof of Lemma 3.1 (leading from (4.12) to (4.19)), we can bound
![]() $\tilde {\mathscr {I} }$
by
$\tilde {\mathscr {I} }$
by
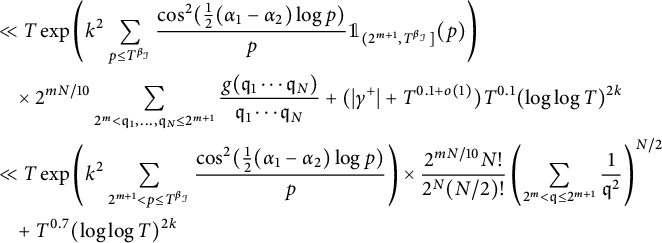
as
![]() $|\gamma ^+|= |\frac {\alpha _1+\alpha _2}{2}|\ll T^{0.6}$
. Hence, by (6.6) and (6.8), combined with (2.2), the left of (6.5) is
$|\gamma ^+|= |\frac {\alpha _1+\alpha _2}{2}|\ll T^{0.6}$
. Hence, by (6.6) and (6.8), combined with (2.2), the left of (6.5) is
 $$ \begin{align} &\ll e^{O(k2^{m/2})} \left(2^{m/5}\cdot 2^{3m/4}\cdot 2^{-m} \right)^{[2^{3m/4}]} T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}} \nonumber\\ &\ll e^{O(k2^{m/2}) -2^{3m/4}} T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}. \end{align} $$
$$ \begin{align} &\ll e^{O(k2^{m/2})} \left(2^{m/5}\cdot 2^{3m/4}\cdot 2^{-m} \right)^{[2^{3m/4}]} T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}} \nonumber\\ &\ll e^{O(k2^{m/2}) -2^{3m/4}} T (\log T)^{\frac{k^2}{2}} \mathcal{F}(T,\alpha_1,\alpha_2)^{\frac{k^2}{2}}. \end{align} $$
Second, we evaluate the contribution from
![]() $t\in \mathcal {T} \cap \mathcal {P}(m)$
with
$t\in \mathcal {T} \cap \mathcal {P}(m)$
with
![]() $ \frac {2\log \log \log T}{\log 2} < m \le \frac {\log \log T}{\log 2}$
. We shall consider
$ \frac {2\log \log \log T}{\log 2} < m \le \frac {\log \log T}{\log 2}$
. We shall consider
Following the previous argument in (6.5) with the exponential factor replaced by
![]() $1$
, one can show that
$1$
, one can show that
![]() $\operatorname {\mathrm {meas}}(\mathcal {T}\cap \mathcal {P}(m))\ll T e^{ -2^{3m/4}}$
. So, for
$\operatorname {\mathrm {meas}}(\mathcal {T}\cap \mathcal {P}(m))\ll T e^{ -2^{3m/4}}$
. So, for
![]() $2^m\ge (\log \log T)^2$
, we see
$2^m\ge (\log \log T)^2$
, we see
![]() $\operatorname {\mathrm {meas}}(\mathcal {T}\cap \mathcal {P}(m))\ll T e^{ -(\log \log T)^{3/2}}$
. In addition, the Cauchy–Schwarz inequality tells us that
$\operatorname {\mathrm {meas}}(\mathcal {T}\cap \mathcal {P}(m))\ll T e^{ -(\log \log T)^{3/2}}$
. In addition, the Cauchy–Schwarz inequality tells us that
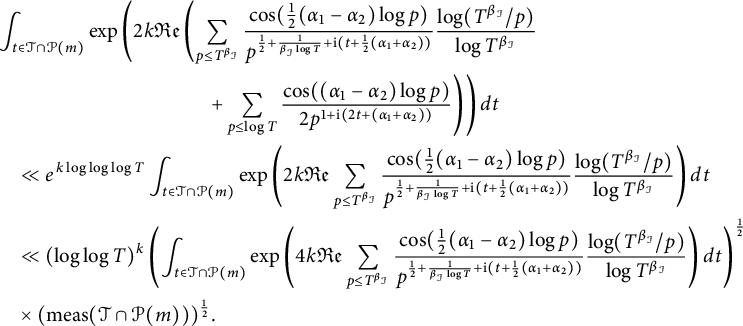 $$ \begin{align} &\int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 2k {\mathfrak{Re}} \left( \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} }\right.\right. \nonumber\\& \left.\left. \qquad\qquad\qquad\qquad\qquad + \sum_{p\le \log T }\frac{\cos( (\alpha_1-\alpha_2) \log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}} \right) \right)dt \nonumber\\&\quad\ll e^{k \log \log \log T } \int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 2k {\mathfrak{Re}} \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \nonumber\\&\quad\ll (\log \log T)^k \left( \int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 4k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right) dt \right)^{\frac{1}{2}} \nonumber\\&\quad\times (\operatorname{\mathrm{meas}}(\mathcal{T}\cap \mathcal{P}(m)))^{\frac{1}{2}}.\nonumber\\ \end{align} $$
$$ \begin{align} &\int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 2k {\mathfrak{Re}} \left( \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} }\right.\right. \nonumber\\& \left.\left. \qquad\qquad\qquad\qquad\qquad + \sum_{p\le \log T }\frac{\cos( (\alpha_1-\alpha_2) \log p)}{2p^{1+ \mathrm{i} (2t+ (\alpha_1+\alpha_2) )}} \right) \right)dt \nonumber\\&\quad\ll e^{k \log \log \log T } \int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 2k {\mathfrak{Re}} \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \nonumber\\&\quad\ll (\log \log T)^k \left( \int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 4k {\mathfrak{Re}}\sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right) dt \right)^{\frac{1}{2}} \nonumber\\&\quad\times (\operatorname{\mathrm{meas}}(\mathcal{T}\cap \mathcal{P}(m)))^{\frac{1}{2}}.\nonumber\\ \end{align} $$
As Lemma 3.1 gives
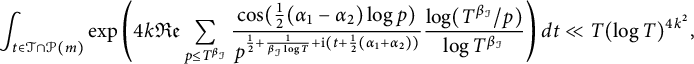 $$ \begin{align*} \int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 4k {\mathfrak{Re}} \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \ll T (\log T)^{4k^2}, \end{align*} $$
$$ \begin{align*} \int_{t\in \mathcal{T}\cap \mathcal{P}(m)} \exp \left( 4k {\mathfrak{Re}} \sum_{ p\le T^{\beta_{\mathcal{I}}}}\frac{\cos( \frac{1}{2}(\alpha_1-\alpha_2) \log p)}{p^{\frac{1}{2}+\frac{1}{\beta_{\mathcal{I}} \log T}+\mathrm{i} (t+ \frac{1}{2}(\alpha_1+\alpha_2) ) } }\frac{\log(T^{\beta_{\mathcal{I}}}/p)}{\log T^{\beta_{\mathcal{I}}} } \right)dt \ll T (\log T)^{4k^2}, \end{align*} $$
we see that (6.10) is bounded by
Finally, we conclude the proof by combining (6.3) with the bounds (6.9) (
![]() $0\le m\le \frac {2\log \log \log T}{\log 2}$
) and (6.11) (
$0\le m\le \frac {2\log \log \log T}{\log 2}$
) and (6.11) (
![]() $ \frac {2\log \log \log T}{\log 2} < m \leq \frac {\log \log T}{\log 2} $
) for
$ \frac {2\log \log \log T}{\log 2} < m \leq \frac {\log \log T}{\log 2} $
) for
![]() $\int _{\mathcal {T} \cap \mathcal {P}(m)} \exp ( \varphi (t))) \, dt$
and the bound (6.4).
$\int _{\mathcal {T} \cap \mathcal {P}(m)} \exp ( \varphi (t))) \, dt$
and the bound (6.4).
Acknowledgment
The authors thank the referees for their helpful comments and suggestions.