2. Steady waves with a cotravelling point-vortex row

It is useful first to review the exact solutions of Crowdy & Roenby (Reference Crowdy and Roenby2014) for a submerged point-vortex row cotravelling with a steady wave. The original derivation (Crowdy & Roenby Reference Crowdy and Roenby2014) employed free streamline theory but a rederivation was given more recently by Crowdy (Reference Crowdy2023) by considering the Schwarz function of the wave. Since the latter method will be generalised here, a brief review of it follows.

For solutions within the case-2 categorisation, it was argued (Crowdy Reference Crowdy2023) that, in a frame of reference cotravelling with the speed $U$ of the wave, the complex conjugate velocity field has the form

(2.1) \begin{equation} u - \textrm {i} v = q \sqrt {S'(z)}, \end{equation}

where $S(z)$ is the Schwarz function of the wave and the prime notation is used to denote differentiation, $S'(z) = {\rm d}S/{\rm d}z$ . The real quantity $q$ is related to the fluid speed on the boundary, which, as a consequence of Bernoulli’s theorem, is constant on the surface of the wave when gravity and surface tension are both absent. For a wave, the Schwarz function $S(z)$ is the function, analytic in a strip neighbourhood enclosing the surface of the wave, with the property $S(z) = \overline {z}$ on the wave surface. For a closed curve, the Schwarz function is a more familiar object (Davis Reference Davis1974): it is the function, analytic in an annular neighbourhood of the curve, with the property $S(z) = \overline {z}$ on the curve. In this paper, the convention is adopted that the parameter $q$ is positive: this will depend on the sign of the circulations chosen, and there is an additional sign indeterminacy in $\sqrt {S'(z)}$ , related to the choice of direction of the complex tangent ${\rm d}z/{\rm d}s=1/\sqrt {S'(z)}$ , where ${\rm d}s$ is the arclength element in the tangent direction. As is customary in fluid dynamics, the orthogonal tangent/normal variables on any boundary will be chosen to correspond to a fluid-inward-pointing normal, as indicated in figure 1. In this cotravelling frame of reference, as $y \to -\infty$ ,

(2.2) \begin{equation} u - \textrm {i} v \to -U, \end{equation}

where $U$ is the speed of the wave.

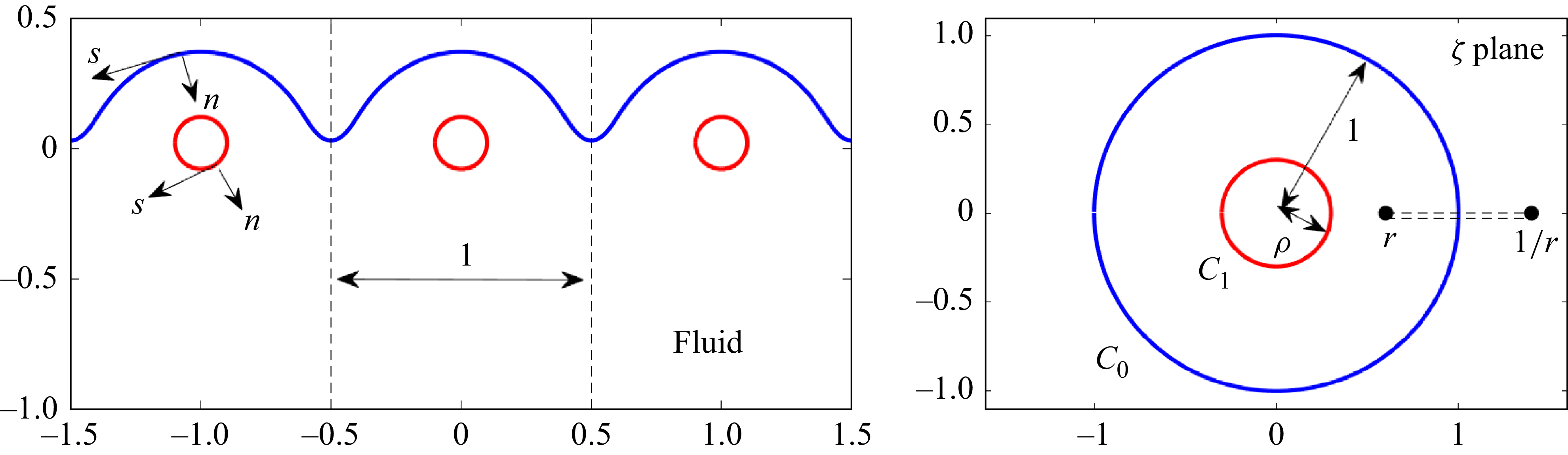
Figure 1. Conformal mapping from the cut unit disc $|\eta |\lt 1$ in a parametric complex $\eta$ plane to a single period of the wave with a submerged point-vortex row. The unit circle $|\eta |=1$ is transplanted to the open curve representing the wave. The two sides of a logarithmic branch cut are transplanted to the two edges of the period window with $\eta =0$ being the preimage of $y \to -\infty$ .

The key to the construction of the steadily travelling wave, and its associated Schwarz function, is use of conformal mapping. Consider the unit disc, $|\eta |\lt 1$ , in a parametric $\eta$ plane which is transplanted to a representative period window of the wave by the conformal mapping

(2.3) \begin{equation} z = {\mathcal Z}(\eta ). \end{equation}

The image of the unit circle $|\eta |=1$ is the open curve constituting the surface of the wave in this representative period window. Figure 1 shows a schematic. By the periodicity of the arrangement, this mapping must have a logarithmic singularity inside the disc, taken to be at $\eta =0$ without loss of generality because of the available degrees of freedom in the Riemann mapping theorem. The two ‘sides’ of a logarithmic branch cut from $\eta =0$ will be transplanted to the two edges of the representative period window. Since, in terms of this variable $\eta$ ,

(2.4) \begin{equation} \sqrt {S'(z)} = {{\rm d} \overline {z} \over {\rm d}s} = \left ( - {\eta ^{-1} \overline {{\mathcal Z}}'\bigl(\eta ^{-1}\bigr) \over \eta {\mathcal Z}'(\eta ) } \right )^{1/2}, \qquad {\mathcal Z}'(\eta ) = {{\rm d}{\mathcal Z} \over{\rm d}\eta }, \end{equation}

then, as shown by Crowdy (Reference Crowdy2023), it is useful to consider the functional form

(2.5) \begin{equation} {\mathcal Z}'(\eta ) = {\textrm {i} R \over \eta } \left ({\eta -c \over \eta -a} \right )^2, \qquad a, R \in \mathbb{R}, \qquad a \gt 1. \end{equation}

The parameter $c$ must have modulus greater than unity so that ${\mathcal Z}'(\eta )$ has no zeros inside the unit $\eta$ disc, a necessary condition for a univalent conformal mapping. Straightforward manipulations lead to

(2.6) \begin{align} \eta {\mathcal Z}'(\eta ) = {\textrm {i} R} \left ({\eta -c \over \eta -a} \right )^2 , \qquad \eta ^{-1} \overline {{\mathcal Z}}'(\eta ^{-1}) &= -{\textrm {i} R} \left ({1-\overline {c} \eta \over 1-a \eta } \right )^2 \end{align}

so that use of these in (2.1) and (2.4) leads to

(2.7) \begin{equation} u - \textrm {i} v = -q {(1-\overline {c} \eta ) (\eta -a) \over (1-a \eta )(\eta -c)}, \end{equation}

where the sign has been chosen to be consistent with positive $q$ if the circulation, $\varGamma$ say, of the point vortex is unity, i.e. $\varGamma =1$ . This complex conjugate velocity field is free of square-root branch points which do not have any natural interpretation as physical singularities. It has a simple pole at $\eta =1/a$ corresponding to a point vortex at $z_a = {\mathcal{Z}}(1/a)$ and, for equilibrium, this point vortex must be stationary in the frame of reference cotravelling with the wave. It is shown by Crowdy (Reference Crowdy2023) that this requires the choice $c=-a$ . Therefore, picking $R$ so that the period of the wave is unity, the solution is

(2.8) \begin{align} z= {\mathcal Z}(\eta ) = {\textrm {i} \over 2\pi } \left ( \log \eta - {4a \over \eta -a} \right )\!, \qquad {\mathcal Z}'(\eta ) = {\textrm {i} \over 2\pi \eta } \left ( {\eta +a \over \eta -a }\right )^2 \!. \end{align}

This coincides with the original solution of Crowdy & Roenby (Reference Crowdy and Roenby2014) who derived it differently. Formula (2.8) is a conformal mapping representation, first derived by Crowdy (Reference Crowdy2000), for the classic pure capillary waves found by Crapper (Reference Crapper1957); Crapper gave his solution in terms of hodograph variables instead. Hur & Wheeler (Reference Hur and Wheeler2020) also made use of a conformal mapping akin to (2.8). The free surface of a steady irrotational wave, without surface tension, cotravelling with a submerged point-vortex row can therefore have exactly the same shape as a pure capillary wave without any cotravelling point vortices. Crowdy (Reference Crowdy2023) has used a Schwarz function approach to rationalise this surprising circumstance.

The parameter $q$ is directly related to the wave speed $U$ . To see this, note from (2.7) that, as $y \to -\infty$ so that $\eta \to 0$ , then

(2.9) \begin{equation} u -\textrm {i} v \to q. \end{equation}

On comparison with (2.2), the speed of the wave $U=-q$ . If the circulation of the point vortex at $z=z_a$ is $\varGamma$ then, locally,

(2.10) \begin{equation} u - \textrm {i} v = - {\textrm {i} \varGamma \over 2\pi (z-z_a)} + \cdots = - {\textrm {i} \varGamma \over 2\pi {\mathcal Z}'(1/a) (\eta -1/a)} + \cdots .\end{equation}

From (2.7),

(2.11) \begin{equation} u - \textrm {i} v \to {2q (1-a^2) \over a(1+a^2)} {1 \over \eta -1/a} + \cdots .\end{equation}

Therefore, it follows that

(2.12) \begin{equation} {2q (1-a^2) \over a(1+a^2)} = - {\textrm {i} \varGamma \over 2 \pi {\mathcal Z}'(1/a)} \end{equation}

or, on use of (2.8),

(2.13) \begin{equation} q = {\varGamma \over 2} \left ({a^2 -1 \over a^2+1} \right )\!. \end{equation}

For a given amplitude parameter $a$ , the wave speed $U=-q$ where $q$ is given by (2.13) and, if $\varGamma =1$ , this is positive because $a\gt 1$ .

3. Hollow-vortex regularisation

If the point vortex is to be regularised as a hollow vortex then the form of the generalised velocity field, in the case-2 setting (Crowdy Reference Crowdy2023) where the flow is irrotational everywhere in the fluid, must be

(3.1) \begin{equation} u-\textrm{i}v = \left \lbrace \!\!\begin{array}{ll} q_0 \sqrt{S_0'(z)} & \textrm {on the wave surface}, \\[5pt] -q_1 \sqrt {S_1'(z)} & \textrm {on the hollow-vortex boundary}, \end{array} \right . \end{equation}

where $S_0(z)$ denotes the Schwarz function of the wave surface and $S_1(z)$ denotes the Schwarz function of the hollow-vortex boundary. As before, the parameters $q_0$ and $q_1$ , both assumed positive, represent the constant fluid speed on the wave surface and on the hollow-vortex boundary, respectively. The form (3.1) simultaneously satisfies the requirements that the two boundaries are streamlines in the cotravelling frame, and, according to Bernoulli’s theorem, are at constant pressure. The signs in these expressions have been chosen to be consistent with the expected flow directions on each boundary; note that, if the circulation of the hollow vortex is unity, as is assumed, the flow direction on its surface will oppose the tangent direction corresponding to the fluid-inward normal indicated in figure 2, and it is this that has been agreed to dictate the sign choice for $\sqrt {S_1'(z)}$ . Since the flow is irrotational, by analytic continuation of $u-\textrm {i}v$ off the two boundaries, it follows from (3.1) that $\sqrt {S_0'(z)}$ must be analytic in the fluid region with

(3.2) \begin{equation} q_0 \sqrt {S_0'(z)} = -q_1 \sqrt {S_1'(z)} \end{equation}

for any point $z$ inside the fluid. The challenge is to construct the two Schwarz functions $S_0(z)$ and $S_1(z)$ with the requisite properties.

Figure 2. Conformal mapping, $z=Z(\zeta )$ , transplants the cut annulus $\rho \lt |\zeta |\lt 1$ to a single period of the hollow-vortex-carrying wave. The unit circle $|\zeta |=1$ , denoted by $C_0$ , is transplanted to the open curve representing the wave surface, the circle $|\zeta |=\rho$ , denoted by $C_1$ , is transplanted to the closed boundary of the hollow vortex. A point $\zeta =r \in \mathbb{R}$ for $\rho \lt r \lt 1$ is the preimage of $y \to -\infty$ .

4. Conformal mapping from an annulus

As done in § 2, the relevant Schwarz functions $S_0(z)$ and $S_1(z)$ are found with the help of conformal mapping theory. The periodicity of the flow in the $x$ direction means it is enough to consider a single period window and, with unit wave period, the representative period window occupies $-1/2 \lt x \lt 1/2$ . Since each period of the fluid domain is now doubly connected, it is necessary to use a preimage domain with the same doubly connected topology.

Consider, therefore, the annulus $\rho \lt |\zeta | \lt 1$ and let $C_0$ denote the unit circle $|\zeta |=1$ with $C_1$ denoting the circle $|\zeta |=\rho$ . It is assumed that $C_0$ is transplanted to the open curve that is a single period of the wave surface, and $C_1$ is transplanted to the closed curve that is the boundary of the hollow vortex. The correspondences are shown colour-coded in figure 2 which features a schematic of corresponding domains in the preimage $\zeta$ plane and in the physical $z$ plane. The interior of the annulus is taken to be in one-to-one correspondence with the fluid region in the representative period window.

In view of the periodicity there must be a logarithmic singularity of $Z(\zeta )$ , and hence a simple pole of $Z'(\zeta )={\rm d}Z/{\rm d}\zeta$ , inside the annulus at some point $\zeta =r$ assumed to be on the positive real $\zeta$ axis (using a rotational degree of freedom in the Riemann mapping theorem). Therefore, $r \in \mathbb{R}$ with $\rho \lt r \lt 1$ . For a one-to-one correspondence between the representative period window and the annulus, it will be necessary to introduce a logarithmic branch cut attached to $\zeta =r$ the two ‘sides’ of which will correspond to the two edges of the period window. A natural choice of this branch cut is made shortly.

Since, on $C_0$ ,

(4.1) \begin{equation} \sqrt {S_0'(z)} = \left ( - {\zeta ^{-1} \overline {Z}'\bigl(\zeta ^{-1}\bigr) \over \zeta Z'(\zeta )} \right )^{1/2} \end{equation}

and, on $C_1$ ,

(4.2) \begin{equation} \sqrt {S_1'(z)} = \left ( - {\rho ^2 \zeta ^{-1} \overline {Z}'\bigl(\rho ^2 \zeta ^{-1}\bigr) \over \zeta Z'(\zeta )} \right )^{1/2} \end{equation}

then, from (3.1),

(4.3) \begin{equation} u-\textrm{i}v = \left \lbrace \!\!\begin{array}{ll} q_0 \left ( - \dfrac {\zeta ^{-1} \overline {Z}'\bigl(\zeta ^{-1}\bigr)}{\zeta Z'(\zeta )} \right )^{1/2}, & \textrm {on}\,|\zeta |=1, \\[6pt] - q_1 \left ( - \dfrac{\rho ^2 \zeta ^{-1} \overline {Z}'\bigl(\rho ^2 \zeta ^{-1}\bigr)}{\zeta Z'(\zeta )} \right )^{1/2}, & \textrm {on}\,|\zeta |=\rho . \end{array} \right . \end{equation}

Consider a conformal mapping $z=Z(\zeta )$ from the annulus with derivative of the form reported earlier in (1.1). All parameters $R,\ b$ and $r$ are assumed to be real. This restricts the search to waves that are symmetric about the crests and troughs. The simple poles at $\zeta =r,1/r$ will lead to logarithmic singularities of the mapping function $Z(\zeta )$ , and a branch cut is taken along the real axis between them, as shown in figure 2. It is evident from (1.1) and (1.2) that an infinity of equivalent pairs of logarithmic branch points of the mapping also exist, and it is assumed that corresponding branch cut choices are made so that none pass through the principal annulus $\rho \lt |\zeta | \lt 1/\rho$ . The parameter $b$ , which is the location of a second-order zero of the derivative of the mapping function, is not allowed inside the annulus $\rho \lt |\zeta | \lt 1$ since $Z'(\zeta )$ must not vanish there. To set the period of the waves to unity, the constant $R$ in (1.1) is chosen to be

(4.4) \begin{equation} R = - {\hat P(1,\rho ) P\big(r^2,\rho \big) \over 2 \pi r P(r/b,\rho )^2}. \end{equation}

After some elementary manipulations, the infinite product definition (1.2) can be used to verify the two functional identities:

(4.5) \begin{equation} P(1/\zeta ,\rho ) = -\zeta ^{-1}P(\zeta ,\rho ), \qquad P\big(\rho ^2 \zeta , \rho \big) = -\zeta ^{-1}P(\zeta ,\rho ). \end{equation}

The infinite product (1.2), once truncated after a sufficiently large number of terms for the required accuracy, can also be used to evaluate $P(\zeta ,\rho )$ . There is a rapidly convergent infinite sum representation of $P(\zeta ,\rho )$ that can also be used, as explained in Chapter 14 of Crowdy (Reference Crowdy2020) which gives additional background theory on $P(\zeta ,\rho )$ and the closely related prime function of the annulus.

The parameter $\rho$ governs the size of the hollow vortex, the parameter $r$ can be viewed as the wave amplitude parameter and $b$ is determined by the condition that the hollow vortex is a closed curve. This requires

(4.6) \begin{equation} \oint _{C_1} Z'(\zeta ) {\rm d}\zeta =0 ,\end{equation}

which turns out to be a single real equation for the single real parameter $b$ . Indeed, it is shown in Appendix A that this integral condition is equivalent to the real equation

(4.7) \begin{equation} {1 \over br} {P(br, \rho ) \over P(r/b,\rho )} = 1. \end{equation}

This equivalent equation, which is nonlinear in $b,\ r$ and $\rho$ , is the more convenient one to solve since it does not involve any integrals.

On $C_0$ ,

(4.8) \begin{equation} \zeta ^{-1} \overline {Z}'(1/\zeta ) = -{\textrm {i} R \over \zeta } \left ( { P(1/(\zeta b), \rho )^2 \over P(1/(\zeta r),\rho ) P( r/\zeta , \rho ) }\right ) = -{\textrm {i} R \over b^2 \zeta } \left ( { P(\zeta b, \rho )^2 \over P(\zeta /r,\rho ) P(\zeta r, \rho ) }\right )\!, \end{equation}

where (4.5) has been used; therefore,

(4.9) \begin{equation} u - \textrm {i} v = q_0 \left [ -{\zeta ^{-1} \overline {Z}'(1/\zeta ) \over \zeta Z'(\zeta )} \right ]^{1/2} = {q_0 \over b \zeta } {P(\zeta b,\rho ) \over P(\zeta /b,\rho )}, \end{equation}

where the sign has been chosen to be consistent with $q_0\gt 0$ and the surface velocity being that generated by a hollow vortex of unit circulation. On $C_1$ , on the other hand,

(4.10) \begin{align} \rho ^2\zeta ^{-1} \overline {Z}'\big(\rho ^2/\zeta \big) &= -{\textrm {i} R \rho ^2 \over \zeta } \!{\kern-.5pt}\left (\! { P\big(\rho ^2/(\zeta b), \rho \big)^2 \over P\big(\rho ^2/(\zeta r),\rho \big) P\big( \rho ^2 r/\zeta , \rho \big) }\!\right )\! = -{\textrm {i} R \rho ^2 \over \zeta } {\kern-.5pt}\!\left (\! { P(\zeta b, \rho )^2 \over P(\zeta /r,\rho ) P(\zeta r, \rho ) }\!\right )\!, \end{align}

where (4.5) has been used again; therefore,

(4.11) \begin{equation} u - \textrm {i} v = -q_1 \left [ -{\rho ^2 \zeta ^{-1} \overline {Z}'(\rho ^2/\zeta ) \over \zeta Z'(\zeta )} \right ]^{1/2} = {\rho q_1 \over \zeta } {P(\zeta b,\rho ) \over P(\zeta /b,\rho )}. \end{equation}

Evidently, (4.9) can be rendered identical with (4.11) – thereby meeting the required analytic continuation condition (3.2) – provided that

(4.12) \begin{equation} q_0 = \rho b q_1. \end{equation}

This is a relation between the fluid speed $q_0$ on the wave and the fluid speed $q_1$ on the hollow-vortex boundary. Since $q_0, q_1 \gt 0$ and $\rho \gt 0$ , then $b$ , which is still unknown, is expected to be real and positive to be consistent with physical expectations. If a real positive parameter $b$ , satisfying (4.7) and lying in $1 \lt b \lt 1/\rho$ can be found, then $u-\textrm {i}v$ is analytic, as a function of $\zeta$ , everywhere in the annulus $\rho \lt |\zeta |\lt 1$ meaning that the flow in the corresponding period window is everywhere irrotational, as required.

It is shown in § 6 that solutions for the parameters $b,\ r$ and $\rho$ , with all the required properties, and furnishing univalent conformal mappings from the annulus to the fluid in a representative period window, can indeed be found. Before presenting this evidence, it is worth documenting formulas that will assist in characterising the resulting solutions.

Reusing $\varGamma$ to denote the circulation of the hollow vortex, and since the speed on the hollow-vortex boundary is constant and in the tangential direction, then

(4.13) \begin{equation} \varGamma = q_1 {\mathcal P}, \end{equation}

where $\mathcal P$ is the perimeter of the hollow vortex given by

(4.14) \begin{equation} {\mathcal P} = \oint _{C_1} |Z'(\zeta )| {\rho {\rm d}\zeta \over \textrm {i} \zeta } \end{equation}

and which is therefore a function of the parameters $R,\ b,\ r$ and $\rho$ . Since the time scale of the flow has been set by insisting that $\varGamma =1$ , then

(4.15) \begin{equation} q_1 = {1 \over {\mathcal P}}, \qquad q_0 = {\rho b \over {\mathcal P}}, \end{equation}

where, in the second equation, (4.12) has been used. The speed of the wave $U$ is found from

(4.16) \begin{equation} \lim _{y \to -\infty } (u-\textrm {i}v) = \lim _{\zeta \to r} \left \lbrace {q_0 \over b \zeta } {P(\zeta b,\rho ) \over P(\zeta /b,\rho )} \right \rbrace = {q_0 \over b r} {P(r b,\rho ) \over P(r/b,\rho )}= q_0= - U, \end{equation}

where (4.7) and (4.9) have been used. Relation (4.16) reveals that the regularised hollow-vortex family of the solutions shares the feature of the solutions of Crowdy & Roenby (Reference Crowdy and Roenby2014) that $|U|=q_0$ .

Streamlines can be plotted as the contours of the streamfunction, $\psi (x,y)$ say. By the chain rule, if $w(z) = \phi + \textrm {i} \psi$ is the complex potential for the flow, where $\phi (x,y)$ is a velocity potential, then

(4.17) \begin{equation} u - \textrm {i} v= {{\rm d}w \over{\rm d}z} = {q_0 \over b \zeta } {P(\zeta b,\rho ) \over P(\zeta /b,\rho )}, \end{equation}

where (4.9) has been used. If $W(\zeta ) \equiv w(Z(\zeta ))$ , then by the chain rule

(4.18) \begin{equation} {{\rm d}w \over {\rm d}z} = {W'(\zeta ) \over Z'(\zeta )}, \qquad \textrm {or} \qquad W'(\zeta ) = {{\rm d}w \over {\rm d}z} Z'(\zeta ). \end{equation}

Consequently, from (4.17) and (1.1),

(4.19) \begin{equation} W'(\zeta ) = {q_0 \over b \zeta } {P(\zeta b,\rho ) \over P(\zeta /b,\rho )} \times \textrm {i} R \left ( { P(\zeta /b, \rho )^2 \over P(\zeta /r,\rho ) P(\zeta r, \rho ) }\right ) = {\textrm {i} q_0 R P(\zeta /b, \rho ) P(\zeta b,\rho ) \over b \zeta P(\zeta /r,\rho ) P(\zeta r, \rho ) }. \end{equation}

Hence, up to an unimportant constant,

(4.20) \begin{equation} W(\zeta ) = \phi + \textrm {i} \psi = {\textrm {i} q_0 R \over b} \int ^\zeta { P(\tilde \zeta /b, \rho ) P(\tilde \zeta b,\rho ) \over P(\tilde \zeta /r,\rho ) P(\tilde \zeta r, \rho ) } {{\rm d} \tilde \zeta \over \tilde \zeta } \end{equation}

from which a parametric representation of the streamfunction $\psi$ in terms of $\zeta$ is readily extracted as the imaginary part. Given (1.1), a similar parametric representation of $z=Z(\zeta )$ can be found and contours of $\psi$ in the physical $z$ plane plotted.

5. The point-vortex limit $\boldsymbol{\rho \to 0}$

Since the hollow-vortex row is supposed to be a regularisation of the point-vortex-row solution of Crowdy & Roenby (Reference Crowdy and Roenby2014) it should be checked that the $\rho \to 0$ limit of the solution of the previous section retrieves that case.

In the point-vortex solution described in § 2 the preimage of $y \to -\infty$ is $\eta =0$ and the preimage of the point vortex is $\eta =1/a$ . By contrast, in the hollow-vortex regularisation just performed, $\zeta$ was used as the parametric conformal mapping variable with $\zeta =r$ as the preimage of $y \to -\infty$ while, as $\rho \to 0$ , the preimage of the hollow vortex degenerates to a single point at $\zeta =0$ . The following automorphism of the unit $\zeta$ disc transplants it to the unit $\eta$ disc while transplanting $\zeta =0$ to $\eta =1/a$ :

(5.1) \begin{equation} \eta = {a \zeta -1 \over \zeta -a} = a + {a^2-1 \over \zeta -a}, \qquad {{\rm d} \eta \over {\rm d} \zeta } = - {\bigl(a^2-1\bigr) \over (\zeta -a)^2}. \end{equation}

In the limit $\rho \to 0$ , it is therefore to be expected that

(5.2) \begin{equation} {\mathcal Z}(\eta ) = {Z}(\zeta ). \end{equation}

By the chain rule,

(5.3) \begin{equation} {{\rm d} {\mathcal Z} \over {\rm d}\eta } = {{\rm d} Z \over {\rm d}\zeta } {{\rm d} \zeta \over {\rm d} \eta }, \qquad \textrm {or} \qquad {{\rm d} {Z} \over {\rm d}\zeta }= {{\rm d} {\mathcal Z} \over {\rm d}\eta } {{\rm d} \eta \over {\rm d}\zeta }. \end{equation}

On substitution of (5.1) into (2.8),

(5.4) \begin{align} {{\rm d}{\mathcal Z} \over {\rm d}\eta } &= {\textrm {i} \over 2\pi \eta } \left ({\eta +a \over \eta -a} \right )^2 = {\textrm {i} (\zeta -a) \over 2\pi (a\zeta -1)} \left ( {a \zeta -1 + a(\zeta -a) \over a \zeta -1 - a(\zeta -a)} \right )^2 \nonumber\\ &= {\textrm {i} \over 2 \pi } \left ({2 a \over a^2-1} \right )^2 {(\zeta -a) \over (a \zeta -1)} \left ( \zeta - {1+a^2 \over 2 a} \right )^2. \end{align}

Use of (5.4) and (5.1) in (5.3) leads to

(5.5) \begin{equation} {{\rm d} {Z} \over {\rm d}\zeta } = - {2 a \textrm {i} \over \pi (a^2-1)} {1 \over (\zeta -1/a) (\zeta - a)} \left ( \zeta - {1+a^2 \over 2 a} \right )^2. \end{equation}

This can be compared with (1.1) in the limit $\rho \to 0$ , i.e.

(5.6) \begin{align} {{\rm d} Z \over {\rm d}\zeta } &= \textrm {i} R \left ( { P(\zeta /b, \rho )^2 \over P(\zeta /r,\rho ) P(\zeta r, \rho ) }\right ) \to \textrm {i} R \left ( { (1-\zeta /b)^2 \over (1-\zeta /r) (1-\zeta r) }\right ) = {\textrm {i} R \over b^2} {(\zeta -b)^2 \over (\zeta -r) (\zeta -1/ r)}. \end{align}

Evidently, (5.5) and (5.6) have identical functional forms with the parameter correspondence

(5.7) \begin{equation} r \mapsto {1 \over a} \qquad b \mapsto {1 \over 2} \left (a+ {1 \over a} \right )\!, \qquad {R \over b^2} \mapsto - {2 a \over \pi (a^2-1)}. \end{equation}

It is emphasised that this is only the correspondence in the $\rho \to 0$ limit. It implies that, for $\rho$ small,

(5.8) \begin{equation} b \approx {1 \over 2} \left (r+ {1 \over r} \right )\!, \end{equation}

which is consistent with the small- $\rho$ expansion of (4.7). To arrange that the wave period is unity in (5.6) it is necessary that

(5.9) \begin{equation} {1 \over 2\pi } =- {r \kern-2pt R \over b^2} {(r-b)^2 \over (1-r^2)}, \qquad \textrm {or} \qquad {R \over b^2} = - {(1-r^2) \over 2\pi r (r-b)^2}. \end{equation}

On substituting for $r$ and $b$ from (5.7) in $R/b^2$ as given in (5.9), the expression for it in (5.7) in terms of $a$ is retrieved, thereby verifying consistency.

On $C_1$ , where $|\zeta |=\rho$ , and if $\rho$ is small then, to a good approximation,

(5.10) \begin{equation} |Z'(\zeta )| \approx |R|. \end{equation}

This means that the radius $\sqrt {{\mathcal A}/\pi }$ of the near-circular image of $C_1$ , assuming small area $\mathcal A$ , is approximately

(5.11) \begin{equation} \sqrt {{\mathcal A} \over \pi } \approx |R| \times \rho = {\rho b^2 \over 2\pi r} {1-r^2 \over (r-b)^2} \end{equation}

yielding the following small-area estimate for $\rho$ as a function of $b$ and $r$ :

(5.12) \begin{equation} \rho \approx {2 r (r-b)^2 \over b^2 (1-r^2)} \sqrt {{\mathcal A} \pi }. \end{equation}

Similarly, it is expected that

(5.13) \begin{equation} {\mathcal P} \approx 2 \pi \sqrt {{\mathcal A} \over \pi } = 2 \pi {\rho b^2 \over 2\pi r} {1-r^2 \over (r-b)^2} = {\rho b^2 \over r} {1-r^2 \over (r-b)^2}. \end{equation}

Therefore,

(5.14) \begin{equation} q_0 = {\rho b \over {\mathcal P}} \approx {r (r-b)^2 \over b (1-r^2)} = {1 \over 2} {a^2 -1 \over a^2+1} = -U, \end{equation}

where (5.7) has been used. The value (5.14) agrees with that given by (2.13) when $\varGamma =1$ .

These calculations confirm that the proposed conformal mapping (1.1), and the velocity fields (3.1) derived from it, indeed furnish a hollow-vortex regularisation of the solutions of Crowdy & Roenby (Reference Crowdy and Roenby2014). The important role played by the prime function (1.2) in this generalisation is evident.

6. Characterisation of the solutions

To characterise the new solutions, it is helpful to think of the point-vortex row, with each vortex of fixed circulation $\varGamma =1$ , as a hollow vortex of zero area ${\mathcal A}=0$ . For a point-vortex row considered in § 2 there is a one-parameter family of waves, the parameter being $a$ which can be viewed as an amplitude parameter. By extension, the unit-circulation hollow-vortex regularisation comprises a two-parameter family of solutions, parametrised by $\rho$ and $r$ . Since $\rho \to 0$ corresponds to the point-vortex row with ${\mathcal A}=0$ , selecting $\rho \gt 0$ can be thought of as increasing the area of each hollow vortex, while $r$ is now the natural choice of amplitude parameter. Indeed, from (5.9), when $\rho =0$ , $r=1/a$ . Another possible choice of amplitude is

(6.1) \begin{equation} \textrm {Im}[Z(1)-Z(-1)] ,\end{equation}

which, it turns out after inspection of the wave profiles, is the crest-to-trough wave height.

The first thing to check is that the parameter $b$ found, for any given $\rho$ and $r$ , by solving (4.7) is real and positive, lying in the interval $1 \lt b \lt 1/\rho$ , all features expected from the preceding analysis. Solving (4.7) is readily done using Newton’s method, and the initial guess provided by (5.8) in the small- $\rho$ limit led to convergence for all cases examined. Figure 3 shows graphs of the $b$ values, found as solutions of (4.7), as a function of $\rho$ , for $r=0.3,\ 0.4,\ 0.4545,\ 0.5,\ 0.6$ and $0.7$ . It is evident that solutions for $b$ with the required properties exist; moreover, an important feature is that, for a fixed $r$ , the graphs are monotonic increasing with $\rho$ . Recall from (1.1) that $b$ is a (second-order) zero of the derivative $Z'(\zeta )$ that, necessarily, lies outside the annulus $\rho \lt |\zeta |\lt 1$ . This is a necessary, but not sufficient, condition for a univalent conformal mapping: indeed, it is known from the pure capillary waves of Crapper (Reference Crapper1957) and Crowdy (Reference Crowdy2000) that, as a zero (at $\eta = -a$ in the analysis of § 2) approaches $C_0$ , the wave shape can lose univalence via a pinchoff event, even before the zero reaches $C_0$ ; indeed, it is known to occur at $a \approx a_{\textit{crit}} = 2.2$ (Crowdy & Roenby Reference Crowdy and Roenby2014). The fact that, as $\rho$ increases – meaning, roughly speaking, that the area of the hollow vortex grows – $b$ moves away from $C_0$ means that regularising a point vortex to a hollow vortex shifts the surface wave away from pinchoff. Indeed it is found that univalent mappings exist for $0 \le \rho \lt 1/r$ provided $r \gt 0.4545$ . This critical value of $r=0.4545$ turns out to equal $1/a_{\textit{crit}}$ ; recall the correspondences given in (5.9) for $\rho \to 0$ which shows $r=1/a$ . This means that, provided $r \lt 1/2.2 \approx 0.4545$ then all the solutions of Crowdy & Roenby (Reference Crowdy and Roenby2014) can be safely regularised by turning the point vortex into a hollow vortex of non-zero area, i.e. by increasing $\rho$ from zero. The values of $b$ corresponding to univalent conformal mappings are shown as bold lines in figure 3.

Figure 3. Graph of $b$ values solving (4.7) as a function of $\rho$ for $r=0.3,\ 0.4,\ 0.4545,\ 0.5,\ 0.6$ and $0.7$ . Parameters corresponding to physically admissible waveforms (i.e. giving univalent conformal mappings) are shown as a bold line. The value $r=1/2.2 \approx 0.4545$ is the critical value above which only a subset of values $\rho \in [\rho _{\textit{crit}}, r)$ provide physically admissible solutions.

However, there are other solutions that are not connected in the same way to the solutions of Crowdy & Roenby (Reference Crowdy and Roenby2014): these are also shown as bold lines in figure 3 but, at a critical $\rho = \rho _{\textit{crit}}$ these bold lines become dashed. These dashed lines still correspond to $b$ values, for the given $\rho$ and $r$ , that solve (4.7), but the corresponding conformal mappings are not univalent. Indeed, they exhibit the same pinchoff characteristic of the solutions of Crowdy & Roenby (Reference Crowdy and Roenby2014). Figure 4 shows a graph of $\rho _{\textit{crit}}$ as a function of $r$ for $1/2.2 \approx 0.4545 \lt r \lt 0.72$ . It is not an easy task to identify mathematically when a pinchoff event occurs; the values shown in figure 4 were found simply by plotting the wave and visually inspecting the resulting profile. The data for $\rho _{\textit{crit}}$ given here should therefore be viewed as approximate. The key point is that it is not possible, for a fixed $r \gt 0.4545$ , to simply decrease $\rho$ until the hollow vortex becomes a point vortex: the surface wave will pinch off before that when the hollow vortex has some critical size.

Figure 4. Graph of $\rho _{\textit{crit}}$ as a function of $r$ for $1/2.2 \approx 0.4545 \lt r \lt 0.72$ .

Figure 5 shows graphs of $b$ , hollow-vortex area $\mathcal A$ , speed on the wave surface $q_0=-U$ and the amplitude parameter (6.1) as a function of $\rho$ for $r=0.4545$ . Since $q_0\gt 0$ then $U \lt 0$ and the waves move steadily to the left. There are five dashed ordinates shown in this figure: the right-most corresponds to $\rho =r$ which is the upper limit allowed for $\rho$ in view of the requirement $\rho \lt r \lt 1$ . The other four ordinates correspond to parameters for which the wave profiles are shown in figure 6 for gradually increasing $\rho$ . For this choice of $r$ , the $\rho =0$ solution is the critical solution of Crowdy & Roenby (Reference Crowdy and Roenby2014). The area of the hollow vortex can be increased by increasing $\rho$ until it nears its maximum possible value $\rho \approx r$ . As $\rho$ draws close to $r$ , there is no evidence of any further breakdown in the solutions (e.g. a loss of univalence) but the conformal mappings are found to exhibit significant crowding and it becomes difficult to plot the profiles accurately without using excessively large numbers of points. As $\rho \to r$ , it is found that the solution for $b \to 1/r$ , as suggested in the upturn of the $b$ graph in figure 5 as it heads towards $b=2.2$ , meaning that the two zeros of $Z'(\zeta )$ in (1.1) are drawing close to its simple pole at $1/r$ resulting in near cancellation of a pole and a zero. This is believed to be the cause of the aforementioned crowding difficulties although the precise nature of how the branch terminates is not clear and merits more careful analysis.

Figure 5. Wave characteristics for $r=1/2.2 \approx 0.4545$ as a function of $\rho$ . The amplitude is that given by formula (6.1).

Figure 6. Wave profiles for $r=1/2.2 \approx 0.4545$ as the hollow-vortex area increases: $\rho = 0.05,\ 0.1,\ 0.2$ and $0.4$ .

While the parameters $\rho ,\ r$ and $b$ are evidently the most convenient mathematical parameters, they do not have a direct physical interpretation. Either $r$ can be used as the amplitude parameter, or some other quantity such as the crest-to-trough height proposed in (6.1). For lack of a convincing reason to pick one over the other, in the following calculations $r$ will continue to serve as the amplitude parameter. Having already explored the solutions as a function of $\rho$ for fixed $r$ , one might now fix $\rho$ and explore the solutions as a function of $r$ . However, it is more natural to specify the hollow-vortex area $\mathcal A$ which will involve finding the corresponding $\rho$ in each case. Consequently, for any chosen $r$ , the following two real nonlinear equations are solved for $\rho$ and $b$ :

(6.2) \begin{equation} {1 \over br} {P(br, \rho ) \over P(r/b,\rho )} = 1, \qquad - {1 \over 2 \textrm {i}} \oint _{C_1} \overline {Z(\zeta )} Z'(\zeta ) {\rm d}\zeta = {\mathcal A}, \end{equation}

where

(6.3) \begin{equation} Z(\zeta ) = \int _{\zeta _0}^\zeta Z'(\tilde \zeta ) {\rm d} \tilde \zeta , \end{equation}

and where the real constant $\zeta _0$ is chosen to that the hollow-vortex centroid or

(6.4) \begin{equation} {1 \over {\mathcal P}} {\oint _{C_1} Z(\zeta ) |Z'(\zeta )| {\rho \,{\rm d} \zeta \over \textrm {i} \zeta }} \end{equation}

is located at the origin. Recall that $Z'(\zeta )$ is given explicitly by (1.1). Once $\mathcal P$ has been determined using the formula (4.14), the surface speeds $q_0$ and $q_1$ are determined a posteriori by (4.15) which also furnishes the wave speed since, from (4.16), $U=-q_0$ .

Figure 7 shows some wave profiles, for fixed hollow-vortex area ${\mathcal A} = \pi (0.1)^2$ and with hollow-vortex centroids fixed at the origin, for $r=0.05,\ 0.1,\ 0.2,\ 0.3,\ 0.4$ and $0.465$ . Figure 8 shows similar profiles for ${\mathcal A} = \pi (0.2)^2$ . In both cases, for fixed hollow-vortex area, there is a critical value of $r$ at which pinchoff occurs. This is to be expected: the same feature is true of the zero-area, or ${\mathcal A} = 0$ , point-vortex row solutions of Crowdy & Roenby (Reference Crowdy and Roenby2014).

Figure 9 shows a typical distribution of streamlines, calculated using (4.20), for ${\mathcal A} = \pi (0.27)^2$ for $r=0.56$ and with hollow-vortex centroid at the origin.

Figure 7. Hollow-vortex-carrying waves with ${\mathcal A}= \pi (0.1)^2 = 0.0314$ and $r=0.05,\ 0.1,\ 0.2,\ 0.3,\ 0.4$ and $0.465$ .

Figure 8. Hollow-vortex-carrying waves with ${\mathcal A}= \pi (0.2)^2$ and $r=0.1,\ 0.2,\ 0.3,\ 0.4,\ 0.45$ and $0.506$ .

Figure 9. Typical streamlines computed using (4.20) for ${\mathcal A} = \pi (0.27)^2$ and $r=0.56$ .