Hostname: page-component-5b777bbd6c-7sgmh Total loading time: 0 Render date: 2025-06-26T01:29:27.081Z Has data issue: false hasContentIssue false
  • English
  • Français

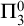A RECURSIVE COLORING FUNCTION WITHOUT $ \Pi _3^0$ SOLUTIONS FOR HINDMAN’S THEOREM

Part of: Computability and recursion theory General logic Proof theory and constructive mathematics

Published online by Cambridge University Press:  29 October 2024

YUKE LIAO
YUKE LIAO*
Affiliation:
DEPARTMENT OF MATHEMATICS NATIONAL UNIVERSITY OF SINGAPORE SINGAPORE 119076
*
E-mail: liao_yuke@u.nus.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that there exists a recursive coloring function c such that any 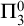$\Pi ^0_3$ set is not a solution to c for Hindman’s theorem. We also show that there exists a recursive coloring function c such that any 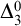$\Delta ^0_3$ set is not a solution to c for Hindman’s theorem restricted to sums of at most three numbers.

Keywords

reverse mathematicsHindman’s theorem

MSC classification

Primary: 03B30: Foundations of classical theories (including reverse mathematics) 03F35: Second- and higher-order arithmetic and fragments 03D80: Applications of computability and recursion theory
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 24
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Blass, A. R., Some questions arising from Hindman’s theorem . Scientiae Mathematicae Japonicae, vol. 62 (2005), no. 2, pp. 331–334.Google Scholar
Blass, A. R., Hirst, J. L., and Simpson, S. G., Logical analysis of some theorems of combinatorics and topological dynamic . Contemporary Mathematics, vol. 65 (1987), pp. 125–156.CrossRefGoogle Scholar
Carlucci, L., “Weak yet strong” restrictions of Hindman’s finite sums theorem . Proceedings of the American Mathematical Society, vol. 146 (2018), no. 2, pp. 819–829.CrossRefGoogle Scholar
Carlucci, L., Restrictions of Hindman’s theorem: An overview , Connecting with Computability: 17th Conference on Computability in Europe, CiE 2021, Virtual Event, Ghent, July 5–9, 2021, Proceedings 17, Springer, Cham, Switzerland, 2021, pp. 94–105.CrossRefGoogle Scholar
Carlucci, L., Kołodziejczyk, L., Lepore, F., and Zdanowski, K., New bounds on the strength of some restrictions of Hindman’s theorem . Computability, vol. 9 (2020), no. 2, pp. 139–153.CrossRefGoogle Scholar
Dzhafarov, D. D., Jockusch, C. G., Solomon, R., and Westrick, L. B., Effectiveness of Hindman’s theorem for bounded sums , Computability and Complexity: Essays Dedicated to Rodney G. Downey on the Occasion of his 60th Birthday (Day, A., Fellows, M., Greenberg, N., Khoussainov, B., Melnikov, A., and Rosamond, F., editors), Springer International Publishing, Cham, Switzerland, 2017, pp. 134–142.CrossRefGoogle Scholar
Dzhafarov, D. D. and Mummert, C., Reverse Mathematics, Springer International Publishing, Cham, Switzerland, 2022.CrossRefGoogle Scholar
Hindman, N., The existence of certain ultra-filters on N and a conjecture of Graham and Rothschild . Proceedings of the American Mathematical Society, vol. 36 (1972), no. 2, pp. 341–346.Google Scholar
Hindman, N., Finite sums from sequences within cells of a partition of N . Journal of Combinatorial Theory, Series A, vol. 17 (1974), no. 1, pp. 1–11.CrossRefGoogle Scholar
Hindman, N., Leader, I., and Strauss, D., Open problems in partition regularity . Combinatorics, Probability and Computing, vol. 12 (2003), nos. 5–6, pp. 571–583.CrossRefGoogle Scholar
Hirst, J. L., Hilbert versus Hindman . Archive for Mathematical Logic, vol. 51 (2012), pp. 123–125.CrossRefGoogle Scholar
Jockusch, C. G., Ramsey’s theorem and recursion theory . The Journal of Symbolic Logic, vol. 37 (1972), no. 2, pp. 268–280.CrossRefGoogle Scholar
Montalbán, A., Open questions in reverse mathematics . The Bulletin of Symbolic Logic, vol. 17 (2011), no. 3, pp. 431–454.CrossRefGoogle Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees: A Study of Computable Functions and Computably Generated Sets, Perspectives in Mathematical Logic, Springer, Berlin, 1987.CrossRefGoogle Scholar