2.1. Governing equations

The assumption of a self-similar stagnation point around axisymmetric ( $\epsilon = 1$ ) or two-dimensional ( $\epsilon = 0$ ) ( $\epsilon$ is a shape parameter) bodies of revolution is employed, with the domain sketch presented in figure 1. In the following analysis, the subscript $\infty$ is used to denote properties of the free stream, $w$ is used to denote wall conditions, and $e$ is used to denote boundary-layer-edge properties. The current work is limited to cases where self-similar theory is appropriate (see Harris & Ii Reference Harris and Ii1982; Tauber Reference Tauber1989; Prévereaud et al. Reference Prévereaud, Vérant and Annaloro2019). This includes the implicit assumption that the boundary-layer edge is in thermochemical equilibrium at all times (Goulard Reference Goulard1958). A body of spherical or cylindrical geometry is assessed as it represents a typical test configuration of material samples and diagnostic probes (Löhle et al. Reference Löhle, Hermann and Zander2018; Lewis et al. Reference Lewis, James, Ravichandran, Morgan and McIntyre2018). It also acts as a canonical geometry case, which can be used to transform the boundary-layer properties to other commonly used geometries in material testing, such as a flat-faced cylinder (Hermann et al. Reference Hermann, Löhle, Zander and Fasoulas2017b ). The unsteady boundary-layer equations of energy and atomic mass transport are considered. The derivation of Fay & Riddell (Reference Fay and Riddell1958) is adapted, utilising the formulation found in Inger (Reference Inger1963). These equations have been extended to include the appropriate unsteady terms, based on the derivation found in Dorrance (Reference Dorrance2017), yielding

(2.1) \begin{equation} z'' + {\textit{Sc}}f(\eta ) z' - \frac {{\textit{Sc}}}{(1+\epsilon )\beta } \dot {z} = \frac {\alpha _e}{1 + \alpha _e} {\textit{Da}}\, R(z,\theta ) \end{equation}

and

(2.2) \begin{equation} \theta '' + {\textit{Pr}}f(\eta ) \theta ' - \frac {{\textit{Pr}}}{(1+\epsilon )\beta } \dot {\theta } = -\frac {\alpha _e}{1 + \alpha _e} {\textit{Da}}\, H_D \, R(z,\theta ), \end{equation}

with $z = \alpha / \alpha _e$ representing the non-dimensional atomic mass fraction, where $\alpha$ is the atomic mass fraction. Here $\theta = T/T_e$ is the non-dimensional temperature, ${\textit{Sc}}$ designates the Schmidt number, $Pr$ the Prandtl number, $f$ represents the Blasius function, $\beta = ({\rm d}u/{\rm d}s)$ is the stagnation-point velocity gradient, with $s$ denoting the orientation tangential to the surface. The non-dimensional dissociation enthalpy is $H_D = \alpha _e {Le}\, h_D / ( c_{p,M} T_e )$ , $Le$ is the Lewis number, $c_{p,M}$ is the specific heat at constant pressure of the molecules in the flow, and $h_D$ is the specific dissociation enthalpy of the molecules. A $( \,\dot { }\, )$ symbol refers to the derivative with respect to time, and a ( $'$ ) symbol refers to a derivative with respect to the non-dimensional coordinate normal to the wall,

(2.3) \begin{equation} \eta = \sqrt {\frac {\rho _e(1+\epsilon ) \beta }{C \mu _e}} \int _0^y \frac {\rho }{\rho _e} {\rm d}y, \end{equation}

with the Chapman–Rubesin factor $C = \rho \mu / \rho _e \mu _e = {const}$ , $\rho$ is density, and $\mu$ is dynamic viscosity. The Damkoehler number is

(2.4) \begin{equation} {\textit{Da}} = \frac {4 k_r^{\prime} T_e^{\xi - 2} {\textit{Sc}} }{ (1+\epsilon ) \beta } \left ( \frac {p_e}{R_u} \right )^2, \end{equation}

where the recombination rate constant $K_r$ relates to $k_r^{\prime} = K_r/T^\xi$ , $p_e$ represents the Pitot pressure and $R_u$ is the universal gas constant. The Damkoehler number gives a representation of the ratio of flow time over recombination time. In this work, the exponent for the reaction speed $\xi =-1.5$ is used, according to the works of Fay & Riddell (Reference Fay and Riddell1958) and Dorrance (Reference Dorrance2017). In the current work, a generic mixture of atoms $A$ and diatomic molecules $A_2$ are assumed where the dissociation and recombination reactions are described by

(2.5) \begin{equation} A_2 + M \longleftrightarrow 2 A + M, \end{equation}

with the collision partner $M$ . This generic description is based on the work of Lighthill (Reference Lighthill1957) and was subsequently used by Fay & Riddell (Reference Fay and Riddell1958) in their analysis on stagnation-point heating. The approach lends itself to the current work, as a general theoretical framework is sought to be established applicable to different diatomic gases. The net reaction term $R$ is a function of both the local temperature and atom concentration and is calculated via the formulation found in Inger (Reference Inger1963):

(2.6) \begin{equation} R(z,\theta ) = \theta ^{\xi -2} \left ( \frac {1 + \alpha _e}{1 + \alpha _e z} \right ) \left ( z^2 - \frac {1 - \alpha _e^2 z^2}{1 - \alpha _e^2 } \exp \left ( -\frac {\theta _D}{\theta } \left ( 1 - \theta \right ) \right ) \right ), \end{equation}

where $\theta _D = h_D / (R_M T_e)$ is the dissociation temperature, and $R_M$ is the specific gas constant of the molecules.

Equations (2.1) and (2.2) are a coupled set of non-linear partial differential equations and require a numerical solution to accurately capture the flow behaviour in the boundary layer. The approach presented in this work is an approximation of these equations using analytical solutions of special cases and connecting these with an empirical correlation that captures the essential flow physics in unsteady reacting non-equilibrium boundary layers. This is achieved by investigating two simplified cases, the diffusion-dominated regime and the reaction-dominated regime. These two special cases will be derived in the following sections, followed by their application in a generalised correlation.

2.2. Diffusion-dominated regime

This special case considers a flow dominated by the effects of unsteady diffusion. Convective transport ( ${\textit{Sc}}f(\eta ) z'$ ) and reaction terms ( $({\alpha _e}/{1 + \alpha _e}) {\textit{Da}}\, R(z,\theta )$ ) are neglected. These simplifications allow a closed analytical solution to this case which is used in the following semi-empirical correlation. Equation (2.1) becomes

(2.7) \begin{equation} z'' - \frac {{\textit{Sc}}}{(1+\epsilon )\beta } \dot {z} = 0. \end{equation}

This represents the boundary layer as a non-moving slab of fluid where reactions do not take place, i.e. frozen conditions (Wang, Yu & Bao (Reference Wang, Yu and Bao2018)). Neglecting convective transport has to be compensated by using an appropriate choice of boundary-layer thickness, which will be discussed in § 2.4. This formulation is used in part due to its linear time-invariant properties, allowing solutions to be superimposed. This property is exploited by employing the Fourier transform, yielding

(2.8) \begin{equation} \tilde {z}'' - \frac { {\rm i} \omega {\textit{Sc}}}{(1+\epsilon )\beta } \tilde {z} = 0, \end{equation}

where $\tilde {z}$ is the Fourier-transformed non-dimensional concentration and $\omega$ is a frequency. A general solution to (2.8) is

(2.9) \begin{equation} \tilde {z}= C_1\, \exp \left ( \left ( 1+ {\rm i} \right ) \sqrt {\frac {\omega \,{\textit{Sc}}}{2 (1+\epsilon )\beta }}\, \eta \right ) + C_2\, \exp \left ( - \left ( 1+ {\rm i} \right ) \sqrt {\frac {\omega \,{\textit{Sc}}}{2 (1+\epsilon )\beta }} \, \eta \right ), \end{equation}

where the coefficients $C_{1,2}$ are calculated based on the boundary conditions

(2.10) \begin{equation} z(\delta _c) = 1 + \Delta z_\infty \, \cos (\omega t);\,\,\,\,\,\,\,\,\,\,\,\, z'(0)= \sigma z(0). \end{equation}

The first term in (2.10) describes the conditions found at the edge of the concentration boundary layer thickness at $\eta = \delta _c$ . A harmonic oscillation of frequency $\omega$ and amplitude $\Delta z_\infty$ is imposed originating from concentration fluctuations in the free stream. A single frequency is investigated, as arbitrary time-dependent boundary-layer fluctuations can be decomposed into a range of frequencies via Fourier analysis. The linear nature of the investigated problem allows their superposition, not restricting the generality of boundary-layer-edge fluctuation conditions. These unsteady fluctuations could occur due to electrical power supplies varying in input power, turbulent fluctuations in the flow, flow entrainment and large scale eddies, etc. (Hermann et al. Reference Hermann, Löhle, Fasoulas and Andrianatos2016; Capponi et al. Reference Capponi, Padovan, Elliott, Panesi, Bodony and Panerai2024). The boundary-layer profile will consist of a steady-state mean profile and a superimposed oscillating component, due to the linearity of (2.8). The employed solution (2.9) considers only the transient behaviour and omits the superimposed steady-state contribution. This simplifies the solution slightly and does not restrict the generality of the approach. Additionally, this simplifies the boundary-layer-edge condition to $ z(\delta _c) = \Delta z_\infty \cos (\omega t)$ . At the wall, a material with catalytic recombination coefficient $\gamma$ is assumed to be present. The factor $\sigma$ relates to this via

(2.11) \begin{equation} \sigma = \frac { {\textit{Sc}} \, K_w }{\mu _w} \sqrt {\frac {2 C \rho _e \mu _e}{(1+\epsilon ) \beta }}, \end{equation}

where $\mu$ is the dynamic viscosity, $\rho$ is the density, and $K_w$ is the speed of atom recombination at the surface,

(2.12) \begin{equation} K_w = \gamma \sqrt {R_M T_w / \pi }. \end{equation}

The factor $\sigma$ can be interpreted as an inverse non-dimensional length scale, denoted as

(2.13) \begin{equation} l_w = \frac {1}{\sigma }. \end{equation}

Fully catalytic surface conditions (all incoming atoms recombine) results in a very small $l_w$ , while non-catalytic conditions result in an infinity large $l_w$ .

The goal of the following analysis is to relate the fluctuation amplitude at the wall $\Delta z_w$ to the fluctuation amplitude at the boundary-layer edge $\Delta z_\infty$ . To simplify solution (2.9), all terms including $\textrm i$ are dropped, as they do not contribute to the amplitude change, but describe the time-dependent behaviour. This yields for the oscillation amplitudes,

(2.14) \begin{equation} \tilde {\Delta} z(\eta ) = \tilde {\Delta} z_\infty \frac { \left ( 1/\delta _S + 1/l_w \right ) \exp \left ( \eta /\delta _S \right ) + \left ( 1/\delta _S - 1/l_w \right ) \exp \left ( -\eta /\delta _S \right ) }{ \left ( 1/\delta _S + 1/l_w \right ) \exp \left ( \delta _c/\delta _S \right ) + \left ( 1/\delta _S - 1/l_w \right ) \exp \left ( -\delta _c/\delta _S \right ) }. \end{equation}

For the fluctuation amplitude at the wall $(\eta =0)$ , this simplifies to

(2.15) \begin{equation} \frac {\tilde {\Delta} z_w}{\tilde {\Delta} z_\infty } = \frac {\Delta z_w}{\Delta z_\infty } = 2 \left [ \left ( 1 + \frac {\delta _S}{l_w} \right ) \exp \left ( \frac {\delta _c}{\delta _S} \right ) + \left ( 1 - \frac {\delta _S}{l_w} \right ) \exp \left ( -\frac {\delta _c}{\delta _S} \right ) \right ]^{-1} , \end{equation}

with

(2.16) \begin{equation} \delta _S = \sqrt {\frac {2 (1+\epsilon )\beta }{\omega \,{\textit{Sc}}}}, \end{equation}

which can be interpreted as the Stokes-layer thickness of an unsteady concentration problem. This is analogous to other Stokes layers of oscillating transport phenomena, such as momentum and heat (Pal & Chakraborty Reference Pal and Chakraborty2015; Schlichting & Gersten Reference Schlichting and Gersten2017). The Stokes-layer thickness describes a measure for the penetration depth of a wave with frequency $\omega$ . As the frequency increases, the diffusive inertia of the medium will attenuate the propagation of this wave, decreasing its penetration depth (Hermann Reference Hermann2025). Equation (2.15) describes the relative amplitude of a concentration fluctuation of frequency $\omega$ at the wall. For the case of $\omega = 0$ , the Stokes-layer thickness $\delta _S$ becomes infinite, yielding the limiting solution of (2.15) as

(2.17) \begin{equation} \lim _{\delta _S \to \infty } \frac {\Delta z_w}{\Delta z_\infty } = \frac {1}{1 + \frac {\delta _c}{l_w}}. \end{equation}

The solution (2.15) relies on the specification of a mass diffusion boundary-layer thickness $\delta _c$ , representing the interface between boundary layer and inviscid external flow. This boundary-layer thickness is defined in relation to the thermal boundary layer, analogous to Hermann (Reference Hermann2025). In this work, the conduction length,

(2.18) \begin{equation} \delta _{T,L} = \frac {1 - \theta _w}{ \left ( \frac {\partial \theta }{\partial \eta }\right )_w } \end{equation}

is considered alongside the thermal-boundary-layer thickness,

(2.19) \begin{equation} \delta _{T,T} = 2 \frac {1 - \theta _w}{ \left ( \frac {\partial \theta }{\partial \eta }\right )_w }. \end{equation}

Here $\delta _{T,L}$ represents the thickness required for a solid medium to conduct the same heat flux as the boundary layer (Smith & Spalding Reference Smith and Spalding1958; Smith Reference Smith1979); $\delta _{T,T}$ , instead, represents the thermal-boundary-layer thickness required to fulfil the Reynolds analogy for Prandtl numbers close to unity, if a Pohlhausen velocity–boundary-layer profile is present (Schlichting & Gersten Reference Schlichting and Gersten2017). Using the correlation between mass diffusion and thermal boundary-layer thicknesses found in Dorrance (Reference Dorrance2017) for a Prandtl number close to unity, the diffusion boundary layer is calculated as

(2.20) \begin{equation} \delta _c = \frac {\delta _T}{ \sqrt { {Le}}}, \end{equation}

where $\delta _T$ is determined by either (2.18) or (2.19). A schematic of a typical boundary-layer profile is provided in figure 2, which illustrates the considered length scales. Equation (2.15) developed in this section can be interpreted as a frequency-resolved impulse response of the boundary layer to a change in external flow conditions, if diffusion is the dominant transport mechanism. This approach allows the use of Duhamel’s theorem to superimpose solutions based on arbitrary boundary-layer-edge fluctuations.

Figure 2. Schematic of boundary-layer atomic concentration profile, with characteristic length scales of diffusion problem.

2.3. Reaction-dominated regime

In this regime, the rate of atomic consumption through recombination reactions is far higher than the local rate of change, i.e. the storage term $({{\textit{Sc}}}/{(1+\epsilon )\beta }) \dot {z}$ is small compared with the reaction term $({\alpha _e}/{1 + \alpha _e}) {\textit{Da}}\, R(z,\theta )$ . Equation (2.1) is simplified to

(2.21) \begin{equation} z'' + {\textit{Sc}}f z' = \frac {\alpha _e}{1 + \alpha _e} {\textit{Da}}\, R(z,\theta ) \end{equation}

resulting in a quasi-steady solution of the boundary layer. These solutions assume that the influence of boundary-layer-edge conditions is instantaneously transported to the wall. In this case, boundary conditions are

(2.22) \begin{equation} z(\delta _c) = 1 ;\,\,\,\,\,\,\,\,\,\,\,\, z'(0)= \sigma z(0) \end{equation}

for nominal conditions without external fluctuations, and

(2.23) \begin{equation} z(\delta _c) = 1 + \Delta z_\infty ;\,\,\,\,\,\,\,\,\,\,\,\, z'(0)= \sigma z(0) \end{equation}

for perturbed conditions with perturbation magnitude $\Delta z_\infty$ . These conditions are identical to the case used in (2.10), apart from dropping the oscillation term. This is due to the fact that an instantaneous transport is assumed, and the temporal rate of change of boundary-layer-edge conditions therefore becomes irrelevant. Extending the work of Inger (Reference Inger1963), a solution to (2.21) is achieved by double integration of (2.21) with an integrating factor of $\exp ( {\textit{Sc}} \int _{0}^{\eta } f \mathrm {d}\eta )$ , yielding

(2.24) \begin{equation} z(\eta ) = z_F(\eta ) - \frac {\alpha _e}{1 + \alpha _e} {\textit{Da}} \left ( \frac {z_F(\eta )}{z_F(\delta _c)} g(\delta _c) - g(\eta ) \right ) \end{equation}

with

(2.25) \begin{equation} g(\eta ) = \int _{0}^{\eta } \exp \left ( - {\textit{Sc}} \int _{0}^{\eta } f \mathrm {d}\eta \right )\left ( \int _{0}^{\eta } \exp \left ( {\textit{Sc}} \int _{0}^{\eta } f \mathrm {d}\eta \right ) R \mathrm {d}\eta \right ) \mathrm {d}\eta , \end{equation}

where $z_F$ refers to the frozen boundary-layer profile, $g$ is a boundary layer integral factor, i.e. the solution of the ordinary differential equation

(2.26) \begin{equation} z_F'' + {\textit{Sc}}f z_F' = 0, \end{equation}

where the boundary conditions (2.22) and (2.23) also apply to this case. The frozen-wall condition can be determined analytically using Goulard (Reference Goulard1958), by employing a double integration, yielding

(2.27) \begin{equation} z_F(0) = \frac {z_F(\delta _c)}{\sigma I(\delta _c) + 1} \end{equation}

with

(2.28) \begin{equation} I(\delta _c) = \int _{0}^{\delta _c} \exp \left ( - {\textit{Sc}} \int _{0}^{\delta _c} f \mathrm {d}\eta \right ) \mathrm {d}\eta . \end{equation}

The integral can be transformed slightly into a new non-dimensional spatial domain $\tilde {\eta } = \eta / \delta _c$ which equals to unity at the boundary-layer edge:

(2.29) \begin{equation} \tilde {I} = \int _{0}^{1} \delta _c \,\exp \left ( - {\textit{Sc}} \int _{0}^{1} f \mathrm {d}\tilde {\eta } \right ) \mathrm {d}\tilde {\eta } = I(\delta _c) /\delta _c. \end{equation}

This normalisation is conducted to non-dimensionalise the derived solution. Evaluating (2.24) at the wall ( $\eta =0$ ) with the nominal (unperturbed) boundary condition $z_F(\delta _c) = 1$ yields

(2.30) \begin{equation} z(0) = z_F(0) \left ( 1 - \frac {\alpha _e}{1 + \alpha _e} {\textit{Da}} \, g(\delta _c) \right ). \end{equation}

Using the perturbed boundary condition $z_F(\delta _c) = 1 +\Delta z_\infty$ to denote the increase of external concentration by the relative fraction $\Delta z_\infty$ , yields the solution

(2.31) \begin{equation} z^\Delta (0) = z_F^\Delta (0) \left ( 1 - \frac {\alpha _e}{(1 + \alpha _e) (1 + \Delta z_\infty )} {\textit{Da}} \, g^\Delta (\delta _c) \right ). \end{equation}

Quantities denoted by ( $^\Delta$ ) relate to boundary conditions (2.23), while all other cases refer to boundary conditions (2.22). Utilising (2.27) and (2.29) yields

(2.32) \begin{equation} z_F(0) = \frac {1}{\frac {\delta _c}{l_w} \tilde {I} + 1} \,\,\,\,\,\,\, \mathrm{and} \,\,\,\,\,\,\, z_F^\Delta (0) = \frac {1+\Delta z_\infty }{\frac {\delta _c}{l_w} \tilde {I} + 1}. \end{equation}

Using this, the difference between (2.30) and (2.31), corresponding to the difference in wall concentration for a given boundary-layer-edge concentration perturbation of $\Delta z_\infty$ , is

(2.33) \begin{equation} \Delta z_w = z^\Delta (0) - z(0) = z_F(0) \left ( \Delta z_\infty - \frac {\alpha _e}{(1 + \alpha _e)} {\textit{Da}} \, \left ( g^\Delta (\delta _c) - g(\delta _c) \right ) \right ). \end{equation}

The $g$ -integrals, given with (2.25), are an implicit function of $z$ , which would require an iterative solution to (2.33). To avoid this recursive solution procedure, an empirical correlation is proposed. It has been found that the approximation

(2.34) \begin{equation} \frac {\alpha _e}{(1 + \alpha _e)} {\textit{Da}} \, \left ( g^\Delta (\delta _c) - g(\delta _c) \right ) \approx \Delta z_\infty \left ( 1 - \frac {z(0)}{z_F(0)} \right ) \end{equation}

gives a satisfactory prediction of the difference between the two integral terms. The accuracy is better than 10.4 % for all investigated cases in this work (see § 3.2 for details). The fraction $z(0) / z_F(0)$ is mainly a function of Damkoehler number, and can be calculated by solving the nonlinear ordinary differential (2.21) to obtain $z(0)$ , and utilising (2.32) for $z_F(0)$ . Alternatively, this ratio can be determined analytically using Inger (Reference Inger1963) which utilises only steady-state frozen solutions, which is more in keeping with the approach taken in this work. Either way, the final solution for the wall concentration change under quasi-steady conditions is

(2.35) \begin{equation} \Delta z_w = \Delta z_\infty \frac { \frac {z(0)}{z_F(0)} }{\frac {\delta _c}{l_w} \tilde {I} + 1 } = \Delta z_\infty \, z(0). \end{equation}

The special cases of diffusion- and reaction-dominated regimes build the basis of the generalised correlation derived in this work, which is presented in the following.

2.4. Generalised correlation

The hypothesis utilised in the current work is based on the assumption that effects due to chemical reactions are separable from diffusion. This allows the formulation of a general correlation:

(2.36) \begin{equation} \frac {\Delta z_w}{\Delta z_\infty } = F_{\textit{Diff.}} \boldsymbol{\cdot }G_{\textit{Chem.}}, \end{equation}

where $F_{\textit{Diff.}}$ describes the attenuation of fluctuations due to the inertia of boundary-layer mass transport, and $G_{\textit{Chem.}}$ describes the suppression of fluctuations due to chemical reactions, foremost recombination. The variable $F_{\textit{Diff.}}$ utilises (2.15) normalised by its limit for $\omega = 0$ , given in (2.17), leading to

(2.37) \begin{equation} A = \frac {\frac {\Delta z_w}{\Delta z_\infty }|_{\textit{Diff.}} }{ \lim _{\delta _S \to \infty } \frac {\Delta z_w}{\Delta z_\infty }|_{\textit{Diff.}} } = \frac { 2 + 2 \frac {\delta _c}{l_w} }{ \left ( 1 + \frac {\delta _S}{l_w} \right ) \exp \left ( \frac {\delta _c}{\delta _S} \right ) + \left ( 1 - \frac {\delta _S}{l_w} \right ) \exp \left ( -\frac {\delta _c}{\delta _S} \right ) } . \end{equation}

This function describes the attenuation of mass transport relative to the maximum possible wall value. It is further used to define

(2.38) \begin{equation} F_{\textit{Diff.}} = A \left ( \delta _{T,L} \right ) - \frac { A\left ( \delta _{T,L} \right ) - A\left ( \delta _{T,T} \right ) }{ 1 + 8.2 \left ( \frac {{\textit{Sc}} \omega }{ \beta (1+\epsilon ) } \right )^{-3} } . \end{equation}

Equation (2.38) utilises an empirical correlation which is based on the data analysis presented in § 3.1, where respective details are discussed in greater depth. It utilises the definitions in (2.18) and (2.19) for the thermal boundary-layer thickness, which in turn determine the concentration boundary-layer thickness through (2.20). This is finally used in (2.37).

The second term in (2.36), describing wall concentration attenuation due to chemical reactions utilises (2.35):

(2.39) \begin{equation} G_{\textit{Chem.}} = \frac { \frac {z(0)}{z_F(0)} }{\frac {\delta _c}{l_w} \tilde {I} + 1 } , \end{equation}

resulting in the full correlation

(2.40) \begin{equation} \frac {\Delta z_w}{\Delta z_\infty } = \left [ A \left ( \delta _{T,L} \right ) - \frac { A\left ( \delta _{T,L} \right ) - A\left ( \delta _{T,T} \right ) }{ 1 + 8.2 \left ( \frac {{\textit{Sc}} \omega }{ \beta (1+\epsilon ) } \right )^{-3} } \right ] \left [ \frac { \frac {z(0)}{z_F(0)} }{\frac {\delta _c}{l_w} \tilde {I} + 1 } \right ]. \end{equation}

The correlation features a few noteworthy properties that give insight into the behaviour of the fluid mechanics. All functions involved are only dependent on the steady-state frozen boundary-layer solution, which can be readily obtained using either simple numerical simulations or classical theory (Goulard Reference Goulard1958; Dorrance Reference Dorrance2017). Another useful aspect is that this correlation retains the linear time-invariant property found in § 2.2. As such, this approach can be viewed as an approximate linearisation of the inherently nonlinear flow physics. The linear time-invariant property allows the calculation of a frequency-resolved impulse response which can then be applied to arbitrary temporal boundary conditions at the boundary-layer edge using Duhamel’s theorem.

Furthermore, several special cases exist for components in correlation (2.40) that lead to substantial simplification. These are (i) either very fast or slow flow oscillations, (ii) fully or non-catalytic surface behaviour and (iii) frozen or fully equilibrated flow. The diffusion term $A$ depends only on the catalytic and frequency aspects and can be simplified as follows.

High frequency (small $\delta _S$ ) and fully catalytic wall (small $l_w$ ):

(2.41) \begin{equation} \lim _{\delta _S \to 0, \,\, l_w \to 0} A = \frac { \frac {\delta _c}{l_w} }{ \mathrm{sinh} \left (\frac {\delta _c}{\delta _S} \right ) } . \end{equation}

High frequency (small $\delta _S$ ) and non-catalytic wall (large $l_w$ ):

(2.42) \begin{equation} \lim _{\delta _S \to 0, \,\, l_w \to \infty } A = \frac { 1 }{ \mathrm{sinh} \left (\frac {\delta _c}{\delta _S} \right ) } . \end{equation}

Low frequency (large $\delta _S$ ) and fully catalytic wall (small $l_w$ ):

(2.43) \begin{equation} \lim _{\delta _S \to \infty , \,\, l_w \to 0} A= 1 . \end{equation}

Low frequency (large $\delta _S$ ) and non-catalytic wall (large $l_w$ ):

(2.44) \begin{equation} \lim _{\delta _S \to \infty , \,\, l_w \to \infty } A = 1 . \end{equation}

Furthermore, using the fringe cases presented in Inger (Reference Inger1963) for close to frozen conditions ( ${\textit{Da}}\lt \lt 1$ ),

(2.45) \begin{equation} \frac {z(0)}{z_F(0)} \approx 1 - \frac {{\textit{Da}}^{*}}{1+\alpha _e z_F(0)}, \end{equation}

where ${\textit{Da}}^{*}$ is a composite Damkoehler number, as defined in Inger (Reference Inger1963). This number is entirely dependent on steady-state frozen-flow properties. Alternatively close to equilibrium ( ${\textit{Da}}\gt \gt 1$ ) conditions can be approximated with

(2.46) \begin{equation} \frac {z(0)}{z_F(0)} = \left ( {\textit{Da}}^{*} \right )^{-1/2} \approx \left ({\textit{Da}}\right )^{-1/2} . \end{equation}

In the following, the individual components of the derivation are investigated with respect to their accuracy for a fully coupled unsteady simulation.

3.1. Investigation of diffusion-dominated regime

This section concentrates on the special case of a diffusion-dominated regime, described in § 2.2. For these simulations, the Damkoehler number is set to zero, excluding any influence of chemical reactions in the boundary layer. As described in the previous section, the amplitude of the concentration fluctuation $\Delta z_w$ is extracted and normalised by the amplitude imposed through the boundary-layer-edge condition $\Delta z_\infty$ . This ratio describes the attenuation of these fluctuations, which is investigated for a variety of different test cases. The parameters summarised in § 3 are used, while the following parameters are varied to facilitate a range of different flow conditions. (i) The free-stream oscillation frequency $\omega$ was varied in 20 steps between $10^{1.5}$ s $^{-1}$ and $10^{6}$ s $^{-1}$ , keeping an equidistant logarithmic spacing. (ii) The wall temperature $\theta _w$ was varied in 6 steps between $0.01$ and $0.35$ , keeping a linear equidistant spacing. (iii) The wall catalycity factor $\sigma$ was varied in 6 steps between $10^{-2}$ and $10^{4}$ , keeping an equidistant logarithmic spacing. This resulted in $20 \times 6 \times 6 = 720$ unique transient numerical simulations.

Figure 7. Comparison between analytical correlation (2.15) and numerical simulation results for variations of wall temperature $\theta _w$ and surface catalycity $\sigma$ .

The results for the normalised wall-fluctuation amplitude are shown as circles in figure 7, and are compared with the analytical solution (2.15) where either the conduction or thermal-boundary-layer thicknesses given in (2.18) and (2.19) are used as the boundary-layer reference length. For small frequencies, the Stokes-layer thickness is large and penetrates deep into or beyond the boundary-layer thickness. This means that the fluctuations are not attenuated by the boundary layer whatsoever. As frequencies become larger, the diffusive inertia of the boundary layer rapidly attenuates the magnitude of the fluctuation. This behaviour is entirely analogous to the classical second Stokes problem in momentum and heat transfer, an unsurprising observation as the partial differential equations are identical, albeit with different transport properties (Schlichting & Gersten Reference Schlichting and Gersten2017; Hermann Reference Hermann2025). The second observation relates to the strong influence of the surface catalycity. For small frequencies, a close to non-catalytic surface (e.g. $\sigma = 0.01$ ) results in a full transmission of the fluctuations to the wall, i.e. $\Delta z_w/\Delta z_\infty \approx 1$ . The limiting maximum value for each catalycity factor $\sigma$ can be determined via (2.17). If the surface tends towards higher catalytic efficiency, this maximum possible value decreases significantly. At $\sigma = 10\,000$ , the fluctuation magnitude at the wall is over four orders of magnitude lower than the corresponding free-stream value. The reason for this behaviour is the fast consumption of atoms at the surface. Even in cases of low-frequency oscillations, where the diffusive inertia is small, atoms are immediately consumed through wall recombination reactions. These reactions, controlled through the boundary condition $z'(0)= \sigma z(0)$ , drive a strong concentration gradient to the surface supplying this flux of atoms. This behaviour is illustrated in the boundary-layer profile of figure 4. The fast consumption of atoms suppresses any significant fluctuations and therefore leads to extremely small $\Delta z_w/\Delta z_\infty$ values. Lastly, the wall temperature variation has no influence whatsoever. Each plotted datapoint is in fact six points with different $\theta _w$ values sharing the identical $\Delta z_w/\Delta z_\infty$ value. This is unsurprising, as the only coupling between energy and mass diffusion equations occurs via the reaction term $R(z,\theta )$ , controlled by the magnitude of the Damkoehler number. As ${\textit{Da}} = 0$ is used in these cases, this coupling is absent. It is, however, noteworthy that the different values of wall temperature also do not have an effect on the thermal-boundary-layer thickness, calculated via (2.18) or (2.19). This is apparent as the analytical correlation (2.15) is equally unaffected by the choice of $\theta _w$ .

Figure 7 also shows how correlation (2.15) compares against the simulations. If the conduction layer thickness $\delta _{T,L}$ is chosen, the correlation agrees extremely well for cases where the Stokes-layer thickness is large, i.e. for low frequencies. In this regime, the modelling of the boundary layer as a solid diffusion slug provides a very good approximation. If the Stokes layer is smaller, i.e. for high frequencies, the data points tend to be better correlated by using the thermal-boundary-layer thickness $\delta _{T,T}$ . This behaviour is again analogous to thermal-boundary-layer oscillations as shown in Hermann (Reference Hermann2025), where additional discussion is provided on this topic. If each case of a given $\sigma$ is normalised by its maximum possible value given in (2.17), the simulated data collapses to a single function. This behaviour motivates the use of an empirical bridging function that connects the asymptotes of $\delta _{T} = \delta _{T,T}$ for high frequencies and $\delta _{T} = \delta _{T,L}$ for low frequencies. It is found that (2.38) follows the numerical data points within reasonable accuracy. The bridging function is shown for each simulated case as a dotted line in figure 7. The correlation becomes less accurate at high frequencies. However, at that point the boundary layer attenuates the propagation of oscillations so severely that these values have no practical significance due to their extremely small magnitude. The correlation provides a good fit for all investigated cases.

3.2. Investigation of reaction-dominated regime

In this section, the accuracy of the approximate theory derived in § 2.3 is investigated. This is achieved by numerically solving (2.21) and extracting the magnitude of the wall concentration. This procedure is carried out with boundary conditions

(3.3) \begin{align}& z(\infty ) = 1 + \Delta z_\infty ;\,\,\,\,\,\,\,\,\,\,\,\, z'(0)= \sigma z(0), \end{align}

(3.4) \begin{align}&\qquad \theta (\infty ) = 1 ;\,\,\,\,\,\,\,\,\,\,\,\, \theta (0)= \theta _w, \end{align}

where $\Delta z_\infty$ is either finite to investigate the perturbed case, or zero to investigate the nominal case. The difference between the two respective wall values is denoted $\Delta z_w$ . In contrast to the analysis, these simulations are steady-state cases and simulate a situation where the boundary layer reacts infinitely fast to changes imposed by the free stream. Due to the coupling of energy and mass diffusion equations, this test case is highly nonlinear and depends on a variety of different parameters. To assess the approximate solution (2.35) against the fully coupled numerical solution, a base test case is constructed with the following values: $\Delta z_\infty = 0.1$ , $\theta _D = 10$ , $\xi = -1.5$ , $\theta _w = 0.15$ , $\sigma = 0.1$ , ${\textit{Sc}} = 0.5$ , ${\textit{Pr}} = 0.71$ , $\alpha _e = 0.6$ , $\beta = 7500$ s $^{-1}$ , $R_M=287$ J kg $^{-1}$ K $^{-1}$ , $c_{p,M}=1004.5$ J kg $^{-1}$ K $^{-1}$ . Of this set of values $\sigma$ , $\alpha _e$ , $\theta _D$ and $\theta _w$ are varied one at a time. For instance, the wall temperature $\theta _w$ is varied between 0.01 and 0.35 in six equally spaced intervals. For each of these intervals, the Damkoehler number is varied between $10^{-5}$ and $10^{3.2}$ with 25 logarithmically equal spacings. This results in a set of $25 \times 6 \times 4 = 600$ unique solutions.

The results of these simulations and the respective comparison with correlation (2.35) is shown in figure 8. In all cases, a significant influence of the Damkoehler number on the relative wall concentration augmentation $\Delta z_w / \Delta z_\infty$ is evident. Small Damkoehler numbers, where the flow can be considered frozen, do not affect the wall concentration in most cases. In the frozen-flow domain, chemical reactions do not take part and an exact solution of the wall concentration can be obtained with (2.32). These wall conditions depend only on the catalytic wall value $\sigma$ , the boundary-layer thickness $\delta _c$ , the Blasius function $f$ and the Schmidt number $Sc$ . This is the reason why several solutions become degenerate for small Damkoehler numbers (see figure 8 a,b). Large Damkoehler numbers suggest a flow close to chemical equilibrium. Under these conditions, any deviation from the nominal boundary-layer profile is immediately suppressed by recombination reactions, hence reducing $\Delta z_w / \Delta z_\infty$ significantly. The local equilibrium condition is mainly influenced by the temperature $\theta$ . Even though the temperature distribution $\theta (\eta )$ changes under perturbed external conditions, this effect is only weak and the frozen temperature $\theta _F(\eta )$ distribution is a good approximation in all considered cases (Inger Reference Inger1963).

Figure 8. Comparison between analytical correlation (2.35) and numerical simulation results for variations of different domain properties. (a) Boundary-layer-edge atomic mass fraction $\alpha e$ , (b) Dissociation temperature $\theta D$ , (c) Wall temperature $\theta w$ , and (d) Wall catalycity $\sigma$ .

Figures 8(a) and 8(c) reveal that the boundary-layer-edge atomic mass fraction $\alpha _e$ and the dissociation temperature $\theta _D$ affect $\Delta z_w / \Delta z_\infty$ only weakly. Some deviation from the correlation is seen for smaller values of $\theta _D$ which occur for Damkoehler numbers greater than $10^{-2}$ . However, overall the agreement between correlation (2.35) and the numerical solution is good. Figure 8(b) reveals that the wall temperature exerts a significant influence on $\Delta z_w / \Delta z_\infty$ . In fact, the curve shown for $\theta _w = 0.01$ , corresponding to a highly cooled wall, provides the only aberration from the trend of degenerate solutions at small Damkoehler numbers. Low temperatures near the wall significantly increase the reaction term given in (2.6), where the term $\theta ^{\xi -2}$ dominates. This nonlinear term results in such a strong rate of recombination that even small Damkoehler numbers lead to significant changes in the atomic wall concentration. It can be observed that the point where $\Delta z_w / \Delta z_\infty$ deviates from $1$ is delayed to larger Damkoehler numbers as the wall temperature is increased. This occurs as the larger wall temperature results in a smaller $R(z,\theta )$ and a larger Damkoehler number is needed to affect the flow. The largest influence on $\Delta z_w / \Delta z_\infty$ is exerted by the wall catalycity factor $\sigma$ , as seen in figure 8(d). As discussed in § 3.1, highly catalytic surfaces lead to a significant suppression of the wall concentration augmentation. Overall, given the wide and diverse range of flow conditions investigated, correlation (2.35) provides a very good fit to the numerical data for the majority of cases.

3.3. Investigation of fully coupled unsteady behaviour

Figure 9. Comparison between analytical correlation (2.40) and numerical simulation results. (a) For variation in Da,(b) For variation in $\delta c/\delta S$ ,(c) For variation in $\delta c/lw$ and (d) For variation in $\delta S/lw$ .

In this section, the full unsteady problem given in (2.1) and (2.2) with boundary conditions

(3.5) \begin{align}& z(\infty ) = 1 + \Delta z_\infty \, \cos (\omega t);\,\,\,\,\,\,\,\,\,\,\,\, z'(0)= \sigma z(0), \end{align}

(3.6) \begin{align}&\qquad\qquad \theta (\infty ) = 1 ;\,\,\,\,\,\,\,\,\,\,\,\, \theta (0)= \theta _w \end{align}

is solved numerically. Based on the two previous sections, it is found that the most impactful parameters controlling the wall concentration are the oscillation frequency $\omega$ , the Damkoehler number $Da$ , the wall catalycity factor $\sigma$ , and the wall temperature $\theta _w$ . The four parameters are varied with $10^{-2}\lt \omega \lt 10^{6}$ ; $10^{-5}\lt {\textit{Da}}\lt 10^{3.2}$ ; $10^{-2}\lt \sigma \lt 10^{4}$ ; $0.01\lt \theta _w\lt 0.35$ , each probing 10 values in the respective range. Every possible combination is tested resulting in $10^4 = 10\,000$ unique transient simulations. The remaining salient parameters are $\Delta z_\infty = 0.1$ , $\theta _D = 10$ , $\xi = -1.5$ , ${\textit{Sc}} = 0.5$ , ${\textit{Pr}} = 0.71$ , $\alpha _e = 0.6$ , $\beta = 7500\,\textrm {s}^{-1}$ , $R_M=287\,\textrm {J}\,\textrm {kg}^{-1}\,\textrm {K}^{-1}$ , $c_{p,M}=1004.5\,\textrm {J}\,\textrm {kg}^{-1}\,\textrm {K}^{-1}$ .

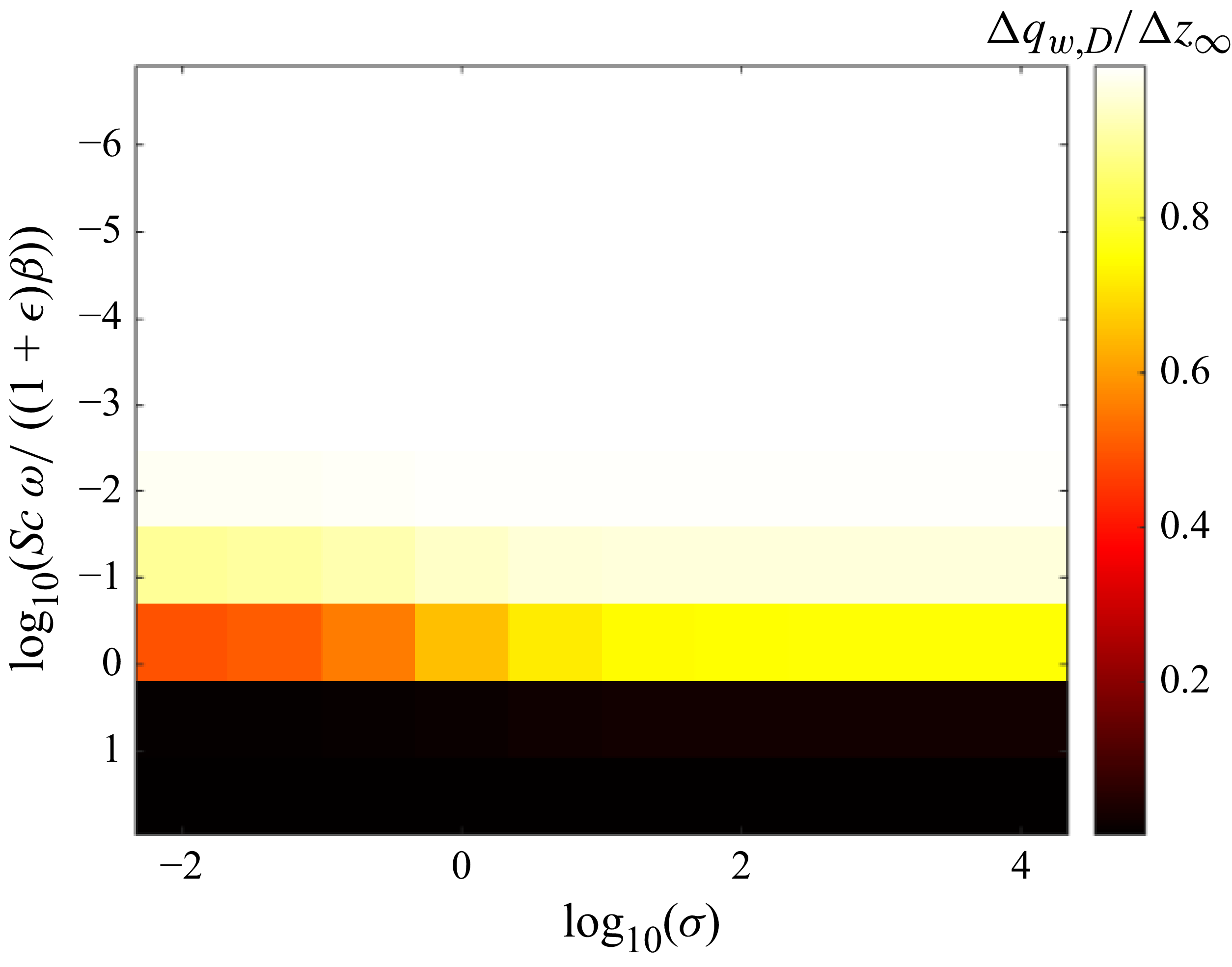
The correlation in (2.40) reveals that the problem is mostly dependent on four non-dimensional parameters: the three length-scale ratios $\delta _c/l_w$ , $\delta _S/l_w$ , $\delta _c/\delta _S$ and the Damkoehler number $Da$ . For this reason, the results obtained from the numerical simulation are plotted against these four scaling parameters. The results are shown in figure 9, where the % difference between numerical solution and correlation (2.40) is presented. All four figures present the same dataset, and it can be seen that the largest deviation amounts to $-12.5$ % and $9$ %. Given the approximate engineering approach taken, this level of agreement is adequate. The agreement is especially good at high frequencies (small Stokes-layer thickness $\delta _S$ ), large Damkoehler numbers and highly catalytic surface conditions. Each of these effects reduces the magnitude of wall fluctuations to very small values, which is accurately captured by the correlation. The good agreement between simulation and correlation is due to the fact that diffusion processes very quickly limit the penetration depth, i.e. the Stokes-layer thickness, such that the oscillation amplitude is attenuated already close to the boundary-layer edge. This then effectively reduces the boundary-layer-edge perturbation magnitude for a quasi-equilibrium case. This behaviour motivated the use of a simple multiplication of diffusion and chemical attenuation terms, as employed in § 2.4.