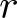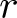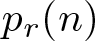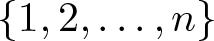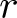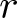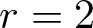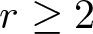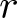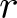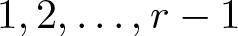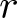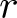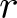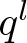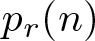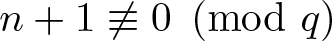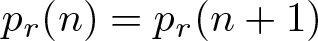1. Introduction
This paper is concerned with a duality between 
$r$-regular permutations and 
$r$-cycle permutations, which are closely related to permutations with an 
$r$th root, see, e.g., [Reference Bolker and Gleason6, Reference Bóna, McLennan and White8, Reference Külshammer, Olsson and Robinson14]. For an integer 
$r \ge 2$, a cycle is called 
$r$-regular if its length is not divisible by 
$r$ and 
$r$-singular otherwise (i.e., if its length is divisible by 
$r$). Suppose that permutations are represented in the cycle notation. A permutation is called 
$r$-regular provided that all of its cycles are 
$r$-regular, and an 
$r$-cycle permutation is a permutation where all cycles are 
$r$-singular. These terms were introduced by Külshammer, Olsson, and Robinson [Reference Külshammer, Olsson and Robinson14]. As usual, for 
$n\geq 1$, 
$S_n$ stands for the set of permutations of 
$[n]=\{1,2,\ldots, n\}$. Given a permutation 
$\sigma \in S_n$, it is said to have an 
$r$th root if there exists a permutation 
$\pi \in S_n$ such that 
$\pi^r = \sigma$. Permutations with an 
$r$th root can be characterized in terms of their cycle types [Reference Wilf20, p. 158]. For the number of such permutations, one may refer to the sequence A247005 in the OEIS [18]. The exponential generating function for this count was discussed in Bender [Reference Bender2], see also [Reference Wilf20, p. 159].
We shall follow the terminology in [Reference Külshammer, Olsson and Robinson14]. Throughout the paper, 
${\rm Reg}_r(n)$ and 
${\rm Cyc}_r(n)$ will stand for the set of 
$r$-regular permutations of 
$[n]$ and the set of 
$r$-cycle permutations of 
$[n]$, respectively. Note that 
${\rm NODIV}_r(n)$ and 
${\rm PERM}_r(n)$ are used in [Reference Bóna, McLennan and White8]. For 
$r\geq 2$ and 
$n=0$, set 
$\left\lvert{\rm Reg}_r(0)\right\rvert=\left\lvert{\rm Cyc}_r(0)\right\rvert=1$. Clearly, 
$\left\lvert{\rm Cyc}_r(n)\right\rvert=0$ whenever 
$n \not\equiv 0 \pmod r$.
The enumeration of 
$r$-regular permutations dates back to Erdős and Turán [Reference Erdős and Turán11]. By using generating functions, they showed that for 
$n\geq 1$, and 
$r$ a prime power, the proportion of 
$r$-regular permutations in 
$S_n$ equals
\begin{equation*}
\prod_{k=1}^{\lfloor n/r \rfloor}\frac{rk-1}{rk}.
\end{equation*} It was later observed that the above formula remains true for an arbitrary integer 
$r \ge 2$, for example, see [Reference Maróti17].
There are various ways to count 
${\rm Reg}_r(n)$ and 
${\rm Cyc}_r(n)$, see [Reference Beals, Leedham-Green, Niemeyer, Praeger and Seress1, Reference Bertram and Gordon4, Reference Bolker and Gleason6, Reference Bóna, McLennan and White8, Reference Glasby12, Reference Maróti17, Reference Wilf20]. In particular, for 
$r\geq 2$, Bóna, McLennan and White [Reference Bóna, McLennan and White8] presented a bijective argument to deduce the number of 
$r$-regular permutations of 
$[n]$ from the number of 
$r$-regular permutations of 
$[n-1]$. As a consequence, they confirmed the conjecture of Wilf [Reference Wilf20] that the probability 
$p_2(n)$ for a random permutation of 
$[n]$ to have a square root is monotonically nonincreasing in 
$n$. Such permutations have been called square permutations [Reference Blum5]. For example, 
$(1\ 2\ 3\ 4)\,(5\ 6\ 7\ 8)$ is a square permutation and it has a square root 
$(1\ 5\ 2\ 6\ 3\ 7\ 4\ 8)$. Beyond the case 
$r=2$, they proved that, more generally, for any prime 
$r$, the probability 
$p_r(n)$ that a random permutation of 
$[n]$ has an 
$r$th root is nonincreasing in 
$n$.
Notice that the monotone property does not hold in general. For example, when 
$r=6$, we have 
$p_6(4)=1/6$ but 
$p_6(5)=1/3$. Nonetheless, Bóna, McLennan and White [Reference Bóna, McLennan and White8] showed that for any 
$r\geq 2$,
\begin{align*}
p_r(n) \to 0,
\end{align*} as 
$n \to \infty$.
Table 1 exhibits the values of 
$p_r(n)$ for 
$r=2,3,5$ and 
$1\leq n \leq 12$.
Table 1. The values of 
$p_r(n)$.
As set forth by Bóna, McLennan and White, their proof of the monotone property is mostly combinatorial, and they left the question of seeking a fully combinatorial reasoning, which amounts to a combinatorial understanding of the following inequality
\begin{equation}
\left\lvert\mbox{Cyc}_{r^2}(mr^2) \right\rvert \le \left\lvert \mbox{Reg}_r(mr^2)\right\rvert,
\end{equation}which we shall call the Bóna-McLennan-White inequality, or the BMW inequality, for short.
Note that for 
$r=2$, 
${\rm Reg}_2(n)$ and 
${\rm Cyc}_2(n)$ are usually written as 
${\rm Odd}(n)$ and 
${\rm Even}(n)$, respectively. In the literature, 
$2$-regular permutations are also known as odd order permutations, which are related to ballot permutations, see, for example, [Reference Bernardi, Duplantier and Nadeau3, Reference Lin, Wang and Zhao16, Reference Spiro19]. However, even order permutations refer to permutations with at least one even cycle. These terms originated from the notion of the order of an element in a group.
It is a known result that 
${\rm Odd}(2n)$ and 
${\rm Even}(2n)$ share the same cardinality, 
$((2n-1)!!)^2$, see A001818 in the OEIS [18]. The equality of their cardinalities entails the existence of a bijection between 
${\rm Odd}(2n)$ and 
${\rm Even}(2n)$; however, this mapping is not immediately evident upon first inspection. A specific correspondence was found by Sayag based on the canonical representation of permutations, see Bóna [Reference Bóna7, Lemma 6.20]. An intermediate structure, which we call nearly odd order permutations, was introduced in [Reference Chen9]. It induces incremental transforms from a permutation in 
${\rm Odd}(2n)$ to a permutation in 
${\rm Even}(2n)$.
It is natural to ask whether the correspondence between 
${\rm Odd}(2n)$ and 
${\rm Even}(2n)$ can be extended to any 
$r \ge 2$? In this paper, we introduce the structure of enriched permutations, and we find a bijection between 
$r$-regular permutations of 
$[rn]$ and enriched 
$r$-cycle permutations of 
$[rn]$. As an immediate consequence, we achieve a combinatorial comprehension of the BMW inequality, or a stronger version, strictly speaking. This answers the question of Bóna, McLennan and White for any prime 
$r \geq 3$. As for the case 
$r=2$, we fill up with some discussions for the sake of completeness.
While the monotone property of 
$p_r(n)$ does not hold for general 
$r$, we show that it is valid for prime powers 
$r=q^l$. The proof relies on a stronger version of the Bóna-McLennan-White inequality and the characterization of permutations with an 
$r$th root, for a prime power 
$r$, due to A. Knopfmacher and R. Warlimont [Reference Wilf20, p. 158].
2. 
$r$-Enriched permutations
The aim of this section is to provide a bijection between 
$r$-regular permutations of 
$[rn]$ and enriched 
$r$-singular permutations of 
$[rn]$, for 
$r\geq 2$ and 
$n\geq 1$. Given 
$r \ge 2$, by saying that a permutation is 
$r$-enriched we mean that each 
$r$-singular cycle is coloured by one of the colours in the set 
$\{1, 2, \dots, r-1\}$. Later, we simply call such a permutation enriched. Bear in mind that 
$r$-regular cycles are never coloured.
Given 
$r \ge 2 $, we shall use the symbol 
$*$ to signify the enriched structure. For example, 
${\rm Cyc}^*_r(rn)$ denotes the set of enriched 
$r$-cycle permutations of 
$[rn]$. Throughout, we represent each permutation in cycle notation, where each cycle is written as a linear order starting with its smallest element, and the cycles are arranged in increasing order of their minima. We use the subscript of a cycle to denote the colour assigned to it. For example, for 
$r=3$, 
$(1\ 2\ 4)_2\,(3)\,(5\ 6)$ represents an 
$3$-enriched permutation for which the 
$3$-singular cycle 
$(1\ 2\ 4)$ is coloured by 
$2$.
To transform an 
$r$-regular permutation of 
$[rn]$ to an enriched 
$r$-singular permutation of 
$[rn]$, we introduce an intermediate structure like nearly odd permutations emerging in [Reference Chen9]. For 
$n\geq 1$, we say that a permutation 
$\sigma$ of 
$[n]$ is nearly 
$r$-regular if its cycles are all 
$r$-regular except that the one containing 
$1$ is 
$r$-singular. The notation 
${\rm NReg}_r(n)$ stands for the set of nearly 
$r$-regular permutations of 
$[n]$. For example, 
$(1\ 2\ 4)\,(3)\,(5\ 6)$ is a nearly 
$3$-regular permutation.
Enriched nearly 
$r$-regular permutations serve as an intermediate structure linking 
$r$-regular and enriched 
$r$-cycle permutations. More precisely, we manipulate the cycle structures to construct a bijection between 
${\rm Reg}_r(rn)$ and 
${\rm Cyc}^*_r(rn)$. For 
$r=2$, it reduces to a bijection between 
${\rm Odd}(2n)$ and 
${\rm Even}(2n)$.
Theorem 2.1. For any 
$r \ge 2$, there is a bijection 
$\Phi$ from 
${\rm Reg}_r(rn)$ to 
${\rm Cyc}^*_r(rn)$. Moreover, if 
$\sigma \in {\rm Reg}_r(rn)$ and the cycle containing 
$1$ in 
$\sigma$ has length 
$l=rk+i$, 
$1 \le i \le r-1$, then 
$\Phi(\sigma) \in {\rm Cyc}^*_r(rn)$, where the cycle containing 
$1$ in 
$\Phi(\sigma)$ has length 
$rk+r$.
To prove the theorem, let 
$Q_{r,\,k}(n)$ denote the set of permutations of 
$[n]$ for which the length of the cycle containing 
$1$ is 
$k$, and the other cycles are 
$r$-regular. We first build a bijection between 
$Q_{r,\,k}(n)$ and 
$Q_{r,\,k+1}(n)$ by applying an elegant bijection of Bóna, McLennan and White in [Reference Bóna, McLennan and White8, Lemma 2.1], which is a paradigm of a recursive algorithm.
Lemma 2.2. For all 
$r \geq 2$ and 
$n+1 \not\equiv 0 \pmod r$, there is a bijection 
$\Psi$ from 
${\rm Reg}_r(n) \times[n+1]$ to 
${\rm Reg}_r(n+1)$.
Practically, to make use of the bijection, it is unnecessary to adjust the elements of the underlying sets to fit in the above canonical form. It seems to be convenient to harness the following more generic formulation, and it might be informative to reproduce the proof as such. For a nonempty set 
$S$, we use 
${\rm Reg}_r(S)$ to denote the set of 
$r$-regular permutations of 
$S$. When 
$S=\emptyset$, the empty permutation is considered both 
$r$-regular and 
$r$-singular.
Lemma 2.3. Let 
$S$ be a nonempty finite set and 
$r$ an integer such that 
$r\geq 2$. If 
$\lvert S \rvert\not \equiv 0 \pmod{r}$, then there is a bijection 
$\Delta$ from 
${\rm Reg}_r(S)$ to the set of pairs 
$(x, \pi)$ such that 
$x\in S$ and 
$\pi$ is in 
${\rm Reg}_r(S
\setminus \{x\})$.
Proof. Assume that 
$\sigma$ belongs to 
${\rm Reg}_r(S)$ and 
$\lvert S \rvert \not\equiv 0 \pmod r$. From now on, we shall use 
$\lvert \sigma \rvert$ to denote the number of elements of 
$\sigma$. Let 
$D_1$ denote the first cycle of 
$\sigma$, 
$l$ be its length, 
$x$ be the last entry in 
$D_1$, and let 
$\tilde{\sigma}$ be 
$\sigma$ with 
$D_1$ being removed. In effect, the map 
$\Delta$ will remove 
$x$ in 
$D_1$ and turn it into a distinguished element. We encounter three cases.
Case 1: 
$l=1$. Then set 
$\Delta(\sigma)=(x, \tilde{\sigma})$. By construction, the element 
$x$ is smaller than every element of 
$\tilde{\sigma}$.
Case 2: 
$l \not\equiv 1 \pmod r$. Then remove 
$x$ from 
$D_1$ to get 
$C_1$ and set 
$\Delta(\sigma)=(x, C_1\,\tilde{\sigma})$. Contrary to the previous case, the element 
$x$ is greater than the smallest element of 
$C_1\,\tilde{\sigma}$. Since 
$l \not\equiv 0, 1 \pmod r$, we have 
$\left\lvert C_1 \right\rvert = l-1 \not\equiv -1,0 \pmod r$, which ensures that the resulting permutation is 
$r$-regular.
Case 3: 
$l \equiv 1 \pmod r$ and 
$l \neq 1$. Let 
$\tilde{x}$ be the second-to-last element in 
$D_1$ and 
$C_1$ be the cycle obtained from 
$D_1$ by removing 
$x$ and 
$\tilde{x}$. Since 
$\left\lvert \tilde{\sigma}\right\rvert+1
=\lvert \sigma \rvert-l+1 \not\equiv 0 \pmod r$, we can apply 
$\Delta^{-1}$ to 
$(\tilde{x}, \tilde{\sigma})$ to get 
$\tilde{\pi}$. Then set 
$\Delta(\sigma)=(x, C_1\, \tilde{\pi})$. In this situation, the element 
$x$ is greater than the smallest element of 
$C_1\, \tilde{\pi}$ and 
$\left\lvert C_1\right\rvert = l-2 \equiv -1 \pmod r$.
It remains to verify that 
$\Delta$ is a bijection. Given a pair 
$(x,\pi)$ where 
$x\in S$ and 
$\pi$ is an 
$r$-regular permutation of 
$S
\setminus \{x\}$ with 
$\lvert \pi \rvert+1
\not\equiv 0 \pmod r$. Let 
$C_1$ denote the first cycle of 
$\pi$, 
$l$ be its length and let 
$\tilde{\pi}$ be permutation 
$\pi$ with 
$C_1$ being removed. Conversely, the map 
$\Delta^{-1}$ will place 
$x$ as the last entry in the first cycle of 
$\Delta^{-1}(x,\pi)$. Accordingly, we face three possibilities.
Case 1: The element 
$x$ is smaller than every element of 
$\pi$. Then set 
$\Delta^{-1}(x,\pi)=(x) \, \pi$. In this case, 
$\left\lvert D_1\right\rvert$=1.
Case 2: The element 
$x$ is greater than the smallest element of 
$\pi$ and 
$l \not\equiv -1 \pmod r$. Let 
$D_1$ be 
$C_1$ with 
$x$ appended to the end of 
$C_1$. Then set 
$\Delta^{-1}(x,\pi)=D_1 \, \tilde{\pi}$. Notice that 
$l \not\equiv -1, 0 \pmod r$, and so 
$\left\lvert D_1 \right\rvert=l+1 \not\equiv 0, 1 \pmod r$.
Case 3: The element 
$x$ is greater than the smallest element of 
$\pi$ and 
$l \equiv -1 \pmod r$. Under the conditions 
$\lvert \pi \rvert-l \equiv \lvert \pi \rvert+1 \pmod r$ and 
$\lvert \pi \rvert +1 \not\equiv 0 \pmod r$, we have 
$\left\lvert \tilde{\pi} \right\rvert=\lvert \pi \rvert-l \not\equiv 0 \pmod r$. Thus we can apply 
$\Delta$ to 
$\tilde{\pi}$ to get 
$(\tilde{x}, \tilde{\sigma})$. Let 
$D_1$ be the permutation obtained from 
$C_1$ with 
$\tilde{x}x$ appended to the end. Then set 
$\Delta^{-1}(x,\pi)=D_1 \, \tilde{\sigma}$. Notice that in this case 
$\left\lvert D_1 \right\rvert = l +2 \equiv 1 \pmod r$ and 
$\left\lvert D_1 \right\rvert \neq 1$, completing the proof.
For example, when 
$r=3$, consider
\begin{equation*} \sigma = (1\ 8\ 2\ 5)\,(3)\,(4)\,(6\ 7).\end{equation*} Since the length of the first cycle is congruent to 
$1 \pmod 3$, we are in Case 
$3$. Hence,
\begin{align*}
\Delta(\sigma)=(5,(1\ 8)\,\tilde{\pi}),
\end{align*}where
\begin{align*}
\tilde{\pi}=\Delta^{-1}(2,(3)\,(4)\,(6\ 7)).
\end{align*} Because the element 
$2$ is smaller than every element in 
$\tilde{\pi}$, we are in Case 
$1$ of 
$\Delta^{-1}$. Therefore,
\begin{align*}
\Delta^{-1}\left(2,(3)\,(4)\,(6\ 7)\right)=(2)\,(3)\,(4)\,(6\ 7).
\end{align*}Consequently,
\begin{align*}
\Delta(\sigma)=(5,(1\ 8)\,(2)\,(3)\,(4)\,(6\ 7)).
\end{align*} We now turn to the description of the bijection 
$\varphi$. The following lemma is the building block of the correspondence between 
$r$-regular permutations and enriched 
$r$-cycle permutations. It rests on the Lemma of Bóna, McLennan and White, as restated in Lemma 2.3.
Lemma 2.4. Let 
$n, r, k$ be integers such that 
$n \ge 0, r \ge 2, k \ge 1$ and 
$n -k \not\equiv 0 \pmod r$. Then there is a bijection 
$\varphi$ from 
$Q_{r,\,k}(n)$ to 
$Q_{r,\,k+1}(n)$.
Proof. We proceed to construct a map 
$\varphi$ from 
$Q_{r,\,k}(n)$ to 
$Q_{r,\,k+1}(n)$ by employing the above bijection 
$\Delta$. Assume that 
$n -k \not\equiv 0 \pmod r$ and 
$k \ge 1$. Let 
$\sigma \in Q_{r,\,k}(n)$, and denote by 
$C_1$ the cycle containing 
$1$. Define 
$\tilde{\sigma} = \sigma - C_1$, by which we mean the permutation obtained from 
$\sigma$ by removing 
$C_1$. Since 
$\left\lvert\tilde{\sigma}\right\rvert=n-k \not\equiv 0 \pmod r$ and 
$\tilde{\sigma}$ is an 
$r$-regular permutation, applying the map 
$\Delta$, we get 
$\Delta(\tilde{\sigma})=(x, \tilde{\pi})$. Now, let 
$D$ denote the cycle obtained from 
$C_1$ with 
$x$ attached at the end. Set 
$\varphi (\sigma) = D\, \tilde{\pi}$, which is readily seen to lie in 
$Q_{r,\,k+1}(n)$.
Conversely, let us define a map 
$\alpha$ from 
$Q_{r,\,k+1}(n)$ to 
$Q_{r,\,k}(n)$. Given 
$\pi \in Q_{r,\,k+1}(n)$, where 
$n-k \not\equiv 0 \pmod r$ and 
$k \ge 1$, let 
$C_1$ be the first cycle of 
$\pi$, and let 
$D$ be the cycle obtained from 
$C_1$ by removing its last entry 
$x$. Define 
$\tilde{\pi}$ be the permutation obtained from 
$\pi$ with 
$C_1$ being removed. Note that 
$\left\lvert \tilde{\pi} \right\rvert +1=n-k \not\equiv 0 \pmod r$ and 
$ \tilde{\pi}$ is an 
$r$-regular permutation. Then set
\begin{equation*} \alpha(\pi) = D \, \Delta^{-1}(x, \tilde{\pi}),\end{equation*} which belongs to 
$Q_{r,\,k}(n)$.
It is straightforward to verify that the maps 
$\varphi$ and 
$\alpha$ are well-defined and are inverses of each other. Thus 
$\varphi$ is a bijection.
For example, if 
$r=3$, then 
$\varphi((3)\,(5\ 6))=(3\ 6)\,(5)$ and 
$\varphi((3 \ 6)\,(5))=(3\ 6\ 5)$.
Writing 
$n-k=mr+d$ with 
$0 \lt d \lt r $, it is known that, see [Reference Beals, Leedham-Green, Niemeyer, Praeger and Seress1, Reference Bertram and Gordon4, Reference Bolker and Gleason6, Reference Bóna, McLennan and White8, Reference Glasby12, Reference Maróti17, Reference Wilf20],
\begin{align*}
\left\lvert {\rm Reg}_{r}(n-k)\right\rvert = (n-k)! \, \frac{(r-1)\, (2r-1)\cdots(mr-1)}{r^m m!},
\end{align*}from which we deduce that
\begin{equation}
\left\lvert Q_{r,\,k}(n)\right\rvert = \left\lvert Q_{r,\,k+1}(n)\right\rvert = (n-1)! \, \frac{(r-1)\, (2r-1)\cdots(mr-1)}{r^m m!}.
\end{equation} For 
$k \ge 1$, let 
$A_{n,\,2k-1}$ denote the set of permutations of 
$[n]$ with only odd cycles for which the element 
$1$ appears in a cycle of length 
$2k-1$, and let 
$P_{n,\,2k}$ denote the set of permutations of 
$[n]$ with odd cycles except that the element 
$1$ is contained in an even cycle of length 
$2k$. When 
$r=2$, we come to the following correspondence. Notice that the construction in [Reference Chen9] by way of breaking cycles does not possess this refined property.
Corollary 2.5. For 
$k \ge 1$, the map 
$\varphi$ defined in Lemma 2.4 gives a bijection between 
$A_{2n,\, 2k-1}$ and 
$P_{2n, \,2k}$, as well as a bijection between 
$P_{2n+1,\, 2k}$ and 
$A_{2n+1,\, 2k+1}$.
For example, when 
$r=2$, given 
$\sigma = (1\ 2\ 3\ 4\ 6)\,(5\ 10\ 8)\,(7)\,(9) \in A_{10,\,5}$, we have
\begin{align*}
\Delta((5\ 10\ 8)\,(7)\,(9))=(8,(5)\,(7\ 9\ 10)).
\end{align*}Thus
\begin{align*}
\varphi(\sigma) & = (1\ 2\ 3\ 4\ 6\ 8) \,(5) \, (7\ 9\ 10) \in P_{10,\,6}.
\end{align*}Below are the explicit formulas:
\begin{equation}
\left\lvert A_{2n,\,2k-1} \right\rvert = \left\lvert P_{2n,\,2k}\right\rvert=\frac{(2n-1)!}{(2n-2k)!}\, \left((2n-2k-1))!!\right)^2,
\end{equation}
\begin{equation}
\left\lvert P_{2n+1,\,2k}\right\rvert = \left\lvert A_{2n+1,\,2k+1} \right\rvert=\frac{(2n)!}{(2n-2k)!}\, \left((2n-2k-1))!!\right)^2.
\end{equation} Exploiting the bijection 
$\varphi$, we are led to the following incremental transformation 
$\Lambda$.
Theorem 2.6. For all 
$r \ge 2$, there is a bijection 
$\Lambda$ from 
${\rm Reg}_r(rn)$ to 
${\rm NReg}^*_r(rn)$. Moreover, if 
$\sigma \in {\rm Reg}_r(rn)$ and the cycle containing 
$1$ in 
$\sigma$ has length 
$l=rk+i$, 
$1 \le i \le r-1$, then 
$\Lambda(\sigma) \in {\rm NReg}^*_r(rn)$, where the cycle containing 
$1$ in 
$\Lambda(\sigma)$ has length 
$rk+r$.
Proof. Let 
$\sigma$ in 
${\rm Reg}_r(rn)$. Assume that its first cycle length is 
$rk+i$, where 
$1 \le i \le r-1$. Since 
$rn \not\equiv rk+i \pmod r$, we can apply the bijection 
$\varphi$ in Lemma 2.4 to 
$\sigma$ to get a permutation 
$\pi$. There are two possibilities with regard to the length of the first cycle of 
$\pi$.
If 
$\pi$ is in 
${\rm NReg}_r(rn)$, in which case, 
$i+1=r$, we colour its first cycle with 
$r-1$ to obtain 
$\Lambda(\sigma) \in {\rm NReg}^*_r(rn)$.
If 
$\pi$ stays in 
${\rm Reg}_r(rn)$ with the length of the first cycle increased by 
$1$ in comparison with 
$\sigma$, that is, the length of the first cycle of 
$\pi$ equals 
$rk+i+1$ with 
$rk+i+1 \not\equiv 0 \pmod r$. Again, since 
$rn \not\equiv rk+i+1 \pmod r$, we may move on to apply the bijection 
$\varphi$ once more. The procedure continues until we obtain a permutation 
$\pi$ in 
${\rm NReg}_r(rn)$. Colour 
$\pi$’s first cycle with 
$i$ and define the resulting enriched permutation to be 
$\Lambda(\sigma)$, which lies in 
${\rm NReg}^*_r(rn)$. Apparently, it takes 
$r-i$ steps to reach this point.
As an example, for 
$r=3$, we have
\begin{equation*}\Lambda\left((3)\,(5\ 6)\right)=(3\ 6\ 5)_1\end{equation*}and
\begin{equation*}\Lambda\left((1\ 2)\,(3\ 4)\,(5\ 6)\right) = (1\ 2\ 4)_2\,(3)\,(5\ 6). \end{equation*} It is readily seen that the process is reversible because the colour of the 
$r$-singular cycle keeps track of the number of times that the map 
$\varphi$ is applied. Thus 
$\Lambda$ is a bijection.
Proof of Theorem 2.1
We proceed to define a map 
$\Phi$ from 
${\rm Reg}_r(rn)$ to 
${\rm Cyc}_r^*(rn)$ by successively applying the map 
$\Lambda$ in Theorem 2.6.
Given an 
$r$-regular permutation 
$\sigma$, our goal is to create a sequence of coloured 
$r$-singular cycles 
$C_i^*$. At the first step, applying the bijection 
$\Lambda$ to 
$\sigma$, we get
\begin{equation*}\Lambda(\sigma)=C_1^*\, \sigma_1,\end{equation*} where 
$C_1^*$ is a coloured 
$r$-singular cycle and 
$\sigma_1$ is an 
$r$-regular permutation (possibly empty), and 
$C_1^* \sigma_1$ stands for the permutation obtained by putting together the coloured cycle 
$C_1^*$ and the cycles in 
$\sigma_1$. If 
$\sigma_1$ is empty, then we set 
$\Phi(\sigma)=C_1^*$; otherwise, applying 
$\Lambda$ again to 
$\sigma_1$ gives
\begin{equation*}\Lambda(\sigma_1)=C_2^*\, \sigma_2.\end{equation*} If 
$\sigma_2$ is empty, we define 
$\Phi(\sigma)=C_1^*\, C_2^*$; otherwise, we may apply 
$\Lambda$ to 
$\sigma_2$.
We may iterate the procedure as follows. Assume that we have obtained a nonempty permutation 
$\sigma_i$ for some 
$i$. Applying 
$\Lambda$ to 
$\sigma_i$ yields
\begin{equation*}\Lambda(\sigma_i)=C_{i+1}^* \sigma_{i+1},\end{equation*} where 
$C_{i+1}^*$ is a coloured 
$r$-singular cycle and 
$\sigma_{i+1}$ is an 
$r$-regular permutation (possibly empty). If 
$\sigma_{i+1}$ is not empty, we apply 
$\Lambda$ again; otherwise, we stop. Clearly, the above process will terminate at some point when 
$\sigma_{i+1}$ is empty. Now define
\begin{equation*}\Phi(\sigma)=C_1^*\, \cdots \, C_{i+1}^*.\end{equation*} Since 
$\Lambda$ is bijective, so is 
$\Phi$.
For example, for 
$r=3$, let
\begin{equation*}\sigma=(1\ 2)\,(3\ 4)\,(5\ 6).\end{equation*} Applying 
$\Lambda$ to 
$\sigma$ yields
\begin{equation*}\Lambda \left((1\ 2)\,(3\ 4)\,(5\ 6)\right) = (1\ 2\ 4)_2\,(3)\,(5\ 6);\end{equation*} at this stage, the permutation still contains 
$r$-regular cycles 
$(3), (5\;6)$, so we need to repeat the above procedure. One more round of iteration gives
\begin{equation*}\Lambda \left((3)\,(5\ 6)\right) = (3\ 6\ 5)_1,\end{equation*}thus we finally obtain
\begin{equation*}
\Phi\left((1\ 2)\,(3\ 4)\,(5\ 6)\right)= (1\ 2\ 4)_2\,(3\ 6\ 5)_1.
\end{equation*}3. The Bóna-McLennan-White inequality
In the proof of the following monotone property, there is an inequality that demands a combinatorial explanation. As will be seen, the structure of enriched cycle permutations entails a combinatorial interpretation of this inequality. Recall that 
$p_r(n)$ is the probability for a random permutation of 
$[n]$ to have an 
$r$th root.
Theorem 3.1. (Bóna, McLennan and White [Reference Bóna, McLennan and White8])
For all positive integers 
$n$ and all primes 
$r$, we have,
\begin{align*}
p_r(n) \ge p_r(n+1).
\end{align*} The above assertion consists of three circumstances contingent to modulo conditions on 
$n+1$.
Theorem 3.2. (Bóna, McLennan and White [Reference Bóna, McLennan and White8])
Let 
$r$ be a prime. Then we have the following.
(i) If
$n+1 \not\equiv 0 \pmod r$, then
$p_r(n)=p_r(n+1)$.(ii) If
$n+1 \equiv 0 \pmod {r}$ but
$n+1 \not\equiv 0 \pmod {r^{2}}$, then
\begin{align*}
p_r(n) \geq \frac{n+1}{n}p_r(n+1)
\end{align*}with equality only when
$n+1=kr$, where
$k=1,2,\ldots,r-1$.(iii) If
$n+1 \equiv 0 \pmod {r^{2}}$, then
$p_r(n) \ge p_r(n+1)$ with equality only when
$r=2$ and
$n=3$.
The proof of the above theorem builds upon a special case of the characterization of permutations with an 
$r$th root, due to Knopfmacher and Warlimont, see [Reference Wilf20, p. 158]. In particular, when 
$r$ is prime, a permutation has an 
$r$th root if and only if for any positive integer 
$i$, the number of cycles of length 
$ir$ is a multiple of 
$r$. Making use of the bijection 
$\Psi$ as restated in Lemma 2.3, Bóna, McLennan and White gave an entirely combinatorial proof of (i) and (ii). However, in order to have a fully combinatorial understanding of (iii), one needs a combinatorial interpretation of the following inequality, see [Reference Bóna, McLennan and White8, Lemma 3.3], which we call the Bóna-McLennan-White inequality, or the BMW inequality, for short.
Lemma 3.3. For all 
$r \geq 2$ and 
$m \ge 1$,
\begin{equation}
\left\lvert {\rm Cyc}_{r^2}(mr^2) \right\rvert \lt \left\lvert {\rm Reg}_r(mr^2)\right\rvert .
\end{equation} The BMW-inequality was proved in [Reference Bóna, McLennan and White8] by means of generating functions. In fact, we observe that a stronger version of (3.1), i.e., Theorem 3.4, holds, which can be deduced from the following known formulas, see [Reference Beals, Leedham-Green, Niemeyer, Praeger and Seress1, Reference Bertram and Gordon4, Reference Bolker and Gleason6, Reference Bóna, McLennan and White8, Reference Glasby12, Reference Maróti17, Reference Wilf20]. For 
$r \ge 2$ and 
$m \ge 1$,
\begin{equation}
\left\lvert{\rm Cyc}_{r}(rm)\right\rvert =(rm)!\frac{(1+r)\,(1+2r)\cdots(1+(m-1)r)}{r^m m!},
\end{equation}
\begin{equation}
\left\lvert{\rm Reg}_{r}(rm)\right\rvert =(rm)!\frac{(r-1)\, (2r-1)\cdots(mr-1)}{r^m m!}.
\end{equation}On the other hand, it is transparent from a combinatorial point of view.
Theorem 3.4. For 
$r \geq 2$ and 
$n\geq 1$,
\begin{equation}
\left\lvert{\rm Cyc}_r(n)\right\rvert \le \left\lvert{\rm Reg}_r(n)\right\rvert,
\end{equation} where the equality holds only when 
$r=2$ and 
$n$ is even.
Proof. When 
$n \not\equiv 0 \pmod r$, we have 
$\left\lvert{\rm Cyc}_{r}(n)\right\rvert=0$, nothing needs to be done. When 
$n = rm$, by restricting 
$r$ to only one colour, we see that
\begin{equation}
\left\lvert{\rm Cyc}_r(rm)\right\rvert \leq \left\lvert{\rm Cyc}^*_r(rm)\right\rvert.
\end{equation} But Theorem 2.1 says that 
$ \left\lvert{\rm Reg}_{r}(rm)\right\rvert= \left\lvert{\rm Cyc}^*_r(rm)\right\rvert$, and so (3.4) follows. The equality holds only when 
$r=2$ and 
$n$ is even. This concludes the proof.
To see that the BMW inequality (3.1) stems from (3.4), just observe that for 
$r\geq 2$,
\begin{align*}
{\rm Cyc}_{r^2}(mr^2) \subset {\rm Cyc}_r(mr^2).
\end{align*} This inequality, together with the combinatorial reasoning in [Reference Bóna, McLennan and White8] gives rise to the conclusion that 
$p_r(n) \gt p_r(n+1)$ for any prime 
$r \ge 3$ and 
$n+1 \equiv 0 \pmod {r^2}$.
As defined before, 
$\left\lvert{\rm Reg}_r(0)\right\rvert=1$ and 
$\left\lvert{\rm Cyc}_r(0)\right\rvert=1$. With Lemma 2.2 in hand, it is easy to get the following recurrence of 
$\left\lvert{\rm Reg}_r(rm)\right\rvert$. For details, we refer to Lemma 2.1 and Lemma 2.6 in [Reference Bóna, McLennan and White8].
Lemma 3.5. For all 
$r \ge 2$ and 
$m \ge 1$, we have
\begin{equation}
\left\lvert{\rm Reg}_r(rm)\right\rvert = (rm-1)\, (rm-1)_{r-1} \left\lvert{\rm Reg}_r(rm-r)\right\rvert,
\end{equation} where 
$(x)_{m}$ stands for the lower factorial 
$x(x-1)\cdots(x-m+1)$.
The above relation can also be deduced inductively by using the recursive generation of permutations in the cycle notation, see, for example, [Reference Beals, Leedham-Green, Niemeyer, Praeger and Seress1, Reference Herrera13]. In [Reference Beals, Leedham-Green, Niemeyer, Praeger and Seress1], it has been shown that
\begin{align*}
\begin{split}\left\lvert {\rm Reg}_r(rm)\right\rvert &= \sum_{1 \le l \le r-1} (rm-1)_{l-1}\left\lvert {\rm Reg}_r(rm-l)\right\rvert \\[3pt]
& \qquad + (rm-1)_{r} \left\lvert {\rm Reg}_r(rm-r)\right\rvert,
\end{split}
\end{align*} and by an easy induction on 
$n$, it can be shown that for 
$1\leq l\leq r-1$,
\begin{align*}
\left\lvert{\rm Reg}_r(rm-l)\right\rvert=(rm-l)_{r-l} \left\lvert{\rm Reg}_r(rm-r)\right\rvert.\end{align*}This proves (3.6).
Similarly, we have the following recurrence relation for 
${\rm Cyc}_r(rm)$.
Lemma 3.6. For all 
$r \ge 2$ and 
$m \ge 1$, we have
\begin{equation}
\left\lvert{\rm Cyc}_r(rm)\right\rvert = (rm-1)_{r-1}(rm-r+1) \left\lvert{\rm Cyc}_r(rm-r)\right\rvert.
\end{equation}Proof. Let 
$\sigma$ be a permutation in 
${\rm Cyc}_r(rm)$. Let 
$l$ be the length of the first cycle of 
$\sigma$. If 
$l = r$, we have 
$(rm-1)_{r-1}$ choices to form the first cycle, which gives a total of 
$(rm-1)_{r-1}\left\lvert{\rm Cyc}_r(rm-r)\right\rvert$ choices. If the first cycle contains more than 
$r$ elements, say 
$(1\ \cdots\ j_r\ j_{r+1}\ \cdots)$, we can break the first cycle into two segments 
$ 1\ \cdots\ j_r $ and 
$j_{r+1}\ \cdots$. The second segment can be viewed as a cycle with a distinguished element 
$j_{r+1}$. Combining this cycle with a distinguished element and other cycles, we find a permutation in 
${\rm Cyc}_r(rm-r)$ with a distinguished element. There are 
$(rm-1)_{r-1}$ choices for the first segment 
$ 1\ \cdots\ j_r $ and there are 
$rm-r$ choices for the distinguished element 
$j_{r+1}$. Hence
\begin{align*}
\left\lvert{\rm Cyc}_r(rm)\right\rvert & = (rm-1)_{r-1} \left\lvert{\rm Cyc}_r(rm-r)\right\rvert \\
& \quad {}+ (rm-1)_{r-1} (rm-r) \left\lvert{\rm Cyc}_r(rm-r)\right\rvert,
\end{align*}which gives (3.7).
As per the recurrence relations (3.6) and (3.7), one can derive the formulas for 
$\left\lvert{\rm Reg}_r(rm)\right\rvert$ and 
$\left\lvert{\rm Cyc}_r(rm)\right\rvert$, which result in the stronger version of the BMW inequality, i.e., (3.4). Thus, for a prime 
$r\ge 3$, we obtain another combinatorial explanation of the monotone property.
As noted in [Reference Bóna, McLennan and White8], the case 
$r=2$ requires a stronger inequality, which can be justified using generating functions.
Lemma 3.7. For 
$m \ge 4$, we have
\begin{equation}
2\left\lvert{\rm Cyc}_4(4m)\right\rvert \lt \left\lvert{\rm Reg}_2(4m)\right\rvert.
\end{equation}Proof. For 
$m \ge 1$, by Lemmas 3.5 and 3.6, we obtain that
\begin{equation}
\left\lvert{\rm Reg}_2(4m)\right\rvert = (4m-1)^2\,(4m-3)^2 \left\lvert{\rm Reg}_2(4m-4)\right\rvert,
\end{equation}
\begin{equation}
\left\lvert{\rm Cyc}_4(4m)\right\rvert = (4m-1)\,(4m-2)\,(4m-3)^2 \left\lvert{\rm Cyc}_4(4m-4)\right\rvert.
\end{equation} In fact, the proofs of Lemmas 3.5 and 3.6 reveal that there is a bijection from 
${\rm Reg}_2(4m)$ to 
$[4m-1]^2\times[4m-3]^2\times{\rm Reg}_2(4m-4)$, and there is also a bijection from 
${\rm Cyc}_4(4m)$ to 
$[4m-1] \times[4m-2]\times[4m-3]^2 \times {\rm Cyc}_4(4m-4)$. Clearly, the coefficient in (3.9) is greater than that in (3.10), and it is just a matter of formality to make this comparison in combinatorial terms. Consequently, if
\begin{align*}
2\left\lvert{\rm Cyc}_4(4m)\right\rvert \lt \left\lvert{\rm Reg}_2(4m)\right\rvert
\end{align*} holds for some value 
$m_0$, then it holds for all 
$m\geq m_0$. It is easily verified that we can choose 
$m_0=4$, since from (3.9) and (3.10), we have
\begin{equation*}
\frac{\left\lvert{\rm Reg}_2(4m_0)\right\rvert}{\left\lvert{\rm Cyc}_4(4m_0) \right\rvert}=\frac{15}{14}\cdot\frac{11}{10}\cdot\frac{7}{6}\cdot\frac{3}{2}\cdot\frac{\left\lvert{\rm Reg}_2(0)\right\rvert}{\left\lvert{\rm Cyc}_4(0)\right\rvert}=\frac{33}{16} \gt 2.
\end{equation*}So the Lemma is proved.
In view of the above argument, inequality (3.8) admits a combinatorial interpretation. Appealing to this inequality, we deduce that 
$p_2(n+1) \lt p_2(n)$ whenever 
$n+1 \equiv 0 \pmod {4}$, with the only exceptions for 
$n=3,7,11$, see [Reference Bóna, McLennan and White8]. For these three special cases, we can look up the data in [Reference Bóna, McLennan and White8] or the sequence A247005 in the OEIS [18]. The values of 
$p_2(n)$ for 
$n=3,4,7,8,11,12$ are given as follows
\begin{align*}
\frac{1}{2}, \,\frac{1}{2}, \, \frac{3}{8}, \,\frac{17}{48}, \,\frac{29}{96}, \,\frac{209}{720}.
\end{align*} Thus for 
$n=3,7,11$, the inequality 
$p_2(n+1) \le p_2(n)$ is valid with equality attained only when 
$n=3$. Therefore, for any prime 
$r$, a full combinatorial analysis is achieved.
4. The monotone property for prime powers
Whereas the monotone property of 
$p_r(n)$ does not hold in general, numerical evidence raises hopes that it might hold for prime powers, as indicated in Table 2 for 
$r=4, 8, 9$ and 
$1\leq n \leq 12$.
Table 2. The values of 
$p_r(n)$.
The main result of this section is as follows.
Theorem 4.1. Let 
$n$ be a positive integer and 
$r=q^l$, where 
$q$ is a prime and 
$l \ge 1$, then 
$p_r(n) \ge p_r(n+1)$.
Like the case for primes, this monotone property stands on the following cases subject to modulo conditions on 
$n+1$. First, we recall an equality concerning 
$p_r(n)$ when 
$r$ is a prime power. Chernoff [Reference Chernoff10] established the following equality, and Leaños, Moreno and Rivera-Martínez [Reference Leaños, Moreno and Rivera–Martínez15] presented two proofs, with one using generating functions and the other being combinatorial.
Theorem 4.2. Let 
$q$ be a prime and 
$r=q^l$, 
$l \ge 1$. If 
$n+1 \not\equiv 0 \pmod q$, then 
$p_r(n)=p_r(n+1)$.
For the remaining cases, we obtain the following relations.
Theorem 4.3. Let 
$q$ be a prime, and 
$r=q^l$, 
$l \ge 1$.
(i) If
$n+1 \equiv 0 \pmod {q}$ but
$n+1 \not\equiv 0 \pmod {qr}$, then
(4.1)\begin{equation}
p_r(n) \geq \frac{n+1}{n}p_r(n+1),
\end{equation}with equality only when
$n+1=kq$, where
$k=1,2,\ldots,r-1$.(ii) If
$n+1 \equiv 0 \pmod {qr}$, then
$p_r(n) \ge p_r(n+1)$ with equality only when
$r=2$ and
$n=3$.
To prove the above theorem, it is helpful to prepare some auxiliary inequalities. Even though these estimates can be considerably improved, we will be content with the coarse lower bounds in order to keep the proofs brief. Recall that for any 
$r$, permutations with an 
$r$th root can be characterized in terms of the cycle type by Knopfmacher and Warlimont, see Wilf [Reference Wilf20, p. 158]. In particular, we need the following criterion when 
$r$ is a prime power.
Proposition 4.4. If 
$r=q^l$ with 
$q$ being a prime number and 
$l \ge 1$, then a permutation has an 
$r$th root if and only if for any integer 
$i$, the number of cycles of length 
$iq$ is a multiple of 
$r$.
Next, we show that the two inequalities in Lemma 3.2 and Lemma 3.3 in [Reference Bóna, McLennan and White8] for a prime 
$r$ can be extended to a prime power. With the common notation 
$S_n^r$ for the set of permutations of 
$[n]$ with an 
$r$th root, by Proposition 4.4, we have for a prime power 
$r=q^l$,
\begin{equation}
{\rm Reg}_q(n) \subseteq S^r_n .
\end{equation} Let 
${\rm Cyc}_{q,\,r}(n)$ denote the set of permutations such that each cycle length is a multiple of 
$q$ and each cycle length occurs a multiple of 
$r$ times. The following relation is an extension of Lemma 3.2 in [Reference Bóna, McLennan and White8].
Lemma 4.5. For any 
$m \ge 1$, let 
$r=q^l$, where 
$q \ge 2$ (not necessarily a prime) and 
$l \ge 1$, we have
\begin{equation}
\frac{\left\lvert {\rm Cyc}_{qr}(mqr)\right\rvert}{\left\lvert {\rm Cyc}_{q,\,r}(mqr)\right\rvert } \ge (mq)^{r-1}.
\end{equation}Proof. Let 
$\pi \in {\rm Cyc}_{q,\,r}(mqr)$. By definition, we assume that 
$\pi$ contains 
$k_ir$ cycles of length 
$iq $, where 
$k_i \geq 0$. For each 
$i$ with 
$k_i \neq 0$, partition the cycles of length 
$iq$ into 
$k_i$ classes with each class containing 
$r$ cycles. For each class 
$F$ of 
$r$ cycles of length 
$iq$, we proceed to generate a cycle of length 
$iqr$ out of the elements in 
$F$. Running over all such classes 
$F$, we obtain permutations in 
${\rm Cyc}_{qr}(mqr)$.
First, let 
$A_1, A_2, \ldots, A_{r}$ be the cycles in 
$F$, where every cycle has length 
$iq$, that is, arrange the cycles in 
$F$ in any specific linear order. To form a cycle of length 
$iqr$, we represent 
$A_1$ with the minimum element at the beginning. Then break the cycles 
$A_2, A_2, \ldots, A_r$ into linear orders by starting with any element. There are 
$iq$ ways to break a cycle of length 
$iq$ into a linear order. Assume that 
$A_2', A_3', \ldots, A_r'$ are in linear order by breaking the cycles 
$A_2, A_3, \ldots, A_r$, respectively. Now we can form a cycle of length 
$iqr$ by adjoining 
$A_2', A_3', \ldots, A_r'$ successively at the end of 
$A_1$. Evidently, the cycles formed in this way are all distinct, and there are 
$(iq)^{r-1}$ of them that can be generated in this manner.
Taking into account all classes 
$F$, we may produce certain permutations in 
${\rm Cyc}_{qr}(mqr)$. The number of permutations generated this way equals 
$\prod_i(iq )^{(r-1)k_i}$. Moreover, the range of 
$i$ in 
$\prod_i(iq)^{(r-1)k_i}$ can be restricted to those such that 
$k_i\geq 1$. Given that 
$q\geq 2$, for any 
$k_i \ge 1$, we have 
$(iq)^{k_i} \geq i qk_i$ and
\begin{equation*} \prod_i iq{k_i} \ge \sum_i iqk_i.\end{equation*}Thus we see that
\begin{equation*}\prod_i(iq)^{(r-1)k_i} \ge \left(\sum_i iqk_i\right)^{r-1}=(mq)^{r-1}, \end{equation*}where we have used the relation
\begin{equation*} \sum_{i} iqk_i = m q, \end{equation*}because
\begin{equation*}\sum_iiqk_ir=mqr.\end{equation*}So the Lemma is proved.
The following lemma is an extension of Lemma 3.3 in [Reference Bóna, McLennan and White8].
Lemma 4.6. Let 
$r=q^l$, where 
$q \ge 2$ (not necessarily a prime) and 
$l \ge 1$. Then, for any integer 
$m \ge 1$, we have
\begin{equation}
\frac{\left\lvert{\rm Reg}_{q}(mqr)\right\rvert}{\left\lvert{\rm Cyc}_{q,\,r}(mqr)\right\rvert} \gt (mq)^{r-1}.
\end{equation}Proof. By definition, we have
\begin{align*}
{\rm Cyc}_{qr}(mqr) \subset {\rm Cyc}_{q}(mqr),
\end{align*} and hence 
$\left\lvert{\rm Cyc}_{qr}(mqr) \right \rvert \lt \left\lvert{\rm Cyc}_{q}(mqr) \right\rvert$. In light of the stronger version of the BMW inequality (3.4), we see that
\begin{equation}
\frac{\left\lvert{\rm Reg}_{q}(mqr)\right\rvert}{\left\lvert{\rm Cyc}_{qr}(mqr)\right\rvert} = \frac{\left\lvert{\rm Reg}_{q}(mqr)\right\rvert}{\left\lvert{\rm Cyc}_{q}(mqr)\right\rvert} \cdot \frac{\left\lvert{\rm Cyc}_{q}(mqr)\right\rvert}{\left\lvert{\rm Cyc}_{qr}(mqr)\right\rvert} \gt 1.
\end{equation}Comparing with (4.3) shows that
\begin{align*}
\frac{\left\lvert{\rm Reg}_{q}(mqr)\right\rvert}{\left\lvert{\rm Cyc}_{q,\,r}(mqr)\right\rvert} =\frac{\left\lvert {\rm Cyc}_{qr}(mqr)\right\rvert}{\left\lvert {\rm Cyc}_{q,\,r}(mqr)\right\rvert } \cdot\frac{\left\lvert{\rm Reg}_{q}(mqr)\right\rvert}{\left\lvert{\rm Cyc}_{qr}(mqr)\right\rvert} \gt (mq)^{r-1},
\end{align*}as required.
The following lower bound of 
$\left\lvert S_{mqr}^r \right\rvert$ will also be needed in the proof of Theorem 4.3.
Lemma 4.7. Let 
$r=q^l$ be a prime power greater than 
$2$. For any 
$m \ge 1$, we have
\begin{equation}
\left\lvert S_{mqr}^r \right\rvert \gt mqr \left\lvert{\rm Cyc}_{q,\,r}(mqr)\right\rvert .
\end{equation}Proof. For the conditions stated in the lemma, we obtain
\begin{equation*}r-1=q^{l}-1 \ge l+1,\end{equation*} thus, 
$(mq)^{r-1} \ge mq^{l+1}$. Thanks to (4.4), we find that
\begin{align*}
\frac{\left\lvert{\rm Reg}_{q}(mqr)\right\rvert}{\left\lvert{\rm Cyc}_{q,\,r}(mqr)\right\rvert} \gt (mq)^{r-1} \ge mq^{l+1}=mqr.
\end{align*}Recalling (4.2), we get
\begin{align*}
\left\lvert S_{mqr}^r \right\rvert \ge \left\lvert {\rm Reg}_{q} (mqr)\right\rvert \gt mqr \left\lvert{\rm Cyc}_{q,\,r}(mqr)\right\rvert,
\end{align*}as claimed.
For now, we still need one more inequality, that is, Corollary 2.16 in [Reference Bóna, McLennan and White8]. Given a permutation 
$\sigma$, we may partition its set of cycles into two classes. Let 
$R_q(\sigma)$ and 
$S_{q}(\sigma)$ denote the permutation consisting of the 
$q$-regular cycles and the permutation consisting of the 
$q$-singular cycles of 
$\sigma$, respectively, in lieu of 
$\sigma_{(\sim q)}$ and 
$\sigma_{(q)}$ as used in [Reference Bóna, McLennan and White8]. We call 
$R_q(\sigma)$ and 
$S_{q}(\sigma)$ the 
$q$-regular part and 
$q$-singular part of 
$\sigma$, respectively.
The cycle type 
$\rho$ of a permutation is defined to be the multiset of its cycle lengths, often denoted by 
$1^{k_1} 2^{k_2} \cdots n^{k_n}$, meaning that there are 
$k_i$ cycles of length 
$i$ for 
$1\leq i \leq n$. We write 
$\lvert \rho \rvert$ for the sum of the cycle lengths in 
$\rho$.
Let 
$S_{\rho, \, q}(n)$, in place of 
${\rm DIV}_{\rho,\,q}(n)$ as used in [Reference Bóna, McLennan and White8], denote the set of permutations of 
$[n]$ whose 
$q$-singular part has cycle type 
$\rho$. In particular, 
$S_{\emptyset, \, q}(n)$ is the set of 
$q$-regular permutations, i.e., 
${\rm Reg}_q(n)$. For instance, the permutation 
$\sigma=(1\ 2)\,(3\ 4)\,(5\ 9\ 7\ 8)\,(6\ 10\ 11\ 13)\,(12)$ belongs to 
$S_{2^2 4^2,\,2}(13)$.
The inequality in [Reference Bóna, McLennan and White8] can be restated as follows.
Proposition 4.8. Let 
$n \geq 1$, 
$q\geq 2$ (not necessarily a prime), and let 
$\rho$ be a cycle type with 
$\lvert \rho \rvert \leq n$. If 
$n+1$ is a multiple of 
$q$, then
\begin{align*}
\left\lvert S_{\rho, \, q}(n)\right\rvert \geq \frac{1}{n} \left\lvert S_{\rho, \, q}(n+1)\right\rvert,
\end{align*} where equality is attained if and only if 
$\rho=\emptyset$.
In the event that 
$\rho=\emptyset$, the equality states that if 
$n+1$ is a multiple of 
$q$, then
\begin{equation*} n\left\lvert{\rm Reg}_q(n)\right\rvert=\left\lvert{\rm Reg}_q(n+1)\right\rvert, \end{equation*} which follows from the bijection between 
${\rm Reg}_q(n) \times [n]$ and 
${\rm Reg}_q(n+1)$ constructed by Bóna, McLennan and White, see Lemma 2.6 in [Reference Bóna, McLennan and White8].
We are now ready to prove Theorem 4.3.
Proof of Theorem 4.3
Given positive integers 
$q,r$, we say that a cycle type 
$\rho$ is 
$(q,r)$-divisible, denoted by 
$(q,r) \mid \rho$, if every cycle length in 
$\rho$ is divisible by 
$q$, and for any integer 
$i$, the number of cycles of length 
$iq$ is a multiple of 
$r$. We also set 
$(q,r) \mid \emptyset$ by convention.
Since 
$r$ is a prime power 
$q^l$, Proposition 4.4 implies that a permutation of 
$[n]$ belongs to 
$S_{n}^r$ if and only if the cycle type of its 
$q$-singular part is 
$(q,r)$-divisible. So we have
\begin{align*}
S_{n}^r=\bigcup_{\substack{\lvert\rho\rvert \le n
\\[2pt] (q,\,r)\,\mid\,\rho}} S_{\rho, \,q}(n) .
\end{align*}Hence
\begin{equation}
\left\lvert S_{n}^r \right\rvert=\sum_{\substack{\lvert\rho\rvert \le n
\\ (q,\,r)\,\mid\,\rho}} \left\lvert S_{\rho, \,q}(n)\right\rvert .
\end{equation} Again, by Proposition 4.4, a permutation of 
$[n+1]$ is in 
$S_{n+1}^r$ if and only if its 
$q$-singular cycle type is 
$(q,r)$-divisible, namely,
\begin{align*}
S_{n+1}^r = \bigcup_{\substack{\lvert\rho\rvert
\le n+1 \\[2pt] (q,\,r)\,\mid\,\rho }} S_{\rho, \,q}(n+1) .
\end{align*} Considering the range of 
$\rho$, we get
\begin{equation}
\left\lvert S_{n+1}^r\right\rvert =
\sum_{\substack{\lvert\rho\rvert \le n
\\ (q,\,r)\,\mid\,\rho}} \left \lvert S_{\rho, \,q} (n+1) \right\rvert
+ \sum_{\substack{\lvert\rho\rvert = n+1 \\ (q,\,r)\,\mid\,\rho}}
\left\lvert S_{\rho, \,q}(n+1) \right\rvert.
\end{equation} Concerning the terms in (4.7) and in the first sum in (4.8), given any cycle type 
$\rho$ with 
$\lvert \rho\rvert \le n$ and 
$(q,r) \mid \rho$, Proposition 4.8 asserts that if 
$n+1$ is a multiple of 
$q$, then
\begin{equation}
\left\lvert S_{\rho, \, q}(n)\right\rvert \geq \frac{1}{n} \left\lvert S_{\rho, \, q}(n+1)\right\rvert,
\end{equation} where equality is attained if and only if 
$\rho=\emptyset$. Therefore,
\begin{align*}
\lvert S_{n}^r \rvert
&=\sum_{\substack{\left\lvert \rho \right\rvert \le n \\[2pt] (q,\,r)\,\mid\,\rho}} \left\lvert
S_{\rho, \,q}(n) \right\rvert
\\[6pt]
&\ge \frac{1}{n} \sum_{\substack{\lvert\rho\rvert \le n \\[2pt] (q,\,r)\,\mid\,\rho}}
\left\lvert S_{\rho, \, q}(n+1)\right\rvert
\\[6pt]
&=\frac{1}{n} \, \Bigg(\left\lvert S_{n+1}^r \right\rvert
- \sum_{\substack{\left\lvert \rho \right\rvert = n+1 \\[2pt] (q,\,r)\,\mid\,\rho}} \left\lvert S_{\rho, \,q} (n+1) \right\rvert \Bigg).
\end{align*}Consequently,
\begin{equation}
n\left\lvert S_{n}^r \right\rvert \ge \left\lvert S_{n+1}^r \right\rvert - \sum_{\substack{\lvert\rho\rvert = n+1 \\ (q,\,r)\,\mid\,\rho}} \left\lvert S_{\rho, \,q} (n+1) \right\rvert.
\end{equation} We now proceed to prove (i). Assume that 
$n+1$ is a multiple of 
$q$ but not a multiple of 
$qr$. We claim that for a cycle type 
$\rho$ with 
$\left\lvert \rho \right\rvert = n+1$ and 
$(q,r)\mid\rho$,
\begin{equation}
S_{\rho, \,q} (n+1) =\emptyset.
\end{equation} Suppose to the contrary that there exists a permutation in 
$S_{\rho, \,q} (n+1)$. Under the condition that 
$\rho$ is 
$(q,r)$-divisible, we have 
$\left\lvert\rho \right\rvert$ is a multiple of 
$qr$, but we also have 
$\left\lvert\rho \right\rvert = n+1$, which contradicts the condition that 
$n+1$ is not a multiple of 
$qr$. Utilizing the property (4.11) and the relation (4.10), we get
\begin{align*}
n\left\lvert S_{n}^r \right\rvert \ge \left\lvert S_{n+1}^r \right\rvert,
\end{align*}which is equivalent to (4.1). This proves (i).
To prove (ii), assume that 
$n+1=mqr$. We shall proceed in the same fashion as the argument given in [Reference Bóna, McLennan and White8] when 
$r$ is a prime. The case 
$r=2$ has been taken care of in the preceding section. So we may set our mind on the case when 
$r$ is a prime power greater than 
$2$.
In the notation 
$(q,r)\mid\rho$, we can write
\begin{equation}
{\rm Cyc}_{q,\,r}(mqr) =\bigcup_{\substack{\lvert\rho\rvert = mqr \\
(q,\, r)\,\mid\,\rho}} S_{\rho, \,q} (mqr).
\end{equation}Inserting (4.12) into (4.10), we find that
\begin{equation}
(mqr-1)\left\lvert S_{mqr-1}^r \right\rvert \ge \left\lvert S_{mqr}^r \right\rvert - \left\lvert{\rm Cyc}_{q,\,r}(mqr)\right\rvert.
\end{equation}Putting (4.6) into (4.13) yields
\begin{align*}
(mqr-1)\left\lvert S^r_{mqr-1} \right\rvert \gt \left(1-\frac{1}{mqr}\right)\left\lvert S^r_{mqr} \right\rvert.
\end{align*}It follows that
\begin{align*}
mqr\left\lvert S^r_{mqr-1} \right\rvert \gt \left\lvert S^r_{mqr} \right\rvert.
\end{align*} Thus we conclude that 
$p_r(n) \gt p_r(n+1)$ when 
$n+1 \equiv 0 \pmod {qr}$. This proves (ii).
The conditions under which equality holds in (i) and (ii) are readily discerned, and so the theorem is proved.
To conclude, we note that the monotonicity of 
$p_r(n)$ for prime powers 
$r$, as stated in Theorem 4.1, is immediate from Theorems 4.2 and 4.3.
Acknowledgements
We are deeply indebted to the referees for their close scrutiny of the manuscript and for their constructive suggestions.
