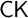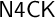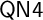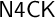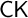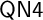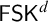1 Introduction
The present article is a study of the relation between the relatively new system of conditional logic
![]() $\mathsf {N4CK}$
, introduced recently in [Reference Olkhovikov11] by the author and the paraconsistent version
$\mathsf {N4CK}$
, introduced recently in [Reference Olkhovikov11] by the author and the paraconsistent version
![]() $\mathsf {QN4}$
of Nelson’s logic of strong negation.Footnote
1
The main result of the article says that a natural notion of the standard first-order translation of conditional formulas provides a faithful embedding of
$\mathsf {QN4}$
of Nelson’s logic of strong negation.Footnote
1
The main result of the article says that a natural notion of the standard first-order translation of conditional formulas provides a faithful embedding of
![]() $\mathsf {N4CK}$
into
$\mathsf {N4CK}$
into
![]() $\mathsf {QN4}$
modulo the assumption of a certain first-order theory encoding the notion of a conditional model.
$\mathsf {QN4}$
modulo the assumption of a certain first-order theory encoding the notion of a conditional model.
Since this embedding is, in a sense, the same embedding that obtains in the case of
![]() $\mathsf {CK}$
, the minimal classical conditional logic, relative to the classical first-order logic
$\mathsf {CK}$
, the minimal classical conditional logic, relative to the classical first-order logic
![]() $\mathsf {QCL}$
, one can view this result as showing that
$\mathsf {QCL}$
, one can view this result as showing that
![]() $\mathsf {N4CK}$
as conditional logic is the same logic as
$\mathsf {N4CK}$
as conditional logic is the same logic as
![]() $\mathsf {CK}$
, only read non-classically, that is to say, read in terms of Nelson’s logic of strong negation rather than classical logic. In this capacity,
$\mathsf {CK}$
, only read non-classically, that is to say, read in terms of Nelson’s logic of strong negation rather than classical logic. In this capacity,
![]() $\mathsf {N4CK}$
can be viewed as a natural candidate for the role of the minimal normal conditional logic extending
$\mathsf {N4CK}$
can be viewed as a natural candidate for the role of the minimal normal conditional logic extending
![]() $\mathsf {N4}$
, the propositional fragment of
$\mathsf {N4}$
, the propositional fragment of
![]() $\mathsf {QN4}$
.
$\mathsf {QN4}$
.
One can better appreciate the true meaning of this result if one views it as the final piece in the mosaic of results relating the classical, the intuitionistic, and the Nelsonian modal and conditional logics to their corresponding fragments of first-order reasoning by way of standard translation embeddings—but also to one another. In order to supply this richer context, we have to do quite a bit of preliminary work before we get to the main proof, if this article is to be reasonably self-contained. Our strife towards this goal explains most of our choices related both to the structure of the article and to its length. We did our best to compensate for the latter shortcoming by making our explanations as lucid and easy to follow as possible. The more technical and tedious parts of our reasoning are systematically shifted to numerous appendices to be found at the end of the article.
The rest of the article is organized as follows. Section 2 introduces the notational preliminaries, after which Section 3 defines a notion of logic which is wide enough to cover every system to be mentioned below. We then proceed to introduce three first-order logics in Section 4, namely,
![]() $\mathsf {QCL}$
,
$\mathsf {QCL}$
,
![]() $\mathsf {QN4}$
, and
$\mathsf {QN4}$
, and
![]() $\mathsf {QIL}^+$
, the positive fragment of the first-order intuitionistic logic
$\mathsf {QIL}^+$
, the positive fragment of the first-order intuitionistic logic
![]() $\mathsf {QIL}$
. The main work in this section is directed towards familiarizing the reader with some elementary results about
$\mathsf {QIL}$
. The main work in this section is directed towards familiarizing the reader with some elementary results about
![]() $\mathsf {QN4}$
, which is the least known of the three logics. To facilitate our main proof, we also need to define a novel sheaf semantics for
$\mathsf {QN4}$
, which is the least known of the three logics. To facilitate our main proof, we also need to define a novel sheaf semantics for
![]() $\mathsf {QN4}$
, and we show its adequacy for the logic.
$\mathsf {QN4}$
, and we show its adequacy for the logic.
The propositional fragments of the logics dealt with in Section 4 will not be introduced separately but will in each case be referred to by omitting the initial
![]() $\mathsf {Q}$
in the name of the corresponding logic, so that we will be mentioning
$\mathsf {Q}$
in the name of the corresponding logic, so that we will be mentioning
![]() $\mathsf {CL}$
,
$\mathsf {CL}$
,
![]() $\mathsf {N4}$
,
$\mathsf {N4}$
,
![]() $\mathsf {IL}^+$
, and
$\mathsf {IL}^+$
, and
![]() $\mathsf {IL}$
below without further explanation. All of the propositional fragments of the first-order logics are assumed to be given over the set
$\mathsf {IL}$
below without further explanation. All of the propositional fragments of the first-order logics are assumed to be given over the set
![]() $Prop$
to be introduced in Section 5.
$Prop$
to be introduced in Section 5.
The main task of the latter section, however, is to provide the context for the main result of the article by recalling several classical definitions and results about the standard translation of modal logics into first-order logics. This is followed by Section 6, where we introduce the classical conditional logic
![]() $\mathsf {CK}$
and show how its properties can be viewed as a natural continuation of the properties of the modal logics laid out in the previous section. After that, Section 7 introduces the main system of the article,
$\mathsf {CK}$
and show how its properties can be viewed as a natural continuation of the properties of the modal logics laid out in the previous section. After that, Section 7 introduces the main system of the article,
![]() $\mathsf {N4CK}$
, and proves our main result. The proof procedure explained in Section 7 has the additional merit in that it allows to improve on some known results about the standard translation embeddings of
$\mathsf {N4CK}$
, and proves our main result. The proof procedure explained in Section 7 has the additional merit in that it allows to improve on some known results about the standard translation embeddings of
![]() $\mathsf {N4}$
-based modal logics. Finally, Section 8 sums up the broader meaning of the results obtained, as well as offers concluding remarks; we also chart several avenues for further research.
$\mathsf {N4}$
-based modal logics. Finally, Section 8 sums up the broader meaning of the results obtained, as well as offers concluding remarks; we also chart several avenues for further research.
2 Preliminaries
We use this section to fix some notations to be used throughout the article.
We will use IH as the abbreviation for Induction Hypothesis in the inductive proofs, and we will write
![]() $\alpha :=\beta $
to mean that we define
$\alpha :=\beta $
to mean that we define
![]() $\alpha $
as
$\alpha $
as
![]() $\beta $
. We will use the usual notations for sets and functions. The set of all subsets of X will be denoted by
$\beta $
. We will use the usual notations for sets and functions. The set of all subsets of X will be denoted by
![]() $\mathcal {P}(X)$
. The natural numbers are understood as the finite von Neumann ordinals, and
$\mathcal {P}(X)$
. The natural numbers are understood as the finite von Neumann ordinals, and
![]() $\omega $
as the smallest infinite ordinal. Given an
$\omega $
as the smallest infinite ordinal. Given an
![]() $n \in \omega $
and a tuple
$n \in \omega $
and a tuple
![]() $\alpha = (x_1,\ldots ,x_n)$
of any sort of objects, we will refer to
$\alpha = (x_1,\ldots ,x_n)$
of any sort of objects, we will refer to
![]() $\alpha $
by
$\alpha $
by
![]() $\bar {x}_n$
and will denote by
$\bar {x}_n$
and will denote by
![]() $init(\alpha )$
and
$init(\alpha )$
and
![]() $end(\alpha )$
the initial and final elements of
$end(\alpha )$
the initial and final elements of
![]() $\alpha $
, that is to say,
$\alpha $
, that is to say,
![]() $x_1$
and
$x_1$
and
![]() $x_n$
, respectively. More generally, given any
$x_n$
, respectively. More generally, given any
![]() $i < \omega $
such that
$i < \omega $
such that
![]() $1 \leq i \leq n$
, we set that
$1 \leq i \leq n$
, we set that
![]() $\pi ^i(\alpha ):= x_i$
, i.e., that
$\pi ^i(\alpha ):= x_i$
, i.e., that
![]() $\pi ^i(\alpha )$
denotes the i-th projection of
$\pi ^i(\alpha )$
denotes the i-th projection of
![]() $\alpha $
. Given another tuple
$\alpha $
. Given another tuple
![]() $\beta = \bar {y}_m$
, we will denote by
$\beta = \bar {y}_m$
, we will denote by
![]() $(\alpha )^\frown (\beta )$
the concatenation of the two tuples, i.e., the tuple
$(\alpha )^\frown (\beta )$
the concatenation of the two tuples, i.e., the tuple
![]() $(x_1,\ldots ,x_n,y_1,\ldots ,y_m)$
. The empty tuple will be denoted by
$(x_1,\ldots ,x_n,y_1,\ldots ,y_m)$
. The empty tuple will be denoted by
![]() $\Lambda $
.
$\Lambda $
.
We will extensively use ordered couples of sets, which we will call bi-sets. Relations are understood as sets of ordered tuples. Given binary relations
![]() $R \subseteq X \times Y$
and
$R \subseteq X \times Y$
and
![]() $S\subseteq Y\times Z$
, we denote their composition by
$S\subseteq Y\times Z$
, we denote their composition by
![]() $R\circ S:= \{(a,c)\mid \text { for some }b \in Y,\,(a, b)\in R,\,(b,c)\in S\}$
.
$R\circ S:= \{(a,c)\mid \text { for some }b \in Y,\,(a, b)\in R,\,(b,c)\in S\}$
.
We view functions as relations with special properties; we write
![]() $f:X \to Y$
to denote a function
$f:X \to Y$
to denote a function
![]() $f \subseteq X\times Y$
such that its left projection is all of X. If
$f \subseteq X\times Y$
such that its left projection is all of X. If
![]() $f: X \to Y$
and
$f: X \to Y$
and
![]() $Z\subseteq X,$
then we will denote the image of Z under f by
$Z\subseteq X,$
then we will denote the image of Z under f by
![]() $f(Z)$
. In view of our previous convention for relations, for any given two functions
$f(Z)$
. In view of our previous convention for relations, for any given two functions
![]() $f:X\to Y$
and
$f:X\to Y$
and
![]() $g:Y\to Z$
, we will denote the function
$g:Y\to Z$
, we will denote the function
![]() ${x\mapsto g(f(x))}$
by
${x\mapsto g(f(x))}$
by
![]() $f\circ g$
, even though, in the existing literature, this function is often denoted by
$f\circ g$
, even though, in the existing literature, this function is often denoted by
![]() $g\circ f$
instead.
$g\circ f$
instead.
Given a set X, we will denote by
![]() $id[X]$
the identity function on X, i.e., the function
$id[X]$
the identity function on X, i.e., the function
![]() $f:X\to X$
such that
$f:X\to X$
such that
![]() $f(x) = x$
for every
$f(x) = x$
for every
![]() $x \in X$
. In relation to compositions, functions of the form
$x \in X$
. In relation to compositions, functions of the form
![]() $id[X]$
have a special importance as a limiting case. More precisely, given a set X and a family F of functions from X to X, we will assume that the composition of the empty tuple of functions from F is just
$id[X]$
have a special importance as a limiting case. More precisely, given a set X and a family F of functions from X to X, we will assume that the composition of the empty tuple of functions from F is just
![]() $id[X]$
.
$id[X]$
.
Furthermore, if
![]() $f:X\to Y$
is any function,
$f:X\to Y$
is any function,
![]() $x \in X$
and
$x \in X$
and
![]() $y \in Y$
, we will denote by
$y \in Y$
, we will denote by
![]() $f[x/y]$
the unique function
$f[x/y]$
the unique function
![]() $g:X\to Y$
such that, for a given
$g:X\to Y$
such that, for a given
![]() $z \in X$
we have
$z \in X$
we have
 $$ \begin{align*}g(z):=\begin{cases} y,\text{ if }z = x;\\ f(z),\text{ otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*}g(z):=\begin{cases} y,\text{ if }z = x;\\ f(z),\text{ otherwise. } \end{cases} \end{align*} $$
3 Logics
We are going to give a notion of logic that is wide enough to cover every formal system to be considered below, without aspiring to give any sort of ultimate generalization of this notion.
Logics are based on languages, and in this article we confine ourselves to considering languages of two types: the propositional language with an added conditional or modal operator(s) and the first-order relational languages with equality. Speaking generally, a language
![]() $\mathcal {L}$
is simply a certain set. The elements of languages are called their formulas. The languages are often generated from certain sets of atoms by repeated application of connectives and quantifiers. Every language considered in this article will include at least the binary connectives
$\mathcal {L}$
is simply a certain set. The elements of languages are called their formulas. The languages are often generated from certain sets of atoms by repeated application of connectives and quantifiers. Every language considered in this article will include at least the binary connectives
![]() $\to $
,
$\to $
,
![]() $\wedge $
, and
$\wedge $
, and
![]() $\vee $
. One consequence of this is that we can assume the standard reading of equivalence
$\vee $
. One consequence of this is that we can assume the standard reading of equivalence
![]() $\phi \leftrightarrow \psi $
as the abbreviation for
$\phi \leftrightarrow \psi $
as the abbreviation for
![]() $(\phi \to \psi )\wedge (\psi \to \phi )$
for every language considered below.
$(\phi \to \psi )\wedge (\psi \to \phi )$
for every language considered below.
In this article, we will treat the sets of formulas generated by different sets of atoms over the same set of logical symbols as different languages rather than different versions of the same language.
Although one and the same logic can be formulated over different versions of the same language (or, in our terminology, over different languages), in this article we will abstract away from such subtleties, and will simply treat a logic as a consequence relation, or, in other words, as a set of consecutions over a particular language
![]() $\mathcal {L}$
. More precisely, a logic is a set
$\mathcal {L}$
. More precisely, a logic is a set
![]() $\mathsf {L} \subseteq \mathcal {P}(\mathcal {L})\times \mathcal {P}(\mathcal {L})$
, for some language
$\mathsf {L} \subseteq \mathcal {P}(\mathcal {L})\times \mathcal {P}(\mathcal {L})$
, for some language
![]() $\mathcal {L}$
, where
$\mathcal {L}$
, where
![]() $(\Gamma , \Delta )\in \mathsf {L}$
iff
$(\Gamma , \Delta )\in \mathsf {L}$
iff
![]() $\Delta\ \mathsf {L}$
-follows from
$\Delta\ \mathsf {L}$
-follows from
![]() $\Gamma $
(we will also denote this by
$\Gamma $
(we will also denote this by
![]() $\Gamma \models _{\mathsf {L}}\Delta $
). We will say that
$\Gamma \models _{\mathsf {L}}\Delta $
). We will say that
![]() $(\Gamma , \Delta )$
is
$(\Gamma , \Delta )$
is
![]() $\mathsf {L}$
-satisfiable iff
$\mathsf {L}$
-satisfiable iff
![]() ${(\Gamma , \Delta )\notin \mathsf {L}}$
. Given a
${(\Gamma , \Delta )\notin \mathsf {L}}$
. Given a
![]() $\phi \in \mathcal {L}$
,
$\phi \in \mathcal {L}$
,
![]() $\phi $
is
$\phi $
is
![]() $\mathsf {L}$
-valid or a theorem of
$\mathsf {L}$
-valid or a theorem of
![]() $\mathsf {L}$
(we will also write
$\mathsf {L}$
(we will also write
![]() $\phi \in \mathsf {L}$
) iff
$\phi \in \mathsf {L}$
) iff
![]() $(\emptyset , \{\phi \}) \in \mathsf {L}$
.
$(\emptyset , \{\phi \}) \in \mathsf {L}$
.
Every logic considered in this article will be introduced either by its intended semantics, or by a complete Hilbert-style axiomatization; for most logics in this article, we will mention both.
The semantics of various logics considered in this article is going to be laid out according to the following general scheme. Recall that, given a classically flavored logic
![]() $\mathsf {L}$
, we typically define
$\mathsf {L}$
, we typically define
![]() $\mathsf {L}$
by setting that
$\mathsf {L}$
by setting that
![]() $(\Gamma , \Delta )\in \mathsf {L}$
iff the truth of every
$(\Gamma , \Delta )\in \mathsf {L}$
iff the truth of every
![]() $\phi \in \Gamma $
implies the truth of some
$\phi \in \Gamma $
implies the truth of some
![]() $\psi \in \Delta $
. In the more general setting of our article, if
$\psi \in \Delta $
. In the more general setting of our article, if
![]() $\mathcal {L}$
is a language, then a semantics for
$\mathcal {L}$
is a language, then a semantics for
![]() $\mathcal {L}$
is a pair
$\mathcal {L}$
is a pair
![]() $\sigma = (EP_\sigma , \models _\sigma )$
, where
$\sigma = (EP_\sigma , \models _\sigma )$
, where
![]() $EP_\sigma $
is a (definable) class called the class of
$EP_\sigma $
is a (definable) class called the class of
![]() $\sigma $
-evaluation points. The other element of the semantics is a (class-)relation
$\sigma $
-evaluation points. The other element of the semantics is a (class-)relation
![]() $\models _\sigma \subseteq EP_\sigma \times \mathcal {L}$
called the (
$\models _\sigma \subseteq EP_\sigma \times \mathcal {L}$
called the (
![]() $\sigma $
-)satisfaction relation.
$\sigma $
-)satisfaction relation.
In case
![]() $(pt, \phi ) \in \models _\sigma $
, we write
$(pt, \phi ) \in \models _\sigma $
, we write
![]() $pt\models _\sigma \phi $
, and say that
$pt\models _\sigma \phi $
, and say that
![]() $pt\ \sigma $
-satisfies
$pt\ \sigma $
-satisfies
![]() $\phi $
. More generally, given any
$\phi $
. More generally, given any
![]() $\Gamma , \Delta \subseteq \mathcal {L}$
, and a
$\Gamma , \Delta \subseteq \mathcal {L}$
, and a
![]() $pt \in EP_\sigma $
, we say that
$pt \in EP_\sigma $
, we say that
![]() $pt \sigma $
-satisfies
$pt \sigma $
-satisfies
![]() $(\Gamma , \Delta )$
and write
$(\Gamma , \Delta )$
and write
![]() $pt\models _\sigma (\Gamma , \Delta )$
iff:
$pt\models _\sigma (\Gamma , \Delta )$
iff:
More conventionally, we say that
![]() $pt$
satisfies
$pt$
satisfies
![]() $\Gamma $
, and write
$\Gamma $
, and write
![]() $pt\models _\sigma \Gamma $
, iff
$pt\models _\sigma \Gamma $
, iff
![]() $pt\models _\sigma (\Gamma , \emptyset )$
. This latter format is in fact sufficient to set up a semantics as long as our logics can express Boolean negation. However, this is not the case for many logics to be considered in this article. For such logics the “double-entry” format for satisfaction relation proves to be more convenient and flexible.
$pt\models _\sigma (\Gamma , \emptyset )$
. This latter format is in fact sufficient to set up a semantics as long as our logics can express Boolean negation. However, this is not the case for many logics to be considered in this article. For such logics the “double-entry” format for satisfaction relation proves to be more convenient and flexible.
Next, given any
![]() $\Gamma , \Delta \cup \{\phi \} \subseteq \mathcal {L}$
, we say that
$\Gamma , \Delta \cup \{\phi \} \subseteq \mathcal {L}$
, we say that
![]() $(\Gamma , \Delta )$
(resp.,
$(\Gamma , \Delta )$
(resp.,
![]() $\Gamma $
,
$\Gamma $
,
![]() $\phi $
) is
$\phi $
) is
![]() $\sigma $
-satisfiable iff, for some
$\sigma $
-satisfiable iff, for some
![]() $pt \in EP_\sigma $
,
$pt \in EP_\sigma $
,
![]() $pt$
satisfies
$pt$
satisfies
![]() $(\Gamma , \Delta )$
(resp.,
$(\Gamma , \Delta )$
(resp.,
![]() $\Gamma $
,
$\Gamma $
,
![]() $\phi $
). Finally,
$\phi $
). Finally,
![]() $\Delta \sigma $
-follows from
$\Delta \sigma $
-follows from
![]() $\Gamma $
(written
$\Gamma $
(written
![]() $\Gamma \models _\sigma \Delta $
) iff
$\Gamma \models _\sigma \Delta $
) iff
![]() $(\Gamma , \Delta )$
is
$(\Gamma , \Delta )$
is
![]() $\sigma $
-unsatisfiable, in other words, if every
$\sigma $
-unsatisfiable, in other words, if every
![]() $\sigma $
-evaluation point satisfying every formula from
$\sigma $
-evaluation point satisfying every formula from
![]() $\Gamma $
, also satisfies at least one formula from
$\Gamma $
, also satisfies at least one formula from
![]() $\Delta $
.
$\Delta $
.
We now say that, for a given language
![]() $\mathcal {L}$
, a semantics
$\mathcal {L}$
, a semantics
![]() $\sigma $
over
$\sigma $
over
![]() $\mathcal {L}$
induces the logic
$\mathcal {L}$
induces the logic
![]() $\mathsf {L}$
over
$\mathsf {L}$
over
![]() $\mathcal {L}$
and write
$\mathcal {L}$
and write
![]() $\mathsf {L} = \mathbb {L}(\sigma )$
iff for all
$\mathsf {L} = \mathbb {L}(\sigma )$
iff for all
![]() $\Gamma , \Delta \subseteq \mathcal {L}$
, we have
$\Gamma , \Delta \subseteq \mathcal {L}$
, we have
![]() $(\Gamma , \Delta ) \in \mathsf {L}$
iff
$(\Gamma , \Delta ) \in \mathsf {L}$
iff
![]() $(\Gamma , \Delta )$
is
$(\Gamma , \Delta )$
is
![]() $\sigma $
-unsatisfiable; in other words,
$\sigma $
-unsatisfiable; in other words,
![]() $\mathsf {L} = \mathbb {L}(\sigma )$
means that, for all
$\mathsf {L} = \mathbb {L}(\sigma )$
means that, for all
![]() $\Gamma , \Delta \subseteq \mathcal {L}$
,
$\Gamma , \Delta \subseteq \mathcal {L}$
,
![]() $\Delta\ \mathsf {L}$
-follows from
$\Delta\ \mathsf {L}$
-follows from
![]() $\Gamma $
iff
$\Gamma $
iff
![]() $\Delta\ \sigma $
-follows from
$\Delta\ \sigma $
-follows from
![]() $\Gamma $
. In case
$\Gamma $
. In case
![]() $\sigma $
is also used to introduce
$\sigma $
is also used to introduce
![]() $\mathsf {L}$
by definition, we write
$\mathsf {L}$
by definition, we write
![]() $\mathsf {L} := \mathbb {L}(\sigma )$
.
$\mathsf {L} := \mathbb {L}(\sigma )$
.
As for the Hilbert-style systems, all of them will be given by a finite number of axiomatic schemas
![]() $\alpha _1,\ldots ,\alpha _n$
augmented with a finite number of inference rules
$\alpha _1,\ldots ,\alpha _n$
augmented with a finite number of inference rules
![]() $\rho _1,\ldots ,\rho _m$
, such a system will be denoted by
$\rho _1,\ldots ,\rho _m$
, such a system will be denoted by
![]() $\Sigma (\bar {\alpha }_n; \bar {\rho }_m)$
. Every Hilbert-style system considered below happens to extend a certain minimal system which we will denote by
$\Sigma (\bar {\alpha }_n; \bar {\rho }_m)$
. Every Hilbert-style system considered below happens to extend a certain minimal system which we will denote by
![]() $\mathfrak {IL}^+$
.Footnote
2
We have
$\mathfrak {IL}^+$
.Footnote
2
We have
![]() $\mathfrak {IL}^+:= \Sigma (\alpha _1-\alpha _8;\text{(MP)})$
, where
$\mathfrak {IL}^+:= \Sigma (\alpha _1-\alpha _8;\text{(MP)})$
, where
 $$ \begin{align*} &\phi \to(\psi\to\phi)\,(\alpha_1),\quad(\phi\to(\psi\to\chi))\to((\phi\to\psi)\to(\phi\to\chi))\,(\alpha_2),\\&\quad(\phi\wedge\psi)\to\phi\,(\alpha_3),\quad(\phi\wedge\psi)\to\psi\,(\alpha_4),\quad \phi\to(\psi\to (\phi\wedge\psi))\,(\alpha_5),\\&\quad\phi\to(\phi\vee \psi)\,(\alpha_6),\quad\psi\to(\phi\vee \psi)\,(\alpha_7),\\ &\quad (\phi\to\chi)\to((\psi \to \chi) \to ((\phi\vee\psi)\to \chi))\,(\alpha_8) \end{align*} $$
$$ \begin{align*} &\phi \to(\psi\to\phi)\,(\alpha_1),\quad(\phi\to(\psi\to\chi))\to((\phi\to\psi)\to(\phi\to\chi))\,(\alpha_2),\\&\quad(\phi\wedge\psi)\to\phi\,(\alpha_3),\quad(\phi\wedge\psi)\to\psi\,(\alpha_4),\quad \phi\to(\psi\to (\phi\wedge\psi))\,(\alpha_5),\\&\quad\phi\to(\phi\vee \psi)\,(\alpha_6),\quad\psi\to(\phi\vee \psi)\,(\alpha_7),\\ &\quad (\phi\to\chi)\to((\psi \to \chi) \to ((\phi\vee\psi)\to \chi))\,(\alpha_8) \end{align*} $$
and
It is therefore important for our purposes to be able to refer to Hilbert-style systems as extensions of other systems. If
![]() $\mathfrak {Ax} = \Sigma (\bar {\alpha }_n; \bar {\rho }_m)$
, and
$\mathfrak {Ax} = \Sigma (\bar {\alpha }_n; \bar {\rho }_m)$
, and
![]() $\beta _1,\ldots ,\beta _k$
are some new axiomatic schemes and
$\beta _1,\ldots ,\beta _k$
are some new axiomatic schemes and
![]() $\sigma _1,\ldots ,\sigma _r$
are some new rules, then we will write
$\sigma _1,\ldots ,\sigma _r$
are some new rules, then we will write
![]() $\mathfrak {Ax}+(\bar {\beta }_k;\bar {\sigma }_r)$
to denote the system
$\mathfrak {Ax}+(\bar {\beta }_k;\bar {\sigma }_r)$
to denote the system
![]() $\Sigma ((\bar {\alpha }_n)^\frown (\bar {\beta }_k);(\bar {\rho }_m)^\frown (\bar {\sigma }_r))$
.
$\Sigma ((\bar {\alpha }_n)^\frown (\bar {\beta }_k);(\bar {\rho }_m)^\frown (\bar {\sigma }_r))$
.
Axiomatic systems can be viewed as operators generating logics when applied to languages. More precisely, if
![]() $\mathfrak {Ax} = \Sigma (\bar {\alpha }_n; \bar {\rho }_m)$
and
$\mathfrak {Ax} = \Sigma (\bar {\alpha }_n; \bar {\rho }_m)$
and
![]() $\mathcal {L}$
is a language, then
$\mathcal {L}$
is a language, then
![]() $\mathsf {L} = \mathfrak {Ax}(\mathcal {L})$
can be described as follows. We say that a
$\mathsf {L} = \mathfrak {Ax}(\mathcal {L})$
can be described as follows. We say that a
![]() $\phi \in \mathcal {L}$
is provable in
$\phi \in \mathcal {L}$
is provable in
![]() $\mathfrak {Ax}(\mathcal {L})$
iff there exists a finite sequence
$\mathfrak {Ax}(\mathcal {L})$
iff there exists a finite sequence
![]() $\bar {\psi }_k\in \mathcal {L}^k$
such that every formula in this sequence is either a substitution instance of one of
$\bar {\psi }_k\in \mathcal {L}^k$
such that every formula in this sequence is either a substitution instance of one of
![]() $\bar {\alpha }_n$
or results from an application of one of
$\bar {\alpha }_n$
or results from an application of one of
![]() $\bar {\rho }_m$
to some earlier formulas in the sequence and
$\bar {\rho }_m$
to some earlier formulas in the sequence and
![]() $\psi _k = \phi $
; we will say that
$\psi _k = \phi $
; we will say that
![]() $(\Gamma , \Delta ) \in \mathfrak {Ax}(\mathcal {L})$
iff
$(\Gamma , \Delta ) \in \mathfrak {Ax}(\mathcal {L})$
iff
![]() $(\Gamma , \Delta ) \in \mathcal {P}(\mathcal {L})\times \mathcal {P}(\mathcal {L})$
and there exists a sequence
$(\Gamma , \Delta ) \in \mathcal {P}(\mathcal {L})\times \mathcal {P}(\mathcal {L})$
and there exists a sequence
![]() $\bar {\chi }_r\in \mathcal {L}^r$
such that every formula in it is either in
$\bar {\chi }_r\in \mathcal {L}^r$
such that every formula in it is either in
![]() $\Gamma $
, or is provable in
$\Gamma $
, or is provable in
![]() $\mathfrak {Ax}(\mathcal {L})$
or results from an application of (MP) to a pair of earlier formulas in the sequence, and, for some
$\mathfrak {Ax}(\mathcal {L})$
or results from an application of (MP) to a pair of earlier formulas in the sequence, and, for some
![]() $\theta _1,\ldots ,\theta _s\in \Delta $
we have
$\theta _1,\ldots ,\theta _s\in \Delta $
we have
![]() $\chi _r = \theta _1\vee \cdots \vee \theta _s$
. This definition makes sense in the context of our article, since every language that we are going to consider contains
$\chi _r = \theta _1\vee \cdots \vee \theta _s$
. This definition makes sense in the context of our article, since every language that we are going to consider contains
![]() $\vee $
, and every axiomatic system that we are going to consider contains (MP). We will also express the fact that
$\vee $
, and every axiomatic system that we are going to consider contains (MP). We will also express the fact that
![]() $(\Gamma , \Delta ) \in \mathfrak {Ax}(\mathcal {L})$
by writing
$(\Gamma , \Delta ) \in \mathfrak {Ax}(\mathcal {L})$
by writing
![]() $\Gamma \vdash _{\mathfrak {Ax}(\mathcal {L})}\Delta $
. If also
$\Gamma \vdash _{\mathfrak {Ax}(\mathcal {L})}\Delta $
. If also
![]() $\mathsf {L} = \mathfrak {Ax}(\mathcal {L})$
, then we can write
$\mathsf {L} = \mathfrak {Ax}(\mathcal {L})$
, then we can write
![]() $\Gamma \vdash _{\mathsf {L}}\Delta $
instead of
$\Gamma \vdash _{\mathsf {L}}\Delta $
instead of
![]() $\Gamma \vdash _{\mathfrak {Ax}(\mathcal {L})}\Delta $
. In the latter case we will also have, for every
$\Gamma \vdash _{\mathfrak {Ax}(\mathcal {L})}\Delta $
. In the latter case we will also have, for every
![]() $\phi \in \mathcal {L}$
, that
$\phi \in \mathcal {L}$
, that
![]() $\phi \in \mathsf {L}$
iff
$\phi \in \mathsf {L}$
iff
![]() $\vdash _{\mathfrak {Ax}(\mathcal {L})}\phi $
iff
$\vdash _{\mathfrak {Ax}(\mathcal {L})}\phi $
iff
![]() $\phi $
is provable in
$\phi $
is provable in
![]() $\mathfrak {Ax}(\mathcal {L})$
.
$\mathfrak {Ax}(\mathcal {L})$
.
4 The first-order languages and their logics
We start by defining a handful of first-order languages (relational with equality; the latter is denoted by
![]() $\equiv $
) according to the scheme laid out in the previous section. First, we let
$\equiv $
) according to the scheme laid out in the previous section. First, we let
![]() $\Pi $
denote the set
$\Pi $
denote the set
![]() $\{p^1_n\mid n\in \omega \}\cup \{S^1, O^1, E^2, R^3\}$
. In case
$\{p^1_n\mid n\in \omega \}\cup \{S^1, O^1, E^2, R^3\}$
. In case
![]() $\Omega \subseteq \Pi $
, we set
$\Omega \subseteq \Pi $
, we set
![]() $\Omega ^\pm := \{(P_+)^n, (P_-)^n\mid P^n\in \Omega \}$
. For instance, if
$\Omega ^\pm := \{(P_+)^n, (P_-)^n\mid P^n\in \Omega \}$
. For instance, if
![]() $\Omega = \{S^1, R^3, p^1_0\}$
, then
$\Omega = \{S^1, R^3, p^1_0\}$
, then
![]() $\Omega ^\pm = \{S^1_+, R^3_+, (p_0)^1_+, S^1_-, R^3_-, (p_0)^1_- \}$
.
$\Omega ^\pm = \{S^1_+, R^3_+, (p_0)^1_+, S^1_-, R^3_-, (p_0)^1_- \}$
.
Next, we define
![]() $Sign:= \Pi \cup \Pi ^\pm \cup \{\epsilon ^2\}$
. The elements of
$Sign:= \Pi \cup \Pi ^\pm \cup \{\epsilon ^2\}$
. The elements of
![]() $Sign$
will serve as predicateFootnote
3
letters; their superscripts denote their arities. In order to define the first-order atoms, we also need to supply the set
$Sign$
will serve as predicateFootnote
3
letters; their superscripts denote their arities. In order to define the first-order atoms, we also need to supply the set
![]() $Ind:= \{v_n\mid n \in \omega \}$
of individual variables.
$Ind:= \{v_n\mid n \in \omega \}$
of individual variables.
If now
![]() $\Omega \subseteq Sign$
, then the set
$\Omega \subseteq Sign$
, then the set
![]() $At(\Omega ):= \{x \equiv y,\, Q\bar {x}_n\mid Q^n\in \Omega ,\,x,y, \bar {x}_n \in Ind\}$
is called the set of
$At(\Omega ):= \{x \equiv y,\, Q\bar {x}_n\mid Q^n\in \Omega ,\,x,y, \bar {x}_n \in Ind\}$
is called the set of
![]() $\Omega $
-atoms. The set
$\Omega $
-atoms. The set
![]() $Lit(\Omega ):= At(\Omega )\cup \{\sim \phi \mid \phi \in At(\Omega )\}$
is called the set of
$Lit(\Omega ):= At(\Omega )\cup \{\sim \phi \mid \phi \in At(\Omega )\}$
is called the set of
![]() $\Omega $
-literals. Our definition of atoms entails, among other things, that the arity superscripts are not a part of predicate letters; strictly speaking, they are assigned by
$\Omega $
-literals. Our definition of atoms entails, among other things, that the arity superscripts are not a part of predicate letters; strictly speaking, they are assigned by
![]() $\Omega $
to the predicate letters, so that, viewed more formally,
$\Omega $
to the predicate letters, so that, viewed more formally,
![]() $\Omega $
must be understood as a function from the set of predicate letters into
$\Omega $
must be understood as a function from the set of predicate letters into
![]() $\omega $
. This is why the arity superscripts do not appear in actual formulas. To take our previous example,
$\omega $
. This is why the arity superscripts do not appear in actual formulas. To take our previous example,
![]() $\Omega = \{S^1, R^3, p^1_0\}$
is, strictly speaking, a function and could have been alternatively written in the form
$\Omega = \{S^1, R^3, p^1_0\}$
is, strictly speaking, a function and could have been alternatively written in the form
![]() $\Omega = \{(S, 1), (R,3), (p_0, 1)\}$
; examples of
$\Omega = \{(S, 1), (R,3), (p_0, 1)\}$
; examples of
![]() $\Omega $
-atoms in this case are given by
$\Omega $
-atoms in this case are given by
![]() $S(v_0)$
and
$S(v_0)$
and
![]() $R(v_0,v_0, v_3)$
rather than, say,
$R(v_0,v_0, v_3)$
rather than, say,
![]() $S^1(v_0)$
.
$S^1(v_0)$
.
The first-order language
![]() $\mathcal {FO}(\Omega )$
is then generated on the basis of
$\mathcal {FO}(\Omega )$
is then generated on the basis of
![]() $At(\Omega )$
by the following BNF (where
$At(\Omega )$
by the following BNF (where
![]() $x \in Ind$
):
$x \in Ind$
):
The positive first-order language
![]() $\mathcal {FO}^+(\Omega )$
is the (
$\mathcal {FO}^+(\Omega )$
is the (
![]() $\sim $
)-free subset of
$\sim $
)-free subset of
![]() $\mathcal {FO}(\Omega )$
.
$\mathcal {FO}(\Omega )$
.
Given an
![]() $\Omega \subseteq Sign$
and a formula
$\Omega \subseteq Sign$
and a formula
![]() $\phi \in \mathcal {FO}(\Omega )$
, we denote by
$\phi \in \mathcal {FO}(\Omega )$
, we denote by
![]() $Sub(\phi )$
the set of subformulas of
$Sub(\phi )$
the set of subformulas of
![]() $\phi $
assuming its standard definition by induction on the construction of
$\phi $
assuming its standard definition by induction on the construction of
![]() $\phi $
. Furthermore, we can inductively define for
$\phi $
. Furthermore, we can inductively define for
![]() $\phi $
its set of free variables in a standard way (see, e.g., [Reference van Dalen4, p. 64]). This set, denoted by
$\phi $
its set of free variables in a standard way (see, e.g., [Reference van Dalen4, p. 64]). This set, denoted by
![]() $FV(\phi )$
, is always finite. Given an
$FV(\phi )$
, is always finite. Given an
![]() $n \in \omega $
, and a
$n \in \omega $
, and a
![]() $\bar {x}_n \in Ind^n$
, we will denote by
$\bar {x}_n \in Ind^n$
, we will denote by
![]() $\mathcal {FO}(\Omega )^{\bar {x}_n}$
the set
$\mathcal {FO}(\Omega )^{\bar {x}_n}$
the set
![]() $\{\phi \in \mathcal {FO}(\Omega )\mid FV(\phi ) \subseteq \{\bar {x}_n\}\}$
. If
$\{\phi \in \mathcal {FO}(\Omega )\mid FV(\phi ) \subseteq \{\bar {x}_n\}\}$
. If
![]() $\phi \in \mathcal {FO}(\Omega )^\emptyset $
, then
$\phi \in \mathcal {FO}(\Omega )^\emptyset $
, then
![]() $\phi $
is called an
$\phi $
is called an
![]() $\Omega $
-sentence. Finally, given some
$\Omega $
-sentence. Finally, given some
![]() $x,y \in Ind$
, we assume a standard definition for the property of y being substitutable for x in
$x,y \in Ind$
, we assume a standard definition for the property of y being substitutable for x in
![]() $\phi $
; in case this property holds, we define the result
$\phi $
; in case this property holds, we define the result
![]() $\phi [x/y]$
of this substitution simply as the result of replacing all free occurrences of x in
$\phi [x/y]$
of this substitution simply as the result of replacing all free occurrences of x in
![]() $\phi $
with the occurrences of y.
$\phi $
with the occurrences of y.
We are going to define three first-order logics, the classical logic
![]() $\mathsf {QCL}$
, the positive intuitionistic logic
$\mathsf {QCL}$
, the positive intuitionistic logic
![]() $\mathsf {QIL}^+$
, and, finally, the logic
$\mathsf {QIL}^+$
, and, finally, the logic
![]() $\mathsf {QN4}$
, which represents the paraconsistent variant of Nelson’s first-order logic of strong negation. Each of these logics will be defined over a different set of the first-order language variants. Among the three logics, the classical logic has the simplest semantics. We describe it as follows.
$\mathsf {QN4}$
, which represents the paraconsistent variant of Nelson’s first-order logic of strong negation. Each of these logics will be defined over a different set of the first-order language variants. Among the three logics, the classical logic has the simplest semantics. We describe it as follows.
Definition 1. Given an
![]() $\Omega \subseteq Sign$
, a classical first-order model over
$\Omega \subseteq Sign$
, a classical first-order model over
![]() $\Omega $
(also called classical first-order
$\Omega $
(also called classical first-order
![]() $\Omega $
-model) is a tuple
$\Omega $
-model) is a tuple
![]() $\mathcal {M} = (U^{\mathcal {M}}, \{P^{\mathcal {M}}\mid P^n \in \Omega , n \in \omega \})$
, where
$\mathcal {M} = (U^{\mathcal {M}}, \{P^{\mathcal {M}}\mid P^n \in \Omega , n \in \omega \})$
, where
![]() $U \neq \emptyset $
is called the domain of
$U \neq \emptyset $
is called the domain of
![]() $\mathcal {M}$
and, for every
$\mathcal {M}$
and, for every
![]() $P^n \in \Omega $
,
$P^n \in \Omega $
,
![]() $P^{\mathcal {M}} \subseteq U^n$
. The class of all classical first-order
$P^{\mathcal {M}} \subseteq U^n$
. The class of all classical first-order
![]() $\Omega $
-models will be denoted by
$\Omega $
-models will be denoted by
![]() $\mathbb {C}(\Omega )$
.
$\mathbb {C}(\Omega )$
.
We will also need the following notion relating classical models.
Definition 2. Let
![]() $\Omega \subseteq Sign$
, and let
$\Omega \subseteq Sign$
, and let
![]() $\mathcal {M}, \mathcal {N} \in \mathbb {C}(\Omega )$
. Then a function
$\mathcal {M}, \mathcal {N} \in \mathbb {C}(\Omega )$
. Then a function
![]() ${f:U^{\mathcal {M}}\to U^{\mathcal {N}}}$
is called a homomorphism from
${f:U^{\mathcal {M}}\to U^{\mathcal {N}}}$
is called a homomorphism from
![]() $\mathcal {M}$
to
$\mathcal {M}$
to
![]() $\mathcal {N}$
(written
$\mathcal {N}$
(written
![]() $f:\mathcal {M}\to \mathcal {N}$
) iff
$f:\mathcal {M}\to \mathcal {N}$
) iff
![]() $\bar {a}_n \in P^{\mathcal {M}}$
implies
$\bar {a}_n \in P^{\mathcal {M}}$
implies
![]() $f(\bar {a}_n) \in P^{\mathcal {N}}$
for every
$f(\bar {a}_n) \in P^{\mathcal {N}}$
for every
![]() $n \in \omega $
, every
$n \in \omega $
, every
![]() $\bar {a}_n \in (U^{\mathcal {M}})^n$
, and every
$\bar {a}_n \in (U^{\mathcal {M}})^n$
, and every
![]() $P^n\in \Omega $
. The set of all homomorphisms from
$P^n\in \Omega $
. The set of all homomorphisms from
![]() $\mathcal {M}$
to
$\mathcal {M}$
to
![]() $\mathcal {N}$
will be denoted by
$\mathcal {N}$
will be denoted by
![]() $Hom(\mathcal {M},\mathcal {N})$
.
$Hom(\mathcal {M},\mathcal {N})$
.
The class
![]() $EP_c(\Omega )$
of classical
$EP_c(\Omega )$
of classical
![]() $\Omega $
-evaluation points is then the class
$\Omega $
-evaluation points is then the class
We now define
![]() $\mathsf {QCL}(\Omega ):=\mathbb {L}(EP_c(\Omega ), \models _c)$
, where
$\mathsf {QCL}(\Omega ):=\mathbb {L}(EP_c(\Omega ), \models _c)$
, where
![]() $\models _c$
is the classical first-order satisfaction relation. We will often write
$\models _c$
is the classical first-order satisfaction relation. We will often write
![]() $\mathcal {M}\models _{c}\phi [f]$
instead of
$\mathcal {M}\models _{c}\phi [f]$
instead of
![]() $(\mathcal {M}, f)\models _{c}\phi $
(also for the non-classical first-order logics). The relation itself is defined by the following induction on the construction of
$(\mathcal {M}, f)\models _{c}\phi $
(also for the non-classical first-order logics). The relation itself is defined by the following induction on the construction of
![]() $\phi $
:
$\phi $
:
 $$ \begin{align*} \mathcal{M}\models_{c}P\bar{x}_n[f] &\text{ iff } f(\bar{x}_n)\in P^{\mathcal{M}} &&P^n\in \Omega\\\mathcal{M}\models_{c}x\equiv y[f] &\text{ iff } f(x) = f(y)\\\mathcal{M}\models_{c}(\psi\wedge\chi)[f] &\text{ iff } \mathcal{M}\models_{c}\psi[f]\text{ and }\mathcal{M}\models_{c}\chi[f]\\\mathcal{M}\models_{c}(\psi\vee\chi)[f] &\text{ iff } \mathcal{M}\models_{c}\psi[f]\text{ or }\mathcal{M}\models_{c}\chi[f]\\\mathcal{M}\models_{c}(\psi\to\chi)[f] &\text{ iff } \mathcal{M}\not\models_{c}\psi[f]\text{ or }\mathcal{M}\models_{c}\chi[f]\\\mathcal{M}\models_{c}\sim\psi[f] &\text{ iff } \mathcal{M}\not\models_{c}\psi[f]\\\mathcal{M}\models_{c}\exists x\psi[f] &\text{ iff } (\exists a\in U^{\mathcal{M}})(\mathcal{M}\models_{c}\psi[f[x/a]])\\\mathcal{M}\models_{c}\forall x\psi[f] &\text{ iff } (\forall a\in U^{\mathcal{M}})(\mathcal{M}\models_{c}\psi[f[x/a]]). \end{align*} $$
$$ \begin{align*} \mathcal{M}\models_{c}P\bar{x}_n[f] &\text{ iff } f(\bar{x}_n)\in P^{\mathcal{M}} &&P^n\in \Omega\\\mathcal{M}\models_{c}x\equiv y[f] &\text{ iff } f(x) = f(y)\\\mathcal{M}\models_{c}(\psi\wedge\chi)[f] &\text{ iff } \mathcal{M}\models_{c}\psi[f]\text{ and }\mathcal{M}\models_{c}\chi[f]\\\mathcal{M}\models_{c}(\psi\vee\chi)[f] &\text{ iff } \mathcal{M}\models_{c}\psi[f]\text{ or }\mathcal{M}\models_{c}\chi[f]\\\mathcal{M}\models_{c}(\psi\to\chi)[f] &\text{ iff } \mathcal{M}\not\models_{c}\psi[f]\text{ or }\mathcal{M}\models_{c}\chi[f]\\\mathcal{M}\models_{c}\sim\psi[f] &\text{ iff } \mathcal{M}\not\models_{c}\psi[f]\\\mathcal{M}\models_{c}\exists x\psi[f] &\text{ iff } (\exists a\in U^{\mathcal{M}})(\mathcal{M}\models_{c}\psi[f[x/a]])\\\mathcal{M}\models_{c}\forall x\psi[f] &\text{ iff } (\forall a\in U^{\mathcal{M}})(\mathcal{M}\models_{c}\psi[f[x/a]]). \end{align*} $$
Our next logic is the positive intuitionistic logic
![]() $\mathsf {QIL}^+$
. Its semantics (defined here for every
$\mathsf {QIL}^+$
. Its semantics (defined here for every
![]() $\Omega \subseteq Sign$
over the language
$\Omega \subseteq Sign$
over the language
![]() $\mathcal {FO}^+(\Omega )$
) is somewhat more involved, and exists in several variants. By far the most popular one is the so-called Kripke semantics (see, e.g., [Reference Gabbay, Shehtman and Skvortsov6, Chapter 3]). However, the proof of our main result proceeds more conveniently on the basis of a somewhat involved semantics of Kripke sheaves which we define next.
$\mathcal {FO}^+(\Omega )$
) is somewhat more involved, and exists in several variants. By far the most popular one is the so-called Kripke semantics (see, e.g., [Reference Gabbay, Shehtman and Skvortsov6, Chapter 3]). However, the proof of our main result proceeds more conveniently on the basis of a somewhat involved semantics of Kripke sheaves which we define next.
Definition 3. Given an
![]() $\Omega \subseteq Sign$
, an intuitionistic Kripke
$\Omega \subseteq Sign$
, an intuitionistic Kripke
![]() $\Omega $
-sheaf is any structure of the form
$\Omega $
-sheaf is any structure of the form
![]() $\mathcal {S} = (W, \leq , \mathtt {M}, \mathtt {H})$
, such that:
$\mathcal {S} = (W, \leq , \mathtt {M}, \mathtt {H})$
, such that:
-
1.
 $W \neq \emptyset $
is the set of worlds, or nodes.
$W \neq \emptyset $
is the set of worlds, or nodes. -
2.
 $\leq $
is a reflexive and transitive relation (also called a preorder) on W.
$\leq $
is a reflexive and transitive relation (also called a preorder) on W. -
3.
 $\mathtt {M}:W\to \mathbb {C}(\Omega )$
.
$\mathtt {M}:W\to \mathbb {C}(\Omega )$
. -
4.
 $\mathtt {H}:\{(\mathbf {w},\mathbf {v})\in W^2\mid \mathbf {w}\leq \mathbf {v}\}\to Hom(\mathtt {M}(\mathbf {w}), \mathtt {M}(\mathbf {v}))$
such that the following holds:
$\mathtt {H}:\{(\mathbf {w},\mathbf {v})\in W^2\mid \mathbf {w}\leq \mathbf {v}\}\to Hom(\mathtt {M}(\mathbf {w}), \mathtt {M}(\mathbf {v}))$
such that the following holds:-
(a)
 $\mathtt {H}(\mathbf {w},\mathbf {w}) = id[U^{\mathtt {M}(\mathbf {w})}]$
for every
$\mathtt {H}(\mathbf {w},\mathbf {w}) = id[U^{\mathtt {M}(\mathbf {w})}]$
for every
 $\mathbf {w} \in W$
.
$\mathbf {w} \in W$
. -
(b)
 $\mathtt {H}(\mathbf {w},\mathbf {v})\circ \mathtt {H}(\mathbf {v},\mathbf {u}) = \mathtt {H}(\mathbf {w},\mathbf {u})$
for all
$\mathtt {H}(\mathbf {w},\mathbf {v})\circ \mathtt {H}(\mathbf {v},\mathbf {u}) = \mathtt {H}(\mathbf {w},\mathbf {u})$
for all
 $\mathbf {w},\mathbf {v},\mathbf {u} \in W$
such that
$\mathbf {w},\mathbf {v},\mathbf {u} \in W$
such that
 $\mathbf {w} \leq \mathbf {v} \leq \mathbf {u}$
.
$\mathbf {w} \leq \mathbf {v} \leq \mathbf {u}$
.
-
We will often write
![]() $\mathtt {M}_{\mathbf {w}}$
,
$\mathtt {M}_{\mathbf {w}}$
,
![]() $\mathtt {H}_{\mathbf {w}\mathbf {v}}$
in place of
$\mathtt {H}_{\mathbf {w}\mathbf {v}}$
in place of
![]() $\mathtt {M}(\mathbf {w})$
,
$\mathtt {M}(\mathbf {w})$
,
![]() $\mathtt {H}(\mathbf {w},\mathbf {v})$
, respectively.
$\mathtt {H}(\mathbf {w},\mathbf {v})$
, respectively.
The class of all intuitionistic Kripke
![]() $\Omega $
-sheaves will be denoted by
$\Omega $
-sheaves will be denoted by
![]() $\mathbb {I}(\Omega )$
.
$\mathbb {I}(\Omega )$
.
Remark 1. In this article we will introduce multiple notions of model-like structure; in every case, we will assume that the default representation of the structure is given in the definition and that all decorations applied to the default notation for a structure of a given sort are also inherited by the elements of its default structure, unless explicitly stated otherwise. For example, in the case of intuitionistic sheaves this means that every
![]() $\mathcal {S}\in \mathbb {I}(\Omega )$
is given as
$\mathcal {S}\in \mathbb {I}(\Omega )$
is given as
![]() $(W, \leq , \mathtt {M}, \mathtt {H})$
and that
$(W, \leq , \mathtt {M}, \mathtt {H})$
and that
![]() $\mathcal {S}_n, \mathcal {S}' \in \mathbb {I}(\Omega )$
are always given as
$\mathcal {S}_n, \mathcal {S}' \in \mathbb {I}(\Omega )$
are always given as
![]() $(W_n, \leq _n, \mathtt {M}_n, \mathtt {H}_n)$
and
$(W_n, \leq _n, \mathtt {M}_n, \mathtt {H}_n)$
and
![]() $(W', \leq ', \mathtt {M}', \mathtt {H}')$
, respectively, unless explicitly stated otherwise.
$(W', \leq ', \mathtt {M}', \mathtt {H}')$
, respectively, unless explicitly stated otherwise.
For any
![]() $\Omega \subseteq Sign$
, the class
$\Omega \subseteq Sign$
, the class
![]() $EP_{i}(\Omega )$
of intuitionistic evaluation points is the class
$EP_{i}(\Omega )$
of intuitionistic evaluation points is the class
The satisfaction relation
![]() $\models _{i}$
is then defined by the following induction:
$\models _{i}$
is then defined by the following induction:
 $$ \begin{align*} \mathcal{S},\mathbf{w}\models_{i}P\bar{x}_n[f] &\text{ iff } \mathtt{M}_{\mathbf{w}}\models_{c}P(\bar{x}_n)[f] \text{ iff } f(\bar{x}_n)\in P^{\mathtt{M}_{\mathbf{w}}} && P^n\in \Omega\\\mathcal{S},\mathbf{w}\models_ix \equiv y &\text{ iff } f(x) = f(y)\\\mathcal{S},\mathbf{w}\models_i(\psi\wedge\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models_i\psi[f]\text{ and }\mathcal{S},\mathbf{w}\models_i\chi[f]\\\mathcal{S},\mathbf{w}\models_i(\psi\vee\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models_i\psi[f]\text{ or }\mathcal{S},\mathbf{w}\models_i\chi[f]\\\mathcal{S},\mathbf{w}\models_i(\psi\to\chi)[f] &\text{ iff } (\forall \mathbf{v}\geq \mathbf{w})(\mathcal{S},\mathbf{v}\not\models_i\psi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}, \mathbf{v}\models_i\chi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}])\\\mathcal{S},\mathbf{w}\models_i\exists x\psi[f] &\text{ iff } (\exists a\in U^{\mathtt{M}_{\mathbf{w}}})(\mathcal{S},\mathbf{w}\models_i\psi[f[x/a]])\\\mathcal{S},\mathbf{w}\models_i\forall x\psi[f] &\text{ iff } (\forall \mathbf{v}\geq \mathbf{w})(\forall a\in U^{\mathtt{M}_{\mathbf{v}}})(\mathcal{S},\mathbf{v}\models_i\psi[(f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}})[x/a]]). \end{align*} $$
$$ \begin{align*} \mathcal{S},\mathbf{w}\models_{i}P\bar{x}_n[f] &\text{ iff } \mathtt{M}_{\mathbf{w}}\models_{c}P(\bar{x}_n)[f] \text{ iff } f(\bar{x}_n)\in P^{\mathtt{M}_{\mathbf{w}}} && P^n\in \Omega\\\mathcal{S},\mathbf{w}\models_ix \equiv y &\text{ iff } f(x) = f(y)\\\mathcal{S},\mathbf{w}\models_i(\psi\wedge\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models_i\psi[f]\text{ and }\mathcal{S},\mathbf{w}\models_i\chi[f]\\\mathcal{S},\mathbf{w}\models_i(\psi\vee\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models_i\psi[f]\text{ or }\mathcal{S},\mathbf{w}\models_i\chi[f]\\\mathcal{S},\mathbf{w}\models_i(\psi\to\chi)[f] &\text{ iff } (\forall \mathbf{v}\geq \mathbf{w})(\mathcal{S},\mathbf{v}\not\models_i\psi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}, \mathbf{v}\models_i\chi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}])\\\mathcal{S},\mathbf{w}\models_i\exists x\psi[f] &\text{ iff } (\exists a\in U^{\mathtt{M}_{\mathbf{w}}})(\mathcal{S},\mathbf{w}\models_i\psi[f[x/a]])\\\mathcal{S},\mathbf{w}\models_i\forall x\psi[f] &\text{ iff } (\forall \mathbf{v}\geq \mathbf{w})(\forall a\in U^{\mathtt{M}_{\mathbf{v}}})(\mathcal{S},\mathbf{v}\models_i\psi[(f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}})[x/a]]). \end{align*} $$
We now define
![]() $\mathsf {QIL}^+(\Omega ) := \mathbb {L}(EP_{i}(\Omega ), \models _i)$
for any
$\mathsf {QIL}^+(\Omega ) := \mathbb {L}(EP_{i}(\Omega ), \models _i)$
for any
![]() $\Omega \subseteq Sign$
. See [Reference Gabbay, Shehtman and Skvortsov6, Section 3.6 ff] for a proof that we indeed get a correct semantics for the positive intuitionistic logic in this way, the fact is also mentioned in [Reference van Dalen4, Corollary 5.3.16].
$\Omega \subseteq Sign$
. See [Reference Gabbay, Shehtman and Skvortsov6, Section 3.6 ff] for a proof that we indeed get a correct semantics for the positive intuitionistic logic in this way, the fact is also mentioned in [Reference van Dalen4, Corollary 5.3.16].
Sheaf semantics is a generalization of Kripke semantics in that the latter can be obtained from sheaf semantics as long as we assume in Definition 3 that
![]() $\mathtt {H}_{\mathbf {w}\mathbf {v}} = id[U^{\mathtt {M}_{\mathbf {w}}}]$
for all
$\mathtt {H}_{\mathbf {w}\mathbf {v}} = id[U^{\mathtt {M}_{\mathbf {w}}}]$
for all
![]() $\mathbf {w},\mathbf {v} \in W$
such that
$\mathbf {w},\mathbf {v} \in W$
such that
![]() $\mathbf {w}\leq \mathbf {v}$
. Therefore, most of the properties and constructions available in the usual Kripke semantics have obvious counterparts in the sheaf semantics. The following lemma mentions some of these properties.
$\mathbf {w}\leq \mathbf {v}$
. Therefore, most of the properties and constructions available in the usual Kripke semantics have obvious counterparts in the sheaf semantics. The following lemma mentions some of these properties.
Lemma 1. For every
![]() $\Omega \subseteq Sign$
,
$\Omega \subseteq Sign$
,
![]() $(\mathcal {S}, \mathbf {w}, f)\in EP_{i}(\Omega )$
, and
$(\mathcal {S}, \mathbf {w}, f)\in EP_{i}(\Omega )$
, and
![]() $\phi \in \mathcal {FO}^+(\Omega )$
, we have:
$\phi \in \mathcal {FO}^+(\Omega )$
, we have:
-
1. If
 $\mathbf {v}\geq \mathbf {w}$
, and
$\mathbf {v}\geq \mathbf {w}$
, and
 $\mathcal {S},\mathbf {w}\models _{i}\phi [f]$
, then
$\mathcal {S},\mathbf {w}\models _{i}\phi [f]$
, then
 $\mathcal {S},\mathbf {v}\models _{i}\phi [f\circ \mathtt {H}_{\mathbf {w}\mathbf {v}}]$
.
$\mathcal {S},\mathbf {v}\models _{i}\phi [f\circ \mathtt {H}_{\mathbf {w}\mathbf {v}}]$
. -
2. The generated sub-sheaf
 $\mathcal {S}|_{\mathbf {w}} = (W|_{\mathbf {w}}, \leq |_{\mathbf {w}}, \mathtt {M}|_{\mathbf {w}}, \mathtt {H}|_{\mathbf {w}})\in \mathbb {I}(\Omega )$
is defined by
$\mathcal {S}|_{\mathbf {w}} = (W|_{\mathbf {w}}, \leq |_{\mathbf {w}}, \mathtt {M}|_{\mathbf {w}}, \mathtt {H}|_{\mathbf {w}})\in \mathbb {I}(\Omega )$
is defined by
 $W|_{\mathbf {w}}:= \{\mathbf {v}\in W\mid \mathbf {v}\geq \mathbf {w}\}$
,
$W|_{\mathbf {w}}:= \{\mathbf {v}\in W\mid \mathbf {v}\geq \mathbf {w}\}$
,
 $\leq |_{\mathbf {w}}:= \leq \cap (W|_{\mathbf {w}}\times W|_{\mathbf {w}})$
,
$\leq |_{\mathbf {w}}:= \leq \cap (W|_{\mathbf {w}}\times W|_{\mathbf {w}})$
,
 $\mathtt {M}|_{\mathbf {w}}:= \mathtt {M}\upharpoonright (W|_{\mathbf {w}})$
, and
$\mathtt {M}|_{\mathbf {w}}:= \mathtt {M}\upharpoonright (W|_{\mathbf {w}})$
, and
 $\mathtt {H}|_{\mathbf {w}}:= \mathtt {H}\upharpoonright (W|_{\mathbf {w}}\times W|_{\mathbf {w}})$
. With this definition, we get for every
$\mathtt {H}|_{\mathbf {w}}:= \mathtt {H}\upharpoonright (W|_{\mathbf {w}}\times W|_{\mathbf {w}})$
. With this definition, we get for every $$ \begin{align*}\mathcal{S}|_{\mathbf{w}},\mathbf{v}\models_{i}\phi[f]\text{ iff } \mathcal{S},\mathbf{v}\models_{i}\phi[f] \end{align*} $$
$$ \begin{align*}\mathcal{S}|_{\mathbf{w}},\mathbf{v}\models_{i}\phi[f]\text{ iff } \mathcal{S},\mathbf{v}\models_{i}\phi[f] \end{align*} $$
 $\mathbf {v}\geq \mathbf {w}$
and every
$\mathbf {v}\geq \mathbf {w}$
and every
 $f:Ind\to U^{\mathtt {M}_{\mathbf {v}}} = U^{(\mathtt {M}|_{\mathbf {w}})_{\mathbf {v}}}$
.
$f:Ind\to U^{\mathtt {M}_{\mathbf {v}}} = U^{(\mathtt {M}|_{\mathbf {w}})_{\mathbf {v}}}$
.
Proof We proceed by a straightforward induction on the construction of
![]() $\phi \in \mathcal {FO}^+(\Omega )$
in both cases, the reasoning is quite similar to the case of intuitionistic Kripke semantics.
$\phi \in \mathcal {FO}^+(\Omega )$
in both cases, the reasoning is quite similar to the case of intuitionistic Kripke semantics.
Alternatively, one can define
![]() $\mathsf {QIL}^+$
by its complete Hilbert-style axiomatization. More precisely, consider the following set of axiomatic schemes:
$\mathsf {QIL}^+$
by its complete Hilbert-style axiomatization. More precisely, consider the following set of axiomatic schemes:
plus the following rules of inference:
where
![]() $x, z \in Ind$
and
$x, z \in Ind$
and
![]() $y \in Ind\setminus FV(\psi )$
are such that
$y \in Ind\setminus FV(\psi )$
are such that
![]() $z, y$
are substitutable for x in
$z, y$
are substitutable for x in
![]() $\phi $
. We then let
$\phi $
. We then let
![]() $\mathfrak {QIL}^+:= \mathfrak {IL}^++((\alpha_9),\ldots ,(\alpha_12);(R\forall),(R\exists))$
. It is well-known that for every
$\mathfrak {QIL}^+:= \mathfrak {IL}^++((\alpha_9),\ldots ,(\alpha_12);(R\forall),(R\exists))$
. It is well-known that for every
![]() $\Omega \subseteq Sign$
, we have
$\Omega \subseteq Sign$
, we have
![]() $\mathsf {QIL}^+(\Omega ) = \mathfrak {QIL}^+(\mathcal {FO}(\Omega ))$
.
$\mathsf {QIL}^+(\Omega ) = \mathfrak {QIL}^+(\mathcal {FO}(\Omega ))$
.
We now turn to the paraconsistent variant of Nelson’s logic of strong negation, which we denote by
![]() $\mathsf {QN4}$
and which we only define over
$\mathsf {QN4}$
and which we only define over
![]() $\mathcal {FO}(\Omega )$
for
$\mathcal {FO}(\Omega )$
for
![]() $\Omega \subseteq \Pi $
. Our main goal in this section is to set up a sheaf semantics also for
$\Omega \subseteq \Pi $
. Our main goal in this section is to set up a sheaf semantics also for
![]() $\mathsf {QN4}$
. Since no variants of sheaf semantics were yet (to the best of our knowledge) proposed for this logic in the existing literature, we cannot use our proposed semantics to define
$\mathsf {QN4}$
. Since no variants of sheaf semantics were yet (to the best of our knowledge) proposed for this logic in the existing literature, we cannot use our proposed semantics to define
![]() $\mathsf {QN4}$
. Instead, we extend
$\mathsf {QN4}$
. Instead, we extend
![]() $\mathfrak {QIL}^+$
with the following axiomatic schemes:
$\mathfrak {QIL}^+$
with the following axiomatic schemes:
In doing so, we obtain the system
![]() $\mathfrak {QN4}:= \mathfrak {QIL}^++\textrm{(An1)},\ldots ,\textrm{(An6)};)$
which represents the most standard way to axiomatize
$\mathfrak {QN4}:= \mathfrak {QIL}^++\textrm{(An1)},\ldots ,\textrm{(An6)};)$
which represents the most standard way to axiomatize
![]() $\mathsf {QN4}$
known in the existing literature on the subject (see, e.g., [Reference Odintsov, Wansing, Hendricks and Malinowski9, p. 313]). We can therefore set
$\mathsf {QN4}$
known in the existing literature on the subject (see, e.g., [Reference Odintsov, Wansing, Hendricks and Malinowski9, p. 313]). We can therefore set
![]() $\mathsf {QN4}(\Omega ):= \mathfrak {QN4}(\mathcal {FO}(\Omega ))$
for every
$\mathsf {QN4}(\Omega ):= \mathfrak {QN4}(\mathcal {FO}(\Omega ))$
for every
![]() $\Omega \subseteq \Pi $
.
$\Omega \subseteq \Pi $
.
This definition makes it obvious that
![]() $\mathsf {QN4}$
is a sublogic of
$\mathsf {QN4}$
is a sublogic of
![]() $\mathsf {QCL}$
and extends
$\mathsf {QCL}$
and extends
![]() $\mathsf {QIL}^+$
. We retain these observations for future reference.
$\mathsf {QIL}^+$
. We retain these observations for future reference.
Lemma 2. Let
![]() $\Omega \subseteq \Pi $
. Every substitution instance of a
$\Omega \subseteq \Pi $
. Every substitution instance of a
![]() $\mathsf {QIL}^+(\Omega )$
-theorem is a theorem of
$\mathsf {QIL}^+(\Omega )$
-theorem is a theorem of
![]() $\mathsf {QN4}(\Omega )$
and every inference rule that is deducible in
$\mathsf {QN4}(\Omega )$
and every inference rule that is deducible in
![]() $\mathsf {QIL}^+(\Omega )$
is also deducible in
$\mathsf {QIL}^+(\Omega )$
is also deducible in
![]() $\mathsf {QN4}(\Omega )$
. In particular, the following derived rules hold:
$\mathsf {QN4}(\Omega )$
. In particular, the following derived rules hold:
Lemma 3. Let
![]() $\Omega \subseteq \Pi $
. Then
$\Omega \subseteq \Pi $
. Then
![]() $\mathsf {QN4}(\Omega )\subseteq \mathsf {QCL}(\Omega )$
and every inference rule that is deducible
$\mathsf {QN4}(\Omega )\subseteq \mathsf {QCL}(\Omega )$
and every inference rule that is deducible
![]() $\mathsf {QN4}$
is also deducible in
$\mathsf {QN4}$
is also deducible in
![]() $\mathsf {QCL}$
.
$\mathsf {QCL}$
.
We observe, further, that, for every
![]() $\Omega \subseteq \Pi $
,
$\Omega \subseteq \Pi $
,
![]() $\mathsf {QN4}(\Omega )$
is embeddable into
$\mathsf {QN4}(\Omega )$
is embeddable into
![]() $\mathsf {QIL}^+(\Omega ^\pm \cup \{\epsilon ^2\})$
and that the corresponding embedding
$\mathsf {QIL}^+(\Omega ^\pm \cup \{\epsilon ^2\})$
and that the corresponding embedding
![]() $Tr:\mathcal {FO}(\Omega )\to \mathcal {FO}^+(\Omega ^\pm \cup \{\epsilon ^2\})$
can be defined by the following induction on the construction of
$Tr:\mathcal {FO}(\Omega )\to \mathcal {FO}^+(\Omega ^\pm \cup \{\epsilon ^2\})$
can be defined by the following induction on the construction of
![]() $\phi \in \mathcal {FO}(\Pi )$
:
$\phi \in \mathcal {FO}(\Pi )$
:
 $$ \begin{align*} Tr(P\bar{x}_n)&:= P_+\bar{x}_n;&&Tr(\sim P\bar{x}_n):= P_-\bar{x}_n;\\Tr(x\equiv y)&:= x\equiv y;&&Tr(\sim(x \equiv y)):= \epsilon xy;\\Tr(\sim\sim\phi)&:= Tr(\phi);\\Tr(\phi\star\psi)&:= Tr(\phi)\star Tr(\psi);&&Tr(\sim(\phi\star\psi)):= Tr(\sim\phi)\ast Tr(\sim\psi);\\Tr(\phi\to\psi)&:= Tr(\phi)\to Tr(\psi);&& Tr(\sim(\phi\to\psi)):= Tr(\phi)\wedge Tr(\sim\psi);\\Tr(Qx\phi)&:= QxTr(\phi);&& Tr(\sim Qx\phi):= Q'xTr(\sim\phi) \end{align*} $$
$$ \begin{align*} Tr(P\bar{x}_n)&:= P_+\bar{x}_n;&&Tr(\sim P\bar{x}_n):= P_-\bar{x}_n;\\Tr(x\equiv y)&:= x\equiv y;&&Tr(\sim(x \equiv y)):= \epsilon xy;\\Tr(\sim\sim\phi)&:= Tr(\phi);\\Tr(\phi\star\psi)&:= Tr(\phi)\star Tr(\psi);&&Tr(\sim(\phi\star\psi)):= Tr(\sim\phi)\ast Tr(\sim\psi);\\Tr(\phi\to\psi)&:= Tr(\phi)\to Tr(\psi);&& Tr(\sim(\phi\to\psi)):= Tr(\phi)\wedge Tr(\sim\psi);\\Tr(Qx\phi)&:= QxTr(\phi);&& Tr(\sim Qx\phi):= Q'xTr(\sim\phi) \end{align*} $$
for all
![]() $n \in \omega $
, all
$n \in \omega $
, all
![]() $P^n \in \Pi $
, all
$P^n \in \Pi $
, all
![]() $\bar {x}_n, x, y \in Ind$
, and all
$\bar {x}_n, x, y \in Ind$
, and all
![]() $\star , \ast , Q,$
and
$\star , \ast , Q,$
and
![]() $Q'$
such that both
$Q'$
such that both
![]() $\{\star , \ast \} = \{\wedge , \vee \}$
and
$\{\star , \ast \} = \{\wedge , \vee \}$
and
![]() $\{Q,Q'\} = \{\forall , \exists \}$
. More precisely, the following proposition holds.
$\{Q,Q'\} = \{\forall , \exists \}$
. More precisely, the following proposition holds.
Proposition 1. For all
![]() $\Gamma , \Delta \subseteq \mathcal {FO}(\Pi )$
,
$\Gamma , \Delta \subseteq \mathcal {FO}(\Pi )$
,
![]() $\Gamma \models _{\mathsf {QN4}}\Delta $
iff
$\Gamma \models _{\mathsf {QN4}}\Delta $
iff
![]() $Tr(\Gamma )\models _{\mathsf {QIL}^+}Tr(\Delta )$
.
$Tr(\Gamma )\models _{\mathsf {QIL}^+}Tr(\Delta )$
.
Proposition 1 is a well-known result about
![]() $\mathsf {QN4}$
(see, e.g., [Reference Odintsov, Wansing, Hendricks and Malinowski9, Proposition 7] for a sketch of a proof). To keep this article reasonably self-contained, we also give its proof in Appendix A.1.
$\mathsf {QN4}$
(see, e.g., [Reference Odintsov, Wansing, Hendricks and Malinowski9, Proposition 7] for a sketch of a proof). To keep this article reasonably self-contained, we also give its proof in Appendix A.1.
We proceed to define a sheaf semantics for
![]() $\mathsf {QN4}$
that we will presently show to be adequate for this logic. We start by defining the structures that we will call Nelsonian sheaves.
$\mathsf {QN4}$
that we will presently show to be adequate for this logic. We start by defining the structures that we will call Nelsonian sheaves.
Definition 4. Let
![]() $\Omega \subseteq \Pi $
. A Nelsonian
$\Omega \subseteq \Pi $
. A Nelsonian
![]() $\Omega $
-sheaf is any structure of the form
$\Omega $
-sheaf is any structure of the form
![]() $\mathcal {S} = (W, \leq , \mathtt {M}^+, \mathtt {M}^-, \mathtt {H})$
, such that:
$\mathcal {S} = (W, \leq , \mathtt {M}^+, \mathtt {M}^-, \mathtt {H})$
, such that:
-
1.
 $\mathcal {S}^+ = (W, \leq , \mathtt {M}^+, \mathtt {H}) \in \mathbb {I}(\Omega )$
.
$\mathcal {S}^+ = (W, \leq , \mathtt {M}^+, \mathtt {H}) \in \mathbb {I}(\Omega )$
. -
2.
 $\mathcal {S}^- =(W, \leq , \mathtt {M}^-, \mathtt {H}) \in \mathbb {I}(\Omega \cup \{\epsilon ^2\})$
.
$\mathcal {S}^- =(W, \leq , \mathtt {M}^-, \mathtt {H}) \in \mathbb {I}(\Omega \cup \{\epsilon ^2\})$
.The intuitionistic sheaves
 $\mathcal {S}^+$
and
$\mathcal {S}^+$
and
 $\mathcal {S}^-$
, defined above, will be called the positive and the negative components of the Nelsonian sheaf
$\mathcal {S}^-$
, defined above, will be called the positive and the negative components of the Nelsonian sheaf
 $\mathcal {S}$
.
$\mathcal {S}$
.
The class of all Nelsonian
![]() $\Omega $
-sheaves will be denoted by
$\Omega $
-sheaves will be denoted by
![]() $\mathbb {N}4(\Omega )$
.
$\mathbb {N}4(\Omega )$
.
Since the family
![]() $\mathtt {H}$
of canonical homomorphisms is shared by
$\mathtt {H}$
of canonical homomorphisms is shared by
![]() $\mathcal {S}^+$
and
$\mathcal {S}^+$
and
![]() $\mathcal {S}^-$
, it follows that
$\mathcal {S}^-$
, it follows that
![]() $U^{\mathtt {M}^+_{\mathbf {w}}} = U^{\mathtt {M}^-_{\mathbf {w}}}$
for every
$U^{\mathtt {M}^+_{\mathbf {w}}} = U^{\mathtt {M}^-_{\mathbf {w}}}$
for every
![]() $\mathbf {w} \in W$
; we can therefore set
$\mathbf {w} \in W$
; we can therefore set
![]() $U_{\mathbf {w}}:= U^{\mathtt {M}^+_{\mathbf {w}}} = U^{\mathtt {M}^-_{\mathbf {w}}}$
for every
$U_{\mathbf {w}}:= U^{\mathtt {M}^+_{\mathbf {w}}} = U^{\mathtt {M}^-_{\mathbf {w}}}$
for every
![]() $\mathbf {w} \in W$
. As for the Nelsonian sheaf evaluation points, they are defined similarly to the intuitionistic ones:
$\mathbf {w} \in W$
. As for the Nelsonian sheaf evaluation points, they are defined similarly to the intuitionistic ones:
![]() $EP_{n}(\Omega ):= \{(\mathcal {S}, \mathbf {w}, f)\mid \mathcal {M}\in \mathbb {N}4(\Omega ),\,(\mathcal {S}^+, \mathbf {w}, f)\in EP_{i}(\Omega )\}$
.
$EP_{n}(\Omega ):= \{(\mathcal {S}, \mathbf {w}, f)\mid \mathcal {M}\in \mathbb {N}4(\Omega ),\,(\mathcal {S}^+, \mathbf {w}, f)\in EP_{i}(\Omega )\}$
.
One peculiarity of
![]() $\mathsf {QN4}$
consists in the fact that its semantics is usually constructed on the basis of two satisfaction relations,
$\mathsf {QN4}$
consists in the fact that its semantics is usually constructed on the basis of two satisfaction relations,
![]() $\models ^+_{n}$
and
$\models ^+_{n}$
and
![]() $\models ^-_{n}$
, instead of just one.Footnote
4
The informal interpretation of the two relations is that whenever
$\models ^-_{n}$
, instead of just one.Footnote
4
The informal interpretation of the two relations is that whenever
![]() $\mathcal {S}, \mathbf {w}\models ^+_{n}\phi [f]$
holds,
$\mathcal {S}, \mathbf {w}\models ^+_{n}\phi [f]$
holds,
![]() $\phi $
is verified at
$\phi $
is verified at
![]() $(\mathcal {S}, \mathbf {w}, f)$
, and when
$(\mathcal {S}, \mathbf {w}, f)$
, and when
![]() $\mathcal {M}, \mathbf {w}\models ^-_{n}\phi [f]$
holds,
$\mathcal {M}, \mathbf {w}\models ^-_{n}\phi [f]$
holds,
![]() $\phi $
is falsified at the same triple. These two relations are defined by simultaneous induction on the construction of
$\phi $
is falsified at the same triple. These two relations are defined by simultaneous induction on the construction of
![]() $\phi \in \mathcal {FO}(\Omega )$
:
$\phi \in \mathcal {FO}(\Omega )$
:
 $$ \begin{align*} \mathcal{S},\mathbf{w}\models^\ast_nP\bar{x}_n[f] &\text{ iff } \mathcal{S}^\ast,\mathbf{w}\models_iP\bar{x}_n[f]\text{ iff } \mathtt{M}^\ast_{\mathbf{w}}\models_c P\bar{x}_n[f]\text{ iff } f(\bar{x}_n)\in P^{\mathtt{M}^\ast_{\mathbf{w}}}\\& \qquad\qquad\qquad\qquad\qquad\qquad\qquad P^n\in \Omega,\,\ast\in \{+,-\}\\\mathcal{S},\mathbf{w}\models^+_nx \equiv y[f] &\text{ iff } \mathcal{S}^+,\mathbf{w}\models_ix \equiv y[f]\text{ iff } \mathtt{M}^+_{\mathbf{w}}\models_{c}x \equiv y[f]\text{ iff } f(x) = f(y)\\\mathcal{S},\mathbf{w}\models^-_nx \equiv y[f] &\text{ iff } \mathcal{S}^-,\mathbf{w}\models_i\epsilon xy[f]\text{ iff } \mathtt{M}^-_{\mathbf{w}}\models_{c}\epsilon xy[f]\\\mathcal{S},\mathbf{w}\models^+_n(\psi\wedge\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^+_n\psi[f]\text{ and }\mathcal{S},\mathbf{w}\models^+_n\chi[f]\\\mathcal{S},\mathbf{w}\models^-_n(\psi\wedge\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^-_n\psi[f]\text{ or }\mathcal{S},\mathbf{w}\models^-_n\chi[f]\\\mathcal{S},\mathbf{w}\models^+_n(\psi\vee\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^+_n\psi[f]\text{ or }\mathcal{S},\mathbf{w}\models^+_n\chi[f]\\\mathcal{S},\mathbf{w}\models^-_n(\psi\vee\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^-_n\psi[f]\text{ and }\mathcal{S},\mathbf{w}\models^-_n\chi[f]\\\mathcal{S},\mathbf{w}\models^+_n(\psi\to\chi)[f] &\text{ iff } (\forall \mathbf{v}\geq \mathbf{w})(\mathcal{S},\mathbf{v}\not\models^+_n\psi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}, \mathbf{v}\models^+_n\chi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}])\\\mathcal{S},\mathbf{w}\models^-_n(\psi\to\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^+_n\psi[f]\text{ and }\mathcal{S},\mathbf{w}\models^-_n\chi[f]\\\mathcal{S},\mathbf{w}\models^+_n\sim\psi[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^-_n\psi[f]\\\mathcal{S},\mathbf{w}\models^-_n\sim\psi[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^+_n\psi[f]\\\mathcal{S},\mathbf{w}\models^+_n\exists x\psi[f] &\text{ iff } (\exists a\in U_{\mathbf{w}})(\mathcal{S},\mathbf{w}\models^+_n\psi[f[x/a]])\\\mathcal{S},\mathbf{w}\models^-_n\exists x\psi[f] &\text{ iff } (\forall \mathbf{v}\geq \mathbf{w})(\forall a\in U_{\mathbf{v}})(\mathcal{S},\mathbf{v}\models^-_n\psi[(f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}})[x/a]])\\\mathcal{S},\mathbf{w}\models^+_n\forall x\psi[f] &\text{ iff } (\forall \mathbf{v}\geq \mathbf{w})(\forall a\in U_{\mathbf{v}})(\mathcal{S},\mathbf{v}\models^+_n\psi[(f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}})[x/a]])\\\mathcal{S},\mathbf{w}\models^-_n\forall x\psi[f] &\text{ iff } (\exists a\in U_{\mathbf{w}})(\mathcal{S},\mathbf{w}\models^-_n\psi[f[x/a]]). \end{align*} $$
$$ \begin{align*} \mathcal{S},\mathbf{w}\models^\ast_nP\bar{x}_n[f] &\text{ iff } \mathcal{S}^\ast,\mathbf{w}\models_iP\bar{x}_n[f]\text{ iff } \mathtt{M}^\ast_{\mathbf{w}}\models_c P\bar{x}_n[f]\text{ iff } f(\bar{x}_n)\in P^{\mathtt{M}^\ast_{\mathbf{w}}}\\& \qquad\qquad\qquad\qquad\qquad\qquad\qquad P^n\in \Omega,\,\ast\in \{+,-\}\\\mathcal{S},\mathbf{w}\models^+_nx \equiv y[f] &\text{ iff } \mathcal{S}^+,\mathbf{w}\models_ix \equiv y[f]\text{ iff } \mathtt{M}^+_{\mathbf{w}}\models_{c}x \equiv y[f]\text{ iff } f(x) = f(y)\\\mathcal{S},\mathbf{w}\models^-_nx \equiv y[f] &\text{ iff } \mathcal{S}^-,\mathbf{w}\models_i\epsilon xy[f]\text{ iff } \mathtt{M}^-_{\mathbf{w}}\models_{c}\epsilon xy[f]\\\mathcal{S},\mathbf{w}\models^+_n(\psi\wedge\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^+_n\psi[f]\text{ and }\mathcal{S},\mathbf{w}\models^+_n\chi[f]\\\mathcal{S},\mathbf{w}\models^-_n(\psi\wedge\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^-_n\psi[f]\text{ or }\mathcal{S},\mathbf{w}\models^-_n\chi[f]\\\mathcal{S},\mathbf{w}\models^+_n(\psi\vee\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^+_n\psi[f]\text{ or }\mathcal{S},\mathbf{w}\models^+_n\chi[f]\\\mathcal{S},\mathbf{w}\models^-_n(\psi\vee\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^-_n\psi[f]\text{ and }\mathcal{S},\mathbf{w}\models^-_n\chi[f]\\\mathcal{S},\mathbf{w}\models^+_n(\psi\to\chi)[f] &\text{ iff } (\forall \mathbf{v}\geq \mathbf{w})(\mathcal{S},\mathbf{v}\not\models^+_n\psi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}, \mathbf{v}\models^+_n\chi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}])\\\mathcal{S},\mathbf{w}\models^-_n(\psi\to\chi)[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^+_n\psi[f]\text{ and }\mathcal{S},\mathbf{w}\models^-_n\chi[f]\\\mathcal{S},\mathbf{w}\models^+_n\sim\psi[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^-_n\psi[f]\\\mathcal{S},\mathbf{w}\models^-_n\sim\psi[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^+_n\psi[f]\\\mathcal{S},\mathbf{w}\models^+_n\exists x\psi[f] &\text{ iff } (\exists a\in U_{\mathbf{w}})(\mathcal{S},\mathbf{w}\models^+_n\psi[f[x/a]])\\\mathcal{S},\mathbf{w}\models^-_n\exists x\psi[f] &\text{ iff } (\forall \mathbf{v}\geq \mathbf{w})(\forall a\in U_{\mathbf{v}})(\mathcal{S},\mathbf{v}\models^-_n\psi[(f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}})[x/a]])\\\mathcal{S},\mathbf{w}\models^+_n\forall x\psi[f] &\text{ iff } (\forall \mathbf{v}\geq \mathbf{w})(\forall a\in U_{\mathbf{v}})(\mathcal{S},\mathbf{v}\models^+_n\psi[(f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}})[x/a]])\\\mathcal{S},\mathbf{w}\models^-_n\forall x\psi[f] &\text{ iff } (\exists a\in U_{\mathbf{w}})(\mathcal{S},\mathbf{w}\models^-_n\psi[f[x/a]]). \end{align*} $$
However, the negative satisfaction relation
![]() $\models ^-_{n}$
is often viewed within this pair as a subsidiary one, which, among other things, is due to the fact that the satisfaction clauses for negation allow to completely reflect the structure of
$\models ^-_{n}$
is often viewed within this pair as a subsidiary one, which, among other things, is due to the fact that the satisfaction clauses for negation allow to completely reflect the structure of
![]() $\models ^-_{n}$
within
$\models ^-_{n}$
within
![]() $\models ^+_{n}$
. Therefore, one can still capture
$\models ^+_{n}$
. Therefore, one can still capture
![]() $\mathsf {QN4}$
according to our usual pattern. In other words, we are going to prove the following.
$\mathsf {QN4}$
according to our usual pattern. In other words, we are going to prove the following.
Proposition 2. For every
![]() $\Omega \subseteq \Pi $
,
$\Omega \subseteq \Pi $
,
![]() $\mathsf {QN4}(\Omega ) = \mathbb {L}(EP_n(\Omega ), \models ^+_n)$
.
$\mathsf {QN4}(\Omega ) = \mathbb {L}(EP_n(\Omega ), \models ^+_n)$
.
The proof of this proposition makes a substantial use of the embedding
![]() $Tr$
defined above.Footnote
5
We sketch it in Appendix A.2. Another consequence of the tight relation between
$Tr$
defined above.Footnote
5
We sketch it in Appendix A.2. Another consequence of the tight relation between
![]() $\mathsf {QN4}$
and
$\mathsf {QN4}$
and
![]() $\mathsf {QIL}^+$
is that Lemma 1 carries over to Nelsonian sheaves.
$\mathsf {QIL}^+$
is that Lemma 1 carries over to Nelsonian sheaves.
Lemma 4. Let
![]() $\Omega \subseteq \Pi $
. For every
$\Omega \subseteq \Pi $
. For every
![]() $\ast \in \{+, -\}$
,
$\ast \in \{+, -\}$
,
![]() $(\mathcal {S}, \mathbf {w}, f)\in EP_{n}(\Omega )$
, and
$(\mathcal {S}, \mathbf {w}, f)\in EP_{n}(\Omega )$
, and
![]() $\phi \in \mathcal {FO}(\Omega )$
, we have:
$\phi \in \mathcal {FO}(\Omega )$
, we have:
-
1. If
 $\mathbf {v}\geq \mathbf {w}$
, and
$\mathbf {v}\geq \mathbf {w}$
, and
 $\mathcal {S},\mathbf {w}\models ^\ast _{n}\phi [f]$
, then
$\mathcal {S},\mathbf {w}\models ^\ast _{n}\phi [f]$
, then
 $\mathcal {S},\mathbf {v}\models ^\ast _{n}\phi [f\circ \mathtt {H}_{\mathbf {w}\mathbf {v}}]$
.
$\mathcal {S},\mathbf {v}\models ^\ast _{n}\phi [f\circ \mathtt {H}_{\mathbf {w}\mathbf {v}}]$
. -
2. The Nelsonian generated sub-sheaf
 $\mathcal {S}|_{\mathbf {w}} = (W|_{\mathbf {w}}, \leq |_{\mathbf {w}}, \mathtt {M}^+|_{\mathbf {w}}, \mathtt {M}^-|_{\mathbf {w}}, \mathtt {H}|_{\mathbf {w}})\in \mathbb {N}4(\Omega )$
is such that both
$\mathcal {S}|_{\mathbf {w}} = (W|_{\mathbf {w}}, \leq |_{\mathbf {w}}, \mathtt {M}^+|_{\mathbf {w}}, \mathtt {M}^-|_{\mathbf {w}}, \mathtt {H}|_{\mathbf {w}})\in \mathbb {N}4(\Omega )$
is such that both
 $(\mathcal {S}|_{\mathbf {w}})^+$
and
$(\mathcal {S}|_{\mathbf {w}})^+$
and
 $(\mathcal {S}|_{\mathbf {w}})^-$
are the generated sub-sheaves of
$(\mathcal {S}|_{\mathbf {w}})^-$
are the generated sub-sheaves of
 $\mathcal {S}^+$
and
$\mathcal {S}^+$
and
 $\mathcal {S}^-$
, respectively. Then, for every
$\mathcal {S}^-$
, respectively. Then, for every $$ \begin{align*}\mathcal{S}|_{\mathbf{w}},\mathbf{v}\models^\ast_{n}\phi[f]\text{ iff } \mathcal{S},\mathbf{v}\models^\ast_{n}\phi[f] \end{align*} $$
$$ \begin{align*}\mathcal{S}|_{\mathbf{w}},\mathbf{v}\models^\ast_{n}\phi[f]\text{ iff } \mathcal{S},\mathbf{v}\models^\ast_{n}\phi[f] \end{align*} $$
 $\mathbf {v}\geq \mathbf {w}$
and every
$\mathbf {v}\geq \mathbf {w}$
and every
 $f:Ind\to U_{\mathbf {v}}$
.
$f:Ind\to U_{\mathbf {v}}$
.
Proof of the lemma is relegated to Appendix A.3.
Remark 2. For the rest of the article, we will be suppressing
![]() $\Pi $
in notations like
$\Pi $
in notations like
![]() $\mathcal {FO}(\Pi )$
,
$\mathcal {FO}(\Pi )$
,
![]() $\mathbb {N}4(\Pi )$
,
$\mathbb {N}4(\Pi )$
,
![]() $EP_n(\Pi )$
, and
$EP_n(\Pi )$
, and
![]() $\mathsf {QN4}(\Pi )$
.
$\mathsf {QN4}(\Pi )$
.
In the remaining part of the section we develop
![]() $\mathsf {QN4}$
to an extent that is sufficient for the subsequent sections. As usual, it follows from our semantic definitions that the truth value of a formula
$\mathsf {QN4}$
to an extent that is sufficient for the subsequent sections. As usual, it follows from our semantic definitions that the truth value of a formula
![]() $\phi \in \mathcal {FO}$
only depends on the values assigned by f to the values of the variables in
$\phi \in \mathcal {FO}$
only depends on the values assigned by f to the values of the variables in
![]() $FV(\phi )$
. We will therefore write, for any
$FV(\phi )$
. We will therefore write, for any
![]() $\ast \in \{+, -\}$
,
$\ast \in \{+, -\}$
,
![]() $\mathcal {S}, \mathbf {w}\models ^\ast _{n}\phi [x_1/a_1,\ldots ,x_n/a_n]$
iff
$\mathcal {S}, \mathbf {w}\models ^\ast _{n}\phi [x_1/a_1,\ldots ,x_n/a_n]$
iff
![]() $\mathcal {S} \in \mathbb {N}4$
,
$\mathcal {S} \in \mathbb {N}4$
,
![]() $\mathbf {w} \in W$
,
$\mathbf {w} \in W$
,
![]() $\phi \in \mathcal {FO}^{\bar {x}_n}$
, and
$\phi \in \mathcal {FO}^{\bar {x}_n}$
, and
![]() $\mathcal {S}, \mathbf {w}\models ^\ast _{n}\phi [f]$
for every (equivalently, any) f such that both
$\mathcal {S}, \mathbf {w}\models ^\ast _{n}\phi [f]$
for every (equivalently, any) f such that both
![]() $(\mathcal {S}, \mathbf {w}, f) \in EP_{n}$
and
$(\mathcal {S}, \mathbf {w}, f) \in EP_{n}$
and
![]() $f(x_i) = a_i$
for every
$f(x_i) = a_i$
for every
![]() $1 \leq i \leq n$
. In particular, we will write
$1 \leq i \leq n$
. In particular, we will write
![]() $\mathcal {S}, \mathbf {w}\models ^\ast _{n}\phi $
iff
$\mathcal {S}, \mathbf {w}\models ^\ast _{n}\phi $
iff
![]() $\phi \in \mathcal {FO}^\emptyset $
and we have
$\phi \in \mathcal {FO}^\emptyset $
and we have
![]() $\mathcal {S}, \mathbf {w}\models ^\ast _{n}\phi [f]$
for every (equivalently, any) function f such that
$\mathcal {S}, \mathbf {w}\models ^\ast _{n}\phi [f]$
for every (equivalently, any) function f such that
![]() $(\mathcal {S}, \mathbf {w}, f) \in EP_{n}$
; we will write
$(\mathcal {S}, \mathbf {w}, f) \in EP_{n}$
; we will write
![]() $\mathcal {S}\models ^\ast _{n}\phi $
iff
$\mathcal {S}\models ^\ast _{n}\phi $
iff
![]() $\mathcal {S}, \mathbf {w}\models ^\ast _{n}\phi $
for every
$\mathcal {S}, \mathbf {w}\models ^\ast _{n}\phi $
for every
![]() $\mathbf {w}\in W$
. The conventions of this paragraph also extend to sets and bi-sets of formulas in an obvious way; furthermore, in what follows, we will also apply these notational conventions to both intuitionistic and classical semantics of the first-order languages.
$\mathbf {w}\in W$
. The conventions of this paragraph also extend to sets and bi-sets of formulas in an obvious way; furthermore, in what follows, we will also apply these notational conventions to both intuitionistic and classical semantics of the first-order languages.
Next, we introduce the following abbreviations for all
![]() $\phi , \psi \in \mathcal {FO}$
:
$\phi , \psi \in \mathcal {FO}$
:
-
•
 $\phi \Rightarrow \psi $
(strong implication) for
$\phi \Rightarrow \psi $
(strong implication) for
 $(\phi \to \psi )\wedge (\sim \psi \to \sim \phi )$
.
$(\phi \to \psi )\wedge (\sim \psi \to \sim \phi )$
. -
•
 $\phi \Leftrightarrow \psi $
(strong equivalence) for
$\phi \Leftrightarrow \psi $
(strong equivalence) for
 $(\phi \Rightarrow \psi )\wedge (\psi \Rightarrow \phi )$
, or, (equivalently, in view of Lemma 2), for
$(\phi \Rightarrow \psi )\wedge (\psi \Rightarrow \phi )$
, or, (equivalently, in view of Lemma 2), for
 $(\phi \leftrightarrow \psi )\wedge (\sim \phi \leftrightarrow \sim \psi )$
.
$(\phi \leftrightarrow \psi )\wedge (\sim \phi \leftrightarrow \sim \psi )$
. -
•
 $\phi \,\&\,\psi $
(ampersand) for
$\phi \,\&\,\psi $
(ampersand) for
 $\sim (\phi \to \sim \psi )$
.
$\sim (\phi \to \sim \psi )$
.
The following lemma lists some properties of these derived connectives.
Lemma 5. Let
![]() $\phi , \psi , \chi , \theta \in \mathcal {FO}$
be chosen arbitrarily. Then all of the following theorems hold in
$\phi , \psi , \chi , \theta \in \mathcal {FO}$
be chosen arbitrarily. Then all of the following theorems hold in
![]() $\mathsf {QN4}$
:
$\mathsf {QN4}$
:
Observe that (T9)–(T12) strengthen (in view of (T2)) the axioms (An1)–(An2) and (An5)–(An6), respectively. That this strengthening is non-trivial, follows from the fact that the converses of both (T1) and (T2) fail in general; moreover, one cannot replace
![]() $\leftrightarrow $
with
$\leftrightarrow $
with
![]() $\Leftrightarrow $
in (An4), (T15), or (T16).
$\Leftrightarrow $
in (An4), (T15), or (T16).
Finally, note that the following schemes are not, in general, valid in
![]() $\mathsf {QN4}$
:
$\mathsf {QN4}$
:
We sketch the proof in Appendix A.4.
Thus, even though our defined connectives wouldn’t make much sense in
![]() $\mathsf {QCL}$
as they are classically equivalent to
$\mathsf {QCL}$
as they are classically equivalent to
![]() $\to $
,
$\to $
,
![]() $\leftrightarrow $
, and
$\leftrightarrow $
, and
![]() $\wedge $
, respectively, we see that the situation is different in the context of
$\wedge $
, respectively, we see that the situation is different in the context of
![]() $\mathsf {QN4}$
. Indeed, whereas
$\mathsf {QN4}$
. Indeed, whereas
![]() $\to $
and
$\to $
and
![]() $\leftrightarrow $
in
$\leftrightarrow $
in
![]() $\mathsf {QN4}$
cannot be contraposed,
$\mathsf {QN4}$
cannot be contraposed,
![]() $\Rightarrow $
and
$\Rightarrow $
and
![]() $\Leftrightarrow $
define stronger (and contraposable) analogues to
$\Leftrightarrow $
define stronger (and contraposable) analogues to
![]() $\to $
and
$\to $
and
![]() $\leftrightarrow $
, respectively. Finally, the ampersand is especially convenient for handling the falsity conditions of restricted existential quantification in the context of
$\leftrightarrow $
, respectively. Finally, the ampersand is especially convenient for handling the falsity conditions of restricted existential quantification in the context of
![]() $\mathsf {QN4}$
. We provide a motivation for this use of ampersand in Appendix A.5.
$\mathsf {QN4}$
. We provide a motivation for this use of ampersand in Appendix A.5.
Note, furthermore, that the failure of theorems like
![]() $(\phi \leftrightarrow \psi )\to (\sim \phi \leftrightarrow \sim \psi )$
implies that provably equivalent formulas in general fail to be substitutable for one another in
$(\phi \leftrightarrow \psi )\to (\sim \phi \leftrightarrow \sim \psi )$
implies that provably equivalent formulas in general fail to be substitutable for one another in
![]() $\mathsf {QN4}$
. However, this failure does not extend to the strong equivalence; to the contrary, one can even prove that a substitution of strongly equivalent formulas results in a formula that is also strongly equivalent to the original one.
$\mathsf {QN4}$
. However, this failure does not extend to the strong equivalence; to the contrary, one can even prove that a substitution of strongly equivalent formulas results in a formula that is also strongly equivalent to the original one.
As is well-known, a substitution of one formula for another in a first-order context can lead to rather complicated definitions. For the purposes of our article it is sufficient to confine ourselves to the following one simple case.
If
![]() $\phi , \psi \in \mathcal {FO}$
then we denote by
$\phi , \psi \in \mathcal {FO}$
then we denote by
![]() $\phi /\psi $
the result of replacing every occurrence of
$\phi /\psi $
the result of replacing every occurrence of
![]() $v_0\equiv v_0$
in
$v_0\equiv v_0$
in
![]() $\phi $
by
$\phi $
by
![]() $\psi $
. The replacement operationFootnote
6
then commutes with all the connectives and quantifiers, and, for
$\psi $
. The replacement operationFootnote
6
then commutes with all the connectives and quantifiers, and, for
![]() $\phi \in At$
, we stipulate that:
$\phi \in At$
, we stipulate that:
 $$ \begin{align*}\phi/\psi:=\begin{cases} \psi,\text{ if }\phi = (v_0\equiv v_0)\\ \phi,\text{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}\phi/\psi:=\begin{cases} \psi,\text{ if }\phi = (v_0\equiv v_0)\\ \phi,\text{ otherwise.} \end{cases} \end{align*} $$
Then the following holds (see Appendix A.6 for a proof).
Lemma 6. For all
![]() $\phi , \psi , \chi \in \mathcal {FO}$
, we have
$\phi , \psi , \chi \in \mathcal {FO}$
, we have
An immediate consequence of Lemma 6 is that disjunction can also be understood as defined connective.
Corollary 1. For all
![]() $\phi , \psi , \chi \in \mathcal {FO}$
, we have
$\phi , \psi , \chi \in \mathcal {FO}$
, we have
![]() $\vdash _{\mathsf {QN4}}(\chi /(\phi \vee \psi ))\Leftrightarrow (\chi /(\sim (\sim \phi \wedge \sim \psi ))).$
$\vdash _{\mathsf {QN4}}(\chi /(\phi \vee \psi ))\Leftrightarrow (\chi /(\sim (\sim \phi \wedge \sim \psi ))).$
The formulas of the form
![]() $(\forall x)(\chi \to (\phi \Leftrightarrow \psi ))$
will play a prominent role in the subsequent sections. We would like, therefore, also to take a moment to spell out their truth conditions in terms of Nelsonian sheaf semantics.
$(\forall x)(\chi \to (\phi \Leftrightarrow \psi ))$
will play a prominent role in the subsequent sections. We would like, therefore, also to take a moment to spell out their truth conditions in terms of Nelsonian sheaf semantics.
Corollary 2. Let
![]() $x,y \in Ind$
be pairwise distinct, let
$x,y \in Ind$
be pairwise distinct, let
![]() $\phi \in \mathcal {FO}^{x,y}$
and let
$\phi \in \mathcal {FO}^{x,y}$
and let
![]() $\psi , \chi \in \mathcal {FO}^y$
. For every
$\psi , \chi \in \mathcal {FO}^y$
. For every
![]() $\mathcal {S}\in \mathbb {N}4$
, every
$\mathcal {S}\in \mathbb {N}4$
, every
![]() $\mathbf {w} \in W$
, and every
$\mathbf {w} \in W$
, and every
![]() $a \in U_{\mathbf {w}}$
, we have
$a \in U_{\mathbf {w}}$
, we have
iff, for every
![]() $\mathbf {v} \geq \mathbf {w}$
and every
$\mathbf {v} \geq \mathbf {w}$
and every
![]() $b \in U_{\mathbf {v}}$
such that
$b \in U_{\mathbf {v}}$
such that
![]() $\mathcal {S}, \mathbf {v}\models ^+_n \chi [x/b]$
we have both
$\mathcal {S}, \mathbf {v}\models ^+_n \chi [x/b]$
we have both
and
Proof By application of the definitions.
Moreover, we would like to state an application of Lemma 6 to formulas of this type as a separate corollary.
Corollary 3. For all
![]() $\phi , \psi , \chi , \theta \in \mathcal {FO}$
, we have
$\phi , \psi , \chi , \theta \in \mathcal {FO}$
, we have
Proof We reason as follows:
 $$ \begin{align} \vdash_{\mathsf{QN4}}(\chi\to (\phi\Leftrightarrow\psi))&\to (\chi\to((\theta/\phi)\Leftrightarrow(\theta/\psi)))\nonumber\\&\quad \text{by}\ ({T17}), \text{Lm}\ ({2}) \end{align} $$
$$ \begin{align} \vdash_{\mathsf{QN4}}(\chi\to (\phi\Leftrightarrow\psi))&\to (\chi\to((\theta/\phi)\Leftrightarrow(\theta/\psi)))\nonumber\\&\quad \text{by}\ ({T17}), \text{Lm}\ ({2}) \end{align} $$
5 Modal logics and their standard translation embeddings
Although modal logics are not the main subject of this article, they are so tightly connected to conditional logics based on the so-called Chellas semantics that a review of their standard translation embedding properties provides the best possible introduction to our main result. We start by setting
![]() $Prop:= \Pi \setminus \{S^1, O^1, E^2, R^3\} = \{p^1_n\mid n \in \omega \}$
. The modal language
$Prop:= \Pi \setminus \{S^1, O^1, E^2, R^3\} = \{p^1_n\mid n \in \omega \}$
. The modal language
![]() $\mathcal {MD}$
is generated from
$\mathcal {MD}$
is generated from
![]() $Prop$
by the following BNF:
$Prop$
by the following BNF:
where
![]() $p^1 \in Prop$
. In case we want to have
$p^1 \in Prop$
. In case we want to have
![]() $\Diamond \phi $
as an elementary modality rather than an abbreviation for
$\Diamond \phi $
as an elementary modality rather than an abbreviation for
![]() $\sim \Box \sim \phi $
, we obtain the language
$\sim \Box \sim \phi $
, we obtain the language
![]() $\mathcal {MD}^\Diamond $
. The Kripke semantics for this language uses the class
$\mathcal {MD}^\Diamond $
. The Kripke semantics for this language uses the class
![]() $pMod$
of pointed Kripke models as evaluation points and the modal satisfaction relation
$pMod$
of pointed Kripke models as evaluation points and the modal satisfaction relation
![]() $\models _m$
; the definitions of both can be easily found in any of the numerous textbooks, e.g., in [Reference Chagrov and Zakharyaschev2, Chapter 3.2]. The minimal normal modal logic
$\models _m$
; the definitions of both can be easily found in any of the numerous textbooks, e.g., in [Reference Chagrov and Zakharyaschev2, Chapter 3.2]. The minimal normal modal logic
![]() $\mathsf {K}$
can then be defined by
$\mathsf {K}$
can then be defined by
![]() $\mathsf {K}:= \mathbb {L}(pMod, \models _m)$
.
$\mathsf {K}:= \mathbb {L}(pMod, \models _m)$
.
If we now set
![]() $\mu := Prop\cup \{E^2\}$
and assume that, for every
$\mu := Prop\cup \{E^2\}$
and assume that, for every
![]() $x\in Ind$
we have fixed a
$x\in Ind$
we have fixed a
![]() $y\in Ind$
which is distinct from x, then the mapping
$y\in Ind$
which is distinct from x, then the mapping
![]() $\sigma \tau _x:\mathcal {MD}\to \mathcal {FO}(\mu )^x$
is definedFootnote
7
by induction on the construction of
$\sigma \tau _x:\mathcal {MD}\to \mathcal {FO}(\mu )^x$
is definedFootnote
7
by induction on the construction of
![]() $\phi \in \mathcal {MD}$
and is called the modal standard x-translation:
$\phi \in \mathcal {MD}$
and is called the modal standard x-translation:
 $$ \begin{align*} \sigma\tau_x(p)&:= px&&p^1 \in Prop\\ \sigma\tau_x(\sim\psi)&:= \sim \sigma\tau_x(\psi)\\ \sigma\tau_x(\psi\ast\chi)&:= \sigma\tau_x(\psi)\ast \sigma\tau_x(\chi)&&\ast\in \{\wedge, \vee, \to\}\\ \sigma\tau_x(\Box\psi) &:= \forall y(Exy\to \sigma\tau_{y}(\psi)). \end{align*} $$
$$ \begin{align*} \sigma\tau_x(p)&:= px&&p^1 \in Prop\\ \sigma\tau_x(\sim\psi)&:= \sim \sigma\tau_x(\psi)\\ \sigma\tau_x(\psi\ast\chi)&:= \sigma\tau_x(\psi)\ast \sigma\tau_x(\chi)&&\ast\in \{\wedge, \vee, \to\}\\ \sigma\tau_x(\Box\psi) &:= \forall y(Exy\to \sigma\tau_{y}(\psi)). \end{align*} $$
The following lemma is then often presented without any proof in the existing literature.
Lemma 7. For every
![]() $x\in Ind$
, every
$x\in Ind$
, every
![]() $\phi \in \mathcal {MD,}$
and every
$\phi \in \mathcal {MD,}$
and every
![]() $(\mathcal {M}, \mathbf {w})\in pMod$
, we have
$(\mathcal {M}, \mathbf {w})\in pMod$
, we have
![]() $\mathcal {M}, \mathbf {w}\models _m\phi $
iff
$\mathcal {M}, \mathbf {w}\models _m\phi $
iff
![]() $\mathcal {M} \models _c\sigma \tau _x(\phi )[x/\mathbf {w}]$
.
$\mathcal {M} \models _c\sigma \tau _x(\phi )[x/\mathbf {w}]$
.
Lemma 7 comes across as very natural, indeed, almost self-evident: the class of Kripke models for modal logic is just another name for
![]() $\mathbb {C}(\mu )$
,
$\mathbb {C}(\mu )$
,
![]() $x\in Ind$
chooses a point, turning it into a pointed structure, and the definition of
$x\in Ind$
chooses a point, turning it into a pointed structure, and the definition of
![]() $\sigma \tau _x$
is just a direct formalization of the inductive definition of
$\sigma \tau _x$
is just a direct formalization of the inductive definition of
![]() $\models _m$
in first-order logic.
$\models _m$
in first-order logic.
It is then just a small step to get from Lemma 7 to the following.
Proposition 3. For all
![]() $\Gamma , \Delta \subseteq \mathcal {MD}$
and for every
$\Gamma , \Delta \subseteq \mathcal {MD}$
and for every
![]() $x \in Ind$
, we have
$x \in Ind$
, we have
![]() $\Gamma \models _{\mathsf {K}} \Delta $
iff
$\Gamma \models _{\mathsf {K}} \Delta $
iff
![]() $\sigma \tau _x(\Gamma )\models _{\mathsf {QCL}}\sigma \tau _x(\Delta )$
.
$\sigma \tau _x(\Gamma )\models _{\mathsf {QCL}}\sigma \tau _x(\Delta )$
.
In other words, we find that
![]() $\sigma \tau _x$
faithfully embeds
$\sigma \tau _x$
faithfully embeds
![]() $\mathsf {K}$
into
$\mathsf {K}$
into
![]() $\mathsf {QCL}(\mu )$
for every
$\mathsf {QCL}(\mu )$
for every
![]() $x\in Ind$
.
$x\in Ind$
.
The main line of thought presented in the article can be viewed as a natural continuation of this very idea. However, before we get to it, we need to observe that things become more complicated as soon as we replace the classical propositional basis of
![]() $\mathsf {K}$
with some non-classical logic. For example, the basic intuitionistic modal logic
$\mathsf {K}$
with some non-classical logic. For example, the basic intuitionistic modal logic
![]() $\mathsf {IK}$
(see, e.g., [Reference Fischer-Servi and Chiara5]) is supplied with a Kripke semantics of bi-relational models over a classical metalanguage. This immediately results in an analogue of Proposition 3 saying that a straightforward formalization of this semantics amounts to defining an embedding of
$\mathsf {IK}$
(see, e.g., [Reference Fischer-Servi and Chiara5]) is supplied with a Kripke semantics of bi-relational models over a classical metalanguage. This immediately results in an analogue of Proposition 3 saying that a straightforward formalization of this semantics amounts to defining an embedding of
![]() $\mathsf {IK}$
into a classical first-order correspondence language based on two binary predicates.Footnote
8
However, and much more interestingly,
$\mathsf {IK}$
into a classical first-order correspondence language based on two binary predicates.Footnote
8
However, and much more interestingly,
![]() $\sigma \tau _x$
turns out to be useful for
$\sigma \tau _x$
turns out to be useful for
![]() $\mathsf {IK}$
, too, as it happens to embed it into
$\mathsf {IK}$
, too, as it happens to embed it into
![]() $\mathsf {QIL}(\mu )$
. This result, which is far from being trivial (one version of its proof can found in [Reference Simpson13, Chapter 5]), suggests that
$\mathsf {QIL}(\mu )$
. This result, which is far from being trivial (one version of its proof can found in [Reference Simpson13, Chapter 5]), suggests that
![]() $\mathsf {IK}$
carves out exactly the same fragment of
$\mathsf {IK}$
carves out exactly the same fragment of
![]() $\mathsf {QIL}(\mu )$
as the one carved out by
$\mathsf {QIL}(\mu )$
as the one carved out by
![]() $\mathsf {K}$
in
$\mathsf {K}$
in
![]() $\mathsf {QCL}(\mu )$
; and the latter circumstance provides a strong argument in favor of viewing
$\mathsf {QCL}(\mu )$
; and the latter circumstance provides a strong argument in favor of viewing
![]() $\mathsf {IK}$
as the correct intuitionistic analogue of
$\mathsf {IK}$
as the correct intuitionistic analogue of
![]() $\mathsf {K}$
.
$\mathsf {K}$
.
One may picture this situation as follows: assume that an intuitionist gets interested in modal logic, and asks a classicist colleague to explain them
![]() $\mathsf {K}$
. It is natural to expect that this explanation, if it is to be given in precise terms, will end up mentioning
$\mathsf {K}$
. It is natural to expect that this explanation, if it is to be given in precise terms, will end up mentioning
![]() $\sigma \tau _x$
at some point. Of course, the intuitionist will read the definition of
$\sigma \tau _x$
at some point. Of course, the intuitionist will read the definition of
![]() $\sigma \tau _x$
in terms of
$\sigma \tau _x$
in terms of
![]() $\mathsf {QIL}$
rather than
$\mathsf {QIL}$
rather than
![]() $\mathsf {QCL}$
and thus will end up with
$\mathsf {QCL}$
and thus will end up with
![]() $\mathsf {IK}$
. In a sense then,
$\mathsf {IK}$
. In a sense then,
![]() $\mathsf {IK}$
is nothing but
$\mathsf {IK}$
is nothing but
![]() $\mathsf {K}$
read intuitionistically.
$\mathsf {K}$
read intuitionistically.
Moreover, it is easy to see that at most one intuitionistic modal logic can be faithfully embedded by
![]() $\sigma \tau _x$
into
$\sigma \tau _x$
into
![]() $\mathsf {QIL}(\mu )$
. In this sense,
$\mathsf {QIL}(\mu )$
. In this sense,
![]() $\mathsf {IK}$
can be called the correct intuitionistic counterpart to
$\mathsf {IK}$
can be called the correct intuitionistic counterpart to
![]() $\mathsf {K}$
. We may even try to elevate this to a general criterion: given a non-classical logic
$\mathsf {K}$
. We may even try to elevate this to a general criterion: given a non-classical logic
![]() $Q\nu $
such that
$Q\nu $
such that
![]() $Q\nu $
is a proper sublogic of
$Q\nu $
is a proper sublogic of
![]() $\mathsf {QCL}$
and its propositional fragment
$\mathsf {QCL}$
and its propositional fragment
![]() $\nu $
is a proper sublogic of
$\nu $
is a proper sublogic of
![]() $\mathsf {CL}$
, a modal extension
$\mathsf {CL}$
, a modal extension
![]() $\nu \mathsf {K}$
of
$\nu \mathsf {K}$
of
![]() $\nu $
is the
$\nu $
is the
![]() $\nu $
-based counterpart of
$\nu $
-based counterpart of
![]() $\mathsf {K}$
iff
$\mathsf {K}$
iff
![]() $\sigma \tau _x$
faithfully embeds
$\sigma \tau _x$
faithfully embeds
![]() $\nu \mathsf {K}$
into
$\nu \mathsf {K}$
into
![]() $\mathsf {Q}\nu (\mu )$
.
$\mathsf {Q}\nu (\mu )$
.
Yet, the very deep and enlightening result about
![]() $\mathsf {IK}$
is not without its little annoying wrinkles. Observe that
$\mathsf {IK}$
is not without its little annoying wrinkles. Observe that
![]() $\mathsf {IK}$
is formulated over
$\mathsf {IK}$
is formulated over
![]() $\mathcal {MD}^\Diamond $
rather than
$\mathcal {MD}^\Diamond $
rather than
![]() $\mathcal {MD}$
as the diamond is no longer definable in terms of box. Therefore, the above definition of
$\mathcal {MD}$
as the diamond is no longer definable in terms of box. Therefore, the above definition of
![]() $\sigma \tau _x$
is no longer sufficient, as it has to include
$\sigma \tau _x$
is no longer sufficient, as it has to include
as an additional clause. Of course, this clause is implied by the above definition of
![]() $\sigma \tau _x$
over
$\sigma \tau _x$
over
![]() $\mathsf {QCL}$
and thus adding it to the definition of
$\mathsf {QCL}$
and thus adding it to the definition of
![]() $\sigma \tau _x$
results in a classically equivalent reformulation
$\sigma \tau _x$
results in a classically equivalent reformulation
![]() $\sigma \tau ^i_x$
of
$\sigma \tau ^i_x$
of
![]() $\sigma \tau _x$
. However, other classically equivalent formulations of
$\sigma \tau _x$
. However, other classically equivalent formulations of
![]() $\sigma \tau _x$
are also possible, and some of them make the analogue of Proposition 3 fail for
$\sigma \tau _x$
are also possible, and some of them make the analogue of Proposition 3 fail for
![]() $\mathsf {IK}$
and
$\mathsf {IK}$
and
![]() $\mathsf {QIL}$
. Think, for example, of the extension
$\mathsf {QIL}$
. Think, for example, of the extension
![]() $\sigma \tau ^j_x$
of
$\sigma \tau ^j_x$
of
![]() $\sigma \tau _x$
with the following clause:
$\sigma \tau _x$
with the following clause:
The choice of a right classical reformulation of
![]() $\sigma \tau _x$
can therefore affect the truth of our analogue of Proposition 3 in the intuitionistic case. Its precise formulation, then, goes as follows.
$\sigma \tau _x$
can therefore affect the truth of our analogue of Proposition 3 in the intuitionistic case. Its precise formulation, then, goes as follows.
Proposition 4. There exists a classically equivalent reformulation
![]() $\sigma \tau ^i_x$
of
$\sigma \tau ^i_x$
of
![]() $\sigma \tau _x$
such that, for all
$\sigma \tau _x$
such that, for all
![]() $\Gamma , \Delta \subseteq \mathcal {MD}^\Diamond $
and for every
$\Gamma , \Delta \subseteq \mathcal {MD}^\Diamond $
and for every
![]() $x \in Ind$
, we have
$x \in Ind$
, we have
![]() $\Gamma \models _{\mathsf {IK}} \Delta $
iff
$\Gamma \models _{\mathsf {IK}} \Delta $
iff
![]() $\sigma \tau ^i_x(\Gamma )\models _{\mathsf {QIL}}\sigma \tau ^i_x(\Delta )$
.
$\sigma \tau ^i_x(\Gamma )\models _{\mathsf {QIL}}\sigma \tau ^i_x(\Delta )$
.
Of course, the required classical reformulation is pretty clear in the case of
![]() $\mathsf {IK}$
; in fact, it is so clear that one is tempted to dismiss the existential quantifier in the formulation of Proposition 4 as mere pedantry and to speak of just
$\mathsf {IK}$
; in fact, it is so clear that one is tempted to dismiss the existential quantifier in the formulation of Proposition 4 as mere pedantry and to speak of just
![]() $\sigma \tau _x$
instead. However, we need to be mindful of the fact that our caveat ‘up to a classically equivalent reformulation’ reflects a very real possibility that (to continue with our metaphorical scenario) in explaining the semantics of
$\sigma \tau _x$
instead. However, we need to be mindful of the fact that our caveat ‘up to a classically equivalent reformulation’ reflects a very real possibility that (to continue with our metaphorical scenario) in explaining the semantics of
![]() $\mathsf {K}$
to an interested intuitionist, the classicist modal logician might slip up and explain the semantics of diamond according to (6) rather than (5), which might lead, on the side of the intuitionist colleague, to a logic that is distinct from
$\mathsf {K}$
to an interested intuitionist, the classicist modal logician might slip up and explain the semantics of diamond according to (6) rather than (5), which might lead, on the side of the intuitionist colleague, to a logic that is distinct from
![]() $\mathsf {IK}$
. In other words, our caveat uncovers the fact that
$\mathsf {IK}$
. In other words, our caveat uncovers the fact that
![]() $\mathsf {IK}$
is the result of the intuitionistic reading of
$\mathsf {IK}$
is the result of the intuitionistic reading of
![]() $\mathsf {K}$
only up to a certain wording of
$\mathsf {K}$
only up to a certain wording of
![]() $\mathsf {K}$
.
$\mathsf {K}$
.
Given these considerations, our tentative principle for seeking out non-classical counterparts for
![]() $\mathsf {K}$
needs to be corrected as follows: given a non-classical logic
$\mathsf {K}$
needs to be corrected as follows: given a non-classical logic
![]() $Q\nu $
such that
$Q\nu $
such that
![]() $Q\nu $
is a proper sublogic of
$Q\nu $
is a proper sublogic of
![]() $\mathsf {QCL}$
and its propositional fragment
$\mathsf {QCL}$
and its propositional fragment
![]() $\nu $
is a proper sublogic of
$\nu $
is a proper sublogic of
![]() $\mathsf {CL}$
, a modal extension
$\mathsf {CL}$
, a modal extension
![]() $\nu \mathsf {K}$
of
$\nu \mathsf {K}$
of
![]() $\nu $
is a
$\nu $
is a
![]() $\nu $
-based counterpart of
$\nu $
-based counterpart of
![]() $\mathsf {K}$
iff some classically equivalent reformulation of
$\mathsf {K}$
iff some classically equivalent reformulation of
![]() $\sigma \tau _x$
faithfully embeds
$\sigma \tau _x$
faithfully embeds
![]() $\nu \mathsf {K}$
into
$\nu \mathsf {K}$
into
![]() $\mathsf {Q}\nu (\mu )$
; the comparative merits of different
$\mathsf {Q}\nu (\mu )$
; the comparative merits of different
![]() $\nu $
-based counterparts of
$\nu $
-based counterparts of
![]() $\mathsf {K}$
will then have to be judged on the basis of other properties of
$\mathsf {K}$
will then have to be judged on the basis of other properties of
![]() $Q\nu $
.
$Q\nu $
.
Apart from
![]() $\mathsf {IL}$
,
$\mathsf {IL}$
,
![]() $\mathsf {N4}$
provides another possible instantiation of
$\mathsf {N4}$
provides another possible instantiation of
![]() $\nu $
in the above principle; in fact we are not the first to notice this, as the paper [Reference Odintsov, Wansing and Hendricks10] by S. Odintsov and H. Wansing both defines several
$\nu $
in the above principle; in fact we are not the first to notice this, as the paper [Reference Odintsov, Wansing and Hendricks10] by S. Odintsov and H. Wansing both defines several
![]() $\mathsf {N4}$
-based analogues of
$\mathsf {N4}$
-based analogues of
![]() $\mathsf {K}$
and looks into their standard translation embeddings into
$\mathsf {K}$
and looks into their standard translation embeddings into
![]() $\mathsf {QN4}(\mu )$
. In the context of this article, the most interesting of these results is [Reference Odintsov, Wansing and Hendricks10, Proposition 7], which shows that the
$\mathsf {QN4}(\mu )$
. In the context of this article, the most interesting of these results is [Reference Odintsov, Wansing and Hendricks10, Proposition 7], which shows that the
![]() $\mathsf {N4}$
-based modal logic
$\mathsf {N4}$
-based modal logic
![]() $\mathsf {FSK}^d$
is faithfully embedded into
$\mathsf {FSK}^d$
is faithfully embedded into
![]() $\mathsf {QN4}(\mu )$
by a standard translation
$\mathsf {QN4}(\mu )$
by a standard translation
![]() $T^{\prime }_x$
which provides yet another classical equivalent to
$T^{\prime }_x$
which provides yet another classical equivalent to
![]() $\sigma \tau _x$
. Although [Reference Odintsov, Wansing and Hendricks10] defines
$\sigma \tau _x$
. Although [Reference Odintsov, Wansing and Hendricks10] defines
![]() $\mathsf {FSK}^d$
over
$\mathsf {FSK}^d$
over
![]() $\mathcal {MD}^\Diamond $
, the logic also derives the classical definition of
$\mathcal {MD}^\Diamond $
, the logic also derives the classical definition of
![]() $\Diamond $
in terms of
$\Diamond $
in terms of
![]() $\Box $
which makes it possible to alternatively define
$\Box $
which makes it possible to alternatively define
![]() $\mathsf {FSK}^d$
and
$\mathsf {FSK}^d$
and
![]() $T^{\prime }_x$
over
$T^{\prime }_x$
over
![]() $\mathcal {MD}$
.Footnote
9
The result of [Reference Odintsov, Wansing and Hendricks10] can then be reformulated in the terminology of this article as follows.
$\mathcal {MD}$
.Footnote
9
The result of [Reference Odintsov, Wansing and Hendricks10] can then be reformulated in the terminology of this article as follows.
Proposition 5. There exists a classically equivalent reformulation
![]() $T^{\prime }_x$
of
$T^{\prime }_x$
of
![]() $\sigma \tau _x$
such that, for all
$\sigma \tau _x$
such that, for all
![]() $\Gamma , \Delta \subseteq \mathcal {MD}$
and for every
$\Gamma , \Delta \subseteq \mathcal {MD}$
and for every
![]() $x \in Ind$
, we have
$x \in Ind$
, we have
![]() $\Gamma \models _{\mathsf {FSK}^d} \Delta $
iff
$\Gamma \models _{\mathsf {FSK}^d} \Delta $
iff
![]() $T^{\prime }_x(\Gamma )\models _{\mathsf {QN4}}T^{\prime }_x(\Delta )$
.
$T^{\prime }_x(\Gamma )\models _{\mathsf {QN4}}T^{\prime }_x(\Delta )$
.
Unfortunately,
![]() $T^{\prime }_x$
looks a bit clumsy in that it fails to commute (up to a strong equivalence) with the propositional connectives of
$T^{\prime }_x$
looks a bit clumsy in that it fails to commute (up to a strong equivalence) with the propositional connectives of
![]() $\mathsf {N4}$
. For example, given a
$\mathsf {N4}$
. For example, given a
![]() $p^1 \in Prop$
, we have
$p^1 \in Prop$
, we have
![]() $T^{\prime }_x(\Box p) = \forall y(Rxy \to py)$
, but also
$T^{\prime }_x(\Box p) = \forall y(Rxy \to py)$
, but also
![]() ${T^{\prime }_x(\sim \Box p) = \exists y(Rxy \wedge \sim py)}$
, whereas
${T^{\prime }_x(\sim \Box p) = \exists y(Rxy \wedge \sim py)}$
, whereas
![]() $\sim T^{\prime }_x(\Box p) = \sim \forall y(Rxy \to py)$
, and the latter formula is clearly equivalent to
$\sim T^{\prime }_x(\Box p) = \sim \forall y(Rxy \to py)$
, and the latter formula is clearly equivalent to
![]() $\exists y(Rxy\,\&\,\sim py)$
rather than
$\exists y(Rxy\,\&\,\sim py)$
rather than
![]() $T^{\prime }_x(\sim \Box p)$
. Whereas (T15) ensures that
$T^{\prime }_x(\sim \Box p)$
. Whereas (T15) ensures that
![]() $\exists y(Rxy\,\&\,\sim py)\leftrightarrow \exists y(Rxy \wedge \sim py)$
, we fail to get the strong equivalence between the two formulas.
$\exists y(Rxy\,\&\,\sim py)\leftrightarrow \exists y(Rxy \wedge \sim py)$
, we fail to get the strong equivalence between the two formulas.
Still, Proposition 5 shows that some sort of an
![]() $\mathsf {N4}$
-based analogue to Propositions 3 and 4 is possible and that
$\mathsf {N4}$
-based analogue to Propositions 3 and 4 is possible and that
![]() $\mathsf {FSK}^d$
, at least to some extent, can be viewed as an
$\mathsf {FSK}^d$
, at least to some extent, can be viewed as an
![]() $\mathsf {N4}$
-based counterpart of
$\mathsf {N4}$
-based counterpart of
![]() $\mathsf {K}$
.
$\mathsf {K}$
.
6
 $\mathsf {CK}$
, the minimal classical logic of conditionals
$\mathsf {CK}$
, the minimal classical logic of conditionals
In this section we will introduce the language of conditional propositional logic (conditional language for short), which we will denote by
![]() $\mathcal {CN}$
. The language is generated from
$\mathcal {CN}$
. The language is generated from
![]() $Prop$
by the following BNF:
$Prop$
by the following BNF:
where
![]() $p^1 \in Prop$
. The new connective
$p^1 \in Prop$
. The new connective ![]() will be referred to as would-conditional or simply conditional; the elements of
will be referred to as would-conditional or simply conditional; the elements of
![]() $\mathcal {CN}$
will be called conditional formulas. We will apply to the conditional formulas all of the abbreviations introduced earlier for the connectives in
$\mathcal {CN}$
will be called conditional formulas. We will apply to the conditional formulas all of the abbreviations introduced earlier for the connectives in
![]() $\mathcal {FO}$
, plus the following new one:
$\mathcal {FO}$
, plus the following new one:
-
•
 (might-conditional) for
(might-conditional) for  .
.
One relatively popular and well-researched semantics for
![]() $\mathcal {CN}$
is the so-called Chellas semantics. In this article, we will use Chellas semantics to define two logics over
$\mathcal {CN}$
is the so-called Chellas semantics. In this article, we will use Chellas semantics to define two logics over
![]() $\mathcal {CN}$
, denoted by
$\mathcal {CN}$
, denoted by
![]() $\mathsf {CK}$
and
$\mathsf {CK}$
and
![]() $\mathsf {N4CK}$
, respectively. We begin by defining our models.
$\mathsf {N4CK}$
, respectively. We begin by defining our models.
Definition 5. A classical conditional model is a structure of the form
![]() $\mathcal {M} = (W, R, V)$
, such that:
$\mathcal {M} = (W, R, V)$
, such that:
-
1.
 $W \neq \emptyset $
is a set of worlds, or nodes.
$W \neq \emptyset $
is a set of worlds, or nodes. -
2.
 $R \subseteq W \times \mathcal {P}(W)\times W$
is the accessibility relation. Thus, for every
$R \subseteq W \times \mathcal {P}(W)\times W$
is the accessibility relation. Thus, for every
 $X \subseteq W$
, R induces a binary relation
$X \subseteq W$
, R induces a binary relation
 $R_X$
on W such that, for all
$R_X$
on W such that, for all
 $\mathbf {w},\mathbf {v} \in W$
,
$\mathbf {w},\mathbf {v} \in W$
,
 $R_X(\mathbf {w},\mathbf {v})$
iff
$R_X(\mathbf {w},\mathbf {v})$
iff
 $R(\mathbf {w}, X, \mathbf {v})$
.
$R(\mathbf {w}, X, \mathbf {v})$
. -
3.
 $V:Prop\to \mathcal {P}(W)$
, called evaluation function.
$V:Prop\to \mathcal {P}(W)$
, called evaluation function.
The class of all classical conditional models will be denoted by
![]() $\mathbb {CK}$
.
$\mathbb {CK}$
.
The absence of bound variables in
![]() $\mathcal {CN}$
allows for a shorter definition of evaluation points compared to the one we had in the first-order case: we simply set
$\mathcal {CN}$
allows for a shorter definition of evaluation points compared to the one we had in the first-order case: we simply set
The satisfaction relation (denoted by
![]() $\models _{ck}$
) is then supplied by the following definition:
$\models _{ck}$
) is then supplied by the following definition:

where
![]() $\|\psi \|^{ck}_{\mathcal {M}} := \{\mathbf {w}\in W\mid \mathcal {M}, \mathbf {w}\models _{ck}\psi \}$
. Having thus defined the intended semantics for the classical conditional logic, we set
$\|\psi \|^{ck}_{\mathcal {M}} := \{\mathbf {w}\in W\mid \mathcal {M}, \mathbf {w}\models _{ck}\psi \}$
. Having thus defined the intended semantics for the classical conditional logic, we set
![]() $\mathsf {CK} = \mathbb {L}(EP_{ck}, \models _{ck})$
.
$\mathsf {CK} = \mathbb {L}(EP_{ck}, \models _{ck})$
.
It is easy to see that
![]() $\mathsf {CK}$
extends
$\mathsf {CK}$
extends
![]() $\mathsf {CL}$
. Furthermore, our semantics represents conditionals as a sort of modal sentences where the box is indexed by the antecedent; in other words, it generates a binary
$\mathsf {CL}$
. Furthermore, our semantics represents conditionals as a sort of modal sentences where the box is indexed by the antecedent; in other words, it generates a binary
![]() $\phi $
-accessibility relation for every
$\phi $
-accessibility relation for every
![]() $\phi \in \mathcal {CN}$
and reads a conditional ‘if
$\phi \in \mathcal {CN}$
and reads a conditional ‘if
![]() $\phi $
then
$\phi $
then
![]() $\psi $
’ as something like ‘it is
$\psi $
’ as something like ‘it is
![]() $\phi $
-necessary that
$\phi $
-necessary that
![]() $\psi $
’. This connection leads to some obvious correspondences between normal modal logics and conditional logics based on Chellas semantics: indeed, one can meaningfully ask what kind of modalities are we dealing with when we view the conditionals of a given logic as nothing but formula-indexed modal boxes, and these considerations lead us to the notion of a modal companion of a given conditional logic. For example, the formula-indexed boxes assumed by the conditionals in
$\psi $
’. This connection leads to some obvious correspondences between normal modal logics and conditional logics based on Chellas semantics: indeed, one can meaningfully ask what kind of modalities are we dealing with when we view the conditionals of a given logic as nothing but formula-indexed modal boxes, and these considerations lead us to the notion of a modal companion of a given conditional logic. For example, the formula-indexed boxes assumed by the conditionals in
![]() $\mathsf {CK}$
can be viewed as
$\mathsf {CK}$
can be viewed as
![]() $\mathsf {K}$
-boxes, which, for every
$\mathsf {K}$
-boxes, which, for every
![]() $\phi \in \mathcal {CN}$
, is attested by the existence of the faithful embedding
$\phi \in \mathcal {CN}$
, is attested by the existence of the faithful embedding
![]() $\eta _\phi $
of
$\eta _\phi $
of
![]() $\mathsf {K}$
into
$\mathsf {K}$
into
![]() $\mathsf {CK}$
which commutes with the propositional connectives and reads modal boxes as conditionals with
$\mathsf {CK}$
which commutes with the propositional connectives and reads modal boxes as conditionals with
![]() $\phi $
as the antecedent.
$\phi $
as the antecedent.
Thus the idea of standard translation, at least for the conditional logics based on Chellas semantics, readily suggests itself. Of course, our accessibility relation is now ternary, so we have to use
![]() $R^3$
instead of
$R^3$
instead of
![]() $E^2$
in the correspondence language. An additional difficulty is that our binary accessibility relations are generated from
$E^2$
in the correspondence language. An additional difficulty is that our binary accessibility relations are generated from
![]() $R^3$
by truth-sets of the conditional formulas, therefore, our semantics has to say something not only about particular nodes in a Kripke model, but also about certain subsets of this model. Thus we must allow for two kinds of items in the first-order correspondence language, the nodes of the corresponding Kripke model and the subsets thereof; we need, therefore, to add two additional unary predicates to our correspondence language. In our article we denote them
$R^3$
by truth-sets of the conditional formulas, therefore, our semantics has to say something not only about particular nodes in a Kripke model, but also about certain subsets of this model. Thus we must allow for two kinds of items in the first-order correspondence language, the nodes of the corresponding Kripke model and the subsets thereof; we need, therefore, to add two additional unary predicates to our correspondence language. In our article we denote them
![]() $S^1$
and
$S^1$
and
![]() $O^1$
(for ‘sets’ and ‘objects’). Next, we must be able to express that some sets are in fact truth sets of certain conditional formulas, that is to say that an item of the object kind is their element iff this item verifies a given conditional formula, which further means that we have to allow the elementhood relation into the correspondence language. In what follows, we will denote this relation by
$O^1$
(for ‘sets’ and ‘objects’). Next, we must be able to express that some sets are in fact truth sets of certain conditional formulas, that is to say that an item of the object kind is their element iff this item verifies a given conditional formula, which further means that we have to allow the elementhood relation into the correspondence language. In what follows, we will denote this relation by
![]() $E^2$
. To sum up, our correspondence language turns out to be just
$E^2$
. To sum up, our correspondence language turns out to be just
![]() $\mathcal {FO}(\Pi ) = \mathcal {FO}$
.
$\mathcal {FO}(\Pi ) = \mathcal {FO}$
.
Given this informal interpretation of the predicates in
![]() $\Pi $
, the following definition is just a straightforward first-order formalization of the inductive definition of
$\Pi $
, the following definition is just a straightforward first-order formalization of the inductive definition of
![]() $\models _{ck}$
. For every
$\models _{ck}$
. For every
![]() $x \in Ind$
, let us fix
$x \in Ind$
, let us fix
![]() $y,z,w \in Ind$
such that
$y,z,w \in Ind$
such that
![]() $x,y,z,w$
are pairwise distinct. Moreover, for any given
$x,y,z,w$
are pairwise distinct. Moreover, for any given
![]() $\phi \in \mathcal {FO}$
let
$\phi \in \mathcal {FO}$
let
![]() $(\forall x)_O\phi $
abbreviate
$(\forall x)_O\phi $
abbreviate
![]() $\forall x(Ox\to \phi )$
. The classical standard x-translation
$\forall x(Ox\to \phi )$
. The classical standard x-translation
![]() $st_x:\mathcal {CN} \to \mathcal {FO}^x$
is given by induction on the construction of a
$st_x:\mathcal {CN} \to \mathcal {FO}^x$
is given by induction on the construction of a
![]() $\phi \in \mathcal {CN}$
:
$\phi \in \mathcal {CN}$
:

Of course, in order for
![]() $st_x$
to work correctly, the interaction between S,
$st_x$
to work correctly, the interaction between S,
![]() $O,$
and E must in fact resemble the interaction between sets of worlds and worlds in a classical conditional model. Although E does not need to be a ‘real’ elementhood verifying anything like ZFC, we can at least expect that E satisfies a variant of the extensionality axiom in that we do not have multiple copies of the same truth-set; moreover, sufficiently many instances of set-theoretic comprehension must hold in order to guarantee that at least one copy of a truth-set for any given
$O,$
and E must in fact resemble the interaction between sets of worlds and worlds in a classical conditional model. Although E does not need to be a ‘real’ elementhood verifying anything like ZFC, we can at least expect that E satisfies a variant of the extensionality axiom in that we do not have multiple copies of the same truth-set; moreover, sufficiently many instances of set-theoretic comprehension must hold in order to guarantee that at least one copy of a truth-set for any given
![]() $\phi \in \mathcal {CN}$
is contained in the extension of the S predicate. The following first-order theory
$\phi \in \mathcal {CN}$
is contained in the extension of the S predicate. The following first-order theory
![]() $Th_{ck}\subseteq \mathcal {FO}^\emptyset $
sums up these requirements:
$Th_{ck}\subseteq \mathcal {FO}^\emptyset $
sums up these requirements:
It is easy to show that this, relatively lightweight, encoding of the subset structure of a classical conditional model is sufficient to turn
![]() $st_x$
into a faithful embedding of
$st_x$
into a faithful embedding of
![]() $\mathsf {CK}$
into
$\mathsf {CK}$
into
![]() $\mathsf {QCL}$
. Although the proof of the fact that
$\mathsf {QCL}$
. Although the proof of the fact that
![]() $st_x$
faithfully embeds
$st_x$
faithfully embeds
![]() $\mathsf {CK}$
into
$\mathsf {CK}$
into
![]() $\mathsf {QCL}$
under the assumption of
$\mathsf {QCL}$
under the assumption of
![]() $Th_{ck}$
provides no principal difficulty, we could not find it in the existing literature, so we devote the rest of this section to sketching it. In other words,Footnote
10
we claim the following.
$Th_{ck}$
provides no principal difficulty, we could not find it in the existing literature, so we devote the rest of this section to sketching it. In other words,Footnote
10
we claim the following.
Proposition 6. For all
![]() $\Gamma , \Delta \subseteq \mathcal {CN}$
and for every
$\Gamma , \Delta \subseteq \mathcal {CN}$
and for every
![]() $x \in Ind$
,
$x \in Ind$
,
![]() $\Gamma \models _{\mathsf {CK}}\Delta $
iff
$\Gamma \models _{\mathsf {CK}}\Delta $
iff
![]() $Th_{ck}\cup st_x(\Gamma )\models _{\mathsf {QCL}}st_x(\Delta )$
.
$Th_{ck}\cup st_x(\Gamma )\models _{\mathsf {QCL}}st_x(\Delta )$
.
The proof of this proposition employs the following technical lemmas.
Lemma 8. For every
![]() $\phi \in \mathcal {CN}$
, we have
$\phi \in \mathcal {CN}$
, we have
![]() $Th_{ck}\models _{\mathsf {QCL}}\exists y(Sy\wedge (\forall x)_O(Exy \leftrightarrow st_y(\phi )))$
.
$Th_{ck}\models _{\mathsf {QCL}}\exists y(Sy\wedge (\forall x)_O(Exy \leftrightarrow st_y(\phi )))$
.
Proof We can simply repeat the proof that we give for Lemma 12 below, and observe that
![]() $Th$
is clearly equivalent to
$Th$
is clearly equivalent to
![]() $Th_{ck}$
over
$Th_{ck}$
over
![]() $\mathsf {QCL}$
. Our lemma then follows by Lemma 3.
$\mathsf {QCL}$
. Our lemma then follows by Lemma 3.
Lemma 9. Let
![]() $\mathcal {M}\in \mathbb {CK}$
and let
$\mathcal {M}\in \mathbb {CK}$
and let
![]() $\mathcal {M}^{cl} \in \mathbb {C}$
be such that:
$\mathcal {M}^{cl} \in \mathbb {C}$
be such that:
-
•
 $U^{\mathcal {M}^{cl}} := W \cup \mathcal {P}(W)$
.
$U^{\mathcal {M}^{cl}} := W \cup \mathcal {P}(W)$
. -
• For every
 $p^1 \in Prop$
,
$p^1 \in Prop$
,
 $p^{\mathcal {M}^{cl}} := V(p)$
.
$p^{\mathcal {M}^{cl}} := V(p)$
. -
•
 $O^{\mathcal {M}^{cl}}:= W$
.
$O^{\mathcal {M}^{cl}}:= W$
. -
•
 $S^{\mathcal {M}^{cl}}:= \mathcal {P}(W)$
.
$S^{\mathcal {M}^{cl}}:= \mathcal {P}(W)$
. -
•
 $E^{\mathcal {M}^{cl}}:= \{(w, X)\in W\times \mathcal {P}(W)\mid w \in X\}$
.
$E^{\mathcal {M}^{cl}}:= \{(w, X)\in W\times \mathcal {P}(W)\mid w \in X\}$
. -
•
 $R^{\mathcal {M}^{cl}}:= \{(w, X,v)\in W\times \mathcal {P}(W)\times W\mid R(w, X, v)\}$
.
$R^{\mathcal {M}^{cl}}:= \{(w, X,v)\in W\times \mathcal {P}(W)\times W\mid R(w, X, v)\}$
.
Then the following statements hold:
-
1.
 $\mathcal {M}^{cl}\models _{c} Th_{ck}$
.
$\mathcal {M}^{cl}\models _{c} Th_{ck}$
. -
2. For every
 $\phi \in \mathcal {CN}$
, every
$\phi \in \mathcal {CN}$
, every
 $x \in Ind$
, and every
$x \in Ind$
, and every
 $\mathbf {w} \in W$
, we have
$\mathbf {w} \in W$
, we have
 $\mathcal {M}, \mathbf {w} \models _{ck} \phi $
iff
$\mathcal {M}, \mathbf {w} \models _{ck} \phi $
iff
 $\mathcal {M}^{cl}\models _{c}st_x(\phi )[x/\mathbf {w}]$
.
$\mathcal {M}^{cl}\models _{c}st_x(\phi )[x/\mathbf {w}]$
.
Proof (a sketch)
Part 1 is straightforward (even though somewhat tedious) to check. As for Part 2, we argue by induction on the construction of
![]() $\phi \in \mathcal {CN}$
in which we only consider a couple of cases.
$\phi \in \mathcal {CN}$
in which we only consider a couple of cases.
Basis. Assume that
![]() $\phi = p$
where
$\phi = p$
where
![]() $p^1 \in Prop$
. Then we have
$p^1 \in Prop$
. Then we have
Induction step. The Boolean cases are straightforward. In case ![]() for some
for some
![]() $\psi , \chi \in \mathcal {CN}$
, and pairwise distinct
$\psi , \chi \in \mathcal {CN}$
, and pairwise distinct
![]() $x,y,z, w \in Ind$
, we begin by noting that IH for
$x,y,z, w \in Ind$
, we begin by noting that IH for
![]() $\psi $
implies that:
$\psi $
implies that:
We now reason as follows:
 $$ \begin{align*} \mathcal{M}, \mathbf{w} \models_{ck} \phi &\text{ iff } (\forall \mathbf{v} \in W)(R_{\|\psi\|^{ck}_{\mathcal{M}}}(\mathbf{w},\mathbf{v})\text{ implies }\mathcal{M}, \mathbf{v}\models_{ck} \chi)\\&\text{ iff } (\forall \mathbf{v} \in W)(R^{\mathcal{M}^{cl}}(\mathbf{w},\|\psi\|^{ck}_{\mathcal{M}},\mathbf{v})\text{ implies}\\& \quad \mathcal{M}^{cl}\models_{c} st_{w}(\chi)[w/\mathbf{v}])&&\text{by IH}\\&\text{ iff } (\forall \mathbf{v} \in W\ \cup \mathcal{P}(W))(R^{\mathcal{M}^{cl}}(\mathbf{w},\|\psi\|^{ck}_{\mathcal{M}},\mathbf{v})\\& \quad \text{implies }\mathcal{M}^{cl}\models_{c} st_{w}(\chi)[w/\mathbf{v}])&&\text{by def. of } R^{\mathcal{M}^{cl}}\\&\text{ iff } (\forall \mathbf{v} \in U^{\mathcal{M}^{cl}})(R^{\mathcal{M}^{cl}}(\mathbf{w},\|\psi\|^{ck}_{\mathcal{M}},\mathbf{v})\text{ implies}\\& \quad \mathcal{M}^{cl}\models_{c} st_{w}(\chi)[w/\mathbf{v}])\\&\text{ iff } \mathcal{M}^{cl}\models_{c} \forall w(Rxyw \to st_{w}(\chi))[x/\mathbf{w}, y/\|\psi\|^{ck}_{\mathcal{M}}]. \end{align*} $$
$$ \begin{align*} \mathcal{M}, \mathbf{w} \models_{ck} \phi &\text{ iff } (\forall \mathbf{v} \in W)(R_{\|\psi\|^{ck}_{\mathcal{M}}}(\mathbf{w},\mathbf{v})\text{ implies }\mathcal{M}, \mathbf{v}\models_{ck} \chi)\\&\text{ iff } (\forall \mathbf{v} \in W)(R^{\mathcal{M}^{cl}}(\mathbf{w},\|\psi\|^{ck}_{\mathcal{M}},\mathbf{v})\text{ implies}\\& \quad \mathcal{M}^{cl}\models_{c} st_{w}(\chi)[w/\mathbf{v}])&&\text{by IH}\\&\text{ iff } (\forall \mathbf{v} \in W\ \cup \mathcal{P}(W))(R^{\mathcal{M}^{cl}}(\mathbf{w},\|\psi\|^{ck}_{\mathcal{M}},\mathbf{v})\\& \quad \text{implies }\mathcal{M}^{cl}\models_{c} st_{w}(\chi)[w/\mathbf{v}])&&\text{by def. of } R^{\mathcal{M}^{cl}}\\&\text{ iff } (\forall \mathbf{v} \in U^{\mathcal{M}^{cl}})(R^{\mathcal{M}^{cl}}(\mathbf{w},\|\psi\|^{ck}_{\mathcal{M}},\mathbf{v})\text{ implies}\\& \quad \mathcal{M}^{cl}\models_{c} st_{w}(\chi)[w/\mathbf{v}])\\&\text{ iff } \mathcal{M}^{cl}\models_{c} \forall w(Rxyw \to st_{w}(\chi))[x/\mathbf{w}, y/\|\psi\|^{ck}_{\mathcal{M}}]. \end{align*} $$
The latter implies, by (7), that
in other words, that ![]() . Conversely, assuming (8), we can find an
. Conversely, assuming (8), we can find an
![]() $X \in U^{\mathcal {M}^{cl}}$
such that
$X \in U^{\mathcal {M}^{cl}}$
such that
![]() $X \in S^{\mathcal {M}^{cl}} = \mathcal {P}(W)$
and we have
$X \in S^{\mathcal {M}^{cl}} = \mathcal {P}(W)$
and we have
But then, by (7) and Part 1, it follows that
![]() $X = \|\psi \|^{ck}_{\mathcal {M}}$
so that
$X = \|\psi \|^{ck}_{\mathcal {M}}$
so that
![]() $ \mathcal {M}^{cl}\models _{c} \forall w(Rxyw \to st_{w}(\chi ))[x/\mathbf {w}, y/\|\psi \|^{ck}_{\mathcal {M}}]$
follows.
$ \mathcal {M}^{cl}\models _{c} \forall w(Rxyw \to st_{w}(\chi ))[x/\mathbf {w}, y/\|\psi \|^{ck}_{\mathcal {M}}]$
follows.
Yet another lemma provides for the converse direction of Proposition 6.
Lemma 10. Let
![]() $\mathcal {M}\in \mathbb {C}$
be such that
$\mathcal {M}\in \mathbb {C}$
be such that
![]() $\mathcal {M}\models _{c} Th_{ck}$
, and let
$\mathcal {M}\models _{c} Th_{ck}$
, and let
![]() $\mathcal {M}^{ck} \in \mathbb {CK}$
be such that:
$\mathcal {M}^{ck} \in \mathbb {CK}$
be such that:
-
•
 $W^{ck} := U^{\mathcal {M}}$
.
$W^{ck} := U^{\mathcal {M}}$
. -
•
 $R^{ck}(\mathbf {w}, X, \mathbf {v})\text { iff } (\exists a \in S^{\mathcal {M}})(X \cap O^{\mathcal {M}} = \{b \in O^{\mathcal {M}}\mid E^{\mathcal {M}}(b,a)\}\text { and} R^{\mathcal {M}}(\mathbf {w}, a, \mathbf {v}))$
.
$R^{ck}(\mathbf {w}, X, \mathbf {v})\text { iff } (\exists a \in S^{\mathcal {M}})(X \cap O^{\mathcal {M}} = \{b \in O^{\mathcal {M}}\mid E^{\mathcal {M}}(b,a)\}\text { and} R^{\mathcal {M}}(\mathbf {w}, a, \mathbf {v}))$
. -
• For every
 $p^1 \in Prop$
,
$p^1 \in Prop$
,
 $V^{ck}(p) := p^{\mathcal {M}}$
.
$V^{ck}(p) := p^{\mathcal {M}}$
.
Then, for every
![]() $\phi \in \mathcal {CN}$
, every
$\phi \in \mathcal {CN}$
, every
![]() $x \in Ind$
, and every
$x \in Ind$
, and every
![]() $\mathbf {w} \in W^{ck} = U^{\mathcal {M}}$
, we have
$\mathbf {w} \in W^{ck} = U^{\mathcal {M}}$
, we have
![]() $\mathcal {M}^{ck}, \mathbf {w} \models _{ck} \phi $
iff
$\mathcal {M}^{ck}, \mathbf {w} \models _{ck} \phi $
iff
![]() $\mathcal {M}\models _{c}st_x(\phi )[x/\mathbf {w}]$
.
$\mathcal {M}\models _{c}st_x(\phi )[x/\mathbf {w}]$
.
Proof (a sketch)
It is clear that
![]() $\mathcal {M}^{ck} \in \mathbb {CK}$
; as for the main statement of the lemma, we proceed by induction on the construction of
$\mathcal {M}^{ck} \in \mathbb {CK}$
; as for the main statement of the lemma, we proceed by induction on the construction of
![]() $\phi \in \mathcal {CN}$
.
$\phi \in \mathcal {CN}$
.
Basis. Assume that
![]() $\phi = p$
where
$\phi = p$
where
![]() $p^1 \in Prop$
. Then we have
$p^1 \in Prop$
. Then we have
Induction step. The Boolean cases are straightforward by IH. If ![]() , assume
, assume
![]() $x,y,z, w \in Ind$
to be pairwise distinct. By Lemma 8, we know that for some
$x,y,z, w \in Ind$
to be pairwise distinct. By Lemma 8, we know that for some
![]() $a \in S^{\mathcal {M}}$
we have
$a \in S^{\mathcal {M}}$
we have
For the left-to-right half of the lemma, assume that
![]() $\mathcal {M}^{ck}, \mathbf {w} \models _{ck} \phi $
. Then
$\mathcal {M}^{ck}, \mathbf {w} \models _{ck} \phi $
. Then
![]() $(\forall \mathbf {v} \in W^{ck})(R^{ck}_{\|\psi \|^{ck}_{\mathcal {M}^{ck}}}(\mathbf {w},\mathbf {v})\text { implies }\mathcal {M}^{ck}, \mathbf {v}\models _{ck} \chi )$
. If now
$(\forall \mathbf {v} \in W^{ck})(R^{ck}_{\|\psi \|^{ck}_{\mathcal {M}^{ck}}}(\mathbf {w},\mathbf {v})\text { implies }\mathcal {M}^{ck}, \mathbf {v}\models _{ck} \chi )$
. If now
![]() $\mathbf {v} \in U^{\mathcal {M}} = W^{ck}$
is such that
$\mathbf {v} \in U^{\mathcal {M}} = W^{ck}$
is such that
![]() $R^{\mathcal {M}}(\mathbf {w}, a, \mathbf {v})$
, then, by IH and the choice of a, we must have
$R^{\mathcal {M}}(\mathbf {w}, a, \mathbf {v})$
, then, by IH and the choice of a, we must have
![]() $R^{ck}_{\|\psi \|^{ck}_{\mathcal {M}^{ck}}}(\mathbf {w},\mathbf {v})$
, whence also
$R^{ck}_{\|\psi \|^{ck}_{\mathcal {M}^{ck}}}(\mathbf {w},\mathbf {v})$
, whence also
![]() $\mathcal {M}^{ck}, \mathbf {v}\models _{ck} \chi $
, and, by IH,
$\mathcal {M}^{ck}, \mathbf {v}\models _{ck} \chi $
, and, by IH,
![]() $\mathcal {M}\models _{c} st_{w}(\chi )[w/\mathbf {v}]$
. Thus we have shown that
$\mathcal {M}\models _{c} st_{w}(\chi )[w/\mathbf {v}]$
. Thus we have shown that
![]() $\mathcal {M}\models _{c}\forall w(Rxyw\to st_{w}(\chi )))[x/\mathbf {w}, y/a]$
, which, together with (10), yields that
$\mathcal {M}\models _{c}\forall w(Rxyw\to st_{w}(\chi )))[x/\mathbf {w}, y/a]$
, which, together with (10), yields that ![]() .
.
For the converse, assume that ![]() . Then there must exist a
. Then there must exist a
![]() $b \in S^{\mathcal {M}}$
such that both
$b \in S^{\mathcal {M}}$
such that both
and
If now
![]() $\mathbf {v} \in W^{ck} = U^{\mathcal {M}}$
is such that
$\mathbf {v} \in W^{ck} = U^{\mathcal {M}}$
is such that
![]() $R^{ck}_{\|\psi \|^{ck}_{\mathcal {M}^{ck}}}(\mathbf {w},\mathbf {v})$
, then, by IH, we can choose a
$R^{ck}_{\|\psi \|^{ck}_{\mathcal {M}^{ck}}}(\mathbf {w},\mathbf {v})$
, then, by IH, we can choose a
![]() $c\in U^{\mathcal {M}}$
such that both
$c\in U^{\mathcal {M}}$
such that both
![]() $R^{\mathcal {M}}(\mathbf {w},c,\mathbf {v})$
and
$R^{\mathcal {M}}(\mathbf {w},c,\mathbf {v})$
and
Now, (11) and (13), together with (Thc1), imply that
![]() $b = c$
so that
$b = c$
so that
![]() $R^{\mathcal {M}}(\mathbf {w},b,\mathbf {v})$
also follows. The latter entails
$R^{\mathcal {M}}(\mathbf {w},b,\mathbf {v})$
also follows. The latter entails
![]() $\mathcal {M}\models _{c} st_{w}(\chi )[w/\mathbf {v}]$
by (12). By IH, we must have
$\mathcal {M}\models _{c} st_{w}(\chi )[w/\mathbf {v}]$
by (12). By IH, we must have
![]() $\mathcal {M}^{ck}, \mathbf {v}\models _{ck} \chi $
. Thus we have shown that
$\mathcal {M}^{ck}, \mathbf {v}\models _{ck} \chi $
. Thus we have shown that ![]() .
.
If we attempt to adapt the general criterion for seeking out non-classical counterparts to
![]() $\mathsf {K}$
that was formulated in the previous section, to the context of conditional logic, the following principle suggests itself: given a non-classical logic
$\mathsf {K}$
that was formulated in the previous section, to the context of conditional logic, the following principle suggests itself: given a non-classical logic
![]() $Q\nu $
such that
$Q\nu $
such that
![]() $Q\nu $
is a proper sublogic of
$Q\nu $
is a proper sublogic of
![]() $\mathsf {QCL}$
and its propositional fragment
$\mathsf {QCL}$
and its propositional fragment
![]() $\nu $
is a proper sublogic of
$\nu $
is a proper sublogic of
![]() $\mathsf {CL}$
, a conditional extension
$\mathsf {CL}$
, a conditional extension
![]() $\nu \mathsf {CK}$
of
$\nu \mathsf {CK}$
of
![]() $\nu $
is a
$\nu $
is a
![]() $\nu $
-based counterpart of
$\nu $
-based counterpart of
![]() $\mathsf {CK}$
iff some classically equivalent reformulation of
$\mathsf {CK}$
iff some classically equivalent reformulation of
![]() $\sigma \tau _x$
faithfully embeds
$\sigma \tau _x$
faithfully embeds
![]() $\nu \mathsf {CK}$
into
$\nu \mathsf {CK}$
into
![]() $\mathsf {Q}\nu (\Pi )$
modulo the assumption of some classically equivalent reformulation of
$\mathsf {Q}\nu (\Pi )$
modulo the assumption of some classically equivalent reformulation of
![]() $Th_{ck}$
; the comparative merits of different
$Th_{ck}$
; the comparative merits of different
![]() $\nu $
-based counterparts of
$\nu $
-based counterparts of
![]() $\mathsf {CK}$
will then have to be judged on the basis of other properties of
$\mathsf {CK}$
will then have to be judged on the basis of other properties of
![]() $Q\nu $
.
$Q\nu $
.
Approaching with this principle to
![]() $\mathsf {QIL}$
, we have defined an intuitionistic counterpart
$\mathsf {QIL}$
, we have defined an intuitionistic counterpart
![]() $\mathsf {IntCK}$
of
$\mathsf {IntCK}$
of
![]() $\mathsf {CK}$
in [Reference Olkhovikov12], and we have shown, in [Reference Olkhovikov12, Theorem 2], that
$\mathsf {CK}$
in [Reference Olkhovikov12], and we have shown, in [Reference Olkhovikov12, Theorem 2], that
![]() $\mathsf {IntCK}$
is an intuitionistic counterpart to
$\mathsf {IntCK}$
is an intuitionistic counterpart to
![]() $\mathsf {CK}$
according to the above criterion.Footnote
11
Very conveniently, the reformulation
$\mathsf {CK}$
according to the above criterion.Footnote
11
Very conveniently, the reformulation
![]() $st^i_x$
of
$st^i_x$
of
![]() $st_x$
used in [Reference Olkhovikov12] is similar to the reformulation
$st_x$
used in [Reference Olkhovikov12] is similar to the reformulation
![]() $\sigma \tau ^i_x$
of
$\sigma \tau ^i_x$
of
![]() $\sigma \tau _x$
, described in the previous section in that the change consists in adding the standard translation of
$\sigma \tau _x$
, described in the previous section in that the change consists in adding the standard translation of ![]() as a separate clause. Moreover, [Reference Olkhovikov12, Proposition 4] shows that, if we also add a clause for diamonds to the mapping
as a separate clause. Moreover, [Reference Olkhovikov12, Proposition 4] shows that, if we also add a clause for diamonds to the mapping
![]() $\eta _\phi $
mentioned in the beginning of this section, then we get an embedding of
$\eta _\phi $
mentioned in the beginning of this section, then we get an embedding of
![]() $\mathsf {IK}$
into
$\mathsf {IK}$
into
![]() $\mathsf {IntCK}$
. Thus,
$\mathsf {IntCK}$
. Thus,
![]() $\mathsf {K}$
,
$\mathsf {K}$
,
![]() $\mathsf {CK}$
,
$\mathsf {CK}$
,
![]() $\mathsf {IK}$
, and
$\mathsf {IK}$
, and
![]() $\mathsf {IntCK}$
are tied to one another by natural embeddings forming, as it were, a tightly connected system. The main aim of the next section, and of this article in general, is to extend this system with
$\mathsf {IntCK}$
are tied to one another by natural embeddings forming, as it were, a tightly connected system. The main aim of the next section, and of this article in general, is to extend this system with
![]() $\mathsf {N4}$
-based modal and conditional logics.
$\mathsf {N4}$
-based modal and conditional logics.
7
 $\mathsf {N4CK}$
, the basic Nelsonian conditional logic
$\mathsf {N4CK}$
, the basic Nelsonian conditional logic
Another logic based on
![]() $\mathcal {CN}$
extends
$\mathcal {CN}$
extends
![]() $\mathsf {N4}$
rather than
$\mathsf {N4}$
rather than
![]() $\mathsf {CL}$
. It was introduced in [Reference Olkhovikov11], and its semantics is based on the following notion.
$\mathsf {CL}$
. It was introduced in [Reference Olkhovikov11], and its semantics is based on the following notion.
Definition 6. A Nelsonian conditional model is a structure of the form
![]() $\mathcal {M} = (W, \leq , R, V^+, V^-)$
such that:
$\mathcal {M} = (W, \leq , R, V^+, V^-)$
such that:
-
1.
 $W \neq \emptyset $
is the set of worlds, or nodes.
$W \neq \emptyset $
is the set of worlds, or nodes. -
2.
 $\leq $
is a pre-order on W.
$\leq $
is a pre-order on W. -
3.
 $R \subseteq W \times (\mathcal {P}(W)\times \mathcal {P}(W))\times W$
is the conditional accessibility relation. Thus, for all
$R \subseteq W \times (\mathcal {P}(W)\times \mathcal {P}(W))\times W$
is the conditional accessibility relation. Thus, for all
 $X,Y \subseteq W$
, R induces a binary relation
$X,Y \subseteq W$
, R induces a binary relation
 $R_{(X,Y)}$
on W such that, for all
$R_{(X,Y)}$
on W such that, for all
 $\mathbf {w},\mathbf {v} \in W$
,
$\mathbf {w},\mathbf {v} \in W$
,
 $R_{(X,Y)}(\mathbf {w},\mathbf {v})$
iff
$R_{(X,Y)}(\mathbf {w},\mathbf {v})$
iff
 $R(\mathbf {w}, (X,Y),\mathbf {v})$
. Moreover, the following conditions must be satisfied for all
$R(\mathbf {w}, (X,Y),\mathbf {v})$
. Moreover, the following conditions must be satisfied for all
 $X, Y \subseteq W$
: (c1)
$X, Y \subseteq W$
: (c1) $$ \begin{align} (\leq^{-1}\circ R_{(X,Y)}) &\subseteq (R_{(X,Y)}\circ\leq^{-1}) \end{align} $$
(c2)
$$ \begin{align} (\leq^{-1}\circ R_{(X,Y)}) &\subseteq (R_{(X,Y)}\circ\leq^{-1}) \end{align} $$
(c2) $$ \begin{align} (R_{(X,Y)}\circ\leq) &\subseteq (\leq\circ R_{(X,Y)}). \end{align} $$
$$ \begin{align} (R_{(X,Y)}\circ\leq) &\subseteq (\leq\circ R_{(X,Y)}). \end{align} $$
-
4.
 $V^+, V^-:Prop \to \mathcal {P}^\leq (W) = \{X\subseteq W\mid (\forall \mathbf {w}\in X)(\forall \mathbf {v}\geq \mathbf {w})(\mathbf {v}\in X)\}$
.
$V^+, V^-:Prop \to \mathcal {P}^\leq (W) = \{X\subseteq W\mid (\forall \mathbf {w}\in X)(\forall \mathbf {v}\geq \mathbf {w})(\mathbf {v}\in X)\}$
.
The class of all Nelsonian conditional models will be denoted by
![]() $\mathbb {NC}$
.
$\mathbb {NC}$
.
Conditions (c1) and (c2) can be reformulated as requirements to complete the dotted parts of each of the two diagrams given in Figure 1 once the respective straight-line part is given.
The evaluation points for
![]() $\mathsf {N4CK}$
are then defined as in
$\mathsf {N4CK}$
are then defined as in
![]() $\mathsf {CK}$
, in other words, we set
$\mathsf {CK}$
, in other words, we set
![]() $EP:= \{(\mathcal {M}, \mathbf {w})\mid \mathcal {M}\in \mathbb {NC},\,\mathbf {w} \in W\}$
.
$EP:= \{(\mathcal {M}, \mathbf {w})\mid \mathcal {M}\in \mathbb {NC},\,\mathbf {w} \in W\}$
.
Just as in other Nelsonian logics, we find in
![]() $\mathsf {N4CK}$
two satisfaction relations
$\mathsf {N4CK}$
two satisfaction relations
![]() $\models ^+$
and
$\models ^+$
and
![]() $\models ^-$
, representing verifications and falsifications of the conditional formulas, respectively. Their inductive definition runs as follows:
$\models ^-$
, representing verifications and falsifications of the conditional formulas, respectively. Their inductive definition runs as follows:

where we assume, for any given
![]() $\phi \in \mathcal {CN}$
, that:
$\phi \in \mathcal {CN}$
, that:
To set up the semantics for
![]() $\mathsf {N4CK}$
it only remains to define that
$\mathsf {N4CK}$
it only remains to define that
![]() $\mathsf {N4CK}:= \mathbb {L}(EP, \models ^+)$
.
$\mathsf {N4CK}:= \mathbb {L}(EP, \models ^+)$
.
The following lemma is then straightforward to prove.
Lemma 11. For every
![]() $\mathcal {M}\in \mathbb {NC}$
, all
$\mathcal {M}\in \mathbb {NC}$
, all
![]() $\mathbf {w},\mathbf {v}\in W$
such that
$\mathbf {w},\mathbf {v}\in W$
such that
![]() $\mathbf {w}\leq \mathbf {v}$
, for every
$\mathbf {w}\leq \mathbf {v}$
, for every
![]() $\ast \in \{+, -\}$
, and for every
$\ast \in \{+, -\}$
, and for every
![]() $\phi \in \mathcal {CN}$
,
$\phi \in \mathcal {CN}$
,
![]() $\mathbf {w}\in \|\phi \|^\ast _{\mathcal {M}}$
implies
$\mathbf {w}\in \|\phi \|^\ast _{\mathcal {M}}$
implies
![]() $\mathbf {v}\in \|\phi \|^\ast _{\mathcal {M}}$
.
$\mathbf {v}\in \|\phi \|^\ast _{\mathcal {M}}$
.
Among other things, [Reference Olkhovikov11] considered the question of a complete Hilbert-style axiomatization of
![]() $\mathsf {N4CK}$
. It turns out (see [Reference Olkhovikov11, Theorem 1]) that we have
$\mathsf {N4CK}$
. It turns out (see [Reference Olkhovikov11, Theorem 1]) that we have
![]() $\mathsf {N4CK} = \mathfrak {N4CK}(\mathcal {CN})$
for
$\mathsf {N4CK} = \mathfrak {N4CK}(\mathcal {CN})$
for
![]() $\mathfrak {N4CK} = \mathfrak {IL}^+ +((An1)\text {--}(An6),(Ax1)\text {--}(Ax4);(RA\Box),(RC\Box1),(RC\Box2))$
, where we assume that:
$\mathfrak {N4CK} = \mathfrak {IL}^+ +((An1)\text {--}(An6),(Ax1)\text {--}(Ax4);(RA\Box),(RC\Box1),(RC\Box2))$
, where we assume that:
In what follows, we will write
![]() $\vdash $
to denote
$\vdash $
to denote
![]() $\vdash _{\mathfrak {N4CK}}$
.
$\vdash _{\mathfrak {N4CK}}$
.
The completeness of
![]() $\mathfrak {N4CK}$
relative to
$\mathfrak {N4CK}$
relative to
![]() $\mathsf {N4CK}$
was shown in [Reference Olkhovikov11] by the rather standard method of constructing a universal model; we would like to recall this construction in some detail as we plan to use it below. More precisely, we say that, for any given
$\mathsf {N4CK}$
was shown in [Reference Olkhovikov11] by the rather standard method of constructing a universal model; we would like to recall this construction in some detail as we plan to use it below. More precisely, we say that, for any given
![]() $\Gamma , \Delta \subseteq \mathcal {CN}$
, the pair
$\Gamma , \Delta \subseteq \mathcal {CN}$
, the pair
![]() $(\Gamma , \Delta )$
is maximal iff
$(\Gamma , \Delta )$
is maximal iff
![]() $\Gamma \not \vdash \Delta $
and
$\Gamma \not \vdash \Delta $
and
![]() $\Gamma \cup \Delta = \mathcal {CN}$
. Our universal model can now be defined as follows.
$\Gamma \cup \Delta = \mathcal {CN}$
. Our universal model can now be defined as follows.
Definition 7. The structure
![]() $\mathcal {M}_c$
is the tuple
$\mathcal {M}_c$
is the tuple
![]() $(W_c, \leq _c, R_c, V^+_c, V^-_c)$
is such that:
$(W_c, \leq _c, R_c, V^+_c, V^-_c)$
is such that:
-
•
 $W_c:=\{(\Gamma , \Delta )\in \mathcal {P}(\mathcal {CN})\times \mathcal {P}(\mathcal {CN})\mid (\Gamma , \Delta )\text { is maximal}\}$
.
$W_c:=\{(\Gamma , \Delta )\in \mathcal {P}(\mathcal {CN})\times \mathcal {P}(\mathcal {CN})\mid (\Gamma , \Delta )\text { is maximal}\}$
. -
•
 $(\Gamma _0,\Delta _0)\leq _c(\Gamma _1,\Delta _1)$
iff
$(\Gamma _0,\Delta _0)\leq _c(\Gamma _1,\Delta _1)$
iff
 $\Gamma _0\subseteq \Gamma _1$
for all
$\Gamma _0\subseteq \Gamma _1$
for all
 $(\Gamma _0,\Delta _0),(\Gamma _1,\Delta _1)\in W_c$
.
$(\Gamma _0,\Delta _0),(\Gamma _1,\Delta _1)\in W_c$
. -
• For all
 $(\Gamma _0,\Delta _0),(\Gamma _1,\Delta _1)\in W_c$
and
$(\Gamma _0,\Delta _0),(\Gamma _1,\Delta _1)\in W_c$
and
 $X, Y \subseteq W_c$
, we have
$X, Y \subseteq W_c$
, we have
 $((\Gamma _0,\Delta _0), (X,Y),(\Gamma _1,\Delta _1)) \in R_c$
iff there exists a
$((\Gamma _0,\Delta _0), (X,Y),(\Gamma _1,\Delta _1)) \in R_c$
iff there exists a
 $\phi \in \mathcal {CN}$
, such that all of the following holds:
$\phi \in \mathcal {CN}$
, such that all of the following holds:-
–
 $X = \{(\Gamma ,\Delta )\in W_c\mid \phi \in \Gamma \}$
.
$X = \{(\Gamma ,\Delta )\in W_c\mid \phi \in \Gamma \}$
. -
–
 $Y = \{(\Gamma ,\Delta )\in W_c\mid \sim \phi \in \Gamma \}.$
$Y = \{(\Gamma ,\Delta )\in W_c\mid \sim \phi \in \Gamma \}.$
-
–
 .
. -
–
 .
.
-
-
•
 $V^+_c(p):=\{(\Gamma ,\Delta )\in W_c\mid p\in \Gamma \}$
for every
$V^+_c(p):=\{(\Gamma ,\Delta )\in W_c\mid p\in \Gamma \}$
for every
 $p^1 \in Prop$
.
$p^1 \in Prop$
. -
•
 $V^-_c(p):=\{(\Gamma ,\Delta )\in W_c\mid \sim p\in \Gamma \}$
for every
$V^-_c(p):=\{(\Gamma ,\Delta )\in W_c\mid \sim p\in \Gamma \}$
for every
 $p^1 \in Prop$
.
$p^1 \in Prop$
.
It follows from [Reference Olkhovikov11, Proposition 7] that:
Proposition 7. For every
![]() $\phi \in \mathcal {CN}$
, the following statements are true:
$\phi \in \mathcal {CN}$
, the following statements are true:
-
1.
 $\mathcal {M}_c \in \mathbb {NC}$
.
$\mathcal {M}_c \in \mathbb {NC}$
. -
2. For every
 $(\Gamma , \Delta )\in W_c$
, we have:
$(\Gamma , \Delta )\in W_c$
, we have:-
(a)
 $ \mathcal {M}_c,(\Gamma ,\Delta )\models ^+\phi $
iff
$ \mathcal {M}_c,(\Gamma ,\Delta )\models ^+\phi $
iff
 $\phi \in \Gamma $
.
$\phi \in \Gamma $
. -
(b)
 $ \mathcal {M}_c,(\Gamma ,\Delta )\models ^-\phi $
iff
$ \mathcal {M}_c,(\Gamma ,\Delta )\models ^-\phi $
iff
 $\sim \phi \in \Gamma $
.
$\sim \phi \in \Gamma $
.
-
The main result of this article is that an analogue of Proposition 6 can be proven for
![]() $\mathsf {N4CK}$
and
$\mathsf {N4CK}$
and
![]() $\mathsf {QN4}$
, respectively, which considerably strengthens the claim that
$\mathsf {QN4}$
, respectively, which considerably strengthens the claim that
![]() $\mathsf {N4CK}$
is the correct minimal conditional logic on the Nelsonian propositional basis. In order to do that, we first need to define the right classical equivalents for
$\mathsf {N4CK}$
is the correct minimal conditional logic on the Nelsonian propositional basis. In order to do that, we first need to define the right classical equivalents for
![]() $Th_{ck}$
and
$Th_{ck}$
and
![]() $st_x$
, respectively. Since these equivalents are at least syntactically different from
$st_x$
, respectively. Since these equivalents are at least syntactically different from
![]() $Th_{ck}$
and
$Th_{ck}$
and
![]() $st_x$
, we will introduce for them separate notations, namely,
$st_x$
, we will introduce for them separate notations, namely,
![]() $Th$
and
$Th$
and
![]() $ST_x$
.
$ST_x$
.
As for the first component in this pair, we assume that
![]() $Th \subseteq \mathcal {FO}^\emptyset $
contains all and only the following first-order sentences:
$Th \subseteq \mathcal {FO}^\emptyset $
contains all and only the following first-order sentences:
It is easy to see that
![]() $Th$
is classically equivalent to
$Th$
is classically equivalent to
![]() $Th_{ck}$
. The only difference between the two theories is the replacement of equivalences encoding the set extensions in
$Th_{ck}$
. The only difference between the two theories is the replacement of equivalences encoding the set extensions in
![]() $Th_{ck}$
with the strong equivalences which allows for a replacement of a definable set with its definition in
$Th_{ck}$
with the strong equivalences which allows for a replacement of a definable set with its definition in
![]() $\mathsf {QN4}$
. In view of the considerations given in Appendix A.5, one could also argue for replacing conjunctions with ampersands in (Th2)–(Th5); however, this is not necessary, since
$\mathsf {QN4}$
. In view of the considerations given in Appendix A.5, one could also argue for replacing conjunctions with ampersands in (Th2)–(Th5); however, this is not necessary, since
![]() $Th$
only imposes the truth of its components and never says anything about their falsity conditions. We have seen, however, that the differences between
$Th$
only imposes the truth of its components and never says anything about their falsity conditions. We have seen, however, that the differences between
![]() $\wedge $
and
$\wedge $
and
![]() $\&$
only become apparent when the treatment of the falsity component of a restricted existential quantification comes into question. Therefore, the distinction between
$\&$
only become apparent when the treatment of the falsity component of a restricted existential quantification comes into question. Therefore, the distinction between
![]() $\wedge $
and
$\wedge $
and
![]() $\&$
can no longer be overlooked when it comes to the definition of the standard translation which is supposed to faithfully represent both the truth and the falsity conditions of a translated formula. As a result, we obtain, for every given
$\&$
can no longer be overlooked when it comes to the definition of the standard translation which is supposed to faithfully represent both the truth and the falsity conditions of a translated formula. As a result, we obtain, for every given
![]() $x \in Ind$
, the standard translation
$x \in Ind$
, the standard translation
![]() $ST_x:\mathcal {CN}\to \mathcal {FO}^x$
defined by the following induction on the construction of a
$ST_x:\mathcal {CN}\to \mathcal {FO}^x$
defined by the following induction on the construction of a
![]() $\phi \in \mathcal {CN}$
(assuming the same choice of
$\phi \in \mathcal {CN}$
(assuming the same choice of
![]() $x,y,z,w$
as in
$x,y,z,w$
as in
![]() $st_x$
):
$st_x$
):

The following proposition provides the ‘easy’ direction of the faithfulness claim.
Proposition 8. Let
![]() $\Gamma , \Delta \subseteq \mathcal {CN}$
, and let
$\Gamma , \Delta \subseteq \mathcal {CN}$
, and let
![]() $x \in Ind$
. If
$x \in Ind$
. If
![]() $\Gamma \models _{\mathsf {N4CK}} \Delta $
, then
$\Gamma \models _{\mathsf {N4CK}} \Delta $
, then
![]() $Th\cup ST_x(\Gamma )\models _{\mathsf {QN4}} ST_x(\Delta )$
.
$Th\cup ST_x(\Gamma )\models _{\mathsf {QN4}} ST_x(\Delta )$
.
Its proof is analogous to the proof of the corresponding half of Proposition 6 given in the previous section. We start by proving the following technical lemmas.
Lemma 12. For every
![]() $\phi \in \mathcal {CN}$
, we have
$\phi \in \mathcal {CN}$
, we have
![]() $Th\models _{\mathsf {QN4}}\exists y(Sy\wedge (\forall x)_O(Exy \Leftrightarrow ST_x(\phi )))$
.
$Th\models _{\mathsf {QN4}}\exists y(Sy\wedge (\forall x)_O(Exy \Leftrightarrow ST_x(\phi )))$
.
The proof of the lemma is relegated to Appendix B.
Definition 8. Given an
![]() $\mathcal {S}\in \mathbb {N}4$
, we define
$\mathcal {S}\in \mathbb {N}4$
, we define
![]() $\mathcal {M}_{\mathcal {S}}$
as follows:
$\mathcal {M}_{\mathcal {S}}$
as follows:
-
1.
 $W_{\mathcal {S}} := \{(\mathbf {w}, a)\mid \mathbf {w} \in W,\,a\in U_{\mathbf {w}}\}$
.
$W_{\mathcal {S}} := \{(\mathbf {w}, a)\mid \mathbf {w} \in W,\,a\in U_{\mathbf {w}}\}$
. -
2.
 $(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v},b)$
iff
$(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v},b)$
iff
 $\mathbf {w}\leq \mathbf {v}$
and
$\mathbf {w}\leq \mathbf {v}$
and
 $\mathtt {H}_{\mathbf {w}\mathbf {v}}(a) = b$
.
$\mathtt {H}_{\mathbf {w}\mathbf {v}}(a) = b$
. -
3.
 $R_{\mathcal {S}}((\mathbf {w},a), (X, Y), (\mathbf {v},b))$
iff
$R_{\mathcal {S}}((\mathbf {w},a), (X, Y), (\mathbf {v},b))$
iff
 $\mathbf {w} = \mathbf {v}$
and
$\mathbf {w} = \mathbf {v}$
and  $$ \begin{align*} (\exists c \in S^{\mathtt{M}^+_{\mathbf{w}}})&((\forall \mathbf{u} \geq \mathbf{w})(\forall d \in O^{\mathtt{M}^+_{\mathbf{u}}})(((\mathbf{u},d)\in X\text{ iff }E^{\mathtt{M}^+_{\mathbf{u}}}(d,\mathtt{H}_{\mathbf{w}\mathbf{u}}(c)))\\ &\text{ and }((\mathbf{u},d)\in Y\text{ iff }E^{\mathtt{M}^-_{\mathbf{u}}}(d,\mathtt{H}_{\mathbf{w}\mathbf{u}}(c))))\text{ and }R^{\mathtt{M}^+_{\mathbf{w}}}(a,c,b)). \end{align*} $$
$$ \begin{align*} (\exists c \in S^{\mathtt{M}^+_{\mathbf{w}}})&((\forall \mathbf{u} \geq \mathbf{w})(\forall d \in O^{\mathtt{M}^+_{\mathbf{u}}})(((\mathbf{u},d)\in X\text{ iff }E^{\mathtt{M}^+_{\mathbf{u}}}(d,\mathtt{H}_{\mathbf{w}\mathbf{u}}(c)))\\ &\text{ and }((\mathbf{u},d)\in Y\text{ iff }E^{\mathtt{M}^-_{\mathbf{u}}}(d,\mathtt{H}_{\mathbf{w}\mathbf{u}}(c))))\text{ and }R^{\mathtt{M}^+_{\mathbf{w}}}(a,c,b)). \end{align*} $$
-
4. For every
 $p^1 \in Prop$
,
$p^1 \in Prop$
,
 $V^+_{\mathcal {S}}(p) := \{(\mathbf {w},a)\in W_{\mathcal {S}}\mid a \in p^{\mathtt {M}^+_{\mathbf {w}}}\}$
and
$V^+_{\mathcal {S}}(p) := \{(\mathbf {w},a)\in W_{\mathcal {S}}\mid a \in p^{\mathtt {M}^+_{\mathbf {w}}}\}$
and
 $V^-_{\mathcal {S}}(p) := \{(\mathbf {w},a)\in W_{\mathcal {S}}\mid a \in p^{\mathtt {M}^-_{\mathbf {w}}}\}$
.
$V^-_{\mathcal {S}}(p) := \{(\mathbf {w},a)\in W_{\mathcal {S}}\mid a \in p^{\mathtt {M}^-_{\mathbf {w}}}\}$
.
In order to avoid the clutter, we introduce the notation
![]() $\Xi ((\mathbf {w},c), (X,Y))$
for the main universally quantified bi-conditional in Definition 8.3; this part of the definition can then be re-written as
$\Xi ((\mathbf {w},c), (X,Y))$
for the main universally quantified bi-conditional in Definition 8.3; this part of the definition can then be re-written as
 $$ \begin{align*}&R_{\mathcal{S}}((\mathbf{w},a), (X, Y), (\mathbf{v},b))\\& \quad \text{ iff }\mathbf{w} = \mathbf{v}\text{ and }(\exists c \in S^{\mathtt{M}^+_{\mathbf{w}}})(\Xi((\mathbf{w},c), (X,Y))\text{ and }R^{\mathtt{M}^+_{\mathbf{w}}}(a,c,b)). \end{align*} $$
$$ \begin{align*}&R_{\mathcal{S}}((\mathbf{w},a), (X, Y), (\mathbf{v},b))\\& \quad \text{ iff }\mathbf{w} = \mathbf{v}\text{ and }(\exists c \in S^{\mathtt{M}^+_{\mathbf{w}}})(\Xi((\mathbf{w},c), (X,Y))\text{ and }R^{\mathtt{M}^+_{\mathbf{w}}}(a,c,b)). \end{align*} $$
Lemma 13. Let
![]() $\mathcal {S}\in \mathbb {N}4$
be such that
$\mathcal {S}\in \mathbb {N}4$
be such that
![]() $\mathcal {S}\models ^+_{n} Th$
, and let
$\mathcal {S}\models ^+_{n} Th$
, and let
![]() $\mathcal {M}_{\mathcal {S}}$
be given according to Definition 8. Then
$\mathcal {M}_{\mathcal {S}}$
be given according to Definition 8. Then
![]() $\mathcal {M}_{\mathcal {S}}\in \mathbb {NC}$
.
$\mathcal {M}_{\mathcal {S}}\in \mathbb {NC}$
.
Proof The transitivity and reflexivity of
![]() $\leq _{\mathcal {S}}$
easily follow from the same properties of
$\leq _{\mathcal {S}}$
easily follow from the same properties of
![]() $\leq $
. As for the monotonicity of
$\leq $
. As for the monotonicity of
![]() $V^+_{\mathcal {S}}$
relative to
$V^+_{\mathcal {S}}$
relative to
![]() $\leq _{\mathcal {S}}$
, assume that
$\leq _{\mathcal {S}}$
, assume that
![]() $p^1 \in Prop$
, and that
$p^1 \in Prop$
, and that
![]() $(\mathbf {w},a), (\mathbf {v},b) \in W_{\mathcal {S}}$
are such that
$(\mathbf {w},a), (\mathbf {v},b) \in W_{\mathcal {S}}$
are such that
![]() $(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v},b)$
. Then
$(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v},b)$
. Then
![]() $\mathbf {w} \leq \mathbf {v}$
and
$\mathbf {w} \leq \mathbf {v}$
and
![]() $\mathtt {H}_{\mathbf {w}\mathbf {v}}(a) = b$
. If now
$\mathtt {H}_{\mathbf {w}\mathbf {v}}(a) = b$
. If now
![]() $(\mathbf {w},a) \in V^+_{\mathcal {S}}(p)$
, then
$(\mathbf {w},a) \in V^+_{\mathcal {S}}(p)$
, then
![]() $a \in p^{\mathtt {M}^+_{\mathbf {w}}}$
, and, since
$a \in p^{\mathtt {M}^+_{\mathbf {w}}}$
, and, since
![]() $\mathtt {H}_{\mathbf {w}\mathbf {v}}\in Hom(\mathtt {M}^+_{\mathbf {w}}, \mathtt {M}^+_{\mathbf {v}})$
, also
$\mathtt {H}_{\mathbf {w}\mathbf {v}}\in Hom(\mathtt {M}^+_{\mathbf {w}}, \mathtt {M}^+_{\mathbf {v}})$
, also
![]() $b = \mathtt {H}_{\mathbf {w}\mathbf {v}}(a) \in p^{\mathtt {M}^+_{\mathbf {v}}}$
, which, in turn, means that
$b = \mathtt {H}_{\mathbf {w}\mathbf {v}}(a) \in p^{\mathtt {M}^+_{\mathbf {v}}}$
, which, in turn, means that
![]() $(\mathbf {v},b) \in V^+_{\mathcal {S}}(p)$
. We argue similarly for the monotonicity of
$(\mathbf {v},b) \in V^+_{\mathcal {S}}(p)$
. We argue similarly for the monotonicity of
![]() $V^-_{\mathcal {S}}$
.
$V^-_{\mathcal {S}}$
.
It only remains to check the conditions imposed on R. As for (c1), assume that
![]() $(\mathbf {w},a), (\mathbf {v},b), (\mathbf {u},c) \in W_{\mathcal {S}}$
and
$(\mathbf {w},a), (\mathbf {v},b), (\mathbf {u},c) \in W_{\mathcal {S}}$
and
![]() $X, Y \subseteq W_{\mathcal {S}}$
are such that both
$X, Y \subseteq W_{\mathcal {S}}$
are such that both
![]() $(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v},b)$
and
$(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v},b)$
and
![]() $R_{\mathcal {S}}((\mathbf {w},a), (X, Y), (\mathbf {u},c))$
. Then
$R_{\mathcal {S}}((\mathbf {w},a), (X, Y), (\mathbf {u},c))$
. Then
![]() $\mathbf {w} = \mathbf {u}$
and
$\mathbf {w} = \mathbf {u}$
and
![]() $\mathbf {w} \leq \mathbf {v}$
, whence
$\mathbf {w} \leq \mathbf {v}$
, whence
![]() $(\mathbf {u},c) = (\mathbf {w},c)\leq _{\mathcal {S}}(\mathbf {v},\mathtt {H}_{\mathbf {w}\mathbf {v}}(c))\in W_{\mathcal {S}}$
. On the other hand,
$(\mathbf {u},c) = (\mathbf {w},c)\leq _{\mathcal {S}}(\mathbf {v},\mathtt {H}_{\mathbf {w}\mathbf {v}}(c))\in W_{\mathcal {S}}$
. On the other hand,
![]() $\mathtt {H}_{\mathbf {w}\mathbf {v}}(a) = b$
, and there exists a
$\mathtt {H}_{\mathbf {w}\mathbf {v}}(a) = b$
, and there exists a
![]() $d \in S^{\mathtt {M}^+_{\mathbf {w}}}$
such that both
$d \in S^{\mathtt {M}^+_{\mathbf {w}}}$
such that both
![]() $R^{\mathtt {M}^+_{\mathbf {w}}}(a,d,c)$
and, for all
$R^{\mathtt {M}^+_{\mathbf {w}}}(a,d,c)$
and, for all
![]() $\mathbf {w}'\geq \mathbf {w}$
and all
$\mathbf {w}'\geq \mathbf {w}$
and all
![]() $g \in O^{\mathtt {M}^+_{\mathbf {w}'}}$
we have
$g \in O^{\mathtt {M}^+_{\mathbf {w}'}}$
we have
Now, consider
![]() $\mathtt {H}_{\mathbf {w}\mathbf {v}}(d)\in S^{\mathtt {M}^+_{\mathbf {v}}}$
. Since
$\mathtt {H}_{\mathbf {w}\mathbf {v}}(d)\in S^{\mathtt {M}^+_{\mathbf {v}}}$
. Since
![]() $\mathtt {H}_{\mathbf {w}\mathbf {v}}\in Hom(\mathtt {M}^+_{\mathbf {w}}, \mathtt {M}^+_{\mathbf {v}})$
, we must have that
$\mathtt {H}_{\mathbf {w}\mathbf {v}}\in Hom(\mathtt {M}^+_{\mathbf {w}}, \mathtt {M}^+_{\mathbf {v}})$
, we must have that
![]() $R^{\mathtt {M}^+_{\mathbf {v}}}(\mathtt {H}_{\mathbf {w}\mathbf {v}}(a),\mathtt {H}_{\mathbf {w}\mathbf {v}}(d),\mathtt {H}_{\mathbf {w}\mathbf {v}}(c))$
, in other words, that
$R^{\mathtt {M}^+_{\mathbf {v}}}(\mathtt {H}_{\mathbf {w}\mathbf {v}}(a),\mathtt {H}_{\mathbf {w}\mathbf {v}}(d),\mathtt {H}_{\mathbf {w}\mathbf {v}}(c))$
, in other words, that
![]() $R^{\mathtt {M}^+_{\mathbf {v}}}(b,\mathtt {H}_{\mathbf {w}\mathbf {v}}(d),\mathtt {H}_{\mathbf {w}\mathbf {v}}(c))$
. Moreover, if
$R^{\mathtt {M}^+_{\mathbf {v}}}(b,\mathtt {H}_{\mathbf {w}\mathbf {v}}(d),\mathtt {H}_{\mathbf {w}\mathbf {v}}(c))$
. Moreover, if
![]() $\mathbf {v}'\geq \mathbf {v}$
and
$\mathbf {v}'\geq \mathbf {v}$
and
![]() $k\in O^{\mathtt {M}^+_{\mathbf {v}'}}$
, then transitivity implies
$k\in O^{\mathtt {M}^+_{\mathbf {v}'}}$
, then transitivity implies
![]() $\mathbf {v}'\geq \mathbf {w}$
, and Definition 4 implies that
$\mathbf {v}'\geq \mathbf {w}$
, and Definition 4 implies that
![]() $\mathtt {H}_{\mathbf {v}\mathbf {v}'}(\mathtt {H}_{\mathbf {w}\mathbf {v}}(d)) = \mathtt {H}_{\mathbf {w}\mathbf {v}'}(d)$
, whence, by (14), we must have
$\mathtt {H}_{\mathbf {v}\mathbf {v}'}(\mathtt {H}_{\mathbf {w}\mathbf {v}}(d)) = \mathtt {H}_{\mathbf {w}\mathbf {v}'}(d)$
, whence, by (14), we must have
Therefore, we must also have
![]() $R_{\mathcal {S}}((\mathbf {v},b), X, Y, (\mathbf {v}, \mathtt {H}_{\mathbf {w}\mathbf {v}}(c)))$
, and (c1) is shown to hold.
$R_{\mathcal {S}}((\mathbf {v},b), X, Y, (\mathbf {v}, \mathtt {H}_{\mathbf {w}\mathbf {v}}(c)))$
, and (c1) is shown to hold.
The argument for (c2) is similar.
Since Definition 8.3 is relatively involved, we look a bit deeper into its consequences, before proceeding further.
Lemma 14. Let
![]() $\mathcal {S}\in \mathbb {N}4$
and let
$\mathcal {S}\in \mathbb {N}4$
and let
![]() $\phi \in \mathcal {CN}$
. Then the following statements hold:
$\phi \in \mathcal {CN}$
. Then the following statements hold:
-
1. Assume that, for every
 $\star \in \{+, -\}$
, every
$\star \in \{+, -\}$
, every
 $x \in Ind$
, and every
$x \in Ind$
, and every
 $(\mathbf {w},a) \in W_{\mathcal {S}}$
, we have
$(\mathbf {w},a) \in W_{\mathcal {S}}$
, we have
 $\mathcal {M}_{\mathcal {S}}, (\mathbf {w},a) \models ^\star \phi $
iff
$\mathcal {M}_{\mathcal {S}}, (\mathbf {w},a) \models ^\star \phi $
iff
 $\mathcal {S}, \mathbf {w}\models ^\star _{n}ST_x(\phi )[x/a]$
. Then, for every
$\mathcal {S}, \mathbf {w}\models ^\star _{n}ST_x(\phi )[x/a]$
. Then, for every
 $(\mathbf {v}, b)\in W_{\mathcal {S}}$
and all distinct
$(\mathbf {v}, b)\in W_{\mathcal {S}}$
and all distinct
 $y,z \in Ind$
we have
$y,z \in Ind$
we have  $$ \begin{align*}\mathcal{S}, \mathbf{v}\models^+_n (\forall z)_O(Ezy \Leftrightarrow ST_z(\phi))[y/b] \text{ iff }\Xi((\mathbf{v},b), \|\phi\|_{\mathcal{M}_{\mathcal{S}}}). \end{align*} $$
$$ \begin{align*}\mathcal{S}, \mathbf{v}\models^+_n (\forall z)_O(Ezy \Leftrightarrow ST_z(\phi))[y/b] \text{ iff }\Xi((\mathbf{v},b), \|\phi\|_{\mathcal{M}_{\mathcal{S}}}). \end{align*} $$
-
2. For all
 $(\mathbf {w},a), (\mathbf {v}, b) \in W_{\mathcal {S}}$
, if
$(\mathbf {w},a), (\mathbf {v}, b) \in W_{\mathcal {S}}$
, if
 $(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v}, b)$
and
$(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v}, b)$
and
 $\Xi ((\mathbf {w},a), \|\phi \|_{\mathcal {M}_{\mathcal {S}}})$
, then
$\Xi ((\mathbf {w},a), \|\phi \|_{\mathcal {M}_{\mathcal {S}}})$
, then
 $\Xi ((\mathbf {v},b), \|\phi \|_{\mathcal {M}_{\mathcal {S}}})$
.
$\Xi ((\mathbf {v},b), \|\phi \|_{\mathcal {M}_{\mathcal {S}}})$
.
Proof (Part 1) Assume the premises. We have
![]() $\mathcal {S}, \mathbf {v}\models ^+_n (\forall z)_O(Ezy \Leftrightarrow ST_z(\phi ))[y/b]$
iff, by Corollary 2, we have
$\mathcal {S}, \mathbf {v}\models ^+_n (\forall z)_O(Ezy \Leftrightarrow ST_z(\phi ))[y/b]$
iff, by Corollary 2, we have
 $$ \begin{align*} (\forall \mathbf{u} \geq \mathbf{v})(\forall d \in O^{\mathtt{M}^+_{\mathbf{u}}})&((\mathcal{S},\mathbf{u}\models^+_n ST_z(\phi)[z/d]\text{ iff }\mathcal{S},\mathbf{u}\models^+_n Ezy[y/\mathtt{H}_{\mathbf{w}\mathbf{u}}(b), z/d])\nonumber\\ &\text{ and }(\mathcal{S},\mathbf{u}\models^-_n ST_z(\phi)[z/d]\text{ iff }\mathcal{S},\mathbf{u}\models^-_n Ezy[y/\mathtt{H}_{\mathbf{w}\mathbf{u}}(b), z/d])). \end{align*} $$
$$ \begin{align*} (\forall \mathbf{u} \geq \mathbf{v})(\forall d \in O^{\mathtt{M}^+_{\mathbf{u}}})&((\mathcal{S},\mathbf{u}\models^+_n ST_z(\phi)[z/d]\text{ iff }\mathcal{S},\mathbf{u}\models^+_n Ezy[y/\mathtt{H}_{\mathbf{w}\mathbf{u}}(b), z/d])\nonumber\\ &\text{ and }(\mathcal{S},\mathbf{u}\models^-_n ST_z(\phi)[z/d]\text{ iff }\mathcal{S},\mathbf{u}\models^-_n Ezy[y/\mathtt{H}_{\mathbf{w}\mathbf{u}}(b), z/d])). \end{align*} $$
By our hypothesis about
![]() $\phi $
, the latter statement is equivalent to
$\phi $
, the latter statement is equivalent to
 $$ \begin{align*} (\forall \mathbf{u} \geq \mathbf{v})(\forall d \in O^{\mathtt{M}^+_{\mathbf{u}}})(((\mathbf{u}, z)&\in \|\phi\|^+_{\mathcal{M}_{\mathcal{S}}}\text{ iff } E^{\mathtt{M}^+_{\mathbf{u}}}(d,\mathtt{H}_{\mathbf{w}\mathbf{u}}(b)))\nonumber\\ &\text{ and }((\mathbf{u}, z)\in \|\phi\|^-_{\mathcal{M}_{\mathcal{S}}}\text{ iff }E^{\mathtt{M}^-_{\mathbf{u}}}(d,\mathtt{H}_{\mathbf{w}\mathbf{u}}(b)))) \end{align*} $$
$$ \begin{align*} (\forall \mathbf{u} \geq \mathbf{v})(\forall d \in O^{\mathtt{M}^+_{\mathbf{u}}})(((\mathbf{u}, z)&\in \|\phi\|^+_{\mathcal{M}_{\mathcal{S}}}\text{ iff } E^{\mathtt{M}^+_{\mathbf{u}}}(d,\mathtt{H}_{\mathbf{w}\mathbf{u}}(b)))\nonumber\\ &\text{ and }((\mathbf{u}, z)\in \|\phi\|^-_{\mathcal{M}_{\mathcal{S}}}\text{ iff }E^{\mathtt{M}^-_{\mathbf{u}}}(d,\mathtt{H}_{\mathbf{w}\mathbf{u}}(b)))) \end{align*} $$
that is to say, to
![]() $\Xi ((\mathbf {v},b), \|\phi \|_{\mathcal {M}_{\mathcal {S}}})$
.
$\Xi ((\mathbf {v},b), \|\phi \|_{\mathcal {M}_{\mathcal {S}}})$
.
(Part 2) Assume that
![]() $(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v}, b)$
; then
$(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v}, b)$
; then
![]() $\mathbf {w} \leq \mathbf {v}$
and
$\mathbf {w} \leq \mathbf {v}$
and
![]() $\mathtt {H}_{\mathbf {w}\mathbf {v}}(a) = b$
. If now
$\mathtt {H}_{\mathbf {w}\mathbf {v}}(a) = b$
. If now
![]() $\Xi ((\mathbf {w},a), \|\phi \|_{\mathcal {M}_{\mathcal {S}}})$
, this means, by Part 1, that
$\Xi ((\mathbf {w},a), \|\phi \|_{\mathcal {M}_{\mathcal {S}}})$
, this means, by Part 1, that
![]() $\mathcal {S}, \mathbf {w}\models ^+_n (\forall z)_O(Ezy \Leftrightarrow ST_z(\phi ))[y/a]$
, whence, by Lemma 4.1,
$\mathcal {S}, \mathbf {w}\models ^+_n (\forall z)_O(Ezy \Leftrightarrow ST_z(\phi ))[y/a]$
, whence, by Lemma 4.1,
![]() $\mathcal {S}, \mathbf {v}\models ^+_n (\forall z)_O(Ezy \Leftrightarrow ST_z(\phi )) [y/\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)]$
, whence, again by Part 1,
$\mathcal {S}, \mathbf {v}\models ^+_n (\forall z)_O(Ezy \Leftrightarrow ST_z(\phi )) [y/\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)]$
, whence, again by Part 1,
![]() $\Xi ((\mathbf {v},b), \|\phi \|_{\mathcal {M}_{\mathcal {S}}})$
.
$\Xi ((\mathbf {v},b), \|\phi \|_{\mathcal {M}_{\mathcal {S}}})$
.
Lemma 15. Let
![]() $\mathcal {S}\in \mathbb {N}4$
be such that
$\mathcal {S}\in \mathbb {N}4$
be such that
![]() $\mathcal {S}\models ^+_{n} Th$
, and let
$\mathcal {S}\models ^+_{n} Th$
, and let
![]() $\mathcal {M}_{\mathcal {S}}\in \mathbb {NC}$
be given according to Definition 8. Then, for every
$\mathcal {M}_{\mathcal {S}}\in \mathbb {NC}$
be given according to Definition 8. Then, for every
![]() $\phi \in \mathcal {CN}$
,
$\phi \in \mathcal {CN}$
,
![]() $\star \in \{+, -\}$
,
$\star \in \{+, -\}$
,
![]() $x \in Ind$
, and
$x \in Ind$
, and
![]() $(\mathbf {w},a) \in W_{\mathcal {S}}$
, we have
$(\mathbf {w},a) \in W_{\mathcal {S}}$
, we have
![]() $\mathcal {M}_{\mathcal {S}}, (\mathbf {w},a) \models ^\star \phi $
iff
$\mathcal {M}_{\mathcal {S}}, (\mathbf {w},a) \models ^\star \phi $
iff
![]() $\mathcal {S}, \mathbf {w}\models ^\star _{n}ST_x(\phi )[x/a]$
.
$\mathcal {S}, \mathbf {w}\models ^\star _{n}ST_x(\phi )[x/a]$
.
Proof We argue by induction on the construction of
![]() $\phi \in \mathcal {CN}$
.
$\phi \in \mathcal {CN}$
.
Basis. If
![]() $\phi = p$
for some
$\phi = p$
for some
![]() $p^1 \in Prop$
, then we have, for every
$p^1 \in Prop$
, then we have, for every
![]() $\star \in \{+, -\}$
and
$\star \in \{+, -\}$
and
![]() $(\mathbf {w},a) \in W_{\mathcal {S}}$
, that
$(\mathbf {w},a) \in W_{\mathcal {S}}$
, that
![]() $\mathcal {M}_{\mathcal {S}}, (\mathbf {w},a) \models ^\star p$
iff
$\mathcal {M}_{\mathcal {S}}, (\mathbf {w},a) \models ^\star p$
iff
![]() $(\mathbf {w},a)\in V^\star _{\mathcal {S}}(p)$
iff
$(\mathbf {w},a)\in V^\star _{\mathcal {S}}(p)$
iff
![]() $a \in p^{\mathtt {M}^\star _{\mathbf {w}}}$
iff
$a \in p^{\mathtt {M}^\star _{\mathbf {w}}}$
iff
![]() $\mathcal {S}, \mathbf {w}\models ^\star _n px[x/a]$
.
$\mathcal {S}, \mathbf {w}\models ^\star _n px[x/a]$
.
Induction step. The following cases arise.
Case 1. If
![]() $\phi = \psi \wedge \chi $
, then we have, on the one hand,
$\phi = \psi \wedge \chi $
, then we have, on the one hand,
 $$ \begin{align*} \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^+ \psi \wedge \chi &\text{ iff } \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^+ \psi\text{ and }\mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^+\chi&&\text{ by IH}\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^+_n ST_x(\psi)[x/a]\text{ and }\\& \quad\ \, \mathcal{S}, \mathbf{w}\models^+_n ST_x(\chi)[x/a]\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^+_n ST_x(\psi)\wedge ST_x(\chi)[x/a]\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^+_n ST_x(\psi\wedge\chi)[x/a]. \end{align*} $$
$$ \begin{align*} \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^+ \psi \wedge \chi &\text{ iff } \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^+ \psi\text{ and }\mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^+\chi&&\text{ by IH}\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^+_n ST_x(\psi)[x/a]\text{ and }\\& \quad\ \, \mathcal{S}, \mathbf{w}\models^+_n ST_x(\chi)[x/a]\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^+_n ST_x(\psi)\wedge ST_x(\chi)[x/a]\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^+_n ST_x(\psi\wedge\chi)[x/a]. \end{align*} $$
On the other hand, we have
 $$ \begin{align*} \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^- \psi \wedge \chi &\text{ iff } \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^- \psi\text{ or }\mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^-\chi\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^-_n ST_x(\psi)[x/a]\text{ or } \\& \quad\ \, \mathcal{S}, \mathbf{w}\models^-_n ST_x(\chi)[x/a]&&\text{ by IH}\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^-_n ST_x(\psi)\wedge ST_x(\chi)[x/a]\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^-_n ST_x(\psi\wedge\chi)[x/a]. \end{align*} $$
$$ \begin{align*} \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^- \psi \wedge \chi &\text{ iff } \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^- \psi\text{ or }\mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^-\chi\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^-_n ST_x(\psi)[x/a]\text{ or } \\& \quad\ \, \mathcal{S}, \mathbf{w}\models^-_n ST_x(\chi)[x/a]&&\text{ by IH}\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^-_n ST_x(\psi)\wedge ST_x(\chi)[x/a]\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^-_n ST_x(\psi\wedge\chi)[x/a]. \end{align*} $$
Case 2 and Case 3, where we assume that
![]() $\phi = \psi \vee \chi $
and
$\phi = \psi \vee \chi $
and
![]() $\phi = \sim \psi $
, respectively, are solved similarly to Case 1.
$\phi = \sim \psi $
, respectively, are solved similarly to Case 1.
Case 4. If
![]() $\phi = \psi \to \chi $
, then assume that
$\phi = \psi \to \chi $
, then assume that
![]() $ \mathcal {M}_{\mathcal {S}}, (\mathbf {w},a) \models ^+ \psi \to \chi $
, and let
$ \mathcal {M}_{\mathcal {S}}, (\mathbf {w},a) \models ^+ \psi \to \chi $
, and let
![]() $\mathbf {v}\geq \mathbf {w}$
be such that
$\mathbf {v}\geq \mathbf {w}$
be such that
![]() $\mathcal {S}, \mathbf {v}\models ^+_n ST_x(\psi )[x/\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)]$
. Then, by IH,
$\mathcal {S}, \mathbf {v}\models ^+_n ST_x(\psi )[x/\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)]$
. Then, by IH,
![]() $\mathcal {M}_{\mathcal {S}}, (\mathbf {v},\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)) \models ^+ \psi $
, and we also have
$\mathcal {M}_{\mathcal {S}}, (\mathbf {v},\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)) \models ^+ \psi $
, and we also have
![]() $(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v},\mathtt {H}_{\mathbf {w}\mathbf {v}}(a))$
, whence, by our assumption,
$(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v},\mathtt {H}_{\mathbf {w}\mathbf {v}}(a))$
, whence, by our assumption,
![]() $\mathcal {M}_{\mathcal {S}}, (\mathbf {v},\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)) \models ^+ \chi $
. Again by IH,
$\mathcal {M}_{\mathcal {S}}, (\mathbf {v},\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)) \models ^+ \chi $
. Again by IH,
![]() $\mathcal {S}, \mathbf {v}\models ^+_n ST_x(\chi )[x/\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)]$
. Since
$\mathcal {S}, \mathbf {v}\models ^+_n ST_x(\chi )[x/\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)]$
. Since
![]() $\mathbf {v}\geq \mathbf {w}$
was chosen arbitrarily, we conclude that
$\mathbf {v}\geq \mathbf {w}$
was chosen arbitrarily, we conclude that
In the other direction, assume that (15) holds. If
![]() $(\mathbf {v},b) \in W_{\mathcal {S}}$
is such that
$(\mathbf {v},b) \in W_{\mathcal {S}}$
is such that
![]() $(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v},b)$
, then
$(\mathbf {w},a)\leq _{\mathcal {S}}(\mathbf {v},b)$
, then
![]() $\mathbf {w} \leq \mathbf {v}$
and
$\mathbf {w} \leq \mathbf {v}$
and
![]() $\mathtt {H}_{\mathbf {w}\mathbf {v}}(a) = b$
. If, moreover, we have
$\mathtt {H}_{\mathbf {w}\mathbf {v}}(a) = b$
. If, moreover, we have
![]() $\mathcal {M}_{\mathcal {S}}, (\mathbf {v},b) \models ^+ \psi $
, then, by IH,
$\mathcal {M}_{\mathcal {S}}, (\mathbf {v},b) \models ^+ \psi $
, then, by IH,
![]() $\mathcal {S}, \mathbf {v}\models ^+_n ST_x(\psi )[x/\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)]$
, whence, by (15),
$\mathcal {S}, \mathbf {v}\models ^+_n ST_x(\psi )[x/\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)]$
, whence, by (15),
![]() $\mathcal {S}, \mathbf {v}\models ^+_n ST_x(\chi )[x/\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)]$
. Applying IH again, we get that
$\mathcal {S}, \mathbf {v}\models ^+_n ST_x(\chi )[x/\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)]$
. Applying IH again, we get that
![]() $\mathcal {M}_{\mathcal {S}}, (\mathbf {v},\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)) \models ^+ \psi $
, in other words, that
$\mathcal {M}_{\mathcal {S}}, (\mathbf {v},\mathtt {H}_{\mathbf {w}\mathbf {v}}(a)) \models ^+ \psi $
, in other words, that
![]() $\mathcal {M}_{\mathcal {S}}, (\mathbf {v},b) \models ^+ \psi $
. By the choice of
$\mathcal {M}_{\mathcal {S}}, (\mathbf {v},b) \models ^+ \psi $
. By the choice of
![]() $(\mathbf {v},b) \in W_{\mathcal {S}}$
, we obtain that
$(\mathbf {v},b) \in W_{\mathcal {S}}$
, we obtain that
![]() $ \mathcal {M}_{\mathcal {S}}, (\mathbf {w},a) \models ^+ \psi \to \chi $
, as desired.
$ \mathcal {M}_{\mathcal {S}}, (\mathbf {w},a) \models ^+ \psi \to \chi $
, as desired.
Finally, observe that we have
 $$ \begin{align*} \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^- \psi \to \chi &\text{ iff } \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^+ \psi\text{ and }\mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^-\chi\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^+_n ST_x(\psi)[x/a]\text{ and } \\& \quad\ \, \mathcal{S}, \mathbf{w}\models^-_n ST_x(\chi)[x/a]&&\text{ by IH}\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^-_n ST_x(\psi)\to ST_x(\chi)[x/a]\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^-_n ST_x(\psi\to\chi)[x/a]. \end{align*} $$
$$ \begin{align*} \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^- \psi \to \chi &\text{ iff } \mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^+ \psi\text{ and }\mathcal{M}_{\mathcal{S}}, (\mathbf{w},a) \models^-\chi\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^+_n ST_x(\psi)[x/a]\text{ and } \\& \quad\ \, \mathcal{S}, \mathbf{w}\models^-_n ST_x(\chi)[x/a]&&\text{ by IH}\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^-_n ST_x(\psi)\to ST_x(\chi)[x/a]\\&\text{ iff } \mathcal{S}, \mathbf{w}\models^-_n ST_x(\psi\to\chi)[x/a]. \end{align*} $$
Case 5. If ![]() , then assume that
, then assume that
By Lemma 12, we can choose a
![]() $b \in U_{\mathbf {w}}$
such that:
$b \in U_{\mathbf {w}}$
such that:
Moreover, choose any
![]() $\mathbf {v} \in W$
and any
$\mathbf {v} \in W$
and any
![]() $c \in U_{\mathbf {v}}$
such that:
$c \in U_{\mathbf {v}}$
such that:
We now reason as follows:
By the choice of
![]() $\mathbf {v}$
and c, we obtain that:
$\mathbf {v}$
and c, we obtain that:
Now (29), together with (17), allows us to conclude that
For the converse, assume (30) and choose any
![]() $b \in U_{\mathbf {w}}$
such that both (17) and (29) hold. Consider any
$b \in U_{\mathbf {w}}$
such that both (17) and (29) hold. Consider any
![]() $(\mathbf {v},c),(\mathbf {u},d) \in W_{\mathcal {S}}$
such that
$(\mathbf {v},c),(\mathbf {u},d) \in W_{\mathcal {S}}$
such that
By (32) and Definition 8.3, there must be an
![]() $e \in U_{\mathbf {v}}$
such that all of the following holds:
$e \in U_{\mathbf {v}}$
such that all of the following holds:
We now reason as follows:
Since
![]() $(\mathbf {v},c),(\mathbf {u},d) \in W_{\mathcal {S}}$
were chosen arbitrarily under the conditions (31) and (32), it follows that
$(\mathbf {v},c),(\mathbf {u},d) \in W_{\mathcal {S}}$
were chosen arbitrarily under the conditions (31) and (32), it follows that ![]() , as desired.
, as desired.
Next, assume that
This means that, for some
![]() $(\mathbf {v}, b) \in W_{\mathcal {S}}$
, we have
$(\mathbf {v}, b) \in W_{\mathcal {S}}$
, we have
By (47), we can choose a
![]() $c \in U_{\mathbf {w}}$
such that all of the following holds:
$c \in U_{\mathbf {w}}$
such that all of the following holds:
Assume, next, that some
![]() $\mathbf {u}'\geq \mathbf {u}\geq \mathbf {w}$
and some
$\mathbf {u}'\geq \mathbf {u}\geq \mathbf {w}$
and some
![]() $d\in U_{\mathbf {u}}$
are such that
$d\in U_{\mathbf {u}}$
are such that
We now reason as follows:
It follows from the above reasoning, by the choice of
![]() $\mathbf {u}'\geq \mathbf {u}$
, that we must have
$\mathbf {u}'\geq \mathbf {u}$
, that we must have
the latter implies, by the definition of
![]() $\&$
, that
$\&$
, that
whence, by the choice of
![]() $\mathbf {u}$
and d, it follows that
$\mathbf {u}$
and d, it follows that
or, in other words, that ![]() , as desired.
, as desired.
On the other hand, if we have
this means that, for every
![]() $(\mathbf {v}, b) \in W_{\mathcal {S}}$
, we have
$(\mathbf {v}, b) \in W_{\mathcal {S}}$
, we have
By Lemma 12, we can choose a
![]() $c \in U_{\mathbf {w}}$
, such that:
$c \in U_{\mathbf {w}}$
, such that:
We choose, next, any
![]() $d \in U_{\mathbf {w}}$
and reason as follows:
$d \in U_{\mathbf {w}}$
and reason as follows:
This reasoning, by the choice of
![]() $d \in U_{\mathbf {w}}$
, shows that we have
$d \in U_{\mathbf {w}}$
, shows that we have
which, together with (68), implies that
whence we get, by definition of
![]() $\&$
, that
$\&$
, that
the latter implies that
or, in other words, that ![]() , as desired.
, as desired.
We are now in a position to prove Proposition 8.
Proof of Proposition 8
We argue by contraposition. Assume that
![]() $Th\cup ST_x(\Gamma )\not \models _{\mathsf {QN4}}ST_x(\Delta )$
. Then there must exist an
$Th\cup ST_x(\Gamma )\not \models _{\mathsf {QN4}}ST_x(\Delta )$
. Then there must exist an
![]() $\mathcal {S}\in \mathbb {N}4$
, a
$\mathcal {S}\in \mathbb {N}4$
, a
![]() $\mathbf {w} \in W$
, and an
$\mathbf {w} \in W$
, and an
![]() $a\in U_{\mathbf {w}}$
such that
$a\in U_{\mathbf {w}}$
such that
![]() $\mathcal {S}, \mathbf {w}\models ^+_n(Th\cup ST_x(\Gamma ), ST_x(\Delta ))[x/a]$
. By Lemma 4.2, we have
$\mathcal {S}, \mathbf {w}\models ^+_n(Th\cup ST_x(\Gamma ), ST_x(\Delta ))[x/a]$
. By Lemma 4.2, we have
![]() $\mathcal {S}_{\mathbf {w}}\models ^+_n Th$
and
$\mathcal {S}_{\mathbf {w}}\models ^+_n Th$
and
![]() $\mathcal {S}_{\mathbf {w}}, \mathbf {w}\models ^+_n(ST_x(\Gamma ), ST_x(\Delta ))[x/a]$
. By Lemma 13, the structure
$\mathcal {S}_{\mathbf {w}}, \mathbf {w}\models ^+_n(ST_x(\Gamma ), ST_x(\Delta ))[x/a]$
. By Lemma 13, the structure
![]() $\mathcal {M}_{\mathcal {S}_{\mathbf {w}}}$
given as in Definition 8 is a Nelsonian conditional model, and, by Lemma 15, we have
$\mathcal {M}_{\mathcal {S}_{\mathbf {w}}}$
given as in Definition 8 is a Nelsonian conditional model, and, by Lemma 15, we have
![]() $\mathcal {M}_{\mathcal {S}_{\mathbf {w}}},(\mathbf {w}, a)\models ^+ (\Gamma , \Delta )$
. But then also
$\mathcal {M}_{\mathcal {S}_{\mathbf {w}}},(\mathbf {w}, a)\models ^+ (\Gamma , \Delta )$
. But then also
![]() $\Gamma \not \models _{\mathsf {N4CK}}\Delta $
.
$\Gamma \not \models _{\mathsf {N4CK}}\Delta $
.
We now wish to prove a converse of Proposition 8. This task also requires a series of preliminary constructions that develop the potential of the universal model
![]() $\mathcal {M}_c$
of
$\mathcal {M}_c$
of
![]() $\mathsf {N4CK}$
given in Definition 7.
$\mathsf {N4CK}$
given in Definition 7.
Definition 9. For any
![]() $n \in \omega $
, a sequence
$n \in \omega $
, a sequence
![]() $\alpha = ((\Gamma _0,\Delta _0),\phi _1,\ldots ,\phi _n, (\Gamma _n, \Delta _n))$
is called a
$\alpha = ((\Gamma _0,\Delta _0),\phi _1,\ldots ,\phi _n, (\Gamma _n, \Delta _n))$
is called a
![]() $(\Gamma _0,\Delta _0)$
-standard sequence of length
$(\Gamma _0,\Delta _0)$
-standard sequence of length
![]() $n + 1$
iff
$n + 1$
iff
![]() $(\Gamma _0,\Delta _0),\ldots ,(\Gamma _n, \Delta _n)\in W_c$
,
$(\Gamma _0,\Delta _0),\ldots ,(\Gamma _n, \Delta _n)\in W_c$
,
![]() $\phi _1,\ldots ,\phi _n \in \mathcal {CN}$
, and we have
$\phi _1,\ldots ,\phi _n \in \mathcal {CN}$
, and we have
Given a
![]() $(\Gamma , \Delta )\in W_c$
, the set of all
$(\Gamma , \Delta )\in W_c$
, the set of all
![]() $(\Gamma ,\Delta )$
-standard sequences will be denoted by
$(\Gamma ,\Delta )$
-standard sequences will be denoted by
![]() $Seq(\Gamma ,\Delta )$
. The set
$Seq(\Gamma ,\Delta )$
. The set
![]() $Seq$
of all standard sequences is then given by
$Seq$
of all standard sequences is then given by
![]() ${Seq := \bigcup \{Seq(\Gamma ,\Delta )\mid (\Gamma , \Delta )\in W_c\}}$
.
${Seq := \bigcup \{Seq(\Gamma ,\Delta )\mid (\Gamma , \Delta )\in W_c\}}$
.
Finally, given a
![]() $\beta = ((\Xi _0,\Theta _0),\psi _1,\ldots ,\psi _m, (\Xi _m, \Theta _m))\in Seq$
, we say that
$\beta = ((\Xi _0,\Theta _0),\psi _1,\ldots ,\psi _m, (\Xi _m, \Theta _m))\in Seq$
, we say that
![]() $\beta $
extends
$\beta $
extends
![]() $\alpha $
and will write
$\alpha $
and will write
![]() $ \alpha \mathrel {\prec }\beta $
iff (1)
$ \alpha \mathrel {\prec }\beta $
iff (1)
![]() $m = n$
, (2)
$m = n$
, (2)
![]() $\phi _1 = \psi _1,\ldots , \phi _n = \psi _n (= \psi _m)$
, and
$\phi _1 = \psi _1,\ldots , \phi _n = \psi _n (= \psi _m)$
, and
(3)
![]() $(\Gamma _0,\Delta _0)\leq _c (\Xi _0,\Theta _0),\ldots , (\Gamma _n,\Delta _n)\leq _c (\Xi _n,\Theta _n)(= (\Xi _m,\Theta _m))$
.
$(\Gamma _0,\Delta _0)\leq _c (\Xi _0,\Theta _0),\ldots , (\Gamma _n,\Delta _n)\leq _c (\Xi _n,\Theta _n)(= (\Xi _m,\Theta _m))$
.
Given any
![]() $(\Gamma , \Delta ), (\Xi , \Theta )\in W_c$
such that
$(\Gamma , \Delta ), (\Xi , \Theta )\in W_c$
such that
![]() $(\Gamma ,\Delta )\leq _c (\Xi ,\Theta )$
, a function
$(\Gamma ,\Delta )\leq _c (\Xi ,\Theta )$
, a function
![]() $f:Seq(\Gamma ,\Delta )\to Seq(\Xi ,\Theta )$
is called a local
$f:Seq(\Gamma ,\Delta )\to Seq(\Xi ,\Theta )$
is called a local
![]() $((\Gamma ,\Delta ),(\Xi ,\Theta ))$
-choice function iff
$((\Gamma ,\Delta ),(\Xi ,\Theta ))$
-choice function iff
![]() $(\forall \alpha \in Seq(\Gamma ,\Delta ))(\alpha \mathrel {\prec }f(\alpha ))$
. The set of all local
$(\forall \alpha \in Seq(\Gamma ,\Delta ))(\alpha \mathrel {\prec }f(\alpha ))$
. The set of all local
![]() $((\Gamma ,\Delta ),(\Xi ,\Theta ))$
-choice functions will be denoted by
$((\Gamma ,\Delta ),(\Xi ,\Theta ))$
-choice functions will be denoted by
![]() $\mathfrak {F}((\Gamma ,\Delta ),(\Xi ,\Theta ))$
.
$\mathfrak {F}((\Gamma ,\Delta ),(\Xi ,\Theta ))$
.
However,
![]() $((\Gamma ,\Delta ),(\Xi ,\Theta ))$
-choice functions will mostly interest us as restrictions of global choice functions. More precisely,
$((\Gamma ,\Delta ),(\Xi ,\Theta ))$
-choice functions will mostly interest us as restrictions of global choice functions. More precisely,
![]() $F: Seq \to Seq$
is a global choice function iff for every
$F: Seq \to Seq$
is a global choice function iff for every
![]() $(\Gamma , \Delta ) \in W_c$
there exists a
$(\Gamma , \Delta ) \in W_c$
there exists a
![]() $(\Xi , \Theta )\in W_c$
such that
$(\Xi , \Theta )\in W_c$
such that
![]() $(\Gamma ,\Delta )\leq _c (\Xi ,\Theta )$
and
$(\Gamma ,\Delta )\leq _c (\Xi ,\Theta )$
and
![]() $F\upharpoonright Seq(\Gamma ,\Delta ) \in \mathfrak {F}((\Gamma ,\Delta ),(\Xi ,\Theta ))$
. The set of all global choice functions will be denoted by
$F\upharpoonright Seq(\Gamma ,\Delta ) \in \mathfrak {F}((\Gamma ,\Delta ),(\Xi ,\Theta ))$
. The set of all global choice functions will be denoted by
![]() $\mathfrak {G}$
. The following lemma sums up some useful properties of global choice functions.
$\mathfrak {G}$
. The following lemma sums up some useful properties of global choice functions.
Lemma 16. Let
![]() $(\Gamma , \Delta ) \in W_c$
. Then the following statements hold:
$(\Gamma , \Delta ) \in W_c$
. Then the following statements hold:
-
1. For every
 $(\Xi , \Theta )\in W_c$
such that
$(\Xi , \Theta )\in W_c$
such that
 $(\Gamma ,\Delta )\leq _c (\Xi ,\Theta )$
and for every
$(\Gamma ,\Delta )\leq _c (\Xi ,\Theta )$
and for every
 $f \in \mathfrak {F}((\Gamma ,\Delta ),(\Xi ,\Theta ))$
, there exists an
$f \in \mathfrak {F}((\Gamma ,\Delta ),(\Xi ,\Theta ))$
, there exists an
 $F \in \mathfrak {G}$
such that
$F \in \mathfrak {G}$
such that
 $F\upharpoonright Seq(\Gamma ,\Delta ) = f$
.
$F\upharpoonright Seq(\Gamma ,\Delta ) = f$
. -
2. For every
 $\alpha \in Seq(\Gamma ,\Delta )$
and every
$\alpha \in Seq(\Gamma ,\Delta )$
and every
 $(\Xi , \Theta )\in W_c$
such that
$(\Xi , \Theta )\in W_c$
such that
 $end(\alpha ) \leq _c (\Xi , \Theta )$
, there exists a
$end(\alpha ) \leq _c (\Xi , \Theta )$
, there exists a
 $\beta \in Seq$
such that
$\beta \in Seq$
such that
 $end(\beta ) = (\Xi , \Theta )$
, and an
$end(\beta ) = (\Xi , \Theta )$
, and an
 $F\in \mathfrak {G}$
such that
$F\in \mathfrak {G}$
such that
 $F(\alpha ) = \beta $
.
$F(\alpha ) = \beta $
. -
3.
 $id[Seq]\in \mathfrak {G}$
.
$id[Seq]\in \mathfrak {G}$
. -
4. Given any
 $n \in \omega $
and any
$n \in \omega $
and any
 $F_1,\ldots ,F_n \in \mathfrak {G}$
we also have that
$F_1,\ldots ,F_n \in \mathfrak {G}$
we also have that
 ${F_1\circ \dots \circ F_n \in \mathfrak {G}}$
.
${F_1\circ \dots \circ F_n \in \mathfrak {G}}$
. -
5. For every
 $\alpha \in Seq$
and every
$\alpha \in Seq$
and every
 $F \in \mathfrak {G}$
, we have
$F \in \mathfrak {G}$
, we have
 $\alpha \mathrel {\prec }F(\alpha )$
.
$\alpha \mathrel {\prec }F(\alpha )$
.
The proof of Lemma 16 repeats the proof of [Reference Olkhovikov12, Lemma 19] almost word-for-word; however, for the sake of completeness, we also include this proof in Appendix C.
The global choice functions are the basis for another type of sequences, that, along with the standard sequences, is necessary for the main model-theoretic construction of the present section. We will call them global sequences. A global sequence is any sequence of the form
![]() $(F_1,\ldots , F_n) \in \mathfrak {G}^n$
, where
$(F_1,\ldots , F_n) \in \mathfrak {G}^n$
, where
![]() $n \in \omega $
(thus
$n \in \omega $
(thus
![]() $\Lambda $
is also a global sequence with
$\Lambda $
is also a global sequence with
![]() $n = 0$
). Given two global sequences
$n = 0$
). Given two global sequences
![]() $(F_1,\ldots , F_k)$
and
$(F_1,\ldots , F_k)$
and
![]() $(G_1,\ldots , G_m)$
, we say that
$(G_1,\ldots , G_m)$
, we say that
![]() $(G_1,\ldots , G_m)$
extends
$(G_1,\ldots , G_m)$
extends
![]() $(F_1,\ldots , F_k)$
and write
$(F_1,\ldots , F_k)$
and write
![]() $(F_1,\ldots , F_k)\mathrel {\sqsubseteq }(G_1,\ldots , G_m)$
iff
$(F_1,\ldots , F_k)\mathrel {\sqsubseteq }(G_1,\ldots , G_m)$
iff
![]() $k \leq m$
and
$k \leq m$
and
![]() $F_1 = G_1,\ldots , F_k = G_k$
. Furthermore, we will denote by
$F_1 = G_1,\ldots , F_k = G_k$
. Furthermore, we will denote by
![]() $Glob$
the set
$Glob$
the set
![]() $\bigcup _{n \in \omega }\mathfrak {G}^n$
, that is to say, the set of all global sequences.
$\bigcup _{n \in \omega }\mathfrak {G}^n$
, that is to say, the set of all global sequences.
The final item in this series of preliminary model-theoretic constructions is a certain equivalence relation on
![]() $\mathcal {CN}$
. Namely, given any
$\mathcal {CN}$
. Namely, given any
![]() $\phi ,\psi \in \mathcal {CN}$
, we define that:
$\phi ,\psi \in \mathcal {CN}$
, we define that:
For any
![]() $\phi \in \mathcal {CN}$
, we will denote its equivalence class relative to
$\phi \in \mathcal {CN}$
, we will denote its equivalence class relative to
![]() $\simeq $
by
$\simeq $
by
![]() $[\phi ]_\simeq $
.
$[\phi ]_\simeq $
.
We now proceed to define an
![]() $\mathcal {S}_c \in \mathbb {N}4$
induced by
$\mathcal {S}_c \in \mathbb {N}4$
induced by
![]() $\mathcal {M}_c\in \mathbb {NC}$
of Definition 7.
$\mathcal {M}_c\in \mathbb {NC}$
of Definition 7.
Definition 10. We set
![]() $\mathcal {S}_c:= (Glob, \sqsubseteq , \mathbb {M}^+, \mathbb {M}^-,\mathbb {F})$
, where:
$\mathcal {S}_c:= (Glob, \sqsubseteq , \mathbb {M}^+, \mathbb {M}^-,\mathbb {F})$
, where:
-
• For every
 $\bar {F} \in Glob$
,
$\bar {F} \in Glob$
,
 $\mathbb {M}^+_{\bar {F}} := \mathbb {M}^+$
,
$\mathbb {M}^+_{\bar {F}} := \mathbb {M}^+$
,
 $\mathbb {M}^-_{\bar {F}} := \mathbb {M}^-$
, i.e., every global sequence gets assigned the same positive model
$\mathbb {M}^-_{\bar {F}} := \mathbb {M}^-$
, i.e., every global sequence gets assigned the same positive model
 $\mathbb {M}^+\in \mathbb {C}(\Pi )$
(resp., the same negative model
$\mathbb {M}^+\in \mathbb {C}(\Pi )$
(resp., the same negative model
 $\mathbb {M}^-\in \mathbb {C}(\Pi \cup \{\epsilon ^2\})$
). As for the components of these models, we set:
$\mathbb {M}^-\in \mathbb {C}(\Pi \cup \{\epsilon ^2\})$
). As for the components of these models, we set:-
–
 $U^{\mathbb {M}^+} = U^{\mathbb {M}^-} = U := Seq \cup \{[\phi ]_{\simeq }\mid \phi \in \mathcal {CN}\}$
.
$U^{\mathbb {M}^+} = U^{\mathbb {M}^-} = U := Seq \cup \{[\phi ]_{\simeq }\mid \phi \in \mathcal {CN}\}$
. -
–
 $p^{\mathbb {M}^+} := \{\beta \in Seq\mid p\in \pi ^1(end(\beta ))\}$
and
$p^{\mathbb {M}^+} := \{\beta \in Seq\mid p\in \pi ^1(end(\beta ))\}$
and
 $p^{\mathbb {M}^-} := \{\beta \in Seq\mid \sim p\in \pi ^1(end(\beta ))\}$
for every
$p^{\mathbb {M}^-} := \{\beta \in Seq\mid \sim p\in \pi ^1(end(\beta ))\}$
for every
 $p^1 \in Prop$
.
$p^1 \in Prop$
. -
–
 $S^{\mathbb {M}^+} :=\{[\phi ]_{\simeq }\mid \phi \in \mathcal {CN}\}$
and
$S^{\mathbb {M}^+} :=\{[\phi ]_{\simeq }\mid \phi \in \mathcal {CN}\}$
and
 $S^{\mathbb {M}^-} :=Seq$
.
$S^{\mathbb {M}^-} :=Seq$
. -
–
 $O^{\mathbb {M}^+} :=Seq$
and
$O^{\mathbb {M}^+} :=Seq$
and
 $O^{\mathbb {M}^-} := \{[\phi ]_{\simeq }\mid \phi \in \mathcal {CN}\}$
.
$O^{\mathbb {M}^-} := \{[\phi ]_{\simeq }\mid \phi \in \mathcal {CN}\}$
. -
–
 $E^{\mathbb {M}^+} := \{(\beta , [\phi ]_{\simeq })\in O^{\mathbb {M}^+}\times S^{\mathbb {M}^+}\mid \phi \in \pi ^1(end(\beta ))\}$
and
$E^{\mathbb {M}^+} := \{(\beta , [\phi ]_{\simeq })\in O^{\mathbb {M}^+}\times S^{\mathbb {M}^+}\mid \phi \in \pi ^1(end(\beta ))\}$
and
 $E^{\mathbb {M}^-} := \{(\beta , [\phi ]_{\simeq })\in O^{\mathbb {M}^+}\times S^{\mathbb {M}^+}\mid \sim \phi \in \pi ^1(end(\beta ))\}$
.
$E^{\mathbb {M}^-} := \{(\beta , [\phi ]_{\simeq })\in O^{\mathbb {M}^+}\times S^{\mathbb {M}^+}\mid \sim \phi \in \pi ^1(end(\beta ))\}$
. -
–
 $R^{\mathbb {M}^+} := \{(\beta , [\phi ]_{\simeq }, \gamma )\in O^{\mathbb {M}^+}\times S^{\mathbb {M}^+}\times O^{\mathbb {M}^+}\mid (\exists (\Xi , \Theta ) \in W_c)(\exists \psi \in [\phi ]_{\simeq })(\gamma = \beta ^\frown (\psi , (\Xi , \Theta )))\}$
and
$R^{\mathbb {M}^+} := \{(\beta , [\phi ]_{\simeq }, \gamma )\in O^{\mathbb {M}^+}\times S^{\mathbb {M}^+}\times O^{\mathbb {M}^+}\mid (\exists (\Xi , \Theta ) \in W_c)(\exists \psi \in [\phi ]_{\simeq })(\gamma = \beta ^\frown (\psi , (\Xi , \Theta )))\}$
and
 $R^{\mathbb {M}^-} := \emptyset $
.
$R^{\mathbb {M}^-} := \emptyset $
. -
–
 $\epsilon ^{\mathbb {M}^-}:= \{([\phi ]_{\simeq },[\psi ]_{\simeq })\in S^{\mathbb {M}^+}\times S^{\mathbb {M}^+}\mid [\phi ]_{\simeq }\neq [\psi ]_{\simeq }\}$
.
$\epsilon ^{\mathbb {M}^-}:= \{([\phi ]_{\simeq },[\psi ]_{\simeq })\in S^{\mathbb {M}^+}\times S^{\mathbb {M}^+}\mid [\phi ]_{\simeq }\neq [\psi ]_{\simeq }\}$
.
-
-
• For any
 $\bar {F}, \bar {G} \in Glob$
such that, for some
$\bar {F}, \bar {G} \in Glob$
such that, for some
 $k \leq m$
we have
$k \leq m$
we have
 $\bar {F} = (F_1,\ldots , F_k)$
and
$\bar {F} = (F_1,\ldots , F_k)$
and
 $\bar {G} = (F_1,\ldots , F_m)$
we have
$\bar {G} = (F_1,\ldots , F_m)$
we have
 $\mathbb {F}_{\bar {F}\bar {G}}:U\to U$
, where we set:
$\mathbb {F}_{\bar {F}\bar {G}}:U\to U$
, where we set:  $$ \begin{align*}\mathbb{F}_{\bar{F}\bar{G}}(\gamma):= \begin{cases} (F_{k + 1}\circ\dots\circ F_m)(\gamma),\text{ if }\gamma \in Seq;\\ \gamma,\text{ otherwise. } \end{cases} \end{align*} $$
$$ \begin{align*}\mathbb{F}_{\bar{F}\bar{G}}(\gamma):= \begin{cases} (F_{k + 1}\circ\dots\circ F_m)(\gamma),\text{ if }\gamma \in Seq;\\ \gamma,\text{ otherwise. } \end{cases} \end{align*} $$
The first thing to show is that we, indeed, have
![]() $\mathcal {S}_c\in \mathbb {N}4$
. Again, we begin by establishing another technical fact.
$\mathcal {S}_c\in \mathbb {N}4$
. Again, we begin by establishing another technical fact.
Lemma 17. For all
![]() $\bar {F}, \bar {G}\in Glob$
such that
$\bar {F}, \bar {G}\in Glob$
such that
![]() $\bar {F}\mathrel {\sqsubseteq }\bar {G}$
, it is true that:
$\bar {F}\mathrel {\sqsubseteq }\bar {G}$
, it is true that:
-
1.
 $\mathbb {F}_{\bar {F}\bar {G}}\upharpoonright Seq \in \mathfrak {G}$
.
$\mathbb {F}_{\bar {F}\bar {G}}\upharpoonright Seq \in \mathfrak {G}$
. -
2. For every
 $\alpha \in Seq$
we have
$\alpha \in Seq$
we have
 $\alpha \mathrel {\prec }\mathbb {F}_{\bar {F}\bar {G}}(\alpha )$
; in particular, we have
$\alpha \mathrel {\prec }\mathbb {F}_{\bar {F}\bar {G}}(\alpha )$
; in particular, we have
 $end(\alpha )\leq _c end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha ))$
, or, equivalently,
$end(\alpha )\leq _c end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha ))$
, or, equivalently,
 $\pi ^1(end(\alpha ))\subseteq \pi ^1(end (\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
.
$\pi ^1(end(\alpha ))\subseteq \pi ^1(end (\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
.
Proof Assume the hypothesis; we may also assume, wlog, that, for some
![]() $k \leq m < \omega $
,
$k \leq m < \omega $
,
![]() $\bar {F}$
and
$\bar {F}$
and
![]() $\bar {G}$
are given in the following form:
$\bar {G}$
are given in the following form:
In this case, we also get the following representation for
![]() $\mathbb {F}_{\bar {F}\bar {G}}$
:
$\mathbb {F}_{\bar {F}\bar {G}}$
:
Part 1 now easily follows from (
![]() $ \text{def1-}\mathbb{F}_{\bar{F}\bar{G}}$
) and Lemma 16.4. As for Part 2, we observe that, if
$ \text{def1-}\mathbb{F}_{\bar{F}\bar{G}}$
) and Lemma 16.4. As for Part 2, we observe that, if
![]() $\alpha \in Seq$
, then
$\alpha \in Seq$
, then
![]() $ \mathbb {F}_{\bar {F}\bar {G}}(\alpha ) = (id[U]\circ F_{k + 1}\circ \dots \circ F_m)(\alpha )\in Seq$
. Now Part 1 and Lemma 16.5 together imply that
$ \mathbb {F}_{\bar {F}\bar {G}}(\alpha ) = (id[U]\circ F_{k + 1}\circ \dots \circ F_m)(\alpha )\in Seq$
. Now Part 1 and Lemma 16.5 together imply that
![]() $\alpha \mathrel {\prec }\mathbb {F}_{\bar {F}\bar {G}}(\alpha )$
. By Definition 9, this means that
$\alpha \mathrel {\prec }\mathbb {F}_{\bar {F}\bar {G}}(\alpha )$
. By Definition 9, this means that
![]() $end(\alpha )\leq _c end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha ))$
, or, equivalently, that
$end(\alpha )\leq _c end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha ))$
, or, equivalently, that
![]() $\pi ^1(end(\alpha ))\subseteq \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
.
$\pi ^1(end(\alpha ))\subseteq \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
.
Lemma 18.
![]() $\mathcal {S}_c$
is a Nelsonian sheaf.
$\mathcal {S}_c$
is a Nelsonian sheaf.
Proof It is clear that
![]() $Glob$
is non-empty and that
$Glob$
is non-empty and that
![]() $\sqsubseteq $
defines a pre-order on
$\sqsubseteq $
defines a pre-order on
![]() $Glob$
. It is also clear that
$Glob$
. It is also clear that
![]() $\mathbb {M}^+\in \mathbb {C}(\Theta )$
,
$\mathbb {M}^+\in \mathbb {C}(\Theta )$
,
![]() $\mathbb {M}^-\in \mathbb {C}(\Theta \cup \{\epsilon ^2\})$
, and that, for
$\mathbb {M}^-\in \mathbb {C}(\Theta \cup \{\epsilon ^2\})$
, and that, for
![]() $\bar {F}, \bar {G}\in Glob$
,
$\bar {F}, \bar {G}\in Glob$
,
![]() $\bar {F}\mathrel {\sqsubseteq }\bar {G}$
implies
$\bar {F}\mathrel {\sqsubseteq }\bar {G}$
implies
![]() $\mathbb {F}_{\bar {F}\bar {G}}:U\to U$
. We need to show that
$\mathbb {F}_{\bar {F}\bar {G}}:U\to U$
. We need to show that
![]() $\mathcal {S}^+_c = (Glob, \sqsubseteq , \mathbb {M}^+, \mathbb {F})\in \mathbb {I}(\Theta )$
and that
$\mathcal {S}^+_c = (Glob, \sqsubseteq , \mathbb {M}^+, \mathbb {F})\in \mathbb {I}(\Theta )$
and that
![]() $\mathcal {S}^-_c =(Glob, \sqsubseteq , \mathbb {M}^+, \mathbb {F})\in \mathbb {I}(\Theta \cup \{\epsilon ^2\})$
.
$\mathcal {S}^-_c =(Glob, \sqsubseteq , \mathbb {M}^+, \mathbb {F})\in \mathbb {I}(\Theta \cup \{\epsilon ^2\})$
.
As for the conditions imposed by Definition 3.4 on the functions of the form
![]() $\mathbb {F}_{\bar {F}\bar {G}}$
, it is clear from Definition 10 and from our convention on compositions of empty families of functions that (1) for any
$\mathbb {F}_{\bar {F}\bar {G}}$
, it is clear from Definition 10 and from our convention on compositions of empty families of functions that (1) for any
![]() $\bar {F}\in Glob$
we will have in
$\bar {F}\in Glob$
we will have in
![]() $\mathbb {F}_{\bar {F}\bar {F}} = id[U]$
and that (2) if
$\mathbb {F}_{\bar {F}\bar {F}} = id[U]$
and that (2) if
![]() $\bar {F}, \bar {G}, \bar {H}\in Glob$
are such that
$\bar {F}, \bar {G}, \bar {H}\in Glob$
are such that
![]() $\bar {F}\mathrel {\sqsubseteq }\bar {G}\mathrel {\sqsubseteq }\bar {H}$
, then
$\bar {F}\mathrel {\sqsubseteq }\bar {G}\mathrel {\sqsubseteq }\bar {H}$
, then
![]() $\mathbb {F}_{\bar {F}\bar {G}}\circ \mathbb {F}_{\bar {G}\bar {H}} = \mathbb {F}_{\bar {F}\bar {H}}$
.
$\mathbb {F}_{\bar {F}\bar {G}}\circ \mathbb {F}_{\bar {G}\bar {H}} = \mathbb {F}_{\bar {F}\bar {H}}$
.
It remains to establish that, for each pair
![]() $\bar {F}, \bar {G}\in Glob$
such that
$\bar {F}, \bar {G}\in Glob$
such that
![]() $\bar {F}\mathrel {\sqsubseteq }\bar {G}$
, we have
$\bar {F}\mathrel {\sqsubseteq }\bar {G}$
, we have
![]() $\mathbb {F}_{\bar {F}\bar {G}}\in Hom(\mathbb {M}^+,\mathbb {M}^+)\cap Hom(\mathbb {M}^-,\mathbb {M}^-)$
. The latter claim boils down to showing that the
$\mathbb {F}_{\bar {F}\bar {G}}\in Hom(\mathbb {M}^+,\mathbb {M}^+)\cap Hom(\mathbb {M}^-,\mathbb {M}^-)$
. The latter claim boils down to showing that the
![]() $\mathbb {M}^+$
-extension of every predicate in
$\mathbb {M}^+$
-extension of every predicate in
![]() $\Pi $
and the
$\Pi $
and the
![]() $\mathbb {M}^-$
-extension of every predicate in
$\mathbb {M}^-$
-extension of every predicate in
![]() $\Pi \cup \{\epsilon ^2\}$
is preserved by
$\Pi \cup \{\epsilon ^2\}$
is preserved by
![]() $\mathbb {F}_{\bar {F}\bar {G}}$
. In doing so, we will assume that, for some appropriate
$\mathbb {F}_{\bar {F}\bar {G}}$
. In doing so, we will assume that, for some appropriate
![]() $k \leq m < \omega $
,
$k \leq m < \omega $
,
![]() $\bar {F}$
,
$\bar {F}$
,
![]() $\bar {G}$
, and
$\bar {G}$
, and
![]() $\mathbb {F}_{\bar {F}\bar {G}}$
are given in a form that satisfies (def-F̅), (def-Ḡ
), (
$\mathbb {F}_{\bar {F}\bar {G}}$
are given in a form that satisfies (def-F̅), (def-Ḡ
), (
![]() $ \text{def1-}\mathbb{F}_{\bar{F}\bar{G}}$
), and (
$ \text{def1-}\mathbb{F}_{\bar{F}\bar{G}}$
), and (
![]() $ \text{def2-}\mathbb{F}_{\bar{F}\bar{G}}$
). So let
$ \text{def2-}\mathbb{F}_{\bar{F}\bar{G}}$
). So let
![]() $\mathbb {X} \in \Pi \cup \{\epsilon ^2\}$
; the following cases have to be considered:
$\mathbb {X} \in \Pi \cup \{\epsilon ^2\}$
; the following cases have to be considered:
Case 1.
![]() $\mathbb {X} \in \{O^1, S^1, \epsilon ^2\}$
. Trivial by (
$\mathbb {X} \in \{O^1, S^1, \epsilon ^2\}$
. Trivial by (
![]() $ \text{def1-}\mathbb{F}_{\bar{F}\bar{G}}$
) and (
$ \text{def1-}\mathbb{F}_{\bar{F}\bar{G}}$
) and (
![]() $ \text{def2-}\mathbb{F}_{\bar{F}\bar{G}}$
).
$ \text{def2-}\mathbb{F}_{\bar{F}\bar{G}}$
).
Case 2.
![]() $\mathbb {X} = p^1 \in Prop$
. If
$\mathbb {X} = p^1 \in Prop$
. If
![]() $\alpha \in U$
is such that
$\alpha \in U$
is such that
![]() $\alpha \in p^{\mathbb {M}^+}$
, then, by Definition 10 and Lemma 17, we must have all of the following: (1)
$\alpha \in p^{\mathbb {M}^+}$
, then, by Definition 10 and Lemma 17, we must have all of the following: (1)
![]() $\alpha , \mathbb {F}_{\bar {F}\bar {G}}(\alpha ) \in Seq$
, (2)
$\alpha , \mathbb {F}_{\bar {F}\bar {G}}(\alpha ) \in Seq$
, (2)
![]() $\pi ^1(end(\alpha ))\subseteq \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, and (3)
$\pi ^1(end(\alpha ))\subseteq \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, and (3)
![]() $p\in \pi ^1(end(\alpha ))$
. But then clearly also
$p\in \pi ^1(end(\alpha ))$
. But then clearly also
![]() $p \in \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, whence, further,
$p \in \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, whence, further,
![]() $\mathbb {F}_{\bar {F}\bar {G}}(\alpha ) \in p^{\mathbb {M}^+}$
, as desired. Similarly, if
$\mathbb {F}_{\bar {F}\bar {G}}(\alpha ) \in p^{\mathbb {M}^+}$
, as desired. Similarly, if
![]() $\alpha \in U$
is such that
$\alpha \in U$
is such that
![]() $\alpha \in p^{\mathbb {M}^-}$
, then, by Definition 10 and Lemma 17, we must have (1) and (2) as given above, plus
$\alpha \in p^{\mathbb {M}^-}$
, then, by Definition 10 and Lemma 17, we must have (1) and (2) as given above, plus
![]() $\sim p\in \pi ^1(end(\alpha ))$
. But then clearly also
$\sim p\in \pi ^1(end(\alpha ))$
. But then clearly also
![]() $\sim p \in \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, whence, further,
$\sim p \in \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, whence, further,
![]() $\mathbb {F}_{\bar {F}\bar {G}}(\alpha ) \in p^{\mathbb {M}^-}$
, as desired
$\mathbb {F}_{\bar {F}\bar {G}}(\alpha ) \in p^{\mathbb {M}^-}$
, as desired
Case 3.
![]() $\mathbb {X} = E^2$
. If
$\mathbb {X} = E^2$
. If
![]() $\alpha , \beta \in U$
are such that
$\alpha , \beta \in U$
are such that
![]() $(\alpha , \beta ) \in E^{\mathbb {M}^+}$
, then, arguing as in Case 2, we must have: (1)
$(\alpha , \beta ) \in E^{\mathbb {M}^+}$
, then, arguing as in Case 2, we must have: (1)
![]() $\alpha , \mathbb {F}_{\bar {F}\bar {G}}(\alpha ) \in Seq$
, (2)
$\alpha , \mathbb {F}_{\bar {F}\bar {G}}(\alpha ) \in Seq$
, (2)
![]() $\beta \in S^{\mathbb {M}^+}$
, in other words,
$\beta \in S^{\mathbb {M}^+}$
, in other words,
![]() $\beta = [\phi ]_{\simeq }$
for some
$\beta = [\phi ]_{\simeq }$
for some
![]() $\phi \in \mathcal {CN}$
, (3)
$\phi \in \mathcal {CN}$
, (3)
![]() $\pi ^1(end(\alpha ))\subseteq \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, and (4)
$\pi ^1(end(\alpha ))\subseteq \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, and (4)
![]() $\phi \in \pi ^1(end(\alpha ))\subseteq \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, so that we also have, by (
$\phi \in \pi ^1(end(\alpha ))\subseteq \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, so that we also have, by (
![]() $ \text{def2-}\mathbb{F}_{\bar{F}\bar{G}}$
), that
$ \text{def2-}\mathbb{F}_{\bar{F}\bar{G}}$
), that
![]() $ (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),\mathbb {F}_{\bar {F}\bar {G}}(\beta )) = (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),\mathbb {F}_{\bar {F}\bar {G}}([\phi ]_{\simeq })) = (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),[\phi ]_{\simeq }) \in E^{\mathbb {M}^+}$
. On the other hand, if
$ (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),\mathbb {F}_{\bar {F}\bar {G}}(\beta )) = (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),\mathbb {F}_{\bar {F}\bar {G}}([\phi ]_{\simeq })) = (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),[\phi ]_{\simeq }) \in E^{\mathbb {M}^+}$
. On the other hand, if
![]() $(\alpha , \beta ) \in E^{\mathbb {M}^-}$
, then we must have (1)–(3) as above plus
$(\alpha , \beta ) \in E^{\mathbb {M}^-}$
, then we must have (1)–(3) as above plus
![]() $\sim \phi \in \pi ^1(end(\alpha ))\subseteq \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, so that we also have, by (
$\sim \phi \in \pi ^1(end(\alpha ))\subseteq \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, so that we also have, by (
![]() $ \text{def2-}\mathbb{F}_{\bar{F}\bar{G}}$
), that
$ \text{def2-}\mathbb{F}_{\bar{F}\bar{G}}$
), that
![]() $ (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),\mathbb {F}_{\bar {F}\bar {G}}(\beta )) = (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),\mathbb {F}_{\bar {F}\bar {G}}([\phi ]_{\simeq })) = (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),[\phi ]_{\simeq }) \in E^{\mathbb {M}^-}$
.
$ (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),\mathbb {F}_{\bar {F}\bar {G}}(\beta )) = (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),\mathbb {F}_{\bar {F}\bar {G}}([\phi ]_{\simeq })) = (\mathbb {F}_{\bar {F}\bar {G}}(\alpha ),[\phi ]_{\simeq }) \in E^{\mathbb {M}^-}$
.
Case 4.
![]() $\mathbb {X} = R^3$
. Then for no
$\mathbb {X} = R^3$
. Then for no
![]() $\alpha , \beta , \gamma \in U$
can we have
$\alpha , \beta , \gamma \in U$
can we have
![]() $(\alpha , \beta , \gamma ) \in R^{\mathbb {M}^-}$
. If
$(\alpha , \beta , \gamma ) \in R^{\mathbb {M}^-}$
. If
![]() $\alpha , \beta , \gamma \in U$
are such that
$\alpha , \beta , \gamma \in U$
are such that
![]() $(\alpha , \beta , \gamma ) \in R^{\mathbb {M}^+}$
, then, arguing as in Case 2, we must have: (1)
$(\alpha , \beta , \gamma ) \in R^{\mathbb {M}^+}$
, then, arguing as in Case 2, we must have: (1)
![]() $\alpha , \gamma , \mathbb {F}_{\bar {F}\bar {G}}(\alpha ), \mathbb {F}_{\bar {F}\bar {G}}(\gamma )\in Seq$
, (2)
$\alpha , \gamma , \mathbb {F}_{\bar {F}\bar {G}}(\alpha ), \mathbb {F}_{\bar {F}\bar {G}}(\gamma )\in Seq$
, (2)
![]() $\beta \in S^{\mathbb {M}^+}$
, in other words,
$\beta \in S^{\mathbb {M}^+}$
, in other words,
![]() $\beta = [\phi ]_{\simeq }$
for some
$\beta = [\phi ]_{\simeq }$
for some
![]() $\phi \in \mathcal {CN}$
, (3)
$\phi \in \mathcal {CN}$
, (3)
![]() $\alpha \mathrel {\prec }\mathbb {F}_{\bar {F}\bar {G}}(\alpha )$
, and
$\alpha \mathrel {\prec }\mathbb {F}_{\bar {F}\bar {G}}(\alpha )$
, and
![]() $\gamma \mathrel {\prec }\mathbb {F}_{\bar {F}\bar {G}}(\gamma )$
, and, finally, (4) for some
$\gamma \mathrel {\prec }\mathbb {F}_{\bar {F}\bar {G}}(\gamma )$
, and, finally, (4) for some
![]() $(\Xi ,\Theta )\in W_c$
and some
$(\Xi ,\Theta )\in W_c$
and some
![]() $\psi \in [\phi ]_{\simeq }$
, we must have
$\psi \in [\phi ]_{\simeq }$
, we must have
![]() $\gamma = \alpha ^\frown (\psi , (\Xi , \Theta ))$
. Now, Definition 9 implies that, for some
$\gamma = \alpha ^\frown (\psi , (\Xi , \Theta ))$
. Now, Definition 9 implies that, for some
![]() $(\Xi ',\Theta ')\in W_c$
such that
$(\Xi ',\Theta ')\in W_c$
such that
![]() $(\Xi ,\Theta )\leq _c(\Xi ',\Theta ')$
we must have
$(\Xi ,\Theta )\leq _c(\Xi ',\Theta ')$
we must have
![]() $\mathbb {F}_{\bar {F}\bar {G}}(\gamma ) = \mathbb {F}_{\bar {F}\bar {G}}(\alpha )^\frown (\psi , (\Xi ', \Theta '))$
. Therefore, by Definition 10, we must have
$\mathbb {F}_{\bar {F}\bar {G}}(\gamma ) = \mathbb {F}_{\bar {F}\bar {G}}(\alpha )^\frown (\psi , (\Xi ', \Theta '))$
. Therefore, by Definition 10, we must have
We will eventually have to show that the Nelsonian sheaf
![]() $\mathcal {S}_c$
satisfies (Th1)–(Th5). The following lemma shows the satisfaction of (Th1).
$\mathcal {S}_c$
satisfies (Th1)–(Th5). The following lemma shows the satisfaction of (Th1).
Lemma 19.
![]() $\mathcal {S}_c \models ^+_{n} (Th1)$
.
$\mathcal {S}_c \models ^+_{n} (Th1)$
.
Proof Let
![]() $\bar {F} \in Glob$
and let
$\bar {F} \in Glob$
and let
![]() $a, b \in U$
be such that
$a, b \in U$
be such that
![]() $ \mathcal {S}_c,\bar {F} \models ^+_n Sx\wedge Sz\wedge (\forall y)_O (Eyx\Leftrightarrow Eyz)[x/a, z/b]$
. Then
$ \mathcal {S}_c,\bar {F} \models ^+_n Sx\wedge Sz\wedge (\forall y)_O (Eyx\Leftrightarrow Eyz)[x/a, z/b]$
. Then
![]() $a,b \in S^{\mathbb {M}^+}$
, that is to say, for some
$a,b \in S^{\mathbb {M}^+}$
, that is to say, for some
![]() $\phi , \psi \in \mathcal {CN}$
, we must have
$\phi , \psi \in \mathcal {CN}$
, we must have
![]() $a = [\phi ]_{\simeq }$
and
$a = [\phi ]_{\simeq }$
and
![]() $b = [\psi ]_{\simeq }$
. Assume, towards contradiction, that
$b = [\psi ]_{\simeq }$
. Assume, towards contradiction, that
![]() $a = [\phi ]_{\simeq }\neq [\psi ]_{\simeq } = b$
, then we must have
$a = [\phi ]_{\simeq }\neq [\psi ]_{\simeq } = b$
, then we must have
![]() $(\phi \Leftrightarrow \psi )\notin \mathsf {N4CK}$
; in view of Proposition 7, we can suppose, wlog, that for some
$(\phi \Leftrightarrow \psi )\notin \mathsf {N4CK}$
; in view of Proposition 7, we can suppose, wlog, that for some
![]() $(\Gamma , \Delta ) \in W_c$
we either have
$(\Gamma , \Delta ) \in W_c$
we either have
![]() $\phi \in \Gamma $
but
$\phi \in \Gamma $
but
![]() $\psi \notin \Gamma $
or we have
$\psi \notin \Gamma $
or we have
![]() $\sim \phi \in \Gamma $
but
$\sim \phi \in \Gamma $
but
![]() $\sim \psi \notin \Gamma $
. Since we clearly have
$\sim \psi \notin \Gamma $
. Since we clearly have
![]() $(\Gamma , \Delta ) \in Seq \subseteq U$
, it follows from Definition 10 that in the former case we must have both
$(\Gamma , \Delta ) \in Seq \subseteq U$
, it follows from Definition 10 that in the former case we must have both
![]() $ \mathcal {S}_c,\bar {F} \models ^+_{n} Oy\wedge Eyx[x/a, y/(\Gamma , \Delta )]$
, and
$ \mathcal {S}_c,\bar {F} \models ^+_{n} Oy\wedge Eyx[x/a, y/(\Gamma , \Delta )]$
, and
![]() $\mathcal {S}_c,\bar {F} \not \models ^+_{n} Eyz[y/(\Gamma , \Delta ), z/b]$
, which contradicts our assumption. Similarly, in the latter case we must have both
$\mathcal {S}_c,\bar {F} \not \models ^+_{n} Eyz[y/(\Gamma , \Delta ), z/b]$
, which contradicts our assumption. Similarly, in the latter case we must have both
![]() $ \mathcal {S}_c,\bar {F} \models ^+_{n} Oy\wedge \sim Eyx[x/a, y/(\Gamma , \Delta )]$
, and
$ \mathcal {S}_c,\bar {F} \models ^+_{n} Oy\wedge \sim Eyx[x/a, y/(\Gamma , \Delta )]$
, and
![]() $\mathcal {S}_c,\bar {F} \not \models ^+_{n} \sim Eyz[y/(\Gamma , \Delta ), z/b]$
, which, again, contradicts our assumption. Therefore, we must have
$\mathcal {S}_c,\bar {F} \not \models ^+_{n} \sim Eyz[y/(\Gamma , \Delta ), z/b]$
, which, again, contradicts our assumption. Therefore, we must have
![]() $a = b$
.
$a = b$
.
We will also need the following corollary to Lemma 19.
Corollary 4. Let
![]() $x,y,z \in Ind$
be pairwise distinct, let
$x,y,z \in Ind$
be pairwise distinct, let
![]() $\phi \in \mathcal {FO}^y$
,
$\phi \in \mathcal {FO}^y$
,
![]() $\bar {F}\in Glob$
, and
$\bar {F}\in Glob$
, and
![]() $a,b \in U$
be such that both
$a,b \in U$
be such that both
![]() $\mathcal {S}_c,\bar {F}\models ^+_{n} Sx\wedge (\forall y)_O(Eyx\Leftrightarrow \phi )[x/a]$
and
$\mathcal {S}_c,\bar {F}\models ^+_{n} Sx\wedge (\forall y)_O(Eyx\Leftrightarrow \phi )[x/a]$
and
![]() $\mathcal {S}_c,\bar {F}\models ^+_{n} Sx\wedge (\forall y)_O(Eyx\Leftrightarrow \phi )[x/b]$
. Then
$\mathcal {S}_c,\bar {F}\models ^+_{n} Sx\wedge (\forall y)_O(Eyx\Leftrightarrow \phi )[x/b]$
. Then
![]() $a = b$
.
$a = b$
.
Proof Assume the premises. Renaming the variables, we get that
![]() $\mathcal {S}_c,\bar {F}\models ^+_{n} Sz\wedge (\forall y)_O(Ezx\Leftrightarrow \phi )[z/b]$
, whence, by (T18) we obtain that
$\mathcal {S}_c,\bar {F}\models ^+_{n} Sz\wedge (\forall y)_O(Ezx\Leftrightarrow \phi )[z/b]$
, whence, by (T18) we obtain that
![]() $\mathcal {S}_c,\bar {F}\models ^+_{n} Sx \wedge Sz\wedge (\forall y)_O(Eyx\Leftrightarrow Eyz)[x/a,z/b]$
. It follows, by Lemma 19, that
$\mathcal {S}_c,\bar {F}\models ^+_{n} Sx \wedge Sz\wedge (\forall y)_O(Eyx\Leftrightarrow Eyz)[x/a,z/b]$
. It follows, by Lemma 19, that
![]() $a = b$
.
$a = b$
.
The next lemma can be seen as a version of a ‘truth lemma’ for
![]() $\mathcal {S}_c$
.
$\mathcal {S}_c$
.
Lemma 20. Let
![]() $\bar {F} \in Glob$
,
$\bar {F} \in Glob$
,
![]() $\alpha \in Seq$
,
$\alpha \in Seq$
,
![]() $x \in Ind$
, and let
$x \in Ind$
, and let
![]() $\phi \in \mathcal {CN}$
. Then the following statements hold:
$\phi \in \mathcal {CN}$
. Then the following statements hold:
-
1.
 $\mathcal {S}_c,\bar {F} \models ^+_n ST_x(\phi )[x/\alpha ] \text { iff } \phi \in \pi ^1(end(\alpha ))$
.
$\mathcal {S}_c,\bar {F} \models ^+_n ST_x(\phi )[x/\alpha ] \text { iff } \phi \in \pi ^1(end(\alpha ))$
. -
2.
 $\mathcal {S}_c,\bar {F} \models ^-_n ST_x(\phi )[x/\alpha ] \text { iff } \sim \phi \in \pi ^1(end(\alpha ))$
.
$\mathcal {S}_c,\bar {F} \models ^-_n ST_x(\phi )[x/\alpha ] \text { iff } \sim \phi \in \pi ^1(end(\alpha ))$
. -
3.
 $\mathcal {S}_c,\bar {F}\models ^+_{n} Sx\wedge (\forall y)_O(Eyx\Leftrightarrow ST_y(\phi ))[x/[\phi ]_{\simeq }]$
.
$\mathcal {S}_c,\bar {F}\models ^+_{n} Sx\wedge (\forall y)_O(Eyx\Leftrightarrow ST_y(\phi ))[x/[\phi ]_{\simeq }]$
.
Proof We observe, first, that, for any given
![]() $\phi \in \mathcal {CN}$
, Parts 1 and 2 together clearly imply Part 3. Indeed, we must have
$\phi \in \mathcal {CN}$
, Parts 1 and 2 together clearly imply Part 3. Indeed, we must have
![]() $\mathcal {S}_c,\bar {F}\models ^+_{n} Sx[x/[\phi ]_{\simeq }]$
. As for the other conjunct, if Parts 1 and 2 hold for a given
$\mathcal {S}_c,\bar {F}\models ^+_{n} Sx[x/[\phi ]_{\simeq }]$
. As for the other conjunct, if Parts 1 and 2 hold for a given
![]() $\phi $
and for all instantiations of
$\phi $
and for all instantiations of
![]() $\bar {F}$
,
$\bar {F}$
,
![]() $\alpha $
, and x, then assume that a
$\alpha $
, and x, then assume that a
![]() $\bar {G} \in Glob$
is such that
$\bar {G} \in Glob$
is such that
![]() $\bar {F}\mathrel {\sqsubseteq }\bar {G}$
. Then, by Part 1, we must have, for every
$\bar {F}\mathrel {\sqsubseteq }\bar {G}$
. Then, by Part 1, we must have, for every
![]() $\beta \in Seq$
:
$\beta \in Seq$
:
and, by Part 2, we will have, for every
![]() $\beta \in Seq$
,
$\beta \in Seq$
,
Since we have
![]() $[\phi ]_{\simeq } = \mathbb {F}_{\bar {F}\bar {G}}([\phi ]_{\simeq })$
, Corollary 2 allows us to conclude that
$[\phi ]_{\simeq } = \mathbb {F}_{\bar {F}\bar {G}}([\phi ]_{\simeq })$
, Corollary 2 allows us to conclude that
![]() $ \mathcal {S}_c,\bar {F}\models ^+_{n} (\forall y)_O(Eyx\Leftrightarrow ST_y(\phi )))[x/[\phi ]_{\simeq }]$
.
$ \mathcal {S}_c,\bar {F}\models ^+_{n} (\forall y)_O(Eyx\Leftrightarrow ST_y(\phi )))[x/[\phi ]_{\simeq }]$
.
We will therefore prove all the three parts simultaneously by induction on the construction of
![]() $\phi \in \mathcal {CN}$
; but, in view of the foregoing observation, we will only argue for Parts 1 and 2.
$\phi \in \mathcal {CN}$
; but, in view of the foregoing observation, we will only argue for Parts 1 and 2.
Basis. Assume that
![]() $\phi = p$
for some
$\phi = p$
for some
![]() $p^1 \in Prop$
. Then
$p^1 \in Prop$
. Then
![]() $ST_x(\phi ) = px$
and Definition 10 implies that we have (for Part 1)
$ST_x(\phi ) = px$
and Definition 10 implies that we have (for Part 1)
![]() $\mathcal {S}_c,\bar {F}\models ^+_{n} px[x/\alpha ]$
iff
$\mathcal {S}_c,\bar {F}\models ^+_{n} px[x/\alpha ]$
iff
![]() $\alpha \in p^{\mathbb {M}^+}$
iff
$\alpha \in p^{\mathbb {M}^+}$
iff
![]() $p \in \pi ^1(end(\alpha ))$
, and (for Part 2)
$p \in \pi ^1(end(\alpha ))$
, and (for Part 2)
![]() $\mathcal {S}_c,\bar {F}\models ^-_{n} px[x/\alpha ]$
iff
$\mathcal {S}_c,\bar {F}\models ^-_{n} px[x/\alpha ]$
iff
![]() $\alpha \in p^{\mathbb {M}^-}$
iff
$\alpha \in p^{\mathbb {M}^-}$
iff
![]() $\sim p \in \pi ^1(end(\alpha ))$
.
$\sim p \in \pi ^1(end(\alpha ))$
.
Induction step. Again, several cases are possible:
Case 1.
![]() $\phi = \psi \wedge \chi $
. Then
$\phi = \psi \wedge \chi $
. Then
![]() $ST_x(\phi ) = ST_x(\psi )\wedge ST_x(\chi )$
and we have, for Part 1, by IH and Proposition 7:
$ST_x(\phi ) = ST_x(\psi )\wedge ST_x(\chi )$
and we have, for Part 1, by IH and Proposition 7:
 $$ \begin{align*} &\mathcal{S}_c,\bar{F}\models^+_{n} (ST_x(\psi)\wedge ST_x(\chi))[x/\alpha]\\& \quad \text{iff } \mathcal{S}_c,\bar{F}\models^+_{n} ST_x(\psi)[x/\alpha]\text{ and }\mathcal{S}_c,\bar{F}\models^+_{n} ST_x(\chi)[x/\alpha]\\& \quad \text{iff } \psi\in \pi^1(end(\alpha))\text{ and }\chi\in \pi^1(end(\alpha))\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^+ \psi\text{ and } \mathcal{M}_c, end(\alpha)\models^+ \chi\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^+ \psi\wedge\chi\\& \quad \text{iff } \psi\wedge\chi\in \pi^1(end(\alpha)) \end{align*} $$
$$ \begin{align*} &\mathcal{S}_c,\bar{F}\models^+_{n} (ST_x(\psi)\wedge ST_x(\chi))[x/\alpha]\\& \quad \text{iff } \mathcal{S}_c,\bar{F}\models^+_{n} ST_x(\psi)[x/\alpha]\text{ and }\mathcal{S}_c,\bar{F}\models^+_{n} ST_x(\chi)[x/\alpha]\\& \quad \text{iff } \psi\in \pi^1(end(\alpha))\text{ and }\chi\in \pi^1(end(\alpha))\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^+ \psi\text{ and } \mathcal{M}_c, end(\alpha)\models^+ \chi\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^+ \psi\wedge\chi\\& \quad \text{iff } \psi\wedge\chi\in \pi^1(end(\alpha)) \end{align*} $$
and, for Part 2,
 $$ \begin{align*} &\mathcal{S}_c,\bar{F}\models^-_{n} (ST_x(\psi)\wedge ST_x(\chi))[x/\alpha]\\& \quad \text{iff } \mathcal{S}_c,\bar{F}\models^-_{n} ST_x(\psi)[x/\alpha]\text{ or }\mathcal{S}_c,\bar{F}\models^-_{n} ST_x(\chi)[x/\alpha]\\& \quad \text{iff } \sim\psi\in \pi^1(end(\alpha))\text{ or }\sim\chi\in \pi^1(end(\alpha))\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^- \psi\text{ or } \mathcal{M}_c, end(\alpha)\models^- \chi\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^- \psi\wedge\chi\\& \quad \text{iff } \sim(\psi\wedge\chi)\in \pi^1(end(\alpha)). \end{align*} $$
$$ \begin{align*} &\mathcal{S}_c,\bar{F}\models^-_{n} (ST_x(\psi)\wedge ST_x(\chi))[x/\alpha]\\& \quad \text{iff } \mathcal{S}_c,\bar{F}\models^-_{n} ST_x(\psi)[x/\alpha]\text{ or }\mathcal{S}_c,\bar{F}\models^-_{n} ST_x(\chi)[x/\alpha]\\& \quad \text{iff } \sim\psi\in \pi^1(end(\alpha))\text{ or }\sim\chi\in \pi^1(end(\alpha))\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^- \psi\text{ or } \mathcal{M}_c, end(\alpha)\models^- \chi\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^- \psi\wedge\chi\\& \quad \text{iff } \sim(\psi\wedge\chi)\in \pi^1(end(\alpha)). \end{align*} $$
Case 2
![]() $\phi = \psi \vee \chi $
and Case 3
$\phi = \psi \vee \chi $
and Case 3
![]() $\phi = \sim \psi $
are similar to Case 1.
$\phi = \sim \psi $
are similar to Case 1.
Case 4.
![]() $\phi = \psi \to \chi $
. By Proposition 7, we know that:
$\phi = \psi \to \chi $
. By Proposition 7, we know that:
 $$ \begin{align} \psi\to&\chi\in \pi^1(end(\alpha)) \text{ iff } \mathcal{M}_c, end(\alpha)\models^+ \psi\to\chi\nonumber\\&\text{ iff }(\forall(\Xi,\Theta)\in W_c)(end(\alpha)\leq_c(\Xi,\Theta)\text{ and}\nonumber\\& \quad \mathcal{M}_c, (\Xi,\Theta)\models^+ \psi\text{ implies }\mathcal{M}_c, (\Xi,\Theta)\models^+ \chi)\nonumber\\&\text{ iff }(\forall(\Xi,\Theta)\in W_c)(end(\alpha)\leq_c(\Xi,\Theta)\text{ and }\psi \in \Xi \text{ implies }\chi\in \Xi). \end{align} $$
$$ \begin{align} \psi\to&\chi\in \pi^1(end(\alpha)) \text{ iff } \mathcal{M}_c, end(\alpha)\models^+ \psi\to\chi\nonumber\\&\text{ iff }(\forall(\Xi,\Theta)\in W_c)(end(\alpha)\leq_c(\Xi,\Theta)\text{ and}\nonumber\\& \quad \mathcal{M}_c, (\Xi,\Theta)\models^+ \psi\text{ implies }\mathcal{M}_c, (\Xi,\Theta)\models^+ \chi)\nonumber\\&\text{ iff }(\forall(\Xi,\Theta)\in W_c)(end(\alpha)\leq_c(\Xi,\Theta)\text{ and }\psi \in \Xi \text{ implies }\chi\in \Xi). \end{align} $$
We have
![]() $ST_x(\phi ) = ST_x(\psi )\to ST_x(\chi )$
, and we argue as follows for Part 1.
$ST_x(\phi ) = ST_x(\psi )\to ST_x(\chi )$
, and we argue as follows for Part 1.
First, assume that
![]() $\psi \to \chi \in \pi ^1(end(\alpha ))$
, and let
$\psi \to \chi \in \pi ^1(end(\alpha ))$
, and let
![]() $\bar {G} \in Glob$
be such that
$\bar {G} \in Glob$
be such that
![]() $\bar {F}\mathrel {\sqsubseteq }\bar {G}$
. Then, by Lemma 17.2,
$\bar {F}\mathrel {\sqsubseteq }\bar {G}$
. Then, by Lemma 17.2,
![]() $end(\alpha )\leq _c end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha ))$
, so that, by (→),
$end(\alpha )\leq _c end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha ))$
, so that, by (→),
![]() $ \psi \in \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
entails
$ \psi \in \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
entails
![]() $\chi \in \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, whence, by IH, it follows that
$\chi \in \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, whence, by IH, it follows that
Since
![]() $\bar {G}\sqsupseteq \bar {F}$
was chosen in
$\bar {G}\sqsupseteq \bar {F}$
was chosen in
![]() $Glob$
arbitrarily, we have shown that
$Glob$
arbitrarily, we have shown that
![]() $\mathcal {S}_c,\bar {F}\models ^+_{n} (ST_x(\psi )\to ST_x(\chi ))[x/\alpha ]$
, or, equivalently, that
$\mathcal {S}_c,\bar {F}\models ^+_{n} (ST_x(\psi )\to ST_x(\chi ))[x/\alpha ]$
, or, equivalently, that
![]() $\mathcal {S}_c,\bar {F}\models ^+_{n} ST_x(\phi )[x/\alpha ]$
.
$\mathcal {S}_c,\bar {F}\models ^+_{n} ST_x(\phi )[x/\alpha ]$
.
For the converse, we argue by contraposition. Assume that
![]() $\psi \to \chi \notin \pi ^1(end(\alpha ))$
. By (→), there must be a
$\psi \to \chi \notin \pi ^1(end(\alpha ))$
. By (→), there must be a
![]() $(\Xi ,\Theta )\in W_c$
such that
$(\Xi ,\Theta )\in W_c$
such that
![]() $end(\alpha )\leq _c(\Xi ,\Theta )$
,
$end(\alpha )\leq _c(\Xi ,\Theta )$
,
![]() $\psi \in \Xi $
, and
$\psi \in \Xi $
, and
![]() $\chi \notin \Xi $
. By Lemma 16.2, we can choose a
$\chi \notin \Xi $
. By Lemma 16.2, we can choose a
![]() $\beta \in Seq$
such that
$\beta \in Seq$
such that
![]() $end(\beta ) = (\Xi ,\Theta )$
, and an
$end(\beta ) = (\Xi ,\Theta )$
, and an
![]() $F \in \mathfrak {G}$
such that
$F \in \mathfrak {G}$
such that
![]() $F(\alpha ) = \beta $
. But then we can set
$F(\alpha ) = \beta $
. But then we can set
![]() $\bar {G} := \bar {F}^\frown (F) \in Glob$
; we clearly have
$\bar {G} := \bar {F}^\frown (F) \in Glob$
; we clearly have
![]() $\bar {G}\sqsupseteq \bar {F}$
,
$\bar {G}\sqsupseteq \bar {F}$
,
![]() $\mathbb {F}_{\bar {F}\bar {G}}(\alpha ) = F(\alpha ) = \beta $
, and
$\mathbb {F}_{\bar {F}\bar {G}}(\alpha ) = F(\alpha ) = \beta $
, and
![]() $\pi ^1(end(\beta )) = \Xi $
. Therefore, under these settings, we also get that
$\pi ^1(end(\beta )) = \Xi $
. Therefore, under these settings, we also get that
![]() $\psi \in \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, but
$\psi \in \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
, but
![]() $\chi \notin \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
. Thus we must have, by IH, that
$\chi \notin \pi ^1(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )))$
. Thus we must have, by IH, that
![]() $\mathcal {S}_c,\bar {G}\models ^+_n ST_x(\psi )[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha )]$
but
$\mathcal {S}_c,\bar {G}\models ^+_n ST_x(\psi )[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha )]$
but
![]() $\mathcal {S}_c,\bar {G}\not \models ^+_n ST_x(\chi )[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha )]$
. The latter means that
$\mathcal {S}_c,\bar {G}\not \models ^+_n ST_x(\chi )[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha )]$
. The latter means that
![]() $\mathcal {S}_c,\bar {F}\not \models ^+_n (ST_x(\psi )\to ST_x(\chi ))[x/\alpha ]$
, or, equivalently, that
$\mathcal {S}_c,\bar {F}\not \models ^+_n (ST_x(\psi )\to ST_x(\chi ))[x/\alpha ]$
, or, equivalently, that
![]() $\mathcal {S}_c,\bar {F}\not \models ^+_n ST_x(\phi )[x/\alpha ]$
.
$\mathcal {S}_c,\bar {F}\not \models ^+_n ST_x(\phi )[x/\alpha ]$
.
As for Part 2, we have, by IH and Proposition 7,
 $$ \begin{align*} &\mathcal{S}_c,\bar{F}\models^-_{n} (ST_x(\psi)\to ST_x(\chi))[x/\alpha]\\& \quad \text{iff } \mathcal{S}_c,\bar{F}\models^+_{n} ST_x(\psi)[x/\alpha]\text{ and }\mathcal{S}_c,\bar{F}\models^-_{n} ST_x(\chi)[x/\alpha]\\& \quad \text{iff } \psi\in \pi^1(end(\alpha))\text{ and }\sim\chi\in \pi^1(end(\alpha))\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^+ \psi\text{ and } \mathcal{M}_c, end(\alpha)\models^- \chi\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^- \psi\to\chi\\& \quad \text{iff } \sim(\psi\to\chi)\in \pi^1(end(\alpha)). \end{align*} $$
$$ \begin{align*} &\mathcal{S}_c,\bar{F}\models^-_{n} (ST_x(\psi)\to ST_x(\chi))[x/\alpha]\\& \quad \text{iff } \mathcal{S}_c,\bar{F}\models^+_{n} ST_x(\psi)[x/\alpha]\text{ and }\mathcal{S}_c,\bar{F}\models^-_{n} ST_x(\chi)[x/\alpha]\\& \quad \text{iff } \psi\in \pi^1(end(\alpha))\text{ and }\sim\chi\in \pi^1(end(\alpha))\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^+ \psi\text{ and } \mathcal{M}_c, end(\alpha)\models^- \chi\\& \quad \text{iff } \mathcal{M}_c, end(\alpha)\models^- \psi\to\chi\\& \quad \text{iff } \sim(\psi\to\chi)\in \pi^1(end(\alpha)). \end{align*} $$
Case 5. ![]() . Then we have
. Then we have
We argue for Part 1 first. By Proposition 7, we know that:

Assume first that ![]() ; let
; let
![]() $\beta \in Seq$
, and let
$\beta \in Seq$
, and let
![]() $\bar {G} \in Glob$
be such that
$\bar {G} \in Glob$
be such that
![]() $\bar {F}\mathrel {\sqsubseteq }\bar {G}$
. If
$\bar {F}\mathrel {\sqsubseteq }\bar {G}$
. If
![]() $(\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), [\psi ]_{\simeq },\beta ) \in R^{\mathbb {M}^+}$
, then we must have, by Definition 10, that, for some
$(\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), [\psi ]_{\simeq },\beta ) \in R^{\mathbb {M}^+}$
, then we must have, by Definition 10, that, for some
![]() $(\Gamma , \Delta )\in W_c$
and some
$(\Gamma , \Delta )\in W_c$
and some
![]() $\theta \in [\psi ]_{\simeq }$
, we have
$\theta \in [\psi ]_{\simeq }$
, we have
![]() $\beta = \mathbb {F}_{\bar {F}\bar {G}}(\alpha )^\frown (\theta , (\Gamma , \Delta ))$
. But then, by Definition 9, also
$\beta = \mathbb {F}_{\bar {F}\bar {G}}(\alpha )^\frown (\theta , (\Gamma , \Delta ))$
. But then, by Definition 9, also
![]() $R_c(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )), \|\theta \|_{\mathcal {M}_c}, (\Gamma , \Delta ))$
; and, since
$R_c(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )), \|\theta \|_{\mathcal {M}_c}, (\Gamma , \Delta ))$
; and, since
![]() $\theta \in [\psi ]_{\simeq }$
, Proposition 7 implies that
$\theta \in [\psi ]_{\simeq }$
, Proposition 7 implies that
![]() $\|\theta \|_{\mathcal {M}_c} = \|\psi \|_{\mathcal {M}_c}$
, so that
$\|\theta \|_{\mathcal {M}_c} = \|\psi \|_{\mathcal {M}_c}$
, so that
![]() $R_c(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )), \|\psi \|_{\mathcal {M}_c}, (\Gamma , \Delta ))$
. By Lemma 17.2, we must further have
$R_c(end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha )), \|\psi \|_{\mathcal {M}_c}, (\Gamma , \Delta ))$
. By Lemma 17.2, we must further have
![]() $end(\alpha )\leq _c end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha ))$
, and now (□→) yields that
$end(\alpha )\leq _c end(\mathbb {F}_{\bar {F}\bar {G}}(\alpha ))$
, and now (□→) yields that
![]() $\chi \in \Gamma = \pi ^1(end(\beta ))$
. Therefore, it follows by IH that
$\chi \in \Gamma = \pi ^1(end(\beta ))$
. Therefore, it follows by IH that
![]() $\mathcal {S}_c,\bar {G}\models ^+_{n} ST_w(\chi )[w/\beta ]$
.
$\mathcal {S}_c,\bar {G}\models ^+_{n} ST_w(\chi )[w/\beta ]$
.
Since the choice of
![]() $\beta \in Seq$
and
$\beta \in Seq$
and
![]() $\bar {G} \in Glob$
such that
$\bar {G} \in Glob$
such that
![]() $\bar {F}\mathrel {\sqsubseteq }\bar {G}$
was made arbitrarily, we have shown that
$\bar {F}\mathrel {\sqsubseteq }\bar {G}$
was made arbitrarily, we have shown that
![]() $ \mathcal {S}_c,\bar {F}\models ^+_n \forall w(Rxyw\to ST_w(\chi ))[x/\alpha , y/[\psi ]_{\simeq }]$
. Moreover, IH for Part 3 implies that
$ \mathcal {S}_c,\bar {F}\models ^+_n \forall w(Rxyw\to ST_w(\chi ))[x/\alpha , y/[\psi ]_{\simeq }]$
. Moreover, IH for Part 3 implies that
![]() $ \mathcal {S}_c,\bar {F}\models ^+_n Sy\wedge (\forall z)_O(Ezy\Leftrightarrow ST_z(\psi )))[y/[\psi ]_{\simeq }]$
. Summing up the two conjuncts and applying (α10) and (T15), we obtain that:
$ \mathcal {S}_c,\bar {F}\models ^+_n Sy\wedge (\forall z)_O(Ezy\Leftrightarrow ST_z(\psi )))[y/[\psi ]_{\simeq }]$
. Summing up the two conjuncts and applying (α10) and (T15), we obtain that:
or, in other words, that
![]() $\mathcal {S}_c,\bar {F}\models ^+_n ST_x(\phi )[x/\alpha ]$
, as desired.
$\mathcal {S}_c,\bar {F}\models ^+_n ST_x(\phi )[x/\alpha ]$
, as desired.
For the converse, we argue by contraposition. Assume that ![]() . In this case, (□→) implies the existence of
. In this case, (□→) implies the existence of
![]() $(\Xi ,\Theta ),(\Xi ',\Theta ')\in W_c$
such that
$(\Xi ,\Theta ),(\Xi ',\Theta ')\in W_c$
such that
![]() $end(\alpha )\leq _c(\Xi ,\Theta )$
,
$end(\alpha )\leq _c(\Xi ,\Theta )$
,
![]() $R_c((\Xi ,\Theta ), \|\psi \|_{\mathcal {M}_c}, (\Xi ',\Theta '))$
, and
$R_c((\Xi ,\Theta ), \|\psi \|_{\mathcal {M}_c}, (\Xi ',\Theta '))$
, and
![]() ${\chi \notin \Xi '}$
. By Lemma 16.2, there exists a
${\chi \notin \Xi '}$
. By Lemma 16.2, there exists a
![]() $\beta \in Seq$
such that
$\beta \in Seq$
such that
![]() $end(\beta ) = (\Xi ,\Theta )$
and an
$end(\beta ) = (\Xi ,\Theta )$
and an
![]() $F \in \mathfrak {G}$
such that
$F \in \mathfrak {G}$
such that
![]() $F(\alpha ) = \beta $
. But then clearly
$F(\alpha ) = \beta $
. But then clearly
![]() $\bar {G} = \bar {F}^\frown (F) \in Glob$
and
$\bar {G} = \bar {F}^\frown (F) \in Glob$
and
![]() $\bar {F}\mathrel {\sqsubseteq }\bar {G}$
. Moreover, Definition 10 implies that
$\bar {F}\mathrel {\sqsubseteq }\bar {G}$
. Moreover, Definition 10 implies that
![]() $\mathbb {F}_{\bar {F}\bar {G}}(\alpha ) = \beta $
. Next,
$\mathbb {F}_{\bar {F}\bar {G}}(\alpha ) = \beta $
. Next,
![]() $R_c((\Xi ,\Theta ), \|\psi \|_{\mathcal {M}_c}, (\Xi ',\Theta '))$
implies that
$R_c((\Xi ,\Theta ), \|\psi \|_{\mathcal {M}_c}, (\Xi ',\Theta '))$
implies that
![]() $\gamma = \beta ^\frown (\psi , (\Xi ',\Theta ')) \in Seq$
, whence, by Definition 10,
$\gamma = \beta ^\frown (\psi , (\Xi ',\Theta ')) \in Seq$
, whence, by Definition 10,
![]() $(\beta , [\psi ]_\simeq , \gamma )\in R^{\mathbb {M}^+}$
. So, all in all we get that
$(\beta , [\psi ]_\simeq , \gamma )\in R^{\mathbb {M}^+}$
. So, all in all we get that
![]() $ \mathcal {S}_c,\bar {G}\models ^+_n Rxyw[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), y/[\psi ]_\simeq , w/\gamma ]$
, and, on the other hand, since
$ \mathcal {S}_c,\bar {G}\models ^+_n Rxyw[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), y/[\psi ]_\simeq , w/\gamma ]$
, and, on the other hand, since
![]() $\chi \notin \Xi ' = \pi ^1(end(\gamma ))$
, IH for Part 1 implies that
$\chi \notin \Xi ' = \pi ^1(end(\gamma ))$
, IH for Part 1 implies that
![]() $ \mathcal {S}_c,\bar {G}\not \models ^+_n ST_w(\chi )[w/\gamma ]$
. Therefore, given that
$ \mathcal {S}_c,\bar {G}\not \models ^+_n ST_w(\chi )[w/\gamma ]$
. Therefore, given that
![]() $\bar {F}\mathrel {\sqsubseteq }\bar {G}$
, it follows that:
$\bar {F}\mathrel {\sqsubseteq }\bar {G}$
, it follows that:
If now
![]() $a \in U$
is such that we have
$a \in U$
is such that we have
then note that, by IH for Part 3 we also have
![]() $ \mathcal {S}_c,\bar {F}\models ^+_nSy\wedge (\forall z)_O(Ezy\Leftrightarrow ST_z(\psi ))[y/[\psi ]_\simeq ]$
. By Corollary 4 and (‡), it follows that we must have
$ \mathcal {S}_c,\bar {F}\models ^+_nSy\wedge (\forall z)_O(Ezy\Leftrightarrow ST_z(\psi ))[y/[\psi ]_\simeq ]$
. By Corollary 4 and (‡), it follows that we must have
![]() $a = [\psi ]_\simeq $
in this case. But then (†) implies that we must have
$a = [\psi ]_\simeq $
in this case. But then (†) implies that we must have
![]() $\mathcal {S}_c,\bar {F}\not \models ^+_n \forall w(Rxyw\to ST_w(\chi ))[x/\alpha , y/a]$
. Since
$\mathcal {S}_c,\bar {F}\not \models ^+_n \forall w(Rxyw\to ST_w(\chi ))[x/\alpha , y/a]$
. Since
![]() $a\in U$
was chosen arbitrarily under the condition given by (‡), we conclude that
$a\in U$
was chosen arbitrarily under the condition given by (‡), we conclude that
whence, by Lemma 2 and (T15), it follows that
![]() $\mathcal {S}_c,\bar {F}\not \models ^+_n ST_x(\phi )[x/\alpha ]$
, as desired.
$\mathcal {S}_c,\bar {F}\not \models ^+_n ST_x(\phi )[x/\alpha ]$
, as desired.
It remains to consider Part 2. By Proposition 7, we know that:

Assume, first, that ![]() . Then, by (□→−
), we can choose a
. Then, by (□→−
), we can choose a
![]() $(\Xi ,\Theta )\in W_c$
such that both
$(\Xi ,\Theta )\in W_c$
such that both
![]() $R_c(end(\alpha ), \|\psi \|_{\mathcal {M}_c}, (\Xi ,\Theta ))$
and
$R_c(end(\alpha ), \|\psi \|_{\mathcal {M}_c}, (\Xi ,\Theta ))$
and
![]() $\sim \chi \in \Xi $
. The former means, by Definition 9, that
$\sim \chi \in \Xi $
. The former means, by Definition 9, that
![]() $\beta = \alpha ^\frown (\psi , (\Xi ,\Theta )) \in Seq$
, and the latter means that
$\beta = \alpha ^\frown (\psi , (\Xi ,\Theta )) \in Seq$
, and the latter means that
![]() $\sim \chi \in \pi ^1(end(\beta ))$
whence, by IH for Part 2, it follows that
$\sim \chi \in \pi ^1(end(\beta ))$
whence, by IH for Part 2, it follows that
![]() $\mathcal {S}_c,\bar {F}\models ^-_n ST_w(\chi )[w/\beta ]$
.
$\mathcal {S}_c,\bar {F}\models ^-_n ST_w(\chi )[w/\beta ]$
.
Next, Definition 10 implies that
![]() $\mathcal {S}_c,\bar {F}\models ^+_n Rxyw[x/\alpha , y/[\psi ]_\simeq , w/\beta ]$
and that, by IH for Part 3, we have
$\mathcal {S}_c,\bar {F}\models ^+_n Rxyw[x/\alpha , y/[\psi ]_\simeq , w/\beta ]$
and that, by IH for Part 3, we have
![]() $\mathcal {S}_c,\bar {F}\models ^+_n Sy\wedge (\forall z)_O (Ezy\Leftrightarrow ST_z(\psi ))[y/[\psi ]_\simeq ]$
.
$\mathcal {S}_c,\bar {F}\models ^+_n Sy\wedge (\forall z)_O (Ezy\Leftrightarrow ST_z(\psi ))[y/[\psi ]_\simeq ]$
.
If now
![]() $\bar {G}\in Glob$
is such that
$\bar {G}\in Glob$
is such that
![]() $\bar {G}\sqsupseteq \bar {F}$
and
$\bar {G}\sqsupseteq \bar {F}$
and
![]() $a \in U$
is such that
$a \in U$
is such that
![]() $\mathcal {S}_c,\bar {G}\models ^+_n Sy\wedge (\forall z)_O (Ezy\Leftrightarrow ST_z(\psi ))[y/a]$
, then, by Lemma 4.1, we must have
$\mathcal {S}_c,\bar {G}\models ^+_n Sy\wedge (\forall z)_O (Ezy\Leftrightarrow ST_z(\psi ))[y/a]$
, then, by Lemma 4.1, we must have
![]() $\mathcal {S}_c,\bar {G}\models ^+_n Sy\wedge (\forall z)_O (Ezy\Leftrightarrow ST_z(\psi ))[y/[\psi ]_\simeq ]$
. By Corollary 4, we get that
$\mathcal {S}_c,\bar {G}\models ^+_n Sy\wedge (\forall z)_O (Ezy\Leftrightarrow ST_z(\psi ))[y/[\psi ]_\simeq ]$
. By Corollary 4, we get that
![]() $a = [\psi ]_\simeq $
. Moreover, Lemma 4.1 also implies that
$a = [\psi ]_\simeq $
. Moreover, Lemma 4.1 also implies that
![]() $\mathcal {S}_c,\bar {G}\models ^+_n Rxyw[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), y/a, w/\mathbb {F}_{\bar {F}\bar {G}}(\beta )]$
and
$\mathcal {S}_c,\bar {G}\models ^+_n Rxyw[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), y/a, w/\mathbb {F}_{\bar {F}\bar {G}}(\beta )]$
and
![]() $\mathcal {S}_c,\bar {G}\models ^-_n ST_w(\chi )[w/\mathbb {F}_{\bar {F}\bar {G}}(\beta )]$
. It follows that
$\mathcal {S}_c,\bar {G}\models ^-_n ST_w(\chi )[w/\mathbb {F}_{\bar {F}\bar {G}}(\beta )]$
. It follows that
![]() $ \mathcal {S}_c,\bar {G}\models ^-_n \forall w(Rxyw\to ST_w(\chi ))[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), y/a]$
, in other words, that:
$ \mathcal {S}_c,\bar {G}\models ^-_n \forall w(Rxyw\to ST_w(\chi ))[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), y/a]$
, in other words, that:
In view of the choice of
![]() $\bar {G}\in Glob$
and
$\bar {G}\in Glob$
and
![]() $a \in U$
, we have shown that:
$a \in U$
, we have shown that:
which, by (T8) and (T17), is the same as
It remains to apply the definition of ampersand and (An5) to get that
![]() $\mathcal {S}_c,\bar {F}\models ^+_n \sim ST_x(\phi )[x/\alpha ]$
, or, equivalently that
$\mathcal {S}_c,\bar {F}\models ^+_n \sim ST_x(\phi )[x/\alpha ]$
, or, equivalently that
![]() $\mathcal {S}_c,\bar {F}\models ^-_n ST_x(\phi )[x/\alpha ]$
, as desired.
$\mathcal {S}_c,\bar {F}\models ^-_n ST_x(\phi )[x/\alpha ]$
, as desired.
As for the converse of Part 2, we again argue by contraposition. Assume that ![]() . In this case, (□→−
) implies that for every
. In this case, (□→−
) implies that for every
![]() $(\Xi ,\Theta )\in W_c$
such that
$(\Xi ,\Theta )\in W_c$
such that
![]() $R_c(end(\alpha ), \|\psi \|_{\mathcal {M}_c}, (\Xi ,\Theta ))$
, we must have
$R_c(end(\alpha ), \|\psi \|_{\mathcal {M}_c}, (\Xi ,\Theta ))$
, we must have
![]() $\sim \chi \notin \Xi $
. Now, if
$\sim \chi \notin \Xi $
. Now, if
![]() $\beta \in Seq$
is such that
$\beta \in Seq$
is such that
![]() $(\alpha , [\psi ]_\simeq , \beta ) \in R^{\mathbb {M}^+}$
, then, by Definition 10, there must exist a
$(\alpha , [\psi ]_\simeq , \beta ) \in R^{\mathbb {M}^+}$
, then, by Definition 10, there must exist a
![]() $(\Gamma , \Delta ) \in W_c$
and a
$(\Gamma , \Delta ) \in W_c$
and a
![]() $\theta \in [\psi ]_\simeq $
such that
$\theta \in [\psi ]_\simeq $
such that
![]() $\beta = \alpha ^\frown (\theta , (\Gamma , \Delta ))$
. Since
$\beta = \alpha ^\frown (\theta , (\Gamma , \Delta ))$
. Since
![]() $\beta \in Seq$
, Definition 9 implies that
$\beta \in Seq$
, Definition 9 implies that
![]() $R_c(end(\alpha ), \|\theta \|_{\mathcal {M}_c}, (\Gamma , \Delta ))$
; but, since
$R_c(end(\alpha ), \|\theta \|_{\mathcal {M}_c}, (\Gamma , \Delta ))$
; but, since
![]() $\theta \in [\psi ]_\simeq $
, the latter means that we must have
$\theta \in [\psi ]_\simeq $
, the latter means that we must have
![]() $R_c(end(\alpha ), \|\psi \|_{\mathcal {M}_c}, (\Gamma , \Delta ))$
. But then our assumption implies that
$R_c(end(\alpha ), \|\psi \|_{\mathcal {M}_c}, (\Gamma , \Delta ))$
. But then our assumption implies that
![]() $\sim \chi \notin \Gamma = \pi ^1(end(\beta ))$
, whence, by IH for Part 2, we must have
$\sim \chi \notin \Gamma = \pi ^1(end(\beta ))$
, whence, by IH for Part 2, we must have
![]() $\mathcal {S}_c,\bar {F}\not \models ^-_n ST_w(\chi )[w/\beta ]$
. Thus we have shown that
$\mathcal {S}_c,\bar {F}\not \models ^-_n ST_w(\chi )[w/\beta ]$
. Thus we have shown that
![]() $\mathcal {S}_c,\bar {F}\not \models ^+_n Rxyw\wedge \sim ST_w(\chi )[x/\alpha , y/[\psi ]_\simeq , w/\beta ]$
for every
$\mathcal {S}_c,\bar {F}\not \models ^+_n Rxyw\wedge \sim ST_w(\chi )[x/\alpha , y/[\psi ]_\simeq , w/\beta ]$
for every
![]() $\beta \in Seq$
, which, by definition of
$\beta \in Seq$
, which, by definition of
![]() $R^{\mathbb {M}^+}$
, implies that
$R^{\mathbb {M}^+}$
, implies that
![]() $\mathcal {S}_c,\bar {F}\not \models ^-_n Rxyw\to ST_w(\chi )[x/\alpha , y/[\psi ]_\simeq , w/b]$
for every
$\mathcal {S}_c,\bar {F}\not \models ^-_n Rxyw\to ST_w(\chi )[x/\alpha , y/[\psi ]_\simeq , w/b]$
for every
![]() $b \in U$
. In view of the
$b \in U$
. In view of the
![]() $\mathsf {QN4}$
semantics of
$\mathsf {QN4}$
semantics of
![]() $\forall $
and
$\forall $
and
![]() $\sim $
, the latter can be equivalently reformulated as
$\sim $
, the latter can be equivalently reformulated as
![]() $\mathcal {S}_c,\bar {F}\not \models ^+_n \sim \forall w(Rxyw\to ST_w(\chi ))[x/\alpha , y/[\psi ]_\simeq ]$
. Since, by IH for Part 3, we also have
$\mathcal {S}_c,\bar {F}\not \models ^+_n \sim \forall w(Rxyw\to ST_w(\chi ))[x/\alpha , y/[\psi ]_\simeq ]$
. Since, by IH for Part 3, we also have
![]() $\mathcal {S}_c,\bar {F}\models ^+_n Sy\wedge (\forall z)_O (Ezy\Leftrightarrow ST_z(\psi ))[y/[\psi ]_\simeq ]$
, we have shown that
$\mathcal {S}_c,\bar {F}\models ^+_n Sy\wedge (\forall z)_O (Ezy\Leftrightarrow ST_z(\psi ))[y/[\psi ]_\simeq ]$
, we have shown that
which, in view of the definition of ampersand, is the same as
The latter, by the
![]() $\mathsf {QN4}$
semantics of the existential quantifier, entails that
$\mathsf {QN4}$
semantics of the existential quantifier, entails that
in other words, that
![]() $\mathcal {S}_c,\bar {F}\not \models ^-_n ST_x(\phi )[x/\alpha ]$
, as desired.
$\mathcal {S}_c,\bar {F}\not \models ^-_n ST_x(\phi )[x/\alpha ]$
, as desired.
Before we move on, we would like to draw a corollary from our lemma.
Corollary 5. Let
![]() $\bar {F} \in Glob$
,
$\bar {F} \in Glob$
,
![]() $\alpha \in Seq$
,
$\alpha \in Seq$
,
![]() $x \in Ind$
, and let
$x \in Ind$
, and let
![]() $\psi ,\chi \in \mathcal {CN}$
. Then:
$\psi ,\chi \in \mathcal {CN}$
. Then:
Proof We show, first, that
Right-to-left direction is trivial by Lemma 20.3. As for the converse, if ![]() , then we can choose an
, then we can choose an
![]() $a \in U$
such that:
$a \in U$
such that:
But then, by Corollary 4 and Lemma 20.3, we must have
![]() $a = [\psi ]_\simeq $
, so that
$a = [\psi ]_\simeq $
, so that
![]() $\mathcal {S}_c,\bar {F} \models ^+_n \forall w(R(x,y,w)\to ST_w(\chi ))[x/\alpha , y/[\psi ]_\simeq ]$
follows. We need to show, next, that
$\mathcal {S}_c,\bar {F} \models ^+_n \forall w(R(x,y,w)\to ST_w(\chi ))[x/\alpha , y/[\psi ]_\simeq ]$
follows. We need to show, next, that
The left-to-right direction easily follows by (An1), (An5), and Lemma 20.3. If
![]() $\mathcal {S}_c,\bar {F} \models ^-_n \forall w(R(x,y,w)\to ST_w(\chi ))[x/\alpha , y/[\psi ]_\simeq ]$
, then let
$\mathcal {S}_c,\bar {F} \models ^-_n \forall w(R(x,y,w)\to ST_w(\chi ))[x/\alpha , y/[\psi ]_\simeq ]$
, then let
![]() $\bar {G} \in Glob$
and an
$\bar {G} \in Glob$
and an
![]() $a \in U$
be such that
$a \in U$
be such that
![]() $\bar {G}\sqsupseteq \bar {F}$
and
$\bar {G}\sqsupseteq \bar {F}$
and
![]() $ \mathcal {S}_c,\bar {G}\models ^+_n Sy \wedge (\forall z)_O(Ezy\Leftrightarrow ST_z(\psi ))[y/a]$
. By Lemma 4.1, we also have
$ \mathcal {S}_c,\bar {G}\models ^+_n Sy \wedge (\forall z)_O(Ezy\Leftrightarrow ST_z(\psi ))[y/a]$
. By Lemma 4.1, we also have
![]() $ \mathcal {S}_c,\bar {G} \models ^-_n \forall w(R(x,y,w)\to ST_w(\chi ))[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), y/[\psi ]_\simeq ]$
. Next, Corollary 4 and Lemma 20.3 imply that
$ \mathcal {S}_c,\bar {G} \models ^-_n \forall w(R(x,y,w)\to ST_w(\chi ))[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), y/[\psi ]_\simeq ]$
. Next, Corollary 4 and Lemma 20.3 imply that
![]() $a = [\psi ]_\simeq $
, so that
$a = [\psi ]_\simeq $
, so that
![]() $\mathcal {S}_c,\bar {G} \models ^-_n \forall w(R(x,y,w)\to ST_w(\chi ))[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), y/a]$
follows. Since
$\mathcal {S}_c,\bar {G} \models ^-_n \forall w(R(x,y,w)\to ST_w(\chi ))[x/\mathbb {F}_{\bar {F}\bar {G}}(\alpha ), y/a]$
follows. Since
![]() $\bar {G}\sqsupseteq \bar {F}$
and
$\bar {G}\sqsupseteq \bar {F}$
and
![]() $a \in U$
were chosen arbitrarily, it follows that
$a \in U$
were chosen arbitrarily, it follows that
or, equivalently, that ![]() .
.
It only remains now to show that
![]() $\mathcal {S}_c$
is a model of
$\mathcal {S}_c$
is a model of
![]() $Th$
.
$Th$
.
Lemma 21. For every
![]() $\bar {F} \in Glob$
, we have
$\bar {F} \in Glob$
, we have
![]() $\mathcal {S}_c, \bar {F}\models ^+_n Th$
.
$\mathcal {S}_c, \bar {F}\models ^+_n Th$
.
Proof That the Nelsonian sheaf
![]() $\mathcal {S}_c$
satisfies (Th1) was shown in Lemma 19. The satisfaction of (Th2) follows from Lemma 20.3 (one needs to instantiate y to
$\mathcal {S}_c$
satisfies (Th1) was shown in Lemma 19. The satisfaction of (Th2) follows from Lemma 20.3 (one needs to instantiate y to
![]() $[p]_\simeq $
). We consider the remaining parts of
$[p]_\simeq $
). We consider the remaining parts of
![]() $Th$
in more detail below:
$Th$
in more detail below:
(Th4). Let
![]() $\ast \in \{\wedge , \to \}$
,
$\ast \in \{\wedge , \to \}$
,
![]() $\bar {F} \in Glob$
, and
$\bar {F} \in Glob$
, and
![]() $a, b \in S^{\mathbb {M}^+}$
. Then, by Definition 10, there must exist some
$a, b \in S^{\mathbb {M}^+}$
. Then, by Definition 10, there must exist some
![]() $\phi , \psi \in \mathcal {CN}$
such that
$\phi , \psi \in \mathcal {CN}$
such that
![]() $a = [\phi ]_\simeq $
and
$a = [\phi ]_\simeq $
and
![]() $b = [\psi ]_\simeq $
. But then Lemma 20.3 implies that we have all of the following:
$b = [\psi ]_\simeq $
. But then Lemma 20.3 implies that we have all of the following:
 $$ \begin{align} \mathcal{S}_c, \bar{F}&\models^+_n Sy \wedge (\forall w)_O(Ewy\Leftrightarrow ST_w(\psi))[y/b]\\ \mathcal{S}_c, \bar{F}&\models^+_n Sz \wedge (\forall w)_O(Ewz\Leftrightarrow ST_w(\phi)\ast ST_w(\psi))[z/[\phi\ast\psi]_\simeq]\nonumber \end{align} $$
$$ \begin{align} \mathcal{S}_c, \bar{F}&\models^+_n Sy \wedge (\forall w)_O(Ewy\Leftrightarrow ST_w(\psi))[y/b]\\ \mathcal{S}_c, \bar{F}&\models^+_n Sz \wedge (\forall w)_O(Ewz\Leftrightarrow ST_w(\phi)\ast ST_w(\psi))[z/[\phi\ast\psi]_\simeq]\nonumber \end{align} $$
whence
![]() $\mathcal {S}_c, \bar {F}\models _{fo} (Th4)$
clearly follows by (T18). The argument for the satisfaction of (Th3) is similar.
$\mathcal {S}_c, \bar {F}\models _{fo} (Th4)$
clearly follows by (T18). The argument for the satisfaction of (Th3) is similar.
(Th5). Again, let
![]() $\bar {F} \in Glob$
and
$\bar {F} \in Glob$
and
![]() $a, b \in S^{\mathbb {M}^+}$
. Then let
$a, b \in S^{\mathbb {M}^+}$
. Then let
![]() $\phi , \psi \in \mathcal {CN}$
be such that
$\phi , \psi \in \mathcal {CN}$
be such that
![]() $a = [\phi ]_\simeq $
and
$a = [\phi ]_\simeq $
and
![]() $b = [\psi ]_\simeq $
. Lemma 20.3 implies that both (§) and (¶) hold, and that we have:
$b = [\psi ]_\simeq $
. Lemma 20.3 implies that both (§) and (¶) hold, and that we have:
By Corollary 5 and (T18), it follows now that we must have
whence
![]() $\mathcal {S}_c, \bar {F}\models ^+_n (Th5)$
clearly follows.
$\mathcal {S}_c, \bar {F}\models ^+_n (Th5)$
clearly follows.
We are now finally in a position to prove a converse to Proposition 8.
Proposition 9. For all
![]() $\Gamma , \Delta \subseteq \mathcal {CN}$
and for every
$\Gamma , \Delta \subseteq \mathcal {CN}$
and for every
![]() $x \in Ind$
, if
$x \in Ind$
, if
![]() $Th\cup ST_x(\Gamma )\models _{\mathsf {QN4}}ST_x(\Delta )$
, then
$Th\cup ST_x(\Gamma )\models _{\mathsf {QN4}}ST_x(\Delta )$
, then
![]() $\Gamma \models _{\mathsf {N4CK}} \Delta $
.
$\Gamma \models _{\mathsf {N4CK}} \Delta $
.
Proof We argue by contraposition. If
![]() $\Gamma \not \models _{\mathsf {N4CK}} \Delta $
, then
$\Gamma \not \models _{\mathsf {N4CK}} \Delta $
, then
![]() $(\Gamma , \Delta )$
must be
$(\Gamma , \Delta )$
must be
![]() $\mathsf {N4CK}$
-satisfiable, and therefore, applying the standard Lindenbaum construction (cf. [Reference Olkhovikov11, Lemma 8]), we can find a
$\mathsf {N4CK}$
-satisfiable, and therefore, applying the standard Lindenbaum construction (cf. [Reference Olkhovikov11, Lemma 8]), we can find a
![]() $(\Gamma ', \Delta ')\in W_c$
such that
$(\Gamma ', \Delta ')\in W_c$
such that
![]() $(\Gamma ', \Delta ')\supseteq (\Gamma , \Delta )$
. By Definition 9, we have
$(\Gamma ', \Delta ')\supseteq (\Gamma , \Delta )$
. By Definition 9, we have
![]() $(\Gamma ', \Delta ')\in Seq$
, therefore, Lemmas 20.1 and 21 together imply that
$(\Gamma ', \Delta ')\in Seq$
, therefore, Lemmas 20.1 and 21 together imply that
![]() $\mathcal {S}_c, \Lambda \models ^+_n (Th \cup ST_x(\Gamma ), ST_x(\Delta )[x/(\Gamma ', \Delta ')]$
, or, equivalently, that
$\mathcal {S}_c, \Lambda \models ^+_n (Th \cup ST_x(\Gamma ), ST_x(\Delta )[x/(\Gamma ', \Delta ')]$
, or, equivalently, that
![]() $Th\cup ST_x(\Gamma )\not \models _{\mathsf {QN4}}ST_x(\Delta )$
, as desired.
$Th\cup ST_x(\Gamma )\not \models _{\mathsf {QN4}}ST_x(\Delta )$
, as desired.
We can now formulate and prove the main result of this section.
Theorem 1. For all
![]() $\Gamma , \Delta \subseteq \mathcal {CN}$
and for every
$\Gamma , \Delta \subseteq \mathcal {CN}$
and for every
![]() $x \in Ind$
, we have
$x \in Ind$
, we have
![]() $\Gamma \models _{\mathsf {N4CK}} \Delta $
iff
$\Gamma \models _{\mathsf {N4CK}} \Delta $
iff
![]() $Th\cup ST_x(\Gamma )\models _{\mathsf {QN4}}ST_x(\Delta )$
.
$Th\cup ST_x(\Gamma )\models _{\mathsf {QN4}}ST_x(\Delta )$
.
Before we end this section, we would like to mention that the proof of Theorem 1 not only allows us to completely mirror, on the level of conditional logic, the selection of the embedding results for modal logic reported in Section 5, but also to improve on [Reference Odintsov, Wansing and Hendricks10, Proposition 7] for the
![]() $\mathsf {N4}$
-based modal logic
$\mathsf {N4}$
-based modal logic
![]() $\mathsf {FSK}^d$
; namely, if we repeat the constructions of this section adapting them to the modal case (basically, using
$\mathsf {FSK}^d$
; namely, if we repeat the constructions of this section adapting them to the modal case (basically, using
![]() $\sigma \tau _x$
in place of
$\sigma \tau _x$
in place of
![]() $ST_x$
and throwing away all the parts dealing with
$ST_x$
and throwing away all the parts dealing with
![]() $Th$
and the existence of formula-defined truth-sets) then we arrive at the following.
$Th$
and the existence of formula-defined truth-sets) then we arrive at the following.
Theorem 2. For all
![]() $\Gamma , \Delta \subseteq \mathcal {MD}$
and for every
$\Gamma , \Delta \subseteq \mathcal {MD}$
and for every
![]() $x \in Ind$
, we have
$x \in Ind$
, we have
![]() $\Gamma \models _{\mathsf {FSK}^d} \Delta $
iff
$\Gamma \models _{\mathsf {FSK}^d} \Delta $
iff
![]() $\sigma \tau _x(\Gamma )\models _{\mathsf {QN4}}\sigma \tau _x(\Delta )$
.
$\sigma \tau _x(\Gamma )\models _{\mathsf {QN4}}\sigma \tau _x(\Delta )$
.
This alternative embedding result shows that the very definition of translation used for the classical logic
![]() $\mathsf {K}$
, also embeds
$\mathsf {K}$
, also embeds
![]() $\mathsf {FSK}^d$
into
$\mathsf {FSK}^d$
into
![]() $\mathsf {QN4}$
; and this time our embedding commutes, up to the strong equivalence, with the propositional connectives of
$\mathsf {QN4}$
; and this time our embedding commutes, up to the strong equivalence, with the propositional connectives of
![]() $\mathsf {N4}$
.
$\mathsf {N4}$
.
That such a result would fall out from our proof of Theorem 1 should not surprise us, as
![]() $\mathsf {FSK}^d$
was shown to be the modal companion to
$\mathsf {FSK}^d$
was shown to be the modal companion to
![]() $\mathsf {N4CK}$
in [Reference Olkhovikov11, Lemma 16].
$\mathsf {N4CK}$
in [Reference Olkhovikov11, Lemma 16].
8 Discussion, conclusion, and future work
Theorem 1 shows that
![]() $\mathsf {N4CK}$
is faithfully embedded into
$\mathsf {N4CK}$
is faithfully embedded into
![]() $\mathsf {QN4}$
by a (classically equivalent) variant of the classical formalization of the Chellas semantics for
$\mathsf {QN4}$
by a (classically equivalent) variant of the classical formalization of the Chellas semantics for
![]() $\mathsf {CK}$
based on the pair
$\mathsf {CK}$
based on the pair
![]() $(Th, ST_x)$
for any given
$(Th, ST_x)$
for any given
![]() $x \in Ind$
. The conditional logic
$x \in Ind$
. The conditional logic
![]() $\mathsf {N4CK}$
can thus be seen as a result of a Nelsonian reading of the classical conditional logic
$\mathsf {N4CK}$
can thus be seen as a result of a Nelsonian reading of the classical conditional logic
![]() $\mathsf {CK}$
, and, therefore, as one plausible counterpart to
$\mathsf {CK}$
, and, therefore, as one plausible counterpart to
![]() $\mathsf {CK}$
on the basis of Nelson’s logic of strong negation. This result allows us to view
$\mathsf {CK}$
on the basis of Nelson’s logic of strong negation. This result allows us to view
![]() $\mathsf {N4CK}$
as a strong candidate for the role of a natural minimal
$\mathsf {N4CK}$
as a strong candidate for the role of a natural minimal
![]() $\mathsf {N4}$
-based logic of conditionals, and thus completes a series of other arguments to that effect presented earlier in [Reference Olkhovikov11].
$\mathsf {N4}$
-based logic of conditionals, and thus completes a series of other arguments to that effect presented earlier in [Reference Olkhovikov11].
Our nearest research plans include an extension of this series to other non-classical constructive logics. An especially fitting candidate for such an extension appears to be the negation-inconsistent constructive logic
![]() $\mathsf {C}$
introduced by H. Wansing in [Reference Wansing, Schmidt, Pratt-Hartmann, Reynolds and Wansing14], given especially that the subject of conditional logics on the basis of the propositional fragment of
$\mathsf {C}$
introduced by H. Wansing in [Reference Wansing, Schmidt, Pratt-Hartmann, Reynolds and Wansing14], given especially that the subject of conditional logics on the basis of the propositional fragment of
![]() $\mathsf {C}$
has already seen its first rather intriguing steps in [Reference Wansing and Unterhuber15], and that the methods of the current article seem to open a way to a considerable refinement of these first results. However, one should also keep in mind that
$\mathsf {C}$
has already seen its first rather intriguing steps in [Reference Wansing and Unterhuber15], and that the methods of the current article seem to open a way to a considerable refinement of these first results. However, one should also keep in mind that
![]() $\mathsf {C}$
is not a sublogic of
$\mathsf {C}$
is not a sublogic of
![]() $\mathsf {CL}$
and is therefore not in the scope of the general criterion put forward in the final paragraphs of Section 6.
$\mathsf {CL}$
and is therefore not in the scope of the general criterion put forward in the final paragraphs of Section 6.
Before we end this article, we would like to observe that
![]() $Th$
is but one of the infinitely many theories that can be used to prove results like Theorem 1. More precisely, let us call a
$Th$
is but one of the infinitely many theories that can be used to prove results like Theorem 1. More precisely, let us call a
![]() $T\subseteq \mathcal {FO}^\emptyset\ \mathsf {N4}$
-conditional iff it can be substituted for
$T\subseteq \mathcal {FO}^\emptyset\ \mathsf {N4}$
-conditional iff it can be substituted for
![]() $Th$
in Theorem 1 above, in other words, iff for all
$Th$
in Theorem 1 above, in other words, iff for all
![]() $\Gamma , \Delta \subseteq \mathcal {CN}$
and for every
$\Gamma , \Delta \subseteq \mathcal {CN}$
and for every
![]() $x \in Ind$
, it is true that
$x \in Ind$
, it is true that
![]() $\Gamma \models _{\mathsf {N4CK}} \Delta $
iff
$\Gamma \models _{\mathsf {N4CK}} \Delta $
iff
![]() $T\cup ST_x(\Gamma )\models _{\mathsf {QN4}}ST_x(\Delta )$
. Then Theorem 1 can be reformulated as stating that
$T\cup ST_x(\Gamma )\models _{\mathsf {QN4}}ST_x(\Delta )$
. Then Theorem 1 can be reformulated as stating that
![]() $Th$
is
$Th$
is
![]() $\mathsf {N4}$
-conditional. But we can also show that:
$\mathsf {N4}$
-conditional. But we can also show that:
Corollary 6. Let
![]() $Th'\subseteq \mathcal {FO}^\emptyset $
be such that
$Th'\subseteq \mathcal {FO}^\emptyset $
be such that
![]() $\mathcal {S}_c\models ^+_n Th'\supseteq Th$
. Then
$\mathcal {S}_c\models ^+_n Th'\supseteq Th$
. Then
![]() $Th'$
is
$Th'$
is
![]() $\mathsf {N4}$
-conditional.
$\mathsf {N4}$
-conditional.
Proof Assume the hypothesis. If
![]() $\Gamma , \Delta \subseteq \mathcal {CN}$
and
$\Gamma , \Delta \subseteq \mathcal {CN}$
and
![]() $x \in Ind$
are such that
$x \in Ind$
are such that
![]() $\Gamma \models _{\mathsf {N4CK}} \Delta $
, then, by Proposition 8, we must have
$\Gamma \models _{\mathsf {N4CK}} \Delta $
, then, by Proposition 8, we must have
![]() $Th\cup ST_x(\Gamma )\models _{\mathsf {QN4}}ST_x(\Delta )$
, whence, by monotonicity of
$Th\cup ST_x(\Gamma )\models _{\mathsf {QN4}}ST_x(\Delta )$
, whence, by monotonicity of
![]() $\models _{\mathsf {QN4}}$
and
$\models _{\mathsf {QN4}}$
and
![]() $Th'\supseteq Th$
, also
$Th'\supseteq Th$
, also
![]() $Th'\cup ST_x(\Gamma )\models _{\mathsf {QN4}}ST_x(\Delta )$
. In the other direction, we can just repeat the proof of Proposition 9 using the fact that
$Th'\cup ST_x(\Gamma )\models _{\mathsf {QN4}}ST_x(\Delta )$
. In the other direction, we can just repeat the proof of Proposition 9 using the fact that
![]() $\mathcal {S}_c\models ^+_n Th'$
.
$\mathcal {S}_c\models ^+_n Th'$
.
Corollary 6 allows us to strengthen the connection between Theorem 1 and the earlier embedding result [Reference Olkhovikov12, Theorem 2] reported for the intuitionistic conditional logic
![]() $\mathsf {IntCK}$
. Namely, we can define a theory
$\mathsf {IntCK}$
. Namely, we can define a theory
![]() $Th^i\supseteq Th$
which is both
$Th^i\supseteq Th$
which is both
![]() $\mathsf {N4}$
-conditional and classically equivalent to the theory mentioned in [Reference Olkhovikov12]. To obtain
$\mathsf {N4}$
-conditional and classically equivalent to the theory mentioned in [Reference Olkhovikov12]. To obtain
![]() $Th^i$
, we need to extend
$Th^i$
, we need to extend
![]() $Th$
with the following sentences, for every
$Th$
with the following sentences, for every
![]() $p^1 \in Prop$
:
$p^1 \in Prop$
:
 $$ \begin{align*} \forall x(Sx\vee Ox),\,&\forall x\sim(Sx\wedge Ox),\,\forall x(px\to Ox),\, \forall x\forall y(Exy\to (Ox\wedge Sy))\\ &\forall x\forall y\forall z(Rxyz\to (Ox\wedge Sy\wedge Oz)). \end{align*} $$
$$ \begin{align*} \forall x(Sx\vee Ox),\,&\forall x\sim(Sx\wedge Ox),\,\forall x(px\to Ox),\, \forall x\forall y(Exy\to (Ox\wedge Sy))\\ &\forall x\forall y\forall z(Rxyz\to (Ox\wedge Sy\wedge Oz)). \end{align*} $$
It is clear that all of these sentences are in the scope of Corollary 6; but they are by no means the only interesting additions to
![]() $Th$
made available by the said corollary. It is easy to see, for example, that we can also replace the main
$Th$
made available by the said corollary. It is easy to see, for example, that we can also replace the main
![]() $\to $
in (Th1) with
$\to $
in (Th1) with
![]() $\Rightarrow $
without affecting Theorem 1.
$\Rightarrow $
without affecting Theorem 1.
Of course, the same trick is possible w.r.t. Proposition 6 which was our blueprint for Theorem 1. Indeed, we can call a
![]() $T\subseteq \mathcal {FO}^\emptyset\ \mathsf {CL}$
-conditional iff for all
$T\subseteq \mathcal {FO}^\emptyset\ \mathsf {CL}$
-conditional iff for all
![]() $\Gamma , \Delta \subseteq \mathcal {CN}$
and for every
$\Gamma , \Delta \subseteq \mathcal {CN}$
and for every
![]() $x \in Ind$
, it is true that
$x \in Ind$
, it is true that
![]() $\Gamma \models _{\mathsf {CK}} \Delta $
iff
$\Gamma \models _{\mathsf {CK}} \Delta $
iff
![]() ${T\cup st_x(\Gamma )\models _{\mathsf {CL}}st_x(\Delta )}$
. Then Proposition 6 shows us that
${T\cup st_x(\Gamma )\models _{\mathsf {CL}}st_x(\Delta )}$
. Then Proposition 6 shows us that
![]() $Th_{ck}$
is
$Th_{ck}$
is
![]() $\mathsf {CL}$
-conditional; denoting by
$\mathsf {CL}$
-conditional; denoting by
![]() $\mathcal{M}^{cl}$
the classical first-order model that arises, according to the definition given in Lemma 9, from the universal model of
$\mathcal{M}^{cl}$
the classical first-order model that arises, according to the definition given in Lemma 9, from the universal model of
![]() $\mathsf{CK}$
, we can also strengthen it as follows.
$\mathsf{CK}$
, we can also strengthen it as follows.
Corollary 7. Let
![]() $T\subseteq \mathcal {FO}^\emptyset $
be such that
$T\subseteq \mathcal {FO}^\emptyset $
be such that
![]() $\mathcal {M}^{cl}\models _c T\supseteq Th_{ck}$
. Then T is
$\mathcal {M}^{cl}\models _c T\supseteq Th_{ck}$
. Then T is
![]() $\mathsf {CL}$
-conditional.
$\mathsf {CL}$
-conditional.
The proof is similar to the above proof of Corollary 6. However, now that we have established the polymorphism of both
![]() $\mathsf {N4}$
-conditional and
$\mathsf {N4}$
-conditional and
![]() $\mathsf {CL}$
-conditional first-order theories, further (and increasingly deeper) questions suggest themselves. For example, what is the relation between the theories mentioned in Corollary 6 to the theories mentioned in Corollary 7? It appears that at least the following is highly plausible.
$\mathsf {CL}$
-conditional first-order theories, further (and increasingly deeper) questions suggest themselves. For example, what is the relation between the theories mentioned in Corollary 6 to the theories mentioned in Corollary 7? It appears that at least the following is highly plausible.
Conjecture 1. Let
![]() $Th'\subseteq \mathcal {FO}^\emptyset $
be such that
$Th'\subseteq \mathcal {FO}^\emptyset $
be such that
![]() $\mathcal {S}_c\models ^+_n Th'\supseteq Th$
. Then
$\mathcal {S}_c\models ^+_n Th'\supseteq Th$
. Then
![]() $\mathcal {M}^{cl}\models _c Th'$
; in particular,
$\mathcal {M}^{cl}\models _c Th'$
; in particular,
![]() $Th'$
is also
$Th'$
is also
![]() $\mathsf {CL}$
-conditional.
$\mathsf {CL}$
-conditional.
If the above conjecture is true, then it might still be the case, that some subtheories of the complete theory of
![]() $\mathcal {M}^{cl}$
that extend
$\mathcal {M}^{cl}$
that extend
![]() $Th_{ck}$
are such that none of their classical equivalents both extends
$Th_{ck}$
are such that none of their classical equivalents both extends
![]() $Th$
and is a subtheory of the complete
$Th$
and is a subtheory of the complete
![]() $\mathsf {N4}$
-theory of
$\mathsf {N4}$
-theory of
![]() $\mathcal {S}_c$
. Moreover, this discrepancy between the two sets of theories can be either coincidental or necessary. Indeed, notice that the definitions of
$\mathcal {S}_c$
. Moreover, this discrepancy between the two sets of theories can be either coincidental or necessary. Indeed, notice that the definitions of
![]() $\mathcal {M}^{cl}$
and
$\mathcal {M}^{cl}$
and
![]() $\mathcal {S}_c$
are not completely forced by our main result: at least the definition of
$\mathcal {S}_c$
are not completely forced by our main result: at least the definition of
![]() $\mathbb {M}^-$
could have been given differently without affecting Theorem 1. So is it possible to revise those definitions in such a way that one gets a perfect match between the theories arising in the two structures? We sum these considerations up as the following.
$\mathbb {M}^-$
could have been given differently without affecting Theorem 1. So is it possible to revise those definitions in such a way that one gets a perfect match between the theories arising in the two structures? We sum these considerations up as the following.
Open Question 1. Assume the truth of the above conjecture. Is it true that for every
![]() $T\subseteq \mathcal {FO}^\emptyset $
we have
$T\subseteq \mathcal {FO}^\emptyset $
we have
![]() $\mathcal {M}^{cl}\models _c T\supseteq Th_{ck}$
iff there exists a
$\mathcal {M}^{cl}\models _c T\supseteq Th_{ck}$
iff there exists a
![]() $T'\subseteq \mathcal {FO}^\emptyset $
such that
$T'\subseteq \mathcal {FO}^\emptyset $
such that
![]() $T'$
is equivalent to T over
$T'$
is equivalent to T over
![]() $\mathsf {CL}$
and
$\mathsf {CL}$
and
![]() $\mathcal {S}_c\models ^+_n T'\supseteq Th$
? If not, then is it possible to tweak the definitions of both
$\mathcal {S}_c\models ^+_n T'\supseteq Th$
? If not, then is it possible to tweak the definitions of both
![]() $\mathcal {M}^{cl}$
and
$\mathcal {M}^{cl}$
and
![]() $\mathcal {S}_c$
in such a way that the answer to this question becomes affirmative and both Proposition 6 and Theorem 1 are still true relative to these new definitions?
$\mathcal {S}_c$
in such a way that the answer to this question becomes affirmative and both Proposition 6 and Theorem 1 are still true relative to these new definitions?
However, the above question may seem a bit too narrow in that we only ask about the relation between the theories arising in two particular structures (even when we allow those structures to differ from
![]() $\mathcal {M}^{cl}$
and
$\mathcal {M}^{cl}$
and
![]() $\mathcal {S}_c$
as defined above). A much more interesting question is whether we can establish any meaningful relation between the
$\mathcal {S}_c$
as defined above). A much more interesting question is whether we can establish any meaningful relation between the
![]() $\mathsf {N4}$
-conditional theories and
$\mathsf {N4}$
-conditional theories and
![]() $\mathsf {CL}$
-conditional theories in general. In other words:
$\mathsf {CL}$
-conditional theories in general. In other words:
Open Question 2. Let
![]() $T\subseteq \mathcal {FO}^\emptyset $
be
$T\subseteq \mathcal {FO}^\emptyset $
be
![]() $\mathsf {N4}$
-conditional. Is it then also
$\mathsf {N4}$
-conditional. Is it then also
![]() $\mathsf {CL}$
-conditional?
$\mathsf {CL}$
-conditional?
Open Question 3. Let
![]() $T\subseteq \mathcal {FO}^\emptyset $
be
$T\subseteq \mathcal {FO}^\emptyset $
be
![]() $\mathsf {CL}$
-conditional. Is it always the case that there exists some
$\mathsf {CL}$
-conditional. Is it always the case that there exists some
![]() $T'\subseteq \mathcal {FO}^\emptyset $
which is equivalent to T over
$T'\subseteq \mathcal {FO}^\emptyset $
which is equivalent to T over
![]() $\mathsf {CL}$
and also
$\mathsf {CL}$
and also
![]() $\mathsf {N4}$
-conditional?
$\mathsf {N4}$
-conditional?
It is much harder to formulate the right inverses to the open questions 2 and 3. It seems that not all
![]() $\mathsf {CL}$
-conditional theories are also
$\mathsf {CL}$
-conditional theories are also
![]() $\mathsf {N4}$
-conditional: one example is likely to be provided by
$\mathsf {N4}$
-conditional: one example is likely to be provided by
![]() $Th_{ck}$
itself. However, some sort of a canonical reformulation
$Th_{ck}$
itself. However, some sort of a canonical reformulation
![]() $\rho (T)$
of a classical theory T might be still possible with the effect that
$\rho (T)$
of a classical theory T might be still possible with the effect that
![]() $\rho (T)$
and T are classically equivalent and, in case T is
$\rho (T)$
and T are classically equivalent and, in case T is
![]() $\mathsf {CL}$
-conditional,
$\mathsf {CL}$
-conditional,
![]() $\rho (T)$
is
$\rho (T)$
is
![]() $\mathsf {N4}$
-conditional. In case such a reformulation technique is found and given in an effective way, the above conjectures and open questions can be extended by similar items asking about the format of the possible match-up between
$\mathsf {N4}$
-conditional. In case such a reformulation technique is found and given in an effective way, the above conjectures and open questions can be extended by similar items asking about the format of the possible match-up between
![]() $\mathsf {CL}$
-conditional theories and their canonical reformulations.
$\mathsf {CL}$
-conditional theories and their canonical reformulations.
A Proofs of some results about
 $\mathsf {QN4}$
$\mathsf {QN4}$
To simplify the notation, we fix an
![]() $\Omega \subseteq \Pi $
and set
$\Omega \subseteq \Pi $
and set
![]() $\mathcal {FO}^+:= \mathcal {FO}^+(\Omega ^\pm \cup \{\epsilon ^2\})$
,
$\mathcal {FO}^+:= \mathcal {FO}^+(\Omega ^\pm \cup \{\epsilon ^2\})$
,
![]() $\mathbb {I}:= \mathbb {I}(\Omega ^\pm \cup \{\epsilon ^2\})$
,
$\mathbb {I}:= \mathbb {I}(\Omega ^\pm \cup \{\epsilon ^2\})$
,
![]() $EP_i:= EP_i(\Omega ^\pm \cup \{\epsilon ^2\})$
,
$EP_i:= EP_i(\Omega ^\pm \cup \{\epsilon ^2\})$
,
![]() $\mathsf {QIL}^+:= \mathsf {QIL}^+(\Omega ^\pm \cup \{\epsilon ^2\})$
, and
$\mathsf {QIL}^+:= \mathsf {QIL}^+(\Omega ^\pm \cup \{\epsilon ^2\})$
, and
![]() $\mathfrak {QIL}^+:= \mathfrak {QIL}^+(\mathcal {FO}^+)$
. Moreover, we set
$\mathfrak {QIL}^+:= \mathfrak {QIL}^+(\mathcal {FO}^+)$
. Moreover, we set
![]() $\mathcal {FO}:= \mathcal {FO}(\Omega )$
,
$\mathcal {FO}:= \mathcal {FO}(\Omega )$
,
![]() $At:= At(\Omega )$
,
$At:= At(\Omega )$
,
![]() $Lit:= Lit(\Omega )$
,
$Lit:= Lit(\Omega )$
,
![]() $\mathbb {N}4:= \mathbb {N}4(\Omega )$
, and
$\mathbb {N}4:= \mathbb {N}4(\Omega )$
, and
![]() $EP_n:= EP_i(\Omega )$
for this Appendix.
$EP_n:= EP_i(\Omega )$
for this Appendix.
A.1 Proof of Proposition 1
The proof of Proposition 1 is complicated by the fact that
![]() $Tr$
is not injective; we have, for example,
$Tr$
is not injective; we have, for example,
Therefore, we need to choose a subset of
![]() $\mathcal {FO}$
which can both serve as a representative for the whole set
$\mathcal {FO}$
which can both serve as a representative for the whole set
![]() $\mathcal {FO}$
and provide a basis for an injective restriction of
$\mathcal {FO}$
and provide a basis for an injective restriction of
![]() $Tr$
. The next definition singles out this class.
$Tr$
. The next definition singles out this class.
Definition 11. A
![]() $\phi \in \mathcal {FO}$
is in negation normal form iff, for every
$\phi \in \mathcal {FO}$
is in negation normal form iff, for every
![]() $\sim \psi \in Sub(\phi )$
it is true that
$\sim \psi \in Sub(\phi )$
it is true that
![]() $\psi \in At$
.
$\psi \in At$
.
The following lemma sums up the properties of negation normal forms in
![]() $\mathsf {QN4}$
required for our argument.
$\mathsf {QN4}$
required for our argument.
Lemma 22. The following statements hold:
-
1.
 $tr:= Tr\upharpoonright \{\phi \in \mathcal {FO}\mid \phi \text { is in negation normal form}\}$
is a bijection.
$tr:= Tr\upharpoonright \{\phi \in \mathcal {FO}\mid \phi \text { is in negation normal form}\}$
is a bijection. -
2. For every
 $\phi \in \mathcal {FO}$
, define
$\phi \in \mathcal {FO}$
, define
 $NNF(\phi )\in \mathcal {FO}$
by the following induction on the construction of
$NNF(\phi )\in \mathcal {FO}$
by the following induction on the construction of
 $\phi $
: Then
$\phi $
: Then $$ \begin{align*} NNF(\phi)&:= \phi &&\phi \text{ is a literal}\\ NNF(\psi\ast\chi)&:= NNF(\psi)\ast NNF(\chi)&&\ast \in \{\wedge, \vee, \to\}\\ NNF(Qx\psi)&:= QxNNF(\psi)&&Q \in \{\forall, \exists\}\\ NNF(\sim\sim\psi)&:= NNF(\psi)\\ NNF(\sim(\psi\star\chi))&:= NNF(\sim\psi)\ast NNF(\sim\chi) &&\{\star, \ast\} = \{\wedge, \vee\}\\ NNF(\sim(\psi\to\chi))&:= NNF(\psi)\wedge NNF(\sim\chi);\\ NNF(\sim Qx\psi)&:= Q'xNNF(\sim\psi) &&\{Q,Q'\} = \{\forall, \exists\}. \end{align*} $$
$$ \begin{align*} NNF(\phi)&:= \phi &&\phi \text{ is a literal}\\ NNF(\psi\ast\chi)&:= NNF(\psi)\ast NNF(\chi)&&\ast \in \{\wedge, \vee, \to\}\\ NNF(Qx\psi)&:= QxNNF(\psi)&&Q \in \{\forall, \exists\}\\ NNF(\sim\sim\psi)&:= NNF(\psi)\\ NNF(\sim(\psi\star\chi))&:= NNF(\sim\psi)\ast NNF(\sim\chi) &&\{\star, \ast\} = \{\wedge, \vee\}\\ NNF(\sim(\psi\to\chi))&:= NNF(\psi)\wedge NNF(\sim\chi);\\ NNF(\sim Qx\psi)&:= Q'xNNF(\sim\psi) &&\{Q,Q'\} = \{\forall, \exists\}. \end{align*} $$
 $NNF(\phi )$
is in negation normal form, and
$NNF(\phi )$
is in negation normal form, and
 $\phi \leftrightarrow NNF(\phi )\in \mathsf {QN4}$
.
$\phi \leftrightarrow NNF(\phi )\in \mathsf {QN4}$
.
-
3. For every
 $\phi \in \mathcal {FO}$
, we have
$\phi \in \mathcal {FO}$
, we have
 $Tr(\phi ) = Tr(NNF(\phi ))$
.
$Tr(\phi ) = Tr(NNF(\phi ))$
.
Proof (a sketch)
(Part 1) Observe that
![]() $Tr$
is injective on literals and commutes with the connectives and quantifiers for the non-negated complex formulas. As for the surjectivity, a simple induction on the construction of
$Tr$
is injective on literals and commutes with the connectives and quantifiers for the non-negated complex formulas. As for the surjectivity, a simple induction on the construction of
![]() $\phi \in \mathcal {FO}^+(\Pi ^\pm \cup \{\epsilon ^2\})$
shows that every such
$\phi \in \mathcal {FO}^+(\Pi ^\pm \cup \{\epsilon ^2\})$
shows that every such
![]() $\phi $
must have a
$\phi $
must have a
![]() $tr$
-preimage.
$tr$
-preimage.
(Part 2) That
![]() $NNF(\phi )$
is in the negation normal form is immediate from the definition. As for the provability of
$NNF(\phi )$
is in the negation normal form is immediate from the definition. As for the provability of
![]() $\phi \leftrightarrow NNF(\phi )$
, we reason by induction on the construction of
$\phi \leftrightarrow NNF(\phi )$
, we reason by induction on the construction of
![]() $\phi \in \mathcal {FO}$
, using Lemma 2 plus the axioms (An1)–(An6).
$\phi \in \mathcal {FO}$
, using Lemma 2 plus the axioms (An1)–(An6).
(Part 3) By a straightforward induction on the construction of
![]() $\phi \in \mathcal {FO}$
.
$\phi \in \mathcal {FO}$
.
We are now ready to prove our proposition.
Proof of Proposition 1
(Left-to-right) Assume that
![]() $\Gamma \models _{\mathsf {QN4}}\Delta $
and choose any
$\Gamma \models _{\mathsf {QN4}}\Delta $
and choose any
![]() $\mathfrak {QN4}$
-deduction
$\mathfrak {QN4}$
-deduction
![]() $\bar {\chi }_r$
from the premises in
$\bar {\chi }_r$
from the premises in
![]() $\Gamma $
such that, for some
$\Gamma $
such that, for some
![]() $\psi _1,\ldots ,\psi _s\in \Delta $
we have
$\psi _1,\ldots ,\psi _s\in \Delta $
we have
![]() $\chi _r = \psi _1\vee \cdots \vee \psi _s$
. Consider
$\chi _r = \psi _1\vee \cdots \vee \psi _s$
. Consider
![]() $Tr(\bar {\chi }_r)$
: the translation of every axiom of
$Tr(\bar {\chi }_r)$
: the translation of every axiom of
![]() $\mathfrak {QIL}^+$
is again an instance of the same axiom and the same is true for the applications of every rule in
$\mathfrak {QIL}^+$
is again an instance of the same axiom and the same is true for the applications of every rule in
![]() $\mathfrak {QIL}^+$
. Finally, all the instances of (An1)–(An6) get translated into formulas of the form
$\mathfrak {QIL}^+$
. Finally, all the instances of (An1)–(An6) get translated into formulas of the form
![]() $\psi \leftrightarrow \psi $
for an appropriate
$\psi \leftrightarrow \psi $
for an appropriate
![]() $\psi \in \mathcal {FO}^+$
; all of these translations are also clearly provable in
$\psi \in \mathcal {FO}^+$
; all of these translations are also clearly provable in
![]() $\mathfrak {QIL}^+$
. Therefore,
$\mathfrak {QIL}^+$
. Therefore,
![]() $Tr(\bar {\chi }_r)$
is straightforwardly extendable to a
$Tr(\bar {\chi }_r)$
is straightforwardly extendable to a
![]() $\mathfrak {QIL}^+$
-deduction of
$\mathfrak {QIL}^+$
-deduction of
![]() $Tr(\chi _r) = Tr(\psi _1\vee \cdots \vee \psi _s) = Tr(\psi _1)\vee \cdots \vee Tr(\psi _s)$
from premises in
$Tr(\chi _r) = Tr(\psi _1\vee \cdots \vee \psi _s) = Tr(\psi _1)\vee \cdots \vee Tr(\psi _s)$
from premises in
![]() $Tr(\Gamma )$
. We have thus shown that
$Tr(\Gamma )$
. We have thus shown that
![]() $Tr(\Gamma )\models _{\mathsf {QIL}^+}Tr(\Delta )$
.
$Tr(\Gamma )\models _{\mathsf {QIL}^+}Tr(\Delta )$
.
(Right-to-left) Assume that
![]() $Tr(\Gamma )\models _{\mathsf {QIL}^+}Tr(\Delta )$
and choose any
$Tr(\Gamma )\models _{\mathsf {QIL}^+}Tr(\Delta )$
and choose any
![]() $\mathfrak {QIL}^+$
-deduction
$\mathfrak {QIL}^+$
-deduction
![]() $\bar {\chi }_r$
from the premises in
$\bar {\chi }_r$
from the premises in
![]() $Tr(\Gamma )$
such that, for some
$Tr(\Gamma )$
such that, for some
![]() $\psi _1,\ldots ,\psi _s\in \Delta $
we have
$\psi _1,\ldots ,\psi _s\in \Delta $
we have
![]() $\chi _r = Tr(\psi _1)\vee \cdots \vee Tr(\psi _s)$
. Consider
$\chi _r = Tr(\psi _1)\vee \cdots \vee Tr(\psi _s)$
. Consider
![]() $tr^{-1}(\bar {\chi }_r)$
. Again, every instance of a
$tr^{-1}(\bar {\chi }_r)$
. Again, every instance of a
![]() $\mathfrak {QIL}^+$
-axiom is transferred by
$\mathfrak {QIL}^+$
-axiom is transferred by
![]() $tr^{-1}$
into an instance of the same axiom and the applications of all the rules in
$tr^{-1}$
into an instance of the same axiom and the applications of all the rules in
![]() $\mathfrak {QIL}^+$
are likewise preserved by
$\mathfrak {QIL}^+$
are likewise preserved by
![]() $tr^{-1}$
. Therefore,
$tr^{-1}$
. Therefore,
![]() $tr^{-1}(\bar {\chi }_r)$
must be a deduction of
$tr^{-1}(\bar {\chi }_r)$
must be a deduction of
![]() $tr^{-1}(\chi _r)$
in
$tr^{-1}(\chi _r)$
in
![]() $\mathfrak {QIL}^+$
and hence also in
$\mathfrak {QIL}^+$
and hence also in
![]() $\mathfrak {QN4}$
. Note, next, that for every
$\mathfrak {QN4}$
. Note, next, that for every
![]() $\theta \in \mathcal {FO}$
we have
$\theta \in \mathcal {FO}$
we have
 $$ \begin{align*} tr^{-1}(Tr(\theta)) &= tr^{-1}(Tr(NNF(\theta))) &&\text{by Lemma}\ {22}.3\\ &= tr^{-1}(tr(NNF(\theta)))&&\text{by Lemma}\ {22}.2\\ &= NNF(\theta)&&\text{by Lemma}\ {22}.1. \end{align*} $$
$$ \begin{align*} tr^{-1}(Tr(\theta)) &= tr^{-1}(Tr(NNF(\theta))) &&\text{by Lemma}\ {22}.3\\ &= tr^{-1}(tr(NNF(\theta)))&&\text{by Lemma}\ {22}.2\\ &= NNF(\theta)&&\text{by Lemma}\ {22}.1. \end{align*} $$
Therefore
![]() $tr^{-1}(\bar {\chi }_r)$
is a
$tr^{-1}(\bar {\chi }_r)$
is a
![]() $\mathfrak {QN4}$
-deduction of
$\mathfrak {QN4}$
-deduction of
 $$ \begin{align*}tr^{-1}(\chi_r) &= tr^{-1}(Tr(\psi_1)\vee\cdots\vee Tr(\psi_s)) = tr^{-1}Tr(\psi_1)\vee\cdots\vee tr^{-1}Tr(\psi_s)\\& = NNF(\psi_1)\vee\cdots\vee NNF(\psi_s) \end{align*} $$
$$ \begin{align*}tr^{-1}(\chi_r) &= tr^{-1}(Tr(\psi_1)\vee\cdots\vee Tr(\psi_s)) = tr^{-1}Tr(\psi_1)\vee\cdots\vee tr^{-1}Tr(\psi_s)\\& = NNF(\psi_1)\vee\cdots\vee NNF(\psi_s) \end{align*} $$
from premises in
![]() $NNF(\Gamma )$
. In view of Lemma 22.2, it is straightforward to extend
$NNF(\Gamma )$
. In view of Lemma 22.2, it is straightforward to extend
![]() $tr^{-1}(\bar {\chi }_r)$
to a
$tr^{-1}(\bar {\chi }_r)$
to a
![]() $\mathfrak {QN4}$
-deduction of
$\mathfrak {QN4}$
-deduction of
![]() $\psi _1\vee \cdots \vee \psi _s$
from the premises in
$\psi _1\vee \cdots \vee \psi _s$
from the premises in
![]() $\Gamma $
.
$\Gamma $
.
A.2 Proof of Proposition 2
Proposition 2 follows from Proposition 1 together with the following two lemmas.
Lemma 23. Let
![]() $\mathcal {S}\in \mathbb {N}4$
, and let
$\mathcal {S}\in \mathbb {N}4$
, and let
![]() $\mathcal {S}^i = (W^i, \leq ^i, \mathtt {M}^i, \mathtt {H}^i)$
be such that
$\mathcal {S}^i = (W^i, \leq ^i, \mathtt {M}^i, \mathtt {H}^i)$
be such that
![]() $W^i := W$
,
$W^i := W$
,
![]() $\leq ^i:= \leq $
,
$\leq ^i:= \leq $
,
![]() $\mathtt {H}^i:= \mathtt {H}$
, and that, for every
$\mathtt {H}^i:= \mathtt {H}$
, and that, for every
![]() $\mathbf {w} \in W^i = W$
, we have
$\mathbf {w} \in W^i = W$
, we have
![]() $U^{\mathtt {M}^i_{\mathbf {w}}}:= U_{\mathbf {w}} = U^{\mathtt {M}^+_{\mathbf {w}}} = U^{\mathtt {M}^-_{\mathbf {w}}}$
. Finally, for all
$U^{\mathtt {M}^i_{\mathbf {w}}}:= U_{\mathbf {w}} = U^{\mathtt {M}^+_{\mathbf {w}}} = U^{\mathtt {M}^-_{\mathbf {w}}}$
. Finally, for all
![]() $\mathbf {w} \in W$
and
$\mathbf {w} \in W$
and
![]() $P^n \in \Pi $
, we set that
$P^n \in \Pi $
, we set that
Then all of the following statements hold:
-
1.
 $\mathcal {S}^i \in \mathbb {I}$
.
$\mathcal {S}^i \in \mathbb {I}$
. -
2. For every
 $\mathbf {w} \in W$
and every function f, we have
$\mathbf {w} \in W$
and every function f, we have
 $(\mathcal {S}, \mathbf {w}, f) \in EP_{n}$
iff
$(\mathcal {S}, \mathbf {w}, f) \in EP_{n}$
iff
 $(\mathcal {S}^i, \mathbf {w}, f) \in EP_{i}$
.
$(\mathcal {S}^i, \mathbf {w}, f) \in EP_{i}$
. -
3. For every
 $\mathbf {w} \in W$
, every f such that
$\mathbf {w} \in W$
, every f such that
 $(\mathcal {S}, \mathbf {w}, f) \in EP_{n}$
, and every
$(\mathcal {S}, \mathbf {w}, f) \in EP_{n}$
, and every
 $\phi \in \mathcal {FO}$
, we have
$\phi \in \mathcal {FO}$
, we have
 $\mathcal {S}, \mathbf {w}\models ^+_{n} \phi [f]$
iff
$\mathcal {S}, \mathbf {w}\models ^+_{n} \phi [f]$
iff
 $\mathcal {S}^i, \mathbf {w}\models _i Tr(\phi )[f]$
.
$\mathcal {S}^i, \mathbf {w}\models _i Tr(\phi )[f]$
.
Proof Parts 1 and 2 follow trivially by definition. Part 3 is proved by a straightforward induction on the construction of
![]() $\phi \in \mathcal {FO}$
for all
$\phi \in \mathcal {FO}$
for all
![]() $\mathbf {w}$
and f such that
$\mathbf {w}$
and f such that
![]() $(\mathcal {S}, \mathbf {w}, f) \in EP_n$
. We consider some typical cases in this induction in more detail.
$(\mathcal {S}, \mathbf {w}, f) \in EP_n$
. We consider some typical cases in this induction in more detail.
Case 1.
![]() $\phi = P\bar {x}_m$
for some
$\phi = P\bar {x}_m$
for some
![]() $m \in \omega $
,
$m \in \omega $
,
![]() $P^m \in \Pi $
and
$P^m \in \Pi $
and
![]() $\bar {x}_m\in Ind^m$
. But then:
$\bar {x}_m\in Ind^m$
. But then:
 $$ \begin{align*} \mathcal{S}, \mathbf{w}\models^+_n \phi[f] &\text{ iff } f(\bar{x}_m)\in P^{\mathtt{M}^+_{\mathbf{w}}} \text{ iff } f(\bar{x}_m)\in P_+^{\mathtt{M}^i_{\mathbf{w}}}\\& \text{ iff } \mathcal{S}^i, \mathbf{w}\models_i P_+(\bar{x}_m)[f]\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
$$ \begin{align*} \mathcal{S}, \mathbf{w}\models^+_n \phi[f] &\text{ iff } f(\bar{x}_m)\in P^{\mathtt{M}^+_{\mathbf{w}}} \text{ iff } f(\bar{x}_m)\in P_+^{\mathtt{M}^i_{\mathbf{w}}}\\& \text{ iff } \mathcal{S}^i, \mathbf{w}\models_i P_+(\bar{x}_m)[f]\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
On the other hand, we have
 $$ \begin{align*} \mathcal{S}, \mathbf{w}\models^{+}_{n} \sim\phi[f] &\text{ iff } \mathcal{S}, \mathbf{w}\models^{-}_{n} \phi[f] \text{ iff } f(\bar{x}_m)\in P^{\mathtt{M}^{-}_{\mathbf{w}}} \text{ iff } f(\bar{x}_m)\in P_{-}^{\mathtt{M}^i_{\mathbf{w}}}\\&\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i P_-(\bar{x}_{m})[f]\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\sim\phi)[f]. \end{align*} $$
$$ \begin{align*} \mathcal{S}, \mathbf{w}\models^{+}_{n} \sim\phi[f] &\text{ iff } \mathcal{S}, \mathbf{w}\models^{-}_{n} \phi[f] \text{ iff } f(\bar{x}_m)\in P^{\mathtt{M}^{-}_{\mathbf{w}}} \text{ iff } f(\bar{x}_m)\in P_{-}^{\mathtt{M}^i_{\mathbf{w}}}\\&\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i P_-(\bar{x}_{m})[f]\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\sim\phi)[f]. \end{align*} $$
Case 2.
![]() $\phi = (\psi \to \chi )$
. Then we have
$\phi = (\psi \to \chi )$
. Then we have
 $$ \begin{align*} &\mathcal{S}, \mathbf{w}\models^+_n \phi[f]\\&\quad \text{ iff }(\forall \mathbf{v}\geq \mathbf{w})(\mathcal{S},\mathbf{v}\not\models^+_{n}\psi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}, \mathbf{v}\models^+_{n}\chi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}])\\&\quad \text{ iff }(\forall \mathbf{v}\geq^i \mathbf{w})(\mathcal{S}^i,\mathbf{v}\not\models_iTr(\psi)[f\circ\mathtt{H}^i_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}^i, \mathbf{v}\models_iTr(\chi)[f\circ\mathtt{H}^i_{\mathbf{w}\mathbf{v}}])&&\text{by IH}\\&\quad \text{ iff } \mathcal{S}^i, \mathbf{w}\models_i (Tr(\psi)\to Tr(\chi))[f] \text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
$$ \begin{align*} &\mathcal{S}, \mathbf{w}\models^+_n \phi[f]\\&\quad \text{ iff }(\forall \mathbf{v}\geq \mathbf{w})(\mathcal{S},\mathbf{v}\not\models^+_{n}\psi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}, \mathbf{v}\models^+_{n}\chi[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}])\\&\quad \text{ iff }(\forall \mathbf{v}\geq^i \mathbf{w})(\mathcal{S}^i,\mathbf{v}\not\models_iTr(\psi)[f\circ\mathtt{H}^i_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}^i, \mathbf{v}\models_iTr(\chi)[f\circ\mathtt{H}^i_{\mathbf{w}\mathbf{v}}])&&\text{by IH}\\&\quad \text{ iff } \mathcal{S}^i, \mathbf{w}\models_i (Tr(\psi)\to Tr(\chi))[f] \text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
On the other hand, we have
 $$ \begin{align*} \mathcal{S}, \mathbf{w}\models^+_n \sim\phi[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^+_{n}\psi[f]\text{ and }\mathcal{S}, \mathbf{v}\models^-_{n}\chi[f]\\&\text{ iff } \mathcal{S},\mathbf{w}\models^+_{n}\psi[f]\text{ and }\mathcal{S}, \mathbf{w}\models^+_{n}\sim\chi[f]\\&\text{ iff } \mathcal{S}^i,\mathbf{w}\models_iTr(\psi)[f]\text{ and }\mathcal{S}^i, \mathbf{w}\models_iTr(\sim\chi)[f]&&\!\!\text{by IH}\\&\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\psi)\wedge Tr(\sim\chi)\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
$$ \begin{align*} \mathcal{S}, \mathbf{w}\models^+_n \sim\phi[f] &\text{ iff } \mathcal{S},\mathbf{w}\models^+_{n}\psi[f]\text{ and }\mathcal{S}, \mathbf{v}\models^-_{n}\chi[f]\\&\text{ iff } \mathcal{S},\mathbf{w}\models^+_{n}\psi[f]\text{ and }\mathcal{S}, \mathbf{w}\models^+_{n}\sim\chi[f]\\&\text{ iff } \mathcal{S}^i,\mathbf{w}\models_iTr(\psi)[f]\text{ and }\mathcal{S}^i, \mathbf{w}\models_iTr(\sim\chi)[f]&&\!\!\text{by IH}\\&\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\psi)\wedge Tr(\sim\chi)\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
Case 3.
![]() $\phi = \forall x\psi $
. Then we have
$\phi = \forall x\psi $
. Then we have
 $$ \begin{align*} \mathcal{S}, \mathbf{w}\models^+_n \phi[f] &\text{ iff } (\forall\mathbf{v}\geq \mathbf{w})(\forall a\in U_{\mathbf{v}})(\mathcal{S},\mathbf{v}\models^+_{n}\psi[(f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}})[x/a]])\\&\text{ iff } (\forall\mathbf{v}\geq^i \mathbf{w})(\forall a\in U^{\mathtt{M}^i_{\mathbf{v}}})(\mathcal{S}^i,\mathbf{v}\models_iTr(\psi)[(f\circ\mathtt{H}^i_{\mathbf{w}\mathbf{v}})[x/a]])&&\text{by IH}\\&\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i \forall xTr(\psi)[f]\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
$$ \begin{align*} \mathcal{S}, \mathbf{w}\models^+_n \phi[f] &\text{ iff } (\forall\mathbf{v}\geq \mathbf{w})(\forall a\in U_{\mathbf{v}})(\mathcal{S},\mathbf{v}\models^+_{n}\psi[(f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}})[x/a]])\\&\text{ iff } (\forall\mathbf{v}\geq^i \mathbf{w})(\forall a\in U^{\mathtt{M}^i_{\mathbf{v}}})(\mathcal{S}^i,\mathbf{v}\models_iTr(\psi)[(f\circ\mathtt{H}^i_{\mathbf{w}\mathbf{v}})[x/a]])&&\text{by IH}\\&\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i \forall xTr(\psi)[f]\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
On the other hand, we have
 $$ \begin{align*} \mathcal{S}, \mathbf{w}\models^+_n \sim\phi[f] &\text{ iff } (\exists a\in U_{\mathbf{w}})(\mathcal{S},\mathbf{w}\models^-_{n}\psi[f[x/a]])\\&\text{ iff } (\exists a\in U_{\mathbf{w}})(\mathcal{S},\mathbf{w}\models^+_{n}\sim\psi[f[x/a]])\\&\text{ iff } (\exists a\in U^{\mathtt{M}^i_{\mathbf{w}}})(\mathcal{S}^i,\mathbf{w}\models_iTr(\sim\psi)[f[x/a]])&&\text{by IH}\\&\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i \exists xTr(\sim\psi)[f]\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
$$ \begin{align*} \mathcal{S}, \mathbf{w}\models^+_n \sim\phi[f] &\text{ iff } (\exists a\in U_{\mathbf{w}})(\mathcal{S},\mathbf{w}\models^-_{n}\psi[f[x/a]])\\&\text{ iff } (\exists a\in U_{\mathbf{w}})(\mathcal{S},\mathbf{w}\models^+_{n}\sim\psi[f[x/a]])\\&\text{ iff } (\exists a\in U^{\mathtt{M}^i_{\mathbf{w}}})(\mathcal{S}^i,\mathbf{w}\models_iTr(\sim\psi)[f[x/a]])&&\text{by IH}\\&\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i \exists xTr(\sim\psi)[f]\text{ iff } \mathcal{S}^i, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
The remaining cases are trivial, or similar to the cases considered above, or both.
Lemma 24. Let
![]() $\mathcal {S}\in \mathbb {I}$
and let
$\mathcal {S}\in \mathbb {I}$
and let
![]() $\mathcal {S}^n = (W^n, \leq ^n, \mathtt {M}^{n+}, \mathtt {M}^{n-}, \mathtt {H}^n)$
be such that
$\mathcal {S}^n = (W^n, \leq ^n, \mathtt {M}^{n+}, \mathtt {M}^{n-}, \mathtt {H}^n)$
be such that
![]() $W^n := W$
,
$W^n := W$
,
![]() $\leq ^n:= \leq $
,
$\leq ^n:= \leq $
,
![]() $\mathtt {H}^n:= \mathtt {H}$
, and that, for every
$\mathtt {H}^n:= \mathtt {H}$
, and that, for every
![]() $\mathbf {w} \in W^n = W$
, we have
$\mathbf {w} \in W^n = W$
, we have
![]() $U^n_{\mathbf {w}} = U^{\mathtt {M}^{n+}_{\mathbf {w}}} = U^{\mathtt {M}^{n-}_{\mathbf {w}}}:= U^{\mathtt {M}_{\mathbf {w}}}$
. Finally, for all
$U^n_{\mathbf {w}} = U^{\mathtt {M}^{n+}_{\mathbf {w}}} = U^{\mathtt {M}^{n-}_{\mathbf {w}}}:= U^{\mathtt {M}_{\mathbf {w}}}$
. Finally, for all
![]() $\mathbf {w} \in W$
and
$\mathbf {w} \in W$
and
![]() $P^m \in \Pi $
, we set that
$P^m \in \Pi $
, we set that
Then all of the following statements hold:
-
1.
 $\mathcal {S}^n \in \mathbb {N}4$
.
$\mathcal {S}^n \in \mathbb {N}4$
. -
2. For every
 $\mathbf {w} \in W$
and every function f, we have
$\mathbf {w} \in W$
and every function f, we have
 $(\mathcal {S}, \mathbf {w}, f) \in EP_{i}$
iff
$(\mathcal {S}, \mathbf {w}, f) \in EP_{i}$
iff
 $(\mathcal {S}^n, \mathbf {w}, f) \in EP_{n}$
.
$(\mathcal {S}^n, \mathbf {w}, f) \in EP_{n}$
. -
3. For every
 $\mathbf {w} \in W$
, every f such that
$\mathbf {w} \in W$
, every f such that
 $(\mathcal {S}, \mathbf {w}, f) \in EP_{n}$
, and every
$(\mathcal {S}, \mathbf {w}, f) \in EP_{n}$
, and every
 $\phi \in \mathcal {FO}$
, we have
$\phi \in \mathcal {FO}$
, we have
 $\mathcal {S}^n, \mathbf {w}\models ^+_n \phi [f]$
iff
$\mathcal {S}^n, \mathbf {w}\models ^+_n \phi [f]$
iff
 $\mathcal {S}, \mathbf {w}\models _i Tr(\phi )[f]$
.
$\mathcal {S}, \mathbf {w}\models _i Tr(\phi )[f]$
.
Proof Again, the first two parts are trivial and Part 3 is proved by an induction on the construction of
![]() $\phi \in \mathcal {FO}$
. We illustrate the idea using the same selection of cases as in the previous proof:
$\phi \in \mathcal {FO}$
. We illustrate the idea using the same selection of cases as in the previous proof:
Case 1.
![]() $\phi = P\bar {x}_m$
for some
$\phi = P\bar {x}_m$
for some
![]() $m \in \omega $
,
$m \in \omega $
,
![]() $P^m \in \Pi $
and
$P^m \in \Pi $
and
![]() $\bar {x}_m\in Ind^m$
. But then:
$\bar {x}_m\in Ind^m$
. But then:
 $$ \begin{align*} \mathcal{S}^n, \mathbf{w}\models^+_n \phi[f] &\text{ iff } f(\bar{x}_m)\in P^{\mathtt{M}^{n+}_{\mathbf{w}}}\text{ iff } f(\bar{x}_m)\in P_+^{\mathtt{M}_{\mathbf{w}}}\\& \text{ iff } \mathcal{S}, \mathbf{w}\models_i P_+(\bar{x}_m)[f]\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
$$ \begin{align*} \mathcal{S}^n, \mathbf{w}\models^+_n \phi[f] &\text{ iff } f(\bar{x}_m)\in P^{\mathtt{M}^{n+}_{\mathbf{w}}}\text{ iff } f(\bar{x}_m)\in P_+^{\mathtt{M}_{\mathbf{w}}}\\& \text{ iff } \mathcal{S}, \mathbf{w}\models_i P_+(\bar{x}_m)[f]\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
On the other hand, we have
 $$ \begin{align*} \mathcal{S}^n, \mathbf{w}\models^+_n \sim\phi[f] &\text{ iff } \mathcal{S}^n, \mathbf{w}\models^-_n \phi[f] \text{ iff } f(\bar{x}_m)\in P^{\mathtt{M}^{n-}_{\mathbf{w}}} \text{ iff } f(\bar{x}_m)\in P_-^{\mathtt{M}_{\mathbf{w}}}\\ &\text{ iff } \mathcal{S}, \mathbf{w}\models_i P_-(\bar{x}_m)[f]\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\sim\phi)[f]. \end{align*} $$
$$ \begin{align*} \mathcal{S}^n, \mathbf{w}\models^+_n \sim\phi[f] &\text{ iff } \mathcal{S}^n, \mathbf{w}\models^-_n \phi[f] \text{ iff } f(\bar{x}_m)\in P^{\mathtt{M}^{n-}_{\mathbf{w}}} \text{ iff } f(\bar{x}_m)\in P_-^{\mathtt{M}_{\mathbf{w}}}\\ &\text{ iff } \mathcal{S}, \mathbf{w}\models_i P_-(\bar{x}_m)[f]\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\sim\phi)[f]. \end{align*} $$
Case 2.
![]() $\phi = (\psi \to \chi )$
. Then we have
$\phi = (\psi \to \chi )$
. Then we have
 $$ \begin{align*} &\mathcal{S}^n, \mathbf{w}\models^+_n \phi[f]\\&\quad \text{ iff }(\forall \mathbf{v} \geq^n \mathbf{w} )(\mathcal{S}^n,\mathbf{v}\not\models^+_{n}\psi[f\circ\mathtt{H}^n_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}^n, \mathbf{v}\models^+_{n}\chi[f\circ\mathtt{H}^n_{\mathbf{w}\mathbf{v}}])\\&\quad \text{ iff }(\forall \mathbf{v} \geq \mathbf{w})(\mathcal{S},\mathbf{v}\not\models_iTr(\psi)[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}, \mathbf{v}\models_iTr(\chi)[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}])&&\text{by IH}\\&\quad \text{ iff } \mathcal{S}, \mathbf{w}\models_i (Tr(\psi)\to Tr(\chi))[f] \text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
$$ \begin{align*} &\mathcal{S}^n, \mathbf{w}\models^+_n \phi[f]\\&\quad \text{ iff }(\forall \mathbf{v} \geq^n \mathbf{w} )(\mathcal{S}^n,\mathbf{v}\not\models^+_{n}\psi[f\circ\mathtt{H}^n_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}^n, \mathbf{v}\models^+_{n}\chi[f\circ\mathtt{H}^n_{\mathbf{w}\mathbf{v}}])\\&\quad \text{ iff }(\forall \mathbf{v} \geq \mathbf{w})(\mathcal{S},\mathbf{v}\not\models_iTr(\psi)[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}]\text{ or }\mathcal{S}, \mathbf{v}\models_iTr(\chi)[f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}}])&&\text{by IH}\\&\quad \text{ iff } \mathcal{S}, \mathbf{w}\models_i (Tr(\psi)\to Tr(\chi))[f] \text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
On the other hand, we have
 $$ \begin{align*} \mathcal{S}^n, \mathbf{w}\models^+_n \sim\phi[f] &\text{ iff } \mathcal{S}^n,\mathbf{w}\models^+_{n}\psi[f]\text{ and }\mathcal{S}^n, \mathbf{w}\models^-_{n}\chi[f]\\&\text{ iff } \mathcal{S}^n,\mathbf{w}\models^+_{n}\psi[f]\text{ and }\mathcal{S}^n, \mathbf{w}\models^+_{n}\sim\chi[f]\\&\text{ iff } \mathcal{S},\mathbf{w}\models_iTr(\psi)[f]\text{ and }\mathcal{S}, \mathbf{w}\models_iTr(\sim\chi)[f]&&\text{by IH}\\&\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\psi)\wedge Tr(\sim\chi)\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
$$ \begin{align*} \mathcal{S}^n, \mathbf{w}\models^+_n \sim\phi[f] &\text{ iff } \mathcal{S}^n,\mathbf{w}\models^+_{n}\psi[f]\text{ and }\mathcal{S}^n, \mathbf{w}\models^-_{n}\chi[f]\\&\text{ iff } \mathcal{S}^n,\mathbf{w}\models^+_{n}\psi[f]\text{ and }\mathcal{S}^n, \mathbf{w}\models^+_{n}\sim\chi[f]\\&\text{ iff } \mathcal{S},\mathbf{w}\models_iTr(\psi)[f]\text{ and }\mathcal{S}, \mathbf{w}\models_iTr(\sim\chi)[f]&&\text{by IH}\\&\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\psi)\wedge Tr(\sim\chi)\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
Case 3.
![]() $\phi = \forall x\psi $
. Then we have
$\phi = \forall x\psi $
. Then we have
 $$ \begin{align*} \mathcal{S}^n, \mathbf{w}\models^+_n \phi[f] &\text{ iff } (\forall \mathbf{v} \geq^n \mathbf{w})(\forall a\in U^n_{\mathbf{v}})(\mathcal{S}^n,\mathbf{v}\models^+_{n}\psi[(f\circ\mathtt{H}^n_{\mathbf{w}\mathbf{v}})[x/a]])\\ &\text{ iff } (\forall \mathbf{v} \geq \mathbf{w})(\forall a\in U^{\mathtt{M}_{\mathbf{v}}})(\mathcal{S},\mathbf{v}\models_iTr(\psi)[(f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}})[x/a]])&&\text{by IH}\\ &\text{ iff } \mathcal{S}, \mathbf{w}\models_i \forall xTr(\psi)[f]\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
$$ \begin{align*} \mathcal{S}^n, \mathbf{w}\models^+_n \phi[f] &\text{ iff } (\forall \mathbf{v} \geq^n \mathbf{w})(\forall a\in U^n_{\mathbf{v}})(\mathcal{S}^n,\mathbf{v}\models^+_{n}\psi[(f\circ\mathtt{H}^n_{\mathbf{w}\mathbf{v}})[x/a]])\\ &\text{ iff } (\forall \mathbf{v} \geq \mathbf{w})(\forall a\in U^{\mathtt{M}_{\mathbf{v}}})(\mathcal{S},\mathbf{v}\models_iTr(\psi)[(f\circ\mathtt{H}_{\mathbf{w}\mathbf{v}})[x/a]])&&\text{by IH}\\ &\text{ iff } \mathcal{S}, \mathbf{w}\models_i \forall xTr(\psi)[f]\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\phi)[f]. \end{align*} $$
On the other hand, we have
 $$ \begin{align*} \mathcal{S}^n, \mathbf{w}\models^+_n \sim\phi[f] &\text{ iff } (\exists a\in U^n_{\mathbf{w}})(\mathcal{S}^n,\mathbf{w}\models^-_{n}\psi[f[x/a]])\\ &\text{ iff } (\exists a\in U^n_{\mathbf{w}})(\mathcal{S}^n,\mathbf{w}\models^+_{n}\sim\psi[f[x/a]])\\ &\text{ iff } (\exists a\in U^{\mathtt{M}_{\mathbf{w}}})(\mathcal{S},\mathbf{w}\models_iTr(\sim\psi)[f[x/a]])&&\text{by IH}\\ &\text{ iff } \mathcal{S}, \mathbf{w}\models_i \exists xTr(\sim\psi)[f]\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\phi)[f].\\[-37pt] \end{align*} $$
$$ \begin{align*} \mathcal{S}^n, \mathbf{w}\models^+_n \sim\phi[f] &\text{ iff } (\exists a\in U^n_{\mathbf{w}})(\mathcal{S}^n,\mathbf{w}\models^-_{n}\psi[f[x/a]])\\ &\text{ iff } (\exists a\in U^n_{\mathbf{w}})(\mathcal{S}^n,\mathbf{w}\models^+_{n}\sim\psi[f[x/a]])\\ &\text{ iff } (\exists a\in U^{\mathtt{M}_{\mathbf{w}}})(\mathcal{S},\mathbf{w}\models_iTr(\sim\psi)[f[x/a]])&&\text{by IH}\\ &\text{ iff } \mathcal{S}, \mathbf{w}\models_i \exists xTr(\sim\psi)[f]\text{ iff } \mathcal{S}, \mathbf{w}\models_i Tr(\phi)[f].\\[-37pt] \end{align*} $$
We can now prove our proposition.
Proof of Proposition 2
For all
![]() $\Gamma , \Delta \subseteq \mathcal {FO}$
it is true that:
$\Gamma , \Delta \subseteq \mathcal {FO}$
it is true that:
 $$ \begin{align*} \Gamma\models_{\mathsf{QN4}}\Delta &\text{ iff } Tr(\Gamma)\models_{\mathsf{QIL}^+}Tr(\Delta) &&\text{by Proposition}\ {1}\\ &\text{ iff } Tr(\Gamma)\models_{i}Tr(\Delta) &&\text{by definition of }\mathsf{QIL}^+\\ &\text{ iff } \Gamma\models^+_{n}\Delta &&\text{by Lemmas}\ {23}\ \text{and}\ {24}.\\[-41pt] \end{align*} $$
$$ \begin{align*} \Gamma\models_{\mathsf{QN4}}\Delta &\text{ iff } Tr(\Gamma)\models_{\mathsf{QIL}^+}Tr(\Delta) &&\text{by Proposition}\ {1}\\ &\text{ iff } Tr(\Gamma)\models_{i}Tr(\Delta) &&\text{by definition of }\mathsf{QIL}^+\\ &\text{ iff } \Gamma\models^+_{n}\Delta &&\text{by Lemmas}\ {23}\ \text{and}\ {24}.\\[-41pt] \end{align*} $$
A.3 Proof of Lemma 4
(Part 1) If
![]() $\mathbf {w}\leq \mathbf {v}$
and
$\mathbf {w}\leq \mathbf {v}$
and
![]() $\mathcal {S},\mathbf {w}\models ^+_{n}\phi [f]$
, then, by Lemma 23, we must have
$\mathcal {S},\mathbf {w}\models ^+_{n}\phi [f]$
, then, by Lemma 23, we must have
![]() $\mathcal {S}^i,\mathbf {w}\models ^+_{i}Tr(\phi )[f]$
, whence
$\mathcal {S}^i,\mathbf {w}\models ^+_{i}Tr(\phi )[f]$
, whence
![]() $\mathcal {S}^i,\mathbf {v}\models ^+_{i}Tr(\phi )[f\circ \mathtt {H}^ i_{\mathbf {w}\mathbf {v}}]$
by Lemma 1.1 and
$\mathcal {S}^i,\mathbf {v}\models ^+_{i}Tr(\phi )[f\circ \mathtt {H}^ i_{\mathbf {w}\mathbf {v}}]$
by Lemma 1.1 and
![]() $\mathcal {S},\mathbf {v}\models ^+_{n}\phi [f\circ \mathtt {H}_{\mathbf {w}\mathbf {v}}]$
, again by Lemma 23. In case
$\mathcal {S},\mathbf {v}\models ^+_{n}\phi [f\circ \mathtt {H}_{\mathbf {w}\mathbf {v}}]$
, again by Lemma 23. In case
![]() $\mathcal {S},\mathbf {w}\models ^-_{n}\phi [f]$
, we must have
$\mathcal {S},\mathbf {w}\models ^-_{n}\phi [f]$
, we must have
![]() $\mathcal {S},\mathbf {w}\models ^+_{n}\sim \phi [f]$
, whence
$\mathcal {S},\mathbf {w}\models ^+_{n}\sim \phi [f]$
, whence
![]() $\mathcal {S},\mathbf {v}\models ^+_{n}\sim \phi [f\circ \mathtt {H}_{\mathbf {w}\mathbf {v}}]$
which is the same as
$\mathcal {S},\mathbf {v}\models ^+_{n}\sim \phi [f\circ \mathtt {H}_{\mathbf {w}\mathbf {v}}]$
which is the same as
![]() $\mathcal {S},\mathbf {v}\models ^-_{n}\phi [f\circ \mathtt {H}_{\mathbf {w}\mathbf {v}}]$
.
$\mathcal {S},\mathbf {v}\models ^-_{n}\phi [f\circ \mathtt {H}_{\mathbf {w}\mathbf {v}}]$
.
(Part 2) We note that we clearly have
![]() $(\mathcal {S}|_{\mathbf {w}})^i = (\mathcal {S}^i)|_{\mathbf {w}}$
. Thus, by Lemma 23, we have
$(\mathcal {S}|_{\mathbf {w}})^i = (\mathcal {S}^i)|_{\mathbf {w}}$
. Thus, by Lemma 23, we have
![]() $\mathcal {S}|_{\mathbf {w}}, \mathbf {v}\models ^+_{n}\phi [f]$
iff
$\mathcal {S}|_{\mathbf {w}}, \mathbf {v}\models ^+_{n}\phi [f]$
iff
![]() $(\mathcal {S}|_{\mathbf {w}})^i, \mathbf {v}\models _{i}Tr(\phi )[f]$
iff
$(\mathcal {S}|_{\mathbf {w}})^i, \mathbf {v}\models _{i}Tr(\phi )[f]$
iff
![]() $(\mathcal {S}^i)|_{\mathbf {w}}, \mathbf {v}\models _{i}Tr(\phi )[f]$
iff, by Lemma 1.2, we have
$(\mathcal {S}^i)|_{\mathbf {w}}, \mathbf {v}\models _{i}Tr(\phi )[f]$
iff, by Lemma 1.2, we have
![]() $\mathcal {S}^i, \mathbf {v}\models _{i}Tr(\phi )[f]$
, iff, again by Lemma 23,
$\mathcal {S}^i, \mathbf {v}\models _{i}Tr(\phi )[f]$
, iff, again by Lemma 23,
![]() $\mathcal {S}, \mathbf {v}\models ^+_{n}\phi [f]$
.
$\mathcal {S}, \mathbf {v}\models ^+_{n}\phi [f]$
.
On the other hand, we have
![]() $\mathcal {S}|_{\mathbf {w}}, \mathbf {v}\models ^-_{n}\phi [f]$
iff
$\mathcal {S}|_{\mathbf {w}}, \mathbf {v}\models ^-_{n}\phi [f]$
iff
![]() $\mathcal {S}|_{\mathbf {w}}, \mathbf {v}\models ^+_{n}\sim \phi [f]$
iff
$\mathcal {S}|_{\mathbf {w}}, \mathbf {v}\models ^+_{n}\sim \phi [f]$
iff
![]() $\mathcal {S}, \mathbf {v}\models ^+_{n}\sim \phi [f]$
iff
$\mathcal {S}, \mathbf {v}\models ^+_{n}\sim \phi [f]$
iff
![]() $\mathcal {S}, \mathbf {v}\models ^-_{n}\phi [f]$
.
$\mathcal {S}, \mathbf {v}\models ^-_{n}\phi [f]$
.
A.4 Proof of Lemma 5
The claims of Lemma 5 can be easily verified on the basis of the Nelsonian sheaf semantics. Also, it is pretty straightforward to obtain the proofs of (T1)–(T16) in
![]() $\mathfrak {QN4}$
. As an example, we sketch the following proofs.
$\mathfrak {QN4}$
. As an example, we sketch the following proofs.
(T13). We consider the case when
![]() $\ast = \to $
. We start by building the following chains of
$\ast = \to $
. We start by building the following chains of
![]() $\mathsf {QN4}$
-valid implications:
$\mathsf {QN4}$
-valid implications:
 $$ \begin{align*} ((\phi \Leftrightarrow \psi) \wedge (\chi \Leftrightarrow \theta))&\to ((\phi \leftrightarrow \psi) \wedge (\chi \leftrightarrow \theta))&&\text{ by Lemma}\ {2},\ \text{def. of }\Leftrightarrow\\ &\to (\phi \to \chi)\leftrightarrow (\psi \to \theta)&&\text{ by Lemma}\ {2} \end{align*} $$
$$ \begin{align*} ((\phi \Leftrightarrow \psi) \wedge (\chi \Leftrightarrow \theta))&\to ((\phi \leftrightarrow \psi) \wedge (\chi \leftrightarrow \theta))&&\text{ by Lemma}\ {2},\ \text{def. of }\Leftrightarrow\\ &\to (\phi \to \chi)\leftrightarrow (\psi \to \theta)&&\text{ by Lemma}\ {2} \end{align*} $$
and
 $$ \begin{align*} ((\phi \Leftrightarrow \psi) \wedge (\chi \Leftrightarrow \theta))&\to ((\phi \leftrightarrow \psi) \wedge (\sim\chi \leftrightarrow \sim\theta))&&\text{ by Lemma {2}, def. of }\Leftrightarrow\\ &\to (\phi \wedge \sim\chi)\leftrightarrow (\psi \wedge \sim\theta)&&\text{ by Lemma {2}}\\ &\to \sim(\phi \to \chi)\leftrightarrow \sim(\psi \to \theta) &&\text{ by Lemma {2}, }\text{({An4})}. \end{align*} $$
$$ \begin{align*} ((\phi \Leftrightarrow \psi) \wedge (\chi \Leftrightarrow \theta))&\to ((\phi \leftrightarrow \psi) \wedge (\sim\chi \leftrightarrow \sim\theta))&&\text{ by Lemma {2}, def. of }\Leftrightarrow\\ &\to (\phi \wedge \sim\chi)\leftrightarrow (\psi \wedge \sim\theta)&&\text{ by Lemma {2}}\\ &\to \sim(\phi \to \chi)\leftrightarrow \sim(\psi \to \theta) &&\text{ by Lemma {2}, }\text{({An4})}. \end{align*} $$
We thus have shown that
whence (T13) for
![]() $\ast = \to $
follows by the definition of
$\ast = \to $
follows by the definition of
![]() $\Leftrightarrow $
.
$\Leftrightarrow $
.
(T14). We consider the case when
![]() $Q = \exists $
. Again, we build two valid implication chains (the commentary applies to both chains simultaneously):
$Q = \exists $
. Again, we build two valid implication chains (the commentary applies to both chains simultaneously):
 $$ \begin{align*} (\phi \Leftrightarrow \psi) &\to (\phi \leftrightarrow \psi)&& (\phi \Leftrightarrow \psi)\to (\sim\phi \leftrightarrow \sim\psi)&&\text{ by Lemma {2}, def. of }\Leftrightarrow\\ &\to (\exists x\phi\leftrightarrow \exists x\psi)&&\qquad\qquad\to (\forall x\sim\phi\leftrightarrow\forall x\sim\psi)&&\text{ by Lemma {2}}\\ & &&\qquad\qquad\to(\sim\exists x\phi\leftrightarrow\sim\exists x\psi)&&\text{ by Lemma {2}, }\text{(An5)}. \end{align*} $$
$$ \begin{align*} (\phi \Leftrightarrow \psi) &\to (\phi \leftrightarrow \psi)&& (\phi \Leftrightarrow \psi)\to (\sim\phi \leftrightarrow \sim\psi)&&\text{ by Lemma {2}, def. of }\Leftrightarrow\\ &\to (\exists x\phi\leftrightarrow \exists x\psi)&&\qquad\qquad\to (\forall x\sim\phi\leftrightarrow\forall x\sim\psi)&&\text{ by Lemma {2}}\\ & &&\qquad\qquad\to(\sim\exists x\phi\leftrightarrow\sim\exists x\psi)&&\text{ by Lemma {2}, }\text{(An5)}. \end{align*} $$
Combining the two implication chains yields that
whence (T14) for
![]() $Q = \exists $
follows by the definition of
$Q = \exists $
follows by the definition of
![]() $\Leftrightarrow $
.
$\Leftrightarrow $
.
A.5 The use of ampersand in
 $\mathsf {QN4}$
$\mathsf {QN4}$
In this appendix, we quickly motivate the usefulness of ampersand. Ampersand is especially convenient for handling the restricted existential quantification in the context of
![]() $\mathsf {QN4}$
. The latter statement can be easily motivated as long as one is prepared to assume that the states of any given Nelsonian sheaf
$\mathsf {QN4}$
. The latter statement can be easily motivated as long as one is prepared to assume that the states of any given Nelsonian sheaf
![]() $\mathcal {S}$
can be seen as knowledge states so that an object
$\mathcal {S}$
can be seen as knowledge states so that an object
![]() $a \in U_{\mathbf {w}}$
is understood as an object known to exist at
$a \in U_{\mathbf {w}}$
is understood as an object known to exist at
![]() $\mathbf {w}$
; the states that are accessible from
$\mathbf {w}$
; the states that are accessible from
![]() $\mathbf {w}$
are then to be understood as future knowledge states that are possible in
$\mathbf {w}$
are then to be understood as future knowledge states that are possible in
![]() $\mathbf {w}$
.
$\mathbf {w}$
.
Indeed, when we say that some object has some property, say
![]() $p_0$
, this is true iff at least one currently known object verifies
$p_0$
, this is true iff at least one currently known object verifies
![]() $p_0$
; this is false iff every object that is either currently known or will become known in the future falsifies
$p_0$
; this is false iff every object that is either currently known or will become known in the future falsifies
![]() $p_0$
. Let us now try to formalize this idea: if our current state of knowledge, located in the web of other possible knowledge states, is faithfully captured by some world
$p_0$
. Let us now try to formalize this idea: if our current state of knowledge, located in the web of other possible knowledge states, is faithfully captured by some world
![]() $\mathbf {w}$
in some Nelsonian sheaf
$\mathbf {w}$
in some Nelsonian sheaf
![]() $\mathcal {S}$
, then we will say that our existence claim is true at
$\mathcal {S}$
, then we will say that our existence claim is true at
![]() $(\mathcal {S}, \mathbf {w})$
iff
$(\mathcal {S}, \mathbf {w})$
iff
![]() $U_{\mathbf {w}} \cap p^{\mathtt {M}_{\mathbf {w}}^+}_0\neq \emptyset $
; and false at
$U_{\mathbf {w}} \cap p^{\mathtt {M}_{\mathbf {w}}^+}_0\neq \emptyset $
; and false at
![]() $(\mathcal {S}, \mathbf {w})$
iff, for every
$(\mathcal {S}, \mathbf {w})$
iff, for every
![]() $\mathbf {v} \geq \mathbf {w}$
, we have
$\mathbf {v} \geq \mathbf {w}$
, we have
![]() $U_{\mathbf {v}} \subseteq p^{\mathtt {M}_{\mathbf {v}}^-}_0$
. It is easy to see now that both the truth and the falsity condition of our existence claim are exactly those of the sentence
$U_{\mathbf {v}} \subseteq p^{\mathtt {M}_{\mathbf {v}}^-}_0$
. It is easy to see now that both the truth and the falsity condition of our existence claim are exactly those of the sentence
![]() $\exists xp_0x$
, which is also how one usually formalizes simple existence claims classically.
$\exists xp_0x$
, which is also how one usually formalizes simple existence claims classically.
Suppose now that we would like to restrict our claim about the existence of an object with the property
![]() $p_0$
to the family of objects that verify some additional property
$p_0$
to the family of objects that verify some additional property
![]() $p_1$
. At least one natural way to understand such a restriction is to say that our claim is true iff at least one object that is currently known to have
$p_1$
. At least one natural way to understand such a restriction is to say that our claim is true iff at least one object that is currently known to have
![]() $p_1$
also verifies
$p_1$
also verifies
![]() $p_0$
. As for the falsity condition, our claim must be false iff every object that is either currently known or will be known in the future to have
$p_0$
. As for the falsity condition, our claim must be false iff every object that is either currently known or will be known in the future to have
![]() $p_1$
also falsifies
$p_1$
also falsifies
![]() $p_0$
. Turning again to possible formalizations, we are looking for a formula that must be true at
$p_0$
. Turning again to possible formalizations, we are looking for a formula that must be true at
![]() $(\mathcal {S}, \mathbf {w})$
iff
$(\mathcal {S}, \mathbf {w})$
iff
![]() $(U_{\mathbf {w}}\cap p^{\mathtt {M}_{\mathbf {w}}^+}_1) \cap p^{\mathtt {M}_{\mathbf {w}}^+}_0\neq \emptyset $
and false at
$(U_{\mathbf {w}}\cap p^{\mathtt {M}_{\mathbf {w}}^+}_1) \cap p^{\mathtt {M}_{\mathbf {w}}^+}_0\neq \emptyset $
and false at
![]() $(\mathcal {S}, \mathbf {w})$
iff, for every
$(\mathcal {S}, \mathbf {w})$
iff, for every
![]() $\mathbf {v} \geq \mathbf {w}$
, we have
$\mathbf {v} \geq \mathbf {w}$
, we have
![]() $(U_{\mathbf {v}}\cap p^{\mathtt {M}_{\mathbf {v}}^+}_1)\subseteq p^{\mathtt {M}_{\mathbf {v}}^-}_0$
.
$(U_{\mathbf {v}}\cap p^{\mathtt {M}_{\mathbf {v}}^+}_1)\subseteq p^{\mathtt {M}_{\mathbf {v}}^-}_0$
.
Now the classical formalization of this sort of restricted existential quantification is given by
![]() $\exists x(p_1x\wedge p_0x)$
, and it is easy to see that in the context of
$\exists x(p_1x\wedge p_0x)$
, and it is easy to see that in the context of
![]() $\mathsf {QN4}$
this sentence has exactly the truth condition that we have given above. However, its falsity condition is different, namely, the sentence is false at
$\mathsf {QN4}$
this sentence has exactly the truth condition that we have given above. However, its falsity condition is different, namely, the sentence is false at
![]() $(\mathcal {S}, \mathbf {w})$
iff, for every
$(\mathcal {S}, \mathbf {w})$
iff, for every
![]() $\mathbf {v} \geq \mathbf {w}$
, we have
$\mathbf {v} \geq \mathbf {w}$
, we have
![]() $U_{\mathbf {v}} \subseteq (p^{\mathtt {M}_{\mathbf {v}}^-}_1\cup p^{\mathtt {M}_{\mathbf {v}}^-}_0)$
. Note that in the semantics of Nelsonian sheaves,
$U_{\mathbf {v}} \subseteq (p^{\mathtt {M}_{\mathbf {v}}^-}_1\cup p^{\mathtt {M}_{\mathbf {v}}^-}_0)$
. Note that in the semantics of Nelsonian sheaves,
![]() $p^{\mathtt {M}_{\mathbf {v}}^-}_1$
and
$p^{\mathtt {M}_{\mathbf {v}}^-}_1$
and
![]() $p^{\mathtt {M}_{\mathbf {v}}^+}_1$
are, generally speaking, completely independent from one another and, therefore, the latter condition is also independent from the requirement that
$p^{\mathtt {M}_{\mathbf {v}}^+}_1$
are, generally speaking, completely independent from one another and, therefore, the latter condition is also independent from the requirement that
![]() $(U_{\mathbf {v}}\cap p^{\mathtt {M}_{\mathbf {v}}^+}_1)\subseteq p^{\mathtt {M}_{\mathbf {v}}^-}_0$
for every
$(U_{\mathbf {v}}\cap p^{\mathtt {M}_{\mathbf {v}}^+}_1)\subseteq p^{\mathtt {M}_{\mathbf {v}}^-}_0$
for every
![]() $\mathbf {v} \geq \mathbf {w}$
.
$\mathbf {v} \geq \mathbf {w}$
.
We are doing much better, though, if in the above formalization we replace conjunction with ampersand. The truth condition then remains the same, since Lemma 2 and (T13) together imply that
![]() $ \exists x(p_1x\,\&\, p_0x)\leftrightarrow \exists x(p_1x\wedge p_0x)$
.
$ \exists x(p_1x\,\&\, p_0x)\leftrightarrow \exists x(p_1x\wedge p_0x)$
.
However, the falsity condition looks different, since, by Lemma 2, (T2), (T11), and (T14), it follows that
![]() $ \sim \exists x(p_1x\,\&\, p_0x)\leftrightarrow \forall x(p_1x\to \sim p_0x)$
.
$ \sim \exists x(p_1x\,\&\, p_0x)\leftrightarrow \forall x(p_1x\to \sim p_0x)$
.
In other words, our alternative formalization is false at
![]() $(\mathcal {S}, \mathbf {w})$
iff, for every
$(\mathcal {S}, \mathbf {w})$
iff, for every
![]() $\mathbf {v} \geq \mathbf {w}$
, we have
$\mathbf {v} \geq \mathbf {w}$
, we have
![]() $(U_{\mathbf {v}}\cap p^{\mathtt {M}_{\mathbf {v}}^+}_1)\subseteq p^{\mathtt {M}_{\mathbf {v}}^-}_0$
, which is exactly what we wanted initially.
$(U_{\mathbf {v}}\cap p^{\mathtt {M}_{\mathbf {v}}^+}_1)\subseteq p^{\mathtt {M}_{\mathbf {v}}^-}_0$
, which is exactly what we wanted initially.
Note that ampersand becomes necessary for our representations of restricted existential quantifications only insofar as we get interested in what happens when a statement is false. This is not always the case, though. For example, if one is formulating a theory in
![]() $\mathsf {QN4}$
and would like to ensure the existence of an object with the property
$\mathsf {QN4}$
and would like to ensure the existence of an object with the property
![]() $p_0$
among those objects that happen to satisfy
$p_0$
among those objects that happen to satisfy
![]() $p_1$
, then it might make perfect sense to formalize this part of one’s theory by requiring that
$p_1$
, then it might make perfect sense to formalize this part of one’s theory by requiring that
![]() $\exists x(p_1x\wedge p_0x)$
as long as one is only interested in the models where this claim is true and is indifferent to the models where the claim happens to be false.
$\exists x(p_1x\wedge p_0x)$
as long as one is only interested in the models where this claim is true and is indifferent to the models where the claim happens to be false.
A.6 A proof of Lemma 6
We proceed by induction on the construction of
![]() $\chi \in \mathcal {FO}$
.
$\chi \in \mathcal {FO}$
.
Basis. If
![]() $\chi \in At$
, then the following cases are possible:
$\chi \in At$
, then the following cases are possible:
Case 1.
![]() $\chi = (v_0 \equiv v_0)$
. Then (T17) assumes the form
$\chi = (v_0 \equiv v_0)$
. Then (T17) assumes the form
![]() $ (\phi \Leftrightarrow \psi )\to (\phi \Leftrightarrow \psi )$
, and is a theorem of
$ (\phi \Leftrightarrow \psi )\to (\phi \Leftrightarrow \psi )$
, and is a theorem of
![]() $\mathsf {QN4}$
by Lemma 2.
$\mathsf {QN4}$
by Lemma 2.
Case 2.
![]() $\chi \neq (v_0 \equiv v_0)$
. Then (T17) is just
$\chi \neq (v_0 \equiv v_0)$
. Then (T17) is just
![]() $(\phi \Leftrightarrow \psi )\to (\chi \Leftrightarrow \chi )$
, and is a theorem of
$(\phi \Leftrightarrow \psi )\to (\chi \Leftrightarrow \chi )$
, and is a theorem of
![]() $\mathsf {QN4}$
by (T5) and Lemma 2.
$\mathsf {QN4}$
by (T5) and Lemma 2.
Induction step. The following cases are possible:
Case 1.
![]() $\chi = (\chi _0\ast \chi _1)$
for some
$\chi = (\chi _0\ast \chi _1)$
for some
![]() $\ast \in \{\wedge , \vee , \to \}$
. Then we reason as follows:
$\ast \in \{\wedge , \vee , \to \}$
. Then we reason as follows:
 $$ \begin{align} \vdash_{\mathsf{QN4}}(((\chi_0/\phi)&\Leftrightarrow(\chi_0/\psi))\wedge((\chi_1/\phi)\Leftrightarrow(\chi_1/\psi)))\to\nonumber\\ &\qquad\qquad\to(((\chi_0\ast\chi_1)/\phi)\Leftrightarrow((\chi_0\ast\chi_1)/\psi))&&\text{by (T13)} \end{align} $$
$$ \begin{align} \vdash_{\mathsf{QN4}}(((\chi_0/\phi)&\Leftrightarrow(\chi_0/\psi))\wedge((\chi_1/\phi)\Leftrightarrow(\chi_1/\psi)))\to\nonumber\\ &\qquad\qquad\to(((\chi_0\ast\chi_1)/\phi)\Leftrightarrow((\chi_0\ast\chi_1)/\psi))&&\text{by (T13)} \end{align} $$
Case 2.
![]() $\chi = \sim \chi _0$
or
$\chi = \sim \chi _0$
or
![]() $\chi = Qx\chi _0$
for some
$\chi = Qx\chi _0$
for some
![]() $Q\in \{\forall , \exists \}$
and some
$Q\in \{\forall , \exists \}$
and some
![]() $x \in Ind$
. We reason as in Case 1 applying (T4) (resp., (T14)) in place of (T13).
$x \in Ind$
. We reason as in Case 1 applying (T4) (resp., (T14)) in place of (T13).
B Proof of Lemma 12
We proceed by induction on the construction of
![]() $\phi \in \mathcal {CN}$
. The basis of induction follows from (Th2). As for the induction step, we need to consider the following cases:
$\phi \in \mathcal {CN}$
. The basis of induction follows from (Th2). As for the induction step, we need to consider the following cases:
Case 1.
![]() $\phi = \psi \ast \chi $
, where
$\phi = \psi \ast \chi $
, where
![]() $\ast \in \{\wedge , \to \}$
. We consider the following derivation D1 from premises in
$\ast \in \{\wedge , \to \}$
. We consider the following derivation D1 from premises in
![]() $\mathsf {QN4}$
:
$\mathsf {QN4}$
:
We now reason as follows:
 $$ \begin{align*} &Th, \text{({B.1}), ({B.2})} \models_{n} \exists z(\text{{B.3}})\\& \quad \to \exists z(Sz\wedge (\forall w)_O(Ewz\Leftrightarrow ST_w(\psi\ast\chi)))&&(\text{D1, {DT}, }({\text{B}\exists})) \\&Th, \text{({B.1}), ({B.2})} \models_{n} Sx\wedge Sy &&\text{(trivially)} \\&Th, \text{({B.1}), ({B.2})} \models_{n} (Sx\wedge Sy )\to \exists z\text{({B.3})}&&\text{({Th4})} \\&Th, \text{({B.1}), ({B.2})} \models_{n}\exists z(Sz{\kern-1pt}\wedge{\kern-1pt} (\forall w)_O(Ewz{\kern-1pt}\Leftrightarrow{\kern-1pt} ST_w(\psi{\kern-1pt}\ast{\kern-1pt}\chi)))&&\text{({MP})} \\&Th\models_{n} \exists x(\text{{B.1}}) \to (\exists y\text{({B.2})}\\& \quad \to \exists z(Sz\wedge (\forall w)_O(Ewz\Leftrightarrow ST_w(\psi\ast\chi))))&&\text{({DT}), }({\text{B}\exists}) \\&Th\models_{n} \exists x\text{({B.1})} \wedge \exists y(\text{{B.2}})&&\text{(IH)} \\&Th\models_{n}\exists z(Sz\wedge (\forall w)_O(Ewz\Leftrightarrow ST_w(\psi\ast\chi))).&&\text{({MP})} \end{align*} $$
$$ \begin{align*} &Th, \text{({B.1}), ({B.2})} \models_{n} \exists z(\text{{B.3}})\\& \quad \to \exists z(Sz\wedge (\forall w)_O(Ewz\Leftrightarrow ST_w(\psi\ast\chi)))&&(\text{D1, {DT}, }({\text{B}\exists})) \\&Th, \text{({B.1}), ({B.2})} \models_{n} Sx\wedge Sy &&\text{(trivially)} \\&Th, \text{({B.1}), ({B.2})} \models_{n} (Sx\wedge Sy )\to \exists z\text{({B.3})}&&\text{({Th4})} \\&Th, \text{({B.1}), ({B.2})} \models_{n}\exists z(Sz{\kern-1pt}\wedge{\kern-1pt} (\forall w)_O(Ewz{\kern-1pt}\Leftrightarrow{\kern-1pt} ST_w(\psi{\kern-1pt}\ast{\kern-1pt}\chi)))&&\text{({MP})} \\&Th\models_{n} \exists x(\text{{B.1}}) \to (\exists y\text{({B.2})}\\& \quad \to \exists z(Sz\wedge (\forall w)_O(Ewz\Leftrightarrow ST_w(\psi\ast\chi))))&&\text{({DT}), }({\text{B}\exists}) \\&Th\models_{n} \exists x\text{({B.1})} \wedge \exists y(\text{{B.2}})&&\text{(IH)} \\&Th\models_{n}\exists z(Sz\wedge (\forall w)_O(Ewz\Leftrightarrow ST_w(\psi\ast\chi))).&&\text{({MP})} \end{align*} $$
Case 2.
![]() $\phi = \sim \psi $
. Similar to Case 1, but using (Th3) in place of (Th4).
$\phi = \sim \psi $
. Similar to Case 1, but using (Th3) in place of (Th4).
Case 3.
![]() $\phi = \psi \vee \chi $
. Note that by Cases 1 and 2 we know that
$\phi = \psi \vee \chi $
. Note that by Cases 1 and 2 we know that
![]() $Th\models _{\mathsf {QN4}}\exists y(Sy\wedge (\forall x)_O(Exy \Leftrightarrow \sim (\sim ST_x(\psi )\wedge \sim ST_x(\chi ))))$
(which can be equivalently re-written as
$Th\models _{\mathsf {QN4}}\exists y(Sy\wedge (\forall x)_O(Exy \Leftrightarrow \sim (\sim ST_x(\psi )\wedge \sim ST_x(\chi ))))$
(which can be equivalently re-written as
![]() $Th\models _{\mathsf {QN4}}\exists y(Sy\wedge (\forall x)_O(Exy \Leftrightarrow v_0\equiv v_0))/\theta $
for
$Th\models _{\mathsf {QN4}}\exists y(Sy\wedge (\forall x)_O(Exy \Leftrightarrow v_0\equiv v_0))/\theta $
for
![]() $\theta : = \sim (\sim ST_x(\psi )\wedge \sim ST_x(\chi ))$
); now, Corollary 1, together with Lemma 6, implies that
$\theta : = \sim (\sim ST_x(\psi )\wedge \sim ST_x(\chi ))$
); now, Corollary 1, together with Lemma 6, implies that
![]() $Th\models _{\mathsf {QN4}}\exists y(Sy\wedge (\forall x)_O(Exy \Leftrightarrow (ST_x(\psi )\vee ST_x(\chi ))))$
.
$Th\models _{\mathsf {QN4}}\exists y(Sy\wedge (\forall x)_O(Exy \Leftrightarrow (ST_x(\psi )\vee ST_x(\chi ))))$
.
Case 4. ![]() . We consider the following deductions from premises in
. We consider the following deductions from premises in
![]() $\mathsf {QN4}$
, letting
$\mathsf {QN4}$
, letting
![]() $T:= Th \cup \{Sy'\wedge (\forall w)_O(Ewy'\Leftrightarrow ST_w(\psi ))\} = Th \cup \{\theta \}$
.
$T:= Th \cup \{Sy'\wedge (\forall w)_O(Ewy'\Leftrightarrow ST_w(\psi ))\} = Th \cup \{\theta \}$
.
Deduction D2+:
 $$\begin{align} &\exists y((Sy\wedge(\forall w)_O(Ewy\Leftrightarrow ST_w(\psi))) \nonumber\\&\qquad\qquad\qquad \&\ \forall w(Rxyw\to ST_w(\chi))) && \text{by } \theta, (\text{{B.9}), }({\alpha_{10}}),\text{ ({T15})}\end{align}$$
$$\begin{align} &\exists y((Sy\wedge(\forall w)_O(Ewy\Leftrightarrow ST_w(\psi))) \nonumber\\&\qquad\qquad\qquad \&\ \forall w(Rxyw\to ST_w(\chi))) && \text{by } \theta, (\text{{B.9}), }({\alpha_{10}}),\text{ ({T15})}\end{align}$$
Deduction D2–:
 $$\begin{align} &\forall y((Sy\wedge(\forall w)_O(Ewy\Leftrightarrow ST_w(\psi)))\to\nonumber\\&\qquad\qquad\qquad\to\sim\forall w(Rxyw\to ST_w(\chi)))\qquad\qquad\text{by ({B.12}), (An5), (T16)} \end{align}$$
$$\begin{align} &\forall y((Sy\wedge(\forall w)_O(Ewy\Leftrightarrow ST_w(\psi)))\to\nonumber\\&\qquad\qquad\qquad\to\sim\forall w(Rxyw\to ST_w(\chi)))\qquad\qquad\text{by ({B.12}), (An5), (T16)} \end{align}$$
Deduction D3+:
Deduction D3–:
We sum up the intermediate results of these deductions:

We now feed these results into the next deduction D4:
We now finish our reasoning as follows:

C Proof of Lemma 16
In order to prove the lemma, we will need to prove a couple of technical results first.
Lemma 25. The following statements hold:
-
1. If
 $\alpha , \beta \in Seq$
are such that
$\alpha , \beta \in Seq$
are such that
 $\alpha \mathrel {\prec }\beta $
, and
$\alpha \mathrel {\prec }\beta $
, and
 $\phi \in \mathcal {CN}$
,
$\phi \in \mathcal {CN}$
,
 $(\Gamma , \Delta ) \in W_c$
are such that
$(\Gamma , \Delta ) \in W_c$
are such that
 $\alpha ' = \alpha ^\frown (\phi , (\Gamma , \Delta )) \in Seq$
, then there exists a
$\alpha ' = \alpha ^\frown (\phi , (\Gamma , \Delta )) \in Seq$
, then there exists a
 $\beta ' = \beta ^\frown (\phi , (\Xi , \Theta )) \in Seq$
and
$\beta ' = \beta ^\frown (\phi , (\Xi , \Theta )) \in Seq$
and
 $\alpha '\mathrel {\prec }\beta '$
.
$\alpha '\mathrel {\prec }\beta '$
. -
2. For all
 $(\Gamma ,\Delta ), (\Xi ,\Theta ) \in W_c$
such that
$(\Gamma ,\Delta ), (\Xi ,\Theta ) \in W_c$
such that
 $(\Gamma ,\Delta )\leq _c (\Xi ,\Theta )$
, and every
$(\Gamma ,\Delta )\leq _c (\Xi ,\Theta )$
, and every
 $\alpha \in Seq(\Gamma ,\Delta )$
, there exists a
$\alpha \in Seq(\Gamma ,\Delta )$
, there exists a
 $\beta \in Seq(\Xi , \Theta )$
such that
$\beta \in Seq(\Xi , \Theta )$
such that
 $\alpha \mathrel {\prec }\beta $
.
$\alpha \mathrel {\prec }\beta $
. -
3. For all
 $(\Gamma ,\Delta ), (\Xi ,\Theta ) \in W_c$
and
$(\Gamma ,\Delta ), (\Xi ,\Theta ) \in W_c$
and
 $\alpha \in Seq(\Gamma ,\Delta )$
such that
$\alpha \in Seq(\Gamma ,\Delta )$
such that
 $end(\alpha )\leq _c(\Xi ,\Theta )$
, there exists a
$end(\alpha )\leq _c(\Xi ,\Theta )$
, there exists a
 $\beta \in Seq$
such that
$\beta \in Seq$
such that
 $\alpha \mathrel {\prec }\beta $
and
$\alpha \mathrel {\prec }\beta $
and
 $end(\beta ) = (\Xi ,\Theta )$
.
$end(\beta ) = (\Xi ,\Theta )$
.
Proof (Part 1) Assume the hypothesis. Since
![]() $\alpha \mathrel {\prec }\beta $
, we must have
$\alpha \mathrel {\prec }\beta $
, we must have
![]() $end(\alpha )\leq _c end(\beta )$
, and, since
$end(\alpha )\leq _c end(\beta )$
, and, since
![]() $\alpha ' = \alpha ^\frown (\phi , (\Gamma , \Delta )) \in Seq$
, we must have
$\alpha ' = \alpha ^\frown (\phi , (\Gamma , \Delta )) \in Seq$
, we must have
![]() $R_c(end(\alpha ),\|\phi \|_{\mathcal {M}_c}, (\Gamma , \Delta ))$
. Since
$R_c(end(\alpha ),\|\phi \|_{\mathcal {M}_c}, (\Gamma , \Delta ))$
. Since
![]() $\mathcal {M}_c$
satisfies condition (c1) of Definition 6, there must exist some
$\mathcal {M}_c$
satisfies condition (c1) of Definition 6, there must exist some
![]() $(\Xi , \Theta )\in W_c$
such that both
$(\Xi , \Theta )\in W_c$
such that both
![]() $(\Gamma , \Delta )\mathrel {\leq _c}(\Xi , \Theta )$
and
$(\Gamma , \Delta )\mathrel {\leq _c}(\Xi , \Theta )$
and
![]() $R_c(end(\beta ),\|\phi \|_{\mathcal {M}_c}, (\Xi , \Theta ))$
. The latter means that we have both
$R_c(end(\beta ),\|\phi \|_{\mathcal {M}_c}, (\Xi , \Theta ))$
. The latter means that we have both
![]() $\beta ' = \beta ^\frown (\phi , (\Xi , \Theta )) \in Seq$
and
$\beta ' = \beta ^\frown (\phi , (\Xi , \Theta )) \in Seq$
and
![]() $\alpha '\mathrel {\prec }\beta '$
.
$\alpha '\mathrel {\prec }\beta '$
.
(Part 2) By induction on the length of
![]() $\alpha $
. If
$\alpha $
. If
![]() $\alpha $
has length
$\alpha $
has length
![]() $1$
, then we can set
$1$
, then we can set
![]() $\beta := (\Xi ,\Theta )$
. If
$\beta := (\Xi ,\Theta )$
. If
![]() $\alpha $
has length
$\alpha $
has length
![]() $k + 1$
for some
$k + 1$
for some
![]() $1 \leq k < \omega $
, then we apply IH and Part 1.
$1 \leq k < \omega $
, then we apply IH and Part 1.
(Part 3) Again, we proceed by induction on the length of
![]() $\alpha $
. If
$\alpha $
. If
![]() $\alpha $
has length
$\alpha $
has length
![]() $1$
, then we can set
$1$
, then we can set
![]() $\beta := (\Xi ,\Theta )$
. If
$\beta := (\Xi ,\Theta )$
. If
![]() $\alpha $
has length
$\alpha $
has length
![]() $k + 1$
for some
$k + 1$
for some
![]() $1 \leq k < \omega $
, then for some
$1 \leq k < \omega $
, then for some
![]() $\alpha ' \in Seq$
of length k and some
$\alpha ' \in Seq$
of length k and some
![]() $\phi \in \mathcal {CN}$
, we must have
$\phi \in \mathcal {CN}$
, we must have
![]() $\alpha = ((\Gamma , \Delta ), \phi )^\frown (\alpha ')$
, with
$\alpha = ((\Gamma , \Delta ), \phi )^\frown (\alpha ')$
, with
![]() $end(\alpha ) = end(\alpha ')$
. Applying now IH to
$end(\alpha ) = end(\alpha ')$
. Applying now IH to
![]() $\alpha '$
, we find some
$\alpha '$
, we find some
![]() $\beta ' \in Seq$
such that
$\beta ' \in Seq$
such that
![]() $end(\beta ') = (\Xi ,\Theta )$
and
$end(\beta ') = (\Xi ,\Theta )$
and
![]() $\alpha '\mathrel {\prec }\beta '$
. But then, in particular, we must have
$\alpha '\mathrel {\prec }\beta '$
. But then, in particular, we must have
![]() $init(\alpha ') \leq _c init(\beta ')$
. Moreover, since
$init(\alpha ') \leq _c init(\beta ')$
. Moreover, since
![]() $\alpha = ((\Gamma , \Delta ), \phi )^\frown (\alpha ') \in Seq$
, we must also have
$\alpha = ((\Gamma , \Delta ), \phi )^\frown (\alpha ') \in Seq$
, we must also have
![]() $R_c((\Gamma , \Delta ),\|\phi \|_{\mathcal {M}_c}, init(\alpha '))$
. But then, since
$R_c((\Gamma , \Delta ),\|\phi \|_{\mathcal {M}_c}, init(\alpha '))$
. But then, since
![]() $\mathcal {M}_c$
satisfies condition (c2) of Definition 6, there must exist some
$\mathcal {M}_c$
satisfies condition (c2) of Definition 6, there must exist some
![]() $(\Gamma ', \Delta ')\in W_c$
such that both
$(\Gamma ', \Delta ')\in W_c$
such that both
![]() $(\Gamma , \Delta )\mathrel {\leq _c}(\Gamma ', \Delta ')$
and
$(\Gamma , \Delta )\mathrel {\leq _c}(\Gamma ', \Delta ')$
and
![]() $R_c((\Gamma ', \Delta '),\|\phi \|_{\mathcal {M}_c},init(\beta '))$
. For
$R_c((\Gamma ', \Delta '),\|\phi \|_{\mathcal {M}_c},init(\beta '))$
. For
![]() $\beta := ((\Gamma ', \Delta '), \phi )^\frown (\beta ')$
we have
$\beta := ((\Gamma ', \Delta '), \phi )^\frown (\beta ')$
we have
![]() $\beta \in Seq$
,
$\beta \in Seq$
,
![]() $end(\beta ) = end(\beta ') = (\Xi ,\Theta )$
, and
$end(\beta ) = end(\beta ') = (\Xi ,\Theta )$
, and
![]() $\alpha \mathrel {\prec }\beta $
.
$\alpha \mathrel {\prec }\beta $
.
The following lemma sums up some facts about local choice functions.
Lemma 26. Let
![]() $(\Gamma , \Delta ) \in W_c$
. Then the following statements hold:
$(\Gamma , \Delta ) \in W_c$
. Then the following statements hold:
-
1. For every
 $(\Xi , \Theta )\in W_c$
such that
$(\Xi , \Theta )\in W_c$
such that
 $(\Gamma ,\Delta )\leq _c (\Xi ,\Theta )$
, we have
$(\Gamma ,\Delta )\leq _c (\Xi ,\Theta )$
, we have
 $\mathfrak {F}((\Gamma ,\Delta ), (\Xi ,\Theta ))\neq \emptyset $
.
$\mathfrak {F}((\Gamma ,\Delta ), (\Xi ,\Theta ))\neq \emptyset $
. -
2. For every
 $\alpha \in Seq(\Gamma ,\Delta )$
and every
$\alpha \in Seq(\Gamma ,\Delta )$
and every
 $(\Xi , \Theta )\in W_c$
such that
$(\Xi , \Theta )\in W_c$
such that
 $end(\alpha ) \leq _c (\Xi , \Theta )$
, there exist a
$end(\alpha ) \leq _c (\Xi , \Theta )$
, there exist a
 $\beta \in Seq$
such that
$\beta \in Seq$
such that
 $end(\beta ) = (\Xi , \Theta )$
, and an
$end(\beta ) = (\Xi , \Theta )$
, and an
 $f\in \mathfrak {F}((\Gamma ,\Delta ),init(\beta ))$
such that
$f\in \mathfrak {F}((\Gamma ,\Delta ),init(\beta ))$
such that
 $f(\alpha ) = \beta $
.
$f(\alpha ) = \beta $
. -
3. For every
 $(\Xi , \Theta )\in W_c$
,
$(\Xi , \Theta )\in W_c$
,
 $id[Seq(\Xi ,\Theta )]\in \mathfrak {F}((\Xi ,\Theta ),(\Xi ,\Theta ))$
.
$id[Seq(\Xi ,\Theta )]\in \mathfrak {F}((\Xi ,\Theta ),(\Xi ,\Theta ))$
. -
4. Given an
 $n \in \omega $
, any
$n \in \omega $
, any
 $(\Gamma _0,\Delta _0),\ldots ,(\Gamma _n, \Delta _n)\in W_c$
such that
$(\Gamma _0,\Delta _0),\ldots ,(\Gamma _n, \Delta _n)\in W_c$
such that
 $(\Gamma _0,\Delta _0)\leq _c\ldots \leq _c(\Gamma _n, \Delta _n)$
, and any
$(\Gamma _0,\Delta _0)\leq _c\ldots \leq _c(\Gamma _n, \Delta _n)$
, and any
 $f_1,\ldots ,f_n$
such that for every
$f_1,\ldots ,f_n$
such that for every
 $i < n$
we have
$i < n$
we have
 $f_{i + 1}\in \mathfrak {F}((\Gamma _i, \Delta _i),(\Gamma _{i + 1}, \Delta _{i + 1}))$
, we also have that
$f_{i + 1}\in \mathfrak {F}((\Gamma _i, \Delta _i),(\Gamma _{i + 1}, \Delta _{i + 1}))$
, we also have that
 $f_1\circ \dots \circ f_n \in \mathfrak {F}((\Gamma _0, \Delta _0),(\Gamma _{n}, \Delta _{n}))$
.
$f_1\circ \dots \circ f_n \in \mathfrak {F}((\Gamma _0, \Delta _0),(\Gamma _{n}, \Delta _{n}))$
.
Proof (Part 1) By Lemma 25.2 and the Axiom of Choice.
(Part 2) Assume the hypothesis. By Lemma 25.3, we can find a
![]() $\beta \in Seq$
such that both
$\beta \in Seq$
such that both
![]() $\alpha \mathrel {\prec }\beta $
and
$\alpha \mathrel {\prec }\beta $
and
![]() $end(\beta ) = (\Xi , \Theta )$
are satisfied. Trivially, we must also have
$end(\beta ) = (\Xi , \Theta )$
are satisfied. Trivially, we must also have
![]() $\beta \in Seq(init(\beta ))$
. Assume, wlog, that
$\beta \in Seq(init(\beta ))$
. Assume, wlog, that
![]() $\alpha = ((\Gamma _0,\Delta _0),\phi _1,\ldots ,\phi _n, (\Gamma _n, \Delta _n))$
and that
$\alpha = ((\Gamma _0,\Delta _0),\phi _1,\ldots ,\phi _n, (\Gamma _n, \Delta _n))$
and that
![]() $\beta = ((\Xi _0,\Theta _0),\phi _1,\ldots ,\phi _n, (\Xi _n, \Theta _n))$
. We now set
$\beta = ((\Xi _0,\Theta _0),\phi _1,\ldots ,\phi _n, (\Xi _n, \Theta _n))$
. We now set
![]() $f((\Gamma _0,\Delta _0),\phi _1,\ldots ,\phi _i, (\Gamma _i, \Delta _i)):= ((\Xi _0,\Theta _0),\phi _1,\ldots ,\phi _i, (\Xi _i, \Theta _i))$
for every
$f((\Gamma _0,\Delta _0),\phi _1,\ldots ,\phi _i, (\Gamma _i, \Delta _i)):= ((\Xi _0,\Theta _0),\phi _1,\ldots ,\phi _i, (\Xi _i, \Theta _i))$
for every
![]() $i \leq n$
and, proceeding by induction on the length of a standard sequence, extend this partial function to other elements of
$i \leq n$
and, proceeding by induction on the length of a standard sequence, extend this partial function to other elements of
![]() $Seq(\Gamma ,\Delta )$
in virtue of Lemma 25.1. The resulting function f clearly has the desired properties.
$Seq(\Gamma ,\Delta )$
in virtue of Lemma 25.1. The resulting function f clearly has the desired properties.
Part 3 is trivial, and an easy induction on
![]() $n \in \omega $
also yields us Part 4.
$n \in \omega $
also yields us Part 4.
Proof of Lemma 16
(Part 1) Note that we have
![]() $Seq(\Gamma _0,\Delta _0) \cap Seq(\Gamma _1,\Delta _1) = \emptyset $
whenever
$Seq(\Gamma _0,\Delta _0) \cap Seq(\Gamma _1,\Delta _1) = \emptyset $
whenever
![]() $(\Gamma _0,\Delta _0), (\Gamma _1,\Delta _1) \in W_c$
are such that
$(\Gamma _0,\Delta _0), (\Gamma _1,\Delta _1) \in W_c$
are such that
![]() $(\Gamma _0,\Delta _0)\neq (\Gamma _1,\Delta _1)$
. Therefore, we can define the global choice function in question by
$(\Gamma _0,\Delta _0)\neq (\Gamma _1,\Delta _1)$
. Therefore, we can define the global choice function in question by
![]() $F:= (\bigcup \{Id[Seq(\Gamma _0,\Delta _0)]\mid (\Gamma _0,\Delta _0)\neq (\Gamma ,\Delta )\}) \cup f$
. Lemma 26.3 then implies that
$F:= (\bigcup \{Id[Seq(\Gamma _0,\Delta _0)]\mid (\Gamma _0,\Delta _0)\neq (\Gamma ,\Delta )\}) \cup f$
. Lemma 26.3 then implies that
![]() $F\in \mathfrak {G}$
.
$F\in \mathfrak {G}$
.
(Part 2) Assume the hypothesis. By Lemma 26.2, we can choose a
![]() $\beta \in Seq$
such that
$\beta \in Seq$
such that
![]() $end(\beta ) = (\Xi , \Theta )$
, and an
$end(\beta ) = (\Xi , \Theta )$
, and an
![]() $f\in \mathfrak {F}((\Gamma ,\Delta ),init(\beta ))$
such that
$f\in \mathfrak {F}((\Gamma ,\Delta ),init(\beta ))$
such that
![]() $f(\alpha ) = \beta $
. By Part 1, we can find an
$f(\alpha ) = \beta $
. By Part 1, we can find an
![]() $F\in \mathfrak {G}$
such that
$F\in \mathfrak {G}$
such that
![]() $F\upharpoonright Seq(\Gamma ,\Delta ) = f$
and thus also
$F\upharpoonright Seq(\Gamma ,\Delta ) = f$
and thus also
![]() $F(\alpha ) = f(\alpha ) = \beta $
. Parts 3 and 4 are, again, straightforward.
$F(\alpha ) = f(\alpha ) = \beta $
. Parts 3 and 4 are, again, straightforward.
As for Part 5, note that we must have both
![]() $\alpha \in Seq(init(\alpha ))$
and, for an appropriate
$\alpha \in Seq(init(\alpha ))$
and, for an appropriate
![]() $(\Gamma , \Delta ) \in W_c$
, that
$(\Gamma , \Delta ) \in W_c$
, that
![]() $F\upharpoonright Seq(init(\alpha )) \in \mathfrak {F}(init(\alpha ), (\Gamma , \Delta ))$
. But then we must have
$F\upharpoonright Seq(init(\alpha )) \in \mathfrak {F}(init(\alpha ), (\Gamma , \Delta ))$
. But then we must have
![]() $\alpha \mathrel {\prec }(F\upharpoonright Seq(init(\alpha )))(\alpha ) = F(\alpha )$
by definition of a local choice function.
$\alpha \mathrel {\prec }(F\upharpoonright Seq(init(\alpha )))(\alpha ) = F(\alpha )$
by definition of a local choice function.
Acknowledgments
The author would like to thank the reviewers of this article for the numerous incisive and helpful comments. The author is also thankful to Heinrich Wansing, who saw this article in one of its earlier versions and made several useful comments. Hrafn Valtýr Oddsson is the person who initially introduced the author to the ampersand and its role in Nelsonian logic; he also read parts of the article including an early version of Appendix A.5; however the author remains fully responsible for its contents, especially for any possible mistakes.
Funding
This research has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme, grant agreement ERC-2020-ADG, 101018280, ConLog.