1. Introduction
Flow around and downstream of two-dimensional (2-D) porous media has received significant attention due to its practical importance in engineering and environmental applications. From an engineering perspective, porous media offer enhanced aerodynamic properties, such as reductions in drag force (Klausmann & Ruck Reference Klausmann and Ruck2017; Geyer Reference Geyer2020), noise (Sato & Hattori Reference Sato and Hattori2021) and vortex-induced vibration (Yuan et al. Reference Yuan, Laima, Gao, Chen and Li2021). These characteristics make porous media promising for passive flow control, with applications in the design of aircraft landing gear (Merino-Martínez et al. Reference Merino-Martínez, Kennedy and Bennett2021; Selivanov et al. Reference Selivanov, Silnikov, Markov, Popov and Pusev2021), high-speed train pantographs (Sueki, Ikeda & Takaishi Reference Sueki, Ikeda and Takaishi2009), subsea pipeline systems (Wen et al. Reference Wen, Jeng, Wang and Zhou2012) and unmanned aerial vehicle frames (Klippstein et al. Reference Klippstein, Hassanin, Diaz De Cerio Sanchez, Zweiri and Seneviratne2018). From an environmental perspective, emergent aquatic vegetation, modelled as arrays of 2-D circular cylinders, serves as an example of flows through porous media. Such vegetation plays a critical role in river ecosystems by providing habitats for aquatic organisms, improving water quality and influencing morphodynamic processes such as sedimentation and erosion (Gacia & Duarte Reference Gacia and Duarte2001; Bouma et al. Reference Bouma, Van Duren, Temmerman, Claverie, Blanco-Garcia, Ysebaert and Herman2007; Moore Reference Moore2009).
The flow characteristics of porous media, including wake manipulation, are primarily governed by bleeding flow, defined as the flow passing through the porous media. In 2-D porous configurations, bleeding occurs in both the longitudinal and lateral directions, typically characterized by the velocity at the trailing edge and along the lateral surfaces, respectively (Taddei, Manes & Ganapathisubramani Reference Taddei, Manes and Ganapathisubramani2016). These components interact to collectively modify the downstream flow structure (Yu et al. Reference Yu, Zeng, Lee, Bai and Low2010; Nicolle & Eames Reference Nicolle and Eames2011; Cummins et al. Reference Cummins, Viola, Mastropaolo and Nakayama2017; Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). For instance, longitudinal bleeding has been shown to reduce the size of recirculation bubbles, displace them downstream, weaken shear layer intensity and shift the shear layer convergence point farther downstream (Chen et al. Reference Chen, Ortiz, Zong and Nepf2012; Zong & Nepf Reference Zong and Nepf2012; Tang et al. Reference Tang, Yu, Shan and Chen2019). In contrast, lateral bleeding increases the boundary-layer thickness along the side of the porous body by reducing the streamwise momentum of the external flow and vertically displacing the shear layer away from the wake core (Nicolai et al. Reference Nicolai, Taddei, Manes and Ganapathisubramani2020; Seol, Kim & Kim Reference Seol, Kim and Kim2024). These flow manipulation mechanisms are governed by the bleeding flux, which is intrinsically linked to the porosity and permeability of the porous medium.
Although porosity and permeability are interdependent, most experimental studies have treated porosity as the primary control parameter for bleeding, due to its ease of manipulation (Zong & Nepf Reference Zong and Nepf2012; Tang et al. Reference Tang, Yu, Shan and Chen2019; Kim et al. Reference Kim, Blois, Best and Christensen2020; Xu et al. Reference Xu, Chang, Yu, Chen and Gao2022; Cicolin et al. Reference Cicolin, Chellini, Usherwood, Ganapathisubramani and Castro2024; Kim et al. Reference Kim, Best, Christensen and Blois2025). For example, Xu et al. (Reference Xu, Chang, Yu, Chen and Gao2022) demonstrated experimentally that increasing the porosity of circular cylinders suppressed vortex shedding and reduced drag at high Reynolds numbers (
![]() $ \textit{Re}=2.02\times 10^4$
,
$ \textit{Re}=2.02\times 10^4$
,
![]() $ \textit{Re}=U_eD/\nu$
, where
$ \textit{Re}=U_eD/\nu$
, where
![]() $U_e$
is the upstream velocity,
$U_e$
is the upstream velocity,
![]() $D$
is the cylinder width and
$D$
is the cylinder width and
![]() $\nu$
is the kinematic viscosity). Similarly, Cicolin et al. (Reference Cicolin, Chellini, Usherwood, Ganapathisubramani and Castro2024) reported that higher porosity in rectangular porous plates weakened shear layers, resulting in more diffuse vortices and reduced shedding intermittency. Zong & Nepf (Reference Zong and Nepf2012) further examined the effect of porosity on wake development using patches of 2-D circular cylinders. Their results showed that longitudinal bleeding occurs in the region between shear layers and becomes stronger with increasing patch porosity, shifting the shear layer convergence point farther downstream. This finding highlights the crucial role of longitudinal bleeding in shaping the wake, particularly through its influence on shear layer interactions and velocity recovery in the near wake.
$\nu$
is the kinematic viscosity). Similarly, Cicolin et al. (Reference Cicolin, Chellini, Usherwood, Ganapathisubramani and Castro2024) reported that higher porosity in rectangular porous plates weakened shear layers, resulting in more diffuse vortices and reduced shedding intermittency. Zong & Nepf (Reference Zong and Nepf2012) further examined the effect of porosity on wake development using patches of 2-D circular cylinders. Their results showed that longitudinal bleeding occurs in the region between shear layers and becomes stronger with increasing patch porosity, shifting the shear layer convergence point farther downstream. This finding highlights the crucial role of longitudinal bleeding in shaping the wake, particularly through its influence on shear layer interactions and velocity recovery in the near wake.
Despite these experimental advances, previous studies have not explicitly established a direct relationship between porosity and the aerodynamic or wake characteristics of porous bluff bodies. This limitation stems from the intrinsic coupling between porosity and permeability. While porosity quantifies the void fraction, it is permeability that characterizes the resistance to internal flow and more directly controls the bleeding flux through the medium.
In contrast to porosity, permeability has often been systemically varied in numerical studies, particularly through macroscopic frameworks such as the Darcy–Brinkman–Forchheimer (DBF) model (Yu et al. Reference Yu, Zeng, Lee, Bai and Low2010; Cummins et al. Reference Cummins, Viola, Mastropaolo and Nakayama2017; Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018) or homogenization-based approach (Mei & Auriault Reference Mei and Auriault1991; Zampogna & Bottaro Reference Zampogna and Bottaro2016). In DBF-based studies of 2-D porous configurations, the Darcy number (
![]() $ \textit{Da}=K/D^2$
, where
$ \textit{Da}=K/D^2$
, where
![]() $K$
is the physical permeability and
$K$
is the physical permeability and
![]() $D$
denotes the cylinder diameter) is commonly used to characterize the degree of flow blockage and its effect on the flow field. For instance, Yu et al. (Reference Yu, Zeng, Lee, Bai and Low2010) performed finite-volume simulations to investigate flow past porous square cylinders over a wide range of Darcy numbers (
$D$
denotes the cylinder diameter) is commonly used to characterize the degree of flow blockage and its effect on the flow field. For instance, Yu et al. (Reference Yu, Zeng, Lee, Bai and Low2010) performed finite-volume simulations to investigate flow past porous square cylinders over a wide range of Darcy numbers (
![]() $10^{-6}\lt Da\lt 10^{-1}$
). Their study revealed strong correlations between permeability and wake structure. Cummins et al. (Reference Cummins, Viola, Mastropaolo and Nakayama2017) conducted direct numerical simulations (DNS) at low Reynolds numbers (
$10^{-6}\lt Da\lt 10^{-1}$
). Their study revealed strong correlations between permeability and wake structure. Cummins et al. (Reference Cummins, Viola, Mastropaolo and Nakayama2017) conducted direct numerical simulations (DNS) at low Reynolds numbers (
![]() $1\lt \textit{Re} \lt 130$
) and identified distinct flow regimes, characterized by changes in recirculation patterns as a function of
$1\lt \textit{Re} \lt 130$
) and identified distinct flow regimes, characterized by changes in recirculation patterns as a function of
![]() $ \textit{Da} $
. Similarly, Ledda et al. (Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018) showed that the drag coefficient (
$ \textit{Da} $
. Similarly, Ledda et al. (Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018) showed that the drag coefficient (
![]() $C_{\kern-1pt D}$
) depends on both
$C_{\kern-1pt D}$
) depends on both
![]() $ \textit{Re} $
and
$ \textit{Re} $
and
![]() $ \textit{Da} $
, highlighting the dominant role of permeability in wake dynamics.
$ \textit{Da} $
, highlighting the dominant role of permeability in wake dynamics.
Beyond these macroscopic approaches, recent studies have employed pore-resolved simulations to investigate flow behaviour near the porous interface (Nair et al. Reference Nair, Kazemi, Curet and Verma2023; He et al. Reference He, An, Ghisalberti, Draper, Ren, Branson and Cheng2024). These works showed that the internal arrangement of solid elements within a fixed-porosity matrix strongly influence drag, vortex formation and wake recirculation even when porosity remains constant. In particular, Nair et al. (Reference Nair, Kazemi, Curet and Verma2023) observed that vorticity production is highly sensitive to the local configuration of internal structures. He et al. (Reference He, An, Ghisalberti, Draper, Ren, Branson and Cheng2024) further confirmed that a change in internal arrangement geometry can significantly affect drag and bleeding behaviour.
Despite these contributions, a major limitation of both macroscopic and pore-resolved numerical studies is their predominant focus on low Reynolds number regimes (
![]() $ \textit{Re}\sim O(10^2)$
). Consequently, the influence of permeability on bleeding characteristics at high Reynolds numbers remains poorly understood. This knowledge gap poses a significant challenge to developing a comprehensive understanding of flow past porous media and limits the assessment of their feasibility in practical applications.
$ \textit{Re}\sim O(10^2)$
). Consequently, the influence of permeability on bleeding characteristics at high Reynolds numbers remains poorly understood. This knowledge gap poses a significant challenge to developing a comprehensive understanding of flow past porous media and limits the assessment of their feasibility in practical applications.
To address this challenge, our recent experimental studies introduced a novel design of porous structures based on a uniform and scalable simple cubic lattice (Seol et al. Reference Seol, Hong and Kim2023, Reference Seol, Kim and Kim2024). This design enables independent control of permeability while maintaining constant porosity, made possible through high-resolution three-dimensional (3-D) printing. This approach facilitated the first experimental study of permeability effects on flow past porous square cylinders over a wide range of Darcy numbers (
![]() $2.4\times 10^{-5}\lt Da\lt 2.9\times 10^{-3}$
) at a high Reynolds number (
$2.4\times 10^{-5}\lt Da\lt 2.9\times 10^{-3}$
) at a high Reynolds number (
![]() $ \textit{Re} = 3.1\times 10^4$
). In particular, Seol et al. (Reference Seol, Kim and Kim2024) demonstrated that the interaction between longitudinal and lateral bleeding significantly alters the shear layers and associated wake structures, depending on
$ \textit{Re} = 3.1\times 10^4$
). In particular, Seol et al. (Reference Seol, Kim and Kim2024) demonstrated that the interaction between longitudinal and lateral bleeding significantly alters the shear layers and associated wake structures, depending on
![]() $ \textit{Da} $
. They further identified four distinct flow regimes downstream of porous square cylinders, each corresponding to a different range of Darcy numbers. These findings highlight the critical role of permeability in shaping wake topology and governing bleeding flow characteristics.
$ \textit{Da} $
. They further identified four distinct flow regimes downstream of porous square cylinders, each corresponding to a different range of Darcy numbers. These findings highlight the critical role of permeability in shaping wake topology and governing bleeding flow characteristics.
Building on the structural features of longitudinal bleeding observed in Seol et al. (Reference Seol, Hong and Kim2023, Reference Seol, Kim and Kim2024), we note that the downstream evolution of the longitudinal bleeding, originating from an array of pores, is analogous to that of parallel plane jets, wherein multiple shear layers develop and eventually merge. This structural similarity motivates a conceptual model of longitudinal bleeding as a quasi-2-D jet, which itself shares characteristics with the far wake of a solid cylinder (Bradbury Reference Bradbury1965). As a result, for 2-D porous cylinders with uniform and periodic internal geometry, we hypothesize that the longitudinal jets issuing from individual pores can be interpreted within the framework of multiple plane jets, where the interaction between adjacent shear layers governs the downstream flow evolution in the presence of an external flow. In other words, the flow behind porous square cylinders can be understood by integrating two distinct structural behaviours: quasi-2-D jet-like structures in the near wake and turbulent boundary-layer-like flow in the far wake.
In classical multiple plane jet configurations, individual jets undergo a merging and combining process in the near wake, eventually evolving into a single jet-like structure as they develop downstream (Tanaka Reference Tanaka1974; Nasr & Lai Reference Nasr and Lai1997; Morris et al. Reference Morris, Aleyasin, Biswas and Tachie2020). The merging region refers to the initial zone in which distinct jets begin to interact and redistribute momentum. Beyond this, in the combined region, the jets have fully coalesced into a single structure, where the flow evolves primarily through lateral diffusion and momentum decay (Miller & Comings Reference Miller and Comings1960; Zhao & Wang Reference Zhao and Wang2018).
The structural development of multiple plane jets is known to depend strongly on nozzle configuration, such as spacing (Tanaka Reference Tanaka1970; Tanaka & Nakata Reference Tanaka and Nakata1975) and nozzle orientation (Morris et al. Reference Morris, Aleyasin, Biswas and Tachie2020). While the fully combined region resembles a canonical turbulent plane jet in structure, its overall momentum and turbulence intensity often differ, depending on jet configuration (Tanaka Reference Tanaka1974; Morris et al. Reference Morris, Aleyasin, Biswas and Tachie2020). In particular, the presence of a central jet plays a critical role in flow development, leading to the classification of dual jets (no central jet) and triple jets (with a central jet) as canonical configurations for studying jet interactions. For example, dual jets are characterized by inward entrainment towards the centreline, driven by a low-pressure region between the side jets (Tanaka Reference Tanaka1970, Reference Tanaka1974; Nasr & Lai Reference Nasr and Lai1997). In contrast, triple jets exhibit enhanced lateral momentum diffusion due to the merging of the central jet with adjacent side jets (Tanaka & Nakata Reference Tanaka and Nakata1975; Nouali & Mataoui Reference Nouali and Mataoui2016; Morris et al. Reference Morris, Aleyasin, Biswas and Tachie2020). This distinction is particularly relevant to the structured porous cylinders considered in the present study. Specifically, the arrangement of lattice pores at the trailing edge may lead to wake structures resembling either dual- or triple-jet-like configurations. Consequently, the presence or absence of a central pore plays a significant role in determining the structural characteristics of bleeding flows.
From the perspective of the boundary-layer framework, Bradbury (Reference Bradbury1965) showed that, in the far field of a turbulent plane jet, the flow becomes self-similar. This indicates that velocity profiles collapse onto a universal shape when appropriately scaled. This self-similarity arises because, at a sufficient distance downstream, the effect of initial conditions at the jet exit diminishes. In this regime, the jet spreads at a predictable rate with a characteristic decay in centreline velocity, a condition referred to as the boundary-layer assumption.
More recently, this assumption has been extended from canonical plane jets to porous bluff-body wakes. For instance, Nicolai et al. (Reference Nicolai, Taddei, Manes and Ganapathisubramani2020) experimentally investigated the wake of a wall-mounted porous patch composed of an array of circular cylinders, fully immersed in a turbulent boundary layer. Despite the inherent three-dimensionality and wall interference in their configuration, they observed that beyond the immediate near-wake region (approximately 1
![]() ${-}$
2 patch diameters downstream), the velocity deficit profiles evolved towards a self-similar form. These results suggest that the wake transitions into a shear-layer-dominated state, where the boundary layer assumption becomes asymptotically valid, even in geometrically complex, wall-bounded environments.
${-}$
2 patch diameters downstream), the velocity deficit profiles evolved towards a self-similar form. These results suggest that the wake transitions into a shear-layer-dominated state, where the boundary layer assumption becomes asymptotically valid, even in geometrically complex, wall-bounded environments.
Based on our recent study (Seol et al. Reference Seol, Kim and Kim2024), this work reports the first experimental investigation into the structural characteristics of longitudinal bleeding jets downstream of porous square cylinders, with a focus on the effect of cylinder permeability and pore configuration. In particular, the behaviour of longitudinal bleeding is interpreted within the framework of turbulent plane jets under the influence of an external flow. Furthermore, an analytical model is developed to predict the key dynamics of bleeding flow evolution, formulated by integrating the momentum equation with the DBF model and the boundary-layer assumption. To this end, we fabricated porous square cylinders composed of a periodic and scalable simple cubic lattice structure using high-resolution 3-D printing. This unique design, initially proposed in our earlier work (Seol, Hong & Kim Reference Seol, Hong and Kim2023), enables the independent control of permeability and porosity. A comprehensive set of experiments was conducted over a broad range of Darcy numbers, using particle image velocimetry (PIV) to systematically investigate the impact of permeability and pore configuration on the longitudinal bleeding flow and the corresponding wake dynamics.
The DBF model effectively captures flow dynamics both within and around porous media based on the macroscopic effects of viscosity, inertia and permeability. In this regard, the DBF model has been widely used in numerical simulations of flow around porous bluff bodies, particularly at low Reynolds numbers (Yu et al. Reference Yu, Zeng, Lee, Bai and Low2010; Cummins et al. Reference Cummins, Viola, Mastropaolo and Nakayama2017; Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). More recently, the DBF model has been extended to high-Reynolds-number flows in both experimental and computational studies with thorough validations (Seol et al. Reference Seol, Kim and Kim2024; Hao & García-Mayoral Reference Hao and García-Mayoral2025).
For example, Seol et al. (Reference Seol, Kim and Kim2024) demonstrated the successful application of a DBF-based analytical model in characterizing the streamwise flow adjustment behind porous square cylinders for
![]() $ \textit{Re}\approx 3.1\times 10^4$
. Their analytical model captured the permeability-induced source terms and predicted the flow adjustment length across a wide range of Darcy numbers (
$ \textit{Re}\approx 3.1\times 10^4$
. Their analytical model captured the permeability-induced source terms and predicted the flow adjustment length across a wide range of Darcy numbers (
![]() $10^{-5}\lt Da\lt 10^{-3}$
). Their model predictions were in close agreement with experimental data from PIV measurements. This result indicates that the DBF model remains valid when used to capture macroscopic momentum loss associated with porous media under turbulent conditions. Moreover, the recent DNS study by Hao & García-Mayoral (Reference Hao and García-Mayoral2025) provides further theoretical and computational justification. In this work, they investigated turbulent channel flows over porous substrates with Reynolds numbers up to
$10^{-5}\lt Da\lt 10^{-3}$
). Their model predictions were in close agreement with experimental data from PIV measurements. This result indicates that the DBF model remains valid when used to capture macroscopic momentum loss associated with porous media under turbulent conditions. Moreover, the recent DNS study by Hao & García-Mayoral (Reference Hao and García-Mayoral2025) provides further theoretical and computational justification. In this work, they investigated turbulent channel flows over porous substrates with Reynolds numbers up to
![]() $ \textit{Re}_\tau \approx 550$
(
$ \textit{Re}_\tau \approx 550$
(
![]() $ \textit{Re}_\tau = u_\tau h/\nu$
, where
$ \textit{Re}_\tau = u_\tau h/\nu$
, where
![]() $u_\tau$
and
$u_\tau$
and
![]() $h$
are the friction velocity and the channel half-height, respectively). Particularly, they employed analytical solutions to the Darcy–Brinkman equation to estimate the permeability-dependent shear penetration and subsurface velocity field. These solutions served as boundary conditions for the overlying DNS. They were found to be in good agreement with the simulated near-interface velocity fields. Their analysis confirms that the Darcy–Brinkman model provides a physically consistent framework for representing bulk momentum transport and interface conditions even in wall-bounded turbulent flows.
$h$
are the friction velocity and the channel half-height, respectively). Particularly, they employed analytical solutions to the Darcy–Brinkman equation to estimate the permeability-dependent shear penetration and subsurface velocity field. These solutions served as boundary conditions for the overlying DNS. They were found to be in good agreement with the simulated near-interface velocity fields. Their analysis confirms that the Darcy–Brinkman model provides a physically consistent framework for representing bulk momentum transport and interface conditions even in wall-bounded turbulent flows.
Therefore, the primary objective of this study is to characterize the evolution of longitudinal bleeding flow with respect to permeability and pore configuration. First, we investigate how permeability alters wake topology to establish its role in governing downstream flow structures. Next, we assess structural variation in longitudinal bleeding induced by changes in permeability and pore arrangement, leading to a refined description of jet merging and decay processes. Particularly, this work presents the first experimental evidence that longitudinal bleeding can be modelled as interacting multiple plane jets, providing a new conceptual framework for interpreting porous-body wakes. Finally, we proposed a new analytical model to predict the merging length of longitudinal bleeding jets, explicitly incorporating permeability as a governing parameter, and validated the model against experimental data. This analytical approach extends the applicability of DBF-based models to jet-interaction regimes not previously addressed in porous media flow studies.
2. Experiments
2.1. Cylinder models
The porous cylinders investigated in this study utilize a simple cubic lattice structure characterized by the unit cell length (
![]() $d_1$
) and the strut width (
$d_1$
) and the strut width (
![]() $d_2$
). As depicted in figure 1(a), this lattice design ensures isotropic permeability, with its porosity (
$d_2$
). As depicted in figure 1(a), this lattice design ensures isotropic permeability, with its porosity (
![]() $\varPhi$
) determined by the ratio of
$\varPhi$
) determined by the ratio of
![]() $d_2$
to
$d_2$
to
![]() $d_1$
in a unit cell as
$d_1$
in a unit cell as

Figure 1. (a) Simple cubic lattice structure serving as a base porous structure; (b) schematic representation illustrating of decoupling process of permeability (
![]() $K$
) from porosity (
$K$
) from porosity (
![]() $\varPhi$
); (c) dimensions of the porous square cylinder utilized in the experiments; (d) sample images of the porous square cylinders with different designs; detailed design parameters outlined in the schematic cross-sections for (e) case A3 and (f) case A5 (see table 1).
$\varPhi$
); (c) dimensions of the porous square cylinder utilized in the experiments; (d) sample images of the porous square cylinders with different designs; detailed design parameters outlined in the schematic cross-sections for (e) case A3 and (f) case A5 (see table 1).
A key feature of this design is that while porosity remains constant (i.e. constant
![]() $d_2/d_1$
), decreasing
$d_2/d_1$
), decreasing
![]() $d_1$
leads to a reduction in permeability (
$d_1$
leads to a reduction in permeability (
![]() $K$
), thereby enabling the decoupling of permeability effect from those of porosity (see figure 1
b). This experimental configuration allows for a controlled investigation of permeability-driven flow phenomena, which have predominantly been explored though computational studies due to the challenges associated with independently varying permeability in experimental settings. Within this unit-cell design, the pore-to-pore spacing equals the lattice length
$K$
), thereby enabling the decoupling of permeability effect from those of porosity (see figure 1
b). This experimental configuration allows for a controlled investigation of permeability-driven flow phenomena, which have predominantly been explored though computational studies due to the challenges associated with independently varying permeability in experimental settings. Within this unit-cell design, the pore-to-pore spacing equals the lattice length
![]() $d_1$
. Accordingly, at fixed porosity
$d_1$
. Accordingly, at fixed porosity
![]() $\varPhi$
, varying permeability
$\varPhi$
, varying permeability
![]() $K$
by uniform unit-cell scaling necessarily changes the spacing in proportion. Jet spacing is thus not treated as an independent control parameter in this study. Its influence is accounted for implicitly through the scale-separation parameter
$K$
by uniform unit-cell scaling necessarily changes the spacing in proportion. Jet spacing is thus not treated as an independent control parameter in this study. Its influence is accounted for implicitly through the scale-separation parameter
![]() $\epsilon =d_1/D$
(Mei & Auriault Reference Mei and Auriault1991; Zampogna & Bottaro Reference Zampogna and Bottaro2016), as discussed in §§ 3.1–3.2. The precise fabrication of these geometries was achieved using advanced stereolithography 3-D printing techniques, ensuring high resolution and surface quality.
$\epsilon =d_1/D$
(Mei & Auriault Reference Mei and Auriault1991; Zampogna & Bottaro Reference Zampogna and Bottaro2016), as discussed in §§ 3.1–3.2. The precise fabrication of these geometries was achieved using advanced stereolithography 3-D printing techniques, ensuring high resolution and surface quality.
In this study, 2-D square cylinders were chosen due to their alignment with the Cartesian coordinate system. Compared with cylinders with circular cross-sections, 2-D square cylinders with rectangular cross-sections are better suited for manipulating permeability due to their tensor nature. For simplicity, the aspect ratio of the rectangular cross-section was set to unity, resulting in square cylinders. Additionally, it is worth noting that the pore configuration of the porous cylinders can vary between odd and even numbers of pores along the cylinder width (
![]() $D$
), as illustrated in figure 1(e) and 1(f). These specific configurations play a crucial role in the behaviour of longitudinal bleedings near the trailing edge and their downstream structural evolution, depending on whether a central pore aligns with the lateral centreline (Seol et al. Reference Seol, Hong and Kim2023). For clarity, we refer to these configurations as the odd and even cases, respectively. All cylinders, both porous and solid, were fabricated using an advanced stereolithography 3-D printer (Anycubic Photon Mono X), with a width
$D$
), as illustrated in figure 1(e) and 1(f). These specific configurations play a crucial role in the behaviour of longitudinal bleedings near the trailing edge and their downstream structural evolution, depending on whether a central pore aligns with the lateral centreline (Seol et al. Reference Seol, Hong and Kim2023). For clarity, we refer to these configurations as the odd and even cases, respectively. All cylinders, both porous and solid, were fabricated using an advanced stereolithography 3-D printer (Anycubic Photon Mono X), with a width
![]() $D$
of 40 mm (or 42 mm) and a length of 320 mm, as depicted in figure 1(c). Detailed specifications of each cylinder are provided in table 1 and further discussed in previous studies (Seol et al. Reference Seol, Kim and Kim2024).
$D$
of 40 mm (or 42 mm) and a length of 320 mm, as depicted in figure 1(c). Detailed specifications of each cylinder are provided in table 1 and further discussed in previous studies (Seol et al. Reference Seol, Kim and Kim2024).
2.2. Permeability measurements
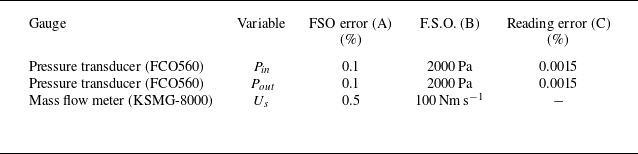
Permeability measurements were carried out in a 3.5 m-long acrylic pipe with an internal diameter of 65 mm, as shown in figure 2(a). Porous disks with the same lattice structure used in this study were fabricated via 3-D printing. To ensure that the maximum pressure drop did not exceed 2000 Pa at a superficial velocity (
![]() $U_s$
) of 15 m s−1, the thickness of the disks was varied between 20 and 60 mm. The disks were securely mounted 1.2 m downstream from the inlet to guarantee a fully developed flow. Pressure drop (
$U_s$
) of 15 m s−1, the thickness of the disks was varied between 20 and 60 mm. The disks were securely mounted 1.2 m downstream from the inlet to guarantee a fully developed flow. Pressure drop (
![]() $\Delta{\kern-1pt}P$
) across the disks was measured using a high-resolution differential pressure transmitter (FCO560, Furness Control) with a sampling rate of 1 kHz over a 2 min period, using pressure taps placed before and after the disks. At a distance of 0.4 m from the outlet, the superficial velocity (
$\Delta{\kern-1pt}P$
) across the disks was measured using a high-resolution differential pressure transmitter (FCO560, Furness Control) with a sampling rate of 1 kHz over a 2 min period, using pressure taps placed before and after the disks. At a distance of 0.4 m from the outlet, the superficial velocity (
![]() $U_s$
) was measured using a thermal mass flow meter (KSMG-8000, pressure and temperature compensated) over the same 2 min period, with
$U_s$
) was measured using a thermal mass flow meter (KSMG-8000, pressure and temperature compensated) over the same 2 min period, with
![]() $U_s$
ranging from 0.15 to 15 m s−1. By plotting
$U_s$
ranging from 0.15 to 15 m s−1. By plotting
![]() $\Delta{\kern-1pt}P$
against
$\Delta{\kern-1pt}P$
against
![]() $U_s$
for all the porous samples, the permeability (
$U_s$
for all the porous samples, the permeability (
![]() $K$
) was determined by fitting the data to the Forchheimer equation (Dukhan & Minjeur Reference Dukhan and Minjeur2011). The resulting permeability (
$K$
) was determined by fitting the data to the Forchheimer equation (Dukhan & Minjeur Reference Dukhan and Minjeur2011). The resulting permeability (
![]() $K$
) and the corresponding non-dimensional Darcy numbers (
$K$
) and the corresponding non-dimensional Darcy numbers (
![]() $ \textit{Da} $
) are listed in table 1.
$ \textit{Da} $
) are listed in table 1.

Figure 2. Experimental set-up for (a) permeability measurements, featuring sample porous disks and associated equipment, including a thermal mass flow meter, differential pressure transmitter and pressure taps for
![]() $\Delta{\kern-1pt}P$
measurement; (b) PIV measurements using two PIV cameras arranged in tandem; (c) schematic representation of the field of view (FoV) for PIV measurements, with the darker shaded area in the middle indicating the overlap between the two fields of view.
$\Delta{\kern-1pt}P$
measurement; (b) PIV measurements using two PIV cameras arranged in tandem; (c) schematic representation of the field of view (FoV) for PIV measurements, with the darker shaded area in the middle indicating the overlap between the two fields of view.
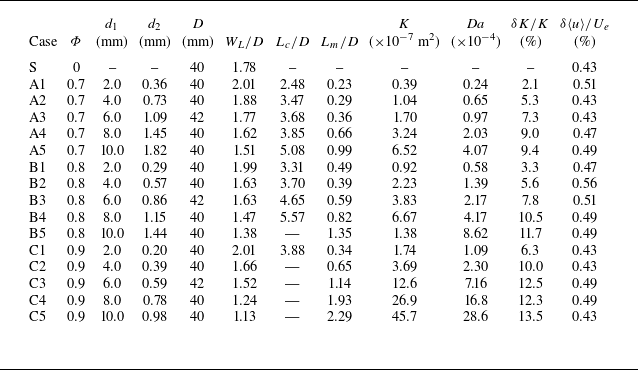
Table 1. Parameters for the structured porous square cylinders:
![]() $\varPhi$
, porosity;
$\varPhi$
, porosity;
![]() $d_1$
, length of the unit cell;
$d_1$
, length of the unit cell;
![]() $d_2$
, strut width;
$d_2$
, strut width;
![]() $D$
, cylinder width;
$D$
, cylinder width;
![]() $W_L$
, lateral wake extent;
$W_L$
, lateral wake extent;
![]() $L_{c}$
and
$L_{c}$
and
![]() $L_m$
, longitudinal extent of combined and merging region, respectively;
$L_m$
, longitudinal extent of combined and merging region, respectively;
![]() $K$
, permeability;
$K$
, permeability;
![]() $ \textit{Da} $
, Darcy number;
$ \textit{Da} $
, Darcy number;
![]() $\delta K/K$
, relative total uncertainty in permeability;
$\delta K/K$
, relative total uncertainty in permeability;
![]() $\delta \langle u \rangle / U_e$
: relative total uncertainty in mean longitudinal velocity.
$\delta \langle u \rangle / U_e$
: relative total uncertainty in mean longitudinal velocity.

2.3. The PIV measurements
Particle image velocimetry was employed to assess the flow behaviour for all cylinder cases at an upstream velocity of 11.5 m s−1 (corresponding to
![]() $ \textit{Re} \approx 3.1 \times 10^4$
). The free stream turbulence intensity in the test section was less than 0.8
$ \textit{Re} \approx 3.1 \times 10^4$
). The free stream turbulence intensity in the test section was less than 0.8
![]() $\,\%$
over the velocity range
$\,\%$
over the velocity range
![]() $3{-}20$
m s−1, as reported previously for the same facility (Seol et al. Reference Seol, Hong and Kim2023). The operating condition of the present measurements lies within this range. Measurements were taken at two downstream positions in the
$3{-}20$
m s−1, as reported previously for the same facility (Seol et al. Reference Seol, Hong and Kim2023). The operating condition of the present measurements lies within this range. Measurements were taken at two downstream positions in the
![]() $x$
–
$x$
–
![]() $y$
plane to capture the extended wake structures, using two 12 MP TSI Powerview cameras (
$y$
plane to capture the extended wake structures, using two 12 MP TSI Powerview cameras (
![]() $4k \times 3k$
, eight-bit) fitted with 105 mm Nikkor lenses. These cameras provided a FoV of
$4k \times 3k$
, eight-bit) fitted with 105 mm Nikkor lenses. These cameras provided a FoV of
![]() $6D \times 3D$
(figure 2
a,b). A Quantel Evergreen Nd:YAG double-pulsed laser (200 mJ per pulse) was used to generate a 1 mm-thick laser sheet, and data were acquired at a frequency of 5 Hz for all cases. For each cylinder case, 2000 independent image pairs were recorded. The final interrogation window size was 32
$6D \times 3D$
(figure 2
a,b). A Quantel Evergreen Nd:YAG double-pulsed laser (200 mJ per pulse) was used to generate a 1 mm-thick laser sheet, and data were acquired at a frequency of 5 Hz for all cases. For each cylinder case, 2000 independent image pairs were recorded. The final interrogation window size was 32
![]() $\times$
32 pixels with 50
$\times$
32 pixels with 50
![]() $\,\%$
overlap, resulting in a grid resolution of 890
$\,\%$
overlap, resulting in a grid resolution of 890
![]() $ \unicode{x03BC}\rm m$
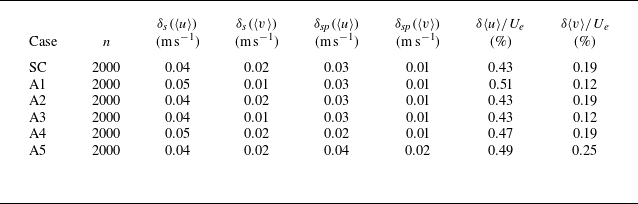
. Considering the random error in PIV measurements, which results from both sampling error in the turbulent velocity signal and the subpixel accuracy of the PIV system, the total random error in the mean velocity for the current measurements is estimated to be
$ \unicode{x03BC}\rm m$
. Considering the random error in PIV measurements, which results from both sampling error in the turbulent velocity signal and the subpixel accuracy of the PIV system, the total random error in the mean velocity for the current measurements is estimated to be
![]() $\pm 0.05$
m s−1. This corresponds to an uncertainty of 0.1
$\pm 0.05$
m s−1. This corresponds to an uncertainty of 0.1
![]() $\,\%$
when normalized by the free stream velocity (
$\,\%$
when normalized by the free stream velocity (
![]() $U_e$
). For further details on permeability and PIV measurements, readers are referred to our previous studies (Seol et al. Reference Seol, Hong and Kim2023, Reference Seol, Kim and Kim2024).
$U_e$
). For further details on permeability and PIV measurements, readers are referred to our previous studies (Seol et al. Reference Seol, Hong and Kim2023, Reference Seol, Kim and Kim2024).
3. Results and discussion
3.1. Downstream wake topology
Since the velocity deficit serves as a useful indicator of the downstream wake topology behind bluff bodies, we computed the velocity deficit, which is defined as the difference between the incoming mean flow and the mean longitudinal velocity around the porous cylinders,
![]() $(U_e- \langle u\rangle )/U_e$
. Figure 3 displays selected contour maps of the velocity deficit alongside a schematic representation of the porous cylinders at the origin. This facilitates in understanding the cross-section of the cylinder and the effect of permeability. For a baseline of comparison, a solid case is included to highlight the influence of permeability on the downstream wake topology. The coordinate system is normalized by the cylinder width,
$(U_e- \langle u\rangle )/U_e$
. Figure 3 displays selected contour maps of the velocity deficit alongside a schematic representation of the porous cylinders at the origin. This facilitates in understanding the cross-section of the cylinder and the effect of permeability. For a baseline of comparison, a solid case is included to highlight the influence of permeability on the downstream wake topology. The coordinate system is normalized by the cylinder width,
![]() $D$
.
$D$
.

Figure 3. Selected contour maps of the normalized velocity deficit,
![]() $(U_e - \langle u \rangle )/U_e$
, illustrating the wake topology behind the cylinders. Panels (
$(U_e - \langle u \rangle )/U_e$
, illustrating the wake topology behind the cylinders. Panels (
![]() $a$
)–(
$a$
)–(
![]() $f$
) depict the variation in velocity deficit behaviour with increasing Darcy number (
$f$
) depict the variation in velocity deficit behaviour with increasing Darcy number (
![]() $ \textit{Da} $
).
$ \textit{Da} $
).
Figure 3 illustrates the evolution of the velocity deficit with increasing
![]() $ \textit{Da} $
, which highlights the main flow features influenced by the permeable nature of the cylinders. A representative subset of configurations (S, A1, B2, A4, B5, C5) is shown to span the tested
$ \textit{Da} $
, which highlights the main flow features influenced by the permeable nature of the cylinders. A representative subset of configurations (S, A1, B2, A4, B5, C5) is shown to span the tested
![]() $ \textit{Da} $
range and to sample both odd and even pore arrangements. The remaining cases exhibit similar trends and are omitted here for clarity. It should be noted that in figure 3 contour levels less than 0.5 were omitted to clearly identify the downstream wake topology imposed by the current porous cylinders. This means that at the edge of the coloured regions in the contour maps, the streamwise velocity has recovered 50
$ \textit{Da} $
range and to sample both odd and even pore arrangements. The remaining cases exhibit similar trends and are omitted here for clarity. It should be noted that in figure 3 contour levels less than 0.5 were omitted to clearly identify the downstream wake topology imposed by the current porous cylinders. This means that at the edge of the coloured regions in the contour maps, the streamwise velocity has recovered 50
![]() $\,\%$
of its undisturbed value upstream of the cylinders.
$\,\%$
of its undisturbed value upstream of the cylinders.
As shown in figure 3, the velocity deficit and its spatial evolution behind the cylinders are clearly dictated by the permeability and the characteristics of the bleedings through the porous structure. Even with the smallest permeability (i.e.
![]() $ \textit{Da}=2.44 \times 10^{-5}$
) considered in this study (see figure 3
b), the downstream wake structure is significantly altered compared with the solid case shown in figure 3(a). Specifically, the overall shape of the wake becomes elongated in both longitudinal and lateral directions due to the presence of bleeding flows in these directions, featuring a smaller magnitude of velocity deficit near the porous-fluid interface compared with the solid case. With increasing
$ \textit{Da}=2.44 \times 10^{-5}$
) considered in this study (see figure 3
b), the downstream wake structure is significantly altered compared with the solid case shown in figure 3(a). Specifically, the overall shape of the wake becomes elongated in both longitudinal and lateral directions due to the presence of bleeding flows in these directions, featuring a smaller magnitude of velocity deficit near the porous-fluid interface compared with the solid case. With increasing
![]() $ \textit{Da} $
, the downstream wake topology is remarkably modified, as shown in figure 3(c–f). The lateral extent of the wake appears to decrease, and the magnitude of velocity deficit diminishes with increasing
$ \textit{Da} $
, the downstream wake topology is remarkably modified, as shown in figure 3(c–f). The lateral extent of the wake appears to decrease, and the magnitude of velocity deficit diminishes with increasing
![]() $ \textit{Da} $
. This observation is consistent with the findings of Nicolai et al. (Reference Nicolai, Taddei, Manes and Ganapathisubramani2020), reporting similar trends in flows through cylinder arrays at high Reynolds numbers (
$ \textit{Da} $
. This observation is consistent with the findings of Nicolai et al. (Reference Nicolai, Taddei, Manes and Ganapathisubramani2020), reporting similar trends in flows through cylinder arrays at high Reynolds numbers (
![]() $ \textit{Re} = 1.3\times 10^5$
). This topological change in the wake is due to the fact that the higher permeability allows more fluid to pass through the porous cylinder, reducing the momentum deficit and resulting in a structural alteration of the downstream wake (Taddei et al. Reference Taddei, Manes and Ganapathisubramani2016).
$ \textit{Re} = 1.3\times 10^5$
). This topological change in the wake is due to the fact that the higher permeability allows more fluid to pass through the porous cylinder, reducing the momentum deficit and resulting in a structural alteration of the downstream wake (Taddei et al. Reference Taddei, Manes and Ganapathisubramani2016).
Furthermore, the dependence of lateral wake extent on permeability observed here is in close agreement with previous studies of porous plates at lower Reynolds numbers. For example, Castro (Reference Castro1971) reported that increasing longitudinal bleeding through porous plates leads to a reduction in the lateral wake width, which is a consistent pattern with the present results. Similarly, Steiros, Bempedelis & Ding (Reference Steiros, Bempedelis and Ding2021) provided both theoretical and experimental analysis of wakes behind porous plates, showing that increased longitudinal bleeding reduces wake width by weakening the momentum deficit in the wake region. Their results indicated that the reduction in wake width results from attenuated velocity gradients across the shear layer, reducing downstream wake entrainment and suppressing lateral wake growth. This mechanism has also been supported in other studies involving porous geometries (Zong & Nepf Reference Zong and Nepf2012; Taddei et al. Reference Taddei, Manes and Ganapathisubramani2016; Ciuti et al. Reference Ciuti, Zampogna, Gallaire, Camarri and Ledda2021). The current results in figure 3 exhibit a similar structural trend, supporting the notion that enhanced permeability mitigates the momentum deficit and effectively reduces the lateral wake extent. The agreement between the present results and previous studies suggests that this trend is robust across different configurations of porous bluff-body and Reynolds number conditions.
It should be also noted that figure 3 captures the structural features of longitudinal bleeding flow immediately downstream of the porous cylinders depending on the pore size and the corresponding permeability. For the porous cylinders with a sufficiently small permeability, as shown in figure 3(b,c), the longitudinal bleeding appears to behave as a combined single jet. In contrast, as pore size increases, inherently leading to higher permeability, the longitudinal bleeding transitions into discrete jet structures emitted from each lattice pore. These discrete jets are demarcated by the internal boundaries of the coloured contours within the wake topology (see figure 3 d–f).
The observed transition in wake structure – from a single, combined jet to spatially discrete bleeding jets – can be further interpreted through the framework of homogenization theory (Mei & Auriault Reference Mei and Auriault1991; Zampogna & Bottaro Reference Zampogna and Bottaro2016). Classical homogenization assumes a strong scale separation between the microscopic porescale and the macroscopic domain size, quantified by the scale separation parameter
![]() $\epsilon =d_1/D$
, where
$\epsilon =d_1/D$
, where
![]() $d_1$
is the unit cell size and
$d_1$
is the unit cell size and
![]() $D$
is the cylinder width. When
$D$
is the cylinder width. When
![]() $\epsilon \ll 1$
, the flow through the porous medium can be approximated as spatially uniform, thereby justifying the emergence of a homogenized jet-like structure in the near wake, as illustrated in figure 3(b,c). However, in the present study, the scale separation parameter spans the range
$\epsilon \ll 1$
, the flow through the porous medium can be approximated as spatially uniform, thereby justifying the emergence of a homogenized jet-like structure in the near wake, as illustrated in figure 3(b,c). However, in the present study, the scale separation parameter spans the range
![]() $0.05\lt \epsilon \lt 0.25$
, and for cases with larger pore size (i.e.
$0.05\lt \epsilon \lt 0.25$
, and for cases with larger pore size (i.e.
![]() $\epsilon \gt 0.1$
, see figure 3
d–f), the assumption of homogenization breaks down. The pores are macroscopically resolvable, and the flow exhibits discrete jet-like features aligned with the pore geometry. This breakdown highlights the limitation of homogenization theory in high-permeability regimes, where pore-resolved effects, such as localized bleeding and wake variability, become significant.
$\epsilon \gt 0.1$
, see figure 3
d–f), the assumption of homogenization breaks down. The pores are macroscopically resolvable, and the flow exhibits discrete jet-like features aligned with the pore geometry. This breakdown highlights the limitation of homogenization theory in high-permeability regimes, where pore-resolved effects, such as localized bleeding and wake variability, become significant.
It is also worth noting that porescale inertial effects play a critical role in determining the flow characteristics particularly under the homogenization framework (Zampogna & Bottaro Reference Zampogna and Bottaro2016). These effects can be quantified using the microscopic-scale Reynolds number
![]() $ \textit{Re}_l=U^*l/\nu$
, where
$ \textit{Re}_l=U^*l/\nu$
, where
![]() $U^*$
is the characteristic internal velocity through the porous matrix, and
$U^*$
is the characteristic internal velocity through the porous matrix, and
![]() $\nu$
is the kinematic viscosity (Zampogna & Bottaro Reference Zampogna and Bottaro2016). However, in our current experimental set-up, the internal velocity cannot be captured using a standard PIV system. Accurate measurement would require advanced techniques such as refractive-index matching (Blois et al. Reference Blois, Bristow, Kim, Best and Christensen2020) or magnetic resonance velocimetry (Elkins & Alley Reference Elkins and Alley2007). In this regard, we are currently unable to systematically assess the inertial contribution at the pore level. Nonetheless, the scale-separation parameter
$\nu$
is the kinematic viscosity (Zampogna & Bottaro Reference Zampogna and Bottaro2016). However, in our current experimental set-up, the internal velocity cannot be captured using a standard PIV system. Accurate measurement would require advanced techniques such as refractive-index matching (Blois et al. Reference Blois, Bristow, Kim, Best and Christensen2020) or magnetic resonance velocimetry (Elkins & Alley Reference Elkins and Alley2007). In this regard, we are currently unable to systematically assess the inertial contribution at the pore level. Nonetheless, the scale-separation parameter
![]() $\epsilon$
remains a useful metric for evaluating the applicability of homogenization in porous bluff-body flows and provides an important physical basis for interpreting the observed transition from homogenized to discrete bleeding behaviour.
$\epsilon$
remains a useful metric for evaluating the applicability of homogenization in porous bluff-body flows and provides an important physical basis for interpreting the observed transition from homogenized to discrete bleeding behaviour.

Figure 4. (a) Schematic representation of the lateral wake extent,
![]() $W_L$
, for case A1. (b) Variation of the lateral wake extent,
$W_L$
, for case A1. (b) Variation of the lateral wake extent,
![]() $W_L$
, as a function of
$W_L$
, as a function of
![]() $ \textit{Da} $
. The crosses bounding the symbols indicate the sensitivity of the wake extent to the threshold level (set at 50
$ \textit{Da} $
. The crosses bounding the symbols indicate the sensitivity of the wake extent to the threshold level (set at 50
![]() $\%$
) used to define the wake edge.
$\%$
) used to define the wake edge.
To further examine the influence of permeability on the wake size, the wake extent is evaluated. In this study, the lateral wake extent is only considered since the longitudinal extents for the porous cylinders are beyond the present PIV FoV under 50
![]() $\,\%$
of the cutoff defining the wake edge. The lateral wake extent
$\,\%$
of the cutoff defining the wake edge. The lateral wake extent
![]() $W_L$
, defined as the maximum lateral distance reached by the wake edge, is illustrated in figure 4(a). In figure 4(b), the measured
$W_L$
, defined as the maximum lateral distance reached by the wake edge, is illustrated in figure 4(a). In figure 4(b), the measured
![]() $W_L$
for all porous cases is plotted against
$W_L$
for all porous cases is plotted against
![]() $ \textit{Da} $
, with uncertainty indicated by cross symbols. The uncertainty in
$ \textit{Da} $
, with uncertainty indicated by cross symbols. The uncertainty in
![]() $W_L$
was quantified by performing a sensitivity analysis, varying the threshold level used to define the wake edge by
$W_L$
was quantified by performing a sensitivity analysis, varying the threshold level used to define the wake edge by
![]() $50 \pm 10\,\%$
(Nicolai et al. Reference Nicolai, Taddei, Manes and Ganapathisubramani2020), resulting in a maximum variation of
$50 \pm 10\,\%$
(Nicolai et al. Reference Nicolai, Taddei, Manes and Ganapathisubramani2020), resulting in a maximum variation of
![]() $\pm 2.46\,\%$
in
$\pm 2.46\,\%$
in
![]() $W_L$
.
$W_L$
.
As seen in figure 4(b),
![]() $W_L$
expands laterally up to approximately twice the cylinder width
$W_L$
expands laterally up to approximately twice the cylinder width
![]() $D$
for the lowest
$D$
for the lowest
![]() $ \textit{Da} $
(i.e. case A1) and decreases progressively with increasing
$ \textit{Da} $
(i.e. case A1) and decreases progressively with increasing
![]() $ \textit{Da} $
. This reduction in
$ \textit{Da} $
. This reduction in
![]() $W_L$
with increasing
$W_L$
with increasing
![]() $ \textit{Da} $
is attributed to the effect of lateral bleeding, a phenomenon previously shown to strongly influence the wake size in the
$ \textit{Da} $
is attributed to the effect of lateral bleeding, a phenomenon previously shown to strongly influence the wake size in the
![]() $y$
-direction (Taddei et al. Reference Taddei, Manes and Ganapathisubramani2016). Nicolai et al. (Reference Nicolai, Taddei, Manes and Ganapathisubramani2020) also observed a decreasing trend in wake extent related to cylinder porosity
$y$
-direction (Taddei et al. Reference Taddei, Manes and Ganapathisubramani2016). Nicolai et al. (Reference Nicolai, Taddei, Manes and Ganapathisubramani2020) also observed a decreasing trend in wake extent related to cylinder porosity
![]() $\varPhi$
, although the relation in their study was implicit. In contrast, the present observations in figure 4(b) reveal an explicit log–linear relationship between
$\varPhi$
, although the relation in their study was implicit. In contrast, the present observations in figure 4(b) reveal an explicit log–linear relationship between
![]() $W_L$
and
$W_L$
and
![]() $ \textit{Da} $
. This result further emphasize the role of permeability as an important control parameter for the wake structures induced by porous cylinders (Cummins et al. Reference Cummins, Viola, Mastropaolo and Nakayama2017; Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018; Seol et al. Reference Seol, Hong and Kim2023).
$ \textit{Da} $
. This result further emphasize the role of permeability as an important control parameter for the wake structures induced by porous cylinders (Cummins et al. Reference Cummins, Viola, Mastropaolo and Nakayama2017; Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018; Seol et al. Reference Seol, Hong and Kim2023).
Based on the observations in figures 3 and 4, several noteworthy points emerge. First, bleeding flows in both longitudinal and lateral directions significantly affect shear layer development and wake formation behind porous square cylinders. For example, it has been documented that longitudinal bleeding contributes to the weakening of shear layer intensity, while lateral bleeding causes the vertical displacement of the top and bottom shear layers away from the wake core (Taddei et al. Reference Taddei, Manes and Ganapathisubramani2016; Nicolai et al. Reference Nicolai, Taddei, Manes and Ganapathisubramani2020). In this study, figure 3 illustrates a substantial decrease in velocity deficit with increasing
![]() $ \textit{Da} $
, indicating a significant attenuation in shear layer intensity. Simultaneously, figure 4 demonstrates a decreasing pattern in lateral wake extent with increasing
$ \textit{Da} $
, indicating a significant attenuation in shear layer intensity. Simultaneously, figure 4 demonstrates a decreasing pattern in lateral wake extent with increasing
![]() $ \textit{Da} $
, reflecting weakened lateral bleeding. These findings are consistent with recent observations from both qualitative and quantitative perspectives (Taddei et al. Reference Taddei, Manes and Ganapathisubramani2016; Zhou & Venayagamoorthy Reference Zhou and Venayagamoorthy2019; Nicolai et al. Reference Nicolai, Taddei, Manes and Ganapathisubramani2020), reaffirming that cylinder permeability and the associated bleeding characteristics predominantly control the flow structures downstream of the porous cylinders.
$ \textit{Da} $
, reflecting weakened lateral bleeding. These findings are consistent with recent observations from both qualitative and quantitative perspectives (Taddei et al. Reference Taddei, Manes and Ganapathisubramani2016; Zhou & Venayagamoorthy Reference Zhou and Venayagamoorthy2019; Nicolai et al. Reference Nicolai, Taddei, Manes and Ganapathisubramani2020), reaffirming that cylinder permeability and the associated bleeding characteristics predominantly control the flow structures downstream of the porous cylinders.
Second, discrete longitudinal bleeding jets observed in cases with larger pores and higher permeability (figure 3
d–f) evolve structurally, resembling multiple plane jets as they move downstream (Miller & Comings Reference Miller and Comings1960; Zhao & Wang Reference Zhao and Wang2018). This structural similarity suggests that the discrete jets behind the porous square cylinders can be classified into two distinct regions based on their streamwise location: merging and combined regions. In the merging region, as seen in figure 3(d), individual jets curve towards the symmetry plane (i.e.
![]() $y/D=0$
) and begin to merge. As they move downstream, these jets interact further and coalesce into a single jet in the combined region. Notably, the pore configuration of the cylinder significantly influences local flow structures immediately behind the cylinder. For instance, in the case of cylinders with odd pore configuration (figure 3
d), the momentum of the longitudinal bleeding reaches its maximum at
$y/D=0$
) and begin to merge. As they move downstream, these jets interact further and coalesce into a single jet in the combined region. Notably, the pore configuration of the cylinder significantly influences local flow structures immediately behind the cylinder. For instance, in the case of cylinders with odd pore configuration (figure 3
d), the momentum of the longitudinal bleeding reaches its maximum at
![]() $y/D=0$
and decreases laterally due to the presence of a central pore along the lateral centreline. In contrast, cylinders with even pore configuration (figure 3
e) generate dual jet-like structure, with the highest momentum occurring along the off-centreline, due to the locally impermeable boundary at
$y/D=0$
and decreases laterally due to the presence of a central pore along the lateral centreline. In contrast, cylinders with even pore configuration (figure 3
e) generate dual jet-like structure, with the highest momentum occurring along the off-centreline, due to the locally impermeable boundary at
![]() $y/D=0$
. These differences in the longitudinal bleeding patterns and their interactions lead to complex flow dynamics within the merging region before the jets fully combine into a single structure.
$y/D=0$
. These differences in the longitudinal bleeding patterns and their interactions lead to complex flow dynamics within the merging region before the jets fully combine into a single structure.
Lastly, drawing an analogy from multiple plane jets (Miller & Comings Reference Miller and Comings1960; Zhao & Wang Reference Zhao and Wang2018), the current observations of the permeability effect on longitudinal bleeding provide a basis for developing an analytical model linking the structural characteristics of bleeding jets to permeability. Specifically, the combined point on the centreline marks where the jets coalesce into a single entity. Beyond this point, the effects of the initial conditions have largely dissipated, and the influence of permeability, as a global factor, prevails in the downstream bleeding flow. In our previous work (Seol et al. Reference Seol, Kim and Kim2024), we successfully proposed an analytical model for downstream flow adjustment behind porous square cylinders in relation to permeability. We believe that the connection between the structural behaviour of the bleeding (i.e. the combined point) and permeability can be analytically approached. This relationship will be discussed in further detail in § 3.3.
3.2. Structural characteristics of longitudinal bleeding
As discussed in the previous section, bleeding flows play a pivotal role in shaping the wake structures downstream of porous square cylinders. The structural features of longitudinal bleeding are dictated by the permeability and pore configuration of the porous cylinders, which in turn exert a significant influence on the development of the downstream flow. To gain further insight into the fundamental physics governing these flows, it is essential to investigate how the structural characteristics of longitudinal bleeding evolve with permeability and pore configuration. In this section, we examine the downstream evolution of longitudinal bleeding jets, drawing on an analogy with multiple plane turbulent jets, with particular emphasis on the merging and coalescence behaviour of the jets (Miller & Comings Reference Miller and Comings1960; Zhao & Wang Reference Zhao and Wang2018).

Figure 5. (a) Evolution of the longitudinal velocity profiles at multiple downstream positions (
![]() $x/D = 1.5$
, 3, 4.5 and 6) for cases S, A1, B2, C4 and C5, corresponding to increasing
$x/D = 1.5$
, 3, 4.5 and 6) for cases S, A1, B2, C4 and C5, corresponding to increasing
![]() $ \textit{Da} $
. (b) Schematic illustration of the development of longitudinal bleeding jets, interacting with surrounding shear layers. The diagram highlights the merging, combined, and wake regions for the odd pore configuration.
$ \textit{Da} $
. (b) Schematic illustration of the development of longitudinal bleeding jets, interacting with surrounding shear layers. The diagram highlights the merging, combined, and wake regions for the odd pore configuration.
Figure 5(a) shows the lateral profiles of the mean longitudinal velocity,
![]() $\langle u \rangle /U_e$
, at several downstream positions for selected porous cases, emphasizing the structural evolution of bleeding flows. Four porous cases (A1, B2, C4 and C5) are selected as representative configurations to capture distinct structural patterns across pore arrangement and permeability. The solid square (case S) is included as a baseline without bleeding. These cases cover the tested
$\langle u \rangle /U_e$
, at several downstream positions for selected porous cases, emphasizing the structural evolution of bleeding flows. Four porous cases (A1, B2, C4 and C5) are selected as representative configurations to capture distinct structural patterns across pore arrangement and permeability. The solid square (case S) is included as a baseline without bleeding. These cases cover the tested
![]() $ \textit{Da} $
range and represent both odd and even pore configurations. Other tested configurations exhibit the same qualitative behaviour and are therefore omitted for clarity.
$ \textit{Da} $
range and represent both odd and even pore configurations. Other tested configurations exhibit the same qualitative behaviour and are therefore omitted for clarity.
As evident in figure 5(a), the flow structure downstream of porous cylinders differs considerably from that of the solid cylinder due to the influence of bleeding flows. In the solid case, the centreline velocity reaches its minimum around
![]() $x/D=1.95$
(not shown for brevity), marking the onset of cylinder-scale vortex formation, followed by velocity recovery. In contrast, for porous cases, longitudinal bleedings shifts the minimum velocity point farther downstream, delaying the formation of large-scale vortices (Zong & Nepf Reference Zong and Nepf2012). In figure 5(a), the near-wake (
$x/D=1.95$
(not shown for brevity), marking the onset of cylinder-scale vortex formation, followed by velocity recovery. In contrast, for porous cases, longitudinal bleedings shifts the minimum velocity point farther downstream, delaying the formation of large-scale vortices (Zong & Nepf Reference Zong and Nepf2012). In figure 5(a), the near-wake (
![]() $x/D=1.5$
) exhibits more pronounced longitudinal bleeding, with individual bleeding jets becoming increasingly distinct and aligned with the lattice pores as pore size and permeability increase. These velocity profiles in the near-wake quantitatively confirm that the formation of the bleeding jet structure is strongly influenced by the pore configuration whether it corresponds to an odd or even case, as noted in the wake topologies (see figure 3). Interestingly, for the cases with larger pores (i.e. C4 and C5), figure 5(a) illustrates the merging of multiple parallel jets, emitted from each lattice pore, as they propagate downstream. These jets eventually combine into a single structure, which spreads and decays farther downstream. In contrast, for smaller pore cases (i.e. A1 and B2), their velocity profiles at
$x/D=1.5$
) exhibits more pronounced longitudinal bleeding, with individual bleeding jets becoming increasingly distinct and aligned with the lattice pores as pore size and permeability increase. These velocity profiles in the near-wake quantitatively confirm that the formation of the bleeding jet structure is strongly influenced by the pore configuration whether it corresponds to an odd or even case, as noted in the wake topologies (see figure 3). Interestingly, for the cases with larger pores (i.e. C4 and C5), figure 5(a) illustrates the merging of multiple parallel jets, emitted from each lattice pore, as they propagate downstream. These jets eventually combine into a single structure, which spreads and decays farther downstream. In contrast, for smaller pore cases (i.e. A1 and B2), their velocity profiles at
![]() $x/D=1.5$
resemble a single jet, indicating rapid flow adjustment immediately behind the porous cylinder (Seol et al. Reference Seol, Kim and Kim2024).
$x/D=1.5$
resemble a single jet, indicating rapid flow adjustment immediately behind the porous cylinder (Seol et al. Reference Seol, Kim and Kim2024).
The observations from figure 5(a) suggest a new conceptual model of bleeding flows behind porous square cylinders, analogous to the behaviour observed in parallel plane jets (Miller & Comings Reference Miller and Comings1960; Zhao & Wang Reference Zhao and Wang2018), although with distinct shear layer dynamics due to the influence of a strong external flow. Figure 5(b) illustrates this proposed model, which divides the longitudinal bleeding domain into three distinct flow regions based on their structural attributes. The first region, termed the merging region, situated near the jet exit where individual jets begin to interact and merge, leading to significant mixing and causing the flow to lose its individual jet characteristics. This is followed by the combined region, where the coalesced jets behave as a single, unified flow that progressively spreads and decays while interacting with the top and bottom shear layers induced by the cylinder. Finally, the wake region is located downstream of the combined region, where the combined jet fully dissipates and transitions into a wake characterized by the onset of wake recovery process. This conceptual framework captures the complex evolution of longitudinal bleedings behind porous square cylinders, offering a detailed understanding of how these jets shape the downstream flow structure under the influence of surrounding shear layers.

Figure 6. Selected contour maps of the normalized mean longitudinal velocity,
![]() $\langle u \rangle /U_e$
, superimposed with streamlines for case B, where
$\langle u \rangle /U_e$
, superimposed with streamlines for case B, where
![]() $ \textit{Da} $
varies while maintaining a constant porosity of
$ \textit{Da} $
varies while maintaining a constant porosity of
![]() $\varPhi =0.8$
. Red dashed circles indicate the main recirculation bubble at
$\varPhi =0.8$
. Red dashed circles indicate the main recirculation bubble at
![]() $y/D=0$
, while yellow dashed circles highlight the second recirculation bubble attached to the cylinder trailing edge.
$y/D=0$
, while yellow dashed circles highlight the second recirculation bubble attached to the cylinder trailing edge.
To investigate the overall behaviour of longitudinal bleeding flows and their influence on downstream flow structures, contour maps of the mean longitudinal velocity (
![]() $\langle u \rangle /U_e$
) with streamlines are presented in figure 6. Here,
$\langle u \rangle /U_e$
) with streamlines are presented in figure 6. Here,
![]() $\langle \boldsymbol{\cdot }\rangle$
denotes the ensemble average of a quantity. The analysis focuses on porous cylinders from case B, where permeability varies with unit-cell scaling while maintaining a constant porosity of
$\langle \boldsymbol{\cdot }\rangle$
denotes the ensemble average of a quantity. The analysis focuses on porous cylinders from case B, where permeability varies with unit-cell scaling while maintaining a constant porosity of
![]() $\varPhi =0.8$
. For clarity, a side view of the cylinder cross-section is included at the origin to aid in understanding the structural features of the longitudinal bleeding flows.
$\varPhi =0.8$
. For clarity, a side view of the cylinder cross-section is included at the origin to aid in understanding the structural features of the longitudinal bleeding flows.
Figure 6 reveals the presence of longitudinal bleeding flow along the symmetric plane (
![]() $y/D=0$
) for all porous cases due to the permeable nature of the cylinders. However, both the momentum and the longitudinal extent of this bleeding flow are strongly influenced by cylinder permeability (
$y/D=0$
) for all porous cases due to the permeable nature of the cylinders. However, both the momentum and the longitudinal extent of this bleeding flow are strongly influenced by cylinder permeability (
![]() $ \textit{Da} $
), which in turn modifies the main recirculation bubble. As highlighted by the red dashed circles in figure 6, increasing permeability leads to a reduction in the size of the main recirculation bubble and causes it to shift farther downstream, consistent with the findings of Ledda et al. (Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). When reaches its critical value (
$ \textit{Da} $
), which in turn modifies the main recirculation bubble. As highlighted by the red dashed circles in figure 6, increasing permeability leads to a reduction in the size of the main recirculation bubble and causes it to shift farther downstream, consistent with the findings of Ledda et al. (Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). When reaches its critical value (
![]() $ \textit{Da}_c=2\times 10^{-4}$
), as reported in our previous work (Seol et al. Reference Seol, Kim and Kim2024), the reverse flow in the downstream region vanishes. Instead, a steady wake region with positive and nearly constant velocity develops, as seen in figure 6(e) and 6(f) (Zong & Nepf Reference Zong and Nepf2012). Based on this structural behaviour, Seol et al. (Reference Seol, Kim and Kim2024) categorized flows into two regimes: high flow-blockage cases (
$ \textit{Da}_c=2\times 10^{-4}$
), as reported in our previous work (Seol et al. Reference Seol, Kim and Kim2024), the reverse flow in the downstream region vanishes. Instead, a steady wake region with positive and nearly constant velocity develops, as seen in figure 6(e) and 6(f) (Zong & Nepf Reference Zong and Nepf2012). Based on this structural behaviour, Seol et al. (Reference Seol, Kim and Kim2024) categorized flows into two regimes: high flow-blockage cases (
![]() $ \textit{Da} \lt Da_c$
) and low flow-blockage cases (
$ \textit{Da} \lt Da_c$
) and low flow-blockage cases (
![]() $ \textit{Da} \gt Da_c$
).
$ \textit{Da} \gt Da_c$
).
Additionally, figure 6 captures a second pair of recirculation bubbles attached to the trailing edge of the porous cylinders, highlighted by the yellow dashed circles. These bubbles have been reported in past numerical and experimental studies (Fang et al. Reference Fang, Yang, Ma and Li2020; Seol et al. Reference Seol, Kim and Kim2024) and attributed to the shear layer interactions between the separated external flow and the longitudinal bleeding flow. The second recirculation bubble represents a low-pressure zone that envelops the longitudinal bleeding flow near the trailing edge. These second bubble pairs thus influence the structural development of the longitudinal bleeding, inducing local acceleration and deceleration as the flow convects downstream in the near wake. Consequently, the observations in figure 6 suggest that the coupled effects of the main and second recirculation bubbles play a role in governing the structural behaviour of longitudinal bleeding flows downstream of the porous cylinders.

Figure 7. Selected contour maps of the normalized Reynolds shear stress,
![]() $-\langle u'v' \rangle /U_e^2$
, for the same cases shown in figure 6.
$-\langle u'v' \rangle /U_e^2$
, for the same cases shown in figure 6.
To further explore the structural evolution of longitudinal bleeding flows and their resulting shear layers as a function of permeability, contour maps of Reynolds shear stress,
![]() $-\langle u'v' \rangle$
, normalized by
$-\langle u'v' \rangle$
, normalized by
![]() $U_e^2$
are presented in figure 7. Here,
$U_e^2$
are presented in figure 7. Here,
![]() $u'$
and
$u'$
and
![]() $v'$
are the fluctuating velocity components in the longitudinal and lateral directions, respectively. For consistency, the same porous cases as in figure 6 are considered. A schematic representation of the cylinder cross-section is included to facilitate understanding of the structural characteristics of the bleeding shear layers, which are influenced by pore size and the corresponding permeability. Here, the term bleeding shear layer refers to the shear layers generated by longitudinal bleeding jets immediately downstream of the porous cylinders. This terminology is introduced intentionally to avoid confusion with the shear layers originating from flow separation at the leading edge of the cylinders. For reference, the solid cylinder case is also included to highlight the modifications in shear layer structure induced by the permeable nature of the cylinders and the resulting bleeding flows.
$v'$
are the fluctuating velocity components in the longitudinal and lateral directions, respectively. For consistency, the same porous cases as in figure 6 are considered. A schematic representation of the cylinder cross-section is included to facilitate understanding of the structural characteristics of the bleeding shear layers, which are influenced by pore size and the corresponding permeability. Here, the term bleeding shear layer refers to the shear layers generated by longitudinal bleeding jets immediately downstream of the porous cylinders. This terminology is introduced intentionally to avoid confusion with the shear layers originating from flow separation at the leading edge of the cylinders. For reference, the solid cylinder case is also included to highlight the modifications in shear layer structure induced by the permeable nature of the cylinders and the resulting bleeding flows.
Figure 7 clearly illustrates the impact of permeability on the intensity and development of the primary shear layers shed from the leading edge of the cylinders. As
![]() $ \textit{Da} $
increases, the magnitude of
$ \textit{Da} $
increases, the magnitude of
![]() $-\langle u'v' \rangle$
diminishes, indicating suppression of the unsteady wake and a reduction in turbulent mixing intensity. This trend suggests that the presence of bleeding flows attenuates the shear layer development compared with the solid case. Furthermore, the merging point of the two primary shear layers shifts progressively downstream with increasing
$-\langle u'v' \rangle$
diminishes, indicating suppression of the unsteady wake and a reduction in turbulent mixing intensity. This trend suggests that the presence of bleeding flows attenuates the shear layer development compared with the solid case. Furthermore, the merging point of the two primary shear layers shifts progressively downstream with increasing
![]() $ \textit{Da} $
, emphasizing the role of permeability in modulating the downstream flow dynamics.
$ \textit{Da} $
, emphasizing the role of permeability in modulating the downstream flow dynamics.
In addition to the primary shear layers, figure 7 reveals the development of bleeding shear layers for the porous cylinders. These shear layers exhibit distinct structural behaviour: their growth remains constrained by the primary shear layers, confining them within the outer boundaries of the main flow structures. Initially, the bleeding shear layers expand near the cylinder trailing edge but subsequently diminish in both size and intensity as they convect downstream. At the location where the primary shear layers merge, the bleeding shear layers dissipate entirely, as observed in figure 7. Moreover, it should be noted that the structural characteristics of the bleeding shear layers are closely related to the pore size and resulting permeability. For cases with larger pores and higher permeability (figure 7 d–f), multiple discrete bleeding shear layers are evident, corresponding to the individual jets emitted from each lattice pore. These discrete layers undergo merging and interaction processes, starting immediately behind the porous cylinder, consistent with the behaviour illustrated in figure 5(b). In contrast, cases with smaller pores and lower permeability (figure 7 b,c) exhibit a continuous mixing layer formed by a combined jet that undergoes lateral spreading near the cylinder trailing edge. This distinction highlights the critical role of pore configuration and permeability in shaping the evolution of bleeding shear layers within the primary wake.

Figure 8. Lateral profiles of the mean longitudinal velocity
![]() $\langle u \rangle /U_e$
(blue circles) and the Reynolds shear stress
$\langle u \rangle /U_e$
(blue circles) and the Reynolds shear stress
![]() $\langle u'v' \rangle /U_e^2$
(red solid line) at several downstream positions (
$\langle u'v' \rangle /U_e^2$
(red solid line) at several downstream positions (
![]() $1 \leqslant x/D \leqslant 3.5$
) for each porous cylinder configurations shown in figures 6 and 7.
$1 \leqslant x/D \leqslant 3.5$
) for each porous cylinder configurations shown in figures 6 and 7.
To provide further insight into the structural evolution of longitudinal bleeding flows, figure 8 presents lateral profiles of the mean longitudinal velocity (
![]() $\langle u \rangle$
, blue circles) and Reynolds shear stress (
$\langle u \rangle$
, blue circles) and Reynolds shear stress (
![]() $-\langle u'v' \rangle$
, red lines) at various downstream positions within the range
$-\langle u'v' \rangle$
, red lines) at various downstream positions within the range
![]() $1\leqslant x/D \leqslant 3.5$
for the porous cylinder cases shown in figure 6 and 7. Both
$1\leqslant x/D \leqslant 3.5$
for the porous cylinder cases shown in figure 6 and 7. Both
![]() $\langle u \rangle$
and
$\langle u \rangle$
and
![]() $-\langle u'v' \rangle$
are normalized by their respective scaling factors to highlight overall trends with respect to
$-\langle u'v' \rangle$
are normalized by their respective scaling factors to highlight overall trends with respect to
![]() $ \textit{Da} $
and streamwise location. Within the bleeding shear layer, rapid velocity change induced by longitudinal bleeding gives rise to intense turbulence, as evidenced by the
$ \textit{Da} $
and streamwise location. Within the bleeding shear layer, rapid velocity change induced by longitudinal bleeding gives rise to intense turbulence, as evidenced by the
![]() $-\langle u'v' \rangle$
profiles. The centres of both the primary and bleeding shear layers can be identified either by the inflection points in the velocity profiles or the local maxima in the Reynolds shear stress profiles, providing insights into the complex interaction between the longitudinal bleeding flows and the surrounding mixing layers.
$-\langle u'v' \rangle$
profiles. The centres of both the primary and bleeding shear layers can be identified either by the inflection points in the velocity profiles or the local maxima in the Reynolds shear stress profiles, providing insights into the complex interaction between the longitudinal bleeding flows and the surrounding mixing layers.
The evolution of the bleeding shear layers, as depicted in figure 8, offers a detailed view of the structural change of longitudinal bleeding jets as they propagate downstream from the porous cylinders. Consistent with the velocity structures presented in figure 5(a), figure 8 reveals a distinct merging process of the bleeding shear layers, followed by gradual dissipation as the bleeding jets weaken. These structural changes can be described with respect to the flow regions identified in figure 5(b). Specifically, in the merging region, multiple bleeding shear layers originating from the individual pores of the porous cylinders are discernible. As these shear layers progress downstream into the combined region, they coalesce into a single pair of shear layers with opposing signs, symmetrically aligned along
![]() $y/D=0$
, indicating the formation of a combined bleeding jet. In the wake region, the bleeding shear layers fully dissipate as the primary shear layers merge, marking the final phase of the structural evolution.
$y/D=0$
, indicating the formation of a combined bleeding jet. In the wake region, the bleeding shear layers fully dissipate as the primary shear layers merge, marking the final phase of the structural evolution.
The structural characteristics of longitudinal bleeding flows, as shown in figure 8, provide a framework for quantitatively assessing the extents of the merging and combined regions downstream of the porous cylinders, denoted as
![]() $L_m$
and
$L_m$
and
![]() $L_c$
, respectively (see figure 5
b). These extents can be determined by analysing the longitudinal velocity and Reynolds shear stress profiles along the centreline, offering a deeper understanding of the flow dynamics behind the porous cylinders. In the context of parallel plane jets, it is well established that the merging region ends at the combined point, where two jets coalesce into a single jet flow along the centreline (Zhao & Wang Reference Zhao and Wang2018). Applying this concept to the present study,
$L_c$
, respectively (see figure 5
b). These extents can be determined by analysing the longitudinal velocity and Reynolds shear stress profiles along the centreline, offering a deeper understanding of the flow dynamics behind the porous cylinders. In the context of parallel plane jets, it is well established that the merging region ends at the combined point, where two jets coalesce into a single jet flow along the centreline (Zhao & Wang Reference Zhao and Wang2018). Applying this concept to the present study,
![]() $L_m$
can be defined as the streamwise distance from the cylinder trailing edge to the combined point in the flow past porous cylinders. Conversely, the merging and dissipation processes of the longitudinal bleeding jets, as observed in figure 8, suggest that the longitudinal extent of the combined region,
$L_m$
can be defined as the streamwise distance from the cylinder trailing edge to the combined point in the flow past porous cylinders. Conversely, the merging and dissipation processes of the longitudinal bleeding jets, as observed in figure 8, suggest that the longitudinal extent of the combined region,
![]() $L_c$
, aligns with the merging point of the primary shear layers along the centreline. For instance, Zong & Nepf (Reference Zong and Nepf2012) noted that following the merging of the primary shear layers, the centreline velocity begins to recover. This observation implies that the streamwise location where the centreline velocity reaches its minimum corresponds to the point where the primary shear layers merge, thereby defining the extent of the combined region,
$L_c$
, aligns with the merging point of the primary shear layers along the centreline. For instance, Zong & Nepf (Reference Zong and Nepf2012) noted that following the merging of the primary shear layers, the centreline velocity begins to recover. This observation implies that the streamwise location where the centreline velocity reaches its minimum corresponds to the point where the primary shear layers merge, thereby defining the extent of the combined region,
![]() $L_c$
.
$L_c$
.

Figure 9. Profiles of the normalized mean longitudinal velocity,
![]() $\langle u \rangle /U_e$
, along the centreline for the same cases shown in figure 6. Red crosses denote the local minima of the profiles, indicating the combined region length,
$\langle u \rangle /U_e$
, along the centreline for the same cases shown in figure 6. Red crosses denote the local minima of the profiles, indicating the combined region length,
![]() $L_c$
. (b) Variation of the measured
$L_c$
. (b) Variation of the measured
![]() $L_c$
as a function of
$L_c$
as a function of
![]() $ \textit{Da} $
, for all possible porous cases. The crosses bounding the symbols indicate the sensitivity of the
$ \textit{Da} $
, for all possible porous cases. The crosses bounding the symbols indicate the sensitivity of the
![]() $L_c$
based on the uncertainty of the longitudinal velocity,
$L_c$
based on the uncertainty of the longitudinal velocity,
![]() $\delta \langle u \rangle / U_e$
.
$\delta \langle u \rangle / U_e$
.
Figure 9 illustrates the method used to determine the combined region length,
![]() $L_c$
, by analysing centreline profiles of the mean longitudinal velocity
$L_c$
, by analysing centreline profiles of the mean longitudinal velocity
![]() $\langle u \rangle$
, normalized by the free stream velocity
$\langle u \rangle$
, normalized by the free stream velocity
![]() $U_e$
, as a function of the streamwise position
$U_e$
, as a function of the streamwise position
![]() $x/D$
. The shaded region in figure 9(a) represents the physical domain occupied by the porous cylinder (
$x/D$
. The shaded region in figure 9(a) represents the physical domain occupied by the porous cylinder (
![]() $0\lt x/D\lt 1$
). To maintain consistency with figures 6–8, the same porous cases (B1–B5) with a fixed porosity
$0\lt x/D\lt 1$
). To maintain consistency with figures 6–8, the same porous cases (B1–B5) with a fixed porosity
![]() $\varPhi =0.8$
are examined. For comparison, the solid cylinder case (S) is included to highlight the wake behaviour in the absence of bleeding effects. Unlike previous studies (Seol et al. Reference Seol, Hong and Kim2023, Reference Seol, Kim and Kim2024), the present analysis focuses exclusively on the longitudinal velocity at
$\varPhi =0.8$
are examined. For comparison, the solid cylinder case (S) is included to highlight the wake behaviour in the absence of bleeding effects. Unlike previous studies (Seol et al. Reference Seol, Hong and Kim2023, Reference Seol, Kim and Kim2024), the present analysis focuses exclusively on the longitudinal velocity at
![]() $y/D=0$
, avoiding spatial averaging across the lateral direction (i.e.
$y/D=0$
, avoiding spatial averaging across the lateral direction (i.e.
![]() $0 \leqslant y/d_1 \leqslant 1$
, where
$0 \leqslant y/d_1 \leqslant 1$
, where
![]() $d_1$
is the unit cell length, as depicted in figure 1
f).
$d_1$
is the unit cell length, as depicted in figure 1
f).
As shown in figure 9(a), the centreline velocity downstream of the porous cylinders is strongly influenced by permeability. With increasing
![]() $ \textit{Da} $
, the magnitude of the negative velocity associated with the recirculation bubble decreases, and the bubble shifts farther downstream. This trend is consistent with observations by Ledda et al. (Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). Furthermore, the velocity gradient in the near wake, reflecting the flow adjustment process, is progressively weakened as
$ \textit{Da} $
, the magnitude of the negative velocity associated with the recirculation bubble decreases, and the bubble shifts farther downstream. This trend is consistent with observations by Ledda et al. (Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). Furthermore, the velocity gradient in the near wake, reflecting the flow adjustment process, is progressively weakened as
![]() $ \textit{Da} $
increases in agreement with findings by Zong & Nepf (Reference Zong and Nepf2012). As
$ \textit{Da} $
increases in agreement with findings by Zong & Nepf (Reference Zong and Nepf2012). As
![]() $ \textit{Da} $
increases, the local minimum in the centreline velocity (marked by red crosses in figure 9
a) shifts downstream, leading to an elongation of the combined region. This behaviour indicates that higher permeability promotes stronger longitudinal bleeding flow, delaying velocity recovery farther downstream.
$ \textit{Da} $
increases, the local minimum in the centreline velocity (marked by red crosses in figure 9
a) shifts downstream, leading to an elongation of the combined region. This behaviour indicates that higher permeability promotes stronger longitudinal bleeding flow, delaying velocity recovery farther downstream.
To quantify the influence of permeability on the combined region length
![]() $L_c$
, figure 9(b) presents
$L_c$
, figure 9(b) presents
![]() $L_c$
as a function of
$L_c$
as a function of
![]() $ \textit{Da} $
. The results reveal a clear log–linear relationship, demonstrating that
$ \textit{Da} $
. The results reveal a clear log–linear relationship, demonstrating that
![]() $L_c$
increases systematically with increasing
$L_c$
increases systematically with increasing
![]() $ \textit{Da} $
. This strong correlation indicates that enhanced longitudinal bleeding flows with higher permeability are the dominant factor driving the expansion of the combined region. It is worth noting that for the cases with exceptionally high permeability (e.g. B5, C2–C5),
$ \textit{Da} $
. This strong correlation indicates that enhanced longitudinal bleeding flows with higher permeability are the dominant factor driving the expansion of the combined region. It is worth noting that for the cases with exceptionally high permeability (e.g. B5, C2–C5),
![]() $L_c$
exceeds
$L_c$
exceeds
![]() $6D$
, surpassing the FoV of the current PIV measurements. While these cases could not be fully captured (see table 1), the trend remains consistent and robust. Based on these observations, figure 9 reaffirms that the combined region length
$6D$
, surpassing the FoV of the current PIV measurements. While these cases could not be fully captured (see table 1), the trend remains consistent and robust. Based on these observations, figure 9 reaffirms that the combined region length
![]() $L_c$
is intrinsically linked to the strength of longitudinal bleeding flows induced by permeability. Furthermore, this elongation of the combined region has direct implications for the aerodynamic drag of the porous cylinders, following a consistent log–linear relation, as recently reported by (Seol et al. Reference Seol, Kim and Kim2024).
$L_c$
is intrinsically linked to the strength of longitudinal bleeding flows induced by permeability. Furthermore, this elongation of the combined region has direct implications for the aerodynamic drag of the porous cylinders, following a consistent log–linear relation, as recently reported by (Seol et al. Reference Seol, Kim and Kim2024).
The merging region length,
![]() $L_m$
, is generally defined as the streamwise distance from the cylinder trailing edge to the combined point, where multiple bleeding jets coalesce into a single, unified jet along the centreline. To quantitatively assess
$L_m$
, is generally defined as the streamwise distance from the cylinder trailing edge to the combined point, where multiple bleeding jets coalesce into a single, unified jet along the centreline. To quantitatively assess
![]() $L_m$
, it is crucial to understand the overall merging behaviour of these jets in the near wake, where intense mixing of porescale jets occurs. Within this region, additional local pressure drops around the longitudinal bleeding flows lead to a complex diffusion process, distinct from the combined region. To simplify the analysis of these interactions, we introduce two primary assumptions.
$L_m$
, it is crucial to understand the overall merging behaviour of these jets in the near wake, where intense mixing of porescale jets occurs. Within this region, additional local pressure drops around the longitudinal bleeding flows lead to a complex diffusion process, distinct from the combined region. To simplify the analysis of these interactions, we introduce two primary assumptions.
First, the combined point is assumed to reside along the lateral centreline (
![]() $y/D=0$
), and thus, our evaluation in the following sections focuses solely on this axis. Second, the boundary layer assumption for turbulent plane jets (Bradbury Reference Bradbury1965) is applied:
$y/D=0$
), and thus, our evaluation in the following sections focuses solely on this axis. Second, the boundary layer assumption for turbulent plane jets (Bradbury Reference Bradbury1965) is applied:
This assumption implies that at sufficient distances from the cylinder, where the jet flow becomes self-similar, advective transport of longitudinal momentum dominates over lateral turbulent and viscous transport, justifying the boundary layer approximation. The validity of this assumption in the wake region is supported by recent experimental findings (Nicolai et al. Reference Nicolai, Taddei, Manes and Ganapathisubramani2020), which demonstrated self-similar characteristics of the flow in the far-wake region of wall-mounted porous cylinders. Thus, the boundary layer assumption provides a practical framework for simplifying the analysis of the merging region by focusing on the lateral diffusion process, which predominantly governs the streamwise development of jet velocity profiles as the flow propagates downstream. Accordingly, the lateral gradient of Reynolds shear stress,
![]() $\partial \langle u'v' \rangle /\partial y$
, evaluated at
$\partial \langle u'v' \rangle /\partial y$
, evaluated at
![]() $y/D=0$
, serves as a representation for the diffusion process in the wake and facilitates the determination of
$y/D=0$
, serves as a representation for the diffusion process in the wake and facilitates the determination of
![]() $L_m$
.
$L_m$
.

Figure 10. Streamwise profiles of the lateral gradient of Reynolds shear stress,
![]() $\partial \langle u'v' \rangle / \partial y$
, and normalized longitudinal velocity,
$\partial \langle u'v' \rangle / \partial y$
, and normalized longitudinal velocity,
![]() $\langle u \rangle /U_e$
, at the centreline (
$\langle u \rangle /U_e$
, at the centreline (
![]() $y/D=0$
): (a) case B1, (b) case A3, (c) case B5 and (d) case B4. Red and black symbols represent
$y/D=0$
): (a) case B1, (b) case A3, (c) case B5 and (d) case B4. Red and black symbols represent
![]() $\partial \langle u'v' \rangle / \partial y$
and
$\partial \langle u'v' \rangle / \partial y$
and
![]() $\langle u \rangle /U_e$
, respectively. The vertical dashed line indicates the extent of the merging region,
$\langle u \rangle /U_e$
, respectively. The vertical dashed line indicates the extent of the merging region,
![]() $L_m$
. The red shading denotes the uncertainty in
$L_m$
. The red shading denotes the uncertainty in
![]() $\partial \langle u'v' \rangle /\partial y$
, as described in Appendix A.
$\partial \langle u'v' \rangle /\partial y$
, as described in Appendix A.
Figure 10 illustrates
![]() $\partial \langle u'v' \rangle /\partial y$
along the centreline (red symbols) for four representative cases, capturing the influence of pore configuration and permeability on the lateral diffusion process downstream of the porous cylinders. To complement this analysis, the centreline profiles of the mean longitudinal velocity
$\partial \langle u'v' \rangle /\partial y$
along the centreline (red symbols) for four representative cases, capturing the influence of pore configuration and permeability on the lateral diffusion process downstream of the porous cylinders. To complement this analysis, the centreline profiles of the mean longitudinal velocity
![]() $\langle u \rangle /U_e$
(black symbols), are included to provide insights into key structural behaviour such as the presence of the main recirculation bubbles or the steady wake region behind the cylinders. For consistency, the analysis mainly considers porous cylinders from case B, with the exception of case A3 (figure 10
b). This is because case B3 does not meet the criteria for both high permeability (
$\langle u \rangle /U_e$
(black symbols), are included to provide insights into key structural behaviour such as the presence of the main recirculation bubbles or the steady wake region behind the cylinders. For consistency, the analysis mainly considers porous cylinders from case B, with the exception of case A3 (figure 10
b). This is because case B3 does not meet the criteria for both high permeability (
![]() $ \textit{Da} \gt Da_c = 2.0\times 10^{-4}$
) and an odd pore configuration. Instead, case A3, which satisfies both conditions, is included. Figure 10(a,b) corresponds to high flow-blockage cases (
$ \textit{Da} \gt Da_c = 2.0\times 10^{-4}$
) and an odd pore configuration. Instead, case A3, which satisfies both conditions, is included. Figure 10(a,b) corresponds to high flow-blockage cases (
![]() $ \textit{Da}\lt Da_c$
), while figure 10(c,d) represents low flow-blockage cases (
$ \textit{Da}\lt Da_c$
), while figure 10(c,d) represents low flow-blockage cases (
![]() $ \textit{Da}\gt Da_c$
). Figure 10(a,c) depicts cases with even pore configurations, where the momentum peaks of the longitudinal bleeding jets are positioned off-centre at half the unit cell length (
$ \textit{Da}\gt Da_c$
). Figure 10(a,c) depicts cases with even pore configurations, where the momentum peaks of the longitudinal bleeding jets are positioned off-centre at half the unit cell length (
![]() $d_1/2$
). Conversely, figure 10(b,d) illustrates odd pore configurations, where the momentum peak aligns with the centreline due to the presence of a central pore.
$d_1/2$
). Conversely, figure 10(b,d) illustrates odd pore configurations, where the momentum peak aligns with the centreline due to the presence of a central pore.
It is important to note that the lateral gradient of Reynolds shear stress in figure 10 is intentionally presented in its dimensional form, as it is directly incorporated into the analytical model in (3.3) (§ 3.3). Since the model is formulated based on a dimensional representation of the lateral diffusion of longitudinal momentum, retaining the dimensional form of
![]() $\partial \langle u'v' \rangle /\partial y$
ensures a direct, one-to-one correspondence between the experimentally measured values and their role in determining the merging region length,
$\partial \langle u'v' \rangle /\partial y$
ensures a direct, one-to-one correspondence between the experimentally measured values and their role in determining the merging region length,
![]() $L_m$
, without the need for additional normalization.
$L_m$
, without the need for additional normalization.
In figure 10, the influence of pore configuration on
![]() $\partial \langle u'v' \rangle /\partial y$
profiles within the merging region is evident. For cylinders with even pore configurations (figures 10
a and 10
c), a negative gradient emerges immediately downstream of the cylinder, initially decreasing before increasing farther downstream. This negative gradient reflects inward lateral diffusion towards the centreline (Oskouie, Tachie & Wang Reference Oskouie, Tachie and Wang2020), indicating lateral energy transfer driven by off-centred bleeding jets. This behaviour arises from the momentum deficit between adjacent jets, with local maxima in velocity located at
$\partial \langle u'v' \rangle /\partial y$
profiles within the merging region is evident. For cylinders with even pore configurations (figures 10
a and 10
c), a negative gradient emerges immediately downstream of the cylinder, initially decreasing before increasing farther downstream. This negative gradient reflects inward lateral diffusion towards the centreline (Oskouie, Tachie & Wang Reference Oskouie, Tachie and Wang2020), indicating lateral energy transfer driven by off-centred bleeding jets. This behaviour arises from the momentum deficit between adjacent jets, with local maxima in velocity located at
![]() $y/d_1=\pm 1/2$
(see figure 8
f). As the jets diverge and subsequently converge in the merging region, inward momentum transfer is initially enhanced and then attenuates, as indicated by the
$y/d_1=\pm 1/2$
(see figure 8
f). As the jets diverge and subsequently converge in the merging region, inward momentum transfer is initially enhanced and then attenuates, as indicated by the
![]() $\partial \langle u'v' \rangle /\partial y$
profiles in figure 10(a) and 10(c). In contrast, for cylinders with odd pore configurations (figure 10
b and 10
d), the lateral gradient is positive immediately behind the cylinder and gradually decreases in magnitude farther downstream. This positive value in
$\partial \langle u'v' \rangle /\partial y$
profiles in figure 10(a) and 10(c). In contrast, for cylinders with odd pore configurations (figure 10
b and 10
d), the lateral gradient is positive immediately behind the cylinder and gradually decreases in magnitude farther downstream. This positive value in
![]() $\partial \langle u'v' \rangle /\partial y$
corresponds to outward momentum diffusion from the central bleeding jet at
$\partial \langle u'v' \rangle /\partial y$
corresponds to outward momentum diffusion from the central bleeding jet at
![]() $y/D=0$
. As the longitudinal bleedings converge along the centreline, this outward momentum transfer weakens progressively.
$y/D=0$
. As the longitudinal bleedings converge along the centreline, this outward momentum transfer weakens progressively.
Following the structural patterns dictated by pore configurations, the impact of permeability on the
![]() $\partial \langle u'v' \rangle /\partial y$
profiles becomes evident when comparing high flow-blockage cases (figure 10
a and 10
b) with low flow-blockage cases (figure 10
c and 10
d). In high flow-blockage cases, a distinct positive hump in
$\partial \langle u'v' \rangle /\partial y$
profiles becomes evident when comparing high flow-blockage cases (figure 10
a and 10
b) with low flow-blockage cases (figure 10
c and 10
d). In high flow-blockage cases, a distinct positive hump in
![]() $\partial \langle u'v' \rangle /\partial y$
appears downstream of a local minimum, followed by a subsequent negative hump farther downstream. These patterns arise from interactions between primary and second recirculation bubbles, as illustrated in figure 6. These low-pressure zones are strongly influenced by permeability (Fang et al. Reference Fang, Yang, Ma and Li2020; Seol et al. Reference Seol, Hong and Kim2023), driving complex energy transfer along the centreline. For even pore configuration (figure 10
a), recirculation bubbles change the direction of lateral momentum diffusion, as evidenced by the sign change in
$\partial \langle u'v' \rangle /\partial y$
appears downstream of a local minimum, followed by a subsequent negative hump farther downstream. These patterns arise from interactions between primary and second recirculation bubbles, as illustrated in figure 6. These low-pressure zones are strongly influenced by permeability (Fang et al. Reference Fang, Yang, Ma and Li2020; Seol et al. Reference Seol, Hong and Kim2023), driving complex energy transfer along the centreline. For even pore configuration (figure 10
a), recirculation bubbles change the direction of lateral momentum diffusion, as evidenced by the sign change in
![]() $\partial \langle u'v' \rangle /\partial y$
at
$\partial \langle u'v' \rangle /\partial y$
at
![]() $x/D \sim 1.5$
. For odd configuration (figure 10
b), reversed flows enhance outward momentum transfer from the central jet, as shown by the rapid increase following a positive local minimum at
$x/D \sim 1.5$
. For odd configuration (figure 10
b), reversed flows enhance outward momentum transfer from the central jet, as shown by the rapid increase following a positive local minimum at
![]() $x/D \sim 1.4$
. Conversely, for low flow-blockage cylinders (figure 10
c and 10
d),
$x/D \sim 1.4$
. Conversely, for low flow-blockage cylinders (figure 10
c and 10
d),
![]() $\partial \langle u'v' \rangle /\partial y$
profiles approach zero farther downstream, corresponding to the development of a steady wake region.
$\partial \langle u'v' \rangle /\partial y$
profiles approach zero farther downstream, corresponding to the development of a steady wake region.
Based on these observations, the extent of the merging region,
![]() $L_{m}$
, can be experimentally quantified according to the structural patterns of lateral diffusion in the bleeding flow behind the porous cylinders. Despite various structural scenarios arising from differences in cylinder permeability and pore configurations, it is consistently observed that the merging region extends up to the combined point, where the bleeding jets coalesce into a single entity, indicating the stoppage of lateral momentum transfer at this point (Oskouie et al. Reference Oskouie, Tachie and Wang2020). In light of this,
$L_{m}$
, can be experimentally quantified according to the structural patterns of lateral diffusion in the bleeding flow behind the porous cylinders. Despite various structural scenarios arising from differences in cylinder permeability and pore configurations, it is consistently observed that the merging region extends up to the combined point, where the bleeding jets coalesce into a single entity, indicating the stoppage of lateral momentum transfer at this point (Oskouie et al. Reference Oskouie, Tachie and Wang2020). In light of this,
![]() $L_{m}$
can be defined as the distance from the trailing edge to the streamwise location where the lateral gradient change diminishes to
$L_{m}$
can be defined as the distance from the trailing edge to the streamwise location where the lateral gradient change diminishes to
![]() $|\partial ^2 \langle u'v' \rangle /\partial x\partial y| \lt 0.1$
for low flow-blockage cylinders, independent of pore configuration. For high flow-blockage cylinders, however,
$|\partial ^2 \langle u'v' \rangle /\partial x\partial y| \lt 0.1$
for low flow-blockage cylinders, independent of pore configuration. For high flow-blockage cylinders, however,
![]() $L_{m}$
for even and odd pore configurations can be defined differently: for the even case, it is the distance from the trailing edge to the point where
$L_{m}$
for even and odd pore configurations can be defined differently: for the even case, it is the distance from the trailing edge to the point where
![]() $\partial \langle u'v' \rangle /\partial y \approx 0$
; for the odd case, it is the distance to the first local minimum in
$\partial \langle u'v' \rangle /\partial y \approx 0$
; for the odd case, it is the distance to the first local minimum in
![]() $\partial \langle u'v' \rangle /\partial y$
as indicated in figure 10(a) and 10(b), respectively.
$\partial \langle u'v' \rangle /\partial y$
as indicated in figure 10(a) and 10(b), respectively.
Consequently, from the analysis of the merging and combined regions and their corresponding structural features shown in figure 10, both permeability and pore configuration are found to play critical roles in shaping the structural patterns within the merging region. In contrast, the downstream flow structures in the combined region are predominantly governed by permeability. This distinction highlights why the lateral diffusion term,
![]() $\partial \langle u'v' \rangle / \partial y$
, used to evaluate
$\partial \langle u'v' \rangle / \partial y$
, used to evaluate
![]() $L_m$
, depends on both the permeability and pore configuration of the porous square cylinders. As the longitudinal bleeding flow transitions through the merging region, losing its individual jet characteristics and evolving into a single, unified jet within the combined region, the flow behaviour becomes increasingly dependent on cylinder permeability. This dependency on permeability is reflected in the trend of
$L_m$
, depends on both the permeability and pore configuration of the porous square cylinders. As the longitudinal bleeding flow transitions through the merging region, losing its individual jet characteristics and evolving into a single, unified jet within the combined region, the flow behaviour becomes increasingly dependent on cylinder permeability. This dependency on permeability is reflected in the trend of
![]() $\partial \langle u'v' \rangle / \partial y$
observed in figure 10. Specifically, for low flow-blockage cases, the
$\partial \langle u'v' \rangle / \partial y$
observed in figure 10. Specifically, for low flow-blockage cases, the
![]() $\partial \langle u'v' \rangle / \partial y$
profile stabilizes and becomes constant farther downstream, indicating a steady wake (Zong & Nepf Reference Zong and Nepf2012). Conversely, high flow-blockage cases exhibit a more complex
$\partial \langle u'v' \rangle / \partial y$
profile stabilizes and becomes constant farther downstream, indicating a steady wake (Zong & Nepf Reference Zong and Nepf2012). Conversely, high flow-blockage cases exhibit a more complex
![]() $\partial \langle u'v' \rangle / \partial y$
profile, even within the combined region, due to the presence of downstream recirculation bubbles (Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). These results emphasize the complex interplay between permeability and pore configuration in lateral momentum transfer and the structural evolution of longitudinal bleeding flows downstream of porous square cylinders.
$\partial \langle u'v' \rangle / \partial y$
profile, even within the combined region, due to the presence of downstream recirculation bubbles (Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). These results emphasize the complex interplay between permeability and pore configuration in lateral momentum transfer and the structural evolution of longitudinal bleeding flows downstream of porous square cylinders.
3.3. Analytical approach for longitudinal bleeding
The results presented in § 3.2 suggest a promising approach for developing an analytical model to estimate the extent of the merging region,
![]() $L_m$
. This approach integrates the momentum equation incorporating the DBF model (Yu et al. Reference Yu, Zeng, Lee, Bai and Low2010; Anirudh & Dhinakaran Reference Anirudh and Dhinakaran2018) with the boundary layer assumption (Bradbury Reference Bradbury1965). The DBF model, embedded within the momentum equation, has been demonstrated to effectively capture flow dynamics both within and around porous media across a range of Reynolds numbers and flow conditions, including bluff body flows to turbulent boundary layers (Kuwata & Suga Reference Kuwata and Suga2017; Rosti, Brandt & Pinelli Reference Rosti, Brandt and Pinelli2018; Chavarin et al. Reference Chavarin, Efstathiou, Vijay and Luhar2020; Seol et al. Reference Seol, Kim and Kim2024).
$L_m$
. This approach integrates the momentum equation incorporating the DBF model (Yu et al. Reference Yu, Zeng, Lee, Bai and Low2010; Anirudh & Dhinakaran Reference Anirudh and Dhinakaran2018) with the boundary layer assumption (Bradbury Reference Bradbury1965). The DBF model, embedded within the momentum equation, has been demonstrated to effectively capture flow dynamics both within and around porous media across a range of Reynolds numbers and flow conditions, including bluff body flows to turbulent boundary layers (Kuwata & Suga Reference Kuwata and Suga2017; Rosti, Brandt & Pinelli Reference Rosti, Brandt and Pinelli2018; Chavarin et al. Reference Chavarin, Efstathiou, Vijay and Luhar2020; Seol et al. Reference Seol, Kim and Kim2024).
In this context, the DBF model characterizes the flow structure within the merging region by accounting for viscous, inertial and porous effects. The boundary layer assumption, on the other hand, provides a robust framework for describing the structural behaviour of bleeding jets in the combined region, where streamwise gradients are negligible compared with lateral gradients. This dual approach establishes a connection between the merging and combined regions, with
![]() $L_m$
defined as the streamwise position of the combined point, which serves as the boundary between these two regions. Consequently, integrating the DBF model with the boundary layer assumption offers a systematic framework for analytically determining the combined point and, in turn, facilitates the development of an analytical model for
$L_m$
defined as the streamwise position of the combined point, which serves as the boundary between these two regions. Consequently, integrating the DBF model with the boundary layer assumption offers a systematic framework for analytically determining the combined point and, in turn, facilitates the development of an analytical model for
![]() $L_m$
.
$L_m$
.
To develop an analytical model for the longitudinal extent of the merging region (
![]() $L_m$
), which corresponds to the streamwise location of the combined point, two separate governing equations are considered for the merging and combined regions:
$L_m$
), which corresponds to the streamwise location of the combined point, two separate governing equations are considered for the merging and combined regions:
 \begin{align} \frac {1}{\varPhi ^2} \left (\langle u \rangle \frac {\partial \langle u \rangle }{\partial x} + \langle v \rangle \frac {\partial \langle u \rangle }{\partial y} \right ) & = -\frac {1}{\rho } \frac {\partial p}{\partial x} + \underbrace {\frac {\mu }{\rho \varPhi } \left (\frac {\partial ^2 \langle u \rangle }{\partial x^2} + \frac {\partial ^2 \langle u \rangle }{\partial y^2} \right )}_{\text{Brinkman term}} - \underbrace {\frac {\mu }{\rho K}\langle u \rangle }_{\text{Darcy term}} \nonumber \\ - \underbrace {\frac {F}{\sqrt {K}} \langle u \rangle \left (\langle u \rangle ^2+ \langle v \rangle ^2 \right )^{1/2}}_{\text{Forchheimer term}}, \\[-12pt] \nonumber \end{align}
\begin{align} \frac {1}{\varPhi ^2} \left (\langle u \rangle \frac {\partial \langle u \rangle }{\partial x} + \langle v \rangle \frac {\partial \langle u \rangle }{\partial y} \right ) & = -\frac {1}{\rho } \frac {\partial p}{\partial x} + \underbrace {\frac {\mu }{\rho \varPhi } \left (\frac {\partial ^2 \langle u \rangle }{\partial x^2} + \frac {\partial ^2 \langle u \rangle }{\partial y^2} \right )}_{\text{Brinkman term}} - \underbrace {\frac {\mu }{\rho K}\langle u \rangle }_{\text{Darcy term}} \nonumber \\ - \underbrace {\frac {F}{\sqrt {K}} \langle u \rangle \left (\langle u \rangle ^2+ \langle v \rangle ^2 \right )^{1/2}}_{\text{Forchheimer term}}, \\[-12pt] \nonumber \end{align}
Equation (3.2) represents the longitudinal momentum equation integrated with the DBF model, where
![]() $p$
is the intrinsic average pressure,
$p$
is the intrinsic average pressure,
![]() $\mu$
is the fluid dynamic viscosity,
$\mu$
is the fluid dynamic viscosity,
![]() $\varPhi$
is the porosity,
$\varPhi$
is the porosity,
![]() $F(=1.75/\sqrt {150\varPhi ^3})$
is the inertial factor (Vafai Reference Vafai1984) and
$F(=1.75/\sqrt {150\varPhi ^3})$
is the inertial factor (Vafai Reference Vafai1984) and
![]() $(u^2+v^2)^{1/2}$
is the resultant velocity. Equation (3.3) is the boundary layer equation, where
$(u^2+v^2)^{1/2}$
is the resultant velocity. Equation (3.3) is the boundary layer equation, where
![]() $u'$
and
$u'$
and
![]() $v'$
denote the fluctuating velocity components in the longitudinal and lateral directions, respectively.
$v'$
denote the fluctuating velocity components in the longitudinal and lateral directions, respectively.
In the momentum equation, the Brinkman term (also known as the Reynolds stress term) is considered negligible compared with the remaining terms within the merging region, as a part of the downstream flow adjustment (Rominger & Nepf Reference Rominger and Nepf2011). Therefore, it is omitted from the governing equation. Additionally, under high-Reynolds-number conditions, the Darcy term is small compared with the Forchheimer term and can also be neglected in (3.2) (Seol et al. Reference Seol, Kim and Kim2024).
For both (3.2) and (3.3), the analysis focuses along the lateral centre,
![]() $y/D=0$
, reducing the problem to a one-dimensional approach since the combined point resides along this axis. We assume that
$y/D=0$
, reducing the problem to a one-dimensional approach since the combined point resides along this axis. We assume that
![]() $\langle u \rangle = \langle u \rangle _{y/D=0} = U_o$
,
$\langle u \rangle = \langle u \rangle _{y/D=0} = U_o$
,
![]() $\langle v \rangle = \langle v \rangle _{y/D=0} \approx 0$
and
$\langle v \rangle = \langle v \rangle _{y/D=0} \approx 0$
and
![]() $\partial \langle u'v' \rangle /\partial y = \partial \langle u'v' \rangle _{y/D=0}/\partial y$
. Furthermore, the pressure gradient in (3.2) is scaled as
$\partial \langle u'v' \rangle /\partial y = \partial \langle u'v' \rangle _{y/D=0}/\partial y$
. Furthermore, the pressure gradient in (3.2) is scaled as
![]() $\partial p/\partial x = \Delta p/D$
, reflecting the pressure difference between the upstream and downstream regions of the porous square cylinders. Based on these considerations, the governing equations simplify to
$\partial p/\partial x = \Delta p/D$
, reflecting the pressure difference between the upstream and downstream regions of the porous square cylinders. Based on these considerations, the governing equations simplify to
 \begin{align} U_o \frac {\partial U_o}{\partial x} \sim -\frac {\partial \langle u'v' \rangle }{\partial y}\bigg \rvert _{y/D=0} \\[-2pt] \nonumber \end{align}.
\begin{align} U_o \frac {\partial U_o}{\partial x} \sim -\frac {\partial \langle u'v' \rangle }{\partial y}\bigg \rvert _{y/D=0} \\[-2pt] \nonumber \end{align}.
It is worth noting that in the context of canonical turbulent twin jets, the combined point is often identified at the location where the mean centreline velocity,
![]() $U_o$
, reaches its maximum (Nasr & Lai Reference Nasr and Lai1997; Durve et al. Reference Durve, Patwardhan, Banarjee, Padmakumar and Vaidyanathan2012). However, this approach is not suitable for the present study due to the distinct structural characteristics of longitudinal bleedings, which vary with pore configuration. Instead, (3.5) indicates that the local maximum in
$U_o$
, reaches its maximum (Nasr & Lai Reference Nasr and Lai1997; Durve et al. Reference Durve, Patwardhan, Banarjee, Padmakumar and Vaidyanathan2012). However, this approach is not suitable for the present study due to the distinct structural characteristics of longitudinal bleedings, which vary with pore configuration. Instead, (3.5) indicates that the local maximum in
![]() $U_o$
corresponds to
$U_o$
corresponds to
![]() $\partial U_o/\partial x=0$
, and thus to
$\partial U_o/\partial x=0$
, and thus to
![]() $\partial \langle u'v' \rangle /\partial y\rvert _{y/D=0}$
. This relationship provides a more fundamental and robust method for determining the combined point, based on the structural characteristics of lateral diffusion, and thereby facilitates the determination of
$\partial \langle u'v' \rangle /\partial y\rvert _{y/D=0}$
. This relationship provides a more fundamental and robust method for determining the combined point, based on the structural characteristics of lateral diffusion, and thereby facilitates the determination of
![]() $L_m$
.
$L_m$
.
For the current flow configuration, it is also important to emphasize that the primary contribution to cylinder drag arises from pressure drag rather than friction drag. This observation allows the pressure term in (3.4) to be reformulated as
![]() $\Delta p \approx \rho C_{\kern-1pt D} U_e^2$
, based on the explicit relationship between the cylinder drag and the pressure drop across the structured porous media (Seol et al. Reference Seol, Hong and Kim2023). Substituting this expression into (3.4), the equation can be rewritten as
$\Delta p \approx \rho C_{\kern-1pt D} U_e^2$
, based on the explicit relationship between the cylinder drag and the pressure drop across the structured porous media (Seol et al. Reference Seol, Hong and Kim2023). Substituting this expression into (3.4), the equation can be rewritten as
This reformulation of the momentum equation reduces it to a first-order ordinary differential equation, which can be solved explicitly using separation of variables and integration by substitution over the range
![]() $D \leqslant x \leqslant L_m + D$
. The resulting solution is expressed as
$D \leqslant x \leqslant L_m + D$
. The resulting solution is expressed as
 \begin{align} L_m \sim \frac {\sqrt {K}}{F\varPhi ^2} \ln {\left [ \frac {\varPhi ^2 \big\{C_{\kern-1pt D} U_e^2/D + F U_o^2(D)/\sqrt {K} \big\}}{\varPhi ^2 \big\{C_{\kern-1pt D} U_e^2/D + F U_o^2(L_m+D)/\sqrt {K} \big\}} \right ]} .\end{align}
\begin{align} L_m \sim \frac {\sqrt {K}}{F\varPhi ^2} \ln {\left [ \frac {\varPhi ^2 \big\{C_{\kern-1pt D} U_e^2/D + F U_o^2(D)/\sqrt {K} \big\}}{\varPhi ^2 \big\{C_{\kern-1pt D} U_e^2/D + F U_o^2(L_m+D)/\sqrt {K} \big\}} \right ]} .\end{align}
To further evaluate
![]() $L_m$
, appropriate boundary conditions must be applied at
$L_m$
, appropriate boundary conditions must be applied at
![]() $x = D$
and
$x = D$
and
![]() $x = L_m+D$
, corresponding to the cylinder trailing edge and the streamwise position of the combined point, respectively. At
$x = L_m+D$
, corresponding to the cylinder trailing edge and the streamwise position of the combined point, respectively. At
![]() $x=D$
, the centreline velocity,
$x=D$
, the centreline velocity,
![]() $U_o(x=D)$
, represents the exit longitudinal velocity,
$U_o(x=D)$
, represents the exit longitudinal velocity,
![]() $U_{o, \textit{exit}}$
, immediately behind the porous medium. In general, this exit velocity is substantially smaller than
$U_{o, \textit{exit}}$
, immediately behind the porous medium. In general, this exit velocity is substantially smaller than
![]() $U_e$
, leading to the approximation
$U_e$
, leading to the approximation
![]() $U_{o, \textit{exit}}^2/U_e^2 \approx 0$
, consistent with the findings of Zong & Nepf (Reference Zong and Nepf2012) and Nicolai et al. (Reference Nicolai, Taddei, Manes and Ganapathisubramani2020). At
$U_{o, \textit{exit}}^2/U_e^2 \approx 0$
, consistent with the findings of Zong & Nepf (Reference Zong and Nepf2012) and Nicolai et al. (Reference Nicolai, Taddei, Manes and Ganapathisubramani2020). At
![]() $x=L_m+D$
, the combined point characterizes the boundary between the merging and combined regions. At this position, the momentum (3.7) transitions to being equivalent to the boundary layer (3.5), as described by
$x=L_m+D$
, the combined point characterizes the boundary between the merging and combined regions. At this position, the momentum (3.7) transitions to being equivalent to the boundary layer (3.5), as described by
 \begin{align} U_o(L_m+D) \frac {\partial U_o(L_m+D)}{\partial x} \sim -\varPhi ^2 \left [ \frac {C_{\kern-1pt D} U_e^2}{D} + \frac {F}{\sqrt {K}}U_o^2(L_m+D) \right ] \nonumber \\ = -\frac {\partial \langle u'v' \rangle (L_m+D,0)}{\partial y} .\end{align}
\begin{align} U_o(L_m+D) \frac {\partial U_o(L_m+D)}{\partial x} \sim -\varPhi ^2 \left [ \frac {C_{\kern-1pt D} U_e^2}{D} + \frac {F}{\sqrt {K}}U_o^2(L_m+D) \right ] \nonumber \\ = -\frac {\partial \langle u'v' \rangle (L_m+D,0)}{\partial y} .\end{align}
In this study, the lateral diffusion term,
![]() $\partial \langle u'v' \rangle /\partial y$
, at the combined point is empirically determined, as illustrated in figure 10. It is observed that for most porous cylinder cases, the magnitude of this term spans the range
$\partial \langle u'v' \rangle /\partial y$
, at the combined point is empirically determined, as illustrated in figure 10. It is observed that for most porous cylinder cases, the magnitude of this term spans the range
![]() $0 \lt \partial \langle u'v' \rangle /\partial y \lt 100$
, with typical values around
$0 \lt \partial \langle u'v' \rangle /\partial y \lt 100$
, with typical values around
![]() $\partial \langle u'v' \rangle /\partial y \approx O(10)$
at the combined point. This experimental observation allows for a simplification in the present analytical model, setting
$\partial \langle u'v' \rangle /\partial y \approx O(10)$
at the combined point. This experimental observation allows for a simplification in the present analytical model, setting
![]() $\varPhi ^2 [ ({C_{\kern-1pt D} U_e^2}/{D} )+ ({F}/{\sqrt {K}})U_o^2(L_m+D) ] = \partial \langle u'v' \rangle /\partial y \approx 10$
. By substituting this result into (3.8), (3.7) can now be further simplified to
$\varPhi ^2 [ ({C_{\kern-1pt D} U_e^2}/{D} )+ ({F}/{\sqrt {K}})U_o^2(L_m+D) ] = \partial \langle u'v' \rangle /\partial y \approx 10$
. By substituting this result into (3.8), (3.7) can now be further simplified to
To finalize the analytical model for the longitudinal extent of the merging region,
![]() $L_m$
, it is essential to determine the drag coefficient,
$L_m$
, it is essential to determine the drag coefficient,
![]() $C_{\kern-1pt D}$
, of the porous cylinder. In general, the drag coefficient of a 2-D porous cylinder is inversely correlated with the non-dimensional permeability,
$C_{\kern-1pt D}$
, of the porous cylinder. In general, the drag coefficient of a 2-D porous cylinder is inversely correlated with the non-dimensional permeability,
![]() $ \textit{Da} $
(Cummins et al. Reference Cummins, Viola, Mastropaolo and Nakayama2017; Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). However, recent experimental observations by Seol et al. (Reference Seol, Kim and Kim2024) have shown that
$ \textit{Da} $
(Cummins et al. Reference Cummins, Viola, Mastropaolo and Nakayama2017; Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). However, recent experimental observations by Seol et al. (Reference Seol, Kim and Kim2024) have shown that
![]() $C_{\kern-1pt D}$
can be more effectively characterized by the non-dimensional flow-blockage factor,
$C_{\kern-1pt D}$
can be more effectively characterized by the non-dimensional flow-blockage factor,
![]() $1/(2\sqrt {Da})$
, which represents the ratio of two key length scales: the cylinder half-width,
$1/(2\sqrt {Da})$
, which represents the ratio of two key length scales: the cylinder half-width,
![]() $D/2$
, and the drag length scale,
$D/2$
, and the drag length scale,
![]() $\sqrt {K}$
. This finding aligns well with earlier studies on flow past 2-D porous bluff bodies (Chen et al. Reference Chen, Ortiz, Zong and Nepf2012; Zong & Nepf Reference Zong and Nepf2012). Seol et al. (Reference Seol, Kim and Kim2024) explicitly demonstrated that
$\sqrt {K}$
. This finding aligns well with earlier studies on flow past 2-D porous bluff bodies (Chen et al. Reference Chen, Ortiz, Zong and Nepf2012; Zong & Nepf Reference Zong and Nepf2012). Seol et al. (Reference Seol, Kim and Kim2024) explicitly demonstrated that
![]() $C_{\kern-1pt D}$
is logarithmically proportional to
$C_{\kern-1pt D}$
is logarithmically proportional to
![]() $1/(2\sqrt {Da})$
across a broad range of cylinder permeabilities. This explicit relationship allows the drag coefficient to be expressed as
$1/(2\sqrt {Da})$
across a broad range of cylinder permeabilities. This explicit relationship allows the drag coefficient to be expressed as
![]() $C_{\kern-1pt D} \sim \log (1/(2\sqrt {Da}))$
for the present analysis. Additionally, the inertial factor,
$C_{\kern-1pt D} \sim \log (1/(2\sqrt {Da}))$
for the present analysis. Additionally, the inertial factor,
![]() $F$
, in (3.9) is approximated as
$F$
, in (3.9) is approximated as
![]() $F=1.75/\sqrt {150\varPhi ^3} \approx 1/(7\sqrt {\varPhi ^3})$
(Vafai Reference Vafai1984). Substituting these relationships into (3.9), the final expression for
$F=1.75/\sqrt {150\varPhi ^3} \approx 1/(7\sqrt {\varPhi ^3})$
(Vafai Reference Vafai1984). Substituting these relationships into (3.9), the final expression for
![]() $L_m$
is given by
$L_m$
is given by

Figure 11. Variation of the merging region length,
![]() $L_m$
, as a function of
$L_m$
, as a function of
![]() $ \textit{Da} $
. Here,
$ \textit{Da} $
. Here,
![]() $L_{m,\textit{fit}}$
is obtained from the analytical model (3.10), while
$L_{m,\textit{fit}}$
is obtained from the analytical model (3.10), while
![]() $L_{m,exp}$
is determined experimentally. The blue shaded area represents the 95
$L_{m,exp}$
is determined experimentally. The blue shaded area represents the 95
![]() $\%$
confidence interval for (3.10). Panel (a) highlights the influence of porosity, considering values of
$\%$
confidence interval for (3.10). Panel (a) highlights the influence of porosity, considering values of
![]() $\varPhi =0.7$
, 0.8 and 0.9. Panel (b) investigates the effect of the lateral diffusion term,
$\varPhi =0.7$
, 0.8 and 0.9. Panel (b) investigates the effect of the lateral diffusion term,
![]() $\partial \langle u'v' \rangle /\partial y$
, at the combined point, with values of 1, 10 and 100 used in (3.10).
$\partial \langle u'v' \rangle /\partial y$
, at the combined point, with values of 1, 10 and 100 used in (3.10).
The longitudinal extent of the merging region,
![]() $L_m$
, normalized by the cylinder width,
$L_m$
, normalized by the cylinder width,
![]() $D$
, is presented in figure 11 as a function of
$D$
, is presented in figure 11 as a function of
![]() $ \textit{Da} $
using both the analytical model (3.10) and experimental data. In both figure 11(a) and 11(b), the black solid line represents
$ \textit{Da} $
using both the analytical model (3.10) and experimental data. In both figure 11(a) and 11(b), the black solid line represents
![]() $L_{m,\textit{fit}}$
, which is calculated from the analytical model (3.10). For consistency, the porosity is set to
$L_{m,\textit{fit}}$
, which is calculated from the analytical model (3.10). For consistency, the porosity is set to
![]() $\varPhi =0.8$
in (3.10), reflecting the midrange value of
$\varPhi =0.8$
in (3.10), reflecting the midrange value of
![]() $\varPhi$
for the porous cylinders used in this study. The blue shaded region denotes the 95
$\varPhi$
for the porous cylinders used in this study. The blue shaded region denotes the 95
![]() $\,\%$
confidence interval for (3.10). Using this reference line from the analytical model, the effect of porosity (
$\,\%$
confidence interval for (3.10). Using this reference line from the analytical model, the effect of porosity (
![]() $\varPhi$
) and the lateral diffusion (
$\varPhi$
) and the lateral diffusion (
![]() $\partial \langle u'v'\rangle /\partial y$
) at the combined point are examined in figure 11(a) and 11(b), respectively.
$\partial \langle u'v'\rangle /\partial y$
) at the combined point are examined in figure 11(a) and 11(b), respectively.
In figure 11(a),
![]() $\varPhi =0.7$
and
$\varPhi =0.7$
and
![]() $\varPhi =0.9$
are applied to (3.10) to define the upper and lower bounds, represented by the red dashed and dashed–dot lines. In contrast, figure 11(b) explores the variability in
$\varPhi =0.9$
are applied to (3.10) to define the upper and lower bounds, represented by the red dashed and dashed–dot lines. In contrast, figure 11(b) explores the variability in
![]() $\partial \langle u'v' \rangle /\partial y$
, where values of 1 and 100 are substituted for the nominal value of 10 in the denominator of (3.10), reflecting the observed experimental fluctuation range. These substitutions result in the red dashed line (upper boundary,
$\partial \langle u'v' \rangle /\partial y$
, where values of 1 and 100 are substituted for the nominal value of 10 in the denominator of (3.10), reflecting the observed experimental fluctuation range. These substitutions result in the red dashed line (upper boundary,
![]() $\partial \langle u'v' \rangle /\partial y=1$
) and the red dashed–dot line (lower boundary,
$\partial \langle u'v' \rangle /\partial y=1$
) and the red dashed–dot line (lower boundary,
![]() $\partial \langle u'v'\rangle /\partial y=100$
) for the analytical model in figure 11(b). Experimental measurements of the merging region length,
$\partial \langle u'v'\rangle /\partial y=100$
) for the analytical model in figure 11(b). Experimental measurements of the merging region length,
![]() $L_{m,exp}$
, are included in both figure 11(a) and 11(b) for comparison. Specifically,
$L_{m,exp}$
, are included in both figure 11(a) and 11(b) for comparison. Specifically,
![]() $L_{m,exp}$
is defined as the distance from the cylinder trailing edge to the combined point, which is identified based on the lateral diffusion characteristics at
$L_{m,exp}$
is defined as the distance from the cylinder trailing edge to the combined point, which is identified based on the lateral diffusion characteristics at
![]() $y/D=0$
, as influenced by flow blockage and pore configurations, as illustrated in figure 10.
$y/D=0$
, as influenced by flow blockage and pore configurations, as illustrated in figure 10.
Figure 11 demonstrates strong agreement between the experimental data and the analytical model (black solid line) across the measured range of
![]() $ \textit{Da} $
, revealing a log–log relationship between
$ \textit{Da} $
, revealing a log–log relationship between
![]() $L_m$
and
$L_m$
and
![]() $ \textit{Da} $
. Notably,
$ \textit{Da} $
. Notably,
![]() $L_m$
increases systematically with increasing
$L_m$
increases systematically with increasing
![]() $ \textit{Da} $
, indicating that the combined point shifts farther downstream as the momentum of the bleeding flow increases with
$ \textit{Da} $
, indicating that the combined point shifts farther downstream as the momentum of the bleeding flow increases with
![]() $ \textit{Da} $
. This trend is consistent with the past observations related to structural modification in the downstream flow. Examples include the relocation of the downstream recirculation bubble with increasing longitudinal bleeding momentum (Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018) and the corresponding enhancement of flow adjustment length (Seol et al. Reference Seol, Kim and Kim2024). Since longitudinal bleeding momentum is inherently linked to the permeability of the porous cylinder, permeability emerges as a critical parameter in determining the extent of the merging region and the resulting flow structures. Although porosity (
$ \textit{Da} $
. This trend is consistent with the past observations related to structural modification in the downstream flow. Examples include the relocation of the downstream recirculation bubble with increasing longitudinal bleeding momentum (Ledda et al. Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018) and the corresponding enhancement of flow adjustment length (Seol et al. Reference Seol, Kim and Kim2024). Since longitudinal bleeding momentum is inherently linked to the permeability of the porous cylinder, permeability emerges as a critical parameter in determining the extent of the merging region and the resulting flow structures. Although porosity (
![]() $\varPhi$
) appears in (3.10) and may influence
$\varPhi$
) appears in (3.10) and may influence
![]() $L_m$
, figure 11(a) reveals that the effect of permeability dominates over porosity. This result is consistent with Seol et al. (Reference Seol, Kim and Kim2024), which emphasized the crucial role of permeability in controlling wake dynamics behind porous square cylinders.
$L_m$
, figure 11(a) reveals that the effect of permeability dominates over porosity. This result is consistent with Seol et al. (Reference Seol, Kim and Kim2024), which emphasized the crucial role of permeability in controlling wake dynamics behind porous square cylinders.
Some experimental data points deviate from the model predictions (black solid line), primarily due to underestimation or overestimation of the lateral diffusion term,
![]() $\partial \langle u'v'\rangle /\partial y$
, at the combined point. As shown in figure 11(b), varying this term by two orders of magnitude introduces upper and lower prediction bounds, illustrating its sensitivity. This result suggests that the magnitude of
$\partial \langle u'v'\rangle /\partial y$
, at the combined point. As shown in figure 11(b), varying this term by two orders of magnitude introduces upper and lower prediction bounds, illustrating its sensitivity. This result suggests that the magnitude of
![]() $\partial \langle u'v' \rangle /\partial y$
plays a role in determining
$\partial \langle u'v' \rangle /\partial y$
plays a role in determining
![]() $L_m$
. Nonetheless, all data points in figure 11(b) fall within the predicted boundaries, supporting the robustness of the proposed model and its applicability to the experimental results.
$L_m$
. Nonetheless, all data points in figure 11(b) fall within the predicted boundaries, supporting the robustness of the proposed model and its applicability to the experimental results.
These findings suggest that the DBF model, incorporated into the momentum equation, effectively captures the volume-averaged resistance of the porous medium and its impact on the near-wake region. It is important to note that the DBF model used herein is not intended to resolve porescale details near the fluid-porous interface. Instead, it serves as a macroscale closure, consistent with prior studies that have shown its validity in turbulent flows (Seol et al. Reference Seol, Kim and Kim2024; Hao & García-Mayoral Reference Hao and García-Mayoral2025).
While figure 11 supports the validity of the analytical model, it is equally important to clarify that the jet-based interpretation adopted in this study is not proposed as a replacement for classical porous-media models such as the DBF equation (Yu et al. Reference Yu, Zeng, Lee, Bai and Low2010), particularly in regimes where strong scale separation exists and homogenization theory is valid (Zampogna & Bottaro Reference Zampogna and Bottaro2016). Our objective is not to claim the superiority of the jet-based framework, but to highlight its complementary role, especially in high-permeability cases where scale separation weakens and porescale effects become non-negligible.
In this context, figure 11 illustrates that the proposed analytical model plays as a bridge between pore-resolved jet dynamics and volume-averaged porous media models. It combines the DBF model for near-wake momentum loss with a boundary-layer approximation in the far wake. As a result, the present framework should not be viewed as a purely jet-based model, but rather as a hybrid approach that accounts for both macroscale permeability effects and lateral momentum diffusion in predicting the merging point,
![]() $L_m$
, in high-Reynolds-number flows past porous bluff bodies.
$L_m$
, in high-Reynolds-number flows past porous bluff bodies.
Lastly, it is worth noting that the jet-merging framework developed here is intended for porous bodies with periodic, isotropic lattices in a high-
![]() $ \textit{Re} $
external flow, in which coherent porescale jets emerge at the trailing edge. Its validity is bounded by the scale separation
$ \textit{Re} $
external flow, in which coherent porescale jets emerge at the trailing edge. Its validity is bounded by the scale separation
![]() $\epsilon =d_1/D$
(Zampogna & Bottaro Reference Zampogna and Bottaro2016) and the permeability
$\epsilon =d_1/D$
(Zampogna & Bottaro Reference Zampogna and Bottaro2016) and the permeability
![]() $ \textit{Da} $
: in the present configurations
$ \textit{Da} $
: in the present configurations
![]() $0.05 \lt \epsilon \lt 0.25$
and
$0.05 \lt \epsilon \lt 0.25$
and
![]() $2.4\times 10^{-5} \lt Da \lt 2.9\times 10^{-3}$
. In this regime, discrete jets are macroscopically resolvable when
$2.4\times 10^{-5} \lt Da \lt 2.9\times 10^{-3}$
. In this regime, discrete jets are macroscopically resolvable when
![]() $\epsilon \gt 0.1$
and interact to form a merged structure downstream. In contrast, for
$\epsilon \gt 0.1$
and interact to form a merged structure downstream. In contrast, for
![]() $\epsilon \lt 0.1$
the outflow becomes effectively homogenized and can be adequately described by the DBF formulation alone. The interpretation presumes geometric regularity at the trailing edge (even/odd pore configurations corresponding to dual/triple-jet analogies) and is not claimed to extend to random foams or strongly anisotropic/fibrous media. At a qualitative level, increasing
$\epsilon \lt 0.1$
the outflow becomes effectively homogenized and can be adequately described by the DBF formulation alone. The interpretation presumes geometric regularity at the trailing edge (even/odd pore configurations corresponding to dual/triple-jet analogies) and is not claimed to extend to random foams or strongly anisotropic/fibrous media. At a qualitative level, increasing
![]() $ \textit{Re} $
is likely to enhance shear-layer inertia and tends to increase the merging length (
$ \textit{Re} $
is likely to enhance shear-layer inertia and tends to increase the merging length (
![]() $L_m$
), while lower
$L_m$
), while lower
![]() $ \textit{Re} $
may promote homogenization and weaken the plane-jet analogy.
$ \textit{Re} $
may promote homogenization and weaken the plane-jet analogy.
4. Summary
In this study, we investigated the bleeding flow characteristics and the resulting wake structures induced by isotropic porous square cylinders at high Reynolds numbers (
![]() $ \textit{Re} \sim O(10^4)$
). By utilizing a novel decoupling approach to independently vary permeability (
$ \textit{Re} \sim O(10^4)$
). By utilizing a novel decoupling approach to independently vary permeability (
![]() $K$
) while maintaining constant porosity (
$K$
) while maintaining constant porosity (
![]() $\varPhi$
), isotropic porous cylinders spanning two decades of Darcy number (
$\varPhi$
), isotropic porous cylinders spanning two decades of Darcy number (
![]() $2.4\times 10^{-5} \lt Da \lt 2.9\times 10^{-3}$
) were fabricated using high-resolution 3-D printing. This design allowed for a detailed examination of the individual role of permeability and pore configuration in shaping downstream flow structures.
$2.4\times 10^{-5} \lt Da \lt 2.9\times 10^{-3}$
) were fabricated using high-resolution 3-D printing. This design allowed for a detailed examination of the individual role of permeability and pore configuration in shaping downstream flow structures.
High-resolution PIV measurements, performed on these porous square cylinders, revealed a strong dependence of wake structures on permeability, demonstrating an explicit log–linear relationship. The transition of longitudinal bleeding jets from combined to discrete structures, as permeability increases, significantly alters downstream wake topology. These findings reaffirm the critical role of bleeding flows in shaping wake structures downstream of porous square cylinders, consistent with previous works (Taddei et al. Reference Taddei, Manes and Ganapathisubramani2016; Nicolai et al. Reference Nicolai, Taddei, Manes and Ganapathisubramani2020).
The structural characteristics of longitudinal bleeding flows were further interpreted through an analogy with multiple plane turbulent jets (Miller & Comings Reference Miller and Comings1960; Zhao & Wang Reference Zhao and Wang2018). Despite the influence of strong external shear layers, the evolution of longitudinal bleeding jets downstream of the porous cylinder was found to exhibit behaviours similar to those of interacting parallel plane jets. Based on this analogy, we classified the downstream flow into three distinct regions: (i) a merging region, where individual jets interact and merge, leading to intense mixing; (ii) a combined region, characterized by a unified jet interacting with cylinder-induced shear layers; (iii) a wake region, where the velocity recovery dominates.
The merging and combined regions were characterized using the mean longitudinal velocity
![]() $\langle u \rangle$
and the lateral diffusion
$\langle u \rangle$
and the lateral diffusion
![]() $\partial \langle u'v' \rangle / \partial y$
. Our results revealed distinct governing mechanisms for each region. In the merging region, both permeability and pore configuration play critical roles in defining the structural pattern of longitudinal bleeding. In contrast, the combined region is predominantly influenced by permeability. This distinction highlights the complex interplay between porescale geometry and macroscopic permeability in lateral momentum transfer and flow evolution. The characteristic lengths of the merging and combined regions,
$\partial \langle u'v' \rangle / \partial y$
. Our results revealed distinct governing mechanisms for each region. In the merging region, both permeability and pore configuration play critical roles in defining the structural pattern of longitudinal bleeding. In contrast, the combined region is predominantly influenced by permeability. This distinction highlights the complex interplay between porescale geometry and macroscopic permeability in lateral momentum transfer and flow evolution. The characteristic lengths of the merging and combined regions,
![]() $L_m$
and
$L_m$
and
![]() $L_c$
, were quantified based on these observations.
$L_c$
, were quantified based on these observations.
To describe the flow evolution in each region, we applied different governing frameworks. In the merging region, the DBF model (Yu et al. Reference Yu, Zeng, Lee, Bai and Low2010; Anirudh & Dhinakaran Reference Anirudh and Dhinakaran2018) was incorporated into the momentum equation to represent the macroscopic resistance effect in and around porous media. For the combined region, the boundary-layer approximation (Bradbury Reference Bradbury1965) was adopted, based on the assumption that streamwise gradients are small relative to lateral gradients (Nicolai et al. Reference Nicolai, Taddei, Manes and Ganapathisubramani2020). In this context, the merging point, located at
![]() $x=L_m$
, serves as the transition between these two regimes.
$x=L_m$
, serves as the transition between these two regimes.
Building on this dual framework, we developed an analytical model to predict the merging length
![]() $L_m$
by integrating the DBF model with the boundary-layer assumption. The model captures the key dynamics of bleeding flow development and provides accurate predictions of
$L_m$
by integrating the DBF model with the boundary-layer assumption. The model captures the key dynamics of bleeding flow development and provides accurate predictions of
![]() $L_m$
, in good agreement with experimental data. Therefore, this study advances our understanding of wake dynamics behind porous bluff bodies, revealing that pore configuration and its associated permeability are critical in governing wake behaviour. These findings offer a predictive framework for permeability-driven flow control, with broad implications including drag reduction, heat transfer optimization and flow management involving porous media.
$L_m$
, in good agreement with experimental data. Therefore, this study advances our understanding of wake dynamics behind porous bluff bodies, revealing that pore configuration and its associated permeability are critical in governing wake behaviour. These findings offer a predictive framework for permeability-driven flow control, with broad implications including drag reduction, heat transfer optimization and flow management involving porous media.
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (RS-2025-23524733, RS-2024-00406514).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Uncertainty analysis for two primary experimental measurements
Here, we present the uncertainty analysis associated with two primary experimental activities: (i) the determination of permeability for structured porous media and (ii) the characterization of the associated wake structures via PIV measurements around porous square cylinders.
First, we performed an uncertainty analysis of the measured permeability using Moffat’s error propagation method (Moffat Reference Moffat1988; Ifti et al. Reference Ifti, Hermann, McGilvray, Larrimbe, Hedgecock and Vandeperre2022), which is defined as
 \begin{align} \delta X = \sqrt {\sum _{i=1}^{N} \left ( \frac {\partial X}{\partial Y_i} \delta Y_i \right )^2 }, \end{align}
\begin{align} \delta X = \sqrt {\sum _{i=1}^{N} \left ( \frac {\partial X}{\partial Y_i} \delta Y_i \right )^2 }, \end{align}
where
![]() $X=X(Y_1,Y_2,\ldots ,Y_N)$
is a variable derived from experimental measurements
$X=X(Y_1,Y_2,\ldots ,Y_N)$
is a variable derived from experimental measurements
![]() $Y_i$
, and
$Y_i$
, and
![]() $\delta Y_i$
are the associated uncertainties based on the manufacturer specifications (see table 2). In this context,
$\delta Y_i$
are the associated uncertainties based on the manufacturer specifications (see table 2). In this context,
![]() $X$
denotes the permeability
$X$
denotes the permeability
![]() $K$
, and
$K$
, and
![]() $Y$
corresponds to the pressure drop
$Y$
corresponds to the pressure drop
![]() $\Delta{\kern-1pt}P$
across the porous medium.
$\Delta{\kern-1pt}P$
across the porous medium.
Table 2. Apparatus uncertainties (FSO, full-scale output).

For compressible gas flow through a porous material, the pressure drop is given by
where
![]() $P_{\textit{in}}$
and
$P_{\textit{in}}$
and
![]() $P_{\textit{out}}$
represent the absolute inlet and outlet pressures, respectively, measured using high-resolution pressure transducer (FCO560, Furness Controls) in a circular pipe test section. The thickness of the porous disk along the flow direction is denoted by
$P_{\textit{out}}$
represent the absolute inlet and outlet pressures, respectively, measured using high-resolution pressure transducer (FCO560, Furness Controls) in a circular pipe test section. The thickness of the porous disk along the flow direction is denoted by
![]() $L$
. Permeability was then estimated using the Forchheimer equation, which captures the nonlinear relationship between pressure drop and superficial velocity
$L$
. Permeability was then estimated using the Forchheimer equation, which captures the nonlinear relationship between pressure drop and superficial velocity
![]() $U_s$
(Dukhan & Minjeur Reference Dukhan and Minjeur2011),
$U_s$
(Dukhan & Minjeur Reference Dukhan and Minjeur2011),
where
![]() $\mu$
is the dynamic viscosity of the working fluid,
$\mu$
is the dynamic viscosity of the working fluid,
![]() $\rho$
is its density and
$\rho$
is its density and
![]() $C$
is an empirical form drag coefficient. For the purpose of the uncertainty analysis, we focused on the Darcian regime in which the permeability is expressed as
$C$
is an empirical form drag coefficient. For the purpose of the uncertainty analysis, we focused on the Darcian regime in which the permeability is expressed as
![]() $K=(\mu U_s L)/\Delta P$
.
$K=(\mu U_s L)/\Delta P$
.
Accordingly, the propagated uncertainty in permeability is given by
 \begin{align} \delta K = \sqrt {\left ( \frac {\partial K}{\partial P_{\textit{in}}} \delta P \right )^2 + \left ( \frac {\partial K}{\partial P_{\textit{out}}} \delta P \right )^2}, \end{align}
\begin{align} \delta K = \sqrt {\left ( \frac {\partial K}{\partial P_{\textit{in}}} \delta P \right )^2 + \left ( \frac {\partial K}{\partial P_{\textit{out}}} \delta P \right )^2}, \end{align}
where
![]() $\delta P = ((B\times A)^2+(B \times C)^2 )^{0.5}$
accounts for the full-scale output and reading errors from the pressure measurement system (refer to table 2).
$\delta P = ((B\times A)^2+(B \times C)^2 )^{0.5}$
accounts for the full-scale output and reading errors from the pressure measurement system (refer to table 2).
Figure 12(a) shows the variation in permeability
![]() $K$
with error bars as a function of superficial velocity
$K$
with error bars as a function of superficial velocity
![]() $U_s$
for selected cases (A1–A5). As seen in this figure, the uncertainty in permeability increases significantly as
$U_s$
for selected cases (A1–A5). As seen in this figure, the uncertainty in permeability increases significantly as
![]() $U_s$
approaches zero. This is because smaller velocity conditions produce lower pressure differentials across the porous medium, making the fixed transducer error relatively more significant. Furthermore, media with higher permeability (e.g. case A5) exhibit larger uncertainty due to the inherently smaller pressure drop at a given flow rate. These trends indicate that the uncertainty in permeability is inherently linked to its magnitude.
$U_s$
approaches zero. This is because smaller velocity conditions produce lower pressure differentials across the porous medium, making the fixed transducer error relatively more significant. Furthermore, media with higher permeability (e.g. case A5) exhibit larger uncertainty due to the inherently smaller pressure drop at a given flow rate. These trends indicate that the uncertainty in permeability is inherently linked to its magnitude.
To summarize the total uncertainty for each case, we computed the root-mean-square of pointwise uncertainty values across all
![]() $U_s$
. These updated values have been included in table 1. Figure 12(b) presents the relative uncertainty
$U_s$
. These updated values have been included in table 1. Figure 12(b) presents the relative uncertainty
![]() $\delta K/K$
as a function of permeability
$\delta K/K$
as a function of permeability
![]() $K$
. A clear increasing trend is observed: more permeable media exhibit greater uncertainty due to the reduced pressure drop for a given flow rate. In particular, this trend is approximately log–linear, which is consistent with previously reported permeability-flow relationships (see figure 4
b and 9
b). This result supports the robustness of the uncertainty analysis and may also serve as a useful diagnostic feature when assessing aerodynamic performance, flow structure and experimental resolution in porous media flows.
$K$
. A clear increasing trend is observed: more permeable media exhibit greater uncertainty due to the reduced pressure drop for a given flow rate. In particular, this trend is approximately log–linear, which is consistent with previously reported permeability-flow relationships (see figure 4
b and 9
b). This result supports the robustness of the uncertainty analysis and may also serve as a useful diagnostic feature when assessing aerodynamic performance, flow structure and experimental resolution in porous media flows.

Figure 12. (a) Variation in permeability
![]() $K$
with error bars for each data point as a function of the corresponding superficial velocity
$K$
with error bars for each data point as a function of the corresponding superficial velocity
![]() $U_s$
shown for representative porous media (cases A1–A5). (b) Relative total uncertainty in permeability,
$U_s$
shown for representative porous media (cases A1–A5). (b) Relative total uncertainty in permeability,
![]() $\delta K/K$
, plotted against the measured permeability
$\delta K/K$
, plotted against the measured permeability
![]() $K$
for all cases.
$K$
for all cases.
In addition to the pressure-based uncertainty analysis, we also addressed the uncertainty associated with the PIV measurements. In the context of turbulent flows, the dominant source of error in 2-D PIV arises from the random nature of velocity fluctuations and particle image processing. For this reason, we focused on the quantification of random errors, which are more critical than systematic biases in the present set-up.
Following Mejia-Alvarez (Reference Mejia-Alvarez2010), the total random error in the measured velocity field was expressed as
where
![]() $\delta _s (\langle u \rangle )$
represents the sampling error due to finite ensemble size, and
$\delta _s (\langle u \rangle )$
represents the sampling error due to finite ensemble size, and
![]() $\delta _{\textit{sp}} (\langle u \rangle )$
denotes the subpixel resolution error in particle displacement estimation. The sampling error
$\delta _{\textit{sp}} (\langle u \rangle )$
denotes the subpixel resolution error in particle displacement estimation. The sampling error
![]() $\delta _s (\langle u \rangle )$
was estimated as
$\delta _s (\langle u \rangle )$
was estimated as
where
![]() $u'$
is the fluctuating velocity component and n is the number of PIV samples (here, n = 2000 for all cases). Given the spatial variation of turbulence intensity in the wake, we conservatively used the maximum value of
$u'$
is the fluctuating velocity component and n is the number of PIV samples (here, n = 2000 for all cases). Given the spatial variation of turbulence intensity in the wake, we conservatively used the maximum value of
![]() $\langle u'^2 \rangle ^{1/2}$
in each field to represent the upper bound of the sampling error.
$\langle u'^2 \rangle ^{1/2}$
in each field to represent the upper bound of the sampling error.
The subpixel error
![]() $\delta _{\textit{sp}}(\langle u \rangle )$
results from inaccuracies in the estimation of the subpixel displacement. According to Prasad et al. (Reference Prasad, Adrian, Landreth and Offutt1992), this error is approximately 5
$\delta _{\textit{sp}}(\langle u \rangle )$
results from inaccuracies in the estimation of the subpixel displacement. According to Prasad et al. (Reference Prasad, Adrian, Landreth and Offutt1992), this error is approximately 5
![]() $\,\%$
of the particle image diameter, which corresponds to
$\,\%$
of the particle image diameter, which corresponds to
![]() $\delta _{\textit{sp}}(\Delta \xi )_{\textit{max}}=0.15$
in the current work as an upper boundary of the uncertainty (particle image diameter taken here as 3 pixels). Note that the subpixel accuracy is inversely proportional to the sample size in the same manner as the sampling error in (A6) due to its random nature. Thus, the subpixel uncertainty can be expressed as
$\delta _{\textit{sp}}(\Delta \xi )_{\textit{max}}=0.15$
in the current work as an upper boundary of the uncertainty (particle image diameter taken here as 3 pixels). Note that the subpixel accuracy is inversely proportional to the sample size in the same manner as the sampling error in (A6) due to its random nature. Thus, the subpixel uncertainty can be expressed as
Once the particle displacement
![]() $\Delta \xi$
is translated into velocity, (A7) can be rewritten as
$\Delta \xi$
is translated into velocity, (A7) can be rewritten as
where
![]() $M$
and
$M$
and
![]() $\Delta t$
are the magnification and the time-delay between PIV image pairs, respectively. Consequently, the total random error of the ensemble velocity components in all cases through the present 2-D PIV measurements is summarized in table 3.
$\Delta t$
are the magnification and the time-delay between PIV image pairs, respectively. Consequently, the total random error of the ensemble velocity components in all cases through the present 2-D PIV measurements is summarized in table 3.
Table 3. Random errors on an ensemble basis for cases A of the 2-D PIV measurements.

To estimate the uncertainty in the Reynolds shear stress
![]() $\langle u'v' \rangle$
, we employ a root-mean-square error propagation formula as
$\langle u'v' \rangle$
, we employ a root-mean-square error propagation formula as
where each term is estimated based on the ensemble statistics of the velocity fields.
Then the lateral gradient
![]() $\partial \langle u'v' \rangle / \partial y$
is computed using a second-order central finite difference scheme as
$\partial \langle u'v' \rangle / \partial y$
is computed using a second-order central finite difference scheme as
The associated uncertainty is propagated using standard error analysis for finite differences as
To address the convergence of the velocity statistics, we also conducted progressive averaging analysis of the turbulence quantities
![]() $\langle u' \rangle ^2$
and
$\langle u' \rangle ^2$
and
![]() $\langle u'v' \rangle$
. These quantities were evaluated at the location of the local maximum in
$\langle u'v' \rangle$
. These quantities were evaluated at the location of the local maximum in
![]() $\langle u'v' \rangle$
. This region corresponds to highly fluctuating flow where convergence rate could be minimum. As shown in figure 13, both quantities converge well within 2000 samples, confirming the statistical reliability of the PIV measurements.
$\langle u'v' \rangle$
. This region corresponds to highly fluctuating flow where convergence rate could be minimum. As shown in figure 13, both quantities converge well within 2000 samples, confirming the statistical reliability of the PIV measurements.

Figure 13. Example showing the convergence of turbulent quantities as a function of sample size for selected porous cylinder cases.

Figure 14. (a) Drag coefficient
![]() $C_{\kern-1pt D}$
against Darcy number
$C_{\kern-1pt D}$
against Darcy number
![]() $ \textit{Da} $
: present measurements at
$ \textit{Da} $
: present measurements at
![]() $ \textit{Re}_D \approx 3.1\times 10^4$
(open circles) compared with Ledda et al. (Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). The horizontal solid line indicates
$ \textit{Re}_D \approx 3.1\times 10^4$
(open circles) compared with Ledda et al. (Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018). The horizontal solid line indicates
![]() $C_{\kern-1pt D}$
for a solid square at
$C_{\kern-1pt D}$
for a solid square at
![]() $ \textit{Re}_D \approx 3.1\times 10^4$
. (b) Longitudinal wake length
$ \textit{Re}_D \approx 3.1\times 10^4$
. (b) Longitudinal wake length
![]() $W_r$
as a function of
$W_r$
as a function of
![]() $ \textit{Da}/Da_c$
: present measurements (open circles) compared with the recirculation length of Cummins et al. (Reference Cummins, Viola, Mastropaolo and Nakayama2017) at
$ \textit{Da}/Da_c$
: present measurements (open circles) compared with the recirculation length of Cummins et al. (Reference Cummins, Viola, Mastropaolo and Nakayama2017) at
![]() $ \textit{Re}=10, 30$
and
$ \textit{Re}=10, 30$
and
![]() $130$
. Here
$130$
. Here
![]() $W_r$
is the centreline distance between the two saddle points determining the size of the main recirculation bubbles, and
$W_r$
is the centreline distance between the two saddle points determining the size of the main recirculation bubbles, and
![]() $ \textit{Da}_c$
denotes the critical Darcy number for the onset of a steady wake.
$ \textit{Da}_c$
denotes the critical Darcy number for the onset of a steady wake.
Appendix B. Comparative anchoring and data alignment
To provide comparative context for the high-Re measurements reported in the represent study, figure 14(a,b) present the drag coefficient
![]() $C_{\kern-1pt D}$
and a longitudinal wake length metric against the permeability
$C_{\kern-1pt D}$
and a longitudinal wake length metric against the permeability
![]() $ \textit{Da} $
. In this case, our goal is to assess whether the direction and structure of the permeability dependence established here are consistent with representative DBF-based simulations at low Reynolds number.
$ \textit{Da} $
. In this case, our goal is to assess whether the direction and structure of the permeability dependence established here are consistent with representative DBF-based simulations at low Reynolds number.
First, the drag-permeability trend for the current cylinders at
![]() $ \textit{Re}_D\approx 3.1\times 10^4$
has already been established in Seol et al. (Reference Seol, Kim and Kim2024) and is reproduced in figure 14(a), showing a monotonic decrease of
$ \textit{Re}_D\approx 3.1\times 10^4$
has already been established in Seol et al. (Reference Seol, Kim and Kim2024) and is reproduced in figure 14(a), showing a monotonic decrease of
![]() $C_{\kern-1pt D}$
with
$C_{\kern-1pt D}$
with
![]() $ \textit{Da} $
. In this study, we further superimpose the result of Ledda et al. (Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018), which present DBF-based simulations for porous rectangular cylinders at
$ \textit{Da} $
. In this study, we further superimpose the result of Ledda et al. (Reference Ledda, Siconolfi, Viola, Gallaire and Camarri2018), which present DBF-based simulations for porous rectangular cylinders at
![]() $ \textit{Re}=20$
and
$ \textit{Re}=20$
and
![]() $30$
, plotted on the same
$30$
, plotted on the same
![]() $x$
-coordinate,
$x$
-coordinate,
![]() $ \textit{Da} $
. Despite differences in Reynolds number and cross-sectional geometry, both datasets exhibit the same qualitative dependence: increasing
$ \textit{Da} $
. Despite differences in Reynolds number and cross-sectional geometry, both datasets exhibit the same qualitative dependence: increasing
![]() $ \textit{Da} $
reduces pressure drag. As expected from Reynolds number and geometric effects, the absolute values differ, but the direction and curvature of the trend remain consistent.
$ \textit{Da} $
reduces pressure drag. As expected from Reynolds number and geometric effects, the absolute values differ, but the direction and curvature of the trend remain consistent.
Next, the longitudinal wake length,
![]() $W_r$
, is defined as the centreline distance between the two saddle points that bound the main recirculation bubble. The same quantity for identical porous square cylinder configurations was previously measured and reported in Seol et al. (Reference Seol, Hong and Kim2023) and differs from the lateral wake extent
$W_r$
, is defined as the centreline distance between the two saddle points that bound the main recirculation bubble. The same quantity for identical porous square cylinder configurations was previously measured and reported in Seol et al. (Reference Seol, Hong and Kim2023) and differs from the lateral wake extent
![]() $W_L$
introduced in the present study. Using this definition, we compare our measurements of
$W_L$
introduced in the present study. Using this definition, we compare our measurements of
![]() $W_r$
with the recirculation length reported by Cummins et al. (Reference Cummins, Viola, Mastropaolo and Nakayama2017) for permeable rectangles at
$W_r$
with the recirculation length reported by Cummins et al. (Reference Cummins, Viola, Mastropaolo and Nakayama2017) for permeable rectangles at
![]() $ \textit{Re}=10, 30$
and
$ \textit{Re}=10, 30$
and
![]() $130$
, as shown in figure 14(b). In this comparison, the
$130$
, as shown in figure 14(b). In this comparison, the
![]() $x$
-coordinate
$x$
-coordinate
![]() $ \textit{Da} $
is normalized by the critical Darcy number
$ \textit{Da} $
is normalized by the critical Darcy number
![]() $ \textit{Da}_c$
, corresponding to the onset of a steady wake. Despite differences in Reynolds number and bluff body geometry, the two datasets display the same qualitative trend. For example, as
$ \textit{Da}_c$
, corresponding to the onset of a steady wake. Despite differences in Reynolds number and bluff body geometry, the two datasets display the same qualitative trend. For example, as
![]() $ \textit{Da} $
approaches
$ \textit{Da} $
approaches
![]() $ \textit{Da}_c$
, the recirculation bubble collapses to zero, whereas for
$ \textit{Da}_c$
, the recirculation bubble collapses to zero, whereas for
![]() $ \textit{Da}\lt Da_c$
,
$ \textit{Da}\lt Da_c$
,
![]() $W_r$
increases as permeability decreases. We emphasize that this comparison serves as an anchor rather than a strict validation because (i) the present experiments involve porous square cylinders at high
$W_r$
increases as permeability decreases. We emphasize that this comparison serves as an anchor rather than a strict validation because (i) the present experiments involve porous square cylinders at high
![]() $ \textit{Re} $
and (ii) the reference data correspond to low-
$ \textit{Re} $
and (ii) the reference data correspond to low-
![]() $ \textit{Re} $
numerical simulations of permeable rectangles. With these limitations, the observed consistency in the trend and structure of the permeability dependence supports the physical interpretation developed in §§ 3.1–3.3.
$ \textit{Re} $
numerical simulations of permeable rectangles. With these limitations, the observed consistency in the trend and structure of the permeability dependence supports the physical interpretation developed in §§ 3.1–3.3.