1. Introduction
Amorphous materials lie at the intersection of solids and liquids (Nicolas et al. Reference Nicolas, Ferrero, Martens and Barrat2018). Under small stresses, amorphous materials deform elastically, whereas under large stresses, they yield and start to flow plastically, and consequently they are also referred to as yield stress materials (Nicolas et al. Reference Nicolas, Ferrero, Martens and Barrat2018; Lin et al. Reference Lin, Lerner, Rosso and Wyart2014a ). In athermal amorphous materials such as dense granular suspensions, foams and emulsions, the effects of Brownian motion on the response of the material to deformation are negligible (Amon et al. Reference Amon, Bruand, Crassous and Clément2012). On the contrary, thermal fluctuations can play a key role in the dynamics of thermal amorphous materials such as colloidal gels, colloidal glasses and metallic glasses (Chattoraj, Caroli & Lemaître Reference Chattoraj, Caroli and Lemaître2010). The yielding transition has been extensively studied for athermal materials (Ritort & Sollich Reference Ritort and Sollich2003; Biroli & Bouchaud Reference Biroli and Bouchaud2012; Lin et al. Reference Lin, Gueudré, Rosso and Wyart2015; Ozawa et al. Reference Ozawa, Berthier, Biroli, Rosso and Tarjus2018). However, the origin of this transition and its connection to molecular-level information remains poorly understood, especially in thermal systems.
Unlike crystalline solids in which plasticity is a consequence of dislocations (Hill Reference Hill1998), amorphous materials are in an arrested, glassy state, and plasticity occurs through localized rearrangements of constituent particles as they break the cages created by their neighbours (Argon Reference Argon1979; Falk & Langer Reference Falk and Langer1998). More specifically, glassy materials have a rough free energy landscape meaning that the particles are in metastable configurations (energy wells) due to the presence of their neighbours. The particles can hop to another energy well by thermal activation. This is the underlying physics of trap models developed for glasses (Bouchaud Reference Bouchaud1992; Monthus & Bouchaud Reference Monthus and Bouchaud1996). Following in the footsteps of Monthus & Bouchaud (Reference Monthus and Bouchaud1996), Sollich et al. (Reference Sollich, Lequeux, Hébraud and Cates1997) developed the soft glassy rheology (SGR) model to incorporate elasticity into trap models and describe the rheology of foams and dense emulsions (so-called soft glassy materials (Dollet & Graner Reference Dollet and Graner2007; Dollet, Scagliarini & Sbragaglia Reference Dollet, Scagliarini and Sbragaglia2015)). This model divides the material into mesoscopic elements (each with a specific energy well and thus a yield threshold) and assumes that under mechanical loading, the elements (particles) deform elastically within their energy wells. This stored elastic energy reduces the energy barrier to hop. Since foams and emulsions are athermal, the yielding of elements is activated by the stress redistributed by the structural relaxation of other elements. This activation is modelled by an ad hoc noise temperature in the SGR model (Sollich et al. Reference Sollich, Lequeux, Hébraud and Cates1997; Sollich Reference Sollich1998). Hébraud & Lequeux (Reference Hébraud and Lequeux1998) further formalized the idea of dividing the material into mesoscopic elements leading to the emergence of numerous elastoplastic models (EPMs) which consider an elastic response, a local yield criterion, stress redistribution after yielding and a recovery of the local stress after a plastic event (Lin et al. Reference Lin, Lerner, Rosso and Wyart2014a ,Reference Lin, Saade, Lerner, Rosso and Wyart b , Reference Lin, Gueudré, Rosso and Wyart2015; Lin & Wyart Reference Lin and Wyart2016).
These models provide illuminating insights into the elasticity and the mechanical noise generated by plasticity in amorphous materials. However, they exhibit deficiencies in two significant regards: first, they are developed for athermal materials, while many amorphous materials have nanoscopic elements and activated dynamics, e.g. biological tissues (Bi et al. Reference Bi, Yang, Marchetti and Manning2016), cytoskeleton networks in living cells (Bursac et al. Reference Bursac, Lenormand, Fabry, Oliver, Weitz, Viasnoff, Butler and Fredberg2005), calcium-protein assembly in the casein matrix of cheese (Gillies Reference Gillies2019), nanofilms at fluid interfaces (Krishnaswamy & Sood Reference Krishnaswamy and Sood2010), among others. An activated version of the Hébraud–Lequeux model is proposed by Popović et al. (Reference Popović, de, Tom, Ji and Wyart2021), which shows that thermal fluctuations change the distribution of local stress, referred to as rounding of the yielding transition. They also proposed scaling laws for the yielding transition that were further analysed and explained by Ferrero, Kolton & Jagla (Reference Ferrero, Kolton and Jagla2021). Both of these studies, however, were limited to steady-state flows and applied stresses only slightly below the yield stress. Second, the currently available elastoplastic modelling only connects the mesoscopic properties (such as distribution of local stress, mechanical noise, etc.) to the bulk response while neglecting the molecular-level properties. This is despite the fact that the free energy landscape and the local barriers, which are a result of molecular-level information, dictate the dynamics of amorphous materials (Pica Ciamarra et al. Reference Ciamarra, Massimo and Wyart2024).
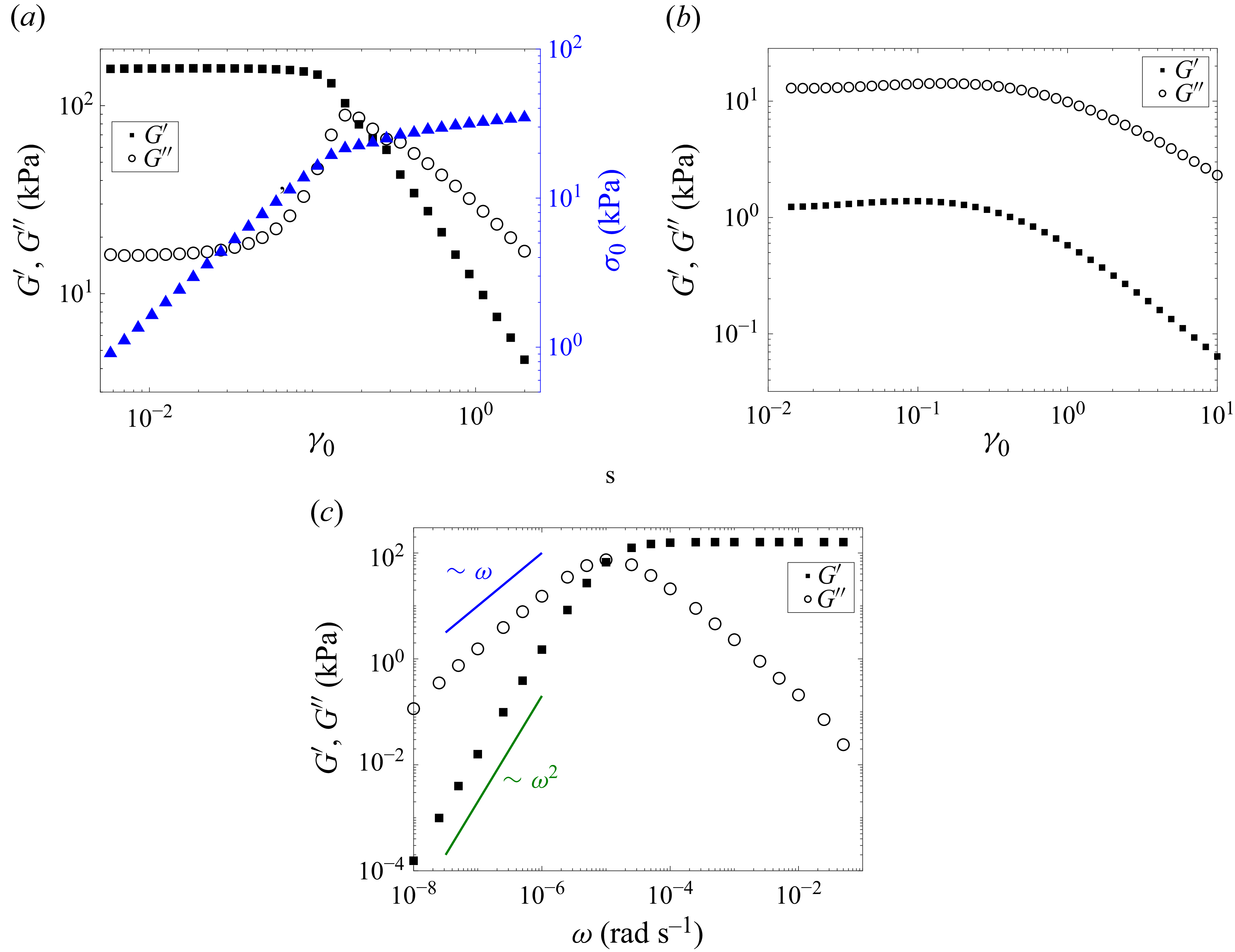
Unlike simple liquids, soft amorphous materials exhibit complex nonlinear rheology (Goyon et al. Reference Goyon, Colin, Ovarlez, Ajdari and Bocquet2008; Bonn et al. Reference Bonn, Denn, Berthier, Divoux and Manneville2017; Khabaz, Cloitre & Bonnecaze Reference Khabaz, Cloitre and Bonnecaze2020). Some common rheological features of these materials are: (i) a rate-dependent stress overshoot in the stress–strain curve of a start-up shear test depending on the initial state of the material and direction of the shear (Derec et al. Reference Derec, Ducouret, Ajdari and Lequeux2003; Moorcroft, Cates & Fielding Reference Moorcroft, Cates and Fielding2011); (ii) a peak in the loss modulus and a decrease in the storage modulus in a strain sweep test when an oscillatory shear strain is applied (Mason, Bibette & Weitz Reference Mason, Bibette and Weitz1995; Rogers et al. Reference Rogers, Erwin, Vlassopoulos and Cloitre2011; Dimitriou, Ewoldt & McKinley Reference Dimitriou, Ewoldt and McKinley2013); (iii) history-dependent behaviour (Khabaz et al. Reference Khabaz, Di, Flavio, Cloitre and Bonnecaze2021; Di Dio et al. Reference Di, Flavio, Khabaz, Bonnecaze and Cloitre2022); (iv) ageing (Liu, Martens & Barrat Reference Liu, Martens and Barrat2018; Parley, Fielding & Sollich Reference Parley, Fielding and Sollich2020); (v) shear banding (Kabla, Scheibert & Debregeas Reference Kabla, Scheibert and Debregeas2007; Coussot & Ovarlez Reference Coussot and Ovarlez2010; Fielding Reference Fielding2014), among others. The SGR model can qualitatively reproduce these rheological features for athermal amorphous materials by changing the parameters of the model (Fielding et al. Reference Fielding, Sollich and Cates2000, Reference Fielding, Cates and Sollich2009). Quantitative agreement between the model and experiments might be achieved provided that the model is linked to molecular-level information about the material to achieve physical and meaningful values for the parameters.
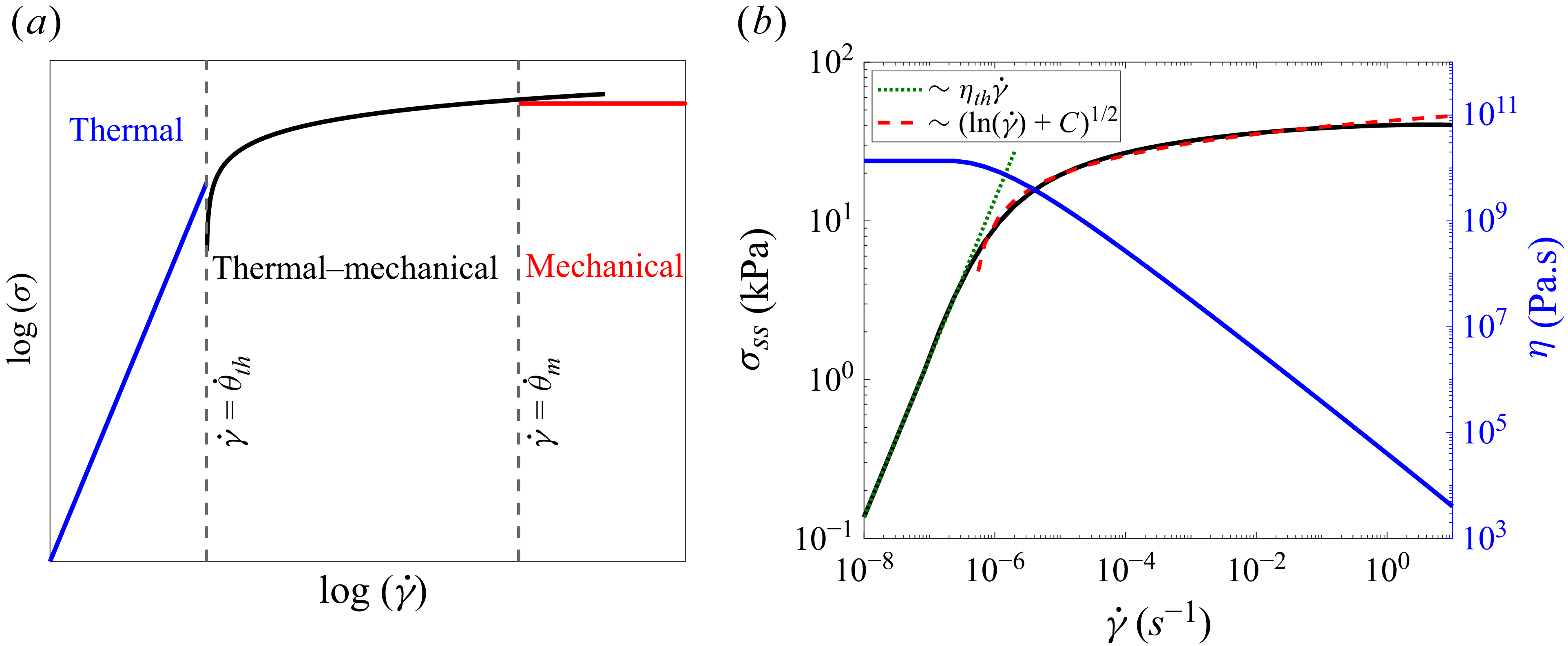
An important question is how the presence of thermal fluctuations affects this nonlinear rheology. The first consideration when including the thermal fluctuations is the time scale of thermally activated structural relaxations (
![]() $\tau _{\textit{th}}$
) that competes with the time scale of mechanical loading (
$\tau _{\textit{th}}$
) that competes with the time scale of mechanical loading (
![]() $1/\dot \gamma$
). Further richness may arise when one considers a time scale for plasticity (single rearrangement) (Ferrero, Martens & Barrat Reference Ferrero, Martens and Barrat2014) and a time scale for avalanches of rearrangements (multiple plastic events which are triggered by an initial event) (Nicolas et al. Reference Nicolas, Puosi, Mizuno and Barrat2015). The complex interplay between mechanical loading and thermal fluctuations might completely alter both transient and steady-state responses, depending on the system under deformation. For example, the flow curve, indicating the stress as a function of shear rate in steady shear, in athermal amorphous materials usually follows a Herschel–Bulkley law (Lin et al. Reference Lin, Lerner, Rosso and Wyart2014a
; Sen, Morales & Ewoldt Reference Sen, Morales and Ewoldt2020), while at vanishing shear rates, thermal fluctuations give rise to a Newtonian stress instead of a stress plateau in dense colloidal suspensions (Fuchs & Cates Reference Fuchs and Cates2002). Furthermore, molecular dynamics simulations of a two-dimensional Lennard-Jones glass (Chattoraj et al. Reference Chattoraj, Caroli and Lemaître2010) and thermally activated creep tests using kinetic Monte Carlo simulations on a square lattice (Merabia & Detcheverry Reference Merabia and Detcheverry2016) show that thermal fluctuations introduce a logarithmic dependence of the steady-state stress on the shear rate. An activated version of the Hébraud–Lequeux model also predicts a logarithmic flow curve for large stresses just below the yield stress in the limit of small temperatures (Popović et al. Reference Popović, de, Tom, Ji and Wyart2021). Prior studies on the role of thermal fluctuations in amorphous materials have only focused on steady-state situations under large applied deformation. However, thermal amorphous materials can flow over a long time scale even under very small deformation while showing solid-like behaviour on limited time scales (Schröter & Donth Reference Schröter and Donth2000; Lu, Ravichandran & Johnson Reference Lu, Ravichandran and Johnson2003; Agarwal, Qi & Archer Reference Agarwal, Qi and Archer2010; Riechers et al. Reference Riechers, Das, Rashidi, Dufresne and Maaß2025). A comprehensive theoretical understanding of the intricate physics governing this complex behaviour is yet to be established. Thus, to better understand and characterize the combined effects of mechanical loading and thermal fluctuations on both the transient and steady-state rheology, it is essential to have a thermally activated constitutive model. To test the model, it would be crucial to study a well-characterized thermal amorphous material.
$1/\dot \gamma$
). Further richness may arise when one considers a time scale for plasticity (single rearrangement) (Ferrero, Martens & Barrat Reference Ferrero, Martens and Barrat2014) and a time scale for avalanches of rearrangements (multiple plastic events which are triggered by an initial event) (Nicolas et al. Reference Nicolas, Puosi, Mizuno and Barrat2015). The complex interplay between mechanical loading and thermal fluctuations might completely alter both transient and steady-state responses, depending on the system under deformation. For example, the flow curve, indicating the stress as a function of shear rate in steady shear, in athermal amorphous materials usually follows a Herschel–Bulkley law (Lin et al. Reference Lin, Lerner, Rosso and Wyart2014a
; Sen, Morales & Ewoldt Reference Sen, Morales and Ewoldt2020), while at vanishing shear rates, thermal fluctuations give rise to a Newtonian stress instead of a stress plateau in dense colloidal suspensions (Fuchs & Cates Reference Fuchs and Cates2002). Furthermore, molecular dynamics simulations of a two-dimensional Lennard-Jones glass (Chattoraj et al. Reference Chattoraj, Caroli and Lemaître2010) and thermally activated creep tests using kinetic Monte Carlo simulations on a square lattice (Merabia & Detcheverry Reference Merabia and Detcheverry2016) show that thermal fluctuations introduce a logarithmic dependence of the steady-state stress on the shear rate. An activated version of the Hébraud–Lequeux model also predicts a logarithmic flow curve for large stresses just below the yield stress in the limit of small temperatures (Popović et al. Reference Popović, de, Tom, Ji and Wyart2021). Prior studies on the role of thermal fluctuations in amorphous materials have only focused on steady-state situations under large applied deformation. However, thermal amorphous materials can flow over a long time scale even under very small deformation while showing solid-like behaviour on limited time scales (Schröter & Donth Reference Schröter and Donth2000; Lu, Ravichandran & Johnson Reference Lu, Ravichandran and Johnson2003; Agarwal, Qi & Archer Reference Agarwal, Qi and Archer2010; Riechers et al. Reference Riechers, Das, Rashidi, Dufresne and Maaß2025). A comprehensive theoretical understanding of the intricate physics governing this complex behaviour is yet to be established. Thus, to better understand and characterize the combined effects of mechanical loading and thermal fluctuations on both the transient and steady-state rheology, it is essential to have a thermally activated constitutive model. To test the model, it would be crucial to study a well-characterized thermal amorphous material.
As a class of polymer nanocomposites and a promising thermal model material, self-suspended polymer-grafted nanoparticles consist of hard inorganic nanocores densely grafted with polymer chains. Even in the absence of a dispersing medium, these polymer-grafted nanoparticles can exhibit fluid behaviour as the grafted polymers fill the interstitial space between the cores like an incompressible fluid (Bourlinos et al. Reference Bourlinos, Herrera, Chalkias, Jiang, Zhang, Archer and Giannelis2005a , Reference Bourlinos, Ray Chowdhury, Herrera, Jiang, Zhang, Archer and Giannelisb ; Rodriguez et al. Reference Rodriguez, Herrera, Archer and Giannelis2008). Strong van der Waals forces usually lead to irreversible aggregation of nanoscale suspensions making the material properties unpredictable (Russel et al. Reference Russel, Russel, Saville and Schowalter1991). However, polymer-grafted nanoparticles are a novel class of polymer nanocomposites in which particle aggregation is suppressed since the configurational entropy of the grafted polymers is much greater than the van der Waals interactions between the cores (Yu & Koch Reference Yu and Koch2010; Chremos et al. Reference Chremos, Panagiotopoulos, Yu and Koch2011; Yu et al. Reference Yu, Srivastava, Archer and Koch2014).
Experiments have shown that due to the interactions of the grafted polymers, solvent-free polymer-grafted nanoparticles exhibit rheological characteristics similar to those of soft glassy materials, e.g. slow dynamics, yield stress, rate-dependent behaviour (Agarwal et al. Reference Agarwal, Qi and Archer2010; Agarwal & Archer Reference Agarwal and Archer2011; Srivastava et al. Reference Srivastava, Shin and Archer2012b
). This stems from the cooperation of the grafted polymers to fill the interstitial space which creates local cages around the nanocores. More specifically, in solvent-free polymer-grafted nanoparticles, the entropy of the space-filling grafted polymers controls the core configuration, and there is a large energy penalty to alter this configuration. Thus, solvent-free polymer-grafted nanoparticles are in arrested states and relax very slowly exhibiting an apparent yield stress over extended time periods (Agarwal, Srivastava & Archer Reference Agarwal, Srivastava and Archer2011; Liu et al. Reference Liu, Utomo, Zhao, Zheng, Zhang and Archer2020). Interestingly, polymer-grafted nanoparticles can display glassy behaviour at very low core volume fraction (
![]() $\phi \approx 0.1{-}0.2$
) (Yu & Koch Reference Yu and Koch2014; Srivastava et al. Reference Srivastava, Choudhury, Agrawal and Archer2017), which allows thermal fluctuations to relax their nanostructures towards local equilibrium states. This is in contrast to dense colloidal suspensions in which the large particle volume fraction prevents thermal relaxation to a local equilibrium state (Nazockdast & Morris Reference Nazockdast and Morris2012; Lu & Weitz Reference Lu and Weitz2013). Understanding the complex rheology of a thermal amorphous materials like polymer-grafted nanoparticles requires knowledge of the molecular-level physics.
$\phi \approx 0.1{-}0.2$
) (Yu & Koch Reference Yu and Koch2014; Srivastava et al. Reference Srivastava, Choudhury, Agrawal and Archer2017), which allows thermal fluctuations to relax their nanostructures towards local equilibrium states. This is in contrast to dense colloidal suspensions in which the large particle volume fraction prevents thermal relaxation to a local equilibrium state (Nazockdast & Morris Reference Nazockdast and Morris2012; Lu & Weitz Reference Lu and Weitz2013). Understanding the complex rheology of a thermal amorphous materials like polymer-grafted nanoparticles requires knowledge of the molecular-level physics.
Theoretical calculations (Yu & Koch Reference Yu and Koch2010) and scattering experiments (Bourlinos et al. Reference Bourlinos, Ray Chowdhury, Herrera, Jiang, Zhang, Archer and Giannelis2005b ; Agarwal et al. Reference Agarwal, Qi and Archer2010) have shown that the grafted polymers in solvent-free polymer-grafted nanoparticles act as an incompressible fluid, indicating that each core and its tethered polymers must exclude exactly one neighbouring core and its tethered polymers. This means that each particle carries its own share of the fluid attached to it making monodisperse, solvent-free polymer-grafted nanoparticles an incompressible single-component fluid for which the static structure factor at zero wavenumber is theoretically zero (Yu & Koch Reference Yu and Koch2010). Small angle X-ray scattering experiments on these materials show that due to polydispersity in core size, polymer molecular weight and grafting density, the static structure factor at zero wavenumber is slightly above zero but still substantially smaller than that for a hard-sphere suspension with the same core volume fraction. This means that long-range density fluctuations in solvent-free polymer-grafted nanoparticles are suppressed, making them disordered hyperuniform materials as the grafted polymers uniformly fill the interstitial space between the cores (Yu et al. Reference Yu, Srivastava, Archer and Koch2014; Chremos & Douglas Reference Chremos and Douglas2018). This cooperation between grafted polymers to fill the space leads to a non-pairwise-additive interparticle potential, interpenetration of polymer brushes from neighbouring particles, creation of cages around the cores and slowing-down of the relaxation dynamics (Yu & Koch Reference Yu and Koch2010; Goyal & Escobedo Reference Goyal and Escobedo2011; Chremos, Panagiotopoulos & Koch Reference Chremos, Panagiotopoulos and Koch2012). As a result, the incompressibility constraint alters the probability distribution of the grafted polymers and thus their free energy (Tai, Pan & Yu Reference Tai, Pan and Yu2019). Generally, the probability distribution of surface-tethered polymers can be obtained by using a self-consistent field theory (SCFT) (Park et al. Reference Park, Kim, Yong, Choe, Bang and Kim2018), polymer reference interaction site model (Martin et al. Reference Martin, Gartner, Jones, Snyder and Jayaraman2018), classical density functional theory (DFT) (Chen et al. Reference Chen, Tang, Qiu and Shi2015), molecular dynamics (Chang & Yu Reference Chang and Yu2021) or Monte Carlo (Ohno et al. Reference Ohno, Sakamoto, Minagawa and Okabe2007) simulations. Among these techniques, the polymer SCFT (Matsen Reference Matsen2002) and classical DFT (Yu & Koch Reference Yu and Koch2013) can effectively impose the incompressibility constraint and capture the entropic interactions between the grafted polymers. However, modelling an incompressibility constraint with polymer SCFT is numerically challenging as it results in solving a set of stiff integrodifferential equations, while classical DFT is more analytically favourable (Tai et al. Reference Tai, Pan and Yu2019).
In this paper, we first focus on thermodynamics at the molecular scale and study how the free energy of the nanostructure evolves under deformation using a classical DFT discussed in § 2. The outcome will be the free energy landscape of a solvent-free polymer-grafted nanoparticle system as a function of material properties such as core volume fraction, and molecular weight and grafting density of the polymers. In § 3, a thermally activated SGR model is proposed which takes the free energy landscape as an input and connects the thermodynamics to the bulk rheology of the material. In § 4, we delve into the molecular-level information and explain that the shape of the energy well is an outcome of the competition between the translational and configurational entropy of the grafted polymers. In § 5, we note that depending on the energy landscape and the rate of deformation, structural rearrangements activated by thermal hops can regulate the macroscopic rheology. Furthermore, a detailed characterization of the interplay between mechanical loading and thermal fluctuations is provided by modelling different shear tests and including a deformation history.
2. A classical DFT
We model the polymer chains as beads–springs tethered to the surface of the cores and assume linear and massless springs with zero rest length. The spring energy is defined as
![]() $F_{\textit{spring}} = ({1}/{2}) \xi x^2$
where
$F_{\textit{spring}} = ({1}/{2}) \xi x^2$
where
![]() $\xi$
is the spring constant and
$\xi$
is the spring constant and
![]() $x$
is the displacement of the spring from its rest length. The spring constant is chosen to be related to the radius of gyration,
$x$
is the displacement of the spring from its rest length. The spring constant is chosen to be related to the radius of gyration,
![]() $R_g$
, of an ideal, unattached linear chain as
$R_g$
, of an ideal, unattached linear chain as
![]() $\xi = ({k_{\!B} T}/{2R_g^2})$
, where
$\xi = ({k_{\!B} T}/{2R_g^2})$
, where
![]() $k_{\!B}$
is the Boltzmann constant and
$k_{\!B}$
is the Boltzmann constant and
![]() $T$
is the temperature. The spring energy models the configurational entropy of an ideal chain. To achieve the relaxation of the core configuration, all the grafted polymers have to move, whereas for polymer relaxation, only one polymer has to move. As a result, we assume that polymers are at equilibrium since they can relax much faster than the cores. Previous studies have tested the validity of these assumptions (Yu & Koch Reference Yu and Koch2010; Chremos et al. Reference Chremos, Panagiotopoulos, Yu and Koch2011; Yu et al. Reference Yu, Srivastava, Archer and Koch2014; Tai et al. Reference Tai, Pan and Yu2019). For solvent-free polymer-grafted nanoparticles, the free energy of the grafted polymers includes the entropy of the beads and the spring energy of the chains. Furthermore, the incompressibility condition is imposed by requiring all the grafted polymers to uniformly fill the interstitial space. Thus, the total free energy,
$T$
is the temperature. The spring energy models the configurational entropy of an ideal chain. To achieve the relaxation of the core configuration, all the grafted polymers have to move, whereas for polymer relaxation, only one polymer has to move. As a result, we assume that polymers are at equilibrium since they can relax much faster than the cores. Previous studies have tested the validity of these assumptions (Yu & Koch Reference Yu and Koch2010; Chremos et al. Reference Chremos, Panagiotopoulos, Yu and Koch2011; Yu et al. Reference Yu, Srivastava, Archer and Koch2014; Tai et al. Reference Tai, Pan and Yu2019). For solvent-free polymer-grafted nanoparticles, the free energy of the grafted polymers includes the entropy of the beads and the spring energy of the chains. Furthermore, the incompressibility condition is imposed by requiring all the grafted polymers to uniformly fill the interstitial space. Thus, the total free energy,
![]() $F$
, of the polymers can be written as
$F$
, of the polymers can be written as
 \begin{align} \frac {F}{k_{\textit{B}}T} = \int _V \int _A \left [P(\boldsymbol{r},\boldsymbol{r_0}) \big [\ln \big (P(\boldsymbol{r},\boldsymbol{r_0})\varLambda _b^3 \big ) - 1 \big ] + P(\boldsymbol{r},\boldsymbol{r_0})\frac {|\boldsymbol{r}-\boldsymbol{r}_0|^2}{4R_g^2}\right ] {\text{d}}\boldsymbol{r}_0 \, {\text{d}}\boldsymbol{r} \notag \\ + \dfrac {\alpha }{2}\int _V \, \left (n(\boldsymbol{r})-n_0 \right )^2 {\text{d}}\boldsymbol{r}. \end{align}
\begin{align} \frac {F}{k_{\textit{B}}T} = \int _V \int _A \left [P(\boldsymbol{r},\boldsymbol{r_0}) \big [\ln \big (P(\boldsymbol{r},\boldsymbol{r_0})\varLambda _b^3 \big ) - 1 \big ] + P(\boldsymbol{r},\boldsymbol{r_0})\frac {|\boldsymbol{r}-\boldsymbol{r}_0|^2}{4R_g^2}\right ] {\text{d}}\boldsymbol{r}_0 \, {\text{d}}\boldsymbol{r} \notag \\ + \dfrac {\alpha }{2}\int _V \, \left (n(\boldsymbol{r})-n_0 \right )^2 {\text{d}}\boldsymbol{r}. \end{align}
In the above formulation,
![]() $P(\boldsymbol{r},\boldsymbol{r}_0)$
is the probability density of finding a polymer bead position
$P(\boldsymbol{r},\boldsymbol{r}_0)$
is the probability density of finding a polymer bead position
![]() $\boldsymbol{r}$
provided that it is grafted at a position
$\boldsymbol{r}$
provided that it is grafted at a position
![]() $\boldsymbol{r}_0$
on the particle surface. Therefore, the integrals over
$\boldsymbol{r}_0$
on the particle surface. Therefore, the integrals over
![]() $\boldsymbol{r}$
and
$\boldsymbol{r}$
and
![]() $\boldsymbol{r}_0$
are integrals over volume (denoted by
$\boldsymbol{r}_0$
are integrals over volume (denoted by
![]() $V$
) of the system and over the surface (denoted by
$V$
) of the system and over the surface (denoted by
![]() $A$
) of the cores, respectively. All the lengths are non-dimensionalized by the diameter of the cores,
$A$
) of the cores, respectively. All the lengths are non-dimensionalized by the diameter of the cores,
![]() $d$
. In the first integral, the first term is the ideal gas Helmholtz free energy of the beads which models the translational entropy of the polymers where
$d$
. In the first integral, the first term is the ideal gas Helmholtz free energy of the beads which models the translational entropy of the polymers where
![]() $\varLambda _b$
is the thermal de Broglie wavelength of the monomer beads, and the second term represents the spring energy of the grafted polymers which models the configurational entropy of the polymer chains. The last term is the space-filling (incompressibility) constraint. The number density,
$\varLambda _b$
is the thermal de Broglie wavelength of the monomer beads, and the second term represents the spring energy of the grafted polymers which models the configurational entropy of the polymer chains. The last term is the space-filling (incompressibility) constraint. The number density,
![]() $n(\boldsymbol{r})$
, of the grafted polymers at every point in the void space is given by
$n(\boldsymbol{r})$
, of the grafted polymers at every point in the void space is given by
and
![]() $n_0$
is the mean number density of the grafted polymers defined as
$n_0$
is the mean number density of the grafted polymers defined as
![]() $n_0 = {N}/{V_{v\textit{oid}}}$
, where
$n_0 = {N}/{V_{v\textit{oid}}}$
, where
![]() $N$
is the total number of chains and
$N$
is the total number of chains and
![]() $V_{v\textit{oid}}$
is the void volume in the system. We impose the space-filling constraint as a free energy penalty term by defining a space-filling parameter,
$V_{v\textit{oid}}$
is the void volume in the system. We impose the space-filling constraint as a free energy penalty term by defining a space-filling parameter,
![]() $\alpha$
. When
$\alpha$
. When
![]() $\alpha \rightarrow \infty$
, there is a very large free energy penalty for having a number density at any point in space that differs from the mean value. This corresponds to a solvent-free case in which the tethered polymers are modelled as an incompressible fluid. The case
$\alpha \rightarrow \infty$
, there is a very large free energy penalty for having a number density at any point in space that differs from the mean value. This corresponds to a solvent-free case in which the tethered polymers are modelled as an incompressible fluid. The case
![]() $\alpha =0$
can be viewed as a system with excess implicit, theta solvent. Here, there is no requirement for the grafted polymers to fill the void space, because we assume that the void volume is occupied primarily by the solvent. By choosing a reference state consisting of excess theta solvent, we omit considerations of the excluded volume interactions that lead to extended brush heights at large polymer grafting densities (Alexander Reference Alexander1977; de Gennes Reference de Gennes1980). For intermediate values of
$\alpha =0$
can be viewed as a system with excess implicit, theta solvent. Here, there is no requirement for the grafted polymers to fill the void space, because we assume that the void volume is occupied primarily by the solvent. By choosing a reference state consisting of excess theta solvent, we omit considerations of the excluded volume interactions that lead to extended brush heights at large polymer grafting densities (Alexander Reference Alexander1977; de Gennes Reference de Gennes1980). For intermediate values of
![]() $\alpha$
, we can view the energy penalty modelling the finite compressibility of tethered polymers in a solvent-free system. This form of the energy penalty is related to the free energy variation of a Lennard-Jones liquid of monomer beads (Betancourt-Cárdenas et al. Reference Betancourt-Cárdenas, Galicia-Luna and Sandler2008; Chremos et al. Reference Chremos, Panagiotopoulos, Yu and Koch2011) with
$\alpha$
, we can view the energy penalty modelling the finite compressibility of tethered polymers in a solvent-free system. This form of the energy penalty is related to the free energy variation of a Lennard-Jones liquid of monomer beads (Betancourt-Cárdenas et al. Reference Betancourt-Cárdenas, Galicia-Luna and Sandler2008; Chremos et al. Reference Chremos, Panagiotopoulos, Yu and Koch2011) with
![]() $\alpha$
being related to the ratio of the interbead potential to the thermal energy. In a typical liquid, the attractive and repulsive potential forces maintain nearly constant molecular density so that typical values of
$\alpha$
being related to the ratio of the interbead potential to the thermal energy. In a typical liquid, the attractive and repulsive potential forces maintain nearly constant molecular density so that typical values of
![]() $\alpha$
are very large but not infinite. In this case, the incompressibility constraint replaces considerations of monomer excluded volume typically included in solvent-swollen polymer brushes (Alexander Reference Alexander1977; de Gennes Reference de Gennes1980). By minimizing the free energy, we can find the probability density of the grafted polymers at equilibrium,
$\alpha$
are very large but not infinite. In this case, the incompressibility constraint replaces considerations of monomer excluded volume typically included in solvent-swollen polymer brushes (Alexander Reference Alexander1977; de Gennes Reference de Gennes1980). By minimizing the free energy, we can find the probability density of the grafted polymers at equilibrium,
 \begin{equation} \frac {\delta\! F}{\delta\! P} = 0 \rightarrow P(\boldsymbol{r},\boldsymbol{r}_0) = K(\boldsymbol{r}_0)\exp\! {\left [\!-\frac {|\boldsymbol{r}-\boldsymbol{r}_0|^2}{4R_g^2}\right ]} \exp {[-\alpha (n(\boldsymbol{r})-n_0)]} ,\end{equation}
\begin{equation} \frac {\delta\! F}{\delta\! P} = 0 \rightarrow P(\boldsymbol{r},\boldsymbol{r}_0) = K(\boldsymbol{r}_0)\exp\! {\left [\!-\frac {|\boldsymbol{r}-\boldsymbol{r}_0|^2}{4R_g^2}\right ]} \exp {[-\alpha (n(\boldsymbol{r})-n_0)]} ,\end{equation}
where
![]() $K(\boldsymbol{r}_0)$
is a normalization coefficient related to the grafting density of the polymers, given by
$K(\boldsymbol{r}_0)$
is a normalization coefficient related to the grafting density of the polymers, given by
Polymer-grafted nanoparticles are usually made of silica nanocores with a diameter of
![]() $d \approx 5{-}10 \, \mathrm{nm}$
and polyethylene glycol (PEG) as the grafted polymer (Agarwal et al. Reference Agarwal, Qi and Archer2010; Srivastava et al. Reference Srivastava, Agarwal and Archer2012a
). A schematic of an arbitrary configuration of solvent-free polymer-grafted nanoparticles and the bead–spring representation of the grafted polymers are shown in figure 1(a) and 1(b), respectively. We obtain the free energy landscape by shearing the system of nanocores and grafted polymers, and at each strain, we calculate the free energy of the system. This requires solving a highly coupled system of equations for the probability density and number density for every point in the space, at each strain and for each value of the space-filling parameter. Furthermore, to study the effect of material properties like core volume fraction, polymer molecular weight, etc., we have to repeat this procedure. Therefore, it is computationally expensive to solve this system multiple times for millions of polymer-grafted particles in a real sample. To ameliorate this situation, we consider a face-centred-cubic (FCC) arrangement of the cores, shown in figure 1(c), to limit the calculations to a unit cell by using periodic boundary conditions. This calculation is used to estimate the typical energy barrier to rearrange the local configuration of a nanoparticle and its neighbours. This energy barrier can then be placed into an EPM designed to approximately describe the rheology of amorphous materials to provide predictions that incorporate molecular-scale information. As mentioned previously, in the solvent-free case, each particle carries an equal amount of the grafted polymeric fluid. This leads to a disordered structure but with equal Voronoi volumes around each particle (Singh, Walsh & Koch Reference Singh, Walsh and Koch2015). The FCC lattice provides equal Voronoi volumes but in an ordered structure.
$d \approx 5{-}10 \, \mathrm{nm}$
and polyethylene glycol (PEG) as the grafted polymer (Agarwal et al. Reference Agarwal, Qi and Archer2010; Srivastava et al. Reference Srivastava, Agarwal and Archer2012a
). A schematic of an arbitrary configuration of solvent-free polymer-grafted nanoparticles and the bead–spring representation of the grafted polymers are shown in figure 1(a) and 1(b), respectively. We obtain the free energy landscape by shearing the system of nanocores and grafted polymers, and at each strain, we calculate the free energy of the system. This requires solving a highly coupled system of equations for the probability density and number density for every point in the space, at each strain and for each value of the space-filling parameter. Furthermore, to study the effect of material properties like core volume fraction, polymer molecular weight, etc., we have to repeat this procedure. Therefore, it is computationally expensive to solve this system multiple times for millions of polymer-grafted particles in a real sample. To ameliorate this situation, we consider a face-centred-cubic (FCC) arrangement of the cores, shown in figure 1(c), to limit the calculations to a unit cell by using periodic boundary conditions. This calculation is used to estimate the typical energy barrier to rearrange the local configuration of a nanoparticle and its neighbours. This energy barrier can then be placed into an EPM designed to approximately describe the rheology of amorphous materials to provide predictions that incorporate molecular-scale information. As mentioned previously, in the solvent-free case, each particle carries an equal amount of the grafted polymeric fluid. This leads to a disordered structure but with equal Voronoi volumes around each particle (Singh, Walsh & Koch Reference Singh, Walsh and Koch2015). The FCC lattice provides equal Voronoi volumes but in an ordered structure.

Figure 1. (a) A schematic of a random configuration of polymer-grafted nanoparticles. For clarity, only a few grafted chains per nanocore are illustrated. (b) A schematic of solvent-free polymer-grafted nanoparticles with the bead–spring model under shear deformation. (c) The FCC arrangement assumed for the nanocores.
Due to the impenetrability of the cores, we exclude the space inside the nanocores from the volume integrals (polymers are grafted to the surface of the cores). For computational convenience, we model the impenetrability of the cores using a soft potential such that the integrands become zero inside the cores. As
![]() $\alpha$
increases, the problem becomes more stiff and as a result is more prone to instabilities. To solve for
$\alpha$
increases, the problem becomes more stiff and as a result is more prone to instabilities. To solve for
![]() $\alpha \rightarrow \infty$
, we use the solution for
$\alpha \rightarrow \infty$
, we use the solution for
![]() $\alpha =0$
as an initial guess and then gradually increase
$\alpha =0$
as an initial guess and then gradually increase
![]() $\alpha$
and use the solution for each
$\alpha$
and use the solution for each
![]() $\alpha$
as the initial guess for the next
$\alpha$
as the initial guess for the next
![]() $\alpha$
. Another important point to ensure stability of the calculations is to use under-relaxation to update the solution. It is worth mentioning that a fourth-order accurate, six-point quadrature rule in three dimensions is used for the volume integrals (Hughes Reference Hughes2003) and Lebedev quadrature rule is used for the surface integrals over the spherical particles (Ericson & Zinoviev Reference Ericson and Zinoviev2001).
$\alpha$
. Another important point to ensure stability of the calculations is to use under-relaxation to update the solution. It is worth mentioning that a fourth-order accurate, six-point quadrature rule in three dimensions is used for the volume integrals (Hughes Reference Hughes2003) and Lebedev quadrature rule is used for the surface integrals over the spherical particles (Ericson & Zinoviev Reference Ericson and Zinoviev2001).
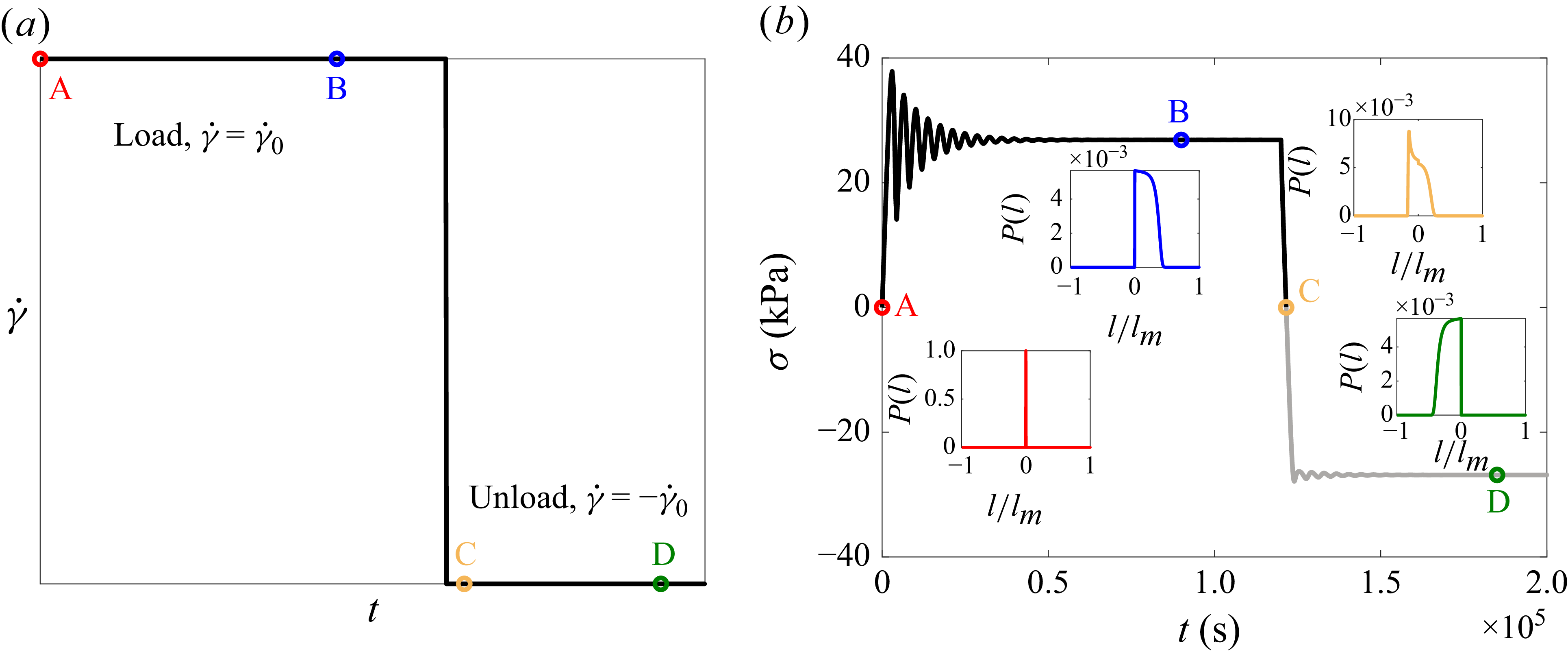
3. Thermal SGR model
In the last section, we elaborated on how to obtain the free energy as a function of the applied shear strain. The output will be the energy landscape and the corresponding energy barrier to structural relaxation. In this section, we connect the obtained energy landscape to the bulk rheology by introducing a thermal SGR model. Similar to the original SGR model, we conceptually divide the material into a large number of mesoscopic elements and assign a local scalar strain (and thus a local stress) and a local yield energy to each element (Sollich et al. Reference Sollich, Lequeux, Hébraud and Cates1997; Sollich Reference Sollich1998). The elements are sheared with the same rate as the macroscopic shear rate, and they store elastic energy. Mechanical loading reduces the energy barrier thus facilitating hops out of the trap by thermal fluctuations, which we call a thermally induced microstructural relaxation. Therefore, the energy barrier to hop at each local strain,
![]() $l$
, is equal to
$l$
, is equal to
![]() $\mathcal{R} = E-F(l)$
, where
$\mathcal{R} = E-F(l)$
, where
![]() $F(l)$
is the locally stored elastic energy at strain
$F(l)$
is the locally stored elastic energy at strain
![]() $l$
, and
$l$
, and
![]() $E$
is the local yield energy (the maximum energy barrier) both of which are predicted by our DFT calculations. We use this energy barrier,
$E$
is the local yield energy (the maximum energy barrier) both of which are predicted by our DFT calculations. We use this energy barrier,
![]() $\mathcal{R}$
, as the activation energy for an Arrhenius law to predict the rate of thermal hops. We assume that elements mechanically yield once
$\mathcal{R}$
, as the activation energy for an Arrhenius law to predict the rate of thermal hops. We assume that elements mechanically yield once
![]() $F(l)\geqslant E$
, similar to the local yield criterion in athermal EPMs. After relaxation, whether mechanical or thermal, the elements rearrange to a new configuration corresponding to a new energy well and zero local strain. Thus, the probability,
$F(l)\geqslant E$
, similar to the local yield criterion in athermal EPMs. After relaxation, whether mechanical or thermal, the elements rearrange to a new configuration corresponding to a new energy well and zero local strain. Thus, the probability,
![]() $P(E,l,t)$
of having an element with a local strain
$P(E,l,t)$
of having an element with a local strain
![]() $l$
and yield energy
$l$
and yield energy
![]() $E$
at time
$E$
at time
![]() $t$
evolves as the following:
$t$
evolves as the following:
The first term on the right-hand side represents the elastic deformation with the applied macroscopic shear rate,
![]() $\dot \gamma$
. The second term is the thermally activated relaxation, and
$\dot \gamma$
. The second term is the thermally activated relaxation, and
![]() $\varGamma _0$
is the attempt frequency for hopping. The third term is the mechanical relaxation. Here
$\varGamma _0$
is the attempt frequency for hopping. The third term is the mechanical relaxation. Here
![]() $\mathcal{H}$
is the Heaviside function denoting that once the entire local barrier is surmounted, the element relaxes over a time scale of
$\mathcal{H}$
is the Heaviside function denoting that once the entire local barrier is surmounted, the element relaxes over a time scale of
![]() $1/\varGamma _m$
. Finally, the last term is the rearrangement of elements after yielding to a new configuration which is unstrained and randomly chosen from the distribution of energy wells,
$1/\varGamma _m$
. Finally, the last term is the rearrangement of elements after yielding to a new configuration which is unstrained and randomly chosen from the distribution of energy wells,
![]() $\rho (E)$
. The prefactor is the total yielding rate which is the average of local yielding rates:
$\rho (E)$
. The prefactor is the total yielding rate which is the average of local yielding rates:
The stress response of the material,
![]() $\sigma (t)$
, is the average over all the local stresses,
$\sigma (t)$
, is the average over all the local stresses,
![]() $\sigma _{\textit{loc}}$
, multiplied by the number density of the particles,
$\sigma _{\textit{loc}}$
, multiplied by the number density of the particles,
![]() $n_c$
, as the following:
$n_c$
, as the following:
We take each core with its attached polymers as an element of the thermal SGR model. Also, we calculate the local stresses as
![]() $\sigma _{\textit{loc}} = ({d\!F}/{dl})$
from the locally stored elastic energies. The thermal SGR model is connected to our free energy calculations through the energy landscape. Since we used a FCC arrangement in our DFT calculations, the energy landscape has only one unique energy well, and thus
$\sigma _{\textit{loc}} = ({d\!F}/{dl})$
from the locally stored elastic energies. The thermal SGR model is connected to our free energy calculations through the energy landscape. Since we used a FCC arrangement in our DFT calculations, the energy landscape has only one unique energy well, and thus
![]() $\rho (E) = \delta (E-E_0)$
with
$\rho (E) = \delta (E-E_0)$
with
![]() $E_0$
being the depth of the single energy well in the landscape. This single-well assumption allows us to probe the effect of thermal fluctuations on the rheology as the only factor to produce a steady-state response. We also use a Gaussian distribution of the yield energies to account for heterogeneity in the energy landscape. A Gaussian distribution of yield energies is assumed in polymer glasses (Hasan & Boyce Reference Hasan and Boyce1995), supercooled liquids (Xia & Wolynes Reference Xia and Wolynes2001), metallic glasses (Schirmacher, Ruocco & Mazzone Reference Schirmacher, Ruocco and Mazzone2015) and active cytoskeletal networks (Woillez, Kafri & Gov Reference Woillez, Kafri and Gov2020). Also, a Gaussian distribution of yield energies is argued to result in stretched exponential relaxations (Monthus & Bouchaud Reference Monthus and Bouchaud1996; Xia & Wolynes Reference Xia and Wolynes2001), which are observed experimentally in solvent-free polymer-grafted nanoparticles (Agarwal & Archer Reference Agarwal and Archer2011).
$E_0$
being the depth of the single energy well in the landscape. This single-well assumption allows us to probe the effect of thermal fluctuations on the rheology as the only factor to produce a steady-state response. We also use a Gaussian distribution of the yield energies to account for heterogeneity in the energy landscape. A Gaussian distribution of yield energies is assumed in polymer glasses (Hasan & Boyce Reference Hasan and Boyce1995), supercooled liquids (Xia & Wolynes Reference Xia and Wolynes2001), metallic glasses (Schirmacher, Ruocco & Mazzone Reference Schirmacher, Ruocco and Mazzone2015) and active cytoskeletal networks (Woillez, Kafri & Gov Reference Woillez, Kafri and Gov2020). Also, a Gaussian distribution of yield energies is argued to result in stretched exponential relaxations (Monthus & Bouchaud Reference Monthus and Bouchaud1996; Xia & Wolynes Reference Xia and Wolynes2001), which are observed experimentally in solvent-free polymer-grafted nanoparticles (Agarwal & Archer Reference Agarwal and Archer2011).
To achieve thermally induced structural relaxation, the particle has to diffuse some distance to change its neighbours. The attempt frequency,
![]() $\varGamma _0$
, for hopping that is the inverse of the bare hopping time,
$\varGamma _0$
, for hopping that is the inverse of the bare hopping time,
![]() $\tau _0$
, is calculated as
$\tau _0$
, is calculated as
![]() $\varGamma _0 = D/h^2$
, where
$\varGamma _0 = D/h^2$
, where
![]() $D$
is a diffusion coefficient and
$D$
is a diffusion coefficient and
![]() $h$
is the interparticle distance between the cores. The diffusion coefficient is approximated by the Stokes–Einstein relation for a single particle diffusing through a polymer melt with the same molecular weight as the grafted polymers. Therefore, this formulation connects the attempt frequency to the core particle radius, the polymer molecular weight and the core volume fraction. An increase in the polymer molecular weight leads to an increase in the viscosity of the polymer melt,
$h$
is the interparticle distance between the cores. The diffusion coefficient is approximated by the Stokes–Einstein relation for a single particle diffusing through a polymer melt with the same molecular weight as the grafted polymers. Therefore, this formulation connects the attempt frequency to the core particle radius, the polymer molecular weight and the core volume fraction. An increase in the polymer molecular weight leads to an increase in the viscosity of the polymer melt,
![]() $\mu _{\!p}$
, which hinders the diffusion and thus reduces the attempt frequency. Increasing the core volume fraction corresponds to smaller interparticle distances and consequently shorter time scales for the particle to diffuse relative to its neighbours. Note that the actual time scale for thermally induced rearrangements also includes the barrier as expressed by an Arrhenius law,
$\mu _{\!p}$
, which hinders the diffusion and thus reduces the attempt frequency. Increasing the core volume fraction corresponds to smaller interparticle distances and consequently shorter time scales for the particle to diffuse relative to its neighbours. Note that the actual time scale for thermally induced rearrangements also includes the barrier as expressed by an Arrhenius law,
![]() $\tau = \tau _0 \, \exp ({\mathcal{R}}/{k_{\textit{B}}T} )$
. All the calculations are performed assuming a temperature of
$\tau = \tau _0 \, \exp ({\mathcal{R}}/{k_{\textit{B}}T} )$
. All the calculations are performed assuming a temperature of
![]() $T = 100 \, ^\circ \mathrm{C}$
, which is above the melting point of the solvent-free polymer-grafted nanoparticles of interest (Agarwal et al. Reference Agarwal, Qi and Archer2010). Another time scale in the model is the mechanical relaxation of the stress once the barrier is removed by mechanical deformation. In this work, we assume that this relaxation happens instantly thus eliminating
$T = 100 \, ^\circ \mathrm{C}$
, which is above the melting point of the solvent-free polymer-grafted nanoparticles of interest (Agarwal et al. Reference Agarwal, Qi and Archer2010). Another time scale in the model is the mechanical relaxation of the stress once the barrier is removed by mechanical deformation. In this work, we assume that this relaxation happens instantly thus eliminating
![]() $\varGamma _m$
from the model.
$\varGamma _m$
from the model.
Equation (3.1) is solved numerically using finite volume method to discretize the strain space for each value of
![]() $E$
. The coupling between different values of
$E$
. The coupling between different values of
![]() $E$
is achieved through the yielding rate (3.2) which is solved separately. The discontinuity introduced by the Dirac delta function is numerically challenging to resolve, and thus to ensure stability and accuracy a total variation diminishing (TVD) scheme is used. In TVD schemes, the total variation of the solution is always non-increasing in time. The TVD schemes are usually defined for homogeneous partial differential equations. Therefore, to apply this scheme to (3.1), which is a hyperbolic equation with a source term (thermally induced rearrangements), we split the equation into a homogeneous hyperbolic equation and an ordinary differential equation for the source term. In this way, we first solve the homogeneous partial differential equation by applying the TVD scheme and using the initial condition of the problem, and then we use the solution to this equation as an initial condition to solve the ordinary differential equation for the source term. This process is repeated at each time step. To update the solution in time, the second-order explicit Runge–Kutta method is used (Toro Reference Toro2013). The last two terms in (3.1) are treated as boundary conditions. Lastly, the composite midpoint rule is used as the quadrature routine for numerical integration.
$E$
is achieved through the yielding rate (3.2) which is solved separately. The discontinuity introduced by the Dirac delta function is numerically challenging to resolve, and thus to ensure stability and accuracy a total variation diminishing (TVD) scheme is used. In TVD schemes, the total variation of the solution is always non-increasing in time. The TVD schemes are usually defined for homogeneous partial differential equations. Therefore, to apply this scheme to (3.1), which is a hyperbolic equation with a source term (thermally induced rearrangements), we split the equation into a homogeneous hyperbolic equation and an ordinary differential equation for the source term. In this way, we first solve the homogeneous partial differential equation by applying the TVD scheme and using the initial condition of the problem, and then we use the solution to this equation as an initial condition to solve the ordinary differential equation for the source term. This process is repeated at each time step. To update the solution in time, the second-order explicit Runge–Kutta method is used (Toro Reference Toro2013). The last two terms in (3.1) are treated as boundary conditions. Lastly, the composite midpoint rule is used as the quadrature routine for numerical integration.
4. Molecular-level information
We shear the system of polymer-grafted nanoparticles in the
![]() $x$
direction while the shear gradient is in the
$x$
direction while the shear gradient is in the
![]() $z$
direction. Since the system under shear is a unit cell, once it is displaced by its size, we reproduce the same configuration. The configuration with a shear strain of
$z$
direction. Since the system under shear is a unit cell, once it is displaced by its size, we reproduce the same configuration. The configuration with a shear strain of
![]() $\gamma = 1$
results in the most deviation from the initial configuration (
$\gamma = 1$
results in the most deviation from the initial configuration (
![]() $\gamma = 0$
) since the unit cell is displaced by half of its size. As a result, we can detect all the possible configurations in a shearing cycle, by shearing the unit cell only from
$\gamma = 0$
) since the unit cell is displaced by half of its size. As a result, we can detect all the possible configurations in a shearing cycle, by shearing the unit cell only from
![]() $\gamma = 0$
to
$\gamma = 0$
to
![]() $\gamma = 1$
.
$\gamma = 1$
.
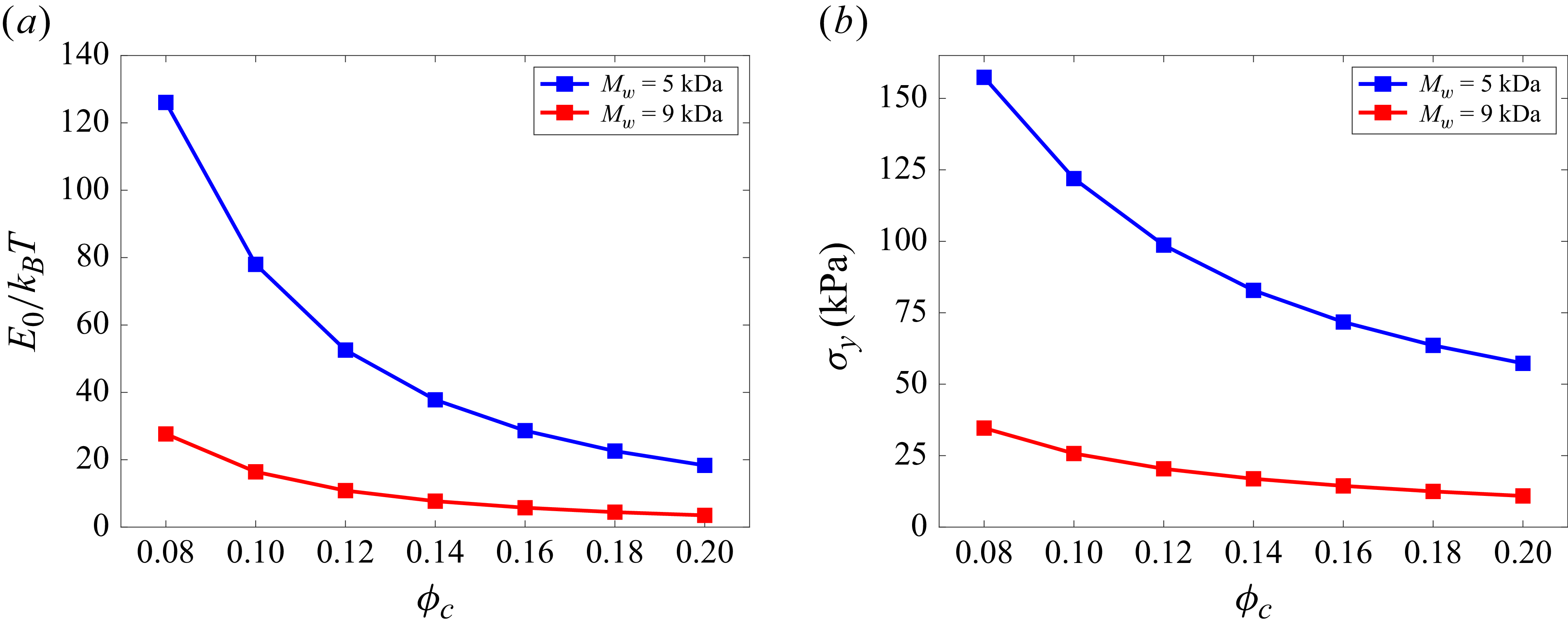
Table 1 lists the dimensional and dimensionless parameters used in this work. We assume a range of core volume fractions and two different polymer molecular weights. The void volume per core depends on the core volume fraction as
![]() ${(1-\phi _c)}/{n_c}$
where
${(1-\phi _c)}/{n_c}$
where
![]() $n_c$
is the number density of the cores. Since the grafted polymers must be able to fill the void volume, the number of grafted polymers is found by defining a volume per polymer molecule as
$n_c$
is the number density of the cores. Since the grafted polymers must be able to fill the void volume, the number of grafted polymers is found by defining a volume per polymer molecule as
![]() $({M_w}/{\rho _p N_{\!A}})$
, where
$({M_w}/{\rho _p N_{\!A}})$
, where
![]() $N_{\!A}$
is Avogadro’s number. As the core volume fraction is decreased, there is more void space in the system for polymers to fill. As a result, the number of grafted polymers (and thus the grafting density) has to increase. For a fixed core volume fraction, increasing the molecular weight of the grafted polymers decreases the grafting density. This stems from the fact that a higher molecular weight provides a larger volume per polymer molecule, and thus a smaller number of polymers is needed to fill the void space. The range of the core volume fraction and polymer molecular weights that we use in this work lead to a range of grafting densities,
$N_{\!A}$
is Avogadro’s number. As the core volume fraction is decreased, there is more void space in the system for polymers to fill. As a result, the number of grafted polymers (and thus the grafting density) has to increase. For a fixed core volume fraction, increasing the molecular weight of the grafted polymers decreases the grafting density. This stems from the fact that a higher molecular weight provides a larger volume per polymer molecule, and thus a smaller number of polymers is needed to fill the void space. The range of the core volume fraction and polymer molecular weights that we use in this work lead to a range of grafting densities,
![]() $\sigma _g = 0.45{-}2.3 \, \mathrm{chains}\,\text{nm}^{-2}$
, which is experimentally achievable (Srivastava et al. Reference Srivastava, Choudhury, Agrawal and Archer2017). The viscosity of molten PEG is also reported in table 1 for the two different molecular weights. These values will be used in the thermal SGR model to calculate the attempt frequency as described in § 3.
$\sigma _g = 0.45{-}2.3 \, \mathrm{chains}\,\text{nm}^{-2}$
, which is experimentally achievable (Srivastava et al. Reference Srivastava, Choudhury, Agrawal and Archer2017). The viscosity of molten PEG is also reported in table 1 for the two different molecular weights. These values will be used in the thermal SGR model to calculate the attempt frequency as described in § 3.
Table 1. Dimensional and dimensionless parameters used in this study. Two different polymer molecular weights are used which lead to two different radii of gyration and viscosities of melt. A range of grafting densities and number of polymer chains per particle is due to a range of core volume fractions and two different molecular weights.

4.1. Number density profiles
As shown in (2.1), a competition between the translational entropy of the polymers (captured by the beads) and the configurational entropy of the polymers (captured by the spring energy) in conjunction with the space-filling constraint (depending on the value of
![]() $\alpha$
) determines the free energy of the polymers. Figure 2 shows the number density of the grafted polymers in a system with a core volume fraction of
$\alpha$
) determines the free energy of the polymers. Figure 2 shows the number density of the grafted polymers in a system with a core volume fraction of
![]() $\phi _c=0.1$
, a grafting density of
$\phi _c=0.1$
, a grafting density of
![]() $\sigma _g = 1.8 \, \mathrm{chains}\,\text{nm}^{-2}$
and polymer molecular weight of
$\sigma _g = 1.8 \, \mathrm{chains}\,\text{nm}^{-2}$
and polymer molecular weight of
![]() $M_w = 5000 \, \mathrm{Da}$
. The number densities are shown at different points in space for the solvent-free case (
$M_w = 5000 \, \mathrm{Da}$
. The number densities are shown at different points in space for the solvent-free case (
![]() $\alpha \rightarrow \infty$
) and the case with solvent (
$\alpha \rightarrow \infty$
) and the case with solvent (
![]() $\alpha =0$
) under shear deformation. The dark blue regions display the cores where there is zero probability of finding a polymer.
$\alpha =0$
) under shear deformation. The dark blue regions display the cores where there is zero probability of finding a polymer.

Figure 2. The number density of the grafted polymers (normalized by the mean number density) at each point of the unit cell under shear deformation with different applied strains and different values of the space-filling parameter: (a)
![]() $\alpha = 0$
and
$\alpha = 0$
and
![]() $\gamma = 0$
, (b)
$\gamma = 0$
, (b)
![]() $\alpha = 0$
and
$\alpha = 0$
and
![]() $\gamma = 1$
, (c)
$\gamma = 1$
, (c)
![]() $\alpha \rightarrow \infty$
and
$\alpha \rightarrow \infty$
and
![]() $\gamma = 0$
and (d)
$\gamma = 0$
and (d)
![]() $\alpha \rightarrow \infty$
and
$\alpha \rightarrow \infty$
and
![]() $\gamma = 1$
. In all of the profiles, the core volume fraction is
$\gamma = 1$
. In all of the profiles, the core volume fraction is
![]() $\phi _c = 0.1$
, the grafting density is
$\phi _c = 0.1$
, the grafting density is
![]() $\sigma _g = 1.8 \, \mathrm{chains}\,\text{nm}^{-2}$
, and the PEG molecular weight is
$\sigma _g = 1.8 \, \mathrm{chains}\,\text{nm}^{-2}$
, and the PEG molecular weight is
![]() $M_w = 5000 \, \mathrm{Da}$
.
$M_w = 5000 \, \mathrm{Da}$
.
For
![]() $\alpha =0$
at no shear deformation (figure 2
a), the polymers are most likely found around the grafting points as they form a cloud around each core. The number density in these relatively thin clouds is larger than the mean number density. The green regions between the clouds represent a mild polymer–polymer interpenetration where the polymers from neighbouring cores meet. In regions far away from any grafting points, the number density decreases, and only a few polymers can be found. One can assume that these regions are filled with solvent molecules although their contribution to the free energy of the system is not explicitly modelled. When
$\alpha =0$
at no shear deformation (figure 2
a), the polymers are most likely found around the grafting points as they form a cloud around each core. The number density in these relatively thin clouds is larger than the mean number density. The green regions between the clouds represent a mild polymer–polymer interpenetration where the polymers from neighbouring cores meet. In regions far away from any grafting points, the number density decreases, and only a few polymers can be found. One can assume that these regions are filled with solvent molecules although their contribution to the free energy of the system is not explicitly modelled. When
![]() $\alpha =0$
, there is no constraint requiring the polymers to stretch and fill the interstitial space, and they are free to occupy interstitial space in a manner that maximizes the sum of their translational and configurational entropies. To fill the entire void space, the polymers have to highly stretch which causes a large spring energy contribution to the free energy. As a result, the polymers remain near their grafting points and avoid stretching in order to minimize their spring energy. For
$\alpha =0$
, there is no constraint requiring the polymers to stretch and fill the interstitial space, and they are free to occupy interstitial space in a manner that maximizes the sum of their translational and configurational entropies. To fill the entire void space, the polymers have to highly stretch which causes a large spring energy contribution to the free energy. As a result, the polymers remain near their grafting points and avoid stretching in order to minimize their spring energy. For
![]() $\alpha =0$
under maximum deformation (figure 2
b), polymers would need to stretch and increase their spring energy to fill the additional space along the extensional axis. Thus, the polymers avoid filling the added volume along the extensional axis to minimize their free energy resulting in an almost zero number density along this axis. As a result, the polymers from neighbouring particles accumulate along the compressional axis leading to a very non-uniform number density profile in the shear plane. Since the plane
$\alpha =0$
under maximum deformation (figure 2
b), polymers would need to stretch and increase their spring energy to fill the additional space along the extensional axis. Thus, the polymers avoid filling the added volume along the extensional axis to minimize their free energy resulting in an almost zero number density along this axis. As a result, the polymers from neighbouring particles accumulate along the compressional axis leading to a very non-uniform number density profile in the shear plane. Since the plane
![]() $z=0$
undergoes no shear deformation, the polymers in this plane form the thin clouds around the cores which are the hallmark of the case with
$z=0$
undergoes no shear deformation, the polymers in this plane form the thin clouds around the cores which are the hallmark of the case with
![]() $\alpha =0$
and zero applied strain (figure 2
a).
$\alpha =0$
and zero applied strain (figure 2
a).
When
![]() $\alpha \rightarrow \infty$
, the space-filling constraint is imposed and the polymers stretch and uniformly fill the entire interstitial space under both minimum (figure 2
c) and maximum (figure 2
d) deformation. In this case, the polymers are not compressed as, at each point, they have a number density equal to the mean number density corresponding to an incompressible single-component fluid. This is corroborated by scattering experiment, theoretical and molecular simulation results for the structure factor showing that density fluctuations are highly suppressed in solvent-free polymer-grafted nanoparticles (Yu & Koch Reference Yu and Koch2010; Chremos et al. Reference Chremos, Panagiotopoulos, Yu and Koch2011; Yu et al. Reference Yu, Srivastava, Archer and Koch2014). This situation corresponds to many-body interactions between the cores as their grafted polymers cooperate to fill the void space. Although filling the entire void space is accompanied by a large spring energy, the penalty for not filling the entire space is much larger than the spring energy when
$\alpha \rightarrow \infty$
, the space-filling constraint is imposed and the polymers stretch and uniformly fill the entire interstitial space under both minimum (figure 2
c) and maximum (figure 2
d) deformation. In this case, the polymers are not compressed as, at each point, they have a number density equal to the mean number density corresponding to an incompressible single-component fluid. This is corroborated by scattering experiment, theoretical and molecular simulation results for the structure factor showing that density fluctuations are highly suppressed in solvent-free polymer-grafted nanoparticles (Yu & Koch Reference Yu and Koch2010; Chremos et al. Reference Chremos, Panagiotopoulos, Yu and Koch2011; Yu et al. Reference Yu, Srivastava, Archer and Koch2014). This situation corresponds to many-body interactions between the cores as their grafted polymers cooperate to fill the void space. Although filling the entire void space is accompanied by a large spring energy, the penalty for not filling the entire space is much larger than the spring energy when
![]() $\alpha \rightarrow \infty$
. Therefore, to minimize their free energy, the polymers have to satisfy the space-filling constraint and consequently
$\alpha \rightarrow \infty$
. Therefore, to minimize their free energy, the polymers have to satisfy the space-filling constraint and consequently
![]() $n(\boldsymbol{r}) \approx n_0$
at any point in the void space (the number density profiles of figure 2
c and 2
d). The origin of the slow dynamics of solvent-free polymer-grafted nanoparticles can be found in the space-filling constraint and will be discussed in depth in § 4.2 and § 4.3. This observation is supported by experiments (Agarwal et al. Reference Agarwal, Qi and Archer2010, Reference Agarwal, Srivastava and Archer2011) and molecular dynamics simulations (Midya et al. Reference Midya, Rubinstein, Kumar and Nikoubashman2020) on solvent-free polymer-grafted nanoparticles indicating a high degree of polymer interpenetration in the system and formation of cages around the cores which slow down the relaxation. To understand how the system evolves under shear from figure 2(a) and 2(c), to figure 2(b) and 2(d), respectively, we quantitatively demonstrate the different contributions to the free energy along with the effects of the space-filling penalty in a cycle of shear.
$n(\boldsymbol{r}) \approx n_0$
at any point in the void space (the number density profiles of figure 2
c and 2
d). The origin of the slow dynamics of solvent-free polymer-grafted nanoparticles can be found in the space-filling constraint and will be discussed in depth in § 4.2 and § 4.3. This observation is supported by experiments (Agarwal et al. Reference Agarwal, Qi and Archer2010, Reference Agarwal, Srivastava and Archer2011) and molecular dynamics simulations (Midya et al. Reference Midya, Rubinstein, Kumar and Nikoubashman2020) on solvent-free polymer-grafted nanoparticles indicating a high degree of polymer interpenetration in the system and formation of cages around the cores which slow down the relaxation. To understand how the system evolves under shear from figure 2(a) and 2(c), to figure 2(b) and 2(d), respectively, we quantitatively demonstrate the different contributions to the free energy along with the effects of the space-filling penalty in a cycle of shear.
4.2. Free energy and entropy of the grafted polymers
Figure 3 illustrates how the free energy of the polymers grafted on a single core changes with respect to the shear deformation and the space-filling parameter in a system with a core volume fraction of
![]() $\phi _c = 0.1$
, a grafting density of
$\phi _c = 0.1$
, a grafting density of
![]() $\sigma _g = 1.8 \, \mathrm{chains\,nm^{-2}}$
and a PEG molecular weight of
$\sigma _g = 1.8 \, \mathrm{chains\,nm^{-2}}$
and a PEG molecular weight of
![]() $M_w = 5000 \, \mathrm{Da}$
. Since the entropic free energy is
$M_w = 5000 \, \mathrm{Da}$
. Since the entropic free energy is
![]() $-T\Delta S$
, where
$-T\Delta S$
, where
![]() $S$
is the entropy, figure 3 also shows how the translational entropy of the beads changes with respect to the space-filling parameter and shear deformation. Positive changes in the entropic free energy correspond to negative changes in the translational entropy of the beads and vice versa. Increasing
$S$
is the entropy, figure 3 also shows how the translational entropy of the beads changes with respect to the space-filling parameter and shear deformation. Positive changes in the entropic free energy correspond to negative changes in the translational entropy of the beads and vice versa. Increasing
![]() $\alpha$
, regardless of the value of the shear strain, monotonically increases the total free energy of the polymers (figure 3
a) and the translational entropy of the beads until they reach a plateau. For
$\alpha$
, regardless of the value of the shear strain, monotonically increases the total free energy of the polymers (figure 3
a) and the translational entropy of the beads until they reach a plateau. For
![]() $\alpha \gt 0.4$
, the state of the system appears to be insensitive to the value of
$\alpha \gt 0.4$
, the state of the system appears to be insensitive to the value of
![]() $\alpha$
, implying that the space-filling constraint is satisfied. This can be regarded as the solvent-free case, i.e.
$\alpha$
, implying that the space-filling constraint is satisfied. This can be regarded as the solvent-free case, i.e.
![]() $\alpha \rightarrow \infty$
.
$\alpha \rightarrow \infty$
.

Figure 3. (a) The changes in the free energy of the polymers as a function of the space-filling parameter relative to the values at
![]() $\alpha =0$
(open symbols,
$\alpha =0$
(open symbols,
![]() $\gamma = 0$
; filled symbols,
$\gamma = 0$
; filled symbols,
![]() $\gamma = 1$
). (b) The evolution of the total free energy and different contributions to the free energy with shear strain relative to the values at
$\gamma = 1$
). (b) The evolution of the total free energy and different contributions to the free energy with shear strain relative to the values at
![]() $\gamma =0$
(open symbols,
$\gamma =0$
(open symbols,
![]() $\alpha = 0$
; filled symbols,
$\alpha = 0$
; filled symbols,
![]() $\alpha \rightarrow \infty$
). The core volume fraction is
$\alpha \rightarrow \infty$
). The core volume fraction is
![]() $\phi _c = 0.1$
, the grafting density is
$\phi _c = 0.1$
, the grafting density is
![]() $\sigma _g = 1.8 \, \mathrm{chains}\,\text{nm}^{-2}$
, and the PEG molecular weight is
$\sigma _g = 1.8 \, \mathrm{chains}\,\text{nm}^{-2}$
, and the PEG molecular weight is
![]() $M_w = 5000 \, \mathrm{Da}$
.
$M_w = 5000 \, \mathrm{Da}$
.
The polymers always choose the configurations that minimize their free energy. In the absence of the space-filling constraint, all the configurations are allowed corresponding to a large configurational entropy for the chains. The configurations that lead to a small spring energy are preferred due to the free energy minimization. Thus, the polymers choose the configurations that avoid stretching as much as possible, shown in figure 2(a) and 2(b). However, these configurations lead to a small translational entropy since the probabilities of finding the polymers in the void space are highly inhomogeneous. On the other hand, when the space-filling constraint is imposed, the polymers are forced to choose only between the configurations that result in a relatively large stretch. This reduces the number of allowed configurations for the chains and greatly suppresses their configurational entropy. In this case, the chains are ‘frustrated’ because their conformational space is extremely limited. This entropic frustration of the chain configurations, which is a unique characteristic of solvent-free polymer-grafted nanoparticles (Agarwal, Kim & Archer Reference Agarwal, Kim and Archer2012; Yu et al. Reference Yu, Srivastava, Archer and Koch2014), manifests itself here through the drastic increase in the spring energy as the space-filling constraint is enforced (figure 3
a). However, satisfying the space-filling constraint brings about an advantage for the translational entropy. In this situation, the number density (and thus the probability distribution) of the polymers is uniform in the void space (figure 2
c and 2d
) correlating with a large translational entropy for the polymers. Therefore, the role of the space-filling parameter in the configurational entropy of the polymers (spring energy) and in the translational entropy of the polymers can be interpreted as unfavourable and favourable, respectively. Since the effects on the configurational entropy are more pronounced, the total free energy increases with
![]() $\alpha$
.
$\alpha$
.
The free energy penalty is zero when
![]() $\alpha = 0$
and also when the polymers uniformly fill the interstitial space since
$\alpha = 0$
and also when the polymers uniformly fill the interstitial space since
![]() $n(\boldsymbol{r}) \approx n_0$
at any point (see (2.1)). However, one should note that changing
$n(\boldsymbol{r}) \approx n_0$
at any point (see (2.1)). However, one should note that changing
![]() $\alpha$
alters the probabilities and thus the free energy and entropy, as described earlier and evidenced by figure 3 and number density profiles in figure 2. An interesting observation is the non-zero values of the free energy penalty for small, non-zero values of
$\alpha$
alters the probabilities and thus the free energy and entropy, as described earlier and evidenced by figure 3 and number density profiles in figure 2. An interesting observation is the non-zero values of the free energy penalty for small, non-zero values of
![]() $\alpha$
. Since
$\alpha$
. Since
![]() $\alpha$
is small, the space-filling constraint is mildly enforced and thus the number density at each point still deviates from the mean value. This can be considered as a compressible system in which the thermal energy of the polymers can cause variations in their number density. However, large variations are not allowed as they lead to a large free energy penalty. In this case, the polymers have more freedom in choosing different configurations compared with when
$\alpha$
is small, the space-filling constraint is mildly enforced and thus the number density at each point still deviates from the mean value. This can be considered as a compressible system in which the thermal energy of the polymers can cause variations in their number density. However, large variations are not allowed as they lead to a large free energy penalty. In this case, the polymers have more freedom in choosing different configurations compared with when
![]() $\alpha \rightarrow \infty$
. Therefore, decreasing
$\alpha \rightarrow \infty$
. Therefore, decreasing
![]() $\alpha$
(increasing the compressibility of the system) releases the entropic frustration of the chain configurations.
$\alpha$
(increasing the compressibility of the system) releases the entropic frustration of the chain configurations.
Figure 3(b) shows that by starting from the initial configuration, the free energy and the translational entropy change with shear strain until they reach a maximum difference (at
![]() $\gamma = 1$
) where the cores experience the most deviation from their initial configuration. The core configuration has mirror symmetry about the
$\gamma = 1$
) where the cores experience the most deviation from their initial configuration. The core configuration has mirror symmetry about the
![]() $zy$
plane such that shearing beyond
$zy$
plane such that shearing beyond
![]() $\gamma =1$
yields configurations in which strain of
$\gamma =1$
yields configurations in which strain of
![]() $1+\delta \gamma$
is the mirror image (with equal free energy) of that with strain of
$1+\delta \gamma$
is the mirror image (with equal free energy) of that with strain of
![]() $1-\delta \gamma$
.
$1-\delta \gamma$
.
Figure 3(b) indicates that, at
![]() $\alpha =0$
, the spring energy decreases under shear deformation corresponding to the polymers being less stretched as they leave the extensional axis. Since shearing in this case leads to even less homogeneous probabilities (transition from figure 2
a to 2b
), the translational entropy of the polymers decreases under deformation. Thus, at
$\alpha =0$
, the spring energy decreases under shear deformation corresponding to the polymers being less stretched as they leave the extensional axis. Since shearing in this case leads to even less homogeneous probabilities (transition from figure 2
a to 2b
), the translational entropy of the polymers decreases under deformation. Thus, at
![]() $\alpha =0$
, shearing the unit cell is favourable to the configurational entropy (spring energy) but unfavourable to the translational entropy. As a result, a free energy barrier emerges in this situation due to the limited translational entropy of the polymers. For the solvent-free system, shear deformation will further stretch the polymers filling the space near the extensional axis and reduce the number of allowed configurations for the chains compared with the unstrained system. This creates a large free-energy barrier due to limited configurational entropy of the polymers. Noticeably, this barrier is lowered by the increased translational entropy of the polymers under shear. Figure 3(b) shows that shear deformation is favourable to the translational entropy of the polymers when
$\alpha =0$
, shearing the unit cell is favourable to the configurational entropy (spring energy) but unfavourable to the translational entropy. As a result, a free energy barrier emerges in this situation due to the limited translational entropy of the polymers. For the solvent-free system, shear deformation will further stretch the polymers filling the space near the extensional axis and reduce the number of allowed configurations for the chains compared with the unstrained system. This creates a large free-energy barrier due to limited configurational entropy of the polymers. Noticeably, this barrier is lowered by the increased translational entropy of the polymers under shear. Figure 3(b) shows that shear deformation is favourable to the translational entropy of the polymers when
![]() $\alpha \rightarrow \infty$
. This can be explained by the probability density of finding the polymer bead within the shear plane conditioned on the grafting location being along the extensional axis, shown in figure 4. Although shearing the solvent-free system does not alter the number density profile (see figure 2
c and 2
d), it stretches the polymers grafted on the points along the extensional axis. Thus, the transition from figure 4(a) to figure 4(b) due to the applied shear, creates a more uniform probability distribution for the polymers over a large volume which correlates with an increase in their translational entropy.
$\alpha \rightarrow \infty$
. This can be explained by the probability density of finding the polymer bead within the shear plane conditioned on the grafting location being along the extensional axis, shown in figure 4. Although shearing the solvent-free system does not alter the number density profile (see figure 2
c and 2
d), it stretches the polymers grafted on the points along the extensional axis. Thus, the transition from figure 4(a) to figure 4(b) due to the applied shear, creates a more uniform probability distribution for the polymers over a large volume which correlates with an increase in their translational entropy.

Figure 4. The probability density of finding the polymer bead within the shear plane conditioned on the grafting location being along the extensional axis for solvent-free polymer-grafted nanoparticles at (a)
![]() $\gamma = 0$
and (b)
$\gamma = 0$
and (b)
![]() $\gamma = 1$
.
$\gamma = 1$
.
Although we focused on a fixed core volume fraction, polymer molecular weight and grafting density, our findings are applicable to other parameter sets in solvent-free polymer-grafted nanoparticle systems, as demonstrated in the subsequent section. Similarly, for each set of parameters, the polymer configuration will be determined based on the amount of the void space around each core and the polymer length. The distinction between mushroom and brush configurations for polymers does not apply to the solvent-free systems we consider. This distinction applies to polymer brushes in a good solvent where there is a competition between the configurational entropy of the chain (favouring the mushroom state) and the enthalpic interactions of the chains with the solvent or effective excluded volume of the monomers in the chain (favouring an extended brush). Here, the effective excluded volume is zero as the polymer brush sees a melt of polymers of the same species and they act as ideal chains which we model with a linear spring. The changes in polymer configuration are then governed by the requirement that the chains from all cores collectively preserve the melt state throughout the interstitial space.
4.3. Energy well and mechanical yield stress
We demonstrated that the interplay between the configurational and translational entropy of the polymers, which is strongly influenced by the space-filling parameter, determines the shape of the energy well depicted in figure 3(b). In this section, we generalize our findings for solvent-free polymer-grafted nanoparticles to explore the effects of the core volume fraction, grafting density and molecular weight of the polymers on the energy well and consequently the mechanical yield stress.

Figure 5. (a) The depth of the energy well (energy barrier) and (b) the mechanical yield stress as a function of the core volume fraction for different molecular weights of the grafted polymers in solvent-free polymer-grafted nanoparticles.
An estimate of the mechanical yield stress of the material is possible based on the energy landscape. We can define the mechanical yield stress as the minimum stress necessary to continually deform the periodic array, i.e.
![]() $\sigma _y = ({\rm d}/{\rm d\gamma })({\Delta F}/{V})|_{\textit{max}}$
, where
$\sigma _y = ({\rm d}/{\rm d\gamma })({\Delta F}/{V})|_{\textit{max}}$
, where
![]() $V$
is the volume of an element or a typical rearrangement in the system. This definition does not take into account the thermal fluctuations of the cores, and thus we refer to it as the mechanical yield stress. This is a crude estimate of the mechanical yield stress of the material since it does not include amorphous structures, and it assumes that the elements are independent. Figure 5 displays how the depth of the energy well and the mechanical yield stress change with the polymer molecular weight and the core volume fraction. Similar trends are observed for the depth of the energy well and the mechanical yield stress as a function of the core volume fraction and polymer molecular weight as expected based on the definition of the mechanical yield stress. Interestingly, decreasing the core volume fraction increases the depth of the energy well and consequently the mechanical yield stress. This seems counterintuitive since in dense colloidal suspensions, the yield stress increases as the system becomes more packed with particles (Petekidis, Vlassopoulos & Pusey Reference Petekidis, Vlassopoulos and Pusey2004). In those systems, as the volume fraction of colloidal particles increases, the particles become more strongly confined in cages formed by their neighbours, and the system becomes dynamically arrested above the packing volume fraction (Bonn et al. Reference Bonn, Denn, Berthier, Divoux and Manneville2017). However, solvent-free grafted nanoparticles exhibit glassy behaviour even at low core volume fractions, and increasing the core volume fraction is favourable for the grafted polymers. In § 4.2, we interpreted the difficulty of filling the space by grafted polymers as the entropic frustration of the chain configuration and observed that more frustrated chains have a much larger free energy. Increasing the core volume fraction leads to a smaller void volume for the grafted polymers to fill. Thus, the polymers are less stretched, and their conformational space is less limited as they can choose between a larger number of allowed configurations. As a result, the energy barrier and the mechanical yield stress decrease with increased core volume fraction. We anticipate this trend to be valid up to a maximum volume fraction,
$V$
is the volume of an element or a typical rearrangement in the system. This definition does not take into account the thermal fluctuations of the cores, and thus we refer to it as the mechanical yield stress. This is a crude estimate of the mechanical yield stress of the material since it does not include amorphous structures, and it assumes that the elements are independent. Figure 5 displays how the depth of the energy well and the mechanical yield stress change with the polymer molecular weight and the core volume fraction. Similar trends are observed for the depth of the energy well and the mechanical yield stress as a function of the core volume fraction and polymer molecular weight as expected based on the definition of the mechanical yield stress. Interestingly, decreasing the core volume fraction increases the depth of the energy well and consequently the mechanical yield stress. This seems counterintuitive since in dense colloidal suspensions, the yield stress increases as the system becomes more packed with particles (Petekidis, Vlassopoulos & Pusey Reference Petekidis, Vlassopoulos and Pusey2004). In those systems, as the volume fraction of colloidal particles increases, the particles become more strongly confined in cages formed by their neighbours, and the system becomes dynamically arrested above the packing volume fraction (Bonn et al. Reference Bonn, Denn, Berthier, Divoux and Manneville2017). However, solvent-free grafted nanoparticles exhibit glassy behaviour even at low core volume fractions, and increasing the core volume fraction is favourable for the grafted polymers. In § 4.2, we interpreted the difficulty of filling the space by grafted polymers as the entropic frustration of the chain configuration and observed that more frustrated chains have a much larger free energy. Increasing the core volume fraction leads to a smaller void volume for the grafted polymers to fill. Thus, the polymers are less stretched, and their conformational space is less limited as they can choose between a larger number of allowed configurations. As a result, the energy barrier and the mechanical yield stress decrease with increased core volume fraction. We anticipate this trend to be valid up to a maximum volume fraction,
![]() $\phi _m$
, beyond which there are no pathways for the nanocores to rearrange. In this situation, all the mobilized parts of the polymer chains are replaced by the nanocores, and there is only a thin layer of immobilized polymers around each nanocore which prevents the particle aggregation. Due to the immobilized polymers, we expect that
$\phi _m$
, beyond which there are no pathways for the nanocores to rearrange. In this situation, all the mobilized parts of the polymer chains are replaced by the nanocores, and there is only a thin layer of immobilized polymers around each nanocore which prevents the particle aggregation. Due to the immobilized polymers, we expect that
![]() $\phi _m \lt \phi _g = 0.58$
, where
$\phi _m \lt \phi _g = 0.58$
, where
![]() $\phi _g$
corresponds to the transition from a supercooled liquid to a glass in colloidal systems (Hunter & Weeks Reference Hunter and Weeks2012).
$\phi _g$
corresponds to the transition from a supercooled liquid to a glass in colloidal systems (Hunter & Weeks Reference Hunter and Weeks2012).
Another interesting observation is a decline in the energy barrier and the mechanical yield stress upon increasing the molecular weight of the grafted polymers. The reason again lies in the requirement for the grafted polymers to fill the space. At a fixed core volume fraction (fixed void volume between the cores), longer polymers, compared with shorter chains, can fill the void space more easily as they undergo less stretch to do so. Thus, increasing the molecular weight of the grafted polymers facilitates space filling and releases the entropic frustration of the polymers. Experimental results show that increasing the polymer molecular weight decreases the loss modulus maximum at yielding which in turn is connected to the cage breakage (Agrawal et al. Reference Agrawal, Yu, Srivastava, Choudhury, Narayanan and Archer2015; Srivastava et al. Reference Srivastava, Choudhury, Agrawal and Archer2017). The observed peak in the loss modulus in strain-sweep oscillatory shear test on soft glassy materials manifests an enhanced energy dissipation due to continuous cage breakage and rearrangements of particles. A less pronounced peak is associated with less energy dissipation resulting from smaller locally stored energies before the cage breakage. Therefore, we would expect that increasing the polymer molecular weight leads to smaller values of the elastic modulus as the capacity of cages to store elastic energy decreases. Another experimental observation is the decrease in the yield strain with increasing the core volume fraction which can be related to the space-filling constraint (Liu et al. Reference Liu, Utomo, Zhao, Zheng, Zhang and Archer2020).
The trends in figure 5 will remain the same if, for a fixed core volume fraction, both the core radius and polymer radius of gyration change in the same proportion. This stems from the fact that in solvent-free polymer-grafted nanoparticles, the free energy of the polymers is determined by the requirement to fill the void space. As long as the void volume remains constant, only the ratio of the polymer radius of gyration to the core radius is important. It is worth mentioning that changing both the core radius and polymer radius of gyration in the same proportion while keeping the core volume fraction fixed will result in a slightly different number of polymer chains per particle and thus a slightly different free energy. One can fix the number of polymer chains per particle by fixing the volume per polymer molecule through using a different linear polymer (with a different mass density). Therefore, our theory is applicable to all linear polymers, a wide range of particle sizes and a wide range polymer radii of gyration.
5. Macroscopic rheology
In this section, we use the energy profiles obtained from our DFT calculations to predict the macroscopic response of the material to different rheological tests. Our thermal version of the SGR model (3.1) allows an examination of the effects of thermal fluctuations of the cores and the rate of deformation on the transient and nonlinear rheology. This includes an apparent yield stress that may differ from the mechanical yield stress derived in § 4 when experiments are performed over time periods shorter than the very large terminal relaxation time of the material. For the sake of brevity, unless otherwise stated, the results shown in this section belong to solvent-free grafted nanoparticles with a polymer molecular weight of
![]() $M_w = 5 \, \mathrm{kDa}$
and a core volume fraction of
$M_w = 5 \, \mathrm{kDa}$
and a core volume fraction of
![]() $\phi _c = 0.2$
. However, we obtain the yield stress values for all the samples (different core volume fraction and polymer molecular weight) and perform scaling analysis based on the energy well and the attempt frequency for hopping that are applicable to all thermal amorphous materials.
$\phi _c = 0.2$
. However, we obtain the yield stress values for all the samples (different core volume fraction and polymer molecular weight) and perform scaling analysis based on the energy well and the attempt frequency for hopping that are applicable to all thermal amorphous materials.
5.1. Start-up shear test
Applying a constant shear rate is a simple and yet highly informative rheological probe as it allows us to monitor the evolution of the macroscopic stress versus strain (or time) in both linear and nonlinear regimes and determine the effects of the rate of deformation on the structural relaxations. In this section, we assume that the material has been at rest for a long time prior to performing the test. This corresponds to no history of deformation as all the elements start from zero local stress. We later address the effects of the history of deformation on the stress–strain curve.
Figures 6(a) to 6(c) show the stress–strain curves for different applied shear rates. For very small deformation, the stress increases linearly with strain as the material behaves like an elastic solid. However, for large deformation, the material flows like a liquid, and the stress is no longer a function of the applied strain but the applied rate of strain. The transition from solid-like to liquid-like behaviour, which is the hallmark of amorphous materials, is highly dependent on the rate of deformation. The sample in this section has a local energy barrier of around
![]() $E_0 \approx 20 \, k_{\textit{B}}T$
. When the energy barrier is large compared with
$E_0 \approx 20 \, k_{\textit{B}}T$
. When the energy barrier is large compared with
![]() $k_{\textit{B}}T$
, activation by thermal fluctuations requires either a significant amount of time or a considerable decrease in the energy barrier. For very small shear rates (figure 6
a), at short times (small strains), the thermal hops do not result in local yielding as the activation energy is still large, and the mechanical relaxation is also not achieved since the deformation of the elements is very small. As a result, the elements deform elastically and accumulate stress in their cages. As time progresses, more thermally induced attempts at relaxation occur and also a larger proportion of those attempts are successful owing to the decrease in the remaining energy barrier resulting from the work done on the system. Thus, after a short time of no structural relaxation, a few elements hop and relax their local stresses. The number of thermally induced structural relaxations increases over time based on the above argument. Thus, the stress–strain curve deviates from linearity, and this deviation increases over time as the number of thermally induced relaxations increase. When the build up of the local stress by shear is faster than stress relaxation by thermal fluctuations, an overshoot appears in the stress–strain curve. After the overshoot, the stress decreases due to continuous plastic events. Thus, the stress overshoot in the stress–strain curve can be regarded as a measure of the material’s static yield stress (Balmforth, Frigaard & Ovarlez Reference Balmforth, Frigaard and Ovarlez2014). At the steady state the stress plateaus, corresponding to plastic flow with a constant rate of plastic rearrangements in the system. In this situation, the rate of stress increase in the system due to the applied shear is equal to the rate of stress relaxation.
$k_{\textit{B}}T$
, activation by thermal fluctuations requires either a significant amount of time or a considerable decrease in the energy barrier. For very small shear rates (figure 6
a), at short times (small strains), the thermal hops do not result in local yielding as the activation energy is still large, and the mechanical relaxation is also not achieved since the deformation of the elements is very small. As a result, the elements deform elastically and accumulate stress in their cages. As time progresses, more thermally induced attempts at relaxation occur and also a larger proportion of those attempts are successful owing to the decrease in the remaining energy barrier resulting from the work done on the system. Thus, after a short time of no structural relaxation, a few elements hop and relax their local stresses. The number of thermally induced structural relaxations increases over time based on the above argument. Thus, the stress–strain curve deviates from linearity, and this deviation increases over time as the number of thermally induced relaxations increase. When the build up of the local stress by shear is faster than stress relaxation by thermal fluctuations, an overshoot appears in the stress–strain curve. After the overshoot, the stress decreases due to continuous plastic events. Thus, the stress overshoot in the stress–strain curve can be regarded as a measure of the material’s static yield stress (Balmforth, Frigaard & Ovarlez Reference Balmforth, Frigaard and Ovarlez2014). At the steady state the stress plateaus, corresponding to plastic flow with a constant rate of plastic rearrangements in the system. In this situation, the rate of stress increase in the system due to the applied shear is equal to the rate of stress relaxation.

Figure 6. The stress–strain curve for applied shear rates of (a)
![]() $\dot \gamma = 10^{-6} \, \text{s}^{-1}$
, (b)
$\dot \gamma = 10^{-6} \, \text{s}^{-1}$
, (b)
![]() $\dot \gamma = 10^{-4} \, \text{s}^{-1}$
and (c)
$\dot \gamma = 10^{-4} \, \text{s}^{-1}$
and (c)
![]() $\dot \gamma = 10^{-2} \, \text{s}^{-1}$
in the start-up shear test. (d) The steady-state probability distribution of the local strain (scaled by the maximum local strain).
$\dot \gamma = 10^{-2} \, \text{s}^{-1}$
in the start-up shear test. (d) The steady-state probability distribution of the local strain (scaled by the maximum local strain).
The emergence of a stress overshoot followed by a monotonic decrease and then a plateau at steady state is experimentally observed in soft glassy materials at all shear rates (Bonn et al. Reference Bonn, Denn, Berthier, Divoux and Manneville2017). However, in the stress–strain curves of figure 6, the decrease in the stress from the overshoot to the steady state is not monotonic and is followed by a number of oscillations, especially at larger shear rates (figure 6
b and 6
c). In the stress–strain curves of figure 6, all the elements start from zero local stress, they are all in the same energy well, and they have the same elasticity. As a result, they are all sheared together and have the same evolution of the local stress in the elastic regime. We refer to this situation as having ‘synchronized’ elements. At higher shear rates, there is a smaller chance for thermal relaxation since the time scale of the shear deformation (
![]() $1/\dot \gamma$
) is smaller than the time scale for thermal relaxation. However, shear deformation reduces the time scale for thermally induced relaxation. Thus, all the elements build-up stress in their cages with little chance for thermally induced plastic events and then release this stress through thermal relaxations once the system is sheared enough so the activation energy is reduced. In other words, thermally induced plastic events start to occur once the time scale of mechanical relaxation and thermal relaxation become comparable. The number of thermally induced relaxations increases upon further shear due to further reduction in the local energy barriers. Since the evolution of the free energy is the same in all the elements, the stress relaxation is almost synchronized as thermally induced structural relaxations occur over a short time scale. This corresponds to a sudden decrease in the stress after the overshoot. Since at this state, many elements start from zero local stress in the same energy well, they are again synchronized leading to the same pattern. Each structural relaxation by thermal hops desynchronizes the free energy evolution and thus the yielding events. Thus, the oscillations in the stress die down over time due to thermal relaxations leading to a constant steady-state stress. Increasing the shear rate shrinks the time scale over which the thermally induced relaxations occur leading to more oscillations before reaching the steady state due to more synchronized elements.
$1/\dot \gamma$
) is smaller than the time scale for thermal relaxation. However, shear deformation reduces the time scale for thermally induced relaxation. Thus, all the elements build-up stress in their cages with little chance for thermally induced plastic events and then release this stress through thermal relaxations once the system is sheared enough so the activation energy is reduced. In other words, thermally induced plastic events start to occur once the time scale of mechanical relaxation and thermal relaxation become comparable. The number of thermally induced relaxations increases upon further shear due to further reduction in the local energy barriers. Since the evolution of the free energy is the same in all the elements, the stress relaxation is almost synchronized as thermally induced structural relaxations occur over a short time scale. This corresponds to a sudden decrease in the stress after the overshoot. Since at this state, many elements start from zero local stress in the same energy well, they are again synchronized leading to the same pattern. Each structural relaxation by thermal hops desynchronizes the free energy evolution and thus the yielding events. Thus, the oscillations in the stress die down over time due to thermal relaxations leading to a constant steady-state stress. Increasing the shear rate shrinks the time scale over which the thermally induced relaxations occur leading to more oscillations before reaching the steady state due to more synchronized elements.
Two time scales are associated with these transient stress oscillations. The first time scale is the interval between two consecutive peaks of the oscillations,
![]() $\tau _{\!p}$
, while the second time scale corresponds to the inverse of the rate at which the oscillation amplitude decays,
$\tau _{\!p}$
, while the second time scale corresponds to the inverse of the rate at which the oscillation amplitude decays,
![]() $\tau _d$
. In the start-up shear test on identical elements starting from rest and in the absence of thermal fluctuations, the stress will elastically increase up to a maximum value (local yield stress) and then will suddenly relax to zero, and this pattern keeps repeating. Thus,
$\tau _d$
. In the start-up shear test on identical elements starting from rest and in the absence of thermal fluctuations, the stress will elastically increase up to a maximum value (local yield stress) and then will suddenly relax to zero, and this pattern keeps repeating. Thus,
![]() $\tau _{\!p}$
is the time scale of stress build up between two consecutive synchronized yielding events. This time scale shrinks (the stress build up occurs faster) as
$\tau _{\!p}$
is the time scale of stress build up between two consecutive synchronized yielding events. This time scale shrinks (the stress build up occurs faster) as
![]() $\dot \gamma$
increases. In this case, the oscillations will continue forever. However, introducing thermal hops dampens the oscillations as seen in figure 6(a) to 6(c). As a result,
$\dot \gamma$
increases. In this case, the oscillations will continue forever. However, introducing thermal hops dampens the oscillations as seen in figure 6(a) to 6(c). As a result,
![]() $\tau _d$
originates from the variability of the local strains caused by thermally induced structural relaxations and it is the time scale over which the elements dissipate their stored energies (elastic stresses) to reach their steady-state energies (stresses). Increasing the shear rate reduces the local energy barriers (
$\tau _d$
originates from the variability of the local strains caused by thermally induced structural relaxations and it is the time scale over which the elements dissipate their stored energies (elastic stresses) to reach their steady-state energies (stresses). Increasing the shear rate reduces the local energy barriers (
![]() $\mathcal{R} = E-F(l)$
) and thus decreases
$\mathcal{R} = E-F(l)$
) and thus decreases
![]() $\tau _d$
. The situations where numerous oscillations occur correspond to
$\tau _d$
. The situations where numerous oscillations occur correspond to
![]() $\tau _{\!p} \lt \tau _d$
as the stress builds up faster than the desynchronization by thermally induced relaxations. The ratio
$\tau _{\!p} \lt \tau _d$
as the stress builds up faster than the desynchronization by thermally induced relaxations. The ratio
![]() $\tau _d/\tau _{\!p}$
increases with shear rate leading to a greater number of oscillations prior to the steady state. Both these time scales increase with
$\tau _d/\tau _{\!p}$
increases with shear rate leading to a greater number of oscillations prior to the steady state. Both these time scales increase with
![]() $E/k_{\textit{B}}T$
as the stress build up and relaxation become slower. For a fixed shear rate, the ratio
$E/k_{\textit{B}}T$
as the stress build up and relaxation become slower. For a fixed shear rate, the ratio
![]() $\tau _d/\tau _{\!p}$
increases (more pronounced oscillations) as
$\tau _d/\tau _{\!p}$
increases (more pronounced oscillations) as
![]() $E/k_{\textit{B}}T$
increases.
$E/k_{\textit{B}}T$
increases.
The stress oscillations are usually not observed in experiments since the local elements are not synchronized due to several reasons: (i) the elements have different initial conditions due to a history of deformation; (ii) there is a distribution of the energy barriers in the material; (iii) each local yielding event redistributes the stress and affects other elements based on their distance from the event; (iv) the element might not fully relax to its new equilibrium state resulting in a non-zero local stress after yielding. We study the effects of the first two factors on the stress response of the material.
The steady-state probability distribution of the local strains is shown in figure 6(d) for different applied shear rates. From the local strain of the elements,
![]() $l$
, we can define a new strain variable,
$l$
, we can define a new strain variable,
![]() $\bar l = (l_m-l)/l_m$
, where
$\bar l = (l_m-l)/l_m$
, where
![]() $l_m=1$
is the maximum local strain of the energy well which is obtained from our DFT calculations. Thus,
$l_m=1$
is the maximum local strain of the energy well which is obtained from our DFT calculations. Thus,
![]() $\bar l$
is a measure of the distance to the local free energy maximum as it ranges from
$\bar l$
is a measure of the distance to the local free energy maximum as it ranges from
![]() $\bar l = 0$
(at the local free energy maximum) to
$\bar l = 0$
(at the local free energy maximum) to
![]() $\bar l = 1$
(no mechanical deformation or the local free energy minimum). Negative values of
$\bar l = 1$
(no mechanical deformation or the local free energy minimum). Negative values of
![]() $\bar l$
are not physical as the element transitions to a new energy well after
$\bar l$
are not physical as the element transitions to a new energy well after
![]() $l = l_m$
. Also,
$l = l_m$
. Also,
![]() $\bar l \gt 1$
is not achieved since the material is sheared in the positive direction.
$\bar l \gt 1$
is not achieved since the material is sheared in the positive direction.
In athermal systems, the local elements are sheared until a local yielding point (a maximum local strain) and undergo rearrangement through a sharp transition. On the other hand, thermally induced relaxations occur over a range of local strains which can be much below the maximum local strain. Therefore, in thermal systems, the yielding transition becomes rounded, and the elements might not access the entire local strain space due to thermal hops. In figure 6(d), we observe that the peak of the probability density is at
![]() $l = 0$
(or
$l = 0$
(or
![]() $\bar l = 1$
) due to the incoming flux of the rearranged elements. As
$\bar l = 1$
) due to the incoming flux of the rearranged elements. As
![]() $\bar l$
decreases from
$\bar l$
decreases from
![]() $\bar l = 1$
to
$\bar l = 1$
to
![]() $\bar l = 0$
, the local energy barrier declines, and thus there is a higher chance for thermally induced plastic events. The shape of the probability distribution of the local strain depends on the applied rate of deformation. At low shear rates, the dynamics are slow, and thermally induced relaxations occur before the elements are significantly sheared. As a result, we observe zero probability densities for even moderately large values of the local strain. However, at higher shear rates, the local strains increase rapidly before the thermally activated rearrangements take place. Therefore, almost no thermally induced plastic event happens over a relatively wide region of local strain values leading to a uniform probability distribution. Larger shear rates broaden this uniform distribution as the mechanical deformation dominates over thermal fluctuations. This distribution is followed by a rounded transition where the local strains become large and increase the number of thermally induced plastic events. We can deduce that the regime of pure mechanical relaxations can be achieved when
$\bar l = 0$
, the local energy barrier declines, and thus there is a higher chance for thermally induced plastic events. The shape of the probability distribution of the local strain depends on the applied rate of deformation. At low shear rates, the dynamics are slow, and thermally induced relaxations occur before the elements are significantly sheared. As a result, we observe zero probability densities for even moderately large values of the local strain. However, at higher shear rates, the local strains increase rapidly before the thermally activated rearrangements take place. Therefore, almost no thermally induced plastic event happens over a relatively wide region of local strain values leading to a uniform probability distribution. Larger shear rates broaden this uniform distribution as the mechanical deformation dominates over thermal fluctuations. This distribution is followed by a rounded transition where the local strains become large and increase the number of thermally induced plastic events. We can deduce that the regime of pure mechanical relaxations can be achieved when
![]() $\dot \gamma \rightarrow \infty$
. This corresponds to a very short time scale for mechanical relaxation which dominates over the relatively large time scale for thermal relaxation. In this situation, we recover our DFT predictions of the mechanical yield stress.
$\dot \gamma \rightarrow \infty$
. This corresponds to a very short time scale for mechanical relaxation which dominates over the relatively large time scale for thermal relaxation. In this situation, we recover our DFT predictions of the mechanical yield stress.
Figure 7 shows the maximum stress and the corresponding strain in the start-up shear tests for different samples subjected to a wide range of shear rates. The maximum stress corresponds to the point where plastic events occur most frequently. Thus, this point signifies the transition from solid-like to liquid-like behaviour in the start-up shear test and can be a measure of the material’s apparent yield stress. We showed that when the stress builds up faster than relaxation by thermal fluctuations, a stress overshoot is observed as the maximum stress. As explained in the following, in some cases, thermal fluctuations completely dominate over mechanical loading. In these situations, the stress does not overshoot, and thus the maximum stress will be equal to the steady-state value. Figure 7 shows that how the maximum stress or apparent yield stress deviates from the mechanical yield stresses predicted by our DFT calculations depending on the applied rate of deformation. This apparent yield stress is consistent with that from other sources such as the oscillatory shear test and is observed over limited time scales. In § 5.3, we will show that thermal amorphous materials do not have a true yield stress, and even under very small deformation, they will flow over very long time scales due to thermally driven structural rearrangements.
In figure 7(a) and 7(b), thermal fluctuations play a minor role in samples with small core volume fraction since the activation energy is very large compared with
![]() $k_{\textit{B}}T$
(see figure 5
a). In these samples, in order to observe the effects of thermal fluctuations, one has to wait for a very long time. Thus, these materials are essentially athermal over experimental time scales and, under deformation, all the elements reach their maximum local stress before they rearrange. Therefore, the maximum stress (and the corresponding strain) is not affected by the thermal fluctuations. In this case, the apparent yield stresses predicted by the thermal SGR model converge to the mechanical yield stresses obtained from the DFT calculations. Note that in this work, we only focus on the interplay between mechanical deformation and thermal fluctuations to probe the effects of thermal fluctuations on the rheology. When thermal fluctuations are inactive, the yield stress becomes independent of the shear rate as there will be no competing time scales in the model. Therefore, for the athermal limit, we encourage the readers to follow athermal EPMs (Nicolas et al. Reference Nicolas, Ferrero, Martens and Barrat2018). It is worth mentioning that even in the samples with very large energy barriers, the thermal fluctuations will eventually cause structural rearrangements and change the maximum stress if the material is sheared extremely slowly (even smaller than the smallest shear rate
$k_{\textit{B}}T$
(see figure 5
a). In these samples, in order to observe the effects of thermal fluctuations, one has to wait for a very long time. Thus, these materials are essentially athermal over experimental time scales and, under deformation, all the elements reach their maximum local stress before they rearrange. Therefore, the maximum stress (and the corresponding strain) is not affected by the thermal fluctuations. In this case, the apparent yield stresses predicted by the thermal SGR model converge to the mechanical yield stresses obtained from the DFT calculations. Note that in this work, we only focus on the interplay between mechanical deformation and thermal fluctuations to probe the effects of thermal fluctuations on the rheology. When thermal fluctuations are inactive, the yield stress becomes independent of the shear rate as there will be no competing time scales in the model. Therefore, for the athermal limit, we encourage the readers to follow athermal EPMs (Nicolas et al. Reference Nicolas, Ferrero, Martens and Barrat2018). It is worth mentioning that even in the samples with very large energy barriers, the thermal fluctuations will eventually cause structural rearrangements and change the maximum stress if the material is sheared extremely slowly (even smaller than the smallest shear rate
![]() $\dot \gamma = 10^{-8} \, \mathrm{s^{-1}}$
shown in figure 7). However, these shear rates are beyond the time scales of usual rheological characterizations and are not studied here.
$\dot \gamma = 10^{-8} \, \mathrm{s^{-1}}$
shown in figure 7). However, these shear rates are beyond the time scales of usual rheological characterizations and are not studied here.

Figure 7. The maximum stress and the corresponding strain in start-up shear tests for a range of core volume fractions and rates of deformation. Panels (a) and (b) are for polymer molecular weights of
![]() $M_w = 5 \, \mathrm{kDa}$
, and panels (c) and (d) for polymer molecular weights of
$M_w = 5 \, \mathrm{kDa}$
, and panels (c) and (d) for polymer molecular weights of
![]() $M_w = 9 \, \mathrm{kDa}$
. The square symbols are the purely mechanical results predicted by the DFT calculations for different samples.
$M_w = 9 \, \mathrm{kDa}$
. The square symbols are the purely mechanical results predicted by the DFT calculations for different samples.
A decline in the energy barrier (with increasing core volume fraction and/or the polymer molecular weight), leads to more pronounced effects of the thermal fluctuations on the maximum stress (figure 7). The yield stress decreases when the thermal fluctuations are active, since the elements hop in anticipation before reaching the mechanical yielding point. For a fixed shear rate, in systems with larger energy barriers, the elements need to store more elastic energy before being activated by the thermal hops. Thus, the elements with larger barriers hop at a larger local strain (stress). In systems with larger energy barriers, this point is reached at a larger local stress resulting in a larger maximum stress. The effects of the shear rate on the maximum stress are more noticeable for samples with smaller energy barriers. This stems from the fact that smaller barriers favour the thermal hops which in turn affect the interplay between mechanical loading and thermal relaxations and consequently the rheology. In figure 6, we observed that slowly shearing the system provides more time for thermal activations. As a result, the elements rearrange at a much smaller local stress if they are sheared more slowly. This corresponds to a drastic decrease in the maximum stress by decreasing the applied shear rate. On the other hand, if the system is sheared very fast, by the time that thermal hops trigger a rearrangement, the elements have stored a considerable amount of elastic energy (local stress). As a result, at high shear rates, the maximum stress approaches the mechanical limit which corresponds to the maximum stored elastic energy at the time of the local rearrangement.
Based on figure 5(a), polymer-grafted nanoparticles with a core volume fraction of
![]() $\phi _c = 0.16$
and a polymer molecular weight of
$\phi _c = 0.16$
and a polymer molecular weight of
![]() $M_w = 5 \, \mathrm{kDa}$
(sample 1) have almost the same energy barrier as the ones with a core volume fraction of
$M_w = 5 \, \mathrm{kDa}$
(sample 1) have almost the same energy barrier as the ones with a core volume fraction of
![]() $\phi _c = 0.08$
and a polymer molecular weight of
$\phi _c = 0.08$
and a polymer molecular weight of
![]() $M_w = 9 \, \mathrm{kDa}$
(sample 2). However, interestingly, they show a noticeably different maximum stress at various shear rates (figure 7
a and 7
c). Although these two samples have almost the same local energy barrier, they have different local hopping rates due to different attempt frequencies. As explained in § 3, the attempt frequency increases with increasing core volume fraction and decreasing polymer molecular weight. Thus, the sample with a larger core volume fraction and smaller molecular weight can hop over the same barrier more easily. This is illustrated in the results of figures 7
a and 7
c. The maximum stress in sample 1 shows a noticeable decrease due to activated hops as the shear rate is reduced, while in sample 2, the maximum stress remains almost constant for the range of studied shear rates. This indicates that the thermal fluctuations are weaker in sample 2, and to observe their effects on the dynamics, we need to reduce the shear rate even further.
$M_w = 9 \, \mathrm{kDa}$
(sample 2). However, interestingly, they show a noticeably different maximum stress at various shear rates (figure 7
a and 7
c). Although these two samples have almost the same local energy barrier, they have different local hopping rates due to different attempt frequencies. As explained in § 3, the attempt frequency increases with increasing core volume fraction and decreasing polymer molecular weight. Thus, the sample with a larger core volume fraction and smaller molecular weight can hop over the same barrier more easily. This is illustrated in the results of figures 7
a and 7
c. The maximum stress in sample 1 shows a noticeable decrease due to activated hops as the shear rate is reduced, while in sample 2, the maximum stress remains almost constant for the range of studied shear rates. This indicates that the thermal fluctuations are weaker in sample 2, and to observe their effects on the dynamics, we need to reduce the shear rate even further.
The obtained results suggest that based on the energy well, the attempt frequency and the applied shear rate, the thermal SGR model can show a broad spectrum of behaviour from glassy regimes with slow dynamics and high apparent yield stresses to flow regimes with very low or no apparent yield stresses. To characterize this behaviour, we perform scaling analyses in the following.
5.2. Scaling analysis for the potential energy landscape and the relaxation time
To study how the stress response is scaled, we first need to understand how the local free energy and the relaxation time scale as the material is sheared. In EPMs, linear elasticity is assumed corresponding to a parabolic shape of the energy well. In this case, the potential energy landscape is ‘cuspy’ as it results from concatenation of parabolic energy wells. In a cuspy or parabolic potential, the interparticle force is discontinuous at the yielding transition. However, it has been shown that in molecular systems under mechanical deformation, the yielding transition is smooth resulting in a smooth potential energy landscape (Maloney & Lacks Reference Maloney and Lacks2006). Both potentials scale quadratically near the local free energy minima, and they deviate close to the local free energy maxima. Previous studies in mean field suggest that the flow exponent in athermal amorphous materials depends on the shape of the potential since different shapes of the potential result in different local free energies especially when the elements reach the local free energy maxima (Jagla Reference Jagla2017; Aguirre & Jagla Reference Aguirre and Jagla2018). To the best of our knowledge, such a characterization of the flow curve has not being reported for thermal amorphous materials.

Figure 8. (a) The shape of the energy profile predicted by DFT fitted with smooth and parabolic potentials. (b) The local free energy scaled by the maximum free energy as a function of the distance to the free energy maximum for smooth and parabolic potentials. (c) The hopping time as a function of the distance to the free energy maximum for smooth and parabolic potentials.
Figure 8(a) illustrates that our DFT predicts a smooth potential for solvent-free polymer-grafted nanoparticles. The results show a quadratic scaling of the potential near the free energy minima corresponding to linear elastic behaviour for local elements under small to moderate deformation. However, linear elasticity is not valid for large deformation since the evolution of the free energy deviates from a parabolic potential. Thus, the assumption of linear elasticity in the original SGR model might not be valid for soft glassy materials such as polymer-grafted nanoparticles. The elements mechanically yield around
![]() $l \approx 0.5$
where there is a continuous change in the sign of the curvature of the potential. The parabolic potential overpredicts the value of the yield stress and yield strain due to the assumption that the elements deform perfectly linear up until the transition to the next energy well (rearrangement). It is worth mentioning that, in a smooth potential, the element is still in its current energy well even after the mechanical yield point, and although it is mechanically unstable, it is smoothly transitioning to a new energy well. In a parabolic potential, on the other hand, the element abruptly transitions to a new state at the mechanical yield point, unless one specifies a time required for this transition to be completed. In the presence of thermal fluctuations, the yielding transition occurs in anticipation before reaching the maximum local free energy. Depending on the energy barrier, the attempt frequency and the rate of deformation, activation by thermal hops is achieved at different local strain values. If the element hops out of the trap before the inflection point of the potential, the choice of smooth or parabolic potential does not make much difference. However, if the element is mechanically driven beyond this point, a parabolic potential overestimates the amount of stored elastic energy. Note that this argument is valid in the absence of any interactions between elements. If one includes such interactions, a more complex analysis is needed based on the type of the stress redistribution after yielding.
$l \approx 0.5$
where there is a continuous change in the sign of the curvature of the potential. The parabolic potential overpredicts the value of the yield stress and yield strain due to the assumption that the elements deform perfectly linear up until the transition to the next energy well (rearrangement). It is worth mentioning that, in a smooth potential, the element is still in its current energy well even after the mechanical yield point, and although it is mechanically unstable, it is smoothly transitioning to a new energy well. In a parabolic potential, on the other hand, the element abruptly transitions to a new state at the mechanical yield point, unless one specifies a time required for this transition to be completed. In the presence of thermal fluctuations, the yielding transition occurs in anticipation before reaching the maximum local free energy. Depending on the energy barrier, the attempt frequency and the rate of deformation, activation by thermal hops is achieved at different local strain values. If the element hops out of the trap before the inflection point of the potential, the choice of smooth or parabolic potential does not make much difference. However, if the element is mechanically driven beyond this point, a parabolic potential overestimates the amount of stored elastic energy. Note that this argument is valid in the absence of any interactions between elements. If one includes such interactions, a more complex analysis is needed based on the type of the stress redistribution after yielding.
Figure 8(b) shows the free energy as a function of the distance to the free energy maximum. This can be regarded as the distance to the next energy well (residual load needed for transitioning to the next configuration) in the absence of thermal hops. As expected, a parabolic potential assumes that the barrier height linearly depends on the residual load, near the local free energy maxima. On the contrary, our DFT calculations predict a quadratic dependence. The smooth potential predicted in this work and the corresponding scaling near the free energy maximum are a result of the periodic structure considered in the DFT calculations. This is in contrast to the smooth potential in amorphous structures for which a scaling of
![]() $F(l)/E_0 \thicksim \bar l^{\,1.5}$
is predicted by molecular simulations (Maloney & Lacks Reference Maloney and Lacks2006). Although the DFT calculations can capture the smooth transition, the exponent depends on the structure of the particles. We expect that for an amorphous structure in DFT calculations, the predicted scaling will be close to
$F(l)/E_0 \thicksim \bar l^{\,1.5}$
is predicted by molecular simulations (Maloney & Lacks Reference Maloney and Lacks2006). Although the DFT calculations can capture the smooth transition, the exponent depends on the structure of the particles. We expect that for an amorphous structure in DFT calculations, the predicted scaling will be close to
![]() $\thicksim \bar l^{\,1.5}$
. Using the scaling in figure 8(b), we can scale the hopping time as a function of the distance to the local free energy maximum (figure 8
c). At the undeformed state (
$\thicksim \bar l^{\,1.5}$
. Using the scaling in figure 8(b), we can scale the hopping time as a function of the distance to the local free energy maximum (figure 8
c). At the undeformed state (
![]() $\bar l = 1$
), thermal fluctuations have to overcome the maximum energy barrier and thus
$\bar l = 1$
), thermal fluctuations have to overcome the maximum energy barrier and thus
![]() $\tau = \tau _0 \, \exp (E_0/k_{\textit{B}}T)$
. In the limit of vanishing residual load (
$\tau = \tau _0 \, \exp (E_0/k_{\textit{B}}T)$
. In the limit of vanishing residual load (
![]() $\bar l \rightarrow 0$
), the barrier vanishes and thus
$\bar l \rightarrow 0$
), the barrier vanishes and thus
![]() $\tau \rightarrow \tau _0 = \varGamma _0^{-1}$
. Near the top of the energy well, the logarithm of the hopping time scales linearly and quadratically with the distance to the free energy maximum for the parabolic and smooth potentials, respectively. At the same residual load, thermally induced relaxation is achieved much faster in a smooth potential compared with a parabolic potential. The reason is that at the same residual load, the barrier is much smaller in the smooth potential compared with the parabolic one.
$\tau \rightarrow \tau _0 = \varGamma _0^{-1}$
. Near the top of the energy well, the logarithm of the hopping time scales linearly and quadratically with the distance to the free energy maximum for the parabolic and smooth potentials, respectively. At the same residual load, thermally induced relaxation is achieved much faster in a smooth potential compared with a parabolic potential. The reason is that at the same residual load, the barrier is much smaller in the smooth potential compared with the parabolic one.
5.3. Scaling analysis for the steady-state stress
We demonstrated that the time scale for the activation by thermal hops depends on the local free energy barrier, which in turn depends on the amount of locally stored elastic energy. Based on figures 6 and 7, the applied shear rate changes the interplay between mechanical loading and thermal fluctuations, resulting in a wide range of macroscopic responses. The time scale for mechanical deformation is given by the applied shear rate (
![]() $1/\dot \gamma$
). To achieve mechanical yielding, the element must reach its maximum local strain (maximum local free energy). Thus, we can define the time scale for mechanical relaxation as
$1/\dot \gamma$
). To achieve mechanical yielding, the element must reach its maximum local strain (maximum local free energy). Thus, we can define the time scale for mechanical relaxation as
![]() $\tau _m = ({l_m-l}/{\dot \gamma }) = ( {\Delta l}/{\dot \gamma })$
which depends on the current local strain of the element. Larger local strains lead to a shorter time needed to achieve mechanical yielding. The competing time scale for relaxation is the one for thermally activated hops, given as
$\tau _m = ({l_m-l}/{\dot \gamma }) = ( {\Delta l}/{\dot \gamma })$
which depends on the current local strain of the element. Larger local strains lead to a shorter time needed to achieve mechanical yielding. The competing time scale for relaxation is the one for thermally activated hops, given as
![]() $\tau _{\textit{th}} = (\varGamma _0 \, e^{-(E-F(l))/k_{\textit{B}}T})^{-1}$
which also depends on the local strain through the local free energy. Larger local strains correspond to larger local free energies and thus shorter time scale for the activation by thermal hops. Therefore, the applied shear rate not only determines the time scale of mechanical deformation but also changes the time scale of thermal relaxation as it determines the amount of locally stored energy,
$\tau _{\textit{th}} = (\varGamma _0 \, e^{-(E-F(l))/k_{\textit{B}}T})^{-1}$
which also depends on the local strain through the local free energy. Larger local strains correspond to larger local free energies and thus shorter time scale for the activation by thermal hops. Therefore, the applied shear rate not only determines the time scale of mechanical deformation but also changes the time scale of thermal relaxation as it determines the amount of locally stored energy,
![]() $F(l)$
, at each time. For a thermal amorphous material, depending on the value of the applied shear rate, we propose three different regimes of relaxation as thermal, thermal–mechanical and mechanical. In the following, we characterize each regime and provide scalings for the steady-state response in each regime.
$F(l)$
, at each time. For a thermal amorphous material, depending on the value of the applied shear rate, we propose three different regimes of relaxation as thermal, thermal–mechanical and mechanical. In the following, we characterize each regime and provide scalings for the steady-state response in each regime.
5.3.1. Purely thermal relaxation
Purely thermal relaxation occurs when the elements hop out of their energy wells before they are noticeably sheared. As a result, the stored elastic energy is almost zero (
![]() $F(l) \approx 0$
), and the elements have to overcome their maximum local barrier to hop. This situation is achieved when the time scale for thermal relaxation is much smaller than the time scale of the applied shear deformation. Thus, purely thermal relaxation requires small
$F(l) \approx 0$
), and the elements have to overcome their maximum local barrier to hop. This situation is achieved when the time scale for thermal relaxation is much smaller than the time scale of the applied shear deformation. Thus, purely thermal relaxation requires small
![]() $\dot \gamma$
such that
$\dot \gamma$
such that
The rate of change of the local strain between thermally induced plastic events is very small since
![]() $\dot l = \dot \gamma$
. Therefore, the elements hop from their current configuration with a very small local strain to a new configuration with zero local strain. In other words, the elements are negligibly sheared before activation by thermal hops (for a time
$\dot l = \dot \gamma$
. Therefore, the elements hop from their current configuration with a very small local strain to a new configuration with zero local strain. In other words, the elements are negligibly sheared before activation by thermal hops (for a time
![]() $t = \tau _{\textit{th}}$
), and thus the local strain scales as
$t = \tau _{\textit{th}}$
), and thus the local strain scales as
 \begin{equation} l \thicksim \dot \gamma \tau _{\textit{th}} \thicksim \frac {\dot \gamma }{\varGamma _0 \, \exp\! \left (\dfrac {-E}{k_{\textit{B}}T} \right )} \ll 1. \end{equation}
\begin{equation} l \thicksim \dot \gamma \tau _{\textit{th}} \thicksim \frac {\dot \gamma }{\varGamma _0 \, \exp\! \left (\dfrac {-E}{k_{\textit{B}}T} \right )} \ll 1. \end{equation}
In this situation, the elements are always near the bottom of their local energy wells where the free energy scales quadratically with the local strain. Assuming
![]() $F(l) = ( {1}/{2}) kl^2$
, where
$F(l) = ( {1}/{2}) kl^2$
, where
![]() $k$
is the local spring constant or shear modulus of the element, the macroscopic stress scales as
$k$
is the local spring constant or shear modulus of the element, the macroscopic stress scales as
 \begin{equation} \sigma _{\textit{ss}} \thicksim kl \thicksim \frac {k}{\varGamma _0 \, \exp\! \left (\dfrac {-E}{k_{\textit{B}}T} \right )} \dot \gamma, \end{equation}
\begin{equation} \sigma _{\textit{ss}} \thicksim kl \thicksim \frac {k}{\varGamma _0 \, \exp\! \left (\dfrac {-E}{k_{\textit{B}}T} \right )} \dot \gamma, \end{equation}
corresponding to a Newtonian response with a constant viscosity
which is linked to the molecular-level information of the material. In this regime, the viscosity of the material depends on three different material-specific parameters. The local energy barrier,
![]() $E$
, can be interpreted as the resistance to flow, the attempt frequency,
$E$
, can be interpreted as the resistance to flow, the attempt frequency,
![]() $\varGamma _0$
, as the ability of the material to flow, and the local shear modulus,
$\varGamma _0$
, as the ability of the material to flow, and the local shear modulus,
![]() $k$
, as the stiffness of the material under shear deformation. The Newtonian regime is a high-viscous flow which requires a long time scale. Our scaling analysis sheds lights on the origin of the Newtonian fluid behaviour observed experimentally in polymer-grafted nanoparticles under extremely small applied shear rates (Agarwal et al. Reference Agarwal, Qi and Archer2010; Wen, Schaefer & Archer Reference Wen, Schaefer and Archer2015).
$k$
, as the stiffness of the material under shear deformation. The Newtonian regime is a high-viscous flow which requires a long time scale. Our scaling analysis sheds lights on the origin of the Newtonian fluid behaviour observed experimentally in polymer-grafted nanoparticles under extremely small applied shear rates (Agarwal et al. Reference Agarwal, Qi and Archer2010; Wen, Schaefer & Archer Reference Wen, Schaefer and Archer2015).
5.3.2. Purely mechanical relaxation
To achieve purely mechanical relaxation, the local strain of the element has to exceed its maximum local strain. This regime is attainable if the element is sheared close to the top of the energy well where there is almost no local barrier, i.e.
![]() $E - F(l) \approx k_{\textit{B}}T$
, and thus the time scale for thermal relaxation is approximately
$E - F(l) \approx k_{\textit{B}}T$
, and thus the time scale for thermal relaxation is approximately
![]() $\tau _{\textit{th}} \approx \varGamma _0^{-1}$
. The criterion for purely mechanical relaxation follows
$\tau _{\textit{th}} \approx \varGamma _0^{-1}$
. The criterion for purely mechanical relaxation follows
stating that the element has to mechanically yield and transition to the new configuration before it has time to hop over the barrier. Equation (5.5) indicates a minimum shear rate to reach purely mechanical relaxation implying that this regime requires extremely large applied shear rates. However, adopting a criterion based on the distance to yielding is rather vague. Figure 8
b and 8
c reveal that depending on the shape of the potential (parabolic or smooth), the free energy scales linearly or quadratically with the distance to yielding,
![]() $\Delta l$
, near the local free energy maximum. We first focus on the parabolic potential, i.e.
$\Delta l$
, near the local free energy maximum. We first focus on the parabolic potential, i.e.
![]() $F(l) = ( {1}/{2}) kl^2$
. At the top of the energy well, the free energy scales linearly with the distance to yielding which gives
$F(l) = ( {1}/{2}) kl^2$
. At the top of the energy well, the free energy scales linearly with the distance to yielding which gives
![]() $k\Delta l \thicksim k_{\textit{B}}T$
. The local spring constant,
$k\Delta l \thicksim k_{\textit{B}}T$
. The local spring constant,
![]() $k$
, is of the order of the local energy barrier, and thus we have
$k$
, is of the order of the local energy barrier, and thus we have
![]() $\Delta l \thicksim k_{\textit{B}}T/E$
. A similar argument can be deployed for the smooth potential used in this study. Since the barrier scales quadratically with the distance to the free energy maxima, we have
$\Delta l \thicksim k_{\textit{B}}T/E$
. A similar argument can be deployed for the smooth potential used in this study. Since the barrier scales quadratically with the distance to the free energy maxima, we have
![]() $\Delta l \thicksim (k_{\textit{B}}T/E)^{1/2}$
. We can summarize the criteria for purely mechanical relaxation as follows:
$\Delta l \thicksim (k_{\textit{B}}T/E)^{1/2}$
. We can summarize the criteria for purely mechanical relaxation as follows:
where
![]() $\zeta = 1$
in parabolic potential and
$\zeta = 1$
in parabolic potential and
![]() $\zeta = 0.5$
in smooth potential for a periodic array. Since in amorphous materials
$\zeta = 0.5$
in smooth potential for a periodic array. Since in amorphous materials
![]() $E \gt k_{\textit{B}}T$
, (5.6) shows that in a parabolic potential, the regime of purely mechanical relaxation can be achieved more easily (at a smaller shear rate) than in a smooth potential. This is another manifestation of the fact that a smooth potential is more favourable to activation by thermal hops in comparison with a parabolic potential. In this regime, the macroscopic stress approaches the value predicted by the DFT calculations, and thus we have
$E \gt k_{\textit{B}}T$
, (5.6) shows that in a parabolic potential, the regime of purely mechanical relaxation can be achieved more easily (at a smaller shear rate) than in a smooth potential. This is another manifestation of the fact that a smooth potential is more favourable to activation by thermal hops in comparison with a parabolic potential. In this regime, the macroscopic stress approaches the value predicted by the DFT calculations, and thus we have
which states that the steady-state stress is independent of applied shear rate once it is above the criteria mentioned in (5.6). This is an outcome of the fact that the thermal SGR model in its current form (3.1) does not distinguish between different applied shear rates in the athermal limit. All the elements are sheared, and they instantly yield once the local free energy is greater than the energy barrier.
5.3.3. Thermal–mechanical relaxation
Based on (5.1) and (5.6), we can define characteristic shear rates for purely thermal relaxation,
![]() $\dot {\theta }_{\textit{th}}$
, and purely mechanical relaxation,
$\dot {\theta }_{\textit{th}}$
, and purely mechanical relaxation,
![]() $\dot {\theta }_{m}$
, as
$\dot {\theta }_{m}$
, as
 \begin{equation} \begin{aligned} & \dot {\theta }_{\textit{th}} = \varGamma _0 \, \exp\! \left (\frac {-E}{k_{\textit{B}}T} \right )\!, & \\ & \dot {\theta }_{m} = \varGamma _0 \! \left (\frac {k_{\textit{B}}T}{E}\right )^\zeta\!, & \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & \dot {\theta }_{\textit{th}} = \varGamma _0 \, \exp\! \left (\frac {-E}{k_{\textit{B}}T} \right )\!, & \\ & \dot {\theta }_{m} = \varGamma _0 \! \left (\frac {k_{\textit{B}}T}{E}\right )^\zeta\!, & \end{aligned} \end{equation}
where
![]() $\zeta$
depends on the potential as explained earlier. These characteristic values depend on the molecular level information such as the energy landscape and the bare hopping time which are a function of the material properties (e.g. the core volume fraction, polymer molecular weight, grafting density, solvent, etc., in polymer-grafted nanoparticles of interest in this work). The interpretation of these characteristic shear rates is as follows: for shear rates much below
$\zeta$
depends on the potential as explained earlier. These characteristic values depend on the molecular level information such as the energy landscape and the bare hopping time which are a function of the material properties (e.g. the core volume fraction, polymer molecular weight, grafting density, solvent, etc., in polymer-grafted nanoparticles of interest in this work). The interpretation of these characteristic shear rates is as follows: for shear rates much below
![]() $\dot {\theta }_{\textit{th}}$
, we expect the structural relaxations to be purely thermal. In other words, the mechanical loading becomes important once the applied shear rate is comparable to or greater than
$\dot {\theta }_{\textit{th}}$
, we expect the structural relaxations to be purely thermal. In other words, the mechanical loading becomes important once the applied shear rate is comparable to or greater than
![]() $\dot {\theta }_{\textit{th}}$
. On the other hand, for shear rates much larger than
$\dot {\theta }_{\textit{th}}$
. On the other hand, for shear rates much larger than
![]() $\dot {\theta }_{m}$
, the relaxations are purely mechanical, and thermal fluctuations become unimportant. For all other values of the applied shear rate, the response is in the thermal–mechanical regime, where both mechanical loading and thermal fluctuations are important. We can summarize the mentioned argument in the criterion for thermal–mechanical regime of relaxation as follows:
$\dot {\theta }_{m}$
, the relaxations are purely mechanical, and thermal fluctuations become unimportant. For all other values of the applied shear rate, the response is in the thermal–mechanical regime, where both mechanical loading and thermal fluctuations are important. We can summarize the mentioned argument in the criterion for thermal–mechanical regime of relaxation as follows:
which, in general, we expect to be valid for a wide range of shear rates accessible in experiments.
In the thermal–mechanical regime, the steady state is the outcome of the balance between the applied mechanical loading (
![]() $1/\dot \gamma$
) and the hopping time (
$1/\dot \gamma$
) and the hopping time (
![]() $\tau _{\textit{th}}$
). Balancing the flux of the applied mechanical loading and the flux of the thermally induced plastic events, we have
$\tau _{\textit{th}}$
). Balancing the flux of the applied mechanical loading and the flux of the thermally induced plastic events, we have
This regime corresponds to relaxation at moderate local strain values. Thus, at steady state, the local strain is
![]() $0 \lt l \lt l_m$
. Based on figure 8(a), we can still expect similar results for both parabolic and smooth potentials as they deviate dramatically near the top of the energy well. Thus, for the sake of simplicity, we assume
$0 \lt l \lt l_m$
. Based on figure 8(a), we can still expect similar results for both parabolic and smooth potentials as they deviate dramatically near the top of the energy well. Thus, for the sake of simplicity, we assume
![]() $F(l) \approx ({1}/{2}) kl^2$
leading to
$F(l) \approx ({1}/{2}) kl^2$
leading to
 \begin{equation} l \thicksim \left (\frac {2\!\left ( \ln\! \left(\dfrac {\dot \gamma }{\varGamma _0}\right) + E/k_{\textit{B}}T \right )}{k/k_{\textit{B}}T}\right )^{1/2}\!, \end{equation}
\begin{equation} l \thicksim \left (\frac {2\!\left ( \ln\! \left(\dfrac {\dot \gamma }{\varGamma _0}\right) + E/k_{\textit{B}}T \right )}{k/k_{\textit{B}}T}\right )^{1/2}\!, \end{equation}
which can be referred to as the steady-state local strain at which most of the thermally induced relaxations occur. This clearly shows that at the steady state, as the shear rate increases, most of the thermally induced relaxations are achieved at a larger local strain. For small shear rates (
![]() $\dot \gamma \approx \dot {\theta }_{\textit{th}}$
), it takes a long time for the local strain to increase and during this time, thermally induced attempts at relaxation occur. Thus, for small shear rates, the activation by thermal hops occurs at small strains. However, increasing the shear rate pushes the elements up their energy landscape faster which leads to a larger local strain at the time of hopping. Finally, the steady-state stress in this regime scales as
$\dot \gamma \approx \dot {\theta }_{\textit{th}}$
), it takes a long time for the local strain to increase and during this time, thermally induced attempts at relaxation occur. Thus, for small shear rates, the activation by thermal hops occurs at small strains. However, increasing the shear rate pushes the elements up their energy landscape faster which leads to a larger local strain at the time of hopping. Finally, the steady-state stress in this regime scales as
 \begin{equation} \sigma _{\textit{ss}} \thicksim kl \thicksim k\! \left (\frac {2\!\left ( \ln\! \left(\dfrac {\dot \gamma }{\varGamma _0}\right) + E/k_{\textit{B}}T \right )}{k/k_{\textit{B}}T}\right )^{1/2}\!, \end{equation}
\begin{equation} \sigma _{\textit{ss}} \thicksim kl \thicksim k\! \left (\frac {2\!\left ( \ln\! \left(\dfrac {\dot \gamma }{\varGamma _0}\right) + E/k_{\textit{B}}T \right )}{k/k_{\textit{B}}T}\right )^{1/2}\!, \end{equation}
indicating a logarithmic flow curve of the form
![]() $\sigma _{\textit{ss}} \thicksim (\ln (\dot \gamma ) + C)^{0.5}$
, where the constant
$\sigma _{\textit{ss}} \thicksim (\ln (\dot \gamma ) + C)^{0.5}$
, where the constant
![]() $C$
depends on the energy barrier, local shear modulus, attempt frequency for hopping and temperature.
$C$
depends on the energy barrier, local shear modulus, attempt frequency for hopping and temperature.
5.3.4. Steady-state flow curve and viscosity
Based on the mentioned scaling analysis, the steady-state flow curve includes three different regimes depending on the applied rate of deformation. Figure 9(a) outlines the scaling of the flow curve in the three regimes, and figure 9(b) shows the steady-state flow curve and viscosity predicted by the thermal SGR model for solvent-free polymer-grafted nanoparticles with a core volume fraction of
![]() $\phi _c = 0.2$
and polymer molecular weight of
$\phi _c = 0.2$
and polymer molecular weight of
![]() $M_w = 5\,\mathrm{kDa}$
. Each point in the graph is the steady state of a start-up shear test. The dotted and dashed lines are fits based on our scaling analysis. As mentioned, at very small shear rates, the response of the material is entirely governed by thermal fluctuations which result in a Newtonian flow. The effects of mechanical loading become noticeable as the shear rate is increased leading to the emergence of the thermal–mechanical regime with a logarithmic flow curve. Finally, at very large shear rates, mechanical loading dominates over thermal fluctuations. It is worth mentioning that solvent-free polymer-grafted nanoparticles with other core volume fractions and polymer molecular weights also qualitatively follow the same flow curve as figure 9. However, the values will be different since different samples have quantitatively different energy landscapes and bare hopping times as shown earlier. Although the scaling analysis is performed for a unique energy well in the energy landscape, it can be also extended to the case with a Gaussian distribution of energy barriers. In the presence of a distribution of energy barriers, the purely thermal regime of relaxation is achieved when most of the relaxations across the system are entirely driven by thermal fluctuations rather than mechanical loading. Whereas the purely mechanical regime of relaxation corresponds to very fast applied shear rates such that the time scale of mechanical yielding is smaller than most of the thermally mechanically activated hopping times across the sample. Consequently, for a Gaussian distribution of energy barriers centred at the single-well energy barrier, the characteristic shear rate,
$M_w = 5\,\mathrm{kDa}$
. Each point in the graph is the steady state of a start-up shear test. The dotted and dashed lines are fits based on our scaling analysis. As mentioned, at very small shear rates, the response of the material is entirely governed by thermal fluctuations which result in a Newtonian flow. The effects of mechanical loading become noticeable as the shear rate is increased leading to the emergence of the thermal–mechanical regime with a logarithmic flow curve. Finally, at very large shear rates, mechanical loading dominates over thermal fluctuations. It is worth mentioning that solvent-free polymer-grafted nanoparticles with other core volume fractions and polymer molecular weights also qualitatively follow the same flow curve as figure 9. However, the values will be different since different samples have quantitatively different energy landscapes and bare hopping times as shown earlier. Although the scaling analysis is performed for a unique energy well in the energy landscape, it can be also extended to the case with a Gaussian distribution of energy barriers. In the presence of a distribution of energy barriers, the purely thermal regime of relaxation is achieved when most of the relaxations across the system are entirely driven by thermal fluctuations rather than mechanical loading. Whereas the purely mechanical regime of relaxation corresponds to very fast applied shear rates such that the time scale of mechanical yielding is smaller than most of the thermally mechanically activated hopping times across the sample. Consequently, for a Gaussian distribution of energy barriers centred at the single-well energy barrier, the characteristic shear rate,
![]() $\dot {\theta }_{\textit{th}}$
will be smaller while
$\dot {\theta }_{\textit{th}}$
will be smaller while
![]() $\dot {\theta }_{m}$
will be larger, compared with the single-well scenario. Therefore, the thermal–mechanical regime of relaxation spans a larger range of shear rates compared with the single-well case.
$\dot {\theta }_{m}$
will be larger, compared with the single-well scenario. Therefore, the thermal–mechanical regime of relaxation spans a larger range of shear rates compared with the single-well case.

Figure 9. (a) A schematic of scaling analysis for the flow curve and (b) the flow curve and viscosity of solvent-free polymer-grafted nanoparticles with a core volume fraction of
![]() $\phi _c = 0.2$
and polymer molecular weight of
$\phi _c = 0.2$
and polymer molecular weight of
![]() $M_w = 5 \, \mathrm{kDa}$
predicted by the thermal SGR model.
$M_w = 5 \, \mathrm{kDa}$
predicted by the thermal SGR model.
The flow curve in athermal amorphous materials usually follows a Herschel–Bulkley law which predicts a stress plateau (considered as the yield stress) at small shear rates. The presence of thermal fluctuations has led to a variety of non-Herschel–Bulkley flow curves. For example, in molecular dynamics simulations of a two-dimensional Lennard-Jones glass (Chattoraj et al. Reference Chattoraj, Caroli and Lemaître2010), kinetic Monte Carlo simulations of thermal amorphous materials on a square lattice (Merabia & Detcheverry Reference Merabia and Detcheverry2016) and Hamiltonian description of the yielding transition (Ferrero et al. Reference Ferrero, Kolton and Jagla2021), a logarithmic dependence on the shear rate emerges in the flow curve with different exponents depending on the details of the model. Here we observed that the thermal SGR model predicts a thermally activated, Newtonian flow prior to the emergence of the logarithmic flow curve. This interesting observation which is in complete agreement with experiments on polymer-grafted nanoparticles (Agarwal et al. Reference Agarwal, Qi and Archer2010; Wen et al. Reference Wen, Schaefer and Archer2015) is the outcome of the observable (although relatively long) time scale of thermal flow in such systems. This behaviour might not be observable over time scales of usual rheological characterization in many other amorphous materials such as molecular and metallic glasses. Thus, in those systems, in order to observe a flow, one has to apply a considerable amount of load on the material so that the thermal–mechanical regime of relaxation in the flow curve can be accessed. This results in the absence of observable flow at small shear rates suggesting the presence of a yield stress. On the other hand, figure 9 shows that solvent-free polymer-grafted nanoparticles flow even at very small applied shear rates. However, these materials show characteristics of a yield stress (e.g. the overshoot in the start-up shear test or the peak in the viscous modulus accompanied by a decrease in the storage modulus in strain-sweep oscillatory shear test which will be studied below). We refer to this yield stress as an apparent yield stress, depending on the time scale of observation.
We can calculate the steady-state viscosity based on the flow curve (figure 9
b). As expected from the scaling analysis, in the limit of small shear rates, the thermal SGR model predicts a Newtonian viscosity. The very large value of the viscosity is due to the large energy barrier (5.4), resembling glassy-like behaviour (Mauro et al. Reference Mauro, Yue, Ellison, Gupta and Allan2009). In glassy materials, this behaviour usually emerges from the jammed packing of the particles. Interestingly, in solvent-free polymer-grafted nanoparticles, glassy behaviour is observed at very low particle volume fractions (
![]() $\phi _c \approx 0.1-0.2$
) as it originates from the space-filling constraint for the grafted polymers rather than packing of the particles. As a result, the interparticle distance is large allowing Brownian relaxation to equilibrium on an observable time scale. Increasing the applied rate of deformation facilitates the thermally induced relaxation by reducing the barrier. Thus, the material flows more easily as the mechanical loading increases, which can be the origin of the shear-thinning behaviour observed here and in experiments (Agarwal et al. Reference Agarwal, Qi and Archer2010; Wen et al. Reference Wen, Schaefer and Archer2015).
$\phi _c \approx 0.1-0.2$
) as it originates from the space-filling constraint for the grafted polymers rather than packing of the particles. As a result, the interparticle distance is large allowing Brownian relaxation to equilibrium on an observable time scale. Increasing the applied rate of deformation facilitates the thermally induced relaxation by reducing the barrier. Thus, the material flows more easily as the mechanical loading increases, which can be the origin of the shear-thinning behaviour observed here and in experiments (Agarwal et al. Reference Agarwal, Qi and Archer2010; Wen et al. Reference Wen, Schaefer and Archer2015).
5.4. Effects of the history of deformation
In thixotropic yield stress materials, the history of deformation becomes important since it determines the initial microstructure of the system and hence affects the rheology (Bonn et al. Reference Bonn, Denn, Berthier, Divoux and Manneville2017). As a result, before performing each experimental measurement, one has to create a new history for the sample (based on a prescribed cycle of preshear) which is known and reproducible. The first step is to remove any unknown, previous history of the material for example by applying steady shear (imposing a constant
![]() $\dot \gamma = \dot \gamma _0$
to reach a steady state, point
$\dot \gamma = \dot \gamma _0$
to reach a steady state, point
![]() $\mathrm{S}$
shown in figure 10
a). A common approach to create a new history in shear-rate controlled experiments with athermal systems is to suddenly stop the flow and set the applied shear rate to zero. This causes a sudden relaxation of the stress to some residual value. This state can be used as the initial microstructure of the system to perform various rheological tests (Bonn et al. Reference Bonn, Denn, Berthier, Divoux and Manneville2017). However, in the flow-cessation experiment with thermal materials, the stress relaxes to zero instead of a non-zero residual stress observed in athermal materials. The relaxation process predicted by the thermal SGR model is shown in figure 10(b), in which the stress eventually almost relaxes to zero (point
$\mathrm{S}$
shown in figure 10
a). A common approach to create a new history in shear-rate controlled experiments with athermal systems is to suddenly stop the flow and set the applied shear rate to zero. This causes a sudden relaxation of the stress to some residual value. This state can be used as the initial microstructure of the system to perform various rheological tests (Bonn et al. Reference Bonn, Denn, Berthier, Divoux and Manneville2017). However, in the flow-cessation experiment with thermal materials, the stress relaxes to zero instead of a non-zero residual stress observed in athermal materials. The relaxation process predicted by the thermal SGR model is shown in figure 10(b), in which the stress eventually almost relaxes to zero (point
![]() $\mathrm{R}$
in the figure). The relaxation process in figure 10(b) can be explained by the activated dynamics due to thermal hops. The shear rate before the stress relaxation in figure 10(b) is set to
$\mathrm{R}$
in the figure). The relaxation process in figure 10(b) can be explained by the activated dynamics due to thermal hops. The shear rate before the stress relaxation in figure 10(b) is set to
![]() $\dot \gamma _0 = 10^{-5} \, s^{-1}$
. Upon flow cessation (
$\dot \gamma _0 = 10^{-5} \, s^{-1}$
. Upon flow cessation (
![]() $\dot \gamma = 0$
), the dynamics is purely governed by thermal hops. The elements with higher locally stored elastic energies (smaller energy barriers) have a shorter time scale for thermally induced relaxation. As a result, they relax relatively fast compared with other elements which have a larger remaining energy barrier. This results in a drastic stress relaxation over a relatively short time scale corresponding to a high yielding rate of structural rearrangements. For elements with lower stored elastic energies, thermally induced relaxations require a larger time scale since the barrier is much larger than
$\dot \gamma = 0$
), the dynamics is purely governed by thermal hops. The elements with higher locally stored elastic energies (smaller energy barriers) have a shorter time scale for thermally induced relaxation. As a result, they relax relatively fast compared with other elements which have a larger remaining energy barrier. This results in a drastic stress relaxation over a relatively short time scale corresponding to a high yielding rate of structural rearrangements. For elements with lower stored elastic energies, thermally induced relaxations require a larger time scale since the barrier is much larger than
![]() $k_{\textit{B}}T$
. Thus, after the sudden stress relaxation, thermally induced relaxations occur slowly over a long time interval (very low yielding rate) and the stress decays over a very long time scale.
$k_{\textit{B}}T$
. Thus, after the sudden stress relaxation, thermally induced relaxations occur slowly over a long time interval (very low yielding rate) and the stress decays over a very long time scale.

Figure 10. (a) The imposed shear rate during the loading phase and the relaxation process. (b) The stress relaxation predicted by the thermal SGR model for
![]() $\dot \gamma _0 = 10^{-5} \, \text{s}^{-1}$
which follows a stretched exponential form (
$\dot \gamma _0 = 10^{-5} \, \text{s}^{-1}$
which follows a stretched exponential form (
![]() $\sigma (t) = \sigma _0 \, \exp [-(t_r/\tau _r)^{\beta _r}]$
). The inset represents the same plot on a log–log scale. (c) Stress relaxation as a function of non-dimensionalized time for different applied
$\sigma (t) = \sigma _0 \, \exp [-(t_r/\tau _r)^{\beta _r}]$
). The inset represents the same plot on a log–log scale. (c) Stress relaxation as a function of non-dimensionalized time for different applied
![]() $\dot \gamma _0$
. (d) The characteristic relaxation time and the stretching exponent as a function of
$\dot \gamma _0$
. (d) The characteristic relaxation time and the stretching exponent as a function of
![]() $\dot \gamma _0$
.
$\dot \gamma _0$
.
A broad distribution of relaxation times is observed in a vast range of soft matter systems, including but not limited to colloidal glasses and suspensions, gels and biological networks (Song, Holten-Andersen & McKinley Reference Song, Holten-Andersen and McKinley2023). However, its origin is poorly understood. Here, we observed that a distribution of local strain (or stress) prior to the relaxation results in a wide distribution of relaxation times. The distribution of local strain (or stress) corresponds to a distribution of local free energy and thus a spectrum of relaxation times across the system. Here, since all the elements are in the same energy well, the only factor to create a distribution of relaxation times is the distribution of local stress prior to relaxation. However, in a thermal soft glassy system, even in an unstrained condition, the material has an inherent distribution of relaxation times due to the energy landscape having many different local minima. Furthermore, each plastic event triggers a redistribution of the stress in the system changing the relaxation time of other elements. We expect that these complexities might change the distribution of relaxation times both quantitatively and qualitatively depending on the soft matter system and the history of deformation prior to relaxation.
The original SGR model which is primarily developed for athermal systems such as foams and emulsions, predicts a power-law decay of the stress during relaxation in both its scalar (Fielding, Sollich & Cates Reference Fielding, Sollich and Cates2000) and tensorial descriptions (Cates & Sollich Reference Cates and Sollich2004). However, for either flow cessation after steady shear or relaxation after a step strain, a variety of amorphous materials such as glasses (Phillips Reference Phillips1996), polymer-grafted nanoparticles (Agarwal & Archer Reference Agarwal and Archer2011), tissues (Chaudhuri et al. Reference Chaudhuri2016), gels (Erk & Douglas Reference Erk and Douglas2012) and surfactants (Cates & Candau Reference Cates and Candau1990) exhibit a stretched exponential relaxation of the Kohlrausch–Williams–Watts form, i.e.
![]() $\sigma (t) = \sigma _0 \, \exp [-(t/\tau _r)^{\beta _r}]$
, where
$\sigma (t) = \sigma _0 \, \exp [-(t/\tau _r)^{\beta _r}]$
, where
![]() $t$
is the elapsed time after the step or steady shear,
$t$
is the elapsed time after the step or steady shear,
![]() $\sigma _0$
is the zero time value of the stress,
$\sigma _0$
is the zero time value of the stress,
![]() $\tau _r$
is a characteristic relaxation time of the material and
$\tau _r$
is a characteristic relaxation time of the material and
![]() $\beta _r$
is the stretching exponent. We observe that unlike the power-law decay predicted by the original SGR model, our thermal SGR model predicts a stretched exponential relaxation function (figure 10
b). The original SGR model assumes an exponential distribution of the energy wells. However, the stretched exponential relaxation is associated with a Gaussian distribution of barriers. The thermal SGR model in this work assumes only a single energy well. This is similar to a Gaussian distribution with a very small standard deviation. We envision that a wide range of amorphous materials might possess a Gaussian distribution of barriers in the energy landscape. Furthermore, our results show that given the right set of conditions, the SGR framework is able to predict either a power-law or a stretched exponential decay of the stress in relaxation experiments.
$\beta _r$
is the stretching exponent. We observe that unlike the power-law decay predicted by the original SGR model, our thermal SGR model predicts a stretched exponential relaxation function (figure 10
b). The original SGR model assumes an exponential distribution of the energy wells. However, the stretched exponential relaxation is associated with a Gaussian distribution of barriers. The thermal SGR model in this work assumes only a single energy well. This is similar to a Gaussian distribution with a very small standard deviation. We envision that a wide range of amorphous materials might possess a Gaussian distribution of barriers in the energy landscape. Furthermore, our results show that given the right set of conditions, the SGR framework is able to predict either a power-law or a stretched exponential decay of the stress in relaxation experiments.
Figure 10(c) illustrates that the stretched exponential relaxation occurs for different values of the steady shear rate applied prior to the relaxation. To provide a meaningful comparison between the relaxation dynamics after different applied steady shear rates, the time in the relaxation process is non-dimensionalized by the respective values of steady shear rate. This shows that for different initial microstructure in the material, the shape of the relaxation is consistent.
Increasing the load before the relaxation leads to a larger initial stress at the beginning of the relaxation process. These observations are in agreement with the original SGR model (Cates & Sollich Reference Cates and Sollich2004) and also experiments on polymer-grafted nanoparticles (Agarwal & Archer Reference Agarwal and Archer2011). The parameters predicted by the Kohlrausch–Williams–Watts fits for different applied shear rates are plotted in figure 10(d). The values of the shear rate in the loading process,
![]() $\dot \gamma _0$
, are chosen to access both the thermal and thermal–mechanical regimes of steady state prior to the relaxation process. In figure 9, we observed that at very low shear rates, the dynamics are purely governed by thermal hops. When
$\dot \gamma _0$
, are chosen to access both the thermal and thermal–mechanical regimes of steady state prior to the relaxation process. In figure 9, we observed that at very low shear rates, the dynamics are purely governed by thermal hops. When
![]() $\dot \gamma _0 \leqslant 10^{-7} \, \mathrm{s^{-1}}$
(for the sample of interest here which has a core volume fraction of
$\dot \gamma _0 \leqslant 10^{-7} \, \mathrm{s^{-1}}$
(for the sample of interest here which has a core volume fraction of
![]() $\phi _c = 0.2$
and a polymer molecular weight of
$\phi _c = 0.2$
and a polymer molecular weight of
![]() $M_w = 5 \,\mathrm{kDa}$
), the steady state lies in the thermal regime. Therefore, in this situation, the elements are near their local free energy minima at the beginning of the relaxation process leading to
$M_w = 5 \,\mathrm{kDa}$
), the steady state lies in the thermal regime. Therefore, in this situation, the elements are near their local free energy minima at the beginning of the relaxation process leading to
![]() $\mathcal{R} \approx E$
in (3.1). As a result, the relaxation dynamics in the thermal regime is exponential (
$\mathcal{R} \approx E$
in (3.1). As a result, the relaxation dynamics in the thermal regime is exponential (
![]() $\beta _r = 1$
) with an almost constant characteristic relaxation time of
$\beta _r = 1$
) with an almost constant characteristic relaxation time of
![]() $\tau _r \approx \tau _0 \, \exp (E/k_{\textit{B}}T)$
, where
$\tau _r \approx \tau _0 \, \exp (E/k_{\textit{B}}T)$
, where
![]() $\tau _0$
is the bare hopping time. This characteristic relaxation time can simply be approximated by the inherent relaxation time of the material due to thermal fluctuations. As expected, in the thermal–mechanical regime, increasing
$\tau _0$
is the bare hopping time. This characteristic relaxation time can simply be approximated by the inherent relaxation time of the material due to thermal fluctuations. As expected, in the thermal–mechanical regime, increasing
![]() $\dot \gamma _0$
makes the subsequent relaxation process faster. This stems from the fact that increasing the amount of load results in larger local stresses at the steady state of the loading process (or beginning of the relaxation process, point
$\dot \gamma _0$
makes the subsequent relaxation process faster. This stems from the fact that increasing the amount of load results in larger local stresses at the steady state of the loading process (or beginning of the relaxation process, point
![]() $\mathrm{S}$
in figure 10
a). Thus, the elements have larger local free energies (smaller barriers) which lead to shorter relaxation times. Equivalently, this can also be viewed in terms of the accumulated strain during the loading process before the onset of relaxation. Based on figure 6, higher shear rates lead to larger locally stored elastic strains which in turn accelerate the relaxation process. The deviation from the thermal regime is also evident in the stretching exponent whose deviation from
$\mathrm{S}$
in figure 10
a). Thus, the elements have larger local free energies (smaller barriers) which lead to shorter relaxation times. Equivalently, this can also be viewed in terms of the accumulated strain during the loading process before the onset of relaxation. Based on figure 6, higher shear rates lead to larger locally stored elastic strains which in turn accelerate the relaxation process. The deviation from the thermal regime is also evident in the stretching exponent whose deviation from
![]() $\beta _r = 1$
grows as the rate of the previous deformation increases. We can further characterize the relationship between the applied shear rate in the loading process and the relaxation time in the relaxation process. The relaxation time follows the time scale for thermal relaxation which scales as
$\beta _r = 1$
grows as the rate of the previous deformation increases. We can further characterize the relationship between the applied shear rate in the loading process and the relaxation time in the relaxation process. The relaxation time follows the time scale for thermal relaxation which scales as
![]() $\tau _r \thicksim \tau _{\textit{th}} \thicksim \exp ((E-({1}/{2}) kl^2)/k_{\textit{B}}T)$
with the local strain. Based on our scaling analysis (§ 5.3), the local strain in the thermal–mechanical regime of relaxation follows (5.10), resulting in a power-law behaviour between
$\tau _r \thicksim \tau _{\textit{th}} \thicksim \exp ((E-({1}/{2}) kl^2)/k_{\textit{B}}T)$
with the local strain. Based on our scaling analysis (§ 5.3), the local strain in the thermal–mechanical regime of relaxation follows (5.10), resulting in a power-law behaviour between
![]() $\tau _r$
and
$\tau _r$
and
![]() $1/\dot \gamma _0$
. This is apparent in figure 10(d), which confirms the strain accelerated dynamics in thermal amorphous materials (Agarwal & Archer Reference Agarwal and Archer2011).
$1/\dot \gamma _0$
. This is apparent in figure 10(d), which confirms the strain accelerated dynamics in thermal amorphous materials (Agarwal & Archer Reference Agarwal and Archer2011).
As mentioned earlier, one approach to create a history of deformation is to impose zero shear rate, wait for the material to relax the stress to a constant value and then perform the rheological test from the reproducible microstructure achieved in this manner. However, we observed that in thermal amorphous materials, this approach might not be very practical. Although the material relaxes to a constant stress (which is zero due to thermal relaxations), this process happens over a large time scale. Thus, reproducing this microstructure might be highly time-consuming in experiments. As an alternative, one could interrupt the relaxation at a certain time. However, this introduces ageing effects based on the finite waiting time which will add to the complexity of the analysis. In this work, we will not focus on ageing effects in thermal amorphous materials. Instead, we propose a different approach to create a known initial microstructure. Following a steady state with an imposed non-zero
![]() $\dot \gamma = \dot \gamma _0$
, we instantly reverse the direction of the load (
$\dot \gamma = \dot \gamma _0$
, we instantly reverse the direction of the load (
![]() $\dot \gamma = -\dot \gamma _0$
), which we refer to as unloading. This procedure is shown in figure 11(a). Starting from point
$\dot \gamma = -\dot \gamma _0$
), which we refer to as unloading. This procedure is shown in figure 11(a). Starting from point
![]() $\mathrm{A}$
where all the elements have zero local stress, a start-up shear test with
$\mathrm{A}$
where all the elements have zero local stress, a start-up shear test with
![]() $\dot \gamma = 10^{-4} \, \mathrm{s^{-1}}$
is performed to reach a steady state (point
$\dot \gamma = 10^{-4} \, \mathrm{s^{-1}}$
is performed to reach a steady state (point
![]() $\mathrm{B}$
). This process was previously explained in detail in § 5.1. Then, the direction of the applied shear rate is reversed. This can be regarded as a similar start-up shear test, but with a different initial microstructure (point
$\mathrm{B}$
). This process was previously explained in detail in § 5.1. Then, the direction of the applied shear rate is reversed. This can be regarded as a similar start-up shear test, but with a different initial microstructure (point
![]() $\mathrm{B}$
). Since
$\mathrm{B}$
). Since
![]() $\dot l = \dot \gamma \lt 0$
, the elements are sheared in the negative direction, and the local stresses decrease. This results in a distribution of negative and positive local stresses in the system. The elements that had zero or small local stress before shear reversal now have a negative local stress, and the ones that had large initial local stress find a smaller positive local stress. At some point (point
$\dot l = \dot \gamma \lt 0$
, the elements are sheared in the negative direction, and the local stresses decrease. This results in a distribution of negative and positive local stresses in the system. The elements that had zero or small local stress before shear reversal now have a negative local stress, and the ones that had large initial local stress find a smaller positive local stress. At some point (point
![]() $\mathrm{C}$
), this distribution of positive and negative local stresses leads to zero macroscopic (average) stress. Continuing the shear in the negative direction, the macroscopic stress becomes negative, and the material eventually reaches a new steady state (point
$\mathrm{C}$
), this distribution of positive and negative local stresses leads to zero macroscopic (average) stress. Continuing the shear in the negative direction, the macroscopic stress becomes negative, and the material eventually reaches a new steady state (point
![]() $\mathrm{D}$
). This new steady state is exactly the opposite of the previous steady state since both tests are performed with the same shear rate but in different directions. However, the transient processes are distinct. The reason lies in the initial microstructure. Although both cases (shearing from point
$\mathrm{D}$
). This new steady state is exactly the opposite of the previous steady state since both tests are performed with the same shear rate but in different directions. However, the transient processes are distinct. The reason lies in the initial microstructure. Although both cases (shearing from point
![]() $\mathrm{A}$
to point
$\mathrm{A}$
to point
![]() $\mathrm{B}$
versus shearing from point
$\mathrm{B}$
versus shearing from point
![]() $\mathrm{C}$
to point
$\mathrm{C}$
to point
![]() $\mathrm{D}$
) have zero initial macroscopic stress, the initial distribution of local stresses are strikingly different as shown in the insets of figure 11(b), resulting in different transient dynamics. As explained in § 5.1, since at point
$\mathrm{D}$
) have zero initial macroscopic stress, the initial distribution of local stresses are strikingly different as shown in the insets of figure 11(b), resulting in different transient dynamics. As explained in § 5.1, since at point
![]() $\mathrm{A}$
the elements are synchronized, the transient response is accompanied by noticeable oscillations in the stress. In contrast, at point
$\mathrm{A}$
the elements are synchronized, the transient response is accompanied by noticeable oscillations in the stress. In contrast, at point
![]() $\mathrm{C}$
, the elements are quite desynchronized leading to a substantial decrease in the number of oscillations.
$\mathrm{C}$
, the elements are quite desynchronized leading to a substantial decrease in the number of oscillations.

Figure 11. (a) The imposed shear rate during the loading phase and the unloading phase. (b) The stress response in a loading–unloading cycle with a constant shear rate
![]() $\dot \gamma _0$
. The insets show the probability distribution of local strains (normalized by the maximum local strain) at different stages.
$\dot \gamma _0$
. The insets show the probability distribution of local strains (normalized by the maximum local strain) at different stages.
We consider the preshear cycle from point
![]() $\mathrm{A}$
to point
$\mathrm{A}$
to point
![]() $\mathrm{C}$
in figure 11. This creates a known and reproducible history of deformation with zero macroscopic stress to facilitate probing the elasticity of the material. We choose two different values for the preshear rate,
$\mathrm{C}$
in figure 11. This creates a known and reproducible history of deformation with zero macroscopic stress to facilitate probing the elasticity of the material. We choose two different values for the preshear rate,
![]() $\dot \gamma _0$
, to study the effects of the initial microstructure on the macroscopic response. Figure 12(a) shows the distribution of the local strain at the end of the preshear cycle with two different shear rates. These two distributions correspond to a point equivalent to point
$\dot \gamma _0$
, to study the effects of the initial microstructure on the macroscopic response. Figure 12(a) shows the distribution of the local strain at the end of the preshear cycle with two different shear rates. These two distributions correspond to a point equivalent to point
![]() $\mathrm{C}$
in figure 11(b). The results can be interpreted based on our arguments in § 5.3 regarding the interplay between mechanical loading and thermal fluctuations. The mechanical loading is more dominant in the preshear cycle with
$\mathrm{C}$
in figure 11(b). The results can be interpreted based on our arguments in § 5.3 regarding the interplay between mechanical loading and thermal fluctuations. The mechanical loading is more dominant in the preshear cycle with
![]() $\dot \gamma _0 = 10^{-2} \, \mathrm{s^{-1}}$
compared with the one with
$\dot \gamma _0 = 10^{-2} \, \mathrm{s^{-1}}$
compared with the one with
![]() $\dot \gamma _0 = 10^{-4} \, \mathrm{s^{-1}}$
which pushes the elements towards larger local strains both in the loading and unloading processes. The peaks on the left-hand side of both distributions are due to the elements with zero local strain at the steady state of the loading process (e.g. point
$\dot \gamma _0 = 10^{-4} \, \mathrm{s^{-1}}$
which pushes the elements towards larger local strains both in the loading and unloading processes. The peaks on the left-hand side of both distributions are due to the elements with zero local strain at the steady state of the loading process (e.g. point
![]() $\mathrm{B}$
in figure 11
b), which are sheared to negative strains in the unloading process. A smaller
$\mathrm{B}$
in figure 11
b), which are sheared to negative strains in the unloading process. A smaller
![]() $\dot \gamma _0$
results in a larger number of elements with zero local strain at the steady state of the loading process which in turn leads to a more pronounced peak at the end of the preshear cycle. Zero local strain correlates with zero local free energy, and thus when the material is sheared in the negative direction, the elements with zero local strain (at the steady state of the loading process) have to overcome a large barrier to hop in the unloading process. Thus, their stress relaxation by thermal hops takes a long time. Over time, due to shear from the steady state in the loading process to the end of the preshear cycle in the unloading process, the free energy of these elements increases, and this reduces the time scale of thermally induced relaxations. However, the time scale associated with the transition from the previous steady state to the end of the preshear cycle is relatively short, as shown in figure 11, thereby not allowing for many thermally induced relaxations to occur during the unloading process. This time scale is determined by
$\dot \gamma _0$
results in a larger number of elements with zero local strain at the steady state of the loading process which in turn leads to a more pronounced peak at the end of the preshear cycle. Zero local strain correlates with zero local free energy, and thus when the material is sheared in the negative direction, the elements with zero local strain (at the steady state of the loading process) have to overcome a large barrier to hop in the unloading process. Thus, their stress relaxation by thermal hops takes a long time. Over time, due to shear from the steady state in the loading process to the end of the preshear cycle in the unloading process, the free energy of these elements increases, and this reduces the time scale of thermally induced relaxations. However, the time scale associated with the transition from the previous steady state to the end of the preshear cycle is relatively short, as shown in figure 11, thereby not allowing for many thermally induced relaxations to occur during the unloading process. This time scale is determined by
![]() $\dot \gamma _0$
. Larger preshear rates lead to a shorter time for the activation by thermal hops. The secondary peak in the distribution obtained by
$\dot \gamma _0$
. Larger preshear rates lead to a shorter time for the activation by thermal hops. The secondary peak in the distribution obtained by
![]() $\dot \gamma _0 = 10^{-4} \, \mathrm{s^{-1}}$
results from the small number of elements which have hopped during the unloading process. For this small shear rate, the flux of thermally induced relaxations is a bit larger than the flux of mechanical shear, resulting in a minor peak at zero strain. Since at
$\dot \gamma _0 = 10^{-4} \, \mathrm{s^{-1}}$
results from the small number of elements which have hopped during the unloading process. For this small shear rate, the flux of thermally induced relaxations is a bit larger than the flux of mechanical shear, resulting in a minor peak at zero strain. Since at
![]() $\dot \gamma _0 = 10^{-2} \, \mathrm{s^{-1}}$
, the dynamics is faster and mechanical loading is stronger, such a secondary peak does not emerge.
$\dot \gamma _0 = 10^{-2} \, \mathrm{s^{-1}}$
, the dynamics is faster and mechanical loading is stronger, such a secondary peak does not emerge.

Figure 12. (a) The distribution of local strain at the end of the preshear cycle with two different shear rates. Materials with these initial states are sheared with
![]() $\dot \gamma = 10^{-4} \, \mathrm{s^{-1}}$
in positive and negative directions leading to the stress responses shown in (b). PS denotes pre-shear and SS denotes steady-state shear.
$\dot \gamma = 10^{-4} \, \mathrm{s^{-1}}$
in positive and negative directions leading to the stress responses shown in (b). PS denotes pre-shear and SS denotes steady-state shear.
Now, we use the distributions in figure 12(a) as the initial distributions to perform start-up shear tests. Having the two initial states (two different
![]() $\dot \gamma _0$
), the material is sheared in either the positive or negative direction. Figure 12(b) summarizes the results of the stress–strain curve. These results can be compared with figure 6(b) in which the initial state corresponds to all the elements with zero local strain. We observe that having a history of deformation leads to a substantial decrease in the oscillations observed in the stress–strain curve. These oscillations are due to synchronization of the elements. In figure 12, many elements are initially desynchronized while in figure 6(b), all the elements are initially synchronized. We attribute the small oscillations in figure 12(b) to the facts that there is still a single unique energy well, there is no redistribution of stress after yielding, and all the elements are reset to zero local stress after yielding. All these factors lead to moderate synchronization and thus oscillations in the stress–strain curve. Although in all the tests in figure 12(b) we observe the same steady state due to the same magnitude of applied shear rate, the transient responses are very different due to different initial states. In addition, we observe that even with the same initial state, shearing in the positive and negative directions lead to different transient responses, especially for
$\dot \gamma _0$
), the material is sheared in either the positive or negative direction. Figure 12(b) summarizes the results of the stress–strain curve. These results can be compared with figure 6(b) in which the initial state corresponds to all the elements with zero local strain. We observe that having a history of deformation leads to a substantial decrease in the oscillations observed in the stress–strain curve. These oscillations are due to synchronization of the elements. In figure 12, many elements are initially desynchronized while in figure 6(b), all the elements are initially synchronized. We attribute the small oscillations in figure 12(b) to the facts that there is still a single unique energy well, there is no redistribution of stress after yielding, and all the elements are reset to zero local stress after yielding. All these factors lead to moderate synchronization and thus oscillations in the stress–strain curve. Although in all the tests in figure 12(b) we observe the same steady state due to the same magnitude of applied shear rate, the transient responses are very different due to different initial states. In addition, we observe that even with the same initial state, shearing in the positive and negative directions lead to different transient responses, especially for
![]() $\dot \gamma _0 = 10^{-4} \, \mathrm{s^{-1}}$
. This stems from the fact that the initial state of the system in this case is highly anisotropic, causing direction-dependent behaviour in the transient stress response. On the other hand, for an isotropic initial state, the stress response is not a function of the direction of the shear (e.g. shearing from point
$\dot \gamma _0 = 10^{-4} \, \mathrm{s^{-1}}$
. This stems from the fact that the initial state of the system in this case is highly anisotropic, causing direction-dependent behaviour in the transient stress response. On the other hand, for an isotropic initial state, the stress response is not a function of the direction of the shear (e.g. shearing from point
![]() $\mathrm{A}$
in figure 11 to positive and negative directions yields the same results). These interesting observations are also seen in experiments on soft particle glasses (Di Dio et al. Reference Di, Flavio, Khabaz, Bonnecaze and Cloitre2022). Furthermore, we observe that a history of deformation considerably changes the stress overshoot in the start-up shear test. This implies that the yield stress is a function of the history of deformation, a result which is observed in thixotropic yield stress materials such as polymer gels (Møller et al. Reference Møller, Rodts, Michels and Bonn2008), attractive glasses (Moller et al. Reference Moller, Fall, Chikkadi, Derks and Bonn2009), soft colloidal glasses (Bonn et al. Reference Bonn, Coussot, Huynh, Bertrand and Debrégeas2002) and hard-sphere colloidal glasses (Møller et al. Reference Møller, Fall and Bonn2009).
$\mathrm{A}$
in figure 11 to positive and negative directions yields the same results). These interesting observations are also seen in experiments on soft particle glasses (Di Dio et al. Reference Di, Flavio, Khabaz, Bonnecaze and Cloitre2022). Furthermore, we observe that a history of deformation considerably changes the stress overshoot in the start-up shear test. This implies that the yield stress is a function of the history of deformation, a result which is observed in thixotropic yield stress materials such as polymer gels (Møller et al. Reference Møller, Rodts, Michels and Bonn2008), attractive glasses (Moller et al. Reference Moller, Fall, Chikkadi, Derks and Bonn2009), soft colloidal glasses (Bonn et al. Reference Bonn, Coussot, Huynh, Bertrand and Debrégeas2002) and hard-sphere colloidal glasses (Møller et al. Reference Møller, Fall and Bonn2009).
5.5. Oscillatory shear test
A well-known rheological characterization involves performing an oscillatory cycle of shear, calculating the elastic (storage) and viscous (loss) moduli of the material, and observing the transition from solid-like to liquid-like behaviour (Donley et al. Reference Donley, de, John, McKinley and Rogers2019). To model this test, we prescribe an applied strain of
![]() $\gamma = \gamma _0 \, \cos (\omega t)$
, where
$\gamma = \gamma _0 \, \cos (\omega t)$
, where
![]() $\gamma _0$
is the strain amplitude and
$\gamma _0$
is the strain amplitude and
![]() $\omega$
is the frequency of the oscillations. Then, by solving the thermal SGR model ((3.1)–(3.3)), the macroscopic stress response of the material is calculated and the elastic and viscous moduli are extracted. Figure 13(a) represents the steady-state strain-sweep oscillatory tests performed at a frequency of
$\omega$
is the frequency of the oscillations. Then, by solving the thermal SGR model ((3.1)–(3.3)), the macroscopic stress response of the material is calculated and the elastic and viscous moduli are extracted. Figure 13(a) represents the steady-state strain-sweep oscillatory tests performed at a frequency of
![]() $\omega = 10^{-4} \, \mathrm{rad\,s}^{-1}$
. The specific evolution of the elastic and viscous moduli shown in figure 13(a), is one of the hallmarks of soft glassy materials. For small shear strain amplitudes, both moduli are constant with the elastic modulus being much larger than the viscous modulus indicating solid-like behaviour. Increasing the strain amplitude triggers a decrease in the elastic modulus and a pronounced peak in the viscous modulus which is followed by the viscous modulus dominating over the elastic modulus (liquid-like behaviour).
$\omega = 10^{-4} \, \mathrm{rad\,s}^{-1}$
. The specific evolution of the elastic and viscous moduli shown in figure 13(a), is one of the hallmarks of soft glassy materials. For small shear strain amplitudes, both moduli are constant with the elastic modulus being much larger than the viscous modulus indicating solid-like behaviour. Increasing the strain amplitude triggers a decrease in the elastic modulus and a pronounced peak in the viscous modulus which is followed by the viscous modulus dominating over the elastic modulus (liquid-like behaviour).

Figure 13. Oscillatory shear test results. (a) Strain-sweep performed at a frequency of
![]() $\omega = 10^{-4} \, \mathrm{rad}\, \text{s}^{-1}$
. The left-hand
$\omega = 10^{-4} \, \mathrm{rad}\, \text{s}^{-1}$
. The left-hand
![]() $\mathrm{y}$
-axis shows the elastic and viscous moduli, and the right-hand
$\mathrm{y}$
-axis shows the elastic and viscous moduli, and the right-hand
![]() $\mathrm{y}$
-axis shows the stress amplitude as a function of the strain amplitude. (b) Strain-sweep performed at a frequency of
$\mathrm{y}$
-axis shows the stress amplitude as a function of the strain amplitude. (b) Strain-sweep performed at a frequency of
![]() $\omega = 10^{-6} \, \mathrm{rad}\, \text{s}^{-1}$
. (c) Frequency-sweep oscillatory test performed for small amplitude oscillatory shear. The blue and green lines are guides to the eye which show the scalings at very small frequencies.
$\omega = 10^{-6} \, \mathrm{rad}\, \text{s}^{-1}$
. (c) Frequency-sweep oscillatory test performed for small amplitude oscillatory shear. The blue and green lines are guides to the eye which show the scalings at very small frequencies.
The transition from linear elastic behaviour to nonlinear flow behaviour is a sign of macroscopic yielding. This transition is also clearly evident in the stress amplitude as a function of the strain amplitude, shown in blue symbols in figure 13(a). The apparent yield stress predicted by this test is of the same order of magnitude as the experimental yield stress measured for polymer-grafted nanoparticles of interest (Agarwal et al. Reference Agarwal, Qi and Archer2010). However, the apparent yield stress is observed over a limited time scale which is governed by the competition between thermally induced structural relaxations and the applied rate of deformation. As mentioned in § 5.3, the material flows and does not show a yield stress when probed over long time scales. Therefore, when subjected to the same strain-sweep oscillatory test at a much smaller frequency, the material acts as a viscoelastic fluid with no yield stress, as shown in figure 13(b).
Another useful characterization based on this test is studying the evolution of the moduli as a function of frequency for a fixed amplitude of oscillation. Figure 13(c) shows our predictions in the limit of small amplitude oscillatory shear. A transition from liquid-like to solid-like behaviour is also depicted in this test. For low frequencies, the viscous modulus dominates over the elastic modulus while for higher frequencies, this trend is reversed. We observe that at very low frequencies, the elastic modulus scales with
![]() $G^{\prime } \thicksim \omega ^2$
, and the viscous modulus scales with
$G^{\prime } \thicksim \omega ^2$
, and the viscous modulus scales with
![]() $G^{\prime \prime } \thicksim \omega$
, suggesting a crossover to Maxwellian viscoelastic fluid behaviour in this limit. We can extract a characteristic relaxation time predicted by the Maxwell model as
$G^{\prime \prime } \thicksim \omega$
, suggesting a crossover to Maxwellian viscoelastic fluid behaviour in this limit. We can extract a characteristic relaxation time predicted by the Maxwell model as
![]() $\tau _{\textit{Max}w\textit{ell}} = \lim _{\omega \to 0} G^{\prime }/(G^{\prime \prime } \omega )$
. Based on our calculations, we obtain a relaxation time of
$\tau _{\textit{Max}w\textit{ell}} = \lim _{\omega \to 0} G^{\prime }/(G^{\prime \prime } \omega )$
. Based on our calculations, we obtain a relaxation time of
![]() $\tau _{\textit{Max}w\textit{ell}} \approx 10^5 \, \mathrm{s}$
, which is equal to the relaxation time predicted by our flow-cessation tests in the thermal regime of relaxations (figure 10
d). This result suggests that at the limit of very low frequencies and strain amplitudes, the material flows like a viscoelastic fluid. However, this flow is associated with a very large viscosity and is a result of thermally activated structural relaxations in the system.
$\tau _{\textit{Max}w\textit{ell}} \approx 10^5 \, \mathrm{s}$
, which is equal to the relaxation time predicted by our flow-cessation tests in the thermal regime of relaxations (figure 10
d). This result suggests that at the limit of very low frequencies and strain amplitudes, the material flows like a viscoelastic fluid. However, this flow is associated with a very large viscosity and is a result of thermally activated structural relaxations in the system.
Although in this section we reported a single relaxation time for the material, in reality thermal amorphous materials like polymer-grafted nanoparticles have many different relaxation times due to the history of deformation (as shown in § 5.4) and the heterogeneity in the energy landscape (which will be discussed in the next section). The single relaxation time reported here is obtained by assuming a single energy well in the system. This corresponds to a relaxation time of
![]() $\tau _r \approx \tau _0 \, \exp (E/k_{\textit{B}}T)$
which is approximately
$\tau _r \approx \tau _0 \, \exp (E/k_{\textit{B}}T)$
which is approximately
![]() $\tau _r \approx 10^5 \, \mathrm{s}$
for the sample chosen for this test. In the case of a distribution of different energy barriers, the material has a distribution of relaxation times with an average relaxation time,
$\tau _r \approx 10^5 \, \mathrm{s}$
for the sample chosen for this test. In the case of a distribution of different energy barriers, the material has a distribution of relaxation times with an average relaxation time,
![]() $\tau _{\textit{avg}}$
, given by
$\tau _{\textit{avg}}$
, given by
The linear viscoelastic regime lies in the purely thermal regime of relaxations and thus we can neglect the dependence on the local strain (§ 5.3.1) and therefore
For a Gaussian distribution of energy barriers,
![]() $\rho (E) = ({1}/{\sqrt {2\pi\! s^2}}) \exp{} (-{(E-E_{0,g})^2}/{2s^2})$
, where
$\rho (E) = ({1}/{\sqrt {2\pi\! s^2}}) \exp{} (-{(E-E_{0,g})^2}/{2s^2})$
, where
![]() $E_{0,g}$
is the mean energy barrier and
$E_{0,g}$
is the mean energy barrier and
![]() $s$
is the standard deviation, the integral in (5.14) converges as the Gaussian distribution decays faster than
$s$
is the standard deviation, the integral in (5.14) converges as the Gaussian distribution decays faster than
![]() $\exp (E/k_{\textit{B}}T)$
. Therefore, in this case, the average relaxation time is finite, although it might be extremely large. Consequently, the material will reach equilibrium over long time scales due to thermal fluctuations. For an exponential distribution of barriers,
$\exp (E/k_{\textit{B}}T)$
. Therefore, in this case, the average relaxation time is finite, although it might be extremely large. Consequently, the material will reach equilibrium over long time scales due to thermal fluctuations. For an exponential distribution of barriers,
![]() $\rho (E) = \exp (-E/E_{0,e})$
, where
$\rho (E) = \exp (-E/E_{0,e})$
, where
![]() $E_{0,e}$
is an energy constant, the integral in (5.14) converges if
$E_{0,e}$
is an energy constant, the integral in (5.14) converges if
![]() $E_{0,e} \leqslant k_{\textit{B}}T$
and diverges if
$E_{0,e} \leqslant k_{\textit{B}}T$
and diverges if
![]() $E_{0,e} \gt k_{\textit{B}}T$
. As a result, the average relaxation time is finite and thermal fluctuations can lead to equilibrium only when
$E_{0,e} \gt k_{\textit{B}}T$
. As a result, the average relaxation time is finite and thermal fluctuations can lead to equilibrium only when
![]() $E_{0,e} \leqslant k_{\textit{B}}T$
. However, if the energy distribution is cut off above a maximum energy barrier, the average relaxation time is finite regardless of the distribution of energy barriers below the cutoff.
$E_{0,e} \leqslant k_{\textit{B}}T$
. However, if the energy distribution is cut off above a maximum energy barrier, the average relaxation time is finite regardless of the distribution of energy barriers below the cutoff.
When the average relaxation time is finite, the dynamic modulus can be obtained as an average over Maxwell modes with different relaxation times. In order to access this regime, the frequency of oscillations has to be much smaller than the average relaxation rate,
![]() $\tau _{\textit{avg, th}}^{-1}$
, to allow for thermally driven structural rearrangements. Experiments on polymer-grafted nanoparticles have also shown a Maxwell-like behaviour over long time scales suggesting a Gaussian distribution of barriers in the material (Wen et al. Reference Wen, Schaefer and Archer2015). In § 5.4, we demonstrated how stress relaxation tests can provide insights into the distribution of energy barriers in the system. Here, we observed that the linear viscoelastic response can also be used to extract information about the energy landscape. However, this regime is associated with very long time scales and might not be accessible experimentally.
$\tau _{\textit{avg, th}}^{-1}$
, to allow for thermally driven structural rearrangements. Experiments on polymer-grafted nanoparticles have also shown a Maxwell-like behaviour over long time scales suggesting a Gaussian distribution of barriers in the material (Wen et al. Reference Wen, Schaefer and Archer2015). In § 5.4, we demonstrated how stress relaxation tests can provide insights into the distribution of energy barriers in the system. Here, we observed that the linear viscoelastic response can also be used to extract information about the energy landscape. However, this regime is associated with very long time scales and might not be accessible experimentally.
5.6. Effects of the distribution of energy barriers
All the results presented thus far assume that the energy landscape has only one unique energy well. This assumption was made to simplify the analyses and provide insight into the complex interplay between mechanical loading and thermal fluctuations in thermal amorphous materials. However, the energy landscape in amorphous materials has many local minima, and a single energy well cannot represent the entire landscape. As addressed in § 5.4, the energy barriers in many amorphous materials possess a Gaussian distribution. Therefore, in this section, we assume a Gaussian distribution for the energy barriers with a mean value equal to the single energy barrier obtained previously,
![]() $E_0$
, and a standard deviation of
$E_0$
, and a standard deviation of
![]() $0.2E_0$
. We assume that the shape of the energy well remains fixed, and we only scale up/down the energy profiles based on the value of the energy barrier compared with the mean value. Thus, this landscape is a simplification based on the shape of the single energy well obtained from our DFT calculations. Predicting the details of the entire landscape based on the molecular-level information is beyond the scope of this work.
$0.2E_0$
. We assume that the shape of the energy well remains fixed, and we only scale up/down the energy profiles based on the value of the energy barrier compared with the mean value. Thus, this landscape is a simplification based on the shape of the single energy well obtained from our DFT calculations. Predicting the details of the entire landscape based on the molecular-level information is beyond the scope of this work.

Figure 14. (a) Stress–strain curve in the start-up shear test with
![]() $\dot \gamma = 10^{-4} \, \mathrm{s^{-1}}$
assuming a Gaussian energy distribution. (b) The probability distribution of local strain and energy barrier at steady state.
$\dot \gamma = 10^{-4} \, \mathrm{s^{-1}}$
assuming a Gaussian energy distribution. (b) The probability distribution of local strain and energy barrier at steady state.
Figure 14(a) shows the stress–strain curve with an applied shear rate of
![]() $\dot \gamma = 10^{-4} \, \mathrm{s^{-1}}$
assuming the mentioned Gaussian distribution for the energy barriers. Comparing this plot with figure 6(b), we clearly observe that the oscillations in the stress–strain curve are due to the synchronization of the elements. A distribution of the barriers desynchronizes the yielding events since: (i) the elements are initially in different energy wells and thus desynchronized, and (ii) every time an element yields, it randomly chooses a new energy well from the Gaussian distribution instead of being reborn in the same energy well. This desynchronization eliminates the oscillations in the stress–strain curve. It is evident that further broadening the distribution of energy barriers leads to more desynchronization. Although a broad distribution of barriers might completely eliminate the oscillations at low shear rates, we expect to observe some oscillations at higher shear rates. We attribute the small oscillations after the overshoot to the absence of interactions between different elements in the system. A redistribution of the stress after yielding further desynchronizes the elements as they receive positive and negative random stress kicks (Nicolas et al. Reference Nicolas, Ferrero, Martens and Barrat2018).
$\dot \gamma = 10^{-4} \, \mathrm{s^{-1}}$
assuming the mentioned Gaussian distribution for the energy barriers. Comparing this plot with figure 6(b), we clearly observe that the oscillations in the stress–strain curve are due to the synchronization of the elements. A distribution of the barriers desynchronizes the yielding events since: (i) the elements are initially in different energy wells and thus desynchronized, and (ii) every time an element yields, it randomly chooses a new energy well from the Gaussian distribution instead of being reborn in the same energy well. This desynchronization eliminates the oscillations in the stress–strain curve. It is evident that further broadening the distribution of energy barriers leads to more desynchronization. Although a broad distribution of barriers might completely eliminate the oscillations at low shear rates, we expect to observe some oscillations at higher shear rates. We attribute the small oscillations after the overshoot to the absence of interactions between different elements in the system. A redistribution of the stress after yielding further desynchronizes the elements as they receive positive and negative random stress kicks (Nicolas et al. Reference Nicolas, Ferrero, Martens and Barrat2018).
Figure 14(b) displays the probability distribution,
![]() $P(E,l)$
, of the elements being trapped in an energy well,
$P(E,l)$
, of the elements being trapped in an energy well,
![]() $E$
, and possessing a local strain,
$E$
, and possessing a local strain,
![]() $l$
, at the steady state for
$l$
, at the steady state for
![]() $\dot \gamma = 10^{-4} \, \mathrm{s^{-1}}$
. Since the distribution of
$\dot \gamma = 10^{-4} \, \mathrm{s^{-1}}$
. Since the distribution of
![]() $E$
, i.e.
$E$
, i.e.
![]() $\rho (E)$
, is Gaussian, most of the elements have an energy well around the mean value. More specifically, the probability distribution,
$\rho (E)$
, is Gaussian, most of the elements have an energy well around the mean value. More specifically, the probability distribution,
![]() $P(E,l)$
, is Gaussian with respect to
$P(E,l)$
, is Gaussian with respect to
![]() $E$
for very small
$E$
for very small
![]() $l$
(near the free energy minima). However, for larger local strains, the number of elements trapped in small barriers diminishes. When the barrier is small, the elements easily hop out of the trap, while thermal fluctuations cannot overcome larger energy barriers. As a result, these elements get sheared more, access larger local strains and contain a larger portion of the global stress. However, even for the largest trap assumed, the elements hop before reaching the maximum local strain. Increasing the shear rate will lead to accessing larger local strains, as discussed in figure 6(d).
$l$
(near the free energy minima). However, for larger local strains, the number of elements trapped in small barriers diminishes. When the barrier is small, the elements easily hop out of the trap, while thermal fluctuations cannot overcome larger energy barriers. As a result, these elements get sheared more, access larger local strains and contain a larger portion of the global stress. However, even for the largest trap assumed, the elements hop before reaching the maximum local strain. Increasing the shear rate will lead to accessing larger local strains, as discussed in figure 6(d).
As mentioned earlier in this section, here the shape of the energy wells is assumed to follow the shape obtained from our DFT calculations for a periodic array of particles. This results in the same mechanical yield strain for different energy wells in the landscape. However, in amorphous materials, the distribution of local environments would likely lead to different yield strains as well as different energy barriers. Having a distribution of yield strains as well as energy barriers would lead to a qualitative change in the results. The distribution of yield strains would help to reduce the oscillations of stress even at large shear rates whereas the distribution of energy barriers only does this at lower shear rates. We expect that changes in the shape of the free energy profile in other ways would be more a matter of quantitative changes of behaviour rather than qualitative.
6. Conclusion
In this work, we proposed an innovative approach to connect molecular-level information to the bulk rheology of thermal amorphous materials. Our results demonstrate the ability of classical DFT to predict the energy landscape of amorphous materials. This energy landscape can be integrated into mesoscopic models to bridge the gap between the molecular-level structure and the macroscopic response and accurately explain the complex behaviour of these materials across a vast range of length and time scales. The findings in this study shed light on the underlying physics of deformation in thermal amorphous materials and on the role of thermal fluctuations in the rheology. We tested our framework with a model thermal elastoplastic material consisting of solvent-free polymer-grafted nanoparticles. We showed that the wide range of complex rheological behaviours exhibited by this material can be understood in terms of the interplay between the time scale of mechanical deformation and the time scale of thermally induced structural relaxations. This interplay is mainly governed by the energy landscape and attempt frequency for hops.
In the first part of the paper, we studied the molecular-level physics of solvent-free polymer-grafted nanoparticles using a classical DFT. We used a bead–spring model to represent the grafted polymers and demonstrated that the free energy of the polymers is determined by the competition between the configurational and translational entropy of the grafted polymers. The absence of a solvent forces the grafted polymers to fill the void space between the nanocores leading to a significant loss in the configurational entropy of the polymers. As a result, strong cages are created around each nanocore strongly retarding structural relaxations. Interestingly, these cages are found to be particularly strong at small core volume fractions and polymer molecular weights leading to especially slow dynamics for cases that exhibit small stresses and rapid relaxation in the absence of polymer tethering. This molecular-scale information is encoded in the energy landscape of the material.
Our thermally activated EPM, which we refer to as the thermal SGR model, draws upon concepts from Bouchaud’s trap model for glasses (Bouchaud Reference Bouchaud1992; Monthus & Bouchaud Reference Monthus and Bouchaud1996) and the phenomenological SGR model developed for athermal soft glassy materials (Sollich et al. Reference Sollich, Lequeux, Hébraud and Cates1997; Sollich Reference Sollich1998). The thermal SGR model facilitates incorporation of molecular-level information by allowing any functional form for the energy landscape, e.g. smooth or parabolic, and it replaces the non-physical noise temperature in the original SGR model with the thermodynamic temperature. Even in its simplest form, i.e. with all elements possessing the same energy well and no elastic interactions among the elements in the system, the thermal SGR model can accurately explain and reproduce a variety of rheological experiments based solely on the interplay between mechanical loading and thermal fluctuations.
The thermal SGR model predicts a soft glassy behaviour with an apparent yield stress when probed over limited time scales. The presence of thermal fluctuations reduces the stress overshoot in the stress–strain curve or the apparent yield stress of the material since the elements hop out of their traps in anticipation. The apparent yield stress strongly depends on the history of deformation and the applied shear rate since both alter the dynamics of relaxation by thermal hops. Although we did not focus on ageing, we anticipate that the thermal SGR model would predict ageing behaviour characterized by an increase in the stress overshoot as a function of the waiting time as the elements hop into deeper traps over time. These history-dependent behaviours are signatures of thixotropy in soft glassy materials (Agarwal et al. Reference Agarwal, Sharma, Shankar and Joshi2021; Bhattacharyya et al. Reference Bhattacharyya, Jacob, Petekidis and Joshi2023). In contrast to athermal amorphous materials, thermal amorphous materials can flow and act like a liquid with no yield stress over sufficiently long times. Based on our scaling analyses, for small shear rates at steady state, our model reveals a thermal regime of relaxations which results in Newtonian flow over long time scales with a high viscosity. For intermediate shear rates however, a logarithmic flow curve emerges due to thermal–mechanical relaxations.
As suggested by the typical molecular-level structure of amorphous materials, we assumed a Gaussian distribution for energy barriers and showed that, in this case, the thermal SGR model predicts a stretched exponential relaxation of the kind observed experimentally in many amorphous materials. On the other hand, the original SGR model assumes an exponential distribution of barriers and predicts a power-law stress relaxation, which is also observed for some amorphous materials. This confirms that once informed by the molecular-scale physics, the SGR framework in general can capture the complexities of a wide range of amorphous materials under shear deformation.
In this work, we focused on amorphous materials that can relax towards equilibrium states due to thermal fluctuations. Such a behaviour has been observed in polymer-grafted nanoparticles (Agarwal et al. Reference Agarwal, Qi and Archer2010; Agarwal & Archer Reference Agarwal and Archer2011), supercooled glass-forming liquids (Laughlin & Uhlmann Reference Laughlin and Uhlmann1972; Schröter & Donth Reference Schröter and Donth2000) and metallic glasses (Kawamura, Nakamura & Inoue Reference Kawamura, Nakamura and Inoue1998; Lu et al. Reference Lu, Ravichandran and Johnson2003; Riechers et al. Reference Riechers, Das, Rashidi, Dufresne and Maaß2025). We expect that the creep flow associated with the solid-like behaviour in these systems will be eventually followed by fluidization and a steady-state flow. For stresses just below the yield stress, prior theoretical (Popović et al. Reference Popović, de, Tom, Ji and Wyart2021) and experimental (Grenard et al. Reference Grenard, Divoux, Taberlet and Manneville2014) studies show that the time scale over which the material behaves as a solid decreases exponentially with increasing applied stress. For very small stresses, this time scale will become quite large and thus might not be accessible within the time window of experiments and simulations. The flow in this situation is entirely driven by thermal fluctuations. As supported by our scaling analysis and oscillatory shear tests, this indicates that the average relaxation time of the material is finite, although it might be extremely large. Therefore, non-equilibrium behaviours become important over limited time scales while the material reaches equilibrium over long time scales. A glassy behaviour here refers to exhibiting an apparent yield stress over extended time periods and is different from the true glassy behaviour of systems with no equilibrium states.
Extending our free energy calculations to account for an amorphous structure will provide illuminating insights on the energy landscape in amorphous materials. This is a challenging task as it involves a system with millions of particles, many-body interactions and intrinsic disorder. Although promising, the thermal SGR model in its current form has some limitations. The model assumes independent elements while in amorphous materials, the elements are highly coupled through stress redistribution after local yielding events (Nicolas et al. Reference Nicolas, Ferrero, Martens and Barrat2018). Furthermore, a tensorial description of the energy landscape along with the local and macroscopic stresses would be valuable.
Acknowledgements
The authors thank F. Blanc, G. Ovarlez and S. Rassouli for discussions.
Funding
This work was supported by National Science Foundation (CBET: Fluid Dynamics Award 2135617).
Declaration of interests
The authors report no conflict of interest.