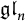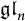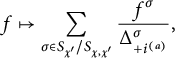1 Introduction
In this article, we discuss three different perspectives on a category which has shown up in several guises in recent years. We can organize these perspectives as (1) diagrammatic, (2) representation-theoretic, and (3) geometric.
For the diagrammatic perspective, work of Khovanov and Lauda [Reference Khovanov and LaudaKL09] initiated a great burst of different algebras spanned by diagrams with locally defined relations; while no rubric can contain all of this efflorescence, the author introduced weighted Khovanov–Lauda–Rouquier algebras [Reference WebsterWeb19] which include the algebras discussed in this article (and many others we will not consider here). The special case of interest to us was considered in recent work of Khovanov–Lauda–Sussan–Yonezawa [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18]; in their terminology, this is a deformed Webster algebra. In the spirit of compromise, we will follow the terminology suggested by our collaborators in [Reference Kamnitzer, Tingley, Webster, Weekes and YacobiKTW+19], and write KLRW algebras.
As suggested by the title, we will focus on the case which is relevant to symmetric Howe duality; specifically, we consider the algebras that categorify
![]() $\mathfrak {sl}_\infty $
-weight spaces of the symmetric power
$\mathfrak {sl}_\infty $
-weight spaces of the symmetric power
![]() $U(\mathfrak {n})\otimes \operatorname {Sym}^n({\mathbb{C}}^{\infty }\otimes {\mathbb{C}}^{m})$
, where
$U(\mathfrak {n})\otimes \operatorname {Sym}^n({\mathbb{C}}^{\infty }\otimes {\mathbb{C}}^{m})$
, where
![]() $\mathfrak {n}\subset \mathfrak {sl}_{m}$
is the Lie algebra of strictly upper-triangular matrices. We can identify the
$\mathfrak {n}\subset \mathfrak {sl}_{m}$
is the Lie algebra of strictly upper-triangular matrices. We can identify the
![]() $\mathfrak {sl}_\infty $
weights appearing with increasing n-tuples
$\mathfrak {sl}_\infty $
weights appearing with increasing n-tuples
![]() $\chi =(\chi _1\leq \chi _2\leq \cdots \leq \chi _n)$
, and we denote the algebra categorifying this weight space by
$\chi =(\chi _1\leq \chi _2\leq \cdots \leq \chi _n)$
, and we denote the algebra categorifying this weight space by
![]() $\mathbb{\tilde {T}}^\chi $
. One can easily verify that as an
$\mathbb{\tilde {T}}^\chi $
. One can easily verify that as an
![]() $\mathfrak {sl}_m$
-module, this weight space can be identified with
$\mathfrak {sl}_m$
-module, this weight space can be identified with
![]() $U(\mathfrak {n})\otimes \operatorname {Sym}^{g_1}({\mathbb{C}}^m)\otimes \cdots \otimes \operatorname {Sym}^{g_k}({\mathbb{C}}^m)$
, where
$U(\mathfrak {n})\otimes \operatorname {Sym}^{g_1}({\mathbb{C}}^m)\otimes \cdots \otimes \operatorname {Sym}^{g_k}({\mathbb{C}}^m)$
, where
![]() $g_*$
are multiplicities with which the distinct elements of
$g_*$
are multiplicities with which the distinct elements of
![]() $\chi $
repeat. The algebra
$\chi $
repeat. The algebra
![]() $\mathbb{\tilde {T}}^\chi $
is a deformed version of the algebra
$\mathbb{\tilde {T}}^\chi $
is a deformed version of the algebra
![]() $\tilde {T}^{\underline {\boldsymbol {\lambda }}}$
as introduced in [Reference WebsterWeb17b, Section 4] which is shown there to give a categorification of this tensor product. In [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18], Khovanov–Lauda–Sussan–Yonezawa consider the case
$\tilde {T}^{\underline {\boldsymbol {\lambda }}}$
as introduced in [Reference WebsterWeb17b, Section 4] which is shown there to give a categorification of this tensor product. In [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18], Khovanov–Lauda–Sussan–Yonezawa consider the case
![]() $m=2$
and construct the Howe dual categorical
$m=2$
and construct the Howe dual categorical
![]() $\mathfrak {sl}_\infty $
-action on the categories of
$\mathfrak {sl}_\infty $
-action on the categories of
![]() $\mathbb{\tilde {T}}^\chi $
-modules. In this article, we will generalize this result to all values of m.
$\mathbb{\tilde {T}}^\chi $
-modules. In this article, we will generalize this result to all values of m.
We achieve this by considering the other perspectives mentioned above, where the Howe dual actions are consequences of previously constructed
![]() $\mathfrak {sl}_\infty $
-actions. From the representation-theoretic perspective, we consider the category of Gelfand–Tsetlin modules over
$\mathfrak {sl}_\infty $
-actions. From the representation-theoretic perspective, we consider the category of Gelfand–Tsetlin modules over
![]() $\mathfrak {gl}_n$
. Recall that a Gelfand–Tsetlin module over
$\mathfrak {gl}_n$
. Recall that a Gelfand–Tsetlin module over
![]() $\mathfrak {gl}_n$
is one on which the center of
$\mathfrak {gl}_n$
is one on which the center of
![]() $U(\mathfrak {gl}_k)$
for all
$U(\mathfrak {gl}_k)$
for all
![]() $k\leq n$
acts locally finitely; we will also sometimes want to consider pro-Gelfand–Tsetlin modules, by which we mean topological modules where the action is only topologically locally finite. This category has received a great deal of interest in recent years [Reference Futorny, Grantcharov and RamirezFGR17, Reference Futorny, Grantcharov, Ramirez and ZadunaiskyFGRZ20, Reference Ramírez and ZadunaiskyRZ18] but its objects have remained relatively mysterious. Recent work of the author and collaborators [Reference Kamnitzer, Tingley, Webster, Weekes and YacobiKTW+19, Reference WebsterWeba] gave a classification of the simples in a block of this category in general, but the combinatorics of the general case is somewhat complicated; some data on the complexity of the
$k\leq n$
acts locally finitely; we will also sometimes want to consider pro-Gelfand–Tsetlin modules, by which we mean topological modules where the action is only topologically locally finite. This category has received a great deal of interest in recent years [Reference Futorny, Grantcharov and RamirezFGR17, Reference Futorny, Grantcharov, Ramirez and ZadunaiskyFGRZ20, Reference Ramírez and ZadunaiskyRZ18] but its objects have remained relatively mysterious. Recent work of the author and collaborators [Reference Kamnitzer, Tingley, Webster, Weekes and YacobiKTW+19, Reference WebsterWeba] gave a classification of the simples in a block of this category in general, but the combinatorics of the general case is somewhat complicated; some data on the complexity of the
![]() $\mathfrak {sl}_3$
and
$\mathfrak {sl}_3$
and
![]() $\mathfrak {sl}_4$
case are presented in [Reference Silverthorne and WebsterSW24]. One of our motivations in this article is to draw out the structure of this category in the most interesting case, that of an integral central character. We’ll show here (based on the techniques in [Reference WebsterWeba]) that the algebras
$\mathfrak {sl}_4$
case are presented in [Reference Silverthorne and WebsterSW24]. One of our motivations in this article is to draw out the structure of this category in the most interesting case, that of an integral central character. We’ll show here (based on the techniques in [Reference WebsterWeba]) that the algebras
![]() $\mathbb{\tilde {T}}^\chi $
attached to the zero weight space for the action of
$\mathbb{\tilde {T}}^\chi $
attached to the zero weight space for the action of
![]() $\mathfrak {sl}_{m}$
control the category
$\mathfrak {sl}_{m}$
control the category
![]() $\mathcal {GT}_\chi $
of integral Gelfand–Tsetlin modules where now we interpret
$\mathcal {GT}_\chi $
of integral Gelfand–Tsetlin modules where now we interpret
![]() $\chi $
as a central character of
$\chi $
as a central character of
![]() $Z_n=Z(U(\mathfrak {gl}_n))$
. We can also associate a parabolic
$Z_n=Z(U(\mathfrak {gl}_n))$
. We can also associate a parabolic
![]() $P_\chi $
to
$P_\chi $
to
![]() $\chi $
, whose block sizes are the multiplicities of entries in
$\chi $
, whose block sizes are the multiplicities of entries in
![]() $\chi $
which coincide.
$\chi $
which coincide.
The algebras
![]() $\mathbb{\tilde {T}}^\chi $
also have a topological interpretation in terms of convolution algebras and perverse sheaves. We can view this as a generalization of the well-known theorem of Beilinson–Ginzburg–Soergel, which shows that the Koszul dual of an integral block
$\mathbb{\tilde {T}}^\chi $
also have a topological interpretation in terms of convolution algebras and perverse sheaves. We can view this as a generalization of the well-known theorem of Beilinson–Ginzburg–Soergel, which shows that the Koszul dual of an integral block
![]() $\mathcal {O}_\chi $
of the deformed category
$\mathcal {O}_\chi $
of the deformed category
![]() $\mathcal {O}$
is the category of P-equivariant perverse sheaves on
$\mathcal {O}$
is the category of P-equivariant perverse sheaves on
![]() $GL_n/B,$
where
$GL_n/B,$
where
![]() $P=P_\chi $
corresponds to the central character
$P=P_\chi $
corresponds to the central character
![]() $\chi $
of the block. Our main theorem explains how to extend this to Gelfand–Tsetlin modules.
$\chi $
of the block. Our main theorem explains how to extend this to Gelfand–Tsetlin modules.
Consider the vector space V defined by the set of quiver representations on the vector spaces
![]() ${\mathbb{C}}^1\overset {f_1}\to {\mathbb{C}}^2\overset {f_2}\to \cdots \overset {f_{n-2}}\to {\mathbb{C}}^{n-1}\overset {f_{n-1}}\to {\mathbb{C}}^{n}$
divided by the group G that changes bases arbitrarily on
${\mathbb{C}}^1\overset {f_1}\to {\mathbb{C}}^2\overset {f_2}\to \cdots \overset {f_{n-2}}\to {\mathbb{C}}^{n-1}\overset {f_{n-1}}\to {\mathbb{C}}^{n}$
divided by the group G that changes bases arbitrarily on
![]() ${\mathbb{C}}^1,\dots , {\mathbb{C}}^{n-1}$
and on
${\mathbb{C}}^1,\dots , {\mathbb{C}}^{n-1}$
and on
![]() ${\mathbb{C}}^{n}$
by elements of the group
${\mathbb{C}}^{n}$
by elements of the group
![]() $P\subset GL_n$
(that is, preserving the standard partial flag corresponding to P). That is,
$P\subset GL_n$
(that is, preserving the standard partial flag corresponding to P). That is,
with
![]() $G^0=GL_{{n-1}}\times \cdots \times GL_{1}$
. Note that on an open subset of V, the maps
$G^0=GL_{{n-1}}\times \cdots \times GL_{1}$
. Note that on an open subset of V, the maps
![]() $f_i$
are all injective, and the subspaces
$f_i$
are all injective, and the subspaces
give a complete flag. Thus, we can identify this open subset of
![]() $V/G^0$
with the flag variety
$V/G^0$
with the flag variety
![]() $\operatorname {Fl}=GL_n/B$
. In this article, we will study G-equivariant sheaves on V as an enlargement of the category of P-equivariant sheaves on
$\operatorname {Fl}=GL_n/B$
. In this article, we will study G-equivariant sheaves on V as an enlargement of the category of P-equivariant sheaves on
![]() $\operatorname {Fl}$
.
$\operatorname {Fl}$
.
We let
![]() $G_{\chi }=P_{\chi }\times G^0$
and consider the usual
$G_{\chi }=P_{\chi }\times G^0$
and consider the usual
![]() $G_{\chi }$
-equivariant derived category of
$G_{\chi }$
-equivariant derived category of
![]() ${\mathbb{C}}$
-vector spaces
${\mathbb{C}}$
-vector spaces
![]() $D^{b}_{G_{\chi }}(V)$
; we’ll show that this category has a graded lift
$D^{b}_{G_{\chi }}(V)$
; we’ll show that this category has a graded lift
![]() $D^{b,\operatorname {mix}}_{G_{\chi }}(V)$
.
$D^{b,\operatorname {mix}}_{G_{\chi }}(V)$
.
Theorem 1 We have equivalences of categories between:
-
(1) the category of weakly gradable finite-dimensional
 $\mathbb{\tilde {T}}^\chi $
-modules;
$\mathbb{\tilde {T}}^\chi $
-modules; -
(2) the category
 $\mathcal {GT}_\chi $
of integral Gelfand–Tsetlin modules.
$\mathcal {GT}_\chi $
of integral Gelfand–Tsetlin modules.
Thus, the category
![]() $\mathbb{\tilde {T}}^\chi \operatorname {-gmod}$
of all finitely generated graded
$\mathbb{\tilde {T}}^\chi \operatorname {-gmod}$
of all finitely generated graded
![]() $\mathbb{\tilde {T}}^\chi $
-modules is a graded lift
$\mathbb{\tilde {T}}^\chi $
-modules is a graded lift
![]() $\widetilde {\mathcal {GT}}_\chi $
of the category of pro-Gelfand–Tsetlin modules.
$\widetilde {\mathcal {GT}}_\chi $
of the category of pro-Gelfand–Tsetlin modules.
We also have an equivalence of categories between:
-
(1’) the category of linear complexes of projectives over
 $\mathbb{\tilde {T}}^\chi $
;
$\mathbb{\tilde {T}}^\chi $
; -
(3) the category of
 $P_\chi $
-equivariant perverse sheaves on V.
$P_\chi $
-equivariant perverse sheaves on V.
The categories
![]() $(1)$
and
$(1)$
and
![]() $(1')$
are in a certain sense Koszul dual, so the same is true of
$(1')$
are in a certain sense Koszul dual, so the same is true of
![]() $(2)$
and
$(2)$
and
![]() $(3)$
. These equivalences are induced by equivalences of derived categories
$(3)$
. These equivalences are induced by equivalences of derived categories
Just as with the original Koszul duality of Beilinson–Ginzburg–Soergel, this result seems to be a manifestation of the self-duality of
![]() $T^*GL_n/B$
under three-dimensional mirror symmetry [Reference Webster and YooWY23]. In particular, the Koszul duality of (2) and (3) is a special case of [Reference WebsterWebb, Proposition 4.7], which relates versions of these categories for arbitrary Higgs and Coulomb branches of three-dimensional gauge theories.
$T^*GL_n/B$
under three-dimensional mirror symmetry [Reference Webster and YooWY23]. In particular, the Koszul duality of (2) and (3) is a special case of [Reference WebsterWebb, Proposition 4.7], which relates versions of these categories for arbitrary Higgs and Coulomb branches of three-dimensional gauge theories.
Furthermore, this equivalence matches two natural actions of 2-categories on the categories appearing in the theorem above. As discussed previously, we can interpret
![]() $\chi $
as a weight of
$\chi $
as a weight of
![]() $\mathfrak {sl}_\infty $
, and
$\mathfrak {sl}_\infty $
, and
![]() $K^0(\mathbb{\tilde {T}}^\chi )$
as a weight space of an
$K^0(\mathbb{\tilde {T}}^\chi )$
as a weight space of an
![]() $\mathfrak {sl}_\infty $
-module. Thus, it’s a natural question whether this can be extended to a categorical
$\mathfrak {sl}_\infty $
-module. Thus, it’s a natural question whether this can be extended to a categorical
![]() $\mathfrak {sl}_{\infty }$
-action. Not only is this possible, but in fact, the resulting action is one already known in both the representation-theoretic and geometric perspectives.
$\mathfrak {sl}_{\infty }$
-action. Not only is this possible, but in fact, the resulting action is one already known in both the representation-theoretic and geometric perspectives.
For Gelfand–Tsetlin modules, this action is by translation functors. The functors of
![]() $\mathsf {E}(M)={\mathbb{C}}^n\otimes M$
and
$\mathsf {E}(M)={\mathbb{C}}^n\otimes M$
and
![]() $\mathsf {F}(M)=({\mathbb{C}}^n)^*\otimes M$
act on the category of Gelfand–Tsetlin modules, and define an action of the level 0 Heisenberg category (also called the affine oriented Brauer category in [Reference Brundan, Comes and KujawaBCK19]) on the category of all Gelfand–Tsetlin modules. These functors decompose according to how they act on blocks, and by [Reference Brundan, Savage and WebsterBSW, Theorem A], the summands of this functor define a categorical
$\mathsf {F}(M)=({\mathbb{C}}^n)^*\otimes M$
act on the category of Gelfand–Tsetlin modules, and define an action of the level 0 Heisenberg category (also called the affine oriented Brauer category in [Reference Brundan, Comes and KujawaBCK19]) on the category of all Gelfand–Tsetlin modules. These functors decompose according to how they act on blocks, and by [Reference Brundan, Savage and WebsterBSW, Theorem A], the summands of this functor define a categorical
![]() $\mathfrak {sl_\infty }$
action on the sum of the integral blocks
$\mathfrak {sl_\infty }$
action on the sum of the integral blocks
![]() $\mathcal {GT}_\chi $
.
$\mathcal {GT}_\chi $
.
On the other hand, as is always true for equivariant sheaves for different subgroups of a single group, the
![]() $G_{\chi }=P_\chi \times G^0$
equivariant derived categories of V for different
$G_{\chi }=P_\chi \times G^0$
equivariant derived categories of V for different
![]() $\chi $
carry an action by convolution of the derived categories
$\chi $
carry an action by convolution of the derived categories
![]() $D^b_{P_{\chi '}\times P_\chi } ( GL_n)$
where these subgroups act by left and right multiplication. This is essentially an action of the category
$D^b_{P_{\chi '}\times P_\chi } ( GL_n)$
where these subgroups act by left and right multiplication. This is essentially an action of the category
![]() $\mathsf {Perv}$
from [Reference WebsterWeb17a, Definition 5] with minor notational changes to account for working with
$\mathsf {Perv}$
from [Reference WebsterWeb17a, Definition 5] with minor notational changes to account for working with
![]() $\mathfrak {sl}_\infty .$
There is a 2-functor
$\mathfrak {sl}_\infty .$
There is a 2-functor
![]() $\Phi $
from the 2-Kac–Moody algebra for
$\Phi $
from the 2-Kac–Moody algebra for
![]() $\mathfrak {sl}_\infty $
to
$\mathfrak {sl}_\infty $
to
![]() $\mathsf {Perv}$
introduced in [Reference WebsterWeb17a], uniquely characterized by the property that it agrees with Khovanov and Lauda’s original functor from [Reference Khovanov and LaudaKL10] to modules over the cohomology rings of
$\mathsf {Perv}$
introduced in [Reference WebsterWeb17a], uniquely characterized by the property that it agrees with Khovanov and Lauda’s original functor from [Reference Khovanov and LaudaKL10] to modules over the cohomology rings of
![]() $GL_n/P_\chi $
.
$GL_n/P_\chi $
.
Both these actions must have an algebraic description in terms of bimodules over
![]() $\mathbb{\tilde {T}}^{\chi '}$
and
$\mathbb{\tilde {T}}^{\chi '}$
and
![]() $\mathbb{\tilde {T}}^{\chi }$
. In fact, the resulting bimodules are the ladder bimodules defined in [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18] in the case of
$\mathbb{\tilde {T}}^{\chi }$
. In fact, the resulting bimodules are the ladder bimodules defined in [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18] in the case of
![]() $\mathfrak {sl}_2$
. Our comparison of these with the geometric action gives an easy and conceptual proof of the fact that these bimodules induce a categorical
$\mathfrak {sl}_2$
. Our comparison of these with the geometric action gives an easy and conceptual proof of the fact that these bimodules induce a categorical
![]() $\mathfrak {sl}_\infty $
action in the case not just of
$\mathfrak {sl}_\infty $
action in the case not just of
![]() $\mathfrak {sl}_2$
(as is shown in [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18]), but the more general case of
$\mathfrak {sl}_2$
(as is shown in [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18]), but the more general case of
![]() $\mathfrak {sl}_n$
.
$\mathfrak {sl}_n$
.
Theorem 2 The equivalences of Theorem 1 match:
-
(1) the categorical
 $\mathfrak {sl}_\infty $
-action on
$\mathfrak {sl}_\infty $
-action on
 $\oplus _\chi \mathbb{\tilde {T}}^\chi \operatorname {-mod}$
defined by ladder bimodules as in [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18];
$\oplus _\chi \mathbb{\tilde {T}}^\chi \operatorname {-mod}$
defined by ladder bimodules as in [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18]; -
(2) the categorical
 $\mathfrak {sl}_\infty $
-action on
$\mathfrak {sl}_\infty $
-action on
 $\oplus _\chi \mathcal {GT}_\chi $
defined by translation functors;
$\oplus _\chi \mathcal {GT}_\chi $
defined by translation functors; -
(3) the categorical
 $\mathfrak {sl}_\infty $
-action on
$\mathfrak {sl}_\infty $
-action on
 $\oplus _\chi D^{b,\operatorname {mix}}_{G_{\chi }}(V)$
defined by convolution with sheaves in
$\oplus _\chi D^{b,\operatorname {mix}}_{G_{\chi }}(V)$
defined by convolution with sheaves in
 $\mathsf {Perv}$
.
$\mathsf {Perv}$
.
The actions (1) and (3) make sense when we replace (1.1a) and (1.1b) with more general dimension vectors, as we’ll discuss below, but (2) really depends on the identification with the universal enveloping algebra. Theorems 1 and 2 extend essentially without change to the comparison of the equivariant derived category and
![]() $\mathbb{\tilde {T}}$
, and the match of the categorical
$\mathbb{\tilde {T}}$
, and the match of the categorical
![]() $\mathfrak {sl}_\infty $
-actions. The extension of the action (2) will require more effort, though it should be possible in some cases where the quantum Coulomb branch is a finite W-algebra using Brundan and Kleshchev’s definition of translation functors for W-algebras in [Reference Brundan and KleshchevBK08, Section 4.4].
$\mathfrak {sl}_\infty $
-actions. The extension of the action (2) will require more effort, though it should be possible in some cases where the quantum Coulomb branch is a finite W-algebra using Brundan and Kleshchev’s definition of translation functors for W-algebras in [Reference Brundan and KleshchevBK08, Section 4.4].
Finally, we discuss the slightly tangled relationship of this construction to previous work relating diagrammatic categories and the representation theory of Lie algebras.
2 Diagrammatic algebras
2.1 Algebras
In this section, we introduce the algebraic construction that will unify the perspectives appearing here. These algebras have appeared in many previous works of the author and collaborators [Reference Kamnitzer, Tingley, Webster, Weekes and YacobiKTW+19, Reference WebsterWeba, Reference WebsterWeb15, Reference WebsterWeb16, Reference WebsterWeb17b, Reference WebsterWeb19], as well as the line of research of Khovanov, Lauda, Sussan, and Yonezawa [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18, Reference Khovanov and SussanKS18].
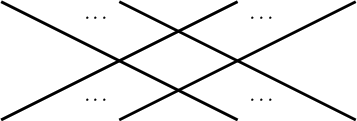
Definition 2.1 A KLRW diagram is a collection of finitely many oriented curves in
![]() $\mathbb{R}\times [0,1]$
whose projection to the second factor is a diffeomorphism. Each curve is either:
$\mathbb{R}\times [0,1]$
whose projection to the second factor is a diffeomorphism. Each curve is either:
-
• colored red and labeled with the integer m and decorated with finitely many dots;
-
• colored black and labeled with
 $i\in [1,m-1]$
and decorated with finitely many dots. Let
$i\in [1,m-1]$
and decorated with finitely many dots. Let
 $v_i$
be the number of black strands with label i.
$v_i$
be the number of black strands with label i.
The diagram must be locally of the form

with each curve oriented in the negative direction. In particular, no red strands can ever cross. Each curve must meet both
![]() $y=0$
and
$y=0$
and
![]() $y=1$
at distinct points from the other curves.
$y=1$
at distinct points from the other curves.
Readers familiar with the conventions of [Reference WebsterWeb16, Reference WebsterWeb17b], etc. might be surprised to see dots on red strands as well as black. This corresponds to the “canonical deformation” discussed in [Reference WebsterWeb19, Section 2.7] or the “redotting” of [Reference Khovanov and SussanKS18].
We’ll only consider KLRW diagrams up to isotopy. Since the orientation on a diagram is clear, we typically won’t draw it.
We call the lines
![]() $y=0,1$
the bottom and top of the diagram. Reading across the bottom and top from left to right, we obtain a sequence
$y=0,1$
the bottom and top of the diagram. Reading across the bottom and top from left to right, we obtain a sequence
![]() $\mathbf {i}=(i_1, \dots , i_V)$
of elements of
$\mathbf {i}=(i_1, \dots , i_V)$
of elements of
![]() $[1,m]$
labeling both red and black strands, where V is the total number of strands.
$[1,m]$
labeling both red and black strands, where V is the total number of strands.
Definition 2.2 Given KLRW diagrams a and b, their composition
![]() $ab$
is given by stacking a on top of b and attempting to join the bottom of a and top of b. If the sequences from the bottom of a and top of b don’t match, then the composition is not defined and by convention is 0, which is not a KLRW diagram, just a formal symbol.
$ab$
is given by stacking a on top of b and attempting to join the bottom of a and top of b. If the sequences from the bottom of a and top of b don’t match, then the composition is not defined and by convention is 0, which is not a KLRW diagram, just a formal symbol.
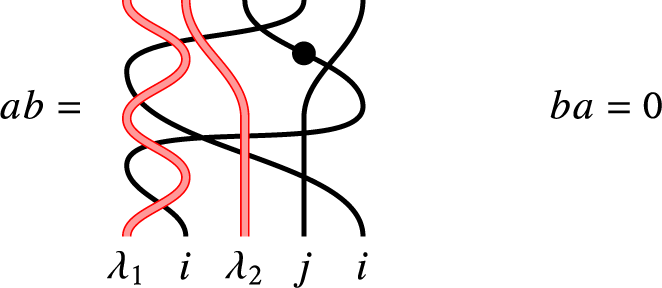
Fix a field ![]() and let
and let
![]() ${\tilde {{\tilde {\mathbb{T}}}}}$
be the formal span over
${\tilde {{\tilde {\mathbb{T}}}}}$
be the formal span over ![]() of KLRW diagrams (up to isotopy). The composition law induces an algebra structure on
of KLRW diagrams (up to isotopy). The composition law induces an algebra structure on
![]() ${\tilde {{\tilde {\mathbb{T}}}}}$
.
${\tilde {{\tilde {\mathbb{T}}}}}$
.
Let
![]() $e(\mathbf {i})$
be the unique crossingless, dotless diagram where the sequence at top and bottom are both
$e(\mathbf {i})$
be the unique crossingless, dotless diagram where the sequence at top and bottom are both
![]() $\mathbf {i}$
.
$\mathbf {i}$
.
Definition 2.3 The degree of a KLRW diagram is the sum over crossings and dots in the diagram of:
-
•
 $-\langle \alpha _i,\alpha _j\rangle $
for each crossing of a black strand labeled i with one labeled j;
$-\langle \alpha _i,\alpha _j\rangle $
for each crossing of a black strand labeled i with one labeled j; -
•
 $2$
for each dot on a red strand or a black strand;
$2$
for each dot on a red strand or a black strand; -
•
 $\langle \alpha _i,\lambda \rangle =\lambda ^i$
for each crossing of a black strand labeled i with a red strand labeled
$\langle \alpha _i,\lambda \rangle =\lambda ^i$
for each crossing of a black strand labeled i with a red strand labeled
 $\lambda $
.
$\lambda $
.
The degree of diagrams is additive under composition. Thus, the algebra
![]() ${\tilde {{\tilde {\mathbb{T}}}}}$
inherits a grading from this degree function.
${\tilde {{\tilde {\mathbb{T}}}}}$
inherits a grading from this degree function.
Throughout, we fix integers
![]() $m,n,$
and
$m,n,$
and
![]() $\chi $
an integral weight
$\chi $
an integral weight
![]() $(\chi _1,\dots , \chi _n)\in \mathbb{Z}^n$
such that
$(\chi _1,\dots , \chi _n)\in \mathbb{Z}^n$
such that
![]() $\chi _1\leq \cdots \leq \chi _n$
. Fix a dimension vector
$\chi _1\leq \cdots \leq \chi _n$
. Fix a dimension vector
![]() $\mathbf {v}=(v_1,\dots , v_{m-1})\in \mathbb{Z}_{\geq 0}^{m-1}$
; by convention, we take
$\mathbf {v}=(v_1,\dots , v_{m-1})\in \mathbb{Z}_{\geq 0}^{m-1}$
; by convention, we take
![]() $v_{m}=n$
. Consider the set
$v_{m}=n$
. Consider the set
![]() $\Omega =\{(i,j) \mid i\in [1,m], j\in [1,v_i]\}$
. Let
$\Omega =\{(i,j) \mid i\in [1,m], j\in [1,v_i]\}$
. Let
![]() $\prec $
be a total order on
$\prec $
be a total order on
![]() $\Omega $
such that
$\Omega $
such that
This is equivalent to choosing a word
![]() $\mathbf {i} =(i_1,\dots , i_{N}),$
where
$\mathbf {i} =(i_1,\dots , i_{N}),$
where
![]() $N=|\Omega |$
and
$N=|\Omega |$
and
![]() $i_k=i$
for
$i_k=i$
for
![]() $v_i$
different indices k.
$v_i$
different indices k.
We will want to weaken this definition a bit and allow
![]() $\preceq $
to be a total preorder (that is, a relation which is transitive and reflexive, but not necessarily anti-symmetric). In this case, we have an induced equivalence relation
$\preceq $
to be a total preorder (that is, a relation which is transitive and reflexive, but not necessarily anti-symmetric). In this case, we have an induced equivalence relation
![]() $(i,k)\approx (j,\ell )$
if
$(i,k)\approx (j,\ell )$
if
![]() $(i,k)\preceq (j,\ell )$
and
$(i,k)\preceq (j,\ell )$
and
![]() $(i,k)\succeq (j,\ell )$
. We assume that our preorder satisfies the condition that
$(i,k)\succeq (j,\ell )$
. We assume that our preorder satisfies the condition that
We can still attach a word
![]() $\mathbf {i}$
to such a preorder; two equivalent elements give the same letter in the word
$\mathbf {i}$
to such a preorder; two equivalent elements give the same letter in the word
![]() $\mathbf {i}$
, so it doesn’t matter whether they have a chosen order. We can thus think of a preorder as corresponding to a word in the generators with some subsets where the same letter appears multiple times together grouped together. We can represent this within the word itself by replacing
$\mathbf {i}$
, so it doesn’t matter whether they have a chosen order. We can thus think of a preorder as corresponding to a word in the generators with some subsets where the same letter appears multiple times together grouped together. We can represent this within the word itself by replacing
![]() $(i,\dots , i)$
with
$(i,\dots , i)$
with
![]() $i^{(a)}$
. Thus, for our purposes,
$i^{(a)}$
. Thus, for our purposes,
![]() $(3,2,2,3,1,3)$
and
$(3,2,2,3,1,3)$
and
![]() $(3,2^{(2)},3,1,3)$
are different words with different associated preorders. Every such word has a unique totalization satisfying (2.1).
$(3,2^{(2)},3,1,3)$
are different words with different associated preorders. Every such word has a unique totalization satisfying (2.1).
Definition 2.4 We say the preorder
![]() $\prec $
and word
$\prec $
and word
![]() $\mathbf {i}$
is
$\mathbf {i}$
is
![]() $\chi $
-parabolic if whenever
$\chi $
-parabolic if whenever
![]() $\chi _k=\chi _{k+1}$
then
$\chi _k=\chi _{k+1}$
then
![]() $(m,k)\approx (m,k+1)$
. In particular, the corresponding appearances of m in
$(m,k)\approx (m,k+1)$
. In particular, the corresponding appearances of m in
![]() $\mathbf {i}$
are consecutive.
$\mathbf {i}$
are consecutive.
Definition 2.5 Let
![]() $\mathbb{\tilde {T}}$
be the quotient of
$\mathbb{\tilde {T}}$
be the quotient of
![]() ${\tilde {{\tilde {\mathbb{T}}}}}$
by the following local relations between KLRW diagrams. We draw these below as black, but the same relations apply to red strands (always taken with the label m):
${\tilde {{\tilde {\mathbb{T}}}}}$
by the following local relations between KLRW diagrams. We draw these below as black, but the same relations apply to red strands (always taken with the label m):




Let
![]() $e_\chi $
be the idempotent given by summing
$e_\chi $
be the idempotent given by summing
![]() $e(\mathbf {i})$
for all
$e(\mathbf {i})$
for all
![]() $\chi $
-parabolic total orders satisfying (2.1). For a non-total order satisfying (2.1) and (2.2), we associate the “divided power” idempotent
$\chi $
-parabolic total orders satisfying (2.1). For a non-total order satisfying (2.1) and (2.2), we associate the “divided power” idempotent
![]() $e'(\mathbf {i})$
which acts on each equivalence class of consecutive strands by a primitive idempotent in the nilHecke algebra (for example, that introduced in [Reference Khovanov, Lauda, Mackaay and StošićKLMS12, (2.18)]). So, for example, we associate to
$e'(\mathbf {i})$
which acts on each equivalence class of consecutive strands by a primitive idempotent in the nilHecke algebra (for example, that introduced in [Reference Khovanov, Lauda, Mackaay and StošićKLMS12, (2.18)]). So, for example, we associate to
![]() $(3,2^{(2)},3,1,3)$
the idempotent
$(3,2^{(2)},3,1,3)$
the idempotent

Let
![]() $S_\chi $
be the stabilizer of
$S_\chi $
be the stabilizer of
![]() $\chi $
in
$\chi $
in
![]() $S_n$
; this naturally acts on the subalgebra
$S_n$
; this naturally acts on the subalgebra
![]() $e_\chi \mathbb{\tilde {T}} e_\chi $
by permuting groups of red strands (or equivalently, dots on those red strands).
$e_\chi \mathbb{\tilde {T}} e_\chi $
by permuting groups of red strands (or equivalently, dots on those red strands).
Definition 2.6 Let
![]() $\mathbb{\tilde {T}}^\chi =(e_\chi \mathbb{\tilde {T}} e_{\chi })^{S_\chi }$
be the invariants of
$\mathbb{\tilde {T}}^\chi =(e_\chi \mathbb{\tilde {T}} e_{\chi })^{S_\chi }$
be the invariants of
![]() $S_\chi $
acting on the subalgebra
$S_\chi $
acting on the subalgebra
![]() $(e_\chi \mathbb{\tilde {T}} e_{\chi })^{S_\chi }$
.
$(e_\chi \mathbb{\tilde {T}} e_{\chi })^{S_\chi }$
.
This is a canonical deformation of the algebra
![]() $\tilde {T}^{{\underline {\boldsymbol {\lambda }}}}$
of [Reference WebsterWeb17b] attached to the sequence of dominant weights
$\tilde {T}^{{\underline {\boldsymbol {\lambda }}}}$
of [Reference WebsterWeb17b] attached to the sequence of dominant weights
![]() ${\underline {\boldsymbol {\lambda }}}=(g_1\omega _{m-1},\dots , g_k\omega _{m-1})$
, where
${\underline {\boldsymbol {\lambda }}}=(g_1\omega _{m-1},\dots , g_k\omega _{m-1})$
, where
![]() $g_1,\dots , g_k$
are the sizes of the blocks of consecutive equal entries in
$g_1,\dots , g_k$
are the sizes of the blocks of consecutive equal entries in
![]() $\chi $
, i.e.,
$\chi $
, i.e.,
![]() $S_\chi =S_{g_1}\times \cdots \times S_{g_k}$
.
$S_\chi =S_{g_1}\times \cdots \times S_{g_k}$
.
Note that this algebra breaks up into a sum of subalgebras where we fix the number of strands with each label; as usual, we let
![]() $v_i$
denote the number with label i. We’ll be particularly interested in the case when
$v_i$
denote the number with label i. We’ll be particularly interested in the case when
![]() $v_1\leq v_2\leq \dots \leq v_m$
. This is the condition that the corresponding weight of
$v_1\leq v_2\leq \dots \leq v_m$
. This is the condition that the corresponding weight of
![]() $\mathfrak {sl}_m$
is dominant; in our usual correspondence, it corresponds to the n-tuple
$\mathfrak {sl}_m$
is dominant; in our usual correspondence, it corresponds to the n-tuple
![]() $\nu $
where
$\nu $
where
![]() $(1,\dots , 1,2,\dots , 2,\dots ,)$
where i appears
$(1,\dots , 1,2,\dots , 2,\dots ,)$
where i appears
![]() $v_i-v_{i-1}$
times. This same algebra is considered in [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18, Section 4] in the case
$v_i-v_{i-1}$
times. This same algebra is considered in [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18, Section 4] in the case
![]() $m=2$
and is denoted
$m=2$
and is denoted
![]() $W(\mathbf {g},v_1)$
(using our
$W(\mathbf {g},v_1)$
(using our
![]() $g_*$
and
$g_*$
and
![]() $v_*$
as above).
$v_*$
as above).
From its realization as a weighted KLR algebra, the algebra
![]() $\mathbb{\tilde {T}}$
inherits a polynomial representation.
$\mathbb{\tilde {T}}$
inherits a polynomial representation.
Definition 2.7 The polynomial representation of
![]() $\mathbb{\tilde {T}}$
is the vector space
$\mathbb{\tilde {T}}$
is the vector space
with sum running over total orders on
![]() $\Omega $
satisfying (2.1). The action is given by the rules:
$\Omega $
satisfying (2.1). The action is given by the rules:
-
•
 $e({\mathbf {i}})$
acts by projection to the corresponding summand;
$e({\mathbf {i}})$
acts by projection to the corresponding summand; -
• a dot on the kth strand from the left acts by multiplication by
 $Y_k$
;
$Y_k$
; -
• a crossing of the kth and
 $k+1$
st strands with
$k+1$
st strands with
 $\mathbf {i}$
at the bottom and
$\mathbf {i}$
at the bottom and
 $\mathbf {i}'$
at top acts by:
$\mathbf {i}'$
at top acts by:-
– If
 $i_k=i_{k+1}$
, the divided difference operator
$i_k=i_{k+1}$
, the divided difference operator  $$\begin{align*}fe_{\mathbf{i}}\mapsto \frac{f^{(k,k+1)}-f}{Y_{k+1}-Y_k}e_{\mathbf{i}'}.\end{align*}$$
$$\begin{align*}fe_{\mathbf{i}}\mapsto \frac{f^{(k,k+1)}-f}{Y_{k+1}-Y_k}e_{\mathbf{i}'}.\end{align*}$$
-
– If
 $i_k+1=i_{k+1}$
, the permutation
$i_k+1=i_{k+1}$
, the permutation
 $(k,k+1)$
followed by a multiplication
$(k,k+1)$
followed by a multiplication  $$\begin{align*}fe_{\mathbf{i}}\mapsto (Y_{k+1}-Y_k) f^{(k,k+1)}e_{\mathbf{i}'}.\end{align*}$$
$$\begin{align*}fe_{\mathbf{i}}\mapsto (Y_{k+1}-Y_k) f^{(k,k+1)}e_{\mathbf{i}'}.\end{align*}$$
-
– Otherwise, the permutation
 $(k,k+1)$
$(k,k+1)$
 $$\begin{align*}fe_{\mathbf{i}}\mapsto f^{(k,k+1)}e_{\mathbf{i}'}.\end{align*}$$
$$\begin{align*}fe_{\mathbf{i}}\mapsto f^{(k,k+1)}e_{\mathbf{i}'}.\end{align*}$$
-
The polynomial representation
![]() $\mathscr {P}^\chi $
for
$\mathscr {P}^\chi $
for
![]() $\mathbb{\tilde {T}}^\chi $
is given by
$\mathbb{\tilde {T}}^\chi $
is given by
![]() $(e_\chi \mathscr {P})^{S_\chi }$
, where
$(e_\chi \mathscr {P})^{S_\chi }$
, where
![]() $S_\chi $
acts by permuting red dots as usual.
$S_\chi $
acts by permuting red dots as usual.
2.2 Violating quotients
Definition 2.8 We call an idempotent
![]() $e(\mathbf {i})$
violating if
$e(\mathbf {i})$
violating if
![]() $i_1\neq m$
; that is, if
$i_1\neq m$
; that is, if
![]() $(m,1)$
is not minimal in
$(m,1)$
is not minimal in
![]() $\prec $
. Let
$\prec $
. Let
![]() $\mathbb{T}^\chi $
be the quotient of
$\mathbb{T}^\chi $
be the quotient of
![]() $\mathbb{\tilde {T}}^\chi $
by the 2-sided ideal generated by all violating idempotents.
$\mathbb{\tilde {T}}^\chi $
by the 2-sided ideal generated by all violating idempotents.
The algebra
![]() $\mathbb{T}^\chi $
is not precisely the algebra
$\mathbb{T}^\chi $
is not precisely the algebra
![]() $T^\chi $
defined in [Reference WebsterWeb17b], but a deformation of it which we’ve considered in several contexts, in particular, in [Reference WebsterWebc, Section 4]. This deformation is flat, since it is a special case of deforming the polynomials defining the KLRW algebra (as discussed in [Reference WebsterWeb19, Proposition 2.23]); in the case
$T^\chi $
defined in [Reference WebsterWeb17b], but a deformation of it which we’ve considered in several contexts, in particular, in [Reference WebsterWebc, Section 4]. This deformation is flat, since it is a special case of deforming the polynomials defining the KLRW algebra (as discussed in [Reference WebsterWeb19, Proposition 2.23]); in the case
![]() $m=2$
, this is the redotted algebra discussed by Khovanov–Sussan in [Reference Khovanov and SussanKS18]. The algebra
$m=2$
, this is the redotted algebra discussed by Khovanov–Sussan in [Reference Khovanov and SussanKS18]. The algebra
![]() $T^\chi $
is the quotient of
$T^\chi $
is the quotient of
![]() $\mathbb{T}^\chi $
by all red dots. Since the red dots are central, and the polynomial ring is graded local, every gradable simple
$\mathbb{T}^\chi $
by all red dots. Since the red dots are central, and the polynomial ring is graded local, every gradable simple
![]() $\mathbb{T}^\chi $
-module factors through
$\mathbb{T}^\chi $
-module factors through
![]() $T^\chi $
, and so the Grothendieck group of
$T^\chi $
, and so the Grothendieck group of
![]() $T^\chi \operatorname {-wgmod}$
agrees with the Grothendieck group of
$T^\chi \operatorname {-wgmod}$
agrees with the Grothendieck group of
![]() $\mathbb{T}^\chi \operatorname {-wgmod}$
. From [Reference WebsterWebc, Section 4], we have the following theorem.
$\mathbb{T}^\chi \operatorname {-wgmod}$
. From [Reference WebsterWebc, Section 4], we have the following theorem.
Theorem 2.9 The categories of
![]() $\mathbb{T}^\chi $
-modules and
$\mathbb{T}^\chi $
-modules and
![]() $T^\chi $
-modules are categorifications of
$T^\chi $
-modules are categorifications of
![]() $\operatorname {Sym}^{\mathbf {g}}({\mathbb{C}}^m)$
, with the categorical
$\operatorname {Sym}^{\mathbf {g}}({\mathbb{C}}^m)$
, with the categorical
![]() $\mathfrak {sl}_m$
-action given by induction and restriction functors changing the number of black strands.
$\mathfrak {sl}_m$
-action given by induction and restriction functors changing the number of black strands.
2.3 Ladder bimodules
In our notation, we identify the dominant weight
![]() $\chi $
with a weight of
$\chi $
with a weight of
![]() $\mathfrak {sl}_\infty $
by
$\mathfrak {sl}_\infty $
by
![]() ${\mu _{\chi }=\sum _{i=1}^n \epsilon _{\chi _i}}$
. This is an injective map, but is far from surjective, since it only hits weights where the coefficients of the
${\mu _{\chi }=\sum _{i=1}^n \epsilon _{\chi _i}}$
. This is an injective map, but is far from surjective, since it only hits weights where the coefficients of the
![]() $\epsilon _i$
’s are positive and sum to n (in the usual parlance, they are level n). In particular,
$\epsilon _i$
’s are positive and sum to n (in the usual parlance, they are level n). In particular,
Definition 2.10 Let
![]() $\chi ^{+ i}$
denote
$\chi ^{+ i}$
denote
![]() $\chi $
with an entry i increased to
$\chi $
with an entry i increased to
![]() $i+1$
if such a dominant weight exists, and
$i+1$
if such a dominant weight exists, and
![]() $\chi ^{-i}$
denote
$\chi ^{-i}$
denote
![]() $\chi $
with an entry
$\chi $
with an entry
![]() $i+1$
decreased to i if such a dominant weight exists. Let
$i+1$
decreased to i if such a dominant weight exists. Let
![]() $\chi ^{\pm i^a}$
be the result of doing this operation a times.
$\chi ^{\pm i^a}$
be the result of doing this operation a times.
These operations are uniquely characterized by the following fact.
Lemma 2.11 If
![]() $\mu _{\chi ^{\pm i}}$
and
$\mu _{\chi ^{\pm i}}$
and
![]() $\mu _{\chi }$
exist, then
$\mu _{\chi }$
exist, then
![]() $\mu _{\chi ^{\pm i}}=\mu _{\chi }\pm \alpha _i$
.
$\mu _{\chi ^{\pm i}}=\mu _{\chi }\pm \alpha _i$
.
Proof If
![]() $\chi ^{+ i}$
exists, then for some k, we have
$\chi ^{+ i}$
exists, then for some k, we have
![]() $i=\chi _k<\chi _{k+1}$
. In this case, the dominant weight
$i=\chi _k<\chi _{k+1}$
. In this case, the dominant weight
satisfies
 $$\begin{align*}\alpha_j^\vee(\chi+\epsilon_k)=\begin{cases} \alpha_j^\vee(\mu_{\chi})-1 & j=\chi_k\pm 1,\\ \alpha_j^\vee(\mu_{\chi})+2 & j=\chi_k,\\ \alpha_j^\vee(\mu_{\chi}) & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}\alpha_j^\vee(\chi+\epsilon_k)=\begin{cases} \alpha_j^\vee(\mu_{\chi})-1 & j=\chi_k\pm 1,\\ \alpha_j^\vee(\mu_{\chi})+2 & j=\chi_k,\\ \alpha_j^\vee(\mu_{\chi}) & \text{otherwise}. \end{cases} \end{align*}$$
Thus, we have that
![]() $\mu _{\chi +\epsilon _k}=\mu _\chi +\alpha _{i}$
as desired. The second half of the result follows from the fact that
$\mu _{\chi +\epsilon _k}=\mu _\chi +\alpha _{i}$
as desired. The second half of the result follows from the fact that
![]() $(\chi ^{+ i})^{-i}=\chi $
.
$(\chi ^{+ i})^{-i}=\chi $
.
Assume that i appears at least a times in
![]() $\chi $
. Let
$\chi $
. Let
![]() $\chi '=\chi ^{+i^a}$
be the dominant weight obtained by changing a instances of i to
$\chi '=\chi ^{+i^a}$
be the dominant weight obtained by changing a instances of i to
![]() $i+1$
. Let
$i+1$
. Let
![]() $S_{\chi ,\chi '}=S_{\chi }\cap S_{\chi '}$
.
$S_{\chi ,\chi '}=S_{\chi }\cap S_{\chi '}$
.
Definition 2.12 The ladder bimodules are the subspace
![]() $\mathbb{E}_i^{(a)}=(e_\chi \mathbb{\tilde {T}} e_{\chi '})^{S_{\chi ,\chi '}}$
considered as a
$\mathbb{E}_i^{(a)}=(e_\chi \mathbb{\tilde {T}} e_{\chi '})^{S_{\chi ,\chi '}}$
considered as a
![]() $\mathbb{\tilde {T}}^{\chi '}$
-
$\mathbb{\tilde {T}}^{\chi '}$
-
![]() $\mathbb{\tilde {T}}^\chi $
bimodule, and similarly
$\mathbb{\tilde {T}}^\chi $
bimodule, and similarly
![]() $\mathbb{F}_i^{(a)}=(e_{\chi '} \mathbb{\tilde {T}} e_\chi )^{S_{\chi ,\chi '}}$
simply swaps the roles of
$\mathbb{F}_i^{(a)}=(e_{\chi '} \mathbb{\tilde {T}} e_\chi )^{S_{\chi ,\chi '}}$
simply swaps the roles of
![]() $\chi $
and
$\chi $
and
![]() $\chi '$
.
$\chi '$
.
These are generalizations of the ladder bimodules defined in [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18, Section 5.2]. We draw these by pinching together the red strands in a single equivalence class under the
![]() $\chi $
-parabolic preorder giving an idempotent into a single red strand. Thus, elements of this bimodule look like:
$\chi $
-parabolic preorder giving an idempotent into a single red strand. Thus, elements of this bimodule look like:

These bimodules have a “representation” as well. By a representation of a bimodule B over algebras
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, we mean a representation of the Morita context:
$A_2$
, we mean a representation of the Morita context:
 $$\begin{align*}A_B=\begin{bmatrix} A_1 & B \\ 0& A_2\end{bmatrix}\end{align*}$$
$$\begin{align*}A_B=\begin{bmatrix} A_1 & B \\ 0& A_2\end{bmatrix}\end{align*}$$
with the obvious matrix multiplication. That is, a left module
![]() $V_i$
of
$V_i$
of
![]() $A_i$
, and a bimodule map
$A_i$
, and a bimodule map ![]() . In our case, we will use the polynomial representations
. In our case, we will use the polynomial representations
![]() $\mathscr {P}^\chi $
of
$\mathscr {P}^\chi $
of
![]() $\mathbb{\tilde {T}}^\chi $
. Diagrams other than the split and join of red strands act by the formulas in Definition 2.7. The formulas for splitting and joining are the same as in [Reference Stroppel and WebsterSW]:
$\mathbb{\tilde {T}}^\chi $
. Diagrams other than the split and join of red strands act by the formulas in Definition 2.7. The formulas for splitting and joining are the same as in [Reference Stroppel and WebsterSW]:
-
• split corresponds to the inclusion
 $\mathscr {P}^\chi \hookrightarrow \mathscr {P}^{\chi ,\chi '}$
, where the latter is the invariants under
$\mathscr {P}^\chi \hookrightarrow \mathscr {P}^{\chi ,\chi '}$
, where the latter is the invariants under
 $S_{\chi ,\chi '}\subset S_{\chi }$
;
$S_{\chi ,\chi '}\subset S_{\chi }$
; -
• merge corresponds to the divided difference operator
 $\mathscr {P}^{\chi ,\chi '}\to \mathscr {P}^{\chi '}$
given by where
$\mathscr {P}^{\chi ,\chi '}\to \mathscr {P}^{\chi '}$
given by where $$\begin{align*}f\mapsto \sum_{\sigma\in S_{\chi'}/S_{\chi,\chi'}}\frac{\displaystyle f^{\sigma}}{\Delta_{+i^{(a)}}^\sigma},\end{align*}$$
$$\begin{align*}f\mapsto \sum_{\sigma\in S_{\chi'}/S_{\chi,\chi'}}\frac{\displaystyle f^{\sigma}}{\Delta_{+i^{(a)}}^\sigma},\end{align*}$$
 $\Delta _{+i^{(a)}}$
is the product of
$\Delta _{+i^{(a)}}$
is the product of
 $Y_k-Y_\ell $
, where k ranges over the red strands with
$Y_k-Y_\ell $
, where k ranges over the red strands with
 $\lambda _{n,j}=i+1$
, and
$\lambda _{n,j}=i+1$
, and
 $\ell $
over the red strands in the “rung” of the ladder. This corresponds to the operator in equivariant cohomology which integrates a
$\ell $
over the red strands in the “rung” of the ladder. This corresponds to the operator in equivariant cohomology which integrates a
 $P_{\chi ,\chi '}$
-equivariant class over
$P_{\chi ,\chi '}$
-equivariant class over
 $P_{\chi '}/P_{\chi ,\chi '}$
to give a
$P_{\chi '}/P_{\chi ,\chi '}$
to give a
 $P_{\chi '}$
-equivariant class. In terms of the nilHecke algebra, this corresponds to the diagram:
$P_{\chi '}$
-equivariant class. In terms of the nilHecke algebra, this corresponds to the diagram: 
Lemma 2.13 The formulas above define a representation of the bimodule
![]() $\mathbb{E}_i^{(a)}$
.
$\mathbb{E}_i^{(a)}$
.
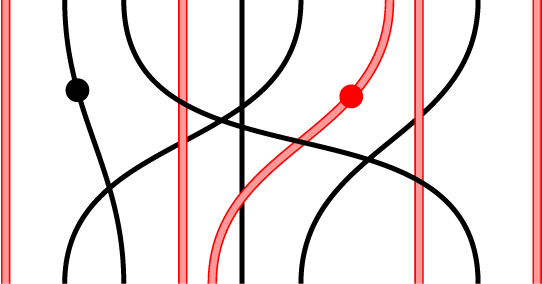
Proof Here, we use the fact that
![]() $\mathbb{E}_i$
by definition is the subbimodule of
$\mathbb{E}_i$
by definition is the subbimodule of
![]() $e_{\chi '}\mathbb{\tilde {T}} e_{\chi }$
invariant under
$e_{\chi '}\mathbb{\tilde {T}} e_{\chi }$
invariant under
![]() $S_{\chi ,\chi '}$
. This embedding corresponds to taking a diagram as in (2.3), and simply expanding red strands.
$S_{\chi ,\chi '}$
. This embedding corresponds to taking a diagram as in (2.3), and simply expanding red strands.
This does not precisely match the operators above, but it does after we add a crossing of the red strands that joined at the top:

The action of this in the usual polynomial representation of the KLR algebra of
![]() $A_{m}$
matches the formulas we have given. The fact that this is a bimodule map follows from the faithfulness of the polynomial representations.
$A_{m}$
matches the formulas we have given. The fact that this is a bimodule map follows from the faithfulness of the polynomial representations.
3 The geometry of quivers and perverse sheaves
3.1 Quiver representations
As in the previous section, we fix
![]() $m,n$
, and
$m,n$
, and
![]() $\chi $
. We can think of this as giving a cocharacter into
$\chi $
. We can think of this as giving a cocharacter into
![]() $GL_n$
, and let
$GL_n$
, and let
![]() $P_\chi \subset GL_n$
be the parabolic whose Lie algebra is the non-positive weight space for this cocharacter. This is the standard Borel if
$P_\chi \subset GL_n$
be the parabolic whose Lie algebra is the non-positive weight space for this cocharacter. This is the standard Borel if
![]() $\chi _i\neq \chi _j$
for all
$\chi _i\neq \chi _j$
for all
![]() $i,j$
, and in general is block upper-triangular matrices, with blocks corresponding to the consecutive
$i,j$
, and in general is block upper-triangular matrices, with blocks corresponding to the consecutive
![]() $\chi _i$
which are equal.
$\chi _i$
which are equal.
Fix a dimension vector
![]() $\mathbf {v}=(v_1,\dots , v_{m-1})\in \mathbb{Z}_{\geq 0}^{m-1}$
as in the previous section. Consider the representation
$\mathbf {v}=(v_1,\dots , v_{m-1})\in \mathbb{Z}_{\geq 0}^{m-1}$
as in the previous section. Consider the representation
of the group
![]() $G=G_{\chi }=P_\chi \times GL_{v_1}\times \cdots \times GL_{v_{m-1}}$
. Recall that we introduced the notation
$G=G_{\chi }=P_\chi \times GL_{v_1}\times \cdots \times GL_{v_{m-1}}$
. Recall that we introduced the notation
![]() $G^0=GL_{v_1}\times \cdots \times GL_{v_{m-1}}$
in the introduction. In the notation popular with physicists, this corresponds to the following quiver:
$G^0=GL_{v_1}\times \cdots \times GL_{v_{m-1}}$
in the introduction. In the notation popular with physicists, this corresponds to the following quiver:

Attached to the space V with the action of G, we have an equivariant derived category
![]() $D^b_G(V)$
as introduced in [Reference Bernstein and LuntsBL94]; in modern terminology, we would think of this as the derived category of constructible sheaves on the quotient stack
$D^b_G(V)$
as introduced in [Reference Bernstein and LuntsBL94]; in modern terminology, we would think of this as the derived category of constructible sheaves on the quotient stack
![]() $V/G$
. There are various other avatars of this category, such as strongly equivariant D-modules, but we will only use a few basic facts about this category, such as the decomposition theorem and the computation of Ext-algebras as Borel–Moore homology familiar from [Reference Chriss and GinzburgCG97, Section 8.6].
$V/G$
. There are various other avatars of this category, such as strongly equivariant D-modules, but we will only use a few basic facts about this category, such as the decomposition theorem and the computation of Ext-algebras as Borel–Moore homology familiar from [Reference Chriss and GinzburgCG97, Section 8.6].
First, we simply need to classify the orbits of
![]() $P_\chi $
in V. Recall that a segment in
$P_\chi $
in V. Recall that a segment in
![]() $[1,m]$
is a list of consecutive integers
$[1,m]$
is a list of consecutive integers
![]() $(k,k+1,\dots , \ell )$
, and a multi-segment is a multi-set of segments. The dimension vector of a segment is the vector
$(k,k+1,\dots , \ell )$
, and a multi-segment is a multi-set of segments. The dimension vector of a segment is the vector
![]() $(0,\dots , 1,\dots , 1,\dots , 0)\in \mathbb{Z}^{m}$
with 1 in every position in
$(0,\dots , 1,\dots , 1,\dots , 0)\in \mathbb{Z}^{m}$
with 1 in every position in
![]() $[k,\ell ]$
and 0 in all others, and the dimension vector of a multi-segment is the sum of those for the constituent segments. That is, it is the vector that records how many times an index
$[k,\ell ]$
and 0 in all others, and the dimension vector of a multi-segment is the sum of those for the constituent segments. That is, it is the vector that records how many times an index
![]() $i\in [1,m]$
appears in the constituent segments.
$i\in [1,m]$
appears in the constituent segments.
Definition 3.1 A flavored segment is a pair consisting of a segment and an integer
![]() $\beta \in \mathbb{Z}$
. A
$\beta \in \mathbb{Z}$
. A
![]() $\chi $
-flavored multi-segment is a multi-segment with a choice of flavoring on each segment with
$\chi $
-flavored multi-segment is a multi-segment with a choice of flavoring on each segment with
![]() $\ell =m$
(and no additional information about other segments) such that the flavors of the different segments agree with
$\ell =m$
(and no additional information about other segments) such that the flavors of the different segments agree with
![]() $\chi $
up to permutation.
$\chi $
up to permutation.
We call the segments with
![]() $\ell =m$
flavored and those with
$\ell =m$
flavored and those with
![]() $\ell <m$
unflavored.
$\ell <m$
unflavored.
Example 1 If
![]() $n=2$
and
$n=2$
and
![]() $m=2$
and
$m=2$
and
![]() $v_1=1$
, then there are two multisegments with the correct dimension vector:
$v_1=1$
, then there are two multisegments with the correct dimension vector:
![]() $\{(1), (2),(2)\}$
and
$\{(1), (2),(2)\}$
and
![]() $\{(1,2), (2)\}$
. There is only one way of flavoring
$\{(1,2), (2)\}$
. There is only one way of flavoring
![]() $\{(1), (2),(2)\}$
, mapping the two copies of
$\{(1), (2),(2)\}$
, mapping the two copies of
![]() $(2)$
to the two coordinates of
$(2)$
to the two coordinates of
![]() $\chi $
.
$\chi $
.
On the other hand, for
![]() $\{(1,2), (2)\}$
, there are two different possible flavors, as long as
$\{(1,2), (2)\}$
, there are two different possible flavors, as long as
![]() $\chi _1\neq \chi _2$
, depending on the bijection we choose between the sets
$\chi _1\neq \chi _2$
, depending on the bijection we choose between the sets
![]() $\{(1,2), (2)\}$
and
$\{(1,2), (2)\}$
and
![]() $\{\chi _1,\chi _2\}$
. If
$\{\chi _1,\chi _2\}$
. If
![]() $\chi _1=\chi _2$
, then we are back to having a single possible choice of flavor.
$\chi _1=\chi _2$
, then we are back to having a single possible choice of flavor.
These are relevant because of the following fact from the appendix.
Theorem 3.2 (Lemmas A.2 and A.3)
The
![]() $P_\chi $
-orbits in V are in bijection with
$P_\chi $
-orbits in V are in bijection with
![]() $\chi $
-flavored multi-segments with the corresponding dimension vector. Each of these orbits is equivariantly simply connected.
$\chi $
-flavored multi-segments with the corresponding dimension vector. Each of these orbits is equivariantly simply connected.
We view the subset
![]() $\{(i,1),\dots ,(i,v_i)\}\subset \Omega $
as corresponding to an ordered basis
$\{(i,1),\dots ,(i,v_i)\}\subset \Omega $
as corresponding to an ordered basis
![]() $\{b_{(i,1)},\dots , b_{(i,v_i)}\}$
of
$\{b_{(i,1)},\dots , b_{(i,v_i)}\}$
of
![]() ${\mathbb{C}}^{v_i}$
. Giving this copy of
${\mathbb{C}}^{v_i}$
. Giving this copy of
![]() ${\mathbb{C}}^{v_i}$
degree i, we can view
${\mathbb{C}}^{v_i}$
degree i, we can view
as a graded vector space, and we can view a degree 1 map
![]() $f\colon {\mathbb{C}}^\Omega \to {\mathbb{C}}^\Omega $
as an element of V, that is, of quiver representation of
$f\colon {\mathbb{C}}^\Omega \to {\mathbb{C}}^\Omega $
as an element of V, that is, of quiver representation of
![]() $A_{m}$
with dimension vector
$A_{m}$
with dimension vector
![]() $(v_1,\dots , v_{m})$
.
$(v_1,\dots , v_{m})$
.
3.2 Quiver flag varieties and the equivariant derived category
As before, consider a total preorder
![]() $\preceq $
satisfying (2.1) and (2.2). This choice of preorder induces a flag
$\preceq $
satisfying (2.1) and (2.2). This choice of preorder induces a flag
![]() $F^{\prec }_\bullet $
, with each subspace given by the formula:
$F^{\prec }_\bullet $
, with each subspace given by the formula:
If the preorder is not an order, equivalent elements give the same subspace, so this flag will have some redundancies in it. We say that a flag on
![]() ${\mathbb{C}}^\Omega $
indexed by the equivalence classes has type
${\mathbb{C}}^\Omega $
indexed by the equivalence classes has type
![]() $\preceq $
or type
$\preceq $
or type
![]() $\mathbf {i}$
if it is conjugate to a flag of this form under
$\mathbf {i}$
if it is conjugate to a flag of this form under
![]() $G^0$
, and let
$G^0$
, and let
![]() $\operatorname {Fl}(\mathbf {i})$
be the set of such flags. Note that
$\operatorname {Fl}(\mathbf {i})$
be the set of such flags. Note that
![]() $G^0$
acts on this space transitively, with the stabilizer of
$G^0$
acts on this space transitively, with the stabilizer of
![]() $F^{\prec }_\bullet $
given by a parabolic
$F^{\prec }_\bullet $
given by a parabolic
![]() $P_0$
, which only depends on the equivalence relation of
$P_0$
, which only depends on the equivalence relation of
![]() $\preceq $
; in particular, for any total order, we get the same Borel
$\preceq $
; in particular, for any total order, we get the same Borel
![]() $B_0$
. Consider the
$B_0$
. Consider the
![]() $G^0$
-space
$G^0$
-space
Lemma 3.3 If
![]() $\mathbf {i}$
is
$\mathbf {i}$
is
![]() $\chi $
-parabolic, then
$\chi $
-parabolic, then
![]() $X(\mathbf {i})$
has an action of
$X(\mathbf {i})$
has an action of
![]() $P_\chi $
by the post-composition action on V and the trivial action on
$P_\chi $
by the post-composition action on V and the trivial action on
![]() $\operatorname {Fl}(\mathbf {i})$
. This commutes with the
$\operatorname {Fl}(\mathbf {i})$
. This commutes with the
![]() $G^0$
-action, inducing a
$G^0$
-action, inducing a
![]() $P_\chi \times G^0$
action for which projection to V is equivariant.
$P_\chi \times G^0$
action for which projection to V is equivariant.
Proof Assume that
![]() $\mathbf {i}$
is
$\mathbf {i}$
is
![]() $\chi $
-parabolic. Thus, we have that if
$\chi $
-parabolic. Thus, we have that if
![]() $\chi _k=\chi _{k+1}$
, then
$\chi _k=\chi _{k+1}$
, then
![]() $F^{\prec }_{(m,k+1)}=F^{\prec }_{(m,k)}+{\mathbb{C}}\cdot b_{m,k+1}$
. By degree considerations,
$F^{\prec }_{(m,k+1)}=F^{\prec }_{(m,k)}+{\mathbb{C}}\cdot b_{m,k+1}$
. By degree considerations,
![]() $f(b_{m,k+1})=0$
, so
$f(b_{m,k+1})=0$
, so
![]() $f(F^{\prec }_{(m,k)})\subset F^{\prec }_{(m,k)}$
, then automatically, we have
$f(F^{\prec }_{(m,k)})\subset F^{\prec }_{(m,k)}$
, then automatically, we have
Thus, for a
![]() $\chi $
-parabolic flag, we only need to check that
$\chi $
-parabolic flag, we only need to check that
![]() $f(F^{\prec }_{(i,k)})\subset F^{\prec }_{(i,k)}$
for
$f(F^{\prec }_{(i,k)})\subset F^{\prec }_{(i,k)}$
for
![]() $i<m$
or when
$i<m$
or when
![]() $i=m$
and
$i=m$
and
![]() $\chi _k\neq \chi _{k-1}$
.
$\chi _k\neq \chi _{k-1}$
.
Consider
![]() $(f,F_\bullet )\in X(\mathbf {i})$
and
$(f,F_\bullet )\in X(\mathbf {i})$
and
![]() $g\in P_\chi $
. Consider the map
$g\in P_\chi $
. Consider the map
![]() $gf\colon {\mathbb{C}}^{\Omega } \to {\mathbb{C}}^{\Omega }$
. This is again a quiver representation, which is compatible with the flag
$gf\colon {\mathbb{C}}^{\Omega } \to {\mathbb{C}}^{\Omega }$
. This is again a quiver representation, which is compatible with the flag
![]() $gF^{\prec }_{(i,k)}$
. Since
$gF^{\prec }_{(i,k)}$
. Since
![]() $g\in P_\chi $
, we have that
$g\in P_\chi $
, we have that
![]() $gF^{\prec }_{(i,k)}=F^{\prec }_{(i,k)}$
if
$gF^{\prec }_{(i,k)}=F^{\prec }_{(i,k)}$
if
![]() $i<m$
or if
$i<m$
or if
![]() $i=m$
and
$i=m$
and
![]() $\chi _k\neq \chi _{k-1}$
. Thus, by our observation above, our original flag is still compatible with
$\chi _k\neq \chi _{k-1}$
. Thus, by our observation above, our original flag is still compatible with
![]() $gf$
. The fact that this commutes with
$gf$
. The fact that this commutes with
![]() $G^0$
is clear.
$G^0$
is clear.
For each segment
![]() $(k,\dots , \ell )$
, let
$(k,\dots , \ell )$
, let
![]() $\mathbf {i}_{(k,\dots , \ell )}=(\ell , \ell -1,\dots , k)$
be the word where we list the entries in reverse order.
$\mathbf {i}_{(k,\dots , \ell )}=(\ell , \ell -1,\dots , k)$
be the word where we list the entries in reverse order.
Definition 3.4 For a
![]() $\chi $
-flavored multi-segment
$\chi $
-flavored multi-segment
![]() $\mathbf {Q}$
, the corresponding good word
$\mathbf {Q}$
, the corresponding good word
![]() $\mathbf {i}_{\mathbf {Q}}$
is the result of concatenating:
$\mathbf {i}_{\mathbf {Q}}$
is the result of concatenating:
-
(1) the words for the unflavored segments in increasing lexicographic order (with the convention that attaching any suffix makes a word lower);
-
(2) the words for the flavored segments sorted first by the attached flavor (in increasing order), and with the entries of the words for a single flavor shuffled together in decreasing order.
Example 2 Let
![]() $n=2,m=3$
and consider the multi-segment
$n=2,m=3$
and consider the multi-segment
If
![]() $\chi _1>\chi _2$
, a flavoring of this multi-segment is a bijection between the sets
$\chi _1>\chi _2$
, a flavoring of this multi-segment is a bijection between the sets
![]() $\{(3,2,1) ,(3,2)\}$
and
$\{(3,2,1) ,(3,2)\}$
and
![]() $\{\chi _1,\chi _2\}$
. In this case, good words for this multi-segment with the flavorings for the order we’ve written the sets above and its opposite are, respectively:
$\{\chi _1,\chi _2\}$
. In this case, good words for this multi-segment with the flavorings for the order we’ve written the sets above and its opposite are, respectively:
On the other hand, if
![]() $\chi _1=\chi _2$
, there is only one possible flavoring with
$\chi _1=\chi _2$
, there is only one possible flavoring with
Lemma 3.5 The good word
![]() $\mathbf {i}_{\mathbf {Q}}$
is always
$\mathbf {i}_{\mathbf {Q}}$
is always
![]() $\chi $
-parabolic, and the image of
$\chi $
-parabolic, and the image of
![]() $X(\mathbf {i}_{\mathbf {Q}})$
is precisely the closure of the corresponding
$X(\mathbf {i}_{\mathbf {Q}})$
is precisely the closure of the corresponding
![]() $G_{\chi }$
-orbit.
$G_{\chi }$
-orbit.
Proof We prove this by induction on the number of segments. Note that since
![]() $X(\mathbf {i})$
is irreducible, the same is true of its image in V, so its image is the closure of some orbit.
$X(\mathbf {i})$
is irreducible, the same is true of its image in V, so its image is the closure of some orbit.
Consider the segment
![]() $(k,\dots , \ell )$
which appears first in the good word; if any unflavored segments appear in
$(k,\dots , \ell )$
which appears first in the good word; if any unflavored segments appear in
![]() $\mathbf {Q}$
, then this will be unflavored. Assume for now that
$\mathbf {Q}$
, then this will be unflavored. Assume for now that
![]() $\ell < m$
. This portion of the word gives a submodule
$\ell < m$
. This portion of the word gives a submodule
![]() $M\subset {\mathbb{C}}^\Omega $
, and on an open subset of
$M\subset {\mathbb{C}}^\Omega $
, and on an open subset of
![]() $X(\mathbf {i})$
, this submodule is the unique indecomposable module with this dimension vector. Also, by assumption, the quotient
$X(\mathbf {i})$
, this submodule is the unique indecomposable module with this dimension vector. Also, by assumption, the quotient
![]() ${\mathbb{C}}^\Omega /M$
gives a point in
${\mathbb{C}}^\Omega /M$
gives a point in
![]() $X(\mathbf {i}')$
, the good word obtained by removing this segment. By induction, on an open subset of
$X(\mathbf {i}')$
, the good word obtained by removing this segment. By induction, on an open subset of
![]() $X(\mathbf {i})$
, the quotient
$X(\mathbf {i})$
, the quotient
![]() ${\mathbb{C}}^\Omega /M$
has the representation type given by
${\mathbb{C}}^\Omega /M$
has the representation type given by
![]() $\mathbf {Q}$
with this segment removed.
$\mathbf {Q}$
with this segment removed.
By the lexicographic condition
![]() $\operatorname {Ext}^1({\mathbb{C}}^\Omega /M,M)=0$
, so on the open set where both M and
$\operatorname {Ext}^1({\mathbb{C}}^\Omega /M,M)=0$
, so on the open set where both M and
![]() ${\mathbb{C}}^\Omega /M$
have the correct representation type, we have a split extension, and the result follows.
${\mathbb{C}}^\Omega /M$
have the correct representation type, we have a split extension, and the result follows.
We need to be a bit careful in the case of a flavored word with
![]() $\chi _1=\chi _{2}=\cdots =\chi _{p}$
; in this case, we don’t have a single segment appearing at the bottom, but rather a word of the form
$\chi _1=\chi _{2}=\cdots =\chi _{p}$
; in this case, we don’t have a single segment appearing at the bottom, but rather a word of the form
![]() $(m,\dots , m,m-1,\dots , m-1,\dots )$
, which again has a corresponding subrepresentation M, which by construction satisfies
$(m,\dots , m,m-1,\dots , m-1,\dots )$
, which again has a corresponding subrepresentation M, which by construction satisfies
![]() $M\cap {\mathbb{C}}^n=\operatorname {span}(b_{m,1},\dots , b_{m,p})$
. The generic representation with this dimension vector lies in the orbit given by the corresponding multi-segment, and by induction, the same is true
$M\cap {\mathbb{C}}^n=\operatorname {span}(b_{m,1},\dots , b_{m,p})$
. The generic representation with this dimension vector lies in the orbit given by the corresponding multi-segment, and by induction, the same is true
![]() ${\mathbb{C}}^\Omega /M$
. In particular,
${\mathbb{C}}^\Omega /M$
. In particular,
![]() ${\mathbb{C}}^{\Omega }/M$
is compatible as desired with the action of
${\mathbb{C}}^{\Omega }/M$
is compatible as desired with the action of
![]() $P_{\chi '}$
where
$P_{\chi '}$
where
![]() $\chi '=(\chi _{p+1},\dots , \chi _n)$
. As before, we have
$\chi '=(\chi _{p+1},\dots , \chi _n)$
. As before, we have
![]() $\operatorname {Ext}^1({\mathbb{C}}^\Omega /M,M)=0$
, so generically on
$\operatorname {Ext}^1({\mathbb{C}}^\Omega /M,M)=0$
, so generically on
![]() $X(\mathbf {i})$
, we have a split extension, and the desired generic representation type.
$X(\mathbf {i})$
, we have a split extension, and the desired generic representation type.
Let
![]() $\pi ^{\mathbf {i}}\colon X(\mathbf {i})\to V$
be the projection map, and
$\pi ^{\mathbf {i}}\colon X(\mathbf {i})\to V$
be the projection map, and
![]() $\mathscr {F}_{\mathbf {i}}=\pi _*^{\mathbf {i}}{\mathbb{C}}_{X(\mathbf {i})}[\dim X(\mathbf {i})]$
be the pushforward of the sheaf of locally constant
$\mathscr {F}_{\mathbf {i}}=\pi _*^{\mathbf {i}}{\mathbb{C}}_{X(\mathbf {i})}[\dim X(\mathbf {i})]$
be the pushforward of the sheaf of locally constant
![]() ${\mathbb{C}}$
-valued functions on
${\mathbb{C}}$
-valued functions on
![]() $X(\mathbf {i})$
.
$X(\mathbf {i})$
.
Lemma 3.6 If
![]() $\mathbf {i}'$
is the totalization of
$\mathbf {i}'$
is the totalization of
![]() $\mathbf {i}$
, then there is a natural map
$\mathbf {i}$
, then there is a natural map
![]() $\phi \colon X(\mathbf {i}')\to X(\mathbf {i})$
satisfying
$\phi \colon X(\mathbf {i}')\to X(\mathbf {i})$
satisfying
![]() $\pi ^{\mathbf {i}}\circ \phi =\pi ^{\mathbf {i}'}$
. The map
$\pi ^{\mathbf {i}}\circ \phi =\pi ^{\mathbf {i}'}$
. The map
![]() $\phi $
is a fiber bundle with fiber given by a product of complete flag varieties. Thus,
$\phi $
is a fiber bundle with fiber given by a product of complete flag varieties. Thus,
![]() $\mathscr {F}_{\mathbf {i}'}$
is a sum of copies of shifts of
$\mathscr {F}_{\mathbf {i}'}$
is a sum of copies of shifts of
![]() $\mathscr {F}_{\mathbf {i}}$
.
$\mathscr {F}_{\mathbf {i}}$
.
Proof The map
![]() $\phi $
is defined by forgetting the spaces attached to elements which are not maximal in their equivalence class in
$\phi $
is defined by forgetting the spaces attached to elements which are not maximal in their equivalence class in
![]() $\mathbf {i}$
. This indeed gives an element of
$\mathbf {i}$
. This indeed gives an element of
![]() $X(\mathbf {i})$
and a point in the fiber over a given point in
$X(\mathbf {i})$
and a point in the fiber over a given point in
![]() $X(\mathbf {i})$
is given by choosing a total flag in the subquotient of consecutive spaces in the flag. This has an induced grading, for which it is homogeneous of a single degree. Thus, the induced action of f is trivial for degree reasons, and any choice of total flag gives an element of
$X(\mathbf {i})$
is given by choosing a total flag in the subquotient of consecutive spaces in the flag. This has an induced grading, for which it is homogeneous of a single degree. Thus, the induced action of f is trivial for degree reasons, and any choice of total flag gives an element of
![]() $X(\mathbf {i}').$
$X(\mathbf {i}').$
Since the map
![]() $\phi $
is a fiber bundle whose fiber is a smooth projective variety, the pushforward
$\phi $
is a fiber bundle whose fiber is a smooth projective variety, the pushforward
![]() $\phi _*{\mathbb{C}}_{X(\mathbf {i}')}[\dim X(\mathbf {i}')]$
is a sum of shifts of local systems by the Hodge theorem. The space
$\phi _*{\mathbb{C}}_{X(\mathbf {i}')}[\dim X(\mathbf {i}')]$
is a sum of shifts of local systems by the Hodge theorem. The space
![]() $X(\mathbf {i}')$
is homotopy equivalent to
$X(\mathbf {i}')$
is homotopy equivalent to
![]() $G^0/P_0$
, which is simply connected, so these local systems are all trivial. This gives the result.
$G^0/P_0$
, which is simply connected, so these local systems are all trivial. This gives the result.
Recall that for each
![]() $G_{\chi }$
-orbit, there is a unique
$G_{\chi }$
-orbit, there is a unique
![]() $G_{\chi }$
-equivariant perverse sheaf
$G_{\chi }$
-equivariant perverse sheaf
![]() $\mathbf {IC}_{\mathbf {Q}}$
which extends the trivial local system on the orbit.
$\mathbf {IC}_{\mathbf {Q}}$
which extends the trivial local system on the orbit.
Theorem 3.7 Every simple
![]() $G_{\chi }$
-equivariant perverse sheaf on V is the intersection cohomology complex
$G_{\chi }$
-equivariant perverse sheaf on V is the intersection cohomology complex
![]() $\mathbf {IC}_{\mathbf {Q}}$
for the orbit of a flavored multi-segment with the trivial local system, and
$\mathbf {IC}_{\mathbf {Q}}$
for the orbit of a flavored multi-segment with the trivial local system, and
![]() $\mathbf {IC}_{\mathbf {Q}}$
is a summand of
$\mathbf {IC}_{\mathbf {Q}}$
is a summand of
![]() $\mathscr {F}_{\mathbf {i}_{\mathbf {Q}}}$
up to shift.
$\mathscr {F}_{\mathbf {i}_{\mathbf {Q}}}$
up to shift.
Proof The fact that
![]() $\mathbf {IC}_{\mathbf {Q}}$
is a complete list of simple perverse sheaves follows from the classification of orbits and their equivariant 1-connectedness.
$\mathbf {IC}_{\mathbf {Q}}$
is a complete list of simple perverse sheaves follows from the classification of orbits and their equivariant 1-connectedness.
Since
![]() $\pi ^{\mathbf {i}}$
is a proper
$\pi ^{\mathbf {i}}$
is a proper
![]() $G_{\chi }$
-equivariant map with
$G_{\chi }$
-equivariant map with
![]() $X(\mathbf {i})$
smooth, the Decomposition Theorem shows that
$X(\mathbf {i})$
smooth, the Decomposition Theorem shows that
![]() $\mathscr {F}_{\mathbf {i}}$
is a Verdier self-dual direct sum of shifts of perverse sheaves supported on the orbit closure
$\mathscr {F}_{\mathbf {i}}$
is a Verdier self-dual direct sum of shifts of perverse sheaves supported on the orbit closure
![]() $\overline {\mathbb{O}_{\mathbf {Q}}}$
.
$\overline {\mathbb{O}_{\mathbf {Q}}}$
.
At least one of these summands must have support precisely equal to
![]() $\overline {\mathbb{O}_{\mathbf {Q}}}$
, and
$\overline {\mathbb{O}_{\mathbf {Q}}}$
, and
![]() $\mathbf {IC}_{\mathbf {Q}}$
is the only such option. Thus, it must appear as a summand up to shift.
$\mathbf {IC}_{\mathbf {Q}}$
is the only such option. Thus, it must appear as a summand up to shift.
3.3 Graded lifts
Let
![]() $\mathscr {F}_{\chi }=\oplus _{\mathbf {i}}\mathscr {F}_{\mathbf {i}}$
, where
$\mathscr {F}_{\chi }=\oplus _{\mathbf {i}}\mathscr {F}_{\mathbf {i}}$
, where
![]() $\mathbf {i}$
ranges over totalizations of
$\mathbf {i}$
ranges over totalizations of
![]() $\chi $
-parabolic words and
$\chi $
-parabolic words and
![]() ${X_{\chi }=\sqcup _{\mathbf {i}} X(\mathbf {i})}$
. As usual, by [Reference Chriss and GinzburgCG97], we have that
${X_{\chi }=\sqcup _{\mathbf {i}} X(\mathbf {i})}$
. As usual, by [Reference Chriss and GinzburgCG97], we have that
as dg-algebras, where we give the left-hand side a non-standard grading.
The sheaves
![]() $\mathscr {F}_{\chi }$
have an additional structure which is hard to see directly on the sheaf level: they are the solutions of complexes of D-modules
$\mathscr {F}_{\chi }$
have an additional structure which is hard to see directly on the sheaf level: they are the solutions of complexes of D-modules
![]() $\mathsf {F}_{\chi }$
which carry a mixed Hodge structure. See [Reference SaitoSai] for more details on mixed Hodge structures. We don’t need much of the full power of this mixed Hodge structure, but as in [Reference WebsterWebb, Section 2.8], this gives us a natural dgg (differential-graded and graded) structure on
$\mathsf {F}_{\chi }$
which carry a mixed Hodge structure. See [Reference SaitoSai] for more details on mixed Hodge structures. We don’t need much of the full power of this mixed Hodge structure, but as in [Reference WebsterWebb, Section 2.8], this gives us a natural dgg (differential-graded and graded) structure on
![]() $A_{\chi }$
. A dgg-algebra A is a dg-algebra in the category of graded vector spaces; that is, A has a homological grading and an internal grading, with the differential having degree
$A_{\chi }$
. A dgg-algebra A is a dg-algebra in the category of graded vector spaces; that is, A has a homological grading and an internal grading, with the differential having degree
![]() $(1,0)$
. Given a dgg-algebra A, we let
$(1,0)$
. Given a dgg-algebra A, we let
![]() $A\operatorname {-dggmod}$
be the category of representations of A, again, in the category of graded vector spaces, that is, dg-modules over A equipped with an additional grading. These form a graded dg-category where the morphism complexes are the degree
$A\operatorname {-dggmod}$
be the category of representations of A, again, in the category of graded vector spaces, that is, dg-modules over A equipped with an additional grading. These form a graded dg-category where the morphism complexes are the degree
![]() $(*,0)$
part of the usual morphism complexes of dg-modules – again, this just means that we only use degree 0 morphisms between graded vector spaces.
$(*,0)$
part of the usual morphism complexes of dg-modules – again, this just means that we only use degree 0 morphisms between graded vector spaces.
One useful observation is that a dgg-algebra where the internal grading coincides with the homological grading is necessarily formal, since it is quasi-isomorphic to a graded
![]() $A_{\infty }$
algebra, and all the higher operations are trivial for grading reasons (see [Reference WebsterWebb, Theorem 2.38] and [Reference Cirici and Sopena-GilboyCSG, Proposition 5.4]).
$A_{\infty }$
algebra, and all the higher operations are trivial for grading reasons (see [Reference WebsterWebb, Theorem 2.38] and [Reference Cirici and Sopena-GilboyCSG, Proposition 5.4]).
We can use this dgg-algebra structure to construct a graded lift.
Definition 3.8 A grading on an object M in
![]() $D^{b}_{G_{\chi }}(V)$
is a dgg-module N over
$D^{b}_{G_{\chi }}(V)$
is a dgg-module N over
![]() $A_{\chi }$
and a quasi-isomorphism of
$A_{\chi }$
and a quasi-isomorphism of
![]() $A_{\chi }$
dg-modules
$A_{\chi }$
dg-modules
![]() $\mathrm {Hom}^{\bullet }(\mathscr {F}_{\chi },M)\cong N$
, forgetting the second grading on N. We can define a graded lift of
$\mathrm {Hom}^{\bullet }(\mathscr {F}_{\chi },M)\cong N$
, forgetting the second grading on N. We can define a graded lift of
![]() $D^{b,\operatorname {mix}}_{G_{\chi }}(V)$
whose:
$D^{b,\operatorname {mix}}_{G_{\chi }}(V)$
whose:
-
• objects are graded objects in
 $D^{b}_{G_{\chi }}(V)$
;
$D^{b}_{G_{\chi }}(V)$
; -
• morphisms are degree 0 morphisms in
 $D^{b,\operatorname {mix}}_{G_{\chi }}(V)$
under the isomorphism That is, the functor sending a graded sheaf to the corresponding dgg-module is fully faithful.
$D^{b,\operatorname {mix}}_{G_{\chi }}(V)$
under the isomorphism That is, the functor sending a graded sheaf to the corresponding dgg-module is fully faithful. $$\begin{align*}\mathrm{Hom}^{\bullet}_{D^{b}_{G_{\chi}}(V)}(M,M')\cong \mathrm{Hom}^{\bullet}_{A\operatorname{-dg-mod}}(N,N').\end{align*}$$
$$\begin{align*}\mathrm{Hom}^{\bullet}_{D^{b}_{G_{\chi}}(V)}(M,M')\cong \mathrm{Hom}^{\bullet}_{A\operatorname{-dg-mod}}(N,N').\end{align*}$$
Remark 3.9 It should be more geometrically natural to define a grading as a Hodge, or perhaps twistor, structure on the sheaf M. Unfortunately, the existence of non-Tate Hodge/twistor structures means that there are “too many” such structures lifting a given dgg-module structure. It seems likely that a canonical “most Tate” choice of Hodge structure exists, but constructing it is too complicated a job for this paper. This comes down to the question of whether the Hodge structure on
![]() $A_{\chi }$
makes this into a formal dg-algebra in the category of mixed Hodge structures. See [Reference WebsterWebb, Remark 2.59] for more discussion of this phenomenon.
$A_{\chi }$
makes this into a formal dg-algebra in the category of mixed Hodge structures. See [Reference WebsterWebb, Remark 2.59] for more discussion of this phenomenon.
By [Reference WebsterWeb19, Theorem 4.5], we have the following theorem.
Theorem 3.10 For any preorders
![]() $\mathbf {i},\mathbf {j}$
satisfying (2.1) and (2.2), we have an isomorphism
$\mathbf {i},\mathbf {j}$
satisfying (2.1) and (2.2), we have an isomorphism
matching convolution product with multiplication in
![]() $\mathbb{\tilde {T}}^\chi $
, the red dots with the cohomology ring
$\mathbb{\tilde {T}}^\chi $
, the red dots with the cohomology ring
![]() $H^*(BP_\chi )$
and the black dots with Chern classes of the tautological bundles on
$H^*(BP_\chi )$
and the black dots with Chern classes of the tautological bundles on
![]() $X(\mathbf {i})$
. In particular, we have an isomorphism
$X(\mathbf {i})$
. In particular, we have an isomorphism
![]() $A_\chi \cong \mathbb{\tilde {T}}^\chi $
.
$A_\chi \cong \mathbb{\tilde {T}}^\chi $
.
It might seem strange that in the definition of the algebra
![]() $A_\chi $
, we used only honest orders, not preorders, when the first sentence of the theorem covers preorders. This is needed to match the usual definition of
$A_\chi $
, we used only honest orders, not preorders, when the first sentence of the theorem covers preorders. This is needed to match the usual definition of
![]() $\mathbb{\tilde {T}}^\chi $
. If we incorporated preorders, the result would be a larger, Morita equivalent algebra which contained thick strands as in the extended graphical calculus of [Reference Khovanov, Lauda, Mackaay and StošićKLMS12, Reference Stroppel and WebsterSW]. It is much more difficult to give a nice presentation of this larger algebra.
$\mathbb{\tilde {T}}^\chi $
. If we incorporated preorders, the result would be a larger, Morita equivalent algebra which contained thick strands as in the extended graphical calculus of [Reference Khovanov, Lauda, Mackaay and StošićKLMS12, Reference Stroppel and WebsterSW]. It is much more difficult to give a nice presentation of this larger algebra.
These results combine to show that the algebra
![]() $\mathbb{\tilde {T}}^\chi $
controls the derived category
$\mathbb{\tilde {T}}^\chi $
controls the derived category
![]() $D^b_{G_{\chi }}(V)$
.
$D^b_{G_{\chi }}(V)$
.
Theorem 3.11 The object
![]() $\mathscr {F}_{\chi }$
is a compact generator of
$\mathscr {F}_{\chi }$
is a compact generator of
![]() $D^b_{G_{\chi }}(V)$
. Thus, the functor
$D^b_{G_{\chi }}(V)$
. Thus, the functor
![]() $\operatorname {Ext}(\mathscr {F}_{\chi },-)$
induces equivalences:
$\operatorname {Ext}(\mathscr {F}_{\chi },-)$
induces equivalences:
The functor of forgetting graded structure corresponds to the functor considering a complex of graded modules as a dg-module by collapsing gradings.
3.4 The categorical action
Consider the 2-category
![]() $\mathsf {Perv}$
whose:
$\mathsf {Perv}$
whose:
-
• objects are dominant integral weights
 $\chi =(\chi _1\leq \cdots \leq \chi _n)$
;
$\chi =(\chi _1\leq \cdots \leq \chi _n)$
; -
• 1-morphisms
 $\chi \to \chi '$
are sums of shifts of semi-simple
$\chi \to \chi '$
are sums of shifts of semi-simple
 $P_{\chi '}\times P_{\chi }$
-equivariant perverse sheaves on
$P_{\chi '}\times P_{\chi }$
-equivariant perverse sheaves on
 $GL_n$
, or equivalently,
$GL_n$
, or equivalently,
 $GL_n$
-equivariant perverse sheaves on
$GL_n$
-equivariant perverse sheaves on
 $GL_n/P_{\chi '}\times GL_n/P_{\chi '}$
with composition given by convolution;
$GL_n/P_{\chi '}\times GL_n/P_{\chi '}$
with composition given by convolution; -
• 2-morphisms in the equivariant derived category.
As discussed in [Reference WebsterWeb17a, Theorem 6], this equivalent to the category
![]() $\mathsf {Flag}$
whose:
$\mathsf {Flag}$
whose:
-
• objects are dominant integral weights
 $\chi =(\chi _1\leq \cdots \leq \chi _n)$
;
$\chi =(\chi _1\leq \cdots \leq \chi _n)$
; -
• 1-morphisms
 $\chi \to \chi '$
are sums of singular Soergel
$\chi \to \chi '$
are sums of singular Soergel
 $H^*(BP_{\chi '})\operatorname {-}H^*(BP_{\chi })$
-bimodules;
$H^*(BP_{\chi '})\operatorname {-}H^*(BP_{\chi })$
-bimodules; -
• 2-morphisms are degree 0 homomorphisms of bimodules.
via the functor that takes hypercohomology of a sum of shifts of equivariant perverse sheaves. For technical reasons, we add to these categories an object
![]() $\emptyset $
, which has Hom with any other object given by the zero category.
$\emptyset $
, which has Hom with any other object given by the zero category.
Consider the fiber product
where the action is via
![]() $(p',p)\cdot (g,v)=(p'gp^{-1},pv)$
. This is, of course, equipped with an action map
$(p',p)\cdot (g,v)=(p'gp^{-1},pv)$
. This is, of course, equipped with an action map
and as usual, we define convolution of sheaves
![]() $\mathcal {F}\in D^b_{P_{\chi '}\times P_\chi }(GL_n)$
and
$\mathcal {F}\in D^b_{P_{\chi '}\times P_\chi }(GL_n)$
and
![]() $\mathcal {G}\in D^b_{G_{\chi }}(V)$
as
$\mathcal {G}\in D^b_{G_{\chi }}(V)$
as
![]() $\mathcal {F}\star \mathcal {G}=a_* (\mathcal {F}\boxtimes \mathcal {G}).$
$\mathcal {F}\star \mathcal {G}=a_* (\mathcal {F}\boxtimes \mathcal {G}).$
Lemma 3.12 Convolution of sheaves induces a representation of
![]() $\mathsf {Perv}$
in
$\mathsf {Perv}$
in
![]() $\mathsf {Cat}$
sending
$\mathsf {Cat}$
sending
![]() $\chi \mapsto D^b_{G_{\chi }}(V)$
.
$\chi \mapsto D^b_{G_{\chi }}(V)$
.
The category
![]() $\mathsf {Flag}$
carries a well-known categorical action defined by Khovanov and Lauda [Reference Khovanov and LaudaKL10, Section 6]. We define
$\mathsf {Flag}$
carries a well-known categorical action defined by Khovanov and Lauda [Reference Khovanov and LaudaKL10, Section 6]. We define
![]() $\mathcal {U}$
to be the 2-category categorifying the quantum group of
$\mathcal {U}$
to be the 2-category categorifying the quantum group of
![]() $\mathfrak {sl}_\infty $
(following the definition of [Reference BrundanBru16, Definition 1.1] which unifies all previous definitions). In this category:
$\mathfrak {sl}_\infty $
(following the definition of [Reference BrundanBru16, Definition 1.1] which unifies all previous definitions). In this category:
-
• objects are integral weights of
 $\mathfrak {sl}_\infty $
, that is, finite sums of the unit vectors
$\mathfrak {sl}_\infty $
, that is, finite sums of the unit vectors
 $\epsilon _k$
for
$\epsilon _k$
for
 $k\in \mathbb{Z}$
;
$k\in \mathbb{Z}$
; -
• 1-morphisms are generated by formal symbols

-
• 2-morphisms are given by certain string diagrams modulo the relations in [Reference BrundanBru16].
As discussed in [Reference WebsterWeb17a, Section 2.2], we thus have a 2-functor
![]() $\Phi _{\mathsf {P}}\colon \mathcal {U}\to \mathsf {Perv}$
sending
$\Phi _{\mathsf {P}}\colon \mathcal {U}\to \mathsf {Perv}$
sending
![]() $\mu _\chi \to \chi $
for weights of the correct form, and to
$\mu _\chi \to \chi $
for weights of the correct form, and to
![]() $\emptyset $
otherwise.
$\emptyset $
otherwise.
If
![]() $\chi '=\chi ^{+i^a}$
, then the
$\chi '=\chi ^{+i^a}$
, then the
![]() $P_{\chi }\times P_{\chi '}$
-orbits on G are in bijection with orbits of double cosets for
$P_{\chi }\times P_{\chi '}$
-orbits on G are in bijection with orbits of double cosets for
![]() $(S_\chi ',S_\chi )$
. In particular, there is a unique closed orbit, given by the product
$(S_\chi ',S_\chi )$
. In particular, there is a unique closed orbit, given by the product
![]() $P_{\chi ',\chi }=P_{\chi '}P_{\chi }$
. The cohomology
$P_{\chi ',\chi }=P_{\chi '}P_{\chi }$
. The cohomology
![]() $H^*_{P_{\chi '}\times P_{\chi }}(P_{\chi ',\chi })$
of this orbit gives the action of [Reference Khovanov and LaudaKL10, Section 6]. As discussed below the proof of Theorem 6 in [Reference WebsterWeb17a, Section 2.2], we have the following lemma.
$H^*_{P_{\chi '}\times P_{\chi }}(P_{\chi ',\chi })$
of this orbit gives the action of [Reference Khovanov and LaudaKL10, Section 6]. As discussed below the proof of Theorem 6 in [Reference WebsterWeb17a, Section 2.2], we have the following lemma.
Lemma 3.13 The image ![]() is the Verdier-self-dual shift of the constant sheaf
is the Verdier-self-dual shift of the constant sheaf
![]() ${\mathbb{C}}_{\chi ',\chi }$
on
${\mathbb{C}}_{\chi ',\chi }$
on
![]() $P_{\chi ',\chi }$
. Similarly,
$P_{\chi ',\chi }$
. Similarly, ![]() is the same sheaf with the role of the factors switched.
is the same sheaf with the role of the factors switched.
For us, the important new ingredient here is that since we have an algebraic manifestation of the category
![]() $D^b_{P_\chi }(V)$
given by the algebra
$D^b_{P_\chi }(V)$
given by the algebra
![]() $\mathbb{\tilde {T}}^\chi $
, the action of the 2-category
$\mathbb{\tilde {T}}^\chi $
, the action of the 2-category
![]() $\mathcal {U}$
has a similar manifestation.
$\mathcal {U}$
has a similar manifestation.
For every 1-morphism
![]() $\mathcal {F}\colon \chi \to \chi '$
in the 2-category
$\mathcal {F}\colon \chi \to \chi '$
in the 2-category
![]() $\mathsf {Perv}$
, we can define a bimodule
$\mathsf {Perv}$
, we can define a bimodule
By Theorem 3.11, we have a commutative diagram

Lemma 3.14 For any sum of shifts of semi-simple perverse sheaves
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $D^b_{P_{\chi '}\times P_{\chi }}(GL_n)$
, the bimodule
$D^b_{P_{\chi '}\times P_{\chi }}(GL_n)$
, the bimodule
![]() $B_{\mathcal {F}}$
is sweet, that is, it is projective as a left module over
$B_{\mathcal {F}}$
is sweet, that is, it is projective as a left module over
![]() $\mathbb{\tilde {T}}^{\chi '}$
and as a right module over
$\mathbb{\tilde {T}}^{\chi '}$
and as a right module over
![]() $\mathbb{\tilde {T}}^\chi $
.
$\mathbb{\tilde {T}}^\chi $
.
Proof Since the anti-automorphism of taking inverse switches left and right module structures, it’s enough to prove this for the left module structure.
Note that for any flavored multi-segment
![]() $\mathbf {Q}$
for
$\mathbf {Q}$
for
![]() $\chi '$
, we have that
$\chi '$
, we have that
![]() $\mathbf {IC}_{\mathbf {Q}}$
is a summand of
$\mathbf {IC}_{\mathbf {Q}}$
is a summand of
![]() $\mathscr {F}_{\chi '}$
by Theorem 3.7. Thus,
$\mathscr {F}_{\chi '}$
by Theorem 3.7. Thus,
![]() $\operatorname {Ext}_{D^b_{G_{\chi '}}(V)}(\mathscr {F}_{\chi '}, \mathbf {IC}_{\mathbf {Q}})$
is a projective as a left module over
$\operatorname {Ext}_{D^b_{G_{\chi '}}(V)}(\mathscr {F}_{\chi '}, \mathbf {IC}_{\mathbf {Q}})$
is a projective as a left module over
![]() $\mathbb{\tilde {T}}^{\chi '}$
; in fact, it is of the form
$\mathbb{\tilde {T}}^{\chi '}$
; in fact, it is of the form
![]() $\mathbb{\tilde {T}}^{\chi '} e_{\mathbf {Q}}$
for an idempotent projecting to
$\mathbb{\tilde {T}}^{\chi '} e_{\mathbf {Q}}$
for an idempotent projecting to
![]() $\mathbf {IC}_{\mathbf {Q}}$
as a summand of
$\mathbf {IC}_{\mathbf {Q}}$
as a summand of
![]() $\mathscr {F}_{\chi '}$
.
$\mathscr {F}_{\chi '}$
.
Since
![]() $\mathcal {F}$
is semi-simple, by the Decomposition Theorem, the complex
$\mathcal {F}$
is semi-simple, by the Decomposition Theorem, the complex
![]() $\mathcal {F}\star \mathscr {F}_{\chi }$
is a sum of shifts of simple perverse sheaves in
$\mathcal {F}\star \mathscr {F}_{\chi }$
is a sum of shifts of simple perverse sheaves in
![]() $D^b_{G_{\chi '}}(V)$
. Thus,
$D^b_{G_{\chi '}}(V)$
. Thus,
![]() $B_{\mathcal {F}}=\operatorname {Ext}_{D^b_{G_{\chi '}}(V)}(\mathscr {F}_{\chi '}, \mathcal {F}\star \mathscr {F}_{\chi })$
is a sum of projective left
$B_{\mathcal {F}}=\operatorname {Ext}_{D^b_{G_{\chi '}}(V)}(\mathscr {F}_{\chi '}, \mathcal {F}\star \mathscr {F}_{\chi })$
is a sum of projective left
![]() $\mathbb{\tilde {T}}^{\chi '}$
-modules, and thus projective.
$\mathbb{\tilde {T}}^{\chi '}$
-modules, and thus projective.
It follows immediately that the functor of tensor product with
![]() $B_{\mathcal {F}}$
is exact. It also follows that
$B_{\mathcal {F}}$
is exact. It also follows that
Lemma 3.15
![]() $B_{\mathcal {F}\star \mathcal {G}}\cong B_{\mathcal {F}}\overset {L}{\otimes } B_{\mathcal {G}}=B_{\mathcal {F}}\otimes B_{\mathcal {G}}$
.
$B_{\mathcal {F}\star \mathcal {G}}\cong B_{\mathcal {F}}\overset {L}{\otimes } B_{\mathcal {G}}=B_{\mathcal {F}}\otimes B_{\mathcal {G}}$
.
Theorem 3.16 If
![]() $\chi '=\chi ^{+i^a}$
, then we have that
$\chi '=\chi ^{+i^a}$
, then we have that
![]() $B_{{\mathbb{C}}_{\chi ',\chi }}=\mathbb{E}_i^{(a)}$
and
$B_{{\mathbb{C}}_{\chi ',\chi }}=\mathbb{E}_i^{(a)}$
and
![]() $B_{{\mathbb{C}}_{\chi ,\chi '}}=\mathbb{F}_i^{(a)}$
.
$B_{{\mathbb{C}}_{\chi ,\chi '}}=\mathbb{F}_i^{(a)}$
.
Proof Of course, we only need to check one idempotent at a time. That is, let
![]() $\mathbf {i}$
be a
$\mathbf {i}$
be a
![]() $\chi $
-parabolic word, and
$\chi $
-parabolic word, and
![]() $\mathbf {i}'$
a
$\mathbf {i}'$
a
![]() $\chi '$
parabolic. We only need to show that
$\chi '$
parabolic. We only need to show that
Note that this isomorphism is only correct up to grading shift due to the need to shift
![]() ${\mathbb{C}}_{\chi ',\chi }$
to make it Verdier-self-dual. Since
${\mathbb{C}}_{\chi ',\chi }$
to make it Verdier-self-dual. Since
![]() ${\mathbb{C}}_{\chi ^{\prime },\chi }\star -$
is the composition of restriction of
${\mathbb{C}}_{\chi ^{\prime },\chi }\star -$
is the composition of restriction of
![]() $\mathscr {F}_{\mathbf {i}}$
to the
$\mathscr {F}_{\mathbf {i}}$
to the
![]() $P_\chi \cap P_{\chi ^{\prime }}$
-equivariant derived category, with the induction to the
$P_\chi \cap P_{\chi ^{\prime }}$
-equivariant derived category, with the induction to the
![]() $P_{\chi '}$
-equivariant derived category, we can use adjunction to show that
$P_{\chi '}$
-equivariant derived category, we can use adjunction to show that
Of course, by Theorem 3.10 in the case where
![]() $P_\chi =B$
, we have
$P_\chi =B$
, we have
Thus, combining (3.1) and (3.2), we find that:
Combining Lemma 3.15 and Theorem 3.16, we find the following.
Corollary 3.17 We have a representation of the category
![]() $\mathcal {U}$
sending
$\mathcal {U}$
sending
![]() $\mu _\chi \mapsto \mathbb{\tilde {T}}^\chi \operatorname {-mod}$
where any 1-morphism u acts by tensor product with the bimodule
$\mu _\chi \mapsto \mathbb{\tilde {T}}^\chi \operatorname {-mod}$
where any 1-morphism u acts by tensor product with the bimodule
![]() $B_{\Phi _{\mathsf {P}}(u)}$
, and in particular,
$B_{\Phi _{\mathsf {P}}(u)}$
, and in particular, ![]() act by the bimodules
act by the bimodules
![]() $\mathbb{E}_i^{(a)},\mathbb{F}_i^{(a)}$
.
$\mathbb{E}_i^{(a)},\mathbb{F}_i^{(a)}$
.
This generalizes [Reference Khovanov, Lauda, Sussan and YonezawaKLSY18, Theorem 9.1], which is the special case where
![]() $m=2$
, and avoids the long computation required by the direct proof given in that paper.
$m=2$
, and avoids the long computation required by the direct proof given in that paper.
3.5 Restriction to the flag variety
Assume now that
![]() $v_1\leq v_2\leq \cdots \leq v_n$
. In this case, the stack
$v_1\leq v_2\leq \cdots \leq v_n$
. In this case, the stack
![]() $V/G^0$
contains an open subset where the compositions
$V/G^0$
contains an open subset where the compositions
![]() $f_{i;1}=f_i\dots f_1$
are injective for all i. On this open subset,
$f_{i;1}=f_i\dots f_1$
are injective for all i. On this open subset,
gives a partial flag. As before, we let
![]() $\nu =(1,\dots , 1,2, \dots , 2,\dots )\in \mathbb{Z}^n$
be the unique increasing sequence with i occuring
$\nu =(1,\dots , 1,2, \dots , 2,\dots )\in \mathbb{Z}^n$
be the unique increasing sequence with i occuring
![]() $v_i-v_{i-1}$
times. We can then describe our space of partial flags as exactly
$v_i-v_{i-1}$
times. We can then describe our space of partial flags as exactly
![]() $GL_n/P_{\nu }.$
Thus, we obtain a functor
$GL_n/P_{\nu }.$
Thus, we obtain a functor
by restriction to this open set. This is, of course, compatible with the natural action of
![]() $\mathsf {Perv}$
.
$\mathsf {Perv}$
.
Theorem 3.18 We have an equivalence of categories
such that we have a commutative diagram:

Proof This is essentially a restatement of [Reference WebsterWeb17c, Corollary 5.4], but let us be a bit more careful about the details of this point. We have a map
![]() $\mathbb{\tilde {T}}^\chi \to \operatorname {Ext}^*(\operatorname {Res}(\mathscr {F}_{\chi }), \operatorname {Res}(\mathscr {F}_{\chi }))$
induced by the functor
$\mathbb{\tilde {T}}^\chi \to \operatorname {Ext}^*(\operatorname {Res}(\mathscr {F}_{\chi }), \operatorname {Res}(\mathscr {F}_{\chi }))$
induced by the functor
![]() $\operatorname {Res}$
.
$\operatorname {Res}$
.
If
![]() $\mathbf {i}$
is violating, then
$\mathbf {i}$
is violating, then
![]() $(i_1,1)\prec (m,1)$
. For any point in
$(i_1,1)\prec (m,1)$
. For any point in
![]() $\operatorname {Fl}(\mathbf {i})$
, by assumption, we have
$\operatorname {Fl}(\mathbf {i})$
, by assumption, we have
![]() $f_{m-1;i_1}F_{\preceq (i_1,1)}=0$
, and so one of
$f_{m-1;i_1}F_{\preceq (i_1,1)}=0$
, and so one of
![]() $f_k$
is not injective. This shows that
$f_k$
is not injective. This shows that
![]() $\operatorname {Res}(\mathscr {F}_{\mathbf {i}})=0$
. On the other hand, if
$\operatorname {Res}(\mathscr {F}_{\mathbf {i}})=0$
. On the other hand, if
![]() $\operatorname {Res}(\mathbf {IC}_{\mathbf {Q}})=0$
, then
$\operatorname {Res}(\mathbf {IC}_{\mathbf {Q}})=0$
, then
![]() $\mathbf {Q}$
must be a multi-segment that includes a segment without m, so the corresponding good word
$\mathbf {Q}$
must be a multi-segment that includes a segment without m, so the corresponding good word
![]() $\mathbf {i}_{\mathbf {Q}}$
is violating. Thus,
$\mathbf {i}_{\mathbf {Q}}$
is violating. Thus,
![]() ${\operatorname {Res}(\mathbf {IC}_{\mathbf {Q}})=0}$
if and only if
${\operatorname {Res}(\mathbf {IC}_{\mathbf {Q}})=0}$
if and only if
![]() $\mathbf {IC}_{\mathbf {Q}}$
is a summand of
$\mathbf {IC}_{\mathbf {Q}}$
is a summand of
![]() $\mathscr {F}_{\mathbf {i}}$
.
$\mathscr {F}_{\mathbf {i}}$
.
The usual formalism of recollement shows that
![]() $D^{b,\operatorname {mix}}_{P_\chi }(GL_n/P_\nu )$
(after suitable enhancement) is a dg-quotient of
$D^{b,\operatorname {mix}}_{P_\chi }(GL_n/P_\nu )$
(after suitable enhancement) is a dg-quotient of
![]() $D^{b,\operatorname {mix}}_{G_{\chi }}(V)$
by the subcategory of objects killed by
$D^{b,\operatorname {mix}}_{G_{\chi }}(V)$
by the subcategory of objects killed by
![]() $\operatorname {Res}$
; by the paragraph above, this is exactly the subcategory generated by
$\operatorname {Res}$
; by the paragraph above, this is exactly the subcategory generated by
![]() $\mathscr {F}_{\mathbf {i}}$
for
$\mathscr {F}_{\mathbf {i}}$
for
![]() $\mathbf {i}$
violating. Since
$\mathbf {i}$
violating. Since
![]() $\mathbb{\tilde {T}}^\chi $
is quasi-isomorphic to
$\mathbb{\tilde {T}}^\chi $
is quasi-isomorphic to
![]() $\operatorname {Ext}^*(\mathscr {F}_{\chi }, \mathscr {F}_{\chi })$
as a formal dg-algebra, taking dg-quotient by the projectives
$\operatorname {Ext}^*(\mathscr {F}_{\chi }, \mathscr {F}_{\chi })$
as a formal dg-algebra, taking dg-quotient by the projectives
![]() $\mathbb{\tilde {T}}^\chi e(\mathbf {i})$
for
$\mathbb{\tilde {T}}^\chi e(\mathbf {i})$
for
![]() $\mathbf {i}$
violating has the effect of simply modding out by the corresponding 2-sided ideal. Thus, the map above induces an isomorphism
$\mathbf {i}$
violating has the effect of simply modding out by the corresponding 2-sided ideal. Thus, the map above induces an isomorphism
By dg-Morita theory, this completes the proof.
Of course, we can also interpret
![]() $D^b_{P_{\chi }}(GL_n/P_\nu )$
as a Hom-category in the equivalent 2-categories
$D^b_{P_{\chi }}(GL_n/P_\nu )$
as a Hom-category in the equivalent 2-categories
![]() $\mathsf {Flag}\cong \mathsf {Perv}$
, and this identification intertwines the left regular action on
$\mathsf {Flag}\cong \mathsf {Perv}$
, and this identification intertwines the left regular action on
![]() $\mathsf {Perv}$
with the action we’ve discussed on
$\mathsf {Perv}$
with the action we’ve discussed on
![]() $D^b_{P_{\chi }}(GL_n/P_\nu )$
.
$D^b_{P_{\chi }}(GL_n/P_\nu )$
.
To fix this equivalence algebraically, we need to describe the image of the identity. This corresponds to the constant sheaf on
![]() $P_\nu /P_\nu \subset GL_n/P_{\nu }$
. Consider the flavored multi-segment where we take the segment
$P_\nu /P_\nu \subset GL_n/P_{\nu }$
. Consider the flavored multi-segment where we take the segment
![]() $(i,\dots ,m)$
exactly
$(i,\dots ,m)$
exactly
![]() $v_i-v_{i-1}$
times, and flavor these with i.
$v_i-v_{i-1}$
times, and flavor these with i.
The corresponding word is
Lemma 3.19 We have an isomorphism
![]() $\operatorname {Res}(\mathscr {F}_{\mathbf {i}_\nu })\cong {\mathbb{C}}_{P_{\nu }/P_{\nu }}$
.
$\operatorname {Res}(\mathscr {F}_{\mathbf {i}_\nu })\cong {\mathbb{C}}_{P_{\nu }/P_{\nu }}$
.
Proof Consider the space
![]() ${\mathbb{C}}^{v_{i}}$
. If f is injective on
${\mathbb{C}}^{v_{i}}$
. If f is injective on
![]() ${\mathbb{C}}^{v_j}$
for all
${\mathbb{C}}^{v_j}$
for all
![]() $j<m$
, then
$j<m$
, then
![]() $f^{m-i}({\mathbb{C}}^{v_{i}})$
is a
$f^{m-i}({\mathbb{C}}^{v_{i}})$
is a
![]() $v_i$
-dimensional subspace in
$v_i$
-dimensional subspace in
![]() ${\mathbb{C}}^n$
. Furthermore, this subspace must lie in the span of
${\mathbb{C}}^n$
. Furthermore, this subspace must lie in the span of
![]() $b_{m,j}$
with
$b_{m,j}$
with
![]() $(m,j)\prec (i,v_i),$
since
$(m,j)\prec (i,v_i),$
since
![]() $F_{\preceq (i,v_i)}$
is a submodule containing
$F_{\preceq (i,v_i)}$
is a submodule containing
![]() ${\mathbb{C}}^{v_i}.$
In the word
${\mathbb{C}}^{v_i}.$
In the word
![]() $\mathbf {i}_{\nu }$
, we have
$\mathbf {i}_{\nu }$
, we have
![]() $(m,1) \preceq \cdots \preceq (m,v_i)\prec (i,v_i)\prec (m,v_{i+1}).$
This shows that the image of
$(m,1) \preceq \cdots \preceq (m,v_i)\prec (i,v_i)\prec (m,v_{i+1}).$
This shows that the image of
![]() $f^{m-i}$
must be exactly the
$f^{m-i}$
must be exactly the
![]() $v_i$
-dimensional space in the standard flag; this completes the proof.
$v_i$
-dimensional space in the standard flag; this completes the proof.
Corollary 3.20 The category of graded projective
![]() $\mathbb{T}^\chi _\nu $
-modules is equivalent to the category
$\mathbb{T}^\chi _\nu $
-modules is equivalent to the category
![]() $\mathrm {Hom}_{\mathsf {Flag}}(\chi ,\nu )$
of singular Soergel bimodules for the singularity
$\mathrm {Hom}_{\mathsf {Flag}}(\chi ,\nu )$
of singular Soergel bimodules for the singularity
![]() $(\chi ,\nu )$
. This equivalence is characterized by:
$(\chi ,\nu )$
. This equivalence is characterized by:
-
(1) sending the diagonal bimodule in
 $\mathrm {Hom}_{\mathsf {Flag}}(\nu ,\nu )$
to the module
$\mathrm {Hom}_{\mathsf {Flag}}(\nu ,\nu )$
to the module
 $\mathbb{T}^\nu _\nu e(\mathbf {i}_{\nu })$
;
$\mathbb{T}^\nu _\nu e(\mathbf {i}_{\nu })$
; -
(2) intertwining the action of
 $\mathsf {Flag}\cong \mathsf {Perv}$
by ladder bimodules with the left regular action on singular Soergel bimodules;
$\mathsf {Flag}\cong \mathsf {Perv}$
by ladder bimodules with the left regular action on singular Soergel bimodules; -
(3) intertwining the action of
 $\mathsf {Flag}$
by induction and restriction functors with the right regular action on singular Soergel bimodules.
$\mathsf {Flag}$
by induction and restriction functors with the right regular action on singular Soergel bimodules.
This generalizes the main theorem of [Reference Khovanov and SussanKS18]. Of course, the category of Soergel bimodules has a “reversing functor” where one swaps the left and right actions; this is an equivalence
![]() $\mathrm {Hom}_{\mathsf {Flag}}(\chi ,\nu )\cong \mathrm {Hom}_{\mathsf {Flag}}(\nu ,\chi )$
which is anti-monoidal. Applying Corollary 3.20, we find the following.
$\mathrm {Hom}_{\mathsf {Flag}}(\chi ,\nu )\cong \mathrm {Hom}_{\mathsf {Flag}}(\nu ,\chi )$
which is anti-monoidal. Applying Corollary 3.20, we find the following.
Corollary 3.21 We have a Morita equivalence between
![]() $\mathbb{T}^\chi _\nu $
and
$\mathbb{T}^\chi _\nu $
and
![]() $\mathbb{T}^\nu _\chi $
, which swaps the action of
$\mathbb{T}^\nu _\chi $
, which swaps the action of
![]() $\mathsf {Flag}$
via ladder bimodules with the action via induction and restriction functors.
$\mathsf {Flag}$
via ladder bimodules with the action via induction and restriction functors.
Of course, this Morita equivalence is realized by a bimodule over these two algebras. It should be possible to capture this equivalence via a diagrammatic bimodule, but the author has not yet been successful in producing a workable description of it. One important special case is that relating
![]() $\mathbb{T}^\nu _\nu $
to itself. This is, of course, true tautologically, but there are two ways of relating the ring
$\mathbb{T}^\nu _\nu $
to itself. This is, of course, true tautologically, but there are two ways of relating the ring
![]() $e(\mathbf {i}_{\nu })\mathbb{T}^\nu _\nu e(\mathbf {i}_{\nu })$
to the ring
$e(\mathbf {i}_{\nu })\mathbb{T}^\nu _\nu e(\mathbf {i}_{\nu })$
to the ring
![]() $H^*_{P_{\nu }\times P_{\nu }}(P_\nu )$
. The one naturally arising from the left action of
$H^*_{P_{\nu }\times P_{\nu }}(P_\nu )$
. The one naturally arising from the left action of
![]() $P_{\nu }$
is given by polynomials on the red strands, which are symmetrized on each strand. In the diagram, we insert symmetric polynomials in alphabets with sizes given by
$P_{\nu }$
is given by polynomials on the red strands, which are symmetrized on each strand. In the diagram, we insert symmetric polynomials in alphabets with sizes given by
![]() $v_1,v_2-v_1,\dots v_m-v_{m-1}$
at each point marked by a
$v_1,v_2-v_1,\dots v_m-v_{m-1}$
at each point marked by a
![]() $*$
on the red strands:
$*$
on the red strands:
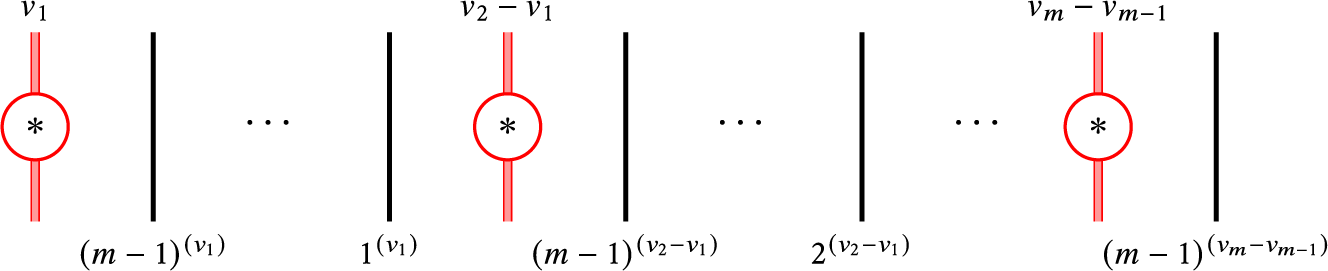
That arising from the right action is given by the same polynomials on the rightmost strand with each label:

Geometrically, these correspond to polynomials in the Chern classes of tautological bundles: in the first case, of the associated bundles for the action of
![]() $P_{\nu }$
on simple subquotients of
$P_{\nu }$
on simple subquotients of
![]() ${\mathbb{C}}^n$
under the left action of
${\mathbb{C}}^n$
under the left action of
![]() $P_{\nu }$
; in the second case on
$P_{\nu }$
; in the second case on
![]() ${\mathbb{C}}^{v_k}/f({\mathbb{C}}^{v_{k-1}})$
. These are the same, since as discussed in the proof of Lemma 3.19, the corresponding vector bundles are isomorphic.
${\mathbb{C}}^{v_k}/f({\mathbb{C}}^{v_{k-1}})$
. These are the same, since as discussed in the proof of Lemma 3.19, the corresponding vector bundles are isomorphic.
4 Gelfand–Tsetlin modules
Let
![]() $U=U(\mathfrak {gl}_n)$
. As mentioned in the introduction, we let
$U=U(\mathfrak {gl}_n)$
. As mentioned in the introduction, we let
![]() $\Gamma \subset U(\mathfrak {gl}_n)$
be the Gelfand–Tsetlin subalgebra generated by the centers
$\Gamma \subset U(\mathfrak {gl}_n)$
be the Gelfand–Tsetlin subalgebra generated by the centers
![]() $Z_k=Z(U(\mathfrak {gl}_k))$
for
$Z_k=Z(U(\mathfrak {gl}_k))$
for
![]() $k=1,\dots , n$
, where
$k=1,\dots , n$
, where
![]() $\mathfrak {gl}_k\subset \mathfrak {gl}_n$
is embedded as the top left corner. In this section, we’ll discuss how
$\mathfrak {gl}_k\subset \mathfrak {gl}_n$
is embedded as the top left corner. In this section, we’ll discuss how
![]() $U(\mathfrak {gl}_n)$
and its representation theory relate to the algebras
$U(\mathfrak {gl}_n)$
and its representation theory relate to the algebras
![]() $\mathbb{\tilde {T}}^\chi $
in the case where
$\mathbb{\tilde {T}}^\chi $
in the case where
![]() $v_i=i$
for
$v_i=i$
for
![]() $i=1,\dots , n$
. In this case,
$i=1,\dots , n$
. In this case,
![]() $\Omega =\{(i,j) \mid 1\leq j\leq i\leq n\}$
.
$\Omega =\{(i,j) \mid 1\leq j\leq i\leq n\}$
.
For the dominant weight
![]() $\chi $
, we have a maximal ideal
$\chi $
, we have a maximal ideal
![]() $\mathfrak {m}_\chi $
of
$\mathfrak {m}_\chi $
of
![]() $Z_n $
defined by the kernel of the action on the Verma module with highest weight
$Z_n $
defined by the kernel of the action on the Verma module with highest weight
Definition 4.1 A Gelfand–Tsetlin module is a finitely generated
![]() $U(\mathfrak {gl}_n)$
-module on which the action of
$U(\mathfrak {gl}_n)$
-module on which the action of
![]() $\Gamma $
is locally finite.
$\Gamma $
is locally finite.
Of course, by standard commutative algebra, if M is a Gelfand–Tsetlin module then M breaks up as a direct sum over the maximal ideals in
![]() $\operatorname {MaxSpec}(\Gamma )$
. Every maximal ideal of
$\operatorname {MaxSpec}(\Gamma )$
. Every maximal ideal of
![]() $\Gamma $
is generated by maximal ideals in
$\Gamma $
is generated by maximal ideals in
![]() $Z_k$
for each k, which we index with an unordered k-tuple
$Z_k$
for each k, which we index with an unordered k-tuple
![]() $\lambda _k=(\lambda _{k,1},\dots , \lambda _{k,k})$
; as above, we match this with the maximal ideal in
$\lambda _k=(\lambda _{k,1},\dots , \lambda _{k,k})$
; as above, we match this with the maximal ideal in
![]() $Z_k$
acts trivially on the Verma module over
$Z_k$
acts trivially on the Verma module over
![]() $U(\mathfrak {gl}_k)$
with highest weight
$U(\mathfrak {gl}_k)$
with highest weight
![]() ${\lambda _k-\rho _k=(\lambda _{k,1}-1,\dots , \lambda _{k,k}-k).}$
Let
${\lambda _k-\rho _k=(\lambda _{k,1}-1,\dots , \lambda _{k,k}-k).}$
Let
![]() $\mathsf {m}_{\lambda }\subset \Gamma $
be the corresponding maximal ideal. Thus, for any Gelfand–Tsetlin module, we have a decomposition
$\mathsf {m}_{\lambda }\subset \Gamma $
be the corresponding maximal ideal. Thus, for any Gelfand–Tsetlin module, we have a decomposition
Remark 4.2 To help the reader fix notation in their mind, this means that the maximal ideals that appear in finite-dimensional modules with
![]() $\chi \in \mathbb{Z}^n$
are given by
$\chi \in \mathbb{Z}^n$
are given by
![]() $\lambda _k\in \mathbb{Z}^k$
with
$\lambda _k\in \mathbb{Z}^k$
with
![]() $\lambda _n=\chi $
that satisfy
$\lambda _n=\chi $
that satisfy
for
![]() $k=1,\dots , n-1$
. Readers will recognize this as the condition that
$k=1,\dots , n-1$
. Readers will recognize this as the condition that
![]() $\lambda _k-\rho _k$
form a Gelfand–Tsetlin pattern. Under this correspondence, the trivial module gives
$\lambda _k-\rho _k$
form a Gelfand–Tsetlin pattern. Under this correspondence, the trivial module gives
![]() $\lambda _k=(1,2,\dots , k).$
$\lambda _k=(1,2,\dots , k).$
Definition 4.3 Let
![]() $\operatorname {MaxSpec}_{\mathbb{Z}}(\Gamma )\subset \operatorname {MaxSpec}(\Gamma )$
be the subset where
$\operatorname {MaxSpec}_{\mathbb{Z}}(\Gamma )\subset \operatorname {MaxSpec}(\Gamma )$
be the subset where
![]() $\lambda _{k,i}\in \mathbb{Z}$
for all
$\lambda _{k,i}\in \mathbb{Z}$
for all
![]() $(k,i)\in \Omega $
, and
$(k,i)\in \Omega $
, and
![]() $\operatorname {MaxSpec}_{\mathbb{Z},\chi }(\Gamma )\subset \operatorname {MaxSpec}_{\mathbb{Z}}(\Gamma )$
the subset where
$\operatorname {MaxSpec}_{\mathbb{Z},\chi }(\Gamma )\subset \operatorname {MaxSpec}_{\mathbb{Z}}(\Gamma )$
the subset where
![]() $\lambda _{n,i}=\chi _i$
for all i. An integral Gelfand–Tsetlin module is one where
$\lambda _{n,i}=\chi _i$
for all i. An integral Gelfand–Tsetlin module is one where ![]() if
if
![]() $\lambda \notin \operatorname {MaxSpec}_{\mathbb{Z}}(\Gamma )$
.
$\lambda \notin \operatorname {MaxSpec}_{\mathbb{Z}}(\Gamma )$
.
Let
![]() $\mathcal {GT}_\chi $
be the category of integral Gelfand–Tsetlin modules over
$\mathcal {GT}_\chi $
be the category of integral Gelfand–Tsetlin modules over
![]() $U(\mathfrak {gl}_n)$
on which the ideal
$U(\mathfrak {gl}_n)$
on which the ideal
![]() $\mathfrak {m}_\chi \subset Z_n$
acts nilpotently, i.e., those where
$\mathfrak {m}_\chi \subset Z_n$
acts nilpotently, i.e., those where ![]() if
if
![]() $\lambda \notin \operatorname {MaxSpec}_{\mathbb{Z},\chi }(\Gamma )$
.
$\lambda \notin \operatorname {MaxSpec}_{\mathbb{Z},\chi }(\Gamma )$
.
Lemma 4.4 Let
![]() $V,M$
be
$V,M$
be
![]() $U(\mathfrak {gl}_n)$
-modules with M Gelfand–Tsetlin and V finite-dimensional. The module
$U(\mathfrak {gl}_n)$
-modules with M Gelfand–Tsetlin and V finite-dimensional. The module
![]() $V\otimes M$
is Gelfand–Tsetlin, and if
$V\otimes M$
is Gelfand–Tsetlin, and if
![]() $M\in \mathcal {GT}_\chi $
, then
$M\in \mathcal {GT}_\chi $
, then
![]() $V\otimes M$
is a sum of objects in
$V\otimes M$
is a sum of objects in
![]() $\mathcal {GT}_{\chi +\mu }$
for
$\mathcal {GT}_{\chi +\mu }$
for
![]() $\mu $
a weight of V.
$\mu $
a weight of V.
Proof Since
![]() $\Gamma $
is commutative, it is enough to show local finiteness separately under a set of generating subalgebras. That is, it suffices to check that
$\Gamma $
is commutative, it is enough to show local finiteness separately under a set of generating subalgebras. That is, it suffices to check that
![]() $V\otimes M$
is locally finite under
$V\otimes M$
is locally finite under
![]() $Z_k=Z(U(\mathfrak {gl}_k))$
for all
$Z_k=Z(U(\mathfrak {gl}_k))$
for all
![]() $k\leq n$
. This follows from [Reference Bernstein and Gel’fandBG80, Corollary 2.6(ii)], which shows that
$k\leq n$
. This follows from [Reference Bernstein and Gel’fandBG80, Corollary 2.6(ii)], which shows that
![]() $V\otimes M$
is locally finite under
$V\otimes M$
is locally finite under
![]() $Z_k$
whenever M is locally finite under
$Z_k$
whenever M is locally finite under
![]() $Z_k$
.
$Z_k$
.
By [Reference Bernstein and Gel’fandBG80, Theorem 2.5(ii)], the set of modules with integral central character is closed under tensor product, so if M is integral Gelfand–Tsetlin, then
![]() $V\otimes M$
is as well. Finally, applying [Reference Bernstein and Gel’fandBG80, Theorem 2.5(ii)] again implies the statement on characters under
$V\otimes M$
is as well. Finally, applying [Reference Bernstein and Gel’fandBG80, Theorem 2.5(ii)] again implies the statement on characters under
![]() $Z_n$
.
$Z_n$
.
In particular, we have functors
![]() $E(M)={\mathbb{C}}^n\otimes M$
and
$E(M)={\mathbb{C}}^n\otimes M$
and
![]() $F(M)=({\mathbb{C}}^n)^*\otimes M$
on the category of Gelfand–Tsetlin modules with integral central character
$F(M)=({\mathbb{C}}^n)^*\otimes M$
on the category of Gelfand–Tsetlin modules with integral central character
![]() $\chi \in \mathbb{Z}^n$
. Lemma 4.4 shows the following.
$\chi \in \mathbb{Z}^n$
. Lemma 4.4 shows the following.
Corollary 4.5 If
![]() $M\in \mathcal {GT}_\chi $
, then
$M\in \mathcal {GT}_\chi $
, then
![]() $E(M)$
is a sum of objects in
$E(M)$
is a sum of objects in
![]() $\mathcal {GT}_{\chi ^{+i}}$
for
$\mathcal {GT}_{\chi ^{+i}}$
for
![]() $i\in \{\chi _1,\dots , \chi _n\}$
and
$i\in \{\chi _1,\dots , \chi _n\}$
and
![]() $F(M)$
is a sum of objects in
$F(M)$
is a sum of objects in
![]() $\mathcal {GT}_{\chi ^{-i}}$
for
$\mathcal {GT}_{\chi ^{-i}}$
for
![]() $i\in \{\chi _1-1,\dots , \chi _n-1\}$
.
$i\in \{\chi _1-1,\dots , \chi _n-1\}$
.
Since decomposing according to the spectrum of
![]() $Z_n$
is functorial, we can define functors
$Z_n$
is functorial, we can define functors
![]() $E_i$
(resp.,
$E_i$
(resp.,
![]() $F_i$
) such that for
$F_i$
) such that for
![]() $M\in \mathcal {GT}_{\chi }$
, we have that
$M\in \mathcal {GT}_{\chi }$
, we have that
![]() $E_i(M)\subset E(M)$
(resp.,
$E_i(M)\subset E(M)$
(resp.,
![]() $F_i(M)\subset F(M)$
) is the unique maximal summand that lies in the category
$F_i(M)\subset F(M)$
) is the unique maximal summand that lies in the category
![]() $\mathcal {GT}_{\chi ^{\pm i}}$
. These are also the generalized weight spaces of the Casimir operator on
$\mathcal {GT}_{\chi ^{\pm i}}$
. These are also the generalized weight spaces of the Casimir operator on
![]() $V\otimes M$
(this follows, for example, by [Reference Brundan, Savage and WebsterBSW, Lemma 4.5]). This gives a decomposition of these functors acting on integral Gelfand–Tsetlin modules:
$V\otimes M$
(this follows, for example, by [Reference Brundan, Savage and WebsterBSW, Lemma 4.5]). This gives a decomposition of these functors acting on integral Gelfand–Tsetlin modules:
It is well-known that the functors
![]() $E_i, F_i$
define categorical actions (for example, see the discussion of category
$E_i, F_i$
define categorical actions (for example, see the discussion of category
![]() $\mathcal {O}$
in [Reference Chuang and RouquierCR08, Section 7.5]) on various categories of
$\mathcal {O}$
in [Reference Chuang and RouquierCR08, Section 7.5]) on various categories of
![]() $\mathfrak {gl}_n$
-modules, but due to artifacts of the proofs, it is not obvious that these apply to the category of Gelfand–Tsetlin modules. Recent work of Brundan, Savage, and the author shows how to unify these proofs.
$\mathfrak {gl}_n$
-modules, but due to artifacts of the proofs, it is not obvious that these apply to the category of Gelfand–Tsetlin modules. Recent work of Brundan, Savage, and the author shows how to unify these proofs.
Lemma 4.6 The functors E and F define an action of the level 0 Heisenberg category of [Reference BrundanBru18] (also called the affine oriented Brauer category in [Reference Brundan, Comes and KujawaBCK19]). The functors
![]() $E_i$
and
$E_i$
and
![]() $F_i$
for
$F_i$
for
![]() $i\in \mathbb{Z}$
give an induced categorical Kac–Moody action of
$i\in \mathbb{Z}$
give an induced categorical Kac–Moody action of
![]() $\mathfrak {sl}_\infty $
, and these actions are related by [Reference Brundan, Savage and WebsterBSW, Theorem A].
$\mathfrak {sl}_\infty $
, and these actions are related by [Reference Brundan, Savage and WebsterBSW, Theorem A].
Note that the formulas of [Reference Brundan, Savage and WebsterBSW, Theorem 4.11] give explicit formulas for the action of
![]() $\mathcal {U}$
in terms of swapping factors in tensor products and the Casimir element, but these formulas are not needed for our purposes.
$\mathcal {U}$
in terms of swapping factors in tensor products and the Casimir element, but these formulas are not needed for our purposes.
Let us note another perspective on this result. Recall that we call a U-U bimodule Harish-Chandra if it is locally finite for the adjoint action and pro-Harish-Chandra if it satisfies this property in the topological sense.
The most important example of a Harish-Chandra bimodule is the tensor product
![]() $V\otimes U$
for V a finite-dimensional U-module, with the right action by right multiplication on the second factor, and the left action via the coproduct. That is, for
$V\otimes U$
for V a finite-dimensional U-module, with the right action by right multiplication on the second factor, and the left action via the coproduct. That is, for
![]() $v\in {\mathbb{C}}^n,u\in U, X_1,X_2\in \mathfrak {gl}_n$
, we have
$v\in {\mathbb{C}}^n,u\in U, X_1,X_2\in \mathfrak {gl}_n$
, we have
The resulting bimodule structure on
![]() $V\otimes U$
is Harish-Chandra. Thus, the functor
$V\otimes U$
is Harish-Chandra. Thus, the functor
![]() $E_i\colon \mathcal {GT}_{\chi }\to \mathcal {GT}_{\chi ^{+i}}$
is given by tensor product with a pro-Harish-Chandra U-U bimodule
$E_i\colon \mathcal {GT}_{\chi }\to \mathcal {GT}_{\chi ^{+i}}$
is given by tensor product with a pro-Harish-Chandra U-U bimodule
![]() $\mathscr {E}_i$
, formed by completing the left and right actions of
$\mathscr {E}_i$
, formed by completing the left and right actions of
![]() $Z_n$
on
$Z_n$
on
![]() ${\mathbb{C}}^n\otimes M$
with respect to the appropriate maximal ideal. Let
${\mathbb{C}}^n\otimes M$
with respect to the appropriate maximal ideal. Let
![]() $\mathsf {HC}$
be the 2-category such that:
$\mathsf {HC}$
be the 2-category such that:
-
• objects are dominant integral weights
 $\chi =(\chi _1\leq \cdots \leq \chi _n)$
;
$\chi =(\chi _1\leq \cdots \leq \chi _n)$
; -
• 1-morphisms
 $\chi \to \chi '$
are sums of pro-Harish-Chandra bimodules where the maximal ideal
$\chi \to \chi '$
are sums of pro-Harish-Chandra bimodules where the maximal ideal
 $\mathfrak {m}_{\chi '}\subset Z_n$
acts topologically nilpotently on the left and
$\mathfrak {m}_{\chi '}\subset Z_n$
acts topologically nilpotently on the left and
 $\mathfrak {m}_\chi \subset Z_n$
acts topologically nilpotently on the right;
$\mathfrak {m}_\chi \subset Z_n$
acts topologically nilpotently on the right; -
• 2-morphisms are homomorphisms of bimodules.
By [Reference Brundan, Savage and WebsterBSW, Theorem A], we have a 2-functor
![]() $\mathcal {U}^*\to \mathsf {HC}$
sending
$\mathcal {U}^*\to \mathsf {HC}$
sending ![]() and similarly with
and similarly with
![]() $\mathscr {F}$
. Note that Soergel sketches the construction of a functor
$\mathscr {F}$
. Note that Soergel sketches the construction of a functor
![]() $\mathsf {Flag}\to \mathsf {HC}$
which can be used to relate this to Khovanov and Lauda’s action in the final paragraph of [Reference SoergelSoe92].
$\mathsf {Flag}\to \mathsf {HC}$
which can be used to relate this to Khovanov and Lauda’s action in the final paragraph of [Reference SoergelSoe92].
4.1 Presentation of the category
 $\mathcal {GT}_{\chi }$
$\mathcal {GT}_{\chi }$
A choice of integral
![]() $\lambda \in \operatorname {MaxSpec}_{\mathbb{Z},\chi }(\Gamma )$
can be used to give a total preorder
$\lambda \in \operatorname {MaxSpec}_{\mathbb{Z},\chi }(\Gamma )$
can be used to give a total preorder
![]() $\prec $
on the set
$\prec $
on the set
![]() $\Omega $
as in previous sections for the dimension vector
$\Omega $
as in previous sections for the dimension vector
![]() $v_i=i$
for
$v_i=i$
for
![]() $m=n$
. We set
$m=n$
. We set
![]() $(i,k) \preceq (j,\ell )$
if and only if
$(i,k) \preceq (j,\ell )$
if and only if
![]() $\lambda _{i,k}< \lambda _{j,\ell }$
or
$\lambda _{i,k}< \lambda _{j,\ell }$
or
![]() $\lambda _{i,k}= \lambda _{j,\ell }$
and
$\lambda _{i,k}= \lambda _{j,\ell }$
and
![]() $i\geq j$
. Note that the resulting preorder satisfies (2.1) by assumption and (2.2) since if
$i\geq j$
. Note that the resulting preorder satisfies (2.1) by assumption and (2.2) since if
![]() $(i,k) \approx (j,\ell )$
, then we must have
$(i,k) \approx (j,\ell )$
, then we must have
![]() $\lambda _{i,k}=\lambda _{j,\ell }$
and
$\lambda _{i,k}=\lambda _{j,\ell }$
and
![]() $i=j$
.
$i=j$
.
Definition 4.7 We let
![]() $\mathbf {i}(\lambda )$
define the corresponding word in
$\mathbf {i}(\lambda )$
define the corresponding word in
![]() $[1,m+1]$
and
$[1,m+1]$
and
![]() $e'(\lambda )$
be the corresponding idempotent in
$e'(\lambda )$
be the corresponding idempotent in
![]() $\mathbb{\tilde {T}}^\chi $
.
$\mathbb{\tilde {T}}^\chi $
.
Note that [Reference WebsterWeba, Proposition 5.4] shows that any maximal ideals giving the same preorder on
![]() $\Omega $
give isomorphic functors on
$\Omega $
give isomorphic functors on
![]() $\mathcal {GT}_\chi $
. If we change the order by swapping pairs
$\mathcal {GT}_\chi $
. If we change the order by swapping pairs
![]() $(i,k) $
and
$(i,k) $
and
![]() $(j,\ell )$
, this is called a neutral swap, and more generally, neutral swaps don’t change the functor given by two maximal ideals. For example, two Gelfand–Tsetlin patterns with the same
$(j,\ell )$
, this is called a neutral swap, and more generally, neutral swaps don’t change the functor given by two maximal ideals. For example, two Gelfand–Tsetlin patterns with the same
![]() $\chi $
don’t necessarily give the same order, but they differ by neutral swaps, and indeed they give isomorphic functors.
$\chi $
don’t necessarily give the same order, but they differ by neutral swaps, and indeed they give isomorphic functors.
Example 3 The action of
![]() $\Gamma $
on the trivial representation gives the weight
$\Gamma $
on the trivial representation gives the weight
![]() $\lambda _{i,k}=k$
. Thus, the resulting word is
$\lambda _{i,k}=k$
. Thus, the resulting word is
As mentioned before, every Gelfand–Tsetlin pattern gives an ordering that differs from this one by neutral swaps.
On the other hand, a weight like
![]() $\lambda _3=(1,2,3), \lambda _2=(4,4), \lambda _1=(1)$
gives
$\lambda _3=(1,2,3), \lambda _2=(4,4), \lambda _1=(1)$
gives
![]() $(3,1,3,3,2^{(2)})$
, whereas if
$(3,1,3,3,2^{(2)})$
, whereas if
![]() $\lambda _2=(4,5)$
, then we have
$\lambda _2=(4,5)$
, then we have
![]() $(3,1,3,3,2,2).$
This is an example of a maximal ideal of the Gelfand–Tsetlin subalgebra that appears in no finite-dimensional module.
$(3,1,3,3,2,2).$
This is an example of a maximal ideal of the Gelfand–Tsetlin subalgebra that appears in no finite-dimensional module.
Using the techniques of [Reference Kamnitzer, Tingley, Webster, Weekes and YacobiKTW+19, Reference WebsterWeba, Reference WebsterWebb], we can give an algebraic presentation of the category
![]() $\mathcal {GT}_{\chi }$
. This is accomplished by presenting the algebra of natural transformations of the functors
$\mathcal {GT}_{\chi }$
. This is accomplished by presenting the algebra of natural transformations of the functors ![]() Let
Let
![]() $\widehat {\mathbb{\tilde {T}}}_\chi $
be the completion of the algebra
$\widehat {\mathbb{\tilde {T}}}_\chi $
be the completion of the algebra
![]() $\mathbb{\tilde {T}}_{\chi }$
with respect to its grading. See [Reference WebsterWeb20, Section 2] for more discussion of the induced topology (in particular, the continuity of multiplication in it).
$\mathbb{\tilde {T}}_{\chi }$
with respect to its grading. See [Reference WebsterWeb20, Section 2] for more discussion of the induced topology (in particular, the continuity of multiplication in it).
Theorem 4.8 We have an isomorphism compatible with multiplication
This is extremely closely related to [Reference Kamnitzer, Tingley, Webster, Weekes and YacobiKTW+19, Theorem 5.2], but slightly different, since that result is for Gelfand–Tsetlin modules with honest central character, which corresponds in
![]() $\widehat {\mathbb{\tilde {T}}}_\chi $
to setting red dots to 0. Under this isomorphism, the red dots give the nilpotent parts of certain (complicated) elements of the center of
$\widehat {\mathbb{\tilde {T}}}_\chi $
to setting red dots to 0. Under this isomorphism, the red dots give the nilpotent parts of certain (complicated) elements of the center of
![]() $U(\mathfrak {gl}_n).$
In [Reference Silverthorne and WebsterSW24, Lemma 3.3 and Proposition 3.4], we give a more direct algebraic proof of this theorem.
$U(\mathfrak {gl}_n).$
In [Reference Silverthorne and WebsterSW24, Lemma 3.3 and Proposition 3.4], we give a more direct algebraic proof of this theorem.
Proof This follows from [Reference WebsterWeba, Theorem 4.4]. The space ![]() is exactly the bimodule
is exactly the bimodule
![]() ${}_{\lambda '}\hat {U}_{\lambda }=\varprojlim U/(\mathsf {m}_{\lambda '}^NU+U\mathsf {m}^N_{\lambda })$
, and by [Reference WebsterWeba, (4.5)], this is exactly the completion with respect to grading of
${}_{\lambda '}\hat {U}_{\lambda }=\varprojlim U/(\mathsf {m}_{\lambda '}^NU+U\mathsf {m}^N_{\lambda })$
, and by [Reference WebsterWeba, (4.5)], this is exactly the completion with respect to grading of
![]() $\operatorname {Ext}(\mathscr {F}_{\mathbf {i}(\lambda )},\mathscr {F}_{\mathbf {i}(\lambda ')}).$
On the other hand, by Theorem 3.10, we have an isomorphism
$\operatorname {Ext}(\mathscr {F}_{\mathbf {i}(\lambda )},\mathscr {F}_{\mathbf {i}(\lambda ')}).$
On the other hand, by Theorem 3.10, we have an isomorphism
![]() $\operatorname {Ext}(\mathscr {F}_{\mathbf {i}(\lambda )},\mathscr {F}_{\mathbf {i}(\lambda ')})\cong e'(\lambda ') {\mathbb{\tilde {T}}}_\chi e'(\lambda ).$
After applying completion, this induces an isomorphism
$\operatorname {Ext}(\mathscr {F}_{\mathbf {i}(\lambda )},\mathscr {F}_{\mathbf {i}(\lambda ')})\cong e'(\lambda ') {\mathbb{\tilde {T}}}_\chi e'(\lambda ).$
After applying completion, this induces an isomorphism
![]() ${}_{\lambda '}\hat {U}_{\lambda }\cong e'(\lambda ') \widehat {\mathbb{\tilde {T}}}_\chi e'(\lambda )$
. Both of these isomorphisms are compatible with multiplication, so this completes the proof.
${}_{\lambda '}\hat {U}_{\lambda }\cong e'(\lambda ') \widehat {\mathbb{\tilde {T}}}_\chi e'(\lambda )$
. Both of these isomorphisms are compatible with multiplication, so this completes the proof.
Definition 4.9 Let
![]() $\mathbb{\tilde {T}}^\chi \operatorname {-wgmod}$
be the category of finite-dimensional
$\mathbb{\tilde {T}}^\chi \operatorname {-wgmod}$
be the category of finite-dimensional
![]() $\mathbb{\tilde {T}}^\chi $
-modules M which are weakly gradable, that is, M has a finite filtration with gradable subquotients.
$\mathbb{\tilde {T}}^\chi $
-modules M which are weakly gradable, that is, M has a finite filtration with gradable subquotients.
These are precisely the modules that extend to finite-dimensional modules over the completion
![]() $\widehat {\mathbb{\tilde {T}}}_\chi $
with the discrete topology.
$\widehat {\mathbb{\tilde {T}}}_\chi $
with the discrete topology.
Corollary 4.10 We have an equivalence of categories
![]() $\boldsymbol {\Theta }\colon \mathcal {GT}_\chi \cong {\mathbb{\tilde {T}}}_\chi \operatorname {-wgmod}$
such that
$\boldsymbol {\Theta }\colon \mathcal {GT}_\chi \cong {\mathbb{\tilde {T}}}_\chi \operatorname {-wgmod}$
such that ![]() for all integral maximal ideals
for all integral maximal ideals
![]() $\lambda \in \operatorname {MaxSpec}_{\mathbb{Z},\chi } (\Gamma )$
.
$\lambda \in \operatorname {MaxSpec}_{\mathbb{Z},\chi } (\Gamma )$
.
Proof As
![]() $\lambda $
runs over
$\lambda $
runs over
![]() $\operatorname {MaxSpec}_{\mathbb{Z},\chi } (\Gamma )$
, we only get finitely many different idempotents as
$\operatorname {MaxSpec}_{\mathbb{Z},\chi } (\Gamma )$
, we only get finitely many different idempotents as
![]() $e(\lambda )$
; if we let
$e(\lambda )$
; if we let
![]() $\mathsf {S}$
be a set of maximal ideals that contains one representative of each idempotent, then this is complete in the sense of [Reference WebsterWeba, Definition 2.24]. Let
$\mathsf {S}$
be a set of maximal ideals that contains one representative of each idempotent, then this is complete in the sense of [Reference WebsterWeba, Definition 2.24]. Let
![]() $\bar {e}$
be the sum of these idempotents. Then, [Reference WebsterWeba, Definition 2.23] shows that the functor
$\bar {e}$
be the sum of these idempotents. Then, [Reference WebsterWeba, Definition 2.23] shows that the functor ![]() is an equivalence of categories
is an equivalence of categories
![]() $\mathcal {GT}_\chi \cong \bar {e}\widehat {\mathbb{\tilde {T}}}_\chi \bar {e}\operatorname {-wgmod}$
with the desired properties. As argued in [Reference WebsterWeba, Proposition 5.12], no simple object in
$\mathcal {GT}_\chi \cong \bar {e}\widehat {\mathbb{\tilde {T}}}_\chi \bar {e}\operatorname {-wgmod}$
with the desired properties. As argued in [Reference WebsterWeba, Proposition 5.12], no simple object in
![]() $\widehat {\mathbb{\tilde {T}}}_\chi \operatorname {-mod}$
is killed by
$\widehat {\mathbb{\tilde {T}}}_\chi \operatorname {-mod}$
is killed by
![]() $\bar {e}$
, so
$\bar {e}$
, so
![]() $\bar {e}$
defines a Morita equivalence giving the desired result.
$\bar {e}$
defines a Morita equivalence giving the desired result.
Note that if
![]() $\chi _i \ll \chi _{i+1}$
, then
$\chi _i \ll \chi _{i+1}$
, then
![]() $\bar {e}$
is the identity in
$\bar {e}$
is the identity in
![]() $\mathbb{\tilde {T}}^\chi $
and this last step is not needed. The general case can be deduced from this one using translation functors, but we appeal to [Reference WebsterWeba, Proposition 5.12] since we have not yet discussed compatibility with translation functors.
$\mathbb{\tilde {T}}^\chi $
and this last step is not needed. The general case can be deduced from this one using translation functors, but we appeal to [Reference WebsterWeba, Proposition 5.12] since we have not yet discussed compatibility with translation functors.
Together with Theorem 3.10, this establishes Theorem 1.
Let us record how this equivalence matches various properties of interest for Gelfand–Tsetlin modules.
Lemma 4.11 A Gelfand–Tsetlin module M satisfies:
-
(1)
 $U(\mathfrak {n})\subset U(\mathfrak {gl}_n)$
acts locally finitely if and only if
$U(\mathfrak {n})\subset U(\mathfrak {gl}_n)$
acts locally finitely if and only if
 $\Theta (M)$
factors through
$\Theta (M)$
factors through
 $\mathbb{T}^{\chi }_\nu $
.
$\mathbb{T}^{\chi }_\nu $
. -
(2) The Gelfand–Tsetlin subalgebra acts semi-simply if and only if all dots, red and black, act trivially.
-
(3) The Cartan
 $\mathfrak {h}$
acts semi-simply if and only if the sum
$\mathfrak {h}$
acts semi-simply if and only if the sum
 $h_{i,1}$
of all dots on strands with label i acts trivially, for all i.
$h_{i,1}$
of all dots on strands with label i acts trivially, for all i. -
(4) The center
 $Z_n$
acts semi-simply if and only if all positive degree homogeneous polynomials in the red dots act trivially.
$Z_n$
acts semi-simply if and only if all positive degree homogeneous polynomials in the red dots act trivially.
In particular, the modules over
![]() $\mathbb{\tilde {T}}^\chi _\nu $
which factor through the quotient by all red dots and by violating strands is the category
$\mathbb{\tilde {T}}^\chi _\nu $
which factor through the quotient by all red dots and by violating strands is the category
![]() $\mathcal {O}^{\prime }_\chi $
of modules locally finite under
$\mathcal {O}^{\prime }_\chi $
of modules locally finite under
![]() $U(\mathfrak {n})$
and semi-simple for the action of the center with central character
$U(\mathfrak {n})$
and semi-simple for the action of the center with central character
![]() $\chi $
; such a module is automatically a generalized weight module, but not necessarily an honest weight module, and so not necessarily in category
$\chi $
; such a module is automatically a generalized weight module, but not necessarily an honest weight module, and so not necessarily in category
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
On the other hand, the modules that factor through the quotient of
![]() $\mathbb{T}^{\chi }_\nu $
by the symmetric polynomials
$\mathbb{T}^{\chi }_\nu $
by the symmetric polynomials
![]() $h_{i,1}$
for all i, are those which lie in the usual category
$h_{i,1}$
for all i, are those which lie in the usual category
![]() $\mathcal {O}$
. Note that we showed in [Reference WebsterWeb17b, Corollary 9.10] that
$\mathcal {O}$
. Note that we showed in [Reference WebsterWeb17b, Corollary 9.10] that
![]() $T^{\nu }_\chi \operatorname {-mod}$
was equivalent to
$T^{\nu }_\chi \operatorname {-mod}$
was equivalent to
![]() $\mathcal {O}_\chi $
with the translation functors matched with the induction–restriction action. Thus, this is related to our result using the Morita equivalence of Corollary 3.21 between
$\mathcal {O}_\chi $
with the translation functors matched with the induction–restriction action. Thus, this is related to our result using the Morita equivalence of Corollary 3.21 between
![]() $T^{\nu }_\chi $
and this quotient of
$T^{\nu }_\chi $
and this quotient of
![]() $\mathbb{T}^\chi _\nu $
.
$\mathbb{T}^\chi _\nu $
.
4.2 Translation functors
Now, let us consider how this perspective interacts with translation functors. This requires studying the bimodule
![]() ${\mathbb{C}}^n\otimes U$
.
${\mathbb{C}}^n\otimes U$
.
Lemma 4.12 As a
![]() $U\operatorname {-}U$
-bimodule,
$U\operatorname {-}U$
-bimodule,
![]() ${\mathbb{C}}^n\otimes U$
is isomorphic to the sub-bimodule
${\mathbb{C}}^n\otimes U$
is isomorphic to the sub-bimodule
![]() $U'$
in
$U'$
in
![]() $U(\mathfrak {gl}_{n+1})$
generated by
$U(\mathfrak {gl}_{n+1})$
generated by
![]() $e_n$
.
$e_n$
.
Proof Both these bimodules have an induced adjoint
![]() $\mathfrak {gl}_n$
-module structure (which exists for any Hopf algebra). The subspace
$\mathfrak {gl}_n$
-module structure (which exists for any Hopf algebra). The subspace
![]() ${\mathbb{C}}^n\subset {\mathbb{C}}^n\otimes U$
is a submodule with this module structure. Similarly,
${\mathbb{C}}^n\subset {\mathbb{C}}^n\otimes U$
is a submodule with this module structure. Similarly,
![]() $e_n$
generates a copy of
$e_n$
generates a copy of
![]() ${\mathbb{C}}^{n}$
inside the adjoint module over
${\mathbb{C}}^{n}$
inside the adjoint module over
![]() $\mathfrak {gl}_{n+1}$
restricted to
$\mathfrak {gl}_{n+1}$
restricted to
![]() $\mathfrak {gl}_n$
. Sending
$\mathfrak {gl}_n$
. Sending
![]() $e_n\mapsto (0,\dots , 0,1)$
induces a unique isomorphism
$e_n\mapsto (0,\dots , 0,1)$
induces a unique isomorphism
![]() $\psi $
between these subspaces.
$\psi $
between these subspaces.
In any
![]() $U\operatorname {-}U$
bimodule, a generating subspace for the bimodule action which is closed under the adjoint action is already generating for the right action. The module
$U\operatorname {-}U$
bimodule, a generating subspace for the bimodule action which is closed under the adjoint action is already generating for the right action. The module
![]() ${\mathbb{C}}^n\otimes U$
is freely generated by
${\mathbb{C}}^n\otimes U$
is freely generated by
![]() ${\mathbb{C}}^n$
as a right U-module by definition, and the same is true for
${\mathbb{C}}^n$
as a right U-module by definition, and the same is true for
![]() $U'$
by the PBW theorem. Thus,
$U'$
by the PBW theorem. Thus,
![]() $\psi $
canonically extends to a right-module homomorphism, which is also a left-module homomorphism since
$\psi $
canonically extends to a right-module homomorphism, which is also a left-module homomorphism since
![]() $\psi $
is adjoint equivariant.
$\psi $
is adjoint equivariant.
Fix
![]() $\chi \in \operatorname {MaxSpec}(Z_n)$
, and assume that
$\chi \in \operatorname {MaxSpec}(Z_n)$
, and assume that
![]() $\chi ^{+i}$
exists. Consider
$\chi ^{+i}$
exists. Consider
Theorem 4.13 We have an isomorphism compatible with bimodule structure:
Proof Note that
![]() $e_n$
commutes with
$e_n$
commutes with
![]() $Z_k$
for
$Z_k$
for
![]() $k<n$
, embedded in
$k<n$
, embedded in
![]() $U(\mathfrak {gl}_{n+1})$
via the standard inclusion. Thus,
$U(\mathfrak {gl}_{n+1})$
via the standard inclusion. Thus,
![]() $e_n$
only has non-zero image if
$e_n$
only has non-zero image if
![]() $\lambda _{i,k}=\lambda ^{\prime }_{i,k}$
for all
$\lambda _{i,k}=\lambda ^{\prime }_{i,k}$
for all
![]() $i<n$
. We therefore can describe the desired map by specifying the image of
$i<n$
. We therefore can describe the desired map by specifying the image of
![]() $e_n$
in this case.
$e_n$
in this case.
As in [Reference Kamnitzer, Tingley, Webster, Weekes and YacobiKTW+19, Reference WebsterWebb], we can read this off by carefully studying the polynomial representation of
![]() $U(\mathfrak {gl}_{n+1})$
, induced by its realization as an orthogonal Gelfand–Zetlin algebra.Footnote
1
This was originally given in [Reference MazorchukMaz99], though it might be easier to follow the notation in [Reference WebsterWeba, Section 5.1]. Let
$U(\mathfrak {gl}_{n+1})$
, induced by its realization as an orthogonal Gelfand–Zetlin algebra.Footnote
1
This was originally given in [Reference MazorchukMaz99], though it might be easier to follow the notation in [Reference WebsterWeba, Section 5.1]. Let
![]() $\Gamma _{(n+1)}$
be the Gelfand–Tsetlin subalgebra of
$\Gamma _{(n+1)}$
be the Gelfand–Tsetlin subalgebra of
![]() $U(\mathfrak {gl}_{n+1})$
, which we identify with the space of symmetric polynomials in the alphabets
$U(\mathfrak {gl}_{n+1})$
, which we identify with the space of symmetric polynomials in the alphabets
![]() $\{x_{i,1},\dots , x_{i,i}\}$
for
$\{x_{i,1},\dots , x_{i,i}\}$
for
![]() $i=1,\dots , i+1$
.
$i=1,\dots , i+1$
.
Let
![]() $\varphi _{i,j}$
be the translation on all polynomials in these alphabets satisfying
$\varphi _{i,j}$
be the translation on all polynomials in these alphabets satisfying
We then have a representation of
![]() $\mathfrak {gl}_{n+1}$
, where
$\mathfrak {gl}_{n+1}$
, where
![]() $E_i$
and
$E_i$
and
![]() $F_i$
act by the operators
$F_i$
act by the operators
 $$\begin{align*}X^\pm_i=\mp\sum_{j=1}^{i}\frac{\displaystyle\prod_{k=1}^{v_{i\pm 1}} (x_{i,j}-x_{i\pm 1,k})}{\displaystyle\prod_{k\neq j} (x_{i,j}-x_{i,k})}\varphi_{i,j}^{\pm 1}.\end{align*}$$
$$\begin{align*}X^\pm_i=\mp\sum_{j=1}^{i}\frac{\displaystyle\prod_{k=1}^{v_{i\pm 1}} (x_{i,j}-x_{i\pm 1,k})}{\displaystyle\prod_{k\neq j} (x_{i,j}-x_{i,k})}\varphi_{i,j}^{\pm 1}.\end{align*}$$
Thus,
![]() $U'$
embeds into the bimodule of operators
$U'$
embeds into the bimodule of operators
![]() $\Gamma _{(n+1)}$
when this space is made into a module over
$\Gamma _{(n+1)}$
when this space is made into a module over
![]() $U(\mathfrak {gl}_{n})$
as the subspace generated by the operator
$U(\mathfrak {gl}_{n})$
as the subspace generated by the operator
 $$\begin{align*}X^+_n=-\sum_{j=1}^{n}\frac{\displaystyle\prod_{k=1}^{{n+ 1}} (x_{n,j}-x_{n+ 1,k})}{\displaystyle\prod_{k\neq j} (x_{n,j}-x_{n,k})}\varphi_{n,j}.\end{align*}$$
$$\begin{align*}X^+_n=-\sum_{j=1}^{n}\frac{\displaystyle\prod_{k=1}^{{n+ 1}} (x_{n,j}-x_{n+ 1,k})}{\displaystyle\prod_{k\neq j} (x_{n,j}-x_{n,k})}\varphi_{n,j}.\end{align*}$$
Consider
![]() $P'=\varprojlim U'/U'\mathsf {m}_{\lambda }^N$
. This is a left module over U, and clearly pro-Gelfand–Tsetlin, since for any element of
$P'=\varprojlim U'/U'\mathsf {m}_{\lambda }^N$
. This is a left module over U, and clearly pro-Gelfand–Tsetlin, since for any element of
![]() $u\in U'$
, the sub-bimodule
$u\in U'$
, the sub-bimodule
![]() $\Gamma u\Gamma $
lies in the left
$\Gamma u\Gamma $
lies in the left
![]() $\Gamma $
module generated by finitely many translations (this is a version of the Harish-Chandra property discussed in [Reference Drozd, Futorny and OvsienkoDFO94]). This means that
$\Gamma $
module generated by finitely many translations (this is a version of the Harish-Chandra property discussed in [Reference Drozd, Futorny and OvsienkoDFO94]). This means that
![]() $\Gamma u\Gamma \otimes _{\Gamma }\Gamma /\mathsf {m}_{\lambda }^N$
is finite-dimensional so
$\Gamma u\Gamma \otimes _{\Gamma }\Gamma /\mathsf {m}_{\lambda }^N$
is finite-dimensional so
![]() $U'/U'\mathsf {m}_{\lambda }^N$
is Gelfand–Tsetlin. Thus,
$U'/U'\mathsf {m}_{\lambda }^N$
is Gelfand–Tsetlin. Thus,
![]() $P'$
decomposes into pieces
$P'$
decomposes into pieces
![]() $P'=\oplus _{i\in \mathbb{Z}} P_i'$
on which
$P'=\oplus _{i\in \mathbb{Z}} P_i'$
on which
![]() $Z_n$
acts by
$Z_n$
acts by
![]() $\chi ^{+i}$
for i ranging over the values of
$\chi ^{+i}$
for i ranging over the values of
![]() $\chi _g$
; note that
$\chi _g$
; note that
![]() $P_i'=E_i(\varprojlim U/U\mathsf {m}_{\lambda }^N)$
.
$P_i'=E_i(\varprojlim U/U\mathsf {m}_{\lambda }^N)$
.
Consider the image of
![]() $X^+_n$
in
$X^+_n$
in
![]() $P^{\prime }_i$
. If we let
$P^{\prime }_i$
. If we let
![]() $I_i=\{j\mid \lambda _{n,j}=i\}$
, then we have that this image is given by
$I_i=\{j\mid \lambda _{n,j}=i\}$
, then we have that this image is given by
 $$\begin{align*}\sum_{j\in I_{i+1}} \frac{\displaystyle\prod_{k=1}^{{n+ 1}} (x_{n,j}-x_{n+ 1,k})}{\displaystyle\prod_{k\in [1,n]\setminus \{j\}} (x_{n,j}-x_{n,k})} \varphi_{n,j}.\end{align*}$$
$$\begin{align*}\sum_{j\in I_{i+1}} \frac{\displaystyle\prod_{k=1}^{{n+ 1}} (x_{n,j}-x_{n+ 1,k})}{\displaystyle\prod_{k\in [1,n]\setminus \{j\}} (x_{n,j}-x_{n,k})} \varphi_{n,j}.\end{align*}$$
Note that if
![]() $k\notin I_{i+1}$
, then the corresponding factor in the denominator is invertible in the local ring
$k\notin I_{i+1}$
, then the corresponding factor in the denominator is invertible in the local ring
![]() $\varprojlim \Gamma _{n}/\Gamma _{n}\mathsf {m}_{\lambda '}^N$
, using the geometric series
$\varprojlim \Gamma _{n}/\Gamma _{n}\mathsf {m}_{\lambda '}^N$
, using the geometric series
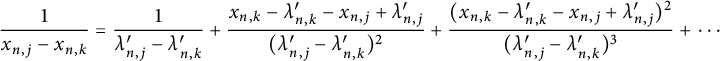 $$\begin{align*}\frac{1}{x_{n,j}-x_{n,k}}=\frac{1}{\lambda_{n,j}'-\lambda^{\prime}_{n,k}}+\frac{x_{n,k}-\lambda^{\prime}_{n,k}-x_{n,j}+\lambda^{\prime}_{n,j}}{(\lambda_{n,j}'-\lambda^{\prime}_{n,k})^2}+\frac{(x_{n,k}-\lambda^{\prime}_{n,k}-x_{n,j}+\lambda^{\prime}_{n,j})^2}{(\lambda_{n,j}'-\lambda^{\prime}_{n,k})^3}+\cdots\end{align*}$$
$$\begin{align*}\frac{1}{x_{n,j}-x_{n,k}}=\frac{1}{\lambda_{n,j}'-\lambda^{\prime}_{n,k}}+\frac{x_{n,k}-\lambda^{\prime}_{n,k}-x_{n,j}+\lambda^{\prime}_{n,j}}{(\lambda_{n,j}'-\lambda^{\prime}_{n,k})^2}+\frac{(x_{n,k}-\lambda^{\prime}_{n,k}-x_{n,j}+\lambda^{\prime}_{n,j})^2}{(\lambda_{n,j}'-\lambda^{\prime}_{n,k})^3}+\cdots\end{align*}$$
Thus, we can write the image of
![]() $X^+_n$
as a sum of operators of the form
$X^+_n$
as a sum of operators of the form
 $$\begin{align*}X_{i}^{(p,s)}=-\sum_{j\in I_{i+1}} \frac{\displaystyle\prod_{k=1}^{{n+ 1}} (x_{n,j}-x_{n+ 1,k})}{\displaystyle\prod_{p\in I_{i+1}\setminus \{j\}} (x_{n,j}-x_{n,p})} (x_{n,j}-i-1)^sp(x_{n,1},\dots, x_{n,n})\varphi_{n,j},\end{align*}$$
$$\begin{align*}X_{i}^{(p,s)}=-\sum_{j\in I_{i+1}} \frac{\displaystyle\prod_{k=1}^{{n+ 1}} (x_{n,j}-x_{n+ 1,k})}{\displaystyle\prod_{p\in I_{i+1}\setminus \{j\}} (x_{n,j}-x_{n,p})} (x_{n,j}-i-1)^sp(x_{n,1},\dots, x_{n,n})\varphi_{n,j},\end{align*}$$
where p is a polynomial symmetric in the alphabets
![]() $I_i$
.
$I_i$
.
We can identify p with a polynomial in the red dots at the bottom of the diagram, with the shifted variables
![]() $\{x_{n,j}-i\}_{j\in I_i}$
sent to the red dots on the corresponding strand with
$\{x_{n,j}-i\}_{j\in I_i}$
sent to the red dots on the corresponding strand with
![]() $i=\chi _j$
. We then send
$i=\chi _j$
. We then send
![]() $X_{i}^{(p)}$
to the element of
$X_{i}^{(p)}$
to the element of
![]() $\mathbb{E}_i$
, where we place the polynomial p applied to the red dots at the bottom of the diagram and “sandwich” s red dots on the middle strand of the ladder, with all black strands are straight vertical at positions determined by
$\mathbb{E}_i$
, where we place the polynomial p applied to the red dots at the bottom of the diagram and “sandwich” s red dots on the middle strand of the ladder, with all black strands are straight vertical at positions determined by
![]() $\lambda $
. That is,
$\lambda $
. That is,
We claim that this defines a map
First, let us match the completion ![]() with the completed polynomial ring
with the completed polynomial ring
![]() $\varprojlim \Gamma /\Gamma \mathsf {m}_\lambda ^N$
by matching
$\varprojlim \Gamma /\Gamma \mathsf {m}_\lambda ^N$
by matching
![]() $Y_r$
with
$Y_r$
with
![]() $x_{p,j}-\lambda _{p,j}$
if the rth strand from the left is the jth (from the left) with label p; let us simplify notation by writing
$x_{p,j}-\lambda _{p,j}$
if the rth strand from the left is the jth (from the left) with label p; let us simplify notation by writing
![]() $Y_{p,j}:=Y_r$
in this case. Under this isomorphism,
$Y_{p,j}:=Y_r$
in this case. Under this isomorphism,
![]() $X_i^{(p,s)}$
transforms to
$X_i^{(p,s)}$
transforms to
 $$\begin{align*}\mathscr{X}_{i}^{(p,s)}=-\sum_{j\in I_{i+1}} \frac{\displaystyle\prod_{k=1}^{{n+ 1}} (Y_{n,j}+\lambda_{n,j}-x_{n+ 1,k})}{\displaystyle\prod_{p\in I_{i+1}\setminus \{j\}} (Y_{n,j}-Y_{n,p})} (Y_{n,j})^sp(Y_{n,1}+\lambda_{n,1},\dots, Y_{n,n}+\lambda_{n,1})\varphi_{n,j}.\end{align*}$$
$$\begin{align*}\mathscr{X}_{i}^{(p,s)}=-\sum_{j\in I_{i+1}} \frac{\displaystyle\prod_{k=1}^{{n+ 1}} (Y_{n,j}+\lambda_{n,j}-x_{n+ 1,k})}{\displaystyle\prod_{p\in I_{i+1}\setminus \{j\}} (Y_{n,j}-Y_{n,p})} (Y_{n,j})^sp(Y_{n,1}+\lambda_{n,1},\dots, Y_{n,n}+\lambda_{n,1})\varphi_{n,j}.\end{align*}$$
This is exactly
![]() $C=\prod _{k=1}^{{n+ 1}} (Y_{n,j}+\lambda _{n,j}-x_{n+ 1,k})$
times the action in the polynomial representation of
$C=\prod _{k=1}^{{n+ 1}} (Y_{n,j}+\lambda _{n,j}-x_{n+ 1,k})$
times the action in the polynomial representation of
![]() $\mathbb{E}_i$
given the diagram on the left-hand side of (4.2) in Lemma 2.13. Multiplication by C commutes with the left and right actions on this bimodule, so this shows that the representations of bimodules match.
$\mathbb{E}_i$
given the diagram on the left-hand side of (4.2) in Lemma 2.13. Multiplication by C commutes with the left and right actions on this bimodule, so this shows that the representations of bimodules match.
This shows that (4.2) defines a homomorphism, which must be injective by the faithfulness of both representations. Obviously, every bare ladder is in the image of this map, so it must be surjective as well.
Corollary 4.14 The equivalence of Corollary 4.10 intertwines the action of the translation functors
![]() $E_i$
on
$E_i$
on
![]() $\mathcal {GT}_\chi $
and the bimodules
$\mathcal {GT}_\chi $
and the bimodules
![]() $\mathbb{E}_i$
on
$\mathbb{E}_i$
on
![]() ${\mathbb{\tilde {T}}}_\chi \operatorname {-mod}$
.
${\mathbb{\tilde {T}}}_\chi \operatorname {-mod}$
.
Together with Theorem 3.16, this establishes Theorem 2, completing the main results of the paper.
A The classification of orbits
by Jerry Guan and Ben Webster
In this appendix, we discuss the classification of orbits of
![]() $P_\chi $
on V, using the notation introduced earlier.
$P_\chi $
on V, using the notation introduced earlier.
Recall the definition of a
![]() $\chi $
-flavored multi-segment from Definition 3.1. A subsegment of
$\chi $
-flavored multi-segment from Definition 3.1. A subsegment of
![]() $\Omega $
is a subset S such that
$\Omega $
is a subset S such that
![]() $S=\{ (k,j_k),(k+1,j_{k+1}),\dots , (\ell ,j_{\ell })\} $
for a segment
$S=\{ (k,j_k),(k+1,j_{k+1}),\dots , (\ell ,j_{\ell })\} $
for a segment
![]() $(k,k+1,\dots , \ell )$
. A subsegment carries a canonical charge: if
$(k,k+1,\dots , \ell )$
. A subsegment carries a canonical charge: if
![]() $\ell < m$
, this requires no new information, and if
$\ell < m$
, this requires no new information, and if
![]() $\ell =m$
, then we use
$\ell =m$
, then we use
![]() $\chi _{j_{m}}$
as our flavor. A segmentation of the set
$\chi _{j_{m}}$
as our flavor. A segmentation of the set
![]() $\Omega $
is a partition of
$\Omega $
is a partition of
![]() $\Omega $
into subsegments. Every segmentation gives a choice of flavored multisegment.
$\Omega $
into subsegments. Every segmentation gives a choice of flavored multisegment.
Definition A.1 For each segmentation
![]() $\Sigma $
of
$\Sigma $
of
![]() $\Omega $
, there is a canonical map
$\Omega $
, there is a canonical map
![]() ${f_{\Sigma }\colon {\mathbb{C}}^\Omega \to {\mathbb{C}}^{\Omega }}$
sending
${f_{\Sigma }\colon {\mathbb{C}}^\Omega \to {\mathbb{C}}^{\Omega }}$
sending
![]() $f(b_{k,j_k})=b_{k+1,j_{k+1}}$
when
$f(b_{k,j_k})=b_{k+1,j_{k+1}}$
when
![]() $(k,j_{k})$
and
$(k,j_{k})$
and
![]() $(k+1,j_{k+1})$
lie in a subsegment together, and
$(k+1,j_{k+1})$
lie in a subsegment together, and
![]() $f(b_{k,j})=0$
if there is no element
$f(b_{k,j})=0$
if there is no element
![]() $(k+1,j')$
in the same subsegment.
$(k+1,j')$
in the same subsegment.
Lemma A.2 Every
![]() $G_{\chi }$
-orbit on V contains
$G_{\chi }$
-orbit on V contains
![]() $f_{\Sigma }$
for some segmentation
$f_{\Sigma }$
for some segmentation
![]() $\Sigma $
, and
$\Sigma $
, and
![]() $f_{\Sigma }$
and
$f_{\Sigma }$
and
![]() $f_{\Sigma '}$
are in the same orbit if and only if they have the same
$f_{\Sigma '}$
are in the same orbit if and only if they have the same
![]() $\chi $
-flavored multisegment. Thus, we have a bijection between
$\chi $
-flavored multisegment. Thus, we have a bijection between
![]() $G_{\chi }$
-orbits and
$G_{\chi }$
-orbits and
![]() $\chi $
-flavored multi-segments with the corresponding dimension vector.
$\chi $
-flavored multi-segments with the corresponding dimension vector.
Note that we can think this as a generalization of Gabriel’s theorem on the representations of type A quivers: if
![]() $v_{m-1}=0$
, then orbits correspond to isomorphism types of quiver representations, which are classified by multi-segments.
$v_{m-1}=0$
, then orbits correspond to isomorphism types of quiver representations, which are classified by multi-segments.
Proof Obviously, if two segmentations
![]() $\Sigma , \Sigma '$
correspond to the same
$\Sigma , \Sigma '$
correspond to the same
![]() $\chi $
-flavored multisegment, then there is a permutation
$\chi $
-flavored multisegment, then there is a permutation
![]() $\sigma $
of
$\sigma $
of
![]() $\Omega $
with
$\Omega $
with
![]() $\sigma (\Sigma )=\Sigma '$
which preserves the first index, such that if
$\sigma (\Sigma )=\Sigma '$
which preserves the first index, such that if
![]() $\sigma ((m,i))=(m,j)$
, then
$\sigma ((m,i))=(m,j)$
, then
![]() $\chi _i=\chi _j$
. The induced linear map
$\chi _i=\chi _j$
. The induced linear map
![]() ${\mathbb{C}}^{\Omega }\to {\mathbb{C}}^\Omega $
lies in
${\mathbb{C}}^{\Omega }\to {\mathbb{C}}^\Omega $
lies in
![]() $G_{\chi }$
and witnesses the fact that these are in the same orbit.
$G_{\chi }$
and witnesses the fact that these are in the same orbit.
Now, we turn to showing that if
![]() $\Sigma $
and
$\Sigma $
and
![]() ${\Sigma '}$
are segmentations, where
${\Sigma '}$
are segmentations, where
![]() $f_\Sigma $
and
$f_\Sigma $
and
![]() $f_{\Sigma '}$
are in the same orbit, then the corresponding
$f_{\Sigma '}$
are in the same orbit, then the corresponding
![]() $\chi $
-flavored multisegment is the same.
$\chi $
-flavored multisegment is the same.
We’ll prove this by induction on m. As before, let
![]() $f_{i;j}=f_{i-1}\dots f_j\colon {\mathbb{C}}^{v_j}\to {\mathbb{C}}^{v_i}$
. Consider the map
$f_{i;j}=f_{i-1}\dots f_j\colon {\mathbb{C}}^{v_j}\to {\mathbb{C}}^{v_i}$
. Consider the map
![]() $f_{m;1}\colon {\mathbb{C}}^{v_1}\to {\mathbb{C}}^{v_{m}}$
. The space
$f_{m;1}\colon {\mathbb{C}}^{v_1}\to {\mathbb{C}}^{v_{m}}$
. The space
![]() ${\mathbb{C}}^{v_{m}}$
has a unique finest partial flag that is invariant under
${\mathbb{C}}^{v_{m}}$
has a unique finest partial flag that is invariant under
![]() $P_\chi $
. This is of the form
$P_\chi $
. This is of the form
![]() $0\subset F_{p_1}\subset \cdots \subset F_{p_\ell }$
, where
$0\subset F_{p_1}\subset \cdots \subset F_{p_\ell }$
, where
![]() $p_k$
ranges over the integers which appear as values
$p_k$
ranges over the integers which appear as values
![]() $\chi _i$
. The dimension
$\chi _i$
. The dimension
![]() $\dim F_{p_k}/F_{p_{k-1}}=g_k$
is the number of indices i such that
$\dim F_{p_k}/F_{p_{k-1}}=g_k$
is the number of indices i such that
![]() $p_k=\chi _i$
. Thus, consider the flag
$p_k=\chi _i$
. Thus, consider the flag
For
![]() $f_\Sigma $
, obviously,
$f_\Sigma $
, obviously,
![]() $\dim f_{m;1}^{-1}(F_{p_1})/\ker f_{m;1}$
is the number of segments of the form
$\dim f_{m;1}^{-1}(F_{p_1})/\ker f_{m;1}$
is the number of segments of the form
![]() $(1,\dots , m)$
of charge
$(1,\dots , m)$
of charge
![]() $p_1$
, and
$p_1$
, and
![]() $\dim f_{m;1}^{-1}(F_{p_k})/f_{m;1}^{-1}(F_{p_{k-1}})$
is the number of charge
$\dim f_{m;1}^{-1}(F_{p_k})/f_{m;1}^{-1}(F_{p_{k-1}})$
is the number of charge
![]() $p_k$
. Since these dimensions are the same on orbits of
$p_k$
. Since these dimensions are the same on orbits of
![]() $G_{\chi }$
, the segmentations
$G_{\chi }$
, the segmentations
![]() $\Sigma $
and
$\Sigma $
and
![]() ${\Sigma '}$
must have the same number of segments of the form
${\Sigma '}$
must have the same number of segments of the form
![]() $(1,\dots , m)$
of each given charge.
$(1,\dots , m)$
of each given charge.
Similarly, the rank of the map
![]() $f_{m-1;1}\colon \ker f_{m;1}\subset {\mathbb{C}}^{v_1}\to {\mathbb{C}}^{v_{m-1}}$
is the number of segments of the form
$f_{m-1;1}\colon \ker f_{m;1}\subset {\mathbb{C}}^{v_1}\to {\mathbb{C}}^{v_{m-1}}$
is the number of segments of the form
![]() $(1,\dots , m-1).$
More generally, the rank of the map
$(1,\dots , m-1).$
More generally, the rank of the map
![]() $f_{k;1}\colon \ker f_{k+1;1}\subset {\mathbb{C}}^{v_1}\to {\mathbb{C}}^{v_{k}}$
gives the number of segments of the form
$f_{k;1}\colon \ker f_{k+1;1}\subset {\mathbb{C}}^{v_1}\to {\mathbb{C}}^{v_{k}}$
gives the number of segments of the form
![]() $(1,\dots , k)$
.
$(1,\dots , k)$
.
This shows that each flavored segment containing a 1 appears with the same multiplicity in the multisegments for
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma '$
. Thus, if
$\Sigma '$
. Thus, if
![]() $w,w'\subset {\mathbb{C}}^{\Omega }$
are the subrepresentations generated by
$w,w'\subset {\mathbb{C}}^{\Omega }$
are the subrepresentations generated by
![]() ${\mathbb{C}}^{v_1}$
under
${\mathbb{C}}^{v_1}$
under
![]() $f_\Sigma $
and
$f_\Sigma $
and
![]() $f_{\Sigma '}$
, the induced representations on
$f_{\Sigma '}$
, the induced representations on
![]() ${\mathbb{C}}^{\Omega }/W$
and
${\mathbb{C}}^{\Omega }/W$
and
![]() ${\mathbb{C}}^{\Omega }/W'$
are of the form
${\mathbb{C}}^{\Omega }/W'$
are of the form
![]() $f_{\bar {\Sigma }}$
and
$f_{\bar {\Sigma }}$
and
![]() $f_{\bar {\Sigma }'}$
for
$f_{\bar {\Sigma }'}$
for
![]() $\bar {\Sigma }$
and
$\bar {\Sigma }$
and
![]() $\bar {\Sigma }'$
segmentations obtained by throwing out all subsegments containing a
$\bar {\Sigma }'$
segmentations obtained by throwing out all subsegments containing a
![]() $(1,k)$
(and reindexing by decreasing all indices). By induction,
$(1,k)$
(and reindexing by decreasing all indices). By induction,
![]() $\bar {\Sigma }$
and
$\bar {\Sigma }$
and
![]() $\bar {\Sigma }'$
have the same flavored multisegment, so the same is true of
$\bar {\Sigma }'$
have the same flavored multisegment, so the same is true of
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma '$
.
$\Sigma '$
.
This shows that we have an injective map from flavored multi-segments with the right dimension vector to the set of orbits. Now, we need to show that this map is also surjective.
Consider the flag
Choose a ordered basis of
![]() ${\mathbb{C}}^{v_1}$
compatible with this flag, and let
${\mathbb{C}}^{v_1}$
compatible with this flag, and let
![]() $g_1\in GL({\mathbb{C}}^{v_1})$
be a matrix mapping this basis to
$g_1\in GL({\mathbb{C}}^{v_1})$
be a matrix mapping this basis to
![]() $b_{1,1},\dots , b_{1,v_1}.$
By construction, the non-zero images of this set under
$b_{1,1},\dots , b_{1,v_1}.$
By construction, the non-zero images of this set under
![]() $f_{k;1}$
form a linearly independent set, which span
$f_{k;1}$
form a linearly independent set, which span
![]() $\operatorname {image}(f_{k;1})$
compatibly with the intersection with the flag
$\operatorname {image}(f_{k;1})$
compatibly with the intersection with the flag
Thus, we can choose a basis of
![]() $\ker f_{3;2}\subset {\mathbb{C}}^{v_2}$
whose union with the non-zero images
$\ker f_{3;2}\subset {\mathbb{C}}^{v_2}$
whose union with the non-zero images
![]() $f(g_1^{-1}b_{1,*})$
is still linearly independent; we then in turn extend this in turn to bases of
$f(g_1^{-1}b_{1,*})$
is still linearly independent; we then in turn extend this in turn to bases of
to obtain a basis containing all non-zero vectors of the form
![]() $f_{1}(g_1^{-1}b_{1,*})$
which is compatible with the flag (A.1) in the case
$f_{1}(g_1^{-1}b_{1,*})$
which is compatible with the flag (A.1) in the case
![]() $k=2$
. Let
$k=2$
. Let
![]() $g_2$
be a matrix that maps this basis to
$g_2$
be a matrix that maps this basis to
![]() $b_{2,*}$
.
$b_{2,*}$
.
Now, apply the same process in
![]() ${\mathbb{C}}^{v_3}$
, to construct a basis compatible with the flag (A.1) in the case
${\mathbb{C}}^{v_3}$
, to construct a basis compatible with the flag (A.1) in the case
![]() $k=3$
, and so on to construct such a basis in
$k=3$
, and so on to construct such a basis in
![]() ${\mathbb{C}}^{v_{k+1}}$
compatible with
${\mathbb{C}}^{v_{k+1}}$
compatible with
![]() $f_k(g_k^{-1}b_{k,*})$
and the flag (A.1) in the general case, with
$f_k(g_k^{-1}b_{k,*})$
and the flag (A.1) in the general case, with
![]() $g_{k+1}$
mapping this to the standard basis.
$g_{k+1}$
mapping this to the standard basis.
Note that in
![]() ${\mathbb{C}}^{v_{m}}$
, this just gives a basis compatible with
${\mathbb{C}}^{v_{m}}$
, this just gives a basis compatible with
![]() $0\subset F_{p_1}\subset \cdots \subset F_{p_\ell }= {\mathbb{C}}^{v_{m}}$
; whereas for previous bases, we have been able to choose any bijection of our basis to the standard basis, we have to ensure that
$0\subset F_{p_1}\subset \cdots \subset F_{p_\ell }= {\mathbb{C}}^{v_{m}}$
; whereas for previous bases, we have been able to choose any bijection of our basis to the standard basis, we have to ensure that
![]() $g_{m}\in P_\chi $
, which is, of course, possible since our basis is compatible with the partial flag.
$g_{m}\in P_\chi $
, which is, of course, possible since our basis is compatible with the partial flag.
Thus, the bases
![]() $\{g_k^{-1}b_{k,*}\}$
satisfy the property that f sends each of these basis vectors to another basis vector or to 0. This shows that
$\{g_k^{-1}b_{k,*}\}$
satisfy the property that f sends each of these basis vectors to another basis vector or to 0. This shows that
![]() $(g_1^{-1},\dots , g_{m}^{-1})\cdot f=f_{\Sigma }$
for a segmentation
$(g_1^{-1},\dots , g_{m}^{-1})\cdot f=f_{\Sigma }$
for a segmentation
![]() $\Sigma .$
This completes the proof.
$\Sigma .$
This completes the proof.
Lemma A.3 Each of these orbits is
![]() $G_{\chi }$
-equivariantly simply connected.
$G_{\chi }$
-equivariantly simply connected.
Proof To show this, we only need to show that the stabilizer of
![]() $f_{\Sigma }$
in
$f_{\Sigma }$
in
![]() $G_{\chi }$
is simply connected.
$G_{\chi }$
is simply connected.
We can think about this stabilizer as follows. The element
![]() $g_1$
acting on
$g_1$
acting on
![]() ${\mathbb{C}}^{v_1}$
must preserve the flag (A.1), but otherwise can be chosen freely. This is a connected parabolic subgroup. This choice determines how
${\mathbb{C}}^{v_1}$
must preserve the flag (A.1), but otherwise can be chosen freely. This is a connected parabolic subgroup. This choice determines how
![]() $g_2$
acts on the image of f in
$g_2$
acts on the image of f in
![]() ${\mathbb{C}}^{v_2}$
, but on the complement U to this image (given by the span of the appropriate vectors), we can freely choose an isomorphism of U to itself compatible with the intersection with the flag (A.1) (again a connected parabolic), and any map
${\mathbb{C}}^{v_2}$
, but on the complement U to this image (given by the span of the appropriate vectors), we can freely choose an isomorphism of U to itself compatible with the intersection with the flag (A.1) (again a connected parabolic), and any map
![]() $U \to \operatorname {image}(f)$
compatible with this flag (a contractible set).
$U \to \operatorname {image}(f)$
compatible with this flag (a contractible set).
Applying this inductively, we find that the stabilizer is topologically a product of these parabolics (always connected) with affine spaces. Paying attention to the group structure, we have a product of general linear groups (with ranks given by the multiplicities with which given flavored segments appear) extended by a unipotent radical. Thus, as a quotient, the orbit is homotopic to a product of classifying spaces
![]() $BGL_{*}$
and, in particular, is simply connected.
$BGL_{*}$
and, in particular, is simply connected.
Index of Notation
This index of notation gives a brief description of the main notation used in the paper, together with the section and page where the notation is defined.