2. One-dimensional shallow water waves due to a source

Given a single body of length $L$ propelling itself forward using WDP, we wish to study the conditions to produce maximal forward thrust. We will consider a surface region where there is a pressure disturbance induced by the motion of the body. To begin, we will consider zero horizontal velocity $U$ of the body. This will be referred to as the start-up phase where a body is beginning to propel itself forward from rest. Following this, the horizontal velocity will be introduced in three different regimes: subcritical velocities ( $0\lt v\lt 1$ ), critical velocities ( $v=1$ ) and finally supercritical velocities ( $v\gt 1$ ), where $v=U/c$ is the drift velocity divided by the wave speed $c$ . The following work will operate in the shallow water regime where the wave speed is defined as $c=\sqrt {\textit{gH}}$ which means that our dimensionless velocity $v$ is related to two dimensionless numbers, the Froude number and the Mach number ${\textit{Fr}} = {U}/{\sqrt {\textit{gH}}} = {U}/{c} = {\textit{Ma}}$ .

As mentioned, we will operate within the shallow water approximation and a one-dimensional set-up as shown in figure 1. Mathematically, we enforce this to gain insight into the conditions for optimal thrust with a simplified linear model that allows us to focus purely on the surface waves and avoids complexities such as dispersive waves. Meanwhile, our model is also motivated physically by the larger-scale examples mentioned in § 1 in the case where there is a long aspect ratio ( $\textit{kH}\ll 1$ ).

Mathematically, a pressure source $P(x,t)$ is applied at the surface of an otherwise undisturbed body of shallow water where the fluid is in the region $0\leqslant z\leqslant H$ in the steady state. The source induces a perturbation, so the surface of the water is at $z=H+h(x,t)$ , where $h(x,t)\ll H$ . The shape of the surface perturbed by the pressure is encapsulated in $h(x,t)$ . Unlike the honeybee and the water strider which produce gravity-capillary waves, here, we focus on gravity waves and ignore the effect of surface tension.

Figure 1. Diagram of the shallow water set-up ( $\textit{kH}\ll 1$ ) where there is a pressure source $P(x,t)$ , over a region of length $L$ , acting on the surface of the shallow water, with depth $H$ . This induces waves on the fluid surface, denoted by $h(x,t)$ , resulting in locomotion with a drift velocity $U$ .

As described in Appendix A.1, the perturbed wave field $z=h(x,t)$ satisfies the one-dimensional wave equation

(2.1) \begin{equation} \frac {\partial ^2h}{\partial x^2} - \frac {1}{c^2}\frac {\partial ^2h}{\partial t^2} = -Q(x,t), \hspace {1cm} -\infty \lt x \lt \infty , \end{equation}

where $c=\sqrt {\textit{gH}}$ is the wave speed and $Q(x,t) = P_{xx}(x,t)/\rho g$ is the pressure source term. The source is defined to be non-zero in the region $x\in [-{L}/{2},{L}/{2} ]$ and zero outside this. Since this investigation is concerned with a single body undergoing periodic oscillations, with a frequency $\omega$ , the variables will be rescaled as follows:

(2.2) \begin{align} h, x \sim \frac {c}{\omega }, \quad t\sim \frac {1}{\omega }, \quad Q \sim \frac { \omega }{c}. \end{align}

After considering these scalings, we arrive at the dimensionless wave equation with a source,

(2.3) \begin{equation} \frac {\partial ^2h}{\partial x^2} - \frac {\partial ^2h}{\partial t^2} = -Q(x,t), \hspace {1cm} -\infty \lt x \lt \infty . \end{equation}

In dimensionless form, the source $Q$ is defined to be non-zero on the interval $[-{l}/{2},{l}/{2} ]$ , where $l$ is the dimensionless body length $l = L\omega /c$ . A periodically oscillating source and wave field are assumed, since there is a single body and the surface is otherwise undisturbed. Therefore, the source and wave field can be decomposed as follows:

(2.4) \begin{align} h(x,t) = \mathrm{Re}\big[\hat {h}(x)\textrm{e}^{\textit{it}}\big], \quad Q(x,t) = \mathrm{Re} \big[\hat {Q}(x)\textrm{e}^{\textit{it}}\big]. \end{align}

The above expressions in (2.4) are used to reduce the Partial Differential Equation (PDE) for $h(x,t)$ in (2.3) to an Ordinary Differential Equation (ODE) for the complex function  $\hat {h}(x)$

(2.5) \begin{equation} \hat {h}''(x)+\hat {h}(x) = -\hat {Q}(x). \end{equation}

The ODE has a general solution that is calculated using Green’s functions

(2.6) \begin{equation} \hat {h}(x) = \textit{A}\textrm{e}^{\textit{ix}} + \textit{B}\textrm{e}^{\textit{-ix}} + \frac {i}{2}\int ^{x}_{-\frac {l}{2}}\hat {Q}(X)\Big (\textrm{e}^{\text{i}\left (x-X\right )} - \textrm{e}^{\text{i}\left (X-x\right )}\Big )\,\mathrm{d}X, \end{equation}

where $A,B\in \mathbb{C}$ are constants to be found. We note that although there is a dependence on $x$ in the integral, for $x\gt {l}/{2}$ the upper bound will be ${l}/{2}$ since $\hat {Q}(X\gt {l}/{2})=0$ . Likewise for $x\lt - {l}/{2}$ the integral is zero since $\hat Q(X\lt -{l}/{2}) = 0$ . The following Sommerfeld boundary conditions will be used, where $k_{\pm }$ is the wavenumber:

(2.7) \begin{align} \hat {h}'\! \left (\pm \frac {l}{2}\right ) = \mp \textit{ik}_{\pm }\hat {h}\! \left (\pm \frac {l}{2} \right )\!, \end{align}

and $k_{\pm }=1$ for the start-up case. This is equivalent to imposing that waves only radiate away from the source. Through application of the boundary conditions, $A$ and $B$ are found to be

(2.8) \begin{align} A = -\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{-\textrm{i}X}\, \mathrm{d}X, \quad B = 0, \end{align}

and the resulting solution for the wave field is

(2.9) \begin{equation} \hat {h}(x) = -\frac {i}{2}\int ^{\frac {l}{2}}_{x}\hat {Q}(X)\textrm{e}^{i\left (x-X\right )}\,\mathrm{d}X - \frac {i}{2}\int ^{x}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{i\left (X-x\right )}\,\mathrm{d}X. \end{equation}

This solution is therefore composed only of a left-travelling wave for $x\lt - {l}/{2}$ and a right-travelling wave for $x\gt {l}/{2}$ .

The problem we aim to solve is to find a $\hat {Q}$ such that it gives maximal thrust. Therefore, an expression for the thrust is required. The thrust force is not immediately obvious to define but can be derived through manipulation of the wave equation (2.3) to recover the thrust as in (1.1) where a difference in fore–aft amplitude squared is indicative of a net flow of excess momentum in the horizontal direction of the larger wave. Multiplying (2.3) by $h_x$ and taking an integral with respect to $x$ (see Appendix A.2), we derive the following equivalence:

(2.10) \begin{equation} -\frac {1}{2}\big [k|\hat {h}|^2\big ]^{+}_{-} = \langle \hat {Q},\hat {h}'\rangle , \end{equation}

where the $+$ and $-$ symbols in (2.10) represent values for $x$ that are on the right- and left-hand side of the $[-{l}/{2},{l}/{2}]$ region respectively and $\langle \boldsymbol{\cdot },\boldsymbol{\cdot }\rangle$ is the time-averaged inner product defined as

(2.11) \begin{equation} \langle f,g\rangle := \frac {1}{T}\int ^{T}_{0}\int ^{\frac {l}{2}}_{-\frac {l}{2}} \textrm {Re}\big [f(x)\textrm{e}^{\textit{it}}\big ]\,\textrm {Re}\big [g(x)\textrm{e}^{\textit{it}}\big ]\,\textrm {d}x\,\textrm {d}t = \frac {1}{4}\int ^{\frac {l}{2}}_{-\frac {l}{2}} f\,g^{*} + f^{*}g\,\textrm {d}x. \end{equation}

The left-hand side of (2.10) has included differing fore–aft wavenumbers $k_{\pm }$ , but in the start-up case $k_+=k_- = 1$ . This will be more important when velocity is introduced to apply a correction due to the Doppler shift introduced through operating in the moving frame. Relating back to the radiation stress, we interpret (2.10) as an equivalence relation between the force injected and the resulting asymmetrical wave field that induces thrust. Motivated by (2.10) the time-averaged thrust is taken to be

(2.12) \begin{equation} \bar {F}_T \big (\hat {Q}(x)\big ) := \int ^{\frac {l}{2}}_{-\frac {l}{2}}\overline {Qh_x}\,\mathrm{d}x = \langle \hat {Q},\hat {h}'\rangle . \end{equation}

Some constraints will be required in the optimal control problem. One case that will be investigated is when the time-averaged power is bounded. To derive an expression for the power, we begin with the energy of the wave as the sum of the dimensionless kinetic and potential energy integrated over the whole domain

(2.13) \begin{equation} E(t) = \int ^{+}_{-} \left (\frac {1}{2}h_{t}^2+\frac {1}{2}h_x^2 \right ) \mathrm{d}x. \end{equation}

Power is given as $\mathrm{Pow} = {\mathrm{d}E}/{\mathrm{d}t}$ . Since we are working with periodic oscillations, the time-averaged power is $\overline {\mathrm{Pow}} =E(T) - E(0) = 0$ , which means the energy is conserved over a period. The right-hand side of (2.13) can be differentiated with respect to time and (2.3) is substituted and then time-averaged to generate another equivalence relationship (see Appendix A.3)

(2.14) \begin{equation} \int ^{\frac {l}{2}}_{-\frac {l}{2}} \overline {Qh_t}\, \mathrm{d}x =-\left [\overline {h_th_x}\right ]^{+}_{-}\!. \end{equation}

The average power injected by the pressure source on the left-hand side of (2.14) is related by equality to the average power radiated at the boundaries of the pressure source on the right-hand side of (2.14). Since this is an idealised system where no power inputted is lost due to external effects, this is expected. Motivated by (2.14) we take the time-averaged power injected to be

(2.15) \begin{equation} \overline {\mathrm{Pow}} := \int ^{\frac {l}{2}}_{-\frac {l}{2}} \overline {Qh_t}\, \,\mathrm{d}x= \langle \hat {Q},i\hat {h}\rangle . \end{equation}

Furthermore, we can substitute (2.4) into the right-hand side of (2.14) to show

(2.16) \begin{equation} \frac {1}{2}\big [k_{+}|\hat {h}_{+}|^2 + k_{-}|\hat {h}_{-}|^2\big ] = \langle \hat {Q},i\hat {h}\rangle . \end{equation}

As such, while the thrust is the difference in fore–aft amplitude squared, the power is the sum.

Now, we can proceed with posing the optimal control problem. In the work so far, the body is taken to be at rest. The thrust would introduce movement itself but, for now, we will restrict the problem to that of ‘start-up’, with the horizontal drift velocity close to zero, $U\approx 0$ .

3. Optimal locomotion on start-up

We wish to pose an optimal control problem to maximise the thrust as it is defined in (2.12). The control function $\hat {Q}(x)$ is in the expression for $\hat {h}(x)$ in (2.9) which implicitly enforces that the wave ODE (2.5) and its boundary conditions (2.7) must be satisfied. Some sort of regularisation to the problem is required. In this paper we will use two different constraints. Firstly we will bound the time-averaged norm of the control

(3.1) \begin{equation} \langle \hat {Q},\hat {Q}\rangle \leqslant \varepsilon , \end{equation}

for some dimensionless $\varepsilon \gt 0$ . Secondly, we will bound the time-averaged power, as it is seen in (2.15),

(3.2) \begin{equation} \langle \hat {Q},i\hat {h}\rangle \leqslant \delta , \end{equation}

for some dimensionless $\delta \gt 0$ . We define $\varepsilon = \hat {\varepsilon }c/\omega$ , $\delta = \hat {\delta }\omega/\rho g\!H^{2}c$ where $\hat {\varepsilon}, \hat {\delta}$ are dimensional bounds. It is worth noting that, neither constraint requires that $\hat {Q}$ be continuous at the boundary and jumps may be present at $x=\pm {l}/{2}$ .

Along with an analytical approach, a numerical optimisation approach is taken to validate the results using the Ipopt solver that is part of the JuMP package in Julia (Lubin et al. Reference Lubin, Dowson, Dias Garcia, Huchette, Legat and Vielma2023). To pose the problem numerically, the inputs are divided into variables, objective and constraints. There are four arrays of variables to represent the real and imaginary parts of $\hat {Q}$ and $\hat {h}$ which are discretised in space. The thrust (2.12), discretised using the trapezium rule, is the objective function we wish to maximise. As for the constraints, these are the boundary conditions (2.7), the discretised ODE for $\hat {h}(x)$ (2.5) and either the bounded norm of $\hat {Q}$ , or the bounded power. In the interest of comparing the analytical and numerical work, we take $\varepsilon ,\delta =1$ . These will be dealt with separately in the subsections that follow.

3.1. Case 1 – bounded norm

To be physically plausible, the source $Q$ can be regularised by bounding the $L_2$ norm which will provide us with well-behaved solutions for $\hat {Q}$ . In (3.1) the value $\varepsilon =1$ is taken to compare the analytical and numerical approaches. The variational calculus approach in Appendix B.1 results in the following condition to be an optimal solution:

(3.3) \begin{equation} \mathcal{L}_0\hat {Q} = 0, \end{equation}

where the (one-dimensional Helmholtz) differential operator $\mathcal{L}_0 = \partial _{xx} + \mathbb{I}$ applied to $\hat {Q}$ implies wave-like solutions

(3.4) \begin{equation} \hat {Q}(x) = D_{{L}}\,\textrm{e}^{\textit{ix}} +D_{\!{R}}\,\textrm{e}^{\textit{-ix}}, \end{equation}

where $D_{{L}},D_{\!{R}}\in \mathbb{C}$ . In Appendix B.1, we go a step further and find the constants $D_{{L}}$ and $D_{\!{R}}$ in terms of $\lambda$ , the Lagrange multiplier, which is also found. The constraint on the modulus squared of the constants is

(3.5) \begin{equation} \begin{aligned} |D_{{L}}|^2 = 4\left (l+\frac {l\sin ^2(l)}{(2\lambda -l)^2}+\frac {2\sin ^2(l)}{2\lambda -l}\right )^{-1}\!, \quad |D_{\!{R}}|^2 = |D_{{L}}|^2\frac {\sin ^2(l)}{(2\lambda -l)^2}, \end{aligned} \end{equation}

where $\lambda$ is

(3.6) \begin{equation} \lambda _{\pm } = \pm \frac {\sqrt {l^2- \sin ^2(l)}}{2}. \end{equation}

The $(\pm )$ in the expression for $\lambda$ corresponds to the choice of thrust direction. To move in the positive direction (right) corresponds to taking the negative part in $\lambda$ , thus maximising positive thrust. Since $\lambda$ is the Lagrange multiplier, $\lambda \in \mathbb{R}$ is required. We have the condition

(3.7) \begin{equation} l^2 - \sin ^2(l)\geqslant 0, \end{equation}

which is true for all real values of $l\gt 0$ , so $\lambda$ is always real. Hence, in (B9) we note $D_{{L}}$ and $D_{\!{R}}$ are related via multiplication by a real number meaning the two waves are in phase.

A periodic source $\hat {Q}$ that is composed of a left-travelling and/or right-travelling waves of this form will produce optimum thrust. There are infinitely many such solutions which differ by an arbitrary choice of phase $\mathrm{Arg}(D)$ . An example of one such $\hat {Q}(x)$ , found numerically, is displayed in figure 2 along with the resulting wave field, $\hat {h}(x)$ . In figure 2 we see a larger wave on the left-hand side which corresponds to positive thrust and hence start-up locomotion in the right-travelling direction is achieved.

Figure 2. (a) An example of a source, $\hat {Q}(x)$ , that results in the optimal thrust under the bounded norm constraint where $v=0$ and $l=3\pi /2$ . (b) The corresponding wave field, $\hat {h}(x)$ , under the same conditions.

The expressions for $|D_{{L}}|^2$ and $|D_{\!{R}}|^2$ in (3.5) are validated numerically for a given  $l$ . Using (B16) allows us to use the right and left waves to relate $|D_{{L}}|^2,|D_{\!{R}}|^2$ to the information we have on $\hat {Q}$ from the numerical result, which is one of infinite solutions that satisfy

(3.8) \begin{align} \left |\frac {1}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{-\text{i}X}\,\mathrm{d}X\right |^2 = \lambda ^2|D_{{L}}|^2, \quad \left |\frac {1}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{iX}\,\mathrm{d}X \right |^2 = \lambda ^2|D_{\!{R}}|^2. \end{align}

We note that $\lambda ^2|D_{{L}}|^2$ and $\lambda ^2|D_{\!{R}}|^2$ are related to the amplitude squared of the left- and right-travelling waves ( $|\hat {h}_{{L}}|^2,|\hat {h}_{{R}}|^2$ ), respectively. For $l=3\pi /2$ , the relative error between the analytical and numerical expressions was found to be $0.003\,\%$ for $\lambda |D_{{L}}|^2$ and $0.014\,\%$ for $\lambda ^2|D_{\!{R}}|^2$ . Given the aforementioned arbitrary choice of phase, the numerical scheme will converge to one of an infinite set of solutions. If we use (B16), we find the numerical values for $D_{{L}}$ and $D_{\!{R}}$ and use them in conjunction with (3.4) to demonstrate correspondence between the numerical and analytical results in figure 2.

The dependence of the expressions on the length scale $l$ , which is related to $\omega$ , motivates that we investigate how the resulting thrust depends on $l$ . The thrust can be written (see Appendix B.1) in terms of the constants that have been found

(3.9) \begin{equation} \bar {F}_T = \frac {1}{2}\big (\lambda ^2|D_{{L}}|^2 - \lambda ^2|D_{\!{R}}|^2\big ). \end{equation}

Plotting the force that results from the numerical optimisation, we see that it increases with $l$ (figure 3), which is a property we will return to in § 4.

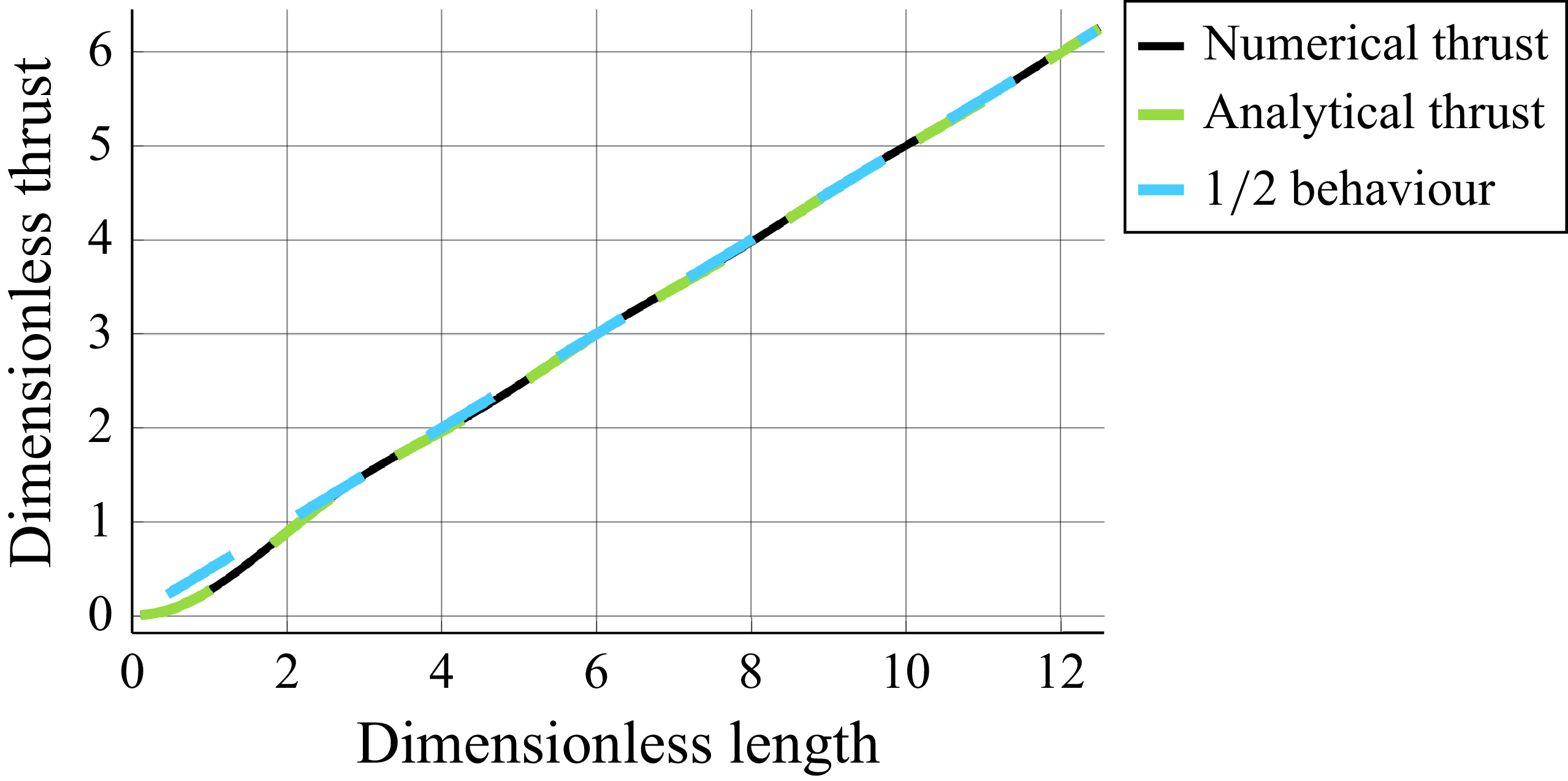
Figure 3. Plot of the time-averaged thrust $\bar {F}_T$ vs the dimensionless length scale $l$ resulting from the bounded norm optimisation on start-up $v\approx 0$ . It can also be seen that as $l$ increases, the dimensional thrust tends to scale with ${l}/{2}$ which is the same behaviour found in (3.9) for $l\gg 1$ .

We also note that the condition $|D_{\!{R}}|^2=0$ depends on $l$ in (3.5), resulting in

(3.10) \begin{align} \sin ^2(l) = 0 \,\implies \, l = n\pi , \end{align}

where $n\in \mathbb{N}$ . These points correspond to a discrete number of wavelengths being contained within the body region, i.e. a harmonic. Due to the thrust being written in terms of the difference in fore–aft amplitude squared and power being the sum, we see equality between the two in the absence of the front wave. This will have consequences on maximising efficiency as will be expanded upon in § 4.

3.2. Case 2 – bounded power

Rather than bounding the norm of $\hat {Q}$ , let us instead bound the power (2.15). A body on the water propelling itself through vertical oscillations has control over the power it inputs to generate thrust. Mathematically, the power is bounded by $\overline {\textrm {Pow}} \leqslant \delta$ , where $\delta =1$ is chosen for the following work. The variational calculus approach in Appendix B.2 is taken and the optimal condition is a first-order homogeneous ODE

(3.11) \begin{equation} \left (\partial _{x} + i\lambda \right )\left (\!-\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{i(X-x)}\,\mathrm{d}X - \frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{i(x-X)}\,\mathrm{d}X\right ) = 0, \end{equation}

which results in two solutions depending on the eigenvalue, $\lambda \in \mathbb{R}$ , which again corresponds to the Lagrange multiplier in the variational calculus. The two solutions for $\lambda$ will be denoted as $\lambda _1$ and $\lambda _2$ and the corresponding solutions to the ODE (3.11) are given as follows:

(3.12) \begin{align} C_{\!{L}}\,\textrm{e}^{\textit{ix}} + C_{\!{R}}\,\textrm{e}^{\textit{-ix}} = C\,\textrm{e}^{\textit{ix}}\quad &\textrm {for} \quad \lambda _{1}=-1, \end{align}

(3.13) \begin{align} C_{\!{L}}\,\textrm{e}^{\textit{ix}} + C_{\!{R}}\,\textrm{e}^{\textit{-ix}} = C\,\textrm{e}^{\textit{-ix}} \quad &\textrm {for} \quad \lambda _{2} = 1, \end{align}

where $C_{\!{L}},C_{\!{R}} \in \mathbb{C}$ . This gives us the option of a purely left- or purely right-travelling wave and to illuminate this fact, the left and right wave amplitudes have been labelled $C_{\!{L}}$ and $C_{\!{R}}$ , respectively. The constants are found, by equating coefficients, to be

(3.14) \begin{align} C_{\!{L}} = -\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{-\text{i}X}\,\mathrm{d}X, \quad C_{\!{R}} = -\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{iX}\,\mathrm{d}X. \end{align}

Similar to the bounded norm case, we can note that $C_{\!{L}}$ and $C_{\!{R}}$ correspond the fore–aft wave heights, respectively. Before making a choice of $\lambda$ and discussing that solution, we recall that the bounded power (2.15), when written in terms of the above constants, gives a condition on $|C_{\!{L}}|^2$ and $|C_{\!{R}}|^2$

(3.15) \begin{equation} \frac {1}{2}\big (\left |C_{\!{L}} \right |^2 + \left |C_{\!{R}}\right |^2\big ) = 1. \end{equation}

To achieve a positive thrust, a purely left-travelling wave is chosen ( $\lambda =-1$ ), meaning $C_{\!{L}} = C$ and $C_{\!{R}} = 0$ (see Appendix B.2). Using (3.15) the condition for optimal thrust is

(3.16) \begin{align} \left |-\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{-\text{i}X}\,\mathrm{d}X\right |^2 = 2, \quad \mathrm{and} \quad \left |-\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{iX}\,\mathrm{d}X\right |^2 = 0. \end{align}

These equations are two linear constraints on the function $\hat {Q}$ , constituting thus an underdetermined system. Therefore, there are infinitely many possible solutions that satisfy this. To verify that there is indeed a positive thrust, the conditions (3.16) are substituted into the thrust formula (2.12) to give

(3.17) \begin{equation} \bar {F}_T = 1. \end{equation}

This makes physical sense, since to get a motion in a right-travelling direction, a left-travelling wave would be required. The absence of a wave in the rightward direction agrees with this intuition since a wave on the right-hand side would reduce the difference in fore–aft amplitude squared and decrease the thrust while wasting a portion of the power injected.

Figure 4. (a) Resulting plots for the real and imaginary parts of the source $\hat {Q}$ for the bounded power case where ${U}/{c}=v=0$ and ${L\omega }/{c}= l=3\pi /2$ . (b) A similar plot for the wave field $\hat {h}$ for the same case. There is no wave on the right implying this is the optimum result to start and travel rightward.

To validate the numerical result with the analytical expression, we want to do something similar to what was done in § 3.1. This time, we have less information because the constraints do not give us information on $\hat {Q}$ like (3.8). Therefore, as an ansatz we will prescribe $\hat {Q}$ to be a step function of the form

(3.18) \begin{equation} \hat {Q} = \begin{cases} \alpha , & \textrm {if }\, x\in \big [-\frac {l}{2},0\big ), \nonumber\\[-12pt]\\ \beta , & \textrm {if }\, x\in \big [0,\frac {l}{2}\big ], \nonumber\\[-12pt]\\ 0, & \textrm {otherwise}, \end{cases} \end{equation}

and use the numerical optimisation to find $\alpha , \beta \in \mathbb{C}$ which can then be used to validate $\hat {h}$ . This will show that there is no wave on the right-hand side as is the case in (3.16). Given the step function in figure 4, the wave field is found analytically and numerically and their comparison is demonstrated in figure 4. To fully validate the result, the condition for the left-travelling wave in (3.16) and the thrust (3.17) are compared using relative error, which were within $0.008\,\%$ and $0.007\,\%$ , respectively. To validate the right-hand wave, the relative error is undefined since the value we are comparing with is zero. We will instead present the absolute difference in the numerical value, which is $5.9\times 10^{-8}$ . Given the prescribed step function can be substituted into (3.16), we can get constraints on $\alpha$ and $\beta$ . However, we leave this calculation for § 4.2 in the case of general subcritical $v$ .

4. Subcritical motion $\boldsymbol{0\lt v \lt 1}$

Up to now, all that has been considered is the start-up case. This section will introduce a velocity $U$ as in figure 1. In dimensionless form, the source is moving at a velocity $v = {U}/{c}$ . The body velocity is scaled by the velocity of the waves emitted $c$ such that the Froude number can be interpreted like a Mach number, ${\textit{Fr}} = {U}/{\sqrt {\textit{gH}}} = {U}/{c} = {\textit{Ma}}$ . With this scaling, the dimensionless velocity is split into three different regimes: subcritical velocities ( $0\lt v\lt 1$ ) where the source is travelling slower than the waves it emits, supercritical velocities ( $v\gt 1$ ) where the source moves quicker than the waves it produces and the critical velocity ( $v=1$ ). We will discuss the latter two in §§ 6 and 5, respectively. To begin, we will rewrite the optimisation problem to include a subcritical velocity and discuss the two choices of bound similar to the previous section.

As was the case in § 3, the assumption of a periodic source is applied. Due to a moving body in a static frame, expressions for the wave field and the source are

(4.1) \begin{align} h(x,t) = \mathrm{Re}\big [\hat {h}(x-vt)\textrm{e}^{\textit{it}}\big ], \quad Q(x,t) = \mathrm{Re}\big [\hat {Q}(x-vt)\textrm{e}^{\textit{it}}\big ]. \end{align}

A Galilean transformation is applied to work in the rest frame of the source. The Galilean transformation will define new spatial and temporal coordinates $\tilde {x}$ and $\tilde {t}$

(4.2) \begin{align} \tilde {x} = x-vt \quad \tilde {t} = t. \end{align}

As such, the PDE in (2.3) is reduced to a modified ODE

(4.3) \begin{equation} (1-v^2)\hat {h}''(\tilde {x}) + 2iv\hat {h}'(\tilde {x}) +\hat {h}(\tilde {x}) = -\hat {Q}(\tilde {x}). \end{equation}

This is solved with the same Green’s function approach as before

(4.4) \begin{equation} \hat {h}(\tilde {x}) = \textit{A}\textrm{e}^{\frac {i\tilde {x}}{1+v}} + \textit{B}\textrm{e}^{-\frac {i\tilde {x}}{1-v}} + \frac {i}{2}\int ^{\tilde {x}}_{-\frac {l}{2}}\hat {Q}(X)\left (\textrm{e}^{\frac {\text{i}\left (\tilde {x}-X\right )}{1+v}} - \textrm{e}^{\frac {\text{i}\left (X-\tilde {x}\right )}{1-v}}\right )\mathrm{d}X, \end{equation}

where $A,B\in \mathbb{C}$ are constants to be found. Sommerfeld boundary conditions will be used again, but they now take a Doppler-shifted form

(4.5) \begin{align} \hat {h}'\left (\pm \frac {l}{2}\right ) = \mp \textit{ik}_{\pm }\hat {h}\left (\pm \frac {l}{2} \right )\!, \end{align}

where $k_+ = {1}/({1-v})$ , $k_- = {1}/({1+v})$ are the right- and left-travelling Doppler-shifted wavenumbers, respectively. The resulting wave field is given by

(4.6) \begin{equation} \hat {h}(\tilde {x}) = -\frac {i}{2}\int ^{\frac {l}{2}}_{\tilde {x}}\hat {Q}(X)\textrm{e}^{\frac {\text{i}\left (\tilde {x}-X\right )}{1+v}}\,\mathrm{d}X - \frac {i}{2}\int ^{\tilde {x}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{\frac {\text{i}\left (X-\tilde {x}\right )}{1-v}}\,\mathrm{d}X. \end{equation}

An equivalent expression for the thrust can be derived (see Appendix A.2) using the same method as was done to get (2.10) and $\bar {F}_T$ will be as in (2.12). In this case $k_{\pm }$ are the same as in (4.5) and are interpreted as a correction due to the Doppler shift in the moving frame. Similarly, the time-averaged power in the moving case can be found. Following the steps taken in Appendix A.3, the resulting expression for the time-averaged injected power is

(4.7) \begin{equation} \overline {\mathrm{Pow}} = \langle \hat {Q},i\hat {h}\rangle - v\langle \hat {Q},\hat {h}'\rangle , \end{equation}

where the second term is proportional to the thrust as in (2.12).

Given that we have the power and thrust, the efficiency $\eta$ can be discussed next. The efficiency will tell us how much of the injected power is used as thrust. In dimensionless form, all that is required is (2.12) and (4.7) to provide this information

(4.8) \begin{equation} \eta = \frac {\bar {F}_T}{\overline {\mathrm{Pow}}} = \frac {\langle \hat {Q},\hat {h}'\rangle }{\langle \hat {Q},i\hat {h}\rangle - v\langle \hat {Q},\hat {h}'\rangle }. \end{equation}

Note that, in dimensional form, we see that the efficiency is given as $\eta = \bar {F}_T\boldsymbol{\cdot }c/\overline {\mathrm{Pow}}$ , because the energy is being radiated at speed $c$ . In the start-up case, where the power was bounded to be $\overline {\mathrm{Pow}} = 1$ the resulting force was $\bar {F}_T=1$ . Hence, the efficiency is $\eta =1$ when $\hat {Q}$ is optimised. If we had a purely symmetric source, the difference in fore–aft amplitude squared would be zero, resulting in $\bar {F}_T=0$ and hence $\eta =0$ . We will revisit the efficiency in the discussion of the results for the bounded norm and power in the subcritical case.

4.1. Case 1 – bounded norm

Similar to the start-up case (§ 3.1), an analytical approach shows us that to be an optimal solution the source $\hat {Q}(\tilde {x})$ must satisfy

(4.9) \begin{equation} \mathcal{L}_v\hat {Q} = 0, \end{equation}

where $\mathcal{L}_v = (1-v^2)\partial _{\tilde {x}\tilde {x}} + 2iv\partial _{\tilde {x}} +\mathbb{I}$ . This means that the source must be composed of a rightward and leftward Doppler-shifted wave

(4.10) \begin{equation} \hat {Q}(\tilde {x}) = D_{{L}}\textrm{e}^{\frac {\text{i}\tilde {x}}{1+v}}+D_{\!{R}}\textrm{e}^{-\frac {\text{i}\tilde {x}}{1-v}}, \end{equation}

where conditions on $D_{{L}},D_{\!{R}}\in \mathbb{C}$ are found in Appendix B.1. These are summarised as follows:

(4.11) \begin{equation} |D_{{L}}|^2 = 4\left (l+\frac {l(1-v^2)^2}{\left (2\lambda (1-v)-l\right )^2}\sin ^2\! \left (\frac {l}{1-v^2}\right )+\frac {2(1-v^2)^2}{2\lambda (1-v)-l}\sin ^2\! \left (\frac {l}{1-v^2}\right )\right )^{-1}\!, \end{equation}

(4.12) \begin{equation} |D_{\!{R}}|^2 = \frac {|D_{{L}}|^2(1-v^2)^2}{\big (2(1-v)\lambda -l\big )^2}\sin ^2\! \left (\frac {l}{1-v^2}\right )\!. \end{equation}

Again, $\lambda \in \mathbb{R}$ is the Lagrange multiplier associated with the variational calculus, with eigenvalues

(4.13) \begin{equation} \lambda _{\pm } = \frac {vl \pm \sqrt { l^2 - (1-v^2)^3\sin ^2\! \left (\dfrac {l}{1-v^2}\right )}}{2(1-v^2)}. \end{equation}

It is worth noting than given $\lambda \in \mathbb{R}$ , the constants $D_{{L}}$ and $D_{\!{R}}$ are in phase as they are related via multiplication by a real scalar (see (B9)). As was the case on start-up, the negative sign is taken to maximise the thrust for a body moving in the positive (right) direction. We validate that $\lambda \in \mathbb{R}$ , since

(4.14) \begin{equation} l^2-(1-v^2)^3\sin ^2\left (\frac {l}{1-v^2}\right )\geqslant 0, \end{equation}

is satisfied for all real $l,v\gt 0$ .

Figure 5. (a) Comparison between the analytically and numerically calculated left and (b) right wave amplitudes squared for $l=3\pi /2$ over both subcritical and supercritical velocities. For the right wave, the numerical scheme becomes unstable close to $v=1$ and hence it has been hatched.

The expressions for $D_{{L}}$ and $D_{\!{R}}$ can be validated numerically. Using (B16) we recover $\lambda ^2|D_{{L}}|^2$ and $\lambda ^2|D_{\!{R}}|^2$ in a similar way to (3.8), we show correspondence within $0.221\,\%$ and $0.0005$ , respectively. The latter error is an absolute value since the right wave can have zero amplitude. This is reflected in figures 5(a) and 5(b).

In the moving frame a Doppler shift contracts and stretches the right and left waves respectively in (4.10). In figure 5(b) we note that the forward wave appears to have zero amplitude at certain subcritical values of $v$ . This relates back to the harmonics introduced in § 3.1 where a discrete number of half-waves can be contained in the body region. Using (4.12), we find

(4.15) \begin{equation} \sin ^2\left (\frac {l}{1-v^2}\right ) = 0 \,\implies \, v = \left (1- \frac {l}{n\pi }\right )^{\frac {1}{2}}\!. \end{equation}

The positive square root is taken to study right-travelling subcritical velocities. The subcritical harmonics can be found for all $n\gt {l}/{\pi }$ and are plotted in figure 5(b). The first harmonic may occur at $n\gt 1$ in the case $l\gt \pi$ as seen when $l=3\pi /2$ .

We now have two different ways of finding harmonics, by varying the length or by varying the velocity. Both of these achieve the same phenomenon. Since there is no forward wave in some conditions, we ask, is there an optimal $l$ for a given $v$ ? The contour plots in figure 6 best illuminate that the same trend as in figure 3 continues for subcritical values of $v$ . For a given $v$ , maximal thrust is achieved at maximal $l$ . However, there is an interesting behavioural difference between smaller and larger length scales. For a fixed  $l$ that is large, the force is maximal close to $v=0$ , but as we shrink the length scale, the optimum begins to move towards $v=1$ , which is demonstrated in figure 6(b). For a given short $l$ , the time-averaged thrust may be non-monotonic with velocity, which is demonstrated in the subcritical part of figure 7(b). The efficiency is also plotted showing that $\eta =1$ is achieved for a small set of velocities close to $v=1$ for small $l$ . This will be shown in greater detail in § 6.

Figure 6. (a) Contour plot where colour corresponds to the magnitude of the force. For a given $v$ , a larger time-averaged thrust can be achieved with a larger $l$ . (b) The same heat map over a range of smaller $l$ denoted by the red box in (a) to convey the trend for smaller length scales, demonstrating maximal thrust at dimensionless velocities closer to 1.

Figure 7. (a) Time-averaged thrust over velocities from $v=0$ to $v=3$ for $l=3\pi /2$ . The efficiency is also plotted on the right axis showing the reduction after the last harmonic. (b) A similar plot for $l=\pi /6$ demonstrates that the region of maximal efficiency reduces due to the last and first harmonics being closer to $v=1$ for smaller values of $l$ .

4.2. Case 2 – bounded power

The general approach taken while moving is the same as it is in the start-up case. The variational calculus approach (Appendix B.2) produces two results depending on the choice of the solution for the Lagrange multiplier, $\lambda$ ,

(4.16) \begin{align} C_{\!{L}}\,\textrm{e}^{\frac {i\tilde {x}}{1+v}} + C_{\!{R}}\,\textrm{e}^{-\frac {\text{i}\tilde {x}}{1-v}} = C\,\textrm{e}^{\frac {\text{i}\tilde {x}}{1+v}} \quad &\textrm { for } \quad \lambda _1 = -1, \end{align}

(4.17) \begin{align} C_{\!{L}}\,\textrm{e}^{\frac {\text{i}\tilde {x}}{1+v}} + C_{\!{R}}\,\textrm{e}^{-\frac {\text{i}\tilde {x}}{1-v}} = C\,\textrm{e}^{-\frac {\text{i}\tilde {x}}{1-v}} \quad &\textrm { for } \quad \lambda _2 = 1 , \end{align}

where

(4.18) \begin{align} C_{\!{L}} = -\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{-\frac {\text{i}X}{1+v}}\,\textrm {d}X,\quad & C_{\!{R}} = -\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{\frac {\text{i}X}{1-v}}\,\textrm {d}X. \end{align}

The choice of $\lambda$ governs whether we are going to maximise the thrust in the positive or negative direction. Given that the subcritical velocity is positive ( $0\lt v\lt 1$ ), to maximise thrust in the positive direction, $\lambda _1$ is chosen. Using (4.16), $C_{\!{L}}=C$ and $C_{\!{R}}=0$ . The power constraint (4.7) is then used to give

(4.19) \begin{align} \left |-\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{-\frac {\text{i}X}{1+v}}\,\textrm {d}X\right |^2 = 2(1+v), \quad & \left |-\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{\frac {\text{i}X}{1-v}}\,\textrm {d}X\right |^2 = 0, \end{align}

and this can be used to show that, for all subcritical $v$ ,

(4.20) \begin{equation} \bar {F}_T = \frac {1}{2}\left (\frac {1}{1+v}\left |C_{\!{L}}\right |^2 - \frac {1}{1-v}\left |C_{\!{R}}\right |^2\right ) = 1. \end{equation}

The above results can be verified numerically over the interval $0\leqslant v\lt 1$ . The condition for the left-travelling wave (4.19) was tested and the infinity norm of the relative error at each point sampled was taken to show that all the points were within $0.0010\,\%$ . Through a similar test the force (4.20) was shown to be within $0.0011\,\%$ . As discussed in § 3.2, the right-hand wave condition of zero (4.19) does not permit the calculation of the relative error so we will just provide the infinity norm of the absolute difference between the analytical and numerical solution, which is $1.11\times 10^{-5}$ .

This is a very general solution since there are infinite solutions for $\hat {Q}$ that satisfy (4.19). It is also interesting that we are free to choose any $l$ and still maintain an optimal solution that has $\bar {F}_T = 1$ . This corresponds to an efficiency of $\eta =1$ since the power and force are found to be equal.

To shed some light onto what an example solution would look like, we will return to the example used in § 3.2 where $\hat {Q}(\tilde {x})$ is defined as a step function in the non-zero domain (3.18). The conditions (4.19) become

(4.21) \begin{align} \left |-\frac {i}{2}\left (\alpha \int ^{0}_{-\frac {l}{2}} \textrm{e}^{-\frac {\text{i}X}{1+v}}\,\textrm {d}X+\beta \int ^{\frac {l}{2}}_{0} \textrm{e}^{-\frac {\text{i}X}{1+v}}\,\textrm {d}X\right )\right |^2 &= 2(1+v), \end{align}

(4.22) \begin{align} \left |-\frac {i}{2}\left (\alpha \int ^{0}_{-\frac {l}{2}} \textrm{e}^{\frac {\text{i}X}{1-v}}\,\textrm {d}X + \beta \int ^{\frac {l}{2}}_{0} \textrm{e}^{\frac {\text{i}X}{1-v}}\,\textrm {d}X\right )\right |^2&=0. \end{align}

Equation (4.22) gives us

(4.23) \begin{equation} \alpha = \beta\! \left (\frac {1-\textrm{e}^{\frac {il}{2(1-v)}}}{1-\textrm{e}^{-\frac {il}{2(1-v)}}} \right ) = \beta \zeta , \end{equation}

where $\zeta \in \mathbb{C}$ . This can be substituted back into (4.21) to show that

(4.24) \begin{equation} |\beta |^2 = 4\left (\left |\zeta \left (1-\textrm{e}^{\frac {il}{2(1+v)}}\right ) + \textrm{e}^{-\frac {il}{2(1+v)}} -1\right |^2\right )^{-1}\!. \end{equation}

If we wish to prescribe that $\hat {Q}$ be a step function of this form, the constants $\alpha$ and $\beta$ are constrained to satisfy the condition on their modulus squared, and are only defined up to an arbitrary phase, similar to the bounded norm case. In contrast to the bounded norm case, there is a phase difference between $\alpha$ and $\beta$ since $\zeta \in \mathbb{C}$ .

5. The critical case ( $\boldsymbol{v=1}$ )

In order to study the whole range of velocities, the critical velocity case ( $v=1$ ) must be studied separately. This is a simple case because (4.3) reduces to a first-order ODE

(5.1) \begin{equation} 2i\hat {h}'(\tilde {x}) +\hat {h}(\tilde {x}) = -\hat {Q}(\tilde {x}). \end{equation}

The sole boundary condition required is that the fluid to the right of the body is unperturbed, since the body is now moving as quickly as the waves that it emits. The boundary condition takes the form

(5.2) \begin{align} \hat {h}= 0: \,\,\,\tilde {x} \gt \frac {l}{2}. \end{align}

The resulting particular solution for the wave field $\hat {h}(\tilde {x})$ is

(5.3) \begin{equation} \hat {h}(\tilde {x}) = -\frac {i}{2}\int ^{\frac {l}{2}}_{\tilde {x}} \hat {Q}(X)\textrm{e}^{\frac {\text{i}(\tilde {x}-X)}{1+v}}\,\mathrm{d}X, \end{equation}

where $v=1$ . Given this expression for $\hat {h}$ , we can recover the scaled thrust as done previously

(5.4) \begin{equation} \frac {1}{2}k_{-}|\hat {h}_{-}|^2 = \langle \hat {Q},\hat {h}'\rangle , \end{equation}

where $k_{-}={1}/({1+v})$ is the wavenumber for the left-travelling wave with amplitude $|\hat {h}_{-}|$ . This is the same form as (2.10), but the fore wave is zero.

The same analytical and numerical methods are used as the subcritical case and we will briefly outline the results. In the bounded norm case there will only be a wave in the aft direction which from the variational calculus is generated by $\hat {Q}$ such that

(5.5) \begin{equation} \hat {Q}(\tilde {x}) = D_{{L}}\textrm{e}^{\frac {\text{i}\tilde {x}}{2}}, \end{equation}

where $D_{{L}}$ is found to satisfy

(5.6) \begin{equation} |D_{{L}}|^2 = \frac {4}{l}. \end{equation}

Since there is no forward wave, we will not study the harmonics discussed in the subcritical case. Efficiency of $\eta =1$ is always achieved in this case. The Lagrange multiplier is found to be $\lambda = -{l}/{4}$ and the condition in (5.6) can be tested using expressions found in a similar way to (B16) and $\lambda ^2|D_{{L}}|^2$ is found to have a relative error of $0.0002\,\%$ .

For the bounded power case, the condition is the first equation in (4.19) when $v=1$ (the second condition is automatically satisfied due to the impossibility of a wave on the right-hand side). Hence, our condition is

(5.7) \begin{equation} \Bigg |-\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}} \hat {Q}(X)\textrm{e}^{-\frac {\text{i}X}{2}}\,\mathrm{d}X\Bigg |^2 = 4. \end{equation}

The resulting force is again $\bar {F}_T =1$ . These two results are validated with the numerical approach with relative errors of $0.037\,\%$ and $6.07\times 10^{-12}\,\%$ , respectively.

6. Supercritical motion $\boldsymbol{v\gt 1}$

The final part of our study is the supercritical velocity regime. If we recall, the dimensionless velocity, $v=U/c$ , is the ratio of the body velocity and the emitted wave velocity. The $v\gt 1$ case, corresponds to the body moving faster than the waves that it emits. Hence, any wave emitted will immediately be overtaken by the body. Similar to the subcritical case, a Galilean transformation into the moving frame is done using the transformation in (4.2).

The radiative boundary conditions applied in §§ 3 and 4 are no longer suitable because no wave can possibly propagate on the right-hand side and the left-hand side will be composed of two waves of differing wavenumbers. We can use the fact that there is no wave on the right to our advantage by applying the following boundary conditions:

(6.1) \begin{align} \hat {h} = \hat {h}' = 0: \,\,\, \tilde {x} \gt \frac {l}{2}. \end{align}

The Green’s function approach to solving (4.3) is applied again to calculate the solution for the wave field, $\hat {h}(\tilde {x})$ ,

(6.2) \begin{equation} \hat {h}(\tilde {x}) = -\frac {i}{2}\int ^{\frac {l}{2}}_{\tilde {x}} \hat {Q}(X)\textrm{e}^{\frac {\text{i}(\tilde {x}-X)}{1+v}}\,\textrm {d}X +\frac {i}{2}\int ^{\frac {l}{2}}_{\tilde {x}} \hat {Q}(X)\textrm{e}^{\frac {\text{i}(\tilde {x}-X)}{v-1}}\,\textrm {d}X, \end{equation}

where we have swapped $-(1-v)$ with $v-1$ to emphasise that this solution is now composed of two left-travelling waves in the rest frame of the body.

A similar approach of recovering the thrust as in Appendix A.2 is applied. The following equivalence relation is recovered:

(6.3) \begin{equation} -\frac {1}{2}\big [k|\hat {h}|^2\big ]^{\rightarrow }_{\leftarrow } = \langle \hat {Q},\hat {h}'\rangle , \end{equation}

where $\rightarrow$ and $\leftarrow$ denote the right- and left-travelling waves in the rest frame, respectively. This choice of notation represents a subtlety of the supercritical case where both waves are left-travelling waves in the moving frame. But once we translate back into the rest frame, there is a forward and backwards wave. As such, $k$ represents the Doppler-shifted wavenumber in the moving frame where $k_{\leftarrow }= {1}/({1+v})$ and $k_{\rightarrow } = {1}/({v-1})$ .

Variational calculus is undertaken in a similar way to the subcritical case. The bounded norm and power cases will be studied again, but since there are only minor changes, rather than being split into sections, we simply summarise the results.

In the bounded norm case the optimal condition again is that $\hat {Q}(\tilde {x})$ is composed of wave-like parts as was the case in (4.10). This time the corresponding $|D_{{L}}|^2$ , $|D_{\!{R}}|^2$ and $\lambda$ are

(6.4) \begin{equation} |D_{{L}}|^2 = 4\left (l+\frac {l(v^2-1)^2}{\left (2\lambda (v-1)-l\right )^2}\sin ^2\! \left (\frac {l}{v^2-1}\right )+\frac {2(v^2-1)^2}{2\lambda (v-1)-l}\sin ^2\! \left (\frac {l}{v^2-1}\right )\right )^{-1}\!, \end{equation}

(6.5) \begin{equation} |D_{\!{R}}|^2 = \frac {|D_{{L}}|^2(v^2-1)^2}{\big (2(v-1)\lambda -l\big )^2}\sin ^2\! \left (\frac {l}{v^2-1}\right )\!, \end{equation}

(6.6) \begin{equation} \lambda _{\pm } = \frac {l \pm \sqrt {v^2l^2 - (v^2-1)^3\sin ^2\! \left (\dfrac {l}{v^2-1}\right )}}{2(v^2-1)}. \end{equation}

Similar to before, to maximise the force in the positive direction, the negative sign is taken in the expression for $\lambda \in \mathbb{R}$ . The analytical and numerical results are verified as they were in the subcritical case. Previously, we saw the forward wave demonstrates harmonic behaviour where at certain velocities it has zero amplitude. Using the fact that $\sin ^2(l/(v^2-1)) = \sin ^2(l/(1-v^2))$ , we solve for harmonic velocities in (6.5)

(6.7) \begin{align} \sin ^2\left (\frac {l}{1-v^2}\right ) = 0 \, \implies\,v = \left (1-\frac {l}{n\pi }\right )^{\frac {1}{2}}\!, \end{align}

and we see that supercritical harmonics are for all integers $n\lt 0$ while subcritical harmonics were for all integers $n\gt {l}/{\pi }$ .

We have shown that for a given $l$ , we can find values of $v$ for which the forward wave will be zero. Inspired by the bounded power results, we can use this to our advantage in the interest of efficiency. For supercritical velocities this will be

(6.8) \begin{equation} \eta = \frac {\bar {F}_T}{\overline {\mathrm{Pow}}} = \frac {-2(v-1)\lambda ^2|D_{\!{R}}|^2 + 2(1+v)\lambda ^{2}|D_{{L}}|^2}{2(v-1)\lambda ^2|D_{\!{R}}|^2 + 2(1+v)\lambda ^{2}|D_{{L}}|^2}. \end{equation}

It is clear from (6.8) that $|D_{\!{R}}|=0$ will produce maximal efficiency (see figure 7 a at the values of $v$ where $\eta =1$ ) which is achieved by wasting no power on the wave that inhibits thrust. For supercritical harmonics, the largest harmonic velocity will always be found at $n=-1$ . Both waves are now getting stretched behind the raft and $n=-1$ corresponds to the point where the source has been stretched to only have one half-wavelength within the body length. Past this velocity, there is a decline in thrust because there is insufficient oscillation along the body length. A longer body will be able to contain more than half a wavelength for larger velocities as the contrast between figures 7(a) and 7(b) demonstrates.

In contrast, the bounded power case will continue to follow the same result in (4.19) where the only change is a ${i}/{2}$ rather than $-({i}/{2})$ preceding the second integral. Since the absolute value is taken, this has no effect. After inserting these optimal conditions into the expressions for the force, we find that $\bar {F}_T=1$ still holds. Hence, the bounded power case results in $\eta =1$ for all $v\gt 0$ . The ansatz (3.18) can be used again here but we do not include the results since they are similar.

7. Quasi-periodic theory for a changing $\boldsymbol{v}$

We have studied the optimal solution for a given velocity and found that in the bounded power case the time-averaged thrust is a constant ( $\bar {F}_T=1$ ). All this work has been done in the absence of acceleration. We can now ask if we could create a model that introduces a small acceleration to move between different velocities while maintaining the optimal solution and the assumption that the waves are periodic? A dimensional acceleration such that $\dot {U}\ll \omega c$ , permits the use of the previous results where acceleration can be interpreted as changing from one moving frame to the next.

In order to make sense of moving between different velocities, the cruising velocity  $v_\star$ must be known. For a given set of conditions, the thrust $F_T$ and drag $F_D$ appear in Newton’s second law

(7.1) \begin{equation} m\ddot {X} = F_{T}-F_{D}, \end{equation}

where $X(t)$ is the horizontal position. Our work thus far has been in a time-averaged setting. With a similar treatment here, the inertial term cancels out over a period leaving us with $\bar {F}_{T}=\bar {F}_{D}$ . Focusing purely on WDP, the result from bounding the power will be used to create the force balance with drag and the intercept will be $v_{\star }$ . The form of $v_\star$ can then be used to understand how slowly varying the parameters of the problem can be used to move from $v=0$ to $v\gt 1$ .

To find $v_\star$ , we need to introduce a drag force. It is important to note that the true drag may contain contributions from wave drag, form drag due to shape and shallow water resonance, but we skip these details here since they are not the focus of the study. Instead, we use a simple drag law to demonstrate how the force changes with velocity. Therefore, the dimensional drag will be considered to be

(7.2) \begin{equation} \bar {F}_{D} = \frac {1}{2}C_{D} \rho U^2 L, \end{equation}

where $C_D$ is a constant drag coefficient. As mentioned in the introduction, we do not model vertical dynamics, instead focusing solely on horizontal drag. Similar to Benham et al. (Reference Benham, Devauchelle and Thomson2024) we assume $\mathrm{Re}$ is sufficiently large such that small variations in velocity $v_{\star }$ will not change the drag coefficient considerably.

To get the drag in dimensionless form, the dimensional drag is set equal to the dimensional thrust

(7.3) \begin{equation} \bar {F}_T = \rho g H^2 \langle \hat {Q},\hat {h}'\rangle . \end{equation}

Hence, by dividing by $\rho g H^2$ , the corresponding time-averaged dimensionless drag is found to be

(7.4) \begin{equation} \bar {F}_D = \frac {1}{2}C_Dv^2\frac {L}{H}. \end{equation}

In the previous sections we chose $\delta =1$ for the bounded power case to compare with the numerical work. In this section we will return to the general result $\overline {\textrm {Pow}}\leqslant \delta$ . The resulting optimal time-averaged thrust is $\bar {F}_T = \delta$ which gives us the cruising velocity $v_\star$

(7.5) \begin{equation} \begin{aligned} \delta = \frac {1}{2}C_D v^2\frac {L}{H} \quad &\implies \ v_{\star }(\delta ) = \sqrt {\frac {2H\delta }{\textit{LC}_D}}. \end{aligned} \end{equation}

The drag coefficient $C_D$ , the body length $L$ and the fluid height $H$ are fixed, which leaves the power injected $\delta$ as the only parameter to control the velocity. The velocity and power injected are related by $v_\star \sim \delta ^{ {1}/{2}}$ . Using the thrust result $\bar {F}_T=\delta$ , the optimal conditions on the wave amplitudes squared can be shown to also increase with $\delta$ (see (7.6) below). In terms of $\delta$ and $v_{\star }$ , the variational calculus produces the following conditions:

(7.6) \begin{align} \left |-\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{-\frac {\text{i}X}{1+v_{\star }}}\,\mathrm{d}X\right |^2 = 2\delta (1+v_{\star }(\delta )), \quad \left |-\frac {i}{2}\int ^{\frac {l}{2}}_{-\frac {l}{2}}\hat {Q}(X)\textrm{e}^{\frac {\text{i}X}{1-v_{\star }}}\,\mathrm{d}X\right |^2=0. \end{align}

Hence, as the velocity increases, we need a larger wave to equilibrate the drag. Of course, the scaling here is limited by the assumption that $C_{D}$ is a constant, and if the velocity fluctuation were to affect the drag coefficient, we would need to amend the scaling. However, the same behaviour where a larger wave is required to achieve a higher velocity would still be expected.

Given a small acceleration we can vary the cruising velocity $v_{\star }$ with the time-averaged power injected $\delta$ . From here we can make two observations. To move quicker, one has to provide more power and to remain moving efficiently, the aft wave gets larger while the fore wave remains zero. This makes physical sense because the faster velocity requires that we generate more thrust, which requires a bigger difference in fore–aft amplitude as is the case in (2.10). Modifications can be made to delve further into the conditions for accelerating from start-up. Motivated by previous sections, we could prescribe $\hat {Q}$ . For example, if we used a step function like (3.18), we could study how the conditions for $\alpha$ and $\beta$ evolve in terms of the changing speed $v_{\star }$ . We could also study adding in another constraint on top of the bounded power. If the norm is bounded simultaneously, there will be an upper bound on the magnitude of the source and hence there will come a point where the thrust will diminish from achieving $\bar {F}_T = \delta$ and efficiency will suffer. Since this section is a demonstration of a simple theory, these modifications will not be investigated here.

To conclude this section, we will take this opportunity to look at the time evolution of the solutions. We will reintroduce the temporal part and study the wave field $h(x,t)$ as it is in (4.1) to produce a graph showing one whole period of oscillation. The numerically optimised bounded power solution is plotted over one period in figure 8(a) (note, this is just one optimal $\hat {Q}$ out of infinitely many that satisfy (4.19)). To visualise the results of (7.6), a comparison between a faster cruising velocity is shown in figure 8(b). Here, we can see that the amplitude of oscillation is required to be greater to maintain optimal efficiency at the larger velocity.

Figure 8. (a) Demonstration of the one period of oscillation where $v_{\star }=0.2$ and $l=3\pi /2$ . The body is defined as the region between the vertical lines ( $\tilde {x}\in [-l/2,l/2]$ ). The period is divided into $10$ instances where the first half-period is in blue and the latter in red. (b) A similar plot showing the time evolution at $v_{\star }=0.3$ demonstrating that the amplitude must increase to maintain the optimal solution at the larger velocity.