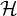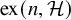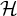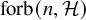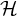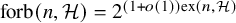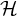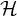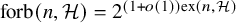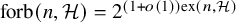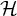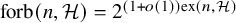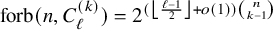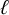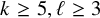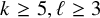1 Introduction
1.1 History
In extremal combinatorics, the problem of enumerating the number of discrete structures that avoid given substructures has a very rich history. One of the most natural questions one may ask is as follows: given a fixed graph H, how many n-vertex (labelled) graphs are there that contain no copy of H? Formally, given a fixed graph H, we say that a graph G is H-free if it does not contain H as a subgraph. For each natural number n, we let
![]() ${\mathrm {Forb}}(n,H)$
denote the family of all labeled H-free graphs on the vertex set
${\mathrm {Forb}}(n,H)$
denote the family of all labeled H-free graphs on the vertex set
![]() $[n]:=\{1,\dots , n\}$
and let
$[n]:=\{1,\dots , n\}$
and let
![]() ${\mathrm { forb}}(n,H)=|{\mathrm {Forb}}(n,H)|$
. The problem is to determine or estimate
${\mathrm { forb}}(n,H)=|{\mathrm {Forb}}(n,H)|$
. The problem is to determine or estimate
![]() ${\mathrm { forb}}(n,H)$
. This function is closely related to another classic function studied in extremal graph theory, namely the extremal number
${\mathrm { forb}}(n,H)$
. This function is closely related to another classic function studied in extremal graph theory, namely the extremal number
![]() $\mathrm {ex}(n,H)$
, defined as the maximum number of edges in an n-vertex H-free graph. Indeed, if we take a maximum n-vertex H-free graph G and take all the subgraphs of it we get
$\mathrm {ex}(n,H)$
, defined as the maximum number of edges in an n-vertex H-free graph. Indeed, if we take a maximum n-vertex H-free graph G and take all the subgraphs of it we get
![]() $2^{\mathrm {ex}(n,H)}$
many H-free graphs. On the other hand, for each
$2^{\mathrm {ex}(n,H)}$
many H-free graphs. On the other hand, for each
![]() $0\leq i \leq \mathrm {ex}(n,H)$
there are at most
$0\leq i \leq \mathrm {ex}(n,H)$
there are at most
![]() $\binom {\binom {n}{2}}{i}$
many n-vertex H-free graphs with i edges. Hence, we trivially have
$\binom {\binom {n}{2}}{i}$
many n-vertex H-free graphs with i edges. Hence, we trivially have
 $$ \begin{align} 2^{\mathrm{ex}(n,H)}\leq {\mathrm{ forb}}(n,H)\leq \sum_{i\leq \mathrm{ex}(n,H)} \binom{\binom{n}{2}}{i}=n^{O(\mathrm{ex}(n,H))}. \end{align} $$
$$ \begin{align} 2^{\mathrm{ex}(n,H)}\leq {\mathrm{ forb}}(n,H)\leq \sum_{i\leq \mathrm{ex}(n,H)} \binom{\binom{n}{2}}{i}=n^{O(\mathrm{ex}(n,H))}. \end{align} $$
For non-bipartite graphs H, the upper bound in (1) was significantly sharpened by Erdős, Frankl, and Rödl [Reference Erdős, Frankl and Rödl10], extending the earlier seminal work of Erdős, Kleitman, and Rothschild [Reference Erdős, Kleitman and Rothschild11] for complete graphs, showing that
![]() ${\mathrm { forb}}(n,H)\leq 2^{\mathrm {ex}(n,H)+o(n^k)}$
. Therefore, for any non-bipartite H,
${\mathrm { forb}}(n,H)\leq 2^{\mathrm {ex}(n,H)+o(n^k)}$
. Therefore, for any non-bipartite H,
For bipartite graphs H, estimating
![]() ${\mathrm { forb}}(n,H)$
is much more difficult, even for the few bipartite H whose extremal numbers
${\mathrm { forb}}(n,H)$
is much more difficult, even for the few bipartite H whose extremal numbers
![]() $\mathrm {ex}(n,H)$
are relatively well-understood. The first breakthrough in this area was made by Kleitman and Winston [Reference Kleitman and Winston27], who showed that the number of
$\mathrm {ex}(n,H)$
are relatively well-understood. The first breakthrough in this area was made by Kleitman and Winston [Reference Kleitman and Winston27], who showed that the number of
![]() $C_4$
-free graphs was
$C_4$
-free graphs was
![]() $2^{O(\mathrm {ex}(n, C_4))}$
. For complete bipartite graphs, this was extended by Balogh and Samotij first for symmetric [Reference Balogh and Samotij4] and then asymmetric [Reference Balogh and Samotij5] versions, showing that the number of
$2^{O(\mathrm {ex}(n, C_4))}$
. For complete bipartite graphs, this was extended by Balogh and Samotij first for symmetric [Reference Balogh and Samotij4] and then asymmetric [Reference Balogh and Samotij5] versions, showing that the number of
![]() $K_{s, t}$
-free graphs is no more than
$K_{s, t}$
-free graphs is no more than
![]() $2^{O(n^{2 - 1/ s})}$
, a near optimal result for t sufficiently large compared to s. For even cycles, this was extended by Morris and Saxton [Reference Morris and Saxton32] in a breakthrough work, showing that the number of
$2^{O(n^{2 - 1/ s})}$
, a near optimal result for t sufficiently large compared to s. For even cycles, this was extended by Morris and Saxton [Reference Morris and Saxton32] in a breakthrough work, showing that the number of
![]() $C_{2 \ell }$
-free graphs is no more than
$C_{2 \ell }$
-free graphs is no more than
![]() $2^{O(n^{1 + \frac {1}{\ell }})}$
. In a more recent breakthrough, Ferber, McKinley, and Samotij [Reference Ferber, McKinley and Samotij14] showed that for all bipartite graphs satisfying a mild condition (see their Theorem 5),
$2^{O(n^{1 + \frac {1}{\ell }})}$
. In a more recent breakthrough, Ferber, McKinley, and Samotij [Reference Ferber, McKinley and Samotij14] showed that for all bipartite graphs satisfying a mild condition (see their Theorem 5),
![]() ${\mathrm { forb}}(n,H)=2^{O(\mathrm {ex}(n, H))}$
holds. Until recently, it was believed that in fact
${\mathrm { forb}}(n,H)=2^{O(\mathrm {ex}(n, H))}$
holds. Until recently, it was believed that in fact
![]() ${\mathrm { forb}}(n,H)=2^{(1+o(1))\mathrm {ex}(n,H)}$
should hold for all bipartite graphs that contain a cycle just as it does for non-bipartite H. But this was disproved by Morris and Saxton [Reference Morris and Saxton32], who showed that
${\mathrm { forb}}(n,H)=2^{(1+o(1))\mathrm {ex}(n,H)}$
should hold for all bipartite graphs that contain a cycle just as it does for non-bipartite H. But this was disproved by Morris and Saxton [Reference Morris and Saxton32], who showed that
![]() ${\mathrm { forb}}(n,C_6)\geq 2^{(1+c)\mathrm {ex}(n,C_6)}$
for some positive c. Thus, unlike for non-bipartite graphs, for bipartite H, the trivial lower bound of
${\mathrm { forb}}(n,C_6)\geq 2^{(1+c)\mathrm {ex}(n,C_6)}$
for some positive c. Thus, unlike for non-bipartite graphs, for bipartite H, the trivial lower bound of
![]() $2^{\mathrm {ex}(n,H)}$
is not always asymptotically tight.
$2^{\mathrm {ex}(n,H)}$
is not always asymptotically tight.
One may consider the natural extension of the problem to the setting of uniform hypergraphs. For an integer
![]() $k\geq 2$
, a k-uniform hypergraph (or k-graph) is pair
$k\geq 2$
, a k-uniform hypergraph (or k-graph) is pair
![]() $(V,E)$
of finite sets, where the edge set E is a family of k-element subsets of the vertex set V. For a fixed k-graph
$(V,E)$
of finite sets, where the edge set E is a family of k-element subsets of the vertex set V. For a fixed k-graph
![]() $\mathcal {H}$
, one defines the extremal number
$\mathcal {H}$
, one defines the extremal number
![]() $\mathrm {ex}(n,\mathcal {H})$
and
$\mathrm {ex}(n,\mathcal {H})$
and
![]() ${\mathrm { forb}}(n,\mathcal {H})$
analogously as in the graph setting. As for graphs, for any k-graph
${\mathrm { forb}}(n,\mathcal {H})$
analogously as in the graph setting. As for graphs, for any k-graph
![]() $\mathcal {H}$
, we trivially have
$\mathcal {H}$
, we trivially have
 $$ \begin{align} 2^{\mathrm{ex}(n,\mathcal{H})}\leq {\mathrm{ forb}}(n,\mathcal{H})\leq \sum_{i\leq \mathrm{ex}(n,\mathcal{H})} \binom{\binom{n}{k}}{i}=n^{O(\mathrm{ex}(n,\mathcal{H}))}. \end{align} $$
$$ \begin{align} 2^{\mathrm{ex}(n,\mathcal{H})}\leq {\mathrm{ forb}}(n,\mathcal{H})\leq \sum_{i\leq \mathrm{ex}(n,\mathcal{H})} \binom{\binom{n}{k}}{i}=n^{O(\mathrm{ex}(n,\mathcal{H}))}. \end{align} $$
A k-graph
![]() $\mathcal {H}$
is k-partite (or degenerate) if its vertex can be partitioned into k parts
$\mathcal {H}$
is k-partite (or degenerate) if its vertex can be partitioned into k parts
![]() $X_1,\dots , X_k$
so that each edge contains exactly one vertex in each part. We call
$X_1,\dots , X_k$
so that each edge contains exactly one vertex in each part. We call
![]() $(X_1,\dots , X_k)$
a k-partition of
$(X_1,\dots , X_k)$
a k-partition of
![]() $\mathcal {H}$
. It is easy to see that when
$\mathcal {H}$
. It is easy to see that when
![]() $\mathcal {H}$
is not k-partite,
$\mathcal {H}$
is not k-partite,
![]() $\mathrm {ex}(n,\mathcal {H})=\Theta (n^k)$
. When
$\mathrm {ex}(n,\mathcal {H})=\Theta (n^k)$
. When
![]() $\mathcal {H}$
is k-partite, it follows from a result of Erdős [Reference Erdős8] that
$\mathcal {H}$
is k-partite, it follows from a result of Erdős [Reference Erdős8] that
![]() $\mathrm {ex}(n,\mathcal {H})=O(n^{k-c})$
, for some constant
$\mathrm {ex}(n,\mathcal {H})=O(n^{k-c})$
, for some constant
![]() $c>0$
. Extending the work of Erdős, Frankl and Rödl [Reference Erdős, Frankl and Rödl10], Nagle, Rödl, and Schacht [Reference Nagle, Rödl and Schacht37] showed that for any fixed k-graph
$c>0$
. Extending the work of Erdős, Frankl and Rödl [Reference Erdős, Frankl and Rödl10], Nagle, Rödl, and Schacht [Reference Nagle, Rödl and Schacht37] showed that for any fixed k-graph
![]() $\mathcal {H}$
,
$\mathcal {H}$
,
![]() $\mathrm {forb}(n, \mathcal {H}) \leq 2^{\mathrm {ex}(n, \mathcal {H}) + o(n^k)}$
. Hence, for any k-graph
$\mathrm {forb}(n, \mathcal {H}) \leq 2^{\mathrm {ex}(n, \mathcal {H}) + o(n^k)}$
. Hence, for any k-graph
![]() $\mathcal {H}$
that is not k-partite, we have
$\mathcal {H}$
that is not k-partite, we have
When
![]() $\mathcal {H}$
is k-partite, however, the bound
$\mathcal {H}$
is k-partite, however, the bound
![]() ${\mathrm { forb}}(n,\mathcal {H})\leq 2^{\mathrm {ex}(n,\mathcal {H})+o(n^k)}$
becomes too weak. To improve this trivial upper bound for k-partite k-graphs, a natural approach is to first study the problem for some prototypical examples of k-partite k-graphs. It follows from the work of Balogh et al [Reference Balogh, Das, Delcourt, Liu and Sharifzadeh1] on the typical structures of t-intersecting families that
${\mathrm { forb}}(n,\mathcal {H})\leq 2^{\mathrm {ex}(n,\mathcal {H})+o(n^k)}$
becomes too weak. To improve this trivial upper bound for k-partite k-graphs, a natural approach is to first study the problem for some prototypical examples of k-partite k-graphs. It follows from the work of Balogh et al [Reference Balogh, Das, Delcourt, Liu and Sharifzadeh1] on the typical structures of t-intersecting families that
![]() ${\mathrm { forb}}(n,\mathcal {F}_{k,t})=2^{(1+o(1))\mathrm {ex}(n,\mathcal {F}_{k,t})}$
, where
${\mathrm { forb}}(n,\mathcal {F}_{k,t})=2^{(1+o(1))\mathrm {ex}(n,\mathcal {F}_{k,t})}$
, where
![]() $\mathcal {F}_{k,t}$
is the family of k-graphs each of which consists of two edges sharing at least t vertices in common. (Their actual estimate is in fact even sharper than stated, see their Theorem 1.4). Mubayi and Wang [Reference Mubayi and Wang34] investigated
$\mathcal {F}_{k,t}$
is the family of k-graphs each of which consists of two edges sharing at least t vertices in common. (Their actual estimate is in fact even sharper than stated, see their Theorem 1.4). Mubayi and Wang [Reference Mubayi and Wang34] investigated
![]() ${\mathrm { forb}}(n,C^{(k)}_{\ell })$
for
${\mathrm { forb}}(n,C^{(k)}_{\ell })$
for
![]() $k\geq 3$
, where
$k\geq 3$
, where
![]() $C^{(k)}_\ell $
is the so-called k-uniform linear cycle of length
$C^{(k)}_\ell $
is the so-called k-uniform linear cycle of length
![]() $\ell $
which is the k-graph obtained from a graph
$\ell $
which is the k-graph obtained from a graph
![]() $\ell $
-cycle by expanding each edge with
$\ell $
-cycle by expanding each edge with
![]() $k-2$
degree
$k-2$
degree
![]() $1$
vertices. It follows from the work of Füredi and Jiang [Reference Füredi and Jiang21] and of Kostochka, Mubayi and Verstraëte [Reference Kostochka, Mubayi and Verstraëte29] that for all
$1$
vertices. It follows from the work of Füredi and Jiang [Reference Füredi and Jiang21] and of Kostochka, Mubayi and Verstraëte [Reference Kostochka, Mubayi and Verstraëte29] that for all
![]() $k,\ell \geq 3, \mathrm {ex}(n,C^{(k)}_\ell )\sim \left \lfloor \frac {\ell -1}{2} \right \rfloor \binom {n}{k-1}$
. Mubayi and Wang [Reference Mubayi and Wang34] showed that
$k,\ell \geq 3, \mathrm {ex}(n,C^{(k)}_\ell )\sim \left \lfloor \frac {\ell -1}{2} \right \rfloor \binom {n}{k-1}$
. Mubayi and Wang [Reference Mubayi and Wang34] showed that
![]() ${\mathrm { forb}}(n, C^{(3)}_\ell )=2^{O(n^{k-1})}$
for all even
${\mathrm { forb}}(n, C^{(3)}_\ell )=2^{O(n^{k-1})}$
for all even
![]() $\ell \geq 4$
and further conjectured that
$\ell \geq 4$
and further conjectured that
![]() ${\mathrm { forb}}(n,C^{(k)}_\ell )=2^{O(n^{k-1})}$
for all
${\mathrm { forb}}(n,C^{(k)}_\ell )=2^{O(n^{k-1})}$
for all
![]() $k,\ell \geq 3$
. Their conjecture was subsequently settled by Balogh, Narayanan and Skokan [Reference Balogh, Narayanan and Skokan3], who then posed the natural question of whether
$k,\ell \geq 3$
. Their conjecture was subsequently settled by Balogh, Narayanan and Skokan [Reference Balogh, Narayanan and Skokan3], who then posed the natural question of whether
![]() ${\mathrm { forb}}(n, C^{(k)}_\ell )=2^{(1+o(1))\mathrm {ex}(n,C^{(k)}_\ell )}$
holds for all
${\mathrm { forb}}(n, C^{(k)}_\ell )=2^{(1+o(1))\mathrm {ex}(n,C^{(k)}_\ell )}$
holds for all
![]() $k,\ell \geq 3$
. More recently, in the same paper mentioned earlier, Ferber, McKinley, and Samotij [Reference Ferber, McKinley and Samotij14] established the very general result that for all k-partite k-graphs H that satisfy a mild condition (see their Theorem 9)
$k,\ell \geq 3$
. More recently, in the same paper mentioned earlier, Ferber, McKinley, and Samotij [Reference Ferber, McKinley and Samotij14] established the very general result that for all k-partite k-graphs H that satisfy a mild condition (see their Theorem 9)
thus significantly sharpening the trivial upper bound in (3), while also retrieving the results of Mubayi and Wang and of Balogh, Narayan and Skokan on
![]() $\mathrm {ex}(n,C^{(k)}_\ell )$
. In spite of this remarkable progress, it remains an intriguing question whether the bounds can be further sharpened, and in particular, in view of (4) and the question of Balogh, Narayanan and Skokan [Reference Balogh, Narayanan and Skokan3] whether there exists some nontrivial infinite family of k-partite k-graphs for which
$\mathrm {ex}(n,C^{(k)}_\ell )$
. In spite of this remarkable progress, it remains an intriguing question whether the bounds can be further sharpened, and in particular, in view of (4) and the question of Balogh, Narayanan and Skokan [Reference Balogh, Narayanan and Skokan3] whether there exists some nontrivial infinite family of k-partite k-graphs for which
![]() ${\mathrm { forb}}(n,\mathcal {H})=2^{1+o(1))\mathrm {ex}(n,\mathcal {H})}$
holds.
${\mathrm { forb}}(n,\mathcal {H})=2^{1+o(1))\mathrm {ex}(n,\mathcal {H})}$
holds.
In this paper, we establish a large and the first known family of degenerate k-graphs, for which
![]() ${\mathrm { forb}}(n,\mathcal {H})=2^{(1+o(1))\mathrm {ex}(n,\mathcal {H})}$
holds. As an immediate consequence of our main result, we settled the question of Balogh, Narayanan and Skokan [Reference Balogh, Narayanan and Skokan3] in the affirmative for all
${\mathrm { forb}}(n,\mathcal {H})=2^{(1+o(1))\mathrm {ex}(n,\mathcal {H})}$
holds. As an immediate consequence of our main result, we settled the question of Balogh, Narayanan and Skokan [Reference Balogh, Narayanan and Skokan3] in the affirmative for all
![]() $k\geq 5, \ell \geq 3$
.
$k\geq 5, \ell \geq 3$
.
Theorem 1.1. For all integers,
![]() $k\geq 5, \ell \geq 3$
, we have
$k\geq 5, \ell \geq 3$
, we have
To state our main results, we need a few definitions and history, which we detail next.
1.2 Main Result
First, we define hypertrees recursively as follows. A single edge E is a hypertree. In general, a hypergraph
![]() $\mathcal {H}$
with at least two edges is a hypertree if there exists an edge E such that
$\mathcal {H}$
with at least two edges is a hypertree if there exists an edge E such that
![]() $\mathcal {H}':=\mathcal {H}\setminus E$
is a hypertree and there exists an edge F in
$\mathcal {H}':=\mathcal {H}\setminus E$
is a hypertree and there exists an edge F in
![]() $\mathcal {H}'$
such that
$\mathcal {H}'$
such that
![]() $E\cap V(\mathcal {H}')=E\cap F$
; we call such an edge E a leaf edge of
$E\cap V(\mathcal {H}')=E\cap F$
; we call such an edge E a leaf edge of
![]() $\mathcal {H}$
and call F a parent edge of E in
$\mathcal {H}$
and call F a parent edge of E in
![]() $\mathcal {H}'$
. It follows from the definition above that if
$\mathcal {H}'$
. It follows from the definition above that if
![]() $\mathcal {H}$
is a hypertree with
$\mathcal {H}$
is a hypertree with
![]() $m\geq 2$
edges, there exists an ordering of its edges as
$m\geq 2$
edges, there exists an ordering of its edges as
![]() $E_1,\dots , E_m$
such that for each
$E_1,\dots , E_m$
such that for each
![]() $i=2,\dots , m$
,
$i=2,\dots , m$
,
![]() $\mathcal {H}_i:=\{E_1,\dots , E_i\}$
is a tree and
$\mathcal {H}_i:=\{E_1,\dots , E_i\}$
is a tree and
![]() $E_i$
is a leaf edge of
$E_i$
is a leaf edge of
![]() $\mathcal {H}_i$
. We call such an edge-ordering a tree-defining ordering for
$\mathcal {H}_i$
. We call such an edge-ordering a tree-defining ordering for
![]() $\mathcal {H}$
. If k is a positive integer, we will call a k-uniform hypertree a k-tree. As a simple example, a k-uniform matching is a k-tree. It is easy to show by induction that every k-tree is k-partite. Given a positive integer
$\mathcal {H}$
. If k is a positive integer, we will call a k-uniform hypertree a k-tree. As a simple example, a k-uniform matching is a k-tree. It is easy to show by induction that every k-tree is k-partite. Given a positive integer
![]() $t\leq k-1$
, we say that a k-graph
$t\leq k-1$
, we say that a k-graph
![]() $\mathcal {H}$
is t-contractible if each edge of
$\mathcal {H}$
is t-contractible if each edge of
![]() $\mathcal {H}$
contains t vertices of degree
$\mathcal {H}$
contains t vertices of degree
![]() $1$
and a t-contraction of
$1$
and a t-contraction of
![]() $\mathcal {H}$
is the
$\mathcal {H}$
is the
![]() $(k-t)$
-uniform multi-hypergraph obtained by deleting t degree
$(k-t)$
-uniform multi-hypergraph obtained by deleting t degree
![]() $1$
vertices from each edge of
$1$
vertices from each edge of
![]() $\mathcal {H}$
. The notion of t-contractibility is more general than that of the k-uniform expansion of a graph. The latter has been quite extensively studied, as detailed in the survey by Mubayi and Verstraëte [Reference Mubayi and Verstraëte33]. Specifically, the k-expansion of a graph G is the k-graph
$\mathcal {H}$
. The notion of t-contractibility is more general than that of the k-uniform expansion of a graph. The latter has been quite extensively studied, as detailed in the survey by Mubayi and Verstraëte [Reference Mubayi and Verstraëte33]. Specifically, the k-expansion of a graph G is the k-graph
![]() $G^{(k)}$
obtained from G by expanding each edge into a k-set by adding
$G^{(k)}$
obtained from G by expanding each edge into a k-set by adding
![]() $k-2$
degree
$k-2$
degree
![]() $1$
vertices. Thus, for instance, the k-uniform linear cycle
$1$
vertices. Thus, for instance, the k-uniform linear cycle
![]() $C^{(k)}_\ell $
is the k-expansion of a graph
$C^{(k)}_\ell $
is the k-expansion of a graph
![]() $\ell $
-cycle. Hence, the k-expansion of a graph G is a
$\ell $
-cycle. Hence, the k-expansion of a graph G is a
![]() $(k-2)$
-contractible k-graph whose
$(k-2)$
-contractible k-graph whose
![]() $(k-2)$
-contraction is a simple hypergraph with no repeated edges, whereas for a general
$(k-2)$
-contraction is a simple hypergraph with no repeated edges, whereas for a general
![]() $(k-2)$
-contractible k-graph
$(k-2)$
-contractible k-graph
![]() $\mathcal {H}$
, its
$\mathcal {H}$
, its
![]() $(k-2)$
-contraction is allowed to be a multigraph.
$(k-2)$
-contraction is allowed to be a multigraph.
Given a hypergraph
![]() $\mathcal {H}$
, a set
$\mathcal {H}$
, a set
![]() $S\subseteq V(\mathcal {H})$
is called a cross-cut of
$S\subseteq V(\mathcal {H})$
is called a cross-cut of
![]() $\mathcal {H}$
if each edge of
$\mathcal {H}$
if each edge of
![]() $\mathcal {H}$
intersects S in exactly one vertex. If
$\mathcal {H}$
intersects S in exactly one vertex. If
![]() $\mathcal {H}$
has a cross-cut then we denote the minimum size of a cross-cut of it by
$\mathcal {H}$
has a cross-cut then we denote the minimum size of a cross-cut of it by
![]() $\sigma (\mathcal {H})$
, and call it the cross-cut number of
$\sigma (\mathcal {H})$
, and call it the cross-cut number of
![]() $\mathcal {H}$
. Note that every k-partite k-graph
$\mathcal {H}$
. Note that every k-partite k-graph
![]() $\mathcal {H}$
has a cross-cut, for instance by taking any part in a k-partition of
$\mathcal {H}$
has a cross-cut, for instance by taking any part in a k-partition of
![]() $\mathcal {H}$
. Generalizing a long line of work [Reference Füredi20, Reference Füredi and Jiang21, Reference Füredi, Jiang and Seiver23, Reference Kostochka, Mubayi and Verstraëte29, Reference Kostochka, Mubayi and Verstaëte30] for k-graphs with
$\mathcal {H}$
. Generalizing a long line of work [Reference Füredi20, Reference Füredi and Jiang21, Reference Füredi, Jiang and Seiver23, Reference Kostochka, Mubayi and Verstraëte29, Reference Kostochka, Mubayi and Verstaëte30] for k-graphs with
![]() $k\geq 5$
, Füredi and Jiang [Reference Füredi and Jiang22] established the following sharp results on the extremal number of any subgraph of a
$k\geq 5$
, Füredi and Jiang [Reference Füredi and Jiang22] established the following sharp results on the extremal number of any subgraph of a
![]() $2$
-contractible k-tree for
$2$
-contractible k-tree for
![]() $k\geq 5$
.
$k\geq 5$
.
Theorem 1.2 [Reference Füredi and Jiang22].
Let
![]() $k\geq 4$
be an integer. For any k-graph
$k\geq 4$
be an integer. For any k-graph
![]() $\mathcal {H}$
that is a subgraph of a
$\mathcal {H}$
that is a subgraph of a
![]() $2$
-contractible k-tree, we have
$2$
-contractible k-tree, we have
 $$\begin{align*}\mathrm{ex}(n,\mathcal{H})=(\sigma(\mathcal{H})-1+o(1))\binom{n}{k-1}.\end{align*}$$
$$\begin{align*}\mathrm{ex}(n,\mathcal{H})=(\sigma(\mathcal{H})-1+o(1))\binom{n}{k-1}.\end{align*}$$
In particular, Theorem 1.2 implies that for
![]() $k \geq 5$
and
$k \geq 5$
and
![]() $\ell \geq 3$
,
$\ell \geq 3$
,
![]() $\mathrm {ex}(n, C_\ell ^{(k)}) = \left \lfloor \frac {\ell - 1}{2} \right \rfloor \binom {n}{k - 1}$
. Indeed, for
$\mathrm {ex}(n, C_\ell ^{(k)}) = \left \lfloor \frac {\ell - 1}{2} \right \rfloor \binom {n}{k - 1}$
. Indeed, for
![]() $k\geq 5$
, it is easy to see that
$k\geq 5$
, it is easy to see that
![]() $C_\ell ^{(k)}$
is a subgraph of a k-tree and
$C_\ell ^{(k)}$
is a subgraph of a k-tree and
![]() $\sigma (C_\ell ^{(k)})=\left \lfloor \frac {\ell +1}{2} \right \rfloor $
(see [Reference Füredi and Jiang21] for instance for details). The authors of [Reference Füredi and Jiang22] also demonstrated existence of
$\sigma (C_\ell ^{(k)})=\left \lfloor \frac {\ell +1}{2} \right \rfloor $
(see [Reference Füredi and Jiang21] for instance for details). The authors of [Reference Füredi and Jiang22] also demonstrated existence of
![]() $1$
-contractible hypertrees for which the conclusion is no longer valid. The main method used in [Reference Füredi and Jiang22] is the so-called Delta system method, which is a powerful tool for studying extremal problems on set systems.
$1$
-contractible hypertrees for which the conclusion is no longer valid. The main method used in [Reference Füredi and Jiang22] is the so-called Delta system method, which is a powerful tool for studying extremal problems on set systems.
In this paper, we develop a supersaturation variant of the Delta system method and use it in conjunction with the container method to establish the following sharp enumeration result.
Theorem 1.3 (Main Theorem).
Let
![]() $k\geq 4$
be an integer. For every
$k\geq 4$
be an integer. For every
![]() $2$
-contractible k-tree
$2$
-contractible k-tree
![]() $\mathcal {H}$
, we have
$\mathcal {H}$
, we have
This gives the first known family of degenerate k-graphs
![]() $\mathcal {H}$
for which
$\mathcal {H}$
for which
![]() ${\mathrm { forb}}(n,\mathcal {H})=2^{(1+o(1))\mathrm {ex}(n,\mathcal {H})}$
holds.
${\mathrm { forb}}(n,\mathcal {H})=2^{(1+o(1))\mathrm {ex}(n,\mathcal {H})}$
holds.
Furthermore, as a by-product of the supersaturation variant of the Delta-system method, we also get an optimal supersaturation result for the family of
![]() $2$
-contractible k-trees for
$2$
-contractible k-trees for
![]() $k\geq 4$
, which may be of independent interest (see Theorem 4.4).
$k\geq 4$
, which may be of independent interest (see Theorem 4.4).
As an immediate corollary of Theorem 1.3, we obtain Theorem 1.1, which answers the question of Balogh, Narayanan and Skokan [Reference Balogh, Narayanan and Skokan3] affirmatively for all
![]() $k\geq 5,\ell \geq 3$
. Indeed, as mentioned earlier,
$k\geq 5,\ell \geq 3$
. Indeed, as mentioned earlier,
![]() $\sigma (C^{(k)}_\ell )= \left \lfloor \frac {\ell +1}{2} \right \rfloor $
, and by considering
$\sigma (C^{(k)}_\ell )= \left \lfloor \frac {\ell +1}{2} \right \rfloor $
, and by considering
![]() $\ell $
even and
$\ell $
even and
![]() $\ell $
odd cases separately it is not hard to construct a k-tree
$\ell $
odd cases separately it is not hard to construct a k-tree
![]() $T^{(k)}_\ell $
with cross-cut number
$T^{(k)}_\ell $
with cross-cut number
![]() $\left \lfloor \frac {\ell +1}{2} \right \rfloor $
that contains
$\left \lfloor \frac {\ell +1}{2} \right \rfloor $
that contains
![]() $C^{(k)}_\ell $
. Thus, by Theorem 1.3,
$C^{(k)}_\ell $
. Thus, by Theorem 1.3,
![]() ${\mathrm { forb}}(n, C^{(k)}_\ell )\leq {\mathrm { forb}}(n, T^{(k)}_\ell ) \leq 2^{(\left \lfloor \frac {\ell -1}{2} \right \rfloor +o(1))\binom {n}{k-1}}$
, for all
${\mathrm { forb}}(n, C^{(k)}_\ell )\leq {\mathrm { forb}}(n, T^{(k)}_\ell ) \leq 2^{(\left \lfloor \frac {\ell -1}{2} \right \rfloor +o(1))\binom {n}{k-1}}$
, for all
![]() $k \geq 5$
and
$k \geq 5$
and
![]() $\ell \geq 3$
, from which Theorem 1.1 follows.
$\ell \geq 3$
, from which Theorem 1.1 follows.
1.3 Applications to the random Turán problem
The methods used in establishing our main theorem also readily yield some sharp results on the so-called random Turán problem. Let
![]() $k\geq 2$
be an integer. We let
$k\geq 2$
be an integer. We let
![]() $G_{n, p}^{(k)}$
be the so-called Erdős-Rényi random graph formed by keeping each edge of
$G_{n, p}^{(k)}$
be the so-called Erdős-Rényi random graph formed by keeping each edge of
![]() $K_n^{(k)}$
uniformly at random with probability p. The random Turán problem is to study the random variable
$K_n^{(k)}$
uniformly at random with probability p. The random Turán problem is to study the random variable
![]() $\mathrm {ex}(G_{n, p}^{(k)}, H)$
that counts the maximum number of edges in an H-free subgraph of
$\mathrm {ex}(G_{n, p}^{(k)}, H)$
that counts the maximum number of edges in an H-free subgraph of
![]() $G_{n,p}^{(k)}$
. For a thorough introduction to the random Turán problem, the reader is referred to the excellent survey by Rödl and Schacht [Reference Rödl and Schacht41], though we will offer a brief summary here.
$G_{n,p}^{(k)}$
. For a thorough introduction to the random Turán problem, the reader is referred to the excellent survey by Rödl and Schacht [Reference Rödl and Schacht41], though we will offer a brief summary here.
The random Turán problem for non-k-partite k-graphs was essentially solved in breakthrough works by Conlon and Gowers [Reference Conlon and Gowers6] and by Schacht [Reference Schacht43], who showed that when
![]() $p\gg n^{-1/m_k(H)}$
, almost surely
$p\gg n^{-1/m_k(H)}$
, almost surely
![]() $\mathrm {ex}(n,G(n,p)^{(k)}) =p(\mathrm {ex}(n,H)+o(n^k))$
, as
$\mathrm {ex}(n,G(n,p)^{(k)}) =p(\mathrm {ex}(n,H)+o(n^k))$
, as
![]() $n\to \infty $
, where
$n\to \infty $
, where
![]() $m_k(H)=\max _{F\subseteq H, e(F)\geq 2} \frac {e(F)-1}{v(F)-k}$
. The theorem was then reproved using the container method by Balogh, Morris and Samotij [Reference Balogh, Morris and Samotij2] and independently by Saxton and Thomason [Reference Saxton and Thomason42].
$m_k(H)=\max _{F\subseteq H, e(F)\geq 2} \frac {e(F)-1}{v(F)-k}$
. The theorem was then reproved using the container method by Balogh, Morris and Samotij [Reference Balogh, Morris and Samotij2] and independently by Saxton and Thomason [Reference Saxton and Thomason42].
For k-partite k-graphs (which are also called degenerate k-graphs) much less is known. For degenerate graphs, early results due to Haxell, Kohayakawa, and Łuczak [Reference Haxell, Kohayakawa and Łuczak25] and Kohayakawa, Kreuter, and Steger [Reference Kohayakawa, Kreuter and Steger28] essentially solved the problem for even graph cycles for small values of p. For dense ranges, Morris and Saxton [Reference Morris and Saxton32] solved the problem for cycles and complete bipartite graphs, and McKinley and Spiro [Reference McKinley and Spiro36] extended their result for theta graphs. For dense p, some general upper bounds are obtained in [Reference Jiang and Longbrake26].
Even less is known for degenerate hypergraphs. For k-uniform even linear cycles, Mubayi and Yepremyan [Reference Mubayi and Yepremyan35] and independently Nie [Reference Nie39] proved
Theorem 1.4 [Reference Mubayi and Yepremyan35, Reference Nie39].
For every
![]() $\ell \geq 2$
and
$\ell \geq 2$
and
![]() $k\geq 4$
with high probability, the following holds:
$k\geq 4$
with high probability, the following holds:
 $$ \begin{align*}\mathrm{ex}\left(G_{n,p}^{(k)}, C_{2\ell}^{(k)}\right) = \begin{cases} \Theta(pn^{k-1}), & \text{if } { p \geq n^{-(k-2)+\frac{1}{2\ell-1}+o(1)}} \\ n^{1+\frac{1}{2\ell-1}+o(1)}, & \text{if } {n^{-(k-1)+\frac{1}{2\ell-1}+o(1)}\leq p\leq n^{-(k-2)+\frac{1}{2\ell-1}+o(1)}} \\ (1-o(1))pn^k, & \text{if } {n^{-k} \ll p\ll n^{-(k-1)+\frac{1}{2\ell-1}}}. \end{cases}\end{align*} $$
$$ \begin{align*}\mathrm{ex}\left(G_{n,p}^{(k)}, C_{2\ell}^{(k)}\right) = \begin{cases} \Theta(pn^{k-1}), & \text{if } { p \geq n^{-(k-2)+\frac{1}{2\ell-1}+o(1)}} \\ n^{1+\frac{1}{2\ell-1}+o(1)}, & \text{if } {n^{-(k-1)+\frac{1}{2\ell-1}+o(1)}\leq p\leq n^{-(k-2)+\frac{1}{2\ell-1}+o(1)}} \\ (1-o(1))pn^k, & \text{if } {n^{-k} \ll p\ll n^{-(k-1)+\frac{1}{2\ell-1}}}. \end{cases}\end{align*} $$
For other classes of hypergraphs, near optimal results were obtained by Nie [Reference Nie38] for k-expansions of subgraphs of tight p-trees and of
![]() $K_p^{p-1}$
, where
$K_p^{p-1}$
, where
![]() $k\geq p\geq 3$
, which includes both odd and even linear cycles. Nie and Spiro [Reference Nie and Spiro40] also were able to get near optimal bounds for expansions of theta-graphs. Furthermore, for any k-uniform hypergraph H, which satisfies that for every k-uniform G there are at least
$k\geq p\geq 3$
, which includes both odd and even linear cycles. Nie and Spiro [Reference Nie and Spiro40] also were able to get near optimal bounds for expansions of theta-graphs. Furthermore, for any k-uniform hypergraph H, which satisfies that for every k-uniform G there are at least
![]() $e(G)^{e(H)}v(G)^{v(H) - k e(H)}$
many homomorphisms from
$e(G)^{e(H)}v(G)^{v(H) - k e(H)}$
many homomorphisms from
![]() $H \rightarrow G$
, they proved that there is some
$H \rightarrow G$
, they proved that there is some
![]() $r_0 \geq k$
such that for every
$r_0 \geq k$
such that for every
![]() $r \geq r_0$
, tight bounds on the random Turán number of r-expansions of H hold.
$r \geq r_0$
, tight bounds on the random Turán number of r-expansions of H hold.
As an immediate byproduct of our main result, for dense p and for
![]() $C^{(k)}_\ell $
with
$C^{(k)}_\ell $
with
![]() $k \geq 5$
, we are able to sharpen the bound
$k \geq 5$
, we are able to sharpen the bound
![]() $pn^{k-1+o(1)}$
to the correct bound
$pn^{k-1+o(1)}$
to the correct bound
![]() $p(\left \lfloor \frac {\ell -1}{2} \right \rfloor +o(1))\binom {n}{k-1}=p(1+o(1)) \mathrm {ex}(n,C^{(k)}_\ell )$
, albeit for a slightly more restricted range of p. This comes as an immediate corollary to the following more general theorem. A hypergraph
$p(\left \lfloor \frac {\ell -1}{2} \right \rfloor +o(1))\binom {n}{k-1}=p(1+o(1)) \mathrm {ex}(n,C^{(k)}_\ell )$
, albeit for a slightly more restricted range of p. This comes as an immediate corollary to the following more general theorem. A hypergraph
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $\ell $
-overlapping if for any two edges
$\ell $
-overlapping if for any two edges
![]() $E,F$
in
$E,F$
in
![]() $\mathcal {H}$
,
$\mathcal {H}$
,
![]() $|E\cap F|\leq \ell $
.
$|E\cap F|\leq \ell $
.
Theorem 1.5. Let
![]() $k\geq 4$
be an integer. Let
$k\geq 4$
be an integer. Let
![]() $\mathcal {H}$
be a
$\mathcal {H}$
be a
![]() $2$
-contractible
$2$
-contractible
![]() $\ell $
-overlapping k-tree. When
$\ell $
-overlapping k-tree. When
![]() $p \gg \frac {\log (n)^2}{n^{ k -\ell - 1}}$
, with high probability
$p \gg \frac {\log (n)^2}{n^{ k -\ell - 1}}$
, with high probability
 $$\begin{align*}\mathrm{ex}(G(n,p)^{(k)}, \mathcal{H})= (\sigma(\mathcal{H}) - 1 +o(1))p \binom{n}{k - 1} = p(1+o(1))\mathrm{ex}(n,\mathcal{H}).\end{align*}$$
$$\begin{align*}\mathrm{ex}(G(n,p)^{(k)}, \mathcal{H})= (\sigma(\mathcal{H}) - 1 +o(1))p \binom{n}{k - 1} = p(1+o(1))\mathrm{ex}(n,\mathcal{H}).\end{align*}$$
As mentioned earlier, for all
![]() $k\geq 5, \ell \geq 3$
, there exists a
$k\geq 5, \ell \geq 3$
, there exists a
![]() $2$
-contractible k-tree
$2$
-contractible k-tree
![]() $T^{(k)}_\ell $
containing
$T^{(k)}_\ell $
containing
![]() $C^{(k)}_\ell $
with
$C^{(k)}_\ell $
with
![]() $\sigma (T^{(k)}_\ell )=\sigma (C^{(k)}_\ell )=\left \lfloor \frac {\ell +1}{2} \right \rfloor $
. Hence, Theorem 1.5 immediately implies
$\sigma (T^{(k)}_\ell )=\sigma (C^{(k)}_\ell )=\left \lfloor \frac {\ell +1}{2} \right \rfloor $
. Hence, Theorem 1.5 immediately implies
Corollary 1.6. For all
![]() $k\geq 5, \ell \geq 3$
and
$k\geq 5, \ell \geq 3$
and
![]() $p \gg \log (n)^2 n^{ -(k - 3)}$
, with high probability,
$p \gg \log (n)^2 n^{ -(k - 3)}$
, with high probability,
 $$\begin{align*}\mathrm{ex}(G(n,p)^{(k)}, C^{(k)}_\ell) = p\left(\left\lfloor \frac{\ell-1}{2} \right\rfloor+o(1)\right )\binom{n}{k-1} =p(1+o(1))\mathrm{ex}(n,C^{(k)}_\ell).\end{align*}$$
$$\begin{align*}\mathrm{ex}(G(n,p)^{(k)}, C^{(k)}_\ell) = p\left(\left\lfloor \frac{\ell-1}{2} \right\rfloor+o(1)\right )\binom{n}{k-1} =p(1+o(1))\mathrm{ex}(n,C^{(k)}_\ell).\end{align*}$$
1.4 Overiew of methodology and organization of the paper
At the heart of our work is the so-called optimal balanced supersaturation at the Turán threshold. Several long-standing conjectures of Erdős and Simonovits [Reference Erdős and Simonovits12] addressed the question of how many copies of a graph H we can guarantee in a dense enough host graph G. Loosely speaking, the conjectures say that the number of copies of H we expect in G should be at least on the same order of magnitude as the number of copies of H we expect in a random graph with the same edge-density as G. These are referred to as supersaturation conjectures. The strongest of the Erdős-Simonovits supersaturation conjectures says that the conjectured bound on the number of copies of H should already hold as soon as an n-vertex graph G has just barely asymptotically a bit more edges than what is enough to guarantee a single copy of H, namely when
![]() $e(G)\geq (1+\varepsilon ) \mathrm {ex}(n,H)$
for any small real
$e(G)\geq (1+\varepsilon ) \mathrm {ex}(n,H)$
for any small real
![]() $\varepsilon>0$
. We will refer to this phenomenon as optimal supersaturation at the Turán threshold. Establishing optimal supersaturation at the Turán threshold turns out to be a very difficult task for degenerate (i.e., bipartite) graphs, with the problem being unsolved except for very few bipartite graphs.
$\varepsilon>0$
. We will refer to this phenomenon as optimal supersaturation at the Turán threshold. Establishing optimal supersaturation at the Turán threshold turns out to be a very difficult task for degenerate (i.e., bipartite) graphs, with the problem being unsolved except for very few bipartite graphs.
In the last decade or so, the development of the container method has brought enhanced importance to the supersaturation problem. Specifically, the container method allows one to obtain tight enumeration results for
![]() ${\mathrm { forb}}(n,H)$
once one is able to obtain supersaturation of H with the additional feature that the copies of H found are evenly distributed in a sense. While this paved the way for several breakthroughs mentioned earlier, naturally developing optimal supersaturation at the Turán threshold with the added balanced feature is an even more difficult task than the one without the additional balanced requirement, as witnessed by the fact this has not been done even for the
${\mathrm { forb}}(n,H)$
once one is able to obtain supersaturation of H with the additional feature that the copies of H found are evenly distributed in a sense. While this paved the way for several breakthroughs mentioned earlier, naturally developing optimal supersaturation at the Turán threshold with the added balanced feature is an even more difficult task than the one without the additional balanced requirement, as witnessed by the fact this has not been done even for the
![]() $4$
-cycle, whose extremal number is very well-understood [Reference Füredi19] and for whom supersaturation at the Turán threshold has been achieved [Reference Erdős and Simonovits13].
$4$
-cycle, whose extremal number is very well-understood [Reference Füredi19] and for whom supersaturation at the Turán threshold has been achieved [Reference Erdős and Simonovits13].
Our main results crucially build on the optimal balanced supersaturation at the Turán threshold for
![]() $2$
-contractible hypertrees. Given the difficulty with the optimal balanced supersaturation at the Turán threshold for graphs, it does come as a surprise that one is able to establish it for a large family of degenerate hypergraphs. This is in a strong sense attributed to the power of the method we use, known as the Delta system method for set-systems. However, while the Delta system method has been successfully used on Turán type problem for hypergraphs, it has not been tailored for supersaturation problems before. In that regard, the most important innovative aspect of our work is the development of a supersaturation variant of the Delta system method and applying it successfully with the container method to get tight enumeration results. We believe that this variant of the Delta system method will find future applications.
$2$
-contractible hypertrees. Given the difficulty with the optimal balanced supersaturation at the Turán threshold for graphs, it does come as a surprise that one is able to establish it for a large family of degenerate hypergraphs. This is in a strong sense attributed to the power of the method we use, known as the Delta system method for set-systems. However, while the Delta system method has been successfully used on Turán type problem for hypergraphs, it has not been tailored for supersaturation problems before. In that regard, the most important innovative aspect of our work is the development of a supersaturation variant of the Delta system method and applying it successfully with the container method to get tight enumeration results. We believe that this variant of the Delta system method will find future applications.
We organize the rest of the paper as follows. In Section 2, we give some notation. In Section 3, we develop a supersaturation variant of the Delta system method and develop a structural dichotomy for all k-graphs with
![]() $\Theta (n^{k-1})$
edges, both of which may be of independent interest. In Section 4, we develop optimal supersaturation at the Turán threshold for
$\Theta (n^{k-1})$
edges, both of which may be of independent interest. In Section 4, we develop optimal supersaturation at the Turán threshold for
![]() $2$
-contractible hypertrees. In Section 5, we develop optimal balanced supersaturation at the Turán threshold for
$2$
-contractible hypertrees. In Section 5, we develop optimal balanced supersaturation at the Turán threshold for
![]() $2$
-contractible hypertrees. In Section 6, we prove our main theorem, Theorem 1.3, as well as Theorem 1.5.
$2$
-contractible hypertrees. In Section 6, we prove our main theorem, Theorem 1.3, as well as Theorem 1.5.
2 Notation
Let
![]() $\mathcal {F}$
be a hypergraph on
$\mathcal {F}$
be a hypergraph on
![]() $V=V(\mathcal {F})$
. For each integer
$V=V(\mathcal {F})$
. For each integer
![]() $i\geq 0$
, we define the i-shadow of
$i\geq 0$
, we define the i-shadow of
![]() $\mathcal {F}$
to be
$\mathcal {F}$
to be
The Lovász’ [Reference Lovász31] version of the Kruskal-Katona theorem states that if
![]() $\mathcal {F}$
is a k-graph of size
$\mathcal {F}$
is a k-graph of size
![]() $|\mathcal {F}|=\binom {x}{k}$
, where
$|\mathcal {F}|=\binom {x}{k}$
, where
![]() $x\geq k-1$
is a real number, then for all i with
$x\geq k-1$
is a real number, then for all i with
![]() $1\leq i \leq k-1$
one has
$1\leq i \leq k-1$
one has
 $$ \begin{align} |\partial_i(\mathcal{F})|\geq \binom{x}{i}. \end{align} $$
$$ \begin{align} |\partial_i(\mathcal{F})|\geq \binom{x}{i}. \end{align} $$
Given
![]() $D\subseteq V(\mathcal {F})$
, we define the link of D in
$D\subseteq V(\mathcal {F})$
, we define the link of D in
![]() $\mathcal {F}$
to be
$\mathcal {F}$
to be
Note that we allow
![]() $\emptyset $
to be a member of
$\emptyset $
to be a member of
![]() $\mathcal {L}_{\mathcal {F}}(D)$
. We define the degree of D in
$\mathcal {L}_{\mathcal {F}}(D)$
. We define the degree of D in
![]() $\mathcal {F}$
to be
$\mathcal {F}$
to be
![]() $d_{\mathcal {F}}(D):=|\mathcal {L}_{\mathcal {F}}(D)|$
.
$d_{\mathcal {F}}(D):=|\mathcal {L}_{\mathcal {F}}(D)|$
.
Given a k-graph
![]() $\mathcal {F}$
where
$\mathcal {F}$
where
![]() $k\geq 2$
is an integer and integer i with
$k\geq 2$
is an integer and integer i with
![]() $1\leq i\leq k-1$
, let
$1\leq i\leq k-1$
, let
We call
![]() $\delta _i(\mathcal {F})$
the proper minimum i-degree of
$\delta _i(\mathcal {F})$
the proper minimum i-degree of
![]() $\mathcal {F}$
. By definition, every i-set in
$\mathcal {F}$
. By definition, every i-set in
![]() $\mathcal {F}$
either has degree
$\mathcal {F}$
either has degree
![]() $0$
or has degree at least
$0$
or has degree at least
![]() $\delta _i(\mathcal {F})$
. Let
$\delta _i(\mathcal {F})$
. Let
![]() $\mathcal {F}$
be a k-graph and
$\mathcal {F}$
be a k-graph and
![]() $S\subseteq V(\mathcal {F})$
, we let
$S\subseteq V(\mathcal {F})$
, we let
![]() $\mathcal {F}-S:=\{F\setminus S: F\in \mathcal {F}\}$
$\mathcal {F}-S:=\{F\setminus S: F\in \mathcal {F}\}$
3 A variant of the Delta system method and a structural dichotomy for k graphs of size
 $\Theta (n^{k - 1})$
$\Theta (n^{k - 1})$
The delta system method, originated by Deza, Erdős and Frankl [Reference Deza, Erdős and Frankl7] and others, is a powerful tool for solving extremal set problems. A particularly versatile tool within the method, which one may call the intersection semilattice lemma was developed by Füredi [Reference Füredi18] (Theorem 1’). The delta system method, particularly aided by the semilattice lemma, has been very successfully used to obtain a series of sharp results on extremal set problems (see for instance [Reference Frankl and Füredi16, Reference Frankl and Füredi17, Reference Füredi18, Reference Füredi20, Reference Füredi and Jiang21, Reference Füredi, Jiang and Seiver23]). However, despite its effectiveness in determining the threshold on the size of a hosting hypergraph beyond which a certain subgraph occurs, it does not readily allow us to effectively count the number of such subgraphs (known as the supersaturation problem). In this section, we develop a variant of Füredi’s intersection semilattice lemma, Theorem 3.1 below, to also address hypergraph supersaturation.
Let
![]() $k\geq 2$
be an integer. Let
$k\geq 2$
be an integer. Let
![]() $\mathcal {F}$
be a k-partite k-graph
$\mathcal {F}$
be a k-partite k-graph
![]() $\mathcal {F}$
with a fixed k-partition
$\mathcal {F}$
with a fixed k-partition
![]() $(X_1,\dots , X_k)$
. For each
$(X_1,\dots , X_k)$
. For each
![]() $J\subseteq [k]$
and
$J\subseteq [k]$
and
![]() $F\in \mathcal {F}$
, we define the J-projection of F, denoted by
$F\in \mathcal {F}$
, we define the J-projection of F, denoted by
![]() $F_J$
to be
$F_J$
to be
Conversely, for any
![]() $D\in \bigcup _{i=1}^k \partial _i(\mathcal {F})$
, we define the pattern of D, denoted by
$D\in \bigcup _{i=1}^k \partial _i(\mathcal {F})$
, we define the pattern of D, denoted by
![]() $\pi (D)$
, to be
$\pi (D)$
, to be
Note that since
![]() $\mathcal {F}$
is k-partite,
$\mathcal {F}$
is k-partite,
![]() $|\pi (D)|=|D|$
for each
$|\pi (D)|=|D|$
for each
![]() $D\in \bigcup _{i=1}^k \partial _i(\mathcal {F})$
.
$D\in \bigcup _{i=1}^k \partial _i(\mathcal {F})$
.
Given a positive integer
![]() $s\geq 2$
, a nonempty hypergraph
$s\geq 2$
, a nonempty hypergraph
![]() $\mathcal {H}$
is called s-diverse if
$\mathcal {H}$
is called s-diverse if
Note that implicitly an s-diverse hypergraph necessarily contains more than s edges.
Let
Theorem 3.1 (Super-homogeneous Subfamily Lemma).
Let
![]() $s, k\geq 2$
be integers where
$s, k\geq 2$
be integers where
![]() $s \geq 2k$
. Let
$s \geq 2k$
. Let
![]() $c(k,s) = \frac {k!}{k^k (2s(1 + 2^{k}))^{2^k}}$
. Let
$c(k,s) = \frac {k!}{k^k (2s(1 + 2^{k}))^{2^k}}$
. Let
![]() $\mathcal {F}$
be a k-graph on
$\mathcal {F}$
be a k-graph on
![]() $[n]$
. Then there exists a k-partite subgraph
$[n]$
. Then there exists a k-partite subgraph
![]() $\mathcal {F}' \subseteq \mathcal {F}$
with some k-partition
$\mathcal {F}' \subseteq \mathcal {F}$
with some k-partition
![]() $(X_1,\dots , X_k)$
such that the following holds:
$(X_1,\dots , X_k)$
such that the following holds:
-
1.
 $|\mathcal {F}'|\geq c(k,s) |\mathcal {F}|$
.
$|\mathcal {F}'|\geq c(k,s) |\mathcal {F}|$
. -
2. For every
 $F\in \mathcal {F}'$
and
$F\in \mathcal {F}'$
and
 $J\in \mathrm {Int}(\mathcal {F}')$
,
$J\in \mathrm {Int}(\mathcal {F}')$
,
 $\mathcal {L}_{\mathcal {F}'}(F_J)$
is s-diverse.
$\mathcal {L}_{\mathcal {F}'}(F_J)$
is s-diverse. -
3. For every
 $F\in \mathcal {F}'$
and
$F\in \mathcal {F}'$
and
 $J\in \mathrm {Int}(\mathcal {F}')$
,
$J\in \mathrm {Int}(\mathcal {F}')$
,
 $d_{\mathcal {F}'}(F_J)\geq \max \{s, \frac {1}{2k}\frac {|\mathcal {F}'|}{n^{|J|} }\}$
.
$d_{\mathcal {F}'}(F_J)\geq \max \{s, \frac {1}{2k}\frac {|\mathcal {F}'|}{n^{|J|} }\}$
.
We call such a k-graph
![]() $\mathcal {F}' s$
-super-homogeneous.
$\mathcal {F}' s$
-super-homogeneous.
Proof. By a well-known result of Erdős and Kleitman [Reference Erdős and Kleitman9],
![]() $\mathcal {F}$
contains a k-partite subgraph
$\mathcal {F}$
contains a k-partite subgraph
![]() $\mathcal {F}_0$
with
$\mathcal {F}_0$
with
![]() $|\mathcal {F}_0|\geq \frac {k!}{k^k}|\mathcal {F}|$
. Let
$|\mathcal {F}_0|\geq \frac {k!}{k^k}|\mathcal {F}|$
. Let
![]() $(X_1, X_2, \dots X_k)$
be a fixed k-partition of
$(X_1, X_2, \dots X_k)$
be a fixed k-partition of
![]() $\mathcal {F}_0$
. If
$\mathcal {F}_0$
. If
![]() $\mathcal {F}_0$
satisfies conditions 2 and 3, then the theorem holds with
$\mathcal {F}_0$
satisfies conditions 2 and 3, then the theorem holds with
![]() $\mathcal {F}'=\mathcal {F}_0$
. Otherwise, let
$\mathcal {F}'=\mathcal {F}_0$
. Otherwise, let
![]() $\mathcal {G}_0=\mathcal {F}_0$
. We perform a so-called filtering process on
$\mathcal {G}_0=\mathcal {F}_0$
. We perform a so-called filtering process on
![]() $\mathcal {G}_0$
as follows. Let
$\mathcal {G}_0$
as follows. Let
![]() $\mathcal {W}_0=\emptyset $
. For each
$\mathcal {W}_0=\emptyset $
. For each
![]() $J\in \mathrm {Int}(\mathcal {G}_0)$
, let
$J\in \mathrm {Int}(\mathcal {G}_0)$
, let
![]() $\mathcal {A}_J=\emptyset $
. We iteratively modify
$\mathcal {A}_J=\emptyset $
. We iteratively modify
![]() $\mathcal {G}_0$
,
$\mathcal {G}_0$
,
![]() $\mathcal {W}_0$
and the
$\mathcal {W}_0$
and the
![]() $\mathcal {A}_J$
’s for
$\mathcal {A}_J$
’s for
![]() $J\in \mathrm {Int}(\mathcal {G}_0)$
as follows. Whenever there is an edge
$J\in \mathrm {Int}(\mathcal {G}_0)$
as follows. Whenever there is an edge
![]() $F\in \mathcal {G}_0$
and a
$F\in \mathcal {G}_0$
and a
![]() $J\in \mathrm {Int}(\mathcal {G}_0)$
such that
$J\in \mathrm {Int}(\mathcal {G}_0)$
such that
![]() $\mathcal {L}_{\mathcal {G}_0}(F_J)$
is nonempty and not s-diverse, we remove all the edges of
$\mathcal {L}_{\mathcal {G}_0}(F_J)$
is nonempty and not s-diverse, we remove all the edges of
![]() $\mathcal {G}_0$
containing
$\mathcal {G}_0$
containing
![]() $F_J$
and add them to
$F_J$
and add them to
![]() $\mathcal {A}_J$
. Whenever there is an edge
$\mathcal {A}_J$
. Whenever there is an edge
![]() $F\in \mathcal {G}_0$
and a
$F\in \mathcal {G}_0$
and a
![]() $J\in \mathrm {Int}(G_0)$
such that
$J\in \mathrm {Int}(G_0)$
such that
![]() $\mathcal {L}_{\mathcal {G}_0}(F_j)$
is s-diverse but
$\mathcal {L}_{\mathcal {G}_0}(F_j)$
is s-diverse but
![]() $d_{\mathcal {G}_0}(F_J)<\frac {1}{2k}\frac {|\mathcal {F}_0|}{n^{|J|}}$
, we remove all the edges of
$d_{\mathcal {G}_0}(F_J)<\frac {1}{2k}\frac {|\mathcal {F}_0|}{n^{|J|}}$
, we remove all the edges of
![]() $\mathcal {G}_0$
containing
$\mathcal {G}_0$
containing
![]() $F_J$
and add them to
$F_J$
and add them to
![]() $\mathcal {W}_0$
. Let
$\mathcal {W}_0$
. Let
![]() $\mathcal {G}^*_0$
denote the final
$\mathcal {G}^*_0$
denote the final
![]() $\mathcal {G}_0$
at the end of the filtering process. By definition, if
$\mathcal {G}_0$
at the end of the filtering process. By definition, if
![]() $\mathcal {G}^*_0$
is nonempty, then
$\mathcal {G}^*_0$
is nonempty, then
![]() $\mathcal {G}^*_0$
satisfies conditions 2 and 3.
$\mathcal {G}^*_0$
satisfies conditions 2 and 3.
Note that
![]() $|\mathcal {W}_0|\leq |\mathcal {F}_0|/2$
. This is because for any fixed
$|\mathcal {W}_0|\leq |\mathcal {F}_0|/2$
. This is because for any fixed
![]() $j=1,\dots , k-1$
, there are at most
$j=1,\dots , k-1$
, there are at most
![]() $\binom {n}{j}$
different
$\binom {n}{j}$
different
![]() $F_J$
’s. When all edges containing some
$F_J$
’s. When all edges containing some
![]() $F_J$
are moved to
$F_J$
are moved to
![]() $\mathcal {W}_0$
, by definition, fewer than
$\mathcal {W}_0$
, by definition, fewer than
![]() $\frac {1}{2k}\frac {|\mathcal {F}_0|}{n^{|J|}}$
edges are moved. Hence
$\frac {1}{2k}\frac {|\mathcal {F}_0|}{n^{|J|}}$
edges are moved. Hence
![]() $|\mathcal {F}_0\setminus \mathcal {W}_0|\geq |\mathcal {F}_0|/2$
. If
$|\mathcal {F}_0\setminus \mathcal {W}_0|\geq |\mathcal {F}_0|/2$
. If
![]() $|\mathcal {G}_0^*|\geq \frac {1}{1+2^k} |\mathcal {F}_0\setminus \mathcal {W}_0|$
, we let
$|\mathcal {G}_0^*|\geq \frac {1}{1+2^k} |\mathcal {F}_0\setminus \mathcal {W}_0|$
, we let
![]() $\mathcal {F}'=\mathcal {G}^*_0$
. Otherwise, by the pigeonhole principle, there exists some
$\mathcal {F}'=\mathcal {G}^*_0$
. Otherwise, by the pigeonhole principle, there exists some
![]() $J\in \mathrm {Int}(\mathcal {G}_0)$
such that
$J\in \mathrm {Int}(\mathcal {G}_0)$
such that
![]() $|\mathcal {A}_J|\geq \frac {1}{1+2^k} |\mathcal {F}_0\setminus \mathcal {W}_0|$
. Note that edges were added to
$|\mathcal {A}_J|\geq \frac {1}{1+2^k} |\mathcal {F}_0\setminus \mathcal {W}_0|$
. Note that edges were added to
![]() $\mathcal {A}_J$
in batches, with each batch consisting of edges F with the same J-projection and different batches have different J-projections. Consider any batch
$\mathcal {A}_J$
in batches, with each batch consisting of edges F with the same J-projection and different batches have different J-projections. Consider any batch
![]() $\mathcal {B}$
added to
$\mathcal {B}$
added to
![]() $\mathcal {A}_J$
. Let D denote the common J-projection of the edges in
$\mathcal {A}_J$
. Let D denote the common J-projection of the edges in
![]() $\mathcal {B}$
. By definition,
$\mathcal {B}$
. By definition,
![]() $\mathcal {L}_{\mathcal {B}}(D)=\mathcal {L}_{\mathcal {G}_0}(F_J)$
is nonempty and not s-diverse at the moment
$\mathcal {L}_{\mathcal {B}}(D)=\mathcal {L}_{\mathcal {G}_0}(F_J)$
is nonempty and not s-diverse at the moment
![]() $\mathcal {B}$
was added to
$\mathcal {B}$
was added to
![]() $\mathcal {A}_J$
. By definition, there exists a vertex v in
$\mathcal {A}_J$
. By definition, there exists a vertex v in
![]() $\mathcal {L}_{\mathcal {B}}(D)$
that lies in at least
$\mathcal {L}_{\mathcal {B}}(D)$
that lies in at least
![]() $(1/s)|\mathcal {L}_{\mathcal {B}}(D)|$
of the edges. Let
$(1/s)|\mathcal {L}_{\mathcal {B}}(D)|$
of the edges. Let
![]() $\mathcal {B}'$
denote the subset of edges in
$\mathcal {B}'$
denote the subset of edges in
![]() $\mathcal {B}$
that also contain v. We now remove
$\mathcal {B}$
that also contain v. We now remove
![]() $\mathcal {B}$
from
$\mathcal {B}$
from
![]() $\mathcal {A}_J$
and replace it with
$\mathcal {A}_J$
and replace it with
![]() $\mathcal {B}'$
. We do this for each batch of edges that were added to
$\mathcal {B}'$
. We do this for each batch of edges that were added to
![]() $\mathcal {A}_J$
, and denote the resulting subgraph of
$\mathcal {A}_J$
, and denote the resulting subgraph of
![]() $\mathcal {A}_J$
by
$\mathcal {A}_J$
by
![]() $\mathcal {A}^{\prime }_J$
. Then
$\mathcal {A}^{\prime }_J$
. Then
![]() $|\mathcal {A}^{\prime }_J|\geq (1/s)|\mathcal {A}_J|$
. Furthermore, it is easy to see that
$|\mathcal {A}^{\prime }_J|\geq (1/s)|\mathcal {A}_J|$
. Furthermore, it is easy to see that
![]() $J\notin \mathrm {Int}(\mathcal {A}^{\prime }_J)$
. We let
$J\notin \mathrm {Int}(\mathcal {A}^{\prime }_J)$
. We let
![]() $\mathcal {F}_1=\mathcal {A}^{\prime }_J$
. Then
$\mathcal {F}_1=\mathcal {A}^{\prime }_J$
. Then
Now, let
![]() $\mathcal {G}_1=\mathcal {F}_1$
, let
$\mathcal {G}_1=\mathcal {F}_1$
, let
![]() $\mathcal {W}_1=\emptyset $
and set
$\mathcal {W}_1=\emptyset $
and set
![]() $\mathcal {A}_J=\emptyset $
for all
$\mathcal {A}_J=\emptyset $
for all
![]() $J\in \mathrm {Int}(\mathcal {G}_1)$
. We then perform the same filtering on
$J\in \mathrm {Int}(\mathcal {G}_1)$
. We then perform the same filtering on
![]() $\mathcal {G}_1$
to iteratively modify
$\mathcal {G}_1$
to iteratively modify
![]() $\mathcal {G}_1$
,
$\mathcal {G}_1$
,
![]() $\mathcal {W}_1$
and the
$\mathcal {W}_1$
and the
![]() $\mathcal {A}_J$
’s for
$\mathcal {A}_J$
’s for
![]() $J\in \mathrm {Int}(\mathcal {G}_1)$
. Let
$J\in \mathrm {Int}(\mathcal {G}_1)$
. Let
![]() $\mathcal {G}^*_1$
denote the final
$\mathcal {G}^*_1$
denote the final
![]() $\mathcal {G}_1$
at the end of the filtering process. By definition,
$\mathcal {G}_1$
at the end of the filtering process. By definition,
![]() $\mathcal {G}^*_1$
satisfies conditions 2 and 3. If
$\mathcal {G}^*_1$
satisfies conditions 2 and 3. If
![]() $|\mathcal {G}_1^*|\geq \frac {1}{1+2^k}|\mathcal {F}_1\setminus \mathcal {W}_1|$
, we let
$|\mathcal {G}_1^*|\geq \frac {1}{1+2^k}|\mathcal {F}_1\setminus \mathcal {W}_1|$
, we let
![]() $\mathcal {F}'=\mathcal {G}_1^*$
. Otherwise, as before, there exists some
$\mathcal {F}'=\mathcal {G}_1^*$
. Otherwise, as before, there exists some
![]() $J\in \mathrm {Int}(\mathcal {G}_1)$
and a subgraph
$J\in \mathrm {Int}(\mathcal {G}_1)$
and a subgraph
![]() $\mathcal {A}^{\prime }_J\subseteq \mathcal {A}_J$
with
$\mathcal {A}^{\prime }_J\subseteq \mathcal {A}_J$
with
![]() $|\mathcal {A}^{\prime }_J|\geq \frac {1}{2s(1+2^k)} |\mathcal {F}_1|$
such that
$|\mathcal {A}^{\prime }_J|\geq \frac {1}{2s(1+2^k)} |\mathcal {F}_1|$
such that
![]() $|\mathrm {Int}(\mathcal {A}^{\prime }_J)|\leq |\mathrm {Int}(\mathcal {G}_1)|-1$
. We let
$|\mathrm {Int}(\mathcal {A}^{\prime }_J)|\leq |\mathrm {Int}(\mathcal {G}_1)|-1$
. We let
![]() $\mathcal {F}_2=\mathcal {A}^{\prime }_J$
.
$\mathcal {F}_2=\mathcal {A}^{\prime }_J$
.
We continue like this, obtaining a sequence
![]() $\mathcal {F}_0, \mathcal {F}_1,\dots $
. Since
$\mathcal {F}_0, \mathcal {F}_1,\dots $
. Since
![]() $|\mathrm {Int}(\mathcal {F}_i)|$
strictly decreases with i, the sequence must end with
$|\mathrm {Int}(\mathcal {F}_i)|$
strictly decreases with i, the sequence must end with
![]() $\mathcal {F}_m$
for some
$\mathcal {F}_m$
for some
![]() $m\leq 2^k-1$
. Since
$m\leq 2^k-1$
. Since
![]() $\mathcal {F}_{m+1}$
is undefined, this must mean that
$\mathcal {F}_{m+1}$
is undefined, this must mean that
 $$\begin{align*}|\mathcal{G}_m^*|\geq \frac{1}{1+2^k}|\mathcal{F}_m\setminus \mathcal{W}_m|\geq \frac{1}{2(1+2^k)}|\mathcal{F}_m|\geq \frac{1}{[2s(1+2^k)]^{2^k}}|\mathcal{F}_0|\geq c(k,s)|\mathcal{F}|,\end{align*}$$
$$\begin{align*}|\mathcal{G}_m^*|\geq \frac{1}{1+2^k}|\mathcal{F}_m\setminus \mathcal{W}_m|\geq \frac{1}{2(1+2^k)}|\mathcal{F}_m|\geq \frac{1}{[2s(1+2^k)]^{2^k}}|\mathcal{F}_0|\geq c(k,s)|\mathcal{F}|,\end{align*}$$
where
![]() $c(k,s)=\frac {k!}{k^k}\cdot \frac {1}{[2s(1+2^k)]^{2^k}}$
. Let
$c(k,s)=\frac {k!}{k^k}\cdot \frac {1}{[2s(1+2^k)]^{2^k}}$
. Let
![]() $\mathcal {F}'=\mathcal {G}^*_m$
. Then
$\mathcal {F}'=\mathcal {G}^*_m$
. Then
![]() $|\mathcal {F}'|\geq c(k,s)|\mathcal {F}|$
and
$|\mathcal {F}'|\geq c(k,s)|\mathcal {F}|$
and
![]() $\mathcal {F}'$
also satisfies conditions 2 and 3, by the definition of
$\mathcal {F}'$
also satisfies conditions 2 and 3, by the definition of
![]() $\mathcal {G}^*_m$
.
$\mathcal {G}^*_m$
.
Throughout the rest of the paper, whenever we consider an s-super-homogeneous k-graph
![]() $\mathcal {F}$
, we always implicitly fix a k-partition associated with
$\mathcal {F}$
, we always implicitly fix a k-partition associated with
![]() $\mathrm {Int}(\mathcal {F})$
.
$\mathrm {Int}(\mathcal {F})$
.
Next, we collect some useful facts about s-super-homogeneous families, for which we need the following definition.
Definition 3.2. Let k be a positive integer. Given a family
![]() $\mathcal {J}$
of proper subsets of
$\mathcal {J}$
of proper subsets of
![]() $[k]$
, let
$[k]$
, let
We call
![]() $r(\mathcal {J})$
the rank of
$r(\mathcal {J})$
the rank of
![]() $\mathcal {J}$
.
$\mathcal {J}$
.
Lemma 3.3. Let
![]() $s , k \geq 2$
be integers with
$s , k \geq 2$
be integers with
![]() $s \geq 2k$
. Let
$s \geq 2k$
. Let
![]() $\mathcal {F}$
be an s-super-homogeneous k-partite k-graph on
$\mathcal {F}$
be an s-super-homogeneous k-partite k-graph on
![]() $[n]$
with some fixed k-partition
$[n]$
with some fixed k-partition
![]() $(X_1,\dots , X_k)$
. Then, the following hold.
$(X_1,\dots , X_k)$
. Then, the following hold.
-
1. For each
 $J\subsetneq [k]$
where
$J\subsetneq [k]$
where
 $J\notin \mathrm {Int}(\mathcal {F})$
and each
$J\notin \mathrm {Int}(\mathcal {F})$
and each
 $F\in \mathcal {F}$
, there is no
$F\in \mathcal {F}$
, there is no
 $F'\in \mathcal {F}$
satisfying
$F'\in \mathcal {F}$
satisfying
 $F\cap F'=F_J$
.
$F\cap F'=F_J$
. -
2. For all
 $ J,J'\in \mathrm {Int}(\mathcal {F})$
,
$ J,J'\in \mathrm {Int}(\mathcal {F})$
,
 $J\cap J'\in \mathrm {Int}(\mathcal {F})$
, that is,
$J\cap J'\in \mathrm {Int}(\mathcal {F})$
, that is,
 $\mathrm {Int}(\mathcal {F})$
is closed under intersection.
$\mathrm {Int}(\mathcal {F})$
is closed under intersection. -
3. If
 $\mathrm {Int}(\mathcal {F})$
has rank m, then
$\mathrm {Int}(\mathcal {F})$
has rank m, then
 $|\mathcal {F}|\leq \binom {n}{m}$
.
$|\mathcal {F}|\leq \binom {n}{m}$
.
Proof. Statement 1 follows from definition of
![]() $\mathrm {Int}(\mathcal {F})$
. For statement 2, let
$\mathrm {Int}(\mathcal {F})$
. For statement 2, let
![]() $J,J'\in \mathrm {Int}(\mathcal {F})$
with
$J,J'\in \mathrm {Int}(\mathcal {F})$
with
![]() $J\neq J'$
. Let
$J\neq J'$
. Let
![]() $F\in \mathcal {F}$
. By our assumption
$F\in \mathcal {F}$
. By our assumption
![]() $\mathcal {L}_{\mathcal {F}}(F_J)$
is s-diverse. So the vertices in
$\mathcal {L}_{\mathcal {F}}(F_J)$
is s-diverse. So the vertices in
![]() $F\setminus F_J$
block fewer than
$F\setminus F_J$
block fewer than
![]() $k(1/s)|\mathcal {L}_{\mathcal {F}}(F_J)| \leq |\mathcal {L}_{\mathcal {F}}(F_J)|$
of the edges in
$k(1/s)|\mathcal {L}_{\mathcal {F}}(F_J)| \leq |\mathcal {L}_{\mathcal {F}}(F_J)|$
of the edges in
![]() $\mathcal {L}_{\mathcal {F}}(F_J)$
. So there exists
$\mathcal {L}_{\mathcal {F}}(F_J)$
. So there exists
![]() $F'\in \mathcal {F}$
with
$F'\in \mathcal {F}$
with
![]() $F\cap F'=F_J$
. By a similar reasoning, since
$F\cap F'=F_J$
. By a similar reasoning, since
![]() $2k(1/s)|\mathcal {L}_{\mathcal {F}}(F^{\prime }_{J'})| \leq |\mathcal {L}_{\mathcal {F}}(F^{\prime }_{J'})|$
there exists
$2k(1/s)|\mathcal {L}_{\mathcal {F}}(F^{\prime }_{J'})| \leq |\mathcal {L}_{\mathcal {F}}(F^{\prime }_{J'})|$
there exists
![]() $F"\in \mathcal {F}$
containing
$F"\in \mathcal {F}$
containing
![]() $F^{\prime }_{J'}$
that avoids vertices in
$F^{\prime }_{J'}$
that avoids vertices in
![]() $(F\setminus F')\cup (F'\setminus F^{\prime }_{J'})$
. Now,
$(F\setminus F')\cup (F'\setminus F^{\prime }_{J'})$
. Now,
![]() $\pi (F\cap F")=J\cap J'$
. Hence,
$\pi (F\cap F")=J\cap J'$
. Hence,
![]() $J\cap J'\in \mathrm {Int}(\mathcal {F})$
.
$J\cap J'\in \mathrm {Int}(\mathcal {F})$
.
For statement 3, suppose
![]() $\mathrm {Int}(\mathcal {F})$
has rank m. Then
$\mathrm {Int}(\mathcal {F})$
has rank m. Then
![]() $\exists D\subseteq [k]$
with
$\exists D\subseteq [k]$
with
![]() $|D|=m$
such that D is not contained in any member of
$|D|=m$
such that D is not contained in any member of
![]() $\mathrm {Int}(\mathcal {F})$
. Consider any
$\mathrm {Int}(\mathcal {F})$
. Consider any
![]() $F,F'\in \mathcal {F}$
, where
$F,F'\in \mathcal {F}$
, where
![]() $F\neq G$
. If
$F\neq G$
. If
![]() $F[D]=F'[D]$
, then
$F[D]=F'[D]$
, then
![]() $\pi (F\cap F')$
is a member of
$\pi (F\cap F')$
is a member of
![]() $\mathrm {Int}(\mathcal {F})$
that contains D, a contradiction. So, the D-projections of members of
$\mathrm {Int}(\mathcal {F})$
that contains D, a contradiction. So, the D-projections of members of
![]() $\mathcal {F}$
are all distinct. This implies that
$\mathcal {F}$
are all distinct. This implies that
![]() $|\mathcal {F}|\leq \binom {n}{m}$
.
$|\mathcal {F}|\leq \binom {n}{m}$
.
The following structural lemma strengthens Lemma 7.1 of [Reference Frankl and Füredi17] (see also Lemma 4.2 of [Reference Füredi and Jiang22]) and leads to a structural dichotomy theorem (Theorem 3.5) that is important for our main arguments.
Lemma 3.4. Let
![]() $k\geq 3$
be an integer. Let
$k\geq 3$
be an integer. Let
![]() $\mathcal {J}\subseteq 2^{[k]}$
be a family of proper subsets of
$\mathcal {J}\subseteq 2^{[k]}$
be a family of proper subsets of
![]() $[k]$
that is closed under intersection. Suppose
$[k]$
that is closed under intersection. Suppose
![]() $\mathcal {J}$
has rank at least
$\mathcal {J}$
has rank at least
![]() $k-1$
. Then one of the following must hold.
$k-1$
. Then one of the following must hold.
-
1. There exists
 $B\subseteq [k]$
, with
$B\subseteq [k]$
, with
 $|B|=k-2$
, such that
$|B|=k-2$
, such that
 $2^B\subseteq \mathcal {J}$
.
$2^B\subseteq \mathcal {J}$
. -
2. There exists a unique
 $i\in [k]$
such that
$i\in [k]$
such that
 $\forall D\subsetneq [k]$
with
$\forall D\subsetneq [k]$
with
 $i\in D$
we have
$i\in D$
we have
 $D\in \mathcal {J}$
and for every
$D\in \mathcal {J}$
and for every
 $D\subseteq [k]\setminus \{i\}$
with
$D\subseteq [k]\setminus \{i\}$
with
 $|D|\geq k-2$
we have
$|D|\geq k-2$
we have
 $D\notin \mathcal {J}$
. We call i the central index for
$D\notin \mathcal {J}$
. We call i the central index for
 $\mathcal {J}$
.
$\mathcal {J}$
.
If condition 1 holds for
![]() $\mathcal {J}$
, we say that
$\mathcal {J}$
, we say that
![]() $\mathcal {J}$
is of type 1. If condition 2 holds for
$\mathcal {J}$
is of type 1. If condition 2 holds for
![]() $\mathcal {J}$
, we say that
$\mathcal {J}$
, we say that
![]() $\mathcal {J}$
is of type 2.
$\mathcal {J}$
is of type 2.
Proof. If
![]() $r(\mathcal {J})=k$
then
$r(\mathcal {J})=k$
then
![]() $[k]\setminus \{j\}\in \mathcal {J}$
for each
$[k]\setminus \{j\}\in \mathcal {J}$
for each
![]() $j\in [k]$
. Since
$j\in [k]$
. Since
![]() $\mathcal {J}$
is closed under intersection, we see that
$\mathcal {J}$
is closed under intersection, we see that
![]() $S\in \mathcal {J}$
for each proper subset S of
$S\in \mathcal {J}$
for each proper subset S of
![]() $[k]$
. Hence statement 1 clearly holds. Next, suppose
$[k]$
. Hence statement 1 clearly holds. Next, suppose
![]() $r(\mathcal {J})=k-1$
. Then some
$r(\mathcal {J})=k-1$
. Then some
![]() $(k-1)$
-subset of
$(k-1)$
-subset of
![]() $[k]$
is not in
$[k]$
is not in
![]() $\mathcal {J}$
. Without loss of generality, suppose
$\mathcal {J}$
. Without loss of generality, suppose
![]() $[k]\setminus \{j\}\notin \mathcal {J}$
for
$[k]\setminus \{j\}\notin \mathcal {J}$
for
![]() $j=1,\dots , t$
and
$j=1,\dots , t$
and
![]() $[k]\setminus \{j\}\in \mathcal {J}$
for
$[k]\setminus \{j\}\in \mathcal {J}$
for
![]() $j=t+1,\dots , k$
, for some
$j=t+1,\dots , k$
, for some
![]() $1\leq t\leq k$
.
$1\leq t\leq k$
.
First, suppose
![]() $t=1$
. Then
$t=1$
. Then
![]() $[k]\setminus \{1\}\notin \mathcal {J}$
and
$[k]\setminus \{1\}\notin \mathcal {J}$
and
![]() $[k]\setminus \{2\},\dots , [k]\setminus \{k\}\in \mathcal {J}$
. Since
$[k]\setminus \{2\},\dots , [k]\setminus \{k\}\in \mathcal {J}$
. Since
![]() $\mathcal {J}$
is closed under intersection, every proper subset of
$\mathcal {J}$
is closed under intersection, every proper subset of
![]() $[k]$
that contains
$[k]$
that contains
![]() $1$
is in
$1$
is in
![]() $\mathcal {J}$
. We already have
$\mathcal {J}$
. We already have
![]() $[k]\setminus \{1\}\notin \mathcal {J}$
. Suppose there is a
$[k]\setminus \{1\}\notin \mathcal {J}$
. Suppose there is a
![]() $(k-2)$
-subset B of
$(k-2)$
-subset B of
![]() $[k]\setminus \{1\}$
that is in
$[k]\setminus \{1\}$
that is in
![]() $\mathcal {J}$
. Let S be any subset of B. By earlier discussion
$\mathcal {J}$
. Let S be any subset of B. By earlier discussion
![]() $S\cup \{1\}\in \mathcal {J}$
. Since
$S\cup \{1\}\in \mathcal {J}$
. Since
![]() $\mathcal {J}$
is closed under intersection, we have
$\mathcal {J}$
is closed under intersection, we have
![]() $S=(S\cup \{1\})\cap B\in \mathcal {J}$
. Hence,
$S=(S\cup \{1\})\cap B\in \mathcal {J}$
. Hence,
![]() $2^B\subseteq \mathcal {J}$
. So statement 1 holds in this case. Hence, we may assume that no
$2^B\subseteq \mathcal {J}$
. So statement 1 holds in this case. Hence, we may assume that no
![]() $(k-2)$
-subset of
$(k-2)$
-subset of
![]() $[k]\setminus \{1\}$
is in
$[k]\setminus \{1\}$
is in
![]() $\mathcal {J}$
. Then statement 2 holds for
$\mathcal {J}$
. Then statement 2 holds for
![]() $i=1$
. It is easy to see that if an i satisfies the requirements, it can only be
$i=1$
. It is easy to see that if an i satisfies the requirements, it can only be
![]() $1$
.
$1$
.
Next, suppose
![]() $t\geq 2$
. Observe that for any
$t\geq 2$
. Observe that for any
![]() $1\leq i<j\leq t$
, we must have
$1\leq i<j\leq t$
, we must have
![]() $[k]\setminus \{i,j\}\in \mathcal {J}$
, as otherwise
$[k]\setminus \{i,j\}\in \mathcal {J}$
, as otherwise
![]() $[k]\setminus \{i,j\}$
is not contained in any member of
$[k]\setminus \{i,j\}$
is not contained in any member of
![]() $\mathcal {J}$
, contradicting
$\mathcal {J}$
, contradicting
![]() $r(\mathcal {J})\geq k-1$
. Also, by our assumption for every
$r(\mathcal {J})\geq k-1$
. Also, by our assumption for every
![]() $t+1\leq j\leq k$
we have
$t+1\leq j\leq k$
we have
![]() $[k]\setminus \{j\}\in \mathcal {J}$
. Since
$[k]\setminus \{j\}\in \mathcal {J}$
. Since
![]() $\mathcal {J}$
is closed under intersection, we see that every subset of
$\mathcal {J}$
is closed under intersection, we see that every subset of
![]() $[k]\setminus \{1,2\}$
is in
$[k]\setminus \{1,2\}$
is in
![]() $\mathcal {J}$
. So statement 1 holds.
$\mathcal {J}$
. So statement 1 holds.
Now, we describe our structural theorem that gives a dichotomy of n-vertex k-graphs with
![]() $\Theta (n^{k-1})$
edges. We believe that it is also of independent interest.
$\Theta (n^{k-1})$
edges. We believe that it is also of independent interest.
Theorem 3.5. Let
![]() $a, \varepsilon $
be fixed positive reals with
$a, \varepsilon $
be fixed positive reals with
![]() $\varepsilon < \min \{1, a^{ k - 2}\}$
. Let
$\varepsilon < \min \{1, a^{ k - 2}\}$
. Let
![]() $k,s$
be fixed positive integers with
$k,s$
be fixed positive integers with
![]() $s \geq 2k$
. Let n be sufficiently large in terms of
$s \geq 2k$
. Let n be sufficiently large in terms of
![]() $a,\varepsilon , k,s$
. Let
$a,\varepsilon , k,s$
. Let
![]() $\mathcal {F}$
be a k-graph on
$\mathcal {F}$
be a k-graph on
![]() $[n]$
with
$[n]$
with
![]() $|\mathcal {F}|=a\binom {n}{k-1}$
. Then one of the following two holds:
$|\mathcal {F}|=a\binom {n}{k-1}$
. Then one of the following two holds:
-
1.
 $\mathcal {F}$
contains an s-super-homogeneous k-partite subgraph
$\mathcal {F}$
contains an s-super-homogeneous k-partite subgraph
 $\mathcal {F}'$
such that
$\mathcal {F}'$
such that
 $|\mathcal {F}'|\geq \frac {1}{2}c(k,s)\varepsilon |\mathcal {F}|$
and
$|\mathcal {F}'|\geq \frac {1}{2}c(k,s)\varepsilon |\mathcal {F}|$
and
 $\mathrm {Int}(\mathcal {F}')$
is of type 1, where
$\mathrm {Int}(\mathcal {F}')$
is of type 1, where
 $c(k,s)$
is the constant as in Theorem 3.1.
$c(k,s)$
is the constant as in Theorem 3.1. -
2. There exist a
 $W \subseteq [n]$
and a subgraph
$W \subseteq [n]$
and a subgraph
 $\mathcal {F}"\subseteq \mathcal {F}$
satisfying the following:
$\mathcal {F}"\subseteq \mathcal {F}$
satisfying the following:-
(a)
 $|W|\leq \left (\frac {10}{c(k,s)\varepsilon ^2}\right )^{k-1}$
.
$|W|\leq \left (\frac {10}{c(k,s)\varepsilon ^2}\right )^{k-1}$
. -
(b)
 $|\mathcal {F}"|\geq (1-\varepsilon ) |\mathcal {F}|$
.
$|\mathcal {F}"|\geq (1-\varepsilon ) |\mathcal {F}|$
. -
(c) Every
 $F \in \mathcal {F}"$
satisfies
$F \in \mathcal {F}"$
satisfies
 $|W \cap F| = 1$
.
$|W \cap F| = 1$
.
-
Proof. First we apply Lemma 3.1 to
![]() $\mathcal {F}$
to get an s-super-homogeneous subgraph
$\mathcal {F}$
to get an s-super-homogeneous subgraph
![]() $\mathcal {F}_1$
of size at least
$\mathcal {F}_1$
of size at least
![]() $c(k,s)|\mathcal {F}|$
. If
$c(k,s)|\mathcal {F}|$
. If
![]() $|\mathcal {F}\setminus \mathcal {F}_1|\leq \frac {1}{2} \varepsilon |\mathcal {F}|$
, then we stop. Otherwise, we apply the lemma to
$|\mathcal {F}\setminus \mathcal {F}_1|\leq \frac {1}{2} \varepsilon |\mathcal {F}|$
, then we stop. Otherwise, we apply the lemma to
![]() $\mathcal {F}\setminus \mathcal {F}_1$
to find an s-super-homogeneous subgraph
$\mathcal {F}\setminus \mathcal {F}_1$
to find an s-super-homogeneous subgraph
![]() $\mathcal {F}_2$
of size at least
$\mathcal {F}_2$
of size at least
![]() $c(k,s)|\mathcal {F}\setminus \mathcal {F}_1|$
. In general, as long as
$c(k,s)|\mathcal {F}\setminus \mathcal {F}_1|$
. In general, as long as
![]() $|\mathcal {F}\setminus (\mathcal {F}_1\cup \cdots \cup \mathcal {F}_i)|>\frac {1}{2}\varepsilon |\mathcal {F}|$
, we let
$|\mathcal {F}\setminus (\mathcal {F}_1\cup \cdots \cup \mathcal {F}_i)|>\frac {1}{2}\varepsilon |\mathcal {F}|$
, we let
![]() $\mathcal {F}_{i+1}$
be an s-super-homogeneous subgraph of
$\mathcal {F}_{i+1}$
be an s-super-homogeneous subgraph of
![]() $\mathcal {F}\setminus (\mathcal {F}_1\cup \cdots \cup \mathcal {F}_i)$
of size at least
$\mathcal {F}\setminus (\mathcal {F}_1\cup \cdots \cup \mathcal {F}_i)$
of size at least
![]() $c(k,s)|\mathcal {F}\setminus (\mathcal {F}_1\cup \cdots \cup \mathcal {F}_i)|$
, which exists by Lemma 3.1. Suppose the sequence of subgraphs we constructed are
$c(k,s)|\mathcal {F}\setminus (\mathcal {F}_1\cup \cdots \cup \mathcal {F}_i)|$
, which exists by Lemma 3.1. Suppose the sequence of subgraphs we constructed are
![]() $\mathcal {F}_1,\dots , \mathcal {F}_m$
.
$\mathcal {F}_1,\dots , \mathcal {F}_m$
.
By our algorithm, for each
![]() $i\in [m]$
,
$i\in [m]$
,
![]() $|\mathcal {F}_i|\geq \frac {1}{2}c(k,s) \varepsilon |\mathcal {F}|$
. Note that this implies that
$|\mathcal {F}_i|\geq \frac {1}{2}c(k,s) \varepsilon |\mathcal {F}|$
. Note that this implies that
![]() $m\leq \frac {2}{c(k,s)\varepsilon }$
. For each
$m\leq \frac {2}{c(k,s)\varepsilon }$
. For each
![]() $i\in [m]$
, by Lemma 3.3 part 3,
$i\in [m]$
, by Lemma 3.3 part 3,
![]() $r(\mathrm {Int}(\mathcal {F}_i))\geq k-1$
and by Lemma 3.3 part 2 and Lemma 3.4,
$r(\mathrm {Int}(\mathcal {F}_i))\geq k-1$
and by Lemma 3.3 part 2 and Lemma 3.4,
![]() $\mathrm {Int}(\mathcal {F}_i)$
is either of type 1 or is of type 2. If for some
$\mathrm {Int}(\mathcal {F}_i)$
is either of type 1 or is of type 2. If for some
![]() $i\in [m]$
,
$i\in [m]$
,
![]() $\mathrm {Int}(\mathcal {F}_i)$
is of type 1, then we let
$\mathrm {Int}(\mathcal {F}_i)$
is of type 1, then we let
![]() $\mathcal {F}'=\mathcal {F}_i$
for such an i and Statement 1 holds. Hence, we may assume that for each
$\mathcal {F}'=\mathcal {F}_i$
for such an i and Statement 1 holds. Hence, we may assume that for each
![]() $i\in [m]$
,
$i\in [m]$
,
![]() $\mathrm {Int}(\mathcal {F}_i)$
is of type 2. Let
$\mathrm {Int}(\mathcal {F}_i)$
is of type 2. Let
![]() $\mathcal {F}^*=\bigcup _{j=1}^m \mathcal {F}_j$
. Then
$\mathcal {F}^*=\bigcup _{j=1}^m \mathcal {F}_j$
. Then
Set
 $h=\left \lfloor \left (\frac {5m}{\varepsilon }\right )^{k-1} \right \rfloor $
. Since
$h=\left \lfloor \left (\frac {5m}{\varepsilon }\right )^{k-1} \right \rfloor $
. Since
![]() $m\leq \frac {2}{c(k,s)\varepsilon }$
, we have
$m\leq \frac {2}{c(k,s)\varepsilon }$
, we have
 $$ \begin{align} h\leq \left(\frac{10}{c(k,s)\varepsilon^2}\right)^{k-1}. \end{align} $$
$$ \begin{align} h\leq \left(\frac{10}{c(k,s)\varepsilon^2}\right)^{k-1}. \end{align} $$
For each
![]() $j\in [m]$
, let
$j\in [m]$
, let
![]() $i_j\in [k]$
denote the central index for
$i_j\in [k]$
denote the central index for
![]() $\mathrm {Int}(\mathcal {F}_j)$
and for each
$\mathrm {Int}(\mathcal {F}_j)$
and for each
![]() $F\in \mathcal {F}_j$
, let
$F\in \mathcal {F}_j$
, let
![]() $c(F) = F_{\{i_j\}}$
. We call
$c(F) = F_{\{i_j\}}$
. We call
![]() $c(F)$
the central vertex of F. We partition
$c(F)$
the central vertex of F. We partition
![]() $\mathcal {F}^*$
according to
$\mathcal {F}^*$
according to
![]() $c(F)$
. For each
$c(F)$
. For each
![]() $i \in [n]$
, let
$i \in [n]$
, let
Clearly, for each
![]() $i\in [n]$
we have
$i\in [n]$
we have
![]() $|\mathcal {A}_i|=|\mathcal {A}^{\prime }_i|$
. For each
$|\mathcal {A}_i|=|\mathcal {A}^{\prime }_i|$
. For each
![]() $j \in [m]$
, let
$j \in [m]$
, let
Then, in particular:
 $$\begin{align*}\bigcup_{i = 1}^n \mathcal{A}_i' = \bigcup_{j = 1}^m \mathcal{F}_j'. \end{align*}$$
$$\begin{align*}\bigcup_{i = 1}^n \mathcal{A}_i' = \bigcup_{j = 1}^m \mathcal{F}_j'. \end{align*}$$
The next claim is crucial to our argument.
Claim 3.6. For each
![]() $j\in [m]$
, we have
$j\in [m]$
, we have
 $$\begin{align*}|\partial_{k-2}(\mathcal{F}_j')|=\sum_{i = 1}^n |\partial_{k - 2} (\mathcal{A}_i' \cap \mathcal{F}_j')|.\end{align*}$$
$$\begin{align*}|\partial_{k-2}(\mathcal{F}_j')|=\sum_{i = 1}^n |\partial_{k - 2} (\mathcal{A}_i' \cap \mathcal{F}_j')|.\end{align*}$$
Proof of Claim 3.6.
Let
![]() $(X_1,\dots , X_k)$
denote the k-partition associated with
$(X_1,\dots , X_k)$
denote the k-partition associated with
![]() $\mathrm {Int}(\mathcal {F}_j)$
. Recall that
$\mathrm {Int}(\mathcal {F}_j)$
. Recall that
![]() $i_j\in [k]$
denotes the central index for
$i_j\in [k]$
denotes the central index for
![]() $\mathrm {Int}(\mathcal {F}_j)$
. Without loss of generality, we may assume
$\mathrm {Int}(\mathcal {F}_j)$
. Without loss of generality, we may assume
![]() $i_j=1$
. To prove the claim, it suffices to show that for any
$i_j=1$
. To prove the claim, it suffices to show that for any
![]() $a,b\in X_1$
where
$a,b\in X_1$
where
![]() $a\neq b$
, we have
$a\neq b$
, we have
![]() $\partial _{k-2}(\mathcal {A}^{\prime }_a\cap \mathcal {F}^{\prime }_j)\cap \partial _{k-2}(\mathcal {A}^{\prime }_b\cap \mathcal {F}^{\prime }_j)=\emptyset $
. Suppose for contradiction that there exists
$\partial _{k-2}(\mathcal {A}^{\prime }_a\cap \mathcal {F}^{\prime }_j)\cap \partial _{k-2}(\mathcal {A}^{\prime }_b\cap \mathcal {F}^{\prime }_j)=\emptyset $
. Suppose for contradiction that there exists
![]() $S\in \partial _{k-2}(\mathcal {A}^{\prime }_a\cap \mathcal {F}^{\prime }_j)\cap \partial _{k-2}(\mathcal {A}^{\prime }_b\cap \mathcal {F}^{\prime }_j)$
. Then there exist
$S\in \partial _{k-2}(\mathcal {A}^{\prime }_a\cap \mathcal {F}^{\prime }_j)\cap \partial _{k-2}(\mathcal {A}^{\prime }_b\cap \mathcal {F}^{\prime }_j)$
. Then there exist
![]() $F_a\in \mathcal {A}_a\cap \mathcal {F}_j, F_b\in \mathcal {A}_b\cap \mathcal {F}_j$
such that
$F_a\in \mathcal {A}_a\cap \mathcal {F}_j, F_b\in \mathcal {A}_b\cap \mathcal {F}_j$
such that
![]() $F_a\cap F_b\supseteq S$
. By definition,
$F_a\cap F_b\supseteq S$
. By definition,
![]() $\pi (F_a\cap F_b)\in \mathrm {Int}(\mathcal {F}_j)$
. But
$\pi (F_a\cap F_b)\in \mathrm {Int}(\mathcal {F}_j)$
. But
![]() $\pi (F_a\cap F_b)$
is a subset of
$\pi (F_a\cap F_b)$
is a subset of
![]() $[k]\setminus \{1\}$
with size at least
$[k]\setminus \{1\}$
with size at least
![]() $k-2$
. This contradicts
$k-2$
. This contradicts
![]() $\mathrm {Int}(\mathcal {F}_j)$
being of type 2 (see Lemma 3.4 (2)). The claim immediately follows.
$\mathrm {Int}(\mathcal {F}_j)$
being of type 2 (see Lemma 3.4 (2)). The claim immediately follows.
Note that trivially
![]() $|\partial _{k - 2} (\mathcal {F}_j')| \leq \binom {n}{k - 2}$
. Now, we have
$|\partial _{k - 2} (\mathcal {F}_j')| \leq \binom {n}{k - 2}$
. Now, we have
 $$ \begin{align} \sum_{i = 1}^n |\partial_{k - 2}(\mathcal{A}_i')| \leq \sum_{i = 1}^n\sum_{j = 1}^m |\partial_{k - 2}(\mathcal{A}_i' \cap \mathcal{F}_j')|= \sum_{j = 1}^m \sum_{i = 1}^n|\partial_{k - 2}(\mathcal{A}_i' \cap \mathcal{F}_j')| = \sum_{j =1}^m |\partial_{k - 2} (\mathcal{F}_j')|\leq m \binom{n}{k - 2} \end{align} $$
$$ \begin{align} \sum_{i = 1}^n |\partial_{k - 2}(\mathcal{A}_i')| \leq \sum_{i = 1}^n\sum_{j = 1}^m |\partial_{k - 2}(\mathcal{A}_i' \cap \mathcal{F}_j')|= \sum_{j = 1}^m \sum_{i = 1}^n|\partial_{k - 2}(\mathcal{A}_i' \cap \mathcal{F}_j')| = \sum_{j =1}^m |\partial_{k - 2} (\mathcal{F}_j')|\leq m \binom{n}{k - 2} \end{align} $$
For each
![]() $i \in [n]$
, let
$i \in [n]$
, let
![]() $x_i$
be the real such that
$x_i$
be the real such that
![]() $|\partial _{k - 2}(\mathcal {A}_i')| = \binom {x_i}{k - 2}$
, where without loss of generality,
$|\partial _{k - 2}(\mathcal {A}_i')| = \binom {x_i}{k - 2}$
, where without loss of generality,
![]() $x_1 \geq x_2 \dots \geq x_n$
. By (6), for each
$x_1 \geq x_2 \dots \geq x_n$
. By (6), for each
![]() $i\in [n]$
we have
$i\in [n]$
we have
![]() $|\mathcal {A}_i'| \leq \binom {x_i}{k - 1}$
.
$|\mathcal {A}_i'| \leq \binom {x_i}{k - 1}$
.
By (8),
![]() $\sum _{i=1}^n\binom {x_i}{k-2}\leq m\binom {n}{k-2}$
. Thus,
$\sum _{i=1}^n\binom {x_i}{k-2}\leq m\binom {n}{k-2}$
. Thus,
![]() $\binom {x_{h+1}}{k - 2} \leq \frac {m}{h+1} \binom {n}{ k - 2}$
, which yields
$\binom {x_{h+1}}{k - 2} \leq \frac {m}{h+1} \binom {n}{ k - 2}$
, which yields
Thus, we have
 $$ \begin{align*} \sum_{i> h} |\mathcal{A}_i| =\sum_{i>h}|\mathcal{A}^{\prime}_i|&\leq \sum_{i = h + 1}^n \binom{x_i}{k - 1} \\&=\sum_{h+1}^n \frac{x_i-k+2}{k-1}\binom{x_i}{k-2}\\&\leq \frac{x_{h+1} - k +2 }{k - 1} \sum_{i = h + 1}^{n} \binom{x_i}{k - 2} \\&\leq \left( \frac{m}{h+1 } \right)^{ 1 / (k - 2)} \frac{nm}{k - 1} \binom{n}{k - 2} \quad \quad \text{(by (}{8}\text{) and (}{9}))\\\end{align*} $$
$$ \begin{align*} \sum_{i> h} |\mathcal{A}_i| =\sum_{i>h}|\mathcal{A}^{\prime}_i|&\leq \sum_{i = h + 1}^n \binom{x_i}{k - 1} \\&=\sum_{h+1}^n \frac{x_i-k+2}{k-1}\binom{x_i}{k-2}\\&\leq \frac{x_{h+1} - k +2 }{k - 1} \sum_{i = h + 1}^{n} \binom{x_i}{k - 2} \\&\leq \left( \frac{m}{h+1 } \right)^{ 1 / (k - 2)} \frac{nm}{k - 1} \binom{n}{k - 2} \quad \quad \text{(by (}{8}\text{) and (}{9}))\\\end{align*} $$
By our choice of h,
![]() $h+1\geq (\frac {5m}{\varepsilon })^{k-1}$
. So we have
$h+1\geq (\frac {5m}{\varepsilon })^{k-1}$
. So we have
![]() $\sum _{i>h} |\mathcal {A}_i|<\left (\frac {\varepsilon }{5}\right )^{1 + \frac {1}{k - 2}}\frac {n}{k-1}\binom {n}{k-2}\leq \frac {\varepsilon }{4} a\binom {n}{k-1}$
, for sufficiently large n and by our assumption
$\sum _{i>h} |\mathcal {A}_i|<\left (\frac {\varepsilon }{5}\right )^{1 + \frac {1}{k - 2}}\frac {n}{k-1}\binom {n}{k-2}\leq \frac {\varepsilon }{4} a\binom {n}{k-1}$
, for sufficiently large n and by our assumption
![]() $a \geq \varepsilon ^{\frac {1}{ k - 2}}$
. Let
$a \geq \varepsilon ^{\frac {1}{ k - 2}}$
. Let
![]() $W := [h]$
. Let
$W := [h]$
. Let
![]() $\mathcal {G}_1:= \{ F \in \mathcal {F}^*: c(F) \not \in W\}$
and
$\mathcal {G}_1:= \{ F \in \mathcal {F}^*: c(F) \not \in W\}$
and
![]() $\mathcal {G}_2:= \{F \in \mathcal {F}^*: |F \cap W| \geq 2\}$
.
$\mathcal {G}_2:= \{F \in \mathcal {F}^*: |F \cap W| \geq 2\}$
.
Then by the argument above,
![]() $|\mathcal {G}_1|=\sum _{i>h}|\mathcal {A}_i| \leq \frac {\varepsilon }{4} a \binom {n}{k - 1}$
. Also, for n sufficiently large, we have
$|\mathcal {G}_1|=\sum _{i>h}|\mathcal {A}_i| \leq \frac {\varepsilon }{4} a \binom {n}{k - 1}$
. Also, for n sufficiently large, we have
![]() $|\mathcal {G}_2| \leq \binom {W}{2} \binom {n}{ k - 2} \leq \frac {\varepsilon }{4} a\binom {n}{k-1}$
. Let
$|\mathcal {G}_2| \leq \binom {W}{2} \binom {n}{ k - 2} \leq \frac {\varepsilon }{4} a\binom {n}{k-1}$
. Let
![]() $\mathcal {F}":= \mathcal {F}^* \setminus (\mathcal {G}_1 \cup \mathcal {G}_2)$
. We can readily check that
$\mathcal {F}":= \mathcal {F}^* \setminus (\mathcal {G}_1 \cup \mathcal {G}_2)$
. We can readily check that
![]() $\mathcal {F}"$
satisfy all of conditions 1,2,3.
$\mathcal {F}"$
satisfy all of conditions 1,2,3.
Let us close this section by noting that a structural dichotomy like Theorem 3.5 was used in earlier works such as [Reference Füredi20, Reference Füredi and Jiang21, Reference Füredi and Jiang22]. However, in those papers, such a dichotomy was made possible only under the extra assumption that
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $\mathcal {H}$
-free, where
$\mathcal {H}$
-free, where
![]() $\mathcal {H}$
is a
$\mathcal {H}$
is a
![]() $2$
-contractible tree. Here, Theorem 3.5 is applicable to any k-graph with
$2$
-contractible tree. Here, Theorem 3.5 is applicable to any k-graph with
![]() $\Theta (n^{k-1})$
edges. Since we will aim to count number of copies of
$\Theta (n^{k-1})$
edges. Since we will aim to count number of copies of
![]() $\mathcal {H}$
in a hosting graph
$\mathcal {H}$
in a hosting graph
![]() $\mathcal {F}$
, the removal of the
$\mathcal {F}$
, the removal of the
![]() $\mathcal {H}$
-free condition is essential for our overall arguments.
$\mathcal {H}$
-free condition is essential for our overall arguments.
4 Optimal Supersaturation at the Turán threshold
In this section, we develop an asymptotically tight bound on the number of copies of a
![]() $2$
-contractible tree
$2$
-contractible tree
![]() $\mathcal {H}$
in a host graph with size just beyond the Turán threshold for
$\mathcal {H}$
in a host graph with size just beyond the Turán threshold for
![]() $\mathcal {H}$
, which provides the most important foundation on which the rest of our work is built. It may also be of independent interest as a supersaturation result. We start with the following two folklore lemmas. Recall the definition of
$\mathcal {H}$
, which provides the most important foundation on which the rest of our work is built. It may also be of independent interest as a supersaturation result. We start with the following two folklore lemmas. Recall the definition of
![]() $\delta _i(\mathcal {F})$
from Section 2.
$\delta _i(\mathcal {F})$
from Section 2.
Lemma 4.1. Let
![]() $k\geq 2$
be an integer. Let
$k\geq 2$
be an integer. Let
![]() $\mathcal {F}$
be a k-graph. Then
$\mathcal {F}$
be a k-graph. Then
![]() $\mathcal {F}$
contains a nonempty subgraph
$\mathcal {F}$
contains a nonempty subgraph
![]() $\mathcal {F}'$
with at least
$\mathcal {F}'$
with at least
![]() $\frac {1}{2} |\mathcal {F}|$
edges such that for each
$\frac {1}{2} |\mathcal {F}|$
edges such that for each
![]() $i=1,\dots , k-1$
,
$i=1,\dots , k-1$
,
![]() $\delta _i(\mathcal {F}')\geq \frac {1}{2k}\frac {|\mathcal {F}|}{\binom {n}{i}}$
.
$\delta _i(\mathcal {F}')\geq \frac {1}{2k}\frac {|\mathcal {F}|}{\binom {n}{i}}$
.
Proof. We iteratively remove edges of
![]() $\mathcal {F}$
to form
$\mathcal {F}$
to form
![]() $\mathcal {F}'$
in accordance with the following process. Whenever there is some
$\mathcal {F}'$
in accordance with the following process. Whenever there is some
![]() $B \subseteq V(\mathcal {F})$
with
$B \subseteq V(\mathcal {F})$
with
![]() $|B|\leq k-1$
such that B is contained in at least one but fewer than
$|B|\leq k-1$
such that B is contained in at least one but fewer than
![]() $\frac {1}{2 k } \frac {|\mathcal {F}|}{\binom {n}{|B|}}$
edges, we mark B and remove all edges containing B from
$\frac {1}{2 k } \frac {|\mathcal {F}|}{\binom {n}{|B|}}$
edges, we mark B and remove all edges containing B from
![]() $\mathcal {F}'$
. Clearly at some point this process will terminate. We denote the final graph by
$\mathcal {F}'$
. Clearly at some point this process will terminate. We denote the final graph by
![]() $\mathcal {F}'$
.
$\mathcal {F}'$
.
Let us count now how many edges
![]() $\mathcal {F}'$
has. For each
$\mathcal {F}'$
has. For each
![]() $i=1,\dots , k-1$
, there are at most
$i=1,\dots , k-1$
, there are at most
![]() $\binom {n}{i}$
marked i-sets. For each marked i-set, we have removed at most
$\binom {n}{i}$
marked i-sets. For each marked i-set, we have removed at most
![]() $\frac {1}{2k}\frac {|\mathcal {F}|}{\binom {n}{i}}$
edges from
$\frac {1}{2k}\frac {|\mathcal {F}|}{\binom {n}{i}}$
edges from
![]() $\mathcal {F}$
. Summing over
$\mathcal {F}$
. Summing over
![]() $i=1, \dots , k-1$
, we see that we have removed at most
$i=1, \dots , k-1$
, we see that we have removed at most
![]() $\frac {1}{2} |\mathcal {F}|$
edges. Hence,
$\frac {1}{2} |\mathcal {F}|$
edges. Hence,
![]() $|\mathcal {F}'| \geq \frac {1}{2} |\mathcal {F}|$
. Since the process terminates with a nonempty
$|\mathcal {F}'| \geq \frac {1}{2} |\mathcal {F}|$
. Since the process terminates with a nonempty
![]() $\mathcal {F}'$
, it must be the case that for each
$\mathcal {F}'$
, it must be the case that for each
![]() $i=1,\dots , k-1$
and any i-set contained in an edge of
$i=1,\dots , k-1$
and any i-set contained in an edge of
![]() $\mathcal {F}'$
it is in at least
$\mathcal {F}'$
it is in at least
![]() $\frac {1}{2k}\frac {|\mathcal {F}|}{\binom {n}{i}}$
edges, completing the proof.
$\frac {1}{2k}\frac {|\mathcal {F}|}{\binom {n}{i}}$
edges, completing the proof.
Lemma 4.2. Let
![]() $k,s,t$
be positive integers, where
$k,s,t$
be positive integers, where
![]() $k,s\geq 2$
,
$k,s\geq 2$
,
![]() $t\geq 1$
. Let
$t\geq 1$
. Let
![]() $\mathcal {H}$
be a k-tree on s vertices with t edges. Let
$\mathcal {H}$
be a k-tree on s vertices with t edges. Let
![]() $\mathcal {F}$
be a k-graph on
$\mathcal {F}$
be a k-graph on
![]() $[n]$
, where
$[n]$
, where
![]() $|\mathcal {F}|=a \binom {n}{k - 1}$
and
$|\mathcal {F}|=a \binom {n}{k - 1}$
and
![]() $a \geq 8sk !$
. Then there exists a constant
$a \geq 8sk !$
. Then there exists a constant
![]() $\eta>0$
such that
$\eta>0$
such that
![]() $\mathcal {F}$
contains at least
$\mathcal {F}$
contains at least
![]() $\eta a^{t} n^{s - t}$
copies of
$\eta a^{t} n^{s - t}$
copies of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Proof. By picking
![]() $\eta $
sufficiently small, we may assume n is sufficiently large in terms of s and k. By Lemma 4.1,
$\eta $
sufficiently small, we may assume n is sufficiently large in terms of s and k. By Lemma 4.1,
![]() $\mathcal {F}$
contains a subgraph
$\mathcal {F}$
contains a subgraph
![]() $\mathcal {F}'$
such that
$\mathcal {F}'$
such that
![]() $|\mathcal {F}'|\geq \frac {1}{2}|\mathcal {F}|$
and for each
$|\mathcal {F}'|\geq \frac {1}{2}|\mathcal {F}|$
and for each
![]() $i\in [k-1]$
,
$i\in [k-1]$
,
![]() $\delta _i(\mathcal {F}')\geq \frac {1}{2k} \frac {|\mathcal {F}|}{\binom {n}{i}}=\frac {a}{2k}\frac {\binom {n}{k-1}}{\binom {n}{i}}$
. Let
$\delta _i(\mathcal {F}')\geq \frac {1}{2k} \frac {|\mathcal {F}|}{\binom {n}{i}}=\frac {a}{2k}\frac {\binom {n}{k-1}}{\binom {n}{i}}$
. Let
![]() $E_1,\dots , E_t$
be a tree-defining ordering of
$E_1,\dots , E_t$
be a tree-defining ordering of
![]() $\mathcal {H}$
. For each
$\mathcal {H}$
. For each
![]() $j\in [t]$
, let
$j\in [t]$
, let
![]() $\mathcal {H}_j=\{E_1,\dots , E_j\}$
. We prove by induction that for each
$\mathcal {H}_j=\{E_1,\dots , E_j\}$
. We prove by induction that for each
![]() $j=1,\dots , t$
,
$j=1,\dots , t$
,
![]() $\mathcal {F}$
contains at least
$\mathcal {F}$
contains at least
![]() $(\frac {a}{8k!})^jn^{v(\mathcal {H}_j)-j}$
copies of
$(\frac {a}{8k!})^jn^{v(\mathcal {H}_j)-j}$
copies of
![]() $\mathcal {H}_j$
.
$\mathcal {H}_j$
.
For the base case,
![]() $\mathcal {F}'$
contains at least
$\mathcal {F}'$
contains at least
![]() $\frac {1}{2}|\mathcal {F}|=\frac {a}{2}\binom {n}{k-1}\geq \frac {a}{8k!} n^{v(\mathcal {H}_1)-1}$
copies of
$\frac {1}{2}|\mathcal {F}|=\frac {a}{2}\binom {n}{k-1}\geq \frac {a}{8k!} n^{v(\mathcal {H}_1)-1}$
copies of
![]() $\mathcal {H}_1$
. So the claim holds. For the induction step, let
$\mathcal {H}_1$
. So the claim holds. For the induction step, let
![]() $1\leq j\leq t-1$
and suppose
$1\leq j\leq t-1$
and suppose
![]() $\mathcal {F}'$
contains at least
$\mathcal {F}'$
contains at least
![]() $(\frac {a}{8k!})^j n^{v(\mathcal {H}_j)-j} $
copies of
$(\frac {a}{8k!})^j n^{v(\mathcal {H}_j)-j} $
copies of
![]() $\mathcal {H}_j$
. Let F denote a parent edge of
$\mathcal {H}_j$
. Let F denote a parent edge of
![]() $E_{j+1}$
in
$E_{j+1}$
in
![]() $\mathcal {H}_j$
. Let
$\mathcal {H}_j$
. Let
![]() $L=F\cap E_{j+1}=V(\mathcal {H}_j)\cap E_{j+1}$
and
$L=F\cap E_{j+1}=V(\mathcal {H}_j)\cap E_{j+1}$
and
![]() $\ell =|L|$
. Let
$\ell =|L|$
. Let
![]() $\mathcal {H}'$
denote a copy of
$\mathcal {H}'$
denote a copy of
![]() $\mathcal {H}_j$
in
$\mathcal {H}_j$
in
![]() $\mathcal {F}'$
and
$\mathcal {F}'$
and
![]() $L'$
the image of L in
$L'$
the image of L in
![]() $\mathcal {H}'$
. By our assumptions of
$\mathcal {H}'$
. By our assumptions of
![]() $\mathcal {F}'$
,
$\mathcal {F}'$
,
![]() $\deg _{\mathcal {F}'}(L') \geq \frac {a}{2k} \frac {\binom {n}{k - 1}}{\binom {n}{\ell }}$
. For each vertex
$\deg _{\mathcal {F}'}(L') \geq \frac {a}{2k} \frac {\binom {n}{k - 1}}{\binom {n}{\ell }}$
. For each vertex
![]() $v \in V(\mathcal {H}')$
, we have that v is contained in at most
$v \in V(\mathcal {H}')$
, we have that v is contained in at most
![]() $\binom {n - \ell - 1}{k - \ell - 1}$
edges which contain
$\binom {n - \ell - 1}{k - \ell - 1}$
edges which contain
![]() $L'$
. As there are at most s vertices in
$L'$
. As there are at most s vertices in
![]() $\mathcal {H}_j$
, we have that for sufficiently large n the number of edges of
$\mathcal {H}_j$
, we have that for sufficiently large n the number of edges of
![]() $\mathcal {F}'$
that contain
$\mathcal {F}'$
that contain
![]() $L'$
but do not intersect
$L'$
but do not intersect
![]() $\mathcal {H}'$
somewhere else is at least
$\mathcal {H}'$
somewhere else is at least
 $$ \begin{align*} \frac{a}{2k} \frac{\binom{n}{k - 1}}{\binom{n}{\ell}} - s \binom{n - \ell - 1}{k - \ell - 1} \geq \frac{a \ell !}{4 k!} n^{k - 1 - \ell} - \frac{s}{(k - \ell - 1)!} n^{k - \ell - 1} \geq \frac{a}{8k!}n^{k - 1 - \ell}, \end{align*} $$
$$ \begin{align*} \frac{a}{2k} \frac{\binom{n}{k - 1}}{\binom{n}{\ell}} - s \binom{n - \ell - 1}{k - \ell - 1} \geq \frac{a \ell !}{4 k!} n^{k - 1 - \ell} - \frac{s}{(k - \ell - 1)!} n^{k - \ell - 1} \geq \frac{a}{8k!}n^{k - 1 - \ell}, \end{align*} $$
where we used the fact that
![]() $a\geq 8sk!$
. Hence
$a\geq 8sk!$
. Hence
![]() $\mathcal {H}'$
can be extended to at least
$\mathcal {H}'$
can be extended to at least
![]() $\frac {a}{8k!} n^{k-1-\ell }$
copies of
$\frac {a}{8k!} n^{k-1-\ell }$
copies of
![]() $\mathcal {H}_{j+1}$
in
$\mathcal {H}_{j+1}$
in
![]() $\mathcal {F}'$
. Therefore,
$\mathcal {F}'$
. Therefore,
![]() $\mathcal {F}'$
contains at least
$\mathcal {F}'$
contains at least
![]() $(\frac {a}{8k!})^{j+1}n^{v(\mathcal {H}_j)-j+k-1-\ell }=\frac {a}{8k!}^{j+1}n^{v(\mathcal {H}_{j+1})- (j+1)}$
copies of
$(\frac {a}{8k!})^{j+1}n^{v(\mathcal {H}_j)-j+k-1-\ell }=\frac {a}{8k!}^{j+1}n^{v(\mathcal {H}_{j+1})- (j+1)}$
copies of
![]() $\mathcal {H}_{j+1}$
. This completes the induction and the proof.
$\mathcal {H}_{j+1}$
. This completes the induction and the proof.
Before we prove the supersaturation theorem, we first deal with one of the cases.
Lemma 4.3. Let
![]() $k\geq 4$
be an integer. Let
$k\geq 4$
be an integer. Let
![]() $\mathcal {H}$
be a
$\mathcal {H}$
be a
![]() $2$
-contractible k-tree with s vertices and t edges. Let
$2$
-contractible k-tree with s vertices and t edges. Let
![]() $\mathcal {F}$
be an s-super-homogeneous k-graph on
$\mathcal {F}$
be an s-super-homogeneous k-graph on
![]() $[n]$
such that
$[n]$
such that
![]() $|\mathcal {F}|\geq \varepsilon n^{k - 1}$
and
$|\mathcal {F}|\geq \varepsilon n^{k - 1}$
and
![]() $\mathrm {Int}(\mathcal {F})$
is of type 1. Then,
$\mathrm {Int}(\mathcal {F})$
is of type 1. Then,
![]() $\mathcal {F}$
contains at least
$\mathcal {F}$
contains at least
![]() $(\frac {\varepsilon }{2ks})^t n^{s - t}$
many copies of
$(\frac {\varepsilon }{2ks})^t n^{s - t}$
many copies of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Proof. Let
![]() $(X_1,\dots , X_k)$
be a k-partition associated with
$(X_1,\dots , X_k)$
be a k-partition associated with
![]() $\mathrm {Int}(\mathcal {F})$
. Without loss of generality, suppose
$\mathrm {Int}(\mathcal {F})$
. Without loss of generality, suppose
![]() $2^{[k-2]}\subseteq \mathrm {Int}(\mathcal {F})$
. Since
$2^{[k-2]}\subseteq \mathrm {Int}(\mathcal {F})$
. Since
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $2$
-contractible, each edge E contains at least two vertices of degree
$2$
-contractible, each edge E contains at least two vertices of degree
![]() $1$
. We will designate two of them as expansion vertices for E.
$1$
. We will designate two of them as expansion vertices for E.
Let
![]() $E_1,\cdots , E_t$
be a tree-defining ordering of
$E_1,\cdots , E_t$
be a tree-defining ordering of
![]() $\mathcal {H}$
. For each
$\mathcal {H}$
. For each
![]() $i\in [t]$
, let
$i\in [t]$
, let
![]() $\mathcal {H}_i=\{E_1,\dots , E_i\}$
,
$\mathcal {H}_i=\{E_1,\dots , E_i\}$
,
![]() $v_i=|V(\mathcal {H}_i)|$
, and let
$v_i=|V(\mathcal {H}_i)|$
, and let
![]() $\Pi _i$
denote the set of injective homomorphisms
$\Pi _i$
denote the set of injective homomorphisms
![]() $\varphi ^i$
of
$\varphi ^i$
of
![]() $\mathcal {H}_i$
into
$\mathcal {H}_i$
into
![]() $\mathcal {F}$
that maps all the expansion vertices in
$\mathcal {F}$
that maps all the expansion vertices in
![]() $\mathcal {H}_i$
into
$\mathcal {H}_i$
into
![]() $X_{k-1}\cup X_k$
. We will prove by induction the stronger statement that for each
$X_{k-1}\cup X_k$
. We will prove by induction the stronger statement that for each
![]() $i\in [t]$
,
$i\in [t]$
,
![]() $|\Pi _i|\geq (\frac {\varepsilon }{2ks})^i n^{v_i-i}$
. The base step
$|\Pi _i|\geq (\frac {\varepsilon }{2ks})^i n^{v_i-i}$
. The base step
![]() $i=1$
is trivial since
$i=1$
is trivial since
![]() $\mathcal {F}$
has at least
$\mathcal {F}$
has at least
![]() $\varepsilon n^{k-1}$
edges E and for each E we can define an embedding
$\varepsilon n^{k-1}$
edges E and for each E we can define an embedding
![]() $\varphi ^1$
of
$\varphi ^1$
of
![]() $\mathcal {H}_1$
to E where the expansion vertices are mapped to
$\mathcal {H}_1$
to E where the expansion vertices are mapped to
![]() $X_{k-1}\cup X_k$
. For the induction step, let
$X_{k-1}\cup X_k$
. For the induction step, let
![]() $1\leq i\leq t-1$
and suppose
$1\leq i\leq t-1$
and suppose
![]() $|\Pi _i|\geq (\frac {\varepsilon }{2ks})^i n^{v_i-i}$
. Let F be a parent edge of
$|\Pi _i|\geq (\frac {\varepsilon }{2ks})^i n^{v_i-i}$
. Let F be a parent edge of
![]() $E_{i+1}$
in
$E_{i+1}$
in
![]() $\mathcal {H}_i$
. Consider any
$\mathcal {H}_i$
. Consider any
![]() $\varphi ^i\in \Pi _i$
. Since vertices in
$\varphi ^i\in \Pi _i$
. Since vertices in
![]() $F\cap E_{i+1}$
have degree at least two in
$F\cap E_{i+1}$
have degree at least two in
![]() $\mathcal {H}$
and are not expansion vertices in
$\mathcal {H}$
and are not expansion vertices in
![]() $\mathcal {H}_i$
, we have
$\mathcal {H}_i$
, we have
![]() $\varphi ^i(F\cap E_{i+1})\subseteq \bigcup _{j=1}^{k-2} X_j$
. Since
$\varphi ^i(F\cap E_{i+1})\subseteq \bigcup _{j=1}^{k-2} X_j$
. Since
![]() $2^{[k-2]}\subseteq \mathrm {Int}(\mathcal {F})$
, we have
$2^{[k-2]}\subseteq \mathrm {Int}(\mathcal {F})$
, we have
![]() $\pi (\varphi ^i(F\cap E_{i+1})) \in \mathrm {Int}(\mathcal {F})$
. So,
$\pi (\varphi ^i(F\cap E_{i+1})) \in \mathrm {Int}(\mathcal {F})$
. So,
![]() $\mathcal {L}_{\mathcal {F}}(\varphi ^i(F \cap E_{i+1}))$
is s-diverse. Therefore, there are at least
$\mathcal {L}_{\mathcal {F}}(\varphi ^i(F \cap E_{i+1}))$
is s-diverse. Therefore, there are at least
![]() $\frac {s -v_i}{s} | \mathcal {L}_{\mathcal {F}}( \varphi ^i (F\cap E_{i+1}))|\geq \frac {1}{s} | \mathcal {L}_{\mathcal {F}}( \varphi ^i (F\cap E_{i+1}))|$
edges of
$\frac {s -v_i}{s} | \mathcal {L}_{\mathcal {F}}( \varphi ^i (F\cap E_{i+1}))|\geq \frac {1}{s} | \mathcal {L}_{\mathcal {F}}( \varphi ^i (F\cap E_{i+1}))|$
edges of
![]() $\mathcal {F}$
that contain
$\mathcal {F}$
that contain
![]() $\varphi ^i(F\cap E_{i+1})$
and do not intersect the rest of
$\varphi ^i(F\cap E_{i+1})$
and do not intersect the rest of
![]() $\varphi ^i(\mathcal {H}_i)$
. Let
$\varphi ^i(\mathcal {H}_i)$
. Let
![]() $\ell =|F\cap E_{i+1}|$
. Since
$\ell =|F\cap E_{i+1}|$
. Since
![]() $\mathcal {F}$
is s-super-homogeneous with
$\mathcal {F}$
is s-super-homogeneous with
![]() $\mathrm {Int}(\mathcal {F})\supseteq 2^{[k-2]}$
and
$\mathrm {Int}(\mathcal {F})\supseteq 2^{[k-2]}$
and
![]() $\pi (\varphi ^i(F\cap E_{i+1}))\in \mathrm {Int}(\mathcal {F})$
, by the conditions of s-super-homogeneous given in Theorem 3.1,
$\pi (\varphi ^i(F\cap E_{i+1}))\in \mathrm {Int}(\mathcal {F})$
, by the conditions of s-super-homogeneous given in Theorem 3.1,
![]() $|\mathcal {L}(\varphi ^i (F \cap E_{i+1}))| \geq \frac {|\mathcal {F}|}{2kn^\ell } \geq \frac {\varepsilon }{2k} n^{ k - \ell -1}$
. Hence each mapping
$|\mathcal {L}(\varphi ^i (F \cap E_{i+1}))| \geq \frac {|\mathcal {F}|}{2kn^\ell } \geq \frac {\varepsilon }{2k} n^{ k - \ell -1}$
. Hence each mapping
![]() $\varphi _i$
in
$\varphi _i$
in
![]() $\Pi _i$
can be extended to at least
$\Pi _i$
can be extended to at least
![]() $\frac {\varepsilon }{2ks} n^{ k -\ell - 1}$
injective mappings
$\frac {\varepsilon }{2ks} n^{ k -\ell - 1}$
injective mappings
![]() $\varphi ^{i+1}$
of
$\varphi ^{i+1}$
of
![]() $\mathcal {H}_{i+1}$
, by mapping
$\mathcal {H}_{i+1}$
, by mapping
![]() $E_{i+1}$
to an edge
$E_{i+1}$
to an edge
![]() $F'$
of
$F'$
of
![]() $\mathcal {F}$
that contains
$\mathcal {F}$
that contains
![]() $\varphi ^i(F\cap E_{i+1})$
and avoids the rest of
$\varphi ^i(F\cap E_{i+1})$
and avoids the rest of
![]() $\varphi ^i(\mathcal {H}_i)$
. Furthermore, we can require
$\varphi ^i(\mathcal {H}_i)$
. Furthermore, we can require
![]() $\varphi ^{i+1}$
to map the two designated expansion vertices of
$\varphi ^{i+1}$
to map the two designated expansion vertices of
![]() $E_{i+1}$
to
$E_{i+1}$
to
![]() $X_{k-1}\cup X_k$
. Hence,
$X_{k-1}\cup X_k$
. Hence,
![]() $|\Pi _{i+1}|\geq |\Pi _i|\cdot \frac {\varepsilon }{2ks} n^{ k -\ell - 1} \geq (\frac {\varepsilon }{2ks})^{i+1} n^{v_{i+1}-(i+1)}$
. This completes the induction step and the proof.
$|\Pi _{i+1}|\geq |\Pi _i|\cdot \frac {\varepsilon }{2ks} n^{ k -\ell - 1} \geq (\frac {\varepsilon }{2ks})^{i+1} n^{v_{i+1}-(i+1)}$
. This completes the induction step and the proof.
We are now ready to prove our first supersaturation theorem.
Theorem 4.4. Let
![]() $k\geq 4$
be an integer. Let
$k\geq 4$
be an integer. Let
![]() $0<\gamma <1$
, and let
$0<\gamma <1$
, and let
![]() $\mathcal {H}$
be a
$\mathcal {H}$
be a
![]() $2$
-contractible k-tree with s vertices and t edges. Then, there exists
$2$
-contractible k-tree with s vertices and t edges. Then, there exists
![]() $\beta> 0$
, depending on
$\beta> 0$
, depending on
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\gamma $
, such that the following holds. Let
$\gamma $
, such that the following holds. Let
![]() $\mathcal {F}$
be a k-graph on
$\mathcal {F}$
be a k-graph on
![]() $[n]$
with
$[n]$
with
![]() $|\mathcal {F}|= a \binom {n}{k - 1}$
, where
$|\mathcal {F}|= a \binom {n}{k - 1}$
, where
![]() $a \geq \sigma (\mathcal {H}) - 1 + \gamma $
. Then,
$a \geq \sigma (\mathcal {H}) - 1 + \gamma $
. Then,
![]() $\mathcal {F}$
contains at least
$\mathcal {F}$
contains at least
![]() $\beta a^t n^{s - t}$
many copies of
$\beta a^t n^{s - t}$
many copies of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Proof. For convenience, let
![]() $\sigma =\sigma (\mathcal {H})$
. Note that if
$\sigma =\sigma (\mathcal {H})$
. Note that if
![]() $a \geq 8 s k!$
, we may apply Lemma 4.2, so at the cost of a constant factor on
$a \geq 8 s k!$
, we may apply Lemma 4.2, so at the cost of a constant factor on
![]() $\beta $
, we will assume
$\beta $
, we will assume
![]() $a = \sigma - 1 + \gamma $
. We apply Theorem 3.5 to
$a = \sigma - 1 + \gamma $
. We apply Theorem 3.5 to
![]() $\mathcal {F}$
with
$\mathcal {F}$
with
![]() $\varepsilon = \frac {\gamma }{4 \sigma }$
if
$\varepsilon = \frac {\gamma }{4 \sigma }$
if
![]() $\sigma \geq 2$
and
$\sigma \geq 2$
and
![]() $\varepsilon = \frac {1}{4} \gamma ^{k - 2}$
if
$\varepsilon = \frac {1}{4} \gamma ^{k - 2}$
if
![]() $\sigma = 1$
. Then one of the following two cases holds.
$\sigma = 1$
. Then one of the following two cases holds.
Case 1.
![]() $\mathcal {F}$
contains an s-super-homogeneous subgraph
$\mathcal {F}$
contains an s-super-homogeneous subgraph
![]() $\mathcal {F}'$
such that
$\mathcal {F}'$
such that
![]() $|\mathcal {F}'|\geq \frac {1}{2} c(k,s)\varepsilon |\mathcal {F}|$
and
$|\mathcal {F}'|\geq \frac {1}{2} c(k,s)\varepsilon |\mathcal {F}|$
and
![]() $\mathrm {Int}(\mathcal {F}')$
is of type 1.
$\mathrm {Int}(\mathcal {F}')$
is of type 1.
By Lemma 4.3,
![]() $\mathcal {F}'$
contains
$\mathcal {F}'$
contains
![]() $\left ( \frac {\varepsilon c(k, s) }{2 ks}\right )^t n^{s - t}$
copies of
$\left ( \frac {\varepsilon c(k, s) }{2 ks}\right )^t n^{s - t}$
copies of
![]() $\mathcal {H}$
. So the claim holds.
$\mathcal {H}$
. So the claim holds.
Case 2. There exists a
![]() $W \subseteq [n]$
and
$W \subseteq [n]$
and
![]() $\mathcal {F}" \subseteq \mathcal {F}$
satisfying the following:
$\mathcal {F}" \subseteq \mathcal {F}$
satisfying the following:
-
(a)
 $$ \begin{align*}|W| \leq \left( \frac{160 \sigma^2}{c(k,s) \gamma^{2k - 4}} \right)^{k - 1}.\end{align*} $$
$$ \begin{align*}|W| \leq \left( \frac{160 \sigma^2}{c(k,s) \gamma^{2k - 4}} \right)^{k - 1}.\end{align*} $$
-
(b)
 $$ \begin{align*}|\mathcal{F}"| \geq \left(1-\frac{\gamma}{4\sigma}\right)|\mathcal{F}|.\end{align*} $$
$$ \begin{align*}|\mathcal{F}"| \geq \left(1-\frac{\gamma}{4\sigma}\right)|\mathcal{F}|.\end{align*} $$
-
(c) Every
 $F \in \mathcal {F}"$
satisfies
$F \in \mathcal {F}"$
satisfies
 $|W \cap F| = 1$
.
$|W \cap F| = 1$
.
Observe that in
![]() $\sigma = 1$
case, Theorem 3.5 gives the upper bound
$\sigma = 1$
case, Theorem 3.5 gives the upper bound
![]() $W \leq \left ( \frac {160}{c(k, s) \gamma ^{ 2k - 4} } \right )^{ k -1}$
and in
$W \leq \left ( \frac {160}{c(k, s) \gamma ^{ 2k - 4} } \right )^{ k -1}$
and in
![]() $\sigma \geq 2$
case, gives the bound
$\sigma \geq 2$
case, gives the bound
![]() $W \leq \left ( \frac {160 \sigma ^2}{c(k, s) \gamma ^{ 2} } \right )^{ k -1} $
. In both cases, the written upper bound holds. For simplicity, observe that for both choices of
$W \leq \left ( \frac {160 \sigma ^2}{c(k, s) \gamma ^{ 2} } \right )^{ k -1} $
. In both cases, the written upper bound holds. For simplicity, observe that for both choices of
![]() $\varepsilon $
,
$\varepsilon $
,
![]() $|\mathcal {F}"| \geq (1 - \varepsilon )|\mathcal {F}| \geq \left ( 1 - \frac {\gamma }{4 \sigma }\right ) |\mathcal {F}|$
.
$|\mathcal {F}"| \geq (1 - \varepsilon )|\mathcal {F}| \geq \left ( 1 - \frac {\gamma }{4 \sigma }\right ) |\mathcal {F}|$
.
For each
![]() $S\in \binom {W}{\sigma }$
, let
$S\in \binom {W}{\sigma }$
, let
![]() $\mathcal {L}^*(S) = \bigcap _{v \in S} \mathcal {L}_{\mathcal {F}"}(v)$
. We say a set
$\mathcal {L}^*(S) = \bigcap _{v \in S} \mathcal {L}_{\mathcal {F}"}(v)$
. We say a set
![]() $S \in \binom {W}{\sigma }$
is good, if
$S \in \binom {W}{\sigma }$
is good, if
![]() $|\mathcal {L}^*(S)| \geq 8s (k - 1)! \binom {n}{k-2}$
; otherwise we say S is bad. Let
$|\mathcal {L}^*(S)| \geq 8s (k - 1)! \binom {n}{k-2}$
; otherwise we say S is bad. Let
![]() $\mathcal {D}$
denote the set of
$\mathcal {D}$
denote the set of
![]() $(k-1)$
-sets D in
$(k-1)$
-sets D in
![]() $[n]\setminus W$
with
$[n]\setminus W$
with
![]() $d_{\mathcal {F}"}(D)\geq \sigma $
. Since each edge of
$d_{\mathcal {F}"}(D)\geq \sigma $
. Since each edge of
![]() $\mathcal {F}"$
contains one vertex in W and a
$\mathcal {F}"$
contains one vertex in W and a
![]() $(k-1)$
-set in
$(k-1)$
-set in
![]() $[n]\setminus W$
, via double counting, we get
$[n]\setminus W$
, via double counting, we get
 $$ \begin{align} \sum_{S \in \binom{W}{\sigma}} |\mathcal{L}^*(S)| = \sum_{D \in \mathcal{D}} \binom{d_{\mathcal{F}"}(D)}{\sigma}. \end{align} $$
$$ \begin{align} \sum_{S \in \binom{W}{\sigma}} |\mathcal{L}^*(S)| = \sum_{D \in \mathcal{D}} \binom{d_{\mathcal{F}"}(D)}{\sigma}. \end{align} $$
By our assumption,
![]() $|\mathcal {F}"|\geq (1-\frac {\gamma }{4 \sigma })|\mathcal {F}|\geq (1-\frac {\gamma }{4\sigma })(\sigma -1+\gamma )\binom {n}{k-1}\geq (\sigma -1+\frac {\gamma }{2})\binom {n}{k-1}$
. This implies that
$|\mathcal {F}"|\geq (1-\frac {\gamma }{4 \sigma })|\mathcal {F}|\geq (1-\frac {\gamma }{4\sigma })(\sigma -1+\gamma )\binom {n}{k-1}\geq (\sigma -1+\frac {\gamma }{2})\binom {n}{k-1}$
. This implies that
![]() $m:=\sum _{D\in \mathcal {D}} d_{\mathcal {F}"} (D)\geq \frac {\gamma }{2}\binom {n}{k-1}$
. Observe that for all
$m:=\sum _{D\in \mathcal {D}} d_{\mathcal {F}"} (D)\geq \frac {\gamma }{2}\binom {n}{k-1}$
. Observe that for all
![]() $D \in \mathcal {D}$
,
$D \in \mathcal {D}$
,
![]() $\binom {d_{\mathcal {F}"}(D)}{\sigma } \geq \frac {d_{\mathcal {F}"}(D)}{\sigma } $
.
$\binom {d_{\mathcal {F}"}(D)}{\sigma } \geq \frac {d_{\mathcal {F}"}(D)}{\sigma } $
.
Thus,
 $$ \begin{align*}\sum_{S \in \binom{W}{\sigma}} |\mathcal{L}^*(S)| \geq \frac{m}{\sigma} \geq \frac{\gamma}{2 \sigma }\binom{n}{ k - 1}.\end{align*} $$
$$ \begin{align*}\sum_{S \in \binom{W}{\sigma}} |\mathcal{L}^*(S)| \geq \frac{m}{\sigma} \geq \frac{\gamma}{2 \sigma }\binom{n}{ k - 1}.\end{align*} $$
On the other hand, the contribution to the left-hand side of (10) from the bad
![]() $\sigma $
-sets of W is at most
$\sigma $
-sets of W is at most
![]() $\binom {|W|}{\sigma } 8s(k-1)!\binom {n}{k-2}<\frac {\gamma }{4\sigma }\binom {n}{k-1}$
, for sufficiently large n. Hence, we have
$\binom {|W|}{\sigma } 8s(k-1)!\binom {n}{k-2}<\frac {\gamma }{4\sigma }\binom {n}{k-1}$
, for sufficiently large n. Hence, we have
 $$\begin{align*}\sum_{S\in \binom{W}{\sigma}, \, S \text{ good}} |\mathcal{L}^*(S)| \geq \frac{\gamma}{4\sigma} \binom{n}{ k - 1}.\end{align*}$$
$$\begin{align*}\sum_{S\in \binom{W}{\sigma}, \, S \text{ good}} |\mathcal{L}^*(S)| \geq \frac{\gamma}{4\sigma} \binom{n}{ k - 1}.\end{align*}$$
Fix any
![]() $S\in \binom {|W|}{\sigma }$
that is good, let
$S\in \binom {|W|}{\sigma }$
that is good, let
![]() $d(S) = \frac {|\mathcal {L}^*(S)|}{\binom {n}{ k - 2}}$
, in particular, since S is good,
$d(S) = \frac {|\mathcal {L}^*(S)|}{\binom {n}{ k - 2}}$
, in particular, since S is good,
![]() $d(S) \geq 8s (k - 1)!$
. Let R be a minimum cross-cut of
$d(S) \geq 8s (k - 1)!$
. Let R be a minimum cross-cut of
![]() $\mathcal {H}$
. Let
$\mathcal {H}$
. Let
![]() $\mathcal {H}'=\mathcal {H}-R$
. It is easy to see that
$\mathcal {H}'=\mathcal {H}-R$
. It is easy to see that
![]() $\mathcal {H}'$
is a
$\mathcal {H}'$
is a
![]() $(k-1)$
-tree. Observe that any copy of
$(k-1)$
-tree. Observe that any copy of
![]() $\mathcal {H}'$
in
$\mathcal {H}'$
in
![]() $\mathcal {L}^*(S)$
corresponds to a copy of
$\mathcal {L}^*(S)$
corresponds to a copy of
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\mathcal {F}$
by joining it to S and different copies of
$\mathcal {F}$
by joining it to S and different copies of
![]() $\mathcal {H}'$
in
$\mathcal {H}'$
in
![]() $\mathcal {L}^*(S)$
give rise to different copies of
$\mathcal {L}^*(S)$
give rise to different copies of
![]() $\mathcal {H}$
. Let
$\mathcal {H}$
. Let
![]() $t'=|\mathcal {H}'|$
and note that
$t'=|\mathcal {H}'|$
and note that
![]() $v(\mathcal {H}')=s-\sigma $
. By Lemma 4.2, for every good S, there are at least
$v(\mathcal {H}')=s-\sigma $
. By Lemma 4.2, for every good S, there are at least
![]() $\eta d(S)^{t'}n^{s - \sigma - t'}$
many copies of
$\eta d(S)^{t'}n^{s - \sigma - t'}$
many copies of
![]() $\mathcal {H}'$
in
$\mathcal {H}'$
in
![]() $\mathcal {L}^*(S)$
. Thus, the number of copies of
$\mathcal {L}^*(S)$
. Thus, the number of copies of
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\mathcal {F}$
is at least:
$\mathcal {F}$
is at least:
 $$ \begin{align*} \sum_{S\in \binom{W}{\sigma}, \, S \text{ good }} \eta d(S)^{t'} n^{s - \sigma - t'} &\geq \eta n^{s - \sigma - t' - (k - 2)t'} \sum_{S\in \binom{W}{\sigma},\, S \text{ good }} |\mathcal{L}^*(S))|^{t'} \\ &\geq \eta n^{s - \sigma - t' - (k - 2)t'} |W|^{\sigma} \left( \frac{1}{|W|^{\sigma}} \sum_{S \text{ good }} |\mathcal{L}^*(S)|\right) ^{t'}\\ &\geq \eta n^{s - \sigma - t' - (k - 2)t'} |W|^{\sigma} \left( \frac{1}{|W|^{\sigma}} \frac{\gamma}{4 \sigma} \binom{n}{ k - 1}\right) ^{t'}\\ &\geq \beta a^t n^{s - \sigma}\geq \beta a^t n^{s-t}, \end{align*} $$
$$ \begin{align*} \sum_{S\in \binom{W}{\sigma}, \, S \text{ good }} \eta d(S)^{t'} n^{s - \sigma - t'} &\geq \eta n^{s - \sigma - t' - (k - 2)t'} \sum_{S\in \binom{W}{\sigma},\, S \text{ good }} |\mathcal{L}^*(S))|^{t'} \\ &\geq \eta n^{s - \sigma - t' - (k - 2)t'} |W|^{\sigma} \left( \frac{1}{|W|^{\sigma}} \sum_{S \text{ good }} |\mathcal{L}^*(S)|\right) ^{t'}\\ &\geq \eta n^{s - \sigma - t' - (k - 2)t'} |W|^{\sigma} \left( \frac{1}{|W|^{\sigma}} \frac{\gamma}{4 \sigma} \binom{n}{ k - 1}\right) ^{t'}\\ &\geq \beta a^t n^{s - \sigma}\geq \beta a^t n^{s-t}, \end{align*} $$
for some constant
![]() $\beta>0$
, where we used the fact that
$\beta>0$
, where we used the fact that
![]() $a=\sigma -1+\gamma $
is a constant and
$a=\sigma -1+\gamma $
is a constant and
![]() $|W|$
is bounded by a constant.
$|W|$
is bounded by a constant.
Note that the bound obtained in Theorem 4.4 is tight up to a constant factor, as shown by considering
![]() $G(n,p)^{(k)}$
, with
$G(n,p)^{(k)}$
, with
![]() $p=|\mathcal {F}|/\binom {n}{k}$
.
$p=|\mathcal {F}|/\binom {n}{k}$
.
5 Optimal Balanced Supersaturation at the Turán Threshold
In this section, we develop a balanced version of the supersaturation theorem of Section 4. In the next section, we will use this balanced supersaturation theorem to obtain almost tight bounds on the number of
![]() $\mathcal {H}$
-free graphs.
$\mathcal {H}$
-free graphs.
Let
![]() $d>0$
be a real. A t-uniform hypergraph
$d>0$
be a real. A t-uniform hypergraph
![]() $\mathcal {K}$
is called d-graded if for all sets
$\mathcal {K}$
is called d-graded if for all sets
![]() $S \subseteq V(\mathcal {K})$
with
$S \subseteq V(\mathcal {K})$
with
![]() $1\leq |S|\leq t$
, we have
$1\leq |S|\leq t$
, we have
We say
![]() $S \subseteq V(\mathcal {K})$
is saturated by
$S \subseteq V(\mathcal {K})$
is saturated by
![]() $\mathcal {K}$
if
$\mathcal {K}$
if
![]() $d_{\mathcal {K}}(S) = \left \lfloor d^{t - |S|} \right \rfloor $
. We say S is admissible if no subset of it is saturated, and inadmissible otherwise. For each admissible
$d_{\mathcal {K}}(S) = \left \lfloor d^{t - |S|} \right \rfloor $
. We say S is admissible if no subset of it is saturated, and inadmissible otherwise. For each admissible
![]() $S\subseteq V(\mathcal {K})$
, let
$S\subseteq V(\mathcal {K})$
, let
Lemma 5.1. Let
![]() $d \geq 2$
be a real and
$d \geq 2$
be a real and
![]() $\mathcal {K}$
be a d-graded t-uniform hypergraph of size less than
$\mathcal {K}$
be a d-graded t-uniform hypergraph of size less than
![]() $d^{t - 1} M$
. Then, the set of vertices
$d^{t - 1} M$
. Then, the set of vertices
![]() $v \in V(\mathcal {K})$
satisfying
$v \in V(\mathcal {K})$
satisfying
![]() $d_{\mathcal {K}}(v) = \left \lfloor d^{t - 1} \right \rfloor $
is less than
$d_{\mathcal {K}}(v) = \left \lfloor d^{t - 1} \right \rfloor $
is less than
![]() $2 t M$
. Furthermore, any admissible set S of size
$2 t M$
. Furthermore, any admissible set S of size
![]() $|S| \leq t - 1$
, satisfies
$|S| \leq t - 1$
, satisfies
Proof. Let
![]() $B = \{ v\in V(\mathcal {K}): d_{\mathcal {K}}(v) = \left \lfloor d^{t - 1} \right \rfloor \}$
. Then clearly,
$B = \{ v\in V(\mathcal {K}): d_{\mathcal {K}}(v) = \left \lfloor d^{t - 1} \right \rfloor \}$
. Then clearly,
Since
![]() $|\mathcal {K}|\leq d^{t-1}M$
, we have
$|\mathcal {K}|\leq d^{t-1}M$
, we have
![]() $|B| \leq 2 t M $
.
$|B| \leq 2 t M $
.
Now, consider any admissible set
![]() $S\subseteq V(\mathcal {K})$
with
$S\subseteq V(\mathcal {K})$
with
![]() $|S|\leq t - 1$
. For every
$|S|\leq t - 1$
. For every
![]() $D \subseteq S$
, let
$D \subseteq S$
, let
![]() $\mathcal {B}(D) := \{ v \in V(\mathcal {K}) : D \cup \{ v\} \text { is saturated} \}$
. By definition,
$\mathcal {B}(D) := \{ v \in V(\mathcal {K}) : D \cup \{ v\} \text { is saturated} \}$
. By definition,
![]() $\mathcal {Z}_{\mathcal {K}}(S) = \bigcup _{D \subseteq S, D \neq \emptyset } \mathcal {B}(D)$
. Consider a fixed nonempty
$\mathcal {Z}_{\mathcal {K}}(S) = \bigcup _{D \subseteq S, D \neq \emptyset } \mathcal {B}(D)$
. Consider a fixed nonempty
![]() $D\subseteq S$
. Note that
$D\subseteq S$
. Note that
since each edge of
![]() $\mathcal {K}$
containing D is counted at most t times in the sum on the left-hand side. Since S is admissible, D is not saturated. Thus,
$\mathcal {K}$
containing D is counted at most t times in the sum on the left-hand side. Since S is admissible, D is not saturated. Thus,
![]() $d_{\mathcal {K}}(D) \leq d^{t - |D|}$
. On the other hand, for every
$d_{\mathcal {K}}(D) \leq d^{t - |D|}$
. On the other hand, for every
![]() $v \in \mathcal {B}(D)$
,
$v \in \mathcal {B}(D)$
,
![]() $D\cup \{v\}$
is saturated. So,
$D\cup \{v\}$
is saturated. So,
![]() $d_{\mathcal {K}}(D \cup \{v\}) = \left \lfloor d^{t - |D| - 1} \right \rfloor $
. By (11), we get
$d_{\mathcal {K}}(D \cup \{v\}) = \left \lfloor d^{t - |D| - 1} \right \rfloor $
. By (11), we get
![]() $|\mathcal {B}(D)|\left \lfloor d^{t-|D|-1} \right \rfloor \leq t d^{t-|D|}$
, implying
$|\mathcal {B}(D)|\left \lfloor d^{t-|D|-1} \right \rfloor \leq t d^{t-|D|}$
, implying
Summing over all
![]() $D \subseteq S$
with
$D \subseteq S$
with
![]() $D \neq \emptyset $
, we get
$D \neq \emptyset $
, we get
![]() $|\mathcal {Z}(S)|\leq t2^{t+1}d$
.
$|\mathcal {Z}(S)|\leq t2^{t+1}d$
.
We say that a hypergraph
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $\ell $
-overlapping if every two edges
$\ell $
-overlapping if every two edges
![]() $E, F \in \mathcal {H}$
satisfy that
$E, F \in \mathcal {H}$
satisfy that
![]() $|E \cap F| \leq \ell $
. The next lemma says for any
$|E \cap F| \leq \ell $
. The next lemma says for any
![]() $2$
-contractible,
$2$
-contractible,
![]() $\ell $
-overlapping k-tree
$\ell $
-overlapping k-tree
![]() $\mathcal {H}$
, a sufficiently dense k-graph
$\mathcal {H}$
, a sufficiently dense k-graph
![]() $\mathcal {F}$
always contains a dense balanced collection of copies of
$\mathcal {F}$
always contains a dense balanced collection of copies of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Lemma 5.2. Let
![]() $k\geq 4$
be an integer. Let
$k\geq 4$
be an integer. Let
![]() $\mathcal {H}$
be a
$\mathcal {H}$
be a
![]() $2$
-contractible,
$2$
-contractible,
![]() $\ell $
-overlapping k-tree with t edges. There exists
$\ell $
-overlapping k-tree with t edges. There exists
![]() $a_0$
and
$a_0$
and
![]() $\beta $
such that the following holds if n is sufficiently large. Let
$\beta $
such that the following holds if n is sufficiently large. Let
![]() $\mathcal {F}$
be a k-graph on
$\mathcal {F}$
be a k-graph on
![]() $[n]$
that has size
$[n]$
that has size
![]() $a\binom {n}{ k - 1}$
, with
$a\binom {n}{ k - 1}$
, with
![]() $a \geq a_0$
. Then, there exists a collection
$a \geq a_0$
. Then, there exists a collection
![]() $\mathcal {K}$
of copies of
$\mathcal {K}$
of copies of
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\mathcal {F}$
such that:
$\mathcal {F}$
such that:
-
1.
 $$ \begin{align*}|\mathcal{K}| \geq \beta an^{ k - 1} (\beta an^{k - \ell - 1})^{t - 1}\end{align*} $$
$$ \begin{align*}|\mathcal{K}| \geq \beta an^{ k - 1} (\beta an^{k - \ell - 1})^{t - 1}\end{align*} $$
-
2. For all
 $S \subseteq \mathcal {F}$
with
$S \subseteq \mathcal {F}$
with
 $1\leq |S|\leq t$
,
$1\leq |S|\leq t$
,  $$ \begin{align*}d_{\mathcal{K}}(S) \leq (\beta an^{k - \ell - 1})^{t - |S|}.\end{align*} $$
$$ \begin{align*}d_{\mathcal{K}}(S) \leq (\beta an^{k - \ell - 1})^{t - |S|}.\end{align*} $$
Proof. Let
![]() $\beta $
be sufficiently small and
$\beta $
be sufficiently small and
![]() $a_0$
be sufficiently large. Let
$a_0$
be sufficiently large. Let
![]() $\mathcal {K}$
be maximal collection of copies of
$\mathcal {K}$
be maximal collection of copies of
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\mathcal {F}$
that satisfies condition 2. Since any collection that consists of a single copy of
$\mathcal {F}$
that satisfies condition 2. Since any collection that consists of a single copy of
![]() $\mathcal {H}$
satisfies condition 2,
$\mathcal {H}$
satisfies condition 2,
![]() $\mathcal {K}$
exists. We show that
$\mathcal {K}$
exists. We show that
![]() $\mathcal {K}$
must also satisfy condition 1. Suppose on the contrary that
$\mathcal {K}$
must also satisfy condition 1. Suppose on the contrary that
![]() $|\mathcal {K}| < \beta ^t n^{ k - 1} (a n^{k - \ell })^{t - 1}$
. To derive a contradiction, it suffices to show that
$|\mathcal {K}| < \beta ^t n^{ k - 1} (a n^{k - \ell })^{t - 1}$
. To derive a contradiction, it suffices to show that
![]() $\mathcal {F}$
contains a copy
$\mathcal {F}$
contains a copy
![]() $\mathcal {H}^*$
of
$\mathcal {H}^*$
of
![]() $\mathcal {H}$
that is admissible relative to
$\mathcal {H}$
that is admissible relative to
![]() $\mathcal {K}$
. Indeed, if we found such an
$\mathcal {K}$
. Indeed, if we found such an
![]() $\mathcal {H}^*$
, in particular, it would not be saturated by
$\mathcal {H}^*$
, in particular, it would not be saturated by
![]() $\mathcal {K}$
. Hence,
$\mathcal {K}$
. Hence,
![]() $d_{\mathcal {K}}(\mathcal {H}^*) < (\beta a n^{k-\ell -1})^{t-t}=1$
. So,
$d_{\mathcal {K}}(\mathcal {H}^*) < (\beta a n^{k-\ell -1})^{t-t}=1$
. So,
![]() $\mathcal {H}^*\notin \mathcal {K}$
. Furthermore, for all
$\mathcal {H}^*\notin \mathcal {K}$
. Furthermore, for all
![]() $S \subseteq \mathcal {H}^*$
, we would have
$S \subseteq \mathcal {H}^*$
, we would have
![]() $d_{\mathcal {K}}(S) \leq \left \lfloor (\beta a n^{k - \ell })^{t - |S|} \right \rfloor - 1$
. Thus,
$d_{\mathcal {K}}(S) \leq \left \lfloor (\beta a n^{k - \ell })^{t - |S|} \right \rfloor - 1$
. Thus,
![]() $d_{\mathcal {K}\cup \mathcal {H}^*}(S)\leq (\beta a n^{k - \ell })^{t - |S|}$
. Therefore,
$d_{\mathcal {K}\cup \mathcal {H}^*}(S)\leq (\beta a n^{k - \ell })^{t - |S|}$
. Therefore,
![]() $\mathcal {K}\cup \{\mathcal {H}^*\}$
would still satisfy condition 2, which would contradict the maximality of
$\mathcal {K}\cup \{\mathcal {H}^*\}$
would still satisfy condition 2, which would contradict the maximality of
![]() $\mathcal {K}$
and complete the proof. Thus, it suffices to find such an admissible
$\mathcal {K}$
and complete the proof. Thus, it suffices to find such an admissible
![]() $\mathcal {H}^*$
.
$\mathcal {H}^*$
.
Since
![]() $\mathcal {K}$
satisfies condition 2,
$\mathcal {K}$
satisfies condition 2,
![]() $\mathcal {K}$
is
$\mathcal {K}$
is
![]() $\beta a n^{ k- \ell - 1}$
-graded. Recall that a set
$\beta a n^{ k- \ell - 1}$
-graded. Recall that a set
![]() $S \subseteq \mathcal {F}$
is saturated by
$S \subseteq \mathcal {F}$
is saturated by
![]() $\mathcal {K}$
if
$\mathcal {K}$
if
![]() $d_{\mathcal {K}}(S) = \left \lfloor (\beta an^{k - \ell })^{t - |S|} \right \rfloor $
. Let
$d_{\mathcal {K}}(S) = \left \lfloor (\beta an^{k - \ell })^{t - |S|} \right \rfloor $
. Let
![]() $\mathcal {F}_{\mathrm {heavy}} := \{F \in \mathcal {F}: d_{\mathcal {K}}(F) = \left \lfloor (\beta an^{k - \ell })^{t - 1} \right \rfloor \}$
, so that
$\mathcal {F}_{\mathrm {heavy}} := \{F \in \mathcal {F}: d_{\mathcal {K}}(F) = \left \lfloor (\beta an^{k - \ell })^{t - 1} \right \rfloor \}$
, so that
![]() $\mathcal {F}_{\mathrm {heavy}}$
consists of all the saturated edges of
$\mathcal {F}_{\mathrm {heavy}}$
consists of all the saturated edges of
![]() $\mathcal {F}$
. By Lemma 5.1,
$\mathcal {F}$
. By Lemma 5.1,
![]() $|\mathcal {F}_{\mathrm {heavy}}| \leq 2t \beta a n^{ k - 1}$
. Let
$|\mathcal {F}_{\mathrm {heavy}}| \leq 2t \beta a n^{ k - 1}$
. Let
![]() $\mathcal {F}^* = \mathcal {F} \setminus \mathcal {F}_{\mathrm {heavy}}$
. Then
$\mathcal {F}^* = \mathcal {F} \setminus \mathcal {F}_{\mathrm {heavy}}$
. Then
![]() $|\mathcal {F}^*|\geq \frac {1}{2}|\mathcal {F}|$
, as long as
$|\mathcal {F}^*|\geq \frac {1}{2}|\mathcal {F}|$
, as long as
![]() $\beta < \frac {1}{8 t (k - 1)!}$
. By definition, every edge in
$\beta < \frac {1}{8 t (k - 1)!}$
. By definition, every edge in
![]() $\mathcal {F}^*$
is admissible relative to
$\mathcal {F}^*$
is admissible relative to
![]() $\mathcal {K}$
. By Lemma 4.1, there exists
$\mathcal {K}$
. By Lemma 4.1, there exists
![]() $\mathcal {F}' \subseteq \mathcal {F}^*$
such that
$\mathcal {F}' \subseteq \mathcal {F}^*$
such that
![]() $|\mathcal {F}'| \geq \frac {1}{4} |\mathcal {F}|$
and for each
$|\mathcal {F}'| \geq \frac {1}{4} |\mathcal {F}|$
and for each
![]() $i\in [k-1]$
,
$i\in [k-1]$
,
![]() $\delta _i(\mathcal {F}')\geq \frac {a}{4 k } \frac {\binom {n}{k - 1}}{\binom {n}{ i}}$
.
$\delta _i(\mathcal {F}')\geq \frac {a}{4 k } \frac {\binom {n}{k - 1}}{\binom {n}{ i}}$
.
For each
![]() $i\in [t]$
, let
$i\in [t]$
, let
![]() $\mathcal {H}_i=\{E_1,\dots , E_i\}$
. We will inductively find embeddings
$\mathcal {H}_i=\{E_1,\dots , E_i\}$
. We will inductively find embeddings
![]() $\varphi ^i$
of
$\varphi ^i$
of
![]() $\mathcal {H}_i$
into
$\mathcal {H}_i$
into
![]() $\mathcal {F}'$
, such that
$\mathcal {F}'$
, such that
![]() $\varphi ^i(\mathcal {H}_i)$
is admissible relative to
$\varphi ^i(\mathcal {H}_i)$
is admissible relative to
![]() $\mathcal {K}$
. First, let
$\mathcal {K}$
. First, let
![]() $F_1$
be any edge of
$F_1$
be any edge of
![]() $\mathcal {F}'$
and let
$\mathcal {F}'$
and let
![]() $\varphi ^1$
be any bijection from the vertices of
$\varphi ^1$
be any bijection from the vertices of
![]() $E_1$
to the vertices of
$E_1$
to the vertices of
![]() $F_1$
. Since
$F_1$
. Since
![]() $F_1$
is admissible relative to
$F_1$
is admissible relative to
![]() $\mathcal {K}$
,
$\mathcal {K}$
,
![]() $\varphi ^1(\mathcal {H}_1)$
is admissible. Let
$\varphi ^1(\mathcal {H}_1)$
is admissible. Let
![]() $1\leq i\leq t-1$
and suppose we have defined an embedding
$1\leq i\leq t-1$
and suppose we have defined an embedding
![]() $\varphi ^i$
of
$\varphi ^i$
of
![]() $\mathcal {H}_i$
into
$\mathcal {H}_i$
into
![]() $\mathcal {F}'$
such that
$\mathcal {F}'$
such that
![]() $\varphi ^i(\mathcal {H}_i)$
admissible relative to
$\varphi ^i(\mathcal {H}_i)$
admissible relative to
![]() $\mathcal {K}$
. Let F denote a parent edge of
$\mathcal {K}$
. Let F denote a parent edge of
![]() $E_{i+1}$
in
$E_{i+1}$
in
![]() $\mathcal {H}_i$
. Let
$\mathcal {H}_i$
. Let
![]() $p=|F\cap E_{i+1}|$
. Since
$p=|F\cap E_{i+1}|$
. Since
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $\ell $
-overlapping,
$\ell $
-overlapping,
![]() $p\leq \ell $
. By our conditions on
$p\leq \ell $
. By our conditions on
![]() $\mathcal {F}'$
, we have
$\mathcal {F}'$
, we have
![]() $d_{\mathcal {F}'}(\varphi ^i(F\cap E_{i + 1})) \geq \frac {a}{4k} \frac {\binom {n}{k - 1}}{\binom {n}{p}}$
. The number of edges of
$d_{\mathcal {F}'}(\varphi ^i(F\cap E_{i + 1})) \geq \frac {a}{4k} \frac {\binom {n}{k - 1}}{\binom {n}{p}}$
. The number of edges of
![]() $\mathcal {F}'$
that contain
$\mathcal {F}'$
that contain
![]() $\varphi ^i(F\cap E_{i + 1})$
and some other vertex of
$\varphi ^i(F\cap E_{i + 1})$
and some other vertex of
![]() $\varphi ^i(\mathcal {H}_i)$
is at most
$\varphi ^i(\mathcal {H}_i)$
is at most
![]() $kt \binom {n}{ k - p - 1}$
. Since
$kt \binom {n}{ k - p - 1}$
. Since
![]() $\mathcal {K}$
is
$\mathcal {K}$
is
![]() $\beta a n^{ k- \ell - 1}$
-graded, by Lemma 5.1, we have
$\beta a n^{ k- \ell - 1}$
-graded, by Lemma 5.1, we have
![]() $\mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i)),$
the set of edges E of
$\mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i)),$
the set of edges E of
![]() $\mathcal {F}'$
such that
$\mathcal {F}'$
such that
![]() $\{E\} \cup \varphi ^i(\mathcal {H}_i)$
is inadmissible relative to
$\{E\} \cup \varphi ^i(\mathcal {H}_i)$
is inadmissible relative to
![]() $\mathcal {K}$
, has size at most
$\mathcal {K}$
, has size at most
![]() $t 2^{t + 1} \beta a n^{ k -\ell - 1}$
.
$t 2^{t + 1} \beta a n^{ k -\ell - 1}$
.
Therefore as long as
![]() $\beta $
and a satisfy the following inequality:
$\beta $
and a satisfy the following inequality:
 $$ \begin{align*}\frac{a}{4 k} \frac{\binom{n}{k - 1}}{\binom{n}{p}}> kt \binom{n}{ k - p - 1} + 2^{ t + 1} t \beta a n^{ k - \ell - 1},\end{align*} $$
$$ \begin{align*}\frac{a}{4 k} \frac{\binom{n}{k - 1}}{\binom{n}{p}}> kt \binom{n}{ k - p - 1} + 2^{ t + 1} t \beta a n^{ k - \ell - 1},\end{align*} $$
there is some edge E of
![]() $\mathcal {F}'\setminus \mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))$
that contains
$\mathcal {F}'\setminus \mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))$
that contains
![]() $\varphi ^i(F\cap E_{i+1})$
but does not intersect the rest of
$\varphi ^i(F\cap E_{i+1})$
but does not intersect the rest of
![]() $\varphi ^i(\mathcal {H}_i)$
. Picking some
$\varphi ^i(\mathcal {H}_i)$
. Picking some
![]() $a_0$
sufficiently large in terms of
$a_0$
sufficiently large in terms of
![]() $k, \ell , t$
and
$k, \ell , t$
and
![]() $\beta $
sufficiently small in terms of
$\beta $
sufficiently small in terms of
![]() $k, \ell , t$
, the inequality holds and such E exists. We extend
$k, \ell , t$
, the inequality holds and such E exists. We extend
![]() $\varphi ^i$
to an embedding
$\varphi ^i$
to an embedding
![]() $\varphi ^{i+1}$
of
$\varphi ^{i+1}$
of
![]() $\mathcal {H}_{i+1}$
into
$\mathcal {H}_{i+1}$
into
![]() $\mathcal {F}'$
by mapping the vertices of
$\mathcal {F}'$
by mapping the vertices of
![]() $E_{i+1}\setminus (F\cap E_{i+1})$
injectively to the vertices of
$E_{i+1}\setminus (F\cap E_{i+1})$
injectively to the vertices of
![]() $E\setminus \varphi ^i (F\cap E_{i+1})$
so that
$E\setminus \varphi ^i (F\cap E_{i+1})$
so that
![]() $\varphi ^{i+1}(E_{i+1})=E$
. Note that
$\varphi ^{i+1}(E_{i+1})=E$
. Note that
![]() $\varphi ^{i+1}(\mathcal {H}_{i+1})=\varphi ^i(\mathcal {H}_i)\cup \{E\}$
. Since
$\varphi ^{i+1}(\mathcal {H}_{i+1})=\varphi ^i(\mathcal {H}_i)\cup \{E\}$
. Since
![]() $E \not \in \mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))$
and
$E \not \in \mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))$
and
![]() $\varphi ^{i + 1}(\mathcal {H}_{i+1})$
is admissible relative to
$\varphi ^{i + 1}(\mathcal {H}_{i+1})$
is admissible relative to
![]() $\mathcal {K}$
. This completes the induction. Now,
$\mathcal {K}$
. This completes the induction. Now,
![]() $\varphi ^t(\mathcal {H}_t)$
is a copy of
$\varphi ^t(\mathcal {H}_t)$
is a copy of
![]() $\mathcal {H}$
that is admissible relative to
$\mathcal {H}$
that is admissible relative to
![]() $\mathcal {K}$
, completing our proof.
$\mathcal {K}$
, completing our proof.
Next, we seek to prove a similar result for
![]() $|\mathcal {F}| = a \binom {n}{k - 1}$
with
$|\mathcal {F}| = a \binom {n}{k - 1}$
with
![]() $\sigma (\mathcal {H}) - 1 + \gamma \leq a \leq a_0$
, where
$\sigma (\mathcal {H}) - 1 + \gamma \leq a \leq a_0$
, where
![]() $\gamma $
is any given small positive real. At the cost of a constant, we will prove a balanced supersaturation lemma only for
$\gamma $
is any given small positive real. At the cost of a constant, we will prove a balanced supersaturation lemma only for
![]() $a = \sigma (\mathcal {H}) - 1 + \gamma $
.
$a = \sigma (\mathcal {H}) - 1 + \gamma $
.
Lemma 5.3. Let
![]() $k\geq 4$
be an integer. Let
$k\geq 4$
be an integer. Let
![]() $\mathcal {H}$
be a
$\mathcal {H}$
be a
![]() $2$
-contractible
$2$
-contractible
![]() $\ell $
-overlapping k-tree with t edges. Let
$\ell $
-overlapping k-tree with t edges. Let
![]() $\gamma> 0$
be a positive real. There exists a
$\gamma> 0$
be a positive real. There exists a
![]() $\beta> 0$
such that the following holds if n is sufficiently large. Let
$\beta> 0$
such that the following holds if n is sufficiently large. Let
![]() $\mathcal {F}$
be a k-graph on
$\mathcal {F}$
be a k-graph on
![]() $[n]$
with
$[n]$
with
![]() $|\mathcal {F}|\geq (\sigma (\mathcal {H}) -1 + \gamma ) \binom {n}{ k - 1}$
. Then, there exists a collection
$|\mathcal {F}|\geq (\sigma (\mathcal {H}) -1 + \gamma ) \binom {n}{ k - 1}$
. Then, there exists a collection
![]() $\mathcal {K}$
of copies of
$\mathcal {K}$
of copies of
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\mathcal {F}$
such that:
$\mathcal {F}$
such that:
-
1.
 $$ \begin{align*}|\mathcal{K}| \geq \beta n^{ k - 1} (\beta n^{k - \ell - 1})^{t - 1}\end{align*} $$
$$ \begin{align*}|\mathcal{K}| \geq \beta n^{ k - 1} (\beta n^{k - \ell - 1})^{t - 1}\end{align*} $$
-
2. For all
 $S \subseteq \mathcal {F}$
with
$S \subseteq \mathcal {F}$
with
 $1\leq |S|\leq t$
,
$1\leq |S|\leq t$
,  $$\begin{align*}d_{\mathcal{K}}(S) \leq (\beta n^{k - \ell - 1})^{t - |S|}.\end{align*}$$
$$\begin{align*}d_{\mathcal{K}}(S) \leq (\beta n^{k - \ell - 1})^{t - |S|}.\end{align*}$$
Proof. For convenience, let
![]() $\sigma =\sigma (\mathcal {H})$
. Let
$\sigma =\sigma (\mathcal {H})$
. Let
![]() $\beta $
be sufficiently small and
$\beta $
be sufficiently small and
![]() $a_0$
be sufficiently large. Let
$a_0$
be sufficiently large. Let
![]() $\mathcal {K}$
be maximal collection of copies of
$\mathcal {K}$
be maximal collection of copies of
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\mathcal {F}$
that satisfies condition 2. Since any collection consisting of a single copy of
$\mathcal {F}$
that satisfies condition 2. Since any collection consisting of a single copy of
![]() $\mathcal {H}$
satisfies condition 2,
$\mathcal {H}$
satisfies condition 2,
![]() $\mathcal {K}$
exists. We show that
$\mathcal {K}$
exists. We show that
![]() $\mathcal {K}$
must also satisfy condition 1. Suppose on the contrary that
$\mathcal {K}$
must also satisfy condition 1. Suppose on the contrary that
![]() $|\mathcal {K}| < \beta ^t n^{ k - 1} (n^{k - \ell })^{t - 1}$
. To derive a contradiction, as in the proof Lemma 5.2, it suffices to show that
$|\mathcal {K}| < \beta ^t n^{ k - 1} (n^{k - \ell })^{t - 1}$
. To derive a contradiction, as in the proof Lemma 5.2, it suffices to show that
![]() $\mathcal {F}$
contains a copy
$\mathcal {F}$
contains a copy
![]() $\mathcal {H}^*$
of
$\mathcal {H}^*$
of
![]() $\mathcal {H}$
that is admissible relative to
$\mathcal {H}$
that is admissible relative to
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
By definition,
![]() $\mathcal {K}$
is
$\mathcal {K}$
is
![]() $\beta n^{ k- \ell - 1}$
-graded. Recall that a set
$\beta n^{ k- \ell - 1}$
-graded. Recall that a set
![]() $S \subseteq \mathcal {F}$
is saturated with respect to
$S \subseteq \mathcal {F}$
is saturated with respect to
![]() $\mathcal {K}$
if
$\mathcal {K}$
if
![]() $\deg _{\mathcal {K}}(S) = \left \lfloor (\beta n^{k - \ell })^{t - |S|} \right \rfloor $
. Let
$\deg _{\mathcal {K}}(S) = \left \lfloor (\beta n^{k - \ell })^{t - |S|} \right \rfloor $
. Let
![]() $\mathcal {F}_{\mathrm {heavy}} := \{F \in \mathcal {F}: \deg _{\mathcal {K}}(F) = \left \lfloor (\beta n^{k - \ell })^{t - 1} \right \rfloor \}$
. Note that
$\mathcal {F}_{\mathrm {heavy}} := \{F \in \mathcal {F}: \deg _{\mathcal {K}}(F) = \left \lfloor (\beta n^{k - \ell })^{t - 1} \right \rfloor \}$
. Note that
![]() $\mathcal {F}_{\mathrm {heavy}}$
consists of all the saturated edges. By Lemma 5.1,
$\mathcal {F}_{\mathrm {heavy}}$
consists of all the saturated edges. By Lemma 5.1,
![]() $|\mathcal {F}_{\mathrm {heavy}}| \leq 2t \beta n^{ k - 1}<\frac {\gamma }{2} \binom {n}{k-1}$
, if
$|\mathcal {F}_{\mathrm {heavy}}| \leq 2t \beta n^{ k - 1}<\frac {\gamma }{2} \binom {n}{k-1}$
, if
![]() $\beta $
is sufficiently small. Let
$\beta $
is sufficiently small. Let
![]() $\widehat {\mathcal {F}} := \mathcal {F} - \mathcal {F}_{\mathrm {heavy}}$
. Then
$\widehat {\mathcal {F}} := \mathcal {F} - \mathcal {F}_{\mathrm {heavy}}$
. Then
![]() $|\widehat {\mathcal {F}}| \geq (\sigma -1 + \frac {\gamma }{2}) \binom {n}{ k - 1}.$
By definition, all edges of
$|\widehat {\mathcal {F}}| \geq (\sigma -1 + \frac {\gamma }{2}) \binom {n}{ k - 1}.$
By definition, all edges of
![]() $\widehat {\mathcal {F}}$
are admissible relative to
$\widehat {\mathcal {F}}$
are admissible relative to
![]() $\mathcal {K}$
. Let
$\mathcal {K}$
. Let
![]() $s = v(\mathcal {H})$
. Now we apply Theorem 3.5 to
$s = v(\mathcal {H})$
. Now we apply Theorem 3.5 to
![]() $\widehat {\mathcal {F}}$
with
$\widehat {\mathcal {F}}$
with
There are two cases to consider:
Case 1.
![]() $\widehat {\mathcal {F}}$
satisfies case (1) of Theorem 3.5.
$\widehat {\mathcal {F}}$
satisfies case (1) of Theorem 3.5.
In this case, we find an
![]() $\mathcal {F}' \subseteq \widehat {\mathcal {F}}$
which is s-super-homogeneous,
$\mathcal {F}' \subseteq \widehat {\mathcal {F}}$
which is s-super-homogeneous,
![]() $|\mathcal {F}'|\geq \frac {c(k, s) \gamma ^{ k -2}}{2^{k - 1} \sigma } \binom {n}{ k - 1}$
, and
$|\mathcal {F}'|\geq \frac {c(k, s) \gamma ^{ k -2}}{2^{k - 1} \sigma } \binom {n}{ k - 1}$
, and
![]() $\mathrm {Int}(\mathcal {F}')$
is of type 1, where without loss of generality
$\mathrm {Int}(\mathcal {F}')$
is of type 1, where without loss of generality
![]() $2^{[ k - 2]} \subseteq \mathrm {Int}(\mathcal {F}')$
. Let
$2^{[ k - 2]} \subseteq \mathrm {Int}(\mathcal {F}')$
. Let
![]() $(X_1,\dots , X_k)$
be the k-partition associated with
$(X_1,\dots , X_k)$
be the k-partition associated with
![]() $\mathrm {Int}(\mathcal {F}')$
. Since
$\mathrm {Int}(\mathcal {F}')$
. Since
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $2$
-contractible, each edge contains at least two vertices of degree
$2$
-contractible, each edge contains at least two vertices of degree
![]() $1$
. We will designate two of them as expansion vertices for E.
$1$
. We will designate two of them as expansion vertices for E.
Let
![]() $E_1,\cdots , E_t$
be a tree-defining ordering of the edges of
$E_1,\cdots , E_t$
be a tree-defining ordering of the edges of
![]() $\mathcal {H}$
. For each
$\mathcal {H}$
. For each
![]() $i\in [t]$
, let
$i\in [t]$
, let
![]() $\mathcal {H}_i=\{E_1,\dots , E_i\}$
. Let
$\mathcal {H}_i=\{E_1,\dots , E_i\}$
. Let
![]() $\Pi _i$
denote the set of embeddings
$\Pi _i$
denote the set of embeddings
![]() $\varphi ^i$
of
$\varphi ^i$
of
![]() $\mathcal {H}_i$
into
$\mathcal {H}_i$
into
![]() $\mathcal {F}'$
satisfying that
$\mathcal {F}'$
satisfying that
![]() $\varphi ^i(\mathcal {H}_i)$
is admissible relative to
$\varphi ^i(\mathcal {H}_i)$
is admissible relative to
![]() $\mathcal {K}$
and
$\mathcal {K}$
and
![]() $\varphi ^i$
maps all expansion vertices in
$\varphi ^i$
maps all expansion vertices in
![]() $\mathcal {H}_i$
to
$\mathcal {H}_i$
to
![]() $X_{k-1}\cup X_k$
. We use induction on i to prove that for each
$X_{k-1}\cup X_k$
. We use induction on i to prove that for each
![]() $i\in [t]$
,
$i\in [t]$
,
![]() $\Pi _i\neq \emptyset $
.
$\Pi _i\neq \emptyset $
.
For the base step, we let
![]() $F_1$
be any edge of
$F_1$
be any edge of
![]() $\mathcal {F}'$
. Let
$\mathcal {F}'$
. Let
![]() $\varphi ^1$
be a bijection that maps the vertices of
$\varphi ^1$
be a bijection that maps the vertices of
![]() $E_1$
to the vertices of
$E_1$
to the vertices of
![]() $F_1$
such that the two expansion vertices are mapped to
$F_1$
such that the two expansion vertices are mapped to
![]() $F_1\cap X_{k-1}$
and
$F_1\cap X_{k-1}$
and
![]() $F_1\cap X_k$
, respectively. Since all edges of
$F_1\cap X_k$
, respectively. Since all edges of
![]() $\mathcal {F}'$
are admissible,
$\mathcal {F}'$
are admissible,
![]() $\varphi ^1(\mathcal {H}_1)$
is admissible. Hence,
$\varphi ^1(\mathcal {H}_1)$
is admissible. Hence,
![]() $\Pi _1\neq \emptyset $
.
$\Pi _1\neq \emptyset $
.
For the induction step, let
![]() $1\leq i\leq t-1$
and suppose that
$1\leq i\leq t-1$
and suppose that
![]() $\Pi _i\neq \emptyset $
. Let
$\Pi _i\neq \emptyset $
. Let
![]() $\varphi ^i\in \Pi _i$
. Let F be a parent edge of
$\varphi ^i\in \Pi _i$
. Let F be a parent edge of
![]() $E_{i+1}$
in
$E_{i+1}$
in
![]() $\mathcal {H}_i$
. Since vertices in
$\mathcal {H}_i$
. Since vertices in
![]() $F\cap E_{i+1}$
have degree at least two in
$F\cap E_{i+1}$
have degree at least two in
![]() $\mathcal {H}$
, they are not expansion vertices in
$\mathcal {H}$
, they are not expansion vertices in
![]() $\mathcal {H}_i$
. Hence,
$\mathcal {H}_i$
. Hence,
![]() $\varphi ^i(F\cap E_{i+1})\subseteq \bigcup _{j=1}^{k-2} X_j$
. Since
$\varphi ^i(F\cap E_{i+1})\subseteq \bigcup _{j=1}^{k-2} X_j$
. Since
![]() $2^{[k-2]}\subseteq \mathrm {Int}(\mathcal {F})$
, we have
$2^{[k-2]}\subseteq \mathrm {Int}(\mathcal {F})$
, we have
![]() $\pi (\varphi ^i(F \cap E_{i+1})) \in \mathrm {Int}(\mathcal {F})$
. So, in particular that
$\pi (\varphi ^i(F \cap E_{i+1})) \in \mathrm {Int}(\mathcal {F})$
. So, in particular that
![]() $\mathcal {L}_{\mathcal {F}}(\varphi ^i(F \cap E_{i+1}))$
is s-diverse. Therefore, we have that at least
$\mathcal {L}_{\mathcal {F}}(\varphi ^i(F \cap E_{i+1}))$
is s-diverse. Therefore, we have that at least
![]() $1 - \frac {v(H_i)}{s} \geq \frac {1}{s}$
proportion of the edges in
$1 - \frac {v(H_i)}{s} \geq \frac {1}{s}$
proportion of the edges in
![]() $\mathcal {L}_{\mathcal {F}}( \varphi ^i(F \cap E_i))$
do not intersect the rest of
$\mathcal {L}_{\mathcal {F}}( \varphi ^i(F \cap E_i))$
do not intersect the rest of
![]() $\varphi ^i(\mathcal {H}_i)$
. Furthermore, by Lemma 5.1, with
$\varphi ^i(\mathcal {H}_i)$
. Furthermore, by Lemma 5.1, with
![]() $d=\beta n^{k-\ell -1}$
,
$d=\beta n^{k-\ell -1}$
,
![]() $|\mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))| \leq t 2^{ t + 1} \beta n^{ k - \ell - 1}$
. Let
$|\mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))| \leq t 2^{ t + 1} \beta n^{ k - \ell - 1}$
. Let
![]() $p=|F\cap E_{i+1}|$
. Since
$p=|F\cap E_{i+1}|$
. Since
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $\ell $
-overlapping,
$\ell $
-overlapping,
![]() $p\leq \ell $
. Since
$p\leq \ell $
. Since
![]() $\mathcal {F}'$
is s-super-homogoneus and
$\mathcal {F}'$
is s-super-homogoneus and
![]() $\pi (F\cap E_{i+1})\in \mathrm {Int}(\mathcal {F}')$
,
$\pi (F\cap E_{i+1})\in \mathrm {Int}(\mathcal {F}')$
,
By picking
![]() $\beta $
sufficiently small in terms of
$\beta $
sufficiently small in terms of
![]() $\gamma $
and
$\gamma $
and
![]() $\mathcal {H}$
, we can ensure that
$\mathcal {H}$
, we can ensure that
Hence,
![]() $\mathcal {F}'\setminus \mathcal {Z}(\varphi ^i(\mathcal {H}_i))$
contains an edge E that contains
$\mathcal {F}'\setminus \mathcal {Z}(\varphi ^i(\mathcal {H}_i))$
contains an edge E that contains
![]() $\varphi ^i(F\cap E_{i+1})$
but does not intersect the rest of
$\varphi ^i(F\cap E_{i+1})$
but does not intersect the rest of
![]() $\varphi ^i(\mathcal {H}_i)$
. We extend
$\varphi ^i(\mathcal {H}_i)$
. We extend
![]() $\varphi ^i$
to an embedding of
$\varphi ^i$
to an embedding of
![]() $\mathcal {H}_{i+1}$
in
$\mathcal {H}_{i+1}$
in
![]() $\mathcal {F}'$
by mapping the vertices of
$\mathcal {F}'$
by mapping the vertices of
![]() $E_{i+1}\setminus (F\cap E_{i+1})$
injectively into
$E_{i+1}\setminus (F\cap E_{i+1})$
injectively into
![]() $E\setminus \varphi ^i(F\cap E_{i+1})$
, so that
$E\setminus \varphi ^i(F\cap E_{i+1})$
, so that
![]() $\varphi ^{i+1}(E_{i+1})=E$
and the expansion vertices of E are mapped into
$\varphi ^{i+1}(E_{i+1})=E$
and the expansion vertices of E are mapped into
![]() $X_{k - 1}$
and
$X_{k - 1}$
and
![]() $X_k$
. Since
$X_k$
. Since
![]() $E \not \in \mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))$
,
$E \not \in \mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))$
,
![]() $\varphi ^{i + 1}(\mathcal {H}_{i + 1})$
is admissible relative to
$\varphi ^{i + 1}(\mathcal {H}_{i + 1})$
is admissible relative to
![]() $\mathcal {K}$
. This completes the induction. Now,
$\mathcal {K}$
. This completes the induction. Now,
![]() $\varphi ^t(\mathcal {H}_t)$
is a copy of
$\varphi ^t(\mathcal {H}_t)$
is a copy of
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\mathcal {F}'$
that is admissible relative to
$\mathcal {F}'$
that is admissible relative to
![]() $\mathcal {K}$
. This completes the proof for Case 1.
$\mathcal {K}$
. This completes the proof for Case 1.
Case 2.
![]() $\widehat {\mathcal {F}}$
satisfies case (2) of Theorem 3.5.
$\widehat {\mathcal {F}}$
satisfies case (2) of Theorem 3.5.
In this case, there exist a
![]() $W \subseteq [n]$
and
$W \subseteq [n]$
and
![]() $\mathcal {F}" \subseteq \widehat {\mathcal {F}}$
satisfying
$\mathcal {F}" \subseteq \widehat {\mathcal {F}}$
satisfying
-
(a)
 $|W| \leq \left ( \frac {5\cdot 2^{2k - 2} \sigma ^2}{c(k,s) \gamma ^{2k - 4}} \right )^{k - 1}.$
$|W| \leq \left ( \frac {5\cdot 2^{2k - 2} \sigma ^2}{c(k,s) \gamma ^{2k - 4}} \right )^{k - 1}.$
-
(b)
 $|\mathcal {F}"| \geq (1-\frac {\gamma ^{k - 2}}{ 2^{ k - 2} \cdot \sigma } )|\widehat {\mathcal {F}}|\geq (1-\frac {\gamma }{4\sigma })(\sigma -1+\frac {\gamma }{2}) \binom {n}{k-1} \geq (\sigma - 1 + \frac {\gamma }{8} ) \binom {n}{k - 1} .$
$|\mathcal {F}"| \geq (1-\frac {\gamma ^{k - 2}}{ 2^{ k - 2} \cdot \sigma } )|\widehat {\mathcal {F}}|\geq (1-\frac {\gamma }{4\sigma })(\sigma -1+\frac {\gamma }{2}) \binom {n}{k-1} \geq (\sigma - 1 + \frac {\gamma }{8} ) \binom {n}{k - 1} .$
-
(c) Every
 $F \in \mathcal {F}"$
satisfies
$F \in \mathcal {F}"$
satisfies
 $|W \cap F| = 1$
.
$|W \cap F| = 1$
.
For each
![]() $S\in \binom {W}{\sigma }$
, let
$S\in \binom {W}{\sigma }$
, let
![]() $\mathcal {L}^*(S) = \bigcap _{v \in S} \mathcal {L}_{\mathcal {F}"}(v)$
. Let
$\mathcal {L}^*(S) = \bigcap _{v \in S} \mathcal {L}_{\mathcal {F}"}(v)$
. Let
![]() $\mathcal {D}$
denote the set of
$\mathcal {D}$
denote the set of
![]() $(k-1)$
-sets D in
$(k-1)$
-sets D in
![]() $[n]\setminus W$
with
$[n]\setminus W$
with
![]() $d_{\mathcal {F}"}(D)\geq \sigma $
. Since each edge of
$d_{\mathcal {F}"}(D)\geq \sigma $
. Since each edge of
![]() $\mathcal {F}"$
contains one vertex in W and a
$\mathcal {F}"$
contains one vertex in W and a
![]() $(k-1)$
-set in
$(k-1)$
-set in
![]() $[n]\setminus W$
, via double counting, we get
$[n]\setminus W$
, via double counting, we get
 $$\begin{align*}\sum_{S \in \binom{W}{\sigma}} |\mathcal{L}^*(S)| = \sum_{D \in \mathcal{D}} \binom{d_{\mathcal{F}"}(D)}{\sigma}.\end{align*}$$
$$\begin{align*}\sum_{S \in \binom{W}{\sigma}} |\mathcal{L}^*(S)| = \sum_{D \in \mathcal{D}} \binom{d_{\mathcal{F}"}(D)}{\sigma}.\end{align*}$$
By our assumption,
![]() $|\mathcal {F}"|\geq (\sigma -1+\frac {\gamma }{8})\binom {n}{k-1}$
. This implies that
$|\mathcal {F}"|\geq (\sigma -1+\frac {\gamma }{8})\binom {n}{k-1}$
. This implies that
![]() $m:=\sum _{D\in \mathcal {D}} d_{\mathcal {F}"} (D)\geq \frac {\gamma }{8}\binom {n}{k-1}$
. Thus, by observing that if
$m:=\sum _{D\in \mathcal {D}} d_{\mathcal {F}"} (D)\geq \frac {\gamma }{8}\binom {n}{k-1}$
. Thus, by observing that if
![]() $d_{\mathcal {F}"}(D) \geq \sigma $
,
$d_{\mathcal {F}"}(D) \geq \sigma $
,
![]() $\binom {d_{\mathcal {F}"}(D)}{\sigma } \geq \frac {d_{\mathcal {F}"}(D)}{\sigma }$
, the right-hand side is at least
$\binom {d_{\mathcal {F}"}(D)}{\sigma } \geq \frac {d_{\mathcal {F}"}(D)}{\sigma }$
, the right-hand side is at least
![]() $\frac {\gamma }{8 \sigma } \binom {n}{k -1}$
.
$\frac {\gamma }{8 \sigma } \binom {n}{k -1}$
.
Hence, there exists a
![]() $S \in \binom {W}{\sigma }$
, such that
$S \in \binom {W}{\sigma }$
, such that
 $$ \begin{align} |\mathcal{L}^*(S)| \geq\frac{\gamma}{8 \sigma |W|^\sigma} \binom{n}{ k - 1}. \end{align} $$
$$ \begin{align} |\mathcal{L}^*(S)| \geq\frac{\gamma}{8 \sigma |W|^\sigma} \binom{n}{ k - 1}. \end{align} $$
We fix such an S. By Lemma 4.1,
![]() $\mathcal {L}^*(S)$
contains a subgraph
$\mathcal {L}^*(S)$
contains a subgraph
![]() $\mathcal {L}'$
such that
$\mathcal {L}'$
such that
![]() $|\mathcal {L}'|\geq \frac {1}{2}|\mathcal {L}^*(S)|$
and for each
$|\mathcal {L}'|\geq \frac {1}{2}|\mathcal {L}^*(S)|$
and for each
![]() $i\in [k-1]$
,
$i\in [k-1]$
,
![]() $\delta _i(\mathcal {L}')\geq \frac {1}{2k}\frac {|\mathcal {L}^*(S)|}{\binom {n}{i}}$
. Note that since
$\delta _i(\mathcal {L}')\geq \frac {1}{2k}\frac {|\mathcal {L}^*(S)|}{\binom {n}{i}}$
. Note that since
![]() $\mathcal {L}'\subseteq \mathcal {L}^*(S)$
, for each
$\mathcal {L}'\subseteq \mathcal {L}^*(S)$
, for each
![]() $D\in \mathcal {L}'$
and each
$D\in \mathcal {L}'$
and each
![]() $v\in S$
,
$v\in S$
,
![]() $D\cup \{v\}\in \mathcal {F}"$
.
$D\cup \{v\}\in \mathcal {F}"$
.
Let
![]() $E_1,\dots , E_t$
be a tree-defining order of
$E_1,\dots , E_t$
be a tree-defining order of
![]() $\mathcal {H}$
. For each
$\mathcal {H}$
. For each
![]() $i\in [t]$
, let
$i\in [t]$
, let
![]() $\mathcal {H}_i=\{E_1,\dots , E_i\}$
. Let R be a minimum cross-cut of
$\mathcal {H}_i=\{E_1,\dots , E_i\}$
. Let R be a minimum cross-cut of
![]() $\mathcal {H}$
. For each
$\mathcal {H}$
. For each
![]() $i\in [t]$
, let
$i\in [t]$
, let
![]() $\{v_i\}=E_i\cap R$
and
$\{v_i\}=E_i\cap R$
and
![]() $E^{\prime }_i=E_i\setminus \{v_i\}$
. Let
$E^{\prime }_i=E_i\setminus \{v_i\}$
. Let
![]() $\mathcal {H}' = \mathcal {H} - R$
. It is easy to see by definition that
$\mathcal {H}' = \mathcal {H} - R$
. It is easy to see by definition that
![]() $\mathcal {H}'$
is a
$\mathcal {H}'$
is a
![]() $(k-1)$
-tree for which
$(k-1)$
-tree for which
![]() $E^{\prime }_1,\dots , E^{\prime }_t$
is a tree-defining ordering of
$E^{\prime }_1,\dots , E^{\prime }_t$
is a tree-defining ordering of
![]() $\mathcal {H}'$
. Furthermore, since each
$\mathcal {H}'$
. Furthermore, since each
![]() $E_i$
contains two degree
$E_i$
contains two degree
![]() $1$
vertices,
$1$
vertices,
![]() $E^{\prime }_1,\dots , E^{\prime }_t$
are all distinct.
$E^{\prime }_1,\dots , E^{\prime }_t$
are all distinct.
For each
![]() $i\in [t]$
, let
$i\in [t]$
, let
![]() $\Pi _i$
denote the collection of embeddings of
$\Pi _i$
denote the collection of embeddings of
![]() $\varphi ^i$
of
$\varphi ^i$
of
![]() $\mathcal {H}_i$
into
$\mathcal {H}_i$
into
![]() $\mathcal {F}'$
such that
$\mathcal {F}'$
such that
![]() $\varphi (\mathcal {H}_i)$
is admissible relative to
$\varphi (\mathcal {H}_i)$
is admissible relative to
![]() $\mathcal {K}$
. We prove by induction on i that
$\mathcal {K}$
. We prove by induction on i that
![]() $\Pi _i\neq \emptyset $
. Let g be any bijection from R to S. For the base step, let
$\Pi _i\neq \emptyset $
. Let g be any bijection from R to S. For the base step, let
![]() $D_1$
be any edge of
$D_1$
be any edge of
![]() $\mathcal {L}'$
. We define
$\mathcal {L}'$
. We define
![]() $\varphi ^1$
to be any mapping from
$\varphi ^1$
to be any mapping from
![]() $V(\mathcal {H}_1)$
to
$V(\mathcal {H}_1)$
to
![]() $V(\mathcal {F}")$
that maps
$V(\mathcal {F}")$
that maps
![]() $v_1$
to
$v_1$
to
![]() $g(v_1)$
and
$g(v_1)$
and
![]() $E^{\prime }_1$
to
$E^{\prime }_1$
to
![]() $D_1$
. By earlier discussion,
$D_1$
. By earlier discussion,
![]() $\varphi ^1(E_1)= D_1\cup \{v_1\}$
is an edge in
$\varphi ^1(E_1)= D_1\cup \{v_1\}$
is an edge in
![]() $\mathcal {F}"$
. Since all edges in
$\mathcal {F}"$
. Since all edges in
![]() $\widehat {\mathcal {F}}$
are admissible, all edges in
$\widehat {\mathcal {F}}$
are admissible, all edges in
![]() $\mathcal {F}"$
are admissible. Hence,
$\mathcal {F}"$
are admissible. Hence,
![]() $\varphi ^1(\mathcal {H}_1)= \varphi ^1(E_1)$
is admissible relative to
$\varphi ^1(\mathcal {H}_1)= \varphi ^1(E_1)$
is admissible relative to
![]() $\mathcal {K}$
. For the induction step, let
$\mathcal {K}$
. For the induction step, let
![]() $1\leq i\leq t-1$
and suppose
$1\leq i\leq t-1$
and suppose
![]() $\Pi _i\neq \emptyset $
. Let
$\Pi _i\neq \emptyset $
. Let
![]() $\varphi ^i\in \Pi _i$
. Suppose a parent edge of
$\varphi ^i\in \Pi _i$
. Suppose a parent edge of
![]() $E^{\prime }_{i+1}$
in
$E^{\prime }_{i+1}$
in
![]() $\mathcal {H}^{\prime }_i$
is
$\mathcal {H}^{\prime }_i$
is
![]() $E^{\prime }_j$
, for some
$E^{\prime }_j$
, for some
![]() $j\leq i$
. Let
$j\leq i$
. Let
![]() $p=|E_j\cap E^{\prime }_{i+1}|$
. Since
$p=|E_j\cap E^{\prime }_{i+1}|$
. Since
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $\ell $
-overlapping,
$\ell $
-overlapping,
![]() $\mathcal {H}'$
is
$\mathcal {H}'$
is
![]() $\ell $
-overlapping. So
$\ell $
-overlapping. So
![]() $p\leq \ell $
. By (12) and subsequent discussion,
$p\leq \ell $
. By (12) and subsequent discussion,
![]() $d_{\mathcal {L}'}(\varphi ^i(E^{\prime }_j\cap E^{\prime }_{i+1}))\geq \frac {\gamma }{16\sigma |W|^\sigma }\frac {\binom {n}{k-1}}{\binom {n}{p}}$
. The number of edges of
$d_{\mathcal {L}'}(\varphi ^i(E^{\prime }_j\cap E^{\prime }_{i+1}))\geq \frac {\gamma }{16\sigma |W|^\sigma }\frac {\binom {n}{k-1}}{\binom {n}{p}}$
. The number of edges of
![]() $\mathcal {L}'$
containing
$\mathcal {L}'$
containing
![]() $\varphi ^i(E^{\prime }_j\cap E^{\prime }_{i + 1})$
and intersect the rest of
$\varphi ^i(E^{\prime }_j\cap E^{\prime }_{i + 1})$
and intersect the rest of
![]() $\varphi ^i(\mathcal {H}_i)$
is at most
$\varphi ^i(\mathcal {H}_i)$
is at most
![]() $kt \binom {n}{ k - p - 2}$
. Furthermore, by Lemma 5.1, with
$kt \binom {n}{ k - p - 2}$
. Furthermore, by Lemma 5.1, with
![]() $d=\beta n^{k-\ell -1}$
,
$d=\beta n^{k-\ell -1}$
,
![]() $|\mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))|\leq 2^{ t + 1} t \beta n^{ k - \ell -1}$
. Let
$|\mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))|\leq 2^{ t + 1} t \beta n^{ k - \ell -1}$
. Let
![]() $\mathcal {Z}'=\{E\setminus R: E\in \mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))\}$
. Then
$\mathcal {Z}'=\{E\setminus R: E\in \mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))\}$
. Then
![]() $|\mathcal {Z}'|\leq 2^{t+1}t\beta n^{k-\ell -1}$
. By choosing
$|\mathcal {Z}'|\leq 2^{t+1}t\beta n^{k-\ell -1}$
. By choosing
![]() $\beta $
small enough, for sufficiently large n, we have
$\beta $
small enough, for sufficiently large n, we have
 $$\begin{align*}\frac{\gamma}{16 k \sigma |W|^\sigma } \frac{\binom{n}{k - 1}}{\binom{n}{p}}> kt \binom{n}{ k - p - 2} + 2^{ t + 1} t \beta n^{ k - \ell -1},\end{align*}$$
$$\begin{align*}\frac{\gamma}{16 k \sigma |W|^\sigma } \frac{\binom{n}{k - 1}}{\binom{n}{p}}> kt \binom{n}{ k - p - 2} + 2^{ t + 1} t \beta n^{ k - \ell -1},\end{align*}$$
where we used the fact that
![]() $|W|$
is bounded by a constant.
$|W|$
is bounded by a constant.
Hence,
![]() $\mathcal {L}'\setminus Z'$
contains an edge D that contains
$\mathcal {L}'\setminus Z'$
contains an edge D that contains
![]() $\varphi ^i(E_j'\cap E_{i+1}')$
but does not intersect the rest of
$\varphi ^i(E_j'\cap E_{i+1}')$
but does not intersect the rest of
![]() $\varphi ^i(\mathcal {H}_i)$
. We extend
$\varphi ^i(\mathcal {H}_i)$
. We extend
![]() $\varphi ^i$
to an embedding of
$\varphi ^i$
to an embedding of
![]() $\mathcal {H}_{i+1}$
in
$\mathcal {H}_{i+1}$
in
![]() $\mathcal {F}'$
by mapping the vertices of
$\mathcal {F}'$
by mapping the vertices of
![]() $E^{\prime }_{i+1}\setminus (E^{\prime }_j\cap E^{\prime }_{i+1})$
injectively into
$E^{\prime }_{i+1}\setminus (E^{\prime }_j\cap E^{\prime }_{i+1})$
injectively into
![]() $D\setminus \varphi ^i(E^{\prime }_j\cap E^{\prime }_{i+1})$
and mapping
$D\setminus \varphi ^i(E^{\prime }_j\cap E^{\prime }_{i+1})$
and mapping
![]() $v_{i+1}$
to
$v_{i+1}$
to
![]() $g(v_{i + 1})$
so that
$g(v_{i + 1})$
so that
![]() $\varphi ^{i+1}(E_{i+1})=D \cup \{ g(v_{i + 1})\}$
. Since
$\varphi ^{i+1}(E_{i+1})=D \cup \{ g(v_{i + 1})\}$
. Since
![]() $D \not \in \mathcal {Z}'$
,
$D \not \in \mathcal {Z}'$
,
![]() $\varphi ^{i+1}(E_{i+1})\notin \mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))$
, and hence
$\varphi ^{i+1}(E_{i+1})\notin \mathcal {Z}_{\mathcal {K}}(\varphi ^i(\mathcal {H}_i))$
, and hence
![]() $\varphi ^{i + 1}(\mathcal {H}_{i + 1})$
is admissible relative to
$\varphi ^{i + 1}(\mathcal {H}_{i + 1})$
is admissible relative to
![]() $\mathcal {K}$
. This completes the induction. Now,
$\mathcal {K}$
. This completes the induction. Now,
![]() $\varphi ^t(\mathcal {H}_t)$
is a copy of
$\varphi ^t(\mathcal {H}_t)$
is a copy of
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\mathcal {F}"$
that is admissible relative to
$\mathcal {F}"$
that is admissible relative to
![]() $\mathcal {K}$
. This completes the proof for Case 2.
$\mathcal {K}$
. This completes the proof for Case 2.
Lemma 5.2 and Lemma 5.3 together imply the following:
Theorem 5.4. Let
![]() $k\geq 4$
. Let
$k\geq 4$
. Let
![]() $\varepsilon> 0$
. Let
$\varepsilon> 0$
. Let
![]() $\mathcal {H}$
be a
$\mathcal {H}$
be a
![]() $2$
-contractible
$2$
-contractible
![]() $\ell $
-overlapping k-tree with t edges. There exist
$\ell $
-overlapping k-tree with t edges. There exist
![]() $c=c(\varepsilon , \mathcal {H}), c'=c'(\varepsilon ,\mathcal {H})>0$
such that the following holds. Let
$c=c(\varepsilon , \mathcal {H}), c'=c'(\varepsilon ,\mathcal {H})>0$
such that the following holds. Let
![]() $\mathcal {F}$
be a k-graph on
$\mathcal {F}$
be a k-graph on
![]() $[n]$
with
$[n]$
with
![]() $|\mathcal {F}|=a\binom {n}{k-1}$
, where
$|\mathcal {F}|=a\binom {n}{k-1}$
, where
![]() $a\geq \sigma (\mathcal {H}) - 1 + \varepsilon $
. Then, there exists a collection
$a\geq \sigma (\mathcal {H}) - 1 + \varepsilon $
. Then, there exists a collection
![]() $\mathcal {K}$
of copies of
$\mathcal {K}$
of copies of
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $|\mathcal {K}| \geq c' an^{k-1}(an^{k-\ell -1})^{t-1}$
and for all
$|\mathcal {K}| \geq c' an^{k-1}(an^{k-\ell -1})^{t-1}$
and for all
![]() $1 \leq b \leq t$
:
$1 \leq b \leq t$
:
where
![]() $\tau (\mathcal {F}) := \frac {1}{ a n^{k - \ell - 1}}$
.
$\tau (\mathcal {F}) := \frac {1}{ a n^{k - \ell - 1}}$
.
Observe that the size of the collection
![]() $\mathcal {K}$
returned by Theorem 5.4 matches the bound in Theorem 4.4 if the intersection of each edge of
$\mathcal {K}$
returned by Theorem 5.4 matches the bound in Theorem 4.4 if the intersection of each edge of
![]() $\mathcal {H}$
and its parent edge has size exactly
$\mathcal {H}$
and its parent edge has size exactly
![]() $\ell $
. Thus, it can be viewed as a direct strengthening of Theorem 4.4 for such
$\ell $
. Thus, it can be viewed as a direct strengthening of Theorem 4.4 for such
![]() $2$
-contractible hypertrees.
$2$
-contractible hypertrees.
6 Number of
 $\mathcal {H}$
-free hypergraphs
$\mathcal {H}$
-free hypergraphs
In this section, we prove Theorem 1.3 and Theorem 1.5. First, we recall the celebrated Container Lemma as follows.
Lemma 6.1 [Reference Balogh, Morris and Samotij2, Reference Saxton and Thomason42].
For every
![]() $t \in \mathbb {N}$
and every
$t \in \mathbb {N}$
and every
![]() $c> 0$
, there exists a
$c> 0$
, there exists a
![]() $\delta> 0$
such that the following holds for all
$\delta> 0$
such that the following holds for all
![]() $N \in \mathbb {N}$
. Let
$N \in \mathbb {N}$
. Let
![]() $\mathcal {K}$
be a t-uniform hypergraph on N vertices such that for all
$\mathcal {K}$
be a t-uniform hypergraph on N vertices such that for all
![]() $1 \leq b \leq t$
,
$1 \leq b \leq t$
,
Then there exists a collection
![]() $\mathcal {C}$
of subsets of
$\mathcal {C}$
of subsets of
![]() $V(\mathcal {K})$
such that the following holds:
$V(\mathcal {K})$
such that the following holds:
-
1. For every
 $I \in \mathcal {I}(\mathcal {K})$
, there is a
$I \in \mathcal {I}(\mathcal {K})$
, there is a
 $C \in \mathcal {C}$
such that
$C \in \mathcal {C}$
such that
 $I \subseteq C$
.
$I \subseteq C$
. -
2.
 $|\mathcal {C}| \leq \binom {N}{\leq t \tau N}$
.
$|\mathcal {C}| \leq \binom {N}{\leq t \tau N}$
. -
3. For every
 $C \in \mathcal {C}$
,
$C \in \mathcal {C}$
,
 $|V(C)| \leq (1 - \delta )|V(\mathcal {K})|$
.
$|V(C)| \leq (1 - \delta )|V(\mathcal {K})|$
.
Applying Lemma 6.1 with Theorem 5.4, we have the following:
Lemma 6.2. Let
![]() $k\geq 4$
be an integer. Let
$k\geq 4$
be an integer. Let
![]() $\mathcal {H}$
be a
$\mathcal {H}$
be a
![]() $2$
-contractible
$2$
-contractible
![]() $\ell $
-overlapping k-tree with t edges and cross-cut number
$\ell $
-overlapping k-tree with t edges and cross-cut number
![]() $\sigma $
. Then, for every
$\sigma $
. Then, for every
![]() $\varepsilon> 0$
, there exists a
$\varepsilon> 0$
, there exists a
![]() $\delta>0$
such that the following holds. Let
$\delta>0$
such that the following holds. Let
![]() $\mathcal {F}$
be a k-graph on
$\mathcal {F}$
be a k-graph on
![]() $[n]$
with
$[n]$
with
![]() $|\mathcal {F}|\geq (\sigma - 1 + \varepsilon )\binom {n}{k - 1}$
. Then, there is a collection
$|\mathcal {F}|\geq (\sigma - 1 + \varepsilon )\binom {n}{k - 1}$
. Then, there is a collection
![]() $\mathcal {C} \subseteq 2^{\mathcal {F}}$
satisfying
$\mathcal {C} \subseteq 2^{\mathcal {F}}$
satisfying
-
1. For every
 $\mathcal {H}$
-free subgraph
$\mathcal {H}$
-free subgraph
 $I \subseteq \mathcal {F}$
, there is a
$I \subseteq \mathcal {F}$
, there is a
 $C \in \mathcal {C}$
such that
$C \in \mathcal {C}$
such that
 $I \subseteq C$
.
$I \subseteq C$
. -
2.
 $|\mathcal {C}| \leq \binom {\binom {n}{k}}{\leq \frac {t}{n^{k - \ell - 1}} \binom {n}{ k - 1} }$
.
$|\mathcal {C}| \leq \binom {\binom {n}{k}}{\leq \frac {t}{n^{k - \ell - 1}} \binom {n}{ k - 1} }$
. -
3. For every
 $C \in \mathcal {C}$
,
$C \in \mathcal {C}$
,
 $|V(C)| \leq (1 - \delta ) |\mathcal {F}|$
.
$|V(C)| \leq (1 - \delta ) |\mathcal {F}|$
.
Proof. Given
![]() $\mathcal {F}$
, let
$\mathcal {F}$
, let
![]() $\mathcal {K}$
be the collection of copies of
$\mathcal {K}$
be the collection of copies of
![]() $\mathcal {H}$
returned by Theorem 5.4. We will view
$\mathcal {H}$
returned by Theorem 5.4. We will view
![]() $\mathcal {K}$
as a t-uniform hypergraph with
$\mathcal {K}$
as a t-uniform hypergraph with
![]() $V(\mathcal {K})=E(\mathcal {F})$
whose hyperedges are the copies of
$V(\mathcal {K})=E(\mathcal {F})$
whose hyperedges are the copies of
![]() $\mathcal {H}$
in the collection. By the conditon on
$\mathcal {H}$
in the collection. By the conditon on
![]() $\mathcal {K}$
, we have that for all
$\mathcal {K}$
, we have that for all
![]() $1\leq b\leq t$
$1\leq b\leq t$
where
![]() $\tau (\mathcal {F}) := \frac {1}{n^{k - \ell - 1}} \frac {\binom {n}{k - 1}}{|\mathcal {F}|}$
.
$\tau (\mathcal {F}) := \frac {1}{n^{k - \ell - 1}} \frac {\binom {n}{k - 1}}{|\mathcal {F}|}$
.
Then, applying Lemma 6.1, there is a
![]() $\delta $
and a collection
$\delta $
and a collection
![]() $\mathcal {C} \subseteq 2^{E(\mathcal {F})}$
satisfying:
$\mathcal {C} \subseteq 2^{E(\mathcal {F})}$
satisfying:
-
1. For every independent set
 $I \subseteq \mathcal {H}$
, there is a
$I \subseteq \mathcal {H}$
, there is a
 $C \in \mathcal {C}$
such that
$C \in \mathcal {C}$
such that
 $I \subseteq C$
.
$I \subseteq C$
. -
2.
 $|\mathcal {C}| \leq \binom {n}{\leq \frac {t}{n^{k - \ell - 1}} \binom {n}{ k - 1} }$
.
$|\mathcal {C}| \leq \binom {n}{\leq \frac {t}{n^{k - \ell - 1}} \binom {n}{ k - 1} }$
. -
3. For every
 $C \in \mathcal {C}$
,
$C \in \mathcal {C}$
,
 $|V(C)| \leq (1 - \delta )|\mathcal {F}|$
.
$|V(C)| \leq (1 - \delta )|\mathcal {F}|$
.
Noting that every
![]() $\mathcal {H}$
-free subfamily of
$\mathcal {H}$
-free subfamily of
![]() $\mathcal {F}$
corresponds to an independent set in
$\mathcal {F}$
corresponds to an independent set in
![]() $\mathcal {K}$
, the result follows.
$\mathcal {K}$
, the result follows.
We now apply Lemma 6.2 repeatedly to derive the following lemma.
Lemma 6.3. Let
![]() $k\geq 4$
be an integer. Let
$k\geq 4$
be an integer. Let
![]() $\mathcal {H}$
be a
$\mathcal {H}$
be a
![]() $2$
-contractible
$2$
-contractible
![]() $\ell $
-overlapping k-tree with t edges and cross-cut number
$\ell $
-overlapping k-tree with t edges and cross-cut number
![]() $\sigma $
. Let
$\sigma $
. Let
![]() $\varepsilon> 0$
. Then there exists a constant K such that there is a collection
$\varepsilon> 0$
. Then there exists a constant K such that there is a collection
![]() $\mathcal {C}$
of size at most
$\mathcal {C}$
of size at most
 $$ \begin{align*}\exp\left(\frac{K \log^2(n)}{n^{k - \ell - 1}} \binom{n}{k - 1}\right)\end{align*} $$
$$ \begin{align*}\exp\left(\frac{K \log^2(n)}{n^{k - \ell - 1}} \binom{n}{k - 1}\right)\end{align*} $$
subgraphs of
![]() $K_{n}^{(k)}$
such that for every
$K_{n}^{(k)}$
such that for every
![]() $\mathcal {H}$
-free subgraph I of
$\mathcal {H}$
-free subgraph I of
![]() $K_{n}^{(k)}$
, there is a
$K_{n}^{(k)}$
, there is a
![]() $C \in \mathcal {C}$
with
$C \in \mathcal {C}$
with
![]() $I \subseteq C$
and every
$I \subseteq C$
and every
![]() $C \in \mathcal {C}$
has size at most
$C \in \mathcal {C}$
has size at most
![]() $(\sigma - 1 + \varepsilon ) \binom {n}{k - 1}$
.
$(\sigma - 1 + \varepsilon ) \binom {n}{k - 1}$
.
Proof. Let
![]() $\delta := \delta (\varepsilon , \mathcal {H})$
be the constant given by Lemma 6.2 and choose K large enough depending on
$\delta := \delta (\varepsilon , \mathcal {H})$
be the constant given by Lemma 6.2 and choose K large enough depending on
![]() $\varepsilon , \delta , t$
. Let n be sufficiently large.
$\varepsilon , \delta , t$
. Let n be sufficiently large.
We will build a sequence of auxiliary rooted trees
![]() $\mathcal {A}_1, \dots , \mathcal {A}_m$
such that leaves of
$\mathcal {A}_1, \dots , \mathcal {A}_m$
such that leaves of
![]() $\mathcal {A}_m$
will be our containers. We begin by fixing
$\mathcal {A}_m$
will be our containers. We begin by fixing
![]() $\mathcal {A}_1$
to be the tree with a single vertex, the root
$\mathcal {A}_1$
to be the tree with a single vertex, the root
![]() $K_n^{(k)}$
. To construct
$K_n^{(k)}$
. To construct
![]() $\mathcal {A}_2$
, we apply Lemma 6.2 to
$\mathcal {A}_2$
, we apply Lemma 6.2 to
![]() $K_n^{(k)}$
to find a collection
$K_n^{(k)}$
to find a collection
![]() $\mathcal {C}$
of subgraphs of
$\mathcal {C}$
of subgraphs of
![]() $K_n^{(k)}$
. We form
$K_n^{(k)}$
. We form
![]() $\mathcal {A}_2$
by adding each container
$\mathcal {A}_2$
by adding each container
![]() $C \in \mathcal {C}$
as a vertex and connect it to the root
$C \in \mathcal {C}$
as a vertex and connect it to the root
![]() $K_n^{(k)}$
. Observe that in
$K_n^{(k)}$
. Observe that in
![]() $\mathcal {A}_2$
,
$\mathcal {A}_2$
,
![]() $K_n^{(k)}$
has no more than
$K_n^{(k)}$
has no more than
 $$ \begin{align*}\binom{\binom{n}{k}}{\frac{2t}{n^{k - \ell - 1} }\binom{n}{k - 1}}\end{align*} $$
$$ \begin{align*}\binom{\binom{n}{k}}{\frac{2t}{n^{k - \ell - 1} }\binom{n}{k - 1}}\end{align*} $$
children, every
![]() $\mathcal {H}$
-free subgraph of
$\mathcal {H}$
-free subgraph of
![]() $K_n^{(k)}$
is contained in one of the children, and every child has size no more than
$K_n^{(k)}$
is contained in one of the children, and every child has size no more than
![]() $(1 - \delta ) \binom {n}{k - 1}$
.
$(1 - \delta ) \binom {n}{k - 1}$
.
To find
![]() $\mathcal {A}_{i + 1}$
from
$\mathcal {A}_{i + 1}$
from
![]() $\mathcal {A}_i$
, we first check to see if any leaf has size greater than
$\mathcal {A}_i$
, we first check to see if any leaf has size greater than
![]() $(\sigma - 1 + \varepsilon ) \binom {n}{k - 1}$
. If not, we terminate the process then. For every leaf
$(\sigma - 1 + \varepsilon ) \binom {n}{k - 1}$
. If not, we terminate the process then. For every leaf
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $\mathcal {A}_i$
which does have size greater than
$\mathcal {A}_i$
which does have size greater than
![]() $( \sigma - 1 + \varepsilon ) \binom {n}{k - 1}$
(we call such
$( \sigma - 1 + \varepsilon ) \binom {n}{k - 1}$
(we call such
![]() $\mathcal {F}$
dense), we apply Lemma 6.2 to find a collection
$\mathcal {F}$
dense), we apply Lemma 6.2 to find a collection
![]() $\mathcal {C}_{\mathcal {F}} \subseteq 2^{\mathcal {F}}$
such that the following holds:
$\mathcal {C}_{\mathcal {F}} \subseteq 2^{\mathcal {F}}$
such that the following holds:
-
1. For every
 $\mathcal {H}$
-free subgraph
$\mathcal {H}$
-free subgraph
 $I \subseteq \mathcal {F}$
, there is there is a
$I \subseteq \mathcal {F}$
, there is there is a
 $C \in \mathcal {C}_{\mathcal {F}}$
such that
$C \in \mathcal {C}_{\mathcal {F}}$
such that
 $I \subseteq C$
.
$I \subseteq C$
. -
2.
 $|\mathcal {C}_{\mathcal {F}}| \leq \binom {n}{\frac {2t }{n^{k - \ell - 1}} \binom {n}{ k - 1} }$
.
$|\mathcal {C}_{\mathcal {F}}| \leq \binom {n}{\frac {2t }{n^{k - \ell - 1}} \binom {n}{ k - 1} }$
. -
3. For every
 $C \in \mathcal {C}_{\mathcal {F}}$
,
$C \in \mathcal {C}_{\mathcal {F}}$
,
 $|V(C)| \leq (1 - \delta )|\mathcal {F}|$
.
$|V(C)| \leq (1 - \delta )|\mathcal {F}|$
.
Then, from
![]() $\mathcal {A}_i$
, we add every C in
$\mathcal {A}_i$
, we add every C in
![]() $\mathcal {C}_{\mathcal {F}}$
as a leaf below
$\mathcal {C}_{\mathcal {F}}$
as a leaf below
![]() $\mathcal {F}$
for each dense
$\mathcal {F}$
for each dense
![]() $\mathcal {F}$
to form
$\mathcal {F}$
to form
![]() $\mathcal {A}_{i+1}$
. Since for every
$\mathcal {A}_{i+1}$
. Since for every
![]() $\mathcal {H}$
-free graph
$\mathcal {H}$
-free graph
![]() $I \subseteq \mathcal {F}$
, there is some
$I \subseteq \mathcal {F}$
, there is some
![]() $C \in \mathcal {C}_{\mathcal {F}}$
such that
$C \in \mathcal {C}_{\mathcal {F}}$
such that
![]() $I \subseteq C$
, we have that every
$I \subseteq C$
, we have that every
![]() $\mathcal {H}$
-free graph contained in
$\mathcal {H}$
-free graph contained in
![]() $\mathcal {F}$
is contained in some child of
$\mathcal {F}$
is contained in some child of
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathcal {A}_{i+1}$
. Furthermore, by construction, we have that there are no more than
$\mathcal {A}_{i+1}$
. Furthermore, by construction, we have that there are no more than
 $$ \begin{align*}\binom{\binom{n}{k}}{\frac{2t}{n^{k - \ell - 1} }\binom{n}{k - 1}}\end{align*} $$
$$ \begin{align*}\binom{\binom{n}{k}}{\frac{2t}{n^{k - \ell - 1} }\binom{n}{k - 1}}\end{align*} $$
children below each such
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
We will terminate this process when every leaf has size less than
![]() $(\sigma - 1+ \varepsilon ) \binom {n}{k - 1}$
. Let
$(\sigma - 1+ \varepsilon ) \binom {n}{k - 1}$
. Let
![]() $\mathcal {A}_m$
be the final such tree. Observe that (3) implies the height of
$\mathcal {A}_m$
be the final such tree. Observe that (3) implies the height of
![]() $\mathcal {A}_m$
is no more than
$\mathcal {A}_m$
is no more than
![]() $O(\log n )$
, (1) implies that every
$O(\log n )$
, (1) implies that every
![]() $\mathcal {H}$
-free subgraph of
$\mathcal {H}$
-free subgraph of
![]() $K^{(k)}_n$
is contained in some leaf of
$K^{(k)}_n$
is contained in some leaf of
![]() $\mathcal {A}_m$
, and the height condition with (2) implies that the number of leaves of
$\mathcal {A}_m$
, and the height condition with (2) implies that the number of leaves of
![]() $\mathcal {A}_m$
is no more than
$\mathcal {A}_m$
is no more than
 $$ \begin{align*}\prod_{i = 1}^{m} \binom{\binom{n}{k}}{\frac{2t}{n^{k - \ell - 1} }\binom{n}{k - 1}} \leq \exp \left( \frac{K \log^2(n)}{n^{k - \ell - 1} } \binom{n}{ k -1} \right),\end{align*} $$
$$ \begin{align*}\prod_{i = 1}^{m} \binom{\binom{n}{k}}{\frac{2t}{n^{k - \ell - 1} }\binom{n}{k - 1}} \leq \exp \left( \frac{K \log^2(n)}{n^{k - \ell - 1} } \binom{n}{ k -1} \right),\end{align*} $$
for some large enough constant K depending on
![]() $\varepsilon , t, k, \ell $
.
$\varepsilon , t, k, \ell $
.
We are now ready to prove Theorem 1.3 and Theorem 1.5.
Theorem 6.4 (Restatement of Theorem 1.3).
Let
![]() $k \geq 4$
be an integer. Let
$k \geq 4$
be an integer. Let
![]() $\mathcal {H}$
be a
$\mathcal {H}$
be a
![]() $2$
-contractible k-tree with cross-cut number
$2$
-contractible k-tree with cross-cut number
![]() $\sigma $
. The number of
$\sigma $
. The number of
![]() $\mathcal {H}$
-free k-graphs on
$\mathcal {H}$
-free k-graphs on
![]() $[n]$
is at most
$[n]$
is at most
![]() $2^{(\sigma - 1 + o(1))\binom {n}{ k- 1}}.$
$2^{(\sigma - 1 + o(1))\binom {n}{ k- 1}}.$
Proof. Since
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $2$
-contractible, it is
$2$
-contractible, it is
![]() $(k - 2)$
-overlapping. Fix some
$(k - 2)$
-overlapping. Fix some
![]() $\varepsilon> 0$
, and let
$\varepsilon> 0$
, and let
![]() $\mathcal {C}$
be the collection returned by Theorem 6.3 with
$\mathcal {C}$
be the collection returned by Theorem 6.3 with
![]() $\ell =k-2$
. Then every
$\ell =k-2$
. Then every
![]() $\mathcal {H}$
-free k-graph I on
$\mathcal {H}$
-free k-graph I on
![]() $[n]$
is a subgraph of some C in
$[n]$
is a subgraph of some C in
![]() $\mathcal {C}$
. The number of such I is at most
$\mathcal {C}$
. The number of such I is at most
![]() $|\mathcal {C}| 2^{(\sigma - 1 + \varepsilon )\binom {n}{ k- 1}}$
.
$|\mathcal {C}| 2^{(\sigma - 1 + \varepsilon )\binom {n}{ k- 1}}$
.
Taking n sufficiently large, we have that
![]() $|\mathcal {C}| \leq 2^{\varepsilon \binom {n}{k - 1}}$
, and thus the number of
$|\mathcal {C}| \leq 2^{\varepsilon \binom {n}{k - 1}}$
, and thus the number of
![]() $\mathcal {H}$
-free k-graphs on
$\mathcal {H}$
-free k-graphs on
![]() $[n]$
is at most
$[n]$
is at most
![]() $2^{(\sigma - 1 + 2 \varepsilon )\binom {n}{k - 1}}$
. As this holds for all
$2^{(\sigma - 1 + 2 \varepsilon )\binom {n}{k - 1}}$
. As this holds for all
![]() $\varepsilon $
, the result follows.
$\varepsilon $
, the result follows.
Theorem 6.5 (Restatement of Theorem 1.5).
Let
![]() $k \geq 4$
be an integer. Let
$k \geq 4$
be an integer. Let
![]() $\mathcal {H}$
be a
$\mathcal {H}$
be a
![]() $2$
-contractible
$2$
-contractible
![]() $\ell $
-overlapping k-tree with cross-cut number
$\ell $
-overlapping k-tree with cross-cut number
![]() $\sigma $
. Then if
$\sigma $
. Then if
![]() $p \gg \frac {\log ^2 (n)}{n^{ k -\ell - 1}}$
, with high probability
$p \gg \frac {\log ^2 (n)}{n^{ k -\ell - 1}}$
, with high probability
![]() $\mathrm {ex}( G(n, p), \mathcal {H}) = (1 - o(1)) (\sigma - 1 + o(1)) \binom {n}{ k - 1}$
.
$\mathrm {ex}( G(n, p), \mathcal {H}) = (1 - o(1)) (\sigma - 1 + o(1)) \binom {n}{ k - 1}$
.
Proof. Fix some
![]() $\varepsilon> 0$
, and let
$\varepsilon> 0$
, and let
![]() $\mathcal {C}$
be the collection returned by Theorem 6.3. Then, let X be the number of members
$\mathcal {C}$
be the collection returned by Theorem 6.3. Then, let X be the number of members
![]() $C \in \mathcal {C}$
such that
$C \in \mathcal {C}$
such that
![]() $|C \cap G^{(k)}(n, p)| \geq (\sigma - 1 + 2 \varepsilon ) p \binom {n}{k - 1}$
.
$|C \cap G^{(k)}(n, p)| \geq (\sigma - 1 + 2 \varepsilon ) p \binom {n}{k - 1}$
.
The probability that a specific member of
![]() $C \in \mathcal {C}$
satisfies
$C \in \mathcal {C}$
satisfies
![]() $|C \cap G^{(k)}(n, p)| \geq (\sigma - 1 + 2 \varepsilon ) p \binom {n}{k - 1}$
is at most
$|C \cap G^{(k)}(n, p)| \geq (\sigma - 1 + 2 \varepsilon ) p \binom {n}{k - 1}$
is at most
![]() $\exp \left ( - \frac {\varepsilon ^2}{6 \sigma } p \binom {n}{k - 1}\right )$
by Chernoff’s Inequality. Thus, the expected size
$\exp \left ( - \frac {\varepsilon ^2}{6 \sigma } p \binom {n}{k - 1}\right )$
by Chernoff’s Inequality. Thus, the expected size
![]() $\mathbb {E}(X)$
of X is at most
$\mathbb {E}(X)$
of X is at most
 $$ \begin{align*}\exp\left(\frac{K \log^2(n)}{n^{k - \ell - 1}} \binom{n}{k - 1}\right) \exp\left( - \frac{\varepsilon^2}{6 \sigma} p \binom{n}{k - 1}\right),\end{align*} $$
$$ \begin{align*}\exp\left(\frac{K \log^2(n)}{n^{k - \ell - 1}} \binom{n}{k - 1}\right) \exp\left( - \frac{\varepsilon^2}{6 \sigma} p \binom{n}{k - 1}\right),\end{align*} $$
which goes to zero as
![]() $n \rightarrow \infty $
since
$n \rightarrow \infty $
since
![]() $p \gg \frac {\log ^2 (n)}{n^{ k -\ell - 1}}$
. Applying Markov’s inequality, this implies that with high probability,
$p \gg \frac {\log ^2 (n)}{n^{ k -\ell - 1}}$
. Applying Markov’s inequality, this implies that with high probability,
![]() $X = 0$
. Hence, with high probability, the largest
$X = 0$
. Hence, with high probability, the largest
![]() $\mathcal {H}$
-free subgraph of
$\mathcal {H}$
-free subgraph of
![]() $G^{(k)}(n, p)$
is of size at most
$G^{(k)}(n, p)$
is of size at most
![]() $(\sigma - 1 +2 \varepsilon )p \binom {n}{k - 1}$
. As this holds for all
$(\sigma - 1 +2 \varepsilon )p \binom {n}{k - 1}$
. As this holds for all
![]() $\varepsilon $
, the upper bound follows.
$\varepsilon $
, the upper bound follows.
A simple lower bound follows from the following: let
![]() $\mathcal {L}$
be the k-graph on
$\mathcal {L}$
be the k-graph on
![]() $[n]$
vertices with the edge set
$[n]$
vertices with the edge set
![]() $\{ \{i_1, i_2, \dots , i_k\} : i_i \in [\sigma - 1], \{i_2, \dots i_{k} \in \binom {[n] \setminus [\sigma ]}{k - 1}\} $
. Observe
$\{ \{i_1, i_2, \dots , i_k\} : i_i \in [\sigma - 1], \{i_2, \dots i_{k} \in \binom {[n] \setminus [\sigma ]}{k - 1}\} $
. Observe
![]() $\mathcal {L}$
contains no copy of
$\mathcal {L}$
contains no copy of
![]() $\mathcal {H}$
and furthermore has
$\mathcal {H}$
and furthermore has
![]() $(\sigma - 1) \binom {n - \sigma + 1}{k - 1}$
edges. Note that as
$(\sigma - 1) \binom {n - \sigma + 1}{k - 1}$
edges. Note that as
![]() $|G^{k}(n, p) \cap \mathcal {L}| \geq (\sigma - 1 - \varepsilon )p \binom {n}{k -1}$
with probability
$|G^{k}(n, p) \cap \mathcal {L}| \geq (\sigma - 1 - \varepsilon )p \binom {n}{k -1}$
with probability
![]() $1 - \exp \left ( - \frac {\varepsilon ^2}{6 \sigma } p \binom {n}{k - 1}\right )$
by Chernoff’s Inequality, the lower bound follows.
$1 - \exp \left ( - \frac {\varepsilon ^2}{6 \sigma } p \binom {n}{k - 1}\right )$
by Chernoff’s Inequality, the lower bound follows.
Competing interests
The authors have no competing interest to declare.
Financial support
The first author’s research was supported by the NSF grant DMS-1855542.