2.1. Experimental set-up

Figure 2 shows the experimental set-up, which is identical to that of Grift et al. (Reference Grift, Vijayaragavan, Tummers and Westerweel2019). It consists of a rectangular plate with an aspect ratio of 1 : 2 (AR = 2) with a width $\ell _a$ of 0.200 m, a height $\ell _b$ of 0.100 m and thickness $\ell _c$ of 4 mm, connected to an industrial gantry robot (Reis Robotics RL50). The plate is translated through a 2.00 $\times$ 2.00 $\times$ 0.60 m $^3$ water-filled tank, with a water height of 0.50 m. The top of this plate is 1.5 $\ell _b$ below the water surface, so that it can be considered fully submerged (Grift et al. Reference Grift, Vijayaragavan, Tummers and Westerweel2019). With a frontal area of $A$ = $\ell _a\times \ell _b$ = 0.020 m $^2$ , the blockage ratio is 0.02, which is well below the value of 0.06 for which walls may begin to influence the drag force (West & Apelt Reference West and Apelt1982). In addition to this rectangular plate, a square plate and a circular plate, both with $A$ = 200.0 cm $^2$ , are also tested, in addition to AR = 2 rectangular plates with frontal areas of 312.5 and 112.5 cm $^2$ , respectively, see § 4.2. All plates are made of acrylic and have the same thickness, i.e. 4 mm.

Figure 2. Schematic of the experimental set-up, viewed from the side (a) and from above (b), consisting of a large water-filled tank, with a gantry robot moving a plate with a prescribed motion. A light sheet illuminates a planar cross-section of the flow through the middle of the plate. A digital high-speed camera is positioned below the water-filled tank and observes the flow through a $45^\circ$ mirror. The shaded area represents the field-of-view of the camera. For the measurements in the water–glycerol mixtures at elevated viscosities a smaller tank, outlined by the dotted line, is placed inside the larger tank, see text for further details. Photographs of the experimental set-up are available as Supplementary material at https://doi.org/10.1017/jfm.2025.11107.

The use of thin plates, instead of streamlined bodies, has the advantage that the quasisteady drag coefficient $C_{\!D}$ in (1.1) hardly varies with the Reynolds number ${\textit{Re}}$ when ${\textit{Re}}$ $\gt 10^3$ (Blevins Reference Blevins2003), see also § 3.1.

In this paper we focus on measurements of the drag force on AR = 2 rectangular plates, following Ringuette, Milano & Gharib (Reference Ringuette, Milano and Gharib2007), Grift et al. (Reference Grift, Vijayaragavan, Tummers and Westerweel2019) and Reijtenbagh et al. (Reference Reijtenbagh, Tummers and Westerweel2023). One can argue that it makes more sense to primarily consider a circular plate, and later test for other geometries. There are two main reasons for using the rectangular AR = 2 plate. As shown by Fernando & Rival (Reference Fernando and Rival2016) and Grift et al. (Reference Grift, Vijayaragavan, Tummers and Westerweel2019), there are clear peaks in the drag force at certain values of $t^*$ that occur due to significant changes in the originally formed vortex ring behind a circular plate. Also, Fernando & Rival (Reference Fernando and Rival2016) and Fernando et al. (Reference Fernando, Weymouth and Rival2020) show that circular plates show a large decrease of $F_D$ after the acceleration phase until $t^* \approx 20$ , even below what is expected from a steady-state drag force. With this in mind, one could question the validity of (1.1) during the relaxation phase of the motion, and even during the acceleration phase. These complications do not appear to occur for rectangular plates, where the drag force $F_D$ during the relaxation phase decays more or less gradually to the expected steady-state value, see figure 1.

The robot is programmed to move the plates through the fluid along a straight path in the middle of the tank. The start and end positions of the plate are at least three times the plate height from the front and rear facing tank walls. Previously Grift et al. (Reference Grift, Vijayaragavan, Tummers and Westerweel2019) showed that the flow remains unperturbed over a distance 2.4 times the plate height in front of the plate.

Additional measurements are performed in a smaller tank (with dimensions of 1.50 $\times$ 0.75 $\times$ 0.60 m $^3$ ) for three different water–glycerol mixtures to investigate the effect of the fluid viscosity $\nu$ , see table 1. The smaller tank is designed such that the plates can reach a final velocity $V_{{a}}$ of 0.90 m s⁻¹ for a large range of accelerations without any wall effects by keeping the blockage ratio of the rectangular plate below 0.06. The finite length of the smaller tank limits the final plate velocity $V_{{a}}$ to 0.90 m s⁻¹. The full range of experiments with constant accelerations is given by table 2. The motions in experiments with non-constant accelerations are shown in figure 3 and details of these experiments are given in table 3.

Table 1. The dynamic viscosity $\mu$ , density $\rho$ and kinematic viscosity $\nu$ of water (V1) and water–glycerol mixtures (V2–4).

Table 2. Overview of the accelerations $a$ and final velocities $V_{{a}}$ in the constant-acceleration experiments with the AR = 2 rectangular plate. Crosses indicate the combinations of acceleration and velocity that are done with water only; dots indicate the combinations of acceleration and velocity with water and water–glycerol mixtures at higher viscosities. The Reynolds number ${\textit{Re}}$ is given by the velocity $V_{{a}}$ , the plate height $\ell _b$ and the kinematic viscosity $\nu$ of the fluid, i.e. either water (V1) or the water–glycerol mixtures (V2–V4), see table 1.

The plate is connected to the gantry robot with a streamlined strut. We use either of two force sensors between the robot and the plate, where one sensor (ATI Gamma 32-2.5) is used for measurements with lower final velocities ( $V_{{a}}\lt$ 0.6 m s⁻¹), while the other sensor (ATI Delta 660-60) is used for those with higher velocities ( $V_{{a}}\geqslant$ 0.6 m s⁻¹). The force signals are filtered using a low-pass filter with a 15 Hz cutoff frequency to reduce noise in the measured signal that originates from the robot (Grift et al. Reference Grift, Vijayaragavan, Tummers and Westerweel2019). The drag force $F_D(t)$ is found from the measured force $F(t)$ by subtracting the inertia $m_pa(t)$ of the plate and the strut, where $m_p$ is their combined mass, and the (very small) measured drag imposed by the strut.

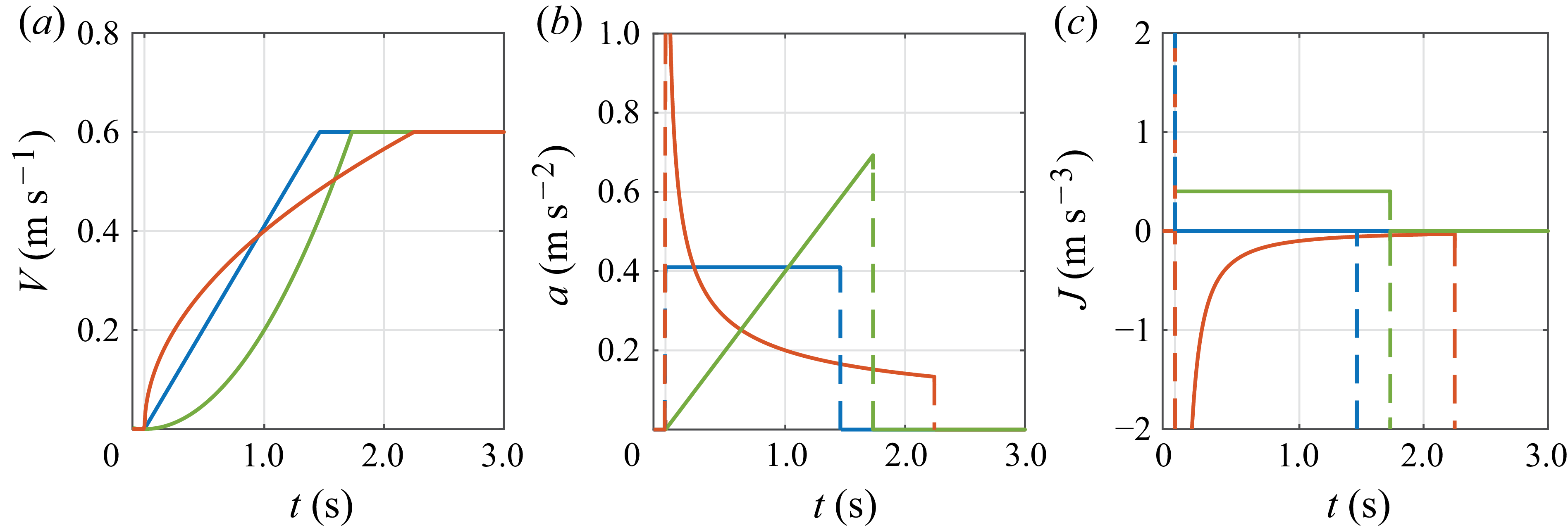
Figure 3. Examples of the programmed plate motions with prescribed (a) velocity $V(t)$ , (b) acceleration $a(t)$ and (c) jerk $J(t)$ : constant acceleration (blue); quadratic velocity motion (green); square-root velocity motion (red). Dashed lines indicate discontinuities in acceleration or jerk. In this example, the final velocity is $V_{{a}}$ = 0.6 m s⁻¹, see tables 2 and 3 for an overview of all motions.

2.2. Particle image velocimetry

Planar particle image velocimetry (PIV) is used to characterize the flow around the plates. A high-speed camera (Phantom VEO 640 L) is used to record 2560 $\times$ 1600 pixel images at a rate of 1000 frames per second of small neutrally buoyant fluorescent tracer particles (Cospheric UVPMS-BR-0.995, with 53–63 $\unicode{x03BC}$ m diameter) suspended in the water-filled tank. A 4 mm-thick light sheet from a frequency-doubled Nd:YLF pulsed laser (Litron LDY304-PIV, 527 nm light wavelength) illuminates the tracer particles in a planar cross-section of the tank. The camera and laser sheet are set up to ensure that the field of view is through the centre of the plate in a horizontal plane. This two-dimensional field is representative of the three-dimensional flow around the plate. The field of view has dimensions of 913 $\times$ 477 mm $^2$ , which is sufficient to capture the full width of the wake and to follow the plate over a distance of more than six times the plate height (i.e. $t^* \gt 6)$ .

Table 3. Overview of three accelerating motions with velocity $V \propto t^n$ and acceleration $a \propto t^{n-1}$ , with $n$ = 1, 2 and $\textstyle 1/2$ ; these correspond to ‘zero jerk’ ( $J=0$ ), ‘positive jerk’ ( $J\gt 0$ ) and ‘negative jerk’ ( $J\lt 0$ ) motions, respectively. The scaling for the force $F_{{a}}$ is according to the model in (3.1) proposed by Reijtenbagh et al. (Reference Reijtenbagh, Tummers and Westerweel2023).

The PIV images are analysed using commercial software (Davis 10.2, LaVision GmbH), using a multipass sliding sum-of-correlation method between the $n$ th frame and ( $n$ + 2)th frame, with 48 $\times$ 48-pixel interrogation regions at the initial pass to 24 $\times$ 24-pixel windows at the final pass, and with 50 % overlap between adjacent interrogations windows. The final result for the velocity fields has a data spacing of 4.19 mm (i.e. 8.37 mm spatial resolution). The velocities in the final results pass a universal outlier detection test (Westerweel & Scarano Reference Westerweel and Scarano2005), indicating that the results contain at least 99.8 % valid data; rejected interrogation results are replaced by linear interpolation.

3.1. Background

Our point of departure is Morison’s equation (1.1) as modified by Reijtenbagh et al. (Reference Reijtenbagh, Tummers and Westerweel2023) to describe the drag force on an accelerating plate. The quasisteady force remains unchanged, and instead of the conventional inviscid added mass for the acceleration drag force $F_{{a}}(t)$ we use a history-based acceleration drag force. Reijtenbagh et al. (Reference Reijtenbagh, Tummers and Westerweel2023) showed that this gives a better representation of the total drag force. Figure 4 shows the flow field around the plate at different dimensionless times. Figure 4(a) shows the potential flow solution for a moving plate, which resembles the measured flow field at $t^*=0.05$ in figure 4(b). This indicates that at these short times potential flow, and therefore inviscid added mass, remains a good approximation of the flow and drag force on the plate, although evidence of vorticity at the plate edges is visible. However, note that here $t^*$ = 0.05 corresponds to a plate displacement of 5 mm that is just slightly larger than the plate thickness (4 mm).

Figure 4. The flow around an accelerating AR = 2 rectangular plate. (a) Potential flow around a flat plate, with streamlines in blue. The measured flow around the plate for $a$ = 0.82 m s⁻² and $V_{{a}}$ = 0.40 m s⁻¹ (corresponding to ${\textit{Re}}$ = 40 $\times$ 10 $^3$ ) at dimensionless times: $t^*$ = 0.05 (b), 0.10 (c), 0.20 (d) and 0.75 (e), respectively, in a fixed frame of reference. The panels (b–e) correspond to the roman numerals I–IV in figure 1. Panels (f–i) represent the same data as (b–e), but now represented in a frame of reference moving with the plate. The colour scale indicates dimensionless out-of-plane component of the vorticity $\omega ^* = \omega _z \ell _b / V_{{a}}$ . Dimensions ( $x$ , $y$ ) are made dimensionless with the plate height $\ell _b$ . For clarity only one out of four velocity vectors is shown.

When the plate further progresses during the acceleration the flow starts to separate and a starting vortex loop is created (Grift et al. Reference Grift, Vijayaragavan, Tummers and Westerweel2019), visible as the vortex pair in figure 4(c). Here, potential flow is no longer appropriate to describe the flow, and therefore is not a proper basis for estimating the acceleration drag force $F_{{a}}(t)$ . This is in line with earlier derivations (Burgers Reference Burgers1921; Biesheuvel & Hagmeijer Reference Biesheuvel and Hagmeijer2006; Limacher et al. Reference Limacher, Morton and Wood2018) where the acceleration drag force is equal to inviscid added mass at early stages only, without flow separation, and where the vorticity is only present in a thin boundary layer close to the plate. This boundary layer is readily visible in figure 4(d–e) (see also figure 18 in Appendix B) and figure 4(h–i), where the flow field is represented in a frame of reference that moves with the plate. The incoming flow impinging on the plate resembles a Hiemenz flow (Emanuel Reference Emanuel2000), which is that of a stationary irrotational outer flow that resembles a stagnation point flow with a viscous boundary layer with a thickness that is inversely proportional to the square root of the flow Reynolds number. The moving plate in the fluid generates vorticity at the surface that diffuses into the fluid and then advects to the edges of the plate where it accumulates in the vortex (Burgers Reference Burgers1921; Biesheuvel & Hagmeijer Reference Biesheuvel and Hagmeijer2006). Figure 5 shows the further development of the instantaneous flow to illustrate the transition of the flow into that of a turbulent wake.

Reijtenbagh et al. (Reference Reijtenbagh, Tummers and Westerweel2023) use Stokes’ first problem as an ansatz for a model that incorporates the generation and diffusion of vorticity for an accelerating plate. This is then generalized to account for the advection of vorticity along the plate surface, which leads to a model where the acceleration drag force $F_{{a}}(t)$ is proportional to $\sqrt {aV}$ . The derivation of this model is summarized in Appendix B.

Figure 5. The instantaneous flow field around an accelerating AR = 2 rectangular plate in the same experiment as in figure 4, at dimensionless times $t^*$ = 2.0 (a), 3.0 (b), 4.0 (c), 5.0 (d) and 7.0 (e), respectively. Dimensions ( $x$ , $y$ ) are made dimensionless with the plate height $\ell _b$ . For clarity only one out of four velocity vectors is shown. The colours represent the dimensionless out-of-plane component of the vorticity $\omega ^* = \omega _z\ell _b/V_{{a}}$ . The roman numerals correspond to those in figure 1.

3.2. Acceleration drag force

Combining the results of Xu & Nitsche (Reference Xu and Nitsche2015) and Reijtenbagh et al. (Reference Reijtenbagh, Tummers and Westerweel2023) we find for the acceleration drag force $F_{{a}}(t)$ ,

(3.1) \begin{equation} F_{{a}}(t) = \underbrace {C\frac {a^{1/4}\ell ^{3/4}}{\nu ^{1/2}}}_{C_{{a}}}\rho A \sqrt {\nu a V}, \end{equation}

where $C$ is an empirical constant and $\ell$ an appropriate length scale. Note that $\sqrt {aV} = at^{1/2}$ for a constant acceleration $a$ . Rewriting (3.1) by eliminating $\sqrt \nu$ gives

(3.2) \begin{equation} F_{{a}}(t) \cong m_{{h}}(t) a, \quad \text{with}\quad m_{{h}}(t) = \rho A \ell _{{h}}(t), \end{equation}

where $\ell _{{h}}(t)$ ( $=Ca^{1/4}\ell ^{3/4}t^{1/2}$ ) absorbs the time dependency of (3.1) and other remaining constants, and $m_{{h}}(t)$ represents a time-dependent ‘hydrodynamic mass’ of the accelerating plate (Grift et al. Reference Grift, Vijayaragavan, Tummers and Westerweel2019). The length scale $\ell _{{h}}(t)$ would represent the dimension of the ‘volume of fluid’ $A\ell _{{h}}(t)$ that is thought to be accelerated along with the moving plate (Batchelor Reference Batchelor1967). Evidently, the acceleration drag force is not constant, as opposed to the conventional inviscid added mass force obtained from potential flow, which implies $m_{{h}}(t)$ grows during acceleration, and (3.2) would represent a generalized approach where the flow can also be rotational. However, the concept of hydrodynamic mass in (3.2) would also imply that $F_{{a}}(t)$ vanishes when $a=0$ , which is evidently not the case, see figure 1. Therefore, the association of $F_{{a}}(t)$ with a ‘hydrodynamic mass’ does not seem appropriate in this context.

The dimensionless prefactor $C_ {{a}}$ in (3.1) is rewritten as

(3.3) \begin{equation} C_{{a}} = C\frac {a^{1/4}\ell ^{3/4}}{\nu ^{1/2}} = C\left (\frac {a\ell }{V^2}\right )^{1/4} \frac {V^{1/2}\ell ^{1/2}}{\nu ^{1/2}} = C\left (a^*\right )^{1/4}{\textit{Re}}^{1/2}, \end{equation}

where $a^* = a\ell /V^2$ is the dimensionless acceleration defined with respect to the velocity $V$ of the moving plate, and ${\textit{Re}}$ the Reynolds number defined by the velocity $V$ , the plate dimension $\ell$ and the kinematic viscosity $\nu$ . The constant $C$ is determined experimentally, see § 4.1. It depends on the plate geometry, i.e. AR = 2 rectangular, square or circular plate, but also on the motion; it absorbs the constants $C_n$ , with $n$ = 1, 2 and 1/2, that arise from the history-based model explained in Appendix B.

Hence, the acceleration drag force $F_{{a}}(t)$ for constant acceleration motion ( $n=1$ ), $V(t)=at$ ; constant jerk motion ( $n=2$ ), $V(t) = \textstyle (1/2) Jt^2$ ; ‘square-root velocity’ motion ( $n=1/2$ ), $V(t)=Q\sqrt {t}$ , given by the history-based model become

(3.4) \begin{equation} F_{{a}}(t) = C_{{a}}\rho A \sqrt \nu \begin{cases} at^{1/2} & n=1,\\ Jt^{3/2} &n=2,\\ Qt^0 &n=\textstyle \dfrac 12. \end{cases} \end{equation}

When the motions are expressed in terms of $t^*$ , defined in (1.2), we find

(3.5)

Note that for the square-root velocity motion ( $n$ = 1/2), $t^*$ = $\textstyle ( 2/3)(Q/\ell _b)t^{3/2}$ .

3.3. Acceleration Reynolds number

The expression in (3.3) can be written as

(3.6) \begin{equation} C_{{a}} = C\sqrt {{\textit{Re}}_{{a}}}, \end{equation}

where ${\textit{Re}}_{{a}}$ is given by

(3.7) \begin{equation} {\textit{Re}}_{{a}} = \sqrt {a^*} Re. \end{equation}

This definition of an acceleration Reynolds number ${\textit{Re}}_{{a}}$ is convenient since it eliminates the velocity $V$ , so what is left is a Reynolds number ${\textit{Re}}_{{a}}$ that only depends on acceleration. This Reynolds number is equivalent to the acceleration-based Reynolds number introduced by Freymuth, Bank & Palmer (Reference Freymuth, Bank and Palmer1983) and generalized by Xu & Nitsche (Reference Xu and Nitsche2015) and is equal to the square root of the dimensionless acceleration $\alpha = a \ell ^3 / \nu ^2$ defined by Koumoutsakos & Shiels (Reference Koumoutsakos and Shiels1996).

The dimensionless acceleration $a^* = a\ell /V^2$ requires further clarification, especially for the non-constant accelerations of the plate. Our point of departure is the Morison equation, which has two terms: one is the quasisteady drag force $F_{\textit{QS}}$ and the other one is the acceleration drag force $F_{{a}}$ that is due to the acceleration of the surrounding fluid. In the original expression $F_{{a}}$ is taken equal to the inviscid added mass force $F_{\textit{AM}}$ that is associated with potential flow. For a fully submerged AR = 2 rectangular plate, with $A$ = $\ell _a\times \ell _b$ , the drag coefficient is $C_{\!D}$ = 1.3 (Grift et al. Reference Grift, Vijayaragavan, Tummers and Westerweel2019). For thin plates the drag coefficient $C_{\!D}$ is effectively constant over a large range of Reynolds numbers ${\textit{Re}} \gg 10^3$ (Hoerner Reference Hoerner1965; Blevins Reference Blevins2003). The inviscid added mass force $F_{\textit{AM}}$ for a rectangular plate is (Brennen Reference Brennen1982)

(3.8) \begin{equation} F_{\textit{AM}} = 0.84\frac \pi 4\rho \ell _a\ell _b^2a. \end{equation}

The ratio of the added mass force and the quasisteady drag force, with $C_{\!D}=1.3$ , is then

(3.9) \begin{equation} \frac {F_{\textit{AM}}}{F_{\textit{QS}}} = \frac {0.84\dfrac \pi 4\rho \ell _a\ell _b^2a}{1.3\times \textstyle \dfrac 12\rho V^2\ell _a\ell _b} = \underbrace {\frac {0.84\dfrac \pi 4}{1.3\times \textstyle \frac 12}}_{1.01}\frac {a\ell _b}{V^2} \cong a^*, \end{equation}

where $\ell _b$ is the short dimension of the plate, here referred to as the plate height; the numerical prefactor is close to unity, and therefore ignored here. Hence, the dimensionless acceleration $a^*$ can be interpreted as the ratio of the added mass force relative to the quasisteady drag force.

We can take the same approach for the cases with non-constant accelerations, where both $a_n$ and $V_n$ vary in time (see table 3), such that for $n=2$

(3.10) \begin{equation} a_2 = Jt \quad \text{and}\quad V_2(t) = \frac {1}{2}Jt^2, \end{equation}

where $J$ is the jerk in $\rm [m\,s^{-3}]$ and $n=1/2$ gives

(3.11) \begin{equation} a_{1/2}(t) = \frac {1}{2}Qt^{-1/2}, \quad \text{and}\quad V_{1/2}(t) = Qt^{1/2}. \end{equation}

Substituting (3.10) and (3.11) in the definition for $a^*$ gives

(3.12) \begin{equation} a^*_2 = \frac {a_2\ell _b}{V_2^2}=\frac {Jt\ell _b}{\frac {1}{4}J^2t^{4}}=\frac {4\ell _b}{J} \frac {1}{t^{3}}, \quad \text{and}\quad a^*_{1/2} = \frac {a_{1/2}\ell _b}{V_{1/2}^2}=\frac {\dfrac {1}{2}Qt^{-1/2}\ell _b}{Q^2t}=\frac {\ell _b}{2Q} \frac {1}{t^{3/2}}, \end{equation}

respectively. Evidently, the dimensionless accelerations $a^*_2$ and $a^*_{1/2}$ should be independent of time, and therefore only a function of $J$ or $Q$ , the velocity $V$ and the plate height $\ell _b$ . Substituting $V$ back into the time dependent part from (3.12) for $a^*_2$ and $a^*_{1/2}$ results in

(3.13) \begin{equation} a^*_2 = \frac {\sqrt 2 \ell _b}{J^{-1/2}} \frac {1}{\frac {1}{2}^{3/2}J^{3/2}t^{3}} = \frac {\sqrt 2 \ell _b J^{1/2}}{V_J^{3/2}}, \quad \text{and}\quad a^*_{1/2} = \frac {\ell _bQ^{2}}{2} \frac {1}{Q^3t^{3/2}} = \frac {\ell _bQ^{2}} {2V_Q^{3}}, \end{equation}

respectively. In addition, it is desirable to maintain a numerator that is proportional to $V^2$ , similar to $a^*$ for constant accelerations, so that in (3.7) the velocity is effectively cancelled in the definition of ${\textit{Re}}_a$ while maintaining its scaling with the reciprocal of $\sqrt {\nu }$ . To ensure this, $a^*_2$ in (3.13) is raised to the power $4/3$ and $a^*_{1/2}$ to the power $2/3$ ,

(3.14) \begin{equation} a^*_2 = \frac {(4\ell _b^4 J^2)^{1/3}}{V^2}, \quad \text{and}\quad a^*_{1/2} = \frac {\left(\dfrac 14\ell _b^2 Q^4\right)^{1/3}}{V^2}. \end{equation}

Finally, these expressions for $a^*_{n}$ for non-constant accelerations can be used in (3.7) to find specific Reynolds numbers ${\textit{Re}}_{{a}}^n$ for the constant jerk motion and ‘square-root velocity’ motion,

(3.15) \begin{equation} {\textit{Re}}_{{a}}^{n=2} = \frac {(2 \ell _b^5 J)^{1/3}}{\nu }, \quad \text{and}\quad {\textit{Re}}_{{a}}^{n=1/2} = \frac {\left(\dfrac 12 \ell _b^4 Q^2\right)^{1/3}}{\nu }. \end{equation}

These expressions for the acceleration Reynolds number ${\textit{Re}}_{{a}}^n$ are used to determine $C_{{a}}$ for different plate motions with different values for $Q$ and $J$ . The acceleration Reynolds numbers ${\textit{Re}}_{{a}}$ in (3.3) for the constant-acceleration motion and in (3.15) for the constant-jerk and ‘square-root velocity’ motions, respectively, are each constants during the specified motions. Hence, they can be used for normalizing the acceleration drag forces $F_{{a}}(t)$ during each of these motions; this is demonstrated in § 5. They replace the conventional Reynolds number that is defined by the instantaneous velocity, which would constantly change during the motion as the velocity increases during the acceleration phase. In earlier numerical studies of impulsively started plates, i.e. where a plate attains a fixed velocity $V_{{a}}$ for $t\gt 0$ , the velocity-based Reynolds number is used to characterize the flow. In this case the plate velocity is increased discontinuously, and the plate does not experience an acceleration phase. This motion is not physical, and in reality any plate that starts to move from rest towards a certain final velocity $V_{{a}}$ must experience a finite-duration acceleration phase where the velocity of the plate remains continuous.

4.1. Acceleration phase

The numerical value of the proportionality constant $C$ in (3.1), and consequently $C_{{a}}$ in (3.3), is found by a least-squares fit of the model to the measured acceleration drag force $F_{{a}}(t)$ = $F_D(t)\!-\!F_{\textit{QS}}(t)$ during the acceleration phase for all measurements in table 2. Figure 6 compares the model with the corresponding fit of $C_{{a}} = C {\textit{Re}}_{{a}}^{1/2}$ in (3.1) with the measured acceleration drag force $F_{{a}}(t)$ during a constant-acceleration motion with acceleration $a = 1.03\,{\textrm {m}\,\textrm {s}^{-2}}$ and final velocity $V_{{a}} = 0.75\,\textrm {m}\,\textrm {s}^{-1}$ . Figure 6 shows that the force $F_{{a}}(t)$ grows proportional to $t^{1/2}$ , or equivalently $(t^*)^{1/4}$ , see (3.5). Evidently $F_{{a}}(t)$ exceeds the (constant) inviscid added mass force $F_{\textit{AM}}$ . Note that $F_{{a}}$ at $t^* = 0$ increases almost discontinuously to the value of $F_{AM}$ . This implies that no distinction can be made between the inviscid added mass $F_{AM}$ and the history-based model for $F_{{a}}(t)$ at the start of the motion.

When the acceleration ceases and the plate assumes a constant velocity, there is an apparent sharp drop $\Delta F$ in $F_{{a}}$ . The magnitude of this drop is also predicted by the model, but is not included in the fitting of the model. This is further discussed in § 4.3.

The resulting values of $C_{{a}}$ defined according to (3.3) for accelerations $a$ between 0.41 and 1.64 m s⁻² and final velocities $V_{{a}}$ between 0.30 and 1.35 m s⁻¹ are shown in figure 7. The curves in the graph represent $C_{{a}}$ in (3.3), with $C$ = 1.5 for different values of the Reynolds number ${\textit{Re}}$ = $V_{{a}}\ell _b/\nu$ , where $V_{{a}}$ is the final plate velocity at the end of the acceleration phase. This result supports the scaling of $C_{{a}} \propto (a^*)^{1/4}$ ; this rather weak dependence results in a nearly constant value for $C_{{a}}$ for the measurements represented in figure 7. These results replace the results previously presented by Reijtenbagh et al. (Reference Reijtenbagh, Tummers and Westerweel2023), where $C_{{a}}$ was considered to be constant for the range of Reynolds numbers ${\textit{Re}}$ and values of the dimensionless acceleration $a^*$ for the 200 $\times$ 100 mm $^2$ rectangular plate and different constants $C_{{a}}$ for circular and square plates. The values for $C$ in $C_{{a}}$ for different geometries are described in § 4.2.

Figure 6. The measured acceleration drag force $F_{{a}}(t)=F_D(t)\!-\!F_{\textit{QS}}(t)$ as a function of the dimensionless time $t^*$ , defined in (1.2), during a constant-acceleration motion of an AR = 2 rectangular plate (blue line) with acceleration $a$ = 1.03 m s⁻² until the plate reaches a final velocity $V_{{a}}$ = 0.75 m s⁻¹. Here $F_{{a}}(t)$ is proportional to $(t^*)^{1/4}$ , see (3.5). The data highlighted in the bold section is used for fitting the model (3.1), represented by the solid black line, to determine the constant $C$ in (3.3). The dashed black line represents the model in (B8) for $F_{{a}}(t)$ during the relaxation phase ‘R’ after the acceleration ceases, where it drops with a magnitude $\Delta F$ , see § 4.3. The dash–dotted line represents the inviscid added mass force $F_{\textit{AM}}$ given by Payne (Reference Payne1981). The top axis indicates corresponding dimensional time $t$ ; note that this is a nonlinear axis. The grey area corresponds to the variation in acceleration during the motion, as indicated in figure 17 of Appendix A.

Figure 7. Acceleration drag coefficient $C_{{a}}$ as a function of the dimensionless acceleration $a^*$ = $a\ell _b/V_{{a}}^2$ , where $a$ is the acceleration, $\ell _b$ the plate height and $V_{{a}}$ the final velocity at the end of the acceleration phase. The symbols represent the values of $C_{{a}}$ determined experimentally for an AR = 2 rectangular plate with a constant-acceleration motion with acceleration $a$ . The curves represent $C_{{a}}$ according to (3.3) at constant Reynolds number ${\textit{Re}}$ = $V_{{a}}\ell _b/\nu$ , where $\nu$ is the kinematic viscosity. The colours represent $V_{{a}}$ = 0.30 (blue), 0.45 (orange), 0.60 (yellow), 0.75 (purple), 0.90 (green), 1.05 (cyan), 1.20 (maroon) and 1.35 m s⁻¹ (lilac), respectively.

The acceleration drag coefficient $C_{{a}} = C(a^*)^{1/4}{\textit{Re}}^{1/2}$ in (3.1) requires further justification. Given the no-slip boundary condition on the plate, which effectively results in the production of vorticity at the plate surface, involves the finite viscosity of the fluid. Reijtenbagh et al. (Reference Reijtenbagh, Tummers and Westerweel2023) present $C_{{a}}$ as a constant that depends on the plate geometry, and is interpreted as a ‘Nusselt number’ for the advective transport of vorticity over the diffusive transport. Hence, a factor $\sqrt {\nu }$ appears in their expression for $F_{{a}}$ , but this serves to dimensionally balance the equation; evidently, a factor $1/\sqrt {\nu }$ should be included in $C_{{a}}$ , as in (3.1), to account for the effect of the flow Reynolds number in the ‘Nusselt number’ for the ratio of advective transport over diffusive transport, see also Appendix B. To investigate this we also conduct measurements in a smaller tank (with dimensions of 1.50 $\times$ 0.75 $\times$ 0.60 m $^3$ ) filled with different water–glycerol mixtures that is placed inside the larger tank, see figure 2.

The properties of the different mixtures are shown in table 1. The water–glycerol mixtures are prepared such that the kinematic viscosity is approximately 2, 3 and 4 times that of water. The resulting values for the measured acceleration drag coefficients $C_{{a}}$ for the fluid viscosities in table 1 are shown in figure 8(a), where the acceleration drag coefficient $C_{{a}}$ is plotted as a function of the Reynolds number ${\textit{Re}} = V_{{a}}\ell _b/\nu$ . This shows that the value of $C_{{a}}$ , when considering the data for a single fluid with constant kinematic viscosity $\nu$ , remains constant over a considerable range of Reynolds numbers. Note that the values of $C_{{a}}$ are elevated as the acceleration $a$ increases, corresponding to its expected scaling proportional to $(a^*)^{1/4}$ . When considering fluids with increasing kinematic viscosity $\nu$ , the values of $C_{{a}}$ drop in proportion to the increase in $\nu$ , but remain more or less constant as a function of ${\textit{Re}}$ . For the same value of the Reynolds number, ${\textit{Re}} = V_{{a}}\ell _b/\nu$ , the value of $C_{{a}}$ depends only on the value of $\nu$ ; this is in agreement with Hiemenz flow (Emanuel Reference Emanuel2000), where the thickness of the boundary layer, for constant approaching velocity and constant length scale, only depends on the value of $\nu$ . While it is tempting to fit a line in the graph of figure 8(a) that follows $C_{{a}} \propto {\textit{Re}}^{1/2}$ , this does not lead to the correct scaling of $C_{{a}}$ . The data points in figure 8(a) are modified by $C a^{1/4}\ell _b^{3/4}$ in figure 8(b), with $C = 1.5$ , to adjust for the variation in $C_{{a}}$ due to acceleration. The variation in $C_{{a}}$ is greatly reduced and matches very well with $1/\sqrt {\nu }$ . It is noted that the data points in both figures 8(a) and 8(b) for each viscosity appear to display a similar systematic variation; we attribute this to the fact that two different force sensors are used in the measurement (see § 2.1) that have different measurement ranges and accuracy.

Figure 9 summarizes all measurements of $C_{{a}}$ as a function of the acceleration Reynolds number ${\textit{Re}}_{{a}} = \sqrt {a^*}Re$ , defined in (3.6). The shaded area indicates the variation in $C_{{a}}$ throughout the range of measurements. The data appear to follow a curve $C_{{a}} = C\sqrt {{\textit{Re}}_{{a}}}$ , with $C = 1.50\!\pm \!0.12$ for the AR = 2 rectangular plate. In § 4.2 it is described how the proportionality constant $C$ varies with plate geometry.

Figure 8. (a) The measured acceleration drag coefficient $C_{{a}}$ as a function of the Reynolds number ${\textit{Re}} = V_{{a}}\ell _b/\nu$ , where $V_{{a}}$ is the final velocity at the end of the acceleration phase, for different accelerations $a$ . The colours indicate four different fluid kinematic viscosities: $\nu$ = 1.0 (blue), 2.4 (orange), 3.2 (purple) and 4.5 mm $^2$ s⁻¹ (green), see table 1. (b) The same data now represented as $C_{{a}} / [Ca^{1/4}\ell _b^{3/4}]$ , cf. (3.3), compared with $1/\sqrt {\nu }$ , represented by the dashed lines.

Figure 9. The acceleration drag coefficient $C_{{a}}$ as a function of the acceleration Reynolds number ${\textit{Re}}_{{a}} = \sqrt {a^*} Re$ for four different kinematic viscosities, indicated by different colours, as in figure 8. Symbols indicate the median value of results with different final velocities $V_{{a}}$ and equal dimensionless acceleration $a^*$ and ${\textit{Re}}_{{a}}$ , see figure 8. The black line represents $C_{{a}} = C\sqrt {{\textit{Re}}_{{a}}}$ , with $C = 1.50\!\pm \!0.12$ for an AR = 2 rectangular plate; the shaded region represents the variation of the empirical constant $C$ .

Figure 10. The empirical constant $C$ in (3.1) as a function of the Reynolds number ${\textit{Re}} = V_{{a}}\ell _b/\nu$ , where $V_{{a}}$ is the final velocity at the end of the acceleration phase, defined in (3.7), for different sets of parameters: (a) $C$ for a 200 $\times$ 100 mm $^2$ rectangular plate at four different viscosities; (b) $C$ for different AR = 2 rectangular plates with different dimensions in water; (c) $C$ for a 141.4 $\times$ 141.4 mm $^2$ square plate at four different fluid viscosities; (d) $C$ for a circular plate with a diameter of 159.6 mm at four different viscosities.

4.2. Plate geometry

In the previous section the drag force is considered for an AR = 2 rectangular plate, in correspondence to the plates used in earlier works (Ringuette et al. Reference Ringuette, Milano and Gharib2007; Grift et al. Reference Grift, Vijayaragavan, Tummers and Westerweel2019; Reijtenbagh et al. Reference Reijtenbagh, Tummers and Westerweel2023). To validate the generality of the developed model and scaling behaviour, we also consider a circular plate, a square plate and AR = 2 rectangular plates with varying dimensions. The circular and square plates both have a frontal area that is equal to that of the rectangular plate, i.e. $A$ = 200.0 cm $^2$ . In addition, we test AR = 2 rectangular plates with frontal areas $A$ of 25.0 $\times$ 12.5 cm $^2$ and 15.0 $\times$ 7.5 cm $^2$ .

For each measurement the empirical coefficient $C$ is determined by fitting the model in (3.1) to the measured acceleration drag force $F_{{a}}(t)$ = $F_D(t)\!-\!F_{\textit{QS}}(t)$ during the acceleration phase of the motion, see figure 6. The results are summarized in figure 10. All results for the AR = 2 rectangular plate with $A$ = 200.0 cm $^2$ for four different fluid viscosities are plotted in figure 10(a), which correspond to the data in figure 8. This shows that $C = 1.50\pm 0.12$ . Figure 10(b) shows the variation in $C$ for AR = 2 rectangular plates with different dimensions. The same value of $C \cong 1.5$ is found for all three dimensions of the AR = 2 plates. There appears to be a slight systematic variation in $C$ with the plate dimensions, which may be attributed to the ratio of the plate thickness over plate height that is not identical as all plates have the same thickness. Also, the results are affected by using two different force sensors, see § 2.

Figures 10(c) and 10(d) show the results for $C$ for the square and circular plate, respectively, using the side length and plate diameter as the characteristic length to determine ${\textit{Re}}_{{a}}$ for the square and circular plate, respectively. Similar to the rectangular plate, $C$ seems to be constant for Reynolds numbers between 10 $\times$ 10 $^3$ and 150 $\times$ 10 $^3$ . For the circular plate we find $C \cong 1.04$ , and for the rectangular plate $C \cong 1.14$ . The ratios of $C$ for rectangular, circular and square plates, i.e. 1.50 : 1.04 : 1.14, are remarkably similar to the ratios of the steady-state drag coefficients $C_{\!D}$ at high Reynolds numbers for these plates: 1.30 : 1.14 : 1.25 (Blevins Reference Blevins2003; Grift et al. Reference Grift, Vijayaragavan, Tummers and Westerweel2019).

4.3. Relaxation phase

After the acceleration phase ceases (at time $t_{{a}} = V_{{a}}/a$ ) the acceleration drag force $F_{{a}}(t)$ drops sharply. This is shown in figure 1 as $F_D$ decays towards a constant force $F_{\textit{QS}}$ and in figure 6 as $F_{{a}}$ decays towards zero. This drop, indicated as $\Delta F$ in figure 6, appears to be comparable to $F_{\textit{AM}}$ in magnitude, and it is tempting to consider the drop in the drag force to be caused by the vanishing of $F_{\textit{AM}}$ when the acceleration ceases, i.e. $\Delta F = -F_{\textit{AM}}$ . However, the change in the flow field between the moment when the plate still accelerates and when it has assumed a constant velocity is not irrotational. As a matter of fact, vorticity maintains to be created at the surface of the plate and the vortex loop at the plate edge continues to accumulate circulation, albeit at a lower rate, see Reijtenbagh et al. (Reference Reijtenbagh, Tummers and Westerweel2023, figure 4)

The history-based model described in Appendix B predicts a drop in the force $F_{{a}}(t)$ that is proportional to $(t-t_{{a}})^{-1/2}$ , see (B8). Indeed, this also implies a sharp drop in $F_{{a}}(t)$ at $t=t_{{a}}$ , and the force $F_{{a}}(t)$ initially appears to follow the model, see figure 6. This $t^{-1/2}$ decay is in line with an early theoretical result for the history force on spherical particles at low Reynolds number (Odar & Hamilton Reference Odar and Hamilton1964). However, later investigations (Mei & Adrian Reference Mei and Adrian1992; Lovalenti & Brady Reference Lovalenti and Brady1993) on spherical particles starting from rest showed that for small Reynolds numbers the decay of the history force does not scale as $t^{-1/2}$ , but rather as $t^{-2}$ . This is in line with the findings of Grift et al. (Reference Grift, Vijayaragavan, Tummers and Westerweel2019) for the drag force on a plate at high Reynolds number during the relaxation phase.

For longer dimensionless times in the relaxation phase, other effects, such as the detachment and disintegration of the vortex loop, and subsequent transition to a turbulent wake and shedding of vorticity, determine the actual relaxation of the drag force. This typically occurs for dimensionless times $t^* \gt 4$ (Grift et al. Reference Grift, Vijayaragavan, Tummers and Westerweel2019).

5.1. Velocity relation $V\propto t^2$

We consider a plate that is started from rest and is then accelerated with a constant jerk $J$ , so that the acceleration increases linearly with time, i.e. $a = Jt$ , and the velocity increases quadratically with time, i.e. $V = ( 1/2) Jt^2$ .

An example of the measured drag force $F_D(t)$ is shown in figure 11. The measured force is compared with the quasisteady drag force $F_{\textit{QS}}(t)$ , which is now proportional to $t^4$ , and the inviscid added mass force $F_{\textit{AM}}$ , which is now directly proportional to $t$ ; in figure 11, $F_{\textit{AM}}$ doubles in magnitude from $t$ = 0.7 s to 1.4 s. As for the constant-acceleration motion, it is evident that the total drag force during the acceleration phase is higher than the sum of $F_{\textit{QS}}\!+\!F_{\textit{AM}}$ . Instead, the sum of the quasisteady force $F_{\textit{QS}}(t)$ and the history-based model for the acceleration drag force $F_{{a}}(t)$ gives a proper description of the drag force during the acceleration phase, where $F_{{a}}(t)$ is given by (3.4), i.e.

(5.1) \begin{align} F_{{a}}(t) = C_{{a}}\rho A \sqrt {\nu }t^{3/2}, \quad \text{with} \quad C_{{a}} = C\sqrt {{\textit{Re}}_a}, \end{align}

where ${\textit{Re}}_{{a}}$ = ${\textit{Re}}_{{a}}^{n=2}$ is the acceleration Reynolds number, defined in (3.15). We note that the empirical constant $C$ has a numerical value $C$ = $1.5(C_2/C_1) \approx 1.0$ , see Appendix B.

This motion provides a smoother start that avoids large discontinuities in velocity and acceleration. It mitigates the initial peak in the measured force due to the robot engagement (see Appendix A), although the effects of robot engagement and a small jump in acceleration at $t=0$ could not be fully avoided. However, the magnitude of the initial peak in the force signal is considerably smaller compared with those in the measurements with a constant-acceleration motion, cf. figures 1 and 6.

The history-based model also provides a reasonable description of the drag force during the relaxation phase. The decay of $F_{{a}}(t)$ during the relaxation phase for the history-based model does not have an analytical expression, and is computed numerically, see Appendix B. Yet, it follows a similar decay as during the relaxation phase for the constant-acceleration motion.

Figure 11. Example of the measured drag force $F_D(t)$ (blue solid line) as a function of time $t$ for a motion with constant jerk $J$ = 0.4 m s⁻³ until a final velocity $V_{{a}}$ = 0.6 m s⁻¹ is reached. The red solid line represents the quasisteady drag force $F_{\textit{QS}}$ = $C_{\!D}\textstyle ( 1/2)\rho V^2(t) A$ ; the red dash–dotted line represents the inviscid added mass force $F_{\textit{AM}}$ = $m_{{h}}a(t)$ that follows from potential flow; the red dashed line is the sum $F_{\textit{QS}}+F_{\textit{AM}}$ . The black dashed line is the sum $F_{\textit{QS}}+F_{{a}}$ , where $F_{{a}}(t)$ is the model for the acceleration drag force in (3.4) during the acceleration phase; the relaxation phase is determined numerically as described in Appendix B. The top axis indicates the dimensionless time $t^*$ , equivalent to the number of plate heights $\ell _b$ travelled by the plate. The acceleration phase is indicated by ‘A’, and the relaxation phase with ‘R’ ; the shaded region (‘E’) indicates the engagement phase of the robot. The vertical green bars indicate where the inviscid added mass $F_{\textit{AM}}$ has doubled in magnitude.

Figure 12(a) shows the result for the measured acceleration drag force $F_{{a}}(t)$ = $F_D(t)\!-\!F_{\textit{QS}}(t)$ for values of the jerk $J$ between 0.1 and 0.8 m s⁻ $^3$ . The measurements are compared with the model prediction for $F_{{a}}(t)$ . The same measurement data and model predictions are shown in figure 12(b), but now plotted as a function of the dimensionless time $t^*$ . For each value of the jerk $J$ the acceleration drag force $F_{{a}}$ grows proportional to $(t^*)^{1/2}$ , see (3.5). Note that the initial peak due to the robot engagement, visible in figure 12(a), nearly coincides with the vertical axis $t^* \approx 0$ in figure 12(b), and thus does not appear to make a significant contribution during the plate motion as a whole.

The agreement between the measured data and the model is remarkably good, taking into consideration the fluctuations in the measured force signals that are the result of the somewhat noisy signal from the force sensor. The prediction is more accurate for short times ( $t^* \lt 4$ ), where we observe a concentrated vortex loop near the plate edges (see figure 4). For longer times ( $t^* \gt 4$ ) the vortex loop detaches from the plate and the wake starts to become more complicated, as can be seen in the PIV snapshots indicated by the roman numerals in figure 12. The development of the vortex loop into a turbulent wake is not included in the history-based model.

Figure 12. (a) The measured acceleration drag force $F_{{a}}(t) = F_D(t)\!-\!F_{\textit{QS}}(t)$ as a function of time $t$ for the constant jerk motion of an AR = 2 rectangular plate with acceleration $a = Jt$ for different values of the jerk $J$ between 0.1 and 0.8 m s⁻³, see table 2. The final velocity is $V_{{a}}$ = 0.60 m s⁻¹ for all measurements. The initial peak is due to the engagement of the robot that moves the plate. The dashed lines correspond to the forces predicted by the model (3.4) with $F_{{a}} \propto t^{3/2}$ . (b) Same data as in (a), but presented as a function of the dimensionless time $t^*$ . Below are four PIV snapshots at $t^*$ = 2.0 (I), 3.0 (II), 4.0 (III) and 5.0 (IV), respectively, for the motion with $J = 0.4$ m s⁻³, as indicated by the roman numerals in (b). The colour indicates the dimensionless out-of-plane vorticity $\omega ^* = \omega _z\ell _b/V_{{a}}$ .

5.2. Velocity relation $V\propto \sqrt {t}$

Figure 13. Example of the measured drag force $F_D(t)$ (blue line) as a function of time $t$ for an accelerating motion of an AR = 2 rectangular flat plate with a velocity $V(t) = Qt^{1/2}$ with $Q^2$ = 0.36 m $^2$ s⁻ $^3$ until the plate reaches a final velocity $V_{{a}}$ = 0.60 m s⁻¹. The solid red line represents the quasisteady drag force $F_{\textit{QS}}(t)$ = $C_{\!D}\textstyle (1/2)\rho V^2(t)A$ . Note that $F_{\textit{QS}}$ is not exactly linear at the start of the motion, which is due to the robot engagement and finite jerk that can be employed. The red dash–dotted line represents the added mass force $F_{\textit{AM}}$ = $m_{{h}}a(t)$ that follows from potential flow; the red dashed line is the combination $F_{\textit{QS}}+F_{\textit{AM}}$ . The black dashed line is the sum $F_{\textit{QS}}+F_{{a}}$ , where $F_{{a}}(t)$ is the model for the acceleration drag force in (3.4) according to the actual plate motion, rather than the prescribed motion. The top axis indicates the dimensionless time $t^*$ , equivalent to the number of plate heights $\ell _b$ travelled by the plate. The acceleration phase is indicated by ‘A’, and the relaxation phase with ‘R’ ; the shaded region (‘E’) indicates the engagement phase of the robot. The vertical green bars indicate where the amplitude of the inviscid added mass $F_{\textit{AM}}$ has reduced to approximately one half, one third and one quarter in magnitude.

Here we consider a motion where the velocity $V(t)$ increases with the square root of time, i.e. $V(t) = Qt^{1/2}$ . This motion implies that the kinetic energy of the plate increases at a constant rate, i.e. $\textstyle ( 1/2) m_P V^2 = \textstyle (1/2) m_P Q^2 t$ , where $m_P$ is the mass of the plate and the strut. Hence, the square of the parameter $Q$ can be interpreted as constant ‘power per unit mass’ (with a dimension m $^2$ s⁻ $^3$ ) added to the plate kinetic energy. For this motion the acceleration $a$ is equal to $a(t) = \textstyle (1/2) Q t^{-1/2}$ , which implies an infinite acceleration at the start of the motion. This is evidently not realistic, and in practice the start of the motion is limited by the finite jerk and maximum acceleration that can be achieved by the robot. For this motion the history-based model predicts an acceleration drag force $F_{{a}}$ that is constant, i.e.

(5.2) \begin{align} F_{{a}}\propto \sqrt {aV} = \left ( \dfrac 12 Q t^{-1/2}\times Qt^{1/2} \right )^{1/2} = \frac {1}{\sqrt {2}}Q. \end{align}

This implies that during this motion the acceleration drag force $F_{{a}}(t)$ , given in (3.4), remains constant while the acceleration decreases with time, i.e.

(5.3) \begin{align} F_{{a}}(t) = C_{{a}}\rho A \sqrt {\nu }Q, \quad \text{with}\quad C_{{a}} = C\sqrt {{\textit{Re}}_{{a}}}, \end{align}

where ${\textit{Re}}_{{a}} = {\textit{Re}}_a ^ {n=1/2}$ is the acceleration Reynolds number defined in (3.15). We note that the empirical constant $C$ has a numerical value $C$ = $1.5(C_{1/2}/C_1) \approx 1.2$ , see Appendix B.

The result that $F_{{a}}(t)$ is expected to remain constant, while the magnitude of the acceleration $a(t)$ decreases, is evidently in contrast to the inviscid added mass force $F_{\textit{AM}}$ . Hence, this can be considered as a critical test for the history-based model to predict the drag force $F_D(t)$ , and in particular the contribution of $F_{{a}}(t)$ .

Figure 14. (a) The acceleration drag force $F_{{a}}(t) = F_D(t)\!-\!F_{\textit{QS}}(t)$ as a function of time $t$ for the motion of an AR = 2 rectangular plate that moves with a velocity $V(t) = Qt^{1/2}$ for different values of $Q^2$ between 0.16 and 0.64 m $^2$ s⁻³, see table 2. The final velocity is $V_{{a}}$ = 0.60 m s⁻¹ for all measurements. The dashed lines correspond to the forces $F_{{a}}(t)$ predicted by the model (3.4) with constant $F_{{a}} \propto Q$ during the acceleration phase of the motion. (b) Same data as in (a), but presented as a function of the dimensionless time $t^*$ . Below are four PIV snapshots at $t^*$ = 2.0 (I), 3.0 (II), 4.0 (III) and 5.0 (IV), respectively, of the motion with $Q^2$ = 0.25 m $^2$ s⁻ $^3$ , as indicated by the roman numerals in (b). The colour indicates the dimensionless out-of-plane vorticity $\omega ^* = \omega _z\ell _b/V_{{a}}$ . Note the deviation between the measured acceleration drag force $F_{{a}}$ and the modelled force after $t^* \approx 4$ , caused by the detachment and breakup of the vortex loop.

Figure 13 shows an example of the measured drag force $F_D(t)$ . Given that the velocity $V(t)$ increases proportionally to $V\propto t^{1/2}$ , the quasisteady drag force $F_{\textit{QS}}$ increases linearly with time. In this figure it can be seen that this is not exactly the case for the initial part of the motion. This is due to the robot engagement and the finite maximum jerk and acceleration that the robot can achieve. However, it is evident that the measured acceleration drag force $F_{{a}}(t)$ = $F_D(t)\!-\!F_{QS}(t)$ remains constant in magnitude during the accelerating phase of the motion.

The force $F_{{a}}(t)$ during the relaxation phase of this motion is determined numerically (see Appendix B). The predicted values for $F_{{a}}(t)$ during the relaxation phase is less accurate, but we note that the motion during the relaxation phase is already beyond $t^*$ = 4 (see top axis in figure 13); we already noted that, due to the change in structure of the wake for $t^*\gt 4$ , the history-based model is no longer accurate. We also note that during the robot engagement, i.e. the shaded area adjacent to $t^*$ = 0, the magnitude of the drag force $F_D(t)$ is practically equal to that given by the inviscid added mass force $F_{\textit{AM}}$ , but the same magnitude is given by the numerical result for the history-based model for $F_{{a}}(t)$ . However, while the inviscid added mass force $F_{\textit{AM}}$ rapidly drops in accordance with the decreasing magnitude of the acceleration, both the measured drag force and the predicted drag force $F_{\textit{QS}}(t)\!+\!F_{{a}}(t)$ closely resemble each other.

Figure 14(a) summarizes the results for the measured acceleration drag force $F_{{a}}(t)$ = $F_D(t)-F_{\textit{QS}}(t)$ for values of $Q^2$ between 0.16 and 0.64 m $^2$ s⁻³ and with a final velocity of $V_{{a}}$ = 0.60 m s⁻¹ for all measurements. These results further support the model prediction of a constant acceleration drag force $F_{{a}}$ . It can be seen that the agreement is not as good for motions with higher values of $Q^2$ . This can be attributed to inaccuracies in the imposed motion due to the mechanical limitations of the robot, see Appendix A. At longer times the measured force $F_{{a}}(t)$ drops below the predicted values for the lower values of $Q^2$ . When the same data are presented as a function of dimensionless time $t^*$ , as in figure 14(b), it shows that the measured force data drop below the theoretical results when the dimensionless time $t^*$ becomes larger than 4, even during the acceleration phase. This can again be associated with the detachment of the vortex loop from the plate edges, the transition to a turbulent wake, and shedding of vorticity from the wake. This is also observed in the experiments of Grift et al. (Reference Grift, Vijayaragavan, Tummers and Westerweel2019), but for a value of $t^*$ = 6. The value of $t^* = 4$ where this begins to occur may be attributed to optimal vortex formation (Dabiri Reference Dabiri2009).

Figure 15. Overview of velocity $V$ and acceleration $a$ for experiments with different motions with a final velocity $V_a = 0.6 \,\mathrm{m\,s^{- 1}}$ . Blue lines show the experiments with constant accelerations, with the acceleration $a$ increasing in the direction of the arrow. Green lines show the experiments with increasing acceleration, with the jerk $J$ increasing in the direction of the arrow. Red lines indicate experiments with decreasing accelerations, with $Q^2$ increasing in the direction of the arrow. Thick lines indicate the experiments with the lowest value of $a$ , $J$ and $Q^2$ , respectively. Black stars indicate where experiments with all three motion types have (almost) identical values for the velocity and acceleration of the plate. The black circle indicates the identical motion states considered in figure 16.

5.3. Equivalent motion states

The two terms in the original Morison equation (1.1) are the quasisteady drag force $F_{\textit{QS}}(t)$ and an acceleration drag force $F_{{a}}(t)$ that is taken equal to the added mass force $F_{\textit{AM}}(t) = m_{{h}}a(t)$ , where $m_{{h}}$ is the added mass given by the potential flow solution (e.g. Brennen Reference Brennen1982). Note that $F_{\textit{QS}}$ and $F_{\textit{AM}}$ only depend on the instantaneous velocity $V$ and acceleration $a$ , respectively. Hence, this suggests that the (total) drag force $F_D$ can be determined without further knowledge of the underlying flow field or the motion history. It is demonstrated in previous sections that the acceleration drag force $F_{{a}}(t)$ is not properly described by the inviscid added mass force $F_{\textit{AM}}$ . Instead, the history-based model (Reijtenbagh et al. Reference Reijtenbagh, Tummers and Westerweel2023) in (3.1) implies that the actual acceleration drag force $F_a(t)$ that is added to the quasisteady drag force $F_{\textit{QS}}$ depends on the flow history. In this section we illustrate this by combining all motions for the AR = 2 rectangular plate considered in this paper, and identify the cases for which the velocity and acceleration are (nearly) equal but were reached by different motions, i.e. different flow (acceleration) histories.

Figure 16. The acceleration drag force $F_{{a}}(t)$ as a function of time $t$ and PIV velocity fields for the three different plate motions in table 3, with (a–b) constant-acceleration motion with $a$ = 0.62 m s⁻ $^2$ ; (c–d) $V(t) = (1/2)Jt^2$ with $J$ = 0.40 m s⁻ $^3$ ; and (e–f) $V(t) = Qt^{1/2}$ with $Q^2$ = 0.49 m $^2$ s⁻ $^3$ . The * symbols in (a), (c) and (e) indicate the instants when the velocity and the acceleration are equal for all three motions: $a \cong$ 0.64 m s⁻² and $V \cong$ 0.50 m s⁻¹, see figure 15. The dashed lines represent $F_{{a}}(t)$ according to the history-based model in (3.4) for the acceleration phase, and for the relaxation phase, i.e. (B8) for $n$ = 1, and otherwise numerically computed, as described in Appendix B. Panels (b), (d) and (f) show PIV snapshots of the measured velocity field in the midplane of the plate. The colour indicates the dimensionless out-of-plane vorticity $\omega ^* = \omega _z\ell _b/V_{{a}}$ .

Figure 15 shows all motions considered in this paper, i.e. constant acceleration ( $J = 0$ ), increasing acceleration ( $J \gt 0$ ) and decreasing acceleration ( $J \lt 0$ ). Six cases can be identified where instantaneous velocity and acceleration are (almost) equal. However, the acceleration histories are very different between the three different motions. For the case marked by the circle in figure 15, the three measured acceleration drag forces $F_{{a}}(t)$ and the three corresponding flow fields are compared in figure 16. Only the force $F_{{a}}$ needs to be considered, as the quasisteady drag force $F_{\textit{QS}}(t)$ is equal for all three cases due to equal instantaneous velocity $V(t)$ . The Supplementary material provides a video that visualizes the PIV flow fields and acceleration drag force $F_{{a}}(t)$ simultaneously for the three motions considered here. This case was chosen because the time instants that are compared occur near the end of the acceleration phase of each motion, giving the highest values for $F_{{a}}(t)$ and consequently also the largest differences in both the measured drag force and velocity field. In all three cases, velocity and acceleration are equal, i.e. $V$ = 0.50 m s⁻¹ and $a$ = 0.64 m s⁻ $^2$ , but the measured acceleration drag forces differ significantly by almost 20 %; the acceleration drag force for the ‘square-root motion’ (with negative jerk $J \lt 0$ and $V(t) \propto t^{1/2}$ ) is the highest in our measurements, while it is the lowest for the ‘quadratic motion’ (with positive jerk $J \gt 0$ and $V(t) \propto t^2$ ), and with the result for the constant-acceleration motion ( $J = 0$ and $V(t) \propto t$ ) between the two.

We note that a significant part of the drag originates from the vorticity in the wake. This vorticity has been created at the plate surface since it was brought into motion from rest. Therefore, the history of the motion needs to be taken into account.