2. Theory and experimental verification

The geometry of the set-up is shown in figure 1(b): a wire loop of radius $R$ held at a distance less than $d_{\textit{max}}$ above a soap solution ( $d_{\textit{max}}=0.663R$ is the critical height of a half-catenoid) supports a soap film whose shape is the function $\zeta (z)$ surrounding a central cylinder of radius $r_0=0.553R$ , the corresponding critical neck radius. The initial condition of the surface is the critical half-catenoid where the contact line of the surface with the cylinder coincides with the surface of the bath. When the loop is moved beyond $d_{\textit{max}}$ the SPB detaches from the bath and begins its motion up the cylinder.

While the motion of the soap film is a moving boundary problem in which the shape of the film is to be determined as part of the dynamics, we explore the simplest possibility, a quasistatic approximation in which, at every instant of time, the moving film is taken to be an (unstable) equilibrium catenoid that connects the present location of the SPB to the wire loop above. The motion is then governed by a balance between the film’s capillary force and the viscous drag within the moving SPB.

Figure 2.

Geometry of Plateau borders for two topologically equivalent situations. (a) Relaxation of a half-catenoid. (b) Relaxation of a bubble with an embedded ring in a tube. (c) Pathway of smooth interconversion between (a) and (b).

We adopt a coordinate system with the origin on the plane of the loop, with positive $z$ downwards, as in figure 1(b). Let $d(t)$ be the time-dependent SPB location measured from the origin, $z=0$ . Under the quasistatic approximation the shape of the moving surface can be found by a standard analysis. The general form of the catenoid is

(2.1) \begin{align} \zeta (z)=a\cosh \left (\frac {z-c}{a}\right ) \!, \end{align}

where the constants $a$ and $c$ are determined by the boundary conditions. These are $\zeta (0)=R$ and, for all $d\equiv d(t)\leqslant d_{{max}}$ , $\zeta (d)=r_0$ . We adopt a system of units made dimensionless with the loop radius $R$ and define

(2.2) \begin{align} \alpha =\frac {a}{R}, \ \ \ \ \beta =\frac {r_0}{R}, \ \ \ \ D=\frac {\textrm{d}}{R}, \end{align}

and find from the boundary conditions the result

(2.3) \begin{align} \beta =\cosh \left (\frac {D}{\alpha }\right )-\sqrt {1-\alpha ^2}\sinh \left (\frac {D}{\alpha }\right )\!. \end{align}

Writing the hyperbolic functions as exponentials and multiplying by $x=e^{D/\alpha }$ , this result can be recast as a quadratic equation for $x$ , whose two roots yield transcendental equations defining two branches of solution $D_\pm (\alpha )$

(2.4) \begin{align} D_\pm =\alpha \ln \left [\frac {\beta \pm \sqrt {\beta ^2-\alpha ^2}}{1-\sqrt {1-\alpha ^2}}\right ]\!. \end{align}

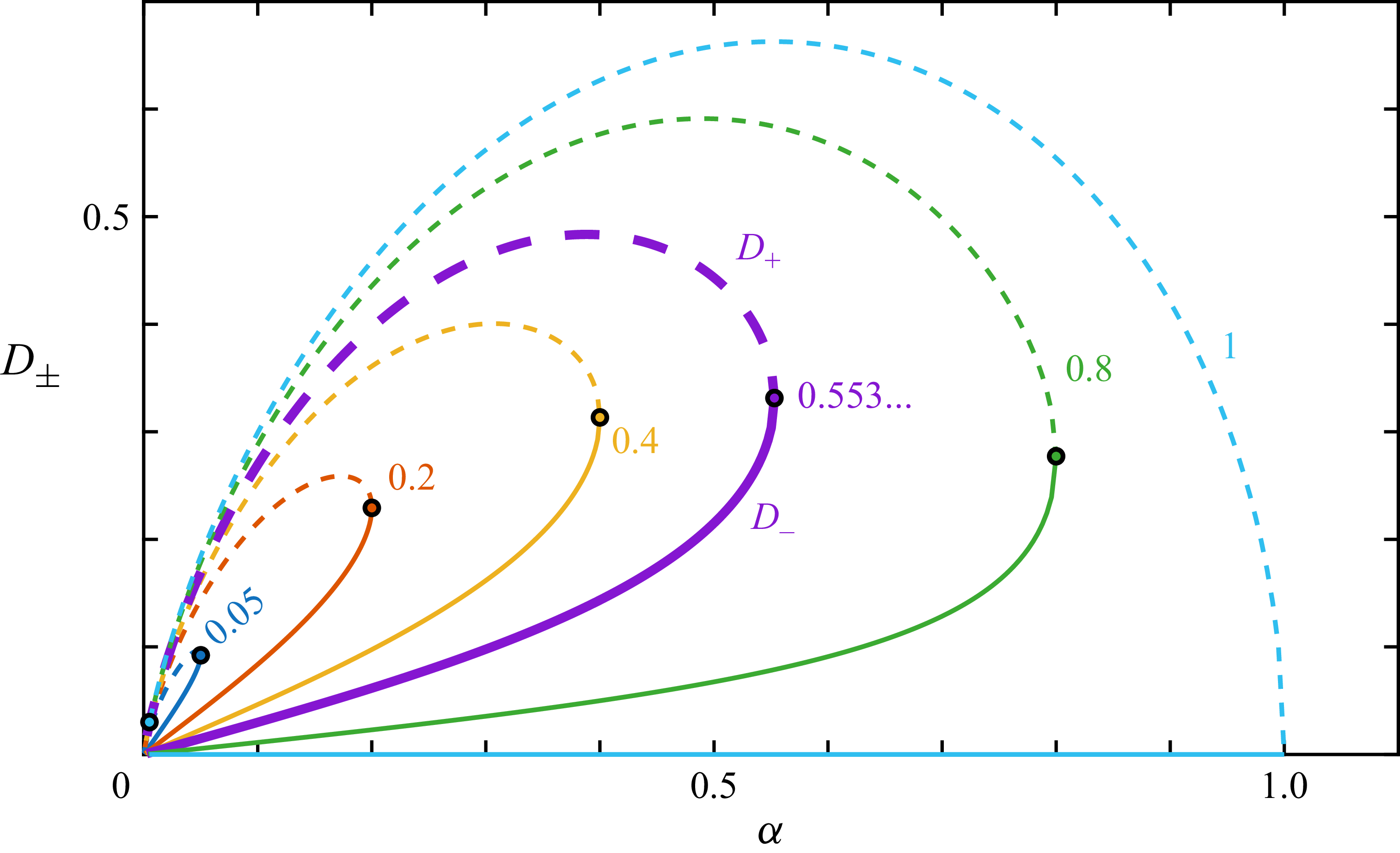
As shown in figure 3, these two branches combine to give a loop in the $\alpha D$ -plane. As in the treatment of a full catenoid spanning two identical loops (Goldstein et al. Reference Goldstein, Pesci, Raufaste and Shemilt2021), of the two branches $D_\pm$ one ( $D_-$ ) is the physically attainable one because it is the one that minimises the area, while the other ( $D_+$ ) is a local maximum of the area. Hence, we choose the branch $D_-$ . The contact angle $\theta$ at the SPB, defined to be $0$ when the film is tangent to the cylinder as in figure 1(b), is given by

(2.5) \begin{align} \theta =-\tan ^{-1}\left [\sinh \left (\frac {D_-}{\alpha }-\cosh ^{-1}\left (\frac {1}{\alpha }\right )\right )\right ]\!. \end{align}

Figure 3.

The two branches of solutions $D_\pm (\alpha )$ in (2.4) for various values of $\beta$ . The physical branch $D_-$ (solid) and unphysical branch $D_+$ (dashed) meet at the black circles. Heavy curve for critical size of inner cylinder.

The motion of the soap film arises from a balance between the capillary force $\gamma \cos \theta$ per unit length of SPB with $\theta$ given by (2.5) and we set $\gamma =2\sigma$ , with $\sigma$ the surface tension of each side of the soap film, and frictional forces that arise from flows within the Plateau border. The latter have been considered previously by Cantat, Kern & Delannay (Reference Cantat, Kern and Delannay2004), Cantat & Delannay (Reference Cantat and Delannay2005), Terriac, Etrillard & Cantat (Reference Terriac, Etrillard and Cantat2006) and Clerget et al. (Reference Clerget, Delvert, Courbin and Panizza2021), who noted in both steady-state and dynamical problems that Bretherton’s law holds. As shown in figure 2, the Plateau border problems of a moving bubble in a tube and the present situation are related by topological inversion. Thus we expect that, per unit length of the contact line between the film and the cylinder, there is a frictional force of the form previously used to describe the motion of bubbles attached to surfaces, with a general exponent $q$

(2.6) \begin{align} f=A \gamma \left (\frac {\mu v}{\gamma }\right )^{\!q} \! , \end{align}

where $A$ is a dimensionless constant and $q=2/3$ corresponds to Bretherton’s law. We take $A$ to be fixed as the geometry changes, while recognising that in a more detailed analysis there may be higher-order corrections as the angle $\theta$ evolves. For the case of interest ( $q=2/3$ ), we define a rescaled time $T=\gamma t/(\mu \textit{RA}^{1/q})$ , and making use of the relation $\cos (\arctan (x))=1/\sqrt {1+x^2}$ , the scaled SPB position obeys the equation

(2.7) \begin{align} \frac {{\rm d}D}{{\rm d}T}=-\cos (\theta (D))^{1/q}=-\left (\frac {\alpha (D)}{\beta }\right )^{\! 1/q} \!, \end{align}

after some straightforward but lengthy algebra, and $\alpha (D)$ is given implicitly by (2.4). While it is possible to obtain an implicit solution for $T(\alpha )$ in terms of hypergeometric functions for any power $q\leqslant 1$ , the result is not particularly illuminating and a numerical solution is straightforward. The function $D(T)$ is shown in figure 3 for $q=2/3,1$ . At large $T$ , as $D\to 0$ , its asymptotic behaviour, obtained from (2.4), is $D=-\alpha \ln \beta + {\cdots}$ . Upon substitution into (2.7) one finds $D\sim T^{-2}$ when $q=2/3$ , which contrasts strongly with exponential decay obtained when the frictional law is linear in the capillary number ( $q=1$ ), as would be the case when there is no wetting layer with its associated flows.

Figure 4.

Time dependence of the SPB position in scaled coordinates. Data points (squares and circles) are from two distinct experimental sets, with error bars representing standard deviations. Blue line is the solution to (2.7) for $q=2/3$ , and red dashed line is for $q=1$ .

To test which power-law exponent $q$ governs the SPB motion, we employed an apparatus consisting of a $50\,$ ml Falcon tube (diameter $39\,$ mm) attached by its threaded end to a large plastic Petri dish (inner diameter $135\,$ mm, height $15\,$ mm). The upper loop supporting the soap film is a section of Tygon tubing (diameter $8\,$ mm) attached to a shelf extending out from the bottom of a plastic cylinder that fits tightly around the Falcon tube and smoothly slides along it. The shelf is perforated in order to allow free circulation of air in and out of the half-catenoid region. The Petri dish was filled with a soap solution to ${\sim} 2\,$ mm below the top. The soap solution was a mixture of Fairy liquid detergent, glycerol and water using published proportions (recipe C in Lalli et al. (Reference Lalli, Shen, Dini and Giusti2023)).

Videos of the meniscus motion were captured at $200\,$ frames sec^–1 using a Phantom V641 high-speed camera equipped with a Zeiss macro lens ( $f=60\,$ mm). The SPB motion was tracked by hand from those videos using Image J. Figure 4 shows the average data from two independent sessions, consisting respectively of $8$ and $10$ independent runs, plotted against the scaled time $T$ from theory. At long times, the data clearly favour $q=2/3$ . The deviations visible at early times may arise from a breakdown of the quasi-static approximation when the film separates from the bath. Taking the value $q=2/3$ , there is one free parameter to compare experiment and theory, the characteristic time $\tau$ that maps the dimensional time $t$ to the scaled time $T$ via $T=t/\tau$ , where $\tau =RA^{3/2}\mu /\gamma$ . We find $\tau =0.1{-}0.3\,$ s. Using $R=4\,$ cm, $\mu =2\,$ cP and the estimated $\sigma =25\,$ dyn cm⁻¹, we find $A=16{-}30$ , consistent in scale with previous observations by Cantat et al. (Reference Cantat, Kern and Delannay2004) and Clerget et al. (Reference Clerget, Delvert, Courbin and Panizza2021), who found values of ${\sim} 40$ and suggested that the discrepancy between these values and the significantly smaller theoretical estimates of ${\sim} 10$ arises from the greater dissipation within the fluid due to the existence of rigid air–water interfaces arising from the presence of surfactants.

The agreement between theory and experiment reported provides further validation of the applicability of Bretherton’s law to the motion of Plateau borders, and also shows the validity of force estimates obtained from the geometry of unstable minimal surfaces. This therefore suggests a pathway forward in the quantitative description of more complex topological rearrangements of soap films (Goldstein et al. Reference Goldstein, McTavish, Moffatt and Pesci2014) in which the Plateau border undergoes a reconnection at the moment of singularity (Goldstein et al. Reference Goldstein, Moffatt, Pesci and Ricca2010).