2. Preliminaries

In the whole paper, we use the convention $\frac{1}{\infty} = 0$ and $0\cdot \infty = 0$. When $E\subseteq (0, \infty)$ is Lebesgue measurable, we denote by $\lambda(E)$ its Lebesgue measure.

Let $(R, \mu)$ be a σ-finite nonatomic measure space. By $\mathcal{M}(R, \mu)$ we will denote the class of all µ-measurable functions on R whose values lie in $\mathbb{R} \cup \{- \infty, \infty\}$. We will denote the class of all µ-measurable functions on R whose values lie in $[0, \infty]$ by $\mathcal{M}^{+}(R, \mu)$. And the class of all functions in $\mathcal{M}(R, \mu)$ that are finite µ-almost everywhere in R will be denoted by $\mathcal{M}_{0}(R, \mu)$.

Now we introduce rearrangement-invariant Banach function spaces and their basic properties. The theory that is presented here except of the Sobolev spaces follows the first three chapters of [Reference Bennett and Sharpley2].

Let $f \in \mathcal{M}(R, \mu)$. The distribution function of the function f is the function $f_{\ast, \mu} \colon [0, \infty) \to [0, \infty]$ defined by

\begin{align*} f_{\ast, \mu}(\lambda) = \mu(\{x \in R; \lvert f(x) \rvert \gt \lambda \}), \, \, \, \, \lambda \in [0, \infty). \end{align*}

Furthermore, the nonincreasing rearrangement of the function f is the function $f^{\ast}_{\mu} \colon (0, \infty) \to [0, \infty]$ defined by

\begin{align*} f^{\ast}_{\mu}(t) = \inf\left\{\lambda \in [0, \infty); f_{\ast, \mu}(\lambda) \leq t \right\}, \, \, \, \, t \in (0, \infty). \end{align*}

The functions $f_{\ast, \mu}(\lambda)$ and $f^{\ast}_{\mu}$ are both nonincreasing and right-continuous. If $f \in \mathcal{M}(R, \mu)$, $g \in \mathcal{M}(S, \nu)$ satisfy

(2.1)\begin{align} f^{\ast}_{\mu}(t) = g^{\ast}_{\nu}(t), \, \, \, \, t \in (0, \infty), \end{align}

we say that f and g are equimeasurable. For instance, the functions f and $f^{\ast}_{\mu}$ are equimeasurable.

A mapping ρ on $\mathcal{M}^{+}(R, \mu)$ with values in $[0, \infty]$ is called a rearrangement-invariant Banach function norm if all the following properties are satisfied for all $f, g \in \mathcal{M}^{+}(R, \mu)$, $\{f_{k}; k \in \mathbb{N}\} \subseteq \mathcal{M}^{+}(R, \mu)$, $c \in [0, \infty)$ and $A \subseteq R$ such that A is µ-measurable.

1. (i) the norm axiom: $\rho(f) = 0$ if and only if f = 0 µ-almost everywhere in R, $\rho(cf) = c\rho(f)$, $\rho(f + g) \leq \rho(f) + \rho(g)$;

2. (ii) the lattice axiom: if $g \leq f$ µ-almost everywhere in R, then $\rho(g) \leq \rho(f)$;

3. (iii) the Fatou axiom: if $f_{k} \uparrow f$ µ-almost everywhere in R, then $\rho(f_{k}) \uparrow \rho(f)$;

4. (iv) the nontriviality axiom: if $\mu({A}) \lt \infty$, then $\rho(\chi_{A}) \lt \infty$;

5. (v) the local embedding in L¹: if $\mu(A) \lt \infty$, then

   (2.2)\begin{align} \int_{A} f \, d\mu \leq K_{A}\rho(f), \end{align}

   where $K_{A} \geq 0$ is a constant which may depend on A but which does not depend on f;

6. (vi) the rearrangement-invariance axiom: if $f^{\ast}_{\mu} = g^{\ast}_{\mu}$, then $\rho(f) = \rho(g)$.

The collection of all functions $f \in \mathcal{M}(R, \mu)$ such that $\rho(\lvert f \rvert) \lt \infty$ is called a rearrangement-invariant Banach function space. We will denote it by $X(\rho)$, $X(R, \mu)$ or just by X.

As their name suggests, rearrangement-invariant Banach function spaces are Banach spaces. Textbook examples of rearrangement-invariant spaces are the Lebesgue spaces $L^p(R, \mu)$ for $p\in[1, \infty]$. Every rearrangement-invariant space contains simple functions (i.e., linear combinations of characteristic functions of µ-measurable sets of finite measure) and is contained in $\mathcal{M}_{0}(R, \mu)$.

Now we present some notation and conventions used in the rest of this paper. Throughout the rest of this paper, we assume that $n\in{\mathbb{N}}$, $n\geq2$, is the dimension of ${\mathbb{R}}^n$. Furthermore, we assume that Σ is a nonempty open convex cone with vertex at the origin, i.e., $\Sigma \subseteq {\mathbb{R}}^{n}$ is a nonempty open convex set such that for every $x \in \Sigma$ and for every r > 0, we have $rx \in \Sigma$. We also assume that $w \colon \overline{\Sigma} \rightarrow [0, \infty)$ is a nonnegative continuous function that is not identically zero. Furthermore, we assume that w is α-homogeneous for some α > 0, i.e., for every $x \in \overline{\Sigma}$ and for every s > 0, we have $w(s x) = s^{\alpha} w(x)$. Finally, we assume that the function $w^{\frac{1}{\alpha}}$ is concave in Σ. We set

(2.3)\begin{align} D = n + \alpha. \end{align}

We assume that $m\in{\mathbb{N}}$ is such that

(2.4)\begin{align} 1\leq m \lt D. \end{align}

We define the weighted measure µ on Σ as

\begin{equation*} \mu(E) = \int\limits_{E} w(x) \, dx \end{equation*}

for every Lebesgue measurable set $E \subseteq \Sigma$.

We now introduce the Sobolev spaces that we will work with. Let $k \in \mathbb{N}$ and let $u \colon \Sigma \rightarrow {\mathbb{R}} $ be k-times weakly differentiable function in Σ (i.e., it has all weak derivatives up to the k-th order). We denote by $\nabla^l u$, $l \in \{1, \dots, k\}$, the vector of all l-th order weak derivatives of u. We also set $\nabla^0 u = u$.

Let $X(\Sigma, \mu)$ be a rearrangement-invariant space. We say that u belongs to the space $V^{k}X(\Sigma, \mu)$ if

\begin{equation*} \left\lvert \nabla^{k} u \right\rvert \in X(\Sigma, \mu). \end{equation*}

We say that u belongs to the space $V^{k}_{0}X(\Sigma, \mu)$ if $u \in V^{k}X(\Sigma, \mu)$ and for every $l \in \{0, 1, \dots, k-1 \}$ and for every λ > 0 it holds that

\begin{equation*} \mu\left(\left\{x \in \Sigma; \left\lvert \nabla^{l} u(x) \right\rvert \gt \lambda \right\}\right) \lt \infty. \end{equation*}

For short, we will write $\|\nabla^k u\|_{X(\Sigma, \mu)}$ instead of $\|\, |\nabla^k u| \,\|_{X(\Sigma, \mu)}$.

We will also encounter Sobolev space $W^{1,1}(\Sigma, \mu)$, which is a weighted counterpart of the classical Sobolev space $W^{1,1}(\Sigma)$. We say that a function u belongs to the space $W^{1,1}(\Sigma, \mu)$ if it is weakly differentiable in Σ, $u\in L^1(\Sigma, \mu)$ and $| \nabla u | \in L^1(\Sigma, \mu)$.

Now we turn back to the theory of rearrangement-invariant spaces. We present here their other important properties which we will need in what follows.

To every rearrangement-invariant space X, there is associated another rearrangement-invariant space, which is related to its continuous dual, but which is usually more useful in the theory of Banach function spaces. The mapping $\rho'$ defined on $\mathcal{M}^{+}(R, \mu)$ by

(2.5)\begin{align} \rho'(g) = \sup\limits_{f \in \mathcal{M}^{+}(R, \mu), \rho(f) \leq 1}\int_{R} fg \, d\mu, \, \, \, \, g \in \mathcal{M}^{+}(R, \mu), \end{align}

is the associate norm of the function norm ρ. We say that the space $X(\rho')$ is the associate space to the space $X(\rho)$ and we detone this space by X ^ʹ.

For example, when $X = L^p(R, \mu)$ for $p\in[1, \infty]$, then $X' = L^{p'}(R, \mu)$. Here $p'\in[1, \infty]$ is the dual index defined by $\frac{1}{p} + \frac{1}{p'} = 1$.

An important property of Banach function spaces is that, if X is a Banach function space, then $(X')' = X$.

For every Banach function norm ρ, the Hölder inequality

\begin{align*} \int_{R} \left\lvert fg \right\rvert \, d\mu \leq \rho(f) \rho'(g) \end{align*}

holds for every $f, g \in \mathcal{M}(R, \mu)$.

For every $f \in \mathcal{M}(R, \mu)$ and $t \in (0, \infty)$, we have

(2.6)\begin{align} \mu(\{x \in R; |f(x)| \gt f^{\ast}_{\mu}(t)\}) \leq t. \end{align}

Furthermore, if $f^{\ast}_{\mu}(t) \lt \infty$ and $\mu(\{x \in R; |f(x)| \gt f^{\ast}_{\mu}(t) - \varepsilon\}) \lt \infty$ for some ɛ > 0, then

(2.7)\begin{align} \mu(\{x \in R; |f(x)| \geq f^{\ast}_{\mu}(t)\}) \geq t. \end{align}

The fundamental function $\varphi_{X} \colon [0, \mu(R)] \to [0, \infty]$ of the rearrangement-invariant space X is the mapping defined by

\begin{align*} \varphi_{X}(t) = \left\lVert \chi_{E} \right\rVert_{X}, \,\,\,\, t \in [0, \mu(R)], \end{align*}

where $E \subseteq R$ is an arbitrary set satisfying $\mu(E) = t$. The definition is correct since if $E, F \subseteq R$ are sets such that $\mu(E) = \mu(F)$, then their characteristic functions χ_E and χ_F are equimeasurable.

Furthermore, if $g \in \mathcal{M}(R, \mu)$ and if ρ is a rearrangement-invariant norm, we have

(2.8)\begin{align} \rho'(g) = \sup\limits_{f \in \mathcal{M}^{+}(R, \mu), \rho(f) \leq 1} \int_{0}^{\infty} f^{\ast}(t) g^{\ast}(t) \, dt. \end{align}

The Hardy–Littlewood inequality is very important in the theory of rearrangement-invariant spaces. It states that

\begin{align*} \int_{R} \left\lvert fg \right\rvert \, d\mu \leq \int\limits_{0}^{\infty} f^{\ast}(t) g^{\ast}(t) \, dt \end{align*}

for every $f, g \in \mathcal{M}(R, \mu)$. In particular, by taking $g = \chi_E$, we have

(2.9)\begin{align} \int_{E} \left\lvert f\right\rvert \, d\mu \leq \int\limits_{0}^{\mu(E)} f^{\ast}(t) \, dt \end{align}

for each µ-measurable set $E \subseteq R$.

Another important result in the theory of rearrangement-invariant spaces is the Hardy–Littlewood–Pólya principle. For every rearrangement-invariant norm ρ, if $f, g \in \mathcal{M}^{+}(R, \mu)$ are such that

\begin{align*} \int_{0}^{t} f^{\ast}(\tau) \, d\tau \leq \int_{0}^{t} g^{\ast}(\tau) \, d\tau \end{align*}

for every $t \in (0, \infty)$, then

(2.10)\begin{align} \rho(f) \leq \rho(g). \end{align}

We will also need the following facts. For every $t \in (0, \mu(R))$ and for every $f \in \mathcal{M}(R, \mu)$, we have

(2.11)\begin{align} \int_{0}^{t}f^{\ast}(\tau) \; d\tau = \sup\left(\left\{\int_{E} \left\lvert f\right\rvert \; d\mu; E \subseteq R, E \, \, \mu-\text{measurable}, \mu(E) = t \right\}\right). \end{align}

Each rearrangement-invariant space on $(R, \mu)$ can be represented as a rearrangement-invariant space on $(0, \mu(R))$. More precisely, if $X(R, \mu)$ is a rearrangement-invariant space, then there exists the unique rearrangement-invariant space $X(0, \mu(R))$ such that for every function $f \in X(R, \mu)$ it holds that

\begin{align*} \left\lVert f \right\rVert_{X(R, \mu)} = \left\lVert f^{\ast}_{\mu} \right\rVert_{X(0, \mu(R))}. \end{align*}

The rearrangement-invariant space $X(0, \mu(R))$ is called the representation space of $X(R, \mu)$. For example, if $X(R, \mu) = L^p(R, \mu)$, then $X(0, \mu(R)) = L^p(0, \mu(R))$.

On the other hand, for every $f \in \mathcal{M}(0, \mu(R))$, there exists a function $u \in \mathcal{M}(R, \mu)$ such that $f^{\ast}_{\lambda}(t) = u^{\ast}_{\mu}(t)$ for every $t \in (0, \infty)$.

Closely related to the nonincreasing rearrangement is the maximal nonincreasing rearrangement. The maximal nonincreasing operator

\begin{align*} P_{\mu} \colon \mathcal{M}(R, \mu) \rightarrow \mathcal{M}^{+}(0, \infty) \end{align*}

is defined by

\begin{align*} P_{\mu}(f)(t) = \frac{1}{t} \int_{0}^{t} f^{\ast}_{\mu}(\tau)\, d\tau, \, \, \, \, f \in \mathcal{M}(R, \mu), t \in (0, \infty). \end{align*}

The image of a function $f \in \mathcal{M}(R, \mu)$ under the maximal nonincreasing operator P_µ is also commonly denoted by $f^{\ast \ast}_{\mu}$, and it is called the maximal nonincreasing function. The maximal nonincreasing function is nonincreasing and we have $f^{\ast} \leq f^{\ast \ast}$.

If $X(0, \mu(R))$ is a rearrangement-invariant space and $h \in \mathcal{M}^{+}(0, \mu(R))$ is a nonincreasing function, we know thanks to (2.8) that

\begin{align*} \left\lVert h \right\rVert_{X'(0, \mu(R))} = \sup\limits_{g \in \mathcal{M}^{+}(0, \mu(R)), \left\lVert g \right\rVert_{X(0, \mu(R))} \leq 1}\int_{0}^{\mu(R)} h(t)g^{\ast}(t) \, dt. \end{align*}

In general, when $h \in \mathcal{M}^{+}(0, \mu(R))$ is not necessarily nonincreasing, we only have

(2.12)\begin{align} \left\lVert h \right\rVert_{X'(0, \mu(R))} \geq \sup\limits_{g \in \mathcal{M}^{+}(0, \mu(R)), \left\lVert g \right\rVert_{X(0, \mu(R))} \leq 1} \int_{0}^{\mu(R)} h(t)g^{\ast}(t) \, dt \end{align}

owing to (2.5). However, it follows from [Reference Cianchi, Pick and Slavíková13, theorem 9.5] and [Reference Peša38, theorem 3.10] that

(2.13)\begin{align} \left\lVert t^{\alpha}f^{\ast \ast}(t) \right\rVert_{X'(0, \mu(R))} \leq 4 \sup\limits_{g \in \mathcal{M}^{+}(0, \mu(R)), \left\lVert g \right\rVert_{X(0, \mu(R))} \leq 1}\int_{0}^{\mu(R)} t^{\alpha}f^{\ast \ast}(t)g^{\ast}(t) \, dt \end{align}

for every $\alpha \in [0, 1]$ and $f\in \mathcal{M}(R, \mu)$. Inequalities (2.12) and (2.13) mean that the norm of $t^{\alpha}f^{\ast \ast}(t)$ can be approached, up to a multiplicative constant, by nonincreasing functions in this case even though the function $t^{\alpha}f^{\ast \ast}(t)$ does not have to be nonincreasing.

We will continue by introducing the dilation operator. Let $\alpha \in (0, \infty)$. The dilation operator $D_{\alpha} \colon \mathcal{M}^{+}(0, \infty) \rightarrow \mathcal{M}^{+}(0, \infty)$ is defined by $(D_{\alpha} f)(t) = f(\alpha t)$ for each $f \in \mathcal{M}^{+}(0, \infty)$ and $t \in (0, \infty)$. This operator is bounded on every rearrangement-invariant space over $(0, \infty)$. More precisely, there exists a constant $0 \lt C \leq \max\{1, \frac{1}{\alpha}\}$ such that

(2.14)\begin{align} \left\lVert D_{\alpha} f \right\rVert_{X(0, \infty)} \leq C\left\lVert f \right\rVert_{X(0, \infty)} \end{align}

for every $f \in \mathcal{M}^{+}(0, \infty)$, every $\alpha \in (0, \infty)$ and every rearrangement-invariant space $X(0, \infty)$.

We conclude this section by introducing the continuous embedding. We say that $X(R, \mu)$ is continuously embedded into $Y(R, \mu)$ if for every function $u \in X(R,\mu)$ it holds that $u \in Y(R,\mu)$ and that $\left\lVert u \right\rVert_{Y(R, \mu)} \leq C \left\lVert u \right\rVert_{X(R, \mu)}$, where C is a constant that does not depend on u. We denote the fact that $X(R, \mu)$ is continuously embedded into $Y(R, \mu)$ by $X(R, \mu) \hookrightarrow Y(R, \mu)$. In fact, inclusion between Banach function spaces is always continuous in the sense that $X(R, \mu) \hookrightarrow Y(R, \mu)$ if and only if $X(R, \mu) \subseteq Y(R, \mu)$. If $X(R, \mu), Y(R, \mu)$ are Banach function spaces, it holds that $X(R, \mu) \hookrightarrow Y(R, \mu)$ if and only if $Y'(R, \mu) \hookrightarrow X'(R, \mu)$.

In the rest of the paper, we will denote by $C, K, C_{i}, K_{i}$ positive finite constants whose exact values are not important for our purposes.

3. Reduction principle and optimality

3.1. Reduction principle

The goal of this subsection is to prove a suitable reduction principle. To prove it we need to derive a variant of the Pólya–Szegő inequality. The proof of this theorem is at the end of this section.

Proposition 3.1. Pólya–Szegő inequality

Let X be a rearrangement-invariant space over $(\Sigma, \mu)$ and $u \in V^{1}_{0}X(\Sigma, \mu)$. Then $u^{\ast}_{\mu}$ is a locally absolutely continuous function on the interval $(0, \infty)$, and it holds that

(3.1)\begin{align} \left\lVert t^{\frac{D - 1}{D}} \frac{d u^{\ast}_{\mu}}{dt}(t) \right\rVert_{X(0, \infty)} \leq C \left\lVert \nabla u \right\rVert_{X(\Sigma, \mu)}, \end{align}

where C is a positive constant independent of u.

In the remaining part of this section, we prove the reduction principle. Recall that the parameters m and D were introduced in (2.3) and (2.4).

Theorem 3.2 Reduction principle

Let X and Y be rearrangement-invariant spaces over $(\Sigma, \mu)$. Then the following two statements are equivalent.

1. (i) For all functions $v \in V^{m}_{0}X(\Sigma, \mu)$ it holds that

   (3.2)\begin{align} \left\lVert v \right\rVert_{Y(\Sigma, \mu)} \leq C_{1} \left\lVert \nabla^{m} v \right\rVert_{X(\Sigma, \mu)}. \end{align}

2. (ii) For all functions $f \in \mathcal{M}^{+}(0, \infty)$ it holds that

   (3.3)\begin{align} \left\lVert \int_{t}^{\infty} f(\tau)\tau^{\frac{m}{D}-1} \; d\tau \right\rVert_{Y(0, \infty)} \leq C_{2} \left\lVert f \right\rVert_{X(0, \infty)}. \end{align}

Here, C ₁ and C ₂ are positive constants independent of v and f, respectively.

The proof of this theorem will be divided into two steps, proposition 3.5 and proposition 3.7.

Remark 3.3. As an easy consequence of the definition of the associate norm, we obtain the fact that (3.3) is equivalent to the following assertion:

1. 1. (2*) For all functions $g \in \mathcal{M}^{+}(0, \infty)$ it holds that

   (3.4)\begin{align} \left\lVert t^{\frac{m}{D}} g^{\ast \ast}(t) \right\rVert_{X'(0, \infty)} \leq C_{2} \left\lVert g \right\rVert_{Y'(0, \infty)}. \end{align}

Remark 3.4. We have

\begin{align*} \begin{aligned} & \left\lVert \chi_{(0, 1)}(t) \right\rVert_{Y(0, \infty)} \left\lVert t^{\frac{m}{D}-1} \chi_{(1, \infty)}(t) \right\rVert_{X'(0, \infty)} \\ & = \left\lVert \chi_{(0, 1)}(t) \right\rVert_{Y(0, \infty)} \sup\limits_{h \geq 0, \left\lVert h\right\rVert_{X(0, \infty)} \leq 1} \int_{1}^{\infty} \tau^{\frac{m}{D}-1} h(\tau) \,d\tau \\ & \leq \sup\limits_{h \geq 0, \left\lVert h\right\rVert_{X(0, \infty)} \leq 1} \left\lVert \chi_{(0, 1)}(t) \int_{t}^{\infty} \tau^{\frac{m}{D}-1} h(\tau) \,d\tau \right\rVert_{Y(0, \infty)}, \end{aligned} \end{align*}

so, (3.3) implies that

\begin{align*} t^{\frac{m}{D}-1} \chi_{(1, \infty)}(t) \in X'(0, \infty). \end{align*}

Proposition 3.5. Let $X, Y$ be rearrangement-invariant spaces over $(\Sigma, \mu)$. Assume that there exists a positive constant C ₁ such that for all functions $v \in V^{m}_{0}X(\Sigma, \mu)$ it holds that

\begin{align*} \left\lVert v \right\rVert_{Y(\Sigma, \mu)} \leq C_{1} \left\lVert \nabla^{m} v \right\rVert_{X(\Sigma, \mu)}. \end{align*}

Then there exists a positive constant C ₂ such that for all functions $f \in \mathcal{M}^{+}(0, \infty)$ it holds that

(3.5)\begin{align} \left\lVert \int_{t}^{\infty} f(\tau)\tau^{\frac{m}{D}-1} \; d\tau \right\rVert_{Y(0, \infty)} \leq C_{2} \left\lVert f \right\rVert_{X(0, \infty)}. \end{align}

The constant C ₂ depends only on the constant C ₁, on m, and on D.

Owing to this proposition the n-dimensional part of the reduction principle ((3.2) in theorem 3.2) implies the one-dimensional part ((3.3) in theorem 3.2). In the proof of the proposition, we need to use the following technical lemma, whose proof is straightforward and omitted.

Lemma 3.6. Let $f \in \mathcal{M}^{+}(0, \infty) \cap L^{\infty}(0, \infty)$ be a function with a bounded support. Let $g \colon [0, \infty) \rightarrow [0, \infty)$ be the function defined by

(3.6)\begin{align} g(t) = \int_{t}^{\infty} f(\tau) \tau^{\frac{m}{D} - m} (\tau - t)^{m-1} \; d\tau, \; \; \; \; t \in [0, \infty). \end{align}

Then $g \in \mathcal{C}^{m-1}(0, \infty)$ and

\begin{align*} g^{(j)}(t) = (-1)^{j}\frac{(m-1)!}{(m-j-1)!} \int_{t}^{\infty} f(\tau) \tau^{\frac{m}{D} - m} (\tau - t)^{m-j-1} \; d\tau, \; \; \; \; t \in (0, \infty) \end{align*}

for every $j \in \{1, \dots, m-1\}$. Moreover, $g^{(m-1)}$ is locally Lipschitz on $(0, \infty)$ and

\begin{align*} g^{(m)}(t) = (-1)^{m}(m-1)! f(t) t^{\frac{m}{D}-m} \end{align*}

for almost every $t \in (0, \infty)$.

We denote by B_µ the µ-measure of the intersection of the unit ball in ${\mathbb{R}^n}$ with Σ, i.e.,

\begin{align*} B_{\mu} = \mu(\{x \in \Sigma; \left\lvert x \right\rvert \leq 1 \}). \end{align*}

Now we prove proposition 3.5.

Proof. Proof of Proposition 3.5

Choose an arbitrary function $f \in \mathcal{M}^{+}(0, \infty)$. Observe that it is enough to prove the proposition for $\left\lVert f \right\rVert_{X(0, \infty)} \lt \infty$. Firstly, assume that the function f belongs to $L^{\infty}(0, \infty)$ and that it has a bounded support. Define the function $v \colon \Sigma \rightarrow [0, \infty)$ by

(3.7)\begin{align} v(x) = \int_{{B_{\mu}} \left\lvert x \right\rvert^{D}}^{\infty} f(\tau)\tau^{\frac{m}{D}-m}\left(\tau - {B_{\mu}} \left\lvert x \right\rvert^{D}\right)^{m-1} \, d\tau, \, \, \, \, x \in \Sigma. \end{align}

Now define the function $\sigma \colon \Sigma \rightarrow [0, \infty)$ by $\sigma(x) = {B_{\mu}} \left\lvert x \right\rvert^{D}$, $x \in \Sigma$. It holds that $\sigma \in \mathcal{C}^{\infty}(\Sigma)$. Clearly $v(x) = (g \circ \sigma)(x), x \in \Sigma$, where g is the function from (3.6), so $v \in \mathcal{C}^{m-1}(\Sigma)$ owing to lemma 3.6 and the mth order weak partial derivatives exist (see [Reference Leoni25, theorem 10.35]) and are linear combinations of the functions

(3.8)\begin{align} x \mapsto \int_{{B_{\mu}} \left\lvert x \right\rvert^{D}}^{\infty} f(\tau)\tau^{\frac{m}{D}-m}\left(\tau - {B_{\mu}} \left\lvert x \right\rvert^{D}\right)^{m-l_{1}-1} \, d\tau \left\lvert x \right\rvert^{l_{1}(D-2) -2l_{2}} \prod\limits_{j=1}^{2(l_{1}+l_{2})-k} x_{i_{j}} \end{align}

and

(3.9)\begin{align} x \mapsto f\left({B_{\mu}} \left\lvert x \right\rvert^{D}\right) \left\lvert x \right\rvert^{-m} \prod\limits_{j=1}^{m} x_{i_{j}} \end{align}

for the parametres $l_{1}, l_{2}$ satisfying $l_{1} \in \mathbb{N}, l_{1} \leq m-1, l_{2} \in \{0, \dots, m\}, 2(l_{1} + l_{2}) \geq m$. Since f has a bounded support, we also have

(3.10)\begin{align} \left\lvert \nabla^{m} v(x) \right\rvert \leq K_{1} \left(f\left({B_{\mu}} \left\lvert x \right\rvert^{D}\right) + \sum\limits_{l = 1}^{m-1} \int_{{B_{\mu}} \left\lvert x \right\rvert^{D}}^{\infty} f(\tau) \tau^{\frac{m}{D}-l-1} \, d\tau \left\lvert x \right\rvert^{lD - m}\right) \end{align}

for µ-almost every $x \in \Sigma$ thanks to (3.8) and (3.9).

For every $l \in \{1, \dots m-1\}$, we now define the operator

\begin{align*} F_{l} \colon (L^{1} + L^{\infty})(0, \infty) \rightarrow (L^{1} + L^{\infty})(0, \infty) \end{align*}

by

\begin{align*} F_{l}(\varphi)(t) = t^{l-\frac{m}{D}}\int_{t}^{\infty} \varphi(\tau) \tau^{\frac{m}{D}-l-1} \, d\tau, \, \, t \in (0, \infty), \, \, \varphi \in (L^{1} + L^{\infty})(0, \infty). \end{align*}

For an arbitrary $l \in \{1, \dots m-1\}$ we have $\left\lVert F_{l} \right\rVert_{L^{\infty} \rightarrow L^{\infty}} \leq \frac{D}{Dl-m}$ and $\left\lVert F_{l} \right\rVert_{L^{1} \rightarrow L^{1}} \leq \frac{D}{Dl-m+D}$. So, we obtain the fact that the operator F_l is, owing to [Reference Bennett and Sharpley2, Chapter 3, theorem 2.2], bounded on the space $X(0, \infty)$.

Now define the functions $h \colon (0, \infty) \rightarrow [0, \infty)$ and $\omega \colon \Sigma \rightarrow [0, \infty)$. The function h is defined by

\begin{align*} h(t) = f(t) + \sum_{l=1}^{m-1} F_{l}(f)(t), \, \, \, \, t \in (0, \infty). \end{align*}

The function ω is defined by

\begin{align*} \omega(x) = (h \circ \sigma)(x), \, \, \, \, x \in \Sigma. \end{align*}

Owing to (3.10) we obtain

\begin{align*} \left\lvert \nabla^{m} v \right\rvert^{\ast}_{\mu}(t) \leq K_{2} \omega^{\ast}_{\mu}(t), \, \, \, \, t \in (0, \infty). \end{align*}

The functions h and ω are equimeasurable. So, we have

\begin{align*} \left\lvert \nabla^{m} v \right\rvert^{\ast}_{\mu}(t) \leq K_{2} h^{\ast}(t), \, \, \, \, t \in (0, \infty), \end{align*}

thanks to (Reference Mihula2.1). Now we obtain

(3.11)\begin{align} \begin{aligned} & \left\lVert \nabla^{m} v \right\rVert_{X(\Sigma, \mu)} \leq K_{2} \left\lVert h \right\rVert_{X(0, \infty)} \\ & \leq K_{2} \left(\left\lVert f \right\rVert_{X(0, \infty)} + \sum_{l = 1}^{m-1} \left\lVert F_{l}(f) \right\rVert_{X(0, \infty)}\right) \leq K_{3} \left\lVert f \right\rVert_{X(0, \infty)}. \end{aligned} \end{align}

From (3.11) it follows that $ v \in V^{m}X(\Sigma, \mu)$. Since the function f has a bounded support, we obtain the fact that $v \in V^{m}_{0}X(\Sigma, \mu)$ owing to (3.7).

Now, we know that the functions v and g are equimeasurable since the mapping σ is a measure-preserving transformation of the spaces $(\Sigma, \mu)$ and $([0, \infty), \lambda)$ (see [Reference Bennett and Sharpley2, section 2.7]). We obtain the fact that

(3.12)\begin{align} & \left\lVert v \right\rVert_{Y(\Sigma, \mu)} = \left\lVert g \right\rVert_{Y(0, \infty)} \geq \left\lVert \int_{2t}^{\infty} f(\tau)\tau^{\frac{m}{D}-m}\left(\tau - t \right)^{m-1} \, d\tau \right\rVert_{Y(0, \infty)}\\ & \geq 2^{1-m} \left\lVert \int_{2t}^{\infty} f(\tau)\tau^{\frac{m}{D}-m}\tau^{m-1} \, d\tau \right\rVert_{Y(0, \infty)} = 2^{1-m} \left\lVert \int_{2t}^{\infty} f(\tau)\tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{Y(0, \infty)}. \notag \end{align}

Finally, we have

\begin{align*} \begin{aligned} & \left\lVert \int_{t}^{\infty} f(\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{Y(0, \infty)} \leq 2 \left\lVert \int_{2t}^{\infty} f(\tau) \tau^{\frac{m}{D}-1}\, d\tau \right\rVert_{Y(0, \infty)} \leq 2^{m} \left\lVert v \right\rVert_{Y(\Sigma, \mu)} \\ & \leq 2^{m} C_{1} \left\lVert \nabla^{m} v \right\rVert_{X(\Sigma, \mu)} \leq 2^{m} C_{1} K_{3} \left\lVert f \right\rVert_{X(0, \infty)}. \end{aligned} \end{align*}

The first inequality holds by virtue of (2.14). The second inequality holds thanks to (3.12). The last inequality holds owing to (3.11). So, we have proved the inequality (3.5) for bounded functions with bounded support. Now let f be general. Define a sequence $\{f_{k}\}_{k=1}^{\infty}$ of functions from  $\mathcal{M}^{+}(0, \infty)$ by $f_{k}(t) = \min\{f(t), k\}\chi_{(0, k)}(t), t \in (0, \infty), k \in \mathbb{N}$. Since (3.5) holds for every $f_{k}, k \in \mathbb{N}$, we obtain the fact that (3.5) also holds for f thanks to the Fatou axiom of Banach function norms.

Now we prove the remaining implication in theorem 3.2.

Proposition 3.7. Let $X, Y$ be rearrangement-invariant spaces over $(\Sigma, \mu)$. Assume that there exists a positive constant C ₂ such that for all functions $f \in \mathcal{M}^{+}(0, \infty)$ it holds that

(3.13)\begin{align} \left\lVert \int_{t}^{\infty} f(\tau)\tau^{\frac{m}{D}-1} \; d\tau \right\rVert_{Y(0, \infty)} \leq C_{2} \left\lVert f \right\rVert_{X(0, \infty)}. \end{align}

Then there exists a positive constant C ₁ such that for every $u \in V^{m}_{0}X(\Sigma, \mu)$ it holds that

\begin{align*} \left\lVert u \right\rVert_{Y(\Sigma, \mu)} \leq C_{1} \left\lVert \nabla^{m} u \right\rVert_{X(\Sigma, \mu)}. \end{align*}

The constant C ₁ depends only on the constant C ₂, on m, and on D.

Proof. The mapping $\sigma_{m, X} \colon \mathcal{M}^{+}(\Sigma, \mu) \rightarrow [0, \infty]$ defined by

(3.14)\begin{align} \sigma_{m, X}(v) = \left\lVert t^{\frac{m}{D}} v^{\ast \ast}_{\mu}(t) \right\rVert_{X'(0, \infty)}, \, \, \, \, v \in \mathcal{M}^{+}(\Sigma, \mu), \end{align}

is a rearrangement-invariant Banach function norm if and only if

(3.15)\begin{align} t^{\frac{m}{D}-1} \chi_{(1, \infty)}(t) \in X'(0, \infty) \end{align}

(see [Reference Cianchi, Pick and Slavíková13, theorem 5.4] and [Reference Edmunds, Mihula, Musil and Pick18, theorem 4.4]). Since (3.13) holds we have the fact that (3.15) is true thanks to remark 3.4. Hence $\sigma_{m, X}$ is a rearrangement-invariant Banach function norm. We denote the respective space by $Z_{m}X(\Sigma, \mu)$.

We want to prove that for every function $u \in V^{m}_{0}X(\Sigma, \mu)$ it holds that

(3.16)\begin{align} \left\lVert u \right\rVert_{Y(\Sigma, \mu)} \leq C_{2} \left\lVert u \right\rVert_{Z'_{m}X(\Sigma, \mu)} \leq C_{2}K_{m} \left\lVert \nabla^{m} u \right\rVert_{X(\Sigma, \mu)}, \end{align}

where K_m is a positive constant. The first inequality follows from (3.4). We prove the second inequality by induction on m. Firstly, we assume that m = 1. Choose an arbitrary function $u \in V_{0}^{1}X(\Sigma, \mu)$. We have

\begin{align*} \begin{aligned} & \left\lVert u \right\rVert_{Z'_{1}X(\Sigma, \mu)} = \left\lVert u^{\ast}_{\mu} \right\rVert_{Z'_{1}X(0, \infty)} = \left\lVert - \int_{t}^{\infty} \frac{d u^{\ast}_{\mu}}{d\tau}(\tau) \, d\tau \right\rVert_{Z'_{1}X(0, \infty)} \\ & = \left\lVert \int_{t}^{\infty} \left ( \tau^{\frac{D-1}{D}} \frac{d u^{\ast}_{\mu}}{d\tau}(\tau) \right ) \tau^{\frac{1-D}{D}} \, d\tau \right\rVert_{Z'_{1}X(0, \infty)} \leq \left\lVert t^{\frac{D-1}{D}} \frac{d u^{\ast}_{\mu}}{d t}(t) \right\rVert_{X(0, \infty)} \\ & \leq C_{3} \left\lVert \nabla u \right\rVert_{X(\Sigma, \mu)}. \end{aligned} \end{align*}

The second equality is true owing to the fact that $u^{\ast}_{\mu}$ is locally absolutely continuous on $(0, \infty)$ (see proposition 3.1) and the fact that $u^{\ast}_{\mu}(\infty) = 0$. The first inequality holds by virtue of (3.4) and the second one is true thanks to the Pólya–Szegő inequality (proposition 3.1). So, we proved (3.16) for m = 1.

Now assume that $1 \lt m \lt D$ is arbitrary and that (3.16) holds for m − 1. Choose an arbitrary function $u \in V_{0}^{m}X(\Sigma, \mu)$ and $i \in \{1, \dots, n\}$. Then the weak partial derivative $\frac{\partial u}{\partial x_{i}}$ belongs to $V_{0}^{m-1}X(\Sigma, \mu)$. So, we can use the induction hypothesis to obtain

\begin{align*} \left\lVert \frac{\partial u}{\partial x_{i}} \right\rVert_{Z'_{m-1}X(\Sigma, \mu)} \leq K_{m-1} \left\lVert \nabla^{m-1} \frac{\partial u}{\partial x_{i}} \right\rVert_{X(\Sigma, \mu)} \leq K_{m-1} \left\lVert \nabla^{m} u \right\rVert_{X(\Sigma, \mu)}. \end{align*}

It means that

(3.17)\begin{align} \left\lVert \nabla u \right\rVert_{Z'_{m-1}X(\Sigma, \mu)} \leq n K_{m-1} \left\lVert \nabla^{m} u \right\rVert_{X(\Sigma, \mu)} \lt \infty. \end{align}

It follows that u belongs to $V_{0}^{1}Z'_{m-1}X(\Sigma, \mu)$. Now it can be straightforwardly proved that

\begin{align*} t^{\frac{1}{D}-1}\chi_{(1, \infty)}(t) \in Z_{m-1}X(0, \infty), \end{align*}

(for details see [3.23, theorem 2.2]), which means that the mapping $u \mapsto \left\lVert t^{\frac{1}{D}} u^{\ast \ast}_{\mu_{D}}(t) \right\rVert_{Z_{m-1}X(0, \infty)} = \left\lVert u \right\rVert_{Z_{1}(Z_{m-1}X)(0, \infty)}$ is a rearrangement-invariant Banach function norm (cf. (3.15)). From the case m = 1 it now follows that

(3.18)\begin{align} \left\lVert u \right\rVert_{(Z_{1}(Z_{m-1}X))'(\Sigma, \mu)} \leq C_{3} \left\lVert \nabla u \right\rVert_{Z'_{m-1}X(\Sigma, \mu)}. \end{align}

Owing to [Reference Cianchi and Pick12, theorem 3.4] and [Reference Mihula29, proposition 5.1] (cf. [Reference Cianchi, Pick and Slavíková13, theorem 9.5]), we obtain

\begin{align*} \begin{aligned} & \left\lVert v \right\rVert_{Z_{1}(Z_{m-1}X)(\Sigma, \mu)} = \left\lVert t^{\frac{m-1}{D}} \left(\tau^{\frac{1}{D}} v^{\ast \ast}_{\mu}(\tau)\right)^{\ast \ast}(t) \right\rVert_{X'(0, \infty)} \\ & \leq C_{4} \left\lVert t^{\frac{m}{D}} v^{\ast \ast}_{\mu}(t) \right\rVert_{X'(0, \infty)} = C_{4} \left\lVert v \right\rVert_{Z_{m}X(\Sigma, \mu)} \end{aligned} \end{align*}

for every $v \in \mathcal{M}^{+}(\Sigma, \mu)$. From the previous inequality we obtain

(3.19)\begin{align} \left\lVert v \right\rVert_{Z'_{m}X(\Sigma, \mu)} \leq C_ {5} \left\lVert v \right\rVert_{(Z_{1}(Z_{m-1}X))'(\Sigma, \mu)} \end{align}

for every $v \in \mathcal{M}^{+}(\Sigma, \mu)$. By virtue of (3.17), (3.18), and (3.19), we obtain the fact that (3.16) holds for m.

At the end of the section, we prove proposition 3.1. The proof is based on the proofs of theorems [Reference Cianchi and Pick10, lemma 4.1], [Reference Cianchi and Pick11, lemma 3.3], and [Reference Talenti47, lemma 1.E].

Proof. Proof of Proposition 3.5

Firstly, we prove the proposition for nonnegative u. We start with the proof of the local absolute continuity of the function $u^{\ast}_{\mu}$. Let $\{(a_{m}, b_{m})\}_{m\in M}$ be a countable system of pairwise disjoint nonempty bounded intervals. For each $m \in M$ define the function $f_{m} \colon \mathbb{R} \rightarrow \mathbb{R}$ in the following way:

\begin{equation*} f_{m}(y) = \left \{ \begin{array}{ll} 0 & \text{if} \, \, y \leq u^{\ast}_{\mu}(b_{m}), \\ y - u^{\ast}_{\mu}(b_{m}) & \text{if} \, \, u^{\ast}_{\mu}(b_{m}) \lt y \lt u^{\ast}_{\mu}(a_{m}), \\ u^{\ast}_{\mu}(a_{m}) - u^{\ast}_{\mu}(b_{m}) & \text{if} \, \, u^{\ast}_{\mu}(a_{m}) \leq y. \\ \end{array} \right. \end{equation*}

For each $m \in M$ we now set $v_{m} = f_{m} \circ u$. It also holds that

(3.20)\begin{align} \mu(\{x \in \Sigma; u(x) \gt u^{\ast}_{\mu}(b_{m})\}) \lt \infty \end{align}

since $u \in V^{1}_{0}X(\Sigma, \mu)$. So, the function v_m is bounded and can be nonzero in a set of finite µ-measure only. We obtain the fact that $v_{m} \in L^{1}(\Sigma, \mu)$. Now we use the chain rule for Sobolev functions to obtain the fact that v_m is weakly differentiable in Σ and $\nabla v_{m} = \nabla u \chi_{\{u^{\ast}_{\mu}(b_{m}) \lt u \lt u^{\ast}_{\mu}(a_{m})\}}$ µ-almost everywhere in Σ. From this equality we get $\left\lvert \nabla v_{m} \right\rvert = 0$ µ-almost everywhere in the set $\{x \in\Sigma; u(x) \leq u^{\ast}_{\mu}(b_{m})\}$. We know that $\nabla u \in X(\Sigma, \mu)$. So, by virtue of (2.2) it follows that $\nabla u \in L^{1}(E, \mu)$ for every µ-measurable set $E \subseteq \Sigma, \mu(E) \lt \infty$. We can now again use (3.20) to obtain $\nabla v_{m} \in L^{1}(\Sigma, \mu)$.

Now we can use the coarea formula (see [Reference Maly, Swanson and Ziemer27], [Reference Swanson46]) for the functions v_m, $m \in M$, and the isoperimetric inequality (see [Reference Cabré, Ros-Oton and Serra7, theorem 1.3]). We obtain

(3.21)\begin{align} \begin{aligned} & \int_{\bigcup_{m \in M} \{u^{\ast}_{\mu}(b_{m}) \lt u \lt u^{\ast}_{\mu}(a_{m})\}} \left\lvert \nabla u(x) \right\rvert \, d\mu(x) \\ & \geq C_{iso} \sum\limits_{m \in M} \int^{u^{\ast}_{\mu}(a_{m}) - u^{\ast}_{\mu}(b_{m})}_{0} \mu(\{x \in \Sigma ; v_{m}(x) \gt t\})^{\frac{D-1}{D}} \, dt \\ & = C_{iso} \sum\limits_{m \in M} \int^{u^{\ast}_{\mu}(a_{m})}_{u^{\ast}_{\mu}(b_{m})} \mu(\{x \in \Sigma; u(x) \gt t \})^{\frac{D-1}{D}} \, dt, \end{aligned} \end{align}

where C_iso is the isoperimetric constant. Now we derive an upper estimate of

\begin{align*} \int_{\bigcup_{m \in M} \{u^{\ast}_{\mu}(b_{m}) \lt u \lt u^{\ast}_{\mu}(a_{m})\}} \left\lvert \nabla u(x) \right\rvert \, d\mu(x). \end{align*}

We obtain the fact that

(3.22)\begin{align} \begin{aligned} & \int_{\bigcup_{m \in M} \{u^{\ast}_{\mu}(b_{m}) \lt u \lt u^{\ast}_{\mu}(a_{m})\}} \left\lvert \nabla u(x) \right\rvert \, d\mu(x) \\ & \leq \int^{\sum\limits_{m \in M} \mu(\{u^{\ast}_{\mu}(b_{m}) \lt u \lt u^{\ast}_{\mu}(a_{m})\})}_{0} \left\lvert \nabla u \right\rvert^{\ast}_{\mu}(t) \, dt \leq \int^{\sum\limits_{m \in M} (b_{m} - a_{m})}_{0} \left\lvert \nabla u \right\rvert^{\ast}_{\mu}(t) \, dt. \end{aligned} \end{align}

The first inequality holds by virtue of the Hardy–Littlewood inequality (2.9). We can verify the last inequality in the following way. We have

\begin{align*} \begin{aligned} & \mu(\{u_{\mu}^{\ast}(b_{m}) \lt u \lt \mu_{\mu}^{\ast}(a_{m})\}) = \mu(\{u_{\mu}^{\ast}(b_{m}) \lt u \}) - \mu(\{u_{\mu}^{\ast}(a_{m}) \leq u\}) \\ & \leq b_{m} - a_{m}, \end{aligned} \end{align*}

where we used (2.6) and (2.7).

In the following part of the proof, we will assume that all the intervals $(a_{m}, b_{m}), m \in M$, are contained in an interval $[a, b] \subseteq (0, \infty)$. We prove that the function $u^{\ast}_{\mu}$ is absolutely continuous on the interval $[a, b]$. We can assume that $u_{\mu}^{\ast}(a) \gt 0$. We set

\begin{align*} K = \mu(\{x \in \Sigma; u(x) \geq u^{\ast}_{\mu}(a) \}). \end{align*}

Then we have $K \lt \infty$ since $u \in V^{1}_{0}X(\Sigma, \mu)$. Since $u_{\mu}^{\ast}(a) \gt 0$, we can use (2.7) to obtain K > 0. Owing to (3.21) we obtain the fact that

(3.23)\begin{align} \begin{aligned} & \int_{\bigcup_{m \in M} \{u^{\ast}_{\mu}(b_{m}) \lt u \lt u^{\ast}_{\mu}(a_{m})\}} \left\lvert \nabla u(x) \right\rvert \, d\mu(x) \\ & \geq C_{iso}\sum\limits_{m \in M} \int_{u^{\ast}_{\mu}(b_{m})}^{u^{\ast}_{\mu}(a_{m})} \mu(\{x \in \Sigma; u(x) \geq u^{\ast}_{\mu}(a)\})^{\frac{D-1}{D}} \, dt \\ & = C_{iso} K^{\frac{D-1}{D}} \sum\limits_{m \in M} (u^{\ast}_{\mu}(a_{m}) - u^{\ast}_{\mu}(b_{m})). \end{aligned} \end{align}

It follows that

(3.24)\begin{align} \begin{aligned} & \sum\limits_{m \in M} (u^{\ast}_{\mu}(a_{m}) - u^{\ast}_{\mu}(b_{m})) \\ & \leq C_{iso}^{-1} K^{\frac{1-D}{D}} \int_{\bigcup_{m \in M} \{u^{\ast}_{\mu}(b_{m}) \lt u \lt u^{\ast}_{\mu}(a_{m})\}} \left\lvert \nabla u(x) \right\rvert \, d\mu(x) \\ & \leq C_{iso}^{-1} K^{\frac{1-D}{D}} \int^{\sum\limits_{m \in M} (b_{m} - a_{m})}_{0} \left\lvert \nabla u \right\rvert^{\ast}_{\mu}(t) \, dt. \end{aligned} \end{align}

The first inequality holds due to (3.23). The second inequality holds by virtue of (3.22).

Next, we want to prove that

(3.25)\begin{align} \int_{0}^{t} \left\lvert \nabla u \right\rvert^{\ast}_{\mu} (\tau) \, d\tau \lt \infty \end{align}

for every $t \in (0, \infty)$. Since $\left\lvert \nabla u \right\rvert \in (L^{1} + L^{\infty})(\Sigma, \mu)$, it follows that $\left\lvert \nabla u \right\rvert^{\ast}_{\mu} \in L^{1}(0, t)$. So, (3.25) is true.

Since we know that $\left\lvert \nabla u \right\rvert^{\ast}_{\mu}$ is integrable over an arbitrary bounded interval $(0, t)$, we can use (3.24) to obtain the fact that the function $u^{\ast}_{\mu}$ is absolutely continuous on the interval $[a, b]$. It follows that it is locally absolutely continuous on the interval $(0, \infty)$, which is the desired result.

It remains to prove the inequality (3.1). From now we do not anymore assume that the intervals $(a_{m}, b_{m})$ are contained in $[a, b]$. Define the function $\phi \colon (0, \infty) \rightarrow [0, \infty)$ by 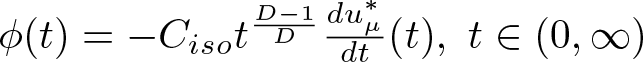$\phi(t) = - C_{iso} t^{\frac{D-1}{D}} \frac{du^{\ast}_{\mu}}{dt}(t), \, \, t \in (0, \infty)$. We show that

(3.26)\begin{equation} \int_{0}^{t}\phi^{\ast}(\tau) \; d\tau \leq \int_{0}^{t}\left\lvert \nabla u \right\rvert^{\ast}_{\mu} (\tau) \; d\tau, \, \, \, \, t \in (0, \infty). \end{equation}

Choose $t \in (0, \infty)$ arbitrarily. By virtue of (2.11), we know that it is enough to prove that for every measurable set $E \subseteq (0, \infty)$ such that $\lambda(E) = t$, it holds that

(3.27)\begin{align} \int_{E} \phi(\tau)\; d\tau \leq \int_{0}^{t}\left\lvert \nabla u \right\rvert^{\ast}_{\mu} (\tau) \; d\tau. \end{align}

Now choose an arbitrary $m \in M$. We have

(3.28)\begin{align} \int_{a_{m}}^{b_{m}} \phi(\tau) \, d\tau = - \int_{a_{m}}^{b_{m}} C_{iso} \tau^{\frac{D-1}{D}}\frac{du^{\ast}_{\mu}}{d\tau}(\tau) \, d\tau. \end{align}

Since the function $u^{\ast}_{\mu}$ is absolutely continuous and nonincreasing on the interval $[a_{m}, b_{m}]$, and the function $\tau \mapsto \mu(\{x \in \Sigma; u(x) \gt \tau\})^{\frac{D-1}{D}}, \tau \in (0, \infty),$ is nonnegative on the interval $(a_{m}, b_{m})$, we obtain the fact that (see [Reference Rudin42, page 156])

(3.29)\begin{align} \begin{aligned} & \int_{u^{\ast}_{\mu}(b_{m})}^{u^{\ast}_{\mu}(a_{m})} C_{iso} \mu(\{x \in \Sigma; u(x) \gt s \})^{\frac{D-1}{D}} \; ds \\ & = -\int_{a_{m}}^{b_{m}} C_{iso} \mu(\{x \in \Sigma; u(x) \gt u^{\ast}_{\mu}(\tau)\})^{\frac{D-1}{D}} \frac{du^{\ast}_{\mu}}{d\tau}(\tau) \; d\tau. \end{aligned} \end{align}

Now we observe that

(3.30)\begin{align} \begin{aligned} & \int_{a_{m}}^{b_{m}} C_{iso} \mu(\{x \in \Sigma; u(x) \gt u^{\ast}_{\mu}(\tau)\})^{\frac{D-1}{D}} \frac{du^{\ast}_{\mu}}{d\tau}(\tau) \; d\tau \\ & = \int_{a_{m}}^{b_{m}} C_{iso} \tau^{\frac{D-1}{D}} \frac{du^{\ast}_{\mu}}{d\tau}(\tau) \; d\tau. \end{aligned} \end{align}

Owing to (2.6) we know that for every $\tau \in (a_{m}, b_{m})$ it holds that

\begin{align*} \mu(\{x \in \Sigma; u(x) \gt u^{\ast}_{\mu}(\tau)\}) \leq \tau. \end{align*}

Choose an arbitrary $\tau \in (a_{m}, b_{m})$ such that the function $u^{\ast}_{\mu}$ is differentiable at τ. Assume that

\begin{align*} \mu(\{x \in \Sigma; u(x) \gt u^{\ast}_{\mu}(\tau)\}) \lt \tau. \end{align*}

Then there exists δ > 0, such that for every $s \in (\tau - \delta, \tau)$ it holds that

\begin{align*} \mu(\{x \in \Sigma; u(x) \gt u^{\ast}_{\mu}(\tau)\}) \lt s. \end{align*}

From this inequality, we obtain the fact that for each $s \in (\tau - \delta, \tau)$

\begin{align*} \begin{aligned} & u^{\ast}_{\mu}(s) = \inf\left\{\alpha \gt 0; \mu(\{x \in \Sigma; u(x) \gt \alpha\}) \leq s\right\} \\ & \leq u^{\ast}_{\mu}(\tau). \end{aligned} \end{align*}

Because the function  $u^{\ast}_{\mu}$ is nonincreasing it holds that $u^{\ast}_{\mu}(s) = u^{\ast}_{\mu}(\tau)$ for all $s \in (\tau - \delta, \tau)$. Since the function $u^{\ast}_{\mu}$ is differentiable at τ, we have $\frac{du^{\ast}_{\mu}}{d\tau}(\tau) = 0$. So, we have just proved (3.30). By (3.28), (3.29), and (3.30) we have

(3.31)\begin{align} \int_{a_{m}}^{b_{m}} \phi(\tau) \, d\tau = \int_{u^{\ast}_{\mu}(b_{m})}^{u^{\ast}_{\mu}(a_{m})} C_{iso} \mu(\{x \in \Sigma; u(x) \gt \tau \})^{\frac{D-1}{D}} \; d\tau. \end{align}

Now we obtain

(3.32)\begin{align} \begin{aligned} & \int_{\bigcup_{m \in M}(a_{m}, b_{m})} \phi(\tau) \, d\tau = \sum\limits_{m \in M} \int_{u^{\ast}_{\mu}(b_{m})}^{u^{\ast}_{\mu}(a_{m})} C_{iso} \mu(\{x \in \Sigma; u(x) \gt \tau \})^{\frac{D-1}{D}} \; d\tau \\ & \leq \int_{\bigcup_{m \in M} \{u^{\ast}_{\mu}(b_{m}) \lt u \lt u^{\ast}_{\mu}(a_{m})\}} \left\lvert \nabla u(x) \right\rvert \, d\mu(x) \\ & \leq \int^{\sum\limits_{m \in M} (b_{m} - a_{m})}_{0} \left\lvert \nabla u \right\rvert^{\ast}_{\mu}(\tau) \, d\tau. \end{aligned} \end{align}

The equality holds thanks to (3.31) and to the fact that all the intervals $(a_{m}, b_{m}), m \in M$, are pairwise disjoint. The first inequality holds thanks to (3.21). The second inequality is true by virtue of (3.22). Now choose an arbitrary measurable set $E \subseteq (0, \infty), \lambda(E) = t$. Then for every ɛ > 0, there exists a countable system $\{(a_{m}, b_{m})\}_{m \in M}$ of pairwise disjoint nonempty bounded intervals such that

\begin{align*} E \subseteq \bigcup_{m \in M} (a_{m}, b_{m}) \; \; \; \text{and} \; \; \; \lambda\left(\bigcup_{m \in M} (a_{m}, b_{m}) \setminus E \right) \lt \varepsilon. \end{align*}

So, choose an arbitrary ɛ > 0, and let $\{(a_{m}, b_{m})\}_{m \in M}$ be such a system of intervals. From (3.32) we obtain

\begin{align*} \int_{E} \phi(\tau)\, d\tau \leq \int_{\bigcup_{m \in M}(a_{m}, b_{m})} \phi(\tau) \, d\tau \leq \int^{t + \varepsilon}_{0} \left\lvert \nabla u \right\rvert^{\ast}_{\mu}(\tau) \, d\tau. \end{align*}

We already know from (3.25) that for all $s \in (0, \infty)$ the function $\left\lvert \nabla u \right\rvert^{\ast}_{\mu}$ is integrable over $(0, s)$. So, we obtain

\begin{align*} \int_{E} \phi(\tau) \, d\tau \leq \int^{t}_{0} \left\lvert \nabla u \right\rvert^{\ast}_{\mu}(\tau) \, d\tau. \end{align*}

This means that (3.27) is true. So, we have just proved (3.26). The inequality (3.1) now follows from the Hardy–Littlewood–Pólya principle (2.10).

We have proved the proposition for nonnegative u. Now let $u \in V_{0}^{1}X(\Sigma, \mu)$ be general. It is true that $\left\lvert u \right\rvert \in V_{0}^{1}X(\Sigma, \mu)$. So, the proposition holds for $\left\lvert u \right\rvert$. Since $u^{\ast}_{\mu} = \left\lvert u \right\rvert^{\ast}_{\mu}$, the proposition holds also for the function u.

3.2. Optimality

In this subsection, we will describe the smallest target space in the inequality (3.2) among all spaces $Y(\Sigma, \mu)$ for a given space $X(\Sigma, \mu)$ and the largest domain space in the inequality (3.2) among all spaces $X(\Sigma, \mu)$ for a given space $Y(\Sigma, \mu)$.

Firstly we describe the optimal target space in the following theorem.

Theorem 3.8 Let X be a rearrangement-invariant space over $(\Sigma, \mu)$. Assume that

(3.33)\begin{align} t^{\frac{m}{D}-1}\chi_{(1, \infty)}(t) \in X'(0, \infty). \end{align}

Then there exists a positive constant C, which depends only on m and on D, such that

(3.34)\begin{align} \left\lVert u \right\rVert_{Z'_{m}X(\Sigma, \mu)} \leq C \left\lVert \nabla^{m} u \right\rVert_{X(\Sigma, \mu)}, \, \, \, \, u \in V^{m}_{0}X(\Sigma, \mu), \end{align}

where the space $Z'_{m}X(\Sigma, \mu)$ is the associate space to the space $Z_{m}X(\Sigma, \mu)$, which is defined by (3.14). Moreover, the space $Z'_{m}X(\Sigma, \mu)$ is the optimal space in the previous inequality among all rearrangement-invariant spaces in the following way. If $Y(\Sigma, \mu)$ is a rearrangement-invariant space satisfying

(3.35)\begin{align} \left\lVert u \right\rVert_{Y(\Sigma, \mu)} \leq \widetilde{C} \left\lVert \nabla^{m} u \right\rVert_{X(\Sigma, \mu)}, \, \, \, \, u \in V^{m}_{0}X(\Sigma, \mu), \end{align}

with a positive constant $\widetilde{C}$ that does not depend on u, then

(3.36)\begin{align} Z'_{m}X(\Sigma, \mu) \hookrightarrow Y(\Sigma, \mu). \end{align}

On the other hand, if (3.33) is not true, then the inequality (3.35) does not hold for any rearrangement-invariant space $Y(\Sigma, \mu)$.

Proof. The inequality (3.34) follows from the proof of proposition 3.7. Assume that (3.33) holds and that $Y(\Sigma, \mu)$ is a rearrangement-invariant space satisfying (3.35). Owing to proposition 3.5 we obtain the fact that $Y(\Sigma, \mu)$ satisfies the inequality (3.3). It means that we can use the first inequality in (3.16) to obtain the embedding (3.36).

Now, assume that (3.33) is not true. Then there does not exist any rearrangement-invariant space $Y(\Sigma, \mu)$ such that (3.3) holds thanks to remark 3.4. Then by proposition 3.5 there is not any rearrangement-invariant space $Y(\Sigma, \mu)$ such that (3.35) is true.

Let Y be a rearrangement-invariant space over $(\Sigma, \mu)$. Assume that

(3.37)\begin{align} \inf\limits_{t \in [1, \infty)} \frac{t^{1-\frac{m}{D}}}{\varphi_{Y}(t)} \gt 0, \end{align}

where φ_Y is the fundamental function of the space $Y(\Sigma, \mu)$. Then the mapping $\nu_{m, Y} \colon \mathcal{M}^{+}(\Sigma, \mu) \rightarrow [0, \infty]$ defined by

\begin{align*} \nu_{m, Y}(u) = \sup\limits_{v \sim u, v \geq 0} \left\lVert \int_{t}^{\infty} v(\tau) \tau^{\frac{m}{D} -1} \, d\tau \right\rVert_{Y(0, \infty)}, \end{align*}

where the supremum is taken over all functions $v \in \mathcal{M}^{+}(0, \infty)$ equimeasurable with u, is a rearrangement-invariant Banach function norm (for the proof see [Reference Edmunds, Mihula, Musil and Pick18, theorem 4.1]). The respective space will be denoted by $U_{m}Y(\Sigma, \mu)$.

Now we can finally describe the largest domain space.

Theorem 3.9 Let Y be a rearrangement-invariant space over $(\Sigma, \mu)$. Assume that the condition (3.37) is satisfied. Then there exists a positive constant C, which depends only on m and on D, such that

(3.38)\begin{align} \left\lVert u \right\rVert_{Y(\Sigma, \mu)} \leq C \left\lVert \nabla^{m} u \right\rVert_{U_{m}Y(\Sigma, \mu)}, \, \, \, \, u \in V^{m}_{0}U_{m}Y(\Sigma, \mu). \end{align}

Moreover, the space $U_{m}Y(\Sigma, \mu)$ is the optimal space in the previous inequality among all rearrangement-invariant spaces in the following way. If $X(\Sigma, \mu)$ is a rearrangement-invariant space satisfying

(3.39)\begin{align} \left\lVert u \right\rVert_{Y(\Sigma, \mu)} \leq \widetilde{C} \left\lVert \nabla^{m} u \right\rVert_{X(\Sigma, \mu)}, \, \, \, \, u \in V^{m}_{0}X(\Sigma, \mu), \end{align}

with a positive constant $\widetilde{C}$ that does not depend on u, then

(3.40)\begin{align} X(\Sigma, \mu) \hookrightarrow U_{m}Y(\Sigma, \mu). \end{align}

On the other hand, if (3.37) is not true, then the inequality (3.39) does not hold for any rearrangement-invariant space $X(\Sigma, \mu)$.

Proof. Let $f \in \mathcal{M}^{+}(0, \infty)$. Then

\begin{align*} \begin{aligned} & \left\lVert \int_{t}^{\infty} f(\tau) \tau^{\frac{m}{D} -1} \, d\tau \right\rVert_{Y(0, \infty)} \leq \sup\limits_{g \sim f, g \geq 0} \left\lVert \int_{t}^{\infty} g(\tau) \tau^{\frac{m}{D} -1} \, d\tau \right\rVert_{Y(0, \infty)} \\ & = \left\lVert f \right\rVert_{U_{m}Y(0, \infty)}, \end{aligned} \end{align*}

so, the inequality (3.38) follows from proposition 3.7.

Now, assume that $X(\Sigma, \mu)$ is a rearrangement-invariant space satisfying (3.39) and let $f, g \in \mathcal{M}^{+}(0, \infty)$ be equimeasurable. Then, by virtue of proposition 3.5, we obtain

\begin{align*} \begin{aligned} & \left\lVert f \right\rVert_{U_{m}Y(0, \infty)} = \sup\limits_{g \sim f, g \geq 0} \left\lVert \int_{t}^{\infty} g(\tau) \tau^{\frac{m}{D} -1} \, d\tau \right\rVert_{Y(0, \infty)} \leq K \sup\limits_{g \sim f, g \geq 0} \left\lVert g \right\rVert_{X(0, \infty)} \\ & = K \left\lVert f \right\rVert_{X(0, \infty)}. \end{aligned} \end{align*}

It means that (3.40) is true.

On the other hand, if the condition (3.37) is not satisfied, then it can be proved analogously as in the proof of [Reference Edmunds, Mihula, Musil and Pick18, theorem 4.1] that for each $u \in \mathcal{M}^{+}(\Sigma, \mu)$ such that $u^{\ast}_{\mu} = \chi_{(0, 1)}$ it holds that

\begin{align*} \nu_{m, Y}(u) = \sup\limits_{v \sim u, v \geq 0} \left\lVert \int_{t}^{\infty} v(\tau) \tau^{\frac{m}{D} -1} \, d\tau \right\rVert_{Y(0, \infty)} = \infty. \end{align*}

By the nontriviality axiom of the Banach function norm, we know that u belongs to an arbitrary rearrangement-invariant space $X(\Sigma, \mu)$. So, we obtain the fact that (3.3) does not hold for any rearrangement-invariant space $X(\Sigma, \mu)$. It means that the inequality (3.39) does not hold for any rearrangement-invariant space $X(\Sigma, \mu)$ owing to the reduction principle (theorem 3.2).

4. Examples

In this section, we will show some examples. We will describe the optimal space $Z'_{m}(\Sigma, \mu)$ when $X(\Sigma, \mu)$ is a Lorentz–Karamata space $L^{p, q, b}(\Sigma, \mu)$ with $p \in \left[1, \frac{D}{m}\right]$.

Now we introduce the theory of Lorentz–Karamata spaces. For proofs and more information see [Reference Edmunds and Evans16, Reference Edmunds, Kerman and Pick17, Reference Neves34, Reference Peša39]. The class of Lorentz–Karamata spaces contains a lot of classical function spaces, such as the Lebesgue spaces, Lorentz spaces, Lorentz-Zygmund spaces or Orlicz spaces of the type $L_{\exp}$ or $L^{p}(\log L)^{\alpha}$.

We start with the concept of slowly varying functions. Let $f, g \colon (0, \infty) \to (0, \infty)$ be functions. We say that the function f is equivalent to the function g if there exist constants $C_{1} \gt 0$ and $C_{2} \gt 0$ such that $C_{2} g(t) \leq f(t) \leq C_{1} g(t)$ for every $t \in (0, \infty)$.

We say that a measurable function $b \colon (0, \infty) \rightarrow (0, \infty)$ is slowly varying if for every ɛ > 0 there exists a nondecreasing function φ_ɛ and a nonincreasing function $\varphi_{- \varepsilon}$ such that $t^{\varepsilon}b(t)$ is equivalent to $\varphi_{\varepsilon}(t)$ on $(0, \infty)$ and that $t^{- \varepsilon}b(t)$ is equivalent to $\varphi_{- \varepsilon}$ on $(0, \infty)$. A positive measurable function on $(0, \infty)$ that is equivalent to a positive constant function is a trivial example of a slowly varying function. Functions of logarithmic type constitute less trivial and very important examples of slowly varying functions. For $k\in{\mathbb{N}}$, the function $\ell_k\colon (0, \infty) \to (0, \infty)$ defined as

\begin{equation*} \ell_k(t) = \begin{cases} 1 + |\log t| \quad &\text{if}\ k = 1, \\ 1 + \log \ell_{k - 1}(t) \quad &\text{if}\ k \gt 1, \end{cases} \end{equation*}

$t\in(0, \infty)$, is slowly varying. More generally, the function $\ell_k^{\mathbb{A}}\colon (0, \infty) \to (0, \infty)$ defined as

\begin{equation*} \ell_k^{\mathbb{A}}(t) = \begin{cases} \ell_k^{\alpha_0}(t) \quad &\text{if}\ t\in(0, 1), \\ \ell_k^{\alpha_\infty}(t) \quad &\text{if}\ t\in[1, \infty), \end{cases} \end{equation*}

where $\mathbb {A} = (\alpha_0, \alpha_\infty)\in{\mathbb{R}}^2$, is slowly varying.

Note that by b ⁻¹ we will denote the function $\frac{1}{b}$.

Now we finally introduce Lorentz–Karamata spaces. Let b be a slowly varying function. Let $p, q \in [1, \infty]$. We define the Lorentz–Karamata functionals by

\begin{align*} \left\lVert f \right\rVert _{p, q, b} = \left\lVert t^{\frac{1}{p}-\frac{1}{q}} b(t) f^{\ast}_{\mu}(t) \right\rVert_{L^{q}(0, \infty)} \end{align*}

and by

\begin{align*} \left\lVert f \right\rVert _{(p, q, b)} = \left\lVert t^{\frac{1}{p}-\frac{1}{q}} b(t) f^{\ast \ast}_{\mu}(t) \right\rVert_{L^{q}(0, \infty)} \end{align*}

for every $f \in \mathcal{M}(\Sigma, \mu)$. The Lorentz–Karamata spaces are defined as

\begin{align*} L^{p, q, b}(\Sigma, \mu) = \left\{f \in \mathcal{M}(\Sigma, \mu); \left\lVert f \right\rVert _{p, q, b} \lt \infty \right\} \end{align*}

and as

\begin{align*} L^{(p, q, b)}(\Sigma, \mu) = \left\{f \in \mathcal{M}(\Sigma, \mu); \left\lVert f \right\rVert _{(p, q, b)} \lt \infty \right\}. \end{align*}

If we take p = q and $b\equiv1$ in the definition of $L^{p, q, b}(\Sigma, \mu)$, we obtain the Lebesgue spaces. More generally, we obtain the Lorentz spaces $L^{p,q}(\Sigma, \mu)$ and $L^{(p,q)}(\Sigma, \mu)$ by taking $b\equiv 1$. Furthermore, Lorentz–Karamata spaces also include the Lorentz–Zygmund spaces, which were thoroughly studied in [Reference Opic and Pick36]. We obtain them by taking slowly varying functions of logarithmic type as above.

Even though we refer to Lorentz–Karamata spaces as spaces, they are not always rearrangement-invariant spaces.

The space $L^{(p, q, b)}(R, \mu)$ is a rearrangement-invariant Banach function space if and only if $q\in[1, \infty]$ and one of the following conditions holds:

1. (i) $p \in (1, \infty)$,

2. (ii) p = 1 and $\left\lVert t^{-\frac{1}{q}} b(t) \chi_{(1, \infty)}(t) \right\rVert_{L^{q}(0, \infty)} \lt \infty$,

3. (iii) $p = \infty$ and $\left\lVert t^{-\frac{1}{q}} b(t) \chi_{(0, 1)}(t) \right\rVert_{L^{q}(0, \infty)} \lt \infty$.

The Lorentz–Karamata functional $\left\lVert \cdot \right\rVert_{p, q, b}$ is equivalent to a rearrangement-invariant Banach function norm if and only if $q\in[1, \infty]$ and one of the following conditions is satisfied:

1. (i) $p \in (1, \infty)$,

2. (ii) $p = q =1$ and b is equivalent to a nonincreasing function on $(0, \infty)$,

3. (iii) $p = \infty$ and $\left\lVert t^{-\frac{1}{q}} b(t) \chi_{(0, 1)}(t) \right\rVert_{L^{q}(0, \infty)} \lt \infty$.

In what follows we will also use the fact that if p > 1, then the spaces $L^{p, q, b}(\Sigma, \mu)$ and $L^{(p, q, b)}(\Sigma, \mu)$ are equivalent. Note that for an arbitrary slowly varying function b, there exists a slowly varying function c that is equivalent to b on $(0, \infty)$ and that has continuous classical derivatives of all orders, i.e., $c \in \mathcal{C}^{\infty}(0, \infty)$ (see [Reference Peša40]). This means that we can assume without loss of generality that the slowly varying function in the definition of the Lorentz–Karamata space is always smooth.

Now we describe the optimal target space for the Lorentz–Karamata space $L^{p, q, b}(\Sigma, \mu)$.

The function space $\Lambda^1(d')(\Sigma, \mu)$ is an example of a classical Lorentz space (e.g., see [Reference Pick, Kufner, John and Fučík41, Chapter 10]). It is defined as the collection of all functions $f\in\mathcal M(\Sigma, \mu)$ such that $\|d'(t)f_{\mu}^*(t)\|_{L^1(0, \infty)} \lt \infty$.

Proof. First of all, we prove that the space $Z'_{m}X(\Sigma, \mu)$ is the optimal space. Owing to [Reference Peša39, section 3.7] we obtain the fact that the space $\left(L^{p, q, b}(\Sigma, \mu) \right)'$ is equivalent to the space $L^{p', q', b^{-1}}(\Sigma, \mu)$. So, in the view of theorem 3.8, it is enough to prove that

(4.3)\begin{align} \left\lVert t^{\frac{m}{D}-1}\chi_{(1, \infty)}(t) \right\rVert_{L^{p', q', b^{-1}}(0, \infty)} = \left\lVert t^{\frac{1}{p'}-\frac{1}{q'}} (t+1)^{\frac{m}{D}-1} b^{-1}(t) \right\rVert_{L^{q'}(0, \infty)} \lt \infty. \end{align}

If $p \in [1, \frac{D}{m})$, then (4.3) follows from the basic properties of slowly varying functions (see [Reference Peša39, lemma 2.16]). If $p = \frac{D}{m}$ then (4.3) follows from (4.1).

It remains to describe the space $Z'_{m}X(\Sigma, \mu)$. Firstly, assume that $p \in \left (1, \frac{D}{m} \right)$. Owing to [Reference Peša39, section 3.5] the maximal nonincreasing operator P_µ is bounded on the space $L^{p, q, b}(0, \infty)$. Now we show that the norm of the space $Z_{m}X(\Sigma, \mu)$ is equivalent to the functional

(4.4)\begin{align} u \mapsto \left\lVert t^{\frac{1}{q}-\frac{1}{p}} b^{-1}(t) \int_{t}^{\infty} u^{\ast \ast}_{\mu} (\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{L^{q'}(0, \infty)}, \, \, \, \, u \in \mathcal{M}^{+}(\Sigma, \mu). \end{align}

By virtue of [Reference Peša39, section 3.7] we can rewrite the functional in the form

\begin{align*} \begin{aligned} & \left\lVert \int_{t}^{\infty}u^{\ast \ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{(L^{p, q, b})'(0, \infty)} \\ & = \sup\limits_{\left\lVert g \right\rVert_{L^{p, q, b}(0, \infty)} \leq 1} \int_{0}^{\infty} g^{\ast}(t) \int_{t}^{\infty}u^{\ast \ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau dt \\ & = \sup\limits_{\left\lVert g \right\rVert_{L^{p, q, b}(0, \infty)} \leq 1} \int_{0}^{\infty}u^{\ast \ast}_{\mu}(\tau) \tau^{\frac{m}{D}} g^{\ast \ast}(\tau) \, d\tau. \end{aligned} \end{align*}

By virtue of (2.13), we obtain the first inequality

\begin{align*} \begin{aligned} & \left\lVert u \right\rVert_{Z_{m}X(\Sigma, \mu)} = \left\lVert t^{\frac{m}{D}} u^{\ast \ast}_{\mu}(t) \right\rVert_{(L^{p, q, b})'(0, \infty)} \\ & \leq 4 \sup\limits_{\left\lVert g \right\rVert_{L^{p, q, b}(0, \infty)} \leq 1} \int_{0}^{\infty} g^{\ast \ast}(\tau) \tau^{\frac{m}{D}} u^{\ast \ast}_{\mu}(\tau) \, d\tau, \end{aligned} \end{align*}

while the second inequality follows directly from the boundedness of the operator P_µ. The norm of the associate space $\left( L^{\frac{Dp}{D-mp}, q, b}(\Sigma, \mu) \right)'$ is equivalent to the functional

(4.5)\begin{align} u \mapsto \left\lVert t^{\frac{1}{q} - \frac{1}{p} + \frac{m}{D}} b^{-1}(t) u^{\ast \ast}_{\mu}(t) \right\rVert_{L^{q'}(0, \infty)}, \, \, \, \, u \in \mathcal{M}^{+}(\Sigma, \mu), \end{align}

owing to [Reference Peša39, section 3.7]. It remains to prove that the functionals (4.4) and (4.5) are equivalent. Since

\begin{align*} t^{\frac{m}{D}} = \frac{m}{D \left(1-2^{-\frac{m}{D}}\right)} \int_{\frac{t}{2}}^{t} \tau^{\frac{m}{D}-1} \, d\tau, \end{align*}

we obtain

(4.6)\begin{align} \begin{aligned} & t^{\frac{m}{D}} u^{\ast \ast}_{\mu}(t) \leq \frac{m}{D \left(1-2^{-\frac{m}{D}}\right)} \int_{\frac{t}{2}}^{t} u^{\ast \ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau \\ & \leq \frac{m}{D \left(1-2^{-\frac{m}{D}}\right)} \int_{\frac{t}{2}}^{\infty} u^{\ast \ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau \end{aligned} \end{align}

for every $u \in \mathcal{M}^{+}(\Sigma, \mu)$ and for every $t \in (0, \infty)$. By virtue of (4.6) and [Reference Peša39, lemma 2.16] , we obtain the existence of a positive constant C ₁ such that

(4.7)\begin{align} t^{\frac{1}{q} - \frac{1}{p} + \frac{m}{D}} b^{-1}(t) u^{\ast \ast}_{\mu}(t) \leq \frac{2^{\frac{1}{q}-\frac{1}{p}}mC_{1}}{D \left(1-2^{-\frac{m}{D}}\right)} \left( \frac{t}{2} \right)^{\frac{1}{q}-\frac{1}{p}} b^{-1}\left(\frac{t}{2} \right) \int_{\frac{t}{2}}^{\infty} u^{\ast \ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau \end{align}

for every $u \in \mathcal{M}^{+}(\Sigma, \mu)$ and for every $t \in (0, \infty)$. Owing to (2.14) and (4.7) we obtain the existence of a positive constant C ₂ such that

\begin{align*} \left\lVert t^{\frac{1}{q} - \frac{1}{p} + \frac{m}{D}} b^{-1}(t) u^{\ast \ast}_{\mu} \right\rVert_{L^{q'}(0, \infty)} \leq C_{2} \left\lVert t^{\frac{1}{q}-\frac{1}{p}} b^{-1}(t) \int_{t}^{\infty} u^{\ast \ast}_{\mu} (\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{L^{q'}(0, \infty)} \end{align*}

for every $u \in \mathcal{M}^{+}(\Sigma, \mu)$. Now we prove the opposite inequality, i.e., we prove that there exists a constant $K_{1} \gt 0$ such that

(4.8)\begin{align} \begin{aligned} & \left\lVert t^{\frac{1}{q}-\frac{1}{p}} b^{-1}(t) \int_{t}^{\infty} u^{\ast \ast}_{\mu} (\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{L^{q'}(0, \infty)} \\ & \leq K_{1} \left\lVert t^{\frac{1}{q} - \frac{1}{p} + \frac{m}{D}} b^{-1}(t) u^{\ast \ast}_{\mu}(t) \right\rVert_{L^{q'}(0, \infty)}, \end{aligned} \end{align}

for every $u \in \mathcal{M}^{+}(\Sigma, \mu)$. By virtue of the weighted Hardy inequality [Reference Muckenhoupt32, theorem 2], the inequality (4.8) is valid if and only if

\begin{align*} \sup\limits_{t \in (0, \infty)} \left\lVert \tau^{\frac{1}{q}-\frac{1}{p}} b^{-1}(\tau) \right\rVert_{L^{q'}(0, t)} \left\lVert \tau^{\frac{1}{p} - \frac{1}{q} - 1} b(\tau) \right\rVert_{L^{q}(t, \infty)} \lt \infty, \end{align*}

which is not hard to verify (see [Reference Peša39, lemma 2.16]).

It remains to derive the description of the space $Z'_{m}X(\Sigma, \mu)$ in case of $p = q = 1$ and b is equivalent to a nonincreasing function on $(0, \infty)$ or $ p = \frac{D}{m}$ and $q \in [1, \infty]$. Thanks to [Reference Peša39, section 3.5 and section 3.7] it is sufficient to prove that $Z_{m}X(\Sigma, \mu)$ with the norm satisfying

\begin{align*} \left\lVert u \right\rVert_{Z_{m}X(\Sigma, \mu)} = \left\lVert t^{\frac{m}{D}} u^{\ast \ast}_{\mu}(t) \right\rVert_{L^{p', q', b^{-1}}(0, \infty)} \end{align*}

for each $u \in \mathcal{M}^{+}(\Sigma, \mu)$ is equivalent to $L^{(r, q', b^{-1})}(\Sigma, \mu)$, where r = 1 if $p = \frac{D}{m}$ and $r = \frac{D}{m}$ if p = 1. Note that in the case of $p = \frac{D}{m}, q = 1$, we also exploit the fact that d ⁻¹ is locally absolutely continuous on $(0, \infty)$. Now, for every $u \in \mathcal{M}^{+}(\Sigma, \mu)$ we have

\begin{align*} \begin{aligned} & \left\lVert u\right\rVert_{Z_{m}X(\Sigma, \mu)} = \left\lVert t^{\frac{m}{D}} u^{\ast \ast}_{\mu}(t) \right\rVert_{L^{p', q', b^{-1}}(0, \infty)} \leq \left\lVert \sup\limits_{\tau \in [t, \infty)} \tau^{\frac{m}{D}} u^{\ast \ast}_{\mu}(\tau) \right\rVert_{L^{p', q', b^{-1}}(0, \infty)} \notag \\ & = \left\lVert t^{\frac{1}{p'} - \frac{1}{q'}} b^{-1}(t) \sup\limits_{\tau \in [t, \infty)} \tau^{\frac{m}{D}} u^{\ast \ast}_{\mu}(\tau) \right\rVert_{L^{q'}(0, \infty)} \\ & \leq K_{2} \left\lVert t^{\frac{1}{r} - \frac{1}{q'}} b^{-1}(t) u^{\ast \ast}_{\mu}(t) \right\rVert_{L^{q'}(0, \infty)} \notag = \left\lVert u \right\rVert_{L^{(r, q', b^{-1})}(\Sigma, \mu)}, \end{aligned} \end{align*}

where K ₂ is a positive constant that does not depend on u. If $p = q = 1$, then the last inequality follows from the fact that b ⁻¹ is equivalent to a nonincreasing function on $(0, \infty)$. If $p = \frac{D}{m}, q = 1$, then the last inequality follows from the fact that $t^{1 - \frac{m}{D}}b^{-1}(t)$ is equivalent to a nonincreasing function on $(0, \infty)$. If q > 1, then we use [Reference Gogatishvili, Opic and Pick19, theorem 3.2] to prove the last inequality. Owing to this theorem the last inequality is valid if and only if for every $t \in (0, \infty)$ it is true that

\begin{align*} t^{\frac{m}{D}} \left\lVert \tau^{\frac{D-m}{D} - \frac{1}{q'}} b^{-1}(\tau) \right\rVert_{L^{q'}(0, t)} \leq K \left\lVert \tau^{1 - \frac{1}{q'}} b^{-1}(\tau) \right\rVert_{L^{q'}(0, t)}, \end{align*}

where K > 0 is a constant that does not depend on t, which is satisfied thanks to [Reference Peša39, lemma 2.16]. So, we have proved the first inequality. For every $u \in \mathcal{M}^{+}(\Sigma, \mu)$ we have now

\begin{align*} \begin{aligned} & \left\lVert u \right\rVert_{L^{(r, q', b^{-1})}(\Sigma, \mu)} = \left\lVert t^{\frac{1}{r} - \frac{1}{q'}} b^{-1}(t) u^{\ast \ast}_{\mu}(t) \right\rVert_{L^{q'}(0, \infty)} \\ & \leq \left\lVert t^{\frac{1}{r} - \frac{m}{D} - \frac{1}{q'}} b^{-1}(t) \sup\limits_{\tau \in [t, \infty)} \tau^{\frac{m}{D}} u^{\ast \ast}_{\mu}(\tau) \right\rVert_{L^{q'}(0, \infty)} \\ & = \left\lVert \sup\limits_{\tau \in [t, \infty)} \tau^{\frac{m}{D}} u^{\ast \ast}_{\mu}(\tau) \right\rVert_{L^{p', q', b^{-1}}(0, \infty)} \leq C \left\lVert t^{\frac{m}{D}} u^{\ast \ast}_{\mu}(t) \right\rVert_{L^{p', q', b^{-1}}(0, \infty)} \\ & = C \left\lVert u\right\rVert_{Z_{m}X(\Sigma, \mu)}, \end{aligned} \end{align*}

where C is a positive constant that does not depend on u. To prove the second inequality, we exploit [Reference Edmunds, Mihula, Musil and Pick18, lemma 4.10] since the function $t \mapsto t^{\frac{m}{D}}, t \in [0, \infty),$ is quasiconcave.

Finally, we describe the optimal domain space in the view of theorem 3.9 for a given Lorentz–Karamata space.

Proof. For every $f \in \mathcal{M}(0, \infty)$, we define the operator $T_{\frac{m}{D}}(f)$ by

\begin{align*} T_{\frac{m}{D}}(f)(t) = t^{-\frac{m}{D}} \sup\limits_{\tau \in [t, \infty)} \tau^{\frac{m}{D}} f^{\ast}_{\mu}(\tau), \,\,\,\, t \in (0, \infty). \end{align*}

Owing to [Reference Edmunds, Mihula, Musil and Pick18, theorem 4.7 and remark 4.8], we obtain the fact that the operator $T_{\frac{m}{D}} \colon Y'(0, \infty) \to Y'(0, \infty)$ is bounded if and only if the norm of the space $U_{m}Y(\Sigma, \mu)$ is equivalent to

(4.9)\begin{align} \left\lVert \int_{t}^{\infty} f^{\ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{Y(0, \infty)}. \end{align}

So, we prove the fact that the operator $T_{\frac{m}{D}}$ is bounded on the space $\left(L^{p, q, b}(0, \infty)\right)'$. Firstly, assume that $p \lt \infty$ or $q \lt \infty$. We use [Reference Peša39, section 3.7] to describe the space $\left(L^{p, q, b}(0, \infty)\right)'$. If $p \in \left [\frac{D}{D-m}, \infty \right) $, then we obtain the fact that $\left(L^{p, q, b}(\Sigma, \mu) \right)'$ is equivalent to $ L^{(p', q', b^{-1})}(\Sigma, \mu)$. If $p = \infty$ and $q \in [1, \infty)$, then $\left(L^{\infty, q, b}(\Sigma, \mu) \right)'$ is equivalent to $L^{(1, q', a)}(\Sigma, \mu)$, where a is the slowly varying function given by

\begin{align*} a(t) = \left( \int\limits_{0}^{t} \tau^{-1} b^{q}(\tau) \, d\tau \right)^{-1} b^{q-1}(t), \,\,\,\, t \in (0, \infty). \end{align*}

In what follows we will write c instead of b ⁻¹ and a since the estimates are the same in both cases. Then, for every $f \in \mathcal{M}(0, \infty)$, we obtain

(4.10)\begin{align} \begin{aligned} & \left\lVert T_{\frac{m}{D}}(f) \right\rVert_{L^{(p', q', c)}(0, \infty)} = \left\lVert t^{\frac{1}{p'} - \frac{1}{q'}} c(t) \left(T_{\frac{m}{D}}(f)\right)^{\ast \ast}_{\mu}(t) \right\rVert_{L^{q'}(0, \infty)} \\ & \leq C_{2} \left\lVert t^{\frac{1}{p'} - \frac{1}{q'}} c(t) T_{\frac{m}{D}}(f^{\ast \ast}_{\mu})(t) \right\rVert_{L^{q'}(0, \infty)} \\ & = C_{2} \left\lVert t^{\frac{1}{p'} - \frac{1}{q'}} c(t) t^{-\frac{m}{D}} \sup\limits_{\tau \in [t, \infty)} \tau^{\frac{m}{D}} f^{\ast \ast}_{\mu}(\tau) \right\rVert_{L^{q'}(0, \infty)} \\ & \leq C_{3} \left\lVert t^{\frac{1}{p'} - \frac{1}{q'}} c(t) f^{\ast \ast}_{\mu}(t) \right\rVert_{L^{q'}(0, \infty)} = C_{3} \left\lVert f \right\rVert_{L^{(p', q', c)}(0, \infty)}. \end{aligned} \end{align}

The first inequality is true thanks to [Reference Musil and Olhava33, lemma 4.1]. Now we prove the second inequality. If q > 1, then we use [Reference Gogatishvili, Opic and Pick19, theorem 3.2] to prove it. Owing to this theorem the second inequality is valid if and only if for every $t \in (0, \infty)$ it is true that

(4.11)\begin{align} t^{\frac{m}{D}} \left\lVert \tau^{\frac{1}{p'} - \frac{1}{q'} - \frac{m}{D}} c(\tau) \right\rVert_{L^{q'}(0, t)} \leq K \left\lVert \tau^{\frac{1}{p'} - \frac{1}{q'}} c(\tau) \right\rVert_{L^{q'}(0, t)}, \end{align}

where K > 0 is a constant that does not depend on t, which is not hard to verify (see [Reference Peša39, lemma 2.16]). If q = 1, then $q' = \infty$, so the second inequality in (4.10) is of the form

\begin{align*} \begin{aligned} & C_{2} \sup\limits_{t \in (0, \infty)} t^{\frac{1}{p'} - \frac{m}{D}} c(t) \sup\limits_{\tau \in [t, \infty)} \tau^{\frac{m}{D}} f^{\ast \ast}_{\mu}(\tau) = C_{2} \sup\limits_{\tau \in (0, \infty)} \tau^{\frac{m}{D}} f^{\ast \ast}_{\mu}(\tau) \sup\limits_{t \in (0, \tau]} t^{\frac{1}{p'} - \frac{m}{D}} c(t) \\ & \leq C_{3} \sup\limits_{t \in (0, \infty)} t^{\frac{1}{p'}} c(t) f^{\ast \ast}_{\mu}(t) = C_{3} \left\lVert f \right\rVert_{L^{(p', \infty, c)}(0, \infty)}. \end{aligned} \end{align*}

Note that we used the fact that b ⁻¹ is equivalent to a nondecreasing function on $(0, \infty)$ if $p = \frac{D}{D-m}$. It means that (4.10) is true. So, the operator $T_{\frac{m}{D}}$ is bounded on the space $\left(L^{p, q, b}(0, \infty)\right)'$. If $p = q = \infty$, then we use [Reference Peša39, proposition 3.3 and theorem 3.31] to obtain the fact that $\left(L^{\infty, \infty, b}(\Sigma, \mu) \right)'$ is equivalent to $L^{1, 1, h^{-1}}(\Sigma, \mu)$, where h is the slowly varying function given by $h(t) = \sup\limits_{\tau \in (0, t)} b(\tau)$, $t \in (0, \infty)$. The boundedness of the operator $T_{\frac{m}{D}}$ in this case can be proved similarly as in the preceding cases, hence we omit the proof. Now it follows from the proof of [Reference Edmunds, Mihula, Musil and Pick18, theorem 4.1] that the condition (3.37) is satisfied. It means that the norm of the optimal space $U_{m}Y(\Sigma, \mu)$ given by theorem 3.9 is equivalent to (4.9). So, we have proved the assertion (iii) of the theorem.

It remains to prove that (4.9) is equivalent to the norm of the space $U_{m}Y(\Sigma, \mu)$ in the first two cases. For each $f \in \mathcal{M}(0, \infty)$ we obtain

\begin{align*} \begin{aligned} & \left\lVert \int_{t}^{\infty} f^{\ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{L^{p, q, b}(0, \infty)} = \left\lVert t^{\frac1{p} - \frac1{q}} b(t) \int_{t}^{\infty} f^{\ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{L^{p, q, b}(0, \infty)} \\ &\geq \left\lVert t^{\frac1{p} - \frac1{q}} b(t) \int_{t}^{2t} f^{\ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{L^{p, q, b}(0, \infty)} \geq C_{4} \left\lVert t^{\frac{1}{p} - \frac{1}{q} + \frac{m}{D}} b(t) f^{\ast}_{\mu}(2t) \right\rVert_{L^{q}(0, \infty)} \\ &\geq C_{5} \left\lVert t^{\frac{1}{p} - \frac{1}{q} + \frac{m}{D}} b(t) f^{\ast}_{\mu}(t) \right\rVert_{L^{q}(0, \infty)} = C_{5}\left\lVert f \right\rVert_{L^{\frac{Dp}{D + mp}, q, b}(0, \infty)}. \end{aligned} \end{align*}

In the third inequality, we used the boundedness of the dilation operator (see (2.14)). On the other hand, for every $f \in \mathcal{M}(0, \infty)$ we have

\begin{align*} \begin{aligned} & \left\lVert \int_{t}^{\infty} f^{\ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{L^{p, q, b}(0, \infty)} = \left\lVert t^{\frac{1}{p} - \frac{1}{q}} b(t) \int_{t}^{\infty} f^{\ast}_{\mu}(\tau) \tau^{\frac{m}{D}-1} \, d\tau \right\rVert_{L^{q}(0, \infty)} \\ & \leq C_{6} \left\lVert t^{\frac{1}{p} - \frac{1}{q} + \frac{m}{D}} b(t) f^{\ast}_{\mu}(t)\right\rVert_{L^{q}(0, \infty)} = C_{6} \left\lVert f \right\rVert_{L^{\frac{Dp}{D + mp}, q, b}(0, \infty)}. \end{aligned} \end{align*}

By virtue of the weighted Hardy inequality [Reference Muckenhoupt32, theorem 2], the preceding inequality is valid if and only if

\begin{align*} \sup\limits_{t \in (0, \infty)} \left\lVert \tau^{\frac{1}{p}-\frac{1}{q}} b(\tau) \right\rVert_{L^{q}(0, t)} \left\lVert \tau^{\frac{1}{q} - \frac{1}{p} - 1} b^{-1}(\tau) \right\rVert_{L^{q'}(t, \infty)} \lt \infty, \end{align*}

which is not hard to verify (see [Reference Peša39, lemma 2.16]).

Remark. It is a natural question of what we can say about the optimal domain space for the Lorentz–Karamata space $Y(\Sigma, \mu)= L^{p, q, b}(\Sigma, \mu)$ in the case $p = \frac{D}{D-m}, q \in (1, \infty]$. In this case we have

(4.12)\begin{align} \frac{t^{1-\frac{m}{D}}}{\varphi_{Y}(t)} = \frac{t^{1-\frac{m}{D}}}{\left\lVert \chi_{(0, t)} \right\rVert_{L^{\frac{D}{D-m}, q, b}(0, \infty)}} = \frac{t^{1-\frac{m}{D}}}{\left\lVert \tau^{1 - \frac{m}{D} - \frac{1}{q}} b(\tau) \right\rVert_{L^{q }(0, t)}}. \end{align}

It can be proved by [Reference Peša39, lemma 2.16] and elementary computations that the right-hand side of (4.12) is equivalent to b ⁻¹ on $(0, \infty)$. It means that the condition (3.37) is satisfied if and only if b is equivalent to a nonincreasing function on $(1, \infty)$. By theorem 3.9 we conclude that the optimal domain space for $Y(\Sigma, \mu) = L^{\frac{D}{D-m}, q, b}(\Sigma,\mu)$ exists if and only if b is equivalent to a nonincreasing function on $(1, \infty)$. Furthermore, if this is not the case, then there is no domain space X with which (3.39) is valid.

On the other hand, it can be proved by [Reference Gogatishvili, Opic and Pick19, theorem 3.2] that the operator $T_{\frac{m}{D}}$ is not bounded on the space $\left(L^{\frac{D}{D-m}, q, b}\right)'(0, \infty)$, which is equivalent to $L^{\frac{D}{m}, q', b^{-1}}(0, \infty)$ owing to [Reference Peša39, section 3.7]. In particular, notice that the condition (4.11) is not satisfied, which is not hard to verify thanks to [Reference Peša39, lemma 2.16]). The unboundedness of $T_{\frac{m}{D}}$ on $\left(L^{\frac{D}{D-m}, q, b}\right)'(0, \infty)$ means that we cannot simplify the norm of the optimal space $U_{m}Y(\Sigma, \mu)$ ([Reference Edmunds, Mihula, Musil and Pick18, theorem 4.7 and remark 4.8]).