1. Introduction
A premixed laminar flame propagating in a quiescent, gravity-free environment can develop intrinsic flamefront cellular instability, which renders the otherwise smooth flamefront wrinkled with a wide range of cell sizes. The instability can be one of two modes, namely, the Darrieus–Landau hydrodynamic instability, caused by the sharp density gradient across the flamefront and promoted at higher pressures owing to reduced flame thickness and increased reactivity; and diffusional-thermal instability, which is promoted in mixtures with weaker thermal diffusion compared to mass diffusion and can be identified by a sub-unity Lewis number, ![]() $Le<1$, defined as the ratio of thermal to mass diffusivities. Irrespective of the instability mode, once the cellular structure appears on the flamefront, the continuous generation and evolution of new cells will increase the flame surface area and hence, the burning rate, a process known as self-acceleration. Owing to its capability to accelerate without external sources, such as turbulence, these laminar self-accelerating flames have been extensively studied (Gostintsev, Istratov & Shulenin Reference Gostintsev, Istratov and Shulenin1988; Ashurst Reference Ashurst1997; Clanet & Searby Reference Clanet and Searby1998; Bradley Reference Bradley1999; Truffaut & Searby Reference Truffaut and Searby1999; Wu, Jomaas & Law Reference Wu, Jomaas and Law2013; Yang et al. Reference Yang, Saha, Wu and Law2016; Beeckmann et al. Reference Beeckmann, Hesse, Kruse, Berens, Peters, Pitsch and Matalon2017). Furthermore, it has also been suggested that a self-accelerating laminar flame could attain a ‘turbulence-like’ behaviour, a phenomenon termed self-turbulization, which in turn could become supersonic through a process termed deflagration-to-detonation transition, or DDT (Sivashinsky Reference Sivashinsky1977; Oran & Gamezo Reference Oran and Gamezo2007; Vasil'ev Reference Vasil'ev2012; Clavin & Searby Reference Clavin and Searby2016), which has been analytically and numerically studied (Zeldovich & Rozlovskii Reference Zeldovich and Rozlovskii1947; Khokhlov, Oran & Wheeler Reference Khokhlov, Oran and Wheeler1997; Akkerman, Law & Bychkov Reference Akkerman, Law and Bychkov2011; Kagan & Sivashinsky Reference Kagan and Sivashinsky2017; Kiverin, Yakovenko & Fortov Reference Kiverin, Yakovenko and Fortov2019). The issue of self-turbulization, within this proposed trilogy of events, that is, from self-acceleration, to self-turbulization to DDT, has not been adequately examined and is the subject of the present study.
$Le<1$, defined as the ratio of thermal to mass diffusivities. Irrespective of the instability mode, once the cellular structure appears on the flamefront, the continuous generation and evolution of new cells will increase the flame surface area and hence, the burning rate, a process known as self-acceleration. Owing to its capability to accelerate without external sources, such as turbulence, these laminar self-accelerating flames have been extensively studied (Gostintsev, Istratov & Shulenin Reference Gostintsev, Istratov and Shulenin1988; Ashurst Reference Ashurst1997; Clanet & Searby Reference Clanet and Searby1998; Bradley Reference Bradley1999; Truffaut & Searby Reference Truffaut and Searby1999; Wu, Jomaas & Law Reference Wu, Jomaas and Law2013; Yang et al. Reference Yang, Saha, Wu and Law2016; Beeckmann et al. Reference Beeckmann, Hesse, Kruse, Berens, Peters, Pitsch and Matalon2017). Furthermore, it has also been suggested that a self-accelerating laminar flame could attain a ‘turbulence-like’ behaviour, a phenomenon termed self-turbulization, which in turn could become supersonic through a process termed deflagration-to-detonation transition, or DDT (Sivashinsky Reference Sivashinsky1977; Oran & Gamezo Reference Oran and Gamezo2007; Vasil'ev Reference Vasil'ev2012; Clavin & Searby Reference Clavin and Searby2016), which has been analytically and numerically studied (Zeldovich & Rozlovskii Reference Zeldovich and Rozlovskii1947; Khokhlov, Oran & Wheeler Reference Khokhlov, Oran and Wheeler1997; Akkerman, Law & Bychkov Reference Akkerman, Law and Bychkov2011; Kagan & Sivashinsky Reference Kagan and Sivashinsky2017; Kiverin, Yakovenko & Fortov Reference Kiverin, Yakovenko and Fortov2019). The issue of self-turbulization, within this proposed trilogy of events, that is, from self-acceleration, to self-turbulization to DDT, has not been adequately examined and is the subject of the present study.
In the 1970s, Sivashinsky (Reference Sivashinsky1977) first suggested the term self-turbulization when he theoretically derived the growth rate of instability in laminar premixed flames subjected to cellular instability, and demonstrated that the propagation speed exceeds that of a stable flame owing to the cellular structure, a behaviour commonly associated with turbulent flames. Later, Bradley (Bradley & Harper Reference Bradley and Harper1994; Bradley Reference Bradley1999) conjectured that the non-uniformity of the flamefront could lead to an inhomogeneity in the adjacent flow due to baroclinic torque leading to a ‘turbulent’ flow. In attempts to address the existence of self-turbulization, a large number of theoretical (Bradley Reference Bradley1999; Addabbo, Bechtold & Matalon Reference Addabbo, Bechtold and Matalon2002), computational (Filyand, Sivashinsky & Frankel Reference Filyand, Sivashinsky and Frankel1994; Ashurst Reference Ashurst1997) and experimental (Gostintsev et al. Reference Gostintsev, Istratov and Shulenin1988; Wu et al. Reference Wu, Jomaas and Law2013; Yang et al. Reference Yang, Saha, Wu and Law2016) investigations have studied the self-similarity nature of flame propagation, and evaluated the acceleration exponent as well as the associated fractal dimension of the flamefront and compared with those of flames in Kolmogorov turbulence. The acceleration exponent, ![]() $\alpha$, for cellularly unstable expanding flames is defined through
$\alpha$, for cellularly unstable expanding flames is defined through ![]() $R_f \sim t^\alpha$, where
$R_f \sim t^\alpha$, where ![]() $R_f$ is the mean flame radius and
$R_f$ is the mean flame radius and ![]() $t$ the time from ignition. The possible attainment of self-turbulization is assessed by evaluating whether the fractal dimension of the wrinkled two-dimensional (2-D) flamefront reaches the theoretical value of Kolmogorov turbulence,
$t$ the time from ignition. The possible attainment of self-turbulization is assessed by evaluating whether the fractal dimension of the wrinkled two-dimensional (2-D) flamefront reaches the theoretical value of Kolmogorov turbulence, ![]() $7/3$ (Sreenivasan & Meneveau Reference Sreenivasan and Meneveau1986; Sreenivasan, Ramshankar & Meneveau Reference Sreenivasan, Ramshankar and Meneveau1989), or equivalently whether
$7/3$ (Sreenivasan & Meneveau Reference Sreenivasan and Meneveau1986; Sreenivasan, Ramshankar & Meneveau Reference Sreenivasan, Ramshankar and Meneveau1989), or equivalently whether ![]() $\alpha$ reaches a critical value of
$\alpha$ reaches a critical value of ![]() $1.5$ (Gostintsev et al. Reference Gostintsev, Istratov and Shulenin1988). It is then of interest to note that experimental results (Gostintsev et al. Reference Gostintsev, Istratov and Shulenin1988; Wu et al. Reference Wu, Jomaas and Law2013; Yang et al. Reference Yang, Saha, Wu and Law2016), obtained by measuring the flame radius
$1.5$ (Gostintsev et al. Reference Gostintsev, Istratov and Shulenin1988). It is then of interest to note that experimental results (Gostintsev et al. Reference Gostintsev, Istratov and Shulenin1988; Wu et al. Reference Wu, Jomaas and Law2013; Yang et al. Reference Yang, Saha, Wu and Law2016), obtained by measuring the flame radius ![]() $R_f$ as function of time, have not shown acceleration exponents exceeding
$R_f$ as function of time, have not shown acceleration exponents exceeding ![]() $1.5$. Here, we note that the aforementioned tests, through evolution of the flame radius, is an indirect approach, which inherently assumes that self-tubulization should lead to Kolmogorov turbulence-like behaviour, although originally, this was not suggested by Sivashinsky (Reference Sivashinsky1977). Indeed, while a direct test is to measure the characteristics of the flow field induced by the wrinkled flamefront and examine if it resembles that of a turbulent flow, experimental measurement of such flow structures has not been systematically attempted, ostensibly due to inherent complications in the measurement. Furthermore, it is also noted that most of the numerical studies (Rastigejev & Matalon Reference Rastigejev and Matalon2006; Yu, Bai & Bychkov Reference Yu, Bai and Bychkov2015; Creta et al. Reference Creta, Lapenna, Lamioni, Fogla and Matalon2020) have focused on the effects of cellular instability on flame propagation and flame wrinkling, with several (Fogla, Creta & Matalon Reference Fogla, Creta and Matalon2015; Lamioni et al. Reference Lamioni, Lapenna, Troiani and Creta2018) discussing the flow patterns for cellular flames propagating in turbulence. Consequently, they are unrelated to the issues of self-turbulization.
$1.5$. Here, we note that the aforementioned tests, through evolution of the flame radius, is an indirect approach, which inherently assumes that self-tubulization should lead to Kolmogorov turbulence-like behaviour, although originally, this was not suggested by Sivashinsky (Reference Sivashinsky1977). Indeed, while a direct test is to measure the characteristics of the flow field induced by the wrinkled flamefront and examine if it resembles that of a turbulent flow, experimental measurement of such flow structures has not been systematically attempted, ostensibly due to inherent complications in the measurement. Furthermore, it is also noted that most of the numerical studies (Rastigejev & Matalon Reference Rastigejev and Matalon2006; Yu, Bai & Bychkov Reference Yu, Bai and Bychkov2015; Creta et al. Reference Creta, Lapenna, Lamioni, Fogla and Matalon2020) have focused on the effects of cellular instability on flame propagation and flame wrinkling, with several (Fogla, Creta & Matalon Reference Fogla, Creta and Matalon2015; Lamioni et al. Reference Lamioni, Lapenna, Troiani and Creta2018) discussing the flow patterns for cellular flames propagating in turbulence. Consequently, they are unrelated to the issues of self-turbulization.
Recognizing the lack of, and hence the need for, understanding the issue of self-turbulization, in this study we present an experimental investigation to provide useful information on the flow induced by cellular flames. Specifically, in the context of expanding cellular flames, we set out to answer the following three questions: (i) What are the primary characteristics of the flow induced by cellularly unstable flames? (ii) Because the flow is induced by the wrinkled flamefront, is there a connection between the cellular flamefront and the flow structure? (iii) Do cellular flames induce a turbulent flow?
2. Experiments
We conducted our experiments in a well-vetted, dual-chamber combustion vessel, in which propagation of a centrally ignited, outwardly propagating globally spherical premixed flame could be studied in a constant and high-pressure environment, triggering the Darrieus–Landau instability. The apparatus consists of two cylindrical chambers. The inner chamber of almost unity aspect ratio and filled with the test mixture is situated in an outer chamber of a much larger volume (inner diameter: 114 mm, outer diameter: 167 mm; length: 127 mm) and filled with nitrogen (N![]() $_{2}$) having the same pressure as that of the test mixture. The flat ends of the inner chamber are sealed with thick quartz windows for optical access. The connection between the chambers is controlled by four valves (sliding sleeve with multiple holes) which are opened when the test mixture is spark ignited and allowed the expanding flame to come in contact with the inert gas in the outer chamber to quench. Thus, the expansion process mimicks an isobaric process owing to the small volume of the inner chamber compared to the outer chamber. Figure 1 shows the schematic of the apparatus. More details of the chamber can be found in our previous publications (Chaudhuri et al. Reference Chaudhuri, Wu, Zhu and Law2012; Yang et al. Reference Yang, Saha, Wu and Law2016; Liu et al. Reference Liu, Unni, Chaudhuri, Law and Saha2020) and in the Supplementary material available at https://doi.org/10.1017/jfm.2021.330. The flame propagation was studied using two diagnostic techniques. High-speed Schlieren imaging was used to capture the flame morphology, the propagation speed and the acceleration exponent, as shown in figures 2(a) and 2(b). High-speed (8 kHz) 2-D particle image velocimetry (PIV) was used to measure the flow dynamics. The mixtures were seeded with a small amount of di-ethyl-hexyl-sebacat droplets (
$_{2}$) having the same pressure as that of the test mixture. The flat ends of the inner chamber are sealed with thick quartz windows for optical access. The connection between the chambers is controlled by four valves (sliding sleeve with multiple holes) which are opened when the test mixture is spark ignited and allowed the expanding flame to come in contact with the inert gas in the outer chamber to quench. Thus, the expansion process mimicks an isobaric process owing to the small volume of the inner chamber compared to the outer chamber. Figure 1 shows the schematic of the apparatus. More details of the chamber can be found in our previous publications (Chaudhuri et al. Reference Chaudhuri, Wu, Zhu and Law2012; Yang et al. Reference Yang, Saha, Wu and Law2016; Liu et al. Reference Liu, Unni, Chaudhuri, Law and Saha2020) and in the Supplementary material available at https://doi.org/10.1017/jfm.2021.330. The flame propagation was studied using two diagnostic techniques. High-speed Schlieren imaging was used to capture the flame morphology, the propagation speed and the acceleration exponent, as shown in figures 2(a) and 2(b). High-speed (8 kHz) 2-D particle image velocimetry (PIV) was used to measure the flow dynamics. The mixtures were seeded with a small amount of di-ethyl-hexyl-sebacat droplets (![]() ${\sim }$1–2
${\sim }$1–2 ![]() $\mathrm {\mu }$m) before ignition. A planar 2-D laser sheet, which was generated using a high-speed Nd-YLF dual-pulsed laser and associated optics, was placed at the centre of the chamber. During propagation of the flame, the droplets evaporated in the burned side due to high temperature, which resulted in a clear flame boundary in the Mie scattering images captured by a high-speed camera orthogonally placed and synchronized with the laser sheet (shown in figure 2c). The flamefront in this study, therefore, is essentially the isothermal surface at the droplet boiling point, which does not vary significantly across the prevailing pressure condition. The mean flame radius
$\mathrm {\mu }$m) before ignition. A planar 2-D laser sheet, which was generated using a high-speed Nd-YLF dual-pulsed laser and associated optics, was placed at the centre of the chamber. During propagation of the flame, the droplets evaporated in the burned side due to high temperature, which resulted in a clear flame boundary in the Mie scattering images captured by a high-speed camera orthogonally placed and synchronized with the laser sheet (shown in figure 2c). The flamefront in this study, therefore, is essentially the isothermal surface at the droplet boiling point, which does not vary significantly across the prevailing pressure condition. The mean flame radius ![]() $R_f$ is defined based on the area (
$R_f$ is defined based on the area (![]() $A_f$) enclosed by the flamefronts in the 2-D Mie scattering images,
$A_f$) enclosed by the flamefronts in the 2-D Mie scattering images, ![]() $R_f=\sqrt {A_f/{\rm \pi} }$. The DaVis PIV algorithm and in-house MATLAB codes were used to extract the velocity field around the flamefront (shown in figure 2d), which was then analysed to yield the specific flow characteristics. The uncertainty of the velocity measurement was evaluated to be less than
$R_f=\sqrt {A_f/{\rm \pi} }$. The DaVis PIV algorithm and in-house MATLAB codes were used to extract the velocity field around the flamefront (shown in figure 2d), which was then analysed to yield the specific flow characteristics. The uncertainty of the velocity measurement was evaluated to be less than ![]() $4\,\%$. In this study, we solely focused on the effect of the Darrieus–Landau hydrodynamic cellular instability, and hence used diffusively neutral (
$4\,\%$. In this study, we solely focused on the effect of the Darrieus–Landau hydrodynamic cellular instability, and hence used diffusively neutral (![]() $Le\approx 1$) stoichiometric (equivalence ratio,
$Le\approx 1$) stoichiometric (equivalence ratio, ![]() $\phi =1$) hydrogen(H
$\phi =1$) hydrogen(H![]() $_{2}$)/oxygen(O
$_{2}$)/oxygen(O![]() $_{2}$)/nitrogen(N
$_{2}$)/nitrogen(N![]() $_{2}$) mixtures at a flame temperature of 2400 K to minimize stabilization/destabilization effects of diffusional-thermal instability. We also note that the effects of Rayleigh–Taylor instability were rather weak for our experimental conditions (Bell et al. Reference Bell, Day, Rendleman, Woosley and Zingale2004; Abarzhi et al. Reference Abarzhi, Ilyin, Goddard and Anisimov2019) and hence, the reported flame dynamics solely arose from Darrieus–Landau instability.
$_{2}$) mixtures at a flame temperature of 2400 K to minimize stabilization/destabilization effects of diffusional-thermal instability. We also note that the effects of Rayleigh–Taylor instability were rather weak for our experimental conditions (Bell et al. Reference Bell, Day, Rendleman, Woosley and Zingale2004; Abarzhi et al. Reference Abarzhi, Ilyin, Goddard and Anisimov2019) and hence, the reported flame dynamics solely arose from Darrieus–Landau instability.

Figure 1. Experimental setup: Dual chamber vessel with high-speed camera, optics and laser used for high-speed particle image velocimetry.

Figure 2. (a) Schlieren image. The inset bar indicates 10 mm. (b) Three-stage behaviour of flame propagation. Here, ![]() $Pe$, Péclet number;
$Pe$, Péclet number; ![]() $\widetilde {S_{L,b}}$, flame propagation speed normalized by laminar unstretched flame speed (burned side). Replotted from data presented in Yang et al. (Reference Yang, Saha, Liu and Law2018). (c) Mie scattering image with edge detection. (d) Vector field from particle image velocimetry. Colour represents magnitude of local velocity.
$\widetilde {S_{L,b}}$, flame propagation speed normalized by laminar unstretched flame speed (burned side). Replotted from data presented in Yang et al. (Reference Yang, Saha, Liu and Law2018). (c) Mie scattering image with edge detection. (d) Vector field from particle image velocimetry. Colour represents magnitude of local velocity.
The fundamental flame properties, such as the laminar unstretched flame speed (![]() $S_{L,0}$) and adiabatic flame temperature (
$S_{L,0}$) and adiabatic flame temperature (![]() $T_f$), were calculated numerically using the CHEMKIN one-dimensional flame solver and a reaction model of H
$T_f$), were calculated numerically using the CHEMKIN one-dimensional flame solver and a reaction model of H![]() $_{2}$-oxidation proposed by Burke et al. (Reference Burke, Chaos, Ju, Dryer and Klippenstein2012). The experimental conditions and corresponding flame properties are listed in table 1. In this study, we defined the planar flame thickness based on diffusivity,
$_{2}$-oxidation proposed by Burke et al. (Reference Burke, Chaos, Ju, Dryer and Klippenstein2012). The experimental conditions and corresponding flame properties are listed in table 1. In this study, we defined the planar flame thickness based on diffusivity, ![]() $\delta _{L,0} = D_T/S_{L,0}$, where
$\delta _{L,0} = D_T/S_{L,0}$, where ![]() $D_T$ is the thermal diffusivity of the mixture. The instantaneous propagation speed of the expanding flame,
$D_T$ is the thermal diffusivity of the mixture. The instantaneous propagation speed of the expanding flame, ![]() $S_{L,b}=\textrm {d} R_f/\textrm {d} t$, was obtained from the time derivative of the mean flame radius,
$S_{L,b}=\textrm {d} R_f/\textrm {d} t$, was obtained from the time derivative of the mean flame radius, ![]() $R_f$. To study a wide range of
$R_f$. To study a wide range of ![]() $Pe$, we experimented with a broad range (
$Pe$, we experimented with a broad range (![]() $1$–
$1$–![]() $7$ atm) of ambient pressures.
$7$ atm) of ambient pressures.
Table 1. Experimental conditions with corresponding flame parameters. The parameters are ![]() $\phi$, equivalence ratio;
$\phi$, equivalence ratio; ![]() $Y_i$, mole fraction of species
$Y_i$, mole fraction of species ![]() $i$ in unburned mixture; Le, Lewis number; P, pressure;
$i$ in unburned mixture; Le, Lewis number; P, pressure; ![]() $S_{L,0}$, flame speed of laminar planar flame;
$S_{L,0}$, flame speed of laminar planar flame; ![]() $\delta _{L,0}$, thickness of laminar planar flame.
$\delta _{L,0}$, thickness of laminar planar flame.

3. Results
3.1. Global propagation
In our previous study (Yang et al. Reference Yang, Saha, Wu and Law2016), it was shown that the propagation of cellularly unstable expanding flames at various pressures can be unified when the normalized flame propagation speed is plotted with the normalized radius, or Péclet number, ![]() $Pe=R_f/\delta _{L,0}$, somewhat similar to turbulent flames (Chaudhuri et al. Reference Chaudhuri, Wu, Zhu and Law2012). Figure 2(b) shows such a normalized plot for the current experiments, which identifies a three-stage behaviour with two critical
$Pe=R_f/\delta _{L,0}$, somewhat similar to turbulent flames (Chaudhuri et al. Reference Chaudhuri, Wu, Zhu and Law2012). Figure 2(b) shows such a normalized plot for the current experiments, which identifies a three-stage behaviour with two critical ![]() $Pe$'s. Specifically, the flamefront in the smooth expansion stage,
$Pe$'s. Specifically, the flamefront in the smooth expansion stage, ![]() $Pe < Pe_{c1} \approx 1000$, is free from instabilities (inset of figure 2b) and hence the propagation is stretch controlled. As the cellular instability is triggered at
$Pe < Pe_{c1} \approx 1000$, is free from instabilities (inset of figure 2b) and hence the propagation is stretch controlled. As the cellular instability is triggered at ![]() $Pe=Pe_{c1}$, the flame shows sharp acceleration, and over a short
$Pe=Pe_{c1}$, the flame shows sharp acceleration, and over a short ![]() $Pe$ range, new cells start appearing and spreading over the entire flamefront (inset of figure 2b), which marks a transition stage (
$Pe$ range, new cells start appearing and spreading over the entire flamefront (inset of figure 2b), which marks a transition stage (![]() $Pe_{c1}<Pe<Pe_{c2}$). At the saturated stage (
$Pe_{c1}<Pe<Pe_{c2}$). At the saturated stage (![]() $Pe>Pe_{c2}\approx 1900$), the flamefront becomes fully covered with cells (inset of figure 2b) and the acceleration attains self-similarity. Yang et al. (Reference Yang, Saha, Wu and Law2016) showed that for a wide range of conditions, the acceleration exponent (
$Pe>Pe_{c2}\approx 1900$), the flamefront becomes fully covered with cells (inset of figure 2b) and the acceleration attains self-similarity. Yang et al. (Reference Yang, Saha, Wu and Law2016) showed that for a wide range of conditions, the acceleration exponent (![]() $\alpha$) lies in the range 1.2–1.4 and the corresponding fractal excess (
$\alpha$) lies in the range 1.2–1.4 and the corresponding fractal excess (![]() $d=1-1/\alpha$) is within 0.2–0.3. In a similar, but larger chamber, Huo et al. (Reference Huo, Saha, Ren and Law2018, Reference Huo, Saha, Shu, Ren and Law2019) also observed the three-stage behaviour with a similar global acceleration exponent. However they noticed an oscillation in the mean propagation speed in the saturated stage. We note that such pulsation occurs for a larger flame and was not observed in our experiments. Furthermore, in this study, we will be analysing the energy spectra from local velocity fluctuation and, as such, oscillation in mean propagation speed or mean velocity is expected to have an insignificant effect on the reported statistics.
$d=1-1/\alpha$) is within 0.2–0.3. In a similar, but larger chamber, Huo et al. (Reference Huo, Saha, Ren and Law2018, Reference Huo, Saha, Shu, Ren and Law2019) also observed the three-stage behaviour with a similar global acceleration exponent. However they noticed an oscillation in the mean propagation speed in the saturated stage. We note that such pulsation occurs for a larger flame and was not observed in our experiments. Furthermore, in this study, we will be analysing the energy spectra from local velocity fluctuation and, as such, oscillation in mean propagation speed or mean velocity is expected to have an insignificant effect on the reported statistics.
3.2. Flow statistics
Next, we focus our attention on the flow field ahead of the propagating cellular flamefront measured by PIV. To characterize the flow generated by the flame, we first explore the variation of the radial (![]() $U_r(r,\theta )$) and azimuthal (
$U_r(r,\theta )$) and azimuthal (![]() $U_{\theta }(r,\theta )$) components of the velocity in the radial direction. To present the radial variation of these velocities at various flame conditions, we take the azimuthal average of these velocities at any fixed
$U_{\theta }(r,\theta )$) components of the velocity in the radial direction. To present the radial variation of these velocities at various flame conditions, we take the azimuthal average of these velocities at any fixed ![]() $r$ (averaged quantities denoted as
$r$ (averaged quantities denoted as ![]() $\langle \cdot \rangle _{\theta }$) and normalize the averaged velocity with the flame propagation speed,
$\langle \cdot \rangle _{\theta }$) and normalize the averaged velocity with the flame propagation speed, ![]() $S_{L,b}$ (normalized quantities presented as
$S_{L,b}$ (normalized quantities presented as ![]() $\overline {(\cdot )}$). In figure 3(a), we compare the averaged normalized radial velocity,
$\overline {(\cdot )}$). In figure 3(a), we compare the averaged normalized radial velocity, ![]() $\langle \overline {U_r} \rangle _\theta$, as function of distance from the flamefront,
$\langle \overline {U_r} \rangle _\theta$, as function of distance from the flamefront, ![]() ${\rm \Delta} R$, for various
${\rm \Delta} R$, for various ![]() $Pe$. For all
$Pe$. For all ![]() $Pe$,
$Pe$, ![]() $\langle \overline {U_r} \rangle _\theta$ is maximum adjacent to the flamefront and decay monotonically with
$\langle \overline {U_r} \rangle _\theta$ is maximum adjacent to the flamefront and decay monotonically with ![]() ${\rm \Delta} R$ as the effect of flame propagation weakens away from the flamefront. Interestingly, the averaged normalized radial velocity at the flamefront (
${\rm \Delta} R$ as the effect of flame propagation weakens away from the flamefront. Interestingly, the averaged normalized radial velocity at the flamefront (![]() $\langle \overline {U_r} \rangle _\theta |_{{\rm \Delta} R=0}$) shows a non-monotonic dependence on
$\langle \overline {U_r} \rangle _\theta |_{{\rm \Delta} R=0}$) shows a non-monotonic dependence on ![]() $Pe$, in that at low
$Pe$, in that at low ![]() $Pe$ (smooth expansion stage,
$Pe$ (smooth expansion stage, ![]() $Pe<Pe_{c1}$) and high
$Pe<Pe_{c1}$) and high ![]() $Pe$ (saturated stage,
$Pe$ (saturated stage, ![]() $Pe>Pe_{c2}$), it is smaller compared to that at intermediate
$Pe>Pe_{c2}$), it is smaller compared to that at intermediate ![]() $Pe$ (transition stage,
$Pe$ (transition stage, ![]() $Pe_{c1}<Pe<Pe_{c2}$), as shown in the inset of figure 3(a). At the onset of the transition stage, the flamefront becomes unstable and hence experiences sudden acceleration (figure 2b), and thereby increasing the radial velocity adjacent to the flamefront significantly before the far field flow could respond. Such dramatic increase, however, is attenuated at the saturated stage, as the cellular structure and flamefront morphology become saturated and the acceleration becomes ‘steady’, which in turn reduces
$Pe_{c1}<Pe<Pe_{c2}$), as shown in the inset of figure 3(a). At the onset of the transition stage, the flamefront becomes unstable and hence experiences sudden acceleration (figure 2b), and thereby increasing the radial velocity adjacent to the flamefront significantly before the far field flow could respond. Such dramatic increase, however, is attenuated at the saturated stage, as the cellular structure and flamefront morphology become saturated and the acceleration becomes ‘steady’, which in turn reduces ![]() $\langle \overline {U_r} \rangle _\theta |_{{\rm \Delta} R=0}$ to the original value.
$\langle \overline {U_r} \rangle _\theta |_{{\rm \Delta} R=0}$ to the original value.

Figure 3. (a) Averaged normalized radial velocity, ![]() $\langle \overline {U_r} \rangle _{\theta }$, versus distance away from flamefront,
$\langle \overline {U_r} \rangle _{\theta }$, versus distance away from flamefront, ![]() ${\rm \Delta} R$, at different
${\rm \Delta} R$, at different ![]() $Pe$. Inset: Averaged normalized radial velocity,
$Pe$. Inset: Averaged normalized radial velocity, ![]() $\langle \overline {U_r} \rangle _{\theta }$, on the flamefront (
$\langle \overline {U_r} \rangle _{\theta }$, on the flamefront (![]() ${\rm \Delta} R = 0$) versus
${\rm \Delta} R = 0$) versus ![]() $Pe$. (b) Averaged normalized azimuthal velocity,
$Pe$. (b) Averaged normalized azimuthal velocity, ![]() $\langle \overline {U_{\theta }} \rangle _{\theta }$, versus distance away from flamefront,
$\langle \overline {U_{\theta }} \rangle _{\theta }$, versus distance away from flamefront, ![]() ${\rm \Delta} R$, at different
${\rm \Delta} R$, at different ![]() $Pe$. (c) Root-mean-square (RMS) of normalized radial and azimuthal velocity fluctuation
$Pe$. (c) Root-mean-square (RMS) of normalized radial and azimuthal velocity fluctuation ![]() $\overline {u_r}$,
$\overline {u_r}$,![]() $\overline {u_{\theta }}$ versus distance away from flamefront,
$\overline {u_{\theta }}$ versus distance away from flamefront, ![]() ${\rm \Delta} R$, in the saturated stage. The uncertainties (shown in c) for radial and azimuthal velocities are within
${\rm \Delta} R$, in the saturated stage. The uncertainties (shown in c) for radial and azimuthal velocities are within ![]() ${\pm }6\,\%$.
${\pm }6\,\%$.
The averaged normalized azimuthal velocity, ![]() $\langle \overline {U_\theta } \rangle _\theta$, however, is much weaker than
$\langle \overline {U_\theta } \rangle _\theta$, however, is much weaker than ![]() $\langle \overline {U_r} \rangle _\theta$ and does not show any correlated variation along the radial direction, as shown in figure 3(b). The flow structure generated by the flamefront is consumed by the propagating flamefront before it is convected to the far field and hence no particular correlation between near field and far field was observed. This can be further shown through the velocity fluctuations in the radial (
$\langle \overline {U_r} \rangle _\theta$ and does not show any correlated variation along the radial direction, as shown in figure 3(b). The flow structure generated by the flamefront is consumed by the propagating flamefront before it is convected to the far field and hence no particular correlation between near field and far field was observed. This can be further shown through the velocity fluctuations in the radial (![]() ${u_r}$) and azimuthal (
${u_r}$) and azimuthal (![]() $u_{\theta }$) directions. The RMS of
$u_{\theta }$) directions. The RMS of ![]() $\overline {u_r}$ and
$\overline {u_r}$ and ![]() $\overline {u_{\theta }}$ monotonically decrease with
$\overline {u_{\theta }}$ monotonically decrease with ![]() ${\rm \Delta} R$, as shown in figure 3(c). Such monotonic decay suggests that the flow far away from the flame is dominated by the mean radial flow generated by thermal expansion and does not possess strong velocity fluctuations.
${\rm \Delta} R$, as shown in figure 3(c). Such monotonic decay suggests that the flow far away from the flame is dominated by the mean radial flow generated by thermal expansion and does not possess strong velocity fluctuations.
Recognizing that the flame-generated flow structures were mostly confined in the vicinity of the flamefront, we focus the rest of the analysis on the flow vectors conditioned on the wrinkled flamefront, and analysed them in a flame-coordinate system using the normal and tangential directions of the flamefront. Figure 4 shows the one-dimensional energy spectra ![]() $\phi _{nn}, \phi _{tt}$ of the fluctuation velocity in the normal,
$\phi _{nn}, \phi _{tt}$ of the fluctuation velocity in the normal, ![]() $u_n$, and tangential,
$u_n$, and tangential, ![]() $u_t$, directions, respectively, measured along the flamefront for five values of
$u_t$, directions, respectively, measured along the flamefront for five values of ![]() $Pe$ spanning all three stages of propagation. We observe that
$Pe$ spanning all three stages of propagation. We observe that ![]() $\phi _{nn}(k)$ shows a similar shape at the different stages of the propagation. Furthermore, the energy is large at small wavenumbers (large scales) and rapidly decayed at large wavenumbers (small scales). Although the shape of
$\phi _{nn}(k)$ shows a similar shape at the different stages of the propagation. Furthermore, the energy is large at small wavenumbers (large scales) and rapidly decayed at large wavenumbers (small scales). Although the shape of ![]() $\phi _{tt}$ is similar to
$\phi _{tt}$ is similar to ![]() $\phi _{nn}$ at low
$\phi _{nn}$ at low ![]() $Pe$, there are some characteristic changes with
$Pe$, there are some characteristic changes with ![]() $Pe$ (figure 4b). First, the spectra shifts to higher energy values as
$Pe$ (figure 4b). First, the spectra shifts to higher energy values as ![]() $Pe$ increases and the flame moves from the smooth expansion stage (
$Pe$ increases and the flame moves from the smooth expansion stage (![]() $Pe=587$) to the transition stage (
$Pe=587$) to the transition stage (![]() $Pe=1235$) to the saturated stage (
$Pe=1235$) to the saturated stage (![]() $Pe=3005$,
$Pe=3005$, ![]() $3552$ and
$3552$ and ![]() $4372$) with the flamefront becoming progressively more wrinkled owing to the appearance of the cellular structure. Moreover, at the saturated stage, the spectra almost overlap (
$4372$) with the flamefront becoming progressively more wrinkled owing to the appearance of the cellular structure. Moreover, at the saturated stage, the spectra almost overlap (![]() $Pe=3005$,
$Pe=3005$, ![]() $3552$ and
$3552$ and ![]() $4372$) at various
$4372$) at various ![]() $Pe$ and as such, become independent of
$Pe$ and as such, become independent of ![]() $Pe$. They also attains a power-law dependence, i.e.
$Pe$. They also attains a power-law dependence, i.e. ![]() $\phi _{tt}(k)\sim k^{-\beta }$, where
$\phi _{tt}(k)\sim k^{-\beta }$, where ![]() $\beta$ was measured to be approximately
$\beta$ was measured to be approximately ![]() $2.6$ (the dashed line). The power-law behaviour is observed for length scales,
$2.6$ (the dashed line). The power-law behaviour is observed for length scales, ![]() $2{\rm \pi} /k$, roughly from the flame radius (
$2{\rm \pi} /k$, roughly from the flame radius (![]() $R_f\sim \textit{O}(10\ \textrm {mm})$) to the smallest scales we can resolve in the experiments, which is
$R_f\sim \textit{O}(10\ \textrm {mm})$) to the smallest scales we can resolve in the experiments, which is ![]() $\textit{O}(0.1\ \textrm {mm}) \sim 20 \delta _{L,0}$. We note that theoretical analyses (Pelce & Clavin Reference Pelce and Clavin1982; Bychkov & Liberman Reference Bychkov and Liberman2000) have shown that the cut-off limit of Darrieus–Landau instability is approximately
$\textit{O}(0.1\ \textrm {mm}) \sim 20 \delta _{L,0}$. We note that theoretical analyses (Pelce & Clavin Reference Pelce and Clavin1982; Bychkov & Liberman Reference Bychkov and Liberman2000) have shown that the cut-off limit of Darrieus–Landau instability is approximately ![]() $k_{cut-off}\approx 2{\rm \pi} /(20\delta _{L,0}$), which is close to the experimental resolution. Nevertheless, whether the power-law scaling holds for larger wavenumbers is still to be investigated. The turbulent Reynolds number based on the largest scale (
$k_{cut-off}\approx 2{\rm \pi} /(20\delta _{L,0}$), which is close to the experimental resolution. Nevertheless, whether the power-law scaling holds for larger wavenumbers is still to be investigated. The turbulent Reynolds number based on the largest scale (![]() $Re_t=u_{rms}R_f/\nu$) at the saturated stage was in the range of 1500–4000, where
$Re_t=u_{rms}R_f/\nu$) at the saturated stage was in the range of 1500–4000, where ![]() $\nu$ is the kinematic viscosity of unburned gas.
$\nu$ is the kinematic viscosity of unburned gas.

Figure 4. (a) Energy spectra of normal velocity fluctuation ![]() $u_n$ on the flamefront at different
$u_n$ on the flamefront at different ![]() $Pe$. (b) Energy spectra of tangential velocity fluctuation
$Pe$. (b) Energy spectra of tangential velocity fluctuation ![]() $u_t$ on the flamefront at different
$u_t$ on the flamefront at different ![]() $Pe$. Here,
$Pe$. Here, ![]() $Pe=587$, smooth expansion stage;
$Pe=587$, smooth expansion stage; ![]() $Pe=1235$, transition stage; the rest, saturated stage. The uncertainty of the power spectral density is approximately
$Pe=1235$, transition stage; the rest, saturated stage. The uncertainty of the power spectral density is approximately ![]() ${\pm }12\,\%$.
${\pm }12\,\%$.
It should be noted that the flow statistics were measured in the meridional plane of the cellularly unstable expanding flame and as such, were 2-D in nature. However, these flames are statistically spherical (Chaudhuri, Wu & Law Reference Chaudhuri, Wu and Law2013; Chaudhuri, Saha & Law Reference Chaudhuri, Saha and Law2015) and as such, orientation of the measurement plane does not affect the statistics.
3.3. Scaling analysis
Next, we explore the origin of the power-law dependence observed in the flame-generated flow. Here, we note that in our experiments, the flame propagates in a quiescent environment and as such, the observed energy spectra of the flow adjacent to the flamefront is generated by the wrinkling of the flamefront. Consequently, we present a scaling analysis to connect the energy spectra with the cellular structure. In the Landau limit, every point on the flamefront propagates individually in the normal direction at the speed of ![]() $S_{L,0}$. Defining
$S_{L,0}$. Defining ![]() $S_w$ as the projected propagation speed on the mean spherical flamefront for every local infinitesimal flame segment, we can write
$S_w$ as the projected propagation speed on the mean spherical flamefront for every local infinitesimal flame segment, we can write ![]() $S_w/S_{L,0}=|\boldsymbol {\nabla } G|=\sqrt {1+\boldsymbol {\nabla } g \boldsymbol {\cdot } \boldsymbol {\nabla } g}$, where
$S_w/S_{L,0}=|\boldsymbol {\nabla } G|=\sqrt {1+\boldsymbol {\nabla } g \boldsymbol {\cdot } \boldsymbol {\nabla } g}$, where ![]() $G$ is the scalar describing the flamefront in the well-known G-equation (Peters Reference Peters1999). We can also define
$G$ is the scalar describing the flamefront in the well-known G-equation (Peters Reference Peters1999). We can also define ![]() $G = R_f+g-r$, where
$G = R_f+g-r$, where ![]() $g$ is the fluctuation of the flamefront from the mean surface for a mildly wrinkled flamefront, and
$g$ is the fluctuation of the flamefront from the mean surface for a mildly wrinkled flamefront, and ![]() $r$ is the radial distance from the centre of the flame. Such a definition ensures
$r$ is the radial distance from the centre of the flame. Such a definition ensures ![]() $G>0$ in the unburned side,
$G>0$ in the unburned side, ![]() $G<0$ in the burned side and
$G<0$ in the burned side and ![]() $G=0$ on the flamefront, a convention commonly followed in the G-equation representation. Because the flow is induced by the flame, the kinetic energy of the flow (
$G=0$ on the flamefront, a convention commonly followed in the G-equation representation. Because the flow is induced by the flame, the kinetic energy of the flow (![]() $E$) must arise from flame propagation, or
$E$) must arise from flame propagation, or ![]() $E\sim S_w^2$. Considering the contribution from the flow velocity in the normal
$E\sim S_w^2$. Considering the contribution from the flow velocity in the normal ![]() $U_n$ and tangential
$U_n$ and tangential ![]() $U_t$ components, we can write
$U_t$ components, we can write
In the Landau limit, for adjacent fluid particles, ![]() $U_n^2$ scales as
$U_n^2$ scales as ![]() $S_{L,0}^2$, which, along with (3.1), suggests that
$S_{L,0}^2$, which, along with (3.1), suggests that ![]() $U_t^2 \sim S_{L,0}^2 \boldsymbol {\nabla } g \boldsymbol {\cdot }\boldsymbol {\nabla } g$. We notice that
$U_t^2 \sim S_{L,0}^2 \boldsymbol {\nabla } g \boldsymbol {\cdot }\boldsymbol {\nabla } g$. We notice that ![]() $U_n^2$ is independent of
$U_n^2$ is independent of ![]() $g$ or the geometry of the wrinkled flamefront at all stages of propagation or
$g$ or the geometry of the wrinkled flamefront at all stages of propagation or ![]() $Pe$ (figure 4a). Consequently, fluctuation of the normal velocity
$Pe$ (figure 4a). Consequently, fluctuation of the normal velocity ![]() $u_n$ is mainly determined by the disturbance on the large scales in the system, while decaying rapidly on the small scales. This explains the similar energy spectra at all values of
$u_n$ is mainly determined by the disturbance on the large scales in the system, while decaying rapidly on the small scales. This explains the similar energy spectra at all values of ![]() $Pe$, as the disturbance on the large scale is independent of the development of the cellular instability. For fluctuation of the tangential velocity
$Pe$, as the disturbance on the large scale is independent of the development of the cellular instability. For fluctuation of the tangential velocity ![]() $u_t$ at low
$u_t$ at low ![]() $Pe$ when the flame is free from instability, the energy spectra is the same as that from disturbance. However, as
$Pe$ when the flame is free from instability, the energy spectra is the same as that from disturbance. However, as ![]() $Pe$ increases, cellular instability induces strong tangential velocity structures and the influence of disturbance is suppressed.
$Pe$ increases, cellular instability induces strong tangential velocity structures and the influence of disturbance is suppressed.
Now, we closely explore the relation between ![]() $U_t^2$ and the flame geometry or
$U_t^2$ and the flame geometry or ![]() $g$. First we note that the scaling
$g$. First we note that the scaling ![]() $U_t^2 \sim \boldsymbol {\nabla } g \boldsymbol {\cdot }\boldsymbol {\nabla } g$ suggests that the power spectral density (
$U_t^2 \sim \boldsymbol {\nabla } g \boldsymbol {\cdot }\boldsymbol {\nabla } g$ suggests that the power spectral density (![]() $PSD$) of
$PSD$) of ![]() $U_t$ should scale with the
$U_t$ should scale with the ![]() $PSD$ of
$PSD$ of ![]() $|\boldsymbol {\nabla } g|$, denoted as
$|\boldsymbol {\nabla } g|$, denoted as ![]() $P_{g'}$. Since
$P_{g'}$. Since ![]() $PSD$ of the tangential velocity
$PSD$ of the tangential velocity ![]() $U_t$ and its fluctuation
$U_t$ and its fluctuation ![]() $u_t=U_t-\langle U_t \rangle$ is equivalent for
$u_t=U_t-\langle U_t \rangle$ is equivalent for ![]() $k>0$, we have
$k>0$, we have ![]() $\phi _{tt}(k)\sim P_{g'}(k)$. From the experiments, we measured
$\phi _{tt}(k)\sim P_{g'}(k)$. From the experiments, we measured ![]() $g$ (shown in figure 5a) and evaluated
$g$ (shown in figure 5a) and evaluated ![]() $|\boldsymbol {\nabla } g|$ and
$|\boldsymbol {\nabla } g|$ and ![]() $P_{g'}(k)$, as shown in figure 5(b). At low
$P_{g'}(k)$, as shown in figure 5(b). At low ![]() $Pe$ (smooth expansion stage), the flame edge (
$Pe$ (smooth expansion stage), the flame edge (![]() $g$) possesses less oscillation while at large
$g$) possesses less oscillation while at large ![]() $Pe$ (saturated stage), it becomes highly oscillating (figure 5a). It is then interesting to note that
$Pe$ (saturated stage), it becomes highly oscillating (figure 5a). It is then interesting to note that ![]() $P_{g'}$ (figure 5b) also shows a power-law dependence with wavenumber in the form of
$P_{g'}$ (figure 5b) also shows a power-law dependence with wavenumber in the form of ![]() $k^{-2.6}$, which is very similar to
$k^{-2.6}$, which is very similar to ![]() $\phi _{tt}$, hence confirming our scaling.
$\phi _{tt}$, hence confirming our scaling.

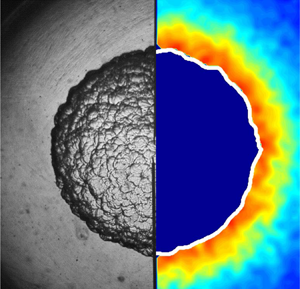
Figure 5. (a) Flamefront fluctuation ![]() $g$ versus
$g$ versus ![]() $\theta$ in the smooth expansion stage and the saturated stage. In the smooth expansion stage, only large cracks are present on the flamefront, while in the saturated stage, small cellular structures are generated on the flamefront. (b) Power spectra density of
$\theta$ in the smooth expansion stage and the saturated stage. In the smooth expansion stage, only large cracks are present on the flamefront, while in the saturated stage, small cellular structures are generated on the flamefront. (b) Power spectra density of ![]() $\textrm {d} g/{\textrm {d}x}$ of the flamefront. Here wavenumber
$\textrm {d} g/{\textrm {d}x}$ of the flamefront. Here wavenumber ![]() $k$ is based on the distance along the flamefront. The smallest resolved scale is controlled by the resolution of the Mie scattering images. The uncertainty for edge detection is approximately
$k$ is based on the distance along the flamefront. The smallest resolved scale is controlled by the resolution of the Mie scattering images. The uncertainty for edge detection is approximately ![]() ${\pm }1\,\%$, and for
${\pm }1\,\%$, and for ![]() $PSD$ is
$PSD$ is ![]() ${\pm }2\,\%$.
${\pm }2\,\%$.
Next, we attempt another scaling analysis to assess the theoretical approximation of ![]() $\beta$ in the scaling of
$\beta$ in the scaling of ![]() $\phi _{tt}(k)\sim P_{g'}(k)\sim k^{-\beta }$. Studies (Liberman et al. Reference Liberman, Ivanov, Peil, Valiev and Eriksson2004; Yu et al. Reference Yu, Bai and Bychkov2015; Yang et al. Reference Yang, Saha, Wu and Law2016) have confirmed that cellularly unstable laminar flamefronts are fractal in nature. The perimeter,
$\phi _{tt}(k)\sim P_{g'}(k)\sim k^{-\beta }$. Studies (Liberman et al. Reference Liberman, Ivanov, Peil, Valiev and Eriksson2004; Yu et al. Reference Yu, Bai and Bychkov2015; Yang et al. Reference Yang, Saha, Wu and Law2016) have confirmed that cellularly unstable laminar flamefronts are fractal in nature. The perimeter, ![]() $L$, of the 2-D cross-section of such a wrinkled fractal expanding flame scales with the mean radius
$L$, of the 2-D cross-section of such a wrinkled fractal expanding flame scales with the mean radius ![]() $R_f$, as
$R_f$, as ![]() $L \sim R_f^D$, where
$L \sim R_f^D$, where ![]() $D$ is the fractal dimension of the flame edge. Here,
$D$ is the fractal dimension of the flame edge. Here, ![]() $L$ can be obtained by integrating the arc length of the flamefront
$L$ can be obtained by integrating the arc length of the flamefront ![]() $R_f+g(\theta )$ in the polar coordinate (Strang Reference Strang1991),
$R_f+g(\theta )$ in the polar coordinate (Strang Reference Strang1991),
 \begin{equation} L=\int_{0}^{2{\rm \pi}}\sqrt{(R_f+g)^2+\left(\frac{\textrm{d}(R_f+g)}{\textrm{d}\theta}\right)^2}\textrm{d}\theta. \end{equation}
\begin{equation} L=\int_{0}^{2{\rm \pi}}\sqrt{(R_f+g)^2+\left(\frac{\textrm{d}(R_f+g)}{\textrm{d}\theta}\right)^2}\textrm{d}\theta. \end{equation}
Because the cellularly unstable flamefronts are mildly wrinkled, i.e. ![]() $R_f \gg g$, and
$R_f \gg g$, and ![]() $R_f$ is independent of
$R_f$ is independent of ![]() $\theta$, we find
$\theta$, we find
 \begin{equation} L\approx \int_{0}^{2{\rm \pi}}\sqrt{R_f^2+\left(\frac{\textrm{d} g}{\textrm{d}\theta}\right)^2}\textrm{d}\theta = R_f\int_{0}^{2{\rm \pi}}\sqrt{1+\frac{1}{R_f^2}\left(\frac{\textrm{d} g}{\textrm{d}\theta}\right)^2}\textrm{d}\theta. \end{equation}
\begin{equation} L\approx \int_{0}^{2{\rm \pi}}\sqrt{R_f^2+\left(\frac{\textrm{d} g}{\textrm{d}\theta}\right)^2}\textrm{d}\theta = R_f\int_{0}^{2{\rm \pi}}\sqrt{1+\frac{1}{R_f^2}\left(\frac{\textrm{d} g}{\textrm{d}\theta}\right)^2}\textrm{d}\theta. \end{equation}
Using ![]() $L\sim R_f^D$, (3.3) can be reduced to
$L\sim R_f^D$, (3.3) can be reduced to
 \begin{equation} \int_{0}^{2{\rm \pi}}\sqrt{1+\left(\frac{\textrm{d} g}{R_f\textrm{d}\theta}\right)^2}\textrm{d}\theta \sim R_f^{D-1} \end{equation}
\begin{equation} \int_{0}^{2{\rm \pi}}\sqrt{1+\left(\frac{\textrm{d} g}{R_f\textrm{d}\theta}\right)^2}\textrm{d}\theta \sim R_f^{D-1} \end{equation}
One can show that ![]() $(1/R_f)({\textrm {d} g}/{\textrm {d}\theta }) \sim R_f^{D-1}$, as it is the only term on the left-hand side of (3.4), which is a function of
$(1/R_f)({\textrm {d} g}/{\textrm {d}\theta }) \sim R_f^{D-1}$, as it is the only term on the left-hand side of (3.4), which is a function of ![]() $R_f$. As a result, we have
$R_f$. As a result, we have
The cellular structure on the flamefront is bounded by two length scales, the flame thickness scale (![]() $\delta _{L,0}$) and the flame radius scale (
$\delta _{L,0}$) and the flame radius scale (![]() $R_f$) (Matalon Reference Matalon2007), and as such, the spectrum of
$R_f$) (Matalon Reference Matalon2007), and as such, the spectrum of ![]() $g$, which describes the flamefront geometry, can be expressed as
$g$, which describes the flamefront geometry, can be expressed as
 \begin{equation} g(\theta) \sim \int_{2{\rm \pi}/R_f}^{2{\rm \pi}/\delta_{L,0}}A(k)\sin(kR_f\theta+\psi_k)\,\textrm{d} k, \end{equation}
\begin{equation} g(\theta) \sim \int_{2{\rm \pi}/R_f}^{2{\rm \pi}/\delta_{L,0}}A(k)\sin(kR_f\theta+\psi_k)\,\textrm{d} k, \end{equation}
where ![]() $k$ represents the wavenumber along the flamefront and
$k$ represents the wavenumber along the flamefront and ![]() $\psi _k$ is the phase angle. Assuming
$\psi _k$ is the phase angle. Assuming ![]() $A(k)$, the amplitude at wavenumber
$A(k)$, the amplitude at wavenumber ![]() $k$ follows a power law
$k$ follows a power law ![]() $A(k) \sim k^{-\gamma }$. By differentiating it with respect to
$A(k) \sim k^{-\gamma }$. By differentiating it with respect to ![]() $\theta$ and substituting
$\theta$ and substituting ![]() $A(k) \sim k^{-\gamma }$, we obtain
$A(k) \sim k^{-\gamma }$, we obtain
 \begin{equation} \frac{\textrm{d} g}{\textrm{d}\theta} \sim R_f\int_{2{\rm \pi}/R_f}^{2{\rm \pi}/\delta_{L,0}}k^{1-\gamma} \cos(kR_f\theta+\psi_k)\,\textrm{d} k \end{equation}
\begin{equation} \frac{\textrm{d} g}{\textrm{d}\theta} \sim R_f\int_{2{\rm \pi}/R_f}^{2{\rm \pi}/\delta_{L,0}}k^{1-\gamma} \cos(kR_f\theta+\psi_k)\,\textrm{d} k \end{equation}
The amplitude of ![]() $\textrm {d} g/\textrm {d}\theta$ at wavenumber
$\textrm {d} g/\textrm {d}\theta$ at wavenumber ![]() $k$ scales with
$k$ scales with ![]() $k^{1-\gamma }$, thus,
$k^{1-\gamma }$, thus, ![]() $PSD$ of
$PSD$ of ![]() $\textrm {d} g/\textrm {d}\theta$ has a
$\textrm {d} g/\textrm {d}\theta$ has a ![]() $k^{2(1-\gamma )}$ dependence; in other words,
$k^{2(1-\gamma )}$ dependence; in other words, ![]() $\beta =-2(1-\gamma )$. Now rearranging (3.7) and substituting
$\beta =-2(1-\gamma )$. Now rearranging (3.7) and substituting ![]() $\lambda = kR_f$ as a normalized wavenumber, we have
$\lambda = kR_f$ as a normalized wavenumber, we have
It can be shown (see Supplementary material) that the integral in (3.8) converges to a constant value for any ![]() $\theta$ and
$\theta$ and ![]() $\psi$ for
$\psi$ for ![]() $\gamma >1$ at large
$\gamma >1$ at large ![]() $Pe$, and hence is independent of
$Pe$, and hence is independent of ![]() $R_f$. This leads to
$R_f$. This leads to ![]() $|dg/(R_fd\theta )| \sim R_f^{\gamma -2}$, and by comparing with (3.5), we find
$|dg/(R_fd\theta )| \sim R_f^{\gamma -2}$, and by comparing with (3.5), we find ![]() $\gamma = D+1$ or
$\gamma = D+1$ or ![]() $\beta =2D$. Using the experimentally measured fractal dimension (
$\beta =2D$. Using the experimentally measured fractal dimension (![]() $D = 1+d \approx 1.25 \pm 0.05$) in the saturated stage for our flames (Yang et al. Reference Yang, Saha, Wu and Law2016), we expect
$D = 1+d \approx 1.25 \pm 0.05$) in the saturated stage for our flames (Yang et al. Reference Yang, Saha, Wu and Law2016), we expect ![]() $\beta = 2.5 \pm 0.1$, which is close to the observed value of
$\beta = 2.5 \pm 0.1$, which is close to the observed value of ![]() $2.6$ shown in figures 4(b) and 5(b).
$2.6$ shown in figures 4(b) and 5(b).
4. Concluding remarks
We conclude by revisiting the questions posed at the beginning. In terms of flow characteristics, we have shown that for an expanding cellularly (Darrieus–Landau) unstable flame, the far field flow is dominated by a radial mean flow, owing to thermal expansion, and the RMS of the velocity is rather weak. Close to the flame, however, the flow shows turbulence-like behaviour. In particular, the energy spectra from the tangential velocity component approach a power-law behaviour in the saturated stage of the propagation. The spectra from the normal component of velocity, however, remains unaltered between the stable and unstable flames. Further analysis based on the G-equation shows that the spectra from the tangential velocity arise from the wrinkling of the cellular flamefronts. We identify that the observed power-law dependence in the energy spectra in the flow is directly related to the fractal dimension of the wrinkled flamefront. We end this exposition with the understanding that the flow adjacent to a cellularly unstable flamefront does become ‘turbulent’. Such turbulence, generated by the propagating wrinkled flamefront, has a strong directionality and hence, is anisotropic.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2021.330.
Acknowledgements
The authors sincerely thank Prof C. Sun, Prof M. Mueller, Prof L. Deike and Dr K. Kokmanian for helpful discussions.
Funding
This work was supported by the US National Science Foundation (CBET, grant no. 1827287).
Declaration of interests
The authors report no conflict of interest.