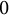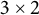1 Introduction
In the last few years, local stability, as developed by Hrushovski and Pillay [Reference Hrushovski and Pillay21], has found several applications [Reference Conant11, Reference Conant, Pillay and Terry12, Reference Martin-Pizarro, Palacín and Wolf30, Reference Terry and Wolf42] to questions on asymptotic behavior in additive combinatorics. Recall that a subset A of a group G is k-stable if its Cayley graph
induces no half-graph of height k, that is, there is no sequence
![]() $(a_1,b_1,\ldots ,a_k,b_k)$
in
$(a_1,b_1,\ldots ,a_k,b_k)$
in
![]() $G^{2k}$
such that the pair
$G^{2k}$
such that the pair
![]() $a_i ^{-1}\cdot b_j$
belongs to A if and only if
$a_i ^{-1}\cdot b_j$
belongs to A if and only if
![]() $i\le j$
.
$i\le j$
.
Although the notion of stability has played and continues to play a crucial role in the development of model theory, from a combinatorial perspective, it is exceptionally sensitive: the slightest perturbation of the set (adding a single instance of a half-graph) has the potential to destroy it. Motivated by this, we introduce a relaxation of stability which takes such perturbations into account. Given finite sets X and Y, a relation
![]() $S\subseteq X\times Y$
is almost surely k-stable if there are few (in the sense of the counting measure associated with
$S\subseteq X\times Y$
is almost surely k-stable if there are few (in the sense of the counting measure associated with
![]() $X\times Y$
) half-graphs of height k induced by S (see Definition 4.3). Similar attempts to quantify stability appeared in earlier work of Terry and the third author [Reference Terry and Wolf43, Section 5] and Coregliano and Malliaris [Reference Coregliano and Malliaris13, Definition 3.5].Footnote
1
$X\times Y$
) half-graphs of height k induced by S (see Definition 4.3). Similar attempts to quantify stability appeared in earlier work of Terry and the third author [Reference Terry and Wolf43, Section 5] and Coregliano and Malliaris [Reference Coregliano and Malliaris13, Definition 3.5].Footnote
1
Our purpose for this work is twofold: on the one hand, we aim to develop the notion of almost sure stability from a model-theoretic point of view.Footnote 2 On the other hand, we hope to further cement the relevance of stability to classical questions in arithmetic combinatorics (in both the abelian and the non-commutative case). The article thus focuses on the existence of certain two-dimensional shapes, such as corners and squares, in dense subsets of groups.
Given an abelian group G, a (nontrivial) corner in a subset
![]() $S\subseteq G\times G$
is given by a pair
$S\subseteq G\times G$
is given by a pair
![]() $(x, y)$
in
$(x, y)$
in
![]() $G^2$
along with
$G^2$
along with
![]() $d\ne 0_G$
in G with the property that all three pairs
$d\ne 0_G$
in G with the property that all three pairs
![]() $(x,y)$
,
$(x,y)$
,
![]() $(x+d, y)$
, and
$(x+d, y)$
, and
![]() $(x,y+d)$
lie in S. It is well known [Reference Solymosi41] that the existence of nontrivial corners for dense subsets in
$(x,y+d)$
lie in S. It is well known [Reference Solymosi41] that the existence of nontrivial corners for dense subsets in
![]() $G\times G$
implies Roth’s theorem [Reference Roth36] on
$G\times G$
implies Roth’s theorem [Reference Roth36] on
![]() $3$
-term arithmetic progressions in dense subsets A of G. Indeed, a nontrivial corner in
$3$
-term arithmetic progressions in dense subsets A of G. Indeed, a nontrivial corner in
![]() $\mathrm {Cay}(G,A)\subseteq G\times G$
determined by
$\mathrm {Cay}(G,A)\subseteq G\times G$
determined by
![]() $(x, y)$
and d gives rise, by a simple projection, to the nontrivial
$(x, y)$
and d gives rise, by a simple projection, to the nontrivial
![]() $3$
-term arithmetic progression
$3$
-term arithmetic progression
![]() $x-y-d, x-y, x-y+d$
in A.
$x-y-d, x-y, x-y+d$
in A.
The existence of corners in subsets S of
![]() $G\times G$
of positive density follows straight from the multidimensional Szemerédi theorem. The latter was first proved qualitatively in [Reference Furstenberg and Katznelson16], and quantitative versions (albeit with poor bounds) follow from the hypergraph regularity lemmas of Gowers [Reference Gowers18] and Nagle, Rödl, Schacht, and Skokan [Reference Nagle, Rödl and Schacht32, Reference Rödl and Skokan35]. However, finding corners is not quite as difficult as resolving the full multidimensional Szemerédi theorem, and indeed some remarkable progress has been made toward a strongly quantitative resolution [Reference Ajtai and Szemerédi1, Reference Green19, Reference Lacey and McClain27, Reference Shkredov39, Reference Shkredov40].Footnote
3
$G\times G$
of positive density follows straight from the multidimensional Szemerédi theorem. The latter was first proved qualitatively in [Reference Furstenberg and Katznelson16], and quantitative versions (albeit with poor bounds) follow from the hypergraph regularity lemmas of Gowers [Reference Gowers18] and Nagle, Rödl, Schacht, and Skokan [Reference Nagle, Rödl and Schacht32, Reference Rödl and Skokan35]. However, finding corners is not quite as difficult as resolving the full multidimensional Szemerédi theorem, and indeed some remarkable progress has been made toward a strongly quantitative resolution [Reference Ajtai and Szemerédi1, Reference Green19, Reference Lacey and McClain27, Reference Shkredov39, Reference Shkredov40].Footnote
3
In the case of a non-abelian group G, we distinguish between so-called naive corners, that is, configurations of the form
![]() $(x, y), (x \cdot g, y), (x, y \cdot g)$
with
$(x, y), (x \cdot g, y), (x, y \cdot g)$
with
![]() $g\neq 1_G$
, and BMZ corners (for Bergelson, McCutcheon, and Zhang [Reference Bergelson, McCutcheon and Zhang4]), which are of the form
$g\neq 1_G$
, and BMZ corners (for Bergelson, McCutcheon, and Zhang [Reference Bergelson, McCutcheon and Zhang4]), which are of the form
![]() $(x, y), (x \cdot g, y), (x \cdot g, y\cdot g)$
with
$(x, y), (x \cdot g, y), (x \cdot g, y\cdot g)$
with
![]() $g\neq 1_G$
. Note that the latter configuration can also be written as
$g\neq 1_G$
. Note that the latter configuration can also be written as
![]() $(x, y), (g \cdot x, y), (x, y\cdot g)$
, by first writing
$(x, y), (g \cdot x, y), (x, y\cdot g)$
, by first writing
![]() $z=x\cdot g$
and then replacing the set
$z=x\cdot g$
and then replacing the set
![]() $S\subseteq G\times G$
with its image after applying the inverse operation in the first coordinate. Similarly, naive corners can be expressed as
$S\subseteq G\times G$
with its image after applying the inverse operation in the first coordinate. Similarly, naive corners can be expressed as
![]() $(x,y)$
,
$(x,y)$
,
![]() $(g\cdot x,y)$
,
$(g\cdot x,y)$
,
![]() $(g\cdot x, y\cdot g)$
.
$(g\cdot x, y\cdot g)$
.
In abelian groups, naive and BMZ corners are easily seen to be equivalent. Some abelian techniques can be adapted to the non-abelian context for BMZ corners, but do not seem to apply to naive corners [Reference Bergelson, McCutcheon and Zhang4], and an extensive literature now exists [Reference Austin2, Reference Bergelson, Robertson and Zorin-Kranich5, Reference Solymosi41].
Other two-dimensional shapes are of interest in abelian groups, for instance, squares, which are configurations given by
![]() $(x, y)\in G^2$
together with
$(x, y)\in G^2$
together with
![]() $d\neq 0_G$
in G such that all of
$d\neq 0_G$
in G such that all of
![]() $(x,y)$
,
$(x,y)$
,
![]() $(x+d, y)$
,
$(x+d, y)$
,
![]() $(x,y+d)$
,
$(x,y+d)$
,
![]() $(x+d,y+d)$
lie in S. We observe that the non-abelian formulation of a square, where we require
$(x+d,y+d)$
lie in S. We observe that the non-abelian formulation of a square, where we require
to lie in S, actually contains both a naive and a BMZ corner (and could have been expressed in a number of equivalent ways).
In the presence of almost sure stability, that is, when few half-graphs of height k are induced by the subset S of
![]() $G\times G$
, we are able to obtain qualitative asymptotic bounds on the density of S that guarantees the existence of a square in S. In fact, our methods work in both abelian and non-abelian finite groups (see Corollary 5.5).
$G\times G$
, we are able to obtain qualitative asymptotic bounds on the density of S that guarantees the existence of a square in S. In fact, our methods work in both abelian and non-abelian finite groups (see Corollary 5.5).
Moreover, we prove the following strengthening in the setting of finite groups of bounded exponent (see Corollary 5.6).
Theorem A Given integers
![]() $k, r\ge 1$
and real numbers
$k, r\ge 1$
and real numbers
![]() $\delta , \epsilon>0,$
there exists an integer
$\delta , \epsilon>0,$
there exists an integer
![]() $N=N(k, r, \delta , \epsilon )\ge 1$
and real numbers
$N=N(k, r, \delta , \epsilon )\ge 1$
and real numbers
![]() $\theta =\theta (k, r, \delta , \epsilon )>0$
and
$\theta =\theta (k, r, \delta , \epsilon )>0$
and
![]() $\eta =(k, r, \delta , \epsilon )>0$
with the following property.
$\eta =(k, r, \delta , \epsilon )>0$
with the following property.
Let G be a finite group of exponent at most r, and consider a relation
![]() $S\subseteq G\times G$
of size
$S\subseteq G\times G$
of size
![]() $|S|\ge \delta |G|^{2}$
such that the collection
$|S|\ge \delta |G|^{2}$
such that the collection
![]() $\mathcal {H}_k(S)$
of all half-graphs of height k induced by S on G has size
$\mathcal {H}_k(S)$
of all half-graphs of height k induced by S on G has size
![]() $|\mathcal {H}_k(S)|\le \theta |G|^{2k}$
. For an element g in G, set
$|\mathcal {H}_k(S)|\le \theta |G|^{2k}$
. For an element g in G, set
Then, there exists a subgroup H of G of index at most N such that
Going beyond corners, in a recent breakthrough, Peluse [Reference Peluse34] obtained the first reasonable bound for the existence of so-called L-shapes (where each of the pairs
![]() $(x,y)$
,
$(x,y)$
,
![]() $(x+d, y)$
,
$(x+d, y)$
,
![]() $(x,y+d)$
,
$(x,y+d)$
,
![]() $(x,y+2d)$
belongs to S) in dense subsets of
$(x,y+2d)$
belongs to S) in dense subsets of
![]() $\mathbb {F}_p^n\times \mathbb {F}_p^n$
.
$\mathbb {F}_p^n\times \mathbb {F}_p^n$
.
In the presence of almost sure stability, we are able to establish the existence of even larger two-dimensional patterns, including
![]() $3\times 2$
-grids (see Corollary 6.4).
$3\times 2$
-grids (see Corollary 6.4).
Theorem B Given an integer
![]() $k\ge 1$
and a real number
$k\ge 1$
and a real number
![]() $\delta>0$
, there is an integer
$\delta>0$
, there is an integer
![]() $N(k, \delta )\ge 1$
and real numbers
$N(k, \delta )\ge 1$
and real numbers
![]() $\theta =\theta (k, \delta )>0$
and
$\theta =\theta (k, \delta )>0$
and
![]() $\epsilon =\epsilon (k, \delta )>0$
with the following property.
$\epsilon =\epsilon (k, \delta )>0$
with the following property.
Let G be a finite abelian group of odd order with
![]() $|G|\ge N$
, and consider a relation
$|G|\ge N$
, and consider a relation
![]() $S\subseteq G\times G$
of size
$S\subseteq G\times G$
of size
![]() $|S|\ge \delta |G|^{2}$
such that the collection
$|S|\ge \delta |G|^{2}$
such that the collection
![]() $\mathcal {H}_k(S)$
of all half-graphs of height k induced by S on G has size
$\mathcal {H}_k(S)$
of all half-graphs of height k induced by S on G has size
![]() $|\mathcal {H}_k(S)|\le \theta |G|^{2k}$
.
$|\mathcal {H}_k(S)|\le \theta |G|^{2k}$
.
Then, the set
has size
![]() $|\Lambda _{3\times 2}(S)| \ge \epsilon |G|^{3}$
. In particular, the relation S contains an L-shape.
$|\Lambda _{3\times 2}(S)| \ge \epsilon |G|^{3}$
. In particular, the relation S contains an L-shape.
The techniques used to prove Theorems A and B are of a model-theoretic flavor, and rely heavily on a stationarity result for almost surely stable relations (see Theorem 4.7). In forthcoming work, we establish some of the results presented here in the language of additive combinatorics. While the techniques used will be different, the structure of the proofs will follow a similar pattern. The present article should therefore be viewed as an effort to highlight the close interactions and foster stronger synergies between model theory and additive combinatorics.
In order to render the presentation of this first work more accessible to an audience who may not be versed in the language of model theory, we have adapted the results using some of the (perhaps more familiar) machinery of ultraproducts, with the aim of keeping the presentation as self-contained as possible. This choice should not present an obstacle for the model-theoretic reader, who will easily translate the terminology and techniques to the more general setting.
Outline of the article. Sections 2 and 3 introduce the background needed for the remainder of the article. In Section 4, we define almost sure stability and prove a stationarity principle for almost stable relations. The main theorems concerning corners and squares are derived in Section 5, while Section 6 considers more complex two-dimensional configurations.
2 Non-standard f inite groups and Loeb measures
Recall that a non-principal ultrafilter
![]() $\mathfrak {U}$
on
$\mathfrak {U}$
on
![]() $\mathbb {N}$
is a non-empty collection of infinite sets closed under finite intersections and with the property that either a subset of
$\mathbb {N}$
is a non-empty collection of infinite sets closed under finite intersections and with the property that either a subset of
![]() $\mathbb {N}$
or its complement belongs to
$\mathbb {N}$
or its complement belongs to
![]() $\mathfrak {U}$
. Such ultrafilters exist and each one induces a finitely additive probability measure on all subsets of
$\mathfrak {U}$
. Such ultrafilters exist and each one induces a finitely additive probability measure on all subsets of
![]() $\mathbb {N}$
, taking values
$\mathbb {N}$
, taking values
![]() $0$
and
$0$
and
![]() $1$
only, such that no finite subset has measure
$1$
only, such that no finite subset has measure
![]() $1$
.
$1$
.
Definition 2.1 A non-standard finite group (sometimes referred to in the literature as a hyperfinite group) has as underlying set
![]() $\prod _{n\to \mathfrak {U}} G_n$
for some collection
$\prod _{n\to \mathfrak {U}} G_n$
for some collection
![]() $(G_n)_{n\in \mathbb {N}}$
of finite groups of strictly increasing size (that is,
$(G_n)_{n\in \mathbb {N}}$
of finite groups of strictly increasing size (that is,
![]() $|G_n|<|G_{n+1}|$
for all n in
$|G_n|<|G_{n+1}|$
for all n in
![]() $\mathbb {N}$
) and some non-principal ultrafilter
$\mathbb {N}$
) and some non-principal ultrafilter
![]() $\mathfrak {U}$
on
$\mathfrak {U}$
on
![]() $\mathbb {N}$
, where the set
$\mathbb {N}$
, where the set
![]() $\prod _{n\to \mathfrak {U}} G_n$
consists of the infinite Cartesian product
$\prod _{n\to \mathfrak {U}} G_n$
consists of the infinite Cartesian product
![]() $\prod _{n\in \mathbb {N}} G_n$
modulo the equivalence relation
$\prod _{n\in \mathbb {N}} G_n$
modulo the equivalence relation
That is, we identify two sequences if they are equal
![]() $\mathfrak {U}$
-almost everywhere (with respect to the measure induced by
$\mathfrak {U}$
-almost everywhere (with respect to the measure induced by
![]() $\mathfrak {U}$
on all subsets of
$\mathfrak {U}$
on all subsets of
![]() $\mathbb {N}$
).
$\mathbb {N}$
).
If we denote the class of
![]() $(g_n)_{n\in \mathbb {N}}$
modulo
$(g_n)_{n\in \mathbb {N}}$
modulo
![]() $\sim _{\mathfrak {U}}$
by
$\sim _{\mathfrak {U}}$
by
![]() $[(g_n)_{n\in \mathbb {N}}]_{\mathfrak {U}}$
, it follows immediately from the definition of the non-principal ultrafilter
$[(g_n)_{n\in \mathbb {N}}]_{\mathfrak {U}}$
, it follows immediately from the definition of the non-principal ultrafilter
![]() $\mathfrak {U}$
that the quotient
$\mathfrak {U}$
that the quotient
![]() $\prod _{n\to \mathfrak {U}} G_n$
is a group, where
$\prod _{n\to \mathfrak {U}} G_n$
is a group, where
is well-defined and has neutral element
![]() $1_{\prod _{\mathfrak {U}} G_n} = [(1_{G_n})_{n\in \mathbb {N}}]_{\mathfrak {U}}$
. Furthermore, the inverse
$1_{\prod _{\mathfrak {U}} G_n} = [(1_{G_n})_{n\in \mathbb {N}}]_{\mathfrak {U}}$
. Furthermore, the inverse
![]() $[(g_n)_{n\in \mathbb {N}}]_{\mathfrak {U}} ^{-1}= [(g_n ^{-1})_{n\in \mathbb {N}}]_{\mathfrak {U}}$
.
$[(g_n)_{n\in \mathbb {N}}]_{\mathfrak {U}} ^{-1}= [(g_n ^{-1})_{n\in \mathbb {N}}]_{\mathfrak {U}}$
.
Note that a finite Cartesian product of non-standard finite groups is again a non-standard finite group.
Definition 2.2 A subset X of a non-standard finite group
![]() $\prod _{n\to \mathfrak {U}} G_n$
is internal if there exists a collection
$\prod _{n\to \mathfrak {U}} G_n$
is internal if there exists a collection
![]() $(X_n)_{n\in \mathbb {N}}$
such that each
$(X_n)_{n\in \mathbb {N}}$
such that each
![]() $X_n$
is a subset of
$X_n$
is a subset of
![]() $G_n$
and
$G_n$
and
 $$\begin{align*}X= \left\{ [(g_n)_{n\in\mathbb{N}}]_{\mathfrak{U}} \in \prod_{n\to \mathfrak{U}} G_n : \ g_n \text{ belongs to } X_n \text{ for }\mathfrak{U}-\text{almost all } n \text{ in } \mathbb{N} \right\}.\end{align*}$$
$$\begin{align*}X= \left\{ [(g_n)_{n\in\mathbb{N}}]_{\mathfrak{U}} \in \prod_{n\to \mathfrak{U}} G_n : \ g_n \text{ belongs to } X_n \text{ for }\mathfrak{U}-\text{almost all } n \text{ in } \mathbb{N} \right\}.\end{align*}$$
Given an internal subset X of
![]() $G=\prod _{n\to \mathfrak {U}} G_n$
induced from the collection
$G=\prod _{n\to \mathfrak {U}} G_n$
induced from the collection
![]() $(X_n)_{n\in \mathbb {N}}$
as above, we will denote the subset
$(X_n)_{n\in \mathbb {N}}$
as above, we will denote the subset
![]() $X_n$
of
$X_n$
of
![]() $G_n$
by
$G_n$
by
![]() $X(G_n)$
. Likewise, we will sometimes denote the internal set X by
$X(G_n)$
. Likewise, we will sometimes denote the internal set X by
![]() $\prod _{n\to \mathfrak {U}} X_n$
.
$\prod _{n\to \mathfrak {U}} X_n$
.
Remark 2.1
-
(1) Every finite subset of a non-standard finite group is internal.
-
(2) The collection of internal sets is closed under Boolean combinations and projections. Given a (group) word
 $w=w(u, v_1,\ldots , v_n)$
and a tuple
$w=w(u, v_1,\ldots , v_n)$
and a tuple
 $\bar a=(a_1,\ldots , a_n)$
in a non-standard finite group G, the set
$\bar a=(a_1,\ldots , a_n)$
in a non-standard finite group G, the set  $$\begin{align*}X=\left\{ g\in G : \ w(g, \bar a)=1_G\right\} \end{align*}$$
$$\begin{align*}X=\left\{ g\in G : \ w(g, \bar a)=1_G\right\} \end{align*}$$
is internal.
-
(3) Given internal subsets
 $X_1,\ldots ,X_n$
of a non-standard finite group G, the Cartesian product
$X_1,\ldots ,X_n$
of a non-standard finite group G, the Cartesian product
 $X_1\times \dots \times X_n$
is an internal subset of the nth Cartesian product
$X_1\times \dots \times X_n$
is an internal subset of the nth Cartesian product
 $G^n=G\times \dots \times G$
.
$G^n=G\times \dots \times G$
. -
(4) Given an internal set X of G, the subset
 $$\begin{align*}\left\{ (x,y) \in G\times G : \ x\cdot y\in X \right\} \end{align*}$$
$$\begin{align*}\left\{ (x,y) \in G\times G : \ x\cdot y\in X \right\} \end{align*}$$
is an internal subset of
 $G\times G$
. In particular, every translate (left or right) of an internal set is internal.
$G\times G$
. In particular, every translate (left or right) of an internal set is internal. -
(5) In this particular set-up, Łoś’s Theorem becomes tautologically immediate: given an internal set X in a non-standard finite group
 $G= \prod _{n\to \mathfrak {U}} G_n$
, we have that
$G= \prod _{n\to \mathfrak {U}} G_n$
, we have that  $$\begin{align*}X\ne \emptyset \ \Longleftrightarrow \ X(G_n) \ne \emptyset \text{ for } \mathfrak{U}\text{-almost all } n \text{ in } \mathbb{N}. \end{align*}$$
$$\begin{align*}X\ne \emptyset \ \Longleftrightarrow \ X(G_n) \ne \emptyset \text{ for } \mathfrak{U}\text{-almost all } n \text{ in } \mathbb{N}. \end{align*}$$
Every non-standard finite group arising as a limit of finite groups has cardinality continuum and so it has continuum many internal sets. However, whenever we restrict our attention to only countably many internal sets non-standard finite groups have the following remarkable property, which in model-theoretic terms is called
![]() $\aleph _1$
-saturation.
$\aleph _1$
-saturation.
Fact 2.2 (
 $\aleph _1$
-saturation)
$\aleph _1$
-saturation)
Let G be a non-standard finite group. Every internal countable cover of an internal set admits a finite sub-covering: given an internal subset X of G and a countable family
![]() $(Y_n)_{n\in \mathbb {N}}$
of internal subsets of G such that
$(Y_n)_{n\in \mathbb {N}}$
of internal subsets of G such that
![]() $X=\bigcup _{n\in \mathbb {N}} Y_n$
, there is some natural number k such that
$X=\bigcup _{n\in \mathbb {N}} Y_n$
, there is some natural number k such that
Equivalently, a countable intersection of internal sets is non-empty whenever every finite sub-intersection is.
In particular, every infinite internal subset of a non-standard finite group must be uncountable.
Every non-standard finite group is equipped with a finitely additive probability measure on the Boolean algebra of internal sets, induced by the normalized counting measure on every finite group.
Definition 2.3 The Loeb or non-standard counting measure of the non-standard finite group
![]() $G=\prod _{n\to \mathfrak {U}} G_n$
is defined for every internal subset X of G as
$G=\prod _{n\to \mathfrak {U}} G_n$
is defined for every internal subset X of G as
 $$\begin{align*}\mu_G (X) = \lim_{n\to \mathfrak{U}} \frac{|X(G_n)|}{|G_n|}. \end{align*}$$
$$\begin{align*}\mu_G (X) = \lim_{n\to \mathfrak{U}} \frac{|X(G_n)|}{|G_n|}. \end{align*}$$
In an abuse of notation, we call the value
![]() $\mu _G(X)$
the density of X.
$\mu _G(X)$
the density of X.
Note that for every real number r in the interval
![]() $[0,1]$
, the measure
$[0,1]$
, the measure
![]() $\mu _G(X)\ge r$
whenever
$\mu _G(X)\ge r$
whenever
![]() $|X(G_n)|\ge r|G_n|$
for
$|X(G_n)|\ge r|G_n|$
for
![]() $\mathfrak {U}$
-almost all n in
$\mathfrak {U}$
-almost all n in
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Remark 2.3 Given an internal subset Z of the non-standard finite group
![]() $G^{k+m}$
and a real number r in
$G^{k+m}$
and a real number r in
![]() $[0,1]$
, there is an internal subset
$[0,1]$
, there is an internal subset
![]() $Y_r$
of
$Y_r$
of
![]() $G^m$
such that
$G^m$
such that
where
![]() $Z_y=\{x \in G^k : \ (x,y)\in Z\}$
denotes the fiber of Z over y. Namely, set
$Z_y=\{x \in G^k : \ (x,y)\in Z\}$
denotes the fiber of Z over y. Namely, set
We include the following easy result to demonstrate how information about the measure of non-standard finite objects allows us to provide asymptotic bounds on the cardinalities of the corresponding sequence of finite objects.
Lemma 2.4 Consider a family
![]() $(G_n,X_n)_{n\in \mathbb {N}}$
, where
$(G_n,X_n)_{n\in \mathbb {N}}$
, where
![]() $X_n$
is a subset of the finite group
$X_n$
is a subset of the finite group
![]() $G_n$
. The following are equivalent for every real number r in
$G_n$
. The following are equivalent for every real number r in
![]() $[0,1]$
:
$[0,1]$
:
-
(1) For every
 $\epsilon>0,$
there is some
$\epsilon>0,$
there is some
 $n_0=n_0(r, \epsilon )$
in
$n_0=n_0(r, \epsilon )$
in
 $\mathbb {N}$
such that
$\mathbb {N}$
such that
 $|X_n| \le (r+\epsilon ) |G_n|$
for all
$|X_n| \le (r+\epsilon ) |G_n|$
for all
 $n> n_0$
.
$n> n_0$
. -
(2) For every non-principal ultrafilter
 $\mathfrak {U}$
on
$\mathfrak {U}$
on
 $\mathbb {N}$
, we have that
$\mathbb {N}$
, we have that
 $\mu _G(X) \le r$
for the internal set
$\mu _G(X) \le r$
for the internal set
 $X=\prod _{n\to \mathfrak {U}} X_n$
in the non-standard finite group
$X=\prod _{n\to \mathfrak {U}} X_n$
in the non-standard finite group
 $\prod _{n\to \mathfrak {U}}G_n$
.
$\prod _{n\to \mathfrak {U}}G_n$
.
Proof
![]() $(a)\Rightarrow (b):$
No finite set lies in a non-principal ultrafilter
$(a)\Rightarrow (b):$
No finite set lies in a non-principal ultrafilter
![]() $\mathfrak {U}$
. Hence, by the way, the non-standard counting measure on the non-standard finite group
$\mathfrak {U}$
. Hence, by the way, the non-standard counting measure on the non-standard finite group
![]() $G=\prod _{n\to \mathfrak {U}} G_n$
has been defined, it follows from (a) that
$G=\prod _{n\to \mathfrak {U}} G_n$
has been defined, it follows from (a) that
![]() $\mu _G(X)\le r+\epsilon $
for every
$\mu _G(X)\le r+\epsilon $
for every
![]() $\epsilon>0$
, so
$\epsilon>0$
, so
![]() $\mu _G(X)\le r$
, as desired.
$\mu _G(X)\le r$
, as desired.
![]() $(b)\Rightarrow (a):$
If (a) is false, negating quantifiers, there is some value
$(b)\Rightarrow (a):$
If (a) is false, negating quantifiers, there is some value
![]() $\epsilon>0$
such that for every natural number
$\epsilon>0$
such that for every natural number
![]() $n_0\ge 1$
, we find some
$n_0\ge 1$
, we find some
![]() $n> n_0$
with
$n> n_0$
with
![]() $|X_n|> (r+ \epsilon ) |G_n|$
. Hence, the subset
$|X_n|> (r+ \epsilon ) |G_n|$
. Hence, the subset
is infinite. Choose a non-principal ultrafilter
![]() $\mathfrak {U}$
containing each
$\mathfrak {U}$
containing each
![]() $Q_\epsilon $
(which exists). By definition of the non-standard counting measure on the non-standard finite group
$Q_\epsilon $
(which exists). By definition of the non-standard counting measure on the non-standard finite group
![]() $G=\prod _{n\to \mathfrak {U}} G_n$
, we deduce
$G=\prod _{n\to \mathfrak {U}} G_n$
, we deduce
 $$\begin{align*}\mu_G(X) = \lim_{n\to\mathfrak{U}} \frac{|X(G_n)|}{|G_n|} \ge \lim_{n\to\mathfrak{U}} r+\epsilon = r +\epsilon. \end{align*}$$
$$\begin{align*}\mu_G(X) = \lim_{n\to\mathfrak{U}} \frac{|X(G_n)|}{|G_n|} \ge \lim_{n\to\mathfrak{U}} r+\epsilon = r +\epsilon. \end{align*}$$
Thus,
![]() $\mu _G(X)> r$
, which yields the desired contradiction.
$\mu _G(X)> r$
, which yields the desired contradiction.
Remark 2.5 Taking set-theoretic complements, it follows from Lemma 2.4 that the following two conditions are equivalent:
-
(1) For every
 $\epsilon>0,$
there is some
$\epsilon>0,$
there is some
 $n_0=n_0(r, \epsilon )$
in
$n_0=n_0(r, \epsilon )$
in
 $\mathbb {N}$
such that
$\mathbb {N}$
such that
 $|X_n| \ge (r-\epsilon )|G_n|$
for all
$|X_n| \ge (r-\epsilon )|G_n|$
for all
 $n> n_0$
.
$n> n_0$
. -
(2) For every non-principal ultrafilter
 $\mathfrak {U}$
on
$\mathfrak {U}$
on
 $\mathbb {N}$
, we have that
$\mathbb {N}$
, we have that
 $\mu _G(X) \ge r$
for the internal set
$\mu _G(X) \ge r$
for the internal set
 $X=\prod _{n\to \mathfrak {U}} X_n$
in the non-standard finite group
$X=\prod _{n\to \mathfrak {U}} X_n$
in the non-standard finite group
 $\prod _{n\to \mathfrak {U}}G_n$
.
$\prod _{n\to \mathfrak {U}}G_n$
.
Remark 2.6 (cf. [Reference Bergelson and Tao6, Section 2])
Carathéodory’s Extension Criterion is satisfied by the Loeb measure by
![]() $\aleph _1$
-saturation (Fact 2.2). Therefore, the Loeb measure
$\aleph _1$
-saturation (Fact 2.2). Therefore, the Loeb measure
![]() $\mu _G$
extends to a unique
$\mu _G$
extends to a unique
![]() $\sigma $
-additive measure on the
$\sigma $
-additive measure on the
![]() $\sigma $
-algebra generated by the internal subsets of G. Abusing notation, we will not distinguish between
$\sigma $
-algebra generated by the internal subsets of G. Abusing notation, we will not distinguish between
![]() $\mu _G$
and its unique extension.
$\mu _G$
and its unique extension.
Furthermore, the family of measures
![]() $\{\mu _{G^k}\}_{k\ge 1}$
satisfies the Fubini–Tonelli Theorem [Reference Bergelson and Tao6, Theorem 19], meaning that for any internal subset Z of
$\{\mu _{G^k}\}_{k\ge 1}$
satisfies the Fubini–Tonelli Theorem [Reference Bergelson and Tao6, Theorem 19], meaning that for any internal subset Z of
![]() $G^{n+m}$
, the following holds:
$G^{n+m}$
, the following holds:
-
• The function
 $y\mapsto \mu _{G^n}(Z_y)$
, resp.,
$y\mapsto \mu _{G^n}(Z_y)$
, resp.,
 $x\mapsto \mu _{G^m}(Z_x)$
, is
$x\mapsto \mu _{G^m}(Z_x)$
, is
 $\mu _{G^m}$
-measurable, resp.,
$\mu _{G^m}$
-measurable, resp.,
 $\mu _{G^n}$
-measurable.
$\mu _{G^n}$
-measurable. -
• We have the equality
 $$\begin{align*}\mu_{G^{n+m}}(Z) = \int_{G^n} \mu_{G^m}(Z_x) \, \mathrm{d}\mu_{G^n} =\int_{G^m} \mu_{G^n}(Z_y) \, \mathrm{d}\mu_{G^m}. \end{align*}$$
$$\begin{align*}\mu_{G^{n+m}}(Z) = \int_{G^n} \mu_{G^m}(Z_x) \, \mathrm{d}\mu_{G^n} =\int_{G^m} \mu_{G^n}(Z_y) \, \mathrm{d}\mu_{G^m}. \end{align*}$$
3 Tame families and dense subsets
In view of
![]() $\aleph _1$
-saturation (Fact 2.2), we introduce the following notion, which appears in [Reference Bays and Breuillard3] as
$\aleph _1$
-saturation (Fact 2.2), we introduce the following notion, which appears in [Reference Bays and Breuillard3] as
![]() $\bigwedge $
-internal and in [Reference van den Dries14] as
$\bigwedge $
-internal and in [Reference van den Dries14] as
![]() $\Pi $
-definable. For readers familiar with model theory, this corresponds to type-definable sets over a countable parameter set in a countable language.
$\Pi $
-definable. For readers familiar with model theory, this corresponds to type-definable sets over a countable parameter set in a countable language.
Definition 3.1 A subset X of G is
![]() $\omega $
-internal if it is a countable intersection of internal subsets of G.
$\omega $
-internal if it is a countable intersection of internal subsets of G.
Remark 3.1
-
(1) Internal sets are
 $\omega $
-internal.
$\omega $
-internal. -
(2) Every countable decreasing chain
 $(Y_n)_{n\in \mathbb {N}}$
of infinite internal subsets of a non-standard finite group G yields a non-empty
$(Y_n)_{n\in \mathbb {N}}$
of infinite internal subsets of a non-standard finite group G yields a non-empty
 $\omega $
-internal set. By
$\omega $
-internal set. By
 $\aleph _1$
-saturation (Fact 2.2), this
$\aleph _1$
-saturation (Fact 2.2), this
 $\omega $
-internal set is uncountable.
$\omega $
-internal set is uncountable. -
(3) The projection of an
 $\omega $
-internal subset of
$\omega $
-internal subset of
 $G^{n+m}$
onto the first n coordinates is
$G^{n+m}$
onto the first n coordinates is
 $\omega $
-internal in
$\omega $
-internal in
 $G^n$
. Indeed, if X is a countable intersection of a decreasing family
$G^n$
. Indeed, if X is a countable intersection of a decreasing family
 $(X_k)_{k\in \mathbb {N}}$
of internal subsets of
$(X_k)_{k\in \mathbb {N}}$
of internal subsets of
 $G^{n+1}$
, Fact 2.2 gives immediately that
$G^{n+1}$
, Fact 2.2 gives immediately that
 $\pi (X)$
equals
$\pi (X)$
equals
 $\bigcap _{k\in \mathbb {N}} \pi (X_k)$
.
$\bigcap _{k\in \mathbb {N}} \pi (X_k)$
.
Example 3.2 Let G be the non-standard finite group
![]() $\prod _{n\to \mathfrak {U}} \mathbb {Z}/2^n\mathbb {Z}$
, for some non-principal ultrafilter
$\prod _{n\to \mathfrak {U}} \mathbb {Z}/2^n\mathbb {Z}$
, for some non-principal ultrafilter
![]() $\mathfrak {U}$
. For every natural number
$\mathfrak {U}$
. For every natural number
![]() $k\ge 1$
, the function
$k\ge 1$
, the function
![]() $f_k:x\mapsto 2^k\cdot x$
from G to G is an internal function, that is, its graph is an internal set. Each internal subgroup
$f_k:x\mapsto 2^k\cdot x$
from G to G is an internal function, that is, its graph is an internal set. Each internal subgroup
![]() $\mathrm {Im}(f_k)$
has finite index in G and they form a strictly decreasing chain, which yields an
$\mathrm {Im}(f_k)$
has finite index in G and they form a strictly decreasing chain, which yields an
![]() $\omega $
-internal uncountable subgroup of G which is
$\omega $
-internal uncountable subgroup of G which is
![]() $2$
-divisible.
$2$
-divisible.
In view of Fact 2.2, we will need to restrict our attention to suitable countable families of internal sets. Model-theoretically, this is done by fixing a suitable countable first-order language and considering the corresponding definable sets, which are always internal (see, for example, [Reference Bays and Breuillard3, Reference Hrushovski20, Reference Palacín33, Reference van den Dries14]). For the sake of the presentation, we will avoid introducing the terminology of first-order formulas and provide an approach tailored to our purposes.
Definition 3.2 Let
![]() $G=\prod _{n\to \mathfrak {U}} G_n$
be a non-standard finite group. A family
$G=\prod _{n\to \mathfrak {U}} G_n$
be a non-standard finite group. A family
![]() $\mathcal F=\bigcup _{n\in \mathbb {N}} \mathcal F_n$
, where each
$\mathcal F=\bigcup _{n\in \mathbb {N}} \mathcal F_n$
, where each
![]() $\mathcal F_n$
consists of internal subsets of
$\mathcal F_n$
consists of internal subsets of
![]() $G^n$
, is tame if it satisfies the following conditions:
$G^n$
, is tame if it satisfies the following conditions:
-
(1) Every internal set of the form:
 $$\begin{align*}X_w=\left\{ (g_1,\ldots,g_n)\in G^n : \ w(g_1,\ldots,g_n)=1_G\right\}, \end{align*}$$
$$\begin{align*}X_w=\left\{ (g_1,\ldots,g_n)\in G^n : \ w(g_1,\ldots,g_n)=1_G\right\}, \end{align*}$$
where
 $w=w(u_1,\ldots ,u_n)$
is a (group) word, belongs to
$w=w(u_1,\ldots ,u_n)$
is a (group) word, belongs to
 $\mathcal F_n$
.
$\mathcal F_n$
. -
(2)
 $\mathcal F$
is closed under finite Cartesian products, Boolean combinations, projections, and permutations of the coordinates.
$\mathcal F$
is closed under finite Cartesian products, Boolean combinations, projections, and permutations of the coordinates. -
(3) Given an internal subset Z of
 $G^n$
in
$G^n$
in
 $\mathcal F_n$
, the internal set
$\mathcal F_n$
, the internal set  $$\begin{align*}\left\{ (x,y)\in G^n\times G^n : \ x\cdot y\in Z \right\} \end{align*}$$
$$\begin{align*}\left\{ (x,y)\in G^n\times G^n : \ x\cdot y\in Z \right\} \end{align*}$$
belongs to
 $\mathcal F_{2n}$
.
$\mathcal F_{2n}$
. -
(4) Given an internal subset Z of
 $G^{k+m}$
in
$G^{k+m}$
in
 $\mathcal F_{k+m}$
and a rational number q in
$\mathcal F_{k+m}$
and a rational number q in
 $[0,1]$
, there is an internal set
$[0,1]$
, there is an internal set
 $Y_q$
in
$Y_q$
in
 $\mathcal F_m$
such that
$\mathcal F_m$
such that  $$\begin{align*}\left\{ y \in G^m : \ \mu_{G^k} (Z_y)> q \right\} \subseteq Y _q \subseteq \left\{ y \in G^m : \ \mu_{G^k} (Z_y)\ge q \right\}, \end{align*}$$
$$\begin{align*}\left\{ y \in G^m : \ \mu_{G^k} (Z_y)> q \right\} \subseteq Y _q \subseteq \left\{ y \in G^m : \ \mu_{G^k} (Z_y)\ge q \right\}, \end{align*}$$
as in Remark 2.3. In particular, for every internal subset Z of
 $G^{k+m}$
in
$G^{k+m}$
in
 $\mathcal F_{k+m}$
, the subset
$\mathcal F_{k+m}$
, the subset  $$\begin{align*}\left\{ y \in G^m : \ \mu_{G^k} (Z_y) =0 \right\}=\bigcap\limits_{n\ge 1} \left(G^m\setminus Y_{\frac{1}{n}} \right)\end{align*}$$
$$\begin{align*}\left\{ y \in G^m : \ \mu_{G^k} (Z_y) =0 \right\}=\bigcap\limits_{n\ge 1} \left(G^m\setminus Y_{\frac{1}{n}} \right)\end{align*}$$
is
 $\omega $
-internal and given by a countable intersection of internal subsets in
$\omega $
-internal and given by a countable intersection of internal subsets in
 $\mathcal F_m$
.
$\mathcal F_m$
.
Remark 3.3 The reader familiar with the notion of first-order formulas in a given language containing the language of groups will notice that a tame family
![]() $\mathcal F$
induces a first-order language
$\mathcal F$
induces a first-order language
![]() $\mathcal L$
containing the language of groups after adding, for every internal subset X of
$\mathcal L$
containing the language of groups after adding, for every internal subset X of
![]() $G^n$
in
$G^n$
in
![]() $\mathcal F$
, a distinguished predicate
$\mathcal F$
, a distinguished predicate
![]() $R_X$
such that its interpretation in G equals X.
$R_X$
such that its interpretation in G equals X.
Analogously, every language
![]() $\mathcal L_0$
containing the language of groups can be enlarged to a language
$\mathcal L_0$
containing the language of groups can be enlarged to a language
![]() $\mathcal L\supseteq \mathcal L_0$
(as in [Reference Hrushovski20, Section 2.6]) with
$\mathcal L\supseteq \mathcal L_0$
(as in [Reference Hrushovski20, Section 2.6]) with
![]() $|\mathcal L|\le \max (|\mathcal L_0|,\aleph _0)$
such that
$|\mathcal L|\le \max (|\mathcal L_0|,\aleph _0)$
such that
![]() $\mathcal L$
induces a tame family of internal sets, by setting
$\mathcal L$
induces a tame family of internal sets, by setting
for every
![]() $\mathcal L$
-formula
$\mathcal L$
-formula
![]() $\psi (x_1,\ldots , x_n)$
.
$\psi (x_1,\ldots , x_n)$
.
With this translation in mind, we see that certain internal sets automatically belong to a tame family
![]() $\mathcal F$
, without having to write them explicitly as a Boolean combination of suitable projections. For example, if the subset S of
$\mathcal F$
, without having to write them explicitly as a Boolean combination of suitable projections. For example, if the subset S of
![]() $G\times G$
is in
$G\times G$
is in
![]() $\mathcal F$
(and thus definable), then so is the set of BMZ-corners
$\mathcal F$
(and thus definable), then so is the set of BMZ-corners
To obtain an example of a countable tame family of internal sets, it suffices to close the family of internal sets given by group words under countably many instances of properties (II)–(IV). More generally, the following holds.
Fact 3.4 Given any countable family
![]() $\mathcal F_0$
of internal sets, there is a countable tame family
$\mathcal F_0$
of internal sets, there is a countable tame family
![]() $\mathcal F$
of internal sets extending
$\mathcal F$
of internal sets extending
![]() $\mathcal F_0$
.
$\mathcal F_0$
.
Remark 3.5 By Fact 3.4, whenever we want to apply Lemma 2.4 to a distinguished internal set X in a non-standard finite group, we may always assume that X belongs to a countable tame family.
If the tame family
![]() $\mathcal F$
arises as the family of definable sets with respect to a fixed language
$\mathcal F$
arises as the family of definable sets with respect to a fixed language
![]() $\mathcal L$
as explained in Remark 3.3, then the following notion of richness corresponds to the classical model-theoretic notion of an elementary substructure in that particular language.
$\mathcal L$
as explained in Remark 3.3, then the following notion of richness corresponds to the classical model-theoretic notion of an elementary substructure in that particular language.
Definition 3.3 A subset M of a non-standard finite group G is rich with respect to the tame family
![]() $\mathcal {F}$
if every non-empty fiber
$\mathcal {F}$
if every non-empty fiber
![]() $X_{a}$
of
$X_{a}$
of
![]() $G^n$
, where a is tuple in M and X is an internal subset of
$G^n$
, where a is tuple in M and X is an internal subset of
![]() $G^{n+|a|}$
in
$G^{n+|a|}$
in
![]() $\mathcal {F}$
, contains an n-tuple whose coordinates all lie in M, i.e.,
$\mathcal {F}$
, contains an n-tuple whose coordinates all lie in M, i.e.,
![]() $X_a(M)=X_a\cap M^n\neq \emptyset $
.
$X_a(M)=X_a\cap M^n\neq \emptyset $
.
A straightforward chain argument, mimicking the proof of Downward Löwenheim–Skolem for first-order languages, yields the following result.
Remark 3.6 (Downward Löwenheim–Skolem)
Given a countable tame family
![]() $\mathcal {F}$
and a countable subset A of a non-standard finite group G, there is a countable subset M of G containing A which is rich with respect to
$\mathcal {F}$
and a countable subset A of a non-standard finite group G, there is a countable subset M of G containing A which is rich with respect to
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Notice that every rich subset is, in particular, an infinite subgroup of G. However, a countable rich subset M no longer satisfies the
![]() $\aleph _1$
-saturation condition for covers of internal subsets. Indeed, the M-points of the internal set given by
$\aleph _1$
-saturation condition for covers of internal subsets. Indeed, the M-points of the internal set given by
![]() $x=x$
can be covered by countably many singletons (running through every point in M), yet it does not admit a finite cover.
$x=x$
can be covered by countably many singletons (running through every point in M), yet it does not admit a finite cover.
Henceforth, we fix a countable tame family
![]() $\mathcal {F}$
of internal sets. All internal and
$\mathcal {F}$
of internal sets. All internal and
![]() $\omega $
-internal sets we shall consider belong to this particular family.
$\omega $
-internal sets we shall consider belong to this particular family.
Given a subset A of a non-standard finite group G, we will denote by
![]() $\mathcal {F}(A)$
the collection of all fibers
$\mathcal {F}(A)$
the collection of all fibers
![]() $Y_{a}$
of
$Y_{a}$
of
![]() $G^{n}$
, with n running over all possible natural numbers, where a is a tuple in A and Y is an internal subset of
$G^{n}$
, with n running over all possible natural numbers, where a is a tuple in A and Y is an internal subset of
![]() $G^{n+|a|}$
in
$G^{n+|a|}$
in
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Definition 3.4 With the previous notation, the internal subsets in
![]() $\mathcal {F}(A)$
are said to be defined over A.
$\mathcal {F}(A)$
are said to be defined over A.
An
![]() $\omega $
-internal set
$\omega $
-internal set
![]() $X=\bigcap _{n\in \mathbb {N}} X_n$
is defined over A if each one of the internal sets
$X=\bigcap _{n\in \mathbb {N}} X_n$
is defined over A if each one of the internal sets
![]() $X_n$
is defined over the parameter set A.
$X_n$
is defined over the parameter set A.
Remark 3.7 Note that for every internal set Z of
![]() $G^{k+m}$
and every rational number q in
$G^{k+m}$
and every rational number q in
![]() $[0,1]$
, there exists an internal set
$[0,1]$
, there exists an internal set
![]() $Y_q$
as in Condition (IV) of Definition 3.2, which is defined over the same parameters as Z.
$Y_q$
as in Condition (IV) of Definition 3.2, which is defined over the same parameters as Z.
Definition 3.5 Consider a non-standard finite group G and a countable subset A of G. Given a tuple b of elements of G, its type over A is the
![]() $\omega $
-internal set
$\omega $
-internal set

Since the set
![]() $\mathcal {F}(A)$
is countable, by Remark 3.1(b), the type
$\mathcal {F}(A)$
is countable, by Remark 3.1(b), the type
![]() $\operatorname {tp}(b/A)$
is an uncountable
$\operatorname {tp}(b/A)$
is an uncountable
![]() $\omega $
-internal set whenever b does not lie in a finite fiber defined over A of some internal set in
$\omega $
-internal set whenever b does not lie in a finite fiber defined over A of some internal set in
![]() $\mathcal {F}$
(that is, in model-theoretic terms, whenever the type is not algebraic). Note that
$\mathcal {F}$
(that is, in model-theoretic terms, whenever the type is not algebraic). Note that
![]() $\operatorname {tp}(b'/A) = \operatorname {tp}(b/A)$
if and only if
$\operatorname {tp}(b'/A) = \operatorname {tp}(b/A)$
if and only if
![]() $b'$
belongs to
$b'$
belongs to
![]() $\operatorname {tp}(b/A)$
.
$\operatorname {tp}(b/A)$
.
Remark 3.8 Consider a countable subset A of parameters in a non-standard finite group G. Given two tuples
![]() $(b, c)$
and
$(b, c)$
and
![]() $b'$
such that
$b'$
such that
![]() $b'$
belongs to
$b'$
belongs to
![]() $\operatorname {tp}(b/A)$
, there is some tuple
$\operatorname {tp}(b/A)$
, there is some tuple
![]() $c'$
of length
$c'$
of length
![]() $k=|c|$
such that
$k=|c|$
such that
![]() $(b', c')$
belongs to
$(b', c')$
belongs to
![]() $\operatorname {tp}((b, c)/A)$
(denoted henceforth, as is standard, by
$\operatorname {tp}((b, c)/A)$
(denoted henceforth, as is standard, by
![]() $\operatorname {tp}(b,c/A)$
for brevity). While for model-theorists, this is an easy consequence of
$\operatorname {tp}(b,c/A)$
for brevity). While for model-theorists, this is an easy consequence of
![]() $\aleph _1$
-saturation, we will include a quick proof for the sake of completeness. Indeed, by
$\aleph _1$
-saturation, we will include a quick proof for the sake of completeness. Indeed, by
![]() $\aleph _1$
-saturation, it suffices to show that every finite intersection
$\aleph _1$
-saturation, it suffices to show that every finite intersection
is non-empty, where each of the
![]() $Y_j$
varies over all internal sets in
$Y_j$
varies over all internal sets in
![]() $\operatorname {tp}(b, c/A)$
. Now, the intersection
$\operatorname {tp}(b, c/A)$
. Now, the intersection
![]() $\bigcap _{j=1}^n Y_j$
belongs to
$\bigcap _{j=1}^n Y_j$
belongs to
![]() $\operatorname {tp}(b,c/A)$
and thus contains the tuple
$\operatorname {tp}(b,c/A)$
and thus contains the tuple
![]() $(b, c)$
. Hence, by Definition 3.2, the projection onto the first
$(b, c)$
. Hence, by Definition 3.2, the projection onto the first
![]() $|b|$
coordinates of
$|b|$
coordinates of
![]() $\bigcap _{j=1}^n Y_j$
is an internal set defined over A which contains b. Since
$\bigcap _{j=1}^n Y_j$
is an internal set defined over A which contains b. Since
![]() $b'$
belongs to
$b'$
belongs to
![]() $\operatorname {tp}(b/A)$
, there exists some d such that
$\operatorname {tp}(b/A)$
, there exists some d such that
![]() $(b', d)$
belongs to
$(b', d)$
belongs to
![]() $\bigcap _{j=1}^n Y_j$
, as desired (note that the element d need not be
$\bigcap _{j=1}^n Y_j$
, as desired (note that the element d need not be
![]() $c'$
).
$c'$
).
A classical Ramsey argument and the
![]() $\aleph _1$
-saturation argument in Remark 3.8 allow us to produce, out of a given infinite sequence and a countable set of parameters, a new sequence with a remarkable property known as indiscernibility.
$\aleph _1$
-saturation argument in Remark 3.8 allow us to produce, out of a given infinite sequence and a countable set of parameters, a new sequence with a remarkable property known as indiscernibility.
Definition 3.6 We say that a sequence
![]() $(a_i)_{i\in \mathbb N}$
is indiscernible over the countable subset A (or A-indiscernible) if for every natural number n and every increasing enumeration
$(a_i)_{i\in \mathbb N}$
is indiscernible over the countable subset A (or A-indiscernible) if for every natural number n and every increasing enumeration
![]() $i_0<\dots <i_{n-1}$
, we have that
$i_0<\dots <i_{n-1}$
, we have that
![]() $\operatorname {tp}(a_0,\ldots , a_{n-1} / A )$
equals
$\operatorname {tp}(a_0,\ldots , a_{n-1} / A )$
equals
![]() $\operatorname {tp}(a_{i_0},\ldots , a_{i_{n-1}} / A )$
, that is,
$\operatorname {tp}(a_{i_0},\ldots , a_{i_{n-1}} / A )$
, that is,
for every internal subset X in
![]() $\mathcal {F}(A)$
of the appropriate arity.
$\mathcal {F}(A)$
of the appropriate arity.
We also define a notion of density for a non-standard finite group.
Definition 3.7 Let G be a non-standard finite group.
-
• An
 $\omega $
-internal subset is dense if it is not contained in any internal set of density
$\omega $
-internal subset is dense if it is not contained in any internal set of density
 $0$
(see Definition 2.3).
$0$
(see Definition 2.3). -
• Given a countable subset A of G and a tuple b of elements of G, we say that b is dense over A if the
 $\omega $
-internal subset
$\omega $
-internal subset
 $\operatorname {tp}(b/A)$
is dense.
$\operatorname {tp}(b/A)$
is dense.
Remark 3.9
-
(1) An internal subset X is dense if and only if it intersects every internal subset of density
 $1$
. Notice that the internal set X is dense (seen as an
$1$
. Notice that the internal set X is dense (seen as an
 $\omega $
-internal subset) if and only if it has positive density. However, an
$\omega $
-internal subset) if and only if it has positive density. However, an
 $\omega $
-internal set can be dense and yet have density
$\omega $
-internal set can be dense and yet have density
 $0$
(with respect to the extension of the Loeb measure to the
$0$
(with respect to the extension of the Loeb measure to the
 $\sigma $
-algebra generated by all internal sets, see [Reference Bergelson and Tao6, Remark 16]).
$\sigma $
-algebra generated by all internal sets, see [Reference Bergelson and Tao6, Remark 16]). -
(2) If an
 $\omega $
-internal set
$\omega $
-internal set
 $X=\bigcap _{n\in \mathbb {N}} X_n$
is given by a decreasing chain, then the set X is dense if and only if each internal set
$X=\bigcap _{n\in \mathbb {N}} X_n$
is given by a decreasing chain, then the set X is dense if and only if each internal set
 $X_n$
is. Indeed, if X were not dense, this would be witnessed by an internal set Y of density
$X_n$
is. Indeed, if X were not dense, this would be witnessed by an internal set Y of density
 $0$
. Thus, the decreasing intersection
$0$
. Thus, the decreasing intersection  $$\begin{align*}\bigcap_{n\in \mathbb{N}} (X_n \setminus Y) = \emptyset,\end{align*}$$
$$\begin{align*}\bigcap_{n\in \mathbb{N}} (X_n \setminus Y) = \emptyset,\end{align*}$$
which, by
 $\aleph _1$
-saturation, would yield that some
$\aleph _1$
-saturation, would yield that some
 $X_n\setminus Y$
must be empty.
$X_n\setminus Y$
must be empty. -
(3) If b is dense over A, then so is every element in
 $\operatorname {tp}(b/A)$
.
$\operatorname {tp}(b/A)$
. -
(4) If b is dense over
 $A\cup \{g\}$
, then so are
$A\cup \{g\}$
, then so are
 $b\cdot g$
and
$b\cdot g$
and
 $g\cdot b$
.
$g\cdot b$
.
Lemma 3.10 Let X be an
![]() $\omega $
-internal dense subset of a non-standard finite group G defined over a countable subset A. If B is a countable subset of parameters extending A, then there exists some element in X which is dense over B.
$\omega $
-internal dense subset of a non-standard finite group G defined over a countable subset A. If B is a countable subset of parameters extending A, then there exists some element in X which is dense over B.
In particular, if c is dense over A, then there is some
![]() $c'$
in
$c'$
in
![]() $\operatorname {tp}(c/A)$
which is dense over B.
$\operatorname {tp}(c/A)$
which is dense over B.
Proof Write
![]() $X=\bigcap _{n\in \mathbb {N}} X_n$
. By
$X=\bigcap _{n\in \mathbb {N}} X_n$
. By
![]() $\aleph _1$
-saturation, it suffices to show that
$\aleph _1$
-saturation, it suffices to show that
for every
![]() $m\ge 1$
, where
$m\ge 1$
, where
![]() $Y_1, \dots , Y_m$
are fibers of internal sets in
$Y_1, \dots , Y_m$
are fibers of internal sets in
![]() $\mathcal {F}$
defined over B and of density
$\mathcal {F}$
defined over B and of density
![]() $0$
. If the above intersection were empty, then
$0$
. If the above intersection were empty, then
![]() $ X_1\cap \dots \cap X_m$
would have density
$ X_1\cap \dots \cap X_m$
would have density
![]() $0$
, and X would not be dense.
$0$
, and X would not be dense.
Lemma 3.11 Consider a countable set of parameters A and a finite tuple
![]() $(b,c)$
in a non-standard finite group G such that b is dense over
$(b,c)$
in a non-standard finite group G such that b is dense over
![]() $A\cup \{c\}$
. If
$A\cup \{c\}$
. If
![]() $(b',c')$
belongs to
$(b',c')$
belongs to
![]() $\operatorname {tp}(b,c/A)$
, then
$\operatorname {tp}(b,c/A)$
, then
![]() $b'$
is dense over
$b'$
is dense over
![]() $A\cup \{c'\}$
.
$A\cup \{c'\}$
.
Proof Assume for a contradiction that
![]() $b'$
is not dense over
$b'$
is not dense over
![]() $A\cup \{c'\}$
. By Remark 3.9, there exists a fiber X of an internal set defined over
$A\cup \{c'\}$
. By Remark 3.9, there exists a fiber X of an internal set defined over
![]() $A\cup \{c'\}$
of density
$A\cup \{c'\}$
of density
![]() $0$
and containing
$0$
and containing
![]() $b'$
. Write
$b'$
. Write
![]() $X=Z_{c'}$
for some internal set
$X=Z_{c'}$
for some internal set
![]() $Z\subset G^{k+m}$
defined over A, where
$Z\subset G^{k+m}$
defined over A, where
![]() $k=|b|=|b'|$
and
$k=|b|=|b'|$
and
![]() $m=|c|=|c'|$
. By Remark 3.7 (after taking set-theoretic complements), there is for every natural number
$m=|c|=|c'|$
. By Remark 3.7 (after taking set-theoretic complements), there is for every natural number
![]() $n\ge 1$
an internal set
$n\ge 1$
an internal set
![]() $Y_{\frac {1}{n}}$
defined over A such that
$Y_{\frac {1}{n}}$
defined over A such that
Now, the internal set
![]() $\widetilde Z_n=Z\cap \big (G^{k}\times Y_{\frac {1}{n}}\big )$
is defined over A for every natural number
$\widetilde Z_n=Z\cap \big (G^{k}\times Y_{\frac {1}{n}}\big )$
is defined over A for every natural number
![]() $n\ge 1$
and contains
$n\ge 1$
and contains
![]() $(b',c')$
, so
$(b',c')$
, so
![]() $(b,c)$
also belongs to the intersection of all the
$(b,c)$
also belongs to the intersection of all the
![]() $\widetilde Z_n$
. We conclude that b is not dense over
$\widetilde Z_n$
. We conclude that b is not dense over
![]() $A\cup \{c\}$
, witnessed by the fiber
$A\cup \{c\}$
, witnessed by the fiber
![]() $\widetilde {Z}_{c}$
, as desired.
$\widetilde {Z}_{c}$
, as desired.
Model-theoretically, it is convenient to capture the global behavior of an internal (or definable) set in terms of a suitable (dense) element in the set. An example of this translation is the following result, which follows from the Fubini–Tonelli Theorem and Caratheodory’s Extension Theorem for the Loeb measure.
Fact 3.12 [Reference Martin-Pizarro and Palacín28, Lemma 1.10 as well as Remarks 1.13 and 1.14 and Lemma 1.15]
Let G be a non-standard finite group and X be an
![]() $\omega $
-internal subset of
$\omega $
-internal subset of
![]() $G^n$
defined over a countable subset A. The following are equivalent:
$G^n$
defined over a countable subset A. The following are equivalent:
-
(1) There exists some
 $(b_1,\ldots ,b_n)$
in X in good position over A, that is, each
$(b_1,\ldots ,b_n)$
in X in good position over A, that is, each
 $b_i$
is dense over
$b_i$
is dense over
 $A\cup \{b_j:j<i\}$
.
$A\cup \{b_j:j<i\}$
. -
(2) The set X is dense.
Furthermore, every tuple as in (a) is dense over A with respect to the Loeb measure on
![]() $G^n$
.
$G^n$
.
Note that if a tuple is in good position, then so is every subtuple.
Definition 3.8 Two internal subsets X and Y of
![]() $G^n$
are comparable if the set
$G^n$
are comparable if the set
![]() $X\triangle Y$
has Loeb measure
$X\triangle Y$
has Loeb measure
![]() $0$
.
$0$
.
Remark 3.13 By Lemma 3.10, two internal sets X and Y, both defined over A, are comparable if and only if they contain the same dense elements over A.
By the Fubini–Tonelli Theorem, two internal subsets X and Y of
![]() $G^{m+n}$
are comparable if and only if for
$G^{m+n}$
are comparable if and only if for
![]() $\mu _{G^n}$
-almost all elements b in
$\mu _{G^n}$
-almost all elements b in
![]() $G^n$
, the fibers
$G^n$
, the fibers
![]() $X_b$
and
$X_b$
and
![]() $Y_b$
are comparable.
$Y_b$
are comparable.
4 Stability and almost sure stability
Let
![]() $k\ge 1$
be a natural number. A half-graph of height k induced by the relation
$k\ge 1$
be a natural number. A half-graph of height k induced by the relation
![]() $S \subseteq X\times Y$
consists of a sequence
$S \subseteq X\times Y$
consists of a sequence
![]() $(a_1,b_1,\ldots ,a_k,b_k)$
with
$(a_1,b_1,\ldots ,a_k,b_k)$
with
![]() $a_i$
in X and
$a_i$
in X and
![]() $b_i$
in Y for each
$b_i$
in Y for each
![]() $i=1,\dots , k$
, such that the pair
$i=1,\dots , k$
, such that the pair
![]() $(a_i,b_j)$
belongs to S if and only if
$(a_i,b_j)$
belongs to S if and only if
![]() $i\le j$
. We denote by
$i\le j$
. We denote by
![]() $\mathcal {H}_k(S)$
the collection of all half-graphs of height k induced by S. Note that for each sequence
$\mathcal {H}_k(S)$
the collection of all half-graphs of height k induced by S. Note that for each sequence
![]() $(a_1,b_1,\ldots ,a_k,b_k)$
in
$(a_1,b_1,\ldots ,a_k,b_k)$
in
![]() $\mathcal {H}_k(S)$
, the elements
$\mathcal {H}_k(S)$
, the elements
![]() $a_i$
must be pairwise distinct and similarly for the elements
$a_i$
must be pairwise distinct and similarly for the elements
![]() $b_i$
.
$b_i$
.
Definition 4.1 The relation
![]() $S \subseteq X\times Y$
is k-stable if it induces no half-graph of height k, or equivalently, if
$S \subseteq X\times Y$
is k-stable if it induces no half-graph of height k, or equivalently, if
![]() $\mathcal {H}_k(S)=\emptyset $
. A subset A of a group G is k-stable if the relation given by the Cayley graph of A in G
$\mathcal {H}_k(S)=\emptyset $
. A subset A of a group G is k-stable if the relation given by the Cayley graph of A in G
is k-stable, or equivalently, if the relation
is k-stable.
Example 4.1 A non-empty subset A of a group G is
![]() $2$
-stable if and only if it is a coset of a subgroup of G. Indeed, cosets are clearly
$2$
-stable if and only if it is a coset of a subgroup of G. Indeed, cosets are clearly
![]() $2$
-stable. To verify the other direction, it suffices to show that
$2$
-stable. To verify the other direction, it suffices to show that
![]() $a\cdot b ^{-1}\cdot c$
belongs to A for every a, b, and c in A. Sidon subsets of abelian groups, such as
$a\cdot b ^{-1}\cdot c$
belongs to A for every a, b, and c in A. Sidon subsets of abelian groups, such as
![]() $2^{\mathbb N}$
in
$2^{\mathbb N}$
in
![]() $\mathbb {Z}$
, are easily seen to be
$\mathbb {Z}$
, are easily seen to be
![]() $3$
-stable [Reference Sanders37, Lemma 1.3].
$3$
-stable [Reference Sanders37, Lemma 1.3].
Remark 4.2 Consider a non-standard finite group
![]() $G=\prod _{n\to \mathfrak {U}} G_n$
and an internal relation S on
$G=\prod _{n\to \mathfrak {U}} G_n$
and an internal relation S on
![]() $G\times G$
defined over a countable subset A. By Łoś’ Theorem (see Remark 2.1(e)), the relation S is k-stable if and only if
$G\times G$
defined over a countable subset A. By Łoś’ Theorem (see Remark 2.1(e)), the relation S is k-stable if and only if
![]() $S(G_n)$
is k-stable in
$S(G_n)$
is k-stable in
![]() $G_n$
for
$G_n$
for
![]() $\mathfrak {U}$
-almost all n in
$\mathfrak {U}$
-almost all n in
![]() $\mathbb {N}$
. Furthermore, a straightforward
$\mathbb {N}$
. Furthermore, a straightforward
![]() $\aleph _1$
-saturation argument yields that the internal relation S is k-stable for some
$\aleph _1$
-saturation argument yields that the internal relation S is k-stable for some
![]() $k\ge 2$
if and only if there is no A-indiscernible sequence
$k\ge 2$
if and only if there is no A-indiscernible sequence
![]() $(a_i,b_i)_{i\in \mathbb {N}}$
such that the pair
$(a_i,b_i)_{i\in \mathbb {N}}$
such that the pair
![]() $(a_i,b_j)$
belongs to S if and only if
$(a_i,b_j)$
belongs to S if and only if
![]() $i\le j$
.
$i\le j$
.
The previous remark motivates the following definition.
Definition 4.2 Consider a non-standard finite group
![]() $G=\prod _{n\to \mathfrak {U}} G_n$
. An
$G=\prod _{n\to \mathfrak {U}} G_n$
. An
![]() $\omega $
-internal relation S on
$\omega $
-internal relation S on
![]() $G\times G$
defined over the countable subset A is stable if there is no infinite A-indiscernible sequence
$G\times G$
defined over the countable subset A is stable if there is no infinite A-indiscernible sequence
![]() $(a_i,b_i)_{i\in \mathbb {N}}$
such that the pair
$(a_i,b_i)_{i\in \mathbb {N}}$
such that the pair
![]() $(a_i,b_j)$
belongs to S if and only if
$(a_i,b_j)$
belongs to S if and only if
![]() $i\le j$
.
$i\le j$
.
Using the Krein–Milman theorem on the locally compact Hausdorff topological real vector space of all
![]() $\sigma $
-additive probability measures, Hrushovski [Reference Hrushovski20, Proposition 2.25] proved the following result. Roughly speaking, it asserts that the relation
$\sigma $
-additive probability measures, Hrushovski [Reference Hrushovski20, Proposition 2.25] proved the following result. Roughly speaking, it asserts that the relation
![]() $R(a,b)$
defined by requiring the measure of the intersection of two associated internal sets
$R(a,b)$
defined by requiring the measure of the intersection of two associated internal sets
![]() $X_a$
and
$X_a$
and
![]() $Y_b$
to exceed a certain threshold is stable. For the purpose of this work, we will state an adapted version of [Reference Hrushovski20, Lemma 2.10], extracting it from the formulation in [Reference Martin-Pizarro and Palacín29, Fact 2.2 and Corollary 2.3].
$Y_b$
to exceed a certain threshold is stable. For the purpose of this work, we will state an adapted version of [Reference Hrushovski20, Lemma 2.10], extracting it from the formulation in [Reference Martin-Pizarro and Palacín29, Fact 2.2 and Corollary 2.3].
Fact 4.3 Let G be a non-standard finite group and let
![]() $\alpha $
be a real number in
$\alpha $
be a real number in
![]() $[0,1]$
.
$[0,1]$
.
-
(1) Given two internal subsets X of
 $G^{n+r}$
and Y of
$G^{n+r}$
and Y of
 $G^{n+s}$
in
$G^{n+s}$
in
 $\mathcal {F}$
, the relation
$\mathcal {F}$
, the relation
 $R^\alpha _{X,Y}$
of
$R^\alpha _{X,Y}$
of
 $G^r\times G^s$
defined by
$G^r\times G^s$
defined by  $$\begin{align*}R^\alpha_{X,Y}(a,b) \ \Leftrightarrow \ \mu_{G^n}(X_a \cap Y_b) \le \alpha \end{align*}$$
$$\begin{align*}R^\alpha_{X,Y}(a,b) \ \Leftrightarrow \ \mu_{G^n}(X_a \cap Y_b) \le \alpha \end{align*}$$
is stable. Notice that
 $R^\alpha _{X,Y}$
is
$R^\alpha _{X,Y}$
is
 $\omega $
-internal by Definition 3.2(IV), and definable over the same parameters needed to define both X and Y, by Remark 3.7.
$\omega $
-internal by Definition 3.2(IV), and definable over the same parameters needed to define both X and Y, by Remark 3.7. -
(2) If the two subsets X of
 $G^{n+r}$
and Y of
$G^{n+r}$
and Y of
 $G^{n+s}$
are
$G^{n+s}$
are
 $\omega $
-internal and defined over A, the relation
$\omega $
-internal and defined over A, the relation
 $R_{X,Y}$
of
$R_{X,Y}$
of
 $G^r\times G^s$
defined by
$G^r\times G^s$
defined by  $$\begin{align*}R_{X,Y}(a,b) \ \Leftrightarrow \ \text{ the } \omega-\text{internal subset } X_a \cap Y_b \text{ of } G^n \text{ is not dense}\end{align*}$$
$$\begin{align*}R_{X,Y}(a,b) \ \Leftrightarrow \ \text{ the } \omega-\text{internal subset } X_a \cap Y_b \text{ of } G^n \text{ is not dense}\end{align*}$$
is equational, that is, there is no A-indiscernible sequence
 $(a_i, b_i)_{i\in \mathbb {N}}$
such that
$(a_i, b_i)_{i\in \mathbb {N}}$
such that
 $X_{a_0} \cap Y_{b_0}$
is dense yet
$X_{a_0} \cap Y_{b_0}$
is dense yet
 $X_{a_0} \cap Y_{b_1}$
is not.
$X_{a_0} \cap Y_{b_1}$
is not. -
(3) Equationality implies the following (see [Reference Martin-Pizarro and Palacín29, Remark 2.1 and Corollary 2.3]). For every
 $\omega $
-internal subset X of
$\omega $
-internal subset X of
 $G^{n+r}$
defined over a countable rich subset M, if the fiber
$G^{n+r}$
defined over a countable rich subset M, if the fiber
 $X_a$
is dense for some a which is itself dense over M, then so is the intersection
$X_a$
is dense for some a which is itself dense over M, then so is the intersection
 $\bigcap _{i=0}^m X_{b_i}$
for every m in
$\bigcap _{i=0}^m X_{b_i}$
for every m in
 $\mathbb {N}$
and every tuple
$\mathbb {N}$
and every tuple
 $(b_0, \ldots , b_m)$
of elements in
$(b_0, \ldots , b_m)$
of elements in
 $\operatorname {tp}(a/M)$
in good position over M, as in Fact 3.12(a), that is, the element
$\operatorname {tp}(a/M)$
in good position over M, as in Fact 3.12(a), that is, the element
 $b_i$
is dense over
$b_i$
is dense over
 $M\cup \{b_j:j<i\}$
for
$M\cup \{b_j:j<i\}$
for
 $i\le m$
.
$i\le m$
.
While the notion of stability has proved highly profitable in model theory, from a more combinatorial perspective, it is open to the criticism that whether or not a relation is stable is very sensitive to minor perturbations. In particular, modifications by an internal set of measure
![]() $0$
can destroy stability, as the following example illustrates.
$0$
can destroy stability, as the following example illustrates.
Example 4.4 For some non-principal ultrafilter
![]() $\mathfrak {U}$
, consider the non-standard finite group
$\mathfrak {U}$
, consider the non-standard finite group
![]() $G=\prod _{n\to \mathfrak {U}} \mathbb {Z}/n^2\mathbb {Z}$
as well as the internal set
$G=\prod _{n\to \mathfrak {U}} \mathbb {Z}/n^2\mathbb {Z}$
as well as the internal set
![]() $X=\prod _{n\to \mathfrak {U}} \{\overline 0,\ldots , \overline {n-1}\}$
and the internal relation S on
$X=\prod _{n\to \mathfrak {U}} \{\overline 0,\ldots , \overline {n-1}\}$
and the internal relation S on
![]() $X\times X$
arising from the standard linear order of
$X\times X$
arising from the standard linear order of
![]() $\mathbb {Z}$
restricted to the set of representatives
$\mathbb {Z}$
restricted to the set of representatives
![]() $\{0,\ldots , n-1\}$
. By Łoś’s theorem (see Remark 2.1(e)), the collection
$\{0,\ldots , n-1\}$
. By Łoś’s theorem (see Remark 2.1(e)), the collection
![]() $\mathcal {H}_k(S)$
of induced half-graphs of height k is non-empty for every natural number
$\mathcal {H}_k(S)$
of induced half-graphs of height k is non-empty for every natural number
![]() $k\ge 1$
, so the internal relation S is never stable. However, for every index
$k\ge 1$
, so the internal relation S is never stable. However, for every index
![]() $k\ge 1$
, the internal set
$k\ge 1$
, the internal set
![]() $\mathcal {H}_k(S)$
has
$\mathcal {H}_k(S)$
has
![]() $\mu _{G^{2k}}$
-measure
$\mu _{G^{2k}}$
-measure
![]() $0$
, so it is comparable to the empty relation, which in turn is k-stable.
$0$
, so it is comparable to the empty relation, which in turn is k-stable.
Motivated by the above example, we introduce a weakening of stability, which is combinatorially robust with respect to perturbations by sets of measure
![]() $0$
.
$0$
.
Definition 4.3 Consider a non-standard finite group G as well as two internal subsets X of
![]() $G^{n}$
and Y of
$G^{n}$
and Y of
![]() $G^{m}$
. Given a natural number
$G^{m}$
. Given a natural number
![]() $k\geq 1$
, an internal relation
$k\geq 1$
, an internal relation
![]() $S \subseteq X\times Y$
is almost surely k-stable if
$S \subseteq X\times Y$
is almost surely k-stable if
![]() $\mu _{G^{(n+m)k}}(\mathcal {H}_k(S))=0$
, that is, the collection of all half-graphs of height k induced by S is negligible in
$\mu _{G^{(n+m)k}}(\mathcal {H}_k(S))=0$
, that is, the collection of all half-graphs of height k induced by S is negligible in
![]() $G^{(n+m)k}$
with respect to the non-standard counting measure.
$G^{(n+m)k}$
with respect to the non-standard counting measure.
Remark 4.5
-
(1) It is immediate that almost sure stability is preserved by finite Boolean combinations as well as by permutation of the variables: if
 $S\subseteq X\times Y$
is almost surely k-stable, then so is the inverse relation
$S\subseteq X\times Y$
is almost surely k-stable, then so is the inverse relation  $$\begin{align*}S^{\mathrm{opp}}=\{(y,x)\in Y\times X : \ (x,y) \in S\}.\end{align*}$$
$$\begin{align*}S^{\mathrm{opp}}=\{(y,x)\in Y\times X : \ (x,y) \in S\}.\end{align*}$$
-
(2) Fact 3.12 yields that the internal relation S defined over the countable subset A is not almost surely k-stable if and only if it induces a half-graph of height k witnessed by a dense tuple
 $(a_1, b_1, \ldots , a_k, b_k)$
in good position over A.
$(a_1, b_1, \ldots , a_k, b_k)$
in good position over A.As a consequence, whenever a relation S is comparable to an internal k-stable or even an almost surely k-stable relation
 $S'$
, Remark 3.13 yields that S is almost surely k-stable.
$S'$
, Remark 3.13 yields that S is almost surely k-stable.
We will see in Proposition 4.9 below that every almost surely stable relation
![]() $S\subseteq X\times Y$
can be approximated for every
$S\subseteq X\times Y$
can be approximated for every
![]() $\epsilon>0$
by a finite union of internal boxes of the form
$\epsilon>0$
by a finite union of internal boxes of the form
![]() $X'\times Y'$
. Hence, the almost surely k-stable relation is
$X'\times Y'$
. Hence, the almost surely k-stable relation is
![]() $\epsilon $
-comparable to a stable relation
$\epsilon $
-comparable to a stable relation
![]() $S'$
, although our methods do not allow us to compute the degree of stability of
$S'$
, although our methods do not allow us to compute the degree of stability of
![]() $S'$
.
$S'$
.
In fact, the (bipartite version of the) induced removal lemma [Reference Erdős, Frankl and Rödl15] implies that every almost surely k-stable must be comparable to a k-stable relation, but we do not know how to give a model-theoretic proof of this result. So we ask the following:
Question Is there a model-theoretic account that every almost surely k-stable internal relation is comparable (or
![]() $\epsilon $
-comparable) to an internal k-stable relation?
$\epsilon $
-comparable) to an internal k-stable relation?
A straightforward application of Lemma 2.4 (with
![]() $r=0$
) yields an analog of almost sure stability for families of finite groups in terms of their asymptotic behavior.
$r=0$
) yields an analog of almost sure stability for families of finite groups in terms of their asymptotic behavior.
Remark 4.6 Consider a family
![]() $(G_\ell , X_\ell , Y_\ell , S_\ell )_{\ell \in \mathbb {N}}$
, where for each
$(G_\ell , X_\ell , Y_\ell , S_\ell )_{\ell \in \mathbb {N}}$
, where for each
![]() $\ell \in \mathbb {N}$
,
$\ell \in \mathbb {N}$
,
![]() $G_\ell $
is a finite group,
$G_\ell $
is a finite group,
![]() $X_\ell \subseteq G_\ell ^n$
and
$X_\ell \subseteq G_\ell ^n$
and
![]() $Y_\ell \subseteq G_\ell ^m$
for some
$Y_\ell \subseteq G_\ell ^m$
for some
![]() $n,m\in \mathbb {N}$
, and
$n,m\in \mathbb {N}$
, and
![]() $S_\ell \subseteq X_\ell \times Y_\ell $
. The following are equivalent for every natural number
$S_\ell \subseteq X_\ell \times Y_\ell $
. The following are equivalent for every natural number
![]() $k\ge 1$
:
$k\ge 1$
:
-
(1) For every
 $\theta>0,$
there is some
$\theta>0,$
there is some
 $\ell _0=\ell _0(k,\theta )$
in
$\ell _0=\ell _0(k,\theta )$
in
 $\mathbb {N}$
such that
$\mathbb {N}$
such that
 $|\mathcal {H}_k(S_\ell )| \le \theta |G_\ell |^{k(n+m)}$
for all
$|\mathcal {H}_k(S_\ell )| \le \theta |G_\ell |^{k(n+m)}$
for all
 $\ell \ge \ell _0$
, where
$\ell \ge \ell _0$
, where
 $\mathcal {H}_k(S_\ell )$
is the collection of all half-graphs of height k induced by
$\mathcal {H}_k(S_\ell )$
is the collection of all half-graphs of height k induced by
 $S_\ell $
on the finite group
$S_\ell $
on the finite group
 $G_\ell $
.
$G_\ell $
. -
(2) For every non-principal ultrafilter
 $\mathfrak {U}$
on
$\mathfrak {U}$
on
 $\mathbb {N}$
, the internal relation
$\mathbb {N}$
, the internal relation
 $S=\prod _{n\to \mathfrak {U}} S_\ell $
is almost surely k-stable.
$S=\prod _{n\to \mathfrak {U}} S_\ell $
is almost surely k-stable.
If (a) holds, we say that
![]() $(G_\ell , X_\ell , Y_\ell , S_\ell )_{\ell \in \mathbb {N}}$
is an almost surely k-stable family.
$(G_\ell , X_\ell , Y_\ell , S_\ell )_{\ell \in \mathbb {N}}$
is an almost surely k-stable family.
A key feature of stable relations is that they are stationary [Reference Hrushovski20, Lemma 2.3], in the sense that their truth value is constant along the set of pairs of realizations which are non-forking independent. Non-forking independence is a fundamental notion in model theory, originally due to Shelah, defined in combinatorial terms for any structure [Reference Shelah38, Chapter III.1, Definition 1.4]. We will not need to introduce non-forking independence in this article. Instead, inspired by classical results in model theory, we will show that the truth value of an almost surely stable relation remains constant along the set of pairs of realizations for which one coordinate is dense over the other.
Before stating the corresponding result, we introduce some notation.
Definition 4.4 Fix two types
![]() $\operatorname {tp}(a/M)$
and
$\operatorname {tp}(a/M)$
and
![]() $\operatorname {tp}(b/M)$
over a countable rich subset M. We denote by
$\operatorname {tp}(b/M)$
over a countable rich subset M. We denote by
![]() $\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
the set of all pairs
$\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
the set of all pairs
![]() $(a',b')$
with
$(a',b')$
with
![]() $a'$
in
$a'$
in
![]() $\operatorname {tp}(a/M)$
and
$\operatorname {tp}(a/M)$
and
![]() $b'$
in
$b'$
in
![]() $\operatorname {tp}(b/M)$
such that
$\operatorname {tp}(b/M)$
such that
![]() $(a',b')$
or
$(a',b')$
or
![]() $(b',a')$
is in good position over M (see Fact 3.12).
$(b',a')$
is in good position over M (see Fact 3.12).
Note that the set
![]() $\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
is empty exactly if one of the types
$\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
is empty exactly if one of the types
![]() $\operatorname {tp}(a/M)$
or
$\operatorname {tp}(a/M)$
or
![]() $\operatorname {tp}(b/M)$
is not dense, by Lemma 3.10. Moreover,
$\operatorname {tp}(b/M)$
is not dense, by Lemma 3.10. Moreover,
Theorem 4.7 Consider a non-standard finite group G as well as two internal subsets X of
![]() $G^{n}$
and Y of
$G^{n}$
and Y of
![]() $G^{m}$
and an internal relation S on
$G^{m}$
and an internal relation S on
![]() $X\times Y$
, all defined over a countable rich subset M.
$X\times Y$
, all defined over a countable rich subset M.
If S is almost surely k-stable for some
![]() $k\ge 1$
, then for every two (dense) types
$k\ge 1$
, then for every two (dense) types
![]() $\operatorname {tp}(a/M)$
and
$\operatorname {tp}(a/M)$
and
![]() $\operatorname {tp}(b/M)$
, the set
$\operatorname {tp}(b/M)$
, the set
![]() $\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
is either contained in S or disjoint from S.
$\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
is either contained in S or disjoint from S.
Proof If a does not lie in X, neither does any element of
![]() $\operatorname {tp}(a/M)$
, and likewise if b does not lie in Y. In this case,
$\operatorname {tp}(a/M)$
, and likewise if b does not lie in Y. In this case,
![]() $X\times Y$
(and thus S) is clearly disjoint from
$X\times Y$
(and thus S) is clearly disjoint from
![]() $\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
. So we may assume that
$\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
. So we may assume that
![]() $\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
is a subset of
$\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
is a subset of
![]() $X\times Y$
.
$X\times Y$
.
Suppose now that S is not disjoint from
![]() $\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
. Up to relabeling, we may assume by Remark 4.5(a) that
$\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
. Up to relabeling, we may assume by Remark 4.5(a) that
![]() $(a,b)$
lies in S, with
$(a,b)$
lies in S, with
![]() $(a, b)$
in good position, that is, the element b is dense over
$(a, b)$
in good position, that is, the element b is dense over
![]() $M\cup \{a\}$
(keeping in mind that a is already dense over M).
$M\cup \{a\}$
(keeping in mind that a is already dense over M).
Claim All pairs
![]() $(c, d)$
in
$(c, d)$
in
![]() $\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
with
$\operatorname {GP}(\operatorname {tp}(a/M),\operatorname {tp}(b/M))$
with
![]() $(d, c)$
in good position over M are contained in S.
$(d, c)$
in good position over M are contained in S.
Proof of Claim
Suppose to the contrary that there is a pair
![]() $(c, d)$
with c dense over
$(c, d)$
with c dense over
![]() $M\cup \{d\}$
not contained in S. By Remark 3.8 (using the fact that d belongs to the type
$M\cup \{d\}$
not contained in S. By Remark 3.8 (using the fact that d belongs to the type
![]() $\operatorname {tp}(b/M)$
), there is a pair
$\operatorname {tp}(b/M)$
), there is a pair
![]() $(a',b)$
in
$(a',b)$
in
![]() $\operatorname {tp}(c, d/M)$
. So the original tuple
$\operatorname {tp}(c, d/M)$
. So the original tuple
![]() $(a, b)$
belongs to S but
$(a, b)$
belongs to S but
![]() $(a', b)$
does not lie in S (for S is definable over M). In particular, we have two pairs
$(a', b)$
does not lie in S (for S is definable over M). In particular, we have two pairs
![]() $(a, b)$
and
$(a, b)$
and
![]() $(a', b)$
satisfying the following:
$(a', b)$
satisfying the following:
-
• the type
 $\operatorname {tp}(a/M)=\operatorname {tp}(a'/M)$
is dense;
$\operatorname {tp}(a/M)=\operatorname {tp}(a'/M)$
is dense; -
• the element b is dense over
 $M \cup \{a\}$
and
$M \cup \{a\}$
and
 $a'$
is dense over
$a'$
is dense over
 $M \cup \{b\}$
(by Lemma 3.11);
$M \cup \{b\}$
(by Lemma 3.11); -
• the pair
 $(a, b)$
belongs to S but
$(a, b)$
belongs to S but
 $(a', b)$
does not.
$(a', b)$
does not.
We will now construct inductively, for every n in
![]() $\mathbb {N}$
, a dense sequence
$\mathbb {N}$
, a dense sequence
![]() $(a_0, b_0, \ldots , a_n, b_n)_{0\le i\le n}$
in good position over M witnessing that S induces a half-graph of height n such that
$(a_0, b_0, \ldots , a_n, b_n)_{0\le i\le n}$
in good position over M witnessing that S induces a half-graph of height n such that
![]() $a_i$
belongs to
$a_i$
belongs to
![]() $\operatorname {tp}(a/M)$
and
$\operatorname {tp}(a/M)$
and
![]() $b_i$
to
$b_i$
to
![]() $\operatorname {tp}(b/M)$
for each
$\operatorname {tp}(b/M)$
for each
![]() $i\le n$
. In particular, the case
$i\le n$
. In particular, the case
![]() $n=k$
contradicts the almost sure stability of S by Remark 4.5(b).
$n=k$
contradicts the almost sure stability of S by Remark 4.5(b).
For
![]() $n=0$
, set
$n=0$
, set
![]() $a_0=a$
and
$a_0=a$
and
![]() $b_0=b$
, so
$b_0=b$
, so
![]() $(a_0, b_0)$
is in good position over M and lies in S, as desired. Suppose now that the sequence
$(a_0, b_0)$
is in good position over M and lies in S, as desired. Suppose now that the sequence
![]() $(a_0, b_0, \ldots , a_r, b_r)$
has already been constructed for some
$(a_0, b_0, \ldots , a_r, b_r)$
has already been constructed for some
![]() $r< n$
. Consider the
$r< n$
. Consider the
![]() $\omega $
-internal set
$\omega $
-internal set
which is defined over M. Clearly,
![]() $(a', b)$
belongs to Z, so the fiber
$(a', b)$
belongs to Z, so the fiber
![]() $Z_b\subseteq X$
is dense. By Fact 4.3(c), so is the intersection
$Z_b\subseteq X$
is dense. By Fact 4.3(c), so is the intersection
![]() $ Z_{b_0}\cap \cdots \cap Z_{b_r}$
, since the subtuple
$ Z_{b_0}\cap \cdots \cap Z_{b_r}$
, since the subtuple
![]() $(b_0,\ldots , b_r)$
is also in good position over M and all coordinates lie in
$(b_0,\ldots , b_r)$
is also in good position over M and all coordinates lie in
![]() $\operatorname {tp}(b/M)$
. Hence, there is an element
$\operatorname {tp}(b/M)$
. Hence, there is an element
![]() $a_{r+1}$
in the above intersection which is dense over
$a_{r+1}$
in the above intersection which is dense over
![]() $M\cup \{a_i, b_i\}_{0\le i\le r}$
. In particular, the element
$M\cup \{a_i, b_i\}_{0\le i\le r}$
. In particular, the element
![]() $a_{r+1}$
lies in
$a_{r+1}$
lies in
![]() $\operatorname {tp}(a/M)$
but
$\operatorname {tp}(a/M)$
but
![]() $(a_{r+1}, b_i)$
does not lie in S for
$(a_{r+1}, b_i)$
does not lie in S for
![]() $i\le r$
.
$i\le r$
.
Similarly, the
![]() $\omega $
-internal set
$\omega $
-internal set
is also defined over M and the fiber
![]() $W_a\subseteq Y$
is dense, since
$W_a\subseteq Y$
is dense, since
![]() $(a, b)$
lies in W. Thus, there exists an element
$(a, b)$
lies in W. Thus, there exists an element
![]() $b_{r+1}$
in
$b_{r+1}$
in
![]() $\operatorname {tp}(b/M)$
contained in
$\operatorname {tp}(b/M)$
contained in
![]() $W_{a_0}\cap \cdots \cap W_{a_{r+1}}$
dense over
$W_{a_0}\cap \cdots \cap W_{a_{r+1}}$
dense over
![]() $M\cup \{a_i, b_i\}_{0\le i\le r} \cup \{a_{r+1}\}$
, which yields that the tuple
$M\cup \{a_i, b_i\}_{0\le i\le r} \cup \{a_{r+1}\}$
, which yields that the tuple
is in good position over M by Fact 3.12 and satisfies the desired properties.
By the previous claim, choose any pair
![]() $(a',b')$
in
$(a',b')$
in
![]() $S\cap \operatorname {GP}(\operatorname {tp}(a/M), \operatorname {tp}(b/M))$
such that
$S\cap \operatorname {GP}(\operatorname {tp}(a/M), \operatorname {tp}(b/M))$
such that
![]() $a'$
is dense over
$a'$
is dense over
![]() $M\cup \{b'\}$
. The pair
$M\cup \{b'\}$
. The pair
![]() $(b',a')$
is in good position over M and it belongs to the inverse relation
$(b',a')$
is in good position over M and it belongs to the inverse relation
![]() $S^{\mathrm {opp}}$
, which is again almost surely k-stable, by Remark 4.5(a). We conclude by the Claim (applied to
$S^{\mathrm {opp}}$
, which is again almost surely k-stable, by Remark 4.5(a). We conclude by the Claim (applied to
![]() $S^{\mathrm {opp}}$
inverting the roles of X and Y) that all pairs
$S^{\mathrm {opp}}$
inverting the roles of X and Y) that all pairs
![]() $(b", a")$
in
$(b", a")$
in
![]() $\operatorname {GP}(\operatorname {tp}(b/M), \operatorname {tp}(a/M))$
with
$\operatorname {GP}(\operatorname {tp}(b/M), \operatorname {tp}(a/M))$
with
![]() $b"$
dense over
$b"$
dense over
![]() $M\cup \{a"\}$
must be contained in
$M\cup \{a"\}$
must be contained in
![]() $S^{\mathrm {opp}}$
. Hence, all pairs
$S^{\mathrm {opp}}$
. Hence, all pairs
![]() $(a", b")$
in
$(a", b")$
in
![]() $\operatorname {GP}(\operatorname {tp}(a/M), \operatorname {tp}(b/M))$
in good position over M belong to S, so the set
$\operatorname {GP}(\operatorname {tp}(a/M), \operatorname {tp}(b/M))$
in good position over M belong to S, so the set
![]() $\operatorname {GP}(\operatorname {tp}(a/M), \operatorname {tp}(b/M))$
is fully contained in S, as desired.
$\operatorname {GP}(\operatorname {tp}(a/M), \operatorname {tp}(b/M))$
is fully contained in S, as desired.
Corollary 4.8 Consider a non-standard finite group G as well as two internal subsets X of
![]() $G^{n}$
and Y of
$G^{n}$
and Y of
![]() $G^{m}$
and an internal relation S on
$G^{m}$
and an internal relation S on
![]() $X\times Y$
, all defined over a countable rich subset M. If S is almost surely k-stable for some
$X\times Y$
, all defined over a countable rich subset M. If S is almost surely k-stable for some
![]() $k\ge 1$
, then the fibers
$k\ge 1$
, then the fibers
![]() $S_a$
and
$S_a$
and
![]() $S_{a'}$
are comparable whenever
$S_{a'}$
are comparable whenever
![]() $a'$
belongs to the dense type
$a'$
belongs to the dense type
![]() $\operatorname {tp}(a/M)$
.
$\operatorname {tp}(a/M)$
.
Proof If the set-theoretic difference
![]() $S_a \setminus S_{a'}$
were dense for some choice a and
$S_a \setminus S_{a'}$
were dense for some choice a and
![]() $a'$
, both in the same dense type over M, then it would contain some element b which is dense over
$a'$
, both in the same dense type over M, then it would contain some element b which is dense over
![]() $M\cup \{a, a '\}$
. In particular, both
$M\cup \{a, a '\}$
. In particular, both
![]() $(a, b)$
and
$(a, b)$
and
![]() $(a', b)$
would lie in
$(a', b)$
would lie in
![]() $\operatorname {GP}(\operatorname {tp}(a/M), \operatorname {tp}(b/M))$
, yet
$\operatorname {GP}(\operatorname {tp}(a/M), \operatorname {tp}(b/M))$
, yet
![]() $(a,b)$
belongs to S but
$(a,b)$
belongs to S but
![]() $(a', b)$
does not, which contradicts Theorem 4.7.
$(a', b)$
does not, which contradicts Theorem 4.7.
Proposition 4.9 Consider a non-standard finite group G as well as two internal subsets X of
![]() $G^{n}$
and Y of
$G^{n}$
and Y of
![]() $G^{m}$
and an internal relation S on
$G^{m}$
and an internal relation S on
![]() $X\times Y$
, all defined over a countable rich subset M. If S is almost surely k-stable for some
$X\times Y$
, all defined over a countable rich subset M. If S is almost surely k-stable for some
![]() $k\ge 1$
, then for every
$k\ge 1$
, then for every
![]() $\epsilon>0,$
there is a finite (possibly empty) union of boxes
$\epsilon>0,$
there is a finite (possibly empty) union of boxes
 $$\begin{align*}U=\bigcup\limits_{i=1}^\ell (X_i\times Y_i),\end{align*}$$
$$\begin{align*}U=\bigcup\limits_{i=1}^\ell (X_i\times Y_i),\end{align*}$$
with all
![]() $X_i\times Y_i \subseteq X\times Y$
, defined over M, such that
$X_i\times Y_i \subseteq X\times Y$
, defined over M, such that
![]() $\mu (U\triangle S) < \epsilon $
.
$\mu (U\triangle S) < \epsilon $
.
Note that every box is
![]() $2$
-stable and thus the finite union U is r-stable for some r, which can be explicitly computed in terms of the number
$2$
-stable and thus the finite union U is r-stable for some r, which can be explicitly computed in terms of the number
![]() $\ell $
of boxes occurring in U. However, at the time of writing, we are unable to give an explicit bound on
$\ell $
of boxes occurring in U. However, at the time of writing, we are unable to give an explicit bound on
![]() $\ell $
or show that U and S are actually comparable.
$\ell $
or show that U and S are actually comparable.
Proof If S is not dense in
![]() $G^{n+m}$
, then it suffices to take U to be the empty union of boxes. Thus, we may assume that the internal subset S of
$G^{n+m}$
, then it suffices to take U to be the empty union of boxes. Thus, we may assume that the internal subset S of
![]() $G^{n+m}$
is dense.
$G^{n+m}$
is dense.
Claim 1 Consider an arbitrary subset Z of S in the
![]() $\sigma $
-algebra of internal sets defined over M. (Note that Z need not be
$\sigma $
-algebra of internal sets defined over M. (Note that Z need not be
![]() $\omega $
-internal, but it is measurable with respect to the extension of the Loeb measure.) If Z has positive measure, then there exists a dense element a in
$\omega $
-internal, but it is measurable with respect to the extension of the Loeb measure.) If Z has positive measure, then there exists a dense element a in
![]() $G^n$
such that the fiber
$G^n$
such that the fiber
![]() $Z_a$
is dense and satisfies the following property (
$Z_a$
is dense and satisfies the following property (
![]() $\star $
): for every internal subset W of Y defined over M, if
$\star $
): for every internal subset W of Y defined over M, if
![]() $\mu _{G^m}(W\setminus S_a)=0$
, then
$\mu _{G^m}(W\setminus S_a)=0$
, then
Proof of Claim 1
By Fubini–Tonelli (Remark 2.6), the measurable set
has positive measure (since
![]() $\mu _{G^{n+m}} (Z)$
is not zero). For every internal subset W of Y defined over M, set
$\mu _{G^{n+m}} (Z)$
is not zero). For every internal subset W of Y defined over M, set
Notice that there are only countably many such sets
![]() $D_W$
. Consider the subfamily
$D_W$
. Consider the subfamily
![]() $\mathcal D$
of all sets
$\mathcal D$
of all sets
![]() $D_W$
of measure
$D_W$
of measure
![]() $0$
. Similarly, let
$0$
. Similarly, let
![]() $\mathcal E$
be the countable family of all internal subsets
$\mathcal E$
be the countable family of all internal subsets
![]() $X'$
of
$X'$
of
![]() $G^n$
defined over M of measure
$G^n$
defined over M of measure
![]() $0$
. By
$0$
. By
![]() $\sigma $
-additivity of the (extension of the) Loeb measure, the set
$\sigma $
-additivity of the (extension of the) Loeb measure, the set
has positive measure, so it is non-empty. Now choose some element a in the above set-theoretic difference. By the choice of
![]() $\mathcal E$
, the type
$\mathcal E$
, the type
![]() $\operatorname {tp}(a/M)$
is dense and so is the fiber
$\operatorname {tp}(a/M)$
is dense and so is the fiber
![]() $Z_a$
(since a lies in
$Z_a$
(since a lies in
![]() $Z_1$
). Furthermore, the element a satisfies (
$Z_1$
). Furthermore, the element a satisfies (
![]() $\star $
) by our choice of the family
$\star $
) by our choice of the family
![]() $\mathcal D$
.
$\mathcal D$
.
As the internal set S is dense, it has positive measure. By the previous claim, there is an element a which is dense over M satisfying
![]() $(\star )$
with respect to
$(\star )$
with respect to
![]() $Z=S$
such that the fiber
$Z=S$
such that the fiber
![]() $S_a$
is dense. Thus, the fiber
$S_a$
is dense. Thus, the fiber
![]() $S_a$
contains an element b which is dense over
$S_a$
contains an element b which is dense over
![]() $M\cup \{a\}$
. By Fact 3.12, the dense pair
$M\cup \{a\}$
. By Fact 3.12, the dense pair
![]() $(a,b)$
is in good position over M and clearly lies in S.
$(a,b)$
is in good position over M and clearly lies in S.
Claim 2 For every pair
![]() $(a, b)$
in S in good position over M such that a satisfies (
$(a, b)$
in S in good position over M such that a satisfies (
![]() $\star $
), there are an internal subset
$\star $
), there are an internal subset
![]() $Y'$
of Y and an
$Y'$
of Y and an
![]() $\omega $
-internal subset
$\omega $
-internal subset
![]() $X'$
of X, both defined over M, such that
$X'$
of X, both defined over M, such that
![]() $(a,b)$
lies in
$(a,b)$
lies in
![]() $X'\times Y'$
and
$X'\times Y'$
and
![]() $\mu ((X'\times Y')\setminus S)=0$
.
$\mu ((X'\times Y')\setminus S)=0$
.
Proof of Claim 2
By Theorem 4.7, there is no element in
![]() $\operatorname {tp}(b/M)$
dense over
$\operatorname {tp}(b/M)$
dense over
![]() $M\cup \{a\}$
outside of
$M\cup \{a\}$
outside of
![]() $S_a$
, so the
$S_a$
, so the
![]() $\omega $
-internal subset
$\omega $
-internal subset
![]() $\operatorname {tp}(b/M) \setminus S_a$
of Y is not dense. By
$\operatorname {tp}(b/M) \setminus S_a$
of Y is not dense. By
![]() $\aleph _1$
-saturation, there is some internal subset
$\aleph _1$
-saturation, there is some internal subset
![]() $Y'$
of Y defined over M containing b with
$Y'$
of Y defined over M containing b with
![]() $\mu _{G^m}(Y'\setminus S_a)=0$
. We deduce by
$\mu _{G^m}(Y'\setminus S_a)=0$
. We deduce by
![]() $(\star )$
that
$(\star )$
that
![]() $\mu _{G^n}(X')>0$
, where
$\mu _{G^n}(X')>0$
, where
is an
![]() $\omega $
-internal subset (by Definition 3.2(IV)) containing a (this set is
$\omega $
-internal subset (by Definition 3.2(IV)) containing a (this set is
![]() $D_{Y'}$
with
$D_{Y'}$
with
![]() $Z=S$
in the notation of Claim 1).
$Z=S$
in the notation of Claim 1).
A straightforward computation using Fubini–Tonelli yields
as desired.
Consider now the countable collection
![]() $\mathcal B_S$
of all subsets
$\mathcal B_S$
of all subsets
![]() $X'\times Y'$
as in Claim 2, that is, the set
$X'\times Y'$
as in Claim 2, that is, the set
![]() $Y'$
is internal while
$Y'$
is internal while
![]() $X'$
is
$X'$
is
![]() $\omega $
-internal, both are defined over M and
$\omega $
-internal, both are defined over M and
so
![]() $\mu _{G^{n+m}}((X'\times Y')\setminus S)=0$
. By
$\mu _{G^{n+m}}((X'\times Y')\setminus S)=0$
. By
![]() $\sigma $
-additivity, we have that
$\sigma $
-additivity, we have that
 $$\begin{align*}\left(\bigcup_{X'\times Y'\in \mathcal B_S} (X'\times Y') \right)\setminus S \end{align*}$$
$$\begin{align*}\left(\bigcup_{X'\times Y'\in \mathcal B_S} (X'\times Y') \right)\setminus S \end{align*}$$
has measure
![]() $0$
(with respect to the extension of the Loeb measure). Observe further that the set
$0$
(with respect to the extension of the Loeb measure). Observe further that the set
belongs to the
![]() $\sigma $
-algebra of internal sets defined over M. If Z has positive measure, we deduce as in the discussion right after Claim 1 that Z contains a pair
$\sigma $
-algebra of internal sets defined over M. If Z has positive measure, we deduce as in the discussion right after Claim 1 that Z contains a pair
![]() $(a,b)$
in good position over M with a satisfying
$(a,b)$
in good position over M with a satisfying
![]() $(\star )$
. It follows from Claim 2 that
$(\star )$
. It follows from Claim 2 that
![]() $(a,b)$
lies in some box
$(a,b)$
lies in some box
![]() $X'\times Y'$
in
$X'\times Y'$
in
![]() $\mathcal B_S$
, contradicting the choice of Z. Thus, S and
$\mathcal B_S$
, contradicting the choice of Z. Thus, S and
![]() $\bigcup _{X'\times Y'\in \mathcal B_S} (X'\times Y')$
are comparable with respect to the extension of the Loeb measure. We need only show that we can replace the latter union, modulo an
$\bigcup _{X'\times Y'\in \mathcal B_S} (X'\times Y')$
are comparable with respect to the extension of the Loeb measure. We need only show that we can replace the latter union, modulo an
![]() $\epsilon $
-error, by an actual finite union of internal boxes defined over M.
$\epsilon $
-error, by an actual finite union of internal boxes defined over M.
Given
![]() $\epsilon>0$
, by continuity of the Loeb measure, there is some integer
$\epsilon>0$
, by continuity of the Loeb measure, there is some integer
![]() $\ell $
and subsets
$\ell $
and subsets
![]() $X^{\prime }_1\times Y_1,\ldots , X^{\prime }_\ell \times Y_\ell $
in
$X^{\prime }_1\times Y_1,\ldots , X^{\prime }_\ell \times Y_\ell $
in
![]() $\mathcal B_S$
such that
$\mathcal B_S$
such that
 $$\begin{align*}\mu_{G^{n+m}}\left( S\setminus \bigcup\limits_{i=1}^\ell (X^{\prime}_i\times Y_i)\right)<\frac{\epsilon}{2}.\end{align*}$$
$$\begin{align*}\mu_{G^{n+m}}\left( S\setminus \bigcup\limits_{i=1}^\ell (X^{\prime}_i\times Y_i)\right)<\frac{\epsilon}{2}.\end{align*}$$
Note that
![]() $\ell>0$
, since
$\ell>0$
, since
![]() $\mathcal B_S$
is non-empty, for S is assumed to be dense. For each
$\mathcal B_S$
is non-empty, for S is assumed to be dense. For each
![]() $1\le i\le \ell $
, the
$1\le i\le \ell $
, the
![]() $\omega $
-internal subset
$\omega $
-internal subset
![]() $(X^{\prime }_i\times Y_i)\setminus S$
has measure
$(X^{\prime }_i\times Y_i)\setminus S$
has measure
![]() $0$
, so we can find internal subsets
$0$
, so we can find internal subsets
![]() $X_i$
, with each
$X_i$
, with each
![]() $X_i$
containing
$X_i$
containing
![]() $X^{\prime }_i$
, such that
$X^{\prime }_i$
, such that
Note that
![]() $X_i$
is again internal and defined over M. Now set
$X_i$
is again internal and defined over M. Now set
![]() $U=\bigcup _{i=1}^\ell (X_i\times Y_i)$
, so U contains
$U=\bigcup _{i=1}^\ell (X_i\times Y_i)$
, so U contains
![]() $\bigcup _{i=1}^\ell (X^{\prime }_i\times Y_i)$
, and it follows that
$\bigcup _{i=1}^\ell (X^{\prime }_i\times Y_i)$
, and it follows that
 $$ \begin{align*} \mu_{G^{n+m}}\left(S \triangle U\right) & = \mu_{G^{n+m}} (S \setminus U) + \mu_{G^{n+m}}(U\setminus S) \\ & \le \mu_{G^{n+m}} \left(S \setminus \bigcup_{i=1}^\ell (X_i'\times Y_i) \right) + \sum_{i=1}^{\ell} \mu_{G^{n+m}}\left((X_i\times Y_i)\setminus S \right) \\ & < \frac{\epsilon}{2} + \ell\cdot \frac{\epsilon}{2\ell} = \epsilon. \end{align*} $$
$$ \begin{align*} \mu_{G^{n+m}}\left(S \triangle U\right) & = \mu_{G^{n+m}} (S \setminus U) + \mu_{G^{n+m}}(U\setminus S) \\ & \le \mu_{G^{n+m}} \left(S \setminus \bigcup_{i=1}^\ell (X_i'\times Y_i) \right) + \sum_{i=1}^{\ell} \mu_{G^{n+m}}\left((X_i\times Y_i)\setminus S \right) \\ & < \frac{\epsilon}{2} + \ell\cdot \frac{\epsilon}{2\ell} = \epsilon. \end{align*} $$
This completes the proof of Proposition 4.9.
5 Corners and squares
Observe that the results in Section 4 did not make use of the underlying group structure. In this section, on the other hand, the group structure will play a fundamental role in guaranteeing the existence of certain two-dimensional patterns in a dense almost surely stable relation.
Given a countable rich subset M, the group
![]() $G(M)=G\cap M$
of M-rational points of G naturally acts on the collection of types over M by
$G(M)=G\cap M$
of M-rational points of G naturally acts on the collection of types over M by
This is a right action, but there is also a natural left action, defined analogously. With respect to the previous right action, we can thus consider the stabilizer in
![]() $G(M)$
of a type. This subgroup need not be definable in general. However, in the presence of stability, the stabilizer of a type becomes
$G(M)$
of a type. This subgroup need not be definable in general. However, in the presence of stability, the stabilizer of a type becomes
![]() $\omega $
-internal (or type-definable), though we will not need this for the purpose of this article.
$\omega $
-internal (or type-definable), though we will not need this for the purpose of this article.
Since the seminal work of Kim and Pillay [Reference Kim and Pillay25] on simple theories, many notions and techniques from geometric stability have been adapted successfully to other contexts. Pushing beyond simplicity, in groundbreaking work [Reference Hrushovski20], Hrushovski established the existence of an
![]() $\omega $
-internal subgroup of a non-standard finite group that plays the role of the stabilizer of every dense type over the countable rich substructure M. This subgroup is known in model theory as the connected component of G over M and denoted by
$\omega $
-internal subgroup of a non-standard finite group that plays the role of the stabilizer of every dense type over the countable rich substructure M. This subgroup is known in model theory as the connected component of G over M and denoted by
![]() $G_{M}^{00}$
.
$G_{M}^{00}$
.
The next fact summarizes the content of Hrushovski’s stabilizer theorem, tailored to our particular context. For ease of reference, the presentation largely follows the formulation of [Reference Montenegro, Onshuus and Simon31, Theorem 2.12].
Fact 5.1 ([Reference Hrushovski20, Theorem 3.5] & [Reference Montenegro, Onshuus and Simon31, Theorem 2.12])
Let M be a countable rich subset of a non-standard finite group G. Then, there exists an
![]() $\omega $
-internal normal subgroup
$\omega $
-internal normal subgroup
![]() $G_{M}^{00}$
defined over M with the following properties:
$G_{M}^{00}$
defined over M with the following properties:
-
(1) The
 $\omega $
-internal subset
$\omega $
-internal subset
 $G_{M}^{00}$
equals a countable intersection of internal generic symmetric neighborhoods
$G_{M}^{00}$
equals a countable intersection of internal generic symmetric neighborhoods
 $Z_n$
of the identity, each defined over M, that is,
$Z_n$
of the identity, each defined over M, that is,-
• each
 $Z_n=Z_n ^{-1}$
is symmetric and contains the identity element
$Z_n=Z_n ^{-1}$
is symmetric and contains the identity element
 $1_G$
;
$1_G$
; -
• finitely many translates of each
 $Z_n$
cover the group G;
$Z_n$
cover the group G; -
•
 $Z_{n+1}\cdot Z_{n+1}\subseteq Z_n$
for all n in
$Z_{n+1}\cdot Z_{n+1}\subseteq Z_n$
for all n in
 $\mathbb {N}$
.
$\mathbb {N}$
.
-
-
(2) Whenever
 $(a, b)$
is in good position over M with b in
$(a, b)$
is in good position over M with b in
 $\operatorname {tp}(a/M)$
, the dense element
$\operatorname {tp}(a/M)$
, the dense element
 $b\cdot a ^{-1}$
over M belongs to
$b\cdot a ^{-1}$
over M belongs to
 $G_{M}^{00}$
. In particular, the
$G_{M}^{00}$
. In particular, the
 $\omega $
-internal set
$\omega $
-internal set
 $G_{M}^{00}$
is dense.
$G_{M}^{00}$
is dense. -
(3) Whenever a is dense over M and g in
 $G_{M}^{00}$
is dense over M, the
$G_{M}^{00}$
is dense over M, the
 $\omega $
-internal set is again dense, that is, there exists some
$\omega $
-internal set is again dense, that is, there exists some $$\begin{align*}\operatorname{tp}(a/M)\cap \operatorname{tp}(a/M)\cdot g\end{align*}$$
$$\begin{align*}\operatorname{tp}(a/M)\cap \operatorname{tp}(a/M)\cdot g\end{align*}$$
 $a'$
in
$a'$
in
 $\operatorname {tp}(a/M)$
which is dense over
$\operatorname {tp}(a/M)$
which is dense over
 $M\cup \{g\}$
such that
$M\cup \{g\}$
such that
 $a'\cdot g$
belongs to
$a'\cdot g$
belongs to
 $\operatorname {tp}(a/M)$
.
$\operatorname {tp}(a/M)$
.
Similarly, the
 $\omega $
-internal set
$\omega $
-internal set
 $\operatorname {tp}(a/M)\cap g\cdot \operatorname {tp}(a/M)$
is also dense, so there exists some
$\operatorname {tp}(a/M)\cap g\cdot \operatorname {tp}(a/M)$
is also dense, so there exists some
 $a"$
in
$a"$
in
 $\operatorname {tp}(a/M)$
which is dense over
$\operatorname {tp}(a/M)$
which is dense over
 $M\cup \{g\}$
such that
$M\cup \{g\}$
such that
 $g\cdot a"$
belongs to
$g\cdot a"$
belongs to
 $\operatorname {tp}(a/M)$
.
$\operatorname {tp}(a/M)$
. -
(4) If N is a countable rich subset of G containing M, then
 $G_{N}^{00}$
is a subgroup of
$G_{N}^{00}$
is a subgroup of
 $G_{M}^{00}$
.
$G_{M}^{00}$
.
Furthermore, it follows that if G has finite exponent, then
![]() $G_{M}^{00}$
is a countable intersection of internal subgroups, each defined over M and of finite index: Indeed, we can equip the quotient group
$G_{M}^{00}$
is a countable intersection of internal subgroups, each defined over M and of finite index: Indeed, we can equip the quotient group
![]() $G/ G_{M}^{00}$
with the so-called logic topology, according to which a subset in the quotient is closed if its preimage is
$G/ G_{M}^{00}$
with the so-called logic topology, according to which a subset in the quotient is closed if its preimage is
![]() $\omega $
-internal and defined over M. The quotient group
$\omega $
-internal and defined over M. The quotient group
![]() $G/ G_{M}^{00}$
is a compact Hausdorff topological group of finite exponent, and thus profinite by [Reference Iltis22, Theorem 4.5]. Since M and
$G/ G_{M}^{00}$
is a compact Hausdorff topological group of finite exponent, and thus profinite by [Reference Iltis22, Theorem 4.5]. Since M and
![]() $\mathcal F$
are countable, the logic topology is second countable, so there is a fundamental system of open normal subgroups
$\mathcal F$
are countable, the logic topology is second countable, so there is a fundamental system of open normal subgroups
![]() $H_n/ G_{M}^{00}$
with
$H_n/ G_{M}^{00}$
with
![]() $G_{M}^{00}=\bigcap _n H_n$
. Now, each quotient
$G_{M}^{00}=\bigcap _n H_n$
. Now, each quotient
![]() $H_n/G_{M}^{00}$
is closed of finite index, by topological compactness, and thus the preimage
$H_n/G_{M}^{00}$
is closed of finite index, by topological compactness, and thus the preimage
![]() $H_n$
is internal and defined over M, as desired.
$H_n$
is internal and defined over M, as desired.
Since the
![]() $\omega $
-internal normal subgroup
$\omega $
-internal normal subgroup
![]() $G_{M}^{00}$
equals a countable intersection of internal generic symmetric neighborhoods
$G_{M}^{00}$
equals a countable intersection of internal generic symmetric neighborhoods
![]() $Z_n$
, each defined over M, the elements
$Z_n$
, each defined over M, the elements
![]() $a'$
of any given type
$a'$
of any given type
![]() $\operatorname {tp}(a/M)$
all lie in the same coset
$\operatorname {tp}(a/M)$
all lie in the same coset
![]() $a\cdot G_{M}^{00}$
. Indeed, we need only show that
$a\cdot G_{M}^{00}$
. Indeed, we need only show that
![]() $a ^{-1} \cdot a'$
belongs to
$a ^{-1} \cdot a'$
belongs to
![]() $Z_n$
for every n in
$Z_n$
for every n in
![]() $\mathbb {N}$
. Now, the subset M is rich, so finitely many translates of each
$\mathbb {N}$
. Now, the subset M is rich, so finitely many translates of each
![]() $Z_n$
by elements of
$Z_n$
by elements of
![]() $G(M)$
cover G. In particular, the element a belongs to
$G(M)$
cover G. In particular, the element a belongs to
![]() $g \cdot Z_{n+1}$
for some g in
$g \cdot Z_{n+1}$
for some g in
![]() $G(M)$
and therefore so does
$G(M)$
and therefore so does
![]() $a'$
. Hence, we deduce that
$a'$
. Hence, we deduce that
belongs to
![]() $(Z_{n+1}) ^{-1}\cdot Z_{n+1}=Z_{n+1}\cdot Z_{n+1}\subset Z_n$
, as desired.
$(Z_{n+1}) ^{-1}\cdot Z_{n+1}=Z_{n+1}\cdot Z_{n+1}\subset Z_n$
, as desired.
We now have all the ingredients in order to state our main result.
Theorem 5.2 Consider a non-standard finite group G along with an internal relation S on
![]() $G\times G$
defined over a countable rich subset M. If S is dense and almost surely k-stable for some
$G\times G$
defined over a countable rich subset M. If S is dense and almost surely k-stable for some
![]() $k\ge 1$
, then for every g in
$k\ge 1$
, then for every g in
![]() $G_{M}^{00}$
which is dense over M, the internal set
$G_{M}^{00}$
which is dense over M, the internal set
has positive density.
Proof Fix some element g in
![]() $G_{M}^{00}$
which is dense over M. In order to show that the internal set
$G_{M}^{00}$
which is dense over M. In order to show that the internal set
![]() $\Lambda _\Box (S)_g$
has positive density, we need only show that
$\Lambda _\Box (S)_g$
has positive density, we need only show that
![]() $\Lambda _\Box (S)_g$
contains a pair
$\Lambda _\Box (S)_g$
contains a pair
![]() $(a, b)$
dense over
$(a, b)$
dense over
![]() $M\cup \{g\}$
. We do so with the help of the following auxiliary claims.
$M\cup \{g\}$
. We do so with the help of the following auxiliary claims.
Claim 3 There is a tuple
![]() $(c, d)$
in good position over M with c and d in
$(c, d)$
in good position over M with c and d in
![]() $\operatorname {tp}(g/M)$
such that
$\operatorname {tp}(g/M)$
such that
![]() $g=c ^{-1}\cdot d$
.
$g=c ^{-1}\cdot d$
.
Proof of Claim 3
By Fact 5.1 applied to the dense element
![]() $g ^{-1}$
of
$g ^{-1}$
of
![]() $G_{M}^{00}$
and the dense type
$G_{M}^{00}$
and the dense type
![]() $\operatorname {tp}(g/M)$
, we deduce that there exists some element
$\operatorname {tp}(g/M)$
, we deduce that there exists some element
![]() $a'$
in
$a'$
in
![]() $\operatorname {tp}(g/M)$
dense over
$\operatorname {tp}(g/M)$
dense over
![]() $M\cup \{g\}$
such that
$M\cup \{g\}$
such that
![]() $g"=g ^{-1} \cdot a'$
belongs to
$g"=g ^{-1} \cdot a'$
belongs to
![]() $\operatorname {tp}(g/M)$
. Hence, for the element
$\operatorname {tp}(g/M)$
. Hence, for the element
![]() $g"$
in
$g"$
in
![]() $\operatorname {tp}(g/M),$
there are two elements
$\operatorname {tp}(g/M),$
there are two elements
![]() $c'=g$
and
$c'=g$
and
![]() $d'=a'$
in
$d'=a'$
in
![]() $\operatorname {tp}(g/M)$
with
$\operatorname {tp}(g/M)$
with
![]() $(c', d')$
in good position over M such that
$(c', d')$
in good position over M such that
![]() $g"=(c') ^{-1} \cdot d'$
. By Remark 3.8 and Lemma 3.11, we deduce that the same is true for every element in
$g"=(c') ^{-1} \cdot d'$
. By Remark 3.8 and Lemma 3.11, we deduce that the same is true for every element in
![]() $\operatorname {tp}(g"/M)=\operatorname {tp}(g/M)$
. We thus obtain the desired tuple
$\operatorname {tp}(g"/M)=\operatorname {tp}(g/M)$
. We thus obtain the desired tuple
![]() $(c, d)$
as in the statement with
$(c, d)$
as in the statement with
![]() $g=c ^{-1}\cdot d$
.
$g=c ^{-1}\cdot d$
.
Claim 4 The internal set
![]() $S\cap S\cdot (1_G, g ^{-1}) $
is dense.
$S\cap S\cdot (1_G, g ^{-1}) $
is dense.
Proof of Claim 4
Recall that S is dense and thus so is
![]() $S\cdot (1_G, g ^{-1})$
. Hence, by Fact 4.3(c), so is the intersection
$S\cdot (1_G, g ^{-1})$
. Hence, by Fact 4.3(c), so is the intersection
![]() $S\cdot (1_G, c ^{-1})\cap S\cdot (1_G, d ^{-1})$
, since the tuple
$S\cdot (1_G, c ^{-1})\cap S\cdot (1_G, d ^{-1})$
, since the tuple
![]() $(c, d)$
as in Claim 3 is in good position over M and both c and d lie in the dense type
$(c, d)$
as in Claim 3 is in good position over M and both c and d lie in the dense type
![]() $\operatorname {tp}(g/M)$
. Multiplying on the right by
$\operatorname {tp}(g/M)$
. Multiplying on the right by
![]() $(1_G, c)$
, we deduce that
$(1_G, c)$
, we deduce that
![]() $S\cap S \cdot (1_G, g ^{-1})$
is dense, as desired.
$S\cap S \cdot (1_G, g ^{-1})$
is dense, as desired.
By Claim 4 and Fact 3.12, there is a pair
![]() $(a_0, b)$
in good position over
$(a_0, b)$
in good position over
![]() $M\cup \{g\}$
contained in
$M\cup \{g\}$
contained in
![]() $S\cap S\cdot (1_G, g ^{-1})$
. That is, both pairs
$S\cap S\cdot (1_G, g ^{-1})$
. That is, both pairs
![]() $(a_0, b)$
and
$(a_0, b)$
and
![]() $(a_0, b\cdot g)$
belong to S.
$(a_0, b\cdot g)$
belong to S.
Note that we have not yet used that S is almost surely stable. The idea is to replace
![]() $a_0$
by a suitable realization a such that the product
$a_0$
by a suitable realization a such that the product
![]() $ a\cdot g$
lies again in
$ a\cdot g$
lies again in
![]() $\operatorname {tp}(a/M)$
.
$\operatorname {tp}(a/M)$
.
Indeed, Fact 5.1(c) yields that there is some a in
![]() $\operatorname {tp}(a_0/M)$
dense over
$\operatorname {tp}(a_0/M)$
dense over
![]() $M\cup \{g\}$
such that
$M\cup \{g\}$
such that
![]() $a\cdot g$
lies again in
$a\cdot g$
lies again in
![]() $\operatorname {tp}(a_0/M)$
. We may assume that a is dense over
$\operatorname {tp}(a_0/M)$
. We may assume that a is dense over
![]() $M\cup \{b,g\}$
, by Lemma 3.10. Clearly, each of the pairs
$M\cup \{b,g\}$
, by Lemma 3.10. Clearly, each of the pairs
![]() $(b, a)$
,
$(b, a)$
,
![]() $(b, a\cdot g)$
,
$(b, a\cdot g)$
,
![]() $(b\cdot g, a)$
, and
$(b\cdot g, a)$
, and
![]() $(b\cdot g, a\cdot g)$
is in good position over M.
$(b\cdot g, a\cdot g)$
is in good position over M.
Theorem 4.7 implies that
since the pair
![]() $(a_0, b)$
lies in S and is in good position over M. Thus, both pairs
$(a_0, b)$
lies in S and is in good position over M. Thus, both pairs
![]() $(a, b)$
and
$(a, b)$
and
![]() $(a\cdot g, b)$
lie in S.
$(a\cdot g, b)$
lie in S.
Now, the pair
![]() $(a_0, b\cdot g)$
also lies in S and is in good position over M. Again by Theorem 4.7, the pairs
$(a_0, b\cdot g)$
also lies in S and is in good position over M. Again by Theorem 4.7, the pairs
![]() $(a, b\cdot g)$
and
$(a, b\cdot g)$
and
![]() $(a\cdot g, b\cdot g)$
of
$(a\cdot g, b\cdot g)$
of
![]() $\operatorname {GP}(\operatorname {tp}(a'/M), \operatorname {tp}(b\cdot g/M))$
must lie in S. In particular, the pair
$\operatorname {GP}(\operatorname {tp}(a'/M), \operatorname {tp}(b\cdot g/M))$
must lie in S. In particular, the pair
![]() $(a, b)$
is dense over
$(a, b)$
is dense over
![]() $M\cup \{g\}$
and belongs to the internal set
$M\cup \{g\}$
and belongs to the internal set
![]() $\Lambda _\Box (S)_g$
, as desired.
$\Lambda _\Box (S)_g$
, as desired.
A straightforward application of Fubini–Tonnelli (Remark 2.6) yields the following corollary.
Corollary 5.3 Consider a non-standard finite group G along with an internal relation S on
![]() $G\times G$
defined over a countable rich subset M. If S is dense and almost surely k-stable for some
$G\times G$
defined over a countable rich subset M. If S is dense and almost surely k-stable for some
![]() $k\ge 1$
, then the internal set
$k\ge 1$
, then the internal set
has positive density.
In particular, S contains a dense collection of both BMZ and naive corners, as remarked in the introduction. Moreover, if G is abelian, then there is a dense collection of triples
![]() $(x, y, d)$
in
$(x, y, d)$
in
![]() $G^3$
such that
$G^3$
such that
![]() $(x, y)$
,
$(x, y)$
,
![]() $(x+d, y)$
,
$(x+d, y)$
,
![]() $(x, y+d)$
,
$(x, y+d)$
,
![]() $(x+d, y+d)$
form a square in S.
$(x+d, y+d)$
form a square in S.
In the special case of a binary relation given by the Cayley graph of a subset A of G, the proof of Theorem 5.2 yields a stronger result, since every dense element g in
![]() $G_{M}^{00}$
is a popular side length for many corners.
$G_{M}^{00}$
is a popular side length for many corners.
Proposition 5.4 Consider a non-standard finite group G and an internal almost surely k-stable dense subset A of G defined over a countable rich subset M. For every g in
![]() $G_{M}^{00}$
which is dense over M, the sets A and
$G_{M}^{00}$
which is dense over M, the sets A and
![]() $g\cdot A$
are comparable, that is,
$g\cdot A$
are comparable, that is,
In particular, whenever the element a in A is dense over
![]() $M\cup \{g\}$
,
$M\cup \{g\}$
,
![]() $g^m\cdot a$
belongs to A for all m in
$g^m\cdot a$
belongs to A for all m in
![]() $\mathbb {Z}$
. Hence, the
$\mathbb {Z}$
. Hence, the
![]() $\omega $
-internal set
$\omega $
-internal set
![]() $\bigcap _{m\in \mathbb {Z}} g^m\cdot A$
is dense with measure
$\bigcap _{m\in \mathbb {Z}} g^m\cdot A$
is dense with measure
![]() $\mu _G(A)>0$
.
$\mu _G(A)>0$
.
Proof As in Claim 3 of Theorem 5.2, write
![]() $g=c ^{-1} \cdot d$
, where
$g=c ^{-1} \cdot d$
, where
![]() $(c, d)$
are in good position over M and both lie in the same type
$(c, d)$
are in good position over M and both lie in the same type
![]() $\operatorname {tp}(g/M)$
. Suppose toward a contradiction that
$\operatorname {tp}(g/M)$
. Suppose toward a contradiction that
![]() $\mu _G(A\triangle (g\cdot A))>0$
, or equivalently, that
$\mu _G(A\triangle (g\cdot A))>0$
, or equivalently, that
Without loss of generality, we may assume that
![]() $(c\cdot A)\setminus (d\cdot A)$
is dense, so it contains some element b which is dense over
$(c\cdot A)\setminus (d\cdot A)$
is dense, so it contains some element b which is dense over
![]() $M\cup \{c,d\}$
. This means that
$M\cup \{c,d\}$
. This means that
![]() $c ^{-1}\cdot b$
belongs to A but
$c ^{-1}\cdot b$
belongs to A but
![]() $d ^{-1} \cdot b$
does not, or equivalently, the pair
$d ^{-1} \cdot b$
does not, or equivalently, the pair
![]() $(c, b)$
belongs to the almost surely k-stable relation
$(c, b)$
belongs to the almost surely k-stable relation
![]() $\mathrm {Cay}(G,A)$
, but
$\mathrm {Cay}(G,A)$
, but
![]() $(d, b)$
does not. Since both pairs belong to
$(d, b)$
does not. Since both pairs belong to
![]() $\operatorname {GP}(\operatorname {tp}(g/M), \operatorname {tp}(b/M) )$
, this contradicts Theorem 4.7.
$\operatorname {GP}(\operatorname {tp}(g/M), \operatorname {tp}(b/M) )$
, this contradicts Theorem 4.7.
To prove the final part, observe that since A and
![]() $g\cdot A$
are comparable, so are A and
$g\cdot A$
are comparable, so are A and
![]() $g ^{-1} \cdot A$
. By continuity, we need only show that each intersection
$g ^{-1} \cdot A$
. By continuity, we need only show that each intersection
has constant measure
![]() $\mu _G(A)$
for all m in
$\mu _G(A)$
for all m in
![]() $\mathbb {Z}$
. Otherwise, the internal set
$\mathbb {Z}$
. Otherwise, the internal set
is dense, so by Lemma 3.10, we may choose an element a in A which is dense over
![]() $M\cup \{g\}$
. Remark 3.13 implies that a must belong to both
$M\cup \{g\}$
. Remark 3.13 implies that a must belong to both
![]() $g\cdot A$
and
$g\cdot A$
and
![]() $g ^{-1} \cdot A$
, and inductively, we conclude that a belongs to
$g ^{-1} \cdot A$
, and inductively, we conclude that a belongs to
![]() $g^{i} \cdot A$
for all
$g^{i} \cdot A$
for all
![]() $-m\le i\le m$
, which gives the desired contradiction.
$-m\le i\le m$
, which gives the desired contradiction.
We conclude this section by deducing a finitary (albeit ineffective) version of Corollary 5.3, using Lemma 2.4 and the accompanying Remark 2.5, and strengthening it in two special cases.
Corollary 5.5 Given an integer
![]() $k\ge 1$
and a real number
$k\ge 1$
and a real number
![]() $\delta>0$
, there is an integer
$\delta>0$
, there is an integer
![]() $\ell _0(k, \delta )\ge 1$
and real numbers
$\ell _0(k, \delta )\ge 1$
and real numbers
![]() $\theta =\theta (k, \delta )>0$
and
$\theta =\theta (k, \delta )>0$
and
![]() $\epsilon =\epsilon (k, \delta )>0$
with the following property.
$\epsilon =\epsilon (k, \delta )>0$
with the following property.
Let G be a finite group of order
![]() $|G|\ge \ell _0$
and let
$|G|\ge \ell _0$
and let
![]() $S\subseteq G\times G$
be a relation of size
$S\subseteq G\times G$
be a relation of size
![]() $|S|\ge \delta |G|^{2}$
such that the collection
$|S|\ge \delta |G|^{2}$
such that the collection
![]() $\mathcal {H}_k(S)$
of all half-graphs of height k induced by S on G has size
$\mathcal {H}_k(S)$
of all half-graphs of height k induced by S on G has size
![]() $|\mathcal {H}_k(S)|\le \theta |G|^{2k}$
. Then,
$|\mathcal {H}_k(S)|\le \theta |G|^{2k}$
. Then,
![]() $\Lambda _\Box (S)$
has size at least
$\Lambda _\Box (S)$
has size at least
![]() $\epsilon |G|^{3}$
.
$\epsilon |G|^{3}$
.
In particular, the relation S contains a (nontrivial) square provided that
![]() $|G|\geq 1/\epsilon $
.
$|G|\geq 1/\epsilon $
.
Proof The proof proceeds by contradiction. Suppose there are
![]() $k\ge 1$
and
$k\ge 1$
and
![]() $\delta>0$
such that for every
$\delta>0$
such that for every
![]() $\ell \ge 1$
(setting
$\ell \ge 1$
(setting
![]() $\theta =\epsilon =1/\ell $
), we can find a finite group
$\theta =\epsilon =1/\ell $
), we can find a finite group
![]() $G_\ell $
of order at least
$G_\ell $
of order at least
![]() $\ell $
and a relation
$\ell $
and a relation
![]() $S_\ell \subseteq G_\ell \times G_\ell $
of density
$S_\ell \subseteq G_\ell \times G_\ell $
of density
![]() $\delta $
such that
$\delta $
such that
![]() $\mathcal {H}_k(S_\ell )\le \frac {1}{\ell } |G_\ell |^{2k}$
, yet
$\mathcal {H}_k(S_\ell )\le \frac {1}{\ell } |G_\ell |^{2k}$
, yet
![]() $|\Lambda _\Box (S_\ell )|<|G_\ell ^{3}|/\ell $
.
$|\Lambda _\Box (S_\ell )|<|G_\ell ^{3}|/\ell $
.
In particular, the family
![]() $(G_\ell , S_\ell )_{\ell \in \mathbb {N}}$
is almost surely k-stable, as in Remark 4.6. Take a non-principal ultrafilter
$(G_\ell , S_\ell )_{\ell \in \mathbb {N}}$
is almost surely k-stable, as in Remark 4.6. Take a non-principal ultrafilter
![]() $\mathfrak {U}$
on
$\mathfrak {U}$
on
![]() $\mathbb {N}$
and consider the non-standard finite group
$\mathbb {N}$
and consider the non-standard finite group
![]() $G=\prod _{\ell \to \mathfrak {U}} G_\ell $
as well as the internal set
$G=\prod _{\ell \to \mathfrak {U}} G_\ell $
as well as the internal set
![]() $ S=\prod _{\ell \to \mathfrak {U}} S_\ell $
. By Remark 2.5, the set S has Loeb measure
$ S=\prod _{\ell \to \mathfrak {U}} S_\ell $
. By Remark 2.5, the set S has Loeb measure
![]() $\mu _{G^{2}}(S)\ge \delta $
and is almost surely k-stable by Remark 4.6. Choose any countable rich subset M. Corollary 5.3 yields that
$\mu _{G^{2}}(S)\ge \delta $
and is almost surely k-stable by Remark 4.6. Choose any countable rich subset M. Corollary 5.3 yields that
![]() $\mu _{G^{3}}(\Lambda _\Box (S))$
is at least
$\mu _{G^{3}}(\Lambda _\Box (S))$
is at least
![]() $\eta $
for some
$\eta $
for some
![]() $\eta>0$
.
$\eta>0$
.
Remark 2.4 applied to
![]() $r=\eta $
yields the desired contradiction, since
$r=\eta $
yields the desired contradiction, since
![]() $\Lambda _\Box (S_\ell )$
has size at most
$\Lambda _\Box (S_\ell )$
has size at most
![]() $\eta |G_\ell |^{3}/2$
for sufficiently large
$\eta |G_\ell |^{3}/2$
for sufficiently large
![]() $\ell $
.
$\ell $
.
In the particular case that the group in question has bounded exponent, we can strengthen Corollary 5.5 using Fact 5.1 to obtain a subgroup of bounded index almost all of whose elements witness the existence of a square.
Corollary 5.6 Given integers
![]() $k, r\ge 1$
and real numbers
$k, r\ge 1$
and real numbers
![]() $\delta , \epsilon>0$
, there is an integer
$\delta , \epsilon>0$
, there is an integer
![]() $\ell =\ell (k, r, \delta , \epsilon )\ge 1$
and real numbers
$\ell =\ell (k, r, \delta , \epsilon )\ge 1$
and real numbers
![]() $\theta =\theta (k, r, \delta , \epsilon )>0$
and
$\theta =\theta (k, r, \delta , \epsilon )>0$
and
![]() $\eta =\eta (k, r, \delta , \epsilon )>0$
with the following property.
$\eta =\eta (k, r, \delta , \epsilon )>0$
with the following property.
Let G be a finite group of exponent bounded by r, and consider a relation
![]() $S\subseteq G\times G$
of size
$S\subseteq G\times G$
of size
![]() $|S|\ge \delta |G|^{2}$
such that the collection
$|S|\ge \delta |G|^{2}$
such that the collection
![]() $\mathcal {H}_k(S)$
of all half-graphs of height k induced by S on G has size
$\mathcal {H}_k(S)$
of all half-graphs of height k induced by S on G has size
![]() $|\mathcal {H}_k(S)|\le \theta |G|^{2k}$
. Then, there exists a subgroup H of G of index at most
$|\mathcal {H}_k(S)|\le \theta |G|^{2k}$
. Then, there exists a subgroup H of G of index at most
![]() $\ell $
such that
$\ell $
such that
where
![]() $\Lambda _\Box (S)_g\subseteq S$
is as in Theorem 5.2.
$\Lambda _\Box (S)_g\subseteq S$
is as in Theorem 5.2.
Proof As in the proof of Corollary 5.5, negating quantifiers, we deduce that for a fixed choice of
![]() $k, r, \delta ,$
and
$k, r, \delta ,$
and
![]() $\epsilon $
, for every
$\epsilon $
, for every
![]() $\ell $
in
$\ell $
in
![]() $\mathbb {N}$
(setting
$\mathbb {N}$
(setting
![]() $\theta =\eta =1/\ell $
), there is a finite group
$\theta =\eta =1/\ell $
), there is a finite group
![]() $G_\ell $
of exponent at most r and a relation
$G_\ell $
of exponent at most r and a relation
![]() $S_\ell \subseteq G_\ell \times G_\ell $
of density
$S_\ell \subseteq G_\ell \times G_\ell $
of density
![]() $\delta $
such that
$\delta $
such that
yet for every subgroup
![]() $H\leqslant G_\ell $
of index at most
$H\leqslant G_\ell $
of index at most
![]() $\ell $
, the subset of elements g in H with
$\ell $
, the subset of elements g in H with
has size at least
![]() $\epsilon |H|$
. In particular, the group
$\epsilon |H|$
. In particular, the group
![]() $G_\ell $
has size at least
$G_\ell $
has size at least
![]() $\ell $
, by taking H the trivial subgroup of
$\ell $
, by taking H the trivial subgroup of
![]() $G_\ell $
.
$G_\ell $
.
Take a non-principal ultrafilter
![]() $\mathfrak {U}$
on
$\mathfrak {U}$
on
![]() $\mathbb {N}$
and consider the non-standard finite group
$\mathbb {N}$
and consider the non-standard finite group
![]() $G=~\prod _{\ell \to \mathfrak {U}} G_\ell $
as well as the internal set
$G=~\prod _{\ell \to \mathfrak {U}} G_\ell $
as well as the internal set
![]() $ S=\prod _{\ell \to \mathfrak {U}} S_\ell $
. By Remark 2.5, the set S has Loeb measure
$ S=\prod _{\ell \to \mathfrak {U}} S_\ell $
. By Remark 2.5, the set S has Loeb measure
![]() $\mu _{G^{2}}(S)\ge \delta $
and is almost surely k-stable by Remark 4.6. Choose any countable rich subset M. Notice that the exponent of the non-standard finite group G is bounded by r by Łoś’s Theorem (Theorem 2.1). Fact 5.1 yields that the subgroup
$\mu _{G^{2}}(S)\ge \delta $
and is almost surely k-stable by Remark 4.6. Choose any countable rich subset M. Notice that the exponent of the non-standard finite group G is bounded by r by Łoś’s Theorem (Theorem 2.1). Fact 5.1 yields that the subgroup
![]() $G_{M}^{00}$
is a countable intersection of internal subgroups
$G_{M}^{00}$
is a countable intersection of internal subgroups
![]() $H_n$
, each of finite index and defined over M. We may assume that
$H_n$
, each of finite index and defined over M. We may assume that
![]() $H_{n+1}\subseteq H_n$
for every n in
$H_{n+1}\subseteq H_n$
for every n in
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Definition 3.2 tells us that the set
 $$\begin{align*}Z=\{g \in G_{M}^{00} : \ \mu_{G^{2}}(\Lambda_\Box(S)_g)=0\} = \bigcap\limits_{\substack{n\in \mathbb{N} \\ 0\ne m\in \mathbb{N}}} \left\{g \in H_n : \ \mu_{G^{2}}(\Lambda_\Box(S)_g)<\frac{1}{m}\right\} \end{align*}$$
$$\begin{align*}Z=\{g \in G_{M}^{00} : \ \mu_{G^{2}}(\Lambda_\Box(S)_g)=0\} = \bigcap\limits_{\substack{n\in \mathbb{N} \\ 0\ne m\in \mathbb{N}}} \left\{g \in H_n : \ \mu_{G^{2}}(\Lambda_\Box(S)_g)<\frac{1}{m}\right\} \end{align*}$$
is
![]() $\omega $
-internal.
$\omega $
-internal.
Fact 3.12 and Theorem 5.2 imply that Z is not dense, so by
![]() $\aleph _1$
-saturation and Remark 3.9, we deduce that for some
$\aleph _1$
-saturation and Remark 3.9, we deduce that for some
![]() $0\ne m$
in
$0\ne m$
in
![]() $\mathbb {N}$
and some finite-index internal subgroup
$\mathbb {N}$
and some finite-index internal subgroup
![]() $H=H_n$
defined over M, the set
$H=H_n$
defined over M, the set
![]() $\{g \in H : \ \mu _{G^{2}}(\Lambda _\Box (S))_g) < \frac {1}{m}\}$
is contained in some internal set of density
$\{g \in H : \ \mu _{G^{2}}(\Lambda _\Box (S))_g) < \frac {1}{m}\}$
is contained in some internal set of density
![]() $0$
.
$0$
.
Choose some
![]() $\ell _0$
in
$\ell _0$
in
![]() $\mathbb {N}$
with
$\mathbb {N}$
with
such that for
![]() $\mathfrak {U}$
-almost all
$\mathfrak {U}$
-almost all
![]() $\ell \ge \ell _0$
, the subgroup
$\ell \ge \ell _0$
, the subgroup
![]() $H(G_{\ell })$
has index
$H(G_{\ell })$
has index
![]() $[G:H]\le \ell _0$
. Now, Definition 3.2 yields an internal set W with
$[G:H]\le \ell _0$
. Now, Definition 3.2 yields an internal set W with
whence
![]() $\mu _G(W)=0$
and
$\mu _G(W)=0$
and
![]() $ \mu _G(W)<\epsilon \cdot \mu _G(H)=\epsilon /[G:H]$
. Therefore, for
$ \mu _G(W)<\epsilon \cdot \mu _G(H)=\epsilon /[G:H]$
. Therefore, for
![]() $\mathfrak {U}$
-almost all
$\mathfrak {U}$
-almost all
![]() $\ell \ge \ell _0$
, we have that
$\ell \ge \ell _0$
, we have that
 $$\begin{align*}\left|\left\{g \in H(G_\ell) : \ |\Lambda_\Box(S_\ell)_g| < \frac{|S_\ell|}{\ell} \right\} \right| \le |W(G_\ell)|< \frac{\epsilon}{[G:H]} |G_\ell| = \epsilon |H(G_\ell)|.\end{align*}$$
$$\begin{align*}\left|\left\{g \in H(G_\ell) : \ |\Lambda_\Box(S_\ell)_g| < \frac{|S_\ell|}{\ell} \right\} \right| \le |W(G_\ell)|< \frac{\epsilon}{[G:H]} |G_\ell| = \epsilon |H(G_\ell)|.\end{align*}$$
This contradicts our choice of
![]() $G_\ell $
, as desired.
$G_\ell $
, as desired.
Mimicking the proof above, together with Proposition 5.4, we deduce the following finitary statement concerning the existence of arbitrary long arithmetic progressions in almost surely stable dense sets.
Corollary 5.7 Given integers
![]() $k, m, r\ge 1$
and real numbers
$k, m, r\ge 1$
and real numbers
![]() $\delta , \epsilon , \eta>0$
, there is an integer
$\delta , \epsilon , \eta>0$
, there is an integer
![]() $n=n(k, m, r, \delta , \epsilon , \eta )\ge 1$
and a real number
$n=n(k, m, r, \delta , \epsilon , \eta )\ge 1$
and a real number
![]() $\theta =\theta (k, m, r, \delta , \epsilon , \eta )>0$
with the following property.
$\theta =\theta (k, m, r, \delta , \epsilon , \eta )>0$
with the following property.
Let G be a finite group of exponent bounded by r, and let
![]() $A\subseteq G$
be subset of G of size
$A\subseteq G$
be subset of G of size
![]() $|A|\geq \delta |G|$
such that the collection
$|A|\geq \delta |G|$
such that the collection
![]() $\mathcal {H}_k(\mathrm {Cay}(G,A))$
of all half-graphs of height k induced by its Cayley graph on G has size
$\mathcal {H}_k(\mathrm {Cay}(G,A))$
of all half-graphs of height k induced by its Cayley graph on G has size
![]() $|\mathcal {H}_k(\mathrm {Cay}(G,A))|\le \theta |G|^{2k}$
. Then, there exists a subgroup H of G of index at most n such that
$|\mathcal {H}_k(\mathrm {Cay}(G,A))|\le \theta |G|^{2k}$
. Then, there exists a subgroup H of G of index at most n such that
where
![]() $\text {m-}\mathrm {AP}(A)_h= \{ a\in A : \ \{a,h\cdot a,\ldots ,h^{m-1}\cdot a\} \subseteq A\}$
.
$\text {m-}\mathrm {AP}(A)_h= \{ a\in A : \ \{a,h\cdot a,\ldots ,h^{m-1}\cdot a\} \subseteq A\}$
.
6 Grids and L-shapes
In the preceding section, we saw that almost sure stability was sufficient to imply the existence of squares in dense subsets of Cartesian products of arbitrary finite groups. In order to extend the previous results to other two-dimensional shapes, such as L-shapes or
![]() $3\times 2$
-grids, we will need to impose some (mild) conditions on the nature of the groups in question.
$3\times 2$
-grids, we will need to impose some (mild) conditions on the nature of the groups in question.
As mentioned in the introduction, in recent work [Reference Peluse34], Peluse obtained the first reasonable upper bound on the density of two-dimensional subsets of
![]() $\mathbb F_p^n$
without L-shaped configurations. We will show how to obtain a qualitative version of her result valid in finite abelian groups of odd order under the assumption of almost sure stability.
$\mathbb F_p^n$
without L-shaped configurations. We will show how to obtain a qualitative version of her result valid in finite abelian groups of odd order under the assumption of almost sure stability.
Given a subset X of G, every solution
![]() $(x, y, z)$
in
$(x, y, z)$
in
![]() $X^3$
to the equation
$X^3$
to the equation
with
![]() $x\ne y$
determines a generalized arithmetic progression of length
$x\ne y$
determines a generalized arithmetic progression of length
![]() $3$
in X. Indeed, if
$3$
in X. Indeed, if
![]() $x\cdot y=z^2$
with
$x\cdot y=z^2$
with
![]() $x\ne y$
, then
$x\ne y$
, then
![]() $g= x ^{-1}\cdot z= y\cdot z ^{-1}$
is nontrivial and satisfies that all three elements
$g= x ^{-1}\cdot z= y\cdot z ^{-1}$
is nontrivial and satisfies that all three elements
![]() $x, x\cdot g$
and
$x, x\cdot g$
and
![]() $g\cdot x\cdot g$
belong to X. If the group G is abelian, this is an arithmetic progression in the classical sense, for
$g\cdot x\cdot g$
belong to X. If the group G is abelian, this is an arithmetic progression in the classical sense, for
![]() $g\cdot x\cdot g=g^2\cdot x$
. In what follows, we denote by
$g\cdot x\cdot g=g^2\cdot x$
. In what follows, we denote by
![]() $\mathcal {E}(X)$
the set
$\mathcal {E}(X)$
the set
Definition 6.1 The non-standard finite group G is suitable for the equation
![]() $x\cdot y=z^2$
if the following conditions hold:
$x\cdot y=z^2$
if the following conditions hold:
-
(i) Squaring preserves dense elements (cf. [Reference Martin-Pizarro and Palacín28, Definition 3.12]), that is, for every element a and every countable set of parameters B, we have that a is dense over B if and only if the element
 $a^2$
is dense over B.
$a^2$
is dense over B. -
(ii) For every dense internal subset X of G, the internal set
 $\mathcal {E}(X)$
has positive density in
$\mathcal {E}(X)$
has positive density in
 $G^2$
.
$G^2$
.
While (i) implies (ii) in any non-standard finite group G (see [Reference Martin-Pizarro and Palacín28, Theorem 3.14]), for the sake of a self-contained presentation, we have decided to impose (ii) as an additional condition, since the examples we are most interested in already verify this condition by classical results in additive combinatorics, as the next remark shows.
Remark 6.1 Every non-standard finite group G obtained as a non-principal ultraproduct of a family
![]() $(G_\ell )_{\ell \in \mathbb {N}}$
of finite abelian groups of odd order is suitable for the equation
$(G_\ell )_{\ell \in \mathbb {N}}$
of finite abelian groups of odd order is suitable for the equation
![]() $x\cdot y=z^2$
. Indeed, in such a non-standard finite abelian group G as above, there are no involutions, so a is the only element in the fiber of
$x\cdot y=z^2$
. Indeed, in such a non-standard finite abelian group G as above, there are no involutions, so a is the only element in the fiber of
![]() $a^2$
with respect to the group homomorphism
$a^2$
with respect to the group homomorphism
![]() $x\mapsto x^2$
. Thus, density of elements is preserved by Fubini–Tonelli (Remark 2.6).
$x\mapsto x^2$
. Thus, density of elements is preserved by Fubini–Tonelli (Remark 2.6).
There is a plethora of explicit lower bounds for
![]() $\mathcal {E}(X)$
for finite abelian groups of odd order. For instance, Bloom and Sisask showed in [Reference Bloom and Sisask7, Theorem 2.1] that whenever a finite subset
$\mathcal {E}(X)$
for finite abelian groups of odd order. For instance, Bloom and Sisask showed in [Reference Bloom and Sisask7, Theorem 2.1] that whenever a finite subset
![]() $X_\ell $
of a finite abelian group
$X_\ell $
of a finite abelian group
![]() $G_\ell $
of odd order has density
$G_\ell $
of odd order has density
![]() $|X_\ell |/|G_\ell |\ge \sigma $
, then
$|X_\ell |/|G_\ell |\ge \sigma $
, then
![]() $|\mathcal {E}(X_\ell )|\ge f(\sigma ) |G_\ell |^2$
, with
$|\mathcal {E}(X_\ell )|\ge f(\sigma ) |G_\ell |^2$
, with
for some absolute constant
![]() $C>0$
.Footnote
4
It follows easily from Łoś’s Theorem that for every internal subset X of density
$C>0$
.Footnote
4
It follows easily from Łoś’s Theorem that for every internal subset X of density
![]() $\mu _G(X)\ge \sigma $
in the non-standard finite abelian group G,
$\mu _G(X)\ge \sigma $
in the non-standard finite abelian group G,
![]() $\mu _{G^2}(\mathcal {E}(X))\ge f(\sigma )>0$
, as desired.
$\mu _{G^2}(\mathcal {E}(X))\ge f(\sigma )>0$
, as desired.
Theorem 6.2 Consider a non-standard finite group G suitable for the equation
![]() $x\cdot y=z^2$
along with an internal relation S on
$x\cdot y=z^2$
along with an internal relation S on
![]() $G\times G$
defined over a countable rich subset M of G. If S is dense and almost surely k-stable for some
$G\times G$
defined over a countable rich subset M of G. If S is dense and almost surely k-stable for some
![]() $k\ge 1$
, then there is a tuple
$k\ge 1$
, then there is a tuple
![]() $(a, g, b)$
of
$(a, g, b)$
of
![]() $G^3$
in good position over M such that
$G^3$
in good position over M such that
![]() $(a, b, g)$
belongs to the internal set
$(a, b, g)$
belongs to the internal set
In particular, the set
![]() $\Lambda _{3\times 2}(S)$
has positive density in
$\Lambda _{3\times 2}(S)$
has positive density in
![]() $G^3$
, by Fact 3.12 and Definition 3.2(II).
$G^3$
, by Fact 3.12 and Definition 3.2(II).
Proof Set
![]() $\delta =\mu _{G^{2}}(S)/2>0$
. By Definition 3.2, there is an internal set
$\delta =\mu _{G^{2}}(S)/2>0$
. By Definition 3.2, there is an internal set
![]() $Y_\delta $
defined over M such that
$Y_\delta $
defined over M such that
where
![]() $S_y=\{x\in G : \ (x, y) \in S\}$
denotes the fiber of S over y. By Fubini–Tonelli (Remark 2.6), the internal set
$S_y=\{x\in G : \ (x, y) \in S\}$
denotes the fiber of S over y. By Fubini–Tonelli (Remark 2.6), the internal set
![]() $Y_\delta $
is dense. Hence, choose some c in G dense over M with
$Y_\delta $
is dense. Hence, choose some c in G dense over M with
![]() $\mu _G(S_{c})\ge \delta $
. By Remark 3.6, there is a countable rich subset N containing
$\mu _G(S_{c})\ge \delta $
. By Remark 3.6, there is a countable rich subset N containing
![]() $M\cup \{c\}$
. Notice that the internal dense subset
$M\cup \{c\}$
. Notice that the internal dense subset
![]() $S_{c}\subseteq G$
is defined over N.
$S_{c}\subseteq G$
is defined over N.
Claim There exists a tuple
![]() $(a_1, a_2, a_3)$
in
$(a_1, a_2, a_3)$
in
![]() $S_c^3$
such that
$S_c^3$
such that
-
(i)
 $a_1\cdot a_2=a_3^2$
;
$a_1\cdot a_2=a_3^2$
; -
(ii) the difference
 $g=a_1 ^{-1} \cdot a_3=a_2\cdot a_3 ^{-1}$
is dense over N and belongs to
$g=a_1 ^{-1} \cdot a_3=a_2\cdot a_3 ^{-1}$
is dense over N and belongs to
 $G_{N}^{00}$
;
$G_{N}^{00}$
; -
(iii) the pair
 $(a_1, g)$
is in good position over N.
$(a_1, g)$
is in good position over N.
Proof of Claim
It suffices to find a triple satisfying (i) and (ii) in the statement of the claim with
![]() $(a_1,a_3)$
in good position over N, or equivalently, with
$(a_1,a_3)$
in good position over N, or equivalently, with
![]() $(a_1,a_2)$
in good position over N, since squaring preserves dense elements.
$(a_1,a_2)$
in good position over N, since squaring preserves dense elements.
Write
![]() $G_{N}^{00}$
as a countable intersection of internal generic symmetric neighborhoods
$G_{N}^{00}$
as a countable intersection of internal generic symmetric neighborhoods
![]() $Z_j$
, with j in
$Z_j$
, with j in
![]() $\mathbb {N}$
, defined over N as in Fact 5.1(a). In particular, for each
$\mathbb {N}$
, defined over N as in Fact 5.1(a). In particular, for each
![]() $Z_j$
, there are finitely many elements
$Z_j$
, there are finitely many elements
![]() $t_1(j),\ldots , t_{n_j}(j)$
in G such that
$t_1(j),\ldots , t_{n_j}(j)$
in G such that
Note that we may find such elements
![]() $t_r(j)$
in N, since N is a rich subset of G. Moreover, the product set
$t_r(j)$
in N, since N is a rich subset of G. Moreover, the product set
![]() $Z_{j+1}\cdot Z_{j+1}$
is a subset of
$Z_{j+1}\cdot Z_{j+1}$
is a subset of
![]() $Z_j$
. Assume toward a contradiction that there is no triple as required, and consider the
$Z_j$
. Assume toward a contradiction that there is no triple as required, and consider the
![]() $\omega $
-internal set
$\omega $
-internal set
 $$\begin{align*}\mathcal Z= \bigcap\limits_{\substack{j\in \mathbb{N} \\ \mathcal X \in \mathcal F}} \left\{ (x,y,z) \in S_c^{3} : \ x\cdot y= z^2 \text{ with} x ^{-1} \cdot z=y\cdot z ^{-1} in Z_j \text{ and } (x,y) \notin \mathcal X \right\}, \end{align*}$$
$$\begin{align*}\mathcal Z= \bigcap\limits_{\substack{j\in \mathbb{N} \\ \mathcal X \in \mathcal F}} \left\{ (x,y,z) \in S_c^{3} : \ x\cdot y= z^2 \text{ with} x ^{-1} \cdot z=y\cdot z ^{-1} in Z_j \text{ and } (x,y) \notin \mathcal X \right\}, \end{align*}$$
where
![]() $\mathcal F$
is the countable collection of all internal subsets
$\mathcal F$
is the countable collection of all internal subsets
![]() $\mathcal X$
of
$\mathcal X$
of
![]() $G^2$
defined over N of density
$G^2$
defined over N of density
![]() $0$
. Notice that the projection
$0$
. Notice that the projection
![]() $\pi $
of
$\pi $
of
![]() $\mathcal Z$
onto the first two coordinates is again
$\mathcal Z$
onto the first two coordinates is again
![]() $\omega $
-internal by Remark 3.1 and empty, for otherwise, it would contain a pair
$\omega $
-internal by Remark 3.1 and empty, for otherwise, it would contain a pair
![]() $(a_1,a_2)$
in good position over N, by Fact 3.12, but such a pair would yield a triple as in the statement. Therefore, the
$(a_1,a_2)$
in good position over N, by Fact 3.12, but such a pair would yield a triple as in the statement. Therefore, the
![]() $\omega $
-internal set
$\omega $
-internal set
![]() $\mathcal Z$
must be empty as well, since
$\mathcal Z$
must be empty as well, since
![]() $\pi (\mathcal Z)=\emptyset $
. By Fact 2.2, there are finitely many sets
$\pi (\mathcal Z)=\emptyset $
. By Fact 2.2, there are finitely many sets
![]() $\mathcal X_1, \ldots , \mathcal X_r$
in
$\mathcal X_1, \ldots , \mathcal X_r$
in
![]() $\mathcal F$
and some j in
$\mathcal F$
and some j in
![]() $\mathbb {N}$
such that the internal set
$\mathbb {N}$
such that the internal set
is covered by
![]() $\bigcup _{i=1}^r \pi ^{-1}(\mathcal X_i)$
. Now, the internal set
$\bigcup _{i=1}^r \pi ^{-1}(\mathcal X_i)$
. Now, the internal set
![]() $S_c$
is dense, so there is some
$S_c$
is dense, so there is some
![]() $t_r(j+1)$
in N such that
$t_r(j+1)$
in N such that
![]() $S_c\cap (Z_{j+1}\cdot t_r(j+1))$
is dense as well. It follows from the suitability of G that the corresponding set
$S_c\cap (Z_{j+1}\cdot t_r(j+1))$
is dense as well. It follows from the suitability of G that the corresponding set
![]() $\mathcal {E}(S_c\cap (Z_{j+1}\cdot t_r(j+1))$
must have positive density. Hence, there is a dense pair
$\mathcal {E}(S_c\cap (Z_{j+1}\cdot t_r(j+1))$
must have positive density. Hence, there is a dense pair
![]() $(u_1,u_2)$
over N with each
$(u_1,u_2)$
over N with each
![]() $u_i$
in
$u_i$
in
![]() $S_c\cap (Z_{j+1}\cdot t_r(j+1))$
such that
$S_c\cap (Z_{j+1}\cdot t_r(j+1))$
such that
Now, the pair
![]() $(u_1,u_2)$
avoids all
$(u_1,u_2)$
avoids all
![]() $\mathcal X_i$
and the common difference
$\mathcal X_i$
and the common difference
 $$\begin{align*}u_1 ^{-1}\cdot u_3 &= u_2\cdot u_3 ^{-1}=u_2\cdot (t_r(j+1) ^{-1} \cdot t_r(j+1) ) \cdot u_3 ^{-1}\\ & =( u_2\cdot t_r(j+1) ^{-1} ) \cdot (u_3\cdot t_r(j+1) ^{-1}) ^{-1} \end{align*}$$
$$\begin{align*}u_1 ^{-1}\cdot u_3 &= u_2\cdot u_3 ^{-1}=u_2\cdot (t_r(j+1) ^{-1} \cdot t_r(j+1) ) \cdot u_3 ^{-1}\\ & =( u_2\cdot t_r(j+1) ^{-1} ) \cdot (u_3\cdot t_r(j+1) ^{-1}) ^{-1} \end{align*}$$
belongs to
![]() $Z_{j+1}\cdot Z_{j+1}\subseteq Z_j$
. Thus, the triple
$Z_{j+1}\cdot Z_{j+1}\subseteq Z_j$
. Thus, the triple
![]() $(u_1,u_2, u_3)$
belongs to
$(u_1,u_2, u_3)$
belongs to
![]() $\widetilde {\mathcal Z}$
and thus to some
$\widetilde {\mathcal Z}$
and thus to some
![]() $\pi ^{-1}(\mathcal X_j)$
. This implies that the dense pair
$\pi ^{-1}(\mathcal X_j)$
. This implies that the dense pair
![]() $(u_1,u_2)$
over N belongs to the internal set
$(u_1,u_2)$
over N belongs to the internal set
![]() $\mathcal X_j$
defined over N of density
$\mathcal X_j$
defined over N of density
![]() $0$
, which yields the desired contradiction.
$0$
, which yields the desired contradiction.
Choose now a tuple
![]() $(a_1,a_2,a_3)$
in
$(a_1,a_2,a_3)$
in
![]() $S_c^{3}$
as in the Claim with
$S_c^{3}$
as in the Claim with
![]() $a_1\cdot a_2 = a_3^2$
, where
$a_1\cdot a_2 = a_3^2$
, where
![]() $g=a_1 ^{-1} \cdot a_3=a_2\cdot a_3 ^{-1}$
lies in
$g=a_1 ^{-1} \cdot a_3=a_2\cdot a_3 ^{-1}$
lies in
![]() $G_{N}^{00}$
and
$G_{N}^{00}$
and
![]() $(a_1,g)$
in good position over N. By Fact 5.1(d), we have that g, viewed as an element of
$(a_1,g)$
in good position over N. By Fact 5.1(d), we have that g, viewed as an element of
![]() $G_{M}^{00}$
, is dense over M. Fact 5.1(c) yields that for some b in
$G_{M}^{00}$
, is dense over M. Fact 5.1(c) yields that for some b in
![]() $\operatorname {tp}(c/M)$
dense over
$\operatorname {tp}(c/M)$
dense over
![]() $M\cup \{a_1, a_2,a_3\}$
, the product
$M\cup \{a_1, a_2,a_3\}$
, the product
![]() $b\cdot g$
also belongs to
$b\cdot g$
also belongs to
![]() $\operatorname {tp}(c/M)$
(and is dense over
$\operatorname {tp}(c/M)$
(and is dense over
![]() $M\cup \{a_1, a_2, a_3\}$
). Hence, the triple
$M\cup \{a_1, a_2, a_3\}$
). Hence, the triple
![]() $(a_1,g, b)$
is in good position over M. We need only verify that
$(a_1,g, b)$
is in good position over M. We need only verify that
![]() $(a_1, b, g)$
belongs to
$(a_1, b, g)$
belongs to
![]() $\Lambda _{3\times 2}(S)$
.
$\Lambda _{3\times 2}(S)$
.
By construction, the points
all lie in the almost surely k-stable internal relation S. As each pair (with the order of coordinates reversed) is in good position over M, Theorem 4.7 implies that for each
![]() $i=1,2,3$
,
$i=1,2,3$
,
so the pairs
all lie in the almost surely k-stable internal relation S. Analogously, using now that the element
![]() $b\cdot g$
of
$b\cdot g$
of
![]() $\operatorname {tp}(b/M)$
is also dense over
$\operatorname {tp}(b/M)$
is also dense over
![]() $M\cup \{a_1, a_1\cdot g, g\cdot a_1\cdot g\}$
, we conclude again by Theorem 4.7 that each of the pairs
$M\cup \{a_1, a_1\cdot g, g\cdot a_1\cdot g\}$
, we conclude again by Theorem 4.7 that each of the pairs
lies in the almost surely k-stable internal relation S, as desired.
Remark 6.1 immediately yields the following result.
Corollary 6.3 If the non-standard finite group G is obtained as an ultraproduct of finite abelian groups of odd order, then for every almost surely k-stable dense internal relation S of
![]() $G\times G$
, the collection of
$G\times G$
, the collection of
![]() $3\times 2$
grids
$3\times 2$
grids
has positive density in
![]() $G^3$
.
$G^3$
.
In particular, every dense almost surely k-stable subset Z of G (see Definition 4.1) contains a
![]() $4$
-term arithmetic progression
$4$
-term arithmetic progression
![]() $\{z, z+d, z+2d, z+3d\}$
given by a dense pair
$\{z, z+d, z+2d, z+3d\}$
given by a dense pair
![]() $(z, d)$
(with
$(z, d)$
(with
![]() $d\ne 0$
).
$d\ne 0$
).
Just like Theorem 5.2 gives rise to the finitary Corollary 5.6, Theorem 6.2 yields a finitary version for sufficiently large abelian groups of odd order.
Corollary 6.4 Given an integer
![]() $k\ge 1$
and a real number
$k\ge 1$
and a real number
![]() $\delta>0$
, there is an integer
$\delta>0$
, there is an integer
![]() $\ell _0(k, \delta )\ge 1$
and real numbers
$\ell _0(k, \delta )\ge 1$
and real numbers
![]() $\theta =\theta (k, \delta )>0$
and
$\theta =\theta (k, \delta )>0$
and
![]() $\epsilon =\epsilon (k, \delta )>0$
with the following property.
$\epsilon =\epsilon (k, \delta )>0$
with the following property.
Let G be a finite abelian group of odd order with
![]() $|G|\ge \ell _0$
, and consider a relation
$|G|\ge \ell _0$
, and consider a relation
![]() $S\subseteq G\times G$
of size
$S\subseteq G\times G$
of size
![]() $|S|\ge \delta |G|^{2}$
such that the collection
$|S|\ge \delta |G|^{2}$
such that the collection
![]() $\mathcal {H}_k(S)$
of all half-graphs of height k induced by S on G has size
$\mathcal {H}_k(S)$
of all half-graphs of height k induced by S on G has size
![]() $|\mathcal {H}_k(S)|\le \theta |G|^{2k}$
. Then, the set
$|\mathcal {H}_k(S)|\le \theta |G|^{2k}$
. Then, the set
has size
![]() $|\Lambda _{3\times 2}(S)| \ge \epsilon |G|^{3}$
. In particular, the relation S contains an L-shape.
$|\Lambda _{3\times 2}(S)| \ge \epsilon |G|^{3}$
. In particular, the relation S contains an L-shape.
Remark 6.5 The astute reader will have noticed that we used very little about the particular equation
![]() $x\cdot y=z^2$
in Theorem 6.2. Indeed, if the non-standard finite group G is built as an ultraproduct of finite groups
$x\cdot y=z^2$
in Theorem 6.2. Indeed, if the non-standard finite group G is built as an ultraproduct of finite groups
![]() $(G_\ell )_{\ell \in \mathbb {N}}$
such that for every finite subset
$(G_\ell )_{\ell \in \mathbb {N}}$
such that for every finite subset
![]() $X_\ell $
of
$X_\ell $
of
![]() $G_\ell $
of density
$G_\ell $
of density
![]() $\sigma $
, the collection of tuples
$\sigma $
, the collection of tuples
![]() $(a_1,\ldots , a_{m+1})$
in
$(a_1,\ldots , a_{m+1})$
in
![]() $X_\ell ^{m+1}$
satisfying a certain pattern has size at least
$X_\ell ^{m+1}$
satisfying a certain pattern has size at least
![]() $f(\sigma )|G_\ell ^m|$
for some function
$f(\sigma )|G_\ell ^m|$
for some function
![]() $f:\mathbb R\to \mathbb R$
which is uniform in the family
$f:\mathbb R\to \mathbb R$
which is uniform in the family
![]() $(G_\ell )_{\ell \in \mathbb {N}}$
, then we could reproduce the proof of Theorem 6.2 verbatim to obtain grids using differences
$(G_\ell )_{\ell \in \mathbb {N}}$
, then we could reproduce the proof of Theorem 6.2 verbatim to obtain grids using differences
![]() $g=a_i-a_j$
for any suitable choice of coordinates.
$g=a_i-a_j$
for any suitable choice of coordinates.
This applies in particular to the pattern given by the equation
![]() $n_1x_1+\cdots +n_mx_m=k z$
with
$n_1x_1+\cdots +n_mx_m=k z$
with
![]() $k=\sum _{j=1}^m n_j$
in
$k=\sum _{j=1}^m n_j$
in
![]() $\mathbb Z/p\mathbb Z$
, asymptotically as p is large (see, for instance, [Reference Kościuszko26, Theorem 3]).
$\mathbb Z/p\mathbb Z$
, asymptotically as p is large (see, for instance, [Reference Kościuszko26, Theorem 3]).
Acknowledgements
The authors are grateful to the anonymous referee for helpful comments and corrections.