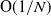1. Introduction
We focus on approximating the stationary distribution for a finite Wright–Fisher Markov chain with parent-independent mutation, where the population has fixed size N and a fixed number of allele types K. We represent this model as a discrete-time Markov chain (DTMC)
![]() $\{{\boldsymbol{U}}(t) \,:\,t \in \mathbb{Z}_+\}$
taking values in
$\{{\boldsymbol{U}}(t) \,:\,t \in \mathbb{Z}_+\}$
taking values in
 \begin{align*}\nabla^{K} = \left\{{\boldsymbol{u}} \in \delta \mathbb{Z}^{K-1} \,:\,u_i \geq 0, \sum_{i=1}^{K-1}u_i \leq 1\right\},\end{align*}
\begin{align*}\nabla^{K} = \left\{{\boldsymbol{u}} \in \delta \mathbb{Z}^{K-1} \,:\,u_i \geq 0, \sum_{i=1}^{K-1}u_i \leq 1\right\},\end{align*}
where
![]() $\delta = 1/N$
is a scaling parameter,
$\delta = 1/N$
is a scaling parameter,
![]() $U_i(t)$
denotes the fraction of genes that are of type
$U_i(t)$
denotes the fraction of genes that are of type
![]() $1 \leq i \leq K-1$
, and
$1 \leq i \leq K-1$
, and
![]() $1 -\sum_{i=1}^{K-1}U_i(t)$
is the fraction of genes of type K. For any
$1 -\sum_{i=1}^{K-1}U_i(t)$
is the fraction of genes of type K. For any
![]() ${\boldsymbol{u}}, {\boldsymbol{y}} \in \nabla^{K}$
and probabilities
${\boldsymbol{u}}, {\boldsymbol{y}} \in \nabla^{K}$
and probabilities
![]() $p_1,\ldots, p_K$
such that
$p_1,\ldots, p_K$
such that
![]() $\sum_{i=1}^K p_i \leq 1$
, the transition probabilities
$\sum_{i=1}^K p_i \leq 1$
, the transition probabilities
![]() $P_{{\boldsymbol{u}}}({\boldsymbol{y}}) = \mathbb{P}(U(1) ={\boldsymbol{y}} | U(0) = {\boldsymbol{u}})$
of this process satisfy
$P_{{\boldsymbol{u}}}({\boldsymbol{y}}) = \mathbb{P}(U(1) ={\boldsymbol{y}} | U(0) = {\boldsymbol{u}})$
of this process satisfy
 \begin{align}P_{{\boldsymbol{u}}}({\boldsymbol{y}}) =&\ \left(\begin{array}{cc}N\\ N y_1, \ldots, N y_{K-1}\end{array}\right)\prod_{j=1}^{K-1} \Big( u_{j} \big(1 - \sum_{i=1}^{K} p_{i}\big) + p_{j} \Big)^{N y_j}.\end{align}
\begin{align}P_{{\boldsymbol{u}}}({\boldsymbol{y}}) =&\ \left(\begin{array}{cc}N\\ N y_1, \ldots, N y_{K-1}\end{array}\right)\prod_{j=1}^{K-1} \Big( u_{j} \big(1 - \sum_{i=1}^{K} p_{i}\big) + p_{j} \Big)^{N y_j}.\end{align}
Our DTMC is irreducible, aperiodic, and positive recurrent because its state space is finite, and we let
![]() ${\boldsymbol{U}}$
denote the vector having the unique stationary distribution.
${\boldsymbol{U}}$
denote the vector having the unique stationary distribution.
As it will be useful later, we informally give a common interpretation of the model and how it models changes in allele types over time. In each generation of fixed size N, given the parent generation, each individual in the offspring population independently chooses a parent, uniformly at random. In addition to this random genealogy structure, a random mutation structure is added such that each individual offspring independently has a probability of mutating to type i with probability
![]() $p_i$
. Otherwise, with probability
$p_i$
. Otherwise, with probability
![]() $1 - \sum_{i=1}^K p_i$
, the offspring does not mutate and takes on the type of their parent. Note that in this structure each child could mutate to the same type as their respective parent.
$1 - \sum_{i=1}^K p_i$
, the offspring does not mutate and takes on the type of their parent. Note that in this structure each child could mutate to the same type as their respective parent.
The Wright–Fisher DTMC, while easy to formulate, is known to be relatively intractable, and hence, the limiting diffusion process as
![]() $N \to \infty$
is of particular interest. The limiting diffusion in this case is the well known Wright–Fisher diffusion, defined later in (1.8). Using the tools of [Reference Stroock and Varadhan21], one can show that the Markov chain converges weakly to the diffusion process. Rates of convergence to the diffusion have been studied as well. In [Reference Ethier and Norman11] the authors obtained an explicit bound of order
$N \to \infty$
is of particular interest. The limiting diffusion in this case is the well known Wright–Fisher diffusion, defined later in (1.8). Using the tools of [Reference Stroock and Varadhan21], one can show that the Markov chain converges weakly to the diffusion process. Rates of convergence to the diffusion have been studied as well. In [Reference Ethier and Norman11] the authors obtained an explicit bound of order
![]() $\mathrm{O} (1/N)$
when
$\mathrm{O} (1/N)$
when
![]() $K = 2$
, but required bounded sixth derivatives on test functions. A similar result can be found in the more recent work of [Reference Kasprzak16], where the author builds on the approach for Gaussian process approximation via Stein’s method in [1] to establish a rate of convergence for the Moran model (a continuous-time cousin of the Wright–Fisher DTMC) to the limiting Wright–Fisher diffusion. The result in [Reference Kasprzak16] is for the transient distribution of the Moran model and, like [Reference Ethier and Norman11], requires
$K = 2$
, but required bounded sixth derivatives on test functions. A similar result can be found in the more recent work of [Reference Kasprzak16], where the author builds on the approach for Gaussian process approximation via Stein’s method in [1] to establish a rate of convergence for the Moran model (a continuous-time cousin of the Wright–Fisher DTMC) to the limiting Wright–Fisher diffusion. The result in [Reference Kasprzak16] is for the transient distribution of the Moran model and, like [Reference Ethier and Norman11], requires
![]() $K = 2$
. The rate of convergence obtained there is of order
$K = 2$
. The rate of convergence obtained there is of order
![]() $\mathrm{O}(1/N^{1/4})$
.
$\mathrm{O}(1/N^{1/4})$
.
In [Reference Gan, Röllin and Ross13] bounds for quantities of the form
![]() $\vert\mathbb{E}h({\boldsymbol{U}}) - \mathbb{E} h({\boldsymbol{Z}})\vert$
are derived, where
$\vert\mathbb{E}h({\boldsymbol{U}}) - \mathbb{E} h({\boldsymbol{Z}})\vert$
are derived, where
![]() ${\boldsymbol{Z}}$
is an appropriately chosen Dirichlet random variable, and h is any general test function with two bounded derivatives and a bounded Lipschitz constant on the second derivative. Under the typical assumption for these models that the mutation probabilities are rare, in the sense that
${\boldsymbol{Z}}$
is an appropriately chosen Dirichlet random variable, and h is any general test function with two bounded derivatives and a bounded Lipschitz constant on the second derivative. Under the typical assumption for these models that the mutation probabilities are rare, in the sense that
![]() $p_i = \mathrm{O}(1/N)$
, [Reference Gan, Röllin and Ross13] establish an upper bound on
$p_i = \mathrm{O}(1/N)$
, [Reference Gan, Röllin and Ross13] establish an upper bound on
![]() $\vert\mathbb{E} h({\boldsymbol{U}}) - \mathbb{E}h({\boldsymbol{Z}})\vert$
that is of order
$\vert\mathbb{E} h({\boldsymbol{U}}) - \mathbb{E}h({\boldsymbol{Z}})\vert$
that is of order
![]() $\mathrm{O}(1 /\sqrt N)$
. It has been anecdotally conjectured to the authors that this bound may not be of the optimal order, and that the correct order may be of order
$\mathrm{O}(1 /\sqrt N)$
. It has been anecdotally conjectured to the authors that this bound may not be of the optimal order, and that the correct order may be of order
![]() $\mathrm{O}(1/N)$
, as suggested, for example, by the results of [Reference Ethier and Norman11]. In this paper we derive a bound of order
$\mathrm{O}(1/N)$
, as suggested, for example, by the results of [Reference Ethier and Norman11]. In this paper we derive a bound of order
![]() $\mathrm{O} (1/N)$
for approximating the stationary distribution assuming four bounded derivatives. Before we present the main result, we first define the Dirichlet distribution and our approximating metric.
$\mathrm{O} (1/N)$
for approximating the stationary distribution assuming four bounded derivatives. Before we present the main result, we first define the Dirichlet distribution and our approximating metric.
Let
![]() $\bar \nabla^{K} = \{{\boldsymbol{u}} \in \mathbb{R}^{K-1} \,:\,x \geq 0,\sum_{i=1}^{K-1}x_i \leq 1\}$
. We define the Dirichlet distribution with parameters
$\bar \nabla^{K} = \{{\boldsymbol{u}} \in \mathbb{R}^{K-1} \,:\,x \geq 0,\sum_{i=1}^{K-1}x_i \leq 1\}$
. We define the Dirichlet distribution with parameters
![]() $\boldsymbol\beta = (\beta_1, \ldots, \beta_K)$
, where
$\boldsymbol\beta = (\beta_1, \ldots, \beta_K)$
, where
![]() $\beta_1 > 0,\ldots, \beta_K > 0$
, to be supported on the
$\beta_1 > 0,\ldots, \beta_K > 0$
, to be supported on the
![]() $(K-1)$
-dimensional open simplex
$(K-1)$
-dimensional open simplex
 \begin{align*}\text{int$(\bar \nabla^{K})$} = \left\{ {\boldsymbol{x}} = (x_1, \ldots, x_{K-1})\,:\,x_1 > 0, \ldots, x_{K-1} > 0, \sum_{i=1}^{K-1}x_i < 1 \right\} \subset \mathbb{R}^{K-1}.\end{align*}
\begin{align*}\text{int$(\bar \nabla^{K})$} = \left\{ {\boldsymbol{x}} = (x_1, \ldots, x_{K-1})\,:\,x_1 > 0, \ldots, x_{K-1} > 0, \sum_{i=1}^{K-1}x_i < 1 \right\} \subset \mathbb{R}^{K-1}.\end{align*}
The Dirichlet distribution has density
 \begin{align}\psi_\beta(x_1, \ldots x_{K-1}) = \frac{ \Gamma(s)}{\prod_{i=1}^K \Gamma(\beta_i)} \prod_{i=1}^K x_i^{\beta_i - 1}, \quad {\boldsymbol{x}} \in \text{int$(\bar \nabla^{K})$},\end{align}
\begin{align}\psi_\beta(x_1, \ldots x_{K-1}) = \frac{ \Gamma(s)}{\prod_{i=1}^K \Gamma(\beta_i)} \prod_{i=1}^K x_i^{\beta_i - 1}, \quad {\boldsymbol{x}} \in \text{int$(\bar \nabla^{K})$},\end{align}
where
![]() $s = \sum_{i=1}^K \beta_i$
, and we set
$s = \sum_{i=1}^K \beta_i$
, and we set
![]() $x_K = 1 - \sum_{i=1}^{K-1}x_i$
. We assume that our mutation probabilities
$x_K = 1 - \sum_{i=1}^{K-1}x_i$
. We assume that our mutation probabilities
![]() $p_{i}$
satisfy
$p_{i}$
satisfy
for some fixed
![]() $\boldsymbol\beta$
and all
$\boldsymbol\beta$
and all
![]() $N > 0$
.
$N > 0$
.
The metric we will be using is the Lipschitz type metric defined as follows. For any vector
![]() ${\boldsymbol{a}} \in \mathbb{Z}^{K-1}$
consisting of nonnegative integer values and a function
${\boldsymbol{a}} \in \mathbb{Z}^{K-1}$
consisting of nonnegative integer values and a function
![]() $f\,:\,\mathbb{R}^{K-1} \to\mathbb{R}$
, let
$f\,:\,\mathbb{R}^{K-1} \to\mathbb{R}$
, let
and define
Then for any random vectors
![]() ${\boldsymbol{V}},{\boldsymbol{V}}' \in \mathbb{R}^{K-1}$
, set
${\boldsymbol{V}},{\boldsymbol{V}}' \in \mathbb{R}^{K-1}$
, set
Lemma 2.2 of [Reference Mackey and Gorham18] proves that
![]() $\mathcal{M}_{3}$
is a convergence-determining class; i.e.
$\mathcal{M}_{3}$
is a convergence-determining class; i.e.
![]() $d_{\mathcal{M}_{3}}({\boldsymbol{V}},{\boldsymbol{V}}') \to 0$
implies that
$d_{\mathcal{M}_{3}}({\boldsymbol{V}},{\boldsymbol{V}}') \to 0$
implies that
![]() ${\boldsymbol{V}}$
and
${\boldsymbol{V}}$
and
![]() ${\boldsymbol{V}}'$
converge in distribution. Their result can be readily extended to show that
${\boldsymbol{V}}'$
converge in distribution. Their result can be readily extended to show that
![]() $\mathcal{M}_{4}$
, the class of functions used in this paper, is also convergence determining.
$\mathcal{M}_{4}$
, the class of functions used in this paper, is also convergence determining.
Theorem 1.1. Let
![]() ${\boldsymbol{U}}$
denote the random vector with stationary distribution for the transition function (1.1), assume that the mutation probabilities satisfy (1.3) for some
${\boldsymbol{U}}$
denote the random vector with stationary distribution for the transition function (1.1), assume that the mutation probabilities satisfy (1.3) for some
![]() $\boldsymbol\beta>0$
, set
$\boldsymbol\beta>0$
, set
![]() $s = \sum_{i=1}^K \beta_i$
, and let
$s = \sum_{i=1}^K \beta_i$
, and let
![]() ${\boldsymbol{Z}}$
be a Dirichlet random variable with parameter vector
${\boldsymbol{Z}}$
be a Dirichlet random variable with parameter vector
![]() $\boldsymbol\beta$
. Then for all N such that
$\boldsymbol\beta$
. Then for all N such that
![]() $s/2N < 1$
and
$s/2N < 1$
and
![]() $N > 100K^2$
,
$N > 100K^2$
,
 \begin{align*}d_{\mathcal{M}_{4}}({\boldsymbol{U}} ,{\boldsymbol{Z}}) \leq\ &C(K) \Bigg[ \frac{1}{N^4} + \frac{2K^2(1+s)^2 + 20 K^3 1595^K(1+s)^3+ 2K^4 1595^K (1+s)^4}{Ns}\\&\hskip8mm+ \frac{1}{ N^{ \beta_K/2 -3}} \frac{K^3 (10K)^{\beta_K}(4 + 6s) \Gamma(s)}{s\Gamma(s - \beta_K)\Gamma(\beta_K)\beta_K}\Big( 1 + \frac{1}{(1-1/\sqrt{N})^{\vert s-\beta_{K} -1\vert}} \Big)\\&\hskip8mm+ \frac{16\cdot 1595^K K^5(4K+1)2^{4K} N^{8K-5}}{s(s-\beta_K)^{4K}} \Big( 1- \frac{10K(\sqrt{N}-1)(1-s/2N)}{N}\Big)^{N}\Bigg]\\&+ C(K)^2 \Bigg[ \frac{Ks + 6K^2(1+s^2)}{N^2s} + \frac{K}{N^3}\Bigg],\end{align*}
\begin{align*}d_{\mathcal{M}_{4}}({\boldsymbol{U}} ,{\boldsymbol{Z}}) \leq\ &C(K) \Bigg[ \frac{1}{N^4} + \frac{2K^2(1+s)^2 + 20 K^3 1595^K(1+s)^3+ 2K^4 1595^K (1+s)^4}{Ns}\\&\hskip8mm+ \frac{1}{ N^{ \beta_K/2 -3}} \frac{K^3 (10K)^{\beta_K}(4 + 6s) \Gamma(s)}{s\Gamma(s - \beta_K)\Gamma(\beta_K)\beta_K}\Big( 1 + \frac{1}{(1-1/\sqrt{N})^{\vert s-\beta_{K} -1\vert}} \Big)\\&\hskip8mm+ \frac{16\cdot 1595^K K^5(4K+1)2^{4K} N^{8K-5}}{s(s-\beta_K)^{4K}} \Big( 1- \frac{10K(\sqrt{N}-1)(1-s/2N)}{N}\Big)^{N}\Bigg]\\&+ C(K)^2 \Bigg[ \frac{Ks + 6K^2(1+s^2)}{N^2s} + \frac{K}{N^3}\Bigg],\end{align*}
where
![]() $C(K) \leq (K^4 + 7975^K) (4 \times 12^K + K\cdot 11404^{5} 1595^K +1)$
and
$C(K) \leq (K^4 + 7975^K) (4 \times 12^K + K\cdot 11404^{5} 1595^K +1)$
and
![]() $\Gamma(x) =\int_{0}^{\infty} t^{x-1} \textrm{e}^{-t} dt$
.
$\Gamma(x) =\int_{0}^{\infty} t^{x-1} \textrm{e}^{-t} dt$
.
We make two remarks. First, most of the terms are
![]() $\mathrm{O}(1/N)$
except for the one involving
$\mathrm{O}(1/N)$
except for the one involving
![]() $N^{ 3 -\beta_K/2 }$
. The latter is also
$N^{ 3 -\beta_K/2 }$
. The latter is also
![]() $\mathrm{O}(1/N)$
when
$\mathrm{O}(1/N)$
when
![]() $\beta_{K} \geq 8$
(without loss of generality, we can assume that
$\beta_{K} \geq 8$
(without loss of generality, we can assume that
![]() $\beta_{K}$
is the largest of all the betas). We believe it to be an artifact of our methodology and expect that it can be removed, although at considerable effort. Second, the constants of the form
$\beta_{K}$
is the largest of all the betas). We believe it to be an artifact of our methodology and expect that it can be removed, although at considerable effort. Second, the constants of the form
![]() $C^{K}$
(such as
$C^{K}$
(such as
![]() $1595^K$
, not to be confused with C(K)) are again a result of our prelimit generator approach and are not a fundamental part of the Wright–Fisher diffusion approximation error. Though tracking error terms more carefully would result in a modest decrease of the value of C in
$1595^K$
, not to be confused with C(K)) are again a result of our prelimit generator approach and are not a fundamental part of the Wright–Fisher diffusion approximation error. Though tracking error terms more carefully would result in a modest decrease of the value of C in
![]() $C^{K}$
, the presence of these terms is an inevitable side effect of our prelimit approach. We expand on both remarks at the end of this section after introducing the prelimit approach.
$C^{K}$
, the presence of these terms is an inevitable side effect of our prelimit approach. We expand on both remarks at the end of this section after introducing the prelimit approach.
The primary tool used in this paper to prove the main results is Stein’s method. Stein’s method is a powerful tool in probability theory that is used to derive an explicit bound for the difference between two probability distributions. Typically, one aims to use it to find an upper bound on the errors incurred when approximating an intractable target distribution with a commonly used simple reference distribution. It was first developed for the normal distribution in [Reference Stein20] to bound the approximation errors when applying the central limit theorem, and it has since been developed for numerous distributions, such as Poisson [Reference Barbour, Holst and Janson4, Reference Chen9], beta [Reference Döbler10, Reference Goldstein and Reinert15], Dirichlet [Reference Gan, Röllin and Ross13], Poisson-Dirichlet [Reference Gan and Ross14], negative binomial [Reference Brown and Phillips7], exponential [Reference Fulman and Ross12] to just name a few. For many more examples and applications, see, for example, the surveys or monographs [Reference Barbour and Chen3, Reference Chatterjee8, Reference Ley, Reinert and Swan17, Reference Ross19]. In the following we give a brief introduction to Stein’s method.
To successfully apply Stein’s method, one of the main approaches is what is known as the generator method, first pioneered in [Reference Barbour2]. Below we give a brief description of Stein’s method in general, with a particular focus on the generator method, and details of our approach. In this brief description we discuss the univariate case, but note that the multivariate case is analogous. Our goal is to bound the difference between the typically unknown or intractable law of our target random variable X with the law of a well understood and simple reference random variable Z. Stein’s method can usually be summarised in the following three main steps.
-
1. Identify a characterising operator
 $\mathcal{G}_Z$
or identity that is satisfied only by the distribution of the reference random variable Z. In the generator method, the characterising operator is a generator of a Markov chain or diffusion process, and the reference distribution is the associated stationary distribution. The generator characterises its associated stationary distribution through the identity that
$\mathcal{G}_Z$
or identity that is satisfied only by the distribution of the reference random variable Z. In the generator method, the characterising operator is a generator of a Markov chain or diffusion process, and the reference distribution is the associated stationary distribution. The generator characterises its associated stationary distribution through the identity that
 $\mathbb{E}\mathcal{G}_Zf(Z) = 0$
for all suitable functions f if and only if Z follows the stationary distribution.
$\mathbb{E}\mathcal{G}_Zf(Z) = 0$
for all suitable functions f if and only if Z follows the stationary distribution. -
2. For any arbitrary function h, solve for the function
 $f_h$
that satisfies (1.6)Then by setting
$f_h$
that satisfies (1.6)Then by setting \begin{align}\mathcal{G}_Z f_h(x) = h(x) - \mathbb{E} h(Z).\end{align}
\begin{align}\mathcal{G}_Z f_h(x) = h(x) - \mathbb{E} h(Z).\end{align}
 $x = X$
and taking expectations, (1.7)Properties of the function
$x = X$
and taking expectations, (1.7)Properties of the function \begin{align}\vert \mathbb{E} \mathcal{G}_Z f_h(X)\vert = \vert \mathbb{E} h(X) - \mathbb{E} h(Z)\vert.\end{align}
\begin{align}\vert \mathbb{E} \mathcal{G}_Z f_h(X)\vert = \vert \mathbb{E} h(X) - \mathbb{E} h(Z)\vert.\end{align}
 $f_h$
turn out to be crucial to derive a good bound with Stein’s method. Typically, one will require good bounds on
$f_h$
turn out to be crucial to derive a good bound with Stein’s method. Typically, one will require good bounds on
 $f_h$
and its derivatives or differences if Z is continuous or discrete. Using the generator method, one can usually express
$f_h$
and its derivatives or differences if Z is continuous or discrete. Using the generator method, one can usually express
 $f_h$
in terms of the semi-group of the process defined by
$f_h$
in terms of the semi-group of the process defined by
 $\mathcal{G}_Z$
, and exploit properties and couplings of the process that found such bounds.
$\mathcal{G}_Z$
, and exploit properties and couplings of the process that found such bounds.
-
3. The goal is to bound (1.7) for all h from a rich enough family of test functions
 $\mathcal H$
, where
$\mathcal H$
, where
 $\mathcal H$
is typically a convergence-determining class. Rather than directly bounding
$\mathcal H$
is typically a convergence-determining class. Rather than directly bounding
 $\vert\mathbb{E} h(X) - \mathbb{E} h(Z)\vert$
, which would typically require knowledge of the unknown density or distribution function of X, the final step is to derive a bound for
$\vert\mathbb{E} h(X) - \mathbb{E} h(Z)\vert$
, which would typically require knowledge of the unknown density or distribution function of X, the final step is to derive a bound for
 $\vert \mathbb{E} \mathcal{G}_Z f_h(X)\vert$
that is more tractable. Standard approaches often involve Taylor expansions and couplings.
$\vert \mathbb{E} \mathcal{G}_Z f_h(X)\vert$
that is more tractable. Standard approaches often involve Taylor expansions and couplings.
In [Reference Gan, Röllin and Ross13] the above approach is used where
![]() $\mathcal{G}_{\boldsymbol{Z}}$
is the generator of the Wright–Fisher diffusion,
$\mathcal{G}_{\boldsymbol{Z}}$
is the generator of the Wright–Fisher diffusion,
 \begin{align}\mathcal{G}_{\boldsymbol{Z}} f({\boldsymbol{z}}) \,:\!= \frac{1}{2}\left[\sum_{i,j=1}^{K-1} z_i(\delta_{i j}-z_j) \frac{\partial f}{\partial z_i \partial z_j}({\boldsymbol{z}})+\sum_{i=1}^{K-1}(\beta_i-s z_i)\frac{\partial f}{\partial z_i}({\boldsymbol{z}})\right], \quad {\boldsymbol{z}} \in \text{int}(\bar \nabla^{K}), \end{align}
\begin{align}\mathcal{G}_{\boldsymbol{Z}} f({\boldsymbol{z}}) \,:\!= \frac{1}{2}\left[\sum_{i,j=1}^{K-1} z_i(\delta_{i j}-z_j) \frac{\partial f}{\partial z_i \partial z_j}({\boldsymbol{z}})+\sum_{i=1}^{K-1}(\beta_i-s z_i)\frac{\partial f}{\partial z_i}({\boldsymbol{z}})\right], \quad {\boldsymbol{z}} \in \text{int}(\bar \nabla^{K}), \end{align}
where
![]() $s = \sum_{i=1}^K \beta_i$
and
$s = \sum_{i=1}^K \beta_i$
and
![]() $\delta_{ij}$
denotes the Kronecker delta function. The stationary distribution associated to this generator is the Dirichlet distribution on
$\delta_{ij}$
denotes the Kronecker delta function. The stationary distribution associated to this generator is the Dirichlet distribution on
![]() $\text{int}(\bar \nabla^{K})$
with parameters
$\text{int}(\bar \nabla^{K})$
with parameters
![]() $\beta_1, \ldots, \beta_K$
. Recalling the definition of
$\beta_1, \ldots, \beta_K$
. Recalling the definition of
![]() ${\boldsymbol{U}}$
as the stationary distribution associated with (1.1), letting
${\boldsymbol{U}}$
as the stationary distribution associated with (1.1), letting
![]() ${\boldsymbol{Z}} \sim {\rm{Dir}}(\beta_1,\ldots, \beta_K)$
, a bound for
${\boldsymbol{Z}} \sim {\rm{Dir}}(\beta_1,\ldots, \beta_K)$
, a bound for
![]() $\vert\mathbb{E} h({\boldsymbol{U}}) -\mathbb{E} h ({\boldsymbol{Z}})\vert$
is derived by finding a bound for
$\vert\mathbb{E} h({\boldsymbol{U}}) -\mathbb{E} h ({\boldsymbol{Z}})\vert$
is derived by finding a bound for
![]() $\vert \mathbb{E} \mathcal{G}_Z f_h({\boldsymbol{U}})\vert$
. The following (Stein) lemma formalises the link between
$\vert \mathbb{E} \mathcal{G}_Z f_h({\boldsymbol{U}})\vert$
. The following (Stein) lemma formalises the link between
![]() $\mathcal{G}_{\boldsymbol{Z}}$
and
$\mathcal{G}_{\boldsymbol{Z}}$
and
![]() ${\boldsymbol{Z}}$
.
${\boldsymbol{Z}}$
.
Lemma 1.1. The random vector
![]() ${\boldsymbol{Z}} \sim {\rm{Dir}}(\beta_1, \ldots, \beta_K)$
if and only if, for all
${\boldsymbol{Z}} \sim {\rm{Dir}}(\beta_1, \ldots, \beta_K)$
if and only if, for all
![]() $f \in C^{2}(\bar \nabla^{K})$
with bounded partial derivatives up to the second order and Lipschitz continuous second-order partial derivatives,
$f \in C^{2}(\bar \nabla^{K})$
with bounded partial derivatives up to the second order and Lipschitz continuous second-order partial derivatives,
In [Reference Braverman5] a variation of the generator method was innovated, namely the prelimit generator comparison approach, which is the approach we use in this paper. We briefly describe the general idea of the approach and how it compares with the traditional generator method. The full details of our approach are contained in the appendices. The traditional generator comparison approach works by noting that (1.7) yields
where
![]() $\mathcal{G}_X$
is a characterising operator/generator for X, and hence,
$\mathcal{G}_X$
is a characterising operator/generator for X, and hence,
![]() $\mathbb{E} \mathcal{G}_X f_h(X) = 0$
. Typically, X will be a discrete object and Z will be its continuous limit. The generator comparison approach then follows the intuition that if X is approximately equal to Z then the operators
$\mathbb{E} \mathcal{G}_X f_h(X) = 0$
. Typically, X will be a discrete object and Z will be its continuous limit. The generator comparison approach then follows the intuition that if X is approximately equal to Z then the operators
![]() $\mathcal{G}_X$
and
$\mathcal{G}_X$
and
![]() $\mathcal{G}_Z$
should also be approximately equal, and the distributional distance between X and Z can be quantified by the differences in
$\mathcal{G}_Z$
should also be approximately equal, and the distributional distance between X and Z can be quantified by the differences in
![]() $\mathcal{G}_X$
and
$\mathcal{G}_X$
and
![]() $\mathcal{G}_Z$
. In a sense, this approach takes the discrete object X and evaluates it with respect to the continuous operator
$\mathcal{G}_Z$
. In a sense, this approach takes the discrete object X and evaluates it with respect to the continuous operator
![]() $\mathcal G_Z$
. The prelimit generator comparison approach swaps the roles of the continuous and discrete terms.
$\mathcal G_Z$
. The prelimit generator comparison approach swaps the roles of the continuous and discrete terms.
Let
![]() $h\,:\,\delta \mathbb{Z}^d \mapsto \mathbb R$
, where
$h\,:\,\delta \mathbb{Z}^d \mapsto \mathbb R$
, where
![]() $\delta > 0$
is a test function defined on the lattice
$\delta > 0$
is a test function defined on the lattice
![]() $\delta \mathbb{Z}^d$
. For a random vector
$\delta \mathbb{Z}^d$
. For a random vector
![]() ${\boldsymbol{U}}$
that takes values on
${\boldsymbol{U}}$
that takes values on
![]() $\delta \mathbb{Z}^d$
, suppose there is a characterising operator
$\delta \mathbb{Z}^d$
, suppose there is a characterising operator
![]() $\mathcal G_{\boldsymbol{U}}$
and given h one can find the solution to the Stein equation
$\mathcal G_{\boldsymbol{U}}$
and given h one can find the solution to the Stein equation
Then, naively speaking at least, for some continuous
![]() ${\boldsymbol{Z}}$
and its characterising operator
${\boldsymbol{Z}}$
and its characterising operator
![]() $\mathcal{G}_{\boldsymbol{Z}}$
,
$\mathcal{G}_{\boldsymbol{Z}}$
,
The general approach remains similar to the typical generator approach, the bound is reliant upon
![]() $\mathcal{G}_{\boldsymbol{U}}$
and
$\mathcal{G}_{\boldsymbol{U}}$
and
![]() $\mathcal{G}_{\boldsymbol{Z}}$
being close. One can now see however that in comparison to the standard generator comparison method, we are putting the continuous object
$\mathcal{G}_{\boldsymbol{Z}}$
being close. One can now see however that in comparison to the standard generator comparison method, we are putting the continuous object
![]() ${\boldsymbol{Z}}$
into the discrete (state-space) generator for
${\boldsymbol{Z}}$
into the discrete (state-space) generator for
![]() ${\boldsymbol{U}}$
. This can be advantageous if the solution
${\boldsymbol{U}}$
. This can be advantageous if the solution
![]() $f_h$
to the Stein equation (1.9) with respect to the discrete generator is tractable. Unfortunately, (1.10) is not that straightforward as
$f_h$
to the Stein equation (1.9) with respect to the discrete generator is tractable. Unfortunately, (1.10) is not that straightforward as
![]() $\mathcal{G}_{\boldsymbol{U}}$
is only defined on the lattice
$\mathcal{G}_{\boldsymbol{U}}$
is only defined on the lattice
![]() $\delta \mathbb{Z}^d$
, but we wish to input the continuous object
$\delta \mathbb{Z}^d$
, but we wish to input the continuous object
![]() ${\boldsymbol{Z}}$
. To address this issue, a smoothing interpolation operator for
${\boldsymbol{Z}}$
. To address this issue, a smoothing interpolation operator for
![]() $\mathcal{G}_{\boldsymbol{U}}$
is required, which will be described in detail in this paper.
$\mathcal{G}_{\boldsymbol{U}}$
is required, which will be described in detail in this paper.
Although the task of interpolating
![]() $\mathcal{G}_{\boldsymbol{U}}$
is conceptually straightforward, its execution is nontrivial. Thus, examples of the prelimit approach in practice are crucial for its proliferation. To date, only two examples exist. A simple single-server queue (
$\mathcal{G}_{\boldsymbol{U}}$
is conceptually straightforward, its execution is nontrivial. Thus, examples of the prelimit approach in practice are crucial for its proliferation. To date, only two examples exist. A simple single-server queue (
![]() $M/M/1$
model) is considered in [Reference Braverman5], while [Reference Braverman6] considers a much more involved queueing model—a load-balancing model under the join-the-shortest-queue policy. The former is a simple one-dimensional model that does not fully illustrate the challenges of interpolating
$M/M/1$
model) is considered in [Reference Braverman5], while [Reference Braverman6] considers a much more involved queueing model—a load-balancing model under the join-the-shortest-queue policy. The former is a simple one-dimensional model that does not fully illustrate the challenges of interpolating
![]() $\mathcal{G}_{\boldsymbol{U}}$
, while the latter example is extremely involved due to the complicated dynamics of the queueing model. The Wright–Fisher model we consider falls nicely between these two examples in terms of difficulty—our model is multi-dimensional, highlighting all the challenges of interpolating
$\mathcal{G}_{\boldsymbol{U}}$
, while the latter example is extremely involved due to the complicated dynamics of the queueing model. The Wright–Fisher model we consider falls nicely between these two examples in terms of difficulty—our model is multi-dimensional, highlighting all the challenges of interpolating
![]() $\mathcal{G}_{\boldsymbol{U}}$
, whilst the task of bounding the Stein factors, which is unrelated to interpolation, is relatively straightforward. Additionally, this paper refines the original implementation of the prelimit generator approach in [Reference Braverman5]. We present several results in Appendix A that simplify working with the interpolating operator. Specifically, we state and prove Lemma A.1, Lemma A.2, Proposition A.1, and Corollary A.1. We anticipate that these results will help future users of the approach.
$\mathcal{G}_{\boldsymbol{U}}$
, whilst the task of bounding the Stein factors, which is unrelated to interpolation, is relatively straightforward. Additionally, this paper refines the original implementation of the prelimit generator approach in [Reference Braverman5]. We present several results in Appendix A that simplify working with the interpolating operator. Specifically, we state and prove Lemma A.1, Lemma A.2, Proposition A.1, and Corollary A.1. We anticipate that these results will help future users of the approach.
The approach used in [Reference Gan, Röllin and Ross13], follows the traditional generator method described earlier, whereas we use the prelimit generator comparison method in this paper. There are advantages and disadvantages to either approach. If we consider the main three steps in applying Stein’s method discussed earlier, steps 1 and 3 are more or less the same in both approaches. Step 1 is in the traditional approach involves finding a diffusion operator that characterises the Dirichlet distribution. In the prelimit approach, in addition to the same operator, we also require an operator for the discrete population Wright–Fisher Markov chain stationary distribution, which is not difficult. Step 3 in the traditional approach in [Reference Gan, Röllin and Ross13] uses an exchangeable pair coupling, and ultimately the main work involves a series of moment calculations for the discrete stationary distribution. In the prelimit approach, near identical calculations are required. The primary difference between the two approaches lies in step 2. In [Reference Gan, Röllin and Ross13], solving the Stein equation and bounding the derivatives of the solution, known as the Stein factors, is a lengthy process and requires knowledge of coalescent theory and a dual process representation of the Wright–Fisher diffusion process governed by (1.8). These bounds are one of the primary contributions of [Reference Gan, Röllin and Ross13]. In contrast, using the prelimit approach, we instead require Stein factors for the Markov chain associated with (1.1), which we bound in Lemma 2.3. The bounds are simple, elegant and require only a short proof using elementary Markov chain knowledge and couplings. The price we pay to use this simpler approach for the Stein factors is the requirement for an interpolation operator, which leads to numerous technical difficulties, and this is the main trade off between the two approaches.
Lastly, expanding on the two remarks we made following Theorem 1.1, the
![]() $N^{ 3 -\beta_K/2 }$
appears because we use an interpolation operator based on forward differences and, as a result, we have to treat the case when
$N^{ 3 -\beta_K/2 }$
appears because we use an interpolation operator based on forward differences and, as a result, we have to treat the case when
![]() ${\boldsymbol{Z}}$
is close to the ‘right’ boundary of
${\boldsymbol{Z}}$
is close to the ‘right’ boundary of
![]() $\bar \nabla^{K}$
separately. Getting rid of the
$\bar \nabla^{K}$
separately. Getting rid of the
![]() $N^{ 3-\beta_K/2 }$
term would require modifying our interpolation operator to use forward and backward differences when close to the ‘left’ and ‘right’ boundaries of
$N^{ 3-\beta_K/2 }$
term would require modifying our interpolation operator to use forward and backward differences when close to the ‘left’ and ‘right’ boundaries of
![]() $\bar \nabla^{K}$
, respectively, and central differences ‘in the middle’ to smoothly transition between the forward and backward differences. The
$\bar \nabla^{K}$
, respectively, and central differences ‘in the middle’ to smoothly transition between the forward and backward differences. The
![]() $C^{K}$
terms are an inevitable consequence of extending a function defined on the grid
$C^{K}$
terms are an inevitable consequence of extending a function defined on the grid
![]() $\delta \mathbb{Z}^{K}$
to the continuum. For example, see Appendix A.1 where we prove inequalities (A.4) and (A.8) of Theorem A.1.
$\delta \mathbb{Z}^{K}$
to the continuum. For example, see Appendix A.1 where we prove inequalities (A.4) and (A.8) of Theorem A.1.
The remainder of the paper will be as follows. In Section 2 we outline the proof to Theorem 1.1, then provide a number of technical lemmas, and given these lemmas, we prove Theorem 1.1. The proofs of the technical lemmas are relegated to the two appendices.
2. Proof of the main theorem
2.1. Notation
-
1. For any function
 $f \,:\,\nabla^K \to \mathbb{R}$
, and a nonnegative integer valued vector
$f \,:\,\nabla^K \to \mathbb{R}$
, and a nonnegative integer valued vector
 ${\boldsymbol{a}}$
, let (2.1)where
${\boldsymbol{a}}$
, let (2.1)where \begin{align}B_{i} (f) = \sup \{\vert\Delta^{{\boldsymbol{a}}} f({\boldsymbol{u}})\vert \,:\,\Vert{\boldsymbol{a}}\Vert_{1}=i, {\boldsymbol{u}} \in \nabla^{K}, \text{ and } {\boldsymbol{u}} + \delta {\boldsymbol{a}} \in \nabla^{K} \}, \end{align}
\begin{align}B_{i} (f) = \sup \{\vert\Delta^{{\boldsymbol{a}}} f({\boldsymbol{u}})\vert \,:\,\Vert{\boldsymbol{a}}\Vert_{1}=i, {\boldsymbol{u}} \in \nabla^{K}, \text{ and } {\boldsymbol{u}} + \delta {\boldsymbol{a}} \in \nabla^{K} \}, \end{align}
 $\Delta^{\boldsymbol{a}}$
refers to the forwards difference operator with step size
$\Delta^{\boldsymbol{a}}$
refers to the forwards difference operator with step size
 $\delta$
, and analogous to the definition of (1.4),
$\delta$
, and analogous to the definition of (1.4),
 ${\boldsymbol{a}}$
indicates in what directions the forward differences are taken. Note that given
${\boldsymbol{a}}$
indicates in what directions the forward differences are taken. Note that given
 $\Vert{\boldsymbol{a}}\Vert_{1}=i$
,
$\Vert{\boldsymbol{a}}\Vert_{1}=i$
,
 $\Delta^{\boldsymbol{a}}$
is the composition of i forward differences in the directions indicated by the entries of
$\Delta^{\boldsymbol{a}}$
is the composition of i forward differences in the directions indicated by the entries of
 ${\boldsymbol{a}}$
and not a single forward difference in the direction of
${\boldsymbol{a}}$
and not a single forward difference in the direction of
 ${\boldsymbol{a}}$
treated as a whole. For example, if
${\boldsymbol{a}}$
treated as a whole. For example, if
 ${\boldsymbol{a}} = (1,0, \ldots, 0)$
then
${\boldsymbol{a}} = (1,0, \ldots, 0)$
then
 $\Delta^{{\boldsymbol{a}}} f({\boldsymbol{u}}) = f({\boldsymbol{u}} +\delta{\boldsymbol{e}}_1) - f({\boldsymbol{u}})$
and if
$\Delta^{{\boldsymbol{a}}} f({\boldsymbol{u}}) = f({\boldsymbol{u}} +\delta{\boldsymbol{e}}_1) - f({\boldsymbol{u}})$
and if
 ${\boldsymbol{a}} =(1,1,0,\ldots, 0)$
then
${\boldsymbol{a}} =(1,1,0,\ldots, 0)$
then
 $\Delta^{\boldsymbol{a}} f({\boldsymbol{u}}) =f({\boldsymbol{u}} + \delta{\boldsymbol{e}}_1 + \delta{\boldsymbol{e}}_2) -f({\boldsymbol{u}} + \delta{\boldsymbol{e}}_1) - f({\boldsymbol{u}} +\delta{\boldsymbol{e}}_2) + f(\delta{\boldsymbol{u}})$
, where
$\Delta^{\boldsymbol{a}} f({\boldsymbol{u}}) =f({\boldsymbol{u}} + \delta{\boldsymbol{e}}_1 + \delta{\boldsymbol{e}}_2) -f({\boldsymbol{u}} + \delta{\boldsymbol{e}}_1) - f({\boldsymbol{u}} +\delta{\boldsymbol{e}}_2) + f(\delta{\boldsymbol{u}})$
, where
 ${\boldsymbol{e}}_i$
denotes the usual standard basis vector with 1 in the ith component.
${\boldsymbol{e}}_i$
denotes the usual standard basis vector with 1 in the ith component.
-
2. We reserve the variables
 ${\boldsymbol{u}}$
(and
${\boldsymbol{u}}$
(and
 ${\boldsymbol{U}}$
) to emphasise when a function is defined on the lattice
${\boldsymbol{U}}$
) to emphasise when a function is defined on the lattice
 $\nabla^K$
, and
$\nabla^K$
, and
 ${\boldsymbol{x}}$
(and
${\boldsymbol{x}}$
(and
 ${\boldsymbol{X}}$
) when the function is defined on the continuous simplex
${\boldsymbol{X}}$
) when the function is defined on the continuous simplex
 $\bar \nabla^K$
.
$\bar \nabla^K$
. -
3. The vector
 ${\boldsymbol{e}}$
is reserved to denote a K-dimensional vector of ones, that is,
${\boldsymbol{e}}$
is reserved to denote a K-dimensional vector of ones, that is,
 ${\boldsymbol{e}} = (1,1,\ldots,1)$
. Furthermore, any inequalities with respect to
${\boldsymbol{e}} = (1,1,\ldots,1)$
. Furthermore, any inequalities with respect to
 ${\boldsymbol{e}}$
are intended to be element-by-element wise. That is, if
${\boldsymbol{e}}$
are intended to be element-by-element wise. That is, if
 ${\boldsymbol{x}} \leq{\boldsymbol{e}}$
then
${\boldsymbol{x}} \leq{\boldsymbol{e}}$
then
 $x_i \leq e_i$
for all i.
$x_i \leq e_i$
for all i. -
4. We use
 $\Sigma = \sum_{i=1}^K p_i$
to denote the sum of the mutation probabilities in (1.1).
$\Sigma = \sum_{i=1}^K p_i$
to denote the sum of the mutation probabilities in (1.1).
2.2. Outline of the proof
Recall that our goal is to bound
![]() $d_{\mathcal M_4}({\boldsymbol{U}},{\boldsymbol{Z}}) = \sup_{h \in \mathcal M_4} \vert\mathbb{E}h({\boldsymbol{U}}) - \mathbb{E} h({\boldsymbol{Z}})\vert$
. We achieve this bound in three main steps.
$d_{\mathcal M_4}({\boldsymbol{U}},{\boldsymbol{Z}}) = \sup_{h \in \mathcal M_4} \vert\mathbb{E}h({\boldsymbol{U}}) - \mathbb{E} h({\boldsymbol{Z}})\vert$
. We achieve this bound in three main steps.
-
1. Solve the Stein equation: identify a charaterising operator for
 $\mathcal{G}_{\boldsymbol{U}}$
for
$\mathcal{G}_{\boldsymbol{U}}$
for
 ${\boldsymbol{U}}$
and then, for any function
${\boldsymbol{U}}$
and then, for any function
 $h\in \mathcal{M}_4$
, solve for
$h\in \mathcal{M}_4$
, solve for
 $f_h$
that satisfies the Stein equation (2.2)
$f_h$
that satisfies the Stein equation (2.2) \begin{align}\mathcal{G}_{\boldsymbol{U}} f_h({\boldsymbol{u}}) = h({\boldsymbol{u}}) - \mathbb{E} h({\boldsymbol{U}}). \end{align}
\begin{align}\mathcal{G}_{\boldsymbol{U}} f_h({\boldsymbol{u}}) = h({\boldsymbol{u}}) - \mathbb{E} h({\boldsymbol{U}}). \end{align}
-
2. The interpolation operator: we would like to simply substitute
 ${\boldsymbol{u}} = {\boldsymbol{Z}}$
in (2.2) and take expectations, but
${\boldsymbol{u}} = {\boldsymbol{Z}}$
in (2.2) and take expectations, but
 $\mathcal{G}_{\boldsymbol{U}}$
is not well defined for continuous objects as it characterises
$\mathcal{G}_{\boldsymbol{U}}$
is not well defined for continuous objects as it characterises
 ${\boldsymbol{U}}$
that is discrete. We therefore extend
${\boldsymbol{U}}$
that is discrete. We therefore extend
 $f_h({\boldsymbol{u}})$
to take arguments from
$f_h({\boldsymbol{u}})$
to take arguments from
 $\bar\nabla^K$
using a carefully chosen interpolation operator A that satisfies
$\bar\nabla^K$
using a carefully chosen interpolation operator A that satisfies
 $Af_h({\boldsymbol{x}}) = f_h({\boldsymbol{u}})$
for all
$Af_h({\boldsymbol{x}}) = f_h({\boldsymbol{u}})$
for all
 ${\boldsymbol{x}} = {\boldsymbol{u}} \in \nabla^K$
, and A applied to a constant equals that constant. Then by applying A again to (2.2), (2.3)
${\boldsymbol{x}} = {\boldsymbol{u}} \in \nabla^K$
, and A applied to a constant equals that constant. Then by applying A again to (2.2), (2.3) \begin{align}A(\mathcal{G}_{\boldsymbol{U}}(A f_h))({\boldsymbol{x}}) = A h({\boldsymbol{x}}) - \mathbb{E} h({\boldsymbol{U}}). \end{align}
\begin{align}A(\mathcal{G}_{\boldsymbol{U}}(A f_h))({\boldsymbol{x}}) = A h({\boldsymbol{x}}) - \mathbb{E} h({\boldsymbol{U}}). \end{align}
-
3. Generator expansion: noting that
 $\mathbb{E} \mathcal{G}_Z Af_h({\boldsymbol{Z}}) = 0$
, then by setting
$\mathbb{E} \mathcal{G}_Z Af_h({\boldsymbol{Z}}) = 0$
, then by setting
 ${\boldsymbol{x}} ={\boldsymbol{Z}}$
in (2.3) and taking expectations, (2.4)We therefore need to carefully bound the left-hand side. We achieve this via Taylor expansion of
${\boldsymbol{x}} ={\boldsymbol{Z}}$
in (2.3) and taking expectations, (2.4)We therefore need to carefully bound the left-hand side. We achieve this via Taylor expansion of \begin{align}\mathbb{E}[ A \mathcal{G}_{\boldsymbol{U}} A f_h({\boldsymbol{Z}}) - \mathcal{G}_{\boldsymbol{Z}} A f_h({\boldsymbol{Z}})] = \mathbb{E} A h({\boldsymbol{Z}}) - \mathbb{E} h({\boldsymbol{U}}).\end{align}
\begin{align}\mathbb{E}[ A \mathcal{G}_{\boldsymbol{U}} A f_h({\boldsymbol{Z}}) - \mathcal{G}_{\boldsymbol{Z}} A f_h({\boldsymbol{Z}})] = \mathbb{E} A h({\boldsymbol{Z}}) - \mathbb{E} h({\boldsymbol{U}}).\end{align}
 $A \mathcal{G}_{\boldsymbol{U}} A f_h({\boldsymbol{x}})$
. The choice of A plays a crucial role here as we will have specifically chosen A in such a manner that the derivatives of
$A \mathcal{G}_{\boldsymbol{U}} A f_h({\boldsymbol{x}})$
. The choice of A plays a crucial role here as we will have specifically chosen A in such a manner that the derivatives of
 $A f_h$
correspond to the finite differences of
$A f_h$
correspond to the finite differences of
 $f_h$
up to the fourth order.
$f_h$
up to the fourth order.
2.2.1. Solving the Stein equation
As the concept of a generator for a DTMC is relatively uncommon, for the benefit of readers, we spend some time to define the generator and the general form of the solution to its Stein equation.
Definition 2.1 Let
![]() ${\boldsymbol{U}}(t)$
be the Wright–Fisher Markov chain with parent-independent mutation, rescaled to take values on
${\boldsymbol{U}}(t)$
be the Wright–Fisher Markov chain with parent-independent mutation, rescaled to take values on
![]() $\nabla^{K} \subset\delta \mathbb{Z}^d$
. For any function f from a suitable class of test functions
$\nabla^{K} \subset\delta \mathbb{Z}^d$
. For any function f from a suitable class of test functions
![]() $\mathcal F$
, we define the Markov chain generator of this process
$\mathcal F$
, we define the Markov chain generator of this process
![]() $\mathcal{G}_{\boldsymbol{U}}$
as
$\mathcal{G}_{\boldsymbol{U}}$
as
Note that we will use subscript notation on generator operators, for example,
![]() $\mathcal{G}_{\boldsymbol{U}}$
, to associate a generator with its stationary distribution
$\mathcal{G}_{\boldsymbol{U}}$
, to associate a generator with its stationary distribution
![]() ${\boldsymbol{U}}$
.
${\boldsymbol{U}}$
.
Lemma 2.1. Let
![]() ${\boldsymbol{U}}(t)$
denote a Markov chain governed by the generator
${\boldsymbol{U}}(t)$
denote a Markov chain governed by the generator
![]() $\mathcal{G}_{\boldsymbol{U}}$
, then for all
$\mathcal{G}_{\boldsymbol{U}}$
, then for all
![]() $h \in \mathcal{M}_4$
, the function
$h \in \mathcal{M}_4$
, the function
is well defined, and is the solution to
Proof. This can be shown by adapting Lemma 2 of [Reference Braverman5] to the discrete-time setting (see also Lemma 1 of [Reference Barbour2]).
2.2.2. The interpolation operator
Our proof relies on the ability to extend any function
![]() $f\,:\,\delta\mathbb{Z}^{d} \to \mathbb{R}$
to
$f\,:\,\delta\mathbb{Z}^{d} \to \mathbb{R}$
to
![]() $\mathbb{R}^{d}$
in a way that the derivatives of the extension correspond to the finite differences of f. Many such extensions are possible, but we use an interpolating seventh-order Hermite polynomial spline. The spline is a linear operator A acting on functions
$\mathbb{R}^{d}$
in a way that the derivatives of the extension correspond to the finite differences of f. Many such extensions are possible, but we use an interpolating seventh-order Hermite polynomial spline. The spline is a linear operator A acting on functions
![]() $f\,:\,\delta \mathbb{Z}^{d} \to \mathbb{R}$
and returning an extension
$f\,:\,\delta \mathbb{Z}^{d} \to \mathbb{R}$
and returning an extension
![]() $Af\,:\,\mathbb{R}^{d} \to \mathbb{R}$
. When
$Af\,:\,\mathbb{R}^{d} \to \mathbb{R}$
. When
![]() $d = 1$
,
$d = 1$
,
 \begin{align}A f(x) = \sum_{i=0}^{4} \alpha^{k(x)}_{k(x)+i}(x)f(\delta(k(x)+i)), \quad x \in \mathbb{R}, \end{align}
\begin{align}A f(x) = \sum_{i=0}^{4} \alpha^{k(x)}_{k(x)+i}(x)f(\delta(k(x)+i)), \quad x \in \mathbb{R}, \end{align}
where
![]() $k(x) = \lfloor x/\delta\rfloor$
and
$k(x) = \lfloor x/\delta\rfloor$
and
![]() $\alpha_{k+i}^{k}\,: \,\mathbb{R}\to \mathbb{R}$
are weights defined for all
$\alpha_{k+i}^{k}\,: \,\mathbb{R}\to \mathbb{R}$
are weights defined for all
![]() $k \in \mathbb{Z}$
and
$k \in \mathbb{Z}$
and
![]() $i = 0,\ldots, 4$
, making A f(x) a weighted sum of the five points
$i = 0,\ldots, 4$
, making A f(x) a weighted sum of the five points
![]() $f(\delta k(x)), \ldots, f(\delta (k(x)+4))$
. We use five points so that the derivatives of A f(x) capture the finite differences of f(x) up to the fourth order.
$f(\delta k(x)), \ldots, f(\delta (k(x)+4))$
. We use five points so that the derivatives of A f(x) capture the finite differences of f(x) up to the fourth order.
The details about
![]() $\alpha_{k+i}^{k}(x)$
and the definition of A f(x) for
$\alpha_{k+i}^{k}(x)$
and the definition of A f(x) for
![]() $d >1$
are left to Appendix A. For the purposes of this section, it suffices to know that A is a linear operator,
$d >1$
are left to Appendix A. For the purposes of this section, it suffices to know that A is a linear operator,
![]() $Af({\boldsymbol{x}}) = f({\boldsymbol{u}})$
for
$Af({\boldsymbol{x}}) = f({\boldsymbol{u}})$
for
![]() ${\boldsymbol{x}} ={\boldsymbol{u}} \in \delta \mathbb{Z}^{d}$
,
${\boldsymbol{x}} ={\boldsymbol{u}} \in \delta \mathbb{Z}^{d}$
,
![]() $Af({\boldsymbol{x}})$
is twice continuously differentiable, and that A applied to a constant equals that constant.
$Af({\boldsymbol{x}})$
is twice continuously differentiable, and that A applied to a constant equals that constant.
2.2.3. Generator expansion
We first define a discrete analog of
![]() $\mathcal M_j$
. Let
$\mathcal M_j$
. Let
The following lemma, which we prove in Appendix B, shows that the Taylor expansion of
![]() $A (\mathcal{G}_{{\boldsymbol{U}}} (Af_h))({\boldsymbol{x}})$
equals
$A (\mathcal{G}_{{\boldsymbol{U}}} (Af_h))({\boldsymbol{x}})$
equals
![]() $\mathcal{G}_{{\boldsymbol{Z}}} Af_h({\boldsymbol{x}})$
plus an error term on a subset of
$\mathcal{G}_{{\boldsymbol{Z}}} Af_h({\boldsymbol{x}})$
plus an error term on a subset of
![]() $\bar \nabla^{K}$
. To state it, we define
$\bar \nabla^{K}$
. To state it, we define
 \begin{align}\nabla^{K}_{N} =&\ \{{\boldsymbol{u}} \in \nabla^{K} \,:\, u_{K} \geq 10K/\sqrt{N} \} = \{{\boldsymbol{u}} \in \nabla^{K} \,:\,\sum_{i=1}^{K-1} u_i \leq 1 - 10K/\sqrt{N} \}, \end{align}
\begin{align}\nabla^{K}_{N} =&\ \{{\boldsymbol{u}} \in \nabla^{K} \,:\, u_{K} \geq 10K/\sqrt{N} \} = \{{\boldsymbol{u}} \in \nabla^{K} \,:\,\sum_{i=1}^{K-1} u_i \leq 1 - 10K/\sqrt{N} \}, \end{align}
and let
![]() $\bar \nabla^{K}_{N} = \text{Conv}(\nabla^{K}_{N})$
. Note that
$\bar \nabla^{K}_{N} = \text{Conv}(\nabla^{K}_{N})$
. Note that
![]() $\nabla^{K}_{N} \neq \emptyset$
if
$\nabla^{K}_{N} \neq \emptyset$
if
![]() $1 - 10K/\sqrt{N} > 0$
, or
$1 - 10K/\sqrt{N} > 0$
, or
![]() $N > 100K^2$
, which we assume going forward.
$N > 100K^2$
, which we assume going forward.
Lemma 2.2. The extension
![]() $A (\mathcal{G}_{{\boldsymbol{U}}} (A f_h))({\boldsymbol{x}})$
is well defined for all
$A (\mathcal{G}_{{\boldsymbol{U}}} (A f_h))({\boldsymbol{x}})$
is well defined for all
![]() ${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
. Furthermore, if the mutation probabilities satisfy (1.3) for some
${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
. Furthermore, if the mutation probabilities satisfy (1.3) for some
![]() $\boldsymbol\beta>0$
then
$\boldsymbol\beta>0$
then
where
![]() $\mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{x}})$
is defined in (1.8) and, for all
$\mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{x}})$
is defined in (1.8) and, for all
![]() $N > 0$
,
$N > 0$
,

The final main ingredient needed to prove Theorem 1.1 are bounds for the Stein factors
![]() $B_i(f_h)$
.
$B_i(f_h)$
.
Lemma 2.3. Let
![]() $f_h({\boldsymbol{u}})$
be defined as in (2.5), then for all
$f_h({\boldsymbol{u}})$
be defined as in (2.5), then for all
![]() $h \in \mathcal{M}_{\mathrm{disc},4}$
,
$h \in \mathcal{M}_{\mathrm{disc},4}$
,
2.3. Proof of Theorem 1.1
We recall that to prove Theorem 1.1 we need to bound
![]() $d_{\mathcal{M}_{4}}(U,Y)$
. Recall that
$d_{\mathcal{M}_{4}}(U,Y)$
. Recall that
![]() $\delta = 1/N$
. The following lemma relates
$\delta = 1/N$
. The following lemma relates
![]() $\mathcal{M}_{j}$
to
$\mathcal{M}_{j}$
to
![]() $\mathcal{M}_{\mathrm{disc},j}$
. We prove it in Appendix A after stating Proposition A.1.
$\mathcal{M}_{\mathrm{disc},j}$
. We prove it in Appendix A after stating Proposition A.1.
Lemma 2.4. There exists
![]() $C(d)> 0$
such that, for any
$C(d)> 0$
such that, for any
![]() ${\boldsymbol{V}} \in \delta\mathbb{Z}^{d}$
and
${\boldsymbol{V}} \in \delta\mathbb{Z}^{d}$
and
![]() ${\boldsymbol{V}}' \in \mathbb{R}^{d}$
,
${\boldsymbol{V}}' \in \mathbb{R}^{d}$
,
where
![]() $C_{A.11}(d)$
is as in Proposition A.1.
$C_{A.11}(d)$
is as in Proposition A.1.
We require the following auxiliary lemma, which is proved in Appendix A.
Lemma 2.5. Assume that the mutation probabilities satisfy (1.3) for some
![]() $\boldsymbol\beta > 0$
. Then for any
$\boldsymbol\beta > 0$
. Then for any
![]() $h \in \mathcal{M}_{\mathrm{disc},4}$
and
$h \in \mathcal{M}_{\mathrm{disc},4}$
and
![]() ${\boldsymbol{u}} \in \nabla^{K}$
,
${\boldsymbol{u}} \in \nabla^{K}$
,

We are now ready to prove the main theorem.
Proof of Theorem 1.1
. Fix
![]() $h \in \mathcal{M}_{\mathrm{disc},4}$
. As a consequence of Lemma 2.4, it suffices to bound
$h \in \mathcal{M}_{\mathrm{disc},4}$
. As a consequence of Lemma 2.4, it suffices to bound
![]() $\vert\mathbb{E}h({\boldsymbol{U}}) - \mathbb{E} A h({\boldsymbol{Z}})\vert$
to prove Theorem 1.1. Recall the Stein equation (1.9), or
$\vert\mathbb{E}h({\boldsymbol{U}}) - \mathbb{E} A h({\boldsymbol{Z}})\vert$
to prove Theorem 1.1. Recall the Stein equation (1.9), or
Define
![]() $f_h({\boldsymbol{u}}) = 0$
for
$f_h({\boldsymbol{u}}) = 0$
for
![]() ${\boldsymbol{u}} \in \delta\mathbb{Z}^{K-1} \setminus \nabla^{K}$
(this choice is made for convenience), which allows us to define
${\boldsymbol{u}} \in \delta\mathbb{Z}^{K-1} \setminus \nabla^{K}$
(this choice is made for convenience), which allows us to define
![]() $A f_h(x)$
for all
$A f_h(x)$
for all
![]() ${\boldsymbol{x}} \in \mathbb{R}^{K-1}$
. Since
${\boldsymbol{x}} \in \mathbb{R}^{K-1}$
. Since
![]() $A f_h({\boldsymbol{x}}) =f_h({\boldsymbol{u}})$
for
$A f_h({\boldsymbol{x}}) =f_h({\boldsymbol{u}})$
for
![]() ${\boldsymbol{x}} = {\boldsymbol{u}} \in\nabla^{K}$
, the Stein equation yields
${\boldsymbol{x}} = {\boldsymbol{u}} \in\nabla^{K}$
, the Stein equation yields
Note that
![]() $\mathcal{G}_{{\boldsymbol{U}}} (Af_h)({\boldsymbol{u}})$
is only defined for
$\mathcal{G}_{{\boldsymbol{U}}} (Af_h)({\boldsymbol{u}})$
is only defined for
![]() ${\boldsymbol{u}} \in \nabla^{K}$
even though
${\boldsymbol{u}} \in \nabla^{K}$
even though
![]() $Af_h({\boldsymbol{x}})$
is defined on
$Af_h({\boldsymbol{x}})$
is defined on
![]() $\mathbb{R}^{K-1}$
.
$\mathbb{R}^{K-1}$
.
Applying A to
![]() $h({\boldsymbol{u}}) - \mathbb{E} h({\boldsymbol{X}})$
and recalling from Lemma 2.2 that
$h({\boldsymbol{u}}) - \mathbb{E} h({\boldsymbol{X}})$
and recalling from Lemma 2.2 that
![]() $A (\mathcal{G}_{U} (Af_h))({\boldsymbol{x}})$
is well defined for
$A (\mathcal{G}_{U} (Af_h))({\boldsymbol{x}})$
is well defined for
![]() ${\boldsymbol{x}} \in \bar\nabla^{K}_{N}$
, we see that, for any
${\boldsymbol{x}} \in \bar\nabla^{K}_{N}$
, we see that, for any
![]() ${\boldsymbol{x}} \in\mathbb{R}^{K-1}$
,
${\boldsymbol{x}} \in\mathbb{R}^{K-1}$
,
 \begin{align*}A h({\boldsymbol{x}}) - \mathbb{E} h({\boldsymbol{U}}) =&\ A \big( \mathbb{E} h({\boldsymbol{U}}) - h\big)({\boldsymbol{x}}) 1({\boldsymbol{x}} \in \bar \nabla^{K}_{N}) + A \big( \mathbb{E} h({\boldsymbol{U}}) - h\big)({\boldsymbol{x}}) 1({\boldsymbol{x}} \not \in \bar \nabla^{K}_{N}) \notag\\=&\ A (\mathcal{G}_{U} (A f_h))({\boldsymbol{x}}) 1({\boldsymbol{x}} \in \bar \nabla^{K}_{N}) + \big( \mathbb{E} h({\boldsymbol{U}}) - A h({\boldsymbol{x}})\big) 1({\boldsymbol{x}} \not\in \bar \nabla^{K}_{N}).\end{align*}
\begin{align*}A h({\boldsymbol{x}}) - \mathbb{E} h({\boldsymbol{U}}) =&\ A \big( \mathbb{E} h({\boldsymbol{U}}) - h\big)({\boldsymbol{x}}) 1({\boldsymbol{x}} \in \bar \nabla^{K}_{N}) + A \big( \mathbb{E} h({\boldsymbol{U}}) - h\big)({\boldsymbol{x}}) 1({\boldsymbol{x}} \not \in \bar \nabla^{K}_{N}) \notag\\=&\ A (\mathcal{G}_{U} (A f_h))({\boldsymbol{x}}) 1({\boldsymbol{x}} \in \bar \nabla^{K}_{N}) + \big( \mathbb{E} h({\boldsymbol{U}}) - A h({\boldsymbol{x}})\big) 1({\boldsymbol{x}} \not\in \bar \nabla^{K}_{N}).\end{align*}
We claim that
![]() $A f_h({\boldsymbol{x}})$
satisfies the conditions of Lemma 1.1, implying that
$A f_h({\boldsymbol{x}})$
satisfies the conditions of Lemma 1.1, implying that
![]() $ \mathbb{E} \mathcal{G}_{{\boldsymbol{Z}}}A f_h({\boldsymbol{Z}}) = 0$
. Our claim holds because
$ \mathbb{E} \mathcal{G}_{{\boldsymbol{Z}}}A f_h({\boldsymbol{Z}}) = 0$
. Our claim holds because
![]() $Af_h({\boldsymbol{x}})$
is twice continuously differentiable, and
$Af_h({\boldsymbol{x}})$
is twice continuously differentiable, and
![]() $Af_h({\boldsymbol{x}})$
has compact support, which follows by Theorem A.1 of Appendix A since
$Af_h({\boldsymbol{x}})$
has compact support, which follows by Theorem A.1 of Appendix A since
![]() $f_h({\boldsymbol{u}}) = 0$
for
$f_h({\boldsymbol{u}}) = 0$
for
![]() ${\boldsymbol{u}} \in \delta\mathbb{Z}^{K-1} \setminus \nabla^{K}$
. Setting
${\boldsymbol{u}} \in \delta\mathbb{Z}^{K-1} \setminus \nabla^{K}$
. Setting
![]() ${\boldsymbol{x}} ={\boldsymbol{Z}}$
and taking expected values yields
${\boldsymbol{x}} ={\boldsymbol{Z}}$
and taking expected values yields
 \begin{align*}\mathbb{E} A h({\boldsymbol{Z}}) - \mathbb{E} h({\boldsymbol{U}}) =&\ \mathbb{E} \big( A (\mathcal{G}_{{\boldsymbol{U}}} (A f_h))({\boldsymbol{Z}}) - \delta \mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{Z}}) \big) 1({\boldsymbol{Z}} \in \bar \nabla^{K}_{N})\\&+ \mathbb{E} \big( \mathbb{E} h({\boldsymbol{U}}) - A h({\boldsymbol{Z}})- \delta\mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{Z}})\big) 1({\boldsymbol{Z}} \not \in \bar \nabla^{K}_{N})\\=&\ \mathbb{E} \epsilon_{\mathcal{G}}({\boldsymbol{Z}}) 1({\boldsymbol{Z}} \in \bar \nabla^{K}_{N}) + \mathbb{E} \big( \mathbb{E} h({\boldsymbol{U}}) - A h({\boldsymbol{Z}})- \delta\mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{Z}})\big) 1({\boldsymbol{Z}} \not \in \bar \nabla^{K}_{N}).\end{align*}
\begin{align*}\mathbb{E} A h({\boldsymbol{Z}}) - \mathbb{E} h({\boldsymbol{U}}) =&\ \mathbb{E} \big( A (\mathcal{G}_{{\boldsymbol{U}}} (A f_h))({\boldsymbol{Z}}) - \delta \mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{Z}}) \big) 1({\boldsymbol{Z}} \in \bar \nabla^{K}_{N})\\&+ \mathbb{E} \big( \mathbb{E} h({\boldsymbol{U}}) - A h({\boldsymbol{Z}})- \delta\mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{Z}})\big) 1({\boldsymbol{Z}} \not \in \bar \nabla^{K}_{N})\\=&\ \mathbb{E} \epsilon_{\mathcal{G}}({\boldsymbol{Z}}) 1({\boldsymbol{Z}} \in \bar \nabla^{K}_{N}) + \mathbb{E} \big( \mathbb{E} h({\boldsymbol{U}}) - A h({\boldsymbol{Z}})- \delta\mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{Z}})\big) 1({\boldsymbol{Z}} \not \in \bar \nabla^{K}_{N}).\end{align*}
To bound the first term, we recall assumption (1.3), which implies that
![]() $\Sigma = \delta s/2$
. Combining Lemma 2.2 with the Stein factor bounds in Lemma 2.3 then yields
$\Sigma = \delta s/2$
. Combining Lemma 2.2 with the Stein factor bounds in Lemma 2.3 then yields

Note that
![]() $( 1- (10K(\sqrt{N}-1)/N) (1-\Sigma))^{N}$
behaves like
$( 1- (10K(\sqrt{N}-1)/N) (1-\Sigma))^{N}$
behaves like
![]() $\textrm{e}^{-10K\sqrt{N}}$
for large N. Let us bound the second term. Recall that
$\textrm{e}^{-10K\sqrt{N}}$
for large N. Let us bound the second term. Recall that
![]() ${\boldsymbol{Z}}$
has density given by (1.2), which implies that
${\boldsymbol{Z}}$
has density given by (1.2), which implies that
![]() $Z_{K}\sim{\rm Beta}(\beta_{K}, s - \beta_{K})$
. Therefore,
$Z_{K}\sim{\rm Beta}(\beta_{K}, s - \beta_{K})$
. Therefore,

where

Without loss of generality, we may assume that
![]() $h(0) = 0$
. Otherwise, we can replace h(u) by
$h(0) = 0$
. Otherwise, we can replace h(u) by
![]() $h(u) - h(0)$
without affecting the value of
$h(u) - h(0)$
without affecting the value of
![]() $\mathbb{E} h(U) - \mathbb{E} A h(Y)$
. Observe that
$\mathbb{E} h(U) - \mathbb{E} A h(Y)$
. Observe that

In the second inequality we used Lemma 2.5. In the last inequality we used (2.9), the fact that
![]() $\delta < 1$
, the Stein factor bound
$\delta < 1$
, the Stein factor bound
![]() $B_{1}(f_h) \leq \delta/\Sigma$
from Lemma 2.3, and the fact that
$B_{1}(f_h) \leq \delta/\Sigma$
from Lemma 2.3, and the fact that
![]() $\delta/\Sigma = 2/s$
, which follows from (1.3) and the definitions of s and
$\delta/\Sigma = 2/s$
, which follows from (1.3) and the definitions of s and
![]() $\Sigma$
.
$\Sigma$
.
The final bound now follows from choosing C(K) to be a uniform upper bound for
![]() $C_{A.4}(K)$
,
$C_{A.4}(K)$
,
![]() $C_{A.10}(K)$
, and
$C_{A.10}(K)$
, and
![]() $C_{A.11}(K)$
and some routine simplification and rearrangement.
$C_{A.11}(K)$
and some routine simplification and rearrangement.
Appendix A. The interpolator A
The operator A discussed in this appendix is identical to the one introduced in Appendix A of [Reference Braverman5]. We repeat some of its key properties, originally presented in [Reference Braverman5], as they are needed for the proof of Theorem 1.1. We also present several useful technical results about A that are not found in [Reference Braverman5]. Namely, Lemma A.1, Lemma A.2, Proposition A.1, and Corollary A.1.
Building on the discussion in Section 2.2.2, for a one-dimensional function
![]() $f\,:\,\delta \mathbb{Z} \to \mathbb{R}$
, we define
$f\,:\,\delta \mathbb{Z} \to \mathbb{R}$
, we define
 \begin{align*}A f(x) = \sum_{i=0}^{4} \alpha^{k(x)}_{k(x)+i}(x)f(\delta(k(x)+i)),\end{align*}
\begin{align*}A f(x) = \sum_{i=0}^{4} \alpha^{k(x)}_{k(x)+i}(x)f(\delta(k(x)+i)),\end{align*}
where
![]() $k(x) = \lfloor x/\delta\rfloor$
and
$k(x) = \lfloor x/\delta\rfloor$
and
![]() $\alpha_{k+i}^{k}\,:\,\mathbb{R}\to \mathbb{R}$
are weights. Braverman [Reference Braverman5] described how to choose these weights to make Af(x) coincide with
$\alpha_{k+i}^{k}\,:\,\mathbb{R}\to \mathbb{R}$
are weights. Braverman [Reference Braverman5] described how to choose these weights to make Af(x) coincide with
![]() $f(\!\cdot\!)$
on grid points, and also to make it a differentiable function whose derivatives behave like the corresponding finite differences of
$f(\!\cdot\!)$
on grid points, and also to make it a differentiable function whose derivatives behave like the corresponding finite differences of
![]() $f(\!\cdot\!)$
. The idea can be applied to multidimensional grid-valued functions as well. The following result builds on Theorem A.1 of [Reference Braverman5]. We use this as an interface that contains the important properties of A without delving into the low-level details behind its construction.
$f(\!\cdot\!)$
. The idea can be applied to multidimensional grid-valued functions as well. The following result builds on Theorem A.1 of [Reference Braverman5]. We use this as an interface that contains the important properties of A without delving into the low-level details behind its construction.
Theorem A.1. Given a convex set
![]() $K \subset \mathbb{R}^{d}$
, define
$K \subset \mathbb{R}^{d}$
, define
where
![]() $k({\boldsymbol{x}})$
by
$k({\boldsymbol{x}})$
by
![]() $k_{j}({\boldsymbol{x}}) = \lfloor x_j/\delta\rfloor$
. Let
$k_{j}({\boldsymbol{x}}) = \lfloor x_j/\delta\rfloor$
. Let
![]() $\text{Conv}(K_4)$
be the convex hull of
$\text{Conv}(K_4)$
be the convex hull of
![]() $K_4$
and for
$K_4$
and for
![]() ${\boldsymbol{x}} \in \mathbb{R}^{d}$
. There exist weights
${\boldsymbol{x}} \in \mathbb{R}^{d}$
. There exist weights
![]() $\{\alpha_{k+i}^{k} \,:\,\mathbb{R} \to \mathbb{R},\ k \in \mathbb{Z},\ i =0,1,2,3,4\}$
such that, for any
$\{\alpha_{k+i}^{k} \,:\,\mathbb{R} \to \mathbb{R},\ k \in \mathbb{Z},\ i =0,1,2,3,4\}$
such that, for any
![]() $f\,:\,K \cap \delta \mathbb{Z}^{d} \to\mathbb{R}$
, the function
$f\,:\,K \cap \delta \mathbb{Z}^{d} \to\mathbb{R}$
, the function
 \begin{align}A f({\boldsymbol{x}}) =&\ \sum_{i_d = 0}^{4} \alpha_{k_d({\boldsymbol{x}})+i_d}^{k_d({\boldsymbol{x}})}(x_d)\cdots \sum_{i_1 = 0}^{4} \alpha_{k_1({\boldsymbol{x}})+i_1}^{k_1({\boldsymbol{x}})}(x_1) f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) \notag\\=&\ \sum_{i_1, \ldots, i_d = 0}^{4} \bigg(\prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j)\bigg) f(\delta (k({\boldsymbol{x}})+{\boldsymbol{i}})) , \quad {\boldsymbol{x}} \in \text{Conv}(K_4) \end{align}
\begin{align}A f({\boldsymbol{x}}) =&\ \sum_{i_d = 0}^{4} \alpha_{k_d({\boldsymbol{x}})+i_d}^{k_d({\boldsymbol{x}})}(x_d)\cdots \sum_{i_1 = 0}^{4} \alpha_{k_1({\boldsymbol{x}})+i_1}^{k_1({\boldsymbol{x}})}(x_1) f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) \notag\\=&\ \sum_{i_1, \ldots, i_d = 0}^{4} \bigg(\prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j)\bigg) f(\delta (k({\boldsymbol{x}})+{\boldsymbol{i}})) , \quad {\boldsymbol{x}} \in \text{Conv}(K_4) \end{align}
satisfies
![]() $A f({\boldsymbol{x}}) \in C^{3}(\text{Conv}(K_4))$
, where
$A f({\boldsymbol{x}}) \in C^{3}(\text{Conv}(K_4))$
, where
![]() ${\boldsymbol{i}} = (i_1, \ldots, i_d)$
in (A.1). Additionally,
${\boldsymbol{i}} = (i_1, \ldots, i_d)$
in (A.1). Additionally,
![]() $Af({\boldsymbol{x}})$
is infinitely differentiable almost everywhere on
$Af({\boldsymbol{x}})$
is infinitely differentiable almost everywhere on
![]() $\text{Conv}(K_4)$
,
$\text{Conv}(K_4)$
,
and for
![]() $0 \leq \Vert{\boldsymbol{a}}\Vert_{1} \leq 3$
,
$0 \leq \Vert{\boldsymbol{a}}\Vert_{1} \leq 3$
,
where
When
![]() $\Vert{\boldsymbol{a}}\Vert_{1} = 4$
, (A.3) also holds for almost all
$\Vert{\boldsymbol{a}}\Vert_{1} = 4$
, (A.3) also holds for almost all
![]() ${\boldsymbol{x}} \in \text{Conv}(K_4)$
. Additionally, the weights
${\boldsymbol{x}} \in \text{Conv}(K_4)$
. Additionally, the weights
![]() $\{\alpha_{k+i}^{k} \,:\,\mathbb{R} \to \mathbb{R},\ k \in\mathbb{Z},\ i = 0,1,2,3,4\}$
are degree-7 polynomials in
$\{\alpha_{k+i}^{k} \,:\,\mathbb{R} \to \mathbb{R},\ k \in\mathbb{Z},\ i = 0,1,2,3,4\}$
are degree-7 polynomials in
![]() $(x-\delta k)/\delta$
whose coefficients do not depend on k or
$(x-\delta k)/\delta$
whose coefficients do not depend on k or
![]() $\delta$
. For any
$\delta$
. For any
![]() $x \in\mathbb{R}$
, they satisfy
$x \in\mathbb{R}$
, they satisfy
 \begin{align}\sum_{i=0}^{4} \alpha^{k}_{k+i}(x) = 1, \quad k \in \mathbb{Z}, \end{align}
\begin{align}\sum_{i=0}^{4} \alpha^{k}_{k+i}(x) = 1, \quad k \in \mathbb{Z}, \end{align}
We prove (A.4) and (A.8) in Appendix A.1. The rest of Theorem A.1 is identical to Theorem A.1 of [Reference Braverman5]. We now present three useful properties of A. While Theorem A.1 only guarantees that
![]() $Af({\boldsymbol{x}})$
is thrice continuously differentiable, we need to control the fourth-order remainder term in the Taylor expansion of
$Af({\boldsymbol{x}})$
is thrice continuously differentiable, we need to control the fourth-order remainder term in the Taylor expansion of
![]() $Af({\boldsymbol{x}})$
. The following lemma, which would have been trivial if
$Af({\boldsymbol{x}})$
. The following lemma, which would have been trivial if
![]() $Af({\boldsymbol{x}})$
were four-times continuously differentiable, helps with this. Define
$Af({\boldsymbol{x}})$
were four-times continuously differentiable, helps with this. Define
 \begin{align}\mathcal{D}^{d} = \Big\{f \,:\,\mathbb{R}^{d} \to \mathbb{R} \,:\,\text{ for all ${\boldsymbol{x}}, {\boldsymbol{y}} \in \mathbb{R}^{d}$, } \vert f({\boldsymbol{x}}) - f({\boldsymbol{y}})\vert \leq \Vert{\boldsymbol{x}}-{\boldsymbol{y}}\Vert_{1} \sup_{\substack{ \min({\boldsymbol{x}},{\boldsymbol{y}}) \leq {\boldsymbol{z}} \\ {\boldsymbol{z}} \leq \max({\boldsymbol{x}},{\boldsymbol{y}}) \\ \Vert{\boldsymbol{a}}\Vert_{1} = 1}} \vert D^{{\boldsymbol{a}}} f({\boldsymbol{z}})\vert \Big\}, \end{align}
\begin{align}\mathcal{D}^{d} = \Big\{f \,:\,\mathbb{R}^{d} \to \mathbb{R} \,:\,\text{ for all ${\boldsymbol{x}}, {\boldsymbol{y}} \in \mathbb{R}^{d}$, } \vert f({\boldsymbol{x}}) - f({\boldsymbol{y}})\vert \leq \Vert{\boldsymbol{x}}-{\boldsymbol{y}}\Vert_{1} \sup_{\substack{ \min({\boldsymbol{x}},{\boldsymbol{y}}) \leq {\boldsymbol{z}} \\ {\boldsymbol{z}} \leq \max({\boldsymbol{x}},{\boldsymbol{y}}) \\ \Vert{\boldsymbol{a}}\Vert_{1} = 1}} \vert D^{{\boldsymbol{a}}} f({\boldsymbol{z}})\vert \Big\}, \end{align}
where the minimum and maximum are taken elementwise.
Lemma A.1. For any
![]() $f\,:\,\delta \mathbb{Z}^{d} \to \mathbb{R}$
, let
$f\,:\,\delta \mathbb{Z}^{d} \to \mathbb{R}$
, let
![]() $Af({\boldsymbol{x}})$
be as defined in (A.1). Then
$Af({\boldsymbol{x}})$
be as defined in (A.1). Then
![]() $D^{{\boldsymbol{a}}} Af({\boldsymbol{x}}) \in \mathcal{D}^{d}$
for any
$D^{{\boldsymbol{a}}} Af({\boldsymbol{x}}) \in \mathcal{D}^{d}$
for any
![]() ${\boldsymbol{a}} > 0$
with
${\boldsymbol{a}} > 0$
with
![]() $\Vert{\boldsymbol{a}}\Vert_{1} = 3$
.
$\Vert{\boldsymbol{a}}\Vert_{1} = 3$
.
The second lemma is a useful identity for applying A to products of functions.
Lemma A.2. Given
![]() $f,g\,:\,\mathbb{Z}^{d} \to \mathbb{R}$
let
$f,g\,:\,\mathbb{Z}^{d} \to \mathbb{R}$
let
![]() $h({\boldsymbol{u}}) =f({\boldsymbol{u}}) g({\boldsymbol{u}})$
. There exists
$h({\boldsymbol{u}}) =f({\boldsymbol{u}}) g({\boldsymbol{u}})$
. There exists
![]() $\epsilon_{p}:\mathbb{R}^{d} \to \mathbb{R}$
and a constant C(d) such that
$\epsilon_{p}:\mathbb{R}^{d} \to \mathbb{R}$
and a constant C(d) such that

For our third result, let
![]() $f({\boldsymbol{x}})$
be a function defined for all
$f({\boldsymbol{x}})$
be a function defined for all
![]() ${\boldsymbol{x}} \in \mathbb{R}^{d}$
and let
${\boldsymbol{x}} \in \mathbb{R}^{d}$
and let
![]() $f({\boldsymbol{u}})$
denote its restriction to
$f({\boldsymbol{u}})$
denote its restriction to
![]() $\delta \mathbb{Z}^{d}$
. Proposition A.1 provides an upper bound on how well
$\delta \mathbb{Z}^{d}$
. Proposition A.1 provides an upper bound on how well
![]() $Af({\boldsymbol{x}})$
approximates
$Af({\boldsymbol{x}})$
approximates
![]() $f({\boldsymbol{x}})$
. The smoother the function
$f({\boldsymbol{x}})$
. The smoother the function
![]() $f({\boldsymbol{x}})$
, the higher the exponent of
$f({\boldsymbol{x}})$
, the higher the exponent of
![]() $\delta$
in the error bound.
$\delta$
in the error bound.
Proposition A.1. Suppose that
![]() $f \in C^{s-1}(\mathbb{R}^{d})$
for some
$f \in C^{s-1}(\mathbb{R}^{d})$
for some
![]() $s \in \{1,2,3,4\}$
and that
$s \in \{1,2,3,4\}$
and that
![]() $D^{{\boldsymbol{a}}} f({\boldsymbol{x}}) \in \mathcal{D}^{d}$
when
$D^{{\boldsymbol{a}}} f({\boldsymbol{x}}) \in \mathcal{D}^{d}$
when
![]() $\Vert{\boldsymbol{a}}\Vert_{1} = s-1$
. Then
$\Vert{\boldsymbol{a}}\Vert_{1} = s-1$
. Then

The following corollary plays an important role later on in the proof of Lemma B.2.
Corollary A.1. If
![]() $f\,:\,\mathbb{R}^{d} \to \mathbb{R}$
is a polynomial of degree at most three then
$f\,:\,\mathbb{R}^{d} \to \mathbb{R}$
is a polynomial of degree at most three then
![]() $Af({\boldsymbol{x}}) = f({\boldsymbol{x}})$
.
$Af({\boldsymbol{x}}) = f({\boldsymbol{x}})$
.
Proof of Corollary A.1. If f(x) is a polynomial up to the third order, then its fourth-order derivatives are zero. The result follows from applying Proposition A.1 with
![]() $s = 4$
.
$s = 4$
.
We now prove Lemmas A.1 and A.2, and Proposition A.1, in that order.
Proof of Lemma A.1. Given
![]() ${\boldsymbol{x}}, {\boldsymbol{y}} \in \mathbb{R}^{d}$
, define
${\boldsymbol{x}}, {\boldsymbol{y}} \in \mathbb{R}^{d}$
, define
and note that
![]() ${\boldsymbol{x}}^{(1)} = {\boldsymbol{y}}$
and
${\boldsymbol{x}}^{(1)} = {\boldsymbol{y}}$
and
![]() ${\boldsymbol{x}}^{(d)} = {\boldsymbol{x}}$
. Fix
${\boldsymbol{x}}^{(d)} = {\boldsymbol{x}}$
. Fix
![]() ${\boldsymbol{a}} \in \mathbb{Z}^{d}$
with
${\boldsymbol{a}} \in \mathbb{Z}^{d}$
with
![]() ${\boldsymbol{a}} > 0$
and
${\boldsymbol{a}} > 0$
and
![]() $\Vert{\boldsymbol{a}}\Vert_{1} =3$
. Then
$\Vert{\boldsymbol{a}}\Vert_{1} =3$
. Then
 \begin{align*}D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}) - D^{{\boldsymbol{a}}} A f({\boldsymbol{y}}) =&\ D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(d)}) - D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(1)})= \sum_{j=1}^{d-1} D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(j+1)}) - D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(j)}).\end{align*}
\begin{align*}D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}) - D^{{\boldsymbol{a}}} A f({\boldsymbol{y}}) =&\ D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(d)}) - D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(1)})= \sum_{j=1}^{d-1} D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(j+1)}) - D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(j)}).\end{align*}
We now show that
Suppose that
![]() $j = d-1$
; the argument is similar for other values of j. Note that
$j = d-1$
; the argument is similar for other values of j. Note that
 \begin{align*}&D^{{\boldsymbol{a}}} A f({\boldsymbol{x}})\\&\quad= \partial_{d}^{a_{d}} \cdots \partial_{1}^{a_1} \bigg(\sum_{i_d = 0}^{4} \alpha_{k_d({\boldsymbol{x}})+i_d}^{k_d({\boldsymbol{x}})}(x_d)\cdots \sum_{i_1 = 0}^{4} \alpha_{k_1({\boldsymbol{x}})+i_1}^{k_1({\boldsymbol{x}})}(x_1) f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}}))\bigg)\\&\quad= \partial_{d}^{a_d}\sum_{i_d = 0}^{4} \alpha_{k_d(x_d)+i_d}^{k_d(x_d)}(x_d)\\& \hspace{1.3cm} \times \bigg[\partial_{d-1}^{a_{d-1}}\bigg(\sum_{i_{d-1} = 0}^{4} \alpha_{k_{d-1}(x_{d-1})+i_{d-1}}^{k_{d-1}(x_{d-1})}(x_{d-1})\cdots \partial_{1}^{a_1}\bigg(\sum_{i_1 = 0}^{4} \alpha_{k_1(x_1)+i_1}^{k_1(x_1)}(x_1) f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) \bigg)\bigg)\bigg],\end{align*}
\begin{align*}&D^{{\boldsymbol{a}}} A f({\boldsymbol{x}})\\&\quad= \partial_{d}^{a_{d}} \cdots \partial_{1}^{a_1} \bigg(\sum_{i_d = 0}^{4} \alpha_{k_d({\boldsymbol{x}})+i_d}^{k_d({\boldsymbol{x}})}(x_d)\cdots \sum_{i_1 = 0}^{4} \alpha_{k_1({\boldsymbol{x}})+i_1}^{k_1({\boldsymbol{x}})}(x_1) f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}}))\bigg)\\&\quad= \partial_{d}^{a_d}\sum_{i_d = 0}^{4} \alpha_{k_d(x_d)+i_d}^{k_d(x_d)}(x_d)\\& \hspace{1.3cm} \times \bigg[\partial_{d-1}^{a_{d-1}}\bigg(\sum_{i_{d-1} = 0}^{4} \alpha_{k_{d-1}(x_{d-1})+i_{d-1}}^{k_{d-1}(x_{d-1})}(x_{d-1})\cdots \partial_{1}^{a_1}\bigg(\sum_{i_1 = 0}^{4} \alpha_{k_1(x_1)+i_1}^{k_1(x_1)}(x_1) f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) \bigg)\bigg)\bigg],\end{align*}
where the first equality follows the definition of
![]() $A f({\boldsymbol{x}})$
in (A.1). Treating
$A f({\boldsymbol{x}})$
in (A.1). Treating
![]() $x_1, \ldots, x_{d-1}$
as fixed, let us consider the term inside the square brackets as a one-dimensional function in the dth dimension. To be precise, we define
$x_1, \ldots, x_{d-1}$
as fixed, let us consider the term inside the square brackets as a one-dimensional function in the dth dimension. To be precise, we define
![]() $g_{x_1,\ldots,x_{d-1}}\, :\,\delta \mathbb{Z} \to \mathbb{R}$
as
$g_{x_1,\ldots,x_{d-1}}\, :\,\delta \mathbb{Z} \to \mathbb{R}$
as
 \begin{align*}&g_{x_1,\ldots,x_{d-1}}(\delta \ell)\\&\quad= \partial_{d-1}^{a_{d-1}}\bigg(\sum_{i_{d-1} = 0}^{4} \alpha_{k_{d-1}(x_{d-1})+i_{d-1}}^{k_{d-1}(x_{d-1})}(x_{d-1})\cdots \partial_{1}^{a_1}\bigg(\sum_{i_1 = 0}^{4} \alpha_{k_1(x_1)+i_1}^{k_1(x_1)}(x_1)\\& \hspace{3cm} \times f\big(\delta(k(x_1,\ldots,x_{d-1},0)+(i_1,\ldots,i_{d-1},0)) + \delta \ell \big) \bigg)\bigg), \quad \ell \in \mathbb{Z}.\end{align*}
\begin{align*}&g_{x_1,\ldots,x_{d-1}}(\delta \ell)\\&\quad= \partial_{d-1}^{a_{d-1}}\bigg(\sum_{i_{d-1} = 0}^{4} \alpha_{k_{d-1}(x_{d-1})+i_{d-1}}^{k_{d-1}(x_{d-1})}(x_{d-1})\cdots \partial_{1}^{a_1}\bigg(\sum_{i_1 = 0}^{4} \alpha_{k_1(x_1)+i_1}^{k_1(x_1)}(x_1)\\& \hspace{3cm} \times f\big(\delta(k(x_1,\ldots,x_{d-1},0)+(i_1,\ldots,i_{d-1},0)) + \delta \ell \big) \bigg)\bigg), \quad \ell \in \mathbb{Z}.\end{align*}
Then
 \begin{align*}D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}) = \partial_{d}^{a_d}\sum_{i_d =0}^{4} \alpha_{k_d(x_d)+i_d}^{k_d(x_d)}(x_d) g_{x_1,\ldots,x_{d-1}}( \delta(k_{d}(x_d) + i_{d}) ) = \partial^{a_d} A g_{x_1,\ldots,x_{d-1}}(x_{d}).\end{align*}
\begin{align*}D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}) = \partial_{d}^{a_d}\sum_{i_d =0}^{4} \alpha_{k_d(x_d)+i_d}^{k_d(x_d)}(x_d) g_{x_1,\ldots,x_{d-1}}( \delta(k_{d}(x_d) + i_{d}) ) = \partial^{a_d} A g_{x_1,\ldots,x_{d-1}}(x_{d}).\end{align*}
Theorem A.1 states that
![]() $Ag_{x_1,\ldots,x_{d-1}}(x_d)$
is infinitely differentiable almost everywhere. Thus,
$Ag_{x_1,\ldots,x_{d-1}}(x_d)$
is infinitely differentiable almost everywhere. Thus,
 \begin{align*}&\vert D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(d)}) - D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(d-1)})\vert\\&\qquad= \vert\partial^{a_d} A g_{x_1,\ldots,x_{d-1}}(x_{d}) - \partial^{a_d} A g_{x_1,\ldots,x_{d-1}}(y_{d})\vert\\&\qquad= \vert\int_{y_d}^{x_d} \partial^{a_d+1} A g_{x_1,\ldots,x_{d-1}}(x')dx'\vert\\&\qquad\leq \vert x_d - y_d\vert \sup_{(x_d \wedge y_d) \leq z_d \leq (x_d \vee y_{d}) } \vert\partial^{a_d+1} A g_{x_1,\ldots,x_{d-1}}(z_d)\vert\\&\qquad\leq \vert x_d - y_d\vert \max_{\Vert{\boldsymbol{a}}'\Vert_{1} = \Vert{\boldsymbol{a}}\Vert_{1} + 1} \sup_{\substack{ \min({\boldsymbol{x}},{\boldsymbol{y}}) \leq {\boldsymbol{z}}\\{\boldsymbol{z}} \leq \max({\boldsymbol{x}},{\boldsymbol{y}})}} \vert D^{{\boldsymbol{a}}'} A f(z)\vert,\end{align*}
\begin{align*}&\vert D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(d)}) - D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}^{(d-1)})\vert\\&\qquad= \vert\partial^{a_d} A g_{x_1,\ldots,x_{d-1}}(x_{d}) - \partial^{a_d} A g_{x_1,\ldots,x_{d-1}}(y_{d})\vert\\&\qquad= \vert\int_{y_d}^{x_d} \partial^{a_d+1} A g_{x_1,\ldots,x_{d-1}}(x')dx'\vert\\&\qquad\leq \vert x_d - y_d\vert \sup_{(x_d \wedge y_d) \leq z_d \leq (x_d \vee y_{d}) } \vert\partial^{a_d+1} A g_{x_1,\ldots,x_{d-1}}(z_d)\vert\\&\qquad\leq \vert x_d - y_d\vert \max_{\Vert{\boldsymbol{a}}'\Vert_{1} = \Vert{\boldsymbol{a}}\Vert_{1} + 1} \sup_{\substack{ \min({\boldsymbol{x}},{\boldsymbol{y}}) \leq {\boldsymbol{z}}\\{\boldsymbol{z}} \leq \max({\boldsymbol{x}},{\boldsymbol{y}})}} \vert D^{{\boldsymbol{a}}'} A f(z)\vert,\end{align*}
where in the last inequality we used
![]() $\partial^{a_d+1} A g_{x_1,\ldots,x_{d-1}}(x_{d}) = \partial_{d} D^{{\boldsymbol{a}}} A f({\boldsymbol{x}})$
.
$\partial^{a_d+1} A g_{x_1,\ldots,x_{d-1}}(x_{d}) = \partial_{d} D^{{\boldsymbol{a}}} A f({\boldsymbol{x}})$
.
Proof of Lemma A.2. Using (A.1) of Theorem A.1, for
![]() ${\boldsymbol{x}} \in \mathbb{R}^{d}$
,
${\boldsymbol{x}} \in \mathbb{R}^{d}$
,
 \begin{align*}A h({\boldsymbol{x}}) =&\ \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}}))\\=&\ \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) A f({\boldsymbol{x}}) g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}}))\\&+ \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) \big(f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\big) g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})).\end{align*}
\begin{align*}A h({\boldsymbol{x}}) =&\ \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}}))\\=&\ \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) A f({\boldsymbol{x}}) g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}}))\\&+ \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) \big(f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\big) g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})).\end{align*}
By the definition of A,
 \begin{align*}&\sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) A f({\boldsymbol{x}}) g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) = Af({\boldsymbol{x}}) Ag({\boldsymbol{x}}).\end{align*}
\begin{align*}&\sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) A f({\boldsymbol{x}}) g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) = Af({\boldsymbol{x}}) Ag({\boldsymbol{x}}).\end{align*}
Furthermore,
 \begin{align*}& \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) \big(f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\big) g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}}))\\&\qquad = \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) \big(f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\big) \big(g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - g(\delta k({\boldsymbol{x}}))\big),\end{align*}
\begin{align*}& \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) \big(f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\big) g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}}))\\&\qquad = \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) \big(f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\big) \big(g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - g(\delta k({\boldsymbol{x}}))\big),\end{align*}
because again, by the definition of A,
 \begin{align*}\sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) \big(f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\big) g(\delta k({\boldsymbol{x}})) = g(\delta k({\boldsymbol{x}})) (Af({\boldsymbol{x}}) - A f({\boldsymbol{x}})) = 0.\end{align*}
\begin{align*}\sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) \big(f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\big) g(\delta k({\boldsymbol{x}})) = g(\delta k({\boldsymbol{x}})) (Af({\boldsymbol{x}}) - A f({\boldsymbol{x}})) = 0.\end{align*}
Setting
 \begin{align*}\epsilon_{p}({\boldsymbol{x}}) = \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) \big(f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\big) \big(g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - g(\delta k({\boldsymbol{x}}))\big),\end{align*}
\begin{align*}\epsilon_{p}({\boldsymbol{x}}) = \sum_{i_1, \ldots, i_d = 0}^{4} \prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j) \big(f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\big) \big(g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - g(\delta k({\boldsymbol{x}}))\big),\end{align*}
we have shown that
![]() $A h({\boldsymbol{x}}) = Af({\boldsymbol{x}}) A g({\boldsymbol{x}}) + \epsilon_{p}({\boldsymbol{x}})$
. Since
$A h({\boldsymbol{x}}) = Af({\boldsymbol{x}}) A g({\boldsymbol{x}}) + \epsilon_{p}({\boldsymbol{x}})$
. Since
by (A.8), it follows that
To conclude the proof, we argue that

which, when combined with the bound on
![]() $C_{A.4}(d)$
in (A.4), yields
$C_{A.4}(d)$
in (A.4), yields
![]() $C_{A.10}(d) \leq7975^{d}(5^{d} + dC_{A.4}(d) ) \leq 7975^{d}(5^{d} + d11404^{5} 1595^{d})$
. The first inequality follows by rewriting
$C_{A.10}(d) \leq7975^{d}(5^{d} + dC_{A.4}(d) ) \leq 7975^{d}(5^{d} + d11404^{5} 1595^{d})$
. The first inequality follows by rewriting
![]() $g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - g(\delta k({\boldsymbol{x}}))$
as a telescoping series and using the fact that
$g(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - g(\delta k({\boldsymbol{x}}))$
as a telescoping series and using the fact that
![]() ${\boldsymbol{i}} \leq 4{\boldsymbol{e}}$
. Similarly,
${\boldsymbol{i}} \leq 4{\boldsymbol{e}}$
. Similarly,
 \begin{align*}\vert f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\vert \leq&\ \vert f(\delta (k({\boldsymbol{x}})+{\boldsymbol{i}})) - f(\delta k({\boldsymbol{x}}))\vert + \vert f(\delta k({\boldsymbol{x}})) - A f({\boldsymbol{x}})\vert\\\leq&\ 5^{d} \max_{\substack{\Vert{\boldsymbol{a}}\Vert_{1}=1 \\ 0 \leq j \leq 4{\boldsymbol{e}} -{\boldsymbol{a}} }}\vert\Delta^{{\boldsymbol{a}}} f(\delta (k({\boldsymbol{x}}) + {\boldsymbol{j}}) \vert + \vert f(\delta k({\boldsymbol{x}})) - A f({\boldsymbol{x}})\vert,\end{align*}
\begin{align*}\vert f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})) - A f({\boldsymbol{x}})\vert \leq&\ \vert f(\delta (k({\boldsymbol{x}})+{\boldsymbol{i}})) - f(\delta k({\boldsymbol{x}}))\vert + \vert f(\delta k({\boldsymbol{x}})) - A f({\boldsymbol{x}})\vert\\\leq&\ 5^{d} \max_{\substack{\Vert{\boldsymbol{a}}\Vert_{1}=1 \\ 0 \leq j \leq 4{\boldsymbol{e}} -{\boldsymbol{a}} }}\vert\Delta^{{\boldsymbol{a}}} f(\delta (k({\boldsymbol{x}}) + {\boldsymbol{j}}) \vert + \vert f(\delta k({\boldsymbol{x}})) - A f({\boldsymbol{x}})\vert,\end{align*}
and

where the last inequality is due to (A.3) of Theorem A.1.
Fix a function
![]() $f({\boldsymbol{x}})$
satisfying the conditions of Proposition A.1. The following is a key auxiliary lemma, which we prove after proving Proposition A.1.
$f({\boldsymbol{x}})$
satisfying the conditions of Proposition A.1. The following is a key auxiliary lemma, which we prove after proving Proposition A.1.
Lemma A.3. For any
![]() $\delta < 1$
,
$\delta < 1$
,
![]() $s \in \{1,2,3,4\}$
, and
$s \in \{1,2,3,4\}$
, and
![]() $1 \leq\Vert{\boldsymbol{a}}\Vert_{1} \leq s-1$
,
$1 \leq\Vert{\boldsymbol{a}}\Vert_{1} \leq s-1$
,
where, for any
![]() $A \subset \mathbb{R}^{d}$
,
$A \subset \mathbb{R}^{d}$
,
![]() $E^{(s)}(A)$
denotes a quantity that satisfies
$E^{(s)}(A)$
denotes a quantity that satisfies
Proof of Proposition A.1. Throughout the proof we let
![]() $E^{(s)}(A)$
denote a generic quantity that satisfies (A.12), but whose value may change from line to line. Expanding both
$E^{(s)}(A)$
denote a generic quantity that satisfies (A.12), but whose value may change from line to line. Expanding both
![]() $f({\boldsymbol{x}})$
and
$f({\boldsymbol{x}})$
and
![]() $A f({\boldsymbol{x}})$
around
$A f({\boldsymbol{x}})$
around
![]() $\delta k({\boldsymbol{x}})$
yields
$\delta k({\boldsymbol{x}})$
yields
 \begin{align*}A f({\boldsymbol{x}}) - f({\boldsymbol{x}}) =&\ \sum_{j = 1}^{s-1} \frac{1}{j!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = j} \bigg(\prod_{i=1}^{d} (x_{i} - \delta k_{i}({\boldsymbol{x}}))^{a_{i}} \bigg)\big(D^{{\boldsymbol{a}}} A f(\delta k({\boldsymbol{x}})) - D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}}))\big)\\&+ \frac{1}{(s-1)!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = s-1} \bigg(\prod_{i=1}^{d} (x_{i} - \delta k_{i}({\boldsymbol{x}}))^{a_{i}} \bigg) \big( D^{{\boldsymbol{a}}} A f(\boldsymbol{\xi}_{1}) - D^{{\boldsymbol{a}}} Af(\delta k({\boldsymbol{x}}))\big)\\&+ \frac{1}{(s-1)!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = s-1} \bigg(\prod_{i=1}^{d} (x_{i} - \delta k_{i}({\boldsymbol{x}}))^{a_{i}} \bigg) \big( D^{{\boldsymbol{a}}} f(\boldsymbol{\xi}_{2}) - D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}}))\big),\end{align*}
\begin{align*}A f({\boldsymbol{x}}) - f({\boldsymbol{x}}) =&\ \sum_{j = 1}^{s-1} \frac{1}{j!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = j} \bigg(\prod_{i=1}^{d} (x_{i} - \delta k_{i}({\boldsymbol{x}}))^{a_{i}} \bigg)\big(D^{{\boldsymbol{a}}} A f(\delta k({\boldsymbol{x}})) - D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}}))\big)\\&+ \frac{1}{(s-1)!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = s-1} \bigg(\prod_{i=1}^{d} (x_{i} - \delta k_{i}({\boldsymbol{x}}))^{a_{i}} \bigg) \big( D^{{\boldsymbol{a}}} A f(\boldsymbol{\xi}_{1}) - D^{{\boldsymbol{a}}} Af(\delta k({\boldsymbol{x}}))\big)\\&+ \frac{1}{(s-1)!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = s-1} \bigg(\prod_{i=1}^{d} (x_{i} - \delta k_{i}({\boldsymbol{x}}))^{a_{i}} \bigg) \big( D^{{\boldsymbol{a}}} f(\boldsymbol{\xi}_{2}) - D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}}))\big),\end{align*}
where
![]() $\boldsymbol{\xi}_1,\boldsymbol{\xi}_2 \in [\delta k({\boldsymbol{x}}),{\boldsymbol{x}}] \subset [\delta k({\boldsymbol{x}}) ,\delta (k({\boldsymbol{x}}) + {\boldsymbol{e}}))$
. Consider separately each of the three terms on the right-hand side. Since
$\boldsymbol{\xi}_1,\boldsymbol{\xi}_2 \in [\delta k({\boldsymbol{x}}),{\boldsymbol{x}}] \subset [\delta k({\boldsymbol{x}}) ,\delta (k({\boldsymbol{x}}) + {\boldsymbol{e}}))$
. Consider separately each of the three terms on the right-hand side. Since
![]() $\vert x_i - \delta k_i({\boldsymbol{x}})\vert \leq \delta$
, then
$\vert x_i - \delta k_i({\boldsymbol{x}})\vert \leq \delta$
, then
 \begin{align*}& \sum_{j = 1}^{s-1} \frac{1}{j!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = j} \bigg(\prod_{i=1}^{d} (x_{i} - \delta k_{i}({\boldsymbol{x}}))^{a_{i}} \bigg)\big(D^{{\boldsymbol{a}}} A f(\delta k({\boldsymbol{x}})) - D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}}))\big) \\&\qquad\leq \sum_{j = 1}^{s-1} \frac{1}{j!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = j} \delta^{\Vert{\boldsymbol{a}}\Vert_{1}} \delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} 12^{d} E^{(s)}\big([\delta k({\boldsymbol{x}}), \delta ( k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})] \big) \\&\qquad\leq \sum_{j = 1}^{s-1} \frac{1}{j!} d^{j} \delta^{s} 12^{d} E^{(s)}\big([\delta k({\boldsymbol{x}}), \delta ( k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})] \big)\\&\qquad\leq 4 d^{4} 12^{d} \delta^{s} E^{(s)}\big([\delta k({\boldsymbol{x}}), \delta ( k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})] \big).\end{align*}
\begin{align*}& \sum_{j = 1}^{s-1} \frac{1}{j!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = j} \bigg(\prod_{i=1}^{d} (x_{i} - \delta k_{i}({\boldsymbol{x}}))^{a_{i}} \bigg)\big(D^{{\boldsymbol{a}}} A f(\delta k({\boldsymbol{x}})) - D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}}))\big) \\&\qquad\leq \sum_{j = 1}^{s-1} \frac{1}{j!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = j} \delta^{\Vert{\boldsymbol{a}}\Vert_{1}} \delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} 12^{d} E^{(s)}\big([\delta k({\boldsymbol{x}}), \delta ( k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})] \big) \\&\qquad\leq \sum_{j = 1}^{s-1} \frac{1}{j!} d^{j} \delta^{s} 12^{d} E^{(s)}\big([\delta k({\boldsymbol{x}}), \delta ( k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})] \big)\\&\qquad\leq 4 d^{4} 12^{d} \delta^{s} E^{(s)}\big([\delta k({\boldsymbol{x}}), \delta ( k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})] \big).\end{align*}
The first inequality is due to Lemma A.3, the second is due to the fact that there are at most
![]() $d^{j}$
permutations that yield
$d^{j}$
permutations that yield
![]() $\Vert{\boldsymbol{a}}\Vert_{1} = j$
, and the final inequality follows from
$\Vert{\boldsymbol{a}}\Vert_{1} = j$
, and the final inequality follows from
![]() $j < s \leq 4$
.
$j < s \leq 4$
.
For the second term we note that

The second inequality holds because we assumed that
![]() $D^{{\boldsymbol{a}}}f({\boldsymbol{x}}) \in \mathcal{D}^{d}$
when
$D^{{\boldsymbol{a}}}f({\boldsymbol{x}}) \in \mathcal{D}^{d}$
when
![]() $\Vert{\boldsymbol{a}}\Vert_{1} = s-1$
. The third holds because
$\Vert{\boldsymbol{a}}\Vert_{1} = s-1$
. The third holds because
![]() $\Vert\boldsymbol{\xi}_{1}-\delta k({\boldsymbol{x}})\Vert_{1} \leq d\delta$
(since
$\Vert\boldsymbol{\xi}_{1}-\delta k({\boldsymbol{x}})\Vert_{1} \leq d\delta$
(since
![]() $\delta k({\boldsymbol{x}}) \leq \boldsymbol{\xi}_{1} \leq{\boldsymbol{x}} < \delta(k({\boldsymbol{x}}) + {\boldsymbol{e}})$
), and by (A.3). The second-last inequality is a consequence of the fundamental theorem of calculus: suppose that
$\delta k({\boldsymbol{x}}) \leq \boldsymbol{\xi}_{1} \leq{\boldsymbol{x}} < \delta(k({\boldsymbol{x}}) + {\boldsymbol{e}})$
), and by (A.3). The second-last inequality is a consequence of the fundamental theorem of calculus: suppose that
![]() $\Delta^{{\boldsymbol{a}}}f(\delta (k({\boldsymbol{z}})+{\boldsymbol{i}}))= \Delta_{j_s} \cdots \Delta_{j_1} f(\delta(k({\boldsymbol{z}})+{\boldsymbol{i}}))$
for some
$\Delta^{{\boldsymbol{a}}}f(\delta (k({\boldsymbol{z}})+{\boldsymbol{i}}))= \Delta_{j_s} \cdots \Delta_{j_1} f(\delta(k({\boldsymbol{z}})+{\boldsymbol{i}}))$
for some
![]() $1 \leq j_1,\ldots, j_s\leq d$
. By our assumptions that
$1 \leq j_1,\ldots, j_s\leq d$
. By our assumptions that
![]() $f \in C^{s-1}(\mathbb{R}^{d})$
and that
$f \in C^{s-1}(\mathbb{R}^{d})$
and that
![]() $D^{{\boldsymbol{a}}} f({\boldsymbol{x}}) \in \mathcal{D}^{d}$
when
$D^{{\boldsymbol{a}}} f({\boldsymbol{x}}) \in \mathcal{D}^{d}$
when
![]() $\Vert{\boldsymbol{a}}\Vert_{1} = s-1$
, it follows that
$\Vert{\boldsymbol{a}}\Vert_{1} = s-1$
, it follows that
 \begin{align}&\vert\Delta_{j_s} \cdots \Delta_{j_1} f(\delta (k({\boldsymbol{z}})+{\boldsymbol{i}}))\vert \notag\\&\qquad= \Bigg|\Delta_{j_s} \int_{0}^{\delta} \cdots \int_{0}^{\delta} \partial_{j_{s-1}} \cdots \partial_{j_1} f(\delta (k({\boldsymbol{z}})+{\boldsymbol{i}}) + \gamma_{1} e_{j_1} + \cdots + \gamma_{s-1} e_{j_{s-1}}) d \gamma_{1} \cdots d\gamma_{s-1}\Bigg| \notag\\&\qquad\leq \delta^{s} \sup_{\substack{ \delta (k({\boldsymbol{z}})+{\boldsymbol{i}}) \leq {\boldsymbol{z}}' \\ {\boldsymbol{z}}' \leq \delta (k({\boldsymbol{z}})+{\boldsymbol{i}} + {\boldsymbol{a}})}} \vert D^{{\boldsymbol{a}}}f({\boldsymbol{z}}')\vert. \end{align}
\begin{align}&\vert\Delta_{j_s} \cdots \Delta_{j_1} f(\delta (k({\boldsymbol{z}})+{\boldsymbol{i}}))\vert \notag\\&\qquad= \Bigg|\Delta_{j_s} \int_{0}^{\delta} \cdots \int_{0}^{\delta} \partial_{j_{s-1}} \cdots \partial_{j_1} f(\delta (k({\boldsymbol{z}})+{\boldsymbol{i}}) + \gamma_{1} e_{j_1} + \cdots + \gamma_{s-1} e_{j_{s-1}}) d \gamma_{1} \cdots d\gamma_{s-1}\Bigg| \notag\\&\qquad\leq \delta^{s} \sup_{\substack{ \delta (k({\boldsymbol{z}})+{\boldsymbol{i}}) \leq {\boldsymbol{z}}' \\ {\boldsymbol{z}}' \leq \delta (k({\boldsymbol{z}})+{\boldsymbol{i}} + {\boldsymbol{a}})}} \vert D^{{\boldsymbol{a}}}f({\boldsymbol{z}}')\vert. \end{align}
Finally, for the third term, since we assumed that
![]() $D^{{\boldsymbol{a}}}f({\boldsymbol{x}}) \in \mathcal{D}^{d}$
when
$D^{{\boldsymbol{a}}}f({\boldsymbol{x}}) \in \mathcal{D}^{d}$
when
![]() $\Vert{\boldsymbol{a}}\Vert_{1} = s-1$
,
$\Vert{\boldsymbol{a}}\Vert_{1} = s-1$
,
 \begin{align*}&\frac{1}{(s-1)!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = s-1} \bigg(\prod_{i=1}^{d} (x_{i} - \delta k_{i}({\boldsymbol{x}}))^{a_{i}} \bigg) \big( D^{{\boldsymbol{a}}} f(\boldsymbol{\xi}_{2}) - D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}}))\big)\\&\qquad\leq d^{s-1}\delta^{s-1} \Vert\boldsymbol{\xi}_{1}-\delta k({\boldsymbol{x}})\Vert_{1} \sup_{\substack{ \delta k({\boldsymbol{x}}) \leq {\boldsymbol{z}} \\ {\boldsymbol{z}} \leq \delta ( k({\boldsymbol{x}}) + {\boldsymbol{e}}) \\ \Vert{\boldsymbol{a}}\Vert_{1} = s}} \vert D^{{\boldsymbol{a}}} A f({\boldsymbol{z}})\vert\\&\qquad\leq d^{s-1}\delta^{s-1} d \delta E^{(s)}\big([\delta k({\boldsymbol{x}}), \delta ( k({\boldsymbol{x}}) + {\boldsymbol{e}})] \big).\end{align*}
\begin{align*}&\frac{1}{(s-1)!} \sum_{{\boldsymbol{a}} \,:\,\Vert{\boldsymbol{a}}\Vert_{1} = s-1} \bigg(\prod_{i=1}^{d} (x_{i} - \delta k_{i}({\boldsymbol{x}}))^{a_{i}} \bigg) \big( D^{{\boldsymbol{a}}} f(\boldsymbol{\xi}_{2}) - D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}}))\big)\\&\qquad\leq d^{s-1}\delta^{s-1} \Vert\boldsymbol{\xi}_{1}-\delta k({\boldsymbol{x}})\Vert_{1} \sup_{\substack{ \delta k({\boldsymbol{x}}) \leq {\boldsymbol{z}} \\ {\boldsymbol{z}} \leq \delta ( k({\boldsymbol{x}}) + {\boldsymbol{e}}) \\ \Vert{\boldsymbol{a}}\Vert_{1} = s}} \vert D^{{\boldsymbol{a}}} A f({\boldsymbol{z}})\vert\\&\qquad\leq d^{s-1}\delta^{s-1} d \delta E^{(s)}\big([\delta k({\boldsymbol{x}}), \delta ( k({\boldsymbol{x}}) + {\boldsymbol{e}})] \big).\end{align*}
Adding up the bounds on the three terms and using the fact that
![]() $s \leq 4$
yields
$s \leq 4$
yields
To prove Lemma A.3, for
![]() $f\,:\,\mathbb{R}^{d} \to \mathbb{R}$
,
$f\,:\,\mathbb{R}^{d} \to \mathbb{R}$
,
![]() $1 \leq i \leq d$
, and
$1 \leq i \leq d$
, and
![]() ${\boldsymbol{x}} \in \mathbb{R}^{d}$
, we define
${\boldsymbol{x}} \in \mathbb{R}^{d}$
, we define
![]() $\Delta_{i}^{0} f({\boldsymbol{x}}) = f({\boldsymbol{x}})$
,
$\Delta_{i}^{0} f({\boldsymbol{x}}) = f({\boldsymbol{x}})$
,
![]() $\widetilde\Delta_{i}^{(0)} f({\boldsymbol{x}}) = f({\boldsymbol{x}})$
,
$\widetilde\Delta_{i}^{(0)} f({\boldsymbol{x}}) = f({\boldsymbol{x}})$
,
 \begin{gather}\Delta_{i} f({\boldsymbol{x}}) = f({\boldsymbol{x}}+\delta {\boldsymbol{e}}_{i}) - f({\boldsymbol{x}}), \notag\\\widetilde \Delta_{i}^{(1)} f({\boldsymbol{x}})= \Big(\Delta_{i} - \frac{1}{2} \Delta_{i}^2 + \frac{1}{3} \Delta_{i}^3 \Big)f({\boldsymbol{x}}),\notag\\\widetilde \Delta_{i}^{(2)} f({\boldsymbol{x}})= \big(\Delta_{i}^2 - \Delta_{i}^3 \big) f({\boldsymbol{x}}), \quad \widetilde \Delta_{i}^{(3)} f({\boldsymbol{x}})= \Delta_{i}^3 f({\boldsymbol{x}}). \end{gather}
\begin{gather}\Delta_{i} f({\boldsymbol{x}}) = f({\boldsymbol{x}}+\delta {\boldsymbol{e}}_{i}) - f({\boldsymbol{x}}), \notag\\\widetilde \Delta_{i}^{(1)} f({\boldsymbol{x}})= \Big(\Delta_{i} - \frac{1}{2} \Delta_{i}^2 + \frac{1}{3} \Delta_{i}^3 \Big)f({\boldsymbol{x}}),\notag\\\widetilde \Delta_{i}^{(2)} f({\boldsymbol{x}})= \big(\Delta_{i}^2 - \Delta_{i}^3 \big) f({\boldsymbol{x}}), \quad \widetilde \Delta_{i}^{(3)} f({\boldsymbol{x}})= \Delta_{i}^3 f({\boldsymbol{x}}). \end{gather}
Lemma A.4. Given
![]() $f\,:\,\mathbb{R}^{d} \to \mathbb{R}$
and the corresponding
$f\,:\,\mathbb{R}^{d} \to \mathbb{R}$
and the corresponding
![]() $A f({\boldsymbol{x}})$
, for
$A f({\boldsymbol{x}})$
, for
![]() $1 \leq \Vert{\boldsymbol{a}}\Vert_{1} \leq 3$
,
$1 \leq \Vert{\boldsymbol{a}}\Vert_{1} \leq 3$
,
We now prove Lemmas A.3 and A.4.
Proof of Lemma A.3. Fix
![]() $s \in \{1,2,3,4\}$
and
$s \in \{1,2,3,4\}$
and
![]() ${\boldsymbol{a}}$
with
${\boldsymbol{a}}$
with
![]() $1 \leq \Vert{\boldsymbol{a}}\Vert_{1} \leq s-1$
. For any
$1 \leq \Vert{\boldsymbol{a}}\Vert_{1} \leq s-1$
. For any
![]() $A \subset \mathbb{R}^{d}$
, we write
$A \subset \mathbb{R}^{d}$
, we write
![]() $E_{i}^{(s)}(A)$
to denote any quantity satisfying
$E_{i}^{(s)}(A)$
to denote any quantity satisfying
and recall from (A.12) that
![]() $E^{(s)}(A)$
denotes a quantity satisfying
$E^{(s)}(A)$
denotes a quantity satisfying
Suppose we have shown that, for
![]() $1 \leq i \leq d$
and
$1 \leq i \leq d$
and
![]() $1 \leq j \leq s-1$
,
$1 \leq j \leq s-1$
,
Combining (A.15) with Lemma A.4 yields
 \begin{align*}&D^{{\boldsymbol{a}}} A f(\delta k({\boldsymbol{x}}))\\&\quad= \delta^{-\Vert{\boldsymbol{a}}\Vert_{1}} \widetilde \Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d}^{(a_d)} f(\delta k({\boldsymbol{x}})) \notag\\&\quad= \delta^{-\Vert{\boldsymbol{a}}\Vert_{1}} \widetilde\Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})} (\delta^{a_d} \partial_{d}^{a_d} f(\delta k({\boldsymbol{x}})) + 5\delta^{s} E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}}_{d})]) ) \notag\\&\quad= \delta^{-\Vert{\boldsymbol{a}}\Vert_{1}} \delta^{a_d} \widetilde\Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})}\partial_{d}^{a_d} f(\delta k({\boldsymbol{x}})) \\&\qquad+ 5\delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} \widetilde \Delta^{(a_1)}_{1}\cdots \widetilde \Delta_{d-1}^{(a_{d-1})} E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})])\\&\quad= \delta^{-\Vert{\boldsymbol{a}}\Vert_{1}} \delta^{a_d}\widetilde\Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-2}^{(a_{d-2})} (\delta^{a_{d-1}} \partial_{d-1}^{a_{d-1}} \partial_{d}^{a_d} f(\delta k({\boldsymbol{x}})) + 5 \delta^{s} E_{d-1}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d-1})]) )\\&\qquad + 5 \delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} \widetilde\Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})}E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})]).\end{align*}
\begin{align*}&D^{{\boldsymbol{a}}} A f(\delta k({\boldsymbol{x}}))\\&\quad= \delta^{-\Vert{\boldsymbol{a}}\Vert_{1}} \widetilde \Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d}^{(a_d)} f(\delta k({\boldsymbol{x}})) \notag\\&\quad= \delta^{-\Vert{\boldsymbol{a}}\Vert_{1}} \widetilde\Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})} (\delta^{a_d} \partial_{d}^{a_d} f(\delta k({\boldsymbol{x}})) + 5\delta^{s} E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}}_{d})]) ) \notag\\&\quad= \delta^{-\Vert{\boldsymbol{a}}\Vert_{1}} \delta^{a_d} \widetilde\Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})}\partial_{d}^{a_d} f(\delta k({\boldsymbol{x}})) \\&\qquad+ 5\delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} \widetilde \Delta^{(a_1)}_{1}\cdots \widetilde \Delta_{d-1}^{(a_{d-1})} E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})])\\&\quad= \delta^{-\Vert{\boldsymbol{a}}\Vert_{1}} \delta^{a_d}\widetilde\Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-2}^{(a_{d-2})} (\delta^{a_{d-1}} \partial_{d-1}^{a_{d-1}} \partial_{d}^{a_d} f(\delta k({\boldsymbol{x}})) + 5 \delta^{s} E_{d-1}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d-1})]) )\\&\qquad + 5 \delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} \widetilde\Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})}E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})]).\end{align*}
Continuing recursively, we arrive at
 \begin{align}D^{{\boldsymbol{a}}} A f(\delta k({\boldsymbol{x}})) =&\ \delta^{-\Vert{\boldsymbol{a}}\Vert_{1}} \delta^{a_1} \cdots \delta^{a_d} D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}})) \notag\\&+ 5 \delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} \delta^{a_d} \cdots\delta^{a_2} E_{1}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}}_{1})]) \notag\\&+ \cdots \notag\\&+ 5 \delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} \widetilde\Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})}E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})]) \end{align}
\begin{align}D^{{\boldsymbol{a}}} A f(\delta k({\boldsymbol{x}})) =&\ \delta^{-\Vert{\boldsymbol{a}}\Vert_{1}} \delta^{a_1} \cdots \delta^{a_d} D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}})) \notag\\&+ 5 \delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} \delta^{a_d} \cdots\delta^{a_2} E_{1}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}}_{1})]) \notag\\&+ \cdots \notag\\&+ 5 \delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} \widetilde\Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})}E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})]) \end{align}
We now argue that, for any
![]() $1 \leq j \leq d-1$
,
$1 \leq j \leq d-1$
,
because applying (A.17) to (A.16) and using the fact that
![]() $\delta < 1$
yields
$\delta < 1$
yields
 \begin{align*}D^{{\boldsymbol{a}}} A f(\delta k({\boldsymbol{x}})) =&\ D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}})) + 5\delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} \Big(\sum_{j=1}^{d-1} 12^{j-1}\Big) E^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}})])\\=&\ D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}})) + 12^{d}\delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} E^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})])\end{align*}
\begin{align*}D^{{\boldsymbol{a}}} A f(\delta k({\boldsymbol{x}})) =&\ D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}})) + 5\delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} \Big(\sum_{j=1}^{d-1} 12^{j-1}\Big) E^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}})])\\=&\ D^{{\boldsymbol{a}}} f(\delta k({\boldsymbol{x}})) + 12^{d}\delta^{s-\Vert{\boldsymbol{a}}\Vert_{1}} E^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})])\end{align*}
where the second equality follows from
![]() $5 \sum_{j=1}^{d-1} 12^{j-1} \leq12^{d}$
. To prove (A.17), we set
$5 \sum_{j=1}^{d-1} 12^{j-1} \leq12^{d}$
. To prove (A.17), we set
![]() $j = d$
and evaluate
$j = d$
and evaluate
![]() $\widetilde \Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})}E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})])$
. We remind the reader that, for any
$\widetilde \Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})}E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})])$
. We remind the reader that, for any
![]() $1 \leq \ell\leq d-1$
,
$1 \leq \ell\leq d-1$
,
 \begin{align*}&\Delta_{\ell} E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}}_{d})])\\&\qquad= E_{d}^{(s)}([\delta k({\boldsymbol{x}}+\delta{\boldsymbol{e}}_{\ell}), \delta (k({\boldsymbol{x}}+\delta{\boldsymbol{e}}_{\ell}) + 3 {\boldsymbol{e}}_{d})]) - E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})])\\&\qquad= 2 E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) +{\boldsymbol{e}}_{\ell}+ 3{\boldsymbol{e}}_{d})]),\end{align*}
\begin{align*}&\Delta_{\ell} E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}}_{d})])\\&\qquad= E_{d}^{(s)}([\delta k({\boldsymbol{x}}+\delta{\boldsymbol{e}}_{\ell}), \delta (k({\boldsymbol{x}}+\delta{\boldsymbol{e}}_{\ell}) + 3 {\boldsymbol{e}}_{d})]) - E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})])\\&\qquad= 2 E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) +{\boldsymbol{e}}_{\ell}+ 3{\boldsymbol{e}}_{d})]),\end{align*}
where in the second equality we used the fact that
![]() $k({\boldsymbol{x}}+\delta {\boldsymbol{e}}_{\ell}) = k({\boldsymbol{x}})+{\boldsymbol{e}}_{\ell}$
, which follows from the definition of
$k({\boldsymbol{x}}+\delta {\boldsymbol{e}}_{\ell}) = k({\boldsymbol{x}})+{\boldsymbol{e}}_{\ell}$
, which follows from the definition of
![]() $k({\boldsymbol{x}})$
. Similarly,
$k({\boldsymbol{x}})$
. Similarly,
 \begin{align*}\Delta_{\ell}^2 E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}}_{d})]) =&\ 4 E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) +2{\boldsymbol{e}}_{\ell}+3{\boldsymbol{e}}_{d})]),\\\Delta_{\ell}^3 E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}}_{d})]) =&\ 8 E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) +3{\boldsymbol{e}}_{\ell}+3{\boldsymbol{e}}_{d})]).\end{align*}
\begin{align*}\Delta_{\ell}^2 E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}}_{d})]) =&\ 4 E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) +2{\boldsymbol{e}}_{\ell}+3{\boldsymbol{e}}_{d})]),\\\Delta_{\ell}^3 E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}}_{d})]) =&\ 8 E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) +3{\boldsymbol{e}}_{\ell}+3{\boldsymbol{e}}_{d})]).\end{align*}
These expressions, together with the definition of
![]() $\widetilde\Delta_{d-1}^{(a_{d-1})} f({\boldsymbol{x}})$
in (A.14) and the fact that
$\widetilde\Delta_{d-1}^{(a_{d-1})} f({\boldsymbol{x}})$
in (A.14) and the fact that
![]() $0 \leq a_{d-1} \leq 3$
, imply that
$0 \leq a_{d-1} \leq 3$
, imply that
and, similarly,
 \begin{align*}\widetilde \Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})}E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})]) =&\ 12^{d-1} E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})])\\=&\ 12^{d-1} E^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})]),\end{align*}
\begin{align*}\widetilde \Delta^{(a_1)}_{1} \cdots \widetilde \Delta_{d-1}^{(a_{d-1})}E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3{\boldsymbol{e}}_{d})]) =&\ 12^{d-1} E_{d}^{(s)}([\delta k({\boldsymbol{x}}), \delta (k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})])\\=&\ 12^{d-1} E^{(s)}([\delta k({\boldsymbol{x}}), \delta(k({\boldsymbol{x}}) + 3 {\boldsymbol{e}})]),\end{align*}
proving (A.17).
It remains to prove (A.15). Suppose that
![]() $s = 4$
, Taylor expansion yields
$s = 4$
, Taylor expansion yields
 \begin{gather}\Delta_{i} f({\boldsymbol{x}}) = \delta \partial_{i} f({\boldsymbol{x}}) +\frac{1}{2}\delta^2 \partial_{i}^{2} f({\boldsymbol{x}}) +\frac{1}{6}\delta^3 \partial_{i}^{3} f({\boldsymbol{x}}) + \frac{1}{24}\delta^{4} E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + \delta{\boldsymbol{e}}_{i}]), \notag\\\Delta_{i}^2 f({\boldsymbol{x}}) = \delta^2 \partial_{i}^2f({\boldsymbol{x}}) + \delta^3 \partial_{i}^3 f({\boldsymbol{x}}) +\frac{2}{3} \delta^4 E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + 2\delta {\boldsymbol{e}}_{i}]), \notag\\\Delta_{i}^3 f({\boldsymbol{x}}) =\delta^3 \partial_{i}^3f({\boldsymbol{x}}) + \frac{17}{6} \delta^4 E_{i}^{(4)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]), \end{gather}
\begin{gather}\Delta_{i} f({\boldsymbol{x}}) = \delta \partial_{i} f({\boldsymbol{x}}) +\frac{1}{2}\delta^2 \partial_{i}^{2} f({\boldsymbol{x}}) +\frac{1}{6}\delta^3 \partial_{i}^{3} f({\boldsymbol{x}}) + \frac{1}{24}\delta^{4} E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + \delta{\boldsymbol{e}}_{i}]), \notag\\\Delta_{i}^2 f({\boldsymbol{x}}) = \delta^2 \partial_{i}^2f({\boldsymbol{x}}) + \delta^3 \partial_{i}^3 f({\boldsymbol{x}}) +\frac{2}{3} \delta^4 E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + 2\delta {\boldsymbol{e}}_{i}]), \notag\\\Delta_{i}^3 f({\boldsymbol{x}}) =\delta^3 \partial_{i}^3f({\boldsymbol{x}}) + \frac{17}{6} \delta^4 E_{i}^{(4)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]), \end{gather}
The second equality is obtained by applying
![]() $\Delta_{i}$
to both sides of the first equality and observing that
$\Delta_{i}$
to both sides of the first equality and observing that
Similarly, the third equality is obtained by applying
![]() $\Delta_{i}$
to both sides of the second equality. To prove (A.15), we combine (A.18) with the definition of
$\Delta_{i}$
to both sides of the second equality. To prove (A.15), we combine (A.18) with the definition of
![]() $\widetilde \Delta_{i}^{(j)}f({\boldsymbol{x}})$
to obtain
$\widetilde \Delta_{i}^{(j)}f({\boldsymbol{x}})$
to obtain
 \begin{align*}\widetilde \Delta_{i}^{(1)} f({\boldsymbol{x}}) &=\ \delta \partial_{i}f({\boldsymbol{x}}) + \frac{1}{24} \delta^{4}E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + \delta{\boldsymbol{e}}_{i}]) - \frac{1}{2}\times\frac{2}{3} \delta^4E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + 2 \delta{\boldsymbol{e}}_{i}])\\&\hskip4.5mm+ \frac{1}{3}\times\frac{17}{6} \delta^4E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + 3\delta{\boldsymbol{e}}_{i}])\\&= \delta \partial_{i} f({\boldsymbol{x}}) +2\delta^4E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + 3\delta{\boldsymbol{e}}_{i}]),\end{align*}
\begin{align*}\widetilde \Delta_{i}^{(1)} f({\boldsymbol{x}}) &=\ \delta \partial_{i}f({\boldsymbol{x}}) + \frac{1}{24} \delta^{4}E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + \delta{\boldsymbol{e}}_{i}]) - \frac{1}{2}\times\frac{2}{3} \delta^4E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + 2 \delta{\boldsymbol{e}}_{i}])\\&\hskip4.5mm+ \frac{1}{3}\times\frac{17}{6} \delta^4E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + 3\delta{\boldsymbol{e}}_{i}])\\&= \delta \partial_{i} f({\boldsymbol{x}}) +2\delta^4E_{i}^{(4)}([{\boldsymbol{x}}, {\boldsymbol{x}} + 3\delta{\boldsymbol{e}}_{i}]),\end{align*}
and
 \begin{align*}\widetilde \Delta_{i}^{(2)} f({\boldsymbol{x}})=&\ \delta^2 \partial_{i}^2f({\boldsymbol{x}}) + 4\delta^4E_{i}^{(4)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]),\\\widetilde \Delta_{i}^{(3)} f({\boldsymbol{x}})=&\ \delta^3 \partial_{i}^3f({\boldsymbol{x}}) + 3\delta^4E_{i}^{(4)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]).\end{align*}
\begin{align*}\widetilde \Delta_{i}^{(2)} f({\boldsymbol{x}})=&\ \delta^2 \partial_{i}^2f({\boldsymbol{x}}) + 4\delta^4E_{i}^{(4)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]),\\\widetilde \Delta_{i}^{(3)} f({\boldsymbol{x}})=&\ \delta^3 \partial_{i}^3f({\boldsymbol{x}}) + 3\delta^4E_{i}^{(4)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]).\end{align*}
For completeness, we outline the main steps needed to prove (A.15) when
![]() $s<4$
. Suppose that
$s<4$
. Suppose that
![]() $s = 3$
, in which case Taylor expansion yields
$s = 3$
, in which case Taylor expansion yields
 \begin{gather*}\Delta_{i} f({\boldsymbol{x}}) = \delta \partial_{i} f({\boldsymbol{x}}) +\frac{1}{2}\delta^2\partial_{i}^{2} f({\boldsymbol{x}}) + \frac{1}{6}\delta^{3} E_{i}^{(3)}([{\boldsymbol{x}}, {\boldsymbol{x}} + \delta{\boldsymbol{e}}_{i}]),\\\Delta_{i}^2 f({\boldsymbol{x}}) = \delta^2 \partial_{i}^2f({\boldsymbol{x}}) + \frac{4}{3} \delta^3 E_{i}^{(3)}([{\boldsymbol{x}},{\boldsymbol{x}} + 2\delta {\boldsymbol{e}}_{i}]),\\\Delta_{i}^3 f({\boldsymbol{x}}) = \frac{11}{3} \delta^3E_{i}^{(3)}([{\boldsymbol{x}}, {\boldsymbol{x}} + 3\delta{\boldsymbol{e}}_{i}]),\end{gather*}
\begin{gather*}\Delta_{i} f({\boldsymbol{x}}) = \delta \partial_{i} f({\boldsymbol{x}}) +\frac{1}{2}\delta^2\partial_{i}^{2} f({\boldsymbol{x}}) + \frac{1}{6}\delta^{3} E_{i}^{(3)}([{\boldsymbol{x}}, {\boldsymbol{x}} + \delta{\boldsymbol{e}}_{i}]),\\\Delta_{i}^2 f({\boldsymbol{x}}) = \delta^2 \partial_{i}^2f({\boldsymbol{x}}) + \frac{4}{3} \delta^3 E_{i}^{(3)}([{\boldsymbol{x}},{\boldsymbol{x}} + 2\delta {\boldsymbol{e}}_{i}]),\\\Delta_{i}^3 f({\boldsymbol{x}}) = \frac{11}{3} \delta^3E_{i}^{(3)}([{\boldsymbol{x}}, {\boldsymbol{x}} + 3\delta{\boldsymbol{e}}_{i}]),\end{gather*}
which implies that
 \begin{gather*}\widetilde \Delta_{i}^{(1)} f({\boldsymbol{x}}) = \delta \partial_{i}f({\boldsymbol{x}}) + 3\delta^3E_{i}^{(3)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]),\\\widetilde \Delta_{i}^{(2)} f({\boldsymbol{x}})= \delta^2 \partial_{i}^2f({\boldsymbol{x}}) + 5 \delta^3E_{i}^{(3)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]).\end{gather*}
\begin{gather*}\widetilde \Delta_{i}^{(1)} f({\boldsymbol{x}}) = \delta \partial_{i}f({\boldsymbol{x}}) + 3\delta^3E_{i}^{(3)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]),\\\widetilde \Delta_{i}^{(2)} f({\boldsymbol{x}})= \delta^2 \partial_{i}^2f({\boldsymbol{x}}) + 5 \delta^3E_{i}^{(3)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]).\end{gather*}
When
![]() $s = 2$
,
$s = 2$
,
 \begin{gather*}\Delta_{i} f({\boldsymbol{x}}) = \delta\partial_{i} f({\boldsymbol{x}}) +\frac{1}{2}\delta^2 E_{i}^{(2)}([{\boldsymbol{x}}, {\boldsymbol{x}} +\delta {\boldsymbol{e}}_{i}]),\\\Delta_{i}^2 f({\boldsymbol{x}}) = 2\delta^2 E_{i}^{(2)}([{\boldsymbol{x}},{\boldsymbol{x}} + 2\delta {\boldsymbol{e}}_{i}]), \quad \text{ and } \quad\Delta_{i}^3 f({\boldsymbol{x}}) = 4\delta^2 E_{i}^{(2)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]),\end{gather*}
\begin{gather*}\Delta_{i} f({\boldsymbol{x}}) = \delta\partial_{i} f({\boldsymbol{x}}) +\frac{1}{2}\delta^2 E_{i}^{(2)}([{\boldsymbol{x}}, {\boldsymbol{x}} +\delta {\boldsymbol{e}}_{i}]),\\\Delta_{i}^2 f({\boldsymbol{x}}) = 2\delta^2 E_{i}^{(2)}([{\boldsymbol{x}},{\boldsymbol{x}} + 2\delta {\boldsymbol{e}}_{i}]), \quad \text{ and } \quad\Delta_{i}^3 f({\boldsymbol{x}}) = 4\delta^2 E_{i}^{(2)}([{\boldsymbol{x}},{\boldsymbol{x}} + 3\delta {\boldsymbol{e}}_{i}]),\end{gather*}
implying that
Proof of Lemma A.4. Let us first consider the case when
![]() $d = 1$
. According to the original definition of A f(x) in Theorem 1 of [Reference Braverman5],
$d = 1$
. According to the original definition of A f(x) in Theorem 1 of [Reference Braverman5],
where
 \begin{align}P_{k}(x) =&\ f(\delta k) + \Big(\frac{x-\delta k}{\delta} \Big)(\Delta - \frac{1}{2}\Delta^2 + \frac{1}{3}\Delta^3) f(\delta k) \notag\\&+ \frac{1}{2} \Big(\frac{x-\delta k}{\delta} \Big)^2\big(\Delta^2 - \Delta^3\big) f(\delta k) + \frac{1}{6} \Big(\frac{x-\delta k}{\delta} \Big)^3 \Delta^3 f(\delta k)\notag\\& -\frac{23}{3} \Big(\frac{x-\delta k}{\delta} \Big)^4 \Delta^4 f(\delta k) +\frac{41}{2} \Big(\frac{x-\delta k}{\delta} \Big)^5\Delta^4 f(\delta k) \notag\\&- \frac{55}{3} \Big(\frac{x-\delta k}{\delta} \Big)^6\Delta^4 f(\delta k) +\frac{11}{2} \Big(\frac{x-\delta k}{\delta} \Big)^7\Delta^4 f(\delta k) , \quad x \in \mathbb{R}. \end{align}
\begin{align}P_{k}(x) =&\ f(\delta k) + \Big(\frac{x-\delta k}{\delta} \Big)(\Delta - \frac{1}{2}\Delta^2 + \frac{1}{3}\Delta^3) f(\delta k) \notag\\&+ \frac{1}{2} \Big(\frac{x-\delta k}{\delta} \Big)^2\big(\Delta^2 - \Delta^3\big) f(\delta k) + \frac{1}{6} \Big(\frac{x-\delta k}{\delta} \Big)^3 \Delta^3 f(\delta k)\notag\\& -\frac{23}{3} \Big(\frac{x-\delta k}{\delta} \Big)^4 \Delta^4 f(\delta k) +\frac{41}{2} \Big(\frac{x-\delta k}{\delta} \Big)^5\Delta^4 f(\delta k) \notag\\&- \frac{55}{3} \Big(\frac{x-\delta k}{\delta} \Big)^6\Delta^4 f(\delta k) +\frac{11}{2} \Big(\frac{x-\delta k}{\delta} \Big)^7\Delta^4 f(\delta k) , \quad x \in \mathbb{R}. \end{align}
We can also write A f(x) as the weighted sum
 \begin{align*}A f(x) = \sum_{i=0}^{4} \alpha^{k(x)}_{k(x)+i}(x)f(\delta(k(x)+i)),\end{align*}
\begin{align*}A f(x) = \sum_{i=0}^{4} \alpha^{k(x)}_{k(x)+i}(x)f(\delta(k(x)+i)),\end{align*}
where the weights
![]() $\alpha^{k}_{k+i}(x)$
are defined by the corresponding polynomial
$\alpha^{k}_{k+i}(x)$
are defined by the corresponding polynomial
![]() $P_{k}(x)$
. Now
$P_{k}(x)$
. Now
![]() $A f \in C^{3}(\mathbb{R})$
by Theorem A.1, meaning that
$A f \in C^{3}(\mathbb{R})$
by Theorem A.1, meaning that
![]() $\partial^{j} A f(\delta k(x))$
equals the corresponding right derivative of
$\partial^{j} A f(\delta k(x))$
equals the corresponding right derivative of
![]() $P_{k(x)}(x)$
at
$P_{k(x)}(x)$
at
![]() $x =\delta k(x)$
for
$x =\delta k(x)$
for
![]() $1 \leq j \leq 3$
. The result follows immediately by inspecting the derivatives of (A.20).
$1 \leq j \leq 3$
. The result follows immediately by inspecting the derivatives of (A.20).
When
![]() $d > 1$
, the proof is similar. Let us write
$d > 1$
, the proof is similar. Let us write
![]() ${\boldsymbol{k}}$
instead of
${\boldsymbol{k}}$
instead of
![]() $k({\boldsymbol{x}})$
for notational convenience. Since
$k({\boldsymbol{x}})$
for notational convenience. Since
![]() $Af({\boldsymbol{x}}) \in C^{3}(\mathbb{R}^{d})$
by Theorem A.1, we fix
$Af({\boldsymbol{x}}) \in C^{3}(\mathbb{R}^{d})$
by Theorem A.1, we fix
![]() ${\boldsymbol{a}}$
with
${\boldsymbol{a}}$
with
![]() $1 \leq\Vert{\boldsymbol{a}}\Vert_{1} \leq 3$
and consider
$1 \leq\Vert{\boldsymbol{a}}\Vert_{1} \leq 3$
and consider
 \begin{align*}D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}) =&\ D^{{\boldsymbol{a}}}\Bigg( \sum_{i_d = 0}^{4} \alpha_{k_d+i_d}^{k_d}(x_d)\cdots \sum_{i_1 = 0}^{4} \alpha_{k_1+i_1}^{k_1}(x_1) f(\delta({\boldsymbol{k}}+{\boldsymbol{i}}))\Bigg) \\=&\ \Bigg(\sum_{i_d = 0}^{4} \partial_{d}^{a_d}\alpha_{k_d+i_d}^{k_d}(x_d)\cdots \bigg(\sum_{i_2 = 0}^{4} \partial_{2}^{a_2}\alpha_{k_2+i_2}^{k_2}(x_2)\bigg(\sum_{i_1 = 0}^{4} \partial_{1}^{a_1}\alpha_{k_1+i_1}^{k_1}(x_1) f(\delta({\boldsymbol{k}}+{\boldsymbol{i}})) \bigg)\bigg)\Bigg).\end{align*}
\begin{align*}D^{{\boldsymbol{a}}} A f({\boldsymbol{x}}) =&\ D^{{\boldsymbol{a}}}\Bigg( \sum_{i_d = 0}^{4} \alpha_{k_d+i_d}^{k_d}(x_d)\cdots \sum_{i_1 = 0}^{4} \alpha_{k_1+i_1}^{k_1}(x_1) f(\delta({\boldsymbol{k}}+{\boldsymbol{i}}))\Bigg) \\=&\ \Bigg(\sum_{i_d = 0}^{4} \partial_{d}^{a_d}\alpha_{k_d+i_d}^{k_d}(x_d)\cdots \bigg(\sum_{i_2 = 0}^{4} \partial_{2}^{a_2}\alpha_{k_2+i_2}^{k_2}(x_2)\bigg(\sum_{i_1 = 0}^{4} \partial_{1}^{a_1}\alpha_{k_1+i_1}^{k_1}(x_1) f(\delta({\boldsymbol{k}}+{\boldsymbol{i}})) \bigg)\bigg)\Bigg).\end{align*}
The first equality follows from (A.1) of Theorem A.1. If we think of the innermost sum as a one-dimensional function in
![]() $x_1$
only, it follows that
$x_1$
only, it follows that
 \begin{align*}\sum_{i_1 = 0}^{4} \partial_{1}^{a_1}\alpha_{k_1+i_1}^{k_1}(\delta k_1) f(\delta({\boldsymbol{k}}+{\boldsymbol{i}})) = \delta^{-a_1}\widetilde \Delta^{(a_1)}_{1} f\big(\delta ({\boldsymbol{k}}+(0,i_2,\ldots,i_{d}))\big).\end{align*}
\begin{align*}\sum_{i_1 = 0}^{4} \partial_{1}^{a_1}\alpha_{k_1+i_1}^{k_1}(\delta k_1) f(\delta({\boldsymbol{k}}+{\boldsymbol{i}})) = \delta^{-a_1}\widetilde \Delta^{(a_1)}_{1} f\big(\delta ({\boldsymbol{k}}+(0,i_2,\ldots,i_{d}))\big).\end{align*}
Proceeding identically along each of the remaining dimensions yields the result.
Before concluding this section, we prove Lemmas 2.4 and 2.5.
Proof of Lemma 2.4. Fix
![]() $h \in \mathcal{M}_{4}$
and note that
$h \in \mathcal{M}_{4}$
and note that
where
![]() $A h(\!\cdot\!)$
is understood to be the operator A applied to the restriction of
$A h(\!\cdot\!)$
is understood to be the operator A applied to the restriction of
![]() $h({\boldsymbol{x}})$
to
$h({\boldsymbol{x}})$
to
![]() $\delta \mathbb{Z}^{d}$
. Proposition A.1 and the fact that
$\delta \mathbb{Z}^{d}$
. Proposition A.1 and the fact that
![]() $h \in\mathcal{M}_{4}$
imply that
$h \in\mathcal{M}_{4}$
imply that
Furthermore, (A.13) implies that the restriction of
![]() $h({\boldsymbol{x}})$
to
$h({\boldsymbol{x}})$
to
![]() $\delta \mathbb{Z}^{d}$
belongs to
$\delta \mathbb{Z}^{d}$
belongs to
![]() $\mathcal{M}_{\mathrm{disc},4}$
and, therefore,
$\mathcal{M}_{\mathrm{disc},4}$
and, therefore,
Proof of Lemma 2.5. Since
![]() $h \in \mathcal{M}_{\mathrm{disc},4}$
implies that
$h \in \mathcal{M}_{\mathrm{disc},4}$
implies that
![]() $\vert h({\boldsymbol{u}} + \delta {\boldsymbol{e}}_{i}) - h({\boldsymbol{u}})\vert \leq \delta$
for all
$\vert h({\boldsymbol{u}} + \delta {\boldsymbol{e}}_{i}) - h({\boldsymbol{u}})\vert \leq \delta$
for all
![]() $1 \leq i \leq K-1$
, it follows that
$1 \leq i \leq K-1$
, it follows that
Furthermore, (A.3) of Theorem A.1 and the fact that
![]() $h \in \mathcal{M}_{\mathrm{disc},4}$
imply that the first-order partial derivatives of
$h \in \mathcal{M}_{\mathrm{disc},4}$
imply that the first-order partial derivatives of
![]() $A h({\boldsymbol{x}})$
are bounded by
$A h({\boldsymbol{x}})$
are bounded by
![]() $C_{A.4}(d)$
, and therefore,
$C_{A.4}(d)$
, and therefore,
where the last inequality follows from
![]() $A h(0) = h(0)$
and
$A h(0) = h(0)$
and
![]() ${\boldsymbol{Z}} \in \bar \nabla^{K}$
. To bound
${\boldsymbol{Z}} \in \bar \nabla^{K}$
. To bound
![]() $\vert\mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{Z}})\vert$
, we recall that
$\vert\mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{Z}})\vert$
, we recall that
 \begin{align*}\mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{x}}) = \frac{1}{2} \sum_{i=1}^{K-1} (\beta_{i} - s x_{i}) \partial_{i} A f_h({\boldsymbol{x}}) + \frac{1}{2} \sum_{i,j = 1}^{K-1} x_{i}(\delta_{ij} - x_{j}) \partial_{i}\partial_{j} A f_h({\boldsymbol{x}}), \quad {\boldsymbol{x}} \in \bar \nabla^{K}.\end{align*}
\begin{align*}\mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{x}}) = \frac{1}{2} \sum_{i=1}^{K-1} (\beta_{i} - s x_{i}) \partial_{i} A f_h({\boldsymbol{x}}) + \frac{1}{2} \sum_{i,j = 1}^{K-1} x_{i}(\delta_{ij} - x_{j}) \partial_{i}\partial_{j} A f_h({\boldsymbol{x}}), \quad {\boldsymbol{x}} \in \bar \nabla^{K}.\end{align*}
Note that
![]() $\vert\beta_{i} - s x_{i}\vert \leq s$
,
$\vert\beta_{i} - s x_{i}\vert \leq s$
,
![]() $\vert x_{i}(\delta_{ij}-x_{j})\vert \leq 1$
, and that (A.3) of Theorem A.1 implies that
$\vert x_{i}(\delta_{ij}-x_{j})\vert \leq 1$
, and that (A.3) of Theorem A.1 implies that

Recalling from (B.7) that
![]() $\Vert f_h\Vert \leq \delta^{-1} K B_{1}(f_h)$
, we combine the bounds to arrive at
$\Vert f_h\Vert \leq \delta^{-1} K B_{1}(f_h)$
, we combine the bounds to arrive at

where in the last inequality we used
![]() $\delta \leq 1$
.
$\delta \leq 1$
.
Appendix A. Explicit constants in Theorem A.1
Proof of (A.4) and (A.8). We show that

which implies the result. Consider first the case when
![]() $d = 1$
; we want a bound on A f(x) and its first four derivatives. For any
$d = 1$
; we want a bound on A f(x) and its first four derivatives. For any
![]() $f\,:\,\mathbb{Z}\to \mathbb{R}$
, (A.1) of [Reference Braverman5] states that
$f\,:\,\mathbb{Z}\to \mathbb{R}$
, (A.1) of [Reference Braverman5] states that
 \begin{align*}A f(x) = \sum_{i=0}^{4} \alpha^{k(x)}_{k(x)+i}(x)f(\delta(k(x)+i)) = P_{k(x)}(x),\end{align*}
\begin{align*}A f(x) = \sum_{i=0}^{4} \alpha^{k(x)}_{k(x)+i}(x)f(\delta(k(x)+i)) = P_{k(x)}(x),\end{align*}
where
 \begin{align}P_{k}(x) =&\ f(\delta k) + \Big(\frac{x-\delta k}{\delta} \Big)(\Delta - \frac{1}{2}\Delta^2 + \frac{1}{3}\Delta^3) f(\delta k) \notag\\&+ \frac{1}{2} \Big(\frac{x-\delta k}{\delta} \Big)^2\big(\Delta^2 - \Delta^3\big) f(\delta k) + \frac{1}{6} \Big(\frac{x-\delta k}{\delta} \Big)^3 \Delta^3 f(\delta k)\notag\\& -\frac{23}{3} \Big(\frac{x-\delta k}{\delta} \Big)^4 \Delta^4 f(\delta k) +\frac{41}{2} \Big(\frac{x-\delta k}{\delta} \Big)^5\Delta^4 f(\delta k) \notag\\&- \frac{55}{3} \Big(\frac{x-\delta k}{\delta} \Big)^6\Delta^4 f(\delta k) +\frac{11}{2} \Big(\frac{x-\delta k}{\delta} \Big)^7\Delta^4 f(\delta k) , \quad x \in \mathbb{R}. \end{align}
\begin{align}P_{k}(x) =&\ f(\delta k) + \Big(\frac{x-\delta k}{\delta} \Big)(\Delta - \frac{1}{2}\Delta^2 + \frac{1}{3}\Delta^3) f(\delta k) \notag\\&+ \frac{1}{2} \Big(\frac{x-\delta k}{\delta} \Big)^2\big(\Delta^2 - \Delta^3\big) f(\delta k) + \frac{1}{6} \Big(\frac{x-\delta k}{\delta} \Big)^3 \Delta^3 f(\delta k)\notag\\& -\frac{23}{3} \Big(\frac{x-\delta k}{\delta} \Big)^4 \Delta^4 f(\delta k) +\frac{41}{2} \Big(\frac{x-\delta k}{\delta} \Big)^5\Delta^4 f(\delta k) \notag\\&- \frac{55}{3} \Big(\frac{x-\delta k}{\delta} \Big)^6\Delta^4 f(\delta k) +\frac{11}{2} \Big(\frac{x-\delta k}{\delta} \Big)^7\Delta^4 f(\delta k) , \quad x \in \mathbb{R}. \end{align}
To bound
![]() $\vert A f(x)\vert$
, we need to bound each of the terms on the right-hand side of (A.20). For instance,
$\vert A f(x)\vert$
, we need to bound each of the terms on the right-hand side of (A.20). For instance,
 \begin{align*}(\Delta - \frac{1}{2}\Delta^2 + \frac{1}{3}\Delta^3) f(\delta k) =& - f(\delta k) + f(\delta (k+1))\\&- \frac{1}{2}\big( f(\delta k) - 2 f(\delta (k+1)) + f(\delta (k+2))\big)\\&+ \frac{1}{3}\big( \!-f(\delta k) +3 f(\delta (k+1)) -3 f(\delta (k+2)) + f(\delta (k+3))\big),\end{align*}
\begin{align*}(\Delta - \frac{1}{2}\Delta^2 + \frac{1}{3}\Delta^3) f(\delta k) =& - f(\delta k) + f(\delta (k+1))\\&- \frac{1}{2}\big( f(\delta k) - 2 f(\delta (k+1)) + f(\delta (k+2))\big)\\&+ \frac{1}{3}\big( \!-f(\delta k) +3 f(\delta (k+1)) -3 f(\delta (k+2)) + f(\delta (k+3))\big),\end{align*}
implying that
Proceeding similarly with each of the terms on the right-hand side of (A.20), we see that
![]() $\vert A f(x)\vert$
is bounded by
$\vert A f(x)\vert$
is bounded by
 \begin{align*}& \Big(1 + 3\Big(\frac{x-\delta k(x)}{\delta}\Big) + \frac{5}{2} \Big(\frac{x-\delta k(x)}{\delta}\Big)^2 + \frac{1}{2} \Big(\frac{x-\delta k(x)}{\delta}\Big)^3 + \frac{23}{3} \times 6 \Big(\frac{x-\delta k(x)}{\delta}\Big)^4\\&+ \frac{41}{2} \times 6 \Big(\frac{x-\delta k(x)}{\delta}\Big)^5 + \frac{55}{3} \times 6\Big(\frac{x-\delta (x)}{\delta}\Big)^6 + \frac{11}{2} \times 6 \Big(\frac{x-\delta k(x)}{\delta}\Big)^7 \Big) \max_{0 \leq i \leq 4 } \vert f(k(x)+i)\vert\\&\qquad\leq 319 \times 5 \max_{0 \leq i \leq 4 } \vert f(k(x)+i)\vert.\end{align*}
\begin{align*}& \Big(1 + 3\Big(\frac{x-\delta k(x)}{\delta}\Big) + \frac{5}{2} \Big(\frac{x-\delta k(x)}{\delta}\Big)^2 + \frac{1}{2} \Big(\frac{x-\delta k(x)}{\delta}\Big)^3 + \frac{23}{3} \times 6 \Big(\frac{x-\delta k(x)}{\delta}\Big)^4\\&+ \frac{41}{2} \times 6 \Big(\frac{x-\delta k(x)}{\delta}\Big)^5 + \frac{55}{3} \times 6\Big(\frac{x-\delta (x)}{\delta}\Big)^6 + \frac{11}{2} \times 6 \Big(\frac{x-\delta k(x)}{\delta}\Big)^7 \Big) \max_{0 \leq i \leq 4 } \vert f(k(x)+i)\vert\\&\qquad\leq 319 \times 5 \max_{0 \leq i \leq 4 } \vert f(k(x)+i)\vert.\end{align*}
Note that (A.8) follows from a similar argument because
![]() $\alpha_{k+i}^{k}(x)$
is the coefficient corresponding to
$\alpha_{k+i}^{k}(x)$
is the coefficient corresponding to
![]() $f(\delta(k+i))$
. To bound
$f(\delta(k+i))$
. To bound
![]() $\vert \partial A f(x)\vert$
, we differentiate (A.20) once to get
$\vert \partial A f(x)\vert$
, we differentiate (A.20) once to get
 \begin{align*}\partial P_{k}(x) =&\ \frac{1}{\delta} \bigg( (1 - \frac{1}{2}\Delta + \frac{1}{3}\Delta^2) \Delta f(\delta k) \notag\\&\hskip5.5mm+ \frac{1}{2} \times 2 \Big(\frac{x-\delta k}{\delta} \Big)\big(\Delta - \Delta^2\big) ( \Delta f(\delta k)) + \frac{1}{6} \times 3 \Big(\frac{x-\delta k}{\delta} \Big)^2 \Delta^2 ( \Delta f(\delta k))\notag\\&\hskip5.5mm -\frac{23}{3} \times 4 \Big(\frac{x-\delta k}{\delta} \Big)^3 \Delta^3 ( \Delta f(\delta k)) +\frac{41}{2} \times 5 \Big(\frac{x-\delta k}{\delta} \Big)^4\Delta^3 ( \Delta f(\delta k)) \notag\\&\hskip5.5mm- \frac{55}{3} \times 6 \Big(\frac{x-\delta k}{\delta} \Big)^5\Delta^3 ( \Delta f(\delta k)) +\frac{11}{2} \times 7 \Big(\frac{x-\delta k}{\delta} \Big)^6\Delta^3 ( \Delta f(\delta k)) \bigg) , \quad x \in \mathbb{R}.\end{align*}
\begin{align*}\partial P_{k}(x) =&\ \frac{1}{\delta} \bigg( (1 - \frac{1}{2}\Delta + \frac{1}{3}\Delta^2) \Delta f(\delta k) \notag\\&\hskip5.5mm+ \frac{1}{2} \times 2 \Big(\frac{x-\delta k}{\delta} \Big)\big(\Delta - \Delta^2\big) ( \Delta f(\delta k)) + \frac{1}{6} \times 3 \Big(\frac{x-\delta k}{\delta} \Big)^2 \Delta^2 ( \Delta f(\delta k))\notag\\&\hskip5.5mm -\frac{23}{3} \times 4 \Big(\frac{x-\delta k}{\delta} \Big)^3 \Delta^3 ( \Delta f(\delta k)) +\frac{41}{2} \times 5 \Big(\frac{x-\delta k}{\delta} \Big)^4\Delta^3 ( \Delta f(\delta k)) \notag\\&\hskip5.5mm- \frac{55}{3} \times 6 \Big(\frac{x-\delta k}{\delta} \Big)^5\Delta^3 ( \Delta f(\delta k)) +\frac{11}{2} \times 7 \Big(\frac{x-\delta k}{\delta} \Big)^6\Delta^3 ( \Delta f(\delta k)) \bigg) , \quad x \in \mathbb{R}.\end{align*}
Bounding the right-hand side the same way as before yields
 \begin{align*}\vert \partial A f(x)\vert \leq&\ \frac{1}{\delta} \Big( (1+1/2+2/3) + (1+2) \Big(\frac{x-\delta k(x)}{\delta}\Big) + \frac{3}{6}\times 2 \Big(\frac{x-\delta k(x)}{\delta}\Big)^2\\&+ \frac{23}{3} \times 4 \times 3 \Big(\frac{x-\delta k(x)}{\delta}\Big)^3 + \frac{41}{2}\times 5 \times 3 \Big(\frac{x-\delta k(x)}{\delta}\Big)^4\\&+ \frac{55}{3}\times 6 \times 3\Big(\frac{x-\delta (x)}{\delta}\Big)^5 + \frac{11}{2} \times 7 \times 3\Big(\frac{x-\delta k(x)}{\delta}\Big)^6 \Big) \times \max_{0 \leq i \leq 3} \vert\Delta f(k(x)+i)\vert\\\leq&\ \frac{1}{\delta} 852 \times 4 \max_{0 \leq i \leq 3} \vert\Delta f(k(x)+i)\vert.\end{align*}
\begin{align*}\vert \partial A f(x)\vert \leq&\ \frac{1}{\delta} \Big( (1+1/2+2/3) + (1+2) \Big(\frac{x-\delta k(x)}{\delta}\Big) + \frac{3}{6}\times 2 \Big(\frac{x-\delta k(x)}{\delta}\Big)^2\\&+ \frac{23}{3} \times 4 \times 3 \Big(\frac{x-\delta k(x)}{\delta}\Big)^3 + \frac{41}{2}\times 5 \times 3 \Big(\frac{x-\delta k(x)}{\delta}\Big)^4\\&+ \frac{55}{3}\times 6 \times 3\Big(\frac{x-\delta (x)}{\delta}\Big)^5 + \frac{11}{2} \times 7 \times 3\Big(\frac{x-\delta k(x)}{\delta}\Big)^6 \Big) \times \max_{0 \leq i \leq 3} \vert\Delta f(k(x)+i)\vert\\\leq&\ \frac{1}{\delta} 852 \times 4 \max_{0 \leq i \leq 3} \vert\Delta f(k(x)+i)\vert.\end{align*}
Similarly,
 \begin{align*}\partial^{2} P_{k}(x) =&\ \frac{1}{\delta^2} \bigg( \big(1 - \Delta\big) ( \Delta^2 f(\delta k)) + \Big(\frac{x-\delta k}{\delta} \Big) \Delta ( \Delta^2 f(\delta k))\notag\\& -23 \times 4 \Big(\frac{x-\delta k}{\delta} \Big)^2 \Delta^2 ( \Delta^2 f(\delta k)) +81\times 5 \Big(\frac{x-\delta k}{\delta} \Big)^3\Delta^2 ( \Delta^2 f(\delta k)) \notag\\&- \frac{55}{3} \times 6 \times 5 \Big(\frac{x-\delta k}{\delta} \Big)^4\Delta^2 ( \Delta^2 f(\delta k)) \\&+\frac{11}{2} \times 7 \times 6 \Big(\frac{x-\delta k}{\delta} \Big)^5\Delta^2 ( \Delta^2 f(\delta k)) \bigg) , \quad x \in \mathbb{R},\end{align*}
\begin{align*}\partial^{2} P_{k}(x) =&\ \frac{1}{\delta^2} \bigg( \big(1 - \Delta\big) ( \Delta^2 f(\delta k)) + \Big(\frac{x-\delta k}{\delta} \Big) \Delta ( \Delta^2 f(\delta k))\notag\\& -23 \times 4 \Big(\frac{x-\delta k}{\delta} \Big)^2 \Delta^2 ( \Delta^2 f(\delta k)) +81\times 5 \Big(\frac{x-\delta k}{\delta} \Big)^3\Delta^2 ( \Delta^2 f(\delta k)) \notag\\&- \frac{55}{3} \times 6 \times 5 \Big(\frac{x-\delta k}{\delta} \Big)^4\Delta^2 ( \Delta^2 f(\delta k)) \\&+\frac{11}{2} \times 7 \times 6 \Big(\frac{x-\delta k}{\delta} \Big)^5\Delta^2 ( \Delta^2 f(\delta k)) \bigg) , \quad x \in \mathbb{R},\end{align*}
 \begin{align*}\partial^{3} P_{k}(x) =&\ \frac{1}{\delta^3} \bigg( \Delta^3 f(\delta k) -23\! \times 4 \times 2 \Big(\frac{x-\delta k}{\delta} \Big) \Delta ( \Delta^3 f(\delta k)) +81\!\times 5\times 3 \Big(\frac{x-\delta k}{\delta} \Big)^2\Delta ( \Delta^3 f(\delta k)) \notag\\&- \frac{55}{3} \times 6 \times 5 \times 4 \Big(\frac{x-\delta k}{\delta} \Big)^3\Delta ( \Delta^3 f(\delta k)) \\&+\frac{11}{2} \times 7 \times 6 \times 5 \Big(\frac{x-\delta k}{\delta} \Big)^4\Delta ( \Delta^3 f(\delta k)) \bigg) , \quad x \in \mathbb{R},\end{align*}
\begin{align*}\partial^{3} P_{k}(x) =&\ \frac{1}{\delta^3} \bigg( \Delta^3 f(\delta k) -23\! \times 4 \times 2 \Big(\frac{x-\delta k}{\delta} \Big) \Delta ( \Delta^3 f(\delta k)) +81\!\times 5\times 3 \Big(\frac{x-\delta k}{\delta} \Big)^2\Delta ( \Delta^3 f(\delta k)) \notag\\&- \frac{55}{3} \times 6 \times 5 \times 4 \Big(\frac{x-\delta k}{\delta} \Big)^3\Delta ( \Delta^3 f(\delta k)) \\&+\frac{11}{2} \times 7 \times 6 \times 5 \Big(\frac{x-\delta k}{\delta} \Big)^4\Delta ( \Delta^3 f(\delta k)) \bigg) , \quad x \in \mathbb{R},\end{align*}
and
 \begin{align*}\partial^{4} P_{k}(x) =&\ \frac{1}{\delta^4} \bigg( -23 \times 4 \times 2 \Delta^4 f(\delta k) +81\times 5\times 3 \times 2 \Big(\frac{x-\delta k}{\delta} \Big) \Delta^4 f(\delta k) \notag\\&- \frac{55}{3} \times 6 \times 5 \times 4 \times 3 \Big(\frac{x-\delta k}{\delta} \Big)^2 \Delta^4 f(\delta k) \\&+\frac{11}{2} \times 7 \times 6 \times 5 \times 4 \Big(\frac{x-\delta k}{\delta} \Big)^4 \Delta^4 f(\delta k) \bigg) , \quad x \in \mathbb{R},\end{align*}
\begin{align*}\partial^{4} P_{k}(x) =&\ \frac{1}{\delta^4} \bigg( -23 \times 4 \times 2 \Delta^4 f(\delta k) +81\times 5\times 3 \times 2 \Big(\frac{x-\delta k}{\delta} \Big) \Delta^4 f(\delta k) \notag\\&- \frac{55}{3} \times 6 \times 5 \times 4 \times 3 \Big(\frac{x-\delta k}{\delta} \Big)^2 \Delta^4 f(\delta k) \\&+\frac{11}{2} \times 7 \times 6 \times 5 \times 4 \Big(\frac{x-\delta k}{\delta} \Big)^4 \Delta^4 f(\delta k) \bigg) , \quad x \in \mathbb{R},\end{align*}
yield the bounds
 \begin{gather*}\vert \partial^2 A f(x)\vert \leq \frac{1}{\delta^2} 2559 \times 3 \max_{0 \leq i \leq 2} \vert\Delta^2 f(k(x)+i)\vert,\\\vert \partial^3 A f(x)\vert \leq \frac{1}{\delta^3} 4775 \times 2 \max_{0 \leq i \leq 1} \vert\Delta^3 f(k(x)+i)\vert,\\\vert \partial^4 A f(x)\vert \leq \frac{1}{\delta^4} 11404 \vert\Delta^4 f(\delta k(x))\vert.\end{gather*}
\begin{gather*}\vert \partial^2 A f(x)\vert \leq \frac{1}{\delta^2} 2559 \times 3 \max_{0 \leq i \leq 2} \vert\Delta^2 f(k(x)+i)\vert,\\\vert \partial^3 A f(x)\vert \leq \frac{1}{\delta^3} 4775 \times 2 \max_{0 \leq i \leq 1} \vert\Delta^3 f(k(x)+i)\vert,\\\vert \partial^4 A f(x)\vert \leq \frac{1}{\delta^4} 11404 \vert\Delta^4 f(\delta k(x))\vert.\end{gather*}
When
![]() $d > 1$
, we recall from (A.1) that
$d > 1$
, we recall from (A.1) that
 \begin{align*}A f({\boldsymbol{x}}) =&\ \sum_{i_d = 0}^{4} \alpha_{k_d({\boldsymbol{x}})+i_d}^{k_d({\boldsymbol{x}})}(x_d)\cdots \sum_{i_1 = 0}^{4} \alpha_{k_1({\boldsymbol{x}})+i_1}^{k_1({\boldsymbol{x}})}(x_1) f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})).\end{align*}
\begin{align*}A f({\boldsymbol{x}}) =&\ \sum_{i_d = 0}^{4} \alpha_{k_d({\boldsymbol{x}})+i_d}^{k_d({\boldsymbol{x}})}(x_d)\cdots \sum_{i_1 = 0}^{4} \alpha_{k_1({\boldsymbol{x}})+i_1}^{k_1({\boldsymbol{x}})}(x_1) f(\delta(k({\boldsymbol{x}})+{\boldsymbol{i}})).\end{align*}
The result follows by applying the bounds from the
![]() $d=1$
case along each dimension.
$d=1$
case along each dimension.
Appendix B. Generator expansion and Stein factors
This appendix is dedicated to proving Lemmas 2.2 and 2.3. Recall that, for
![]() ${\boldsymbol{x}} \in\mathbb{R}^{K-1}$
, we define
${\boldsymbol{x}} \in\mathbb{R}^{K-1}$
, we define
![]() $k({\boldsymbol{x}})$
by
$k({\boldsymbol{x}})$
by
![]() $k_{j}({\boldsymbol{x}}) = \lfloor x_j/\delta\rfloor$
, that
$k_{j}({\boldsymbol{x}}) = \lfloor x_j/\delta\rfloor$
, that
![]() $\delta = 1/N$
,
$\delta = 1/N$
,
![]() $\nabla^{K}_{N}$
is defined in (2.7), and that
$\nabla^{K}_{N}$
is defined in (2.7), and that
![]() $\bar\nabla^{K}_{N} = \text{Conv}(\nabla^{K}_{N})$
. We may assume without loss of generality that
$\bar\nabla^{K}_{N} = \text{Conv}(\nabla^{K}_{N})$
. We may assume without loss of generality that
![]() $100K^2 < N$
, which implies that
$100K^2 < N$
, which implies that
![]() $\nabla^{K}_{N} \neq\emptyset$
, because the claim in Lemma 2.2 holds trivially for all
$\nabla^{K}_{N} \neq\emptyset$
, because the claim in Lemma 2.2 holds trivially for all
![]() $0 < N \leq 100K^{2}$
(since this covers a finite number of N). We claim that
$0 < N \leq 100K^{2}$
(since this covers a finite number of N). We claim that
We argue this as follows. Since
![]() $0 \leq \delta k({\boldsymbol{x}}) \leq {\boldsymbol{x}}$
, then
$0 \leq \delta k({\boldsymbol{x}}) \leq {\boldsymbol{x}}$
, then
![]() $\delta k({\boldsymbol{x}}) \in \nabla^{K}_{N}$
for any
$\delta k({\boldsymbol{x}}) \in \nabla^{K}_{N}$
for any
![]() ${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
, because
${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
, because
![]() $ \delta \sum_{j=1}^{K-1} k_j({\boldsymbol{x}}) \leq \sum_{j=1}^{K-1} x_j$
. Thus, for all
$ \delta \sum_{j=1}^{K-1} k_j({\boldsymbol{x}}) \leq \sum_{j=1}^{K-1} x_j$
. Thus, for all
![]() $0 \leq i \leq 10{\boldsymbol{e}}$
,
$0 \leq i \leq 10{\boldsymbol{e}}$
,
 \begin{align*}\delta \sum_{j=1}^{K-1} (k_j({\boldsymbol{x}}) + i_j) \leq 1 - 10K/\sqrt{N} + 10K/N < 1,\end{align*}
\begin{align*}\delta \sum_{j=1}^{K-1} (k_j({\boldsymbol{x}}) + i_j) \leq 1 - 10K/\sqrt{N} + 10K/N < 1,\end{align*}
implying (B.1). Combining (B.1) with (A.1) of Theorem A.1 implies that
![]() $A (\mathcal{G}_{{\boldsymbol{U}}} A f_h)({\boldsymbol{x}})$
is well defined if
$A (\mathcal{G}_{{\boldsymbol{U}}} A f_h)({\boldsymbol{x}})$
is well defined if
![]() ${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
. To derive an expression for
${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
. To derive an expression for
![]() $A(\mathcal{G}_{{\boldsymbol{U}}} A f_h)({\boldsymbol{x}})$
, we define
$A(\mathcal{G}_{{\boldsymbol{U}}} A f_h)({\boldsymbol{x}})$
, we define
 \begin{gather*}b_{i}({\boldsymbol{u}}) = \mathbb{E}_{u}(U_i(1) - u_i),\\a_{ij}({\boldsymbol{u}}) = \mathbb{E}_{u}(U_i(1) - u_i)(U_j(1) - u_j),\\c_{ijk}({\boldsymbol{u}}) = \mathbb{E}_{u}(U_i(1) - u_i)(U_j(1) - u_j)(U_{k}(1)-u_{k}),\\\bar d_{ijk\ell}({\boldsymbol{u}}) = \mathbb{E}_{u} \vert(U_i(1) -u_i)(U_j(1) - u_j)(U_{k}(1)-u_{k})(U_{\ell}(1)-u_{\ell})\vert, \quad{\boldsymbol{u}} \in \nabla^{K}.\end{gather*}
\begin{gather*}b_{i}({\boldsymbol{u}}) = \mathbb{E}_{u}(U_i(1) - u_i),\\a_{ij}({\boldsymbol{u}}) = \mathbb{E}_{u}(U_i(1) - u_i)(U_j(1) - u_j),\\c_{ijk}({\boldsymbol{u}}) = \mathbb{E}_{u}(U_i(1) - u_i)(U_j(1) - u_j)(U_{k}(1)-u_{k}),\\\bar d_{ijk\ell}({\boldsymbol{u}}) = \mathbb{E}_{u} \vert(U_i(1) -u_i)(U_j(1) - u_j)(U_{k}(1)-u_{k})(U_{\ell}(1)-u_{\ell})\vert, \quad{\boldsymbol{u}} \in \nabla^{K}.\end{gather*}
Since
![]() $A f_h \in C^{3}(\mathbb{R}^{K-1})$
, by Theorem A.1, we know that, for any
$A f_h \in C^{3}(\mathbb{R}^{K-1})$
, by Theorem A.1, we know that, for any
![]() ${\boldsymbol{u}}\in \nabla^{K}$
,
${\boldsymbol{u}}\in \nabla^{K}$
,
 \begin{align*}\mathcal{G}_{{\boldsymbol{U}}} (A f_h)({\boldsymbol{u}}) &= \mathbb{E}_{{\boldsymbol{u}}} A f_h({\boldsymbol{U}}(1)) - A f_h({\boldsymbol{u}})\\&= \sum_{i=1}^{K-1} b_{i}({\boldsymbol{u}}) \partial_{i} A f_h({\boldsymbol{u}}) + \frac{1}{2}\sum_{i,j=1}^{K-1} a_{ij}({\boldsymbol{u}}) \partial_{i}\partial_{j} A f_h({\boldsymbol{u}})\\& \hskip4mm + \frac{1}{6} \sum_{i,j,k=1}^{K-1} c_{ijk}({\boldsymbol{u}}) \partial_{i}\partial_{j}\partial_{k} A f_h({\boldsymbol{u}}) + \epsilon({\boldsymbol{u}}),\end{align*}
\begin{align*}\mathcal{G}_{{\boldsymbol{U}}} (A f_h)({\boldsymbol{u}}) &= \mathbb{E}_{{\boldsymbol{u}}} A f_h({\boldsymbol{U}}(1)) - A f_h({\boldsymbol{u}})\\&= \sum_{i=1}^{K-1} b_{i}({\boldsymbol{u}}) \partial_{i} A f_h({\boldsymbol{u}}) + \frac{1}{2}\sum_{i,j=1}^{K-1} a_{ij}({\boldsymbol{u}}) \partial_{i}\partial_{j} A f_h({\boldsymbol{u}})\\& \hskip4mm + \frac{1}{6} \sum_{i,j,k=1}^{K-1} c_{ijk}({\boldsymbol{u}}) \partial_{i}\partial_{j}\partial_{k} A f_h({\boldsymbol{u}}) + \epsilon({\boldsymbol{u}}),\end{align*}
where
 \begin{align*}\epsilon({\boldsymbol{u}}) =&\ \frac{1}{6} \sum_{i,j,k=1}^{K-1}\mathbb{E}_{{\boldsymbol{u}}} \Big( (U_i(1) - u_i)(U_j(1) -u_j)(U_{k}(1)-u_{k}) \big(\partial_{i}\partial_{j}\partial_{k}Af_h(\boldsymbol{\xi}) - \partial_{i}\partial_{j}\partial_{k}Af_h({\boldsymbol{u}})\big)\Big),\end{align*}
\begin{align*}\epsilon({\boldsymbol{u}}) =&\ \frac{1}{6} \sum_{i,j,k=1}^{K-1}\mathbb{E}_{{\boldsymbol{u}}} \Big( (U_i(1) - u_i)(U_j(1) -u_j)(U_{k}(1)-u_{k}) \big(\partial_{i}\partial_{j}\partial_{k}Af_h(\boldsymbol{\xi}) - \partial_{i}\partial_{j}\partial_{k}Af_h({\boldsymbol{u}})\big)\Big),\end{align*}
and
![]() $\boldsymbol{\xi}$
is between
$\boldsymbol{\xi}$
is between
![]() ${\boldsymbol{u}}$
and
${\boldsymbol{u}}$
and
![]() ${\boldsymbol{U}}(1)$
. Since A is a linear operator, it follows that, for any
${\boldsymbol{U}}(1)$
. Since A is a linear operator, it follows that, for any
![]() ${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
,
${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
,
 \begin{align}A (\mathcal{G}_{{\boldsymbol{U}}} A f_h)({\boldsymbol{x}}) &= \sum_{i=1}^{K-1} A( b_{i}\partial_{i} A f_h)({\boldsymbol{x}}) + \frac{1}{2}\sum_{i,j =1}^{K-1} A ( a_{ij}\partial_{i}\partial_{j} A f_h)({\boldsymbol{x}}) \notag\\&\hskip4mm + \frac{1}{6} \sum_{i,j,k =1}^{K-1} A ( c_{ijk}\partial_{i}\partial_{j}\partial_{k} A f_h)({\boldsymbol{x}}) + A \epsilon({\boldsymbol{x}}). \end{align}
\begin{align}A (\mathcal{G}_{{\boldsymbol{U}}} A f_h)({\boldsymbol{x}}) &= \sum_{i=1}^{K-1} A( b_{i}\partial_{i} A f_h)({\boldsymbol{x}}) + \frac{1}{2}\sum_{i,j =1}^{K-1} A ( a_{ij}\partial_{i}\partial_{j} A f_h)({\boldsymbol{x}}) \notag\\&\hskip4mm + \frac{1}{6} \sum_{i,j,k =1}^{K-1} A ( c_{ijk}\partial_{i}\partial_{j}\partial_{k} A f_h)({\boldsymbol{x}}) + A \epsilon({\boldsymbol{x}}). \end{align}
We present several lemmas needed to analyze the right-hand side. Recall assumption (1.3) or that
![]() $p_i = \beta_i/(2N) = \delta\beta_{i}/2$
and, subsequently,
$p_i = \beta_i/(2N) = \delta\beta_{i}/2$
and, subsequently,
![]() $\Sigma = \delta s/2$
. Also recall the definition of
$\Sigma = \delta s/2$
. Also recall the definition of
![]() $B_i(\!\cdot\!)$
from (2.1).
$B_i(\!\cdot\!)$
from (2.1).
Lemma B.1. Fix
![]() ${\boldsymbol{u}} \in \nabla^{K}$
and let
${\boldsymbol{u}} \in \nabla^{K}$
and let
![]() $\bar u_{i} = u_{i}\Sigma - p_{i}$
. Then for
$\bar u_{i} = u_{i}\Sigma - p_{i}$
. Then for
![]() $1 \leq i,j \leq K-1$
,
$1 \leq i,j \leq K-1$
,
 \begin{gather*}b_{i}({\boldsymbol{u}}) = - \bar u_{i} \quad \text{ and } \quad a_{ij}({\boldsymbol{u}}) = \bar u_{i}\bar u_{j} + \frac{1}{N}\big(u_{i} - \bar u_{i} \big) \big( \delta_{ij} - ( u_{j} - \bar u_{j})\big),\\B_{1}(b_{i}) \leq \delta^2 s \quad \text{ and } \quad B_{1}(a_{ij}) \leq \delta^2 5(1+s)^2.\end{gather*}
\begin{gather*}b_{i}({\boldsymbol{u}}) = - \bar u_{i} \quad \text{ and } \quad a_{ij}({\boldsymbol{u}}) = \bar u_{i}\bar u_{j} + \frac{1}{N}\big(u_{i} - \bar u_{i} \big) \big( \delta_{ij} - ( u_{j} - \bar u_{j})\big),\\B_{1}(b_{i}) \leq \delta^2 s \quad \text{ and } \quad B_{1}(a_{ij}) \leq \delta^2 5(1+s)^2.\end{gather*}
Furthermore, for any
![]() $1 \leq i,j,k,\ell \leq K-1$
,
$1 \leq i,j,k,\ell \leq K-1$
,
The proof of Lemma B.1 is left to later in this appendix as it essentially has many elementary but tedious moment calculations. Since
![]() $b_{i}({\boldsymbol{u}})$
and
$b_{i}({\boldsymbol{u}})$
and
![]() $a_{ij}({\boldsymbol{u}})$
are polynomials in
$a_{ij}({\boldsymbol{u}})$
are polynomials in
![]() ${\boldsymbol{u}}$
, we let
${\boldsymbol{u}}$
, we let
![]() $b_{i}({\boldsymbol{x}})$
and
$b_{i}({\boldsymbol{x}})$
and
![]() $a_{ij}({\boldsymbol{x}})$
be their natural extensions to
$a_{ij}({\boldsymbol{x}})$
be their natural extensions to
![]() $\bar\nabla^{K}$
. Furthermore, Corollary A.1 implies that
$\bar\nabla^{K}$
. Furthermore, Corollary A.1 implies that
![]() $Ab_{i}({\boldsymbol{x}}) = b_{i}({\boldsymbol{x}})$
and
$Ab_{i}({\boldsymbol{x}}) = b_{i}({\boldsymbol{x}})$
and
![]() $Aa_{ij}({\boldsymbol{x}}) = a_{ij}({\boldsymbol{x}})$
.
$Aa_{ij}({\boldsymbol{x}}) = a_{ij}({\boldsymbol{x}})$
.
Lemma B.2. For any
![]() ${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
,
${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
,
 \begin{gather*}A( b_{i}\partial_{i} A f_h)({\boldsymbol{x}}) = b_i({\boldsymbol{x}}) \partial_{i} A f_{h}({\boldsymbol{x}}) + \tilde \epsilon_{i}({\boldsymbol{x}}), \\A( a_{ij}\partial_{i} A f_h)({\boldsymbol{x}}) = a_{ij}({\boldsymbol{x}})\partial_{i}\partial_{j} A f_{h}({\boldsymbol{x}}) + \tilde \epsilon_{ij}({\boldsymbol{x}}),\\A ( c_{ijk}\partial_{i}\partial_{j}\partial_{k} A f_h)({\boldsymbol{x}}) = \tilde \epsilon_{ijk}({\boldsymbol{x}}),\end{gather*}
\begin{gather*}A( b_{i}\partial_{i} A f_h)({\boldsymbol{x}}) = b_i({\boldsymbol{x}}) \partial_{i} A f_{h}({\boldsymbol{x}}) + \tilde \epsilon_{i}({\boldsymbol{x}}), \\A( a_{ij}\partial_{i} A f_h)({\boldsymbol{x}}) = a_{ij}({\boldsymbol{x}})\partial_{i}\partial_{j} A f_{h}({\boldsymbol{x}}) + \tilde \epsilon_{ij}({\boldsymbol{x}}),\\A ( c_{ijk}\partial_{i}\partial_{j}\partial_{k} A f_h)({\boldsymbol{x}}) = \tilde \epsilon_{ijk}({\boldsymbol{x}}),\end{gather*}
where
Furthermore,

Proof of Lemma 2.2. Assumption (1.3) states that
![]() $p_{i} = \beta_{i}/(2N)$
, which implies that
$p_{i} = \beta_{i}/(2N)$
, which implies that
![]() $\Sigma = s/(2N)$
. Thus,
$\Sigma = s/(2N)$
. Thus,
![]() $\mathcal{G}_{{\boldsymbol{Z}}}f({\boldsymbol{x}})$
, which is defined in (1.8), satisfies
$\mathcal{G}_{{\boldsymbol{Z}}}f({\boldsymbol{x}})$
, which is defined in (1.8), satisfies
 \begin{align*}\delta\mathcal{G}_{{\boldsymbol{Z}}} f({\boldsymbol{x}}) =&\ \sum_{i=1}^{K-1} (p_{i} - \Sigma x_{i}) \partial_{i} f({\boldsymbol{x}}) + \frac{1}{2N} \sum_{i,j = 1}^{K-1} x_{i}(\delta_{ij} - x_{j}) \partial_{i}\partial_{j} f({\boldsymbol{x}})\\=&\ \sum_{i=1}^{K-1} b_{i}({\boldsymbol{x}}) \partial_{i} f({\boldsymbol{x}}) + \frac{1}{2N} \sum_{i,j = 1}^{K-1} x_{i}(\delta_{ij} - x_{j}) \partial_{i}\partial_{j} f({\boldsymbol{x}}), \quad {\boldsymbol{x}} \in \bar \nabla^{K},\end{align*}
\begin{align*}\delta\mathcal{G}_{{\boldsymbol{Z}}} f({\boldsymbol{x}}) =&\ \sum_{i=1}^{K-1} (p_{i} - \Sigma x_{i}) \partial_{i} f({\boldsymbol{x}}) + \frac{1}{2N} \sum_{i,j = 1}^{K-1} x_{i}(\delta_{ij} - x_{j}) \partial_{i}\partial_{j} f({\boldsymbol{x}})\\=&\ \sum_{i=1}^{K-1} b_{i}({\boldsymbol{x}}) \partial_{i} f({\boldsymbol{x}}) + \frac{1}{2N} \sum_{i,j = 1}^{K-1} x_{i}(\delta_{ij} - x_{j}) \partial_{i}\partial_{j} f({\boldsymbol{x}}), \quad {\boldsymbol{x}} \in \bar \nabla^{K},\end{align*}
where the second equality is due to Lemma B.1. Combining Lemma B.2 with (B.2) yields
 \begin{align*}A (\mathcal{G}_{U} A f_h)({\boldsymbol{x}}) &= \sum_{i=1}^{K-1} b_{i}({\boldsymbol{x}})\partial_{i} A f_h ({\boldsymbol{x}}) + \frac{1}{2}\sum_{i,j =1}^{K-1} a_{ij}({\boldsymbol{x}})\partial_{i}\partial_{j} A f_h ({\boldsymbol{x}})\\&\hskip4mm+ \sum_{i=1}^{K-1} \tilde \epsilon_{i}({\boldsymbol{x}}) + \frac{1}{2}\sum_{i,j =1}^{K-1} \tilde \epsilon_{ij}({\boldsymbol{x}}) + \frac{1}{6} \sum_{i,j,k =1}^{K-1} \tilde \epsilon_{ijk}({\boldsymbol{x}}) + A \epsilon({\boldsymbol{x}}).\end{align*}
\begin{align*}A (\mathcal{G}_{U} A f_h)({\boldsymbol{x}}) &= \sum_{i=1}^{K-1} b_{i}({\boldsymbol{x}})\partial_{i} A f_h ({\boldsymbol{x}}) + \frac{1}{2}\sum_{i,j =1}^{K-1} a_{ij}({\boldsymbol{x}})\partial_{i}\partial_{j} A f_h ({\boldsymbol{x}})\\&\hskip4mm+ \sum_{i=1}^{K-1} \tilde \epsilon_{i}({\boldsymbol{x}}) + \frac{1}{2}\sum_{i,j =1}^{K-1} \tilde \epsilon_{ij}({\boldsymbol{x}}) + \frac{1}{6} \sum_{i,j,k =1}^{K-1} \tilde \epsilon_{ijk}({\boldsymbol{x}}) + A \epsilon({\boldsymbol{x}}).\end{align*}
Let us compare the first two terms on the right-hand side to
![]() $\delta \mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{x}})$
. Set
$\delta \mathcal{G}_{{\boldsymbol{Z}}} A f_h({\boldsymbol{x}})$
. Set
![]() $\bar x_{i} = x_{i} \Sigma - p_{i}$
and observe by Lemma B.1 that
$\bar x_{i} = x_{i} \Sigma - p_{i}$
and observe by Lemma B.1 that
 \begin{align*}a_{ij}({\boldsymbol{x}}) =&\ \bar x_{i}\bar x_{j} + \frac{1}{N}\big(x_{i} - \bar x_{i} \big) \big( \delta_{ij} - ( x_{j} - \bar x_{j})\big)\\=&\ \frac{1}{N} x_{i} (\delta_{ij} - x_{j}) - \frac{1}{N}\Big( \bar x_{i}(\delta_{ij} - x_{j}) - x_{i} \bar x_{j} - \bar x_{i} \bar x_{j} \Big) + \bar x_{i}\bar x_{j}.\end{align*}
\begin{align*}a_{ij}({\boldsymbol{x}}) =&\ \bar x_{i}\bar x_{j} + \frac{1}{N}\big(x_{i} - \bar x_{i} \big) \big( \delta_{ij} - ( x_{j} - \bar x_{j})\big)\\=&\ \frac{1}{N} x_{i} (\delta_{ij} - x_{j}) - \frac{1}{N}\Big( \bar x_{i}(\delta_{ij} - x_{j}) - x_{i} \bar x_{j} - \bar x_{i} \bar x_{j} \Big) + \bar x_{i}\bar x_{j}.\end{align*}
Since
![]() $\delta = 1/N$
,
$\delta = 1/N$
,
![]() $\vert\bar x_{i}\vert \leq \Sigma \leq \delta s$
, and
$\vert\bar x_{i}\vert \leq \Sigma \leq \delta s$
, and
![]() $\vert x_i\vert \leq 1$
, it follows that
$\vert x_i\vert \leq 1$
, it follows that

Combining this bound with the bounds on
![]() $\vert\tilde \epsilon_{i}({\boldsymbol{x}})\vert, \ldots, \vert A \epsilon({\boldsymbol{x}})\vert$
from Lemma B.2 yields
$\vert\tilde \epsilon_{i}({\boldsymbol{x}})\vert, \ldots, \vert A \epsilon({\boldsymbol{x}})\vert$
from Lemma B.2 yields

We first state and prove an auxiliary lemma, followed by the proof of Lemma B.2.
Lemma B.3. For any
![]() ${\boldsymbol{u}} \in \nabla^{K}$
and any integer
${\boldsymbol{u}} \in \nabla^{K}$
and any integer
![]() $M \geq0$
,
$M \geq0$
,
Proof of Lemma B.3. Recall that from (1.1),
![]() $N U_{K}(1)|u_{K} \sim{\rm Binomial}(N, u_{K} - \bar u_{K})$
, where
$N U_{K}(1)|u_{K} \sim{\rm Binomial}(N, u_{K} - \bar u_{K})$
, where
![]() $\bar u_{K} = -\Sigma u_{K} + p_{K}$
. For any
$\bar u_{K} = -\Sigma u_{K} + p_{K}$
. For any
![]() $0 \leq j \leq M$
,
$0 \leq j \leq M$
,
 \begin{align*}\mathbb{P}_{{\boldsymbol{u}}}(U_{K}(1) = j/N) =&\ \frac{N!}{j!(N-j)!} (u_{K}(1-\Sigma) + p_{K})^{j} ( 1- u_{K}(1-\Sigma) - p_{K})^{N-j}\\\leq&\ N^{j} ( 1- u_{K}(1-\Sigma) - p_{K})^{N} \frac{1}{( 1- u_{K}(1-\Sigma) - p_{K})^{j}}\\\leq&\ N^{M} ( 1- u_{K}(1-\Sigma))^{N} \frac{1}{( \Sigma - p_{K})^{j}}\\\leq&\ \frac{N^{M}}{( \Sigma - p_{K})^{M}} ( 1- u_{K}(1-\Sigma))^{N},\end{align*}
\begin{align*}\mathbb{P}_{{\boldsymbol{u}}}(U_{K}(1) = j/N) =&\ \frac{N!}{j!(N-j)!} (u_{K}(1-\Sigma) + p_{K})^{j} ( 1- u_{K}(1-\Sigma) - p_{K})^{N-j}\\\leq&\ N^{j} ( 1- u_{K}(1-\Sigma) - p_{K})^{N} \frac{1}{( 1- u_{K}(1-\Sigma) - p_{K})^{j}}\\\leq&\ N^{M} ( 1- u_{K}(1-\Sigma))^{N} \frac{1}{( \Sigma - p_{K})^{j}}\\\leq&\ \frac{N^{M}}{( \Sigma - p_{K})^{M}} ( 1- u_{K}(1-\Sigma))^{N},\end{align*}
where the second inequality follows from
![]() $1- u_{K}(1-\Sigma) - p_{K} \geq \Sigma - p_{K} $
since
$1- u_{K}(1-\Sigma) - p_{K} \geq \Sigma - p_{K} $
since
![]() $u_{K} \leq 1$
. Thus,
$u_{K} \leq 1$
. Thus,
 \begin{align*}\mathbb{P}_{{\boldsymbol{u}}}(U_{K}(1) \leq M/N) = \sum_{j=0}^{M} \mathbb{P}_{{\boldsymbol{u}}}(U_{K}(1) = j/N) \leq \frac{(M+1)N^{M}}{( \Sigma - p_{K})^{M}} ( 1- u_{K}(1-\Sigma) )^{N}.\end{align*}
\begin{align*}\mathbb{P}_{{\boldsymbol{u}}}(U_{K}(1) \leq M/N) = \sum_{j=0}^{M} \mathbb{P}_{{\boldsymbol{u}}}(U_{K}(1) = j/N) \leq \frac{(M+1)N^{M}}{( \Sigma - p_{K})^{M}} ( 1- u_{K}(1-\Sigma) )^{N}.\end{align*}
Proof of Lemma B.2. Let us prove (B.3). Note that
![]() $A b_i({\boldsymbol{x}}) = b_i({\boldsymbol{x}})$
by Corollary A.1. Lemma A.2 then gives us
$A b_i({\boldsymbol{x}}) = b_i({\boldsymbol{x}})$
by Corollary A.1. Lemma A.2 then gives us
where

The constant
![]() $C_{A.10}(K)$
is as in Lemma A.2 and the second inequality is due to the bound on
$C_{A.10}(K)$
is as in Lemma A.2 and the second inequality is due to the bound on
![]() $B_{1}(b_i)$
from Lemma B.1. Now
$B_{1}(b_i)$
from Lemma B.1. Now

where the second-last inequality is due to (A.3) of Theorem A.1. Thus,
To complete the proof of (B.3), note that

The first inequality follows from
![]() $\vert b_i\vert({\boldsymbol{u}}) \leq\Sigma \leq \delta s$
; see Lemma B.1. The second inequality follows from Proposition A.1 with
$\vert b_i\vert({\boldsymbol{u}}) \leq\Sigma \leq \delta s$
; see Lemma B.1. The second inequality follows from Proposition A.1 with
![]() $f({\boldsymbol{x}}) =\partial_{i} A f_h({\boldsymbol{x}})$
and
$f({\boldsymbol{x}}) =\partial_{i} A f_h({\boldsymbol{x}})$
and
![]() $s = 3$
there, and the third inequality follows from (A.3) of Theorem A.1. The proof of (B.4) is similar to that of (B.3). Lemma A.2 and the fact that
$s = 3$
there, and the third inequality follows from (A.3) of Theorem A.1. The proof of (B.4) is similar to that of (B.3). Lemma A.2 and the fact that
![]() $Aa_{ij}({\boldsymbol{x}}) = a_{ij}({\boldsymbol{x}})$
imply that
$Aa_{ij}({\boldsymbol{x}}) = a_{ij}({\boldsymbol{x}})$
imply that
where
We know that
![]() $B_{1}(a_{ij}) \leq \delta^2 5(1+s)^2$
by Lemma B.1, so that repeating the arguments used to bound
$B_{1}(a_{ij}) \leq \delta^2 5(1+s)^2$
by Lemma B.1, so that repeating the arguments used to bound
![]() $\epsilon_{i}({\boldsymbol{x}})$
yields
$\epsilon_{i}({\boldsymbol{x}})$
yields

Furthermore, since
![]() $\vert a_{ij}({\boldsymbol{x}})\vert \leq \Sigma^{2} + \delta \leq \delta(\delta s^2 + 1)$
,
$\vert a_{ij}({\boldsymbol{x}})\vert \leq \Sigma^{2} + \delta \leq \delta(\delta s^2 + 1)$
,

which proves (B.4). Let us prove (B.5). Note that

where the first inequality is due to (A.8) and Lemma B.1, and the second inequality is due to (A.3) of Theorem A.1, and the final inequality is due to (B.1). Lastly, to prove (B.6), we bound
![]() $\vert A \epsilon({\boldsymbol{x}})\vert$
by bounding
$\vert A \epsilon({\boldsymbol{x}})\vert$
by bounding
![]() $\epsilon({\boldsymbol{u}}), {\boldsymbol{u}} \in \nabla^{K}$
and using (A.8).
$\epsilon({\boldsymbol{u}}), {\boldsymbol{u}} \in \nabla^{K}$
and using (A.8).
From (A.1) of Theorem A.1, we see that
![]() $A \epsilon({\boldsymbol{x}})$
depends only on
$A \epsilon({\boldsymbol{x}})$
depends only on
![]() $\epsilon(\delta (k({\boldsymbol{x}})+{\boldsymbol{i}}))$
for
$\epsilon(\delta (k({\boldsymbol{x}})+{\boldsymbol{i}}))$
for
![]() $0 \leq {\boldsymbol{i}} \leq 4{\boldsymbol{e}}$
, so going forward we fix
$0 \leq {\boldsymbol{i}} \leq 4{\boldsymbol{e}}$
, so going forward we fix
![]() ${\boldsymbol{u}} = \delta (k({\boldsymbol{x}})+{\boldsymbol{i}})$
. Recall that
${\boldsymbol{u}} = \delta (k({\boldsymbol{x}})+{\boldsymbol{i}})$
. Recall that
 \begin{align*}\epsilon({\boldsymbol{u}}) =&\ \frac{1}{6}\sum_{i,j,k=1}^{K-1}\mathbb{E}_{{\boldsymbol{u}}} \Big( (U_i(1) -u_i)(U_j(1) - u_j)(U_{k}(1)-u_{k})\big(\partial_{i}\partial_{j}\partial_{k}A f_h(\boldsymbol{\xi}) -\partial_{i}\partial_{j}\partial_{k}A f_h({\boldsymbol{u}})\big)\Big),\end{align*}
\begin{align*}\epsilon({\boldsymbol{u}}) =&\ \frac{1}{6}\sum_{i,j,k=1}^{K-1}\mathbb{E}_{{\boldsymbol{u}}} \Big( (U_i(1) -u_i)(U_j(1) - u_j)(U_{k}(1)-u_{k})\big(\partial_{i}\partial_{j}\partial_{k}A f_h(\boldsymbol{\xi}) -\partial_{i}\partial_{j}\partial_{k}A f_h({\boldsymbol{u}})\big)\Big),\end{align*}
where
![]() $\boldsymbol{\xi}$
is between
$\boldsymbol{\xi}$
is between
![]() ${\boldsymbol{u}}$
and
${\boldsymbol{u}}$
and
![]() ${\boldsymbol{U}}(1)$
. We know that
${\boldsymbol{U}}(1)$
. We know that
![]() $\partial_{i}\partial_{j}\partial_{k}A f_h \in \mathcal{D}^{K-1}$
by Lemma A.1, implying that
$\partial_{i}\partial_{j}\partial_{k}A f_h \in \mathcal{D}^{K-1}$
by Lemma A.1, implying that
 \begin{align*}\vert\partial_{i}\partial_{j}\partial_{k}A f_h(\boldsymbol{\xi}) - \partial_{i}\partial_{j}\partial_{k}A f_h({\boldsymbol{u}})\vert \leq&\ \Vert{\boldsymbol{U}}(1)-{\boldsymbol{u}}\Vert_{1} \sup_{\substack{ \min({\boldsymbol{u}},{\boldsymbol{U}}(1)) \leq {\boldsymbol{z}} \\ {\boldsymbol{z}} \leq \max({\boldsymbol{u}},{\boldsymbol{U}}(1)) \\ \Vert{\boldsymbol{a}}\Vert_{1} = 4}} \vert D^{{\boldsymbol{a}}} Af_h({\boldsymbol{z}})\vert.\end{align*}
\begin{align*}\vert\partial_{i}\partial_{j}\partial_{k}A f_h(\boldsymbol{\xi}) - \partial_{i}\partial_{j}\partial_{k}A f_h({\boldsymbol{u}})\vert \leq&\ \Vert{\boldsymbol{U}}(1)-{\boldsymbol{u}}\Vert_{1} \sup_{\substack{ \min({\boldsymbol{u}},{\boldsymbol{U}}(1)) \leq {\boldsymbol{z}} \\ {\boldsymbol{z}} \leq \max({\boldsymbol{u}},{\boldsymbol{U}}(1)) \\ \Vert{\boldsymbol{a}}\Vert_{1} = 4}} \vert D^{{\boldsymbol{a}}} Af_h({\boldsymbol{z}})\vert.\end{align*}
Consider separately the cases when
![]() $U_{K}(1) > 4K/N$
and
$U_{K}(1) > 4K/N$
and
![]() $U_{K}(1) \leq4K/N$
. If
$U_{K}(1) \leq4K/N$
. If
![]() $U_{K}(1) > 4K/N$
then
$U_{K}(1) > 4K/N$
then

For the last inequality, we used the facts that
![]() $U(1) + \delta {\boldsymbol{a}} \in \nabla^{K}$
and
$U(1) + \delta {\boldsymbol{a}} \in \nabla^{K}$
and
![]() ${\boldsymbol{u}} + \delta {\boldsymbol{a}} \in \nabla^{K}$
for
${\boldsymbol{u}} + \delta {\boldsymbol{a}} \in \nabla^{K}$
for
![]() $\Vert a\Vert_{1} \leq 4$
, because
$\Vert a\Vert_{1} \leq 4$
, because
![]() $U_{K}(1) > 4K/N$
and
$U_{K}(1) > 4K/N$
and
![]() ${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
, respectively. If
${\boldsymbol{x}} \in \bar \nabla^{K}_{N}$
, respectively. If
![]() $U_{K}(1) \leq 4K/N$
, we use the coarse bound of
$U_{K}(1) \leq 4K/N$
, we use the coarse bound of

The last inequality is due to the fact that
which we verify at the end of the proof. Combining the bounds on
![]() $\vert D^{{\boldsymbol{a}}} Af_h({\boldsymbol{z}})\vert$
with the definition of
$\vert D^{{\boldsymbol{a}}} Af_h({\boldsymbol{z}})\vert$
with the definition of
![]() $\epsilon({\boldsymbol{u}})$
yields
$\epsilon({\boldsymbol{u}})$
yields

In the second-last inequality we used the coarse bound of
![]() $\vert U_i(1) -u_i\vert \leq 1$
to bound the second term, and in the last inequality we used the bound on
$\vert U_i(1) -u_i\vert \leq 1$
to bound the second term, and in the last inequality we used the bound on
![]() $\bar d_{ijk\ell}({\boldsymbol{u}})$
from Lemma B.1. Furthermore,
$\bar d_{ijk\ell}({\boldsymbol{u}})$
from Lemma B.1. Furthermore,
![]() ${\boldsymbol{x}} \in \bar\nabla^{K}_{N}$
implies that, for any
${\boldsymbol{x}} \in \bar\nabla^{K}_{N}$
implies that, for any
![]() $0 \leq {\boldsymbol{i}} \leq4{\boldsymbol{e}}$
,
$0 \leq {\boldsymbol{i}} \leq4{\boldsymbol{e}}$
,
 \begin{align*}1 - \sum_{j=1}^{K-1}\delta(k_j({\boldsymbol{x}})+i_j) \geq 1 - \sum_{j=1}^{K-1}\delta k_j({\boldsymbol{x}}) - 4K/N \geq 10K\sqrt{N}/N - 4K/N \geq 10K(\sqrt{N}-1)/N,\end{align*}
\begin{align*}1 - \sum_{j=1}^{K-1}\delta(k_j({\boldsymbol{x}})+i_j) \geq 1 - \sum_{j=1}^{K-1}\delta k_j({\boldsymbol{x}}) - 4K/N \geq 10K\sqrt{N}/N - 4K/N \geq 10K(\sqrt{N}-1)/N,\end{align*}
and, therefore,
![]() $( 1- u_{K}(1-\Sigma))^{N}$
on the right-hand side is bounded by
$( 1- u_{K}(1-\Sigma))^{N}$
on the right-hand side is bounded by
![]() $( 1- (10K(\sqrt{N}-1)/N) (1-\Sigma))^{N}$
.
$( 1- (10K(\sqrt{N}-1)/N) (1-\Sigma))^{N}$
.
Finally, (A.8) yields the upper bound of
 \begin{align*}\vert A \epsilon({\boldsymbol{x}})\vert =&\ \bigg| \sum_{i_1, \ldots, i_{K-1} = 0}^{4} \bigg(\prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j)\bigg) \epsilon(\delta (k({\boldsymbol{x}}) + {\boldsymbol{i}})) \bigg| \leq 5^{K}319^{K} \max_{0 \leq {\boldsymbol{i}} \leq 4{\boldsymbol{e}}} \vert\epsilon(\delta (k({\boldsymbol{x}}) + {\boldsymbol{i}}))\vert,\end{align*}
\begin{align*}\vert A \epsilon({\boldsymbol{x}})\vert =&\ \bigg| \sum_{i_1, \ldots, i_{K-1} = 0}^{4} \bigg(\prod_{j=1}^{d} \alpha_{k_j({\boldsymbol{x}}) +i_j}^{k_j({\boldsymbol{x}}) }(x_j)\bigg) \epsilon(\delta (k({\boldsymbol{x}}) + {\boldsymbol{i}})) \bigg| \leq 5^{K}319^{K} \max_{0 \leq {\boldsymbol{i}} \leq 4{\boldsymbol{e}}} \vert\epsilon(\delta (k({\boldsymbol{x}}) + {\boldsymbol{i}}))\vert,\end{align*}
which proves (B.6). It remains to prove (B.7). Since we chose
![]() $f_h({\boldsymbol{u}}) = 0$
for
$f_h({\boldsymbol{u}}) = 0$
for
![]() ${\boldsymbol{u}}$
outside of
${\boldsymbol{u}}$
outside of
![]() $\nabla^{K}$
, we need to show that
$\nabla^{K}$
, we need to show that
Letting
![]() $\pi({\boldsymbol{u}}) = \mathbb{P}({\boldsymbol{U}} = {\boldsymbol{u}})$
, we have
$\pi({\boldsymbol{u}}) = \mathbb{P}({\boldsymbol{U}} = {\boldsymbol{u}})$
, we have
 \begin{align*}f_h({\boldsymbol{u}}) = \sum_{n=0}^{\infty} \big( \mathbb{E}_{u} h({\boldsymbol{U}}(n)) - \mathbb{E} h({\boldsymbol{U}}) \big) =&\ \sum_{n=0}^{\infty} \sum_{{\boldsymbol{u}}' \in \nabla^{K}} \pi({\boldsymbol{u}}') \big( \mathbb{E}_{{\boldsymbol{u}}} h({\boldsymbol{U}}(n)) - \mathbb{E}_{{\boldsymbol{u}}'} h({\boldsymbol{U}}(n)) \big)\\=&\ \sum_{{\boldsymbol{u}}' \in \nabla^{K}} \sum_{n=0}^{\infty}\pi({\boldsymbol{u}}') \big( \mathbb{E}_{{\boldsymbol{u}}} h({\boldsymbol{U}}(n)) - \mathbb{E}_{{\boldsymbol{u}}'} h({\boldsymbol{U}}(n)) \big),\end{align*}
\begin{align*}f_h({\boldsymbol{u}}) = \sum_{n=0}^{\infty} \big( \mathbb{E}_{u} h({\boldsymbol{U}}(n)) - \mathbb{E} h({\boldsymbol{U}}) \big) =&\ \sum_{n=0}^{\infty} \sum_{{\boldsymbol{u}}' \in \nabla^{K}} \pi({\boldsymbol{u}}') \big( \mathbb{E}_{{\boldsymbol{u}}} h({\boldsymbol{U}}(n)) - \mathbb{E}_{{\boldsymbol{u}}'} h({\boldsymbol{U}}(n)) \big)\\=&\ \sum_{{\boldsymbol{u}}' \in \nabla^{K}} \sum_{n=0}^{\infty}\pi({\boldsymbol{u}}') \big( \mathbb{E}_{{\boldsymbol{u}}} h({\boldsymbol{U}}(n)) - \mathbb{E}_{{\boldsymbol{u}}'} h({\boldsymbol{U}}(n)) \big),\end{align*}
where the interchange is justified by the Fubini–Tonelli theorem because
![]() $\{{\boldsymbol{U}}(n)\}$
is geometrically ergodic. Since
$\{{\boldsymbol{U}}(n)\}$
is geometrically ergodic. Since
it follows that
proving (B.7).
We now prove Lemma B.1. Recall that
where
![]() $\bar u_{i} = u_{i}\Sigma - p_{i}$
. We also require the following result about the moments of the multinomial distribution.
$\bar u_{i} = u_{i}\Sigma - p_{i}$
. We also require the following result about the moments of the multinomial distribution.
Lemma B.4. Let
![]() $X \sim {\rm Multinomial}(N, (p_1, \ldots, p_k))$
. Then for all
$X \sim {\rm Multinomial}(N, (p_1, \ldots, p_k))$
. Then for all
![]() $i \neq j \neq k$
,
$i \neq j \neq k$
,
 \begin{gather*}\mathbb{E}(X_i) = N p_i, \qquad\mathbb{E}(X_i^2) = N(N-1)p_i^2 + Np_i, \qquad\mathbb{E}(X_i X_j) = N(N-1)p_ip_j,\\\mathbb{E}(X_iX_jX_k) = N(N-1)(N-2)p_ip_jp_k,\\\mathbb{E}(X_i^2X_j) = N(N-1)(N-2) p_i^2p_j + N(N-1)p_ip_j,\\\mathbb{E}(X_i^3) = N(N-1)(N-2)p_i^3 + 3N(N-1)p_i^2 - 2Np_i.\end{gather*}
\begin{gather*}\mathbb{E}(X_i) = N p_i, \qquad\mathbb{E}(X_i^2) = N(N-1)p_i^2 + Np_i, \qquad\mathbb{E}(X_i X_j) = N(N-1)p_ip_j,\\\mathbb{E}(X_iX_jX_k) = N(N-1)(N-2)p_ip_jp_k,\\\mathbb{E}(X_i^2X_j) = N(N-1)(N-2) p_i^2p_j + N(N-1)p_ip_j,\\\mathbb{E}(X_i^3) = N(N-1)(N-2)p_i^3 + 3N(N-1)p_i^2 - 2Np_i.\end{gather*}
Proof of Lemma B.1. For convenience, we write
![]() $\mathbb{E}(\!\cdot\!)$
instead of
$\mathbb{E}(\!\cdot\!)$
instead of
![]() $\mathbb{E}_{u}(\!\cdot\!)$
and
$\mathbb{E}_{u}(\!\cdot\!)$
and
![]() $U_{i}$
instead of
$U_{i}$
instead of
![]() $U_{i}(1)$
; e.g. we write
$U_{i}(1)$
; e.g. we write
![]() $\mathbb{E} U_{i}$
instead of
$\mathbb{E} U_{i}$
instead of
![]() $\mathbb{E}_{u} U_{i}(1)$
. Since
$\mathbb{E}_{u} U_{i}(1)$
. Since
![]() $\mathbb{E} N U_i = N(u_{i} - \bar u_{i})$
, it follows from Lemma B.4 that
$\mathbb{E} N U_i = N(u_{i} - \bar u_{i})$
, it follows from Lemma B.4 that
Next, we observe that
Lemma B.4 implies that
![]() $\mathbb{E} U_{j} = (u_{j} - \bar u_{j})$
and
$\mathbb{E} U_{j} = (u_{j} - \bar u_{j})$
and
 \begin{align*}\mathbb{E} ( U_{i} U_{j}) =&\ (1-1/N)(u_i - \bar u_i) (u_j - \bar u_{j})\\=&\ u_i u_j - u_i \bar u_j - u_j \bar u_i + \bar u_i \bar u_j- \frac{1}{N}(u_i - \bar u_i) (u_j - \bar u_{j}),\end{align*}
\begin{align*}\mathbb{E} ( U_{i} U_{j}) =&\ (1-1/N)(u_i - \bar u_i) (u_j - \bar u_{j})\\=&\ u_i u_j - u_i \bar u_j - u_j \bar u_i + \bar u_i \bar u_j- \frac{1}{N}(u_i - \bar u_i) (u_j - \bar u_{j}),\end{align*}
from which it follows that
Similarly,
By Lemma B.4, we know that
 \begin{align*}\mathbb{E} ( U_{i}^2 ) =&\ (1-1/N)(u_i - \bar u_i)^2 + \frac{1}{N} (u_i-\bar u_i)\\=&\ (u_i^2 - 2u_i \bar u_i + \bar u_i^2) + \frac{1}{N} \big( (u_i - \bar u_i) - (u_i - \bar u_i)^2\big),\end{align*}
\begin{align*}\mathbb{E} ( U_{i}^2 ) =&\ (1-1/N)(u_i - \bar u_i)^2 + \frac{1}{N} (u_i-\bar u_i)\\=&\ (u_i^2 - 2u_i \bar u_i + \bar u_i^2) + \frac{1}{N} \big( (u_i - \bar u_i) - (u_i - \bar u_i)^2\big),\end{align*}
and we conclude that
The form of
![]() $b_i({\boldsymbol{u}})$
immediately implies that
$b_i({\boldsymbol{u}})$
immediately implies that
![]() $B_{1}(b_i) = \delta \Sigma \leq \delta^2 s$
. Furthermore, one can check that
$B_{1}(b_i) = \delta \Sigma \leq \delta^2 s$
. Furthermore, one can check that
from which it follows that
The bound is crude but simple, and follows from the facts that
![]() $u_i \leq1$
,
$u_i \leq1$
,
![]() $\delta = 1/N \leq 1$
, and
$\delta = 1/N \leq 1$
, and
![]() $p_i \leq \Sigma \leq \delta s$
. Similarly, one can show that
$p_i \leq \Sigma \leq \delta s$
. Similarly, one can show that
implying the bound on
![]() $B_{1}(a_{ij})$
.
$B_{1}(a_{ij})$
.
To prove
![]() $\vert c_{ijk}({\boldsymbol{u}})\vert \leq 20\delta^2(1+s)^3$
, we compute and then bound
$\vert c_{ijk}({\boldsymbol{u}})\vert \leq 20\delta^2(1+s)^3$
, we compute and then bound
![]() $c_{iii}({\boldsymbol{u}})$
,
$c_{iii}({\boldsymbol{u}})$
,
![]() $c_{iij}({\boldsymbol{u}})$
, and
$c_{iij}({\boldsymbol{u}})$
, and
![]() $c_{ijk}({\boldsymbol{u}})$
, for
$c_{ijk}({\boldsymbol{u}})$
, for
![]() $i \neq j \neq k$
. We begin with
$i \neq j \neq k$
. We begin with
From (B.9), we know that
For the remaining terms, we use Lemma B.4 to see that
 \begin{gather*}\begin{aligned}\mathbb{E} U_{i}^{3} &= (1-1/N)(1-2/N)(u_i - \bar u_i )^3 + \frac{3}{N} (1-1/N)(u_i - \bar u_i )^2 - \frac{2}{N^2} (u_i - \bar u_i)\\&= (u_i - \bar u_i )^3 - \frac{3}{N}(u_i - \bar u_i )^3 + \frac{2}{N^2}(u_i - \bar u_i )^3 + \frac{3}{N} (u_i - \bar u_i )^2 - \frac{3}{N^2}(u_i - \bar u_i )^2 - \frac{2}{N^2}(u_i - \bar u_i ),\end{aligned}\\\begin{aligned}-2u_i \mathbb{E} U_{i}^2 &= -2u_i \Big( (1-1/N) (u_i - \bar u_i )^2 + \frac{1}{N} (u_i - \bar u_i ) \Big)\\&= -2 u_i (u_i - \bar u_i )^2 + 2 u_i \frac{1}{N} (u_i - \bar u_i )^2 - 2u_i \frac{1}{N} (u_i - \bar u_i ),\end{aligned}\\u_i^2 \mathbb{E} U_i = u_i^2 (u_i - \bar u_i).\end{gather*}
\begin{gather*}\begin{aligned}\mathbb{E} U_{i}^{3} &= (1-1/N)(1-2/N)(u_i - \bar u_i )^3 + \frac{3}{N} (1-1/N)(u_i - \bar u_i )^2 - \frac{2}{N^2} (u_i - \bar u_i)\\&= (u_i - \bar u_i )^3 - \frac{3}{N}(u_i - \bar u_i )^3 + \frac{2}{N^2}(u_i - \bar u_i )^3 + \frac{3}{N} (u_i - \bar u_i )^2 - \frac{3}{N^2}(u_i - \bar u_i )^2 - \frac{2}{N^2}(u_i - \bar u_i ),\end{aligned}\\\begin{aligned}-2u_i \mathbb{E} U_{i}^2 &= -2u_i \Big( (1-1/N) (u_i - \bar u_i )^2 + \frac{1}{N} (u_i - \bar u_i ) \Big)\\&= -2 u_i (u_i - \bar u_i )^2 + 2 u_i \frac{1}{N} (u_i - \bar u_i )^2 - 2u_i \frac{1}{N} (u_i - \bar u_i ),\end{aligned}\\u_i^2 \mathbb{E} U_i = u_i^2 (u_i - \bar u_i).\end{gather*}
We begin with the terms with a
![]() $1/N^2$
factor. Since
$1/N^2$
factor. Since
![]() $0 \leq u_i - \bar u_i \leq 1$
, it follows that
$0 \leq u_i - \bar u_i \leq 1$
, it follows that
Let us now consider only those containing
![]() $1/N$
in front of them. Namely,
$1/N$
in front of them. Namely,
 \begin{align*}& - \frac{3}{N}(u_i - \bar u_i )^3+ \frac{3}{N} (u_i - \bar u_i )^2+ 2 u_i \frac{1}{N} (u_i - \bar u_i )^2 - 2u_i \frac{1}{N} (u_i - \bar u_i )- \frac{1}{N} u_{i}\big((u_i - \bar u_i) - (u_i - \bar u_i)^2\big)\\&\qquad= \frac{3}{N} \Big( \!- (u_i - \bar u_i )^3+ (u_i - \bar u_i )^2+ u_i (u_i - \bar u_i )^2 - u_i (u_i - \bar u_i ) \Big)\\&\qquad= \frac{3}{N} \Big( \bar u_i (u_i - \bar u_i )^2 + (u_i - \bar u_i )^2 - u_i (u_i - \bar u_i ) \Big)\\&\qquad= \frac{3}{N} \Big( \bar u_i (u_i - \bar u_i )^2 - \bar u_i (u_i - \bar u_i ) \Big)\\&\qquad= \frac{3}{N} \bar u_i (u_i - \bar u_i ) \Big( (u_i - \bar u_i ) - 1\Big),\end{align*}
\begin{align*}& - \frac{3}{N}(u_i - \bar u_i )^3+ \frac{3}{N} (u_i - \bar u_i )^2+ 2 u_i \frac{1}{N} (u_i - \bar u_i )^2 - 2u_i \frac{1}{N} (u_i - \bar u_i )- \frac{1}{N} u_{i}\big((u_i - \bar u_i) - (u_i - \bar u_i)^2\big)\\&\qquad= \frac{3}{N} \Big( \!- (u_i - \bar u_i )^3+ (u_i - \bar u_i )^2+ u_i (u_i - \bar u_i )^2 - u_i (u_i - \bar u_i ) \Big)\\&\qquad= \frac{3}{N} \Big( \bar u_i (u_i - \bar u_i )^2 + (u_i - \bar u_i )^2 - u_i (u_i - \bar u_i ) \Big)\\&\qquad= \frac{3}{N} \Big( \bar u_i (u_i - \bar u_i )^2 - \bar u_i (u_i - \bar u_i ) \Big)\\&\qquad= \frac{3}{N} \bar u_i (u_i - \bar u_i ) \Big( (u_i - \bar u_i ) - 1\Big),\end{align*}
and note that
Lastly, we collect all the terms without
![]() $1/N$
or
$1/N$
or
![]() $1/N^2$
in front of them. Their sum equals
$1/N^2$
in front of them. Their sum equals
 \begin{align*}&(u_i - \bar u_i )^3 -2 u_i (u_i - \bar u_i )^2 + u_i^2 (u_i - \bar u_i)-u_{i} \bar u_i^2\\&\qquad= u_i^3 - 3\bar u_i u_i^2 + 3 \bar u_i^2 u_i - \bar u_i^3 - 2u_i^3 + 4 u_i^2 \bar u_i - 2 u_i \bar u_i^2 + u_i^3 - u_i^2 \bar u_i - u_i \bar u_i^2\\&\qquad= - 3\bar u_i u_i^2 + 3 \bar u_i^2 u_i - \bar u_i^3 + 4 u_i^2 \bar u_i - 2 u_i \bar u_i^2 - u_i^2 \bar u_i - u_i \bar u_i^2\\&\qquad= 3 \bar u_i^2 u_i - \bar u_i^3 - 2 u_i \bar u_i^2 - u_i \bar u_i^2\\&\qquad= - \bar u_i^3.\end{align*}
\begin{align*}&(u_i - \bar u_i )^3 -2 u_i (u_i - \bar u_i )^2 + u_i^2 (u_i - \bar u_i)-u_{i} \bar u_i^2\\&\qquad= u_i^3 - 3\bar u_i u_i^2 + 3 \bar u_i^2 u_i - \bar u_i^3 - 2u_i^3 + 4 u_i^2 \bar u_i - 2 u_i \bar u_i^2 + u_i^3 - u_i^2 \bar u_i - u_i \bar u_i^2\\&\qquad= - 3\bar u_i u_i^2 + 3 \bar u_i^2 u_i - \bar u_i^3 + 4 u_i^2 \bar u_i - 2 u_i \bar u_i^2 - u_i^2 \bar u_i - u_i \bar u_i^2\\&\qquad= 3 \bar u_i^2 u_i - \bar u_i^3 - 2 u_i \bar u_i^2 - u_i \bar u_i^2\\&\qquad= - \bar u_i^3.\end{align*}
Since
![]() $\vert\bar u_{i}^{3}\vert \leq \Sigma^3 = s^3/(8N^3)$
, we have shown that
$\vert\bar u_{i}^{3}\vert \leq \Sigma^3 = s^3/(8N^3)$
, we have shown that
![]() $\vert c_{iii}(u)\vert \leq 5/N^2 + 3s/(8N^2) + s^3/(8N^3) \leq 20 \delta^2(1+s)^3$
. Next, we bound
$\vert c_{iii}(u)\vert \leq 5/N^2 + 3s/(8N^2) + s^3/(8N^3) \leq 20 \delta^2(1+s)^3$
. Next, we bound
 \begin{align*}c_{iij}({\boldsymbol{u}}) &= \mathbb{E}(U_i-u_i)^2(U_j-u_j)\\&= \mathbb{E} U_i(U_i-u_i)(U_j-u_j) - u_i\mathbb{E}(U_i-u_i)(U_j-u_j)\\&= \mathbb{E} U_{i}^{2} U_{j} - u_{j} \mathbb{E} U_{i}^2 - u_{i}\mathbb{E} U_{i}U_{j} + u_{i}u_{j} \mathbb{E} U_{i} - u_i\mathbb{E}(U_i-u_i)(U_j-u_j).\end{align*}
\begin{align*}c_{iij}({\boldsymbol{u}}) &= \mathbb{E}(U_i-u_i)^2(U_j-u_j)\\&= \mathbb{E} U_i(U_i-u_i)(U_j-u_j) - u_i\mathbb{E}(U_i-u_i)(U_j-u_j)\\&= \mathbb{E} U_{i}^{2} U_{j} - u_{j} \mathbb{E} U_{i}^2 - u_{i}\mathbb{E} U_{i}U_{j} + u_{i}u_{j} \mathbb{E} U_{i} - u_i\mathbb{E}(U_i-u_i)(U_j-u_j).\end{align*}
From (B.8), we know that
and, for the rest of the terms, we use Lemma B.4 to obtain
 \begin{gather*}\begin{aligned}\mathbb{E} U_{i}^{2} U_{j} =&\ (1-1/N)(1-2/N) (u_i - \bar u_i)^2 (u_j - \bar u_j) + \frac{1}{N}(1-1/N) (u_i - \bar u_i) (u_j - \bar u_j)\\=&\ (u_i - \bar u_i)^2 (u_j - \bar u_j) - \frac{3}{N} (u_i - \bar u_i)^2 (u_j - \bar u_j)+ \frac{2}{N^2} (u_i - \bar u_i)^2 (u_j - \bar u_j)\\&+ \frac{1}{N} (u_i - \bar u_i) (u_j - \bar u_j) - \frac{1}{N^2} (u_i - \bar u_i) (u_j - \bar u_j),\\- u_{j} \mathbb{E} U_{i}^2 =&\ -u_{j} \Big( (1-1/N) (u_i - \bar u_i)^2 + \frac{1}{N} (u_i - \bar u_i) \Big)\\=&\ -u_{j} \Big( (u_i - \bar u_i)^2 - \frac{1}{N } (u_i - \bar u_i)^2 + \frac{1}{N} (u_i - \bar u_i) \Big),\end{aligned}\\- u_{i}\mathbb{E} U_{i}U_{j} = - u_{i} \Big( (u_i - \bar u_i) (u_j - \bar u_j) - \frac{1}{N}(u_i - \bar u_i) (u_j - \bar u_j) \Big),\\u_{i}u_{j} \mathbb{E} U_{i} = u_{i}u_{j}(u_i - \bar u_i).\end{gather*}
\begin{gather*}\begin{aligned}\mathbb{E} U_{i}^{2} U_{j} =&\ (1-1/N)(1-2/N) (u_i - \bar u_i)^2 (u_j - \bar u_j) + \frac{1}{N}(1-1/N) (u_i - \bar u_i) (u_j - \bar u_j)\\=&\ (u_i - \bar u_i)^2 (u_j - \bar u_j) - \frac{3}{N} (u_i - \bar u_i)^2 (u_j - \bar u_j)+ \frac{2}{N^2} (u_i - \bar u_i)^2 (u_j - \bar u_j)\\&+ \frac{1}{N} (u_i - \bar u_i) (u_j - \bar u_j) - \frac{1}{N^2} (u_i - \bar u_i) (u_j - \bar u_j),\\- u_{j} \mathbb{E} U_{i}^2 =&\ -u_{j} \Big( (1-1/N) (u_i - \bar u_i)^2 + \frac{1}{N} (u_i - \bar u_i) \Big)\\=&\ -u_{j} \Big( (u_i - \bar u_i)^2 - \frac{1}{N } (u_i - \bar u_i)^2 + \frac{1}{N} (u_i - \bar u_i) \Big),\end{aligned}\\- u_{i}\mathbb{E} U_{i}U_{j} = - u_{i} \Big( (u_i - \bar u_i) (u_j - \bar u_j) - \frac{1}{N}(u_i - \bar u_i) (u_j - \bar u_j) \Big),\\u_{i}u_{j} \mathbb{E} U_{i} = u_{i}u_{j}(u_i - \bar u_i).\end{gather*}
Considering the
![]() $1/N^2$
terms,
$1/N^2$
terms,
Collecting all terms with
![]() $1/N$
in front, the result equals
$1/N$
in front, the result equals
 \begin{align*}& \frac{1}{N} (- 3 (u_i - \bar u_i)^2 (u_j - \bar u_j)+ (u_i - \bar u_i) (u_j - \bar u_j) + u_j (u_i - \bar u_i)^2 - u_j (u_i - \bar u_i)\\& \hskip4mm + u_{i} (u_i - \bar u_i) (u_j - \bar u_j) + u_{i} (u_i - \bar u_i) (u_j - \bar u_j) )\\&\qquad= \frac{1}{N}(u_i - \bar u_i) (- 3 (u_i - \bar u_i) (u_j - \bar u_j)+ (u_j - \bar u_j) + u_j (u_i - \bar u_i) - u_j + 2 u_{i} (u_j - \bar u_j) )\\&\qquad= \frac{1}{N}(u_i - \bar u_i) (- 3 u_i u_j + 3 u_i \bar u_j + 3 u_j \bar u_i - 3 \bar u_i \bar u_j \\&\qquad\qquad\qquad\qquad+ (u_j - \bar u_j) + u_j u_i - u_j \bar u_i - u_j + 2 u_{i} u_j - 2 u_{i} \bar u_j )\\&\qquad= \frac{1}{N}(u_i - \bar u_i) ( 3 u_i \bar u_j + 3 u_j \bar u_i - 3 \bar u_i \bar u_j - \bar u_j - u_j \bar u_i - 2 u_{i} \bar u_j ),\end{align*}
\begin{align*}& \frac{1}{N} (- 3 (u_i - \bar u_i)^2 (u_j - \bar u_j)+ (u_i - \bar u_i) (u_j - \bar u_j) + u_j (u_i - \bar u_i)^2 - u_j (u_i - \bar u_i)\\& \hskip4mm + u_{i} (u_i - \bar u_i) (u_j - \bar u_j) + u_{i} (u_i - \bar u_i) (u_j - \bar u_j) )\\&\qquad= \frac{1}{N}(u_i - \bar u_i) (- 3 (u_i - \bar u_i) (u_j - \bar u_j)+ (u_j - \bar u_j) + u_j (u_i - \bar u_i) - u_j + 2 u_{i} (u_j - \bar u_j) )\\&\qquad= \frac{1}{N}(u_i - \bar u_i) (- 3 u_i u_j + 3 u_i \bar u_j + 3 u_j \bar u_i - 3 \bar u_i \bar u_j \\&\qquad\qquad\qquad\qquad+ (u_j - \bar u_j) + u_j u_i - u_j \bar u_i - u_j + 2 u_{i} u_j - 2 u_{i} \bar u_j )\\&\qquad= \frac{1}{N}(u_i - \bar u_i) ( 3 u_i \bar u_j + 3 u_j \bar u_i - 3 \bar u_i \bar u_j - \bar u_j - u_j \bar u_i - 2 u_{i} \bar u_j ),\end{align*}
the absolute value of which can be bounded by
![]() $15 \Sigma/N$
, because
$15 \Sigma/N$
, because
![]() $\bar u_{i}, \bar u_{j} \leq \Sigma$
. Next, collecting all terms without
$\bar u_{i}, \bar u_{j} \leq \Sigma$
. Next, collecting all terms without
![]() $1/N^2$
or
$1/N^2$
or
![]() $1/N$
yields
$1/N$
yields
 \begin{align*}&(u_i - \bar u_i)^2 (u_j - \bar u_j)- u_{j} (u_i - \bar u_i)^2- u_{i} (u_i - \bar u_i) (u_j - \bar u_j) +u_{i}u_{j}(u_i - \bar u_i)-u_i \bar u_i \bar u_j \\&\qquad= - \bar u_j (u_i - \bar u_i)^2 - u_{i} (u_i - \bar u_i) (u_j - \bar u_j) +u_{i}u_{j}(u_i - \bar u_i)-u_i \bar u_i \bar u_j\\&\qquad= - \bar u_j (u_i - \bar u_i)^2 +u_{i} \bar u_j (u_i - \bar u_i) -u_i \bar u_i \bar u_j\\&\qquad= - \bar u_j ( (u_i - \bar u_i)^2 - u_{i} (u_i - \bar u_i) +u_i \bar u_i )\\&\qquad= - \bar u_j ( - \bar u_i (u_i - \bar u_i) +u_i \bar u_i )\\&\qquad= - \bar u_j \bar u_i^2,\end{align*}
\begin{align*}&(u_i - \bar u_i)^2 (u_j - \bar u_j)- u_{j} (u_i - \bar u_i)^2- u_{i} (u_i - \bar u_i) (u_j - \bar u_j) +u_{i}u_{j}(u_i - \bar u_i)-u_i \bar u_i \bar u_j \\&\qquad= - \bar u_j (u_i - \bar u_i)^2 - u_{i} (u_i - \bar u_i) (u_j - \bar u_j) +u_{i}u_{j}(u_i - \bar u_i)-u_i \bar u_i \bar u_j\\&\qquad= - \bar u_j (u_i - \bar u_i)^2 +u_{i} \bar u_j (u_i - \bar u_i) -u_i \bar u_i \bar u_j\\&\qquad= - \bar u_j ( (u_i - \bar u_i)^2 - u_{i} (u_i - \bar u_i) +u_i \bar u_i )\\&\qquad= - \bar u_j ( - \bar u_i (u_i - \bar u_i) +u_i \bar u_i )\\&\qquad= - \bar u_j \bar u_i^2,\end{align*}
which is bounded by
![]() $\Sigma^{3}$
. Thus, we have shown that
$\Sigma^{3}$
. Thus, we have shown that
Lastly, we consider
 \begin{align*}c_{ijk}({\boldsymbol{u}}) =&\ \mathbb{E}(U_i-u_i)(U_j-u_j) (U_k-u_k)\\=&\ \mathbb{E} U_{k} (U_i-u_i)(U_j-u_j) - u_{k} \mathbb{E} (U_i-u_i)(U_j-u_j)\\=&\ \mathbb{E} U_{k} U_{i} U_{j} - u_{j} \mathbb{E} U_{k} U_{i} - u_{i}\mathbb{E} U_{k} U_{j} + u_{i} u_{j} \mathbb{E} U_{k} - u_{k} \mathbb{E}(U_i-u_i)(U_j-u_j).\end{align*}
\begin{align*}c_{ijk}({\boldsymbol{u}}) =&\ \mathbb{E}(U_i-u_i)(U_j-u_j) (U_k-u_k)\\=&\ \mathbb{E} U_{k} (U_i-u_i)(U_j-u_j) - u_{k} \mathbb{E} (U_i-u_i)(U_j-u_j)\\=&\ \mathbb{E} U_{k} U_{i} U_{j} - u_{j} \mathbb{E} U_{k} U_{i} - u_{i}\mathbb{E} U_{k} U_{j} + u_{i} u_{j} \mathbb{E} U_{k} - u_{k} \mathbb{E}(U_i-u_i)(U_j-u_j).\end{align*}
From (B.8) we have
and from Lemma B.4 we have
 \begin{align*}\mathbb{E} U_{k} U_{i} U_{j} =&\ \Big( 1 - \frac{3}{N} + \frac{2}{N^2} \Big) (u_{i} - \bar u_{i})(u_{j} - \bar u_{j})(u_{k} - \bar u_{k}),\\- u_{j} \mathbb{E} U_{k} U_{i} =&\ - u_{j} \Big( (u_k - \bar u_k) (u_i - \bar u_i) - \frac{1}{N}(u_k - \bar u_k) (u_i - \bar u_i) \Big),\\- u_{i} \mathbb{E} U_{k} U_{j} =&\ - u_{i} \Big( (u_k - \bar u_k) (u_j - \bar u_j) - \frac{1}{N}(u_k - \bar u_k) (u_j - \bar u_j) \Big).\end{align*}
\begin{align*}\mathbb{E} U_{k} U_{i} U_{j} =&\ \Big( 1 - \frac{3}{N} + \frac{2}{N^2} \Big) (u_{i} - \bar u_{i})(u_{j} - \bar u_{j})(u_{k} - \bar u_{k}),\\- u_{j} \mathbb{E} U_{k} U_{i} =&\ - u_{j} \Big( (u_k - \bar u_k) (u_i - \bar u_i) - \frac{1}{N}(u_k - \bar u_k) (u_i - \bar u_i) \Big),\\- u_{i} \mathbb{E} U_{k} U_{j} =&\ - u_{i} \Big( (u_k - \bar u_k) (u_j - \bar u_j) - \frac{1}{N}(u_k - \bar u_k) (u_j - \bar u_j) \Big).\end{align*}
The combined
![]() $1/N^2$
terms can be bounded by
$1/N^2$
terms can be bounded by
![]() $2/N^2$
. Collecting terms with
$2/N^2$
. Collecting terms with
![]() $1/N$
in front yields
$1/N$
in front yields
 \begin{align*}& \frac{1}{N} ( -3(u_{i} - \bar u_{i})(u_{j} - \bar u_{j})(u_{k} - \bar u_{k}) + u_{j} (u_k - \bar u_k) (u_i - \bar u_i)\\& \hskip4mm + u_{i} (u_k - \bar u_k) (u_j - \bar u_j) + u_k (u_i - \bar u_i) (u_j - \bar u_{j}) )\\&\qquad= \frac{1}{N} ( \bar u_j (u_{i} - \bar u_{i})(u_{k} - \bar u_{k}) + \bar u_i (u_{j} - \bar u_{j})(u_{k} - \bar u_{k})+ \bar u_k (u_{j} - \bar u_{j})(u_{i} - \bar u_{i}) ),\end{align*}
\begin{align*}& \frac{1}{N} ( -3(u_{i} - \bar u_{i})(u_{j} - \bar u_{j})(u_{k} - \bar u_{k}) + u_{j} (u_k - \bar u_k) (u_i - \bar u_i)\\& \hskip4mm + u_{i} (u_k - \bar u_k) (u_j - \bar u_j) + u_k (u_i - \bar u_i) (u_j - \bar u_{j}) )\\&\qquad= \frac{1}{N} ( \bar u_j (u_{i} - \bar u_{i})(u_{k} - \bar u_{k}) + \bar u_i (u_{j} - \bar u_{j})(u_{k} - \bar u_{k})+ \bar u_k (u_{j} - \bar u_{j})(u_{i} - \bar u_{i}) ),\end{align*}
and this term can be bounded by
![]() $3 \Sigma /N$
. Similarly, collecting all terms without
$3 \Sigma /N$
. Similarly, collecting all terms without
![]() $1/N^2$
and
$1/N^2$
and
![]() $1/N$
yields
$1/N$
yields
 \begin{align*}&(u_{i} - \bar u_{i})(u_{j} - \bar u_{j})(u_{k} - \bar u_{k}) - u_{j} (u_k - \bar u_k) (u_i - \bar u_i) - u_{i} (u_k - \bar u_k) (u_j - \bar u_j)\\&+ u_{i} u_{j} (u_k - \bar u_k) - u_{k} \bar u_i \bar u_j\\&\qquad= - \bar u_{j} (u_{i} - \bar u_{i}) (u_{k} - \bar u_{k})- u_{i} (u_k - \bar u_k) (u_j - \bar u_j) + u_{i} u_{j} (u_k - \bar u_k) - u_{k} \bar u_i \bar u_j\\&\qquad= - \bar u_{j} ( u_{i} u_k - u_k \bar u_i - u_i \bar u_k + \bar u_i \bar u_k) - u_{i} (u_k u_j -u_k \bar u_j - u_j \bar u_k + \bar u_j \bar u_k) + u_{i} u_{j} u_k\\&\hskip11mm- u_{i} u_{j} \bar u_k - u_{k} \bar u_i \bar u_j\\&\qquad= - \bar u_{j} ( u_{i} u_k - u_k \bar u_i - u_i \bar u_k + \bar u_i \bar u_k) - u_{i} ( -u_k \bar u_j + \bar u_j \bar u_k) - u_{k} \bar u_i \bar u_j\\&\qquad= - \bar u_{j} ( - u_k \bar u_i - u_i \bar u_k + \bar u_i \bar u_k) - u_{i}\bar u_j \bar u_k - u_{k} \bar u_i \bar u_j,\end{align*}
\begin{align*}&(u_{i} - \bar u_{i})(u_{j} - \bar u_{j})(u_{k} - \bar u_{k}) - u_{j} (u_k - \bar u_k) (u_i - \bar u_i) - u_{i} (u_k - \bar u_k) (u_j - \bar u_j)\\&+ u_{i} u_{j} (u_k - \bar u_k) - u_{k} \bar u_i \bar u_j\\&\qquad= - \bar u_{j} (u_{i} - \bar u_{i}) (u_{k} - \bar u_{k})- u_{i} (u_k - \bar u_k) (u_j - \bar u_j) + u_{i} u_{j} (u_k - \bar u_k) - u_{k} \bar u_i \bar u_j\\&\qquad= - \bar u_{j} ( u_{i} u_k - u_k \bar u_i - u_i \bar u_k + \bar u_i \bar u_k) - u_{i} (u_k u_j -u_k \bar u_j - u_j \bar u_k + \bar u_j \bar u_k) + u_{i} u_{j} u_k\\&\hskip11mm- u_{i} u_{j} \bar u_k - u_{k} \bar u_i \bar u_j\\&\qquad= - \bar u_{j} ( u_{i} u_k - u_k \bar u_i - u_i \bar u_k + \bar u_i \bar u_k) - u_{i} ( -u_k \bar u_j + \bar u_j \bar u_k) - u_{k} \bar u_i \bar u_j\\&\qquad= - \bar u_{j} ( - u_k \bar u_i - u_i \bar u_k + \bar u_i \bar u_k) - u_{i}\bar u_j \bar u_k - u_{k} \bar u_i \bar u_j,\end{align*}
and this term can be bounded by
![]() $5\Sigma^2$
. This completes the bound for
$5\Sigma^2$
. This completes the bound for
Finally, we show that
Using the Cauchy–Schwarz inequality twice,
 \begin{align*}&\mathbb{E}\vert(U_i - u_i)(U_j - u_j)(U_k - u_k)(U_{\ell} - u_{\ell})\vert\\&\qquad\leq \left[\mathbb{E}(U_i - u_i)^4\right]^\frac14 \left[\mathbb{E}_u(U_j - u_j)^4\right]^\frac14 \left[\mathbb{E}(U_k - u_k)^4\right]^\frac14 \left[\mathbb{E}_u(U_{\ell} - u_{\ell})^4\right]^\frac14.\end{align*}
\begin{align*}&\mathbb{E}\vert(U_i - u_i)(U_j - u_j)(U_k - u_k)(U_{\ell} - u_{\ell})\vert\\&\qquad\leq \left[\mathbb{E}(U_i - u_i)^4\right]^\frac14 \left[\mathbb{E}_u(U_j - u_j)^4\right]^\frac14 \left[\mathbb{E}(U_k - u_k)^4\right]^\frac14 \left[\mathbb{E}_u(U_{\ell} - u_{\ell})^4\right]^\frac14.\end{align*}
Recalling that
![]() $N U_i | u_i \sim \text{Bin}( N, u_i - \bar u_{i})$
and then using Minkowski’s inequality,
$N U_i | u_i \sim \text{Bin}( N, u_i - \bar u_{i})$
and then using Minkowski’s inequality,
 \begin{align*}\left[\mathbb{E}(U_i - u_i)^4\right]^\frac14 &= \frac{1}{N} \left[\mathbb{E}_u ( NU_i - N(u_i - \bar u_{i}) - N \bar u_{i})^4 \right]^\frac14\\& \leq \frac{1}{N} \left[ \mathbb{E}_u ( NU_i - N(u_i- \bar u_{i}))^4 \right]^\frac14 + \frac{1}{N} N \bar u_{i}.\end{align*}
\begin{align*}\left[\mathbb{E}(U_i - u_i)^4\right]^\frac14 &= \frac{1}{N} \left[\mathbb{E}_u ( NU_i - N(u_i - \bar u_{i}) - N \bar u_{i})^4 \right]^\frac14\\& \leq \frac{1}{N} \left[ \mathbb{E}_u ( NU_i - N(u_i- \bar u_{i}))^4 \right]^\frac14 + \frac{1}{N} N \bar u_{i}.\end{align*}
Noting that, for
![]() $Y \sim \text{Bin}(n,p)$
,
$Y \sim \text{Bin}(n,p)$
,
we conclude that
and the final bound is now clear.
Finally we complete this appendix with the proof of the Stein factor bounds in Lemma 2.3.
Proof of Lemma 2.3. For notational clarity, given
![]() ${\boldsymbol{a}}$
such that
${\boldsymbol{a}}$
such that
![]() $\|{\boldsymbol{a}}\| = k$
, decompose
$\|{\boldsymbol{a}}\| = k$
, decompose
![]() ${\boldsymbol{a}}$
into its components such that
${\boldsymbol{a}}$
into its components such that
![]() ${\boldsymbol{a}} = {\boldsymbol{a}}_1 + \ldots +{\boldsymbol{a}}_k$
, where
${\boldsymbol{a}} = {\boldsymbol{a}}_1 + \ldots +{\boldsymbol{a}}_k$
, where
![]() ${\boldsymbol{a}}_i$
is a standard basis unit vector. Furthermore, for the remainder of this proof, let
${\boldsymbol{a}}_i$
is a standard basis unit vector. Furthermore, for the remainder of this proof, let
![]() ${\boldsymbol{U}}_{\boldsymbol{u}}(t)$
denote the process
${\boldsymbol{U}}_{\boldsymbol{u}}(t)$
denote the process
![]() ${\boldsymbol{U}}(t)$
started at
${\boldsymbol{U}}(t)$
started at
![]() ${\boldsymbol{U}}(0) = {\boldsymbol{u}}$
. We first start with the case where
${\boldsymbol{U}}(0) = {\boldsymbol{u}}$
. We first start with the case where
![]() $\| {\boldsymbol{a}} \| = 1$
. Starting from (2.5), given
$\| {\boldsymbol{a}} \| = 1$
. Starting from (2.5), given
![]() $h \in \mathcal{M}_{\mathrm{disc},4}(C)$
,
$h \in \mathcal{M}_{\mathrm{disc},4}(C)$
,
We couple the two processes
![]() ${\boldsymbol{U}}_{{\boldsymbol{u}} + \delta{\boldsymbol{a}}_1}(t)$
and
${\boldsymbol{U}}_{{\boldsymbol{u}} + \delta{\boldsymbol{a}}_1}(t)$
and
![]() ${\boldsymbol{U}}_{\boldsymbol{u}}(t)$
in the following manner. Index the parents so that the types for individuals in both processes match except for the one entry where the first process will have an individual of type depending on
${\boldsymbol{U}}_{\boldsymbol{u}}(t)$
in the following manner. Index the parents so that the types for individuals in both processes match except for the one entry where the first process will have an individual of type depending on
![]() ${\boldsymbol{a}}_1$
and the second process has an individual of type K. (Recall we reserve the final type K to be the remainder.) Given the current generation, to generate the next generation, take a random sample of size N from the indices
${\boldsymbol{a}}_1$
and the second process has an individual of type K. (Recall we reserve the final type K to be the remainder.) Given the current generation, to generate the next generation, take a random sample of size N from the indices
![]() $\{1,\ldots N\}$
, and use this common random sample to choose parents for the offspring of both processes. Given mutation is parent independent, we also couple the mutations identically across both processes in the obvious manner. Figure 1 illustrates the joint evolution of
$\{1,\ldots N\}$
, and use this common random sample to choose parents for the offspring of both processes. Given mutation is parent independent, we also couple the mutations identically across both processes in the obvious manner. Figure 1 illustrates the joint evolution of
![]() ${\boldsymbol{U}}_{{\boldsymbol{u}} + \delta {\boldsymbol{a}}_1}(t)$
and
${\boldsymbol{U}}_{{\boldsymbol{u}} + \delta {\boldsymbol{a}}_1}(t)$
and
![]() ${\boldsymbol{U}}_{\boldsymbol{u}}(t)$
.
${\boldsymbol{U}}_{\boldsymbol{u}}(t)$
.

Figure 1. An illustration of our coupling at times
![]() $t = 0,1,2$
with population size
$t = 0,1,2$
with population size
![]() $N = 6$
and
$N = 6$
and
![]() $K= 5$
types. Each gene type is colour and number coded; e.g. type 1 is green, type 5 is red, etc. An ‘M’ next to a row represents a mutation, while arrows represent parental relationships; e.g. rows two and three (from the bottom) in the middle plot are children of the first row in the leftmost plot, while row six of the middle plot mutated. Coupling occurs at time
$K= 5$
types. Each gene type is colour and number coded; e.g. type 1 is green, type 5 is red, etc. An ‘M’ next to a row represents a mutation, while arrows represent parental relationships; e.g. rows two and three (from the bottom) in the middle plot are children of the first row in the leftmost plot, while row six of the middle plot mutated. Coupling occurs at time
![]() $t = 2$
since rows two and three in the middle plot have no children.
$t = 2$
since rows two and three in the middle plot have no children.
Given the starting configuration at time 0, let
![]() ${\boldsymbol{V}}(t) =(V_1(t), \ldots, V_N(t))$
denote the process that tracks the ancestry of the original configuration. That is,
${\boldsymbol{V}}(t) =(V_1(t), \ldots, V_N(t))$
denote the process that tracks the ancestry of the original configuration. That is,
![]() $V_j(t)$
tracks the number of individuals at time t that trace their ancestry directly back to individual j at time 0. Note that if a mutation occurs, it is removed from this process, hence,
$V_j(t)$
tracks the number of individuals at time t that trace their ancestry directly back to individual j at time 0. Note that if a mutation occurs, it is removed from this process, hence,
![]() $\|{\boldsymbol{V}}(0)\|_1 = N$
, and
$\|{\boldsymbol{V}}(0)\|_1 = N$
, and
![]() $\lim_{t \to\infty} {\boldsymbol{V}}(t) = 0$
. For readers familiar with coalescent theory, this is analogous to a coalescent process looking forwards in time.
$\lim_{t \to\infty} {\boldsymbol{V}}(t) = 0$
. For readers familiar with coalescent theory, this is analogous to a coalescent process looking forwards in time.
Without loss of generality, we can therefore set
In the context of Figure 1,
![]() $V_1(t)$
is tracking the number of replicates at time t of the pair (5,1) from the final row in the processes at time 0. Therefore, in this particular realisation,
$V_1(t)$
is tracking the number of replicates at time t of the pair (5,1) from the final row in the processes at time 0. Therefore, in this particular realisation,
![]() $V_1(0) =1, V_1(1) = 2, V_1(2) = 0$
. Given
$V_1(0) =1, V_1(1) = 2, V_1(2) = 0$
. Given
![]() $V_1(t-1)$
,
$V_1(t-1)$
,
![]() $V_1(t)$
will be made up of the number of times one of the
$V_1(t)$
will be made up of the number of times one of the
![]() $V_1(t-1)$
individuals are chosen, which will occur with probability
$V_1(t-1)$
individuals are chosen, which will occur with probability
![]() $\delta V_1(t-1)$
, who also do not mutate. Hence, recalling that
$\delta V_1(t-1)$
, who also do not mutate. Hence, recalling that
![]() $\Sigma = \sum_{i=1}^K p_k$
denotes the probability of any mutation occurring,
$\Sigma = \sum_{i=1}^K p_k$
denotes the probability of any mutation occurring,
Observing that
![]() $\mathbb{E}[V_1(1)] = \mathbb{E}[ \mathbb{E}[V_1(1) | V_1(0)]] =\delta\mathbb{E}[V_1(0)](1-\Sigma) = \delta(1-\Sigma)$
, and then applying this recursively we conclude that
$\mathbb{E}[V_1(1)] = \mathbb{E}[ \mathbb{E}[V_1(1) | V_1(0)]] =\delta\mathbb{E}[V_1(0)](1-\Sigma) = \delta(1-\Sigma)$
, and then applying this recursively we conclude that
![]() $\mathbb{E} [V_1(t)] = \delta(1-\Sigma)^t$
for all integers
$\mathbb{E} [V_1(t)] = \delta(1-\Sigma)^t$
for all integers
![]() $t \geq 0$
. Therefore, following on from (B.10), for
$t \geq 0$
. Therefore, following on from (B.10), for
![]() $h\in \mathcal M_{\mathrm{disc},4}(C)$
,
$h\in \mathcal M_{\mathrm{disc},4}(C)$
,
For the second-order difference where
![]() $\|{\boldsymbol{a}}\|=2$
, for
$\|{\boldsymbol{a}}\|=2$
, for
![]() $h \in \mathcal M_{\mathrm{disc},4}(C)$
,
$h \in \mathcal M_{\mathrm{disc},4}(C)$
,
 \begin{align}\vert\Delta^{{\boldsymbol{a}}} f_h({\boldsymbol{u}}) \vert&= \biggl\vert \sum_{t=0}^\infty \mathbb{E} \left[ h ({\boldsymbol{U}}_{{\boldsymbol{u}} + \delta {\boldsymbol{a}}_1 +\delta {\boldsymbol{a}}_2}(t)) - h ({\boldsymbol{U}}_{{\boldsymbol{u}} + \delta {\boldsymbol{a}}_1}(t)) - h ({\boldsymbol{U}}_{{\boldsymbol{u}} + \delta {\boldsymbol{a}}_2}(t)) + h ({\boldsymbol{U}}_{\boldsymbol{u}}(t)) \right] \biggr\vert\notag\\&\leq C \sum_{t=0}^\infty \mathbb{E} \left[\| {\boldsymbol{U}}_{{\boldsymbol{u}} + {\boldsymbol{a}}_1 + {\boldsymbol{a}}_2}(t)- {\boldsymbol{U}}_{{\boldsymbol{u}} + {\boldsymbol{a}}_1}(t)\|_1 \| {\boldsymbol{U}}_{{\boldsymbol{u}} + {\boldsymbol{a}}_2}(t) - {\boldsymbol{U}}_{{\boldsymbol{u}}}(t)\|_1\right], \end{align}
\begin{align}\vert\Delta^{{\boldsymbol{a}}} f_h({\boldsymbol{u}}) \vert&= \biggl\vert \sum_{t=0}^\infty \mathbb{E} \left[ h ({\boldsymbol{U}}_{{\boldsymbol{u}} + \delta {\boldsymbol{a}}_1 +\delta {\boldsymbol{a}}_2}(t)) - h ({\boldsymbol{U}}_{{\boldsymbol{u}} + \delta {\boldsymbol{a}}_1}(t)) - h ({\boldsymbol{U}}_{{\boldsymbol{u}} + \delta {\boldsymbol{a}}_2}(t)) + h ({\boldsymbol{U}}_{\boldsymbol{u}}(t)) \right] \biggr\vert\notag\\&\leq C \sum_{t=0}^\infty \mathbb{E} \left[\| {\boldsymbol{U}}_{{\boldsymbol{u}} + {\boldsymbol{a}}_1 + {\boldsymbol{a}}_2}(t)- {\boldsymbol{U}}_{{\boldsymbol{u}} + {\boldsymbol{a}}_1}(t)\|_1 \| {\boldsymbol{U}}_{{\boldsymbol{u}} + {\boldsymbol{a}}_2}(t) - {\boldsymbol{U}}_{{\boldsymbol{u}}}(t)\|_1\right], \end{align}
where the inequality is due to the fact that, in general,
For one-dimensional functions
![]() $f\,:\,\mathbb{Z} \to \mathbb{R}$
, inequality (B.12) follows from
$f\,:\,\mathbb{Z} \to \mathbb{R}$
, inequality (B.12) follows from
 \begin{align*}&f(x + a + b) - f(x + a) -f(x+b) + f(x)\\&\qquad= \sum_{i=0}^{b-1} \sum_{j=1}^{a-1} \big(f(x +j+ i) - 2 f(x +j-1+ i)+ f(x +j-1+ i -1)\big), \quad x,a,b \in \mathbb{Z}.\end{align*}
\begin{align*}&f(x + a + b) - f(x + a) -f(x+b) + f(x)\\&\qquad= \sum_{i=0}^{b-1} \sum_{j=1}^{a-1} \big(f(x +j+ i) - 2 f(x +j-1+ i)+ f(x +j-1+ i -1)\big), \quad x,a,b \in \mathbb{Z}.\end{align*}
A similar idea can be used to justify (B.12) for multidimensional functions.
We couple the four processes on the right-hand side in an analogous manner to the first difference; i.e. parent selection and mutation are coupled to be identical for all four processes. Figure 2 illustrates their evolution. Similar to the first difference, we need to keep track of any differences between the four processes, which can be achieved by tracking genealogies using the process
![]() ${\boldsymbol{V}}(t)$
where we set
${\boldsymbol{V}}(t)$
where we set
![]() $(V_1(t),V_2(t))$
to jointly track the propagation of the initial two rows in Figure 2.
$(V_1(t),V_2(t))$
to jointly track the propagation of the initial two rows in Figure 2.

Figure 2. An illustration of our second-order difference coupling at times
![]() $t = 0,1,2$
with population size
$t = 0,1,2$
with population size
![]() $N = 6$
and
$N = 6$
and
![]() $K= 5$
types.
$K= 5$
types.
Therefore, we can without loss of generality set
Analogously to the first difference, we can set
![]() $V_1(t)$
and
$V_1(t)$
and
![]() $V_2(t)$
jointly such that
$V_2(t)$
jointly such that
Given
![]() $V_1(0) = V_2(0) = 1$
, we can recursively show, with the help of Lemma B.4, that
$V_1(0) = V_2(0) = 1$
, we can recursively show, with the help of Lemma B.4, that
![]() $\mathbb{E}[N^2 V_1(t) V_2(t)] =N(N-1)\delta^2(1-\Sigma)^{2t}$
. Hence, continuing from (B.11),
$\mathbb{E}[N^2 V_1(t) V_2(t)] =N(N-1)\delta^2(1-\Sigma)^{2t}$
. Hence, continuing from (B.11),
We omit the proof of the bounds when
![]() $\Vert{\boldsymbol{a}}\Vert = 3,4$
, as they follow from exactly the same proof methodology.
$\Vert{\boldsymbol{a}}\Vert = 3,4$
, as they follow from exactly the same proof methodology.
Funding information
There are no funding bodies to thank relating to the creation of this paper.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this paper.