Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hwang, Hsien-Kuei
Chern, Hua-Huai
and
Duh, Guan-Huei
2020.
An asymptotic distribution theory for Eulerian recurrences with applications.
Advances in Applied Mathematics,
Vol. 112,
Issue. ,
p.
101960.


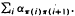 Here, α
Here, α