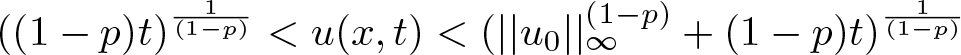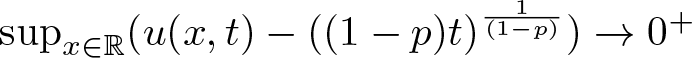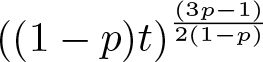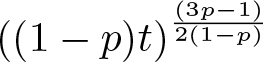1. Introduction
In this paper, we address the classical Fujita problem with sublinear exponent, which takes the form of the following parabolic evolution problem, for 
$T \gt 0$,
\begin{equation}
u_t = u_{xx} + [u^p]^+, ~ \forall ~ (x,t)\in D_T,
\end{equation}
\begin{equation}
u(x,0)=u_0(x)~\forall~x\in \mathbb{R},
\end{equation}
\begin{equation}
u~\text{is bounded on} ~ \overline{D}_T.
\end{equation}Here,
\begin{equation}
D_T = \{(x,t): x\in \mathbb{R}, t\in (0,T] \},
\end{equation} with 
$x$ being the spatial coordinate and 
$t$ being time, whilst the nonlinear reaction function 
$[(\cdot)^p]^+:\mathbb{R}\to\mathbb{R}$ has the simple form,
\begin{equation}
[u^p]^+ =
\begin{cases}
u^p,~~u\ge0,\\
0,~~u \lt 0,
\end{cases}
\end{equation} and we consider the situation when the exponent is sublinear, that is 
$0 \lt p \lt 1$. In the present context the initial data distribution is restricted so that 
$u_0\in C(\mathbb{R}) \cap PC^1(\mathbb{R})$, is nontrivial and nonnegative, and has compact support (without loss of generality, we may set sppt
$(u_0)\subseteq [-1,1]$); for convenience, we henceforth write 
$u_0\in K^+(\mathbb{R})$ (we remark at the end of the paper how this class of initial data may be considerably extended). We refer to this evolution problem as 
$[F(p)]$, and solutions are regarded as classical, so that 
$u\in C(\overline{D}_T) \cap C^{2,1}(D_T)$. For superlinear exponents 
$p \gt 1$ the evolution problem 
$[F(p)]$ is the classical Fujita problem (see Fujita [Reference Fujita4], the reviews of Levine [Reference Levine6] and Deng and Levine [Reference Deng and Levine2], and the many references therein), and, in the superlinear situation, we recall from Fujita [Reference Fujita4] and Hayakawa [Reference Hayakawa5], in one spatial dimension, that there is a critical blow-up exponent 
$p=3$, such that when 
$1 \lt p\le3$, and for any initial data in 
$K^+(\mathbb{R})$, then 
$[F(p)]$ has a unique solution, and this solution undergoes spatially local blow-up (in the supnorm) in finite-
$t$. However, when 
$p \gt 3$, and the initial data has 
$||u_0||_\infty$ sufficiently small, then 
$[F(p)]$ has a unique solution, which is global (that is, exists on 
$\overline{D}_{\infty}$). The situation for sublinear exponents 
$0 \lt p \lt 1$ is significantly different, and this arises due to two features: firstly the reaction function is no longer Lipchitz continuous (due to the behaviour as 
$u \to 0^+$), and so the standard classical theory no longer applies to 
$[F(p)]$ (however, it is Hölder continuous of degree 
$p$); secondly the curvature of the reaction function on 
$u \gt 0$ is now negative rather than positive. A detailed consideration of 
$[F(p)]$ with 
$0 \lt p \lt 1$ has been undertaken in Meyer and Needham [Reference Meyer and Needham7] and Aguirre and Escobedo [Reference Aguirre and Escobedo1]. It is instructive to summarize the relevant key results established therein in the following:
Theorem 1.1 (Aguirre and Escobedo [Reference Aguirre and Escobedo1], Meyer and Needham [Reference Meyer and Needham7])
Let 
$0 \lt p \lt 1$ and 
$u_0\in K^+(\mathbb{R})$. Then for the evolution problem 
$[F(p)]$:
(1) There exists a global solution
$u:\overline{D}_{\infty} \to \mathbb{R}$, and this is unique.(2)
$((1-p)t)^{\frac{1}{(1-p)}} \lt u(x,t) \lt (||u_0||_{\infty}^{(1-p)} + (1-p)t)^{\frac{1}{(1-p)}}$ for all
$(x,t)\in D_{\infty}$.(3) For any
$T \gt 0$, the limit
$u(x,t) \to ((1-p)t)^{\frac{1}{(1-p)}}$ as
$|x|\to \infty$ holds uniformly for
$t\in [0,T]$.(4) The classical parabolic Weak and Strong Comparison Theorems continue to hold.
We observe immediately from the inequality in the second point above that,
\begin{equation}
u(x,t) \sim ((1-p)t)^{\frac{1}{(1-p)}}~\text{as}~t\to \infty,
\end{equation} uniformly for 
$x\in \mathbb{R}$. More specifically, we have,
\begin{equation}
0 \lt u(x,t) - ((1-p)t)^{\frac{1}{(1-p)}} \lt \frac{1}{2}||u_0||_{\infty}^{(1-p)}(1-p)^{-1}((1-p)t)^{\frac{p}{(1-p)}}~\text{as}~t\to \infty,
\end{equation} uniformly for 
$x\in \mathbb{R}$. We remark that the bounds in (4) can be obtained from the theory in [Reference Eom and Ishige3] relating to 
$L^q(\mathbb{R})$ bounds for, amongst others, problem 
$[F(p)]$ (see Theorem 1.1, equation (1.8), on setting 
$\alpha=p, m=1, \lambda=1, q=r=\infty$), but the sharp bounds below cannot. It is also appropriate to note that 
$[F(p)]$ (with a natural modification to the boundedness condition (F3)) has been considered in [Reference Wang and Yin8] for the complementary situation when the initial data is strictly growing at an algebraic rate as 
$|x| \to \infty$, and corresponding bounds have been presented therein. Our objective here is to replace the bounds in (4) with sharp estimates in the algebraic rate. Our principal result can be stated as:
Theorem 1.2 Let 
$0 \lt p \lt 1$ and 
$u:\overline{D}_{\infty}\to \mathbb{R}$ be the solution to 
$[F(p)]$. Then for each 
$u_0\in K^+(\mathbb{R})$, the following lower bound holds:
\begin{equation}
u(x,t) - ((1-p)t)^{\frac{1}{(1-p)}} \ge c_{-}(x,t,p,u_0) ((1-p)t)^{\frac{(3p-1)}{2(1-p)}},
\end{equation} as 
$t\to \infty$ uniformly for 
$x\in \mathbb{R}$. Conversely, for each 
$u_0\in K^+(\mathbb{R})$ the following upper bound holds:
\begin{equation}
u(x,t) - ((1-p)t)^{\frac{1}{(1-p)}} \le c_{+}(x,t,p,u_0) ((1-p)t)^{\frac{(3p-1)}{2(1-p)}},
\end{equation} as 
$t\to \infty$ uniformly for 
$x\in \mathbb{R}$. Here the positive functions 
$c_{\pm}(x,t,p,u_0)$ are bounded as 
$t\to\infty$ uniformly for 
$x\in \mathbb{R}$, and are explicitly given by the the Gaussian convolution forms,
\begin{equation}
c_{-}(x,t,p,u_0) = \frac{(1+||u_0||_{\infty})^{-1}}{2\sqrt{\pi (1-p)}} \int_{-1}^{1}{u_0(s)\exp{\left(-\frac{(s-x)^2}{4t}\right)}}ds,
\end{equation}and
\begin{equation}
c_{+}(x,t,p,u_0) = \frac{(1-p)^{\frac{(1-2p)}{(1-p)}}}{\sqrt{2\pi (1-p)}} \int_{-\infty}^{\infty}{\mathcal{E}(s;p,u_0)\exp{\left(-\frac{(s-x)^2}{4(t-1)}\right)}}ds,
\end{equation} for each 
$x\in \mathbb{R}$ and 
$t \gt 1$, where,
\begin{equation}
\mathcal{E}(s;p,u_0) = ((1-p) + \Delta(s,u_0)^{(1-p)})^{\frac{1}{(1-p)}} - (1-p)^{\frac{1}{(1-p)}},
\end{equation}and
\begin{equation}
\Delta(s,u_0) = \frac{1}{2\sqrt{\pi}} \int_{-1}^{1}{u_0(w)\exp{\left(-\frac{1}{4}(w-s)^2\right)}}dw,
\end{equation} for all 
$s\in \mathbb{R}$.
Remark 1.3. It is worth noting here that the form of the key inequalities (5) and (6) is motivated by considering the formal linearization of 
$[F(p)]$, when 
$0 \lt p \lt 1$, about that nontrivial solution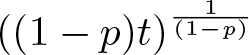 
$((1-p)t)^{\frac{1}{(1-p)}}$ which solves 
$[F(p)]$ when the initial data 
$u_0\equiv 0$. In particular, for initial data with 
$||u_0||_{\infty}$ small we formally write 
$u = ((1-p)t)^{\frac{1}{(1-p)}} + \hat{u}$ for 
$(x,t) \in \mathbb{R} \times [1,\infty)$ and regard 
$||\hat{u}(\cdot,t)||_{\infty}$ as small (at least up to 
$t= 1 + O(1)^+$). On substitution directly into 
$[F(p)]$, expanding the nonlinearity and neglecting terms of quadratic order in 
$\hat{u}$, we obtain the linearized problem governing the perturbation 
$\hat{u}$ as,
\begin{equation}
\hat{u}_t = \hat{u}_{xx} + p((1-p)t)^{-1} \hat{u}~\forall ~ (x,t)\in \mathbb{R} \times (1,\infty),
\end{equation}
\begin{equation}
\hat{u}(x,1) = \hat{u}_1(x) (\equiv u(x,1) - ((1-p))^{\frac{1}{(1-p)}}) ~\forall ~ x\in \mathbb{R},
\end{equation}
\begin{equation}
\hat{u}~\text{is bounded on}~\mathbb{R} \times [1,T]~\text{for each}~T \gt 1.
\end{equation}The (unique) solution to this linear parabolic evolution problem is readily obtained as
\begin{equation}
\hat{u}(x,t) = \frac{(1-p)^{\frac{(1-3p)}{2(1-p)}}((1-p)t)^{\frac{p}{(1-p)}}}{2\sqrt{\pi (1-p)(t-1)}} \int_{-\infty}^{\infty}{\hat{u}_1(s)\exp{\left(-\frac{(s-x)^2}{4(t-1)}\right)}}ds,
\end{equation} for all 
$(x,t) \in \mathbb{R} \times [1,\infty)$. From this it is readily estimated that
\begin{equation}
\hat{u}(x,t) = O\left(
((1-p)t)^{\frac{(3p-1)}{2(1-p)}}
\right),
\end{equation} as 
$t \to \infty$ uniformly for 
$x\in \mathbb{R}$. This calculation motivated our search for the tight bounds in Theorem 1.2.
A consequence of the inequalities (5) and (6) is:
Corollary 1.4. Let 
$0 \lt p \lt 1$, and 
$u:\overline{D}_{\infty}\to \mathbb{R}$ be the solution to 
$[F(p)]$. Then there is a transitional stability exponent 
$p=1/3$, such that,
• when
$0 \lt p \lt 1/3$ and
$u_0\in K^+(\mathbb{R})$ then
$\text{sup}_{x\in\mathbb{R}}(u(x,t) - ((1-p)t)^{\frac{1}{(1-p)}}) \to 0^+$ as
$t\to \infty$, and at a precise algebraic rate of
$((1-p)t)^{\frac{(3p-1)}{2(1-p)}}$;• when
$1/3 \lt p \lt 1$ and
$u_0\in K^+(\mathbb{R})$, then
$\text{sup}_{x\in\mathbb{R}}(u(x,t) - ((1-p)t)^{\frac{1}{(1-p)}}) \to +\infty$ as
$t\to \infty$, and at a precise algebraic rate of
$((1-p)t)^{\frac{(3p-1)}{2(1-p)}}$;• when
$p=1/3$ and
$u_0\in K^+(\mathbb{R})$ then
$\text{sup}_{x\in\mathbb{R}}(u(x,t) - ((1-p)t)^{\frac{1}{(1-p)}})$ is bounded below and above as
$t\to \infty$ by the positive constants
$\overline{c}_-(u_0)$ and
$\overline{c}_+(u_0)$ respectively, which are given by,
(16)\begin{equation}
\overline{c}_{-}(u_0) = \frac{(1+||u_0||_{\infty})^{-1}}{2\sqrt{2\pi/3}} \int_{-1}^{1}{u_0(s)}ds
\end{equation}and
(17)\begin{equation}
\overline{c}_{+}(u_0) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}{\mathcal{E}(s;1/3,u_0)}ds,
\end{equation}with
$\mathcal{E}(s;1/3,u_0)$ as given via (9).
This corollary is a direct consequence of Theorem 1.2 (and needs no further proof) and the results can be interpreted in terms of the spatio-temporal stability of the spatially homogeneous state 
$u=u_h(t)\equiv ((1-p)t)^{\frac{1}{(1-p)}}$:
Remark 1.5. The spatially homogeneous state 
$u=u_h(t)$, when subject to initial disturbances in 
$K^+(\mathbb{R})$, is asymptotically stable when 
$0 \lt p \lt 1/3$, is Liapunov stable when 
$p=1/3$, and is unstable when 
$1/3 \lt p \lt 1$.
We also have:
Remark 1.6. The problem 
$[F(p)]$ can be considered on the higher dimensional spatial domain 
$\mathbb{R}^N$ for 
$N\in\mathbb{N} = 2,3,\ldots$. Theorem 1.1 continues to hold without change. It is also straightforward to adapt Theorem 1.2. The key change is that the algebraic power of 
$t$ on the left hand side of both inequalities now becomes 
$((N+2)p-N)/(2(1-p))$, whilst the integrals in the remaining terms have their natural modification into N-dimensional multiple integrals. The conclusions of Corollary 1.4 continue to hold except now the transitional stability exponent becomes 
$p=p_c^-(N)$ which is given by,
\begin{equation}
p_c^-(N) = N(N+2)^{-1}.
\end{equation} An interesting observation now is that when 
$p \gt 1$, in higher spatial dimensions, the Fujita critical blow-up exponent becomes 
$p=p_c^+(N)$ where,
\begin{equation}
p_c^+(N) = 1 + 2/N.
\end{equation}Thus, we have the interesting reciprocal relationship,
\begin{equation}
p_c^+(N) p_c^-(N) = 1.
\end{equation} We observe that, for small initial data, the critical exponent 
$p_c^+(N)$ is brought about by the balancing of two processes relative to the background trivial equilibrium state: the weak decay due to linear diffusion balancing the weakly nonlinear growth due to the degenerate reaction term. However it is a different balance which determines the transitional exponent 
$p_c^-(N)$ with the background now being the strongly nonlinear nontrivial homogeneous state 
$u_h(t)$ and the balance now being the weak decay due to diffusion with the linearized reaction, both now relative to 
$u_h(t)$. The precise nature of these respective mechanisms results in the exact reciprocity in relation (20). This seems to be the simplest explanation for the occurrence of this exact reciprocity condition; simple transformations on 
$[F(p)]$ do not appear to provide any additional insights.
The remainder of the paper concerns the proof of Theorem 1.2.
2. Preliminary constructions
In this section, we introduce and examine two functions which will play a subsequent role in constructing both a suitable subsolution and supersolution to 
$[F(p)]$. The first is a familiar function which uniquely solves the evolution problem [IVP
$\mathcal{D}$] for the linear diffusion equation, namely,
\begin{equation}
\mathcal{D}_t = \mathcal{D}_{xx},~\forall ~(x,t)\in D_{\infty},
\end{equation}
\begin{equation}
\mathcal{D}(x,0;u_0) = u_0(x),~ \forall ~ x\in \mathbb{R},
\end{equation}
\begin{equation}
\mathcal{D}~\text{is bounded on}~\overline{D}_T~\text{for each}~T \gt 0,
\end{equation}and is given by,
\begin{equation}
\mathcal{D}(x,t;u_0) = \frac{1}{2\sqrt{\pi t}} \int_{-1}^{1}{u_0(s)\exp{\left(-\frac{(s-x)^2}{4t}\right)}}ds
\end{equation} for all 
$(x,t)\in D_{\infty}$. We recall that
\begin{equation}
\mathcal{D}\in C(\overline{D}_{\infty})\cap C^{2,1}(D_{\infty}),
\end{equation}and satisfies the inequalities,
\begin{equation}
0 \lt \mathcal{D}(x,t;u_0) \lt \frac{1}{2\sqrt{\pi t}} \int_{-1}^{1}{u_0(s)}ds,
\end{equation} for all 
$(x,t)\in D_{\infty}$, together with,
\begin{equation}
\mathcal{D}(x,t;u_0) \lt \frac{1}{2\sqrt{\pi t}} \left(\int_{-1}^{1}{u_0(s)}ds\right) \exp{\left(-\frac{(|x|-1)^2}{4t}\right)},
\end{equation} for all 
$(x,t)\in D_\infty$ such that 
$|x|\geq 1$.
Next consider the linear evolution problem [IVP
$\mathcal{W}$], namely,
\begin{equation}
\mathcal{W}_t = \mathcal{W}_{xx} + p((1-p)t)^{-1} \mathcal{W}~\forall ~ (x,t)\in \mathbb{R} \times (1,\infty),
\end{equation}
\begin{equation}
\mathcal{W}(x,1;p,u_0) = \mathcal{E}(x;p,u_0)~\forall ~ x\in \mathbb{R}
\end{equation}
\begin{equation}
\mathcal{W}~\text{is bounded on}~\mathbb{R} \times [1,T]~\text{for each}~T \gt 1,
\end{equation} with 
$\mathcal{E}$ given by (9). We observe that,
\begin{equation}
0 \lt \mathcal{E}(x;p,u_0) \le ((1-p) + ||u_0||_{\infty}^{(1-p)})^{\frac{1}{(1-p)}} - (1-p)^{\frac{1}{(1-p)}},
\end{equation} for all 
$x\in \mathbb{R}$. We note that [IVP
$\mathcal{W}$] has the unique and global solution 
$\mathcal{W} \in C^{2,1}(\mathbb{R} \times [1,\infty))$ given by,
\begin{equation}
\mathcal{W}(x,t;p,u_0) = \frac{t^{\frac{p}{(1-p)}}}{2\sqrt{\pi(t-1)}} \int_{-\infty}^{\infty}{\mathcal{E}(s;p,u_0)\exp{\left(-\frac{(s-x)^2}{4(t-1)}\right)}}ds,
\end{equation} for 
$(x,t)\in \mathbb{R} \times (1,\infty)$.
Remark 2.1. The significance of the linear parabolic PDE in (W1) arises from it being the formal linearization of the PDE in 
$[F(p)]$ about the homogeneous state 
$u=u_h(t)$.
We again readily establish that,
\begin{equation}
\mathcal{W}\in C(\mathbb{R} \times [1,\infty)) \cap C^{2,1}(\mathbb{R} \times (1,\infty)),
\end{equation}whilst we have the bound,
\begin{equation}
||\mathcal{W}(\cdot,t)||_{\infty} \le \text{min}\left(t^{\frac{p}{(1-p)}} ||\mathcal{E}(\cdot;p,u_0)||_{\infty}, \frac{t^{\frac{p}{(1-p)}}}{2\sqrt{\pi(t-1)}}I(p,u_0)\right),
\end{equation} for 
$t\in (1,\infty)$, on using (22). Here
\begin{equation}
I(p,u_0) = \int_{-\infty}^{\infty}{\mathcal{E}(s;p,u_0)}ds.
\end{equation}We now use the above functions in the following constructions.
3. The key subsolution and supersolution to [F(p)]
Throughout this section, for any 
$T \gt T_0\ge0$ and function 
$\psi \in C(\mathbb{R} \times [T_0,T)) \cap C^{2,1}(\mathbb{R} \times (T_0,T))$, we introduce the mapping 
$\mathcal{N}:C^{2,1}(\mathbb{R}\times (T_0,T)) \to C(\mathbb{R}\times (T_0,T))$ as
\begin{equation}
\mathcal{N}(\psi) \equiv \psi_t - \psi_{xx} - [\psi^p]^+.
\end{equation} We next introduce the function 
$\overline{u}^+\in C(\overline{D}_{\infty}) \cap C^{2,1}(D_{\infty})$ such that,
\begin{equation}
\overline{u}^+(x,t) = \left((1-p)t + \mathcal{D}(x,t;u_0)^{(1-p)} \right)^{\frac{1}{(1-p)}},
\end{equation} for all 
$(x,t)\in \overline{D}_{\infty}$. We can now appeal directly to [Reference Meyer and Needham7, Chapter 9, Proposition 9.2] to establish that, for any 
$T \gt 0$, then 
$\overline{u}^+$ is a supersolution to 
$[F(p)]$ on 
$\overline{D}_T$; we then have:
Lemma 3.1. Let 
$0 \lt p \lt 1$ and 
$u:\overline{D}_{\infty} \to \mathbb{R}$ be the solution to 
$[F(p)]$. Then, for any 
$T \gt 0$,
\begin{equation}
u(x,t)\le \left((1-p)t + \mathcal{D}(x,t;u_0)^{(1-p)} \right)^{\frac{1}{(1-p)}},
\end{equation} for all 
$(x,t)\in \overline{D}_T$.
Proof. Recalling that 
$\overline{u}^+$ is a supersolution to 
$[F(p)]$ on 
$\overline{D}_T$, then an application of the Weak Comparison Theorem (which is validated via Theorem 1.1(4)) leads directly to the result.
It follows directly from this inequality and Theorem 1.1(2) that,
\begin{equation}
((1-p))^{\frac{1}{(1-p)}} \lt u(x,1) \le \left((1-p) + \Delta(x,u_0)^{(1-p)} \right)^{\frac{1}{(1-p)}},
\end{equation} for all 
$x\in \mathbb{R}$, and this will be the starting point of the second construction that is developed below.
We now introduce our key subsolution. We have:
Lemma 3.2. For each 
$T \gt 0$ the function 
$\underline{u}: \overline{D}_{\infty} \to \mathbb{R}$, given by
\begin{equation}
\underline{u}(x,t) = \left((1-p)t + (1+||u_0||_{\infty})^{-1}\mathcal{D}(x,t;u_0) \right)^{\frac{1}{(1-p)}},
\end{equation} for all 
$(x,t)\in \overline{D}_{\infty}$, is a subsolution to 
$[F(p)]$ on 
$\overline{D}_T$.
Proof. Fix 
$T \gt 0$ and observe that 
$\underline{u} \in C(\overline{D}_{\infty})\cap C^{2,1}(D_{\infty})$. Next, using the inequalities (23), it is readily confirmed that 
$\underline{u}$ is bounded on 
$\overline{D}_T$. Secondly, since 
$0 \lt p \lt 1$ we have
\begin{align*}
\underline{u}(x,0) & = \left( (1+||u_0||_{\infty})^{-1}\mathcal{D}(x,0;u_0) \right)^{\frac{1}{(1-p)}} \nonumber
\\
& = \left( (1+||u_0||_{\infty})^{-1} u_0(x) \right)^{\frac{1}{(1-p)}}
\nonumber
\\
& \le (1 + ||u_0||_{\infty})^{-1} u_0(x) \nonumber
\\
& \le u_0(x) \nonumber
\end{align*} for all 
$x\in \mathbb{R}$. Finally, for 
$(x,t)\in D _T$,
\begin{align*}
\mathcal{N}(\underline{u})(x,t) & = (\underline{u}_t - \underline{u}_{xx} - [\underline{u}^p]^+)(x,t)
\\
& = -\frac{p}{(1-p)^2} (1 + ||u_0||_{\infty})^{-2} \mathcal{D}_{x}(x,t;u_0)^2 \\
&\quad \times \left( (1-p)t + (1 + ||u_0||_{\infty})^{-1} \mathcal{D}(x,t;u_0)\right)^{\frac{(2p-1)}{(1-p)}}
\\
&\le 0
\end{align*}which completes the proof.
Next we have the key supersolution:
Lemma 3.3. For each 
$T \gt 1$ the function 
$\overline{u}: \mathbb{R} \times [1,\infty) \to \mathbb{R}$, given by
\begin{equation}
\overline{u}(x,t) = ((1-p)t)^{\frac{1}{(1-p)}} + \mathcal{W}(x,t;p,u_0)
\end{equation} for all 
$(x,t)\in \mathbb{R} \times [1,\infty)$, is a supersolution to 
$[F(p)]$ on 
$\mathbb{R}\times [1,T]$.
Proof. Fix 
$T \gt 1$ and observe that 
$\overline{u}\in C(\mathbb{R} \times [1,\infty))\cap C^{2,1} (\mathbb{R} \times (1,\infty))$. It immediately follows from (28) that 
$\overline{u}$ is bounded on 
$\mathbb{R}\times [1,T]$. Next we have,
\begin{align*}
\overline{u}(x,1) & = ((1-p))^{\frac{1}{(1-p)}} + \mathcal{W}(x,1;p,u_0)
\\
& = (1-p)^{\frac{1}{(1-p)}} + \mathcal{E}(x;p,u_0)
\\
& = (1-p)^{\frac{1}{(1-p)}} + \left(((1-p) + \Delta(x,u_0)^{(1-p)})^{\frac{1}{(1-p)}} - (1-p)^{\frac{1}{(1-p)}}\right)
\\
& = ((1-p) + \Delta(x,u_0)^{(1-p)})^{\frac{1}{(1-p)}}
\\
& \ge u(x,1)
\end{align*} for all 
$x\in \mathbb{R}$, via (33). Now, for 
$(x,t) \in \mathbb{R} \times (1,T]$, via (W1) we have
\begin{align*}
\mathcal{N}(\overline{u})(x,t) & = (\overline{u}_t - \overline{u}_{xx} - [\overline{u}^p]^+)(x,t)
\\
& = ((1-p)t)^{\frac{p}{(1-p)}} + (\mathcal{W}_t - \mathcal{W}_{xx})(x,t) \\
&\quad - [(((1-p)t)^{\frac{1}{(1-p)}} + \mathcal{W}(x,t;p,u_0))^p]^+
\\
& = ((1-p)t)^{\frac{p}{(1-p)}} + p((1-p)t)^{-1} \mathcal{W}(x,t) \\
&\quad - [(((1-p)t)^{\frac{1}{(1-p)}} + \mathcal{W}(x,t;p,u_0))^p]^+
\\
& = ((1-p)t)^{\frac{p}{(1-p)}} + p((1-p)t)^{-1} \mathcal{W}(x,t) - (((1-p)t)^{\frac{p}{(1-p)}}
\\
& \quad + p(((1-p)t)^{\frac{1}{(1-p)}}+ \theta (x,t)\mathcal{W}(x,t))^{-(1-p)}\mathcal{W}(x,t))
\\
& \ge 0
\end{align*} since 
$0 \lt p \lt 1$, where we note that 
$\theta(x,t) \in (0,1)$ exists via the Mean Value Theorem. The proof is complete.
We now have:
Corollary 3.4. Let 
$0 \lt p \lt 1$, and 
$u:\overline{D}_{\infty}\to \mathbb{R}$ be the solution to 
$[F(p)]$. Then for each 
$(x,t)\in \mathbb{R}\times [1,\infty)$,
\begin{equation}
\underline{u}(x,t) \le u(x,t) \le \overline{u}(x,t).
\end{equation}Proof. This follows from Lemma 3.2 and Lemma 3.3 on use of the Weak Comparison Theorem (via Theorem 1.1(4)).
It is now straightforward to establish the inequalities (5) and (6) in Theorem 1.2 directly from (34) and (35) (together with the bounds on 
$\mathcal{D}$ and 
$\mathcal{W}$ obtained in section 2), which completes the proof of this theorem. To finish the paper we make the final observation:
Remark 3.5. The containing set 
$K^+(\mathbb{R})$ for initial data in the definition of the evolution problem 
$[F(p)]$ can be considerably broadened to allow for all nontrivial, non-negative functions in 
$C(\mathbb{R}) \cap L^1(\mathbb{R})$ which have zero limit as 
$|x|\to \infty$. This extension follows the above very closely, and requiring only very minor technical modifications. Similarly, modifications to generalize to higher spatial dimensions follow the obvious adaptations.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Open access
